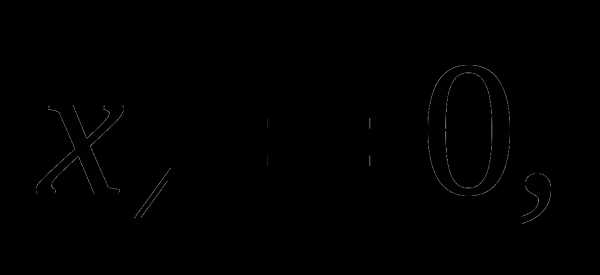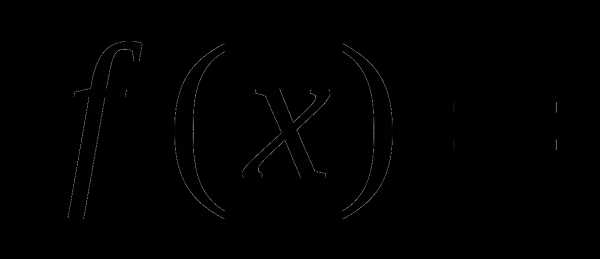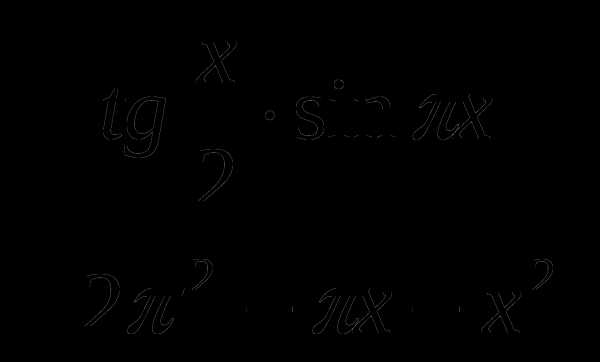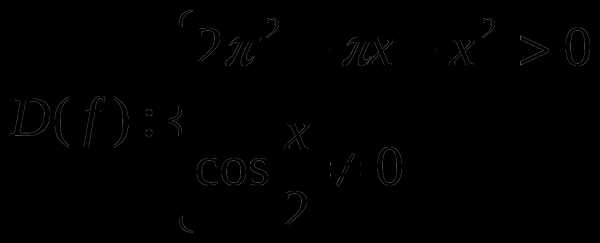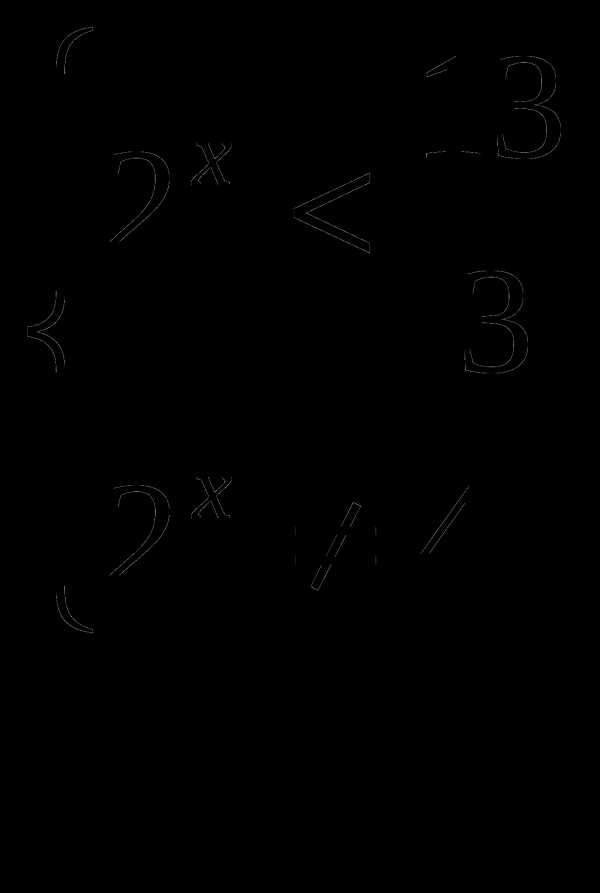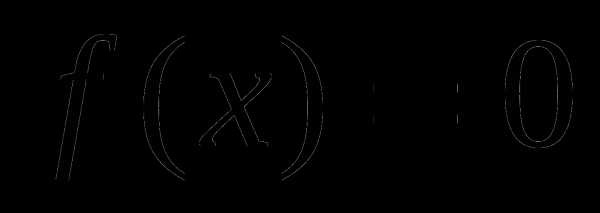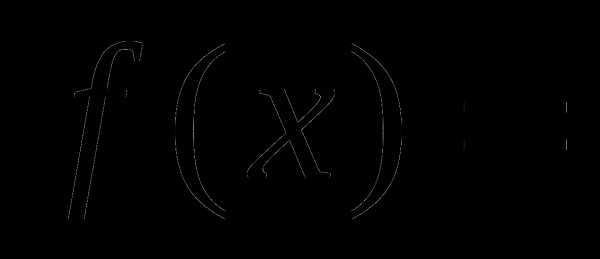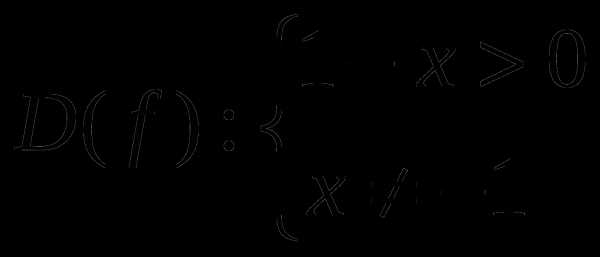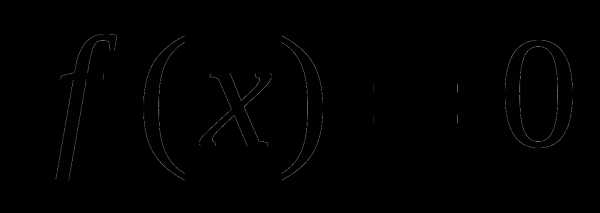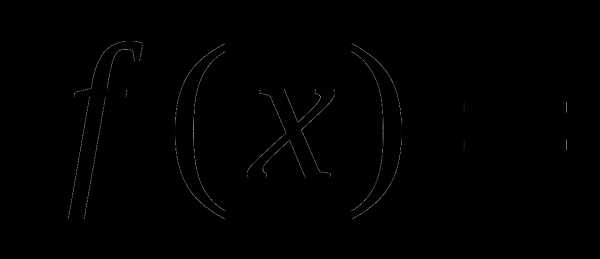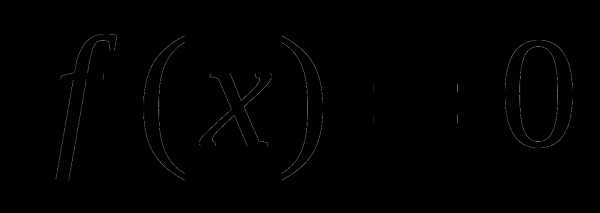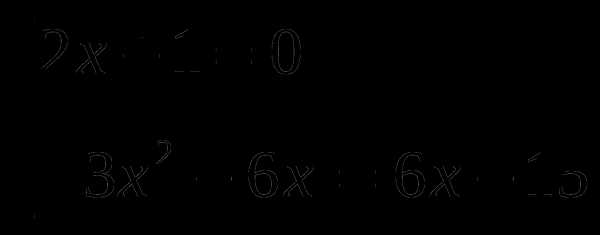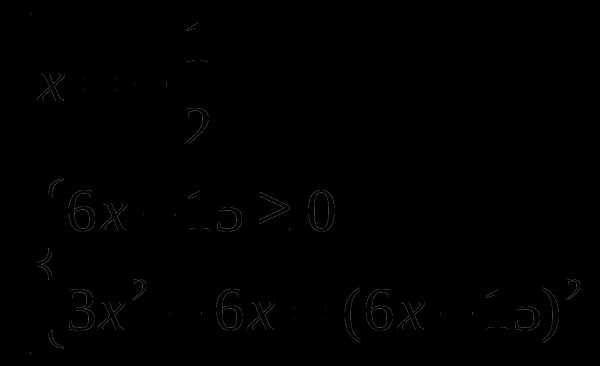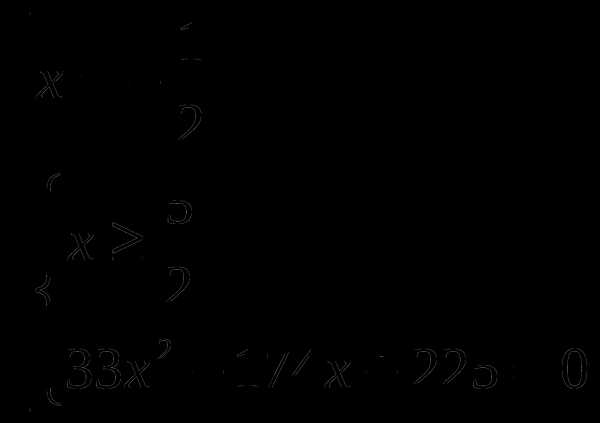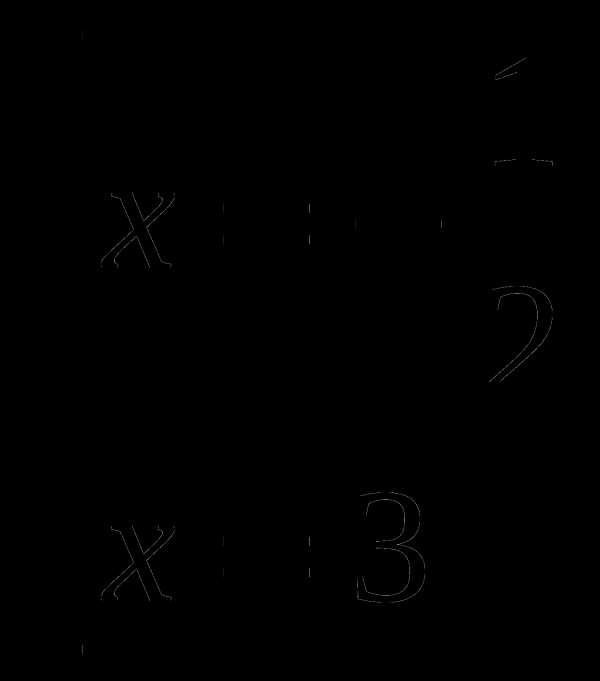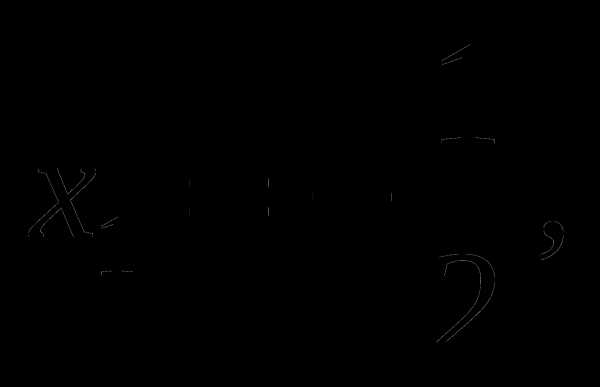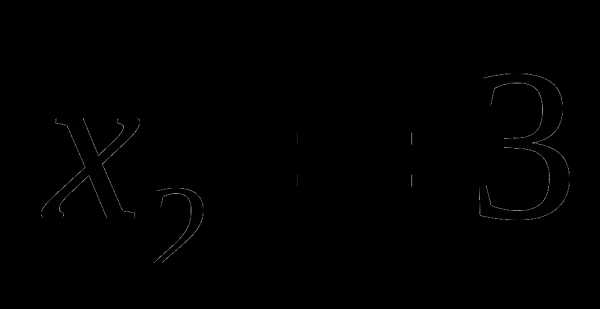Организация итогового повторения по алгебре и началам анализа в 11-м классе
Разделы: Математика
Введение.
Единый государственный экзамен (ЕГЭ) по математике – серьёзное испытание в жизни каждого выпускника школы.
Основная подготовка к ЕГЭ осуществляется на уроках математики.
Особую роль, на наш взгляд, при новой форме проведения выпускного экзамена приобретает организация итогового повторения.
Теперь уже недостаточно привычных обобщения и систематизации знаний и способов действий. Не менее важным нам видится необходимость формирования у выпускников умений:
- быстрее переключаться с одного типа задания на другой;
- выбирать оптимальную стратегию при решении как одной задачи, так и всей работы в целом;
- проверять полученный результат решения.
Основной характеристикой методики проведения обобщающих занятий является активизирующее воздействие на обучаемых – систематическое убеждение их в том, что лишь при активной позиции по отношению к данному предмету можно рассчитывать на успех.
Таким образом, при подготовке выпускников наряду с обычными требованиями важнейшим становится динамика вариативности в выборе методов, развитие системного мышления, вообще – уход от жестких формальных схем и алгоритмов.
С этой целью итоговое повторение разбито на две части:
- Обобщение и систематизация знаний и способов действий;
- Проверка, оценка и коррекция знаний и способов действий.
В первой части идет повторение и систематизация базовых знаний и способов действий при решении стандартных задач. Во второй — в процессе повторения ученики должны последовательно перейти от одного уровня математической деятельности к следующему, более высокому. На этой стадии итогового повторения мы старались составить тестовые задания таким образом, чтобы они максимально содействовали не формальному усвоению программного материала, а глубоко осознанному пониманию его и применению при решении задач на уровне узнавания и соотнесения с базовыми знаниями, способами действий и опорными сигналами.
- разнообразие типов и уровней заданий по данной теме;
- быстрый замер уровня усвоения информации учащимися;
- активизацию обучающей функции при контроле знаний и умений учащихся;
- предоставление учащимся быстрой обратной связи о правильности выполненных заданий;
- предоставление учащимся возможности обсуждение типичных ошибок, их анализа и коррекции.
При составлении тестов мы использовали задания из источников, указанных в библиографии и авторские задания
(Тест1:задания 1,2,3,14; Тест 2: задания 1,2,4,6,10,11,16,17,19; Тест 3: задания 3,5,8,9)
На каждую тему во второй части планирования отводится 3 часа, из них: 2 часа на активную проверку, оценку и коррекцию знаний и способов действий; 1 час на урок-консультацию.
Планирование итогового повторения
(40 часов)
№ | Название темы | Количество часов |
I Обобщение и систематизация знаний и способов действий. | ||
1.1 | Действительные числа | 2 |
1.2 | Тождественные преобразования | 3 |
1.3 | Функции | 4 |
1.4 | Уравнения, неравенства, системы уравнений и неравенств | 10 |
1.5 | Производная, интеграл и их применение | 3 |
II Проверка, оценка и коррекция знаний и способов действий | ||
2.1 | Вычисление и тождественные преобразования рациональных выражений. Рациональные уравнения, неравенства и системы уравнений и неравенств. | 3 |
2.2 | Вычисление и тождественные преобразования выражений, содержащих радикалы. Иррациональные уравнения, неравенства и системы уравнений. | 3 |
2.3 | Вычисление и тождественные преобразования тригонометрических выражений. Тригонометрические функции. Тригонометрические уравнения, неравенства, системы уравнений. | 3 |
2.4 | Вычисление и преобразования выражений, содержащих степени с рациональным показателем. Показательная функция. Показательные уравнения, неравенства, системы уравнений. | 3 |
2.5 | Вычисление и преобразования логарифмических выражений. Логарифмическая функция. Логарифмические уравнения, неравенства, системы уравнений. | 3 |
2.6 | Прогрессии. Тестовые задачи. | 3 |
Урок проверки, оценки и коррекции знаний и способов действий (№ 94- 95)
Тема:
Показательная функция, её свойства и применение.
- выявления и искоренения типичных ошибок учащихся;
- обучения самоконтролю, взаимоконтролю, быстрому переключению с одного типа заданий на другой;
- развития самостоятельности, внимательности, формирования умения выбирать оптимальную стратегию при решении конкретной задачи и работы в целом;
- развития умений аргументировано участвовать в обсуждении решений;
- формирования культуры поведения при работе в парах, уважительного отношения к одноклассникам.
Оборудование:
Компьютеры, мультимедийный проектор, раздаточный материал, презентация.
Структура урока:
- Ознакомление с темой, целью и задачами урока, инструктаж учащихся по организации работы на уроке (5 минут).
- Актуализация знаний и способов действий (10 минут).
- Проверка знаний учащимися основных понятий, правил, свойств и умений объяснять аргументировано результаты своих действий. Обсуждение полученных результатов. (15 минут).
- Проверка умений учащихся самостоятельно применять знания в стандартных ситуациях. Обсуждение полученных результатов (15 минут).
- Проверка умений учащихся применять знания в изменённых, нестандартных условиях. Обсуждение результатов. (35 минут).
- Подведение итогов урока. Объяснение домашнего задания.(5 минут).
- Рефлексия (5 минут).
Ход урока:
Основное содержание учебного материала | Деятельность учителя | Деятельность учащегося |
1. Сообщение темы, целей и задач урока. | ||
| После проверки готовности класса сообщает, что сегодня урок посвящается проверке и оценке знаний и умений по теме. | Записывают тему урока. |
2. Проверка знаний учащимися фактического материала. | ||
Презентация | Актуализация знаний (с использованием компьютера). Организует повторение основного содержания учебного материала.
| Осуществляют самоконтроль: |
3. Проверка умений учащихся самостоятельно применять знания в стандартных условиях. | ||
Тест 1 | Инструктирует учащихся по выполнению Теста 1 на установление истинности (ложности) утверждения. | Выполняют Тест 1 на компьютерах (в парах), получают оценочный результат. |
4. Проверка умений учащихся применять знания в измененных и стандартных условиях. | ||
Тест 2 | Инструктирует учащихся по выполнению Теста 2 на установление истинности (ложности) утверждения. | Выполняют Тест 2 (с учётом опыта Теста 1). |
5. Проверка умений учащихся применять знания в измененных и нестандартных условиях. | ||
Презентация | Инструктирует учащихся по выполнению Теста 3:
Организует проверку правильности полученных результатов посредством коллективного обсуждения (желательно с использованием интерактивной доски). | Выполняют Тест 3. |
6. Подведение итогов учебного занятия. Постановка д/з. | ||
Тест 3 | Комментирует оценки учащихся.
Следующий урок – консультация. | Записывают домашнее задание данное учителем. |
7. Рефлексия. | ||
| Учитель предлагает закончить предложения:
| Дети заканчивают предложения. |
Заключение.
Мы старались спланировать организацию итогового повторения таким образом, чтобы его можно было использовать при работе по учебникам различных авторов, рекомендованных МО РФ.
Предложенную разработку урока можно использовать как урок-конструктор при организации повторения любой темы.
Опыт работы показал, что учащиеся постепенно приобретают «вкус» к работе:
- по классификации заданий по видам;
- по классификации заданий по способам действий;
- по использованию опор;
- по выявлению ошибок и их анализу;
- по оценке результатов своей деятельности и деятельности своих товарищей.
На наш взгляд это движение в нужном направлении математической подготовки выпускников.
Библиография.
- Гин А.А. «Приемы педагогической техники: Свобода выбора. Открытость. Деятельность. Обратная связь. Идеальность». Пособие для учителя. 4-е изд. М.: Вита-Пресс. 2002г.
- Манвелов С.Г. Конструирование современного урока математики. Кн. Для учителя С.Г. Манвелов М. Просвещение. 2002г. (Библиотека учителя).
- Шамова Т.И., Давыденко Т.М. «Управление процессом формирования системы качеств знаний учащихся». Методическое пособие. Москва. 1990г.
- Ф.Ф. Лысенко «Математика ЕГЭ-2008. Вступительные экзамены». Изд. «Легион». 2007г.
- Б.З. Федоренко «Пособие по математике для поступающих в БГТАСМ» Белгород. 2000г.
- А.Г.Клово «Пособие для подготовки к ЕГЭ» Москва. ФЦТ. 2005г.
- «Учебные проекты с использованием Microsoft Office» Изд. «Бином. Лаборатория знаний» 2007г.
- ЕГЭ 2007-2008 Математика. В.В.Кочагин, ФИПИ «Издательство Астрель» 2007г.
Приложение: Тест
13.02.2008
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
План итогового повторения по математике в 11 классе
Итоговое повторение по математике в 11 классе.
Календарно-тематическое планирование.
Название темСодержание уроков
Дата проведения
Кол-во часов
Повторение
Уравнения и неравенства с модулем.
5.04
1
Наибольшее и наименьшее значения функции.
Контрольная работа №11 по теме «Общие методы решения уравнений и неравенств».
7.04
1
Решение уравнений.
Уравнения и неравенства со знаком радикала.
8.04
1
Показательные уравнения.
Уравнения и неравенства со знаком радикала.
9.04
1
Показательные неравенства.
Уравнения и неравенства со знаком радикала.
13.04
1
Системы неравенств.
Иррациональные неравенства.
13.04
1
Формулы приведения.
Доказательство неравенств.
14.04
1
Формулы тригонометрии.
Уравнения с двумя переменными.
14.04
1
Функция , графики функций
Неравенства с двумя переменными.
15.04
1
Функция , графики функций
Системы уравнений.
16.04
1
Тригонометрические уравнения.
Различные методы решения систем уравнений.
20.04
1
Тригонометрические неравенства.
Решение задач на составление уравнений.
20.04
1
Уравнения и неравенства с модулем.
Контрольная работа №12 по теме «Уравнения и неравенства со знаком радикала .Системы уравнений»
21.04
1
Уравнения и неравенства со знаком радикала.
Уравнения и неравенства с модулем.
Простейшие задачи с параметрами.
22.04
1
Определенный интеграл.
Задачи с параметром.
23.04
1
Объем пирамиды, призмы, конуса, цилиндра.
Решение экзаменационных задач с параметрами.
27.04
1
Объем шара и площадь сферы.
Итоговое повторение. Параллельность прямых, прямой и плоскости. Скрещивающиеся прямые.
28.04
1
Перпендикулярность прямой и плоскости. Угол между прямой и плоскостью.
28.04
1
Двугранный угол. Перпендикулярность плоскостей.
30.05
1
Многогранники: параллелепипед, призма, площади их поверхностей.
4.05
1
Комбинации многогранников.
4.05
1
Векторы в пространстве.
5.05
1
Цилиндр, конус, шар, площадь их поверхностей.
5.05
1
Объемы тел.
6.05
1
Преобразование выражений, содержащих радикалы и степени с дробными показателями.
7.05
1
Преобразования тригонометрических выражений.
11.05
1
Преобразование выражений, содержащих степени и логарифмы.
11.05
1
Итоговая контрольная работа
12.05
2
Итоговая контрольная работа
12.05
Степенная, показательная, логарифмическая функции.
13.05
1
Рациональные уравнения и неравенства.
14.05
1
Тригонометрические уравнения и неравенства.
18.05
Показательные уравнения и неравенства.
18.05
Логарифмические уравнения и неравенства.
19.05
Системы тригонометрических, показательных, логарифмических уравнений. уравнений.
19.05
Производная, применение производной.
20.05
Первообразная и интеграл.
21.05
Комбинаторные задачи.
21.05
Итоговое тестирование.
21.05
infourok.ru
Урок математики в 11 классе «Повторение. Подготовка к ЕГЭ»
Урок математики в 11 классе.
Тема: «Повторение. Подготовка к ЕГЭ».
Цель урока:
Повторение материала, подготовка учащихся к экзаменам.
развитие логического мышления, навыков самостоятельной и групповой деятельности.
Воспитание коллективизма.
План урока:
Оргмомент.
Устная работа. Задания типа В2
Повторение темы « Площади». Составление кластера.
Повторение темы «Логарифмы», использование ЭОРов.
Подведение итогов урока
(Тип урока: урок повторения и закрепления пройденного материала.
Методы обучения: словесный, наглядный, практический (частично-поисковый, метод самостоятельной работы).
Средства обучения: наглядный материал (карточки, плакаты, учебное пособие «Банк открытых заданий ЕГЭ»).
Формы работы: групповая, индивидуальная.
Триединая цель урока:
Задачи урока:
Выявить уровень подготовки учащихся по геометрии по данной теме, систематизировать полученные знания с помощью приема «Кластер»
Помочь в развитии и самореализации творческих способностей личности; обучить приемам организации интеллектуального труда
Научить учащихся находить главное
Продолжить воспитание у учащихся уважительного отношения друг к другу, чувства товарищества, культуры общения, чувства ответственности. )
Ход урока.
Оргмомент.
Устные упражнения: Разрешите открыть урок с высказывания Декарта: «Я мыслю, следовательно, существую». Сейчас вам дается возможность проявить свою мысль при выполнении ряда заданий для подготовки к ЕГЭ.
ЕГЭ это вершина ,к которой мы медленно поднимаемся, переходя из класса в класс, изучая одну тему за другой. Задания ЕГЭ это ступени, по которым легче покорить эту вершину. Сегодня на уроке мы преодолеем вместе с вами некоторые из этих ступеней.
Итак , первая ступенька на которую мы с вами сегодня поднимемся -задания В2. Их можно решить устно. Мы сейчас рассмотрим несколько разных заданий этого типа.
Задание B2
На рисунке изображен график осадков в г.Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.
Определите по графику, сколько дней из данного периода осадков выпало между 2 и 8 мм.
Ответ: 3
Задание B2
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году.
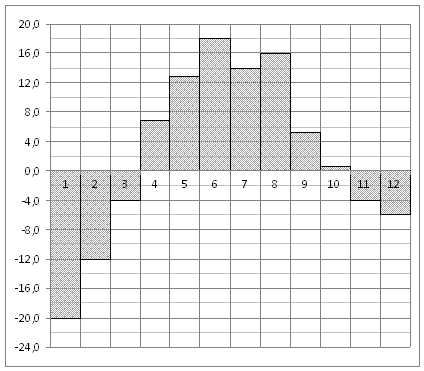
Ответ: 38
Задание B2
Посев семян тыквы рекомендуется проводить в мае при дневной температуре воздуха не менее ° С. На рисунке показан прогноз дневной температуры воздуха в первой и второй декадах мая. Определите, в течение скольких дней за этот период можно производить посев тыквы.

Ответ: 7
Задание B2
На графике показано изменение температуры воздуха в некотором населённом пункте на протяжении трех суток, начиная с 0 часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.

Ответ: 10
Задание B2
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 19 декабря.
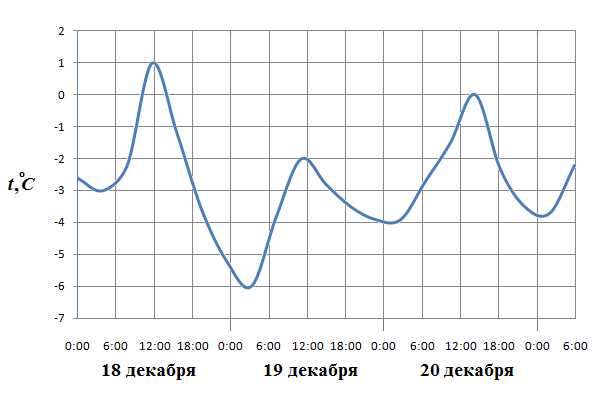
Ответ: 4
Задание B2 (18881)
(показов: 1885, ответов: 1026)
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа выпало наибольшее количество осадков.
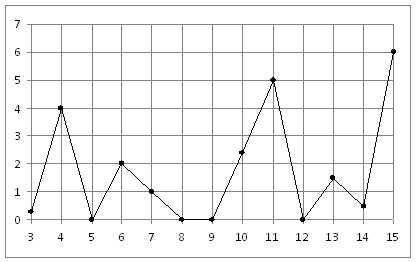
Ответ: 15
Задание B2
На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года.
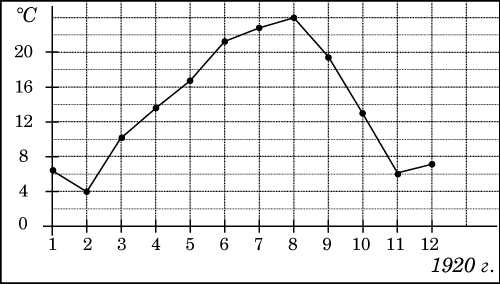
Ответ: 6
Задание B2
На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 1988 году.
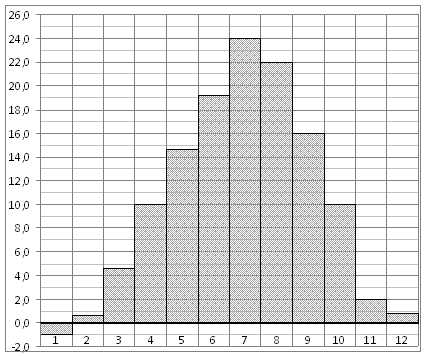
Ответ: 24
Задание B2
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало более 3 миллиметров осадков.

Ответ: 3
Обобщение и коррекция опорных знаний по теме «Площади плоских фигур»
Формулы для кластера
S= аbsinγ S= (d1×d2×sinγ) 2
Формула Геррона S= 1/2ab sinγ S=1/2 r×P S= abc 4R
(круговой сектор) S=πR²α 360
4 n =4, S=a² n=6, S=3√3a² 2 |
(правильная пирамида) Sбок=1/2Pоснd (апофему) (усеченная пирамида) Sбок=1/2(P1 +P2)d (апофему)
Sпол=2πR(R + h)
(прямой призмы) Sбок= Ph
Sпол=πr(l + r) (усеченный конус) Sбок=π (r + r1) l
|
Учащимся предлагается составить кластер по теме «Площади». На столах у каждого находится лист (формат А4).
На листе делается посередине надпись «Площади». Затем учащимся предлагается слева записать виды плоских фигур и их площадей.
Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое обсуждение полученного кластера. Корректировка кластера.
Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач. Работа устно.
Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работать предлагается в парах или индивидуально. Обязательно необходимо подчеркнуть, что при решении задач необходимо применять формулы площадей, можно пользоваться составленным кластером.
После небольшого обсуждения в парах, ответы вслух. Обсуждение.
Учитель показывает чертеж из сборника, дети говорят ответ.
Вопросы, задаваемые при обсуждении задач:
Площадь какой фигуры находили?
Какую формулу применяли?
Можно ли решить данную задачу другим способом?
Предлагаемые задачи для устной работы:
(количество заданий можно увеличить или уменьшить в зависимости от времени урока)
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура. Найдите его площадь.
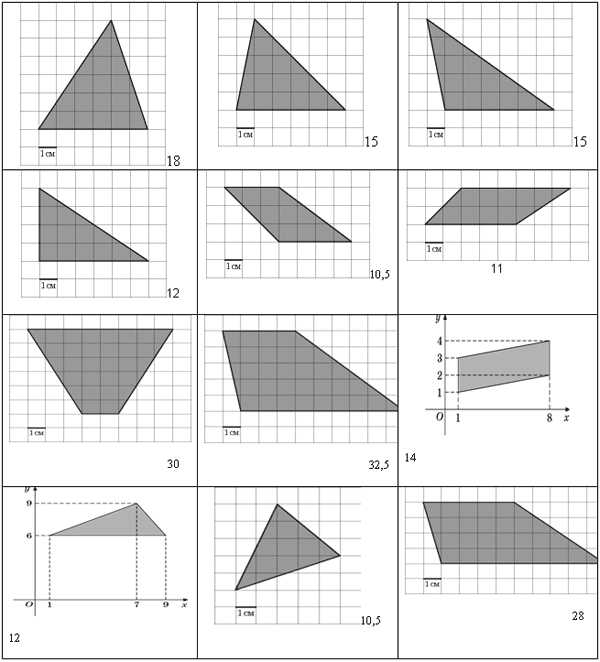
Теперь давайте перейдем к заданиям типа В5, В7. Логарифмы. Перед вами лежат формулы, выражающие свойства логарифмов. При работе можете ими пользоваться.
ЭОРы: а) работа вместе с учителем
Б) самостоятельная работа ученика.
Одновременно класс работает с ним, корректирует знания.
Откройте «Репетитор по математике. Варианты ЕГЭ, 2012 год». Выполняете каждый свой вариант. Начинаем выполнять тест. Результаты тестирования отправьте на печать.
Подведение итогов урока
1. Домашнее задание.
– Задачи из банка открытых задач ЕГЭ: №5061, 5067,5201, 21337.
– Оформить кластер, ответить на вопросы, отмеченные в кластере2. Выставление оценок
3. Рефлексия
– Что дает нам прием «Кластер»?
– Имеет ли практическое значение данная тема?
– Понравился ли вам урок?Сегодня мы проводим урок – отчет самостоятельного решения
задачи. Вы решали одну задачу разными способами. Мы ждем от вас красивого решения, а добиться этого можно лишь в результате кропотливой работы над задачей.
Красивое решение приходит тогда, когда придумано несколько вариантов решения задачи. Метода, который гарантировал бы решение любой задачи – нет. Но все же существуют весьма общие приемы, которые при умелом применении заметно облегчают решение многих трудных задач. Разработка этих приемов называется — эвристика. Слово происходит от знаменитого «Эврика».
«Эврика» — нашел! – воскликнул, согласно легенде, древнегреческий ученый Архимед, выскочив из ванны, он понял как решить, возникшую перед ним задачу.
Стихотворение (читает ученица)
Преданье старинное знает весь свет,
Как, нежась горячею ванной,
Открыл свой великий закон Архимед,
Связав его с выходкой странной.
Сияющий выскочил вон Архимед,
Из ванны горячей, где мылся,
И прямо из бани, как был, неодет,
Куда-то бежать он пустился.
Картина, достойная кисти богов,
По улице, солнцем согретой,
Пунктир оставляя из мокрых следов,
Бежит Архимед неодетый.
Толпа сиракузцев несется во след,
В восторге от бешеной гонки,
И громко ликует, когда Архимед,
Выкрикнул «Эврика» звонко.
«Нашел!» Он нашел тот желанный ответ,
Который искал так упорно.
«Нашел!» В упоенье кричал Архимед,
«Нашел!» — повторяли задорно.
Подобно Архимеду, вы искали решение задачи, каждая группа предлагает свой способ. Когда вы получили задание сделать проект решения задачи, то вы думали, что это невозможно, но сейчас посмотрим, что из этого получилось
Заключение.
Сейчас, прослушав несколько способов решения одной задачи, мы повторили несколько тем. Вы должны выбрать тот способ решения, который вам больше понравился, и если на экзамене вам встретилась задача, которую не можете решить, то вспомните, что можно попытаться решить другим способом.
В этом году вы выпускаетесь из школы и вас ждут большие жизненные испытания. Так вы должны знать, что безвыходных ситуаций не бывает.
В любой ситуации можно найти решение.
Закончим наш урок словами Эйнштейна: «Каждый важный успех приносит новые вопросы».
kopilkaurokov.ru
Урок математики. «Обобщающий урок-повторение», 11-й класс
Разделы: Математика
Цели урока:
- проверка и закрепление ЗУН по решению заданий из КИМов к ЕГЭ;
- закрепление навыков работы в группе;
- воспитание положительной мотивации по подготовке к экзаменам.
Ход урока
1. Организационный момент.
В классе сформированы три группы: по части A, по части B, по части C. Группы можно разбить по принципу: менее подготовленная группа, средняя группа и более сильная группа. В каждой группе выбран ведущий, он распределяет обязанности, готовит учащихся к защите заданий, выставляет групповую оценку, индивидуальную оценку, расписывается в дневниках. За основу берется один из КИМов. Каждая группа получает лист с заданиями и лист с нормами оценивания работы и планом работы. На доске заранее приготовлена таблица для ответов, по мере выполнения заданий учащиеся записывают ответы. Если группа справится с заданием раньше отведенного времени, то каждый может зарабатывать индивидуальную оценку.
2. Работа в творческих группах.
1-я группа
А1. Упростите выражение .
А2. Вычислите: .
А3. Найдите значение выражения .
А4. Функция задана графиком. На каком из
указанных промежутков она возрастает?
1) [-5; -1]
2) [-1; 4]
3) [-2; 2]
4) [-5; 0]
А5. Найдите производную функции .
А6. Найдите множество значений функции .
А7. Функция задана графиком. Укажите промежуток, на котором она принимает только положительные значения.
А8. Решите неравенство .
А9. Решите уравнение
А10. Решите неравенство
2-я группа
В1. Найдите значение выражения .
В2. Решите уравнение .
В3. Решите уравнение .
В4. Найдите значение выражения , если известно, что
В5. Найдите значение выражения .
В6. Решите уравнение .
(Если уравнение имеет более одного корня, то в бланке ответов запишите произведение всех его корней).
3-я группа
С1. Две бригады, работая вместе, ремонтировали дорогу в течение 5 дней, а затем одна вторая бригада закончила ремонт еще за 9 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на 6 дней быстрее, чем одна вторая бригада?
С2. Найдите точки минимума функции
С3. Решите уравнение .
По окончании времени учитель зачитывает верные версии, называет оценку группе. Ведущий в группе выставляет индивидуальные оценки и расписывается в дневниках.
3. Защита заданий у доски.
Представитель от каждой группы проводит анализ решенных заданий, проговаривает формулы и комментирует одно из заданий.
4. Итог урока.
Каждый пишет в тетради, затем один ученик зачитывает, все проверяют. Можно оценить еще одной оценкой.
- На сколько процентов ты готов к ЕГЭ?
- Самая трудная тема для тебя?
- При делении степеней показатели …
- Сумма логарифмов равна логарифму …
- Чему равно основание натурального логарифма?
- Количество букв в отчестве поэта Сергея Есенина?
- Из каких чисел извлекается квадратный корень?
- На какой оси располагаются нули функции?
- Дополни гласными и запиши слово к л б н.
- Каким должно быть выражение под знаком логарифма?
- Какое вещество называют слезами Балтийского моря?
- Дополни гласными и напиши слово н т н м.
- Чему равен угловой коэффициент у касательной в точке касания?
- Дополни гласными и напиши слово д к р т р.
- Дополни гласными и напиши слово к з м т.
Оценки
- “5” — 18-12,
- “4” — 11-10,
- “3” — 9 и менее.
Домашнее задание. Формулы.
17.01.2008
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Рабочая учебная программа элективного курса для 11 класса «Математика. 11 класс. Повторение курса в формате ЕГЭ»
Рабочая учебная программа элективного курса по математике
для 11 класса «Математика. 11 класс. Повторение курса в формате ЕГЭ»
Краткая аннотация программы
Программа элективного курса по математике «Математика. 11 класс. Повторение курса в формате ЕГЭ» предполагает 1 час в неделю с 1 октября 2014 года по май 2015 года. Курс рекомендован учащимся 11 класса и может быть использован при подготовке к ЕГЭ.
Программа составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования на базовом уровне (Приказ МО РФ от 5 марта 2004 года № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего и среднего (полного) общего образования» (далее — ФК ГОС-2004)) и примерной программы среднего (полного) общего образования на базовом уровне по математике (Письмо Министерства образования и науки РФ от 07.07.2005г. № 03-1263 «О примерных программах по учебным предметам федерального базисного учебного плана»).
Каждое занятие посвящено одному или нескольким разделам математики в рамках школьного курса. Каждая тема сопровождается необходимым справочным теоретическим материалом, достаточно полным изложением основных методов решения задач. Разбирается большое количество задач разного уровня сложности. Большое внимание уделено освоению таких сложных для школьников разделов, как «Решение стереометрических и планиметрических задач». Данная методика направлена на более осознанное усвоение математики, высвобождает время для ненужного натаскивания и зазубривания, позволяя тем самым рассмотреть и усвоить методы решения задач путем размышлений и рассуждений.
Обучение на курсе позволит выпускникам общеобразовательных школ обобщить знания по математике, будет способствовать осознанному и более уверенному выходу на экзамен; обеспечит получение достойного балла на ЕГЭ.
Цель курса – создание условий для формирования и развития у обучающихся навыков анализа и систематизации полученных ранее знаний, подготовка к итоговой аттестации в форме ЕГЭ.
Задачи курса:
обеспечение усвоения обучающимися наиболее общих приемов и способов решения задач повышенного уровня сложности;
формирование и развитие у старшеклассников аналитического и логического мышления при проектировании решения задачи;
развитие умений самостоятельно анализировать и решать задачи по образцу и в незнакомой ситуации;
расширение и углубление курса математики, обеспечивающее повышенный уровень изучения математики;
формирование опыта творческой деятельности учащихся через исследовательскую деятельность при решении нестандартных задач;
формирование навыка работы с научной литературой, различными источниками;
развитие коммуникативных и общеучебных навыков работы в Интернете, самостоятельной работы, умений вести дискуссию, аргументировать ответы и т.д.
Виды деятельности на занятиях: консультация, лекция, практикум через сайты, работа с компьютером, в Интернете.
Предполагаемые результаты.
Изучение данного курса дает учащимся возможность:
повторить и систематизировать ранее изученный материал школьного курса математики;
освоить основные приемы решения задач;
овладеть навыками построения и анализа предполагаемого решения поставленной задачи;
познакомиться и использовать на практике нестандартные методы решения задач;
повысить уровень своей математической культуры, творческого развития, познавательной активности;
познакомиться с возможностями использования электронных средств обучения, в том числе Интернет-ресурсов, в ходе подготовки к итоговой аттестации в форме ЕГЭ.
Структура курса:
1. Подготовительный этап: Ликвидация пробелов за курс основной школы.
2. Основной этап. Решение заданий части 1,2.
3. Отработка заданий 15 – 21.
Тематическое планирование:
№ п.п.
Тема
Кол-во часов
Период проведения
1.
Арифметика. Контроль на входе.
1
2.
Простейшие текстовые задачи.
1
3.
Чтение графиков и диаграмм.
1
4.
Планиметрия: вычисление длин и площадей.
1
5.
Выбор оптимального варианта.
1
6.
Очная форма обучения. Промежуточный контроль.
1
7-8
Простейшие уравнения.
2
9-10
Планиметрия: задачи, связанные с углами.
2
11.
Вычисления и преобразования.
1
12-13
Производная и касательная.
2
14
Стереометрия: вычисление длин.
1
15
Начала теории вероятностей.
1
16-17
Задачи по стереометрии.
2
18
Очная форма обучения. Промежуточный контроль.
1
19-20
Задачи с прикладным содержанием .
2
21-22
Текстовые задачи.
2
23
Наибольшее и наименьшее значение функций.
1
24
Очная форма обучения. Промежуточный контроль.
1
25-26
Тригонометрические уравнения.
2
27
Углы и расстояния в пространстве.
1
28-29
Неравенства, содержащие знак корня или логарифма.
2
30
Уравнения, неравенства, системы с параметром.
1
31
Числа и их свойства.
1
32-33
Итоговая работа в форме ЕГЭ
1
34
Анализ итоговой работы. Очная форма
1
Литература:
ЕГЭ 2015. Математика. Типовые тестовые задания. Под ред. Семенова А.Л., Ященко И.В. (2015.) 30 вариантов + 800 заданий Издательство «Экзамен»
ЕГЭ 2015. Математика. Типовые тестовые задания. Под ред. Семенова А.Л., Ященко И.В. 36 вариантов, Издательство Национальное образование
ЕГЭ 2015. Математика. Оптимальный банк заданий для подготовки учащихся. Семенов А.В. и др. (2015, 80с.)
ЕГЭ. Математика. Задание 15 с решениями и ответами А.В. Шевкин, Ю.О. Лукас
Математика. Тесты к ЕГЭ. Клово А.Г. (2012, 220с.)
ЕГЭ. 1000 задач. И.Н.Сергееев. Задания 9-15.
Л.Д.Лаппо Математика. ЕГЭ. Полный курс
ЕГЭ. Тематические тренировочные задания. Супертренинг. Л.Д.Лаппо
infourok.ru
Методическая разработка «Организация повторения по алгебре в 11 профильном классе для подготовки к решению заданий С3 в ЕГЭ»
Муниципальное бюджетное общеобразовательное учреждение лицей № 6
городского округа Тольятти
Методическая разработка
«Организация повторения по алгебре
в 11 профильном классе
для подготовки к решению заданий С3 в ЕГЭ»
Подготовила
Овчинникова Наталья Александровна,
учитель математики высшей категории
МБУ лицея №6 г. о. Тольятти
Тольятти
2014
Тема «Организация повторения по алгебре в 11 профильном классе
для подготовки к решению заданий С3 в ЕГЭ»
Система уроков повторения по теме «Решение неравенств функционально – графическим методом» содержит: примерное планирование учебного времени; краткий анализ знаний и умений учащихся, полученных на уроках повторения по выбранной теме; план-конспект одного из уроков; проверочную работу (в одном варианте).
Примерное планирование учебного времени
Использование области определения функций.(1 час)
Использование монотонности функций.(1 час)
Использование ограниченности функций. (2 часа)
Метод интервалов для непрерывных функций. (2 часа)
Использование графиков функций. (1 час)
Проверочная работа. (1 час)
Краткий анализ и умений знаний учащихся, полученных на уроках повторения по выбранной теме.
В результате повторения данной темы учащиеся должны иметь четкое представление о возможностях функционально-графического подхода к решению неравенств.
Уметь:
решать неравенства с использованием области определения входящих в них функций, свойства монотонности функций;
использовать при решении неравенств свойство ограниченности функции на некотором множестве, уметь находить наибольшее и наименьшее значение функций или их композиций на заданном множестве;
применять метод интервалов при решении неравенств, содержащих различные функции, а также при решении трансцендентных неравенств, используя идею рационализации неравенств;
уметь при решении неравенств рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение неравенства было очевидно;
использовать приобретённые знания и умения в практической деятельности при подготовке к ЕГЭ.
План – конспект урока по теме:
«Метод интервалов для непрерывных функций» (2 часа)
Цели урока:
Обучающие:
обобщить ранее изученный материал о решении неравенств методом
интервалов; возможность применения метода интервалов для
решения неравенств различного типа;выработка умений и навыков в решении неравенств различного типа
методом интервалов;решение трансцендентных неравенств, с использованием метода рационализации.
Развивающие:
повысить интерес учащихся к нестандартным задачам, сформировать у них
положительный мотив учения;развитие у учащихся логического мышления в процессе поиска рациональных методов и алгоритмов решения;
Воспитательные:
формирование нравственных качеств, аккуратности, дисциплинированности, чувства собственного достоинства, ответственного отношения к достижению цели;
развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.
Тип урока: урок обобщения и систематизации знаний.
План урока:
Организационный момент.
Повторение и актуализация опорных знаний.
Решение неравенств методом интервалов.
Подведение итогов. Задание на дом.
Ход урока:
1. Организационный момент.
2. Повторение и актуализация опорных знаний.
Обобщенный метод интервалов.
Применимость метода интервалов не ограничивается решением рациональных неравенств.
Применяя метод интервалов к решению иррациональных, трансцендентных, комбинированных неравенств, говорим об обобщенном методе интервалов.
Алгоритм обобщенного метода интервалов:
Привести неравенство к виду
 . Рассмотреть функцию
. Рассмотреть функцию  .
.Найти область определения функции
 .
.Найти нули функции
 , решив уравнение
, решив уравнение 
Изобразить на числовой прямой область определения и нули функции.
Определить знаки функции на промежутках, входящих в область определения функции.
Записать ответ, включив в него промежутки в соответствии со знаком неравенства (не забыть включить в ответ изолированные точки).
Метод рационализации.
Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x) (в конечном счете, рациональное), при которой неравенство
 равносильно неравенству
равносильно неравенству  в области определения выражения F(x) (символ
в области определения выражения F(x) (символ заменяет один из знаков неравенств: >, ).
заменяет один из знаков неравенств: >, ).Выделим некоторые выражения F и соответствующие им рационализирующие выражения G.
Выражение F(x)
3. Решение неравенств методом интервалов
Каждое задание решает группа учащихся. Затем один из группы записывает решение на доске и поясняет его.
1). Решить неравенство
Используем метод интервалов для решения данного неравенства
Рассмотрим функцию
Найдем область определения функции

Найдем нули функции:






Определим знаки функции на каждом из промежутков
Следовательно, множеством решений исходного неравенства является объединение промежутков
Ответ:
2). Решить неравенство
Используем метод интервалов для решения данного неравенства
Рассмотрим функцию
Найдем область определения функции
Найдем нули функции:

 ,
, 




Определим знаки функции на каждом из промежутков
Следовательно, множеством решений исходного неравенства является объединение промежутков
Ответ:
3). Решить неравенство
Заменим данное неравенство равносильной системой, используя метод рационализации:
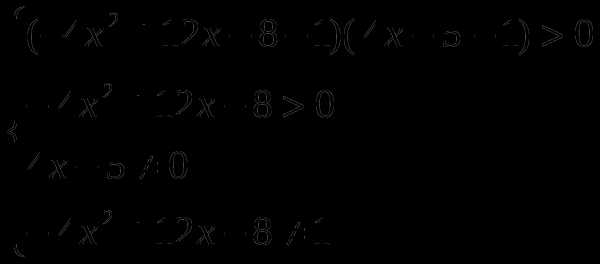
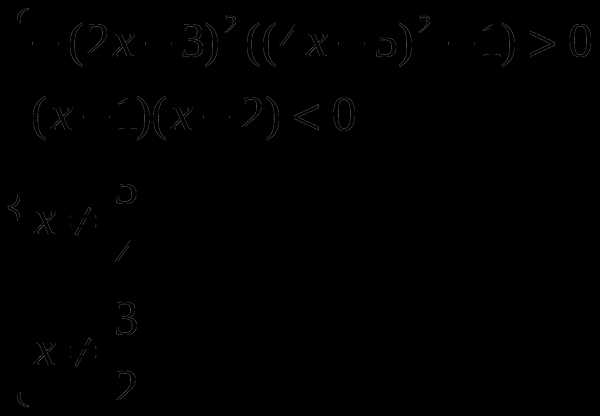
Окончательно получаем,что решением являются все х такие, что

 Ответ:
Ответ: 
4). Решить неравенство 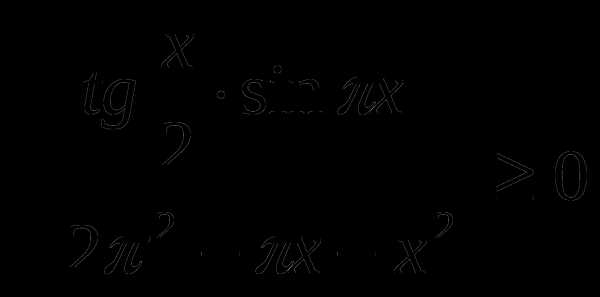
Воспользуемся методом интервалов:
Рассмотрим функцию


Найдем область определения функции

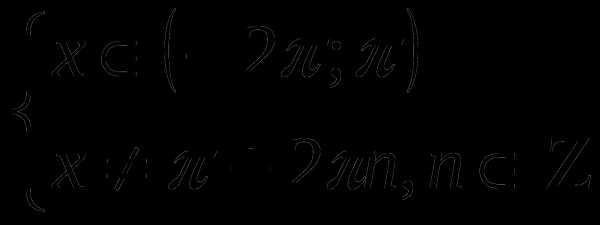
Найдем нули функции:



На промежутке лежат числа:
Определим знаки функции на каждом из промежутков
Множеством решений исходного неравенства является объединение промежутков
Ответ: 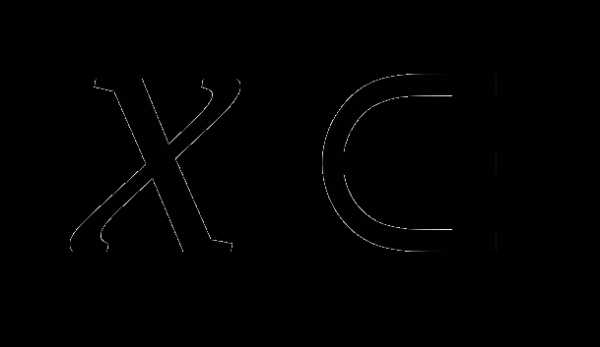
5). Решить неравенство
Используем метод интервалов для решения данного неравенства
Рассмотрим функцию
Найдем область определения функции


Найдем нули функции:

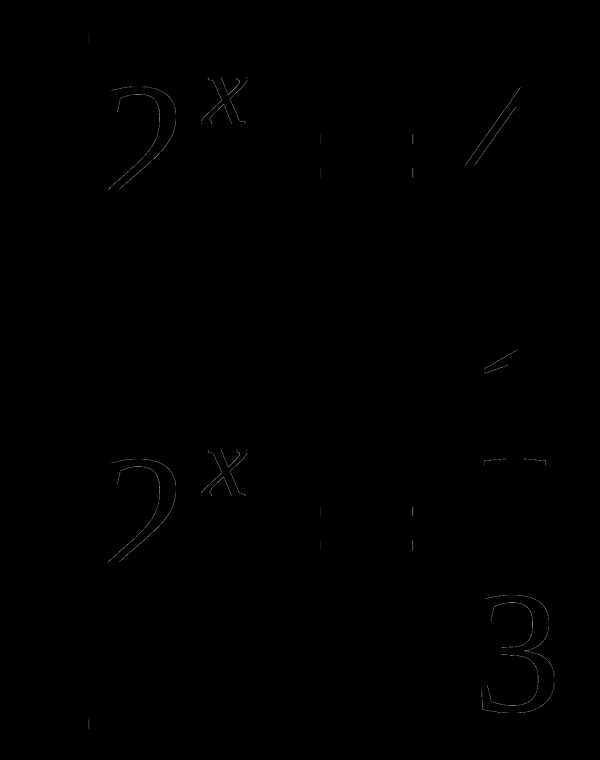

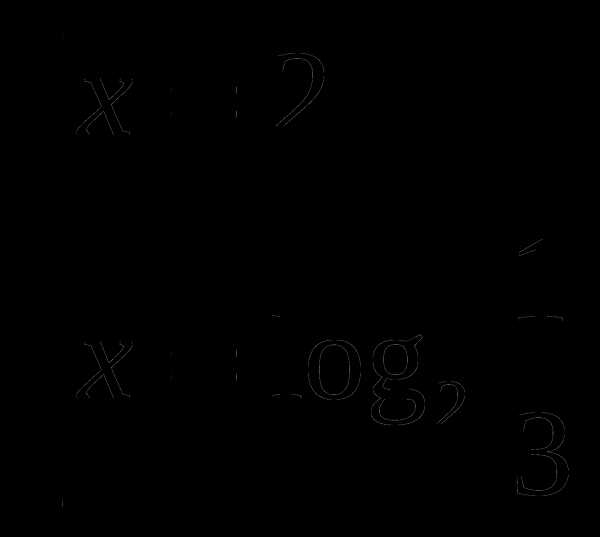

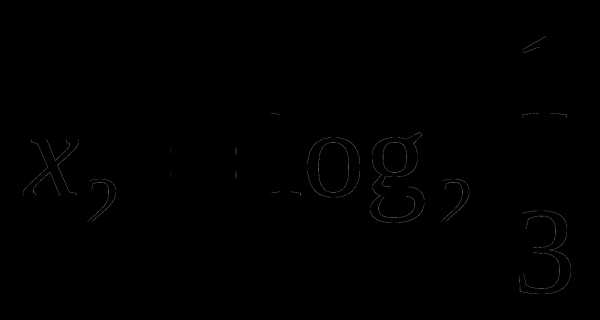
Определим знаки функции на каждом из промежутков
Множеством решений исходного неравенства является объединение промежутков
Ответ:
6). Решить неравенство 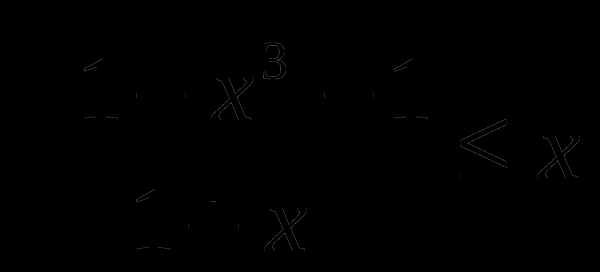
Используем метод интервалов для решения данного неравенства
Рассмотрим функцию

Найдем область определения функции

Найдем нули функции:



Определим знаки функции на промежутках:
Следовательно, множеством решений исходного неравенства является объединение промежутков
Ответ:
7). Решить неравенство 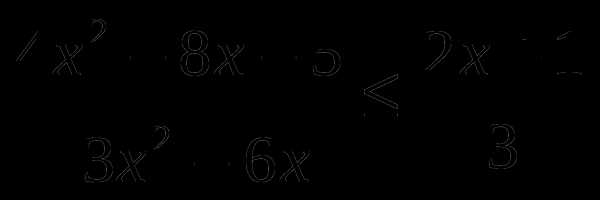
Используем метод интервалов для решения данного неравенства
Рассмотрим функцию

Найдем область определения функции
Найдем нули функции:







Определим знаки функции на промежутках:
, следовательно, множеством решений исходного неравенства является объединение промежутков 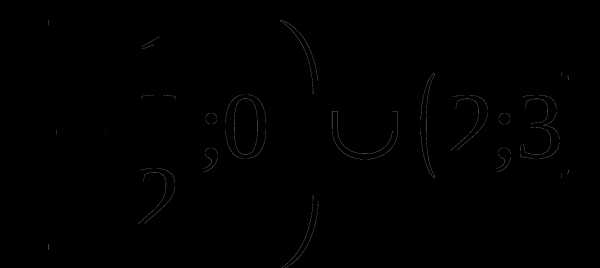
Ответ: 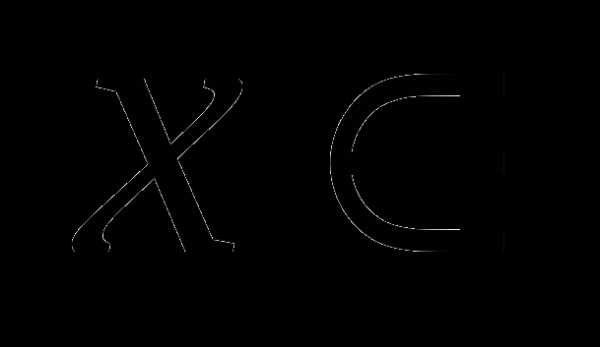
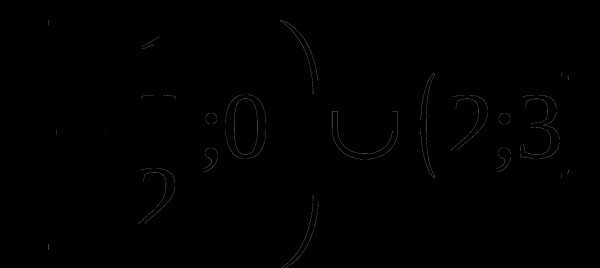
Подведение итогов. Задание на дом
Выводы, оценки.
Решить неравенства:
а) , б) 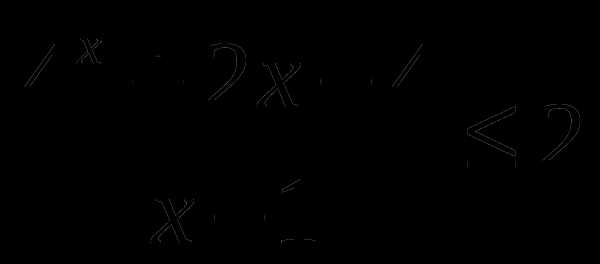
в) г) 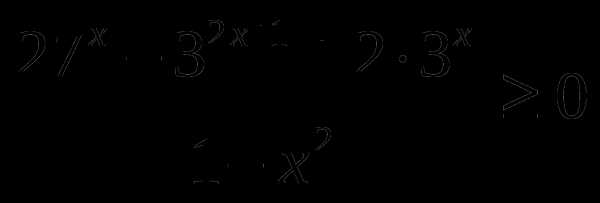
Дополнительно (на оценку):
а) б)
Проверочная работа
Решить неравенства:
2.
4.
5. 6.
Оценка ставится за любые «пять» верно выполненных заданий.
Список использованной литературы
Дорофеев Г. В. Обобщение метода интервалов. – Математика в школе, 1969, №3.
Математика. Алгебра. Начала математического анализа. Профильный уровень: учебник для 10 класса. М. И. Шабунин, А. А. Прокофьев. – М.: БИНОМ. Лаборатория знаний. 2007.
Панферов В. С., Сергеев И. Н. ЕГЭ – 2010. Математика. Задача С3, под редакцией А. Л. Семенова и И. В. Ященко. – М.: МЦНМО, 2010.
Садовничий Ю. В. ЕГЭ. Практикум по математике: Решение уравнений и неравенств. Преобразование алгебраических выражений. – М.: Издательство «Экзамен», 2012.
Выражение G(x) | |
loghf — loghg | (h – 1)(f – g) |
logfh — loggh | (f – 1)(g – 1)(h – 1)(g – f) |
hf — hg | (h – 1)(f – g) |
fh — gh | (f – g)h |
| f | — | g | | (f – g)(f + g) |
loghf · logpg | (f – 1)(g – 1)(h – 1)(p – 1) |
| f- g |
doc4web.ru
11 класс. Алгебра
Рубрика «11 класс. Алгебра»
В алгебре часто решаются задачи на нахождение площади криволинейной трапеции, заключенной между двумя кривыми. Различают два случая: 1) переменная интегрирования х; 2) переменная интегрирования у.
Рассмотрим оба этих случая.
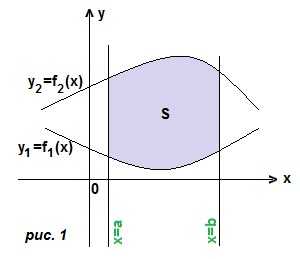 1) переменная интегрирования х. В этом случае трапеция ограничена сверху и снизу двумя кривыми, а слева и справа прямыми х=а, х=b. (рис. 1). Границы интегрирования a и b, а чтобы получить подынтегральную функцию, мы из уравнения верхней линии вычитаем уравнение нижней линии. Тогда площадь трапеции:
1) переменная интегрирования х. В этом случае трапеция ограничена сверху и снизу двумя кривыми, а слева и справа прямыми х=а, х=b. (рис. 1). Границы интегрирования a и b, а чтобы получить подынтегральную функцию, мы из уравнения верхней линии вычитаем уравнение нижней линии. Тогда площадь трапеции:
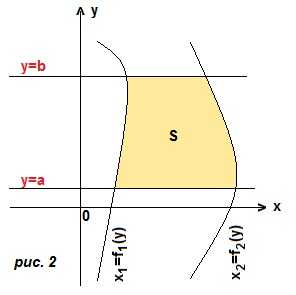 2) переменная интегрирования у. Криволинейная трапеция ограничена справа и слева двумя кривыми, а снизу и сверху прямыми y=a, y=b. (рис. 2). Границы интегрирования a и b. Чтобы получить подынтегральное выражение, мы из уравнения правой линии вычтем уравнение левой линии. Тогда площадь трапеции:
2) переменная интегрирования у. Криволинейная трапеция ограничена справа и слева двумя кривыми, а снизу и сверху прямыми y=a, y=b. (рис. 2). Границы интегрирования a и b. Чтобы получить подынтегральное выражение, мы из уравнения правой линии вычтем уравнение левой линии. Тогда площадь трапеции:
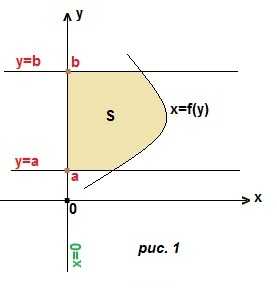 Если криволинейная трапеция прилегает к оси Оу (рис. 1) и ограничена непрерывной кривой x=f (y), осью ординат (прямой х=0) и прямыми y=a, y=b, то ее площадь вычисляется по той же формуле Ньютона-Лейбница (ф. Н-Л), только переменная интегрирования не х, а у:
Если криволинейная трапеция прилегает к оси Оу (рис. 1) и ограничена непрерывной кривой x=f (y), осью ординат (прямой х=0) и прямыми y=a, y=b, то ее площадь вычисляется по той же формуле Ньютона-Лейбница (ф. Н-Л), только переменная интегрирования не х, а у:
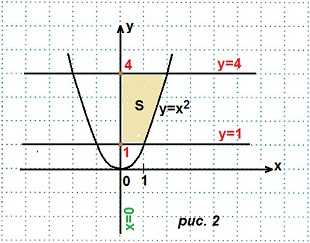 Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=x², y=1, y=4 и осью Оу.
Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=x², y=1, y=4 и осью Оу.
Решение. Построим данную криволинейную трапецию (рис. 2). Выразим х через у:
Искомую площадь S находим по формуле Ньютона-Лейбница (ф. Н-Л). У нас a=1, b=4.
Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница (ф. Н-Л):
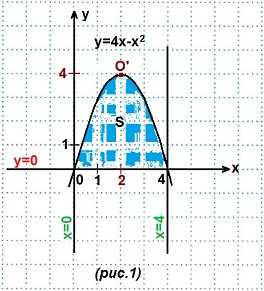 Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.
Пример 1. Найти площадь криволинейной трапеции, ограниченной линиями: y=4x-x²; y=0; x=0; x=4.
Решение. Строим графики данных линий. (рис. 1).
1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент а=-1<0.
Вершина параболы находится
в точке O′(m; n), где
О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:
4х-х²=0.
Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4. Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).
2) y=0 — это ось Ох; 3) х=0 — это ось Оy; 4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.
Площадь построенной криволинейной трапеции находим по (ф. Н-Л). У нас f (x)=4x-x², a=0, b=4.
Кстати, если Вы подсчитаете все целые заштрихованные клетки и добавите к ним половину всех остальных клеток заштрихованной фигуры, то получите приближенное значение искомой площади. Действительно, если единичный отрезок равен одной клетке, то площадь квадратика со стороной, равной 1 клетке, равна 1·1=1 (кв. ед.). Сколько квадратиков — столько квадратных единиц и составляет площадь фигуры.
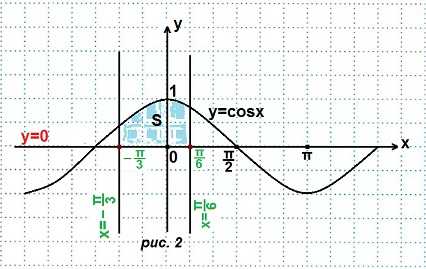
Пример 2. Найти площадь криволинейной трапеции, ограниченной линиями:
Решение. Строим графики данных линий. (рис. 2).
Площадь данной криволинейной трапеции:
Пора познакомиться с мощнейшим средством исследования в математике, физике, механике и других точных дисциплинах. Это средство — определенный интеграл. В средней школе определенный интеграл применяют при вычислениях площадей криволинейных трапеций, объемов тел вращения, нахождении моментов инерции и т.д.
Что такое определенный интеграл? Чем он отличается от неопределенного, с которым мы уже достаточно знакомы.
Сравните:
a и b — это границы, в которых изменяется переменная интегрирования х.
Сравниваем далее:
Неопределенный интеграл графически представляет собой семейство кривых, совмещаемых параллельным переносом (11.1.9).
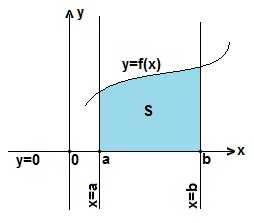 Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми x=a и х=b.
Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми x=a и х=b.
Значение определенного интеграла есть площадь S этой криволинейной трапеции:
Рассмотрим примеры на вычисление определенного интеграла.
Пример 1.
Найдем первообразную F (x) для подынтегральной функции f (x)=3x²-2x+1, а затем применим формулу Ньютона-Лейбница (ф. Н-Л).
Пример 2.
Возникает вопрос: раз определенный интеграл выражает собой площадь криволинейной трапеции, то нельзя ли увидеть эту криволинейную трапецию? А можно! Проиллюстрируем пример 2.
Полученный результат
выражает площадь криволинейной трапеции, ограниченной графиком функции y=(x+1)4, осью Ох и прямыми: х=0 (осью Оy) и х=1.
График функции y=(x+1)4 — парабола, ветви которой направлены вверх,
а вершина находится в точке О′(-1; 0).
Площадь этой криволинейной трапеции:
Вспомним определения:
1. Дифференцируемая функция F (x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство:
F′(x)=f (x).
2. Совокупность всех первообразных F (x)+C функции f (x) на рассматриваемом промежутке называется неопределенным интегралом.
Как можно представить себе неопределенный интеграл
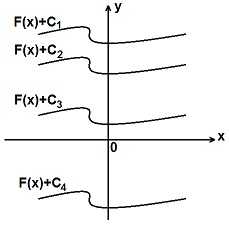 где F (x) — первообразная функции f (x), а С — некоторая постоянная величина?
где F (x) — первообразная функции f (x), а С — некоторая постоянная величина?
Если в данном примере или задаче не даются начальные условия для нахождения величины С, то мы получаем неоднозначную функцию F (x)+С — семейство интегральных кривых. Графики этих кривых можно совместить с помощью параллельного переноса. Из семейства этих кривых нам нужно уметь выделять ту, которая проходит через данную точку.
Пример 1. Найти для функции f (x)=1-2x первообразную, график которой проходит через точку М(3; 2).
Решение.
F (x)=∫(1-2x) dx=∫dx-2∫xdx=x-x²+C.
Так как F (3)=2 по условию, то получаем равенство:
2=3-3²+С;
2=3-9+С;
2=-6+С → С=8.
Тогда F (x)=x-x²+8.
Пример 2. Найти ∫(sinx-cosx) dx, если при π/2 первообразная равна 6.
Решение.
∫(sinx-cosx) dx=∫sinxdx-∫cosxdx=-cosx-sinx+C.
По условию F (π/2)=6. Получаем равенство: -cos (π/2) -sin (π/2)+C=6;
0-1+C=6 → C=6+1; C=7.
Искомая функция F (x)=-cosx-sinx+7.
Пример 3. Найти первообразную для функции
принимает значение, равное нулю.
Решение.

На предыдущем занятии (11.1.7.) мы рассмотрели простые примеры интегралов тригонометрических функций, когда подынтегральное выражение можно было упростить, используя подходящее тригонометрическое тождество, а затем применить соответствующую формулу интеграла тригонометрической функции. Кроме того, во всех примерах предыдущего занятия (11.1.7) мы интегрировали путем подведения под знак интеграла той линейной функции, которая являлась аргументом полученной тождественными преобразованиями тригонометрической функции.
Примеры этого занятия чуть сложнее, так как подынтегральное выражение нельзя будет упростить с помощью тригонометрического тождества. А как же будем решать? Мы продолжим применять тот же метод подведения под знак дифференциала, но уже подводить под знак дифференциала будем не просто линейную функцию, а тригонометрическую функцию, зависящую от линейной функции.
Пример 1. ∫sin7xcosxdx.
Подынтегральное выражение представляет собой произведение степени синуса на производную основания степени – синуса икс: (sinx)’ = cosx.
Воспользуемся способом подведения под знак дифференциала и формулой интеграла степенной функции (формула 1) лист Интегралы). Заменяем cosxdx на d (sinx).
∫sin7xcosxdx =∫sin7xd (sinx) =(1/8) sin8x + C.
Пример 2. (аналогичный). ∫sin7(4x + 5) cos (4x + 5) dx =(¼)∫sin7(4x + 5) d (sin (4x + 5)) =
=(¼)·(1/8)·sin8(4x+5)+C=(1/32) sin8(4x+5)+C.
Пример 3. ∫sin3xcos43xdx. Воспользуемся способом подведения под знак дифференциала и формулой интеграла степени. Один множитель подынтегрального выражения cos43x оставим, а sin3xdx запишем в виде: d (cos3x).
Проверка: d (cos3x) = — 3sin3x. Следовательно, перед знаком интеграла поставим коэффициент: — (1/3).
∫sin3xcos43xdx= — (1/3)∫cos43xd (cos3x) = — (1/3)·(1/5)·cos53x+C = — (1/15) cos53x+C.
Пример 4.
Увидели формулу 4) (лист Интегралы):
В самом деле, u = sinx, du = d (sinx) = cosxdx. Тогда:
Пример 5. (такой же пример со сложным аргументом у тригонометрических функций).
А теперь пример на ту же формулу 4) (лист Интегралы), только в качестве u будет использована функция косинуса, а именно: u=cosx, отсюда du=-sinxdx.
Пример 6.
Пример 7.
В следующих примерах мы также будем подводить функцию под знак интеграла, а затем применять формулу 2) (лист Интегралы):
Пример 8.
Пример 9.
И примеры чуть сложнее:
Пример 10.
Пример 11.
Продолжаем интегрировать тригонометрические функции по простейшим формулам 6) — 9) таблицы интегралов (лист «Интегралы«) Но вот незадача — у нас всего 4 формулы, и нужная формула не всегда сразу «видна»! Как же следует поступать в таких случаях? Нужно постараться упростить подынтегральное выражение, используя подходящие тригонометрические тождества.
Пример 1. ∫(cos²x-sin²x) dx. Такой формулы интегрирования у нас нет, но мы можем упростить подынтегральное выражение, используя тригонометрическую формулу для косинуса двойного аргумента: cos2α=cos²α-sin²α.
Решение.
∫(cos²x-sin²x) dx=∫cos2xdx=½∫cos2xd (2x)=1/2sin2x+C.
При решении мы применяем метод подведения под знак дифференциала (смотрите предыдущие занятия). Так как мы подвели под знак дифференциала 2х и получили выражение под знаком интеграла в 2 раза больше: d (2x)=2dx, то перед знаком интеграла ставим множитель ½. Сделаем проверку.
(F (x)+C)’=(1/2sin2x+C)’=½·cos2x·2=cos2x=cos²x-sin²x=f (x).
Пример 2. ∫(cos²4x-sin²4x) dx (аналогичный).
Решение.
∫(cos²4x-sin²4x) dx=∫cos8xdx=1/8∫cos8xd (8x)=1/8sin8x+C.
Пример 3. ∫(cos²x/2-sin²x/2) dx.
Решение.
∫(cos²x/2-sin²x/2) dx=∫сosxdx=sinx+C.
В примерах 2 и 3 мы так же, как и в примере 1, упрощали подынтегральное выражение по формуле для косинуса двойного аргумента,
а затем применяли формулу 6): ∫cosudu=sinu+C (лист Интегралы).
Пример 4. ∫(sin²x+cos²x) dx.
Решение.
Применяем основное тригонометрическое тождество: sin²α+cos²α=1. (*)
∫(sin²x+cos²x) dx=∫1·dx=∫dx=x+C.
Пример 5. ∫2sinxcosxdx.
Решение.
Используем формулу синуса двойного аргумента: sin2α=2sinαcosα (**) и упростим подынтегральное выражение.
∫2sinxcosxdx=∫sin2xdx=½∫sin2xd (2x)=-1/2cos2x+C.
Пример 6. ∫sin3xcos3xdx. Решаем аналогично примеру 5.
Решение.
∫sin3xcos3xdx=∫1/2sin6xdx=½∫sin6xdx=(½)·(1/6)∫sin6xd (6x)=- (1/12) cos6x+C.
В примерах 5 и 6 мы использовали формулу 7): ∫sinudu=-cosu+C (лист Интегралы), причем, интегрировали путем подведения под знак дифференциала.
Пример 7. ∫(sinx+cosx)²dx.
Решение.
Раскроем скобки, используя формулу квадрата суммы двух выражений: (a+b)²=a²+2ab+b².
∫(sinx+cosx)²dx=∫(sin²x+2sinxcosx+cos²x) dx. Теперь в подынтегральном выражении можно увидеть сразу 2 тригонометрические формулы (*) и (**).
∫(sinx+cosx)²dx=∫(sin²x+2sinxcosx+cos²x) dx=∫(1+sin2x) dx=
=∫dx+∫sin2xdx=∫dx+½∫sin2xd (2x)=x-1/2cos2x+C.
Пример 8. ∫2sin²xdx.
Решение.
Применим тригонометрическую формулу понижения степени для квадрата синуса данного аргумента: 2sin²α=1-cos2α.
∫2sin²xdx=∫(1-cos2x) dx=∫dx-∫cos2xdx=∫dx-½∫cos2xd (2x)=x-1/2sin2x+C.
Пример 9. ∫2cos²xdx.
Решение.
Применяем формулу понижения степени для квадрата косинуса аргумента: 2cos²α=1+cos2α. Тогда:
∫2cos²xdx=∫(1+cos2x) dx=∫dx+∫cos2xdx=∫dx+½∫cos2xd (2x)=x+1/2sin2x+C.
Пример 10 (аналогичный примеру 8). ∫2sin²5xdx.
Решение.
∫2sin²5xdx=∫(1-cos10x) dx=∫dx- (1/10)∫cos10xd (10x)=x- (1/10) sin10x+C.
Пример 11 (аналогичный примеру 9). ∫2cos²(x/2) dx.
Решение.
∫2cos²(x/2) dx=∫(1+cosx) dx=∫dx+∫cosxdx=x+sinx+C.
Пример 12. ∫8sinxcosxcos2xcos4xdx.
Решение.
Преобразуем подынтегральное выражение по формуле (**) — синуса двойного аргумента:
8sinxcosxcos2xcos4x=2·2·2·sinx·cosx·cos2x·cos4x=
=2sinxcosx·2·2·cos2x·cos4x=sin2x·2·2·cos2x·cos4x=
=2sin2xcos2x·2·cos4x=sin4x·2cos4x=sin8x.
Итак, ∫8sinxcosxcos2xcos4xdx=∫sin8xdx=1/8∫sin8xd (8x)=- (1/8) cos8x+C.
Пример 1. ∫sin3xdx.
У нас есть формула 7). Интегралы: ∫sinudu= — cos u + C.
Из этой формулы следует, что какой аргумент у синуса – такой же должна быть и переменная интегрирования. Будем считать, что в нашем случае u = 3x, тогда du = 3dx. Подведем под знак дифференциала 3х, не забыв уравнять обе части равенства.
∫sin3xdx=(1/3)∫sin3xd (3x) = — (1/3) cos 3x + C.
Проверка.
(F (x)+C)’ = ( — 1/3 cos 3x + C)’ = — (1/3) · (cos 3x)’ = — (1/3) · (-3sin 3x) = sin 3x = f (x).
Пример 2. ∫cos (4x+3) dx.
Используем формулу 6). Интегралы: ∫cosudu=sinu+C.
Подводим под знак дифференциала (4х + 3). Так как d (4x + 3) = 4dx, то
∫cos (4x+3) dx=(¼)∫cos (4x+3) d (4x+3) =(¼) sin (4x + 3) + C.
Проверка.
(F (x)+C)’= ( (¼) sin (4x + 3) + C)’ = (¼) · 4 cos (4x + 3) = cos (4x + 3) = f (x).
Пример 3.
Какую формулу напоминает этот пример? Правильно, формулу 8). Интегралы.
Подводим под знак дифференциала (3х+π/4). Тогда d (3x+π/4) = 3dx, значит, чтобы значение данного выражения не изменилось, поставим перед знаком интеграла 1/3.
Пример 4.
Чтобы применить формулу 9). Интегралы, нужно подвести под знак дифференциала (4х- π/5). Отсюда следует: d (4х-π/5)=4dx. Перед знаком интеграла поставим множитель ¼.
При интегрировании путем подведения под знак дифференциала, в предыдущих занятиях, мы подводили под знак дифференциала линейную функцию. На самом деле, вместо переменной u мы каждый раз подразумевали выражение вида kx+b, т.е. полагали: u-kx+b, получали du=kdx, а затем перед знаком интеграла ставили коэффициент 1/k, чтобы не изменилось значение данного интеграла. При решении использовали свойства и таблицу интегралов — лист Интегралы.
А можно ли под знак дифференциала подводить нелинейную функцию? Да, если подынтегральное выражение представляет собой произведение двух множителей: один множитель — сложная функция от какой-то нелинейной функции, а другой множитель есть производная от этой нелинейной функции. Рассмотрим сказанное на примерах.
Найти неопределенные интегралы.
Пример 1. ∫(2x + 1)(x2 + x + 2)5 dx = ∫(x2 + x + 2)5 d (x2 + x + 2) =(x²+x+2)6:6 + C.
Что представляет собой данное подынтегральное выражение? Произведение степенной функции от (х2 + х + 2) и множителя (2х + 1), который равен производной от основания степени: (х2 + х + 2)’ = 2х + 1.
Это и позволило нам подвести (2х + 1) под знак дифференциала:
(2x + 1) dx = d (x2 + x + 2). А далее мы применили формулу:
∫u5du=u6:6+ C. (Формула 1). Интегралы)
Проверка. (F (x)+ C)’ =((x²+x+2)6:6 + C)′=1/6 · 6 (x2 + x + 2)5 · (x2 + x + 2)’ =
=(x2 + x + 2)5 · (2x + 1) = (2x + 1)(x2 + x + 2)5 = f (x).
Пример 2. ∫(3x2 – 2x + 3)(x3 — x2 + 3x + 1)5 dx = ∫(x3 – x2 + 3x + 1)5 d (x3 – x2 + 3x + 1) =
=(x³- x²+3x+1)6:6 + C
И чем этот пример отличается от примера 1? Да ничем! Та же пятая степень с основанием (х3 – х2 + 3х + 1) умножается на трехчлен (3х2 – 2х + 3), который является производной основания степени: (х3 – х2 + 3х + 1)’ = 3х2 – 2х + 3. Это основание степени мы и подвели под знак дифференциала, от чего значение подынтегрального выражения не изменилось, а затем применили ту же формулу 1). (Интегралы)
Пример 3.
Здесь производная от (2х3 – 3х) даст (6х2 – 3), а у нас
имеется (12х2 – 6), то есть выражение в 2 раза большее, значит, подведем (2х3 – 3х) под знак дифференциала, а перед интегралом поставим множитель 2. Применим формулу 2) (лист Интегралы).
Вот что получится:
Сделаем проверку, учитывая, что:
Итак,
Что такое непосредственное интегрирование? Это интегрирование с использованием свойств и простейшей таблицы интегралов (Интегралы). Рассмотренный метод подведения под знак дифференциала (занятие 11.1.3) также относится к непосредственному интегрированию, так как нашей новой переменной служила линейная функция вида u=kx+b, но никаких новых букв мы не использовали, а просто применяли свойство VI (Интегралы), а именно:
Это свойство значительно расширяет таблицу простейших интегралов, так как в силу этого свойства таблица интегралов оказывается справедливой независимо от того, является переменная интегрирования независимой переменной или дифференцируемой функцией. В занятии 11.1.3. мы учились применять метод подведения переменной под знак дифференциала, используя формулы 1) и 2) (Интегралы), причем, прежде чем использовать тот или иной табличный интеграл, мы приводили данный интеграл к виду:
∫f (φ(x))φ′(x) dx=∫f (u) du, где u=φ(x).
Далее, продолжим непосредственное интегрирование с помощью остальных формул таблицы интегралов.
Рассмотрим пример на применение формулы 5) (Интегралы), а именно формулы:
В примере 1 неявно подразумевалось u=9x-2, что и позволило нам применить свойство VI и формулу 5), в результате чего под знак дифференциала мы подвели (9х-2). Перед знаком интеграла стоит множитель 1/9, так как d (9x-2)=9dx.
Рассмотрим пример на применение формулы 4) (Интегралы), а именно, формулы:
В примере 2 неявно подразумевается u=25x-1, поэтому, под знак дифференциала подвели 25х-1, отсюда du=25dx. Вот почему перед интегралом стоит множитель 1/25.
Страница 1 из 41234»www.mathematics-repetition.com

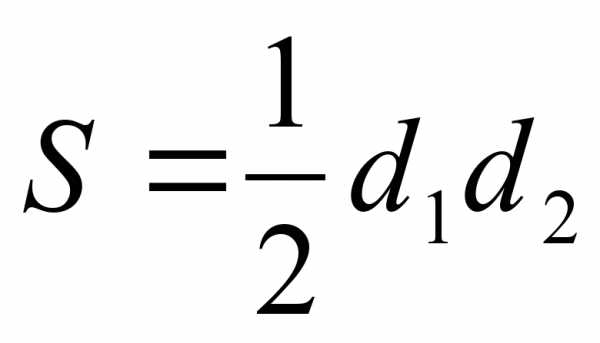
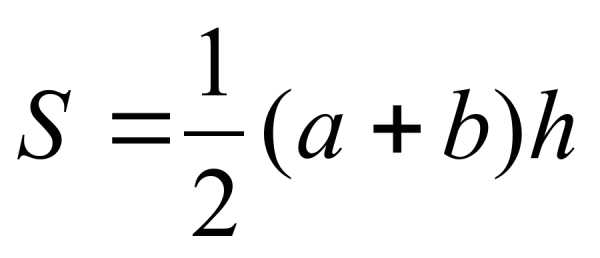
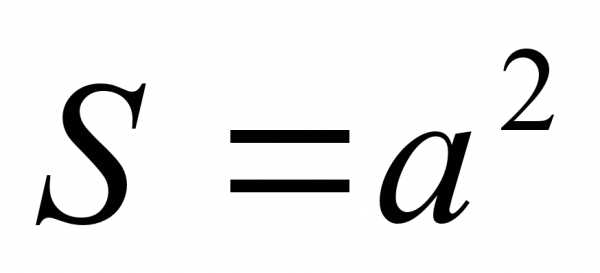
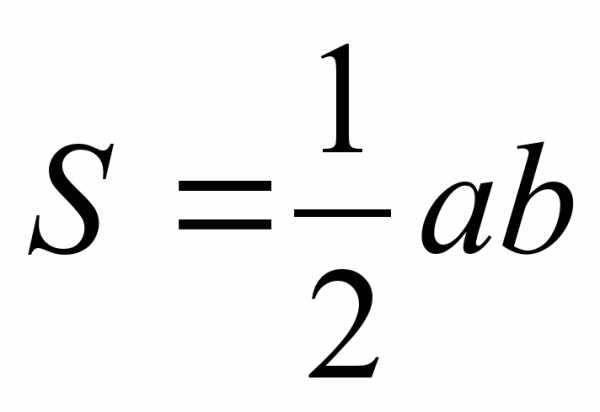
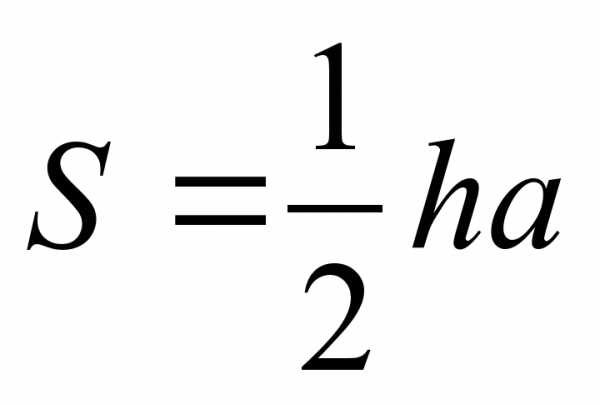
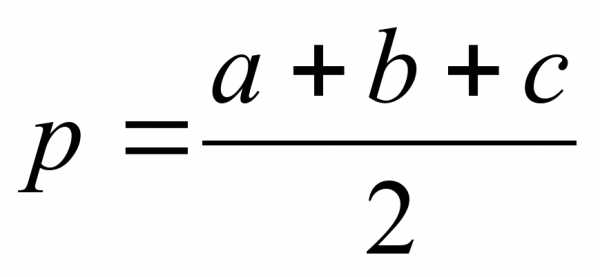
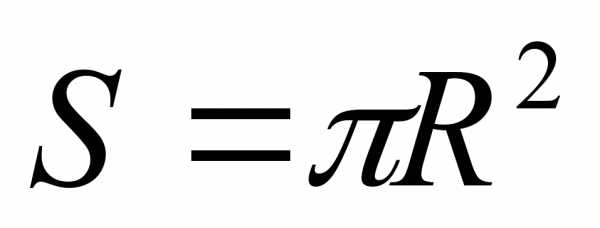
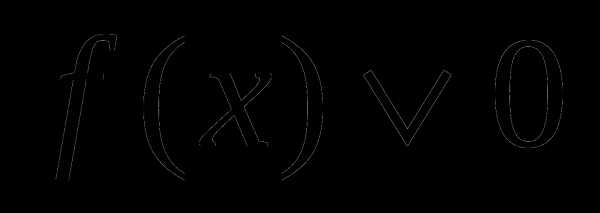 . Рассмотреть функцию
. Рассмотреть функцию 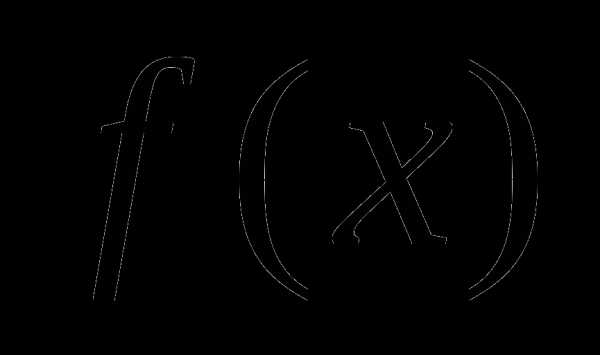 .
.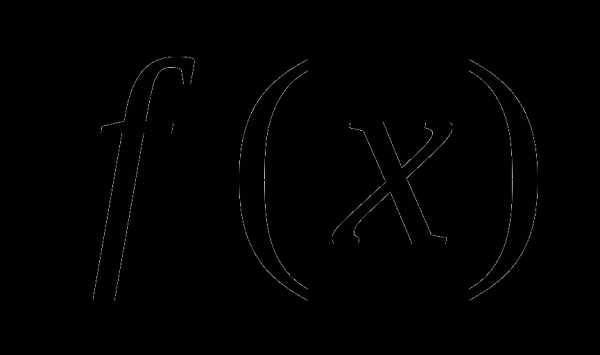 .
.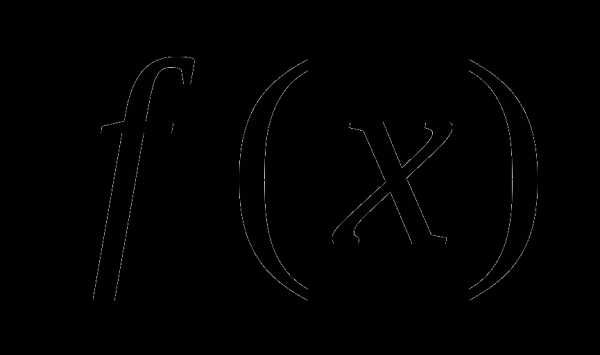 , решив уравнение
, решив уравнение 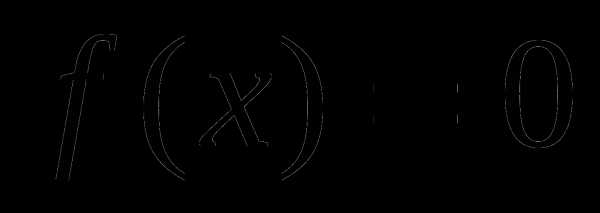
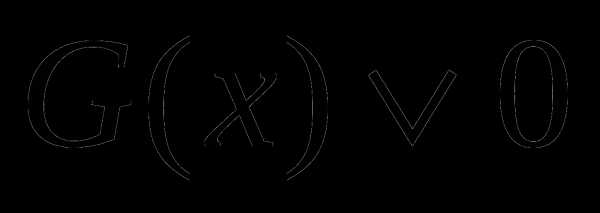 равносильно неравенству
равносильно неравенству 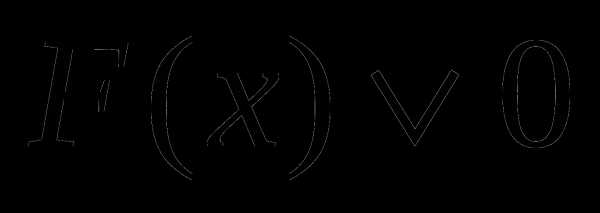 в области определения выражения F(x) (символ
в области определения выражения F(x) (символ заменяет один из знаков неравенств: >, ).
заменяет один из знаков неравенств: >, ).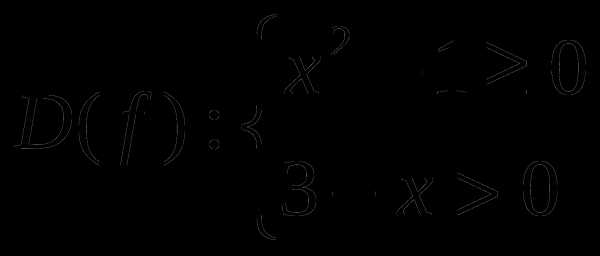
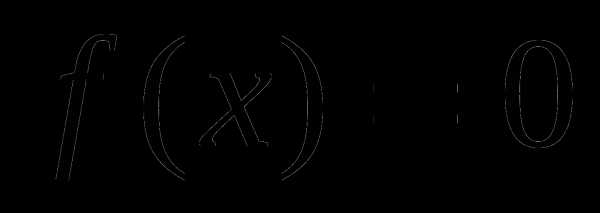
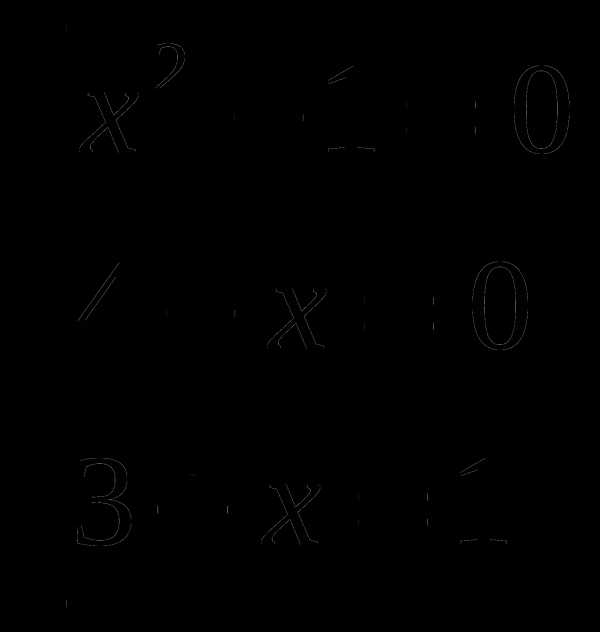




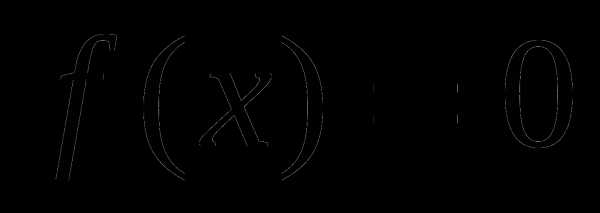
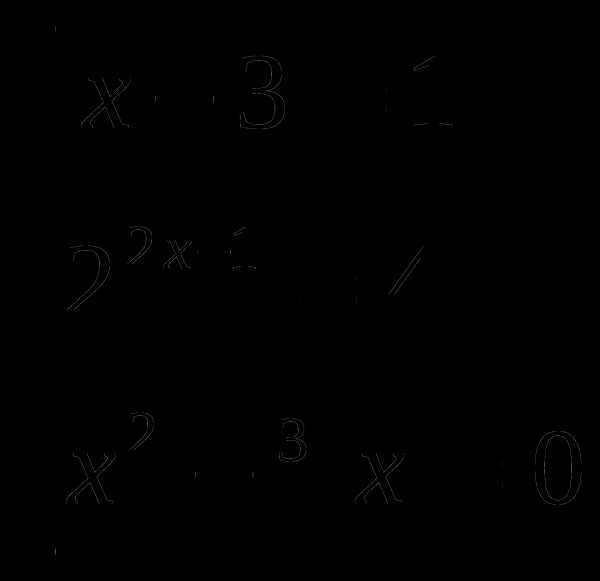 ,
,