ГДЗ Алгебра 11 класс Мордкович, Денищева, Звавич
Алгебра 11 класс
Задачник (Профильный уровень)
Мордкович, Денищева, Звавич
Мнемозина
Не имеет особого значения сколько именно учащиеся проводят в классе, если подача материала поставлена не лучшим образом. Они могут хоть сутками на пролет сидеть и решать бесконечные примеры, но без твердой теоретической базы эти навыки не имеют особого значения, так как быстро выветрятся из памяти. Заниматься же самостоятельно многие школьники не горят особым желанием, поэтому им весьма пригодиться решебник к учебнику «Алгебра и начала математического анализа. Задачник 11 класс (профильный уровень)» Мордкович, Денищева, Звавич.
Что имеется в сборнике.
В пособие вошло тридцать четыре параграфа, а так же задачи на повторении пройденного ранее материала. Авторы приводят детальные решения по всем номерам, давая необходимые пояснения в особо трудных случаях. ГДЗ по алгебре 11 класс Мордкович поможет успешно справляться с текущими заданиями по предмету и лучше понимать все его аспекты.
Зачем им нужно пользоваться.
Реалии современной школьной жизни таковы, что учащиеся большую часть дня проводят в четырех стенах, получая огромные объемы информации. Из-за больших нагрузок какая-то часть этих сведений просто проходит мимо их ушей, а приходя домой учащиеся не стремятся снова садиться за учебники, чтобы восполнить эти пробелы. Постепенно дефицит сведений накапливается и наступает такая точка перелома, когда пройти очередную контрольную работу становится просто не по силам. Чтобы этого не произошло необходимо сразу же разъяснять то, что вызывает заминки при выполнении д/з, ведь хорошо разобранный материал запоминается намного лучше. Осуществить подобную процедуру поможет решебник к учебнику
▶▷▶ учебник и задачник по алгебре 10-11 класс мордкович
▶▷▶ учебник и задачник по алгебре 10-11 класс мордкович| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 07-12-2018 |
учебник и задачник по алгебре 10-11 класс мордкович — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Учебник Алгебра 10 класс АГ Мордкович 2009 Задачник | Вклассе vklasseonline … Алгебра Полный и качественный учебник Алгебра 10 класс АГ Мордкович 2009 Задачник скачать онлайн Доступно на ваших смартфонах читать Задачник Алгебра 10-11 класс Мордкович онлайн newgdzcom/uchebniki- 10-11 -klass/11606-chitat-zadachnik Вот и прочти Задачник Алгебра 10-11 класс Мордкович здесь: это интересно: Категория: Учебники 10,11 класс Учебник по алгебре 10-11 класс Мордкович читать онлайн uchebnik-tetradcom//uchebnik-po-algebre- 10 — 11 -klass Cached Учебник по алгебре 10-11 класс Мордкович читать онлайн Выберите нужную страницу с уроками, заданиями (задачами) и упражнениями из учебника по алгебре за 10-11 класс — Мордкович часть 1 (теория) Учебник И Задачник По Алгебре 10-11 Класс Мордкович — Image Results More Учебник И Задачник По Алгебре 10-11 Класс Мордкович images Алгебра и начала анализа Задачник 10-11 класс, Мордкович АГ domashkasu/gdz/klass11/algebra/book9 Cached Решебник Алгебра и начала анализа Задачник 10-11 класс , Мордкович АГ Готовые домашние задания по алгебре за 11 класс Задачник по алгебре 10-11 класс Мордкович часть 2 читать онлайн uchebnik-tetradcom//zadachnik-po-algebre- 10 — 11 -klass Cached Выберите нужную страницу с уроками, заданиями (задачами) и упражнениями из задачника по алгебре за 10-11 класс — Мордкович Денищева Корешкова Мишустина Семенов Тульчинская часть 2 (практика Решебник по алгебре за 10‐11 класс задачник АГ Мордкович ФГОС gdzguru Алгебра ГДЗ к учебнику по алгебре 10-11 класса Мордкович , Базовый уровень можно скачать здесь Учебник Алгебра 10 класс АГ Мордкович 2009 | Вклассе vklasseonline … Алгебра Полный и качественный учебник Алгебра 10 класс АГ Мордкович 2009 скачать онлайн Доступно на ваших смартфонах ГДЗ задачник по алгебре 10‐11 класс Мордкович часть 2 gdzru/class- 10 /algebra/reshebnik-mordkovich-a-g Cached ГДЗ: Спиши готовые домашние задания задачник по алгебре за 10‐11 класс , решебник АГ Мордкович , Базовый уровень ФГОС, часть 2 онлайн ответы на gdzru ГДЗ по алгебре 10-11 класс Мордкович задачник часть 2 gdz-onlinecom/ 11 -klass/algebra/mordkovich Cached ГДЗ и решебник к задчнику по алгебре за 10-11 класс Мордкович , Александрова, Мишустина, Тульчинская — ответы к учебнику онлайн ГДЗ (решебник) по алгебре 10-11 класс Мордкович задачник reshatorru/ 11 -klass/algebra/mordkovich Cached Здесь в бесплатном доступе выложен решебник по алгебре за 10-11 класс Мордкович , которым легко и удобно пользоваться Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 84,400 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- 2015 год — ФГОС Книгу удобно использовать на уроке
- стоит ли школьникам пользоваться ГДЗ по алгебре 10 – 11 класс Мордкович
- 275 страниц со всеми задачами и упражнениями В конце книги есть ответы и дополнительные задачи Вернуться на главную страницу сайта vpr-klasscom Скрыть 4 Алгебра и начала математического анализа
комбинаторики или тригонометрии? Только тем
Семенов
- easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 84
- 11 класс Учебник по алгебре 10-11 класс Мордкович читать онлайн uchebnik-tetradcom//uchebnik-po-algebre- 10 — 11 -klass Cached Учебник по алгебре 10-11 класс Мордкович читать онлайн Выберите нужную страницу с уроками
- Тульчинская — ответы к учебнику онлайн ГДЗ (решебник) по алгебре 10-11 класс Мордкович задачник reshatorru/ 11 -klass/algebra/mordkovich Cached Здесь в бесплатном доступе выложен решебник по алгебре за 10-11 класс Мордкович
учебник и задачник по алгебре 10-11 класс мордкович — Все результаты ГДЗ задачник по Алгебре за 10-11 класс Мордкович Решебник ГДЗ: Спиши готовые домашние задания задачник по алгебре за 10‐11 класс , решебник АГ Мордкович , Базовый уровень ФГОС, часть 2 онлайн ответы Алгебра 10 класс · Алгебра 11 класс · ГДЗ по алгебре 10‐11 класс А · 11 Алгебра и начала математического анализа, 10—11 класс Часть 2 Алгебра и начала математического анализа, 10—11 класс Часть 2 из 2 Задачник (А Г Мордкович и др) 2009 Страницы учебника : 1, 2, 3, 4, 5, 6, 7, 8, [PDF] Задачник wwwavia-college-uuru/wp-content/uploads//Задачник-10-11-класс-Алгебраpdf Предлагаемый задачник по курсу « Алгебра и начала математического 10 —11 классы В 2 ч Ч 1 Учебник ; А Г Мордкович и др Алгебра и начала Книга: «Алгебра 10-11 классы Учебник В 2-х частях Базовый › › Математика › Математика (10-11 классы) 10-11 классы Учебник Алгебра и начала математического анализа 10-11 классы Учебник и задачник Базовый уровень Домашняя работа по алгебре за 11 класс к учебнику АГ Мордковича и др » Алгебра и начала анализа» 1 Решебник (ГДЗ) к задачнику по алгебре 10 — 11 класс Мордкович › ГДЗ › 10 класс › Алгебра › Мордкович Похожие Подробнейший гдз и решебник к задачнику по алгебре за 11 класс , автор АГ Мордкович 2016 год ГДЗ по алгебре 10-11 класс Мордкович онлайн — MirUrokovru Онлайн ответы на задачники и контрольные работы по алгебре за 10-11 класс автора Мордкович Смотрите готовые домашние задания (ГДЗ) выбрав ГДЗ по алгебре 10-11 класс Мордкович — онлайн решебник ГДЗ по алгебре и началам математического анализа за 10 класс к задачнику АГ Мордковича и др « Алгебра и начала математического анализа 10-11 Мордкович АГ и др Алгебра и начала математического анализа wwwstudmedru › Абитуриентам › Экзамены по математике Мордкович АГ Алгебра и начала анализа 11 класс В 2 ч Часть 2 Учебник Алгебра и начала анализа 10-11 кл Задачник Алгебра и начала анализа Алгебра и начала математического анализа, 10-11 класс › Экзамены › Экзамены по Алгебре 17 июл 2014 г — Алгебра и начала математического анализа, 10-11 класс , Задачник , Часть 2, Мордкович АГ, 2009 Предлагаемый задачник по курсу « Алгебра и начала Смотрите также учебники , книги и учебные материалы: ГДЗ (решебник) по алгебре 10-11 класс Мордкович задачник reshatorru/11-klass/algebra/mordkovich/ Похожие ГДЗ (домашние задания) по алгебре за 10-11 класс к задачнику Мордковича Алгебра Купить книги по низким ценам! Интернет-магазин «Читай Похожие Книги из раздела « Алгебра » по низким ценам в интернет-магазине и математическому анализу с ответами и решениями для 10-11 классов Купить Алгебра 8 класс Учебник Мерзляк А, Полонский В, Якир М комментарии к упражнениям, решение задач раздела «Учимся делать Мордкович А Мегарешеба — ГДЗ по Алгебре за 10‐11 класс Мордкович АГ ГДЗ к учебнику по алгебре 10-11 класса Мордкович , Базовый уровень можно ГДЗ к Задачнику по алгебре за 10 класс Базовый и углубленный уровень Видео 4:09 № 212- Алгебра 10-11 класс Мордкович GDZ Ru YouTube — 31 авг 2017 г 2:40 № 165- Алгебра 10-11 класс Мордкович GDZ Ru YouTube — 20 окт 2017 г Картинки по запросу учебник и задачник по алгебре 10-11 класс мордкович «id»:»Uvr5JZ0w56bQSM:»,»ml»:»600″:»bh»:90,»bw»:61,»oh»:1099,»ou»:» «,»ow»:700,»pt»:»docbazaru/urok/algebra/10/015/cover_bigjpg»,»rh»:»docbazaru»,»rid»:»bsLJPy9ZF9iefM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»DocBazaru»,»th»:105,»tu»:» \u003dtbn:ANd9GcRmDCGEID73ZMM7uFBcu5yWBZr0RFee_DKa6TOAg5_1pXvyP9V6aWpOCSo»,»tw»:66 «id»:»NJ2yy7DNSsJ9WM:»,»ml»:»600″:»bh»:90,»bw»:79,»oh»:2484,»ou»:» «,»ow»:2008,»pt»:»reshatorru/otvety/10-11-klass-mordkovich/1-11png»,»rh»:»reshatorru»,»rid»:»S8x27WkdRZsQpM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:98,»tu»:» \u003dtbn:ANd9GcTmQs_8eSaqz78VEcgVBrCqjp853mESEOTDhR_irQwe6_uCO_di4htpBC8″,»tw»:79 «id»:»rC4wTW5e1RkmJM:»,»ml»:»600″:»bh»:90,»bw»:129,»oh»:1249,»ou»:» «,»ow»:2010,»pt»:»reshatorru/otvety/10-11-klass-mordkovich/2-11png»,»rh»:»reshatorru»,»rid»:»S8x27WkdRZsQpM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:90,»tu»:» \u003dtbn:ANd9GcQqT3odk4te83_YXVnwlrn1D_cYU7HgWQyOR1p3f0-RcPXQOthqnObTYe0″,»tw»:145 «id»:»Lu8HHL_X23FMVM:»,»ml»:»600″:»bh»:90,»bw»:104,»oh»:1809,»ou»:» «,»ow»:1951,»pt»:»reshatorru/otvety/10-11-klass-mordkovich/2-1png»,»rh»:»reshatorru»,»rid»:»S8x27WkdRZsQpM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:96,»tu»:» \u003dtbn:ANd9GcSLkfKOieA31SUb7TLP8yezGGkZvQnkDUnFS8vpQl5XRmxQzpWnH5dhRxk»,»tw»:104 «id»:»tMNdnF3G0clkUM:»,»ml»:»600″:»bh»:90,»bw»:77,»oh»:2500,»ou»:» «,»ow»:2010,»pt»:»reshatorru/otvety/10-11-klass-mordkovich/2-10png»,»rh»:»reshatorru»,»rid»:»S8x27WkdRZsQpM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:96,»tu»:» \u003dtbn:ANd9GcRewYkJzK0G45i9rYvqcRrc77a4Xq9EZaXEk0ItGguc96rCHrW5OxoTxg»,»tw»:77 «id»:»1HK_-H-xD8oa8M:»,»ml»:»600″:»bh»:90,»bw»:130,»oh»:1092,»ou»:» «,»ow»:1943,»pt»:»reshatorru/otvety/10-11-klass-mordkovich/1-3png»,»rh»:»reshatorru»,»rid»:»S8x27WkdRZsQpM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:90,»tu»:» \u003dtbn:ANd9GcQo-yX0W5YhiQ51islW6kfQp94z3BW0Ai_mxc4s25nKY5BU-3Q-jodkZRij»,»tw»:160 Другие картинки по запросу «учебник и задачник по алгебре 10-11 класс мордкович» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Алгебра 9 класс Мордкович А Г 2 часть задачник 10—11 классы / автсост И И Зубарева, А Г Мордкович ; А Г Мордкович , П В Семенов Алгебра 9 класс В 2 ч Ч 1 Учебник ; А Г Мордкович и др Методика обучения математике: компьютерная анимация в среде geogebra Сергей Ларин — 2018 — Mathematics Литература 1 10 11 12 13 Архимед Сочинения — М Физматгиз, 1962 2 Мордкович АГ, Алгебра и начала математического анализа Учебник 10 10 класс Профильный уровень Ч 2 Задачник — М: «Мнемозина», 2008 Педагоги-математики Историко-математические очерки Рамиз Асламов , Ирина Столярова , Наталья Кузина — 2017 — Biography & Autobiography —61 с Мордкович А Г Алгебра 7 класс : методическое пособие для учителя / А Г Учебник для учащихся общеобразовательных учреждений / А Г ГДЗ по алгебре 7 класс Мерзляк, Полонский, Якир › Алгебра › 7 класс Решебник по алгебре за 7 класс авторы Мерзляк, Полонский, Якир издательство Вентана-Граф ГДЗ — самые качественные решебники на Решебами Сайт — РЕШЕБНИК создан исключительно для помощи учащимся в усвоении решать самые тяжёлые задачи из математики, алгебры , геометрии и тд Для ежедневных тренировок рекомендуем использовать учебник математики за 5 класс и 6 класс автора Алгебра 10-11 класс Задачник Мордкович Учебник, задачник Алгебра 10, 11 класс Мордкович купить в › Волгоград › Книги и журналы Объявление о продаже Учебник , задачник Алгебра 10, 11 класс Мордкович в Волгоградской области на Avito Алгебра — Школьные Знанияcom Похожие Срочно, нужно объяснение теми за 7 класс ( алгебра )»Добуток ризници та суми двох виразив» ДАМ 50 БАЛЛОВ! ЧЕСТНО! ТОЛЬКО ОБЪЯСНИТЕ МНЕ Задачник по алгебре 10-11 класс Мордкович часть 2 читать онлайн uchebnik-tetradcom//zadachnik-po-algebre-10-11-klass-mordkovich-chast-2-chitat uchebnik-tetradcom — онлайн учебники и рабочие тетради Задачник по алгебре 10-11 класс Мордкович часть 2 читать онлайн из задачника по алгебре за 10-11 класс — Мордкович Денищева Корешкова Мишустина Семенов Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (28) Показать скрытые результаты В ответ на официальный запрос мы удалили некоторые результаты (3) с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg Вместе с учебник и задачник по алгебре 10-11 класс мордкович часто ищут алгебра 10-11 класс мордкович учебник алгебра 10-11 класс мордкович учебник онлайн читать алгебра 10 класс мордкович профильный уровень гдз по алгебре 10-11 класс мордкович 2007 гдз по алгебре 10 класс алгебра 10 класс мордкович профильный уровень скачать гдз по алгебре и начала анализа 10-11 класс мордкович гдз по алгебре 10-11 класс мордкович 2004 Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Покупки Документы Blogger Hangouts Google Keep Jamboard Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Учебник Алгебра 10 — 11 классы Мордкович 2013 (часть 2) vseuchebnikinet › 10 класс › Школьные учебники и пособия Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Название: Алгебра 10 — 11 классы Автор(ы): АГ Мордкович Год издания: 2013 Издательство: Мнемозина Количество страниц: 279 Читать этот учебник онлайн Загрузка учебника для чтения может занять до 10 секунд — пожалуйста, подождите Смотрите также: Алгебра 10 — 11 классы АГ Мордкович Читать ещё Название: Алгебра 10 — 11 классы Автор(ы): АГ Мордкович Год издания: 2013 Издательство: Мнемозина Количество страниц: 279 Формат: pdf Скачать: algebra_ 10 — 11 _ mordkovich _p2_2013pdf [32,61 Mb] (cкачиваний: 33468) Читать этот учебник онлайн Загрузка учебника для чтения может занять до 10 секунд — пожалуйста, подождите Смотрите также: Алгебра 10 — 11 классы АГ Мордкович Алгебра и начало математического анализа 10 — 11 классы АГ Мордкович Алгебра 10 — 11 класс АГ Мордкович Алгебра 10 класс АГ Мордкович , ПВСемёнов Алгебра 7 класс АГ Мордкович Главная Программы Скрыть 2 ГДЗ (решебник) по алгебре 10 — 11 класс Мордкович reshatorru › 11 класс › Алгебра › Мордкович Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Если сомневаетесь, стоит ли школьникам пользоваться ГДЗ по алгебре 10 – 11 класс Мордкович , то подумайте – многим ли в жизни пригодились школьные знания по основам матанализа, комбинаторики или тригонометрии? Только тем, кто поступил в профильные ВУЗы и нашел работу по специальности Читать ещё Если сомневаетесь, стоит ли школьникам пользоваться ГДЗ по алгебре 10 – 11 класс Мордкович , то подумайте – многим ли в жизни пригодились школьные знания по основам матанализа, комбинаторики или тригонометрии? Только тем, кто поступил в профильные ВУЗы и нашел работу по специальности Решебник позволит остальным не тратить зря время на зубрежку Смотря в нем ответы и подробный ход решения задач, старшеклассники смогут качественно подготовиться к действительно нужным предметам, пообщаться с друзьями, заняться спортом Скрыть 3 Мордкович задачник по алгебре 10 — 11 класс — читать vpr-klasscom › …10-11_klass_mordkovich…zadachnik… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Смотрите онлайн задачник по алгебре и началу математического анализа за 10 — 11 класс — авторы Мордкович , Денищева Книгу удобно использовать на уроке, в задачнике содержится: 10 глав, 60 параграфов, 275 страниц со всеми задачами и Читать ещё Смотрите онлайн задачник по алгебре и началу математического анализа за 10 — 11 класс — авторы Мордкович , Денищева, Корешкова, Мишустина, Семенов, Тульчинская — 2011, 2012, 2013, 2014, 2015 год — ФГОС Книгу удобно использовать на уроке, в задачнике содержится: 10 глав, 60 параграфов, 275 страниц со всеми задачами и упражнениями В конце книги есть ответы и дополнительные задачи Вернуться на главную страницу сайта vpr-klasscom Скрыть 4 Алгебра и начала математического анализа, 10 — 11 класс nasholcom › …i…10-11-klass-zadachnik…2-mordkovich… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Предлагаемый задачник по курсу « Алгебра и начала математического анализа» в 10 — 11 -м классах соответствует одноименному учебнику В каждом параграфе задачника представлена разнообразная система упражнений, включающая четыре уровня — по степени нарастания трудности Примеры Докажите, что Читать ещё Предлагаемый задачник по курсу « Алгебра и начала математического анализа» в 10 — 11 -м классах соответствует одноименному учебнику В каждом параграфе задачника представлена разнообразная система упражнений, включающая четыре уровня — по степени нарастания трудности Примеры Докажите, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними На рисунке 11 изображена часть графика периодической функции у = f(x) на отрезке [-1; 1], длина которого равна периоду функции Постройте график функции: а) на отрезке [1; 3]; б) на отрезке [-3; -1]; в) на от Скрыть 5 читать Задачник Алгебра 10 — 11 класс Мордкович онлайн newgdzcom › Учебники 10 класс › …zadachnik-algebra-10-11… Показать ещё с сайта Пожаловаться Информация о сайте Категория: Учебники 10 , 11 класс На проблемах, с которыми сталкиваются украинские иммигранты, как в Италии так и в Украине ЧИТАТЬ ОНЛАЙН: Вы прочитали Задачник Алгебра 10 — 11 класс Мордкович отличной Вам учебы! Самые популярные статьи: читать Физика Задачник 10 — 11 класс Читать ещё Категория: Учебники 10 , 11 класс На проблемах, с которыми сталкиваются украинские иммигранты, как в Италии так и в Украине, акцентировал внимание присутствующих Олесь Городецкий, председатель Христианского Общества Украинского в Италии На сегодняшний день по официальным данным МВД Италии (2005) на Апеннинский полуострове находится легально более 118000 граждан Украины ЧИТАТЬ ОНЛАЙН: Вы прочитали Задачник Алгебра 10 — 11 класс Мордкович отличной Вам учебы! Самые популярные статьи: читать Физика Задачник 10 — 11 класс Рымкевич онлайн Скрыть 6 Учебник Алгебра 10 класс АГ Мордкович 2009 Задачник vklasseonline › 10…uchebniki…mordkovich…zadachnik Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Учебники за 10 класс Алгебра АГ Мордкович Учебник Алгебра 10 класс АГ Мордкович (2009 год) Задачник Читать ещё Учебники за 10 класс Алгебра АГ Мордкович Учебник Алгебра 10 класс АГ Мордкович (2009 год) Задачник Авторы: АГ Мордкович Год: 2009 | Класс : 10 | Предмет: Алгебра | Похожие учебники (3) + Алгебра 10 класс АГ Мордкович , ПВ Семенов (2009 год) Часть 1 Алгебра 10 класс АГ Мордкович , ПВ Семенов (2009 год) Часть 2 Алгебра 10 класс АГ Мордкович (2009 год) Решебник: Алгебра 10 класс АГ Мордкович (2009 год) Задачник Читать онлайн Скачать учебник Скрыть 7 Задачник по алгебре 10 — 11 класс Мордкович часть uchebnik-tetradcom › …zadachnik…algebre…mordkovich… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Выберите нужную страницу с уроками, заданиями (задачами) и упражнениями из задачника по алгебре за 10 — 11 класс На сайте можно читать, смотреть онлайн и скачать учебники и рабочие тетради по всем предметам за любой класс Главная Математика Читать ещё Выберите нужную страницу с уроками, заданиями (задачами) и упражнениями из задачника по алгебре за 10 — 11 класс — Мордкович Денищева Корешкова Мишустина Семенов Тульчинская часть 2 (практика) Онлайн книгу удобно смотреть (читать) с компьютера и смартфона Электронное учебное пособие подходит к разным годам: от 2011-2012-2013 до 2015-2016-2017 года — создано по стандартам ФГОС На сайте можно читать, смотреть онлайн и скачать учебники и рабочие тетради по всем предметам за любой класс Главная Математика Скрыть 8 ГДЗ задачник по алгебре 10 ‐ 11 класс Мордкович часть 2 GDZru › class-10/algebra/reshebnik-mordkovich-a-g/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ: Спиши готовые домашние задания задачник по алгебре за 10 ‐ 11 класс , решебник АГ Мордкович В 10 классе алгебра становится одним из основных предметов Нагрузка увеличивается, поскольку материала становится все больше Данное пособие содержит шесть разделов, особое внимание в Читать ещё ГДЗ: Спиши готовые домашние задания задачник по алгебре за 10 ‐ 11 класс , решебник АГ Мордкович , Базовый уровень ФГОС, часть 2 онлайн ответы на GDZRU В 10 классе алгебра становится одним из основных предметов Нагрузка увеличивается, поскольку материала становится все больше Данное пособие содержит шесть разделов, особое внимание в которых уделено производной и тригонометрическим функциям Ученик может упростить процесс выполнения домашней работы, пользуясь ГДЗ К самым важным и сложным заданиям приведены дополнительные комментарии и советы по выполнению Скрыть 9 Учебники по алгебре за 10 класс в электронном виде proreshenoru › uchebniki/algebra/10klass Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Задачник для 10 — 11 классов является частью учебно-методического комплекта для старших классов школ с углубленным изучением математики Главы задачника соответствуют главам учебников для 10 и 11 классов Задачи по каждой теме расположены в порядке воз Мордкович 10 Мордкович Читать ещё Задачник для 10 — 11 классов является частью учебно-методического комплекта для старших классов школ с углубленным изучением математики Главы задачника соответствуют главам учебников для 10 и 11 классов Задачи по каждой теме расположены в порядке воз Мордкович 10 Мордкович Показано 1 — 20 из 20 Скрыть 10 Учебник и задачник по алгебре 10-11 класс Мордкович — смотрите картинки ЯндексКартинки › учебник и задачник по алгебре 10-11 класс Пожаловаться Информация о сайте Ещё картинки Решебник (ГДЗ) Алгебра и начала анализа 10 — 11 класс gdzometrby › book975 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Ответы к учебнику по алгебре и началу анализа для 10 — 11 класса Мордкович Добавить книги в список » По запросу «» не найдено ни одной книги Алгебра и начала анализа 10 — 11 класс Читать ещё Ответы к учебнику по алгебре и началу анализа для 10 — 11 класса Мордкович Добавить книги в список » По запросу «» не найдено ни одной книги Алгебра и начала анализа 10 — 11 класс Мордкович А Г « Алгебра и начала анализа 10 — 11 класс » ГДЗ Мордкович А Г Ответы к учебнику по алгебре и началу анализа для 10 — 11 класса Мордкович Алгебра и начала математического анализа 10 — 11 класс Часть 1 Учебник Мордкович А Г, Семенов П В Алгебра и начала математического анализа 10 — 11 класс Часть 2 Задачник Мордкович А Г Алгебра и начала анализа 10 класс Профильный уровень Мордкович А Г, Семенов П В Пособие для учителя 2010г Алгебра и начала анализа 10 — 11 к Скрыть Мордкович АГ « Алгебра 10 — 11 классы [ Учебник / spbdkru spbdkru › Мордкович-А-Г-Алгебр Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Более 120 тыс книг в наличии! Скидки и акции Заказывайте, доставка по всей России! Контактная информация +7 (812) 317-73-45 пн-вс 9:00-21:00 Магазин на Маркете м Невский проспект 18+ Школьные учебники В наличии! / labirintru Лабиринт Пресс Акции Главные книги года Подарочные книги labirintru › учебники Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Учебники 11 класс Почти 20 000 видов Доставка Контактная информация +7 (495) 745-95-25 пн-пт круглосуточно Магазин на Маркете 18+ Скачать: учебник алгебра 10 класс / litresru litresru Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Школьные учебники скачивайте онлайн в электронном формате на ЛитРес Контактная информация +7 (800) 333-27-37 круглосуточно 18+ Вместе с « учебник и задачник по алгебре 10-11 класс мордкович » ищут: учебник и задачник по алгебре 8 класс мордкович учебник и задачник по алгебре 7 класс мордкович учебник и задачник по алгебре 9 класс мордкович скачать бесплатно учебник и задачник по алгебре 7 класс учебник и задачник по алгебре 7 класс мордкович скачать учебник и задачник по алгебре 10 класс мордкович учебник и задачник по php скачать учебник и задачник по php+mysql учебник и задачник по алгебре 8 класс 1 2 3 4 5 дальше Браузер Ускоряет загрузку файлов при медленном соединении 0+ Установить
УМК «Лаборатория А.
 Г. Мордковича». Алгебра и начала математического анализа. 10–11 классы
Г. Мордковича». Алгебра и начала математического анализа. 10–11 классы|
Каталог Поиск книг Электронные приложенияПодписка на рассылку Стихи о нас Богатство Трудности эти уже превратились в смыслы. Тивикова С.К., зав. каф. начального образования НИРО Обратная связь Отправить сообщение с сайта Социальные сети |
Учебники написаны подробно, доступно, хорошим литературным языком, с большим числом тщательно разобранных примеров. Все учебники полностью отвечают требованиям сегодняшнего дня:
|
Контрольные работы по алгебре и началам математического анализа 10-11 класс (базовый уровень). А.Г.Мордкович, В.И.Глизбург | Материал по алгебре (10 класс) на тему:
А.Г.Мордкович, В.И.Глизбург (Москва)
Контрольные работы по алгебре
и началам математического анализа
10-11 класс (базовый уровень)
В статье содержатся по два варианта контрольных работ по курсу «Алгебра и начала математического анализа 10-11 (базовый уровень)», ориентированных на учеб- ный комплект, готовящийся к публикации к началу 2008/09 уч. года издательством «Мнемозина» и включенный в Федеральный перечень учебников с грифом «Рекомен- довано»:
года издательством «Мнемозина» и включенный в Федеральный перечень учебников с грифом «Рекомен- довано»:
А.Г.Мордкович. Алгебра и начала математического анализа 10-11 (базовый уровень), часть 1. Учебник.
А.Г.Мордкович и др.Алгебра и начала математического анализа10-11 (базовый уровень), часть 2. Задачник.
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания условно говоря базового, среднего (обязательного) уровня – до первой черты, задания уровня выше среднего – между первой и второй чертой, задания повышенной сложности – после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий только до первой черты – оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) – оценка 4; ха успешное выполнение заданий всех трех уровней – оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Тематическое планирование было опубликовано в журнале «Математика в школе» ……..
10 класс
Контрольная работа №1 «Действительные числа»
Вариант 1
- Задает ли указанное правило функцию:
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0, 1, 3, – 1;
в) постройте график функции;
г) найдите промежутки монотонности функции.
- Исследуйте функцию на четность.
- На числовой окружности взяты точки Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге АВ. Сделайте чертеж.
- Задайте аналитически и постройте график функции , у которой
______________________________________________________________
5. Найдите функцию, обратную функции . Постройте
на одном чертеже графики указанных двух взаимно обратных функций.
_______________________________________
- Известно, что функция убывает на R. Решите неравенство
.
Вариант 2
1. Задает ли указанное правило функцию:
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0, 4;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге АВ. Сделайте чертеж.
4. Задайте аналитически и постройте график функции , у которой
.
______________________________________________________________
5. Найдите функцию, обратную функции . Постройте
на одном чертеже графики указанных двух взаимно обратных функций.
_______________________________________
6. Известно, что функция возрастает на R. Решите неравенство
Известно, что функция возрастает на R. Решите неравенство
.
Контрольная работа № 2
По теме « Числовые функции»
Вариант 1
- Вычислите: а);
г) ; д) .
- Упростите выражение .
- Решите уравнение: а) ; б) .
____________________________________________________________
- Известно, что .
Найдите __________________________________
5. Расположите в порядке возрастания следующие числа:
.
Вариант 2
1. Вычислите: а);
г) ; д) .
2. Упростите выражение .
3. Решите уравнение: а) ; б) .
____________________________________________________________
4. Известно, что .
Найдите .
___________________________________
5. Расположите в порядке убывания следующие числа:
.
Контрольная работа № 3
По теме «Тригонометрические функции»
Вариант 1
- Не выполняя построения, установите, принадлежит ли графику функции точка: а) ; б) P .

- Исследуйте функцию на четность:
а) ; б) ; в) .
3. Исследуйте функцию на периодичность; укажите
основной период, если он существует.
4. Решите графически уравнение .
____________________________________________________________
5. Постройте график функции а) или б):
а) ; б) .
___________________________________
6. При каком значении параметра неравенство
имеет единственное решение? Найдите это решение.
Вариант 2
1. Не выполняя построения, установите, принадлежит ли графику функции точка: а) M ; б) P .
2. Исследуйте функцию на четность
а) ; б) , в) .
3. Исследуйте функцию на периодичность; укажите
основной период, если он существует.
- Решите графически уравнение .
____________________________________________________________
- Постройте график функции а) или б):
а) ; б) .
___________________________________
6. При каком значении параметра неравенство
имеет единственное решение? Найдите это решение.
Контрольная работа № 4
По теме «Тригонометрические уравнения»
Вариант 1
1. Вычислите: а) ; б) .
2. Решите уравнение: а) ; б) .
3. Найдите корни уравнения принадлежащие полуинтервалу .
____________________________________________________________
4. Решите уравнение .
___________________________________
5. Решите уравнение .
Вариант 2
1. Вычислите: а) ; б) .
2. Решите уравнение: а) ; б) .
3. Найдите корни уравнения принадлежащие
полуинтервалу .
____________________________________________________________
4. Решите уравнение .
___________________________________
- Решите уравнение .
Контрольная работа № 5
По теме «Преобразование тригонометрических выражений»
Вариант 1
1. Вычислите: а) б)
Вычислите: а) б)
в)
2. Упростите выражение .
3. Решите уравнение .
4. Найдите корни уравнения принадлежащие
полуинтервалу.
____________________________________________________________
5. Решите уравнение .
___________________________________
6. Докажите, что для любого x справедливо неравенство .
Вариант 2
1. Вычислите: а) б)
в)
2. Упростите выражение .
3. Решите уравнение .
4. Найдите корни уравнения принадлежащие
промежутку .
____________________________________________________________
5. Решите уравнение .
___________________________________
- Докажите, что для любого x справедливо неравенство
.
Контрольная работа № 6
По теме «правила и формулы отыскания производных»
Вариант 1
- Вычислите первый, пятый и 100-й члены последовательности, если ее n-й член задается формулой .

2. Представьте бесконечную периодическую десятичную дробь 1,(18)
в виде обыкновенной дроби.
3. Найдите производную функции: а)
б) в) г) .
4. Найдите угловой коэффициент касательной к графику функции
в точке с абсциссой .
____________________________________________________________
5. Докажите, что функция удовлетворяет соотношению
_________________________________
6. Найдите знаменатель бесконечно убывающей геометрической
прогрессии, у которой каждый член в 6 раз больше суммы всех ее последующих членов.
Вариант 2
- Вычислите первый, седьмой и 200-й члены последовательности, если ее n-й член задается формулой .
2. Представьте бесконечную периодическую десятичную дробь 2, (27)
в виде обыкновенной дроби.
3. Найдите производную функции: а)
б) в) г) .
4. Найдите угловой коэффициент касательной к графику функции
Найдите угловой коэффициент касательной к графику функции
в точке с абсциссой .
____________________________________________________________
5. Докажите, что функция удовлетворяет соотношению
___________________________________
6. Сумма бесконечной геометрической прогрессии равна 4, а сумма
квадратов ее членов равна 48. Найдите первый член и знаменатель
прогрессии.
Контрольная работа № 7
По теме «Применение производной»
Вариант 1
1. Составьте уравнение касательной к графику функции
в точке
2. Составьте уравнения касательных к графику функции
в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.
____________________________________________________________
3. Исследуйте функцию на монотонность и экстремумы и постройте ее график.
__________________________________
4. Найдите значение параметра , при котором касательная к графику
функции в точке с абсциссой параллельна
биссектрисе первой координатной четверти.
Вариант 2
1. Составьте уравнение касательной к графику функции
в точке
2. Составьте уравнения касательных к графику функции
в точках его пересечения с осью абсцисс.
____________________________________________________________
- Исследуйте функцию на монотонность и экстремумы
и постройте ее график.
___________________________________
4 Найдите значение параметра , при котором касательная к графику
функции в точке с абсциссой параллельна прямой
.
Контрольная работа № 8 (2 часа)
Итоговая контрольная работа
Вариант 1
- Найдите наименьшее и наибольшее значения функции
а) на отрезке ;
б) на отрезке .
2. Найдите диагональ прямоугольника наибольшей площади,
вписанного в прямоугольный треугольник с катетами 18см и 24 см
и имеющего с ним общий прямой угол.
____________________________________________________________
3. Исследуйте функцию на монотонность
Исследуйте функцию на монотонность
и экстремумы.
________________________________
4. При каких значениях параметра уравнение имеет три
корня?
Вариант 2
- Найдите наименьшее и наибольшее значения функции:
а) на отрезке ;
б) на отрезке .
2. В прямоугольном треугольнике с катетами 36 и 48 на гипотенузе взята
точка. Из нее проведены прямые, параллельные катетам. Получился
прямоугольник, вписанный в данный треугольник. Где на гипотенузе
надо взять точку, чтобы площадь такого прямоугольника была
наибольшей?
____________________________________________________________
3. Исследуйте функцию на монотонность
и экстремумы.
___________________________________
- При каких значениях параметра уравнение имеет два
корня?
Решебник к сборнику контрольных работ по алгебре для 11 класса (авт.
 Глизбург В. И.). Профильный уровень ОНЛАЙН
Глизбург В. И.). Профильный уровень ОНЛАЙНРешения контрольных работ по алгебре и началам анализа из сборника для 11 класса Глизбург В. И. (под ред. А.Г. Мордковича). Профильный уровень. Варианты 1,2,3,4. — Рукопись. — 2016.
Настоящее пособие содержит решения контрольных работ из сборника «Глизбург В. И. Алгебра и начала анализа. Контрольные работы для 11 класса общеобразовательных учреждений (профильный уровень) / В. И. Глизбург ; под ред. А. Г. Мордковича. — М. : Мнемозина, 2008. — 55 с.»
Сборник контрольных работ предназначен для тех учителей математики, которые используют в своей преподавательской деятельности УМК, созданный авторским коллективом под руководством А. Г. Мордковича для изучения в 11-м классе профильной старшей школы курса алгебры и начал анализа.
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания базового (обязательного) уровня — до первой черты; задания уровня выше среднего — между первой и второй чертами; задания повышенной сложности — после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий до первой черты — оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) — оценка 4; за успешное выполнение заданий трех уровней — оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий до первой черты — оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) — оценка 4; за успешное выполнение заданий трех уровней — оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Страницы решебника представлены в виде слайдов. Кликните на нужный слайд, чтобы прочитать содержание страницы. Как листать слайды — читайте на странице http://gdz.math-helper.ru/kak-prosmatrivat-slaydyi/
Внимание! Рукопись не проверялась, возможны ошибки!
Содержание
Контрольная работа № 1
Контрольная работа № 2
Контрольная работа № 3
Контрольная работа № 4
Контрольная работа № 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18Контрольная работа № 6
Контрольная работа № 7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Контрольная работа № 8
1 2 3 4 5 6 7 8 9 11 12 13 14 15Алгебра и начала математического анализа, 11 класс, Часть 1, Мордкович, Семенов, 2012
По кнопке выше «Купить бумажную книгу» можно купить эту книгу с доставкой по всей России и похожие книги по самой лучшей цене в бумажном виде на сайтах официальных интернет магазинов Лабиринт, Озон, Буквоед, Читай-город, Литрес, My-shop, Book24, Books. ru.
ru.
По кнопке «Купить и скачать электронную книгу» можно купить эту книгу в электронном виде в официальном интернет магазине «ЛитРес», и потом ее скачать на сайте Литреса.
По кнопке «Найти похожие материалы на других сайтах» можно искать похожие материалы на других сайтах.
Алгебра и начала математического анализа, 11 класс, Часть 1, Мордкович А.Г., Семенов П.В., 2012.
Учебник представляет собой первую часть комплекта из двух книг, предназначенных для изучения курса алгебры и начала анализа в 11-м классе с профильной подготовкой по математике (вторая часть — задачник). Отличительные особенности учебника — доступное изложение материала, большое число подробно решенных примеров, приоритет функционально-графической линии, появление новых тем.
Первообразная и неопределённый интеграл.
Определение первообразной
В курсе алгебры и начал математического анализа 10-го класса мы, руководствуясь различными формулами и правилами, находили производную заданной функции и убедились в том, что производная имеет многочисленные применения: производная — это скорость движения, скорость протекания любого процесса (или, обобщая, скорость изменения функции), производная — это угловой коэффициент касательной к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; производная помогает решать задачи на оптимизацию.
ОГЛАВЛЕНИЕ
Предисловие для учителя 3
Глава 1. Многочлены
§ 1. Многочлены от одной переменной 5
§ 2. Многочлены от нескольких переменных 15
§ 3. Уравнения высших степеней 24
Уравнения высших степеней 24
Глава 2. Степени и корни. Степенные функции
§ 4. Понятие корня п-й степени из действительного числа 31
§ 5. Функции у = n/х, их свойства и графики 36
§ 7. Преобразование иррациональных выражений 46
§ 8. Понятие степени с любым рациональным показателем 50
§ 9. Степенные функции, их свойства и графики 56
§ 10. Извлечение корней из комплексных чисел 67
Глава 3. Показательная и логарифмическая функции
§ 11. Показательная функция, ее свойства и график 81
§ 12. Показательные уравнения 93
§ 13. Показательные неравенства 99
§ 14. Понятие логарифма 102
§ 15. Логарифмическая функция, ее свойства и график 105
§ 16. Свойства логарифмов 112
§ 17. Логарифмические уравнения 121
§ 18. Логарифмические неравенства 127
§ 19. Дифференцирование показательной и логарифмической функций 132
§ 20.
 Первообразная и неопределенный интеграл 140
Первообразная и неопределенный интеграл 140§ 21. Определенный интеграл 149
Глава 5. Элементы теории вероятностей и математической статистики
§ 22. Вероятность и геометрия 162
§ 23. Независимые повторения испытаний с двумя исходами 170
§ 24. Статистические методы обработки информации 179
§ 25. Гауссова кривая. Закон больших чисел 191
Глава 6. Уравнения и неравенства. Системы уравнений и неравенств
§ 26. Равносильность уравнений 201
§ 27. Общие методы решения уравнений 211
§ 29. Уравнения и неравенства с модулями 227
§ 30. Иррациональные уравнения и неравенства 237
§ 31. Доказательство неравенств 246
§ 32. Уравнения и неравенства с двумя переменными 258
§ 33. Системы уравнений 264
§ 34. Задачи с параметрами 273
Приложение 281
Предметный указатель 283.
Купить.
Дата публикации:
Хештеги: #учебник по алгебре :: #алгебра :: #Мордкович :: #Семенов :: #11 класс
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
- Высшая математика, Теория и практика, Курс для экономистов, Часть 1, Ринчино А.
 Л., 2010
Л., 2010 - Высшая математика, Теория и практика, Курс для экономистов, Часть 2, Ринчино А.Л., 2010
- Исследование операций, Писарук Н.Н., 2012
- Алгебра, 11 клас, Академічний рівень, профільний рівень, Нелін Є.П., Долгова О.Є., 2011
Предыдущие статьи:
- Алгебра, 11 клас, Частина 1, Мерзляк А.Г., Номіровський Д.А., 2011
- Дифференциальное исчисление, Кабанова Л.И., 2011
- Колдовство геометрии, Книга 3, Ушаков И.А., 2011
- Теория и практика математического моделирования в современном литейном производстве, Дурина Т.А., 2012
eyellowpage — поиск объявлений
eyellowpage- О проекте
- Политика конфиденциальности
Электроника и современные гаджеты
Домашние животные и товары для них
Одежда, обувь и аксессуары
Автозапчасти
Стройматериалы и инструменты
Оборудование для бизнеса и промышленности
Мебель и интеръер
Техника для дома
Работа
Сервис и услуги
Антиквариат и коллекционирование
Косметика и товары для ухода
Еда и напитки
Музыка и музыкальные инструменты
Товары для детей
Товары для спорта и активного отдыха
Бытовая химия
Книги и журналы
Аренда недвижимости
Продажа недвижимости
© eyellowpage
Домашнее задание на
Математика не относится к творческим предметам, справляется с помощью интуиции. Здесь нужны твердые знания. В обычное школьное время для выполнения практических заданий по алгебре отводится немного. Не у всех есть время списывать решение с доски, не говоря уже о подробностях нюансов примеров и задач. Хорошая практика для семиклассника становится домашним заданием. Вот и воспользуйтесь ГДЗ по алгебре 7 класс — с ними легко ликвидировать пробелы в обучении, принятом в школу.
Здесь нужны твердые знания. В обычное школьное время для выполнения практических заданий по алгебре отводится немного. Не у всех есть время списывать решение с доски, не говоря уже о подробностях нюансов примеров и задач. Хорошая практика для семиклассника становится домашним заданием. Вот и воспользуйтесь ГДЗ по алгебре 7 класс — с ними легко ликвидировать пробелы в обучении, принятом в школу.
Не избегайте решебников, полагаясь на собственные силы. GDZ поможет отточить навыки выполнения примеров, предотвратить досадную ошибку, сделать упражнение в тетради. Готовых заданий, составленных опытными авторами:
- поможет справиться со сложными задачами;
- сможет узнать правильные ответы и наиболее рациональные способы их найти;
- Сформирую привычку работать самостоятельно.
Опытный старшеклассник использует ГДЗ при подготовке к единому государственному экзамену — чтобы посмотреть здесь забытые формулы и правила.Решебник по алгебре для 7 класса — отличный инструмент для самостоятельных занятий. Он будет полезен бедному школьнику и тому, кто собирается на соревнования или олимпиаду.
Он будет полезен бедному школьнику и тому, кто собирается на соревнования или олимпиаду.
 ФГОС Никольский, Потапов Образование
ФГОС Никольский, Потапов Образование ФГОС Звавич, Кузнецова Образование
ФГОС Звавич, Кузнецова Образование М., Саакян С.М., Шварцбург СИМ: Просвещение
М., Саакян С.М., Шварцбург СИМ: Просвещение ГЭФ Попов экзамен
ГЭФ Попов экзаменРабочие тетради
- Мерзляк, Полонский, Якир Вентана График
- Зубарева, Мильштейн Мнемозина
- Миньева, Рослова Просвещение
- Рабочая тетрадь по алгебре 7 класс.
 Часть 1, 2 Потапов, Шевкин Просвещение
Часть 1, 2 Потапов, Шевкин Просвещение - Рабочая тетрадь по алгебре 7 класс. Часть 1, 2. GEF
- Рабочая тетрадь по алгебре 7. Часть 1, 2. ГЭФ Колягин, Ткачева Образование
- Рабочая тетрадь по алгебре 7. Экзамен GEF
- Рабочая тетрадь по алгебре 7. Экзамен GEF
- Рабочая тетрадь по алгебре 7. Часть 1, 2. ГЭФ Ерина. К учебнику Макарычева Экзамен
- Рабочая тетрадь по алгебре 8 класс. Часть 1, 2 Мерзляк, Полонский Вентана График
- Зубарева, Мильштейн Мнемозина
- Рабочая тетрадь по алгебре 8 класс.Часть 1, 2. ГЭФ Миндюк, Шлина Просвещение
- Рабочая тетрадь по алгебре 8 класс. Часть 1, 2. ФГОС Миньева, Рослова Education
- Рабочая тетрадь по алгебре 8 класс. Часть 1, 2. ГЭФ Колягин, Ткачева Education
- Ерина. К учебнику Макарычева Экзамен
- Рабочая тетрадь по алгебре 8 класс. Г.Э.Ф. Журавлев, Перепелкин. К учебнику Никольского Экзамен
- Рабочая тетрадь по алгебре 8 класс. Ч. 1, 2. Ф.
 Э. Ключникова, нарком. К учебнику Мордкович Экзамен
Э. Ключникова, нарком. К учебнику Мордкович Экзамен
ГДЗ по алгебре для 7 класса Макарычев — решебник, и.е. Сборник готовых домашних заданий в одноименном учебнике, составленный коллективом авторитетных российских авторов: Ю.Н. Макарычев, Н. Миндюк, к.и. Нешков, С. Суворов. Он будет помощником родителям и ученикам, желающим разобраться в практическом применении математических примеров.
Решебник по алгебре для 7 класса Макарычев — контроль за учебой школьников
Большинство родителей хотят контролировать академические успехи своего Чада. Однако адекватно проверить задание по такому сложному предмету, как алгебра, далеко не все.Для того, чтобы определить правильность выполнения того или иного примера, можно воспользоваться решебником по алгебре для 7 класса Макарычева.
Пособие будет крайне полезно школьникам, не разобравшимся с правилами выполнения примера на уроке: в связи с тем, что в сборнике не только онлайн-ответы, но и пошаговый алгоритм их расчета.
Наш сайт позаботился об экономии пользовательского времени:
- Вы можете найти ответ на тот или иной пример, воспользовавшись строкой быстрого поиска, где вы можете вбить номер задачи или цитату из ее состояния — и легко выбрать нужный вариант из предлагаемый список;
- Не отвлекайтесь от текущих дел и садитесь за компьютер, а авторизуйтесь с любого электронного гаджета — ноутбука, планшета, смартфона.
На сайте собраны самые актуальные решебники к обучению в общеобразовательных школах России. Есть несколько вариантов ответа на отдельные примеры из разных сборников.
ГДЗ по алгебре в 7 классе: Макарычев, Миндюк, Небков, Суворов — Учебник 2013
Все решения, собранные в сборнике онлайн-ответов на нашем сайте, основаны на задачах учебника по алгебре, выпущенного в 2013 году под редакцией Макарычевой Ю.Н. Пособие включает 46 тем, разделенных на 16 основных параграфов.Изложенный в учебнике материал знакомит учащихся 7 классов с такими темами:
- Преобразование математических выражений и решение уравнений с одной переменной;
- Понятия и типы функций, а также характеристики построения их графиков;
- Формулы сокращенного умножения и практические основы их использования;
- Порядок выполнения математических действий со степенями, простейшими и многочленами;
- Простые системы линейных уравнений и способы их решения.

Разобраться в таком внушительном массиве информации поможет наш сайт, который позволяет научиться решать алгебраические задачи самостоятельно, не привлекая репетитора.
Решебник по алгебре для 7 класса Макарычева от Путина — это сборник готовых решений и ответов на задания и примеры из учебника, составленный коллективом авторитетных российских ученых: Ю.Н. Макарычев, Н. Миндюк, к.и. Нешков, С. Суворов.
ГДЗ по алгебре 7 класс: Макарычев, Миндюк, Небков, Суворов
В 7 классе школьники приступают к углубленному изучению отдельного раздела математики — алгебры.Иногда многие из них начинают испытывать трудности с решением задач и выполнением примеров. Родители в этой ситуации видят только одно решение — нанять репетитора.
Однако проблема решается и без привлечения специалистов со стороны: достаточно использовать ГДЗ по алгебре для 7 класса Макарычева. В книге есть не только готовые ответы, но и пошаговый алгоритм домашнего задания. Это позволит школьникам разбираться дома на непонятных примерах, а их родителям контролировать их читабельность.
В целях оптимизации затрат времени и сил на выполнение алгебраических задач и примеров стоит воспользоваться интерфейсом нашего сайта, который позволяет:
- выбрать нужный номер в таблице и перейти к решенной задаче;
- получить доступ к базе ответов с любого электронного устройства;
- откройте для себя несколько вариантов решения одного и того же примера.
Поскольку база коллекций ГДЗ регулярно обновляется, то школьники могут быть уверены в правильности своего домашнего задания, как с позиции правил языка, так и с точки зрения его оформления.
Решебник по алгебре 7 класс Макарычев — Учебное пособие 2013-2017.
В большинстве образовательных школ России в настоящее время используется учебник 2013 г., составленный группой российских ученых под руководством Макарычева Ю.Н.
Алгебра Макарычева состоит из 46 разделов, распределенных между шестыми основными разделами. Книга знакомит школьников с основными алгебраическими понятиями:
- преобразование выражений и решение уравнений с одной переменной;
- основные типы функций и построение их графиков в декартовой системе координат;
- сокращенных формул умножения: Состав и применение;
- математических действий с простейшими и многочленами;
- системы линейных уравнений и два метода их решения.

Каждая тема преимуществ подкреплена примерами и задачами, как стандартного типа, так и повышенной сложности.
Математика требует скрупулезности, аккуратности и внимания. Чтобы получить правильные ответы на поставленные задачи, вам придется последовательно выполнять множество мелких операций; Ошибка в одном из них приводит к неверному результату. Поэтому в домашних условиях важен контроль. Решебник для 7 класса по алгебре поможет безупречно выполнить все задания, подскажет новые способы решения на примерах, познакомит с научным обоснованием математических задач.ГДЗ — путь к эффективной самостоятельной работе без посторонней помощи, получению отличных оценок, достижению высоких показателей.
Абстрактный язык буквенных выражений и формул лучше подходит тем ученикам, которые не забинтованы, чтобы смотреть задания, выполняемые опытными учителями, и сверяться с их результатами. Решебник полезен тем, что в нем все расписано. Если учитель четко не объясняет или занимает мало времени на практику, GDZ на 7 классе алгебры поможет исправить ситуацию. С ними студент решит достаточное количество примеров для закрепления знаний по:
С ними студент решит достаточное количество примеров для закрепления знаний по:
- функций и графики,
- гоморалы и многочлены
- Основы статистики и теории вероятностей.
ГДЗ снимает стресс, страх перед испытаниями и независимость. Здесь можно списать сложные уравнения, разобраться с аналитическим и графическим представлением функций, узнать формулы сокращенного умножения и тем самым значительно повысить их производительность.
В поисках ОТЗ онлайн. Как найти область определения математических функций? Область допустимых значений — есть раствор
Функция является моделью. Определить x, как набор независимых значений переменных // Независимые — знать любые.
Функция — это правило, по которому для каждого значения независимой переменной из набора X вы можете найти единственное значение зависимой переменной. // т.е. для каждого x есть один y.
Из определения следует, что есть два понятия: независимая переменная (которую мы обозначаем x, и она может принимать любые значения) и зависимая переменная (которую мы обозначаем y или f (x), и она вычисляется из функции, когда мы заменить x).2. (называется Парабола)
3. = 3х + 7. (наим. Прямой)
4. U = √ x. (так называемый филиал Парабола)
Независимая переменная (кат. Обозначается x) имеет имя аргумента функции.
Область определения функции
Набор всех значений, принимающих аргумент функции, называется областью определения функции и обозначается D (F) или D (Y).
Рассмотрим D (y) для 1., 2., 3., 4.
1. D (y) = (∞; 0) and (0; + ∞) // Все много действительных чисел, кроме нуля.
2. D (y) = (∞; + ∞) // Все МН-во действительны.
3. D (y) = (∞; + ∞) // Все MN -в действительны
4. D (y) = ∪∪; Эд. С. А. Теликовский. — 17-е изд. — М .: Просвещение, 2008. — 240 с. : IL. — ISBN 978-5-09-019315-3.
Подробное решение системы неравенства. Система неравенства
Рассмотрим на примерах, как решить систему линейных неравенств.
4x + 29 \ КОНЕЦ (Массив) \ Вправо. \\] «Заголовок =» (! Lang: Rendered by QuickTex.com «>!}
Для решения системы необходима каждая из составляющих ее неравенств. Только решение принимается не отдельно, а вместе, соединяя их фигурной скобкой.
В каждом из неравенств системы неизвестным лицам передать один путь, известный друг другу с противоположным знаком:
Заголовок = «(! Lang: Отрисовано QuickTextEx.com «>!}
После упрощения обеих частей неравенства необходимо разделить число, стоящее перед ix. Первое неравенство делится на положительное число, поэтому знак неравенства не меняется. Второе неравенство делится на отрицательное число, поэтому знак неравенства необходимо поменять на противоположный:
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
Решение неравенств примечание на числовых строках:
В ответ записываем пересечение решений, то есть ту часть, где штриховка находится на обеих прямых.
Ответ: x∈ [-2; 1).
В первом неравенстве мы избавляемся от братства. Для этого обе части умножаются на наименьший общий знаменатель 2. При умножении на положительное число знак неравенства не меняется.
Во втором неравенстве раскрываем скобки. Произведение суммы и разности двух выражений равно разности квадратов этих выражений. В правой части — квадрат разницы двух выражений.
Заголовок = «(! Lang: Отрисовано QuickTextEx.com «>!}
Неизвестные пересадить в одну сторону, знакомую друг другу с обратным знаком и упрощенную:
Обе части неравенства делятся на число перед ix. В первом неравенстве мы делим отрицательное число, поэтому знак неравенства меняется на противоположный. Во втором — делим на положительное число, знак неравенства не меняется:
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
Оба неравенства со знаком «меньше» (не обязательно, чтобы один знак был строго «меньше», а другой не мешал, «меньше или равно»).Мы не можем отмечать оба решения и использовать правило «». Little равно 1, поэтому система сводится к неравенству
Мы отмечаем его решение о числовом прямом:
Ответ: x∈ (-∞; 1].
Открытые брекеты. В первом неравенстве -. Он равен количеству кубиков этих выражений.
Во втором — работа суммы и разности двух выражений, которая равна разнице в квадратах. Поскольку здесь стоит знак «минус», лучше раскрыть знак в два этапа: сначала используйте формулу, и только потом раскрывайте скобки, меняя знак каждой дополнительной на противоположный.
Переход неизвестен в одну сторону, известен — в другую с обратным знаком:
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
Оба подписывают «еще». Используя более длинное правило, мы сводим систему неравенств к одному неравенству. Две большие цифры 5 в соответствии с
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
Решение неравенства отметьте на числовом прямом и запишите ответ:
Ответ: x∈ (5; ∞).
Поскольку алгебра линейных неравенств встречается не только как самостоятельные задачи, но и при решении разного рода уравнений, неравенств и т. Д., Важно вовремя изучить эту тему.
В следующий раз мы рассмотрим примеры решения линейных неравенств в частных случаях, когда одно из неравенств не имеет решений или решением для него является любое число.
Категория: |Эта статья содержит начальную информацию о системах неравенства.Здесь дается определение системы неравенств и определение решения системы неравенств. А также перечислены основные типы систем, с которыми чаще всего работают на уроках алгебры в школе, и приведены примеры.
Страница навигации.
Что такое система неравенства?
Системы неравенства удобно определять аналогично тому, как мы ввели определение системы уравнений, то есть в соответствии с типом записи и смыслом, вложенным в нее.
Определение.
Система неравенств — Это запись, которая представляет собой определенное количество неравенств, записанных друг в друге, объединенных в левой фигурной скобке и обозначающих многие из всех решений, которые одновременно являются решениями для каждого системного неравенства.
Приведем пример системы неравенства. Возьмем два произвольных, например 2 · x-3> 0 и 5 — x≥4 · X-11, запишем их друг под другом
2 · x-3> 0,
5-x≥4 · X-11
и объединяем знак системы — фигурную скобку, в результате получаем систему неравенств такого типа:
Аналогично дается представление о неравенствах в школьных учебниках.Стоит отметить, что определения даны более узко: для неравенств с одной переменной или с двумя переменными.
Основные виды неравенств
Понятно, что различных неравенств можно составить бесконечно много. Чтобы не потеряться в этом многообразии, их желательно рассматривать в группах, имеющих свои особенности. Все неравенства можно разделить на группы по следующим критериям:
- по количеству неравенств в системе;
- по количеству переменных, участвующих в записи;
- согласно самому неравенству.
В число включенных в статью неравенств входят две, три, четыре системы и т. Д. Неравенства. В предыдущем абзаце мы привели пример системы, которая представляет собой систему двух неравенств. Покажем еще один пример системы четырех неравенств.
Отдельно скажем, что нет смысла говорить о системе одного неравенства, в данном случае, по сути, речь идет о самом неравенстве, а не о системе.
Если вы посмотрите на количество переменных, то вы увидите систему неравенств с единицей, двумя, тремя и т. Д.переменные (или, как и везде, неизвестны). Посмотрите на последнюю систему неравенства, зафиксированную двумя абзацами выше. Это система с тремя переменными x, y и z. Обратите внимание, что его два первых неравенства не содержат всех трех переменных, а содержат только одну из них. В контексте этой системы их следует понимать как неравенства с тремя переменными вида X + 0 · Y + 0 · Z≥-2 и 0 · X + Y + 0 · Z≤5 соответственно. Отметим, что в школе основное внимание уделяется неравенствам с одной переменной.
Осталось обсудить, какие типы неравенства задействованы в записях систем. В школе в основном рассматриваются системы двух неравенств (реже — трех, еще реже — четырех и более) с одной или двумя переменными, а сами неравенства обычно составляют целые неравенства Первая или вторая степень (реже — более высокие степени). или дробно-рациональное). Но не удивляйтесь, если в материалах подготовки встретятся системы неравенств, содержащие иррациональные, логарифмические, индикативные и другие неравенства.В качестве примера приведем систему неравенств, из которой она взята.
Что называется решением системы неравенства?
Введем еще одно определение, связанное с системами неравенств — определение решения системы неравенств:
Определение.
Решением системы неравенств с одной переменной Это называется такое значение переменной, которое добавляет каждое из неравенств системы к точному, другими словами, которое является решением каждого системного неравенства.
Поясним на примере. Возьмем систему двух неравенств с одной переменной. Примем значение переменной x равным 8, это решение нашей системы неравенств по определению, так как ее подстановка в системное неравенство дает два точных числовых неравенства 8> 7 и 2-3 · 8≤0. Напротив, единица не является решением системы, так как при ее замене вместо переменной x первое неравенство превратится в неправильное числовое неравенство 1> 7.
Аналогично можно ввести определение решения системы неравенств с двумя, тремя и большим числом переменных:
Определение.
Решением системы неравенств с двумя, тремя и т. Д. Переменными называются парные, тройные и т. Д. Значения этих переменных, которые одновременно являются решением каждого системного неравенства, то есть, сводит каждое системное неравенство к правому числовому неравенству.
Например, пара значений x = 1, y = 2 или другая запись (1, 2) является решением системы неравенств с двумя переменными, как 1 + 2
Системы неравенства могут не иметь решений, могут иметь конечное число решений и может иметь бесконечно много решений. Часто говорят о множестве решений системы неравенств. Когда в системе нет решений, значит, есть пустой набор ее решений. Когда решений является конечным числом, то множество решений содержит конечное число элементов, а когда решений бесконечно много, то множество решений состоит из бесконечного числа элементов.
В некоторых источниках вводятся определения частного и общего решения системы неравенств, как, например, в учебниках Мордковича. Под частное решение системы неравенств Под ней понимается одно отдельное решение. В свою очередь, общих решений. Неравенство систем — это все его частные решения. Однако в этих терминах это имеет смысл только тогда, когда необходимо подчеркнуть, что ясно, что такое решение, но обычно это ясно из контекста, поэтому гораздо чаще они говорят просто «решение системы неравенства».
Из введенных в статье определений неравенств и решений следует, что решение системы неравенств является пересечением множеств решений всех неравенств этой системы.
Список использованной литературы.
- Алгебра: занятий. Для 8 кл. общее образование. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворов]; Эд. С. А. Теликовский. — 16-е изд. — М .: Просвещение, 2008. — 271 с. : IL. — ISBN 978-5-09-019243-9.
- Алгебра: 9 класс: учеб. Для общего образования. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворов]; Эд. С. А. Теликовский. — 16-е изд. — М .: Просвещение, 2009. — 271 с. : IL. — ISBN 978-5-09-021134-5.
- Мордкович А.Г. Алгебра. 9 сорт. По 2 ч. Л. 1. Учебное пособие для учащихся общеобразовательных учреждений / А. Мордкович, П. В. Семенов. — 13-е изд., Чет. — М .: Мнемозина, 2011. — 222 с .: Ил. ISBN 978-5-346-01752-3.
- Мордкович А.Г. Алгебра и начало математического анализа. 11 класс. По 2 ч. Л. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Мордкович, П. В. Семенов. — 2-е изд., Чед. — М .: Мнемозина, 2008. — 287 с .: Ил. ISBN 978-5-346-01027-2.
- ЕГЭ -2013. Математика: Типовые экзамены: 30 вариантов / под ред. Семенова А.Л., Ященко И.В. — М .: Издательство «Народное просвещение», 2012. — 192 с. — (ЕГЭ-2013. ШКОЛА ФИПИ).
Урок и презентация на тему: «Системы неравенства. Примеры решений»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Учебные пособия и тренажеры в интернет-магазине «Интеграл» для 9 класса.
Интерактивное учебное пособие для 9 класса «Правила и упражнения по геометрии»
Электронное учебное пособие «Четкая геометрия» для 7-9 классов
Система неравенств
Ребята, вы изучили линейные и квадратные неравенства, научились решать задачи по этим темам.Теперь перейдем к новому понятию в математике — системе неравенства. Система неравенств аналогична системе уравнений. Вы помните систему уравнений? Система уравнений, которую вы изучали в седьмом классе, постарайтесь вспомнить, как вы их решали. Введем определение системы неравенств.
Несколько неравенств с некоторой вариацией x образуют систему неравенств, если нужно найти все значения x, в которых каждое из неравенств образовано правильным числовым выражением.
Любое значение X, в котором каждое неравенство принимает точное числовое выражение, является решением неравенства. Это также можно назвать частным решением.
А какое конкретное решение? Например, в ответ мы получили выражение x> 7. Тогда x = 8, либо x = 123, либо любое другое число больше семи — частное решение, а выражение X> 7 — общее решение. Общее решение формируется множеством частных решений.
Как мы объединили систему уравнений? Правильно, фигурная скобка, значит, с неравенствами тоже идут.Рассмотрим пример системы неравенств: $ \\ begin (Cases) X + 7> 5 \\\\ X-3
Если система неравенств состоит из одинаковых выражений, например, $ \\ begin (Cases) x + 7> 5 \ x + 7
Так что это значит: найти решение системы неравенств?
Решение неравенства — это множество частных решений неравенства, которые сразу удовлетворяют обоим неравенствам системы.
Общий вид системы неравенств Запишите в виде $ \ begin (Cases) F (x)> 0 \ G (x)> 0 \ End (Cases) $
Обозначим через $ x_1 $ — общее решение неравенства F (x)> 0.
$ X_2 $ — общее решение неравенства G (x)> 0.
$ X_1 $ и $ x_2 $ — это разновидности частных решений.
Решением системы неравенств будут числа, принадлежащие как $ x_1, так и $ x_2 $.
Давайте вспомним операции над наборами. Как нам найти элементы наборов, принадлежащих обоим множественным наборам? Правильно, есть операция пересечения. Итак, решением нашего неравенства будет множество $ a = x_1∩∩ x_2.
Примеры решений систем неравенств
Рассмотрим примеры решений неравенств. Определите систему неравенств.
a) $ \ begin (Cases) 3x-1> 2 \ 5x-10 b) $ \ begin (Cases) 2x-4≤6 \\\\ — X-4
Решение.
а) Каждое неравенство решаю отдельно.
$ 3х-1> 2; \\; 3Х> 3; \\; X> 1.
$ 5x-10
Отметим наши зазоры по той же координате прямой.
Решением системы будет разделение пересечения наших пробелов. Неравенство строгое, тогда отрезок будет открытым.
Ответ: (1; 3).
B) также решите каждое неравенство отдельно.
$ 2x-4≤6; 2x≤ 10; x ≤ 5.
$ -x-4-5 $.
Решением системы будет разделение пересечения наших разрывов. Второе неравенство строгое, тогда отрезок будет открытым слева.
Ответ: (-5; 5].
Подведем итог полученным знаниям.
Допустим, необходимо решить систему неравенств: $ \ begin (Cases) F_1 (X)> F_2 (X) \\\ \ G_1 (x)> G_2 (x) \ End (Cases) $.
Тогда интервал ($ x_1; x_2 $) является решением первого неравенства.
Интервал ($ y_1; y_2 $) — Решение второго неравенства.
Решением системы неравенств является пересечение решений каждого неравенства.
Системы неравенства могут состоять из неравенств не только первого порядка, но и любых других типов неравенств.
Важные правила при решении систем неравенства.
Если одно из неравенств системы не имеет решений, значит, нет решений для всей системы.
Если одно из неравенств выполняется для любых значений вариации, то решением системы будет решение другого неравенства.2 + 4х + 4> 0 \ Конец (Дела) $.
Решение.
а) Первое неравенство имеет решение x> 1.
Находим дискриминант для второго неравенства.
$ D = 16-4 * 2 * 4 = -16 $. $ D Напомним правило, когда одно из неравенств не имеет решений, значит, нет решений у всей системы.
Ответ: Нет решений.
B) Первое неравенство имеет решение x> 1.
Второе неравенство выше нуля Для всех x. Тогда решение системы совпадает с решением первого неравенства.2 + 36
В этом уроке мы начнем изучение систем неравенства. Сначала рассмотрим систему линейных неравенств. В начале урока мы рассмотрим, откуда возникают системы неравенства, откуда неравенство. Далее мы изучим, что значит решить систему, и вспомним ассоциацию и пересечение множеств. В конце решим конкретные примеры по линейным неравенствам.
Тема : Рацион Близнецы и их системы
Урок: Основные концепции, решение линейных неравенств
До сих пор мы решали отдельные неравенства и использовали для них интервальный метод, это могло быть линейных неравенств, , квадратных и рациональных.Теперь перейдем к решению системы неравенств — сначала линейных систем . Рассмотрим пример, в котором берется необходимость учитывать системы неравенства.
Найдите область определения поля
Найдите область определения поля
Функция существует, когда существуют оба квадратных корня, т.е.
Как решить такую систему? Необходимо найти все X, удовлетворяющие как первому, так и второму неравенству.
Рисунки по оси ОХ многих решений первого и второго неравенства.
Пересечение двух лучей и вот наше решение.
Этот метод изображения решения системы неравенств иногда называют методом крыши.
Решение системы — пересечение двух множеств.
Покажите это графически. У нас много и произвольный характер, и многие пересекающиеся произвольно.
Определение: пересечение двух наборов A и B называется таким третьим набором, который состоит из всех элементов, входящих в A и в V.
Рассмотрим на конкретных примерах решения линейных систем неравенств, как найти пересечения множеств решений отдельных неравенств в системе.
Решите систему неравенств:
Ответ: (7; 10].
4. Решите систему
Где может второе неравенство системы? Например, из неравенства
Обозначьте графически решение каждого неравенства и найдите зазор их пересечения.
Таким образом, если у нас есть система, в которой одно из неравенств удовлетворяет любому значению X, его можно исключить.
Ответ: Противоречивая система.
Мы рассмотрели типовые вспомогательные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7.
Иногда линейная система задается двойным неравенством, рассмотрим такой случай.
8.
Мы рассмотрели систему линейных неравенств, поняли, откуда они берутся, рассмотрели типовые системы, к которым относятся все линейные системы, и решили некоторые из них.
1. Мордкович А.Г. и др. Алгебра 9 кл: учеб. Для общего образования. Учреждения. — 4-е изд. — М .: Мнемозина, 2002.-192 с .: Ил.
2. Мордкович А.Г. и др. Алгебра 9 кл .: Задание для учащихся общеобразовательных учреждений / А.А. Мордкович, Т.Н. Мишустина и др. — 4-е изд. — М .: Мнемозина, 2002.-143 с .: Ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: этюд. Для школьников, общеобразовательных. Учреждения / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктисты. — 7-е изд., Акт. и добавить. — М .: Мнемозина, 2008.
.4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16 изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 сорт. По 2 ч. Л. 1. Учебное пособие для учащихся общеобразовательных учреждений / А.Мордкович, П.В. Семенов. — 12-е изд., Чед. — М .: 2010 — 224 с .: Ил.
6. Алгебра. 9 сорт. По 2 ч. Л. 2. Такакон для учащихся общеобразовательных учреждений / А. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др. Под ред. А.Г. Мордкович. — 12-е изд., Акт. — М .: 2010.-223 с .: Ил.
1. Патал естественных наук ().
2. Электронный учебно-методический комплекс Подготовить 10-11 классы к вступительным экзаменам по информатике, математике, русскому языку ().
4. Учебный центр «Технологии обучения» ().
5. Раздел College.ru по математике ().
1. Мордкович А.Г. и др. Алгебра 9 кл .: Задание для учащихся общеобразовательных учреждений / А. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М .: Мнемозина, 2002.-143 с .: Ил. №№ 53; 54; 56; 57.
Неравенство — это два числа или математических выражения, связанных одним из знаков:> (подробнее, в случае строгих неравенств),
Неравенство линейное При тех же условиях, что и уравнение: оно содержит переменные только первой степени и не содержит произведений переменных.
Решение линейных неравенств и систем линейных неравенств неразрывно связано с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость, на которую вся плоскость делит прямую, уравнение которой задается линейным неравенством. Эта полуплоскость, а в случае системы линейных неравенств является частью плоскости, ограниченной несколькими прямыми, ее необходимо найти на чертеже.
Для решения линейных неравенств с большим количеством переменных сокращаются многие экономические задачи, в частности задачи линейного программирования, в которых вы хотите найти максимальную или минимальную функцию.
Решение системы линейных неравенств с любым числом неизвестных
Сначала проанализируем линейные неравенства на плоскости. Рассмотрим одно неравенство с двумя переменными и:
,
где — коэффициенты с переменными (некоторые числа), есть свободный член (тоже некоторые).
Одно неравенство с двумя неизвестными, а также уравнение имеет бесчисленное множество решений. Решением этого неравенства назовем пару чисел, удовлетворяющих этому неравенству.Геометрически многие решения неравенств изображаются в виде полуплоскости, ограниченной прямым
,
, который мы называем границей прямой.
Шаг 1. Постройте прямую, ограничивающую множество решений линейного неравенства
Для этого нужно знать любые две точки этой прямой. Найдите точки пересечения с осями координат. Ордината пересечения A. равна нулю (рисунок 1). Числовые значения по осям на этом рисунке относятся к примеру 1, который будет выглядеть сразу после этого махрового тура.
Я найду абсциссу, решая как системное уравнение, прямое с уравнением оси.
Найдите пересечение с осью:
Подставляя значение в первое уравнение, получаем
Откуда.
Таким образом, найдена точка абсцисс A. .
Найдите координаты точки пересечения с осью.
Absiscuss Point B. равняется нулю. С уравнением границы прямое с уравнением оси координат:
,
следовательно, координаты точки B.:.
Шаг 2. Изобразить прямое, ограничивающее множественное решение неравенства. Правильно A. и B. Пересекая границу непосредственно с осями координат, мы можем провести эту прямую линию. Прямая (снова рис. 1) делит всю плоскость на две части, лежащие справа и слева (сверху и снизу) от этой прямой.
Шаг 3. Установить, какая из полуплоскостей является решением этого неравенства. Для этого необходимо в этом неравенстве подставить начало координат (0; 0).Если координаты стали удовлетворять неравенству, решением неравенства будет полуплоскость, в которой находится начало координат. Если координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, не содержащая начала координат. Решение неравенства в полуплоскости обозначим штрихами от прямой внутренней части полуплоскости, как на рисунке 1.
Если мы решаем систему линейных неравенств , каждый шаг выполняется для каждого из неравенств системы.
Пример 1. Решите неравенство
Решение. Историю прямо
Подставляя в уравнение direct, получаем, а подставляя, получаем. Следовательно, координаты точек пересечения с осями будут A. (3; 0) , Б. (0; 2). Через эти точки мы будем проводить прямые (снова рисунок 1).
Выберем неравенство полуплоскостных решений. Для этого в неравенство подставляем координаты начала (0; 0):
получаем, т.е., координаты стали удовлетворять этому неравенству. Следовательно, решением неравенства является полуплоскость, содержащая начало координат, т.е. левая (она нижняя) полуплоскость.
Если бы это неравенство было строгим, то есть имело бы вид
, то точки прямой границы не были решением, так как они не удовлетворяют неравенству.
Теперь рассмотрим систему линейных неравенств с двумя неизвестными:
Каждое из неравенств этой системы на плоскости определяет полуплоскость.Система линейных неравенств называется коллаборативной, если у нее есть хотя бы одно решение, и неполной, если у нее нет решений. Решением системы линейных неравенств назовем любую пару чисел (), удовлетворяющую всем неравенствам этой системы.
Геометрически решающая система линейных неравенств — это множество точек, удовлетворяющих всем системным неравенствам, то есть суммарной части полученных полупозиций. Поэтому геометрически в целом решение можно изобразить в виде определенного многоугольника, в частном случае — в виде линии, отрезка и даже точки.Если система линейных неравенств неполная, то на плоскости нет ни одной точки, удовлетворяющей всем системным неравенствам.
Пример 2.
Решение. Итак, требуется найти многоугольные решения этой системы неравенств. Границу построим прямую для первого неравенства, т.е. прямую, и границу прямую для второго неравенства, т.е. прямую.
Мы делаем это шаг за шагом, как показано в теоретической справке и в примере 1, тем более что в примере 1 они построили границу непосредственно для неравенства, которая является первой в этой системе.
Решения в полуплоскости, соответствующие неравенствам этой системы на рис. 2, заштрихованы внутри. Общая часть полуплоскостей решений — открытый угол ABC . Это означает, что множество точек плоскости, составляющих открытый угол ABC , является решением как первого, так и второго неравенства системы, то есть является решением системы двух линейных неравенств. Другими словами, владения любой точки из этого множества удовлетворяют обоим неравенствам системы.
Пример 3. Решите линейные неравенства
Решение. Построим граничные прямые соответствующие системные неравенства. Мы делаем это, выполняя шаги, теоретические данные, для каждого неравенства. Теперь определим полуплоскостные решения для каждого неравенства (рисунок 3).
Внутри заштрихованы полуплоскостные решения, соответствующие неравенствам этой системы. Пересечение решений изображено, как показано на рисунке, в виде квадрикуля ABCE .Получено, что многоугольником решения системы линейных неравенств с двумя переменными является квадрика ABCE .
Все описанное выше о системах линейных неравенств с двумя неизвестными относится к системе неравенств с любым числом неизвестных, с той лишь разницей, что решение неравенства с n. Неизвестный будет совокупным n. числа (), удовлетворяющих всем неравенствам, и вместо границы прямой будет граничная гиперплоскость n. — пространственное пространство. Решением будет многогранник решений (симплекс), ограниченный гиперплоскостями.
Умножение многочлена на одно объяснение. Умножение многочлена на один
В данном видеоязыке мы подробно рассмотрим вопрос умножения полинома на любое выражение, которое соответствует определению «моном» или «unrochene». Montomom может действовать с любым свободным числовым значением, представленным натуральным числом (в любой степени, с любым знаком) или определенной переменной (с аналогичными атрибутами).Следует помнить, что многочлен — это набор алгебраических элементов, называемых членами многочлена. Иногда некоторые участники могут быть перечислены и сокращены. Настоятельно рекомендуется проводить процедуру приведения таких членов после операции умножения. Окончательный ответ в этом случае будет стандартизированной формой многочленов.
Как следует из нашего видео, процесс умножения не подчиняется многочленам, его можно рассматривать с двух позиций: линейной алгебры и геометрии.Рассмотрим операцию умножения многочлена на каждую сторону — это способствует универсальности применения правил, особенно в случае комплексных задач.
В алгебраическом понимании умножение многочлена на однополюсное соответствует стандартному правилу умножения: каждый элемент суммы должен быть умножен на заданное значение, а полученное значение алгебраически свернуто. Стоит понимать, что любой многочлен — это подробная алгебраическая сумма.Умножив каждый член многочлена на некоторую значимость, мы получим новую алгебраическую сумму, которую принято приводить к стандартной форме, если возможно, конечно.
Рассмотрим умножение многочлена в этом случае:
3A * (2a 2 + 3c — 3)
Легко понять, что здесь выражение (2a 2 + 3c — 3) является полиномом, а 3a — свободным множителем. Чтобы решить это выражение, достаточно максимизировать каждый из трех членов многочлена до 3a:
Следует помнить, что знак является важным атрибутом переменной справа, и его нельзя потерять.Знак «+», как правило, не записывается, если выражение начинается с него. При умножении числовых выражений умножаются все коэффициенты с переменными переменными. Те же переменные увеличивают степень. Различные переменные остаются неизменными, и записываются в один элемент: A * C = AU. Знание этих простейших правил сложения способствует правильному и быстрому решению любых подобных упражнений.
У нас есть три значения, которые по сути являются членами последнего многочлена, который является ответом на пример.Необходимо только алгебраически сложить значения данных:
6a 3 + 9As + (- 9a) = 6a 3 + 9As — 9A
Скобки раскрывают, сохраняя знаки, так как это алгебраическое сложение, а между мономами по определению стоит знак «плюс». Окончательный стандартный вид многочлена — это правильный ответ на представленный пример.
Геометрический вид умножения многочлена на одно крыло — это процесс нахождения площади прямоугольника. Предположим, у нас есть некий прямоугольник со сторонами a и c.Фигура разбита двумя сегментами на трех прямоугольниках разной площади, так что сторона C у всех общая или одна и та же. А стороны A1, A2 и A3 в сумме дают начальную a. Как известно из аксиоматического определения площади прямоугольника, чтобы найти этот параметр, необходимо стороны умножить: S = a * s. Либо S = (A1 + A2 + A3) * s. Произведем умножение многочлена (образованного сторонами меньших прямоугольников) на однослойной — основной стороне рисунка, и получим выражение для S: A1 * C + A2 * C + A3 * s.Но если внимательно посмотреть, то можно заметить, что этот многочлен представляет собой сумму площадей трех меньших прямоугольников, составляющих исходную фигуру. Действительно, для первого прямоугольника S = A1C (по аксиоме) и т. Д. Алгебраически верность рассуждению при сложении многочлена подтверждается вычислениями линейной алгебры. А геометрически — правила сложения площадей в единую простейшую фигуру.
При проведении манипуляций с умножением полинома на единицу следует помнить, что при этом степени монома и полинома (общие) складываются — и полученное значение является степенью нового полинома (отклика).
Все вышеперечисленные правила вместе с основами алгебраического сложения используются в примерах простейшего упрощения выражений, где совмещение таких членов и умножение элементов осуществляется для упрощения всего полинома.
На унрочене? Как правильно умножать знаки?
Правило.
Чтобы умножить многочлен на, каждый член многочлена умножается на одинарный и результаты складываются.
Удобно записывать перед скобками.
Для правильной расстановки знаков при умножении лучше использовать правила раскрытия скобок, в которых стоит знак «плюс» или знак минус.
Умножение полинома на одно крыло можно изобразить с помощью схемы.
Умножаем на каждый член многочлена, стоящий в скобках («фонтанный»).
Если перед скобками стоит знак «+», знаки в скобках не меняются:
Если перед скобками стоит знак «-», каждый знак в скобках меняется на противоположный:
Рассмотрим, как умножают многочлен на единицу, на конкретных примерах.
Примеры.
Произвести умножение многочлена на одно:
Решение:
Многократно закопченный для каждого члена многочлена, стоящего в скобках. Поскольку перед скобками стоит знак «Плюс», знаки в скобках не меняются:
отдельно, альтернативные номера, отдельно — с одинаковыми базами:
Однократное скручивание умножается на каждый член полинома. Поскольку перед скобками стоит множитель, знак каждого члена, стоящего в скобках, изменится на противоположный:
Обычно пишут короче, умножение степеней и чисел (за исключением обыкновенных дробей и смешанных чисел) выполняют устно.
Если коэффициенты — обыкновенные дроби, то умножаем их по правилу умножения обыкновенных дробей: числитель к числителю, знаменатель — к знаменателю, и сразу записываем их под одной дробной чертой. Если коэффициенты являются смешанными числами, переведите их в неправильную дробь:
Внимание!
Не убавляйте дроби, пока не записали все действия до конца.Как показывает практика, если сразу начать с сокращения дробей, то до остальных компонентов дело не доходит — о них просто забывают.
§ 1 Умножение многочлена на один
Когда дело доходит до умножения многочленов, мы можем иметь дело с двумя типами операций: умножение многочлена на одно и умножение многочлена на многочлен. В этом уроке мы узнаем, как умножить многочлен на однокомнатную.
Основное правило, которое используется при умножении многочлена на единицу, — это свойство распределения умножения.Отзыв:
Чтобы умножить сумму на число, вы можете умножить каждый компонент на это число и полученные работы складываются.
Это свойство умножения применяется к вычету. В алфавитной записи свойство распределения умножения выглядит следующим образом:
(А + В) ∙ С = АС + ВС
(А — В) ∙ С = АС — ВС
Рассмотрим пример: многочлен (5AB — 3A2) умножается на одностворчатый 2b.
Введем новые переменные и обозначим 5Ab — буквой X, 3A2 — буквой C, 2B — буквой C.Тогда наш пример принимает вид:
(5Ab — 3A2) ∙ 2B = (x — y) ∙ с
Согласно закону распределения это равно HS — Us. Теперь вернемся к исходному значению новых переменных. Получаем:
5AB ∙ 2B — 3A2 ∙ 2B
Приведем получившийся многочлен к стандартному виду. Получаем выражение:
Таким образом, можно сформулировать правило:
Чтобы умножить многочлен на одно крыло, каждый член многочлена умножается на этот единственный, и полученные работы складываются.
Действует то же правило, но умножение не убирается с полиномом.
§ 2 Примеры по теме урока
При умножении многочленов на практике, во избежание путаницы, с определением полученных знаков рекомендуется сначала определить и сразу записать знак работы, а уже потом находить и запишите произведение чисел и переменных. Вот как это выглядит на конкретных примерах.
Пример 1. (4A2B — 2A) ∙ (-5AB).
Здесь однослойный — 5Ab нужно умножить на две универсальные составляющие полинома, 4a2b и — 2a. Первая работа будет со знаком «-», а вторая — со знаком «+». Следовательно, решение будет выглядеть так:
(4A2B — 2a) ∙ (-5AB) = — 4A2B ∙ 5AB + 2A ∙ 5AB = -20A3B2 + 10A2B
Пример 2. -st (2x 3ow +5).
Здесь нам нужно будет выполнить три действия умножения, причем знак первой работы будет «-», знак второй «+», знак третьей «-».Решение выглядит так:
Hu (2x — 3a + 5) = -Hh ∙ 2x + Hu ∙ 3ow — Hu ∙ 5 = -2x2u + 3h3 — 5h.
Список литературы:
- Мордкович А.Г., Алгебра 7 класс в 2-х частях, Часть 1, Учебное пособие для общеобразовательных учреждений / А.Г. Мордкович. — 10-е изд., Переработанное — М., Мнемозина, 2007
- Мордкович А.Г., Алгебра 7 класс в 2-х частях, Часть 2, Такакон для общеобразовательных учреждений / [А.Г. Мордкович и др.]; Под редакцией А.Г. Мордковича — издание 10, переработанное — Москва, Мнемозина, 2007
- HER.Тульчинская, алгебра 7 класс. Блиц-опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, Мнемозина, 2008
- Александрова Л.А., алгебра 7 класс. Тематический аудит работ в новой форме для учащихся общеобразовательных учреждений, под ред. А.Г. Мордковича, Москва, Мнемозина, 2011
- Александрова Л.А. Алгебра 7 класс. Самостоятельная работа для учащихся общеобразовательных учреждений под ред. А.Г. Мордковича — 6-е изд., Стереотипное, Москва, «Мнемозина», 2010 г.
И. Для умножения необходимо умножить на этот единственный член многочлена и полученное произведение сложится.
Пример 1. Плавное умножение на многочлен: 2a · (4a 2 -0,5ab + 5a 3).
Решение. Мономер 2А. Умножим каждый односторонний многочлен:
2a · (4a 2 -0,5ab + 5a 3) = 2a ∙ 4a 2 + 2a ∙ (-0,5ab) + 2a ∙ 5a 3 = 8A 3 -A 2 B + 10a 4. Полученный многочлен запишем в стандартном виде:
10A 4 + 8A 3 -A 2 B.
Пример 2. Умножить многочлен на одноразовый: (3XYZ 5 -4,5X 2 Y + 6XY 3 + 2,5Y 2 Z) ∙ (-0,4x 3).
Решение. Все, стоящие в скобках, умножьте на односторонний (-0,4x 3) .
(3XYZ 5 -4,5X 2 Y + 6XY 3 + 2,5Y 2 Z) ∙ (-0,4x 3) =
3XYZ 5 ∙ (-0,4X 3) -4,5X 2 Y ∙ (-0,4x 3) + 6XY 3 ∙ (-0.4х 3) + 2,5Y 2 z ∙ (-0,4х 3) =
= -1,2x 4 yz 5 + 1,8x 5 y-2,4x 4 y 3 -x 3 y 2 z.
II. Представление многочлена в виде работы двух или нескольких многочленов называется разложением многочлена на множители.
III. Создание общего множителя для скобок — это самый простой способ разложить полином на множители.
Пример 3. Исключить многочлены: 5a 3 + 25ab-30A 2.
Решение. Суммирую все члены многочлена для скобок. Это одностворчатый 5А. потому что на 5А. Все члены этого многочлена делятся. Итак, 5А. Перед скобками пишем, а в скобках пишем частное от деления каждой 5A. .
5a 3 + 25ab-30a 2 = 5a · (A 2 + 5B-6A). Проверь себя: умножим ли на 5А. на полиноме в скобках a 2 + 5B-6A, , то мы получаем этот многочлен 5a 3 + 25ab-30A 2 .
Пример 4. Возьмем общий множитель для скобок: (x + 2y) 2 -4 · (x + 2y).
Решение. (x + 2y) 2-4 · (x + 2y) = (x + 2y) (X + 2Y-4).
Общим фактором здесь был двуглавый (X + 2U). Мы сделали это для скобок, и в скобках были записаны частные от деления этих членов (x + 2y) 2 и -4 · (x + 2y) на их общем делителе
(X + 2U). В результате мы представили этот многочлен в виде работы двух многочленов (x + 2y) и (x + 2y-4) Другими словами, мы запустили многочлен (x + 2y) 2 -4 · (x + 2y) для множителей. Ответ: (x + 2y) (X + 2Y-4).
IV. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и записать полученные произведения в виде количества однокрылых.При необходимости приведите аналогичные условия.
Пример 5. Произвести умножение многочленов: (4x 2 -6xy + 9y 2) (2x + 3Y).
Решение. Согласно правилу, мы должны каждый член первого многочлена (4x 2 -6xy + 9y 2) умножить на каждый член второго многочлена (2x + 3Y). Чтобы не запутаться, делайте это всегда: сначала умножьте каждый член первого многочлена на 2x, затем снова каждый член первого многочлена умножьте на 3-й.
(4x 2 -6xy + 9y 2) ( 2x + 3Y. ) = 4x 2 ∙ 2x -6xy ∙ 2x + 9Y 2 ∙ 2x + 4X 2 ∙ 3Y -6xy ∙ 3 года + 9 лет 2 ∙ 3 года =
8x 3 -12x 2 Y + 18XY 2 + 12X 2 Y-18XY 2 + 27Y 3 = 8X 3 + 27Y 3.
Аналогичные члены -12x 2 y и 12x 2 y, а также 18XY 2 и -18XY 2 были противоположными, их суммы равны нулю.
Ответ: 8x 3 + 27y 3.
Страница 1 из 1 1
Класс: 7
назначение :
- Для обеспечения усвоения исходных знаний по теме «Умножение не подчиняется многочлену»;
- Развивать аналитическое и синтезирующее мышление;
- Подчеркните мотивы учения и положительное отношение к знаниям.
Комплектация классной бригады.
Задачи :
- Ознакомьтесь с алгоритмом умножения неназначенного на полином;
- Разработать практическое применение алгоритма.
Оборудование : Карты с заданиями, компьютер, интерактивный проектор.
Тип урока : Комбинированный.
На занятиях I. Организационный момент:Привет, ребята садитесь.
Сегодня мы продолжаем изучать разделы «полиномы» и тему нашего урока «Умножение не подчиняется полиномам». Откройте тетрадь и запишите номер и тему урока «умножение не зависит от полинома».
Задача нашего урока вывести не подчиненное полиномиальное правило умножения и научиться применять его на практике. Полученные сегодня знания необходимы вам на протяжении всего курса алгебры.
У вас есть бланки в ваших таблицах, в которые мы будем заносить ваши баллы, набранные в течение урока, и выставлять оценку.Очки будем изображать в виде смайлов. ( Приложение 1 )
II. Этап обучения студентов активному и осознанному усвоению нового материала.При изучении новой темы нам потребуются знания, полученные на предыдущих уроках.
Ученики выполняют задания по карточкам на тему «Степень и ее свойства». (5-7 минут)
Фасадные работы:
1) Дана два универсальных: 12п 3 и 4п 3
а) сумма;
б) разница;
в) работа;
д) частный;
д) квадрат каждой отдельной.
2) Назовите элементы многочлена и определите степень многочлена:
a) 5. aB — 7 a. 2 + 2 г. — 2,6
б) 6. xY 5 + x 2 Y — 2
3) Сегодня потребуется свойство распределения умножения.
Сформируем это свойство и запишем в алфавит.
III. Этап познания новых знаний.Мы неоднократно повторяли правило одностороннего умножения, свойство распределения умножения.А теперь усложним задачу.
Разделитесь на 4 группы. Каждая группа имеет 4 выражения на карточках. Попробуйте восстановить недостающее звено в цепи и объяснить свою точку зрения.
- 8х 3 (6х 2 — 4х + 3) = …………………. …… = 48х 5 — 32х 4 + 24x 3
- 5a 2 (2a 2 + 3a — 7) = ………………… … … .. = 10a 4 + 15a 3 — 35A 2
- 3Y (9Y 3 — 4Y 2 — 6) = ………………………… = 27Y 4 — 12y 3 — 18лет
- 6Б 4 (6Б 2 + 4Б — 5) =…………. …………… = 36b 6 + 24b 5 — 30b 4
(По одному представителю от каждой группы подходит к экрану, записывает недостающую часть выражения и объясняет свою точку зрения.)
Попробуйте сформулировать правило (алгоритм) умножения многочлена на единичный.
Какое выражение появляется в результате выполнения этих действий?
Чтобы проверить себя, откройте учебное пособие на стр. 126 и прочтите правило (1 человек читает громко).
Совпадают ли наши выводы с правилами в учебнике? Запишите встряхивание правила умножения на многочлен в тетрадь.
IV. Крепление:1. Физкультминтка:
Ребята, сядьте поудобнее, закройте глаза, расслабьтесь, сейчас отдыхаем, мышцы расслаблены, изучаем тему «Умножение не подчинено полиному».
И так мы запоминаем правило и повторяем за мной: для умножения номинальное нужно умножить на каждый член многочлена и записать количество выражений. Открой свои глаза.
2.Работа по учебнику № 614 за доской и в тетрадях;
а) 2x (x 2 — 7x — 3) = 2x 3 — 14x 2 — 6x
б) -4B 2 (5B 2 — 3B — 2) = -20V 4 + 12V 3 + 8V 2
c) ( 3a 3 — a 2 + a) (- 5a 3) = -15a 6 + 5a 5 — 5a 4
d) (в 2 — 2,4U + 6) 1,5U = 1,5U 3 — 3,6U 2 + 9U
d) -0,5x 2 (-2x 2 — 3x + 4) = x 4 + 1,5x 3 — 2x 2
e) (-3u 2 + 0,6U) (- 1,5U 3) \ u003d 4,5U 5 — 0,9U 4
(При выполнении номера анализируются наиболее типичные ошибки)
3.Конкурс вариантов (расшифровка пиктограмм). (Приложение 2)
| 1 опция: | Вариант 2: | |
| 1) -3x 2 (- x 3 + x — 5) 2) 14 х. (3 xY. 2 — х. 2 г. + 5) 3) -0,2 г. 2 п. (10 мН. 2 — 11 г. 3 — 6) 4) (3A 3 — a 2 + 0,1A) (- 5a 2) 5) 1/2 из (6 из 3 d — 10C 2 D 2) 6) 1,4p 3 (3Q — PQ + 5P) 7) 10x 2 y (5,4XY — 7,8Y — 0,4) 8) 3 но b (A 2 — 2AB + B 2) | 1) 3a 4 x (a 2 — 2ach + x 3 — 1) 2) -11A (2A 2 B — A 3 + 5B 2) 3) -0,5 ч. 2 y ( ч. y 3 — 3 ч. + y 2) 4) (6B 4 — b 2 + 0,01) (- 7b 3) 5) 1 / 3м 2 (9м 3 N 2-15 мин) 6) 1.6C 4 (2C 2 D — CD + 5D) 7) 10p 4 (0.7pq — 6,1Q — 3.6) 8) 5XY (x 2 — 3XY + x 3) |
Задачи представлены на отдельных карточках и на экране. Каждый ученик выполняет свою задачу, находит букву и записывает ее на экране напротив выражения, которое он преобразовал.Если получен правильный ответ, то слово будет: Молодец! Очистить 7А.
Объем функции. Примеры. Odz
Любое выражение с переменной имеет свою собственную область допустимых значений, где она существует. При принятии решения всегда необходимо учитывать DLD. При его отсутствии можно получить неверный результат.
Эта статья покажет, как правильно найти ODZ, используйте это на примерах. Также будет учтена важность указания DLD в решении.
Яндекс.RTB R-A-339285-1
Допустимые и недопустимые значения переменных
Это определение связано с допустимыми значениями переменных. Вводя определение, мы увидим, к какому результату оно приведет.
Начиная с 7 класса начинаем работать с числами и числовыми выражениями. Исходные определения с переменными переходят к значениям выражений с выбранными переменными.
Когда есть выражения с выбранными переменными, некоторые из них могут не удовлетворять. Например, выражение вида 1: a, если a = 0, то оно не имеет смысла, так как делить на ноль невозможно.То есть в выражении должны быть такие значения, которые подходят в любом случае и дают ответ. Другими словами, это имеет смысл с доступными переменными.
Определение 1
Если есть выражение с переменными, то оно имеет смысл только тогда, когда при подстановке значение может быть вычислено.
Определение 2
Если есть выражение с переменными, то оно не имеет смысла, когда при подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Определение 3
Существующие допустимые переменные — это те значения, для которых выражение имеет смысл.А если в этом нет смысла, то они считаются недопустимыми.
Чтобы прояснить вышесказанное: если существует более одной переменной, то может быть пара подходящих значений.
Пример 1
В качестве примера рассмотрим выражение вида 1 x — y + z, где есть три переменные. В противном случае можно записать как x = 0, y = 1, z = 2, при этом другая запись имеет вид (0, 1, 2). Эти значения называются действительными, а значит, вы можете найти значение выражения.Получаем, что 1 0 — 1 + 2 = 1 1 = 1. Отсюда видим, что (1, 1, 2) недопустимы. Подстановка приводит к делению на ноль, то есть 1 1-2 + 1 = 1 0.
Что такое DLD?
Диапазон допустимых значений — важный элемент при вычислении алгебраических выражений. Поэтому на это стоит обращать внимание при расчетах.
Определение 4
Область DLD Набор значений, разрешенных для данного выражения.
Рассмотрим пример выражения.
Пример 2
Если у нас есть выражение вида 5 z — 3, то ODZ имеет вид (- ∞, 3) ∪ (3, + ∞). Эта область допустимых значений удовлетворяет переменной z для данного выражения.
Если есть выражения вида z x — y, то можно видеть, что x ≠ y, z принимает любое значение. Это называется выражением ODZ. Это нужно учитывать, чтобы при подстановке не получилось деление на ноль.
Область допустимых значений и область определения имеют то же значение.Только второй из них используется для выражений, а первый — для уравнений или неравенств. Использование DLD имеет смысл, выражение или неравенство. Область определения функции совпадает с областью допустимых значений переменной x до выражения f (x).
Как найти DLD? Примеры, решения
Найти SDL означает найти все допустимые значения, подходящие для данной функции или неравенства. Если эти условия не соблюдены, можно получить неверный результат.Чтобы найти DLD, часто необходимо выполнить преобразования в данном выражении.
Есть выражения, вычисление которых невозможно:
- , если есть деление на ноль;
- извлечение корня из отрицательного числа;
- наличие отрицательного целого числа — только для положительных чисел;
- вычисление логарифма отрицательного числа;
- область определения касательной π 2 + π · k, k ∈ Z, и котангенса π · k, k ∈ Z;
- нахождение значения арксинуса и арккосинуса числа, значение которого не принадлежит [- 1; один ] .
Все это говорит о том, насколько важно наличие DLD.
Пример 3
Найдите выражения ODZ x 3 + 2 · x · y — 4 .
Решение
В кубе можно возвести любое число. В этом выражении нет дроби, поэтому значения x и y могут быть любыми. То есть ОДЗ — это любое число.
Ответ: x и y — любые значения.
Пример 4
Найдите ODZ выражения 1 3 — x + 1 0.
Решение
Видно, что дробь одна, знаменатель которой равен нулю. Это говорит о том, что для любого значения x мы получим деление на ноль. Итак, можно сделать вывод, что данное выражение считается неопределенным, то есть не имеет ОДЗ.
Ответ: ∅.
Пример 5
Найдите ODZ данного выражения x + 2 · y + 3 — 5 · x.
Решение
Наличие квадратного корня предполагает, что это выражение должно быть больше или равно нулю.При отрицательном значении это не имеет смысла. Следовательно, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0. То есть это искомый диапазон допустимых значений.
Ответ: множество x и y, где x + 2 · y + 3 ≥ 0.
Пример 6
Определите выражения ODZ в форме 1 x + 1 — 1 + log x + 8 (x 2 + 3).
Решение
По условию у нас есть дробь, поэтому ее знаменатель не должен быть нулевым.Мы получаем, что x + 1 — 1 ≠ 0. Радикальное выражение всегда имеет смысл, когда оно больше или равно нулю, т.е. x + 1 ≥ 0. Поскольку оно имеет логарифм, его выражение должно быть строго положительным, то есть x 2 + 3> 0. Основание логарифма также должно иметь положительное значение и отличаться от 1, тогда складываем условия x + 8> 0 и x + 8 ≠ 1. Отсюда следует, что искомая ODZ принимает форма:
x + 1-1 0, x + 1 ≥ 0, x 2 + 3> 0, x + 8> 0, x + 8 ≠ 1
Другими словами, они называют систему неравенств с одной переменной.Решение приведет к такому обозначению ODZ [- 1, 0) ∪ (0, + ∞).
Ответ: [- 1, 0) ∪ (0, + ∞)
Почему важно учитывать DLD при трансформации?
При идентичных преобразованиях важно найти ODZ. Бывают случаи, когда существование DLD отсутствует. Чтобы понять, имеет ли решение данное выражение, вам нужно сравнить ODZ переменных исходного выражения и ODZ результирующего.
Преобразования идентичности:
- не может повлиять на DLD;
- может привести к расширению или добавлению DLD;
- может сузить DLD.
Рассмотрим пример.
Пример 7
Если у нас есть выражение вида x 2 + x + 3 · x, то его ODZ определяется для всей области. Даже при сокращении таких членов и упрощении выражения ODL не меняется.
Пример 8
Если мы возьмем пример выражения x + 3 x — 3 x, то все будет по-другому.У нас есть дробное выражение. Но мы знаем, что деление на ноль недопустимо. Тогда ODZ имеет вид (- ∞, 0) ∪ (0, + ∞). Видно, что ноль не является решением, поэтому мы добавляем его в круглые скобки.
Рассмотрим пример с наличием радикального выражения.
Пример 9
Если есть x — 1 · x — 3, то следует обратить внимание на ODZ, так как он должен быть записан в виде неравенства (x — 1) · (x — 3) ≥ 0 Возможно решение интервальным методом, тогда получаем, что ODZ принимает вид (- ∞, 1] ∪ [3, + ∞).После преобразования x — 1 · x — 3 и применения свойства корней получаем, что ODZ можно дополнить и записать в виде системы неравенств вида x — 1 ≥ 0, x — 3 ≥ 0. Решая ее, мы получим [3, + ∞). Следовательно, DLD полностью записывается следующим образом: (- ∞, 1] ∪ [3, + ∞).
Следует избегать преобразований, сужающих DLD.
Пример 10
Рассмотрим на примере выражения x — 1 · x — 3 при x = — 1. При подстановке получаем, что — 1 — 1 · — 1 — 3 = 8 = 2 2.Если преобразовать это выражение и привести его к виду x — 1 · x — 3, то при вычислении получим, что 2 — 1 · 2 — 3 выражение не имеет смысла, так как радикальное выражение не должно быть отрицательным.
Надо придерживаться идентичных преобразований, что ODZ менять не будет.
Если есть примеры, расширяющие его, то его нужно добавить в DLD.
Пример 11
Рассмотрим дробь в форме x x 3 + x в качестве примера. Если мы сократим на x, то получим 1 x 2 + 1.Затем DLD расширяется и становится (- ∞ 0) ∪ (0, + ∞). Причем при вычислении мы уже работаем со второй упрощенной дробью.
С логарифмами дело обстоит немного иначе.
Пример 12
Если существует выражение вида ln x + ln (x + 3), оно заменяется на ln (x · (x + 3)) на основании свойства логарифма. Это показывает, что DLD от (0, + ∞) до (- ∞, — 3) ∪ (0, + ∞). Следовательно, чтобы определить DLD ln (x · (x + 3)), необходимо произвести вычисления на DLD, то есть (0, + ∞) множествах.
При принятии решения всегда необходимо обращать внимание на структуру и внешний вид условно заданного выражения. Если домен определения найден правильно, результат будет положительным.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и дайте нам знать, если у вас возникнут вопросы.
Сбор и использование личной информации
Личная информация — это данные, которые могут быть использованы для идентификации конкретного человека или для связи с ним.
Вас могут попросить предоставить вашу личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы оставляете запрос на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. Д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и сообщать об уникальных предложениях, рекламных акциях и других событиях, а также предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, например, для проведения аудита, анализа данных и различных исследований с целью улучшения предоставляемых нами услуг и предоставления вам рекомендаций относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном рекламном мероприятии, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- При необходимости — в соответствии с законом, судебной системой, в ходе судебного разбирательства и / или на основании публичных запросов или запросов государственных органов в Российской Федерации — раскрывайте вашу личную информацию.Мы также можем раскрыть информацию о вас, если мы определим, что такое раскрытие необходимо или целесообразно в целях безопасности, поддержания правопорядка или в других социально значимых случаях.
- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующей третьей стороне, правопреемнику.
Защита личной информации
Мы принимаем меры предосторожности — включая административные, технические и физические — для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Обеспечение конфиденциальности на уровне вашей компании
Чтобы обеспечить безопасность вашей личной информации, мы сообщаем нашим сотрудникам правила конфиденциальности и безопасности и строго следим за соблюдением мер конфиденциальности.
Решая различные задачи, нам очень часто приходится проводить идентичные преобразования выражений. Но бывает, что в одних случаях допустима какая-то трансформация, в других — нет. Значительную помощь с точки зрения мониторинга допустимости проводимых реформ оказывает ОДЗ.Остановимся на этом подробнее.
Суть подхода заключается в следующем: сравнивая переменные ODZ для исходного выражения с переменными ODZ для выражения, полученного в результате выполнения идентичных преобразований, и по результатам сравнения делаются соответствующие выводы.
В целом преобразования идентичности могут
- не влияет на DLD;
- приведет к расширению междугородней связи;
- приведет к сужению DLD.
Разберем каждый случай на примере.
Рассмотрим выражение x 2 + x + 3 · x, ODZ переменной x для этого выражения — это множество R. Теперь давайте проделаем следующее идентичное преобразование с этим выражением — мы представляем аналогичные термины, в результате форма x 2 + 4 · x. Очевидно, что переменная x DLD этого выражения также является множеством R. Таким образом, преобразование не изменило DLD.
Идем дальше. Возьмем выражение x + 3 / x — 3 / x.В этом случае DLD определяется условием x ≠ 0, что соответствует набору (−∞, 0) ∪ (0, + ∞). Это выражение также содержит аналогичные слагаемые, после сокращения которых мы приходим к выражению x, для которого ODZ равно R. Что мы видим: в результате преобразования произошло расширение ODZ (число ноль было добавлено к ODZ переменной x для исходного выражения).
Осталось рассмотреть пример сужения диапазона допустимых значений после преобразований.Возьмите выражение. DLD переменной x определяется неравенством (x — 1) · (x — 3) ≥0, оно подходит для своего решения, например, в результате имеем (−∞, 1] ∪∪; отредактировано С.А. Теляковского. — 17-е изд. — М .: Просвещение, 2008. — 240 с .: ил. — ISBN 978-5-09-019315-3.
Как найти объем функции? С этой задачей часто приходится сталкиваться ученикам средней школы.
Родители должны помочь своим детям разобраться в этом.
Должностная функция.
Напомним основные термины алгебры. Функция в математике — это зависимость одной переменной от другой. Можно сказать, что это строгий математический закон, который определенным образом связывает два числа.
В математике при анализе формул числовые переменные заменяются буквенными символами. Чаще всего используются x («x») и gamer («y»). Переменная x называется аргументом, а переменная y называется зависимой переменной или функцией от x.
Существуют различные способы определения зависимостей переменных.
Перечислим их:
- Аналитический тип.
- Табличный вид.
- Графический дисплей.
Аналитический метод представлен формулой.Рассмотрим примеры: y = 2x + 3, y = log (x), y = sin (x). Формула y = 2x + 3 типична для линейной функции. Подставляя числовое значение аргумента в данную формулу, получаем значение y.
Табличный метод представляет собой таблицу, состоящую из двух столбцов. Первый столбец предназначен для значений x, а следующий столбец записывает данные игры.
Графический метод считается наиболее интуитивно понятным. Граф — это отображение множества всех точек на плоскости.
Для построения диаграммы используется декартова система координат. Система состоит из двух перпендикулярных линий. На оси укладывают одинаковые сегменты агрегата. Отсчет времени ведется от центральной точки пересечения прямых.
Независимая переменная отображается на горизонтальной линии. Она называется осью абсцисс. Вертикальная линия (ось ординат) отображает числовое значение зависимой переменной. На пересечении перпендикуляров к этим осям отмечаются точки.Соединяя точки вместе, получаем сплошную линию. Это основа расписания.
Типы переменных зависимостей
Определение
В целом зависимость представляется в виде уравнения: y = f (x). Из формулы следует, что для каждого значения числа x существует определенное число y. Значение игры, соответствующее числу x, называется значением функции.
Все возможные значения, требуемые независимой переменной, образуют область определения функции.Соответственно, весь набор чисел зависимой переменной определяет диапазон значений функции. Область видимости — это все значения аргументов, для которых имеет смысл f (x).
Первоначальная задача при изучении математических законов — найти область определения. Этот термин следует правильно определить. В противном случае все дальнейшие расчеты будут бесполезны. Ведь объем ценностей формируется на основе элементов первого набора.
Объем функции напрямую зависит от ограничений.Ограничения связаны с невозможностью выполнять определенные операции. Существуют также ограничения на применение числовых значений.
При отсутствии ограничений областью определения является все числовое пространство. Знак бесконечности имеет горизонтальную восьмерку. Весь набор чисел записывается так: (-∞; ∞).
В некоторых случаях массив данных состоит из нескольких подмножеств. Объем числовых пропусков или пробелов зависит от типа закона изменения параметров.
Перечислим факторы, влияющие на ограничения:
- обратная пропорциональность;
- корень арифметический;
- возведение в степень;
- логарифмическая зависимость;
- тригонометрических форм.
Если таких элементов несколько, то поиск ограничений для каждого из них прекращается. Самая большая проблема — это выявление критических точек и пробелов. Решением проблемы будет объединение всех числовых подмножеств.
Набор и подмножество чисел
О наборах.
Область обозначена как D (f), а знак объединения представлен символом ∪. Все числовые пробелы заключены в квадратные скобки. Если граница участка не входит в набор, то поставить полукруглую скобу. В противном случае, когда число включено в подмножество, используются квадратные скобки.
Обратная пропорциональность выражается формулой y = k / x. График функции представляет собой изогнутую линию, состоящую из двух ветвей.Это обычно называют гиперболой.
Поскольку функция выражается в виде дроби, поиск области определения сводится к анализу знаменателя. Хорошо известно, что деление на ноль запрещено в математике. Решение проблемы — приравнять знаменатель к нулю и найти корни.
Вот пример:
Устанавливается: y = 1 / (x + 4). Найдите прицел.
- Обнулить знаменатель.
х + 4 = 0 - Найдите корень уравнения.
х = -4 - Определяем набор всех возможных значений аргумента.
D (f) = (- ∞; -4) ∪ (-4; + ∞)
Ответ: объем функции — все действительные числа, кроме -4.
Значение числа под знаком квадратного корня не может быть отрицательным. В этом случае определение функции сводится к решению неравенства. Корневое выражение должно быть больше нуля.
Область определения корня связана с четностью корневого индекса.Если показатель делится на 2, то выражение имеет смысл только в том случае, если оно положительное. Нечетный номер индикатора указывает на правильность любого значения радикального выражения: как положительного, так и отрицательного.
Неравенство решается так же, как и уравнение. Есть только одно отличие. После умножения обеих частей неравенства на отрицательное число знак следует поменять местами.
Если в знаменателе стоит квадратный корень, необходимо наложить дополнительное условие.Значение числа не должно быть нулевым. Неравенство переходит в разряд строгих неравенств.
Логарифмические и тригонометрические функции
Логарифмическая форма имеет смысл с положительными числами. Таким образом, область определения логарифмической функции аналогична функции извлечения квадратного корня, за исключением нуля.
Рассмотрим пример логарифмической зависимости: y = log (2x-6). Найдите прицел.
- 2х-6> 0
- 2x> 6
- х> 6/2
Ответ: (3; + ∞).
Область значений y = sin x и y = cos x — это набор всех действительных чисел. Есть ограничения на тангенс и котангенс. Они связаны с делением угла на косинус или синус.
Тангенс угла определяется отношением синуса к косинусу. Указываем значения углов, при которых значение тангенса не существует. Функция y = tg x имеет смысл для всех значений аргумента, кроме x = π / 2 + πn, n∈Z.
Область определения функции y = ctg x — это весь набор действительных чисел, за исключением x = πn, n∈Z. Если аргумент равен числу π или кратно π, синус угла равен нулю. В этих точках (асимптотах) котангенс существовать не может.
Первые задания по определению предметной области начинаются на уроках 7 класса. При первом знакомстве с этим разделом алгебры ученик должен четко понимать тему.
Следует отметить, что этот семестр будет сопровождать студента, а затем и студента на протяжении всего периода обучения.
Функция — это модель. Определяем X как набор значений независимой переменной // независимое означает любое.
Функция — это правило, по которому для каждого значения независимой переменной из множества X можно найти единственное значение зависимой переменной. // т.е. для каждого x есть один y.
Из определения следует, что есть два понятия: независимая переменная (которую мы обозначаем x, и она может принимать любые значения) и зависимая переменная (которую мы обозначаем y или f (x), и она вычисляется из функции, когда мы заменить x).2. (называется параболой)
3.y = 3x + 7. (называется прямым)
4.y = √ x. (называется ветвью параболы)
Независимая переменная (которую мы обозначаем x) называется аргументом функции.
Область определения функции
Набор всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).
Рассмотрим D (y) для 1., 2., 3., 4.
1. D (y) = (∞; 0) and (0; + ∞) // весь набор действительных чисел, кроме нуля.
2. D (y) = (∞; + ∞) // все множество действительных чисел
3. D (y) = (∞; + ∞) // все множество действительных чисел
4. D (y) =)
Система линейных неравенств онлайн-калькулятор. Системы линейных неравенств и выпуклые множества точек
Системой неравенств принято называть любой набор из двух и более неравенств, содержащий неизвестную величину.
Эту формулировку наглядно иллюстрируют, например, такие системы неравенств :
Решите систему неравенств — означает найти все значения неизвестной переменной, для которых реализуется каждое неравенство системы, или доказать, что таких нет.
Следовательно, для каждого отдельного системных неравенств вычисляют неизвестную переменную. Далее из полученных значений выбираются только те, которые верны как для первого, так и для второго неравенства. Следовательно, при замене выбранного значения оба неравенства системы становятся правильными.
Разберем решение нескольких неравенств:
Ставим одну пару числовых прямых под другую; вверху мы применим значение x , для которого первое неравенство примерно ( x > 1) станет истинным, а внизу значение x , которые являются решением второго неравенства ( x > 4).
Сравнивая данные на числовых строках , обратите внимание, что решением для обоих неравенств будет x > 4. Ответ, x > 4.
Пример 2.
Вычислив первое неравенство , получим -3 x x> 2, второе — x > -8, или x xat, что соответствует первому системному неравенству , а по нижней числовой строке все те значения x , для которых реализуется второе неравенство системы.
Сравнивая данные, мы обнаруживаем, что оба неравенства будут реализованы для всех значений x , размещенных от 2 до 8. Наборы значений x обозначают двойное неравенство 2 x
Пример 3. Найдите
Неравенство — это два числа или математических выражения, связанных одним из знаков:> (подробнее, в случае строгих неравенств),
Неравенство является линейным при тех же условиях, что и уравнение: оно содержит переменные только первой степени и не содержит произведений переменных.
Решение линейных неравенств и систем линейных неравенств неразрывно связано с их геометрическим смыслом: решение линейного неравенства представляет собой некую полуплоскость, на которую вся плоскость делится прямой линией, уравнением которой задается линейное неравенство . Эта полуплоскость, а в случае системы линейных неравенств, часть плоскости, ограниченная несколькими прямыми линиями, должна быть найдена на чертеже.
К решению систем линейных неравенств с большим числом переменных сводят многие экономические проблемы, в частности, задачи линейного программирования, в которых требуется найти максимум или минимум функции.
Решение систем линейных неравенств с любым числом неизвестных
Сначала проанализируем линейные неравенства на плоскости. Рассмотрим одно неравенство с двумя переменными и:
,
где — коэффициенты переменных (некоторые числа), — свободный член (также некоторое число).
Одно неравенство с двумя неизвестными, как и уравнение, имеет бесконечное количество решений. Решением этого неравенства является пара чисел, удовлетворяющих этому неравенству.Геометрически множество решений неравенства изображается в виде полуплоскости, ограниченной прямой
,
, который мы будем называть пограничной линией.
Шаг 1. Построить прямую, ограничивающую множество решений линейного неравенства
Для этого нужно знать любые две точки этой прямой. Найдем точки пересечения с осями координат. Ордината пересечения A равна нулю (рисунок 1).Числовые значения по осям на этом рисунке относятся к примеру 1, который мы проанализируем сразу после этого теретического хода.
Мы находим абсциссу, решая уравнение прямой с уравнением оси как системы.
Найдите пересечение с осью:
Подставляя значение в первое уравнение, получаем
Откуда.
Таким образом, мы нашли абсциссу точки A .
Найдите координаты точки пересечения с осью.
Точечная абсцисса B равна нулю. Решим уравнение граничной линии с уравнением координатной оси:
,
отсюда координаты точки B :.
Шаг 2. Проведите линию, ограничивающую множество решений неравенства. Зная точки A и B пересечения линии границы с осями координат, мы можем провести эту линию. Прямая линия (снова рис. 1) делит всю плоскость на две части, лежащие справа и слева (сверху и снизу) от этой прямой.
Шаг 3. Определите, какая полуплоскость является решением этого неравенства. Для этого нужно подставить начало координат (0; 0) в это неравенство. Если координаты начала координат удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой находится начало координат. Если координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, не содержащая начала координат. Полуплоскость решения неравенства обозначим штрихами от прямой к полуплоскости, как на рисунке 1.
Если решать систему линейных неравенств , то каждый шаг выполняется для каждого из неравенств системы.
Пример 1. Решите неравенство
Решение. Нарисуем прямую
Подставляя прямую в уравнение, получаем, а подставляя, получаем. Следовательно, координаты точек пересечения с осями будут A (3; 0) , В (0; 2). Проведите прямую линию через эти точки (снова рисунок 1).
Выберем полуплоскость решений неравенства. Для этого подставляем координаты начала координат (0; 0) в неравенство:
получаем, то есть координаты начала координат удовлетворяют этому неравенству. Следовательно, решением неравенства является полуплоскость, содержащая начало координат, то есть левая (она же нижняя) полуплоскость.
Если бы это неравенство было строгим, то есть имело бы вид
, то точки граничной линии не будут решением, поскольку они не удовлетворяют неравенству.
Теперь рассмотрим систему линейных неравенств с двумя неизвестными:
Каждое из неравенств этой системы на плоскости определяет полуплоскость. Система линейных неравенств называется непротиворечивой, если у нее есть хотя бы одно решение, и несовместимой, если у нее нет решений. Любая пара чисел (), удовлетворяющая всем неравенствам этой системы, называется решением системы линейных неравенств.
Геометрически решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам системы, то есть общая часть полученных полуплоскостей.Поэтому геометрически в общем случае решение можно изобразить в виде некоторого многоугольника, в частном случае это может быть линия, отрезок и даже точка. Если система линейных неравенств несовместна, то на плоскости нет ни одной точки, удовлетворяющей всем неравенствам системы.
Пример 2.
Решение. Итак, требуется найти многоугольник решений этой системы неравенств. Построим граничную линию для первого неравенства, то есть прямую, и граничную линию для второго неравенства, то есть прямую линию.
Мы делаем это шаг за шагом, как показано в теоретической записке и в примере 1, тем более что в примере 1 граничная линия была построена для неравенства, которое является первым в этой системе.
Полуплоскости решений, соответствующие неравенствам этой системы, на рисунке 2 заштрихованы внутрь. Общая часть полуплоскостей решений — открытый угол ABC … Это означает, что множество точек в Плоскость, составляющая открытый угол ABC , является решением как первого, так и второго неравенств системы, то есть является решением системы двух линейных неравенств.Другими словами, координаты любой точки из этого множества удовлетворяют обоим неравенствам системы.
Пример 3. Решите систему линейных неравенств
Решение. Построим граничные линии, соответствующие неравенствам системы. Мы делаем это, следуя шагам, приведенным в теоретических основах для каждого неравенства. Теперь определим полуплоскости решений для каждого неравенства (рисунок 3).
Полуплоскости решений, соответствующие неравенствам этой системы, заштрихованы внутрь.Пересечение полуплоскостей решений изображено, как показано на рисунке, в виде четырехугольника ABCE … Мы обнаружили, что многоугольник решений системы линейных неравенств от двух переменных представляет собой четырехугольник ABCE .
Все, что описано выше о системах линейных неравенств с двумя неизвестными, применимо и к системам неравенств с любым количеством неизвестных, с той лишь разницей, что решением неравенства с n неизвестным будет совокупность n чисел () удовлетворяющие всем неравенствам, и вместо граничной линии будет граничная гиперплоскость n -мерное пространство.Решение представляет собой многогранник решений (симплекс), ограниченный гиперплоскостями.
В этом уроке мы начнем изучать системы неравенства. Сначала рассмотрим системы линейных неравенств. В начале урока мы рассмотрим, где и почему возникают системы неравенств. Далее мы изучим, что значит решить систему, и вспомним объединение и пересечение множеств. В конце мы решим конкретные примеры для систем линейных неравенств.
Тема : Рацион Реальное неравенство и его системы
Урок: Основные концепции, решение систем линейных неравенств
До сих пор мы решали индивидуальные неравенства и применяли к ним метод интервалов, это могло быть линейных неравенств , а также квадратные и рациональные .Теперь перейдем к решению систем неравенств — сначала линейных систем … Рассмотрим пример, откуда возникает необходимость рассматривать системы неравенств.
Найти область определения функции
Найти область определения функции
Функция существует, когда существуют оба квадратных корня, т.е.
Как решить такую систему? Необходимо найти все x, удовлетворяющие как первому, так и второму неравенствам.
На оси Ox начертите множество решений первого и второго неравенств.
Наше решение — интервал пересечения двух лучей.
Этот метод изображения решения системы неравенств иногда называют методом крыши.
Решение системы — пересечение двух множеств.
Изобразим это графически. У нас есть множество A произвольной природы и множество B произвольной природы, которые пересекаются.
Определение: пересечение двух наборов A и B является третьим набором, который состоит из всех элементов, включенных как в A, так и в B.
Рассмотрим на конкретных примерах решения линейных систем неравенств, как найти пересечения множеств решений отдельных неравенств, входящих в систему.
Решите систему неравенств:
Ответ: (7; 10].
4. Решите систему
Откуда взялось второе неравенство системы? Например, из неравенства
Обозначим графически решения каждого неравенства и найдем интервал их пересечения.
Таким образом, если у нас есть система, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.
Ответ: система несовместима.
Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7.
Иногда линейная система задается двойным неравенством; рассмотрим этот случай.
8.
Мы исследовали системы линейных неравенств, поняли, откуда они берутся, изучили типовые системы, к которым относятся все линейные системы, и решили некоторые из них.
1. Мордкович А.Г. и др. Алгебра 9 класс: Учебное пособие. Для общего образования. Учреждения. — 4-е изд. — М .: Мнемосина, 2002.-192 с .: ил.
2. Мордкович А.Г. и др. Алгебра 9 класс: Задача для учащихся общеобразовательных учреждений / А.Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М .: Мнемосина, 2002.-143 с .: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учебник. для учащихся общеобразовательных школ. учреждений / Ю. Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. — 7-е изд., Перераб. И доп. — М .: Мнемосина, 2008.
.4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16 изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 14.00 Часть 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, П. В. Семенов. — 12-е изд., Стер. — М .: 2010. — 224 с .: ил.
6. Алгебра. 9 класс. В 14.00 ч. 2. Задача для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др .; Эд. А.Г. Мордкович. — 12-е изд., Перераб. — М .: 2010.-223 с .: ил.
1. Портал естественных наук ().
2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку ().
4. Учебный центр «Технологии обучения» ().
5. Раздел College.ru по математике ().
1. Мордкович А.Г. и др. Алгебра 9 класс: Задача для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М .: Мнемозина, 2002.-143 с .: ил. № 53; 54; 56; 57.
Эта статья представляет собой введение в системы неравенства. Вот определение системы неравенств и определение решения системы неравенств.В нем также перечислены основные типы систем, с которыми вам чаще всего приходится работать на уроках алгебры в школе, и приведены примеры.
Навигация по страницам.
Что такое система неравенства?
Систему неравенств удобно определять так же, как мы ввели определение системы уравнений, то есть по форме обозначений и заложенному в них смыслу.
Определение.
Система неравенств Обозначение, представляющее ряд неравенств, записанных друг под другом, объединенных фигурной скобкой слева и обозначающее множество всех решений, которые одновременно являются решениями каждого неравенства в системе.
Приведем пример системы неравенств. Возьмите два произвольных, например 2 x — 3> 0 и 5 — x≥4 x — 11, запишите их друг под другом
2 x — 3> 0,
5 — x≥4 x — 11
и объединяем знаком системы — фигурную скобку, в результате получаем систему неравенств следующего вида:
Аналогично дано представление о системах неравенства в школьных учебниках. Следует отметить, что в них определения даны более узко: для неравенств с одной переменной или с двумя переменными.
Основные типы систем неравенств
Понятно, что можно составить бесконечно много различных систем неравенств. Чтобы не потеряться в этом разнообразии, их желательно рассматривать в группах, которые имеют свои отличительные особенности. Все системы неравенства можно разделить на группы по следующим критериям:
- по количеству неравенств в системе;
- по количеству переменных, участвующих в записи;
- по форме самих неравенств.
По количеству включенных в реестр неравенств различают системы двух, трех, четырех и т. Д. неравенства. В предыдущем абзаце мы привели пример системы, которая представляет собой систему двух неравенств. Приведем еще один пример системы четырех неравенств.
Отдельно скажем, что нет смысла говорить о системе одного неравенства, в данном случае, по сути, речь идет о самом неравенстве, а не о системе.
Если мы посмотрим на количество переменных, то у нас есть системы неравенств с одной, двумя, тремя и т. Д. Переменными (или, как говорится, неизвестными). Посмотрите на последнюю систему неравенства, написанную двумя абзацами выше. Это система с тремя переменными x, y и z. Обратите внимание, что его первые два неравенства не содержат всех трех переменных, а содержат только одну из них. В контексте этой системы их следует понимать как неравенства с тремя переменными вида x + 0 y + 0 z≥ — 2 и 0 x + y + 0 z≤5 соответственно.Обратите внимание, что школа фокусируется на неравенстве с одной переменной.
Осталось обсудить, какие виды неравенства присутствуют в системах регистрации. В школе в основном рассматриваются системы двух неравенств (реже — трех, еще реже — четырех и более) с одной или двумя переменными, а сами неравенства обычно представляют собой целые неравенства первой или второй степени (реже — более высоких степеней. или дробно-рациональный). Но не удивляйтесь, если в материалах подготовки к ОГЭ вы встретите системы неравенств, содержащие иррациональные, логарифмические, экспоненциальные и другие неравенства.В качестве примера приведем систему неравенств, она взята из.
Что называется решением системы неравенства?
Введем еще одно определение, связанное с системами неравенств — определение решения системы неравенств:
Определение.
Решением системы неравенств с одной переменной вызывается такое значение переменной, которое превращает каждое из неравенств системы в истинное, другими словами, является решением каждого неравенства в системе.
Поясним на примере. Возьмем систему двух неравенств с одной переменной. Примем значение переменной x равным 8, это решение нашей системы неравенств по определению, так как подстановка ее в неравенства системы дает два истинных числовых неравенства 8> 7 и 2−3 · 8≤0. Напротив, единица не является решением системы, так как при замене ею переменной x первое неравенство превратится в некорректное числовое неравенство 1> 7.
Аналогичным образом мы можем ввести определение решения системы неравенств с двумя, тремя или более переменными:
Определение.
Решением системы неравенств с двумя, тремя и т. Д. Переменными называется пара, три и т. Д. Значений этих переменных, которая одновременно является решением каждого неравенства в системе, то есть переворачивает каждое неравенство в системе в истинное числовое неравенство.
Например, пара значений x = 1, y = 2 или в другой записи (1, 2) является решением системы неравенств с двумя переменными, так как 1 + 2
Системы неравенств могут не иметь решений, могут иметь конечное число решений или могут иметь бесконечно много решений.Мы часто говорим о множестве решений системы неравенств. Когда у системы нет решений, то есть пустой набор ее решений. Когда существует конечное число решений, то множество решений содержит конечное число элементов, а когда существует бесконечно много решений, то множество решений также состоит из бесконечного числа элементов.
В некоторых источниках вводятся определения частного и общего решения системы неравенств, как, например, в учебниках Мордковича.Под частным решением системы неравенств понимают ее одно отдельное решение. В свою очередь общее решение системы неравенств — это все ее частные решения. Однако эти термины имеют смысл только тогда, когда требуется подчеркнуть, какое решение обсуждается, но обычно это ясно из контекста, поэтому гораздо чаще они говорят просто «решение системы неравенств».
Из введенных в данной статье определений системы неравенств и ее решений следует, что решение системы неравенств является пересечением множеств решений всех неравенств этой системы.
Список использованной литературы.
- Алгебра: уч. за 8 кл. общее образование. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; изд. С. А. Теляковский. — 16-е изд. — М .: Просвещение, 2008. — 271 с. : больной. — ISBN 978-5-09-019243-9.
- Алгебра: 9 класс: учебник. для общего образования. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; изд. С. А. Теляковский. — 16-е изд. — М .: Просвещение, 2009.- 271 с. : больной. — ISBN 978-5-09-021134-5.
- А.Г. Мордкович Алгебра. 9 класс. В 14.00 Часть 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, П.В. Семенов. — 13-е изд., Стер. — М .: Мнемозина, 2011. — 222 с .: Илл. ISBN 978-5-346-01752-3.
- Мордкович А.Г. Алгебра и начало математического анализа. 11 класс. В 14.00 Часть 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, П.В.Семенов. — 2-е изд., Стер. — М .: Мнемосина, 2008. — 287 с .: Илл. ISBN 978-5-346-01027-2.
- ЕГЭ -2013. Математика: типовые варианты экзамена: 30 вариантов / под ред. Семенова А.Л., Ященко И.В. — М .: Издательство «Народное просвещение», 2012. — 192 с. — (ЕГЭ-2013. ФИПИ — школа).
Рассмотрим примеры решения системы линейных неравенств.
4х + 29 \ конец (массив) \ вправо. \\] «Заголовок =» (! LANG: визуализируется QuickLaTeX.com «>!}
Для решения системы необходимо каждое из составляющих ее неравенств. Только было принято решение записывать не по отдельности, а вместе, соединив их фигурной скобкой.
В каждом из неравенств системы переносим неизвестные в одну сторону, известные в другую с противоположным знаком:
Заголовок = «(! LANG: Rendered by QuickLaTeX.com»>!}
После упрощения обе части неравенства нужно разделить на число перед x.Разделите первое неравенство на положительное число, чтобы знак неравенства не изменился. Делим второе неравенство на отрицательное число, поэтому знак неравенства нужно поменять на противоположный:
Заголовок = «(! LANG: Rendered by QuickLaTeX.com»>!}
Отмечаем решение неравенств на числовых строках:
В ответ записываем пересечение решений, то есть ту часть, где штриховка находится на обеих линиях.
Ответ: x∈ [-2; 1).
Избавимся от дроби в первом неравенстве. Для этого мы умножаем обе части попарно на наименьший общий знаменатель 2. При умножении на положительное число знак неравенства не меняется.
Раскройте скобки во втором неравенстве. Произведение суммы и разности двух выражений равно разности квадратов этих выражений. Справа квадрат разницы между двумя выражениями.
Заголовок = «(! LANG: Отрисовано QuickLaTeX.com «>!}
Переносим неизвестные в одну сторону, известные в другую с обратным знаком и упрощаем:
Разделим обе части неравенства на число перед x. В первом неравенстве делим на отрицательное число, поэтому знак неравенства меняется на противоположный. Во втором делим на положительное число, знак неравенства не меняется:
Заголовок = «(! LANG: Rendered by QuickLaTeX.com»>!}
Оба неравенства со знаком «меньше» (не обязательно, чтобы один знак был строго меньшим, а другой не строгим, меньшим или равным).Нам не нужно отмечать оба решения, а воспользуемся правилом «». Чем меньше 1, тем система сводится к неравенству
Отметим его решение на числовой прямой:
Ответ: x∈ (-∞; 1].
Раскройте скобки. В первом неравенстве -. Он равен сумме кубиков этих выражений.
Во втором — произведение суммы и разности двух выражений, равное разности квадратов. Так как перед круглыми скобками стоит знак минус, их лучше открывать в два этапа: сначала использовать формулу, а уже потом открывать круглые скобки, меняя знак каждого члена на противоположный.
Перенесем неизвестные в одну сторону, известные в другую с обратным знаком:
Заголовок = «(! LANG: Rendered by QuickLaTeX.com»>!}
Оба больше знаков. Используя правило «больше чем больше», мы сводим систему неравенств к одному неравенству. Большее из двух чисел — 5, следовательно,
.Заголовок = «(! LANG: Rendered by QuickLaTeX.com»>!}
Отмечаем решение неравенства на числовой строке и записываем ответ:
Ответ: x∈ (5; ∞).
Поскольку в алгебре системы линейных неравенств встречаются не только как самостоятельные задачи, но и в процессе решения различного рода уравнений, неравенств и т. Д., Важно вовремя освоить эту тему.
В следующий раз мы рассмотрим примеры решения систем линейных неравенств в частных случаях, когда одно из неравенств не имеет решений или его решением является любое число.
Категория: |Учебная программа по математике в 11 классе | Time4Learning
Посмотреть демо наших уроков!Ожидается, что учащиеся 11 класса продемонстрируют четкое понимание основных алгебраических выражений, функций и навыки сбора и анализа данных.На первом курсе большинство студентов изучают алгебру II, в то время как другие могут изучать геометрию или даже предварительное исчисление.
Какой бы курс математики ни выбрал младший школьник, хорошая учебная программа по математике в 11-м классе должна обеспечивать всесторонние знания основных математических навыков, необходимых для получения высшего образования. Уроки математики, которые являются интерактивными, с упражнениями, которые показывают множество задач и предоставляют множество возможностей для математической практики, чтобы успешно достичь мастерства, имеют решающее значение.
Узнайте, как программа Time4Learning по математике для 11 класса может помочь вашему ученику овладеть важными навыками, которые подготовят его к математике на уровне колледжа.
Какую математику должен знать 11-классник?
Обычно учащиеся 11 класса изучают алгебру II (если они следовали традиционной последовательности курсов: алгебра I в 9 классе и геометрия в 10 классе). Однако некоторые учащиеся могут изучать алгебру I еще в 8-м классе. В таких случаях и 11-й, и 12-й класс становятся открытыми для продвинутых вариантов математики.
В начале 11 класса предполагается, что многие основы алгебры уже освоены.По нашей программе по математике в 11 классе ваш младший ученик выучит:
- Как решать уравнения с использованием квадратичных и комплексных чисел.
- Как представить отношения между величинами с помощью переменных, уравнений и неравенств.
- Правильные операции с многочленами, включая показатели степени и множественные переменные.
- Как складывать, вычитать, умножать и делить рациональные функции и радикальные функции.
- Для оценки и построения графиков тригонометрических функций.
- Как использовать статистику и вероятность для представления и интерпретации данных.
- О построении графиков логарифмических и тригонометрических функций.
- Как представить отношения между величинами с помощью математического моделирования.
- Научитесь пользоваться графическим калькулятором.
Узнайте больше об учебной программе Time4Learning по математике для одиннадцатого класса, изучив объем и последовательность занятий для 11-го класса, а также планы уроков по математике для 11-го класса.
Задачи по математике для 11 класса
На основе типичной последовательности курсов по алгебре II для 11 класса, вот несколько примеров целей и задач по математике:
- Решите линейные неравенства с одной переменной, включая сложные неравенства, и представьте наборы решений графически и алгебраически.
- Найдите сложные решения квадратных уравнений, заполнив квадрат.
- Проанализируйте многочлены, чтобы полностью разложить их на множители.
- Решайте рациональные уравнения и находите посторонние решения.
- Упростите алгебраические выражения, используя свойства рациональных показателей.
- Определите и проанализируйте графики логарифмических функций.
- Создайте распределения вероятностей из набора данных.
- Преобразование между градусами и радианами.
- Используйте функциональные модели, чтобы делать прогнозы относительно ситуаций.
Получите более подробную информацию на нашей странице учебной программы по алгебре 2.
Почему выбирают программу Time4Learning по математике в домашних условиях для 11 класса?
Многие домашние школьники выбирают учебную программу Time4Learning по математике для 11 класса в качестве учебной программы по математике на весь год. Кроме того, некоторые семьи предпочитают использовать учебную программу Time4Learning по математике для 11-х классов в качестве дополнения после школы, чтобы просмотреть материал, улучшить сложные темы или подготовиться к продвинутым курсам или поступлению в колледж / поступлению в колледж.
Узнайте, почему все больше и больше семей обращаются к Time4Learning, чтобы поддержать математические навыки своих детей в 11 классе:
В качестве полной учебной программы
| В качестве дополнения
|

 Приоритетной содержательно-методической линией остаётся функционально-графическая, лучше отвечающая возрастным особенностям учащихся, чем традиционные установки на приоритет алгебраических формул.
Приоритетной содержательно-методической линией остаётся функционально-графическая, лучше отвечающая возрастным особенностям учащихся, чем традиционные установки на приоритет алгебраических формул.



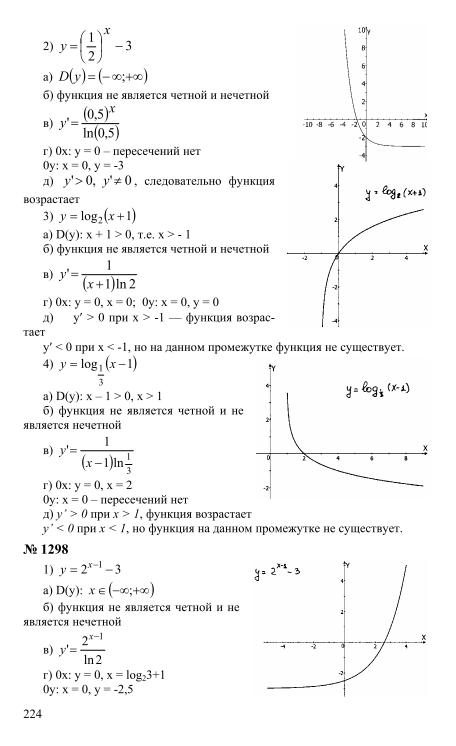 Л., 2010
Л., 2010 Часть 1, 2 Потапов, Шевкин Просвещение
Часть 1, 2 Потапов, Шевкин Просвещение Э. Ключникова, нарком. К учебнику Мордкович Экзамен
Э. Ключникова, нарком. К учебнику Мордкович Экзамен