Решение 11 класс: Решебник (ГДЗ) по алгебре 11 класс – РЕШАТОР!

ГДЗ Алгебра 11 класс Александрова

Алгебра 11 класс

Самостоятельные работы (Базовый уровень)

Александрова

Мнемозина

Как и во все предыдущие годы основной упор в школе идет на результативность. Причем учителей по-прежнему не волнует, как эти результаты будут достигнуты. Учащимся приходится не только осваивать новый материал, но и самостоятельно готовиться ко всем проверочным работам. Учитывая общую сложность и насыщенность учебного процесса, это дается им весьма непросто. Облегчить подобные упражнения поможет решебник к учебнику «Алгебра и начала математического анализа. Самостоятельные работы 11 класс (базовый уровень)» Александрова. Благодаря подробным разъяснениям и обстоятельным наглядным примерам, подростки имеют возможность полноценно освоить все нюансы данного предмета.

Основные моменты издания

В пособии имеется сорок две самостоятельные работы, которые распределены по тематическим разделам. Каждая работа содержит по четыре варианта, что позволит всесторонне подготовиться к подобным испытаниям.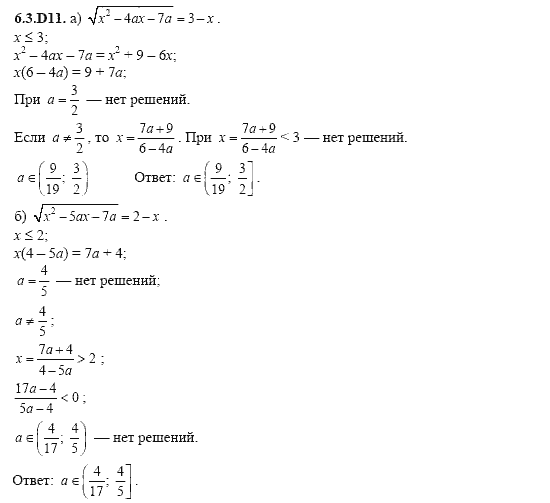

ГДЗ по алгебре 11 класс Александрова включает в себя только исчерпывающие решения и проверенные ответы по всем номерам.

Какие цели преследует его использование

Витая мыслями в мечтах о выпускном, учащиеся могут упустить нечто важное в текущем материале, который становится в этом году чрезвычайно сложным. Логарифмические уравнения и интегралы зачастую никак не воспринимаются школьниками, а ведь хорошее знание этих разделов поможет успешно справиться с большей частью проверочных работ. Кроме того, это необходимо и для экзаменационной части. Поэтому подросткам предстоит приложить много усилий для того, чтобы быть в числе отличников. Подготовиться же ко всем предстоящим испытаниям можно при помощи решебника к учебнику

«Алгебра и начала математического анализа. Самостоятельные работы 11 класс (базовый уровень)» Александрова. «Мнемозина», 2016 г.

Похожие ГДЗ Алгебра 11 класс

Название

Условие

Решение

Общие методы решения уравнений. 11 класс

Конспект урока

по алгебре и началам анализа в 11 классе

по теме «Общие методы решения уравнений.

Замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g

(x)»

Учитель математики

МБОУ гимназии № 9

г. Ставрополь

Устименко Л. И.

2014г.

Цели урока:

1. Образовательная – повторение, обобщение, систематизация знаний об общем методе решения уравнений; проверка усвоения знаний на обязательном уровне;

2. Развивающая – развитие умения работать с тестовыми заданиями, формирование навыков самостоятельной работы с большим объемом информации;

3. Воспитательная – воспитание самооценки, коммуникативных способностей.

Литература:

1. Учебник «Алгебра и начала анализа 10-11 класс» А.Г. Мордкович

«Мнемозина». Москва 2009 год;

2. Задачник «Алгебра и начала анализа 10-11 класс» А.Г. Мордкович

«Мнемозина». Москва 2009 год. 3. Справочные материалы. В.А. Гусев, А.Г. Мордкович. «Просвещение»

Москва 1986 год

4. Типовые тестовые задания для подготовки к ЕГЭ

Оборудование: компьютер, проектор, учебные пособия.

Ход урока.

1. Организационный момент.

Сегодня мы проводим урок по теме «Общие методы решения уравнений.

Замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x)». Повторим алгоритм решения уравнений, теоретический материал. Вспомним, как решаются показательные, логарифмические, иррациональные уравнения. Все уравнения взяты из тестов ЕГЭ. Поэтому сегодняшний урок- это подготовка к сдаче ЕГЭ.

Откройте тетради, запишите дату, тему урока.

2. Повторение теории.

1. Какие уравнения называются равносильными?

2. Сформулируйте теоремы, приводящие к равносильным уравнениям.

3. Перечислите причины расширения области определения уравнения.

4. В каких случаях может произойти потеря корней и как этого избежать?

5. Назовите этапы решения уравнений.

3.Устные задания.

1) Какие из чисел 5; 0; -3; являются корнями уравнения

а) 5^3х =3^5х ответ:0

б) = х + 1 ответ:0

в) ln (x³ – 15) = ln x ответ: ни одно из чисел

2)Равносильны ли уравнения

а) 2^х = 64 и 3х²-18х=0

б) 2^х =256 и log₂ x=3

в) ln x² 5 и 2 ln x=5

3) Решить уравнение

а) =3 ответ: 11

б) log (x-1) =2 ответ: 5

в)= — 9 ответ: нет корней

г) 2^х= 7 ответ: log₂ 7

д) =5 ответ: ±5

3. Решение уравнений из тестов ЕГЭ.

1). 4) —

2).4^х-2^х=0 5)log₃x+1=2log_x3

3)18^х-8·6^х-9·2^х=0

4.Самостоятельная работа.

Вариант 2

25^3-х=0,2

lg(4x-3)=2lg

log₂²x-4log₂x+3=0

15^x-9·5^x-3^x+9=0

4^x-2=0,5

2log=log

(9x-20)

=3

log²₄x-log₄x-2=0

3·9^x-5·6^x+2·4^x=0

5.Проверка самостоятельной работы.

Код правильных ответов

1

2

3

4

5

6

1 вариант

2,5

–5

2

607

2;8

2;0

2 вариант

1,5

7

3

16

16;7

-1;0

Критерии выставления оценок.

“5” – за 6 верных ответов

“4” – за 4 – 5 верных ответов

“3” – за 3 верных ответа

“2” – менее 3 ответов

6. Домашнее задание:

№ 40.25 (б)

№ 55.9 (б,в)

№ 55.16 (б)

№ 56.20 (а,б)

Алгебра и начала математического анализа, 11 класс | Шевкин.Ru

22.03.2017

Алгебра и начала математического анализа. 11 класс : Учебник для общеобразовательных организаций / С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин. – М.: Просвещение, 2019. – 464 с.

Алгебра и начала анализа: Дидактические материалы для 11 класса: Базовый и профильный уровни / М.К.Потапов, А.В.Шевкин. – М.: Просвещение, 2018. – 189 с.

Алгебра и начала математического анализа: Книга для учителя. 11 класс: базовый и профильный уровни / М.К.Потапов, А. В.Шевкин. – М.: Просвещение, 2009. – 256 с.

Небольшие заметки Шевкина А.В. по методике работы с текстовыми задачами, по подготовке к ЕГЭ и др. материалы:

Канал НАБЛЮДАТЕЛЬ на Яндекс Дзен. 

Блог Шевкин А.В. на МЕЛ.фм. 

ПРИМЕРНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

(Учебник «Алгебра и математический анализ, 11» С.М. Никольского и др.)

I вариант — для работы в общеобразовательных классах

(3 ч в неделю, всего 102 ч)

 

1. Функции и их графики (6).
1.1. Элементарные функции (1).
1.2. Область определения и область изменения функции. Ограниченность функции (1).
1.3. Четность, нечетность, периодичность функций (1).
1.4. Промежутки возрастания, убывания, знакопостоянства и нули функции (1).
1.5. Исследование функций и построение их графиков элементарными методами (1).
1.6. Основные способы преобразования графиков (1).
1.7*. Графики функций, связанных с модулем.
1.8*. Графики сложных функций.

 

2. Предел функции и непрерывность (4).
2.1. Понятие предела функции (1).
2.2*. Односторонние пределы.
2.3. Свойства пределов функций (1).
2.4. Понятие непрерывности функции (1).
2.5. Непрерывность элементарных функций (1).
2.6*. Разрывные функции.

 

3. Обратные функции (3).
3.1. Понятие обратной функции (2).
3.2*. Взаимно обратные функции.
3.3*. Обратные тригонометрические функции.
3.4*. Примеры использования обратных тригонометрических функций.
Контрольная работа № 1 (1).

 

4. Производная (10).

4.1. Понятие производной (2).
4.2. Производная суммы. Производная разности (2).
4.3*. Непрерывность функций, имеющих производную. Дифференциал.
4. 4. Производная произведения. Производная частного (2).
4.5. Производные элементарных функций (1).
4.6. Производная сложной функции (2).
4.7*. Производная обратной функции.
Контрольная работа № 2 (1).

 

5. Применение производной (15).
5.1. Максимум и минимум функции (2).
5.2. Уравнение касательной (2).
5.3. Приближенные вычисления (1).
5.4*. Теоремы о среднем.
5.5. Возрастание и убывание функций (2).
5.6. Производные высших порядков (1).
5.7*. Выпуклость и вогнутость графика функции.
5.8. Экстремум функции с единственной критической точкой (2).
5.9. Задачи на максимум и минимум (2).
5.10*.Асимптоты. Дробно-линейная функция.
5.11. Построение графиков функций с применением производной (2).
5.12*. Формула и ряд Тейлора.
Контрольная работа № 3 (1).

 

6. Первообразная и интеграл (11).
6.1. Понятие первообразной (3).
6.2*. Замена переменной. Интегрирование по частям.
6.3. Площадь криволинейной трапеции (1).
6.4. Определенный интеграл (1).
6.5*. Приближенное вычисление определенного интеграла.
6.6. Формула Ньютона – Лейбница (3).
6.7. Свойства определенных интегралов (2).
6.8*. Применение определенных интегралов в геометрических и физических задачах.
6.9*. Понятие дифференциального уравнения.
6.10*. Задачи, приводящие к дифференциальным уравнениям.
Контрольная работа № 4 (1).

 

7. Уравнения-следствия (6).
7.1. Понятие уравнения-следствия (1).
7.2. Возведение уравнения в четную степень (2).
7.3. Потенцирование уравнений (1).
7.4. Другие преобразования, приводящие к уравнению-следствию (1).
7.5. Применение нескольких преобразований, приводящих к уравнению-следствию (1).

 

8. Равносильность уравнений на множествах (7).
8.1. Основные понятия (1).
8.2. Возведение уравнения в натуральную степень (2).
8.3. Потенцирование и логарифмирование уравнений (1).
8.4. Умножение уравнения на функцию (1).
8.5. Другие преобразования уравнений (1).
8.6*. Применение нескольких преобразований.
8.7*. Уравнения с дополнительными условиями.
Контрольная работа № 5 (1).

 

9. Равносильность неравенств на множествах (7).
9.1. Основные понятия (1).
9.2. Возведение неравенств в натуральную степень (2).
9.3. Потенцирование и логарифмирование неравенств (1).
9.4. Умножение неравенства на функцию (1).
9.5. Другие преобразования неравенств (1).
9.6*. Применение нескольких преобразований.
9.7*. Неравенства с дополнительными условиями.
9.8. Нестрогие неравенства (1).

 

10. Метод промежутков для уравнений и неравенств (3).
10.1. Уравнения с модулями (1).
10.2. Неравенства с модулями (1).
10.3*. Метод интервалов для непрерывных функций.
Контрольная работа № 6 (1).

 

11. Равносильность уравнений и неравенств системам (11).
11.1. Основные понятия (1).
11.2. Распадающиеся уравнения (2).
11.3. Решение уравнений с помощью систем (2).
11.4. Уравнения вида f (a(x)) = f (b(x)) (2).
11.5. Решение неравенств с помощью систем (2).
11.6. Неравенства вида f (a(x)) > f (b(x)) (2).

 

12*. Нестандартные методы решения уравнений и неравенств.
12.1*. Использование областей существования функций.
12.2*. Использование неотрицательности функций.
12.3*. Использование ограниченности функций.
12.4*. Использование свойств синуса и косинуса.
12.5*. Использование числовых неравенств.
12.6*. Использование производной для решения уравнений и неравенств.

 

13. Системы уравнений с несколькими неизвестными (7)
13.1. Равносильность систем (2).
13.2. Система–следствие (2).
13.3. Метод замены неизвестных (2).
13.4*. Нестандартные методы решения уравнений и неравенств.
Контрольная работа № 7 (1).

 

14*. Уравнения и неравенства с параметрами
14.1*. Уравнения с параметром.
14.2*. Неравенства с параметром.
14.3*. Системы уравнений с параметром.
14.4*. Задачи с условиями.

 

Дополнение*. Комплексные числа.
1. Алгебраическая форма комплексного числа. 2. Сопряженные комплексные числа. 3. Геометрическая интерпретация комплексного числа. 4. Тригонометрическая форма комплексного числа. 5. Корни из комплексных чисел и их свойства. 6. Корни многочленов. 7*. Показательная форма комплексных чисел.

 

Повторение (12)
Повторение курса алгебры и математического анализа 10–11 классов (10)
Итоговая контрольная работа № 8 (2).

II вариант планирования

для классов с углубленным изучением математики

(5 ч в неделю, всего 170 ч)

 

1. Функции и их графики (8).
2. Предел функции и непрерывность (6).
3. Обратные функции (7).
4. Производная (14).
5. Применение производной (20).
6. Первообразная и интеграл (16).
7. Уравнения-следствия (8).
8. Равносильность уравнений на множествах (9).
9. Равносильность неравенств на множествах (9).
10. Метод промежутков для уравнений и неравенств (4).
11. Равносильность уравнений и неравенств системам (11).
12. Нестандартные методы решения уравнений и неравенств (4).
13. Системы уравнений с несколькими неизвестными (8)
14. Уравнения и неравенства с параметрами (4).
Комплексные числа (15).
Повторение (12)
Повторение курса алгебры и математического анализа 10–11 классов (10)
Итоговая контрольная работа № 8 (2).

Приводим предисловие и оглавление к дидактическим материалам.

 

Предисловие

Дидактические материалы по курсу алгебры и начал анализа содержат 50 самостоятельных и 7 контрольных работ в четырех вариантах, а также тест для самоконтроля в двух вариантах. Ко всем вариантам контрольных работ и к тесту имеются ответы.
Содержание дидактических материалов полностью соответствует учебнику серии «МГУ – школе» для 11 класса (С.М. Никольский, М. К. Потапов, Н.Н. Решетников, А.В. Шевкин) и дополняет его более сложными заданиями, необходимыми для работы в профильных классах. Это дидактические материалы нового типа, содержащие разбор заданий для подготовки к самостоятельным работам, и поэтому не нуждающиеся в «решебниках». Их можно использовать в классе и дома при работе по любым учебникам, а также для восполнения пробелов и самообразования.
Материалы для подготовки к самостоятельным работам содержат подробные объяснения решений заданий, так как имеют целью объяснение выбранных способов действий. Приведенные решения не являются образцами оформления решений учащимися, так как их решения могут быть краткими, в них, как правило, пропускают комментарии при выполнении преобразований уравнений или неравенств. Некоторые типы заданий, например, иррациональные уравнения, встречаются в разных работах, так как в каждой из этих работ предполагается свой способ решения уравнения.
Темы, отмеченные в дидактических материалах звездочкой, не является обязательными для изучения в общеобразовательном классе. Они охватывают программу углубленного изучения математики (профильных классов). Предложенные работы могут использоваться как обучающие самостоятельные работы для классной или домашней работы. Любые из самостоятельных работ учитель может использовать для контроля на отметку. При этом следует учесть, что многие самостоятельные работы и все контрольные работы избыточны по объему. Предполагается, что учитель отберет из них часть заданий с учетом уровня подготовки учащихся своего класса и времени, отводимого на выполнение работы.
Следует учесть, что некоторые задания вариантов III и IV несколько сложнее соответствующих заданий вариантов I и II. Так как в классах с углубленным изучением математики контрольных работ должно быть больше, чем в классе, работающем по общеобразовательной программе, то отдельные самостоятельные работы, отмеченные звездочками, можно провести как контрольные работы.

 

Оглавление

Раздел 1. Материалы для подготовки к самостоятельным работам
1*. Сложная функция
2. Область определения функции
3. Область изменения функции
4. Четные и нечетные функции
5*. Задачи с параметром. Использование четности функций
6. Промежутки монотонности функции. Промежутки знакопостоянства функции
7. Построение графиков функций
8*. Графики функций, содержащих модули
9*. Задачи с параметром. Использование графиков функций
10. Предел функции
11. Обратные функции
12. Производные элементарных функций
13. Производная сложной функции
14*. Производная сложной функции (продолжение)
15. Максимум и минимум функции на отрезке
16. Уравнение касательной к графику функции
17. Приближенные вычисления
18. Исследование функций с помощью производной
19. Задачи на максимум-минимум
20*. Геометрические задачи на максимум-минимум
21*. Задачи на смеси. Нахождение экстремума функции
22. Исследование функции с помощью производной и построение ее графика
23*. Решение задач с помощью производной
24. Первообразная. Неопределенный интеграл
25*. Нахождение неопределенных интегралов с помощью подстановки
26. Геометрический смысл определенного интеграла
27. Формула Ньютона – Лейбница
28. Свойства определенного интеграла
29. Равносильные преобразования уравнений
30. Равносильные преобразования неравенств
31. Уравнения-следствия
32. Уравнения-следствия (продолжение)
33. Решение уравнений с помощью систем
34. Решение уравнений с помощью систем (продолжение)
35*. Уравнения вида f (a(x)) = f (b(x))
36. Решение неравенств с помощью систем
37. Решение неравенств с помощью систем (продолжение)
38*. Неравенства вида f (a(x)) > f (b(x))
39. Равносильность уравнений на множествах
40*. Равносильность уравнений на множествах (продолжение)
41. Равносильность неравенств на множествах
42*. Равносильность неравенств на множествах (продолжение)
43. Уравнения и неравенства с модулями
44*. Уравнения вида f (f (x)) = x
45. Метод интервалов для непрерывных функций
46*. Использование свойств функций при решении уравнений и неравенств
47*. Рассуждения с числовыми значениями при решении уравнений и неравенств
48. Системы уравнений с несколькими неизвестными
49*. Рассуждения с числовыми значениями при решении систем уравнений
50*. Уравнения, неравенства, системы с параметром
Раздел 2. Самостоятельные работы
Раздел 3. Контрольные работы
Тест для самоконтроля
Ответы

Олимпиада по математике 11 класс, задания, уравнения, задачи с ответами

Курс математики в выпускном классе посвящен изучению степеней и корней, знакомству с показательной и логарифмической функцией, интегралами и элементами математической статистикой. Отдельное внимание в 11 классе посвящено повторению изученного за весь курс математики и подготовке к грядущему экзамену.

В связи с этим, для учеников 11 класса особенно важно участие в олимпиадах по математике и дополнительные занятия, посвященные решению заданий различной сложности.

На этой странице собраны задания для подготовки к олимпиаде по математике для 11 класса. Представлены уравнения, задачи и математические загадки с ответами и решениями. Этот материал может быть использован учителями или репетиторами для повышения уровня знания учеников.

Уравнения

1. Решите уравнение: = 3

2. Решите уравнение: ( − 8)² = ( + 9)²

3. Решите уравнение: log2 (5 + ) = log2 (1 − ) + 1

4. Решите уравнение: log5 ( + ) = log5 ( + 9)

5. Решите уравнение: log2 (4 − ) = 7

6. Решите уравнение: − + 72 = 0

7. Решите уравнение: ( + 7)² = ( − 1)²

8. Решите уравнение: ( − 8)² = ( − 2)²

9. Решите уравнение: ( − 6)² = −

10. Решите уравнение: + 9 = ( + 9)²

Задачи

Задача №1
Докажите, что уравнение  xy = 2006 (x + y) имеет решения в целых числах.

Задача №2
Докажите, что если α, β, γ — углы произвольного треугольника, то справедливо тождество cos2α + cos2β + cos2γ + 2 cosα cosβ cosγ = 1.

Задача №3
Три шара радиуса R касаются друг друга и плоскости α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных  шаров. Определите высоту «горки» из четырех шаров.

Задача №4
Докажите неравенство  −< 1/6 на луче [1/4; + ∞).

Задача №5
В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.

Математические загадки

Загадка №1

Сколько лет человеку, если в 2012 году его возраст оказался равным сумме цифр года его рождения.

Загадка №2

Двадцать одна девочка и двадцать один мальчик принимали участие в математическом конкурсе. Каждый участник решил не более шести задач. Для любых девочки и мальчика найдётся хотя бы одна задача, решённая обоими. Докажите, что была задача, которую решили не менее трёх девочек и не менее трёх мальчиков.

Загадка №3

Существует ли многогранник с нечетным числом граней, каждая из которых есть многоугольник с нечетным числом сторон?

Загадка №4

В каждую клетку квадратной таблицы 25 x 25 вписано произвольным образом одно из чисел 1 или -1. Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце. Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке. Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.

Загадка №5

Сумма цифр в десятичной записи натурального числа n равна 100, а сумма цифр числа 44n равна 800.

Чему равна сумма цифр числа 3n?

Ответы к уравнениям

Уравнение	№ 1	№ 2	№ 3	№ 4	№ 5
Ответ	6	8,5 ∈ [8;9)	− 0,25	1,8	-124

Уравнение	№ 6	№ 7	№ 8	№ 9	№ 10
Ответ	9; 8	-1,5	1	-6	-4

Ответы к задачам

Задача 1
Преобразуем уравнение к следующему виду: (x – 2006)(y − 2006) = 20062. Уравнение имеет решения, например, x = y = 4012.

Задача 2
Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π, и применяя формулы: cos² x = (1 + cos 2x)/2, cos x = − cos (π − x), cos x + cos y = (2cos((x + y)/2)) cos((x − y)/2), получим справедливое тождество.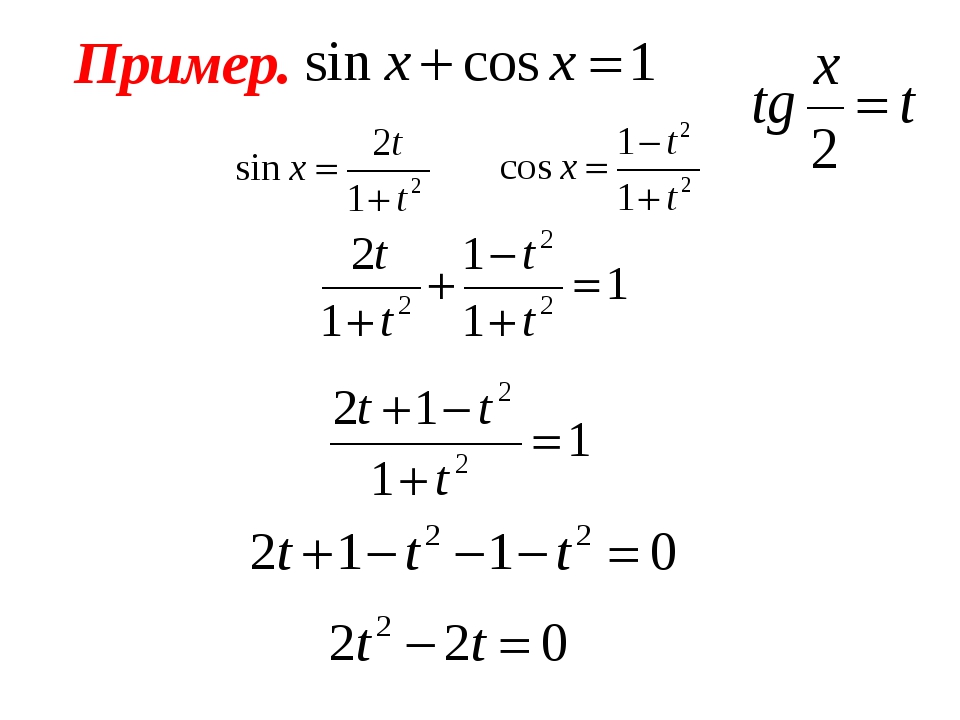

Задача 3
Пусть четыре шара радиуса R c центрами A, B, C, D касаются друг друга и первые три из них – плоскости a в точках A1, B1, C1 . Тогда точки A, B, C, D являются вершинами правильной пирамиды с ребром 2R. Вершина D этой пирамиды проектируется в центр основания О.

Высота «горки» из четырех шаров равна сумме OD + 2R = 2R  + 1

Задача 4
Пусть =  −. Тогда   =  − и с помощью метода интервалов получаем, что  < 0 при всех  >2/9. Но 1/4>2/9, следовательно, функция  убывает на луче [1/4; +∞]. Это значит, что  − < 1/16 − 3/64 = 1/64 < 1/64.

Задача 5
Окружим каждый квадрат полоской шириной 1/2. Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4. Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса  с центром в этой точке не имеет общих точек  ни с одним из квадратов.

Ответ: 175 центов

Ответы на загадки

Загадка 1

1 вар. Человек родился в 19mn году, тогда

          2012 − 19mn= 1 + 9 + m + n

          2012 − 1900 − m − n = 10 + m + n

          102 = 11m + 2n

m = 8, n = 7, значит 1987 год, ему 25 лет.

2 вар. Человек родился в 200n году, тогда

          2012 − 200n = 2 + n

          2012 − 2000 − n = 2 + n

          12 − 2 = 2n

n = 5, значит 2005 год, ему 7 лет.

Загадка 2
Предположим, что нашлась задача, которую решили не более двух девочек или не более двух мальчиков.

Будем считать задачу «красной», если её решили не более двух девочек и «чёрной» в противоположном случае (тогда её решили не более двух мальчиков).

Представим шахматную доску с 21-й строкой, каждая из которых соответствует девочке, и 21-м столбцом, каждый из которых соответствует мальчику.

Тогда каждая клетка соответствует паре «мальчик–девочка». Каждую клетку покрасим в цвет какой-нибудь задачи, которую решили и мальчик-строка и девочка-столбец.

По принципу Дирихле в каком-нибудь столбце найдётся 11 чёрных клеток, или в какой-нибудь строке найдутся 11 красных клеток (потому что иначе получится, что всего клеток не более чем 21 × 10 + 21 × 10 < 21²).

Рассмотрим, например, девочку-строку, содержащую хотя бы 11 чёрных клеток.

Каждой из этих клеток соответствует задача, решённая максимум двумя мальчиками.

Тогда мы можем указать не менее 6 различных задач, решённых этой девочкой. В силу первого условия никаких других задач девочка не решала, но тогда максимум 12 мальчиков имеют общие решённые задачи с этой девочкой, что противоречит второму условию.

Точно также разбирается случай, если в каком-нибудь столбце найдутся 11 красных клеток.

Загадка 3

Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях, тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная. А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно. Получили противоречие. Значит, такого многогранника не существует

Загадка 4
Найдем произведение всех 25 чисел, записанных под каждым столбцом и всех 25 чисел, записанных справа от строчек. Так как в этом произведении каждое из чисел квадратной таблицы входит по два раза, то произведение этих 50 произведений, в каждом из которых стоит по 25 множителей, будет положительным, т. е. равно 1. А так как произведение 50 чисел положительно, то отрицательных сомножителей будет четное число (2, 4, …, 50). Сумма же 50 произведений может быть нулем лишь в случае, когда 25 слагаемых равно 1, а 25 слагаемых равно — 1, т. е. слагаемых с — 1 должно быть нечетное число. А это значит, что сумма 50 написанных произведений не может равняться нулю.

Загадка 5
Заметим, что 44n есть сумма 4 экземпляров числа n и 4 экземпляров числа 10n.

Если складывать эти числа поразрядно, то в каждом разряде окажется сумма учетверённой цифры из этого же разряда числа n и учетверённой цифры из следующего разряда.

Если при этом не происходит никаких переносов, то каждая цифра числа n складывается 8 раз, и сумма цифр во всех разрядах оказывается равной 800. При переносах же сумма цифр, очевидно, уменьшается (так как из одного разряда вычитается 10, а к другому прибавляется только 1). Поэтому в ситуации условия задачи переносов не происходит. Это означает, в частности, что любая цифра числа n не превосходит 2. Тогда при умножении n на 3 просто умножается на 3 каждая его цифра, а, значит, и сумма цифр. Поэтому сумма цифр числа 3n равна 300.

Другие классы

Обновлено: 26/02/2015 , автор: Валерия Токарева

Физика 10-11 класс. Примеры решения задач из учебников Мякишева

Физика 10-11 класс. Примеры решения задач из учебников Мякишева

Задачи по физике — это просто!

Здесь приведены примеры решения задач по физике для учащихся 10-11 классов из учебников «Физика. 10 класс» (авт. Мякишев, Буховцев, Сотский) и «Физика. 11 класс» (авт. Мякишев, Буховцев, Чаругин).

Физика — 10 класс

по теме «Равномерное прямолинейное движение» ………. смотреть
по теме «Сложение скоростей» ………. смотреть
по теме «Движение с постоянным ускорением» ………. смотреть
по теме «Движение с постоянным ускорением свободного падения» ………. смотреть
по теме «Кинематика твёрдого тела» ………. смотреть
по теме «Второй закон Ньютона» ………. смотреть
по теме «Закон всемирного тяготения» ………. смотреть
по теме «Первая космическая скорость» ………. смотреть
по теме «Силы упругости. Закон Гука» ………. смотреть
по теме «Силы трения» ………. смотреть
по теме «Силы трения» (продолжение) . ……… смотреть
по теме «Закон сохранения импульса» ………. смотреть
по теме «Кинетическая энергия и её изменение» ………. смотреть
по теме «Закон сохранения механической энергии» ………. смотреть
по теме «Динамика вращательного движения абсолютно твёрдого тела» ………. смотреть
по теме «Равновесие твёрдых тел» ………. смотреть
по теме «Основные положения МКТ» ………. смотреть
по теме «Основное уравнение молекулярно-кинетической теории» ………. смотреть
по теме «Энергия теплового движения молекул» ………. смотреть
по теме «Уравнение состояния идеального газа» ………. смотреть
по теме «Газовые законы» ………. смотреть
по теме «Определение параметров газа по графикам изопроцессов» ………. смотреть
по теме «Насыщенный пар. Влажность воздуха» ………. смотреть
по теме «Внутренняя энергия. Работа» ………. смотреть
по теме: «Количество теплоты. Уравнение теплового баланса» . ……… смотреть
по теме: «Первый закон термодинамики» ………. смотреть
по теме: «КПД тепловых двигателей» ………. смотреть
по теме «Закон Кулона» ………. смотреть
по теме «Напряжённость электрического поля. Принцип суперпозиции полей» ………. смотреть
по теме «Потенциальная энергия электростатического поля. Разность потенциалов» ………. смотреть
по теме «Электроёмкость. Энергия заряженного конденсатора» ………. смотреть
по теме «Закон Ома. Последовательное и параллельное соединения проводников» ………. смотреть
по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи» ………. смотреть
по теме «Электрический ток в различных средах» ………. смотреть

Физика — 11 класс

по теме «Магнитное поле» ………. смотреть
по теме «Электромагнитная индукция» ………. смотреть
по теме «Механические колебания» ………. смотреть
по теме «Геометрическая оптика» . ……… смотреть
по теме «Волновая оптика» ………. смотреть

Успехов в разборе «полетов»!

Знаете ли вы?

Оптика и живая природа

Оказывается, у человека в глазу хрусталик выполняет роль не только линзы, но и светофильтра. Хрусталик нашего глаза отсекает от видимой части спектра ультрафиолетовые лучи. Не будь у нас его, мы тоже могли бы видать мир в ультрафиолетовых лучах.

В самом деле, люди у которых удален помутневший хрусталик и заменен стеклянной линзой — очками, видят предметы в ультрафиолетовом свете. Они даже читают таблицу для проверки зрения лишь при ультрафиолетовом освещении. Тогда как обычные люди при таком свате совершенно ничего не видят.

Могло бы насекомое, обладающее сложными глазами, воспринимать телевизионную передачу или смотреть кино? Если нам показывать 10 изображений в секунду, мы еще различим отдельные зрительные образы, а если 16, то все сольется в непрерывное действие.

Мухе или пчеле надо 200 смен кадров в секунду, чтобы она восприняла непрерывное движение. Поэтому на наших телевизорах и киноэкранах насекомые видели бы отдельно меняющиеся картинки. А свет ламп дневного света, зажигающихся и гаснущих 50 раз в секунду, который мы воспринимаем как постоянный, для ник представляется всегда мигающим.

Мало кто слышал о сканирующем глазе, который работает по тому же принципу, что и телевизионная трубка. Сканирующий глаз можно найти у маленького членистоногого капилия. Большой красивый хрусталик смотрит на мир. Он фокусирует изображение на… нет, не на сетчатку, а в пустое пространство глазной камеры.

Изображение улавливается всего-навсего одним светочувствительным рецептором, прикрепленным к тонкому мышечному пучку, который перемещает его в глазу, словно электронный луч в светочувствительной трубке телекамеры.

Другие животные обходятся без хрусталика, и глаз у них построен наподобие камеры с точечным отверстием. Головоногий моллюск наутилус, родственник осьминога и кальмара со странными большими глазами м очень маленьким зрачком, как раз использует для своего зрения настоящую камеру Обскура.

У такой камеры-глаза есть большое преимущество: на каком бы расстоянии ни рассматривался предмет, его изображение всегда будет сфокусировано на сетчатке. Жаль только, что через узкое отверстие зрачка проходит мало световых лучей, поэтому при плохом освещении наутилус многого не различает.

Источник: «Юный натуралист»

Объявлены изменения порядка проведения ЕГЭ и государственной итоговой аттестации выпускников 9-х и 11-х классов в 2021 году

Минпросвещения и Рособрнадзор объявили о решениях, которые приняты в отношении порядка проведения ЕГЭ и государственной итоговой аттестации выпускников 9-х и 11-х классов в 2021 году.

Пресс-служба Минпросвещения России

«Мы понимаем, что для ребят, которые сдают ЕГЭ в 2021 году, это год непростой. В связи с принятыми мерами на фоне эпидемиологической ситуации мы внесли изменения в правила сдачи экзаменов. Проведение итогового сочинения или изложения в этом учебном году запланировано на вторую декаду апреля. Государственная итоговая аттестация по образовательным программам среднего общего образования в формате ЕГЭ должна пройти с 31 мая по 2 июля, дополнительный период ЕГЭ – с 12 по 17 июля», – сказал Сергей Кравцов.

Для выпускников 11-х классов и других участников ЕГЭ досрочный период проведения экзаменов в связи с текущей эпидемиологической обстановкой в 2021 году отменяется.

Для получения аттестата о среднем общем образовании выпускникам, которые не планируют поступать в вузы, вместо ЕГЭ нужно будет сдать государственный выпускной экзамен (ГВЭ) по двум предметам – русскому языку и математике.

Выпускникам, которые собираются поступать в вузы и будут сдавать для этого ЕГЭ, чтобы получить аттестат, достаточно сдать на удовлетворительный результат ЕГЭ по русскому языку. ЕГЭ по математике базового уровня в 2021 году проводиться не будет.

ГВЭ для выпускников 11 классов пройдёт в конце мая, а основной период ЕГЭ следом – ориентировочно с 31 мая по 2 июля 2021 года для всех участников экзаменов, в том числе для выпускников прошлых лет.

Для участников ЕГЭ, которые не смогут сдать экзамены в основные сроки по болезни или иной уважительной причине, будет предусмотрен дополнительный период проведения ЕГЭ в середине июля 2021 года. Эти сроки будут увязаны с графиком приемной кампании в вузы – все, кто будет сдавать ЕГЭ в дополнительный период, так же, как и участники основного периода, успеют получить свои результаты и подать документы в выбранные учебные заведения.

Итоговое сочинение и изложение, которые являются для 11-классников допуском к государственной итоговой аттестации, пройдут в середине апреля.

Для 9-классников досрочный период проведения государственной итоговой аттестации также отменён.

Аттестаты за 9-й класс об основном общем образовании будут выданы на основании результатов государственной итоговой аттестации только по двум обязательным предметам – русскому языку и математике. В 2021 году выпускники 9-х классов не будут сдавать на ОГЭ учебные предметы по выбору.

Для девятиклассников также будут проведены контрольные работы по одному учебному предмету по их выбору. Результаты этих контрольных не будут влиять на получение аттестата и допуск к итоговой аттестации. Контрольные работы пройдут с 17 по 25 мая 2021 года. Конкретные даты определят региональные органы управления образованием либо школы.

Государственная итоговая аттестация (ГИА-9) по русскому языку и математике будет проведена в период с 24 по 28 мая 2021 года, резервные сроки проведения основного периода ГИА-9 придутся на начало июня 2021 года. Для девятиклассников, не сдавших экзамены в основной период, ГИА-9 по русскому языку и математике пройдёт повторно в дополнительный сентябрьский период.

«Данные решения приняты в интересах здоровья и безопасности всех участников и организаторов экзаменов, чтобы снизить эпидемиологические риски и сделать проведение итоговой аттестации школьников в 2021 году максимально безопасным. При проведении экзаменов также будут применены все рекомендованные Роспотребнадзором меры эпидемиологической безопасности, которые успешно зарекомендовали себя на ЕГЭ в 2020 году и позволили предупредить новый всплеск заболеваемости после экзаменов», – прокомментировал изменения руководитель Рособрнадзора Анзор Музаев.

Самарский государственный технический университет

27 Января 2021

Продление экзаменационной сессии

Приказом ректора Самарского политеха Дмитрия Быкова №1/32 от 27.01.2021 в нашем университете продлена экзаменационная сессия до 31 января.

В этот день с 12.00 преподаватели университета принимают зачеты и экзамены по всем дисциплинам.

Подробную информацию о месте проведения экзаменов можно узнать в деканатах факультетов, институтов, на кафедрах и в личных кабинетах студентов АИС «Университет».

27 Января 2021

Повышенная академическая стипендия

Для подтверждения участия в конкурсе на назначение стипендии студентам необходимо после
1 февраля в разделе «Студенческий рейтинг» в личном кабинете АИС «Университет» выбрать период «1 полугодие 2020 по 2 полугодие 2020», нажать кнопку «Отчеты», сформировать нужный отчет, распечатать и сдать в деканат. Срок приема документов уточняйте в деканатах.

Подробнее – на сайте ЦИПИ.

27 Января 2021

Конкурс «Мастера гостеприимства»

Студенты приглашаются к участию во всероссийском конкурсе, направленном на повышение престижа профессий в сфере гостеприимства, поиск новых проектов по развитию внутреннего туризма.

Заявки на участие принимаются на сайте до 31 января. Подробная информация – здесь.

26 Января 2021

Конференция
ООО «СамараНИПИнефть»

Студенты и аспиранты приглашаются к участию в XII региональной научно-технической конференции молодых специалистов ООО «СамараНИПИнефть». Она пройдет с 24 февраля по 5 марта.

Работы по секциям принимаются до 12 февраля. Доклад и презентацию необходимо направить по e-mail: [email protected]. Требования к оформлению работ – здесь.

21 Января 2021

День открытых дверей в лицее СамГТУ
⠀
13 февраля состоится день открытых дверей в общеобразовательном архитектурно-техническом лицее Политеха. Детям и родителям расскажут об обучении, о поступлении, ответят на все интересующие вопросы.

Встреча пройдет по адресу:
ул. Молодогвардейская, д.194, аудитория 400. Вход через 12 корпус (угол улиц Ульяновской и Чапаевской). Начало – в 13:00. При себе иметь паспорт и маску.

19 Января 2021

Математическая школа «Талант»

Политех приглашает школьников 5-11 классов на занятия в школе «Талант». Программа направлена на повышение уровня математических знаний и решение олимпиадных заданий.

Занятия проводятся бесплатно в дистанционном формате на сайте два раза в неделю по группам: 5-7 класс, 8-9 класс, 10-11 класс. Видеоуроки доступны в записи на сайте. Обязательна регистрация участников.

18 Января 2021

Военная служба по контракту

Призывники, имеющие высшее или среднее профессиональное образование, вместо службы по призыву могут пройти службу по контракту. Контракт обеспечивает возможности для самореализации и дает ряд гарантий.

Адрес пункта отбора на военную службу: ул. Ленинская, д. 147;
тел.: 8 (846) 332-39-37, 8 (996) 746-42-02;
e-mail: [email protected]. Подробнее – здесь.

15 Января 2021

Лучший студент-исследователь

По итогам 2020 года Политех проводит конкурс «Лучший студент-исследователь ФГБОУ ВО «СамГТУ». Цель – активизация научно-исследовательской работы студентов, выявление талантливой молодежи.

Для участия в конкурсе студентам необходимо в срок до 15 февраля предоставить председателям молодежного научного общества на факультетах конкурсную работу – портфолио.

14 Января 2021

Экскурсия для студентов

29 января духовно-просветительский культурный центр Политеха организует краеведческую экскурсию для студентов с посещением исторического Храма Богоявления, а также сыроварни Fromage de Vera в поселке Курумоч. В программу включен отдых на базе «Актив тайм» – катание на санях, тарзанка.

Количество мест ограничено, запись – у Веры Гридиной. Отправление – в 8:30 от главного корпуса.

24 Декабря 2020

Подготовительные курсы

Абитуриенты приглашаются на подготовительные курсы «Архитектура», «Дизайн», «Математика. Физика. Русский язык», «Конструирование изделий легкой промышленности», «Школа юного архитектора и дизайнера». Сроки обучения: с 11 января по 5 июня.

Занятия – в будни с 16:00 до 19:00. Для иногородних слушателей по направлению «Архитектура» – по субботам с 9:00 до 18:00.

Подробнее – по тел.: (846) 242-13-11, ВКонтакте, на сайте.

21 Декабря 2020

Конкурс Steel2Real’21

Стартовал первый этап международного конкурса студенческих проектов Steel2Real’21, проводимого Ассоциацией развития стального строительства (АРСС).

Командам учащихся архитектурных и строительных специальностей предстоит разработать конструктивные решения для здания общежития со стальным каркасом.

Узнать подробную информацию, а также зарегистрироваться для участия можно на сайте конкурса.

18 Декабря 2020

Курсы для абитуриентов

Политех приглашает на подготовительные курсы старшеклассников, желающих обучаться по направлениям «Дизайн костюма» и «Конструирование изделий легкой промышленности». Занятия – раз в неделю в будни с 16:00 до 19:00.

Заключить договор на обучение можно в будни с 10:00 до 16:00 по адресу: ул. Молодогвардейская, 194, каб. 314.

Подробнее – здесь. Дополнительная информация – по тел.: 8 (846) 242-13-11.

08 Декабря 2020

Конкурс «ШАГ В БУДУЩЕЕ – 2021»

Всероссийский конкурс студенческих идей проводится с целью активизации творческой, познавательной, интеллектуальной инициативы студентов.

Для участия необходимо зарегистрировать конкурсную работу на сайте (вкладка «Конкурс студенческих идей»), а также прислать до 12 марта на e-mail: [email protected] с пометкой «Шаг в будущее-2021».

Подробная информация о конкурсе – здесь.

12 Ноября 2020

Образовательный кредит для студентов

Утверждены новые условия предоставления образовательного кредита. Фиксированная процентная ставка установлена на уровне 3% годовых, льготный период кредитования увеличен с 3 до 9 месяцев, а общий срок пользования кредитом продлен до 15 лет.

Граждане, получившие кредит ранее, могут обратиться в банк и заключить соглашение по переходу на новую процентную ставку. Подробнее – здесь.

12 Февраля 2020

Открыт набор курсантов
ВПК «Тайфун»

Военно-патриотический клуб Политеха «Тайфун» приглашает студентов вступить в свои ряды.

Курсанты проходят начальную военную подготовку, занимаются военно-прикладными видами спорта, участвуют в военно-спортивных соревнованиях, походах, экскурсиях и поисково-краеведческой работе.

Подробнее – в группе ВКонтакте. Подать заявку можно здесь.

Физика 10-11 класс. Примеры решения задач из учебников Мякишева

Физика 10-11 класс. Примеры решения задач из учебников Мякишева

Задачи по физике — это просто!

Здесь приведены примеры решения задач по физике для учащихся 10-11 классов из учебников «Физика. 10 класс» (авт. Мякишев, Буховцев, Сотский) и «Физика. 11 класс» (авт. Мякишев, Буховцев, Чаругин).

Физика — 10 класс

по теме «Равномерное прямолинейное движение». ……… смотреть
по теме «Сложение скоростей» ………. смотреть
по теме «Движение с постоянным ускорением» ………. смотреть
по теме «Движение с постоянным ускорением свободного падения» ………. смотреть
по теме «Кинематика твёрдого тела» ………. смотреть
по теме «Второй закон Ньютона» … ……. смотреть
по теме «Закон всемирного тяготения» ………. смотреть
по теме «Первая космическая скорость» ………. смотреть
по теме « Силы упругости.Закон Гука »………. смотреть
по теме« Силы трения »………. смотреть
по теме« Силы трения »(продолжение) …….. .. смотреть
по теме «Закон сохранения импульса» ………. смотреть
по теме «Кинетическая энергия и её изменение» ………. смотреть
по теме «Закон сохранения механической энергии »………. смотреть
по теме« Динамика вращательного движения абсолютно твёрдого тела »………. смотреть
по теме« Равновесие твёрдого тел »………. смотреть
по теме «Основные положения МКТ» ………. смотреть
по теме «Основное уравнение молекулярно-кинетической теории» ………. смотреть
по теме «Энергия теплового движения смотреть молекулы» ……….
по теме «Уравнение состояния идеального газа» ………. смотреть
по теме «Газовые законы» …… …. смотреть
по теме «Определение параметров газа по графикм изопроцессов» ………. смотреть
по теме «Насыщенный пар. Влажность воздуха »………. смотреть
по теме «Внутренняя энергия. Работа »………. смотреть
по теме:« Количество теплоты. Уравнение теплового баланса »………. смотреть
по теме:« Первый закон термодинамики »………. смотреть
по теме:« КПД тепловых двигателей »…… …. смотреть
по теме «Закон Кулона» ………. смотреть
по теме «Напряжённость электрического поля. Принцип суперпозиции полей »………. смотреть
по теме« Потенциальная энергия электростатического поля.Разность потенциалов ».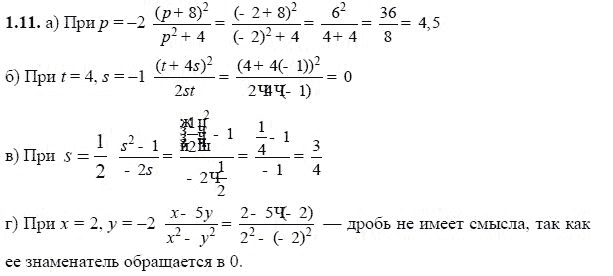 ……… смотреть
по теме« Электроёмкость. Энергия заряженного конденсатора »………. смотреть
по теме« Закон Ома. Последовательное и параллельное соединение проводников »………. смотреть
по теме« Работа и мощность постоянного тока. Закон Ома для полной цепи »………. смотреть
по теме« Электрический ток в различных средах »………. смотреть

Физика — 11 класс

по теме «Магнитное поле» ………. смотреть
по теме «Электромагнитная индукция» ………. смотреть
по теме «Механические колебания» ………. смотреть
по теме «Геометрическая оптика» .. …….. смотреть
по теме «Волновая оптика» ………. смотреть

Успехов в разборе «полетов»!

Знаете ли вы?

Оптика и живая природа

Оказывается, у человека в глазу хрусталик роль не только линзы, но и светофильтра.Хрусталик нашего глаза отсекает от видимой части ультрафиолетовые лучи. Не будь у нас его, мы тоже могли бы видать мир в ультрафиолетовых лучах.

В самом деле, люди у которых удален помутневший хрусталик и заменен стеклянной линзой — очками, видят предметы в ультрафиолетовом свете. Они даже читают таблицу для проверки зрения при ультрафиолетовом освещении. Тогда как обычные люди при таком свате совершенно ничего не видят.

Могло бы насекомое, обладающее сложными глазами, воспринимать телевизионную передачу или смотреть кино? Если нам показывать 10 изображений в секунду, мы еще различим отдельные зрительные образы, а если 16, то все сольется в непрерывное действие.

Мухе или пчеле надо 200 смен кадров в секунду, чтобы она непрерывно продолжала движение. Поэтому на наших телевизорах и киноэкранах насекомые видели бы отдельно меняющиеся картинки. А свет ламп дневного света, зажигающих и гаснущих 50 раз в секунду, который мы воспринимаем как постоянный, для ник представляется всегда мигающим.

Мало кто слышал о сканирующем глазе, который работает по тому же принципу, что и телевизионная трубка. Сканирующий глаз можно найти у маленького членистоногого капилия. Большой красивый хрусталик смотрит на мир. Он фокусирует изображение на … нет, не на сетчатку, а в пустое пространство глазной камеры.

Изображение улавливается всего-навсего одним светочувствительным, прикрепленным к тонкому рецепту мышечному пучку, который перемещает его в глазу, словно электронный луч в светочувствительной трубке телекамеры.

Другие животные обходятся без хрусталика, и они идут наподобие камеры с точечным отверстием. Головоногий моллюск наутилус, родственник осьминога и кальмара со странными глазами м очень маленьким зрачком, как раз использует для своего зрения настоящую камеру Обскура.

У такой камеры-глаза есть большое преимущество: на каком бы расстоянии ни рассматривался предмет, его изображение всегда будет сфокусировано на сетчатке. Жаль только, что через узкое отверстие зрачка проходит мало световых лучей, поэтому при плохом освещении наутилус многого не различает.

Источник: «Юный натуралист»

ГДЗ Алгебра 11 класс Александрова

Алгебра 11 класс

Самостоятельные работы (Базовый уровень)

Александрова

Мнемозина

Как и во все предыдущие основные годы упор в школе идет на результативность. Причем учителей по-прежнему не волнует, как эти результаты будут достигнуты. Учащимся приходится не только осваивать новый материал, но и самостоятельно готовиться ко всем проверочным работам. Учитывая общую сложность и насыщенность учебного процесса, это дается им непросто. Облегчить аналогичные упражнения поможет решебник к учебнику «Алгебра и начала математического анализа. Самостоятельные работы 11 класс (базовый уровень)» Александрова. Благодаря подробным разъяснениям и всесторонним наглядным примерам, подростки имеют возможность полноценно освоить все нюансы данного предмета.

Основные моменты издания

В пособии имеется сорок две самостоятельные работы, которые распределены по тематическим разделам. Каждая работа содержит четыре варианта, предлагаемых всесторонне подготовить к подобным испытаниям. ГДЗ по алгебре 11 класс Александрова включает в себя только исчерпывающие решения и проверенные ответы по всем номерам.

Какие цели преследует его использование

Витая мыслями в мечтах о выпускном, учащиеся может упустить важное в текущем материале, который становится в этом году сложным. Логарифмические уравнения и интегралы зачастую не воспринимаются школьниками, а хорошее знание разделов помогает успешно справиться с большей частью проверочных работ. Кроме того, это необходимо и для экзаменационной части. Поэтому подросткам предстоит приложить много усилий для того, чтобы быть в числе отличников. Подготовиться же ко всем предстоящим испытаниям можно при помощи решебника к учебнику «Алгебра и начала математического анализа. Самостоятельные работы 11 класс (базовый уровень)» Александрова. «Мнемозина», 2016 г.

Похожие ГДЗ Алгебра 11 класс

Название

Условие

Решение

Логарифмические уравнения. 10-11 класс

Стоит напомнить всем, что логарифмическими называют уравнения, в которых переменная или функция от «икс» находится под знаком логарифма.
При равносильных преобразованиях справедливая формула перехода от логарифмического уравнения до уравнения
log _a f (x) = c⇔f (x) = a ^c .
ОДЗ: основание логарифма должно быть больше нуля и не равняться единице,
функция — положительной
{x> 0, x ≠ 1, f (x)> 0}.
Важно знать частные случаи простейших логарифмических соотношений:
правая сторjна равна нулю (с = 0) или единице (с = 1):
правая сторона основания равна единице
c = 1⇔log _a a = 1⇔f (x) = а.
логарифм единицы равенство нулю
c = 1⇔log _a 1 = 0⇔f (x) = 1.
Эти формулы Вы должны знать на память, поскольку их чаще всего применяют при сведении логарифмов до простейшего типа.
С целью научить Вас раскрывать уравнения, а также подготовить к ВНО тестированию решены 40 примеров, которые в полной мере охватывают все известные методы решения логарифмических уравнений, которые Вас учат в 10-11 классе школьной программы, и дальше на первых курсах в ВУЗ -ах.

Схема вычисления логарифмических соотношений

1. , если возможно, выписать область допустимых значений логарифмов и функций, которые в него входят.
2. свести уравнение к простейшему типу элементарных преобразований, заключающиеся в выполнении степени из основания логарифма (или наоборот), логарифмированию и потенцированию (возведение в степень по основанию (экспонента, основы = 10, 2, π)
3. в случаях сложных уравнений вводят замену объединение и сводят к квадратным или другим уравнениям.

Вычисление уравнений с логарифмом

Пример 16.1 Решить уравнение log _a x = c.

Решение: Имеем простейшее логарифмическое уравнение, которое решается методом сведения к одному основанию логарифмов:
log _a x = c
(здесь a> 0, a ≠ 1),
log _a x = c • 1,
log _a x = c • log _a a,
log _a x = log _a a ^c
Здесь использовали свойства логарифма, единицу расписали как логарифм основания, после чего множитель c внесли под логарифм.
Далее опустили основы и приравняли выражения в логарифмах:
x = a ^c .
ОДЗ: x> 0.
Ответ: а ^с — Г.

Пример 16.2 Решить уравнение log _1/2 (x) = — 4.

А	Б	В	Г
							1/16	1/16; 16	16

Решение: ОДЗ функции под логарифмом: x> 0.
Сводим уравнение к одному основанию логарифмов

При равных основах приравниваем выражения под логарифмами:
x = (1/2) ^-4 ,
x = 2 ⁴ ,
x = 16.
Ответ: 16 — Д.

Пример 16.3 Решить уравнение log ₂ (-x) = 5.

А	Б	В	Г	9
			-32	1/32	-1/32

Решение: Выполняем раскрытия логарифмов по данной инструкции:
ОДЗ — -x> 0, x <0.
Упростим уравнения
log ₂ (-x) = 5
log ₂ (-x) = 5 • 1
log ₂ (-x) = 5 • log ₂ 2
log ₂ ( -x) = log ₂ 2 ⁵
опустим основы и приравняем логарифмические выражения:
-x = 2 ⁵ ,
-x = 32,
x = -32.
Ответ: -32 — У.

Пример 16.4 Решить уравнение lg (x ² -x) = 1-lg (5).

А

Б

В

Г

9

; 2

-2; 1

-2; 3

-1; 2

Решение: ОДЗ: x ² -x> 0,
x (x-1)> 0
Решим неравенство методом интервалов
x (x-1) = 0,
x ₁ = 0,
x ₂ = 1.

x∈ (-∞; 1) ∪ (1; + ∞).
На этом множестве значений и ищем решение уравнений, сперва сведя к одной основе логарифмы

по теореме Виета:
x ₁ + x ₂ = 1,
x ₁ • x ₂ = -2.
x ₁ = -1,
x ₂ = 2.
Оба корня принадлежат ОДЗ.
Ответ: -1; 2 — Д.

ОДЗ неравенства могут быть сложнее, чем сами уравнения, тогда достаточно сами корни уравнения подставить в неравенство (или систему неравенств) и определить, принадлежать ли корни области допустимых значений логарифмческого уравнения.

Пример 16.5 Сколько корней имеет уравнение lg (x ⁴ -10x ² ) = lg ₃ x ³ ?

одного

А	Б	В	Г
							два	три

Решение: В логарифме имеет биквадратное выражение, которое при условиях на ОДЗ требует вычислений.
Поэтому пойдем другим путем, сначала решим уравнение с логарифмом, в конце концов удовлетворяют найденные «иксы» ОДЗ:

по теореме Виета:
x ₂ + x ₃ = 3
x ₂ • x ₃ = -10.
x ₂ = -2
x ₃ = 5.
Проверим найденные значения 0; -2; 5 являются решениями.
Выписываем ОДЗ и подставляем «иксы»:

1) 0 = 0, поэтому x ₁ = 0 не принадлежит ОДЗ;

2) (-2) ⁴ -10 • (-2) = 16-40 = -24 <0
x ₂ = -2 не принадлежит ОДЗ.2) = lg ₃ x ³ имеет один корень.
Ответ: один — Б.

Пример 16.6 Решить уравнение log ₆ (x-2) + log ₆ (x-1) = 1 и указать промежуток, которому принадлежит его корень.

Решение: Выпишем систему неровностей для ОДЗ:

По правилам, что сумма логарифмов чисел равна логарифму их произведений ln (a) + ln (b) = ln (a • b) и своеству log ₆ 6 = 1 , сведем логарифмы к общему основанию:

При преобразованиях получено квадратное уравнение, корни которого находим по теореме Виета:
x ₁ + x ₂ = 3
x ₁ • x ₂ = -4.
x ₁ = -1 <2 (не принадлежит ОДЗ)
x ₂ = 4.
x = 4 — единственный корень заданного уравнения, он между промежутком (3,9; 4,1).
Ответ: (3,9; 4,1) — Б.

Пример 16.9 Решить уравнение (log ₂ x) ² -2log ₂ x-3 = 0 и указать сумму его корней.

Решение: ОДЗ: x> 0.
логарифмическое уравнение
(log ₂ x) ² -2log ₂ x-3 = 0
сведем к квадратному заменой log ₂ x = t.
t ² -2 • t-3 = 0
По формулам Виета имеем:
t ₁ + t ₂ = 2 — сумма корней уравнения;
t ₁ • t ₂ = 3 — их произведение, тогда
t ₁ = -1 и t ₂ = 3 — корни квадратного уравнения.
Возвращаемся к замене, и вычисляем простые логарифмические уравнения

Оба корня принадлежат ОДЗ, по условию найдем их сумма:
x ₁ + x ₂ = 0,5 + 8 = 8,5.
Ответ: 8,5 — Д.

С простых примеров на раскрытие логарифмических уравнений Вы увидели, что знать несколько формул и базовые свойства логарифма и уже можно самостоятельно решать уравнения.Для простых условий это работает, но напоминаем, что курс ВНО подготовки содержит 40 примеров, причем ряд задач сочетают в себе не только логарифмы, но и корни, модули, показательные выражения. Вы научитесь сводить уравнения к квадратным, логарифмировать и еще много чего нового.

Общие методы решения уравнений. 11 класс

Конспект урока

по алгебре и начала анализа в 11 классе

по теме «Общие методы решения уравнения.

Замена уравнения h (уравнение f ( x )) = h ( g ( 68) ( x ) = г ( x ) »

Учитель математики

МБОУ гимназии № 9

г. Ставрополь

Устименко Л.И.

2014г.

Цели урока:

1. Образовательное — повторение, обобщение, систематизация знаний об общем методе решения уравнений; проверка усвоения на обязательном уровне;

2. Развивающая — развитие умения работать с тестовыми заданиями, формирование навыков самостоятельной работы с большим объемом информации;

3. Воспитательное — воспитание самооценки, коммуникативных способностей.

Литература:

1. Учебник «Алгебра и начала анализа 10-11 класса» А.Г. Мордкович

«Мнемозина». Москва 2009 год;

2. Задачник «Алгебра и начала анализа 10-11 класс» А.Г. Мордкович

«Мнемозина». Москва 2009 год. 3. Справочные материалы. В.А. Гусев, А.Г. Мордкович. «Просвещение»

Москва 1986 год

4. Типовые тестовые задания для подготовки к ЕГЭ

Оборудование : компьютер, проектор, учебные пособия.

Ход урока.

1. Организационный момент .

Сегодня мы проводим урок по теме «Общие методы решения условий.

Замена уравнения h (f (x)) = h (g (x)) уравнением f (x) = g (x) ». Повторим алгоритм решения уравнения, теоретический материал. Вспомним, как решаются показательные, логарифмические, иррациональные уравнения. Все уравнения взяты из тестов ЕГЭ. Поэтому сегодняшний урок- это подготовка к сдаче ЕГЭ.

Откройте тетради, запишите дату, тему урока.

2. Повторение теории .

1. Какие уравнения называются равносильными?

2. Сформулируйте теоремы, приводящие к равносильным уравнениям.

3. Перечислите причины расширения области определения уравнений.

4. В каких случаях может произойти потеря корней и как этого избежать?

5. Назовите этапы решения решений.

3. Устные задания .

1) Какие из чисел 5; 0; -3; являются корнями уравнения

а) 5 ^3х = 3 ^5х ответ: 0

б) = х + 1 ответ: 0

в) ln ( x ³ -15) = ln x ответ: ни одно из чисел

2) Равносильны ли уравнения

а) 2 ^х = 64 и 3х ² -18х = 0

б) 2 ^х = 256 и log ₂ x = 3

в) ln x ² 5 и 2 ln x = 5

3) Решить уравнение

а) = 3 ответ: 11

б) log (x-1) = 2 ответ : 5

в) = — 9 ответ: нет корней

г) 2 ^х = 7 ответ: журнал ₂ 7

д) = 5 ответ: ± 5

3. Решение уравнения из тестов ЕГЭ .

1). 4) —

2) .4 ^х -2 ^х = 0 5) журнал ₃ x + 1 = 2log _x 3

3) 18 ^х -8 · 6 ^х — 9 · 2 ^х = 0

4. Самостоятельная работа.

Вариант 2

25 ^3-х = 0,2

lg (4x-3) = 2lg

log ₂ ² x-4log ₂ x + 3 = 0

15 ^x -9 · 5 ^x -3 ^x + 9 = 0

4 ^x-2 = 0,5

2log = log (9x-20 )

= 3

log ² ₄ x-log ₄ x-2 = 0

3 · 9 ^x -5 · 6 ^x + 2 · 4 ^x = 0

5.П роверка самостоятельной ра боты.

Код правильных ответов

1

2

3

4

5

6

1 вариант

2,5

–5

2

607

; 2; 0

2 вариант

1,5

7

3

16

16; 7

-1; 0

Критерии выставления оценок.

«5» — за 6 верных ответов

«4» — за 4 — 5 верных ответов

«3» — за 3 верных ответа

«2» — менее 3 ответов

6. Домашнее задание:

№ 40.25 (б)

№ 55.9 (б, в)

№ 55.16 (б)

№ 56.20 (а, б)

Презентация «Решение решений». Повторение 11 класс

«Решение вопросов»

Тема:

Цели урока:

Образовательное — обобщение и повторение основного

алгоритмов решения элементарных соотношений,

66 подготовка к ЕГВА-2015 умения выделять главное,

сравнивать, анализировать.

Воспитательная — воспитание умения работать

в сотрудничестве в парах и группе,

оценивать работу товарища.

Воспитание уверенности в собственных силах.

Уравнение 1

Решение.

Возведем в квадрат:

Далее получаем

откуда

Ответ: -2

Уравнение 2

Решение.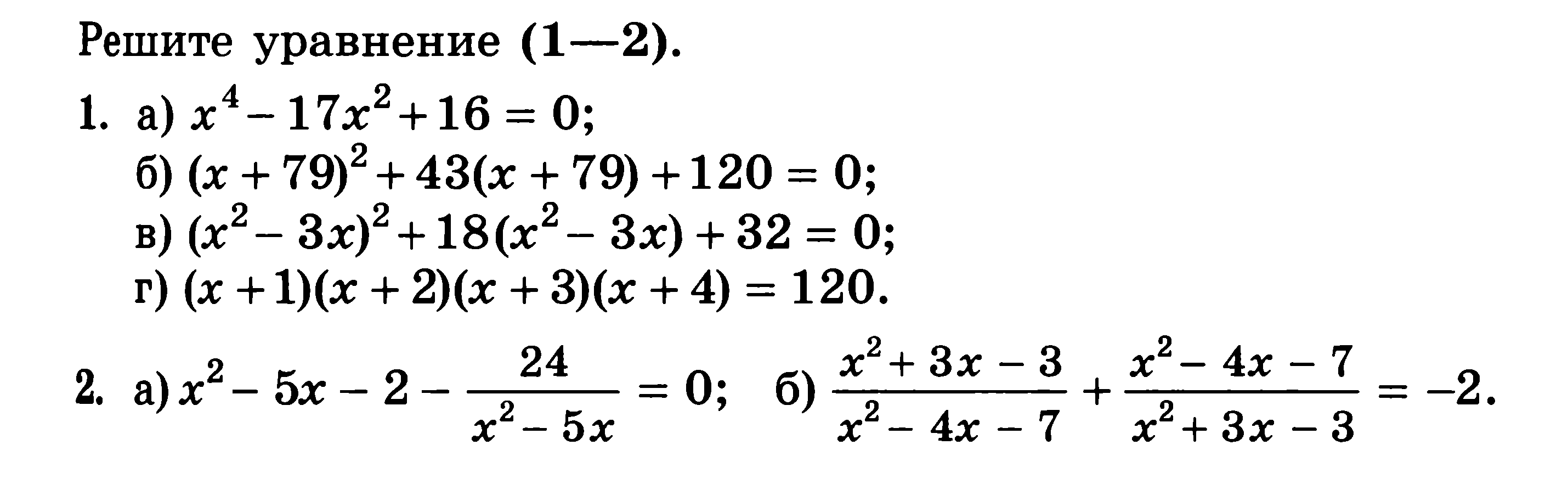 Возведем обе части уравнения в третью степень:

После элементарных преобразований получаем:

Ответ: 23

Уравнение 3

Решение.

Возведя в квадрат обе части уравнения, получим:

Очевидно

откуда

Ответ: 5

Уравнение 4

Решение. Перейдем к одному основанию степени:

От равенства оснований переходим к равенству степеней:

Откуда

Ответ: 3

Уравнение 5

Решение.

Приведя левую и правую части уравнения к степеням числа 6,

получим:

Откуда

значит,

Ответ: 2

Уравнение 6

Решение.

Используя формулу

получаем:

Ответ: 6

Уравнение 7

Решение.

Логарифмы двух выражений равны, если сами выражения выражены и при этом положительны:

Откуда получаем

Ответ: 6

Уравнение 8

Решение.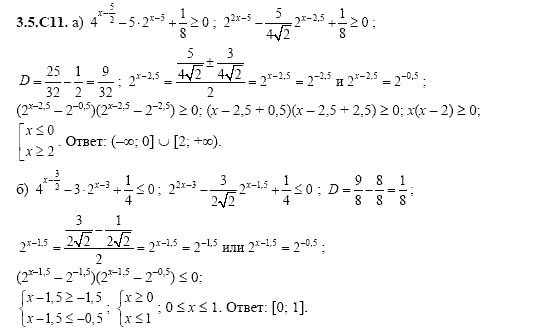

Перепишем уравнение так, чтобы с сторонних сторон

присутствовал логарифм по основанию 4:

Далее, очевидно,

откуда

Ответ: -11

Уравнение 9

Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Решение.

Область допустимых значений: х ≠ 10.

На этой области помножим на знаменатель:

Оба корня лежат в ОДЗ.Меньший из них равенство −3.

Ответ: -3

1.

8.

2.

9.

3.

4.

10.

684

6.

7.

Решить уравнения,

ответить записать в бланки!

журнал 2 (4 — x) = 7

Отдай свой бланк

с ответами соседу!

Проверь соседские ответы!

№ п / п

Ответ

1

103

2

12

3

16

4

10 4

4

6

-5; 5

7

-124

8

0; 18

9

-3

10

-3

Уравнение 10

В ответ укажите наименьший положительный корень

Решение.

Значения

соответствуют большие положительные корни.

Если k = 1 , то x 1 = 6,5 и x 2 = 8,5 . Если k = 0 , то x 3 = 0,5 и x 4 = 2,5 .

Значения

соответствуют меньшие значения корней.

Наименьшим положительным решением является 0,5.

Ответ: 0,5

Уравнения взяты с сайта:

http://reshuege.ru

Сложные функции. Примеры решения методом замены

Дата публикации: 10 апреля 2017 г. .

Ребята, сегодня мы разберем общие методы и наиболее общие идеи, применяемые при решении уравнений.

Замена соотношений $ h (f (x)) = h (g (x)) $ уравнением $ f (x) = g (x) $ .

В общем виде эта формулировка выглядит устрашающе.{g (x)} $, где $ a> 0 $, $ a ≠ 1 $ равносильны уравнению $ f (x) = g (x) $.

Логарифмические уравнения вида: $ log_af (x) = log_ag (x) $, где $ a> 0 $, $ a ≠ 1 $ равносильны уравнению $ f (x) = g (x) $.

Иррациональные уравнения вида: $ \ sqrt [n] {f (x)} = \ sqrt [n] {g (x)} $ равносильны уравнению $ f (x) = g (x) $.

На применение данного метода накладывается серьезное ограничение: функция $ h (x) $ быть строго монотонной, т.е. только возрастать или только убывать (другими словами — одно и тоже значение функция может принимать только один раз).Ребята, вспомните графики показательных, логарифмических иррациональных функций. Они все строго монотонные.
Если функция h (x) — не монотонная, то метод применять нельзя, т.к. возможна потеря корней.

Давайте приведем простой пример. Тригонометрические функции — периодические (между промежутками то возрастают, то убывают).
Уравнение $ sin (15x) = sin (6x) $ — имеет бесконечно много корней. Можно представить два графика и заметить, что они будут бесконечно много раз. Если мы применим метод описанный выше, то получим $ 15х = 6х $. Решением будет $ х = 0 $, т.е. мы потеряли почти все корни.
Итак, применить метод замены $ h (f (x)) = h (g (x)) $ уравнением $ f (x) = g (x) $ можно только в случае строгой монотонности $ h (x) $.

Метод разложения на множители

Уравнения вида $ f (x) * g (x) * h (x) = 0 $, можно заменить совокупностью уравнений: $ f (x) = 0 $, $ g (x) = 0 $, $ h (x) = 0 $. При решении типа уравнения нужно всегда проверять область определения исходного уравнения.2-11x + 30} -1) * ln (x + 9) = 0 $.

Решение.
Используемое уравнение сводится к совокупности уравнений:

Мы вводили уточнения, что стоит проверять область определения. Тогда наша совокупность в самом общем виде сводится к системе:
Эта система имеет довольно громоздкий вид. Можно удобно уравнение и неравенство по отдельности, это кому удобно.
Получилась область допустимых значений: $ x≥2 $. Корни, которые удовлетворяют ОДЗ: $ х = 5 $, $ х = 6 $, $ х = 11 $.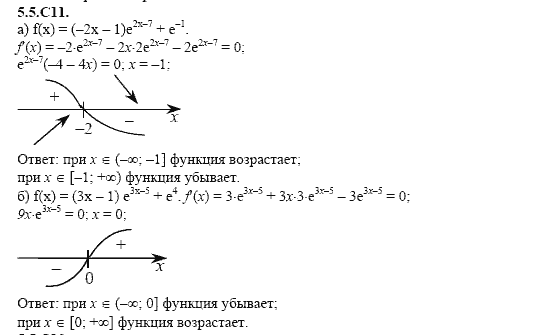

Ответ: 5,6,11.{2} (π + \ frac {x} {2}) — \ frac {1} {2} sin (x) = 0 $.

Поурочные разработки по Геометрии 11 класс

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛАЕ

Глава V. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

§ 1. Координаты точки и координаты вектора

Урок 1. Прямоугольная система координат в пространстве

Урок 2. Координаты вектора

Урок 3. Координаты вектора

Урок 4. Связь между координатами векторов и координат точек

Урок 5.Простейшие задачи в координатах

Урок 6. Простейшие задачи в координатах

Урок 7. Простейшие задачи в координатах. Контрольная работа № 1

§ 2. Скалярное произведение векторов

Урок 8. Угол между векторами. Скалярное произведение векторов

Урок 9. Угол между векторами. Скалярное произведение векторов

Урок 10. Вычисление углов между прямыми и плоскостями

Урок 11. Повторение вопросов теории и решения задач

§ 3. Движения

Урок 12. Движения. Центральная симметрия. Зеркальная симметрия. Осевая симметрия. Параллельный перенос

Урок 13. Решение задач по теме «Движения»

Урок 14. Контрольная работа № 5.2 по теме «Скалярное произведение векторов в косми. Движения »

Урок 15. Зачет по теме «Метод координат в пространстве»

Глава VI. ЦИЛИНДР, КОНУС И ШАР

§ 1. Цилиндр

Урок 16. Понятие цилиндра

Урок 17.Цилиндр. Решение задач

Урок 18. Цилиндр. Решение задач

§ 2. Конус

Урок 19. Конус

Урок 20. Конус

Урок 21. Усеченный конус

§ 3. Сфера

Урок 22. Сфера. Уравнение сферы

Урок 23. Взаимное расположение сферы и плоскости

Урок 24. Касательная плоскость к сфере

Урок 25. Площадь сферы

Урок 26. Разные задачи на многогранники, цилиндр, конус и шар

Урок 27.Разные задачи на многогранники, цилиндр, конус и шар

Урок 28. Разные задачи на многогранники, цилиндр, конус и шар

Урок 29. Зачет по теме: «Тела вращения»

Урок 30. Зачет по теме: «Тела вращения»

Урок 31. Обобщение по теме: «Цилиндр, конус, сфера и шар»

Урок 32. Самостоятельное решение задач

Глава VII. ОБЪЕМЫ ТЕЛ

§ 1. Объемного прямоугольного параллелепипеда

Урок 33. Понятие объема. Объем прямоугольного параллелепипеда

Урок 34.Объем прямоугольного параллелепипеда. Объем прямоугольной призмы, основанием которой является прямоугольный треугольник

Урок 35. Объем прямоугольного параллелепипеда

§ 2. Объем прямой призмы и цилиндра

Урок 36. Объем прямой призмы

Урок 37. Объем цилиндра

Урок 38. Объем цилиндра

§ 3. Объем наклонной призмы, пирамиды и конуса

Урок 39. Вычисление системы тел с помощью интеграла

Урок 40. Объем наклонной призмы

Урок 41.Объем пирамиды

Урок 42. Объем пирамиды

Урок 43. Объем пирамиды

Урок 44. Объем конуса

Урок 45. Решение задач нахождение объема конуса

Урок 46. Контрольная работа № 4

§ 4. Объем шара и площадь сферы

Урок 47. Объем шара

Урок 48. Объем шара

Урок 49. Объем шарового сегмента, шарового слоя, сектора

Урок 50. Объем шарового сегмента, шарового слоя и шарового сектора

Урок 51.Площадь сферы

Урок 52. Решение задач по темам «Объем и шара его частей», «Площадь сферы». Подготовка контр кольной работе

Урок 53. Контрольная работа по темам «Объем шара» и «Площадь сферы»

Урок 54. Зачет по темам «Объем, шара его частей» и «Площадь сферы»

ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ

Урок 55. Аксиомы стереометрии. Повторение

Урок 56. Повторение. Параллельность прямая, параллельность прямая и плоскости.Скрещивающиеся прямые. Параллельность плоскостей

Урок 57. Повторение. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью

Урок 58. Повторение. Двугранный угол. Перпендикулярность плоскостей

Урок 59. Многогранники: параллелепипед, призма, пирамида, площади их поверхностей

Урок 60. Многогранники: параллелепипед, призма, пирамида

Урок 61. Повторение. Векторы в простран. Действия над векторми.Скалярное произведение векторов

Урок 62. Повторение. Цилиндр, конус и шар, площади их поверхностей

Урок 63. Повторение по теме: «Объемы тел»

Основные формулы, используемые в геометрии

Урок 64. Повторение по теме: «Объемы тел»

Урок 65. Повторение по теме: «Многогранники»

Урок 66. Повторение по теме: «Тела вращения»

Урок 67. Повторение по теме: «Комбинации с описанными сферами»

Урок 68. Повторение по теме: «Комбинации с вписанными сферами»

ПРИЛОЖЕНИЕ.КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

Урок 3. Координаты вектора

Урок 5. Простейшие задачи в координатах

Урок 6. Простейшие задачи в координатах

Урок 7. Простейшие задачи в координатах

Урок 9. Угол между векторами. Скалярное произведение векторов

Урок 13. Решение задач по теме «Движения»

Урок 14. Контрольная работа № 5.2 по теме «Скалярное произведение векторов в косми. Движения »

Урок 15.Зачет по теме «Метод в визу»

Урок 18. Цилиндр. Решение задач

Урок 20. Конус

Урок 22. Сфера. Уравнение сферы

Урок 23. Взаимное расположение сферы и плоскости

Урок 28. Разные задачи на многогранники, цилиндр, конус и шар

Урок 29. Зачет по теме: «Тела вращения»

Урок 30. Зачет по теме: «Тела вращения»

Урок 31. Обобщение по теме: «Цилиндр, конус, сфера и шар»

Урок 38.Объем цилиндра

Урок 43. Объем пирамиды

Урок 45. Решение задач нахождение объема конуса

Урок 46. Контрольная работа № 4

Урок 50. Объем шарового сегмента, шарового слоя и шарового сектора

Урок 52. Решение задач по темам «Объем и шара его частей», «Площадь сферы». Подготовка контр кольной работе

Урок 53. Контрольная работа по темам «Объем шара» и «Площадь сферы»

Урок 54. Зачет по темам «Объем, шара его частей» и «Площадь сферы»

Урок 56.Повторение. Параллельность прямая, параллельность прямая и плоскости. Скрещивающиеся прямые. Параллельность плоскостей

Урок 57. Повторение. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью

Урок 60. Многогранники: параллелепипед, призма, пирамида

Урок 65. Повторение по теме «Многогранники»

Урок 66. Повторение по теме: «Тела вращения»

Урок 67. Повторение по теме: «Комбинации с описанными сферами»

Урок 68.Повторение по теме: «Комбинации с вписанными сферами»

.