Материалы школьной программы по математике за 11 класс
В 11 классе заканчивается школьный курс алгебры и основ анализа, а в заключении выпускники сдают экзамен в формате ЕГЭ. Программа 11 класса по математики включает в себя углубленное изучение понятий степени и корня. Кроме того рассматриваются степенная, показательная и логарифмическая функции. Исследуются их графики и выясняются основные свойства.
При изучении логарифмической функции вводится понятие логарифма и его свойства. Рассматриваются основные логарифмические уравнения и неравенства и методы их решения. Помимо этого школьники учатся решать системы уравнений и неравенств.
Курс анализа оканчивается изучением первообразной и определенного интеграла. Изучаются таблица простейших интегралов и применение их для вычисления площадей плоских фигур.
Ниже вы можете найти список материалов по математике для десятиклассников. Каждая отдельная тема написана репетитором и является уникальным образовательным материалом, который поможет ученику разобраться и понять сложные моменты. Данные материалы могут использоваться как учениками и их родителями, так и учителям и репетиторами для своих учеников.
Темы школьной программы 11 класс Математика:
Основное свойство первообразной: теорема и наглядные примерыТри правила нахождения первообразных: алгоритм нахождения и примерыФормула Ньютона — Лейбница: примеры вычисления интеграловПрименение интеграла: нахождение объема тела и вычисление центра масс телаИррациональные уравнения: алгоритм решения и примерыСтепень с рациональным показателем: их основные свойстваПоказательная функция: график и основные свойства функцииРешение показательных уравнений и неравенств: алгоритм решения и примерыЛогарифмы и их свойства: определение и алгоритм решенияЛогарифмическая функция: основные свойства и графикиПонятие об обратной функции: график функции и теоремаПроизводная и первообразная показательной функции: число е и примерыПроизводная и первообразная логарифмической функции: примеры и алгоритмПонятие о дифференциальных уравнениях: примеры использования уравненийНужна помощь в учебе?
Предыдущая тема: Материалы школьной программы по математике за 10 класс
Следующая тема:   Материалы школьной программы по русскому языку за 1 класс
| Твитнуть | Нравится | Нравится |
Все неприличные комментарии будут удаляться.
www.nado5.ru
Рабочая программа по алгебре (11 класс) по теме: Рабочая программа по алгебре для 11 класса
« Рассмотрено и принято» «Согласовано» «Утвердаю»
На заседании МО зам.директора по УВР Директор
Учителей естественно -научного «____»____________2010г Т.Г.Мурыгина/__________/
цикла Архипоской МСО школы№2 Сорокина Н.Е./___________/ «____»____________2010г
Протокол № от
«____»____________2010г
Руководитель МО
Сунцова С.В./___________/
Календарно-тематическое планирование
на 2010-2011 учебный год.
Учебный предмет: Алгебра и начала анализа
Класс 11
Количество часов : в неделю 3 ; всего за год 100
Учитель Сунцова Светлана Владимировна
Планирование составлено на основе программы для общеобразовательных школ ( Министерство образования Р.Ф) и Федерального компонента государственного стандарта общего образования
Используемый учебник Колмогоров А.Н.. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. М., «Просвещение», 2007.
Дополнительная литература
Формы и сроки контроля:
Вид контроля | 1 полугодие | 2 полугодие | год | ||
1 чтв | 2чтв | 3чтв | 4чтв | ||
Контрольные работы | 1 | 2 | 2 | 1 | 6 |
Тесты |
Тематическое планирование составила
Пояснительная записка.
Количество недельных часов 3 Количество часов в год 102
Уровень рабочей программы базовый
Цели и задачи рабочей программы
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
- формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
- овладение языком математики в устной и письменной форме, математическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, продолжения образования и освоения избранной специальности на современном уровне;
- развитие логического мышления, алгоритмической культуры, пространственного воображения, математического мышления и интуиции, творческих способностей, необходимых для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
- воспитание средствами математики культуры личности через знакомство с историей развития математики, эволюцией математических идей; понимания значимости математики для научно-технического прогресса.
Цель изучения курса алгебры и начал анализа в 10-11 классах — систематическое изучение функций как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовка необходимого аппарата для изучения геометрии и физики.
Курс характеризуется содержательным раскрытием понятий, утверждений и методов, относящихся к началам анализа, выявлением их практической значимости.
При изучении вопросов анализа широко используются наглядные соображения. Уровень строгости изложения определяется с учётом общеобразовательной направленности изучения начал анализа и согласуется с уровнем строгости приложений изучаемого материала в смежных дисциплинах. Характерной особенностью курса являются систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков, полученных в курсе алгебры, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения. Учащиеся систематически изучают тригонометрические, показательную и логарифмическую функции и их свойства, тождественные преобразования тригонометрических, показательных и логарифмических выражений и их применение к решению соответствующих уравнений и неравенств, знакомятся с основными понятиями, утверждениями, аппаратом математического анализа в объёме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи.
Нормативные правовые документы, на основании которых разработана рабочая программа:
- Федеральный компонент государственного образовательного стандарта, утвержденный Приказом Минобразования РФ № 1089 от 05.03.2004;
- Примерные программы, созданные на основе федерального компонента государственного образовательного стандарта, рекомендованные Министерством образования и науки РФ приказ № 03-1263 от 07.07.2005. Государственная программа для общеобразовательных школ, гимназий, лицеев. Математика. Составители: Г.М. Кузнецова, Н.Г. Миндюк. Рекомендовано Департаментом образовательных программ и стандартов общего образования Министерства образования Российской Федерации, 2002 год. Программа общеобразовательных учреждений АЛГЕБРА И НАЧАЛА АНАЛИЗА 10-11 классы. Составитель: Т.А. Бурмистрова. Москва «Просвещение», 2009 год.
- Базисный учебный план общеобразовательных учреждений Российской Федерации, утвержденный приказом Минобразования РФ № 1312 от 09.03.2004;
- Федеральный перечень учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2009/2010 учебный год. Утверждён приказом Минобразования РФ № 379 от 09.12.2008.
Данная рабочая программа разработана на основе типовой государственной программы для общеобразовательных школ, гимназий, лицеев. Математика. Составители: Г.М. Кузнецова, Н.Г. Миндюк. Рекомендовано Департаментом образовательных программ и стандартов общего образования Министерства образования Российской Федерации, 2002 год. Использовалась программа общеобразовательных учреждений АЛГЕБРА И НАЧАЛА АНАЛИЗА 10-11 классы. Составитель: Т.А. Бурмистрова. Москва «Просвещение», 2009 год.
СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА
1. Первообразная и интеграл.
Первообразная. Первообразные степенной функции с целым показателем (n ≠ — 1), синуса и косинуса. Простейшие правила нахождения первообразных.
Площадь криволинейной трапеции. Интеграл. Формула Ньютона — Лейбница. Применение интеграла к вычислею площадей и объемов.
Основная цель — ознакомить с интегрированием как операцией, обратной дифференцированию; показать применение интеграла к решению геометрических задач.
Задача отработки навыков нахождения первообразных не ставится, упражнения сводятся к простому применению таблиц и правил нахождения первообразных.
Интеграл вводится на основе рассмотрения задачи о площади криволинейной трапеции и построения интегральных сумм. Формула Ньютона — Лейбница вводится на основе наглядных представлений.
В качестве иллюстрации применения интеграла рассматриваются только задачи о вычислении площадей и объемов. Следует учесть, что формула объема шара выводится при изучении данной темы и используется затем в курсе геометрии.
Материал, касающийся работы переменной силы и нахождения центра масс, не является обязательным.
При изучении темы целесообразно широко применять графические иллюстрации.
2. Показательная и логарифмическая функции.
Понятие о степени с иррациональным показателем. Решение иррациональных уравнений.
Показательная функция, ее свойства и график. Тождественные преобразования показательных уравнений, неравенств и систем.
Логарифм числа. Основные свойства логарифмов. Логарифмическая функция, ее свойства и график. Решение логарифмических уравнений и неравенств.
Производная показательной функции. Число е и натуральный логарифм. Производная степенной функции.
Основная цель — привести в систему и обобщить сведения о степенях; ознакомить с показательной, логарифмической и степенной функциями и их свойствами; научить решать несложные показательные, логарифмические и иррациональные уравнения, их системы.
Следует учесть, что в курсе алгебры девятилетней школы вопросы, связанные со свойствами корней n-й степени и свойствами степеней с рациональным показателем, возможно, не рассматривались, изучение могло быть ограничено действиями со степенями с целым показателем и квадратными корнями. В зависимости от реальной подготовки класса эта тема изучается либо в виде повторения, либо как новый материал.
Серьезное внимание следует уделить работе с основными логарифмическими и показательными тождествами, которые используются как при изложении теоретических вопросов, так и при решении задач.
Исследование показательной, логарифмической и степенной функции производится в соответствии с ранее введённой схемой. Проводится краткий обзор свойств этих функций в зависимости от значений параметров.
Раскрывается роль показательной функции как математической модели, которая находит широкое применение при изучении различных процессов.
Материал об обратной функции не является обязательным.
3. Повторение.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики на профильном уровне в старшей школе ученик должен
знать/понимать:
- значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
- значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
- идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
- значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
- возможности геометрического языка как средства описания свойств реальных предметов и их взаимного расположения;
- универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
- различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
- роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
- вероятностный характер различных процессов и закономерностей окружающего мира.
В результате изучения курса алгебры и начал анализа учащиеся 11 классов должны
уметь:
- находить значения корня, степени, логарифма с помощью таблиц;
- выполнять тождественные преобразования иррациональных, показательных, логарифмических выражений;
- решать иррациональные, показательные, логарифмические уравнения;
- иметь представление о графическом способе решения уравнений и неравенств;
- решать иррациональные, показательные, логарифм и неравенства;
- иметь наглядные представления об основных свойствах функции, иллюстрировать их с помощью графических изображений;
- изображать графики основных элементарных функций; опираясь на график, описывать свойства этих функций; уметь использовать свойства функции для уравнения и оценки её значений;
- представлять комплексное число в алгебраической и тригонометрической формах;
- выполнять операции сложения, вычитания, умножения и деления чисел, записанных в алгебраической форме, операции умножения и деления чисел, представленных в тригонометрической форме;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
- решения прикладных задач, в том числе социально-экономических физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
- построения и исследования простейших математических моделей;
- анализа реальных числовых данных, представленных в виде диаграмм, графиков;
- анализа информации статистического характера;
- описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Цель изучения курса алгебры и начал анализа в 10-11 классах — систематическое изучение функций как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовка необходимого аппарата для изучения геометрии и физики.
Курс характеризуется содержательным раскрытием понятий, утверждений и методов, относящихся к началам анализа, выявлением их практической значимости. При изучении вопросов анализа широко используются наглядные соображения. Уровень строгости изложения определяется с учетом общеобразовательной направленности изучения начал анализа и согласуется с уровнем строгости приложений изучаемого материала в смежных дисциплинах. Характерной особенностью курса является систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков, полученных в курсе алгебры, что осуществляется как при изучении материала, так и при проведении обобщающего повторения.
Учащиеся систематически изучают тригонометрические, показательную и логарифмическую функции и их свойства, тождественные преобразования тригонометрических, показательных и логарифмических выражений и их применение к решению соответствующих уравнений и неравенств, знакомятся с основными понятиями, утверждениями, аппаратом математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
2 | 3 | 4 | 5 | 6 | 9 | 10 | |
Дата | № | Тема урока | Кол-во часов | Ученик должен знать | Ученик должен уметь | Домашнее задание | Примечание |
Повторение | 4 | ||||||
1.09 | Повторение. Применение производной | 1 | Понятия: производная, дифференцирование, непрерывная функция Формулы производных, правила дифференцирования | Находить производные функций, определять промежутки непрерывности функций | П. 12-19 №217 а №219 ав | МУР первый роу | |
3.09 | Повторение. Применение производной | 1 | *№223 а №220 бв | МУР примен. произ | |||
7.09 | Повторение. Применение производной | 1 | П. 18-21 №224 (1) 234 | ||||
8.09 | Повторение. Применение производной | 1 | *№4.178, 5.87 | ||||
10.09 | Повторение. Применение производной | ||||||
Первообразная и интеграл | 11 | ||||||
14.09 | Определение первообразной | 1 | Определение первообразной | Определять является ли заданная функция первообразной | П. 26 № 326 вг 327 вг,330(вг) | цор | |
15.09 | Определение первообразной | 1 | 338(вг) *№330 аб | цор | |||
17.09 | Основное свойство первообразных | 1 | Основное свойство первообразной, геометрический смысл основного свойства первообразной Таблица первообразных для элементарных функций | Основное свойство первообразной, геометрический смысл основного свойства первообразной Таблица первообразных для элементарных функций | П. 27,1,2 №335 аб №336 а *334 а | цор | |
21.09 | Основное свойство первообразных | 1 | П. 26,№337 аб, 336 б | цор | |||
22.09 | Правила нахождения первообразных | 1 | П. 28 №342 аб №343 а | цор | |||
24.09 | Правила нахождения первообразных | 1 | 342(вг),345(вг | цор | |||
28.09 | Правила нахождения первообразных | 1 | 343(вг)344(вг) 346(аб) | цор | |||
29.09 | Правила нахождения первообразных | цор | |||||
1.10 | Площадь криволинейной трапеции | 1 | Формула для нахождения площади криволинейной трапеции | Находить площадь криволинейной трапеции | 353(вг),354(вг | цор | |
5.10 | Площадь криволинейной трапеции | 1 | 355вг,356вг | цор | |||
6.10 | Понятие об определенном интеграле. Формула Ньютона — Лейбница | цор | |||||
8.10 | Применение формулы Ньютона – Лейбница при вычислении площадей | 1 | цор | ||||
12.10 | Контрольная работа №1 по теме «Первообразная и интеграл» | 1 | Ппа 120 | ||||
Обобщение понятия степени | 10 | ||||||
13.10 | Корень n – ой степени и его свойства | 1 | Определение корня n-й степени Условие существования корня п-й степени Свойства корня n-й степени | Вычислять корень n-й степени Решать уравнения вида хn=а | 381вг,382вг,383вг | цор | |
15.10 | Корень n- ой степени и его свойства | 1 | 386вг,387вг,388вг | цор | |||
19.10 | Решение иррациональных уравнений | 1 | Понятие иррациональное уравнение Алгоритм решения иррациональных уравнений | Решать иррациональные уравнения | 417 | цор | |
20.10 | Решение иррациональных уравнений | 1 | 418вг,419вг,420вг | цор | |||
22.10 | Решение иррациональных уравнений | 1 | 422вг,423вг | цор | |||
26.10 | Степень с рациональным показателем | 1 | Определение и свойства степени с рациональным показателем | Представлять корень n-й степени в виде степени с рациональным показателем, степень в виде корня n-й степени Находить значение степени с рациональным показателем | 429вг,430вг,431вг | цор | |
27.10 | Степень с рациональным показателем | 1 | 432вг,433вг | цор | |||
29.10 | Действия над степенями | 1 | Определение и свойства степени с рациональным показателем | 438в,439вг,443вг | цор | ||
II четверть | |||||||
9.11 | Действия над степенями | 1 | 437,438г | ||||
10.11 | Контрольная работа №2 по теме «Обобщение понятия степени» | 1 | Ппа170 | ||||
Показательная и логарифмическая функции | 20 | ||||||
12.11 | Показательная функция | 1 | Определение и свойства показательной функции | Строить график показательной ф-ии Находить область определения показательной ф-ии | 445вг,446вг,448вг | ||
16.11 | Показательная функция | 1 | МУР граики эл-ых ункций | ||||
17.11 | Показательная функция | 450вг,456вг 457вг | цор | ||||
19.11 | Решение показательных уравнений | 1 | Определение и свойства показательной функции | Сравнивать числа, используя свойства показательной ф-ии, упрощать выражения, содержащие степени | 460вг,461вг,462вг | цор | |
23.11 | Решение показательных уравнений | 1 | 464вг,463вг,468вг | цор | |||
24.11 | Решение показательных уравнений | цор | |||||
26.11 | Решение показательных уравнений | цор | |||||
30.11 | Решение показательных неравенств | 1 | Алгоритм решения показательных неравенств | Решать показательные неравентсва, уравнения | 466вг,467вг | цор | |
1.12 | Решение показательных неравенств | 1 | 472вг,473вг | цор | |||
3.12 | Решение показательных неравенств | цор | |||||
7.12 | Решение систем уравнений | 1 | цор | ||||
8.12 | Решение систем уравнений | 1 | цор | ||||
10.12 | Контрольная работа №3 «Показательная функция» | 1 | ппа | ||||
14.12 | Логарифмы и их свойства | 1 | Определение логарифма Понятия: логарифм, десятичный логарифм | Вычислять логарифмы, записывать числа в виде логарифмов, применять свойства логарифмов для упрощения выражений | 499вг,500вг | Цор урок | |
15.12 | Логарифмы и их свойства | 1 | 501вг,503вг,504вг | цор | |||
17.12 | Логарифмы и их свойства | 1 | цор | ||||
21.12 | Логарифмы и их свойства | 1 | цор | ||||
22.12 | Логарифмическая функция, её свойства и график | 1 | Определение и свойства логарифмической ф-ии | Находить область определения логарифмической ф-ии, сравнивать степени | цор | ||
24.12 | Логарифмическая функция, её свойства и график | 1 | |||||
III четверть | |||||||
11.01 | Решение логарифмических уравнений | Общий вид, алгоритм решения простейших логарифмических ур-ий алгоритмы решения логарифмических ур-ий | Решать логарифмические ур-ия | 512вг,513вг,514вг | |||
12.01 | Решение логарифмических уравнений | 1 | 518вг,519вг | ||||
14.01 | Решение логарифмических уравнений | 1 | 520вг,521вг 522а | ||||
18.01 | Решение логарифмических уравнений | 1 | |||||
19.01 | Решение логарифмических уравнений | 1 | |||||
21.01 | Решение логарифмических уравнений | ||||||
25.01 | Решение логарифмических неравенств | 1 | Алгоритм решения логарифмических неравенств | Решать логарифмические неравенства | 516вг,517вг | ||
26.01 | Решение логарифмических неравенств | 1 | 525вг,526вг 527а | ||||
28.01 | Зачет по теме «Показательная и логарифмическая функции» | 1 | |||||
1.02 | Контрольная работа №4 по теме «Показательная и логарифмическая функции» | 1 | |||||
Производная показательной и логарифмической функции | 16 | ||||||
2.02 | Производная показательной функции | 1 | Понятия: натуральный логарифм, экспонента | Находить производную экспоненты, вычислять натуральные логарифмы | 538вг,539вг,540в | ||
4.02 | Производная показательной функции | 1 | 540г,543вг,544б | ||||
8.02 | Производная показательной функции | ||||||
9.02 | Число е. Первообразная показательной функции | 1 | Формулы производной и первообразной показательной функции | Вычислять интегралы, находить производные и первообразные показательной функции | 541вг,542вг | ||
11.02 | Число е. Первообразная показательной функции | 1 | |||||
15.02 | Число е. Первообразная показательной функции | 1 | |||||
16.02 | Исследование функций, вычисление площадей | 1 | |||||
18.02 | Исследование функций, вычисление площадей | 1 | |||||
22.02 | Производная логарифмической функции | 1 | Формула производной логарифмической функции | Находить производные логарифмических функций | 549вг,550вг,552вг | ||
25.02 | Производная логарифмической функции | 1 | 551вг,553вг,555вг | ||||
1.03 | Производная логарифмической функции | ||||||
2.03 | Первообразная функции 1/х | 1 | |||||
4.03 | Исследование функций, вычисление площадей | 1 | |||||
9.03 | Исследование функций, вычисление площадей | 1 | |||||
11.03 | Степенная функция и её производная | 1 | Строить график степенной функции, исследовать степенную функцию | 558вг,560вг | |||
15.03 | Первообразная степенной функции | 1 | 566 | ||||
16.03 | Понятие о дифференциальных уравнениях | 1 | Понятие дифференциальное уравнение | Доказывать, что данная функция является решением дифференциального уравнения | 570,572вг,573вг, | ||
18.03 | Контрольная работа №5 по теме «Производная показательной и логарифмической функций» | 1 | |||||
Повторение | 4 | ||||||
22.03 | Тригонометрические функции и их свойства | ||||||
23.03 | Тригонометрический функции и их свойства | ||||||
IV четверть | |||||||
5.04 | Тригонометрические уравнения | ||||||
6.04 | Тригонометрические уравнения | ||||||
8.04 | Тригонометрические уравнения | ||||||
12.04 | Правила вычисления производных | ||||||
13.04 | Правила вычисления производных | ||||||
15.04 | Правила вычисления производных | ||||||
19.04 | Применение производной | ||||||
20.04 | Применение производной | ||||||
22.04 | Применение производной | ||||||
26.04 | Первообразная и интеграл | ||||||
27.04 | Первообразная и интеграл | ||||||
29.04 | Первообразная и интеграл | ||||||
3.05 | Иррациональные уравнения | ||||||
4.05 | Иррациональные уравнения | ||||||
6.05 | Показательные и логарифмические уравнения | ||||||
10.05 | Показательные и логарифмические уравнения | ||||||
11.05 | Показательные и логарифмические уравнения | ||||||
13.05 | Решение задач на проценты | ||||||
17.05 | Решение задач на проценты | ||||||
18.05 | Чтение графиков. | ||||||
20.05 | Контрольная работа №6 ( итоговая ) | ||||||
24.05 | |||||||
25.05 | Анализ к.р | 2 |
МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КУРСА
Основные учебники:
Алгебра и начала анализа: учеб. для 10—11 кл. общеобразоват.
учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; под.ред. А. Н. Колмогорова. — М.: Просвещение, 2004.
Методические пособия для учителя:
- Программа для общеобразовательных учреждений. Математика. Министерство образования Российской Федерации.
- Федеральный общеобразовательный стандарт. Вестник образования. №12,2004.
- Программы общеобразовательных учреждений. АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА 10-11классы. Составитель: С.А. Бурмистрова. Москва. «Просвещение», 2009 год.
- Алгебра для 9 класса: учебное пособие для учащихся школ и классов с углубленным изучением математики / H. Я. Виленкин, Г. С. Сурвилло, А. С. Симонов, А. И. Кудрявцев; под ред. H. Я. Виленкина. — М.: Просвещение, 2001.
- Алгебра и начала анализа: учебник для 11 классов общеобразовательных учреждений / С. М. Никольский, М. К. Потапов, H. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2003.
- Алгебра и начала анализа: учебник для 10 класса общеобразовательных учреждений / С. М. Никольский, М. К. Потапов, H. H. Решетников, А. В. Шевкин. — М.: Просвещение, 2003.
- Ю. В. Прохоров «Математический энциклопедический словарь», издательство Москва «Советская энциклопедия», 1998 год.
- П.И. Алтынов. Тесты. Издательский дом «Дрофа», 1997.
- А.П.Ершов, В.В. Голобородько. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 класса. «ИЛЕКСА». Москва.2004
- М.А. Максимовская. Тесты. Математика (5-11 кл.). М.:ООО «Агенство «КРПА «Олимп»: ООО «Издательство АСТ», 2002.
- П.И. Алтынов. Математика. 2600 тестов и проверочных заданий для школьников и поступающих в вузы. М., Издательский дом «Дрофа», 1999.
- П.И. Алтынов. Тесты. Алгебра и начала анализа 10-11 классы. М., Издательский дом «Дрофа», 1999.
- Газета «Математика» № 26,2000
- Журнал «Математика в школе» № 6, 2001.
- Л.И. Звавич, Л.Я. Шляпочкин. Контрольные и проверочные работы по алгебре и началам анализа для 10-11 классов. Москва. Издательский дом «Дрофа», 1996.
nsportal.ru
Рабочая программа по алгебре (11 класс) на тему: рабочая программа 11 класс алгебра
№ | Раздел программы | Тема урока | Кол-во часов | Тип урока | Планируемый результат | Вид контроля, измерителя | ЦОР | Материал для сам.работы | Дата |
1 | Повторение по теме «Производная» | 1 | КУ | ||||||
2 | Повторение по теме «Правила дифференцирования» | 1 | КУ | СР | |||||
3 | Повторение по теме «Касательная к графику функции в точке» | 1 | КУ | СР | |||||
4 | Повторение по теме «Наибольшее и наименьшее значение функции. Экстремумы» | 1 | КУ | СР | |||||
5 | Гл.1 Многочлены (10 часов) | Многочлены от одной переменной. Определения и примеры | 1 | УСН | Учащиеся могут выполнять арифметические операции над многочленами от одной переменной, делить многочлен на многочлен с остатком, раскладывать многочлены на множители. | През | |||
6 | Многочлены от одной переменной. Решение упражнений | 1 | УПЗ | ||||||
7 | Многочлены от одной переменной. Систематизация материала | 1 | УОМ | ||||||
8 | Многочлены от нескольких переменных. Определения и примеры | 1 | УНЗ | Учащиеся могут различать однородные, симметрические многочлены от нескольких переменных и их системы, знают способы их решения. Учащиеся могут решать различными способами задания с однородными и симметрическими многочленами от нескольких переменных. | През | ||||
9 | Многочлены от нескольких переменных. Методы решения задач | 1 | УПЗ | ||||||
10 | Многочлены от нескольких переменных. Методы решения задач. Систематизация материала | 1 | УОМ | СР | |||||
11 | Уравнения высших степеней. Теорема Безу | 1 | УСЗ | Учащиеся знают методы решения уравнений высших степеней: метод разложения на множители и метод введения новой переменной; знают метод решения Учащиеся могут применять кроме метода разложения на множители и метода введения новой переменной, при решении уравнений высших степеней, используют различные функционально – графические приемы. возвратных уравнений. | |||||
12 | Уравнений высших степеней. Различные способы нахождения корней | 1 | УПЗ | ||||||
13 | Уравнений высших степеней. Различные способы нахождения корней. Систематизация материала | 1 | УОМ | ||||||
14 | Контрольная работа №1 | 1 | УККЗ | ||||||
15 | Гл. 2 Степени и корни. Степенные функции (24 часа) | Понятие корня n-ой степени из действительного числа | 1 | УНМ | Учащиеся знают определение корня n-ой степени, его свойства, умеют выполнять преобразования выражений, содержащих радикалы, содержащие корни n-ой степени. Умеют вступать в речевое общение. Могут самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. | През | |||
16 | Понятие корня n-ой степени из действительного числа. Решение упражнений | 1 | УПЗ | ||||||
17 | Функции , их свойства и график | 1 | УНЗ | Знают, как определять значение функции по значению аргумента при различных способах задания функции; строить график функции. Используют для решения познавательных задач справочную литературу. Умеют применять свойства функций. Умеют исследовать функцию по схеме, при построении графиков использовать правила преобразования графиков. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. Умеют обосновывать суждения, давать определения, приводить доказательства, примеры. | През | ||||
18 | Функции , их свойства и график. Решение упражнений | 1 | УПЗ | ||||||
19 | Функции , их свойства и график. Систематизация материала | 1 | УОМ | ТЕСТ | |||||
20 | Свойства корня n-ой степени | 1 | УНЗ | Знают свойства корня n-й степени, умеют преобразовывать выражения, содержащие радикалы. Умеют определять понятия, приводить доказательства. Умеют применять свойства корня n-й степени, умеют на творческом уровне пользоваться ими при решении задач. Умеют находить и использовать информацию. | През | ||||
21 | Свойства корня n-ой степени. Решение упражнений | 1 | УПЗ | ||||||
22 | Свойства корня n-ой степени. Систематизация материала | 1 | УОМ | ТЕСТ | |||||
23 | Преобразование выражений, содержащих радикалы | 1 | УНЗ | Знают, как выполнять арифметические действия, сочетая устные и письменные приемы. Знают, как находить значения корня натуральной степени, по известным формулам и правилам преобразования буквенных выражений, включающих радикалы. Умеют выполнять арифметические действия, сочетая устные и письменные приемы; Умеют находить значения корня натуральной степени, по известным формулам и правилам преобразования буквенных выражений, включающих радикалы | |||||
24 | Преобразование выражений, содержащих радикалы. Решение упражнений | 1 | УПЗ | ||||||
25 | Преобразование выражений, содержащих радикалы. Систематизация материала | 1 | УОМ | СР | |||||
26 | Преобразование выражений, содержащих радикалы. Подготовка к контрольной работе | 1 | УКорЗ | ||||||
27 | Контрольная работа №2 | 1 | УКЗ | ||||||
28 | Анализ контрольной работы | 1 | УСМ | През | |||||
29 | Степень с рациональным показателем. Определения и примеры | 1 | УНЗ | Знают, как находить значения степени с рациональным показателем; проводить по известным формулам и правилам преобразования буквенных выражений, Умеют обобщать понятие о показателе степени, выполняя преобразование выражений, содержащих радикалы. Умеют обосновывать суждения, давать определения, приводить доказательства, примеры включающих степени. | |||||
30 | Степень с рациональным показателем. Решение упражнений | 1 | УПЗ | ||||||
31 | Степень с рациональным показателем. Систематизация материала | 1 | УОМ | ТЕСТ | |||||
32 | Степенные функции, график и свойства | 1 | УНЗ | Знают, как строить графики степенных функций при различных значениях показателя; описывают по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения. Умеют строить графики степенных функций при различных значениях показателя; описывают по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения | През | ||||
33 | Степенные функции, график и свойства. Решение упражнений | 1 | УПЗ | ||||||
34 | Степенные функции, график и свойства. Работа с графиками | 1 | УПЗ | ||||||
35 | Степенные функции, график и свойства. Систематизация материала | 1 | УОМ | ТЕСТ | |||||
36 | Извлечение корня из комплексных чисел | 1 | УНЗ | Знают, как выполнять арифметические действия над комплексными числами в разных формах записи. Знают комплексно сопряженные числа, могут извлекать корень из комплексного числа. Могут привести примеры, подобрать аргументы, сформулировать выводы. Умеют составлять текст научного стиля. | |||||
37 | Извлечение корня из комплексных чисел. Подготовка к контрольной работе | 1 | УКорЗ | През | |||||
38 | Контрольная работа №3 | 1 | УКЗ | ||||||
39 | Гл. 3 Показательная и логарифмическая функции (31 час) | Показательная функция, ее свойства и график | 1 | УНЗ | Знают определения показательной функции, умеют формулировать ее свойства, строить схематический график любой показательной функции. Умеют проводить описание свойств показательной функции по заданной формуле, применяя возможные преобразования графиков. Умеют работать с учебником, отбирать и структурировать материал. | През | |||
40 | Показательная функция, ее свойства и график. Решение упражнений | 1 | УПЗ | ||||||
41 | Показательная функция, ее свойства и график. Систематизация материала | 1 | УОМ | ||||||
42 | Решение показательных уравнений и неравенств | 1 | УНЗ | Знают показательные уравнения и умеют решать простейшие показательные уравнения, их системы; использовать для приближенного решения уравнений графический метод. Умеют решать показательные уравнения, применяя комбинацию нескольких алгоритмов. Умеют изображать на координатной плоскости множества решений простейших уравнений, и их систем. Имеют представление о показательном неравенстве и умеют решать простейшие показательные неравенства, их системы; использовать для приближенного решения неравенств графический метод. Умеют решать показательные неравенства, применяя комбинацию нескольких алгоритмов. Умеют изображать на координатной плоскости множества решений простейших неравенств и их систем. | |||||
43 | Решение показательных уравнений | 1 | УПЗ | ||||||
44 | Решение показательных неравенств | 1 | УНЗ | ||||||
45 | Решение показательных уравнений и неравенств. Решение упражнений | УПЗ | |||||||
46 | Решение показательных уравнений и неравенств. Систематизация материала | 1 | УОМ | СР | |||||
47 | Логарифм. Определения и примеры | 1 | УНЗ | Знают, как использовать связь между степенью и логарифмом, понимают их взаимно противоположное значение, умеют вычислять логарифм числа по определению. Умеют передавать информацию сжато, полно, выборочно. Зная понятие логарифма и некоторые его свойства, выполняют преобразования логарифмических выражений и умеют вычислять логарифмы чисел. | През | ||||
48 | Логарифм. Решение упражнений | 1 | УПЗ | ||||||
49 | Логарифмическая функция, ее свойства и график | 1 | УНЗ | Имеют представление об определение логарифмической функции, ее свойства в зависимости от основания. Знают, как применить определение логарифмической функции, ее свойства в зависимости от основания. Умеют определять значение функции по значению аргумента при различных способах задания функции. Умеют применять свойства логарифмической функции. Умеют на творческом уровне исследовать функцию по схеме. Владеют приёмами построения и исследования математических моделей. | През | ||||
50 | Логарифмическая функция, ее свойства и график. Решение упражнений | 1 | УПЗ | ||||||
51 | Логарифмическая функция, ее свойства и график. Подготовка к контрольной работе | 1 | УПЗ | ||||||
52 | Зачет «Логарифмическая функция. Показательные уравнений и неравенства» | 1 | УКорЗ | ТЕСТ | |||||
53 | Контрольная работа №4 | 1 | УКЗ | ||||||
54 | Свойства логарифмов | 1 | УНЗ | Знают свойства логарифмов. Умеют выполнять арифметические действия, сочетая устные и письменные приемы; находить значения логарифма; проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы. Знают формулу перехода к новому основанию и два частных случая формулы перехода к новому основанию логарифма Умеют применять свойства логарифмов. Умеют применять формулу основанию и два частных случая формулы перехода к новому основанию логарифма Умеют на творческом уровне проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы. Умеют обосновывать суждения, давать определения, приводить доказательства, примеры | През | ||||
55 | Свойства логарифмов. Решение упражнений | 1 | УПЗ | ||||||
56 | Свойства логарифмов. Систематизация материала | 1 | УОМ | ТЕСТ | |||||
57 | Свойства логарифмов. Итоговый урок по теме | 1 | КУ | ||||||
58 | Решение логарифмических уравнений и неравенств | 1 | УНЗ | Знают о методах решения логарифмических уравнений. Умеют решать простейшие логарифмические уравнения, их системы; использовать для приближенного решения уравнений графический метод; изображать на координатной плоскости множества решений простейших уравнений и их систем. Знают алгоритм решения логарифмического неравенства в зависимости от основания. Умеют решать простейшие логарифмические неравенства, применяя метод замены переменных для сведении логарифмического неравенства к рациональному виду. Умеют решать простейшие логарифмические неравенства устно, применяют свойства монотонности логарифмической функции при решении более сложных неравенств. Умеют использовать для приближенного решения неравенств графический метод. | През | ||||
59 | Решение простейших логарифмических уравнений и неравенств | 1 | УПЗ | ||||||
60 | Решение логарифмических уравнений | 1 | УПЗ | ||||||
61 | Решение логарифмических неравенств | 1 | УПЗ | ||||||
62 | Решение логарифмических уравнений и неравенств. Решение упражнений | 1 | УПЗ | ||||||
63 | Решение логарифмических уравнений и неравенств. Систематизация материала | 1 | УОМ | ||||||
64 | Решение логарифмических уравнений и неравенств. Итоговый урок по теме | 1 | КУ | ||||||
65 | Производная показательной функции. Число e | 1 | УНЗ | Знают формулы для нахождения производной и первообразной показательной и логарифмической функций. Умеют вычислять производные и первообразные простейших показательных и логарифмических функций. Умеют применять формулы для нахождения производной и первообразной показательной и логарифмической функций. Умеют решать практические задачи с помощью аппарата дифференциального и интегрального исчисления. | През | ||||
66 | Производная логарифмической функции | 1 | УПЗ | ||||||
67 | Производная логарифмической функции | 1 | УПЗ | ||||||
68 | Решение упражнений. Подготовка к контрольной работе | 1 | КУ | ||||||
69 | Контрольная работа №5 | 1 | УКЗ | ||||||
70 | Гл. 4 Первообразная и интеграл (9 часов) | Первообразная и неопределенный интеграл. Определения и примеры | 1 | УНЗ | Знают понятие первообразной и неопределенного интеграла. Умеют находить первообразные для суммы функций и произведения функции на число, используя справочные материалы. Знают, как вычисляются неопределенные интегралы. Умеют пользоваться понятием первообразной и неопределенного интеграла Умеют находить первообразные для суммы функций и произведения функции на число, а также могут применять свойства неопределенных интегралов в сложных творческих задачах. Применяют понятие первообразной и неопределенного интеграла. Умеют находить первообразные для суммы функций и произведения функции на число, используя справочные материалы. Знают, как вычисляются неопределенные интегралы. Умеют пользоваться понятием первообразной и неопределенного интеграла Умеют находить первообразные для суммы функций и произведения функции на число, а также могут применять свойства неопределенных интегралов сложных творческих задачах. | През | |||
71 | Первообразная и неопределенный интеграл. Решение упражнений | 1 | УПЗ | ||||||
72 | Первообразная и неопределенный интеграл. | 1 | КУ | КД | |||||
73 | Определенный интеграл. Определения и примеры | 1 | УНЗ | Знают формулу Ньютона – Лейбница. Умеют вычислять в простейших заданиях площади с использованием первообразной. Умеют извлекать необходимую информацию из учебно-научных текстов. Умеют применять формулу Ньютона – Лейбница. Умеют применять ее для вычисления площади криволинейной трапеции в сложных заданиях. Умеют обосновывать суждения, давать определения, приводить доказательства, примеры. | През | ||||
74 | Определенный интеграл | 1 | КУ | ||||||
75 | Определенный интеграл. Решение упражнений | 1 | УПЗ | ||||||
76 | Определенный интеграл. Систематизация материала | 1 | УОМ | СР | |||||
77 | Определенный интеграл. Подготовка к контрольной работе | 1 | КУ | ||||||
78 | Контрольная работа №6 | 1 | УКЗ | ||||||
79 | Гл.5 Элементы теории вероятностей и математической статистики (9часов) | Вероятность и геометрия | 1 | УНЗ | Знают классическую вероятностную схему для равновозможных испытаниях; знают правило геометрических вероятностей. Используют компьютерные технологии для создания базы данных. Могут по условию текстовой задачи на нахождение вероятности строить геометрическую модель и переходить к корректно поставленной математической задаче. Умеют составлять текст научного стиля. | През | |||
80 | Вероятность и геометрия. Решение упражнений | 1 | УПЗ | ||||||
81 | Независимые повторения испытаний с двумя исходами | 1 | УНЗ | Знают вероятностную схему Бернулли, теорему Бернулли, понятие многогранник распределения. Умеют добывать информацию по заданной теме в источниках различного типа. Учащиеся решают вероятностные задачи, используя вероятностную схему Бернулли, теорему Бернулли, понятие многогранник распределения. Могут привести примеры, подобрать аргументы, сформулировать выводы. | През | ||||
82 | Независимые повторения испытаний с двумя исходами. Решение упражнений | 1 | УПЗ | ||||||
83 | Независимые повторения испытаний с двумя исходами. Систематизация материала | 1 | УОМ | ||||||
84 | Статистические методы обработки информации | 1 | УНЗ | Знают понятия: общий ряд данных, выборка, варианта, кратность варианты, таблица распределения, частота варианты, график распределения частот. Знают способы представления информации. Умеют определять понятия, приводить доказательства. Находят частоту события, используя собственные наблюдения и готовые статистические данные, понимают статистические утверждения, встречающиеся в повседневной жизни. Используют компьютерные технологии для создания базы данных. | През | ||||
85 | Статистические методы обработки информации | УПЗ | |||||||
86 | Гауссова кривая. Закон больших чисел | 1 | УНЗ | Знают график, какой функции называется гауссовой кривой; алгоритм использования кривой нормального распределения и функции площади под гауссовой кривой в приближенных вычислениях, закон больших чисел. Решают вероятностные задачи, используя знания о гауссовой кривой; алгоритм использования кривой нормального распределения и функции площади под гауссовой кривой в приближенных вычислениях, закон больших чисел. | През | ||||
87 | Гауссова кривая. Закон больших чисел. Решение упражнений | 1 | УПЗ | СР | |||||
88 | Гл.6 Уравнения и неравенства. Системы уравнений и неравенств (33 часа) | Равносильность уравнений. Определения и примеры | 1 | УНЗ | Знают основные способы равносильных переходов. Имеют представление о возможных потерях или приобретениях корней и путях исправления данных ошибок, умеют выполнять проверку найденного решения с помощью подстановки и учета области допустимых значений. Умеют производить равносильные переходы с целью упрощения уравнения. Умеют доказывать равносильность уравнений на основе теорем равносильности. Могут самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. | ||||
89 | Равносильность уравнений. | 1 | УПЗ | ||||||
90 | Равносильность уравнений. Решение упражнений | 1 | УПЗ | ||||||
91 | Равносильность уравнений. Систематизация материала | 1 | УОМ | СР | |||||
92 | Общие методы решения уравнений | 1 | УНЗ | Знают основные методы решения алгебраических уравнений: метод разложения на множители и метод введения новой переменной. Умеют применять их при решении рациональных уравнений степени выше 2. Умеют решать рациональные уравнения высших степеней методами разложения на множители или введением новой переменной, решают рациональные уравнения, содержащие модуль. Умеют извлекать необходимую информацию из учебно-научных текстов. | През | ||||
93 | Общие методы решения уравнений. Отработка навыков решения | 1 | УПЗ | ||||||
94 | Общие методы решения уравнений. Систематизация материала | 1 | УОМ | ||||||
95 | Равносильность неравенств. Определения и примеры | 1 | УНЗ | Знают основные способы равносильных переходов. Умеют выполнять проверку найденного решения с помощью подстановки и учета области допустимых значений. Умеют составлять текст научного стиля. Умеют производить равносильные переходы с целью упрощения уравнения. Умеют доказывать равносильность неравенств на основе теорем равносильности. Умеют обосновывать суждения, давать определения, приводить доказательства, примеры. Умеют предвидеть возможную потерю или приобретение корня и находить пути возможного избегания ошибок. | |||||
96 | Равносильность неравенств. Решение упражнений | 1 | УПЗ | ||||||
97 | Равносильность неравенств. Систематизация материала | 1 | УОМ | СР | |||||
98 | Уравнений и неравенства с модулем. Решение простейших уравнений и неравенств | 1 | УНЗ | Знают, как решать уравнения и неравенства с модулем, раскрывая модуль по определению, графически и используя свойства функций входящих в выражение. Умеют находить и использовать информацию. Умеют использовать различные приемы решения уравнений и неравенств с модулем. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. | |||||
99 | Уравнений и неравенства с модулем. Решение более сложных уравнений и неравенств | 1 | УПЗ | ||||||
100 | Уравнений и неравенства с модулем. Систематизация материала | 1 | УОМ | ||||||
101 | Решение упражнений. Подготовка к контрольной работе | 1 | КУ | ||||||
102 | Контрольная работа №7 | 1 | УКЗ | ||||||
103 | Уравнения и неравенства со знаком радикала | 1 | УНЗ | Знают основной метод решения иррациональных уравнений и неравенств – метод возведения обеих частей уравнения в одну и туже степень, а также некоторые специфические приемы (введение новой переменной). Умеют использовать метод возведения обеих частей уравнения в одну и туже степень, а также некоторые специфические приемы. (введение новой переменной). Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. | |||||
104 | Уравнения и неравенства со знаком радикала. Решение упражнений | 1 | УПЗ | ||||||
105 | Уравнения и неравенства со знаком радикала. Систематизация материала | 1 | УОМ | ТЕСТ | |||||
106 | Уравнения и неравенства с двумя переменными | 1 | УНЗ | Знают и понимают решения уравнений и неравенств с двумя переменными Учащиеся умеют изображать на плоскости множество решений уравнений и неравенств с двумя переменными. Знают и умеют решать диофантовое уравнение и систему неравенств с двумя переменными. Умеют обосновывать суждения, давать определения, приводить доказательства, примеры. | През | ||||
107 | Уравнения и неравенства с двумя переменными. Решение упражнений | 1 | УПЗ | ||||||
108 | Доказательство неравенств | 1 | УНЗ | Знают, что доказать неравенства можно с помощью определения, от противного, методом математической индукции, функционально – графическим методом, а также синтетическим методом. Могут привести примеры, подобрать аргументы, сформулировать выводы. Умеют использовать для доказательства неравенства методы: с помощью определения, от противного, метода математической индукции, функционально – графического метода, а также синтетический метод. Умеют составлять текст научного стиля. | |||||
109 | Доказательство неравенств. Решение упражнений | 1 | УПЗ | ||||||
110 | Доказательство неравенств. Систематизация материала | 1 | УОМ | ||||||
111 | Системы уравнений | 1 | УНЗ | Знают, как решать графически и аналитически решать системы, составленные из двух и более уравнений. Умеют работать с учебником, отбирать и структурировать материал. Умеют свободно применять различные способы при решении систем уравнений. Могут самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. | |||||
112 | Системы уравнений. Решение упражнений | 1 | УПЗ | ||||||
113 | Системы уравнений. Отработка навыков решения | 1 | УПЗ | ||||||
114 | Системы уравнений. Систематизация материала | 1 | УОМ | СР | |||||
115 | Решение упражнений. Подготовка к контрольной работе | 1 | КУ | През | |||||
116 | Контрольная работа № 8 | 1 | УКЗ | ||||||
117 | Задачи с параметрами | 1 | УНЗ | Знают, как решать уравнения и неравенства с параметрами. Умеют решать простейшие уравнения с параметрами. Умеют обосновывать суждения, давать определения, приводить доказательства, примеры. Умеют свободно решать уравнения и неравенства с параметрами. Используют для решения познавательных задач справочную литературу. Могут собрать материал для сообщения по заданной теме. Умеют находить и использовать информацию. | |||||
118 | Задачи с параметрами. Решение простейших задач | 1 | УПЗ | ||||||
119 | Задачи с параметрами. Решение более сложных задач | 1 | УПЗ | ||||||
120 | Задачи с параметрами. Систематизация материала | 1 | УОМ | ||||||
121- 136 | Обобщающее повторение (16 часов) | 16 |
nsportal.ru
Уравнения по алгебре 11 класс — математика онлайн
Меню- Обучение
- Закрыть
- Вебинары
- Закрыть
- Все вебинары
- Вебинар#1.ЕГЭ №9,13,18
- Вебинар#2. ЕГЭ №14
- Вебинар#3. ЕГЭ №16
- Вебинар#4.ЕГЭ №17
- Вебинар#5.ЕГЭ №13,18
- Вебинар#6.ЕГЭ №13,18
- Вебинар#7. ЕГЭ №15,18
- Вебинар#8. ЕГЭ. № 13,15
- Вебинар#9. ЕГЭ. №15
- Вебинар#10. ЕГЭ. №14
- Вебинар #11. ЕГЭ №14
- Вебинар#12 .ЕГЭ №16
- Вебинар#13. ЕГЭ №16
- Вебинар#14. ЕГЭ №18
- Вебинар#15. ЕГЭ №18
- Вебинар#16. ЕГЭ №18
- Вебинар#17. ЕГЭ №13
- Вебинар#18. ЕГЭ №15
- Вебинар#19. ЕГЭ №14
- Закрыть
- Пути обучения и темы
- Закрыть
- Пути обучения
- Что такое пути обучения
- Ваш первый учебный путь
- Все пути обучения
- Доступные темы
- Список бесплатных тем
- Полный список доступных тем
- Закрыть
- Подготовка к ЕГЭ
- Закрыть
- ЕГЭ Профиль
- Задание №4
- Задание №5
- Задание №6
- Задание №8
- Задание №9
- Задание №11
- Задание №13
- Задание №14
- Задание №17
- Задание №18
- ЕГЭ База
- Задание №7
- Задание №10
- Пути обучения
- Не помню как работают формулы приведения
- Хочу вспомнить как решать тригонометрические ур.
- Как отбирать корни тригонометрических ур.
- Учимся решать комбинированные ур.
- Учимся решать тригонометрические ур. с параметром
- Объем пирамиды. От простого к сложному.
- Вебинары
- Вебинар#1.ЕГЭ №9,13,18
- Вебинар #2.ЕГЭ №14
- Вебинар#4.ЕГЭ №17
- Вебинар#5.ЕГЭ №13,18
- Вебинар#6.ЕГЭ №13,18
- Вебинар#7. ЕГЭ №15,18
- Вебинар#8.ЕГЭ № 13,15
- Вебинар#9.ЕГЭ. №15
- Вебинар#10. ЕГЭ. №14
- Вебинар #11. ЕГЭ №14
- Вебинар#12. ЕГЭ №16
- Вебинар#13. ЕГЭ №16
- Вебинар#14. ЕГЭ №18
- Вебинар#15. ЕГЭ №18
- Вебинар#16. ЕГЭ №18
- Вебинар#17. ЕГЭ №13
- Вебинар#18. ЕГЭ №15
- Вебинар#19. ЕГЭ №14
- Закрыть
- 11 класс
- Закрыть
- Алгебра
- Уравнения
- Показательные уравнения
- Комбинированные уравнения
- Уравнения
- Геометрия
- Многогранники
- Пути обучения
- Закрыть
- 10 Класс
- Закрыть
- Алгебра
- Повторение 7-9
- Числовые функции
- Тригонометрические уравнения
- Преобразование тригонометрических выражений
- Геометрия
- Введение
- Параллельность прямых и плоскостей
- Перпендикулярность прямых и плоскостей
- Подготовка к ЕГЭ
- Задание №13
- Задание №18
- Пути обучения
- Закрыть
- ОГЭ
- Закрыть
- ОГЭ
- Задание №4
- Задание №9
- Задание №17
- Задание №21
- Задание №22
- Пути обучения
- Закрыть
- 9 Класс
- Закрыть
- Алгебра
- Текстовые задачи
- Геометрия
- Факультатив
- Уравнения
- Уравнения повышенной сложности
- Уравнения
- Пути обучения
- Закрыть
- 8 Класс
- Закрыть
- Алгебра
- Уравнения
- Квадратные уравнения
- Рациональные уравнения
- Текстовые задачи
- Уравнения
- Геометрия
- Окружности
- Факультатив
- Уравнения
- Рациональные уравнения с параметром
- Уравнения
- Пути обучения
- Закрыть
- 7 Класс
- Закрыть
- Алгебра
- Текстовые задачи
- Уравнения
- Линейные уравнения
- Геометрия
- Факультатив
- Уравнения
- Линейные уравнения с параметром
- Уравнения
- Пути обучения
- Закрыть
- Для учителя
- Закрыть
- Алгебра
- Вероятность и статистика
- Повторение 7-9
- Числовые функции
- Текстовые задачи
- Алгебраические уравнения
- Тригонометрические уравнения
- Показательные уравнения
- Иррациональные уравнения
- Комбинированные уравнения
- Преобразование тригонометрических выражений
- Геометрия
- 10 класс Стереометрия
- Многогранники
- Планиметрия
- Закрыть
- Вебинары
- Закрыть
- Информация
- Закрыть
- Учителям и школам
- Для учителей и школ
- Учителям и школам
- Ученикам и родителям
- Для родителей
- Родительский доступ
- Руководство учащегося
- Ученикам и родителям
- Общая информация
- Новости
- Как это работает
- Отзывы
- Акции
- Список слушателей
- Общая информация
- Закрыть
- Вебинары
- Закрыть
- Закрыть
- Вход
- Регистрация
- Как это работает
- Новости
- Поддержка
ВХОД НА САЙТ
Забыл парольЗапомнить
- Регистрация
- Обучение
- Закрыть
- Вебинары
- Закрыть
- Все вебинары
- Вебинар#1.ЕГЭ №9,13,18
- Вебинар#2. ЕГЭ №14
- Вебинар#3. ЕГЭ №16
- Вебинар#4.ЕГЭ №17
- Вебинар#5.ЕГЭ №13,18
- Вебинар#6.ЕГЭ №13,18
- Вебинар#7. ЕГЭ №15,18
- Вебинар#8. ЕГЭ. № 13,15
- Вебинар#10. ЕГЭ. №14
- Вебинар #11. ЕГЭ №14
- Вебинар#12 .ЕГЭ №16
- Вебинар#13. ЕГЭ №16
- Вебинар#14. ЕГЭ №18
- Вебинар#15. ЕГЭ №18
- Вебинар#16. ЕГЭ №18
- Вебинар#17. ЕГЭ №13
- Вебинар#18. ЕГЭ №15
- Вебинар#19. ЕГЭ №14
- Закрыть
- Пути обучения и темы
- Закрыть
- Пути обучения
- Что такое пути обучения
- Ваш первый учебный путь
- Все пути обучения
- Доступные темы
- Список бесплатных тем
- Полный список доступных тем
- Закрыть
- Подготовка к ЕГЭ
- Закрыть
- ЕГЭ Профиль
- Задание №4
- Задание №5
- Задание №6
- Задание №8
- Задание №9
- Задание №11
- Задание №13
- Задание №14
- Задание №17
- Задание №18
- ЕГЭ База
- Задание №7
- Задание №10
- Пути обучения
- Не помню как работают формулы приведения
- Хочу вспомнить как решать тригонометрические ур.
- Как отбирать корни тригонометрических ур.
- Учимся решать комбинированные ур.
- Учимся решать тригонометрические ур. с параметром
- Объем пирамиды. От простого к сложному.
- Вебинары
- Вебинар#1.ЕГЭ №9,13,18
- Вебинар #2.ЕГЭ №14
- Вебинар#3. ЕГЭ №16
- Вебинар#4.ЕГЭ №17
- Вебинар#5.ЕГЭ №13,18
- Вебинар#6.ЕГЭ №13,18
- Вебинар#7. ЕГЭ №15,18
- Вебинар#8.ЕГЭ № 13,15
- Вебинар#9.ЕГЭ. №15
- Вебинар#10. ЕГЭ. №14
- Вебинар #11. ЕГЭ №14
- Вебинар#12. ЕГЭ №16
- Вебинар#13. ЕГЭ №16
- Вебинар#14. ЕГЭ №18
- Вебинар#15. ЕГЭ №18
- Вебинар#16. ЕГЭ №18
- Вебинар#17. ЕГЭ №13
- Вебинар#18. ЕГЭ №15
- Вебинар#19. ЕГЭ №14
- Закрыть
- 11 класс
- Закрыть
- Алгебра
- Уравнения
- Показательные уравнения
- Комбинированные уравнения
- Уравнения
- Геометрия
- Многогранники
- Пути обучения
- Закрыть
- Вебинары
mathcourse.ru
Тренажеры по алгебре по всем темам (11 класс)
Тренажер№1 А – 11. 1.Вычислите приращение функции у=f(x) на промежутке 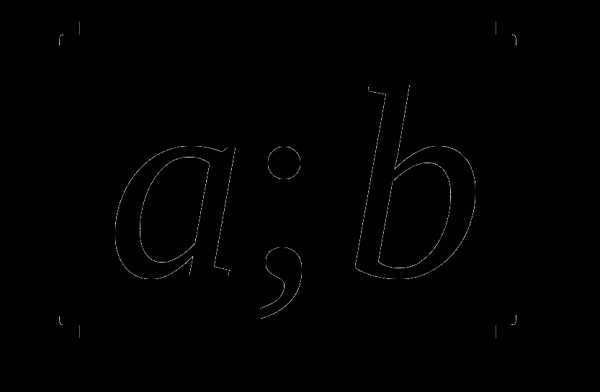
1. f(x)=4х+3, а=0, b=0,2;
2. f(x)=х2 –3х, а=2, b=3;
3. f(x)= , а=1, b=1,5;
, а=1, b=1,5;
4. f(x)=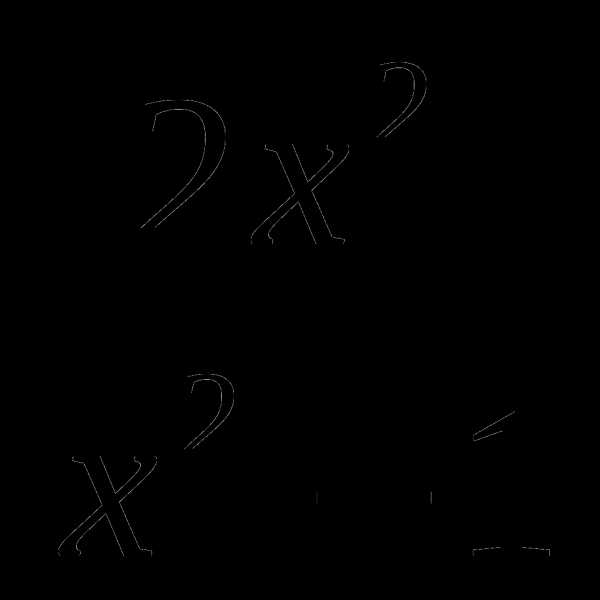 , а=2, b=2,5;
, а=2, b=2,5;
5. f(x)=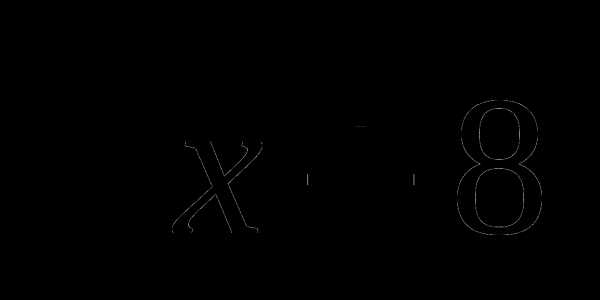 , а=-1, b=-8.
, а=-1, b=-8.
1.Вычислите приращение функции у=f(x) на промежутке 
1. f(x)=2х+3, х=1,5, 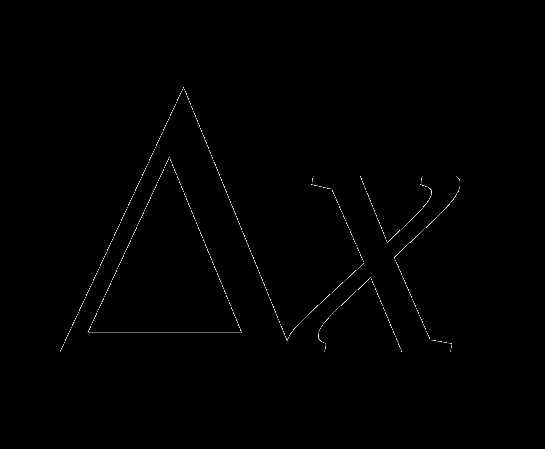 =2,5;
=2,5;
2. f(x)=3х2 –х+1, х=0, 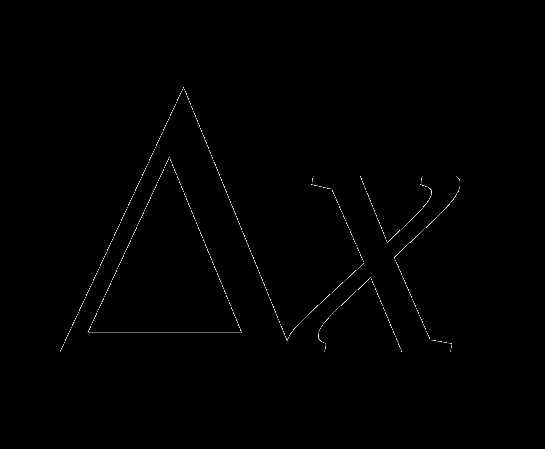 =2;
=2;
3. f(x)=х3 –2х2+х, х=-1, 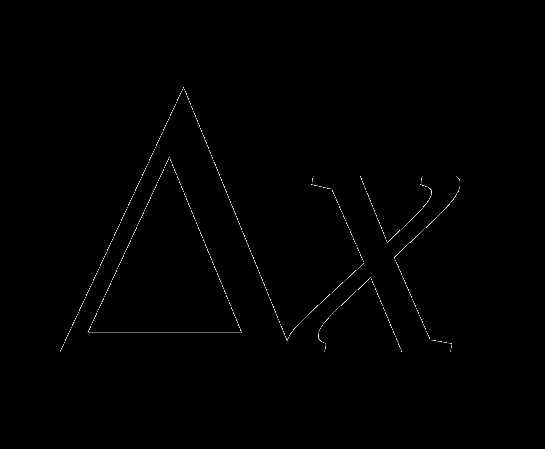 =1;
=1;
4. f(x)=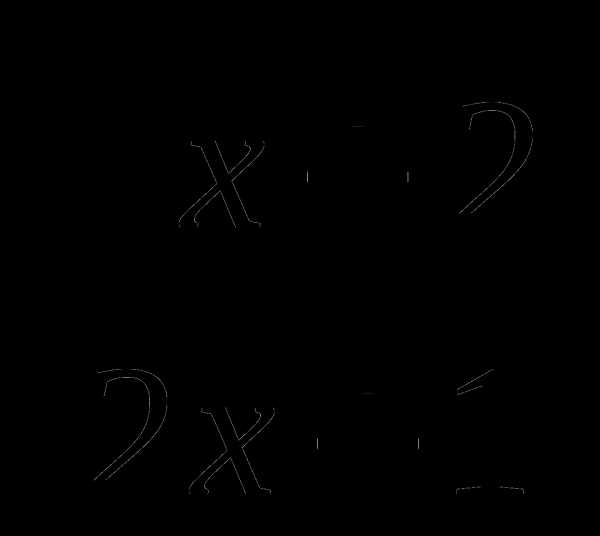 , х=2,
, х=2, 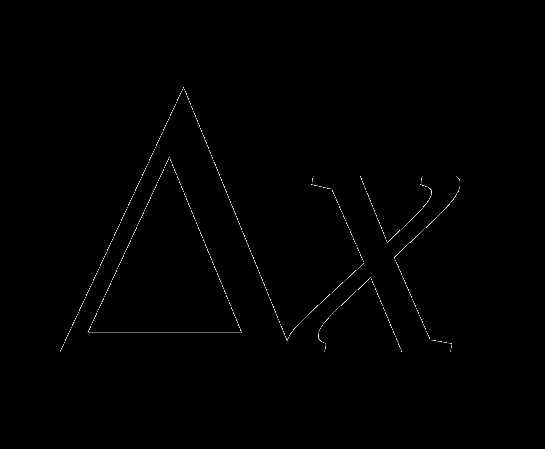 =5;
=5;
5. f(x)=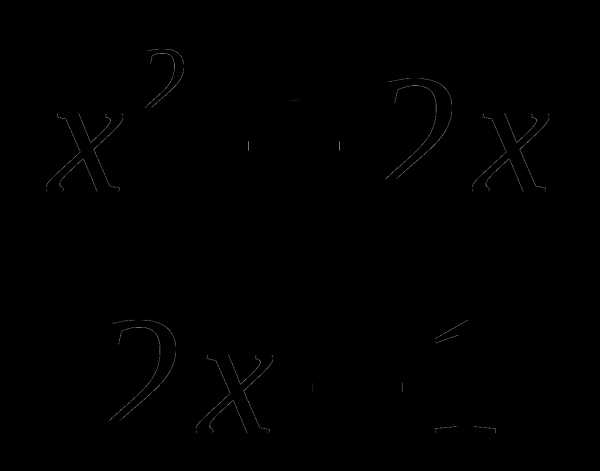 , х=-2,
, х=-2, 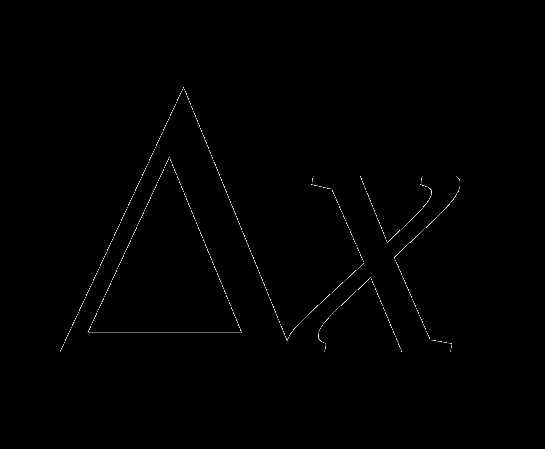 =1.
=1.
3. Вычислите среднюю скорость роста функции у=f(x)
на двух данных промежутках и на промежутке  :
:
1. f(x)=2х+1, ;
2. f(x)= х+3,
х+3, 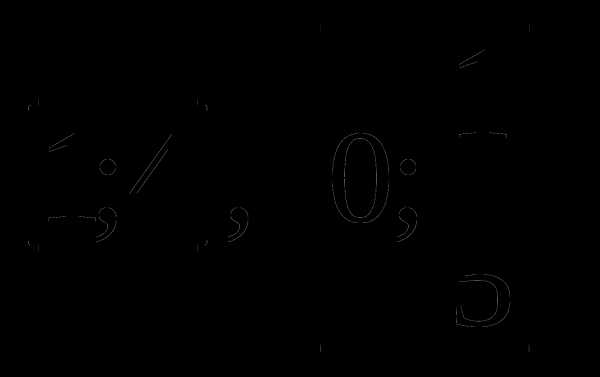 ;
;
3. f(x)=2х2 -1, ;
4. f(x)=2х2 –х-1, ;
5. f(x)=х3 –3х-х, .
Тренажер №2. Производная степенной функции.
Найти производную функции
1. f(x)=2х3
2. h(x)= .
.
3. f(x)=х4-4х3-8х2+13.
4. v(h)=- +3h.
+3h.
5. f(x)=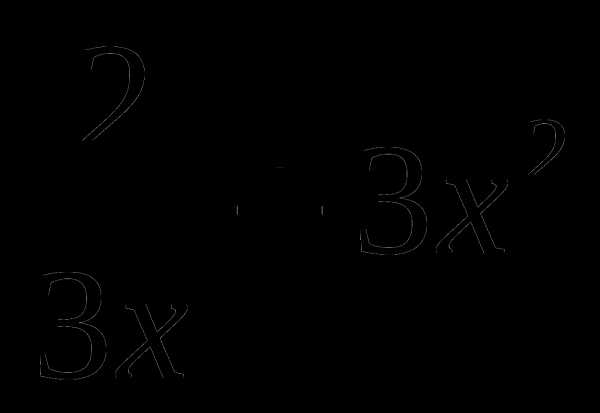 .
.
6. f(x)=.
7. f(x)=-.
8. f(x)=.
9. g(t)=- .
.
10. s(r)=2.
11. у(t)=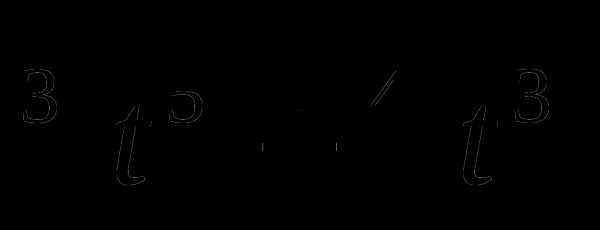 .
.
12. f(x)=х3(5х-1)(1-2х).
13. v(.
14. у(t)=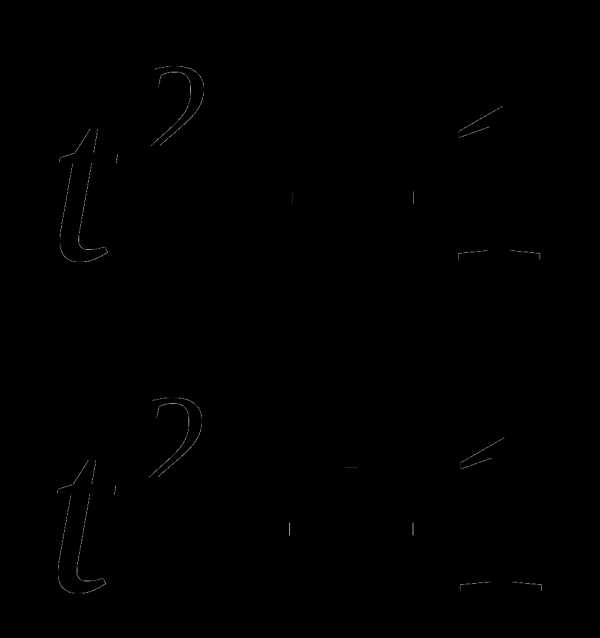 .
.
15. v(h)=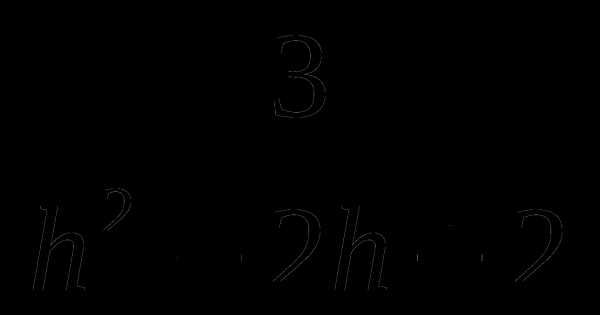 .
.
16. g(t)=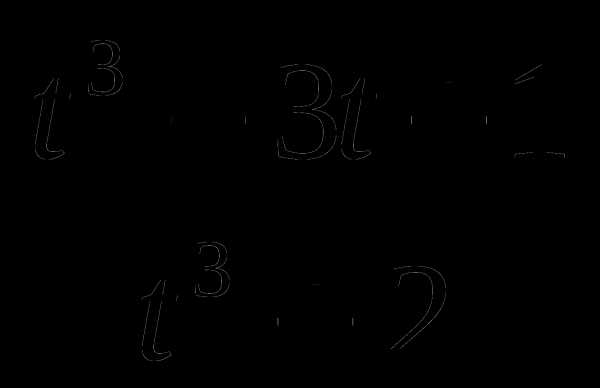 .
.
17. g(t)=(t+4)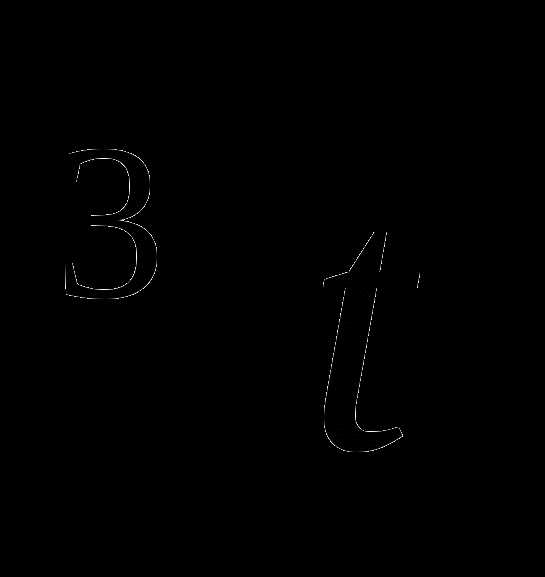 .
.
18. f(u)= .
.
19. f(x)=  .
.
20. f(x)=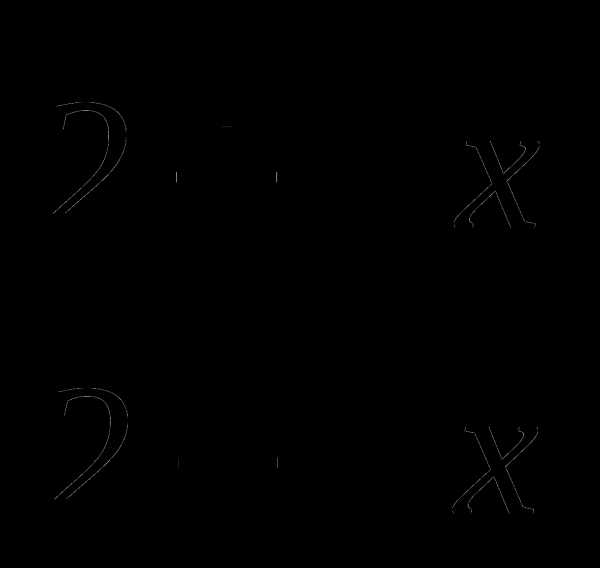 .
.
21. g(x)=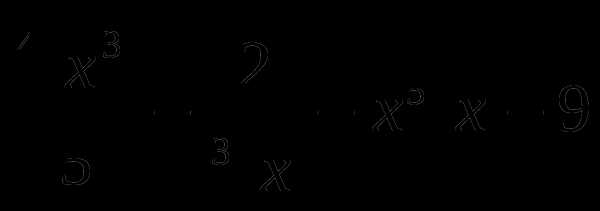 .
.
22. f(x)=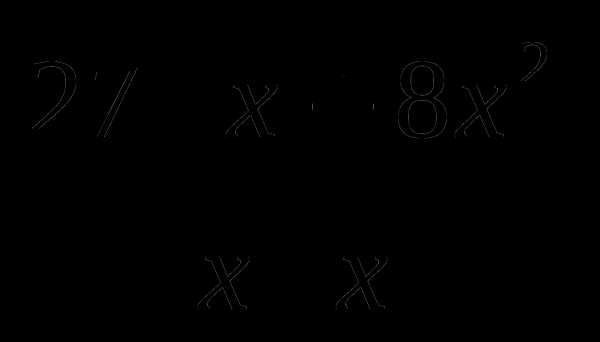 .
.
23. f(x)=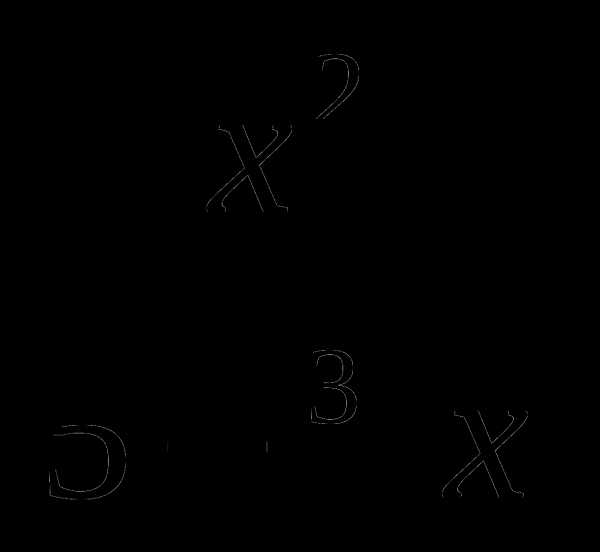 .
.
24. y(t)=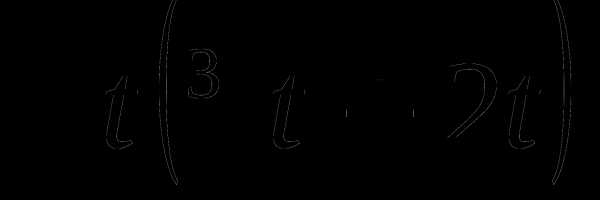 .
.
25. f(x)=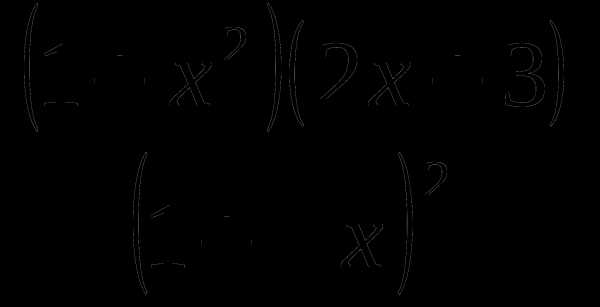 .
.
Тренажер № 3. Производная сложной функции (линейная замена).
Найти производную функции:
1.f(x)= (2х+3)4.
2. g(u)=(-3u+7)3.
3. f(x)=(2x+1)4-(3x-1)6.
4. g(t)=(7t+3)5—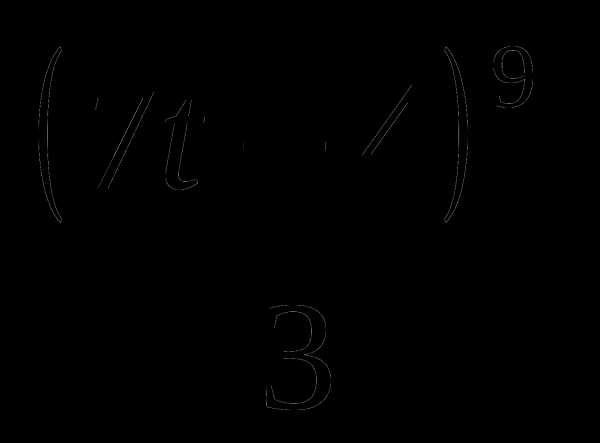 .
.
5. F(l)=(2l+1)4·(2l-1)3.
6. f(x)=a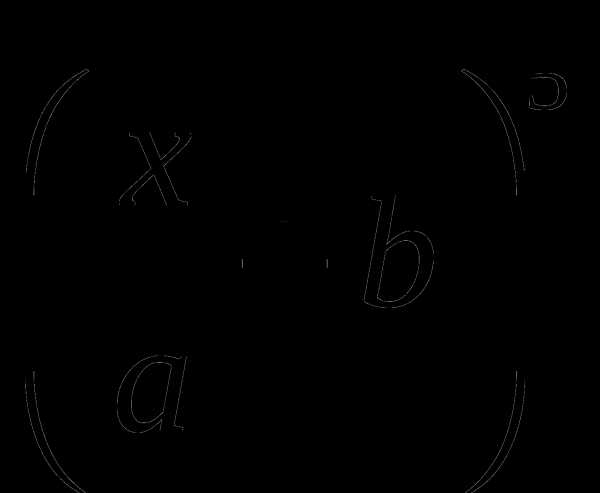 .
.
7. F(j)=2.
8. f(x)=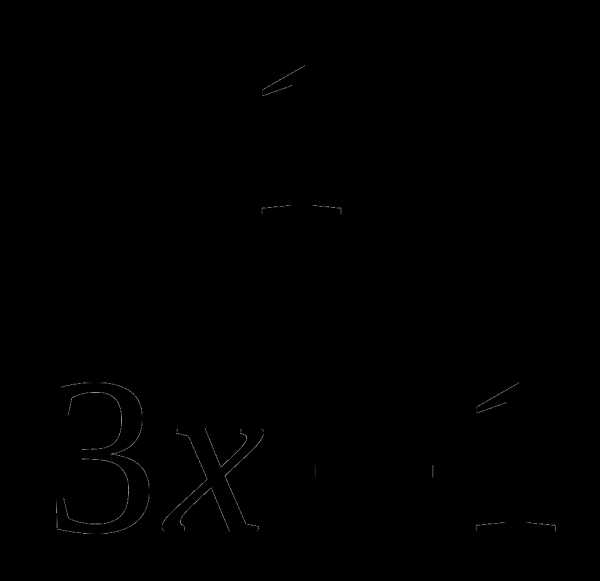 .
.
9. g(x)=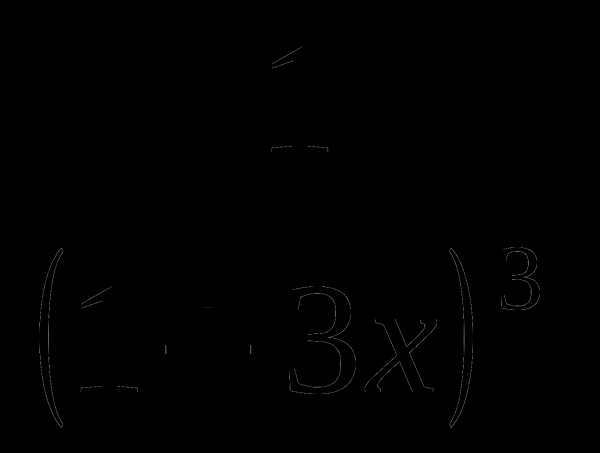 .
.
10. f(x)=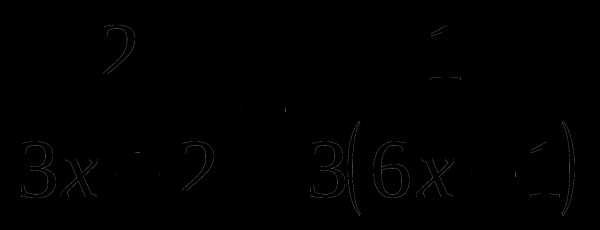 .
.
11. P( )=
)=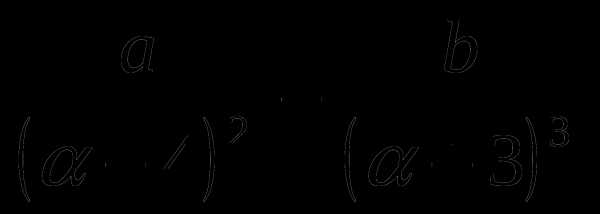 .
.
12. y(x)=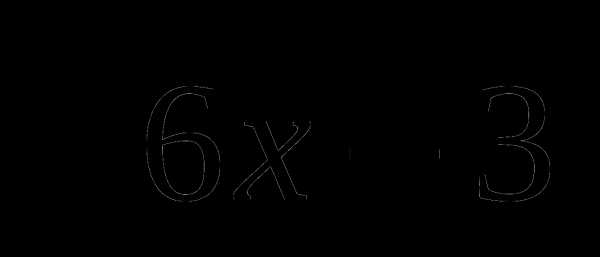 .
.
13. f(x)=3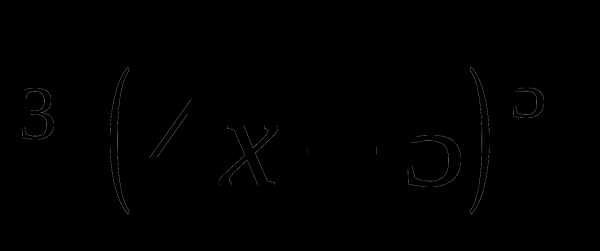 .
.
14. y(t)=.
15. f(x)=.
Тренажер № 4.Уравнение касательной.
Дана функция у=f(x). Найдите:
1) угловой коэффициент касательной к графику этой функции в точке с абсциссой х0;
2) точки, в которых угловой коэффициент касательной равен k;
3) напишите уравнение касательной к графику функции в точке с абсциссой х0:
1. у=х2+4, х0=1, k=4.
2. у= 2х2+х, х0=2, k=-1.
3. у=3х2-6х+1, х0=0, k=6.
4. у=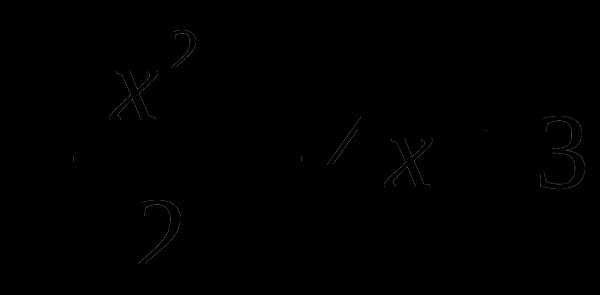 , х0=-1, k=0.
, х0=-1, k=0.
5. у= х3+3х+2, х0=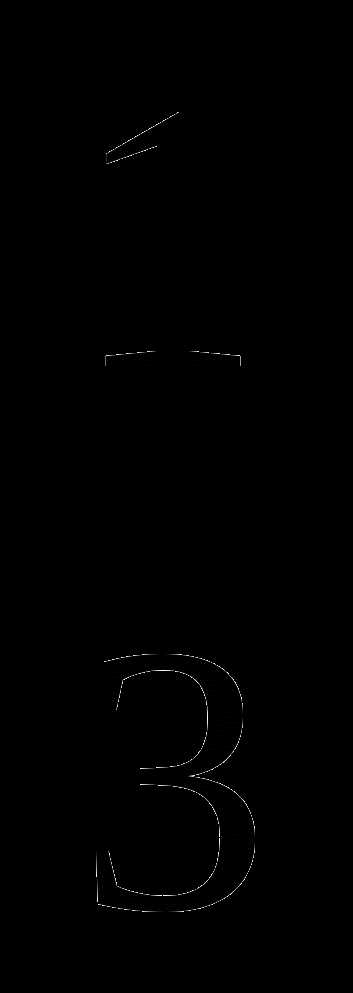 , k=
, k= .
.
6. у= х+ , х0=1, k=
, х0=1, k= .
.
7. у=2х4-х3+1, х0=0, k=0.
8. у=(х-2)2(х+1), х0=1, k=6.
9. у= , х0=1, k=0.
, х0=1, k=0.
10. у=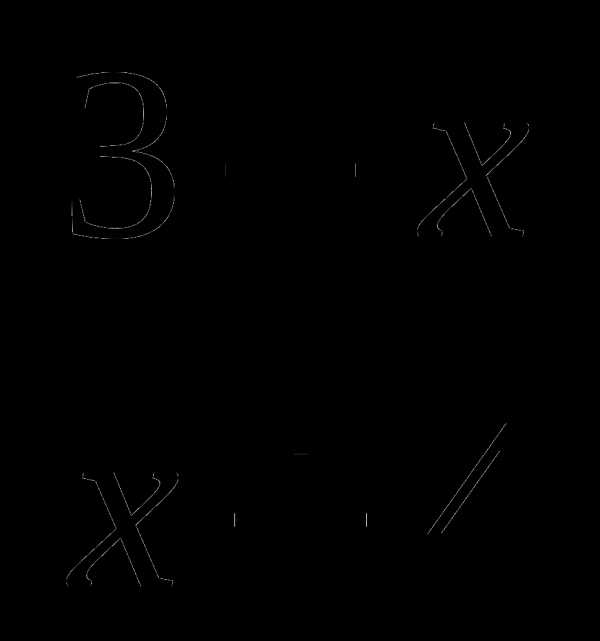 , х0=-3, k=-7.
, х0=-3, k=-7.
11. у=х+2 , х0=1, k=2.
, х0=1, k=2.
12. у=(х+1) , х0=4, k=2.
, х0=4, k=2.
Тренажер № 5. Промежутки монотонности
Найдите промежутки монотонности функции:
1. у=х2-3х+2.
2. у=(2х-1)2.
3. у=6х-х2+5.
4. у=2х3+6х2-1.
5. у=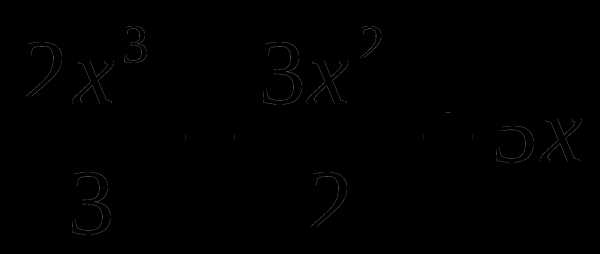 .
.
6. у=2х3—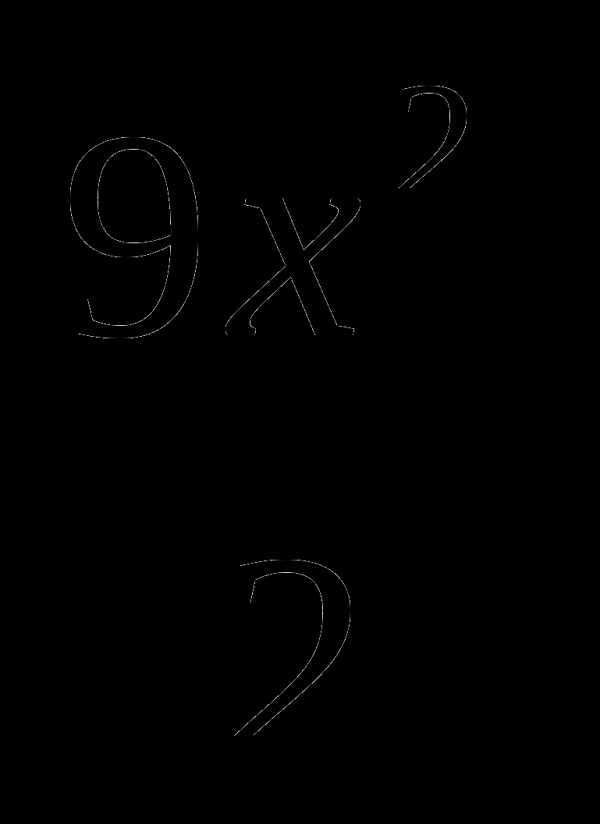 +3х-4.
+3х-4.
7. у=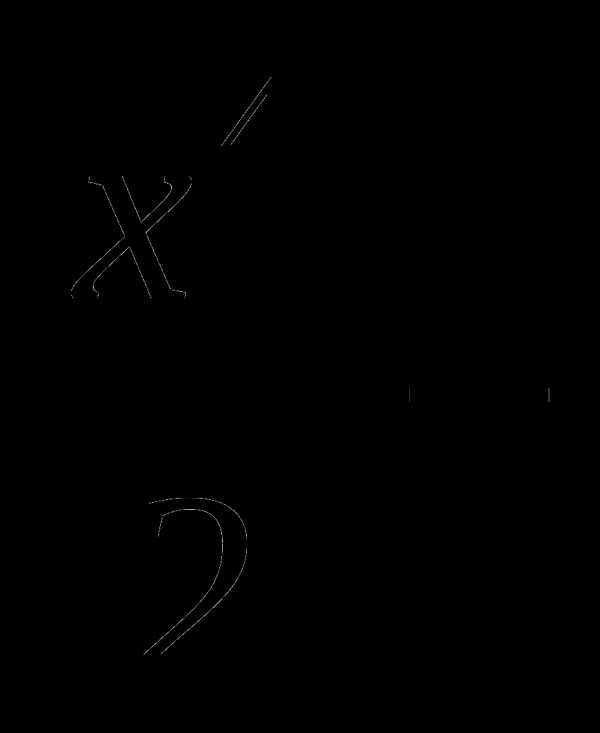 4х2+180.
4х2+180.
8. у=х2-5х3+20х-3.
9. у=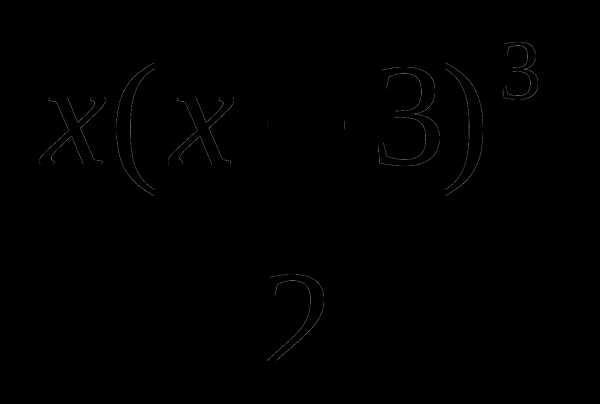 .
.
10. у=х4+ х2-2.
х2-2.
11. у=х5-20х3+1.
12. у=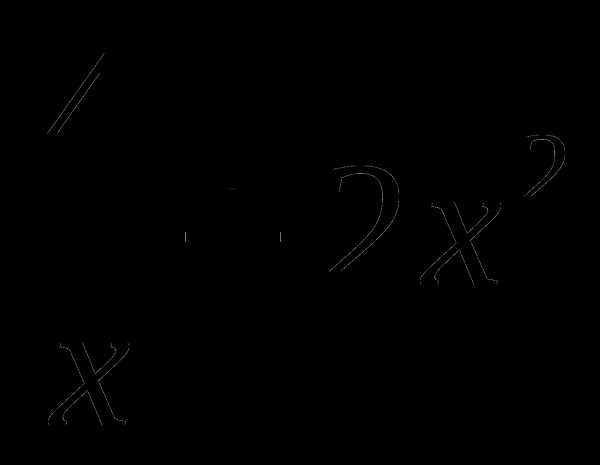 .
.
13. у=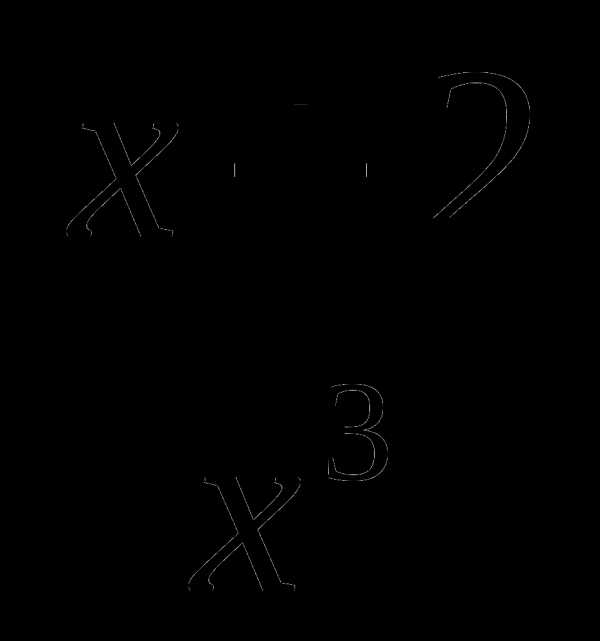 .
.
14. у=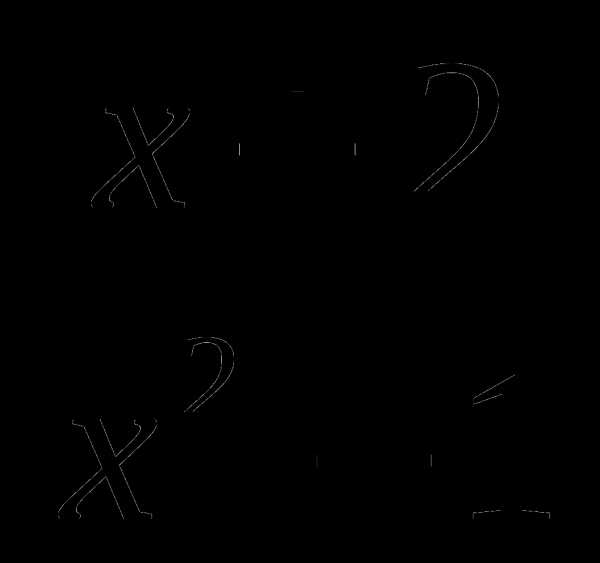 .
.
15. у= .
.
16. у=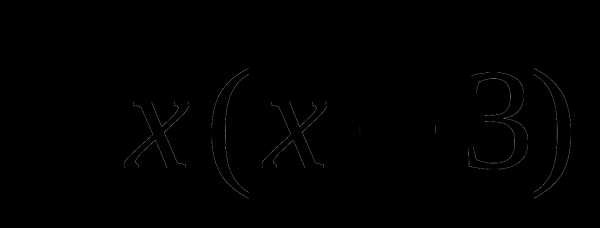 .
.
17. у=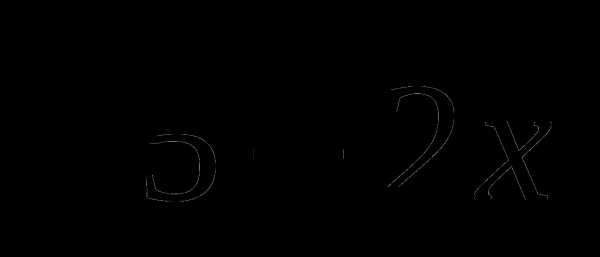 .
.
18. 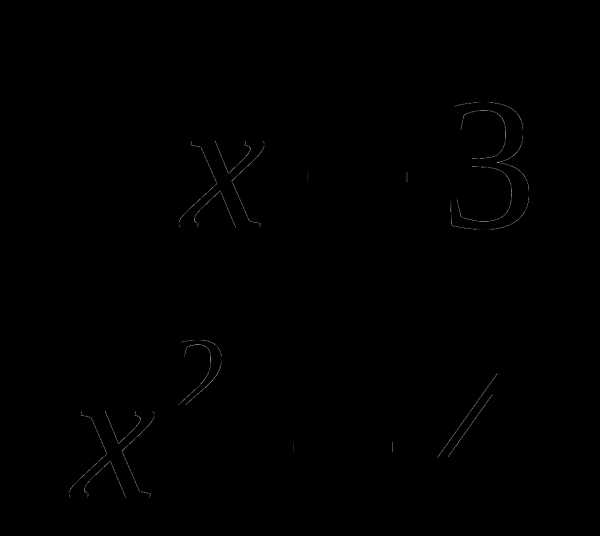 .
.
Тренажер № 6. Экстремум функции.
Найдите точки экстремума функции5
1. у=х2+1.
2. у=3х2-4х.
3. у=х3+3х2.
4. у=2х3-24х+5.
5. у=2х3+3х2-12х+5.
6. у=(х+2)2(3х-1).
7. у=х4-4х3+4х2.
8. у=2х(1-3х)3.
9. у=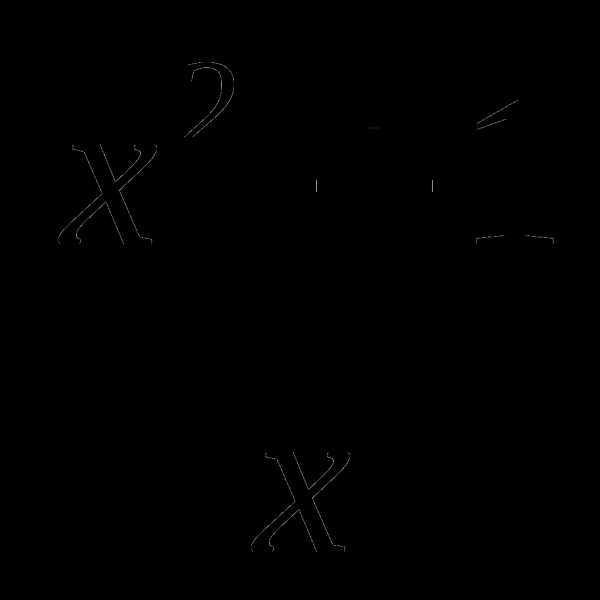 .
.
10. у=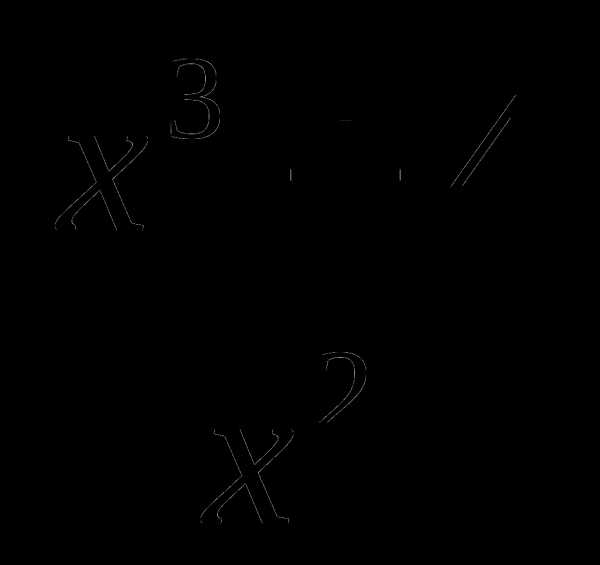 .
.
11. у=х2+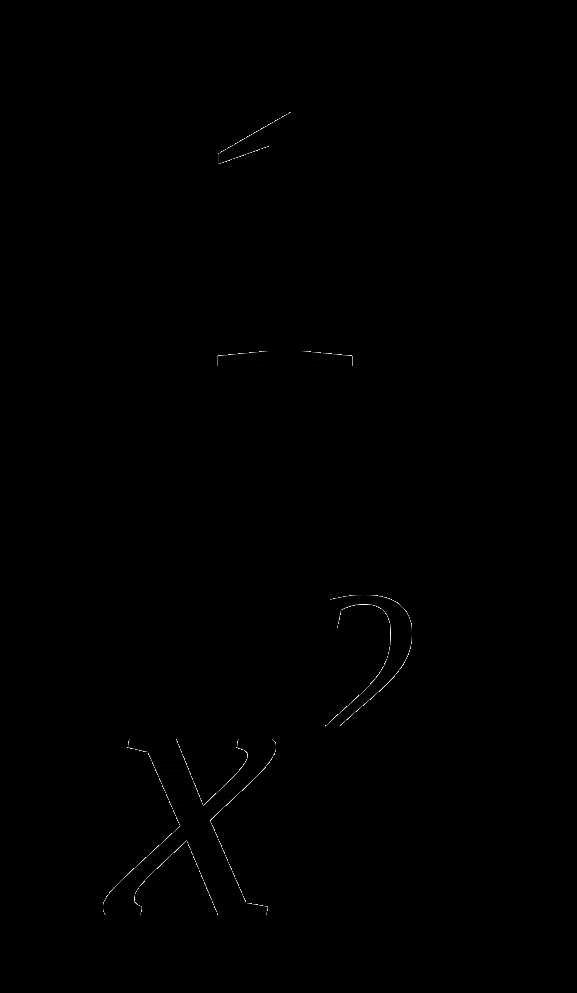 .
.
12. у=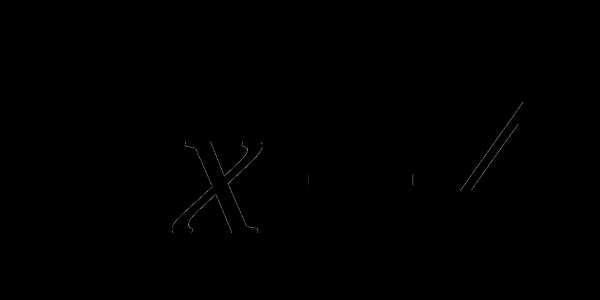 .
.
13. у=х+ .
.
14. у=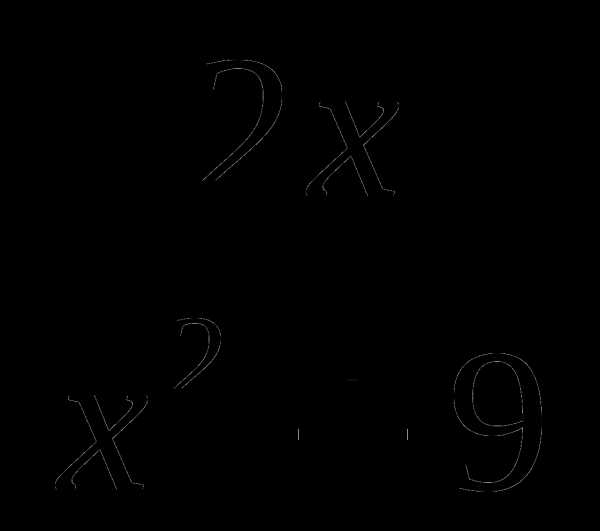 .
.
15. у=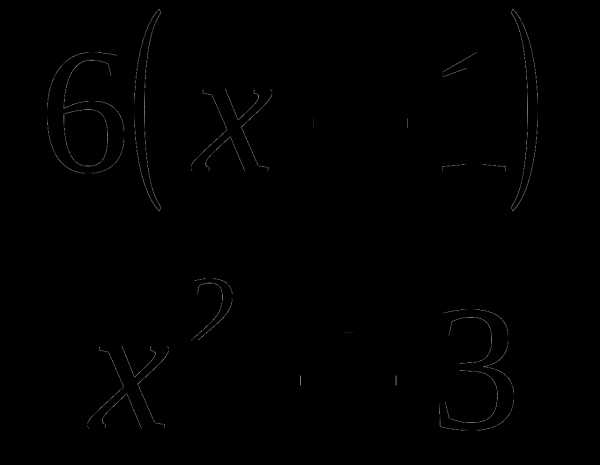 .
.
16. у=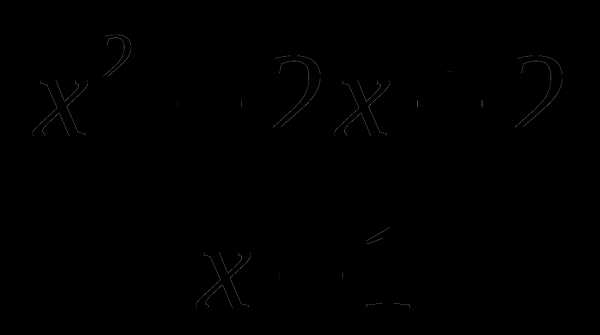 .
.
17. у=(х-1) .
.
18. у=2х2— .
.
19. у=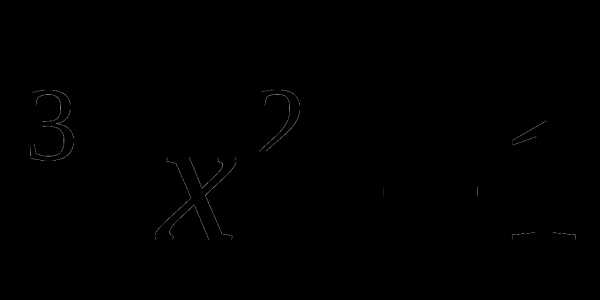 .
.
20. у=х2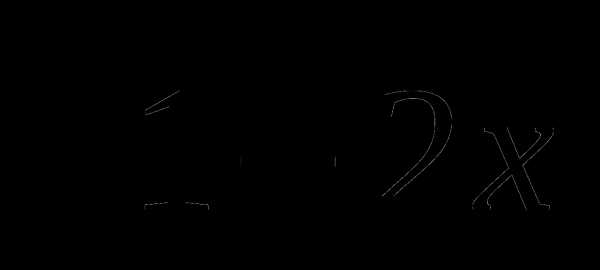 .
.
Тренажер № 7. Исследование функции на отрезке
Найдите наибольшее и наименьшее значение функции у=f(x) на заданных промежутках:
1. у=х3-12х+4 а) 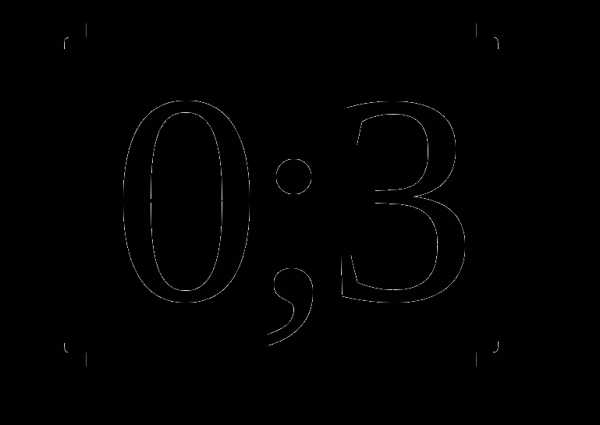 б)
б)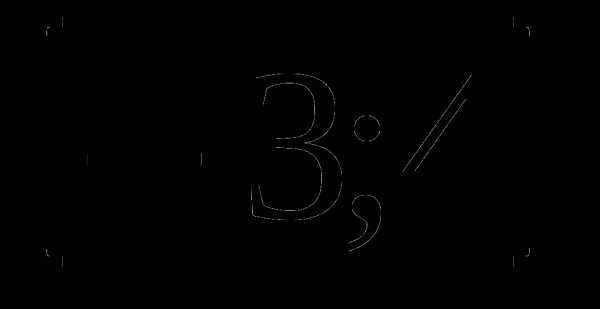
2. у=1+3х-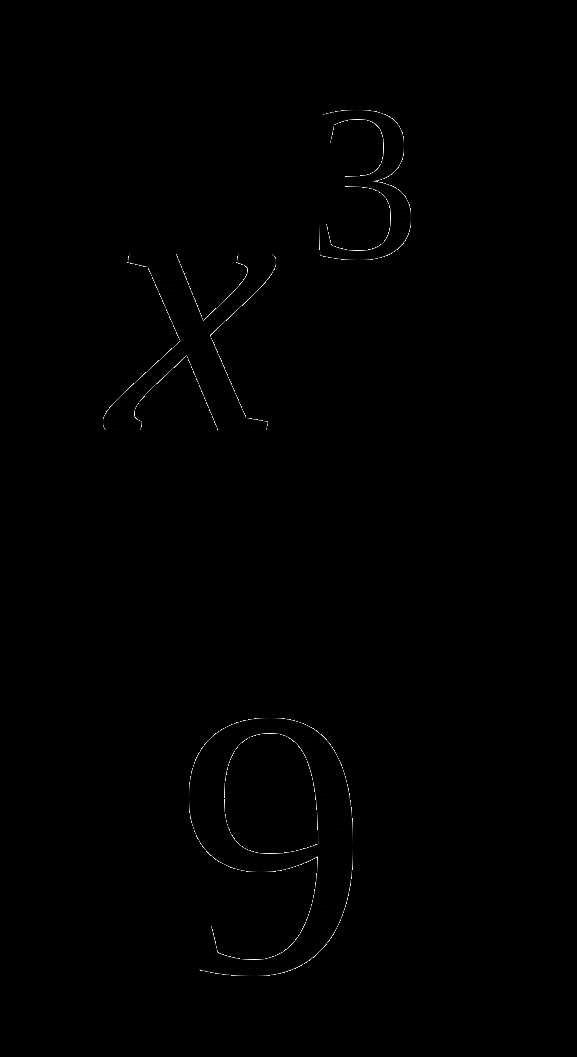 а)
а) 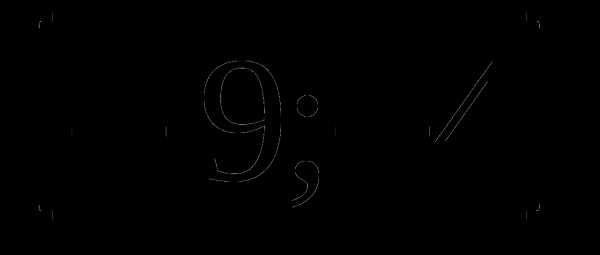 , б)
, б)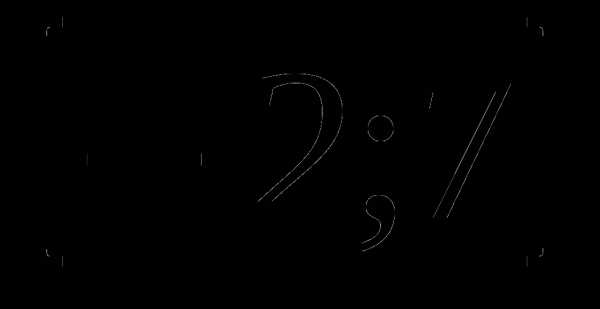
3. у=х3-х2+3х-11 а) 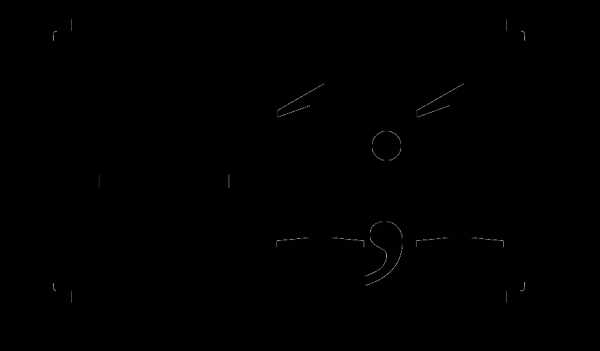 б)
б)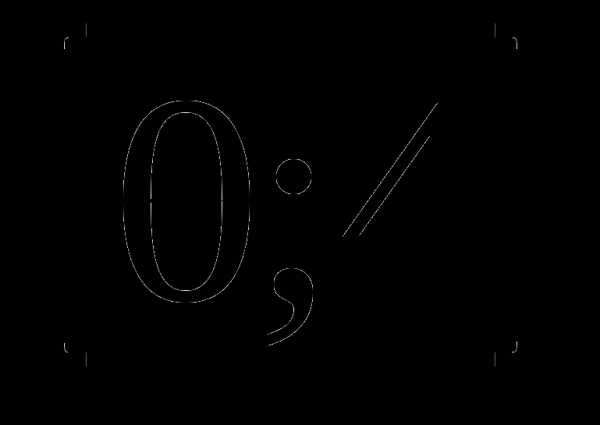
4. у=х4-8х+3 а) 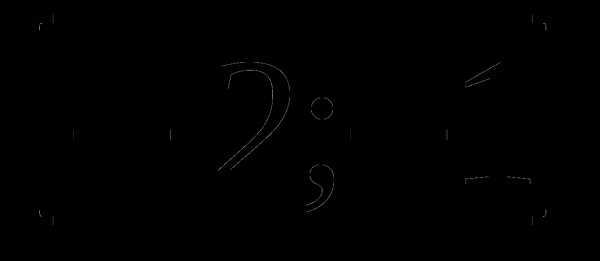 б)
б)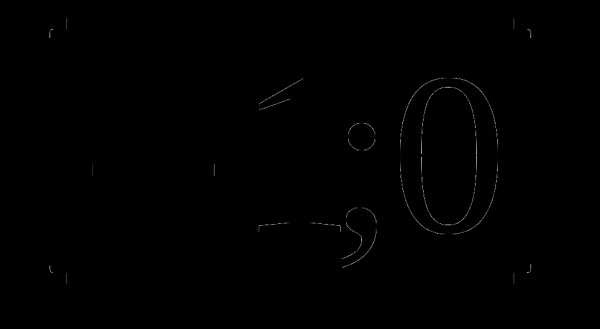
5. у=х4-4х3-8х2+ 13 а) 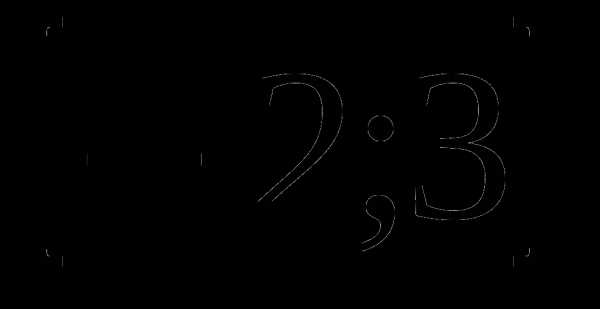 б)
б)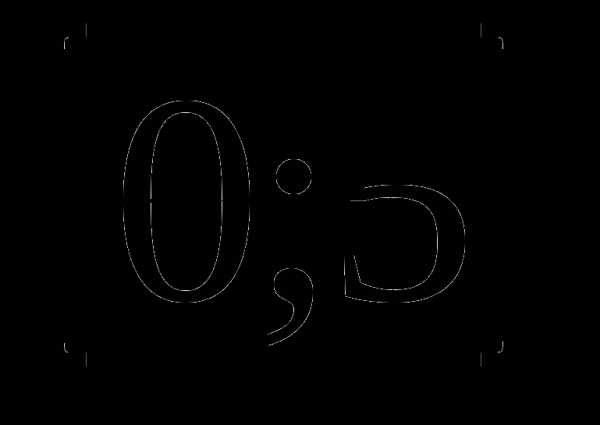
6. у=х+ а)
а) 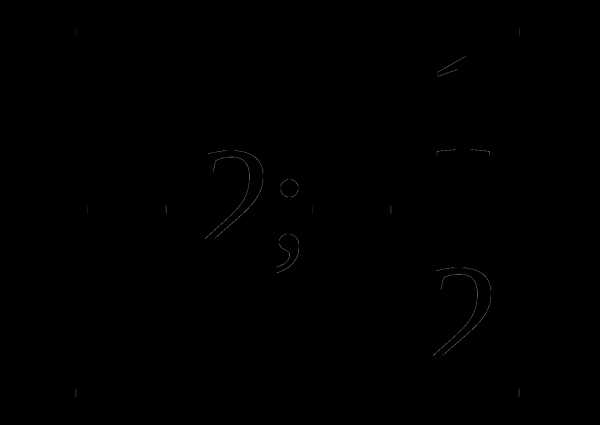 б)
б)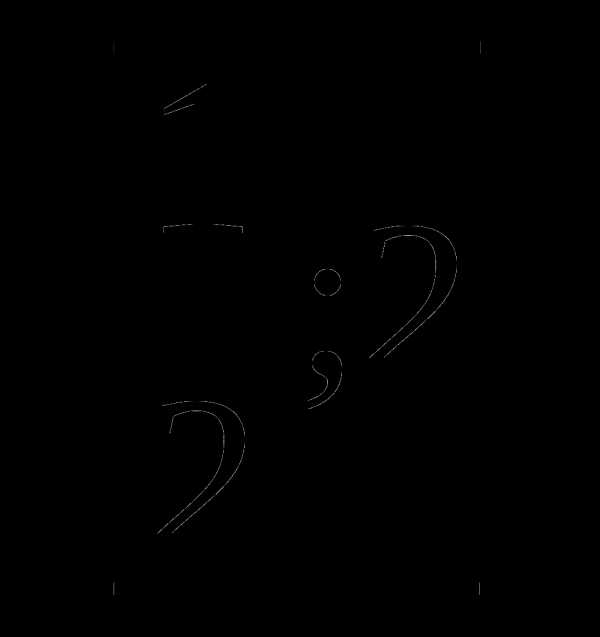
7. у=х2— а)
а)  б)
б)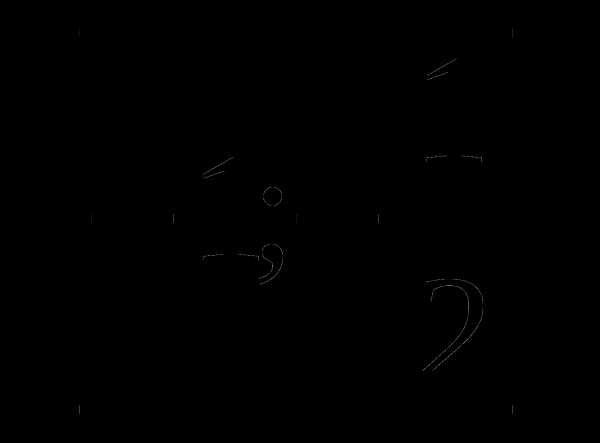
8. у=х2+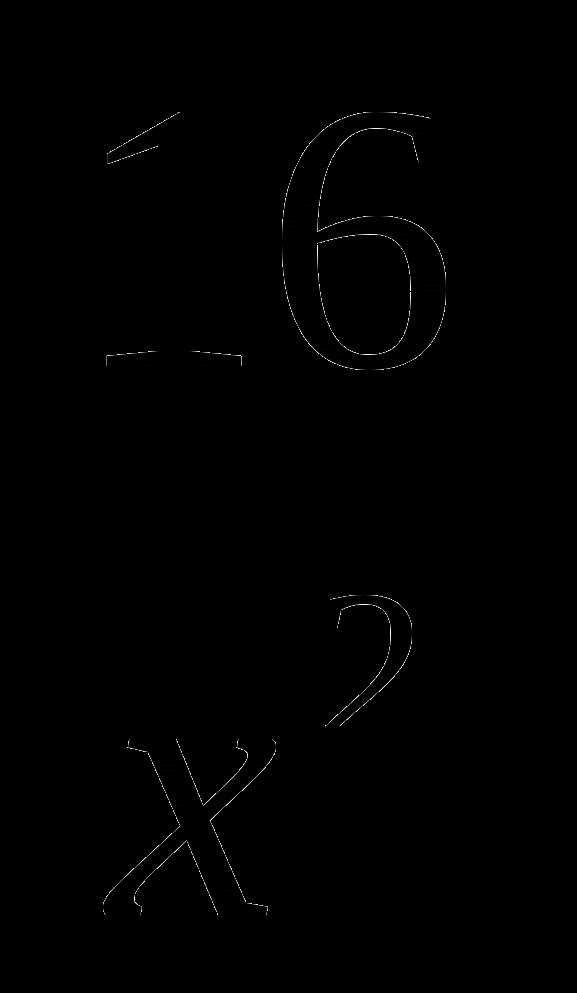 а)
а) 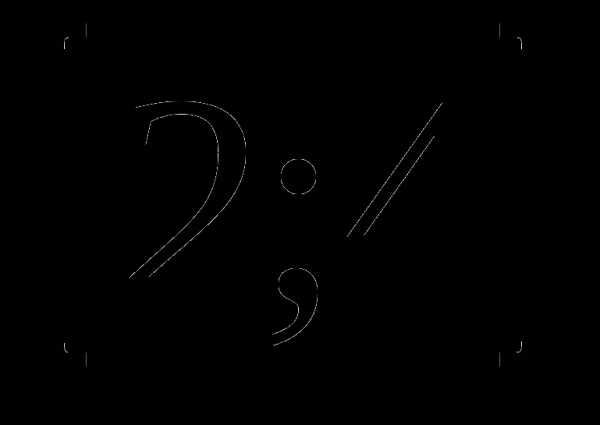 б)
б)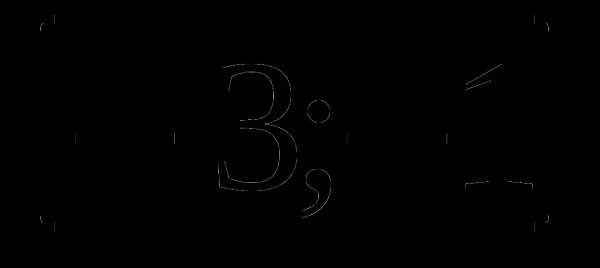
9. у=х- а)
а) 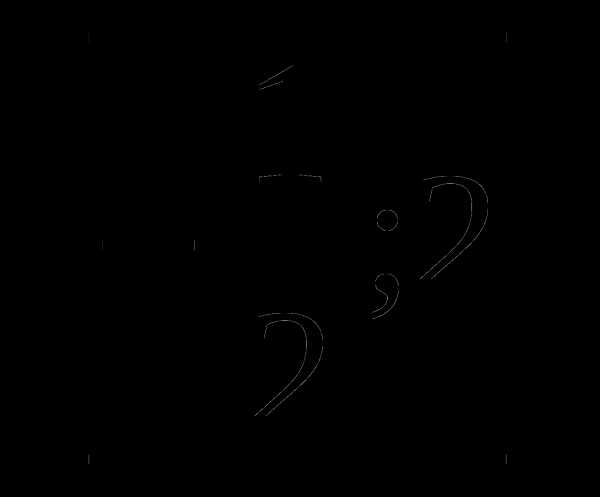 б)
б)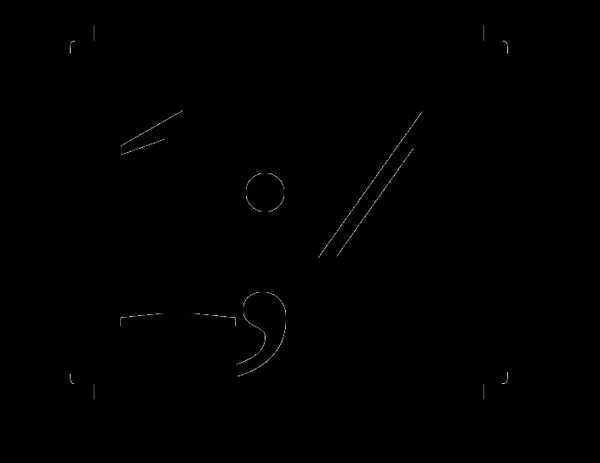
10. у=(х+2)3(х-1) а) 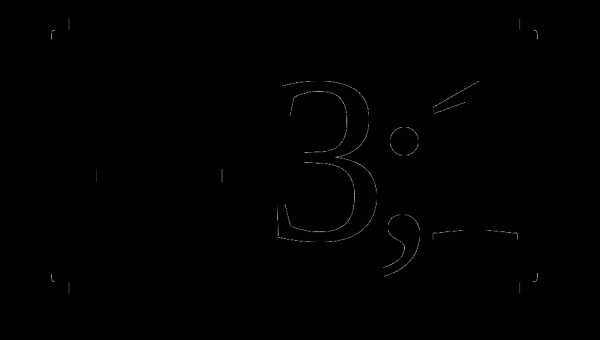 б)
б)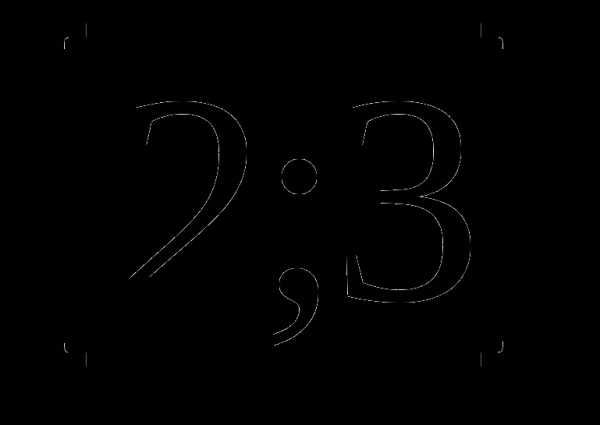
11. у=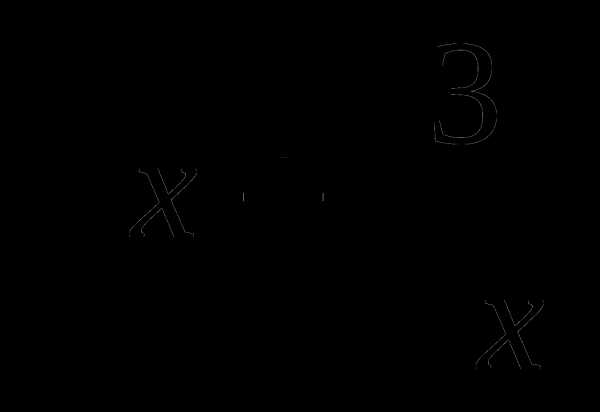 а)
а) 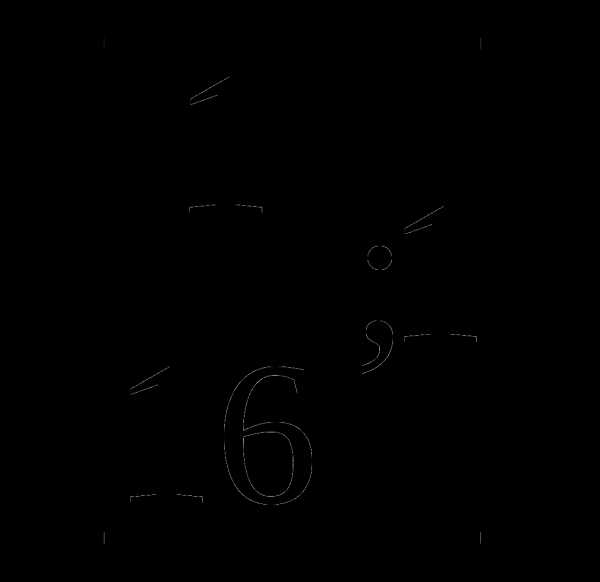 б)
б)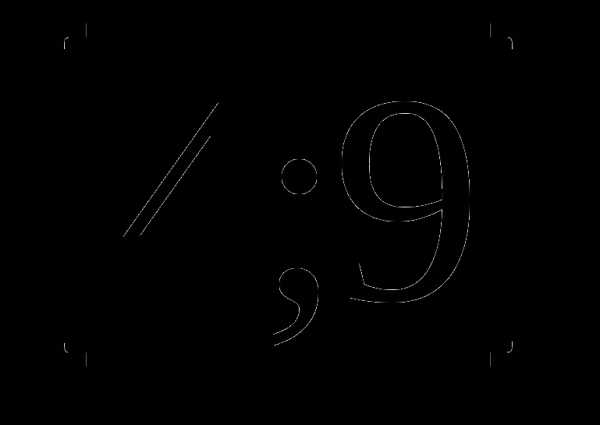
12. у=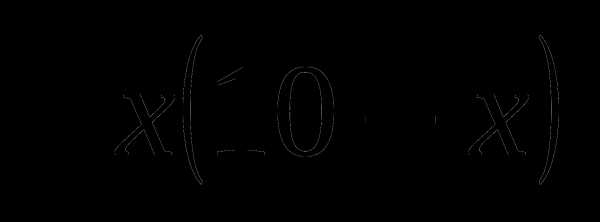 а)
а) 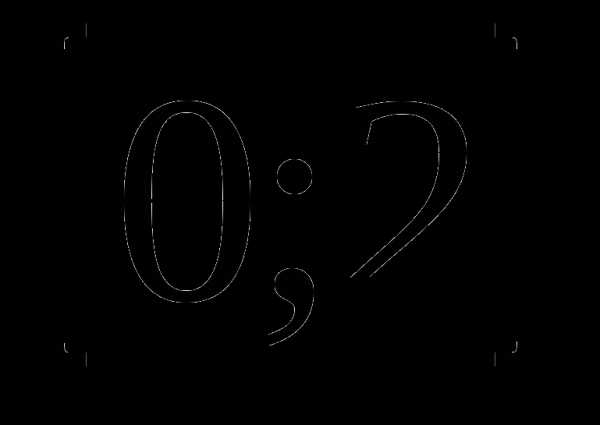 б)
б)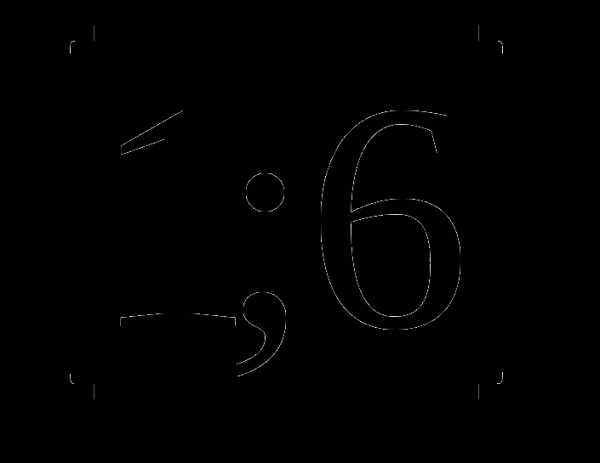 .
.
Тренажер № 8. Вычисление первообразных.
Вычислите первообразную функции:
1. у=х3+1.
2. у=2х2— .
.
3. у=(1-3х)2.
4. у= .
.
5. у=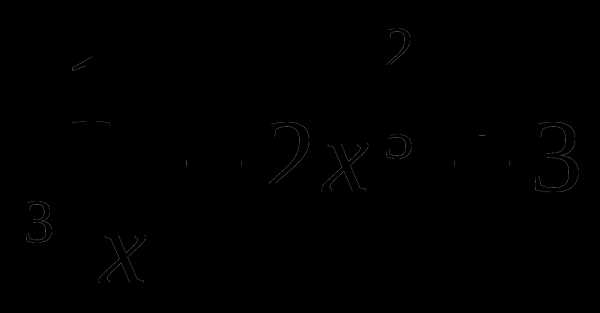 .
.
6. у=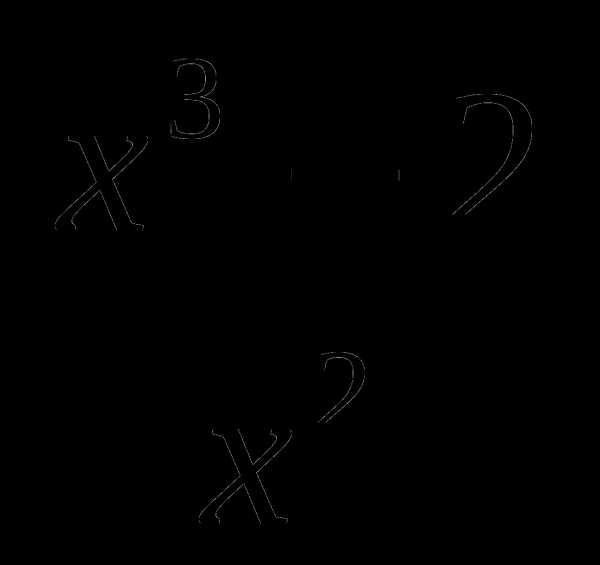 .
.
7. у=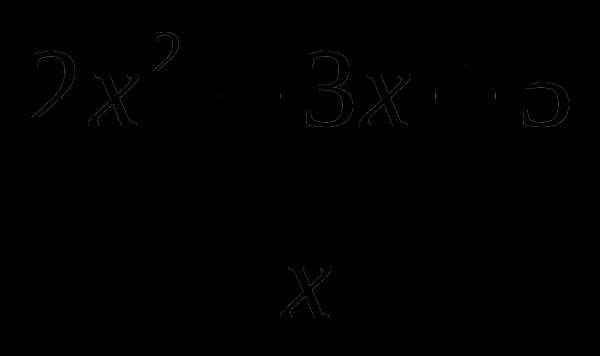 .
.
8. у=.
9. у=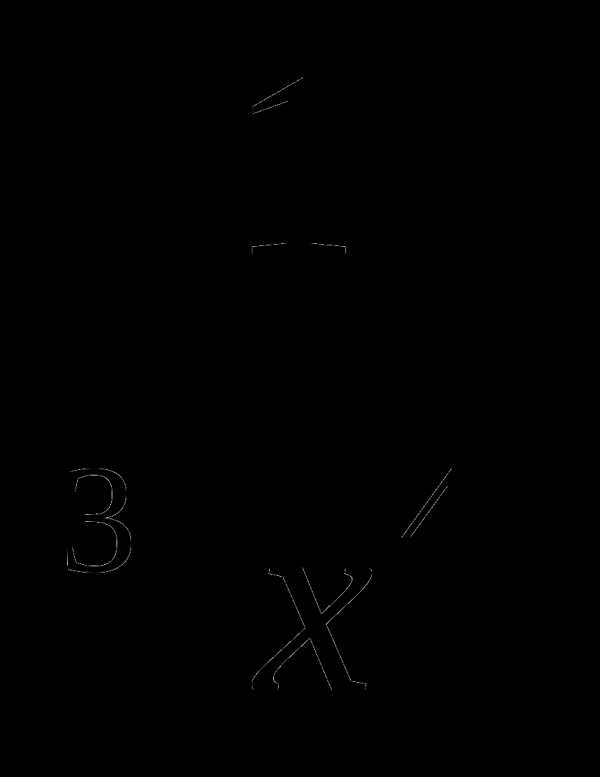 .
.
10. у=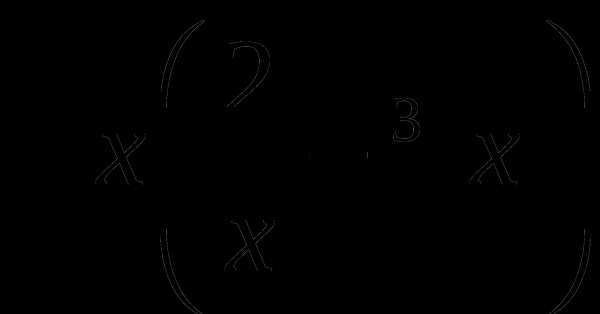
11. у=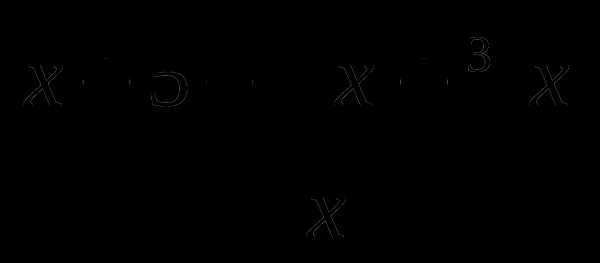 .
.
12. у=(1+х)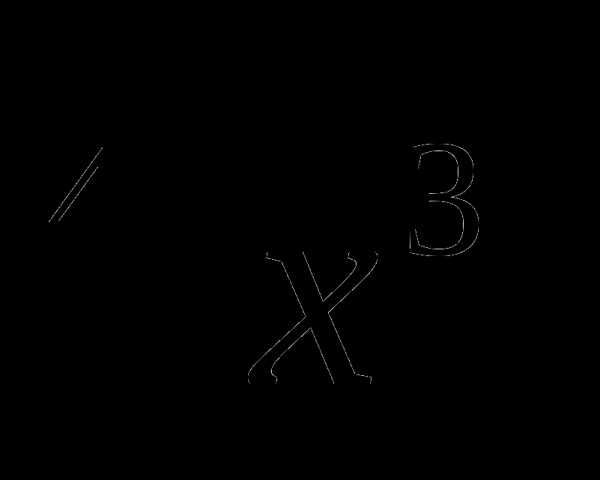 .
.
Тренажер № 10. Вычисление площадей.
Вычислите площадь фигуры, ограниченной линиями:
1. у=х3, у=0, х=1, х=3.
2. у=х2, у=2х,.
3. у=х, у=0, х=3, х=1.
4. у=х2-2х+3, у=0, х=0, х=2.
5. у= , у=х.
, у=х.
6. у=sinx, у=0, х= , х=
, х=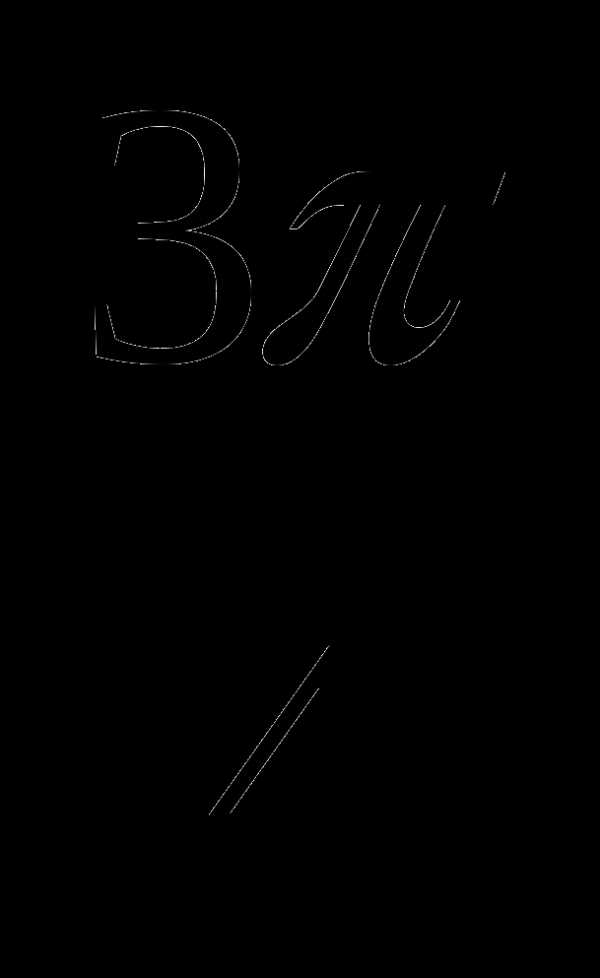 .
.
7. у=sinx, у=0, х= , х=
, х=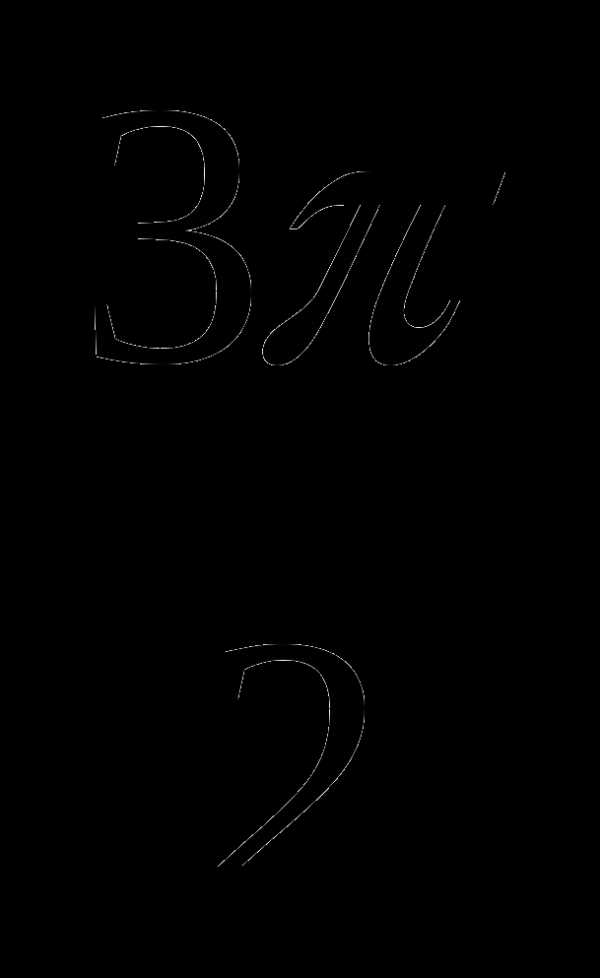 .
.
8. у=2х+1, у=х2.
9. у=х2+2х+2, у=0, х=-1, х=2.
10., у=1, у=х2.
11. у=2х, у=5х, х=1.
12. у=х2 -1, у=0.
13. у=2-х2, у= , х=0.
, х=0.
14. у=-х, у=-х3 ( у 0).
0).
15. у= , у=х, х=2.
, у=х, х=2.
16. у=2-х2, у=х, у=0.
infourok.ru
Рабочая программа по алгебре (11 класс) на тему: Факультативный курс по математике в 11 классе
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №3» пгт. Жешарт
Рекомендовано: Согласовано:
методическим объединением учителей зам.директора по научно-
методической работе
_________________________________ _____________________________
Протокол №____________ от«_______»______________20____г. «______»______________20___г.
Рабочая учебная программа
факультатива по алгебре и началам математического анализа
для 11 класса на 2013-2014 учебный год
Составитель учебной программы-
Суровнева Валентина Михайловна,
учитель математики.
Программа факультативного курса по математике в 11 классе
Пояснительная записка
Программа факультативного курса составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования, методических рекомендаций для поступающих в высшие учебные заведения, требований к ЕГЭ. Факультативный курс построен с опорой на знания и умения, получаемые учащимися при изучении математики в старшей школе.
Материал данного курса содержит нестандартные методы, которые позволяют более эффективно решать различные задачи.
К нестандартным задачам традиционно относятся задачи, которые выделяются необычной формулировкой, а также задачи, для решения которых требуются умения нестандартно мыслить, переносить известные методы решения в непривычные ситуации, проявлять находчивость и сообразительность.
Нестандартные задачи способствуют развитию логического мышления, математической интуиции, творческих способностей, прививают навыки исследовательской работы.
Наряду с основной задачей обучения математике – обеспечение прочного и сознательного овладения учащимися системой математический знаний и умений – данный факультативный курс предусматривает формирование устойчивого интереса к предмету, развитие математических способностей.
Программа факультативного курса предполагает изучение теории и отработку практических навыков по рассматриваемым вопросам и рассчитан на 35 часов
Цели факультативного курса:
- углубление курса алгебры и начал анализа 11 класса;
- изучение современных нестандартных методов решения в соответствии с программой для поступающих в вузы и требованиями, предъявляемыми к выпускникам на едином государственном экзамене;
- развитие логического мышления, пространственного воображения, алгоритмической культуры;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения естественно-научных дисциплин, для получения образования в областях, требующих углубленной математической подготовки;
- воспитание средствами математики культуры личности, знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Задачи факультативного курса:
- повышение математической подготовки учащихся, овладение знаниями и умениями в объеме, необходимом для успешной сдачи экзаменов и продолжения математического образования;
- систематизация нестандартных методов при решении текстовых задач, преобразовании тригонометрических выражений, решение уравнений и неравенств, содержащих обратные тригонометрические функции, показательные и логарифмические функции;
- решение комплексных задач, связанных с построением графиков функций и фигур, вычислением периметров и площадей построенных фигур.
Тематический план
№ п/п | Раздел | Тема | Количество часов |
1. | Решение тригонометрических уравнений и неравенств | Тригонометрические уравнения и неравенств | 2 |
Решение тригонометрических систем уравнений ( задания С-1) | 2 | ||
3. | Текстовые задачи и техника их решения | Классификация и методы решения текстовых задач. Задачи на движение | 1 |
Задачи на совместную работу. | 1 | ||
Задачи на проценты. Задачи экономического содержания | 1 | ||
Задачи на числовые зависимости. | 1 | ||
Задачи аналитического содержания (на смеси, сплавы, растворы). | 1 | ||
Решение заданий В-12 | 1 | ||
4. | Производная, интеграл и их применение | Обобщение темы производная, применение при решении задач и исследовании и построении графика функции | 2 |
Обобщение понятия интеграла | 1 | ||
Площадь криволинейной трапеции | 1 | ||
Применение интеграла | 1 | ||
5. | Алгебраические задачи с параметрами | Тригонометрические уравнения с параметром | 1 |
Задачи с модулями и параметрами. Критические значения параметра | 2 | ||
Решение заданий С-6 | 1 | ||
6. | Общее понятие степени | Корень n-степени и его свойства | 1 |
Иррациональные уравнения и неравенства | 2 | ||
Степень с рациональным показателем | 2 | ||
7. | Показательная и логарифмическая функции | Решение показательных уравнений | 2 |
Решение показательных неравенств | 1 | ||
Решение логарифмических уравнений | 1 | ||
Решение логарифмических неравенств | 1 | ||
8. | Работы ЕГЭ | Дифференциальные уравнения | 1 |
Решение задач на составление систем и геометрические задачи | 1 | ||
Тренировочне работы ЕГЭ (Статград) | 4 | ||
Итого часов: | 35 | ||
СПИСОК УЧЕБНО- МЕТОДИЧЕСКОЙ ЛИТЕРАТУРЫ:
- Математика ЕГЭ, вступительные экзамены ,изд. Легион, 2004г.
- «Алгебра и начала математического анализа 10- 11класс»(базовый уровень) авт. А.Г. Мордкович, изд Мнемозина., 2007-2010г
- Ф.Ф. Лысенко. Математика. Тематические тесты. – Ростов-на-Дону, 2009 г.
- Единая коллекция цифровых образовательных ресурсов / http://school-collection.edu.ru/catalog/search/?text=%DF%E4%E5%F0%ED%FB%E5+%F0%E5%E0%EA%F6%E8%E8.+%D6%E5%EF%ED%E0%FF+%F0%E5%E0%EA%F6%E8%FF+%E4%E5%EB%E5%ED%E8%FF+%FF%E4%E5%F0&tg=&interface=pupi
- Материалы ЕГЭ-2010,201,2012: реальные варианты. М.: АСТ: Астрель, 2007. (Федеральный институт педагогических измерений).
- Работы Статграда .
nsportal.ru
Методическая разработка (алгебра, 11 класс) по теме: рабочая программа по алгебре и началам анализа 11 класса
Начало формы
Конец формы
Устный счет как средство повышения интереса к уроку математики
Тема: “Использование различных видов устных упражнений, как средство
повышения познавательного интереса к уроку математики”.
Оглавление.
Глава I. Анализ методической и психолого-педагогической литературы.
Введение…………………………………………………………………..с 2
1. Понятие интерес………………………………………………………с 4
2. Сущность интереса……………………………………………….…..с 6
3. Виды интересов……………………………………………………….с 7
4. Уровни развития интересов………………………………………….с 8
5. Познавательный интерес, как особый вид интересов………………с 9
6. Стимуляция познавательных интересов у учащихся………………с 12
7. Устные вычисления…………………………………………………..с 16
8. Виды упражнений для устных вычислений ………………………..с 19
9. Формы восприятия устного счета……………………………………с 22
10. Организация занятий по устному счету…………………………..с 23
Глава II. Экспериментальная часть…………………………….с 25
2.1 Констатирующий эксперимент………………………………………с 27
2.2 Формирующий эксперимент………………………………………….с 38
2.3 Контрольный эксперимент……………………………………………с 43
Заключение…………………………………………………………………с 45
Список используемой литературы………………………………………..с 46
Приложения…………………………………………………………………с 48
Я считаю, что эта тема актуальна, так как проходя практику пробных
уроков и наблюдая за уроками математики которые проводили мои одногрупники
и которые проводил я сам мне показалось что детям не интересен это предмет.
В то время как математика является одной из важнейших наук на земле и
именно с ней человек встречается каждый день в своей жизни. Именно поэтому
учителю необходимо развивать у детей интерес к это науке. На наш взгляд,
развивать познавательный интерес к математике возможно с помощью
использования различных видов устного счета.
Поэтому целью нашего исследования стало – доказать результативность
использования различных видов устного счета для повышения познавательного
интереса к урокам математики.
Объект исследования – специально организованный педагогический
процесс, в плане поиска эффективных методов обучения (в частности устных
упражнений).
Предмет исследования – влияние различных видов устного счета на
повышение познавательного интереса к урокам математики у детей 1 класса
занимающихся по традиционной программе (1-4).
Гипотеза исследования состоит в следующем: повышение
познавательного интереса к урокам математики у учащихся 1 класса,
обучающихся по традиционной программе (1-4) в начальной школе может быть
достигнуто, если в обучение будут включены систематически проводящиеся
разнообразные виды устных упражнений.
Задачи:
1) изучить теорию данного вопроса в психолого-педагогической и методической
литературе.
2) подготовить и провести различные виды устных упражнений для повышения
познавательного интереса к урокам математики.
3) сделать выводы, по использованию данных видов устных упражнений.
Методы: анализ психолого-педагогической и методической литературы;
наблюдение; анкетирование; сравнительный анализ;
Глава I. Анализ методической и
психолого-педагогической литературы.
1.1 Понятие интерес.
Одним из важнейших способов воспитания трудолюбия, желания и умения
хорошо учиться является создание условий, обеспечивающих ребенку успех в
учебной работе, ощущение радости на пути продвижения от незнания к знанию,
от неумения к умению. Ещё на рубеже XIX века, известный методист С.И. Шохор-
Троцкий в книге “Чему и как учить на уроках арифметики” писал, что для “…
обогащения интеллекта учащихся математическими знаниями необходимо, чтобы
учащийся испытывал живые эмоции интереса и удовольствия как по поводу
удовлетворения этого интереса, так и по поводу движения работы вперёд и
преодолевания её трудностей.”
Интерес же является сложнейшим психическим образованием. Его нельзя свести
к отдельному психическому акту. Не случайно поэтому так разноречива
трактовка понятия интерес в зарубежной психологии. Философский словарь
Лоланда определяет интерес как самопроизвольное внимание, возбуждающее
состояние легкой и приятной умственной активности, в психологическом
словаре Пьерона интерес представлен как качество вещей, которое привлекает
внимание человека и ориентирует его деятельность. Английский словарь
психологических терминов рассматривает интерес как тенденцию заниматься
вещами из удовольствия, получаемого от самого процесса занятий.
— Интерес выступает как избирательная направленность человека, его
внимания, его мыслей (Т. Рибо, Н.Ф. Добрынин, С.П. Рубенштейн)
— Интерес рассматривается как проявление умственной и эмоциональной
активности (Е.Стронг).
— Интерес трактуется как активатор разнообразных чувств и как своеобразная
чувствительность (Ш. Бюлер, Д. Фрейд).
— В интересе видят тенденцию заниматься деятельностью, вещами, процессами
занятий (Английский словарь психологических терминов).
— Интерес – это активное, познавательное, активно-познавательное отношение
человека к миру (Н.Г. Морозова, В.Г. Иванов).
— Интерес – это активная познавательная направленность, связанная с
положительным эмоционально окрашенным отношением к изучению предмета с
радостью познания, преодоления трудностей, с осознанием успеха, с
самовыражением и утверждением развивающейся личности (Метельский Н.В.)
— Интерес – это одна из психических активностей, характеризующаяся как
общая сознательная устремленность личности к объекту, эмоционально
насыщенная и влияющая на повышение продуктивности деятельности (М.Ф.
Беляев)
Таким образом, психолого-педагогическое понятие интерес отображает
множество значимых процессов: от единичных (внимание), до их совокупности,
он выражается в тенденциях, потребностях, отношениях.
Г.И. Щукина считает, что в действительности интерес выступает перед
нами [8]:
— и как избирательная направленность психических процессов человека на
объекты и явления окружающего мира;
— и как тенденция стремления, потребность личности заниматься именно данной
областью явлений, данной деятельностью, которая приносит удовлетворение;
— и как мощный побудитель активности личности, под влиянием которой все
психические процессы протекают особенно интенсивно и напряженно, а
деятельность становится увлекательной и продуктивной;
— и наконец, как особое избирательное отношение к окружающему миру, к его
объектам, явлениям, процессам.
1.2 Сущность интереса.
Г.И. Щукина считает что интерес – это избирательное отношение
личности к объекту в силу его жизненного значения и эмоциональной
привлекательности.[8]
По мнению Г.И. Щукиной интересы возникают на основе потребностей, но не
сводятся к ним. Потребность выражает необходимость, интерес выражает личную
приязнь к какой-то деятельности.
Формирование интереса не всегда начинается с осознания потребностей,
призвания или общественного долга. Интерес может появиться стихийно и не
осознано вследствие эмоциональной привлекательности объекта, а уже потом
осознается его жизненное значение, которое может определяться многими
причинами: потребностями, общественными требованиями.
Интересы имеют существенное значение в жизни и деятельности
человека. Поэтому и счастье жизни человек испытывает тогда, когда у него
есть интересы. Интересы побуждают к деятельности, активизируют личность,
И.П. Павлов рассматривал интерес как то, что активизирует состояние коры
головного мозга. Работа, отвечающая интересам, осуществляется легко и
продуктивно.
К.Д. Ушинский писал: ”что учение, лишённое всякого интереса и взятое
только силой принуждения, убивает в учении охоту к овладению знаниями.
Вместе с тем, он указывал, что нельзя всё учение свести к интересу. Учение
требует и черновой работы и волевого усилия ”.
1.3 Виды интересов.
Интересы людей чрезвычайно разнообразны, как разнообразна
человеческая деятельность. Интересы различают по их содержанию или
направленности. В этом плане можно выделить математические, общественные и
духовные интересы.
Нас интересуют духовные интересы, так как они характеризуют
высокий уровень развития личности. Это прежде всего познавательные интересы
(в широком смысле слова) к математике, физике, химии, биологии и
т.п. к ним также относятся познавательные интересы к литературе и различным
видам искусства (музыке, живописи).
Г.И. Щукина различает непосредственный и опосредованный
интересы.[8]
Непосредственный интерес – это интерес к самому процессу деятельности:
процессу познания, овладения знаниями, процессу труда.
Опосредованный интерес – это интерес к результатам деятельности.
Наиболее благоприятными для активной и продуктивной деятельности
личности является правильное соотношение непосредственного и
опосредованного интересов.
По уровню действительности Щукина различает пассивные и активные
интересы.[8]
Пассивные – это созерцательные интересы, при которых человек.
1.4 Уровни развития интереса
Г.И. Щукина, выделяет следующие уровни развития интереса [8]:
1) Интерес – любознательность – связанный с эмоциями удивления, изумления,
смешного, любопытства. Этот интерес отличается слабой устойчивостью,
изменчивостью и недостаточной глубиной.
2) Аффективный интерес – основанный на более сильных чувствах
коллективизма, симпатии, долга. Этот интерес отличается большой глубиной и
устойчивостью, но недостаточно дифференцирован и генерализован.
3) Интеллектуальный интерес – связан с пониманием значения объекта, его
связей с другими предметами. Он отличается большой сознательностью и
возрастающим волевым характером.
4) Творчески-волевой интерес – здесь интерес планируется самой личностью и
его устойчивость такова, что он выдерживает трудности и преодолевает
противодейственные влияния.
1.5 Познавательный интерес, как особый вид интересов.
Г.И. Щукина, специально занимавшаяся исследованием познавательных
интересов в педагогике, рассматривает познавательный интерес, как один из
важнейших видов интересов, обладающий особыми свойствами, она определяет
этот интерес следующим образом: “…познавательный интерес выступает перед
нами как избирательная направленность личности, обращенная к области
познания, к её предметной стороне и самому процессу овладения
знаниями”.[10]
Таким образом, особое свойство этого интереса заключается в том, что его
объектом может служить не только содержание предмета, но и процесс
овладения знаниями.
Познавательный интерес относится к различным областям познавательной
деятельности. Он может быть весьма широким, распространяющимся на получение
информации вообще, на изучение нового о различных сторонах предметного мира
и углубленным в определенную область познавания (речь идет о процессе
овладения учащимся научными истинами, закономерностями, системой знаний в
школе).
Познавательный интерес направлен на познавание, овладение знаниями, которые
представлены в школьных предметах. При этом он обращен не только к
содержанию данной предметной области, но и к процессу добывания этих
знаний, к познавательной деятельности. Познавательный интерес может
приобрести характер склонности, если человек усиленно и постоянно
занимается определенным видом деятельности.
В интеллектуальной деятельности, протекающей под влиянием познаватель-ного
интереса, проявляется: активный поиск, догадка, исследовательский подход,
готовность к решению задач.
Эмоциональные проявления вплетенные в познавательный интерес: эмоции
удивления, чувство ожидания нового, чувство успеха.
Ядром познавательного интереса являются мыслительные процессы. По выражению
К.Д. Ушинского, это интерес полный мысли.
Также мы согласны с К.Д. Ушинским в том, что познавательный интерес
составляет важнейший мотив учения, который лежит в основе положи-тельного
отношения учащихся к школе, к знаниям, которые побуждают
учиться с охотой. Важнейшей особенностью
познавательного интереса является и то, что центром его бывает такая
познавательная задача, которая требует от человека активной поисковой или
творческой деятельности, а не элементарной ориентировки на новизну и
неожидан-ность.
“…интерес возникший в процессе обучения, …активизирует умствен-ную
деятельность не только в данный момент, но и направляет её к последующему
решению интеллектуальных задач, т.е. способствует организации последующей
деятельности”.
Б.Г. Ананьев.
Познавательный интерес выступает как ценнейший мотив учебной
деятельности школьников, и это наиболее существенное его проявление. Он
усиливает и углубляет другие познавательные мотивы, с которыми он
переплетается и взаимодействует: возможность получать знания, узнавать
новое, успехи в учении и др.
Также познавательный интерес взаимодействует и с моральными мотивами,
главным образом с чувством долга и ответственности. Познавательный интерес
выступает не только как мотив и средство обучения, но и как устойчивое
качество личности. Пытливость, любознательность, готовность к
познавательной деятельности, “жажда знаний”, все это различные выражения
познавательной направленности личности, в основе которой лежит
познавательный интерес, определяющий активное отношение к миру и к процессу
его познания. Познавательный интерес определяет активность в учении,
инициативу в постановке познавательных целей. Он определяет поисковый,
творческий характер любого вида познавательной деятельности,
благоприятствует формированию способностей к творчеству в самых разных
видах деятельности. Проблема формирования познавательных интересов учащихся
в процессе обучения – одна из центральных. Решение её связано с двумя
главными вопросами: во-первых, содействовать наиболее полноценному
отражению в сознании учащихся явлений науки, проникновению в их
существенные взаимосвязи; во-вторых, на этой почве пробуждать, поддерживать
и подкреплять такое отношение к знаниям, к учению в школе, которое
наполнено готовностью овладеть знаниями, стремлением не скользить по
поверхности, а углубляться все более и более в процессе познавания.
1.6 Стимуляция познавательных интересов у учащихся.
Г.И. Щукина различает три группы условий стимулирующих развитие
познавательных интересов [10]:
Первая — связана с содержанием учебного материала – к ней относится новизна
содержания, обновление уже усвоенных фактов, исторический подход к
сообщаемому материалу.
Вторая – организация процесса обучения – различные формы самостоя-тельной
работы, проблемное обучение, исследовательский подход к изучаемому
материалу, творческие работы.
Третья – определяется отношениями, складывающимися между учениками и
учителем – сюда относят способности учащихся, увлеченность преподавания
самого учителя, его готовность придти на помощь ученикам, вера в их силы и
возможности.
Все условия, стимулирующие возникновение и развитие
математических интересов можно расположить в следующем порядке:
Первая группа – связанная с содержанием.
— задачи повышенной трудности и удовлетворение, получаемое при решении.
— новизна и разнообразие материала школьного курса математики, сведения из
истории науки, обогащение содержания предмета.
— сила и изящество методов вычислений, исследований и доказательств.
Вторая группа – связана с организацией учебного процесса.
— разнообразные системы уроков, нешаблонное их построение, включение по
возможности в каждый урок новых элементов.
— увлекательное проведение уроков, активизация деятельности учащих-ся,
организация творческих работ, соревнований, дидактических игр,
использование Т.С.О.
Третья группа – связана с отношением личности.
— прирожденные математические способности.
— успех в изучении предмета и поощрение.
— влияние родных и близких.
Действие практически всех этих условий в значительной степени
зависит от учителя, его знаний, умений и мастерства. Учитель не определяет
содержание математического образования, но он может обогатить его,
привлекая исторический материал, материал из смежных дисциплин, подчеркивая
красоту и мощь методов математики. Что же касается организации методики
занятий, а также отношений с учениками, то тут всё зависит от учителя.
Задача учителя: сформировать познавательный интерес как устойчивый
мотив познавательной деятельности, что составляет прочную основу и
направленности личности и её отношение к учению, к духовным ценностям.
Учение – основа развития познавательных интересов учащихся. В
учебном процессе, организующем и направляющем познавательную деятельность
школьника, заключены важнейшие условия и возможности прямого и косвенного
влияния на познавательный интерес. Эти влияния, выступающие как стимулы
познавательного интереса систематически и повседневно формируют не только
ситуативный интерес, но и содействуют становлению его как самого значимого
мотива познавательной деятельности.
Стимуляция познавательных интересов в учебном процессе имеет разные
источники и, чтобы управлять формированием интереса, учитель должен ясно
осознавать, что именно способствует их возникновению и укреплению.
По мнению Г.И. Щукиной существует три важнейших источника стимуляции
познавательных интересов [10]:
1) Содержание учебного материала – вызывает удивление перед новыми
открытиями, уважение к науке и её представителям, понимание значи-мости
науки для жизненной и общественной практики.
2) Организация познавательной деятельности – рациональная организация
обучения рождает удовлетворение собственным продвижением, стремление к
преодолению трудностей.
3) Отношения, которые складываются в учебном процессе между учителем и
учащимися – учение с учителем, товарищами, в результате чего складываются
многозначительные отношения, сопутствуют возникнове-нию иного строя
моральных и интеллектуальных переживаний, являющихся также сильными
побудителями познавательного интереса. Здесь возникают коллективные
сопереживания, радость за успех товарища, стремление оказать ему помощь.
Повышение интереса на уроках математики может достигаться следующим
образом:
1) Обогащение содержания материалом по истории науки.
2) Решение задач повышенной трудности и нестандартных задач.
3) Подчеркивание силы и изящества методов вычислений, доказательств,
преобразований и исследований.
4) Разнообразием уроков, нешаблонным их построением, включением в уроки
элементов придающих каждому уроку своеобразный характер, использование
Т.С.О., наглядных пособий, разнообразием устного счета.
5) Активизация познавательной деятельности учащихся на уроке с
использованием форм самостоятельной и творческой работы.
6) Используя различные формы обратной связи: систематическим проведением
опроса, кратковременных устных и письменных контрольных работ, различных
тестов, математических диктантов наряду с контрольными работами
предусмотренными планом.
7) Разнообразие домашнего задания.
8) Установление внутренних и меж предметных связей, показом и разъяснением
применения математики в жизни и в производстве.
Большую роль для формирования интереса к изучению математики играет
личность учителя, причем наиболее важной чертой в этом является его
увлечённость предметом и преподаванием, желание учителя поверить в
возможности ученика, готовность придти ему на помощь. Учитель должен быть
сдержан и терпелив и никогда не допускать грубости по отношению к ученику.
Благотворно влияет на формирование интереса поощрение учителя, его похвала.
1.7 Устные вычисления.
В методике математики различают устные и письменные приемы
вычисления. К устным относят все приемы для случаев вычислений в пределах
100, а также сводящихся к ним приемы вычислений для случаев за пределами
100 ( например прием для случая 900·7 будет устным, так как он сводится к
приему для случая 9·7 ). К письменным, относят приемы для всех других
случаев вычислений над числами большими 100. [1]
Устная работа на уроках математики в начальной школе, а особенно в
первом классе, имеет большое значение – это и беседы учителя с классом или
отдельными учениками, и рассуждения учащихся при выполнении тех или иных
заданий и т.п. Среди этих видов устной работы можно выделить так называемые
устные упражнения. Ранее они сводились в основном к вычислениям, поэтому за
ними закрепилось название “устный счет”. И хотя в современных программах
содержание устных упражнений весьма разнообразно и велико, за счет введения
алгебраического и геометрического материала, а также за счет большого
внимания к свойствам действий над числами и величинами и других вопросов,
название “устный счет” по отношению к устной форме проведения упражнений
сохранилось до сих пор. Это по мнению В.С. Кравченко, приводит к некоторым
неудобствам, так как термин “устный счёт” используется, кроме того, и в
своём естественном смысле, то есть вычисления, производимые устно, в уме,
без записей. В связи с этим вместо термина “устный счёт”, удобнее
пользоваться термином “устные упражнения”.
Как пишет опытный педагог Зайцева О.П. в своей статье “Роль
устного счета в формировании вычислительных навыков и развития личности
ребенка” [5]:важность и необходимость устных упражнений доказывать не
приходиться. Значение их велико в формировании вычислительных навыков и в
совершенствовании знаний по нумерации, и в развитии личностных качеств
ребёнка. Создание определённой системы повторения ранее изученного
материала дает учащимся возможность усвоения знаний на уровне
автоматического навыка. Устные вычисления не могут быть случайным этапом
урока, а должны находиться в методической связи с основной темой и носить
проблемный характер.
Для достижения правильности и беглости устных вычислений в течении
всех трех, четырех лет обучения на каждом уроке математики необходимо
выделять 5 – 10 минут для проведения упражнений в устных вычислениях,
предусмотренных программой каждого класса.
nsportal.ru
