Алгебра 11 класс (базовый уровень)
Описание
Интерактивный онлайн-учебник «Алгебра 11 класс» сможет заменить бумажный учебник или дополнить его. Содержание интерактивных онлайн-курсов соответствует требованиям федеральных государственных образовательных стандартов (ФГОС).
Онлайн-уроки построены таким образом, что перед изучением новой темы, предлагается повторить и закрепить ранее изученный материал Алгебра 10 класса.
Онлайн-уроки подходят для самостоятельного изучения. Ребенок познакомится с теорией, проверит полученные знания с помощью онлайн-тренажеров и интерактивных заданий, подготовится к контрольным и проверочным работам, экзаменам, ОГЭ и ЕГЭ.
Такой формат занятий поможет разобраться в новой теме или подтянуть знания по предмету. Доступ к онлайн-урокам осуществляется через интернет (24/7). Это позволяет заниматься в дороге и дома, во время соревнований, выездов на олимпиады или в оздоровительный лагерь.
Наш сборник — это способ улучшить успеваемость, начать подготовку к экзаменам, повторить пройденный материал во время каникул.
В качестве одной из составляющей курса, ученикам доступен объемный дополнительный материал, позволяющий углубить имеющиеся знания. Различные типы заданий, представленные в онлайн-учебнике — одна из важных составляющих подготовки к будущим экзаменам.
Темы:
- Первообразная
- Применение интеграла
- Степенная функция. Иррациональные уравнения
- Показательная функция
- Логарифмическая функция
- Производная показательной и логарифмической функции
- Алгебраические уравнения, неравенства и их системы
- Повторение. Подготовка к государственному экзамену
- выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа, находить в несложных случаях значения степеней с целыми показателями, находить значения числовых выражений;
- округлять целые числа и десятичные дроби;
- пользоваться основными единицами длины, массы, времени, скорости, площади, объёма;
- составлять буквенные выражения и формулы по условиям задач;
- выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями;
- решать линейные уравнения, системы двух линейных уравнений с двумя переменными;
- решать текстовые задачи алгебраическим методом;
- изображать числа точками на координатной прямой;
- определять координаты точки плоскости, строить точки с заданными координатами;
- выстраивать аргументации при доказательстве и в диалоге;
- извлекать информацию, представленную в таблицах, на диаграммах, графиках, составлять таблицы, строить диаграммы и графики;
- решать учебные и практические задачи, требующие систематического перебора вариантов;
- вычислять средние значения результатов измерений;
- сравнивать шансы наступления случайных событий, оценивать вероятности случайного события в практических ситуациях.

Оглавление
Занятие 1. Первообразная
Интернет-урок 1. Определение первообразной
Интернет-урок 2. Основное свойство первообразной
Интернет-урок 3. Правила нахождения первообразных
Занятие 2. Тематическая контрольная работа № 1
Занятие 3. Применение интеграла
Интернет-урок 1. Площадь криволинейной трапеции
Интернет-урок 2. Интеграл. Формула Ньютона-Лейбница
Интернет-урок 3. Вычисление площадей с помощью интегралов
Интернет-урок 4. Применение интегралов к решению практических задач
Занятие 4. Тематическая контрольная работа № 2
Занятие 5. Степенная функция. Иррациональные уравнения
Интернет-урок 1. Бесконечно убывающая геометрическая прогрессия
Интернет-урок 2. Арифметический корень натуральной степени
Интернет-урок 3. Степень с рациональным показателем
Интернет-урок 4. Степенная функция и её график
Степенная функция и её график
Интернет-урок 5. Взаимно-обратные функции
Интернет-урок 6. Функция корень n-й степени из х
Интернет-урок 7. Иррациональные уравнения
Занятие 6. Тематическая контрольная работа № 3
Занятие 7. Показательная функция
Интернет-урок 1. Показательная функция
Интернет-урок 2. Решение показательных уравнений
Интернет-урок 3. Решение показательных неравенств
Интернет-урок 4. Системы показательных уравнений и неравенств
Занятие 8. Тематическая контрольная работа № 4
Занятие 9. Логарифмическая функция
Интернет-урок 1. Определение логарифма
Интернет-урок 2. Свойства логарифмов
Интернет-урок 3. Десятичные логарифмы. Натуральный логарифм. Формула перехода к новому основанию
Занятие 10. Тематическая контрольная работа № 5
Занятие 11. Логарифмическая функция
Интернет-урок 1. Логарифмическая функция, её свойства и график
Логарифмическая функция, её свойства и график
Интернет-урок 2. Решение логарифмических уравнений
Интернет-урок 3. Решение логарифмических неравенств
Занятие 12. Тематическая контрольная работа № 6
Занятие 13. Производная показательной и логарифмической функции
Интернет-урок 1. Производная показательной функции
Интернет-урок 2. Производная логарифмической функции
Занятие 14. Тематическая контрольная работа № 7
Занятие 15. Алгебраические уравнения, неравенства и их системы
Интернет-урок 1. Решение алгебраических уравнений
Интернет-урок 2. Дробно-рациональные неравенства. Метод интервалов
Интернет-урок 3. Различные способы решения систем уравнений и неравенств
Интернет-урок 4. Решение задач с помощью систем уравнений
Занятие 16. Тематическая контрольная работа № 8
Занятие 17. Повторение. Подготовка к государственному экзамену
Интернет-урок 1.
Интернет-урок 2. Работа с графиками
Интернет-урок 3. Решение уравнений и неравенств
Интернет-урок 4. Задачи по теме «Вероятность»
Интернет-урок 5. Задачи по теме «Производная функции и её применение»
Занятие 18. Тематическая контрольная работа № 9
Рабочая программа к учебнику С.М. Никольского и др. «Алгебра и начала анализа», 11 класс Лунева О.А.
Рабочая программа к учебнику С.М. Никольского и др. «Алгебра и начала анализа», 11 класс Лунева О.А.
Автор: edu1
Методическая копилка — Математика
Рабочая программа
к учебнику С.М. Никольского и др.
«Алгебра и начала анализа», 11 класс (базовый уровень)
Пояснительная записка.
Общая характеристика учебного предмета
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:
В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
знакомство с основными идеями и методами математического анализа.
Цели
Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
- воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.

Общеучебные умения, навыки и способы деятельности
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Тематическое планирование составлено к УМК С.М. Никольского и др. «Алгебра и начала анализа», 11 класс, М. «Просвещение», 2008 год на основе федерального компонента государственного стандарта общего образования с учетом авторского тематического планирования учебного материала, опубликованного в журнале «Математика в школе » №2, 2005.
Тематический план по алгебре и началам анализа в 11 классе
Учебник : «Алгебра и начала анализа, 11»
С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин
3 часа в неделю, всего 102 часа.
|
№ урока |
Содержание учебного материала |
Кол-во часов |
Дата |
|
|
Пример. |
Факт. |
|||
|
1. Функции и их графики |
6 |
|||
|
1 |
Элементарные функции |
1 |
4 сен. |
|
|
2 |
Область определения и область изменения функции. Ограниченность функции |
1 |
6 сен. |
|
|
3 |
Четность , нечетность, периодичность функции |
1 |
9 сен. |
|
|
4 |
Промежутки возрастания , убывания , знакопостоянства и нули функции |
1 |
11 сен. |
|
|
5 |
Исследование функций и построение их графиков элементарными методами |
1 |
13 сен. |
|
|
6 |
Основные способы преобразования графиков |
1 |
16 сен. |
|
|
2. Предел функции и непрерывность. |
1 |
|||
|
7 |
Понятие предела функции |
1 |
18 сен. |
|
|
3. Обратные функции |
3 |
|||
|
8-9 |
Понятие обратной функции |
2 |
20,23 сен. |
|
|
10 |
Контрольная работа №1по теме «Функции и их графики» |
1 |
25 сен. |
|
|
4. Производная |
9 |
|||
|
11-12 |
Понятие производной |
2 |
27,30 сен. |
|
|
13 |
Производная суммы . |
1 |
2 ок. |
|
|
14-15 |
Производная произведения. Производная частного |
2 |
4,7 ок. |
|
|
16 |
Производные элементарных функций |
1 |
9 ок |
|
|
17-18 |
Производная сложной функции |
2 |
11,14 ок. |
|
|
19 |
Контрольная работа №2по теме «Производная» |
1 |
16 ок. |
|
|
5. Применение производной |
15 |
|||
|
20-21 |
Максимум и минимум функции |
2 |
18,21 ок. |
|
|
22-23 |
Уравнение касательной |
2 |
23,25 ок. |
|
|
24 |
Приближенные вычисления |
1 |
28 ок. |
|
|
25-26 |
Возрастание и убывание функций |
2 |
30 ок. 11 нояб. |
|
|
27 |
Производные высших порядков |
1 |
13 нояб. |
|
|
28-29 |
Экстремум функции с единственной критической точкой |
2 |
15,18 нояб. |
|
|
30-31 |
Задачи на максимум и минимум |
2 |
20,22 нояб. |
|
|
32-33 |
Построение графиков функций с применением производной |
2 |
25,27 нояб. |
|
|
34 |
Контрольная работа №3по теме «Применение производной» |
1 |
29 нояб. |
|
|
6. Первообразная и интеграл |
11 |
|||
|
35-37 |
Понятие первообразной |
3 |
2,4,6. дек. |
|
|
38 |
Площадь криволинейной трапеции |
1 |
9 дек. |
|
|
39 |
Определенный интеграл |
1 |
11дек. |
|
|
40-42 |
Формула Ньютона-Лейбница |
3 |
13,16,18 дек. |
|
|
43 |
Свойства определенных интегралов |
1 |
20 дек. |
|
|
44 |
Применение определенных интегралов в геометрических и физических задачах |
1 |
23 дек. |
|
|
45 |
Контрольная работа № 4по теме «Первообразная и интеграл» |
1 |
25 дек. |
|
|
7. Равносильность уравнений и неравенств. |
4 |
|||
|
46-47 |
Равносильные преобразования уравнений. |
2 |
27 дек 13 ян. |
|
|
48-49 |
Равносильные преобразования неравенств |
2 |
15,17 ян. |
|
|
8. |
7 |
|||
|
50 |
Понятие уравнения-следствия. |
1 |
20 ян. |
|
|
51-52 |
Возведение уравнения в четную степень |
2 |
22,24 ян. |
|
|
53 |
Потенцирование уравнений |
1 |
27 ян. |
|
|
54 |
Другие преобразования, приводящие к уравнению- следствию. |
1 |
29 ян. |
|
|
55-56 |
Применение нескольких преобразований, приводящих к уравнению-следствию. |
2 |
31 ян. 3 фев |
|
|
9. Равносильность уравнений и неравенств |
6 |
|||
|
57 |
Основные понятия. |
1 |
5 фев. |
|
|
58-59 |
Решение уравнений с помощью систем. |
2 |
7,10 фев. |
|
|
60 |
Решение уравнений с помощью систем (продолжение) |
1 |
12 фев. |
|
|
61 |
Решение неравенств с помощью систем. |
1 |
14 фев. |
|
|
62 |
Решение неравенств с помощью систем ( продолжение) |
1 |
17 фев. |
|
|
10. Равносильность уравнений на множествах |
3 |
|||
|
63 |
Основные понятия |
1 |
19 фев. |
|
|
64 |
Возведение уравнения в четную степень. |
1 |
21 фев |
|
|
65 |
Контрольная работа №5по теме «Равносильность уравнений и неравенств» |
1 |
24 фев. |
|
|
11. Равносильность неравенств на множествах |
2 |
|||
|
66 |
Основные понятия |
1 |
26 фев |
|
|
67 |
Возведение неравенства в четную степень. |
1 |
28 фев. |
|
|
12 . Метод промежутков для уравнений и неравенств |
4 |
|||
|
68 |
Уравнения с модулями |
1 |
3 мар |
|
|
69 |
Неравенства с модулями |
1 |
5 мар. |
|
|
70 |
Метод интервалов для непрерывных функций |
1 |
7 мар. |
|
|
71 |
Контрольная работа №6 по теме «Метод промежутков для уравнений и неравенств» |
1 |
12 мар. |
|
|
13. Использование свойств функции при решении уравнений и неравенств |
5 |
|||
|
72 |
Использование области существования функций. |
1 |
14 мар. |
|
|
73 |
Использование неотрицательности функции |
1 |
17 мар. |
|
|
74-75 |
Использование ограниченности функции |
2 |
19,21 мар. |
|
|
76 |
Использование монотонности и экстремумов функции. |
1 |
2 апр. |
|
|
77-78 |
Использование свойств синуса и косинуса. |
2 |
4 , 7 ап. |
|
|
14. Системы уравнений с несколькими неизвестными |
7 |
|||
|
79-80 |
Равносильность систем |
2 |
9,11 ап. |
|
|
81-82 |
Система-следствие |
2 |
14,16 ап. |
|
|
83-84 |
Метод замены неизвестных |
2 |
18,21 ап. |
|
|
85 |
Контрольная работа № 7 по теме «Системы уравнений с несколькими неизвестными» |
1 |
23 ап. |
|
|
86- |
Повторение курса алгебры и математического анализа 10-11 классов |
8 |
25 ап- 20 мая |
|
|
Резерв |
3 ч |
|||
СОДЕРЖАНИЕ ОБУЧЕНИЯ
1. Функции и их графики
Функции и их графики
Элементарные функции. Исследование функций и построение их графиков элементарными методами. Основные способы преобразования графиков.
Основная цель — овладеть методами исследования функций и построения их графиков.
Сначала вводятся понятия элементарной функции и суперпозиции функций (сложной функции). Затем исследуются вопросы об области определения и области изменения функции, об ограниченности, четности (или нечетности) и периодичности функции, о промежутках возрастания (убывания) и знакопостоянства функции. Результаты исследования функции применяются для построения ее графика. Далее рассматриваются основные способы преобразования графиков функций — симметрия относительно осей координат, сдвиг вдоль осей, растяжение и сжатие графиков. Все эти способы применяются к построению графика функции у = Af (k (x— а)) + В по графику функции у = f(x).
Рассматривается симметрия графиков функций у = f(x) и х = f(y) относительно прямой у = х. По графику функции у=f{x) строятся графики функций у = \f(x)\ и у = f(\x\). Затем строятся графики функций, являющихся суперпозицией, суммой, произведением функций.
2.Предел функции и непрерывность
Понятие предела функции. Односторонние пределы, свойства пределов. Непрерывность функций в точке, на интервале. Непрерывность элементарных функций.
Основная цель — усвоить понятия предела функции и непрерывности функции в точке и на интервале.
На интуитивной основе вводятся понятия предела функции сначала при х→+∞ , х→- ∞ , затем в точке. Рассматриваются односторонние пределы и свойства пределов функций. Вводится понятие непрерывности функции в точке и на интервале. Выясняются промежутки непрерывности элементарных функций.
Выясняются промежутки непрерывности элементарных функций.
Вводятся понятия непрерывности функции справа (слева) в точке х0и непрерывности функции на отрезке. Приводится также определение предела функции в точке «на языке £ — 8» и «на языке последовательностей». Вводится понятие разрывной функции и рассматриваются примеры разрывных функций.
3.Обратные функции
Понятие обратной функции.
Основная цель — усвоить понятие функции, обратной к данной, и научить находить функцию, обратную к данной.
Сначала на простом примере вводится понятие функции, обратной к данной. Затем определяется функция, обратная
к данной строго монотонной функции. Приводится способ построения графика обратной функции.
Вводится понятие взаимно обратных функций, устанавливается свойство графиков взаимно обратных функций, построенных в одной системе координат. Исследуются основные обратные тригонометрические функции и строятся их графики.
4.Производная
Понятие производной. Производная суммы, разности, произведения и частного двух функций. . Производные элементарных функций. Производная сложной функции.
Основная цель — научить находить производную любой элементарной функции.
Сначала вводится новая операция: дифференцирование функции и ее результат — производная функции. Затем выясняется механический и геометрический смысл производной, после чего находятся производные суммы, разности, произведения, частного и суперпозиции двух функций, а также производные всех элементарных функций. Доказывается непрерывность функции в точке, в которой она имеет производную. Вводится понятие дифференциала функции, доказывается теорема о производной обратной функции и находятся производные для обратных тригонометрических функций.
5.Применение производной
Максимум и минимум функции. Уравнение касательной. Приближенные вычисления. . Возрастание и убывание функций. Производные высших порядков. Задачи на максимум и минимум. Построение графиков функций с применением производной.
Приближенные вычисления. . Возрастание и убывание функций. Производные высших порядков. Задачи на максимум и минимум. Построение графиков функций с применением производной.
Основная цель — научить применять производную при исследовании функций и решении практических задач.
Сначала вводятся понятия локальных максимума и минимума функции, ее критических точек, а затем рассматривается метод нахождения максимума и минимума функции на отрезке. Выводится уравнение касательной к графику функции, исследуется возрастание и убывание функций с помощью производных. Рассматриваются экстремум функции с единственной критической точкой и задачи на максимум и минимум. Проводится исследование функций с помощью производной, строятся их графики.
Доказываются теоремы Ролля и Лагранжа. Обсуждается вопрос о выпуклости вверх (или вниз) графика функции, имеющей вторую производную, т. е. вопрос о геометрическом смысле второй производной. Вводится понятие асимптоты графика функции. Исследуется дробно-линейная функция. Вводятся понятия формулы и ряда Тейлора, показывается их применение при приближенных вычислениях.
Исследуется дробно-линейная функция. Вводятся понятия формулы и ряда Тейлора, показывается их применение при приближенных вычислениях.
6.Первообразная и интеграл
Понятие первообразной. . Площадь криволинейной трапеции. Определенный интеграл. Формула Ньютона — Лейбница. Свойства определенных интегралов. .
Основная цель — знать таблицу первообразных (неопределенных интегралов) основных функций и уметь применять формулу Ньютона — Лейбница при вычислении определенных интегралов и площадей фигур.
Сначала вводится понятие первообразной для функции, непрерывной на интервале, затем понятие неопределенного интеграла, приводятся основные свойства неопределенных «,, интегралов и таблица неопределенных интегралов. Определяется площадь криволинейной трапеции как предел интегральной суммы для неотрицательной функции. Определенный интеграл также вводится как предел интегральной суммы для непрерывной на отрезке функции. Приводится формула Ньютона — Лейбница для вычисления определенных интегралов.
Приводится формула Ньютона — Лейбница для вычисления определенных интегралов.
Рассматриваются способы нахождения неопределенных интегралов — замена переменной и интегрирование по частям, метод трапеций для приближенного вычисления определенных интегралов. Приводятся свойства определенных интегралов и их применение для вычисления площадей фигур на плоскости и для решения геометрических и физических задач. Вводятся понятия дифференциального уравнения, его общего и частного решения. Приводятся способы решения некоторых дифференциальных уравнений.
7.Равносильность уравнений и неравенств
Равносильные преобразования уравнений и неравенств.
Основная цель — научить применять равносильные преобразования при решении уравнений и неравенств.
Сначала перечисляются равносильные преобразования уравнений. Подчеркивается, что при таких преобразованиях множество корней преобразованного уравнения совпадает с множеством корней исходного уравнения. Рассматриваются примеры применения таких преобразований пpи решении уравнений.
Рассматриваются примеры применения таких преобразований пpи решении уравнений.
Затем аналогичным образом рассматриваются равно сильные преобразования неравенств и их применение при] решении неравенств.
8. Уравнения-следствия
Понятие уравнения-следствия. Возведение уравнения в четную степень. Потенцирование логарифмических уравнений. Приведение подобных членов уравнения. Освобождение уравнения от знаменателя.
Основная цель — научить применять преобразования, приводящие к уравнению-следствию.
Сначала вводится понятие уравнения-следствия, перечисляются преобразования, приводящие к уравнению-следствию. Подчеркивается, что при таком способе решение уравнения проверка корней уравнения-следствия является обязательным этапом решения исходного уравнения. Затем рассматриваются многочисленные примеры применения каждого из этих преобразований в отдельности и нескольких таких преобразований.
9.Равносильность уравнений и неравенств системам
Решение уравнений с помощью систем. Решение неравенств с помощью систем.
Решение неравенств с помощью систем.
Основная цель — научить применять переход от уравнения (или неравенства) к равносильной системе.
Сначала вводятся понятия системы, равносильности систем, равносильности уравнения (неравенства) системе или совокупности систем.
Затем перечисляются некоторые уравнения (неравенства) и равносильные им системы. Формулируются утверждения об их равносильности. Приводятся примеры применения этих утверждений.
10.Равносильность уравнений на множествах
Возведение уравнения в четную степень.
Основная цель — научить применять переход к сравнению, равносильному на некотором множестве исходному уравнению.
Сначала вводится понятие равносильности двух уравнений на множестве, описываются те множества чисел, на каждом из которых получается уравнение, равносильное на этом множестве исходному уравнению при возведении уравнения в четную степень, при умножении уравнения на функцию, при логарифмировании, при потенцировании, при приведении подобных членов уравнения, при применении некоторых формул. Для каждого преобразования уравнения формулируются соответствующие утверждения о равносильности и приводятся примеры их применения.
Для каждого преобразования уравнения формулируются соответствующие утверждения о равносильности и приводятся примеры их применения.
11.Равносильность неравенств на множествах
Возведение неравенства в четную степень и умножение неравенства на функцию, потенцирование логарифмических неравенств, приведение подобных членов, применение некоторых формул. Нестрогие неравенства.
Основная цель — научить применять переход к неравенству, равносильному на некотором множестве исходному неравенству.
Вводится понятие равносильности двух неравенств на множестве, описываются те множества чисел, на каждом из которых получается неравенство, равносильное на этом множестве исходному неравенству при возведении уравнения в четную степень, при умножении уравнения на функцию, при потенцировании логарифмического неравенства, при приведении подобных членов неравенства, при применении некоторых формул. Для каждого преобразования неравенства формулируются соответствующие утверждения о равносильности и приводятся примеры их применения. Рассматриваются нестрогие неравенства.
Рассматриваются нестрогие неравенства.
12.Метод промежутков для уравнений и неравенств
Уравнения и неравенства с модулями. Метод интервалов для непрерывных функций.
Основная цель — научить решать уравнения и неравенства с модулями и применять метод интервалов для решения неравенств.
Сначала рассматриваются уравнения с модулями и описывается способ решения таких уравнений переходом к уравнениям, равносильным исходному на некотором множестве и не содержащим модулей. Затем аналогично рассматриваются неравенства с модулями. Наконец, для функций f(x), непрерывных на некоторых интервалах, рассматривается способ решения неравенств f(x) > 0 и f(x) называемый методом интервалов.
При обучении на профильном уровне рассматриваются более сложные уравнения и неравенства.
13.Использование свойств функций при решении уравнений и неравенств
Использование областей существования, неотрицательности, ограниченности, монотонности и экстремумов функции, свойств синуса и косинуса при решении уравнений и неравенств.
Основная цель — научить применять свойства функций при решении уравнений и неравенств.
Приводятся примеры решения уравнений и неравенств с использованием свойств функций.
14.Системы уравнений с несколькими неизвестными
Равносильность систем. Система-следствие. Метод замены неизвестных.
Основная цель — освоить разные способы решения систем уравнений с несколькими неизвестными.
Вводятся понятия системы уравнений, равносильности систем, приводятся утверждения о равносильности систем при тех или иных преобразованиях, рассматриваются основные методы решения систем уравнений: метод подстановки, метод линейных преобразований, метод перехода к системе-следствию, метод замены неизвестных.
Рассматривается решение систем уравнений при помощи рассуждений с числовыми значениями.
сла.
15.Повторение курса алгебры и начал математического анализа за 10—11 классы
ПЕРЕЧЕНЬ ОБЯЗАТЕЛЬНЫХ КОНТРОЛЬНЫХ РАБОТ
1. Контрольная работа №1по теме «Функции и их графики»
Контрольная работа №1по теме «Функции и их графики»
2. Контрольная работа №2по теме «Производная»
3. Контрольная работа №3по теме «Применение производной»
4. Контрольная работа № 4по теме «Первообразная и интеграл»
5. Контрольная работа №5по теме «Равносильность уравнений и неравенств»
6. Контрольная работа №6 по теме «Метод промежутков для уравнений и неравенств»
7. Контрольная работа № 7 по теме «Системы уравнений с несколькими неизвестными»
8. Итоговая контрольная работа.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики на базовом уровне ученик должен
знать/понимать
- значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
- значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
- универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
- вероятностный характер различных процессов окружающего мира.

Алгебра
уметь
- выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
- проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
- вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.

Функции и графики
уметь
- определять значение функции по значению аргумента при различных способах задания функции;
- строить графики изученных функций;
- описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
- решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа
уметь
- вычислять производные и первообразные элементарных функций, используя справочные материалы;
- исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
- вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.

Уравнения и неравенства
уметь
- решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
- составлять уравнения и неравенства по условию задачи;
- использовать для приближенного решения уравнений и неравенств графический метод;
- изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей
уметь
- решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
- вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- анализа реальных числовых данных, представленных в виде диаграмм, графиков;
- анализа информации статистического характера.
Литература
1.Методические рекомендации к учебникам математики для 10-11 классов, журнал «Математика в школе» №2-2005год;
2. Алгебра и начала анализа: учеб. для 11 класса общеобразоват. учреждений /С.М. Никольский и др.- М.: Просвещение, 2007.
3. Дидактические материалы для 11 класса./ М.К. Потапов, А.В. Шевкин, 2008 г.
4. Алгебра и начала анализа. Книга для учителя. 11 класс. /С.М. Никольский и др.- М.: Просвещение, 2009 г.
Алгебра и начала математического анализа, 11 класс | Шевкин.Ru
Алгебра и начала математического анализа. 11 класс : Учебник для общеобразовательных организаций / С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин. – М.: Просвещение, 2019. – 464 с.
Алгебра и начала анализа: Дидактические материалы для 11 класса: Базовый и профильный уровни / М.К.Потапов, А.В.Шевкин. – М.: Просвещение, 2018. – 189 с.
Алгебра и начала математического анализа: Книга для учителя. 11 класс: базовый и профильный уровни / М.К.Потапов, А.В.Шевкин. – М.: Просвещение, 2009. – 256 с.
Небольшие заметки Шевкина А.В. по методике работы с текстовыми задачами, по подготовке к ЕГЭ и др. материалы:
Канал НАБЛЮДАТЕЛЬ на Яндекс Дзен.
Блог Шевкин А.В. на МЕЛ.фм.
ПРИМЕРНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
(Учебник «Алгебра и математический анализ, 11» С.М. Никольского и др.)
I вариант — для работы в общеобразовательных классах
(3 ч в неделю, всего 102 ч)
1. Функции и их графики (6).
1.1. Элементарные функции (1).
1.2. Область определения и область изменения функции. Ограниченность функции (1).
1.3. Четность, нечетность, периодичность функций (1).
1.4. Промежутки возрастания, убывания, знакопостоянства и нули функции (1).
1.5. Исследование функций и построение их графиков элементарными методами (1).
1.6. Основные способы преобразования графиков (1).
1.7*. Графики функций, связанных с модулем.
1.8*. Графики сложных функций.
2. Предел функции и непрерывность (4).
2.1. Понятие предела функции (1).
2.2*. Односторонние пределы.
2.3. Свойства пределов функций (1).
2.4. Понятие непрерывности функции (1).
2.5. Непрерывность элементарных функций (1).
2.6*. Разрывные функции.
3. Обратные функции (3).
3.1. Понятие обратной функции (2).
3.2*. Взаимно обратные функции.
3.3*. Обратные тригонометрические функции.
3.4*. Примеры использования обратных тригонометрических функций.
Контрольная работа № 1 (1).
4. Производная (10).
4.1. Понятие производной (2).
4.2. Производная суммы. Производная разности (2).
4.3*. Непрерывность функций, имеющих производную. Дифференциал.
4.4. Производная произведения. Производная частного (2).
4.5. Производные элементарных функций (1).
4.6. Производная сложной функции (2).
4.7*. Производная обратной функции.
Контрольная работа № 2 (1).
5. Применение производной (15).
5.1. Максимум и минимум функции (2).
5.2. Уравнение касательной (2).
5.3. Приближенные вычисления (1).
5.4*. Теоремы о среднем.
5.5. Возрастание и убывание функций (2).
5.6. Производные высших порядков (1).
5.7*. Выпуклость и вогнутость графика функции.
5.8. Экстремум функции с единственной критической точкой (2).
5.9. Задачи на максимум и минимум (2).
5.10*.Асимптоты. Дробно-линейная функция.
5.11. Построение графиков функций с применением производной (2).
5.12*. Формула и ряд Тейлора.
Контрольная работа № 3 (1).
6. Первообразная и интеграл (11).
6.1. Понятие первообразной (3).
6.2*. Замена переменной. Интегрирование по частям.
6.3. Площадь криволинейной трапеции (1).
6.4. Определенный интеграл (1).
6.5*. Приближенное вычисление определенного интеграла.
6.6. Формула Ньютона – Лейбница (3).
6.7. Свойства определенных интегралов (2).
6.8*. Применение определенных интегралов в геометрических и физических задачах.
6.9*. Понятие дифференциального уравнения.
6.10*. Задачи, приводящие к дифференциальным уравнениям.
Контрольная работа № 4 (1).
7. Уравнения-следствия (6).
7.1. Понятие уравнения-следствия (1).
7.2. Возведение уравнения в четную степень (2).
7.3. Потенцирование уравнений (1).
7.4. Другие преобразования, приводящие к уравнению-следствию (1).
7.5. Применение нескольких преобразований, приводящих к уравнению-следствию (1).
8. Равносильность уравнений на множествах (7).
8.1. Основные понятия (1).
8.2. Возведение уравнения в натуральную степень (2).
8.3. Потенцирование и логарифмирование уравнений (1).
8.4. Умножение уравнения на функцию (1).
8.5. Другие преобразования уравнений (1).
8.6*. Применение нескольких преобразований.
8.7*. Уравнения с дополнительными условиями.
Контрольная работа № 5 (1).
9. Равносильность неравенств на множествах (7).
9.1. Основные понятия (1).
9.2. Возведение неравенств в натуральную степень (2).
9.3. Потенцирование и логарифмирование неравенств (1).
9.4. Умножение неравенства на функцию (1).
9.5. Другие преобразования неравенств (1).
9.6*. Применение нескольких преобразований.
9.7*. Неравенства с дополнительными условиями.
9.8. Нестрогие неравенства (1).
10. Метод промежутков для уравнений и неравенств (3).
10.1. Уравнения с модулями (1).
10.2. Неравенства с модулями (1).
10.3*. Метод интервалов для непрерывных функций.
Контрольная работа № 6 (1).
11. Равносильность уравнений и неравенств системам (11).
11.1. Основные понятия (1).
11.2. Распадающиеся уравнения (2).
11.3. Решение уравнений с помощью систем (2).
11.4. Уравнения вида f (a(x)) = f (b(x)) (2).
11.5. Решение неравенств с помощью систем (2).
11.6. Неравенства вида f (a(x)) > f (b(x)) (2).
12*. Нестандартные методы решения уравнений и неравенств.
12.1*. Использование областей существования функций.
12.2*. Использование неотрицательности функций.
12.3*. Использование ограниченности функций.
12.4*. Использование свойств синуса и косинуса.
12.5*. Использование числовых неравенств.
12.6*. Использование производной для решения уравнений и неравенств.
13. Системы уравнений с несколькими неизвестными (7)
13.1. Равносильность систем (2).
13.2. Система–следствие (2).
13.3. Метод замены неизвестных (2).
13.4*. Нестандартные методы решения уравнений и неравенств.
Контрольная работа № 7 (1).
14*. Уравнения и неравенства с параметрами
14.1*. Уравнения с параметром.
14.2*. Неравенства с параметром.
14.3*. Системы уравнений с параметром.
14.4*. Задачи с условиями.
Дополнение*. Комплексные числа.
1. Алгебраическая форма комплексного числа. 2. Сопряженные комплексные числа. 3. Геометрическая интерпретация комплексного числа. 4. Тригонометрическая форма комплексного числа. 5. Корни из комплексных чисел и их свойства. 6. Корни многочленов. 7*. Показательная форма комплексных чисел.
Повторение (12)
Повторение курса алгебры и математического анализа 10–11 классов (10)
Итоговая контрольная работа № 8 (2).
II вариант планирования
для классов с углубленным изучением математики
(5 ч в неделю, всего 170 ч)
1. Функции и их графики (8).
2. Предел функции и непрерывность (6).
3. Обратные функции (7).
4. Производная (14).
5. Применение производной (20).
6. Первообразная и интеграл (16).
7. Уравнения-следствия (8).
8. Равносильность уравнений на множествах (9).
9. Равносильность неравенств на множествах (9).
10. Метод промежутков для уравнений и неравенств (4).
11. Равносильность уравнений и неравенств системам (11).
12. Нестандартные методы решения уравнений и неравенств (4).
13. Системы уравнений с несколькими неизвестными (8)
14. Уравнения и неравенства с параметрами (4).
Комплексные числа (15).
Повторение (12)
Повторение курса алгебры и математического анализа 10–11 классов (10)
Итоговая контрольная работа № 8 (2).
Приводим предисловие и оглавление к дидактическим материалам.
Предисловие
Дидактические материалы по курсу алгебры и начал анализа содержат 50 самостоятельных и 7 контрольных работ в четырех вариантах, а также тест для самоконтроля в двух вариантах. Ко всем вариантам контрольных работ и к тесту имеются ответы.
Содержание дидактических материалов полностью соответствует учебнику серии «МГУ – школе» для 11 класса (С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин) и дополняет его более сложными заданиями, необходимыми для работы в профильных классах. Это дидактические материалы нового типа, содержащие разбор заданий для подготовки к самостоятельным работам, и поэтому не нуждающиеся в «решебниках». Их можно использовать в классе и дома при работе по любым учебникам, а также для восполнения пробелов и самообразования.
Материалы для подготовки к самостоятельным работам содержат подробные объяснения решений заданий, так как имеют целью объяснение выбранных способов действий. Приведенные решения не являются образцами оформления решений учащимися, так как их решения могут быть краткими, в них, как правило, пропускают комментарии при выполнении преобразований уравнений или неравенств. Некоторые типы заданий, например, иррациональные уравнения, встречаются в разных работах, так как в каждой из этих работ предполагается свой способ решения уравнения.
Темы, отмеченные в дидактических материалах звездочкой, не является обязательными для изучения в общеобразовательном классе. Они охватывают программу углубленного изучения математики (профильных классов). Предложенные работы могут использоваться как обучающие самостоятельные работы для классной или домашней работы. Любые из самостоятельных работ учитель может использовать для контроля на отметку. При этом следует учесть, что многие самостоятельные работы и все контрольные работы избыточны по объему. Предполагается, что учитель отберет из них часть заданий с учетом уровня подготовки учащихся своего класса и времени, отводимого на выполнение работы.
Следует учесть, что некоторые задания вариантов III и IV несколько сложнее соответствующих заданий вариантов I и II. Так как в классах с углубленным изучением математики контрольных работ должно быть больше, чем в классе, работающем по общеобразовательной программе, то отдельные самостоятельные работы, отмеченные звездочками, можно провести как контрольные работы.
Оглавление
Раздел 1. Материалы для подготовки к самостоятельным работам
1*. Сложная функция
2. Область определения функции
3. Область изменения функции
4. Четные и нечетные функции
5*. Задачи с параметром. Использование четности функций
6. Промежутки монотонности функции. Промежутки знакопостоянства функции
7. Построение графиков функций
8*. Графики функций, содержащих модули
9*. Задачи с параметром. Использование графиков функций
10. Предел функции
11. Обратные функции
12. Производные элементарных функций
13. Производная сложной функции
14*. Производная сложной функции (продолжение)
15. Максимум и минимум функции на отрезке
16. Уравнение касательной к графику функции
17. Приближенные вычисления
18. Исследование функций с помощью производной
19. Задачи на максимум-минимум
20*. Геометрические задачи на максимум-минимум
21*. Задачи на смеси. Нахождение экстремума функции
22. Исследование функции с помощью производной и построение ее графика
23*. Решение задач с помощью производной
24. Первообразная. Неопределенный интеграл
25*. Нахождение неопределенных интегралов с помощью подстановки
26. Геометрический смысл определенного интеграла
27. Формула Ньютона – Лейбница
28. Свойства определенного интеграла
29. Равносильные преобразования уравнений
30. Равносильные преобразования неравенств
31. Уравнения-следствия
32. Уравнения-следствия (продолжение)
33. Решение уравнений с помощью систем
34. Решение уравнений с помощью систем (продолжение)
35*. Уравнения вида f (a(x)) = f (b(x))
36. Решение неравенств с помощью систем
37. Решение неравенств с помощью систем (продолжение)
38*. Неравенства вида f (a(x)) > f (b(x))
39. Равносильность уравнений на множествах
40*. Равносильность уравнений на множествах (продолжение)
41. Равносильность неравенств на множествах
42*. Равносильность неравенств на множествах (продолжение)
43. Уравнения и неравенства с модулями
44*. Уравнения вида f (f (x)) = x
45. Метод интервалов для непрерывных функций
46*. Использование свойств функций при решении уравнений и неравенств
47*. Рассуждения с числовыми значениями при решении уравнений и неравенств
48. Системы уравнений с несколькими неизвестными
49*. Рассуждения с числовыми значениями при решении систем уравнений
50*. Уравнения, неравенства, системы с параметром
Раздел 2. Самостоятельные работы
Раздел 3. Контрольные работы
Тест для самоконтроля
Ответы
Открытый урок по алгебре 11 класс по теме «Степень с рациональным показателем»
Открытый урок по алгебре и началам анализа в 11 классе
Тема: «Степень с рациональным показателем»
Математика-это музыка разума.
Музыка-это математика чувств.
(Джеймс Джозеф Сильвестр)
Цели урока:
1. Обобщение и систематизация знаний, умений, навыков.
2. Актуализация опорных знаний в условиях сдачи ЕГЭ.
3. Контроль и самоконтроль знаний, умений, навыков с помощью тестов.
4. Развитие умения сравнивать, обобщать.
План урока.
1. Формулировка цели урока
2. Устная работа «Дополните предложение», «Верю – не верю!»
3. Решение серии примеров на основе демонстрационного варианта ЕГЭ
4. Решение примера на упрощение выражения (из ЕГЭ) с обсуждением наиболее “тонких” мест
5. Физминутка.
6. Самостоятельная работа на основе демонстрационного варианта ЕГЭ
7. Задание на дом (на листочках)
8. Подведение итогов урока.
Оборудование: проектор.
1. Друзья! Перед вашими глазами часть высказывания английского математика Джеймса Джозефа Сильвестра (1814–1897) о математике “Математика – это музыка разума”. Не правда ли, как романтично?
Вопрос. А как вы думаете, как определил он музыку?
“Музыка – это математика чувств”.
К чувствам мы можем отнести различного рода переживания. В этом году одной из причин ваших и моих переживаний является успешная сдача ЕГЭ и, как следствие, поступление в ВУЗ. Очень хочется, чтобы преобладали положительные эмоции. Должна быть уверенность, а это наши знания и навыки. Сегодня на уроке мы продолжим подготовку к ЕГЭ, повторяя и обобщая понятие степени.
Итак, тема сегодняшнего урока –«Степень с рациональным показателем».
2. Устная работа
Дополните предложения:
1. Степень с целочисленным показателем это — :произведение n одинаковых множителей
2. При умножении степеней с одинаковыми основаниями:показатели складываются
3. При делении степеней с одинаковыми основаниями :показатели вычитаются
4. Степень степени равна:произведению показателей
5. Степень числа а, не равного нулю с нулевым показателем равна :1
6. Степень произведения равна :произведению степеней
7. Степень дроби равна :дроби степеней
8. Степень с дробным показателем m\n есть:
9. Степень с любым показателем p\q есть:
«Верю – не верю!»
1. Имеют смысл выражения:
а) б) в) с) д)
2. (да)
3. Уравнение имеет три корня
(нет, корень один: 7, т.к.)
3.Решение серии примеров на основе демонстрационного варианта ЕГЭ
Задания выполняются самостоятельно, с последующей проверкой ответов на доске.
4. Решение примера (из ЕГЭ).
При каком целом положительном x значение выражения
ближе всего к 0,7
Решение.
Вопрос. При каких значениях х данное выражение имеет смысл?
Так как х – целое положительное число, то N,
при .
Проверим, не обращается ли в 0 знаменатель при х = 7.
при х = 7. Следовательно, x > 7.
Преобразуем выражение:
Пусть .
При положительна и возрастает
убывает
возрастает
возрастает
Найдём, при каких значениях х
Так как f(x) –возрастающая функция, то .
Найдём, какое из этих значений ближе лежит к 0,7, для чего сравним
и
Так как , то значение f(26) лежит ближе к 0,7.
5.Физминутка.
6.Самостоятельная работа на основе демонстрационного варианта ЕГЭ с последующей проверкой на доске.
А теперь самое время потренироваться: перед вами примеры из демонстрационного варианта, гр.А 2009 года.
Вы их видите как на доске, так и на листочках. Ваша задача – быстро решить и заполнить таблицы с ответами. Соответствие букв и чисел перед вами. Правильно вычислив или упростив выражения в таблице, вы прочтёте то, что необходимо вам при сдаче ЕГЭ.
Приложение 1.
1 вариант – удача, знания,
2 вариант – уверенность.
7.Задание на дом (на листочках)
№438(а,б), №439.
. При каком целом положительном х значение выражения
ближе всего к (–0,7) ?
8.Подведение итогов урока.
Итак, сегодня на уроке мы увидели насколько широко понятие степени используется при сдаче ЕГЭ. Закрепить полученные навыки вы сможете, выполнив домашнюю работу.
Скачано с www.znanio.ru
Темы исследовательских работ по математике
Внимание! Для повторения и закрепления таблицы умножения и таблицы деления предлагаем наши игровые программы Таблица умножения в мультиках и Таблица деления в мультиках.
На этой странице представлен общий список тем исследовательских работ по математике для 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11 класса, перейти к которым можно по ссылкам и далее на страницах выбрать наиболее подходящую уровню знаний и умений ребенка тему проекта. Проектная деятельность учащегося начинается только после того, как тема научно-исследовательской работы будет одобрена руководителем (учителем).
Приведенные разнообразные темы проектов по математике на этой странице можно брать за основу, дополнять и изменять в соответствии с поставленными целями исследования и идеей проекта.
Правильно выбранные темы проектов по математике для учащихся 5, 6, 7, 8, 9, 10 или 11 класса способствует тому, что работа над ними будет, действительно, увлекательна, познавательна и интересна. Особенно, если данный исследовательский проект по математике выполняется группой детей.
Приведенные ниже темы исследовательских работ и проектов по математике являются примерными, некоторые из них можно объединить в одну тему при наличии общих задач и цели исследования.
Темы исследовательских проектов по математике
Темы проектных работ по математике:
Авторские задачи.
Аликвотные дроби
Арифметика остатков. Сравнения по модулю.
Без мерной линейки
Без мерной линейки, или измерение голыми руками.
Бесконечный мир чисел.
Божественное число
Буква в кубе.
Быстрый счет — легко и просто!
Быстрый счет без калькулятора.
В глубь веков, или Как считали древние.
В мире времени (сборник творческих задач).
В мире ребусов и лабиринтов.
В мире удивительных чисел.
В поисках оптимальных решений.
В царстве чисел-великанов.
Вездесущая математика.
Великие задачи
Великолепная семерка
Великолепные цифры.
Виды задач на логическое мышление.
Виды и свойства движений.
Виды текстовых задач и их решение.
Влияние скорости падения дождевых капель на скорость движения человека во время дождя.
Во всем царит гармонии закон…
Время и его измерение
Время остановить нельзя, а измерить?
Время работать и время отдыхать.
Все есть число
Все о «тройке» и чуть больше…
Все о числе 13
Все о числе 7
Всегда ли 2 х 2 = 4?
Вычисление скорости течения реки.
Галерея замечательных чисел.
Галерея числовых диковинок.
Гармония и математика
Генетический код и квадрат Пифагора.
География чисел
Гипотеза об истоках золотого сечения.
Головоломки со спичками
Графические методы и геометрические соображения при решении задач по математике Графические приемы при решении задач по математике.
Графический метод решения сюжетных задач.
Графический способ умножения чисел.
Два способа решения логических задач
Действия над числами в различных системах счисления.
День рождения нуля
День рождения числа «пи»
Детские задачи для взрослых детей.
Древнерусские задачи
Древние системы счисления.
Древние, но вечно юные простые числа
Дружественные тройки чисел.
Дружественные числа
Жар холодных чисел
Живая математика
Живая природа и симметрия.
Загадка бумажной полоски.
Загадка Рамануджана
Загадки числового ряда
Загадочный мир чисел.
Задачи из старинного учебника.
Задачи из Эфиопии
Задачи на все случаи жизни
Задачи на движение двух объектов.
Задачи на движение по реке
Задачи на клетчатой бумаге. Формула Пика.
Задачи на местном материале
Задачи на наибольшее и наименьшее значение величин и методы их решения.
Задачи на оптимизацию
Задачи на переливание жидкости.
Задачи на разрезание
Задачи на свежем воздухе.
Задачи на чётность
Задачи о лабиринтах
Задачи о четырех красках.
Темы исследовательских работ по математике
Темы исследовательских проектов по математике:
Задачи повышенной трудности «на движение».
Задачи с ограничениями.
Задачи с одинаковыми цифрами.
Задачи с параметрами
Задачи со спичками
Задачи старинные и старые.
Задачи, которые могли бы стать теоремами.
Замечательные числа. Дружественные числа и простые числа-близнецы.
Занимательная логика в математике
Занимательные задачи
Занимательные задачи далекого прошлого.
Занимательные задачи по математике.
Занимательные числа
Заниматика
Занятные стайки простых чисел.
Зарождение и эволюция математической задачи.
Зачем человеку нужны измерения в разные времена?
Знакомое и незнакомое магическое число Пи.
Знакомство с симметрией
Измерение времени.
Изопериметрическая проблема, или Задача Дидоны.
Изучение возможности использования рисунка на уроках математики.
Интересные и быстрые способы и приемы вычислений.
Интересные и интеллектуальные задачки.
Искусство отгадывать числа
Использование математических разрезных игр.
Использование некоторых положений теории чисел для решения задач повышенной трудности.
Использование старинных мер длины и веса для решения и составления задач.
Исследование математических способностей.
Исследование метода решения задач различными способами.
Исследование ряда натуральных чисел.
Исчисление времени
Как велик миллион?
Как измерить время?
Как измерить расстояние между родственниками.
Как найти решение задачи
Как разрезать пирог?
Как считать без компьютера и калькулятора.
Календари времени
Календарная даль веков
Калькуляторы.
Квадратное колесо — правда или миф?
Контактные числа и проблема тринадцати шаров.
Копилка нестандартных задач по математике.
Королева математики
Красивые и быстрые способы вычислений
Красота в симметрии
Красота и математика
Красота через призму науки
Криптограммы — тайнопись прошлого, настоящего и будущего
Криптография
Криптография и криптоанализ.
Криптография и математика
Криптография и стеганография.
Криптография как метод кодирования и декодирования информации.
Криптография, математические алгоритмы при шифровании.
Криптография. Азы шифрования и история развития.
Криптография. Методы ее практического применения.
Криптография. Наука о шифрах
Кристаллография и математика
Крылатые математические выражения.
Курьезы, софизмы, парадоксы в математике.
Ловкий циркуль
Магические тайны числа 7
Магические числа
Магические числа в природе
Магические числа и фигуры
Магическое число «Пи»
Магическое число Шахерезады.
Магия чисел
Магия чисел 3, 11, 13
Математика в жизни: расчёт ремонтных работ помещения.
Математика в моей будущей профессии.
Математика вокруг нас
Математика на шахматной доске.
Математики-вундеркинды
Математическая обработка экспериментальных данных.
Математическая формула прекрасного.
Математические жемчужины
Математические презентации
Математические софизмы.
Математические термины.
Математический бильярд.
Математический календарь школьникам.
Математический маятник
Математический помощник
Математическое моделирование глобального развития человечества.
Математическое моделирование и его практическое применение.
Математическое моделирование как способ решения задач (проблем).
Математическое моделирование окружающей среды.
Математическое моделирование.
Математическое описание случайных явлений.
Математическое путешествие в мир гармонии.
Материалы для математического досуга.
Мир чисел, звуков и цвета
Моделирование составных задач.
Мир больших чисел.
Моделирование текстовых задач.
Наглядная топология
Неизвестное об известном, или Как сделать открытие. Число Пи равно 4?
Некоторые интересные зависимости.
Необычное в обычных числах
Нестандартные задачи
Нестандартные задачи на олимпиадах по математике.
Нуль в математике занимает особое место.
Нумерации и системы счисления.
Нумерология
Нумерология — магия чисел
Нумерология — миф или реальность?
Нумерология — наука о числах в нашей жизни.
Нумерология — современная наука
Нумерология в жизни человека
Нумерология: наука или заблуждение?
Одним росчерком
Описание красоты и гармонии природы математическим отношением.
Определение в курсе математики
Оптические иллюзии и их применение
Орнамент как отпечаток души народа.
Орнаментальное и геометрическое искусство М. Эшера.
Орнаменты
От пальцев до калькулятора
Открытие: случайность или закономерность?
Очарование простых чисел.
Палиндромы в математике
Параметр. Динамические иллюстрации к решению задач.
Письмо с секретом
Планета чисел
По страницам нестареющих русских учебников по математике.
Практические советы математиков.
Преданья старины далёкой (решение старинных задач)
Приборы, инструменты и приспособления для вычислений.
Прикладные задачи
Применение графических методов при решении текстовых задач.
Применение космических снимков на уроке математики.
Проверка вычисления числа «пи».
Проверка на четность
Простые числа
Противоречие непротиворечивого утверждения.
Путешествие к истокам геометрии.
Развитие понятия «бесконечность» в математике.
Разговор о нуле
Различные способы решения текстовых задач.
Реальный мир воображаемых чисел.
Рекуррентные соотношения и их применение.
Решение диофантовых уравнений
Решение задач методом оценки
Решение задач на смеси и сплавы.
Решение задач на соответствие и исключение неверных ответов.
Решение задач по готовым чертежам.
Решение задач по теме «Движение по реке».
Решение оптимизационных задач по математике.
Решение старинных задач
Решение текстовых задач
Решение уравнений в целых числах.
Самое интересное число
Секрет успешного решения задач.
Семь величайших загадок математики.
Серьезное и курьезное в числах
Симметрические простые числа.
Системы счисления
Скрытые модули
Совершенные числа
Совершенные числа. Дружественные числа.
Совершенные числа. Простые числа Мерсенна.
Сокращенное деление с помощью схемы Горнера.
Сохранить здоровье помогут задачи
Способы и приемы быстрых вычислений.
Способы представления чисел в различных системах счисления.
Способы решения задач на движение тел
Способы устного возведения чисел в квадрат.
Сравнительный анализ устойчивости некоторых известных шифров.
Старинные задачи
Старинные задачи древних народов.
Старинные занимательные задачи
Считаем без калькулятора
Тайна чётных чисел
Тайна числа «Пи»
Текстовые задачи в школьном курсе математики.
Текстовые задачи и моделирование.
Текстовые задачи на движение
Текстовые задачи на смеси, сплавы и растворы.
Текстовые задачи на совместную работу.
Учебник математики: вчера, сегодня, завтра
Фигурные числа
Философская тайна чисел
Философские аспекты математики
Финно-угорская система счисления в ряду других систем.
Фольклорные задачи
Целые числа и измерение температуры.
Цена одной минуты
Цепные дроби
Цифра «9» в тувинской нумерологии.
Цифровые корни
Числа в нашей жизни.
Числа вокруг нас
Числа Пифагора и красота мира.
Числа правят миром
Числа правят миром. Можно ли представить себе мир без чисел?
Числа с собственными именами.
Число П.
Число, которое больше Вселенной.
Числовые неравенства
Шестое математическое действие.
Шесть математических действий.
Шифры и криптограммы.
Шифры и математика
Эти удивительные кватернионы.
Перейти к разделам:
Исследовательские работы по математике
Методы исследования
Если Вы хотите разместить ссылку на эту страницу, установите у себя на сайте или форуме один из следующих кодов:
Код ссылки на страницу с темами проектов по математике:
<a href=»http://obuchonok.ru/node/431″ target=»_blank»>Темы исследовательских работ по математике</a>
Код ссылки на форум с темами исследовательских работ по математике:
[URL=http://obuchonok.ru/node/431]Темы исследовательских работ по математике[/URL]
Одиннадцатый класс (11 класс) Функции и алгебра Вопросы для тестов и рабочих листов
Вы можете создавать печатные тесты и рабочие листы из этих 11 класс Функции и алгебра вопроса! Выберите один или несколько вопросов, установив флажки над каждым вопросом. Затем нажмите кнопку добавить выбранные вопросы к тесту перед переходом на другую страницу.
Предыдущая Страница 1 из 70 Следующие Выбрать все вопросы Джереми работает с фундаментальной теоремой алгебры и думает, что нашел исключение.2 [/ math], в результате будет только один корень, [math] x = 1 [/ math]. Следовательно, несмотря на то, что это многочлен второй степени, существует только один корень. Это правильно?- Да, это известное исключение.
- Нет, это не полином, это квадратичная функция.
- Нет, если использовать формулу корней квадратного уравнения, будет найден другой корень.
- Нет, этот корень имеет кратность 2, что означает, что он считается двумя корнями.
| [математика] \ \ \ \ \ \ \ \ \ \ \ mathbf {x} \ \ \ \ \ \ \ \ \ \ \ [/ математика] | [математика] \ \ \ \ \ \ \ \ \ \ \ \ mathbf {f (x)} \ \ \ \ \ \ \ \ \ [/ math] |
| [math] 0 [/ math] | [math] -4 [/ math] |
| [math] 2 [/ math] | [math] 2 [/ math] |
| [math] 4 [/ math] | [math] 8 [/ math] |
| [math] 6 [/ math] | [math] 14 [/ math] |
| [math] 8 [/ math] | [math] 20 [/ math] |
- [math] f (x) [/ math] линейно, потому что разница значений y на равных интервалах постоянна.
- [math] f (x) [/ math] линейно, потому что разница значений x постоянно составляет 2 единицы.
- [math] f (x) [/ math] экспоненциально, потому что соотношение значений y на равных интервалах постоянно.
- Невозможно определить, является ли [math] f (x) [/ math] линейным или экспоненциальным, потому что в таблице нет интервалов только одной единицы.
Математика в 11 классе
Добро пожаловать в 11 класс по математике!
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Мы образовательный сайт ask-math.com, и у нас есть хорошие учебные материалы. Этот год важен, так как студентам необходимо решить, в каком направлении они будут строить свою карьеру. Учебная программа 11 класса по математике охватывает знания по темам, которые входят в математику. Поскольку мы знаем, что у курса нет ограничений, и если все обучение разделено на разные потоки, то определенно ограничение этих потоков для конкретного класса в соответствии с возможностями студентов является обязательным.Таким образом, программа 11-го класса необходима для того, чтобы учащиеся познакомились с темами, и они должны учиться по 11-му стандарту, чтобы база 12-го стандарта была прочной. В Индии. 12-й стандартный процент имеет большое значение в жизни, и прием в старшие классы зависит от этого процента и знаний, и изучение 12-го стандарта может повлиять на знание базы 11-го класса. Так что очень важно знать темы, затронутые 11-м. Спросите-математика.com организовал все темы, включенные в 11-й класс. Чтобы изучить эти темы шаг за шагом, щелкните ссылки внизу этой страницы. Вот список всех тем, изучаемых учениками 11-го класса по математике. Наборы: Понятие набора является базовым во всех разделах математики. Это оказалось особенно важным при формировании отношений и функций.
Отношения и функции: В математике мы сталкиваемся с такими отношениями, как i) линия l параллельна прямой m ii) число m меньше числа n.Во всех этих случаях мы замечаем, что отношение включает пары объектов в определенном порядке. Этот раздел посвящен изучению отношений и функций в математике.
Математическая индукция: Процесс рассуждения от общего к частному и другого известен как процесс индукции. В алгебре или других дисциплинах математики есть определенные результаты или утверждения, которые сформулированы в терминах n, где n — положительное целое число. Чтобы доказать такие утверждения, мы используем особую технику, известную как «Принцип математической индукции».
Логарифмы: Это особый процесс, который сокращает объем работы, связанной с умножением и делением больших чисел.
Комплексные числа: Комплексное число — это число в форме a + ib, где a и b — действительные числа, а i — мнимая единица, имеющая свойство i 2 = -1
Линейные неравенства: 13x <250 такие уравнения называются линейными неравенствами. Изучение неравенств очень полезно при решении задач в области науки, математики, статистики, задач оптимизации, экономики, психологии и т. Д.
Квадратные уравнения: В этом разделе ask-math предоставляет вам квадратные уравнения с действительными коэффициентами, но с отрицательным дискриминантом.
Последовательности и серии: В этом разделе ask-math рассматриваются все типы последовательностей, такие как арифметическая прогрессия (A.P), геометрическая прогрессия (G.P) и гармоническая прогрессия.
Тригонометрические функции: В этом разделе ask-math предоставляет круговую функцию и их свойства. Такие как преобразование углов из радиана в градусы, знаки тригонометрических функций, область определения и диапазон тригонометрических функций, сумма и разность углов и т. Д.
Декартова система прямоугольных координат: В этом разделе представлены формула расстояния, формула сечения, площадь треугольника с использованием координат, параметрическое уравнение линии и т. Д.
Прямая линия и семейство прямых: В этом разделе мы должен вывести различные формы уравнения прямой, включая прямые, параллельные осям, и наклонные.
Наборы:
• Наборы
• Декартово произведение наборов
Функции:
• Круговая функция
• Составные функции
• Вычисление функции обратного косинуса
• Вычисление функции обратного синуса
• Четная и нечетная функция в тригонометрии
График функций :
• График рациональной функции
• График тригонометрической функции
• График y = sin (bx)
• График y = cos (bx)
• График рациональных функций с отверстиями
• Перехват рациональной функции
• Обратный функция касательной
• Функция один к одному
• Функция на
• Периодическая функция в тригонометрии
• Тригонометрические функции в разных квадрантах
Математическая индукция:
• Докажите математической индукцией
Логарифм:
• Общий и натуральный логарифм
• Правила для логарифмы
• Вычисление логарифма
• Изменение логарифма основания
• Применение логарифма
Комплексные числа: 900 91 • Комплексные числа
• Сложение комплексных чисел
• Вычитание комплексных чисел
• Полярная форма комплексных чисел
• Комплексные корни квадратного уравнения
• Сопряженное комплексное число
• Деление комплексных чисел
• Модуль комплексного числа
• Умножение комплексных чисел
• Выполнять операции с комплексными числами
Квадратичные функции:
• Введение квадратного уравнения
• Иррациональные корни квадратного уравнения
• Природа корней квадратного уравнения
• Квадратные уравнения с действительными коэффициентами
• Показать, что квадратное уравнение не может имеют более двух корней
• Квадратные уравнения с комплексными коэффициентами
•
Линейные неравенства:
• Графическое линейное неравенство
• Графическое отображение систем линейных неравенств
• Линейные неравенства
• Решение двухшаговых линейных неравенств
• Решение линейных уравнений алгебры неравенств
• Решение одношаговых уравнений и неравенств
• Системные линейные неравенства словесные задачи
• Система линейных неравенств
Последовательность и серия
• Серия и последовательности
• Что такое арифметические средства
• Арифметическая прогрессия
• Найти термины арифметическая прогрессия
• Свойства арифметической последовательности
• Сумма арифметической прогрессии
• Геометрическая прогрессия
• Свойства геометрическая прогрессия
• Найдите общее отношение, когда дана сумма n членов геометрической прогрессии
• Общий член геометрической прогрессии
• Задача геометрической прогрессии
• Выбор членов в геометрической прогрессии
• Решенные суммы в геометрической прогрессии
• Сумма геометрической прогрессии прогрессия
• S мм бесконечной геометрической прогрессии
• Связь между геометрическим и средним арифметическим
Дом
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Алгебра 2 | 11 класс по математике
Что такое Алгебра 2?
Алгебра 2 развивает у студентов концептуальное понимание, беглость речи и способность применять расширенные функции. Учащиеся проводят связи между типами функций. В частности, учащиеся применяют навыки, полученные в начале года с линейными, квадратичными и полиномиальными функциями, чтобы информировать свое понимание позже в этом году, когда они изучают рациональные, радикальные и тригонометрические функции.Учащиеся выбирают соответствующие функции и ограничения, основываясь на твердом понимании особенностей функций, чтобы создавать функции, моделирующие контекстные ситуации. Свободное владение языком является важной частью Алгебры 2, поскольку способность быстро и легко выполнять процедуры позволяет студентам более глубоко понимать концепции.
Как мы заказывали единицы?
В Блок 1, Линейные функции и приложения , учащиеся изучают особенности функций посредством изучения обратных функций, моделирования контекстных ситуаций и работы с функциями, системами функций и кусочными функциями.Студенты повысят беглость в идентификации и анализе характеристик линейных функций с помощью алгебраических, графических, контекстных и табличных представлений. Студенты будут использовать эти функции, чтобы эффективно моделировать и делать выводы о контекстных ситуациях. Навыки, которые студенты развивают в этом модуле, будут применены и распространены на другие типы функций в течение года, включая квадратичные, полиномиальные, рациональные, экспоненциальные, логарифмические и тригонометрические функции.
В , Блок 2, Квадратичные , студенты пересмотрят концепции, изученные в Алгебре 1, такие как особенности квадратных уравнений, преобразование квадратичных функций, системы квадратичных функций и переход от одной формы уравнения к другой (e.g., форма вершины к стандартной форме, стандартная форма к форме пересечения). Повышенное владение квадратными уравнениями и функциями обеспечивает прочную основу для изучения полиномов, рациональных функций и тригонометрических тождеств. В этом разделе учащиеся также познакомятся с новым типом системы счисления, мнимыми числами, а также будут определять и оперировать мнимыми решениями. Как и в случае с блоком 1, студенты будут применять квадратные уравнения к контекстным ситуациям, системам функций и при переводе между представлениями.Графические калькуляторы широко представлены в этом модуле и будут использоваться до конца года.
В , Блок 3, Полиномы , студенты будут применять навыки из первых двух разделов, чтобы развить понимание особенностей полиномиальных функций. Анализ полиномиальных функций для степени, поведения конца, количества и типа решений основан на работе, проделанной в Блоке 2; это расширенные темы, которые будут применены к будущим типам функций. Учащиеся напишут полиномиальные функции, чтобы раскрыть особенности функций, найти решения систем и применить преобразования, основываясь на блоках 1 и 2.Студенты познакомятся с идеей «идентичности» в этом модуле, а также будут работать с многочленами. Разделение многочленов вводится в этом модуле и будет изучаться с помощью понятий теоремы об остатке, а также предварительных условий для рациональных функций.
В блоке 4 , Рациональные и радикальные функции учащиеся расширят свое понимание обратных функций до функций со степенью выше 1. Наряду с этой концепцией учащиеся будут факторизовать и упростить рациональные выражения и функции, чтобы выявить ограничения и асимптоты предметной области.Студенты научатся свободно оперировать рациональными и радикальными выражениями и использовать структуру для моделирования контекстных ситуаций. В этом модуле учащиеся также вернутся к концепции постороннего решения, впервые представленной в модуле 1, посредством решения радикальных и рациональных уравнений.
В блоке 5 , Экспоненциальное моделирование и логарифмы учащиеся будут моделировать с экспоненциальным ростом и убыванием, включая использование базы непрерывного сложения, e , для решения контекстных проблем в финансах, биологии и других ситуациях.Студенты узнают, что логарифмы являются обратной величиной экспонент, и что они могут свободно оперировать логарифмами и строить графики. Студенты откроют для себя силу логарифмов для определения решений, функций и закономерностей в функциях. Студенты будут использовать экспоненциальные функции и логарифмические функции как часть системы функций в контекстах моделирования.
В блоке 6 «Единичный круг и тригонометрические функции » учащиеся рассмотрят геометрическую тригонометрию как введение в тригонометрические функции.Учащиеся будут использовать наброски тригонометрических функций синуса и косинуса, чтобы развить понимание взаимных триггерных функций, обратных триггерных функций и трансформационных тождеств триггерных функций. Возможности тригонометрических функций, представленные в графическом виде, будут переведены в алгебраические представления, а особенности, уникальные для тригонометрических функций, будут исследованы и использованы в математических и прикладных задачах. Учащиеся познакомятся с единичным кругом, и ожидается, что они легко выведут его.Пифагорейская идентичность будет широко использоваться в этом модуле, и ожидается, что учащиеся будут знать эту идентичность и извлекать другие формы идентичности для использования в задачах. Этот модуль завершает формальное изучение преобразований, обратных систем, свойств функций и использования различных функций для моделирования контекстов, которое началось в модуле 1.
В блоке 7 «Тригонометрические тождества и уравнения » учащиеся разработают основы концепций исчисления, расширив свои представления о тригонометрических функциях и изучив связи между тригонометрическими функциями.Гибкие рассуждения о тригонометрических функциях и видение того, что выражения, которые выглядят по-разному на поверхности, могут фактически одинаково действовать в определенных областях, создают основу для изучения дифференцирования и интегрирования, где периодические функции обладают множеством полезных свойств и действуют как полезные инструменты для изучения исчисления. Студенты также будут применять алгебраические методы к тригонометрии, помогая им лучше понимать тригонометрические функции графически и через единичный круг, а также увидеть силу алгебраических манипуляций и структуры в выражениях.
В блоке 8 «Вероятность и статистический вывод » учащиеся исследуют экспериментальную и условную вероятность в экспериментальном контексте. Акцент на условной вероятности помогает студентам рассуждать о причине и следствии и служит введением в принципы экспериментального анализа. Студенты также изучат возможность делать выводы, уделяя особое внимание нормальному распределению и пониманию результатов случайных процессов, когда они повторяются с течением времени. Наконец, студенты будут использовать распределения, чтобы делать выводы о популяциях на основе выборок и применять понимание изменчивости, чтобы рассуждать о взаимосвязи между выборками и популяциями.
Последний модуль этого курса, Раздел 9, «Пределы и непрерывность» , служит введением в математический анализ. Этот блок включает в себя темы пределов, непрерывности и производных, и он обеспечивает основу для необходимого навыка исчисления — мышления и рассуждений о бесконечно малом и бесконечно большом, а также логической аргументации, основанной на определениях и теоремах. Студенты будут работать с кусочными функциями, графически и алгебраически находить конечные и бесконечные пределы различных типов функций и определять непрерывность.Этот модуль также углубляет знания о различных типах функций, что является важным основополагающим знанием для исчисления.
Этот курс соответствует Основам учебной программы штата Массачусетс 2017 года и включает в себя основополагающий материал из Алгебры 1, где он соответствует действующим стандартам.
Архив 2019-2020 / Архив 2019-20 Математика
Курс № 5491/5492
Класс: 9-12
Предварительные требования: Успешное завершение курса алгебры 8Этот курс охватывает темы фундаментальной алгебры, которые необходимы учащимся для обучения на курсах математики в старших классах, а также для дальнейшей карьеры и образования.Охватываемые темы включают: квадратные уравнения, правила экспонент, дроби с переменными, работу функций, системы линейного программирования и члены полиномиальных функций. Для этого курса требуется графический калькулятор.
(Вернуться наверх)
Курс: 5111/5112
Класс: 9–12Предпосылки: Успешное завершение алгебры 9B
Геометрия — это изучение логических рассуждений, линий, плоскостей и их отношения к треугольникам, четырехугольникам, окружностям и другим плоским фигурам.Особое внимание уделяется написанию дедуктивных доказательств. Студенты будут применять концепции формы, пространства и измерения, чтобы иллюстрировать и описывать физический мир и решать проблемы. Студенты будут использовать измерения прямо или косвенно, изучать уравнения алгебры и графики в двух измерениях.
(Вернуться наверх)
Алгебра IIA / B
Курс: 5031/5032
Оценка: 9-12
Предпосылка: успешное завершение геометрии B
* Студентам рекомендуется завершить этот курс к концу 11 класса, чтобы подготовиться к государственному экзамену MCA по математике.
(Вернуться наверх)
Курс: 5245/5246/5247
Класс: 10-12Пререквизиты: Алгебра IIB
Предварительные исчисления A, B и C предназначены в первую очередь для студентов, которые очень заинтересованы в изучении математики или тех, кто знает, что ему / ей потребуется больше курсов по математике или наука в его / ее образовательном развитии за пределами средней школы.В этом курсе рассматриваются следующие темы: система счисления, математическая индукция, ряды, последовательности, пределы, аналитическая геометрия, функции, комплексные числа, доказательство, процедуры построения графиков, абсолютное значение, функции наклона и тригонометрия. После успешного завершения Pre-Calculus студент будет иметь тригонометрические знания, чтобы перейти к Calculus. Студенты должны иметь графический калькулятор, эквивалентный TI-83 или лучше для этого курса.
(Вернуться наверх)
AP Calculus I A / B
Курс: 5255/5256
Класс: 11-12
Расширенный расчетный курс разработан как расширение и обзор всех ранее пройденных курсов по математике, объединяющий их и применяющий интересными способами.Основная часть этого курса состоит в том, чтобы определить и использовать деривации для поиска наклонов, связанных скоростей и решения задач по максимуму-минимуму. Также будет сосредоточено внимание на антипроизводных и интегралах, нахождение площади под кривыми, длины кривых и изучение трансцендентных функций (тригг., Экспоненциальный, логарифмический и т. Д.). Цель состоит в том, чтобы подготовиться к экзамену Advanced Placement, который проводится в середине мая, что позволит тем, кто имеет проходные баллы, получить кредит колледжа за этот курс. Студенты должны иметь графический калькулятор, эквивалентный TI-83 или лучше для этого курса.Студенты будут готовы к сдаче экзамена AP Calculus AB.
(Вернуться наверх)
AP Calculus II A / B
Курс: 5258/5259
Класс: 11-12
Темы, охваченные AP Calculus BC, включают все темы AP Calculus A и AP Calculus B. Этот курс является расширением предыдущих курсов по математическому анализу. Дополнительные темы, которые будут рассмотрены: полярные, параметрические и векторные функции с использованием производных и интегралов, разработка приближений с использованием рядов Эйлера, Тейлора и Маклорена, правило Л’Опиталса для проверки сходимости, первообразные по частям и частичные дроби, поиск сходимости геометрических, гармонических и чередующийся ряд, радиус и интервал сходимости степенного ряда, оценка ошибки Лагранжа для полиномов Тейлора. После успешного завершения этого курса студенты сдают весенний экзамен AP Calculus BC, который может принести студентам дополнительные баллы колледжа. Они получат оценку за этот тест и дополнительную оценку за уже пройденный тест AP Calculus. Для этого курса требуется графический калькулятор. Студенты будут готовы к сдаче экзамена AP Calculus BC.
(Вернуться наверх)
Тригонометрия
Курс: 5330
Оценка: 10–12Предварительное условие: Успешное завершение Алгебры II B
Тригонометрия — это изучение взаимосвязи между сторонами и углами прямоугольного треугольника.Этот курс разработан, чтобы расширить предварительные знания студента об этом исследовании из геометрии, используя тригонометрические функции и отношения в приложениях и идентичностях. Тригонометрия предназначена для студентов, которые хотят продолжить изучение математики и / или подготовиться к следующему курсу. Для этого курса студенты должны иметь графический калькулятор.
(Вернуться наверх)
Расширенные функции, статистика и геометрия A / B
Курс: 5350/5351
Класс: 10–12Предварительное условие: Успешное завершение Алгебры II A и B
Расширенные функции, статистика и геометрия разработан, чтобы укрепить и расширить понимание учащимся геометрии, статистики и алгебры II.Рассмотренные концепции включают функции, вероятность, статистику и геометрию. Этот курс предназначен для дальнейшей подготовки студентов к экзамену ACT и служит отличным курсом подготовки к экзамену ACT. Пройдя этот курс, студенты обретут уверенность в продолжении обучения в математике и / или смежных областях. Студенты должны иметь графический калькулятор, эквивалентный TI-83 или лучше для этого курса. * Студенты могут сдавать либо AFSG-A, либо AFSG-B, либо оба.
(Вернуться к началу)
Колледж СНГ Алгебра через моделирование A / B
Курс: 5425/5426
Оценка: (11–12)Предварительное условие: Успешное завершение алгебры II A и B с оценкой C или выше.
Высший 50–20-й процентильный класс, или рекомендация учителя
Этот курс знакомит студентов с искусством математического прогнозирования посредством алгебраического моделирования и элементарной теории вероятностей. Класс охватывает методы представления поведения реальных данных с помощью алгебраических уравнений, включая линейные, полиномиальные, экспоненциальные и логарифмические функции. Студенты научатся составлять уравнения, которые точно представляют поведение реальных данных. Задачи взяты из разных дисциплин.В то время как студенты практикуют традиционные алгебраические методы, они также будут широко использовать программу электронных таблиц Excel для исследования поведения наборов данных. Класс также укрепит способность студентов общаться и оценивать математические рассуждения. Этот курс удовлетворяет требованиям университетского математического мышления. Успешное завершение этого курса может позволить студентам получить 3 семестровых кредита в Университете Миннесоты. (CI 1806 College Algebra через моделирование)
(Вернуться к началу)
Введение в C ++
Курс: 5436
Класс: 9-12Пререквизиты: Успешное завершение алгебры 9 A & B
Этот курс научит студентов писать программы на C ++.C ++ — это структурированный язык высокого уровня, позволяющий писать программы для приложений любого типа и размера. Курс будет охватывать шесть основных элементов программирования: ввод, операции с данными, вывод, условное выполнение, циклы и функции.
(Вернуться наверх)
AP Computer Science A / B
Курс: 5445/5446
Класс: 11-12
Это курс информатики на уровне колледжа.Он предназначен для высокомотивированных студентов, интересующихся темами информатики. Информатика включает в себя совокупность технических навыков и научных методов, которые можно использовать для создания высококачественных компьютерных решений реальных проблем. Студенты научатся свободно кодировать в хорошо структурированной манере, используя язык Java. По завершении студенты смогут: применять известные алгоритмы и структуры данных, читать и понимать большие программы, а также понимать процесс проектирования и разработки, ведущий к большой программе.Студентам будет предложено пройти тест Advanced Placement Test, который проводится в середине мая. Многие колледжи и университеты выдают зачетные единицы за высокие достижения по тесту AP. AP Computer Science будет предлагаться только при достаточном количестве учащихся. AP Computer Science не засчитывается как зачет по математике.
(Вернуться наверх)
Статистика AP A / B
Курс: 5449/5450
Класс: 10-12
Цель этого курса — познакомить студентов с основными концепциями и инструментами для сбора, анализа и вывода на основе данных.Студенты знакомятся с четырьмя широкими концептуальными темами: изучение данных, выборка и экспериментирование, прогнозирование закономерностей и статистический вывод. Студенты должны зарегистрироваться на оба семестра и сдают AP экзамен в мае. Студенты должны иметь графический калькулятор, эквивалентный TI 83 или TI 84.
(Вернуться наверх)
Курс: 5030
Класс: 11-12(Требуется рекомендация учителя)
Потребительская математика применяет знания учащегося по арифметике и алгебре в повседневных ситуациях.Темы будут включать личные финансы, валовой и чистый доход, банковское дело для физических лиц, транспорт, потребительский кредит, налоги, жилье, инвестиции и страхование.
(Вернуться наверх)
Базовая и прикладная статистика СНГ A / B
Курс: 5451/5452
Оценка: 10-12
Базовая и прикладная статистика — это вводный курс по статистике, предназначенный для привлечения студентов с использованием методов моделирования и симуляции. Он подчеркивает понимание и применение статистических концепций и процедур с использованием визуальных и количественных методов для представления и анализа данных с использованием методов вывода.Успешное завершение этого курса может позволить студентам заработать 3 семестровых кредита в Университете Миннесоты.(Вернуться наверх)
Алгебра — Введение, различные разделы и часто задаваемые вопросы
Алгебра — один из различных разделов математики. Он имеет дело с символами и переменными. Различные арифметические утверждения и операции, такие как уравнения, термины, выражения, для установления связи между объектами, которые не являются постоянными и меняются с течением времени. Эти объекты в базовой алгебре также называются «переменными».
Алгебра включает несколько форм математических представлений, таких как действительные числа, комплексные числа, векторы, матрицы и т. Д. Уравнения играют важную роль в алгебраических приложениях. Различные алгебраические правила используются для решения элементарных уравнений для изучения переменных.
Введение в алгебру
Говоря о переменных, алгебра используется для определения неизвестных значений, таких как пропорции, банковский процент, процент, расстояние, цена и т. Д. Она также использует символы и буквы для представления математических уравнений.Уравнения состоят из некоторых констант и некоторых переменных. С помощью констант, представленных в уравнении, мы узнаем значение неизвестной / переменной в алгебре.
Учащиеся средних и старших классов средней школы должны понимать, как работает этот раздел математики и как применяются правила. Они должны внимательно изучать алгебру, так как она имеет достаточный вес на выпускных экзаменах. Одна из самых полезных платформ для понимания этого — Веданту.Приложение можно загрузить бесплатно, чтобы понимать алгебру для начинающих, практиковаться в суммах и хорошо сдавать экзамены.
Различные ветви алгебры
Вот список ветвей и подразделов алгебры. Эти ветви применяются соответственно для поиска значений двух или более переменных. Эти алгебраические ветви следующие:
Элементарная алгебра
В этой ветви рассматриваются основные свойства чисел, переменных, констант и отношений между ними.Темы, которые составляют часть элементарной алгебры, включают уравнения, формирование, манипулирование, вычисление выражений, равенства, неравенства, решение уравнений (алгебраических, а также линейных) и т. Д.
Продвинутая алгебра
Это более подробный и промежуточный шаг в алгебре. Уравнения, входящие в эту ветвь, помогают изучать следующее:
Равенства
Неравенства
Матрицы
Конические секции
Последовательности
Последовательности
Полиномиальное уравнение
Графические функции
Рациональное выражение
Вероятность
Абстрактная алгебра
Он имеет дело с истиной, относящейся к алгебраическим приложениям, независимо от ее специфики.Компоненты, включенные в эту ветвь алгебры:
Наборы
Двоичные операции
Идентификационный элемент
Обратный элемент
Ассоциативность
Ассоциативность
109Коммуникативный
Линейная алгебра
Это раздел математики, который имеет дело с линейными уравнениями и их представлениями с помощью векторов и матриц. Линейная алгебра является фундаментальным аспектом для каждого раздела математики.
В этот раздел алгебры включены следующие темы:
Студенты могут изучать различные концепции алгебры онлайн через приложение Vedantu.Алгебраические темы, которые вы можете прочитать в этом приложении:
Основы алгебры.
Сложение, вычитание и умножение алгебраических выражений.
Упрощение алгебраических уравнений с использованием правила BODMAS.
Замена.
Решение неравенств уравнений.
Показатели.
Surds.
Квадратные корни.
Кубикорни.
Законы экспонент.
Упрощающие уравнения.
Алгебраические свойства (ассоциативные свойства, законы распределения, коммуникативные законы).
Перекрестное умножение.
Полиномы.
Сложение, вычитание, умножение и деление многочленов.
Рациональные выражения.
Деление полиномов в столбик.
Конъюгат.
Рационализирующий знаменатель.
Квадратные уравнения.
Приложение Vedantu подробно описывает все упомянутые темы.
Калифорния пытается закрыть пробел в математике, но вызывает обратную реакцию
Если бы все шло по плану, Калифорния в этом месяце утвердила бы новые правила для математического образования в государственных школах.
Но с тех пор, как в феврале проект был открыт для общественного обсуждения, рекомендации вызвали ожесточенные дискуссии не только о том, как преподавать математику, но и о том, как решить проблему, более сложную, чем последняя теорема Ферма: закрытие расового и социально-экономического неравенство в успеваемости, сохраняющееся на всех уровнях математического образования.
Калифорнийские руководящие принципы, которые не являются обязательными, могут полностью изменить подход многих школьных округов к преподаванию математики. В проекте отвергалась идея естественно одаренных детей, рекомендовалось не переводить некоторых учащихся на ускоренные курсы в средней школе и предпринимались попытки продвигать курсы математики высокого уровня, которые могли бы служить альтернативой расчету, например наука о данных или статистика.
В проекте также предлагалось, чтобы математика не была дальтоником и чтобы учителя могли использовать уроки для изучения социальной справедливости — например, обращая внимание на гендерные стереотипы в задачах со словами или применяя математические концепции к таким темам, как иммиграция или неравенство.
Битва за математику происходит в то время, когда политика в области образования по вопросам, включая маски, тестирование и преподавание расизма, оказалась запутанной в ожесточенных спорах. Кандидат от республиканцев в губернаторы Вирджинии Гленн Янгкин ухватился за эти вопросы, чтобы помочь ему добиться победы во вторник. Теперь республиканцы обсуждают, как эти вопросы образования могут помочь им на промежуточных выборах в следующем году.
Даже в сильно демократичной Калифорнии — штате с шестью миллионами учащихся государственных школ и огромным влиянием на издание учебников по всей стране — проект руководящих принципов встретил резкую критику, с обвинениями в том, что эта структура привнесет «пробуждающую» политику в предмет, который должен будьте практичны и точны.
«Люди действительно будут сражаться за математику, чтобы остаться прежними», — сказал Джо Боулер, профессор образования Стэнфордского университета, работающий над пересмотром. «Даже родители, которые ненавидели математику в школе, будут возражать, чтобы их дети оставались неизменными».
Битва за математическую педагогику — сказка стара, как таблица умножения. Идея под названием «новая математика», представленная как более концептуальный подход к предмету, достигла своего расцвета в 1960-х годах. Около десяти лет назад, во время дебатов по поводу национальных стандартов Common Core, многие родители сетовали на математические упражнения, которые, по их словам, сводили на нет построчные вычисления в пользу настоящих иероглифов.
Сегодня битвы за калифорнийские руководящие принципы вращаются вокруг фундаментального вопроса: для чего или для кого нужна математика?
Результаты тестирования регулярно показывают, что студенты-математики в Соединенных Штатах отстают от учащихся других промышленно развитых стран. А внутри страны сохраняется устойчивый расовый разрыв в достижениях. Согласно данным Управления по гражданским правам Министерства образования, чернокожие ученики составляли около 16 процентов старшеклассников, но 8 процентов из них были зачислены на математический факультет в 2015/16 учебном году.Белые и азиатские студенты были перепредставлены на курсах высокого уровня.
«У нас есть государство и нация, которые ненавидят математику и плохо с ней справляются», — сказал д-р Болер.
Критики проекта заявили, что авторы будут наказывать отличников, ограничивая варианты для одаренных программ. В открытом письме, подписанном сотнями калифорнийцев, работающих в сфере науки и технологий, проект описывается как «бесконечная река новых педагогических причуд, которые эффективно искажают и вытесняют настоящую математику».
Уильямсон М.Эверс, старший научный сотрудник Независимого института и бывший сотрудник Департамента образования при администрации Джорджа Буша, был одним из авторов письма и возражал против идеи, что математика может быть инструментом социальной активности.
«Я думаю, что это действительно неправильно, — сказал он в интервью. «Математика есть математика. Два плюс два равно четыре.»
Бедствие по поводу проекта доносилось до Fox News. В мае имя и фотография доктора Болера были показаны в эпизоде «Такера Карлсона сегодня вечером», о котором она не знала, пока не начала получать неприятные письма от незнакомцев.
Как и некоторые попытки реформ прошлых десятилетий, проект Калифорнийских руководящих принципов отдает предпочтение более концептуальному подходу к обучению: больше сотрудничества и решения проблем, меньше запоминания формул.
Это также способствовало так называемой отмене отслеживания, которая удерживает учащихся вместе дольше вместо того, чтобы разделять хорошо успевающих на продвинутые классы перед старшей школой.
Объединенный школьный округ Сан-Франциско уже делает нечто подобное. Там ученики средней школы по математике не делятся на части, а, скорее, проходят интегрированные курсы, предназначенные для того, чтобы из года в год развивать свое понимание, хотя старшеклассники по-прежнему могут выбирать классы высокого уровня, такие как математический анализ.
София Алемайеху, 16 лет, ученица средней школы в Сан-Франциско, продвинулась по этому интегрированному пути, хотя она не всегда считала себя одаренной ученицей математики. Сейчас она занимается углубленным расчетом.
«В восьмом и девятом классах учителя говорили мне:« О, ты действительно хорошо разбираешься в материале », — сказала она. «Так что это заставило меня задуматься, может, я хорошо разбираюсь в математике».
Модель действует с 2014 года и позволяет получать данные об удержании и разнообразии за несколько лет, которые были выбраны экспертами по обе стороны дебатов о недопустимости отслеживания.И хотя данные осложняются многочисленными переменными, среди которых сейчас пандемия, сторонники модели Сан-Франциско говорят, что она привела к тому, что больше студентов и более разнообразный набор студентов прошли курсы повышения квалификации, не снизив при этом отличников.
«Вы слышите, как люди говорят, что это наименьший общий знаменатель, который препятствует развитию одаренных детей», — сказала Элизабет Халл Барнс, математический руководитель округа. «А потом, похоже, нет, наши данные это опровергают».
Но д-р.Эверс, бывший чиновник Министерства образования, указал на исследование, показывающее, что данные об успеваемости по математике в таких местах, как Сан-Франциско, были скорее тщательно отобранными, чем убедительными. Он добавил, что предлагаемая в Калифорнии структура могла бы использовать более тонкий подход к отмене отслеживания, который он рассматривал как грубый инструмент, не учитывающий потребности отдельных районов.
Другие критики отмены отслеживания говорят, что это является тормозом для детей, которым полезен сложный материал, и что это может повредить отстающим учащимся, которым, возможно, потребуется более целенаправленное обучение.
Дивья Чабра, учитель математики в средней школе в Дублине, Калифорния, сказала, что штату следует уделять больше внимания качеству обучения, находя или обучая более сертифицированных, опытных учителей.
Без этого, по ее словам, потенциальные ученики быстро отстанут, и им будет только больно отказываться от возможностей для углубленного обучения. «Мне так жаль этих студентов», — сказала она. «Мы режем ноги ученикам, чтобы они сравнялись с теми, кто не успевает по математике.
Отслеживание — часть более широкой дискуссии о доступе к колледжу. В соответствии с нынешней системой учащиеся, не помещенные на ускоренные курсы в среднюю школу, могут никогда не получить возможность пройти математический анализ, который долгое время был неформальным привратником для приема в избранные школы.
По данным Департамента образования, математический анализ даже не предлагается в большинстве школ, в которых обучается большое количество чернокожих и латиноамериканцев.
Роль математического анализа была предметом обсуждения среди преподавателей математики в течение многих лет, сказала Трена Вилкерсон, президент Национального совета учителей математики.«Если математический анализ — это не главное, то нам нужно, чтобы все понимали, какими могут быть разные пути и как подготовить студентов к будущему», — сказала она.
Рекомендации Калифорнии направлены на расширение возможностей для математики высокого уровня, чтобы студенты могли проходить курсы, например, по науке о данных или статистике, не теряя при этом своих преимуществ при поступлении в колледж. (Этот шаг требует поддержки со стороны колледжей; в последние годы в системе Калифорнийского университета принижается важность расчетных кредитов.)
На данный момент процесс пересмотра достиг своего рода перерыва: проект пересматривается перед очередным раундом общественного обсуждения, и не раньше конца весны или, может быть, лета, совет штата по образованию примет решение о том, будет ли чтобы дать свое одобрение.
Но даже после этого округа смогут по своему усмотрению отказаться от рекомендаций штата. А в тех местах, где они согласны, академические результаты — в виде результатов тестов, показателей удержания и готовности к поступлению в колледж — пополнят бурное море данных о том, какие виды обучения математике работают лучше всего.
Другими словами, разговор еще далек от завершения.
«Нам было очень трудно перестроить обучение математике в этой стране, — сказала Линда Дарлинг-Хаммонд, президент совета по образованию Калифорнии. «Мы не можем ограничить хорошо обученную, вдумчивую математику только нескольким людям. Мы должны сделать его широко доступным. В этом смысле я не возражаю, что это проблема социальной справедливости ».
Аспирантура | Департамент математики Cornell Arts & Sciences
MATH 5080 — Специальное исследование для учителей
Осень 2021 г., Весна 2022 г.1 кредит. Оценка студенческого варианта.
В первую очередь для: учителей средней математики и других лиц, интересующихся вопросами, связанными с преподаванием и изучением средней математики (например, учителей математики, аспирантов математики и математиков). Не открыто для студентов бакалавриата. Встречается с MATH 4980.
Исследует принципы, лежащие в основе содержания учебной программы по математике в средней школе, включая связи с историей математики, технологиями и исследованиями в области математического образования.Один кредит присуждается за посещение двух субботних семинаров (см. Math.cornell.edu/math-5080) и написание статьи.
MATH 5250 — Численный анализ и дифференциальные уравнения
Осень 2021 г. 4 кредита. Оценка студенческого варианта.
Предварительные требования: MATH 2210 или 2940 или эквивалент, один дополнительный курс математики с номером 3000 или выше и знание программирования. Ожидается, что студенты будут довольны доказательствами. Зачисление ограничено: аспирантами. Встречается вместе с MATH 4250.
Введение в основы численного анализа: анализ ошибок, аппроксимация, интерполяция, численное интегрирование. Во второй половине курса вышеизложенное используется для построения приближенных решателей для обыкновенных уравнений и уравнений в частных производных. Особое внимание уделяется пониманию преимуществ, недостатков и ограничений применимости всех описанных методов. Компьютерное программирование требуется для проверки теоретических концепций на протяжении всего курса.
MATH 5410 — Введение в комбинаторику I
Осень 2021 г.4 кредита. Оценка студенческого варианта.
Предварительные требования: MATH 2210, MATH 2230, MATH 2310 или MATH 2940. Ожидается, что учащиеся будут довольны доказательствами. Зачисление ограничено: аспирантами. Встречается с MATH 4410.
Комбинаторика — это изучение дискретных структур, возникающих в различных областях, особенно в других областях математики, информатики и многих других областях. В центре внимания часто бывает подсчет объектов, обладающих определенным свойством (например,g., деревья) или для доказательства существования определенных структур (например, паросочетаний всех вершин в графе). Первый семестр этой последовательности охватывает основные вопросы теории графов, включая теорию экстремальных графов (насколько большим должен быть граф, чтобы он гарантированно имел определенный подграф) и теорию Рамсея (которая показывает, что большие объекты вынуждены иметь структуру). Обсуждаются варианты теории согласования, включая теоремы Дилворта, Холла, Кенига и Биркгофа, а также введение в теорию сетевого потока.Методы перечисления (включение / исключение, обращение Мёбиуса и производящие функции) вводятся и применяются к задачам подсчета перестановок, разбиений и триангуляций.
MATH 5420 — Введение в комбинаторику II
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Предварительные требования: MATH 2210, MATH 2230, MATH 2310 или MATH 2940. Ожидается, что учащиеся будут довольны доказательствами. Зачисление ограничено: аспирантами. Встречается с MATH 4420.
Продолжение MATH 5410, хотя формально не зависит от рассматриваемого там материала. Акцент здесь делается на изучении определенных комбинаторных структур, таких как латинские квадраты и комбинаторные планы (которые используются в статистическом эксперименте), классических конечных геометрий и комбинаторных геометрий (также известных как матроиды, которые возникают во многих областях из алгебры и геометрии). через теорию дискретной оптимизации). Есть введение в частично упорядоченные множества и решетки, включая общую инверсию Мёбиуса и ее применение, а также теорию Пойи счета в присутствии симметрий.
MATH 6110 — Реальный анализ
Осень 2021 г. 4 кредита. Оценка студенческого варианта.
Запрещено перекрытие: из-за перекрытия содержания учащиеся не будут получать баллы за MATH 6110 и MATH 6210.
Необходимое условие: Хорошие результаты на курсе бакалавриата по анализу на уровне MATH 4140 или разрешение преподавателя.
MATH 6110-6120 — это основные курсы анализа в магистерской программе математики. MATH 6110 охватывает измерение, интеграцию и функциональный анализ.
MATH 6120 — Комплексный анализ
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Необходимое условие: Хорошие результаты на курсе бакалавриата по анализу на уровне MATH 4140 или разрешение преподавателя.
MATH 6110-6120 — это основные курсы анализа в магистерской программе математики. MATH 6120 охватывает комплексный анализ, анализ Фурье и теорию распределения.
MATH 6150 — Уравнения в частных производных
Весна 2022 года.4 кредита. Оценка студенческого варианта.
Предварительные требования: MATH 4130, MATH 4140 или аналогичный, либо разрешение преподавателя. Предлагаются альтернативные годы.
Этот курс подчеркивает «классические» аспекты уравнений в частных производных (PDE). Обычные темы включают фундаментальные решения для уравнений Лапласа / Пуассона, тепла и волн в R n , свойства среднего значения, принципы максимума, энергетические методы, принцип Дюамеля и введение в нелинейные уравнения первого порядка, включая потрясения и слабые решения.Дополнительные темы могут включать уравнения Гамильтона-Якоби, теорию распределения и преобразование Фурье.
MATH 6160 — [Уравнения в частных производных]
Осень. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Предварительные требования: MATH 4130, MATH 4140 или аналогичный, либо разрешение преподавателя. Предлагаются альтернативные годы.
Этот курс освещает приложения функционального анализа к теории уравнений в частных производных (PDE).Он охватывает части базовой теории линейных (эллиптических и эволюционных) уравнений в частных производных, включая пространства Соболева, существование и единственность решений, внутреннюю и граничную регулярность, принципы максимума и проблемы собственных значений. Дополнительные темы могут включать: введение в вариационные задачи, уравнения Гамильтона-Якоби и другие современные методы для нелинейных уравнений в частных производных.
MATH 6210 — Теория меры и интегрирование Лебега
Осень 2021 г. 4 кредита. Оценка студенческого варианта.
Запрещено перекрытие: из-за перекрытия содержания учащиеся не будут получать баллы за MATH 6110 и MATH 6210.
Охватывает теорию меры, интегрирование и пространства Lp.
MATH 6220 — Прикладной функциональный анализ
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Излагает основы теории гильбертовых и банаховых пространств и операций над ними. Приложения.
MATH 6230 — [Дифференциальные игры и оптимальное управление]
Осень. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Этот курс представляет собой самостоятельное введение в современную теорию оптимального управления и дифференциальные игры.В динамическом программировании используются уравнения в частных производных (УЧП) Гамильтона-Якоби для кодирования оптимального поведения в задачах совместного и состязательного последовательного принятия решений. Те же PDE имеют альтернативную интерпретацию в контексте задач распространения фронта. Мы показываем, как обе интерпретации полезны при построении эффективных численных методов. Мы также рассматриваем широкий спектр приложений, включая робототехнику, вычислительную геометрию, планирование пути, компьютерное зрение, фотолитографию, экономику, сейсмическую визуализацию, экологию, финансовую инженерию, динамику толпы и предотвращение столкновений самолетов.Предполагает отсутствие предварительных знаний о нелинейных PDE или численном анализе.
MATH 6260 — [Динамические системы]
Осень. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Предлагаемые альтернативные годы.
Темы включают теоремы существования и единственности для ОДУ; Теорема Пуанкаре-Бендиксона и глобальные свойства двумерных потоков; предельные множества, неблуждающие множества, цепная повторяемость, псевдоорбиты и структурная устойчивость; линеаризация в точках равновесия: теорема об устойчивом многообразии и теорема Хартмана-Гробмана; и общие свойства: теорема трансверсальности и теорема Купки-Смейла.Примеры включают расширяющиеся карты и диффеоморфизмы Аносова; гиперболичность: подкова и теорема Биркгофа-Смейла о трансверсальных гомоклинических орбитах; числа вращения; Теорема Германа; и характеристика структурно устойчивых систем.
MATH 6270 — [Прикладные динамические системы]
(также MAE 7760)
Весна. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Необходимое условие: MAE 6750, MATH 6260 или эквивалент.
Темы включают обзор плоских систем (с одной степенью свободы); локальный и глобальный анализ; структурная устойчивость и бифуркации в плоских системах; центральные многообразия и нормальные формы; теорема об усреднении и методы возмущений; Метод Мельникова; дискретные динамические системы, карты и разностные уравнения, гомоклинические и гетероклинические движения, подкова Смейла и другие комплексные инвариантные множества; глобальные бифуркации, странные аттракторы и хаос в уравнениях свободного и вынужденного осцилляторов; и приложения к задачам механики твердого тела и жидкости.
MATH 6310 — Алгебра
Осень 2021 г. 4 кредита. Оценка студенческого варианта.
Необходимое условие: хорошая успеваемость на бакалавриате по курсу абстрактной алгебры на уровне MATH 4340 или разрешение преподавателя.
MATH 6310-6320 — это основные курсы алгебры в магистерской программе математики. MATH 6310 охватывает теорию групп, особенно конечных групп; кольца и модули; теория идеалов в коммутативных кольцах; арифметика и факторизация в областях главных идеалов и областях уникальной факторизации; введение в теорию поля; тензорные произведения и полилинейная алгебра.(Необязательная тема: введение в аффинную алгебраическую геометрию.)
MATH 6320 — Алгебра
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Необходимое условие: MATH 6310 или разрешение преподавателя.
MATH 6320 — второй из двух основных курсов алгебры. Он рассматривает теорию Галуа, теорию представлений конечных групп и ассоциативных алгебр, а также введение в гомологическую алгебру. По большей части эти предметы не рассматриваются глубоко, поскольку цель курса — представить широкий взгляд на несколько тем.
Некоторые темы для обсуждения:
Теория поля и теория Галуа — Расширения полей, степени, поля расщепления, алгебраическое замыкание, нормальные и сепарабельные расширения, фундаментальная теорема теории Галуа, разрешимость уравнений радикалами, круговые расширения, конечные поля.
Гомологическая алгебра — точные последовательности, проективные и инъективные модули, гомологическая размерность, комплексы, гомологии.
Теория представлений конечных групп — простые и полупростые кольца и модули, теорема Веддерберна, представления групп, теорема Машке, характеры конечных групп, отношения ортогональности, взаимность Фробениуса, приложения к теории групп.
MATH 6330 — [Некоммутативная алгебра]
Осень. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Необходимое условие: MATH 6310-MATH 6320 или разрешение преподавателя. Предлагаются альтернативные годы.
Введение в теорию некоммутативных колец и модулей. Темы меняются в зависимости от семестра и включают полупростые модули и кольца, радикал Джекобсона и артиновы кольца, представления групп и групповые алгебры, характеры конечных групп, представления симметрической группы, центральные простые алгебры и группы Брауэра, теорию представлений конечномерных алгебр. , Теория Морита.
MATH 6340 — Коммутативная алгебра с приложениями в алгебраической геометрии
Осень 2021 г. 4 кредита. Оценка студенческого варианта.
Мы рассмотрим темы градуированных колец, функций Гильберта, свободных резольвент, комбинаторной коммутативной алгебры и вычислительной алгебры.
MATH 6350 — Гомологическая алгебра
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Предпосылка: MATH 6310. Предлагаются альтернативные годы.
Первый курс гомологической алгебры.Темы будут включать краткое введение в категории и функторы, цепные и коцепные комплексы, операции над комплексами, (ко) гомологии, стандартные резольвенты (инъективные, проективные, плоские), классические производные функторы, Tor и Ext, интерпретацию Ext Йонедой, гомологическую размерность. , кольца малых размерностей, введение в групповые когомологии, хохшильдовские и циклические гомологии ассоциативных алгебр и (ко) гомологии Шевалле-Эйленберга алгебр Ли.
MATH 6370 — Алгебраическая теория чисел
Весна 2022 года.4 кредита. Оценка студенческого варианта.
Примечание. Описание по умолчанию приводится ниже, но, поскольку это обычно небольшой класс, темы могут быть немного изменены в соответствии с опытом присутствующих. В каталоге упоминается «распределение простых чисел». Но поскольку это в первую очередь аналитическая тема, она не будет рассматриваться, за исключением, возможно, краткого обсуждения теоремы Дирихле о простых числах в арифметических прогрессиях и теоремы Чеботарева о плотности.
Пререквизиты: Курс современной алгебры на уровне MATH 4340 уже пройден или, по крайней мере, одновременно взят.Более низкий уровень подготовки по алгебре затруднит понимание большей части материала.
Темы: Этот курс представляет собой базовое введение в алгебраическую теорию чисел. Ядро его использовалось для изучения идеальной теории дедекиндовских областей применительно к кольцам целых чисел числовых полей (конечным расширениям Q). Основная цель теории — преодолеть недостаток уникальной факторизации на простые числа в этих кольцах. Вторая параллель, исторически более поздняя, пролегает через теорию локальных полей, которая на первый взгляд кажется совершенно иной.Особенно интересно переплетение двух подходов. Из-за нехватки времени мы можем больше сосредоточиться на втором, а также потому, что первое подробно рассматривается во многих классических книгах (например, Сэмюэлса — см. Ниже). Однако мы «сделаем» ключевые теоремы теории идеалов.
Курс также будет охватывать фундаментальные теоремы конечности: конечность идеальной группы классов (через геометрическую теорию чисел Минковского) и структуру (конечное порождение, определение ранга и т. Д.)) группы единиц. Дополнительные темы, которые будут обсуждаться, если позволит время: закон квадратичной взаимности, элементарные диофантовы уравнения, пополнения (p-адические числа).
Текст: Нет. Но для тех, кто любит печатать: Введение Самуэля в алгебраическую теорию чисел коротко и элегантно. Также книга Лэнга по теории чисел охватывает большую часть материала курса (и многое другое).
Оценки: Поскольку нет экзаменов и официальных домашних заданий (в большинстве случаев предлагаемая проблема), оценки не имеют большого значения.Но поскольку необходимо выставить некоторую оценку, моя политика будет полуавтоматической для аспирантов и A- для студентов. Полуавтоматический означает, что должно быть какое-то доказательство того, что вы посещаете и заинтересованы в материале.
ПРИМЕЧАНИЕ. Студентам бакалавриата не разрешается использовать этот курс для выполнения требований по алгебре для математических специальностей. Причина — отсутствие формальных требований (экзамены, hw).
MATH 6390 — [Группы Ли и алгебры Ли]
Осень. Не предлагается: 2021-2022 гг.Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Пререквизиты: продвинутый курс линейной алгебры на уровне MATH 4310 и курс дифференцируемых многообразий.
Излагает основы групп Ли и алгебр Ли. Темы включают в себя действительные и комплексные группы Ли, отношения между группами Ли и алгебрами Ли, экспоненциальное отображение, однородные многообразия и классификацию простых алгебр Ли.
MATH 6410 — Перечислительная комбинаторика
Весна 2022 года.4 кредита. Оценка студенческого варианта.
Необходимое условие: MATH 4410 или разрешение преподавателя. Предлагаются альтернативные годы.
Введение в перечислительную комбинаторику с алгебраической, геометрической и топологической точек зрения. Темы включают, помимо прочего, статистику перестановок, разбиения, производящие функции, различные типы множеств и решеток (распределительные, геометрические и эйлеровы), инверсию Мёбиуса, числа граней, возможность оболочки и отношения с кольцом Стэнли-Райснера.
MATH 6510 — Алгебраическая топология
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Необходимое условие: высокая успеваемость в бакалавриате по курсу абстрактной алгебры на уровне MATH 4340 и топологии с точками на уровне MATH 4530 или разрешение преподавателя.
MATH 6510 – MATH 6520 — это основные курсы по топологии в магистерской программе по математике. MATH 6510 — это вводное исследование определенных геометрических процессов для связывания алгебраических объектов, таких как группы, с топологическими пространствами.Наиболее важными из них являются группы гомологий и гомотопические группы, особенно первая гомотопическая группа или фундаментальная группа, с соответствующими понятиями покрывающих пространств и групповых действий. Развитие теории гомологии сосредоточено на проверке аксиом Эйленберга-Стинрода и на эффективных методах вычислений, таких как симплициальная и клеточная гомология и последовательности Майера-Виеториса. Если позволяет время, можно ввести кольцо когомологий пространства.
MATH 6520 — Дифференцируемые коллекторы
Осень 2021 г.4 кредита. Оценка студенческого варианта.
Необходимое условие: высокие результаты в области анализа (например, MATH 4130 и / или MATH 4140), линейной алгебры (например, MATH 4310) и топологии точек (например, MATH 4530) или разрешение преподавателя.
MATH 6510-MATH 6520 — это основные курсы по топологии в магистерской программе по математике. MATH 6520 — это введение в геометрию и топологию с дифференцированной точки зрения, подходящее для начинающих аспирантов. Объектами исследования являются многообразия и дифференцируемые отображения.Набор всех касательных векторов к многообразию образует касательное расслоение, а сечение касательного расслоения является векторным полем. В качестве альтернативы векторные поля можно рассматривать как дифференциальные операторы первого порядка. В этом курсе изучаются потоки векторных полей и доказывается теорема Фробениуса об интегрируемости. При наличии римановой метрики развивает понятия параллельного переноса, кривизны и геодезических. Исследует тензорное исчисление и внешнее дифференциальное исчисление и доказывает теорему Стокса.Если позволяет время, вводятся когомологии де Рама, теория Морса или другие дополнительные темы.
MATH 6530 — [K-теория и характеристические классы]
Осень. Не предлагается: 2021-2022: Следующее предложение: 2022-2023. 4 кредита. Оценка студенческого варианта.
Необходимое условие: MATH 6510 или разрешение преподавателя.
Введение в топологическую K-теорию и характеристические классы. Топологическая K-теория — это обобщенная теория когомологий, которая на удивление проста и полезна для вычислений, но при этом содержит достаточно структуры для доказательства интересных результатов.Класс начнется с определения K-теории, классов Черна и характера Черна. Дополнительные темы могут включать проблему инварианта Хопфа 1, J-гомоморфизм, классы Штифеля-Уитни и классы Понтрягина, группы кобордизмов и построение экзотических сфер, а также теорему об индексе Атьи-Зингера.
MATH 6540 — Теория гомотопии
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Необходимое условие: MATH 6510 или разрешение преподавателя.
Этот курс представляет собой введение в некоторые основы теории гомотопии.Теория гомотопий изучает пространства с точностью до гомотопической эквивалентности, а не только с точностью до гомеоморфизма. Это позволяет использовать множество алгебраических методов, которые недоступны при работе с гомеоморфизмом. Этот класс изучает основы и инструменты теории гомотопий в прошлом, гомологии и когомологии. Темы могут включать в себя вычисления высших гомотопических групп, симплициальных множеств, категорий моделей, спектральных последовательностей и теории рациональной гомотопии.
MATH 6620 — [Риманова геометрия]
Весна.Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Предлагаемые альтернативные годы.
Темы включают линейные связи, римановы метрики и параллельный перевод; ковариантное дифференцирование и тензоры кривизны; экспоненциальное отображение, лемма Гаусса и полнота метрики; изометрии и пространственные формы, поля Якоби и теорема Картана-Адамара; формулы первой и второй вариаций; индексная форма Морса и теорема Бонне-Майерса; теоремы сравнения Рауха, Гессе и Лапласа; теорема об индексе Морса; конъюгированный и разрезанный локусы; и подмногообразия и вторая основная форма.
MATH 6630 — [Симплектическая геометрия]
Осень. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Необходимое условие: MATH 6510 и MATH 6520 или разрешение преподавателя.
Симплектическая геометрия — это раздел дифференциальной геометрии, изучающий многообразия с невырожденной замкнутой 2-формой. Эта область возникла как математика классической (гамильтоновой) механики и связана (по крайней мере!) Со сложной геометрией, алгебраической геометрией, теорией представлений и математической физикой.В этом введении в симплектическую геометрию класс начнется с линейной симплектической геометрии, обсудит канонические локальные формы (теоремы типа Дарбу) и исследует связанные геометрические структуры, включая почти сложные структуры и кэлеровы метрики. Дополнительные темы могут включать действия симплектических и гамильтоновых групп, метод орбит, топологию и геометрию отображений импульса, торические симплектические многообразия, гамильтонову динамику, группы симплектоморфизмов и проблемы симплектического вложения.
MATH 6640 — Гиперболическая геометрия
Осень 2021 г.4 кредита. Оценка студенческого варианта.
Необходимое условие: MATH 6510 или разрешение преподавателя.
Введение в топологию и геометрию гиперболических многообразий. Класс начнется с геометрии гиперболического $ n $ -пространства, включая верхнее полупространство, диск Пуанкаре и лоренцевы модели. Особое внимание будет уделено случаям $ n = 2 $ и $ n = 3 $. Гиперболические структуры на поверхностях будут параметризованы с использованием пространства Тейхмюллера, и будут обсуждаться дискретные группы изометрий гиперболического пространства.Другие возможные темы включают топологию гиперболических многообразий и орбифолдов; Жесткость Мостова; гиперболическое наполнение Дена; теория деформаций клейновых групп; сложная и кватернионная гиперболическая геометрия; и выпуклые проективные структуры на многообразиях.
MATH 6670 — Алгебраическая геометрия
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Этот курс представляет собой введение в основную алгебраическую геометрию на уровне книги Шафаревича: Основы алгебраической геометрии, том 1.то есть мы ориентируемся на геометрию, а не на понятия схемы или пучка.
Мы рассмотрим многие из наиболее важных геометрических концепций алгебраической геометрии. Темы могут включать следующее (или большую часть следующего):
Глава 1: Основы: аффинные и проективные многообразия, регулярные и рациональные отображения, неприводимые многообразия, раздутие, конечные отображения, замкнутость отображений, слои отображений, произведения, размерность.
Глава 2: локальные свойства: касательное пространство, локальные кольца, особенности, локальные параметры, теорема Бертини, нормальные многообразия.
Глава 3: Дивизоры и дифференциальные формы, дивизоры на кривых, Римана-Роха для кривых, структура бирациональных отображений.
Глава 4: Теория пересечений, в основном для поверхностей.
Один из аспектов этой книги, который мне очень нравится, заключается в том, что в ней нет черного ящика для коммутативной алгебры. Доказывает вещи с нуля. Тем не менее, мы не будем рассматривать всю алгебру в классе: если у вас есть MATH 6340, это должно быть хорошо. В противном случае вы захотите прочитать алгебраические доказательства в книге.
Мы будем рассматривать множество примеров (например, кривые, поверхности, групповые действия, мультипроективные пространства, грассманианы, вложения Сегре и Веронезе, секущие множества, многообразия Калаби-Яу), и мы будем использовать мою систему компьютерной алгебры Macaulay2 для анализа и разбираться в примерах. Мы увидим, как вычислить многие из рассматриваемых нами концепций. Мы попытаемся включить некоторые важные идеи из теории трехмерных многообразий и многообразий более высоких размерностей (например,g конус Мори, конус nef, делители nef). Многие примеры взяты из книги Харриса.
Предварительные требования: MATH 6310 и MATH 6340. (Наличие MATH 6340 очень полезно, но, как упоминалось выше, можно, при некотором дополнительном чтении и усилиях, понять этот материал без этого предварительного условия.)
Домашнее задание: я буду назначать домашнее задание раз в две недели, которое не будет сдаваться, но студенты по очереди будут представлять решения. Очень важно делать примеры и решать задачи, так как это единственный способ по-настоящему изучить алгебраическую геометрию!
MATH 6710 — Теория вероятностей I
Осень 2021 г.4 кредита. Оценка студенческого варианта.
Необходимое условие: знание теории интеграции Лебега, по крайней мере, на реальной линии. Студенты могут изучить этот материал, взяв части MATH 4130-4140 или MATH 6210.
Вводный курс для аспирантов по теории вероятностей. Основные темы включают теоретическую вероятность меры, закон больших чисел, слабую сходимость, характеристические функции и теорию центрального предела. Возможные дополнительные темы включают процессы Пуассона, устойчивые законы, большие отклонения и условное ожидание.(Условное ожидание подробно рассматривается в MATH 6720.)
MATH 6720 — Теория вероятностей II
Весна 2022 года. 4 кредита. Оценка студенческого варианта.
Предпосылка: MATH 6710.
Вторая часть вводного курса по теории вероятностей, продолжение MATH 6710. Основные темы включают условное ожидание, мартингалы, цепи Маркова и их связь с мартингалами, броуновское движение. Если позволит время, будет введение в основы исчисления Ито для броуновского движения.
MATH 6730 — Математическая статистика I
(также STSCI 6730)
Весна 2022г. В титрах.
Предпосылка: STSCI 4090 / BTRY 4090, MATH 6710 или разрешение инструктора.
Этот курс будет сосредоточен на теории конечных выборок статистического вывода с упором на оценку, проверку гипотез и доверительные интервалы. Конкретные темы включают: несмещенные оценки с равномерно минимальной дисперсией, эквивариантные оценки минимального риска, байесовские оценки, минимаксные оценки, теорию проверки гипотез Неймана-Пирсона и построение оптимальных инвариантных тестов.
MATH 6740 — Математическая статистика II
(также STSCI 6740)
Осень 2021 г. 4 кредита. Оценка студенческого варианта.
Предварительные условия: MATH 6710 (теоретическая оценка вероятности) и STSCI 6730 / MATH 6730 или разрешение преподавателя.
Предполагается некоторое знакомство с базовой статистической теорией, то есть с точечной оценкой, проверкой гипотез и доверительными интервалами, а также с концепциями байесовских и минимаксных решений. Курс посвящен современной теории статистического вывода с упором на непараметрические и асимптотические методы.При нахождении оптимальных решений ключевую роль будет играть концепция асимптотической минимаксности. Предварительный список тем (с номерами глав в учебнике): (1) эффективность Фишера (резюме), (2) байесовские и минимаксные оценки (резюме), (3) асимптотическая минимаксность, (4) некоторые нерегулярные статистические эксперименты, ( 8) оценка в непараметрической регрессии, (9) локальная полиномиальная аппроксимация регрессии, (10) оценка регрессии в глобальных нормах, (12) асимптотическая оптимальность в глобальных нормах, (13) оценка функционалов, (15) адаптивное оценивание.
MATH 6810 — [Логика]
Осень или Весна. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Предлагаемые альтернативные годы.
Охватывает основные темы математической логики, включая исчисление высказываний и предикатов; формальная теория чисел и рекурсивные функции; теоремы о полноте и неполноте, компактности и теоремы Сколема-Лёвенгейма. Другие темы, если позволит время.
MATH 6830 — Теория модели
Весна 2022 года.4 кредита. Оценка студенческого варианта.
Предлагаемые альтернативные годы.
Этот курс представляет для выпускников введение в теорию моделей с упором на примеры по алгебре и геометрии. Он будет следовать за текстом Палатки и Зиглера. Рассматриваемые темы будут включать теоремы о компактности и полноте для логики первого порядка, конструкцию Хенкина, теоремы Ловенгейма-Сколема, критерии полноты Воота, аргументы вперед и назад, реализацию и исключение типов, пространства типов, стабильность, пары Вотта и неразличимое.Курс завершится доказательством Болдуина-Лахлана теоремы Морли.
MATH 6840 — Теория рекурсии
Осень 2021 г. 4 кредита. Оценка студенческого варианта.
Предлагаемые альтернативные годы.
Излагает теорию эффективно вычислимых функций; классификация рекурсивно перечислимых множеств; степени рекурсивной неразрешимости; приложения к логике; иерархии; рекурсивные функции ординалов и объектов более высокого типа; обобщенная теория рекурсии.
MATH 6870 — [Теория множеств]
Осень.Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Предлагаемые альтернативные годы.
Первый курс аксиоматической теории множеств на уровне книги Кунена.
MATH 7110 — Темы анализа: лекции по «Геликоидальному методу»
Осень 2021 г. 4 кредита. Только марки S / U.
Это будет продвинутый курс по гармоническому анализу. Его объем состоит в том, чтобы подробно описать то, что мы назвали «геликоидальным методом», повторяющимся и чрезвычайно надежным методом, который, в частности, предоставляет новые парадигмы для доказательства (множественных) векторных оценок, разреженного доминирования и оценок смешанной нормы для многих ( если не большинство) мультиквазилинейных операторов, представляющих интерес в гармоническом анализе.Он был разработан в течение последних восьми лет (или около того) в сотрудничестве с Кристиной Бенеа, которая была аспирантом здесь, в Корнелле, и окончила университет в мае 2015 года.
Презентация будет как можно более замкнутой, но знание основных теорий гармонического анализа явно должно помочь. Я представляю этот класс как класс для людей, которым нравится АНАЛИЗ, даже если их конкретные исследовательские интересы лежат в разных областях, таких как PDE, математическая физика, функциональный анализ, комплексный анализ, геометрическая теория меры, вариационное исчисление, спектральная теория и т. Д. .
MATH 7120 — Темы анализа: геометрия и анализ четырехмерных многообразий
Весна 2022 года. 4 кредита. Только марки S / U.
В этом курсе мы обсудим недавний прогресс в направлении геометрии четырехмерных многообразий. В частности, 4-многообразия Эйнштейна, поток Риччи на 4-многообразиях. Мы также обсудим некоторые классические методы, такие как техника Бохнера, конформная геометрия и их применение к четырехмерным многообразиям.
MATH 7130 — Функциональный анализ
Осень 2021 г.4 кредита. Оценка студенческого варианта.
Предлагаемые альтернативные годы.
Охватывает топологические векторные пространства, банаховы и гильбертовые пространства, а также банаховы алгебры. Дополнительные темы, выбранные инструктором.
MATH 7150 — [Анализ Фурье]
Осень. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Предлагаемые альтернативные годы.
Введение в (в основном евклидовом) гармонический анализ. Темы обычно включают сходимость рядов Фурье, гармонические функции и их сопряженные, преобразование Гильберта, теорию Кальдерона-Зигмунда, теорию Литтлвуда-Пэли, псевдодифференциальные операторы, теорию ограничений преобразования Фурье, связи с PDE.Также могут обсуждаться приложения к теории чисел и / или теории вероятностей, а также к анализу Фурье на группах.
MATH 7160 — Разделы уравнений в частных производных: нелинейные эллиптические уравнения в частных производных
Осень 2021 г. 4 кредита. Только марки S / U.
Темы из: вариационное исчисление (прямые методы) и теория бифуркаций (локальные и теоретико-степенные методы).
MATH 7270 — [Вопросы численного анализа]
Осень или Весна. Не предлагается: 2021-2022 гг.Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Подборка сложных тем из численного анализа. Содержание варьируется.
MATH 7280 — [Разделы динамических систем]
Весна. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Подборка продвинутых тем из динамических систем. Содержание варьируется.
MATH 7290 — Семинар по научным вычислениям и счетам
(также CS 7290)
Осень 2021 г., Весна 2022 г.1 кредит. Только марки S / U.
Беседы о различных методах научных вычислений, анализе их свойств сходимости и вычислительной эффективности, а также их адаптации к конкретным приложениям.
MATH 7310 — [Вопросы по алгебре]
Осень или Весна. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Подборка продвинутых тем по алгебре. Содержание курса варьируется.
MATH 7350 — [Разделы гомологической алгебры]
Осень или Весна.Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Предлагаемые альтернативные годы.
Подборка продвинутых тем по гомологической алгебре. Содержание курса варьируется.
MATH 7370 — Разделы алгебраической теории чисел
Осень 2021 г. 4 кредита. Только марки S / U.
Цель этого курса — научиться понимать теорему Одзаки 2011 г., в которой он доказал, что для каждой конечной p-группы G существует числовое поле K, чье поле p-гильбертова класса Tower равно G.Большая часть курса будет потрачена на понимание утверждений и освоение необходимого базового материала по теории поля классов.
Этот курс предполагает некоторый опыт в теории чисел, примерно на уровне MATH 6370.
MATH 7390 — Темы в группах Ли и алгебрах Ли: симплектические разрешения
Весна 2022 года. 4 кредита. Только марки S / U.
«Симплектические резольвенты» — это определенное семейство голоморфных симплектических многообразий со многими удивительными свойствами.Есть несколько общих построек, каждую из которых мы рассмотрим подробно:
- гиперторических многообразий, которые относятся к расположению гиперплоскостей так же, как торические многообразия относятся к многогранникам;
- колчанов Накадзима, которые обеспечивают «геометрическую теорию представлений» для односвязных алгебр Каца-Муди;
- срезов в аффинных грассманианах, которые обеспечивают «геометрическую теорию представлений» для конечномерных групп Ли;
- Медленные срезы до нильпотентного закрытия орбиты
(Последние три все совпадают в типе A, но расходятся для других групп.* Г / Б. (Недаром Окуньков назвал их «алгебрами Ли XXI века»).
Мы лишь коснемся этой развивающейся темы. Предпосылками являются твердые знания теории представлений и некоторые знания алгебраической геометрии.
MATH 7410 — [Разделы комбинаторики]
Весна.Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Предлагаемые альтернативные годы.
Подборка дополнительных тем по комбинаторике. Содержание курса варьируется.
MATH 7510 — Семинар Берштейна по топологии: потоки Анасова на трехмерных многообразиях
Осень 2021 г. 4 кредита. Только марки S / U.
Мы будем изучать динамические свойства геодезических потоков на поверхностях и, в более общем смысле, потоков Аносова на трехмерных многообразиях. Эти методы основаны на геометрической / низкоразмерной топологии, гиперболической геометрии и гладкой динамике.Есть много интересных построений примеров и результатов существования и изобилия. Мы особенно внимательно рассмотрим примеры на трехмерных гиперболических многообразиях и связанных с ними «квазигеодезических» потоках с целью понять некоторые важные открытые вопросы. Как и на всех семинарах Берштейна, студенты представят основную часть материала и скажут, какие подтемы мы рассматриваем.
Пререквизиты: Как минимум, первый год обучения дифференцируемым многообразиям или эквивалентные знания.В идеале вы должны знать, что такое трехмерное гиперболическое многообразие. Прошлогодний семинар Берштейна по 3-многообразиям — отличная подготовка, но не обязательная (но если бы вы были там, мы могли бы увидеть прекрасные связи с нормой Терстона).
MATH 7520 — [Семинар Берштейна по топологии]
Весна. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Семинар по продвинутой теме топологии или родственной теме. Содержание варьируется. Формат, который обычно представляют участники по очереди.
MATH 7550 — Семинар по топологии и геометрической теории групп
Осень 2021 г. 4 кредита. Только марки S / U.
Еженедельный семинар, на котором приезжие или местные докладчики представляют результаты по топологии, геометрической теории групп или связанным предметам.
MATH 7560 — Семинар по топологии и геометрической теории групп
Весна 2022 года. 4 кредита. Только марки S / U.
Еженедельный семинар, на котором приезжие или местные докладчики представляют результаты по топологии, геометрической теории групп или связанным предметам.
MATH 7580 — Темы топологии
Весна 2022 года. 4 кредита. Только марки S / U.
Этот курс будет посвящен теореме Атьи-Зингера об индексе. Эта теорема описывает прекрасную связь между топологией, дифференциальной геометрией и анализом. Одним из примеров теоремы является теорема Черна-Гаусса-Бонне, которая утверждает, что эйлерова характеристика компактного многообразия может быть вычислена с помощью интеграла класса Эйлера по многообразию; по теории Ходжа эйлерова характеристика — это то же самое, что индекс оператора де Рама-Дирака (эти вещи будут объяснены в курсе).Одна из конечных целей — понять уточнение (только для операторов Дирака) исходной теоремы, называемой теоремой о локальном индексе. Если позволит время, мы изучим обобщения на эквивариантные и семейные настройки.
Предпосылки: предполагаю, что я знаком с темами, затронутыми в MATH 6520 (многообразия, дифференциальные формы, когомологии де Рама, римановы метрики и т. Д.). Предварительное знакомство со связками, соединениями и кривизной было бы преимуществом, так как я планирую, чтобы обсуждение этих тем было кратким.
MATH 7610 — Темы по геометрии: сравнительная геометрия и минимальные поверхности
Осень 2021 г. 4 кредита. Только марки S / U.
Первая часть этого курса будет продолжением Math 6620: Riemannian Geometry, предлагаемого весной 2021 года. Мы обсудим несколько классических теорем сравнения. Вторая часть будет кратким введением в теорию минимальных поверхностей. Темы будут включать первую и вторую формулу вариации, формулу монотонности, принцип максимума и классические оценки кривизны.Когда позволит время, мы обсудим теорию существования и приложения.
MATH 7620 — Темы по геометрии: универсальная жесткость и приложения
Весна 2022 года. 4 кредита. Только марки S / U.
Это введение в теорию жестких каркасов в целом, включая тенсегрити, универсальную жесткость и ее применение к инженерным конструкциям, а также недавнее увлекательное приложение для нахождения порога максимального правдоподобия для оценок максимального правдоподобия в статистике.Каркас — это просто набор точек в евклидовом пространстве, конфигурация, в которой некоторые пары точек, ребра графа, должны находиться на фиксированном расстоянии. Универсальная жесткость — это когда эти ограничения расстояния определяют конфигурацию вплоть до глобального движения в любом более высоком измерении. Существует своего рода обратная связь между существованием универсально жесткой конфигурации для графа в данном измерении и порогом максимального правдоподобия.
MATH 7670 — Темы алгебраической геометрии: неархимедова геометрия
Осень 2021 г.4 кредита. Только марки S / U.
Некогда специализированный предмет, неархимедова геометрия превратилась в основную часть алгебраической и арифметической геометрии. Его цель — распространить концепции и результаты о сложных аналитических пространствах на пространства, определенные над неархимедовыми полями, такими как поля p-адических чисел или поле формальных рядов Лорана. Например, Тейт первоначально сформулировал теорию, расширяющую униформизацию комплексных эллиптических кривых, в которой кривая описывается как фактор группы мультипликативных комплексных чисел по свободной подгруппе, до аналогичной конструкции для эллиптических кривых над более общими не- архимедовы поля.Общая теория неархимедовых пространств с тех пор была развита Рейно, Берковичем, Хубером и многими другими, и она допускает несколько связанных формулировок. Она применялась во многих контекстах: соответствие Ленглендса, топология алгебраических многообразий в высших измерениях, зеркальная симметрия, бирациональная геометрия, p-адическая теория Ходжа, модульность представлений Галуа и т. Д.
Этот курс будет служить введением в неархимедову геометрию, уделяя основное внимание подходам Рейно и Берковича.Мы определим неархимедовы пространства и изучим их основные свойства. Затем мы обсудим теории когерентных когомологий и этальных когомологий на этих пространствах.
MATH 7710 — Разделы теории вероятностей: пределы дискретных случайных структур
Весна 2022 года. 4 кредита. Только марки S / U.
Есть много способов ограничить дискретную структуру (например, случайный граф, остовное дерево или раскраску). Мы рассмотрим некоторые из этих тем:
Случайные блуждания и электрические сети, Гармонические функции, Гауссовское свободное поле, Пределы масштабирования, Пределы бесконечного объема, Пределы графа (Ловаш и Бенджамини-Шрамм), Равномерный остовной лес, Минимальный остовный лес, Ветвящиеся процессы, Континуумное случайное дерево, Неравенства концентрации, Случайное Графы, перколяция, случайная кластерная модель.
Предыстория: для прохождения этого курса вам необходимо знать как минимум один семестр вероятности получения диплома на уровне MATH 6710. Знакомство с мартингейлами и броуновским движением на уровне MATH 6720 является большим плюсом!
Мы будем следовать книге Лайонса и Переса «Вероятность на деревьях и сетях»: https://rdlyons.pages.iu.edu/prbtree/prbtree.html
Я рассчитываю охватить главы 2,4,5,6,7, 9,10,11,12.
Мы также можем охватывать части этих книг !:
Модель случайного кластера, Гриммет: http: // www.statslab.cam.ac.uk/~grg/books/rcm1-1.pdf
Случайные графы, Янсон, Лучак и Ручински: https://onlinelibrary.wiley.com/doi/book/10.1002/9781118032718
Крупные сети и Graph Limits, автор Lovasz: https://web.cs.elte.hu/~%20lovasz/bookxx/hombook-almost.final.pdf
MATH 7720 — Темы в случайных процессах: случайные блуждания в группах
Осень 2021 г. 4 кредита. Только марки S / U.
Этот курс познакомит вас с современными достижениями в изучении случайных блужданий в группах.Значительная часть курса будет посвящена основам случайного блуждания в группах. Вторая часть будет иметь дело с применением этих методов к определенным классам групп: нильпотентным, полициклическим и т. Д. Никаких глубоких знаний теории групп не требуется.
MATH 7740 — [Статистическая теория обучения: классификация, распознавание образов, машинное обучение]
Осень. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Оценка студенческого варианта.
Необходимые условия: базовая математическая статистика (STSCI / MATH 6730 или эквивалент) и теоретическая вероятность измерения (MATH 6710) или разрешение преподавателя.
Целью курса является представление развивающегося интерфейса между теорией машинного обучения и статистикой. Темы включают введение в классификацию и распознавание образов; связь с непараметрической регрессией подчеркивается повсюду. Рассмотрены некоторые классические статистические методологии, такие как дискриминантный анализ и логистическая регрессия, а также понятие восприятия, которое сыграло ключевую роль в развитии теории машинного обучения. Вводится принцип минимизации эмпирического риска и обосновывается его границами Вапника-Червоненкиса.Кроме того, обсуждаются выпуклые мажорирующие функции потерь и маржевые условия, обеспечивающие высокие скорости, и вычислимые алгоритмы. Представлены актуальные сегодня темы многомерных статистических исследований, такие как неравенства оракулов в контексте выбора и агрегирования моделей, оценки типа лассо, регрессия низкого ранга и другие типы задач оценивания разреженных объектов в многомерных пространствах.
MATH 7810 — Семинар по логике: логика групп Томпсона и их родственников
Осень 2021 г.4 кредита. Только марки S / U.
Семинар по логике состоит из лекций студентов по одной теме, дополненных лекциями преподавателей, приглашенных докладчиков и студентов, представляющих свои собственные исследования. В осеннем семестре 2021 года тематический компонент семинара будет «Логика групп Томпсона и их родственников». Ожидается, что студенты, обучающиеся на курсе, прочитают 2-3 лекции по данной теме.
Описание темы семинара: Будучи аспирантом факультета логики в Беркли в 1960-х и 1970-х, Ричард Томпсон представил три группы, теперь известные как $ F $, $ T $ и $ V $.Все три — конечно определенные группы гомеоморфизмов канторова множества. $ T $ и $ V $ были ранними примерами конечно представленных бесконечных простых групп, в то время как $ F $, пожалуй, самый простой пример неэлементарной аменабельной группы, не содержащей свободной группы с двумя образующими.
С 1980-х годов эти группы играли важную роль в теории групп и топологии в основном благодаря своим экзотическим свойствам. Совсем недавно их исследование затронуло разные части логики и теории множеств.В этом семестре мы познакомимся с этими группами, а также с их родственниками, такими как группа кусочно линейных и кусочно проективных гомеоморфизмов единичного интервала. Основное внимание будет уделено их взаимодействию с логикой, от теории множеств до теории доказательств и теории автоматов. На семинаре также будет освещен ряд открытых проблем и направлений текущих исследований.
MATH 7820 — Семинар по логике
Весна 2022 года. 4 кредита. Только марки S / U.
Дважды в неделю семинар по логике.Обычно тема выбирается для каждого семестра, и по крайней мере половина встреч курса посвящена этой теме с презентациями в основном студентов. Студентам и другим людям также предоставляется возможность представить свои собственные работы и другие интересные темы.
MATH 7850 — [Темы по логике]
Осень. Не предлагается: 2021-2022 гг. Следующие предложения: 2022-2023 гг. 4 кредита. Только марки S / U.
Охватывает темы математической логики, которые меняются из года в год, такие как описательная теория множеств или теория доказательств.Может также использоваться для дальнейшего развития материала из теории моделей (MATH 6830), теории рекурсии (MATH 6840) или теории множеств (MATH 6870).
.
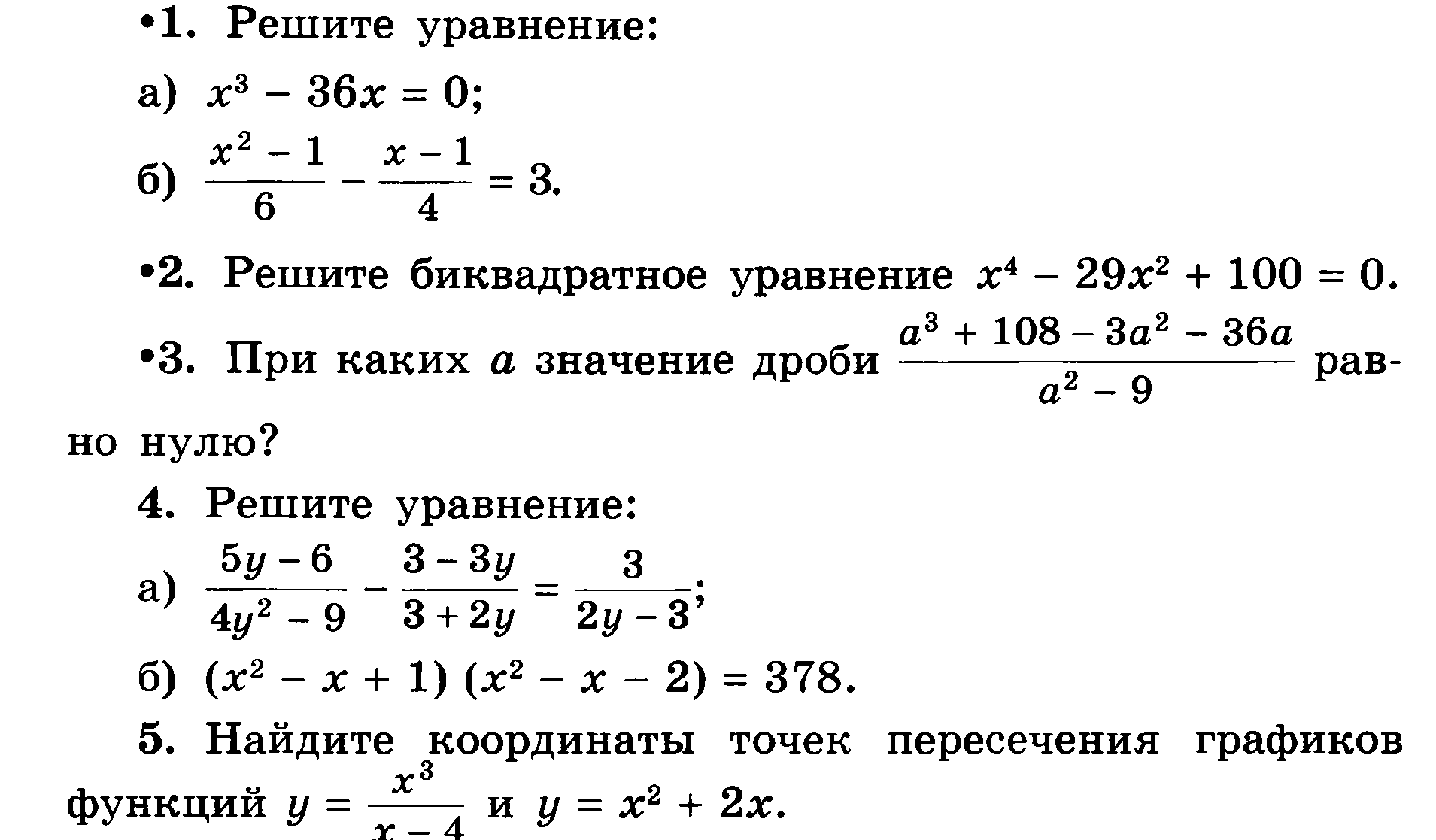





 Производная разности
Производная разности





 Уравнения-следствия.
Уравнения-следствия.