Задания 1 класс математика петерсон: ГДЗ по математике 1 класс Петерсон с бесплатными ответами для 1, 2, 3 частей .

Средняя оценка 5 / 5.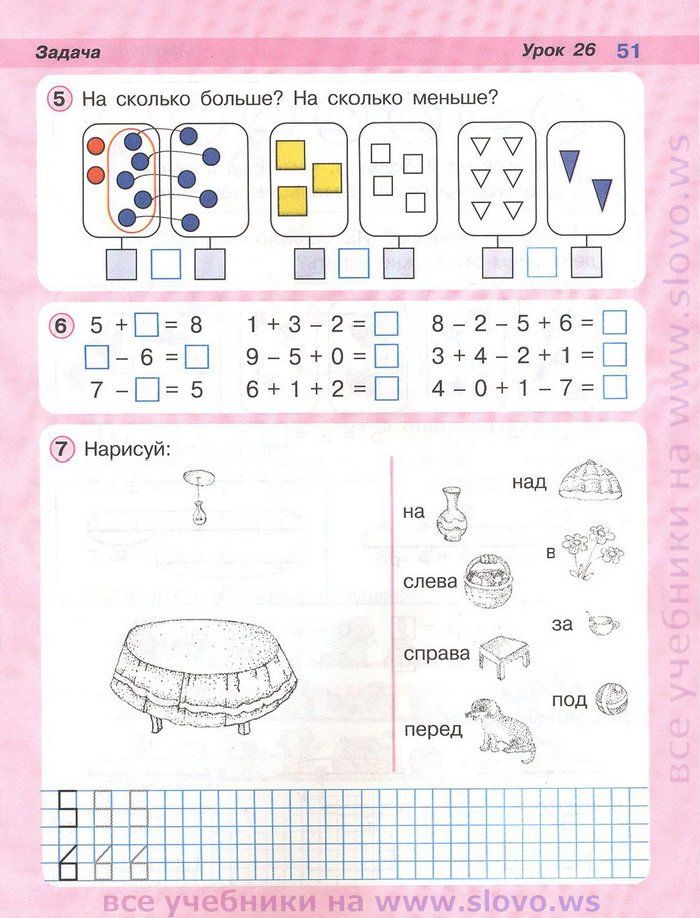 Количество оценок: 1

Оценок пока нет. Поставьте оценку первым.

гдз 1 класс , решебники и ответы онлайн: гдз математика 1 класс

Дополнительная математика 1 класс: geka_luka — LiveJournal

geka_luka (geka_luka) wrote,
2016-03-13 19:23:00 geka_luka
geka_luka
2016-03-13 19:23:00

• Сохранить, занятия математикой

  Оригинал взят у sama_sebe_vesna в Сохранить, занятия математикой Оригинал взят у zalena80 в Сохранить, занятия математикой…

• Математика 7 класс

  Оригинал взят у sm_mama в Математика 7 класс Хочу поделиться накопленными сокровищами)) — ссылками на ресурсы, где ребенок может…

• Книги и ресурсы по математике для школьника — резюме

  Оригинал взят у vorobiev в Книги и ресурсы по математике для школьника — резюме Вчера я попросил помощи зала в создании подборки списка…

Photo

Hint http://pics. livejournal.com/igrick/pic/000r1edq

ГДЗ Математика 1 класс Петерсон

Математика 1 класс

Серия: Перспектива.

Тип пособия: Рабочая тетрадь

Авторы: Петерсон

Издательство: «Ювента»

Похожие ГДЗ Математика 1 класс

Часть 1. Задания: Урок 1

Предыдущее

Следующее

Предыдущее

Следующее

Математика – один из самых важных предметов школьной программы. Она не просто сопровождает школьника с первых дней учебы до выпускных экзаменов, но и пригодится подавляющему большинстве ребят при поступлении в высшие учебные заведения. Основы работы с этим предметом закладываются в первом классе, и главная задача родителей – с самых первых уроков приучать ребенка к полноценной самостоятельной работе.

О роли учебной литературы

Правильно подобранное учебное пособие призвано не только помочь в изучении конкретной дисциплины, но и привить умение использовать вспомогательную литературу. Первоклассник не просто выполняет задание, и проверяет правильность своего ответа: он учится самостоятельно находить свои ошибки и исправлять их. Эти задачи ученику помогает успешно выполнять решебник к пособию «ГДЗ по Математике 1 класс Рабочая тетрадь Петерсон Ювента».

Благодаря сборнику к рабочей тетради, ученик 1 класса

• Научится разбираться в ранее изученном материале.
• Научится определять свои ошибки и исправлять их.
• Выработает свой почерк.
• Забежит дальше учебной программы.

С помощью ГДЗ родители смогут контролировать правильность выполнения домашней работы своего школьника, именно с учетом учебной программы.

О решебнике

Рабочая тетрадь снабжена красочными иллюстрациями, помогающими первокласснику понять смысл задания и сконцентрировать свое внимание на решении. Задания в решебнике соответствуют темам, изучаемым в первом классе:

• Сложение.
• Вычитание.
• Сравнение групп предметов.
• Дециметр.
• Счет десятками и единицами.

Родители при помощи решебника «ГДЗ по Математике 1 класс Рабочая тетрадь Петерсон Ювента» смогут объяснить ребенку, как следует находить алгоритм решения.

Преимущества сборника

Пособие с готовыми ответами «ГДЗ по Математике 1 класс Рабочая тетрадь Петерсон Ювента» – это незаменимый помощник на тернистом пути изучения математической науки. Начальные навыки выполнения самостоятельной работы рекомендуется сопровождать проверкой и анализом результатов первоклассника. Поэтому каждый родитель достойно оценит решебник после совместной работы над домашними задачками.

Главные особенности:

1. Можно приобрести в книжном магазине, а также открыть онлайн.
2. Задания расположены в том же порядке, что и в учебной тетради.
3. Соответствует ФГОС.

Данный решебник прост в использовании и содержит только верные решения с четкими пояснениями, что поможет родителю понимать современную методику обучения.

ГДЗ по математике 1 класс Петерсон для номеров смотреть онлайн.

Часть 1

Урок 1. Свойства предметов (стр. 1):

Урок 2. Свойства предметов (стр. 2–3):

Урок 3. Свойства предметов (стр. 4–5):

Урок 5. Группы предметов (стр. 9):

Урок 6. Группы предметов (стр. 10–11):

Урок 7. Сравнение групп предметов (стр. 12–13):

Урок 8. Сравнение групп предметов (стр. 14–15):

Урок 9. Сложение (стр. 16):

Урок 10. Сложение (стр. 17):

Урок 11. Вычитание (стр. 18):

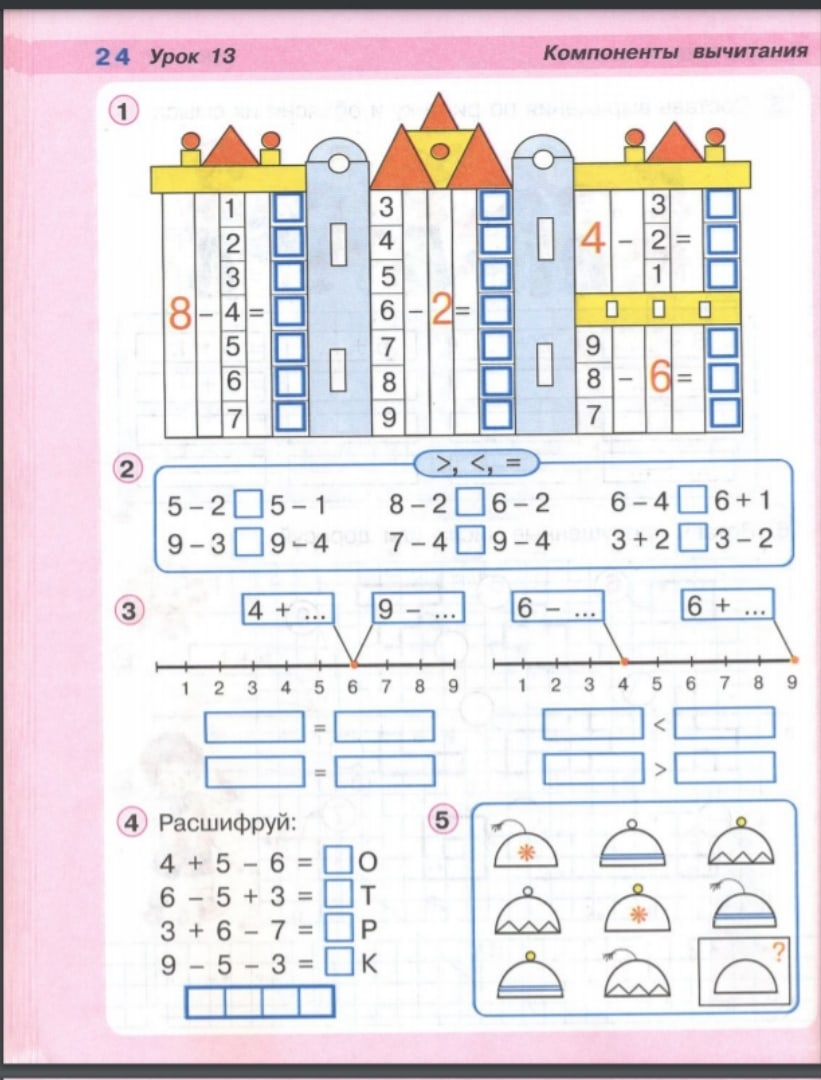
Урок 12. Вычитание (стр. 19):

Урок 13. Выше, ниже (стр. 20–21):

Урок 14. Порядок (стр. 22–23):

Урок 15. Раньше, позже (стр. 24–25):

Урок 16. Один – много (стр. 26–27):

Урок 17. Один (стр. 28):

Урок 18. Два (стр. 29):

Урок 19. Три (стр. 30):

Урок 20. Числа 1 – 3 (стр. 31):

Урок 21. Числа 1 – 3 (стр. 32):

Урок 22. Четыре (стр. 33):

Урок 23. Числа 1 – 4 (стр. 34–35):

Урок 24. Числовой отрезок (стр. 36–37):

Урок 25. Числовой отрезок (стр. 38–39):

Урок 26. Пять (стр. 40–41):

Урок 27. Пять (стр. 42–43):

Урок 28. Столько же (стр. 44–45):

Урок 29. Столько же (стр. 46–47):

Урок 30. Числа 1 – 5 (стр. 48–49):

Урок 31. Больше, меньше (стр. 50):

Урок 32. Больше, меньше (стр. 51):

Урок 33. Шесть (стр. 52–53):

Урок 34. Числа 1 – 6 (стр. 54–55):

Урок 35. Точки и линии (стр. 56–57):

Урок 36. Компоненты сложения (стр. 58–59):

Урок 37. Области и границы (стр. 60–61):

Урок 38. Компоненты вычитания (стр. 62–63):

Часть 2

Урок 1. Отрезок и его части (стр. 1):

Урок 2. Семь (стр. 2–3):

Урок 3. Ломаная линия. Многоугольник (стр. 4–5):

Урок 4. Выражения (стр. 6–7):

Урок 5. Выражения (стр. 8–9):

Урок 6. Выражения (стр. 10–11):

Урок 7. Восемь (стр. 12–13):

Урок 8. Числа 1 – 8 (стр. 14–15):

Урок 9. Числа 1 – 8 (стр. 16–17):

Урок 10. Девять (стр. 18–19):

Урок 11. Таблица сложения (стр. 20–21):

Урок 12. Компоненты сложения (стр. 22–23):

Урок 13. Компоненты вычитания (стр. 24–25):

Урок 14. Части фигур (стр. 26–27):

Урок 15. Части фигур (стр. 28–29):

Урок 16. Нуль (стр. 30–31):

Урок 17. Нуль (стр. 32–33):

Урок 18. Кубик Рубика (стр. 34–35):

Урок 19. Равные фигуры (стр. 36–37):

Урок 20. Равные фигуры (стр. 38–39):

Урок 21. Волшебные цифры (стр. 40–41):

Урок 22. Алфавитная нумерация (стр. 42–43):

Урок 23. Задача (стр. 44–45):

Урок 24. Задача (стр. 46–47):

Урок 25. Задача (стр. 48–49):

Урок 25. Задача (стр. 50–51):

Урок 27. Сравнение чисел (стр. 52–53):

Урок 28. Задачи на сравнение (стр. 54–55):

Урок 29. Задачи на сравнение (стр. 56–57):

Урок 30. Задачи на сравнение (стр. 58–59):

Урок 31. Задачи на сравнение (стр. 60–61):

Урок 32. Повторение (стр. 62–63):

Математические игры (стр. 64):

Часть 3

Урок 1. Величины. Длина (стр. 1):

Урок 2. Величины. Длина (стр. 2–3):

Урок 3. Длина (стр. 4–5):

Урок 4. Масса (стр. 6–7):

Урок 5. Масса (стр. 8–9):

Урок 6. Объем (стр. 10–11):

Урок 7. Свойства величин (стр. 12–13):

Урок 8. Свойства величин (стр. 14–15):

Урок 9. Свойства величин (стр. 16–17):

Урок 10. Решение задач (стр. 18–19):

Урок 11. Уравнения (стр. 20–21):

Урок 12. Уравнения (стр. 22–23):

Урок 13. Уравнения (стр. 24–25):

Урок 14. Уравнения (стр. 26–27):

Урок 15. Уравнения (стр. 28–29):

Урок 16. Уравнения (стр. 30–31):

Урок 17. Уравнения (стр. 32–33):

Урок 18. Единицы счета (стр. 34–35):

Урок 19. Единицы счета (стр. 36–37):

Урок 20. Десять (стр. 38–39):

Урок 21. Десять (стр. 40–41):

Урок 22. Десять (стр. 42–43):

Урок 23. Решение задач (стр. 44–45):

Урок 24. Счет десятками (стр. 46–47):

Урок 25. Круглые числа (стр. 48–49):

Урок 26. Круглые числа (стр. 50–51):

Урок 27. Дециметр (стр. 52–53):

Урок 28. Счет десятками и единицами (стр. 54–55):

Урок 29. Названия чисел до двадцати (стр. 56–57):

Урок 30. Названия чисел до двадцати (стр. 58–59):

Урок 31. Названия чисел до двадцати (стр. 60–61):

Урок 32. Нумерация двузначных чисел (стр. 62–63):

Урок 33. Натуральный ряд (стр. 64–65):

Урок 34. Сравнение чисел (стр. 66–67):

Урок 35. Сложение и вычитание двузначных чисел (стр. 68–69):

Урок 36. Сложение и вычитание двузначных чисел (стр. 70–71):

Урок 37. Сложение и вычитание двузначных чисел (стр. 72–73):

Урок 38. Таблица сложения (стр. 74–75):

Урок 39. Таблица сложения (стр. 76–77):

Урок 40. Таблица сложения (стр. 78–79):

Урок 41. Таблица сложения (стр. 80–81):

Урок 42. Таблица сложения (стр. 82–83):

Урок 43. Таблица сложения (стр. 84–85):

Урок 44. Таблица сложения (стр. 86–87):

Урок 45. Таблица сложения (стр. 88–89):

Повторение (стр. 90–96):

Критическая математика в средней школе района Чикаго, JSTOR

В этой статье приводится пример и уроки преподавания и изучения критической математики в средней школе общественного квартала Чикаго с упором на социальную справедливость. Он рассматривает возможности и проблемы разработки учебных программ и преподавания, исследует обучение студентов и задает вопросы и направления для дальнейших исследований и практики.

Официальный журнал Национального совета учителей математики (NCTM), JRME — ведущий исследовательский журнал в области математического образования, посвященный интересам учителей и исследователей на всех уровнях — от дошкольного до колледжа.

Национальный совет учителей математики — это общественный голос в области математического образования, обеспечивающий видение, руководство и профессиональное развитие для поддержки учителей в обеспечении высочайшего качества обучения математике для всех учащихся. NCTM, насчитывающая около

членов и 250 аффилированных лиц, является крупнейшей в мире организацией, занимающейся совершенствованием математического образования в классах от подготовительных классов до 12 классов.«Принципы и стандарты школьной математики» Совета представляют собой руководящие принципы для достижения совершенства в математическом образовании и призывают всех учащихся заниматься более сложной математикой. NCTM нацелен на постоянный диалог и конструктивное обсуждение со всеми заинтересованными сторонами того, что лучше всего для студентов нашей страны.

Этот предмет является частью коллекции JSTOR.
Условия использования см. В наших Положениях и условиях
Copyright 2016 Национальный совет учителей математики, Inc.
Запросить разрешения

Peterson, James B / Syllabus

Spanish 2A

James Peterson

[email protected]

Обзор курса:

По завершении обзора наиболее важных концепций, изученных на испанском языке I, мы рассмотрим главы 3.2 — 4.2 в нашем учебнике. Новые темы будут включать спорт, путешествия, сезоны и погоду, одежду,

мест в городе, указание маршрута, покупки и торг.Эти темы будут поддерживаться

с грамматическими темами, включая глаголы с изменением основы, фразы тенера, прогрессивное время, команды

и предлоги

Оценка учащихся:

Философия оценок:

Есть две общие взвешенные категории: формирующие оценки (32 процента) и итоговые оценки (68 процентов).

Формирующие оценки лежат в основе преподавания и обучения и предоставляют учащемуся возможность критической обратной связи, которая затем используется учащимся для улучшения своей успеваемости.Примеры включают: викторины, экспертные оценки, письменные абзацы и краткие устные ответы. Не все формирующие оценки будут оцениваться, но когда они будут выставлены, они будут отнесены к взвешенной категории, которая составляет 32 процента итоговой оценки. Формирующие оценки подлежат повторной сдаче. (Более подробную информацию о правилах повторной сдачи см. В разделе «Повторное обучение и повторная сдача» ниже.)

Суммарные оценки считаются очень важными и дают учащимся возможность продемонстрировать навыки и знания, которые они развили с течением времени.Категория итогового оценивания составит 68 процентов итоговой оценки. Эти оценки НЕ подлежат пересдаче. У студентов будет достаточно возможностей попрактиковаться в различных компонентах, составляющих итоговую оценку, и получить целевую обратную связь для улучшения. По этой причине пересдачи не предлагаются. Примеры включают тесты, проекты, письменные эссе, презентации / беседы и выпускные экзамены округа.

Практика учителя

Пропущенные и несвоевременные работы: Ожидается, что все пропущенные работы будут сданы за одну неделю до конца семестра.За опоздание на работу взимается штраф в размере -10% за каждый день опоздания.

Домашнее задание: важно, чтобы учащиеся выполнили все заданные домашние задания, потому что это дает очень важную практику для достижения наших целей обучения и успешной сдачи экзаменов. С родителями свяжутся, если обнаружится, что они не работают.

Повторное обучение и повторная сдача экзаменов: Как отмечалось выше, формирующие экзамены могут быть пересданы ОДИН раз. Будет оставлен наивысший балл. Крайний срок для повторной сдачи — одна неделя после первоначальной оценки.Процесс повторной сдачи:

1. Если возможно, договоритесь о встрече с учителем, чтобы обсудить вашу оценку

до / после школы.

2. Договоритесь с учителем о дате и времени для повторной сдачи — ЭТО НЕ МОЖЕТ БЫТЬ В ТО ЖЕ ДЕНЬ, В КОТОРЫЙ ВЫ ПРОСТО ЗАВЕРШЛИ ПРОВЕРКУ / ПОВТОРНУЮ СЕССИЮ.

3. Пересдайте оценку.

*** Для учащихся с планами IEP или 504 могут быть внесены изменения в оценки.

Дополнительный балл

Дополнительный балл не будет предложен, если он не будет предложен всему классу.Студенты должны сосредоточиться на ожиданиях от курса.

Академическая нечестность

Академическая нечестность (мошенничество) включает копирование чужой работы или разрешение другим копировать вашу работу, участие в несанкционированном сотрудничестве в академической работе, использование онлайн-переводчиков, использование ресурсов, запрещенных во время экзамена или викторины, или плагиат .

Последствия академической недобросовестности:

1. Будет сделан звонок родителю / опекуну.

2. Помощник директора будет уведомлен в письменной форме.

3. Чтобы получить зачет, ученик должен пересдать экзамен под непосредственным наблюдением учителя

.

Руководство по успеху учащихся

Практика вне класса: использование языка во многом похоже на игру в спорте или на игре на музыкальном инструменте: нужно практиковать его, если он хочет его использовать. Поэтому ночные тренировки необходимы и ожидаемы. Если домашнее задание не назначается на конкретный вечер, учащиеся должны использовать это время для изучения своих заметок или изучения словарного запаса, который всегда указывается в конце главы.

Поведение: Учащиеся будут придерживаться правил и кодексов поведения, установленных старшей школой Анока и школьным округом Анока-Хеннепин.

Участие: этот класс требует, чтобы учащиеся по возможности говорили на изучаемом языке. Я веду постоянный подсчет того, как часто учащиеся участвуют в занятиях. Если вы накапливаете очки участия, поднимая руку, вероятность того, что вас вызовут случайным образом, гораздо меньше.

Саморефлексия учащихся: учащимся будет предоставлено множество возможностей для размышлений и самооценки, чтобы отслеживать личный рост и прогресс в достижении результатов обучения.

Отсутствия: когда студент не получает задание из-за отсутствия, он должен выяснить, что он пропустил в тот день, поговорив с инструктором в конце следующего урока. Если учащийся отсутствует в день оценивания, он должен выйти из класса в течение одной недели с момента пропуска первоначальной даты викторины / теста / презентации, чтобы пройти его. .

Помощь: обращайтесь ко мне до или после школы, если вам понадобится дополнительная помощь.За исключением утра среды, я обычно здесь за полчаса до и после школы. Не стесняйтесь записаться на прием, чтобы вам не пришлось ждать своей очереди.

GO Math !: Исследовательские фонды | Houghton Mifflin Harcourt

Достигнуть. (2010). Сравнение общих основных государственных стандартов по математике и основных направлений учебной программы NCTM . Вашингтон, округ Колумбия: Автор. Получено 8 мая 2015 г. с http://www.achieve.org/CCSSandFocalPoints.

Альберт, Л. Р., и Антос, Дж. (2000).Ежедневные журналы связывают математику с реальной жизнью. Преподавание математики в средней школе, 5 (8), 526–531.

Аркави, Авраам. (2003). Роль визуальных представлений в изучении математики. Образовательные исследования по математике, 52 (3). 215–241.

Аспинуолл Л. и Аспинуолл Дж. (2003). Изучение математического мышления с помощью открытых письменных подсказок. Преподавание математики в средней школе, 8 (7), 350–353.

Авалос, Б.(2011). Повышение квалификации в сфере преподавания и педагогического образования более десяти лет. Педагогическое и педагогическое образование, 27 (1). 10–20.

Бахр, Д. Л., Шаха, С. Х., Фарнсворт, Б. Дж., Льюис, В. К., и Бенсон, Л. Ф. (2004). Подготовка учителей завтрашнего дня к использованию технологий: отношение полевого опыта, основанного на технологиях, к кандидатам в предпрофессиональные учителя. Журнал учебной психологии. 31 (2), 88–97.

Бейкер, С., Герстен, Р., и Ли, Д.(2002). Обобщение эмпирических исследований по обучению математике учащимся с низкими успеваемостями. The Elementary School Journal, 103 (1), 67.

Бейкер А., Ширнер К. и Хоффман Дж. (2006). Многоуровневая математика: основы математического обучения детей младшего возраста. Обучение детей математике, 13 (1), 19–21.

Бакстер Дж. А., Вудворд Дж. И Олсон Д. (2005). Письмо по математике: альтернативная форма общения для учащихся с низкой успеваемостью. Исследования и практика нарушений обучаемости, 20 (2), 119–135.

Бэй-Уильямс, Дж. М., и Ливерс, С. (2009). Поддержка приобретения математического словарного запаса. Обучение детей математике, 16 (4), 238–245.

Бин, Дж. А. (1997). Интеграция учебной программы: создание основы демократического образования . Александрия, Вирджиния: Ассоциация по надзору и разработке учебных программ.

Бенсон, Л. Ф., Фарнсворт, Б. Дж., Бар, Д. Л., Льюис, В. К., & Шаха, С. Х. (2004). Влияние обучения технологиям способствовало обучению навыкам и отношению учителей до начала работы. Образование. 124 (4), 649–663.

Бессье, Салли. (2006). Исследование гендерных различий в классах элементарного конструктивизма с использованием инструкций по лего / логотипам. Компьютеры в школах. 22 . 7–19.

Блэк П. и Вильям Д. (1998a). Внутри черного ящика: повышение стандартов посредством оценивания в классе. Дельта Пхи Каппан, 80 (2), 139–148.

Блэк П. и Вильям Д. (1998b). Оценка и обучение в классе. Оценка в образовании: принципы, политика и практика, 5 (1), 7–73.

Боулер Дж. (1998). Открытая и закрытая математика: опыт и понимание студентов. Журнал исследований в области математического образования, 29 , 41–62.

Бодди, М., Уотсон, К., и Обуссон, П. Испытание «Пяти Э»: референтная модель для конструктивистского преподавания и обучения. Исследования в области естественно-научного образования, 33 (1).27–42.

Боссе, М. Дж., И Фолконер, Дж. (2008). Изучение и оценка математики посредством чтения и письма. Школа естественных наук и математики, 108 (1), 8–19.

Бранденбург, старший М. Л. (2002). Продвинутая математика? Напишите! Лидерство в образовании, 60 (3), 67–68.

Брансфорд, Дж. Д., Браун, А. Л., и Кокинг, Р. Р. (ред.). (1999). Как люди учатся: мозг, разум, опыт и школа . Национальный исследовательский совет. Вашингтон, округ Колумбия: Национальная академия прессы.

Брей, В. С., Диксон, Дж. К., и Мартинез, М. (2006). Поощрение общения об измерении площади в переходном языковом классе. Обучение детей математике, 13 (3), 132–138.

Бритт М. и Аглинскас К. (2002). Повышение способности учащихся определять и использовать исходную информацию. Познание и обучение, 20 (4), 485–522.

Браун А. и Кампионе Дж. (1994). Управляемое открытие в сообществе учащихся. В К. МакГилли (Ред.), Классные уроки: объединение когнитивной теории и аудиторной практики (стр. 229–270). Кембридж, Массачусетс: MIT Press.

Buczynski, S., & Hansen, C.B. (2010). Влияние профессионального развития на педагогическую практику: выявление связей. Преподавание и педагогическое образование, 26 (3), 599–607.

Бернс, М. (2004). Пишу по математике. Лидерство в образовании, 62 (2), 30–33.

Бернс, М. К., Эпплтон, Дж. Дж., И Стхаувер, Дж. Д. (2005).Метааналитический обзор исследований реагирования на вмешательство: изучение полевых и реализованных в исследованиях моделей. Журнал психообразовательной оценки, 23 , 381–394.

Bybee, R.J. et al. (2006). Учебная модель BSCS 5E: истоки и эффективность . Колорадо-Спрингс, Колорадо: BSCS.

Кейн Р. Н. и Кейн Г. (1994). Установление связей: обучение и человеческий мозг . Александрия, Вирджиния: Ассоциация по надзору и разработке учебных программ.

Карнеги-Меллон. (2015). Формирующее и итоговое оценивание . (Онлайн). Получено 30 апреля 2015 г. с веб-сайта www.cmu.edu/teaching/assessment/basics/formative-summative.html.

Карпентер, Томас П., Франке, Меган Лоуф и Леви, Линда. (2003). Математическое мышление: интеграция арифметики и алгебры в начальной школе . Портсмут, Нью-Хэмпшир: Хайнеманн.

CDW. (2011). 2011 CDW-G Отчет о классе 21 века . Получено 15 апреля 2015 г. с сайта http: // webobjects.cdw.com/webobjects/media/pdf/newsroom/CDWG-21st-Century-Classroom-Report-0611.pdf.

Чапин, С. Х., О’Коннор, К., и Канаван Андерсон, Н. (2003). Обсуждения в классе: использование разговора по математике для помощи учащимся 1–6 классов . Саусалито, Калифорния: Публикации математических решений.

Чарльз, Рэндалл И. (2005). Большие идеи и понимание как основа математики в начальной и средней школе. Журнал лидерства в математическом образовании. 7 (1). 9–24.

Кристенсон, С.Л., Иселдайк, Дж. Э. и Терлоу, М. Л. (1989). Критические учебные факторы для студентов с легкими физическими недостатками: комплексный обзор. Лечебное и специальное образование, 10 (5), 21–31.

Четти, Р., Фридман, Дж. Н. и Рокофф, Дж. Э. (2012) Отличное преподавание: измерение его влияния на будущие доходы учащихся. Education Next, 12 (3), 58–64.

Cheung, A., & Slavin, R.E. (2011). Эффективность приложений образовательных технологий для повышения успеваемости по математике в классах K-12: метаанализ.Центр исследований и реформ в образовании. Балтимор, Мэриленд: Университет Джона Хопкинса. Получено 17 апреля 2015 г. с сайта http://www.bestevidence.org/word/tech_math_Apr_11_2012.pdf.

Чо, М. и Ратбун, Г. (2013). Реализация ориентированной на учителя онлайн-программы повышения квалификации учителей (oTPD) в высшем образовании: тематическое исследование. Innovations in Education and Teaching International. 50 (2). 144–156.

Кларк Б. и Шинн М. Р. (2004). Предварительное исследование по выявлению и развитию раннего измерения на основе учебной программы по математике. Обзор школьной психологии, 33 (2), 234–248.

Кларк, Ширли, Тимперли, Хелен и Хэтти, Джон. (2004). Разблокировка формирующего оценивания: практические стратегии улучшения обучения учащихся в начальных и средних классах . Окленд, Новая Зеландия: Ходдер Моа Беккет.

Клемент, Л.Л. (2004). Модель для понимания, использования и соединения представлений . Рестон, Вирджиния: Национальный совет учителей математики.

Клементс, Дуглас Х., И Сарама, Джули. (2004). Траектории обучения в математическом образовании. Математическое мышление и обучение. 6 (2). 81–89.

Кобб П. и Джексон К. (2011). Комментарии к книге Портера, МакМакена, Хвана и Янга: оценка качества Общих государственных стандартов по математике. Исследователь в области образования, 40 (4), 183–185.

Коллинз, Дж. К. (2001). От хорошего к отличному: почему одни компании делают рывок, а другие нет . Нью-Йорк, штат Нью-Йорк: HarperBusiness.

Коттон, К. (1995). Эффективная школьная практика: исследование, обновление 1995 г. . Портленд, Орегон: Северо-западная региональная образовательная лаборатория. Получено 10 мая 2015 г. с сайта http://www.kean.edu/~lelovitz/docs/EDD6005/Effective%20School%20Prac.pdf.

Коулсон Д. (2002). BSCS Science: исследовательский подход — результаты оценки 2002 г. . Арнольд, MC: PS International.

Черняк, К. М., Вебер, В. Б., мл., Сандманн, А., и Ахем, Дж. (1999). Обзор литературы по интеграции науки и математики. Школа естественных наук и математики, 99 (8), 421–430.

Демирски Аллан, С., и Годдард, Ю. Л. (2010). Дифференцированная инструкция и RtI: естественное совпадение. Вмешательства, которые работают, 68 (2).

Desimone, Лаура М., Портер, Эндрю К., Гарет, Майкл С., Юн, Кван Сок и Бирман, Беатрис Ф. (2002). Влияние профессионального развития на обучение учителей: результаты трехлетнего лонгитюдного исследования. Оценка образования и анализ политики.24 (2). 81–112.

Дилленбург, П. (2002). Излишнее написание сценариев CSCL: риски сочетания совместного обучения с учебным дизайном. Три мира CSCL. Можем ли мы поддерживать CSCL. 61–91.

Диксон, Дж. К. (1997). Использование компьютера и визуализация в построении учащимися концепций отражения и вращения. Школьные науки и математика, 97 (7), 352–358.

Донован, М. Сюзанна и Брансфорд, ред. (2005). Как учащиеся учатся: история, математика и естественные науки в классе. Национальный исследовательский совет, Комитет по изучению того, как люди учатся: Целевой отчет для учителей . Вашингтон, округ Колумбия: Национальная академия прессы.

Эрп, Н. У. (1970). Наблюдения за обучением чтению по математике. Journal of Reading, 13 , 529–33.

Фоснот, Кэтрин Туми и Джейкоб, Уильям. (2010). Молодые математики за работой: построение алгебры . Портсмут, Нью-Хэмпшир: Хайнеманн.

Franke, M. L., Kazemi, E., & Battey, D.С. (2007). Обучение математике и занятия в классе. В F. K. Lester Jr. (Ed.), Второй справочник исследований по преподаванию и изучению математики (стр. 225–256). Шарлотта, Северная Каролина: информационный век.

Фриман, Б., и Кроуфорд, Л. (2008). Создание учебной программы по математике в средней школе для изучающих английский язык. Лечебное и специальное образование, 29 (1), 9–19.

Фукс, Л. С. (2004). Прошлое, настоящее и будущее измерительных исследований на основе учебных программ. Обзор школьной психологии, 33 , 188–192.

Fuchs, D., & Fuchs, L. S. (2006). Введение в ответ на вмешательство: что, почему и насколько оно достоверно? Reading Research Quarterly, 41 (1), 93–99.

Фукс, Л. С., Фукс, Д., и Холленбек, К. Н. (2007). Повышение отзывчивости к занятиям по математике в первом и третьем классах. Исследования и практика нарушений обучаемости, 22 (1), 13–24.

Фернер, Дж. М., и Даффи, М.Л. (2002). Справедливость для всех учащихся в новом тысячелетии: отключение математической тревожности. Вмешательство в школе и клинике, 38 (2), 67–74.

Гарет, М.С., Портер, А.С., Десимон, Л., Бирман, Б.Ф., и Юн, К.С. (2001). Что делает профессиональное развитие эффективным? Результаты национальной выборки учителей. Американский журнал исследований в области образования. 38 (4), 915.

Герстен, Р., Бекманн, С., Кларк, Б., Фоген, А., Марш, Л., Стар, Дж. Р., и Витцель, Б.(2009). Помощь учащимся, борющимся с математикой: реакция на вмешательство (RtI) для начальных и средних школ . Институт педагогических наук Что работает Информационный центр. Вашингтон, округ Колумбия: Министерство образования США. Получено 9 мая 2015 г. с сайта http://ies.ed.gov/ncee/wwc/pdf/practiceguides/rti_math_pg_042109.pdf.

Герстен Р. и Чард Д. (2001). Чувство чисел: переосмысление арифметических инструкций для учащихся с математическими нарушениями. LD Онлайн .Получено 3 мая 2015 г. с сайта http://www.ldonline.org/article/5838/.

Герстен Р. и Кларк Б. С. (2007). Эффективные стратегии обучения учащихся с трудностями в математике . Краткое руководство по исследованию. Рестон, Вирджиния: Национальный совет учителей математики.

Гинзбург, А., Кук, Г., Лейнванд, С., Ноэл, Дж., И Поллок, Э. (2005). Переоценка международной успеваемости США по математике: новые результаты исследований TIMSS и PISA за 2003 год. Подготовлено для U.S. Служба образовательной политики и программных исследований (PPSS). Вашингтон, округ Колумбия: Американские исследовательские институты (AIR). Получено 8 мая 2015 г. с сайта http://www.air.org/files/TIMSS_PISA_math_study1.pdf.

Голдхабер, Д. (2002). Тайна хорошего обучения: изучение свидетельств об успеваемости учащихся и характеристиках учителей. Education Next, 2 (1), 50–55.

Гонсалес, П., Уильямс, Т., Джоселин, Л., Рой, С., Катсберг, Д., и Бренвальд, С. (2008). Основные моменты TIMSS 2007: Математические и естественные достижения У.S. Учащиеся четвертого и восьмого классов в международном контексте (NCES 2009-001 Revised). Национальный центр статистики образования, Институт педагогических наук. Вашингтон, округ Колумбия: Министерство образования США.

Гуд, Дж. М., и Ван, П. А. (1999). Осмысление педагогической психологии с помощью журналов ответов студентов . Документ, представленный на ежегодном собрании Американской ассоциации исследований в области образования, Монреаль, Канада.

Гриффитс, А., ВанДер Хейден, А.М., Парсон, Л. Б., и Бернс, М. К. (2006). Практическое применение исследования «реакция на вмешательство». Оценка эффективного вмешательства, 32 (1), 50–57.

Холл Т., Стренгман Н. и Мейер А. (2009). Дифференцированная инструкция и последствия для реализации UDL . Уэйкфилд, Массачусетс: Национальный центр доступа к общей учебной программе.

Хармон, Дж. М., Хедрик, В. Б., и Вуд, К. Д. (2005). Исследование словарного запаса в областях содержания: последствия для испытывающих затруднения читателей. Ежеквартально по чтению и письму, 21 , 261–280.

Хатано, Г., Инагаки, К. (1991). Аналогия с ограниченным человеком в биологическом умозаключении маленьких детей. Когнитивное развитие, 6 (2), 219–231.

Хэтти, Дж. (1992). Я-концепция . Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.

Хэтти, Джон А. С. (2009). Видимое обучение: синтез более 800 метаанализов, относящихся к достижению . Нью-Йорк: Рутледж.

Хейстед, Марк У., И Марцано, Роберт Дж. (2009). Метааналитический синтез исследований учебных стратегий, проведенных в Marzano Research Laboratory . Энглвуд, Колорадо: Исследовательская лаборатория Марцано.

Наследие, М. (2007). Формирующее оценивание: что нужно знать и делать учителям? Дельта Пхи Каппан, 89 (2), 140–145.

Hiebert, J., Gallimore, R., Garnier, H., Givvin, K. B., Hollingsworth, H., Jacobs, J., et al. (2003). Преподавание математики в семи странах: результаты видео исследования TIMSS 1999 г. (NCES 2003-2013).Вашингтон, округ Колумбия: Министерство образования США, Национальный центр статистики образования.

Хиберт, Джеймс и Уирн, Диана. (1993). Учебные задания, занятия в классе и обучение учащихся арифметике во втором классе. Американский журнал исследований в области образования, 30 (2). 393–425.

Хиберт, Джеймс, Моррис, Энн К., Берк, Доун и Янсен, Аманда. (2007). Подготовка учителей к обучению на уроках. Журнал педагогического образования, 58 (1), 47–61.

Хиберт, Дж., & Grouws, D.A. (2007). Влияние преподавания математики в классе на учебу учащихся. Второй исследовательский справочник по преподаванию и изучению математики . Рестон, Вирджиния: Национальный совет учителей математики. 371–404.

Хичкок, К., Мейер, А., Роуз, Д., и Джексон, Р. (2002). Обеспечение нового доступа к общеобразовательной программе: Универсальный дизайн для обучения. Обучение выдающихся детей, 35 (2), 8–17.

Хупперт, Дж., Ломаск, С.М., & Лазаровиц Р. (2002). Компьютерное моделирование в старшей школе: этапы познания учащихся, навыки научного процесса и академическая успеваемость по микробиологии. Международный журнал естественнонаучного образования, 24 (8), 803–821.

Хайд, А. (2006). Понимание математики: адаптация стратегий чтения для обучения математике k-6 . Портсмут, Нью-Хэмпшир: Хайнеманн.

Хён, Ынсук и Дэвис, Женевьева. (2005). Беседы воспитанников в классе компьютерных технологий. Коммуникационное образование, 54 , 118–135.

Джексон, М. Б., и Филлипс, Е. Р. (1983). Словарный запас в пропорции и пропорции для семиклассников. Журнал исследований в области математического образования, 14 (5), 337–343.

Джейкобс, Виктория Р., Франке, Меган Лоуф, Карпентер, Томас П., Леви, Линда и Бэтти, Дэн. (2007). Повышение квалификации на основе алгебраических рассуждений детей в начальной школе. Журнал исследований в области математического образования, 38 (3), 258–288.

Джеральд, К. Д. (2001). Еще раз рассеяние мифов . Вашингтон, округ Колумбия: Образовательный фонд.

Джонсон, К. И., и Майер, Р. Э. (2009). Эффект тестирования с мультимедийным обучением. Журнал педагогической психологии, 101 (3), 621–629.

Каллисон, Дж. М. (1986). Влияние организации урока на успеваемость. Американский журнал исследований в области образования, 23 (2), 337–347.

Капур, Ману. (2010). Продуктивный провал в решении математических задач. Инструктаж по науке. 38 (6). 523–550.

Кебричи М., Хируми А. и Бай Х. (2010). Влияние современных математических компьютерных игр на успеваемость по математике и мотивацию в классе. Компьютеры и образование, 55 , 427–443.

Кеттерлин-Геллер, Л. Р., Чард, Д. Дж., И Файн, Х. (2008). Установление связей в математике: вмешательство в концептуальную математику для учащихся с низкой успеваемостью. Лечебное и специальное образование, 29 (1), 33–45.

Кеттерлин-Геллер, Л. Р. и Йованофф, П. (2009). Диагностические оценки по математике для поддержки принятия учебных решений. Практическая оценка, исследования и оценка, 14 (16), 1–11.

Килпатрик Дж., Сваффорд Дж. И Финделл Б., ред. (2001). Комитет по изучению математики, Национальный совет учителей математики .

Коуба, В. Л. (1989). Общее и необычное в математике и терминологии естественных наук. Школа естественных наук и математики, 89 (7), 598.

Ковалик, С. (1994). Интегрированная тематическая инструкция: Модель . Кент, Вашингтон: Сьюзан Ковалик и партнеры.

Кребс А. (2005). Анализ студенческой работы как деятельности по повышению квалификации. Школьные науки и математика, 105 (8), 402–411.

Лаппан, Г., & Брайарс, Д. (1995). Как преподавать математику? В И. М. Карл (ред.), Перспективы школьной математики . Рестон, Вирджиния: Национальный совет учителей математики.131–156.

Ларкин, М. Дж. (2001). Обеспечение поддержки независимости учащихся с помощью инструкций по шаблонам. Обучение выдающихся детей, 34 (1), 30–34.

Leinwand, S., & Fleischman, S. (2004). Учите математику правильно с первого раза. Лидерство в образовании, 62 (1) 88–89.

Лейва, М.А. (2007). Проблема со словами в математике: стратегия дифференцированного обучения . Бостон, Массачусетс: Компания Houghton Mifflin. Получено 20 апреля 2015 г. с сайта http: // www.yond-the-book.com/strategies/strategies_092006.html.

Lembke, E. & Foegen, A. (2005). Выявление показателей раннего владения математикой в ​​детском саду и 1 классе . (Технический отчет № 6). Миннеаполис: Университет Миннесоты. Колледж образования и человеческого развития. Получено 2 мая 2015 г. с сайта www.progressmonitoring.org/pdf/TREarlymath6.pdf.

Леш, Ричард, Пост Том и Бер, Мерлин. (1987). Представления и переводы среди представлений в обучении математике и решении задач.В «Проблемы представления в преподавании и изучении математики» , под редакцией Клода Жанвье, Хиллсдейл, штат Нью-Джерси: Erlbaum, 33–40.

Ли, К., и Ма, X. (2010). Мета-анализ влияния компьютерных технологий на изучение математики школьниками. Обзор педагогической психологии, 22 (3), 215–243.

Лопес, О. С. (2010). Цифровой учебный класс: повышение успеваемости изучающих английский язык по математике и чтению с помощью технологии интерактивной доски. Компьютеры и образование, 54 (4), 901–915.

млн лет назад, Липин. (2010). Знание и преподавание элементарной математики: понимание учителями фундаментальной математики в Китае и США . 2-е изд. Нью-Йорк: Рутледж.

Марцано Р. (2000). Что работает в классе . Александрия, Вирджиния: ASCD.

Марцано, Р. Дж., И Хейстед, М. (2009). Заключительный отчет по оценке технологии Promethean .Энглвуд, Колорадо: Исследовательская лаборатория Марцано.

Марцано Р. Дж., Пикеринг Д. Дж. И Поллок Дж. Э. (2001). Классная инструкция, которая работает: стратегии повышения успеваемости учащихся, основанные на исследованиях . Александрия, Вирджиния: Ассоциация по надзору и разработке учебных программ (ASCD).

Мацумура, Л.С., Слейтер, С.С., Юнкер, Б., Петерсон, М., Бостон, М., Стил, М. и др. (2006). Измерение понимания прочитанного и обучения математике в городских средних школах: экспериментальное исследование оценки качества обучения. .(Технический отчет CSE 691). Лос-Анджелес: Калифорнийский университет в Лос-Анджелесе. Национальный центр исследований в области оценки. Получено 2 мая 2015 г. с https://www.cse.ucla.edu/products/reports/R691.pdf.

Майер Р. Э. (2001, 2009). Мультимедийное обучение . Кембридж: Издательство Кембриджского университета.

Майер Р. Э. (2005). Принципы управления основной обработкой мультимедийного обучения. В R.E. Mayer (Ed.), Кембриджский справочник по мультимедийному обучению (стр.169–182). Нью-Йорк: Издательство Кембриджского университета.

Мэйс Р., Чейз П. Н. и Уокер В. Л. (2008). Дополнительная практика и диагностическая оценка в курсе прикладной алгебры колледжа. Журнал чтения и обучения в колледже, 38 (2), 7–31.

Средство, Б., Тояма, Ю., Мерфи, Р., Бакия, М., и Джонс, К. (2009). Оценка практики онлайн-обучения, основанной на фактах: метаанализ и обзор исследований онлайн-обучения . Вашингтон, округ Колумбия: СШАДепартамент образования, Управление планирования, оценки и разработки политики, Служба исследований политики и программ. Получено 28 апреля 2015 г. с сайта http://www2.ed.gov/rschstat/eval/tech/evidence-based-practices/finalreport.pdf.

Мейерс, М., и Ингварсон, Л. (2005). Изучение связей между профессиональным развитием учителей и результатами обучения студентов. Получено 3 мая 2015 г. с веб-сайта http://www.dest.gov.au/sectors/school_education/publications_resources/profiles/teacher_prof_development_student_learning_outcomes.htm.

Меллард Д. Ф. и Джонсон Э. С. (2008). RTI: Практическое руководство по осуществлению реакции на вмешательство . Таузенд-Оукс, Калифорния: Corwin Press.

Среднеконтинентальные исследования в области образования и обучения (McREL). (2010). Что мы знаем о преподавании и изучении математики, третье издание . Блумингтон, Индиана: Solution Tree Press.

Мири Б., Дэвид Б. К. и Ури З. (2007). Целенаправленное обучение для развития навыков мышления высшего порядка: пример критического мышления. Исследования в области естественно-научного образования, 37 (4), 353–369.

Москаль Б. (2000). Понимание ответов учащихся на открытые задачи. Преподавание математики в средней школе, 5 (8), 500–505.

Национальный совет учителей математики. (2000, 2009). Принципы и стандарты школьной математики . Рестон, Вирджиния: Автор. Получено 8 мая 2015 г. с сайта http://www.nctm.org/standards/content.aspx?id=16909.

Национальный совет учителей математики (2014). Принципы действий: Обеспечение математического успеха для всех . Рестон, Вирджиния: Автор.

Национальная ассоциация губернаторов, Совет директоров школ штата, Achieve, Совет школ большого города и Национальная ассоциация советов по образованию штатов. (2013). Критерии издателей K-8 для Общих государственных стандартов по математике . (Весенний выпуск 2013 г .; 09.04.13). Получено 2 мая 2015 г. с сайта http://www.corestandards.org/assets/Math_Publishers_Criteria_K-8_Spring%202013_FINAL.pdf.

Центр передового опыта Национальной ассоциации губернаторов и Совет директоров государственных школ. (2010a). Общие основные государственные стандарты по математике . Вашингтон, округ Колумбия: Автор. Получено 8 мая 2015 г. с сайта http://www.corestandards.org/the-standards.

Центр передового опыта Национальной ассоциации губернаторов и Совет директоров государственных школ. (2010b). Ключевые моменты математики . Получено 7 мая 2015 г. с сайта http: //www.corestandards.org / other-resources /.

Национальный институт грамотности. (2007). Что учителя предметной области должны знать о подростковой грамотности . Вашингтон, округ Колумбия: ноль, NICHD.

Национальная консультативная группа по математике. (2008). Основы успеха: Заключительный отчет Национальной консультативной группы по математике . Вашингтон, округ Колумбия: Министерство образования США. Получено 2 мая 2015 г. с сайта http://www2.ed.gov/about/bdscomm/list/mathpanel/index.html.

Национальный исследовательский совет.(1999). Как люди учатся: мозг, разум, опыт и школа . Вашингтон, округ Колумбия: Национальная академия прессы.

Национальный исследовательский совет. (2001). Суммируя: Помощь детям в изучении математики . Дж. Килпатрик, Дж. Сваффорд и Б. Финделл (ред.). Комитет по изучению математики, Центр образования, Отдел поведенческих и социальных наук и образования. Вашингтон, округ Колумбия: Национальная академия прессы. Получено 8 мая 2015 г. с сайта http://www.nap.edu/openbook.php?record_id=9822&page=1.

Национальный исследовательский совет. (2005). Как учащиеся учатся: история, математика и естественные науки в классе . Вашингтон, округ Колумбия: Национальная академия прессы.

Национальный исследовательский совет. (2012). Образование для жизни и работы: развитие передаваемых знаний и навыков для 21 века . Вашингтон, округ Колумбия: Национальная академия прессы.

Северо-Центральная региональная учебная лаборатория. (2003). Метаанализ эффективности преподавания и обучения с помощью технологий на успеваемость учащихся .Напервилль, Иллинойс: Северо-Центральная региональная образовательная лаборатория.

О’Нил, Х. Ф., и Браун, Р. С. (1998). Различное влияние форматов вопросов в математической оценке на метапознание и аффект. Прикладные измерения в образовании, 11 (4), 331–351.

Попхэм, У. Дж. (2006). Все об ответственности / фальшивых формирующих оценках: покупатель остерегается. Лидерство в образовании, 64 (3), 86–87.

Пренский М. (2001). Цифровые аборигены, цифровые иммигранты. На горизонте, 9 (5), 1–6.

Критерии издателей. www.corestandards.org

Пугали, Д. К. (2004). Сравнение устных и письменных описаний процессов решения учащимися. Образовательные исследования по математике, 55 , 27–47.

Пугали, Д. К. (2005). Написание для развития математических знаний . Норвуд, Массачусетс: Кристофер-Гордон.

Патнэм Р. (2003). Комментарий к четырем программам элементарной математики. В S. Senk & D. Thompson (Eds.), Учебные программы школьной математики, ориентированные на стандарты: что они говорят об успеваемости учащихся? Махва, Нью-Джерси: Эрлбаум.161–180.

Рид, Д. С. (2009). Есть ли разница в ожиданиях? Образовательный федерализм и демографическое распределение уровней владения языком сокращают. Американский журнал исследований в области образования, 46 (3), 718–742.

Райдаут, В. Дж., Фёр, У. Г., и Робертс, Д. Ф. (2010). Поколение M2: СМИ в жизни детей в возрасте от 8 до 18 лет: исследование фонда семьи Кайзера . Менло-Парк, Калифорния: Фонд семьи Генри Дж. Кайзера. Получено 1 мая 2015 г. с сайта http: //www.kff.org / entmedia / upload / 8010.pdf.

Риентиес, Б., Брауэр, Н., Лиго-Бейкер, С. (2013). Влияние профессионального развития онлайн на убеждения и намерения учителей в отношении упрощения обучения и технологий. Педагогическое и педагогическое образование. 29 , 122–131.

Риттл-Джонсон Б., Сиглер Р. С. и Алибали М. В. (1999). Концептуальные и процедурные знания математики: ведет ли одно к другому. Журнал педагогической психологии, 93 (1), 175–189.

Rosenshine, B. (2012). Принципы обучения: стратегии, основанные на исследованиях, которые должны знать все учителя. Американский педагог , Весна, 12–39.

Russek, B. (1998). Пишу, чтобы изучать математику. Журнал ВАК, 9 , 36–45.

Руссо М., Хехт Д., Бургхардт М. Д., Хакер М. и Саксман Л. (2011). Разработка мультидисциплинарной модели вливания математики в средней школе. Журнал исследований средних классов, 6 (2), 113–128.

Scheuermann, A., & van Garderen, D. (2008). Анализ использования учащимися графических изображений: определение неправильных представлений и шаблонов ошибок для обучения. Преподавание математики в средней школе, 13 (8), 471–477.

Шмидт, В. Х., Ван, Х. С., и Макнайт, К. М. (2005). Согласованность учебной программы: изучение стандартов содержания математики и естественных наук США с международной точки зрения. Journal of Curriculum Studies, 37 , 525–559.

Шнайдер, М. (2007). Национальная оценка образовательного прогресса: сопоставление государственных стандартов квалификации 2005 года с шкалами NAEP . Вашингтон, округ Колумбия: Национальный центр статистики образования IES.

Сигерс, Г., и Боекертс, М. (1993). Мотивация к заданию и достижение математики в реальных заданных ситуациях. Обучение и обучение, 3 (2), 133–150.

Зайферт, К. Л. (1999). Рефлексивное мышление и профессиональное развитие: Учебник .Бостон: Хоутон Миффлин.

Шаха, Стивен и Эллсуорт, Хизер (2013). Квазиэкспериментальное исследование влияния интернет-профессионального обучения по запросу на успеваемость учащихся с участием нескольких штатов. Международный журнал оценки и исследований в области образования. 2 (4). 175–179.

Шеннон, Г. С., и Байлсма, П. (2003). Девять характеристик высокоэффективных школ: научно-исследовательский ресурс для школьных руководящих групп, помогающий в процессе совершенствования школы. .Олимпия, Вашингтон: Управление школьного суперинтенданта общественного обучения.

Шоу Р. А. (2011). Использование универсального дизайна для обучения. Новые направления для обслуживания студентов, 13 (4), 21–33.

Шепард, Л. А. (2000). Роль оценивания в культуре обучения. Образовательные исследования, 29 (7), 4–14.

Скиба Р., Магнуссон Д., Марстон Д. и Эриксон К. (1986). Оценка успеваемости по математике в специальном образовании: успеваемость, квалификационная проверка или формирующая оценка? Миннеаполис: специальные службы, государственные школы Миннеаполиса.

Смит, Э. С., и Джонсон, Л. А. (2011). Ответ на вмешательство в средней школе: история болезни. Журнал средней школы, 42 (3), 24–32.

Шталь, С. А., и Фэрбенкс, М. М. (1986). Эффекты словарного запаса: метаанализ на основе моделей. Обзор исследований в области образования, 56 (1), 72–110.

Стар, Дж. Р. (2005). Реконцептуализация концептуального знания. Журнал исследований в области математического образования , 36 (5), 404–411.

Стетсон Р., Стетсон Э. и Андерсон К. А. (2007). Дифференцированное обучение, основанное на опыте учителей. Директор школы, 8 (64), онлайн. Получено 21 апреля 2015 г. с сайта http://www.aasa.org/SchoolAdministratorArticle.aspx?id=6528.

Стилиану, Деспина А., Сильвер, Эдвард А. (2004). Роль визуальных представлений в решении сложных математических задач: изучение сходств и различий между экспертами и новичками. Математическое мышление и обучение, 6 (4), 353–387.

Штайн П., Конфри Дж., Уилсон П. Х. и Эджингтон К. (2012). Обучение, основанное на траектории обучения: к теории обучения. Исследователь в области образования, 41 (5), 147–156.

Тихенор, Мерседес С., и Тихенор, Джон М. (2005). Понимание точки зрения учителей на профессионализм. Профессиональный педагог, 27 (1–2), 89–95.

Тиене, Дрю и Люфт, Памела. (2001–2002). Динамика класса в среде обучения, богатой технологиями. Обучение и лидерство с помощью технологий .

Томлинсон, К. А. (1997). Удовлетворение потребностей одаренных учеников в обычном классе: видение или заблуждение? Tempo , 17 (1), 1, 10–12.

Томлинсон, К. А. (1999). Дифференцированный класс: удовлетворение потребностей всех учащихся . Александрия, Вирджиния: Ассоциация по надзору и разработке учебных программ.

Томлинсон, К. А., (2000). Примиримые различия: обучение на основе стандартов и дифференциация. Лидерство в образовании, 58 , 6–13.

Томлинсон, К. А., (2001). Как дифференцировать обучение в смешанных классах . (2-е изд.) Александрия, Вирджиния: ASCD.

Томлинсон, К. А., (2005). Путь к дифференциации в развитии персонала. Журнал развития персонала , 26, 8–12.

Томлинсон, К. А., и Аллан, С. Д. (2000). Руководство по дифференциации школ и классных комнат . Александрия, Вирджиния: ASCD.

Уркхарт, В.(2009). Использование письма по математике для углубления обучения учащихся . Денвер, Колорадо: МакРЕЛ. Получено 2 мая 2015 г. с сайта www.mcrel.org.

Выготский, Л. С. (1978). Разум в обществе: развитие высших психологических процессов . Кембридж, Массачусетс: Гарвардский университет.

Вальберг, Х. Дж., Паскаль, Р. А., и Вайнштейн, Т. (1985). Мощное влияние домашнего задания на обучение. Лидерство в образовании, 42 (7), 76–79.

Варшауэр, Хироко Кавагути.(2011). Роль продуктивной борьбы в преподавании и изучении математики в средней школе. Доктор философии, Техасский университет в Остине.

Вайс И., Крамарски Б. и Талис С. (2006). Влияние мультимедийной среды на математические достижения и стиль обучения детей в детском саду. Educational Media International, 43 (1), 3–17.

Вайс И. Р. и Пэсли Дж. Д. (2004). Что такое качественная инструкция? Лидерство в образовании, 61 (5), 24–28.

Вайс, И., Джоан Д. Пэсли, Дж., Смит, П., Баниловер, Э., и Хек, Д. (2003). Взгляд изнутри классной комнаты: исследование K-12 математического и естественнонаучного образования в Соединенных Штатах . Чапел-Хилл, Северная Каролина: Horizons Research, Inc.

Венглинский, Х. (1998). Вычисляет? Взаимосвязь между образовательной технологией и успеваемостью учащихся по математике . Принстон, штат Нью-Джерси: Информационный центр по политике образовательного тестирования. Получено 17 апреля 2015 г. с сайта http: // www.ets.org/research/policy_research_reports/pic-technology.

Уайт, Б.С., & Фредериксен, Дж. Р. (1998). Исследование, моделирование и метапознание: сделать науку доступной для всех учащихся. Познание и обучение, 16 (1), 3–117.

Вильям, Дилан. (2000). Работа представлена ​​рабочей группе 10 международного конгресса по математическому образованию . Макухари, Токио.

Вильям, Дилан. (2011). Встроенная формирующая оценка . Блумингтон, Индиана: Solution Tree Press.

Уильямс, К. М. (2003). Написание о процессе решения проблем для повышения эффективности решения проблем. Учитель математики, 96 (3), 185–187.

Мудрый, А. (1989). Профессиональное обучение: новая парадигма управления образованием. В Т. Дж. Серджиованни и Дж. Х. Мур (ред.). Школа будущего . Бостон, Массачусетс: Аллин и Бэкон. 301–310.

Рабочий лист полиномов с ответами

Рабочий лист полиномов с ответами

рабочий лист полиномов с ответами Мы разделим первый член полинома.Рабочий лист синтетического деления с ответами с рабочими листами со сплошным прошедшим временем в прошедшем времени для класса 3 rea. Разделение многочленов с помощью модели длинного деления Шаг 1: разделить. 4×2 −3x + 2 30 марта, 2021 · Рабочий лист деления многочленов отвечает на вопросы программного обеспечения kuta. Этот набор упражнений 3. 30 марта 2021 г. · Таблица деления многочленов отвечает на вопросы программного обеспечения kuta. Редактировать. Мы умножаем кусок, который мы только что положили как часть ответа (), на весь бином (ð ¥ + 2). Проверьте навыки деления ваших учеников-математиков — и навыки алгебры — с помощью этого видео, которое знакомит с концепцией полиномиального деления.10 июля 2021 г. · Деление многочленов с использованием рабочего листа синтетического деления. Ответ на ключевые слова: полиномы рабочего листа синтетического деления. Мы очень надеемся, что эта коллекция изображений для печати Polynomial Worksheets может быть подсказкой для вас, принести вам больше идей и, самое главное, поможет вам получить отличный день. Полиномиальное деление в длину в алгебре 2 Полиномы в алгебре 2 в длинное деление 30 октября 2021 г. · Рабочий лист класса полиномов 9 с ответами в формате pdf. Разделить: (2 x 2 x 10) (x 3). Уменьшите дроби в каждом члене и примените правило частного, которое гласит, что при делении двух степеней с одинаковым основанием следует вычитать показатели степени.Попробуйте без риска в течение 30 дней. Разделение многочленов с использованием модели длинного деления 30 октября 2021 г. · Рабочий лист класса полиномов 9 с ответами в формате pdf. Вы разделяете концепцию на все поля пропущенного термина с ответами в электронной книге, разделяя два примера, если необходимо, на другие. 30 октября 2021 г. · Рабочий лист класса полиномов 9 с ответами в формате pdf. 3: Рабочий лист «Полиномы деления» также включает: Ключ ответа. ИМЯ ДАТА ПЕРИОД Глава 5 14 Glencoe Algebra 2 Практика деления многочленов 5-2 Получите бесплатно Рабочий лист деления многочленов с ответами Рабочий лист деления многочленов с ответами Да, обзор книги по разделению многочленов с ответами может привести к списку ваших близких друзей.31 шаблонный вопрос, которые начинаются относительно легко и заканчиваются примерно 9 мая 2018 г. · Вот набор практических задач, которые будут сопровождать раздел «Делящие полиномы» главы «Полиномиальные функции» в примечаниях к курсу алгебры Пола Докинза в Университете Ламара. Написано Джоном Л. Рутом, четверг, 26 августа 2021 г. Добавить комментарий. Это написано под исходным многочленом (точно так же, как мы это делали бы в задаче арифметического деления в столбик 0. Это очень похоже на то, что вы делали в elementary, когда пытаетесь разделить большие числа, например, у вас есть 1,723 \ div 5.12 ноя, 2020 · Рабочий лист делящих многочленов. Ответы на одношаговый рабочий лист по уравнениям, по бесконечной алгебре программного обеспечения kuta на множители трехчленов и одношаговый рабочий лист по уравнениям — вот некоторые основные вещи, которые мы хотим представить вам на основе заголовка сообщения. Факторизация многочленов, рабочие листы с ответами и операции с многочленами, рабочие листы, связанные с сложением и вычитанием многочленов, делением и умножением многочленов, распечатываемые рабочие листы, pdf. Далее, как использовать синтетическое деление для деления многочленов.Был указан один фактор. Элементарное умение алгебры делить многочлены делить. 2 × 2 7x 15 x 5 3. 3g −4 3. J: \ LLR \ LearningCentre \ Math-Sci Worksheets \ Final \ Math \ Math071-DivisionOfPolynomials. com Пусть P (x) = 2×3 — 6×2 + 5x + 4 и g (x) = x — 2. В этой статье у нас есть 20 отличных фотографий на листах алгебры 2 с ключом ответа. Если вы действительно хотите узнать, как решать проблемы, подобные тем, которые вы видите на сайте Ответы на листы с долгим делением полиномов, вам следует воспользоваться преимуществами этих веб-сайтов и использовать предлагаемые решения.Какая ширина прямоугольника. 3 x 3 — 0. Затем запишите коэффициенты делимого. Kuta Software — Бесконечная алгебра 1 Имя_ Полиномы деления Дата_ Период_ Деление. 12 апреля 2021 г. · Деление многочленов. Рабочие листы для деления многочленов. Бесплатные задания по математике. Вопросы основаны на делении каждого члена многочлена на одночлен с последующим упрощением. Деление полиномов Рабочие листы для 6 и 7 классов Деление полиномов Чтобы упростить некоторые виды алгебраических дробей, нам понадобится процесс, известный как деление полиномов.П x 3x 3 2x 2 5 7x. Бесплатная рабочая таблица в формате pdf и ключ ответа от 11 июня 2021 г. · Деление на многочлен, содержащий более одного долгосрочного деления. Практические задачи. Наведите указатель мыши на ответ, чтобы отобразить ответ, или щелкните ссылку «Полное решение», чтобы отобразить все шаги, необходимые для деление полиномов в столбик. пользователя x. Ваш профессор дает вам задание, которое вы должны сдать до завтрашнего утра; но у вас уже есть обязательства с друзьями по поводу вечеринки сегодня вечером, и вы можете отступить.Имя учащегося: _____ Оценка: Бесплатные задания по математике @ http: // www. Я могу использовать синтетическое деление для деления многочленов. Полиномиальное деление в длину в алгебре 2 Полиномы в алгебре 2 в длинное деление Отображение всех листов, связанных с — полиномом умножения и деления. Рабочие листы — это сложение и вычитание при сложении, умножение полиномов на период даты, деление полиномов на период даты, умножение одночленов, умножение и деление многочленов на работу, умножение и деление многочленов на работу с ключом ответа, дроби работают на умножение и деление дробей, полиномиальное деление.Чтобы разделить многочлен на многочлен, используйте шаблон деления в столбик. Помните, что складывать и вычитать можно только похожие термины. 4 16×2 −12x + 8 3. Набор упражнений 3 3 Полиномы на деление Рабочий лист 9-го класса 12-й класс Рабочие листы умножения и деления Синтетические рабочие листы деления. 1) (m 2, 8 июля 2018 г. · Ответы на листы с делением полиномов на длинные и синтетические деления, а также на выбор рабочих листов для умножения и деления семейств фактов. Doc Math 071 учебного центра Гордона Вонга — Математическое деление многочленов Мы делим многочлены, используя метод, аналогичный деление в столбик, так что давайте сначала рассмотрим это.Разделим x3 + 2 × 2−3x + 4 x 3 + 2 x 2-3 x + 4 на решение x − 7 x — 7. 16 августа 2021г. 3 на x — 0. Получите бесплатный лист деления многочленов с ответами Рабочий лист деления многочленов с ответами Да, обзор книги по разделению многочленов с ответами может привести к списку ваших близких друзей. Тест и рабочий лист — полиномиальное длинное деление. Имя_____ Период_____ Деление многочленов с помощью синтетического деления Используйте синтетическое деление, чтобы разделить многочлен на линейный коэффициент. 9 мая 2018 г. · Вот набор практических задач, которые будут сопровождать раздел «Делящие полиномы» главы «Полиномиальные функции» в примечаниях к курсу алгебры Пола Докинза в Университете Ламара.Делитель равен (x 3). Полиномиальное деление Практическая деятельность Деление многочленов без остатка для алгебры 2 или предварительных многочленов Полиномы Действия Решение квадратных уравнений. Показаны 8 лучших листов в категории — Деление многочленов с ответами. Викторина представит вам математическую задачу, которая включает многочлены. Лист умножения и деления одночленов. Курс. Деление многочленов на биномиалы ​​Учебный центр Джефферсона Дэвиса, Сандра Петерсон Разделите с помощью деления в столбик или синтетического деления.31 октября 2018 г. · Ответы на листе алгебры 2 деления многочленов. Рабочий лист Kuta Software LLC. Алгебра 2 Деление многочленов Ответы на деление многочленов 1) r2 — r — 42) n2 + 4n + 63) x3 + 6×2 + 7x — 74) v3 + 7v2 — 6v — 5 Деление многочленов на одночлены Jefferson Davis Learning Center , Сандра Петерсон Упростите. Добро пожаловать в блог, по этому поводу я собираюсь научить вас отвечать на вопросы рабочего листа деления многочленов. Деление многочленов на деление. 3 p 2tr −− 12 p 3t 2r — 21 p 2qt r 2-9 p 3tr 3 30 октября 2021 г. · Рабочий лист класса полиномов 9 с ответами pdf.Таблица умножения и деления многочленов с ответами в формате pdf. 11 июня 2021 г. · Деление на многочлен, содержащий более одного члена. Практические задачи с длинным делением. Наведите указатель мыши на ответ, чтобы увидеть ответ, или щелкните ссылку «Полное решение», чтобы просмотреть все шаги, необходимые для деления многочленов в длину. Ответ: — 4 x 2 + 2 x + 3. — 12 x 3 3 x + 6 x 2 3 x + 9 x 3 x. 22 августа 2021 г. · Ответы на листе деления многочленов. Викторина представляет собой сборник математических задач. 21 сообщение, относящееся к листу умножения и деления многочленов с ответами.Как насчет ранее упомянутого изображения? будет в каком офигенном ???. Упражнения в формате Word включены для учащихся старших классов. 02 мая 2021 г. · Бесплатная рабочая таблица (pdf) и ключ ответов по делению многочленов (алгебра 2). Булавка на образовательных крутых инструментах. Этот блок описывает этот процесс. Деление многочленов с использованием модели длинного деления 10 июля 2021 г. · Деление многочленов с использованием таблицы синтетического деления Ответ Ключевые рабочие листы синтетического деления Полиномы. Если нам нужно разделить многочлен на одночлен, метод прост, рассмотрите одночлен как делитель, а многочлен как делимое.Доступна бесплатная пробная версия. Деление многочленов на биномиалы ​​Учебный центр Джефферсона Дэвиса, Сандра Петерсон. Деление делением в столбик или синтетическое деление. Таблицы с дробными числами. Бесплатные рабочие листы для печати. ​​Li Criabooks. Изучите эти распечатываемые рабочие листы умножения многочленов с ключами ответов, которые состоят из набора многочленов, которые должны быть умножены на биномы, трехчлены и многочлены. Определите площадь и объем геометрических фигур, а также неизвестные константы в полиномиальных уравнениях.9 мая 2018 г. · 1. Чтобы помочь вам в этом, модуль 30 марта 2021 г. · Рабочий лист деления многочленов отвечает на вопросы программного обеспечения kuta. Скопируйте первый коэффициент под таблицей от 13 мая 2021 г. · Разделите листы многочленов с электронной книгой ответов, разделите бином на одночлены, разделите другой набор? Готовы для студентов, как скрытый простой, чтобы предотвратить копирование и механику. Контрольный опрос. X 2 23 82 9x 2 x 2 называется делителем, а 23 82 9x 2 называется делимым. Авторское право © Glencoe / McGraw-Hill, подразделение McGraw-Hill Companies, Inc.Расположите коэффициенты в подходящем порядке и выполните обычный процесс, чтобы получить частное и ненулевой остаток. Об этой викторине и рабочем листе. Напишите свой ответ в виде дроби. Листы с ответами на деление многочленов. Рабочий лист «Разделение многочленов» с ответами Попрактикуйтесь в приведенных в рабочем листе вопросах о делении многочлена на одночлен. Рабочий лист полиномов с ответами. -1-Разделить с помощью LONG DIVISION. Разделение многочленов с помощью модели длинного деления. Просмотр справки по домашнему заданию — Деление многочленов с помощью ключа из математической алгебры 1 в средней школе Уоллд-Лейк-Сентрал.N p2c031 b2f tk au gtdaf bs ao5f ptlw gaur mei 4lblsct Ответы на лист синтетического разделения. 20 октября, 2020 по админ. Добавление учеников получит ранний доступ. Это разделение на формат разделения на более подробные решения. Каждая задача решается с использованием обоих методов. Деление в столбик. Рекомендуется, чтобы обучение делению в столбике выполнялось сначала, все задачи решаются с использованием столбца, а затем, чтобы помочь вам сэкономить на бумажных копиях. Шаг 1 Найдите. 2. Ответы 1. Первый шаг — найти то, на что нам нужно умножить первый член делителя x, чтобы получить первый член делимого 2×3.2n + 4 2. Если разделить 2×3 на x, мы получим 2×2. Рабочий лист Kuta Software LLC. Алгебра 2 ПРИМЕРЫ — Деление многочленов с использованием ДЛИННОГО или СИНТЕТИЧЕСКОГО РАЗДЕЛЕНИЯ Имя _____ ID. Деление многочленов на одночлены. Практика рабочего листа b деления. Надеюсь, тебе понравится. 26 августа 2021 г. · Ответы на 32 листа полиномов. Используйте длинное деление, чтобы разделить 3×4 −5×2 +3 3 x 4 — 5 x 2 + 3 на x + 2 x + 2. Еще одно преимущество рабочего листа деления многочленов на одночлены заключается в том, что он поставляется с руководством по ответам. Ответы также включены в файлы PDF.Добавить, вычесть, умножить, разделить многочлены, упростить. Разделение многочленов с использованием модели длинного деления Этот набор упражнений 3. Разделение многочленов с использованием модели длинного деления 22 августа 2021 г. · Ответы на листе деления многочленов. Рабочий лист деления полиномов Ответы Элегантный рабочий лист деления полиномов Edplace. 60 Деление многочленов Длинный синтетический рабочий лист деления Ответы Использование синтетического деления состояние, если данный бином является множителем данного многочлена. Допустим, у нас есть: — 12 x 3 + 6 x 2 + 9 x 3 x.vreodr. 8 3 1 2 4 3 1 1 3 3. Полиномы Сложение и вычитание Разделение Бесплатная рабочая таблица (pdf) и ответ на вопрос по разделению многочленов (алгебра 2). Разделите 2 × 5 + x4−6x + 9 2 x 5. Давайте сначала выполним деление в столбик. 5) Создайте свои собственные рабочие листы, подобные этому, с помощью Infinite Precalculus. Ответы на вопросы содержатся в разделе ответов, начинающемся на странице 26. Попросите старшеклассников разделить каждый член полинома индивидуально на делитель монома. Эти рабочие листы по математике следует выполнять регулярно, и их можно бесплатно загрузить в формате PDF.Разложите дивиденд и делитель в стандартной форме. рабочий лист полиномов с ответами

Педагогика угнетателя | Журнал профессионального образования

Как и более известная программа Teach for America, программа New York Teaching Fellows предоставляет альтернативный путь к государственной сертификации примерно для 1700 новых учителей ежегодно. Когда прошлым летом я встретился с группой ребят, посещающих необходимый класс в образовательной школе, мы начали с обсуждения реформы образования, но вскоре разговор изменился, и многие рассказывали одну ужасную историю за другой из своего тяжелого первого года жизни: хаотичные классы, равнодушные администраторы, учителя-ветераны, которые редко протягивают руку помощи.Вы можете ожидать, что требуемые чтения для этих борющихся новичков будут содержать, скажем, хорошие практические советы по управлению классом или разумные советы по обучению чтению учащихся из неблагополучных семей. Вместо этого единственная книга, которую стипендиаты должны были прочитать полностью, — это «Педагогика угнетенных» бразильского педагога Пауло Фрейре.

Для любого, кто знаком с американскими школами образования, выбор не стал неожиданностью. С момента публикации английского издания в 1970 году книга «Педагогика угнетенных» стала почти знаковой в американских программах подготовки учителей.В 2003 году Дэвид Штайнер и Сьюзан Розен опубликовали исследование, в котором изучались учебные программы 16 учебных заведений, 14 из которых входят в число ведущих учебных заведений в стране, согласно US News and World Report , и обнаружили, что педагогических учебных заведений Угнетенный был одним из наиболее часто задаваемых текстов в их курсах по философии образования. Эти задания курса, несомненно, являются одной из причин того, что, по словам издателя, было продано почти 1 миллион экземпляров, что является значительным числом для книги в области образования.

Странно то, что magnum opus Фрейре, в конце концов, не и не образование — уж точно не образование детей. «Педагогика угнетенных». , самый эффективный способ обучения студентов из малообеспеченных семей. Напротив, этот бестселлер образовательной школы представляет собой утопический политический трактат, призывающий к свержению капиталистической гегемонии и созданию бесклассовых обществ.Учителя, которые перенимают его пагубные идеи, рискуют навредить своим ученикам — и, по иронии судьбы, их ученики из наиболее неблагополучных семей пострадают больше всего.

Чтобы получить представление о приоритетах книги, взгляните на сноски. Фрейре не интересует ведущих мыслителей западной традиции в области образования — ни Руссо, ни Пиаже, ни Джон Дьюи, ни Гораций Манн, ни Мария Монтессори. Он цитирует совсем другой набор фигур: Маркса, Ленина, Мао, Че Гевара и Фиделя Кастро, а также радикальных интеллектуалов Франца Фанона, Режиса Дебре, Герберта Маркуза, Жан-Поля Сартра, Луи Альтюссера и Георга Лукача.И это неудивительно, поскольку основная идея Фрейре состоит в том, что центральное противоречие любого общества находится между «угнетателями» и «угнетенными» и что революция должна разрешить их конфликт. Более того, «угнетенным» суждено разработать «педагогику», которая приведет их к собственному освобождению. Вот как Фрейре объясняет этот освободительный проект в ключевом отрывке:

Педагогика угнетенных [есть] педагогика, которая должна создаваться вместе с угнетенными (будь то отдельные лица или народы), а не для них, в непрекращающейся борьбе за восстановление своей человечности.Эта педагогика делает угнетение и его причины объектами размышления угнетенных, и из этого размышления проистекает их необходимое участие в борьбе за свое освобождение. И в борьбе эта педагогика будет переделана и переделана.

Как ясно видно из этого отрывка, Фрейре никогда не подразумевает, что «педагогика» относится к любому методу обучения в классе, основанному на анализе и исследованиях, или к любым средствам повышения академической успеваемости учащихся. У него есть рыба побольше, которую нужно жарить.Его идиосинкразическая теория школьного образования относится только к растущему самосознанию эксплуатируемых рабочих и крестьян, которые «открывают мир угнетения». Как только они достигают просветления, mirabile dictu , «эта педагогика перестает принадлежать угнетенным и становится педагогикой всех людей в процессе постоянного освобождения».

Фрейре редко обосновывает свое описание столкновения между угнетателями и угнетенными в каком-либо конкретном обществе или историческом периоде, поэтому читателю трудно судить, имеет ли смысл то, что он говорит.Мы не знаем, являются ли угнетатели, которых он осуждает, североамериканскими банкирами, латиноамериканскими земельными баронами или, если уж на то пошло, заурядными бюрократами авторитарного образования. Его язык настолько метафизичен и расплывчат, что с таким же успехом он мог бы описать настольную игру с двумя противоборствующими сторонами: угнетателями и угнетенными. Размышляя над общей борьбой между этими двумя сторонами, он опирается на стандартную формулировку Маркса о том, что «классовая борьба обязательно ведет к диктатуре пролетариата, [и] эта диктатура представляет собой лишь переход к уничтожению всех классов и к власти. бесклассовое общество.”

В одной сноске, однако, Фрейре действительно упоминает общество, которое фактически осуществило «постоянное освобождение», к которому он стремится: оно «кажется фундаментальным аспектом культурной революции Мао». Миллионы китайцев всех классов, которые пострадали и умерли под жестоким гнетом революции, могли не согласиться. Фрейре также дает профессорский совет революционным лидерам, которые «должны воспринимать революцию из-за ее творческого и освободительного характера как акт любви». Образцом этой революционной любви в действии является не кто иной, как пример вооруженного восстания 1960-х годов, Че Гевара, который признал, что «истинный революционер руководствуется сильным чувством любви.Фрейре забывает упомянуть, что Че был одним из самых жестоких проводников кубинской революции, ответственным за казнь сотен политических противников.

После всего этого мутность может быть наименьшей из проблем книги, но тем не менее стоит процитировать первые размышления о книге:

Хотя проблема гуманизации всегда, с аксиологической точки зрения, была центральной проблемой человечества, теперь она принимает характер неизбежного беспокойства.Забота о гуманизации сразу же ведет к признанию дегуманизации не только как онтологической возможности, но и как исторической реальности. И когда человек осознает степень дегуманизации, он или она может спросить, является ли гуманизация реальной возможностью. В истории, в конкретных, объективных контекстах, и гуманизация, и дегуманизация являются возможностями для человека как незавершенного существа, сознающего свою незавершенность.

Примерно переводится: «гуманизация» — это хорошо, «дегуманизация» — это плохо.О, для тех дней, когда революционные трактаты перешли прямо к делу, например: «Призрак бродит по Европе».

Каким образом эту производную, ненаучную книгу об угнетении, классовой борьбе, разграблениях капитализма и необходимости революции когда-либо можно было спутать с трактатом об образовании, который мог бы помочь решить проблемы американских городских школ XXI века? Ответ на этот вопрос начинается в Пернамбуку, бедной провинции на северо-востоке Бразилии. В 1950-х и 1960-х годах Фрейре был профессором университета и радикальным активистом в столице провинции Ресифи, где он организовал кампании по обучению грамоте взрослых бесправных крестьян.Фрейре понял, что проведение ускоренных курсов по обучению грамоте и гражданскому праву было самым эффективным средством мобилизации их для избрания радикальных кандидатов. Таким образом, его «педагогика» началась как кампания по выбору избирателей за получение политической власти.

В 1964 году в Бразилии произошел военный переворот. Фрейре провел некоторое время в тюрьме, а затем был сослан в Чили, где, вдохновленный своей работой с бразильскими крестьянами, он работал над «Педагогика угнетенных» . Отсюда настаивание в книге на том, что школьное обучение никогда не является нейтральным процессом и всегда преследует динамичную политическую цель.И отсюда также один из немногих по-настоящему педагогических моментов в книге: ее противодействие налогообложению студентов любым фактическим академическим содержанием, которое Фрейре высмеивает как «официальное знание», служащее для рационализации неравенства в капиталистическом обществе. Одна из наиболее часто цитируемых метафор Фрейре отвергает инструкции учителя как ошибочную «банковскую концепцию», в которой «объем действий, разрешенных студентам, распространяется только на получение, регистрацию и хранение вкладов». Вместо этого Фрейре предлагает учителям сотрудничать со своими ровесниками, учениками, в «диалогическом» процессе и «решении проблем» до тех пор, пока роли учителя и ученика не сольются в «учитель-ученик» и «ученик-учителя».”

После того, как в 1970 году было опубликовано английское издание книги, Фрейре получил приглашение стать приглашенным лектором в Гарвардской высшей школе образования, и в течение следующего десятилетия он нашел восторженную аудиторию в американских университетах. «Педагогика угнетенных» нашла отклик у прогрессивных педагогов, уже приверженных «ориентированному на ребенка», а не «ориентированному учителем» подходу к обучению в классе. Отказ Фрейре от обучения содержательным знаниям, казалось, подкреплял то, что уже было самой популярной теорией обучения в школах образования, которая утверждала, что учащиеся должны совместно работать над созданием собственных знаний и что учитель должен быть «проводником на стороне», а не помощником. «Шалфей на сцене.”

В «Педагогика угнетенных» Фрейре перечислил десять ключевых характеристик «банковского» метода обучения, которые призваны показать, как он противоречит интересам студентов, находящихся в неблагоприятном положении. Например, «учитель говорит, а ученики кротко слушают»; «Учитель выбирает и добивается своего выбора, а ученики подчиняются»; «Учитель дисциплинирует, а ученики дисциплинированы»; и «преподаватель выбирает содержание программы, а ученики (с которыми не консультировались) адаптируются к нему.Критика Фрейре укрепила еще один заветный миф об американской прогрессивной образовательной системе — что традиционные уроки под руководством учителя оставляют учащихся пассивными и отстраненными, что приводит к более высокому проценту отсева среди меньшинств и бедных. Это описание было больше, чем карикатурой; это была полная выдумка. За последние два десятилетия школы Core Knowledge Э.Д. Хирша снова и снова доказывали, что не только насыщенное содержанием обучение повышает академические достижения детей из бедных семей по стандартизированным тестам, но и что эти учащиеся остаются любопытными, интеллектуально стимулированными и заинтересованными, несмотря на образование школы продолжают игнорировать эти задокументированные успехи.

Конечно, популярность «Педагогика угнетенных» была вызвана не только его педагогической теорией. В семидесятые годы ветераны студенческих протестных и антивоенных движений сложили плакаты и начали свой «долгий марш по институтам», получив докторскую степень и поступив на гуманитарные факультеты. Попав в академию, левые не могли сопротивляться включению своей радикальной политики (марксистской, феминистской или расистской) в свое учение. Прославление Фрейре как крупного мыслителя дало им мощный способ сделать это.Его заявление в «Педагогика угнетенных » о том, что «не существует такой вещи, как нейтральное образование», стало мантрой для левых профессоров, которые могли использовать его для оправдания прозелитизма в адрес ненавистных к Америке причин в классе колледжа.

Кое-где некоторые левые профессора осознавали опасность для академического дискурса в этом уничтожении идеала нейтралитета. В Radical Teacher известный литературный критик Джеральд Графф — бывший президент ультраполитически корректной Ассоциации современного языка — выступил против своих коллег-профессоров, утверждая, что «как бы Фрейре ни настаивал на« постановке проблем », а не на« банковском деле ». В сфере образования цель обучения для Фрейре состоит в том, чтобы приблизить ученика к тому, что Фрейре называет «критическим восприятием мира», и не вызывает сомнений то, что для Фрейре только марксизм или какая-то версия левого радикализма считается подлинным «критическим восприятием».В другом месте Графф пошел еще дальше, отвергнув фрейрианскую модель обучения:

Какое у нас есть право быть самопровозглашенной политической совестью наших студентов? Учитывая неравенство во власти и опыте между учениками и учителями (даже учителями из групп, лишенных прав), ученики часто оправданно боятся бросить вызов нашим политическим взглядам, даже если мы их умоляем. . . . Сделать основной целью обучения «открыть умы студентов для левых, феминистских, антирасистских и квир-идей» и «стимулировать» их (приятный эвфемизм) «работать для эгалитарных изменений» было роковой ошибкой освободительное педагогическое движение от Фрейре в 1960-х годах до наших дней.

Но предостерегающий совет Граффа не был услышан в академии. И не только индоктринация во имя освобождения наводнила американские колледжи, где студенты могли, по крайней мере, выбирать курсы, которые они хотели бы пройти; Благодаря кадрам радикальных профессоров учебных заведений фрейрианская повестка дня пришла и в классы K – 12 в форме расширяющегося движения за «обучение социальной справедливости».

В качестве примера рассмотрим карьеру Роберта Петерсона. Петерсон начал свою карьеру в 1980-х годах как молодой учитель начальной школы в центре Милуоки.Он описал, как он подключил «Педагогика угнетенных» , ища способ применить уроки великого радикального педагога к его собственным двуязычным классам четвертого и пятого классов. Петерсон осознал, что ему пришлось отказаться от «банковского метода» обучения, при котором «учитель и учебные материалы имеют« правильные ответы »и от которых ожидается, что ученики будут периодически срыгивать». Вместо этого он применил фрейрианский подход, который «опирается на опыт ученика.. . . Это означает, что нужно побудить учащихся задуматься о социальном характере знаний и учебной программы ». Петерсон хотел бы, чтобы вы поверили, что его ученики четвертого и пятого классов стали критическими теоретиками, исследующими «природу знания», как младшие ученые Франкфуртской школы.

На самом деле произошло то, что Петерсон использовал фрейрианское обоснование, чтобы стать «самопровозглашенной политической совестью» своих учеников. После одного подразделения по вторжению США в Латинскую Америку Петерсон решил взять детей на митинг протеста против У.С. помощь контрас, выступающим против марксистов-сандинистов в Никарагуа. Дети остались после школы сделать плакаты:

пусть управляют своей землей!

Помогите Центральной Америке не убивать их

Дайте никарагуанцам свободу

Петерсон особенно гордился четвероклассником, который описал ралли в классном журнале. «В дождливый вторник апреля некоторые ученики нашего класса пошли протестовать против контрас», — написал студент.«Люди в Центральной Америке бедны, и их бомбили на голову. Когда мы пошли протестовать, шел дождь, и казалось, что контрас бомбили нас ».

В наши дни Петерсон является редактором Rethinking Schools , ведущего национального издания для преподавателей социальной справедливости. Он также является редактором книги под названием « Переосмысление математики: преподавание социальной справедливости по числам» , в которой даются уроки математики для обучения маленьких детей злу расистской империалистической Америки.Отчасти благодаря усилиям Петерсона движение за социальную справедливость в математике, как и в других академических предметах, полностью развернулось (см. «Последние — и худшие — шалости школ Эд», лето 2006 г.). Он присутствует практически в каждой крупной образовательной школе в стране и пользуется поддержкой некоторых из самых громких имен в области математического образования, в том числе нескольких недавних президентов Американской ассоциации исследований в области образования, состоящей из 25 000 членов, головной организации профессоров в области образования. Десятки псевдонаучных книг, журналов и конференций превозносят предполагаемую пользу для детей из неблагополучных семей, которую Петерсон однажды оказал своим четвероклассникам в Милуоки.

Чтобы противостоять критике, что целью движения является политическая идеологическая обработка, преподаватели социальной справедливости разработали научный аппарат, призванный изобразить преподавание социальной справедливости как еще один разумный подход к образованию, подкрепленный «исследованиями». Так, в недавнем выпуске журнала Teachers College Record Колумбийского университета (который позиционирует себя как «голос исследований в области образования») была опубликована передовая статья профессора математического образования Университета Иллинойса Эрика Гуттштейна, в которой сообщаются результаты «двухлетнего качественного исследования. практическое исследование преподавания и обучения социальной справедливости.«Практическое исследование» полностью состояло из того, что Гуттштейн в течение двух лет наблюдал за своим собственным фрейрианским обучением математике в государственной школе Чикаго, а затем пришел к выводу, что это имело большой успех. Частью доказательства было заявление одного из его учеников: «Я думал, что математика — это просто предмет, который они нам привили только потому, что им так хотелось, но теперь я понимаю, что вы можете использовать математику, чтобы защитить свои права и осознать несправедливость вокруг. ты.» Гутстайн заключает, что «молодежь в классах K – 12 — это больше, чем просто ученики — они, по сути, являются участниками борьбы за социальную справедливость.”

Нет никаких свидетельств того, что фрейрианская педагогика имела большой успех где-либо в странах третьего мира. При этом любимые революционные режимы Фрейре, такие как Китай и Куба, не реформировали свои собственные «банковские» подходы к образованию, при которых наиболее одаренные ученики контролируются, дисциплинируются и наполняются предметными знаниями ради национальных целей — и производства более промышленных менеджеры, инженеры и ученые. Насколько же извращенно то, что только в центральных городах Америки фрейрианским педагогам была предоставлена ​​возможность «освобождать» бедных детей от полностью воображаемого «угнетения» и вербовать их для революции, которая никогда не наступит?

Идеи Фрейре вредны не только для учащихся, но и для учителей, которым доверено их образование.Среди реформаторов образования формируется широкий консенсус в отношении того, что лучший шанс поднять академическую успеваемость детей в национальных школах города — это резко повысить эффективность учителей, закрепленных за этими школами. Повышение квалификации учителей как средство сокращения разрыва в расовых достижениях является одним из основных направлений повестки дня президента Обамы в области образования. Но если качество учителей теперь является главной задачей, это бросает вызов рациональности, что Педагогика угнетенных все еще занимает высокое место в курсах подготовки для тех учителей, которые, несомненно, ничего не узнают о том, как стать лучшими инструкторами из дискредитированных марксистских банальностей. .

В эпоху Обамы, наконец, кажется еще более неприемлемым побуждать учителей из городских районов серьезно относиться к фрейрианской политической повестке дня. Если есть какое-то политическое послание, которое эти учителя должны донести до своих учеников, то его лучше всего сформулировал наш величайший афроамериканский писатель Ральф Эллисон, который подтвердил, что в своих трудах он стремился «увидеть Америку с осознанием ее богатства».