Алгебра 10 класс модули – Методическая разработка по алгебре (10 класс) на тему: Разработка урока по теме «Решение уравнений и неравенств, содержащих модуль» в 10-м классе (профил.уровень) | скачать бесплатно

Элективного курса алгебра модуля 10 класс

г.Сочи

Муниципальное образовательное учреждение

средняя образовательная школа №49

АВТОРСКАЯ ПРОГРАММА

ЭЛЕКТИВНОГО КУРСА

Алгебра модуля

10 класс

Программа составлена учителем математики МОУ СОШ № 49 Величко З.М.

Составитель: Величко З.М.

г.Сочи

2008-2009 г.

Пояснительная записка.

Программа курса рассчитана на 35 часов (1 раз в неделю), содержит углубленное изучение темы «Модуль» и выходит за рамки базовых общеобразовательных программ по математике.

Цели обучения элективного курса ориентированы на формирование личности каждого отдельного ученика. К ним относятся:

1. овладение конкретными математическими знаниями, необходимыми для углубленного изучения предмета, для изучения смежных дисциплин;

2. создание условий для существенной дифференциации при изучении школьниками этого курса;

3. повышение математической культуры в рамках школьной программы по математике.

Задачи курса:

1. Развитие интереса школьников к предмету, к активно-познавательной деятельности;

2. Показать широту и разнообразие применение модуля для решения задач частей В и С экзаменационных вариантов ЕГЭ;

3. Учитывать возрастные особенности каждого учащегося при изучении данного курса.

Элективный курс по математике для учащихся 10 класса посвящен систематическому изложению учебного материала, связанного с понятием модуля числа и аспектами его применения. В нем рассматриваются различные методы решения уравнений и неравенств с модулем, основанные на его определении, свойствах и графической интерпретации. Значительное внимание уделено вопросам приложения модуля к преобразованиям корней.

В последнее время в материалах ЕГЭ предлагаются задания, содержащие модули. Задачи такого типа вызывают затруднений у учащихся, так как практических заданий по данной теме в школьных учебниках мало. В предлагаемом элективном курсе, задачи с модулем рассматриваются как средство обобщения и систематизации знаний учащихся о модуле.

Для курса характерна практическая направленность. Его основное содержание составляют учебные задачи. Часть из них приводится с полным решением, иллюстрирующим тот или иной метод. Другие предлагаются для самостоятельной работы. Правильность выполнения этих заданий контролируется посредством приведенных ответов. Изложение практических приемов решения сопровождается необходимыми теоретическими сведениями.

Элективный курс «Алгебра модуля» направлен на углубление знаний школьников старших классов, так как успешное освоение приведенного учебного материала будет способствовать более полному и глубокому усвоению таких базовых понятий математики как предел и производная. Кроме того, задания единого экзамена по математике предполагают умение оперировать с модулем.

Таким образом, основная роль элективного курса «Алгебра модуля» состоит в подготовке учащихся к успешному обучению в старших классах и позволит им лучше подготовиться к итоговой аттестации в форме ЕГЭ.

Требования к подготовке учащихся по курсу

В результате изучения элективного курса учащиеся должны уметь:

1. решать уравнения, содержащие модуль;

2. решать неравенства, содержащие модуль;

3. показать графическую интерпретацию решения уравнений и неравенств.

Содержание курса

Тема «Определение модуля числа и его применение при решении уравнений»

1. определение модуля.

2. решение линейных уравнений, содержащих модуль.

3. решение квадратных уравнений, содержащих модуль.

Тема «Метод интервалов решения уравнений и неравенств, содержащих модуль»

1. Метод интервалов.

2. решение уравнений с модулем методом интервалов.

3. Решение неравенств с модулем методом интервалов.

Тема «Решение неравенств вида │х│‹ а, │х│› а посредством равносильных переходов»

1. равносильность неравенств │х│‹ а, │х│› а системе неравенств{х‹ а,

х›- а и совокупности неравенств х‹ -а, х›а.

2. решение неравенств с использованием доказанной равносильностью.

Тема «Свойства модуля. Применение свойств модуля при решении уровнений и неравенств»

1. Свойства модуля.

2. Решение уравнений с использованием свойств модуля.

3. Решение неравенств с использованием свойств модуля.

Тема «Решение уравнений неравенств с модулями на координатной прямой»

1. Расстояние между точками на координатной прямой.

2. Геометрическая иллюстрация решений линейных уравнений с модулем.

3. Геометрическая иллюстрация решений линейных неравенств с модулем.

Тема «Модули и преобразование корней»

1. Свойства корня четной степени.

2. Упрощение выражений, содержащих корни.

3. Вычисление значения выражений, содержащих корни.

Тема «Модуль и иррациональные уравнения»

1. Определения иррациональных уравнений.

2. Решение иррациональных уравнений с использованием свойств модуля.

Тема «Решение задач, содержащих модуль заданий части В и С вариантов ЕГЭ.

1. Решение задач части В: на вычисление и упрощение выражений с использованием свойств модуля.

2. Решение задач части С, содержащих модуль или использующих свойства модуля при решении.

Литература для учащихся:

Семенко Е.А. Обобщающее повторение в курсе алгебры основной школы. Краснодар, 2002 г.

Семенко Е.А., Фоменко М.В., Белай Е.Н., Ларкин Г.Н. Тестовые контрольные задания по алгебре и началам анализа. Краснодар, 2005 г.

Симонов Д.С., Бакаев А.Г. и др. Система тренировочных задач и упражнений по математике. М., Просвещение, 1991 г.

Математика. Большой справочник для школьников и поступающих в ВУЗы. Москва, 2006 г.

Литература для учителя.

Семенко Е.А. Обобщающее повторение в курсе алгебры основной школы. Краснодар, 2002 г.

Семенко Е.А., Фоменко М.В., Белай Е.Н., Ларкин Г.Н. Тестовые контрольные задания по алгебре и началам анализа. Краснодар, 2005 г.

Симонов Д.С., Бакаев А.Г. и др. Система тренировочных задач и упражнений по математике. М., Просвещение, 1991 г.

Математика. Большой справочник для школьников и поступающих в ВУЗы. Москва, 2006 г.

Гайдуков И.И. Абсолютная величина: Пособие для учителей. 2-е изд., М., 1968 г.

Зильберберг Н.И. Алгебра для углубленного изучения математики.

Псков, 1992 г.

Литвиненко В.Н., Мордкович А.В. Практикум по решению математических задач: Алгебра. Тригонометрия. М., 1984 г.

Мордкович А.В. Кое-что о радикалах// Квант, 1970, №3.

Шарыгин И.Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 класса средней школы: М., 1989 г.

Учебно-тематический план.

Тема	Кол-во часов	Форма контроля
1. Определение модуля числа и его применение при решении уравнений	2
2. Метод интервалов решения уравнений и неравенств, содержащих модуль	2	Решение контрольных заданий
3. Решение неравенств вида│х│‹ а, │х│› а посредством равносильных переходов	2	Проверка контрольных заданий для домашней работы
4. Свойства модуля. Применение свойств модуля при решении уравнений и неравенств	2	Проверка контрольных заданий для домашней работы
5. Решение уравнений и неравенств с модулями на координатной прямой	2	Математический диктант
6. Модуль и преобразование корней	3	Решение контрольных заданий ЕГЭ
7. Модуль и иррациональные уравнения	4	Решение контрольных заданий ЕГЭ
8. Контрольная работа	1
9. Практикум по решению задач ЕГЭ, содержащих модуль	16	Решение контрольных заданий ЕГЭ. Зачет
10. Контрольная работа	1
ИТОГО	35

textarchive.ru

Урок по алгебре (спецкурс) в 10 классе » Уравнения с модулем»

Учитель Кирилюк Н. А.

Предмет: Спецкурс по математике

Класс – 10-А Дата: 24.03 Урок №

Тема. Решение уравнений с модулем

Цель: обобщить и систематизировать знания о модуле, полученные ранее, познакомить со способами решения уравнеий, формировать умения и навыки решения уравнений с модуле.

развивать логическое мышление, математическую культуру речи и письма , вычислительные навыки;

воспитывать настойчивость, усердие, чувство уверенности в себе, умение работать в коллективе; интерес к изучаемому материалу;

формировать такие виды компетентностей: информационную, познавательную, коммуникативную, социальную.

Планируемые результаты обучения

Учащиеся приобретут следующие умения:

— личностные:

· Развитие инициативности, самостоятельности, навыков сотрудничества в разных видах деятельности;

· Развитие интереса к познанию нового.

— метапредметные:

— Развитие логического мышления;

· Развитие культуры грамотной математической речи;

— предметные:

— Умение выстраивать логическую цепочку рассуждений, аргументировать свои действия, выполнять доказательства.

Формирование УУД (универсальные учебные действия):

Регулятивные: осуществлять итоговый и пошаговый контроль результата; выстраивать алгоритм действий; корректировать деятельность: выделение и осознание того, что уже усвоено и что подлежит усвоению, осознание качества и уровня усвоения.

Личностные:

определять новый уровень отношения к самому себе как субъекту деятельности; формировать способность к мобилизации сил и энергии, к волевому усилию

Познавательные

строить логические рассуждения, включающие установление причинно-следственных связей; строить речевые высказывания в устной и письменной форме; уметь осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от конкретных условий;

Коммуникативные организовывать и планировать учебное сотрудничество с учителем и одноклассниками; формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы

Тип модуля: содержательно — поисковый

Вид модуля: комбинированный

Оборудование: учебник, тетради, раздаточный материал

IV. Изучение нового материала и его первичное закрепление.

Коллективная работа

30 мин.

V. Самостоятельная деятельность

Работа в парах, работа в группах

20 мин

VI. Домашнее завдание

5 мин

VII Итог урока. Рефлексия..

5 мин

Сценарий урока

I. Организационный момент

II. Мотивация учебной деятельности учащихся . Самопостановка целей и задач на урок.

К. С. Станиславский любил рассказывать такую притчу: «Индийский магараджа считал умение сосредоточиться настолько важным, что решил назначить министром того, кто владеет им лучше других. Поэтому он предложил претенденту на эту должность пронести по стене вокруг города большой кувшин с молоком, не пролив ни капли. При этом слуги должны были его всячески отвлекать. Многие пытались пронести кувшин, но терпели неудачу. Только один человек сумел выполнить условие магараджи. «Ты слышал крики?» — спросили его потом. «Нет».— «Ты слышал звуки выстрелов?» — «Нет».— «Ты видел, как вокруг тебя плясали, смеялись, прыгали?» — «Нет. Я ничего не видел и не слышал. Я смотрел на молоко». О чём эта притча? Как вы считаете? (о внимании)

III . Актуализация опорных знаний учеников

1. Проверка домашнего задания(самопроверка). Коррекция знаний учащихся.

2. Повторение. Заполнение пропусков в таблице с теоретическими сведениями

Заполните пропуски в утверждениях:

Модуль произведения двух и более чисел равен

________________________________________.

5.

Постоянный положительный множитель можно выносить ___________________________________

3. Устные упражнения

№ 1.Решить уравнения:

 |x−3|=6
 |x|=2,8
|2x−8|=4
 |3−3x|=6
 |10x+5|=−2

№ 2. Упростить выражение √(2a−6)2 если:

а) а−3≥0
б) a−3<0

IV. Изучение нового материала и его первичное закрепление.

1.Свойства модуля

1. |a| ≥ 0.

2. |a| ≥ a

3. (b≠0)

4. |a|=| —a|

5. |ab| = |a|*|b|

6. | a + b|≤| a|+|b|

7. | a+b|=|a|+|b|, когда ab≥0

8. | a+b|= a + b, когда a≥0, b≥0

9. |a – b| = |a|+|b|, когда ab≤0

10. |a|—|b|≥0, когда

2. Способы решения уравнений с модулем

Решения уравнений вида |f(x)|=b (b≥0)

| f(x)|=b

Пример 1.

|

Решение

=>

Ответ: ; 3; -1.

Решение уравнений с модулем по определению

Пример 2. Решим уравнение

Решение

=> =>

Ответ: -3; -2; 2; 3.

Решение уравнений вида |f(x)|=g(x)

|f(x)|=g(x) или |f(x)|=g(x)

Пример 3. Решим уравнение |3x+1|+x=9

|3x+1|=9-x => =>=>

Ответ:-5;2.

Решение уравнений вида |f(x)|=|g(x)|

|f(x)|=|g(x)| или |f(x)|=|g(x)|

Пример 4.

Решим уравнение |x+5|=|10+x|

Решение

;

10x=-75

X=-7.5

Ответ: -7.5

Решение уравнений с модулем по общей схеме

1) Найти ОДЗ.

2)Найти нули всех функций в модуле.

3)Обозначить нули на ОДЗ и разбить ОДЗ на промежутки.

4)Найти решения в каждом промежутке и проверить, входит ли это решение в рассмотренный промежуток.

Пример 5. Решим уравнение |x-2|+|x-4|=3

Решение

1)ОДЗ: R.

2) x-2=0, x=2

x-4=0, x=4.

3)

x-2 — + +

x-4 — — +

4)Найдем решение в каждом промежутке и проверим, входит ли данное решение в данный промежуток:

a) x

б) x

в) x (4;+; x-2+x-4=3;

Ответ: 1.5; 4.5.

V. Самостоятельная деятельность.

1.Работа в парах.

1) |x+2|=3

2)|x+3|=2x-1

3) |x+1|-|2x-3|=1

4)|x+2|+|x+3|=x

5) |x+5|-|x-3|=8

6)|+3x+2|+4x+10=0

2. Работа в группах .

( по сборнику Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и заданий для тематического оценивания по алгебре и началам анализа для 11 класса. — Харьков, Гимназия, 2006., стр 7)

| || |||

№8 №8 №8

1,2,3 4,5,6 7,8,9

10,11,12 13,14,15 16,17,18

1.|x+4.2|=5.1

2.|3x-5|=4.8

3.||x|-2|=2

10)-5x*-14=0

11)||-8x+4|-3|=7

12)|-3|x|+2|=1

4.|-x-1|=1

5.-|x|-2=0

6) x|x|+8x-7=0

13)|-2x|=3-2x

14) |x|+|x-4|=5

15)|x+1|+|x-3|=4

7) |x-4|+x=8

8) |x+3| —x=2

9) 2+|x-2|-1=0

16) |x|-|x-5|=6

17)|2x-3|-|x+2|=4x+5

18)|-4x+3|+|-5x+6|=1

3. Индивидуальные задания.

№ 1. | 8cos²x – cosx – 6 | + | 8cos²x – cosx – 3 | = 9.

№ 2. | 36^x – 6^x+1 – 3| + | 36^x – 6^x+1 – 13 | = 16.

VI. Домашнее задание

( по сборнику Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и заданий для тематического оценивания по алгебре и началам анализа для 11 класса. — Харьков, Гимназия, 2006.)

Стр.45 на выбор

1 группа №8 (1-4)

2 группа №8 (5-8)

3 группа №8 (9-11)

VII . Итог модуля. Рефлексия

.

Техника «рефлексивная мишень»

Участник ставит метки в сектора соответственно оценке результата: чем ближе к центру мишени, тем ближе к «5», на краях мишени оценка ближе к нулю. 

infourok.ru

«Производная» (алгебра и начала анализа). 10-й класс

Литература, использованная для подготовки модуля по теме “Производная”

Тема урока	Кол-во часов	Тип урока	Форма работы	Форма контроля	Содержание знаний учащихся
1. Приращение функции	1	Вводный урок	Лекция	Составление опорного конспекта	Приращение аргумента и приращение функции, их геометрический смысл
2. Понятие о касательной к графику функции. Производная	2	Формирование ЗУН. Контроль ЗУН. Базовый уровень	Лекция	Составление опорного конспекта. Проверочная работа (Приложение 1)	Понятие производной. Вычисление производных на основе определения производной
Тема урока	Кол-во часов	Тип урока	Форма работы	Форма контроля	Содержание знаний учащихся
3. Понятие о непрерывности предельном переходе	2	Формирование ЗУН	Лекция	Составление опорного конспекта	Правила предельного перехода
4. Правила вычисления производных. Производная сложной функции.	2	Формирование ЗУН	Лекция	Составление опорного конспекта Карточки инструкции (Приложение 2)	Формулы дифференциро-вания
Формулы дифференцирования.	1	Контроль ЗУН Базовый уровень		(Приложение 3)	Применение формул и правил дифференцирования при нахождении производных различных функций.
	2	Урок-практикум. Контроль ЗУН Базовый уровень.	Группо-вая и парная работа.	Составление карточек. Карточки программи-рованного контроля. (Приложение 4)
	2	Урок-практикум.	Парная.	Таблица Функция, ее график и производная. (Приложение 5)
	2+2	Систематиза-ция, обобщение знаний. Контроль ЗУН Продвинутый уровень.	Зачет № 3.	Зачет № 3.(Карточки на 4 варианта). (Приложение 6)
	1	Контроль ЗУН. Продвинутый уровень.	Контро-льная работа.	Контрольная работа № 4 или тест. (Приложение 7. Приложение 8)

xn--i1abbnckbmcl9fb.xn--p1ai

Рабочая программа по элективному курсу для уч-ся 10 класса «Алгебра модуля»

Рабочая программа

по элективному курсу

для уч-ся 10 класса

«Алгебра модуля»

Автор-составитель:

учитель математики МБОУ «Средняя общеобразовательная школа №12 им. С.Н.Перекальского» г. Курска

Лихобабо Л.И.

Пояснительная записка

Основная задача обучения математике в школе — обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин   и продолжения образования.

Наряду с решением основной задачи углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии существенным образом связанных с математикой, подготовку к обучению в вузе.

Основная функция элективного курса– выявление средствами предмета математики направленности личности, её профессиональных интересов. Присутствие такого курса в учебном плане учащегося повышает вероятность того, что выпускник сделает осознанный и успешный выбор профиля, связанного с математикой. Кроме того, задания ЕГЭ по математике предполагают умение оперировать с модулем.

Уравнения, неравенства и другие задачи, связанные с модулем, к сожалению, либо мало, либо вообще не представлены в учебниках для массовых школ.  В последние годы в связи со сменой парадигмы образования, остро стоит вопрос об организации учебного процесса, направленного на развитие творческих способностей и навыков исследовательской деятельности. Решать эти проблемы,  и призван настоящий курс.

Задачи, предлагаемые в данном курсе, интересны и часто не просты в решении, что позволяет повысить учебную мотивацию учащихся и проверить свои способности к математике. Вместе с тем, содержание курса позволяет ученику любого уровня активно включаться в учебно-познавательный процесс и максимально проявить себя: занятия могут проводиться на высоком уровне сложности, но включать в себя вопросы, доступные и интересные всем учащимся.

Элективный курс посвящён систематическому изложению учебного материала, связанного с понятием модуля и аспектами его применения. В нём рассматриваются различные методы решения уравнений и неравенств с модулем, основанные на его определении, свойствах и графической интерпретации.

Для курса характерна практическая направленность. Его основное содержание составляют учебные задачи. Часть их приводится с полным решением, иллюстрирующим тот или иной метод. Другие предлагаются для самостоятельной работы. Правильность выполнения этих заданий контролируется посредством приведённых ответов. Изложение практических приёмов решения сопровождается необходимыми теоретическими сведениями.

Задачи с модулями играют важную роль в формировании логического мышления и математической культуры у школьников, но их решение вызывает значительные трудности. Это связано с тем, что каждое уравнение или неравенство с параметрами представляет собой целый класс обычных уравнений и неравенств, для каждого из которых должно быть получено решение. Поэтому задачи в данном курсе рассматриваются параллельно с изучением соответствующих  вопросов, вместе с тем происходит систематизация знаний и углубление,  как по содержанию, так и по практическому применению и методам обоснований. Т.о. данный курс способствует лучшему усвоению базового курса математики, а с другой — служит для внутрипрофильной дифференциации и построения индивидуального образовательного пути, для раскрытия основных закономерностей построения математической теории. Весь курс строится на решении различных по степени важности и сложности задач.

Учащиеся выполняют индивидуальные и групповые задания по самостоятельному решению задач, за что получают промежуточную оценку за изучение курса. Курс завершается результатом своей исследовательской деятельности и рассчитан на  34 часа.

Цели курса:

обобщение и систематизация, расширение и углубление знаний по теме «Алгебра модуля»;

обретение практических навыков выполнения заданий с модулем;

повышение уровня математической подготовки школьников.

 Задачи курса:

• вооружить учащихся системой знаний по теме «Алгебра модуля»;

• сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;

• подготовить учащихся к ЕГЭ;

• сформировать навыки самостоятельной работы, работы в малых группах;

• сформировать навыки работы со справочной литературой, с компьютером;

• сформировать умения и навыки исследовательской работы;

• способствовать развитию алгоритмического мышления учащихся;

• способствовать формированию познавательного интереса к математике.

Требования к уровню усвоения учебного материала

 

В результате изучения программы элективного курса «Алгебра модуля» учащиеся получают возможность знать и понимать:

• определение абсолютной величины действительного числа;

• основные операции и свойства абсолютной величины;

• правила построения графиков уравнений (в т.ч. функций), содержащих знак абсолютной величины;

• алгоритмы решения уравнений, неравенств, систем уравнений и неравенств, содержащих переменную под знаком модуля.

 Уметь:

• применять определение, свойства абсолютной величины действительного числа к решению конкретных задач;

• читать и строить графики функций, аналитическое выражение которых содержит знак абсолютной величины;

• решать уравнения, неравенства, системы уравнений и неравенств, содержащих переменную под знаком модуля.

Содержание

Тема 1. Определение модуля числа и его применение при решении задач.

Определение модуля. Аналитическая запись определения. Решение уравнений с помощью определения модуля.

Тема 2. Метод интервалов решения уравнений и неравенств, содержащих модуль.

Метод интервалов на примере решения уравнений. Решение неравенств и систем неравенств, содержащих модуль.

Тема 3. Решение неравенств вида /х/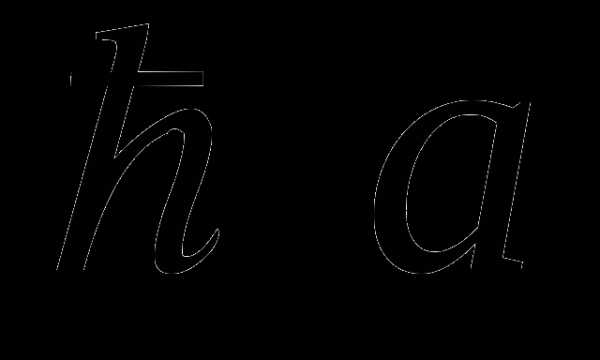, /х/посредством равносильности преобразований.

Равносильные преобразования при решении неравенств с модулем.

Решение неравенств.

Тема 4. Свойства модуля. Применение свойств модуля при решении уравнений и неравенств.

Свойства со знаком равенства. Свойства со знаком неравенства. Применение свойств модуля при решении уравнений и неравенств.

Тема 5. Решение уравнений и неравенств с модулями на координатной прямой.

Запись уравнений с модулем на «языке расстояний». Геометрическая иллюстрация уравнений с модулем. Решение уравнений и неравенств с модулями на координатной прямой.

Тема 6. Модуль и преобразование корней.

Применение понятия модуля при оперировании арифметическими корнями.

Тема 7. Модуль и иррациональные уравнения.

Использование модуля при решении иррациональных уравнений. Решение иррациональных уравнений.

Тема 8. Графики функций и уравнений, содержащих знаки модуля.

Построение графиков функций, содержащих модуль. Построение графиков функций вида:

y = |ƒ(x)| ; y = ƒ |x| ; и уравнений |y| = ƒ(x) ; |y| = |ƒ(x)|. Построение графиков уравнений вида: |y| = ƒ(x) и |y| = |ƒ(x)|.

Тема 9. Решение уравнений и неравенств с модулем.

Тригонометрические уравнения и неравенства с модулем.

Показательные и логарифмические уравнения с модулем.

Уравнения с параметрами, содержащие абсолютные величины.

Предлагаемые темы проектов, творческих работ учащихся

1. История возникновения модуля.

2. «Модуль и его применение».

3. Решение «нестандартных» задач.

4. Модель графиков функций, содержащих модуль и его применение

при построении графиков.

Учебно-тематический план

№

Тема занятия

Коч.час

Форма

контроля

1-2

Определение модуля числа и его применение при решении задач.

2

3

Метод интервалов решения уравнений и неравенств, содержащих модуль.

3

Математич.

диктант

3

Решение неравенств вида /х/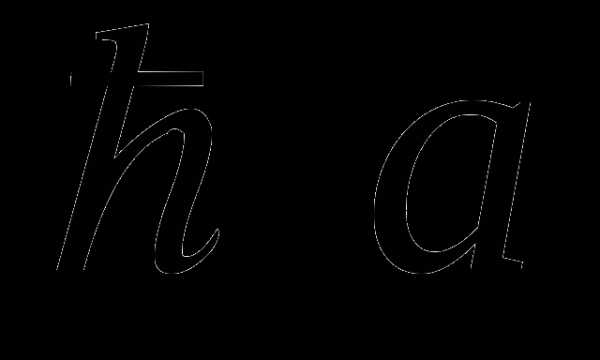, /х/посредством равносильности преобразований.

2

Устный опрос

4

Свойства модуля. Применение свойств модуля при решении уравнений и неравенств.

3

Тест

5

Решение уравнений и неравенств с модулями на координатной прямой.

2

Математич.

диктант

6

Модуль и преобразование корней.

1

7

Модуль и иррациональные уравнения.

3

Самост.работ.

8

Графики функций и уравнений, содержащих знаки модуля.

3

Тест

Тригонометрические уравнения и неравенства с модулем.

2

Домашняя

контр.работа

Показательные и логарифмические уравнения с модулем.

2

Уравнения с параметрами, содержащие абсолютные величины

3

Тест

Модуль в заданиях единого государственного экзамена.

5

Домашняя

контр.работа

9

Проверочная работа.

1

10

Тестирование.

1

11

Творческая работа учащихся

1

Защита проектов

Литература

1. Гайдуков И.И. Абсолютная величина: Пособие для учителей. 2-е изд.- М., 1968.

2. Галицкий М.Л. и др. Сборник задач по алгебре для 8-9 классов: Учебное пособие для учащихся школ и классов с углублённым изучением курса математики.- М. «Просвещение», 1992.

3. Звавич Л.И. и др. Задания для проведения письменного экзамена по математике  в 9 классе: Пособие для учителя.- М. «Просвещение», 1996.

4. Зильберберг Н.И. Алгебра для углубленного изучения математики.- Псков, 1992.

5. Изучение сложных тем курса алгебры в средней школе: Учебно-методические материалы по математике. М.: Илекса, Ставрополь: Сервисшкола, 2002.

6. Колесникова С.И. Математика. Решение сложных задач Единого государственного экзамена.- М.: Айрис-пресс, 2007.

7. Лысенко Ф.Ф. Тематические тесты. Математика ЕГЭ- 2009. Часть 2.- Ростов-на-Дону. Издательство «Легион», 2008.

8. Родионов Е.М. Решение задач с параметрами.- М.П. «Русь – 90»: М. 1995.

9. Симонов А.Я., Бакаев Д.С. и др. Система тренировочных задач и упражнений по математике.- М., «Просвещение», 1991 г.

10. Шарыгин М.Ф. Факультативный курс по математике. Решение задач- М., «Просвещение», 1983.

Рецензия

на рабочую программу по элективному курсу

«Алгебра модуля»

(автор- учитель математики МОУ «Косоржанская средняя общеобразовательная школа» Щигровского района Курской области Лихобабо Л.И.)

Рабочая программа по элективному курсу «Алгебра модуля» разработана в соответствии с Государственным образовательным стандартом по математике, с основными положениями концепции профильной школы. Программа соответствует современным целям общего образования.

Структура рабочей программы соответствует рекомендациям по разработке рабочих программ. Программа состоит из пояснительной записки, тематического плана с указанием затрат времени на изучение каждой темы, содержания и списка рекомендуемой литературы.

В пояснительной записке педагог подчёркивает значение изучаемого курса, обозначает цели и задачи элективного курса, требования к знаниям и умениям обучающихся.

Содержание элективного курса соответствует поставленным целям. Материал программы распределён во времени с учётом его достаточности для качественного изучения знаний и получения запланированного результата.

Рабочая программа по элективному курсу «Параметры в задачах» может быть одобрена и рекомендована к использованию в общеобразовательных учреждениях.

Рецензент-

старший преподаватель кафедры естественно-математического

цикла КИНПО (ПК и ПП) СОО __________________ М.Е.Чаплыгина

infourok.ru

Урок по алгебре(спецкурс) «Уравнения с модулем» в 10 классе.

Учитель Кирилюк Н. А.

Предмет: Спецкурс по математике

Класс – 10-А Дата: 24.03 Урок №

Тема. Решение уравнений с модулем

Цель: обобщить и систематизировать знания о модуле, полученные ранее, познакомить со способами решения уравнеий, формировать умения и навыки решения уравнений с модуле.

развивать логическое мышление, математическую культуру речи и письма , вычислительные навыки;

воспитывать настойчивость, усердие, чувство уверенности в себе, умение работать в коллективе; интерес к изучаемому материалу;

формировать такие виды компетентностей: информационную, познавательную, коммуникативную, социальную.

Планируемые результаты обучения

Учащиеся приобретут следующие умения:

— личностные:

· Развитие инициативности, самостоятельности, навыков сотрудничества в разных видах деятельности;

· Развитие интереса к познанию нового.

— метапредметные:

— Развитие логического мышления;

· Развитие культуры грамотной математической речи;

— предметные:

— Умение выстраивать логическую цепочку рассуждений, аргументировать свои действия, выполнять доказательства.

Формирование УУД (универсальные учебные действия):

Регулятивные: осуществлять итоговый и пошаговый контроль результата; выстраивать алгоритм действий; корректировать деятельность: выделение и осознание того, что уже усвоено и что подлежит усвоению, осознание качества и уровня усвоения.

Личностные: определять новый уровень отношения к самому себе как субъекту деятельности; формировать способность к мобилизации сил и энергии, к волевому усилию

Познавательные

строить логические рассуждения, включающие установление причинно-следственных связей; строить речевые высказывания в устной и письменной форме; уметь осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от конкретных условий;

Коммуникативные организовывать и планировать учебное сотрудничество с учителем и одноклассниками; формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы

Тип модуля: содержательно — поисковый

Вид модуля: комбинированный

Оборудование: учебник, тетради, раздаточный материал

IV. Изучение нового материала и его первичное закрепление.

Коллективная работа

30 мин.

V. Самостоятельная деятельность

Работа в парах, работа в группах

20 мин

VI. Домашнее завдание

5 мин

VII Итог урока. Рефлексия..

5 мин

Сценарий урока

I. Организационный момент

II. Мотивация учебной деятельности учащихся . Самопостановка целей и задач на урок.

К. С. Станиславский любил рассказывать такую притчу: «Индийский магараджа считал умение сосредоточиться настолько важным, что решил назначить министром того, кто владеет им лучше других. Поэтому он предложил претенденту на эту должность пронести по стене вокруг города большой кувшин с молоком, не пролив ни капли. При этом слуги должны были его всячески отвлекать. Многие пытались пронести кувшин, но терпели неудачу. Только один человек сумел выполнить условие магараджи. «Ты слышал крики?» — спросили его потом. «Нет».— «Ты слышал звуки выстрелов?» — «Нет».— «Ты видел, как вокруг тебя плясали, смеялись, прыгали?» — «Нет. Я ничего не видел и не слышал. Я смотрел на молоко». О чём эта притча? Как вы считаете? (о внимании)

III . Актуализация опорных знаний учеников

1. Проверка домашнего задания(самопроверка). Коррекция знаний учащихся.

2. Повторение. Заполнение пропусков в таблице с теоретическими сведениями

Заполните пропуски в утверждениях:

Модуль произведения двух и более чисел равен

________________________________________.

5.

Постоянный положительный множитель можно выносить ___________________________________

3. Устные упражнения

№ 1.Решить уравнения:

 |x−3|=6
 |x|=2,8
|2x−8|=4
 |3−3x|=6
 |10x+5|=−2

№ 2. Упростить выражение √(2a−6)2 если:
а) а−3≥0
б) a−3<0

IV. Изучение нового материала и его первичное закрепление.

1.Свойства модуля

1. |a| ≥ 0.

2. |a| ≥ a

3. (b≠0)

4. |a|=| —a|

5. |ab| = |a|*|b|

6. | a + b|≤| a|+|b|

7. | a+b|=|a|+|b|, когда ab≥0

8. | a+b|= a + b, когда a≥0, b≥0

9. |a – b| = |a|+|b|, когда ab≤0

10. |a|—|b|≥0, когда

2. Способы решения уравнений с модулем

Решения уравнений вида |f(x)|=b (b≥0)

| f(x)|=b

Пример 1.

|

Решение

=>

Ответ: ; 3; -1.

Решение уравнений с модулем по определению

Пример 2. Решим уравнение

Решение

=> =>

Ответ: -3; -2; 2; 3.

Решение уравнений вида |f(x)|=g(x)

|f(x)|=g(x) или |f(x)|=g(x)

Пример 3. Решим уравнение |3x+1|+x=9

|3x+1|=9-x => =>=>

Ответ:-5;2.

Решение уравнений вида |f(x)|=|g(x)|

|f(x)|=|g(x)| или |f(x)|=|g(x)|

Пример 4.

Решим уравнение |x+5|=|10+x|

Решение

;

10x=-75

X=-7.5

Ответ: -7.5

Решение уравнений с модулем по общей схеме

1) Найти ОДЗ.

2)Найти нули всех функций в модуле.

3)Обозначить нули на ОДЗ и разбить ОДЗ на промежутки.

4)Найти решения в каждом промежутке и проверить, входит ли это решение в рассмотренный промежуток.

Пример 5. Решим уравнение |x-2|+|x-4|=3

Решение

1)ОДЗ: R.

2) x-2=0, x=2

x-4=0, x=4.

3)

x-2 — + +

x-4 — — +

4)Найдем решение в каждом промежутке и проверим, входит ли данное решение в данный промежуток:

a) x

б) x

в) x (4;+; x-2+x-4=3;

Ответ: 1.5; 4.5.

V. Самостоятельная деятельность.

1.Работа в парах.

1) |x+2|=3

2)|x+3|=2x-1

3) |x+1|-|2x-3|=1

4)|x+2|+|x+3|=x

5) |x+5|-|x-3|=8

6)|+3x+2|+4x+10=0

2. Работа в группах .

( по сборнику Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и заданий для тематического оценивания по алгебре и началам анализа для 11 класса. — Харьков, Гимназия, 2006., стр 7)

| || |||

№8 №8 №8

1,2,3 4,5,6 7,8,9

10,11,12 13,14,15 16,17,18

1.|x+4.2|=5.1

2.|3x-5|=4.8

3.||x|-2|=2

10)-5x*-14=0

11)||-8x+4|-3|=7

12)|-3|x|+2|=1

4.|-x-1|=1

5.-|x|-2=0

6) x|x|+8x-7=0

13)|-2x|=3-2x

14) |x|+|x-4|=5

15)|x+1|+|x-3|=4

7) |x-4|+x=8

8) |x+3| —x=2

9) 2+|x-2|-1=0

16) |x|-|x-5|=6

17)|2x-3|-|x+2|=4x+5

18)|-4x+3|+|-5x+6|=1

3. Индивидуальные задания.

№ 1. | 8cos²x – cosx – 6 | + | 8cos²x – cosx – 3 | = 9.

№ 2. | 36^x – 6^x+1 – 3| + | 36^x – 6^x+1 – 13 | = 16.

VI. Домашнее задание

( по сборнику Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и заданий для тематического оценивания по алгебре и началам анализа для 11 класса. — Харьков, Гимназия, 2006.)

Стр.45 на выбор

1 группа №8 (1-4)

2 группа №8 (5-8)

3 группа №8 (9-11)

VII . Итог модуля. Рефлексия

.

Техника «рефлексивная мишень»

Участник ставит метки в сектора соответственно оценке результата: чем ближе к центру мишени, тем ближе к «5», на краях мишени оценка ближе к нулю. 

infourok.ru

Сайт учителя математики — Алгебра 10-11 классы

	Рабочие программы
10-11 классы		Рабочая программа по алгебре и началам анализа для 10-11 классов к УМК А.Г. Мордковича (профильный уровень) 5 часов
10-11 классы		Рабочая программа по алгебре и началам анализа для 10-11 классов к УМК А.Г. Мордковича (профильный уровень) 4 часа
10-11 классы		Рабочая программа по математике для 10-11 классов к УМК А.Г. Мордковича, Л.С. Атанасяна (базовый уровень) 5 часов
10 класс		Рабочая программа по алгебре и началам анализа для 10 класса к УМК А.Г. Мордковича (профильный уровень) 5 часов
11 класс		Рабочая программа по алгебре и началам анализа для 11 класса к УМК А.Г. Мордковича (профильный уровень) 5 часов
10 класс		Рабочая программа по математике для 10 класса к УМК А.Г. Мордковича, Л.С. Атанасяна (базовый уровень) 5 часов
	Презентации к урокам
10 класс		Действительные числа
10 класс		Модуль и его приложения
10 класс		Понятие функции. Свойства функций
10 класс		Функции, их свойства и графики
10 класс		Числовые последовательности
10 класс		Понятие производной
10 класс		Производная и ее применение
10 класс		Применение производной
10 класс		Числовая окружность
10 класс		Тригонометрия
10 класс		Построение графиков тригонометрических функций
10 класс		Обратные тригонометрические функции
10 класс		Решение тригонометрических уравнений и неравенств
10 класс		Решение тригонометрических уравнений и неравенств с примерами
10 класс		Преобразование графиков тригонометрических функций
10 класс		Методы решения тригонометрических уравнений
11 класс		Корень n-ой степени. Степень с рациональным показателем
11 класс		Первообразная. Интеграл
11 класс		Многочлены
11 класс		Показательная функция, ее свойства и график. Показательные уравнения и неравенства
11 класс		Логарифмическая функция, ее свойства и график. Логарифмические уравнения и неравенства
11 класс		Комплексные числа
1  2

semenova-klass.moy.su

Алгебра, 10 класс: уроки, тесты, задания

Действительные числа (профильный)

1. Натуральные числа

2. Рациональные числа

3. Иррациональные числа

Числовые функции

1. Обратная функция

2. Периодические функции (профильный)

Тригонометрические функции

1. Числовая окружность

2. Синус и косинус. Тангенс и котангенс

3. Тригонометрические функции числового аргумента

4. Тригонометрические функции углового аргумента

5. Свойства функции y=sinx и её график

6. Свойства функции y=cosx и её график

7. Периодичность тригонометрических функций, чётность, нечётность

8. График гармонического колебания (профильный)

9. Функции y=tgx, y=ctgx, их свойства и график

10. Обратные тригонометрические функции (профильный)

Тригонометрические уравнения

1. Арккосинус и решение уравнения cos х=a

2. Арксинус и решение уравнения sin x=a

3. Арктангенс и арккотангенс. Решение уравнения tg x=a, ctg x=a

4. Методы решения тригонометрических уравнений

Преобразование тригонометрических выражений

1. Синус и косинус суммы и разности аргументов

2. Тангенс суммы и разности аргументов

3. Формулы приведения

4. Формулы двойного аргумента

5. Формулы понижения степени (профильный)

6. Преобразования сумм тригонометрических функций в произведения

7. Преобразование произведений тригонометрических функций в суммы

8. Преобразование выражения A sin x+ B cos x к виду C sin (x+t) (профильный)

Производная

1. Числовые последовательности и их свойства

2. Предел числовой последовательности

3. Cумма бесконечной геометрической прогрессии

4. Предел функции

5. Определение производной

6. Вычисление производных

7. Уравнение касательной к графику функции

8. Применение производной для исследования функций на монотонность и экстремумы

9. Построение графиков функции

10. Применение производной для отыскания наибольших и наименьших величин

www.yaklass.ru