4 класс. Моро. Учебник №1. Ответы к стр. 19
Числа от 1 до 1000
Что узнали. Чему научились
Ответы к стр. 19
12.
600 – 60 : 6 : 2 = 595 960 – 640 : (4 + 4) • 2 = 800
(600 – 60) : 6 : 2 = 595 (960 – 640) : 4 + 4 • 2 = 88
176 + 218 + 206 = 600 295 + 217 + 488 = 1000
13. Для школьной мастерской купили рубанки, отвёртки и молотки. Рубанков 36 штук, отвёртки составляли третью часть числа рубанков, а молотков было в 4 раза больше, чем отвёрток.
Объясни, что обозначают выражения:
36 : 3 36 : 3 + 36 36 : 3 • 4 36 + 36 : 3 • 4
36 : 3 – количество отвёрток
36 : 3 + 36 – количество рубанков и отвёрток
36 : 3 • 4 – количество молотков
36 + 36 : 3 • 4 – количество рубанков и молотков
14.
Измени числа так, чтобы задача решалась двумя способами. Сравни эти способы решения.
1) 38 + 50 = 88 (кг) – всего помидоров собрали
2) 88 : 8 = 11 (ящ.)
В одной теплице собрали 40 кг помидоров, в другой – 48 кг. Все эти помидоры разложили в ящики, по 8 кг в каждый. Сколько таких ящиков потребовалось?
1-й способ – вычислить, сколько ящиков нужно для каждой теплицы, а затем найти их общее количество.
1) 40 : 8 = 5 (ящ.) – нужно для первой теплицы
2) 48 : 8 = 6 (ящ.) – нужно для второй теплицы
О т в е т: потребовалось 11 ящиков.
2-й способ – узнать, сколько всего помидор собрали и найти необходимое количество ящиков.
1) 40 + 48 = 88 (кг) – всего помидор
2) 88 : 8 = 11 (ящ.) – потребуется
О т в е т: потребовалось 11 ящиков.

В пером способе решения задачи выполняется большее количество действий, чем во втором способе, следовательно, второй способ рациональнее.
15. 1) Ученик затратил на решение задачи 6 мин, а на решение каждого из 8 примеров по 3 мин. Сколько всего времени затратил ученик на выполнение этого домашнего задания?
6 + 3 • 8 = 30 (мин)
О т в е т: ученик на выполнение этого домашнего задания затратил 30 мин.
2) Заметь по часам и запиши, сколько времени тебе потребовалось на выполнение домашнего задания по математике.
Самостоятельное выполнение.
1. Как можно получить число, которое следует при счёте сразу за любым данным числом?
Надо к данному числу прибавить единицу.
2. Прочитай, заполняя пропуски.
10 ед. = 1 дес. 1 сот. = 10 ед. 1 тыс. = 1000 ед.
10 дес. = 1 сот. 1 сот. = 10 дес. 1 тыс. = 100 дес.
10 сот. = 1 тыс. 1 тыс.
3. Как по-разному можно прочитать выражения?
320 + 40 – Сумма чисел 320 и 40; 320 увеличить на 40; к 320 прибавить 40; 320 плюс 40.
470 – 300 – Разность чисел 470 и 300; 470 уменьшить на 300; от 470 отнять 300; 470 минус 300.
80 • 5 – Произведение чисел 80 и 5; 80 увеличить в 5 раз; 80 умножить на 5.
900 : 3 – Частное чисел 900 и 3; 900 уменьшить в 3 раза; 900 разделить на 3.
4. Объясни, в каком порядке должны выполняться действия по схематическим записям. обозначает число.
1 2 3 4 5
1) + – + + –
Действия выполняются по порядку.
1 2 3 4
2) • : • •
Действия выполняются по порядку.
3 1 4 2 5
3) + • – : +
Сначала умножение и деление (по порядку слева направо), затем сложение.
2 1 3
4) – ( : ) +
Сначала выполняется действие в скобках, затем вычитание, потом сложение.
3 1 4 2
5) – ( + ) – ( – )
Сначала выполняется действие в скобках (по порядку слева направо), затем вычитание.
3 2 1 4
6) – ( – • ) +
Сначала выполняется действия в скобках (умножение, затем вычитание), потом вычитание и сложение.
4 2 1 3
7) – ( + : ) •
Сначала выполняется действие в скобках (деление, затем сложение), затем умножение и вычитание.
2 1 3
8) : ( – ) •
Сначала выполняется действия в скобках, затем деление, потом умножение.
ЗАДАНИЕ НА ПОЛЯХ:
РЕБУС
999 + 1 = 1000
Проверочные работы, с. 12, 13
Ответы по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
В.
Математика. 4 класс
1.5 / 5 ( 154 голоса )
Страница 99 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
Вернуться к содержанию учебника
Итоговое повторение всего изученного
Вопрос
9. Из 20 кг свежего картофеля получается 6 кг сушёного. Сколько свежего картофеля надо переработать, чтобы получить сушёного картофеля 60 кг? 3 ц? 3 т?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
 При посеве гороха на 100 м2 расходуют 2 кг семян. Сколько килограммов гороха можно собрать с участка прямоугольной формы длиной 60 м и шириной 20 м, если урожай гороха в 16 раз больше, чем его расход при посеве?
При посеве гороха на 100 м2 расходуют 2 кг семян. Сколько килограммов гороха можно собрать с участка прямоугольной формы длиной 60 м и шириной 20 м, если урожай гороха в 16 раз больше, чем его расход при посеве?Реши задачу разными способами.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
11. В два района отправлены учебники одинаковыми пачками: в один — 200 пачек, а в другой — 300 пачек. Сколько учебников отправлено в каждый район, если в первый район отправили на 2000 учебников меньше, чем во второй?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
12. Две бригады рабочих должны посадит 490 лип. Сколько лип посадит каждая бригада, если распределить работу по числу рабочих и если в первой бригаде 34 рабочих, а во второй 36?
Две бригады рабочих должны посадит 490 лип. Сколько лип посадит каждая бригада, если распределить работу по числу рабочих и если в первой бригаде 34 рабочих, а во второй 36?
Подсказка
Повтори случаи внетабличного деления.
Если есть схематический рисунок, таблица или чертёж, краткую запись задачи составлять не нужно.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
13. На двух участках посадили деревья: на одном 18 одинаковых рядов, на другом 14 таких же рядов. Всего посадили 1152 дерева. Сколько деревьев посадили на каждом участке?
Всего посадили 1152 дерева. Сколько деревьев посадили на каждом участке?
Подсказка
Повтори алгоритм письменного умножения и деления многозначных чисел.
Если есть схематический рисунок, таблица или чертёж, краткую запись задачи составлять не нужно.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
14. Одна бригада рабочих может посадить 600 плодовых деревьев за 10 дней, а другая — за 15 дней. За сколько дней могут посадить эти деревья две бригады, работая вместе с такой же производительностью?
Подсказка
Если есть схематический рисунок, таблица или чертёж, краткую запись задачи составлять не нужно.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
15. В детский сад привезли 10 ящиков моркови, по 9 кг в каждом, и 8 одинаковых по массе ящиков свёклы. Всего привезли 170 кг овощей. Сколько килограммов свёклы было в одном ящике?
Составь и реши задачи, обратные данной.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
16. 1) Сестре 12 лет, а брату 7 лет. На сколько лет сестра будет старше брата через 5 лет? через 20 лет?
1) Сестре 12 лет, а брату 7 лет. На сколько лет сестра будет старше брата через 5 лет? через 20 лет?
2) Сыну 9 лет, а его папа на 27 лет старше. Во сколько раз папа старше сына?
Подсказка
Повтори единицу времени — год.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Ребус
Подсказка
Повтори алгоритм письменного деления многозначного числа на двузначное.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Магический квадрат
Подсказка
Магический квадрат — таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
© budu5.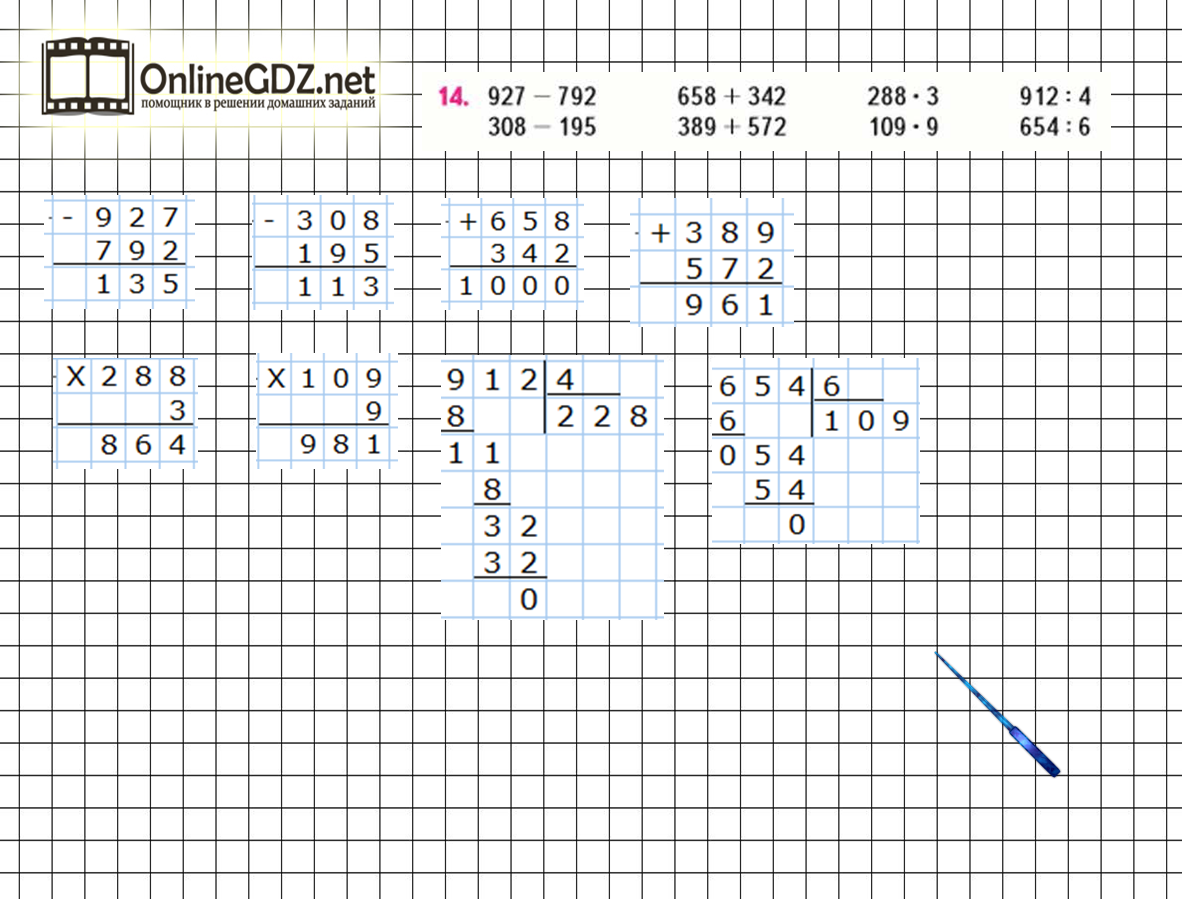 com, 2021
com, 2021
Пользовательское соглашение
Copyright
ВПР 4 класс математика 2021, Ященко. Вариант 14 с ответами
ВПР по математике за 4 класс 2021 года И. В. Ященко — вариант 14
При написании данной работы «ВПР по математике за 4 класс 2021 года И. В. Ященко — вариант 14» было использовано пособие «Всероссийская проверочная работа. Математика 4 класс 25 вариантов. Типовые задания. Г.И. Вольфсон, И.Р. Высоцкий, под редакцией И.В. Ященко 2021 год».
Задание 1
Найди значение выражения 27 + 26.
Решение
27 + 26 = 53
Ответ:
53
Задание 2
Найди значение выражения (17 + 6) * 3 — 6.
Решение
Памятка
Действия выполняются по порядку слева направо, сначала выполняется умножение и деление, а затем – сложение и вычитание. Действия в скобках выполняются в первую очередь.
Действия в скобках выполняются в первую очередь.
17 + 6 = 23
23 * 3 = 69
69 — 6 = 63
Ответ:
63
Задание 3
По правилам авиаперевозок, если багаж весит больше 20 кг, то за перевес нужно доплатить. Рассмотри рисунок с багажом туриста и ответь на вопрос: за сколько килограммов туристу придется доплатить?
Решение
Определим общий вес багажа:
11 + 5 + 6 = 22 (кг) — вес всего багажа
Определим перевес багажа:
22 — 20 = 2 (кг) — вес, за который придется доплатить
Ответ:
Туристу придется доплатить за 2 кг.
Задание 4
Катя родилась в сентябре 2005 года. Сколько полных лет было Кате в марте 2015 года?
Решение
Определим разницу между двумя датами (в годах)
2015 — 2005 = 10 лет
Так как в условии задачи речь идет о марте, то 10-ый год еще не наступил, следовательно Кате было полных 9 лет.
Ответ:
9 лет
Задание 5
- Нарисуй по клеточкам прямоугольник так, чтобы его стороны проходили через все отмеченные точки.

- Найди периметр этого прямоугольника, если сторона клетки — 1 см.
Решение
- Нарисуй по клеточкам прямоугольник так, чтобы его стороны проходили через все отмеченные точки.
- Найди периметр этого прямоугольника, если сторона клетки — 1 см.
одна сторона a равна 5 клеткам, или 5 см
другая сторона b равна 2 клеткам, или 2 см
Определим периметр прямоугольника:
Р = (a + b) * 2 = (5 + 2) * 2 = 7 * 2 = 14
Ответ:
Периметр прямоугольника равен 14 см
Задание 6
В таблице приведены данные о численности населения трёх областей России в разные годы (в тыс. человек). Используя эти данные, ответь на вопросы.
| Область | Численность населения | ||||
| 1970 г. | 1979 г. | 1990 г. | 2000 г. | 2010 г. | |
| Новосибирская | 2505 | 2618 | 2742 | 2725 | 2665 |
| Омская | 1825 | 2140 | 2153 | 2136 | 1975 |
| Иркутская | 2315 | 2560 | 2795 | 2644 | 2430 |
- В каком году численность населения Омской области была наибольшей?
- В какой области численность населения за период с 1970 по 2010 год выросла больше, чем в двух других?
Решение
- В каком году численность населения Омской области была наибольшей?
| Область | Численность населения | ||||
1970 г. | 1979 г. | 1990 г. | 2000 г. | 2010 г. | |
| Новосибирская | 2505 | 2618 | 2742 | 2725 | 2665 |
| Омская | 1825 | 2140 | 2153 | 2136 | 1975 |
| Иркутская | 2315 | 2560 | 2795 | 2644 | 2430 |
В 1990 году численность населения Омской области была наибольшей — 2153 тыс. чел.
- В какой области численность населения за период с 1970 по 2010 год выросла больше, чем в двух других?
Определим разницу между 2010 и 1970 гг для каждой области:
- 2665 — 2505 = 160 (чел.) — Новосибирская обл.
- 1975 — 1825 = 150 (чел.) — Омская обл.
- 2430 — 2315 = 115 (чел) — Иркутская обл.
Больше других выросла численность в Новосибирской области
Ответ:
- в 1990 году
- в Новосибирской области
Задание 7
Найди значение выражения 4004 * 5 — 540 : 6.
Решение
Памятка
Действия выполняются по порядку слева направо, сначала выполняется умножение и деление, а затем – сложение и вычитание. Действия в скобках выполняются в первую очередь.
4004 * 5 = 20020
540 : 6 = 90
20020 — 90 = 19930
Ответ:
19930
Задание 8
Аня и Таня договорились встретиться у четвертого вагона поезда. Аня отсчитывает вагоны с «головы» состава, а Таня — с «хвоста» состава, Тем не менее они подошли к одному и тому же вагону. Сколько вагонов в поезде?
Решение
Аня отсчитала 3 вагона с «головы» состава, а Таня отсчитала 3 вагона с «хвоста», 4-ый вагон оказался общим.
Получается 3 + 1 + 3 = 7 вагонов
Ответ:
В поезде 7 вагонов.
Задание 9
Аня делает открытки к Восьмому марта для родственников: мамы, бабушки и тёти, Сначала она сделала открытку оранжевого цвета, затем — розового, а потом — фиолетового. Известно, что мамин любимый цвет фиолетовый, а бабушка не любит розовый цвет.
- Открытка какого цвета досталась тёте?
- Для кого Аня сделала открытку сразу после открытки для бабушки?
Решение
- 1 открытка — оранжевая
- 2 открытка — розовая
- 3 открытка — фиолетовая
Мамин любимый цвет жёлтый, а бабушка не любит зелёный цвет. Получаем:
- 1 открытка — оранжевая — бабушка не любит розовый цвет, значит эта открытка для неё
- 2 открытка — розовая — открытка для тёти
- 3 открытка — фиолетовая — мамин любимый цвет фиолетовый — эта открытка для мамы
- Открытка какого цвета досталась тёте?
Розовая
- Для кого Аня сделала открытку сразу после открытки для бабушки?
Для тёти
Ответ
- розовая
- для тёти
Задание 10
На столбе висел знак (см. рис. 1). Верхний болт, державший знак, отвалился, и знак перевернулся. Нарисуй, как будет выглядеть знак (рис. 2).
Решение
Задание 11
Петя говорит Васе: «Я легче тебя в три раза». А Вася говорит Пете: «А я тяжелее тебя на 30 килограммов». Оба говорят правду. Сколько весит Петя?
А Вася говорит Пете: «А я тяжелее тебя на 30 килограммов». Оба говорят правду. Сколько весит Петя?
Решение
Решение 1:
Если вес Пети = П, а вес Васи = В, получим:
П = В : 3 — поскольку Петя легче Васи в 3 раза
В = П + 30 — поскольку Вася тяжелее Пети на 30 кг
Из последнего выражения найдем чему равен вес Пети:
В = П + 30
П = В — 30
Мы получили два выражения:
П = В : 3
П = В — 30
Так как оба они равны весу Пети, мы можем их уровнять:
В : 3 = В — 30
В = 3 * (В — 30) = 3В — 90
3В — В = 90
2В = 90
В = 90 : 2 = 45 (кг) — вес Васи
45 : 3 = 15 (кг) — вес Пети
Решение 2:
По условию задачи Вася в три раза тяжелее Пети. Следовательно, если вес Пети взять за 1 часть, то вес Васи будет равен: 1 часть + 1 часть + 1 часть.
Петя легче Васи на 30 кг (т.е. это вес двух частей), следовательно одна часть равна:
30 : 2 = 15 (кг) — вес Пети
Ответ:
Петя весит 15 килограммов.
Страница 21 (учебник Моро 2 часть 4 класс) ответы по математике
10. Начерти окружность, проведи в ней диаметр и соедини концы диаметра с любой точкой окружности. Проверь, какого вида треугольник получился.В результате получится прямоугольный треугольник.
1) a = 7020 и b = 6; 2) а = 17418 и b = 3. 12. Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. Первый мальчик бежал со скоростью 4 м/с. С какой скоростью бежал второй мальчик?
1) 10 * 4 = 40 м пробежал до встречи первый мальчик.
2) 100 — 40 = 60 м пробежал до встречи второй мальчик.
3) 60 : 10 = 6 м/с скорость второго мальчика.Ответ: 6 м/с.
1) 3 + 4 = 7 ч был поезд в пути.
2) 315 : 7 = 45 км/ч скорость поезда.
3) 3 * 45 = 135 км прошел поезд до остановки.
4) 4 * 45 = 180 км прошел поезд после остановки.Ответ: 135 км, 180 км.
1) 90 : 3 = 30 (мм) — одна часть из трёх
2) 30 : 2 = 15 (мм) — одна часть из двух
3) 90 : 15 = 6 (ч.) — всего
4) 90 : 6 = 15 (мм) — шестая частьОтвет: на 6 частей, шестая часть — 15 мм.
1) 56 * 20 = 1120 (кг) было всего масла.
2) 1120 : 7 = 160 (кг) масла продали.
3) 1120 — 160 = 960 (кг) масла осталось.
Ответ: 960 кг.
1) 60 + 15 = 75 (км/ч) — скорость сближения.
2) 150 : 75 = 2 (ч) — время в пути.
3) 15 * 2 = 30 (км) расстояние до встречи.Ответ: 30 км.
1751 : 5 = 350 (ост. 1)
1983 : 9 = 220 (ост. 3)
2930 : 7 = 418 (ост. 6)
40202 : 6 = 6700 (ост. 2)
4527 * 50 − 710037 : 9 = 226350 − 78893 = 147457
(932 + 17692) : 6 * 80 = 18624 : 6 * 80 = 3104 * 80 = 248320
32340 : 10 = 3234
56400 : 100 = 564

5 * 9 = 45
45 * 5 = 225
45 * 9 = 405
225 * 5 = 1125
225 * 9 = 2025
Россия заняла второе место на Международной математической олимпиаде школьников
Анастасия ДолгошеваСтрана и мир 27 Июля 2021
Во времена «новой России» мы бывали первыми – в 1999-м и 2007-м, но советские команды лидировали 14 раз. Тогда тоже случались падения: в 1981-м – до девятого места, но самое сокрушительное было недавно, в 2017-м, 11-е место. Второй год подряд 2-е место в командном зачете – это рост: год назад у российской сборной было два золота и четыре серебра, в этом году – пять золотых наград (две из них – у петербуржцев) и одна серебряная. Ученик Президентского физматлицея № 239 Максим Туревский по личному результату и вовсе второй в мире.
ФОТО Pixabay
На первом месте в командном зачете Китай. Не будем успокаивать себя, дескать, «там народищу столько, что есть из кого выбирать юные таланты». Будем уважать способность китайцев концентрироваться: в 1985-м в командном зачете они были на 32-м месте, а уже на следующий год заняли 4-е. С 1997 года не выпадают из тройки лидеров. 17 раз были первыми.
Задачи на ММО несопоставимы, пожалуй, ни с чем, кроме задач самой ММО, говорит председатель жюри Назар Агаханов, причастный к проведению этой олимпиады на протяжении почти четверти века:
– Задания международных олимпиад не технические, а творческие, на построение логической модели.
Решить задачи для поступления даже в самый «сложный» университет по силам нескольким десяткам школьников страны. На Международной олимпиаде в условии задачи могут фигурировать потешные Чип и Дейл, которые собрали на зиму 2021 орешек, зарыли их в ямки, а потом что-то напутали. .. Но из 600 сильнейших юных математиков со всего мира с самыми сложными задачами ММО могут справиться меньше 20 человек.
.. Но из 600 сильнейших юных математиков со всего мира с самыми сложными задачами ММО могут справиться меньше 20 человек.
– Если рассматривать задачи, которые были на Олимпиаде сорок – пятьдесят лет назад, они чуть легче нынешних, – говорит председатель совета Международной математической олимпиады британец Джефф Смит. – А задачи, которые были на самых первых олимпиадах, сейчас кажутся совсем простыми. Но, честно говоря, легко придумать трудный вопрос. Сложнее найти что-то оригинальное и новое для вопроса «попроще». Но мы стараемся.
В целом олимпиадная задача – это поиск того, как справиться с проблемой, у которой еще нет алгоритма решения. «Именно это нужно в жизни», – констатирует Джефф Смит. Не случайно среди финансовых аналитиков в Нью-Йорке и Лондоне «немало русских ребят, которые побеждали на олимпиаде».
Нынешняя Международная математическая – 62-я по счету. Россия и Советский Союза принимали ее шесть раз, из них четыре раза – Москва. Петербург до прошлого года не принимал никогда, зато как начал, так и не смог остановиться: впервые в истории ММО ее два раза подряд провели в одном городе.
Россия и Советский Союза принимали ее шесть раз, из них четыре раза – Москва. Петербург до прошлого года не принимал никогда, зато как начал, так и не смог остановиться: впервые в истории ММО ее два раза подряд провели в одном городе.
Правда, в прошлом году все надеялись, что в 2021-м наверстают упущенное из-за дистанционного формата. У пандемии оказались другие планы. Участники, как и в прошлом году, сидели в своих странах и решали задачи удаленно, а члены жюри проверяли присланные сканы работ.
– Есть некоторые сложности, потому что школьники находятся в разных часовых поясах, – комментировал а пресс-конференции в ТАСС Джефф Смит. – Мы должны были проводить олимпиаду так, чтобы не получилось, что один участник начинал, когда другой уже закончил. Поэтому в некоторых странах ребята решали задачи в очень позднее время, а, к примеру, в Америке – очень рано.
Еще одна особенность дистанционных олимпиад такого уровня: сложнее утрясти вопросы относительно справедливости оценки. Как поясняет Назар Агаханов, одно дело, когда два математика, от жюри и от национальной сборной, профессионально беседуют, глядя в глаза друг другу. Другое – когда все происходит в переписке, «так сложнее находить общий язык».
Как поясняет Назар Агаханов, одно дело, когда два математика, от жюри и от национальной сборной, профессионально беседуют, глядя в глаза друг другу. Другое – когда все происходит в переписке, «так сложнее находить общий язык».
Общекомандный зачет – штука неофициальная, хотя и показательная. Состязание все равно «личное», и тут у российской сборной отличный результат. Оба представителя Петербурга из Президентского физмат-лицея № 239. Иван Бахарев и Максим Туревский перешли из десятого класса в одиннадцатый, а значит, как отмечает директор лицея Максим Пратусевич, смогут участвовать в ММО в следующем году. Их педагог – создатель математического центра при лицее Сергей Рукшин, на счету которого уже более 100 победителей международных олимпиад еще с советских времен, а руководитель всего тренерского состава – учитель математики этого же лицея Кирилл Сухов.
Джефф Смит определил некоторые тенденции в математическом олимпийском движении: в 1980-е и 1990-е годы очень хорошо выступали страны Центральной и Восточной Европы. В последние годы вперед вырвались Китай, Вьетнам, Южная Корея:
В последние годы вперед вырвались Китай, Вьетнам, Южная Корея:
– Центр математики сместился в Азию. Но не волнуйтесь: Россия хорошо выступает. И Великобритания, кстати, тоже.
Команда из страны Джеффа Смита два года подряд на девятом месте, а перед этим была на 20-м и 12-м. США — на четвертом. Из бывшего Союза выше всех помимо России поднялась Украина: 6-е место – с прошлогоднего 11-го. Казахстан – 20-е место (был на 21-м). Белоруссия в этом году 24-я, но это успех по сравнению с прошлогодним 45-м местом.
Еще одна тенденция – в ММО участвует все больше стран арабского мира: Саудовская Аравия и Египет стали выступать каждый год.
Вот процентное соотношение девчонок в ММО держится пока на планке 10% – хотя, по словам Джеффа Смита, бывают годы, когда барышни оказываются лучшими юными математиками по результатам. Чтобы нарастить представительство девчонок, с 2012 года проводится Европейская математическая олимпиада для девушек – в европейской, впрочем, участвуют школьницы со всего мира. Как говорит Джефф Смит, эффект «девчачьей» олимпиады оценить пока трудно – времени прошло мало, «но впервые за очень долгое время в британскую команду на Международной математической олимпиаде вошли две девочки. Возможно, это результат той работы».
Как говорит Джефф Смит, эффект «девчачьей» олимпиады оценить пока трудно – времени прошло мало, «но впервые за очень долгое время в британскую команду на Международной математической олимпиаде вошли две девочки. Возможно, это результат той работы».
Как говорит Назар Агаханов, для любого государства важно, чтобы наука пополнялась кадрами. Прекрасная половина человечества в этом смысле еще не раскрытый потенциал. Максим Пратусевич отметил: во время Международной матолимпиады 2017 года, которая проходила в Бразилии, пришла горестная весть – после тяжелой болезни умерла 40-летняя Мариам Мирзахани, первая женщина – обладатель математической Филдсовской медали. В память о Мариам была учреждена премия специально для девушек, отличившихся на ММО.
Но в целом, говорит Максим Пратусевич, математику надо развивать и вне олимпийского движения:
– Если мы говорим про цифровую трансформацию нашей жизни, то любой человек, который претендует на что-то большее, чем быть потребителем, без математики не сможет.
Сейчас, по словам директора лицея, если человек в шестом-седьмом классе проседает по математике, для него закрывается примерно половина всех профессиональных возможностей – тех, что связаны с современными технологиями: биоинформатика, химинформатика и все, что на стыке с цифрой.
Следующая ММО пройдет в Норвегии, в Осло. Джефф Смит очень надеется, что она будет «обычная». По нынешним временам это означает – «очная».
Но из Петербурга математика не уходит: в 2022-м город и страна принимут Математический конгресс, главное событие года для математического мира – на нем, в частности, определяют и филдсовских лауреатов.
Материал опубликован в газете «Санкт-Петербургские ведомости» № 136 (6974) от 27.07.2021 под заголовком «Дважды два».
Материалы рубрики
Задания для детей 6 лет, задачи и развивающие задания детям 6 7 лет, распечатать
Дата публикации: .
Развивающие задания детям от 6 до 7 лет. Скачать и распечатать бесплатно в pdf
Представлены задания на: количественный счет предметов, распознавание плоских и объемных геометрических фигур, знание цветов, навыков написания цифр от 1 до 4, сложение и вычитание чисел от 1 до 5.
Ребёнок в 6 лет должен
– Уметь считать от одного до десяти и обратно.
– Знать основные геометрические фигуры (квадрат, прямоугольник, круг, треугольник).
– Уметь сравнивать две группы предметов.
– Группировать предметы по форме и цвету.
– Уметь составлять задачи на счет до 10 и решать их. Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
1. Задания на логическое сравнение предметов
Посмотри внимательно на рисунок.
Выбери шарики, которые должны быть в квадратиках.
Сколько кружек на картинке?
В каком ряду столько же предметов, сколько кружек?
Какого цвета фигура должна быть последней?
2.
 Задание на сложение чисел
Задание на сложение чиселСложи числа.
2 + 6 + 1 = ______ 5 + 1 + 3 = ______ 2 + 9 + 0 = ____
3 + 1 + 4 = ______ 4 + 0 + 2 = ______ 1 + 3 + 3 = ____
2 + 0 + 3 = ______ 6 + 1 + 9 = ______ 4 + 3 + 1 = ____
5 + 0 + 2 = ______ 5 + 8 + 7 = ______ 7 + 6 + 2 = ____
Сложи числа в столбик.
3. Умножение чисел (задания повышенной сложности)
Перемножь числа.
2 х 6 = ______ 5 х 1 = ______ 2 х 0 = ____
3 х 4 = ______ 4 х 0 = ______ 1 х 3 = ____
2 х 3 = ______ 6 х 1 = ______ 4 х 1 = ____
5 х 2 = ______ 5 х 8 = ______ 7 х 2 = ____
Реши задачи на умножение.
1) Книга стоит 1 рубль. Сколько надо заплатить за 3 книги?
2) В корзине лежат 4 яблока. Сколько яблок лежит в двух корзинах?
3) Катя выпивает 3 кружки молока за 1 день. Сколько кружек молока она выпивает за 2 дня?
4. Задания на распознавание геометрических фигур:
Напиши названия геометрических фигур.

Обведи геометрические фигуры. Как они называются?
Обведи фигуры и закрась их как показано. Как они называются?
Назови фигуры и цвета.
Обведи все треугольники и закрась их в красный цвет.
Обведи все окружности и закрась их в синий цвет.
Обведи все звездочки и закрась их в зеленый цвет.
4. Задания на копирование фигур и написание чисел:
Скопируй следующие фигуры. Знаешь как они называются?
Скопируй следующие фигуры. Как они называются и какого они цвета?
Скопируй следующие фигуры. Как они называются и какого они цвета?
Напиши цифру один.
Напиши цифру два.
Напиши цифру три.
Напиши цифру четыре.
Скопируй следующие цифры. Знаешь как они называются?
Распознавание чисел до 5.
1. Подчеркни каждую 2.
1 5 2 3 1 0 1 3 5 3
2. Подчеркни каждую 1.3 3 4 1 1 2 5 4 4 1
3. Подчеркни каждую 3.5 1 0 2 3 2 1 4 3 5
4. Подчеркни каждую 5.
Подчеркни каждую 5.2 0 4 5 3 4 1 1 5 1
5. Подчеркни каждую 2.3 3 4 2 5 0 5 2 4 2
6. Подчеркни каждую 3.2 4 1 4 5 0 2 5 5 2
7. Подчеркни каждую 4.3 2 3 0 1 5 5 0 2 2
8. Подчеркни каждую 5.5 1 3 2 1 3 5 1 1 1
Распознавание чисел до 10.
1. Подчеркни каждую 2.
3 8 6 2 5 8 10 8 1 8
2. Подчеркни каждую 1.5 4 5 4 1 4 0 7 1 8
3. Подчеркни каждую 6.2 2 8 5 2 9 6 0 7 8
4. Подчеркни каждую 9.3 1 6 4 7 6 9 10 8 3
5. Подчеркни каждую 7.1 8 2 5 6 7 9 7 1 1
6. Подчеркни каждую 3.1 0 5 9 1 9 7 4 8 10
7. Подчеркни каждую 8.10 10 8 9 4 10 1 8 3 0
8. Подчеркни каждую 10.9 6 9 3 7 4 7 3 4 3
Распознавание чисел до 20.
1. Подчеркни каждое число равное 12.
12 16 10 14 18 18 12 16 10 14
2. Подчеркни каждое число равное 15.12 19 13 18 12 11 14 13 19 13
3. Подчеркни каждое число равное 13.12 13 10 20 15 19 14 14 13 15
4. Подчеркни каждое число равное 10.20 18 13 20 20 10 15 19 12 13
5. Подчеркни каждое число равное 16.17 20 18 18 10 14 14 20 11 15
6. Подчеркни каждое число равное 17.11 19 11 16 17 10 12 11 16 20
7. Подчеркни каждое число равное 11.17 15 10 18 16 15 19 10 13 11
8. Подчеркни каждое число равное 18.17 14 13 14 13 20 17 19 15 12
4. Задания повышенной сложности на сложение и вычитание чисел:
Стр. 1.
Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||||
| Сложи два однозначных числа. Сумма чисел до 5. | ||||||||||||||||
| 2 | + | 1 | = | __ | 4 | + | 0 | = | __ | 0 | + | 3 | = | __ | ||
| 2 | + | 3 | = | __ | 5 | + | 0 | = | __ | 1 | + | 3 | = | __ | ||
| 2 | + | 3 | = | __ | 1 | + | 2 | = | __ | 3 | + | 2 | = | __ | ||
| 4 | + | 1 | = | __ | 2 | + | 0 | = | __ | 1 | + | 0 | = | __ | ||
| 2 | + | 2 | = | __ | 4 | + | 1 | = | __ | 1 | + | 0 | = | __ | ||
| 3 | + | 2 | = | __ | 5 | + | 0 | = | __ | 3 | + | 2 | = | __ | ||
| 4 | + | 0 | = | __ | 2 | + | 2 | = | __ | 0 | + | 0 | = | __ | ||
| 2 | + | 3 | = | __ | 4 | + | 1 | = | __ | 1 | + | 0 | = | __ | ||
| 2 | + | 1 | = | __ | 4 | + | 1 | = | __ | 2 | + | 0 | = | __ | ||
| 1 | + | 4 | = | __ | 3 | + | 2 | = | __ | 1 | + | 3 | = | __ | ||
| 3 | + | 2 | = | __ | 4 | + | 1 | = | __ | 3 | + | 1 | = | __ | ||
| 0 | + | 4 | = | __ | 4 | + | 0 | = | __ | 0 | + | 2 | = | __ | ||
Стр. 2.
Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||||
| Сложи два однозначных числа. Сумма чисел до 5. | ||||||||||||||||
| 1 | + | 3 | = | __ | 0 | + | 5 | = | __ | 0 | + | 4 | = | __ | ||
| 0 | + | 0 | = | __ | 3 | + | 2 | = | __ | 2 | + | 3 | = | __ | ||
| 4 | + | 1 | = | __ | 2 | + | 3 | = | __ | 3 | + | 0 | = | __ | ||
| 3 | + | 1 | = | __ | 3 | + | 0 | = | __ | 2 | + | 0 | = | __ | ||
| 3 | + | 1 | = | __ | 5 | + | 0 | = | __ | 0 | + | 1 | = | __ | ||
| 2 | + | 2 | = | __ | 1 | + | 1 | = | __ | 2 | + | 0 | = | __ | ||
| 4 | + | 0 | = | __ | 5 | + | 0 | = | __ | 1 | + | 4 | = | __ | ||
| 4 | + | 1 | = | __ | 2 | + | 0 | = | __ | 1 | + | 1 | = | __ | ||
| 0 | + | 4 | = | __ | 0 | + | 0 | = | __ | 1 | + | 2 | = | __ | ||
| 3 | + | 0 | = | __ | 4 | + | 0 | = | __ | 1 | + | 1 | = | __ | ||
| 0 | + | 3 | = | __ | 4 | + | 1 | = | __ | 3 | + | 0 | = | __ | ||
| 4 | + | 1 | = | __ | 1 | + | 4 | = | __ | 1 | + | 1 | = | __ | ||
Стр. 3.
Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||||
| Сложи или вычти два однозначных числа. Числа до 5 | ||||||||||||||||
| 2 | + | 3 | = | __ | 4 | — | 4 | = | __ | 0 | + | 0 | = | __ | ||
| 2 | — | 0 | = | __ | 2 | + | 0 | = | __ | 4 | — | 4 | = | __ | ||
| 3 | + | 2 | = | __ | 0 | — | 0 | = | __ | 5 | + | 0 | = | __ | ||
| 2 | — | 0 | = | __ | 4 | + | 0 | = | __ | 0 | — | 0 | = | __ | ||
| 3 | + | 1 | = | __ | 2 | — | 0 | = | __ | 5 | + | 0 | = | __ | ||
| 4 | — | 4 | = | __ | 2 | + | 0 | = | __ | 5 | — | 2 | = | __ | ||
| 1 | + | 3 | = | __ | 3 | — | 3 | = | __ | 0 | + | 5 | = | __ | ||
| 5 | — | 5 | = | __ | 3 | + | 0 | = | __ | 1 | — | 0 | = | __ | ||
| 0 | + | 0 | = | __ | 0 | — | 0 | = | __ | 3 | + | 1 | = | __ | ||
| 0 | — | 0 | = | __ | 3 | + | 2 | = | __ | 2 | — | 1 | = | __ | ||
| 4 | + | 0 | = | __ | 4 | — | 1 | = | __ | 3 | + | 0 | = | __ | ||
Стр. 4.
Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||||
| Сложи или вычти два однозначных числа. Числа до 5 | ||||||||||||||||
| 4 | + | 1 | = | __ | 0 | — | 0 | = | __ | 1 | + | 3 | = | __ | ||
| 2 | — | 2 | = | __ | 5 | + | 0 | = | __ | 4 | — | 4 | = | __ | ||
| 2 | + | 0 | = | __ | 3 | — | 3 | = | __ | 4 | + | 1 | = | __ | ||
| 1 | — | 1 | = | __ | 5 | + | 0 | = | __ | 4 | — | 3 | = | __ | ||
| 4 | + | 0 | = | __ | 3 | — | 1 | = | __ | 5 | + | 0 | = | __ | ||
| 3 | — | 1 | = | __ | 3 | + | 2 | = | __ | 2 | — | 1 | = | __ | ||
| 3 | + | 1 | = | __ | 4 | — | 3 | = | __ | 4 | + | 1 | = | __ | ||
| 5 | — | 0 | = | __ | 1 | + | 1 | = | __ | 3 | — | 2 | = | __ | ||
| 2 | + | 1 | = | __ | 5 | — | 0 | = | __ | 2 | + | 1 | = | __ | ||
| 4 | — | 0 | = | __ | 4 | + | 1 | = | __ | 1 | — | 0 | = | __ | ||
| 4 | + | 0 | = | __ | 2 | — | 0 | = | __ | 1 | + | 4 | = | __ | ||
Посчитай предметы или животные на картинке. Числа до 5.
1. Сколько всего мальчиков?
2. Сколько всего кенгуру?
3. Сколько всего мороженных?
4. Сколько всего бегемотов?
5. Сколько всего слонов?
Какое число больше или меньше заданного на один.
1.Какое число больше 4 на единицу. 2.Какое число меньше 8 на единицу. 3.Какое число больше 3 на единицу. 4.Какое число меньше 2 на единицу. 5.Какое число больше 2 на единицу. 6.Какое число меньше 7 на единицу. 7.Какое число больше 2 на единицу. 8.Какое число меньше 8 на единицу.
Сравнение двух чисел до 5.
1. Какое число больше? 2. Какое число меньше? 3. Какое число больше? 4. Какое число меньше? 5. Какое число больше? 6. Какое число меньше? 7. Какое число больше?
Сравнение трех чисел до 5.
1. Какое число самое большое? 2. Какое число самое маленькое? 3. Какое число самое большое? 4. Какое число самое маленькое? 5. Какое число самое большое? 6. Какое число самое маленькое? 7. Какое число самое большое?
Общий обзор заданий. Формат А4 (jpg.)
Лицей №1 г.Новотроицка Оренбургской области
2020-2021 учебный годНОВОСТИ!!!!
1. Памятка- «Профилактика совершения несовершеннолетними правонарушений и преступлений»-
********************************************************
22 июня мы отмечаем День памяти и скорби — первый день Великой Отечественной войны. Ежегодно, в этот день зажигаются «Свечи памяти» — дань памяти тем, кто стал жертвой тех страшных лет. В этом году мы можем вспомнить каждого и зажечь 27 000 000 виртуальных свечей. 15-22 июня на сайте деньпамяти.рф можно зажечь свою «Свечу памяти» онлайн, а 20-22 июня — подарить «Свечи памяти» в социальных сетях «Вконтакте» и «Одноклассники».
На сайте деньпамяти.рф так же собрана информация о начале Великой Отечественной войны и воспоминания очевидцев событий 22 июня 1941г.
Министерство образования запустило опрос по вопросам «Дополнительное образование» и «Государственная итоговая аттестация».
Выразите мнение об организации дополнительного образования детей в Оренбургской области, а также об особенностях проведения государственной итоговой аттестации по образовательным программам основного и среднего общего образования в выпускных классах.
Период проведения опросов с 26.05.2021 по 26.11.2021 г.
Для участия в опросе пройдите по ссылке:
– опрос «Дополнительное образование» https://ag.orb.ru/votings/23
– опрос «Государственная итоговая аттестация» https://ag.orb.ru/votings/24.
*******************
Уважаемые родители и выпускники!
С целью успешной реализации приемной кампании в 2021 году Рособрнадзор извещает о возможности подачи заявления на поступление в образовательные организации высшего образования посредством федеральной государственной информационной системы «Единый портал государственных и муниципальных услуг (функций)». !
У выпускников Оренбургской области в этом году есть хорошая перспектива подачи документов в электронной форме. Наряду с предоставлением документов лично и по почте, они смогут подать свои документы и результаты ЕГЭ в пять вузов.
С этого года утверждены соответствующим приказом новые правила приёма в вузы. Они вступают в силу при приёме на обучение в 2021-2022 учебном году. У будущих абитуриентов есть возможность подать документы для зачисления на обучение в государственные образовательные организации высшего образования посредством суперсервиса «Поступление в вузы онлайн».
Напомним, перечень вступительных испытаний утверждён приказом Минобрнауки России от 30.08.2019 г. № 666 и применяется при приёме в вузы уже с 2020-2021 учебного года.
Дополнительные баллы при поступлении на обучение могут самостоятельно устанавливать и вузы. Список достижений, за которые можно получить от 1 до 10 баллов, един для всех вузов. Среди индивидуальных достижений, к примеру, наличие золотого, серебряного или бронзового знака комплекса ГТО, волонтёрская (добровольческая) деятельность, победы в спортивных соревнований, интеллектуальных конкурсах, а также наличие документа об образовании с отличием, оценка вуза по результатам проверки итогового сочинения. *****************************
1) АНКЕТА ДЛЯ РОДИТЕЛЕЙ по удовлетворенностью образовательным процессом в ОО
https://docs.google.com/forms/d/e/1FAIpQLSc4W3JjwEltH_qMlWSM-Y-Q0p84-MeiSRTOF2A-UqmTpnHpbQ/viewform?usp=sf_link2) АНКЕТА ДЛЯ РОДИТЕЛЕЙ по питанию
https://docs.google.com/forms/d/e/1FAIpQLScWcH9ghs39p5zV9c6WldlaZyTFO-L0B40umPNLsl7U8K7gqA/viewform?usp=sf_link
————————————————————-
Минпросвещения России запускает акцию «Мои школьные годы»!
К участию приглашаются школьники, выпускники, родители, бабушки и дедушки. Главная задача – рассказать о школе и своём пути максимально оригинально, креативно или даже трогательно.
Опубликуйте снимок в соцсетях «Вконтакте», Instagram или TikTok с хештегами #Моишкольныегоды #Минпросвещениярф.
Даты проведения: с 19 мая по 30 июня 2021 г.
Регистрация: https://edu.gov.ru/myschool/
Самые креативные и интересные работы будут опубликованы на сайте Министерства просвещения Российской Федерации, авторы трёх лучших работ получат памятные призы, а авторы постов, получивших наибольшее количество лайков, будут отмечены поощрительными призами. Учите, учитесь, берегите себя и близких!
***********************
Генеральная прокуратура РФ выступает организатором Международного молодёжного конкурса социальной антикоррупционной рекламы «Вместе против коррупции!».
Приём работ будет осуществляться с 01.05.2021 по 01.10.2021 на официальном сайте конкурса www.anticorruption.life в двух номинациях – «Лучший плакат» и «Лучший видеоролик». Участниками конкурса могут быть граждане (авторы – физические лица или творческие коллективы) в возрасте от 14 до 35 лет.
************************************
16 мая. Ежегодно в третье воскресенье мая (в этом году 16 мая 2021 г.) отмечается Международный день памяти умерших от СПИДа. Этот день дает возможность почтить память ушедших из жизни людей, поддержать людей, живущих с ВИЧ/СПИДом, их друзей и близких, обратить внимание общества на проблему ВИЧ/СПИДа.
15 мая. Новотройчане отметили День детства.Большая развлекательная программа состоялась 15 мая 2021 г. в городском парке и на площади ДК Металлургов. В нашем регионе этот праздник отмечается в третью субботу мая.
В парке были организованны развлекательные программы от комитета по делам молодежи, станции туризма, станции юных техников и образовательных учреждений города. Для мальчишек, девчонок, а также их родных выступили творческие коллективы.
А в городском парке прошел слет «Туристят». Наш лицей представляла команда 5 «Б» класса (классный руководитель А.О.Непомнящая). Им предстояло пройти по маршруту через все станции, на каждой из которых команду ждали различные испытания. На одной из них, например нужно было ответить на вопросы о своем родном городе.
Наша команда заняла 2 место в старшей группе. За участие в турслете команда была награждена медалями и грамотой.
А у фонтана несколько развлекательно-познавательных зон организовал НФ НИТУ «МИСиС». Здесь 9 «А» класс (классный руководитель А.Б.Ворошилова) приняли участие в профориентационной и развлекательной программе «Мир МИСиС!». Студенты под руководством преподавательского состава показали и рассказали, чем занимаются в МИСиСе, что такое химическая технология, программирование, электроэнергетика, механика и т.д.
Ребята получили грамоту за активное участие в профориентационном мероприятии «Мир МИСиС!»
****************
ПОЗДРАВЛЯЕМ С ПРАЗДНИКОМ ПОБЕДЫ 9 МАЯ!!!
https://nokstv.ru/news/city/society/litseisty-kruzhilis-v-valse-pobedy
7 мая ученики Лицея №1 собрались около своего учебного учреждения, для того, чтобы вспомнить о подвиге советских солдат, подаривших своим потомкам мирную жизнь и гордость за великую Победу.
Победу, оплаченную кровью миллионов солдат красной армии и простых граждан, погибших от рук вторгшихся захватчиков. О тех страшных событиях было написано немало стихов, и несколько из них лицеисты прочли во время мероприятия.
Ученик 2 класса Артем Старостин рассказал стих о молодом, умирающем от ранения на поле боя солдате, давшем на грани жизни и смерти свой последний бой неприятелю.
Другое произведение, прочитанное учеником 9 класса Михаилом Диденко, было о мальчике, переживающем об ушедшем на фронт отце, и защищавшем маму от пришедших в деревню фашистов.
Кульминацией мероприятия стал «Вальс Победы». Юноши и девушки кружились в прекрасном танце, напоминающем о радости советских граждан, услышавших 9 мая новость об окончании войны и победе наших войск
запись вальса — https://cloud.mail.ru/stock/d1DmKn7GEz1Zc4G2jze5BUhZ
Акция «ОкнаПобеды2021» пройдёт с 29 апреля по 9 мая в формате онлайн-флешмоба. Чтобы принять участие в акции нужно:
1.Оформить окна своих квартир/домов/школ рисунками, картинками, фотографиями и надписями, посвящёнными Победе советского народа в Великой Отечественной войне;
2.Опубликовать фотографии получившихся окон в социальных сетях с хештегами #ОкнаПобеды2021 #РДШ #ДеньПобеды со словами благодарности героям, тематическими текстами в преддверии Дня Победы.
Ребята нашего лицея активно приняли участие в детско — юношеской патриотической акции «Рисуем Победу — 2021», посвященной славному ратному и гражданскому подвигу поколения победителей.
«Останови огонь!»
Волонтеры городского движения «Горячие сердца» провели квест-игру в МОАУ Лицей №1 для учеников 5-х классов. В ходе квеста ребята вспомнили знаки пожарной безопасности, повторили всю технику безопасности работы с огнем. А так же для них были проведены три мастер класса:
Правила эвакуации;
Правила разведения костровища;
МК по ознакомлению с оборудованием служб Чрезвычайных Ситуаций.
Отдельное спасибо хотим сказать ВЧС «Следопыт», за оказанную помощь в проведении квеста. В ходе квеста, ребята узнали много новой, интересной и полезной информации. А так же они смогли сфотографироваться с аварийно-спасательным оборудованием
NEW!!!!! 20 апреля
Утверждены билеты к публичному зачету по геометрии в 7, 8 классах.
Приказ+ билеты, процедура проведения
14.04.21 г. сотрудник библиотеки им.М.Горького Н.Н.Турцова, в рамках библиотечного урока рассказала ученикам 4 Б класса (кл. руководитель Л.В.Степанова) об истории малой родины, показала фильм «Город на ладошке», слайды с интересными местами родного города. Полученные знания учащиеся закрепили, отвечая на вопросы викторины.
АПРЕЛЬ
1.Конкурс чтецов9 апреля 2021 г. в лицее прошел школьный этап конкурса чтецов среди 1-4 классов в рамках мероприятий, посвященных году космоса в России.
Итоги
среди 1 — 2 классов
Терехин Иван 2 «В» — 1 место
Шибаев Вячеслав 1 «В» — 1 место
Степанов Дмитрий 1 «А» — 2 место
Стрижак Анастасия 1 «А» — 2 место
Тепляшин Антон 1 «В» — 3 место
Шостак Герман 2 «В» — активное участие
Бодашко Сергей 2 «Б» — активное участие
Мамбетова Аделина 2 «Б» — активное участие
Вагапова Аделина 2 «Б» — активное участие
Шаповалова Кристина – 1 «Б» активное участие
Итоги
среди 3 – 4 классов
Шаранова Маргарита 4 «А» — 1 место
Грошкова Варвара 3 «А» — 2 место
Ганькина Мария 4 «В» — 3 место
Батуев Владислав 4 «В» — активное участие
Постарнак Яна 3 «А» — активное участие
Самохина Екатерина 3 «А» — активное участие
МАРТ
С 10 по 28 марта проходит ежегодный Всероссийский «Урок Цифры». Для участия Вам необходимо зайти по адресу урокцифры.рф , зарегистрироваться в личном кабинете и принять участие:- вы можете просмотреть интересные видеолекции, попробовать себя в программирование- получить сертификат участника, а победители и призеры получать интересные призы!!!!!! Принять участие можно и с родителями и с друзьями в команде.График мероприятий: 10-28 марта- Тема:»Беспилотный транспорт» (Яндекс)
УРОК ЦИФРЫ ЖДЕТ СВОИХ УЧАСТНИКОВ И ПОБЕДИТЕЛЕЙ!!
«Сообщи, где торгуют смертью» — В период 15 по 26 марта и с 18 по 29 октября 2021 г. проводится Общероссийская акция «Сообщи, где торгуют смертью», направленная на объединение усилий органов исполнительной власти и местного самоуправления, общественности и населения в противодействии незаконному обороту наркотиков. В рамках акции гражданам предоставляется возможность сообщить о фактах немедицинского потребления и незаконного оборота наркотиков, а также получить соответствующую консультацию по «телефону доверия» УМВД России по Оренбургской области: 8(3532) 79-02-01.
Всемирный день борьбы с туберкулезом- 24 марта «Всемирный день борьбы с туберкулезом».Не случайно 24 марта выбрано Всемирной организацией здравоохранения (ВОЗ) в качестве Всемирного дня борьбы с туберкулезом. Именно в этот день в 1882 году микробиолог Роберт Кох выступил в Берлине с сенсационной лекцией о своем открытии возбудителя туберкулеза – микобактерии (Mycobacterium), которую впоследствии стали называть палочкой Коха. В рамках Всемирного дня борьбы с туберкулезом в школе прошла акция «Белая ромашка».
Праздник весеннего равноденствия- 22 марта по народному календарю день Жаворонки. По поверьям в этот день прилетают сорок первых птиц и приносят на своих крыльях весну.В нашей школе прошёл праздник для 1 — 4 классов. Учащиеся водили хороводы, отгадывали загадки, кричали веснянки-зазывалки весны. Затем ребятам предложили сделать жаворонков из соленого теста и раскрасить их.Единство – детский онлайн – лагерь. С 22 марта 2021 г. будет работать онлайн детский лагерь «Единство» для 1-4 классов. https://vk.com/club195889732. Регистрироваться вот здесь https://vk.com/topic-195889732_47297252
16.03.2021 в школе прошла профориентационная встреча преподавателей из ОГТИ с обучающимся 9-10 классов. Учащимся рассказали о специальностях и профессиях, факультетах, которые можно получить не только после 11 класса, но и после 9 класса.
«Фестиваль «Крымская весна» С 15 по 21 марта 2021 г. во всех регионах России проходят тематические мероприятия под общим названием «Фестиваль «Крымская весна». 9 А класс принял участие в «Фестивале «Крымская весна», организованный детским технопарком «Кванториум» (кл.рук.Ворошилова А.Б.)
Итоги конкурса чтецов по творчеству М.Джалиля: Поздравляем Полупанову Марию ученицу 5 «А» класса (кл.руководитель Чеботарева Е.Г.), занявшую 1 место в городском конкурсе чтецов, посвященном творчеству М.Джалиля.
Ю.А.Гагарин (09.03.1934 – 27.03.1968)- В 5 «Б» классе (кл.руководитель А.О.Непомнящая) сотрудник библиотеки им. «М. Горького» Н.Н.Турцова провела краеведческий урок «Дорога к звездам», в ходе которого учащиеся познакомились с интересными фактами жизни Ю.А.Гагарина, прослушали отрывки из книги Валентины Гагариной «Мой брат Юрий». Кроме того, школьникам был предложен отрывок из фильма, рассказывающий о детских годах космонавта
ФЕВРАЛЬ
15 февраля 2021 г. День вывода советских войск из Афганистана. В МОАУ «Лицей № 1 г.Новотроицка» состоялись классные часы, посвященные Выводу войск из Афганистана. На классный час был приглашен ветеран боевых действий Карташов Сергей Николаевич. Встреча учеников и Сергея Николаевича проходила в форме беседы с наглядным материалом. А именно, для школьников Сергей Николаевич принес с собой бронежилеты и каски для того, что бы дети могли своими глазами увидеть и потрогать военную амуницию. Ветеран боевых действий в Афганистане, рассказал детям о радостях и тягостях службы. О героизме наших солдат в той, чужой стране. Сам Сергей Николаевич был более 70 раз на боевых заданиях, около 20 раз вступал в бой с противником. Свою службу начал в 1986 году. Ребята затаив дыхание, слушали рассказ ветерана и активно задавали вопросы.
15 февраля 2021г — ежегодно отмечается День памяти о россиянах, исполнявших служебный долг за пределами Отечества. Дата установлена не случайно: в этот день в 1989 году завершился вывод советских войск из Афганистана.В нашей школе в музейном уголке был выставлен Пост № 1. ЮнАрмейцы 8 А и 7 Б класса стояли в почётном карауле.
14 февраля 2021 г.— во всем мире отмечается Международный день дарения книг, это добровольная инициатива, направленная на повышение интереса и доступа детей к книгам. Цель праздника — вдохновить людей по всему миру подарить книгу ребенку. Есть три способа отпраздновать Международный день дарения книг! -Подарить книгу другу или другому члену семьи. -Оставить книгу в зале ожидания или в фойе. -Пожертвовать свои книги в библиотеку.
Пятый год лицеисты принимают участие в праздновании этого дня, в течение месяца фонд библиотеки пополнился на 79 экземпляр.
1 марта была оформлена выставка книг подаренных в библиотеку.
Мы говорим искренне: «Спасибо!» всем тем, кто бескорыстно принес свои дары в нашу библиотеку.
1а. Учащиеся класса-12 экз, Лобыкина В.-22 экз.1в. Учащиеся класса-12 экз. 2а. Старостин А.-1экз.2б. Янина А.-2экз., Якуба Т.-1экз., Воробьева П.-1экз.
3а. Шевченков В.-2экз., Артюшина В.-5экз.3б. Разинкин И.-7экз., Разинкин И.-6экз.4б. Сотникова -1 экз., Проваторова Е.- 1экз.,Чеботарева Н.-2экз.4в. Усманова А.-1экз.5б. Сарсенбаева О.-3экз. Здоровья вам, благополучия и добра!
4-6 февраля Математическая олимпиада имени Эйлера.В этом году впервые учащиеся 8б класса: Соловых Александр, Попов Дмитрий и Попова Елизавета приняли участие в Международной олимпиаде школьников по математике имени Эйлера, которая проходила в г.Оренбурге 5-6 февраля. Олимпиада проходила в два этапа, все задания были высокого уровня сложности. Соперниками наших учащихся были ученики физико-математической школы г. Оренбурга. Тем не менее наши учащиеся показали достойный уровень подготовки в области математики.
МОЛОДЦЫ!!!!!!!
6 февраля — традиционно в первую субботу февраля отмечается День родной школы. В этом году этот день выпал на 6 февраля. В нашей школе в честь этого события были организованы мероприятия под девизом «Здравствуй, школа!». В течение недели с 1 по 5 февраля учащиеся средних классов рисовали «школу будущего». А старшеклассники писали эссе и сочинения на тему «Если бы я был учителем…», «Моя школа – это…». В течение всего дня 5 февраля учащиеся лицея могли принять участие в акции «Педагог – это призвание», в рамках которой они давали свое определение понятию «педагог». Кроме того, выпускники лицея прислали свои видеообращения с рассказом о самом запоминающемся событии из их школьной жизни.
ВНИМАНИЕ!!!!!! ТОНКИЙ ЛЕД (буклет)
**********************************************
АНОНС «Наука. Территория героев»
Изменить будущее можешь только ты. С таким посылом обращаются к школьникам и студентам организаторы про
Книга с дополнительными заданиями для 4–8 классов Возраст 9–14 лет — 287 Головоломки со словами, математические задачи, задачи в лабиринте и многое другое для 4 классов
В этой книге:
- 30 x Word Search
- 30 x Word Hunt
- 30 x Target Puzzles
- 10 x Комплексные криптограммы предложений
Выбранные английские головоломки предназначены для помощи в развитии навыков письма, правописания, словарного запаса, памяти и логических рассуждений.
- 22 листа математических задач с одно-, двух- и трехзначными числами
- 15 математических головоломок с простыми фруктами
- 15 математических головоломок с фруктами среднего размера
- 15 математических головоломок с твердыми фруктами
Эти 45 математических головоломок задействуют и стимулировать способность вашего ребенка решать проблемы путем сложения, вычитания и умножения здоровой пищи.
🍎 🍐 🍍 🍋 🍊 🍏В дошкольном образовании было продемонстрировано, что существует корреляция между уровнем математических способностей ребенка и их будущими академическими успехами. Наблюдалась и обратная ситуация, когда дети, отстающие от математических навыков своих сверстников, продолжают отставать в будущих исследованиях (Pelkowski, et al., 2019). Кроме того, в литературе хорошо известно, что чем больше математика, тем больше математика. возможности обучения, которым открывается ребенок, тем больший рост он будет испытывать в математических знаниях (Piasta, et al.2015).
- 20 x задач распознавания образов
- 50 x головоломок судоку
- 12 x 2D-лабиринтов
- 38 x 3D-лабиринтов
В наш век информации очень важно вооружить учащихся критическим мышлением и навыки логического мышления, позволяющие эффективно расшифровать и осмыслить большие объемы информации (Fitzgerald, 2005). Логические рассуждения помогают в построении концепций и знаний в процессе обучения (Ongcoy, 2016).Эта книга включает в себя логические головоломки, способствующие когнитивному развитию, и логические рассуждения для улучшения их успеваемости в старшей школе и за ее пределами (Bouhnik, Giat, 2009)! Шейер и Адей (1993) обнаружили, что по завершении двухлетней научной программы, разработанной для развития формального оперативного мышления, на Британских национальных экзаменах были замечены улучшения в математике, английском и естественных науках.
Эта книга предназначена для того, чтобы дать возможность учиться, пробудить любопытство и уверенность в себе у детей в возрасте 9–14 лет и направить их на путь к успеху в учебе.📚 📚
ОТВЕТЫ НА ВЫШЕ ВОПРОСЫ
Математика для средней школы (6,7,8 и 9 классы) с бесплатными вопросами и задачами с ответами Математика для средней школы (10, 11 и 12 классы) — бесплатные вопросы и задачи с ответами Главная страница |
Eureka Math 4 класс Модуль 7 Урок 14 Ключ ответов — ответы CCSS Math
Engage NY Eureka Math 4-й класс Модуль 7 Урок 14 Ответы на вопросы
Эврика Математика 4 класс Модуль 7 Урок 14 Набор задач Ключ с ответами
Используйте RDW для решения следующих проблем.
Вопрос 1.
Мультфильм длится \ (\ frac {1} {2} \) час. Фильм в 6 раз длиннее мультфильма. Сколько минут нужно, чтобы посмотреть и мультфильм, и фильм?
Ответ:
Учитывая, что
Продолжительность мультфильма = 1/2 часа = 30 минут
Также дано, что фильм в 6 раз длиннее мультфильма
30 x 6 = 180 минут
Итак, 180 +30 = 210 минут
Следовательно, количество минут, необходимых для просмотра мультфильма и фильма, = 210 минут.
Вопрос 2.
Большая скамья 7 \ (\ frac {1} {6} \) футов в длину. Это на 17 дюймов длиннее, чем более короткая скамья. Сколько дюймов в длину у более короткой скамьи?
Ответ:
Дано,
Длина большой скамьи = 7 1/6 футов
7 1/6 футов =
1 фут = 12 дюймов
Итак, 7 футов = 7 x 12 = 84 дюйма
1/6 футов = 2 дюймов
Итого: 84 + 2 = 86
Также указано,
Более длинная скамья на 17 дюймов длиннее, чем более короткая скамья
Итак, 86 — 17 = 69
Следовательно, длина более короткой скамьи составляет 69 дюймов.
Вопрос 3.
Первый контейнер вмещает 4 галлона 2 литра сока. Второй контейнер может вместить на 1 \ (\ frac {3} {4} \) галлонов больше, чем первый контейнер. В целом, сколько сока могут вместить две емкости?
Ответ:
Учитывая, что
Емкость первого контейнера = 4 галлона 2 кварты или 4 1/2
Также с учетом вместимости второго контейнера на 1 3/4 галлона больше, чем у первого контейнера
Это означает, что 4 1/2 + 1 3/4 = 6 1/4
Итого: 4 1/2 галлона + 6 1/4 галлона
10 галлонов + 3/4 галлона = 10 галлонов 3 кварты
Таким образом, два контейнера могут содержать всего 103/4 галлона.
Вопрос 4.
Рост девушки 3 \ (\ frac {1} {3} \) фута. Рост жирафа в 3 раза больше, чем у девушки. На сколько дюймов жираф выше, чем девочка?
Ответ:
Дано,
Рост девушки = 3 1/3 фута
Рост жирафа в 3 раза больше, чем у девушки
Мы знаем, что 1 фут = 12 дюймов
3 1/3 +3 1/3 = 6 футов 8 дюймов
6 футов = 6 x 12 = 72 дюйма
72 + 8 = 80
Таким образом, девчонка на 80 дюймов выше девушки.
Вопрос 5.
В каждый пакет кладут пять унций кренделей. Сколько пакетов можно сделать из 22 \ (\ frac {3} {4} \) фунтов кренделей?
Ответ:
1 фунт = 16 унций
22 3/4 фунта кренделей =
22 x 16 = 352 унции и
3/4 = 12 унций
Итого: 352 + 12 = 364 унции
Учитывая это, 5 фунтов кренделей хранятся в каждом пакете
Итак, 364/5 = 72
Таким образом, из 22 3/4 фунта кренделей можно сделать 72 пакета.
Вопрос 6.
Для двадцати порций блинов требуется 15 унций смеси для блинов.
а. Сколько блинной смеси нужно на 120 порций?
г. Дополнение: смесь покупается в мешках по 2 \ (\ frac {1} {2} \) фунт. Сколько пакетов понадобится на 120 порций?
Ответ:
Учитывая, что для
Двадцать порций блинов требуется 15 унций смеси для блинов.
20 + 20 + 20 + 20 + 20 + 20 = 120
Итак, 6 x 15 = 90 унций
Следовательно, 90 унций блинов необходимо для 120 порций.
г. 1 фунт = 16 унций
Учитывая, что смесь куплена 2 1/2 фунта
Это означает, что 2 1/2 = 2 x 16 = 32 унции + 8 унций = 40 унций
40 унций x 2 = 80 унций
Следовательно, чтобы сделать Необходимо приобрести 120 порций 3 пакетика смеси.
Потому что из 2 1/2 смеси можно приготовить только 80 унций, а это мало.
Эврика Математика 4 класс Модуль 7 Урок 14 Ключ ответа на входной билет
Используйте RDW для решения следующей проблемы.
Джиджи потребовалось 1 час 20 минут, чтобы завершить велогонку. У Джонни на это ушло вдвое больше времени, потому что у него спустило колесо. Сколько минут понадобилось Джонни, чтобы финишировать?
Ответ:
Время, затраченное Джиджи на завершение велогонки = 1 час 20 минут
Время, затраченное Джонни в два раза больше, потому что он спустил шину =
, что означает
1 час 20 минут + 1 час 20 минут. = 2 часа 40 минут
1 час = 60 минут
2 часа = 2 x 60 = 120 минут
120 минут + 40 минут = 160 минут
Таким образом, Джонни потребовалось 160 минут, чтобы финишировать в велогонке.
Эврика Математика 4 класс Модуль 7 Урок 14 Домашнее задание Ответы на вопросы
Используйте RDW для решения следующих проблем.
Вопрос 1.
Молли испекла пирог 1 час 45 минут. Затем она испекла банановый хлеб на 35 минут меньше, чем пирог. Сколько минут ушло на испекание пирога и хлеба?
Ответ:
Время, в течение которого Молли готовила пирог = 1 час 45 минут
Учитывая, что время, затрачиваемое на выпечку бананового хлеба, на 35 минут меньше
Это означает, что 1 час 45 минут — 35 минут = 1 час 10 минут
Общее время, необходимое для выпечки и пирога, и хлеба:
1 час 45 минут + 1 час 10 минут = 2 часа 55 минут.
Таким образом, на выпечку пирога и бананового хлеба ушло 2 часа 55 минут.
Вопрос 2.
Горка на детской площадке имеет длину 12 \ (\ frac {1} {2} \) футов. Это на 3 фута 7 дюймов длиннее маленькой горки. Какова длина маленького слайда?
Ответ:
Учитывая, что длина более длинного слайда = 12 1/2 = 12 футов 6 дюймов
Длина меньшего слайда на 3 фута 7 дюймов короче более длинного слайда.
Итак,
12 футов 6 дюймов — 3 фута 7 дюймов = 8 футов 11 дюймов
Следовательно, длина меньшего слайда составляет 8 футов 11 дюймов.
Вопрос 3.
Бак для рыбы вмещает 8 галлонов 2 литра воды. Джеффри налил 1 \ (\ frac {3} {4} \) галлон в пустой бак. Сколько еще воды ему еще нужно налить в резервуар, чтобы заполнить его?
Ответ:
Количество воды, которое может вместить аквариум = 8 галлонов 2 кварты
Количество воды, налитой Джеффри в пустой резервуар = 1 3/4 галлона или 1 галлон 3 кварты
Итак,
8 галлонов 2 кварты — 1 галлонов 3 кварты = 6 галлонов 1 кварты
Следовательно, Джеффри нужно налить 6 галлонов 1 кварты воды, чтобы заполнить резервуар.
Вопрос 4.
В кондитерской кладут 10 унций мармеладных мишек в каждую коробку. Сколько коробок им нужно заполнить, если есть 21 \ (\ frac {1} {4} \) фунт мармеладных мишек?
Ответ:
1 фунт = 16 унций
21 1/4 =
21 фунт x 16 = 336 унций
1/4 = 4 унции
Итого: 336 + 4 = 340 унций
Учитывая это,
кондитерская кладет в каждую коробку = 10
Теперь 340/10 = 34
Следовательно, им нужно заполнить 34 коробки.
Вопрос 5.
Мама может сделать 10 пирожных из упаковки на 12 унций.
а. Сколько унций смеси для брауни понадобится для приготовления 50 пирожных?
г. Дополнительная информация: Смесь для брауни также продается в мешках по 1 \ (\ frac {1} {2} \) фунт. Сколько пакетов потребуется, чтобы приготовить 120 пирожных?
Ответ:
а. Учитывая это,
Mom может сделать 10 пирожных из упаковки на 12 унций.
Количество смеси для пирожных, необходимое ей для приготовления 50 пирожных =
12 x 5 = 60
Следовательно, 60 унций смеси для пирожных необходимо для приготовления 50 пирожных
г.1 фунт = 16 унций
1 1/2 =
16 унций + 8 унций = 24 унции
Учитывая, что 10 пирожных сделаны из смеси пирожных на 12 унций
Итак, 10 x 12 = 120
12 x 12 = 144 унции
Теперь, 144 унции / 24 унции = 6
Следовательно, для изготовления 120 пирожных необходимо 6 пакетов.
задач на сложение и вычитание — 14 типов!
Примечание. Эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего предложения членства.
Есть несколько различных типов задач со словами, с которыми могут столкнуться учащиеся. Для каждого из различных типов могут быть дополнительные различия. Например, в задачах со словом, связанных с изменением сумм, может быть неизвестна начальная сумма или окончательная сумма, или сама сумма изменения.
Важно, чтобы учащиеся научились решать все эти различные типы задач, поскольку это продемонстрирует полное понимание значения операций сложения и вычитания.Необходима практика с большим количеством примеров, но это следует делать после того, как вы начнете с большого количества практических занятий с конкретными материалами.
В таблице ниже показаны примеры этих различных типов задач сложения и вычитания. Примечание: таблица основана на Общие ситуации сложения и вычитания в Общих основных стандартах по математике (стр.88)
Различные типы сложения и вычитания| Добавить в | Три утки на пруду.Еще четыре утки приземляются на пруд. Сколько сейчас уток? | 3 + 4 = 7 |
| Три утки плывут по пруду. Еще несколько уток прилетают и приземляются рядом с ними, и теперь их пять. Сколько уток прилетело? | 3 + _ = 7 | |
| Утки плывут по пруду. Рядом с ними приземляются еще четыре утки, и теперь их семь. Сколько уток было на пруду до того, как все четверо приземлились? | _ + 4 = 7 | |
| Забрать | На торте горело семь свечей.Джейк уничтожил троих из них. Сколько осталось гореть? | 7–3 = 4 |
| На торте горело семь свечей. Джейк задул некоторые из них, оставив четыре горящих. Сколько он задул? | 7 — _ = 4 | |
| На торте было несколько свечей. Джейк взорвал четырех из них, оставив троих гореть. Сколько свечей горело на старте? | _ — 4 = 3 | |
| Собранные вместе / Разобрать | В миске четыре красных винограда и три белых винограда.Сколько винограда в миске? | 4 + 3 = _ |
| Семь виноградин в миске. Четыре красные, а остальные белые. Сколько белого винограда в миске? | 4 + _ = 7 7-4 = _ | |
| Сравнить | У Сэма три игры, а у Джека семь игр. Сколько еще игр у Джека? У ORSam есть три игры, а у Джека семь игр. На сколько игр у Сэма меньше? | 3 + _ = 7 7 — 3 = _ |
| У Джека на четыре игры больше, чем у Сэма.У Сэма три игры. Сколько игр у Джека? У ORSam на четыре игры меньше, чем у Джека. У Сэма три игры. Сколько игр у Джека? | 3 + 4 = _ 4 + 3 = _ | |
| У Джека на четыре игры больше, чем у Сэма. У Джека семь игр. Сколько игр у Сэма? У ORSam на четыре игры меньше, чем у Джека. У Джека семь игр. Сколько игр у Джека? | 7-4 = _ _ + 4 = 7 |
Чтобы решить каждый тип описанных выше задач, учащиеся должны владеть словарным запасом сложения и вычитания.например сколько всего, всего вместе, больше, чем разница, сколько нужно.
Решение словесных задач опирается на чтение и языковые навыки, а также развивает их. Знайте уровень чтения ваших детей и используйте возможность развивать эти навыки, работая и обсуждая проблемы. Помогите своим детям определить и понять ключевые слова и термины в проблеме. В таблице ниже приведены лишь несколько примеров.
Ключевые слова и термины для сложения и вычитания| сколько | сколько | осталось больше |
| еще предстоит | вместе | комбинированный |
| оба | добавить | дополнительный |
| сумма | всего | разница |
| изменить | прибавка | уменьшение |
| меньше | подробнее | осталось |
| минус | потрачено | уменьшить |
Дайте вашим детям как можно больше времени и поддержите их, чтобы помочь им понять проблему.Поработайте с ними, чтобы понять проблему и определить необходимую арифметическую операцию, чтобы ее можно было преобразовать в уравнение сложения или вычитания.
Будьте точны при обсуждении проблем и обращайте внимание на проблемы, которые плохо сформулированы. Например, «У Джека 7 консольных игр, а у Сэма 4 консольных игры. Сколько их всего? » лучше было бы сформулировать так: «У Джека есть 7 консольных игр, а у Сэма 4 консольных игры. Сколько всего у них консольных игр, ? »
Когда больше не значит добавитьСтуденты ищут словесные подсказки при решении словесных задач.«Больше» обычно (но не всегда) предполагает сложение, а «меньше» обычно (но не всегда) предполагает вычитание. Обратите внимание на проблемы, в которых эти слова предполагают противоположное тому, что они обычно делают. Например: «В зеленой команде было 14 игроков, что на 2 больше, чем в красной команде. Сколько игроков было в красной команде ». Учащиеся, которые могут интерпретировать это как 14 — 2 = 12, находятся на пути к пониманию сложения и вычитания.
Ошибки, связанные с проблемами текстаНижеследующее основано на работе Энн Ньюман 1 .
Ошибки, которые учащиеся допускают при выполнении текстовых задач, можно разделить на пять типов:
- Чтение — неправильно читаются ключевые слова или символы
- Понимание — непонимание проблемы в целом или ее отдельных частей
- Преобразование — неверное определение операций, необходимых для решения проблемы
- Процедура или факт — неправильный расчет
- Кодировка — решение найдено, но неправильно или полностью указано
Попросите учащихся сделать или ответить следующее, чтобы определить, какой тип ошибки они делают:
- Прочтите вопрос.
- Что вас просили сделать?
- Как вы планировали найти ответ?
- Покажи мне, как ты нашел ответ.
- Что вы ответили?
1. Ньюман, A 1977, «Анализ ошибок шестиклассников при выполнении письменных математических заданий», Бюллетень Викторианского института исследований в области образования, том 39, стр 31–43.
Рабочие листы для задач сложения / вычитания словНа двух листах ниже много проблем со словами.{-1} $} \).
Время определяется путем деления расстояния на скорость.
\ [\ text {time} (t) = \ frac {\ text {distance}} {\ text {speed}} \]Когда струи пересекают друг друга:
\ begin {align *} \ frac {\ text {1 200} — x} {\ text {250}} & = \ frac {x} {\ text {350}} \\ \ text {350} (\ text {1 200} — x) & = \ text {250} x \\ \ text {420 000} — \ text {350} x & = \ text {250} x \\ \ text {600} x & = \ text {420 000} \\ х & = \ текст {700} \ текст {км} \ end {выровнять *}Теперь мы знаем расстояние, которое проходит вторая струя, когда она проходит первую струю, мы можем найти время:
\ begin {align *} t & = \ frac {\ text {700} \ text {km}} {\ text {350} \ text {km · h $ ^ {- 1} $}} \\ & = \ текст {2} \ текст {h} \ end {выровнять *}Самолеты преодолеют друг друга за 2 часа.{-1} $} \). Если обе лодки отправятся в путь одновременно, сколько времени им понадобится, чтобы обогнать друг друга?
Обратите внимание, что сумма расстояний для двух лодок должна быть равна общему расстоянию, когда лодки встречаются: \ (d_ {1} + d_ {2} = d _ {\ text {total}} \ longrightarrow d_ {1} + d_ {2} = \ text {144} \ text {km} \).
Этот вопрос касается расстояний, скорости и времени.Уравнение, связывающее эти значения: \ [\ text {speed} = \ frac {\ text {distance}} {\ text {time}} \ quad \ text {- или -} \ quad \ text {distance} = \ text {speed} \ times \ text {time} \]
Вы хотите знать, сколько времени потребуется лодкам, чтобы встретиться — пусть это время будет \ (t \). Затем вы можете написать выражение для расстояния, которое проходит каждая из лодок: \ begin {align *} \ text {Для лодки 1:} \ quad d_ {1} & = s_ {1} t \\ & = \ текст {63} т \\ \ text {Для лодки 2:} \ quad d_ {2} & = s_ {2} t \\ & = \ текст {81} т \ end {align *}
Теперь мы можем подставить два выражения для расстояний в выражение для общего расстояния:
\ begin {align *} d_ {1} + d_ {2} & = \ text {144} \\ (\ text {63} t) + (\ text {81} t) & = \ text {144} \\ \ text {144} t & = \ text {144} \\ \ поэтому t & = \ frac {\ text {144}} {\ text {144}} \\ & = \ текст {1} \ end {выровнять *}Лодки встретятся через \ (\ text {1} \) час.
Звелибанци и Джессика — друзья. Zwelibanzi берет тестовую работу Джессики по гражданским технологиям и не говорит ей, какова ее оценка. Он знает, что Джессика не любит проблемы со словами, поэтому он решает подразнить ее. Звелибанци говорит: «У меня \ (\ text {12} \) оценок больше, чем у вас, и сумма обеих наших оценок равна \ (\ text {148} \). Какие у нас отметки? »
Пусть отметкой Звелибанци будет \ (z \), а отметкой Джессики будет \ (j \).Затем \ begin {align *} z & = j + \ text {12} \\ z + j & = \ text {148} \ end {align *}
Подставляем первое уравнение во второе уравнение и решаем: \ begin {align *} z + j & = \ text {148} \\ (j + \ text {12}) + j & = \ text {148} \\ 2j & = 148 — \ text {12} \\ \ поэтому j & = \ frac {\ text {136}} {\ text {2}} \\ & = \ текст {68} \ end {align *}
Подстановка этого значения обратно в первое уравнение дает: \ begin {align *} z & = j + \ text {12} \\ & = \ текст {68} + \ текст {12} \\ & = \ текст {80} \ end {выровнять *} Звелибанци получила оценку \ (\ text {80} \), а Джессика получила оценку \ (\ text {68} \).
Кадеш купил \ (\ text {20} \) рубашки на общую сумму \ (\ text {R} \, \ text {980} \). Если большие рубашки стоили \ (\ text {R} \, \ text {50} \), а маленькие — \ (\ text {R} \, \ text {40} \), сколько каждого размера он купить?
Пусть \ (x \) будет количеством больших рубашек и \ (20 — x \) количеством маленьких рубашек.
Далее отметим следующее:
- Он купил \ (x \) большие рубашки за \ (\ text {R} \, \ text {50} \)
- Он купил \ (20 — x \) маленькие рубашки за \ (\ text {R} \, \ text {40} \)
- Он потратил \ (\ text {R} \, \ text {980} \) всего
Мы можем представить стоимость как:
\ begin {align *} 50х + 40 (20 — х) & = 980 \\ 50x + 800 — 40x = & 980 \\ 10x & = 180 \\ х & = 18 \ end {выровнять *}Поэтому Кадеш покупает \ (\ text {18} \) большие рубашки и \ (\ text {2} \) маленькие рубашки.
Диагональ прямоугольника на \ (\ text {25} \) \ (\ text {cm} \) больше его ширины. Длина прямоугольника на \ (\ text {17} \) \ (\ text {cm} \) больше его ширины. Какие размеры у прямоугольника?
Пусть длина \ (= l \), ширина \ (= w \) и диагональ \ (= d \). \ (\, следовательно, d = w + 25 \) и \ (l = w + 17 \).{2} — 16w — 336 & = 0 \\ (ш + 12) (ш — 28) & = 0 \\ w = −12 & \ text {или} w = 28 \ end {выровнять *}
Ширина должна быть положительной, поэтому: width \ (w = \ text {28} \ text {cm} \) length \ (l = (w + 17) = \ text {45} \ text {cm} \) и диагональ \ (d = (w + 25) = \ text {53} \ text {cm} \).
Сумма \ (\ text {27} \) и \ (\ text {12} \) равна \ (\ text {73} \) больше, чем неизвестное число.Найдите неизвестный номер.
Пусть неизвестное число \ (= x \).
\ begin {align *} 27 + 12 & = х + 73 \\ 39 & = х + 73 \\ х & = -34 \ end {выровнять *}Неизвестный номер: \ (- \ text {34} \).
Группа друзей покупает обед. Вот несколько фактов об их обеде:
- молочный коктейль стоит \ (\ text {R} \, \ text {7} \) больше, чем упаковка
- группа покупает 8 молочных коктейлей и 2 упаковки
- общая стоимость обеда \ (\ text {R} \, \ text {326} \)
Пусть молочный коктейль будет \ (m \), а обертка будет \ (w \). Из данной информации получаем следующие уравнения:
\ begin {align *} т & = ш + 7 \\ 8м + 2н & = 326 \ end {выровнять *}Подставляем первое уравнение во второе уравнение и решаем относительно \ (w \):
\ begin {align *} 8м + 2з & = 326 \\ 8 (w + 7) + 2w & = 326 \\ 8w + 56 + 2w & = 326 \\ 10w & = 326 — 56 \\ \ поэтому w & = \ frac {270} {10} \\ & = 27 \ end {выровнять *}Подставьте значение \ (w \) в первое уравнение и решите относительно \ (m \):
\ begin {align *} т & = ш + 7 \\ & = 27 + 7 \\ & = 34 \ end {выровнять *}Следовательно, молочный коктейль стоит \ (\ text {R} \, \ text {34} \), а упаковка — \ (\ text {R} \, \ text {27} \).
Два меньших угла в прямоугольном треугольнике находятся в соотношении \ (1: 2 \). Каковы размеры двух углов?
Пусть \ (x = \) наименьший угол. Следовательно, другой угол \ (= 2x \).
Нам дан третий угол \ (= 90 ° \).
\ begin {align *} x + 2x + 90 ° & = 180 ° \ text {(сумма углов в треугольнике)} \\ 3x & = 90 ° \\ x & = 30 ° \ end {выровнять *}Размеры углов: \ (30 ° \) и \ (60 ° \).
Длина прямоугольника в два раза больше ширины. {2} & = 64 \\ b & = \ pm 8 \ end {выровнять *}
Но ширина должна быть положительной, поэтому \ (b = 8 \).
Подставьте это значение в первое уравнение, чтобы найти \ (l \):
\ begin {align *} l & = 2b \\ & = 2 (8) \\ & = 16 \ end {выровнять *}Следовательно, \ (b = \ text {8} \ text {cm} \) и \ (l = 2b = \ text {16} \ text {cm} \).
Если \ (\ text {4} \) число раз увеличить на \ (\ text {6} \), результат будет на \ (\ text {15} \) меньше квадрата числа. {2} — 4x — 21 & = 0 \\ (х — 7) (х + 3) & = 0 \\ x = 7 & \ text {или} x = −3 \ end {выровнять *}
Нам не сообщают, положительное или отрицательное число.Следовательно, это номер \ (\ text {7} \) или \ (- \ text {3} \).
Длина прямоугольника на \ (\ text {2} \) \ (\ text {cm} \) больше, чем ширина прямоугольника. Периметр прямоугольника равен \ (\ text {20} \) \ (\ text {cm} \). Найдите длину и ширину прямоугольника.
Пусть длина \ (l = x \), ширина \ (w = x — 2 \) и периметр \ (= p \).
\ begin {align *} p & = 2l + 2w \\ & = 2х + 2 (х — 2) \\ 20 & = 2х + 2х — 4 \\ 4x & = 24 \\ х & = 6 \ end {выровнять *}\ (l = \ text {6} \ text {cm} \) и \ (w = l — 2 = \ text {4} \ text {cm} \).
длина: \ (\ text {6} \) \ (\ text {cm} \), ширина: \ (\ text {4} \) \ (\ text {cm} \)У Стивена есть 1 литр смеси, содержащей \ (\ text {69} \% \) соль. Сколько воды нужно добавить Стивену, чтобы получилась \ (\ text {50} \% \) соль? Запишите свой ответ в долях литра.
Новый объем (\ (x \)) смеси должен содержать \ (\ text {50} \% \) соль, следовательно:
\ begin {align *} \ text {0,69} & = \ text {0,5} x \\ \ поэтому x & = \ frac {\ text {0,69}} {\ text {0,5}} \\ х & = 2 (\ текст {0,69}) \\ & = \ текст {1,38} \ end {выровнять *}Объем новой смеси составляет \ (\ text {1,38} \) литр. Количество воды (\ (y \)), которое нужно добавить:
\ begin {align *} у & = х — \ текст {1,00} \\ & = \ text {1,38} — \ text {1,00} \\ & = \ текст {0,38} \ end {выровнять *}Следовательно, необходимо добавить \ (\ text {0,38} \) литров воды.Чтобы записать это в виде доли литра: \ (\ text {0,38} = \ frac {38} {100} = \ frac {19} {50} \ text {литры} \)
Следовательно, необходимо добавить \ (\ frac {19} {50} \ text {литры} \).
Сумма двух подряд идущих нечетных чисел равна \ (\ text {20} \), а их разница равна \ (\ text {2} \). Найдите два числа.
Пусть числа будут \ (x \) и \ (y \).
Тогда два уравнения, описывающие ограничения:
\ begin {align *} х + у & = 20 \\ х — у & = 2 \ end {выровнять *}Добавьте первое уравнение ко второму уравнению:
\ begin {align *} 2x & = 22 \\ х & = 11 \ end {выровнять *}Подставить в первое уравнение:
\ begin {align *} 11 — у & = 2 \\ y & = 9 \ end {выровнять *}Следовательно, два числа — 9 и 11.
Знаменатель дроби на \ (\ text {1} \) больше, чем числитель.Сумма дроби и обратной величины равна \ (\ frac {5} {2} \). Найдите дробь.
Пусть числитель будет \ (x \). Значит, знаменатель равен \ (x + 1 \). {2} + х — 2 & = 0 \\ (х — 1) (х + 2) & = 0 \\ x = 1 & \ text {of} x = −2 \ end {выровнять *}
Отсюда дробь может быть \ (\ frac {1} {2} \) или \ (\ frac {-2} {- 1} \).Для второго решения мы можем упростить дробь до \ (\ text {2} \), и в этом случае знаменатель не на 1 меньше числителя.
Итак, дробь равна \ (\ frac {1} {2} \).
Масинди на \ (\ text {21} \) лет старше своей дочери Муливху. Сумма их возрастов равна \ (\ text {37} \). Сколько лет Муливху?
Пусть Муливху будет \ (x \) лет.Итак, Масинди \ (x + 21 \) год.
\ begin {align *} х + х + 21 & = 37 \\ 2x & = 16 \\ х & = 8 \ end {выровнять *}Муливху \ (\ text {8} \) лет.
Тшамано сейчас в пять раз старше его сына Мурунвы.Через семь лет Тшамано будет в три раза старше своего сына. Найдите их возраст сейчас.
Пусть Мурунве будет \ (x \) лет. Итак, Тшамано \ (5x \) лет.
Через \ (\ text {7} \) лет возраст Мурунвы будет \ (x + 7 \). Возраст Тшамано будет \ (5x + 7 \).
\ begin {align *} 5х + 7 & = 3 (х + 7) \\ 5х + 7 & = 3х + 21 \\ 2x & = 14 \\ х & = 7 \ end {выровнять *}Со Мурунве 7 лет, а Тшамано 35 лет.
\ (\ text {7} \) и \ (\ text {35} \) лет.Если сложение числа от одного до трех совпадает с числом, чему оно равно?
Пусть число будет \ (x \). Тогда:
\ begin {align *} 3х + 1 & = х \\ 2x & = — 1 \\ х & = — \ frac {1} {2} \ end {выровнять *}Если треть суммы числа и единицы эквивалентна дроби, знаменателем которой является число, а в числителе два, то какое число?
Пусть число будет \ (x \). 2 + х — 6 & = 0 \\ (х-2) (х + 3) & = 0 \\ \ поэтому x = 2 & \ text {или} x = -3 \ end {выровнять *}
Владелец магазина покупает 40 мешков риса и муки на сумму \ (\ text {R} \, \ text {5 250} \).Если рис стоит \ (\ text {R} \, \ text {150} \) за мешок, а мука стоит \ (\ text {R} \, \ text {100} \) за мешок, сколько мешков муки еду он купил?
\ begin {align *} х + у & = 40 ~ (1) \\ 150x + 100y & = \ text {5 250} ~ (2) \\ \\ & \ text {посмотрите на} (1) \\ х & = 40 — у ~ (3) \\ (3) & \ text {into} (2) \\ 150 (40 — y) + 100y & = \ text {5 250} \\ -150y + 100y & = \ text {5 250} — \ text {6 000} \\ -50лет & = -750 \\ у & = 15 \\ \ поэтому куплено 15 & \ text {мешков муки мели} \ end {выровнять *}
В коробке 100 кусков синего и зеленого мыла.Синие полосы весят \ (\ text {50} \) \ (\ text {g} \) на полосу, а зеленые полосы \ (\ text {40} \) \ (\ text {g} \) на полосу. Общая масса мыла в ящике составляет \ (\ text {4,66} \) \ (\ text {кг} \). Сколько кусков зеленого мыла в коробке?
\ begin {align *} х + у & = 100 ~ (1) \\ 50x + 40y & = 4660 ~ (2) \\ \\ & \ text {посмотрите на} (1) \\ х & = 100 — у ~ (3) \\ (3) & \ text {into} (2) \\ 50 (100 — лет) & + 40 лет = \ text {4 660} \\ -50y & + 40y = \ text {4 660} — \ text {5 000} \\ -10лет & = -340 \\ у & = 34 \\ \ поэтому куплено 34 & \ text {мешков муки мели} \ end {выровнять *}
У Лизы 170 бусинок.У нее есть синие, красные и фиолетовые бусины весом \ (\ text {13} \) \ (\ text {g} \), \ (\ text {4} \) \ (\ text {g} \) и \ ( \ text {8} \) \ (\ text {g} \) соответственно. Если красных бусинок вдвое больше, чем синих, и все бусинки весят \ (\ text {1,216} \) \ (\ text {kg} \), сколько бусинок каждого типа у Лизы?
\ begin {align *} х + у + г & = 170 \ qquad (1) \\ 13x + 4y + 8z & = \ text {1 216} \ qquad (2) \\ у & = 2х \ qquad (3) \\ \\ (3) & \ text {into} (1) \\ х + (2х) + z & = 170 \\ 3x + z & = 170 \\ z & = 170 — 3x \ qquad (4) \\ (3) & \ text {into} \ qquad (2) \\ 13x + 4 (2x) + 8z & = \ text {1 216} \\ 21x + 8z & = \ text {1 216} \ qquad (5) \\ (4) & \ text {into} (5) \\ 21x + 8 (170 — 3x) & = \ text {1 216} \\ 21x + \ text {1 360} — 24x & = \ text {1 216} \\ -3x & = -144 \\ х & = 48 \\ у & = 2х = 96 \\ z & = 170 — 3x = 26 \\ \\ \ поэтому \ text {у Лизы} & 48 \ text {синие бусинки,} 96 \ text {красные бусинки и} 36 \ text {фиолетовые бусинки,} \ end {выровнять *}
Решение проблем со словами с помощью ленточных диаграмм | пользователя Eureka Math | Eureka Math
Ага! Момент
За 10 лет работы учителем 7-8 классов я ни разу не видел ленточную диаграмму.Я не решался использовать эту модель, но когда я начал по-настоящему изучать ленточные диаграммы и получил возможность использовать ее со студентами всех возрастов, я был поражен ее простотой и красотой. Ленточные диаграммы могут помочь учащимся разобраться в словесных задачах, позволяя им написать уравнение или числовое предложение для представления ситуации.
Давайте посмотрим на несколько примеров того, насколько значимой может быть ленточная диаграмма в вашем классе. Представьте, что ваши 5-классники решают эту задачу без модели:
В классе 32 ученика.3/8 класса приносят свой обед. Сколько студентов приносят обед?
( 5 класс, модуль 4, урок 6)
Если бы эта дробь была дружественной или знакомой дробью, такой как ½ или, учащиеся обычно использовали бы в уме математику и успешно решали бы эту задачу. Но сталкиваясь с дробью, такой как 3/8, студенты обычно полагаются на запоминание алгоритма или поиск ключевых слов, чтобы определить, какую операцию использовать. Кроме того, ленточная диаграмма позволяет учащимся визуализировать проблему и разработать свою стратегию.Используя ленточную диаграмму, учащиеся могут нарисовать изображение, показывающее 3/8 из 32.
Они начинают с рисования модели и разделения ее на 8 частей равного размера, потому что здесь используются восьмые. Целое составляет 32.
Ленточные диаграммы также могут помочь учащимся увидеть разницу между вопросом для 5-го класса, в котором учащихся умножают на дробь, и вопросом для 6-го класса, в котором учащимся предлагается разделить дробь на целое число. Они даже помогают ученикам делить дроби на дроби позже, в Модуле 2 6-го класса.
3/5 пинты сока поровну наливают в 6 стаканов. Сколько сока в каждом стакане?
(6 класс, модуль 2, урок 1)
В каждом стакане 1/10 пинты сока.
Прелесть ленточной диаграммы в том, что учащиеся не будут запоминать правила, которых они не понимают. Заученное правило не поможет ученику, если он не помнит, как его использовать или как применять в различных сценариях. С другой стороны, ленточные диаграммы — это универсальные визуальные инструменты, которые позволяют учащимся лучше понять проблему.Используя их, они могут более эффективно решать проблемы и, в конечном итоге, решать их без рисования модели.
Не забудьте заглянуть в следующий месяц, поскольку мы продолжим обсуждение ленточных диаграмм и их использования при решении алгебраических уравнений.
олимпиады по математике для начальной и средней школы
олимпиады по математике для начальной и средней школыНекоммерческая корпорация, призванная стимулировать энтузиазм, способствовать творчеству, и укрепление интуиции при решении математических задач.Каждый месяц с ноября по март 30-минутный конкурс проводится в вашем школа или другое место на ваше усмотрение. | Команды до 35 студентов изучают математические концепции, развивая гибкость в решении нестандартных задач с множеством путей решения. Наши проблемы подготовит ваших учеников к превышению строгости вашей основной учебной программы развивая навыки решения проблем более высокого порядка. | |||||||||||||||
| ||||||||||||||||
| а | ||||||||||||||||
| ||||||||||||||||
Авторские права © 1998, 2021 MOEMS ®
.
