ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть
❤️️Ответ к странице 34. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.
Номер 129.
Найди ошибки в вычислениях и реши правильно.
Номер 130.
Выполни деление с остатком и проверь решение.
Номер 131.
В ящике помещается 20 кг моркови. Сколько потребуется таких ящиков, чтобы отправить в магазин 675 кг моркови? Сколько килограммов моркови будет в последнем ящике?
1) 675 : 20 = 33 (ост. 15) – морк. Ответ: 33 ящика + 15 кг.
Номер 132.
В каждом ряду кинозала 30 мест. На сеанс продано 942 билета. Сколько полных рядов в этом зале могут занять зрители с билетами?
1) 942 : 30 = 31 (ост. 12) Ответ: 31 ряд могут занять.
Номер 133.
Два лыжника вышли из посёлка одновременно в противоположных направлениях. Один из них шёл со скоростью 12 км/ч, а другой – 10 км/ч.
1) 12 + 10 = 22 (км/ч) – скорость удаления лыж.
2) 44 : 22 = 2 (ч) – будут в пути лыж.
3) 12 ∙ 2 = 24 (км) – прошёл 1-ый лыжник.
4) 10 ∙ 2 = 20 (км) – прошёл 2-ой лыжник.
Ответ: через 2 часа; 1-ый л. – 24 км.; 2-ой л. – 20 км.
Номер 134.
Из двух посёлков выехали одновременно навстречу друг другу два всадника. Первый ехал со скоростью 200 м/мин, а второй проезжал в минуту на 20 м меньше. Всадники встретились через 50 мин. Найди расстояние между посёлками.
1) 200 — 20 = 180 (м/мин) – скорость второго всадника.
2) 200 + 180 = 380 (м/мин) – скорость сближения.
3) 380 ∙ 50 = 19000 (м) – расстояние между посёлками.
19000 м = 19 км
Ответ: 19 км.
Номер 135.
Найди значение выражения 120 : 4 + 2 ∙ 3. Измени порядок действий в этом выражении с помощью скобок так, чтобы его значение стало равно 60; 96; 12.
120 : 4 + 2 ∙ 3 = 36 120 : (4 + 2) ∙ 3 = 60 (120 : 4 + 2) ∙ 3 = 96 120 : (4 + 2 ∙ 3) = 12
Номер 136.
Выполни деление и проверь умножением.
Номер 137.
Номер 138.
1 т — 8 ц = 10 ц — 8 ц = 2 ц 1 ц — 8 кг = 100 кг — 8 кг = 92 кг
1 м² — 10 дм² = 100 дм² — 10 дм² = 90 дм² 1 дм² — 10 см² = 100 см² — 10 см² = 90 см²
Задание на полях страницы
Магический квадрат.
Задание внизу страницы
Проверочные работы с.66 Проверочные работы с.67
№ п/п | Дата | Тема урока | Тип урока | Основные виды учебной деятельности | Планируемые предметные результаты | Универсальные учебные действия | ИКТ | Примечание | ||
Числа от 1 до 1000. Повторение | ||||||||||
1 | 1.09 | Повторение.Нумерация. чисел. | Урок повторения и обобщения | Образовывать числа натурального ряда от 100 до 1000. Совершенствовать вычислительные навыки, решать задачу разными способами; составлять задачи, обратные данной | Называть последовательность чисел в пределах 1000; объяснять, как образуется каждая следующая счётная единица. Называть разряды и классы. | Самостоятельное создание алгоритмов деятельности при решении проблем поискового характера. Установление причинно-следственных связей | ||||
2 | 5.09 | Порядок действий в числовых выражениях. | Урок повторения и обобщения | Применять правила о порядке выполнения действий в числовых выражениях со скобками и без скобок при вычислениях значений числовых выражений | Вычислять значение числового выражения, содержащего 2-3 действия. Понимать правила порядка выполнения действий в числовых выражениях | Планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения | Интер. доска | |||
3 | 6.09 | Нахождение суммы нескольких слагаемых | Урок развития умений и навыков | Выполнять письменные вычисления с натуральными числами. | Вычислять сумму трёх слагаемых. Вычислять значение числового выражения, содержащего 2-3 действия | Самостоятельное создание алгоритмов деятельности при решении проблем поискового характера. Установление причинно-следственных связей | Интер. доска | |||
4 | 7.09 | Алгоритм письменного деления | Урок развития умений и навыков | Выполнять письменное вычитание трёхзначных чисел. Находить значения числовых выражений со скобками и без них | Использовать алгоритм письменного вычитания чисел и выполнять эти действия с числами в пределах 1000 | Актуализировать свои знания для проведения простейших математических доказательств (в том числе с опорой на изученные определения, законы арифметических действий) | ||||
5 | 8. | Умножение трехзначного числа на однозначное | Урок формирования умений и навыков | Умножать письменно в пределах 1000 с переходом через разряд многозначного числа на однозначное. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи | Выполнять письменное умножение в пределах 1000 с переходом через разряд многозначного числа на однозначное. | Самостоятельное создание алгоритмов деятельности при решении проблем поискового характера. Установление причинно-следственных связей | Интер. доска | |||
6 | 12.09 | Свойства умножения | Урок развития умений и навыков | Использовать переместительное свойство умножения. | Выполнять письменное умножение в пределах 1000 с переходом через разряд многозначного числа на однозначное | Делать выводы на основе анализа предъявленного банка данных | ||||
7 | 13.09 | Алгоритм письменного деления | Урок формирования умений и навыков | Применять приём письменного деления многозначного числа на однозначное. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи | Выполнять письменное деление в пределах 1000 | Самостоятельное создание алгоритмов деятельности при решении проблем поискового характера. | ||||
8 | 14.09 | Приёмы письменного деления | Урок формирования умений и навыков | Применять приём письменного деления многозначного числа на однозначное. Использовать свойства деления числа на 1, и нуля на число. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи | Выполнять письменное деление многозначного числа на однозначное по алгоритму | Контролировать свою деятельность: обнаруживать и устранять ошибки логического характера (в ходе решения) и ошибки вычислительного характера | Интер. доска | |||
9 | 15. | Приемы письменного деления | Урок развития умений и навыков | Применять приём письменного деления многозначного числа на однозначное. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи | Выполнять письменное деление многозначного числа на однозначное по алгоритму | Делать выводы на основе анализа предъявленного банка данных | Интер. доска | |||
10 | 19.09 | Приёмы письменного деления | Урок-исследование | Применять приём письменного деления многозначного числа на однозначное, когда в записи частного есть нуль | Выполнять письменное деление многозначного числа на однозначное с объяснением, когда в записи частного есть нуль. | Делать выводы на основе анализа предъявленного банка данных | ||||
11 | 20.09 | Диаграммы | Урок изучения нового материала | Использовать диаграммы для сбора и представления данных | Читать и строить столбчатые диаграммы | Моделировать содержащиеся в тексте данные. Актуализировать свои знания для проведения простейших математических доказательств | Интер. доска | |||
12 | 21.09 | Повторение пройденного. «Что узнали. Чему научились». | Контрольно-обобщающий урок | Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы | ||||
13 14 | 22. 26.09 | Контрольная работа № 1 по теме « Числа от 1 до 1000» Анализ контрольной работы .Страничка для любознательных. | Контроль знаний, умений и навыков | Работать в паре. Находить и исправлять неверные высказывания. Излагать и отстаивать своё мнение, аргументировать свою точку зрения, оценивать точку зрения товарища, обсуждать высказанные мнения | Пользоваться вычислительными навыками, решать составные задачи | Прогнозировать результаты вычислений; контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
Числа, которые больше 1000. Нумерация | ||||||||||
15 | 27. | Класс единиц и класс тысяч | Урок изучения нового материала | Считать предметы десятками, сотнями, тысячами. Выделять количество сотен, десятков, единиц в числе. Совершенствовать вычислительные навыки, умение решать буквенные выражения. Анализировать свои действия и управлять ими | Называть новую счётную единицу – тысячу. Называть разряды, которые составляют первый класс, второй класс | Собирать требуемую информацию из указанных источников; фиксировать результаты разными способами; сравнивать и обобщать информацию | Интер. доска | |||
16 | 28.09 | Чтение многозначных чисел | Урок изучения нового материала | Выделять количество сотен, десятков, единиц в числе. | Читать числа в пределах миллиона | Актуализировать свои знания для проведения простейших математических доказательств | ||||
17 | 29.09 | Запись многозначных чисел | Урок изучения нового материала | Выделять количество сотен, десятков, единиц в числе. Совершенствовать вычислительные навыки | Записывать числа в пределах миллиона | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера | Интер. доска | |||
18 | 3. | Разрядные слагаемые | Урок развития умений и навыков | Заменять многозначное число суммой разрядных слагаемых. Выделять в числе единицы каждого разряда. Определять и называть общее количество единиц любого разряда, содержащихся в числе | Представлять многозначное число суммой разрядных слагаемых. Выполнять устно арифметические действия над числами в пределах сотни и с большими числами в случаях, легко сводимых к действиям в пределах ста | Осознание способов и приёмов действий при решении учебных задач | ||||
19 | 4.10 | Сравнение чисел | Урок развития умений и навыков | Упорядочивать заданные числа. Группировать числа по заданному или самостоятельно установленному признаку, находить несколько вариантов группировки | Сравнивать числа по классам и разрядам. Оценивать правильность составления числовой последовательности | Выделение существенной информации. Осуществление анализа объектов с выделением существенных и несущественных признаков | Интер. доска | |||
20 | 5.10 | Увеличение и уменьшение числа в 10, 100, 1000 раз | Урок формирования умений и навыков | Проверять правильность выполненных вычислений, решать текстовые задачи арифметическим способом, выполнять увеличение и уменьшение числа в 10, 100, 1000 раз | Увеличивать (уменьшать) числа в 10, 100, 1000 раз | Самостоятельное создание алгоритмов деятельности при решении проблем поискового характера. | ||||
21 | 6.10 | Закрепление изученного. | Урок развития умений и навыков | Определять последовательность чисел в пределах 100 000. Читать, записывать и сравнивать числа в пределах 1 000 000. Находить общее количество единиц какого-либо разряда в многозначном числе | Выделять в числе общее количество единиц любого разряда | Самостоятельное создание алгоритмов деятельности при решении проблем поискового характера. Установление причинно-следственных связей | ||||
22 | 10.10 | Класс миллионов. | Урок изучения нового материала | Называть классы и разряды: класс единиц, класс тысяч, класс миллионов. Читать числа в пределах 1 000 000 000 | Называть класс миллионов, класс миллиардов. Читать числа в пределах 1 000 000 000 . Пользоваться вычислительными навыками, решать составные задачи | Приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач | Интер. доска | |||
23 | 11.10 | Странички для любознательных | Комбинированный урок | Собирать информацию о своём городе (селе) и на этой основе создавать математический справочник «Наш город (село) в числах». | Определять цель проекта, работать с известной информацией, собирать дополнительный материал, создавать способы решения проблем творческого и поискового характера, составлять задачи | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера. Поиск и выделение необходимой информации. Контроль и оценка процесса и результатов деятельности | ||||
24 | 12.10 | «Что узнали. Чему научились». | Контроль знаний, умений и навыков | Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Прогнозировать результаты вычислений; контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
25 | 13. | Контрольная работа № 2 по теме «Нумерация» | Контроль знаний, умений и навыков | Выполнять действия, соотносить, сравнивать, оценивать свои знания | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Оценка — выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы | ||||
Величины | ||||||||||
26 27 | 17.10 18.10 | Анализ контрольной работы . Единицы длины. Километр. | Урок изучения нового материала | Переводить одни единицы длины в другие: мелкие в более крупные и крупные в более мелкие, используя соотношения между ними | Называть единицы длины. | Актуализировать свои знания для проведения простейших математических доказательств | ||||
28 | 19.10 | Единицы длины. Закрепление изученного | Урок развития умений и навыков | Переводить одни единицы длины в другие: мелкие в более крупные и крупные в более мелкие, используя соотношения между ними. Измерять и сравнивать длины; упорядочивать их значения | Называть единицы длины. Сравнивать величины по их числовым значениям, выражать данные величины в различных единицах | Делать выводы на основе анализа предъявленного банка данных | Интер. доска | |||
29 | 20.10 | Единицы площади: квадратный километр, квадратный миллиметр | Урок изучения нового материала | Переводить одни единицы длины в другие: мелкие в более крупные и крупные в более мелкие, используя соотношения между ними | Называть единицы площади. Использовать приобретенные знания для сравнения и упорядочения объектов по разным признакам: длине, площади | Приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач | Интер. доска | |||
30 | 24.10 | Таблица единиц площади | Урок развития умений и навыков | Сравнивать значения площадей равных фигур. Переводить одни единицы площади в другие, используя соотношения между ними | Называть результат при переводе одних единиц массы в другие: мелкие в более крупные и крупные в более мелкие | Актуализировать свои знания для проведения простейших математических доказательств | ||||
31 | 25.10 | Измерение площади с помощью палетки | Урок изучения нового материала | Определять площади фигур произвольной формы, используя палетку. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи | Использовать приём измерения площади фигуры с помощью палетки. Сравнивать величины по их числовым значениям, выражать данные величины в различных единицах, решать текстовые задачи арифметическим способом | Учебное сотрудничество с учителем и сверстниками в поиске и сборе информации; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации | ||||
32 | 26.10 | Единицы массы. Тонна, центнер | Урок изучения нового материала | Переводить одни единицы массы в другие, используя соотношения между ними. Приводить примеры и описывать ситуации, требующие перехода от одних единиц измерения к другим (от мелких к более крупным и от крупных к более мелким) | Понимать понятие «масса», называть единицы массы. Сравнивать величины по их числовым значениям | Выделение существенной информации. Осуществление анализа объектов с выделением существенных и несущественных признаков | Интер. доска | |||
33 | 27.10 | Единицы времени. Определение времени по часам | Урок развития умений и навыков | Переводить одни единицы времени в другие. Исследовать ситуации, требующие сравнения событий по продолжительности, упорядочивать их | Использовать таблицу единиц массы. Сравнивать величины по их числовым значениям, выражать данные величины в различных единицах. Решать задачи арифметическим способом | Актуализировать свои знания для проведения простейших математических доказательств | Интер. доска | |||
34 | 7.11 | Определение начала, конца и продолжительности события. Секунда. | Урок повторения и обобщения | Переводить одни единицы времени в другие. Исследовать ситуации, требующие сравнения событий по продолжительности, упорядочивать их | Называть единицы времени: год, месяц, неделя | Выделение существенной информации. Осуществление анализа объектов с выделением существенных и несущественных признаков | ||||
35 | 8.11 | Век. Таблица единиц времени. | Урок формирования умений и навыков | Рассматривать единицу времени – век. Сравнивать величины по их числовым значениям, выражать данные величины в различных единицах | Называть новую единицу измерения времени – век | Самостоятельное выделение и формулирование познавательной цели, создание способов решения проблем поискового характера, инициативное сотрудничество в поиске и сборе информации | Интер. доска | |||
36 | 9.11 | Повторение пройденного. «Что узнали. Чему научились» | Комбинированный урок | Анализировать достигнутые результаты и недочёты, проявлять личную заинтересованность в расширении знаний и способов действий | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
37 | 10.11 | Контрольная работа № 3 по теме «Величины» | Контроль знаний, умений и навыков | Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Оценка — выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения | ||||
Сложение и вычитание | ||||||||||
38 | 14.11 | Анализ контрольной работы .Устные и письменные приёмы вычислений | Урок повторения и обобщения | Проверять усвоение изучаемой темы. Выполнять письменно сложение и вычитание многозначных чисел, опираясь на знание алгоритмов их выполнения. Осуществлять пошаговый контроль правильности выполнения арифметических действий (сложение, вычитание) | Объяснять приёмы письменного сложения и вычитания чисел и выполнять эти действия с числами в пределах 1 000 000 | Актуализировать свои знания для проведения простейших математических доказательств (в том числе с опорой на изученные определения, законы арифметических действий) | Интер. доска | |||
39 | 15.11 | Нахождение неизвестного слагаемого | Урок формирования умений и навыков | Определять, как связаны между собой числа при сложении. Находить неизвестное слагаемое. Объяснять решение уравнений и их проверку. Выполнять вычисления и делать проверку | Использовать правило нахождения неизвестного слагаемого. Пользоваться изученной математической терминологией, проверять правильность выполненных вычислений | Актуализировать свои знания для проведения простейших математических доказательств | ||||
40 | 16.11 | Нахождение неизвестного уменьшаемого, неизвестного вычитаемого | Урок формирования умений и навыков | Определять, как связаны между собой числа при вычитании. Находить неизвестное уменьшаемое, неизвестное вычитаемое. Объяснять решение уравнений и их проверку. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи | Использовать правило нахождения неизвестного уменьшаемого и неизвестного вычитаемого. Вычислять значение числового выражения, содержащего 2-3 действия (со скобками и без них) | Актуализировать свои знания для проведения простейших математических доказательств | Интер. доска | |||
41 | 17.11 | Нахождение нескольких долей целого | Комбинированный урок | Находить, одну долю от целого числа, находить несколько долей от целого числа. Решать уравнения и сравнивать их решения. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи | Находить несколько долей целого. Вычислять значение числового выражения, содержащего 2-3 действия (со скобками и без них) | Прогнозировать результаты вычислений; контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
42 43 | 21.11 22.11 | Решение задач | Комбинированный урок | Использование свойств арифметических действий при выполнении вычислений. Решать задачи, составив уравнения. Ставить скобки в числовом выражении для приведения к верному решению | Решать задачи арифметическим способом. Сравнивать площади фигур | Оценивать правильность выполненного задания на основе сравнения с предыдущими заданиями или на основе различных образцов и критериев. | Интер. доска | |||
44 | 23.12 | Сложение и вычитание величин | Урок формирования умений и навыков | Выполнять действия с величинами, значения которых выражены в разных единицах измерения. Записывать вычисления в строчку и столбиком | Выполнять сложение и вычитание величин | Целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно | ||||
45 | 24.12 | Решение задач
| Комбинированный урок | Моделировать зависимости между величинами в текстовых задачах и решать их. Выполнять сложение и вычитание величин | Решать текстовые задачи арифметическим способом, пользоваться изученной математической терминологией | Развитие навыков формулировки личной оценки, аргументирования своего мнения | ||||
46 | 28.11 | Что узнали. Чему научились. | Комбинированный | Анализировать достигнутые результаты и недочёты, проявлять личную заинтересованность в расширении знаний и способов действий | Анализировать достигнутые результаты и недочёты, проявлять личную заинтересованность в расширении знаний и способов действий | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
47 48 | 29.11 30.11 | Странички для любознательных. Задачи-расчёты Что узнали. Чему научились. | Комбирированный | Выполнять задания творческого и поискового характера, применять знания и способы действий в изменённых условиях. | Использовать приёмы сложения и вычитания многозначных чисел. Решать задачи арифметическим способом | |||||
49 | 1.12 | Контрольная работа № 4 по теме «Сложение и вычитание» | Контроль знаний, умений и навыков | Выполнять задания творческого и поискового характера, применять знания и способы действий в изменённых условиях. Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы | Использовать приёмы сложения и вычитания многозначных чисел. Решать задачи арифметическим способом | Контролировать свою деятельность: обнаруживать и устранять ошибки логического характера (в ходе решения) и ошибки вычислительного характера | ||||
Умножение и деление | ||||||||||
50 | 5.12 | Анализ контрольной работы Свойства умножения | Урок-исследование | Выполнять умножение, используя свойства умножения. Применять при вычислениях свойства умножения на 0 и на 1. Находить значение буквенных выражений | Использовать свойства умножения на 0 и на 1 при выполнении вычислений | Актуализировать свои знания для проведения простейших математических доказательств | Интер. доска | |||
51 52 | 6.12 7.12 | Письменные приемы умножение | Урок развития умений и навыков | Выполнять умножение любого многозначного числа на однозначное так же, как и умножение трёхзначного числа на однозначное. Умножать именованные числа на однозначные | Выполнять письменное умножение многозначного числа на однозначное | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера | ||||
53 | 8.12 | Умножение чисел, запись которых оканчивается нулями. | Урок формирования умений и навыков | Объяснять, как выполнено умножение чисел, запись которых оканчивается нулями. Находить остаток при выполнении деления на однозначное число и проверять вычисления | Объяснять приёмы умножения на однозначное число многозначных чисел, оканчивающихся нулями | Актуализировать свои знания для проведения простейших математических доказательств (в том числе с опорой на изученные определения, законы арифметических действий) | ||||
54 | 12.12 | Нахождение неизвестного множителя, неизвестного делимого, неизвестного делителя | Урок формирования умений и навыков | Определять, как связаны между собой числа при умножении и делении. Находить неизвестный множитель, неизвестное делимое, неизвестный делитель. Объяснять решение уравнений и их проверку. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи | Использовать правило нахождения неизвестного множителя, неизвестного делимого и неизвестного делителя. Вычислять значение числового выражения, содержащего 2-3 действия (со скобками и без них) | Актуализировать свои знания для проведения простейших математических доказательств (в том числе с опорой на изученные определения, законы арифметических действий) | ||||
55 | 13.12 | Деление с числами 0 и 1 | Комбинированный урок | Использовать правила деления суммы на число при решении примеров и задач. Оценивать результаты освоения темы, проявлять личную заинтересованность в приобретении и расширении знаний и способов действий. Анализировать свои действия и управлять ими | Применять правила деления суммы на число и использовать его при решении примеров и задач. Применять полученные знания для решения задач. Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | Интер. доска | |||
56 57 | 14.12 15.12 | Письменные приёмы деления | Урок развития умений и навыков | Объяснять, как выполнено деление многозначного числа на однозначное | Выполнять деление многозначного числа на однозначное с объяснением | Собирать требуемую информацию из указанных источников; фиксировать результаты разными способами; сравнивать и обобщать информацию | ||||
58 | 19.12 | Задачи на увеличение и уменьшение числа в несколько раз, выраженные в косвенной форме | Комбинированный урок | Объяснять, как выполнено деление многозначного числа на однозначное | Выполнять деление многозначного числа на однозначное с объяснением | Собирать требуемую информацию из указанных источников; фиксировать результаты разными способами; сравнивать и обобщать информацию | ||||
59 | 20.12 | Закрепление изученного. Решение задач. | Урок формирования умений и навыков | Составлять план решения текстовых задач и решать их арифметическим способом | Применять полученные знания для решения задач | Моделировать ситуацию, иллюстрирующую данное арифметическое действие | ||||
60 | 21.12 | Письменные приёмы деления. Решение задач. | Урок формирования умений и навыков | Объяснять, как выполнено деление, пользуясь планом. Выполнять деление с объяснением. Составлять план решения текстовых задач и решать их арифметическим способом | Делить многозначное число на однозначное, проверять правильность выполненных вычислений | Собирать требуемую информацию из указанных источников; фиксировать результаты разными способами; сравнивать и обобщать информацию | ||||
61 62 | 22.12 26.12 | Закрепление изученного «Что узнали. Чему научились» | Комбинированный урок | Оценивать результаты усвоения учебного материала, делать выводы, планировать действия по устранению выявленных недочётов, проявлять личностную заинтересованность в расширении знаний и способов действий | Использовать приёмы деления многозначного числа на однозначное. Решать задачи арифметическим способом | Контролировать свою деятельность: обнаруживать и устранять ошибки логического характера (в ходе решения) и ошибки вычислительного характера | ||||
63 | 27.12 | Контрольная работа № 5 по теме «Умножение и деление на однозначное число» | Контроль знаний, умений и навыков | Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Оценка — выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы | ||||
64 65 | 28.12 29.12 | Анализ контрольной работы .Закрепление изученного Умножение и деление на однозначное число | Урок изучения нового материала | Решать задачи арифметическим способом. Находить периметр прямоугольника (квадрата). Решать уравнения. Совершенствовать вычислительные навыки | Применять полученные знания для решения задач | Актуализировать свои знания для проведения простейших математических доказательств | ||||
66 | 10.01 | Скорость. Единицы скорости. Взаимосвязь между скоростью, временем и расстоянием | Урок формирования умений и навыков | Моделировать взаимосвязи между величинами: скорость, время, расстояние. Переводить одни единицы скорости в другие. Находить значение буквенных и числовых выражений | Составлять план действий и определять наиболее эффективные способы решения задачи | Моделировать содержащиеся в тексте задачи зависимости; планировать ход решения задачи | Интер. доска | |||
67 68 69 | 11.01 12.01 16.01 | Решение задач на движение | Урок развития умений и навыков | Записывать задачи с величинами: скорость, время, расстояние в таблицу и решать их. Составлять по выражению задачи с величинами: скорость, время, расстояние. Находить значение уравнений и числовых выражений | Решать задачи с величинами: скорость, время, расстояние. Называть единицы скорости. Понимать взаимосвязь между скоростью, временем и расстоянием | Моделировать содержащиеся в тексте задачи зависимости; планировать ход решения задачи | ||||
70 | 17.01 | Странички для любознательных. | Урок развития умений и навыков | Записывать задачи с величинами: скорость, время, расстояние в таблицу и решать их. Переводить одни единицы длины, массы, времени, площади в другие | Решать задачи с величинами: скорость, время, расстояние. Называть единицы скорости. Понимать взаимосвязь между скоростью, временем и расстоянием | Моделировать содержащиеся в тексте задачи зависимости; планировать ход решения задачи | Интер. доска | |||
71 | 18.01 | Умножение числа на произведение | Урок формирования умений и навыков | Применять свойство умножения числа на произведение в устных и письменных вычислениях. Выполнять умножение числа на произведение разными способами, сравнивать результаты вычислений | Использовать свойства арифметических действий при выполнении вычислений. Находить результат при умножении числа на произведение удобным способом | Постановка и формулирование проблемы, создание алгоритмов деятельности при решении проблем творческого и поискового характера | Интер. доска | |||
72 73 | 19.01 23.01 | Письменное умножение на числа, оканчивающиеся нулями | Урок формирования умений и навыков | Применять свойство умножения числа на произведение в письменных вычислениях, записывать решение столбиком. Решать задачи на одновременное встречное движение | Выполнять письменное умножение на числа, оканчивающиеся нулями | Постановка и формулирование проблемы, создание алгоритмов деятельности при решении проблем творческого и поискового характера | ||||
74 | 24.01 | Письменное умножение на числа, оканчивающиеся нулями | Урок развития умений и навыков | Применять свойство умножения числа на произведение в письменных вычислениях, записывать решение столбиком. Сравнивать именованные числа. Решать задачи на одновременное встречное движение | Выполнять письменное умножение на числа, оканчивающиеся нулями | Делать выводы на основе анализа предъявленного банка данных | ||||
75 | 25.01 | Решение задач | Урок развития умений и навыков | Решать задачи на одновременное встречное движение: выполнять схематические чертежи, сравнивать задачи и их решения | Решать задачи на одновременное встречное движение, развивать навык устного счёта; развивать внимание, творческое мышление | Актуализировать свои знания для проведения простейших математических доказательств | Интер. доска | |||
76 | 26.01 | Перестановка и группировка множителей | Урок развития умений и навыков | Используя переместительное свойство умножения и свойство группировки множителей, находить значение числового выражения. Решать задачи на одновременное встречное движение | Применять свойства умножения при решении числовых выражений | Делать выводы на основе анализа предъявленного банка данных | ||||
77 | 30.01 | Повторение пройденного. «Что узнали. Чему научились». | Контроль знаний, умений и навыков | Оценивать результаты освоения темы, проявлять личную заинтересованность в приобретении и расширении знаний и способов действий. Анализировать свои действия и управлять ими | Решать задачи на одновременное встречное движение, развивать навык устного счёта; развивать внимание, творческое мышление | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
78 79 | 31.01 1.02 | Контрольная работа за первое полугодие Анализ контрольной работы | Контроль знаний, умений и навыков | Оценивать результаты освоения темы, проявлять личную заинтересованность в приобретении и расширении знаний и способов действий. Анализировать свои действия и управлять ими | Решать задачи на одновременное встречное движение, развивать навык устного счёта; развивать внимание, творческое мышление | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
80 | 2.02 | Деление числа на произведение | Урок формирования умений и навыков | Применять свойство деления числа на произведение в устных и письменных вычислениях. Решать тестовые задачи арифметическим способом | Использовать свойства арифметических действий при выполнении вычислений. Находить результат при делении числа на произведение удобным способом | Постановка и формулирование проблемы, создание алгоритмов деятельности при решении проблем творческого и поискового характера | ||||
81 | 6.02 | Деление числа на произведение | Урок развития умений и навыков | Применять свойство деления числа на произведение в устных и письменных вычислениях. Решать тестовые задачи арифметическим способом | Использовать свойства арифметических действий при выполнении вычислений. Находить результат при делении числа на произведение удобным способом | Актуализировать свои знания для проведения простейших математических доказательств | ||||
82 | 7.02 | Деление с остатком на 10, 100, 1 000 | Урок формирования умений и навыков | Выполнять устно и письменно деление с остатком на 10, 100, 1 000. Решать тестовые задачи арифметическим способом. Находить значение буквенных выражений | Применять приём письменного деления многозначного числа на 10, 100, 1 000 с остатком | Постановка и формулирование проблемы, создание алгоритмов деятельности при решении проблем | Интер. доска | |||
83 | 8.02 | Решение задач | Урок формирования умений и навыков | Анализировать задачи, устанавливать зависимости между величинами, составлять план решения задачи, решать текстовые задачи. Записывать равенства и неравенства, выполнять проверку. Выполнять деление с остатком и проверять решение | Применять полученные знания для решения задач | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера | ||||
84 | 9.02 | Письменное деление на числа, оканчивающиеся нулями | Урок формирования умений и навыков | Выполнять устно и письменно деление на числа, оканчивающиеся нулями, объяснять используемые приёмы | Объяснять приём деления на числа, оканчивающиеся нулями | Актуализировать свои знания для проведения простейших математических доказательств | Интер. доска | |||
85 | 13.02 | Письменное деление на числа, оканчивающиеся нулями | Урок развития умений и навыков | Выполнять устно и письменно деление на числа, оканчивающиеся нулями, объяснять используемые приёмы. Совершенствовать вычислительные навыки, умение решать задачи | Объяснять приём деления на числа, оканчивающиеся нулями | Анализ объектов с целью выделения признаков (существенных, несущественных) | ||||
86 | 14.02 | Письменное деление на числа, оканчивающиеся нулями | Урок развития умений и навыков | Выполнять устно и письменно деление на числа, оканчивающиеся нулями, объяснять используемые приёмы. Совершенствовать вычислительные навыки, умение решать задачи | Объяснять приём деления на числа, оканчивающиеся нулями | Анализ объектов с целью выделения признаков (существенных, несущественных) | ||||
87 | 15.02 | Письменное деление на числа, оканчивающиеся нулями | Урок развития умений и навыков | Выполнять устно и письменно деление на числа, оканчивающиеся нулями, объяснять используемые приёмы. Совершенствовать вычислительные навыки, умение решать задачи | Объяснять приём деления на числа, оканчивающиеся нулями | Делать выводы на основе анализа предъявленного банка данных | ||||
88 | 16.02 | Решение задач | Урок формирования умений и навыков | Выполнять схематические чертежи по текстовым задачам на одновременное движение в противоположных направлениях и решать задачи. Составлять план решения. Обнаруживать допущенные ошибки | Применять полученные знания для решения задач. Решать задачи на одновременное движение в противоположных направлениях | Анализ объектов с целью выделения признаков (существенных, несущественных) | ||||
89 90 | 20.02 21.02 | Закрепление изученного. «Что узнали. Чему научились». | Комбинированный урок | Выполнять устно и письменно деление на числа, оканчивающиеся нулями. Совершенствовать вычислительные навыки, умение решать задачи | Выполнять письменное умножение на числа, оканчивающиеся нулями. Использовать приём деления на числа, оканчивающиеся нулями. Решать задачи на одновременное встречное движение, на одновременное движение в противоположных направлениях | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
91 | 22.02 | Контрольная работа № 7по теме «Умножение и деление чисел, оканчивающихся нулями» | Контроль знаний, умений и навыков | Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Выполнять письменное умножение на числа, оканчивающиеся нулями. Использовать приём деления на числа, оканчивающиеся нулями. Решать задачи на одновременное встречное движение, на одновременное движение в противоположных направлениях | Контролировать свою деятельность: обнаруживать и устранять ошибки логического характера (в ходе решения) и ошибки вычислительного характера | ||||
92 | 27.02 | Наши проекты | Урок-проект | Собирать и систематизировать информацию по разделам, отбирать, составлять и решать математические задачи и задания повышенного уровня сложности. Составлять план работы. Составлять сборник математических заданий. Анализировать и оценивать результаты работы | Определять цель проекта, работать с известной информацией, собирать дополнительный материал, создавать способы решения проблем творческого и поискового характера, составлять связный текст | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера. Поиск и выделение необходимой информации. Контроль и оценка процесса и результатов деятельности | ||||
93 | 28.02 | Анализ контрольной работы и работа над ошибками. Умножение числа на сумму | Урок формирования умений и навыков | Применять в вычислениях свойство умножения числа на сумму нескольких слагаемых. Находить значение выражения двумя способами, удобным способом. Сравнивать выражения. Составлять задачу по выражению. | Решать задачи, развивать навык устного счёта; развивать внимание, творческое мышление | Моделировать содержащиеся в тексте задачи зависимости; планировать ход решения задачи. Моделировать ситуацию, иллюстрирующую данное арифметическое действие | ||||
94 | 1.03 | Умножение числа на сумму | Урок развития умений и навыков | Выполнять вычисления с объяснением. Выполнять действия и сравнивать приёмы вычислений. Находить часть от целого. Совершенствовать вычислительные навыки, умение решать задачи | Объяснять, как выполнено умножение числа на сумму | Актуализировать свои знания для проведения простейших математических доказательств | Интер. доска | |||
95 96 | 2.03 6.03 | Письменное умножение на двузначное число | Урок изучения нового материала | Применять алгоритм письменного умножения многозначного числа на двузначное. Осуществлять пошаговый контроль правильности и полноты выполнения алгоритма арифметического действия умножение | Использовать алгоритм письменного умножения многозначного числа на двузначное | Актуализировать свои знания для проведения простейших математических доказательств (в том числе с опорой на изученные определения, законы арифметических действий) | ||||
97 | 7.03 | Решение задач | Урок формирования умений и навыков | Решать задачи на нахождение неизвестного по двум разностям. Анализировать задачи, выполнять прикидку результата, проверять полученный результат. Обнаруживать допущенные ошибки | Составлять план действий и определять наиболее эффективные способы решения задачи | Моделировать содержащиеся в тексте задачи зависимости; планировать ход решения задачи | ||||
98 | 13.03 | Решение задач | Урок развития умений и навыков | Решать задачи арифметическими способами. Объяснять выбор действия для решения. Выполнять вычитание именованных величин. Находить ошибки в примерах на деление, делать проверку | Применять полученные знания для решения задач | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера | ||||
99 100 | 14.03 15.03 | Письменное умножение на трёхзначное число | Урок изучения нового материала | Применять алгоритм письменного умножения многозначного числа на трёхзначное. Осуществлять пошаговый контроль правильности и полноты выполнения алгоритма арифметического действия умножение | Объяснять, как получают каждое неполное произведение при умножении на трёхзначное число | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера. | ||||
101 102 103 | 16.03 20.03 21.03 | Закрепление изученного «Что узнали. Чему научились». | Комбинированный урок | Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Решать задачи, развивать навык устного и письменного счёта; развивать внимание, творческое мышление | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
104 105 | 22.03 23.03 | Контрольная работа № 8 по теме «Умножение на двузначное и трёхзначное число» | Контроль знаний, умений и навыков | Применять свои знания для выполнения итоговой работы Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Оценка — выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы | ||||
105 | 3.04 | Анализ контрольной работы Письменное деление на двузначное число | Урок изучения нового материала | Применять алгоритм письменного деления многозначного числа на двузначное, объяснять каждый шаг | Объяснять алгоритм письменного деления многозначного числа на двузначное, когда цифра в частном находится методом подбора | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера | Интер. доска | |||
106 | 4.04 | Письменное деление на двузначное число | Урок развития умений и навыков | Выполнять деление с остатком на двузначное число, при этом рассуждать так же, как и при делении без остатка, проверять решение. Совершенствовать вычислительные навыки, умение решать задачи | Объяснять алгоритм письменного деления многозначного числа на двузначное с остатком | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера | ||||
107 | 5.04 | Алгоритм письменного деления на двузначное число | Урок изучения нового материала | Применять алгоритм письменного деления многозначного числа на двузначное, объяснять каждый шаг. Выполнять письменное деление многозначных чисел на двузначные, опираясь на знание алгоритмов письменного выполнения действия умножение. Осуществлять пошаговый контроль правильности и полноты выполнения алгоритма арифметического действия деления | Объяснять алгоритм письменного деления многозначного числа на двузначное | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера | ||||
108 109 | 6.04 10.04 | Письменное деление на двузначное число | Урок развития умений и навыков | Применять алгоритм письменного деления многозначного числа на двузначное, объяснять каждый шаг. Объяснять, как выполнено деление по плану. Решать задачи и сравнивать их решения. Проверять, верны ли равенства | Объяснять алгоритм письменного деления многозначного числа на двузначное по плану | Анализ объектов с целью выделения признаков (существенных, несущественных) | Интер. доска | |||
110 111 112 | 11.04 12.04 13.04 | Закрепление изученного Решение задач | Урок развития умений и навыков | Решать задачи арифметическими способами. Выполнять вычитание и сложение именованных величин. Выполнять деление с остатком и делать проверку | Применять полученные знания для решения задач. Объяснять выбор действия для решения | Прогнозировать результаты вычислений; контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
113 | 17.04 | Письменное деление на двузначное число (закрепление) | Урок обобщения и закрепления | Применять алгоритм письменного деления многозначного числа на двузначное, объяснять каждый шаг. Решать задачи арифметическими способами и сравнивать их решения. Объяснять выбор действия для решения. Умножать на именованные числа, решать уравнения | Выполнять письменное деление многозначного числа на однозначное по алгоритму | Контролировать свою деятельность: обнаруживать и устранять ошибки логического характера (в ходе решения) и ошибки вычислительного характера | ||||
114 | 18.04 | Закрепление изученного Решение задач | Урок обобщения и систематизации | Выполнять вычисления и делать проверку. Совершенствовать вычислительные навыки, умение решать задачи | Пользоваться вычислительными навыками, решать составные задачи | Контролировать свою деятельность: обнаруживать и устранять ошибки логического характера (в ходе решения) и ошибки вычислительного характера | ||||
115 | 19.04 | Закрепление изученного Решение задач | Комбинированный урок | Применять алгоритм письменного деления многозначного числа на двузначное, объяснять каждый шаг. Решать задачи арифметическим способом. Выполнять вычитание и сложение именованных величин, решать уравнения | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
116 | 20.04 | Контрольная работа № 9 по теме «Деление на двузначное число» | Контроль знаний, умений и навыков | Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Оценка — выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы | ||||
117 | 24.04 | Анализ контрольной работы | Урок изучения нового материала | Применять алгоритм письменного деления многозначного числа на трёхзначное, объяснять каждый шаг. Выполнять письменное деление многозначных чисел на двузначные, опираясь на знание алгоритмов письменного выполнения действия умножение | Объяснять алгоритм письменного деления многозначного числа на трёхзначное | Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера | ||||
118 | 25.04 | Письменное деление на трёхзначное число | Урок формирования умений и навыков. | Объяснять, как выполнено деление. Называть в каждом случае неполные делимые и рассказывать, как находили цифры частного. Совершенствовать вычислительные навыки, умение решать задачи. | Объяснять алгоритм письменного деления многозначного числа на трёхзначное. | Учебное сотрудничество с учителем и сверстниками в поиске и сборе информации; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. | ||||
119 | 26.04 | Письменное деление на трёхзначное число | Урок развития умений и навыков | Выполнять деление с объяснением и проверять вычисления. Делать чертёж к задаче и решать её. Составлять задачу по выражению. Сравнивать выражения | Объяснять алгоритм письменного деления многозначного числа на трёхзначное, делать проверку | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | Интер. доска | |||
120 | 27.04 | Закрепление изученного | Урок развития умений и навыков | Выполнять деление с объяснением и проверять вычисления. Совершенствовать вычислительные навыки, умение решать задачи | Объяснять алгоритм письменного деления многозначного числа на трёхзначное, делать проверку | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
121 | 3.05 | Деление с остатком | Урок формирования умений и навыков | Проверять, правильно ли выполнено деление с остатком. Находить делимое, если известны: делитель, частное и остаток. Проверять, выполнив деление | Объяснять алгоритм письменного деления многозначного числа на трёхзначное, делать проверку | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
122 123 124 | 4.05 8.05 10.05 | Деление на трёхзначное число. Закрепление Что узнали. Чему научились | Комбинированный урок | Находить ошибки и записывать правильное решение. Совершенствовать вычислительные навыки, умение решать задачи, уравнения | Находить ошибки при делении, исправлять их | Актуализировать свои знания для проведения простейших математических доказательств (в том числе с опорой на изученные определения, законы арифметических действий) | ||||
125 | 11.05 | Решение задач | Комбинированный урок | Находить ошибки и записывать правильное решение. Совершенствовать вычислительные навыки, умение решать задачи, уравнения | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
Итоговое повторение | ||||||||||
126 | 15.05 | Нумерация. | Комбинированный урок | Совершенствовать вычислительные навыки, умение решать задачи. Соотносить результат проведённого самоконтроля с целями, поставленными при изучении темы, оценивать их и делать выводы | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
127 | 16.05 | Итоговая контрольная работа № 11за 4 класс | Контроль знаний, умений и навыков | Применять свои знания для выполнения итоговой работы | Контролировать и оценивать свою работу, её результат, делать выводы на будущее | Контроль и оценка процесса и результатов деятельности | ||||
128 129 | 17.05 18.05 | Выражения и уравнения Арифметические действия: сложение и вычитание | Урок обобщения и систематизации | Оценить результаты освоения темы, проявить личностную заинтересованность в приобретении и расширении знаний и способов действий | Называть числа натурального ряда, которые больше 1 000. Читать и записывать числа, которые больше 1 000, используя правило, по которому составлена числовая последовательность. Решать числовые выражения и уравнения | Актуализировать свои знания для проведения простейших математических доказательств (в том числе с опорой на изученные определения, законы арифметических действий) | Интер. доска | |||
130 131 | 22.05 23.05 | Арифметические действия: умножение и деление Порядок выполнения действий. | Урок обобщения и систематизации | Совершенствовать вычислительные навыки, умение решать задачи | Использовать приёмы сложения и вычитания, умножения и деления чисел, которые больше 1 000 | Контролировать свою деятельность: проверять правильность выполнения вычислений изученными способами | ||||
132 133 | 24.05 25.05 | Величины. Обобщающий урок Игра «В поисках клада» | Урок обобщения и систематизации | Оценить результаты освоения темы, проявить личностную заинтересованность в приобретении и расширении знаний и способов действий Применять полученные знания при выполнении нестандартных задач | Применять правила о порядке выполнения действий в числовых выражениях со скобками и без скобок при вычислениях значений числовых выражений | Собирать требуемую информацию из указанных источников; фиксировать результаты разными способами | Интер. доска | |||
4 класс. Моро. Учебник №1. Ответы к стр. 28
Числа от 1 до 1000
Числа, которые больше 1000
Увеличение и уменьшение числа в 10, 100, 1 000 раз
Ответы к стр. 28
125. 1) Числа 57, 90, 200 увеличь в 10 раз; в 100 раз.
57 • 10 = 570 57 • 100 = 5 700
90 • 10 = 900 90 • 100 = 9 000
200 • 10 = 2 000 200 • 100 = 20 000
2) Числа 4 000, 60 000, 152 000 уменьши в 1 000 раз.
4 000 : 1 000 = 4
60 000 : 1 000 = 60
152 000 : 1 000 = 152
126.
67 000 : 1 000 = 67 39 000 • 10 = 390 000
9 600 : 100 = 96 9 600 • 100 = 960 000
102 000 : 10 = 10 200 102 000 : 100 = 1 020
127. Сравни числа.
99 999 < 100 000 415 760 > 415 670
128. В альбоме 100 листов. Сколько таких альбомов получится из 15 000 листов? Сколько листов в 1 000 таких альбомов?
1) 15 000 : 100 = 15 (ал.)
2) 100 • 1 000 = 100 000 (л.)
О т в е т: из 15 000 листов получится 15 альбомов; в 1 000 таких альбомов 100 000 листов.
129. Сравни пары уравнений. Сравни их решения.
х – 260 = 340 96 : х = 4 16 + х = 80
х = 340 + 260 х = 96 : 4 х = 80 – 16
х = 600 х = 24 х = 64
х + 260 = 340 96 – х = 4 16 • х = 80
х = 340 – 260 х = 96 – 4 х = 80
х = 80 х = 92 х = 5
130. Длина участка прямоугольной формы 70 м, а ширина – 30 м. Сколько шагов надо сделать, чтобы пройти по его периметру? (Два шага составляют 1 м.)
1) (70 + 30) • 2 = 200 (м) – периметр участка
2) 2 • 200 = 400 (ш.)
О т в е т: надо сделать 400 шагов.
131. Начерти: 1) отрезок AB, длина которого равна половине длины отрезка в 1 дм; 2) отрезок CD, длина половины которого равна 2 см.
1) 1 дм = 10 см
10 : 2 = 5 (см)
2) 2 • 2 = 4 (см)
132. Проверь, верны ли равенства.
800 – 296 = 168 • 3 888 : 3 = 703 – 407
504 = 504 296 = 296
133. Записали подряд все трёхзначные числа. Сколько всего цифр записано в этом ряду?
Трёхзначные числа начинаются со 100 и заканчиваются на 999. Их количество: 999 – 100 + 1 = 900 (1 прибавляем, поскольку вычли 100, но оно тоже трёхзначное число). Каждое трёхзначное число содержит 3 цифры. Тогда: 900 • 3 = 2700 – всего цифр в записанном ряду.
34 800 : 10 = 3 480 4 900 : 100 = 49 540 • 10 = 5 400
ЗАДАНИЕ НА ПОЛЯХ:
∧ = 7 = 1
1 :
7 • 1 = 7
7 : 1 = 7
Ответы по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4.8 / 5 ( 42 голоса )
|
Урок математики 4 класс — математика, уроки
Откройте учебники на маршрутных листах и посмотрите какие темы вы уже изучили?
Какие единицы массы вы знаете?
А назовите их в порядке увеличение?
Молодцы.
Какая следующая тема, которую вы изучили?
Чему вы учились на уроке при изучение этой темы?
Какая же следующая тема?
А какие единица S вы знаете?
А какое правило вы знаете для единицы S?
Правильно.
А сегодня на уроке мы с вами будем изучать, новый большой который называется ДЕЛЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ.
И первая наша тема будет Деление- действия, обратное умножению.
Как вы думаете, чему мы будем учиться сегодня на уроке?
Правильно, делить многозначные числа и результат записывать уголком т.е. письменно.
Но сначала повторим связь между умножение и делением.
Откроем учебник на странице 48.
Прочитайте про себя задание №1 (а) и рассмотрите схему № 1.
Давай те рассмотри схему. Какие величины даны в схеме?
Как связаны величины между собой?
Сколько в день состоялось матчей чемпионата по футболу?
Сколько команд принимало участие во встрече?
А если у нас состоялось 8 матчей, то значит сколько команд принимало участие в первый день.?
Сколько игроков в одной команде?
Как же нам узнать общее количество игроков?
Запишите в тетрадях и скажите ответ.
Прочитайте задачу под буквой (б)
Какие величины даны в этой схеме?
Что нам известно?
Сколько?
Сколько игроков в команде?
Как получим число команд?
Запишите в тетрадях.
Как записали ответ?
Итак, посмотрите еще раз на схемы, и скажите, как же связаны умножение и деление?
Выполним №2.(а) (устно)
68:17=4 Как проверим?
Верно.
75:15=7 Проверим.
Неверно.
140:28=5 Верный ли это ответ.
Верно.
204:6=36 Проверим.
Ответ не верен.
Решим под буквой (б) письменно. Методом подбора.
63:21=
72:18=
92:23=
98:14=
74:37=
А теперь давайте немного отдохнем.
Если вам трудно делить, то делить можно выполнить уголком.
Разделим вместе с вами 154:22. Записываем уголком так как записано на доске.
Давайте попробуем определить цифру в частном.
Какой вычислительный разряд в числе 154?
Можем ли мы одну сотню разделить на 22?
Значит делить будем все число 154, и в ответе поставим точку, это значит, что будем однозначное число.
Чтобы удобнее подобрать цифру в частном, округлим 154 до 150, а 22 до 20. Чтобы разделить 150 на 20 достаточно 15:2, это примерно получится 7.
Цифра 7 и будет нашем пробным числом. Проверим ее. Для этого 22*7=20*7 получим, и 2*7 получим 14, 140+14= 154. Вычислим остаток 154-154=0. Закончили деление.
А теперь таким же способом выполним №3.
133:19
Делить будем всё число.
133 округляем до…
19 округлим до……
Значит 130:20, для этого 13:2 получим примерно 6.
Проверим. 19*6= 10*6=60+9*6=54. Значит 60+54=124.
Не правильно. Попробуем число 7. 19*7=10*7=70+9*7=63. 70+63=133. Записываем в частном 7. Делаем проверку 133-133=0. Деление закончили.
Смотри далее.
108:18.
Делить будем все число.
108 округляем до
18 округлим до
100:20, для этого 10:2=5. Проверим .18*5=10*5=50+8*5=40=50+40=90. Неправильно
Возьмем цифру 6.18*6=10*6+8*6=60+48=108.
Делаем проверку. В частном записываем 6. Деление закончено.
Рассмотрим следующий пример.
279:31. Делить будем всё число.
279 округлим до
31 округлим до
200:30=20:3=6. Проверим. 31*6=30*6+1*6=180+6=186.
Неправильно. Возьмем 7. Проверим.31*7=30*7+1*7=210+7=217. Не подходит. Возьмем 9. Проверим. 31*9=30*9+1*9=270+9=279.
В частном запишем 9. Проверим остаток 0. Деление закончено.
Следующий пример попробуйте решить самостоятельно.
Проверим.
168:24=160:20=16:2=8.24*8=20*8+4*8=160+32=192. Много возьмем 7.
24*7=20*7+4*7=140+28=168.
243:27=240:30=24:3=8. Проверим.27*8=20*8+7*8=160+56=216. Не подходит. Берем по 9.27*9=20*9+7*9=180+63=243. Деление закончено.
464:58=400:50=40:5=8. Проверим. 58*8=50*8+8*8=400+64=464.
292:73=200:70=290:7=4. Проверим. 73*4=70*4+3*4=280+12=292.
390:65=300:60=30:6=5. Проверим.65*5=60*5+5*5=300+25=325. Не подходит берем по 6. Проверим. 65*6=60*6+6*5=360+30=390.
420:84=400:80=40:8=5. Проверим. 84*5=80*5+4*5=400+20=420.
Молодцы.
Итак наш урок подошел к концу, давай те вспомним чему мы с вами учились?
Грамм, килограмм, тонна, центнер.
Гр, кг ,ц, т.
Умножать многозначные числа столбиком.
Делить многозначные числа.
Число команд, число игроков в команде, общее число игроков.
8
2
16
11
16*11=176(и)
Ответ: общее кол-во игроков 176
Читают
общее число игроков. Число игроков в команде, число команд.
Общее кол-во игроков
352
11
352:11=32(к)
Число команд=32
4*17=68
7*15=105
5*28=140
36*6=216
3
Сотни.
Нет
130
20
100
20
200
30
336:42. Делим полное
число. Для этого 336
округлим до 300, а 42
до 40. 300: 40=
30: 4=7.Проверим.
42*7=40*7+2*7=
280+14=294.
Не подходит. Возьмем 8. Проверим.42*8=40*8+2*8
=320+16=336. В частном пишем 8. Делаем проверку. Деление закончено.
Делить многозначные числа уголком.
учимся работать с таблицей – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)
1. Информационные таблицы
Информационные таблицы содержат данные, которые ученику нужно использовать при выполнении задания. Могут быть указаны площади стран, сведения из биологии, другие показатели. Дети получают задания: «найди информацию», «классифицируй», «расположи по уменьшению» (и возрастанию), «сделай вычисления», «составь вопросы по таблице» и др. Вычисления производятся отдельно.
Примеры заданий
1 класс
(Из проверочных работ. Задание «со звездочкой»)
На даче собрали урожай ягод. Их количество записали в таблицу
Укажите верные утверждения, составленные по таблице.
- Крыжовника больше, чем малины.
- Черники меньше, чем крыжовника.
- Малины столько же, сколько черники.
- Крыжовника больше, чем черники, но меньше, чем клубники.
2 класс
(Из проверочных работ)
В таблице указано расписание движения поездов
|
|
Номер поезда |
Время отправления |
|
Москва — Сочи |
083С |
20 ч 10 мин |
|
Москва — Уфа |
116Й |
12 ч 26 мин |
|
Москва — Анапа |
109В |
23 ч |
Запиши ответ на вопросы.
- Какой номер поезда Москва — Анапа?
- В какое время отправляется поезд Москва — Сочи?
- В какой город поезд отправляется раньше всех?
3 класс
«Моя телефонная книга»
Составь свою телефонную книгу. Расположи абонентов в алфавитном порядке. Какие телефоны экстренных служб обязательно должны быть занесены в книгу?
|
№ |
Список абонентов |
Телефон |
|
|
|
|
4 класс
Ответьте на вопросы по таблице, в которой записана длина корней некоторых растений.
|
Пшеница |
Фасоль |
Горох |
Лен |
Рожь |
|
150 см |
70 см |
90 см |
80 см |
130 см |
- Какое растение имеет: а) самые длинные корни; б) самые короткие корни?
- Расставь растения в порядке уменьшения длины корней.
- На сколько сантиметров корни пшеницы длиннее, чем корни льна?
- На сколько сантиметров корни гороха короче, чем корни ржи?
Занимательная математика. 1 класс. Рабочая тетрадь
Пособие может быть использовано в начальной школе при проведении занятий математического факультатива, кружка, олимпиады, клуба «Эрудит», интеллектуального марафона и других форм организации внешкольной деятельности учащихся. Задания, включенные в рабочую тетрадь, способствуют формированию у детей самостоятельности, наблюдательности, геометрической зоркости и умения рассуждать, а также создают условия для развития интереса к математике, математического кругозора и эрудиции учащихся.
Купить2. Справочные таблицы
Справочные таблицы в первом классе показывают числа в пределах 20 с разных точек зрения. И далее, они помогают познакомить учеников с названиями чисел, видами вычислений, разрядами чисел, единицами измерения.
Примеры заданий
1 класс
Назови состав числа 5 по рисунку. Заполни домик.
Найди значение выражений, пользуясь составом числа 5.
|
4 + 1 |
3 + 2 |
5 – 1 |
5 – 2 |
|
2 + 3 |
5 – 3 |
1 + 4 |
5 – 4 |
2 класс
Рассмотри таблицу чисел от 1 до 100. Назови числа, которые ты знаешь. По какому правилу составлена таблица? Какие числа пропущены?
- Сколько двузначных чисел начинаются с цифры 7? Назови их.
- Сколько в таблице круглых чисел? Назови их.
- Сколько однозначных чисел? Назови их.
- Сколько двузначных чисел оканчивается цифрой 2? Назови их.
3 класс
Найди значения выражений и запиши их римскими цифрами.
| L – X | CCC + D |
LX – XX |
| D + C | XL + X |
DC – CD |
| XXX – V | CD – C |
|
Арабская нумерация |
1 |
5 |
10 |
50 |
100 |
500 |
|
Римская нумерация |
I |
V |
X |
L |
C |
D |
4 класс
Выполни задание по таблице.
Таблица разрядов и классов
|
Класс миллионов |
Класс тысяч |
Класс единиц |
||||||
|
Сот. |
Дес. |
Ед. |
Сот. |
Дес. |
Ед. |
Сот. |
Дес. |
Ед. |
|
0 |
0 |
0 |
4 |
6 |
5 |
9 |
0 |
7 |
|
3 |
2 |
8 |
0 |
0 |
0 |
6 |
5 |
0 |
|
1 |
7 |
9 |
4 |
5 |
6 |
2 |
0 |
3 |
- Сколько классов в таблице? Сколько разрядов?
- Назови разряды каждого класса.
- Какие цифры записаны в разряде десятков миллионов?
- Какие цифры записаны в разряде: единиц, единиц тысяч, единиц миллионов?
- В каких разрядах записана цифра 3?
- Назови старший разряд каждого числа.
- Прочитай второе число. Какой класс не назван?
3. Логические таблицы
Логические таблицы ставят перед учениками логические задачи: проанализировать данные, найти закономерности. Например: «дополни таблицу нужными элементами» (фигурами/числами), «продолжи запись», «сопоставь числа и формулы», «вставь подходящее число из предложенных и сделай вычисление» и т.д.
Примеры заданий
1 класс
Кто быстрее (ты или твой сосед по парте) нарисует фигуру, которую нужно поставить на свободное девятое место?
3 класс
Какие числа пропущены в таблице, если r — радиус окружности, а d — диаметр этой же окружности?
|
r |
24 м |
|
125 мм |
|
|
d |
|
24 дм |
|
125 см |
4 класс
Какие высказывания о таблице верные?
|
10 |
12 |
74 |
48 |
|
300 |
303 |
330 |
333 |
|
900 |
927 |
956 |
903 |
- В первом столбце записаны круглые числа.
- В первой строке записаны четные двузначные числа.
- В третьей строке записаны трехзначные числа, которые содержат 9 десятков.
- В четвертом столбце записаны числа, которые делятся на 3 без остатка.
- Сумма чисел в первой строке равна 144.
Читайте также:
4. Вычислительные таблицы
Вычислительные таблицы являются формой вычислительного задания, то есть ученики производят вычисления непосредственно в таблице. Так школьники повторяют компоненты действий и составы чисел, работают с множителями, делимыми, разностями, остатками и т.д.
Примеры заданий
1 класс
Какие числа пропущены?
|
Уменьшаемое |
8 |
|
6 |
8 |
|
7 |
|
Вычитаемое |
|
3 |
4 |
|
4 |
|
|
Разность |
1 |
4 |
|
6 |
4 |
1 |
2 класс
Назовите числа, которые пропущены в каждой таблице.
|
Множитель |
2 |
|
2 |
8 |
|
Множитель |
9 |
2 |
3 |
|
|
Произведение |
18 |
10 |
|
16 |
|
Делимое |
12 |
8 |
18 |
|
|
Делитель |
6 |
|
9 |
2 |
|
Частное |
|
4 |
|
7 |
Закончи предложения.
- Если произведение двух чисел разделить на один из множителей, то получится … .
- Если делитель умножить на частное, то получится … .
- Если делимое разделить на частное, то получится … .
- Если делимое разделить на делитель, то получится … .
3 класс
Какие числа пропущены в таблице?
|
Делимое |
19 |
61 |
52 |
|
90 |
236 |
629 |
|
Делитель |
2 |
13 |
|
8 |
|
10 |
100 |
|
Частное |
9 |
|
3 |
100 |
3 |
|
6 |
|
Остаток |
|
9 |
10 |
13 |
12 |
6 |
|
4 класс
Вычисли устно и расшифруй название науки. Что она изучает?
Математика. 4 класс. Итоговая аттестация. Базовый и повышенный уровни сложности.
Рабочая тетрадь предназначена для оценки результатов деятельности выпускников начальной школы по освоению курса математики. В нее включены 10 вариантов заданий на двух уровнях трудности. В основе многих заданий лежат ситуации из реальной жизни. Пособие окажет учителям начальной школы помощь в организации диагностических процедур.
Купить5. Таблицы для решения задач
Таблицы для решения задач подобны вычислительным таблицам, однако используются в заданиях с текстовыми задачами, сопровождаются иллюстрациями, схемами. Такие таблицы часто предусматривают работу с формулами и с пропорциями.
Примеры заданий
1 класс
Составь задачу и реши ее.
2 класс
На пошив спального мешка требуется 4 м ткани. Сколько метров ткани потребуется для 7 спальных мешков? Составь две обратные задачи, используя таблицу.
|
Расход ткани на 1 мешок |
Число мешков |
Расход ткани на все мешки |
|
|
|
|
3 класс
За 5 ластиков Оля заплатила 30 р., а Марина за такие же ластики заплатила 54 р. Сколько ластиков купила Марина?
|
|
Цена (а) |
Количество (n) |
Стоимость (c) |
|
О. |
Одинаковая |
5 шт. |
30 р. |
|
М. |
? шт. |
54 р. |
План решения.
- Найти цену ластика.
- Найти количество ластиков, купленных Мариной.
4 класс
Реши задачу, используя таблицу или схему. Машина в первый день за 8 ч проехала 464 км. Во второй день она была в пути 6 часов и двигалась с той же скоростью. Сколько всего километров проехала машина за два дня?
|
|
V |
t |
S |
|
I |
Одинаковая |
8 ч |
464 км |
|
II |
6 ч |
? км |
|
|
I + II |
(8 + 6) ч |
? км |
Задание с таблицей из демоверсии ВПР по математике (4 класс)
Проверяемые умения в соответствии с ФГОС:
- Умение работать с таблицами, схемами, графиками диаграммами, анализировать и интерпретировать данные.
- Сравнивать и обобщать информацию, представленную в строках и столбцах несложных таблиц и диаграмм.
Задание:
В спортивных соревнованиях по нескольким видам спорта приняли участие 4 команды. Количество медалей, полученных командами, представлено в таблице. Используя эти данные, ответь на вопросы.
|
Команда |
Золотые |
Серебряные |
Бронзовые |
|
«Сириус» |
7 |
8 |
3 |
|
«Орион» |
6 |
4 |
5 |
|
«Заря» |
4 |
6 |
7 |
|
«Весна» |
3 |
2 |
5 |
1) Сколько серебряных медалей завоевала команда «Сириус»? 2) Какая команда заняла 3-е место по сумме всех медалей?
Решение: 1) 7 + 8 + 3 = 18 (м.) — «Сириус»; 2) 6 + 4 + 5 = 15 (м.) — «Орион»; 3) 4 + 6 + 7 = 17 (м.) — «Заря»; 4) 3 + 2 + 5 = 10 (м.) — «Весна».
Ответ: 1) 8; 2) Орион.
Вы можете апробировать учебники «Математика» авторства Г. К. Муравина и О. В. Муравиной. Для этого воспользуйтесь акцией «5 учебников бесплатно».
#ADVERTISING_INSERT#
Страница 34 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
Вернуться к содержанию учебника
Числа, которые больше 1000. Деление на числа, оканчивающиеся нулями
Вопрос
129. Найди ошибки в вычислениях и реши правильно.
Подсказка
Повтори алгоритм письменного деления на двузначные и трёхзначные числа.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
130. Выполни деление с остатком и проверь решение.
| 2856 : 40 | 19217 : 30 | 81569 : 500 | 424807 : 600 |
Подсказка
Повтори алгоритм письменного деления многозначных чисел, а также как выполнять деление с остатком.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
131. В ящике помещается 20 кг моркови. Сколько потребуется таких ящиков, чтобы отправить в магазин 675 кг моркови? Сколько килограммов моркови будет в последнем ящике?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
132. В каждом ряду кинозала 30 мест. На сеанс продано 942 билета. Сколько полных рядов в этом зале могут занять зрители с билетами?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
133. Два лыжника вышли из посёлка одновременно в противоположных направлениях. Один из них шёл со скоростью 12 км/ч, а другой — 10 км/ч. Через сколько часов расстояние между ними будет 44 км? Какое расстояние пройдёт за это время каждый лыжник?
Подсказка
Повтори взаимосвязь между скоростью, временем и расстоянием.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
134. Из двух посёлков выехали одновременно навстречу друг другу два всадника. Первый ехал со скоростью 200 м/мин, а второй проезжал в минуту на 20 м меньше. Всадники встретились через 50 мин. Найди расстояние между посёлками.
Подсказка
Повтори взаимосвязь между скоростью, временем и расстоянием.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
135. Найди значение выражения 120 : 4 + 2 • 3.
Измени порядок действий в этом выражении с помощью скобок так, чтобы его значение стало равно 60; 96; 12.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
136. Выполни деление и проверь умножением.
| 432240 : 60 | 283600 : 400 | 483000 : 700 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
137.
| 10000 — 4500 • 70 : 90 | 276300 : 900 |
| 2099 + 8050 • 20 : 50 | 563500 : 700 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
138.
| 1 ч — 15 мин | 1 т — 8 ц | 1 м2 — 10 дм2 |
| 1 сут. — 15 ч | 1 ц — 8 кг | 1 дм2 — 10 см2 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Магический квадрат
Подсказка
Магический квадрат — таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
На нашем сайте есть решение варианта 1 проверочной работы на странице 66.
На нашем сайте есть решение варианта 2 проверочной работы на странице 67.
Вернуться к содержанию учебника
© budu5.com, 2021
Пользовательское соглашение
Copyright
Описание курсов — Государственный университет Юго-Восточного Миссури
Описание курсов бакалавриата по математике (MA)
MA 003 Контрольный экзамен по математике
Тест по математике. Обязателен для всех специальностей математики (Pure,
Прикладная математика и статистика и среднее образование.
Пререквизиты: специальность математика, 90 кредитных часов.(0)
MA 018 Математика 1 Лаборатория
Курс удовлетворяет требованиям развивающей математики для студентов, обучающихся в
MA128, которые не соответствуют требованиям по математике ACT 22 или выше.
Пре / обязательное условие: оценка по математике MA128 и ACT от 0 до 21; или MA050 с минимальным
сорт НДЦ; заявленное образование по специальности начальное, дошкольное, исключительное
Исследования в области детского, среднего образования или окружающей среды: вариант развития ребенка.(1)
MA 023 Лаборатория математического мышления и моделирования
Курс удовлетворяет требованиям развивающей математики для студентов, обучающихся в
MA123, которые не соответствуют требованиям по математике ACT 22 или выше.
Пре / обязательное условие: оценка по математике MA123 и ACT от 0 до 21; или MA050 с минимальным
сорт НДЦ. (1)
MA 050 Базовые математические навыки
Обзор основных операций арифметики; понимание и выполнение операций
со знаковыми числами; и введение в алгебру.
Необходимое условие: балл ACT по математике 14 или ниже. (3)
MA 055 Лаборатория статистического мышления
Курс удовлетворяет требованиям развивающей математики для студентов, обучающихся в
MA155, которые не соответствуют требованиям по математике ACT 22 или выше.
Пре / обязательное условие: оценка по математике MA155 и ACT от 0 до 21; или MA050 с минимальным
сорт НДЦ.(1)
MA 106 Промежуточная алгебра
Многочлены, факторизация, уравнения и неравенства с одной и двумя переменными, рациональные
выражения, рациональные показатели, квадратные уравнения, графики и системы линейных
уравнения.
Необходимые условия: MA050 с минимальной оценкой NDC или ACT по математике 15-21 или
требуемый балл по соответствующему тесту по математике.(3)
MA 111 Precalculus Review
Обзор полиномиальных, рациональных, экспоненциальных, логарифмических и тригонометрических функций и уравнения с приложениями. Предпосылки: MA133 с минимальной оценкой C (если кредит необходим для MA117) или MA134 с минимальной оценкой C (если кредит требуется для MA116), или MA133 и MA134 с минимальным классом C или MA135 с минимальная оценка C (если кредит необходим для MA137).(1)
MA 115 Precalculus A с интегрированным обзором (начало осени 2018 г.)
Функции и графики, полиномиальные и рациональные функции, экспоненциальные и логарифмические
функции, матрицы. (Общеобразовательный курс) (5)
Пререквизиты: MA 050 с минимальной оценкой NDC, MA095 с минимальной оценкой NDC,
или MA106 или MA102 с минимальной оценкой C, или счетом ACT по математике 15-21, или обязательным
баллы по соответствующему тесту на зачисление на факультет.
MA 116 Precalculus A (начало осени 2018 г.)
Функции и графики, полиномиальные и рациональные функции, экспоненциальные и логарифмические
функции, матрицы. (Общий курс) (3)
Пререквизиты: MA 106 или MA102 с минимальной оценкой C или MA095 с минимальной оценкой
NDC или ACT Math 22 или выше, или требуемый балл на соответствующем факультете
тест на размещение.
MA 117 Precalculus B (начало осени 2018 г.)
Геометрические и тригонометрические рассуждения, необходимые для исчисления. Тригонометрические функции,
тождества, графики и уравнения, векторы, полярные координаты и коники. (3)
Необходимое условие: MA 115 Precalculus A с интегрированной проверкой с минимальной оценкой
C или MA 116 Precalculus A с минимальной оценкой C.
MA 123 Математическое мышление и моделирование
Выборка тем, включая геометрию, вероятность, статистику, финансы с
акцент на реальных приложениях.
Необходимое условие: оценка по математике ACT 15 или выше или MA050 с оценкой «NDC» или
выше или MA 102 с оценкой «C» или выше, или требуемый балл по соответствующему
тест по математике. Студенты, получившие оценку ACT по математике ниже 22 баллов, будут зачисляться совместно.
в MA023. (Общеобразовательный курс) (3)
MA 128 Числа и операции для преподавателей
Вещественные числа и их действия, свойства и приложения, теория чисел, счисление системы, алгебраические свойства, графики, статистика, вероятность и их исторические важность.Предпосылки: Заявленное образование по направлению начальное, раннее детство, исключительные исследования детей, средней школы или окружающей среды: развитие ребенка вариант майор. Оценка ACT по математике 15 или выше или MA050 с оценкой «NDC» или выше или MA 102 с оценкой «C» или выше, или требуемый балл по соответствующему тест по математике. Студенты, получившие оценку ACT по математике ниже 22 баллов, будут зачисляться совместно. в MA018.(Общеобразовательный курс) (4)
MA 133 Плоская тригонометрия
Круговые функции, прямые и наклонные треугольники, тождества и уравнения, комплексные
числа.
Необходимое условие: MA 106 с минимальной оценкой C или MA 102 с минимальной оценкой C
или ACT Math с баллом 15-21 с обязательным баллом по соответствующему положению по математике
тест, или балл ACT Math 22 или выше.(3)
MA 134 Алгебра колледжа
Функции и графики, полиномиальные и рациональные функции, экспоненциальные и логарифмические
функции и последовательности.
Необходимое условие: MA 106 с минимальной оценкой C или MA 102 с минимальной оценкой C
или ACT Math с баллом 15-21 с обязательным баллом по соответствующему положению по математике
тест, или балл ACT Math 22 или выше.(Общеобразовательный курс) (3)
MA 135 Колледж алгебры и тригонометрии
Интегрированный курс студенческой алгебры и плоской тригонометрии. Кредит не может быть получен
для MA 133 или MA 134 и MA 135.
Необходимые условия: MA106 с оценкой «C» или выше или MA102 с оценкой «CR» или
оценка «C» или выше или требуемый балл по соответствующему экзамену по математике
или более 22 баллов по математике ACT.(5)
MA 137 Precalculus
Углубленное изучение полиномиальных, рациональных, экспоненциальных, логарифмических и тригонометрических
функции и уравнения с приложениями. Кредит не может быть получен для MA137 и
любой из следующих: MA 133, MA 134 или MA 135.
Необходимые условия: MA 102 или MA 106 со степенью CR; или MA 095 с минимальной оценкой
из C; или оценка по математике ACT 22 или выше.(Общеобразовательный курс) (5)
MA 138 Дискретная математика
Курс прикладной математики с упором на фундаментальные принципы дискретной математики
и приложения к информатике. Темы включают логику, математическую индукцию,
множества, отношения, функции, алгоритмы, перестановки и комбинации, а также теория графов.
Необходимое условие: MA134 или MA137 с минимальной оценкой C.(3)
MA 139 Прикладное исчисление
Для студентов, изучающих бизнес, общественные науки или науки о жизни. Функции, пределы, дифференциация
и интеграция элементарных функций. Подчеркивает приложения.
Предварительные требования: оценка ACT по математике или 24 балла или MA 134 с минимальной оценкой C. (3)
MA 140 Аналитическая геометрия и исчисление I
Аналитическая геометрия, функции, пределы, производные и интегралы алгебраических, тригонометрических,
и экспоненциальные функции с приложениями.
Предварительные требования: оценка по математике ACT 26 или выше или MA 137 с минимальной оценкой
С. (5)
MA 144 Интегральное исчисление и дифференциальные уравнения
Приложения и методы интегрирования, параметрические уравнения, полярные координаты,
методы решения обыкновенных дифференциальных уравнений, приложения, численные методы,
и преобразования Лапласа.
Пререквизиты: MA 140 с минимальной оценкой C. (5)
MA 145 Аналитическая геометрия и исчисление II
Дифференцирование и интегрирование трансцендентных функций, рядов, конических сечений,
полярные координаты.
Необходимое условие: MA 140 с минимальной оценкой C. (4)
MA 155 Статистическое обоснование
Этот курс познакомит студентов с идеями статистики.Студент достигнет
понимание этих статистических идей, уметь критически относиться к статистическим
аргументы и получить представление о влиянии статистических идей на общественное
политики и в других областях академических исследований.
Предварительное условие: Предварительное условие: оценка ACT по математике 15 или выше или MA050 с оценкой «NDC» или выше или MA 102 с оценкой «C» или выше или
требуемый балл по соответствующему тесту по математике.Студенты с промежуточной оценкой ACT по математике ниже
22 человека будут участвовать в MA055. (Общеобразовательный курс) (3)
MA 223 Элементарная вероятность и статистика
Введение в основные идеи статистики: описательные меры, элементарная вероятность,
распределения, оценка, проверка гипотез, корреляция и линейная регрессия.
Необходимое условие: MA 134 с минимальным баллом «C». (3)
MA 228 Геометрия и измерения для преподавателей
Евклидова геометрия — показательная, координатная, трансформационная; интуитивные отношения,
конструкции, свойства линий, многоугольников, окружностей, трехмерных фигур,
и двумерная неевклидова геометрия.
Необходимое условие: MA 128 с минимальной оценкой C. (4)
MA 244 Аналитическая геометрия и исчисление III
Векторы, твердотельная аналитическая геометрия, частичное дифференцирование, множественное интегрирование и разделы векторного исчисления.
Необходимое условие: MA 145 с минимальной оценкой C. (4)
МА 250 Основы математики
Введение в понимание и написание доказательств с использованием фундаментальных понятий, таких как
как отношения, эквивалентность, разбиения, математическая индукция, функции, развитие
систем счисления и бесконечных множеств.
Пререквизиты: MA 138 с оценкой не ниже C; MA 139 или MA 140 с минимальной оценкой C. (3)
MA 318 Математика II
Разработка системы вещественных чисел, ее свойств и приложений, в том числе
алгебраическая логика, построение графиков, статистика, вероятность и измерения. Можно посчитать
только в качестве факультативного кредита, за исключением программ на получение степени, в которых этот курс явно
обязательный.
Необходимое условие: MA128 с минимальной оценкой C. (3)
MA 334 Математическое программирование
Введение в программирование с использованием системы компьютерной алгебры. Дизайн и реализация
алгоритмов решения математических задач.
Пререквизиты: MA138 с оценкой не ниже C; MA 145 с минимальной оценкой C.
(3)
MA 338 Дискретная математика II
Курс прикладной математики, подчеркивающий фундаментальные принципы дискретной математики.
и их приложения к информатике.Темы включают принцип включения
и исключение, производящие функции, рекуррентные соотношения, теория графов, булева алгебра,
теория кодирования и комбинаторные планы.
Необходимое условие: MA 138 с минимальной оценкой C. (3)
MA 340 Концепции геометрии
Аксиоматическая геометрия, теоремы Менелая и Чевы, гармонические элементы и поперечные отношения,
Теорема Десарка и обращение.
Необходимое условие: MA 250 с минимальной оценкой C. (3)
MA 345 Линейная алгебра
Системы линейных уравнений, матрицы и метод исключения Гаусса, векторные пространства, собственные значения
и собственные векторы, скалярные произведения и ортогональные множества.
Необходимое условие: MA 139 с минимальной оценкой C или MA 140 с минимальной оценкой C. (3)
MA 350 Дифференциальные уравнения I
Теория и методы решения обыкновенных дифференциальных уравнений, приложения, численные
методы, решения рядами, преобразования Лапласа.
Необходимое условие: MA 145 с минимальным баллом C. (3)
MA 375 Теория интереса
Курс охватывает часть экзамена по финансовой математике, проводимого Обществом.
актуариев (SOA) / Emerty Actuarial Society (CAS).
Необходимое условие или сопутствующее условие: MA244 с минимальной оценкой C. (3)
MA 385 Финансовая математика
Продолжение MA 375 с упором на иммунизацию и посвящение, производные,
хеджирование и инвестиционные стратегии.
Требование: MA375 с минимальной оценкой C. (3)
MA 423 Статистический анализ для судебной медицины
Введение в статистический анализ генетических данных, используемых в судебной медицине.
Будут обсуждены основные распределения вероятностей, используемые при анализе генетических данных.
Особое внимание будет уделяться процедурам оценки и статистических выводов в судебной экспертизе.
наука.
Необходимое условие: MA 140 с минимальной оценкой C или согласие преподавателя. (3)
MA 425 Прикладной регрессионный анализ
Использование регрессии для представления взаимосвязи между независимыми переменными и их ответом. Акцент на анализе актуальных
наборы данных. Темы для обсуждения: простая линейная регрессия, множественная регрессия, прогнозирование, выбор переменных,
остаточная диагностика, авторегрессия и логистическая регрессия.
Пререквизиты: MA 223 с оценкой не ниже C; MA 345 с минимальной оценкой C. (3)
MA 440/441 Независимое исследование
Изучите темы математики, не охваченные другими курсами.
Необходимое условие: MA 240 или MA 244 с минимальной оценкой C. (1-2)
MA 443 Элементарная теория чисел
Темы теории чисел, включая фундаментальные законы, диофантовы уравнения, целые числа.
и свойства линейных и квадратичных сравнений.
Необходимое условие: MA 250 с минимальной оценкой C. (3)
MA 445 Современная алгебра
Введение в изучение множеств, колец, полей, групп и векторных пространств.
Необходимое условие: MA 250 с минимальной оценкой C. (3)
MA 449 Решение математических задач
Решение нестандартных задач, чтение, исследование и общение по математике
идеи.
Необходимые условия: MA 250; MA 345; MA 240 или MA 244; минимальная оценка C по всем предпосылкам
курсы. (3)
MA 461/463 Специальные разделы математики
Лекции, дискуссии и / или заданные чтения по различным темам математики. В тема будет меняться в зависимости от предложения. (1-3)
MA 464 Математическая криптография
Курс будет охватывать базовые концепции безопасной связи, классическую криптографию и криптоанализ, моноалфавитные и полиалфавитные шифры, Шеннона.
теория секретности, современные криптосистемы с частным ключом, такие как DES и AES, и криптосистемы с открытым ключом
например RSA.
Необходимые условия: MA 223 или MA 250, или MA 338, или MA 345, или MA 443 с минимальной оценкой C. (3)
MA 486/488 Стажировка по математике
Контролируемое обучение и опыт работы по математике, что способствует повышению успеваемости учащихся.
понимание, признательность и применение математики.
Предпосылки: завершено 45 часов; Средний балл выше 3,0; На 16 часов выше MA 134; согласие
инструктор.(1-3)
UI 438 Природа и развитие математической мысли
Упор на математические идеи как на растущую, изменяющуюся деятельность человека, влияющую на
история обществ, включая сегодняшнюю технологическую культуру.
Предпосылки: Развитие крупной цивилизации; MA 139 или MA 140 с минимумом
оценка C. (общеобразовательный курс) (3)
Математика (MA) Описание курсов для аспирантов
MA 523 Вероятность и статистика I
Введение в вероятность и статистику с использованием инструментов исчисления.Алгебра
вероятность, случайные величины, дискретные и непрерывные распределения.
Обязательное или сопутствующее условие: MA 244 с минимальной оценкой C. (3)
MA 524 Вероятность и статистика II
Продолжение MA 523 с акцентом на двумерные распределения и статистические выводы,
статистическая выборка, оценка, проверка гипотез, параметрические процедуры для однократной выборки
и задачи с двумя выборками.
Необходимое условие: MA 523 с минимальной оценкой C. (3)
MA 526 Актуарный семинар
Решение вероятностных задач, уникальных для актуарной науки.
Необходимое условие: MA 524 с минимальной оценкой C. (3)
МА 532 Основы геометрии
Историческое развитие аксиоматического подхода к евклидовой геометрии и неевклидовой геометрии
геометрии, системы координат для аффинных и проективных плоскостей и метрические постулаты
для евклидовой, гиперболической и эллиптической плоскостей.
Необходимое условие: MA 250 с минимальной оценкой C. (3)
MA 538 История математики
Исторический очерк математики со времен Ньютона и Лейбница до двадцатого века.
века развития.
Необходимое условие: MA 139 или MA 140 с минимальной оценкой C. (3)
MA 540 Проективная геометрия
Неевклидова геометрия, изучение проективной геометрии и ее связи с другими геометриями.
Необходимое условие: MA 250 с минимальной оценкой C. (3)
MA 545 Линейная алгебра и матрицы
Введение в векторные пространства, линейные преобразования, матрицы, собственные значения, собственные векторы
и численные методы в линейной алгебре.
Пререквизиты: MA 250 с минимальной оценкой C; MA 345 с минимальной оценкой C. (3)
MA 546 Расширенный расчет I
Множества, отношения и функции, последовательности действительных чисел и последовательности в R, непрерывные
и дифференцируемые функции на R.
Пререквизиты: MA 244 с минимальной оценкой C; MA 250 с минимальной оценкой C. (3)
MA 547 Расширенный расчет II
Интеграл Римана-Стилтьеса, мера и интеграл Лебега, сходимость бесконечных ряды функций, ряды Фурье, некоторые теории гильбертовых пространств. Пререквизит: MA 546 с минимальной оценкой C. (3)
MA 548 Перечислительная комбинаторика
Изучение основных методов перечисления, рекуррентных соотношений, производящих функций,
принцип включения-исключения, теория Рамсея, частично упорядоченные множества и комбинаторные
конструкции.
Предпосылки: MA145 с оценкой не ниже C; MA 250 с минимальной оценкой C. (3)
MA 549 Теория графов
Основные параметры и свойства графов, представлений, деревьев, связности,
Эйлеровы и гамильтоновы циклы и пути, паросочетания, раскраски ребер и вершин, независимые
множества и клики, плоские графы, ориентированные графы, мультиграфы.
Необходимые условия: MA145 с оценкой не ниже C; MA 250 с минимальной оценкой C.(3)
MA 550 Дифференциальные уравнения II
Теория и методика решения обыкновенных дифференциальных уравнений в частных производных.
уравнения, краевые задачи, приложения, численные методы и устойчивость.
Необходимое условие: MA 350 с минимальной оценкой C. (3)
MA 560 Методы исследования в математике
Обзор методов исследования.Практика в методах составления и решения
проблем.
Необходимое условие: MA 244 с минимальной оценкой C или MA 250 с минимальной оценкой C. (3)
MA 575 Временные ряды и прогнозирование
Введение в анализ финансовых временных рядов с практической оценкой среднего и
условные гетероскедастические процессы с использованием статистических программ.
Пререквизиты: MA 145 с оценкой не ниже C; MA 425 с минимальной оценкой C.(3)
MA 580 Экспериментальный план и дисперсионный анализ
Полностью рандомизированный дизайн и анализ, рандомизированный блочный дизайн и анализ, факторный
эксперименты, дизайн и анализ разделенных участков, эксперименты с повторными измерениями и
анализ, ковариационный анализ.
Необходимое условие: MA 223 с минимальной оценкой C или согласием преподавателя.(3)
MA 585 Введение в непредвиденные обстоятельства жизни
Введение в модели выживания, таблицы дожития, условные платежи и условные платежи.
аннуитетные модели с использованием инструментов математической статистики.
Необходимое условие: MA 524 с минимальной оценкой C. (3)
MA 625 Прикладной регрессионный анализ
Узнайте, как использовать регрессию для представления взаимосвязи между независимыми переменными.
и связанный с ними ответ.Акцент будет сделан на анализе реальных наборов данных. В
будут рассмотрены следующие темы: простая линейная регрессия, множественная регрессия, прогнозирование,
выбор переменных, остаточная диагностика, авторегрессия и логистическая регрессия.
Необходимое условие: MA223 с минимальной оценкой C (3)
MA 630 Основные понятия современной математики
Введение в логику и множества, алгебраические системы и элементарные понятия в геометрии.Предназначен для учителей начальной школы. (3)
МА 632 Основы геометрии
Историческое развитие постуляционного подхода к геометрии, координатизация аффинных и проективных плоскостей и метрических постулатов для евклидовых, гиперболических и эллиптические плоскости. (3)
MA 633 Дифференциальная геометрия
Основные свойства кривых и поверхностей в трехмерном пространстве, длина дуги, кривизна,
кручение.Формулы Френта-Серета, нормаль к поверхности, касательная плоскость, фундаментальные формы
теория поверхности.
Необходимое условие: MA244 с минимальной оценкой C. (3)
MA 635 Топология
Изучение множеств, отношений, функций, произведений, мощности, метрических пространств, топологических пространства, сходимость, непрерывность, аксиомы отделимости, связность, компактность, гомотопия, и фундаментальная группа.(3)
MA 636 Природа математической мысли
Этот курс исследует природу математики, а также ее историческую, социальную и
и культурные аспекты. Студенты познакомятся как с национальными, так и с государственными
принципы и стандарты преподавания и изучения математики. Студенты будут исследовать
Актуальные проблемы и тенденции в математическом образовании.Кредит только для The Missouri Cooperative
Онлайн-степень магистра в области преподавания и обучения — начального образования.
Необходимое условие: Успешное завершение основных курсов программы. (3)
MA 637 Математические процессы
Этот курс исследует как конечные, так и бесконечные математические процессы, используемые при
решение проблем, связанных с дискретными или непрерывными данными. Курс объединяет впечатления
из понятий чисел, алгебры и анализа данных.Кредит только для штата Миссури
Совместная онлайн-степень магистра в области преподавания и обучения — начального образования.
Предпосылки: Успешное завершение основных курсов программы и MA636. (3)
MA 638 История математики
Исторический очерк математики со времен Ньютона и Лейбница до двадцатого века. века развития. (3)
MA 640 Семинар по математике современной школы
Обзор основных вопросов и направлений учебной программы по математике для средних школ
(7-12).
Необходимое условие: опыт преподавания средней математики или согласие преподавателя.
(3)
MA 641 Геометрия и измерения
В этом курсе студенты будут использовать геометрические концепции и отношения для описания моделировать математические идеи и конструкции реального мира и понимать измеримые атрибуты объектов и узлов, систем и процессов измерения.Студент будет формулировать вопросы, на которые можно ответить с помощью данных, и собирать, систематизировать и отображать Соответствующие данные. Кредит только для получения степени магистра в области преподавания в рамках совместной онлайн-программы штата Миссури и обучение — начальное образование. Предпосылки: Успешное завершение программы основные курсы и MA636. (3)
MA 642 Группы и поля
Введение в алгебраическую теорию групп и полей.Использование компьютерной алгебры
система для изучения приложений в связанных областях.
Требование: MA445 с минимальной оценкой C. (3)
MA 643 Теория чисел
Изучение простых чисел, сравнений, квадратичных вычетов и числовых функций.
Необходимое условие: MA 443 с минимальной оценкой C или согласием преподавателя. (3)
MA 644 Кольца и модули
Кольца, идеалы, факторные кольца, домены, полиномиальные кольца, модули, модули над PID,
Коммутативные кольца.
Необходимое условие: MA 445 с минимальной оценкой C. (3)
MA 645 Алгебра
Изучение основных алгебраических (числовых) систем, включая группы, кольца, модули,
и категории.
Предпосылки: MA445 с минимальной оценкой C и MA345 или MA545 с минимальной оценкой
оценка C или согласие преподавателя. (3)
MA 646 Современный реальный анализ
Множества, метрические пространства, интеграл Лебега, гильбертовые пространства.
Требование: MA546 с минимальной оценкой C. (3)
MA 647 Комплексный анализ
Комплексные числа, аналитическая функция, интегралы, степенные ряды, вычеты и полюсы и
конформное отображение.
Пререквизиты: MA244 с минимальной оценкой C. (3)
MA 648 Независимое изучение математики
Изучение тем в специализированной области, не охваченных регулярными курсами.(1)
MA 649 Самостоятельное изучение математики
Изучение тем в специализированной области, не охваченных регулярными курсами. (2)
MA 650 Независимое изучение математики
Изучение тем в специализированной области, не охваченных регулярными курсами. (3)
MA 651 Математика Capstone
В этом курсе студенты будут синтезировать и демонстрировать свое понимание математических
концепции, изученные на трех обязательных курсах математики при успешном завершении
итоговой независимой работы / проекта Другие мероприятия будут назначены для подключения
и расширить существующие математические знания и опыт учащегося.Только кредит
для получения степени магистра в области кооперативного онлайн-обучения штата Миссури в области преподавания и обучения — элементарный
Образование.
Предпосылки: Успешное завершение основных курсов программы и MA636, MA637,
и MA641. (3)
MA 661 Специальные разделы математики
Изучение тем в специализированной области, не охваченных регулярными курсами. (1)
MA 662 Специальные разделы математики
Изучение тем в специализированной области, не охваченных регулярными курсами.(2)
MA 663 Специальные разделы математики
Изучение тем в специализированной области, не охваченных регулярными курсами. (3)
MA 664 Математическая криптография
Классические и современные криптосистемы, эллиптические кривые, хеширование, цифровые подписи,
факторинг, задача дискретного логарифмирования, псевдослучайные числа, идентификация и аутентификация
схемы, приложения.
Необходимое условие: MA443 или MA445 или MA464 с минимальной оценкой C. (3)
MA 670 CAS Семинар
Введение в использование системы компьютерной алгебры (CAS) для изучения продвинутых
математика.
Требование: MA250 с минимальной оценкой C. (1)
MA 678 Математическое моделирование
Введение в математическое описание физических явлений, вычислительные методологии,
и эмпирическая интерпретация числовых данных.
Необходимые условия: MA244 с оценкой не ниже C; MA345 с минимальной оценкой C; MA344
или CS155 или CS177 с минимальной оценкой C. (3)
MA 694 Диссертация
Письменный отчет, основанный на исследовании некоторой темы или завершении творческой проект. См. План диссертации для получения дополнительной информации. (3)
MA 695 Диссертация
Письменный отчет, основанный на исследовании некоторой темы или завершении творческой проект.См. План диссертации для получения дополнительной информации. Второй семестр. (3)
MA 696 Диссертация
Письменный отчет, основанный на исследовании некоторой темы или завершении творческой проект. См. План диссертации для получения дополнительной информации. Второй семестр. (2)
MA 697 Диссертация
Письменный отчет, основанный на исследовании некоторой темы или завершении творческой проект.См. План диссертации для получения дополнительной информации. Второй семестр. (1)
Специалист по элементарной математике (MD) Описание курсов
MD 611 Стажировка по номерам и операциям
Практикум и онлайн-семинары, на которых кандидат приобретает опыт
работа с рядом студентов и взрослых по концепциям числа и операций.
Сопутствующий реквизит: MD 621. (1)
MD 612 Практика рациональных чисел и пропорционального мышления
Практикум и онлайн-семинары, на которых кандидат приобретает опыт
работая с рядом студентов и взрослых учащихся над рациональным числом и пропорциональным
Концепции мышления.
Сопутствующий реквизит: MD 622. (1)
MD 616 Стажировка по геометрии и измерениям
Практикум и онлайн-семинары, на которых кандидат приобретает опыт работа с рядом студентов и взрослых над концепциями геометрии и измерений.Совместный реквизит: MD 626. (1)
MD 617 Стажировка по алгебраическим рассуждениям
Практикум и онлайн-семинары, на которых кандидат приобретает опыт работа с рядом студентов и взрослых над концепциями алгебраического мышления. Совместный реквизит: MD 627. (1)
MD 621 Номера и операции
Курс разработан для развития понимания обучения и преподавания
понятия до числа, подсчет и количество элементов, а также числа и операции в базе
10.Особое внимание будет уделяться тому, как дети думают и изучают эти концепции и
как они вписываются в программу начальной школы.
Сопутствующий реквизит: MD 611. (3)
MD 622 Рациональные числа и пропорциональное мышление
Курс разработан для развития понимания обучения и преподавания
рациональные числа и соотношение и пропорциональные отношения. Акцент будет сделан
к тому, как дети думают и изучают эти концепции, и как они вписываются в элементарный
Школьная программа.
Сопутствующий реквизит: MD 612. (3)
MD 624 Данные и вероятность
Курс разработан для развития понимания вероятностных рассуждений и сбор, исследование и анализ данных. Особое внимание будет уделено тому, как дети подумайте и узнайте об этих концепциях и о том, как они вписываются в программу начальной школы. (3)
MD 626 Геометрия и измерения
Этот курс разработан для развития понимания преподавания и изучения
геометрия и измерения.Особое внимание будет уделяться тому, как дети думают и учатся.
эти концепции и как они вписываются в учебную программу элементарной математики.
Сопутствующий реквизит: MD 616. (3)
MD 627 Алгебраическое мышление
Этот курс будет посвящен содержанию и сложностям преподавания и оценивания алгебраических
рассуждения в настройках 1-6 классов. Содержание курса будет включать проверку представительства
и анализ математических ситуаций и структур.Внимание будет уделено
паттерны, функции и переход от арифметики к алгебре.
Сопутствующий реквизит: MD 617. (3)
множителей 133 — найти простое факторизацию / 133 множителей
Множители 133 — это числа, которые при попарном умножении дают произведение 133. Есть 4 множителя из 133, из которых 133 сами по себе являются наибольшим фактором, а его положительные множители равны 1, 7, 19, 133. Парные множители 133 равны (1, 133), (7, 19), а его простые множители равны 7 × 19.
- Все множители 133: 1, 7, 19 и 133
- Отрицательные множители 133: -1, -7, -19 и -133
- Подводя итоги 133: 7, 19
- Простая факторизация 133: 7 1 × 19 1
- Сумма множителей 133: 160
Какие множители 133?
Факторы 133 — это пары тех чисел, произведение которых дает 133.Эти множители могут быть простыми или составными числами.
Как найти множители 133?
Чтобы найти делители 133, нам нужно будет найти список чисел, которые делили бы 133 без остатка.
- 133/7 = 19; следовательно, 7 — это коэффициент 133, а 19 — также коэффициент 133.
- 133/1 = 133; следовательно, 1 — это коэффициент 133, а 133 — также коэффициент 133.
☛ Также проверьте:
- Множители 13 — Множители 13 равны 1, 13
- Факторы 30 — Факторы 30: 1, 2, 3, 5, 6, 10, 15, 30
- Множители 49 — Множители 49: 1, 7, 49
- Факторы 39 — Факторы 39: 1, 3, 13, 39
- Факторы 32 — Факторы 32 равны 1, 2, 4, 8, 16, 32
Факторы 133 по простому факторизации
Число 133 составное, поэтому оно состоит из простых делителей.Теперь давайте узнаем, как вычислить простые множители 133. Первый шаг — разделить число 133 на наименьший простой множитель, здесь он равен 7. Мы продолжаем делить, пока не получим ненулевой остаток.Дальнейшее деление 19 на 7 дает ненулевой остаток. Итак, мы останавливаем процесс и продолжаем делить число 19 на следующий наименьший простой делитель. В конце концов, мы останавливаемся, если следующего основного фактора не существует или когда мы не можем дальше делиться.
Итак, разложение на простые множители 133 можно записать как 7 1 × 19 1 , где 7, 19 — простые числа.
Факторы 133 в парах
Парные множители 133 — это пары чисел, которые при умножении дают произведение 133. Попарно множители 133 составляют:
- 1 × 133 = (1, 133)
- 7 × 19 = (7, 19)
Отрицательные парные множители 133:
- -1 × -133 = (-1, -133)
- -7 × -19 = (-7, -19)
ПРИМЕЧАНИЕ: Если (a, b) является парным множителем числа, то (b, a) также является парным множителем этого числа.
Факторы 133 решенных примеров
Пример 1: Сколько факторов у 133?
Решение:
Коэффициенты 133 равны 1, 7, 19, 133. Следовательно, 133 имеет 4 фактора.
Пример 2: Найдите наименьшее общее кратное и наибольший общий коэффициент (GCF) 133 и 127.
Решение:
Делители 133 равны 1, 7, 19, 133, а множители 127 — 1, 127.
Следовательно, наименьшее общее кратное 133 и 127 равно 16891, а наибольшее общее кратное (GCF) 133 и 127 равно 1.
Пример 3. Найдите, если 7, 49 и 133 делятся на 133.
Решение:
Когда мы делим 133 на 49, остается остаток. Следовательно, число 49 не делится на 133. Все числа, кроме 49, делятся на 133.
Пример 4: Найдите произведение всех простых делителей 133.
Решение:
Так как простые множители 133 равны 7, 19. Следовательно, произведение простых множителей = 7 × 19 = 133.
перейти к слайду перейти к слайду перейти к слайду
Готовы увидеть мир глазами математиков?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых занятиях и станьте экспертом во всем.
Забронируйте бесплатную пробную версию Класс
Часто задаваемые вопросы по факторам 133
Какие множители 133?
Коэффициенты 133 равны 1, 7, 19, 133, а отрицательные факторы — -1, -7, -19, -133.
Какова сумма всех множителей 133?
Факторы 133 равны 1, 7, 19, 133, а сумма всех этих факторов составляет 1 + 7 + 19 + 133 = 160
Каковы парные множители 133?
Парные множители 133 равны (1, 133), (7, 19).
Какой наибольший общий множитель у 133 и 130?
Множители 133 равны 1, 7, 19, 133, а делители 130 равны 1, 2, 5, 10, 13, 26, 65, 130. 133 и 130 имеют только один общий делитель, равный 1.Это означает, что 133 и 130 совпадают.
Следовательно, наибольший общий коэффициент (GCF) 133 и 130 равен 1.
Сколько множителей 133 также общих для множителей 120?
Так как множители 133 равны 1, 7, 19, 133, а множители 120 равны 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120. Следовательно, 133 и 120 имеют только один общий делитель, равный 1. Следовательно, 133 и 120 совпадают.
Оценка в умножении
Это полный урок с инструкциями и упражнениями по использованию вычислений при умножении, предназначенный для 5-го или 6-го класса.Для оценки ученики округляют двузначные и трехзначные числа перед умножением, но это округление может быть выполнено несколькими способами. Далее следуют различные упражнения и задачи со словами.
Чтобы оценить результат умножения (произведение), округлите числа до некоторые близкие числа, которые вы можете легко умножить мысленно. Один из методов оценки — округлить все
множители к самой большой цифре (разряду), которую они имеют. Например, оценка 365 × 24 . Круглый 365 до ближайшего сто и 24 с точностью до десяти. Итак, 365 ≈ 400, а 24 ≈ 20. Тогда 365 × 24 ≈ 400 × 20 = 8000. Таким образом, умножение выполняется легко, так как это всего лишь состоит из одной цифры (4), умноженной на одну цифру (2), и добавления нулей в конец (000). Посмотрите другие примеры:
|
Практика
1.Оцените продукты, округляя множители до наибольшего числа. стоимость.
а. 158 × 32 ≈ 200 × 30 = 6000 | г. 29 × 94 ≈ ____ × ___ = ____ |
г. 770 × 33 ≈ ____ × ___ = ____ | ф. 88 × 99 ≈ ____ × ___ = ____ |
Дж.486 × 21 ≈ ____ × ___ = ____ | л. 209 × 27 ≈ ____ × ___ = ____ |
2. Одна из целей оценки — выявить грубые ошибки в
расчеты. Например, если вы оцениваете результат в 5000, и вы
вычислите, что это 354, вы знаете, что что-то не так, так как вы далеко.
Какова наилучшая оценка из представленных вариантов?
1.103 × 52 2. 42 × 76 3. 319 × 25 4. 17 × 17 5. 99 × 59 6. 47 × 21 | а. 6500 а. 4000 а. 6000 а. 1000 а. 6000 а. 470 | г. 500 г. 320 г. 750 г.200 г. 900 г. 9700 | г. 5000 г. 4800 г. 9000 г. 400 г. 9000 г. 1000 |
3. Какой продукт больше всего отличается от оценки? Может ты понимаешь почему?
|
Другие методы оценки Если округлить оба множителя до наибольшего разряда, то получится 249 × 34 будет оценено в 6000; но фактический продукт — 8466 — довольно далеко от оценки.
Оценка — это не точная наука, а вопрос округления до конца числа, которые вы можете работать в своей голове. |
4. Сначала оцените, а затем рассчитайте фактический продукт. Ты можешь используйте различные способы оценки по своему усмотрению. Или попробуйте два разных метода оценки и сравнить, что было более точным.
| Оценки: | Реальность: | |
| а. | 143 × 27 ≈ ________ × _________ = __________ | 143 × 27 = _________ |
| б. | 657 × 13 ≈ ________ × _________ = __________ | 657 × 13 = _________ |
| c. | 411 × 9 ≈ ________ × _________ = __________ | 411 × 9 = _________ |
| я. | 406 × 19 ≈ ________ × _________ = __________ | 406 × 19 = _________ |
| k. | 243 × 24 ≈ ________ × _________ = __________ | 243 × 24 = _________ |
| л. | 37 × 258 ≈ ________ × _________ = __________ | 37 × 258 = _________ |
5.Решите проблемы со словом. При необходимости округлите числа, чтобы сделать оценку.
а. Нелли пересчитала спички в спичечной коробке и получила 58.Сколько совпадений примерно в 8 коробках?
Каждый день Нелли использует 10 спичек. Как долго примерно хватит ли ей этих 8 коробок?
б. Куры тети Джини откладывают около 130 яиц в день.
Сможет ли она доставить все яйца в указанную выше школу в течение одной недели?
Обратите внимание, ее куры откладывают яйца 7 дней в неделю.
г. Одна банка (еда) стоит 58 центов, а вы собираетесь купить 18 из
их.
Сделайте оценку стоимости.
По вашей оценке, хватит ли 10 долларов на покупку?
ВЫЧИСЛИТЕЛЬНЫЕ И ПРОГРАММНЫЕ СИСТЕМЫ
CSS 107 Введение в программирование с помощью анимированного повествования (5) VLPA, QSR
Знакомит с основами программирования с использованием повествования в виртуальных мирах; включает создание персонажей, игр, рассказов, раскадровок, трехмерного движения, классов, методов и функций.Современные темы различаются по социальным, научным и этическим вопросам информационных технологий.
Подробная информация о курсе в MyPlan: CSS 107
CSS 110 Введение в кибербезопасность (5) I&S Марк Дж. Дюпюи
Знакомит с темами кибербезопасности, включая взлом, социальные сети, конфиденциальность, криптографию, правовые аспекты, социальные последствия, управление паролями , цифровая криминалистика, компьютерные сети, безопасность беспроводной связи и этические вопросы. Сосредоточен на различных методах и методах устранения угроз кибербезопасности.Никакого технического опыта не требуется.
Подробная информация о курсе в MyPlan: CSS 110
CSS 112 Введение в программирование для научных приложений (4) NW, QSR
Знакомит с концепциями программирования с использованием специализированного компьютерного языка с акцентом на научные приложения. Включает такие темы, как основы программирования (структуры управления, типы и представление данных, операции, функции и параметры) и вводные концепции разработки программного обеспечения (спецификации, дизайн, тестирование).Рекомендуется: STMATH 124 или B MATH 144; и B PHYS 115 или B PHYS 122. Предлагается: WSp.
Подробная информация о курсе в MyPlan: CSS 112
CSS 123 Программирование для науки о данных (3) QSR
Переход от базовых навыков программирования к более продвинутым с упором на использование вычислительных инструментов для решения задач науки о данных. Ознакомьтесь с методами программирования более высокого уровня (рекурсия, абстрактные типы данных, анализ алгоритмов), методами исследования пространства параметров и автоматизации рабочих процессов.Для обучения используется компьютерный язык для конкретной дисциплины. Предварительное условие: минимальная оценка 2.0 в CSS 112, CSS 132, CSS 142 или CSE 142
. Подробности курса в MyPlan: CSS 123
CSS 132 Компьютерное программирование для инженеров I (5) NW, QSR
Знакомит с программированием концепции в социальном, математическом и технологическом контексте. Темы включают основы программирования (управляющие структуры, типы данных, функции и т. Д.), Компьютерную организацию, алгоритмическое мышление, вводные концепции программной инженерии, а также социальные и профессиональные вопросы.Особое внимание уделяется инженерным приложениям. Для обучения используется компьютерный язык, используемый в инженерной практике. Совместное требование: CSSSKL 132.
Подробная информация о курсе в MyPlan: CSS 132
CSS 133 Компьютерное программирование для инженеров II (5) NW, QSR
Переход от базовых навыков программирования к строгому процессу разработки программного обеспечения. Ознакомление с методами программирования более высокого уровня (рекурсия, общее программирование, стеки, очереди, деревья, поиск и сортировка).Подчеркивает связь между алгоритмической мыслью и реализацией. Особое внимание уделяется инженерным приложениям. Совместное требование: CSSSKL 133. Предварительное условие: минимальная оценка 2.0 по CSS 132.
Подробная информация о курсе в MyPlan: CSS 133
CSS 142 Компьютерное программирование I (5) NW, QSR
Знакомит с концепциями программирования в социальных, культурных , научный, математический и технологический контекст. Темы включают основы программирования (управляющие структуры, типы данных и представление, операции, функции и параметры), компьютерную организацию, алгоритмическое мышление, вводные концепции программной инженерии (спецификации, дизайн, тестирование), а также социальные и профессиональные вопросы.Совместное требование: CSSSKL 142.
Подробная информация о курсе в MyPlan: CSS 142
CSS 143 Компьютерное программирование II (5) NW, QSR
Переход от базовых навыков программирования к строгому процессу разработки программного обеспечения. Знакомство с методами программирования более высокого уровня (рекурсия, общее программирование, стеки, очереди, деревья, поиск и сортировка). Подчеркивает связь между алгоритмической мыслью и реализацией. Необходимое условие: минимум 2,7 балла по CSS 161, CSS 142 или CSE 142.Совместное требование: CSSSKL 143.
Подробная информация о курсе в MyPlan: CSS 143
CSS 205 Женщины в STEM Семинар: Студенческая жизнь (1, макс. 6) I&S, DIV
Разработка эффективных академических стратегий для женщин в науке и технологиях , инженерные и математические науки. Исследует представление женщин в STEM, как они изображены в литературе и фильмах. Обсуждает вопросы STEM и гендера, в том числе: наставников и группы поддержки, социальные вопросы, ролевые модели и стереотипы, а также заслужить уважение.Только кредит / без кредита.
Подробная информация о курсе в MyPlan: CSS 205
CSS 211 Компьютеры и общество (5) I&S
Изучение и обсуждение вопросов, связанных с разработкой, поддержкой и использованием компьютерных технологий в современном обществе. Темы меняются каждый квартал, но могут включать такие области, как права интеллектуальной собственности, кибербезопасность, конфиденциальность, свобода слова, ответственность, этика, социальная справедливость, разнообразие и труд.
Подробная информация о курсе в MyPlan: CSS 211
CSS 301 Техническое письмо для профессионалов в области вычислительной техники (5)
Изучены наиболее эффективные методы коммуникации, основанные на общих ожиданиях компьютерных и других инженеров.Исследует различные шаблоны письма, обычно используемые в техническом письме, включая сравнение / противопоставление, убедительность, процесс, инструкции и проблему / решение, а также когда / почему используется. Предварительные требования: B CUSP 135, B WRIT 135, ENGL 141, ENGL 182, ENGL 197, ENGL 198, ENGL 199 или HCDE 231.
Подробная информация о курсе в MyPlan: CSS 301
CSS 305 Survey of Computer Systems for Teachers (5) QSR
Обзор концепций компьютерных систем, чтобы обеспечить контекст и понимание для учителей, создающих учебные программы K-12.Включает проблемы, компромиссы и решения компьютерных систем, включая структуры данных, сети, базы данных, взаимодействие человека с компьютером, разработку программного обеспечения и кибербезопасность. Только специальности, не относящиеся к CSS. Предварительные требования: минимальная оценка 2,7 по CSE 142, CSS 142 или CSS 161; и минимальная оценка 2.0 по CSS 211. Только кредит / без кредита.
Просмотрите подробности курса в MyPlan: CSS 305
CSS 315 Этика, политика и закон кибербезопасности (5) I&S
Изучает этику, политику и закон с точки зрения кибербезопасности, включая такие темы, как: основы этики и философские взгляды; профессиональные этические обязательства; принятие этических решений; этичный взлом; разработка и реализация политики; Конфиденциальность; правовые и нормативные вопросы; государственные, национальные и международные законы о кибербезопасности; интеллектуальная собственность и киберпреступность.Предварительные требования: либо B WRIT 134, либо B WRIT 135.
Просмотреть подробности курса в MyPlan: CSS 315
CSS 320 Digital Forensics (5) NW, QSR
Изучает методы цифровой криминалистики в различных контекстах, например, на компьютерах, мобильных устройствах. устройства, сети, виртуальные машины, социальные сети, облако и электронная почта. Исследуется весь процесс цифровой криминалистики, включая расследования, сбор данных, написание отчетов и свидетельские показания экспертов. Исследуются различные инструменты и методы.Рассмотрены различия в файловых системах Windows, Linux и Macintosh. Условие: один 100-уровневый курс CSS; и либо B WRIT 134, либо B WRIT 135.
Подробная информация о курсе в MyPlan: CSS 320
CSS 340 Прикладная алгоритмика (5)
Расширяет принципы программирования и дискретной математики (например, языки программирования, рекурсия, сортировка, вычислительные сложность, математическая индукция, логические концепции, теория множеств, хеш-таблицы и т. д.) и применяет их для разработки, анализа и реализации структур данных и эффективного программного обеспечения.Предварительное условие: минимальная оценка 2.0 по CSS 123 и CSSSKL 123, либо минимальная оценка 2.5 по CSS 133, CSS 143, CSE 143 или CSS 162; и минимальная оценка 2,5 по STMATH 124 или MATH 124.
Подробная информация о курсе в MyPlan: CSS 340
CSS 342 Структуры данных, алгоритмы и дискретная математика I (5)
Интеграция математических принципов с подробными инструкциями на компьютере программирование. Исследует математические рассуждения и дискретные структуры с помощью объектно-ориентированного программирования.Включает анализ алгоритмов, основные абстрактные типы данных и структуры данных. Не может повториться. Предварительное условие: минимальная оценка 2,8 по CSS 133, CSS 143, CSE 143 или CSS 162; и минимальная оценка 2,5 по STMATH 125 или MATH 125.
Подробная информация о курсе в MyPlan: CSS 342
CSS 343 Структуры данных, алгоритмы и дискретная математика II (5)
Развивает компетенции, связанные с решением задач, алгоритмами , и вычислительные модели. Охватывает абстрактные типы данных и структуры данных, эффективность алгоритмов, представления и обходы двоичного дерева, поиск, словари, очереди приоритетов, хеширование, ориентированные графы и алгоритмы графов, а также языковые грамматики.Предпосылка: минимальная оценка 2.0 по CSS 301; минимальная оценка 2,0 по CSS 342; минимальная оценка 2,0 в STMATH 125 или MATH 125.
Подробная информация о курсе в MyPlan: CSS 343
CSS 350 Принципы управления для специалистов в области вычислительной техники (5) Erdly
В рамках командного программного проекта исследуются важнейшие вопросы межличностного общения , лидерство, принятие решений, социальные и культурные теории, почерпнутые из современных исследований в области антропологии, социологии, психологии и бизнеса.Предпосылка: CSS 301, который можно использовать одновременно; не может повторяться.
Подробная информация о курсе в MyPlan: CSS 350
CSS 360 Разработка программного обеспечения (5)
Обзор процессов, инструментов и методов разработки программного обеспечения, используемых при разработке программного обеспечения и обеспечении качества. Темы включают модели жизненного цикла, моделирование процессов, методы анализа требований и спецификации, методы обеспечения качества, верификацию и валидацию, тестирование, планирование проекта и управление.Предварительные требования: CSS 133, CSS 143, CSE 143, CSS 162 или CSS 173.
Подробная информация о курсе в MyPlan: CSS 360
CSS 370 Анализ и дизайн (5)
Методы и инструменты для сбора и передачи требований, предлагаемые решения и дизайн руководству, клиентам и разработчикам программного обеспечения. Моделирование данных, процессов и объектов с использованием таких языков, как диаграммы потоков данных, диаграммы сущностей / отношений, а также сценарии использования унифицированного языка моделирования и диаграммы классов и последовательностей.Предпосылка: Предпосылка: 2.0 в CSS 301; 2.0 в CSS 342 или CSS 340; 2.0 в CSS 360; не может повторяться.
Подробная информация о курсе в MyPlan: CSS 370
CSS 382 Введение в искусственный интеллект (5) QSR Юсуф Писан
Основные идеи и разработки в области искусственного интеллекта, такие как решение проблем, представление знаний, поиск, рассуждение в условиях неопределенности, обучение и обработка естественного языка. Условие: либо минимум 2 балла.0 в CSS 340 или минимальная оценка 2,0 в CSS 342.
Подробная информация о курсе в MyPlan: CSS 382
CSS 383 Биоинформатика (5) NW Kraemer
Охватывает принципы биоинформатики. Студенты приобретают рабочие знания о вычислительных инструментах для анализа наборов биологических данных, включая базы данных последовательностей ДНК и белков. Включает такие темы, как: поиск в базе данных, выравнивание последовательностей (ДНК, РНК и белок), BLAST, филогения, эволюция, функциональная геномика, экспрессия генов / анализ микрочипов и анализ белков.Предлагается: совместно с B BIO 383.
Подробная информация о курсе в MyPlan: CSS 383
CSS 385 Введение в разработку игр (5) VLPA / NW Sung
Исследует фундаментальные вопросы проектирования и разработки компьютерных видеоигр; творческие и художественные элементы, повествование истории, архитектура программного обеспечения, модель взаимодействия, математика, физика, специальные эффекты и внутриигровая логика ИИ. Знакомство с элементами игрового дизайна: сеттинг, игровой процесс и интерфейс; и опыт реализации игр: концептуализация, прототипирование и игровое тестирование.Предпосылка: STMATH 125 или MATH 125; и CSS 340 или CSS 342. Предлагается: Sp.
Подробная информация о курсе в MyPlan: CSS 385
CSS 405 Женщины в STEM Семинар: карьера / профессиональная жизнь (1, макс. 6) I&S, DIV
Разрабатывает эффективные академические стратегии для женщин в области науки, технологий, инженерии и математики. Исследует представление женщин в STEM, как они изображены в литературе и фильмах. Обсуждает вопросы STEM и гендера, в том числе: завоевание уважения, баланс между работой и личной жизнью, социальные вопросы, связи и сети, поиск работы и технические собеседования.Только кредит / без кредита.
Подробная информация о курсе в MyPlan: CSS 405
CSS 416 Тестирование этического взлома и проникновения (5)
Изучение инструментов, приемов и методов тестирования этического взлома и проникновения. Будет изучать, понимать и выполнять этическое хакерское тестирование и тестирование на проникновение аналогично потенциальному противнику, чтобы впоследствии можно было использовать эффективную защиту для противодействия злонамеренным атакам. Также будут рассмотрены этапы взлома и этические соображения.Предварительные требования: CSS 310, INFO 310 или T INFO 310.
Подробная информация о курсе в MyPlan: CSS 416
CSS 422 Аппаратное обеспечение и организация компьютеров (5)
Введение в архитектуру, работу и организацию современного вычислительная машина. Рассматриваемые темы включают основные логические операции, конечные автоматы, модели регистров, организацию памяти, периферийные устройства и системные проблемы. Язык ассемблера преподается для понимания архитектуры набора команд и модели памяти компьютера.Предпосылка: CSS 342; не может повторяться. Преподаватели: Berger
Подробная информация о курсе в MyPlan: CSS 422
CSS 427 Введение во встроенные системы (5)
Введение в процесс определения и проектирования встроенных систем. Следит за развитием встраиваемых систем; разделение программного и аппаратного обеспечения, выбор процессора, операционные системы реального времени, кодирование на языке ассемблера и C, отладка и тестирование. Лабораторные эксперименты укрепляют фундаментальные концепции с помощью встроенных инструментов проектирования и отладки.Предпосылка: CSS 342; и либо B EE 425, либо CSS 422, которые могут использоваться одновременно.
Подробная информация о курсе в MyPlan: CSS 427
CSS 431 Сетевая архитектура и управление (5) QSR
Изучивает настройку, развертывание, управление, обслуживание и устранение неполадок сетевой инфраструктуры. Эталонные модели OSI и TCP, набор протоколов TCP / IP, LAN, WAN, методологии проектирования, безопасность, межсетевые экраны, VPN, IDS, IPS, VOIP, коммутация пакетов и каналов, конфигурация маршрутизатора, ICMP, SDN, облачный дизайн и операции, центры обработки данных и оптимизация.Ориентирован на работу в сети.
Просмотрите подробности курса в MyPlan: CSS 431
CSS 432 Проектирование и программирование сети (5) QSR
Изучает архитектуру OSI, протоколы TCP / IP, сети передачи данных, коммутацию пакетов, маршрутизацию, протоколы маршрутизации, безопасность, оценку производительности, контроль потока и контроль перегрузки. Сети исследуются в контексте разработки протоколов, реализации, написания функций и средств межпроцессного взаимодействия (например, сокетов, каналов, RPC).Ориентирован на сетевое программирование и эксперименты по оценке производительности. Предпосылка: минимальный балл 2.0 по CSS 343; рекомендуется: CSS 430.
Подробная информация о курсе в MyPlan: CSS 432
CSS 436 Облачные вычисления (5) Роберт Димпси
Прагматичный программно-ориентированный обзор облачных вычислений, охватывающий ключевые облачные технологии и компоненты, которые позволяют и составляют облако (например, виртуализация, вычисления, хранилище, сеть и безопасность). Оценка компромиссов при создании, миграции и использовании облачных сервисов и систем.Исследование архитектурных и теоретических основ облачных сервисов, включая варианты мониторинга, масштабируемости и доступности. Предпосылка: CSS 430 или CSS 432. Предлагается: WSp.
Подробная информация о курсе в MyPlan: CSS 436
CSS 444 Анализ предубеждений в эпоху цифровых данных (5)
Этот курс предназначен для введения в алгоритмы машинного обучения, которые применяются в реальном мире, учитывая систематические ошибки, методологические ограничения и ошибки данных.Он предоставит студентам основу для анализа социальных и политических проблем, позволяя им критически относиться к этическим границам. Темы курса основаны на классической статистике, машинном обучении, этике и конфиденциальности. Предпосылка: CSS 301; и либо CSS 340, либо CSS 342; рекомендуется: иметь опыт программирования нетривиальных функций для работы с наборами данных; и предыдущие курсовые работы по вероятности, статистике и алгоритмам.
Подробная информация о курсе в MyPlan: CSS 444
CSS 449 Дизайн и анализ алгоритмов (5)
Знакомит с фундаментальными методами разработки и анализа алгоритмов, такими как вычислительная сложность, жадные алгоритмы, алгоритмы «разделяй и властвуй», динамическое программирование , алгоритмы на графах, рандомизированные алгоритмы и вычислительная трудоемкость.Предварительное условие: CSS 343.
Подробная информация о курсе в MyPlan: CSS 449
CSS 452 Разработка игрового движка (5)
Изучение технических основ и деталей реализации игрового движка. Темы включают архитектуру программного обеспечения, ввод, управление ресурсами, текстуры, анимацию, системы координат, поведение и взаимодействие объектов, манипуляции с камерой, освещение и специальные эффекты, физику и управление сценой. Предварительные требования: минимальный балл 2.0 в CSS 340 или CSS 342; минимальная оценка 2.0 в CSS 360; и минимальная оценка 2,0 в STMATH 125 или MATH 125.
Подробности курса можно найти в MyPlan: CSS 452
CSS 455 Введение в вычислительную науку и научное программирование (5)
Введение в принципы и фундаментальные алгоритмы научных вычислений, в том числе прикладная линейная алгебра и численные методы. Групповые проекты решают текущие вычислительные проблемы в физических, биологических науках и науках о жизни. Предпосылка: STMATH 125 или MATH 125; а также CSS 133, CSS 143, CSE 143, CSS 162 или CSS 173.
Подробная информация о курсе в MyPlan: CSS 455
CSS 457 Signal Computing (5) Майкл Стибер
Как данные, собранные из реального мира, собираются, представляются, обрабатываются и хранятся на компьютерах. Темы включают оцифровку, цифровую обработку сигналов, фильтрацию, сжатие и то, как обработка сигналов используется как часть более крупных систем, таких как мультимедиа, Интернет вещей и машинное обучение. Предпосылка: CSS 340 или CSS 342; STMATH 308; не может повторяться
См. подробности курса в MyPlan: CSS 457
CSS 461 Управление проектами программного обеспечения (5)
Фундаментальные навыки, необходимые для эффективного управления проектами программного обеспечения, включая планирование и отслеживание проектов, а также управление людьми.Темы включают анализ рисков, объем проекта, планирование, распределение ресурсов, оценку затрат, переговоры, мониторинг и контроль графика, показатели программного обеспечения, управление качеством, улучшение процессов, укомплектование персоналом, лидерство, мотивацию и создание команды. Предпосылка: CSS 360, повторение не допускается.
Подробная информация о курсе в MyPlan: CSS 461
CSS 477 Основы разработки безопасного программного обеспечения (5) QSR
Изучает принципы и методы разработки безопасного программного обеспечения.Принципы безопасного проектирования, проектирования и кодирования представлены с акцентом на широту и глубину, включая такие темы, как жизненный цикл безопасной разработки, известные уязвимости, общие профили атак, моделирование угроз, контроль доступа, методы шифрования, обработка ошибок и обеспечение безопасного качества. Предварительные требования: CSS 343 и CSS 360.
Подробная информация о курсе в MyPlan: CSS 477
Искусственные нейронные сети CSS 485 (5) Майкл Стибер
Применение принципов биологических вычислений для решения машинных задач.Современное состояние искусственных нейронных сетей (ИНС), включая зрение, моторный контроль, обучение, анализ данных. Темы включают в себя архитектуру ИНС, алгоритмы: перцептроны, Уидроу-Хоффа, обратное распространение, сети Хебба. Предпосылка: CSS 343 и STMATH 308; не может повторяться.
Подробная информация о курсе в MyPlan: CSS 485
CSS 503 Системное программирование (4)
Изучает аспекты логического проектирования и программирования операционных систем и сетевого взаимодействия. Темы включают процессы, потоки, синхронизацию, взаимоблокировки, управление памятью, виртуальную память, файловые системы и сетевое программирование клиент-сервер.Предварительное условие: минимальная оценка 2,7 в CSS 502.
Подробная информация о курсе в MyPlan: CSS 503
CSS 514 Безопасность, политика, этика и правовая среда (2)
Рассматриваются этические, правовые и политические рамки, в которых информация профессионалы в области обеспечения гарантий и безопасного жизненного цикла разработки должны практиковаться. Охватывает этические, моральные, правовые и политические вопросы, связанные с компьютерами и телекоммуникационными системами, например, как они влияют на конфиденциальность, честную информационную практику, равенство, контроль контента и свободу электронной речи.
Подробная информация о курсе в MyPlan: CSS 514
CSS 518 Человеческий фактор в кибербезопасности (5)
Люди считаются самым слабым звеном в кибербезопасности. Независимо от надежности технических решений, без понимания и оценки человеческого фактора, по-прежнему будут приходить значительные компромиссы. В этом курсе изучаются человеческие факторы, связанные с кибербезопасностью, включая поведенческие, психологические, социальные, технические компоненты и компоненты удобства использования.
Подробная информация о курсе в MyPlan: CSS 518
CSS 532 Интернет вещей (5) Y.Peng
Изучает фундаментальные знания и технологии, детали реализации и результаты последних исследований Интернета вещей. Темы могут включать компоненты Интернета вещей, архитектуры систем Интернета вещей, услуги облачных вычислений для Интернета вещей, сетевые протоколы и стандарты для Интернета вещей, а также разработку приложений Интернета вещей. Рекомендуется: компьютерные сети, распределенные системы, облачные вычисления.
Подробная информация о курсе в MyPlan: CSS 532
CSS 533 Распределенные вычисления (5)
Основывается на знаниях передовых методологий программирования в распределенных вычислениях.Темы включают передачу сообщений, косвенную связь, удаленный вызов методов, распределенные объекты, многоуровневое серверное программирование, одноранговые системы, распределенную синхронизацию, распределенную контрольную точку и управление репликами.
Подробная информация о курсе в MyPlan: CSS 533
CSS 535 High Performance Computing (5)
Охватывает основные теории, принципы, концепции и практики, связанные с проектированием, внедрением, оценкой и использованием высокопроизводительных вычислительных систем.К ним относятся способы рассуждать о проблемах, возникающих в результате использования однородных и разнородных комбинаций памяти и вычислительных ресурсов (например, центральных и графических процессоров), данных, алгоритмов и доменов приложений.
Подробная информация о курсе в MyPlan: CSS 535
CSS 537 Безопасность сети и системы (5)
Изучает теорию и практику сетевой безопасности, роль криптографии и текущее состояние дел в создании безопасных сетевых систем. Охватывает такие темы, как контроль доступа, аутентификация, защита периметра, межсетевые экраны, виртуальные частные сети, системы обнаружения вторжений, а также инструменты безопасности беспроводной связи и аудита сетевой безопасности.
Подробная информация о курсе в MyPlan: CSS 537
CSS 549 Разработка и анализ алгоритмов (5)
Охватывает фундаментальные методы разработки и анализа алгоритмов, такие как вычислительная сложность, жадные алгоритмы, алгоритмы «разделяй и властвуй», динамическое программирование, алгоритмы на графах, рандомизированные алгоритмы и вычислительная трудоемкость.
Просмотрите подробности курса в MyPlan: CSS 549
CSS 551 Advanced 3D Computer Graphics (5) K. Sung
Изучите темы и проблемы, связанные с проектированием и реализацией графических приложений коммерческого масштаба, включая: системную архитектуру, пользователя модели взаимодействия, проблемы и алгоритмы моделирования, анимации и рендеринга.Предпосылка: не может быть засчитан, если CSS 451 уже принят; рекомендуется: структуры данных, алгоритмы, линейная алгебра
Просмотреть подробности курса в MyPlan: CSS 551
CSS 552 Темы в рендеринге (5)
Изучает основные алгоритмы и технологии в синтезе высококачественных изображений, в том числе: модели камер, 3D-просмотр, выборка и аппроксимация видимости, модели источников света, аппроксимация свойств материала, модели освещения, система человеческого зрения и синтез текстур.Предварительные требования: CSS 451. Преподаватели: Sung Предлагается: W.
Подробная информация о курсе в MyPlan: CSS 552
CSS 553 Архитектура программного обеспечения (5)
Изучение концепций, методов представления, методов разработки и инструментов для структурирования программных систем. Темы включают предметно-ориентированные архитектуры программного обеспечения, языки описания архитектуры, архитектурные стили, архитектуры линейки продуктов и стандарты. Сочетает в себе практический опыт разработки программного обеспечения с пониманием последних разработок в этой области.
Подробная информация о курсе в MyPlan: CSS 553
CSS 566 Управление программным обеспечением (5)
Охватывает теории, принципы и практики, которые позволяют руководителям проектов и другим заинтересованным сторонам оценивать, выбирать и использовать соответствующие структуры. инструменты, методы и показатели, которые помогут программным проектам приблизиться к успешному завершению или завершению.
Подробная информация о курсе в MyPlan: CSS 566
CSS 577 Безопасная разработка программного обеспечения (5)
Изучает безопасный дизайн и принципы, методы и методы безопасного кодирования, включая минимальные привилегии, моделирование угроз и статический анализ.Подробно покрывает распространенные уязвимости, такие как переполнение буфера, целочисленное переполнение, инъекционные атаки, межсайтовый скриптинг и слабая обработка ошибок.
Подробная информация о курсе в MyPlan: CSS 577
CSS 578 Этическое тестирование на проникновение (5)
Изучены этические средства взлома и тестирования на проникновение, анализ и использование уязвимостей, а также методы защиты. Охватывает такие темы, как разведка, идентификация ОС, удаленное сетевое сопоставление, веб-приложения, уязвимости программного обеспечения и сети, анализ поверхности атаки, нечеткое тестирование, использование уязвимостей, сбор учетных данных и повышение привилегий.
Подробная информация о курсе в MyPlan: CSS 578
CSS 581 Машинное обучение (5)
Теория и практическое использование методов машинного обучения, таких как деревья решений, логистическая регрессия, дискриминантный анализ, нейронные сети, наивный байесовский метод, k-ближайший сосед, поддержка векторных машин, совместная фильтрация, кластеризация и ансамбли. Подчеркивает практический опыт работы с реальными наборами данных в сочетании с несколькими проектами программирования.
Подробная информация о курсе в MyPlan: CSS 581
CSS 593 Cybersecurity Engineering Capstone ([1-5] -, макс.10)
Студенты применяют свои знания и навыки, связанные с разработкой кибербезопасности, в завершенном проекте. Предварительное условие: минимальный балл 2,7 по каждому из CSS 514, CSS 517, CSS 519, CSS 527, CSS 537, CSS 577 и CSS 578.
Подробная информация о курсе в MyPlan: CSS 593
Go Math Grade 4 Ответить Ключевое домашнее задание Практика FL Глава 7 Сложение и вычитание дробей — Ответ по математике
Здравствуйте, студенты !!! Вы ищете ответы на вопросы по математике в 4 классе? Если да, то вы попали в нужное место.Учащиеся 4-х классов могут получить «Ответить на ключевые домашние задания для 4-го класса по математике», глава 7, «Сложение и вычитание дробей», FL Глава 7 pdf здесь. Скачайте бесплатно по математике 4 класс. Ответьте на ключевое домашнее задание.
Пойдите по математике 4 класс Ответьте на ключевое домашнее задание Практика FL Глава 7 Сложение и вычитание дробей
Перед тем, как начать подготовку, мы предлагаем студентам ознакомиться с темами Go Math. 4 класс. Ответить на ключевые домашние задания. Практика FL Глава 7: сложение и вычитание дробей.Решения подготовлены экспертами-математиками. Так что вам не нужно беспокоиться о решениях. На все вопросы мы дали краткое объяснение.
Урок: 1 — Сложение и вычитание частей целого
Урок: 2 — Запишите дроби как суммы
Урок: 3 — Сложение дробей с использованием моделей
Урок: 4 — Вычитание дробей с помощью моделей
Урок: 5 — Сложение и вычитание дробей
Урок: 6 — Переименование дробей и смешанных чисел
Урок: 7 — Сложение и вычитание смешанных чисел
Урок: 8 — Вычитание записей с помощью
Урок: 9 — Доли и свойства сложения
Урок: 10 — Прочтите каждую задачу и решите.
Урок 7.1
Common Core — Сложение и вычитание дробей — Стр. № 133
Сложение и вычитание частей целого
Используйте модель, чтобы написать уравнение.
Вопрос 1.
Пояснение:
Глядя на 3 цифры выше, мы можем сказать, что доля затененной части первого круга равна 3/8, а доля второй цифры равна 2/8
Складывая 2 дроби, мы получаем долю от третий круг.
3/8 + 2/8 = 5/8
Вопрос 2.
Введите ниже:
_________
Ответ: 4/5 — 3/5 = 1/5
Пояснение:
Доля затененной части для вышеуказанного прямоугольника составляет 4/5
Доля прямоугольника составляет 3/5
Уравнение для приведенного выше рисунка: 4/5 — 3/5 = 1/5
Вопрос 3.
Введите ниже:
_________
Ответ: 1/4 + 2/4 = 3/4
Пояснение:
Название дроби для заштрихованной части первой цифры — 1/4
Название дроби для заштрихованной части второй цифры — 1/4
Название дроби для заштрихованной части третьей цифры равно 3/4
Итак, уравнение для приведенного выше рисунка: 1/4 + 2/4 = 3/4
Используйте модель, чтобы решить уравнение.
Вопрос 4.
\ (\ frac {2} {6} + \ frac {3} {6} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {2} {6} + \ frac {3} {6} = \ frac {5} {6} \)
Пояснение:
Название дроби для заштрихованной части первой цифры — 2/6
Название дроби для заштрихованной части второй цифры — 3/6
Название дроби для заштрихованной части третьей цифры равно 5/6
Итак, уравнение для приведенного выше рисунка: \ (\ frac {2} {6} + \ frac {3} {6} = \ frac {5} {6} \)
Вопрос 5.
\ (\ frac {3} {5} — \ frac {2} {5} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {3} {5} — \ frac {2} {5} = \ frac {1} {5} \)
Пояснение:
Имя дроби для затененной части рисунка — 3/5
Имя дроби для затененной части закрытого прямоугольника — 2/5
Итак, уравнение для приведенного выше рисунка: \ (\ frac {3} {5} — \ frac {2} {5} = \ frac {1} {5} \)
Решение проблем
Вопрос 6.
Джейк съел \ (\ frac {4} {8} \) пиццы.Милли съела \ (\ frac {3} {8} \) той же пиццы. Сколько пиццы съели Джейк и Милли?
\ (\ frac {□} {□} \)
Ответ: 7/8 пиццы
Пояснение:
Учитывая это,
Джейк съел \ (\ frac {4} {8} \) пиццы.
Милли съела \ (\ frac {3} {8} \) той же пиццы.
Чтобы узнать, сколько пиццы съели Джейк и Милли
Мы должны сложить обе дроби:
\ (\ frac {4} {8} \) + \ (\ frac {3} {8} \) = \ (\ frac {7} {8} \)
Таким образом, доля пиццы, съеденной Джейком и Милли, равна \ (\ frac {7} {8} \)
Вопрос 7.
Кейт съела \ (\ frac {1} {4} \) своего апельсина. Бен съел \ (\ frac {2} {4} \) своего банана. Кейт и Бен съели \ (\ frac {1} {4} + \ frac {2} {4} = \ frac {3} {4} \) их фруктов?
Объясни.
Тип ниже:
__________
Ответ: Нет, одно целое относится к апельсину, а другое целое — к банану.
Common Core — сложение и вычитание дробей — стр. № 134
Проверка урока
Вопрос 1.
Целый пирог разрезается на 8 равных ломтиков. Подаются три ломтика.Сколько пирога осталось?
Опции:
а. \ (\ frac {1} {8} \)
б. \ (\ frac {3} {8} \)
г. \ (\ frac {5} {8} \)
г. \ (\ frac {7} {8} \)
Ответ: \ (\ frac {5} {8} \)
Пояснение:
Дано,
Целый пирог разрезается на 8 равных ломтиков. Подаются три ломтика.
Доля 8 ломтиков составляет 8/8.
из них обслуживаются 3/8.
8/8 — 3/8 = 5/8
Следовательно, \ (\ frac {5} {8} \) пирога осталось.
Таким образом, правильный ответ — вариант c.
Вопрос 2.
Апельсин разделен на 6 равных долек. Джоди съедает 1 дольку. Потом съедает еще 3 дольки. Сколько апельсина съел Джоди?
Опции:
а. \ (\ frac {1} {6} \)
б. \ (\ frac {4} {6} \)
г. \ (\ frac {5} {6} \)
г. \ (\ frac {6} {6} \)
Ответ: \ (\ frac {4} {6} \)
Пояснение:
Дано,
Апельсин разделен на 6 равных долей.
Джоди съедает 1 дольку.
Потом съедает еще 3 дольки.
Доля апельсина, которую ест Джоди, равна \ (\ frac {4} {6} \).
Таким образом, правильный ответ — вариант b.
Обзор спирали
Вопрос 3.
Какой список расстояний в порядке от наименьшего к наибольшему?
Опции:
а. \ (\ frac {1} {8} миля, \ frac {3} {16} миля, \ frac {3} {4} миля \)
b. \ (\ frac {3} {4} миля, \ frac {1} {8} миля, \ frac {3} {16} миля \)
c. \ (\ frac {1} {8} миля, \ frac {3} {4} миля, \ frac {3} {16} миля \)
d. \ (\ frac {3} {16} миля, \ frac {1} {8} миля, \ frac {3} {4} миля \)
Ответ: \ (\ frac {1} {8} \) Миля, \ (\ frac {3} {16} \) Миля, \ (\ frac {3} {4} \) Миля
Пояснение:
Сравните три дроби 1/8, 3/4 и 3/16
Составьте общие знаменатели.
1/8 × 2/2 = 2/16
3/4 × 4/4 = 12/16
Дроби: 2/16, 12/16 и 3/16
Числитель с наибольшим числом будет наибольшим .
Дроби от наименьшей к наибольшей: \ (\ frac {1} {8} \) миля, \ (\ frac {3} {16} \) миля, \ (\ frac {3} {4} \) миля.
Таким образом, правильный ответ — вариант d.
Вопрос 4.
Джереми прошел \ (\ frac {6} {8} \) до школы и пробежал остаток пути. Какая дробь в простейшей форме показывает часть пути, по которой шел Джереми?
Опции:
а.\ (\ frac {1} {4} \)
б. \ (\ frac {3} {8} \)
г. \ (\ frac {1} {2} \)
г. \ (\ frac {3} {4} \)
Ответ: \ (\ frac {3} {4} \)
Пояснение:
Учитывая,
Джереми прошел 6/8 пути до школы и пробежал остаток пути.
Самая простая форма 6/8 — 3/8.
Простейший отрезок пути Джереми — 3/8.
Таким образом, правильный ответ — вариант b.
Вопрос 5.
Лифт поднимается на 100-й этаж здания. Он спускается с 4 этажа каждые 10 секунд.На каком этаже лифт будет через 60 секунд после запуска?
Опции:
а. 60 -й этаж
б. 66 -й этаж
с. 72 -й этаж
д. 76 -й этаж
Ответ: 76 этаж
Пояснение:
Дано,
На 100-м этаже дома идет лифт.
Он спускается с 4 этажа каждые 10 секунд.
4 этажа — 10 секунд
? — 60 секунд
60 × 4/10 = 240/10 = 24 этажа
100 — 24 = 76 этаж
Таким образом, правильный ответ — вариант d.
Вопрос 6.
Для школьного спектакля учитель попросил класс расставить стулья в 20 рядов по 25 стульев в каждом ряду. После расстановки всех стульев их стало не хватать на 5 стульев. Сколько стульев поставил класс?
Опции:
а. 400
г. 450
г. 495
г. 500
Ответ: 495
Пояснение:
Дано,
Для школьного спектакля учитель попросил класс расставить стулья в 20 рядов по 25 стульев в каждом ряду.
После расстановки всех стульев их стало не хватать на 5 стульев.
20 × 25 = 500
500 — 5 = 495
Таким образом, в классе установлено 495 стульев.
Таким образом, правильный ответ c.
Common Core — сложение и вычитание дробей — стр. № 135
Запись дробей как суммы
Запишите дробь как сумму долей единицы.
Вопрос 1.
Ответ: 1/5 + 1/5 + 1/5 + 1/5
Пояснение:
Сумма долей единиц для 4/5 равна 1/5 + 1/5 + 1/5 + 1/5.
Вопрос 2.
\ (\ frac {3} {8} \) =
Введите ниже:
__________
Ответ: 1/8 + 1/8 + 1/8
Пояснение:
Сумма долей единиц для 3/8 составляет 1/8 + 1/8 + 1/8
Вопрос 3.
\ (\ frac {6} {12} \) =
Введите ниже:
__________
Ответ: 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
Пояснение:
Сумма долей единиц для 6/12 составляет 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
Вопрос 4.
\ (\ frac {4} {4} \) =
Введите ниже:
__________
Ответ: 1/4 + 1/4 + 1/4 + 1/4
Пояснение:
Сумма долей единиц для 4/4 составляет 1/4 + 1/4 + 1/4 + 1/4
Запишите дробь как сумму дробей тремя разными способами.
Вопрос 5.
\ (\ frac {7} {10} \)
Введите ниже:
__________
Ответ: 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10
Пояснение:
Сумма долей единиц для 7/10 составляет 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10
Вопрос 6.
\ (\ frac {6} {6} \)
Введите ниже:
__________
Ответ: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6
Пояснение:
Сумма долей единиц для 6/6 составляет 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6
Решение проблем
Вопрос 7.
Учитель Мигеля просит его раскрасить \ (\ frac {4} {8} \) его сетку. Он должен использовать 3 цвета: красный, синий и зеленый. Зеленых участков должно быть больше, чем красных. Как Мигель может раскрасить участки своей сетки, чтобы соблюдать все правила?
Тип ниже:
__________
Ответ: 1/8 красного, 1/8 синего и 2/8 зеленого
Пояснение:
Если есть 8 плиток, раскраска \ (\ frac {4} {8} \) означает раскрашивание 4 плиток. Используя эти три цвета, мы могли бы использовать каждый раз по 1 остатку.Поскольку у нас должно быть больше зеленого, мы будем использовать его дважды; это даст нам 2 зеленых, 1 красный и 1 синий.
Поскольку сетка не обязательно состоит из 8 квадратов, мы должны учесть это, сказав 2/8 зеленого, 1/8 красного и 1/8 синего
Вопрос 8.
Петру предлагается раскрасить \ (\ frac {6} {6} \) ее сетку. Она должна использовать 3 цвета: синий, красный и розовый. Синих участков должно быть больше, чем красных или розовых. Какими способами Петра может раскрашивать участки своей сетки и следовать всем правилам?
Тип ниже:
__________
Ответ: 3/6 синего, 2/6 красного, 1/6 розового
Пояснение:
1.3 синих, 2 красных, 1 розовый.
2. 3 синих, 2 розовых, 1 красный.
3. 4 синих, 1 красный, 1 розовый
Различные способы, которыми Петра может раскрасить участки своей сетки и следовать правилам:
1. 3 синих, 2 красных, 1 розовый.
2. 3 синих, 2 розовых, 1 красный.
3. 4 синих, 1 красный, 1 розовый
Все эти три способа следуют правилам: должно быть три цвета, а также синие участки больше, чем красные или розовые участки.
Common Core — Сложение и вычитание дробей — Стр. № 136
Проверка урока
Вопрос 1.
Хорхе хочет записать \ (\ frac {4} {5} \) как сумму единичных дробей. Что из следующего он должен написать?
Опции:
а. \ (\ frac {3} {5} + \ frac {1} {5} \)
б. \ (\ frac {2} {5} + \ frac {2} {5} \)
c. \ (\ frac {1} {5} + \ frac {1} {5} + \ frac {2} {5} \)
г. \ (\ frac {1} {5} + \ frac {1} {5} + \ frac {1} {5} + \ frac {1} {5} \)
Ответ: \ (\ frac {1} {5} + \ frac {1} {5} + \ frac {1} {5} + \ frac {1} {5} \)
Пояснение:
Учитывая,
Хорхе хочет записать \ (\ frac {4} {5} \) как сумму долей единицы.
Сумма единичной дроби для \ (\ frac {4} {5} \) равна \ (\ frac {1} {5} + \ frac {1} {5} + \ frac {1} {5} + \ frac {1} {5} \)
Таким образом, правильный ответ — вариант d.
Вопрос 2.
Какое выражение эквивалентно \ (\ frac {7} {8} \)?
Опции:
а. \ (\ frac {5} {8} + \ frac {2} {8} + \ frac {1} {8} \)
б. \ (\ frac {3} {8} + \ frac {3} {8} + \ frac {1} {8} + \ frac {1} {8} \)
c. \ (\ frac {4} {8} + \ frac {2} {8} + \ frac {1} {8} \)
г. \ (\ frac {4} {8} + \ frac {2} {8} + \ frac {2} {8} \)
Ответ: \ (\ frac {4} {8} + \ frac {2} {8} + \ frac {1} {8} \)
Пояснение:
Дробь, эквивалентная \ (\ frac {7} {8} \), равна \ (\ frac {4} {8} + \ frac {2} {8} + \ frac {1} {8} \ ).
Таким образом, правильный ответ — вариант c.
Обзор спирали
Вопрос 3.
Яблоко разрезать на 6 равных ломтиков. Нэнси съедает 2 ломтика. Какая часть яблока осталась?
Опции:
а. \ (\ frac {1} {6} \)
б. \ (\ frac {2} {6} \)
г. \ (\ frac {3} {6} \)
г. \ (\ frac {4} {6} \)
Ответ: \ (\ frac {4} {6} \)
Пояснение:
Дано,
Яблоко разрезать на 6 равных ломтиков. Нэнси съедает 2 ломтика.
6 — 2 = 4
\ (\ frac {6} {6} \) — \ (\ frac {2} {6} \) = \ (\ frac {4} {6} \)
Таким образом, правильный ответ это вариант d.
Вопрос 4.
Какое из следующих чисел является простым числом?
Опции:
а. 1
г. 11
г. 21
г. 51
Ответ: 11
Объяснение:
Простое число — это натуральное число больше 1, которое не является произведением двух меньших натуральных чисел.
11 делится на 1 и самого себя.
Таким образом, правильный ответ — вариант b.
Вопрос 5.
У учителя есть мешок из 100 кубиков. Она раздает равное количество кубиков каждой из 7 групп своего класса. Она дает каждой группе столько кубиков, сколько она может
. Сколько единичных кубиков осталось?
Опции:
а. 1
г. 2
г. 3
г. 6
Ответ: 2
Пояснение:
Дано,
У учителя есть мешок из 100 единичных кубиков. Она раздает равное количество кубиков каждой из 7 групп своего класса.
Она дает каждой группе столько кубиков, сколько может.
100 делить на 7 дает 14 r 2, так что остается 2.
Таким образом, правильный ответ — вариант b.
Вопрос 6.
Джесси отсортировала монеты в своем банке. Она сделала 7 стопок по 6 центов и 8 стопок по 5 центов. Затем она нашла 1 цент и 1 цент. Сколько всего десятицентовых монет у Джесси?
Опции:
а. 84
г. 82
г. 80
г. 28
Ответ: 84
Пояснение:
Учитывая,
Джесси отсортировала монеты в своем банке. Она сделала 7 стопок по 6 монет и 8 стопок по 5 монет.
Затем она нашла 1 цент и 1 цент.
43 дайма и 41 никель
43 + 41 = 84
У Джесси всего 84 дайма и никель.
Таким образом, правильный ответ — вариант а.
Common Core — сложение и вычитание дробей — стр. № 137
Сложение дробей с использованием моделей
Найдите сумму. Используйте дробные полоски, чтобы помочь.
Вопрос 1.
Ответ: 3/6
Вопрос 2.
\ (\ frac {4} {10} + \ frac {5} {10} \) = \ (\ frac {□} {□} \)
Ответ: 9/10
Вопрос 3.
\ (\ frac {1} {3} + \ frac {2} {3} \) = \ (\ frac {□} {□} \)
Ответ: 3/3
Вопрос 4.
\ (\ frac {2} {4} + \ frac {1} {4} \) = \ (\ frac {□} {□} \)
Ответ: 3/4
Вопрос 5.
\ (\ frac {2} {12} + \ frac {4} {12} \) = \ (\ frac {□} {□} \)
Ответ: 6/12
Вопрос 6.
\ (\ frac {1} {6} + \ frac {2} {6} \) = \ (\ frac {□} {□} \)
Ответ: 3/6
Вопрос 7.
\ (\ frac {3} {12} + \ frac {9} {12} \) = \ (\ frac {□} {□} \)
Ответ: 12/12
Вопрос 8.
\ (\ frac {3} {8} + \ frac {4} {8} \) = \ (\ frac {□} {□} \)
Ответ: 7/8
Вопрос 9.
\ (\ frac {3} {4} + \ frac {1} {4} \) = \ (\ frac {□} {□} \)
Ответ: 4/4
Вопрос 10.
\ (\ frac {1} {5} + \ frac {2} {5} \) = \ (\ frac {□} {□} \)
Ответ: 3/5
Пояснение:
Решение проблем
Вопрос 11.
Лола идет \ (\ frac {4} {10} \) милю до дома своей подруги. Затем она проходит \ (\ frac {5} {10} \) милю до магазина.Как далеко она вообще заходит?
\ (\ frac {□} {□} \) миля
Ответ: \ (\ frac {9} {10} \) миля
Пояснение:
Учитывая,
Лола идет \ (\ frac {4} {10} \) милю до дома своей подруги.
Затем она идет \ (\ frac {5} {10} \) милю до магазина.
\ (\ frac {4} {10} \) + \ (\ frac {5} {10} \) = \ (\ frac {9} {10} \)
Поэтому она шла \ (\ frac {9} {10} \) миль всего.
Вопрос 12.
Эван съедает \ (\ frac {1} {8} \) кастрюлю с лазаньей, а его брат съедает \ (\ frac {2} {8} \) из нее.Какую часть кастрюли с лазаньей они съедают всего?
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {3} {8} \) противня
Пояснение:
Учитывая,
Эван съедает \ (\ frac {1} {8} \) кастрюли с лазаньей, а его брат съедает \ (\ frac {2} {8} \) из нее.
\ (\ frac {1} {8} \) + \ (\ frac {2} {8} \)
= \ (\ frac {3} {8} \)
Вопрос 13.
Жаклин покупает \ (\ frac {2} {4} \) ярд зеленой ленты и \ (\ frac {1} {4} \) ярд розовой ленты. Сколько всего ярдов ленты она покупает?
\ (\ frac {□} {□} \) двор
Ответ: \ (\ frac {3} {4} \) двор
Пояснение:
Учитывая,
Жаклин покупает \ (\ frac {2} {4} \) ярд зеленой ленты и \ (\ frac {1} {4} \) ярд розовой ленты.
\ (\ frac {2} {4} \) + \ (\ frac {1} {4} \)
= \ (\ frac {3} {4} \)
Таким образом, Жаклин купила \ (\ frac {3 } {4} \) ярдов ленты всего.
Вопрос 14.
Шу смешивает \ (\ frac {2} {3} \) фунт арахиса с \ (\ frac {1} {3} \) фунтом миндаля. Сколько фунтов орехов всего смешивает Шу?
\ (\ frac {□} {□} \) фунт
Ответ: 3/3 фунта
Пояснение:
Дано,
Шу смешивает \ (\ frac {2} {3} \) фунт арахиса с \ (\ frac {1} {3} \) фунтом миндаля.
\ (\ frac {2} {3} \) + \ (\ frac {1} {3} \)
= \ (\ frac {3} {3} \)
Следовательно, Шу смешивает \ (\ frac {3 } {3} \) фунтов орехов всего.
Common Core — Сложение и вычитание дробей — Стр. № 138
Проверка урока
Вопрос 1.
У Мэри Джейн осталось \ (\ frac {3} {8} \) средней пиццы. У Гектора осталось \ (\ frac {2} {8} \) другой средней пиццы. Сколько всего у них пиццы?
Опции:
а. \ (\ frac {1} {8} \)
б.\ (\ frac {4} {8} \)
г. \ (\ frac {5} {8} \)
г. \ (\ frac {6} {8} \)
Ответ: \ (\ frac {5} {8} \)
Пояснение:
Учитывая,
Мэри Джейн осталась \ (\ frac {3} {8} \) пиццы среднего размера.
У Гектора осталось \ (\ frac {2} {8} \) другой средней пиццы.
Чтобы узнать, сколько у них всего пиццы, нам нужно сложить обе дроби.
\ (\ frac {3} {8} \) + \ (\ frac {2} {8} \) = \ (\ frac {5} {8} \)
Следовательно, Мэри Джейн и Гектор имеют \ (\ frac {5} {8} \) пицца вообще.
Таким образом, правильный ответ — вариант c.
Вопрос 2.
Джинни съела \ (\ frac {1} {4} \) яблока. Келли съела \ (\ frac {2} {4} \) яблока. Сколько всего они съели?
Опции:
а. \ (\ frac {1} {4} \)
б. \ (\ frac {2} {8} \)
г. \ (\ frac {3} {8} \)
г. \ (\ frac {3} {4} \)
Ответ: \ (\ frac {3} {4} \)
Пояснение:
Учитывая,
Джинни съела \ (\ frac {1} {4} \) яблока.
Келли съела \ (\ frac {2} {4} \) яблока.
\ (\ frac {1} {4} \) + \ (\ frac {2} {4} \) = \ (\ frac {3} {4} \)
Таким образом, правильный ответ — вариант d.
Обзор спирали
Вопрос 3.
Карен делает 14 различных видов поздравительных открыток. Она делает по 12 штук каждого вида. Сколько открыток она делает?
Опции:
а. 120
г. 132
г. 156
г. 168
Ответ: 168
Пояснение:
Учитывая,
Карен делает 14 различных видов поздравительных открыток.
Она делает по 12 штук каждого вида.
Чтобы узнать, сколько открыток она делает, нам нужно умножить 14 на 12.
14 × 12 = 168.
Таким образом, правильный ответ — вариант d.
Вопрос 4.
Джефферсон работает неполный рабочий день и за четыре недели зарабатывает 1520 долларов. Сколько он зарабатывает каждую неделю?
Опции:
а. 305 $
б. $ 350
c. $ 380
д. $ 385
Ответ: 380 $
Пояснение:
Джефферсон работает неполный рабочий день и за четыре недели зарабатывает 1520 долларов.
1520 — 4 недели
? — 1 неделя
1520/4 = 380 $
Таким образом, правильный ответ — вариант c
Вопрос 5.
Установив эффективную водопроводную арматуру, средний американец может сократить потребление воды примерно до 45 галлонов воды в день. Сколько галлонов воды использовал бы средний американец в декабре, используя такие водопроводные устройства?
Опции:
а. около 1200 галлонов
b. около 1500 галлонов
c. около 1600 галлонов
d. около 2000 галлонов
Ответ: около 1500 галлонов
Пояснение:
Дано,
Установив эффективную водопроводную арматуру, средний американец может сократить потребление воды примерно до 45 галлонов воды в день.
1 день — 45 галлонов
31 день -?
45 × 31 = 1395 галлонов
Число около 1395 — 1500 галлонов.
Таким образом, правильный ответ — вариант b.
Вопрос 6.
Коллин делает доску объявлений и центр заметок. Он использует квадратную пробковую плитку и квадратную плитку сухого стирания. Один из каждых трех квадратов будет пробковым. Если он использует 12 квадратов в качестве центра, сколько будет пробковых квадратов?
Опции:
а. 3
г. 4
г. 6
г. 8
Ответ: 4
Пояснение:
Учитывая это,
Коллин делает доску объявлений и центр заметок.
Он использует квадратные пробковые плитки и квадратные плитки сухого стирания.
Один из каждых трех квадратов будет пробковым.
12/3 = 4
Таким образом, правильный ответ — вариант b.
Common Core — Сложение и вычитание дробей — Стр. № 139
Вычесть дроби с помощью моделей
Вычесть. Используйте дробные полоски, чтобы помочь.
Вопрос 1.
Ответ: 3/5
Пояснение:
Дана дробь, 4/5 и 1/5
Знаменатели обеих дробей одинаковы, поэтому вычтите числители.
4/5 — 1/5 = 3/5
Вопрос 2.
\ (\ frac {3} {4} — \ frac {1} {4} \) = \ (\ frac {□} {□} \)
Ответ: 2/4
Пояснение:
Учитывая дроби \ (\ frac {3} {4} \) и [/ latex] \ frac {1} {4} [/ latex]
Знаменатели обеих дробей одинаковы, поэтому вычтите числители .
\ (\ frac {3} {4} — \ frac {1} {4} = \ frac {2} {4} \)
Вопрос 3.
\ (\ frac {5} {6} — \ frac {1} {6} \) = \ (\ frac {□} {□} \)
Ответ: 4/6
Пояснение:
Учитывая дроби \ (\ frac {5} {6} \) и [/ latex] \ frac {1} {6} [/ latex]
Знаменатели обеих дробей одинаковы, поэтому вычтите числители .
\ (\ frac {5} {6} — \ frac {1} {6} = \ frac {4} {6} \)
Вопрос 4.
\ (\ frac {7} {8} — \ frac {1} {8} \) = \ (\ frac {□} {□} \)
Ответ: 6/8
Пояснение:
Учитывая дроби \ (\ frac {7} {8} \) и [/ latex] \ frac {1} {8} [/ latex]
Знаменатели обеих дробей одинаковы, поэтому вычтите числители .
\ (\ frac {7} {8} — \ frac {1} {8} = \ frac {6} {8} \)
Вопрос 5.
1 — \ (\ frac {2} {3} \) = \ (\ frac {□} {□} \)
Ответ: 1/3
Пояснение:
Учитывая дроби \ (\ frac {1} {3} \) и [/ latex] \ frac {2} {3} [/ latex]
Знаменатели обеих дробей одинаковы, поэтому вычтите числители .
\ (\ frac {1} {3} — \ frac {2} {3} = \ frac {1} {3} \)
Вопрос 6.
\ (\ frac {8} {10} — \ frac {2} {10} \) = \ (\ frac {□} {□} \)
Ответ: 6/10
Пояснение:
Учитывая дроби \ (\ frac {8} {10} \) и [/ latex] \ frac {2} {10} [/ latex]
Знаменатели обеих дробей одинаковы, поэтому вычтите числители .
\ (\ frac {8} {10} — \ frac {2} {10} = \ frac {6} {10} \)
Вопрос 7.
\ (\ frac {3} {4} — \ frac {1} {4} \) = \ (\ frac {□} {□} \)
Ответ: 2/4
Пояснение:
Учитывая дроби \ (\ frac {3} {4} \) и [/ latex] \ frac {1} {4} [/ latex]
Знаменатели обеих дробей одинаковы, поэтому вычтите числители .
\ (\ frac {3} {4} — \ frac {1} {4} = \ frac {2} {4} \)
Вопрос 8.
\ (\ frac {7} {6} — \ frac {5} {6} \) = \ (\ frac {□} {□} \)
Ответ: 2/6
Пояснение:
Учитывая дроби \ (\ frac {7} {6} \) и [/ latex] \ frac {5} {6} [/ latex]
Знаменатели обеих дробей одинаковы, поэтому вычтите числители .
\ (\ frac {7} {6} — \ frac {5} {6} = \ frac {2} {6} \)
Решение проблем
Используйте таблицу для 9 и 10.
Вопрос 9.
Эна делает трейл-микс. Она покупает предметы, указанные в таблице. На сколько фунтов кренделей больше, чем изюма, она купит?
\ (\ frac {□} {□} \)
Ответ: 5/8 фунта
Пояснение:
Учитывая это,
Ena делает трейл-микс.
кренделей = 7/8
Изюм = 2/8
Чтобы найти, на сколько фунтов кренделей больше, чем изюма, она купила
, мы должны вычесть обе дроби.
7/8 — 2/8 = 5/8
Вопрос 10.
На сколько фунтов гранолы больше, чем банановых чипсов, она покупает?
\ (\ frac {□} {□} \)
Ответ: 2/8 фунта
Пояснение:
Гранола = 5/8
Банановые чипсы = 3/8
Чтобы найти, на сколько фунтов гранолы больше, чем банановых чипсов, она покупает, мы должны вычесть обе дроби.
5/8 — 3/8 = 2/8 фунта
Common Core — Сложение и вычитание дробей — Стр. № 140
Проверка урока
Вопрос 1.
Ли читает \ (\ frac {3} {4} \) час утром и \ (\ frac {2} {4} \) час днем.Сколько времени Ли читает утром, чем днем?
Опции:
а. 5 часов
б. \ (\ frac {5} {4} \) часов
c. \ (\ frac {4} {4} \) час
дн. \ (\ frac {1} {4} \) час
Ответ: \ (\ frac {1} {4} \)
Пояснение:
Учитывая, что
Ли читает \ (\ frac {3} {4} \) час утром и \ (\ frac {2} {4} \) час днем.
\ (\ frac {3} {4} \) — \ (\ frac {2} {4} \) = \ (\ frac {1} {4} \)
Ли прочитал \ (\ frac {1} { 4} \) час утром, чем днем.
Таким образом, правильный ответ — вариант d.
Вопрос 2.
Какое уравнение представляет модель ниже?
Опции:
а. \ (\ frac {3} {6} — \ frac {2} {6} = \ frac {1} {6} \)
б. \ (\ frac {2} {6} — \ frac {1} {6} = \ frac {1} {6} \)
c. \ (\ frac {5} {6} — \ frac {3} {6} = \ frac {2} {6} \)
г. 1 — \ (\ frac {3} {6} \) = \ (\ frac {3} {6} \)
Ответ: \ (\ frac {5} {6} — \ frac {3} {6} = \ frac {2} {6} \)
Пояснение:
Из рисунка выше мы можем сказать, что \ (\ frac {5} {6} — \ frac {3} {6} = \ frac {2} {6} \)
Таким образом, правильный ответ — вариант c .
Обзор спирали
Вопрос 3.
В городе выпадает 2 дюйма дождя каждый день в течение 3 дней. Метеоролог сказал, что если бы дождь был снегом, каждый дюйм дождя составлял бы 10 дюймов снега. Сколько снега выпало бы в этом городе за 3 дня?
Опции:
а. 20 дюймов
b. 30 дюймов
c. 50 дюймов
d. 60 дюймов
Ответ: 60 дюймов
Пояснение:
Дано,
Город получал 2 дюйма дождя каждый день в течение 3 дней.
2 × 3 дюйма = 6 дюймов
Метеоролог сказал, что если бы дождь был снегом, каждый дюйм дождя составлял бы 10 дюймов снега.
6 × 10 дюймов = 60 дюймов
Таким образом, город получил 60 дюймов снега за 3 дня.
Таким образом, правильный ответ — вариант d.
Вопрос 4.
На вечеринке было четыре больших сэндвича с подводной лодкой, все одинакового размера. Во время вечеринки \ (\ frac {2} {3} \) сэндвича с курицей, \ (\ frac {3} {4} \) сэндвича с тунцом, \ (\ frac {7} {12} \) бутерброда с ростбифом и \ (\ frac {5} {6} \) овощного бутерброда.В каком бутерброде осталось меньше всего?
Опции:
а. курица
б. тунец
гр. ростбиф
д. вегетарианский
Ответ: вегетарианский
Пояснение:
Дано,
На вечеринке было четыре больших сэндвича с подводными лодками, все одинакового размера. Во время вечеринки \ (\ frac {2} {3} \) сэндвича с курицей, \ (\ frac {3} {4} \) сэндвича с тунцом, \ (\ frac {7} {12} \) бутерброда с ростбифом и \ (\ frac {5} {6} \) овощного бутерброда.
Сравните дроби \ (\ frac {2} {3} \), \ (\ frac {3} {4} \), \ (\ frac {7} {12} \) и \ (\ frac {5} {6} \).
Среди всех фракций овощ имеет наименьшую фракцию.
Таким образом, правильный ответ — вариант d.
Вопрос 5.
Дина использует в рецепте \ (\ frac {3} {8} \) стакан молока и \ (\ frac {2} {8} \) стакан масла. Сколько жидкости она вообще употребляет?
Опции:
а. \ (\ frac {1} {8} \) чашка
б. \ (\ frac {5} {8} \) чашка
c. \ (\ frac {6} {8} \) чашка
d. 5 чашек
Ответ: \ (\ frac {5} {8} \) чашка
Пояснение:
Учитывая, что
Дина использует в рецепте \ (\ frac {3} {8} \) стакан молока и \ (\ frac {2} {8} \) стакан масла.
\ (\ frac {3} {8} \) + \ (\ frac {2} {8} \) = \ (\ frac {5} {8} \) чашка
Поэтому она использовала \ (\ frac {5 } {8} \) всего чашку молока.
Таким образом, правильный ответ — вариант b.
Вопрос 6.
На автомобильной стоянке \ (\ frac {4} {12} \) машины белые, а \ (\ frac {3} {12} \) машины синие. Какая часть автомобилей в партии белые или синие?
Опции:
а. \ (\ frac {1} {12} \)
б. \ (\ frac {7} {24} \)
г. \ (\ frac {7} {12} \)
г. 7
Ответ: \ (\ frac {7} {12} \)
Пояснение:
Дано,
На автомобильной стоянке \ (\ frac {4} {12} \) машины белые, а \ (\ frac {3} {12} \) машины синие.
\ (\ frac {4} {12} \) + \ (\ frac {3} {12} \) = \ (\ frac {7} {12} \)
Таким образом, правильный ответ — вариант c.
Common Core — сложение и вычитание дробей — стр. № 141
Сложить и вычесть дроби
Найдите сумму или разницу.
Вопрос 1.
Ответ: 12/12
Пояснение:
Знаменатели обеих дробей совпадают, поэтому сложите числители.
\ (\ frac {4} {12} \) + \ (\ frac {8} {12} \)
= \ (\ frac {12} {12} \)
Вопрос 2.
\ (\ frac {3} {6} — \ frac {1} {6} \) = \ (\ frac {□} {□} \)
Ответ: 2/6
Пояснение:
Знаменатели обеих дробей совпадают, поэтому вычтите числители.
\ (\ frac {3} {6} \) — \ (\ frac {1} {6} \)
= \ (\ frac {2} {6} \)
Вопрос 3.
\ (\ frac {4} {5} — \ frac {3} {5} \) = \ (\ frac {□} {□} \)
Ответ: 1/5
Пояснение:
Знаменатели обеих дробей совпадают, поэтому вычтите числители.
\ (\ frac {4} {5} \) — \ (\ frac {3} {5} \)
= \ (\ frac {1} {5} \)
Вопрос 4.
\ (\ frac {6} {10} + \ frac {3} {10} \) = \ (\ frac {□} {□} \)
Ответ: 9/10
Пояснение:
Знаменатели обеих дробей совпадают, поэтому сложите числители.
\ (\ frac {6} {10} + \ frac {3} {10} \) = \ (\ frac {9} {10} \)
Вопрос 5.
1 — \ (\ frac {3} {8} \) = \ (\ frac {□} {□} \)
Ответ: 5/8
Пояснение:
Знаменатели обеих дробей совпадают, поэтому вычтите числители.
1 — \ (\ frac {3} {8} \)
= \ (\ frac {8} {8} \) — \ (\ frac {3} {8} \)
= \ (\ frac {5 } {8} \)
Вопрос 6.
\ (\ frac {1} {4} + \ frac {2} {4} \) = \ (\ frac {□} {□} \)
Ответ: 3/4
Пояснение:
Знаменатели обеих дробей совпадают, поэтому сложите числители.
\ (\ frac {1} {4} + \ frac {2} {4} \) = \ (\ frac {3} {4} \)
Вопрос 7.
\ (\ frac {9} {12} — \ frac {5} {12} \) = \ (\ frac {□} {□} \)
Ответ: 12/4
Пояснение:
Знаменатели обеих дробей совпадают, поэтому вычтите числители.
\ (\ frac {9} {12} — \ frac {5} {12} \) = \ (\ frac {4} {12} \)
Вопрос 8.
\ (\ frac {5} {6} — \ frac {2} {6} \) = \ (\ frac {□} {□} \)
Ответ: 3/6
Пояснение:
Знаменатели обеих дробей совпадают, поэтому вычтите числители.
\ (\ frac {5} {6} — \ frac {2} {6} \) = \ (\ frac {3} {6} \)
Вопрос 9.
\ (\ frac {2} {3} + \ frac {1} {3} \) = \ (\ frac {□} {□} \)
Ответ: 3/3 = 1
Пояснение:
Знаменатели обеих дробей совпадают, поэтому сложите числители.
\ (\ frac {2} {3} + \ frac {1} {3} \) = \ (\ frac {3} {3} \) = 1
Решение проблем
Используйте таблицу для 10 и 11.
Вопрос 10.
Парень определяет, как далеко его дом находится от нескольких мест, и показывает таблицу. Насколько дальше от дома Гая библиотека, чем кафе?
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {5} {10} \) миля
Пояснение:
Расстояние от дома Гая до библиотеки составляет \ (\ frac {9} {10} \) милю
Расстояние от дома Гая до кафе составляет \ (\ frac {4} {10} \) милю
. Чтобы определить, насколько дальше от дома Гая находится библиотека, чем кафе, вычтите обе дроби.
\ (\ frac {9} {10} \) — \ (\ frac {4} {10} \) = \ (\ frac {5} {10} \) миля
Вопрос 11.
Если Гай идет из дома в школу и обратно, как далеко он пойдет?
\ (\ frac {□} {□} \)
Ответ: 10/10 миль
Пояснение:
Расстояние от дома Гая до школы = \ (\ frac {5} {10} \) миля
От школы до дома \ (\ frac {5} {10} \) миля
\ (\ frac {5 } {10} \) + \ (\ frac {5} {10} \) = \ (\ frac {10} {10} \) миля
Common Core — сложение и вычитание дробей — стр.142
Проверка урока
Вопрос 1.
Мистер Ангуло покупает \ (\ frac {5} {8} \) фунт красного винограда и \ (\ frac {3} {8} \) фунт зеленого винограда. Сколько фунтов винограда всего купил мистер Ангуло?
Опции:
а. \ (\ frac {1} {8} \) фунт
б. \ (\ frac {2} {8} \) фунт
гр. 1 фунт
д. 2 фунта
Ответ: 1 фунт
Пояснение:
Учитывая это,
г-н Ангуло покупает \ (\ frac {5} {8} \) фунт красного винограда и \ (\ frac {3} {8} \) фунт зеленого винограда.
\ (\ frac {5} {8} \) + \ (\ frac {3} {8} \)
= \ (\ frac {8} {8} \)
= 1
Таким образом, правильный ответ — вариант c.
Вопрос 2.
Какое уравнение представляет модель ниже?
Опции:
а. \ (\ frac {7} {8} + \ frac {2} {8} = \ frac {9} {8} \)
б. \ (\ frac {5} {8} — \ frac {2} {8} = \ frac {3} {8} \)
c. \ (\ frac {8} {8} — \ frac {5} {8} = \ frac {3} {8} \)
г. \ (\ frac {7} {8} — \ frac {2} {8} = \ frac {5} {8} \)
Ответ: \ (\ frac {7} {8} \) — \ (\ frac {2} {8} \) = \ (\ frac {5} {8} \)
Пояснение:
Глядя на рисунок выше, мы можем сказать, что уравнение модели:
\ (\ frac {7} {8} \) — \ (\ frac {2} {8} \) = \ (\ frac {5} {8} \)
Таким образом, правильный ответ — вариант d.
Обзор спирали
Вопрос 3.
В упаковке 6 маффинов. Сколько пакетов понадобится, чтобы накормить 48 человек, если на каждого по 2 кексы?
Опции:
а. 4
г. 8
с. 16
г. 24
Ответ: 16
Пояснение:
В упаковке 6 маффинов.
Количество человек = 48
48/6 = 8
Также с учетом того, что каждый человек получает 2 кексы.
8 × 2 = 16
Таким образом, правильный ответ — вариант c.
Вопрос 4.
Camp Oaks получает 32 коробки апельсинового сока и 56 коробок яблочного сока. Каждая полка в шкафу вмещает 8 коробок сока. Какое наименьшее количество полок
необходимо для всех коробок для сока?
Опции:
а. 4
г. 7
г. 11
г. 88
Ответ: 11
Пояснение:
Учитывая,
Camp Oaks получает 32 коробки апельсинового сока и 56 коробок яблочного сока.
Каждая полка в шкафу вмещает 8 коробок сока.
Сначала добавьте коробки апельсинового и яблочного сока.
32 + 56 = 88 коробок сока
Теперь разделите 88 на 8
88/8 = 11
Таким образом, правильный ответ — вариант c.
Вопрос 5.
Машина производит 18 деталей в час. Если машина работает 24 часа в сутки, сколько деталей она может изготовить за один день
Опции:
a. 302
г. 332
г. 362
г. 432
Ответ: 432
Пояснение:
Дано,
Машина производит 18 деталей каждый час.
Умножьте количество деталей на количество часов.
18 × 24 = 432 детали в сутки.
Таким образом, правильный ответ — вариант d.
Вопрос 6.
Какое уравнение представляет модель ниже?
Опции:
а. \ (\ frac {5} {6} — \ frac {4} {6} = \ frac {1} {6} \)
б. \ (\ frac {4} {5} — \ frac {1} {5} = \ frac {3} {5} \)
c. \ (\ frac {5} {5} — \ frac {4} {5} = \ frac {1} {5} \)
г. \ (\ frac {6} {6} — \ frac {4} {6} = \ frac {2} {6} \)
Ответ: \ (\ frac {5} {6} \) — \ (\ frac {4} {6} \) = \ (\ frac {1} {6} \)
Пояснение:
Наблюдая за фигурой, мы можем сказать, что уравнение имеет вид \ (\ frac {5} {6} \) — \ (\ frac {4} {6} \) = \ (\ frac {1} {6 } \).
Таким образом, правильный ответ — вариант а.
Common Core — сложение и вычитание дробей — стр. № 143
Переименовать дроби и смешанные числа
Запишите смешанное число в виде дроби.
Вопрос 1.
2 \ (\ frac {3} {5} \)
Вопрос 2.
4 \ (\ frac {1} {3} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {13} {3} \)
Пояснение:
\ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {1} {3} \) = \ (\ frac {13} {3} \)
Вопрос 3.
1 \ (\ frac {2} {5} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {7} {5} \)
Пояснение:
\ (\ frac {5} {5} \) + \ (\ frac {2} {5} \) = \ (\ frac {7} {5} \)
Вопрос 4.
3 \ (\ frac {3} {2} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {9} {2} \)
Пояснение:
\ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {1} {2} \) = \ (\ frac {9} {2} \)
Вопрос 5.
4 \ (\ frac {1} {8} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {33} {8} \)
Пояснение:
\ (\ frac {8} {8} \) + \ (\ frac {8} {8} \) + \ (\ frac {8} {8} \) + \ (\ frac {8} {8} \) + \ (\ frac {1} {8} \) = \ (\ frac {33} {8} \)
Вопрос 6.
1 \ (\ frac {7} {10} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {17} {10} \)
Пояснение:
\ (\ frac {10} {10} \) + \ (\ frac {7} {10} \) = \ (\ frac {17} {10} \)
Вопрос 7.
5 \ (\ frac {1} {2} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {11} {2} \)
Пояснение:
\ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {1} {2} \) = \ (\ frac {11} {2} \)
Вопрос 8.
2 \ (\ frac {3} {8} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {19} {8} \)
Пояснение:
\ (\ frac {8} {8} \) + \ (\ frac {8} {8} \) + \ (\ frac {3} {8} \)
Запишите дробь как смешанное число.
Вопрос 9.
\ (\ frac {31} {6} \)
______ \ (\ frac {□} {□} \)
Ответ: 5 \ (\ frac {1} {6} \)
Пояснение:
\ (\ frac {6} {6} \) + \ (\ frac {6} {6} \) + \ (\ frac {6} {6} \) + \ (\ frac {6} {6} \) + \ (\ frac {6} {6} \) + \ (\ frac {1} {6} \)
1 + 1 + 1 + 1 + 1 + \ (\ frac {1} { 6} \) = 5 \ (\ frac {1} {6} \)
Вопрос 10.
\ (\ frac {20} {10} \)
______ \ (\ frac {□} {□} \)
Ответ: 2
Пояснение:
\ (\ frac {10} {10} \) + \ (\ frac {10} {10} \) = 1 + 1 = 2
Вопрос 11.
\ (\ frac {15} {8} \)
______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {7} {8} \)
Пояснение:
\ (\ frac {8} {8} \) + \ (\ frac {7} {8} \)
1 + \ (\ frac {7} {8} \) = 1 \ (\ frac {7} {8} \)
Вопрос 12.
\ (\ frac {13} {6} \)
______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {1} {6} \)
Пояснение:
\ (\ frac {6} {6} \) + \ (\ frac {6} {6} \) + \ (\ frac {1} {6} \)
= 1 + 1 + \ ( \ frac {1} {6} \) = 2 \ (\ frac {1} {6} \)
Вопрос 13.
\ (\ frac {23} {10} \)
______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {3} {10} \)
Пояснение:
\ (\ frac {10} {10} \) + \ (\ frac {10} {10} \) + \ (\ frac {3} {10} \)
1 + 1 + \ (\ гидроразрыв {3} {10} \) = 2 \ (\ frac {3} {10} \)
Вопрос 14.
\ (\ frac {19} {5} \)
______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {4} {5} \)
Пояснение:
\ (\ frac {5} {5} \) + \ (\ frac {5} {5} \) + \ (\ frac {5} {5} \) + \ (\ frac {4} {5} \)
1 + 1 + 1 + \ (\ frac {4} {5} \) = 3 \ (\ frac {4} {5} \)
Вопрос 15.
\ (\ frac {11} {3} \)
______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {2} {3} \)
Пояснение:
\ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {2} {3} \)
= 1 + 1 + 1 \ (\ frac {2} {3} \)
= 3 \ (\ frac {2} {3} \)
Вопрос 16.
\ (\ frac {9} {2} \)
______ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {1} {2} \)
Пояснение:
\ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {1} {2} \)
= 1 + 1 + 1 + 1 + \ (\ frac {1} {2} \)
= 4 \ (\ frac {1} {2} \)
Вопрос 17.
Рецепт требует 2 \ (\ frac {2} {4} \) стаканов изюма, но у Джули есть только мерный стакан с \ (\ frac {1} {4} \) чашками. Сколько \ (\ frac {1} {4} \) чашек нужно Джули, чтобы отмерить 2 \ (\ frac {2} {4} \) чашки изюма?
Ей нужно ______ \ (\ frac {1} {4} \) чашек
Ответ: 10 \ (\ frac {1} {4} \) чашек
Пояснение:
Дано,
Рецепт требует 2 \ (\ frac {2} {4} \) стаканов изюма, но у Джули есть только \ (\ frac {1} {4} \) мерный стаканчик.
\ (\ frac {4} {4} \) + \ (\ frac {4} {4} \) + \ (\ frac {1} {4} \) + \ (\ frac {1} {4} \)
= 10 \ (\ frac {1} {4} \) чашек
Вопрос 18.
Если Джули нужно 3 \ (\ frac {1} {4} \) чашки овсянки, сколько 14 чашек овсянки она использует?
Она будет использовать ______ \ (\ frac {1} {4} \) чашек овсянки
Ответ: 13 \ (\ frac {1} {4} \) чашек овсянки
Пояснение:
\ (\ frac {4} {4} \) + \ (\ frac {4} {4} \) + \ (\ frac {1} {4} \) + \ (\ frac {1} {4} \) + \ (\ frac {1} {4} \)
= 13 \ (\ frac {1} {4} \)
Следовательно, Джули нужно 13 \ (\ frac {1} {4} \) чашки овсянки.
Common Core — сложение и вычитание дробей — стр. № 144
Проверка урока
Вопрос 1.
Что из следующего эквивалентно \ (\ frac {16} {3} \)?
Опции:
а. 3 \ (\ frac {1} {5} \)
б. 3 \ (\ frac {2} {5} \)
c. 5 \ (\ frac {1} {3} \)
г. 5 \ (\ frac {6} {3} \)
Ответ: 5 \ (\ frac {1} {3} \)
Пояснение:
Преобразование неправильной дроби в смешанную.
\ (\ frac {16} {3} \) = \ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {3} {3} \) + \ (\ frac {1} {3} \)
= 5 \ (\ frac {1 } {3} \)
Таким образом, правильный ответ — вариант c.
Вопрос 2.
Стейси наполнила свой мерный стакан \ (\ frac {1} {2} \) семь раз, чтобы было достаточно муки для рецепта торта. Сколько муки требуется в рецепте торта?
Опции:
а. 3 чашки
б. 3 \ (\ frac {1} {2} \) чашки
c. 4 стакана
д. 4 \ (\ frac {1} {2} \) чашки
Ответ: 3 \ (\ frac {1} {2} \) чашки
Пояснение:
Учитывая,
Стейси наполнила свою мерную чашку \ (\ frac {1} {2} \) мерным стаканом семь раз, чтобы было достаточно муки для рецепта торта.
\ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {2} {2} \) + \ (\ frac {1} {2} \)
1 + 1 + 1 + \ (\ frac {1} {2} \)
= 3 \ (\ frac {1} {2} \) чашек
Таким образом, правильный ответ — вариант b.
Обзор спирали
Вопрос 3.
Бекки положила несколько марок в свою книгу коллекции марок. На каждую страницу она поставила по 14 марок. Если она полностью заполнила 16 страниц, сколько марок она поместила в книгу?
Опции:
а. 224
г. 240
г. 272
г. 275
Ответ: 224
Пояснение:
Бекки положила несколько марок в свою книгу коллекций марок.
На каждую страницу поставила по 14 марок.
Если она полностью заполнила 16 страниц
Умножьте 14 на 16 страниц.
14 × 16 = 224 страницы
Таким образом, правильный ответ — вариант а.
Вопрос 4.
Брайан едет 324 мили, чтобы навестить друзей. Он хочет добраться за 6 часов. Сколько миль ему нужно проезжать каждый час?
Опции:
а. 48 миль
б. 50 миль
c. 52 мили
д. 54 миль
Ответ: 54 миль
Пояснение:
Брайан едет 324 мили, чтобы навестить друзей. Он хочет добраться за 6 часов.
Разделите количество миль на часы.
324/6 = 54 мили
Таким образом, правильный ответ — вариант d.
Вопрос 5.
Во время соревнований на велосипеде гонщики должны собирать ленты разного цвета. Каждую \ (\ frac {1} {2} \) милю они собирают красную ленту, каждую \ (\ frac {1} {8} \) милю они собирают зеленую ленту, и каждую \ (\ frac {1} { 4} \) милю они собирают синюю ленточку. Ленты какого цвета будут собраны на отметке \ (\ frac {3} {4} \) мили?
Опции:
а. красный и зеленый
б. красный и синий
c. зелено-синий
д.красный, зеленый и синий
Ответ: зелено-синий
Пояснение:
Дано,
Во время соревнований на велосипеде гонщики должны собирать разноцветные ленты.
Каждую \ (\ frac {1} {2} \) милю они собирают красную ленту, каждую \ (\ frac {1} {8} \) милю они собирают зеленую ленту, и каждая \ (\ frac {1} {4} \) милю они собирают синюю ленточку.
Ленты зеленого и синего цветов будут собраны на отметке \ (\ frac {3} {4} \) мили.
Таким образом, правильный ответ — вариант c.
Вопрос 6.
У Стефани был \ (\ frac {7} {8} \) фунт птичьего семени. Она использовала \ (\ frac {3} {8} \) фунт, чтобы наполнить кормушку для птиц. Сколько семян птицы осталось у Стефани?
Опции:
а. \ (\ frac {3} {8} \) фунт
б. \ (\ frac {4} {8} \) фунт
гр. 1 фунт
д. \ (\ frac {10} {8} \)
Ответ: \ (\ frac {4} {8} \) фунт
Пояснение:
Учитывая, что у
Стефани был \ (\ frac {7} {8} \) фунт птичьего семени.
Она использовала \ (\ frac {3} {8} \) фунт, чтобы наполнить кормушку для птиц.
\ (\ frac {7} {8} \) — \ (\ frac {3} {8} \) = \ (\ frac {4} {8} \) фунт
Таким образом, правильный ответ — вариант b.
Common Core — сложение и вычитание дробей — стр. № 145
Сложить и вычесть смешанные числа
Найдите сумму. Запишите сумму как смешанное число, чтобы дробная часть была меньше 1.
Вопрос 1.
Вопрос 2.
4 \ (\ frac {1} {2} \)
+ 2 \ (\ frac {1} {2} \)
_______ \ (\ frac {□} {□} \)
Ответ: 7
4 \ (\ frac {1} {2} \)
+2 \ (\ frac {1} {2} \)
6 \ (\ frac {2} {2} \) = 6 + 1 = 7
Вопрос 3.
2 \ (\ frac {2} {3} \)
+ 3 \ (\ frac {2} {3} \)
_______ \ (\ frac {□} {□} \)
Ответ: 6 \ (\ frac {1} {3} \)
Пояснение:
2 \ (\ frac {2} {3} \)
+3 \ (\ frac {2} {3} \)
5 \ (\ frac {4} {3} \)
= 5 + 1 \ (\ frac {1} {3} \)
= 6 \ (\ frac {1} {3} \)
Вопрос 4.
6 \ (\ frac {4} {5} \)
+ 7 \ (\ frac {4} {5} \)
_______ \ (\ frac {□} {□} \)
Ответ: 14 \ (\ frac {3} {5} \)
Пояснение:
6 \ (\ frac {4} {5} \)
+7 \ (\ frac {4} {5} \)
13 \ (\ frac {8} {5} \)
13 + 1 \ (\ frac {3} {5} \)
= 14 \ (\ frac {3} {5} \)
Вопрос 5.
9 \ (\ frac {3} {6} \)
+ 2 \ (\ frac {2} {6} \)
_______ \ (\ frac {□} {□} \)
Ответ: 11 \ (\ frac {5} {6} \)
Пояснение:
9 \ (\ frac {3} {6} \)
+2 \ (\ frac {2} {6} \)
11 \ (\ frac {5} {6} \)
Вопрос 6.
8 \ (\ frac {4} {12} \)
+ 3 \ (\ frac {6} {12} \)
_______ \ (\ frac {□} {□} \)
Ответ: 11 \ (\ frac {10} {12} \)
Пояснение:
8 \ (\ frac {4} {12} \)
+3 \ (\ frac {6} {12} \)
11 \ (\ frac {10} {12} \)
Вопрос 7.
4 \ (\ frac {3} {8} \)
+ 1 \ (\ frac {5} {8} \)
_______ \ (\ frac {□} {□} \)
Ответ: 6
Пояснение:
4 \ (\ frac {3} {8} \)
+1 \ (\ frac {5} {8} \)
5 \ (\ frac {8} {8} \)
= 5 + 1 = 6
Вопрос 8.
9 \ (\ frac {5} {10} \)
+ 6 \ (\ frac {3} {10} \)
_______ \ (\ frac {□} {□} \)
Ответ: 15 \ (\ frac {8} {10} \)
Пояснение:
9 \ (\ frac {5} {10} \)
+6 \ (\ frac {3} {10} \)
15 \ (\ frac {8} {10} \)
Найдите разницу.
Вопрос 9.
6 \ (\ frac {7} {8} \)
— 4 \ (\ frac {3} {8} \)
_______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {4} {8} \)
Пояснение:
6 \ (\ frac {7} {8} \)
-4 \ (\ frac {3} {8} \)
2 \ (\ frac {4} {8} \)
Вопрос 10.
4 \ (\ frac {2} {3} \)
— 3 \ (\ frac {1} {3} \)
_______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {1} {3} \)
Пояснение:
4 \ (\ frac {2} {3} \)
-3 \ (\ frac {1} {3} \)
1 \ (\ frac {1} {3} \)
Вопрос 11.
6 \ (\ frac {4} {5} \)
— 3 \ (\ frac {3} {5} \)
_______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {1} {5} \)
Пояснение:
6 \ (\ frac {4} {5} \)
-3 \ (\ frac {3} {5} \)
3 \ (\ frac {1} {5} \)
Вопрос 12.
7 \ (\ frac {3} {4} \)
— 2 \ (\ frac {1} {4} \)
_______ \ (\ frac {□} {□} \)
Ответ: 5 \ (\ frac {1} {2} \)
Пояснение:
7 \ (\ frac {3} {4} \)
-2 \ (\ frac {1} {4} \)
5 \ (\ frac {2} {4} \) = 5 \ ( \ frac {1} {2} \)
Решение проблем
Вопрос 13.
Джеймс хочет отправить два подарка по почте. Один пакет весит 2 \ (\ frac {3} {4} \) фунта. Другой пакет весит 1 \ (\ frac {3} {4} \) фунт. Каков общий вес пакетов?
_______ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {1} {2} \)
Пояснение:
2 \ (\ frac {3} {4} \)
+ 1 \ (\ frac {3} {4} \)
4 \ (\ frac {1} {2} \)
Вопрос 14.
Тьерра купила 4 \ (\ frac {3} {8} \) ярдов синей ленты и 2 \ (\ frac {1} {8} \) ярдов желтой ленты для своего ремесленного проекта. Насколько больше синей ленты, чем желтой, купила Тьерра?
_______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {1} {4} \)
Пояснение:
Дано,
4 \ (\ frac {3} {8} \)
-2 \ (\ frac {1} {8} \)
2 \ (\ frac {1} {4} \)
Common Core — сложение и вычитание дробей — стр.146
Проверка урока
Вопрос 1.
У Брэда два отрезка медных трубок, которые нужно подогнать друг к другу. Один имеет длину 2 \ (\ frac {5} {12} \) футов, а другой — 3 \ (\ frac {7} {12} \) футов. Сколько всего футов трубы у него всего?
Опции:
а. 5 футов
б. 5 \ (\ frac {6} {12} \) футов
c. 5 \ (\ frac {10} {12} \)
г. 6 футов
Ответ: 5 футов
Пояснение:
Учитывая, что у
Brad есть два отрезка медных трубок, которые нужно подогнать друг к другу.Один имеет длину 2 \ (\ frac {5} {12} \) футов, а другой — 3 \ (\ frac {7} {12} \) футов.
Сложите обе длины
2 \ (\ frac {5} {12} \) + 3 \ (\ frac {7} {12} \)
= 5 \ (\ frac {12} {12} \) = 5 футов
Таким образом, правильный ответ — вариант а.
Вопрос 2.
Для выкройки требуется 2 \ (\ frac {1} {4} \) ярда материала и 1 \ (\ frac {1} {4} \) ярд футеровки. Сколько всего требуется ткани?
Опции:
а. 2 \ (\ frac {2} {4} \) ярдов
б. 3 ярда
г. 3 \ (\ frac {1} {4} \) ярдов
д.3 \ (\ frac {2} {4} \) ярдов
Ответ: 3 \ (\ frac {2} {4} \) ярдов
Пояснение:
Дано,
Образец требует 2 \ (\ frac {1} {4} \) ярдов материала и 1 \ (\ frac {1} {4} \) ярдов футеровки.
2 \ (\ frac {1} {4} \) + 1 \ (\ frac {1} {4} \)
= 3 + \ (\ frac {1} {4} \) + \ (\ frac { 1} {4} \)
= 3 \ (\ frac {2} {4} \) ярдов
Таким образом, правильный ответ — вариант d.
Обзор спирали
Вопрос 3.
У Шанис 23 бейсбольных карточки звездных игроков.Она соглашается продать их по 16 долларов за штуку. Сколько она получит за карты?
Опции:
а. $ 258
б. $ 358
c. $ 368
д. $ 468
Ответ: 368 $
Пояснение:
Дано,
Шенис имеет 23 бейсбольных коллекционных карточки звездных игроков. Она соглашается продать их по 16 долларов за штуку.
Чтобы узнать, сколько она получит за карты
23 × 16 = 368
Следовательно, она получит 368 долларов за карты.
Таким образом, правильный ответ — вариант c.
Вопрос 4.
Нанси работает волонтером в приюте для животных.Она хочет проводить равное количество времени, играя с каждой собакой. У нее есть 145 минут, чтобы поиграть со всеми 7 собаками. Примерно сколько времени она может проводить с каждой собакой?
Опции:
а. около 10 минут
б. около 20 минут
c. около 25 минут
д. около 26 минут
Ответ: около 20 минут
Пояснение:
Учитывая,
Нанси работает волонтером в приюте для животных. Она хочет проводить равное количество времени, играя с каждой собакой. У нее есть 145 минут, чтобы поиграть со всеми 7 собаками.
145/7 = 20,7
Следовательно, она может провести с каждой собакой около 20 минут.
Таким образом, правильный ответ — вариант b.
Вопрос 5.
У Фриды 12 красных яблок и 15 зеленых яблок. Она собирается разделить яблоки поровну между 8 людьми, а лишние яблоки оставить себе. Сколько яблок
оставит себе Фрида?
Опции:
а. 3
г. 4
г. 6
г. 7
Ответ: 3
Пояснение:
Дано,
Фрида имеет 12 красных яблок и 15 зеленых яблок.
Она собирается разделить яблоки поровну между 8 людьми, а лишние яблоки оставить себе.
12 + 15 = 27
27/8
27 — 24 = 3
Таким образом, Фрида оставляет себе 3 яблока.
Таким образом, правильный ответ — вариант а.
Вопрос 6.
Семья Линч купила дом за 75 300 долларов. Несколько лет спустя они продали дом за 80 250 долларов. Насколько цена продажи была больше, чем цена покупки?
Опции:
а. 4 950 долларов США
б. 5050 долларов США
c. 5 150 долл. США
d.5 950 долл. США
Ответ: 4950 долларов США
Пояснение:
Дано,
Семья Линч купила дом за 75 300 долларов.
Через несколько лет дом продали за 80 250 долларов.
80 250 долларов — 75 300 долларов = 4 950 долларов
Таким образом, правильный ответ — вариант а.
Common Core — Сложение и вычитание дробей — Стр. № 147
Вычитание записей с помощью
Найдите разницу.
Вопрос 1.
Вопрос 2.
6
— 3 \ (\ frac {2} {5} \)
_______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {3} {5} \)
Пояснение:
Сначала вычтите целые числа
6 — 3 = 3
Затем вычтите дроби,
3 — \ (\ frac {2} {5} \) = 2 \ (\ frac {3} {5} \)
Вопрос 3.
5 \ (\ frac {1} {4} \)
— 2 \ (\ frac {3} {4} \)
_______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {1} {2} \)
Пояснение:
Сначала вычтите целые числа
5 — 2 = 3
Затем вычтите дроби,
\ (\ frac {1} {4} \) — \ (\ frac {3} {4} \) = — \ (\ frac {1} {2} \)
3 — \ (\ frac {1} {2} \)
= 2 \ (\ frac {1} {2} \)
Вопрос 4.
9 \ (\ frac {3} {8} \)
— 8 \ (\ frac {7} {8} \)
_______ \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {2} \)
Пояснение:
Сначала вычтите целые числа
9 — 8 = 1
Затем вычтите дроби,
\ (\ frac {3} {8} \) — \ (\ frac {7} {8} \)
= — \ (\ frac {4} {8} \)
= — \ (\ frac {1} {2} \)
= 1 — \ (\ frac {1} {2} \)
= \ (\ frac { 1} {2} \)
Вопрос 5.
12 \ (\ frac {3} {10} \)
— 7 \ (\ frac {7} {10} \)
_______ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {3} {5} \)
Пояснение:
Сначала вычтите целые числа
12 — 7 = 5
Затем вычтите дроби,
\ (\ frac {3} {10} \) — \ (\ frac {7} {10} \) = — \ (\ frac {4} {10} \)
5 — \ (\ frac {4} {10} \)
5 — \ (\ frac {2} {5} \) = 4 \ (\ frac {3} {5} \)
Вопрос 6.
8 \ (\ frac {1} {6} \)
— 3 \ (\ frac {5} {6} \)
_______ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {1} {3} \)
Пояснение:
Сначала вычтите целые числа
8 — 3 = 5
Затем вычтите дроби,
\ (\ frac {1} {6} \) — \ (\ frac {5} {6} \) = — \ (\ frac {2} {3} \)
5 — \ (\ frac {2} {3} \) = 4 \ (\ frac {1} {3} \)
Вопрос 7.
7 \ (\ frac {3} {5} \)
— 4 \ (\ frac {4} {5} \)
_______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {4} {5} \)
Пояснение:
Сначала вычтите целые числа
7 — 4 = 3
Затем вычтите дроби,
\ (\ frac {3} {5} \) — \ (\ frac {4} {5} \) = — \ (\ frac {1} {5} \)
3 — \ (\ frac {1} {5} \) = 2 \ (\ frac {4} {5} \)
Вопрос 8.
10 \ (\ frac {1} {2} \)
— 8 \ (\ frac {1} {2} \)
_______ \ (\ frac {□} {□} \)
Ответ: 2
Пояснение:
Сначала вычтите целые числа
10-8 = 2
\ (\ frac {1} {2} \) — \ (\ frac {1} {2} \) = 0
Вопрос 9.
7 \ (\ frac {1} {6} \)
— 2 \ (\ frac {5} {6} \)
_______ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {1} {3} \)
Пояснение:
Сначала вычтите целые числа
7 — 2 = 5
Затем вычтите дроби,
\ (\ frac {1} {6} \) — \ (\ frac {5} {6} \) = — \ (\ frac {4} {6} \)
5 — \ (\ frac {4} {6} \) = 4 \ (\ frac {1} {3} \)
Вопрос 10.
9 \ (\ frac {3} {12} \)
— 4 \ (\ frac {7} {12} \)
_______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {2} {3} \)
Пояснение:
Сначала вычтите целые числа
9 — 4 = 5
Затем вычтите дроби,
\ (\ frac {3} {12} \) — \ (\ frac {7} {12} \) = — \ (\ frac {4} {12} \) = — \ (\ frac {1} {3} \)
5 — \ (\ frac {1} {3} \) = 2 \ (\ frac {2} { 3} \)
Вопрос 11.
9 \ (\ frac {1} {10} \)
— 8 \ (\ frac {7} {10} \)
_______ \ (\ frac {□} {□} \)
Ответ: \ (\ frac {2} {5} \)
Пояснение:
Сначала вычтите целые числа
9 — 8 = 1
Затем вычтите дроби,
\ (\ frac {1} {10} \) — \ (\ frac {7} {10} \) = — \ (\ frac {6} {10} \)
1 — \ (\ frac {3} {5} \) = \ (\ frac {2} {5} \)
Вопрос 12.
9 \ (\ frac {1} {3} \)
— \ (\ frac {2} {3} \)
_______ \ (\ frac {□} {□} \)
Ответ: 8 \ (\ frac {2} {3} \)
Пояснение:
9 \ (\ frac {1} {3} \)
— \ (\ frac {2} {3} \)
8 \ (\ frac {2} {3} \)
Вопрос 13.
3 \ (\ frac {1} {4} \)
— 1 \ (\ frac {3} {4} \)
_______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {1} {2} \)
3 \ (\ frac {1} {4} \)
— 1 \ (\ frac {3} {4} \)
1 \ (\ frac {1} {2} \)
Вопрос 14.
4 \ (\ frac {5} {8} \)
— 1 \ (\ frac {7} {8} \)
_______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {3} {4} \)
Пояснение:
Сначала вычтите целые числа
4 — 1 = 3
Затем вычтите дроби,
\ (\ frac {5} {8} \) — \ (\ frac {7} {8} \) = — \ (\ frac {1} {4} \)
3 — \ (\ frac {1} {4} \) = 2 \ (\ frac {3} {4} \)
Вопрос 15.
5 \ (\ frac {1} {12} \)
— 3 \ (\ frac {8} {12} \)
_______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {5} {12} \)
Пояснение:
Сначала вычтите целые числа
5 — 3 = 2
Затем вычтите дроби,
\ (\ frac {1} {12} \) — \ (\ frac {8} {12} \) = — \ (\ frac {7} {12} \)
2 — \ (\ frac {7} {12} \) = 1 \ (\ frac {5} {12} \)
Вопрос 16.
7
— 1 \ (\ frac {3} {5} \)
_______ \ (\ frac {□} {□} \)
Ответ: 5 \ (\ frac {2} {5} \)
Пояснение:
7
— 1 \ (\ frac {3} {5} \)
5 \ (\ frac {2} {5} \)
Решение проблем
Вопрос 17.
Алисия покупает 5-фунтовый мешок камней для аквариума. Она использует 1 \ (\ frac {1} {8} \) фунт для небольшой аквариума. Сколько осталось?
_______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {7} {8} \)
Пояснение:
Учитывая,
Алисия покупает 5-фунтовый мешок камней для аквариума. Она использует 1 \ (\ frac {1} {8} \) фунт для небольшой аквариума.
Сначала вычтите целые числа
5 — 1 = 4
4 — 1 \ (\ frac {1} {8} \)
= 3 \ (\ frac {7} {8} \)
Вопрос 18.
Ксавье сделал для ярмарки 25 фунтов жареного миндаля.У него осталось 3 \ (\ frac {1} {2} \) фунта к концу ярмарки. Сколько фунтов жареного миндаля он продал на ярмарке?
_______ \ (\ frac {□} {□} \)
Ответ: 21 \ (\ frac {1} {2} \)
Пояснение:
Учитывая,
Ксавье сделал для ярмарки 25 фунтов жареного миндаля.
У него осталось 3 \ (\ frac {1} {2} \) фунта к концу ярмарки.
Сначала вычтите целые числа
25 — 3 = 22
22 — \ (\ frac {1} {2} \) = 21 \ (\ frac {1} {2} \)
Common Core — сложение и вычитание дробей — стр.148
Проверка урока
Вопрос 1.
Реджи делает двухслойный торт. Рецепт первого слоя требует 2 \ (\ frac {1} {4} \) стаканов сахара. Рецепт второго слоя требует 1 \ (\ frac {1} {4} \) стакана сахара. У Реджи 5 чашек сахара. Сколько у него останется после приготовления обоих рецептов?
Опции:
а. 1 \ (\ frac {1} {4} \) чашки
б. 1 \ (\ frac {2} {4} \) чашки
c. 2 \ (\ frac {1} {4} \) чашки
г. 2 \ (\ frac {2} {4} \) чашки
Ответ: 1 \ (\ frac {2} {4} \) чашек
Пояснение:
Учитывая,
Реджи делает двухслойный торт.Рецепт первого слоя требует 2 \ (\ frac {1} {4} \) стаканов сахара.
Рецепт второго слоя требует 1 \ (\ frac {1} {4} \) стакана сахара.
У Реджи 5 чашек сахара.
2 \ (\ frac {1} {4} \) + 1 \ (\ frac {1} {4} \) = 3 \ (\ frac {1} {2} \)
5 — 3 \ (\ frac {1} {2} \) = 1 \ (\ frac {2} {4} \) cups
Таким образом, правильный ответ — вариант b.
Вопрос 2.
У Кейт 4 \ (\ frac {3} {8} \) ярда ткани и 2 \ (\ frac {7} {8} \) ярда, чтобы сделать юбку. Сколько лишней ткани у нее останется после изготовления юбки?
Опции:
а.2 \ (\ frac {4} {8} \) ярдов
б. 2 \ (\ frac {2} {8} \) ярдов
гр. 1 \ (\ frac {4} {8} \) ярдов
д. 1 \ (\ frac {2} {8} \) ярдов
Ответ: 1 \ (\ frac {4} {8} \) ярдов
Пояснение:
Учитывая, что
Кейт имеет 4 \ (\ frac {3} {8} \) ярда ткани и ей нужно 2 \ (\ frac {7} {8} \) ярда, чтобы сделать юбку.
Сначала вычтите целые числа
4 — 2 = 2
Затем вычтите дроби,
\ (\ frac {3} {8} \) — \ (\ frac {7} {8} \) = — \ ( \ frac {4} {8} \)
2 — \ (\ frac {4} {8} \) = 1 \ (\ frac {4} {8} \) ярдов
Таким образом, правильный ответ — вариант c.
Обзор спирали
Вопрос 3.
У Пауло есть 128 стеклянных бусин для украшения рамок картин. Он хочет использовать одинаковое количество бусинок на каждом каркасе. Если он украсит 8 рамок для картин, сколько бусинок он наложит на каждую рамку?
Опции:
а. 6
г. 7
г. 14
г. 16
Ответ: 16
Пояснение:
Учитывая, что у
Пауло есть 128 стеклянных бусин, которые можно использовать для украшения рамок для картин. Он хочет использовать одинаковое количество бусинок на каждом кадре
128/8 = 16
Таким образом, правильный ответ — вариант d.
Вопрос 4.
Мэдисон устраивает вечеринки. Она хочет сделать достаточно одолжений, чтобы каждый гость получил одинаковое количество услуг. Она знает, что на вечеринке будет 6 или 8 гостей. Какое наименьшее количество вечеринок должна сделать Мэдисон?
Опции:
а. 18
г. 24
с. 30
г. 32
Ответ: 24
Пояснение:
Учитывая,
Мэдисон делает вечеринку. Она хочет сделать достаточно одолжений, чтобы каждый гость получил одинаковое количество услуг.
Она знает, что на вечеринке будет 6 или 8 гостей.
Чтобы найти наименьшее количество подарков на вечеринке, мы должны учитывать количество гостей.
В этом случае есть две возможности — 6 или 8.
Для 6: 6, 12, 18, 24 (прибавить 6 к каждому числу)
Для 8: 8, 16, 24 (прибавить 8 к каждому числу)
Теперь в обеих сериях наименьшее число (общее) — 24. Следовательно, Мэдисон должен сделать не менее 24 партийных одолжений.
Таким образом, правильный ответ — вариант b.
Вопрос 5.
Автобус-шаттл делает 4 рейса между двумя торговыми центрами каждый день.Автобус вмещает 24 человека. Если автобус полон при каждой поездке в один конец, сколько пассажиров перевозит автобус каждый день?
Опции:
а. 96
г. 162
г. 182
г. 192
Ответ: 96
Пояснение:
Дан,
Маршрутный автобус делает 4 рейса между двумя торговыми центрами каждый день. Автобус вмещает 24 человека.
4 × 24 = 96
Таким образом, правильный ответ — вариант а.
Вопрос 6.
Чтобы приготовить фруктовый салат, Марвин смешивает 1 \ (\ frac {3} {4} \) чашку нарезанных кубиками персиков с 2 \ (\ frac {1} {4} \) чашками нарезанных кубиками груш.Сколько чашек персиков и груш во фруктовом салате?
Опции:
а. 4 чашки
б. 3 \ (\ frac {2} {4} \) чашки
c. 3 \ (\ frac {1} {4} \) чашки
г. 3 чашки
Ответ: 4 чашки
Пояснение:
Дано,
Чтобы приготовить фруктовый салат, Марвин смешивает 1 \ (\ frac {3} {4} \) чашку нарезанных кубиками персиков с 2 \ (\ frac {1} {4} \) чашками нарезанных кубиками груш. .
1 \ (\ frac {3} {4} \) + 2 \ (\ frac {1} {4} \)
= 4 чашки
Таким образом, правильный ответ — вариант а.
Common Core — сложение и вычитание дробей — стр.149
Фракции и свойства добавки
Используйте свойства и математические вычисления, чтобы найти сумму.
Вопрос 1.
Вопрос 2.
\ (10 \ frac {1} {8} + \ left (3 \ frac {5} {8} +2 \ frac {7} {8} \ right) \)
_______ \ (\ frac {□} {□} \)
Ответ: 16 \ (\ frac {5} {8} \)
Пояснение:
Дано,
\ (10 \ frac {1} {8} + \ left (3 \ frac {5} {8} +2 \ frac {7} {8} \ right) \)
Сначала добавьте целые числа в скобках.
3 + 2 = 5
10 \ (\ frac {1} {8} \) + 5 + \ (\ frac {5} {8} \) + \ (\ frac {7} {8} \)
10 \ (\ frac {1} {8} \) + 5 + \ (\ frac {12} {8} \)
10 + 5 = 15
15 + \ (\ frac {1} {8} \) + \ (\ frac {12} {8} \)
15 + \ (\ frac {13} {8} \)
16 \ (\ frac {5} {8} \)
\ (10 \ frac {1} { 8} + \ left (3 \ frac {5} {8} +2 \ frac {7} {8} \ right) \) = 16 \ (\ frac {5} {8} \)
Вопрос 3.
\ (8 \ frac {1} {5} + \ left (3 \ frac {2} {5} +5 \ frac {4} {5} \ right) \)
_______ \ (\ frac {□} {□} \)
Ответ: 17 \ (\ frac {2} {5} \)
Пояснение:
\ (8 \ frac {1} {5} + \ left (3 \ frac {2} {5} +5 \ frac {4} {5} \ right) \)
8 \ (\ frac { 1} {5} \) + 3 \ (\ frac {2} {5} \) + 5 \ (\ frac {4} {5} \)
3 + 5 = 8
8 \ (\ frac {1} {5} \) + 8 + \ (\ frac {2} {5} \) + \ (\ frac {4} {5} \)
8 \ (\ frac {1} {5} \) + 8 + \ (\ frac {6} {5} \)
8 + 8 = 16
16 + \ (\ frac {1} {5} \) + \ (\ frac {6} {5} \)
16 + \ (\ frac {7} {5} \)
17 \ (\ frac {2} {5} \)
\ (8 \ frac {1} {5} + \ left (3 \ frac {2} {5} +5 \ frac {4} {5} \ right) \) = 17 \ (\ frac {2} {5} \)
Вопрос 4.
\ (6 \ frac {3} {4} + \ left (4 \ frac {2} {4} +5 \ frac {1} {4} \ right) \)
_______ \ (\ frac {□} { □} \)
Ответ: 16 \ (\ frac {1} {2} \)
Пояснение:
\ (6 \ frac {3} {4} + \ left (4 \ frac {2} {4} +5 \ frac {1} {4} \ right) \)
Сначала добавьте целые числа в кронштейн.
6 \ (\ frac {3} {4} \) + 4 \ (\ frac {2} {4} \) + 5 \ (\ frac {1} {4} \)
4 + 5 = 9
6 \ (\ frac {3} {4} \) + 9 \ (\ frac {3} {4} \)
6 + 9 = 15
15 + \ (\ frac {3} {4} \) + \ ( \ frac {3} {4} \)
16 \ (\ frac {1} {2} \)
\ (6 \ frac {3} {4} + \ left (4 \ frac {2} {4} + 5 \ frac {1} {4} \ right) \) = 16 \ (\ frac {1} {2} \)
Вопрос 5.
\ (\ left (6 \ frac {3} {6} +10 \ frac {4} {6} \ right) +9 \ frac {2} {6} \)
_______ \ (\ frac {□} { □} \)
Ответ: 26 \ (\ frac {3} {6} \)
Пояснение:
\ (\ left (6 \ frac {3} {6} +10 \ frac {4} {6} \ right) +9 \ frac {2} {6} \)
6 \ (\ frac { 3} {6} \) + 10 \ (\ frac {4} {6} \) + 9 \ (\ frac {2} {6} \)
Сначала сложите целые числа в скобках.
6 + 10 = 16
16 + \ (\ frac {3} {6} \) + \ (\ frac {4} {6} \) + 9 \ (\ frac {2} {6} \)
16 + \ (\ frac {7} {6} \) + 9 \ (\ frac {2} {6} \)
16 + 9 = 25
25 + \ (\ frac {7} {6} \) + \ (\ frac {2} {6} \)
25 + \ (\ frac {9} {6} \)
= 26 \ (\ frac {3} {6} \)
\ (\ left (6 \ frac {3} {6} +10 \ frac {4} {6} \ right) +9 \ frac {2} {6} \) = 26 \ (\ frac {3} {6} \)
Вопрос 6.
\ (\ left (6 \ frac {2} {5} +1 \ frac {4} {5} \ right) +3 \ frac {1} {5} \)
_______ \ (\ frac {□} { □} \)
Ответ: 11 \ (\ frac {2} {5} \)
Пояснение:
\ (\ left (6 \ frac {2} {5} +1 \ frac {4} {5} \ right) +3 \ frac {1} {5} \)
6 \ (\ frac { 2} {5} \) + 1 \ (\ frac {4} {5} \) + 3 \ (\ frac {1} {5} \)
Сначала добавьте целые числа в скобки.
6 + 1 = 7
7 \ (\ frac {2} {5} \) + \ (\ frac {4} {5} \) + 3 \ (\ frac {1} {5} \)
7 + \ (\ frac {6} {5} \) + 3 \ (\ frac {1} {5} \)
7 + 3 = 10
10 + \ (\ frac {6} {5} \) + \ ( \ frac {1} {5} \)
10 + \ (\ frac {7} {5} \) = 11 \ (\ frac {2} {5} \)
Следовательно \ (\ left (6 \ frac { 2} {5} +1 \ frac {4} {5} \ right) +3 \ frac {1} {5} \) = 11 \ (\ frac {2} {5} \)
Вопрос 7.
\ (7 \ frac {7} {8} + \ left (3 \ frac {1} {8} +1 \ frac {1} {8} \ right) \)
_______ \ (\ frac {□} { □} \)
Ответ: 12 \ (\ frac {1} {8} \)
Пояснение:
\ (7 \ frac {7} {8} + \ left (3 \ frac {1} {8} +1 \ frac {1} {8} \ right) \)
7 \ (\ frac { 7} {8} \) + 3 \ (\ frac {1} {8} \) + 1 \ (\ frac {1} {8} \)
Сначала сложите целые числа в скобках.
3 + 1 = 4
7 \ (\ frac {7} {8} \) + 4 + \ (\ frac {1} {8} \) + \ (\ frac {1} {8} \)
7 \ (\ frac {7} {8} \) + 4 + \ (\ frac {2} {8} \)
7 + 4 = 11
11 + \ (\ frac {7} {8} \) + \ (\ frac {2} {8} \)
11 + \ (\ frac {9} {8} \) = 12 \ (\ frac {1} {8} \)
Таким образом, \ (7 \ frac {7} {8} + \ left (3 \ frac {1} {8} +1 \ frac {1} {8} \ right) \) = 12 \ (\ frac {1} {8} \)
Вопрос 8.
\ (14 \ frac {1} {10} + \ left (20 \ frac {2} {10} +15 \ frac {7} {10} \ right) \)
_______ \ (\ frac {□} { □} \)
Ответ: 50
Пояснение:
\ (14 \ frac {1} {10} + \ left (20 \ frac {2} {10} +15 \ frac {7} {10} \ right) \)
Сначала сложите целые числа в кронштейн.
14 \ (\ frac {1} {10} \) + 20 \ (\ frac {2} {10} \) + 15 \ (\ frac {7} {10} \)
20 + 15 = 35
14 \ (\ frac {1} {10} \) + 35 + \ (\ frac {2} {10} \) + \ (\ frac {7} {10} \)
14 \ (\ frac {1} { 10} \) + 35 \ (\ frac {9} {10} \)
49 \ (\ frac {1} {10} \) + \ (\ frac {9} {10} \)
49 + 1 = 50
Таким образом, \ (14 \ frac {1} {10} + \ left (20 \ frac {2} {10} +15 \ frac {7} {10} \ right) \) = 50
Вопрос 9.
\ (\ left (13 \ frac {2} {12} +8 \ frac {7} {12} \ right) +9 \ frac {5} {12} \)
_______ \ (\ frac {□} { □} \)
Ответ: 31 \ (\ frac {2} {12} \)
Пояснение:
\ (\ left (13 \ frac {2} {12} +8 \ frac {7} {12} \ right) +9 \ frac {5} {12} \)
13 \ (\ frac { 2} {12} \) + 8 \ (\ frac {7} {12} \) + 9 \ (\ frac {5} {12} \)
Сначала сложите целые числа в скобках.
13 + 8 = 21
21 + \ (\ frac {2} {12} \) + \ (\ frac {7} {12} \) + 9 \ (\ frac {5} {12} \)
21 + \ (\ frac {9} {12} \) + 9 \ (\ frac {5} {12} \)
30 + \ (\ frac {9} {12} \) + \ (\ frac {5} {12} \) = 31 \ (\ frac {2} {12} \)
Таким образом, \ (\ left (13 \ frac {2} {12} +8 \ frac {7} {12} \ right) +9 \ frac {5} {12} \) = 31 \ (\ frac {2} {12} \)
Решение проблем
Вопрос 10.
В классе Нейта три стола разной длины. Один имеет длину 4 \ (\ frac {1} {2} \) футов, другой — 4 фута, а третий — 2 \ (\ frac {1} {2} \) футов. Какова длина всех трех таблиц, если их сдвинуть встык?
_______ \ (\ frac {□} {□} \)
Ответ: 11
Пояснение:
Учитывая, что в классе
Нейта есть три стола разной длины. Один имеет длину 4 \ (\ frac {1} {2} \) футов, другой — 4 фута, а третий — 2 \ (\ frac {1} {2} \) футов.
4 \ (\ frac {1} {2} \) + 4 + 2 \ (\ frac {1} {2} \)
4 + 4 + 2 = 10
\ (\ frac {1} {2} \ ) + \ (\ frac {1} {2} \) = 1
10 + 1 = 11
Следовательно, длина всех трех таблиц, когда их толкают из конца в конец, составляет 11 футов.
Вопрос 11.
Мистер Уоррен использует 2 \ (\ frac {1} {4} \) мешка с мульчей для своего сада и еще 4 \ (\ frac {1} {4} \) мешка для своего переднего двора. Он также использует сумку \ (\ frac {3} {4} \) вокруг фонтана. Сколько всего мешков с мульчей использует мистер Уоррен?
_______ \ (\ frac {□} {□} \)
Ответ: 7 \ (\ frac {1} {4} \)
Пояснение:
Дано,
г.Уоррен использует 2 \ (\ frac {1} {4} \) мешка с мульчей для своего сада и еще 4 \ (\ frac {1} {4} \) мешка для своего переднего двора.
Он также использует сумку \ (\ frac {3} {4} \) вокруг фонтана.
2 \ (\ frac {1} {4} \) + 4 \ (\ frac {1} {4} \) + \ (\ frac {3} {4} \)
2 + 4 = 6
6 + \ (\ frac {1} {4} \) + \ (\ frac {1} {4} \) + \ (\ frac {3} {4} \)
= 7 \ (\ frac {1} {4 } \)
Common Core — сложение и вычитание дробей — стр. № 150
Проверка урока
Вопрос 1.
Плотник разрезал доску на три части.Один кусок был 2 \ (\ frac {5} {6} \) футов в длину. Второй кусок был длиной 3 \ (\ frac {1} {6} \) футов. Третий кусок был длиной 1 \ (\ frac {5} {6} \) футов. Как долго была доска?
Опции:
а. 6 \ (\ frac {5} {6} \) футов
б. 7 \ (\ frac {1} {6} \) футов
c. 7 \ (\ frac {5} {6} \) футов
г. 8 \ (\ frac {1} {6} \) футов
Ответ: c. 7 \ (\ frac {5} {6} \) футов
Пояснение:
Дано,
Плотник разрезал доску на три части. Один кусок был 2 \ (\ frac {5} {6} \) футов в длину. Второй кусок был длиной 3 \ (\ frac {1} {6} \) футов.
Третий кусок был длиной 1 \ (\ frac {5} {6} \) фут.
Добавьте три штуки.
2 \ (\ frac {5} {6} \) + 3 \ (\ frac {1} {6} \)
= 5 + \ (\ frac {6} {6} \)
= 5 + 1 = 6
6 + 1 \ (\ frac {5} {6} \)
= 7 \ (\ frac {5} {6} \) футов
Таким образом, правильный ответ — вариант c.
Вопрос 2.
Гарри работает в яблоневом саду. В понедельник он собрал 45 \ (\ frac {7} {8} \) фунтов яблок. В среду он собрал 42 \ (\ frac {3} {8} \) фунтов яблок. В пятницу он собрал 54 \ (\ frac {1} {8} \) фунтов яблок.Сколько фунтов яблок Гарри собрал за эти три дня?
Опции:
а. 132 \ (\ frac {3} {8} \) фунтов
б. 141 \ (\ frac {3} {8} \) фунтов
гр. 142 \ (\ frac {1} {8} \) фунтов
г. 142 \ (\ frac {3} {8} \) фунтов
Ответ: 142 \ (\ frac {3} {8} \) фунтов
Пояснение:
Дано,
Гарри работает в яблоневом саду. В понедельник он собрал 45 \ (\ frac {7} {8} \) фунтов яблок.
В среду он собрал 42 \ (\ frac {3} {8} \) фунтов яблок.
В пятницу он собрал 54 \ (\ frac {1} {8} \) фунтов яблок.
45 \ (\ frac {7} {8} \) + 42 \ (\ frac {3} {8} \) + 54 \ (\ frac {1} {8} \)
Складываем первые целые числа
45 + 42 + 54 = 141
141 + \ (\ frac {7} {8} \) + \ (\ frac {3} {8} \) + \ (\ frac {1} {8} \)
141 + 1 \ (\ frac {3} {8} \)
= 142 \ (\ frac {3} {8} \) фунтов
Таким образом, правильный ответ — вариант d.
Обзор спирали
Вопрос 3.
В холодильнике лежало 6 апельсинов. Джои и его друзья съели 3 \ (\ frac {2} {3} \) апельсина. Сколько апельсинов осталось?
Опции:
а.2 \ (\ frac {1} {3} \) апельсины
б. 2 \ (\ frac {2} {3} \) апельсины
c. 3 \ (\ frac {1} {3} \) апельсины
г. 9 \ (\ frac {2} {3} \) апельсины
Ответ: 9 \ (\ frac {2} {3} \) апельсинов
Пояснение:
Дано,
В холодильнике лежало 6 апельсинов.
Джои и его друзья съели 3 \ (\ frac {2} {3} \) апельсина.
6 + 3 \ (\ frac {2} {3} \)
= 9 \ (\ frac {2} {3} \) апельсинов
Таким образом, правильный ответ — вариант d.
Вопрос 4.
Дарлин попросили определить, какое из следующих чисел является простым.Какой номер ей выбрать?
Опции:
а. 2
г. 12
г. 21
г. 39
Ответ: 2
Объяснение:
Простое число — это целое или целое число, состоящее только из двух делителей 1 и самого себя.
В приведенных выше вариантах все являются составными числами, кроме 2.
Следовательно, 2 — простое число.
Таким образом, правильный ответ — вариант а.
Вопрос 5.
У учителя есть 100 стульев для организации собрания. Что из перечисленного НЕ является способом, которым учитель мог бы расставить стулья?
Опции:
а.10 рядов по 10 стульев
б. 8 рядов по 15 стульев
c. 5 рядов по 20 стульев
д. 4 ряда по 25 стульев
Ответ: 8 рядов по 15 стульев
Пояснение:
У учителя есть 100 стульев для организации собрания.
15 × 8 = 120
Итак, 8 рядов по 15 стульев — не способ расставить стулья.
Таким образом, правильный ответ — вариант b.
Вопрос 6.
Ник купил 28 складных стульев по 16 долларов каждое. Сколько денег Ник потратил на стулья?
Опции:
а.196 $
б. $ 348
c. $ 448
д. $ 600
Ответ: c. $ 448
Пояснение:
Дано,
Ник купил 28 складных стульев по 16 долларов каждый.
28 × 16 = 448
Таким образом, правильный ответ — вариант c.
Common Core — сложение и вычитание дробей — стр. № 151
Прочтите каждую проблему и решите.
Вопрос 1.
Каждому ребенку в семье Смитов дали разрезанный апельсин на 8 равных частей. Каждый ребенок съел \ (\ frac {5} {8} \) апельсина.После объединения оставшихся частей миссис Смит отметила, что осталось ровно 3 полных апельсина. Сколько детей в семье Смитов?
Вопрос 2.
Вал проходит 2 \ (\ frac {3} {5} \) мили каждый день. Билл пробегает 10 миль каждые 4 дня. Кто преодолеет большее расстояние за 4 дня?
_________
Ответ: Val
Пояснение:
Учитывая,
Вал проходит 2 \ (\ frac {3} {5} \) мили каждый день. Билл пробегает 10 миль каждые 4 дня.
2 \ (\ frac {3} {5} \) × 4
Преобразование из смешанной дроби в неправильную дробь.
2 \ (\ frac {3} {5} \) = \ (\ frac {13} {5} \) × 4 = 10,4
10,4> 10
Таким образом, Вэл преодолевает большее расстояние.
Вопрос 3.
Чад покупает арахис в двухфунтовых мешках. Он переупаковывает их в мешки, в которых хранится \ (\ frac {5} {6} \) фунт арахиса. Сколько двухфунтовых мешков с арахисом следует купить Чаду, чтобы заполнить \ (\ frac {5} {6} \) -фунтовые мешки, не оставив арахиса?
_________ мешки 2 фунта
Ответ: 5
Пояснение:
Учитывая,
Чад покупает арахис в двухфунтовых мешках.Он переупаковывает их в мешки, в которых хранится \ (\ frac {5} {6} \) фунт арахиса.
\ (\ frac {5} {6} \) + \ (\ frac {5} {6} \) + \ (\ frac {5} {6} \) + \ (\ frac {5} {6} \) + \ (\ frac {5} {6} \)
Таким образом, осталось 5 двухфунтовых мешков арахиса.
Вопрос 4.
У плотника есть несколько досок одинаковой длины. Он отрезает \ (\ frac {3} {5} \) каждой доски. После резки досок плотник замечает, что у него осталось достаточно кусков, чтобы их длина была равна длине 4 исходных досок. Из скольких досок начинал плотник?
_________
Ответ: 10
Пояснение:
Дано,
У плотника есть несколько досок одинаковой длины.Он отрезает \ (\ frac {3} {5} \) каждой доски. После резки досок плотник замечает, что у него осталось достаточно кусков, чтобы их длина была равна длине 4 исходных досок.
4 оригинальных платы имеют общую длину 20 единиц. 5 x 4 = 20.
Поскольку от каждой доски осталось 2/5, вы просто добавляете их, пока 2 не прибавится к 20.
Итак, 2 x 10 = 20. Следовательно, имеется 10 досок 2/5.
Это всего 4 доски, которые составляют 2/5, но это также должно означать, что есть 10 3/5 досок.
30/5 + 20/5 = 50/5 = 10
Common Core — сложение и вычитание дробей — стр. № 152
Проверка урока
Вопрос 1.
Карин разрезает ленту на 4 равных отрезка, каждый длиной 1 \ (\ frac {1} {4} \) фут. Как долго была лента?
Опции:
а. 4 фута
б. 4 \ (\ frac {1} {4} \) футов
c. 5 футов
г. 5 \ (\ frac {1} {4} \) футов
Ответ: 5 футов
Пояснение:
Учитывая, что
Карин разрезает ленту на 4 равных части, каждая длиной 1 \ (\ frac {1} {4} \) фут.
1 \ (\ frac {1} {4} \) × 4
Преобразование смешанной дроби в неправильную дробь.
1 \ (\ frac {1} {4} \) = \ (\ frac {5} {4} \)
\ (\ frac {5} {4} \) × 4 = 5 футов
Таким образом, правильный ответ это вариант c.
Вопрос 2.
У нескольких друзей был \ (\ frac {2} {5} \) мешок с арахисом, оставшийся после бейсбольной игры. Они поняли, что могли бы купить на 2 мешка арахиса меньше. Сколько друзей пошло в игру?
Опции:
а. 6
г. 5
г. 4
г.2
Ответ: 5
Пояснение:
Дано,
У каждого из друзей был \ (\ frac {2} {5} \) мешок с арахисом, оставшийся после бейсбольной игры.
Они поняли, что могли бы купить на 2 мешка арахиса меньше
2 ÷ \ (\ frac {2} {5} \) = 5
Таким образом, правильный ответ — вариант b.
Обзор спирали
Вопрос 3.
Лягушка сделала три прыжка. Первый был 12 \ (\ frac {5} {6} \) дюймов. Второй прыжок составил 8 \ (\ frac {3} {6} \) дюймов.Третий прыжок составил 15 \ (\ frac {1} {6} \) дюймов. На какое общее расстояние прыгнула лягушка?
Опции:
а. 35 \ (\ frac {3} {6} \) дюймов
b. 36 \ (\ frac {1} {6} \) дюймов
c. 36 \ (\ frac {3} {6} \) дюймов
d. 38 \ (\ frac {1} {6} \) дюймов
Ответ: 36 \ (\ frac {3} {6} \) дюймов
Пояснение:
Дано,
Лягушка сделала три прыжка. Первый был 12 \ (\ frac {5} {6} \) дюймов. Второй прыжок составил 8 \ (\ frac {3} {6} \) дюймов. Третий прыжок составил 15 \ (\ frac {1} {6} \) дюймов.
Сначала сложите целые числа
12 + 8 + 15 = 35
Затем сложите дроби,
\ (\ frac {5} {6} \) + \ (\ frac {3} {6} \) + \ (\ frac {1} {6} \) = 1 \ (\ frac {3} {6} \)
35 + \ (\ frac {3} {6} \) = 36 \ (\ frac {3} {6} \) дюймов
Таким образом, правильный ответ — вариант c.
Вопрос 4.
Ладаниан хочет записать дробь \ (\ frac {4} {6} \) как сумму единичных дробей. Какое выражение он должен написать?
Опции:
а. \ (\ frac {1} {6} + \ frac {1} {6} + \ frac {1} {6} + \ frac {1} {6} \)
б. \ (\ frac {2} {6} + \ frac {2} {6} \)
c. \ (\ frac {3} {6} + \ frac {1} {6} \)
г. \ (\ frac {1} {6} + \ frac {1} {6} + \ frac {2} {6} \)
Ответ: \ (\ frac {1} {6} + \ frac {1} {6} + \ frac {1} {6} + \ frac {1} {6} \)
Пояснение:
Учитывая, что
ЛаДаниан хочет записать дробь \ (\ frac {4} {6} \) как сумму единичных дробей.
Дробь единицы для \ (\ frac {4} {6} \) равна \ (\ frac {1} {6} + \ frac {1} {6} + \ frac {1} {6} + \ frac { 1} {6} \)
Таким образом, правильный ответ — вариант а.
Вопрос 5.
Грета сделала дизайн из квадратов. Она покрасила 8 из 12 квадратов в синий цвет. Какую часть квадратов она окрасила в синий цвет?
Опции:
а. \ (\ frac {1} {4} \)
б. \ (\ frac {1} {3} \)
г. \ (\ frac {2} {3} \)
г. \ (\ frac {3} {4} латекс]
Ответ: [латекс] \ frac {2} {3} \)
Пояснение:
Дано,
Грета сделала дизайн из квадратов.Она покрасила 8 из 12 квадратов в синий цвет.
\ (\ frac {8} {12} \)
= \ (\ frac {2} {3} \)
Таким образом, правильный ответ — вариант c.
Вопрос 6.
Учитель дал классу следующую схему: первый семестр — 5, а правило — прибавить 4, вычесть 1. Каждый ученик произносит одно число. Первый ученик говорит 5. Виктор десятый в очереди. Какой номер должен сказать Виктор?
Опции:
а. 17
г. 19
г. 20
г. 21
Ответ:
для
a = 5
d = 4-1 = 3
, чтобы найти t10
tn = a + (n-1) d
t10 = 5 + (10-1) 3
t10 = 5 + 27
t10 = 32
Победитель занимает десятое место в строке, поэтому он должен сказать число 32
Common Core — сложение и вычитание дробей — стр.153
Урок 7.1
Используйте модель, чтобы написать уравнение.
Вопрос 1.
Введите ниже:
_________
Ответ: 1/6 + 3/6 = 4/6
Пояснение:
Из рисунка видно, что заштрихованная доля первого круга равна 1/6.
Заштрихованная доля второго круга — 3/6.
Заштрихованная доля третьего круга — 4/6.
Вопрос 2.
Введите ниже:
_________
Ответ: 5/8
Пояснение:
Из рисунка выше мы можем сказать, что доля затененной части составляет 5/8.
Используйте модель, чтобы решить уравнение.
Вопрос 3.
\ (\ frac {3} {10} + \ frac {5} {10} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {8} {10} \)
Пояснение:
Закрашенная часть первой цифры — 3/10
Затененная часть второй цифры — 5/10
\ (\ frac {3} {10} + \ frac {5} {10} \) = \ (\ frac {8} {10} \)
Вопрос 4.
\ (\ frac {7} {12} — \ frac {6} {12} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {12} \)
Пояснение:
Заштрихованная часть рисунка выше — 7/12.Из них вычитается 6/12.
\ (\ frac {7} {12} — \ frac {6} {12} \) = \ (\ frac {1} {12} \)
Урок 7.2
Запишите дробь как сумму долей единицы.
Вопрос 5.
\ (\ frac {2} {3} \) =
Введите ниже:
_________
Ответ: Доля единицы \ (\ frac {2} {3} \) равна \ (\ frac {1} {3} \) + \ (\ frac {1} {3} \)
Вопрос 6.
\ (\ frac {3} {10} \) =
Введите ниже:
_________
Ответ: Доля единицы \ (\ frac {3} {10} \) равна \ (\ frac {1} {10} \) + \ (\ frac {1} {10} \) + \ (\ frac {1} {10} \)
Вопрос 7.
\ (\ frac {4} {6} \) =
Введите ниже:
_________
Ответ: Доля единицы \ (\ frac {4} {6} \) равна \ (\ frac {1} {6} \) + \ (\ frac {1} {6} \) + \ (\ frac {1} {6} \) + \ (\ frac {1} {6} \)
Вопрос 8.
\ (\ frac {5} {12} \) =
Введите ниже:
_________
Ответ: Единичная доля \ (\ frac {5} {12} \) равна \ (\ frac {1} {12} \) + \ (\ frac {1} {12} \) + \ (\ frac {1} {12} \) + \ (\ frac {1} {12} \) + \ (\ frac {1} {12} \)
Уроки 7.3–7.5
Найдите сумму или разницу.Используйте дробные полоски, чтобы помочь.
Вопрос 9.
\ (\ frac {3} {8} + \ frac {2} {8} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {5} {8} \)
Вопрос 10.
\ (\ frac {4} {5} + \ frac {1} {5} \) =
\ (\ frac {□} {□} \)
Ответ: 1
Вопрос 11.
\ (\ frac {6} {10} + \ frac {1} {10} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {7} {10} \)
Вопрос 12.
\ (\ frac {5} {6} — \ frac {4} {6} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {6} \)
Вопрос 13.
\ (\ frac {3} {4} — \ frac {1} {4} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {2} \)
Вопрос 14.
1 — \ (\ frac {7} {12} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {5} {12} \)
Вопрос 15.
\ (\ frac {7} {10} — \ frac {3} {10} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {4} {10} \)
Вопрос 16.
\ (\ frac {2} {6} + \ frac {4} {6} \) =
\ (\ frac {□} {□} \)
Ответ: 1
Вопрос 17.
\ (\ frac {5} {8} — \ frac {4} {8} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {8} \)
Common Core — сложение и вычитание дробей — стр. № 154
Урок 7.6
Запишите каждое смешанное число как дробь, а каждую дробь как смешанное число.
Вопрос 1.
4 \ (\ frac {2} {3} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {14} {3} \)
Пояснение:
Сначала умножьте 4 и 3
4 × 3 = 12
А затем добавьте 2 к 12
12 + 2 = 14
Таким образом, дробная часть смешанной дроби равна \ (\ frac {14} {3} \).
Вопрос 2.
6 \ (\ frac {1} {4} \) =
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {25} {4} \)
Пояснение:
Сначала умножьте 6 и 4
6 × 4 = 24
А затем добавьте 1 к 24
24 + 1 = 25
Таким образом, дробная часть смешанной дроби будет \ (\ frac {25} {4} \)
Вопрос 3.
\ (\ frac {11} {3} \) =
_______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {2} {3} \)
Пояснение:
Преобразование неправильной дроби в смешанную.
3 × 3 = 9
9 + 2 = 11
\ (\ frac {11} {3} \) = 3 \ (\ frac {2} {3} \)
Вопрос 4.
\ (\ frac {16} {15} \) =
_______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {1} {15} \)
Пояснение:
Дано,
Преобразование неправильной дроби в смешанную дробь.
15 × 1 = 15
15 + 1 = 16
\ (\ frac {16} {15} \) = 1 \ (\ frac {1} {15} \)
Уроки 7.7–7.8
Найдите сумму или разницу.
Вопрос 5.
\ (3 \ frac {1} {4} +2 \ frac {3} {4} \) =
_______ \ (\ frac {□} {□} \)
Ответ: 6
Пояснение:
Дано,
\ (3 \ frac {1} {4} +2 \ frac {3} {4} \)
Сначала сложите целые числа
3 + 2 = 5
\ (\ frac {1} {4} \) + \ (\ frac {3} {4} \) = 1
5 + 1 = 6
\ (3 \ frac {1} {4} +2 \ frac {3} {4} \) = 6
Вопрос 6.
\ (1 \ frac {5} {12} +2 \ frac {1} {12} \) =
_______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {6} {12} \)
Пояснение:
Дано,
\ (1 \ frac {5} {12} +2 \ frac {1} {12} \)
Сначала сложите целые числа
1 + 2 = 3
3 \ (\ frac {5 } {12} \) + \ (\ frac {1} {12} \) = 3 \ (\ frac {6} {12} \)
Вопрос 7.
\ (9 \ frac {5} {6} -7 \ frac {1} {6} \) =
_______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {4} {6} \)
Объяснение:
Дано,
\ (9 \ frac {5} {6} -7 \ frac {1} {6} \)
Сначала вычтите целые числа
9-7 = 2
5/6 — 1/6 = \ (\ frac {4} {6} \)
2 + \ (\ frac {4} {6} \) = 2 \ (\ frac {4} {6} \)
Таким образом, \ (9 \ frac { 5} {6} -7 \ frac {1} {6} \) = 2 \ (\ frac {4} {6} \)
Вопрос 8.
\ (9 \ frac {3} {10} -1 \ frac {7} {10} \) =
_______ \ (\ frac {□} {□} \)
Ответ: 7 \ (\ frac {6} {10} \)
Объяснение:
Дано,
\ (9 \ frac {3} {10} -1 \ frac {7} {10} \)
Сначала вычтите целые числа
9 — 1 = 8
3/10 — 7/10 = — 4/10
8 — 4/10 = 7 \ (\ frac {6} {10} \)
Урок 7.9
Используйте свойства и математические вычисления, чтобы найти сумму.
Вопрос 9.
\ (\ left (1 \ frac {1} {4} +4 \ right) +2 \ frac {3} {4} \)
_______ \ (\ frac {□} {□} \)
Ответ: 8
Пояснение:
Дано,
\ (\ left (1 \ frac {1} {4} +4 \ right) +2 \ frac {3} {4} \)
1 \ (\ frac {1} {4} \) + 4 + 2 \ (\ frac {3} {4} \)
Сложите целые числа
1 + 4 = 5
5 \ (\ frac {1} {4} \) + 2 \ (\ frac { 3} {4} \)
5 + 2 = 7
\ (\ frac {1} {4} \) + \ (\ frac {3} {4} \) = 1
7 + 1 = 8
Вопрос 10.
\ (\ frac {3} {5} + \ left (90 \ frac {2} {5} +10 \ right) \)
_______ \ (\ frac {□} {□} \)
Ответ: 101
Пояснение:
Дано,
\ (\ frac {3} {5} + \ left (90 \ frac {2} {5} +10 \ right) \)
Сложите целые числа
90 + 10 = 100
3 / 5 + 2/5 = 5/5 = 1
100 + 1 = 101
Вопрос 11.
\ (3 \ frac {2} {6} + \ left (2 \ frac {1} {6} + \ frac {4} {6} \ right) \)
_______ \ (\ frac { □} {□} \)
Ответ: 6 \ (\ frac {1} {6} \)
Пояснение:
Дано,
\ (3 \ frac {2} {6} + \ left (2 \ frac {1} {6} + \ frac {4} {6} \ right) \)
1/6 + 4/6 = 5/6
3 \ (\ frac {2} {6} \) + 2 \ (\ frac {5} {6} \) = 6 \ (\ frac {1} {6} \)
Вопрос 12.
\ (\ left (\ frac {5} {8} +2 \ frac {3} {8} \ right) +1 \ frac {3} {8} \)
_______ \ (\ frac {□} {□ } \)
Ответ: 4 \ (\ frac {3} {8} \)
Пояснение:
Дано,
\ (\ left (\ frac {5} {8} +2 \ frac {3} {8} \ right) +1 \ frac {3} {8} \)
5/8 + 3/8 = 8/8 = 1
2 + 1 = 3
3 + 1 3/8 = 4 \ (\ frac {3} {8} \)
Урок 7.10
Вопрос 13.
Адриан каждое утро пробегает \ (\ frac {3} {4} \) милю. За сколько дней он пробежит 3 мили трусцой?
____ дней
Ответ: 4 дня
Пояснение:
Дано,
Адриан пробегает \ (\ frac {3} {4} \) милю каждое утро.
\ (\ frac {3} {4} \) / 3 = 4
Таким образом, ему понадобится 4 дня, чтобы пробежать 3 мили трусцой.
Вопрос 14.
Смесь Trail продается в мешках по 1 фунту. Мэри купит смесь для троп и переупаковывает ее так, чтобы каждый из 15 членов ее походного клуба получил по одной \ (\ frac {2} {5} \) -фунтовой сумке. Сколько килограммовых мешков смеси для трейлов нужно купить Мэри, чтобы у нее было достаточно смеси для трейлов без остатков?
____ Мешки 1 фунт
Ответ: 6 мешков по 1 фунту
Пояснение:
Учитывая, смесь
Trail продается в мешках по 1 фунту.Мэри купит смесь для троп и переупаковывает ее так, чтобы каждый из 15 членов ее походного клуба получил по одной \ (\ frac {2} {5} \) -фунтовой сумке.
15 × \ (\ frac {2} {5} \) = 6
Следовательно, Мэри стоит купить 6 1-фунтовых мешков, чтобы у нее было достаточно смеси без остатков.
Заключение:
Я бы хотел, чтобы информация, предоставленная в формате PDF «Пойди по математике», 4 класс. Проверьте себя, решив задачи в главе 7 «Сложение и вычитание дробей».Следите за обновлениями, чтобы получить PDF-файлы всех глав 4-го класса Go Math Answer Key. Всего наилучшего!!!
Иллюстративная математика
Задача
Соотношение количества мальчиков и девочек в школе составляет 4: 5.
Какая доля учащихся — мальчики?
- Если мальчиков 120, сколько всего учеников?
Комментарий IM
В некоторых учебниках проводится различие между соотношением, которое, как предполагается, имеет общую единицу для обеих величин, и ставкой, которая определяется как частное двух величин с разными единицами измерения (например,г. отношение количества миль к количеству часов). В общем ядре такого различия не делается, и, следовательно, две величины в соотношении могут иметь или не иметь общую единицу. Однако, когда есть общая единица, как в этой задаче, можно сложить две величины, а затем найти отношение каждой величины к целому (часто описывается как отношение части-целого).
Подобные задачи помогают установить соответствующие связи между отношениями и дробями. Студенты часто записывают отношения в виде дробей, но на самом деле мы оставляем за собой дроби для представления чисел или количеств, а не отношений между величинами.Например, если мы рассмотрим соотношение $ 4: 5 $ в этой ситуации, тогда два возможных способа интерпретации $ \ frac45 $ в контексте: сказать,
«Количество мальчиков $ \ frac45 $ количество девочек»
или, скажем,
«Отношение количества мальчиков к количеству девочек $ \ frac45: 1 $.»
Эта вторая интерпретация отражает тот факт, что $ \ frac45 $ — это удельная ставка (то есть число) для отношения $ 4: 5 $.
Решения
Решение: Использование ленточной диаграммы
На каждых 4 мальчиков в школе приходится 5 девочек и 9 учеников.Значит, $ \ frac49 $ учеников — мальчики. $ \ frac49 $ от общего количества студентов составляет 120 человек: $$ \ frac49 \ times? = 120 $$ Если $ \ frac49 $ 120 студентов, то $ \ frac14 $ 120 составляет $ \ frac19 $ от общего числа студентов. Другими словами, $ \ frac14 \ times 120 = 30 $ — это $ \ frac19 $ общее количество студентов. Тогда 9-кратная эта сумма даст общее количество учеников: $$ 9 \ times 30 = 270 $$ Итак, всего в школе 270 учеников. Обратите внимание, что это эквивалентно поиску ответа на проблему деления: $$ 120 \ div \ frac49 =? $$ Все это очень кратко можно увидеть, используя ленточную диаграмму:
Есть 4 единицы мальчиков и 9 единиц студентов.Таким образом, 4/9 студентов — мальчики.
4 шт. = 120
1 единица = 30
9 единиц = 270
Всего обучается 270 человек.
Решение: Использование таблицы
| Мальчики | Девушки | Все студенты |
| 4 | 5 | 9 |
| 40 | 50 | 90 |
| 80 | 100 | 180 |
| 120 | 150 | 270 |
Учащиеся могут умножить числа в первой строке на 10, чтобы получить вторую строку, а затем удвоить это количество, чтобы получить третью строку.Добавление записей во вторую и третью строки дает четвертую строку, в которой есть решение.
В качестве альтернативы, поскольку $ 120 \ div 4 = 30 $, студенты могут просто умножить числа в первой строке на 30, чтобы получить значения в четвертой строке.
- В каждой строке мы видим, что доля мальчиков-школьников составляет $ \ frac {4} {9} $.
- посмотрев на последнюю строку, мы видим, что общее количество студентов будет $ 4 \ times 30 + 5 \ times 30 = 120 + 150 = 270 $.

 Сложение и вычитание
Сложение и вычитание Сложение и вычитание.
Сложение и вычитание. Находить значения числовых выражений со скобками и без них
Находить значения числовых выражений со скобками и без них 09
09 Умножать письменно в пределах 1000 с переходом через разряд многозначное число на однозначное. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи
Умножать письменно в пределах 1000 с переходом через разряд многозначное число на однозначное. Совершенствовать устные и письменные вычислительные навыки, умение решать задачи Установление причинно-следственных связей
Установление причинно-следственных связей 09
09
 09
09 09
09 Совершенствовать вычислительные навыки. Анализировать свои действия и управлять ими
Совершенствовать вычислительные навыки. Анализировать свои действия и управлять ими 10
10 Устанавливать правило, по которому составлена числовая последовательность, продолжать её, восстанавливать пропущенные в ней элементы.
Устанавливать правило, по которому составлена числовая последовательность, продолжать её, восстанавливать пропущенные в ней элементы. Установление причинно-следственных связей
Установление причинно-следственных связей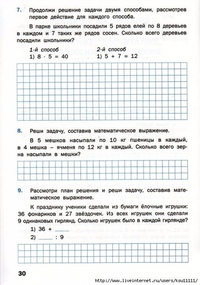 Класс миллиардов .
Класс миллиардов . Использовать материал справочника для составления и решения различных текстовых задач. Сотрудничать с взрослыми и сверстниками. Составлять план работы. Анализировать и оценивать результаты работы
Использовать материал справочника для составления и решения различных текстовых задач. Сотрудничать с взрослыми и сверстниками. Составлять план работы. Анализировать и оценивать результаты работы 10
10 Сравнивать величины по их числовым значениям, выражать данные величины в различных единицах
Сравнивать величины по их числовым значениям, выражать данные величины в различных единицах