Математика. 1 класс. Рабочая тетрадь в 2-х ч. (УМК «Перспектива») ФГОСMOBILE
Дорофеев Г.В.
Аннотация
Рабочая тетрадь переработана с учетом требований ФГОС.
 Задания в тетради расположены в соответствии со структурой учебника и представляют собой систему разнообразных тренировочных и развивающих упражнений, раскрывающих все основные вопросы первого года обучения в начальных классах.
Задания в тетради расположены в соответствии со структурой учебника и представляют собой систему разнообразных тренировочных и развивающих упражнений, раскрывающих все основные вопросы первого года обучения в начальных классах.Дополнительная информация
| Регион (Город/Страна где издана): | |
| Год публикации: | 2016 |
| Страниц: | 96 |
| Ширина издания: | 205 |
| Высота издания: | 260 |
| Язык публикации: | Русский |
| Тип обложки: | |
| Полный список лиц указанных в издании: | Дорофеев Г. В. В. |
Как найти в магазине
С этим товаром покупают
Популярные книги автора
Программа «Перспектива»
Программа «Перспектива»
|
УМК для 1 класса УМК для 2 класса УМК для 3 класса УМК для 4 класса
«Перспектива» — это учебно-методический комплекс (УМК) для начальных классов общеобразовательных учреждений, который представляет собой целостную информционно-образовательную среду, реализующую единые идеологические, дидактические и методические принципы, отвечающие требованиям Федерального государственного образовательного стандарта (ФГОС). |
УМК «Перспектива» состоит из следующих завершенных предметных линий учебников, которые включены в федеральный перечень учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования организациями, осуществляющими образовательную деятельность (приказ Минпросвещения России от 20 мая 2020 г. N 254):
— Русский язык.
Азбука. Авторы: Климанова Л.Ф., Макеева С.Г.
Русский язык. Авторы: Климанова Л.Ф., Макеева С.Г., Бабушкина Т.В.
— Литературное чтение. Авторы: Климанова Л.Ф., Горецкий В.Г., Виноградская Л.А., Бойкина М.В.
— Математика. Авторы: Дорофеев Г.В., Миракова Т.Н., Бука Т.Б.
— Окружающий мир.
 Авторы: Плешаков А.А., Новицкая М.Ю.
Авторы: Плешаков А.А., Новицкая М.Ю.— Изобразительное искусство. Авторы: Шпикалова Т.Я., Ершова Л.В.
— Технология. Авторы: Роговцева Н.И., Богданова Н.В., Фрейтаг И.П., Шипилова Н.В. и др.
— Физическая культура. Автор: Матвеев А.П.
— Физическая культура. Авторы: Винер И.А., Горбулина Н.М., Цыганкова О.Д. (Учебники могут использоваться в составе систем учебников «Школа России» и «Перспектива»).
Все учебники, вошедшие в новый перечень, входили в предыдущий ФПУ 2018г. (приказ Минпросвещения России от 28.12.2018 N 345).
Учебные пособия «Музыка» Сергеевой Г.П. в перечень не вошли. До выхода предыдущего перечня в состав УМК «Перспектива» входили учебники «Музыка» Критской Е.Д., Сергеевой Г.П. и Шмагиной Т.С. Они были переизданы и включены в УМК «Школа России».
Учебники для изучения предметной области «Основы религиозных культур и светской этики» (ОРКСЭ) в 4 классе (могут использоваться в составе систем учебников «Школа России» и «Перспектива»)
— ОРКСЭ. Основы православной культуры. Автор: Кураев А.В.
Основы православной культуры. Автор: Кураев А.В.
— ОРКСЭ. Основы исламской культуры. Авторы: Латышина Д.И., Муртазин М.Ф.
— ОРКСЭ. Основы иудейской культуры. Авторы: Членов М.А., Миндрина Г.А., Глоцер А.В.
— ОРКСЭ. Основы буддийской культуры. Автор: Чимитдоржиев В.Л.
— ОРКСЭ. Основы мировых религиозных культур. Авторы: Беглов А.Л., Саплина Е.В., Токарева Е.С. и др.
— ОРКСЭ. Основы светской этики. Автор: Шемшурина А.И.
Изучение иностранных языков по следующим УМК издательства «Просвещение»:
— Английский язык «Английский в фокусе» («Spotlight»). Быкова Н.И., Дули Д., Поспелова М.Д., Эванс В. (1-4 классы)
— Английский язык «Звездный английский» («Starlight»). Баранова К.М., Дули Д., Копылова В.В., Мильруд Р.П., Эванс В. (углубленное изучение: 1-4 классы)
— Английский язык. Кузовлев В.П., Перегудова Э.Ш., Пастухова С. А., Лапа Н.М., Костина И.П., Дуванова О.В. (2-4 классы) (не включен в новый перечень)
А., Лапа Н.М., Костина И.П., Дуванова О.В. (2-4 классы) (не включен в новый перечень)
— Английский язык. Верещагина И.Н., Бондаренко К.А., Притыкина Т.А., Афанасьева О.В. (углубленное изучение: 2-4 классы)
— Немецкий язык. Бим И.Л., Рыжова Л.И., Фомичева Л.М. (2-4 классы)
— Немецкий язык «Вундеркинды Плюс». Захарова О.Л., Цойнер К.Р. (базовое и углубленное изучение: 2-4 классы)
— Французский язык «Твой друг французский язык». Кулигина А.С., Кирьянова М.Г. (2-4 классы)
— Французский язык «Французский в перспективе». Касаткина Н.М., Белосельская Т.В., Гусева А.В., Береговская Э.М. (углубленное изучение: 2-4 классы)
— Испанский язык. Воинова А.А., Бухарова Ю.А., Морено К.В. (2-4 классы)
УМК программы «Перспектива» создан на концептуальной основе, отражающей современные достижения в области психологии и педагогики, с сохранением при этом тесной связи с лучшими традициями классического школьного образования России.
Главной целью системы учебников «Перспектива» является создание информационно-образовательной среды, обеспечивающей включение каждого ребенка в самостоятельную учебную деятельность, в процессе которой создаются условия для надежного достижения определенных ФГОС личностных, метапредметных и предметных результатов освоения основной образовательной программы начального общего образования посредством формирования универсальных учебных действий как основы ведущей образовательной компетенции — умения учиться.
Основополагающими принципами комплекта являются: гуманистический, принцип историзма, коммуникативный и принцип творческой активности. Такой принципиальный подход позволяет организовать процесс обучения с одной стороны под цель, направленную на получение знаний в соответствии с требованиями нового стандарта, с другой стороны как средство формирования универсальных учебных умений и личностных качеств, т.е. развитие и воспитание ребенка.
Идеологической основой системы учебников «Перспектива» является «Концепция духовно-нравственного развития и воспитания личности гражданина России», направленная на формирование у подрастающего поколения системы ценностей гуманизма, созидания, саморазвития, нравственности как основы успешной самореализации школьника в жизни и труде и как условия безопасности и процветания страны.
Дидактической основой системы учебников «Перспектива» является дидактическая система деятельностного метода (Л. Г. Петерсон), синтезирующая на основе методологического системно-деятельностного подхода неконфликтующие между собой идеи из современных концепций развивающего образования с позиций преемственности научных взглядов с традиционной школой (Заключение РАО от 14.07.2006 года, Премия Президента РФ в области образования за 2002 год).
Г. Петерсон), синтезирующая на основе методологического системно-деятельностного подхода неконфликтующие между собой идеи из современных концепций развивающего образования с позиций преемственности научных взглядов с традиционной школой (Заключение РАО от 14.07.2006 года, Премия Президента РФ в области образования за 2002 год).
Методической основой системы учебников «Перспектива» является методический инструментарий завершенных предметных линии учебников и специально разработанная система информационно-образовательных ресурсов.
Еще одно преимущество обучения по УМК «Перспектива» в том, что, система построения учебного материала позволяет каждому ученику поддерживать и развивать интерес к открытию и изучению нового. В учебниках задания предлагаются в такой форме, чтобы познавательная активность, познавательный интерес и любознательность ребенка переросли в потребность изучать новое, самостоятельно учиться. Ученик на каждом уроке, как бы, приоткрывает для себя содержание будущих тем. Обучение строится по диалектическому принципу, когда введение новых понятий и идей, первоначально представленных в наглядно-образной форме или в виде проблемной ситуации, предшествует их последующему детальному изучению. Каждый учебник снабжен системой заданий, направленных на развитие как логического, так и образного мышления ребенка, его воображения, интуиции. В учебниках системно выстроен теоретический материал, к которому предложены практические, исследовательские и творческие задания, позволяющие активизировать деятельность ребенка, применять полученные знания в практической деятельности, создавать условия для реализации творческого потенциала ученика.
Ученик на каждом уроке, как бы, приоткрывает для себя содержание будущих тем. Обучение строится по диалектическому принципу, когда введение новых понятий и идей, первоначально представленных в наглядно-образной форме или в виде проблемной ситуации, предшествует их последующему детальному изучению. Каждый учебник снабжен системой заданий, направленных на развитие как логического, так и образного мышления ребенка, его воображения, интуиции. В учебниках системно выстроен теоретический материал, к которому предложены практические, исследовательские и творческие задания, позволяющие активизировать деятельность ребенка, применять полученные знания в практической деятельности, создавать условия для реализации творческого потенциала ученика.
Следующая особенность УМК «Перспектива» в контексте его соответствия требованиям ФГОС — это большие возможности для решения воспитательных задач. Реализация в УМК Концепции духовно-нравственного развития и воспитания личности гражданина России направлена на формирование ценностного мировоззрения, воспитание и становление нравственной позиции личности младшего школьника. Эти задачи педагог решает в процессе обсуждения системы вопросов, проблемных и практических ситуаций, текстов, направленных на воспитание самых добрых чувств, любви и интереса к своей семье, малой и большой Родине, традициям и обычаям народов, проживающих на территории России, их культурному и историческому наследию.
Эти задачи педагог решает в процессе обсуждения системы вопросов, проблемных и практических ситуаций, текстов, направленных на воспитание самых добрых чувств, любви и интереса к своей семье, малой и большой Родине, традициям и обычаям народов, проживающих на территории России, их культурному и историческому наследию.
Основой информационно-образовательной среды для начальной школы являются завершенные предметные линии системы учебников «Перспектива». Учебники эффективно дополняют рабочие и творческие тетради, словари, книги для чтения, методические рекомендации для учителей, дидактические материалы, мультимедийные приложения (DVD-видео; DVD-диски со сценариями уроков, реализующих деятельностный метод обучения; CD-ROM диски; презентационные материалы для мультимедийных проекторов; программное обеспечение для интерактивной доски и др.), интернет-поддержка и другие ресурсы по всем предметным областям учебного плана ФГОС (ФГОС, раздел III, п.19.3.). Все это позволяет организовывать различные виды деятельности учащихся, эффективно использовать современные методы и технологии организации учебно-воспитательной работы.
Еще одной отличительной чертой системы учебников «Перспектива», обеспечивающей ему статус ядра информационно-образовательной среды для начальной школы, является разработанная специальная система навигации, позволяющая ученику ориентироваться как внутри УМК, так и выходить за его рамки в поисках других источников информации. Таким образом, система учебников «Перспектива» интегрирована в единую идеологическую, дидактическую и методическую систему, помогающую учителю обеспечивать требования современного образовательного процесса, определяемые ФГОС.
Для УМК «Перспектива» разработано новое методическое сопровождение — «Технологические карты», помогающие учителю реализовывать требования ФГОС в образовательном процессе. «Технологические карты» — это новый методический инструментарий, обеспечивающий учителю качественное преподавание нового учебного курса путем перехода от планирования урока к проектированию изучения темы. В «Технологических картах» определены задачи, планируемые результаты (личностные и метапредметные), указаны возможные межпредметные связи, предложен алгоритм прохождения темы и диагностические работы (промежуточные и итоговые) для определения уровня освоения темы учащимися. Карты размещены на сайте издательства «Просвещение» в разделе ««Перспектива» учителям». Кроме того, для учителей и родителей разработаны дополнительные интернет-ресурсы, включающие разработки уроков, статьи и комментарии, консультативную поддержку учителей и родителей (на вопросы родителей и учителей отвечают психологи, учителя, авторы).
В «Технологических картах» определены задачи, планируемые результаты (личностные и метапредметные), указаны возможные межпредметные связи, предложен алгоритм прохождения темы и диагностические работы (промежуточные и итоговые) для определения уровня освоения темы учащимися. Карты размещены на сайте издательства «Просвещение» в разделе ««Перспектива» учителям». Кроме того, для учителей и родителей разработаны дополнительные интернет-ресурсы, включающие разработки уроков, статьи и комментарии, консультативную поддержку учителей и родителей (на вопросы родителей и учителей отвечают психологи, учителя, авторы).
Для того чтобы обеспечить эффективность использования системы учебников «Перспектива» в практической деятельности учителей, построена многоуровневая система повышения квалификации педагогов разных категорий (учителей начальной и средней школы, воспитателей дошкольных образовательных учреждений, завучей, директоров, методистов, преподавателей педколледжей и педвузов, психологов и др. ), создающая условия для поэтапного освоения ими педагогических инструментов деятельностного обучения как на федеральном уровне (в Центре системно-деятельностной педагогики «Школа 2000…» АПК и ППРО), так и в регионах на основе принципа сетевого взаимодействия.
), создающая условия для поэтапного освоения ими педагогических инструментов деятельностного обучения как на федеральном уровне (в Центре системно-деятельностной педагогики «Школа 2000…» АПК и ППРО), так и в регионах на основе принципа сетевого взаимодействия.
Созданные механизмы повышения качества работы педагогов в соответствии с требованиями ФГОС на единых идеологических, дидактических и методических основаниях открывает перспективу для реального перехода школы к реализации поставленных новых целей и ценностей образования и построения единого образовательного пространства обучения, воспитания и здоровьесбережения школьников.
Официальный сайт издательства «Просвещение»: prosv.ru, old.prosv.ru
Читать по теме:
Учебно-методический комплекс «Перспектива»
Программы начальной школы
Отзывы о программе на нашей странице ВКонтакте
Если материал вам понравился, нажмите кнопку вашей социальной сети:
обзор, слабые и сильные стороны, авторы
Основные сведения
Программа для начальной школы «Перспектива» используется с 2006 года. Она разрабатывалась специально под новый Федеральный государственный образовательный стандарт (ФГОС) по инициативе Людмилы Георгиевны Петерсон — доктора педагогических наук и автора знаменитых учебников по математике.
Она разрабатывалась специально под новый Федеральный государственный образовательный стандарт (ФГОС) по инициативе Людмилы Георгиевны Петерсон — доктора педагогических наук и автора знаменитых учебников по математике.
Авторы проекта — заслуженные учёные и методисты, многие из которых также работали над самым популярным УМК для начальных классов — «Школой России». «Перспектива» занимает второе место по распространению в государственных школах. Основная миссия программы — научить ребёнка учиться: ставить цели, самостоятельно находить ответы и не терять интереса к знаниям.
Особенности программы
Методика «Перспективы» основана на «деятельностном подходе», за разработку которого Людмила Георгиевна получила премию Президента РФ в области образования в 2002 году. Его суть в том, чтобы не давать ребёнку готовые знания, а научить добывать их опытным путём.
Принципы своей программы автор формулирует так:
- «Хочу учиться!».
 Главный двигатель обучения — врождённое любопытство ребёнка. Задания подогревают интерес к теме и стимулируют желание довести её изучение до конца без посторонней помощи. А параллельно учат планировать действия, находить и исправлять свои ошибки.
Главный двигатель обучения — врождённое любопытство ребёнка. Задания подогревают интерес к теме и стимулируют желание довести её изучение до конца без посторонней помощи. А параллельно учат планировать действия, находить и исправлять свои ошибки. - «В здоровом теле — здоровый дух!». Необходимо учить детей беречь здоровье, следить за личной гигиеной и соблюдать правила безопасности. Также школа должна помочь ребёнку сформировать нравственные ценности: умение сопереживать и заботиться о других, беречь созданное природой и человеком.
- «Я в мире, мир во мне!». Важно помочь ребёнку сформировать собственное «я». Научить оценивать свои действия с точки зрения нравственности и культуры. Показать пути к саморазвитию.
- «Я общаюсь — значит, я учусь!». Для успешного обучения важно развивать коммуникативные навыки: умение вести диалог, аргументировать свою позицию и слышать других, находить нужную информацию в источниках.

Обучение происходит по диалектическому принципу: любая тема начинается с проблемы, решая которую ученики получают новые знания. Теоретический материал часто подаётся в необычной форме. Например, правила русского языка в учебнике показываются в виде диалогов между профессором Самоваровым и школьниками Аней и Ваней. Теорию всегда дополняют творческие, исследовательские и практические задачи. Они развивают логику, образное мышление, воображение и интуицию.
Кроме обучения и развития, программа уделяет большое внимание духовно-нравственному воспитанию: семейным ценностям, любви к большой и малой Родине, традициям своего народа, национальной культуре и истории.
<<Форма демодоступа>>
Содержание программы
Примечательно, что учебников самой Л.Г. Петерсон в УМК «Перспектива» нет: в 2009 году Министерство образования и науки РФ исключило их из программы со странной формулировкой: «содержание не способствует формированию патриотизма у школьников». Несмотря на многочисленные требования учителей и родителей вернуть математику Петерсон, сейчас её заменяет курс Г.В. Дорофеева.
Несмотря на многочисленные требования учителей и родителей вернуть математику Петерсон, сейчас её заменяет курс Г.В. Дорофеева.
Учебники программы «Перспектива» выпускает издательство «Просвещение». В состав УМК входят:
- Русский язык
Азбука. Авторы: Климанова Л.Ф., Макеева С.Г.
Русский язык. Авторы: Климанова Л.Ф., Макеева С.Г., Бабушкина Т.В. - Литературное чтение. Авторы: Климанова Л.Ф., Горецкий В.Г., Виноградская Л.А., Бойкина М.В.
- Математика. Авторы: Дорофеев Г.В., Миракова Т.Н., Бука Т.Б.
- Информатика. Авторы: Рудченко Т.А., Семенов А.Л.
- Окружающий мир. Авторы: Плешаков А.А., Новицкая М.Ю.
- Изобразительное искусство. Авторы: Шпикалова Т.Я., Ершова Л.В.
- Технология. Авторы: Роговцева Н.И., Богданова Н.В.
 , Фрейтаг И.П., Шипилова Н.В. и другие.
, Фрейтаг И.П., Шипилова Н.В. и другие. - Физическая культура
Физическая культура Автор: Матвеев А.П.
Физическая культура¹ Авторы: Винер И.А., Горбулина Н.М., Цыганкова О.Д. - Основы религиозных культур и светской этики¹ 4 класс.
Основы православной культуры. Автор: Кураев А.В.
Основы исламской культуры. Авторы: Латышина Д.И., Муртазин М.Ф.
Основы иудейской культуры. Авторы: Членов М.А., Миндрина Г.А., Глоцер А.В.
Основы буддийской культуры. Автор: Чимитдоржиев В.Л.
Основы мировых религиозных культур. Авторы: Беглов А.Л., Саплина Е.В., Токарева Е.С. и другие.
Основы светской этики. Автор: Шемшурина А.И.
Изучение иностранных языков:
- Английский язык¹
«Английский в фокусе» («Spotlight») 1–4 классы. Авторы: Быкова Н.И., Дули Д., Поспелова М.Д., В. Эванс
«Звёздный английский» («Starlight») 1–4 классы: углублённое изучение. Авторы: Баранова К.М., Дули Д., Копылова В.В., Мильруд Р.П., В. Эванс.
Авторы: Баранова К.М., Дули Д., Копылова В.В., Мильруд Р.П., В. Эванс.
Английский язык 2–4 классы. Авторы: Алексеев А.А., Смирнова Е.Ю., Э. Хайн и другие.
Английский язык 2–4 классы: углублённое изучение. Авторы: Верещагина И.Н., Бондаренко К.А., Притыкина Т.А., Афанасьева О.В. - Немецкий язык¹
Немецкий язык 2–4 классы. Авторы: Бим И.Л., Рыжова Л.И., Фомичева Л.М.
«Вундеркинды Плюс» 2–4 классы: углублённое изучение. Авторы: Захарова О.Л., Цойнер К.Р. - Французский язык¹
«Твой друг французский язык» 2–4 классы. Авторы: Кулигина А.С., Кирьянова М.Г.
«Французский в перспективе» 2–4 классы: углублённое изучение. Авторы: Касаткина Н.М., Белосельская Т.В., Гусева А.В., Береговская Э.М. - Испанский язык¹ 2–4 классы. Авторы: Воинова А.А., Бухарова Ю.А., Морено К.В.
¹ — эти учебники также входят в УМК «Школа России».
Учебные курсы дополняют хрестоматии, словари, тетради для самостоятельных и проверочных работ и цифровые носители с обучающими видео, презентациями и программами для мультимедийной доски.
Для учителей разработаны «технологические карты» уроков — электронные методические пособия, которые содержат:
- цели и задачи уроков,
- планируемые результаты,
- алгоритмы ведения уроков,
- связи с другими школьными предметами,
- материалы для проверочных работ.
На официальном сайте издательства также есть комментарии авторов, разработки уроков, статьи по теме и ответы психологов на частые вопросы учителей и родителей. Чтобы использовать программу «Перспектива» онлайн, педагоги повышают квалификацию с помощью многоуровневой системы онлайн-обучения. Ничего подобного нет ни в одном другом школьном УМК.
<<Форма курс 1-4>>
Отзывы о программе
Отзывы о «Перспективе» неоднозначны, одни и те же аспекты разные люди называют как достоинствами, так и недостатками:
- Нестандартная подача информации.
 Одних родителей радует, что учебники напоминают художественные произведения. Других смущает отсутствие правил в рамочках.
Одних родителей радует, что учебники напоминают художественные произведения. Других смущает отсутствие правил в рамочках. - Нет преемственности. УМК разработан только для начальной школы, и некоторые родители жалуются, что после четырёх лет «Перспективы» в пятом классе детям скучно. С другой стороны, это говорит об отличном уровне подготовки.
- Ставка на самостоятельность. Программа не даёт готовых алгоритмов и учит создавать свои. И здесь всё решает искусство учителя: у преподавателей, которые умеют влюбить ученика в предмет, учёба по «Перспективе» будет приносить только положительные эмоции. В ином случае ребёнку будет трудно справляться без посторонней помощи.
- Высокие требования к учителю. Чтобы эффективно преподавать «Перспективу», нужно изучить много методического материала и пройти специальный онлайн-курс. Одни учителя в восторге от такого уровня подготовки, другие заявляют, что не готовы столько учиться.

Безоговорочное достоинство программы — отличная полиграфия. Шрифт в учебниках крупный и чёткий, много красивых иллюстраций. Все книги издаются в мягких, но прочных ламинированных обложках. Это позволило значительно снизить их вес — важный нюанс для младшего школьника.
А недостаток, на котором сходится большинство учителей и родителей, — хаотичная последовательность тем в некоторых курсах. Особенно это касается учебников для первого и второго классов. Например, по математике умножение изучается раньше сложения, а по русскому дети сначала знакомятся с понятием текста и только потом учат буквы. Но чаще всего критикуют курс окружающего мира — за непоследовательность и фактологические ошибки.
Кому подойдёт программа
Рабочая программа «Перспектива» может стать отличной альтернативой другим «массовым» УМК, таким как «Школа России» или «РИТМ». Она подойдёт всем, кто хочет дать детям традиционное образование и хорошую базу для обучения в средней школе. А если вдобавок найти учителя, который знает и любит эту систему — ребёнок точно не растеряет любовь к учёбе и научится мыслить самостоятельно. Поэтому, если вы собираетесь в школу, где учат по «Перспективе», присматривайтесь к педагогу особенно тщательно.
А если вдобавок найти учителя, который знает и любит эту систему — ребёнок точно не растеряет любовь к учёбе и научится мыслить самостоятельно. Поэтому, если вы собираетесь в школу, где учат по «Перспективе», присматривайтесь к педагогу особенно тщательно.
По замыслу авторов программа допускает обучение «с нуля». Но многие отмечают: детям, которые ещё не умеют читать и считать, в первом классе придётся трудновато. Для дошкольной подготовки разработана специальная серия учебников: развитие речи, знакомство с математикой и окружающим миром.
Итоги V Всероссийской научно-практической конференции студентов, аспирантов и школьников «Современная математика и математическое образование в контексте развития края: проблемы и перспективы» :: КГПУ им. В.П. Астафьева
Кафедра математики и методики обучения математике
На базе КГПУ им. В.П. Астафьева 28 апреля 2020 г. в рамках XXI Международного научно-практического форума студентов, аспирантов и молодых ученых «Молодежь и наука XXI века» в заочной форме состоялась V Всероссийская научно-практическая конференция студентов, аспирантов и школьников «Современная математика и математическое образование в контексте развития края: проблемы и перспективы».
Количество участников конференции составило 87 человек, среди них студенты и аспиранты из вузов Красноярска, Ростова-на-Дону, Барнаула, Абакана, Бийска и других городов. Активное участие в конференции приняли школьники из различных образовательных учреждений Красноярского края и Алтая: МАОУ «Лицей № 6 «Перспектива»», МАОУ СШ №150 им. Героя Советского Союза В.С. Молокова, МАОУ «Лицей № 2», МБОУ СШ №149, МБОУ СШ №144, МБОУ СШ №42, КГБОУ «Красноярский кадетский корпус им. А.И. Лебедя», Алтайский краевой педагогический лицей-интернат. В конференции приняли участие многие юные дебютанты: Кейв П.В. (4 класс), Никонов И.А. (4 класс), Сомов И.А. (4 класс). Самому юному участнику исполнилось 10 лет. На протяжении 5 лет конференция пользуется успехом и у постоянных участников, среди которых: Багачук П.С. (5 класс), Шевелёва Д.П. (7 класс), Балахонов В.В. (10 класс) и др.
Результаты исследований, представленных участниками конференции, распределились по следующим секциям:
Секция 1. Математика: современные научные исследования студентов и молодых ученых.
Секция 2. Теория и методика обучения математике: инновационные подходы.
Секция 3. Математические и межпредметные исследования обучающихся (1–11 классы).
Секция 4. ИКТ в математических исследованиях.
Сборник материалов конференции опубликован и выставлен в e-library: https://elibrary.ru/item.asp?id=42741000.
Материалы конференции свидетельствует о возможностях повышения качества математического образования в регионе за счет конструктивного использования имеющихся ресурсов и активного сетевого взаимодействия.
Организационный комитет во главе с его председателем заместителем проректора по науке и сетевому взаимодействию КГПУ им. В.П. Астафьева А.В. Багачук, а также заведующая кафедрой математики и методики обучения математике Л.В. Шкерина выражают благодарность всем участникам конференции и их научным руководителям, нашим партнерам ФГАОУ ВО «Сибирский федеральный университет», МАОУ «Лицей №6 «Перспектива»», МАОУ «Лицей № 2», МБОУ СШ №149, КГБОУ «Красноярский кадетский корпус им. А.И. Лебедя», Алтайский краевой педагогический лицей-интернат, а также студентам и преподавателям ИМФИ КГПУ им. В.П. Астафьева.
Входная контрольная работа по математике для 5 класса
Пояснительная записка
к входной контрольной работе по математике
для учащихся 5 классов
Входная контрольная работа в 5 классах предусматривает проверку знаний учеников по темам: Арифметические действия над натуральными числами, порядок выполнения действий, уравнения, нахождение неизвестного слагаемого. Система заданий адаптирована для данной возрастной категории.
Цель:1. Подготовка учащихся к итоговой аттестации и к независимой оценке качества.
Выявление сформированности учебных умений:
а) контролировать и корректировать собственные действия по ходу выполнения задания;
б) использовать знания в новой нестандартной ситуации.
Объект контроля: знание арифметических действий, порядок выполнения действий. решение задач на движение, площадь прямоугольника, решение уравнений, нахождение неизвестного слагаемого
Время выполнения: один урок (40 минут).
Структура контрольной работы: контрольная работа состоит из 2-х равноценных вариантов, каждый из которых включает в себя 5 заданий
Оценка письменных контрольных работ.
Оценка 5 ставится за работу, выполненную полностью без ошибок и недочетов.
Оценка 4 ставится за работу, выполненную полностью, но при наличии в ней не более одной негрубой ошибки и одного недочета, не более трех недочетов.
Оценка 3 ставится, если ученик правильно выполнил не менее 2/3 всей работы или допустил не более одной грубой ошибки и двух недочетов, не более одной грубой и одной негрубой ошибки, не более трех негрубых ошибок, одной негрубой ошибки и трех недочетов, при наличии четырех-пяти недочетов.
Оценка 2 ставится, если число ошибок и недочетов превысило норму для оценки 3 или правильно выполнено менее 2/3 всей работы
Входная контрольная работа по математике
для 5 класса
Вариант №1
1. Укажите порядок действий и найти значение:
(790 – 17472 : 84) · 64 + 54 · 903.
2. Выполнить действия: а) 80300-5037; в)3800 * 73;
б)769 * 48; г) 20706:34.
3. Расстояние между городами 930 км. Одновременно навстречу друг другу вышли 2 поезда. Скорость одного 45 км/ч, другого 48 км/ч. Через сколько часов поезда встратились?
4. Найди площадь прямоугольника, если его ширина 4 см, а длина в 5 раз больше.
5. Решите уравнение:
а) a · 54 = 12690; б) 474 + a = 500; в) a : 48 = 35; г) 651 – a = 313.
Вариант №2
1. Укажите порядок действий и найти значение:
(591 + 1125 : 75) · 56 – 46 · 702.
2. Выполните действия: а) 83945 – 53927; б)6660 * 59
в) 687 * 39; г)27356 : 7.
3. Из двух городов одновременно навстречу друг другу вышли два поезда и встретились через 7 ч. Скорость одного поезда 54 км/ч, другого – 64 км/ч. Определите расстояние между городами.
4. Найди площадь прямоугольника, если его длина 13 см, а ширина на 4 см больше.
5. Решите уравнения:
а) 48 · а = 624; б) 312 + х = 400 ; в) a : 393 = 15; г) a – 184 = 121.
Есть ли перспективы у растительного молока и мяса — Российская газета
Растительные бургеры, креветки, глазированные сырки и другая альтернативная продукция появляются на полках магазинов. Основные покупатели — молодежь, которая заботится о животных и планете. Правда, делают растительное мясо из обычного гороха или сои, а стоит оно, как натуральный премиальный стейк. Но уже сейчас очевидно: потребление всякого рода заменителей животной продукции не просто дань моде, а устойчивый тренд.
Каждый третий российский потребитель покупает растительные аналоги молока. При этом зачастую эти же люди продолжают пить и традиционное молоко, следует из данных Роскачества. Полностью заменили животное молоко только 6% россиян. Например, в «Магните» продажи растительных аналогов молока в первом полугодии выросли на 35%, рассказала на «круглом столе» в ЕЭК руководитель управления по взаимодействию с государственными органами компании Юлия Храмайкова. К растительному мясу россияне пока относятся настороженно. А для большинства покупателей сейчас на первом месте — качество продуктов и здоровое питание.
Пандемия ускорила развитие этого направления. Разрывы цепочек поставок, опасения передачи инфекции от животных человеку, стремление потребителей к ЗОЖ привели к тому, что инвестиции в стартапы по производству растительного мяса достигли исторических максимумов. Это наслаивается на проблему климатических изменений и попытки государств сократить выбросы парниковых газов (а животноводство — один из серьезных их «производителей»). Растительное мясо едят веганы и в диетических целях, говорит заместитель директора Центра научно-технологического прогнозирования Института статистических исследований и экономики знаний НИУ ВШЭ Ядвига Радомирова. Мировой рынок оценивается в чуть более 5 млрд долларов. Но к 2030 году может превысить 15 млрд долларов.
Заменой животным бургерам растительные не станут, а будут, скорее, интересным дополнением к столу. Но страны ЕАЭС на производстве и экспорте таких растительных аналогов точно могут неплохо заработать. Для этого у нас есть достаточные земельные ресурсы и научный потенциал, считает министр по промышленности и АПК ЕЭК Артак Камалян.
Планы уроков математики для пятого класса
Посмотреть демо наших уроковУчебная программа по математике Time4Learning доступна для учащихся от дошкольных учреждений до двенадцатых классов. Родители могут ожидать, что они увидят охватываемые темы, включая закономерности в алгебре, построение графиков, сравнение и упорядочение десятичных знаков и многое другое.
Подробные планы уроков, представленные ниже, содержат подробный список учебной программы Time4Learning по математике для пятого класса.
Участникичасто используют эту страницу как ресурс для более подробного планирования, как руководство, помогающее выбрать конкретные занятия с помощью средства поиска занятий или сравнить нашу учебную программу с государственными стандартами и законами о домашнем обучении.
Что входит в планы уроков Time4Learning?
- Полная учебная программа для пятого класса по математике с 12 главами, 416+ заданиями, рабочими листами и викторинами
- Глава уроки с подробным описанием пройденного содержания
- Несколько типов заданий для развития навыков, включая задания без баллов, викторины и распечатываемые ключи ответов в викторинах
- Рабочие листы уроков и ключи ответов на представленные материалы
- Легкий доступ к дополнительным главам по каждой теме
- Time4MathFacts, который использует забавные игры, чтобы вовлечь вашего ребенка в изучение основ математики.
Учащиеся пятого класса математической программы Time4Learning будут иметь доступ к урокам как четвертого, так и шестого класса в рамках своего членства, так что они смогут продвигаться вперед или делать повторения в своем собственном темпе.
План урока математики — Учебная программа для пятого класса
Студенты будут использовать римские и греческие цифры.
Студенты будут использовать числовые цифры и слова для чтения и записи чисел до сотен миллиардов.
Студенты покажут числа в стандартной и развернутой форме с точностью до миллиарда.
Учащиеся будут сравнивать и заказывать числа, используя диаграмму разрядов и числовые линии.
Студенты округляют числа до одного миллиарда и используют концепцию округления для решения реальных задач.
Студенты будут использовать стратегии оценки для решения реальных задач, в которых они найдут сумму и разницу.
Учащиеся будут оценивать и оценивать вопросы на предмет разумности и определять разумность данных ответов.
Студенты будут складывать и вычитать целые числа.
Ученики умножают целые числа.
Студенты будут решать задачи умножения, которые включают умножение двух цифр на две цифры, а также умножение трех цифр на две цифры.
Студенты будут решать реальные задачи, связанные с оценкой с умножением двух на две цифры, а также трехзначным умножением на две цифры.
Учащиеся определят наибольший общий делитель данных чисел.
Определить наименьшее общее кратное заданных чисел.
Студенты будут использовать экспоненты для решения задачи.
Учащиеся определяют степень от 10 до 6.
Ученики будут использовать шаблоны при умножении на десять.
Студенты будут изучать экспоненты как многократное умножение.
Студенты разделятся, чтобы решать задачи.
Студенты будут использовать совместимые числа для оценки частных.
Студенты будут применять правила делимости 2, 3, 5, 9 и 10 к различным числам.
Учащиеся интерпретируют остатки и применяют концепции, чтобы определить, что означают остатки.
Студенты будут использовать порядок действий для решения задач.
Студенты будут определять и определять простые и составные числа до 50. Студенты найдут разложение на простые множители чисел до 50.
Студенты будут записывать множители чисел, используя только простые числа и разложенные на простые множители.
Студенты будут решать реальные задачи.
Учащиеся поймут, что цифра в одном месте представляет в 10 раз больше, чем оно представляет в месте справа от него, и одну десятую того, что оно представляет в месте слева.
Учащиеся будут читать и писать числа с точностью до тысячных долей в письменной и стандартной форме и показывать их эквивалентность.
Учащиеся идентифицируют число и ставят в числовой строке данные десятичные дроби.
Учащиеся будут использовать <,> и = для сравнения десятичных и тысячных долей. Студенты упорядочивают десятичные дроби через тысячи.
Учащиеся округляют десятичные дроби до определенного разряда и до ближайшей половины или целого числа.
Учащиеся будут складывать и вычитать десятичные дроби.
Учащиеся оценивают суммы и разницы с десятичными знаками.
Учащиеся умножат десятичные дроби на другие десятичные дроби.
Учащиеся будут делить десятичные дроби на десятичные дроби и целые числа как в делителе, так и в делимом.
Студенты будут оценивать произведения и частные с использованием десятичных знаков.
Студенты определят проц.
Учащиеся найдут процент от числа и решат реальные задачи, используя проценты.
Учащиеся определят неправильные и смешанные числа и продемонстрируют свою способность находить эквиваленты между ними.
Учащиеся определяют наименьший общий знаменатель дробей с разными знаменателями.
Учащиеся упростят дроби, найдя наименьший общий знаменатель.
Студенты найдут эквивалентные формы дробей, за исключением смешанных чисел.
Студенты будут сравнивать и заказывать дроби.
Учащиеся округляют дроби до ближайшей половины или целого числа.
Учащиеся складывают дроби, исключая смешанные числа, с одинаковыми и непохожими знаменателями.
Студенты будут вычитать дроби, не считая смешанных чисел, с одинаковыми и непохожими знаменателями.
Студенты будут решать реальные задачи, связанные с вычитанием дробей с разными знаменателями.
Учащиеся сложат смешанные числа с перегруппировкой и без нее.
Студенты будут вычитать смешанные числа с перегруппировкой и без нее.
Учащиеся представят произведение двух дробей, используя модель площади.
Учащиеся определяют эффект умножения целого числа на дробь меньше 1 и на дробь больше 1.
Учащиеся будут умножать дроби, не считая смешанных чисел, и упрощать ответы.
Учащиеся будут решать задачи, связанные с умножением дроби на смешанное число и умножением смешанного числа на смешанное число.
Студенты будут моделировать деление целых чисел на дробные части и дроби на целые числа.
Студенты будут решать реальные задачи, связанные с делением на единичные дроби.
Учащиеся будут делить дроби, исключая смешанные числа, с помощью обратных чисел и упрощать ответы.
Студенты будут оценивать продукты и частные, используя дроби.
Учащиеся интерпретируют дробь как представляющую деление.
Учащиеся запишут дроби как десятичные.
Учащиеся продемонстрируют свое понимание взаимосвязи между десятичными знаками и дробями и дробями с десятичными знаками и как они эквивалентны процентам.
Студенты выучат дроби как отношения.
Студенты найдут эквивалентные соотношения.
Учащиеся узнают знак процента и поймут процентное значение на сотню. Студенты будут выражать эквивалентности между дробями, десятичными знаками и процентами и знать общие эквиваленты.
Учащиеся будут описывать жизненные ситуации, используя целые числа, и указывать целые числа в числовой строке.
Учащиеся определяют закономерности на рисунках и в таблицах и описывают функциональное правило.
Студенты будут писать и оценивать алгебраические выражения.
Студенты найдут правило в реальных задачах и определят правила функций из таблиц.
Студенты будут решать одношаговые уравнения с целыми, десятичными и дробными числами, включая сложение.
Студенты будут решать одношаговые уравнения с целыми числами, десятичными знаками и дробями с использованием вычитания.
Студенты будут решать одноэтапные уравнения с целыми и десятичными дробями, включая умножение.
Студенты будут решать одношаговые уравнения с целыми и десятичными дробями с делением.
Студенты будут применять формулы для решения обычных задач длины. Учащиеся определят правильные инструменты для решения обычных задач длины и будут применять концепции оценки для получения ответов.
Студенты будут применять формулы для решения обычных задач с весом. Учащиеся определят правильные инструменты для решения обычных задач с весом и будут применять концепции оценки для получения ответов.
Студенты будут применять формулы для решения обычных задач по вместимости. Учащиеся определят правильные инструменты для решения обычных задач, связанных с производительностью, и будут применять концепции оценки для получения ответов.
Студенты будут применять формулы, включающие температуру в градусах Фаренгейта, для решения реальных задач.
Студенты узнают о метрической системе и узнают, как умножение и деление на десять влияет на размещение в системе.
Студенты будут применять формулы для решения задач метрической длины. Учащиеся определят правильные инструменты для решения задач метрической длины и будут применять концепции оценки для получения ответов.
Студенты будут применять формулы для решения задач с метрическим весом. Учащиеся определят правильные инструменты для решения задач с метрическим весом и будут применять концепции оценки для получения ответов.
Студенты будут применять формулы для решения задач метрической вместимости. Студенты определят правильные инструменты для решения задач метрической емкости и будут применять концепции оценки для получения ответов.
Студенты будут применять формулы, включающие температуру в градусах Цельсия, для решения реальных задач.
Студенты решат задачи о затраченном времени.
Студенты будут решать задачи, показывая прошедшее время в днях, неделях, месяцах, годах и столетиях.
Ученики найдут периметр многоугольников и правильных многоугольников с пропущенными значениями и без них.
Ученики найдут площадь квадратов и прямоугольников.
Студенты найдут площадь треугольников.
Студенты найдут объем кубиков и прямоугольных призм.
Учащиеся найдут объем прямоугольной призмы, посчитав единичные кубы.
Учащиеся найдут объем прямоугольной призмы, умножив длину ребер или умножив площадь основания на высоту.
Учащиеся найдут объем прямоугольной призмы, применив формулу V = B × h.
Студенты найдут объем твердой фигуры, состоящей из двух прямоугольных призм.
Учащиеся будут использовать совпадение, коллинеарность, параллельность и перпендикулярность для описания относительной ориентации на координатной сетке.
Учащиеся будут определять параллельные, перпендикулярные, пересекающиеся и наклонные линии.
Студенты будут измерять градусы в прямом, остром, тупом и прямом углах с помощью транспортира.
Студенты будут определять разные виды треугольников.
Учащиеся отсортируют полигоны по атрибутам. Студенты классифицируют четырехугольники как параллелограммы, трапеции, ромбы, прямоугольники и квадраты.
Учащиеся классифицируют четырехугольники как параллелограммы, трапеции, ромбы, прямоугольники и квадраты.
Студенты узнают о трехмерных фигурах.
Учащиеся отсортируют многогранники по их атрибутам.
Учащиеся определяют дугу, хорду, радиус и диаметры окружностей.Учащиеся вычисляют радиус или диаметр круга.
Студенты будут строить трехмерные фигуры из набора видов.
Учащиеся идентифицируют и создают двумерное представление трехмерной фигуры (сетей) на сетке или точечной бумаге.
Студенты найдут измерение углов.
Студенты узнают о заказанных парах.
Учащиеся классифицируют плоские фигуры как имеющие линейную симметрию, точечную симметрию, обе или никакую.
Учащиеся применяют несколько преобразований к плоской фигуре, предсказывают результат и идентифицируют изображение плоской фигуры как результат множественного преобразования, включая поворот на 90 и 180 градусов.
Учащиеся будут использовать масштаб, чтобы показать относительный размер на карте или чертеже.
Ученики будут исследовать сходство, используя конгруэнтные углы. Студенты будут исследовать конгруэнтность, используя конгруэнтные сегменты и конгруэнтные углы.
Студенты будут определять и представлять все возможные результаты для определенного вероятностного события с помощью диаграмм, списков или древовидных диаграмм.
Студенты рассчитают вероятность события.
Студенты будут делать прогнозы на будущие события на основе предыдущих событий.
Студенты будут интерпретировать и анализировать гистограммы.
Студенты интерпретируют линейные графики (интерполяция и экстраполяция).
Студенты будут создавать и интерпретировать круговые диаграммы, используя обычные дроби.
Студенты будут интерпретировать, анализировать и создавать гистограммы.
Студенты будут интерпретировать и анализировать диаграммы Венна.
Студенты выберут наиболее подходящий график для набора данных и сделают выводы из графиков.
Студенты будут сравнивать и переводить данные из информации, счетчиков и данных в график.
Студенты будут собирать, систематизировать и описывать данные с использованием медианы, режима и диапазона.
Учащиеся найдут среднее значение заданного набора чисел.
Учащиеся будут использовать знания о графиках стеблей и листьев для определения среднего, медианного значения, режима и диапазона.
Инструмент поиска учебных занятий
Инструмент для поиска занятий — один из многих полезных инструментов, которые Time4Learning предлагает своим участникам. Средство поиска занятий — это ярлык, с помощью которого родители могут легко просмотреть уроки или найти дополнительную практику для своего ребенка.
Каждому уроку в учебной программе присвоен уникальный номер занятия, который в планах уроков называется «номером LA». Эти числа можно найти либо на страницах содержания и последовательности, либо в планах уроков на родительской информационной панели.
Для получения дополнительной информации посетите наш раздел подсказок и помощи, в котором есть более подробная информация о поисковике действий.
Дополнительные ресурсы по математике для пятого класса
Если вас интересуют планы уроков математики для пятого класса, вас также могут заинтересовать:
Онлайн-программа для домашнего обучения, послешкольного и летнего использования
Если вы только изучаете Time4Learning, мы рекомендуем сначала посмотреть наши интерактивные демонстрации уроков.
Зарегистрируйтесь на Time4Learning и получите доступ к разнообразным образовательным материалам, которые увлекут и побудят вашего ребенка добиться успеха.Сделайте Time4Learning частью ресурсов для домашнего обучения ваших детей.
Советы по математике для 5-го класса
Надеетесь помочь своему пятикласснику с математическими навыками? Вот несколько основных советов, которые специалисты предлагают пятиклассникам.
Подчеркните практическое применение математики
По мере того, как математика, которую они изучают, становится все более сложной и менее очевидно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревога. Важно, чтобы ваш ребенок занимался математикой и помогал ему понять, как в реальной жизни применяются концепции, которые он изучает в школе.Составление бюджета на школьные принадлежности или ежемесячное пособие — это один из способов практиковать сложение и вычитание. Если вы попросите их помочь вам с приготовлением или выпечкой, это покажет им, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.
Связанные
Помогите подготовиться к уроку математики
Помогите своему ребенку снизить стресс из-за математики, ознакомив его с концепциями, которые он будет изучать в классе. Попросите их учителя составить программу и обращайтесь к ней, чтобы каждый вечер предварительно просматривать материал, который будет рассмотрен на уроке математики на следующий день.Просмотрите эти страницы вместе с ними. Нет необходимости тратить время на выяснение смысла понятий или решение примеров задач, хотя вы можете обратиться к глоссарию для определения незнакомых слов. Даже это небольшое улучшение знаний терминов, которые появятся на следующий день, поможет вашему ребенку более уверенно подходить к математике.
Прочитайте задачи вслух
Если ваш ребенок борется с математическими задачами, попросите его прочитать каждую задачу вслух медленно и внимательно, чтобы ваш ребенок мог услышать задачу и подумать о том, о чем его спрашивают.Это помогает им разобраться в проблеме и придумать стратегии ее решения.
Сохраняйте позитивный настрой в математике
Говорите о математике положительно и поощряйте усилия, а не оценки или способности. Подумайте о том, насколько важно чтение и как нам говорят моделировать такое поведение для наших детей. Нам нужно отнести математику к той же категории. Не сбрасывайте со счетов важность математики, говоря: «Я не математик, я никогда не был хорош в математике». Помогите своему ребенку прочитать книги, в которых есть математика, например, «Миллионы кошек» Ванды Гаг или «За миллионом: удивительное математическое путешествие» Дэвида Шварца.
Обратитесь к онлайн-ресурсам
Ознакомьтесь с рядом онлайн-ресурсов, которые могут помочь вашему 5-класснику на практике, и проанализируйте математические концепции, которые они изучают.
Практика вычислений с использованием десятичных дробей
Свяжите работу с десятичными знаками, которую ваш ребенок делает в классе, с реальным миром, поощряя их делать покупки по выгодным ценам. Попросите их разделить стоимость товаров, упакованных оптом, на количество отдельных товаров, чтобы определить стоимость каждого товара. Итак, сколько вы платите за рулон бумажного полотенца или за банку газировки при покупке оптом? Или попросите их подсчитать, сколько вы сэкономите на каждом товаре, если цены со скидкой предполагают оптовые скидки.
Связанные
Практика использования дробей
Помогите своему пятикласснику познакомиться с дробями, попросив его масштабировать рецепты для вашей семьи. Пусть они начнут с того, что уменьшат рецепт вдвое или вдвое. Когда они почувствуют себя комфортно, попросите их преобразовать его на 1 1/2, что позволит рецепту, который должен накормить семью из четырех человек, работать на семью из шести человек.
Откройте банковский счет
Откройте банковский счет для вашего ребенка. Прежде чем вы это сделаете, обсудите с ними основные концепции банковского дела — проценты, текущие и сберегательные счета, кредитные и дебетовые карты и т. Д.Этот опыт поможет им увлечься экономией и приумножением своих денег.
Выделите математику в спорте
Спорт — это увлекательный и увлекательный способ изучения множества математических понятий, начиная с простого сложения. Любой заядлый фанат бейсбола знает, что игру нельзя по-настоящему оценить без понимания некоторых важных статистических данных, таких как средний результат игрока и его результативность. Если ваш ребенок увлечен спортом, поощряйте его изучать его с помощью математики. .
Играйте в математические игры
Играйте в семейные игры, которые помогают развивать математические навыки. К ним относятся карточные игры, такие как Go Fish, где требуется подсчет и сортировка карт по наборам, или настольные игры, такие как «Монополия».
Чтобы узнать, что ваш пятиклассник будет изучать в классе математики, посетите нашу страницу навыков по математике для пятого класса.
Ресурсы TODAY Parenting Guides были разработаны NBC News Learn с помощью профильных экспертов, включая Джойс Эпштейн, директора Центра школьного, семейного и общественного партнерства Университета Джона Хопкинса; Памела Мейсон, директор программы / преподаватель образования, Гарвардская высшая школа образования; Дениз Уолстон, директор отдела математики Совета школ большого города; Нелл Дьюк, профессор Мичиганского университета; Лианна Бейкер, учитель математики на пенсии; Бон Краудер, учитель математики и блогер, MathFour.com; и Робин Шварц, вице-президент Ассоциации учителей математики Нью-Йорка, и соблюдает общепринятые государственные стандарты.
Домыслы и опровержения по математике в 5 классе по JSTOR
АбстрактныйЭта статья вносит вклад в разъяснение того, что такое математическое мышление и как оно выглядит в школьном контексте. В нем описывается один образец рассуждения, наблюдаемый в математической деятельности учащихся 5-го класса, и обсуждается, каким образом этот образец является или не является математическим, чтобы прояснить особенности модели рассуждения, которые важны для вынесения такого суждения.Шаблон включает в себя предположение общего правила, тестирование этого правила, а затем его использование для дальнейшего исследования, отклонение или изменение. Каждый элемент рассуждения в этом шаблоне описывается в терминах используемых способов рассуждения и степени формулировки рассуждения. В математике проводится различие между математическими рассуждениями и научными рассуждениями на основе критериев, используемых для принятия или отклонения рассуждений в каждой области.
Информация о журналеОфициальный журнал Национального совета учителей математики (NCTM), JRME — ведущий исследовательский журнал в области математического образования, посвященный интересам учителей и исследователей на всех уровнях — от дошкольного до колледжа.
Информация об издателеНациональный совет учителей математики — это общественный голос в области математического образования, обеспечивающий видение, руководство и профессиональное развитие для поддержки учителей в обеспечении высочайшего качества обучения математике для всех учащихся. NCTM, насчитывающая около
членов и 250 аффилированных лиц, является крупнейшей в мире организацией, занимающейся совершенствованием математического образования в классах от подготовительных классов до 12 классов.«Принципы и стандарты школьной математики» Совета представляют собой руководящие принципы для достижения совершенства в математическом образовании и призывают всех учащихся заниматься более сложной математикой. NCTM нацелен на постоянный диалог и конструктивное обсуждение со всеми заинтересованными сторонами того, что лучше всего для студентов нашей страны.
Как использовать 5E в дистанционном обучении математике в старших классах
Моя математическая команда в этом году экспериментировала с учебной моделью под названием 5E, которая была разработана в 1987 году командой из отдела изучения учебных программ по биологическим наукам (BSCS).5E — вовлекать, исследовать, объяснять, разрабатывать и оценивать — параллельны модели решения проблем, используемой учеными и математиками для решения реальных проблем: они взаимодействуют с материалами, исследуют возможности путем экспериментов, объясняют и развивают свои наблюдения. , и оценить их новые выводы.
Согласно BSCS, преподаватели могут применять 5E на различных уровнях планирования, включая годичную программу, единицу или в рамках уроков. Одним из преимуществ этого подхода является возможность учащимся построить собственное понимание новой концепции на этапах вовлечения и изучения, а не начинать обучение с объяснения учителя.
Хотя она была разработана для преподавания естественных наук, учебная модель 5E полезна в математике — учителя могут разрабатывать блоки, которые предоставляют своим ученикам значимые возможности для осмысления.
Мое школьное подразделение начало учебный год с дистанционного обучения в основном в асинхронных форматах. В попытке увеличить как равенство, так и сотрудничество в подразделении, были сформированы группы на уровне класса, чтобы разделить работу по планированию между 11 начальными школами. Всем командам, а не только учителям естественных наук, было предложено использовать формат 5E, как мы и планировали.Ниже приводится объяснение того, как мы применили 5E к двухнедельному математическому блоку пятого класса по простым и составным числам.
Занять
На этом этапе учителя задают вопрос, объект или ситуацию, которые фокусируют внимание учащихся и помогают им активировать предыдущие знания. На уроке математики это может быть числовая беседа, связанная с задачей, которую студенты собираются решить, или возможность заметить и удивиться.
Предоставлено Трейси ПроффиттУченики пятого класса, начавшие урок простых и составных чисел, записали то, что они заметили в изображении фигурок Lego.
Наш простое и составное устройство начиналось с изображения 17 фигурок Лего. Мы попросили студентов записать на Google Jamboard то, что они заметили и задались вопросом. Все ответы, как математические, так и нематематические, были приняты и поощрены на этом этапе. Несколько студентов указали на нечетное количество цифр, потому что это была тема уроков на прошлой неделе.
Изучить
Студенты действительно углубляются в задачу на этом этапе. Одна из целей этапа изучения состоит в том, чтобы учащиеся получили общий опыт, который они и учителя могут использовать позже, объясняя новую концепцию или навык.
На очном уроке математики учителя отпускали и позволяли ученикам исследовать сложную задачу с помощью манипуляторов или других моделей. При изучении простых и составных чисел пятиклассников обычно просят создать массивы с разным количеством объектов. Для дистанционного обучения мы попытались смоделировать это физическое манипулирование объектами с помощью рисунков, которые студенты могли перетаскивать в презентацию Google Slides.
Объяснить
Заманчиво думать, что это часть урока или раздела, когда учитель объясняет концепцию или навык.Однако BSCS подчеркивает, что на самом деле именно ученики должны объяснять то, что они наблюдали или узнали, в то время как учитель поддерживает их формальным языком по мере необходимости.
На третий день нашего основного и составного блока студенты использовали Flipgrid, чтобы объяснить, что они обнаружили, исследуя онлайн-инструмент делимости. Flipgrid оказался бесценным ресурсом для студентов и учителей на этом этапе учебной модели 5E. Затем учителя могут записывать видео-комментарии, чтобы прояснить неправильные представления и смоделировать точный математический язык для учащихся.
Разработать
Этап проработки дает учащимся возможность расширить свое мышление и перенести развивающиеся знания в новые ситуации. Это возможность для учащихся избавиться от заблуждений, часто в ходе совместной работы в личных беседах. Во время дистанционного обучения наши учителя предоставили возможности для совместной работы синхронно через Zoom и асинхронно через Desmos.
Руководители наших подразделений призвали учителей использовать этот этап модуля, чтобы расширить возможности обучения для учащихся, которые готовы к более серьезным испытаниям, и для оказания поддержки учащимся, которые еще не усвоили концепцию.Наша команда пятиклассников разработала короткую формирующую оценку и по результатам распределила дифференцированные задачи через Google Classroom. Некоторые студенты применяли свои новые знания, отмечая простые и составные числа в коллекции интересных фотографий и на своих собственных фотографиях.
Другие участники выполнили задачу Open Middle на Google Slides, чтобы объединить рассуждения и решение проблем со своими знаниями простых и составных чисел. Учительница пятого класса Мекензи Шмитт, которая сейчас учится на первом курсе, заметила: «Формирующая оценка в пятницу казалась хорошим показателем того, где должны быть ученики.Участие в этой дифференцированной деятельности было выше, чем обычно. Почти все студенты выполнили поставленную задачу, включая студентов, которые «уже сделали», которые иногда выписываются, и студентов, которые еще не пришли, которые иногда замирают ».
Оценить
На заключительном этапе и ученики, и учителя оценивают обучение учеников. Формирующее оценивание, конечно, должно происходить на протяжении каждого этапа, но итоговое оценивание включено здесь, в конце раздела.
Один из способов, которым наши учителя побуждали учеников оценить их собственное обучение, — это вернуться к тому, что они заметили и задались вопросом об изображении фигурок Lego на этапе вовлечения.Мы побуждали студентов снова замечать и удивляться, на этот раз пытаясь применить новый словарный запас, который они выучили.
Предоставлено Трейси ПроффиттПятиклассники продемонстрировали свое понимание простых и составных чисел ближе к концу единицы.
Учащиеся оставили заметки, подобные тем, которые показаны на изображении выше, которые указывают на различные уровни понимания в данный момент в модуле. Самое замечательное в постановке открытого вопроса заключается в том, что обнаруживается гораздо больше заблуждений по сравнению с основным вопросом вроде «17 простых или составных?»
Следующие шаги
Воспитание в условиях пандемии сложно.Даже с хорошо продуманными планами, ориентированными на студентов, которые наша команда разработала вместе, некоторым студентам все еще приходилось сталкиваться с трудностями в основном и сводном блоке.
Я размышлял со второкурсником Кейтлин Бост об использовании уроков, созданных нашей командой. Она описала студентов, которые не вошли в систему, чтобы выполнить задания, других, которые сразу перешли к задаче, не читая никаких указаний, и тех, у кого не было опыта или комфорта в продуктивной борьбе.
Но Бост не сдается.Она встречается со студентами один на один через Zoom, чтобы пройти с ними эту продуктивную борьбу. Она обдумывает способы редактирования заданий, чтобы ученики не пропустили важные направления, и празднует успехи своих учеников.
Независимо от того, используете ли вы 5E или другую учебную модель, ориентированную на учащихся, в дистанционном обучении математике, связывайте высокие ожидания с учащимися с соответствующей поддержкой и при каждой возможности отмечайте их математическое понимание.
5 новогодних заданий для знакомства своих учеников-математиков
По мере приближения каждого нового года учителя сталкиваются с вопросом, как начать работу со своими новыми учениками. Хотя «как» важно, потратить время на размышления о том, что вашим ученикам нужно знать о себе, вашем классе и ваших ожиданиях, вероятно, поможет пролить свет на метод обучения. Первый день и неделя зададут тон на весь учебный год, поэтому выбор идеальных занятий для знакомства ваших учеников-математиков имеет решающее значение.Выбранные задания передадут учащимся ваши собственные чувства относительно математики, ваших ценностей и ожиданий в классе. Целью каждого учителя должно быть послание: «Мне интересно, кто вы и что вы думаете».
В этой статье вы найдете пять занятий, которые можно использовать в начале нового учебного года как в очном, так и в виртуальном классе.
Создание благоприятного и безопасного пространства, в котором учащиеся чувствуют свою принадлежность, открывает им возможность рисковать, приобретать новые навыки и совместно взаимодействовать друг с другом.Уроки математики часто основываются на продуктивной борьбе, настойчивости в решении проблем и установке на рост, которая позволяет учащимся учиться на своих ошибках. Снова и снова исследования доказывают, что одним из наиболее важных и важных факторов успеха учащихся являются отношения между учителем и учениками. Посещаемость, успеваемость, уровень вовлеченности и улучшенное поведение — все это связано с позитивными отношениями между учителем и учеником. Оптимизация возможностей в первые несколько дней для того, чтобы задать тон в классе и наладить отношения, может иметь решающее значение для вас и ваших учеников.
Следующие пять задач предлагают вам отправную точку для знакомства и продолжения встреч со своими учениками в течение года. Их можно использовать для оценки первоначальных мыслей и отношения студентов к уроку математики, оценки того, как они меняются в течение года, и помочь вам определить любую дополнительную поддержку, которую вы можете предложить!
Если вы будете обучать удаленно, эти PDF-файлы для печати можно преобразовать с помощью Google Диска, чтобы учащиеся могли вводить текст прямо в рабочий лист.Ознакомьтесь с инструкциями Vocab Gal по преобразованию PDF-файлов, чтобы их можно было заполнять онлайн.
Это инструменты, которые задают тон вашему классу, создают чувство общности и развивают понимание того, кем является каждый из ваших учеников. Используя эти упражнения, вы сможете заложить основу для безопасной учебной среды, продуктивных математических дискуссий и совместной групповой работы с самого начала учебного года.
# 1 Опрос «Сделайте математику интересной»
В этом обзоре есть графический органайзер, включающий шесть геометрических фигур.У каждой формы есть разные подсказки, которые позволят вам понять предыдущий математический опыт ваших учеников и их личный стиль обучения. Чтобы использовать это в своем классе, загрузите « Ideas to Make Math Class more Fun» Student Survey и предложите учащимся написать ответы в каждой из различных форм. Вы можете предложить учащимся сначала ответить на вопросы, которые их больше всего интересуют, а затем переходить к другим, пока они не выполнят все шесть. Соберите их графические органайзеры и просмотрите ответы своих учеников, чтобы узнать своих учеников и их мысли о классе математики.Особенно полезно сделать копию и сохранить ее в файле, чтобы вы могли просматривать ее в течение года.
# 2 Математический обзор в стиле Лайкерта
Этот опрос будет генерировать значимую информацию, предлагая учащимся отметить, полностью ли они согласны, согласны, чувствуют себя нейтральными, не согласны или категорически не согласны с каждым утверждением. Вы можете просмотреть ответы студентов, пролистывая их, или ввести результаты в электронную таблицу. Использование электронной таблицы позволит вам увидеть, насколько ваши ученики похожи и / или отличаются друг от друга, отслеживать, как их отношение меняется в течение года, и служить источником данных, который можно использовать для самооценки.Загрузите опрос «Расскажите мне, что вы думаете о математических классах » прямо сейчас.
Если вы преподаете дистанционно, вы можете создать онлайн-опрос с этими вопросами, чтобы студенты могли ответить!
# 3 Math Quotes Discussion Starter
Последнее из заданий нового учебного года для вашего класса математики включает в себя серию из восьми цитат, которые вы можете использовать в качестве подсказки для письма или обсуждения со своими учениками. Эти математические цитаты охватывают широкий спектр математических идей, от постоянства одного и того же до творческого.Мне нравится открывать учебный год таким образом и узнавать, что мои ученики на самом деле думают о математике. Я хочу оценивать их взгляды на математику, влиять на них и даже оспаривать их, помогая им получать удовольствие от предмета и не рассматривать его как обязательный и скучный предмет. Загрузите Каков ваш взгляд на математику? Активность сейчас.
Цитаты могут быть использованы для начала расширенного совместного использования think-pair в следующей предлагаемой последовательности:
Раздайте цитаты.
Призовите разных студентов-добровольцев прочитать цитаты вслух.
Попросите студентов молча обдумать цитаты, выбрать ту, которая им резонирует, и написать пару предложений о том, что они для них значат.
Попросите пары студентов поделиться друг с другом своими цитатами и тем, почему они выбрали их.
Откройте обсуждение в классе, чтобы учащиеся поделились своим мнением о классе математики и математики.
Подсчитайте количество студентов, которые выбрали каждую цитату, чтобы подвести итоги обсуждения в классе различных способов рассмотрения математики.
# 4 Обсуждение номера
Поделившись одним числом (-2, ⅔, 0 и т. Д.) В открытом обсуждении, вы сможете оценить, что ваши ученики помнят из предыдущего года, и начать узнавать об уровне комфорта и способностях каждого из ваши ученики. Беседа с числами — отличный способ для каждого ученика высказаться в классе математики, а для вас — познакомиться с личностями каждой из ваших групп учеников!
Для выполнения этого задания вы можете использовать доску и маркеры сухого стирания или бумагу для плакатов и маркеры, чтобы сохранить мысли каждого класса и показать их по всей комнате.Учащиеся должны думать (без бумаги и карандаша) о том, что приходит в голову, когда они видят число. Попросите их рассмотреть количество, операции, представления и т. Д. В зависимости от того, что подходит для их уровня обучения. После нескольких минут самостоятельного обдумывания обойдите комнату и позвольте каждому ученику поделиться идеей. Примите участие каждого учащегося с положительным подтверждением и запишите его на доске. Во время обмена вы можете сделать паузу и обсудить идеи дальше, связать идеи нескольких студентов или задать вопросы вслух, чтобы еще больше побудить задуматься.
# 5 Математическая автобиография
Последнее из заданий нового учебного года для вашего класса математики — это самостоятельное мероприятие, позволяющее учащимся поделиться с вами о себе и своем прошлом математическом опыте. Понимание того, кто ваши ученики и откуда они пришли, — вот корни, которые позволяют расцветать отношениям между учителем и учеником. В зависимости от количества времени, которое у вас есть, и уровня обучения ваших учеников, эта задача может быть довольно гибкой. Конечный продукт может быть сколь угодно сложным; некоторые учителя могут выбрать, чтобы ученики напечатали свои автобиографии, а затем раскрасили их или наклеили на бумагу, чтобы развесить их в классе.
Попросите учащихся поразмышлять и написать о некоторых или всех этих вопросах и темах либо в классе, либо в качестве домашнего задания:
- Опишите некоторые из самых запоминающихся моментов, которые у вас были в связи с математикой, как хорошей, так и плохой.
- Что вы думаете о математике? Если бы математика была животным, что бы это было и почему?
- Опишите, какой у вас был опыт общения с учителями математики, как хороших, так и плохих
- Как вы себя чувствуете в классе математики? Испуганный? Нервный? В восторге?
- С чем вы больше всего боретесь, когда изучаете математику?
- Что облегчает вам изучение математики?
- Если бы вы дали определение математике тому, кто не знает, что это такое, что бы вы сказали?
- Расскажите мне еще что-нибудь, что вы хотели бы, чтобы я знал о вас!
Резюме
Задания, которые используются в первые несколько дней в школе, заложат основу для взаимоотношений, которые вы сможете построить со своими учениками, и среды, которую вы сможете создать в своем классе математики.Использование этих пяти заданий поможет вам показать своим ученикам, что вы действительно заботитесь о них, и поможет вам узнать своих учеников как людей, так и как изучающих математику.
Виды листов 3D-фигур спереди, сверху и сбоку
Просмотрите эти виды спереди, сверху и сбоку PDF-файлов рабочих листов с трехмерными фигурами, чтобы помочь учащимся 5–8 классов визуализировать объекты под разными углами и создавать двухмерные представления трехмерных объектов с использованием методов ортогональной проекции.Перспектива — это инструмент, с помощью которого мы смотрим на жизнь, ситуации, проблемы, людей с разных точек зрения. Концепция просмотра прямоугольных призм, трехмерных фигур и реальных объектов под разными углами побуждает учащихся понимать, что есть более чем один способ увидеть вещи, которые превратят их в эффективных решателей проблем в более позднем возрасте. Начните с нашего бесплатного рабочего листа.
Прямоугольные призмы, виды спереди, сверху и сбоку
Попросите энергичных бобров 5-го и 6-го классов выбрать двухмерные изображения с разных точек зрения, например, спереди, сверху и сбоку, чтобы описать каждую трехмерную прямоугольную призму.
Затенение твердых блоков в сетках
Сделайте набросок ортогональных проекций: виды спереди, сверху, справа и слева прямоугольных призм и закрасьте правильное количество единичных квадратов на сетке в этом формате PDF для печати.
Сопоставление тел с их ортогональными проекциями
Визуализация каждой прямоугольной призмы в трех основных видах и сопоставление каждого с ее двумерной ортогональной проекцией — это то, что учащиеся 7 и 8 классов делают с этим листом ортогональной проекции сплошных фигур.
Просмотр трехмерных фигур с разных точек зрения
Здесь представлены виды трехмерных фигур, таких как конусы, цилиндры, кубы и т. Д., С разных точек зрения. Определите грань 3D-формы, которая выглядит как 2D-фигура на основе указанного вида.
Визуализация реальных объектов
Изучите виды трехмерных реальных объектов. Визуализируйте и выясните сходство между изображением и его видом.Определите и напишите, является ли это видом 3D-объекта сверху, спереди или сбоку.
Рисование 2D-видов реальных 3D-объектов
Творчество и обучение становятся неотделимыми в этом графическом представлении реальных объектов pdf. Просматривайте каждую трехмерную реальную структуру с заданной точки зрения и создавайте одинаковые двухмерные чертежи.
Какие стратегии работают для учащихся, испытывающих трудности, или учащихся с ограниченными возможностями обучения?
Согласно Национальной оценке успеваемости в образовании 2015 года, две трети восьмиклассников достигли базового или ниже базового уровня владения математикой.Кроме того, более 90 процентов восьмиклассников с ограниченными возможностями достигли базового или ниже базового уровня владения математикой. Эти статистические данные подчеркивают важность серьезной педагогической практики для поддержки учащихся, испытывающих трудности в математике, и учащихся с ограниченными возможностями обучения.
Основываясь на нашем обзоре исследований в этой области, эффективная практика преподавания математики часто включает стратегии, которые включают:
- Систематические и подробные инструкции
- Визуальное представление функций и взаимосвязей, например, манипуляторы, изображения и графики
- Инструктаж с коллегами
- Текущая, формирующая оценка
Наши библиотекари недавно собрали эти легкодоступные, основанные на исследованиях ресурсы, которые дают учителям представление о том, что работает при обучении математике учащихся, испытывающих трудности, и учащихся с ограниченными возможностями обучения.
Практическое руководство Института педагогических наук (IES)
Помощь учащимся, борющимся с математикой: ответ на вмешательство для начальной и средней школы (2009)
Это практическое руководство содержит восемь рекомендаций, которые помогут учителям, директорам и школьным администраторам выявить учащихся, нуждающихся в помощи по математике, и удовлетворить потребности этих учащихся с помощью целенаправленных мероприятий. Каждая рекомендация содержит практические предложения по реализации.
Исследования, посвященные педагогической практике
Интенсивные занятия по математике (2015)
Интенсивное вмешательство — это индивидуальный, требовательный и концентрированный подход к обучению. В этой статье представлены основанные на фактах элементы интенсивного вмешательства, которые учителя должны учитывать при планировании, реализации и мониторинге интенсивного вмешательства в математику.
Практика математического образования для учащихся с ограниченными возможностями и других учащихся, испытывающих трудности: тематические исследования шести школ в двух штатах Северо-Востока и островов (2008)
В этом отчете подробно описывается практика шести школ, которые прилагают целенаправленные усилия для улучшения математического образования учащихся с ограниченными возможностями и других учащихся, испытывающих трудности.В нем изучаются методы каждой школы по улучшению усвоения математики всеми учащимися, а также конкретная поддержка учащихся с ограниченными возможностями и других учащихся, испытывающих трудности, и определяются проблемы, с которыми школы сталкиваются при обслуживании учащихся с различными потребностями.
Инструкции по математике для учащихся с ограниченными возможностями или трудностями в изучении математики: Руководство для учителей (2008)
В этом руководстве описаны семь эффективных методик преподавания математики учащимся K – 12 с нарушением обучаемости, которые были выявлены в синтезе интервенционных исследований Центра обучения, а также включены рекомендации из «Заключительного отчета Национальной консультативной группы по математике».«
Использование предположений при поиске основанных на фактических данных математических практик для разных учащихся (2016)
Этот документ представляет собой руководство для преподавателей, ищущих новейшие научно обоснованные исследования для повышения вероятности улучшения успеваемости по математике для учащихся с математическими отклонениями и для того, чтобы дать учителям определенную степень уверенности в эффективности их обучения.
Дополнительные ресурсы
Какие практические занятия по математике могут использовать учителя?
Этот ресурс от Iris Center охватывает несколько основанных на исследованиях стратегий обучения учащихся, испытывающих трудности в математике.Разделы включают подробные инструкции, визуальные представления, инструкции по схемам, метакогнитивные стратегии и эффективные занятия в классе.
Математика для учащихся с нарушением обучаемости из числа языковых меньшинств: рекомендации по преподаванию
В этой статье исследуются характеристики, а также культурные и лингвистические факторы, имеющие отношение к обучению математике учащихся с ограниченными возможностями обучения из языковых меньшинств. Рекомендации и стратегии представлены с уделением внимания уравновешиванию влияния языка, культуры и инвалидности.Конкретные рекомендации относятся к:
- Оценка математических способностей
- Выбор языка обучения
- От конкретного понимания к абстрактному
- Использование стратегий, помогающих учащимся развивать математические концепции
- Использование математики для развития языка
- Принимая во внимание сильные стороны студентов
10 основных практических занятий по математике для всех начальных школ
В этом кратком ресурсе перечислены концепции и примеры обучения математике, основанные на доказательствах эффективности высококачественных исследований.Вы также можете загрузить прилагаемые 10 основных математических практик для всех средних и старших школ.
Дополнительные исследования
Конкретные нарушения обучаемости по математике: всесторонний обзор (2018)
В этой статье рассматривается изменяющаяся терминология для обозначения конкретных нарушений обучаемости в математике и описываются новые генетические исследования и исследования мозга, которые относятся к людям с математическими нарушениями. Важно сохранять перспективу развития математических нарушений, поскольку представление меняется с возрастом, обучением и различными моделями идентификации (образовательными и медицинскими).Вмешательство требует систематического подхода к скринингу и реабилитации, который развивался благодаря большему количеству научно обоснованной литературы.
Руководство по оценке программ математики, используемых учителями специального образования (2018)
Эта статья предоставляет учителям специального образования практическое руководство по оценке и оценке того, в какой степени математические программы содержат подтвержденные принципы подробного обучения математике.

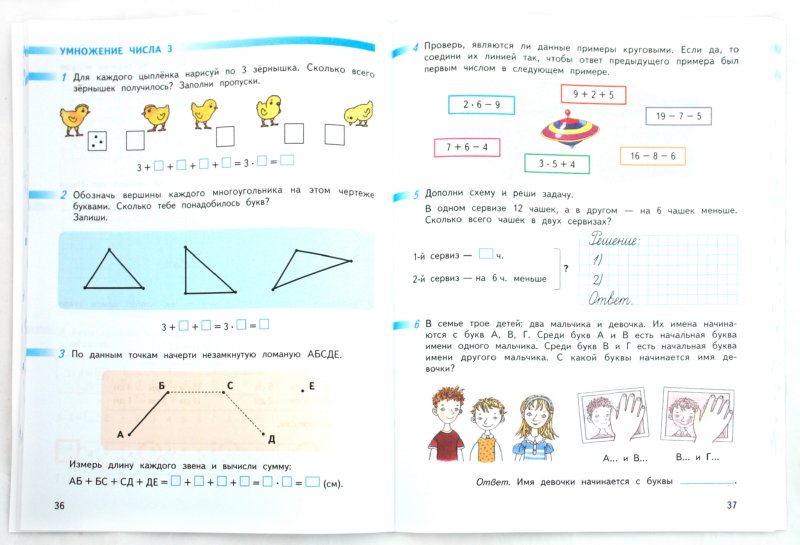
 Главный двигатель обучения — врождённое любопытство ребёнка. Задания подогревают интерес к теме и стимулируют желание довести её изучение до конца без посторонней помощи. А параллельно учат планировать действия, находить и исправлять свои ошибки.
Главный двигатель обучения — врождённое любопытство ребёнка. Задания подогревают интерес к теме и стимулируют желание довести её изучение до конца без посторонней помощи. А параллельно учат планировать действия, находить и исправлять свои ошибки. , Фрейтаг И.П., Шипилова Н.В. и другие.
, Фрейтаг И.П., Шипилова Н.В. и другие.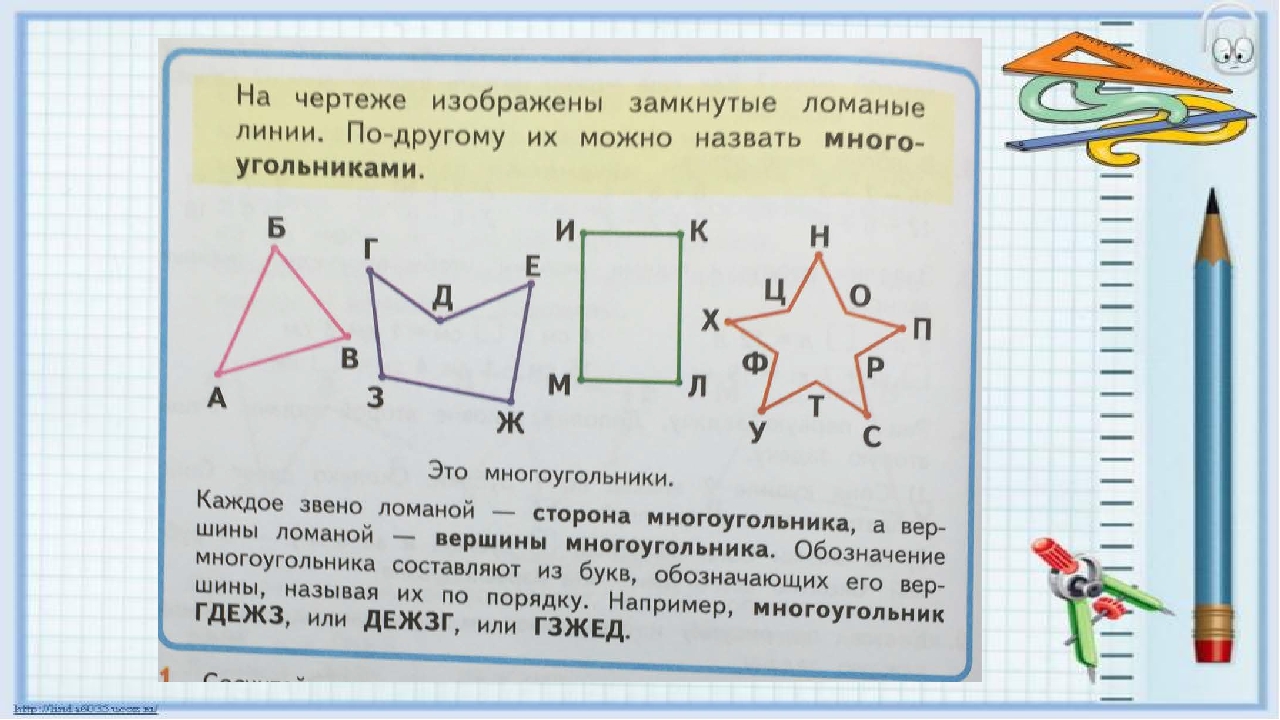 Авторы: Баранова К.М., Дули Д., Копылова В.В., Мильруд Р.П., В. Эванс.
Авторы: Баранова К.М., Дули Д., Копылова В.В., Мильруд Р.П., В. Эванс. Одних родителей радует, что учебники напоминают художественные произведения. Других смущает отсутствие правил в рамочках.
Одних родителей радует, что учебники напоминают художественные произведения. Других смущает отсутствие правил в рамочках.