|
youtube.com/embed/Z62_v8qWJBM?rel=0″ frameborder=»0″ allowfullscreen=»»>
ГДЗ номер 336 математика 5 класс Мерзляк, Полонский
ГДЗ номер 336 математика 5 класс Мерзляк, Полонский Авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. ЯкирСерия: Алгоритм успеха
Тип книги: Учебник
Рекомендуем посмотреть
youtube.com/embed/P7U9_kg_eFo?start=3738″ frameborder=»0″ allowfullscreen=»»/> Подтяни успеваемость и увеличь шансы успешной сдачи экзаменов на
EDN.ru
– мультимедийной платформе для проведения индивидуальных онлайн-занятий с репетиторами!
Решебник 2 / номер / 336Отключить рекламу
Страница не найдена
Новости
27 сен
Директор Лиги безопасности интернета Екатерина Мизулина в стриме RT «Летучка» рассказала, как предотвратить нападения на образовательные учреждения.
27 сен
Счётная палата России отметила сомнения относительно обоснованности освоения средств федерального бюджета, которые были выделены на организацию горячего питания школьников 1-4-х классов в семи регионах на 100%-ном уровне.
Четырёх американских подростков обвинили в заговоре о нападении на среднюю школу в Пенсильвании, которое планировалось совершить в 2024 году в годовщину трагедии в Колумбайн.
25 сен
В Якутске школы и организации дополнительного образования переведены на дистанционную форму обучения в связи с ростом заболеваемости ОРВИ.
Об этом сообщает пресс-служба мэрии Якутска.
24 сен
Саратовские школы переходят на дистанционное обучение из-за роста заболеваемости коронавирусной инфекцией и ОРВИ, сообщила пресс-служба администрации Саратова.
24 сен
Клинический психолог Ирина Коржаева заявила, что возможности нейросети по мониторингу и выявлению опасных учеников ограничены, поскольку программа не сможет вычислить именно стрелков.
24 сен
Новые образовательные центры «Точка роста» открыли ещё более чем в 40 городских округах Московской области.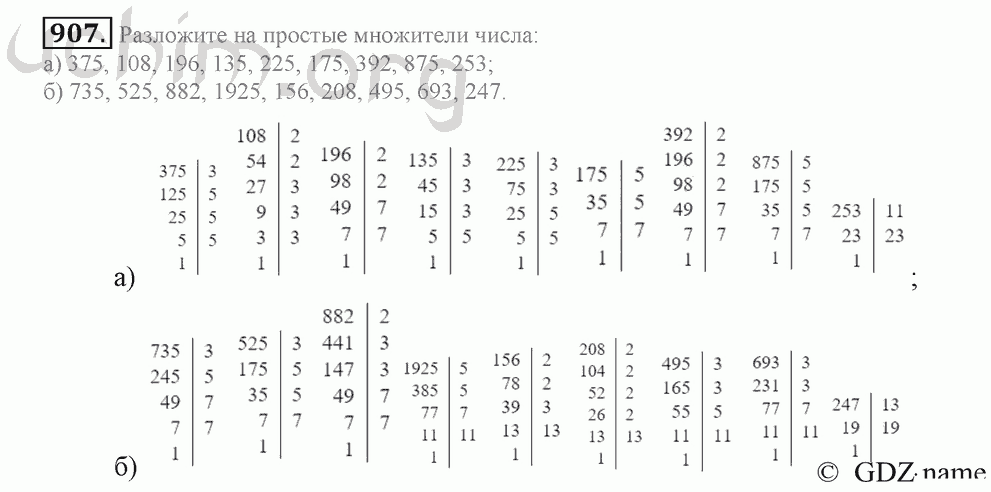
Их число в регионе достигло 242.
Задача 336 математика 5 класси.и.зубарева :: noiturbiowor
12.09.2016 02:37
Готовые домашние задания к учебнику математике за 5 класс Зубарева И.И., Мордкович А.Г. задание номер 336 — на рис. представлено решение задачи №336 — ответы, гдз и решебник онлайн.
5 класс. Зубарева И.И., Мордкович А.Г. Решения примеров и задач учебника: «Математика. 5 класс. Зубарева И.И., Мордкович А.Г.» (Москва: Мнемозина, 2007 — 2013 год).
авторы: И.И. Зубарева, А.Г. Мордкович. издательство: Мнемозина 2015 год. Решебник к книге «Математика. 5 класс Зубаева И.И.» включает в себя ответы на представленные в учебнике задания.
Математика — 5 класс Зубарева Ирина Ивановна, Мордкович Александр Григорьевич (Ответы).
53. Достоверные, невозможные и случайные события 54. Комбинаторные задачи. Домашние контрольные работы.
Математика 5 класс Зубарева. Если вы в 5 классе и занимаетесь математикой по программе авторов И.И. Зубарева, А.Г. Мордкович, то этот гдз для вас. Здесь вы найдёте как условия задач, так и их решения.
ГДЗ(готовые домашние задания) к учебнику Математика 5 класс. Учебник для общеобразовательных учреждений. Зубарева И.И., Мордкович А.Г. На рисунке отображено решение упражнения Задача №336.
Подробный решебник ГДЗ к учебнику по Математике 5 класс Зубарева И.И., Мордкович А.Г. 2015, онлайн ответы на домашнюю работу.
ФГОС Зубарева, Мордкович Мнемозина. Рабочая тетрадь по математике 5 класс. Часть 1, 2 Ерина К учебнику Зубаревой, Мордковича Экзамен.
Авторы: Зубарева, Мордкович Класс: 5 Предмет: Математика. Выберите номер задания учебника. ГДЗ к Рабочей Тетрадиперейти. Решебник по математике для 5 класса Зубарева.
Вы здесь: ГДЗ (решебник) 6 класс МАТЕМАТИКА Зубарева И.И. и др. Зубарева И.
И. Мордкович А.Г. гдз решебник алгебра 6 класс. 336. 337. 338.
Читайте также:
решебник по русскому языку 8 класс львова и львов онлайн
решебник по русскому языку 8 класс львова и львов онлайн
готовые домашние задания по математике 3 класс моро скачать через торрент
Страница 53 №328-336 ГДЗ к учебнику «Математика» 5 класс Виленкин, Жохов, Чесноков
Задание № 328. Найдите значение выражения:
а) 575 : 23 + 15 * 34;
б) (2884 + 1508) : 122 − 22;
в) 37 * 25 − 11 * 12;
г) (237 − 182) * 23 − 13.
Решение
a) 575 : 23 + 15 * 34 = 25 + 510 = 535
б) (2884 + 1508) : 122 − 22 = 36 − 22 = 14
в) 37 * 25 − 11 * 12 = 925 − 132 = 793
г) (237 − 182) * 23 − 13 = 1265 − 13 = 1252
Задание № 329. Составьте выражение для решения задачи и найдите его значение:
«В треугольнике ABC длина стороны АВ равна 5 см, сторона ВС длиннее стороны АВ на 8 см, а длина стороны АС меньше суммы длин сторон АВ и ВС на 6 см.
Найдите периметр треугольника».
Решение
АВ = 5 см;
ВС = АВ + 8 = 5 + 8 = 13 см;
AС = АВ + ВС − 6 = 5 + (5 + 8) − 6 = 12 см;
Р△ABC = АВ + ВС + АС = 5 + 13 + 12 = 30 см.
Задание № 330. Напишите сумму:
а) 256 − 16 и 3 + 14;
б) а + 98 и 49;
в) х + 32 и у + 13;
г) m − 98 и n + 56.
Решение
a) (256 − 16) + (3 + 14) = 257
б) (а + 98) + 49 = а + 147
в) (х + 32) + (у + 13) = х + у + 65
г) (m − 98) + (n + 56) = n + m − 42
Задание № 331. Напишите разность:
а) 13 + 65 и 11 + 54;
б) а + 86 и 91;
в) 181 + b и 195 − х;
г) х − 16 и у − 24.
Решение
a) (13 + 65) − (11 + 54) = 13
б) (а + 86) − 91 = a − 5
в) (181 + b) − (195 − x) = x + b − 14
г) (x − 16) − (у − 24) = x − у + 8
Задание № 332. Продолжительность дня а ч.
Чему равна продолжительность ночи? Составьте выражение. Найдите его значение при а = 8; 10; 12.
Решение
В сутках 24 ч, поэтому продолжительность ночи равна (24 − а) ч.
При а = 8 => 24 − а = 24 − 8 = 16 ч.
При а = 10 => 24 − а = 24 − 10 = 14 ч.
При а = 12 => 24 − а = 24 − 12 = 12 ч.
Задание № 333. Масса одного арбуза 6 кг, а масса другого на n кг меньше. Какова общая масса двух арбузов? Составьте выражение и найдите его значение при n = 2; 3; 4.
Решение
Масса второго арбуза равна (6 − n) кг.
Общая масса двух арбузов: 6 + (6 − n) = (12 − n) кг.
При n = 2 => 12 − n = 12 − 2 = 10 кг,
при n = 3 => 12 − n = 12 − 3 = 9 кг,
при n = 4 => 12 − n = 12 − 4 = 8 кг.
Задание № 334. У Коли m марок, а у Димы n марок. Они сложили их и поделили поровну. Сколько марок досталось каждому?
Напишите выражение и найдите его значение при m = 15, n = 21.
Имеет ли задача смысл, если m = 6, n = 9?
Решение
Каждому мальчику досталось (m + n) : 2 марок.
При m = 15, n = 21 => (m + n) : 2 = (15 + 21) : 2 = 36 : 2 = 18 марок.
При m = 6, n = 9; m + n = 9 + 6 = 15 марок не делятся поровну.
Задание № 335. Решите задачу, составляя выражение:
а) Прямоугольный участок земли имеет длину 85 м и ширину 47 м. Найдите периметр этого участка.
б) Ширина прямоугольного участка земли 47 м, а его длина х м. Чему равен периметр этого участка?
в) Длина прямоугольного участка земли 85 м, а его ширина у м. Чему равен периметр этого участка?
г) Длина прямоугольного участка земли у м, а его ширина х м. Чему равен периметр этого участка?
Решение
а) Периметр прямоугольного участка равен Р = 2 * (а + b), где а − длина участка, b − ширина участка:
при а = 85 м, b = 47 м => Р = 2 * (85 + 47) = 2 * 132 = 264 м.
б) Периметр прямоугольного участка равен Р = 2 * (а + b), где а − длина участка, b − ширина участка:
при а = х м, b = 47 м => Р = 2 * (х + 47) м.
в) Периметр прямоугольного участка равен Р = 2 * (а + b), где а − длина участка, b − ширина участка:
при а = 85 м, b = у м => Р = 2 * (85 + у) м.
г) Периметр прямоугольного участка равен Р = 2 * (а + b), где а − длина участка, b − ширина участка:
при а = у м, b = х м => Р = 2 * (y + х) м.
Задание № 336. Найдите значение выражения:
а) а + 7843, если а = 567; 2415;
б) 88 942 − х, если х = 44 761; 17 942;
в) (а + b) − 674, если а = 830, b = 243; а = 1712, b = 805.
Решение
а) При а = 567 ⇒ 567 + 7843 = 8410;
При а = 2415 ⇒ 2415 + 7843 = 10258.
б) При х = 44 761 ⇒ 88 942 − 44 761 = 44 181;
При х = 17 942 ⇒ 88 942 − 17 942 = 71 000.
в) При а = 830, b = 243 ⇒ (8830 + 243) − 674 = 8399;
При а = 1712, b = 805 ⇒ (1712 + 805) − 674 = 1843.
Номер задания 336 — ГДЗ Математика Никольский учебник 5 класс ξ Super ГДЗ ξ
Математика
- дм Потапов Шевкин
- Тетрадь-тренажер Бунимович
- Тетрадь-экзаменатор Бунимович
- Учебник Никольский
- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
- 6 класс
- 7 класс
- 8 класс
- 9 класс
- 10 класс
- 11 класс
Номер задания 336 — решение из ГДЗ Математика Никольский учебник 5 класс
Номер задания:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897898899900901902903904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934935936937938939940941942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974975976977978979980981982983984985986987988989990991992993994995996997998999100010011002100310041005100610071008100910101011101210131014101510161017101810191020102110221023102410251026102710281029103010311032103310341035103610371038103910401041104210431044104510461047104810491050105110521053105410551056105710581059106010611062106310641065106610671068106910701071107210731074107510761077107810791080108110821083108410851086108710881089109010911092109310941095109610971098109911001101110211031104110511061107110811091110111111121113111411151116111711181119112011211122112311241125112611271128112911301131113211331134113511361137113811391140114111421143114411451146114711481149115011511152115311541155115611571158115911601161116211631164116511661167116811691170117111721173117411751176117711781179118011811182118311841185118611871188118911901191119211931194119511961197119811991200120112021203120412051206120712081209121012111212121312141215Математика 5 клас номер 336
Скачать математика 5 клас номер 336 rtf
Здесь вы найдете учебник по Математике 5 класса авторы: Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд, от издательства: Мнемозина ГДЗ содержит все ответы на вопросы и поможет Вам правильно выполнить домашнее задание. ГДЗ к рабочей тетради по математике за 5 класс Рудницкая В.Н.
можно скачать здесь. ГДЗ к учебнику по математике за 5 класс Виленкин 1, 2 часть (новый, ) можно скачать здесь. ГДЗ к контрольным работам по математике за 5 класс Жохов В.И.
можно скачать здесь. ГДЗ к дидактическим материалам по математике за 5 класс Попов М.А. можно скачать здесь. Введите номер задания. Упражнения. 1. ➜ Ответ к заданию № — готовое решение к учебнику по математике за 5 класс (упражнение ). Авторы: Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. ✔ Бесплатный решебник. Ответы к учебнику по математике за 5 класс Дорофеев, Шарыгин, Суворова — номер Общая оценка: Поделитесь с друзьями. Выбрать другой номер.
Комментарии. Adblock detector. Натуральные числа Сложение и вычитание натуральных чисел Числовые и буквенные выражения Ответы к стр.
53 Найдите значение выражения: а) 23 + 15 • Математика 5 класс. Учебник. Никольский, Потапов, Решетников. Если положить перед ребенком сборник и разрешить ему «скатать» номер, то это естественно породит в нем стремление и дальше поступать аналогичным образом. Поэтому стоит с самого начала приучать ваше чадо к тому, что решебник — это лишь способ самопроверки, который ни в коем случае не заменит изучение материала.
Основные принципы использования ГДЗ. Решебник к пособию «Математика 5 класс Учебник Никольский» рассчитан на то, чтобы дать ученикам более полное представление о текущей программе. При помощи него они могут более детально разобраться в теме и вникнуть в суть решения. В задании надо найти значение трех буквенных выражений. Чтобы сделать это задание без ошибок, воспользуйтесь нашим видео с решением.
Задание № — Математика 5 класс (Виленкин, Жохов).
ГДЗ учебника Математика 5 класс Н. Я. Виленкина, В. И. Жохова, А. С. Чеснокова, С. И. Шварцбурда. Издательство: Мнемозина, серия: Математика. Состоит из одной части (1 часть страниц.) Учебник математики состоит из 8 параграфов, постепенно изучая которые школьники приобретут новые знания по предмету. ГДЗ к учебнику по математике 5 класс Виленкин с углубленным решением всех упражнений, которые Вы найдете на сайте ЯГДЗ, помогут учащимся сполна вникнуть в суть изучаемого материала, сделают процесс познания учебного предмета интересным и увлекательным.
Математика — решебник 5 класс по учебнику Виленкина — Списать решение на задание номер № Данные ответы на задачи также подходят к учебнику , и года (ФГОС). Читать другую версию ГДЗ!!! Решение задания № Смотреть все номера. Решение задания № Смотреть другую домашнюю работу и ГДЗ по математике!. Видео решения задачи № по Математике 5 класс автора Виленкин Н.Я. Если ищете ГДЗ по Математике за 5 класс по № — Математика 5 класс Виленкин. Il y a ans. Видео решение к номеру по математике за 5 класс, авторов Н.Я.
Виленкин, В.И. Жохов, А.С. Чесноков, С.И. № — Математика 5 класс Мерзляк. Il y a ans. Видео решение к номерам по математике за 5 класс, авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир Математика 5 класс Дорофеев, Шарыгин УПР Il y a ans. Видео решение к номеру по математике за 5 класс, авторов Зубарева И.И., Мордокович А.Г. Более подробное гдз к Задание № — Математика 5 класс (Виленкин, Жохов).
Il y a ans.
rtf, fb2, fb2, EPUBПохожее:
из 336 — Найдите простые множители / Факторы 336
Знаете ли вы, что 336 — четное составное число, разложение на простые множители которого состоит из трех простых чисел: 2, 3 и 7? Сумма простых делителей 336 равна 12, что снова является составным числом. В этой главе мы вычислим множители 336, простые множители 336 и множители 336 попарно вместе с решенными примерами и интерактивными вопросами.
- Факторы 336: 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 42, 48, 56, 84, 112, 168 и 336.
- Простое факторизация 336: 336 = 2 4 × 3 × 7
Каковы факторы 336?
Множители 336 — это числа, которые при умножении дают 336. Это числа, которые делят 336, не оставляя остатка. Следовательно, когда мы умножаем любые два целых числа друг на друга и получаем в качестве ответа 336, оба числа считаются делителями 336.
Как вычислить множители 336?
Мы можем вычислить множители 336, найдя все числа, делящие 336, не оставляя остатка.Давайте начнем с проверки делителей 336, начиная с 1. Мы можем выразить 336 как произведение его простых множителей в методе разложения на простые множители, и мы можем разделить 336 на его делители в методе деления. Для чисел, делящих 336 целиком, делители, а также их частные являются множителями 336.
| Числа разделительные 336 | Факторы 336 |
|---|---|
| 336/1 = 336 | 1 и 336 — множители 336 |
| 336/2 = 168 | 2 и 168 — множители 336 |
| 336/3 = 112 | 3 и 112 являются множителями 336 |
| 336/4 = 84 | 4 и 84 — множители 336 |
| 336/6 = 56 | 6 и 56 — множители 336 |
| 336/7 = 48 | 7 и 48 — множители 336 |
| 336/8 = 42 | 8 и 42 — множители 336 |
| 336/12 = 28 | 12 и 28 — множители 336 |
| 336/14 = 24 | 14 и 24 являются множителями 336 |
| 336/16 = 21 | 16 и 21 — множители 336 |
Следовательно, факторов 336 равны 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 42, 48, 56, 84, 112, 168 и 336.
Изучите факторы, используя иллюстрации и интерактивные примеры.
- Факторы 168 — Факторы 168: 1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 28, 42, 56, 84 и 168.
- Факторы 112 — Факторы 112: 1, 2, 4, 7, 8, 14, 16, 28, 56 и 112.
- Факторы 84 — Факторы 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 и 84.
- Факторы 36 — Факторы 36 равны 1, 2, 3, 4, 6, 9, 12, 18 и 36.
- Факторы 42 — Факторы 42 равны 1, 2, 3, 6, 7, 14, 21 и 42.
- Факторы 21 — Факторы 21 равны 1, 3, 7 и 21.
из 336 по прайм-факторизации
Когда составное число выражается как произведение его простых множителей, оно называется факторизацией на простые множители. Чтобы получить разложение 336 на простые множители, мы используем два метода:
- Метод 1: метод факторного дерева
- Метод 2: Метод перевернутого деления
Метод 1: Метод факторного дерева
Факторное дерево 336:
Метод 2: Метод верхнего деления
Делим 336 на наименьший простой делитель, равный 2
.336/2 = 168
168 делится на наименьший простой множитель, и получается частное.Этот процесс повторяется до тех пор, пока мы не получим частное, равное 1. Таким образом, разложение 336 на простые множители будет:
Следовательно, простые делители 336 равны 2, 3 и 7.
Разложение 336 на простые множители дает 2 4 × 3 × 7.
Фактор 336 в парах
Пара чисел, которые при умножении дают 336, являются парами множителей 336. Давайте рассмотрим следующие попарно множители 336. Отрицательные парные множители 336 получаются, когда произведение двух отрицательных чисел берется (- ve × — ve) = + ve.
- Положительные парные факторы числа 336: (1, 336), (2, 168), (3, 112), (4, 84), (6, 56), (7, 48), (8, 42) , (12, 28), (14, 24), (16, 21)
- Отрицательные парные факторы 336: (-1, -336), (-2, -168), (-3, -112), (-4, -84), (-6, -56), (- 7, -48), (-8, -42), (-12, -28), (-14, -24), (-16, -21)
Важные примечания:
- Поскольку 336 оканчивается двумя последними цифрами, так как 36 и 36 делится на 4, мы можем сказать, что 4 является одним из делителей 336.
- Так как сумма цифр 336 равна 12, один из множителей 336 равен 3.
- 336 — не совершенное квадратное число. Следовательно, у него четное количество факторов.
Сложные вопросы:
- Являются ли 672 и 3/4 множителями 336? Почему ты так думаешь?
Часто задаваемые вопросы о факторах 336
Какие множители 336?
Множители 336: 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 42, 48, 56, 84, 112, 168 и 336.
Какие простые делители 336?
Простые множители 336: 2, 3 и 7.
Все множители 336 простые?
Нет, все множители 336 не простые.
Какие общие множители у 336 и 440?
Делители 336: 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 42, 48, 56, 84, 112, 168 и 336.
Множители 440: 1, 2, 4, 5, 8, 10, 11, 20, 22, 40, 44, 55, 88, 110, 220 и 440.
Следовательно, общие множители 336 и 440 равны 1, 2, 4 и 8.
9 является множителем 336?
Нет, 9 не является множителем 336.
% PDF-1.6 % 1167 0 объект> эндобдж xref 1167 143 0000000016 00000 н. 0000009802 00000 н. 0000009940 00000 н. 0000010189 00000 п. 0000010234 00000 п. 0000010366 00000 п. 0000011714 00000 п. 0000011774 00000 п. 0000011825 00000 п. 0000012664 00000 п. 0000013844 00000 п. 0000014057 00000 п. 0000014272 00000 п. 0000015455 00000 п. 0000015500 00000 н. 0000016684 00000 п. 0000016900 00000 н. 0000018477 00000 п. 0000018809 00000 п. 0000018864 00000 п. 0000019080 00000 п. 0000019497 00000 п. 0000020681 00000 п. 0000020738 00000 п. 0000020948 00000 п. 0000022130 00000 н. 0000022292 00000 п. 0000023720 00000 п. 0000044521 00000 п. 0000044734 00000 п. 0000045100 00000 п. 0000045233 00000 п. 0000046654 00000 п. 0000055972 00000 п. 0000056138 00000 п. 0000056210 00000 п. 0000056405 00000 п. 0000057451 00000 п. 0000058475 00000 п. 0000058521 00000 п. 0000059498 00000 п. 0000059551 00000 п. 0000121648 00000 н. 0000121844 00000 н. 0000122176 00000 н. 0000122313 00000 н. 0000123513 00000 н. 0000123568 00000 н. 0000124563 00000 н. 0000125878 00000 н. 0000126270 00000 н. 0000126997 00000 н. 0000127798 00000 н. 0000129726 00000 н. 0000130333 00000 п. 0000130545 00000 н. 0000130753 00000 п. 0000130985 00000 п. 0000131181 00000 н. 0000132008 00000 н. 0000132941 00000 н. 0000136111 00000 п. 0000136315 00000 н. 0000136548 00000 н. 0000137685 00000 н. 0000138755 00000 н. 0000139880 00000 н. 0000141468 00000 н. 0000141699 00000 н. 0000143151 00000 п. 0000155762 00000 н. 0000155813 00000 н. 0000156022 00000 н. 0000156073 00000 н. 0000167071 00000 н. 0000167281 00000 н. 0000167332 00000 н. 0000167384 00000 н. 0000167623 00000 н. 0000167675 00000 н. 0000167914 00000 н. 0000168045 00000 н. 0000168096 00000 н. 0000168228 00000 п. 0000168544 00000 н. 0000168596 00000 н. 0000168648 00000 н. 0000168772 00000 н. 0000168823 00000 н. 0000169145 00000 н. 0000169270 00000 н. 0000169321 00000 н. 0000169560 00000 н. 0000169768 00000 н. 0000169819 00000 н. 0000169870 00000 н. 0000169994 00000 н. 0000170045 00000 н. 0000170097 00000 н. 0000170302 00000 н. 0000170353 00000 п. 0000181056 00000 н. 0000181259 00000 н. 0000181310 00000 н. 0000196038 00000 н. 0000196316 00000 н. 0000196368 00000 н. 0000208557 00000 н. 0000208766 00000 н. 0000208817 00000 н. 0000209398 00000 н. 0000209597 00000 н. 0000209648 00000 н. 0000210226 00000 п. 0000210360 00000 н. 0000210384 00000 п. 0000210408 00000 н. 0000210432 00000 н. 0000210455 00000 н. 0000210479 00000 н. 0000210553 00000 п. 0000210633 00000 н. 0000210720 00000 н. 0000210764 00000 н. 0000210858 00000 п. 0000210902 00000 н. 0000210997 00000 н. 0000211041 00000 н. 0000211135 00000 п. 0000211179 00000 н. 0000211273 00000 н. 0000211317 00000 н. 0000211411 00000 н. 0000211455 00000 н. 0000211549 00000 н. 0000211593 00000 п. 0000211688 00000 н. 0000211732 00000 н. 0000211826 00000 н. 0000211869 00000 н. ֭ ўoI] 3.aSc) DFIOBtͲ | 8G [n4f # r`k>; cHhk «N} pnX ‘\ kt + / p8O / g |% G} ΡX {xC͕ = $ ЫQȸNKwzO 縤 7
Go Math Grade 5 Answer Key Глава 7 Умножение Дроби — ответы по математике CCSS
Если вы ищете ключ ответа на 5-й класс по математике в главе 7, значит, вы попали в нужное место. Мы уже упоминали про умножение дробей для 5-го класса по математике, главу 7, с прямым объяснением всех задач. Родители, которые хотели дать своим детям достаточно практики по принципам умножения дробей, могут дать им ключ к ответу в 5-м классе по математике, глава 7, Умножение дробей.Повысьте свои математические навыки, практикуясь в HMH Go Math Grade 5 Answer Key Ch 7 Multiply Fractions.
Иди по математике, 5 класс. Ключевой ответ Глава 7 Умножение дробей
Считаете ли вы, что концепция умножения дробей трудна? Нет больше с нашим Go Math Answer Key 5 класс Глава 7 Умножение дробей, поскольку в них подробно объяснены концепции. Начните изучать основы прямо с базового уровня с помощью нашего 5-го класса Go Math Answer Key Ch 7 Multiply Fractions. Проверьте свой уровень подготовки, ответив на вопросы в конце ключа ответов для 5-го класса по математике для умножения дробей.Таким образом вы сможете оценить свои стандарты подготовки.
Глава 7 — Урок 1. Найдите часть группы
Глава 7 — Урок 2: Исследование • Умножение дробей и целых чисел
Глава 7 — Урок 3: Умножение дробей и целых чисел
Глава 7 — Урок 4: Исследование • Умножение дробей
Глава 7 — Урок 5: Сравните коэффициенты дроби и продукты
Глава 7 — Урок 6: Умножение дробей
Глава 7 — Контрольная точка в середине
Глава 7 — Урок 7. Расследование • Площадь и смешанные числа
Глава 7 — Урок 8: Сравните смешанные числовые факторы и продукты
Глава 7 — Урок 9: Умножение смешанных чисел
Глава 7 — Урок 10: Решение проблем • Найдите неизвестную длину
Глава 7 — Глава 7 Обзор / тест
Поделиться и показать — Страница No.293
Вопрос 1.
Завершите модель, которую нужно решить.
\ (\ frac {7} {8} \) из 16 или \ (\ frac {7} {8} \) × 16
Сколько рядов счетчиков там?
_____ ряды
Ответ: 8
По рисунку выше можно сказать, что количество счетчиков составляет 8 рядов.
Вопрос 1.
Сколько счетчиков в каждом ряду?
_____ счетчики
Ответ: 2
В каждом ряду по 2 фишки.
Вопрос 1.
Обведите ____ строк, чтобы решить задачу.
_____ ряды
Ответ: 7
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
Вопрос 1.
Сколько счетчиков обведено кружком?
\ (\ frac {7} {8} \) из 16 =
или \ (\ frac {7} {8} \) × 16 =
_____ счетчиков
Ответ: 14
\ (\ frac {7} {8} \) × 16
8 делит 16 на два раза.
Итак, \ (\ frac {7} {8} \) × 16 = 7 × 2 = 14
Следовательно, 14 счетчиков обведены кружком.
Используйте модель для решения.
Вопрос 2.
\ (\ frac {2} {3} \) × 18 = _____
Ответ: 12
Пояснение:
\ (\ frac {2} {3} \) × 18
3 делит 18 шесть раз.
2 × 6 = 12
Вопрос 3.
\ (\ frac {2} {5} \) × 15 = _____
Ответ: 6
Пояснение:
\ (\ frac {2} {5} \) × 15
5 делит 15 на три раза.
2 × 3 = 6
Таким образом, \ (\ frac {2} {5} \) × 15 = 6
Вопрос 4.
\ (\ frac {2} {3} \) × 6 = _____
Ответ: 4
Пояснение:
\ (\ frac {2} {3} \) × 6
3 делит 6 дважды.
\ (\ frac {2} {3} \) × 6
2 × 2 = 4
\ (\ frac {2} {3} \) × 6 = 4
Самостоятельно
Используйте модель для решения.
Вопрос 5.
\ (\ frac {5} {8} \) × 24 = _____
Ответ: 15
Пояснение:
\ (\ frac {5} {8} \) × 24
8 делит 24 на три раза.
5 × 3 = 15
\ (\ frac {5} {8} \) × 24 = 15
Вопрос 6.
\ (\ frac {3} {4} \) × 24 = _____
Ответ: 18
Пояснение:
\ (\ frac {3} {4} \) × 24
4 делит 24 шесть раз.
\ (\ frac {3} {4} \) × 24 = 3 × 6 = 18
Итак, \ (\ frac {3} {4} \) × 24 = 18
Вопрос 7.
\ (\ frac {4} {7} \) × 21 = _____
Ответ: 12
Пояснение:
\ (\ frac {4} {7} \) × 21
7 делит 21 на три раза.
4 × 3 = 12
\ (\ frac {4} {7} \) × 21 = 12
Вопрос 8.
\ (\ frac {2} {9} \) × 27 = _____
Ответ: 6
Пояснение:
\ (\ frac {2} {9} \) × 27
9 делит 27 на три раза.
2 × 3 = 6
\ (\ frac {2} {9} \) × 27 = 6
Вопрос 9.
\ (\ frac {3} {5} \) × 20 = _____
Ответ: 12
Пояснение:
\ (\ frac {3} {5} \) × 20
5 делит 20 четыре раза.
3 × 4 = 12
Таким образом, \ (\ frac {3} {5} \) × 20 = 12
Вопрос 10.
\ (\ frac {7} {11} \) × 22 = _____
Ответ: 14
Пояснение:
\ (\ frac {7} {11} \) × 22
11 делит 22 на два раза.
7 × 2 = 14
\ (\ frac {7} {11} \) × 22 = 14
Решение проблем — Стр. № 294
Используйте таблицу 11-12.
Вопрос 11.
Четыре пятых марок Зака содержат изображения животных. Сколько марок с изображениями животных у Зака? Используйте модель для решения.
_____ марок
Ответ: 24 марки
Пояснение:
При этом четыре пятых марок Зака содержат изображения животных.
Количество марок, которые собрал Зак, составляет 30
30 × \ (\ frac {4} {5} \)
5 делит 30 шесть раз.
6 × 4 = 24
У Зака 24 марки с изображениями животных.
Вопрос 12.
Зак, Тери и Пако объединили иностранные марки из своих коллекций для демонстрации марок. Из их коллекций, \ (\ frac {3} {10} \) марок Зака, \ (\ frac {5} {6} \) марок Тери и \ (\ frac {3} {8} \) марок Пако были из зарубежных стран. Сколько марок было на их витрине? Объясните, как вы решили проблему.
_____ марок
Ответ: 33 марки
Пояснение:
Зак, Тери и Пако объединили иностранные марки из своих коллекций для демонстрации марок.
Из их коллекций, \ (\ frac {3} {10} \) марок Зака, \ (\ frac {5} {6} \) марок Тери и \ (\ frac {3} {8} \ ) марок Пако были из зарубежных стран.
Кол-во марок, собранных Заком = 30
Кол-во марок, собранных Тери = 18
Кол-во марок, собранных Пако = 24
\ (\ frac {3} {10} \) из 30
\ (\ frac {3} {10} \) × 30 = 3 × 3 = 9
\ (\ frac {5} {6} \) × 18 = 5 × 3 = 15
\ (\ frac {3} {8} \) × 24 = 3 × 3 = 9
Теперь сложите все штампы = 9 + 9 + 15 = 33
Вопрос 13.
В коллекции Паулы 24 марки. Среди ее марок \ (\ frac {1} {3} \) есть изображения животных. Из ее марок с изображениями животных \ (\ frac {3} {4} \) этих марок есть изображения птиц. На скольких марках изображены птицы?
_____ марок
Ответ: 6 марок
Пояснение:
В коллекции Паулы 24 марки. Среди ее марок \ (\ frac {1} {3} \) есть изображения животных.
Из ее марок с изображениями животных, \ (\ frac {3} {4} \) этих марок имеют изображения птиц.
\ (\ frac {1} {3} \) × \ (\ frac {3} {4} \) × 24 = 24/4 = 6
Следовательно, на 6 марках есть изображения птиц.
Вопрос 14.
Подготовка к экзамену Барри купил 21 марку в магазине товаров для хобби. Он отдал \ (\ frac {3} {7} \) из них своей сестре. Сколько марок у него осталось?
Опции:
а. 3 марки
б. 6 марок
г. 9 марок
г. 12 марок
Ответ: 9 марок
Пояснение:
Подготовка к экзамену Барри купил 21 марку в магазине товаров для хобби. Он отдал \ (\ frac {3} {7} \) из них своей сестре.
\ (\ frac {3} {7} \) × 21
7 делит 21 три раза.
3 × 3 = 9 марок.
Таким образом, правильный ответ — вариант C.
Используйте модель, чтобы найти товар.
Вопрос 1.
\ (\ frac {5} {6} \) × 3
______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {1} {2} \)
Пояснение:
Поместите три полоски целых фракций рядом.
Найдите шесть полосок дробей с одинаковым знаменателем, который точно соответствует трем целым числам.
Круг \ (\ frac {5} {6} \) из 3 на нарисованной вами модели.
Завершите числовое предложение. \ (\ frac {5} {6} \) из 3
\ (\ frac {5} {6} \) × 3 = \ (\ frac {5} {2} \)
2 \ (\ frac {1 } {2} \)
Вопрос 2.
2 × \ (\ frac {5} {6} \)
______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {2} {3} \)
Пояснение:
Поместите две полоски целых фракций рядом.
Найдите шесть полосок дробей с одинаковым знаменателем, который точно соответствует двум целым числам.
2 из \ (\ frac {5} {6} \) = \ (\ frac {5} {6} \) × 2
\ (\ frac {5} {3} \)
Смешанная фракция \ ( \ frac {5} {3} \) равно 1 \ (\ frac {2} {3} \)
Найдите товар.
Вопрос 3.
\ (\ frac {5} {12} \) × 3 = ______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {1} {4} \)
Пояснение:
\ (\ frac {5} {12} \) × 3
Поместите три полоски целых фракций рядом.
Найдите шесть полосок дробей с одинаковым знаменателем, который точно соответствует двум целым числам.
\ (\ frac {5} {12} \) × 3
3 делит 12 на четыре раза
\ (\ frac {5} {12} \) × 3 = \ (\ frac {5} {4} \)
Смешанная доля \ (\ frac {5} {4} \) равна 1 \ (\ frac {1} {4} \)
\ (\ frac {5} {12} \) × 3 = 1 \ (\ гидроразрыв {1} {4} \)
Вопрос 4.
9 × \ (\ frac {1} {3} \) = ______
Ответ: 3
Пояснение:
9 × \ (\ frac {1} {3} \)
Поместите девять полосок целых дробей рядом.
Найдите три полоски дробей с одинаковым знаменателем, которые точно соответствуют двум целым числам.
9 × \ (\ frac {1} {3} \)
3 делит 9 три раза.
9 × \ (\ frac {1} {3} \) = 3
Таким образом, 9 × \ (\ frac {1} {3} \) = 3
Вопрос 5.
\ (\ frac {7} {8} \) × 4 = ______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {1} {2} \)
Пояснение:
\ (\ frac {7} {8} \) × 4
Поместите четыре полоски целых фракций рядом.
\ (\ frac {7} {8} \) × 4
4 делит 8 дважды.
\ (\ frac {7} {8} \) × 4 = \ (\ frac {7} {2} \)
Смешанная доля \ (\ frac {7} {2} \) равна 3 \ (\ гидроразрыв {1} {2} \)
\ (\ frac {7} {8} \) × 4 = 3 \ (\ frac {1} {2} \)
Вопрос 6.
4 × \ (\ frac {3} {5} \) = ______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {2} {5} \)
Пояснение:
4 × \ (\ frac {3} {5} \)
Поместите четыре полоски целых фракций рядом.
Поместите три полосы \ (\ frac {1} {5} \) дробей с одинаковым знаменателем, который точно соответствует двум целым числам.
4 из \ (\ frac {3} {5} \)
4 × \ (\ frac {3} {5} \) = \ (\ frac {12} {5} \)
Смешанная фракция \ ( \ frac {12} {5} \) равно 2 \ (\ frac {2} {5} \)
Вопрос 7.
\ (\ frac {7} {8} \) × 2 = ______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {3} {4} \)
Пояснение:
\ (\ frac {7} {8} \) × 2
Поместите две полоски целых фракций рядом.
Поместите семь полосок дробей \ (\ frac {1} {8} \) с одинаковым знаменателем, который точно соответствует двум целым числам.
\ (\ frac {7} {8} \) из 2
\ (\ frac {7} {8} \) × 2 = \ (\ frac {7} {4} \)
Смешанная фракция \ ( \ frac {7} {4} \) равно 1 \ (\ frac {3} {4} \)
Вопрос 8.
7 × \ (\ frac {2} {5} \) = ______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {4} {5} \)
Пояснение:
7 × \ (\ frac {2} {5} \)
Поместите семь полосок целых дробей рядом.
Поместите две полосы \ (\ frac {1} {5} \) дробей с одинаковым знаменателем, который точно соответствует двум целым числам.
7 × \ (\ frac {2} {5} \) = \ (\ frac {14} {5} \)
Смешанная фракция \ (\ frac {14} {5} \) = 2 \ (\ гидроразрыв {4} {5} \)
Вопрос 9.
\ (\ frac {3} {8} \) × 4 = ______
Ответ: \ (\ frac {3} {2} \)
Пояснение:
\ (\ frac {3} {8} \) × 4
Поместите четыре полоски целых дробей рядом.
Поместите три полосы \ (\ frac {1} {8} \) дробей с одинаковым знаменателем, который точно соответствует двум целым числам.
Вопрос 10.
11 × \ (\ frac {3} {4} \) = ______ \ (\ frac {□} {□} \)
Ответ: 8 \ (\ frac {1} {4} \)
Пояснение:
11 × \ (\ frac {3} {4} \)
Поместите одиннадцать полосок целых дробей рядом.
Поместите три полосы \ (\ frac {1} {4} \) дробей с одинаковым знаменателем, который точно соответствует двум целым числам.
11 из \ (\ frac {3} {4} \)
11 × \ (\ frac {3} {4} \) = \ (\ frac {33} {4} \)
Преобразуйте неправильную дробь в смешанная фракция.
\ (\ frac {33} {4} \) = 8 \ (\ frac {1} {4} \)
11 × \ (\ frac {3} {4} \) = 8 \ (\ frac {1 } {4} \)
Вопрос 11.
\ (\ frac {4} {15} \) × 5 = ______ \ (\ frac {□} {□} \)
Ответ: 5 \ (\ frac {1} {3} \)
Пояснение:
\ (\ frac {4} {15} \) × 5
Поместите пять полосок целых дробей рядом.
Поместите четыре полосы \ (\ frac {1} {15} \) дробей с одинаковым знаменателем, который точно соответствует двум целым числам.
\ (\ frac {4} {15} \) из 5
\ (\ frac {4} {15} \) × 5 = \ (\ frac {4} {3} \)
Преобразуйте неправильную дробь в смешанная фракция.
\ (\ frac {4} {3} \) = 5 \ (\ frac {1} {3} \)
Вопрос 12.
У Мэтта 5-фунтовый мешок яблок. Чтобы сделать пирог, ему нужно использовать \ (\ frac {3} {5} \) мешка. Сколько фунтов яблок он будет использовать для пирога? Объясните, как может выглядеть модель этой проблемы.
______ фунтов
Ответ: 3 фунта
Пояснение:
Учитывая, что у Мэтта есть пятифунтовый мешок яблок.
Чтобы сделать пирог, ему нужно использовать \ (\ frac {3} {5} \) мешка.
\ (\ frac {3} {5} \) × 5 = 3
Поэтому Мэтт использовал 3 фунта яблок, чтобы сделать пирог.
Решение проблем — Стр. № 298
Задача
Вопрос 13.
Тарик нарисовал модель задачи ниже. Напишите 2 задачи, которые можно решить с помощью этой модели. Одна из ваших задач должна включать умножение целого числа на дробь, а другая проблема должна включать умножение дроби на целое число.
Задачи. Реши свои проблемы.
Как можно изменить модель, чтобы получить ответ 4 \ (\ frac {4} {5} \)?
Объясните и напишите новое уравнение.
Тип ниже:
_________
Ответ:
Пятеро детей в семье Смитов в субботу проводят по 2/5 часа, выполняя домашние дела. Сколько всего времени они потратили на работу по дому?
Умножьте числитель на целое число.
5 × \ (\ frac {2} {5} \) = \ (\ frac {10} {5} \) = 2
Найдите товар. Напишите продукт в простейшей форме.
Вопрос 1.
3 × \ (\ frac {2} {5} \) =
• Умножьте числитель на целое число.Напишите произведение над знаменателем.
• Запишите ответ в виде смешанного числа в простейшей форме.
______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {1} {5} \)
Пояснение:
Умножьте целое число на числитель.
3 \ (\ frac {2} {5} \) = \ (\ frac {6} {5} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {6} {5} \) = 1 \ (\ frac {1} {5} \)
Вопрос 2.
\ (\ frac {2} {3} \) × 5 = ______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {1} {3} \)
Пояснение:
Умножьте целое число на числитель.
\ (\ frac {2} {3} \) × 5 = \ (\ frac {10} {3} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {10} {3} \) = 3 \ (\ frac {1} {3} \)
Вопрос 3.
6 × \ (\ frac {2} {3} \) = ______
Ответ: 4
Пояснение:
6 × \ (\ frac {2} {3} \)
Умножьте целое число на числитель.
6 × \ (\ frac {2} {3} \) = \ (\ frac {12} {3} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {12} {3} \) = 4
Вопрос 4.
\ (\ frac {5} {7} \) × 4 = ______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {6} {7} \)
Пояснение:
\ (\ frac {5} {7} \) × 4
Умножьте целое число на числитель.
\ (\ frac {5} {7} \) × 4 = \ (\ frac {20} {7} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
2 \ (\ frac {6} {7} \)
Таким образом, \ (\ frac {5} {7} \) × 4 = 2 \ (\ frac {6} {7} \)
Самостоятельно
Найдите товар. Напишите продукт в простейшей форме.
Вопрос 5.
5 × \ (\ frac {2} {3} \) = ______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {1} {3} \)
Пояснение:
5 × \ (\ frac {2} {3} \)
Умножьте целое число на числитель.
5 × \ (\ frac {2} {3} \) = \ (\ frac {10} {3} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
3 \ (\ frac {1} {3} \)
5 × \ (\ frac {2} {3} \) = 3 \ (\ frac {1} {3} \)
Вопрос 6.
\ (\ frac {1} {4} \) × 3 = ______ \ (\ frac {□} {□} \)
Ответ: \ (\ frac {3} {4} \)
Пояснение:
\ (\ frac {1} {4} \) × 3
Умножьте целое число на числитель.
\ (\ frac {1} {4} \) × 3 = \ (\ frac {3} {4} \)
Вопрос 7.
7 × \ (\ frac {7} {8} \) = ______ \ (\ frac {□} {□} \)
Ответ: 6 \ (\ frac {1} {8} \)
Пояснение:
7 × \ (\ frac {7} {8} \)
Умножьте целое число на числитель.
\ (\ frac {49} {8} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {49} {8} \) = 6 \ (\ frac {1} {8} \)
Таким образом, 7 × \ (\ frac {7} {8} \) = 6 \ (\ frac {1} {8} \)
Вопрос 8.
2 × \ (\ frac {4} {5} \) = ______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {3} {5} \)
Пояснение:
2 × \ (\ frac {4} {5} \)
Умножьте целое число на числитель.
2 × \ (\ frac {4} {5} \) = \ (\ frac {8} {5} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {8} {5} \) = 1 \ (\ frac {3} {5} \)
Вопрос 9.
4 × \ (\ frac {3} {4} \) = ______
Ответ: 3
Пояснение:
Умножьте целое число на числитель.
4 × \ (\ frac {3} {4} \) = \ (\ frac {12} {4} \)
4 делит 12 три раза.
Итак, \ (\ frac {12} {4} \) = 3
4 × \ (\ frac {3} {4} \) = 3
Вопрос 10.
\ (\ frac {7} {9} \) × 2 = ______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {5} {9} \)
Пояснение:
\ (\ frac {7} {9} \) × 2
Умножьте целое число на числитель.
\ (\ frac {7} {9} \) × 2 = \ (\ frac {14} {9} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {14} {9} \) = 1 \ (\ frac {5} {9} \)
Практика: копирование и решение. Найдите товар. Напишите продукт в простейшей форме.
Вопрос 11.
\ (\ frac {3} {5} \) × 11 = ______ \ (\ frac {□} {□} \)
Ответ: 6 \ (\ frac {3} {5} \)
Пояснение:
\ (\ frac {3} {5} \) × 11
Умножьте целое число на числитель.
\ (\ frac {3} {5} \) × 11 = \ (\ frac {33} {5} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {33} {5} \) = 6 \ (\ frac {3} {5} \)
Вопрос 12.
3 × \ (\ frac {3} {4} \) = ______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {1} {4} \)
Пояснение:
3 × \ (\ frac {3} {4} \)
Умножьте целое число на числитель.
3 × \ (\ frac {3} {4} \) = \ (\ frac {9} {4} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {9} {4} \) = 2 \ (\ frac {1} {4} \)
Вопрос 13.
\ (\ frac {5} {8} \) × 3 = ______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {7} {8} \)
Пояснение:
\ (\ frac {5} {8} \) × 3
Умножьте целое число на числитель.
\ (\ frac {5} {8} \) × 3 = \ (\ frac {15} {8} \)
Теперь запишите неправильную дробь в виде смешанной дроби.
\ (\ frac {15} {8} \) = 1 \ (\ frac {7} {8} \)
Алгебра Найдите неизвестную цифру.
Вопрос 14.
\ (\ frac {■} {2} \) × 8 = 4
■ = ______
Ответ: 1
Пояснение:
\ (\ frac {■} {2} \) × 8 = 4
\ (\ frac {■} {2} \) = 4/8
■ = 4 × 2/8 = 1
■ = 1
Вопрос 15.
■ × \ (\ frac {5} {6} \) = \ (\ frac {20} {6} \) или 3 \ (\ frac {1} {3} \)
■ = ______
Ответ: 4
Пояснение:
■ × \ (\ frac {5} {6} \) = \ (\ frac {20} {6} \)
■ = 20/6 × 6/5
■ = 20/5 = 4
■ = 4
Вопрос 16.
\ (\ frac {1} {■} \) × 18 = 3
■ = ______
Ответ: 6
Пояснение:
\ (\ frac {1} {■} \) × 18 = 3
\ (\ frac {1} {3} \) × 18 = ■
■ = 18/3 = 6
■ = 6
РАЗБЛОКИРОВАТЬ проблему — Страница № 302
Вопрос 17.
Поставщик провизии хочет иметь достаточно индейки, чтобы накормить 24 человека. Если он хочет предоставить \ (\ frac {3} {4} \) фунта индейки на каждого человека, сколько индейки ему нужно?
а. Что вам нужно найти?
Тип ниже:
__________
Ответ: Мне нужно найти, сколько индейки нужно обеспечить кейтерингу на каждого человека.
Вопрос 17.
б. Какую операцию вы будете использовать?
Тип ниже:
__________
Ответ: Я воспользуюсь операцией умножения для решения задачи.
Вопрос 17.
c. Какая информация вам предоставлена?
Тип ниже:
__________
Мне дана информация о количестве людей, которых нужно накормить, и о доле фунтов индейки, которую получает каждый человек.
Вопрос 17.
г. Решать проблему.
Тип ниже:
__________
Ответ:
Поставщик провизии хочет обслужить 24 человека
\ (\ frac {3} {4} \) × 24
4 делит 24 шесть раз.
3 × 6 = 18
Таким образом, поставщику нужно 18 фунтов индейки.
Вопрос 17.
e. Закончите предложения.
Поставщик провизии хочет обслужить 24 человека по _____ фунта индейки каждый.
Ему понадобится ____ × ____, или ______ фунтов индейки.
Тип ниже:
__________
Ответ: \ (\ frac {3} {4} \) × 24
Вопрос 17.
ф. Заполните кружок, чтобы выбрать правильный ответ.
Опции:
а. 72 фунта
б. 24 фунта
гр. 18 фунтов
г.6 фунтов
Ответ: 18 фунтов
Пояснение:
Поставщик провизии хочет обслужить 24 человека
\ (\ frac {3} {4} \) × 24
4 делит 24 шесть раз.
3 × 6 = 18
Правильный ответ — вариант C.
Вопрос 18.
Пэтти хочет пробегать \ (\ frac {5} {6} \) милю каждый день в течение 5 дней. Как далеко она убежит за это время?
Опции:
а. 25 миль
б. 5 миль
г. 4 \ (\ frac {1} {6} \) миль
дн. 1 \ (\ frac {2} {3} \) миль
Ответ: 4 \ (\ frac {1} {6} \) миль
Объяснение:
Пэтти хочет пробегать \ (\ frac {5} {6} \) милю каждый день в течение 5 дней.
\ (\ frac {5} {6} \) × 5 = \ (\ frac {25} {6} \)
Преобразует неправильную дробь в смешанную.
\ (\ frac {25} {6} \) = 4 \ (\ frac {1} {6} \) миль
Таким образом, правильный ответ — вариант C.
Вопрос 19.
У Дуга 33 фута веревки. Он хочет использовать его \ (\ frac {2} {3} \) для своего каноэ. Сколько футов веревки он использует для своего каноэ?
Опции:
а. 11 футов
б. 22 фута
c. 33 фута
г. 66 футов
Ответ: 22 фута
Пояснение:
У Дуга 33 фута веревки.Он хочет использовать его \ (\ frac {2} {3} \) для своего каноэ.
\ (\ frac {2} {3} \) × 33 фута
3 делит 33 одиннадцать раз.
2 × 11 = 22 фута
Правильный ответ — вариант Б.
Используйте модель, чтобы найти товар.
Вопрос 1.
\ (\ frac {3} {5} \ times \ frac {1} {3} = \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {5} \)
Пояснение:
Дробь \ (\ frac {3} {5} \) представляет собой строки и столбцы.
Дробь \ (\ frac {1} {3} \) указывает заштрихованную часть фигуры.
\ (\ frac {3} {5} \) × \ (\ frac {1} {3} \) = \ (\ frac {1} {5} \)
Вопрос 2.
\ (\ frac {2} {3} \ times \ frac {3} {5} = \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {2} {5} \)
Пояснение:
На приведенном выше рисунке показано, что круг разделен на 5 частей, в которых 2 части не закрашены, а 3 части закрашены.
Итак, доля круга равна \ (\ frac {2} {3} \)
Доля затененной части круга равна \ (\ frac {3} {5} \)
\ (\ frac { 2} {3} \) × \ (\ frac {3} {5} \) = \ (\ frac {2} {5} \)
Поделиться и показать — Страница No.305
Найдите товар. Нарисуйте модель.
Вопрос 3.
\ (\ frac {2} {3} \ times \ frac {1} {5} = \) \ (\ frac {□} {□} \)
Ответ: \ (\ frac {2} {15} \)
Пояснение:
\ (\ frac {2} {3} \) × \ (\ frac {1} {5} \)
Умножьте знаменатели обеих дробей.
\ (\ frac {2} {15} \)
\ (\ frac {2} {3} \ times \ frac {1} {5} = \) \ (\ frac {2} {15} \)
Вопрос 4.
\ (\ frac {1} {2} \ times \ frac {5} {6} = \) \ (\ frac {□} {□} \)
Ответ: \ (\ frac {5} {12} \)
Пояснение:
\ (\ frac {1} {2} \) × \ (\ frac {5} {6} \)
Умножьте числители и знаменатели.
\ (\ frac {1} {2} \) × \ (\ frac {5} {6} \) = \ (\ frac {5} {12} \)
\ (\ frac {1} {2} \ times \ frac {5} {6} = \) \ (\ frac {5} {12} \)
Вопрос 5.
\ (\ frac {3} {5} \ times \ frac {1} {3} = \) \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {5} \)
Пояснение:
\ (\ frac {3} {5} \) × \ (\ frac {1} {3} \)
Умножьте знаменатели и числители дробей.
\ (\ frac {3} {5} \) × \ (\ frac {1} {3} \) = \ (\ frac {3} {15} \)
\ (\ frac {3} {15} \) = \ (\ frac {1} {5} \)
\ (\ frac {3} {5} \ times \ frac {1} {3} = \) \ (\ frac {1} {5} \ )
Вопрос 6.
\ (\ frac {3} {4} \ times \ frac {1} {6} = \) \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {8} \)
Пояснение:
\ (\ frac {3} {4} \) × \ (\ frac {1} {6} \)
Умножьте знаменатели и числители дробей.
\ (\ frac {3} {4} \) × \ (\ frac {1} {6} \) = \ (\ frac {3} {24} \)
3 делит 24 восемь раз.
Итак, \ (\ frac {3} {24} \) = \ (\ frac {1} {8} \)
Таким образом, \ (\ frac {3} {4} \ times \ frac {1} {6 } = \) \ (\ frac {1} {8} \)
Вопрос 7.
\ (\ frac {2} {5} \ times \ frac {5} {6} = \) \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {3} \)
Пояснение:
\ (\ frac {2} {5} \) × \ (\ frac {5} {6} \)
Умножьте знаменатели и числители дробей.
\ (\ frac {2} {5} \) × \ (\ frac {5} {6} \) = \ (\ frac {10} {30} \)
10 делит 30 три раза.
\ (\ frac {10} {30} \) = \ (\ frac {1} {3} \)
\ (\ frac {2} {5} \ times \ frac {5} {6} = \) \ (\ frac {1} {3} \)
Вопрос 8.
\ (\ frac {5} {6} \ times \ frac {3} {5} = \) \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {2} \)
Пояснение:
\ (\ frac {5} {6} \) × \ (\ frac {3} {5} \)
Умножьте знаменатели и числители дробей.
\ (\ frac {5} {6} \) × \ (\ frac {3} {5} \) = \ (\ frac {15} {30} \)
\ (\ frac {5} {6} \) × \ (\ frac {3} {5} \) = \ (\ frac {15} {30} \) = \ (\ frac {1} {2} \)
\ (\ frac {5} { 6} \ times \ frac {3} {5} = \) \ (\ frac {1} {2} \)
Решение проблем — стр.306
Что за ошибка?
Вопрос 9.
Шерил и Маркус собираются испечь двухъярусный торт. Меньший уровень равен \ (\ frac {2} {3} \) размеру большего уровня. Рецепт создания нижнего яруса требует \ (\ frac {3} {5} \) стакана воды. Сколько воды им понадобится, чтобы сделать меньший ярус?
Они сделали модель, изображающую проблему. Черил говорит, что им нужен \ (\ frac {6} {9} \) стакан воды. Маркус говорит, что им нужен \ (\ frac {2} {5} \) стакан воды. Кто прав? Объяснять.
Ответ Шерил Ответ Маркуса
Введите ниже:
_________
Ответ: Ответ Маркуса правильный.
Пояснение:
Шерил и Маркус собираются испечь двухъярусный торт.
Меньший уровень равен \ (\ frac {2} {3} \) размеру большего уровня.
Рецепт создания нижнего яруса требует \ (\ frac {3} {5} \) стакана воды.
\ (\ frac {3} {5} \) × \ (\ frac {2} {3} \) = \ (\ frac {2} {5} \)
Заполните утверждение, указав «равно», «больше» или «меньше».
Вопрос 1.
4 × \ (\ frac {7} {8} \) будет ___________ \ (\ frac {7} {8} \)
_________
Ответ: Больше
Пояснение:
4 × \ (\ frac {7} {8} \) = \ (\ frac {7} {2} \)
Знаменатель с большим числом будет наименьшим числом.
Итак, \ (\ frac {7} {2} \) больше, чем \ (\ frac {7} {8} \)
Вопрос 2.
\ (\ frac {3} {5} \ times \ frac {2} {7} \) будет ___________ \ (\ frac {3} {5} \)
Ответ: Менее
Пояснение:
\ (\ frac {3} {5} \) × \ (\ frac {2} {7} \) = \ (\ frac {6} {35} \)
Знаменатель с наибольшим числом будет наименьшая дробь.
Итак, \ (\ frac {6} {35} \) меньше, чем \ (\ frac {3} {5} \)
Вопрос 3.
\ (\ frac {5} {8} \ times 6 \) будет ___________ \ (\ frac {5} {8} \)
Ответ: Больше
Пояснение:
\ (\ frac {5} {8} \) × 6 = \ (\ frac {15} {4} \)
\ (\ frac {15} {4} \) = 3 \ (\ frac {3} {4} \)
3 \ (\ frac {3} {4} \) больше, чем \ (\ frac {5} {8} \)
Вопрос 4.
\ (\ frac {2} {3} \ times \ frac {5} {5} \) будет ___________ \ (\ frac {2} {3} \)
Ответ: равно
Пояснение:
\ (\ frac {2} {3} \) × \ (\ frac {5} {5} \) = \ (\ frac {2} {3} \)
\ (\ frac {2} {3} \) равно \ (\ frac {2} {3} \)
Вопрос 5.
\ (8 \ times \ frac {7} {8} \) будет ___________ 8
Ответ: Менее
Пояснение:
8 × \ (\ frac {7} {8} \) = 7
7 меньше 8.
\ (8 \ times \ frac {7} {8} \) будет меньше 8.
Самостоятельно
Заполните утверждение, указав «равно», «больше» или «меньше».
Вопрос 6.
\ (\ frac {4} {9} \ times \ frac {3} {8} \) будет ___________ \ (\ frac {3} {8} \)
Ответ: Менее
Пояснение:
\ (\ frac {4} {9} \) × \ (\ frac {3} {8} \) = \ (\ frac {12} {72} \)
= \ (\ frac {1 } {6} \)
\ (\ frac {1} {6} \) меньше, чем \ (\ frac {3} {8} \)
\ (\ frac {4} {9} \ times \ frac { 3} {8} \) будет меньше, чем \ (\ frac {3} {8} \)
Вопрос 7.
\ (7 \ times \ frac {9} {10} \) будет ___________ \ (\ frac {9} {10} \)
Ответ: Больше
Пояснение:
7 × \ (\ frac {9} {10} \) = \ (\ frac {63} {10} \)
Знаменатели совпадают, поэтому сравните числители.
\ (\ frac {63} {10} \) больше, чем \ (\ frac {9} {10} \)
Вопрос 8.
\ (5 \ times \ frac {1} {3} \) будет ___________ \ (\ frac {1} {3} \)
Ответ: Больше
Пояснение:
5 × \ (\ frac {1} {3} \) = \ (\ frac {5} {3} \)
Знаменатели совпадают, поэтому сравните числители.
\ (\ frac {5} {3} \) больше, чем \ (\ frac {1} {3} \)
Вопрос 9.
\ (\ frac {6} {11} \ times 1 \) будет ___________ \ (\ frac {6} {11} \)
Ответ: равно
Пояснение:
\ (\ frac {6} {11} \) × 1 = \ (\ frac {6} {11} \)
\ (\ frac {6} {11} \) равно \ (\ гидроразрыв {6} {11} \).
Вопрос 10.
\ (\ frac {1} {6} \ times \ frac {7} {7} \) будет ___________ 1
Ответ: Менее
Пояснение:
\ (\ frac {1} {6} \) × \ (\ frac {7} {7} \) = \ (\ frac {1} {6} \)
\ (\ frac {1} {6} \) меньше 1
Вопрос 11.
\ (4 \ times \ frac {3} {5} \) будет ___________ \ (\ frac {3} {5} \)
Ответ: Больше
Пояснение:
4 × \ (\ frac {3} {5} \) = \ (\ frac {12} {5} \)
Знаменатели совпадают, поэтому сравните числители.
\ (\ frac {12} {5} \) больше, чем \ (\ frac {3} {5} \)
Решение проблем — Стр. № 310
Вопрос 12.
Лола делает куки. Она планирует умножить рецепт на 3, чтобы приготовить достаточно печенья для всего класса. Если рецепт требует \ (\ frac {2} {3} \) стакана сахара, потребуется ли ей больше \ (\ frac {2} {3} \) или меньше \ (\ frac {2} {3 } \) стакан сахара, чтобы приготовить все печенье?
_________ \ (\ frac {2} {3} \) стакан сахара
Ответ: Более
Пояснение:
ola делает куки.Она планирует умножить рецепт на 3, чтобы приготовить достаточно печенья для всего класса.
3 × \ (\ frac {2} {3} \) = 2
Итак, Лоле нужно больше, чем \ (\ frac {2} {3} \) стакан сахара.
Вопрос 13.
Питер планирует потратить \ (\ frac {2} {3} \) на телевизор на этой неделе столько же часов, сколько на прошлой. Собирается ли Питер на этой неделе проводить больше или меньше часов перед телевизором?
_________ часов
Ответ: Меньше
Пояснение:
Питер планирует потратить \ (\ frac {2} {3} \) на телевизор на этой неделе столько же часов, сколько на прошлой.
7 × \ (\ frac {2} {3} \) = \ (\ frac {14} {3} \)
\ (\ frac {14} {3} \) = 4 \ (\ frac {2} {3} \)
Таким образом, на этой неделе Питер будет проводить больше или меньше часов у телевизора.
Вопрос 14.
Подготовка к экзамену Рошель экономит \ (\ frac {1} {4} \) своего суточного. Если она решит начать экономить столько же \ (\ frac {1} {2} \), какое утверждение ниже верно?
Опции:
а. Она будет откладывать такую же сумму.
г. Она будет экономить больше.
г. Она будет меньше экономить.
г. Она сэкономит вдвое больше.
Ответ: она будет копить больше
Пояснение:
Подготовка к экзамену Рошель экономит \ (\ frac {1} {4} \) из своего суточного.
\ (\ frac {1} {4} \) больше, чем \ (\ frac {1} {2} \)
Итак, ответ — вариант B.
Подключиться к Art
Масштабная модель — это представление объекта той же формы, что и реальный объект. Модели могут быть больше или меньше реального объекта, но часто меньше.
Архитекторы часто делают масштабные модели зданий или сооружений, которые они планируют построить.Модели могут дать им представление о том, как будет выглядеть конструкция после завершения. Каждое измерение здания масштабируется вверх или вниз с одинаковым коэффициентом.
Боб строит масштабную модель своего велосипеда. Он хочет, чтобы его модель была \ (\ frac {1} {5} \) такой же длины, как и его велосипед.
Вопрос 15.
Если длина велосипеда Боба составляет 60 дюймов, какой длины будет его модель?
_____ дюйм
Ответ: 12 дюймов
Пояснение:
Учитывая это, Боб строит масштабную модель своего велосипеда.Он хочет, чтобы его модель была \ (\ frac {1} {5} \) такой же длины, как и его велосипед.
Если длина велосипеда Боба 60 дюймов, умножьте его на дробь \ (\ frac {1} {5} \)
\ (\ frac {1} {5} \) × 60 = 12 дюймов
Модель будет 12 дюймов длинный.
Вопрос 16.
Если одно колесо на модели Боба имеет 4 дюйма в поперечнике, сколько дюймов в поперечнике будет фактическим колесом на его велосипеде? Объяснять.
\ (\ frac {□} {□} \) дюйм
Ответ: \ (\ frac {4} {5} \) дюйм
Пояснение:
При этом одно колесо на модели Боба имеет диаметр 4 дюйма.
4 × \ (\ frac {1} {5} \) = \ (\ frac {4} {5} \) дюйм
Найдите товар. Напишите продукт в простейшей форме.
Вопрос 1.
\ (6 \ times \ frac {3} {8} \)
\ (\ frac {6} {1} \ times \ frac {3} {8} \) = \ (\ frac {■ } {■} \)
______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {1} {4} \)
Пояснение:
\ (\ frac {6} {1} \ times \ frac {3} {8} \) = \ (\ frac {■} {■} \)
6 × \ (\ frac {3} { 8} \) = \ (\ frac {18} {8} \) = \ (\ frac {9} {4} \)
\ (\ frac {9} {4} \) = 2 \ (\ frac { 1} {4} \)
2 \ (\ frac {1} {4} \) = \ (\ frac {■} {■} \)
\ (\ frac {■} {■} \) = 2 \ (\ frac {1} {4} \)
Вопрос 2.
\ (\ frac {3} {8} \ times \ frac {8} {9} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {3} \)
Пояснение:
\ (\ frac {3} {8} \ times \ frac {8} {9} \) = \ (\ frac {□} {□} \)
\ (\ frac {3} {8} \) × \ (\ frac {8} {9} \) = \ (\ frac {1} {3} \)
Таким образом, \ (\ frac {3} {8} \ times \ frac {8} {9 } \) = \ (\ frac {1} {3} \)
Вопрос 3.
\ (\ frac {2} {3} \ times 27 \) = ______
Ответ: 18
Пояснение:
27 × \ (\ frac {2} {3} \)
3 делит 27 девять раз.
Таким образом, 27 × \ (\ frac {2} {3} \) = 18
Вопрос 4.
\ (\ frac {5} {12} \ times \ frac {3} {5} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {4} \)
Пояснение:
\ (\ frac {5} {12} \) × \ (\ frac {3} {5} \) = \ (\ frac {3} {12} \)
3 делит 12 на четыре раза.
\ (\ frac {3} {12} \) = \ (\ frac {1} {4} \)
\ (\ frac {5} {12} \ times \ frac {3} {5} \) = \ (\ frac {1} {4} \)
Вопрос 5.
\ (\ frac {1} {2} \ times \ frac {3} {5} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {3} {10} \)
Пояснение:
\ (\ frac {1} {2} \) × \ (\ frac {3} {5} \)
Умножьте числители и знаменатели.
\ (\ frac {1} {2} \) × \ (\ frac {3} {5} \) = \ (\ frac {3} {10} \)
\ (\ frac {1} {2} \ times \ frac {3} {5} \) = \ (\ frac {3} {10} \)
Вопрос 6.
\ (\ frac {2} {3} \ times \ frac {4} {5} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {8} {15} \)
Пояснение:
\ (\ frac {2} {3} \) × \ (\ frac {4} {5} \)
Умножьте числители и знаменатели.
\ (\ frac {2} {3} \) × \ (\ frac {4} {5} \) = \ (\ frac {8} {15} \)
Вопрос 7.
\ (\ frac {1} {3} \ times \ frac {5} {8} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {5} {24} \)
Пояснение:
\ (\ frac {1} {3} \) × \ (\ frac {5} {8} \)
Умножьте числители и знаменатели.
\ (\ frac {1} {3} \ times \ frac {5} {8} \) = \ (\ frac {5} {24} \)
Вопрос 8.
\ (4 \ times \ frac {1} {5} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {4} {5} \)
Пояснение:
Умножьте числитель на целое число.
4 × \ (\ frac {1} {5} \) = \ (\ frac {4} {5} \)
\ (4 \ times \ frac {1} {5} \) = \ (\ frac { 4} {5} \)
Самостоятельно
Найдите товар. Напишите продукт в простейшей форме.
Вопрос 9.
\ (2 \ times \ frac {1} {8} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {4} \)
Пояснение:
Умножьте целое число на числитель.
2 × \ (\ frac {1} {8} \)
2 делит 8 четыре раза.
2 × \ (\ frac {1} {8} \) = \ (\ frac {1} {4} \)
\ (2 \ times \ frac {1} {8} \) = \ (\ frac { 1} {4} \)
Вопрос 10.
\ (\ frac {4} {9} \ times \ frac {4} {5} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {16} {45} \)
Пояснение:
\ (\ frac {4} {9} \) × \ (\ frac {4} {5} \)
Умножьте числители и знаменатели.
\ (\ frac {4} {9} \) × \ (\ frac {4} {5} \) = \ (\ frac {16} {45} \)
\ (\ frac {4} {9} \ times \ frac {4} {5} \) = \ (\ frac {16} {45} \)
Вопрос 11.
\ (\ frac {1} {12} \ times \ frac {2} {3} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {18} \)
Пояснение:
\ (\ frac {1} {12} \) × \ (\ frac {2} {3} \)
Умножьте числители и знаменатели.
\ (\ frac {1} {12} \) × \ (\ frac {2} {3} \) = \ (\ frac {2} {36} \)
\ (\ frac {2} {36} \) = \ (\ frac {1} {18} \)
\ (\ frac {1} {12} \ times \ frac {2} {3} \) = \ (\ frac {1} {18} \ )
Вопрос 12.
\ (\ frac {1} {7} \ times 30 \) = _____ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {2} {7} \)
Пояснение:
30 × \ (\ frac {1} {7} \) = \ (\ frac {30} {7} \)
Преобразование неправильной дроби в смешанную дробь.
\ (\ frac {30} {7} \) = 4 \ (\ frac {2} {7} \)
\ (\ frac {1} {7} \ times 30 \) = 4 \ (\ frac { 2} {7} \)
Вопрос 13.
Из домашних животных на выставке \ (\ frac {5} {6} \) — кошки. \ (\ frac {4} {5} \) кошек — ситцевые кошки. Какую долю домашних животных составляют ситцевые кошки?
\ (\ frac {□} {□} \) ситцевые кошки
Ответ: \ (\ frac {2} {3} \)
Пояснение:
Из питомцев в шоу домашних животных \ (\ frac {5} {6} \) — кошки. \ (\ frac {4} {5} \) кошек — ситцевые кошки.
\ (\ frac {5} {6} \) × \ (\ frac {4} {5} \) = \ (\ frac {20} {30} \) = \ (\ frac {2} {3} \)
\ (\ frac {2} {3} \) часть домашних животных — это ситцевые кошки.
Вопрос 14.
По пять кошек съели \ (\ frac {1} {4} \) чашку еды. Сколько всего они съели еды?
_____ \ (\ frac {□} {□} \) чашек еды
Ответ: 1 \ (\ frac {1} {4} \)
Пояснение:
По пять кошек съели \ (\ frac {1} {4} \) чашку еды.
5 × \ (\ frac {1} {4} \) = \ (\ frac {5} {4} \)
Смешанная доля \ (\ frac {5} {4} \) равна 1 \ (\ гидроразрыв {1} {4} \)
Алгебра Оцените заданное значение.
Вопрос 15.
\ (\ frac {2} {5} \) × c для c = \ (\ frac {4} {7} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {8} {35} \)
Пояснение:
\ (\ frac {2} {5} \) × c = \ (\ frac {4} {7} \)
c = \ (\ frac {4} {7} \) × \ (\ гидроразрыв {2} {5} \)
c = \ (\ frac {8} {35} \)
Вопрос 16.
м × \ (\ frac {4} {5} \) для m = \ (\ frac {7} {8} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {7} {10} \)
Пояснение:
m = \ (\ frac {4} {5} \) × \ (\ frac {7} {8} \)
Умножьте числители и знаменатели.
\ (\ frac {4} {5} \) × \ (\ frac {7} {8} \) = \ (\ frac {7} {10} \)
Вопрос 17.
\ (\ frac {2} {3} \) × t для t = \ (\ frac {1} {8} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {12} \)
Пояснение:
\ (\ frac {2} {3} \) × t для t = \ (\ frac {1} {8} \)
t = \ (\ frac {1} {8} \) × \ (\ frac {2} {3} \)
t = \ (\ frac {1} {12} \)
Вопрос 18.
y × \ (\ frac {2} {3} \) для y = 5
_______
Ответ: 4
Пояснение:
y × \ (\ frac {2} {3} \) для y = 5
6 × \ (\ frac {2} {3} \) = 4
Решение проблем — Стр. № 314
Конькобежный спорт — популярный вид спорта на зимних Олимпийских играх. Многие молодые спортсмены в США участвуют в клубах и лагерях по конькобежному спорту.
Вопрос 19.
В лагере в Грин-Бей, штат Висконсин, \ (\ frac {7} {9} \) участники были из Висконсина.Из этой группы \ (\ frac {3} {5} \) было 12 лет. Какая часть группы была 12-летними жителями Висконсина?
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {7} {15} \)
Пояснение:
Учитывая, что
В лагере в Грин-Бей, Висконсин, \ (\ frac {7} {9} \) участников были из Висконсина.
Из этой группы \ (\ frac {3} {5} \) было 12 лет.
Чтобы найти фракцию группы из Висконсина, возраст которой 12 лет
Мы должны умножить дробь \ (\ frac {7} {9} \) на \ (\ frac {3} {5} \)
\ ( \ frac {7} {9} \) × \ (\ frac {3} {5} \) = \ (\ frac {21} {45} \)
\ (\ frac {21} {45} \) = \ (\ frac {7} {15} \)
Таким образом, часть группы была из Висконсина, а возраст 12 лет — \ (\ frac {7} {15} \).
Вопрос 20.
Марибель хочет проехать 1 \ (\ frac {1} {2} \) милю в понедельник. Если она проедет \ (\ frac {9} {10} \) милю в понедельник утром и \ (\ frac {2} {3} \) эту дистанцию в понедельник днем, достигнет ли она своей цели? Объяснять.
_____
Ответ: Да
Пояснение:
Марибель хочет проехать 1 \ (\ frac {1} {2} \) милю в понедельник.
Чтобы узнать, достигла ли Марибель своей цели, нам нужно умножить дроби \ (\ frac {9} {10} \) и \ (\ frac {2} {3} \).
\ (\ frac {9} {10} \) × \ (\ frac {2} {3} \) = \ (\ frac {3} {5} \)
Таким образом, мы можем сказать, что Марибель достигла своей цели.
Итак, да.
Вопрос 21.
В первый день сбора \ (\ frac {5} {6} \) фигуристы были новичками. Из новичков \ (\ frac {1} {3} \) были девушки. Какая доля фигуристов была девочками и новичками? Объясните, почему ваш ответ разумен.
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {5} {18} \)
Пояснение:
В первый день сбора \ (\ frac {5} {6} \) фигуристы были новичками. Из новичков \ (\ frac {1} {3} \) были девушки.
Умножить долю фигуристов начинали и долю фигуристов составляли девушки.
\ (\ frac {5} {6} \) × latex] \ frac {1} {3} [/ latex] = latex] \ frac {5} {18} [/ latex]
Доля фигуристов была девочки и новички — латекс] \ frac {5} {18} [/ latex]
Вопрос 22.
Подготовка к тесту В среду Даниэль откатала \ (\ frac {2} {3} \) путь по трассе за 2 минуты. Ее младший брат откатал \ (\ frac {3} {4} \) дистанцию Даниэль за 2 минуты. Какую часть трека брат Даниэль закончил за 2 минуты?
Опции:
а. \ (\ frac {1} {3} \)
б. \ (\ frac {1} {2} \)
с.\ (\ frac {5} {7} \)
г. \ (\ frac {3} {4} \)
Ответ: \ (\ frac {1} {2} \)
Пояснение:
Подготовка к тесту В среду Даниэль откатала \ (\ frac {2} {3} \) путь по трассе за 2 минуты.
Ее младший брат откатал \ (\ frac {3} {4} \) дистанцию Даниэль за 2 минуты.
Умножьте долю того, что Даниэль каталась, а ее младший брат катался.
\ (\ frac {2} {3} \) × \ (\ frac {3} {4} \) = \ (\ frac {1} {2} \)
Таким образом, правильный ответ — вариант B.
Контрольный пункт в середине главы — стр.315
Концепция и навыки
Вопрос 1.
Объясните, как вы бы смоделировали 5 × \ (\ frac {2} {3} \)
Введите ниже:
__________
Ответ: \ (\ frac {10} {3} \)
Вопрос 2.
Когда вы умножаете \ (\ frac {2} {3} \) на дробь меньше единицы, как продукт соотносится с факторами?
Тип ниже:
__________
Ответ: \ (\ frac {2} {3} \) × \ (\ frac {1} {2} \)
= \ (\ frac {1} {3} \)
Найдите товар. Напишите продукт в простейшей форме.
Вопрос 3.
\ (\ frac {2} {3} \ times 6 \)
______
Ответ: 4
Пояснение:
6 × \ (\ frac {2} {3} \)
Умножьте числитель на целые числа.
\ (\ frac {1} {3} \)
Вопрос 4.
\ (\ frac {4} {5} \ times 7 \)
______ \ (\ frac {□} {□} \)
Ответ: 5 \ (\ frac {3} {5} \)
Пояснение:
Умножьте числитель на целые числа.
\ (\ frac {4} {5} \ times 7 \)
7 × \ (\ frac {4} {5} \) = \ (\ frac {28} {5} \)
Преобразуйте неправильную дробь в смешанная фракция.
\ (\ frac {28} {5} \) = 5 \ (\ frac {3} {5} \)
\ (\ frac {4} {5} \ times 7 \) = 5 \ (\ frac { 3} {5} \)
Вопрос 5.
\ (8 \ times \ frac {5} {7} \)
______ \ (\ frac {□} {□} \)
Ответ: 5 \ (\ frac {5} {7} \)
Пояснение:
8 × \ (\ frac {5} {7} \)
Умножьте числитель на целые числа.
8 × \ (\ frac {5} {7} \) = \ (\ frac {40} {7} \)
Преобразует неправильную дробь в смешанную дробь.
\ (\ frac {40} {7} \) = 5 \ (\ frac {5} {7} \)
Вопрос 6.
\ (\ frac {7} {8} \ times \ frac {3} {8} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {21} {64} \)
Пояснение:
\ (\ frac {7} {8} \) × \ (\ frac {3} {8} \)
Умножьте числители и знаменатели дробей.
\ (\ frac {7} {8} \) × \ (\ frac {3} {8} \) = \ (\ frac {21} {64} \)
Вопрос 7.
\ (\ frac {1} {2} \ times \ frac {3} {4} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {3} {8} \)
Пояснение:
Умножьте числители и знаменатели дробей.
\ (\ frac {1} {2} \ times \ frac {3} {4} \)
\ (\ frac {1} {2} \) × \ (\ frac {3} {4} \) = \ (\ frac {3} {8} \)
\ (\ frac {1} {2} \ times \ frac {3} {4} \) = \ (\ frac {3} {8} \)
Вопрос 8.
\ (\ frac {7} {8} \ times \ frac {4} {7} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {2} \)
Пояснение:
Умножьте числители и знаменатели дробей.
7 в числителе и 7 в знаменателе будут удалены.
4 делит 8 на два.
Таким образом, дробь равна \ (\ frac {1} {2} \)
\ (\ frac {7} {8} \ times \ frac {4} {7} \) = \ (\ frac {1} {2 } \)
Вопрос 9.
\ (2 \ times \ frac {3} {11} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {6} {11} \)
Пояснение:
Умножьте числитель на целые числа.
2 × \ (\ frac {3} {11} \)
2 × 3 = 6
2 × \ (\ frac {3} {11} \) = \ (\ frac {6} {11} \)
Таким образом, \ (2 \ times \ frac {3} {11} \) = \ (\ frac {6} {11} \)
Вопрос 10.
\ (\ frac {5} {8} \ times \ frac {2} {3} \)
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {5} {12} \)
Пояснение:
\ (\ frac {5} {8} \ times \ frac {2} {3} \)
Умножьте числители и знаменатели дробей.
\ (\ frac {5} {8} \) × \ (\ frac {2} {3} \) = \ (\ frac {10} {24} \)
\ (\ frac {10} {24} \) = \ (\ frac {5} {12} \)
\ (\ frac {5} {8} \ times \ frac {2} {3} \) = \ (\ frac {5} {12} \ )
Вопрос 11.
\ (\ frac {7} {12} \ times 8 \)
______ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {2} {3} \)
Пояснение:
8 × \ (\ frac {7} {12} \)
Умножьте числитель на целые числа.
8 × \ (\ frac {7} {12} \) = \ (\ frac {56} {12} \) = \ (\ frac {14} {3} \)
Преобразование неправильной дроби в смешанную дробь .
\ (\ frac {14} {3} \) = 4 \ (\ frac {2} {3} \)
Заполните утверждение, указав «равно», «больше» или «меньше».
Вопрос 12.
3 × \ (\ frac {2} {3} \) _________ 3
Ответ: Менее
Пояснение:
3 × \ (\ frac {2} {3} \)
Умножьте числитель на целые числа.
3 в знаменателе будут отменены.
3 × \ (\ frac {2} {3} \) = 2
2 меньше 3.
3 × \ (\ frac {2} {3} \) меньше 3.
Вопрос 13.
\ (\ frac {5} {7} \) × 3 _________ \ (\ frac {5} {7} \)
Ответ: Больше
Пояснение:
\ (\ frac {5} {7} \) × 3
Умножьте числитель на целые числа.
\ (\ frac {5} {7} \) × 3 = \ (\ frac {15} {7} \)
Преобразовать в смешанную дробь.
\ (\ frac {15} {7} \) = 2 \ (\ frac {1} {4} \)
2 \ (\ frac {1} {4} \) больше, чем \ (\ frac {5 } {7} \)
Контрольный пункт в середине главы — стр.316
Вопрос 14.
От обеда осталось \ (\ frac {5} {6} \) яблочного пирога. Завтра Виктор планирует съесть \ (\ frac {1} {6} \) оставшегося пирога. Сколько всего пирога останется после того, как он съест завтра?
\ (\ frac {□} {□} \) всего пирога
Ответ: \ (\ frac {25} {36} \) всего пирога
Пояснение:
Гивен,
Яблочный пирог, оставшийся после обеда, — это \ (\ frac {5} {6} \).
Виктор планирует съесть оставшийся пирог, так и \ (\ frac {1} {6} \)
Весь пирог останется после завтрака Виктора =?
Пирог, оставшийся после обеда = \ (\ frac {5} {6} \)
Виктор планирует съесть оставшийся пирог = \ (\ frac {1} {6} \)
\ (\ frac {5} {6 } \) × \ (\ frac {1} {6} \) = \ (\ frac {5} {36} \)
Чтобы найти весь пирог, он останется после завтрака:
\ (\ frac {5 } {6} \) — \ (\ frac {5} {36} \)
LCD = 36
\ (\ frac {5} {6} \) × \ (\ frac {6} {6} \) — \ (\ frac {5} {36} \)
\ (\ frac {30} {36} \) — \ (\ frac {5} {36} \) = \ (\ frac {25} {36} \ )
Таким образом, после того, как Виктор съест завтра, останется весь пирог \ (\ frac {25} {36} \)
Вопрос 15.
Эверетт и Мари собираются сделать фруктовые батончики для воссоединения своей семьи. Они хотят получить в 4 раза больше, чем рецепт. Если рецепт требует \ (\ frac {2} {3} \) стакана масла, сколько масла им потребуется?
______ \ (\ frac {□} {□} \) стакан масла
Ответ: 2 \ (\ frac {2} {3} \)
Пояснение:
Эверетт и Мари собираются сделать фруктовые батончики для воссоединения своей семьи.
Они хотят получить в 4 раза больше, чем рецепт.
4 × \ (\ frac {2} {3} \) = \ (\ frac {8} {3} \)
Смешанная доля \ (\ frac {8} {3} \) равна 2 \ (\ frac {2} {3} \)
Таким образом, Эверетт и Мари нуждаются в нефти Эверетту и Мари.
Вопрос 16.
Мэтт построил модель ниже, чтобы помочь ему решить свою математическую задачу. Напишите выражение, соответствующее модели Мэтта.
Тип ниже:
__________
Ответ: \ (\ frac {3} {4} \) × \ (\ frac {1} {3} \)
Пояснение:
Видя приведенный выше рисунок, мы можем сказать, что дробь для модели Мэтта равна \ (\ frac {3} {4} \) и \ (\ frac {2} {3} \).
Умножаем дроби \ (\ frac {3} {4} \) × \ (\ frac {2} {3} \) = \ (\ frac {1} {4} \)
Поделиться и показать — Страница No.319
Используйте сетку, чтобы найти область. Пусть каждый квадрат представляет \ (\ frac {1} {3} \) метр на \ (\ frac {1} {3} \) метр.
Вопрос 1.
1 \ (\ frac {2} {3} \) × 1 \ (\ frac {1} {3} \)
• Нарисуйте диаграмму для представления размеров.
• Сколько квадратов покрывают диаграмму?
• Какова площадь каждого квадрата?
• Какова площадь диаграммы?
______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {2} {9} \)
Пояснение:
Диаграмма покрыта 20 квадратами.
Каждый квадрат представляет \ (\ frac {1} {9} \) квадратный метр
20 × \ (\ frac {1} {9} \) = \ (\ frac {20} {9} \)
Преобразовать дробь в смешанную фракцию.
\ (\ frac {20} {9} \) = 2 \ (\ frac {2} {9} \)
Таким образом, площадь диаграммы равна 2 \ (\ frac {2} {9} \)
Используйте сетку, чтобы найти область. Пусть каждый квадрат представляет \ (\ frac {1} {4} \) метр на \ (\ frac {1} {4} \) метр.
Вопрос 2.
1 \ (\ frac {3} {4} \) × 1 \ (\ frac {2} {4} \)
______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {5} {8} \)
Пояснение:
Диаграмму покрывают 42 квадрата.
Каждый квадрат представляет \ (\ frac {1} {16} \) квадратных метров.
42 × \ (\ frac {1} {16} \) = \ (\ frac {21} {8} \)
Преобразование дроби в смешанную дробь.
\ (\ frac {21} {8} \) = 2 \ (\ frac {5} {8} \)
Площадь диаграммы составляет 2 \ (\ frac {5} {8} \) квадратный метр.
Вопрос 3.
1 \ (\ frac {1} {4} \) × 1 \ (\ frac {1} {2} \)
______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {7} {8} \)
Пояснение:
Диаграмму покрывают 30 квадратов.
Каждый квадрат представляет \ (\ frac {1} {16} \) квадратных метров.
30 × \ (\ frac {1} {16} \) = \ (\ frac {15} {8} \)
Преобразование дроби в смешанную дробь.
\ (\ frac {15} {8} \) = 1 \ (\ frac {7} {8} \)
Используйте модель области для решения.
Вопрос 4.
1 \ (\ frac {3} {4} \) × 2 \ (\ frac {1} {2} \)
______ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {3} {8} \)
Пояснение:
54 квадрата покрывают диаграмму.
Каждый квадрат представляет \ (\ frac {1} {16} \) квадратных метров.
54 × \ (\ frac {1} {16} \) = \ (\ frac {27} {8} \)
Преобразование дроби в смешанную дробь.
\ (\ frac {27} {8} \) = 4 \ (\ frac {3} {8} \)
Вопрос 5.
1 \ (\ frac {3} {8} \) × 2 \ (\ frac {1} {2} \)
______ \ (\ frac {□} {□} \)
Ответ: 3 \ (\ frac {7} {16} \)
Пояснение:
Диаграмма покрыта 55 квадратами.
Каждый квадрат представляет \ (\ frac {1} {16} \) квадратных метров.
55 × \ (\ frac {1} {16} \) = \ (\ frac {55} {16} \)
Преобразование дроби в смешанную дробь.
\ (\ frac {55} {16} \) = 3 \ (\ frac {7} {16} \)
Вопрос 6.
1 \ (\ frac {1} {9} \) × 1 \ (\ frac {2} {3} \)
______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {23} {27} \)
Пояснение:
130 квадратов диаграммы.
Каждый квадрат представляет \ (\ frac {1} {16} \) квадратных метров.
1 \ (\ frac {1} {9} \) × 1 \ (\ frac {2} {3} \)
\ (\ frac {10} {9} \) × \ (\ frac {5} { 3} \) = \ (\ frac {50} {27} \)
Преобразование дроби в смешанную дробь.
\ (\ frac {50} {27} \) = 1 \ (\ frac {23} {27} \)
Вопрос 7.
Объясните, как определение площади прямоугольника с целыми длинами сторон сравнивается с нахождением площади прямоугольника с дробными длинами сторон.
Тип ниже:
__________
Ответ:
15 квадратов покрывают диаграмму.
Каждый квадрат равен \ (\ frac {1} {16} \) квадратной единице.
Площадь диаграммы составляет \ (\ frac {15} {16} \) квадратных единиц.
Решение проблем — стр. № 320
Задача
Вопрос 8.
Терренс проектирует сад. Он нарисовал следующую схему своего сада. Поставьте задачу, используя смешанные числа, которую можно решить с помощью его диаграммы.
Задайте проблему. Решите вашу проблему.
Опишите, как вы определились с размерами сада Терренса.
Тип ниже:
__________
Ответ:
как нахождение площади прямоугольника со стороной смешанных дробей сравнивается с нахождением площади прямоугольника с дробными длинами сторон.
6 × 1 \ (\ frac {1} {8} \) = \ (\ frac {□} {□} \)
Пусть каждый квадрат представляет \ (\ frac {1} {2} \) метр на \ ( \ frac {1} {2} \)
Из рисунка выше мы можем сказать, что количество квадратов равно 27.
Итак, 27 квадратов покрывают диаграмму.
Каждый квадрат равен \ (\ frac {1} {4} \) квадратной единице.
27 × \ (\ frac {1} {4} \) = \ (\ frac {27} {4} \)
Преобразование дроби в смешанную дробь.
\ (\ frac {27} {4} \) = 6 \ (\ frac {3} {4} \)
Заполните утверждение, указав «равно», «больше» или «меньше».
Вопрос 1.
\ (\ frac {5} {6} \) × 2 \ (\ frac {1} {5} \) будет __________ 2 \ (\ frac {1} {5} \)
Заштрихуйте модель
показывает \ (\ frac {5} {6} \) × 2 \ (\ frac {1} {5} \).
__________
Ответ: Менее
Пояснение:
\ (\ frac {5} {6} \) × 2 \ (\ frac {1} {5} \)
Преобразует смешанную дробь в неправильную дробь.
2 \ (\ frac {1} {5} \) = \ (\ frac {11} {5} \)
\ (\ frac {5} {6} \) × \ (\ frac {11} {5 } \) = \ (\ frac {55} {30} \)
1 \ (\ frac {25} {30} \) = 1 \ (\ frac {5} {6} \)
Таким образом, 1 \ (\ frac {5} {6} \) меньше 2 \ (\ frac {1} {5} \)
Вопрос 2.
1 \ (\ frac {1} {5} \) × 2 \ (\ frac {2} {3} \) будет __________ 2 \ (\ frac {2} {3} \)
Ответ: Больше
Пояснение:
1 \ (\ frac {1} {5} \) × 2 \ (\ frac {2} {3} \)
Сначала преобразуйте смешанную дробь в неправильную дробь.
\ (\ frac {6} {5} \) × \ (\ frac {8} {3} \) = \ (\ frac {48} {15} \)
\ (\ frac {48} {15} \) = 3 \ (\ frac {3} {15} \)
3 \ (\ frac {3} {15} \) больше 2 \ (\ frac {2} {3} \)
Вопрос 3.
\ (\ frac {4} {5} \) × 2 \ (\ frac {2} {5} \) будет __________ 2 \ (\ frac {2} {5} \)
Ответ: Менее
Пояснение:
\ (\ frac {4} {5} \) × \ (\ frac {12} {5} \)
Сначала преобразуйте смешанную дробь в неправильную дробь.
\ (\ frac {4} {5} \) × \ (\ frac {12} {5} \) = \ (\ frac {48} {5} \)
\ (\ frac {48} {5} \) = 9 \ (\ frac {3} {5} \)
9 \ (\ frac {3} {5} \) меньше 2 \ (\ frac {2} {5} \)
Самостоятельно
Заполните утверждение, указав «равно», «больше» или «меньше».
Вопрос 4.
\ (\ frac {2} {2} \) × 1 \ (\ frac {1} {2} \) будет __________ 1 \ (\ frac {1} {2} \)
Ответ: равно
Пояснение:
\ (\ frac {2} {2} \) × \ (\ frac {3} {2} \) = \ (\ frac {6} {4} \)
\ (\ frac {6} {4} \) = 1 \ (\ frac {1} {2} \)
1 \ (\ frac {1} {2} \) равно 1 \ (\ frac {1} {2} \)
\ (\ frac {2} {2} \) × 1 \ (\ frac {1} {2} \) будет равно 1 \ (\ frac {1} {2} \)
Вопрос 5.
\ (\ frac {2} {3} \) × 3 \ (\ frac {1} {6} \) будет __________ 3 \ (\ frac {1} {6} \)
Ответ: Менее
Пояснение:
\ (\ frac {2} {3} \) × 3 \ (\ frac {1} {6} \)
Сначала преобразуйте смешанную дробь в неправильную дробь.
\ (\ frac {2} {3} \) × \ (\ frac {19} {6} \) = \ (\ frac {38} {18} \)
\ (\ frac {38} {18} \) = 2 \ (\ frac {2} {18} \)
2 \ (\ frac {2} {18} \) меньше 3 \ (\ frac {1} {6} \)
\ (\ frac {2} {3} \) × 3 \ (\ frac {1} {6} \) будет меньше 3 \ (\ frac {1} {6} \)
Вопрос 6.
2 × 2 \ (\ frac {1} {4} \) будет __________ 2 \ (\ frac {1} {4} \)
Ответ: Больше
Пояснение:
2 × 2 \ (\ frac {1} {4} \)
Сначала преобразуйте смешанную дробь в неправильную дробь.
2 × \ (\ frac {9} {4} \) = \ (\ frac {18} {4} \)
\ (\ frac {18} {4} \) = 4 \ (\ frac {2} {4} \)
4 \ (\ frac {1} {2} \) больше 2 \ (\ frac {1} {4} \)
Вопрос 7.
4 × 1 \ (\ frac {3} {7} \) будет __________ 1 \ (\ frac {3} {7} \)
Ответ: Больше
Пояснение:
4 × 1 \ (\ frac {3} {7} \)
Сначала преобразуйте смешанную дробь в неправильную дробь.
4 × \ (\ frac {10} {7} \) = \ (\ frac {40} {7} \)
4 × 1 \ (\ frac {3} {7} \) = 5 \ (\ frac {5} {7} \)
5 \ (\ frac {5} {7} \) больше 1 \ (\ frac {3} {7} \)
Алгебра Укажите, меньше ли неизвестный множитель 1 или больше 1.
Вопрос 8.
■ × 1 \ (\ frac {2} {3} \) = \ (\ frac {5} {6} \)
Неизвестный коэффициент: __________ 1.
Ответ: Менее
Пояснение:
■ × 1 \ (\ frac {2} {3} \) = \ (\ frac {5} {6} \)
■ × \ (\ frac {5} {3} \) = \ ( \ frac {5} {6} \)
■ = \ (\ frac {1} {2} \)
Таким образом, неизвестный коэффициент равен \ (\ frac {1} {2} \)
\ (\ frac {1 } {2} \) меньше 1.
Вопрос 9.
■ × 1 \ (\ frac {1} {4} \) = 2 \ (\ frac {1} {2} \)
Неизвестный коэффициент __________ 1.
Ответ: Больше
Пояснение:
■ × 1 \ (\ frac {1} {4} \) = 2 \ (\ frac {1} {2} \)
■ = 2 \ (\ frac {1} {2} \) ÷ 1 \ (\ frac {1} {4} \)
■ = 2 × 2 = 4
■ = 4
Таким образом, неизвестный коэффициент равен 4
4 больше 1.
Решение проблем — Стр. № 324
Вопрос 10.
Кайл рисует в масштабе свою тетрадь по математике. Размеры его рисунка будут \ (\ frac {1} {3} \) размерам его книги. Если ширина его книги составляет 8 \ (\ frac {1} {2} \) дюймов, будет ли ширина его рисунка равна, больше или меньше 8 \ (\ frac {1} {2} \ ) дюймы?
__________
Ответ: Менее
Пояснение:
Учитывая это,
Кайл рисует в масштабе свою книгу по математике.
Размеры его рисунка будут \ (\ frac {1} {3} \) размерам его книги.
\ (\ frac {1} {3} \) × 8 \ (\ frac {1} {2} \)
Сначала преобразуйте смешанную дробь в неправильную дробь.
\ (\ frac {1} {3} \) × \ (\ frac {17} {2} \) = \ (\ frac {17} {6} \)
Преобразует дробь в смешанную дробь.
\ (\ frac {17} {6} \) = 2 \ (\ frac {5} {6} \)
2 \ (\ frac {5} {6} \) меньше 8 \ (\ frac { 1} {2} \) дюймов.
Вопрос 11.
Смысл или ерунда?
Пенни хочет создать модель жука больше, чем в натуральную величину.Пенни говорит, что она собирается использовать коэффициент масштабирования \ (\ frac {7} {12} \). Это имеет смысл или это чепуха? Объяснять.
Тип ниже:
__________
Ответ: Это ерунда, потому что Пенни хочет сделать жука больше, чем в натуральную величину. Таким образом, коэффициент масштабирования \ (\ frac {7} {12} \) не соответствует, потому что, когда мы умножаем любое значение на число меньше 1, мы получаем меньшее число.
Вопрос 12.
Шеннон, Мэри и Джон получают еженедельное пособие. Шеннон зарабатывает сумму, равную \ (\ frac {2} {3} \) от того, что зарабатывает Джон.Мэри зарабатывает 1 \ (\ frac {2} {3} \) того, что зарабатывает Джон. Джон зарабатывает 20 долларов в неделю. Кто получает наибольшее пособие? Кто зарабатывает меньше всего?
__________ получает наибольшее пособие.
__________ получает наименьшее пособие
Ответ:
Мэри получает наибольшее пособие.
Шеннон получает наименьшее содержание.
Пояснение:
Шеннон, Мэри и Джон получают еженедельное пособие.
Шеннон зарабатывает сумму, равную \ (\ frac {2} {3} \) того, что зарабатывает Джон.
Мэри зарабатывает сумму, равную 1 \ (\ frac {2} {3} \) того, что зарабатывает Джон.
Джон зарабатывает 20 долларов в неделю.
\ (\ frac {2} {3} \) ________ 1 \ (\ frac {2} {3} \)
Преобразует смешанную дробь в неправильную дробь.
1 \ (\ frac {2} {3} \) = \ (\ frac {5} {3} \)
\ (\ frac {2} {3} \) меньше 1 \ (\ frac {2 } {3} \)
Таким образом, Шеннон получает наименьшее пособие, а Мэри — наибольшее пособие.
Вопрос 13.
Щенок Test Prep Addie весит в 1 \ (\ frac {2} {3} \) раз больше, чем он весил при рождении.При рождении он весил 1 \ (\ frac {1} {3} \) фунта. Какое из приведенных ниже утверждений верно?
Опции:
а. Щенок весит столько же, сколько при рождении.
г. Щенок весит меньше, чем при рождении.
г. Щенок весит больше, чем при рождении.
г. Щенок весит вдвое больше, чем при рождении.
Ответ: Щенок весит больше, чем при рождении.
Пояснение:
Щенок Test Prep Addie весит в 1 \ (\ frac {2} {3} \) раз больше, чем он весил при рождении.
Он весил 1 \ (\ frac {1} {3} \) фунта при рождении.
1 \ (\ frac {2} {3} \) больше 1 \ (\ frac {1} {3} \).
Итак, щенок весит больше, чем при рождении.
Таким образом, правильный ответ — вариант C.
Найдите товар. Напишите продукт в простейшей форме.
Вопрос 1.
1 \ (\ frac {2} {3} \) × 3 \ (\ frac {4} {5} \) = \ (\ frac {■} {3} \) × \ (\ frac {■} {5} \)
= \ (\ frac {■} {■} \)
=?
_____ \ (\ frac {□} {□} \)
Ответ: 6 \ (\ frac {1} {3} \)
Пояснение:
1 \ (\ frac {2} {3} \) × 3 \ (\ frac {4} {5} \)
\ (\ frac {5} {3} \) × \ (\ frac {19} { 5} \)
\ (\ frac {■} {3} \) × \ (\ frac {■} {5} \) = \ (\ frac {5} {3} \) × \ (\ frac {19 } {5} \)
\ (\ frac {5} {3} \) × \ (\ frac {19} {5} \) = 6 \ (\ frac {1} {3} \)
Вопрос 2.
\ (\ frac {1} {2} \) × 1 \ (\ frac {1} {3} \)
Закрасьте модель, чтобы найти продукт.
\ (\ frac {□} {□} \)
Ответ: \ (\ frac {2} {3} \)
Пояснение:
\ (\ frac {1} {2} \) × 1 \ (\ frac {1} {3} \)
1 \ (\ frac {1} {3} \) = \ (\ frac { 4} {3} \)
\ (\ frac {1} {2} \) × \ (\ frac {4} {3} \) = \ (\ frac {4} {6} \)
Вопрос 3.
\ (1 \ frac {1} {8} \ times 2 \ frac {1} {3} \) = ______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {5} {8} \)
Пояснение:
1 \ (\ frac {1} {8} \) × 2 \ (\ frac {1} {3} \)
\ (\ frac {9} {8} \) × \ (\ frac { 7} {3} \) = \ (\ frac {63} {24} \)
\ (\ frac {63} {24} \) = 2 \ (\ frac {63} {24} \) = 2 \ (\ frac {15} {24} \)
2 \ (\ frac {15} {24} \) = 2 \ (\ frac {5} {8} \)
\ (1 \ frac {1} {8 } \ times 2 \ frac {1} {3} \) = 2 \ (\ frac {5} {8} \)
Вопрос 4.
\ (\ frac {3} {4} \ times 6 \ frac {5} {6} \) = ______ \ (\ frac {□} {□} \)
Ответ: 5 \ (\ frac {1} {8} \)
Пояснение:
\ (\ frac {3} {4} \) × 6 \ (\ frac {5} {6} \)
\ (\ frac {3} {4} \) × \ (\ frac {41 } {6} \)
\ (\ frac {123} {24} \) = \ (\ frac {41} {8} \)
Преобразуйте дробь в смешанную дробь.
\ (\ frac {41} {8} \) = 5 \ (\ frac {1} {8} \)
Вопрос 5.
\ (1 \ frac {2} {7} \ times 1 \ frac {3} {4} \) = ______ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {1} {4} \)
Пояснение:
1 \ (\ frac {2} {7} \) × 1 \ (\ frac {3} {4} \)
Умножьте числители и знаменатели.
Преобразует смешанную дробь в неправильную дробь.
\ (\ frac {9} {7} \) × \ (\ frac {7} {4} \) = \ (\ frac {63} {28} \)
\ (\ frac {63} {28} \) = 2 \ (\ frac {1} {4} \)
\ (1 \ frac {2} {7} \ times 1 \ frac {3} {4} \) = 2 \ (\ frac {1} {4} \)
Вопрос 6.
\ (\ frac {3} {4} \ times 1 \ frac {1} {4} \) = ______ \ (\ frac {□} {□} \)
Ответ: \ (\ frac {15} {16} \)
Пояснение:
\ (\ frac {3} {4} \) × 1 \ (\ frac {1} {4} \)
\ (\ frac {3} {4} \) × \ (\ frac {5 } {4} \) = \ (\ frac {15} {16} \)
\ (\ frac {3} {4} \ times 1 \ frac {1} {4} \) = \ (\ frac {15 } {16} \)
Используйте свойство распределения, чтобы найти продукт.
Вопрос 7.
\ (16 \ times 2 \ frac {1} {2} \) = ______
Ответ: 40
Пояснение:
\ (16 \ times 2 \ frac {1} {2} \)
(16 × 2) + (16 × \ (\ frac {1} {2} \))
32 + 8 = 40
\ (16 \ times 2 \ frac {1} {2} \) = 40
Вопрос 8.
\ (1 \ frac {4} {5} \ times 15 \) = ______
Ответ: 27
Пояснение:
\ (1 \ frac {4} {5} \ times 15 \)
15 × 1 \ (\ frac {4} {5} \)
(1 × 15) + (15 × \ (\ frac {4} {5} \))
15 + \ (\ frac {60} {5} \)
15 + 12 = 27
Таким образом, \ (1 \ frac {4} {5} \ times 15 \) = 27
Самостоятельно
Найдите товар.Напишите продукт в простейшей форме.
Вопрос 9.
\ (\ frac {3} {4} \ times 1 \ frac {1} {2} \) = ______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {1} {8} \)
Пояснение:
\ (\ frac {3} {4} \) × 1 \ (\ frac {1} {2} \)
\ (\ frac {3} {4} \) × \ (\ frac {3 } {2} \) = \ (\ frac {9} {8} \)
Теперь преобразуйте неправильную дробь в смешанную.
\ (\ frac {9} {8} \) = 1 \ (\ frac {1} {8} \)
Вопрос 10.
\ (4 \ frac {2} {5} \ times 1 \ frac {1} {2} \) = ______ \ (\ frac {□} {□} \)
Ответ: 6 \ (\ frac {3} {5} \)
Пояснение:
4 \ (\ frac {2} {5} \) × 1 \ (\ frac {1} {2} \)
Преобразует смешанную дробь в неправильную дробь.
\ (\ frac {22} {5} \) × \ (\ frac {3} {2} \) = \ (\ frac {66} {10} \)
Смешанная фракция \ (\ frac {66 } {10} \) равно 6 \ (\ frac {3} {5} \)
Вопрос 11.
\ (5 \ frac {1} {3} \ times \ frac {3} {4} \) = ______
Ответ: 4
Пояснение:
5 \ (\ frac {1} {3} \) × \ (\ frac {3} {4} \)
Преобразует смешанную дробь в неправильную дробь.
\ (\ frac {16} {3} \) × \ (\ frac {3} {4} \) = \ (\ frac {48} {12} \)
12 делит 48 на четыре раза.
Таким образом, \ (5 \ frac {1} {3} \ times \ frac {3} {4} \) = 4
Вопрос 12.
\ (2 \ frac {1} {2} \ times 5 \ frac {1} {5} \) = ______
Ответ: 13
Пояснение:
2 \ (\ frac {1} {2} \) × 5 \ (\ frac {1} {5} \)
\ (\ frac {5} {2} \) × \ (\ frac { 26} {5} \) = \ (\ frac {130} {10} \)
10 делится на 130 тринадцать раз.
\ (\ frac {130} {10} \) = 13
\ (2 \ frac {1} {2} \ times 5 \ frac {1} {5} \) = 13
Вопрос 13.
\ (12 \ frac {3} {4} \ times 2 \ frac {2} {3} \) = ______
Ответ: 34
Пояснение:
12 \ (\ frac {3} {4} \) × 2 \ (\ frac {2} {3} \)
\ (\ frac {51} {4} \) × \ (\ frac { 6} {3} \)
3 делит 51 семнадцать раз.
17 × 2 = 34
Вопрос 14.
\ (3 \ times 4 \ frac {1} {2} \) = ______ \ (\ frac {□} {□} \)
Ответ: 13 \ (\ frac {1} {2} \)
Пояснение:
3 × 4 \ (\ frac {1} {2} \)
3 × \ (\ frac {9} {2} \) = \ (\ frac {27} {2} \)
Преобразовать дробь в смешанную дробь
\ (\ frac {27} {2} \) = 13 \ (\ frac {1} {2} \)
Вопрос 15.
\ (2 \ frac {3} {8} \ times \ frac {4} {9} \) = ______ \ (\ frac {□} {□} \)
Ответ: 1 \ (\ frac {1} {18} \)
Пояснение:
2 \ (\ frac {3} {8} \) × \ (\ frac {4} {9} \)
\ (\ frac {19} {8} \) × \ (\ frac {4 } {9} \) = \ (\ frac {76} {72} \)
\ (\ frac {76} {72} \) = 1 \ (\ frac {1} {18} \)
\ (2 \ frac {3} {8} \ times \ frac {4} {9} \) = 1 \ (\ frac {1} {18} \)
Вопрос 16.
\ (1 \ frac {1} {3} \ times 1 \ frac {1} {4} \ times 1 \ frac {1} {5} \) = ______
Ответ: 2
Пояснение:
1 \ (\ frac {1} {3} \) × 1 \ (\ frac {1} {4} \) × 1 \ (\ frac {1} {5} \)
\ (\ frac {4} {3} \) × \ (\ frac {5} {4} \) × \ (\ frac {6} {5} \) = 2
\ (1 \ frac {1} {3} \ times 1 \ frac {1} {4} \ times 1 \ frac {1} {5} \) = 2
Используйте свойство распределения, чтобы найти продукт.
Вопрос 17.
\ (10 \ times 2 \ frac {3} {5} \) = ______
Ответ: 26
Пояснение:
10 × 2 \ (\ frac {3} {5} \)
Теперь используйте свойство распределения, чтобы найти продукт.
(10 × 2) + (10 × \ (\ frac {3} {5} \))
20 + \ (\ frac {30} {5} \)
5 делит 30 на 6 раз.
20 + 6 = 26
Вопрос 18.
\ (3 \ frac {3} {4} \ times 12 \) = ______
Ответ: 45
Пояснение:
3 \ (\ frac {3} {4} \) × 12
Теперь используйте свойство распределения, чтобы найти продукт.
(12 × 3) + (12 × \ (\ frac {3} {4} \))
36 + \ (\ frac {36} {4} \)
36 + 9 = 45
\ (3 \ frac {3} {4} \ times 12 \) = 45
Поделиться и показать Подключиться к здоровью — № страницы.328
Смена рецептов
Многие рецепты можно сделать более полезными, уменьшив количество жира, сахара и соли.
У Келли есть рецепт кексов, для которого требуется 1 \ (\ frac {1} {2} \) стакан сахара. Она хочет использовать \ (\ frac {1} {2} \) это количество сахара и побольше корицы и ванили. Сколько сахара она будет употреблять?
Умножьте 1 \ (\ frac {1} {2} \) на \ (\ frac {1} {2} \), чтобы найти, какую часть исходного количества сахара использовать.
Запишите смешанное число в виде дроби больше 1.Затем умножьте.
\ (\ frac {1} {2} \ times 1 \ frac {1} {2} = \ frac {1} {2} \ times \ frac {3} {2} \)
= \ (\ frac { 3} {4} \)
Итак, Келли будет использовать \ (\ frac {3} {4} \) стакан сахара.
Вопрос 19.
У Мишель есть рецепт, который требует 2 \ (\ frac {1} {2} \) стаканов растительного масла. Она хочет использовать \ (\ frac {2} {3} \) это количество масла и использовать яблочное пюре, чтобы заменить остальное. Сколько растительного масла она будет использовать?
______ \ (\ frac {□} {□} \) чашек
Ответ: 1 \ (\ frac {2} {3} \)
Пояснение:
У Мишель есть рецепт, по которому нужно приготовить 2 \ (\ frac {1} {2} \) стакана растительного масла.
Она хочет использовать \ (\ frac {2} {3} \) это количество масла и использовать яблочное пюре, чтобы заменить остальное.
Умножьте 2 \ (\ frac {1} {2} \) на \ (\ frac {2 } {3} \), чтобы узнать, сколько растительного масла она будет использовать.
2 \ (\ frac {1} {2} \) × \ (\ frac {2} {3} \)
Преобразуйте смешанные дроби в дроби.
\ (\ frac {5} {2} \) × \ (\ frac {2} {3} \) = \ (\ frac {10} {6} \)
\ (\ frac {10} {6} \) = \ (\ frac {5} {3} \) = 1 \ (\ frac {2} {3} \)
Она будет использовать 1 \ (\ frac {2} {3} \) стакан растительного масла. .
Вопрос 20.
Рецепт супа Тони требует 1 \ (\ frac {1} {4} \) чайной ложки соли.Он хочет использовать \ (\ frac {1} {2} \) эту сумму. Сколько соли он будет использовать?
\ (\ frac {□} {□} \) чайная ложка
Ответ: \ (\ frac {5} {8} \)
Пояснение:
Рецепт супа Тони требует 1 \ (\ frac {1} {4} \) чайной ложки соли.
Он хочет использовать \ (\ frac {1} {2} \) эту сумму.
Умножьте дроби, чтобы найти, сколько соли он будет использовать в рецепте супа.
1 \ (\ frac {1} {4} \) × \ (\ frac {1} {2} \)
Преобразуйте смешанные дроби в неправильные дроби.
\ (\ frac {5} {4} \) × \ (\ frac {1} {2} \) = \ (\ frac {5} {8} \)
Таким образом, Тони использует \ (\ frac {5} {8} \) чайная ложка соли для супа.
Вопрос 21.
Рецепт Джеффри овсяных маффинов требует 2 \ (\ frac {1} {4} \) стаканов овсяных хлопьев и готовит дюжину маффинов. Если он приготовит 1 \ (\ frac {1} {2} \) дюжину кексов для собрания клуба, сколько овсянки он потратит?
_____ \ (\ frac {□} {□} \) чашек
Ответ: 3 \ (\ frac {3} {8} \)
Пояснение:
Рецепт Джеффри для овсяных маффинов требует 2 \ (\ frac {1} {4} \) стаканов овсяных хлопьев и позволяет приготовить дюжину маффинов.
Чтобы узнать, сколько овсянки он использует, нам нужно умножить дроби.
2 \ (\ frac {1} {4} \) × 1 \ (\ frac {1} {2} \)
Преобразуйте смешанные дроби в неправильные дроби.
\ (\ frac {9} {4} \) × \ (\ frac {3} {2} \)
\ (\ frac {27} {8} \) = 3 \ (\ frac {3} {8 } \)
Таким образом, он будет использовать 3 \ (\ frac {3} {8} \) чашки овсянки, чтобы приготовить овсяные кексы.
Вопрос 22.
Рецепт кексов Кары требует 1 \ (\ frac {1} {2} \) стакана муки для маффинов и \ (\ frac {1} {4} \) стакана муки для начинки. Если она приготовит \ (\ frac {1} {2} \) по первоначальному рецепту, сколько муки она будет использовать?
\ (\ frac {□} {□} \) стакан муки
Ответ: \ (\ frac {7} {8} \)
Пояснение:
Преобразование смешанных дробей в неправильные дроби.
1 \ (\ frac {1} {2} \) = \ (\ frac {3} {2} \)
\ (\ frac {3} {2} \) + \ (\ frac {1} {4 } \) = \ (\ frac {7} {4} \)
Теперь мы можем определить, сколько муки она будет использовать для изготовления \ (\ frac {1} {2} \) по первоначальному рецепту, умножив
\ (\ frac {7} {4} \) от \ (\ frac {1} {2} \)
\ (\ frac {7} {4} \) × \ (\ frac {1} {2} \) = \ (\ frac {7} {8} \)
Вопрос 1.
Когда Паскаль построил собачью будку, он знал, что ему нужно, чтобы пол в доме имел площадь 24 квадратных фута.Он также хотел, чтобы ширина была равна \ (\ frac {2} {3} \) длине. Какие габариты собачьей будки?
Сначала выберите два числа, произведение которых равно 24.
Угадайте: ____ футов и ____ футов
Затем проверьте эти числа. Является ли большее число \ (\ frac {2} {3} \) другим числом?
Чек: \ (\ frac {2} {3} \) × _____ = _____
Я предполагаю ______.
Наконец, если предположение неверно, исправьте его и проверьте еще раз. Продолжайте, пока не найдете правильный ответ.
_____ футов на _____ футов
Ответ: 4 на 6 футов
Пояснение:
Когда Паскаль построил собачью будку, он знал, что ему нужно, чтобы пол в доме имел площадь 24 квадратных фута.
Он также хотел, чтобы ширина была \ (\ frac {2} {3} \) длиной.
Я предполагаю, что 24 квадратных фута составляют 4 фута 6 футов.
Теперь давайте проверим числа.
6 × \ (\ frac {2} {3} \) = 4
Итак, моя догадка верна.
Таким образом, размеры 4 фута на 6 футов
Вопрос 2.
Что, если бы Паскаль хотел, чтобы площадь пола составляла 54 квадратных фута, а ширина по-прежнему равнялась \ (\ frac {2} {3} \) длине? Каких размеров будет пол?
_____ футов на _____ футов
Ответ: 6 футов на 9 футов
Пояснение:
Я предполагаю, что 54 квадратных фута составляют 6 футов 9 футов.
9 × \ (\ frac {2} {3} \)
3 делит 9 три раза.
9 × \ (\ frac {2} {3} \) = 6
Итак, моя догадка верна.
Следовательно, размеры будут 6 футов на 9 футов
Вопрос 3.
Лев хочет нарисовать фреску, которая покрывает стену площадью 1440 квадратных футов. Высота стены равна \ (\ frac {2} {5} \) ее длины. Какая длина и высота стены?
_____ футов на _____ футов
Ответ: 24 на 60 футов
Пояснение:
Лев хочет нарисовать фреску, покрывающую стену площадью 1440 квадратных футов.Высота стены равна \ (\ frac {2} {5} \) ее длины.
Предположение: 1440 квадратных футов = 24 футов × 60 футов
\ (\ frac {2} {5} \) × 60 = 24
Итак, наша догадка верна.
. Таким образом, размеры стены составляют 24 на 60 футов.
Самостоятельно — Стр. № 332
Вопрос 4.
Барри хочет создать рисунок, размер которого равен \ (\ frac {1} {4} \) размеру оригинала. Если дерево на исходном рисунке 14 дюймов в высоту, какой высоты будет дерево на рисунке Барри?
_____ \ (\ frac {□} {□} \) дюймов
Ответ: 3 \ (\ frac {1} {2} \) дюймов
Пояснение:
Дано:
Барри хочет создать рисунок, размер которого равен \ (\ frac {1} {4} \) размеру оригинала.
Высота дерева на чертеже составляет 14 дюймов.
14 × \ (\ frac {1} {4} \) = \ (\ frac {14} {4} \) = \ (\ frac {7} {2} \)
Преобразует дробь в смешанную дробь.
\ (\ frac {7} {2} \) = 3 \ (\ frac {1} {2} \) дюймов
Вопрос 5.
Чертеж — это масштабный чертеж здания. Размеры чертежа кукольного домика Пенни равны \ (\ frac {1} {4} \) размерам настоящего кукольного домика. Пол кукольного домика имеет площадь 864 квадратных дюйма. Если ширина кукольного домика равна \ (\ frac {2} {3} \) длине, каковы размеры пола на чертеже кукольного домика?
_____ дюймов на _____ дюймов
Ответ: 9 на 6 дюймов
Пояснение:
Чертеж — это масштабный чертеж здания.
Размеры чертежа кукольного домика Пенни равны \ (\ frac {1} {4} \) размерам настоящего кукольного домика.
Пол кукольного домика имеет площадь 864 квадратных дюйма.
Площадь кукольного домика составляет 54 квадратных дюйма.
Мое предположение 9 дюймов на 6 дюймов
Давайте проверим числа
9 × \ (\ frac {2} {3} \) = 6
Мое предположение верное.
Следовательно, размеры пола на чертеже кукольного домика 9 дюймов на 6 дюймов
Вопрос 6.
Постановка проблемы Вернитесь к упражнению 4.Напишите аналогичную задачу, используя другое измерение и другую дробь. Тогда реши свою проблему.
Тип ниже:
__________
Ответ:
Кайл производит многоразовые пакеты для продуктов и пакеты для обеда. Она использовала 3/4 ярда ткани, чтобы сделать сумку для продуктов. На пакет для обеда требуется 2/3 ткани от необходимого пакета для продуктов. Сколько ей нужно, чтобы сделать сумку для обеда?
\ (\ frac {3} {4} \) × \ (\ frac {2} {3} \) = \ (\ frac {1} {2} \)
Таким образом, Кайлу нужно \ (\ frac {1} {2} \) продуктового мешка, чтобы сделать ланч-мешок.
Вопрос 7.
Test Prep Фотография Альберта имеет площадь 80 квадратных дюймов. Длина фотографии равна 1 \ (\ frac {1} {4} \) ширине. Что из следующего может быть размером фотографии?
Опции:
а. 5 дюймов на 16 дюймов
b. 12 на 10 дюймов
c. 6 дюймов на 5 дюймов
d. 10 дюймов на 8 дюймов
Ответ: 10 на 8 дюймов
Пояснение:
Фотография Альберта имеет площадь 80 квадратных дюймов.
Длина фотографии равна 1 \ (\ frac {1} {4} \) ширине.
Я предполагаю, что для 80 квадратных дюймов это 10 на 8 дюймов.
Теперь давайте проверим числа.
8 × 1 \ (\ frac {1} {4} \) = 8 × \ (\ frac {5} {4} \) = 10
Таким образом, правильный ответ — вариант D.
Обзор главы / Тест — Стр. № 333
Концепции и навыки
Вопрос 1.
Если умножить 3 \ (\ frac {1} {4} \) на число больше единицы, как получится результат в сравнении с 3 \ (\ frac {1} {4} \)? Объяснять.
Тип ниже:
__________
Ответ:
Ваше произведение будет больше 3 1/4, потому что всякий раз, когда вы умножаете дробь на целое число меньше 1, вы получаете дробь меньше единицы, а каждый раз, когда вы умножаете на дробь и целое число больше единицы, вы получаете ответ больше 1.
Используйте модель для решения.
Вопрос 2.
\ (\ frac {2} {3} \) × 6 = _____
Ответ: 4
Пояснение:
\ (\ frac {2} {3} \) × 6
3 делит 6 дважды.
2 × 2 = 4
\ (\ frac {2} {3} \) × 6 = 4
Вопрос 3.
\ (\ frac {3} {7} \) × 14 = _____
Ответ: 6
Пояснение:
\ (\ frac {3} {7} \) × 14
7 делит 14 на два раза.
3 × 2 = 6
\ (\ frac {3} {7} \) × 14 = 6
Вопрос 4.
\ (\ frac {5} {8} \) × 24 = _____
Ответ: 15
Пояснение:
\ (\ frac {5} {8} \) × 24
8 делит 24 три раза.
5 × 3 = 15
\ (\ frac {5} {8} \) × 24 = 15
Найдите товар. Напишите продукт в простейшей форме.
Вопрос 5.
\ (\ frac {3} {5} \) × 8 = _____ \ (\ frac {□} {□} \)
Ответ: 4 \ (\ frac {4} {5} \)
Пояснение:
\ (\ frac {3} {5} \) × 8 = \ (\ frac {24} {5} \)
Смешанная доля \ (\ frac {24} {5} \) равна 4 \ (\ frac {4} {5} \)
\ (\ frac {3} {5} \) × 8 = 4 \ (\ frac {4} {5} \)
Вопрос 6.
\ (\ frac {1} {4} \) × 10 = _____ \ (\ frac {□} {□} \)
Ответ: 2 \ (\ frac {1} {2} \)
Пояснение:
\ (\ frac {1} {4} \) × 10
2 делит 10 на пять раз.
\ (\ frac {1} {2} \) × 5 = \ (\ frac {5} {2} \)
Смешанная доля \ (\ frac {5} {2} \) равна 2 \ (\ гидроразрыв {1} {2} \)
\ (\ frac {1} {4} \) × 10 = 2 \ (\ frac {1} {2} \)
Вопрос 7.
\ (\ frac {7} {5} \) × 15 = _____
Ответ: 21
\ (\ frac {7} {5} \) × 15
5 делит 15 три раза.
\ (\ frac {7} {5} \) × 15 = 7 × 3 = 21
\ (\ frac {7} {5} \) × 15 = 21
Вопрос 8.
\ (\ frac {5} {6} \) × \ (\ frac {2} {3} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {5} {9} \)
Пояснение:
\ (\ frac {5} {6} \) × \ (\ frac {2} {3} \) = \ (\ frac {10} {18} \)
\ (\ frac {10} {18} \) = \ (\ frac {5} {9} \)
Таким образом, \ (\ frac {5} {6} \) × \ (\ frac {2} {3} \) = \ (\ frac {5} {9} \)
Вопрос 9.
\ (\ frac {1} {5} \) × \ (\ frac {5} {7} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {7} \)
Пояснение:
\ (\ frac {1} {5} \) × \ (\ frac {5} {7} \)
5 в числителе и 5 в знаменателе отменяются.
= \ (\ frac {1} {7} \)
Таким образом, \ (\ frac {1} {5} \) × \ (\ frac {5} {7} \) = \ (\ frac {1} { 7} \)
Вопрос 10.
\ (\ frac {3} {8} \) × \ (\ frac {1} {6} \) = \ (\ frac {□} {□} \)
Ответ: \ (\ frac {1} {16} \)
Пояснение:
\ (\ frac {3} {8} \) × \ (\ frac {1} {6} \)
3 делит 6 дважды на
\ (\ frac {3} {8} \) × \ (\ frac {1} {6} \) = \ (\ frac {1} {8} \) × \ (\ frac {1} {2} \)
Умножьте знаменатели.
= \ (\ frac {1} {16} \)
Таким образом, \ (\ frac {3} {8} \) × \ (\ frac {1} {6} \) = \ (\ frac {1} { 16} \)
Заполните утверждение, указав «равно», «больше» или «меньше».
Вопрос 11.
\ (\ frac {7} {8} \) × \ (\ frac {6} {6} \) будет __________ \ (\ frac {7} {8} \)
Ответ: равно
Пояснение:
\ (\ frac {7} {8} \) × \ (\ frac {6} {6} \)
\ (\ frac {6} {6} \) = 1
\ (\ frac { 7} {8} \) × 1 = \ (\ frac {7} {8} \)
\ (\ frac {7} {8} \) = \ (\ frac {7} {8} \)
Таким образом \ (\ frac {7} {8} \) × \ (\ frac {6} {6} \) будет равно \ (\ frac {7} {8} \)
Вопрос 12.
\ (\ frac {1} {2} \) × \ (\ frac {8} {9} \) будет __________ \ (\ frac {8} {9} \)
Ответ: Менее
Пояснение:
\ (\ frac {1} {2} \) × \ (\ frac {8} {9} \)
Умножьте числители и знаменатели
\ (\ frac {1} {2} \) × \ (\ frac {8} {9} \) = \ (\ frac {4} {9} \)
\ (\ frac {4} {9} \) меньше, чем \ (\ frac {8} {9} \)
Итак, \ (\ frac {1} {2} \) × \ (\ frac {8} {9} \) будет меньше, чем \ (\ frac {8} {9} \)
Обзор / тест главы — стр.334
Полностью закройте кружок, чтобы показать свой ответ.
Вопрос 13.
Вольфганг хочет увеличить созданный им рисунок. Какой из перечисленных ниже факторов увеличил бы (увеличил) его изображение больше всего, если бы он использовал его для умножения его текущих размеров?
Опции:
а. \ (\ frac {7} {8} \)
б. \ (\ frac {14} {14} \)
с. 1 \ (\ frac {4} {9} \)
г. \ (\ frac {3} {2} \)
Ответ: 1 \ (\ frac {4} {9} \)
Пояснение:
Наибольшая дробь среди всех дробей равна 1 \ (\ frac {4} {9} \).
1 \ (\ frac {4} {9} \) больше 1.
Таким образом, правильный ответ — вариант C.
Вопрос 14.
Рэйчел хочет уменьшить размер своей фотографии. Какой из перечисленных ниже факторов больше всего уменьшит (уменьшит) размер ее изображения?
Опции:
а. \ (\ frac {5} {8} \)
б. \ (\ frac {11} {16} \)
с. 1 \ (\ frac {3} {4} \)
г. \ (\ frac {8} {5} \)
Ответ: \ (\ frac {5} {8} \)
Пояснение:
Сравнить со всеми дробями \ (\ frac {5} {8} \) меньше.
Итак, Рэйчел уменьшила бы размер своей фотографии до \ (\ frac {5} {8} \)
Итак, правильный ответ — вариант А.
Вопрос 15.
Мартин хочет сегодня покрасить \ (\ frac {2} {3} \) свою комнату. Она хочет нарисовать \ (\ frac {1} {4} \) из этого до обеда. Какую часть своей комнаты она покрасит сегодня до обеда?
Опции:
а. \ (\ frac {1} {12} \)
б. \ (\ frac {1} {6} \)
с. 1 \ (\ frac {5} {12} \)
г. \ (\ frac {11} {12} \)
Ответ: \ (\ frac {1} {6} \)
Пояснение:
Мартин хочет сегодня покрасить \ (\ frac {2} {3} \) свою комнату.
Она хочет нарисовать \ (\ frac {1} {4} \) из этого до обеда.
\ (\ frac {2} {3} \) × \ (\ frac {1} {4} \) = \ (\ frac {1} {6} \)
Итак, ответ — вариант B.
Обзор главы / Тест — Страница № 335
Полностью закройте кружок, чтобы показать свой ответ.
Вопрос 16.
Автобусный маршрут Гии до школы составляет 5 \ (\ frac {1} {2} \) миль. Автобусный маршрут домой в 1 \ (\ frac {3} {5} \) раз длиннее. Как долго длится автобус Джиа домой?
Опции:
а. 5 \ (\ frac {3} {10} \) миль
б. 8 миль
c. 8 \ (\ frac {4} {5} \) миль
дн.17 \ (\ frac {3} {5} \) миль
Ответ: 8 \ (\ frac {4} {5} \) миль
Пояснение:
Автобусный маршрут от Гии до школы находится в 5 \ (\ frac {1} {2} \) милях. Автобусный маршрут домой в 1 \ (\ frac {3} {5} \) раз длиннее.
5 \ (\ frac {1} {2} \) × 1 \ (\ frac {3} {5} \)
Преобразуйте смешанные дроби в неправильные дроби.
\ (\ frac {11} {2} \) × \ (\ frac {8} {5} \) = \ (\ frac {88} {10} \) = \ (\ frac {44} {5} \)
Смешанная доля \ (\ frac {44} {5} \) составляет 8 \ (\ frac {4} {5} \) миль
Следовательно, ответ — вариант C.
Вопрос 17.
Собака Карла весит в 2 \ (\ frac {1} {3} \) раза больше, чем весит собака Джуди. Если собака Джуди весит 35 \ (\ frac {1} {2} \) фунтов, сколько весит собака Карла?
Опции:
а. 88 \ (\ frac {3} {4} \) фунтов
б. 82 \ (\ frac {5} {6} \) фунтов
гр. 81 \ (\ frac {2} {3} \) фунтов
г. 71 фунт
Ответ: 82 \ (\ frac {5} {6} \) фунтов
Пояснение:
Собака Карла весит в 2 \ (\ frac {1} {3} \) раза больше веса собаки Джуди.
Чтобы найти вес собаки Карла, нам нужно умножить дроби
2 \ (\ frac {1} {3} \) и 35 \ (\ frac {1} {2} \)
\ (\ frac {7} {3} \) × \ (\ frac {71} {2} \) = \ (\ frac {497} {6} \)
Смешанная доля \ (\ frac {497} {6} \) составляет 82 \ (\ frac {5} {6} \) фунтов.
Таким образом, правильный ответ — вариант Б.
Вопрос 18.
В пятом классе у \ (\ frac {4} {5} \) девочек каштановые волосы. Из шатенок \ (\ frac {3} {5} \) девушек имеют длинные волосы. Какая часть девочек в классе имеет длинные каштановые волосы?
Опции:
а. \ (\ frac {1} {20} \)
б. \ (\ frac {1} {5} \)
с. \ (\ frac {3} {5} \)
г. \ (\ frac {1} {4} \)
Ответ: \ (\ frac {1} {5} \)
Пояснение:
В пятом классе у \ (\ frac {4} {5} \) девочек каштановые волосы.Из шатенок \ (\ frac {3} {5} \) девушек имеют длинные волосы.
\ (\ frac {4} {5} \) — \ (\ frac {3} {5} \) = \ (\ frac {1} {5} \)
Правильный ответ — вариант B.
Обзор главы / Тест — Стр. № 336
Построенный ответ
Вопрос 19.
Таша планирует выложить пол в своей комнате квадратными плитками длиной \ (\ frac {1} {4} \) футов. Будет ли она использовать больше или меньше плиток, если она сможет покупать только квадратные плитки длиной \ (\ frac {1} {3} \) футов? Объяснять.
_________ плитки
Ответ: Меньше
Пояснение:
\ (\ frac {1} {4} \) меньше, чем \ (\ frac {1} {3} \)
Таким образом, Таша будет использовать меньше плиток, если она сможет покупать только квадратные плитки, которые \ (\ frac {1} {3} \) долго.
Задача по производительности
Вопрос 20.
Для продажи выпечки Вайолет хочет использовать рецепт, указанный ниже.
А). Если она хочет удвоить рецепт, сколько муки ей понадобится?
_____ \ (\ frac {□} {□} \) стаканов муки
Ответ: 5 \ (\ frac {1} {2} \) стаканов муки
Пояснение:
Чтобы испечь сахарное печенье, ей нужно 2 \ (\ frac {3} {4} \) чашки муки.
Если она хочет удвоить рецепт, ей нужно умножить 2 \ (\ frac {3} {4} \) стакана муки на 2.
2 \ (\ frac {3} {4} \) + 2 \ ( \ frac {3} {4} \) = 5 \ (\ frac {1} {2} \) стаканов муки
Вопрос 20.
B). Бакстер хочет приготовить в 1 \ (\ frac {1} {2} \) раз больше рецепта. Будет ли ему нужно больше или меньше сахара, чем нужно Вайолет, если она удвоит рецепт? Объяснять.
__________ сахар
Ответ: меньше
Пояснение:
Если фиолетовый удваивает рецепт, ему нужно 2 × 1 \ (\ frac {1} {2} \) = 3 чашки сахара
Бакстер хочет приготовить 1 \ (\ frac {1} {2} \) раз рецепт.
1 \ (\ frac {1} {2} \) × \ (\ frac {1} {2} \) = 1 \ (\ frac {3} {4} \)
Бакстеру нужно меньше сахара по сравнению с Вайолет рецепт приготовления.
Вопрос 20.
C). Как показано, рецепт рассчитан на 60 печенек. Хорхе хочет принести 150 печенек. Сколько муки ему понадобится, чтобы приготовить 150 печенек? Объясните, как вы получили ответ. (Подсказка: на что можно умножить 60, чтобы получить 150?)
_____ \ (\ frac {□} {□} \) стаканов муки
Ответ: 2 \ (\ frac {1} {2} \) стакана муки
Пояснение:
По рецепту получается 60 печенек.Хорхе хочет принести 150 печенек.
Пусть количество муки будет x.
60 × x = 150
x = 150/60 = 5/2
Смешанная доля \ (\ frac {5} {2} \) равна 2 \ (\ frac {1} {2} \)
Таким образом, Хорхе нужно 2 \ (\ frac {1} {2} \) стакана муки, чтобы испечь 150 печенек.
Заключение
Получите максимальную отдачу от Ответного ключа по математике для 5-го раздела 7-го класса умножения дробей. Наше руководство по умножению дробей в 5-м классе, глава 7, поможет вам в кратчайшие сроки прояснить связанные концепции. Оставайтесь на связи с нашим сайтом, чтобы получить ответы на вопросы Go Math Answer Key для разных классов в одном месте.
Калькулятор длинного деленияс остатками
Использование калькулятора
Разделите два числа, делимое и делитель, и найдите ответ как частное с остатком. Узнайте, как решать задачи деления в столбик с остатками, или попрактикуйтесь в решении собственных задач деления в столбик и используйте этот калькулятор, чтобы проверить свои ответы.
Деление в столбик с остатками — это один из двух методов ручного деления в столбик.Это несколько проще, чем решить задачу деления, найдя частный ответ с десятичной дробью. Если вам нужно сделать длинное деление с десятичными знаками, используйте наш Калькулятор длинного деления с десятичными знаками.
Что входит в состав подразделения
Для предложения деления 487 ÷ 32 = 15 R 7
- 487 — дивиденд
- 32 — делитель
- 15 — это частная часть ответа
- 7 — это оставшаяся часть ответа
Как сделать длинное деление с остатками
Из приведенного выше примера разделим 487 на 32, показывая работу.
Задайте проблему деления с помощью символа длинного деления или скобки деления. Поместите 487, делимое, на внутреннюю часть скобки. Дивиденд — это число, которое вы делите.
Поместите 32, делитель, на внешнюю сторону кронштейна. Делитель — это число, на которое вы делите.
4, разделенное на 32, равно 0, а остаток равен 4. Остаток пока можно проигнорировать.
Поместите 0 на верхнюю часть скобки деления.Это начало частного ответа.
Затем умножьте 0 на делитель 32 и вставьте результат 0 под первым числом делимого внутри скобок.
0 * 32 = 0
Проведите линию под 0 и вычтите 0 из 4.4 — 0 = 4
Опустите следующее число делимого и вставьте его после 4, чтобы получилось 48.
Разделите 48 на делитель 32. Ответ: 1. Остаток пока можно проигнорировать.48 ÷ 32 = 1
Обратите внимание, что вы можете пропустить все предыдущие шаги с нулями и сразу перейти к этому шагу. Вам просто нужно понять, сколько цифр в дивиденде вам нужно пропустить, чтобы получить первое ненулевое значение в ответе на частное.В этом случае вы можете сразу разделить 32 на 48.
Поместите 1 вверху шкалы деления справа от 0. Затем умножьте 1 на 32 и запишите ответ под 48.1 * 32 = 32
Проведите линию и вычтите 32 из 48.48 — 32 = 16
Опустите следующее число из делимого и вставьте его после 16, чтобы получилось 167.
Разделите 167 на 32. Видите, как возникает закономерность?167 ÷ 32 равно 5 с остатком 7
Поместите цифру 5 вверху полосы деления справа от единицы.Умножьте 5 на 32 и запишите ответ под 167.5 * 32 = 160
Проведите линию и вычтите 160 из 167.167 — 160 = 7
Поскольку 7 меньше 32, деление в столбик сделано.У вас есть свой ответ: частное равно 15, а остаток равен 7.Итак, 487 ÷ 32 = 15 с остатком 7
Для более длинных дивидендов вы должны продолжать повторять шаги деления и умножения, пока вы не уменьшите каждую цифру из divdend и не решите проблему.
Дополнительная литература
Math is Fun также предоставляет пошаговый процесс деления в столбик с Длинное деление с остатками.
Данные испытанийпоказывают влияние потери обучения в связи с пандемией — Гринсборо 101
Для немедленной публикации: 3 сентября 2021 г.
Контактное лицо: Нора Шопто (336) 370-8386
Медиа-стойка (336) 574-5730
Данные испытаний показывают влияние потери обучения в связи с пандемией
Округ, штат см. Снижение уровня владения языком по всем предметам
Гринсборо, Северная Каролина — Как и в других округах штата и страны, школы округа Гилфорд сообщают о значительном снижении уровня знаний учащихся по результатам тестирования в конце класса и в конце курса в 2020-2021 учебном году.Общий уровень владения языком для округа снизился с 55,1 процента в 2019 году, когда проводились прошлогодние тесты, до 42,4 процента в 2021 году, то есть на 12,7 процентных пункта.
Данные, которые были опубликованы в среду вместе с заседанием Совета по образованию штата, показывают двузначное снижение в большинстве проверенных областей. В этом году Северной Каролине был предоставлен отказ от подотчетности по тестам и оценок успеваемости в школе, но от округов по-прежнему требовалось проводить тесты, помогать оценивать степень потери знаний, а также выделять ресурсы и поддержку школам.
Убытки преобладали по всему штату, но GCS занял более высокое место, чем большинство других крупных округов. Только система государственных школ округа Уэйк показала меньшее падение уровня владения языком — 9,8 процентных пункта среди крупнейших округов штата. В масштабах штата уровень владения языком снизился на 13,4 процентных пункта.
«Эти данные подчеркивают важность обеспечения того, чтобы наши студенты и сотрудники оставались здоровыми, чтобы мы могли максимально вовлечь всех студентов в очное обучение», — говорит суперинтендант Шэрон Л.Контрерас. «Этот процесс восстановления не произойдет в одночасье, и мы продолжим использовать проверенные стратегии, такие как частное обучение, чтобы встретить студентов там, где они есть, и помочь им вернуться на правильный путь».
Сильнее всего пострадалибаллов по математике: уровень владения языком упал на 10,5–18,6 процентных пункта по сравнению с 2019 годом. В ожидании, GCS работает с учащимися колледжей и старшеклассниками, чтобы обеспечить их репетиторами по математике с прошлой весны.
Репетиторство с высокой дозировкой — одна из нескольких мер, которые GCS принимает, чтобы помочь студентам начать оправляться от борьбы гибридного и дистанционного обучения за последние 18 месяцев.Округ также привлек более 14 000 учеников к летнему обучению почти во всех школах округа и обновил школьные календари, чтобы увеличить учебное время и повысить квалификацию учителей в 23 школах округа с самыми низкими показателями.
Напротив, оценки по чтению и по английскому языку II были лучше, всего на 3,5 процентных пункта снизился общий балл по английскому языку II. На уровне начальной и средней школы оценки по чтению упали между 7,1 и 17,7 процентных пункта.Оценки по естественным наукам были неоднозначными: оценки в 5-м классе и биологии упали чуть более чем на 16 процентных пунктов каждый, а оценки по естественным наукам в 8-м классе упали на 6,2 процентных пункта.
ВGCS также было две школы, которые успешно оправдали ожидания штата. В колледже Brown Summit Middle и Early College в Гилфорде более 95 процентов учащихся получили баллы, свидетельствующие об уровне владения языком.
Штат также опубликовал данные о количестве выпускников, ставших ярким пятном для школ округа Гилфорд.Округ достиг рекордного уровня выпускников — 91,4 процента, в том числе 12 школ со 100-процентным показателем выпускников. Десять других школ сообщили о том, что процент выпускников составляет не менее 90 процентов, в том числе Северо-Западная средняя школа, в которой был самый большой выпускной класс округа — 479 учеников и 98,4 процента выпускников.
«Мы очень гордимся тем, что достигли рекордного количества выпускников, благодаря нашим учебным центрам, нашей летней программе 5-го квартала, дополнительным консультантам в школах с более низкими показателями выпускников и неустанным усилиям директоров и сотрудников, чтобы оставаться на связи студентам во время пандемии », — говорит Контрерас.
Демографические подгруппы также продемонстрировали значительный рост количества выпускников: рост на четыре процентных пункта среди азиатских студентов и рост более чем на два процентных пункта среди чернокожих и латиноамериканских студентов.
Щелкните здесь, чтобы получить подробные результаты на уровне округа. Www.gcsnc.com/site/handlers/filedownload.ashx?moduleinstanceid=15012&dataid=152956&FileName=2020-2021%20Preterior%20Reporting%20Media%20Presentation%20-%209.3.21.pdf >
О школах округа Гилфорд
Школы округа Гилфорд, третий по величине школьный округ в Северной Каролине и 50-й по величине из более чем 14 000 школ в США, обслуживают 73 000 учащихся PK-12 в 125 школах.В GCS работает около 10 000 сотрудников, и она работает в партнерстве с родителями, предприятиями, колледжами и обществом, чтобы обеспечить образование, которое объединяет интересы и навыки учащихся с карьерой и экономикой нашего будущего здесь и во всем мире. Мы предлагаем варианты образования, отвечающие индивидуальным потребностям учащихся в условиях культурного разнообразия гражданства, и новые возможности, чтобы помочь нашим учащимся достичь величия. Для получения дополнительной информации посетите веб-сайт округа www.gcsnc.comnam05.safelinks.protection.outlook.com/?url=http%3A%2F%2Fwww.gcsnc.com%2F&data=02%7C01%7Csilverj%40gcsnc.com%7C79407275dd6940ec549d08d7e890bf0b%7C9ae2fb1fdea624c4% 7C9ae2fb1fdea624c4c8c8c8c0c7c7c0c8c8c0c8c8c0c7c0c7c08c0c8
Это электронное письмо предназначено исключительно для использования тем лицом, для которого оно предназначено. Если вы не являетесь ни предполагаемым получателем, ни агентом, ответственным за доставку этого электронного письма предполагаемому получателю, любое раскрытие, повторная передача, копирование или принятие мер, полагающихся на эту информацию, строго запрещено.Если вы получили это электронное письмо по ошибке, немедленно сообщите об этом лицу, передающему информацию. Вся электронная корреспонденция, отправляемая и отправляемая на этот адрес электронной почты, может регулироваться Законом NC Public Records, что приводит к мониторингу и раскрытию информации третьим сторонам, включая правоохранительные органы. В соответствии с федеральными законами, школы округа Гилфорд управляют всеми образовательными программами, деятельностью по трудоустройству и приемом без дискриминации по признаку расы, религии, национального или этнического происхождения, цвета кожи, возраста, военной службы, инвалидности или пола, за исключением случаев, когда освобождение уместно и разрешено закон.Полный текст заявления можно найти в Политике AC Совета по вопросам образования и защите окружающей среды от дискриминации. Запросы или жалобы следует направлять сотруднику по соблюдению нормативных требований в школах округа Гилфорд, по адресу: 120 Franklin Boulevard, Greensboro, NC 27401; 336-370-8154
Дом | GTCC
Выберите успех. Выберите GTCC.
ВАШЕ ПУТЕШЕСТВИЕ К ЛУЧШЕЙ ЖИЗНИ НАЧИНАЕТСЯ ЗДЕСЬВы знаете, что образование — ключ к успеху. Теперь вы пытаетесь решить, где получить это образование, и именно поэтому вы здесь.Есть много причин выбрать GTCC, и мы приглашаем вас изучить наш веб-сайт, чтобы узнать их все. Но вот три из лучших — качество, доступность и поддержка. GTCC предлагает вам отличное образование, которое подготовит вас к следующему шагу, каким бы он ни был, к лучшей жизни. GTCC делает это образование возможным для всех с небольшими затратами и финансовой помощью тем, кто в ней нуждается. А у GTCC есть системы поддержки, которые помогут вам не сбиться с пути и сфокусироваться на ваших целях.
Итак, какими бы ни были ваши образовательные цели, выбирайте GTCC.Мы сделаем больше, чем просто поможем вам их достичь — мы поможем вам превзойти их!
60%
Студенты, получающие финансовую помощь
54%
Студенты, получающие гранты Pell
27 572
студентов, обслуживаемых ежегодно
.