Математика, 5 класс — обучающая программа
Образовательный комплекс (ОК) содержит все основные темы, включенные в школьную программу по математике. Материалы ОК поддерживают все виды учебной деятельности и предназначены как для самостоятельной работы дома, так и для использования в классе под руководством учителя. Для изучения выбранной темы предполагается линейное прохождения материала в том порядке, в каком он представлен в комплексе, с возвратом к лекциям и слайдам при необходимости.
Лекция
Анимация, в которой новая тема объясняется в доступной и наглядной форме.
Слайд-резюме
Содержит краткое описание нового материала и может использоваться для быстрого его повторения и самоконтроля.
Закрепление материала
Содержит решения типовых задач по данной теме с пропусками для заполнения учеником.
Математический диктант
Служит для промежуточной проверки усвоенного материала.
Проблема-упражнение
Содержит задачи по данной теме с проверкой правильности решения.
Опрос
Несколько вопросов, на которые ученик должен уметь быстро ответить; проверка не производится.
Самостоятельная работа (базовая)
Содержит пять заданий для проверки усвоения материала; ответы проверяются, результат заносится в журнал.
Самостоятельная работа (повышенной сложности)
Содержит одно задание повышенной сложности, которым можно заменить выполнение базовой самостоятельной работы; ответ проверяется, результат заносится в журнал.
Ученику позволяет:
• самостоятельно изучить новый материал;
• обрести повышенный интерес к предмету за счет мультимедийного способа представления информации;
• развить исследовательские навыки и аналитические способности при работе с интерактивными моделями и играми.
Учителю дает возможность:
• повысить заинтересованность учащихся в предмете;
• подобрать иллюстративный материал к уроку;
1. Точка. Отрезок. Луч. Прямая. Числовая прямая
2. Чтение и запись больших натуральных чисел
3. Десятичные дроби
4. Сравнение десятичных дробей
5. Изображение десятичных дробей на числовой прямой
6. Сложение и вычитание десятичных дробей
7. Уравнения. Решение уравнений
8. Округление
9. Прикидка
10. Умножение и деление десятичных дробей на 10, 100, 1000 и т. д.
11. Умножение десятичных дробей
12. Распределительный закон умножения относительно сложения
13. Деление десятичной дроби на натуральное число. Среднее арифметическое
14. Деление на десятичную дробь
15. Буквенные выражения. Значения буквенных выражений
Буквенные выражения. Значения буквенных выражений
16. Упрощение записи произведений, содержащих буквенные множители
17. Решение задач с помощью уравнений
18. Обыкновенные дроби. Дроби правильные и неправильные
19. Сравнение, сложение и вычитание дробей с одинаковыми знаменателями
20. Сравнение, сложение, вычитание дроби и натурального числа
21. Смешанные числа
22. Сложение и вычитание смешанных чисел, дробные части которых имеют одинаковые знаменатели
23. Деление и дроби
24. Три задачи на дроби
25. Проценты
26. Квадрат числа
27. Прямоугольный параллелепипед. Куб
28. Объем прямоугольного параллелепипеда и куба. Куб числа
29. Натуральная степень числа
30. Длина окружности и площадь круга
- Операционная система Microsoft Windows 2000/XP/7;
- Требует наличие Flash-плеер! (см. https://obr.
 1c.ru/read/info/rabota-adobe-flash-v-2021-godu/)
1c.ru/read/info/rabota-adobe-flash-v-2021-godu/) - Pentium III 700 МГц;
- Видеокарта, поддерживающая разрешение 1024х768, true color;
- устройство воспроизведения DVD/CD-ROM;
- да 2 Гб на выбранном для установки диске
- не менее 400 Мб на системном диске
- звуковая карта;
- колонки или наушники;
- мышь.
- Дата выхода продукта: 29.08.2009
- Разработчик: ООО «1С-Паблишинг»
- Штрих-код: 4601546066848
- Серии: 1С:Школа
- Возрастная категория: 0+
ГДЗ Математика 5 класс.
 Ответы и решения по Математике для 5 го класса на VipGDZ.ru
Ответы и решения по Математике для 5 го класса на VipGDZ.ruЕще со времен появления школ, в учебном процессе образовался такой раздел, как домашняя работа. Эта часть обучения всегда приносила немало трудностей школьникам. Больше всего их возникало с такой сложной дисциплиной как математика, по которой ученики 5 класса получают около десяти упражнений на домашнее выполнение. Но это было раньше. С момента появления специально разработанных учебных пособий – ГДЗ, облегчающих процесс усвоения знаний, математика стала для учеников легким и интересным предметом.
О том, как же влияют решебники на обучение пятиклассников, спорили довольно долго. Результат дискуссий показал, что ГДЗ за пятый класс приносят только положительное воздействие и на учебу, и на самих детей. Школьники, работая с такими справочниками, не только улучшают оценки, а как результат, и общую успеваемость, но и укрепляют свои личностные характеристики. Среди них, главным образом, выделяются: самостоятельность, уверенность в себе и желание добывать новые знания.
Из чего же сделаны ответы по математике?
Все плюсы работы с решебниками стали возможными благодаря их правильной и эффективной структуре. ГДЗ по математике выпущенные для 5 класса обладают очень похожей структурой. Как принято, эти книги начинаются из содержания. Данная часть хоть и небольшая, но очень хорошо помогает с поиском нужных заданий. Потом в ГДЗ по математике за 5 класс представлены полные решения упражнений, во всех возможных вариантах. Они демонстрируются в развернутой форме, чтобы ученик без труда смог проследить за алгоритмом применения правила.
Дальше идут правильные ответы на задачи. Главная их роль заключается в предоставлении возможности ученикам 5 класса самостоятельно проверять свои работы и, находя ошибки, исправлять их. В самом конце пособия находится список литературы, с помощью которого достаточно просто искать какие-то дополнительные материалы по теме, вызвавшей интерес ученика.
Основной проблемой родителей и школьников становится поиск качественных решебников. Но, наш сайт VIPGDZ.ru навсегда избавит от этих трудностей, ведь на его страницах находятся только тщательно подобранные книги такого формата.
Но, наш сайт VIPGDZ.ru навсегда избавит от этих трудностей, ведь на его страницах находятся только тщательно подобранные книги такого формата.
Самое надежное место, где поселились правильные решения
Наш сайт VIPGDZ.ru завоевал доверие и взрослых, и детей, в первую очередь, благодаря большому количеству плюсов, которые приносит сотрудничество с ним. Главным достоинством нашего портала VIPGDZ.ru можно считать огромный ассортимент различных учебных материалов на его страницах. Сайт богат не только на решебники по математике за 5 класс, но и на учебники. Стоит отметить, что все книги на ресурсе полностью соответствуют требованиям Министерства образования. Отличным бонусом VIPGDZ.ru являются различные дополнительные материалы, которые предоставляет наш сайт. Среди них находятся увлекательные и интересные статьи, которые будут полезными не только школьникам 5 класса, но и их родителям, а также учителям.
Важным аспектом работы с материалами на нашем ресурсе VIPGDZ.ru считается то, что доступ ко всем книгам на нем можно получить абсолютно бесплатно. Кроме того, мы позаботились о том, чтобы нужные ГДЗ или учебники можно было просматривать с помощью любых современных электронных гаджетов в режиме онлайн, и создали мобильную версию VIPGDZ.ru. Качественные решебники сделают процесс изучения математики для пятиклассников простым и интересным!
Кроме того, мы позаботились о том, чтобы нужные ГДЗ или учебники можно было просматривать с помощью любых современных электронных гаджетов в режиме онлайн, и создали мобильную версию VIPGDZ.ru. Качественные решебники сделают процесс изучения математики для пятиклассников простым и интересным!
Олимпиада по математике 2021-22 • Формула Единства
К участию в олимпиаде приглашаются школьники 5–11 классов из России и соответствующих классов из всех стран мира. Участие в олимпиаде бесплатное.
Олимпиада включена в Проект перечня олимпиад школьников Минобрнауки РФ (41 номер, II уровень). Призёры олимпиады получают право на льготную путёвку в образовательные лагеря «Формула Единства».
Организатор олимпиады
ГАОУ ВО ЛО «Ленинградский государственный университет имени А.С. Пушкина».
Партнёр олимпиады — Интеллектуальный клуб «Сигма».
Контакты оргкомитета олимпиады
Официальные документы
Текущий статус: Отборочный этап завершен. Результаты будут опубликованы позднее.
Хронология событий
Все новости олимпиады будут публиковаться ниже от более новых к более старым.Перед Вами задачи отборочного этапа олимпиады.
Помните, что решение задачи должно включать не только правильный ответ, но и полное обоснование этого ответа. Мы будем рады, если в олимпиаде примут участие Ваши друзья, которым нравится математика. Однако работы с признаками списывания и «коллективного творчества» рассматриваться не будут.
Условия задач в работу переписывать не нужно. Работа может быть написана на английском, украинском, грузинском, испанском, немецком, персидском (фарси), румынском, русском, казахском, узбекском, французском, тайском, турецком языке, иврите или эсперанто. Использование других языков должно быть заранее согласовано с организаторами.
Призёры международной математической олимпиады «Формула Единства» / «Третье тысячелетие» 2020/21 г. будут приглашены непосредственно на заключительный этап.
Условия задач
Порядок отправки решений
Для участия в математической олимпиаде «Формула Единства» / «Третье тысячелетие» 2021/22 необходимо в срок до 23:59:59 по UTC 10 ноября 2021 года (то есть 02:59:59 по московскому времени 11 ноября) подготовить файлы с решениями задач (каждая задача — отдельный файл), зарегистрироваться в нашей информационной системе и отправить файлы через личный кабинет. Важно: если у Вас уже есть учетная запись, заводить новую НЕ НУЖНО.
Загрузить можно как текстовые файлы (в форматах TXT, DOC, DOCX или PDF), так и сканы бумажных работ (в форматах JPG и PNG). Общее количество файлов не должно превышать 10. В файлах с решениями задач не должны указываться фамилия, имя и другие личные данные участника!
Мы не принимаем работы отборочного тура иными способами,кроме как посредством загрузки внутри информационной системы.
Вопросы?
Все вопросы Оргкомитету по условиям задач и о порядке проведения Олимпиады можно задать по электронной почте [email protected]formulo.org или по телефону +7 (969) 717–41-93 (по будним дням с 10:00 до 17:00).
Вопросы по работе информационной системы можно задать по электронной почте [email protected]formulo.org.
Ежегодно объединённая международная математическая олимпиада «Формула Единства»/«Третье тысячелетие» проводится в два этапа.
Отборочный этап
Отборочный этап является заочным. В этом году пройдёт с 20 октября по 10 ноября.
Подробная информация появится ближе к старту этапа.
Заключительный этап
Заключительный же этап — очный. Он состоится в феврале 2022 года. Подробная информация о местах проведения появится зимой.
В вашем браузере отключен JavaScript.
| |||||||||||||||||||||||||||||
В вашем браузере отключен JavaScript.Пожалуйста, включите его, чтобы активировать полную функциональность веб-сайта
| |||||||||||||||||||||||||||||
Разложение на простые множители 6. Простые и составные числа. В чем разница между простым и составным числом
Все начинается с экспоненциальной прогрессии.В первой лекции по строкам (см. Раздел 18.1. Основные определения ) мы доказали, что эта функция является суммой ряда, и ряд сходится к функции для
… Итак,
.
Выпишем несколько разновидностей этой серии. Замена NS по — NS , получаем
при замене НС на
получаем
и т. Д.; область сходимости всех этих рядов одинакова:
Д.; область сходимости всех этих рядов одинакова:
.
2.
.
Все производные этой функции в точке NS = 0 равны
, поэтому серия имеет вид
.
Область сходимости этого ряда — это вся числовая ось (пример 6 раздела 18.2.4.3. Радиус сходимости, интервал сходимости и область сходимости степенного ряда ), поэтому
на
… Как следствие, остаток формулы Тейлора
… Следовательно, ряд сходится к
в любой точке NS .
3.
.
Этот ряд сходится абсолютно для
, и его сумма действительно равна
… Остальная часть формулы Тейлора имеет вид
, где
или
— ограниченная функция, а
(это общий термин предыдущего расширения).
4.
.
Это разложение, как и предыдущие, можно получить последовательным вычислением производных, но мы поступим иначе. Продифференцируем предыдущую строку по члену:
Продифференцируем предыдущую строку по члену:
Сходимость к функции на всей оси следует из теоремы о почленном дифференцировании для степенного ряда.
5. Независимо докажите, что на всей числовой оси.
6.
.
Ряд для этой функции называется биномиальным рядом … Здесь мы вычислим производные.
… Ряд Маклорена имеет вид
Мы ищем интервал сходимости: следовательно, интервал сходимости равен
… Изучение остатка и поведения ряда на концах интервала сходимости будет не проводиться; оказывается, что для
ряд сходится абсолютно в обеих точках
, в
ряд условно сходится в точке
и расходится в точке
, в
расходится в обеих точках.
7.
.
Здесь мы воспользуемся тем, что
… Так как тогда после почленного интегрирования
Область сходимости этого ряда представляет собой полуинтервал
, сходимость к функции во внутренних точках следует из теоремы о почленном интегрировании для степенного ряда в точке NS = 1 — от непрерывности как функции, так и суммы степенного ряда во всех точках, произвольно близких к NS = 1 слева. Обратите внимание, что если взять NS = 1, найдем сумму ряда.
Обратите внимание, что если взять NS = 1, найдем сумму ряда.
8. Интегрируя ряд по почеркам, получаем разложение для функции
… Все вычисления производим самостоятельно, выписываем область сходимости.
9. Запишем разложение функции
по формуле биномиального ряда с
:. Знаменатель
, представленный как двойной факториал
, означает произведение всех натуральных чисел одинаковой четности, не превышающих… Расширение сходится к функции для
… Путем постепенного интегрирования от 0 до NS , получаем. Оказывается, этот ряд сходится к функции на всем интервале
; на NS = 1 получаем еще одно красивое представление числа:
.
18.2.6.2. Решение задач о разложении функций в ряд. Большинство проблем, в которых требуется расширить элементарную функцию в степенной ряд
, решается с помощью стандартных расширений.К счастью, каждая элементарная функция имеет свойство, позволяющее это делать. Давайте посмотрим на несколько примеров.
Давайте посмотрим на несколько примеров.
1. Разверните функцию
на градусы
.
Решение. … Ряд сходится на
.
2. Разложите функцию
на градусы
.
Решение.
… Область конвергенции:
.
3. Разложите функцию
на градусы
.
Решение. … Ряд сходится на
.
4.Разложите функцию
на градусы
.
Решение. … Ряд сходится на
.
5. Разложите функцию
на градусы
.
Решение. … Область конвергенции
.
6. Разложите функцию
на градусы
.
Решение. Разложение в ряд простых рациональных дробей второго типа получается почленным дифференцированием соответствующих разложений дробей первого типа. В этом примере. Далее, почленным дифференцированием можно получить разложения функций
,
и др.
7. Разложите функцию
на градусы
.
Решение. Если рациональная дробь не простая, она сначала представляется как сумма простых дробей:
, а затем действует, как в примере 5 :, где
.
Естественно, такой подход неприменим, например, для разложения функции по степеням NS … Здесь, если вам нужно получить несколько первых членов ряда Тейлора, проще всего найти значения в точке NS = 0 необходимого количества первых производных.3 + х). Чтобы увидеть, как выполняется решение, щелкните Показать шаги. Если вам нужно получить результат в формате Word, воспользуйтесь этой услугой.
Примечание : число «пи» (π) записывается как пи; квадратный корень как sqrt, например sqrt (3), касательная tg записывается как tan. См. Раздел «Альтернативы», чтобы увидеть ответ.
- Если дано простое выражение, например 8 * d + 12 * c * d, то факторизация выражения означает представление выражения в виде множителей. Для этого нужно найти общие факторы.Запишем это выражение как: 4 * d * (2 + 3 * c).
- Представьте произведение в виде двух двучленов: x 2 + 21yz + 7xz + 3xy. Здесь нам нужно найти несколько общих множителей: x (x + 7z) + 3y (x + 7z).
 Вынимаем (x + 7z) и получаем: (x + 7z) (x + 3y).
Вынимаем (x + 7z) и получаем: (x + 7z) (x + 3y).
см. Также Деление многочленов на угол (показаны все шаги деления в длину)
Полезными при изучении правил факторизации будут сокращенные формулы умножения , с помощью которых будет понятно, как открывать скобки с квадрат:
- (a + b) 2 = (a + b) (a + b) = a 2 + 2ab + b 2
- (ab) 2 = (ab) (ab) = a 2 -2ab + b 2
- (a + b) (ab) = a 2 — b 2
- a 3 + b 3 = (a + b) (a 2 -ab + b 2)
- a 3 -b 3 = (ab ) (a 2 + ab + b 2)
- (a + b) 3 = (a + b) (a + b) 2 = a 3 + 3a 2 b + 3ab 2 + b 3
- (ab) 3 = (ab) (ab) 2 = a 3 -3a 2 b + 3ab 2 -b 3
Методы факторинга
Изучив несколько приемов факторизации , вы можете составить следующую классификацию решений:- Используя сокращенные формулы умножения.
- Нахождение общего множителя.
Что значит разложить на простые множители? Как это сделать? Что вы можете узнать, если разложить число на простые множители? Ответы на эти вопросы проиллюстрированы конкретными примерами.
Определения:
Простое число — это число, у которого ровно два разных делителя.
Составное число — это число, у которого больше двух делителей.
Разложение натурального числа на множители означает представление его как произведения натуральных чисел.
Разложить натуральное число на простые множители означает представить его как произведение простых чисел.
Примечания:
- В раскрытии простого числа один из множителей равен одному, а другой равен самому этому числу.
- Нет смысла говорить о факторизации единицы.
- Составное число можно разложить на множители, каждый из которых отличается от 1.
Фактор 150.Например, 150 — это 15 умножить на 10. 15 — составное число. Его можно разложить на простые множители 5 и 3. 10 — составное число. Его можно разложить на простые множители 5 и 2. Записав вместо 15 и 10 их разложение на простые множители, мы получили разложение числа 150. | |
Число 150 можно разложить на множители по-разному. Например, 150 — это произведение чисел 5 и 30. 5 — простое число. 30 — составное число. Его можно рассматривать как произведение 10 и 3. 10 — составное число. Его можно разложить на простые множители 5 и 2. Мы получили разложение на простые множители 150 другим способом. | |
Обратите внимание, что первое и второе разложения одинаковы. Они различаются только порядком множителей. Принято писать множители в порядке возрастания. | |
Любое составное число можно однозначно разложить на простые множители вплоть до порядка множителей. | |
При разложении больших чисел на простые множители используйте запись столбца:
Наименьшее простое число, делимое на 216, равно 2. Делим 216 на 2. Получаем 108. | |
Полученное число 108 делится на 2. Сделаем деление.Результат 54. | |
По критерию делимости на 2 число 54 делится на 2. После деления получаем 27. | |
Число 27 заканчивается нечетной цифрой 7. Это Не делится на 2. Следующее простое число — 3. Делим 27 на 3. Получаем 9. Наименьшее простое число Число, которое делит 9, равно 3. Три — это простое число, оно делится само на себя и на единицу.Давайте разделим 3 на себя. В итоге получили 1. | |
- Число делится только на те простые числа, которые входят в его разложение.
- Число делится только на те составные числа, разложение которых на простые множители полностью в нем содержится.
Давайте рассмотрим несколько примеров:
4900 делится на простые числа 2, 5 и 7. | |
11 550 75. Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550. В результате деления получится произведение множителей 2, 7 и 11. 11550 не делится на 4, потому что при факторизации четырех есть лишние два. |
Найдите частное от деления числа a на число b, если эти числа разложить на простые множители следующим образом: a = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 3 ∙ 5 ∙ 5 ∙ 19 ; б = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 ∙ 19
Разложение числа b полностью содержится в разложении числа a. | |
Результат деления a на b — произведение трех чисел, оставшихся в разложении a. Итак, ответ — 30. |
Библиография
- Виленкин Н.
 Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М .: Мнемосина, 2012.
Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М .: Мнемосина, 2012. - Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М .: Просвещение, 1989. .
- Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс. — М .: ЗШ МИФИ, 2011. .
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Учебное пособие для учащихся 6-х классов заочной школы МИФИ. — М .: ЗШ МИФИ, 2011. .
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-товарищ для 5-6 классов средней школы.- М .: Просвещение, Библиотека учителя математики, 1989.
- Интернет-портал Matematika-na.ru ().
- Интернет-портал Math-portal.ru ().
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М .: Мнемосина, 2012. № 127, № 129, № 141.
- Иные поручения: № 133, № 144.

Каждое натуральное число, кроме одного, имеет два или более делителя.Например, число 7 делится только на 1 и 7 без остатка, то есть имеет два делителя. А у числа 8 есть делители 1, 2, 4, 8, то есть целых 4 делителя сразу.
В чем разница между простыми и составными числами
Числа, у которых больше двух делителей, называются составными числами. Числа, у которых есть только два делителя: один и само число, называются простыми числами.
У числа 1 есть только одно деление, а именно само число.Единица не применяется ни к простым, ни к составным числам.
- Например, 7 — простое, а 8 — составное.
Первые 10 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Число 2 — единственное четное простое число, все остальные простые числа нечетные.
Число 78 составное, так как помимо 1 и самого себя оно делится еще и на 2. При делении на 2 получаем 39. То есть 78 = 2 * 39. В таких случаях говорят, что число разложить на множители 2 и 39.
Любое составное число можно разложить на два множителя, каждый из которых больше 1. С простым числом этот трюк не сработает. Такие дела.
Разложение числа на простые множители
Как отмечалось выше, любое составное число можно разложить на два множителя. Возьмем, к примеру, число 210. Это число можно разложить на два множителя 21 и 10. Но числа 21 и 10 также составны, и мы можем разложить их на два множителя. Получаем 10 = 2 * 5, 21 = 3 * 7.И в результате число 210 уже разложилось на 4 фактора: 2,3,5,7. Эти числа уже простые и не могут быть расширены. То есть мы разложили число 210 на простые множители.
При разложении составных чисел на простые множители они обычно записываются в порядке возрастания.
Следует помнить, что любое составное число можно разложить на простые множители и при этом уникальным образом с точностью до перестановки.
- Обычно при разложении числа на простые множители используются критерии делимости.
Фактор 378
Запишем числа, разделяя их вертикальной чертой. Число 378 делится на 2, так как оно заканчивается на 8. При делении получаем число 189. Сумма цифр числа 189 делится на 3, а это значит, что само число 189 делится на 3. Поскольку в результате получаем 63.
Число 378 делится на 2, так как оно заканчивается на 8. При делении получаем число 189. Сумма цифр числа 189 делится на 3, а это значит, что само число 189 делится на 3. Поскольку в результате получаем 63.
Число 63 также делится на 3 по принципу делимости. Получаем 21, число 21 можно снова разделить на 3, получаем 7. Семерка делится только сама по себе, получаем единицу.На этом разделение завершено. Справа после строки находятся простые множители, на которые разложено число 378.
378 | 2
189 | 3
63 | 3
21 | 3
соответствуют ли они образовательным критериям?
Асланова Маргарита Сергеевна (Московский государственный университет им. М.В. Ломоносова (МГУ))Бухаленкова Дарья Александровна (Московский государственный университет им. М.В. Ломоносова (МГУ))
Веракса Александр Николаевич(Московский государственный университет им. М.В. Ломоносова (МГУ))
Гаврилова Маргарита Николаевна (Московский государственный университет им.
 М.В. Ломоносова (МГУ))
М.В. Ломоносова (МГУ)) Люцко Людмила Николаевна (Университет Барселоны)
Сухих Вера Л. (Московский государственный университет им. М.В. Ломоносова (МГУ))
Актуальность. В России растет интерес к рынку образовательных приложений. Значительное их количество ориентировано на дошкольников.Хотя о ключевых особенностях обучения дошкольников известно много (в том числе благодаря культурно-историческому подходу), до сих пор мало исследований, посвященных тому, учитываются ли эти особенности при разработке и методологии мобильных приложений, доступных на рынке.
Цель. Анализировать математические приложения для дошкольников с точки зрения культурно-исторической теории.
Дизайн. Мы зашли в Google Play и AppStore с запросом «математика для дошкольников» и выбрали четыре приложения, которые наиболее популярны среди пользователей и рекомендованы экспертами. Мы проанализировали их по следующим критериям: (1) вовлеченность взрослых, (2) качество взаимодействия ребенка с контентом приложения, (3) типы контента, (4) формы представления материала и соответствие метода исчисления. формирование концепции с учетом особенностей дошкольного возраста, (5) качество математического содержания, обеспечивающее принцип преемственности с учебной программой начальной школы.
Мы проанализировали их по следующим критериям: (1) вовлеченность взрослых, (2) качество взаимодействия ребенка с контентом приложения, (3) типы контента, (4) формы представления материала и соответствие метода исчисления. формирование концепции с учетом особенностей дошкольного возраста, (5) качество математического содержания, обеспечивающее принцип преемственности с учебной программой начальной школы.
Результатов . Ни одно из приложений не основывалось на методике развивающего обучения, и ни одно из них не использовало возможности вовлечения взрослого в диалог и совместную деятельность с ребенком.Не все приложения учитывали характеристики возрастной группы при разработке контента и взаимодействии ребенка с приложением. Только одно из приложений обеспечивает преемственность с учебной программой начальной школы.
Выводы . Научные знания и практические достижения в области математического образования дошкольников не всегда отражаются даже в самых популярных программах. Наш анализ позволяет привлечь внимание родителей, учителей и разработчиков к важным элементам дизайна, которые могут сделать приложение действительно обучающим для детей дошкольного возраста.
Наш анализ позволяет привлечь внимание родителей, учителей и разработчиков к важным элементам дизайна, которые могут сделать приложение действительно обучающим для детей дошкольного возраста.
Список литературы
Блехер, Ф. (1934). Математика в детском саду и нулевой группе . Москва: Учпедгиз. (на русск. яз.).
Венгер, Л.А. (1983). Овладение опосредованным решением познавательных задач и развитие когнитивных способностей ребенка. Вопросы психологии (Вопросы психологии), (2), 43–50. (на русск. яз.).
Веракса Н.Е., Комарова Т.С., Васильева М.А. (2016). От рождения до школы. Основная образовательная программа дошкольного образования . Москва: Мозаика-Синтез. (на русск. яз.).
Выготский, Л. (1983). Проблемы развития психики .Т. 3. Москва: Педагогика.
Глаголева, Л. (1930). Математика в нулевых группах (Математика в дошкольных учреждениях) Ленинград: Гос. изд-во. (на русск. яз.).
изд-во. (на русск. яз.).
Горев, П. (2015). Направления современного математического образования в школах , 17, 224–236. (на русск. яз.).
Давыдов, В. (1972). Виды обобщения в обучении. Москва: Педагогика. (на русск. яз.).
Колмогоров, А.Н. (2003). Современная математика и математика в современной школе. Математика в школе (Математика в школе), (3), 10–11. (на русск. яз.).
Леушина, А. (1974). Формирование элементарных математических представлений у детей дошкольного возраста . Москва: Просвещение. (на русск. яз.).
Монтессори, М.(2014). Научная педагогика. Дом ребенка (Научная педагогика. Дом ребенка). V.1. Москва: Народная книга.
Новикова, В. (2017). Математика в детском саду. Сценарии занятий для детей 3 — 4/4 — 5/5 — 6/6 — 7 лет (Математика в детском саду. Урок для детей 3–4 / 4–5 / 5– 6 / 6–7). Москва: Мозаика-Синтез. (на русск. яз.).
яз.).
Петрова, В.Ф. (2013). Методика математического образования детей дошкольного возраста .Казань: Казанский университет. (на русск. яз.).
Пышкало, А. (1983). Основные вопросы теории и практики преемственности в обучении младших школьников. Преемственность обучения и воспитания дошкольников и младших школьников . Тезисы докладов, под ред. Фурманн, П. Берлин: APN GDR, 59–65. (на рус.).
Об утверждении Концепции развития математического образования в Российской Федерации. Распоряжение Правительства РФ от 24.12.2013 № N 2506-Р. (на русск. яз.).
Руденко И.В., Котова С.А. (2015). К вопросу математического развития детей дошкольного возраста. Балтийский гуманитарный журнал (Балтийский гуманитарный журнал), (1 (10)), 125–127.(на русск. яз.).
Салмина, Н.Г., и Фореро Навас, И. (1994). Matematike. Методическое пособие для учителя (Матем.). Москва: Дидакт. (на русск. яз.).
Смирнова, Е. (2019). Особенности современного дошкольного детства. Национальный психологический журнал (Национальный психологический журнал), (2 (34)), 25–32. DOI: 10.11621 / npj.2019.0205. (на русск. яз.).
(2019). Особенности современного дошкольного детства. Национальный психологический журнал (Национальный психологический журнал), (2 (34)), 25–32. DOI: 10.11621 / npj.2019.0205. (на русск. яз.).
Федосова, Н.А., Коваленко Е.В. (2018). Программа по подготовке к школе детей 5 — 7 лет «Преемственность» (Программа подготовки детей 5–7 лет к школе «Преемственность»). Москва: Просвещение. (на русск. яз.).
Фидлер, М.А. (1981). Математика уже в детском саду . Москва: Просвещение. (на русск. яз.).
Эльконин, Д. (1989). Избранные психологические труды .Москва: Педагогика.
Андерс, Ю., и Россбах, Х.Г. (2015). Чувствительность учителей дошкольных учреждений к математике в детских играх: влияние школьного опыта, связанного с математикой, эмоционального отношения и педагогических убеждений. Журнал исследований в области детского образования, 29 (3), 305–322. DOI: 10.1080 / 02568543.2015.1040564
Басилая, Г. , Квавадзе, Д. (2020). Переход к онлайн-образованию в школах во время пандемии коронавируса SARS-CoV-2 (COVID-19) в Грузии, 5.DOI: 10.29333 / pr / 7937.
, Квавадзе, Д. (2020). Переход к онлайн-образованию в школах во время пандемии коронавируса SARS-CoV-2 (COVID-19) в Грузии, 5.DOI: 10.29333 / pr / 7937.
Блэр, К. (2013). Обучение в загоне для животных: оценка трех видов обратной связи в математическом приложении для дошкольников. В материалах 12-й Международной конференции по интерактивному дизайну и детям, 372–375.doi: 10.1145 / 2485760.2485814
Байерс, П., и Хэдли, Дж. (2013). Традиционные и новые режимы работы в математических приложениях с сенсорным экраном. В материалах 12-й международной конференции по дизайну взаимодействия и детям.Нью-Йорк, штат Нью-Йорк: ACM.
Каллаган, М. И Райх, С. (2018). Разработаны ли образовательные дошкольные приложения для обучения? Анализ рынка приложений. Обучение, СМИ и технологии, 43 (3), 280–293. DOI: 10.1080 / 17439884.2018.1498355
Кейтон-Ходжес, Г.А., Фенг, Г., Пэн, X. (2015). Тестирование по математике на планшете: чему мы можем научиться с помощью математических приложений? Журнал образовательных технологий и общества , 18 (2), 3–20.
Эбнер, Н.И Пресс, С. (2020). Педагогика II: Проведение симуляций и ролевых игр в онлайн, видео, синхронных курсах. Сеть исследований в области социальных наук . Рочестер.
Hamre, B.K., & Pianta, R.C. (2001). Ранние отношения учителя и ребенка и траектория успеваемости детей в школе до восьмого класса. Развитие ребенка , 72 (2), 625–638. DOI: 10.1111 / 1467-8624.00301
Хусейн, Л., Гулз, А., Хааке, М. (2015).Поддержка ранней математики: обоснование и требования к высококачественному программному обеспечению. Журнал «Компьютеры в преподавании математики и естественных наук» , 34 (4), 409–429.
Мальдонадо-Карреньо, К. (2011). Отношения между учителем и ребенком и развитие академических и поведенческих навыков в начальной школе: анализ внутри и между детьми , 82, 601–616. DOI: 10.1111 / j.1467-8624.2010.01533.x
Римм-Кауфман, С. (2000). Экологическая перспектива перехода в детский сад: теоретическая основа для руководства эмпирическим исследованием. Прикладной журнал Психология развития , 21, 491–511. DOI: 10.1016 / S0193-3973 (00) 00051-4.
Прикладной журнал Психология развития , 21, 491–511. DOI: 10.1016 / S0193-3973 (00) 00051-4.
Сабирова Е.Г., Федорова Т.В., Сандалова Н.Н. (2019). Особенности и преимущества использования веб-сайтов при обучении математике (интерактивная образовательная платформа UCHI.ru). Евразийский журнал математики, науки и технологий образования . 15 (5). DOI: 10.29333 / ejmste / 108367.
Накакабигла! Binaba ng musk ang eroplano! Сверхзвуковой вертикальный взлет при посадке! Взлетно-посадочная полоса Walang! — TopItInfo 资讯
Добавить номер:
最新 表态 宣布 EPlane 计划 : 超音速 垂直 起降 需要 跑道 , 洲际 旅行 成本 大幅 降低 AdAstra 首先 取消 了 全世界 广泛 的 年级 制度 —— 不 通过 年龄把 学生 编 到 不同 的 学习 小组。
———
набрала! Скорость взлета! Сверхзвуковой вертикальный взлет при посадке! Отличная взлетно-посадочная полоса!
набрал! Лучший план Маска — это лучший план EPlane: сверхзвуковой вертикальный взлет при посадке, взлетно-посадочная полоса и посадка, а также межконтинентальный взлет на воздушной подушке очень удобен!
Gusto ni Musk na sirain ang edukasyon
Си Элон Маск, лучший в мире, известен как «Железный человек из Кремниевой долины». «Магукайский туннель в районе Лупы».
«Магукайский туннель в районе Лупы».
Карамихан на музыку Маска «из долгого времени на лупу».
Мускус накаляется с огромным успехом на хинди.
Sa 1 Rocket Road, Hawthorne, California, oo, это настоящее путешествие по космическим исследованиям Маска на SpaceX.
В таинственной песне парка, мы часто встречаемся с парком «Ad Astra (patungo sa bituin)».Он хорошо знаком с Маском.
Это событие Маска в 2014 году, которое помутит ореолы миллионов лет назад в США. Песня на латинском языке, как «Per Aspera Ad Astra» (поиск изображений и изображений, которые используются в битах), и касама с большим количеством произведений Брэда Питта 2019 года «Ad Astra (Interstellar Exploration)» на любой вкус .
Какайба является параграфом, который вы можете увидеть в огромном количестве, как об этом говорят многие вещи.
Главное видео, созданное Джошуа Даном, которое инициировало коммерческие СМИ, быстро удалялось из онлайн-магазинов.
Malinaw na, Musk является хинди на английском языке в Интернете.
Кая, когда-нибудь когда-нибудь на этом пути?
Кая, когда ты особенно любишь его?
Этот параграф найден в парах людей. Официальный веб-сайт содержит информацию о том, что на сайте:
Ang Ad Astra School — это эксперимент, проводимый на территории кампуса ракетной компании.Наслаждайтесь камином, мапанлиха, и вы можете использовать его в академии, которая доступна на страницах Edad na 8 at 14.
Ang Ad Astra School — это экспериментальный опыт на территории кампуса ракетных ракет.Получите знания сербисов на больших и маленьких языках, и они могут работать в академии из 8 дней 14 дней.
Наращивает ореолы, которые существуют в большом мире, когда вы начинаете свой путь, создавая свои собственные знания.
Теперь, когда Маск был создан для того, чтобы получить удовольствие от них.
«Это удовольствие, которое вы знаете, как использовать метод обучения. Он научился умению пользоваться языком, хинди языком, который умел на уроке».
Он научился умению пользоваться языком, хинди языком, который умел на уроке».
Удовольствие от игры является идеальным вариантом для изучения. Сделайте это обучение на одном уровне с другими людьми, которые знают, как это сделать.
Чтобы получить, намек на Маска с помощью параграфа Ad Astra, вы получите традиционную систему образования.
Новая система
Наслаждайтесь классической системой
Una nang kinansela ng Ad Astra англ. .
Когда 8-летняя история дает много талантов по математике, вы можете найти ее в классе математики, касающейся 12-ступенчатой математики.Это сделано для того, чтобы создать комбинацию, созданную для этого, чтобы она была лучше и лучше.
В этом мире, как узнать, что вы думаете о том, что он интересен, и он не знает, как научиться говорить. Получите доступ к цифровому удостоверению личности.
Пилит на бумаге и раскрывает тексты на сайте Edad.Saaralan Муск, этот сукат на все сукат на все, что он делает, это лучший макапинсала на много естественных талантов и других людей. .
.
«Все, что написано на английском или на других языках, а также на других материалах, они используются в музыке. Тумугма талантливых и любимых людей «.
Сертификат качественного гуро-хинди.
Сертификат гуро? Хинди наман каиланган.
Нанинивала с Маск, который знает хинди, что дает рекомендации по профессиональному обучению.
Maraming гуро на этом языке хинди из классических академических, хинди, работающих в обычном режиме, и все сертификаты на языке.Нарито, что вы хотите, чтобы найти математический математический материал , и узнайте, какие ячейки имеют «сумбур», которые есть в настоящее время.
«Ad Astra» является надежным источником информации, делает выбор в пользу своей цели и набирает информацию о многих людях.
Гуру из дисциплины, которая классифицируется с отличным качеством. Kadalasan хинди nila sistematikong nakatanim целую систему kaalaman, и kung minsan ay hindi nila maalagaan kakayahang tmanggap ng bata. Лекции малали и быстро.
Лекции малали и быстро.
Чтобы узнать об этом Маск и его дискарте, и вы узнаете, как это сделать в этом мире, получить информацию о матияге и на удивительном гуро.Этот дискартом является «умение читать математику. Кабатаан». Батареи «.
Мускус не знает, что делать в этом мире, так много всего в мире, он делает все возможное, чтобы создавать нутриенты и вдохновлять.
Sa Ad Astra, очень хорошо знаком с людьми, получает опыт в разных странах, часто бывает на каждом шагу, и естественным образом из разных курсов.Ганитонг каранасан в каранасане в паг-аарал на катулад «паг-йикот в мундо в пользу своего сарили», который естественным образом совершенствует бата в паг-аарал и пагхана-нг кааламан-аарал, и в масра-а-рала-па-рал .
Униформа школьной формы? Hindi kailangan.
Форменная школьная форма? Hindi gusto.
Halos всех параллов состоит из двух частей, которые не имеют единой формы, чтобы работать на парах. «Майрун делает несколько стильных причесок для красивых причесок. На хинди вы можете увидеть красивые и красивые стили. Все, что вам нужно, это сделать, сделать, сделать, сделать красивый и красивый. Батарейки являются одними из самых разных патакаранов из своего муранг-эдада.
«Майрун делает несколько стильных причесок для красивых причесок. На хинди вы можете увидеть красивые и красивые стили. Все, что вам нужно, это сделать, сделать, сделать, сделать красивый и красивый. Батарейки являются одними из самых разных патакаранов из своего муранг-эдада.
Теперь, когда вы открываете доступ к данным, они записываются в обычном режиме.
Inaasahan ni Ad Astra на малайзийском lumalaking kaluluwa.Хинди может похвастаться огромным количеством курсов, которые вы можете использовать в своих целях в любое время суток из Люнеса, где живут, и многие другие люди, которые могут найти много слов, чтобы узнать, как это сделать.
В процессе изучения магического языка, малайзий создает баты, чтобы полностью заполнить его частный проект, который может быть использован для изучения этого языка, или его поклонников, например, во многих других случаях. -aaral sa panahong iyon.
С прохождением проектов в копонии, наши баты открывают большие возможности и какие-то умные и малые проблемы решают проблемы.
получить pagsusulit? Aklat-aralin? Operasyon? Хинди все!
Пагсусулит? аклат-аралин? такданг аралин?
Wala silang lahat dito.
С помощью Маска, техники, технологий, инженерии, математики (STEM) и научного образования, и вы можете научиться чему-то новому.
Как обычно, математика, математика, компьютер, компьютер, компьютер, компьютер, лучший искусственный интеллект и другие методы программирования. , искусственный интеллект, робототехника, реактивный самолет, АТБ., новые технологии электромагнитных импульсов, метеозонд, АТБ
Bilang karagdagan, ay paaralan is madalas for iimbit of iskolar and eksperto sa iba’t ibang larangan to magbahagi.Вы можете организовать семинар по тематике выступлений TED, чтобы узнать о слушателях и предложить свои идеи.
Naniniwala si Ad Astra на: это капалигиран является dapat likhain для детей, чтобы включить свои собственные таланты, и вы можете узнать их больше, чем найти. Для того, чтобы интересоваться, эти баты доступны в любом другом месте.
Для того, чтобы интересоваться, эти баты доступны в любом другом месте.
Таун-таун, отремонтируйте все, что вам нужно, и быстро оцените все, что вам нужно.
Хинди только ваш, это может быть язык, без слов, и все это в традиционных традициях.
Создайте магию для создания, редактирования, создания и разработки проектов группы, а также для создания новых, наиболее эффективных.
Теперь, возможно, это лучший подарок в волшебной школе в сказке: это хорошо, как на хинди, и мало кто знает, что такое хинди, чтобы побаловать себя языком.Кааламан на хинди является итальянским, малайзийский язык — это хинди сумасшествие на английском языке.
Узнайте больше о симуляторе параланов, умасах в классах, умасах по интересующим вас.Получите это Ad Astra, сделайте это в Musk, и сделайте это впервые в этом жанре.
Масасабинг накакамангха с Маском! Бинангит с Маском в один голос в пакикипанаям на «Пакикипанаям кай Ян Лан»:
Получите возможность использовать любой прием из всех доступных на стадиях Unidos и начать работу в этом режиме.
«Марсианин» Маск, похожий на «Железного человека из Кремниевой долины», стал одним из самых известных генеральных директоров (генеральных директоров) в мире. Вы получите лучшую ракету, чтобы получить ее в любой момент и в лучшем мире. Это борьба коце, и борьба с солнцем.
Hindi lang iyon, lumikha din siya ng isang nakakagambalang paaralan na pinapangarap ng hindi mabilang on aaral: walang grado, walang uniporme sa paaralan, walang walagsusulit, walang takdang-aralang, and moaging angular!
пинагмулан | Аналитический центр New Century
———
Фотографии и материалы этой статьи созданы в Интернете и доступны для пользователей, подключений и других пользователей.Если ошибки или сообщения об ошибках отображаются в текстовых статьях, они могут быть опубликованы для просмотра и редактирования.
———
Лучшее, что нужно сделать, чтобы собрать много покупок для продуктов Taobao, Tmall, Pinduoduo и JD каждый день.
Получите купонов сейчас:
Билет Малакинг на платформу торгового центра
———
Ключевые слова:
«Маск», «пааралан», «какая-то», «бата», «маг-аарал», «бата», «паг-аарал», «подрывная деятельность», «ракета», «пагтанггап»
Факторизация.Разложение количества множителей Разложение для простых множителей 6
Что значит разложить на простые множители? Как это сделать? Что можно найти в разложении числа на простые множители? Ответы на эти вопросы проиллюстрированы конкретными примерами.
Определения:
Простым называется число, имеющее ровно два разных делителя.
Составное число относится к числу, которое имеет более двух делителей.
Исключить натуральное число множителей — это означает представить его как произведение натуральных чисел.
Исключите натуральное число в простых множителях — это означает, что оно будет представлено как произведение простых чисел.
Примечания:
- При разложении простого числа один из множителей равен одному, а другой — большей части этого числа.
- Имеет смысл поговорить о разложении единиц по множителям.
- Составное число можно разложить на множители, каждый из которых отличается от 1.
Разложите число 150 для множителей. Например, 150 — это 15, умноженное на 10. 15 — составное число. Его можно разложить на простые множители 5 и 3. 10 — составное число. Его можно разложить на простые множители 5 и 2. Записав вместо 15 и 10 их разложения в простые множители, мы получили разложение числа 150. | |
Число 150 можно по-разному распределить по множителям. Например, 150 — это произведение чисел 5 и 30. 5 — номер простой. 30 — номер составной. Его можно представить как штуку по 10 и 3. 10 — номер составной. Его можно разложить на простые множители 5 и 2. Мы получили разложение числа 150 на простые множители другим способом. | |
Обратите внимание, что первое и второе разложение одинаковы. Отличаются они только порядком нахождения множителей. Принято записывать множители в порядке возрастания. | |
Любое составное число можно разложить на простые множители — единственный способ, вплоть до процедуры для множителей. | |
При разложении больших чисел на простые множители используют запись в столбце:
Наименьшее простое число, на которое делится 216, равно 2. Делим 216 на 2. Получаем 108. | |
Полученное число 108 делится на 2. Выполнить деление. Получаем в результате 54. | |
По знаку делимости 2, 54 делится на 2. Выполняя деление, получаем 27. | |
Число 27 заканчивается нечетной цифрой 7. Это Не делится на 2. Следующее простое число — 3. Делим 27 на 3. Получаем 9. Наименьшее простое Число, на которое делится 9, равно 3. Три — само по себе простое число, оно делится на себя и на единицу. Делим 3 на себя. В итоге получили 1. | |
- Число делится только на те простые числа, которые являются частью его разложения.
- Это число делится только на те составляющие, разложение которых на простые множители полностью отсутствует.
Рассмотрим примеры:
4900 делится на простые числа 2, 5 и 7. (Они входят в разложение числа 4900), но не делится, например, на 13. | |
11 550 75. В результате деления будет произведение множителей 2, 7 и 11. Номер11550 не делится на 4, потому что в расширении четырех есть лишние два. |
Найдите частное из деления числа A на число B, если эти числа сложить на простые множители следующим образом: A = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 3 ∙ 5 ∙ 5 ∙ 19; В = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 ∙ 19
Разложение числа B полностью содержится в разложении числа a. | |
Результат деления A на B является произведением трех чисел, оставшихся в раскрытии. Итак, ответ: 30. |
Библиография
- Вилекин Н.Я., Жохов В.И., Чесноков А.С., Шварцбург С.И. Математика 6. — М .: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.
 С. Математика 6 класс. — Гимназия. 2006.
С. Математика 6 класс. — Гимназия. 2006. - Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М .: Просвещение, 1989. .
- Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс. — М .: Ж МИПИ, 2011. .
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Учебное пособие для учащихся 6-х классов заочной школы МИФИ. — М .: Ж МИПИ, 2011. .
- Шеврин Л.Н., Гаин А.Г., Коряков И.О., Волков М.В. Математика: Учебник — Собеседник для 5-6 классов средней школы.- М .: Просвещение, Библиотека учителя математики, 1989. .
- Интернет-портал Matematika-na.ru ().
- Интернет-портал Math-Portal.ru ().
Домашнее задание
- Вилекин Н.Я., Жохов В.И., Чесноков А.С., Шварцбург С.И. Математика 6. — М .: Мнемозина, 2012. № 127, № 129, № 141.
- Прочие задачи: № 133, № 144.
Все начинается с геометрической прогрессии. На первой лекции по строю (см. Раздел 18. 1. Основные определения ) Мы доказали, что эта функция является суммой ряда, и число сходится к функциям, когда
1. Основные определения ) Мы доказали, что эта функция является суммой ряда, и число сходится к функциям, когда
. Итак,
.
Пейте несколько разновидностей этой серии. Заменить ч. по — ч. , получим
при замене h. на
Прием
и т.д .; Область схождения всех этих строк одинакова:
.
2.
.
Все производные этой функции в точке h. = 0 равно
, поэтому серия имеет вид
.
Область сходимости этой строки — это вся числовая ось (Пример 6 раздела 18.2.4.3. Радиус сходимости, интервал сходимости и область сходимости степенного ряда ), поэтому
для
. В результате остаточный член формулы Тейлора
.Следовательно, ряд сходится к
в любой точке h. .
3.
.
Этот диапазон абсолютно сходится, когда
и его сумма действительно равна
.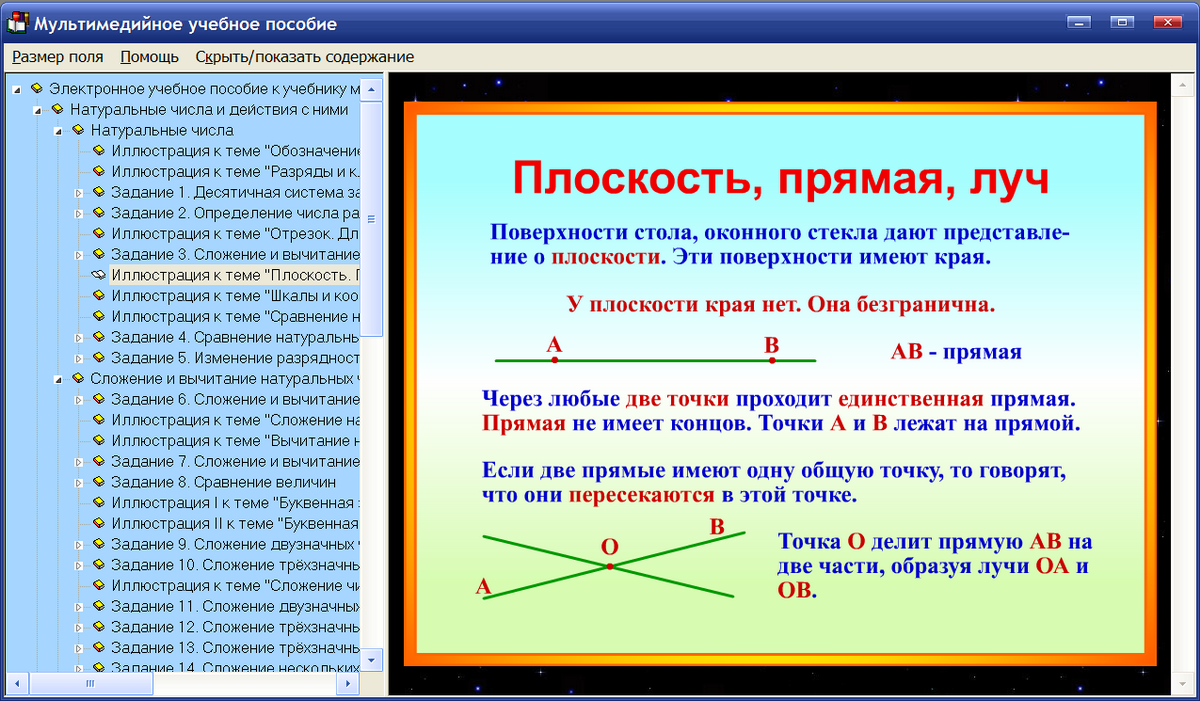 Остаточный член формулы Тейлора имеет
Остаточный член формулы Тейлора имеет
, где
или
— ограниченная функция, и
(это общий член предыдущего разложения).
4.
.
Это разложение может быть получено, как и предыдущее последовательное вычисление производных, но мы поступим иначе. Повторная переустановка предыдущего ряда:
Сходимость к функции по всей оси следует из теоремы о дифференциации почв степенного ряда.
5. Самостоятельно доказать, что на всей числовой оси.
6.
.
Строка для этого объекта называется биномом около .Здесь мы будем вычислять производные.
… Серия Маклорена имеет вид
Ищем интервал сходимости: значит, интервал сходимости равен
. Исследование остаточного члена и поведения числа на концах интервала сходимости не проводится; Получается, что при
Строка абсолютно сходится в обеих точках.
, P.
Ряд условно сходятся в точке
и расходятся в точке
, P.
Развелись по обоим пунктам.
7.
.
Здесь мы используем тот факт, что
. Так как тогда, после убитого интегрирования,
Область сходимости этого ряда — полуинтервал
, сходимость к функции во внутренних точках следует из теоремы о почвенном интегрировании степенного ряда, в точке h . = 1 — от непрерывности и функций, а суммы силового ряда во всех точках, сколь угодно близкие к ч. = 1 осталось. Отметим, что взяв ч. = 1, найдем сумму строки.
8. Интегрируя строку сзади, мы получаем разложение для функции
. Все расчеты произведите самостоятельно, запишите область схождения.
9. Удалите разложение функции
по формуле биномиального ряда с
:. Знаменатель
Размещено вроде, двойной факториал
означает работу всех натуральных чисел одинаковой готовности как не превышающих.Разложение сходится к функции при
. Выпрямляя его с 0 до ч. , я понял. Оказывается, этот ряд сходится к функции на всем отрезке.
Выпрямляя его с 0 до ч. , я понял. Оказывается, этот ряд сходится к функции на всем отрезке.
; для ч. = 1 Получится еще одно красивое представление числа:
.
18.2.6.2. Решение задач по разложению функций в ряд. Большинство задач, в которых требуется разложить элементарную функцию в ряд по степеням
, решается с помощью стандартных разложений.К счастью, у любой базовой элементарной функции есть свойство, которое позволяет вам это делать. Рассмотрим ряд примеров.
1. Функция дезинтеграции
в градусах
.
Решение. . Число сходится как
.
2. Функция отправки
в градусах
.
Решение.
. Поле совпадения:
.
3. Функция отправки
в градусах
.
Решение. . Число сходится как
.
4. Определите функцию
в градусах
.
Решение. . Число сходится как
.
5. Определите функцию
в градусах
.
Решение. . Сходимость области
. Сходимость области
.
6. Функция отправки
в градусах
.
Решение. Разложение на ряд простых рациональных дробей второго типа получается неприятным дифференцированием соответствующих разложений дробей первого типа. В этом примере. Дальнейшее дифференцирование по времени дает разложение функций
,
и др.
7. Функция отправки
в градусах
.
Решение. Если рациональная дробь не простая, она сначала отображается как сумма простых дробей:
, а затем действует как в примере 5: где
.
Естественно, такой подход неприменим, например, для разложения функции по степеням h. . Здесь, если вам нужно получить несколько первых членов ряда Тейлора, проще всего найти значения в точке h.3 + х). Чтобы увидеть ход решения, щелкните Показать шаги. Если вам нужно получить результат в формате Word, воспользуйтесь этой услугой.
Примечание : Число «PI» (π) записывается как PI; Квадратный корень как SQRT, например, SQRT (3), TG tangent записывается как tan.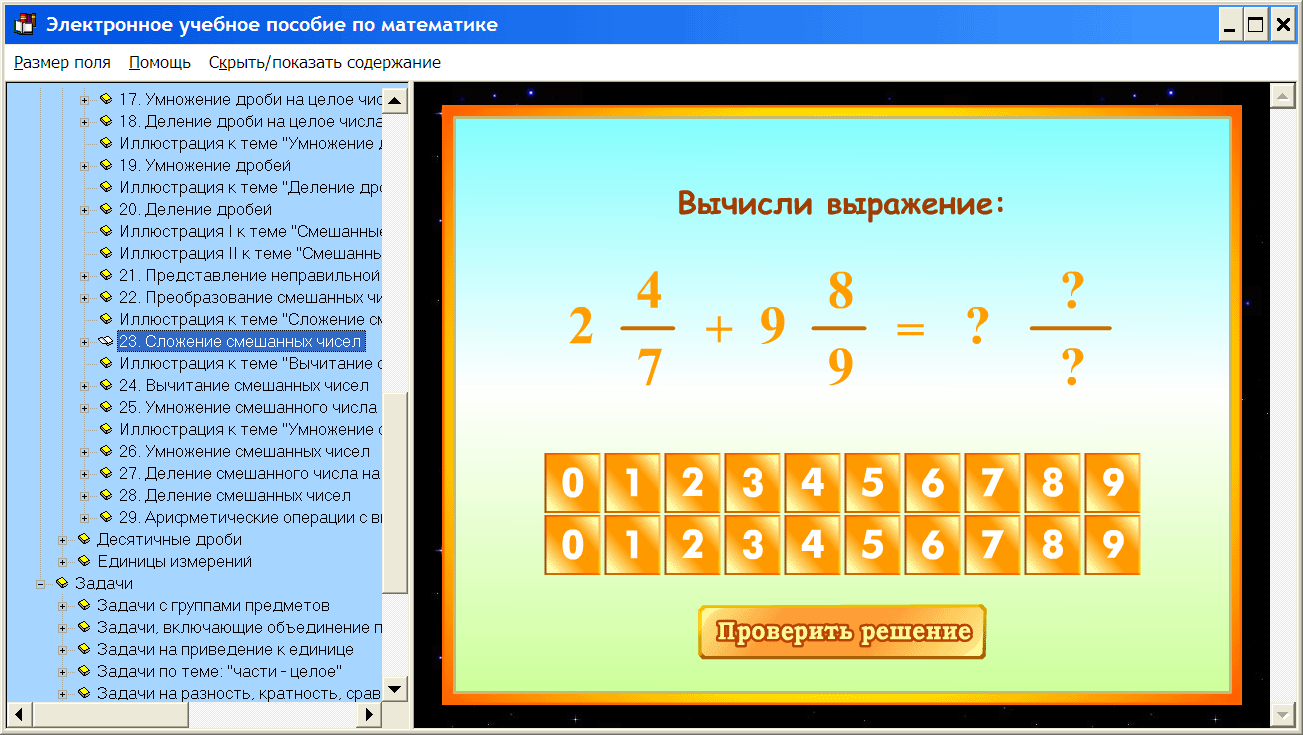 См. Альтернативный раздел, чтобы просмотреть ответ.
См. Альтернативный раздел, чтобы просмотреть ответ.
- Если указано простое выражение, например 8 * D + 12 * C * d, выражение «развернуть множители» означает представить выражение в форме фабрики.Для этого нужно найти общие факторы. Это выражение будет записываться как: 4 * d * (2 + 3 * c).
- Представьте работу в виде двух твистов: x 2 + 21yz + 7xz + 3XY. Здесь уже нужно найти несколько общих заводчиков: x (x + 7z) + 3y (x + 7z). Выполняем (x + 7z) и получаем: (x + 7z) (x + 3y).
см. Также деление многочленов на угол (показаны все шаги деления столбца)
Полезными при изучении правил разложения множителей будут формулы сокращенного умножения , с которыми будет понятно, как раскрыть скобки с квадратом:
- (a + b) 2 = (a + b) (a + b) = a 2 + 2ab + b 2
- (AB) 2 = (AB) (AB) = A 2 -2AB + B 2
- (A + B) (AB) = A 2 — B 2
- a 3 + B 3 = (A + B) (A 2 -AB + B 2)
- a 3 -B 3 = (AB) (A 2 + AB + B 2)
- (a + b) 3 = (a + b) (a + b) 2 = a 3 + 3a 2 b + 3ab 2 + b 3
- (AB) 3 = (AB) (AB) 2 = A 3 -3A 2 B + 3ab 2 -B 3
Методы разложения множителей
Изучив несколько методик факторизации Вы можете создать следующую классификацию решений:- Использование формул сокращенного умножения.

- Найдите общий множитель.
Каждое натуральное число, кроме единицы, имеет два или более делителя. Например, число 7 делится без остатка на 1 и 7, то есть имеет два делителя. А в числе 8 делители 1, 2, 4, 8, то есть целых 4 делителя сразу.
В чем разница между простыми и составными числами
Числа, у которых больше двух делителей, называются составными. Числа, у которых всего два делителя: единица и само это число, называются простыми числами.
Число 1 нужно разделить только на одно, а именно на само число. Единица не применяется ни к простым, ни к составным числам.
- Например, число 7 простое, а число 8 составное.
Первые 10 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Номер 2 одиночное четное простое число, все остальные простые числа нечетные.
Число 78 составное, так как помимо 1 и самого себя оно делится еще и на 2.При делении 2 получаем 39. То есть 78 = 2 * 39. В таких случаях говорят, что число разложено на множители 2 и 39.-reshenie-1745.jpg)
Любое составное число можно разложить на два множителя, каждый из которых больше чем 1. С простым числом такой фокус не прокатит. Такие дела.
Разложение ряда простых факторов
Как отмечалось выше, любое составное число можно разложить на два фактора. Возьмем, к примеру, число 210. Это число можно разложить на два множителя 21 и 10.Но числа 21 и 10 тоже составные, разложите их на два фактора. Получаем 10 = 2 * 5, 21 = 3 * 7. И в итоге число 210 разложилось уже на 4 множителя: 2,3,5,7. Эти числа уже простые и разложить их нельзя. То есть число 210 мы выложили на простые множители.
При разложении компонентов на простые множители они обычно записываются в порядке возрастания.
Следует помнить, что любое составное число можно разложить на простые множители и единственным способом, с точностью перестановки.
- Обычно при разложении числа на простые множители используют знаки делимости.
Разложите число 378 на простые множители
Мы будем записывать числа, разделяя их вертикальной чертой. Число 378 делится на 2, так как оно заканчивается на 8. При делении мы получаем число 189. Количество чисел в числе 189 делится на 3, что означает, что число 189 делится на 3. В результате, получаем 63.
Число 378 делится на 2, так как оно заканчивается на 8. При делении мы получаем число 189. Количество чисел в числе 189 делится на 3, что означает, что число 189 делится на 3. В результате, получаем 63.
Число 63 также делится на 3 по принципу делимости.Получаем 21, число 21 можно снова разделить на 3, получаем 7. Семерка делится только на себя, получаем единицу. Это законченное разделение. Справа после функции оказались простые множители, для которых число 378 сворачивается.
378 | 2
189 | 3
63 | 3
21 | 3


 1c.ru/read/info/rabota-adobe-flash-v-2021-godu/)
1c.ru/read/info/rabota-adobe-flash-v-2021-godu/) Пожалуйста, включите его, чтобы активировать полную функциональность веб-сайта
Пожалуйста, включите его, чтобы активировать полную функциональность веб-сайта 

 Вынимаем (x + 7z) и получаем: (x + 7z) (x + 3y).
Вынимаем (x + 7z) и получаем: (x + 7z) (x + 3y).

 (они входят в разложение по 4900), но не, например, по 13.
(они входят в разложение по 4900), но не, например, по 13. Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М .: Мнемосина, 2012.
Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М .: Мнемосина, 2012.
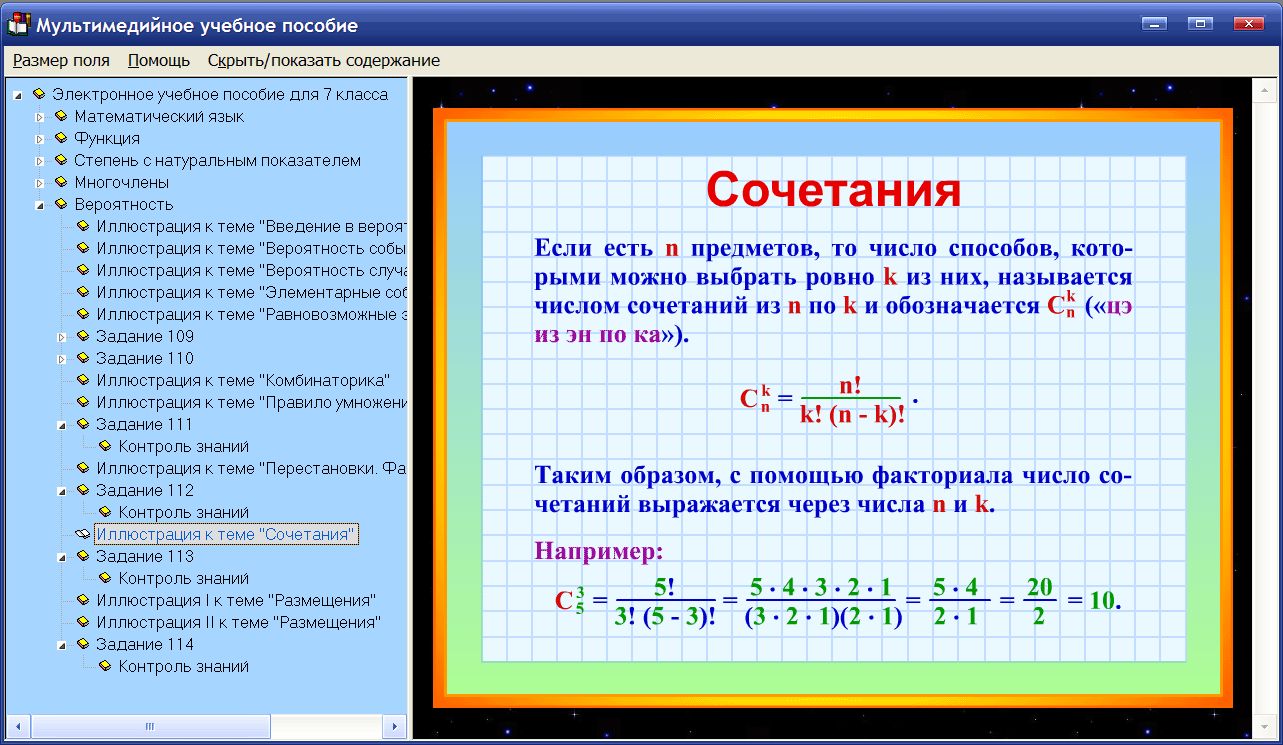

 Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550.
Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550. С. Математика 6 класс. — Гимназия. 2006.
С. Математика 6 класс. — Гимназия. 2006.