Презентация. «Первый урок математики в 5 классе»
библиотека
материалов
Содержание слайдов
Номер слайда 1
Номер слайда 2
 П. Конфорович МАТЕМАТИКА УСТУПАЕТ СВОИ КРЕПОСТИ ЛИШЬ СИЛЬНЫМ И СМЕЛЫМ.
П. Конфорович МАТЕМАТИКА УСТУПАЕТ СВОИ КРЕПОСТИ ЛИШЬ СИЛЬНЫМ И СМЕЛЫМ.Номер слайда 3
А 1. Произведение 9 и 4 2. Разность 57 и 45 3. Сумма 17 и 4 4. На какое число нельзя делить? 5. Частное 105 и 5 Е У Ч А П С Д Х К 13 36 0 21 525 100 12 1 11 17+4=21 57- 45=12 9*4=36 105:5=21 0 У Д А Ч ПРОВЕРКА СНАРЯЖЕНИЯ
Номер слайда 4
ИСТОРИЧЕСКАЯ БУХТА ЗАЛИВ НАТУРАЛЬНЫХ ЧИСЕЛ ОЗЕРО СМЕКАЛКИ ОСТРОВ МАТЕМАТИКА-5
Номер слайда 5
Математика — это язык, на котором написана книга природы .
Номер слайда 6
Математика – самая древняя из наук, она была и остается необходимой людям. Слово «математика» греческого происхождения. Оно обозначает «наука», «размышление».
Первый отечественный учебник по математике вышел в 1703 год. Леонтий Филиппович Магницкий издал «Арифметику». По ней учился М. В. Ломоносов, называвший этот учебник «вратами учёности». Виленкин Н.Я., Жохов В.И. Математика: Учебник для 5 класса общеобразовательных учреждений.
Леонтий Филиппович Магницкий издал «Арифметику». По ней учился М. В. Ломоносов, называвший этот учебник «вратами учёности». Виленкин Н.Я., Жохов В.И. Математика: Учебник для 5 класса общеобразовательных учреждений.
Номер слайда 8
Всё есть число. Пифагорейцы 1,2,3,4,5,6,…- натуральные числа (числа, применяемые при счете). Ноль не относят к натуральным числам. ЗАЛИВ НАТУРАЛЬНЫХ ЧИСЕЛ
Номер слайда 9
Прочитайте числа:
1) Запишите: * наибольшее четырехзначное число * наименьшее трехзначное число * наибольшее девятизначное число * наименьшее семизначное число 9 999 100 999 999 999 1 000 000
+ = 630 г + = 740 г + + = 910 г груша? апельсин? лимон? груша 170 г, апельсин 460 г, лимон 280 г.
Номер слайда 12
Раз – подняться на носки и улыбнуться. Два – согнуться, разогнуться. Три – в ладоши три хлопка, головою три кивка. На четыре – руки шире. Пять – руками помахать. Шесть – за парту тихо сесть.
Номер слайда 13
Смекалка во всяком деле выручит. ОЗЕРО СМЕКАЛКИ
ОЗЕРО СМЕКАЛКИ
6 8 = 70 22 77 7 = 5 6 45 5 = 9 5 2) Поставьте вместо квадратов знаки действий так, чтобы равенства были верными: 1)Найдите неизвестное число: 14 8 42 18 18 7 6 6 ? х — + х : +
3) Поставить знаки действий, если нужно скобки так, чтобы получилось 100. 5 5 5 5 5 = 100 3 3 3 3 3 = 100 1 1 1 1 1 = 100 ( 5 + 5 + 5 + 5 ) * 5 =100 3 3 * 3 + 3 : 3 =100 1 1 1 – 1 1 = 100
5 5 5 5 5 = 100 3 3 3 3 3 = 100 1 1 1 1 1 = 100 ( 5 + 5 + 5 + 5 ) * 5 =100 3 3 * 3 + 3 : 3 =100 1 1 1 – 1 1 = 100
Номер слайда 16
ОТРЕЗОК ЗАДАЧА 4) МАТЕМАТИЧЕСКИЕ РЕБУСЫ
Номер слайда 17
Математику уже затем учить надо, что она ум в порядок приводит. М.В. Ломоносов ОСТРОВ МАТЕМАТИКА-5
М.В. Ломоносов ОСТРОВ МАТЕМАТИКА-5
Номер слайда 18
Натуральные числа Десятичные дроби Обыкновенные дроби Геометрические фигуры
Номер слайда 19
Домашнее задание. Восстановите запись. Одинаковые фигуры обозначают одинаковые цифры. 6 1 2 6 0 3
9
Восстановите запись. Одинаковые фигуры обозначают одинаковые цифры. 6 1 2 6 0 3
9
Номер слайда 20
— Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно. — Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно. — У меня не было желания работать. Сегодня не мой день.
Номер слайда 21
Учебному году положили начало, Желанье учить и учиться совпало. Пусть радостным будет учение ваше, И знаний полученных полная чаша.
Пусть радостным будет учение ваше, И знаний полученных полная чаша.
Ф.И.О. учителя | Кравченко Дмитрий Михайлович | ||||
Предмет | Математика | ||||
Класс | 5 | ||||
Тип урока | Урок закрепления знаний и способов деятельности | ||||
Тема урока | Деление дробей | ||||
Цель урока | Сформировать умение
выполнять действия по делению дробей. | ||||
Задачи урока | образовательные: учить как правильно делить дроби. развивающие: создать условия для развития внимания, инициативы, воображения; вести работу по развитию математической речи, логического мышления; формировать умение анализировать, находить ошибки, делать выводы. воспитательные: содействовать формированию взаимоуважения, умения отстаивать своё мнение, интереса к урокам математики.
| ||||
Планируемые результаты | предметные – моделируют ситуации, требующие замены знака деления дробной чертой и обратно; личностные – проявляют устойчивый и широкий интерес к новой теме и к изучению предмета; метапредметные — регулятивные – обнаруживают проблему «недостатка» знаний для решения заданий, содержащих черту дроби; познавательные
учатся осуществлять выбор наиболее эффективных способов решения
образовательных задач коммуникативные – умеют слушать других, учатся критично относиться
к своему мнению, с достоинством признавать ошибочность своего мнения (если
оно таково) и корректировать его.
| ||||
Формы организации образовательного пространства на уроке | Фронтальная беседа с учащимися; работа с учебником; индивидуальная работа, работа в парах, работа по карточкам-заданиям. | ||||
Риски | Тема урока не заинтересует учащихся. Могут возникнуть трудности при проверке работы товарища; не получится планируемая дискуссия при обсуждении ошибок.
| ||||
Средства обучения | Учебник математики, презентация.
| ||||
Этап урока | Микроцель | Деятельность учителя | Деятельность учащихся | Планируемые результаты | |
1. | Создание положительного эмоционального настроя в классе. | Приветствует учащихся. | Приветствуют учителя. | Включение учащихся в деловой ритм урока. | |
2. Проверка домашней работы | Проверить знания и умения, необходимые для работы на данном уроке.
| Демонстрирует слайд 2,организует работу в парах по взаимопроверке домашней работы | Работа в парах (взаимопроверка домашней работы) | а) познавательные УУД: развитие умения применять математические знания к реальным жизненным ситуациям, проводить наблюдения и делать самостоятельные выводы, применять полученные знания при решении задач; б) коммуникативные УУД: формирование умения работать в коллективе: умение слушать и слышать, отстаивать своё мнение; признавать свои ошибки; в) регулятивные УУД: учить контролировать свою
речь при выражении своей точки зрения; самостоятельно оценивать свои мысли и
высказывания. г) личностные: мотивация к обучению и целенаправленной познавательной деятельности. | |
3. Устная работа
(Актуализация знаний учащихся)
| Повторить учебный материал, необходимый для «открытия нового знания», развивать умение применять черту дроби как знак деления.
| Демонстрирует слайды, организует фронтальную работу с классом. Слайд 3 Какое математическое действие можно обозначить чертой дроби? Найдите значение дроби.
Слайд 4. Представьте число в виде дроби…..
Слайд 5. Сравните дроби. Какие из данных дробей правильные? Неправильные?
Слайд 6. При каких значениях х дробь будет правильной? При каких значениях х дробь будет неправильной?
Слайды 7-11 Как найти дробь от числа? Как найти число по его дроби? | Самостоятельно
находят ответ на поставленный вопрос. Устно отвечают, анализируют ответы одноклассников.
| ||
4.Применение знаний при решении уравнений, содержащих черту дроби. | Подвести к формулированию темы и цели урока.
| Демонстрирует слайды, организует фронтальную работу с классом. Слайд 12. Сравните уравнения правого и левого столбика. Сформулируйте тему урока. Решите уравнения правого столбика.
| Формулируют тему урока, записывают тему урока в тетради. Осваивают способы деятельности в «измененных условиях», т.е. решение уравнений, содержащих дробную черту.
| а)Познавательные УУД: в ходе беседы учащиеся делают вывод, как решить уравнение, содержащее черту дроби; б) регулятивные: формировать целевые установки учебной деятельности; выстраивать алгоритм действий; в) коммуникативные: учить точно и грамотно выражать свои мысли | |
5. |
| №1070(устно) Прочитайте задачу. На сколько частей разделили кусок ткани? Сколько частей пошло на брюки? Сколько частей пошло на куртки? Какая это часть целого?
№1073 Прочитайте задачу. Какой способ решения выберем? Какую величину обозначим через х? Решение задачи у доски с комментированием. | Устно отвечают, анализируют ответы одноклассников.
Записывают решения в тетради. Отвечающий у доски комментирует решение | а) познавательные УУД: Выдвижение гипотезы о связях и закономерностях объектов задачи; организация исследования с целью проверки гипотез; развитие умения делать умозаключения и выводы на основе аргументации б) коммуникативные УУД: Участие в коллективном обсуждении решения задачи; умение слушать и слышать, отстаивать своё мнение; признавать свои ошибки; в) регулятивные УУД: учить контролировать свою
речь при выражении своей точки зрения; самостоятельно оценивать свои мысли и
высказывания. г) личностные: мотивация к обучению и целенаправленной познавательной деятельности. | |
6. Самостоятельная работа (Контроль и самоконтроль.) | Проверка умения применения учащимися нового материала при выполнении практического задания, воспитание самостоятельности.
| №1058 1 вариант (а,б) 2 вариант (в,г) После обсуждения в парах учитель показывает правильное решение на слайде 14 .
№1073(2) После обсуждения в парах учитель показывает правильное решение на слайде 15 .
| Учащиеся самостоятельно выполняют задание, выполняют взаимопроверку, исправляют ошибки соседа.
| Познавательные: формировать умение решать уравнения, содержащие черту дроби, задачи на составление уравнения; регулятивные: формировать способность к мобилизации сил
и энергии, к волевому усилию в преодолении препятствий; коммуникативные: управлять своим поведением (контроль, коррекция, оценка своего
действия).
| |
5. Рефлексия. | Определить соответствие достигнутых результатов учебного занятия поставленным задачам. Оценивается работа класса и конкретных детей на учебном занятии.
| Фронтальная беседа с учащимися. 1.Какое действие заменяет дробная черта в уравнении? 2. Как решить уравнение, содержащее дробную черту?
3.Задание на дом. № 1079; №1080. Спасибо за урок. Урок окончен, до свидания.
| Отвечают на вопросы учителя, подводят итоги своей работы на уроке. Анализируют, что при проверке знаний они проявили самостоятельность, честность, требовательность. При работе в парах оказали взаимопомощь. Во
время урока им потребовалась внимательность, собранность, проявление
смекалки.
Записывают задания в дневник. |
| |
МОУ «СОШ № 5 х. Восточный»
Конспект урока по математике 5 класс
с использованием ИКТ по ФГОС
Обобщение материала по теме: «Натуральные числа»
Разработал учитель – М.А. Холецкая
Цели урока:
Образовательная:
— систематизировать, обобщить и закрепить знания, умения и навыки учащихся, при решении конкретных упражнений и заданий по данной теме;
— повторить и закрепить ранее изученный материал о натуральных числах.
— вспомнить законы умножения;
— научить учащихся выполнять умножение.
Развивающая:
— развитию воображения, творческой активности учащихся, а также памяти, внимания, логического мышления;
— проверить степень усвоения учащимися материала;
— обобщить и систематизировать знания путем создания условий для интеллектуального развития личности ребенка на уроке;
— развивать математическую культуру речи и письма.
Воспитательная:
— воспитывать доброжелательное отношение к коллективу и окружающим;
— дисциплинарные навыки;
— интерес к предмету.
Ожидаемые результаты:
Личностные УУД:
— сформировано положительное отношение к уроку, понимание необходимости учения;
— сформировано следование в поведении моральным и этическим требованиям.
Регулятивные УУД:
— понимать и строить планируемые действия;
— проговаривать и комментировать последовательность производимых действий.
Коммуникативные УУД:
— развивать умения работать с информацией на уроке, связно излагать мысли;
— сохранять и развивать умение сотрудничать в паре, группе; отвечать на вопросы, слушать и слышать товарищей, учителя;
— формулировать, высказывать и обосновывать свою точку зрения.
Познавательные УУД:
— понимать и интегрировать информацию в имеющийся запас знаний, преобразовывать, структурировать и применять;
— извлекать нужную информацию.
Предметные:
— подвести учащихся к открытию и осознанному пониманию основных понятий темы: интонации, логического ударения, паузы, тона голоса;
— формировать умение правильной постановки логического ударения в предложении, тона голоса, интонации, паузы; формировать умение работать с изученными теоретическими сведениями и примянять полученные знания на практике;
— учить формулировать и аргументировать собственную точку зрения по проблеме, поставленной во время изучения материала.
Задачи урока:
- Обобщение и закрепление темы “Натуральные числа», используя различные виды работы.
- Закрепить:
а) умение правильно записывать и выполнять действия с натуральными числами;
б) умение использовать свойства действий при вычислениях.
3. Воспитывать в детях бережное отношение к окружающей природе.
Тип урока: обобщающий урок , урок закрепления и совершенствования знаний.
Оборудование: карточки-задания, компьютер, мультимедийный проектор.
План урока.
1. Проверка домашнего задания.
- История о натуральных числах.
- Свойства действий с натуральными числами.
- Устный счет.
- Решение текстовых задач.
- Самостоятельная работа.
- Подведение итогов урока.
Ход урока.
1. Проверка домашнего задания.
№9 (а) из дидактического материала, стр.42.
(Слайд 1) В одной цистерне было в 3 раза больше бензина, чем в другой. Когда в первую долили 54л, а во вторую-26л, то в двух цистернах стало 200л бензина. Сколько литров бензина было в каждой цистерне первоначально?
(Слайд 2) Решение.
1) 54+26=80(л) бензина долили всего
2) 200-80=120(л) бензина было в двух цистернах
3) 3+1=4(части) составляет весь бензин
4) 120:4=30(л) бензина составляет одна часть или было во второй цистерне
5) 30·3=90(л) бензина было в первой цистерне
Ответ: 90л, 30л.
2. Ребята! Мы с вами учились правильно записывать натуральные числа, выполнять действия с ними, учили свойства действий с натуральными числами.
А сегодня у нас обобщающий урок.
Цель урока: закрепить умение правильно записывать и выполнять действия с натуральными числами, использовать свойства действий при вычислениях, решать задачи на части и на уравнивание.
(Слайд 3) Вспомним, какие числа называются натуральными?
Натуральные числа-числа 1,2,3,4,…употребляемые при счете предметов.
(Слайд 4) А как появились натуральные числа, кто их придумал?
Доклад «История о натуральных числах».
3. Вспомним свойства действий с натуральными числами.
Какие свойства вам известны?
Переместительное, сочетательное и распределительное.
Сформулируйте, пожалуйста, переместительное свойство.
(Слайд 5) От перестановки слагаемых сумма не меняется.
а+в=в+а
От перестановки множителей произведение не меняется.
а·в=в·а
Вспомним сочетательное свойство.
(Слайд 6) Чтобы к сумме двух чисел прибавить третье число, можно к первому прибавить сумму второго и третьего чисел.
(а+в)+с=а+(в+с)
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
(а· в)· с=а· (в· с)
(Слайд 7) Сформулируйте, пожалуйста, распределительное свойство.
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные произведения.
(а+в)· с=а·с + в·с
Чтобы умножить разность двух чисел на третье число, можно уменьшаемое и вычитаемое умножить на это число и из первого результата вычесть второй.
(а-в)·с=а·с — в·с
4. А сейчас выполним устно следующие примеры.
(Слайд 8) Устный счет.
Выполните действия:
23+11+47+29= 110
276+118+324= 718
2·9·5·5·4= 1800
8·4·125·25= 100000
90·25+10·25= 2500
123·27-23·27= 2700
(200+7)·12= 2484
(100-3)·11= 1067
21+22+23+…+29+30= 255
93+83+…+23+13+3= 480
5. Ребята! Вы все знаете, что в жизни без натуральных чисел не обойтись, хотя существуют и другие числа.
Ребята! Вы все знаете, что в жизни без натуральных чисел не обойтись, хотя существуют и другие числа.
А нужны ли числа в окружающей нас природе, например, в экологии?
Да, нужны.
А сейчас мы с вами приступим к решению экологических задач.
(Слайд 9) Задача 1.
За всю историю человечества на сжигание всех видов топлива было израсходовано 290 млрд. тонн кислорода. При этом углекислого газа, отравляющего воздух, образовалось 330 млрд. тонн.
В последние 50 лет масса израсходованного кислорода в среднем в 9 раз больше, чем масса кислорода, израсходованного за все предыдущие годы и в 9 раз больше образованного углекислого газа.
Сколько в среднем расходуется кислорода и образуется углекислого газа в воздухе в последние 50 лет?
(Слайд 10) Решение.
1) 1+9=10(частей) вся масса
2) 290:10=29(млрд. т) 1часть
3) 29·9=261(млрд. т) кислорода расходуется
4) 330:10=33(млрд. т) 1 часть
т) 1 часть
5) 33·9=297(млрд. т) углекислого газа образуется
Ответ: 261млрд.т, 297млрд.т.
Ребята! Сейчас у нас хорошо развита техника, работают фабрики, заводы, и каждый день расходуется много кислорода и образовывается отравляющего газа.
А как решить проблему, чтобы было больше необходимого для жизни кислорода и меньше отравляющего газа?
Сажать деревья. Почему? Потому что деревья, когда растут питаются углекислотой и выделяют кислород.
Решим следующую задачу.
(Слайд 11) Задача №2.
Для прироста 500г сухой массы сосны (без учета воды) дерево поглощает 920г углекислоты из воздуха и выделяет в атмосферу 720г кислорода.
Сколько будет взято углекислоты и будет выделено кислорода, если прирост сухой массы сосны составит 3кг 500г?
(Слайд 12) Решение.
3кг 500г=3500г
1) 3500:500=7(раз) больше стала масса
2) 920·7=6440(г) углекислоты
720·7=5040(г) кислорода
Ответ: 6кг 440г, 5кг 40г.
Ребята! Вы знаете, что город Ставрополь – город « Столица Ставропольского края». А как вы думаете, много в этом городе деревьев?
Да, много.
Сколько человек проживает в городе?
Об этом узнаем, решив задачу.
(Слайд 13) Задача №3.
В городах Ставрополе и Пятигорске проживает 908600 человек. В Ставрополе на 649000 человек больше, чем в Пятигорске.
Сколько человек проживает в каждом городе?
(Слайд 14) Решение.
1) 908600- 649000 =259600 (чел.) всего после уравнивания
2) 259600:2=129800 (чел.) проживает в г. Пятигорск
3) 908600 -129600 =679000 (чел) проживает в г. Ставрополь.
Ответ: 129800 человек, 679000 человек
А теперь решим следующую задачу.
Следующую экологическую задачу вы решите дома.
Задача №4.
Подсчитайте общее потребление кислорода в мире за один год черной металлургией, химической промышленностью и реактивной техникой.
Известно, что черная металлургия потребляет кислорода в 3 раза больше, чем химическая промышленность и в 6 раз больше, чем реактивная техника, которая потребляет кислорода на 6 млрд. м3 меньше, чем химическая промышленность.
Эту задачу вы решите дома. Открыли дневники, запишем задание на дом.
Физкультминутка. (Презентация)
А сейчас выполним самостоятельную работу.
6. Самостоятельная работа.
1) Заполните таблицу «Сумма и разность двух чисел».
1 вариант.
|
а |
213 |
|
189 |
|
312 |
|
в |
85 |
93 |
|
45 |
|
|
а + в |
|
310 |
252 |
|
|
|
а — в |
|
|
|
67 |
105 |
2 вариант.
|
а |
174 |
|
134 |
|
357 |
|
в |
97 |
87 |
|
48 |
|
|
а + в |
|
300 |
211 |
|
|
|
а — в |
|
|
|
57 |
188 |
2) Заполните таблицу «Произведение и частное двух чисел».
1 вариант.
|
а |
84 |
|
85 |
|
135 |
|
в |
3 |
4 |
|
3 |
|
|
а · в |
|
384 |
425 |
|
|
|
а : в |
|
|
|
36 |
27 |
2 вариант.
|
а |
123 |
|
244 |
|
96 |
|
в |
3 |
5 |
|
2 |
|
|
а · в |
|
425 |
976 |
|
|
|
а : в |
|
|
|
32 |
3 |
3) Определите, какой цифрой заканчивается результат вычисления.
1 вариант.
4+24+43+25+57+69+18
5·6·2·4·13·15·21·32·11
22·23+23·24+24·25+25·26+26·27+27·28+28·29
2 вариант.
2+13+25+36+47+58+69
2·4·5·8·12·14·16·18·22
12·13+13·14+14·15+15·16+16·17+17·18+18·19
7.Подведение итогов урока.
Итак, ребята, мы с вами повторили материал о натуральных числах. Узнали, что натуральные числа нам нужны в окружающей нас жизни, в экологии.
Этот урок я хочу закончить словами:
(Слайд 15) Без природы в мире людям
Даже дня прожить нельзя
Так давайте к ней мы будем
Относиться, как друзья.
И при всем честном народе
Добавляем мы потом:
Нужно помогать природе-
Но со знаньем и умом.
- 8. Литература
- Виленкин Н.Я и др. Учебник: Математика 5 класс. – М.
 : Мнемозина, 2007.
: Мнемозина, 2007. - Виленкин Н.Я. и др. Поурочные планы по математике 5 класс. – Волгоград.: Учитель, 2005.
- Суркова О.П. Математика. 5 класс. Тетрадь с печатной основой. – Саратов: Лицей, 2006.
- Пичурин Л.Ф. За страницами учебника математики — М.: Просвещение, 1990.
- Аксенова М.Д. Энциклопедия для детей «Математика — т.11»/.- М.: Аванта + , 2002
- Кордемский Б.А. Увлечь школьников математикой. – М.: Просвещение , 1999.
- Глейзер Г.И. История математики в школе. – М.: Просвещение ,2001.
Предмет: математика
Тема: «Обобщающий урок «Натуральные числа».
«Натуральные числа » – одна из важных тем в курсе математики.
Реальные учебные возможности учащихся данного класса мной учитывались, исходя из возрастных особенностей. При планировании урока я опиралась на такие индивидуальные характеристики учащихся, как мобильность, высокая эмоциональность, желание идти на контакт, любознательность, игровая активность.
Цели урока:
Образовательная:
— систематизировать, обобщить и закрепить знания, умения и навыки учащихся, при решении конкретных упражнений и заданий по данной теме;
— повторить и закрепить ранее изученный материал о натуральных числах.
— вспомнить законы умножения;
— научить учащихся выполнять умножение.
Развивающая:
— способствовать развитию воображения, творческой активности учащихся, а также памяти, внимания, логического мышления;
— проверить степень усвоения учащимися материала;
— обобщить и систематизировать знания путем создания условий для интеллектуального развития личности ребенка на уроке;
— развивать математическую культуру речи и письма.
Воспитательная:
— воспитывать доброжелательное отношение к коллективу и окружающим;
— дисциплинарные навыки;
— интерес к предмету.
Задачи урока:
- Обобщение и закрепление темы “Натуральные числа», используя различные виды работы.

- Закрепить:
а) умение правильно записывать и выполнять действия с натуральными числами;
б) умение использовать свойства действий при вычислениях.
3. Воспитывать в детях бережное отношение к окружающей природе.
Тип урока: обобщающий урок , урок закрепления и совершенствования знаний.
Оборудование: карточки-задания, компьютер, проектор.
Структура урока характерна для данного типа и вида урока и рациональна для достижения поставленных целей.
При планировании урока «Натуральные числа» я обращала внимание на практическую направленность, доступность, выделение главного в содержании, высокую информированность, быстрый темп, развитие навыков самостоятельной работы, использование технических средств обучения.
Для учебной деятельности учащихся при закреплении и совершенствовании знаний по теме «Натуральные числа » характерна большая самостоятельность.
Главный акцент на уроке делался на закрепление навыков учащихся определения натуральных чисел, обобщение и закрепление темы “Натуральные числа», используя различные виды работы , на умение правильно записывать и выполнять действия с натуральными числами; на умение использовать свойства действий при вычислениях, а также на воспитание нравственных качеств: доброты, дружбы, взаимопомощи, бережного отношения к природе.
Методические приемы: в связи с тем, что данная организация урока интересна и класс по своей подготовленности сможет принять активное участие в учебной деятельности, было выбрано сочетание следующих средств и методов работы: проблемный, иллюстративный, частично-поисковый (это поиск скрытой, требующей перестройки информации в ситуации несколько измененной), осмысление и поиск вариантов в выполнении заданий, учащиеся проявляли умение использовать мыслительные операции сравнения, обобщения.
Знания усваивались учащимися и проявлялись только через их деятельность, процесс обучения строился на постепенном усложнении содержания. В ходе решения проблемной задачи учащиеся были настроены на переход к восприятию следующей темы « Натуральные числа»
В ходе решения проблемной задачи учащиеся были настроены на переход к восприятию следующей темы « Натуральные числа»
Формы обучения: самостоятельная работа, работа по карточкам с самопроверкой, работа с наглядным материалом, работа по цепочке, устная работа с классом, решение проблемной задачи.
Такое сочетание форм делает урок закрепления и совершенствования знаний динамичнее, интереснее, не дает накапливаться усталости, однообразию.
Контроль усвоений знаний умений и навыков был предусмотрен в виде карточек-заданий.
На уроке целесообразно использовались возможности компьютерного кабинета, мультимедийного проектора и сделанной мной презентации урока.
Высокая работоспособность и доброжелательная психологическая атмосфера на уроке поддерживалась за счет разнообразия заданий, за счет постоянной смены наглядности, нетрадиционной формы проведения урока, эмоциональной подачи материала, смены деятельности и темпа урока.
Время на различных этапах урока использовалось рационально. Для эмоциональной разгрузки и снятия напряжения учащимся была предложена физкультминутка.
Я думаю, что мне удалось реализовать все поставленные цели и задачи. Ребятам было интересно и комфортно на уроке.
Работа с учебником и работа в тетрадях на уроке проводилась.
Введение в анализ урока
Урок дан в соответствии с тематическим планированием
Использование компьютерной презентации оправданно
Роль компьютера на уроке
Работает для учителя и учащихся на всех этапах урока
Обсуждаемые задания выносятся на компьютер. Учитель, используя компьютер, активно помогает учащимся разобраться в сути заданий, сравнить, проанализировать, сделать выводы, увеличивает процент наглядности, снимает стресс, т. к. ПК является для детей типичным носителем информации
Учителю компьютер — подсказчик, позволяющий четко реализовать замысел урока и соблюсти логику изложения материала, + иллюстратор+ аниматор => повышение уровня усвоения материала учащимися
Компьютер позволяет сделать урок динамичным, что способствует здоровьесбережению.
Программа наблюдения:
|
1. Организационный момент. |
+ использование презентации организовало учащихся, дало положительный настрой на урок |
|
2. Введение в тему |
+ с помощью представленных на экране заданий учителю удалось добиться того, чтобы учащиеся сформулировали тему урока |
|
3.Работа по группам ( поэтапное выполнение заданий) |
+закрепляют полученные знания +активизирует внимание + наличие индивидуальной и групповой работ |
|
|
+ расширение и углубление знаний по предмету +реализация межпредметных связей |
|
4.Чтение и маркировка текста |
+развитие оперативной памяти + умение работать в паре +развитие зрительной памяти |
|
5. |
+умение выбрать правильный ответ |
|
|
+закрепление полученных ранее знаний |
|
6.Дом. задание |
+быстрота выполнения задания + глубина знаний и умений +учащиеся приходят к выводу, как важно иметь прочные знания |
|
Рефлексия урока: отзыв об уроке |
Доволен ли ты как прошёл урок? Да — 100 % учащихся |
|
-было ли тебе интересно? |
Да — 95% |
|
-сумел ли ты закрепить свои знания? |
Да — 100% |
|
— сумел ли ты показать свои знания? |
Да — 90% |
Вывод: учителю в ходе всего урока удалось систематизировать знания учащихся, развивать практические умения и навыки, что говорит о его профессионализме и мастерстве.
Зубарева, Мордкович. Математика 5 класс. Репетитор о новом учебнике
Уже давно работаю с опорой на собственные методические наработки, однако репетитору по математике неизбежно приходится корректировать уроки с оглядкой на типовые программы, продиктованные школой. Вот и сейчас судьба свела с относительно новым комплектом учебников авторов Зубарева/Мордкович для 5-6 класса. Хочу поделиться своими впечатлениями и провести подробный анализ содержащего в них материала.
Репетитор об особенностях учебника по математике Зубарева/Мордкович
Любые книжки для начальной или средней школы должны рассматриваться исключительно комплектами, так как один и тот же набор тем разные авторы разбрасывают по разным классам. Например, как в нашем случае, что то вводится уже в 5 классе, а что то оставляется для 6-го. Поэтому речь пойдет в том числе и об учебнике Зубарева/Мордкович — 6 класс.
Дидактика
Долгие годы Мордковича относился к средней школе (7-9 класс) и его коньком являлась подборка задач. Она отличалась от других программ хорошим объемом и разнообразием упражнений. В ней можно было найти задачки для самых разных целей обучения, что несомненно помогало репетитору по математике в работе с разными учениками. В исследуемом программном комплекте эта традиция нарушилась. Возможно из за того, что коллектив авторов задумал соединить учебник с задачником, что соответственно наложило ограничения на дидактику и снизило ее качество. Однако подчерк Мордковича узнается. По прежнему репетитор найдет в нем отдельные полезные и интересные по формату и типу задания, правда их количество невелико.
Она отличалась от других программ хорошим объемом и разнообразием упражнений. В ней можно было найти задачки для самых разных целей обучения, что несомненно помогало репетитору по математике в работе с разными учениками. В исследуемом программном комплекте эта традиция нарушилась. Возможно из за того, что коллектив авторов задумал соединить учебник с задачником, что соответственно наложило ограничения на дидактику и снизило ее качество. Однако подчерк Мордковича узнается. По прежнему репетитор найдет в нем отдельные полезные и интересные по формату и типу задания, правда их количество невелико.
Методика учебника Мордковича
А вот здесь начинается. Первое что я всегда смотрю — оглавление. Кроме распространенных нестыковок (например в главе «Натуральные числа» присутствует геометрия) есть несколько лишних тем, которые явно не по возрасту: «серединный перпендикуляр», «свойство биссектрисы угла». Задач на отработку и закрепление практически никаких нет, а содержащиеся в параграфах геометрические сведения подаются в довольно сложной для ребенка форме. Авторы пытаются объяснять факты и учить строить выводы, при этом приближаясь к механике взрослых рассуждений с использованием терминологической основы старшей школы (что крайне нежелательно). Подобная акселерация банально отвлекает маленького ученика и его репетитора, мешая сконцентрироваться на формировании главных навыков для 5 класса (вычислительных и образных).
Авторы пытаются объяснять факты и учить строить выводы, при этом приближаясь к механике взрослых рассуждений с использованием терминологической основы старшей школы (что крайне нежелательно). Подобная акселерация банально отвлекает маленького ученика и его репетитора, мешая сконцентрироваться на формировании главных навыков для 5 класса (вычислительных и образных).
P.S. Как Вы думаете, уважаемые репетиторы и родители, пятиклассник разберется в подобном объяснении?
Математика вычислений
Главная роль учебников для 5 и 6 класса — научить работе с разными рациональными дробями в разных практических условиях. Мне не нравится половинчатый стиль изложения, когда тему проходят частично, то есть разбираются не все случаи и не все виды операций, а только какие то самые простые, а затем через некоторое время к этой теме возвращаются. Именно так излагается математика по Мордковичу для 5 класса. Например, в тему «сложение обыкновенных дробей» уже в 5 классе подмешиваются примеры на разные знаменатели (с объяснениями, рассчитанными на смекалку). Полноценный алгоритм приведения к общему знаменателю раскрывается только после отрицательных чисел аж во второй половине 6 класса. Соответствующих упражнений мало и они практически сразу смешиваются с «минусами». Такая же ерунда с темами «умножение и деление дробей на натуральное число». Если уж изучать эти действия, то полностью и с соответствующей базой упражнений.
Полноценный алгоритм приведения к общему знаменателю раскрывается только после отрицательных чисел аж во второй половине 6 класса. Соответствующих упражнений мало и они практически сразу смешиваются с «минусами». Такая же ерунда с темами «умножение и деление дробей на натуральное число». Если уж изучать эти действия, то полностью и с соответствующей базой упражнений.
Рваный характер учебного плана повышает вероятность упущения каких-нибудь важных навыков и является лишней помехой в работе репетиторов по математике. Я не нашел отдельной темы по округлению десятичных дробей, правила заключения в скобки (вынос общего множителя), а также изучения параллелепипеда и куб, хотя встретилась задачка с условием «ребро куба равно 5см…»
Качество объяснений
Про характер геометрических истолкований я уже писал выше. Если касаться главных программных тем, то с их качеством тоже не все хорошо. Частично объяснения (например, в теме «делимость») заимствованы у учебника «Математика, Петерсон, 5 класс», некоторые являются плагиатом программы Виленкина. Те, что сделаны самостоятельно довольно запутанные и неубедительные (в основном это касается 6 класса). Стоит отметить довольно сложный язык, которым написан учебник. Режет слух математика сочетание детского стиля в слове с взрослыми фразами типа «констатация факта», «конфигурация на рисунке» и подобные.
Те, что сделаны самостоятельно довольно запутанные и неубедительные (в основном это касается 6 класса). Стоит отметить довольно сложный язык, которым написан учебник. Режет слух математика сочетание детского стиля в слове с взрослыми фразами типа «констатация факта», «конфигурация на рисунке» и подобные.
Вывод: Попытка написать лучший учебник математики для 5 класса явно провалилась. Я бы поставит этот учебник после группы Виленкин, Петерсон, Мерзляк, Никольский.
С Уважением, репетитор по математике, Колпаков. А.Н Качественные занятия в Строгино.
Метки: Репетиторам по математике, Учебники
МО учителей математикик
МО учителей математики
Цель работы методического объединения:
Формирование инновационной среды школы для успешной реализации ФГОС по математике и информатики
Задачи методического объединения учителей:
1. Обеспечить информационно-методическое сопровождение реализации ФГОС.
Обеспечить информационно-методическое сопровождение реализации ФГОС.
2.Продолжить освоение и внедрение современных образовательных технологий, методов и приемов по формированию личностных, метапредметных результатов.
3.Совершенствовать качество современного урока; повышать его эффективность и направленность на сохранение здоровья учащихся.
4.Стимулировать активность педагогов, вовлекать их в инновационную, творческую, опытно-экспериментальную работу.
Состав методического объединения учителей:
Соболева Любовь Игнатьевна – учитель математики, председатель МО
Педагогический стаж – 33 годf
Категория: высшая квалификационная категория
Пройденные курсы: НИРО «Методика преподавания математики»
Тема по самообразованию:
Повышение эффективности подготовки к сдаче ЕГЭ через внедрение информационных технологий на уроках математики в старших классах
Николаева Татьяна Евгеньевна – учитель математики
Педагогический стаж – 28 лет
Категория: высшая квалификационная категория
Тема по самообразованию:
Применение технологий проектирования на уроках математики
Трапезникова Анна Федоровна – учитель математики
Стаж педагогической работы – 7 лет
Категория: первая квалификационная категория
Тема по самообразованию:
Повышение эффективности подготовки к сдаче ОГЭ через внедрение информационных технологий на уроках математики в 9 классах
Кучина Вера Евгеньевна -(1 категория)
Стаж педагогической работы – 11 лет
тема самооброзования «ИКТ технологии на уроках математики»
Соколова Ксения Сергеевна – учитель математики
Стаж педагогической работы – 2 года
Тема по самообразованию:
Решение нестандартных задач по алгебре
Мельникова Вера Николаевна
общий стаж работы: 42 года
педагогический стаж работы: 26 лет
Категория: первая
Курсы повышения квалификации:
2018 год ГБОУ ДПО НИРО «Теория и методика преподавания информатики в условияз ФГОС»
Зинченко Людмила Леонидовна
общий стаж работы: 33 года
педагогический стаж работы: 31 год
Категория: первая
2014 год ГБОУ ДПО НИРО «Современные информационные технологии в образовании в условиях введения ФГОС»
2016 год ГБОУ ДПО НИРО «Теория и методика преподавания информатики в условияз ФГОС»
2019-2020 учебный год
1) Всероссийская олимпиада школьников (сентябрь-октябрь).
2) Участие в олимпиадах по основам наук (в течение года).
3) Организация и проведение олимпиады «Олимпус» среди учащихся 5-8 классов (осенняя-зимняя сессия).
4) Подготовка обучающихся 9-11 классов к участию в НОУ.
5) Проведение учебных проектов в рамках уроков.
6) Педагогические мастер-классы .
7) Организация и проведение школьной «Недели наук».
Участие в сетевых Интернет проектах
1. Телекоммуникационной олимпиаде по математике при МФТИ в 2019-2020уч. г. Соболева Л.И.- 2 чел.
2. Авторский онлайн-курс: от проектирования до реализации на региональной платформе «Нижегородская дистанционная школа» Ермилова Е.Н.
3. Обобщение и распространение собственного педагогического опыта за 2019-2020 уч.г
Участие в вебинарах, семинарах
Методическое мероприятие (продолжительностью 6 часов) «Повышение качества математического образования: меняем традиционный подход к преподаванию математики в школе»;
· Вебинар (продолжительность 1 час) «Инструменты дизайн мышления в проектной деятельности для школьников»;
· Вебинар (продолжительность 1 час) «Проектная деятельность по математике»;
· Вебинар (продолжительность 1 час) «Финансовые задачи и методы их решения в курсе алгебры и начала анализа 10-11 классов;
· Вебинар (продолжительность 1 час) «Как учить в период каникул»;
· Дистанционное обучение по учебному курсу «Подготовка организаторов ППЭ»;
· Вебинар (продолжительность 2 час) Возможности ЭФУ «Алгебра 7. Углублённый уровень» А. Г. Мордковича, Н. П. Николаева при моделировании онлайн-уроков по алгебре.
Углублённый уровень» А. Г. Мордковича, Н. П. Николаева при моделировании онлайн-уроков по алгебре.
Публикации
на сайте «Инфоурок»:
· Конспект урока «Иррациональные уравнения»;
· Презентация к уроку «Вычитание рациональных чисел»;
· Конспект урока «Вычитание рациональных чисел»;
· Входной контроль по математике 6 класс;
· Научно исследовательская работа «Средние величины: их обоснование и применение»;
· Презентация «Средние величины: их обоснование и применение»;
· Конспект урока Первый признак равенства треугольников;
· Конспект урока Умножение дробей.
Участие в мероприятиях
Федеральный уровень
Всероссийский конкурс для педагогов «Лучшая методическая разработка» на международном интернет – портале. Кучина В.Е.– Диплом 1 место
Участие в тестировании «Я — учитель»
Обмен опытом с учителями по ДО на платформе 1С
Открытый урок «Проектория», проведено 2 урока Зинченко Л. Л.
Л.
Региональный уровень
Участие в Региональной конференции Учи.ру май Мельникова В.Н.
Районный уровень
Участие в качестве экспертов в районном НОУ(Мельникова В.Н.)
Участие в качестве экспертов районная олимпиада по информатике (ЗинченкоЛ.Л., Соболева Л.И.)
Школьный уровень
— Открытки для школьной газеты «Шанс» к Новому году, 8 марта, День победы
Готовимся к итоговой аттестации по информатике
Рекомендации по подготовке к ЕГЭ по информатике
Что нужно знать о ЕГЭ по информатике
Открытый банк заданий ОГЭ — 9 по информатике
Открытый банк заданий ГИА-11 по информатике
График консультаций подготовки к итоговой аттестации в 9,11 классах
| Класс | Предмет | Учитель | Время консультаций |
| 11а, 11б | информатика | Л. Л. Зинченко, ВН. Мельникова Л. Зинченко, ВН. Мельникова | понедельник 14:15-15:00 |
| 9б,9в | информатика | Л.Л. Зинченко | вторник 14:15-15:00 |
| 9а,9б,9в | информатика | В.Н. Мельникова | понедельник 14:15-15:00 |
Мероприятия, проводимые МО:
- Организация и проведение школьных олимпиад;
- Организация научно-исследовательской работы;
- Участие в различных Интернет-олимпиадах, конкурсах, КВН, читательских конференциях;
- Реализация учебных проектов по предмету;
- Организация и проведение школьных предметных недель;
- Индивидуальная работа с учащимися при подготовке к ГИА в 9, 11 классах;
- Осуществление программы развития формирования УУД в рамках ФГОС.
Дидактические материалы по математике 5-11 классы
Участие в олимпиадах и конкурсах:
2018-2019 учебный год
Международный уровень
Международная онлайн-олимпиада «Фоксфорда» сезон XI по информатике
Международная олимпиада по основам наук по математике, информатике.
Результаты 1 тура по математике
Результаты 1 тура по информатике
III Международный открытый конкурс сайтов образовательных учреждений
Школьный уровень
Выставка работ учащихся «Безопасный интернет детям» 5-6-7 классы
Участие во Всемирном Дне библиотек — 10 б класс
Путеводитель по электронным библиотекам
Участие в мероприятиях, посвящённых юбилею И.С. Тургенева
Сайт «Виртуальные прогулки по Тургеневским местам — 11 б класс
2017-2018 учебный год
Региональный конкурс, посвящённый 100-летию заповедной системы России
Работа победителей:
Пифагорка — Ментальная арифметика Мытищи, счеты Соробан, Абакус. Центр развития интеллекта в Мытищах (Московская область) — отзывы, курсы, занятия
Счеты Соробан
Любой родитель хочет видеть своего ребенка счастливым, успешным и самостоятельным
Как это сделать? Где этому учат? Может ли обычный детский сад, школа обеспечить все это?
Мы предлагаем дать шанс самому ребенку!
В основе занятий по ментальной арифметике в г. Мытищи — японская система развития интеллектуальных способностей при помощи счет соробан (абакус).
Мытищи — японская система развития интеллектуальных способностей при помощи счет соробан (абакус).
15 минут ежедневных занятий ментальной арифметикой на счетах соробан помогают заложить новые нейронные связи, развить самостоятельность, способность к принятию решений, внимательность, фотографическую память, а отсюда и дальнейшие успехи в учебе, спорте, работе и жизни.
Вам, наверное, встречалась такая статистика — только 5% людей достигают значительных успехов в жизни. Остальные 95% лишь мечтают об этом, но их мечты почему-то не сбываются.
Всего один навык, полученный до 12 лет, способен изменить будущее вашего ребенка
Почему так происходит, и можем ли мы изменить эту статистику для наших детей?
Наукой доказано: способность к успеху зависит от гармоничного развития правого и левого полушарий мозга. К сожалению, у большей части населения земного шара развитие левого полушария значительно преобладает над правым. Иными словами, логическое мышление развито хорошо. Зато творческое мышление — интуиция, выбор правильных путей и поступков — работает из рук вон плохо.
Иными словами, логическое мышление развито хорошо. Зато творческое мышление — интуиция, выбор правильных путей и поступков — работает из рук вон плохо.
Получается, что если нам с вами развить правое полушарие до уровня левого, то мы обретем способность к успеху?
В какой-то степени — да. Но гораздо более серьезных результатов достигнет здесь не взрослый, а ребенок 5-12 лет. Именно в этом возрасте мозг наиболее пластичен. Поэтому наша методика разработана специально для детей.
Что такое Ментальная арифметика?
Ментальная арифметика высокоэффективная программа развития умственных способностей при помощи арифметических вычислений на счетах (абакус, соробан), так называемый быстрый счет:
подходит для детей от 4 до 16 лет;
развивает самостоятельность, инициативность, умение критически оценивать себя;
работает уже в 52 странах мира (США, Канада, Великобритания, Австрия, Испания, Австралия, Япония, Малайзия, Таиланд, Китай и др.
 ).
).
Счеты называют «древним калькулятором» — их придумали наши предки еще 2500 лет назад. Почему же сегодня эта система вычислений вновь стала популярной?
В отличие от обычной арифметики упражнения на счетах задействуют оба полушария головного мозга. Причем, их развитие происходит согласованно и гармонично.
Как это происходит?
Развитие левого полушария:
- стимуляция мелкой моторики;
- наглядное представление результата арифметических действий.
Развитие правого полушария:
- использование в равной степени правой и левой руки;
- работа в уме с воображаемыми счетами.
«Побочный эффект» методики — быстрый счет в уме
Приведем такой пример: в Японии дети в обязательном порядке изучают соробан (японские счеты) в младших классах. Такой подход к образованию уже дал результаты. Японские школьники из года в год побеждают на международных математических олимпиадах, что стало даже традицией.
Такой подход к образованию уже дал результаты. Японские школьники из года в год побеждают на международных математических олимпиадах, что стало даже традицией.
В Китае решать задачи с трехзначными числами дети умеют уже в детском саду. Взгляните сами — кажется невероятным, но это факт:
Однако смысл Ментальной арифметики вовсе не в навыке считать в уме. Это всего лишь полезный побочный эффект. А сами счеты абакус — не «калькулятор» и даже не математический тренажер.
Ментальная арифметика развивает способность к успеху в любом деле
Занятия Ментальной арифметикой помогают натренировать нейронные связи головного мозга вашего ребенка, развивают скорость и качество его мышления. Это можно сравнить со спортивными тренировками.
Представьте, что вдруг…
Вы оказались среди участников Чемпионата мира по велоспорту. Вот-вот раздастся сигнал старта, а вы в последний раз гоняли на велике в 5-м классе. Есть ли у вас шансы среди спортсменов, тренировавших этот навык несколько лет?
Есть ли у вас шансы среди спортсменов, тренировавших этот навык несколько лет?
Так же и с интеллектом. Проверено: с любыми задачами в учебе, карьере, увлечениях и т.п. тренированный мозг справляется легче и быстрее, чем нетренированный.
Продолжим спортивную аналогию. Чтобы стать олимпийским чемпионом, спортом нужно заниматься с детства. Точно так же и с Ментальной арифметикой и счетами соробан. По заявлению китайских и японских педагогов, если упражняться на счетах одновременно начнут взрослый и ребенок — взрослый не достигнет тех же результатов, что и ребенок. Именно потому важно начать тренировать мозг вовремя.
Что дает вашему ребенку освоение Ментальной арифметики (по отзывам наших родителей)
Программа рассчитана на 2 года, но первые результаты родители обычно замечают уже через 3-4 месяца.
Рост успеваемости в школе (даже в музыкальной)
Математика
Уже после 2-х месяцев обучения оценки по математике у сына заметно улучшились.Однажды мы с мужем на кухне считали вслух какие-то трёхзначные числа, а Кирилл вдруг моментально дал ответ без калькулятора!
Волкова Екатерина Владимировна
Математика и чтение
Никита стал намного лучше считать и читать. Мы видим, что этот уровень выше, чем у сверстников-первоклассников
Лаушкин Олег Александрович
Все предметы
К сожалению, мы занимались только 1 раз в неделю. Но успеваемость уже улучшилась по всем предметам. Этот учебный год мы закончили без троек!
Маринина Елена Анатольевна
Музыка
Мы ещё занимаемся по классу фортепиано (а это мелкая моторика), и Артём стал одинаково успешно играть как левой, так и правой рукой!
Лячина Ирина
Самостоятельность и уверенность в себе
Катя стала собранной и уверенной в себе, говорит: «Я всё равно это сделаю!».
Стала такой самостоятельной, что я могу спокойно доверить ей выполнение сложного школьного задания без моего участия.
Маринина Елена Анатольевна
Ребёнка хвалят, плечи расправились, самооценка поднялась.
Борисова Ольга
Мой сын посещает занятия 3 месяца, поэтому о каких-то глобальных изменениях говорить пока рано. Но то, что он теперь самостоятельно выполняет домашнее задание, это точно.
Лячина Ирина
Победы в конкурсах и олимпиадах (не только математических)
А ещё Макар выиграл Олимпиаду по математике в школе…
Костина Дина Борисовна
Учебный год с Ментальной арифметикой стал для нас особенно успешным. Мой сын Сергей занял призовые места в городском конкурсе научных проектов и конкурсе «Ученик Года»
Пронина Мария Сергеевна
Как проходят занятия по ментальной арифметике в городе Мытищи?
Ваш ребенок тренирует навыки работы со счетами постепенно, с переходом от простого к сложному. Занятия проходят 2 раза в неделю по 1 часу плюс домашние занятия по 15 минут в день. В итоге к концу программы ваш ребенок уже свободно складывает, вычитает, умножает и делит в уме двух-,и даже трехзначные числа.
Занятия проходят 2 раза в неделю по 1 часу плюс домашние занятия по 15 минут в день. В итоге к концу программы ваш ребенок уже свободно складывает, вычитает, умножает и делит в уме двух-,и даже трехзначные числа.
Но вот вопрос: может ли нормальный ребенок прилежно заниматься одним и тем же целый час? Конечно, нет! И поэтому мы придумали вот что…
Особая программа Ментальной арифметики от «Пифагорки»
Традиция упражнений со счетами пришла к нам из Азии, где дети гораздо послушнее, а авторитет старших непререкаем. Там нет понятия «скучно на уроке», зато есть строгая дисциплина. Иное дело — наши дети. Практика показывает, что длительные тренировки на счетах даются им с трудом, возникает утомление и потеря интереса.
Поэтому мы чередуем занятия на счетах играми, заданиями на развитие памяти и внимания, упражнениями для глаз и осанки. Получается двойная польза!
Но и это еще не все.
Обучение Ментальной арифметике часто предлагают по аналогии со школьными уроками — в группах, по общему плану. При этом совершенно не учитываются индивидуальные (генетические) особенности ребенка. Например, один успеет за занятие прорешать 3 страницы учебника, а другой всего 1 или даже половину. Все дети разные, у каждого своя скорость.
При этом совершенно не учитываются индивидуальные (генетические) особенности ребенка. Например, один успеет за занятие прорешать 3 страницы учебника, а другой всего 1 или даже половину. Все дети разные, у каждого своя скорость.
У нас дети тоже занимаются в группах. Но при этом задания даются каждому ребенку индивидуально, с учетом его возможностей. Поэтому у нас весело, интересно и результативно!
В отличие от курсов английского, сын ни разу не сказал про ментальную арифметику: «Мама, а может, не пойдём?». Нас впечатлили результаты, поэтому мы планируем шестилетнюю дочку также записать на этот курс. (Пронина Мария Сергеевна).
Почему ментальную арифметику лучше всего изучать именно в «Пифагорке»?
Вот какие результаты показывают ученики ЦРИ «Пифагорка» в городе Мытищи:
С вашим ребенком занимаются:
педагоги и психологи с опытом работы с детьми в детском саду и школе;
преподаватели высшей категории;
победители областных и всероссийских конкурсов педагогического мастерства.

Все наши педагоги прошли обучение технологии «Ментальная арифметика» в Центрах повышения квалификации.
Приглашаем на обучение успеху!
Не упустите время. Помните — для достижения максимального результата начинать занятия Ментальной арифметикой нужно уже сегодня!
Уникальные результаты по ментальной арифметике в «Пифагорке»
Воспитанница ЦРИ «Пифагорка» (Санкт-Петербург) Виктория Алиева показала удивительные математические способности на ТВ шоу «Удивительные люди».
Остались еще вопросы? Добро пожаловать в раздел Вопросы и ответы по ментальной арифметике.
Также вы можете ознакомиться со статьями по ментальной арифметике.
Учебная программа по математике для 5-х классов — Общие основные уроки и тесты
Что такое математика для 5-х классов?
5 класс фокусируется на трех ключевых достижениях предыдущих лет: (1) развитие беглости с помощью сложения и вычитания дробей и развитие понимания умножения и деления дробей в определенных случаях; (2) интеграция десятичных дробей в систему значений разрядов и развитие свободного владения операциями с целыми числами и десятичными дробями с точностью до сотых; и (3) развитие понимания объема.
Как мы заказывали блоки?
В 4 классе ученики узнали, что в целых числах цифра в одном месте в десять раз больше, чем в месте справа. В 5 классе , блок 1, «Разрядная дробь », учащиеся расширяют это понимание двумя способами. Во-первых, они видят, что похожий образец проявляется с разрядами слева от цифры; а именно они составляют 1/10 стоимости. Во-вторых, учащиеся расширяют это понимание цифры и знаков слева и справа до десятичных чисел.
В блоке 2 «Умножение и деление целых чисел » учащиеся развивают свою работу в 4-м классе, чтобы овладеть свободным владением четырехзначным на двузначное и трехзначным на трехзначное умножение, а также расширить свои знания. понимание деления от однозначных делителей в 4 классе до двузначных делителей в 5 классе.
В блоке 3 , «Фигуры» и «Том » учащиеся изучают двумерные формы, классифицируя их в иерархии в соответствии с их свойствами.Студенты также исследуют трехмерные формы, заполняя прямоугольные призмы единичными кубами, чтобы найти их объем. Затем, видя многослойный характер объема и его связь с формулой для площади прямоугольника, учащиеся применяют недавно приобретенную беглость речи с помощью многозначного умножения, чтобы вычислить объем прямоугольной призмы, и они используют беглость 4-го класса с добавлением найти область составных трехмерных форм.
Затем, видя многослойный характер объема и его связь с формулой для площади прямоугольника, учащиеся применяют недавно приобретенную беглость речи с помощью многозначного умножения, чтобы вычислить объем прямоугольной призмы, и они используют беглость 4-го класса с добавлением найти область составных трехмерных форм.
В блоке 4 «Сложение и вычитание дробей и десятичных знаков » учащиеся обобщают свое понимание сложения и вычитания, которое возможно только при работе с одинаковыми единицами, в контексте дробей и десятичных знаков.Поскольку нужно складывать одинаковые единицы, учащиеся видят, что, прежде чем они смогут вычислить, им может потребоваться найти эквивалентные дроби или быть осторожными, чтобы выровнять единицы (что, в свою очередь, означает выравнивание десятичной точки).
В блоке 5 , Умножение и деление дробей учащиеся развивают более тонкое представление о том, что такое умножение и деление в контексте дробей, и применяют это понимание к новым случаям этих операций, включая умножение дроби на дробь. дробь, деление двух целых чисел, чтобы получить дробь в качестве ответа, и деление единичной дроби на целое число и наоборот.Обладая глубоким пониманием этих операций с дробями, учащиеся выполняют их с десятичными знаками в блоке 6 , умножение и деление десятичных знаков , придавая смысл своим ответам в контексте их понимания разрядов.
дробь, деление двух целых чисел, чтобы получить дробь в качестве ответа, и деление единичной дроби на целое число и наоборот.Обладая глубоким пониманием этих операций с дробями, учащиеся выполняют их с десятичными знаками в блоке 6 , умножение и деление десятичных знаков , придавая смысл своим ответам в контексте их понимания разрядов.
Курс заканчивается блоком 7 , Паттерны и Координатная плоскость , в котором студенты исследуют два числовых паттерна и их взаимосвязь друг с другом. Координатная плоскость помогает визуализировать эти шаблоны, а также другие математические контексты.Это является прекрасным завершением года, намекая на некоторые концепции, которые будут развиваться дальше в средних классах, такие как двумерные данные, соотношения и пропорции.
МАТЕМАТИКА G5: 5 класс по математике
Описание
Пятый класс по математике — около
— Развитие навыков сложения и вычитания дробей, а также развитие понимания умножения дробей и деления дробей в ограниченных случаях (единичные дроби, деленные на целые числа, и целые числа, деленные на единичные дроби)
— Расширение деления на двузначные делители, интеграция десятичных дробей в систему значений разрядов и развитие понимания операций с десятичными дробями до сотых, а также развитие беглости работы с целыми числами и десятичными операциями
— Развитие понимания объема.
О загружаемых ресурсах
История модулей: карта учебной программы и обзор для классов P-5 : дает учителям четкое представление о модулях на каждом уровне от подготовительного до 5-го класса.
Как реализовать рассказ о модулях : предоставляет дополнительную информацию о том, как учителя могут реализовать этот учебный план в своих классах. Он знакомит учителей с «Историей единиц» и описывает общий базовый подход к математике, оцениванию, дифференцированному обучению и математическим моделям.Также подробно описана структура урока, используемая в «Истории единиц», которая включает в себя все три аспекта строгости.
Контрольный список CCLS для истории об учебных модулях : включает диаграммы уровня обучения, позволяющие быстро определить, когда каждый стандарт рассматривается. Обратите внимание, что для классов K – 5 стандарты, включенные в кластеры, обозначенные Департаментом образования штата Нью-Йорк как «Основные акценты», отмечены звездочкой (*).
Scaffolding Instruction for ELLs: Resource Guide for Mathematics : предоставить педагогам руководство по использованию материалов учебной программы на EngageNY и предоставить дополнительные строительные леса для студентов ELL в соответствии с их уровнем владения английским языком.
Загрузки
Могут быть случаи, когда наши загружаемые ресурсы содержат гиперссылки на другие сайты. Эти гиперссылки ведут на веб-сайты, опубликованные или управляемые третьими сторонами. UnboundEd и EngageNY не несут ответственности за содержание, доступность или политику конфиденциальности этих веб-сайтов.
Теги
- Нет тегов для этого ресурса
Кредиты
от EngageNY.org Департамента образования штата Нью-Йорк. 5 класс по математике.
Доступно на сайте engageny.org/resource/grade-5-mat Mathematics; по состоянию на 29 мая 2015 г.
Авторские права © 2015 Great Minds. UnboundEd не связан с правообладателем этой работы.
Рабочие листы по математике для пятого класса (5-й класс): Noetic Learning
Для пятого класса (5-й класс) Задания по математике: Noetic Learning
|
| ||||||||||||||||
52
Авторское право Noetic Learning LLC
Учитель 5-го класса использует игру «Среди нас» для виртуального обучения математике во время пандемии COVID-19.
Учитель 5-го класса из Гамильтона использует вирусную онлайн-игру, чтобы помочь своим ученикам выучить математику.
Эмма Финлейсон, которая работает в школьном совете округа Гамильтон-Вентворт (HWDSB), начала свою первую преподавательскую работу на полную ставку в сентябре с классом из 32 учеников, обучающихся дистанционно.
Финлейсон сказала, что в последний день учебы перед зимними каникулами ее ученики были разделены на группы. Одна группа решила сыграть в популярную многопользовательскую онлайн-игру « среди нас», «» вместо того, чтобы следовать плану урока.
«Я никогда не играл в нее раньше и слышал об этом, поэтому я вошел и сказал им остановиться, и они сказали:« О нет, пожалуйста, это действительно весело », а я такой:« Ребята, я » Я никогда раньше не играла в нее, не могу сказать, подходит ли она для школы », — сказала она.
«Я пошел домой, скачал игру, поиграл, и это весело».
ОГРОМНЫЙ успех в понедельник утром! В 5N мы играли в математическую игру «Среди нас». Студенты вместе выбирали «самозванца» в каждом наборе выражений. Если кому-то нужна копия моего слайд-шоу, я хотел бы поделиться 😀 @HWDSB @HWDSBmath # remotelearning #sus pic.twitter.com/dL1qOr6Q1j
Если кому-то нужна копия моего слайд-шоу, я хотел бы поделиться 😀 @HWDSB @HWDSBmath # remotelearning #sus pic.twitter.com/dL1qOr6Q1j
& mdash; @miss_efinlaysonВ красочной аркадной игре группа до 10 игроков должна выполнить задания на космическом корабле, чтобы вернуться на Землю, но некоторые из них — самозванцы, которые должны убить других и остаться незамеченными.
Хотя Финлейсон не думала, что Среди нас в его нынешней форме подходит для школы, она хотела найти способ включить игру, которой она и ее класс «одержимы», в свое обучение.
Когда ученики собирались вернуться в свою виртуальную школу 4 января, она планировала контрольные упражнения для класса.
«Я задам им вопрос и спрошу:« Вам это нравится? » и это явно неправильно, и они должны попытаться объяснить свои ответы … и я просто подумал о среди нас … и я просто подумал, почему бы мне не поместить вопросы на страницу и не выяснить, кто из них самозванец? » сказал 27-летний учитель в понедельник после того, как представил упражнение в классе.10 вопросы, на один или два из которых есть неправильные ответы. Студенты в одной большой группе должны использовать функцию чата программы, чтобы примерно за одну минуту выяснить, какой ответ неверен. Затем один из учеников обсуждает ответ с учителем.
«Они хотели сыграть снова, поэтому я думаю, что мне придется сделать несколько разных копий этого», — сказал Финлейсон.
«Это была одна из тех сумасшедших вещей, которые я придумал в воскресенье вечером».
ЧАСЫ | Что такое среди нас и насколько это популярно?
Она говорит, что студенты использовали калькуляторы и критическое мышление, чтобы получить ответы. По словам Финлейсона, обсуждение после каждого раунда вопросов также оказалось эффективным, поскольку помогло студентам с разными способностями к обучению понять, почему тот или иной ответ был самозванцем.
По словам Финлейсона, обсуждение после каждого раунда вопросов также оказалось эффективным, поскольку помогло студентам с разными способностями к обучению понять, почему тот или иной ответ был самозванцем.
Финлейсон также заметил, что, как и в реальной онлайн-игре, некоторые ученики меняли свои ответы в зависимости от того, что сказали другие (даже если их первоначальная догадка была правильной).
«Было интересно посмотреть:« Собираюсь ли я взять ответы от группы или я выберу тот, который, как я знаю, правильный? » » она сказала.
Finalyson с тех пор разместила в Твиттере свою презентацию для использования другими преподавателями.
Билл Торренс, руководитель программ HWDSB, сказал, что это знак того, что даже при дистанционном обучении студенты получают необходимые им знания.
«Мы гордимся всеми нашими преподавателями, которые находят инновационные способы взаимодействия со студентами в нашей программе дистанционного обучения», — сказал он.
«Потребности наших студентов удовлетворяются благодаря исключительному преподаванию, которое демонстрируют наши преподаватели».
Вниманию родителей, учеников и учителей: мы хотим услышать от вас!
Мы надеемся, что вы воспользуетесь этой формой, чтобы рассказать нам об условиях в школе, о том, как проходят занятия или о любых других неотложных проблемах, которые у вас на уме в Гамильтоне, Ниагара, Санкт-Петербург.Катаринс и Берлингтон.
Цели изучения математики в 5-м классе
Математика, 5
(OAT) ALT 1 — Числовые выражения
Я умею писать и интерпретировать числовые выражения.
AST 1.1 — Использовать порядок операций : Я могу использовать порядок операций для решения проблем. OA.1
AST 1.2 Числовые выражения : Я могу писать числовые выражения, описанные в задачах со словами, которые могут включать круглые, квадратные и / или фигурные скобки.OA.1 и 2
AST 1.3 — Интерпретация значения числовых выражений : Я могу интерпретировать значение числового выражения, не решая его. OA.2
OA.2
(OAT) ALT 2 — точки графика на координатной плоскости
Я могу анализировать закономерности, взаимосвязи и точки графика на координатной плоскости для решения проблем.
AST 2.1 — 2 числовых паттерна : Я могу создать два числовых паттерна по двум правилам.
AST 2.2 — Связь между шаблонами : Я могу описать отношения между двумя шаблонами.OA.3
AST 2.3 — Формирование упорядоченных пар : Я могу формировать упорядоченные пары из числового шаблона. OA.3
AST 2.4 — Координатная плоскость : я могу разместить пары координат на координатной плоскости в первом квадранте (только положительные числа). G.1-2
AST 2.5 — Графические данные : Я могу решать реальные и математические задачи путем построения графиков данных и интерпретации значений в контексте ситуации. G.2
(NOTB) ALT 3 — разрядная система
Я понимаю систему ценностей.
AST 3.1 — Цифры и 10-кратное значение : Я могу распознать, что в многозначном числе цифра в одном месте представляет в 10 раз больше, чем в месте справа. NBT.1
AST 3.2 — Разрядное значение : Я могу распознать, что в многозначном числе цифра в одном месте представляет 1/10 того, что она представляет в месте слева от него. NBT.1
AST 3.3 — Шаблоны в количестве нулей : Я могу описать шаблоны в количестве нулей в произведении при умножении числа на 10.NBT.2
AST 3.4 — Шаблон описания : Я могу описать шаблон между показателем степени и размещением десятичной дроби при умножении и делении числа на степень 10. NBT.2
AST 3.5 — десятичные дроби с точностью до тысячных долей : Я могу читать и записывать десятичные дроби с точностью до тысячных долей. NBT.3
AST 3.6 — Расширенная форма : Я могу написать и объяснить, что каждая цифра представляет в развернутой форме. NBT.3a
NBT.3a
АСТ 3.7 — Сравните десятичные дроби с разрядами 1000 : Я могу сравнить десятичные дроби с разрядами тысячных. NBT.3b
AST 3.8 — Округление десятичных знаков в любое место : Я могу продемонстрировать свое понимание разряда для округления десятичных знаков в любом месте. NBT.4
AST 3.9 — Преобразование метрических единиц измерения : Я могу преобразовывать метрические единицы измерения разных размеров, используя систему десятичной системы. MD.1
(NOTB) ALT 4 — Выполнение операций
Я умею быстро решать задачи с многозначными целыми числами.
AST 4.1 — Умножение-деление целых чисел : Я могу плавно умножать многозначные целые числа, используя стандартный алгоритм. NBT.5
AST 4.2 — Задачи деления целых чисел : Я могу решать задачи деления целых чисел (до четырехзначных дивидендов и двузначных делителей), используя различные стратегии, такие как: разметка, свойства операций и / или модели площади. NBT.6
NBT.6
AST 4.3 — Взаимосвязь между умножением и делением : Я могу показать взаимосвязь между умножением и делением для решения и объяснения задач деления.NBT.6
(NOTB) ALT 5 — десятичные и сотые знаки
Я умею быстро решать задачи с десятичными знаками с точностью до сотых.
AST 5.1 — Разработка оценки : Я могу разработать оценку, когда мне задают задачу, в которой мне нужно складывать, вычитать, умножать и делить десятичные дроби, чтобы помочь мне приблизиться к ответу. NBT.7
AST 5.2 — Визуальные модели для Add-Sub : я могу создать модель (примеры: сетка, блоки с базой 10, числовая линия, деньги и счетчик), чтобы визуально показать сложение, вычитание, умножение и деление десятичных знаков с точностью до сотых.NBT.7
AST 5.3 — Объяснение стратегии : Я могу написать объяснение стратегии, которую я использовал (для сложения, вычитания, умножения или деления десятичных знаков), и предоставить обоснование ответа на основе используемой модели. NBT.7
NBT.7
AST 5.4 — Преобразование метрических единиц разного размера : Я могу продемонстрировать, как преобразовывать метрические единицы измерения разного размера, используя умножение и деление десятичных знаков. MD.1
(NOF) ALT 6 — Сложение, вычитание дробей
Я могу плавно складывать и вычитать дроби.
AST 6.1 — сложение дробей и вычитание : Я могу найти подобные знаменатели для сложения и вычитания дробей. NF.1
AST 6.2 — Визуальные модели : Я могу создавать и использовать визуальные модели для представления сложения и вычитания дробей. NF.2
AST 6.3 — Определение чисел, контрольные дроби : Я могу использовать числовые и контрольные дроби для оценки сумм и разностей дробей. NF.2
AST 6.4 — Использовать оценки : Я могу использовать свои оценки, чтобы решить, являются ли мои ответы разумными.NF.2
AST 6.5 — Линейный график : я могу построить линейный график для отображения набора данных, включающих доли единицы (1/2, ¼, 1/8). MD.2
MD.2
AST 6.6 — Добавить данные — Вычислить итог : Я могу сложить все данные вместе, чтобы вычислить итог. MD.2
(NOF) ALT 7 — Умножение, деление дробей
Я умею умножать и делить дроби (единичная дробь, деленная на целые числа, и целые числа, деленные на единичные дроби).
АСТ 7.1 — Интерпретация дроби : я могу интерпретировать дробь как результат деления числителя на знаменатель. NF.3
AST 7.2 — Решение задач истории : Я могу решать задачи истории для деления целых чисел на целые числа, которые дают дробные и смешанные частные числа. NF.3
AST 7.3 — Использование визуальных моделей : Я могу использовать визуальные модели, чтобы объяснить умножение на дробь как определение части другого числа. NF.4a
АСТ 7.4 — Выровнять по ширине : я могу обосновать, что площадь прямоугольника с дробными длинами сторон можно найти, умножив длину на ширину. NF.4b
NF.4b
AST 7.5 — Mult Fraction Меньше чем! : Я могу объяснить, почему умножение на дробь меньше 1 дает меньшее число. NF.5
АСТ 7.6. — Создавайте, решайте проблемы реального мира : я могу создавать и решать проблемы реального мира, включая умножение дробей, смешанных чисел и целых чисел.NF.6
AST 7.7 — Единица деления дроби : Я могу решить реальные задачи по делению дроби единицы (, ⅕, ⅙, ⅛ и т. Д.) На целое число и использовать визуальную модель, чтобы показать частное. NF.7a и c
AST 7.8 — Разделение целого числа на единичную дробь : Я могу решить реальные задачи по делению целого числа на единичную дробь (⅓, ⅕, ⅙, ⅛ и т. Д.) И использовать визуальную модель, чтобы показать частное. NF.7b и c
AST 7.9 — Взаимосвязь между разд.и Multip. : Я могу использовать взаимосвязь между делением и умножением, чтобы оправдать свои ответы на задачи деления, связанные с единичными дробями. NF.7a и b
NF.7a и b
(MD) ALT 8 — Концепции тома
Я понимаю и применяю концепции объема.
AST 8.1 — Единичный куб : Я могу определить «единичный куб» и использовать его как инструмент для измерения объема. MD.3a
AST 8.2 -Define Volume : Я могу определить объем как твердую фигуру, заполненную без промежутков.MD.3b
AST 8.3 — Определение объема : Я могу определить объем объекта, используя кубические единицы, кубические дюймы, кубические сантиметры, кубические футы. MD.4
AST 8.4 — Определение объема правого прямоугольника. Призма : я могу определить объем правой прямоугольной призмы, упаковав ее единичными кубами. MD.5a
AST 8.5 — Применить формулу V = l x w x h : Я могу применить формулу V = l x w x h к прямоугольным призмам, чтобы найти объем. MD.5б
AST 8.6 — Решение нерегулярной трехмерной призмы : я могу решать нерегулярные трехмерные объекты, разделяя их на отдельные части, которые являются правильными прямоугольными призмами, находить каждый из их объемов и складывать результаты вместе. MD.5c
MD.5c
(GEO) ALT 9 — Двумерные фигуры
Я могу классифицировать двухмерные фигуры по категориям в зависимости от их свойств.
AST 9.1 — Список атрибутов : я могу перечислить атрибуты (свойства) данного двумерного многоугольника.G.3
AST 9.2 — Категоризация полигонов : я могу классифицировать полигоны на основе их атрибутов. G.3 и 4
AST 9.3 — Создание иерархии : я могу создать иерархию на основе свойства двумерных фигур. G.3 и 4
MP 1 — Обретение смысла
Разбирайтесь в проблемах и настойчиво их решайте.
MP 2 — Причина абстрактно
Размышляйте абстрактно и количественно.
MP 3 — Конструировать аргументы
Создавайте жизнеспособные аргументы и критикуйте рассуждения других.
MP 4 — Модель с математикой
Модель с математикой.
MP 5 — Используйте инструменты
Используйте соответствующие инструменты стратегически.
MP 6 — точность
Будьте внимательны.
MP 7 — Конструкция
Ищите и используйте структуру.
МП 8 — Повторное рассуждение
Ищите и выражайте закономерность в повторении рассуждений.
математических игр для детей 5-х классов в App Store
Мы делаем математику увлекательной и увлекательной.Более 30 миллионов детей используют программу Splash Math, чтобы повысить уверенность в себе, увеличить результаты и добиться прогресса в математике.
Splash Math — это комплексная математическая программа, согласованная с учебным планом, которая усиливает математические концепции с помощью самостоятельной и адаптивной практики.
*** Награды и признание за серию Splash Math *** Программа
Splash Math в настоящее время используется более чем 30 миллионами детей и получила несколько престижных наград.
• Победитель «Gold Stevie Award» (2013) в категории «Образование и рекомендации»
• Победитель «Tabby Awards» (2012) в категории «Лучшее приложение для образования и обучения»
• Победитель «Лучшего приложения для учащихся начальной школы» ( 2011) пользователя BestAppEver. com
com
• В списках Apple — «Любимые сотрудники», «Новые и заслуживающие освещения в печати»
*** Обзоры ***
«Математика для 5-х классов: Общие основные рабочие листы по математике всплеска» — это ресурс с богатым содержанием, наполненный интерактивными рабочими таблицами и несколько аркадных игр. Дети могут использовать приложение, чтобы практиковать навыки, зарабатывая призы, чтобы разблокировать игры «. — Common Sense Media
«Это приложение предоставляет уроки, игры и викторины практически по всем аспектам математики 5-го класса. Дизайн более удобный и продуманный, чем у других виртуальных рабочих тетрадей, которые вы можете загрузить на iPad.»- AppoLearning
» Математика для 5-го класса: Splash Math Worksheets — безусловно, самая полная учебная тетрадь по математике в магазине приложений. Благодаря великолепному интерфейсу и уникальной функции скретчборда это одно из лучших образовательных приложений. «- Famigo
*** Информация о программе ***
Охват содержания: 41+ математических концепций (5 класс)
Учебный план: Common Core State Стандарты
Доступ: iPad, iPhone, настольные компьютеры и ноутбуки
*** Ключевые особенности Splash Math Grade 5 ***
+ Программа самостоятельной математической практики
+ Объяснение неправильных ответов
+ Блокнот для черновой работы
+ Виртуальные награды и игры
+ Отслеживайте прогресс с помощью панели управления прогрессом в реальном времени.
+ Прогресс синхронизируется на нескольких iPad, настольных компьютерах и ноутбуках.
+ HD-графика и звуковые эффекты для потрясающего игрового процесса.
*** ОБЩИЕ ТЕМЫ ***
StudyPad содержит лучшие математические приложения, соответствующие общим основным стандартам, с практически бесконечным количеством вопросов. Это приложение охватывает следующие темы:
1. Разрядное значение — Обобщение понимания разряда с десятичными до тысячных разрядов
2. Чувство числа — Сравнение, порядок и округление десятичных чисел
3. Алгебра — Написание и вычисление числовых выражений, работа с числами Выкройки
4.Умножение — плавно умножайте до трехзначных чисел на двухзначные числа
5. Деление — делите на двузначные числа
6. Дроби — сложение, вычитание и умножение в отличие от дробей, деление с использованием дроби и целого числа
7. Десятичная арифметика — Сложение, вычитание, умножение и деление десятичных дробей с точностью до сотых.
8. Измерения — преобразование величин из одной единицы измерения в другую в рамках той же системы измерения.
Измерения — преобразование величин из одной единицы измерения в другую в рамках той же системы измерения.
9.Геометрия — Координатные плоскости и графики, иерархическая классификация форм, объемов твердых тел
*** Планы подписки ***
• Планы: 29,99 долл. США в квартал или 59,99 долл. США в год
• Бесплатная пробная версия: мы предлагаем бесплатный пробный период, прежде всего планы.
• Отменить в любое время: плата не взимается, если план отменен до окончания пробного периода.
• Продление: автоматическое продление можно отключить в любое время в настройках учетной записи. Подписка автоматически продлевается, если автоматическое продление не отключено по крайней мере за 24 часа до окончания текущего периода.
• Политика конфиденциальности: https://www.splashmath.com/privacy
• Условия использования: https://www.splashmath.com/terms-of-use
*** Политика возврата ***
Пользователь может отменить подписку и автоматически продлить в любое время, и со следующего платежного цикла не будет взиматься дополнительная плата за кредитную карту.



 Организационный
момент
Организационный
момент 

 Работа над задачами.
Работа над задачами.


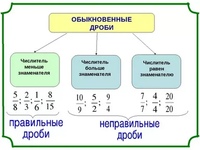 : Мнемозина, 2007.
: Мнемозина, 2007.
 Работа с тестом
Работа с тестом ).
). Однажды мы с мужем на кухне считали вслух какие-то трёхзначные числа, а Кирилл вдруг моментально дал ответ без калькулятора!
Однажды мы с мужем на кухне считали вслух какие-то трёхзначные числа, а Кирилл вдруг моментально дал ответ без калькулятора!  Стала такой самостоятельной, что я могу спокойно доверить ей выполнение сложного школьного задания без моего участия.
Стала такой самостоятельной, что я могу спокойно доверить ей выполнение сложного школьного задания без моего участия. 

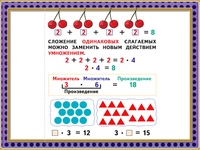 Если кому-то нужна копия моего слайд-шоу, я хотел бы поделиться 😀
Если кому-то нужна копия моего слайд-шоу, я хотел бы поделиться 😀