ГДЗ по Математике 5 класс: Виленкин
Решебник по математике для 5 класса Виленкин – это практическое пособие, которое представляет собой сборник готовых домашних заданий, выполненных по классическому учебнику математики, который используется в большинстве общеобразовательных школ РФ. Авторами учебника выступают авторитетные российские ученые: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
ГДЗ от Путина по математике за 5 класс — Виленкин Н.Я. 2013-2017 год
ГДЗ по математике для 5 класса Виленкин – это не база для бездумного списывания. Это пошаговый алгоритм выполнения расчетов и онлайн-ответы на задания, которые позволяют родителям – контролировать успеваемость детей, а школьникам – проверять правильность выполнения примеров и задач.
Теперь для того чтобы воспользоваться учебником – вовсе не обязательно долго искать нужную страницу. На нашем сайте нужное задание Вы сможете найти, выбрав его номер в приведенной выше таблице.
Дополнительными преимуществами использования ресурса выступают:
- Возможность поиска готовых решений ответов как с ПК, так с планшета и телефона;
- Регулярное обновление версий решебников;
- Наличие сразу нескольких вариантов ответа по одному заданию (из разных решебников).
Наш сайт – серьезное подспорье родителям, которые желают помочь своим детям в выполнении домашних заданий, но не помнят алгоритмов решения арифметических задач.
Решебник по математике 5 класс: Виленкин, Жохов, Чесноков, Шварцбург
В таблице номера ответов соответствуют нумерации заданий в 31-м издании учебника для 5 класса Виленкина Н.Я. Он был издан в 2013 году и включает в себя две большие главы:
- Глава 1 – Натуральные числа;
- Глава 2 – Дробные числа.
В рамках обоих разделов рассматриваются понятия, свойства и признаки, основные математические действия. Отдельные параграфы посвящены расчету площадей и объемов.
Благодаря нашему сайту пятиклассники могут самостоятельно разобраться в сложных арифметических примерах и задачах. Родителям теперь не придется пользоваться дорогостоящими услугами репетиторов: уяснив многоступенчатый алгоритм выполнения заданий, они смогут самостоятельно помочь своим детям.
ГДЗ по математике 5 класс Виленкин Жохов учебник
ГДЗ учебника Математика 5 класс Н.
Я. Виленкина, В. И. Жохова, А. С. Чеснокова, С. И. Шварцбурда. Издательство: Мнемозина, серия: Математика. Состоит из одной части (1 часть -280 страниц.)
Учебник математики состоит из 8 параграфов, постепенно изучая которые школьники приобретут новые знания по предмету. Продолжая освоение математики, пятиклассники познакомятся с натуральными числами, научатся их складывать, вычитать, делить и умножать. Параграф 4 целиком посвящен изучению площадей и объемов. Школьники узнают множество новых формул, благодаря которым смогут производить расчет сложных математических вычислений. Большую часть учебника занимает тема изучения простых и десятичных дробей и действий с ними. Заканчивает курс обучения знакомство с измерительными приборами и правилами пользования ими, в том числе транспортиром. Использование микрокалькулятора, после изучения соответствующего раздела, станет более обширным и необходимым. Представленные в учебнике задания максимально адаптированы под возникающие в реальной жизни ситуации, что поможет школьнику самостоятельно принимать многие решения.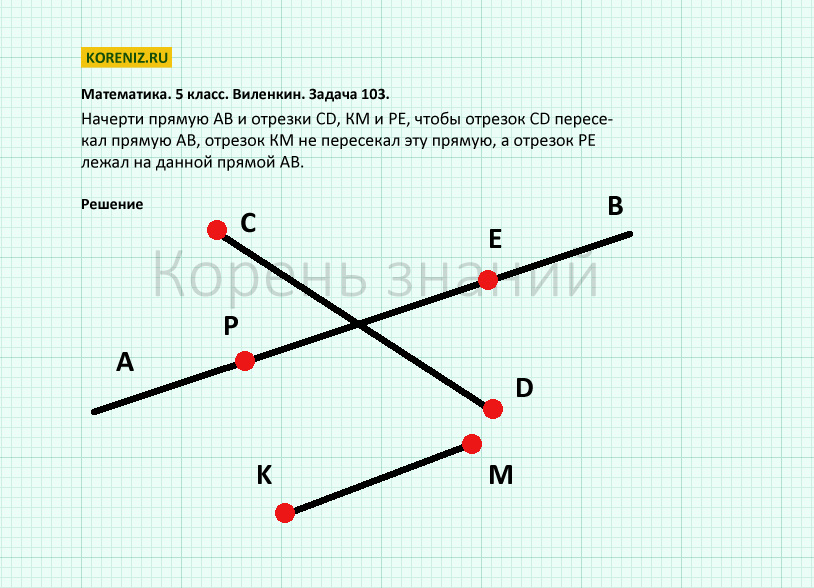
ГДЗ к учебнику по математике 5 класс Виленкин с углубленным решением всех упражнений, которые Вы найдете на сайте ЯГДЗ, помогут учащимся сполна вникнуть в суть изучаемого материала, сделают процесс познания учебного предмета интересным и увлекательным.
Глава 1
Упражнение: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376
Страница 134 №850-856 ГДЗ к учебнику «Математика» 5 класс Виленкин, Жохов, Чесноков
Глава 2.
-reshenie-1460.jpg)
Дробные числа.Ответы к параграфу 22. Окружность и круг
Задание 850. Какие из точек, отмеченных на рисунке 97:
а) лежат на окружности;
в) не лежат на окружности;
г) лежат вне круга?
Решение
а) В, D.
б) А, О, E.
в) А О, Е, С, F.
г) С, F.
Задание 851. Отметьте в тетради точку О. Постройте окружность с центром в этой точке. Измерьте радиус окружности. Чему равен её диаметр?
Задание 852. Начертите окружность и отметьте на ней три точки А, В и С. Назовите дуги, на которые эти точки делят окружность.
Решение
Точки A, В, С делят окружность на дуги АС, АВ, СВ.
Задание 853
Сравните эти расстояния с радиусом круга. Соедините точки А и В отрезком. Пересекается ли он с окружностью?Решение
ОА = 2 см < ОR = 3 см; ОВ = 4,03 см > ОR = 3 см.
Отрезок АВ пересекается с окружностью.
Задание 854. Начертите окружность с центром в точке О и радиусом 3 см 5 мм. Проведите прямую, которая пересекает окружность в точках М и К. На каком расстоянии от центра окружности находятся эти точки?
Решение
ОМ = OK = 3 см 5 мм.
Задание 855. Начертите отрезок CD, равный 5 см. Проведите окружность с центром С и радиусом 3 см, а также другую окружность с центром D и радиусом 4 см. Обозначьте точки пересечения окружностей буквами А и В. Чему равны длины отрезков АС, СВ, DA и BD?
Решение
СK = СM = 3 см, DK = DM = 4 см.
Задание 856. Начертите отрезок MP, равный 6 см.-reshenie-649.jpg)
Найдите две точки А и В, которые находились бы на расстоянии 4 см от точки М и 5 см от точки Р.
(PDF) Заметка о максимальных операторах Виленкина
212 И. БЛАХОТА, Г. ТЕФНАДЗЕ
[14] К. Надь. Аппроксимация средними Норлунда квадратичных частных сумм двойных рядов Фурье Уолша-
. Анальный. Math., 36 (4): 299–319, 2010.
[15] К. Надь. Аппроксимация средними Нёрлунда рядов Уолша-Качмарца-Фурье. Geor-
gian Math. J., 18 (1): 147–162, 2011.
[16] К. Надь. Аппроксимация средними Норлунда двойных рядов Уолша-Фурье для функций Липшица
.Математика. Неравно. Appl., 15 (2): 301–322, 2012.
[17] J. P´al, P. Simon. Об обобщении понятия производной. Acta Math. Акад.
Sci. Hungar., 29 (1-2): 155–164, 1977.
[18] F. Schipp. Некоторые перестановки рядов в системе Уолша. Мат. Заметки,
18 (2): 193–201, 1975.
[19] П. Саймон. Исследования по системе Виленкина.
Анна. Univ. Sci. Будапешт.
E¨otv¨os Sect. Math., 27: 87–101 (1985), 1984.
[20] P.Саймон. Суммируемость по Чезаро по двухпараметрическим системам Уолша. Монатш.
Math., 131 (4): 321–334, 2000.
[21] П. Саймон. Теорема о сильной сходимости для рядов Виленкина-Фурье. J. Math. Анальный. Appl.,
245 (1): 52–68, 2000.
[22] П. Саймон и Ф. Вайс. Слабые неравенства для суммируемости по Чезаро и Рисса рядов Фурье Уолша-
. J. Прибл. Теория, 151 (1): 1–19, 2008.
[23] Г. Тефнадзе. Заметка о коэффициентах Фурье и частичных суммах рядов Виленкина-Фурье
.Acta Math. Акад. Педагог. Ныхази. (Н.С.), 28 (2): 167–176, 2012.
[24] Г. Тефнадзе. О частных суммах рядов Виленкина-Фурье. Изв. Нац. Акад. Наук
Армени матем., 49 (1): 60–72, 2014.
[25] Г. Тефнадзе, Т. Р. Сильная теорема сходимости средних Чезаро относительно
системы Уолша. появляться.
[26] Н. Ю. Виленкин. О классе полных ортонормированных систем.
Амер. Математика. Soc. Пер.
(2), 28: 1–35, 1963.
[27] F.Вайс. Пространства Мартингейла Харди и их приложения в анализе Фурье, том
1568 конспектов лекций по математике. Springer-Verlag, Berlin, 1994.
[28] F. Weisz. Суммируемость по Чезаро одномерного и двумерного рядов Уолша-Фурье. Анальный.
Math., 22 (3): 229–242, 1996.
[29] F. Weisz. Пространства Харди и средние Чезаро двумерных рядов Фурье. В Прибл.
теория имитации и функциональные ряды (Будапешт, 1995), том 5 Bolyai Soc.Математика.
Stud., Страницы 353–367. J´anos Bolyai Math. Soc., Budapest, 1996.
[30] F. Weisz. (C, α) суммируемость рядов Уолша-Фурье. Анальный. Math., 27 (2): 141–155, 2001.
[31] F. Weisz. θ-суммируемость рядов Фурье. Acta Math. Hungar., 103 (1-2): 139–175, 2004.
Поступила 17 ноября 2014 г.
Istv´
an Blahota,
Институт математики и компьютерных наук,
University of Ny
´
ıregyh´
aza,
P.
O. Box 166, Ny
´
ıregyh´
aza, H-4400,
, Венгрия.
Адрес электронной почты: [email protected]
% PDF-1.6
%
440 0 объект
>
эндобдж
xref
440 115
0000000016 00000 н.
0000003518 00000 н.
0000003708 00000 п.
0000003837 00000 н.
0000003873 00000 н.
0000004326 00000 н.
0000004559 00000 н.
0000004706 00000 н.
0000004852 00000 н.
0000005001 00000 н.
0000005151 00000 п.
0000005299 00000 н.
0000005444 00000 н.
0000005593 00000 п.
0000005741 00000 н.
0000005887 00000 н.
0000006036 00000 н.
0000006185 00000 п.
0000006335 00000 н.
0000006481 00000 н.
0000006630 00000 н.
0000006775 00000 н.
0000006924 00000 н.
0000007069 00000 н.
0000007219 00000 н.
0000007371 00000 н.
0000007521 00000 н.
0000007673 00000 н.
0000007823 00000 н.
0000007969 00000 п.
0000008119 00000 п.
0000008264 00000 н.
0000008414 00000 н.
0000008559 00000 н.
0000008708 00000 н.
0000008854 00000 н.
0000009003 00000 н.
0000009177 00000 н.
The Case for Parallel Universe
Примечание редактора: в августовском номере журнала Scientific American космолог 
Здесь сторонники мультивселенной Александр Виленкин и Макс Тегмарк предлагают контрапункты, объясняя, почему мультивселенная объясняет так много особенностей нашей Вселенной — и как это можно проверить.
Добро пожаловать в Мультивселенную
Александр Виленкин
Вселенная в том виде, в каком мы ее знаем, возникла в результате большого взрыва, который мы называем Большим взрывом. В течение почти столетия космологи изучали последствия этого взрыва: как Вселенная расширялась и охлаждалась, и как галактики постепенно сближались под действием силы тяжести. Природа самой челки стала предметом внимания лишь относительно недавно. Это предмет теории инфляции, которая была разработана в начале 1980-х Аланом Гутом, Андреем Линде и другими и привела к радикально новому глобальному взгляду на Вселенную.
Инфляция — это период сверхбыстрого ускоренного расширения в ранней космической истории. Это настолько быстро, что за доли секунды крошечная субатомная частичка пространства раздувается до размеров, намного превышающих размеры всей наблюдаемой в настоящее время области.
В конце инфляции энергия, вызвавшая расширение, воспламеняет горячий огненный шар частиц и излучения. Это то, что мы называем большим взрывом.
Конец инфляции вызван квантовыми вероятностными процессами и не происходит сразу везде.В нашем космическом районе инфляция закончилась 13,7 миллиарда лет назад, но она все еще продолжается в отдаленных частях Вселенной, и постоянно образуются другие «нормальные» регионы, подобные нашей. Новые области выглядят как крошечные микроскопические пузырьки и сразу же начинают расти. Пузыри беспрестанно растут; тем временем они раздвигаются инфляционным расширением, освобождая место для образования большего количества пузырей. Этот нескончаемый процесс называется вечной инфляцией. Мы живем в одном из пузырей и можем наблюдать лишь небольшую его часть.Независимо от того, как быстро мы путешествуем, мы не можем догнать расширяющиеся границы нашего пузыря, поэтому для всех практических целей мы живем в замкнутой пузырьковой вселенной.
Теория инфляции объяснила некоторые загадочные особенности Большого взрыва, которые раньше просто нужно было постулировать.
Он также сделал ряд проверяемых предсказаний, которые затем были убедительно подтверждены наблюдениями. К настоящему времени инфляция стала ведущей космологической парадигмой.
Другой ключевой аспект нового мировоззрения проистекает из теории струн, которая в настоящее время является нашим лучшим кандидатом в фундаментальную теорию природы.Теория струн допускает огромное количество решений, описывающих пузырьковые вселенные с различными физическими свойствами. Величины, которые мы называем константами природы, например массы элементарных частиц, гравитационная постоянная Ньютона и т. Д., Принимают разные значения в разных типах пузырей. Теперь объедините это с теорией инфляции. Каждый тип пузыря имеет определенную вероятность образоваться в надувном пространстве. Так что в процессе вечной инфляции неизбежно будет образовываться неограниченное количество пузырей всех возможных типов.
Эта картина вселенной, или мультивселенная , как ее называют, объясняет давнюю загадку того, почему константы природы, кажется, точно настроены для возникновения жизни.-reshenie-1228.jpg)
Причина в том, что разумные наблюдатели существуют только в тех редких пузырях, в которых по чистой случайности константы оказываются как раз подходящими для развития жизни. Остальная часть мультивселенной остается бесплодной, но некому жаловаться на это.
Некоторые из моих коллег-физиков находят теорию мультивселенной тревожной.Любая теория в физике стоит или падает в зависимости от того, согласуются ли ее предсказания с данными. Но как мы можем проверить существование других пузырьковых вселенных? Пол Стейнхардт и Джордж Эллис утверждали, например, что теория мультивселенной ненаучна, потому что ее нельзя проверить даже в принципе.
Удивительно, но на самом деле возможно проведение наблюдательных тестов изображения мультивселенной. Энтони Агирре, Мэтт Джонсон, Мэтт Клебан и другие указали, что столкновение нашего расширяющегося пузыря с другим пузырем в мультивселенной произведет отпечаток в космическом фоновом излучении — круглое пятно с большей или меньшей интенсивностью излучения.
Обнаружение такого пятна с предсказанным профилем интенсивности предоставит прямое свидетельство существования других пузырьковых вселенных. Поиски сейчас продолжаются, но, к сожалению, нет никакой гарантии, что столкновение пузырей произошло в пределах нашего космического горизонта.
Есть и другой подход, которому можно следовать. Идея состоит в том, чтобы использовать нашу теоретическую модель мультивселенной для предсказания природных констант, которые мы можем ожидать измерить в нашем локальном регионе. Если константы меняются от одной пузырьковой вселенной к другой, их локальные значения нельзя предсказать с уверенностью, но мы все равно можем сделать статистических прогнозов .Мы можем вывести из теории, какие значения констант с наибольшей вероятностью могут быть измерены типичным наблюдателем в мультивселенной. Предполагая, что мы типичны — предположение, что я назвал принципом посредственности — мы можем затем предсказать вероятные значения констант в нашем пузыре.
Эта стратегия была применена к плотности энергии вакуума, также известной как «темная энергия». Стивен Вайнберг отметил, что в регионах, где темная энергия велика, она заставляет Вселенную очень быстро расширяться, предотвращая слипание материи в галактики и звезды.Наблюдатели вряд ли появятся в таких регионах. Расчеты показали, что большинство галактик (и, следовательно, большинство наблюдателей) находятся в областях, где темная энергия примерно такая же, как плотность вещества в эпоху образования галактик. Таким образом, предсказывается, что аналогичное значение должно наблюдаться в нашей части Вселенной.
По большей части физики не воспринимали эти идеи всерьез, но, к их большому удивлению, темная энергия примерно ожидаемой величины была обнаружена в астрономических наблюдениях в конце 1990-х годов.Это может быть нашим первым доказательством того, что действительно существует огромная мультивселенная. Это изменило многие мнения.
Теория мультивселенной все еще находится в зачаточном состоянии, и некоторые концептуальные проблемы еще предстоит решить.
Но, как писал Леонард Сасскинд: «Я готов поспорить, что на рубеже 22-го века философы и физики будут ностальгически смотреть на настоящее и вспоминать золотой век, в котором узкая провинциальная концепция Вселенной 20-го века уступила место большему лучшему. [мультивселенная]… ошеломляющих размеров. »
Мультивселенная наносит ответный удар
Автор: Макс Тегмарк
Вы действительно живете в мультивселенной, или это понятие выходит за рамки науки?
Вдохновленный интересной критикой мультивселенных в августовском номере Scientific American, , написанной пионером теории относительности Джорджем Ф. Р. Эллисом, позвольте мне дать вам сумму в два цента.
Идеи Мультивселенной традиционно не получали должного внимания со стороны истеблишмента: Джордано Бруно с его мультивселенной бесконечного пространства был сожжен на костре в 1600 году, а Хью Эверетт с его квантовой мультивселенной сгорел на рынке труда физиков в 1957 году.-reshenie-1093.jpg)
Я даже почувствовал некоторую жару на собственном опыте, когда старшие коллеги предположили, что мои публикации, связанные с мультивселенной, были сумасшедшими и разрушили мою карьеру. Однако в последние годы произошли кардинальные перемены. Параллельные вселенные сейчас в моде, они появляются в книгах, фильмах и даже в шутках: «Вы сдали экзамен во многих параллельных вселенных, но не в этой».
Это озвучивание идей определенно не привело к консенсусу среди ученых, но оно сделало дискуссию о мультивселенной гораздо более тонкой и, на мой взгляд, более интересной, когда ученые вышли за рамки выкрикивания звуковых фрагментов друг другу и искренне пытались понять противоположные стороны. точки зрения.Новая статья Джорджа Эллиса — отличный тому пример, и я настоятельно рекомендую прочитать ее, если вы еще этого не сделали.
Под нашей Вселенной я имею в виду сферическую область пространства, из которой свет успел достичь нас за 13,7 миллиарда лет с момента нашего большого взрыва.-reshenie-1490.jpg)
Говоря о параллельных вселенных, я считаю полезным различать четыре разных уровня: Уровень I (другие такие области далеко в космосе, где кажущиеся законы физики одинаковы, но где история разыгрывается по-другому, потому что все начиналось по-другому), Уровень II (области пространства, где даже кажущиеся законы физики отличаются), уровень III (параллельные миры в другом месте в так называемом гильбертовом пространстве, где разыгрывается квантовая реальность) и уровень IV (полностью разобщенные реальности, управляемые разными математическими уравнениями) .
В своей критике Джордж классифицирует многие аргументы в пользу этих уровней мультивселенной и утверждает, что все они имеют проблемы. Вот мое резюме его основных аргументов против мультивселенной:
1) Инфляция может быть неправильной (или не вечной)
2) Квантовая механика может быть неправильной (или не унитарной)
3) Теория струн может быть неправильной (или не иметь нескольких решений)
4) Мультивселенные могут быть неверными
5) Некоторые заявленные свидетельства мультивселенной сомнительны
6) Аргументы точной настройки могут предполагать слишком много
7) К еще большим мультивселенным — скользкая дорога
(Джордж на самом деле не упомянул (2) в статье, но я добавляю его здесь, потому что думаю, что он сделал бы, если бы редактор разрешил ему более шести страниц.-reshenie-1080.jpg)
)
Как я отношусь к этой критике? Интересно, что я согласен со всеми этими семью утверждениями — и, тем не менее, я с радостью поставлю свои сбережения на существование мультивселенной!
Начнем с первых четырех. Инфляция естественным образом порождает мультивселенную Уровня I, и если вы добавите теорию струн с ландшафтом возможных решений, вы также получите Уровень II. Квантовая механика в ее простейшей математической («унитарной») форме дает вам уровень III. Так что, если эти теории будут опровергнуты, тогда исчезнут ключевые свидетельства существования этих мультивселенных.
Помните: параллельные вселенные — это не теория — это предсказания определенных теорий.
Для меня ключевым моментом является то, что если теории являются научными, то это законная наука, которая разрабатывает и обсуждает все их последствия, даже если они связаны с ненаблюдаемыми сущностями. Чтобы теория была опровергнута, нам не нужно иметь возможность наблюдать и проверять все ее предсказания, только хотя бы одно из них.
Поэтому мой ответ на (4) таков: то, что можно проверить с научной точки зрения, — это наши математические теории, не обязательно их следствия, и это вполне нормально.Например, поскольку общая теория относительности Эйнштейна успешно предсказала многие вещи, которые мы можем наблюдать, мы также серьезно относимся к ее предсказаниям в отношении вещей, которые мы не можем наблюдать, например, того, что происходит внутри черных дыр.
Точно так же, если мы впечатлены успешными предсказаниями инфляции или квантовой механики до сих пор, то нам нужно серьезно отнестись также к их другим предсказаниям, включая мультивселенную Уровня I и Уровня III. Джордж даже упоминает возможность того, что когда-нибудь вечная инфляция может быть исключена — для меня это просто аргумент, что вечная инфляция — это научная теория.
Теория струн, конечно же, не дошла до инфляции и квантовой механики с точки зрения утверждения себя как проверяемая научная теория. Однако я подозреваю, что мы застрянем с мультивселенной уровня II, даже если теория струн окажется отвлекающим маневром.
Математические уравнения довольно часто имеют несколько решений, и до тех пор, пока существуют фундаментальные уравнения, описывающие нашу реальность, вечная инфляция обычно создает огромные области пространства, которые физически реализуют каждое из этих решений.Например, уравнения, управляющие молекулами воды, которые не имеют ничего общего с теорией струн, допускают три решения, соответствующие пару, жидкой воде и льду, и если само пространство может существовать в разных фазах, инфляция будет стремиться реализовать их все.
Джордж перечисляет ряд наблюдений, якобы поддерживающих теории мультивселенной, которые в лучшем случае сомнительны, например свидетельства того, что определенные природные константы на самом деле не постоянны, свидетельства космического микроволнового фонового излучения столкновений с другими вселенными или странно связанным пространством и т. Д.Я полностью разделяю его скепсис по поводу этих утверждений. Однако во всех этих случаях разногласия касались анализа данных, как и в случае фиаско с холодным синтезом. Для меня сам факт того, что ученые проводят эти измерения и спорят о деталях данных, является еще одним доказательством того, что это находится в пределах поля зрения науки: именно это отличает научную полемику от ненаучной!
Наша Вселенная кажется удивительно приспособленной для жизни в том смысле, что если вы немного измените многие из наших природных констант, жизнь в том виде, в каком мы ее знаем, будет невозможна.Почему? Если существует мультивселенная уровня II, где эти «константы» принимают все возможные значения, неудивительно, что мы оказываемся в одной из редких вселенных, пригодных для обитания, точно так же, как неудивительно, что мы живем на Земле, а не на Меркурии или Нептуне. . Джордж возражает против того факта, что вам нужно принять теорию мультивселенной, чтобы сделать этот вывод, но именно так мы проверяем любую научную теорию: мы предполагаем, что это правда, прорабатываем последствия и отбрасываем теорию, если предсказания не совпадают с наблюдениями. .Некоторые тонкие настройки кажутся достаточно экстремальными, чтобы вызывать затруднения — например, нам нужно настроить темную энергию примерно на 123 знака после запятой, чтобы сделать галактики пригодными для жизни. Для меня необъяснимое совпадение может быть явным признаком пробела в нашем научном понимании. Отклонив его, сказав: «Нам просто повезло — теперь хватит искать объяснения!» не только неудовлетворительно, но и равносильно игнорированию потенциально важной подсказки.
Джордж утверждает, что если мы серьезно отнесемся к тому, что все, что может произойти, действительно произойдет, мы спустимся по скользкой дорожке к еще большим мультивселенным, таким как уровень IV.Так как это мой любимый уровень мультивселенной, и я один из немногих его сторонников, я с радостью скатываюсь по этому склону!
Джордж также упоминает, что мультивселенная может не понравиться бритве Оккама из-за ненужных усложнений. Как физик-теоретик, я сужу об элегантности и простоте теории не по ее онтологии, а по изяществу и простоте ее математических уравнений — и меня весьма поразительно, что математически простейшие теории имеют тенденцию давать нам множественность.Доказано, что написать теорию, которая производит именно ту Вселенную, которую мы видим, и не более того, чрезвычайно сложно.
Наконец, есть аргумент против мультивселенной, которого я рекомендую Джорджу избегать, но который, на мой взгляд, наиболее убедителен для большинства людей: параллельные вселенные кажутся слишком странными, чтобы быть правдой.
Рассмотрев аргументы против мультивселенной, давайте теперь проанализируем случай про-мультивселенной более подробно. Я собираюсь утверждать, что все спорные вопросы исчезнут, если мы примем гипотезу внешней реальности: существует внешняя физическая реальность, полностью независимая от нас, людей.Предположим, что эта гипотеза верна. Тогда большая часть критики мультивселенной основана на некоторой комбинации следующих трех сомнительных предположений:
1) Предположение о всестороннем разделении: физическая реальность должна быть такой, чтобы хотя бы один наблюдатель в принципе мог наблюдать ее всю.
2) Педагогическое допущение реальности: физическая реальность должна быть такой, чтобы все разумно информированные наблюдатели чувствовали, что они интуитивно понимают ее.
3) Предположение об отсутствии копирования: никакой физический процесс не может копировать наблюдателей или создавать субъективно неотличимых наблюдателей.
(1) и (2), по-видимому, мотивированы немногим большим, чем человеческое высокомерие. Предположение о всеведении эффективно переопределяет слово «существует», чтобы оно стало синонимом того, что мы, люди, наблюдаем, подобно страусу, склонившему голову в песок. Те, кто настаивает на допущении педагогической реальности, обычно отвергают успокаивающе знакомые детские понятия, такие как Санта-Клаус, местный реализм, Зубная фея и креационизм — но действительно ли они работали достаточно усердно, чтобы освободиться от успокаивающе знакомых представлений, которые имеют более глубокие корни? По моему личному мнению, наша задача как ученых — попытаться выяснить, как мир работает, не говоря уже о том, как он работает, основываясь на наших философских предубеждениях.
Если предположение о всеядности неверно, то существуют ненаблюдаемые вещи, и мы живем в мультивселенной.
Если допущение педагогической реальности ложно, то возражение о том, что мультивселенная слишком странная, не имеет логического смысла.
Если предположение об отсутствии копий неверно, то нет фундаментальной причины, по которой не может быть ваших копий где-либо еще во внешней реальности — действительно, как вечная инфляция, так и унитарная квантовая механика предоставляют механизмы для их создания.
У нас, людей, есть хорошо задокументированная склонность к высокомерию, высокомерному воображению себя в центре внимания, когда все вращается вокруг нас. Постепенно мы узнали, что вместо этого мы вращаемся вокруг Солнца, которое само вращается вокруг одной галактики среди бесчисленного множества других. Благодаря открытиям в физике мы можем получить еще более глубокое понимание самой природы реальности.
Цена, которую мы должны заплатить, становится все более скромной — что, вероятно, пойдет нам на пользу, — но взамен мы можем оказаться в реальности более грандиозной, чем наши предки мечтали в своих самых смелых мечтах.
Дополнительное чтение:
Многие миры в одном: поиск других вселенных. Алексей Виленкин. Хилл и Ван, 2006.
Космический пейзаж: теория струн и иллюзия разумного замысла . Леонард Сасскинд. Back Bay Books, 2006.
.Скрытая реальность: параллельные вселенные и скрытые законы космоса. Брайан Грин. Кнопф, 2011.
Пересмотр квинтэссенции инфляционной модели Пиблса – Виленкина
Во время фазового перехода от инфляции к кинению образуются частицы.Когда произведенные частицы имеют очень тяжелые массы, которые возникают при мгновенном предварительном нагреве или когда рассматриваются только тяжелые массивные частицы, конформно связанные с гравитацией, эти частицы должны распадаться на легкие частицы, чтобы сформировать релятивистскую плазму в тепловом равновесии, плотность энергии которой в конечном итоге будет доминирующей. чтобы соответствовать горячей вселенной Фридмана. Могут возникнуть два разных случая: когда распад тяжелых массивных частиц происходит до или после окончания режима кинирования.Здесь мы рассмотрим оба случая по отдельности. Также важно учитывать, что в течение этого периода потенциальную энергию поля инфлатона из-за ее низкого значения по сравнению с кинетической энергией можно было безопасно не учитывать, что означает, что динамические уравнения могут быть решены аналитически.
Распад до конца кининирования
Если предположить, что образовавшиеся массивные частицы при фазовом переходе распадаются на более легкие до равенства плотности энергии инфлатона и плотности энергии созданных частиц, то во время повторного нагрева имеем
$$ \ begin {align} \ varphi _ {rh} = \ varphi _ {kin} + \ sqrt {\ frac {2} {3}} M_ {pl} \ ln \ left (\ frac {H_ {kin}} {H_ {rh}} \ right), \ end {align} $$
(8)
и используя это во время разогрева, т.е.2. \ end {align} $$
(11)
Во время фазы преобладания излучения можно продолжать игнорировать градиент потенциала, получая
$$ \ begin {align} \ varphi (t) = \ varphi _ {rh} +2 {\ dot {\ varphi}} _ {rh} t_ {rh} \ left (1- \ sqrt {\ frac {t_ {rh}} {t}} \ right), \ end {align} $$
(12)
и мы должны вычислить значение поля и его производную при равенстве материи и излучения, т.е.4} \ Omega _ {м, 0}. \ end {align} $$
(13)
Таким образом, наблюдательное значение \ (z_ {eq} \) получается из наблюдательных значений \ (H_0 \), \ (\ Omega _ {m, 0} \) и хорошо известной текущей температуры Вселенная \ (T_0 \).
Таким образом, наблюдаемые значения \ (H_0 \) и \ (\ Omega _ {m, 0} \) могут быть получены непосредственно из собственного потенциала \ (V _ {\ alpha} \), однако параметр M полностью вырожден, как сообщается из последних наборов астрономических данных [38], где добавление данных о барионных акустических колебаниях к космическому микроволновому фоновому излучению не может нарушить такое вырождение. {1/4} \ frac {T_ {eq}} {T_ {rh}} \ right) \ nonumber \\\ cong & {} \ varphi _ {rh} +2 \ sqrt {\ frac {2} {3}} M_ {pl} \ cong 24.{-16} \). Однако, если требуется большее значение этого параметра, необходимо рассмотреть более низкие температуры повторного нагрева, удовлетворяющие \ (T_ {rh} \ gtrsim 1 \) МэВ.
Распад после окончания киненирования
В этом случае, который возможен только тогда, когда повторный нагрев происходит из-за образования тяжелых массивных частиц (в случае мгновенного предварительного нагрева это может привести к нежелательной новой инфляционной эре [37, 43 ]), можно получить температуру повторного нагрева, очень близкую к 1 МэВ [38]. Итак, здесь мы рассматриваем \ (T_ {rh} = 1 \) МэВ, что означает, что в эпоху BBN \ (\ Omega _ {\ varphi} (t_ {BBN}) = \ frac {{2}} {3 } \ cong 0.{-13} \).
Пусть \ ({\ bar {t}} \) будет время окончания родства, то есть когда \ (\ rho _ {\ varphi} ({\ bar {t}}) = \ rho _ {\ chi} ({\ bar {t}}) \), где \ (\ rho _ {\ chi} \) обозначает плотность энергии образовавшихся массивных \ (\ chi \) — частиц. 2}, \ end {align} $$
(19)
можно вывести, что \ (H ({\ bar {t}}) = \ sqrt {2} H_ {kin} \ Theta \).Теперь, поскольку во время создания \ (H ({t}) = \ frac {1} {3 {t}} \), можно сделать вывод, что \ ({\ bar {t}} = \ frac {1} {3 \ sqrt {2} H_ {kin} \ Theta} = \ frac {1} {\ sqrt {3 (1+ \ sqrt {3})} m \ Theta} \).
Таблица 1 Приведена сводка начальных условий при равенстве вещества и излучения при различных температурах повторного нагрева.С другой стороны, в конце kination у нас будет
$$ \ begin {align} \ varphi ({\ bar {t}}) = & {} \ varphi _ {kin} + \ sqrt {\ frac {2} {3}} M_ {pl} \ ln \ left (\ frac {{\ bar {t}}} {t_ {kin}} \ right) \ nonumber \\ = & {} \ varphi _ {kin} — \ sqrt {\ frac {2} {3}} M_ {pl} \ ln \ left (\ sqrt {2} \ Theta \ right), \ end {align} $$
(20)
и
$$ \ begin {align} {\ dot {\ varphi}} ({\ bar {t}}) = \ sqrt {\ frac {2} {3}} \ frac {M_ {pl}} {{\ bar {t}}} = \ sqrt {2 (1+ \ sqrt {3})} mM_ {pl} \ Theta. 4} {mM_ {pl} \ Theta }.{-16} \), и, таким образом,
$$ \ begin {align} \ varphi _ {rh} \ cong \ varphi ({\ bar {t}}) + \ sqrt {\ frac {2} {3} } M_ {pl} \ cong 38.18 M_ {pl} \ quad \ text {and} \ quad {\ dot {\ varphi}} _ {rh} \ cong 0. \ end {align} $$
(25)
Наконец, используя соотношения в формуле. (14) получается \ (\ varphi _ {eq} \ cong 39.81 \) и \ ({\ dot {\ varphi}} _ {eq} \ cong 0 \). В следующем разделе мы опишем эволюцию Вселенной после настоящего равенства материи и излучения.
% PDF-1.4 % 106 0 obj> эндобдж xref 106 105 0000000016 00000 н. 0000003562 00000 н. 0000002396 00000 н. 0000003645 00000 н. 0000003835 00000 н. 0000004148 00000 п. 0000004309 00000 н. 0000004691 00000 н. 0000008293 00000 п. 0000008588 00000 н. 0000008855 00000 н. 0000009238 00000 п. 0000016479 00000 п. 0000016879 00000 п. 0000016956 00000 п. 0000017056 00000 п. 0000017359 00000 п. 0000018033 00000 п. 0000018280 00000 п. 0000018438 00000 п. 0000018808 00000 п. 0000021113 00000 п. 0000021402 00000 п. 0000021997 00000 п. 0000022622 00000 п. 0000023068 00000 п. 0000023690 00000 п. 0000024214 00000 п. 0000024379 00000 п. 0000024822 00000 н. 0000025197 00000 п. 0000025651 00000 п. 0000026639 00000 п. 0000027126 00000 п. 0000035658 00000 п. 0000036412 00000 п. 0000036806 00000 п. 0000037166 00000 п. 0000038239 00000 п. 0000038521 00000 п. 0000038962 00000 п. 0000046815 00000 п. 0000047227 00000 п. 0000047544 00000 п. 0000047942 00000 п. 0000050638 00000 п. 0000051080 00000 п. 0000051341 00000 п. 0000051733 00000 п. 0000055689 00000 п. 0000056066 00000 п. 0000056949 00000 п. 0000057591 00000 п. 0000058229 00000 п. 0000059287 00000 п. 0000059508 00000 п. 0000061054 00000 п. 0000061378 00000 п. 0000061468 00000 п. 0000061986 00000 п. 0000062994 00000 п. 0000063460 00000 п. 0000063780 00000 п. 0000065662 00000 п. 0000066007 00000 п. 0000066186 00000 п. 0000067096 00000 п. 0000069804 00000 п. 0000070313 00000 п. 0000070573 00000 п. 0000070884 00000 п. 0000071244 00000 п. 0000071980 00000 п. 0000072575 00000 п. 0000073153 00000 п. 0000073653 00000 п. 0000082545 00000 п. 0000082918 00000 п. 0000083278 00000 п. 0000083609 00000 п. 0000090920 00000 н. 0000091301 00000 п. 0000091494 00000 п. 0000092251 00000 п. 0000092380 00000 п. 0000093331 00000 п. 0000093569 00000 п. 0000093963 00000 н. 0000100680 00000 н. 0000101046 00000 н. 0000101099 00000 н. 0000101384 00000 н. 0000101667 00000 н. 0000101889 00000 н. 0000102007 00000 н. 0000102357 00000 п. 0000104952 00000 н. 0000105210 00000 п. 0000105314 00000 п. 0000105657 00000 н. 0000106982 00000 п. 0000107227 00000 н. 0000107338 00000 н. 0000107685 00000 н. 0000109467 00000 н. трейлер ] >> startxref 0 %% EOF 108 0 obj> поток x ڬ Ile? xx4, m2N, Iq «W! p) dgs ٛ, 4 [SITP! qDp8K င / 0Ɖm g {{3F> B ? #e))? \ gO9t% 8? exC0.k-Se R
\ qP0 (ȓ2rze = vkA (_ V \ 78NGHQ
.