Как понять тему по математике 6 класс: Математика 6 класс

Содержание

Правила по математике 6 класс

Признаки делимости

Простое число – число, у которого имеются два делителя (единица и оно само)

Составное число – число, у которого больше двух делителей.

Сократить дробь, значит разделить числитель и знаменатель на одно и тоже число.

Чтобы умножить дроби, нужно 1. Посмотреть, можем ли мы что-то сократить, 2. Умножить числитель на числитель, знаменатель на знаменатель.

Чтобы найти дробь (часть) от числа, необходимо умножить дробь(часть) на число.

Взаимно обратные числа – числа, произведение которых равно единице.

Чтобы поделить две дроби, необходимо 1. Нужно первую дробь оставить, 2. Деление заменить умножением, 3. Вторую дробь перевернуть, 4. Посмотреть можем ли мы что-то сократить, 5. Умножить числитель на числитель, знаменатель на знаменатель.

Отношение – это частное(деление) двух чисел.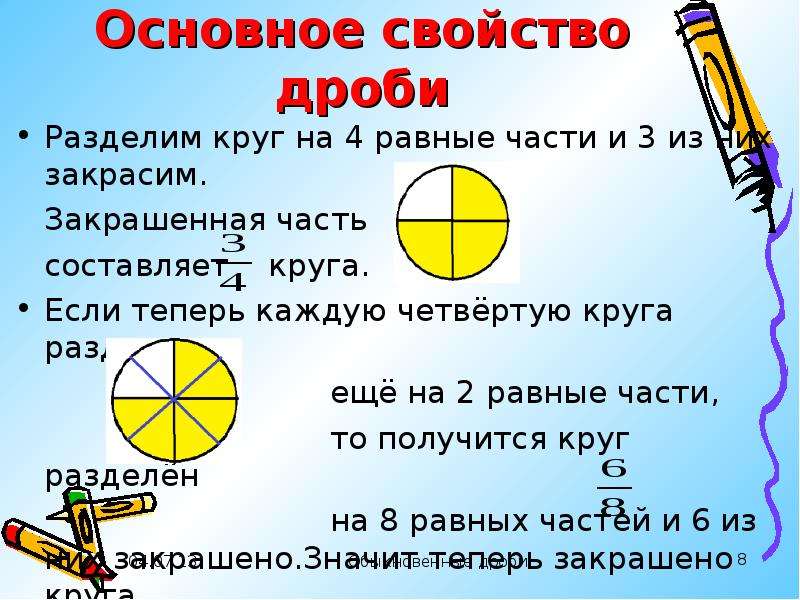

Пропорция – это равенство (=) двух отношений.

Две переменные прямо пропорциональны – когда при увеличении(уменьшении) одной из них в несколько раз другая увеличивается(уменьшается) во столько же раз.

Две переменные обратно пропорциональны – когда при увеличении(уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

Окружность – геометрическая фигура, состоящая из множества точек, находящихся на одинаковом расстоянии от центра.

Радиус – отрезок, соединяющий центр окружности с любой точкой на окружности.

Диаметр – отрезок, соединяющий две точки на окружности, проходящий через центр.

Связь радиуса и диаметра – диаметр равен двум радиусам.

Хорда – отрезок, соединяющий две точки на окружности, не проходящий через центр.

Длина окружности –

Круг – это плоскость, ограниченная окружностью.

Площадь круга –

Целые числа (обозначается буквой Z) – натуральные числа, противоположные им числа и нуль.

Натуральные числа (обозначается буквой N) – числа, которые мы используем при счёте.

Любое отрицательное число меньше любого положительного числа.

Из двух отрицательных чисел меньше то, модуль которого больше.

Нуль больше любого отрицательного числа, но меньше любого положительного.

Чтобы сложить два отрицательных числа, нужно 1) сложить их модули, 2) поставить перед полученным числом знак «—»

Чтобы сложить два числа с разными знаками, нужно 1) из большего модуля слагаемых вычесть меньший, 2) поставить перед полученным числом знак того слагаемого, модуль которого больше.

Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + (– b)

Например, –18 –14 = –18 + (–14)

Противоположные числа — два числа, отличающиеся друг от друга только знаками.
Координатная прямая – прямая с выбранными на ней началом отсчёта, единичным отрезком и направлением.
Число, показывающее положение точки на прямой, называют координатой этой точки.
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
Рациональные числа (обозначается буквой Q) – числа, которые можно записать в виде отношения , где a – целое число, а n – натуральное число.
Свойства действий с рациональными числами:

Переместительный: a + b = b + a

Сочетательный: a + (b + c) = (a + b) + c

Распределительный: (a + b) · c = a · c + b · c

Прибавление нуля: a + 0 = a

Умножение на нуль: a · 0 = 0

Умножение на 1: a · 1 = a

Модуль числа а – расстояние от начала координат до точки А (а).

Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

Две непересекающиеся прямые на плоскости называют параллельными.

Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.

Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
Система координат на плоскости – это две перпендикулярные координатные прямые x и y, которые пересекаются в начале отсчёта – точке О.
Координатная плоскость – плоскость, на которой выбрана система координат.
Начало координат – точка О.
Прямая х – ось абсцисс. Прямая у – ось ординат.
Пусть М – некоторая точка координатной плоскости. Проведем через неё прямую МА, перпендикулярную координатной прямой х, и прямую МВ, перпендикулярную координатной прямой у. Точка А имеет координату 6, а В – координату -5, тогда точка М определяется парой чисел (6, -5). Эта пара чисел называется координаты точки М.
Произведение может быть равно нулю тогда, когда один из множителей равен нуль.

a · b = 0, a = 0 или b=0

Чтобы раскрыть скобки, перед которыми стоит знак « ̶ », нужно оставить знак перед скобками, а в скобках заменить знаки на противоположные.
Если выражение является произведение числа и одной/несколько букв, то это число называют коэффициентом.
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Чтобы сложить подобные слагаемые, нужно сложить их коэффициенты и результат умножить на общую буквенную часть.
Корни уравнения не изменяются, если 1) обе части уравнения умножить или разделить на одно и то же число, не равное нулю, 2) какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

Урок 3. масштаб — Математика — 6 класс

Математика

6 класс

Урок № 3

Масштаб

Перечень рассматриваемых вопросов:

Понятие масштаба.
Находить масштаб по заданному расстоянию на местности и расстоянию на карте (плане).
При заданном масштабе и расстоянии на местности определять расстояние на карте (плане).
При заданном масштабе и расстоянии на карте (плане) определять расстояние на местности.

Тезаурус

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Отношения 2 к 3 и 3 к 2 называются взаимно обратными.

Отношение величин одного наименования (длины, скорости, стоимости и т. д., выраженных одинаковыми единицами измерения) есть число.

Отношение величин различных наименований (пути и времени, стоимости товара и его количества, массы тела и его объёма и т.

д.) есть новая величина.

Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности.

Масштаб, выраженный отношением чисел, называется численным.

Основная литература

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95с.

Теоретический материал для самостоятельного изучения

Сегодня мы с вами разберём, что означает масштаб.

Давайте сначала вспомним, что отношение величин одного наименования – это число.

Составим отношения:

Все мы хорошо знаем, что участки земной поверхности, детали машин и многое другое изображается на бумаге в уменьшенном виде.

Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности.

Рассмотрим пример:

Длина отрезка на карте равна 8 см.

Ответ: 800 м.

Ещё один пример:

Длина отрезка на местности равна 130 километров.

Ответ: 13 см.

Что же означает данный масштаб:

Говорят: карта сделана в масштабе одна двухтысячная. Объект на карте уменьшен в 2000 раз.

Что будет означать такой масштаб:

Рассмотрим ещё несколько примеров.

Огород имеет вид прямоугольника, длина которого 60 м, а ширина 10 м.

Ответ: Огород на плане будет иметь размеры: ширина 20 см, длина 12 см.

Разбор заданий тренировочного модуля

№ 1. Тип задания: Установление соответствий между элементами двух множеств.

Расстояние между двумя городами равно 150 км. Определите расстояние между изображениями этих городов на карте при трёх разных масштабах карты.

№ 2. Тип задания: Выбор элемента из выпадающего списка.

Значит, выбираем ответ 15 км.

Репетитор по математике для 6 класса — Колпаков Александр Николаевич

Индивидуальная работа с преподавателем в 6 классе – распространенное явление. В таком возрасте репетитор по математике набирает учеников раза в 2 чаще, годом ранее. Почему? Дело в том, что программа 6-го класса (по любому учебнику) только на первый взгляд кажется аналогичной пятому. Вроде бы те же дроби и текстовые задачи, те же уравнения и арифметические действия. Но какие? Любой репетитор по математике укажет на значительное увеличение количества алгоритмов и рост числа этапов внутри каждого из них. Кроме этого применение правил более дифференцированное и сильнее зависит от конкретной практической ситуации.

Опыт работы репетитором математики показывает, что тонкости этих ситуации дети улавливают с огромным трудом. По разным причинам. Образцы решений сложнее и дольше запоминаются, а недостаток внимания в паре с низкой скоростью вычислений часто не позволяют решить за урок (45 минут) более 3-4 заадч.

Прежде чем выбрать арифметическое действие для решения задачи, ребенок «примеряет» ее условия к изученным типам, которых к 6 классу накапливается уже немало. Для этого шестикласснику необходим не только опыт работы с ранее изученным, но и определенный уровень мышления в сочетании с надежной и быстрой памятью. В 5 классе и задачи проще и их спектр значительно более узкий.

Проблемы с математикой довольно часто проявляются у шестиклассника. Однако родители не всегда понимают насколько они серьезны, ибо школьная оценка часто завышается. Кроме этого она еще и не стабильна. Сегодня 5, а завтра 2. В чем причина двойки? Ребенок не понял текущий материал, или просто отвлекся на соседа? Именно на такие вопросы должен ответить репетитор по математике. Хороший преподаватель поможет диагностировать наличие проблемы и выявить ее причины.

В пятом классе некоторое непонимание материала еще удается невелировать. Как правило, ученик запонимает некий минимальный набор арифметических действий для 2-3 ситуаций и пытается угадать их появление в текстовых задачах. На малом количестве материала это еще как-то работает. Однако в 6 классе стратегия угадывания не помогает и с определенного момента становится очевидно: ученик не справляется.

Важно не пропустить этот момент и при потоке неудовлетворительных оценкок немедленно обращаться за помощью. Программа на месте не стоит. Материал только усложняется и дальнейшее отставание грозит переходом ученика в категорию безнадежных. Помните, что репетитор по математике, как доктор, спасает только тех больных, которые к нему своевременно обращаются. По статистике подготовка к ЕГЭ по математике с нуля (в 11 классе) обеспечивает в среднем не более чем 35-40 баллов.

Какой репетитор по математике нужен шестикласснику?

Безусловно, это преподаватель с большим школьным опытом и знанием школьных программ. Для одного и того же возраста учебники предлагают разное содержание тем: где-то проходят десятичные дроби, а где то обыкновенные, где-то уже проценты, а где-то еще только уравнения. Во всем этом многообразии нужно разбираться. Кроме знаний специфики учебного материала репетитор по математике должен обладать талантом объяснять простые вещи простым языком, неспеша, но в то же время не затягивая сам процесс.

Я бы не рекомендовал нацеливаться на преподавателя ВУЗа или студента. Несмотря на то, что талантливые репетиторы встречаются и в этих группах, опытный профессиональный педагог имеет куда большие шансы исправить ситуацию. Репетиторы из ВУЗа обычно завышают уровень занятий, а студенты не справляются с точными пояснениями. Кроме этого важен уровень мотивации самого репетитора. Низкая стоимость уроков этот уровень, как правило, снижает.

Репетитор по математике должен жить проблемами своего шестиклассника, понимать и помнить о том, что именно ему можно говорить в конкретной ситуации, а что нельзя. Математике свойственны обобщения и практически любую школьную задачку можно решить общими приемами. Например, уравнение решаемое делением 8:2 формально подходит для применения к нему метода Крамера 🙂

Сравнивая программы

Программу 6-ого класса отличает одно маленькое, но весьма важное свойство: впервые за годы учебы школьник сталкивается с математическими действиями (процессами), практический смысл и реальные модели которых невозможно показать. Например, это относится к действиям с отрицательными числами. Как понять запись или ? Пояснения в учебнике носят весьма упрощенный, поверхностный и логически неточный характер. И даже в таком виде они не всегда доступны слабому школьнику. Обычно репетитор по математике говорит: «делай как показываю и запоминай». Не всегда это оправдано, но здесь я не касаюсь вопросов методики, а просто обозначаю проблему.

Если правила в 5 классе можно сопроводить рисунками и ответ просто увидеть, то в 6 классе репетитор по математике знакомит ученика с «виртуальной математикой», или «с математикой на бумаге». Многое из нее не поддается внятному объяснению. Так школьники работают с формулами вычисления длины окружности и площади круга. Когда я сам учился в 6 классе, наш преподаватель математики сказал, что объяснить формулы и можно будет в старших классах, а когда это время настало, укзал на высшую математику. Из всего класса мне одному посчастливилось столкнуться с доказательствами формул площади и длины, ибо только математические факультеты ВУЗов его в свои программы.

Об учебниках по математике для 6 класса

Наибольшее распространение в школах имеют учебники Петерсона и Виленкина. Первый ориентирован на математические классы, а второй на базовый уровень. Мне не нравится идея, заложенная в Петерсоне. Особенно не нравится навязываение учебника школам, которые не отбирают детей в свои классы. В реальной работе не только репетитор по математике, но и школьный преподаватель пропускает параграфы с кванторами, равносильностью, доказательствами и другими ростками взрослой математики. Не справляются с ними дети. Даже сильные. В старших классах учащиеся переходят на другие программы, в которых точный язык логики высказываний практически не используется. Поэтому, когда ко мне приходит шестиклассник «по Петерсону», я использую книжку только как задачник.

Учебник Виленкина — классический и лучший на сегодяншний день учебник по методическим меркам. Это именно учебник, а не задачник. Его история тянется с далеких 80-х годов и Ваш покорный слуга сам по нему учился в свое время(правда несколько в другом издании) и, как видите, состоялся и без квантеров:)

Виленкин всегда занимал первые места на различных конкурсах пособий для общеобразовательной школы. Еще в советские времена. И это о многом говорит. Единственный минус — не очень богатая база задач, поэтому к учебнику обязательно нужно докупать дидактические материалы.

Подготовка к геометрии

Одно из направлений в работе репетитора по математике 6 классе – постепенное знакомство с понятиями, обозначениями и объектами планиметрии. Для этих целей в Виленкине выделен целый параграф. На тему отводится несколько академических часов и рассматриваются задания практического плана: нарисуйте пересекающие, параллельные , перпендикулярные прямые, найдите и обозначьте пары этих прямых на готовых рисунках, проведите перпендикулярную прямую к заданной и др. Ребенок учится распознавать, строить и обозначать объекты. Не более того. Если репетитор по математике привнесет в тему какие бы то ни было логические законы, то ничего кроме сумятицы и путаницы в голове ученика репетитор не получит.

Нужно понимать, что в 6 классе ученик не воспримет ни аксиомы, ни точные определения понятий параллельности, пересечения, принадлежности. Тем более в мае, когда дети живут мыслями о каникулах. Всему свое время. Я обычно комбинирую творческие задания на изображение прямых линий с темой «координаты».

Репетитор по математике может предложить такое задание: изобразите на координатной плоскости точки А(-3;4), В(2;6) и С(5;4). Проведите через С прямую, параллельную к АВ. Обозначьте буквой D точку ее пересечение с осью OX, а буквой E – точку ее пересечения с осью OY. Найдите координаты точек D и E. В следующем задании репетитор по математике заменяет параллельную прямую на перпендикулярную. И также предлагает найти пересечение с осями. Задания тренируют умение ученика работать с длинными алгоритмами и способствуют повторению сразу несколько правил и операций.

Колпаков А.Н. Репетитор по математике.

математика 6 класс

Автор: edu1

Методическая копилка — Математика

Урок по математике в 6 классе

Учитель математики Бондарь Е. А

Тема урока: “Умножение и деление чисел с разными знаками”.

Цели урока: повторение изученного материала по теме “Умножение и деление чисел с разными знаками”, отработка навыков применения операций умножения и деления положительного числа на отрицательное число и наоборот, а также отрицательного числа на отрицательное число.

Задачи урока:

Образовательные:

Закрепление правил по данной теме;
Формирование умений и навыков работы с операциями умножения и деления чисел с разными знаками.

Развивающие:

Развитие познавательного интереса;
Развитие логического мышления, памяти, внимания;

Воспитательные:

Воспитание активности;
Привитие учащимся навыков самостоятельной работы;
Воспитание настойчивости в достижении цели

Тип урока. Урок-повторения и обобщения.

Вид урока. Урок-игра — учащиеся совершают путешествие на планету положительных и отрицательных чисел для того, чтобы принять участие в конкурсе на “Лучшего математика-вычислителя”. Чтобы совершить путешествие и преодолеть все трудности, которые встречаются на их пути, они должны вспомнить все, что изучалось по теме “Умножение и деление чисел с разными знаками”.

Формы работы на уроке: индивидуальная, групповая, коллективная; устная, письменная.

Оборудование урока:

Наглядный материал: планета, магистр отрицательных наук, космический корабль, горы “Мозгодром”;

Дидактический материал: ветряные мельницы, карточки звездных созвездий, карточки с заданием “Проверь себя сам ”;
Карточки “Маршрутная карта экипажа”.

Литературные источники, использованные при подготовке к уроку.

“Математика 6 класс” Н. А. Виленкин Москва, Просвещение, 2008г.
Детская газета “Вырастайка” №8 2003г.
“Энциклопедический словарь юного астронома”. Составитель Ерпылев Н.ПМосква, Педагогика, 2006 г.
“Дидактические игры на уроках математики”, 2006 г.

План урока.

1.Сообщение темы и постановка целей урока-2 мин.

2.Актуализация знаний учащихся-8 мин.

3 Закрепление знаний (путешествие по планете)-25-30мин.

4.Подведение итогов урока- 4мин.

5.Домашнее задание-1 мин.

Ход урока

I. Сообщение темы и постановка цели урока.

Учитель: Здравствуйте, ребята, я получила приглашение поучаствовать в конкурсе на лучшего математика- счетовода, который проходит сегодня на планете “Отрицательных и положительных чисел”. Магистр отрицательных наук отправил за нами свой личный звездный корабль (приложение (рисунок 1) крепится на доску также на магнитах). Он предлагает вам отправиться в космическое путешествие на эту планету. Прежде чем мы совершим удивительное и увлекательное путешествие, нам необходимо перед полетом проверить готовность нашего экипажа. Итак, проведем экзамен на готовность к полету. Я прошу моих помощников — консультантов взять маршрутные карты экипажа (приложение таблица №1)( Класс работает в три группы- по № рядов, консультанты уже знают, что в этих картах они должны учитывать работу своего экипажа, в конце урока в этой карте будет отслежено, кому из ребят можно поставить оценку).

II. Актуализация знаний учащихся

Проводится фронтальная устная работа. (Консультанты отмечают “+” участие своих членов экипажа в маршрутной карте )

Этапы пути	Фамилия учащихся1 экипажа (1 ряд)
Этапы пути	Шевкун Эльвира	Фидирко Владимир	Дейнеко Анна.
Готовность	+
Ветряные мельницы	+
Звездные созвездия	+
Горы Мозгодром	+
Условия пиратов	+
Оценка	5

Сформулируйте правило умножения и деления чисел с разными знаками.
Даны числа (рисунок 2) Выполните сложение, умножение, деление, вычитание этих чисел. (На доске прикреплены магнитные карточки-лепестки, на них записаны два числа и рядом магнитные карточки с знаками действия. Учащиеся производят вычисление со знаком +, затем знак меняется на -, затем на умножение и, наконец, на деление. Все карточки приклеены к магнитам, удобно менять и данные, и знаки действия.

Ответы: к 1 примеру (90; 150;-3600;-4) ко 2 примеру (-90;-150;-3600, -4)

Вычислите:

-2, 5 х 3= -15, 3:(-3)= -7, 1х10= -20х3=

Ответы(-7, 5; 5, 1; -71;-60)

Даны числа -12 и 3. Назовите:

а) Модули этих чисел

б) Какое из чисел больше

в)Два целых числа, расположенных между ними

г)Два числа, которые меньше данных чисел

д)Два числа, которые больше данных чисел

е) Сумму данных чисел

ж)Разность данных чисел

з)Произведение данных чисел

и) Частное данных чисел?

Учитель: Я думаю, что со всеми заданиями вы справились хорошо. К полету готовы все экипажи. Прошу занять свои места. Корабль держит курс на планету “Отрицательных и положительных чисел” (Звучит космическая музыка).

III Закрепление знаний.

Учитель: Внимание, наш компьютер сообщает, что поступил сигнал SOS: “ С планеты “Отрицательных и положительных чисел” пиратами похищен Магистр отрицательных наук. Просьба ко всем, кто находится близко к зоне похищения, помогите”. Капитанам экипажей принять решение. Решено. Корабль меняет курс к Планете пиратов. Экипажу быть в полной боевой готовности.

Учитель: Внимание. Справа по курсу Планета “Ветряных мельниц”. Пираты побывали и здесь, они испортили механизм мельниц. Необходимо оказать помощь местным жителям. Жители планеты просят, чтобы мы выполнили все действия и решили примеры, этим мы исправим механизм мельниц.

(На доску на магнитах крепятся “ветряные мельницы” рисунок №3>, каждый ряд выполняет задания под своим номером. Консультанты проверяют правильность выполнения задания своего экипажа. Работа групповая.)

Ответы: мельница №I ( -2;8;-2, 5;-10;-40;24)

мельница № II (2;-16;1;-7;-10;16)

мельница № III (9;40;-2.5;0;25;-40)

Учитель. Молодцы! Все справились и с этим заданием. Продолжаем наш полет. Посмотрите в окна иллюминаторов, какие красивые крупные звезды в ночном небе, мы с вами пролетаем через скопление звезд, которые образуют созвездия. Определите, какие созвездия встречаются на нашем пути (На доску прикрепляются магнитные карты 6 созвездий рисунок №4>. Учащиеся выполняют записанные примеры на доске, и по правильным ответам определяют название созвездий.Коллективная работа).

Задание. Чтобы определить название созвездий нужно решить примеры.

Ответы (-1; 71;16;-8/15)

Названия созвездий: Волк – ответ: 16, Кассиопея – ответ: 16, Цефей – ответ: 71, Журавль –ответ: 8/15, Павлин – ответ: 1, Муха – ответ: 71.

Правильные созвездия: Павлин, Муха, Волк, Журавль-это созвездия южного полушария. Остальные созвездия северного полушария.

Учитель: Внимание экипажу: впереди по курсу Планета “Горы Мозгодрома”. Совершаем посадку для разведки.

Задача экипажу: Необходимо подняться на вершину горы, чтобы посмотреть, где находится планета пиратов “Пиратские острова”.Чтобы подняться на вершину, необходимо преодолеть 3 трудности(На доску прикрепляется нарисованная модель горы (рисунок 5) с разными уровнями-трудностями. В каждой группе есть слабые учащиеся, они выполняют задания уровня 2 и уровня 3, сильные учащиеся делают все задания. Дифференцированное задание).

Работа по группам:

Трудность 1. Решить уравнение.

Ответ: х=1.5

Трудность 2. Найти значение выражения.

-42Y при Y=-30;5

Ответ: Y=1260;-210

Трудность 3. Решить уравнение.

Ответ:

Учитель: Внимание, мы подлетаем к Планете “Пиратские острова”. Угадайте, кого уважают пираты. Храбрых? Нет. Сильных? Нет. Ловких? Нет. Неверно. Больше всего пираты любят математику и математиков. Об этом даже в пиратской песне поется:

“Математика-наука мировая,
И главней науки в целом мире нет
Можно все считать от кошки до трамвая
От орехов, между прочим, до конфет”

Без математиков пираты не смогли бы сосчитать сокровища. А сокровища, как известно, любят все. Для переговоров с пиратами высылаем парламентера. Пираты согласны отпустить магистра отрицательных чисел с одним условием, что мы выполним их задания:

Условие 1 Отгадать, как зовут их атамана. (рисунок 7) (Карточки для индивидуальной работы)

Вам предлагается разложить числа в порядке возрастания, чтобы узнать имя.

Ф	Е	М	Н	Л	Ь	С	А	Т
0	0, 5	-13	-0, 5	2	5	-0, 25	-5	12

Ответ:

-13	-5	-0, 5	-0, 25	0	0, 5	2	5	12
М	А	Н	С	Ф	Е	Л	Ь	Т

Условие 2. Помогите решить задачу. Нужно расставить знаки вместо звездочек, чтобы получилось верное равенство.

А) -3, 2*5= -16 б) -9, 1*(-10)=0, 91 в)-73*73=0

Правильные ответы: а) умножение б) деление в) сложение.

Учитель. Молодцы, ребята, вы все сделали правильно, пираты согласились отпустить магистра отрицательных наук (рисунок №6), благодаря вашей помощи, вашим знаниям и находчивости, вашей крепкой дружбе. И в благодарность магистр приглашает нас принять участие в конференции на тему “Отрицательные и положительные числа”. Нам нужно к ней еще хорошо подготовиться, повторить правила, приемы умножения и деления, поэтому мы с вами возвращаемся домой.

Прошу занять свои места. Корабль держит курс на планету “Земля”.

Полет прошел нормально. Посадка прошла успешно.

Вот мы с вами, ребята, и дома. Давайте подведем итоги нашего путешествия.

IV. Итоги урока.

Понравилось путешествовать?

Как вы думаете, какие знания помогали нам в путешествии? Что нужно знать и уметь по данной теме, чтобы принять участие в конференции?

Консультанты подают результаты- карточки, в которых указаны значками “+” все этапы активной работы экипажа, по этим результатам выставляется оценка за урок.

V. Домашнее задание.

Вам предлагается подготовиться к конференции по теме “Положительные и отрицательные числа”. Для этого вам нужно придумать любое разнообразное творческое задание по данной теме, например, тест, сказка, игра, математическое лото, дидактическая карточка, ромашка для устного счета. И кроме этого, конечно, повторить правила по данной теме. Дифференцированное задание: сильным учащимся (группа А) дается задание творческое, слабым (группа С) задание: “Проверь себя сам”, (ключ к заданию дается на следующем уроке) и творческое задание по желанию.

Карточка для домашнего задания

1) Вычислите -12+23= ; -90-67= 345х(-12)= 34-(-56)=

2) Найди значение выражение -12хс = при с= -1234;45

-23-(с) при с =-67;-67.

ГДЗ: Математика 6 класс Никольский, Потапов

Математика 6 класс

Тип: Учебник

Авторы: Никольский, Потапов

Издательство: Просвещение

ГДЗ: МАТЕМАТИКА 6 КЛАСС НИКОЛЬСКИЙ, ПОТАПОВ — УЧЕБНИК

Математика — царица науки, разнообразие которой мы начинаем постигать уже в 6 классе. Учебник математики 6 класса посвящен изучению основ алгебры. Начинается углубленное изучение дробей и действий с ними, отрицательные числа. Решение линейных уравнений, задач на проценты, составление несложных буквенных выражений и формул, знакомство с координатной плоскостью. Школьники узнают геометрические фигуры, вычисляют задачи на нахождение геометрических величин, используя изученные свойства фигур и формулы. Поэтому пробелы в знаниях, полученные на данном этапе, могут сказаться в дальнейшем не только по этому предмету, но и при изучении других школьных дисциплин (физика, химия, астрономия и т.д.).

ПРИЧИНЫ ВОЗНИКНОВЕНИЯ «ПРОБЕЛОВ»

Основными проблемами школьников при усвоении материала являются:

Большое количество тем для изучения.
Недостаточность времени на закрепление материала.
Наличие не устраненных «пробелов» в знаниях.

С каждым годом объем и сложность материала увеличиваются. Все меньше времени уходит на повторение материала и все больше на изучение новых тем. Порой некоторые темы пролетают не оставив и следа в голове школьника. Все это может привести к катастрофическим последствиям. В таких ситуациях родители, вовремя подметив неладное начинают искать выход.

КАК ПОМОЧЬ ШКОЛЬНИКУ

Если ребенок стесняется признаться в классе учителю что не понимает тему, решение вопроса ложится на родителей. Перед ними возникает несколько путей:

Помочь самостоятельно.
Нанять репетитора.
Предоставить ребенку возможность самостоятельно разобраться.

Родителя порой не в силах помочь детям в связи с отсутствием времени, а репетитора может позволить себе не каждый. В таких ситуациях выходом становится использование ГДЗ. На примере решенных заданий, ребенок может самостоятельно разобраться и устранить все недочеты в своих знаниях.

ЧТО СОДЕРЖИТ ГДЗ

В ГДЗ имеются решения задач различной трудности к учебнику «Математика 6 класс Никольского» и рассматриваются все темы, согласно стандартам школьной программы.

НУЖЕН ЛИ РЕШЕБНИК

Предлагаемый решебник к учебнику «Математика 6 класс Никольский» издательство «Просвещение» поможет понять сложные моменты изучения данного материала. Школьник сам может проверить правильность решения задания. А при наличии ошибки, найти на каком этапе решения она была совершена, чтобы в дальнейшем ее не допускать. ГДЗ полезна не только родителям (могут проконтролировать), но и школьникам — для лучшего усвоения школьного курса математики.

ГДЗ по математике 6 класс контрольно-измерительные материалы Попова Решебник

Автор: Попова Л.П.

Издательство: ВАКО 2017

Тип книги: Контрольно-измерительные материалы (КИМ)

Если вам тяжело дается учеба, то можно заглянуть на наш замечательный сервис и отыскать там ГДЗ контрольно-измерительные материалы по математике 6 класс Попова . Конечно, все знают, что самые большие трудности и проблемы у всех возникают с царицей наук. И дело тут не в том, что она неинтересная, скучная или ненужная. Просто для того, чтобы быть успешным, надо учить массу формул, законов, теорем, аксиом, постулатов. Также важно научиться применять эту пройденную теорию на практике, а для этого, в первую очередь, нужно ее понимать, вникать в это. К сожалению, не всегда у учителя получается за 40-45 минут разъяснить обширную и сложную тему всем. Разумеется, некоторые ребята остаются неподготовленными и не знают, как делать работу на дом. В таких ситуациях на помощь и приходит подспорье, доступ к которому открыт круглосуточно!

Какую пользу можно извлечь из учебно-методического комплекса с кимами по математике за шестой класс от Поповой

Предложенный решебник был выпущен знаменитым издательством «Мнемозина» в 2011 году. А его созданием занимались квалифицированные и известные специалисты. Они много лет жизни посвятили преподаванию в школах, гимназиях, лицеях, а некоторые – даже в высших учебных заведениях. Благодаря этому опыту у них есть точное и ясное представление о том, как нужно подавать материал детям, даже самым отстающим. Ведь любого ребенка можно научить и превратить в отличника, главное – желание и старания. Список преимуществ онлайн-решебника по математике контр-измер. матер. за шестой класс от Поповой:

помогает развить метапредметные, предметные и личностные универсальные учебные действия;
полное соответствие с оригинальным печатным учебником и с его структурой;
экономия времени на проверку д/з, что позволит уделять больше внимания другим не менее важным занятиям и секциям;
на сайте представлены пояснения, рассортированные по категориям. Это позволяет без проблем найти нужные ответы и справиться с задачей.

Быстрый поиск

Тест 1. Варианты

Тест 2. Варианты

Тест 3. Варианты

Тест 4. Варианты

Тест 5. Варианты

Тест 6. Варианты

Тест 7. Варианты

Тест 8. Варианты

Тест 9. Варианты

Тест 10. Варианты

Тест 11. Варианты

Тест 12. Варианты

Тест 13. Варианты

Тест 14. Варианты

Тест 15. Варианты

Тест 16. Варианты

Тест 17. Варианты

Тест 18. Варианты

Тест 19. Варианты

Тест 20. Варианты

Тест 21. Варианты

Тест 22. Варианты

Тест 23. Варианты

Тест 24. Варианты

Тест 25. Варианты

Тест 26. Варианты

Тест 27. Варианты

Тест 28. Варианты

Тест 29. Варианты

Тест 30. Варианты

Тест 31. Варианты

Тест 32. Варианты

Тест 33. Варианты

Тест 34. Варианты

Контрольные работы

КР-1. Варианты

КР-2. Варианты

КР-3. Варианты

КР-4. Варианты

КР-5. Варианты

КР-6. Варианты

КР-7. Варианты

КР-8. Варианты

КР-9. Варианты

КР-10. Варианты

КР-11. Варианты

КР-12. Варианты

КР-13. Варианты

КР-14. Варианты

Итоговая контрольная работа. Варианты

На любой ступени обучения школьнику требуется помощь по учёбе. Но иногда ребёнок не хочет получать её от взрослых, желает разобраться самостоятельно. Такое возникает чаще всего в среднем звене ввиду подросткового возраста. Конечно, мамы и папы переживают, некоторые даже нанимают репетиторов. Но ведь далеко не каждая семья может позволить себе такую роскошь. Поэтому мы и предлагаем вам абсолютно бесплатный ресурс, который в любой ситуации сможет помочь.

Почему всем так нравится сборник по математике КИМ за 6 класс от Поповой

Чтобы найти ключ, выполняя домашнее задание, достаточно указать страницу, соответствующую школьному изданию. При выполнении д/з школьнику понадобится оригинальная тетрадь и онлайн-книга, которую можно открыть на телефоне. При выборе номера ученик получит подробное письменное решение и верные ответы. Любой пользователь легко разберется в представленном материале. Наглядные схемы, яркие рисунки помогут донести информацию в более понятной форме. К тому же, навигация у сайта удобна и понятна, в ней сможет разобраться даже младшеклассник. В связи со всем вышеперечисленным процесс обучения станет приятным и веселым, а не скучным и однообразным. Ведь с помощью этого учебно-методического комплекса учитель-предметник сможет составлять интересные и увлекательные задания, а не просто давать упражнения из оригинального печатного учебника. В итоге даже те дети, которые далеко не в восторге от царицы наук, начнут включаться в учебный процесс и познавать все тайны и хитрости. Ведь лучшая награда для преподавателя – это успешные и положительные результаты его учащихся. Также мамы и папы будут радоваться, подписывая каждую неделю дневник своему чаду. Не думайте, что ребята будут просто бездумно переписывать всю инф-цию, объясните им правила работы с онлайн-гдз, и успех не заставит долго ждать! А теперь давайте обратимся к преимуществам, о которых мы еще не успели сказать:

выполнение внеклассных задач проходит качественнее и быстрее, освобождается время для хобби, посещений кружков или просто для активного отдыха;
при самостоятельной подготовке домашнего задания учащийся может проверить свои знания и восполнить пробелы в памяти;
возможность использование ресурса с любого электронного устройства с выходом в интернет.

Содержание пособия по математике для шестого класса авторы: Попова Л. П.

Книга включает главы и параграфы, обязательные для усвоения:

Простые и составные числа.
Приведение дробей к общему знаменателю.
Прямая и обратная пропорциональные зависимости.

Темы исследовательских проектов по математике в 6 классе

На страничке представлены темы проектов по математике для 6 класса школы, по которым учащимися предлагается проведение исследований, связанных с делимостью чисел, наибольшим общим делителем и наименьшим общим кратным, сложением и вычитанием обыкновенных дробей с разными знаменателями, умножением и делением обыкновенных дробей.

Представленные темы проектов по математике для 6 класса позволяют в процессе исследовательской работы более углубленно изучить основные арифметические действия с отрицательными числами, линейные уравнения с одной неизвестной, прорешать более сложные задачи.

Руководитель проекта поможет подстроить представленные темы исследовательских работ по математике для 6 класса школьникам под специфику работы, учитывая индивидуальные особенности автора проекта.

Темы исследовательских работ по математике для 6 класса

Примерные темы исследовательских работ по математике для учащихся 6 класса:

Авторские задачи для учащихся 6-го класса по теме «Проценты».
Алгебра в арифметике.
Арифметика Магницкого
Астрология на координатной плоскости
Влияние математических действий на аликвоты
Веселые математические задачки
Геометрия в национальном костюме народов России.
Действительные числа.
Делимость чисел
Делимость чисел и метод подобия.
Делимость чисел. Принцип Дирихле.
Десятичные дроби
Десятичные дроби и действия над десятичными дробями.
Дроби и единицы измерения.
Дроби и проценты
Дроби. Сравнение дробей.
Египетские дроби
Его величество процент.
Загадочный мир пропорций!
Задачи на делимость чисел.
Задачи на десятичную запись числа.
Задачи на переливание жидкости
Задачи о четных и нечетных числах.
Занимательная математика.
Занимательные задачи по математике для учащихся 6-х классов.
Золотая пропорция
Золотое сечение — высшее совершенство.
Золотое сечение в математике.
Знаменитые задачи древности. Трисекция угла.
Из истории возникновения математических знаков и символов.
Иллюстрации и решения занимательных задач по математике для учеников 6-го класса.
Исследование признаков делимости чисел
История календаря.
История модуля
История Москвы в задачах.
Как люди научились считать?
Как с помощью НОК и НОД решаются разнообразные и интересные задачи.
Координатная плоскость и знаки зодиака
Координатная плоскость и шахматы
Координатная плоскость в рисунках.
Кратные числа
Леонид Филиппович Магницкий.
Летопись открытий в мире чисел и фигур.
Магический квадрат — магия или наука
Магия чисел и знаков.
Магические числа
Масштаб и его применение.
Масштаб. Работа с компасом, GPS-навигация
Математика на клетчатой бумаге
Математическая модель вышивания на окружности.
Математические головоломки.
Меры времени.
Метрическая система мер.
Многоугольники.
Модуль и его свойства
Модуль числа.
«Модуль» – пособие в помощь ученику.
Наименьшее общее кратное взаимно простых чисел.
Начальные понятия теории чисел для шестиклассников.
Начальные сведения о модуле.
НОД и НОК и их практическое применение.
НОД и НОК при решении задач.

Темы проектов по математике для 6 класса

Примерные темы проектов по математике для учащихся 6 класса:

Орнаментальное и геометрическое искусство М. Эшера.
Откуда возникла геометрия?
Отрицательные и положительные числа.
По жизни с дробями
Положительные и отрицательные числа вокруг нас.
Приемы быстрого счета.
Приемы удобного счета.
Признаки делимости многозначных чисел на однозначное число.
Признаки делимости натуральных чисел на числа от 2 до 25 и на 50.
Признаки делимости натуральных чисел.
Признаки делимости чисел.
Применение признаков делимости при решении задач.
Принцип Дирихле.
Про любовь к математике и отрицательные числа.
Пропорции.
Пропорция в жизни человека.
Пропорция в работах великого Леонардо да Винчи.
Пропорция и золотое сечение.
Простые и составные числа.
Решето Эратосфена.
Связь НОК и НОД.
Секрет происхождения арабских цифр
Системы счисления.
Системы счисления разных цивилизаций
Сложение дробей с разными знаменателями.
Сокращение дробей
Сравнение, сложение и вычитание дробей с разными знаменателями.
Сравнения как метод исследования делимости натуральных чисел.
Старинные задачи на дроби
Старинные задачи на составление уравнений.
Старинные задачи.
Старинные математические задачи
Теория вероятностей в задачах.
Теория делимости
Треугольные числа.
Трудные задачи на движение.
Трудные задачи на на работу.
Удивительный мир периодических дробей.
Уравнения с одной переменной.
Числа знакомые и незнакомые.
Числа и их делимость.
Эти «непростые» простые числа.

Перейти к разделу:
Исследовательские проекты по математике
Темы проектов по математике по фгос

Если страница Вам понравилась, поделитесь в социальных сетях:

Что вы изучаете математику в шестом классе?

Математические концепции шестого класса связаны с очень широким спектром математики темы. Тем не менее, это математические концепции, которые студенты должны понимать к концу шестого класса на основе Национального совета учителей математики стандартов.

Что касается концепций Numbers and Operations , то это концепции, которые изучают ученики шестого класса. Студенты изучают дроби, десятичные дроби и проценты. Они используют эти концепции для решения проблем, словесные задачи и уметь правильно разместить их в числовой строке.Они учатся применять и использовать проценты, превышающие 100 и меньше 1. Понимание дробей имеет решающее значение для их способность изучать математику более высокого уровня в старших классах средней школы.

Другая область чисел и операций, которую они изучают, — это использование факторов, кратные, простые числа для решения задач и задач со словами. Они продолжить свою подготовку по элементарной алгебре, используя и применяя распределительное свойство и коммутативное свойство в дополнение и умножение.Затем они дополнительно применяют свойство ассоциативности. и умножение. Их исследования продолжаются в области квадратных корней. чисел, поскольку они применяются к обратным отношениям сложения и вычитание.

В области Геометрия концепций учащиеся шестого класса развивают понимание двух и трехмерных объектов, таких как: квадраты, прямоугольники, конусы, сферы, цилиндры и т. д. Они также изучают многоугольники поскольку они относятся к линиям, которые параллельны и перпендикулярны.Дополнительный области геометрии и форм — в центре внимания трансформации и симметрия форм при их переворачивании, повороте и повороте.

Студенты также узнают, как определять площадь и объем предметов, используя математические формулы. К ним относятся квадраты, призмы, прямоугольники, конусы, круги, сферы, цилиндры и т. д. Они также тратят время на изучение как применять геометрические фигуры в реальных приложениях, а также подключения к предметным областям контента.

Область концепции Измерение сосредоточена на использовании стандарта и нестандартные единицы измерения для определения взаимосвязей между разными объектами.Это также связано с геометрией как они учатся измерять площадь, объем и массу различных геометрические фигуры. Они учатся измерять все аспекты кругов, призмы и пирамиды.

В области концепций Data Analysis and Probability , студенты используйте соответствующий язык для объяснения результатов экспериментов и моделирования. Они учатся составлять вопросы, которые помогут им найти различия. между выборками буксировки в популяции.

Когда дело доходит до Решение задач , ученики разрабатывают задачу стратегии решения, которые помогут им развить фундаментальное понимание математики.Учащиеся используют задачи со словами и другие симуляции реального мира. в проблемных ситуациях.

В концепции Представления , студенты учатся собирать и систематизировать данные. Затем используйте данные для решения проблем. Ответы представлены в виде физических и социальных моделей. Они используют данные рисовать графики, диаграммы, таблицы и другие формы, чтобы объяснить, как они решил проблему.

Для Connection концепций учащиеся учатся устанавливать связи к реальным приложениям и другим предметным областям контента.Это включает в себя установление связей с другими понятиями в математике.

Ученики учатся Передают свои математические идеи в форма предложений, рисунков, плакатов и мультимедийных приложений. Это используется для определения уровня их понимания, когда они объясняют математические понятия другим студентам и учителям.

Студенты используют логическое Reasoning and Proof для объяснения своих математические выводы и методы решения проблем. Эта концепция также используется как метод для студентов, чтобы защитить ответы, которые они получите во время расчетов.Эта концепция используется для улучшения умственных способностей. математические навыки и связи с другими математическими концепциями.

Все эти математические концепции используются для разработки всестороннего базовые знания математических идей и языка по мере успеваемости студентов к более высоким уровням математики.

Четыре основных математических понятия, которые ваши дети изучают в 5–6 классах | Scholastic

С пятого класса на шестой может произойти значительный скачок в знаниях математики, и мне нравится думать об этом как о переходе через мост.Чем больше мы соединим мост, тем лучше наши дети будут чувствовать себя в средней школе. Пятый класс — это кульминация всего, что ученики узнали на начальном уровне, а шестой класс можно рассматривать как отправную точку для средней школы. И независимо от того, как устроена средняя школа вашего ребенка, между этими оценками существует четкая связь. Чем более комфортно дети усваивают эти концепции к концу шестого класса, тем лучше они будут подготовлены к средней школе.

Вот четыре основных математических понятия, которые ваш ребенок усвоит в пятом и шестом классе:

1.Система счисления. В пятом классе ученики сосредотачиваются на сложении, вычитании, умножении и делении целых чисел, дробей и десятичных знаков. Ваш ребенок научится свободно вычислять эти типы чисел и понимать взаимосвязь между ними. Студенты также должны уметь использовать эти числа в реальных сценариях. В шестом классе дети продолжают понимать эти числа, а также знакомятся с отрицательными числами. Они начнут определять рациональные числа и целые числа в числовой строке, а также сравнивать их.Использование моделей значительно улучшит понимание ребенком этих концепций.

Поощряйте своего ребенка:

Распознавайте и вычисляйте, используя дроби и десятичные дроби в реальном мире. Например, попросите ребенка вычислить скидку на распродаже; сумма налога при совершении покупок; найдите кончик счета или объясните спортивную статистику.
Используйте дробные линейки для вычислений (сложение, вычитание, умножение или деление).

Изображение предоставлено: LearnZillion

Найдите примеры положительных и отрицательных чисел в реальном мире (температура, расстояние, уровень моря и т. Д.)) и используйте модели, чтобы понять взаимосвязь между ними.

Изображение предоставлено: положительное влияние Math

2. Коэффициенты. Учащиеся будут использовать свои знания о дробях и десятичных дробях в пятом классе для оценки соотношения разума и оценки задач в шестом классе. Детям нужно будет связать свое понимание умножения и деления с реальными задачами с использованием соотношений. Они будут использовать модели (диаграммы, таблицы, двойные числовые линии и т. Д.), Чтобы помочь им установить эти связи и решить проблемы с удельной стоимостью.Студенты также узнают о процентах и о том, как они соотносятся с дробями и десятичными знаками.

Поощряйте своего ребенка:

Найдите примеры соотношений в реальном мире. Например, « Соотношение крыльев и клювов в скворечнике в зоопарке было 2: 1, потому что на каждые 2 крыла приходился 1 клюв».
Используйте модели, чтобы понять проблемы соотношения и скорости:

Изображение предоставлено: 6-й класс мистера Пратта

Изображение предоставлено: nzmaths.

Создавайте реальные проблемы, используя понимание соотношений. Например, « В этом рецепте соотношение 3 стакана муки к 4 стаканам сахара, поэтому на каждый стакан сахара приходится 3/4 стакана муки».

3. Выражения и уравнения. Учащиеся начинают понимать разницу между выражением и уравнением. Они используют переменные для представления неизвестного числа как в выражениях, так и в уравнениях. Ученики пятого и шестого классов следуют соответствующему порядку действий для решения задач, включая скобки и показатели.Ваши дети начинают читать, интерпретировать и писать выражения и уравнения, а также решать уравнения с одной переменной.

Поощряйте своего ребенка:

Различайте выражение и уравнение и поймите значение знака равенства:

Выражение: 4y + 2
Уравнение: 4y + 2 = 14

Решайте проблемы, используя аббревиатуру PEMDAS:

Изображение предоставлено coolmath.com

Легко читать и писать выражения: Вычтите n из 8 дюймов как 8 — n.
Создавайте и решайте реальные проблемы с помощью переменных. Например: « Аренда катка стоит 100 долларов плюс 5 долларов на человека. Напишите выражение, чтобы найти стоимость для любого количества (n) человек. Сколько стоит 25 человек? Ответ: 100 + 5n; так что для 25 человек = 100 + 5 (25) = 225 ».

4. Геометрия: Учащиеся продолжают классифицировать фигуры по категориям в зависимости от их свойств.Ваш ребенок научится находить площадь треугольников и некоторых четырехугольников. Они научатся вычислять объем трехмерных фигур, используя целые числа и дробные части. Учащиеся начинают использовать представление реальных проблем путем нанесения точек на координатную плоскость.

Поощряйте своего ребенка:

Поймите разницу между поиском площади двухмерной фигуры и поиском объема трехмерной фигуры. Укажите на разные предметы и спросите, найдет ли ваш ребенок площадь или объем этой фигуры.Например, «Вы можете найти площадь или объем этого заднего двора?» Или: «Вы бы нашли объем этого бассейна?»
Используйте соответствующий словарь при описании различных многоугольников и геометрических свойств. Например, «Что такое параллельные прямые?» Ответ: «Две линии на плоскости, которые никогда не пересекаются. Они всегда находятся на одинаковом расстоянии друг от друга».
Используйте их обучение в третьем классе, чтобы понять, как найти площадь прямоугольника или найти значение треугольника:

Изображение предоставлено: Департамент математического образования Университета Джорджии

Развивайте понимание координатной плоскости и начинайте наносить точки, используя реальные сценарии (используя миллиметровую бумагу).Например, «На карте библиотека расположена в (-2, 2), здание мэрии — в (0,2), а средняя школа — в (0,0). Представьте местоположения в виде точек на координатной сетке с единицей измерения 1 миля ».

Не волнуйтесь, если эти концепции поначалу кажутся немного пугающими. Помните, что вы не посещали ежегодные уроки математики, которые опираются друг на друга, как ваши дети. (Сначала может показаться, что ваши дети понимают это лучше, чем вы!)

Но в этом суть нашей серии блогов «Основные математические концепции».Мы хотим, чтобы и были наделены пониманием этих математических концепций. Вы можете быстро начать обучение своих детей, вы можете идти в ногу с ними, но это поможет вам больше общаться со своим ребенком по тому, что часто является сложным предметом.

У вас есть вопросы по этим концепциям или по математике вашего ребенка? Отправьте их Дженнифер здесь, чтобы она могла ответить в следующем блоге. Или поделитесь ими с нами на странице Scholastic Parents в Facebook.

Изображение предоставлено: © Oktay Ortakcioglu / iStockphoto

6 класс по математике

Обзор курса В курсе математики Acellus для 6 класса учащиеся изучают математические концепции, которые помогут им в переходе в среднюю школу и подготовке к предалгебре.Г-н Роджерс воплощает математику в жизнь, предлагая привлекательные и увлекательные приложения из реального мира.

Темы курса включают:

Соотношения, нормы и пропорции
Дроби, десятичные знаки и проценты
Сложение и вычитание десятичных знаков
Умножение и деление десятичных знаков
Умножение и деление на дроби и смешанные числа
Общие и необычные знаменатели
Целые и рациональные числа
Выражения, экспоненты и переменные
Математические свойства и выражения
Одношаговые уравнения
Решение одношаговых уравнений с десятичными, дробными и перекрестными произведениями
Функции и неравенства
Двух- и трехмерные фигуры
Статистика

Математику 6 класса Acellus преподает инструктор Acellus Марк Роджерс.

Пример урока — Ситуации из реального мира

;

Этот курс разработан Международной академией наук. Учить больше

Объем и последовательность

Блок 1 — Передаточные числа Учащиеся начинают курс математики 6-го класса с изучения соотношений — определения и записи соотношений соотношений, а также использования умножения для сравнения чисел. Они исследуют правила делимости, множители, наибольшие общие множители и упрощающие отношения, а также практикуются на реальных примерах. Блок 2 — Нормы и пропорции В этом разделе учащиеся узнают, что подразумевается под расценками. Они практикуются в их поиске, а затем исследуют, как эта концепция используется в реальном мире. Затем они определяют пропорции и упражняются в их написании. Они решают проблемы, используя пропорциональные отношения, и исследуют реальные ситуации, в которых могут использоваться пропорции. Блок 3 — Дроби, десятичные дроби и проценты Студенты изучают основы дробей и десятичных знаков. Они изучают преобразование между этими двумя формами и практикуют преобразование дробей в десятичные и десятичные в дроби. Блок 4 — Проценты Затем студенты изучают проценты. Они учатся записывать проценты как дроби и десятичные дроби, а десятичные и дробные числа — как проценты. Они проверяют проценты больше 100% и меньше 1%. Они учатся использовать гистограмму для вычисления процентов и считают, как дроби, десятичные дроби и проценты связаны друг с другом. Блок 5 — Сложение и вычитание с десятичными знаками Этот блок начинается с принципов, необходимых для добавления десятичных знаков. Студенты учатся складывать целые числа с десятичными и добавлять десятичные к десятичным.Они рассматривают, как эти навыки можно использовать в реальном мире. Они продолжают изучать принципы, используемые для вычитания десятичных знаков, а затем практикуют вычитание десятичных знаков из целых чисел, а также вычитание десятичных знаков из десятичных. Они исследуют, как эти навыки можно применить для решения реальных проблем. Блок 6 — Умножение и деление с десятичными знаками Затем ученики повторяют умножение целых чисел, а затем расширяют свое понимание десятичных дробей, умножая десятичные дроби и целые числа.Они изучают умножение десятичных дробей на десятичные дроби, умножение и деление десятичных дробей на степени десяти. Блок 7 — Больше делений с десятичными знаками Учащиеся изучают стандартный алгоритм деления целых чисел, затем рассматривают деление десятичных дробей на целые числа и исследуют практическое применение этого навыка. Далее они углубляются в деление десятичных знаков на десятичные дроби, а затем сравнивают и сравнивают четыре операции с десятичными знаками. Блок 8 — Умножение дробей и смешанных чисел Уделяя особое внимание умножению дробей, учащиеся изучают умножение дробей на целые числа.Они учатся находить процент числа, умножать дроби на дроби и упрощать перед умножением дробей. Они рассматривают практическое применение этих навыков, а затем обсуждают разницу между смешанными числами и неправильными дробями, а также способы преобразования одного числа в другое и обратно. Они также исследуют, как умножать смешанные числа. Блок 9 — Деление на дроби В этом разделе учащиеся начинают с деления целых чисел на дроби и исследуют практическое применение этого навыка.Они продолжают деление дробей на дроби, деление смешанных чисел и деление смешанных чисел и дробей. Они используют умножение, чтобы убедиться, что десятичные дроби и дроби — это два способа записать одно и то же число. Блок 10 — Общие и необычные знаменатели Начиная с обзора сложения и вычитания дробей, имеющих общие знаменатели, студенты затем повторяют, как найти наименьшее общее кратное. Затем они исследуют сложение и вычитание дробей с необычными знаменателями.Они сравнивают и противопоставляют четыре операции, выполняя их все с одной и той же парой дробей. Блок 11 — Целые и рациональные числа Учащиеся изучают практическое использование целых чисел, а затем изучают графики, абсолютные значения, а также сравнение и упорядочение целых чисел. Затем они определяют рациональные числа и учатся их сравнивать и упорядочивать. Они учатся находить и графически отображать упорядоченные пары, а также исследуют рациональные числа на координатной плоскости. После этого модуля студентам предоставляется промежуточный обзор и экзамен. Блок 12 — Выражения, экспоненты и переменные В этом модуле студенты исследуют переменные. Они обсуждают части выражения и определяют, как записывать словесные фразы как выражения. Они исследуют использование показателей степени и изучают порядок операций. Они обсуждают замену значений переменных и использование подстановки в алгебраических выражениях. Раздел 13 — Математические свойства и выражения Учащиеся обсуждают семь свойств математики и учатся использовать свойство распределения для умножения в уме.Они изучают эквивалентные выражения и используют свойство распределения для перезаписи и факторизации выражений. Они исследуют упрощение, комбинируя похожие термины, и углубляются в эквивалентные выражения. Глава 14 — Одношаговые уравнения Изучив уравнения, учащиеся исследуют их решение с заменой. Они учатся решать и писать уравнения сложения, вычитания, умножения и деления за один шаг, а также практикуются в решении уравнений за один шаг. Блок 15 — Решение десятичных уравнений Продолжая изучение решения уравнений, студенты рассматривают возможность использования десятичных знаков в этой операции.Они учатся использовать десятичные дроби для решения уравнений сложения, вычитания, умножения и деления. Затем они получают дополнительную практику решения уравнений с десятичными знаками. Блок 16 — Решение уравнений с дробями и перекрестными произведениями Дроби — это следующий тип чисел, который студенты изучают в связи с уравнениями. Они изучают и практикуют решение уравнений сложения, вычитания, умножения и деления с дробями. Они также учатся решать процентные задачи и решать уравнения с перекрестными произведениями. Раздел 17 — Функции и неравенства Студенты открывают для себя функции и узнают о таблицах функций. Они исследуют геометрические и арифметические последовательности и правила функций, а также пишут уравнения, представляющие функции. Они исследуют функции на координатной плоскости, графические линейные функции и изучают функции реального мира в виде таблиц и графиков. Затем они рассматривают неравенство и учатся писать и изобразить их. Блок 18 — Двумерные фигуры Начиная с обзора многоугольников, студенты изучают двумерные фигуры.Они учатся находить площадь и применять этот навык к параллелограммам. Они исследуют поиск недостающих длин параллелограммов и определение площади треугольников и трапеций. Они исследуют многоугольники на координатной плоскости и определяют их площадь и периметр. Они также узнают, как найти площадь составных фигур. Блок 19 — Трехмерные фигуры В этом модуле учащиеся анализируют трехмерные фигуры. Они учатся находить объемные прямоугольные и треугольные призмы и применять эти навыки в реальном мире.Также они умеют находить дробные длины сторон. Блок 20 — Больше трехмерных фигур Студенты узнают, что такое площадь поверхности и как ее измерить. Затем их учат, что такое сети и как их использовать для определения площади поверхности. Они применяют эти новые навыки с прямоугольными призмами, треугольными призмами и пирамидами. Раздел 21 — Статистика В этом последнем разделе студенты практикуются в понимании и определении статистических вопросов. Затем они исследуют точечные графики, за которыми следуют меры среднего значения, моды и медианы, а также меры вариации диапазона.Они исследуют среднее абсолютное отклонение и выбирают соответствующие меры, а также анализируют линейные графики, гистограммы, прямоугольные диаграммы и форму данных. За этим блоком следует Заключительный обзор и экзамен. В этом курсе нет разделов.

Учебная программа по математике для 6-х классов | Time4Learning

Посмотреть демо наших уроков!

Для преподавания математики в шестом классе потребуется всеобъемлющая программа обучения математике в шестом классе, которая будет у вас под рукой, чтобы вы могли эффективно обучать своего ребенка, одновременно делая изучение математики увлекательным.

Чтобы ваш ребенок достиг своих целей в обучении, важно, чтобы выбранная вами математическая программа для 6-го класса соответствовала всем государственным стандартам и предоставляла множество возможностей для практики. Это поможет вашему ребенку обрести уверенность в освоении новых математических понятий. Перейдите по ссылкам ниже, чтобы начать:

Что математике должен знать шестиклассник

Основными направлениями математики в учебной программе шестого класса являются определение чисел и операции, алгебра, геометрия и чувство пространства, измерения, функции и вероятность.Хотя эти направления математики могут вас удивить, они охватывают основы того, что должен изучать шестиклассник.

Учащиеся 6-го класса должны уже усвоить математические факты, чтобы помочь им понять более сложные математические концепции. Вот некоторые из навыков, которыми вы должны овладеть ученикам 6-го класса:

Умножение 3-значных чисел на 2-значные числа
Сравнение, округление и выполнение основных операций с десятичными знаками
Дроби: сложение, вычитание, упрощение, сравнение и т. Д.
Анализ данных с использованием гистограмм, линейных графиков, диаграмм Венна и т. Д.
Геометрия: с помощью транспортира, сортировка и классификация треугольников, многоугольников, четырехугольников

Узнайте больше об учебной программе Time4Learning по математике для шестого класса, изучив объем и последовательность занятий, а также планы уроков математики для шестого класса.

Задачи по математике для 6 класса

В начале учебного года вы должны определить некоторые математические цели и задачи для вашего ученика в шестом классе.Ниже приводится общее представление о задачах по математике в шестом классе, над достижением которых должен работать ваш ребенок.

Понимать концепции предалгебры, такие как использование переменных для упрощения выражений
Определить значение десятичного разряда; сравнить и упорядочить десятичные дроби, используя числовую строку
Используйте таблицы частот и определите подходящие интервалы
Знать, как использовать коэффициенты и коэффициенты для сравнения данных
Найдите и нанесите точки на координатный график, используя упорядоченные пары
Поймите соотношение между дробями, десятичными знаками и процентами.

Почему выбирают Time4Learning Программа домашнего обучения математике для шестого класса

Учебную программу по математике для 6-го класса можно использовать в качестве основной программы домашнего обучения или в качестве дополнения к другим учебным программам и для учащихся после школы. Тысячи семей постоянно доверяют Time4Learning, чтобы преподавать все важные концепции, которые студенты должны знать, и помогать им достичь всех своих целей на год.

Ниже приводится еще больше причин, по которым семьи по всей стране выбирают Time4Learning для своих шестиклассников.

В качестве полной учебной программы

Комплексная учебная программа охватывает все математические концепции, которые шестиклассникам необходимо изучить, чтобы построить прочную математическую основу.
Учебная программа представлена в форме, основанной на себе, и разбита на главы, уроки и упражнения.
Возможность изменить курс математики позволяет вашему ребенку пересмотреть концепции предыдущего года или получить фору в седьмом классе.
Возможность повторять уроки и пересдавать тесты и викторины в любом месте и в любое время.
Планировщики занятий и калькуляторы учебных программ помогают учащимся организовываться и работать независимо.
Учебная программа по математике для 6-го класса разработана в соответствии с национальными стандартами.
Родители могут участвовать и наблюдать, как новые математические концепции постепенно вводятся и осваиваются на практике.
Родители могут легко отслеживать успеваемость своего ребенка с помощью автоматической оценки и ведения записей, а распечатанные отчеты упрощают составление портфолио домашнего обучения.

В качестве дополнения

Предлагает множество занятий по математике для шестиклассников, испытывающих трудности в школе.
Уроки занимательные и интерактивные, поэтому учащиеся весело проводят время, осваивая продвинутые математические навыки.
Гибкость для входа в систему в любое время 24/7 делает его идеальным для занятий математикой после школы или на выходных.
Подход, ориентированный на учеников, означает, что ученики могут не торопиться с изучением сложных предметов и учиться в подходящем для них темпе.
Наша программа по математике для 6-го класса способствует развитию алгебраического мышления, чтобы помочь ученикам подготовиться к 7-му классу.
В нашей комплексной математической программе для 6-х классов дети распределяются по порядку в зависимости от их текущих навыков.
В качестве дополнительной математической программы ее можно адаптировать для удовлетворения конкретных потребностей учащихся и закрепить только те математические концепции, с которыми они борются.

Дополнительные ресурсы домашнего образования для 6-го класса

Математика для 6-го класса — Учебная программа, Вопросы по математике для 6-го класса

Учебная программа по математике для 6-го класса

Математика для 6-го класса, несомненно, является шагом вперед по сравнению с тем, что дети изучали в 5-м классе.Но не волнуйтесь, репетиторы Cuemath здесь, чтобы помочь и убедиться, что у вашего ребенка не возникнет проблем с выполнением учебной программы с онлайн-уроками. Многие дети сталкиваются с лежачими полицейскими разного размера на пути к математике. Это особенно верно в 6-м классе, когда так много новых, часто сложных математических теорий и моделей прилетает со всех сторон. Но репетиторы Cuemath могут помочь преодолеть этот страх в вашем ребенке и изменить его обучение.

Почему вашему ребенку в 6 классе нужно дополнительное обучение?

Ученики 6-го класса начинают узнавать много нового и выполнять операции над алгебраическими выражениями.Репетиторы Cuemath позаботятся о том, чтобы ваш ребенок легко перешел из 5-го в 6-й класс, и каждое онлайн-обучение позволит ему узнать что-то новое, будь то периметр, площадь поверхности и объем. Наши онлайн-занятия по математике помогут облегчить процесс обучения ваших детей в 6-м классе. Чего вы ждете, подпишитесь на бесплатное занятие по математике с одним из наших опытных преподавателей, а частные уроки ноу-хау могут повысить ценность вашего обучения. маленький ученик 6-го класса.

Онлайн-обучение математике для вашего чемпиона в 6-м классе

Из соотношения, пропорции, унитарного метода и процентного соотношения нет конца количеству способов, которыми ваш ребенок в 6-м классе может улучшить свои математические навыки.Увлекательные занятия, а не скучные рабочие листы увлекут детей новым опытом обучения, и Cuemath Tutors гарантирует, что сильный акцент делается на концептуальном понимании, а не на повторяющихся упражнениях. Каждое онлайн-обучение вашего ребенка в 6-м классе будет охватывать новую концепцию, и вскоре вы начнете замечать значительные улучшения в их успеваемости.

>> Визуализируйте математику с помощью интерактивных заданий по математике для 6-го класса

Найти репетитора для детей 6-го класса стало еще проще!

Будь то линии, углы, треугольники, четырехугольники и круги, репетиторы Cuemath помогут вам и вашему ребенку открыть для себя лучшее из математики 6-го класса.Большинству детей нелегко понять все сложности математики в 6-м классе, но онлайн-обучение в Cuemath может помочь упростить процесс обучения. Живые и персонализированные репетиторы Cuemath помогают раскрыть лучшее в вашем ребенке.

Чего вы ждете? Помогите своему шестикласснику влюбиться в математику вместо того, чтобы бояться этого предмета. Обучайте его онлайн с Cuemath!

Cuemath позволяет детям творить с помощью кода! Узнайте больше о том, как ученики могут научить детей программировать в Интернете и создать что-нибудь для себя.

Визуализация и исследование больших идей, 6 класс: Булер, Джо, Мансон, Джен, Уильямс, Кэти: 9781119358831: Amazon.com: Книги

Привлекайте своих учеников к визуальному творческому исследованию больших идей в математике

Серия Mindset Mathematics Серия предлагает уникальный, основанный на исследованиях визуальный подход к изучению важных математических идей, которые необходимы для успеха математики в будущем. Этот практический ресурс предназначен для любого учителя, который хочет вовлечь своих шестиклассников в рассуждение и упорство в решении проблем, и предлагает занятия, которые заинтересуют учащихся и покажут им, насколько важна математика в их жизни.

Во время своей работы с десятками тысяч учителей авторы Джо Болер, Джен Мансон и Кэти Уильямс услышали одно и то же сообщение: учителя хотят включить больше науки о мозге в свои инструкции по математике, но им нужно руководство по методам, которые лучше всего подходят для способствовать изучению математических понятий. В этом столь необходимом издании авторы ясно показывают, какие большие идеи есть в этом классе, почему их важно знать и как учащиеся могут лучше всего усвоить эти большие идеи.

Наполненный интересными вопросами, открытыми задачами и четырехцветным наглядным пособием, Mindset Mathematics разработан так, чтобы быть гибким, чтобы его можно было использовать с любой текущей учебной программой. Все упражнения и задачи включают инструкции по запуску в классе, предложения по облегчению динамических дискуссий и рекомендации о том, что нужно искать в мышлении учащихся по мере его развития.

Привлекайте своих учеников к визуальному творческому исследованию больших идей в математике

Серия Mindset Mathematics Серия предлагает уникальный, основанный на исследованиях визуальный подход к изучению важных математических идей, которые необходимы для успеха математики в будущем.Этот практический ресурс предназначен для любого учителя, который хочет вовлечь своих шестиклассников в рассуждение и упорство в решении проблем, и предлагает занятия, которые заинтересуют учащихся и покажут им, насколько важна математика в их жизни.

Во время своей работы с десятками тысяч учителей авторы Джо Болер, Джен Мансон и Кэти Уильямс услышали одно и то же сообщение: учителя хотят включить больше науки о мозге в свои инструкции по математике, но им нужно руководство по методам, которые лучше всего подходят для способствовать изучению математических понятий.В этом столь необходимом издании авторы ясно показывают, какие большие идеи есть в этом классе, почему их важно знать и как учащиеся могут лучше всего усвоить эти большие идеи.

Об авторе

ДЖО БОАЛЕР — профессор математического образования в Стэнфордском университете, соучредитель и директор факультета youcubed. Она работает советником в нескольких компаниях Кремниевой долины и ведет в Белом доме тему девочек и STEM (наука, технологии, инженерия и математика). Автор семи книг, в том числе «Математическое мышление», и многочисленных исследовательских статей, она регулярно пишет новости и радио в Соединенных Штатах и Англии.

ДЖЕН МАНСОН — научный сотрудник Северо-Западного университета, профессиональный разработчик и бывший преподаватель. Она получила докторскую степень по математике в Стэнфордском университете. Ее исследования сосредоточены на гибком и справедливом обучении математике.

КЭТИ УИЛЬЯМС — соучредитель и исполнительный директор youcubed в Стэнфордском университете. До работы в youcubed она была учителем математики в средней школе, а также занималась учебными программами по математике и администрацией в округах и округах Калифорнии.

M / J 6 класс по математике — 1205010

Рациональные числа на Аляске:

Следуйте за Маттео, когда он исследует противоположные числа, положительные и отрицательные рациональные числа и ноль в реальных условиях, планируя круиз по Аляске и отправляясь в него, в этом интерактивном руководстве.

Тип: Оригинальное учебное пособие для учащихся

Математические модели и социальное дистанцирование:

Узнайте, как математические модели могут показать, почему социальное дистанцирование во время эпидемии или пандемии важно, в этом интерактивном руководстве.

Тип: Оригинальное учебное пособие для учащихся

Плавание через вычитание десятичных знаков:

Пройдите через вычитание десятичных знаков до тысячных долей, используя стандартный алгоритм в этом интерактивном руководстве.

Тип: Оригинальное учебное пособие для учащихся

Добавить еще один топпинг: Добавление десятичных знаков:

В этом интерактивном руководстве вы научитесь добавлять десятичные дроби к тысячным с помощью стандартного алгоритма в магазине мороженого.

Тип: Оригинальное учебное пособие для учащихся

Балансировка машины:

Используйте модели для решения задач баланса на космической станции в этом интерактивном учебнике по математике и естествознанию.

Тип: Оригинальное учебное пособие для учащихся

Замки, катапульты и данные: гистограммы, часть 2:

Узнайте, как интерпретировать гистограммы для анализа данных и помочь изобретателю предсказать радиус действия катапульты в части 2 этой серии интерактивных руководств.В частности, вы научитесь описывать форму и распространение распределений данных.

Нажмите ЗДЕСЬ , чтобы открыть часть 1.

Тип: Оригинальное учебное пособие для учащихся

Замки, катапульты и данные: гистограммы, часть 1:

Узнайте, как создать гистограмму для отображения непрерывных данных о снарядах, выпущенных катапультами, в этом интерактивном руководстве.

Это первая часть из 2-х частей. Щелкните ЗДЕСЬ , чтобы открыть часть 2.

Тип: Оригинальное учебное пособие для учащихся

Ферма Маккодера, часть 4: Повторяющиеся циклы:

Изучите компьютерное кодирование на ферме с помощью операторов IF и повторяющихся циклов для вычисления математических выражений.В этом интерактивном руководстве вы также решите проблемы, связанные с неравенством.

Щелкните ниже, чтобы просмотреть другие руководства из этой серии.

Тип: Оригинальное учебное пособие для учащихся

MacCoder’s Farm, часть 3: If Утверждает:

Изучите компьютерное кодирование на ферме с помощью операторов отношения и операторов IF для оценки выражений.В этом интерактивном руководстве вы также решите проблемы, связанные с неравенством.

Щелкните ниже, чтобы просмотреть другие руководства из этой серии.

Тип: Оригинальное учебное пособие для учащихся

MacCoder’s Farm, часть 2: сведения о состоянии:

Изучите компьютерное кодирование на ферме с помощью операторов условия и IF в этом интерактивном руководстве.У вас также будет возможность применить порядок операций при использовании кода для решения проблем.

Щелкните ниже, чтобы просмотреть другие руководства из этой серии.

Тип: Оригинальное учебное пособие для учащихся

MacCoder’s Farm, часть 1: объявление переменных:

Изучите компьютерное кодирование на ферме, объявив и инициализировав переменные в этом интерактивном руководстве.У вас также будет возможность попрактиковаться в своих навыках деления в столбик.

Тип: Оригинальное учебное пособие для учащихся

Движение безумия:

Узнайте, как рассчитать и интерпретировать среднее абсолютное отклонение (MAD) наборов данных в этом интерактивном учебном пособии по статистике, посвященном путешествиям.

Тип: Оригинальное учебное пособие для учащихся

Что на обед?:

Узнайте, как писатели и ораторы создают аргументы, формулируя утверждение и подтверждая его причинами и доказательствами. В этом интерактивном руководстве вы услышите выступления кандидатов в президенты студенческого совета и выполните практические упражнения.

Тип: Оригинальное учебное пособие для учащихся

Это может быть зоопарк данных !:

Узнайте, как рассчитать и интерпретировать среднее, медианное значение, режим и диапазон наборов данных из зоопарка в этом интерактивном руководстве.

Тип: Оригинальное учебное пособие для учащихся

Коэффициент помощи шеф-повара:

Вы систематизируете информацию в таблице и запишите соотношения, эквивалентные заданному соотношению, для решения реальных и математических задач в этом интерактивном руководстве.

Тип: Оригинальное учебное пособие для учащихся

Куда делись все скраб-сойки ?:

Изучите ограничивающие факторы экосистемы Флориды и опишите, как эти ограничивающие факторы влияют на одно коренное население — Флоридскую скраб-сойку — с помощью этого интерактивного учебного пособия.

Тип: Оригинальное учебное пособие для учащихся

По горячим следам:

Изучите, как температура влияет на скорость химических реакций, в этом интерактивном руководстве.

Тип: Оригинальное учебное пособие для учащихся

Да или нет ГМО ?:

Узнайте, что такое генная инженерия и некоторые применения этой технологии.В этом интерактивном руководстве вы получите представление о некоторых преимуществах и потенциальных недостатках генной инженерии. В конечном итоге вы сможете критически относиться к генной инженерии и написать аргумент, описывающий вашу собственную точку зрения на ее влияние.

Тип: Оригинальное учебное пособие для учащихся

Гольф: где отрицательные числа — положительный момент:

Узнайте, как создавать и использовать числовые линии с положительными и отрицательными числами, графически отображать положительные и отрицательные числа, находить их расстояние от нуля, находить противоположность числа, используя числовую линию и знаки, и осознавать, что ноль является своей собственной противоположностью с этим интерактивом, учебник на тему гольфа.

Тип: Оригинальное учебное пособие для учащихся

Решение уравнений: одна и та же переменная, обе стороны, одно решение:

В этой сложной игре вы будете решать уравнения с переменными с обеих сторон.У каждого уравнения есть реальное решение. Используйте кнопку «Научи меня», чтобы просмотреть материалы перед испытанием. После испытания при необходимости просмотрите проблемы. Попробуйте еще раз, чтобы правильно ответить на все вопросы! Наборы вопросов различаются в зависимости от игры, поэтому не стесняйтесь играть в игру несколько раз по мере необходимости! Удачи!

Тип: Обучающая игра

Ice Ice Maybe: игра для оценки операций:

Эта веселая и интерактивная игра помогает отработать навыки оценки, используя различные операции по выбору, включая сложение, вычитание, умножение, деление с использованием десятичных знаков, дробей и процентов.

Различные уровни сложности делают эту игру подходящей для разных возрастов и уровней способностей.

Сложение / Вычитание: Сложение и вычитание целых чисел, сложение и вычитание десятичных знаков.

Умножение / деление: Умножение и сложение целых чисел.

Проценты: Определите процентное соотношение целого числа.

Дроби: Умножайте и делите целое число на дробь, а также применяйте свойства операций.

Тип: Обучающая игра

Сила цветов: игра с упорядочением рациональных чисел:

Это забавная интерактивная игра, которая помогает студентам практиковаться в упорядочивании рациональных чисел, включая десятичные дроби, дроби и проценты.Вы за деньги сажаете и собираете цветы. Позвольте пчеле опылять, и вы сможете приумножить урожай и денежное вознаграждение!

Тип: Обучающая игра

Дроби викторины:

Проверьте свои навыки дроби, отвечая на вопросы на этом сайте.В этом тесте вас просят упростить дроби, преобразовать дроби в десятичные числа и проценты, а также ответить на вопросы по алгебре, связанные с дробями. Вы даже можете выбрать уровень сложности, типы вопросов и ограничение по времени.

Тип: Обучающая игра

Викторина по алгебре на время:

В этом задании на время учащиеся решают линейные уравнения (одно- и двухшаговые) или квадратные уравнения различной сложности в зависимости от выбранных начальных условий.Это упражнение позволяет учащимся попрактиковаться в решении уравнений, в то время как упражнение записывает их баллы, чтобы они могли отслеживать свой прогресс. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.

Тип: Обучающая игра

Алгебра четыре:

В этом упражнении два ученика играют в имитационную игру «Соединение четырех», но для того, чтобы поставить фишку на доску, они должны правильно решить алгебраическое уравнение.Это упражнение позволяет студентам попрактиковаться в решении уравнений различной сложности: одношаговых, двухэтапных или квадратных уравнений и при желании использовать свойство распределения. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с апплетом Java.

Тип: Обучающая игра

Лабиринт игры:

В этом упражнении учащиеся вводят координаты, чтобы проложить путь к цели, избегая мин.Это задание позволяет учащимся изучить декартовы координаты и декартову координатную плоскость. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.

Тип: Обучающая игра

Улыбки:

В этом интерактивном задании по решению проблем учащиеся применяют алгебраические рассуждения для определения «стоимости» отдельных типов лиц по сумме хмурых взглядов, улыбок и нейтральных лиц.На этой странице представлены три графические задачи, связанные с решением систем уравнений, а также советы по обдумыванию проблемы, решения и других подобных проблем.