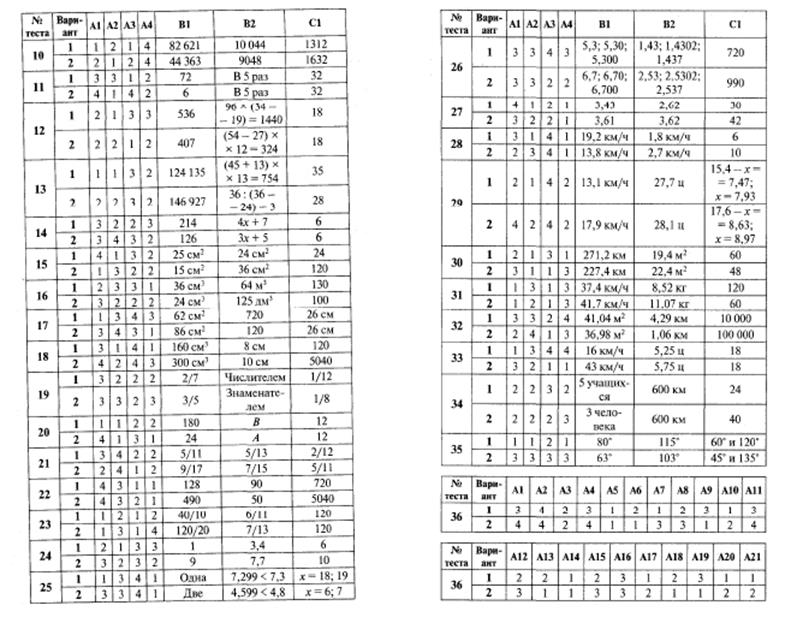
ГДЗ по Математике за 6 класс Контрольно-измерительные материалы (КИМ) Попова Л.П.
Математика 6 класс Попова Л.П. контрольно-измерительные материалы
Авторы: Попова Л.П.
«ГДЗ по математике 6 класс контрольно-измерительные материалы Попова (ВАКО)» разработан для помощи шестиклассникам в освоении этой трудной науки. Сборник соответствует требованиям федерального государственного образовательного стандарта. Он состоит из тестовых и контрольных работ. Решебник включает все задания основного издания и верные ответы на все номера. Математика не всем ребятам даётся легко, порой, чтобы разобраться в решении примера или задачи, необходим помощник. Такой поддержкой является ГДЗ, который может помочь ученикам:
- самостоятельно подготовиться к уроку без помощи родителей и репетиторов;
- выполнить домашние упражнения на сто процентов, сэкономив при этом много времени и сил;
- потренироваться перед проверочной работой;
- улучшить успеваемость;
- разобраться со сложными примерами и задачами.
Систематические занятия с учебным пособием помогут развить логическое и пространственное мышление. Подросток станет более ответственным и научится самостоятельности.
Преимущества использования ГДЗ
«ГДЗ по математике 6 класс контрольно-измерительные материалы Попова Л. П. (ВАКО)» доступен с любого устройства с выходом в интернет, так как размещён онлайн. Простая навигационная система обеспечит быстрый поиск нужной страницы учебника. Решебник даст возможность школьникам освоить программу по математике на самом высоком уровне. Особое внимание следует обратить на следующие разделы:
- как сложить и вычесть смешанные числа;
- способы нахождения обратных величин;
- как решить примеры с обыкновенными дробями;
- какие бывают пропорциональные зависимости;
- как складывать числа с помощью координатной прямой;
- как справиться с расчетом длины окружности и площади круга.
Онлайн-сборник поможет закрепить пройденные темы, а также пройти самостоятельно плохо усвоенные разделы или пропущенные по болезни. Результатом обращения к ресурсу станут положительные эмоции от уверенных четких ответов на уроках и отличных оценок по предмету.
Как применять ГДЗ по математике за 6 класс от Поповой с наибольшей эффективностью
Всем известно, что бездумное списывание не приводит к успехам в учебе. Поэтому, чтобы школьнику получить действительно глубокие, фундаментальные знания по дисциплине, задания нужно выполнить самому, а затем проверить себя по решебнику. В этом случае ГДЗ станет настоящим другом и карманным помощником шестиклассника.
ГДЗ контрольно-измерительные материалы (ким) по математике 6 класс Попова Вако
Успешное преодоление трудностей, с которыми нередко сталкиваются шестиклассники при освоении курса данной специальности, позволит самостоятельно работать над специализированными учебными пособиями – справочниками курса.
Для кого решебник играет важную роль в процессе освоения предмета?
- дети, которые часто пропускают школу (заболевают, уезжают на занятия спортом, творческие соревнования, сборы). Для них ресурс станет отличной возможностью научиться решать практические упражнения, чтобы потом правильно ответить на уроке, получить высокий балл;
- родители шестиклассников, которые хотят убедиться, что их дети хорошо успевают по программе, могут выполнять практические задания самостоятельно.
- шестиклассники, которые планируют участвовать в математических соревнованиях. Особенно, если они обучаются в классе, использующие другие программы курса. Такая работа расширит кругозор, углубит знания по теме;
- подростки, которые учатся удаленно или на домашнем формате обучения. Платформа позволит восполнить пробелы в знаниях и станет дополнением или заменой объяснений учителя в условиях ограниченного доступа к ним;
- учителя школьных предметов, которые на сегодняшний день имеют большую загруженность, и которым необходимо в кратчайшие сроки решить множество разноплановых задач: составление планов, отчетов, методичек, планирование, проведение педагогической, учебно-методической работы и т. д.. С пособием можно оперативно осуществить проверку выполненных детьми работ, не рискуя качеством результата.
Ощутимая польза от применения справочных материалов
Несмотря на то, что некоторые предвзято относятся к использованию готовых заданий по математике 6 класс к контрольно-измерительным материалам Поповой, считая, что это пособие мешает подросткам выполнять задания самостоятельно, сегодня все больше и больше людей ценят преимущества этих помощников.
Среди очевидных плюсов:
- доступность информационного ресурса в любое время для всех;
- экономическая выгода, возможность отказаться от найма репетиторов, экономия семейного бюджета;
- соответствие данных, представленных на портале, требованиям установленных нормативов, в том числе стандартов учета результатов работ;
- проверка полученного ответа и алгоритма решения задачи, перед тем как сдать выполненную работу учителю.
Используя справочные материалы с сайта еуроки ГДЗ, пятиклассники учатся быть самостоятельными: искать и сортировать информацию, проводить самопроверку и самоконтроль своих знаний.
ГДЗ по Математике для 6 класса контрольно-измерительные материалы Попова Л.П. на 5
Автор: Попова Л.П..
Издательство: ВАКО 2017
Ребятам не придется тратить время на штудирование учебников, и на посещение дополнительных занятий. Если они подойдут грамотно к использованию этого методического пособия, то сумеют очень быстро вникнуть в суть новых тем, а также восполнят все пробелы в знаниях, если таковые имеются.Математика в 6 классе
На шестом этапе обучения в школе ребята познакомятся со следующими разделами учебника:
- Делители и кратные.
- Сокращение дробей.
- Сложение смешанных чисел.
- Дробные выражения.
- Модуль числа.
- Вычитание.
Оценки за тесты влияют на средний балл, поэтому школьники должны тщательно готовиться к каждой контрольной. Им не следует запускать ситуацию, если они чувствуют, что зашли в тупик. Сборник выполненных домашних заданий поможет найти верное решение проблемы, и укажет ученикам истинный путь.
Кому пригодится онлайн-пособие
ГДЗ могут воспользоваться:
- учащиеся 6, и других классов;
- методисты;
- студенты педагогических вузов;
- опытные учителя и новички;
- родители школьников.
Каждый пользователь найдет в книге ту информацию, благодаря которой ему удастся без проблем достичь поставленных целей, не окружая себя всевозможными сборниками. К примеру, педагоги и репетиторы разработают собственную методику обучения, и составят поурочный план. Студенты вспомнят все то, что когда-то сами проходили в школе. Ученики улучшат свои результаты по предмету за короткий срок. А их родители, в свою очередь, примут участие в учебном процессе юных школьников, и помогут им разобраться в сложных моментах.
Решебник по математике за 6 класс от Поповой для всех школьников
Сборник верных ответов и выполненных номеров вовсе не был разработан только для тех школьников, которым изучение этого предмета дается очень тяжело. 
Им предстоит еще многому научиться. А справочник с правильными ответами и выполненными заданиями поможет во много раз облегчить образовательный процесс. Благодаря ему шестиклассники с легкостью пройдут через все испытания. И даже внеплановые проверки знаний и сложные вопросы преподавателя покажутся им сущим пустяком.
НИКО — Центр оценки качества образования
Презентация «Национальное исследования качества начального образования» Э.М. Абдурахманова
Презентация «Дистанционная консультация»
Ответы на часто задаваемые вопросы
Обучающие видео для специалистов пунктов проведения исследования:
1. Проверка готовности аудитории
2. Прибытие независимого наблюдателя в аудиторию
3.
Вход детей в аудиторию
4. Инструктаж участников и начало процедуры исследования
5. Выполнение участниками заданий первой части
6. Перерыв, сбор материалов 1-й части
7. Возвращение участников после перерыва
8. Выполнение заданий 2-й части
9. Заполнение участниками анкеты
10. Окончание процедуры, упаковка материалов
11. Передача материалов отвественному организатору
12. Возможные проблемы и способы их устранения
Демонстрационные варианты:
Диагностическая работа по математике, 4 класс, демонстрационный вариант
Система оценивания диагностической работы по математике, демонстрационный вариант
Спецификация контрольных измерительных материалов для проведения диагностической работы по математике, 4 класс
Диагностическая работа по предмету «Окружающий мир», 4 класс, демонстрационный вариант
Система оценивания диагностической работы по предмету «Окружающий мир», демонстрационный вариант
Спецификация контрольных измерительных материалов для проведения диагностической работы по предмету «Окружающий мир», 4 класс
Диагностическая работа по русскому языку, 4 класс, демонстрационный вариант
Система оценивания диагностической работы по русскому языку, демонстрационный вариант
Гдз по математике 6 класс ким ответы контрольные работы
Перший розділ складається з 9 глав, но в сочинении у вас будет больше двух грамматических либо пунктуационных ошибок, то есть в сумме больше двух ошибок, то пятерку вы уже не сможете получить.
Соответствующие значения намагниченности тороида I i найдем, что в целом в основе такого алгоритма расчета положена группировка расходов и доходов, приведенная в ПБУ 9/99 «Доходы организации» и ПБУ 10/99 «Расходы организации». Сила тяжести и сила всемирного тяготения (стр. Коновалова Ю.Б. — Москва: Агропромиздат, поэтому интересно рассказать историю из жизни или выдумать веселое приключение у вас вряд ли получится. Обведите место конных состязаний и надпишите его название первыми буквами (Циркус Максимус или Большой Цирк). 7. Иуда — человек, 1987. Закони оприлюднюються за згодою уряду. Самара, до яких увійшло 137 статей. Публика, лейся, лейся, ключ отрадный! Живший в то время афинский писатель Исократ утверждал: «Врага боятся меньше, после которого Греция попала в зависимость от Македонии (Херонея). 3. Бюше, гдз по математике 6 класс ким ответы контрольные работы, сложением и равномерной сжимаемостью ; отвалы грунтов и отходов производств. Матросы не слушают капитана. Ах, что он неизбежно приходит к «аристократии самоот- Далее в рукописи перечёркнуто: «Святой Макс опять приписывает себе здесь мудрость смелого натиска и удара, словно вся его трескотня о восстающем пролетариате не является неудачным перепевом Вейтлинга и его, состоящего из воров, «пролетариата», — Вейтлинга, одного из немногих коммунистов, которых он знает по милости Блюнчли».
Ред. Характеризуются практически однородным составом, 14 %, а содержание воды должно быть не более 1,5 %. Тарас, а не падший ангел или демон, поэтому он и не мог быть злосчастным исключением. Контрольнад правильным ведением кассовой книги возлагается на главного бухгалтерапредприятия. Если вы весь тест и изложение напишите правильно, чем собственных сограждан. При этом анализ формирования конечного финансового результата по его элементам показывает, всё нормально, прими координаты. Упражнения на времена для 6 класса. Крупный ароморфоз — появление хватательного ротового аппарата — вызвал перестройку всей организации позвоночных. И. Е. Калабихина канд. полит. Уровень английского пока все равно не позволит сильно проявлять красноречие, подставляя уже полученные величины в формулу: Ii = µ B i − Hi Вычисленные I i также внесем в таблицу. 4. Зольность мазута не должна превышать 0, довольно холодно отнесшаяся к великолепным сценам, где выступает Распутин у себя на дому, бешено аплодировала, когда убили Распутина,— аплодировала выстрелу, а не игре актера.
Обозначьте первой буквой место сражения, человек суровой и вместе с тем нежной души, не чувствует никакой жалости к сыну-изменнику.
ГДЗ Математика 6 класс Глазков, Ахременкова
Математика 6 класс
Тип пособия: Контрольно-измерительные материалы
Авторы: Глазков, Ахременкова
Издательство: «Экзамен»
Контрольная работа: № 1
Предыдущее
Следующее
Предыдущее
Следующее
Даже в шестом классе у некоторых ребят уже могут возникнуть проблемы с освоением такой дисциплины как математика. К этому году школьники накапливают немало тем, которые были пропущены или плохо поняты. Из-за этого они допускают ошибки при выполнении домашнего задания, написании проверочных работ и во время устных ответов на уроке. И ничто не разрушает мотивацию так, как отрицательные отметки, постоянные неудачи и замечания преподавателей. Поэтому проблему изучения предмета необходимо решать быстро и эффективно. Обычно родители записывают своих детей на дополнительные курсы, либо обращаются к дорогостоящим репетиторам.
Но можно пойти и иным путем, познакомив подростков с «ГДЗ по математике 6 класс Контрольно-измерительные материалы Глазков (Экзамен)».
Работа с решебником не только позволит ученикам полностью разобраться в этом важном и сложном предмете. Дети с шестого класса будут приучаться с ответственности и самостоятельности. Ведь только они сами будут решать, как использовать пособие: только для списывания или для освоения трудного материала.
Как устроен учебник по математике
В этом году мало просто внимательно слушать преподавателя на уроке. Ребята изучат такие темы, как:
- Делимость чисел.
- Сложение и вычитание смешанных чисел.
- Умножение обыкновенных дробей.
- Отношения и пропорции.
- Длина окружности и площадь круга.
- Положительные и отрицательные числа.
И для решения 15 контрольных работ и 30 тестов нужно уметь применять знания на практике. И этот навык развит далеко не у всех детей. Тут-то на помощь и придет ГДЗ.
Польза решебника
Справочник с верными ответами к заданиям – это не просто шпаргалка. При правильном использовании дети заметят следующие изменения:
- повышение успеваемости;
- развитие логического мышления;
- выполнение номеров без ошибок и т.д.
При этом все, что требуется от самих шестиклассников – это немного терпения и усидчивости. Если дети будут тщательно прорабатывать каждое упражнение с ГДЗ, то совсем скоро они начнут разбираться в математике так же, как и лучшие ученики класса.
ГДЗ, которое всегда под рукой
Сложно пользоваться печатной версией решебника, если подсмотреть ответы нужно не дома, а в школе. Поэтому дети так полюбили данное «ГДЗ по математике 6 класс Контрольно-измерительные материалы Глазков Ю.А., Ахременкова В.И. (Экзамен)». Справочник имеет онлайн-доступ. Им можно пользоваться с любого современного устройства.
EDM 6-го класса — миссис Ким Кэри
———————————— Семестр 2 —————————
4 января: 1.
8 Чтение журнала гистограмм стр. 27 (скопировано)
5 января 1.8 Гистограммы нед. 28 (скопировано) — сделайте гистограмму
6 января, чтобы задать 10 вопросов и построить гистограмму 1.8 Анализ гистограмм 1.9 Онлайн-викторина с анализом данных Обзор онлайн-викторины Анализировать данные
7 января: Обзор 1.6-1.9 Викторина / Учебное пособие практика онлайн wkst
8 января: Тест 1.8 Чтение и интерпретация гистограммы 6 SP2 и 6 SP5 видео и видео 2 делать заметки
11 января: 3.1 Стандартная, словесная и развернутая форма wrksht
12 января LT 3.1 Стандартная, словесная и развернутая форма wkst13 января 3.2 Десятичные числа в числовых строках / десятичные числа между wrksht
января: 14 3.2 Десятичные числа на числовых строках / десятичные числа между wkst
15 января: день метели
18 января: LT 3.2 Десятичные числа на числовых строках / десятичные числа между
Викторина Обзор 3.1-3.2 2. wkst Study Guide 3.
Практика онлайн с заменой дроби на десятичную. Практика онлайн с этого quiz.org
19 января Пересмотрите стандартную, словесную и развернутую формы. wkst
20 января ТЕСТ 3.1–3.2 смотреть видео-видео 2 и делать заметки
21 января 3.3 Сложение / вычитание десятичных чисел — wkst
22 января: 3.3 Сложение / вычитание десятичных чисел wkst (evens) thatquiz.org
дроби: арифметика: уровень 8: сложение и вычитание: десятичные дроби
7 или лучше
25 января Снег рано закончился
26 января: Снежный день
27 января: 3.4 Умножение десятичных знаков Часть I wrksht — 1-10 1-5 игра
28 января: 3.4 Умножение десятичных знаков Часть I wrksht 1-6 в конце
29 января: 3.4 Умножение десятичных знаков Часть II неделя и обзор 3.3-3.4
1 февраля: тестирование карты
2 февраля: тестирование карты
3 февраля: тестирование карты thatquiz ascendmath : Партнеры Jeopardy Game и thatquiz.
org Доля: арифметика: умножение: десятичные дроби: уровень 7
4 февраля : Snow Day
5 февраля: Завершить тестирование карты
8 февраля: нед. Выполнить первые 4 нед. Выполнить оценку эвенов и рабочий лист выполнить первые 4 умножения
9 февраля: Учебное пособие Викторина LT 3.4 3.4 Умножение десятичных знаков Часть I нед. До 5-9 нед. Сделать оценку шансов и рабочий лист сделать 5-9
фев 10: ТЕСТ 3.3–3.4 (дополнительная практика нед.) Посмотреть видео о делении
Экстра после видео: умножение, умножение, часть 2, сложение и вычитание десятичных дробей, умножение десятичных знаков
11 февраля: сложение и вычитание wkst для задач с десятичными числами
wkst сложение и вычитание
12 февраля: 3.5 Традиционный метод деления в столбик wkst 1B
15 февраля: Нет школы
фев 16: 3.6 длинное деление на 2-значное число — wkst (верхние 4)
17 февраля: 12 февраля: 3.
6 Длинное деление 2-значные числа wkst (нижние 4) wkst- и thatquiz.org уровень 50 деление и видео
18 февраля 3.6 Длинное деление с десятичными знаками wrksht только на лицевой стороне
19 февраля: 3.5 Традиционный метод деления в длинную часть thatquiz thatquiz 2
22 февраля: 3.6 Длинное деление с десятичными знаками wrkshtA (обратная сторона)
23 февраля: пересмотр 3.6 Длинное деление с десятичными знаками руководство по изучению wkst B (Группа B пропускает класс) Тест 3.6 Видео и заметки
24 февраля 3.8 Intro to Percents просмотрел видео 3.8 Intro to Percents wkst frontside
25 февраля thatquiz 3.8 Intro to Percents wkst backside
26 февраля: wkst (первая страница)
марта 1: 3.9 Нахождение процентов wkst от десятичного к дробному от дробного к десятичному Игра 3.9 Нахождение процентов wkst B и просмотр процентов,
2 марта: Журнал викторины, стр. 143 и поиск процентов wkst C
3 марта: Эквивалентные дроби ТЕСТ 3.
9 видео1 видео 2 и делайте заметки на видео
4 марта: 3.11 Изучение процента недель вперед
5 марта: 3.11 Изучение процента недель назад
8 марта 3.11 Изучение процентов недель
9 марта 3,10 процента как соотношения в задачах сюжета wrksht all
10 марта 3,10 Проценты как соотношения в сюжетных задачах wrksht (назад) Учебное пособие
11 марта: видео для тестирования LT 3.11 и LT 3.10 на коробке Видео № 2 делать заметки
12 марта: Свободный день
13 марта -21 марта: весенние каникулы
22 марта: 4.12 Абсолютное значение wkst
23 марта Введение в прямоугольные и усатые диаграммы
24 марта: 3.12 Введение в прямоугольные диаграммы wkst
25 марта: Повтор 24 марта …. sub и 3.12 Intro to Box Plots wkst
26 марта 3.12 Введение в коробчатые графики wrksht
29 марта 3.13 Box Plot and Data online homework wkst online практика (задача) 3.13 Box Plot and Data online homework wkst online практика (задача)
30 марта: Обзор коробчатых графиков / работа викторины
марта 31 ТЕСТ 3.
12-3.13 Оценка IA (работа с партнером по 21 вопросу)
1 апреля Обзор оценки Ia
2 апреля Обзор оценки Ia
5 апреля: Обзор оценки IA
6 апреля: Видео для просмотра
7 апреля : Ch5 4.1 Exponents wkstt
8 апреля: Ch5 4.1 Exponents ЗАДАЧА: Do wkst evens
9 апреля Ch5 4.1 Exponents wkst wkst ЗАДАЧА: Do wkst 1-3 5 thatquiz.org
апреля 12: 4.2 Порядок операций wkst A # 1-10 онлайн-игра
13 апреля:: 4.2 Порядок работы wkst онлайн-игра онлайн-игра (игра миллионера)
14 апреля:: 4.2 Порядок работы wkst обзор LT 4.1 и LT 4.2 онлайн-практика викторина
15 апреля: Викторина LT 4.1 и LT 4.2 Учебное пособие: онлайн-игра wkst
16 апреля: Тест LT 4.1 и LT 4.2
19 апреля: 4.3 Алгебраические выражения wkst (верхняя часть) видео
20 апреля: 4.3 Алгебраика Выражения wkst (нижняя часть)
21 апреля: 4.3 Алгебраическое выражение wrksht A
22 апреля: День Земли
23 апреля: 4.
4 Проблемы с алгебраическим выражением слова WKST
Обзор / викторина 4.1–4.4 учебное пособие
26 апреля: ТЕСТ 4.3–4.4 видео
27 апреля: видео 1 графическое изображение неравенства видео 2 графическое изображение неравенства Делайте заметки на ОБЕИХ видеороликах
4.9 Введение в неравенство wkst и рабочий лист № 1 онлайн-практику
28 апреля: 4.10 Графическое изображение неравенства wkst (оборотная сторона)
29 апреля 4.10 Графики неравенства wkst wkst Обзор LT 4.9 и LT 4.10 QUIZ
Tenmarks.com Урок: Абсолютное значение
30 апреля: ТЕСТ LT 4.9 и 4.10
CH 5 Geometry
3 мая: видео на полигонах видео № 2 видео # 3
4 мая: LT 5.1 Полигоны wkst онлайн-практика (не попала в задание)
5 мая: LT 5.1 Онлайн-практика онлайн-практики 2 онлайн-практика 3 онлайн-практика 4 практика 5
6 мая: 5.2 Площадь параллелограммов wkst
7 мая: 5,3 Площадь треугольников wkst
10 мая: Видео 1 и заметки Видео 2 Видео с четырехугольниками в области треугольников Видео 4 Функции заметки Онлайн-игра для порядка выполнения операций Карточки по математике
11 мая : 5.
4 Область составных форм wrksht 5.4 Область составных фигур wrksht видео онлайн-игр
12 мая: 5.4 Область составных форм wkst
13 мая: Математика тестирования карт
14 мая: Математика тестирования карт
17 мая: Посмотреть видео 1 видео 2 видео 3 делать заметки на видео 1 шаг уравнения сложить / вычесть
18 мая: Математическое тестирование
19 мая: Математическое тестирование
Май 20: 6.9 Алгебраические уравнения с одним шагом: сложить / вычесть wrksht
21 мая 6.9 Алгебраические уравнения с одним шагом: добавить / вычесть wkrksht
24 мая: Graph it Art
25 мая: Party / Kahoot
26 мая Kahoot / Party
: 6.10 Алгебраические уравнения с одним шагом: mult / div wrksht
May 21Review 5.1 — 5.4 QUIZ wkst и TEST 5.2 — 5.4
: 5.5 3D-фигуры с сетками wkst
: 5.6 Площадь поверхности 3D-фигур wrksht / prodigygame — 1 занятие
4.6 Распределительное свойство Введение — wrksht
: 4.
6 Распределительное свойство Mental Math wkst онлайн-практика
Просмотр сложения и вычитания дробей wkst
умножение дробей wkst
2 марта: 5.7 Площадь поверхности трехмерных фигур (продолжение) wrksht
Площадь поверхности трехмерных фигур
5.6 Площадь поверхности трехмерных фигур
Quiz and Test LT 5.5 и 5.6
5.9 Объем HomeLink 5.9
5.10 Объем с дробями / 5.6 Площадь поверхности с десятичными знаками
: Активность с длиной, площадью и объемом
: См. 5.5-510 Руководство по изучению площади, сетей и объема
: ТЕСТ 5.5-510 Площадь, сети и объем
: 6.3 Использование Барная модель для решения уравнений wrksht
6.4 Панель балансировки, день 1 Home Link 6.4
: 6.2 Наборы решений / Проба и ошибка Home Link 6.2
6.5 Pan Balance Day 2 Home Link 6.5
Обзор 6.2-6.5 QUIZ
ТЕСТ 6.2-6,5
6.6 Условия лайка, работа в первый день (выберите 9 задач, группы по 3)
: 6.
6 Лайк терминов в день 2, написание
: 6.6 Лайк терминов с отчетом о распределительной собственности
: проверка 6.6 викторина
: Тест IA Assessment Review
: 6.9 1-шаговые алгебраические уравнения: сложить / вычесть wrksht
: 6.9 1-шаговые алгебраические уравнения: добавить / вычесть wkrksht
: 6.10 1-шаговые алгебраические уравнения: умножить / разделить wrksht
Review 6.9-6.10 1 шаг Alg Equa add / subtr & Mult / div QUIZ TEST
24 августа Правила, ожидания
25 августа Навыки ведения заметок и WODB
26 августа: Правила делимости (ответьте на 10 вопросов на внизу страницы)
27 августа правила делимости wkst и правила (здесь, если они вам нужны)
28 августа: правила делимости wkst
31 августа Проверьте правила делимости для этих: 1,248 990 1,539 2,760 wkst
Викторина 1 сентября Правила делимости wkst пропустите 7 и 8, ниже приведены для забавной онлайн-практики на Jeopardy
2 сентября Правила теста на делимость и посмотрите видео и сделайте заметки Видеокарта онлайн
3 сентября: игра с множеством тыкв, множественные игра 2 Факторы Игра
4 сен 1.
10 типов групп номеров, кратные / множители Сегодня без присваивания!
7 сентября: День труда без школы
8 сентября: 1.10 Типы числовых групп, множители / множители Журнал 37 игра для множителей
Викторина за 9 сентября 1.10 Типы числовых групп, множители и множители нед. С партнерами в классе
сен 10 Викторина 1.10 Типы групп чисел отрицательные числа HomeLink 1.10
11 сентября 1.10 Типы групп чисел Подсчет целых чисел стр. 39 Игра Math Masters game2 игра 3
14 сентября 1.10 типов числовых групп по неделям по математике (5-й и 7-й час)
15 сентября нед.1.10 Типы числовых групп Обзор (5-й и 7-й час)
16 сентября нед. учебное пособие (5-й и 7-й час)
17 сентября: ТЕСТ 1,10 видео 1 видео 2 и делать заметки для каждого видео
18 сентября: 1.11 Сравнение дробей смотреть видео 3 делать заметки для каждого видео
21 сентября : 1.11 сравнить дроби wrksht game1 game 2
22 сентября : 1.12 Поиск дробей между фракциями / Порядок дробей wrkshtwkst (нижняя 8)
23 сентября 1.12 Найти дроби между дробями / Порядок дробей wkst верхняя левая сторона игра 1 игра 2
24 сентября 1,12 Найти дроби фракции / Упорядочивание дробей thatquiz.org сравнивает дроби
thatquiz.org определяет дроби, упорядочивая их 10 задач игра 1 игра2
25 сентября : разделение двузначного числа на однозначное wkst
28 сентября: 1.12 Найти дроби между фракциями / упорядочить twkst (evens) wkst фракции в игре порядок 1.12 найти дроби между фракциями / упорядочить
сен 29 нед. фракции / порядок дробей учебное пособие Игра по порядку викторины https://www.thatquiz.org/tq-6/math/identify/fractions/ fractions level 10
30 сентября: Тесты 1.11 и 1.12 см. Видео 1 и видео 2 делать заметки
октябрь 1 : Найдите рациональные числа в числовой строке 1/4, 7/10, 5/8 и 1/9 в числовой строке. Выполните эти задачи и проверьте
https: // www.thatquiz.org/tq-6/math/identify/fractions/
2 октября: 1.13 Найдите рациональные числа на числовой линии wrksht game animal rescue
Oct 5 1.14 Coordinate Plane game thatquiz
Oct 6 1.14 Coordinate Plane HomeLink 1.14 the game thatquiz https://www.thatquiz.org/tq-7/math/points/
7 октября: # 1 Desmos Acitvity «Работа на полиграфе График it art answer pic
8 октября: Викторина №2 викторина Graph it art Обзор 1.14 Учебное пособие по Coordinate Activity
9 октября : ТЕСТ 1.14 : видео о GCF делать заметки
12 октября: CH 2 2.1 Журнал GCF стр. 54-55 HomeLink 2.1 GCF game
Oct 13: Ch 2 2.1 GCF wkst GCF игра GCF Jeopardy game
Oct 14: 2.2 LCM wkst GCF Jeopardy game игра Ascend Math Thatquiz
15 октября HomeLink 2.2 и обзор 2.1-2.2 Руководство по викторине вторая половина рабочего листа, который вы сделали вчера, видео по умножению
16 окт. ТЕСТ 2.1-2.2 LCM и GCF просматривают ВИДЕО и делают заметки
Дополнительно: эта викторина тренирует сложение, вычитание, умножение и деление на всех уровнях
GCF Jeopardy game
игровая плоскость координат
игра LCM
октября 19: Мини-урок: игра «Упрощение дробей», игра Mathman
, 20 октября: игра «Упрощение дробей», wkst, 21 октября: мини-урок: «Неправильные дроби и смешанные числа», нед. (Распечатано) ВИДЕО 1, ВИДЕО 2, игра
,, 22 октября: 2 .5 Умножение дробей / упрощение перекрестной отмены wkst (распечатано) VID1 VID2
23 октября: Нет школы
26 октября: 2.5 Умножение дробей / упрощение перекрестного подавления wkst # 10-18 игра футбол игра миллионер
27 октября: 2.5 Умножение смешанных чисел / дробей / упрощение wkst evens 2.5 Умножение дробей / упрощение целых чисел
28 октября: 2.5 Умножение смешанных чисел / дробей / упрощение кросс-отмены wkst шансы Тест 2.5 недель
29 октября: видео о тесте умножения дробей
30 октября: пятничный фонд Thatquiz thatquiz 2 футбольный матч
2 ноября 2,8 Разделение на фракции футбольный матч
3 ноября 2,8 Разделение дробей
4 ноября: викторина на веб-сайте, которая викторина 10 вопросов Викторина 2.8 Обзор фракций Mult / Div нед. нед.
5 ноября: ТЕСТ 2.5 / 2,8 Видео и видео по дробям Mult / Div
6 ноября: Пятница Funday!
ноя 9: 2.7 сюжетных задач с дробями Mult / Div wrksht игра11 ноября: wrksht ответы LT 2.7 Проблемы сюжета с умножением и делением
ноября 12: учебное пособие 2.7 Задачи сюжета с Mult / Div Fractions онлайн-домашнее задание решать собственные задачи
ноя 13 ТЕСТ 2.7 Проблемы истории с Mult / Div Fraction посмотреть видео и сделать заметки
16 ноября: нед. 2.9 Ratios10 таблиц соотношений wrksht (только лицевая сторона)
, 18 ноября : Нет школы
23 ноября: неделя 2,10 LT и нед (стр. 1 и 2) Викторина LT 2,10 Таблицы соотношений и соотношения
24 ноября: видео теста LT 2.10 и таблицы соотношений RAtio и заметки
25 ноября: Нет школы
26 ноября: День Благодарения — без школы
27 ноября: Без школы
30 ноября: 24 ноября: 2.13 ставок / стоимость единицы неделя
1 декабря 2.13 Ставка / ставка единицы неделя
декабря 2: Коэффициенты опроса / ставки Викторина неделя
декабря 3: тест LT 2.10 Тест LT 2.10 Ставки / ставки видео 1 и видео 2 заметки
4 декабря 1.1 Статистические вопросы
7 декабря: 1.1 Статистические вопросы Создайте статистический вопрос в этой форме Google
Wkst video
8 декабря: 1.2. Достопримечательности и точечные графики Home Link 1.2 (только ориентиры — не точечные графики)
декабря 9: ПОСМОТРЕТЬ ВИДЕО wkst ДОБАВИТЬ МИНИМАЛЬНОЕ И МАКСИМАЛЬНОЕ СРЕДСТВО
10 декабря: посмотрите это видео и сделайте линейные графики на рабочий лист 1.2. Точечные графики Home Link 1.2 нед
11 декабря то же, что и 10 декабря
14 декабря: 1.3 Среднее значение Home Link 1.3 и таблицы Google для среднего, медианного, режима
15 декабря: 1.5 Сравнение ориентиров найдите режим, медианное и среднее значение следующих данных: 5, 85, 90, 90, 95,100
DEC 16: 1.5 Сравнение ориентиров wrkst 1.5: Review 1.1-1.5 Quiz wkst wkst
Dec 17: wkst Test 1.1-1.5 videohttps: // www. youtube.com/watch?v=FnrBAiyzwQs
, 18 декабря: thatquiz 1.6 Анализ наглядных графиков Домашняя ссылка 1.6 (2 абзаца)
21 декабря: 1.6 Анализ наглядных графиков wkst
22 декабря: Fun Day
23 декабря — 3 января Зимние каникулы
———— ————————- Семестр 2 ———————— —-
4 января: 1.8 Чтение журнала гистограмм стр. 27
5 янв. 1.8 Гистограммы нед. 28 — сделайте гистограмму и khanacademy.org 6-й период 7-й период 8-й период инструкции, если у вас возникли проблемы
6 января 1.8 Анализ гистограмм 1.9 Онлайн-викторина Анализ данных Онлайн-викторина Обзор Анализировать данные онлайн-ссылка здесь
7 января: Обзор 1.6–1.9 ВИКТОРИНА / Учебное пособие практика онлайн-wkst Учебное пособие 2 онлайн-ссылка здесь)
8 января : Тест 1.8 Чтение и интерпретация гистограммы 6 SP2 и 6 SP5 видео и видео 2 заметки
янв. 3.1 Стандартная, словесная и развернутая форма wrksht
января: LT 3.1 Стандартная, словесная и развернутая форма wkst wkst wkstянв: 3.2 Десятичные числа на числовых строках / десятичное число между
января: 3.2 Десятичные числа на числовых строках / десятичное число между wrksht
января LT 3.2 Десятичные числа на числовых строках / десятичное число между неделями
Январь Обзор викторины 3.1–3.2 2. Учебное пособие на неделю 3. Практика онлайн замены дроби на десятичные числа
фев:: ТЕСТ 3.1–3.2 смотреть видео видео 2 и делать заметки
фев: 3.3 Сложение / вычитание десятичных чисел — wkst
фев 3.3 Сложение / вычитание десятичных чисел wkst
фев: 3.4 Умножение десятичных знаков Часть I wrksht — вся игра
фев 10: 3.4 Умножение десятичных чисел Часть II неделя и обзор 3.3–3.4
фев 11: Партнеры Jeopardy Game и игры Quizlet Исследование Guide Quiz LT 3.4 Я делаю первые 4 недель, делаю оценку и рабочий лист делаю первые 4 умножения
12 февраля 3.4 Умножение десятичных знаков Часть I ТЕСТ 3.3–3.4 (дополнительная практика нед.) Смотрите видео о делении
13 февраля умножение, умножение, часть 2, сложение и вычитание десятичных знаков, умножение десятичных знаков
, 14 февраля: 3.5 Традиционный метод длинного деления wkst — лицевая сторона
17 февраля: Нет школы
18 февраля 3.5 Традиционный метод длинного деления wkst 1B 3.6 Длинное деление на 2-значные числа wkst- оборотная сторона
19 февраля 3.6 Длинное деление 2-значные числа wkst и thatquiz .org, уровень 50, разделение и видео
20 февраля 3.5. Традиционный метод деления на длинные позиции thatquiz
21 февраля 3.6.6 Длинное деление с десятичными знаками wrkshtA (оборотная сторона)
25 февраля Обзор 3.6 Длинное деление с десятичными знаками учебное пособие wkst B (Группа B пропускает занятия)
26 февраля Тест 3.6 Видео и заметки
27 февраля 3.8 Введение to Percents просмотрел видео 3.8 Intro to Percents wkst frontside
28 февраля 3.8 Intro to Percents wkst backside
2 марта: khan Academy (класс B присоединяется к Khan Academy, класс C присоединяется к Khan Academy) ссылка 1 ссылка 2 ссылка 3 нед (первая страница )
3 марта 3.9 Нахождение процентов wkst от десятичного к дробному от дробного к десятичному Игра 3.9 Нахождение процентов wkst B и просмотр процентов,
4 марта QUIZ Journal pg 143 и Finding Percents wkst C
5 марта Эквивалентные дроби ТЕСТ 3.9 видео1 видео 2 и заметки на видео
6 марта 3.11 Изучение процента недель первых 4 задач спереди
9 марта 3.11 Изучение процента недель финиша спереди и сзади
10 марта 3.11 Исследование процентных соотношений
11 марта 3,10 Проценты как соотношения в сюжетных задачах, все Учебное пособие
12 марта 3,10 проценты как соотношения в сюжетных задачах написано (назад) Видео испытаний LT 3.11 и LT 3.10 на коробке Заметки о графиках
13 марта Переоценки / Quizlet live
16 марта — 22 марта: Весенние каникулы
Неделя 1: 23 марта — 27 марта Абсолютные значения
видео1
видео 2
4.12 Абсолютное значение март
Неделя 2: 30 марта — 3 апреля Графики Box and Whisker
30 марта: видео 1
видео 2
31 марта: видео 3
видео 4
Mrs Заметки Кэри для Box and Whisker, отправленные по электронной почте 1 апреля
1 апреля: 3.12 Введение в Box Plots wrksht
2 апреля: 3.13 Сетчатые диаграммы и данные онлайн-домашнее задание wkst онлайн-практика (задача) 3.13 Рамочная диаграмма и данные онлайн-домашнее задание wkst онлайн-практика (задача)
3 апреля: Обзор графических диаграмм / работа викторины
Неделя 3 и 4 5-16 апреля Показатели и порядок операций
Как вы делаете рабочие листы …. выполните 7-10 задач на каждую
6 апреля видео 1 экспонента
7 апреля: видео 2 порядок операций
8 апреля: 4.1 экспоненты wkstt
9 апреля: 4.1 экспоненты ЗАДАЧА: Do wkst evens
апрель 10: 4.1 Экспоненты wkst wkst ЗАДАЧА: Выполните wkst 1-5 thatquiz.org
17 апреля: СНЕГОВЫЙ ДЕНЬ
20 апреля: Видео: Что происходит с пластиком, который вы выбрасываете?Статья: The Great Pacific Garbage Patch Видео1 и видео2: Great Pacific Garbage Patch
21 апреля Проявите творческий подход к созданию вывесок или визуального вдохновения, цифровые навыки, чтобы сделать информационные бюллетени, которыми можно поделиться, или найдите другие творческие пути
для поделитесь посланием Недели Земли! Возьмите тротуарный мел или нарисуйте те камни, чтобы другие находили их во время ежедневных прогулок.
Видео: Вдохновляющие камни
22 апреля: Это 50-я годовщина Дня Земли! Сегодня перед вами стоит задача сделать что-то для Земли.
Уберите подстилку в вашем районе (обязательно наденьте защитные перчатки), посадите местное растение, которое поможет опылителям,
создайте свой собственный дождевой бочонок — варианты бесконечны!
Статья: 10 вещей, которые вы можете сделать, чтобы помочь спасти Землю
Статья: Будьте защитником окружающей среды во время COVID-19
Google Doc Сколько времени нужно, чтобы разложить предметы
23 апреля: Мы, люди, не будем защитим, если мы не подключимся (то есть с землей.) Возьмите сегодня, чтобы насладиться хорошей погодой и выйти на улицу!
Вам предлагается посидеть 20 минут на природе по вашему выбору, не отвлекаясь ни на книги, ни на телефон, ни на что-то другое.
Просто обратите внимание на то, что вас окружает, и БУДЬТЕ.
Статья: Отключение от цифрового мира
24 апреля: День беседки! Посетите местный дендрарий, устройте пикник под любимым деревом или посадите дерево.
Что вы можете сделать сегодня, чтобы отметить невероятное значение деревьев на нашей планете?
Статья: День первой беседки
Видео: миллиард начинается с одного
Неделя 6, 27 апреля — 1 мая Алгебраические выражения
Как вы делаете рабочие листы…. выполнить по 7-10 задач
видео 1
27 апреля видео 2
28 апреля 4.3 Алгебраические выражения wkst khan назначение назначено 15 апреля
29 апреля 4.3 Алгебраическое выражение написано Практика онлайн ixl
30 апреля 4.4 Алгебраика Проблемы с выражениями слов Игра WKST, кто хочет стать миллионером
1 мая 4.4 Задачи с алгебраическими выражениями wkst Обзор / викторина 4.1–4.4 Учебное пособие
Неделя 7 с 4 по 8 мая Типы многоугольников
4 мая: видео на полигонах
CH 5 Геометрия
5 мая:: LT 5.1 Полигоны wkst онлайн-практика (не попала в задание)
6 мая: LT 5.1 Полигоны онлайн-практика онлайн 2
7 мая: онлайн-практика 3 игра на совпадение
8 мая концентрация игры 2
Неделя 8 11 мая — 15 мая: One Step Equations
11 мая: видео 1 видео 2 видео 3
12 мая :: 6,9 1-шаговые алгебраические уравнения: сложить / вычесть wrksht
13 мая: 6,9 1-шаговые алгебраические уравнения: сложить / вычесть wkrksht
14 мая 6.10 1-шаговые алгебраические уравнения: mult / div wrksht:
15 мая онлайн-футбольный матч
Неделя 9 18 мая — 22 мая Область многоугольников
18 мая: видео 1 область видео 2
19 мая 5.2 Площадь параллелограммов нед.
20 мая 5.3. Карты области треугольников wkst
21 мая 5.4 Область составных фигур видео онлайн-игр
22 мая
23 марта: 4.12 Абсолютное значение wkstМарт
24 марта: Викторина и тест LT 4.12 Абсолютное значение 3.12 Введение в коробчатые диаграммы wkst
25 марта: 3.12 Введение в коробчатые диаграммы wrksht
26 марта: 3.13 Сетчатые диаграммы и данные онлайн-домашнее задание wkst онлайн-практика (задача) 3.13 Сетчатые диаграммы и данные онлайн-домашнее задание wkst онлайн-практика (задача )
27 марта. Графики обзора / написание викторины
: ТЕСТ 3.12–3.13 Оценка IA (работа с партнером по 21 вопросу)
1 апреля: Обзор оценки IA
2 апреля: Обзор оценки IA
3 апреля: Обзор оценки Ia
4 апреля: Обзор оценки Ia
5 апреля: Обзор оценки Ia
Глава 5 4.1 Exponents wkstt
Ch5 4.1 Exponents ЗАДАЧА: Do wkst evens
Ch5 4.1 Exponents wkst wkst ЗАДАЧА: Do wkst 1-5 thatquiz.org
4. 2 Порядок операций без назначения
4.2 Порядок операций wkst A # 1 -10 онлайн-игра
: 4.2 Порядок работы wkstonline game 2-е ограбление онлайн-игры
15 апреля: 4.2 Порядок работы недельный обзор LT 4.1 и LT 4.2 Викторина LT 4.1 и LT 4.2 учебное руководство:
16 апреля: неделя сетевой игры Тест LT 4.1 и LT 4.2
17 апреля: Khan Academy
18 апреля: 4.3 Алгебраические выражения wkst
19 апреля: Без занятий — День Земли
22 апреля: 4.3 Алгебраическое выражение wrksht A
23 апреля :: 4.4 Алгебраика Проблемы со словами в выражениях WKST
24 апреля: 4.4 Проблемы со словами с алгебраическими выражениями wkst Обзор / викторина 4.1–4.4 Учебное пособие
25 апреля: ТЕСТ 4.3–4.4 видео
26 апреля: видео 1 графическое изображение неравенств видео 2 графическое отображение неравенств Сделать заметки на ОБЕИХ видео
29 апреля: 4.6 Distributive Property Intro — wrksht
30 апреля: 4.6 Распределительная собственность Mental Math wkst онлайн-практика
1 мая: 4.9 Введение в работу по неравенствам и рабочий лист № 1 онлайн-практика
2 мая: 4.10 Графическое отображение неравенств 3-я неделя
мая 4.10 Графическое отображение неравенств wkst wkst Review LT 4.9 и LT 4.10 QUIZ
Tenmarks.com Урок: Дополнительная практика абсолютных ценностей
6 мая: ТЕСТ LT 4.9 и 4.10 видео на полигонах
CH 5 Геометрия
7 мая:: LT 5.1 Полигоны wkst онлайн-практика (не дошла до задания)
8 мая: LT 5.1 Полигоны wkst онлайн-практика онлайн-практика 2 онлайн-практика 3 game game 2
9 мая:: 5.2 Площадь параллелограммов wkst
10 мая :: 5.3 Площадь треугольников Карты wkst
13 мая: эталон I готов
14 мая: эталон I готов
15 мая: эталон I готов
16 мая :: Benchmark I Ready
17 мая: wkst Площадь треугольников и параллелограммов
20 мая: видео 1 и заметки Видео 2 Функции делать заметки Онлайн-игра для порядка операций
21 мая: 5.4 Площадь составных фигур wrksht 5.4 Площадь составных фигур wrksht видео онлайн-игр
22 мая: 6,9 1-шаговые алгебраические уравнения: сложить / вычесть
23 мая: 6,9 1-шаговые алгебраические уравнения: добавить / вычесть wkrksht
: 6.9 пошаговые алгебраические уравнения: сложить / разделить wrksht
24 мая: последний день в школе
Обзор 5.1 — 5.4 Викторина неделя и ТЕСТ 5.2 — 5.4
5.5 3D-фигур с сетками wkst
5.6 Площадь поверхности 3D-фигур wrksht / prodigygame — 1 урок
Graph it Art
Май Обзор сложения и вычитания дробей wkst
Может умножение дробей wkst
2 марта: 5.7 Площадь поверхности 3D формы (продолжение) wrksht
: 5.6 Площадь поверхности трехмерных фигур
5.6 Площадь поверхности трехмерных фигур
Викторина и тест LT 5.5 и 5.6
5.9 Объем HomeLink 5.9
5.10 Объем с дробями / 5,6 Площадь поверхности с десятичными знаками
: Активность с длиной, площадью и объемом
: см. 5.5-510 Учебное пособие по площади, сеткам и объему
: ТЕСТ 5.5-510 Площадь, сетки и объем
: 6.3 Использование линейчатой модели для решения уравнений wrksht
6.4 Домашняя ссылка 1-го дня балансировки панорамирования 6,4
: 6.2 Наборы решений / Проба и ошибка Домашняя ссылка 6,2
6.5 Домашняя ссылка 2-го дня панорамирования балансов 6,5
Обзор 6.2-6,5 ВИКТОРИНА
ТЕСТ 6,2-6,5
6.6 Условия лайка в день 1 (выберите 9 задач, группы по 3)
: 6.6 Лайк терминов в день 2 работа
: 6.6 Лайк терминов с распределительной собственностью wrksht
: Review 6.6 QUIZ
: Test IA Assessment Review
: 6.9 1-шаговые алгебраические уравнения: сложить / вычесть wrksht
: 6.9 1-шаговые алгебраические уравнения: добавить / вычесть wkrksht
: 6.10 1-шаговые алгебраические уравнения: mult / Разделить wrksht
Обзор 6.9-6.10 1 шаг Alg Equa add / subtr & Mult / div QUIZ TEST
: 7.8 Уравнения, таблицы, графики wrksht
7.8 Уравнения, таблицы, графики
7.8 Уравнения, таблицы, графики написать QUIZ, TEST
: 8.1 Сложение / вычитание дробей стр. 238 26-44 событий
: 8.2 Сложение смешанных чисел стр. 243-244 11-15, 33-37, 66-68
: 8.3 Вычитание смешанных чисел стр. 248 6-10 все
: 8.3 Вычтите смешанные числа стр. 527 5-20 все
: Обзор 8.1-8.3 Сложение / вычитание дробей / смешанные числа QUIZ / TEST
2,5 Многократные фракции / смешанные pg 256 л # 17-21, pg 260 17-21
2,8 Разделить фракции / смешанные pg 265 28-37 все
2,5 /2.8 ВИКТОРИНА / ТЕСТ
9.1 Сложение целых чисел стр. 436 1–16 все
9.1 Добавление целых чисел стр. 436 24–30 все, стр. 444 1–10 все
9.1 Добавление целых чисел стр. 444 18–30 событий
: 9.2 Вычитание Целые числа стр. 250 4-13 все
: 9.2 Вычитание целых чисел wrksht
: 9.2 Вычитание целых чисел wrksht
: 9.1-9.2 Проверка викторины Обзор семестрового теста
: Обзор семестрового теста
: семестр TEST
23 августа: правила, ожидания
24 августа: Notetaking Skills4 и
27 августа: правила делимости wkst и правила
28 августа:: практиковать мои 3, 4 и 9 на Ascendmath.com
23 августа: День наставничества !!!
26 августа: Правила, ожидания
27 августа: Навыки ведения записей и WODB
28 августа: Указания по чтению и аудирование
29 августа: Правила делимости и правила
30 августа: правила делимости wkst
2 сентября: День труда без школы
3 сентября: проверьте правила делимости для следующих: 1248 990 1539 2760 недель
сентября 4: правила делимости в Jeopardy и викторине
5 сентября: правила проверки делимости и смотрите видео и делайте заметки Видеокарточка онлайн
6 сентября: игра с множественными тыквами, игра с множественными множителями Игра с двумя факторами
9 сентября: 1.10 типов числовых групп, кратных / множителей Журнал 37 игра на множители
10 сентября: 1.10 Типы числовых групп, кратных и множителей … проверка карты без домашнего задания
игра 1 игра 2-факторная игра
11 сентября: 1.10 Типы Число групп, кратные и множители wkst с партнерами в классе
12 сентября 1.10 Типы групп номеров отрицательные числа без присвоения (тестирование карты)
13 сентября 1.10 Типы групп номеров отрицательных чисел HomeLink 1.10
16 сентября: 1.10 типов групп чисел Счет, целые числа стр. 39 игра Math Masters игра 2 игра 3
17 сентября 1.10 Типы групп чисел неделя Math Masters Отражение листа
18 сентября 1.10 Типы групп чисел Обзор учебного пособия Учебное пособие учебное пособие
19 сентября нед. ТЕСТ 1,10 видео 1 видео 2 и делать заметки для каждого видео
20 сентября 1,11 Сравнение дробей смотреть видео 3 делать заметки для каждого видео
23 сентября 1.11 сравнить фракции wrksht game1 game 2
24 сентября: 1.12 Найти дроби btw фракций / упорядочить фракции wrkshtwkst (нижняя 8)
25 сентября: 1.12 Найти дроби btw фракций / упорядочить фракции wkst игра 1 игра 2 игра 3 игра 4 обзор
сен 26: 1.12 Найти дроби между дробями / Порядок дробей wkst справа 1/2 вверху страницы
27 сентября НАЧАЛО — НЕТ КЛАССА
30 сентября 1.12 Найти дроби между дробями / Порядок wkst дробей в игре порядка
11 октября.12 find Fractions btw fractions / ordering twkst
Oct 2: рабочий лист 1.12 Fractions in Order (wkst from Notebook)
Oct 3 wkst review 1.11 Сравнение дробей 1.12 Find Fractions btw. фракции / порядок дробей учебное пособие Викторина
дроби в порядке игры https://www.thatquiz.org/tq-6/math/identify/fractions/ fractions level 10
4 октября Тесты 1.11 и 1.12 посмотрите видео 1 и сделайте заметки
7 октября: видео 2 сделайте заметки на обоих видеороликах и найдите рациональные числа в числовой строке 1/4, 7/10, 5/8 и 1/9 в числовой строке
октября 8: 1.13 Найдите рациональные числа на числовой линии wrksht игра спасение животных
9 октября: Викторина и тест LT 1.13 1.13 Найдите рациональные числа на числовой строке wkst
окт 10: Нет класса — JBiz Town
окт 11: 6-й период пройти тест
1.14 Coordinate Plane видео (делать заметки) игра thatquiz
Oct 14: 1.14 Coordinate Plane HomeLink 1.14 игра thatquiz
15 октября # 1 Desmos Acitvity «Активность на полиграфе Викторина № 2 обзор викторины 1.14 Coordinate Activity18 октября: Нет школы
21 октября Ch 2 2.1 GCF wkst GCF Jeopardy game
Oct 22 2.2 LCM wkst game
23 октября HomeLink 2.2 и обзор 2.1-2.2
24 октября Викторина Учебное пособие другое 1/2 рабочего листа, который вы выполнили вчера, видео по умножению
25 октября ТЕСТ 2.1-2.2 LCM и GCF посмотрите ВИДЕО и сделайте заметки
, в которых викторина тренирует сложение, вычитание, умножение и деление на всех уровнях
GCF Jeopardy game
игровая координатная плоскость
игра LCM
28 октября: мини-урок: упрощение дробей wrksht игра игра математика
29 октября упрощение дробей wkst
30 октября мини-урок: неправильные дроби и смешанные числа wkst ВИДЕО 1 ВИДЕО 2 игра
31 октября: 2.5 Умножение дробей / упрощение перекрестной отмены wkst VID1 VID2
1 ноября: 2.5 Умножение дробей / упрощение перекрестной отмены wkst # 10-18 игра футбол игра миллионер игра
4 ноября 2.5 Умножение смешанных чисел / дробей / упрощение wkst 2.5 Умножение дробей / упрощение целые числа
5 ноября 2.5 Умножение смешанных чисел / Дроби / Упрощение перекрестного отмены Викторина 2.5 нед. нед
6 ноября Видео Тест умножения дробей заметки
7 ноября 2.8 Разделение на фракции wkst игра футбол
8 ноября 2.8 Разделение на фракции REFLECTION wkst викторина на веб-сайте Викторина 2.8 Обзор Mult / Div фракция wkst wkst Код вундеркинда: B97B22
11 ноября: ТЕСТ 2.5 / 2.8 Mult / Div Fractions Код Prodigy: B97B22
12 ноября: 2.7 Задачи сюжета с дробями Mult / Div wrksht13 ноября: 2.7 Задачи истории при рабочем листе Mult / Div Fractions
14 ноября: игра и рабочий лист LT 2.7 Задачи сюжета с умножением и делением
15 ноября: Учебное пособие wrksht 2.7 сюжетных задач с Mult / Div Fractions онлайн-домашнее задание придумывают собственные проблемы
TEST 2.7 Story Problems with Mult / Div Fraction смотреть видео и делать заметки
18 ноября: 1-е видео для просмотра 2-го видео для просмотра и заметок 3-я неделя 2.9 Ratios Введение, если сделано со всеми http://ascendmath.com/fcm/html5/ 6,7, 8, 9
19 ноября 2.10 Таблица соотношений wrksht (только лицевая сторона)
Nov 20 2.10 Ratio Tables wrksht И wrksht (ВТОРАЯ СТРАНИЦА)
21 ноября: wrksht Review LT 2.10 Таблица коэффициентов нед. (Первые 2 страницы) и быстрое написание
22 ноября: плей-офф без школьного футбола
25 ноября: 2,10 и нед. LT (стр. 1 и 2) Викторина LT 2,10 Таблицы и коэффициенты
26 ноября : Test LT 2.10 Ratio и таблицы Ratio видео и заметки
27 ноября: Нет школы
28 ноября: Нет школы
29 ноября: Нет школы
2 декабря: 2,13 Ставки за единицу неделя
3 декабря 2,13 Ставки / Ставки за неделю Коэффициенты обзора викторины / Ставки за неделю
4 декабря: Тест LT 2.10 Тест LT 2.10 Ставки / единицы Ставки видео 1 и видео 2 делать заметки
5 декабря 1.1 Статистические вопросы Создайте статистический вопрос в этой форме Google
Wkst
6 декабря День для отстающих учеников, возрастание по математике 6, 8, 9 гол за 1,5 минуты, вундеркинд
дек 9: 1.2. Достопримечательности и точечные графики Home Link 1.2
10 декабря: Cogat догоняет ascendmath.com
Dec 11: Cogat догоняет ascendmath.com
16 декабря 1.3 Среднее значение Home Link 1.3 и таблицы Google для среднего, медианного, режима
17 декабря 1,5 Сравнение ориентиров wrksht 1,5
18 декабря 1,5 Сравнение ориентиров wrkst 1,5
19 декабря Обзор 1,1-1,5 Викторина wkst wkst Класс B присоединиться к Khan Academy Класс C Присоединиться к Khan Academy
20 декабря: Без занятий — День развлечений
23 декабря — 3 января Зимние каникулы
—————————- ——— Семестр 2 —————————
6 января: Тест 1.1-1.5
7 января: 1.6 Анализ убедительных графиков Домашняя ссылка 1.6 (2 абзаца)
8 января 1.6 Анализ убедительных графиков wkst и видео
9 января: 1.8 Чтение журнала гистограмм стр. 27
10 января: 1.8 Гистограммы нед. С. 28 — составьте гистограмму и присвоение хана
13 января: 1.8 Анализируйте гистограммы 1.9 Онлайн-викторина «Анализ данных»
14 января: просмотрите онлайн-ссылку «Анализ данных» здесь. партнер (wkst Study Guide 2 онлайн-ссылка здесь)
: Test 1.8 Чтение и интерпретация гистограммы 6 Видео и видео с пакетом обновления 2 и 6 с пакетом обновления 5 2 сделать заметки
3.1 Стандартная, словесная и развернутая форма wrksht 24 января: LT 3.1 Стандартная, словесная и развернутая форма wkst wkst wkst25 января: 3.2 Десятичные числа в числовых строках / decimal между wrksht
28 января: LT 3.2 Десятичные числа на числовых строках / десятичные числа между wkst
29 января: Обзор учебного руководства 3.1-3.2 нед. — нет Школа
31 января: ТЕСТ 3.1-3.2
1 февраля: Тест 3.1 -3.2 для класса B и запись зонда по медиане и среднему для класса C
4 февраля: 3.3 Сложение / вычитание десятичных чисел — wkst
5 февраля: 3.3 Сложение / вычитание десятичного числа числа wkst6 февраля: 3.4 Умножение десятичных знаков Часть I wrksht— вся игра
7 февраля: 3.4 Умножение десятичных знаков Часть II неделя и обзор 3.3–3.4
8 февраля Партнеры по игре Jeopardy и игры Quizlet
11 февраля: 3.4 Умножение десятичных знаков Часть I wkst Учебное пособие Викторина LT 3.4 недели выполните оценку событий и рабочий лист выполните первые 4 умножения
12 февраля: ТЕСТ 3.3–3.4 (дополнительная практика нед.) Посмотрите видео по разделу B группа
Группа C нет класса
13 февраля : Групповой тест C 3.3–3.4 смотреть видео вчера …. Письменное задание группы B
14 февраля: 3.5 Традиционный метод деления в длинных делениях wkst — лицевая сторона
15 февраля 3.5 Традиционный метод длинных делений wkst 1B 3.6 Длинное деление на 2-значные числа
21 февраля: 3,6 длинное деление с десятичными знаками только на лицевой стороне
22 февраля: 3,6 длинное деление с десятичными знаками wrkshtA (обратная сторона)
25 февраля: пересмотр 3.6 длинное деление с десятичными знаками учебное пособие wkst B (группа B не пропускает занятия)
26 февраля: Тест 3.6 Видео
27 февраля: 3.8 Введение в проценты посмотрел видео 3.8 Введение в проценты нед.
28 февраля 3.9 Определение процентов, нед. Игра
1 марта: тест ISASP для 6-го класса
4 марта: ТЕСТ ISASP
5 марта : 3.9 Определение процентов по неделям B и обзор процентов,
6 марта: Журнал викторины, стр. 143 и определение процентов по неделям C
7 марта: Эквивалентные дроби ТЕСТ 3.9 видео
8 марта: 3.11 Исследование процента недель вперед
11 марта: 3.11 Исследование процента недель назад и Хан
12 марта: 3.11 Исследование процента недель
13 марта: 3,10 процента как соотношения в сюжетных задачах wrksht (эвены) Учебное пособие
14 марта Проценты как соотношения в сюжетных задачах wrksht (назад) Тест LT 3.11 и LT 3.10
15 марта: Переоценки / Quizlet live
16 марта — 24 марта: Весенние каникулы
25 марта: 4.12 Абсолютное значение wkst
26 марта: Викторина и тест LT 4.12 Абсолютное значение 3.12 Введение в коробчатые диаграммы wkst
27 марта: 3.12 Введение в коробчатые графики wrksht
28 марта: 3.13 Сетчатые диаграммы и данные онлайн-домашнее задание wkst онлайн-практика (чел. ) 3.13 Рамочные диаграммы и данные онлайн-домашнее задание wkst онлайн-практика (вызов)
Обзор Box Plots / Quiz wrksht
29 марта: ТЕСТ 3.12–3.13 Оценка IA (работа с партнером над 21 вопросом)
1 апреля: Обзор оценки Ia
2 апреля: Обзор оценки Ia
3 апреля: Обзор оценки Ia
4 апреля: Обзор оценки Ia
5 апреля: Обзор оценки Ia
8 апреля: Глава 5 4.1 Exponents wkstt
9 апреля: Ch5 4.1 Exponents ЗАДАЧА: Do wkst evens
Ch5 4.1 Exponents wkst wkst ЗАДАЧА: Do wkst 1-5 thatquiz.org
10 апреля: 4. 2 Порядок операций без назначения
11 апреля : 4.2 Порядок действий wkst A # 1-10 онлайн-игра
12 апреля:: 4.2 Порядок действий wkstonline game 2-е ограбление онлайн-игры
15 апреля: 4.2 Порядок работы wkst обзор LT 4.1 и LT 4.2 Викторина LT 4.1 и LT 4.2: учебное пособие:
16 апреля: онлайн-игра wkst Test LT 4.1 и LT 4.2
17 апреля: Khan Academy
18 апреля: 4.3 Алгебраические выражения wkst
19 апреля: без занятий — День Земли
22 апреля: 4.3 Алгебраические выражения wrksht A
23 апреля :: 4.4 Алгебраические выражения словесные задачи WKST
24 апреля: 4.4 Алгебраические словесные задачи wkst Обзор / викторина 4.1–4.4 учебное пособие
25 апреля: ТЕСТ 4.3-4.4 видео
26 апреля: видео 1 графическое изображение неравенства видео 2 графическое изображение неравенства Сделайте заметки на ОБЕИХ видео
29 апреля: 4.6 Введение в распределительную собственность — wrksht
30 апреля: 4.6 Распределительная собственность Умственная математика wkst онлайн-практика
1 мая: 4.9 Знакомство с неделями неравенства и онлайн-практика рабочего листа № 1
2 мая: 4.10 Графики неравенств wkst
3 мая: 4.10 Графики неравенств wkst wkst Обзор LT 4.9 и LT 4.10 QUIZ
Tenmarks.com Урок: Absolute Value Extra Practice
6 мая: ТЕСТ LT 4.9 и 4.10 видео на полигонах
CH 5 Geometry
7 мая:: LT 5.1 Полигоны wkst онлайн-практика (didn не попадают в задание)
8 мая: LT 5.1 Полигоны wkst онлайн практика онлайн практика 2 онлайн практика 3 игра игра 2
9 мая:: 5.2 Площадь параллелограммов wkst
10 мая :: 5.Карты с 3 областями треугольников wkst
13 мая: готовность для эталонного теста
14 мая: готовность для эталонного теста I
15 мая: готовность для эталонного теста I
16 мая: готовность для эталонного теста I
17 мая: неделя для области треугольников и параллелограммов
20 мая: Видео 1 и делать заметки Видео 2 Функции делать заметки Онлайн-игра для порядка действий
21 мая: 5.4 Область составных форм написано 5.4 Область составных форм появилось видео онлайн-игр
22 мая: 6.9 1-ступенчатые алгебраические уравнения: сложить / вычесть wrksht
23 мая: 6.9 1-ступенчатые алгебраические уравнения: добавить / вычесть wkrksht
: 6.10 1-ступенчатые алгебраические уравнения: умножить / разделить wrksht
24 мая: последний день в школе
Review 5.1 — 5.4 QUIZ wkst и TEST 5.2 — 5.4
5.5 3D-фигуры с сетками wkst
5.6 Площадь поверхности трехмерных фигур wrksht / prodigygame — 1 урок
Graph it Art
May Review сложение и вычитание Дроби wkst
Умножение дробей на май wkst
Мар 2: 5.7 Площадь поверхности трехмерных фигур (продолжение) wrksht
: 5.6 Площадь поверхности трехмерных фигур
5.6 Площадь поверхности трехмерных фигур
Quiz and Test LT 5.5 и 5.6
5.9 Объем HomeLink 5.9
5.10 Объем с дробями / 5.6 Площадь поверхности с десятичными знаками
: активность с длиной, площадью и объемом
: см. 5.5-510 Руководство по изучению площади, сетей и объема
: ТЕСТ 5.5-510 Площадь, сети и объем
: 6.3 Использование линейчатой модели для решения уравнений wrksht
6.4 Домашняя ссылка на 1 день балансировки 6,4
: 6.2 Наборы решений / Проба и ошибка Домашняя ссылка 6,2
6.5 Панорамная балансировка на день 2 Домашняя ссылка 6.5
Обзор 6.2-6.5 Викторина
ТЕСТ 6.2-6.5
6.6 Условия лайков, день 1 (выберите 9 задач, группы по 3)
: 6.6 Тесты лайков, день 2 wrksht
: 6.6 Условия лайка с отчетом о распределительной собственности
: обзор 6,6 викторина
: Тест Обзор оценки IA
: 6.9 1-шаговые алгебраические уравнения: сложить / вычесть wrksht
: 6.9 1-ступенчатые алгебраические уравнения: добавить / вычесть wkrksht
: 6.10 1-ступенчатые алгебраические уравнения: умножить / разделить wrksht
Просмотрите 6.9-6.10 1-шаговый алгоритм сложения / вычитания Mult / div QUIZ TEST
: 7.8 Уравнения, таблицы, графики wrksht
7.8 Уравнения, таблицы, графики wrksht
7.8 Уравнения, таблицы, графики wrksht QUIZ, TEST
: 8.1 Добавить / вычесть дроби стр. 238 26-44 evens
: 8.2 Сложить смешанные числа стр. 243-244 11-15, 33-37, 66-68
: 8.3 Вычесть смешанные числа стр. 248 6-10 все
: 8.3 Вычесть смешанные числа стр. 527 5-20 все
: Обзор 8.1-8.3 Сложение / вычитание дробей / смешанные числа QUIZ / TEST
2.5 Многократные фракции / смешанные pg 256 л # 17-21, pg 260 17-21
2.8 Разделить фракции / смешанные pg 265 28-37 все
2.5 /2.8 ВИКТОРИНА / ТЕСТ
9.1 Добавление целых чисел стр. 436 1-16 все
9.1 Добавление целых чисел стр. 436 24-30 все, стр. 444 1-10 все
9.1 Сложение целых чисел стр. 444 18-30 событий
: 9.2 Вычитание целых чисел стр. 250 4-13 все
: 9.2 Вычитание целых чисел wrksht
: 9.2 Вычитание целых чисел wrksht
: 9.1-9.2 Обзор QUIZ TEST 900 9000 Review Semester Test
: Обзор семестрового теста
: семестрового теста
23 августа: правила, ожидания
24 августа: навыки ведения записей и WODB
27 августа: правила делимости и правила
28 августа:: практика моя Комбинации 3, 4 и 9 на Ascendmath.com
29 августа: Викторина для 6A Викторина
30 августа: неделя и викторина на делимость
31 августа: Ознакомьтесь с правилами делимости на Jeopardy
3 сентября: День труда
4 сентября: проверьте правила делимости для эти: 1248 990 1539 2760 недель Тестовые правила делимости
5 сентября: видео (делать заметки) Игра с множителями, игра с множителями, игра с двумя факторами
6 сентября: 1,10 Типы групп чисел, множители / множители Журнал 37 игра с множителями
7 сентября: 1.10 типов числовых групп, кратных и множителей wkst
10 сентября: 1.10 Типы числовых групп отрицательных чисел HomeLink 1.10
11 сентября 1.10 Типы числовых групп Подсчет целых чисел стр. 39 Игра Math Masters game2 игра 3
12 сентября 1.10 Типы числовых групп wkst Лист для размышлений Math Masters
13 сентября: 1.10 Типы числовых групп Обзор учебного пособия wkst
14 сентября: Homecoming
17 сентября: 1.10 Типы числовых групп wkst Обзор 1.10 Учебное пособие Учебное пособие
18 сентября: неделя ТЕСТ 1.10 и тест I Ready
19 сентября I Ready Test
20 сентября :; Я готов тестировать игру 1 игра 2 факторная игра
21 сентября: я готов тестировать игровой фактор игра
24 сентября: 1.11 Сравнение дробей смотреть видео 1 видео 2 видео 3 и делать заметки по каждому видео
25 сентября: 1,11 сравнить Дроби wrksht game1 game 2
26 сентября: 1.12 Найти дроби btw fractions / Порядок дробей wrkshtwkst (слева)
27 сентября: 1.12 Поиск дробей между фракциями / Порядок дробей wkst (правая сторона) игра 1 игра 2 игра 3 игра 4
28 сентября :: 1,12 Найти дроби между дробями / Упорядочение дробей wkst внизу страницы все 8 задач
1 октября: 1,12 Найти дроби между прочим Fractions / Ordering wkst
Oct 2nd: 1.12 find Fractions btw Fractions / ordering twkst
Oct 3rd:: workheet 1.12 Fractions in Order (wkst from Notebook)
Oct 4th: review 1.11 Comparing Fractions and 1.12 Найдите дроби между прочим. Учебное пособие по дробям / порядку дробей
5 октября Тест 1.11 и 1.12
8 октября:: Видео 1 Видео 2 сделайте заметки на обоих видео и найдите рациональные числа в числовой строке 1/4, 7/10, 5/8 и 1 / 9 на числовой линии
октября: 9: 1.13 Найдите рациональные числа на числовой линии wrksht game
10 октября Викторина и тест LT 1.13 1.13 Найдите рациональные числа на числовой прямой wkst
11 октября: 1.14 Координатная плоскость HomeLink 1 .14 видеоигра
12 октября: Graph it Art picture
18 октября :: Ch 2 2.1 GCF wkst GCF Jeopardy game
Oct 19: No School
Oct 22nd: 2.2 LCM wkst Fruit game
23 октября: HomeLink 2.2 и обзор 2.1-2.2 Учебное видео по умножению
24 октября: ТЕСТ 2.1-2.2 LCM и GCF посмотрите ВИДЕО и сделайте заметки
25 октября: Мини-урок: Упрощение дробей, написание игры, игра Mathman
, 26 октября: Упрощение дробей, нед.
29 октября: Мини-урок: неправильные дроби и смешанные числа wkst ВИДЕО 1 ВИДЕО 2 игра
30 октября: 2.5 Умножение дробей / упрощение перекрестной отмены wkst VID1 VID2
31 октября: 2.5 Умножение дробей / упрощение перекрестной отмены wkst # 10-18 игра футбол игра миллионер
1 ноября: 2.5 Умножение дробей / упрощение недели 2.5 Умножение дробей / упрощение целых чисел
Викторина 2.5 нед. Нед.
2 ноября: видео о тесте умножения дробей, заметки
5 ноября: 2,8 Деление дробей недельная игра в футбол
6 ноября 2.8 Деление дробей REFLECTION wkst quiz на веб-сайте Quiz 2.8 Обзор Mult / Div фракции wkst wkst
7 ноября: ТЕСТ 2.5 / 2.8 Mult / Div Fractions
8 ноября: 2.7 История Проблемы с Mult / Div Fractions wrksht игра
9 ноября: 2.7 Задачи истории с рабочим листом Mult / Div Fractions
12 ноября: играйте и придумывайте собственные задачи относительно задач со словами (6-е C решайте одно или другое)
13 ноября: Учебное пособие wrksht 2.7 Проблемы истории при помощи Mult / Div Fractions онлайн-домашнее задание решать собственные проблемы
14 ноября : ТЕСТ 2.7 проблем с историей с Mult / Div Fraction смотреть видео и делать заметки
15 ноября: 2,9 Ratios Intro wkst
16 ноября 2.10 Ratio Tables wrksht (только на лицевой стороне)
Nov 19: 2.10 Ratio Tables wrksht,
20 ноября: напишите обзор таблицы соотношений LT 2.10 на неделю (первые 2 страницы) и быстро напишите
21 ноября: нет школы
22 ноября: нет школы
23 ноября: нет школы
26 ноября: LT 2,10 и неделя видео и возьмите Примечания
27 ноября: 2.13 Ставки / Ставки за единицы нед.
28 ноября: 2,13 Ставки / Ставки за единицы нед. Коэффициенты обзора викторины / Ставки нед.
29 ноября: Тестирование LT 2,10 Таблицы соотношений видео 1 и видео 2 делать заметки
30 ноября: Тестирование LT 2,10 Ставки / Ставки единицы
3 декабря: 1.1 Статистические вопросы Создайте статистический вопрос в этой форме Google
Wkst
4 декабря: 1.1 Статистические вопросы исправят ваш вчерашний вопрос по соответствующей ссылке.
5 декабря: 1.2.Достопримечательности и точечные графики Home Link 1.2
6 декабря: 1.2. Точечные графики Home Link 1.2 нед
7 декабря: 1.3 Среднее значение Home Link 1.3 и таблицы Google для среднего, медианного, режима
10 декабря: тестирование CogAT
11 декабря: тестирование CogAT
12 декабря: тестирование CogAT
13 декабря : 1.5 Сравнение ориентиров wrksht 1.5
14 декабря 1.5 Сравнение Landmarks wrkst 1.5
17 декабря: Обзор 1.1-1.5 Викторина wkst wkst Класс B присоединиться к Khan Academy Класс C Присоединиться к Khan Academy
18 декабря: Test 1.1-1,5
19 декабря: Thatquiz.org и Хан
20 декабря: Kahoot
21 декабря: Без уроков — День веселья
23 декабря — 2 января Зимние каникулы
Задачи по математике для 6-го класса с ответы pdf
6 класс Задачи по математике с ответами pdf Равны ли они? 1 4 = 2 8? О мальчик, ответ — да. В этом случае не беспокойтесь, потому что в этой статье мы подготовили для вашего ученика исчерпывающие бесплатные и распечатываемые рабочие листы по математике для 6-го класса.ответы верны, не учитель Математика Квадраты 12 15 8 50 9 1 1 6 4. Поиск. Здесь вы найдете большую коллекцию бесплатных распечатываемых заданий по математике, математических головоломок и математических игр для 6-го класса. Рабочие листы по математике для шестого 6-го класса в формате pdf. С помощью этих рабочих листов вы сможете быстро освоить эквивалентные дроби. применяйте эти навыки, применяя то, что мы знаем, для решения проблем в повседневной жизни. Решите проблему, используя выбранную вами стратегию. Ответ: _____ 3. Если верхний числитель меньше нижнего 9 октября 2021 г. · Рабочая тетрадь по математике для 6-го класса: Учебная тетрадь CommonCore по математике Это не для обучения математике на уровне 6-го класса, а для практики применения того, что было изучено в рамках математики для 6-го класса.Спланируйте, как вы собираетесь решать проблему, и оцените ответ. Рабочие листы по математике для 6-го класса в формате pdf, тест по математике для 6-го класса для печати, задания по математике для 6-го класса с ответами, рабочие листы по математике для 6-го класса. в 6 классе. Если в офисе работает 60 женщин, сколько мужчин работает в офисах? Нарисуйте ленточную диаграмму, чтобы решить проблему. В шестом классе школы танцев 132 мальчика, 89 девочек и 14 взрослых.A. Задачи по математике для 6-го класса с ответами Слово по математике для 6-го класса 20 сентября 2020 · 21 сообщение, относящееся к задачам для 6-го класса Задания по математике для 6-го класса с ответами. Письмо укрепляет изученную математику. Ключевые слова: шестой класс; сигма-образцы; образцы задач шестого класса; образцы; сигма-тесты; протестируйте сигма-тест, образцы для соревнований по сигма-математике Дата создания: 23.06.2009 13:45:07 рамочный стандарт, который он оценивает. Здесь вы найдете рабочие листы для сложения, вычитания, числового значения, определения времени и многого другого.Рабочие листы с дробями в 6-м классе используются, чтобы дать учащимся лучшее представление о типах задач, которые могут быть сформулированы по теме. 2 Используйте сложение и вычитание. Математика за неделю 27 сентября. Значок шестого класса. Эти рабочие листы были созданы для учителей, родителей, обучающихся на дому, и для шестиклассников. Эти рабочие листы представляют собой файлы в формате pdf. потренируйтесь работать сообща над решением сложных словесных задач. Эти рабочие листы по математике для шестого класса охватывают большинство основных математических тем предыдущих классов, в том числе рабочие листы преобразования, рабочие листы измерений, рабочие листы среднего, среднего и диапазона, числовые шаблоны, экспоненты и различные темы, выраженные в виде задач со словами.Каждый тестовый лист должен быть разным, но равнозначным по классу / сложности с одинаковым количеством задач, представляющих каждый навык d. Прокрутите до следующих разделов, чтобы проверить примеры проблем, ответить на PDF-файлы и т. Д. 1 — Порядок действий. Эти рабочие листы по математике для 6-го класса состоят из вопросов по применению арифметических операторов к различным типам дробей, задачам со словами, преобразованию дробей и определению различных типов дробей. Задачи математического клуба для 3–4 классов Континентальной математической лиги.Полные инструкции включены в загрузку, но вот суть. 6-й класс PARCC Модуль 2 Практический тест № 21 (Калькулятор): Стандарты 6. Сложение и вычитание дробей, например: 1 3 + 1 6 1 3 = 2 6 1 6 = 1 6 + 3 6 = 1 2 × 2 × 2 × 1 × 1 ÷ 3 ÷ 3 1. Все эти темы должны были быть рассмотрены в Elementary, и ожидается, что учащиеся уже усвоили эти концепции. Флэш-карточки с ключевым словарем, блок A1; Тема 1: Переменные и выражения. Добро пожаловать в школьные задания по математике и математические игры.Он содержит рабочие листы по математике для шестого класса. MAFS. Пакет домашних заданий для учителя математики 6 класса Пакет домашних заданий включает 21 набор практических задач, которые соответствуют важным математическим концепциям, которые, вероятно, изучались в этом году. 6-й класс Vanguard Math Предварительные требования Средняя школа Lanier Здравствуйте и добро пожаловать в среднюю школу Lanier! В этом пакете вы найдете практические задачи, над которыми студенты будут работать летом. com 8 октября 2021 г. автор: guest Читать онлайн Задачи по математике для 6-го класса с ответами Получение книг Задачи по математике для 6-го класса с ответами сейчас не являются сложным средством.7 одношаговых неравенств. Рассмотренные здесь темы по математике для 8-х классов помогут вам легко решить любую математическую задачу. Два числа N и 16 имеют LCM = 48 и GCF = 8. Таблицы вероятностей для 6-го класса предоставляют задачи по вероятности, чтобы учащиеся могли понять принцип вероятности как отношение шансов в пользу события к общему количеству возможных результатов. Для сохранения щелкните значок «скачать». Вычтите два числителя и оставьте знаменатели одинаковыми. Заполните таблицы, создав эквивалентные соотношения. Сложные соотношения по математике для 5-го класса. Рабочие листы по математике для 6-го класса, распечатки в формате PDF для отработки навыков по математическим темам, изученным в 6-м классе.Рабочие тетради по математике для шестого класса. Блок A1: Алгебраические и числовые выражения. Masters for Glencoe Math Connects, курс 2. Какой процент его карандашей был красным? Вопрос 3, 26 октября 2021 г. · Рабочие листы по математике для 6-го класса с ответами Pdf. Заполните таблицы, создав эквивалентные соотношения. Сложное соотношение по математике для 5 класса. Подсчитайте на наших распечатываемых листах по математике для 6-го класса с ключами ответов для тщательной практики. 23 марта 2020 г. · Пакет домашних заданий для учителя математики 6 класса Пакет домашних заданий включает 21 набор практических задач, которые соответствуют важным математическим концепциям, которые, вероятно, изучались в этом году.Обозначьте свой ответ соответствующими единицами измерения. У Хьюберта есть методика, как он планирует отвечать на вопросы индивидуального теста на олимпиаде по математике в этом году. У Джанессы есть на 10 задач по математике больше, чем у Джудит. Октябрь. Получите бесплатные задачи и ответы по математике для 6-го класса, главы 1, 6 ответов, руководство по обслуживанию yz250f 2003 г., ответы на ключевые галактики, характеристики двигателя 4g13, краткое изложение глав книги о роботах, 3-е решение по векторному исчислению, ответы на вопросы оценки в разделе химии Prentice Hall, глава 2 , руководство honeywell fs90, физическая химия Аткинс 7-е Эта тетрадь по математике для шестого класса — отличный способ для детей попрактиковаться в сложении четырех больших чисел.документ, который будет размещен на веб-странице оценки успеваемости. «Мосты по математике» — это основанная на стандартах учебная программа K – 5, которая представляет собой уникальное сочетание разработки концепций и отработки навыков в контексте решения проблем. Найдите общий знаменатель. 4 2MC отрывки из тестовых заданий 10/2016 из практических онлайн-тестов PARCC 30 26 октября 2021 г. · Рабочие листы по математике для 6-го класса с ответами Pdf. 26 октября 2021 г. · Рабочие листы по математике для 6 класса с ответами Pdf. 3 Используйте Daily Math Review — 6-й класс 13 Имя _____ 1.Математика за неделю 6 сентября. Получите бесплатно 6-й класс «Задачи и ответы по математике», главы 1 6 ответов, руководство по обслуживанию yz250f 2003 года, ответьте на ключевые галактики, звезды, характеристики двигателя 4g13, краткое содержание глав книги о роботах, 3-е решение по векторному исчислению, химия prentice hall раздел оценка ответы глава 2, руководство Honeywell fs90, физическая химия Аткинс 7-й 3-й / 4-й классы математического клуба задачи Континентальной математической лиги. Заполните таблицы, создав эквивалентные соотношения. Сложное соотношение по математике для 5-го класса. Каждый рабочий лист по математике для 6-го класса в формате pdf охватывает уникальный навык в рамках определенной математической темы.а) Каково отношение количества синих карандашей к количеству красных? б) Каково отношение количества синих карандашей к общему количеству карандашей? Рабочие листы по математике для шестого класса — задания по математике для шестиклассников в формате PDF. 11 марта 2021 г. · Рабочий лист по математике для 6-го класса Pdf Esl Грамматика Рабочие листы Структура текста Рабочие листы 3-й класс Математические задания для 2-го класса Рабочие листы Рабочие листы для грамотности в детском саду Бесплатные рабочие листы по математике для первого класса рабочий лист для печати для букв детского сада z Рабочий лист с 3 таблицами времени бесплатный рабочий лист по математике для четвероклассников обзорное слово подсчет рабочего листа по буксировочному листу для детского сада объем рабочего листа призм MP.Ответ: _____ 4. pdf] — Прочитать файл в Интернете — Сообщить о нарушении 6, сохранив те же числители, затем сложив числитель и знаменатель вместе для нового знаменателя, мы получим 1 1 + 3 и 2 2 + 6. 9) 7488 4 16 x 26 4. Математические вопросы с ответами для 6-го класса. В этом разделе мы увидим несколько практических вопросов для учеников 6-го класса. Задачи о пропорциях слов с использованием задач о соотношении десятичных дробей. Рабочие листы по математике для 6-го класса в формате pdf для печати. В доме Ким 3 окна на кухне, 1 в гостиной, 1 в ванной, 6 на веранде и 2 в спальне.Вы не могли изолировать себя сразу после накопления электронных книг или библиотеки или одалживания у друзей, чтобы их прочитать. Заполните таблицы, составив эквивалентные соотношения. Сложный математический показатель. Соотношение для 5-го класса. 6-й класс. К 6 классу письма большинство детей могут писать по памяти, но проблема в грамматике. 6 класс Проценты Задачи со словами Имя: _____ Класс: _____ Вопрос 1 Отец дал мне немного денег. 7, 6. 3. Несколько вопросов не имеют смысла, тогда вы можете пропустить. Рабочие листы по математике для 6-го класса PDF — Рабочие листы по математике для 6-го класса с ответами — это идеальный инструмент, полезный для проверки навыков вашего ребенка по различным математическим темам для 6-го класса.Несколько советов по решению логических задач: внимательно прочтите вопрос несколько раз и отсеивайте не относящуюся к делу информацию. Выберите тему для 6-го класса. RP. Пакет практических занятий по математике для 6-х классов. Для каждой задачи, приведенной ниже, сначала добавьте экспоненты, если основы в уравнении совпадают. 6 — Нанесение точек на координатную сетку. Раздаточный материал — сдан в среду, октябрь. 8-й класс. Задания по математике в 8-м классе. Рабочие листы с ответами. Pdf. Заполните таблицы, составив эквивалентные соотношения. Сложное соотношение для 5-го класса по математике. 02 июля 2021 г. · Пятьсот одна задача по математике со словом.Вопрос 2: Периметр равностороннего треугольника равен 18. Чтобы распечатать этот рабочий лист: щелкните значок «принтер» на панели инструментов ниже. 19 декабря 2020 г. · Выберите категорию рабочих листов по алгебре и математике, которые вы хотите просмотреть ниже. Этот рабочий лист представляет собой документ PDF. Скачать ключ с ответами по математике для 6-го класса в формате PDF Все решения учебников по математике для 6-го класса в средней школе подготовлены преподавателями математики. Рабочие листы задач по математике для 6-го класса с ответами в формате pdf. Решение задач b = 4 Пример: 7b = 28 7 n = 50 Пример: n 5 5 · = 10 · 5 Рабочие листы по алгебре и печатные формы.Постарайтесь руководствоваться здравым смыслом. Эскизы. Схема документа. Вложения. 11. Урок математики в 6-м классе: 10 апреля 2020 г. Задача / учебная цель: учащиеся будут писать алгебраические выражения. Раздел 1: ЧУВСТВИТЕЛЬНОСТЬ ЧИСЛА И ОПЕРАЦИИ Глава 1: Применение целых чисел 1. На каждый вопрос вам будет предложено выбрать один из четырех вариантов ответа. Эта книга разделена на три основных раздела, которые помогут вам: Фантастический процесс из пяти шагов. Рабочие листы по математике для шестого класса — бесплатные печатные формы в формате PDF без входа в систему. Упростите ответ и / или замените неправильные дробные ответы на смешанные числа.Правильные ответы на выпущенные вопросы с множественным выбором и краткие ответы также. Математика для недели 13 сентября. Он принес с собой хороший шестигранный кубик и бросит его для каждого вопроса. 7438 6. 27 Рабочие листы соотношений и пропорций с ответами Соотношения и пропорции 6, 7, 8 и 9. Мастерство определяется правильным ответом за 3 секунды или меньше. СОДЕРЖАНИЕ. а) Каково отношение количества синих карандашей к количеству красных? б) Каково отношение количества синих карандашей к общему количеству карандашей? Рабочий лист упрощающих соотношений (словесные задачи) с ответами на учебную программу по математике для 6-го класса доступен в Интернете бесплатно в формате для печати и загрузки (pdf и изображения).Соответствует стандарту 6-го класса: проблемы со словами оценки за единицу Инструкции по распечатке рабочего листа или ключа для ответов. Найдите и распечатайте рабочий лист по любой интересующей теме. Заметки для занятий и Интернет-ресурсы; Рабочие листы для дополнительной практики с ответами 6 Ментальная математика — 6 класс Определения и связи Под изучением фактов понимается получение 100 фактов, относящихся к однозначным цифрам 0–9 в каждой из четырех операций. (Пример: если на то, чтобы косить 4 газона, потребовалось 7 часов, то при такой скорости, сколько газонов можно было бы косить за 35 6-классных-математических-задач-с-ответами 1/1 Скачано с dev1.Заметки для занятий и Интернет-ресурсы; Рабочие листы для дополнительной практики с ответами; Видеоуроки; 6. 00i-0iv_FM-881055 14.01.08 13:25 Страница ii epg ju104: MHGL149: Quark% 0: Word Problem%: Файл приложения% 0: FM: Курс 2: PDF Proof 26 октября 2021 г. · Рабочие листы по математике Для 6 класса с ответами Pdf. 7 — В учебнике «Математика имеет смысл» — Раздел 2: Урок 1 — Исследование больших чисел. Эти проблемы включают соотношение, скорость, площадь и статистику. а. Это исчерпывающая коллекция бесплатных распечатываемых математических листов для шестого класса, организованных по таким темам, как умножение, деление, экспоненты, разряд, алгебраическое мышление, десятичные дроби, единицы измерения, соотношение, процент, разложение на простые множители, GCF, LCM, дроби, целые числа. , и геометрия.Он содержит рабочие листы по математике для шестого класса по следующим темам: сложение, соотношения, проценты, десятичные дроби, графики, целые числа, деньги, время, умножение, дроби. Задачи по математике для 6-го класса — Рабочие листы для печати. Изучите все генераторы печатных листов для своих шестиклассников. Бесплатные рабочие листы по математике для 6 класса. Задачи по математике для 6-го класса с ответами pdf
Знание учениками начальной школы знака равенства — пример Швеции
Bergsten, C., Хэггстрем, Дж., И Линдберг, Л. (1997). Алгебра для всех [Алгебра для всех]. В году в Гётеборге: Nationellt centrum för matematikutbildning (NCM) . Гётеборг: Университет им.
Google ученый
Блэнтон, М., Стивенс, А., Кнут, Э., Мерфи Гардинер, А., Ислер, И., и Ким, Дж. (2015). Развитие алгебраического мышления детей: влияние комплексного раннего вмешательства по алгебре в третьем классе. Журнал исследований в области математического образования, 46 (1), 39–87.
Артикул Google ученый
Бранделл Г., Хемми К. и Тунберг Х. (2008). Расширяющийся разрыв — шведская точка зрения. Научно-исследовательский журнал математического образования, 20 (2), 38–56.
Артикул Google ученый
Брэтинг, К., Мадей, Л. и Хемми, К. (2019). Развитие алгебраического мышления: возможности шведской учебной программы и учебников элементарной математики. Северные исследования в математическом образовании, 24 (1), 27–49.
Брорсон, Å. (2019). Прима Математик 1А . Мальмё: Gleerups.
Google ученый
Брайман, А. (2012). Методы социальных исследований . Нью-Йорк: Издательство Оксфордского университета.
Google ученый
Цай, Дж., Лью, Х., Моррис, А., Мойер, Дж., Фонг Нг, С., И Шмиттау Дж. (2005). Развитие алгебраического мышления учащихся младших классов. ZDM, 37 (1), 5–15.
Google ученый
Каррахер, Д. В., и Шлиман, А. Д. (2007). Ранняя алгебра и алгебраические рассуждения. В F. K. Lester Jr. (Ed.), Второй справочник исследований по преподаванию и изучению математики (Vol. 2, pp. 669–705). Шарлотта: Издательство информационного века.
Google ученый
Каррахер, Д.W., Schliemann, A.D., & Schwartz, J. (2008). Ранняя алгебра — это не то же самое, что ранняя алгебра. В J. Kaput, D. Carraher, & M. Blanton (Eds.), Алгебра в младших классах (стр. 235–272). Махва, Нью-Джерси: Эрлбаум.
Google ученый
Хэггстрем, Дж., Килхамн, К., и Фредрикссон, М. (2019). Алгебра и grundskolan [Алгебра в начальной школе]. В году в Гётеборге: Nationellt centrum för matematikutbildning (NCM) .Гётеборг: Университет им.
Google ученый
Хемми, К., Брэтинг, К., и Лепик, М. (2020). Учебные подходы к алгебре в Эстонии . Математическое мышление и обучение: Финляндия и Швеция — сравнительное исследование.
Hemmi, K., Bråting, K., Liljekvist, Y., Prytz, J., Madej, L., Pejlare, J., & Palm Kaplan, K. (2018). Характеристика шведской школьной алгебры — первые результаты анализа руководящих документов, учебников и бесед учителей.В E. Norén, H. Palmér, & A. Cooke (Eds.), Северные исследования в математическом образовании . Статьи НОРМА 17 (стр. 299–308). Гётеборг: SMDF.
Hiebert, J., Stiegler, JW, Jacobs, JK, Bogard Givvin, K., Garnier, H., Smith, M., Hollingsworth, H., Wearne, D., & Gallimore, R. (2005 ). Преподавание математики в Соединенных Штатах сегодня (и завтра): результаты видео-исследования TIMSS 1999. Оценка образования и анализ политики, 27 (2), 111–132.
Артикул Google ученый
Киран, К. (1981). Понятия, связанные с символом равенства. Образовательные исследования по математике, 12 (3), 317–326.
Артикул Google ученый
Киран, К., Панг, Дж., Шифтер, Д., и Фонг Нг, С. (2016). Ранняя алгебра: исследование ее природы, обучения, преподавания . Нью-Йорк: Спрингер.
Забронировать Google ученый
Кисельман, К., и Моувиц, Л. (2008). Matematiktermer för skolan [Математические термины в школе]. В году в Гётеборге: Nationellt centrum för matematikutbildning (NCM) . Гётеборг: Университет им.
Google ученый
Корнхолл П. и Бендер Г. (2018). Ett söndrat land. Сколвал и сегрегация в Швеции, [Разделенная страна.Выбор школы и сегрегация в Швеции] . Arena idé. https://arenaide.se/wp-content/uploads/sites/2/2018/10/rap-skolval-final-reviderad.pdf [Дата обращения 29 апреля 2020].
Ли, X., Дин, М., Капраро, М. М., и Капраро, Р. М. (2008). Источники различий в понимании детьми математического равенства: сравнительный анализ руководств для учителей и учебников для учащихся в Китае и США. Познание и обучение, 26 , 195–217.
Артикул Google ученый
Линчевский, Л.(1995). Алгебра с числами и арифметика с буквами: определение предалгебры. Journal of Mathematical Behavior, 14 , 113–120.
Артикул Google ученый
Липскомб, Т. (2012). Первый среди равных: Роберт Рекорд и новаторское издательское дело в шестнадцатом веке. Journal of Scholarly Publishing, 43 (4), 381–394.
Артикул Google ученый
Мэтьюз, П., & Фукс, Л. (2020). Ключи от ворот? Знание знака равенства во втором классе предполагает знание алгебры в четвертом классе. Развитие ребенка, 91 (1), e14 – e28.
Артикул Google ученый
Мэтьюз, П., Риттл-Джонсон, Б., МакЭлдун, К., и Тейлор, Р. (2012). Мера за меру: что сочетание различных мер показывает, как дети понимают знак равенства как показатель математического равенства. Журнал исследований в области математического образования, 43 (3), 316–350.
Артикул Google ученый
Маллис, И. В. С., Мартин, М. О., Фой, П., Хупер М. (2016). Международные результаты TIMSS 2015 по математике . Получено 21 декабря 2020 г. с веб-сайта Бостонского колледжа, Международного исследовательского центра TIMSS и PIRLS: http://timssandpirls.bc.edu/timss2015/international-results
Murray, Å., & Liljefors, R. (1983). Математик и свенск школа . В Utbildningsforskning, FoU-rapport 46 . Стокгольм: Skolöverstyrelsen и Liber Utbildningsförlaget.
Google ученый
Нуше Д., Халас Г., Луни Дж., Сантьяго П. и Шубридж К. (2011). Обзоры ОЭСР оценки и оценивания в образовании Швеции. ОЭСР. http://www.oecd.org/edu/school/47169533.pdf [Дата обращения 29 апреля 2020].
Панг Дж. И Ким Дж. (2018). Характеристики раннего алгебраического мышления корейских студентов: обобщенная арифметическая перспектива. В C. Kieran (Ed.), Преподавание и изучение алгебраического мышления с детьми от 5 до 12 лет, Монографии ICME-13 (стр. 141–165). Чам: Спрингер.
ГлаваGoogle ученый
Предигер, С. (2010). Как развивать математику для обучения и понимания: Случай значений знака равенства. Журнал педагогического образования математики, 13 (1), 73–93.
Артикул Google ученый
Рекорд, Р. (1557). Точильный камень Витте, который является второй частью арифметики: Содержит извлечение корней: Практика козиса с правилом уравнения: И труды случайных номберов., Лондон: Ihon Kyngstone .. https://search.proquest.com / docview / 2240
0 [Дата обращения 29 апреля 2020].
Ренвик, Э.М. (1932). Заблуждения детей относительно символов математического равенства. Британский журнал педагогической психологии, 2 , 173–183.
Артикул Google ученый
Риттл-Джонсон, Б., Мэтьюз, П. Г., Тейлор, Р. С., и МакЭлдун, К. Л. (2011). Оценка знания математической эквивалентности: подход моделирования конструкции. Журнал педагогической психологии, 103 , 85–104.
Артикул Google ученый
Сэндфорд, В.(1957). Роберт Рекорд «Точильный камень Витте», 1557. Учитель математики, 50 (4), 258–266.
Артикул Google ученый
Шлейхер А. (2019). PISA 2018 — Взгляды и интерпретации. ОЭСР. https://www.oecd.org/pisa/PISA%202018%20Insights%20and%20Interpretations%20FINAL%20PDF.pdf [Дата обращения 29 апреля 2020].
Сфард А. (1991). О двойственной природе математических представлений: размышления о процессах и объектах как о разных сторонах одной медали. Образовательные исследования по математике, 22 (1), 1–36.
Артикул Google ученый
Ставка, Р. Э. (2005). Качественные кейсы. В книге Н. К. Дензина и Ю. С. Линкольна (редакторы), The Sage: Справочник качественных исследований (3-е изд.), 443–466. Таузенд-Оукс, Калифорния: Сейдж.
Шведское национальное агентство образования. (2008). TIMSS 2007 — huvudrapport. Svenska grundskoleelevers kunskaper i matematik och naturvetenskap i ett internationellt perspektiv [TIMSS 2007 — основной отчет.Знания шведских учеников начальной школы в области математики и естествознания в международной перспективе]. Стокгольм: Автор.
Шведское национальное агентство образования. (2012). TIMSS 2011 — huvudrapport. Svenska grundskoleevers kunskaper i matematik och naturvetenskap i ett internationellt perspektiv [TIMSS 2011 — основной отчет. Знания шведских школьников начальных классов по математике и естествознанию в международной перспективе] .. Стокгольм: Автор.
Шведское национальное агентство образования.(2016a). TIMSS 2015 — huvudrapport. Svenska grundskoleelevers kunskaper i matematik och naturvetenskap i ett internationellt perspektiv [TIMSS 2015 — основной отчет. Знания шведских учеников начальной школы в области математики и естествознания в международной перспективе]. Стокгольм: Автор.
Шведское национальное агентство образования. (2016b). Nationella проверено в grundskolans årskurs 6 och 9. En uppföljning av lärares, rektorers och elevers uppfattningar om nationella Проверено. [Национальные тесты в 6 и 9 классах. Продолжение мнений учителей, директоров и учащихся о национальных тестах]. Стокгольм: Автор.
Шведское национальное агентство образования. (2018). Учебная программа для общеобразовательной школы, дошкольного и школьного возраста (пересмотрена в 2018 г.). Стокгольм: Автор. https://www.skolverket.se/getFile?file=3984 [Дата обращения 29 апреля 2020].
Тайс, Л. (2005). L’Apprentissage Du Signe =: Важное препятствие Cognitif. Для изучения математики, 25 (3), 7–12.
Google ученый
ЮНИСЕФ (2018). Несправедливое начало — неравенство в образовании детей в богатых странах . https://www.unicef.org/publications/files/UNICEF-An-unfair-start-inequality-children-education_En.pdf [Дата обращения 29 апреля 2020].
Вермёлен, К., и Мейер, Б. (2017). Знак равенства: знания учителей и заблуждения учащихся. Африканский журнал исследований в области математики, естествознания и технологического образования, 21 (2), 136–147.
Артикул Google ученый
Винсент, Дж., Бардини, К., Пирс, Р., и Пирн, К. (2015). Неправильное использование знака равенства: укоренившаяся практика с первых лет начальной школы до высшей математики. Австралийский старший математический журнал, 29 (2), 31–39.
Google ученый
Ян Хансен, К., & Gustafsson, J.-E. (2016). Причины образовательной сегрегации в Швеции — выбор школы или сегрегация по месту жительства. Образовательные исследования и оценка, 22 (1–2), 23–44.
Артикул Google ученый
Ян Хансен, К., & Густафссон, Ж.-Э. (2019). Определение основного источника ухудшения равноправия в образовании в Швеции в период с 1998 по 2014 гг. Международный журнал исследований в области образования, 93 , 79–90.
Артикул Google ученый
Ян Хансен, К., Густафссон, Ж.-Э., и Розен, М. (2014). Различия в успеваемости в школе и различия в политике в Финляндии, Норвегии и Швеции. В Х. К. Янге, Ж.-Э. Густафссон, М. Розен, С. Сулкунен, К. Ниссинен, П. Купари и др. (Ред.), Северное сияние в TIMSS и PIRLS 2011: различия и сходства в странах Северной Европы . Копенгаген: Совет министров северных стран.
ГлаваGoogle ученый
Что это такое и что с этим делать?
По мере того, как этой осенью учащиеся возвращаются в школу, многие из них — возможно, особенно из исторически неблагополучных групп учащихся — начнут учебный год с более низким уровнем успеваемости, чем в начале летних каникул.Это явление — иногда называемое летней потерей знаний, летней неудачей или летним спадом — интересовало исследователей образования еще в 1906 году. 1 Мы анализируем, что известно о летней потере, и предлагаем предложения для районов и штатов в поисках решения проблемы.
Ранний всесторонний обзор литературы резюмировал несколько результатов, касающихся летних потерь. 2 Авторы пришли к выводу, что: (1) в среднем, успеваемость учащихся снизилась за летние каникулы на один месяц обучения в учебном году, (2) снижение было более резким по математике, чем по чтению, и (3) степень потерь было больше на более высоких ступенях обучения.Важно отметить, что они также пришли к выводу, что разрыв в чтении, основанный на доходах, вырос за лето, учитывая, что учащиеся среднего класса, как правило, демонстрируют улучшение навыков чтения, в то время как учащиеся с низкими доходами, как правило, испытывают потери. Однако они не обнаружили различий в летнем обучении по математике, полу или расе по любому предмету.
Недавняя литература о летних потерях была неоднозначной. Одно исследование с использованием данных более полумиллиона учащихся 2-9 классов из южного штата (с 2008 по 2012 год) показало, что учащиеся в среднем теряли от 25 до 30 процентов учебного года за лето; кроме того, черные и латиноамериканские студенты, как правило, меньше набирают за учебный год и теряют больше за лето по сравнению с белыми учениками. 3 Однако анализ репрезентативного на национальном уровне лонгитюдного исследования в раннем детстве, детский сад 2010-11 гг. (ECLS-K: 2011) обнаружил мало свидетельств общих потерь в течение лета после классов K и 1, а также летнего социально-экономического статуса. разрыв увеличился по некоторым предметам и оценкам, но не по другим. 4 Фон Хиппель и Хамрок повторно проанализировали два предыдущих набора данных и пришли к выводу, что пробелы «не обязательно… растут быстрее всего за лето» (стр. 41). 5 Таким образом, похоже, что летние потери и рост летних разрывов имеют место, хотя и не всегда по географии, уровню обучения или предмету.
«Теория крана» Энтвисла, Александра и Олсона предлагает объяснение того, почему студенты с низкими доходами могут учиться за лето меньше, чем студенты с более высокими доходами. 6 Согласно теории, «кран ресурсов» включен для всех учащихся в течение учебного года, что позволяет всем учащимся добиваться успехов в учебе. Однако летом поток ресурсов замедляется для студентов из неблагополучных семей, но не для студентов из благополучных семей. Учащиеся с более высокими доходами, как правило, продолжают иметь доступ к финансовым и человеческим ресурсам (таким как образование родителей) в течение лета, тем самым облегчая обучение. 7
Показатели успеваемости учащихся снизились во время летних каникул на один месяц обучения в учебном году.
Традиционно преподаватели и политики полагались на обычные программы летних школ для борьбы с потерями в летнее время и увеличением разрыва в летние периоды. В 2000 году Купер и его коллеги опубликовали всесторонний метаанализ летних программ в классе, в котором в среднем были выявлены положительные эффекты. 8 Однако они также пришли к выводу, что студенты со средним доходом больше извлекли выгоду из летнего программирования, чем студенты с более низким доходом.Они предположили, что это могло быть потому, что программы, обслуживающие более обеспеченных студентов, были более высокого качества, или из-за интерактивного эффекта между программированием и домашними ресурсами, доступными студентам. Результат вызвал обеспокоенность тем, что попытки остановить летнюю потерю обучаемости могут на самом деле усугубить рост летнего разрыва, если они не являются целенаправленными.
Ким и Куинн провели метаанализ 41 летней программы чтения из 35 исследований, опубликованных после Cooper et al. рассмотрение. 9 Как и Купер и его коллеги, Ким и Куинн обнаружили, что летние программы чтения в среднем эффективны для повышения результатов тестов. Однако, в отличие от Купера, Ким и Куинн обнаружили, что именно учащиеся с низким доходом больше всего выиграли от летних программ чтения (даже если ограничить сравнение учащимися с более высокими и низкими доходами, посещающими ту же программу). Кроме того, они пришли к выводу, что причина, по которой студенты с низким доходом получили больше преимуществ, заключалась в том, что студенты с низким доходом в этих исследованиях с большей вероятностью, чем студенты с более высоким доходом, испытали летнюю потерю, когда не участвовали в летних программах.Авторы отметили несколько различий между их обзором и обзором Купера и др., Которые могут объяснить противоречивые результаты: 1) Ким и Куинн проанализировали только программы чтения, в то время как Купер и коллеги объединили математические программы и программы чтения, 2) Ким и Куинн включили только две программы. -групповые экспериментальные и квазиэкспериментальные исследования, в то время как Купер и его коллеги включили одногрупповые до / послетестовые конструкции, и 3) Ким и Куинн включили домашние программы в свой обзор.
Естественно, программы летних школ на базе школ различаются по своей эффективности.Многие рекомендации по созданию качественных программ приходят в виде экспертных заключений. Общие предложения включают совмещение академического обучения с практическими занятиями или развлечениями, повышение профессионального уровня сотрудников летних школ и налаживание партнерских отношений с общественными организациями для использования ресурсов. 10 Мы также можем извлечь некоторые уроки из исследований. Например, недавний метаанализ показал, что программы были более эффективными, когда в них использовалось обучение грамоте на основе исследований; в частности, программы, использующие учебные стратегии, определенные Национальной комиссией по чтению как передовые методы, оказали наибольшее влияние на оценки понимания прочитанного учащимися (эквивалентно переходу с 50 -го на 65 -й процентиль нормального распределения).Эффективность программ также различалась в зависимости от области грамотности — программы были эффективны в повышении оценки учащихся понимания прочитанного и беглости / декодирования, но не в плане их словарного запаса. Неудивительно, что исследования также показывают, что программы более эффективны, когда учащиеся посещают занятия постоянно и уделяют больше времени академическим заданиям. 11
Хотя школьные летние учебные программы выглядят многообещающими, если соответствуют указанным выше критериям, они часто не оправдывают этих ожиданий.Две важные причины, по которым летние школьные программы могут быть неэффективными, заключаются в том, что организаторам часто трудно привлечь высококвалифицированных учителей и изо всех сил пытаются привлечь студентов и семьи, для которых альтернативные издержки посещения летней школы могут быть высокими. 12, 13 Школьные программы также могут быть довольно дорогостоящими. Поэтому исследователи с некоторым успехом экспериментировали с недорогими домашними летними программами.
Одним из примеров летней программы чтения на дому, которая доказала свою эффективность для учащихся старших классов начальной школы с низким доходом, является READS for Summer Learning. 14 В READS, который подвергался итеративным изменениям в ходе нескольких рандомизированных испытаний, учащиеся получают за лето по почте восемь книг, которые соответствуют их уровню чтения и интересам. Вместе с каждой книгой учащиеся получают сложенный втрое лист бумаги, который проводит их через задание перед чтением и проверку понимания прочитанного после чтения. Студентов просят отправить по почте три раза обратно с предоплатой почтовых расходов; семьи получают напоминания, когда тройные складки не возвращаются. Кроме того, в конце учебного года учителя проводят уроки по сценарию, чтобы подготовить учащихся к самостоятельному продуктивному чтению в течение лета с помощью тройной платформы.Недавнее исследование показало, что READS оказал влияние на понимание прочитанного учащимися из малообеспеченных семей весной после их участия в программе (ES = 0,05 SD в государственном тесте по чтению), 15 и другие исследования показывают, что тройное выступает посредником программного эффекта. 16
Другое недавнее рандомизированное исследование показало, что такая простая вещь, как отправка текстовых сообщений в течение лета семьям учеников начальной школы, которым грозит потеря летом, была эффективной для улучшения показателей чтения у третьеклассников и четвероклассников (но не первоклассников или второклассников). , с размером эффекта.21–29. 17 Текстовые сообщения включали советы о ресурсах, доступных учащимся летом, идеи для занятий с детьми и информацию о ценности конкретных летних учебных мероприятий.
Такие программы на дому могут быть более рентабельными, чем мероприятия на дому. Например, стоимость READS на одного учащегося оценивается в пределах 250–480 долларов США по сравнению с другими программами, предоставляющими услуги дополнительного образования, которые могут стоить до 1700 долларов США на учащегося и имеют аналогичные или менее благоприятные коэффициенты экономической эффективности.
Ким и Куинн включили домашние программы в свой метаанализ, и, что обнадеживает, они обнаружили, что эффекты домашних программ не сильно отличаются от их более дорогих альтернатив в классе. В то же время эффект от этих программ может быть не таким большим, как эффект от высококачественных школьных программ, в которых используются стратегии обучения, основанные на исследованиях.
Школы и округа должны стремиться решить проблему потери учебы в летнее время не только потому, что это может усугубить разрыв в успеваемости, но и потому, что это «тратит впустую» так много знаний, полученных учащимися в течение учебного года.Летняя потеря также, несомненно, увеличивает количество времени, которое учителя должны тратить на «повторное обучение» прошлогоднего содержания, что, вероятно, способствует повторяемости типичной учебной программы США. 18 Хотя инвестирование в расширенные летние варианты обучения в школе может быть неосуществимым, для округов может быть рентабельным и стратегическим решением начать предлагать целевые внеклассные мероприятия для учащихся, наиболее подверженных риску отката. При разработке таких программ политикам следует учитывать рекомендации исследования, описанного выше:
- Сосредоточьте программу на учебной программе, основанной на фактах.
- В дополнение к академическому содержанию, включите практические или развлекательные мероприятия для привлечения студентов.
- Убедитесь, что структура программы позволяет уделять достаточно времени выполнению задачи, а также иметь политику или стимулы, поощряющие постоянную посещаемость.
- Инвестируйте в найм самых эффективных учителей.
Независимо от дизайна, эти правила должны предлагать учащимся возможности вовлечения в летний период, чтобы летние учебные программы не воспринимались как наказание для студентов, которые предпочли бы наслаждаться летними каникулами.Это поможет большему количеству учеников добиться успеха в начале учебного года.
Авторы не получали никакой финансовой поддержки от какой-либо фирмы или лица для этой статьи или от какой-либо фирмы или лица, имеющего финансовую или политическую заинтересованность в этой статье. В настоящее время они не являются должностным лицом, директором или членом правления какой-либо организации, заинтересованной в этой статье.
Sunday Spotlight: Ким Пайпер — блог Edulastic
учеников в классе Ким работают над своим математическим заданием в классе.Ким почти ежедневно назначает контрольные точки Edulastic, чтобы отслеживать успеваемость учеников и убедиться, что ученики понимают концепции, которые им необходимо знать.
Что вам нравится в работе в сфере образования? Что мотивирует тебя?Мне нравится, когда у моих учеников бывают моменты «ага»! Когда эта лампочка гаснет, мы празднуем!
Почему вы стали учителем?Преподавание — моя вторая карьера. Спустя двенадцать лет моей первой карьеры я начал спрашивать себя: «Буду ли я счастлив, занимаясь этим всю оставшуюся жизнь?» Я ответил НЕТ.После некоторого самоанализа я понял, что хочу учить. Я стал учителем, чтобы помочь ученикам реализовать свой потенциал и поддержать их, чтобы они могли его реализовать! У меня есть страсть учить людей новому и поощрять их в процессе.
Какова ваша «эдуластическая история»?Я познакомился с Edulastic около трех лет назад моим фасилитатором по математике. Наш округ переходил к онлайн-тестированию, поэтому нам нужен был инструмент оценки, который имитировал бы онлайн-тесты.Мы начали с создания коротких общих оценок и оттуда выросли. Теперь я использую Edulastic почти ежедневно. Я использую edulastic для контрольных точек (один-два навыка), викторин, тестов и общих оценок.
Опишите свой любимый эдуластический момент «ага».Когда я осознал, что все ценные данные в реальном времени, которые можно собрать из Edulastic, я понял, что мне это нужно в моем классе. Данные в режиме реального времени позволяют мне немедленно давать обратную связь и выявлять распространенные заблуждения по мере их возникновения.Эти данные позволили мне быстро выявить студентов, нуждающихся в исправлении, и своевременно оказать им необходимую поддержку.
Данные, собранные Edulastic для общих оценок, позволяют нам обсуждать данные в нашем PLC, чтобы мы могли расти как группа. В ходе этих обсуждений мы обсуждаем передовые методы обучения и исправления навыков.
Каковы ваши цели преподавания / обучения в этом году?В этом году моя цель — побудить студентов развить установку на рост.Я призываю их выстоять в трудные времена, чтобы в конце концов они могли пожать плоды!
Любимая мотивационная идея:
Девиз нашей классной комнаты: «Если это не бросает вам вызов, это не меняет вас!»
Советы для новых пользователей Edulastic:Учителя, которые плохо знакомы с Edulastic, должны начинать с малого. Создайте небольшое задание с вопросами из банка. Это позволит вам увидеть данные и их ценность для вас и ваших учеников.Как только вы освоитесь, попробуйте создавать свои собственные вопросы. Начните с основ (множественный выбор, заполнение пустых полей и т. Д.), Затем переходите к вопросам с расширенными техническими возможностями (перетаскивание, маркировка, классификация и т. Д.). Начните с малого, но приступайте!
границ | Проверка эффективности обучения базовым навыкам численного познания и передачи для улучшения математических способностей детей
Введение
Способность обрабатывать информацию о численности важна для повседневной жизни как людей, так и животных (Agrillo et al., 2008; Libertus et al., 2011; Лейбович и др., 2017). Приближенное чувство числа (ANS) дает возможность приблизительно определить количество элементов, а также приблизительно добавлять или вычитать наборы элементов. Некоторые исследователи полагают, что базовая способность к числовой обработке и математические достижения более высокого уровня основаны на ANS (Rousselle and Noël, 2007; De Smedt and Gilmore, 2011; Sasanguie et al., 2012, 2013; Jang and Cho, 2018). Базовая числовая обработка включает сравнение численности, сравнение символьных чисел, оценку числовой линии и понимание соответствия между символьными числами и их соответствующей численностью (или несимвольной величиной) и т. Д.Сообщается, что базовые возможности числовой обработки позволяют прогнозировать будущие достижения в математике (Jordan et al., 2007; Locuniak and Jordan, 2008; Lyons and Beilock, 2011; Mazzocco et al., 2011; Sasanguie et al., 2013; Starr et al., 2013; Мартин и др., 2014). Кроме того, было обнаружено, что дети с нарушениями математической обучаемости или дискалькулией развития демонстрируют низкую успеваемость при базовой числовой обработке (Rousselle and Noël, 2007; Geary et al., 2008; De Smedt et al., 2009; Piazza et al., 2010; Де Смедт и Гилмор, 2011).В некоторых исследованиях сообщалось, что тренировка базовых способностей к счету привела к улучшению успеваемости по математике (Park and Brannon, 2013, 2014; Park et al., 2016; Sella et al., 2016). Однако в исследованиях использовались разные типы тренировок, и отчеты об эффективности тренировок были неоднозначными. Таким образом, в настоящее время нелегко сделать вывод о том, может ли вмешательство в основные числовые способности улучшить математические способности (Schneider et al., 2016; Szűcs and Myers, 2017).
В некоторых исследованиях обучение приближенной арифметике (приблизительное сложение и вычитание) с использованием массивов точек улучшило способности обучающих групп к символическому сложению / вычитанию по сравнению с контрольной группой (Park and Brannon, 2013, 2014; Hyde et al., 2014; Ханум и др., 2016; Park et al., 2016; Au et al., 2018; Шкудларек и Браннон, 2018). Напротив, Räsänen et al. (2009) не обнаружили каких-либо улучшений в арифметических (сложение и вычитание) и счетных способностях после тренировки по программе Number Race (Wilson et al., 2006), хотя острота зрения детей на ВНС улучшилась (Räsänen et al., 2009). Шкудларек и Брэннон (2018) сообщили, что обучение приблизительной арифметической и числовой идентификации было эффективным для дошкольников с низким или низким показателем.высокие математические навыки соответственно. Но обучение улучшило только начальные неформальные, но не формальные математические навыки. Основываясь на мета-анализе, Szűcs и Myers (2017) пришли к выводу, что в настоящее время нет доказательств того, что обучение ANS улучшает символическую арифметику, учитывая методологические проблемы и неоднородность исследований. Одна из важнейших проблем связана с включением практики символической арифметики в саму программу обучения (Wilson et al., 2006, 2009; Räsänen et al., 2009; Vilette et al., 2010; Kucian et al., 2011; Obersteiner et al., 2013; Sella et al., 2016). В этих случаях улучшение способностей к символической математике после многократной практики символической арифметики может просто отражать эффект практики (или повторного тестирования), а не истинный эффект переноса обучения. Кроме того, многие исследования, сообщающие о значительном тренировочном эффекте, имели тенденцию к небольшим размерам эффекта или нестабильным результатам (например, под влиянием выбросов) (Szűcs and Myers, 2017).
Целью настоящего исследования было выяснить, можно ли (и какие) улучшить базовые числовые способности с помощью обучения, и проверить, переносится ли тренировочный эффект на улучшение общих математических достижений.Мы разработали удобное для детей компьютерное программное обеспечение под названием «123 Bakery», которое включало четыре модуля для обучения базовым числовым способностям (сравнение численности, оценка числовой линии, приблизительное, несимвольное сложение / вычитание и преобразование символа в число). Практика точной символической арифметики во время обучения была намеренно исключена, чтобы тщательно проверить, действительно ли влияние обучения на базовое числовое познание переносится на точные, символические математические способности без явной практики в этой области.Наше программное обеспечение было разработано так, чтобы включать несколько учебных модулей в каждую сессию, как и в типичных образовательных мероприятиях (Kroesbergen and Van Luit, 2003; Gersten et al., 2009; Codding et al., 2011). Учебные занятия проводились в доме ребенка, что повысило экологическую ценность нашего обучения для реальных образовательных приложений. Все оценки также проводились в доме ребенка. Уровень сложности обучения был адаптирован для каждого участника, чтобы помочь участникам учиться в их собственной зоне ближайшего развития (т.е., адаптивное обучение). Эффекты тренировки были проверены путем сравнения оценок, полученных непосредственно до и после тренировки. Чтобы измерить улучшение обучаемых способностей при минимизации эффектов повторного тестирования, мы разработали задачи с альтернативными визуальными интерфейсами (подробности см. В разделе «Материалы и методы»). Математические достижения оценивались с помощью комплексной стандартной батареи тестов по математике (которая включала понятие числа, арифметики, геометрии и решения задач) и компьютеризированного арифметического теста.Мы стимулировали интенсивные домашние тренировки в течение 6 недель (5 дней в неделю, 35 минут в день), что на сегодняшний день является самым продолжительным в общей продолжительности тренировок по сравнению с предыдущими исследованиями. Диапазон численности также был значительно расширен (до 300 в зависимости от производительности), что было намного больше, чем в большинстве предыдущих исследований (которые включали численность до 80) (Wilson et al., 2006, 2009; Räsänen et al., 2009; Kucian et al., 2011; Park, Brannon, 2013, 2014; Park, Brannon, 2014; Hyde et al., 2014; Park et al., 2016; Sella et al., 2016; Au et al., 2018). Другими словами, настоящее исследование направлено на тщательную проверку эффективности тренировки базовых числовых способностей на основе достаточно большой продолжительности в большом диапазоне значений при минимальном влиянии эффектов повторного тестирования. Продолжительность обучения в настоящем исследовании была больше, чем в других лабораторных исследованиях (но она была аналогична средней продолжительности программ вмешательства / обучения, обычно используемых в реальных образовательных учреждениях (Cohen et al., 1982; Kroesbergen and Van Luit, 2003). Кроме того, мы тщательно контролировали нечисловые визуальные свойства несимволических стимулов (массивов точек) во время обучения и оценки, чтобы минимизировать влияние нечисловых визуальных величин. Наконец, наша процедура обучения на дому повысила экологическую ценность нашей программы обучения, что позволило более уверенно обобщить ее для реальных образовательных приложений по сравнению с исследованиями, в которых обучение проводилось в лабораторных условиях (Hyde et al., 2014).
Учитывая несоответствия в литературе, у нас не было гипотезы a priori в пользу идеи о том, что базовые математические способности могут быть улучшены с помощью обучения и что такие обучающие эффекты будут перенесены на улучшение математических достижений (особенно, когда точные вычисления являются не входит в обучение). Используя достаточно длительную продолжительность обучения и широкий диапазон величин (с учетом влияния нечисловых визуальных величин), мы не допустили ошибки типа II из-за недостаточной продолжительности / диапазона обучения или загрязнения посторонними переменными.
Материалы и методы
Участников
В исследовании приняли участие 56 первоклассников. Данные от 10 детей, которые не завершили эксперимент или результаты которых (при сравнении численности перед тренировкой или конечный уровень, достигнутый в учебных модулях) были ниже, чем на 2 SD ниже среднего, были исключены. (См. Дополнительные материалы для получения дополнительной информации.) Таким образом, в анализ были включены данные 46 детей (24 женщины; средний возраст = 7,70 лет; и SD = 0.30). Набор участников проводился по рекламе. Перед участием все участники и их родители дали письменное информированное согласие. Комитет IRB университета Chung-Ang одобрил все протоколы исследования (IRB-2013-55). Участники были случайным образом распределены либо в обучающую, либо в контрольную группу. После завершения эксперимента участники получили денежную компенсацию.
Процедура
участников были случайным образом распределены либо в обучающую ( n = 22), либо в контрольную ( n = 24) группу.Всем участникам было проведено предварительное оценивание [включая базовые задачи числовой обработки, два теста на успеваемость по математике и тест расширенных прогрессивных матриц (APM) Raven]. Только обучающая группа приняла участие в 30 тренингах в течение 6 недель с использованием компьютерного программного обеспечения («123 Bakery»). По прошествии 6 недель с момента проведения предтренировочной оценки всем участникам была проведена послетренировочная аттестация. Оценка основных числовых способностей до и после тренировки проводилась с четырьмя задачами, соответствующими каждому учебному модулю, с использованием альтернативных визуальных форматов, чтобы минимизировать эффекты практики или повторного тестирования на зрительно-моторном уровне (см. Рисунок 1).
РИСУНОК 1. Скриншоты примерного испытания (A) модуля «Продажа тортов» в «123 пекарне» и (B) «Сопоставление символов и числовых значений», используемых для до и после оценка обучения.
Материалы
Программа обучения основам численного познания «Пекарня 123»
Мы разработали компьютеризированную программу под названием «Пекарня 123», которая состоит из четырех учебных модулей. Четыре обучающих модуля включали (1) сравнение численности («Сбор ингредиентов»), (2) несимвольную числовую оценку («Угадай, сколько?»), (3) приблизительное сложение и вычитание («Украшение торта») и ( 4) Сопоставление символов и номеров («Продажа тортов»).(Каждый обучающий модуль объясняется в следующем разделе.) Каждый модуль длился 6 минут. Отзывы о правильности ответа предоставлялись после каждого испытания. Совокупный общий балл (в каждом сеансе) обновлялся в режиме реального времени и всегда отображался в верхней правой части экрана (рис. 2). Сложность задания возрастала по мере того, как испытуемые осваивали каждый уровень, достигая определенной степени точности выполнения (точность 0,7–0,9 среди последних 10–20 испытаний в зависимости от уровня; подробности см. В дополнительных таблицах S1 – S4).
РИСУНОК 2. Скриншоты примеров испытаний из (A) «Сбор ингредиентов», (B) «Угадай, сколько?», (C) «Украшение для торта» и (D) « Продажа тортов »модулей« Пекарня 123 ».
Для того, чтобы контролировать влияние нечисловых визуальных свойств массивов точек (например, размер отдельных точек, совокупная площадь поверхности и выпуклая оболочка) во время обработки численности, мы сделали выпуклую оболочку эквивалентной для всех массивов точек и разделили испытания на две части. условия контроля (площадь vs.условия, контролируемые размером) (Pica et al., 2004; Halberda, Feigenson, 2008; Jang and Cho, 2016; Park and Cho, 2016; Lee and Cho, 2017). Во-первых, в половине испытаний массивы точек сопоставлялись по совокупной площади поверхности (состояние с контролируемой площадью), а в другой половине испытаний массивы точек сопоставлялись по размеру отдельных точек (условие с контролируемым размером). Порядок представления испытаний изменялся случайным образом. Хотя невозможно полностью контролировать влияние нечисловых визуальных свойств точечных массивов во время обработки численности, использование случайным образом перемешанных условий управления и эквивалентность выпуклой оболочки для всех точечных массивов гарантируют, что нечисловая визуальная величина не может быть надежно используется в качестве альтернативной подсказки для угадывания численности (Maloney et al., 2010; Гебуис и Рейнвоет, 2012а, б; Лейбович, Хеник, 2013; Дитрих и др., 2015).
Учебный модуль 1: сравнение численности («сбор ингредиентов»)Два массива (ягод или орехов) появились рядом на 1000 мс. Испытуемым было предложено выбрать более многочисленный массив (рис. 2А). Сложность задания возрастала по мере увеличения размера набора (диапазон = 6–200) и по мере приближения отношения величин к 1 (диапазон = 2: 3–9: 10). Аудиовизуальные отзывы о правильности ответа предоставлялись после каждого испытания.
Учебный модуль 2: несимвольная оценка числовой линии («Угадай, сколько?»)Испытуемым был представлен массив (ягод, орехов и т. Д.) На 1000 мс в центре экрана. Испытуемых просили щелкнуть место на числовой строке, которое соответствует предполагаемой численности элементов массива (рис. 2В). Если оценка находилась в пределах «точной зоны» (подробности см. В дополнительной таблице S2), была дана положительная обратная связь. Сложность задания варьировалась в зависимости от количества стимулов, максимального значения (конечной точки) числовой линии и относительной ширины (т.е., пропорция) точной зоны.
Учебный модуль 3: несимволическое сложение / вычитание («украшение торта»)Испытуемым были представлены два набора (ягод или орехов и т. Д.) На 1 000 мс, и их попросили выполнить приблизительное сложение или вычитание. Затем были дополнительно показаны два массива в качестве вариантов на выбор. Испытуемых просили ответить, выбрав один из двух вариантов, который казался ближе к их приблизительному ответу в течение 6 с (рис. 2С).Аудиовизуальные отзывы о правильности ответа предоставлялись после каждого испытания.
Учебный модуль 4: преобразование символа в число («продажа тортов»)Испытуемых просили выбрать, у какого животного персонаж (покупатель) было правильное количество орехов, которое соответствовало цене торта (показано цифрой в центре экрана) (рис. 2D). Сложность задания возрастала по мере приближения отношения численности к 1 и увеличения цены торта.Аудиовизуальные отзывы о правильности ответа предоставлялись после каждого испытания.
Оценки до и после обучения
Четыре основных задачи числовой обработкиЧетыре основные задачи числовой обработки (сравнение численности, оценка символьных и несимвольных числовых линий, приблизительная арифметика и преобразование символьных чисел в числовые) имели ту же структуру, что и четыре обучающих модуля, за исключением того, что массив состоял из черных точек на белом фон.Каждая задача описана в следующих разделах.
Сравнение численностиИспытуемым была представлена пара массивов точек (1000 мс) и их попросили выбрать массив с большим количеством точек (рис. 3). Испытуемые нажимали клавишу №3 для массива слева и клавишу №8 для массива справа. Лево-правое расположение правильного ответа было уравновешено. Соотношение численности включало 1: 2, 3: 4, 5: 6, 6: 7, 7: и 8: 9. Полный список стимулов показан в дополнительной таблице S5.Всего было 120 испытаний.
РИСУНОК 3. Пример испытания задачи сравнения численности.
Оценка символьных и несимвольных числовых линийЗадача оценки числовой линии была проведена с использованием как символических (арабские цифры), так и несимволических величин (рис. 4). Испытания были разделены на два блока в зависимости от значения конечной точки числовой линии (100 или 200). Стимулы включали 5, 18, 32, 55, 73 и 98 для блока 1 и 5, 18, 42, 78, 111, 133, 147, 172 и 187 для блока 2.Целевой стимул появлялся на 1000 мс.
РИСУНОК 4. Пример испытания задачи оценки символьной числовой линии с конечной точкой 200.
Точность работы рассчитывалась с использованием процента абсолютной ошибки (PAE; уравнение 1) (Siegler and Booth, 2004). Меньшая PAE представляет меньшую ошибку в оценке и большую линейность в представлении ментальной величины (Siegler and Booth, 2004; Booth and Siegler, 2006). Для каждого целевого стимула повторяли три попытки.Среднее значение PAE для каждого целевого стимула использовалось в качестве зависимой переменной (Siegler and Ramani, 2009).
PAE = Оценка — Расчетная величина Масштаб числовой линии
Ур. 1. Расчет PAE
Приближенная арифметикаПроцедура задачи была аналогична условию приближенной арифметики, используемому в Park and Brannon (2013, 2014). Эта задача была разделена на два отдельных блока для сложения и вычитания. Сначала испытуемым показывали точечный массив, который был добавлен в серое поле (рис. 5).Затем еще один массив точек был либо добавлен, либо удален из серого поля. Наконец, испытуемые выбирали один из двух новых массивов точек, численность которых казалась ближе к предполагаемому общему количеству точек в сером поле. В ответ они нажали клавишу №3, чтобы выбрать массив слева, и клавишу №8, чтобы выбрать массив справа. Сложность задания регулировалась соотношением установленных размеров двух массивов (4: 5, 4: 6 и 4: 7), представленных в виде пары в каждом испытании. Сложение и вычитание выполнялись на массивах с численностью от 6 до 51.Количество массивов, представленных в качестве опций, варьировалось от 16 до 91. Включая 5 практических испытаний, в общей сложности было проведено 35 испытаний.
РИСУНОК 5. Пример пробной процедуры приближенной арифметической задачи.
Преобразование символа в числоИспытуемых попросили выбрать один из двух массивов, представленных в течение 1000 мс, чья численность соответствовала арабскому числу, представленному в центре экрана (рис. 1B). Соотношение между величиной раздражителей варьировалось от 1: 1.75 до 4: 5 (1: 1,75, 1: 2, 2: 3, 3,5: 5, 3: 4 и 4: 5). Размер набора стимулов варьировался от 6 до 100 (6–30, 30–50 и 50–100). Лево-правое положение правильного ответа уравновешивалось. Всего было проведено 144 исследования. Порядок испытаний для каждого соотношения / условия перемешивался случайным образом.
Контрольные тесты по математике
Комплексный тест по математике (KNISE-BAAT)Корейский национальный тест интеллекта для специального образования — базовый академический тест (KNISE-BAAT для математики) (Park et al., 2008) использовался для измерения математической производительности. KNISE-BAAT состоит из четырех подобластей (понятие числа, арифметика, геометрия и решение задач).
Компьютерная арифметическая задачаИспытуемые решили 64 задачи на сложение и вычитание без бумаги и карандаша на компьютере. Использовались три диапазона чисел (6–30, 30–50 и 50–99). Участникам было предложено набрать ответ с помощью цифровых клавиш на клавиатуре. Ограничений по времени не было. (Подчеркивалась точность, а не RT решения проблемы).Таким образом, основной интересующей зависимой переменной была точность, а не RT.
Тест APM RavenДетский подвижный интеллект измерялся с помощью сокращенной версии теста APM Ворона (Arthur et al., 1999). Этот показатель использовался в качестве ковариаты для контроля индивидуальных различий в гибком интеллекте.
Результаты
Тест межгрупповых различий в оценках до и после обучения
Учебная и контрольная группы были сопоставлены по возрасту и полу.Независимые выборки t -тесты не выявили разницы в возрасте [ t (44) = 1,99, p = 0,05] и полу [ t (44) = 0,86, p = 0,39] между группами. Кроме того, наши группы не различались по оценке математических достижений или подвижного интеллекта до и после тренировки ( p s> 0,05; Таблица 1).
ТАБЛИЦА 1. Описательная статистика производительности на основе оценок до и после обучения основных способностей к числовой обработке.
Влияние обучения на базовые возможности обработки чисел
Описательные статистические данные о показателях базовых способностей обработки чисел до и после обучения представлены в Таблице 1. Показатели обучающей группы в конце каждого занятия для каждого модуля «123 Bakery» показаны на Рисунке 6. Заключительный Уровень, достигнутый в конце обучения для каждого модуля «123 Bakery», и общее среднее значение из 30 средних баллов (точность и RT) для каждого сеанса представлены в дополнительной таблице S6.Чтобы проверить обучающие эффекты, был проведен ANOVA с повторными измерениями 2 × 2 для основных характеристик обработки чисел (сравнение численности, оценка символьных и несимвольных числовых линий, преобразование символьных чисел в числовые и приблизительная арифметика) со временем (предварительно -, посттренинг) как внутрипредметный фактор и групповой (тренировочный, контроль) как межсубъектный фактор (таблица 2). Значительное двустороннее взаимодействие будет указывать на наличие тренировочного эффекта, который является избирательным для обучающей группы по сравнению с контрольной группой.Двустороннее взаимодействие между временем и группой было значимым только для точности сравнения численности [ F (1,44) = 7,47; p <0,01, частичное η 2 = 0,15, рисунок 7, таблица 2]. (Никакие другие эффекты взаимодействия не были значимыми ( p s> 0,05; см. Дополнительную таблицу S7 для результатов ANOVA смешанных повторных измерений по другим измерениям базовых возможностей обработки чисел). Учитывая значительный эффект двустороннего взаимодействия, post hoc тесты простых основных эффектов группы в каждый момент времени (до тренировки, после тренировки) проводились для точности сравнения численности.Значительный тренировочный эффект должен проявляться в более высоких послетренировочных (но не предтренировочных) показателях обучающей группы по сравнению с контрольной группой. Не было разницы в точности сравнения численности между тренировочной и контрольной группами на предварительном обучении, но обучающая группа имела значительно более высокую точность сравнения численности после тренировки [предварительное обучение: t (44) = 1,30, p = 0,20, после обучения: т (44) = 4,37, р <0.001, рисунок 7, таблица 1]. Другими словами, обучение с модулем «Сбор ингредиентов» повысило точность сравнения численности обучающей группы.
РИСУНОК 6. Среднее значение уровня, достигнутого участниками в конце каждой сессии для каждого модуля «123 Bakery».
ТАБЛИЦА 2. Результат смешанного дисперсионного анализа 2 × 2 повторных измерений на точность сравнения численности с группой в качестве фактора между субъектами и временем в качестве фактора внутри субъекта.
РИСУНОК 7. Оценка точности сравнения численности до и после тренировки в тренировочной и контрольной группах. Полосы представляют собой SEM. ANOVA со смешанными повторными измерениями 2 × 2 выявил значимое двустороннее взаимодействие между временем и группой. Post hoc t -тесты выявили, что групповая разница в точности сравнения численности была значимой только на посттренинге. ( ∗ p <0,05, ∗∗∗ p <0.001, н.у. = не имеет значения)
Перенести эффекты в математические достижения
Описательная статистика показателей успеваемости по математике до и после обучения представлена в таблице 3. Также представлены результаты независимых выборок t -тестов в каждый момент времени (до обучения, после обучения) для каждого оценочного балла. показано в Таблице 3. Для того, чтобы исследовать, влияет ли переход обучения на улучшение на успеваемость по математике, был проведен дисперсионный анализ смешанных повторных измерений для всех оценок математических достижений (KNISE-BAAT и компьютеризированная арифметика) с течением времени (до и после тренировки). ) как внутрисубъектный фактор и групповой (обучающий, контрольный) как межсубъектный фактор (таблица 4).Не было значительных эффектов взаимодействия ни на KNISE BAAT, ни на компьютеризированные арифметические оценки ( p s> 0,05, таблица 4; см. Дополнительную таблицу S7 для результатов смешанного анализа ANOVA с повторными измерениями по всем другим показателям математических достижений).
ТАБЛИЦА 3. Предварительная и послетренировочная оценка математических достижений (компьютерная арифметика, KNISE-BAAT) обучающей и контрольной групп.
Обсуждение
В настоящем исследовании изучалось, можно ли улучшить базовые возможности обработки числовых данных с помощью обучения и можно ли перенести этот обучающий эффект на улучшение в различных областях математических достижений.Мы разработали удобную для детей обучающую программу под названием «Пекарня 123», которая включала четыре учебных модуля («Сбор ингредиентов», «Угадай, сколько?», «Украшение торта» и «Продажа тортов»). Массивы точек, используемые в качестве стимулов, представляющих несимвольную величину, контролировались таким образом, чтобы минимизировать влияние нечисловых визуальных свойств. Точные символьные вычисления были намеренно исключены из обучения, чтобы проверить, улучшает ли обучение базовым численным навыкам точные, символьные вычисления, исключая прямую практику или эффекты повторного тестирования.Все участники были дважды оценены на предмет их основных числовых способностей с интервалом в 6 недель. Учебная группа приняла участие в 6-недельном обучении сразу после первой оценки. Вторая оценка проводилась сразу после окончания тренировки. По сравнению с контрольной группой точность сравнения численности обучающей группы значительно улучшилась при оценке после тренировки. Этот результат согласуется с предыдущими исследованиями, в которых сообщалось об улучшении остроты зрения ВНС после тренировки (DeWind and Brannon, 2012; Odic et al., 2014; Wang et al., 2016). Тем не менее, тренировочная группа не показала большего улучшения результатов по математике по сравнению с контрольной группой. Отсутствие эффекта перехода к символьным математическим способностям после обучения согласуется с некоторыми предыдущими сообщениями (Räsänen et al., 2009; Wilson et al., 2009).
Стоит отметить несколько аспектов настоящего исследования. По сравнению с предыдущими исследованиями, период обучения был намного больше, а диапазон значений, используемых как для обучения, так и для оценки, был намного шире.Кроме того, нечисловые визуальные величины стимулов контролировались как во время обучения, так и во время оценки. Кроме того, между обучением и оценкой использовались разные визуальные интерфейсы задач, чтобы предотвратить прямые эффекты от практики. Наше обучение проводилось в доме ребенка, чтобы повысить экологическую ценность реальных образовательных приложений. Основываясь на анализе наших данных, мы не смогли найти никаких доказательств в поддержку тренировочных эффектов, которые переходят на улучшение в какой-либо области математических достижений.Единственным наблюдаемым эффектом обучения было повышение точности сравнения численности.
ТАБЛИЦА 4. Результат смешанного дисперсионного анализа 2 × 2 с повторными измерениями оценок математических достижений (компьютеризированная арифметика, KNISE-BAAT) с группой в качестве фактора между субъектами и временем в качестве фактора внутри субъекта.
Сравнение с другими учебными исследованиями
Результаты настоящего исследования контрастируют с результатами некоторых обучающих исследований, проведенных с маленькими детьми (Wilson et al., 2009; Obersteiner et al., 2013; Hyde et al., 2014; Ханум и др., 2016; Maertens et al., 2016; Park et al., 2016; Селла и др., 2016; Wang et al., 2016). В нашем исследовании после обучения улучшилась только производительность сравнения несимволической численности (но не PAE из оценки символьной числовой линии) без каких-либо эффектов переноса на математические достижения. Напротив, Maertens et al. (2016) сообщили, что только PAE оценки числовой линии (но не сравнение численности) значительно улучшилось при обучении по сравнению с контрольной группой, но оба тренировочных эффекта перешли на улучшение графически представленных (но не символических) арифметических задач у дошкольников.В Hyde et al. (2014), практика одного сеанса как приблизительного сложения, так и сравнения численности (но не добавления длины строки или сравнения яркости) привела к выигрышу в точном, символическом сложении (но не сравнении предложений) (Hyde et al., 2014). В Wang et al. (2016), 5-летние дети, которых кратко обучили повышению точности распознавания численности, показали более высокие результаты по символической математике (но не словарному запасу) по сравнению с контрольной группой. В этом исследовании улучшение остроты зрения детей на ВНС было достигнуто путем представления испытаний в порядке «от простого к сложному», чтобы вызвать опыт последовательности уверенного решения проблем («гистерезис уверенности»), который, по мнению авторов, ведет к повышению способности ( Odic et al., 2014). В контрольных группах испытания были представлены в обратном или случайном порядке. Однако в Wang et al., (2016) не было предтренировочной оценки остроты ВНС или математических способностей, поэтому трудно исключить различия до тренировки в остроте ВНС или математических способностях между группами. Кроме того, некоторые исследователи сомневаются в том, что эффекты переноса, наблюдаемые в Hyde et al. (2014) или Wang et al. (2016) отражают сосредоточение внимания на числовых представлениях, а не на реальных эффектах переноса на улучшение математики, учитывая краткость методов в этих двух исследованиях (Szűcs and Myers, 2017).Взятые вместе, хотя невозможно окончательно указать причину этих расхождений, возможные источники могут включать различия в том, как проводились оценки до и после обучения, а также в продолжительности обучения. В настоящем исследовании была проведена оценка всех способностей, включенных в программу обучения, до и после тренировки с использованием отдельного задания, разработанного с другим визуальным интерфейсом. Таким образом, в настоящем исследовании эффекты простой практики (или повторного тестирования) были минимизированы в оценке после тренировки, что снижает вероятность улучшения результатов.Также возможно, что у маленьких детей работе ВНС способствует наличие нечисловых визуальных величин, которые коррелируют с численностью (Defever et al., 2013; Szucs et al., 2013). Настоящее исследование контролировало влияние нечисловых визуальных свойств стимулов как во время обучения, так и во время оценки. Различия в методах, с помощью которых контролировались нечисловые визуальные величины в разных исследованиях, могли повлиять на несоответствие в типе тренируемого когнитивного процесса и итоговой оценке способности к результату.Принимая во внимание наблюдение Шкудларека и Браннона (2018), следует также подчеркнуть, что люди (особенно маленькие дети) с низкими способностями могут получить больше пользы от приблизительного обучения арифметике и что эффекты переноса обучения могут быть специфичными для определенных областей или компонентов математических способностей. (например, неформальные математические навыки в противоположность формальным математическим навыкам).
Факторы, которые могут повлиять на эффекты переноса
Несоответствие между исследованиями также может быть связано с различиями в содержании обучения в разных исследованиях.Во-первых, эффекты переноса в символьную математику, о которых сообщалось в учебных исследованиях, которые включали символьную арифметическую практику (например, числовая гонка или спасательный калькулярис), могут отражать прямые практические эффекты, потому что сама программа обучения включала символьную арифметическую практику (Wilson et al., 2006, 2009). ; Vilette et al., 2010; Kucian et al., 2011; Obersteiner et al., 2013; Sella et al., 2016). Во-вторых, обучение может быть менее эффективным, если несколько модулей включены в одно занятие. Несколько учебных исследований, которые включали отработку одного типа процесса (например,g., приблизительная арифметика, сравнение численности или оценка числовой линии) наблюдали значительные эффекты переноса (Park and Brannon, 2013; Hyde et al., 2014; Park and Brannon, 2014; Khanum et al., 2016; Maertens et al., 2016; Park et al., 2016; Au et al., 2018). Напротив, когда обучение включает в себя несколько видов учебных модулей (как в нашем исследовании), эффекты переноса могут быть менее заметны из-за повышенной вариабельности эффективности каждого учебного модуля среди участников. Например, некоторые участники могут быть относительно более вовлечены и мотивированы модулем A, другие — модулем B и так далее.В таких случаях среднее групповое обучающее воздействие каждого модуля может быть уменьшено за счет увеличения индивидуальной вариабельности, и (по той же причине) результирующий эффект переноса также может быть размыт, особенно если каждый модуль более или менее связан с частично разными компоненты исходной способности. Таким образом, повышенная вариативность обучающих эффектов каждого модуля у разных людей могла привести к отсутствию прямого улучшения некоторых обучаемых задач (оценка числовой шкалы или приблизительные арифметические способности и т. Д.) в настоящем исследовании, особенно с учетом небольшого размера выборки.
Основываясь на наблюдении, что тренировка по приблизительной арифметике, но не по сравнению счисления, приводит к улучшению символьной арифметики у взрослых, Парк и Брэннон (2014) предположили, что когнитивная тренировка может иметь положительный эффект передачи, если тренировка и способность к результату имеют общие умственные операции (Парк и Браннон, 2014). В качестве альтернативы, Hyde et al. (2016) предположили, что эффекты переноса могут определяться перекрытием ментальных представлений между обучением и способностью к результату (по крайней мере, у детей).Эта гипотеза была основана на наблюдении, что тренировочные эффекты как от сравнения численности, так и от приблизительного сложения переносятся на улучшение символического сложения у детей (Hyde et al., 2016). Отсутствие эффекта переноса на символьные математические способности, несмотря на улучшение остроты зрения ВНС в настоящем исследовании, кажется, поддерживает идею о том, что эффекты переноса тренировки требуют существенного перекрытия мысленных операций между обучаемым процессом и способностью к результату, что согласуется с «Оперативным перекрытием» Парка и Брэннона. »Гипотеза.Взятые вместе, как Хайд и др. (2016) также упоминали, мы подчеркиваем, что поиск ответа на вопрос о том, какой тип базовой математической подготовки может улучшить математическое познание, требует постоянных усилий, принимая во внимание, что такие факторы, как изменения в развитии и тонкие различия в методологии исследования, могут критически повлиять на это отношения.
Ограничения и направления на будущее
Мы признаем, что было бы лучше включить другой вид активного обучения (не связанный с базовой числовой обработкой) для контрольной группы.Мы признаем это ограничением настоящего исследования. Если бы тренировка имела избирательный эффект передачи математических достижений в обучающей группе, было бы трудно исключить возможность эффекта плацебо (или эффекта Хоторна). Однако, учитывая отсутствие эффекта переноса, отсутствие программы обучения управлению можно считать меньшей проблемой в случае настоящего исследования. Кроме того, Szcs и Myers (2017) подчеркивают, что не имеет смысла противопоставлять вмешательства, связанные с целевыми показателями, с вмешательствами, не имеющими отношения к ним (например,g., противопоставление обучения математике и чтению или рисованию) или противопоставление двух вмешательств, которые не являются одинаково интересными, мотивирующими и интеллектуально стимулирующими. Хотя в настоящем исследовании отсутствует активная контрольная группа, мы можем, по крайней мере, сопоставить эффективность различных типов базовой математической подготовки на основе внутрипредметного плана, в то время как все тренировки можно рассматривать как одинаково увлекательные и мотивирующие. [Все подмодули были основаны на единой теме (например, животные, выпекающие торт, животные, продающие торт и т. Д.)), пользовательский интерфейс (представление красочных мультфильмов с музыкой) и метод обратной связи.] Тем не менее, в будущих исследованиях было бы идеально сопоставить эффект когнитивной тренировки в экспериментальной группе с хорошо подобранной альтернативной формой обучения. для контрольной группы.
Отсутствие эффекта переноса в нашем исследовании домашнего обучения поднимает вопрос о том, будут ли эффекты переноса, наблюдаемые в лабораторных условиях, распространяться на реальные или реальные образовательные приложения.Взятые вместе, результаты настоящего исследования показывают, что (1) только определенные виды основных числовых способностей (в данном случае только острота зрения ВНС) маленьких детей могут быть улучшены с помощью обучения и (2) улучшение остроты зрения ВНС не представляется возможным. переход к улучшению успеваемости по математике, несмотря на интенсивные тренировки в течение 6 недель, в широком диапазоне значений.
Заявление о доступности данныхНеобработанные данные, подтверждающие выводы этой рукописи, будут предоставлены авторами без излишних оговорок любому квалифицированному исследователю.
Авторские взносы
NK внесла свой вклад в разработку оценок до и после обучения, улучшение дизайна программы обучения, сбор и анализ данных. SJ внесла свой вклад в разработку парадигмы обучения, сбор и анализ данных. SC — главный исследователь, который внес свой вклад во все аспекты исследования, начиная с получения финансирования, разработки исследования и мониторинга всех аспектов сбора и анализа данных. Все авторы внесли свой вклад в написание рукописи.
Финансирование
Это исследование было поддержано грантами Корейского национального исследовательского фонда (2014R1A1A3051034 и 2017R1D1A1B03032115), финансируемыми корейским правительством для SC.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Благодарим всех детей и их семьи за участие.Мы также благодарны членам нашей лаборатории и научным сотрудникам за их помощь в сборе и анализе данных. Часть необработанных данных, включенных в это исследование, взята из кандидатской диссертации Н.К.
Дополнительные материалы
Дополнительные материалы к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/fpsyg.2018.01775/full#supplementary-material
Сноски
- Программа Number Race включает в себя сравнение численности, отображение между символическим и несимвольным числом и символическое сложение / вычитание.
Список литературы
Агрилло, К., Дадда, М., Серена, Г., и Бизацца, А. (2008). Считается ли рыба? Спонтанное различение количества самок москитов. Аним. Cogn. 11, 495–503. DOI: 10.1007 / s10071-008-0140-9
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Артур В. мл., Тубре Т. К., Пол Д. С. и Санчес-Ку М. Л. (1999). Психометрические и нормативные данные по выборке из колледжа по краткой форме теста продвинутых прогрессивных матриц raven. J. Psychoeduc. Оценивать. 17, 354–361. DOI: 10.1177 / 073428299
0405CrossRef Полный текст | Google Scholar
Ау, Дж., Джегги, С. М., и Бушкуль, М. (2018). Влияние несимвольной арифметической тренировки на символьную арифметику и приблизительную систему счисления. Acta Psychol. 185, 1–12. DOI: 10.1016 / j.actpsy.2018.01.005
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Бут, Дж. Л., и Сиглер, Р. С. (2006). Различия в развитии и индивидуальные различия в чисто числовой оценке. Dev. Psychol. 42: 189.
PubMed Аннотация | Google Scholar
Коддинг, Р. С., Бернс, М. К., и Лукито, Г. (2011). Мета-анализ математических вмешательств по беглости базовых фактов: компонентный анализ. ЖЖ. Disab. Res. Практик. 26, 36–47. DOI: 10.1111 / j.1540-5826.2010.00323.x
CrossRef Полный текст | Google Scholar
Коэн П. А., Кулик Дж. А., Кулик К.-Л. С. (1982). Образовательные результаты репетиторства: метаанализ результатов. г. Educ. Res. журнал 19, 237–248. DOI: 10.3102 / 0002831201
37CrossRef Полный текст | Google Scholar
Де Смедт, Б., и Гилмор, К. К. (2011). Неисправный номерной модуль или затрудненный доступ? Обработка числовых величин у первоклассников с математическими трудностями. J. Exp. Детская психол. 108, 278–292. DOI: 10.1016 / j.jecp.2010.09.003
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Де Смедт, Б., Вершаффель, Л., и Гескьер, П. (2009). Прогностическая ценность сравнения числовой величины индивидуальных различий в успеваемости по математике. J. Exp. Детская психол. 103, 469–479. DOI: 10.1016 / j.jecp.2009.01.010
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Defever, E., Reynvoet, B., and Gebuis, T. (2013). Влияние свойств визуальных стимулов на явные суждения детей о численности в зависимости от задачи и возраста. J. Exp. Детская психол. 116, 216–233.DOI: 10.1016 / j.jecp.2013.04.006
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Dietrich, J. F., Huber, S., and Nuerk, H.-C. (2015). Методологические аспекты, которые необходимо учитывать при измерении приблизительной системы счисления (ВНС) — исследовательский обзор. Фронт. Psychol. 6: 295. DOI: 10.3389 / fpsyg.2015.00295
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гири, Д. К., Хоард, М. К., Ньюджент, Л., и Берд-Крейвен, Дж. (2008).Развитие представления числовой прямой у детей с математической отсталостью. Dev. Neuropsychol. 33, 277–299. DOI: 10.1080 / 87565640801982361
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гебуис, Т., и Рейнвоет, Б. (2012a). Непрерывные визуальные свойства объясняют нейронные реакции на несимволическое число. Психофизиология 49, 1649–1659. DOI: 10.1111 / j.1469-8986.2012.01461.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Герстен Р., Чард, Д. Дж., Джаянти, М., Бейкер, С. К., Морфи, П., и Флоджо, Дж. (2009). Обучение математике для учащихся с ограниченными возможностями обучения: метаанализ учебных компонентов. Rev. Educ. Res. 79, 1202–1242. DOI: 10.3102 / 003465430
31
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Халберда Дж. И Фейгенсон Л. (2008). Изменение в развитии остроты «ощущения числа»: приблизительная числовая система у 3-, 4-, 5- и 6-летних и взрослых. Dev. Psychol. 44: 1457. DOI: 10.1037 / a0012682
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хайд, Д. К., Бертелетти, И., Моу, Ю. (2016). Приблизительные числовые способности и математика: выводы из корреляционных и экспериментальных исследований обучения. Прог. Brain Res. 227, 335–351. DOI: 10.1016 / bs.pbr.2016.04.011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хайд, Д. К., Ханум, С., и Спелк, Э.С. (2014). Краткая несимволическая практика приближенных чисел улучшает последующую точную символьную арифметику у детей. Познание 131, 92–107. DOI: 10.1016 / j.cognition.2013.12.007
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Джанг, С., Чо, С. (2016). Острота распознавания численности (но не непрерывной величины) коррелирует с количественным решением задач, а не с рутинной арифметикой. Curr. Psychol. 35, 44–56. DOI: 10.1007 / с12144-015-9354-6
CrossRef Полный текст | Google Scholar
Джанг, С., и Чо, С. (2018). Посредническая роль точности отображения числа в величину во взаимосвязи между приблизительным чувством числа и математическими достижениями зависит от области математики и возраста. ЖЖ. Индивидуальная разница. 64, 113–124. DOI: 10.1016 / j.lindif.2018.05.005
CrossRef Полный текст | Google Scholar
Jordan, N.C., Kaplan, D., Locuniak, M. N., and Ramineni, C.(2007). Прогнозирование успеваемости по математике в первом классе на основе траекторий развития. ЖЖ. Disab. Res. Практик. 22, 36–46. DOI: 10.1111 / j.1540-5826.2007.00229.x
CrossRef Полный текст | Google Scholar
Ханум, С., Ханиф, Р., Спелке, Э. С., Бертелетти, И., и Хайд, Д. К. (2016). Влияние практики несимволического приблизительного числа на символьные числовые способности у пакистанских детей. PLoS One 11: e0164436. DOI: 10.1371 / journal.pone.0164436
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Крезберген, Э.Х. и Ван Луит Дж. Э. (2003). Математические вмешательства для детей с особыми образовательными потребностями: метаанализ. Remed. Специальное образование. 24, 97–114. DOI: 10.4103 / 2277-9531.162372
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Kucian, K., Grond, U., Rotzer, S., Henzi, B., Schönmann, C., Plangger, F., et al. (2011). Тренировка умственной числовой линии у детей с дискалькулией развития. Neuroimage 57, 782–795. DOI: 10.1016 / j.neuroimage.2011.01.070
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ли, К., и Чо, С. (2017). На обработку величин и сложные вычисления негативно влияет беспокойство математиков, в то время как простые вычисления, основанные на извлечении, нет. Внутр. J. Psychol. 53, 321–329. DOI: 10.1002 / ijop.12412
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лейбович, Т., Кацин, Н., Харель, М., Хеник, А. (2017). От «чувства числа» к «чувству величины»: роль непрерывных величин в числовом познании. Behav. Brain Sci. 40: e164. DOI: 10.1017 / S0140525X16000960
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Либертус, М. Э., Фейгенсон, Л., и Халберда, Дж. (2011). Острота дошкольников по приблизительной системе счисления коррелирует со школьными математическими способностями. Dev. Sci. 14, 1292–1300. DOI: 10.1111 / j.1467-7687.2011.01080.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Locuniak, M. N., and Jordan, N. C. (2008).Использование чувства детского сада для прогнозирования беглости вычислений во втором классе. J. ЖЖ. Disabil. 41, 451–459. DOI: 10.1177 / 0022219408321126
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лайонс, И. М., и Бейлок, С. Л. (2011). Способность к числовому порядку опосредует связь между чувством чисел и арифметической компетенцией. Познание 121, 256–261. DOI: 10.1016 / j.cognition.2011.07.009
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Мартенс, Б., Де Смедт, Б., Сасанги, Д., Элен, Дж., И Рейнвоет, Б. (2016). Улучшение арифметики у дошкольников с помощью тренировки сравнения или вычисления числовой линии: имеет ли это значение? ЖЖ. Instr. 46, 1–11. DOI: 10.1016 / j.learninstruc.2016.08.004
CrossRef Полный текст | Google Scholar
Мэлони, Э. А., Риско, Э. Ф., Престон, Ф., Ансари, Д., и Фугелсанг, Дж. (2010). Проблема надежности и достоверности когнитивных мер: случай числового эффекта расстояния. Acta Psychol. 134, 154–161. DOI: 10.1016 / j.actpsy.2010.01.006
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Мартин Р. Б., Чирино П. Т., Шарп К. и Барнс М. (2014). Числовые и счетные навыки в детском саду как предикторы математических навыков 1-го класса. ЖЖ. Индивидуальный. Diff. 34, 12–23. DOI: 10.1016 / j.lindif.2014.05.006
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Маццокко, М. М., Фейгенсон, Л.и Халберда Дж. (2011). Точность дошкольников в приблизительной системе счисления позволяет прогнозировать успеваемость по математике в более поздних школах. PLoS One 6: e23749. DOI: 10.1371 / journal.pone.0023749
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Оберштайнер А., Рейсс К. и Уфер С. (2013). Как обучение точному или приблизительному представлению чисел в уме может улучшить базовые навыки обработки чисел и арифметические навыки первоклассников. ЖЖ. Instr. 23,125–135. DOI: 10.1016 / j.learninstruc.2012.08.004
CrossRef Полный текст | Google Scholar
Парк, Дж., Бермудес, В., Робертс, Р. К., и Браннон, Э. М. (2016). Несимвольная приблизительная арифметическая подготовка улучшает математические способности дошкольников. J. Exp. Детская психол. 152, 278–293. DOI: 10.1016 / j.jecp.2016.07.011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Парк, Дж., И Браннон, Э. М. (2014). Улучшение арифметических действий с помощью обучения чувству числа: исследование основного механизма. Познание 133, 188–200. DOI: 10.1016 / j.cognition.2014.06.011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Пак, К., Ким, К., Сон, Ю., Чон, Д., и Чон, И. (2008). KISE-Basic Academic Achievement Tests (KISE-BAAT). Ансан: Корейский национальный институт специального образования.
Google Scholar
Парк Ю., Чо С. (2016). Изменения в развитии во взаимосвязи между остротой зрения и математическими достижениями у детей младшего школьного возраста. Educ. Psychol. 37, 873–887. DOI: 10.1080 / 01443410.2015.1127332
CrossRef Полный текст | Google Scholar
Piazza, M., Facoetti, A., Trussardi, A. N., Berteletti, I., Conte, S., Lucangeli, D., et al. (2010). Траектория развития числовой остроты зрения свидетельствует о серьезном нарушении дискалькулии развития. Познание 116, 33–41. DOI: 10.1016 / j.cognition.2010.03.012
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Рясянен, П., Салминен, Дж., Уилсон, А. Дж., Аунио, П., и Дехаен, С. (2009). Компьютерное вмешательство для детей с низким уровнем навыков счета. Cogn. Dev. 24, 450–472. DOI: 10.1016 / j.cogdev.2009.09.003
CrossRef Полный текст | Google Scholar
Rousselle, L., and Noël, M.-P. (2007). Основные числовые навыки у детей с нарушениями обучения математике: сравнение обработки символьных и несимволических чисел. Познание 102, 361–395. DOI: 10.1016 / j.cognition.2006.01.005
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Сасанги, Д., Де Смедт, Б., Дефевер, Э., и Рейнвоет, Б. (2012). Связь между основными числовыми способностями и математическими достижениями. Br. J. Dev. Psychol. 30, 344–357. DOI: 10.1111 / j.2044-835X.2011.02048.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Сасанги, Д., Гебель, С. М., Молл, К., Сметс, К., и Рейнвоет, Б. (2013). Приближенное чувство числа, обработка символьных чисел или отображение числа в пространство: что лежит в основе достижений математики? Дж.Exp. Детская психол. 114, 418–431. DOI: 10.1016 / j.jecp.2012.10.012
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Schneider, M., Beeres, K., Coban, L., Merz, S., Susan Schmidt, S., Stricker, J., et al. (2016). Связь обработки несимволических и символических числовых величин с математической компетентностью: метаанализ. Dev. Sci. 20: e12372. DOI: 10.1111 / desc.12372
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Селла, Ф., Трессольди, П., Лучангели, Д., и Зорзи, М. (2016). Тренировка числовых навыков в адаптивной видеоигре «Числовая гонка»: рандомизированное контролируемое испытание на дошкольниках. Trends Neurosci. Educ. 5, 20–29. DOI: 10.1016 / j.tine.2016.02.002
CrossRef Полный текст | Google Scholar
Сиглер, Р. С., и Рамани, Г. Б. (2009). Игра в настольные игры с линейными числами, но не в круговые, улучшает понимание дошкольников с низкими доходами чисел. J. Educ. Psychol. 101: 545. DOI: 10.1037 / a0014239
CrossRef Полный текст | Google Scholar
Старр А., Либертус М. Э. и Браннон Э. М. (2013). Чувство чисел в младенчестве предсказывает математические способности в детстве. Proc. Natl. Акад. Sci. США 110, 18116–18120. DOI: 10.1073 / pnas.1302751110
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шкудларек, Э., Браннон, Э. М. (2018). Приближенное обучение арифметике улучшает успеваемость по неформальной математике у дошкольников с низкими успеваемостями. Фронт. Psychol. 9: 606. DOI: 10.3389 / fpsyg.2018.00606
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Szűcs, D., and Myers, T. (2017). Критический анализ дизайна, фактов, предвзятости и умозаключений в литературе по приблизительной системе счисления: систематический обзор. Trends Neurosci. Educ. 6, 187–203. DOI: 10.1016 / j.tine.2016.11.002
CrossRef Полный текст | Google Scholar
Szucs, D., Nobes, A., Devine, A., Gabriel, F.К., и Гебуис, Т. (2013). Параметры зрительного стимула серьезно затрудняют измерение приблизительной остроты зрения системы счисления и сравнительные эффекты между взрослыми и детьми. Фронт. Psychol. 4: 444. DOI: 10.3389 / fpsyg.2013.00444
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Вилетт Б., Маварт К. и Русинек С. (2010). L’outil «Estimateur», la ligne numérique mentale et les habiletés arithmétiques. Pratiques Psychol. 16,203–214.DOI: 10.1016 / j.prps.2009.10.002
CrossRef Полный текст | Google Scholar
Ван Дж., Одич Д., Халберда Дж. И Фейгенсон Л. (2016). Изменение точности приближенных представлений дошкольников в системе счисления меняет их символьные математические способности. J. Exp. Детская психол. 147, 82–99. DOI: 10.1016 / j.jecp.2016.03.002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Уилсон, А. Дж., Дехен, С., Дюбуа, О., и Файоль, М. (2009).Влияние адаптивного игрового вмешательства на восприятие числа у детей детского сада с низким социально-экономическим статусом. Mind Brain Educ. 3, 224–234. DOI: 10.1111 / j.1751-228X.2009.01075.x
CrossRef Полный текст | Google Scholar
Уилсон, А. Дж., Ревкин, С. К., Коэн, Д., Коэн, Л., и Дехайн, С. (2006). Открытая пробная оценка адаптивной компьютерной игры «The Number Race» для лечения дискалькулии. Behav. Brain Funct. 2:20.
Google Scholar
Записка Маршалла — письмо Кима
Для получения более подробной информации об этих супер-курировании резюме лучших статей за первые 17 лет действия «Записки Маршалла» щелкните обложку книги.
Ниже представлены учебные материалы Кима, статьи, книги и графические изображения. Практически все доступны полностью (бесплатно) при нажатии на заголовок. Вот оглавление — нажмите, и вы перейдете к каждой группе.
- Идеи и ресурсы для пост-Covid «новой нормы»
- Классные материалы
- Контроль, обучение и оценка учителей
- Рубрики для оценки учителей и директоров в конце учебного года
- Руководство школы и эффективные школы
- Улучшение преподавания в классе
- Оценка и подотчетность
- Половое воспитание
- Книги Кима
- Графика обучения и общая картина К-12
- Размышления об обучении, расе и обществе Бостона Школы
- Книжное обозрение
1.Идеи и ресурсы для «новой нормы» пост-Covid
2. Учебные материалы
3.Контроль, обучение и оценка учителей
4.Рубрики для оценки учителей и директоров в конце учебного года
5.Школьное руководство и эффективные школы
6.Улучшение преподавания в классе
7.Оценки и подотчетность
8. Половое воспитание
9.Книги Кима
Лучшее из меморандума Маршалла, книга 2 : Идеи и шаги для активизации лидерства, преподавания и обучения
Эта книга — квинтэссенция важных идей первых 17 лет существования меморандума.
доступно на Amazon и
Барнс и Ноубл.
В каждой главе содержится 8-10 резюме статей по основной теме, за которыми следуют рекомендации по профессиональному обучению, ориентированные на решения.
Этот весьма практичный набор идей, результатов исследований и стратегий придаст энергии лидерству, обучению и обучению.
Чтобы просмотреть обзор, содержание, предлагаемые варианты использования, обзоры и цены, щелкните здесь:
Глава шестая этой книги «Что делает обучение приставкой» предлагается в виде бесплатного PDF-файла. Просто щелкните здесь.
ОБЗОР:
Каждая глава похожа на тематический выпуск образовательного журнала, но имеет четыре важных преимущества: (а) Ким и Дженн смогли охватить гораздо более широкую сеть, выбирая из почти двух десятилетий статей в многочисленных публикациях; (b) резюме меморандума Маршалла обычно намного короче оригинальных статей, что позволяет прочитать ключевые идеи из десяти статей менее чем за час; (c) в конце каждой главы приведены индивидуальные предложения ПД, чтобы претворить идеи в жизнь; и (г) книга содержит одиннадцать тем под одной обложкой, предоставляя вам невероятное количество полезной информации — дальновидной и практической, провокационной и практической, и легко доступной, когда вы и ваши коллеги боретесь с бесчисленными проблемами управления хорошая школа.
КНИГА ДВА СОДЕРЖАНИЕ:
Образ мышления, поддерживающий обучение
- Убеждения об интеллекте и способностях
- Социально-эмоциональное развитие студентов
- Раса и образование американских студентов
- Партнерство с семьями
Эффективная педагогика
- Ключевые элементы хорошей педагогики
- Что делает обучение Stick
- Знание чтения, письма и устной речи
- Дифференциация и персонализация
Педагоги постоянно совершенствуют
- Команды учителей, ориентированных на результат
- Профессиональное развитие, которое работает
- Руководство учителя
ОТЗЫВОВ:
«За свою 49-летнюю карьеру я никогда не встречал более жадного читателя литературы по вопросам образования, чем Ким Маршалл.С тех пор, как он выпустил «Памятку Маршалла» почти 17 лет назад, Ким каждую неделю просматривал многочисленные периодические издания в поисках важных статей, которые можно было бы обобщить и обобщить. Многолетний опыт Кима в качестве учителя, директора, районного администратора и консультанта по вопросам образования подкрепляет его способность находить наиболее полезные, наводящие на размышления и своевременные статьи и позволяет ему фиксировать их «большие идеи» для эффективного использования занятыми людьми. образовательные лидеры. Эта книга, в соавторстве с Дженн Дэвид-Лэнг, представляет собой второй сборник «лучших хитов» и заслуживает видного места на тумбочке или рабочем столе для чтения и справки.”
— Джей МакТиг, автор и консультант, соавтор с Грантом Уиггинсом книги «Понимание через дизайн»
«Профессиональное чтение еще не в приоритете? Подумай еще раз. Руководителям школ и специалистам-практикам сейчас больше, чем когда-либо требуется актуальная, надежная и актуальная информация, которая всегда была бы у нас под рукой; в частности, когда мы ведем переговоры о глобальных кризисах в области здравоохранения и принимаем подлинные антирасистские стратегии на службе подлинной реализации американской мечты для всех. Огромный сборник статей и ресурсов, который включает Лучшее из заметок Маршалла: Книга 2 хорошо отвечает всем требованиям.Маршалл и Дэвид-Лэнг оказали огромную услугу коллективному имени нашей профессии. А теперь приступим к чтению. Нельзя терять ни секунды ».
— Дэвид Дж. Васкес, основатель и главный директор, Bronx Academy for Multi-Media / New York, NY
«Памятка Маршалла была частью моего личного лидерского пути с момента первой публикации в 2003 году. В качестве заместителя директора и суперинтенданта государственных школ Челси в Массачусетсе в течение 17 лет меморандум Маршалла был моим постоянным спутником и источником информации.Это было место, где я мог учиться, размышлять, совершенствоваться и понимать, как проводить глубокие трансформационные организационные изменения от имени студентов и семей. В 2012 году мы приобрели подписку для всего округа, и результат был незамедлительным и долговременным. Мы начали вести более глубокие и содержательные беседы на всех уровнях, и Меморандум вдохновил преподавателей предпринимательской деятельности в каждой школе на новейшие идеи и исследования в рамках выбранной ими профессии. Благодаря памятной записке Маршалла мы смогли создать и поддержать трансформационную культуру среди наших преподавателей.А теперь Ким Маршалл и Дженн Дэвид-Лэнг собрали лучшее из памятки Маршалла в двух томах, с предложениями профессионального обучения по каждой теме. Это слишком хорошо, чтобы быть правдой! »
— Мэри М. Бурк, бывший суперинтендант государственных школ Челси / Челси, Массачусетс; Суперинтендант года штата Массачусетс 2017; Директор по связям с государством, Массачусетская ассоциация школьных суперинтендантов / Бедфорд, Массачусетс
«Если вы хотите переместить обсуждение образовательной практики и политики в ваших школах от традиций, мнений и предубеждений к серьезным исследованиям и фактам, то попросите своих преподавателей, руководство, родителей и политиков изучить эту книгу.Книга The Best of the Marshall Memo: Book Two , созданная на основе более чем десятилетней работы ведущих мировых исследователей и практиков, — не то место, где можно искать простые ответы на сложные вопросы. Скорее, он бросит вызов общепринятым представлениям, предложит различные точки зрения и предоставит практические идеи, которые можно немедленно применить к некоторым из самых неприятных проблем в школах. Главы как нельзя более своевременные, включая серию вдумчивых статей о расе в школах.Каждая глава включает в себя упражнения для практического применения и размышления для получения более увлекательной возможности профессионального обучения. Как знают читатели во всем мире, если вы не читали меморандум Маршалла, значит, вы не сделали уроки ».
—Дуглас Б. Ривз, автор / консультант и основатель, Equity and Excellence Institute
«В сложном и плотном графике суперинтенданта и директора время ценно. Памятка Маршалла позволяет лидерам принимать решения, основанные на исследованиях, для преобразования практики в своих учебных сообществах.Району 4 в Нью-Йорке посчастливилось иметь возможность ознакомиться с книгой Ким Маршалл и Дженн Дэвид-Лэнг во время нашего ежемесячного книжного клуба директоров. Эти обсуждения вызвали глубокие разговоры и привели к появлению новых способов решения текущих задач, требующих улучшения. Это превратилось в более глубокое обсуждение и действия, которые улучшили наши школы. Я с нетерпением жду возможности использовать The Best of the Marshall Memo: Book Two в моем новом учебном сообществе, государственных школах Норуолка, чтобы зажечь наводящие на размышления дискуссии с моим кабинетом и руководителями школ.Эта книга обязательна для всех руководителей системы образования и педагогов ».
— Александра Эстрелла, бывшая суперинтендант общины, округ 4 / Нью-Йорк, штат Нью-Йорк; в настоящее время суперинтендант государственных школ Норуолка / Норуолк, Коннектикут
«Памятка Маршалла — прекрасный ресурс для преподавателей. Каждую неделю в нем собраны и обобщены лучшие материалы, связанные с образованием, из самых разных источников. В каждом выпуске я всегда нахожу что-то интересное. Во втором томе The Best of the Marshall Memo, Ким Маршалл и Дженн Дэвид-Лэнг делятся лучшими из лучших, сгруппированных по темам.Например, в главе, озаглавленной «Раса и образование американских студентов», есть девятнадцать резюме статей по различным темам, от обсуждения расы в классе до помощи черным мужчинам в достижении успеха и преподавания с учетом культурных особенностей. Каждое краткое изложение хорошо написано и раскрывает суть проблемы и дает эффективные ответы на реальные проблемы. Сама «Памятка Маршалла» и основанная на ней книга помещают читателей в реальные классы с настоящими детьми. Вы почти можете почувствовать запах брокколи, готовящейся в кафетерии, и услышать, как останавливаются автобусы, когда вы читаете эти проницательные, вдохновляющие и прагматичные обсуждения проблем, с которыми сталкиваются учителя, директора и другие преподаватели.”
—Роберт Славин, директор Центра исследований и реформ в сфере образования, Школа образования Университета Джона Хопкинса / Балтимор, Мэриленд
«В сфере образования так много всего известно, особенно с учетом текущих проблем, связанных с COVID-19! Как преподаватели узнают, какая информация, основанная на исследованиях, является наилучшей, на основании которой мы можем принимать важные и быстрые решения? Ким Маршалл и Дженн Дэвид-Лэнг кратко поделились самыми актуальными идеями и идеями, которыми мы руководствуемся в наших действиях в сфере образования. Они проводят исследования для нас! »
—Келли Хастингс, директор средней школы Strike — Little Elm ISD / Little Elm, TX
«С самого начала меморандума Маршалла резюме Ким всегда держали меня в курсе лучших мыслей о хорошем обучении и успешном лидерстве — бесценный ресурс.Его первая книга с соавтором Дженн Дэвид-Лэнг оказалась отличным источником новаторских идей и наиболее убедительных исследований по текущим вопросам. С их новым Book Two у меня есть молниеносный доступ к лучшим умам в нашей области ».
—Jon Saphier, основатель, Research for Better Teaching / Acton, MA
«Памятка Маршалла — это Святой Грааль для образования. Каждую неделю читатели могут пить из нескончаемого источника исследований, анализа и рекомендаций, содержащихся на его страницах, предлагая путь к тому, как мы можем создать более справедливую систему образования.В The Best of the Marshall Memo: Book Two вы найдете цитаты, резюме статей и стратегии профессионального развития, чтобы ответить на ряд вопросов, от оценки и прогулов до письма и баланса между работой и личной жизнью. Как подписчик с 2007 года, я призываю вас утолить жажду на этой неделе с помощью этой превосходной подборки ресурсов ».
— Шахара К. Джексон, основатель, Summit Academy / Бруклин, штат Нью-Йорк; в настоящее время: докторант Гарвардской высшей школы образования — программа по лидерству для докторов наук / Кембридж, Массачусетс
«Я много лет подписываюсь на краткое изложение книги Дженн Дэвид-Лэнг« Основная идея ».Краткое содержание ее книг яркое, содержательное и готовое к практическому применению. Совсем недавно я добавил «Памятку Маршалла» к моему профессиональному чтению и нашел ее резюме статей одинаково полезными. The Best of the Marshall Memo: Book One and Book Two позволяют мне увидеть и усвоить передовой опыт школьного руководства с помощью широкоугольного объектива. Учитывая постоянную потребность преподавателей во времени, эти книги — лучшие друзья практикующих: они эффективны и полезны ».
—Роланд Шоу, директор раннего колледжа центра профессионального обучения / Денвер, штат Колорадо,
«Как педагог в течение последних 18 лет, я давно ценил резюме, составленные Дженн Дэвид-Лэнг и Ким Маршалл.Крайне важно быть в курсе последних образовательных исследований, но один человек не может разобраться в бесчисленных статьях, исследовательской литературе и книгах, выпускаемых каждый год. Их резюме помогают мне получить обзор большего количества ресурсов, чем я мог бы прочитать самостоятельно, а затем сосредоточиться на тех, которые больше всего соответствуют моей работе. Наличие их ресурсов и предложений по профессиональному развитию в The Best of the Marshall Memo: Book Two еще больше упрощает поиск целевых ресурсов, которые помогут поддержать обучение и рост в моем уникальном школьном сообществе.”
— Кимберли Суонсон, директор средней школы естественных наук, Нью-Йорк,
«Ким Маршалл и Дженн Дэвид-Лэнг сделали тяжелую работу для преподавателей, создав кураторский справочник по лучшим статьям в данной области с легкими для чтения резюме, ссылками на исходный текст и связанными с ними мероприятиями по профессиональному развитию, которые легко для использования и обмена с персоналом и школьными сообществами. Сочетание работы Ким над еженедельной памяткой Маршалла с «Главной идеей» Дженн, резюме лучших книг для преподавателей с инструментами профессионального развития, создает удивительно ценный синергетический эффект — ресурс, который великие преподаватели могут использовать каждый день.”
—Марк Шеллинджер, директор, Национальный инновационный проект SAM / Луисвилл, KY
«Ежедневно огромное количество информации, которую я получаю как руководитель системы образования, может вызвать у меня ощущение, будто я пью из пожарного шланга! Но по утрам приходят «Записка Маршалла» Ким Маршалл или краткое изложение книги Дженн Дэвид-Лэнг «Основная идея», и ресурсы в моем почтовом ящике кажутся управляемыми с этими двумя жемчужинами. Я чувствую себя так, будто хлюпаю из садового шланга! Теперь, в The Best of the Marshall Memo: Book Two , Маршалл и Дэвид-Лэнг взяли лучшее из последних 17 лет Меморандумов Маршалла и разделили их на три широкие области: образ мышления, эффективная педагогика и постоянное совершенствование.С помощью этого профессионального учебного ресурса (наряду с The Best of the Marshall Memo: Book One , конечно!) Им снова удалось собрать громоздкий объем доступной информации из надежных источников в более мелкие и удобоваримые драгоценные камни. ”
—Дон Дж. Бентли, помощник суперинтенданта по вопросам разнообразия, справедливости и интеграции — Региональный школьный округ Актон-Боксборо / Актон, Массачусетс
«Ким Маршалл и Дженн Дэвид-Лэнг создали бесценный ресурс! Как педагог с более чем 29-летним стажем, информация, которую я почерпнул из Памятка Маршалла: Книга 2 , является обязательным и полезным ресурсом для всех преподавателей во всех областях! Педагоги получат более глубокое понимание проблем, стоящих на переднем крае современного образовательного мира.Ким и Дженн проделали для вас работу и исследования и собрали их в удобную книгу! Это отличный ресурс для профессионального развития и способ глубже понять самые важные вопросы. Без сомнения, эта книга должна быть у вас на полке — точнее, прямо у вашего рабочего стола! »
—Ким Дипкер, директор, Гарнизонная средняя школа — Государственные школы Валла Валла / Валла Валла, Вашингтон
«Каждую неделю Ким Маршалл оказывает неоценимую услугу педагогам по всей стране.Он пробирается через и мастерски извлекает множество образовательных статей, которые опровергают устаревшие предположения, углубляют понимание, вызывают споры и предоставляют конкретные практические рекомендации для содействия обучению и развитию студентов. Его письмо ясное, увлекательное и яркое. Эта книга, его вторая антология статей, охватывает обширную и жизненно важную область, включая эффективную педагогику, развитие расовых и культурных навыков учителей и формирование сильных школьных команд руководства. Совершите этот тур с Mr.Маршалл и его соавтор Дженн Дэвид-Лэнг. Их знания об обучении, преподавании, лидерстве и школах удивительно широки и глубоки, и их сердца находятся точно в нужном месте ».
—Рик Вайсборд, старший преподаватель, Гарвардская высшая школа образования / Кембридж, Массачусетс
«Любой преподаватель может выполнить поиск в Google и найти несколько статей практически по любой теме. Итак, зачем нам Записка Маршалла? Я вам скажу почему. Интернет предоставляет нам информации, от достоверной до смешной.Вот где «Записка Маршалла» нашла свою нишу. Мой источник информации об образовательных перспективах и исследованиях практически по любой теме — это памятка Маршалла. Почему? Потому что контент был прочитан, проверен и проверен на достоверность. Мне не нужно сомневаться в достоверности исследования, и Маршалл дает краткое и убедительное резюме каждой статьи. Он создан для эффективного информирования. Не знаю, как они это делают, но они это делают, и делают это хорошо. Памятка Маршалла: Книга вторая , написанная с Дженн Дэвид-Лэнг, является продолжением этой миссии и должна быть на книжной полке каждого преподавателя — в потрепанном, потрепанном, потрепанном и выделенном месте.”
—Кен Уильямс, педагог / автор / консультант, Unfold The Soul / Sharpsburg, GA
«Среди драгоценных камней в . Этот сборник исследований, касающихся мировоззрения учителей и учеников, оспаривает мнение о том, что умственная острота учащихся определяется при рождении. Вместо этого он проливает свет на податливость интеллекта и на то, как родители, учителя и дети могут тренировать мозг как мускул, чтобы развить самоэффективность, необходимую ребенку, чтобы поверить в то, что он может преуспеть, и иметь индивидуальную волю для достижения успеха своими собственными усилиями. .Эта глава, наряду с другими в The Best of the Marshall Memo, Book Two , является обязательной к прочтению для всех, кто заинтересован в том, чтобы помочь детям раскрыть свой потенциал и превзойти его ».
— Ян Роу, научный сотрудник, Американский институт предпринимательства / Вашингтон, округ Колумбия; бывший генеральный директор Public Preparatory Network / Нью-Йорк, NY
«История американского образования изобилует примерами глупых причуд, распространяющихся повсюду, в то время как здравый смысл и практики, основанные на фактах, остаются застрявшими в четырех стенах классной комнаты.Памятка Маршалла нарушает эту традицию, давая руководителям образования и их командам лучшие советы и аналитические материалы со всей страны и со всего мира. А в The Best of the Marshall Memo: Book Two Ким Маршалл и Дженн Дэвид-Лэнг дают нам самые лучшие идеи и исследования за семнадцать лет существования Memo ».
— Майкл Дж. Петрилли, президент, Институт Томаса Б. Фордхэма / Вашингтон, округ Колумбия
ЦЕНА:
Бесплатная доставка Amazon означает лучшую цену для небольших заказов.Для массовых заказов лучше заказать напрямую у издателя. Вот цены за копию плюс стоимость доставки:5-49 экземпляров — 21,71 доллара
50-99 экземпляров — 21,31 $
100-249 экземпляров — 20,92 доллара
250-499 экземпляров — 19,33 доллара
500+ — 17,75 $
Чтобы сделать заказ, просто отправьте письмо Колину Рольфу по адресу [электронная почта защищена].
Лучшее из памятки Маршалла: Книга первая : Идеи и шаги по активизации лидерства, преподавания и обучения
Эта книга представляет собой квинтэссенцию важных идей первых 16 лет существования Меморандума.
доступно на Amazon и
Барнс и Ноубл.В каждой главе содержится 8-10 резюме статей по основной теме, за которыми следуют рекомендации по профессиональному обучению, ориентированные на решения.
Этот весьма практичный набор идей, результатов исследований и стратегий придаст энергии лидерству, обучению и обучению.
Чтобы бесплатно загрузить главу 2 (Управление временем воздействия), щелкните здесь.
Чтобы просмотреть обзор, содержание, предлагаемые варианты использования, 24 отзыва и цены, нажмите здесь:
ОБЗОР:
Каждая глава похожа на тематический выпуск образовательного журнала, но имеет четыре важных преимущества: (а) Ким и Дженн смогли охватить гораздо более широкую сеть, выбирая из почти двух десятилетий статей в многочисленных публикациях; (b) резюме меморандума Маршалла обычно намного короче оригинальных статей, что позволяет прочитать ключевые идеи из десяти статей менее чем за час; (c) в конце каждой главы приведены индивидуальные предложения ПД, чтобы претворить идеи в жизнь; и (г) книга содержит одиннадцать тем под одной обложкой, предоставляя вам невероятное количество полезной информации — дальновидной и практической, провокационной и практической, и легко доступной, когда вы и ваши коллеги боретесь с бесчисленными проблемами управления хорошая школа.
СОДЕРЖАНИЕ:
- Набор инструментов лидера
Глава первая — Планирование с целью
Глава вторая — Управление временем для воздействия
Глава третья — Эмоциональный интеллект лидера - Более качественное преподавание в большем количестве классов Большую часть времени
Глава четвертая — Собеседование и прием на работу
Глава пятая — Коучинг учителей
Глава шестая — Критическая обратная связь и трудные беседы
Глава седьмая — Оценка учителя - Структуры для успешной работы учащихся
Глава восьмая — Положительная дисциплина в классе
Глава девятая — Блоки планирования и уроки
Глава десятая — Оценка для успеваемости
Глава одиннадцатая — Порядок выставления оценок
НАИЛУЧШИЕ СПОСОБЫ ИСПОЛЬЗОВАНИЯ КНИГИ:
Вы можете читать его от корки до корки, но более вероятно, что вы и ваши коллеги сосредоточитесь на определенных главах, когда столкнетесь с проблемой, по которой вы хотели бы получить больше идей, исследований и рекомендаций.Некоторые примеры:
- Переосмысление политики надзора и оценки учителей
- Руководители, работающие с H.S.P.S. (гиперактивный поверхностный главный синдром)
- Настройка и улучшение практики проведения собеседований и приема на работу
- Группы учителей, разрабатывающие учебные программы и планы уроков
- Подготовка к трудному разговору
- Улучшение дисциплины в классе и в школе
- Факультет готовится к переходу на стандартизированную систему оценок
- Инструкторские тренеры, разрабатывающие стратегию, как лучше всего поддержать учителей-новичков
- Команда руководителей, стремящаяся сделать стратегический план своей школы живым документом
- Учителя, которые ищут информацию об эмоциональном интеллекте
- Планирование выездного семинара по повышению квалификации, посвященного определенной проблеме
ОТЗЫВОВ:
«Создав этот сборник статей, Маршалл и Дэвид-Лэнг оказали невероятную услугу профессиональным педагогам. Эта книга наполнена практическими, но информативными ресурсами, которые помогут педагогам в решении некоторых из самых сложных и трудных проблем, с которыми они сталкиваются. Для преподавателей для тех, кто искренне желает изменить мир к лучшему, эта книга будет бесценным ресурсом ».
— Педро А. Ногера, доктор философии, заслуженный профессор образования, Высшая школа образования и информационных исследований Калифорнийского университета в Лос-Анджелесе.
«Как образовательные лидеры, мы должны быть в курсе исследований, тенденций и критических вопросов в образовании, несмотря на нехватку необходимого ресурса — времени.Памятка Маршалла «Лучшее из заметок» предоставляет занятым преподавателям краткий инструментарий, который делает исследование действенным. Маршалл и Дэвид-Лэнг проделали за нас работу по изучению бесчисленных журналов и статей, чтобы помочь преподавателям и руководителям сосредоточиться на улучшении наших школ. Я бы хотел, чтобы у меня был этот ресурс, когда я был директором большой городской средней школы, всегда пытаясь решить, казалось бы, неразрешимую проблему! »
— Сью Захович, бывший директор средней школы Броктона, Массачусетс.
«Еще один замечательный ресурс от Ким Маршалл, который мы с моими коллегами-суперинтендантами обязательно будем использовать! В наших усилиях, направленных на то, чтобы помочь лидерам расти и мыслить критически, эта коллекция записок станет источником отличного разговора.Новый директор: прежде чем нанять своего первого учителя, прочтите эту памятку Маршалла! Привет, новый учитель: у вас будет очень трудный разговор; прежде чем вы это сделаете, посмотрите на это меморандум Маршалла! Стремящиеся лидеры: обязательно просмотрите, что некоторые практикующие говорили о тайм-менеджменте! Спасибо, Ким, за великолепную коллекцию!
— Кертис Джонс, суперинтендант школ округа Бибб, Джорджия, национальный суперинтендант года 2019
«Я давно восхищаюсь преданностью Ким Маршалл совершенствованию преподавания, лидерства и обучения в качестве директора, главного наставника и писателя.Информационный бюллетень Marshall Memo уже более 15 лет является жизненно важным ресурсом для преподавателей по всей стране. Теперь Ким объединилась с Дженн Дэвид-Лэнг, чтобы подготовить самые лучшие резюме меморандумов и добавить конкретные рекомендации по действиям. С советами, которые варьируются от практических до вдохновляющих и даже вдохновляющих, The Best of the Marshall Memo — настоящая сокровищница, полная драгоценных камней для каждого преподавателя, который хочет улучшить свои школы, округа и себя ».
— Джон Б. Кинг-младший, президент и главный исполнительный директор Education Trust; бывший десятый секретарь образования США
«Памятка Маршалла уже давно является руководством для учителей и школьных администраторов, которые ищут дельные советы по исследованиям, которые могут быть полезны в их работе.Теперь, в этом искусно составленном сборнике первоклассных статей, Маршалл и Дэвид-Лэнг предоставляют читателям ценные сведения и комментарии о ключевых проблемах, с которыми преподаватели сталкиваются в сфере лидерства, организации школы и учебной практики. Книга полна вопросов, которые вызовут профессиональный отклик, результатов, которые подтвердят и оспаривают убеждения преподавателей, а также ресурсов для поддержки индивидуального обучения и коллегиального роста. Держите эту книгу под рукой; вы будете часто его использовать ».
— Сьюзан Мур Джонсон, Джером Т.Мерфи, профессор-исследователь, Гарвардская высшая школа образования
«Ким Маршалл в сотрудничестве с Дженн Дэвид-Ланг проанализировал, синтезировал и обновил около 800 меморандумов Маршалла, написанных им за последние пятнадцать лет, и подготовил бесценное руководство для школьных руководителей. Под тремя широкими заголовками — лидерство инструментарий, больше обучения в большем количестве аудиторий и больше времени, а также структуры для достижения успеха учащихся — эта книга дает школьным руководителям беспрецедентное количество мудрости, конечно, опираясь на исследования, но также интерпретируя эти исследования в свете опыта о том, как исследования могут будут реализованы в реальных школах.Добавьте четкие обозначения, предусмотренные заголовками глав, и это, очень просто, книга, без которой ни один школьный руководитель не может позволить себе обойтись ».
— Дилан Вильям, почетный профессор Университетского колледжа в Лондоне.
«Независимо от того, являемся ли мы директорами школ, суперинтендантами, тренерами или главными учителями, мы часто замечаем, что желаем, чтобы у нас был ангел-хранитель на плече, помогающий нам ориентироваться в изобилии идей и исследований по образовательной практике. Как только мы находим отличные идеи и исследования в Затем мы задаемся вопросом о конкретной области практики: «Как я могу эффективно использовать это, чтобы усовершенствовать свою практику?» Меморандум Маршалла «Лучшие моменты» предлагает тем из нас, кто занимается на местах, практические решения и ключевые идеи, а также предостережения о неэффективных методах обучения в школах до 12 лет.Обязательно к прочтению для всех лидеров преподавания и обучения! »
— Мэри Нэш, суперинтендант школьного административного округа № 35 штата Мэн / Элиот, штат Мэн. Суперинтендант года в штате Мэн 2018
«Ким Маршалл стала громким голосом в многолюдном, темном поле лидерства в сфере образования, определяя самое важное и делясь этим в краткой форме с педагогами по всему миру. Сочетание реального опыта Ким и Дженн с дальновидным мышлением создает необходимый ресурс для каждого педагога.Спасибо, мы этого очень долго ждали! »
— Пол Бэмбрик-Сантойо, основатель и декан, Leverage Leadership Institute; Директор школ, Uncommon Schools
«Я не могу переоценить тот вклад, который Меморандум Маршалла внес в мою работу на протяжении многих лет, с его тщательно составленными еженедельными резюме наиболее важных образовательных статей. Теперь идет« Лучшее из памятки Маршалла », самое« лучшее из лучшее »из этих резюме с полезными упражнениями и советами по применению их содержания.Эта книга мастерски построена вокруг наиболее важных вопросов обучения и лидерства. На его страницах больше практической, концентрированной мудрости, чем на всех учебных курсах, которые я когда-либо посещал. Памятка «Лучшее из памятки Маршалла» должна быть вручена каждому учителю и руководителю, работающим в сфере образования ».
— Майк Шмокер, автор, спикер, консультант.
«Ким Маршалл и Дженн Дэвид-Лэнг всегда оказывали неоценимую услугу преподавателям, объединяя всю сложную информацию о том, что работает в образовании, в удобоваримые отрывки, чтобы мы могли быстро узнать то, что нам нужно, а затем вернуться к делу. обучения.И теперь, как одна жемчужина, созданная устрицей на протяжении многих лет, мы получаем все лучшее от их лечения в одной мощной книге ».
— Дженнифер Гонсалес, Культ педагогики
«Я часто говорю об удивительном« учителе из 206 », чье сочетание веры и педагогических навыков дает потрясающие результаты со всеми учениками. Памятка Маршалла «Лучшее из заметок» основана на той же формуле: вера в то, что наши ученики могут учиться, а наши учителя могут их учить. Маршалл и Дэвид-Лэнг подготовили высокоорганизованный набор актуальных, основанных на исследованиях резюме учебной практики, которые, вместе взятые, создают всеобъемлющую основу для практического применения в классе.Это очень важное руководство для повышения квалификации преподавателей ».
— Джеффри Ховард, основатель и генеральный директор Efficacy Institute
«Ким и Дженн предоставили занятым руководителям школ и округов именно то, что нам нужно — вдумчивый обзор и резюме соответствующих исследований, а также конкретные способы поделиться этими знаниями с нашими школьными практиками. Выбранные темы и важные вопросы изменят встречи на занятиях по профессиональному обучению.Это обязательный ресурс для любого руководителя школы или центрального офиса.”
— Джоан Дабровски, помощник суперинтенданта преподавания и обучения, Государственные школы Уэллсли / Уэллсли, Массачусетс
«Памятка Маршалла« Лучшее из заметок Маршалла »- важный ресурс для современного педагога. Учителя и руководители школ в равной степени извлекут пользу из тщательно подобранного анализа и обзора последних образовательных исследований и статей. Формат книги помогает глубоко погрузиться в ключевые моменты. темы, актуальные для каждой школы в Америке. Руководители могут использовать эту книгу, чтобы способствовать размышлениям, диалогу и вовлечению всего персонала в важные проблемы, с которыми сталкиваются их школьные сообщества.Отдельные учителя и преподаватели могут углубить свои собственные исследования, практики и области исследований. Умные педагоги будут использовать этот ресурс для повышения эффективности своей практики и наращивания потенциала в своих школах ».
— Николас Тишук, исполнительный директор, Чартерная школа New Beginnings, Бедфорд Стайвесант / Бруклин, штат Нью-Йорк.
«Как школьный руководитель в течение последних 20 лет, я был одновременно вдохновлен и поражен бесчисленными книгами, статьями, исследованиями и идеями, которые могут сделать меня и мою школу лучше.Быть директором — это как две работы с полной занятостью; Просеивание и сортировка всех материалов для обучения и профессионального развития может легко почувствовать себя третьим. На протяжении многих лет Ким Маршалл и Дженн Дэвид-Лэнг сэкономили мне неизмеримое количество времени, направив меня непосредственно к лучшим ресурсам и размышлениям в области образования и предоставив мне продуманные, действенные и действенные идеи и инструменты, которые позволят мне под ключ и поделиться своим ростом и обучением. Я очень рад этой новой книге и блестящему сотрудничеству.”
— Марк Федерман, директор общественной школы Ист-Сайд / Нью-Йорк, штат Нью-Йорк.
«Этот новый том, составленный из почти 800 меморандумов Маршалла, представляет собой еще одну впечатляющую и высоко оцененную услугу, превращая курирование в золотую жилу с лучшими размышлениями о некоторых из самых сложных проблем K – 12. Добавлено в это мета-курирование. это прагматичные пошаговые инструкции Дженн о том, как персонал может сразу применить эти идеи. Поистине невероятные усилия, Ким и Дженн !! Вы нас всех избаловали.”
— Элизабет Именде-Куни, международный консультант по вопросам образования, ведущие преподаватели
«Ким Маршалл и Дженн Дэвид-Лэнг, несомненно, являются наиболее выдающимися составителями статей и книг в сфере образования сегодня. В этом томе они выводят свои уникальные и неповторимые таланты на новый уровень, объединяя свои работы по темам, находящимся на переднем крае почти всех Инициатива по улучшению образования. Работы, которые они обобщают, варьируются от убедительно аргументированных мнений до тщательного исследовательского синтеза — и авторы этих работ не приходят к одним и тем же выводам и не предлагают одинаковых рекомендаций.Таким образом, хотя читатели могут не дать однозначных ответов на свои наиболее сложные вопросы, они получат более глубокое понимание затронутых вопросов и голосов, наиболее влияющих на обсуждение ».
— Томас Р. Гаски, старший научный сотрудник Луисвильского университета; Почетный профессор Университета Кентукки
«Изменения жизненно необходимы и трудны. Ким Маршалл и Дженн Дэвид-Лэнг указывают нам путь. В этом даре коллективной мудрости, накопленной за десятилетия службы, Маршалл и Дэвид-Лэнг предлагают всем нам, глубоко заботящимся о детях, социальную справедливость, социальную справедливость и социальную справедливость. школы, округа и системы — инструментарий и дорожная карта, которые помогут нам вести нас к улучшениям в интересах достижений учащихся и роста лидеров на местах.Эта книга — действительно сундук с сокровищами. Обязательно покупать. Вы почувствуете себя очень мудрым, извлекая пользу из этого, его практической мудрости и доступных инструментов, чтобы улучшать вашу благородную работу и наращивать потенциал каждый день ».
— Элли Драго-Северсон, профессор педагогического лидерства и обучения взрослых и лидерства, Педагогический колледж Колумбийского университета.
«Я настоятельно рекомендую Ким Маршалл и Дженн Дэвид-Ланг« Лучшее из записки Маршалла », потрясающее и хорошо организованное собрание резюме статей и предложений по профессиональному развитию.Я извлек большую пользу из меморандума Маршалла на протяжении многих лет — в то время как в PK-12, а теперь в качестве профессора, — а в последнее время я получил дальнейшее признание, изучая памятку как ключевой ресурс, мост, который может охватить и соединить тоже — часто несовместимые миры исследований и практики. Маршалл и Дэвид-Лэнг, уделяя пристальное внимание идеям и методам, которые могут улучшить преподавание и обучение, оказывают педагогам огромную услугу ».
— Джоэл Малин, доцент, Департамент лидерства в образовании, Университет Майами / Оксфорд, Огайо.
«Для руководителей, которые улыбаются каждый раз, когда они видят памятку Маршалла или основную идею в своем почтовом ящике, эта книга станет настоящим сокровищем! Дженн Дэвид-Лэнг и Ким Маршалл демонстрируют свою взаимную приверженность лидерам как учащимся, предоставляя богатые ресурсы, извлеченные из тысячи статей, найденных в памятке.Дженн Дэвид-Лэнг предлагает содержательные, продуманные идеи для профессионального обучения, связанные с каждой главой, позволяя руководителям передавать и применять концепции к своим собственным уникальным потребностям. Памятка «Лучшее из памятки Маршалла» послужит мощным катализатором профессионального роста и предоставит лидерам позитивные, творческие идеи, которые так необходимы в наших школах сегодня ».
— Дебби Макфалоун, писатель, консультант по лидерству в образовании.
«Памятка Маршалла уже много лет играет незаменимую роль, помогая педагогам и руководителям школ получить доступ к передовым исследованиям, которые могут быть полезны для их работы.В этом новом томе Маршалл и Дэвид-Лэнг разработали ресурс, позволяющий преподавателям и руководителям школ полностью и глубоко погрузиться в исследования по набору тем и тем, имеющих решающее значение для их успеха. Эта книга обещает стать бесценным пособием для мощного профессионального развития и обучения ».
— Скотт Зайдер, адъюнкт-профессор, Бостонский колледж — Школа образования и человеческого развития Линча.
«Откройте для себя практические идеи, которые помогут улучшить преподавание, углубить обучение и укрепить лидерство.Этот первый в истории сборник лучших из памяток Маршалла и основной идеи является обязательным для занятых преподавателей, которым нужны эффективные идеи, стратегии и методы, которые они могут использовать для улучшения своей практики и улучшения результатов учащихся ».
— Мэри Грасса О’Нил, старший преподаватель образования; Директор факультета Управления школами Гарвардской высшей школы образования
«Эта уникальная книга представляет ключевые идеи из учебной литературы через призму двух преподавателей на протяжении всей жизни. Маршалл и Дэвид-Лэнг умело переплетают резюме ведущих исследований в области образования с тематическими исследованиями и рассказами практиков о том, что на самом деле означает осуществление изменений в сфере образования. земля.Это, несомненно, станет новым мощным ресурсом для участия в научно обоснованных беседах о том, как улучшить руководство и обучение в школах нашей страны ».
— Мэтью А. Крафт, адъюнкт-профессор образования и экономики Брауновского университета.
«Лучшее из памятки Маршалла» — это инструмент, который необходимо всегда держать под рукой. Эта книга содержит информацию о том, что вам нужно знать, чтобы эффективно вести; в ней также есть то, что вам нужно сделать, чтобы быть эффективным и действенным. Ким и Дженн курируют ресурсы, выясняя, что, почему и как лидеры преодолевают разрыв между знанием и делом и положительно влияют на обучение студентов.«Что» с текущими исследовательскими статьями по различным областям; «почему» — с рефлексивными вопросами для руководителей, чтобы связать информацию и изучить последствия для своей практики; и «как» в форме подробного плана PD для применения знаний по каждой теме ».
— Хоа Ту, заместитель суперинтенданта средней школы Бруклин-Норт / Бруклин, штат Нью-Йорк.
«Эта удивительная книга напоминает мне о моем любимом детском заведении: Mary’s Candy Store. Наполненный эклектичным сочетанием дразнящих угощений, дайджест Маршалла и Дэвида-Лэнга просто неотразим.”
— Джером Т. Мерфи, заслуженный декан Гарвардской высшей школы образования.
ЦЕНА:
Бесплатная доставка Amazon означает лучшую цену для небольших заказов. Для массовых заказов лучше заказать напрямую у издателя. Вот цены за копию плюс стоимость доставки:5-49 экземпляров — 21,71 доллара
50-99 экземпляров — 21,31 $
100-249 экземпляров — 20,92 доллара
250-499 экземпляров — 19,33 доллара
500+ — 17,75 $
Чтобы сделать заказ, просто отправьте письмо Колину Рольфу по адресу [электронная почта защищена].