Номер (задание) 206 — гдз по математике 6 класс Виленкин, Жохов, Чесноков
Условие / глава 1. / § 1 / тема 7 / 206
206. Решите уравнение: а) (х + 36,1) * 5,1 — 245,82; б) (m — 0,67) * 0,02 = 0,0152; в) (х + 24,3) : 18,3 = 3,1; г) (у — 15,7) : 19,2 = 4,7.
Решебник №1 / глава 1. / § 1 / тема 7 / 206

 / § 1 / тема 7 / 206
/ § 1 / тема 7 / 206Страница 33 №206-210 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 206. Решите уравнение:
а) (х + 36,1) * 5,1 = 245,82;
б) (m − 0,67) * 0,02 = 0,0152;
г) (у − 15,7) : 19,2 = 4,7.
Решение
а) (x + 36,1) * 5,1 = 245,82
x + 36,1 = 245,82 : 5,1
x + 36,1 = 48,2
x = 48,2 − 36,1 = 12,1б) (m − 0,67) * 0,02 = 0,0152
m − 0,67 = 0,0152 : 0,02
m − 0,67 = 0,76
m = 0,76 + 0,67 = 1,43в) (x + 24,3) : 18,3 = 3,1
x + 24,3 = 3,1 * 18,3
x + 24,3 = 56,73
x = 56,73 − 24,3 = 32,43г) (у − 15,7) : 19,2 = 4,7
у − 15,7 = 4,7 * 19,2
у − 15,7 = 105,94
y = 105,94 + 15,7 = 121,64
Задание № 207. Запишите в виде дроби частные:
Запишите в виде дроби частные:
27 : 8;
483 : 18;
1225 : 12 и выделите из них целые части.
Решение
Задание № 208. Найдите среднее арифметическое чисел: 5,24; 6,97; 8,56; 7,32 и 6,23.
Решение
(5,24 + 6,97 + 8,56 + 7,32 + 6,23) : 5 = 34,32 : 5 = 6,864.
Задача № 209. Поезд шёл 3 ч со скоростью 65,2 км/ч и 2 ч со скоростью 83,3 км/ч. Найдите среднюю скорость поезда за эти 5 ч.
Дано:
t1 = 3ч
v1 = 65,2 км/ч
t2 = 2 ч
v2 = 83,3 км/ч
vср = ? км/чРешение
vср = Sвсе : tвсе
vср = (v1 * t1 + v2 * t2) : (t1 + t2)
vср = (65,2 * 3 + 83,3 * 2) : (3 + 2)
vср = (195,6 + 166,6) : 5
vср = 362,2 : 5vср = 72,44 км/ч.
Ответ: vср = 72,44 км/ч.
Задание № 210. Найдите значение выражения:
а) 51 − (3,75 : 3 + 86,45 : 24,7) * 2,4;
б) (650 000 : 3125 − 196,5) * 3,14.
Решение
а) 51 − (3,75 : 3 + 86,45 : 24,7) * 2,4 = 51 − (1,25 = 3,5) * 2,4 = 51 − (1,25 = 3,5) * 2,4 = 51 − 11,4 = 39,64
б) (650 000 : 3125 − 196,5) • 3,14 = (208 − 196,5) • 3,14 = 36,11
ГДЗ: Математика 6 класс Виленкин, Жохов
Математика 6 класс
Тип: Учебник
Авторы: Виленкин, Жохов
Издательство: Мнемозина
ГДЗ: МАТЕМАТИКА 6 КЛАСС ВИЛЕНКИН, ЖОХОВ — УЧЕБНИК
Математика один из основных школьных предметов, изучаемый начиная с первого класса. С каждым годом обучения объем материала для изучения растет и усложняется. Ритм современной жизни учит нас постоянно быть в тонусе, однако детям к этому еще сложно привыкнуть. Поэтому так важно следить за школьником и помогать ему справляться с поставленными в школе задачами.
ОСОБЕННОСТИ ОБУЧЕНИЯ В 6 КЛАССЕ
В 6 классе, согласно стандарту общего образования, на уроках математики начинают изучать основы алгебры и геометрии.
- Скорость изучения материала.
- Недостаточность практических заданий.
- Невнимательность учащихся.
Однако некоторые школьники надеются, что еще успеют наверстать упущенное и разобраться в тонкостях нового предмета. И тогда, пробелы в знании могут негативно отразиться не только на оценках по математике, но и на успеваемости по другим предметам, при проведении необходимых вычислений. Для этих целей как раз и пригодится
ЧТО ВКЛЮЧЕНО В РЕШЕБНИК
В решебнике к пособию «Математика 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд Мнемозина» представлены все темы, изучение которых предусмотрено программой для 6 класса по предмету математика. Сборник поделен на главы, номера заданий соответствуют вышеназванному учебнику.-reshenie-206.jpg)
ЗАЧЕМ НУЖЕН РЕШЕБНИК
Книга полезна многим:
- Учащимся средней школы.
- Родителям.
- Учителям.
- Репетиторам.
Точность, доступность ответов и решений в «ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд Мнемозина» поможет школьникам лучше усвоить материал. При решении сложных примеров или не стандартных задач можно сравнить этапы их решения, последовательность и ответ. Подробно рассмотренные задачи в ГДЗ помогут устранить пробелы по теме. Изучить данный предмет более углубленно самостоятельно. Для родителей ГДЗ это способ сэкономить время на проверке задания, чтобы потом провести его с семьей. Для современного общества свойственна ценность каждой минуты проведенной в кругу семьи, а не за работой. И наконец для учителей данный решебник это источник дополнительных заданий при планировании уроков, а также готовые проверочные работы, для определения уровня знаний учеников.
Алгебры Клиффорда и их приложения в математической физике
Об этой книге
Введение
Уильям Кингдон Клиффорд опубликовал статью с определением его «геометрических алгебр» в 1878 году, за год до своей смерти. Алгебра Клиффорда — это обобщение на n-мерное пространство кватернионов, которое Гамильтон использовал для представления скаляров и векторов в реальном трехмерном пространстве: это также развитие алгебры Грассмана, включающее в фундаментальные отношения скалярные произведения, определенные в терминах метрики космос.Странно, что векторные методы Гиббса Хевисайда стали доминировать в научной и технической литературе, в то время как кватернионы и алгебры Клиффорда, истинные ассоциативные алгебры пространств со скалярными произведениями, почти столетие рассматривались просто как интересные математические курьезы.
Ключевые слова
алгебра исчисление дифференциальное уравнение калибровочная теория математическая физика минимум
Редакторы и филиалы
- 1. Математический институт Кентский университет Кентербери, КентUK
Библиографическая информация
- DOI https: // doi.org / 10.1007 / 978-94-009-4728-3
- Информация об авторских правах Springer Science + Business Media B.V.1986 г.
- Имя издателя Спрингер, Дордрехт
- электронные книги Архив книг Springer
- Печатать ISBN 978-94-010-8602-8
- Интернет ISBN 978-94-009-4728-3
- Серия Печать ISSN 1389-2185
- Купить эту книгу на сайте издателя
Дата | Класс Виды деятельности | Домашнее задание (только нечетные задачи) |
1/20 | Введение (программа) Секция 1. | п. 10: 1-37, 47-57 |
1/25 | Викторина № 1 Разделы 1.2 и 1,3 | п. 17: 1-43, 51 п. 28: 1-29 |
1/27 | Викторина № 2 Раздел 2.1 | с. 43: 1-41 |
2/1 | ||
2/3 | Викторина № 3 Обзор интегралов и раздел 2.2 | Рабочий лист обзора (решения) с. 51: 1-49, 55 |
2/8 | Экзамен №1 (охватывает 1.1 2.2) | |
2/10 | Раздел 2. | с. 61: 1-41, 53 |
15/2 | День без президентов классов | |
2/17 | Викторина № 4 Раздел 2.4 | с. 69: 1-39 |
2/22 | Тест № 5 Разделы 2.5 и 2.6 | с. 74: 1-29, 37 с. 79: 1-3 |
2/24 | Викторина № 6 Раздел 3.1 | с. 90: 1-35, 39-43 |
2/29 | Экзамен №2 (охватывает 2.3 3.1) | |
3/2 | Раздел 4.1 | с. 127: 1-35 |
3/7 | Викторина № 7 Раздел 4. | с. 131: 1-21 (сделать 13 без формулы) |
3/9 | Викторина № 8 Раздел 4.3 | с. 137: 1-61 |
3/14 | Викторина № 9 Раздел 4.4 | с. 147: 1-45 |
3/16 | Викторина № 10 Раздел 4.6 | с. 161: 1-25 |
3/21 | Без класса — Весенние каникулы | |
23/23 | Без класса — Весенние каникулы | |
28/3 | Викторина № 11 Раздел 4.7 | с. 168: 1-45 |
3/30 | Экзамен №3 (охватывает 4. | |
4/4 | Раздел 5.1 | с. 205: 1-37 |
4/6 | Викторина № 12 Раздел 6.1 | с.237: 1-33 |
4/11 | Викторина № 13 Раздел 6.2 | с. 246: 1-25 |
4/13 | Викторина № 14 Раздел 6.3 | с. 255: 1-33 |
4/18 | Экзамен №4 (охватывает 5.1 6.3) | |
4/20 | Раздел 7.1 | с. 280: 1-41 |
4/25 | Викторина № 15 Раздел 7. | п. 288: 1-41 |
4/27 | Викторина № 16 Матрицы | п. APP-18: 1-29, 47-55 |
5/2 | Викторина № 17 Раздел 8.1 | с. 332: 1-25 |
5/4 | Тест № 18 Разделы 8.2.1 и 8.2.2 | с. 346: 1-31 |
5/9 | Викторина № 19 Разделы 8.2.3 и 8.3 | с. 347: 33-45 с. 354: 1-33 |
5/11 | Экзамен №5 (охватывает 7.1 8,3) | |
5/16 | Обзор финала | |
5/18 | Нет класса | |
5/23 | Заключительный экзамен |
Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей (Технический отчет)
Холм, Д. Д. Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей . США: Н. П., 1976.
Интернет. DOI: 10,2172 / 7348957.
Д. Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей . США: Н. П., 1976.
Интернет. DOI: 10,2172 / 7348957.
Холм Д. Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей . Соединенные Штаты. https://doi.org/10.2172/7348957
Холм, Д. Д.Чт.
«Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей». Соединенные Штаты. https://doi.org/10.2172/7348957. https://www.osti.gov/servlets/purl/7348957.
@article {osti_7348957,
title = {Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей},
author = {Holm, D D},
abstractNote = {Физика жидкостей основана на определенных принципах кинематической инвариантности, которые относятся к системам координат, размерам и системе отсчета Галилея. Другие, термодинамические, принципы симметрии вводятся в описании материала. В настоящей работе взаимодействие между этими двумя типами принципов инвариантности используется для решения классов одномерных нестационарных изэнтропических движений жидкости, уравнение состояния которой относится к типу Ми-Грюнайзена. Также на уровне приближения Бюргерса изучается изменение профиля и затухание слабых ударных волн в диссипативной среде с точки зрения лежащей в основе структуры симметрии.Математический метод подхода основан на теории бесконечно малых групп Ли. Движения жидкости охарактеризованы в соответствии с неэквивалентными подгруппами группы полной инвариантности описания течения и представлены точные групповые приводимые решения.},
Другие, термодинамические, принципы симметрии вводятся в описании материала. В настоящей работе взаимодействие между этими двумя типами принципов инвариантности используется для решения классов одномерных нестационарных изэнтропических движений жидкости, уравнение состояния которой относится к типу Ми-Грюнайзена. Также на уровне приближения Бюргерса изучается изменение профиля и затухание слабых ударных волн в диссипативной среде с точки зрения лежащей в основе структуры симметрии.Математический метод подхода основан на теории бесконечно малых групп Ли. Движения жидкости охарактеризованы в соответствии с неэквивалентными подгруппами группы полной инвариантности описания течения и представлены точные групповые приводимые решения.},
doi = {10.2172 / 7348957},
url = {https://www.osti.gov/biblio/7348957},
journal = {},
number =,
объем =,
place = {United States},
год = {1976},
месяц = {7}
}
Записок по математическому образованию в Ленинграде (С. Санкт-Петербург)
Санкт-Петербург)
Примечания к геометрии в Project Maths
Вам необходимо изучить следующие области: Project Maths Geometry Notes (i) Геометрические термины: (ii) Теоремы: (iii) Конструкции: (iv) Расширения: Аксиома, теорема, доказательство, следствие, обратное, подразумевает Экзамен
ПодробнееПланы предварительных уроков в колледже
4-8 января 11-15 января 18-22 января 25-29 января Секции 9.2 Площадь треугольника Раздел смешанных триггерных упражнений 14.1 Раздел сложения матриц и скалярного умножения 14.5 Переход Стр. 342: 1, 3, 7-13,
ПодробнееМАТЕМАТИКА НА ШАХМАТНОЙ ДОСКЕ
МАТЕМАТИКА НА ШАХМАТНОЙ ДОСКЕ Задача 1. Рассмотрим шахматную доску 8 8 и удалите два диаметрально противоположных угловых единичных квадрата. Можно ли покрыть (без нахлеста) оставшиеся 62 квадрата
Рассмотрим шахматную доску 8 8 и удалите два диаметрально противоположных угловых единичных квадрата. Можно ли покрыть (без нахлеста) оставшиеся 62 квадрата
ФИНАЛЬНАЯ ФОРМА ВТОРОЙ ФОРМЫ GENIUS-CUP
МАТЕМАТИКА — АЛГЕБРА 1.Пусть p, q, r — натуральные числа и p + 1 = 26 q + 1 21 r, что из следующего равно p.q.r? A) 18 B) 20 C) 22 D) 24 3. Каково значение 4 (-1 + 2-3 + 4-5 + 6-7 + +1000)? А)
ПодробнееНеделя 1. 1 Что такое комбинаторика?
1 Что такое комбинаторика? Неделя 1 Вопрос о том, что такое комбинаторика, аналогичен вопросу о том, что такое математика. Если мы говорим, что математика — это изучение чисел и фигур, то комбинаторика
ПодробнееРешения задач для класса R5
Международная математическая олимпиада «Формула единства» / Год третьего тысячелетия 016/017. Раунд Решения задач для класса R5 1. Пол рисует точки на листе квадратной бумаги на перекрестках
Раунд Решения задач для класса R5 1. Пол рисует точки на листе квадратной бумаги на перекрестках
2. Девять точек распределяются по кругу таким образом, что когда все ()
1. Сколько кругов на плоскости содержат хотя бы три точки (0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2) , (2, 0), (2, 1), (2, 2)? Решение: имеется () 9 3 = 8 трехэлементных подмножеств, всего
ПодробнееГлава 4 Теория чисел
Глава 4 Теория чисел На протяжении всего изучения чисел учащиеся Á должны определять классы чисел и изучать их свойства.Например, целые числа, которые делятся на 2, называются четными числами
. ПодробнееПриветственный буклет. Версия 5
Приветственный буклет версии 5 Посетите Центр обучения Найдите все ресурсы, необходимые для изучения и использования Sketchpad, видеоролики, руководства, советы, примеры действий и ссылки на онлайн-ресурсы, службы,
ПодробнееМатематика, 8 класс
Сессия 1, вопросы с несколькими вариантами ответов 44084 C 1 13608 C 2 (0. 5) (0,5) (0,5) равно чему из следующего? A. 0,000125 B. 0,00125 C. 0,125 D. 1,25 Категория отчетов для элемента 1: определение числа и операции
5) (0,5) (0,5) равно чему из следующего? A. 0,000125 B. 0,00125 C. 0,125 D. 1,25 Категория отчетов для элемента 1: определение числа и операции
Словарь по геометрии
Словарь по геометрии Единицы 2–4 Стр. 1 Глава 2 Общие характеристики точек геометрии: Характеристики линий: Характеристики плоскости: СВЯЗАННЫЕ ПОСТУЛАТЫ: Через любые две точки существует ровно одна
ПодробнееРаскраска шахматная доска.Томас Хаксли
Раскраска шахматной доски Шахматная доска — это мир, фигуры — явления вселенной, правила игры — это то, что мы называем законами природы. Игрок на другой стороне скрыт от нас.
ПодробнееВ 2 3 = 4 В 2 = 7 В = 14
Бриджит купила в продуктовом магазине пакет яблок. Она отдала Энн половину яблок. Затем она дала Кэсси 3 яблока, оставив себе 4 яблока. Сколько яблок купила Бриджит? (А) 3 (Б) 4 (В) 7
Сколько яблок купила Бриджит? (А) 3 (Б) 4 (В) 7
Проблемы с подсчетом
Проблемы со счетом Проблемы со счетом обычно встречаются где-то в любом курсе математики. Такие проблемы обычно легко сформулировать и даже начать, но насколько далеко они могут зайти, будет варьироваться
ПодробнееДепартамент образования Джорджии
Четвертый класс 4.NOP.1 Умножение и деление; Найдите пары факторов для данного целого числа, меньшего или равного 100; распознавать простые числа как числа больше 1 ровно с одной парой факторов.
ПодробнееСеминар MUMS 24 октября 2008 г.
Семинар MUMS 24 октября 2008 г. Плитка использовалась в искусстве и архитектуре с незапамятных времен. Малыши решают проблемы с укладкой плитки, когда они убирают свои деревянные бруски и средства для ремонта дома
ПодробнееТЕОРИЯ ЧИСЛ AMIN WITNO
ТЕОРИЯ ЧИСЛ АМИН ВИТНО. . ш ш ш w i t n o. c o m Контуры теории чисел и наборы задач Амин Витно Предисловие Эти заметки — просто наброски к курсу Math 313, читаемому в Philadelphia
. ш ш ш w i t n o. c o m Контуры теории чисел и наборы задач Амин Витно Предисловие Эти заметки — просто наброски к курсу Math 313, читаемому в Philadelphia
Размышления о проблеме N + k Куинса
Integre Technical Publishing Co., Inc., College Mathematics Journal 40: 3, 12 марта 2009 г., 14:02 chatham.tex page 204 Размышления о проблеме N + k Куинса Р. Дуглас Чатем Р. Дуглас Чатем (ум[email protected])
ПодробнееАлгебра 1 Онлайн:
Уважаемые студенты, изучающие алгебру 2, В этом пакете вы найдете математические концепции и навыки, полученные в алгебре 1, которые являются фундаментом, на котором построена алгебра 2. Эти концепции необходимо пересмотреть
ПодробнееКритерий Коши
Критерий Коши MATH 464/506, Реальный анализ Дж. Роберт Бьюкенен Департамент математики Лето 2007 г. Определение последовательностей Коши Последовательность X = (x n) действительных чисел является последовательностью Коши, если она удовлетворяет условию
Роберт Бьюкенен Департамент математики Лето 2007 г. Определение последовательностей Коши Последовательность X = (x n) действительных чисел является последовательностью Коши, если она удовлетворяет условию
Конкурс канадских кенгуру по математике
Часть конкурса канадских кенгуру по математике: каждый правильный ответ дает 3 очка 1. Сумма возрастов Тома и Джона составляет 23 года, сумма возрастов Джона и Лекса равна 24, а сумма возрастов Тома и Лекса
ПодробнееЛетний математический пакет с отличием по геометрии
Летний математический пакет с отличием по геометрии Уважаемые ученики! Задачи этого пакета дадут вам возможность попрактиковаться в геометрических навыках с 6-го по 7-й класс.Сделайте все возможное, чтобы выполнить каждую задачу, чтобы
ПодробнееРЕШЕНИЯ ДЛЯ КОМПЛЕКТА ПРОБЛЕМ 4
РЕШЕНИЯ ДЛЯ НАБОРА ПРОБЛЕМ 4 A. Определенное целое число a дает остаток 1 при делении на 2. Что вы можете сказать об остатке, который дает a при делении на 8? РЕШЕНИЕ. Пусть r будет остатком от
Определенное целое число a дает остаток 1 при делении на 2. Что вы можете сказать об остатке, который дает a при делении на 8? РЕШЕНИЕ. Пусть r будет остатком от
12. 6 анекдотов минимальны.
Принцип голубятни Принцип голубятни: когда вы объединяете n вещей в k категорий, в одной из категорий содержится как минимум n / k вещей.Доказательство: если в каждой категории меньше n / k вещей, то
ПодробнееПодготовка к соревнованиям по математике II
WWW.CEMC.UWATERLOO.CA ЦЕНТР ОБРАЗОВАНИЯ ПО МАТЕМАТИКЕ и ВЫЧИСЛИТЕЛЬНОЙ математике Подготовка к соревнованиям II Промежуточные кружки по математике Факультет математики Университет Ватерлоо Дж. П. Претти Среда, 16
ПодробнееПриложения и взаимосвязь с другими разделами математики и физики
400 АЛГЕБР ЛИ И АЛГЕБР ХОПФА
[534] М. Л. Назаров, Янгианы «странных» супералгебр Ли, в изд. П. П. Кулиш, Квантовые группы
Л. Назаров, Янгианы «странных» супералгебр Ли, в изд. П. П. Кулиш, Квантовые группы
, Springer, 1992, 90–97.
[535] Максим Назаров и Виталий Тарасов, Базы Янгиана и Гельфанда-Цетлина, Опубл. RIMS Kyoto
30 (1994), 459–478.
[536] Максим Л. Назаров, Тождества Капелли для супералгебр Ли, 1996; arXiv: 9610032.
[537] Максим Л. Назаров, Янгианы и Тождества Капелли, 1996; arXiv: q-alg / 9601102v2.
[538] М. Нойхль и П.Шауэнбург, Реконструкция в плетеных категориях и понятие мутационной биалгебры com-
, J. of pure and appl. Алгебра 124 (1998), 241–260.
[539] Уоррен Д. Николс, Биалгебры первого типа, Comm. Алгебра 6 (1978), 1521–1552.
[540] Уоррен Николс и Мосс Свидлер, Алгебры Хопфа и комбинаторика, в издании Р. Морриса,
Исчисление умбра и алгебры Хопфа, Amer. математика. Soc., 1982, 49–84.
[541] Эмми Нётер, Проблема инвариантных вариаций, Nachr.K¨onig.Ges.Wiss.Gottingen (1918),
235–257.
[542] Масатоши Нуми, Тору Умеда и Масато Вакаяма, Квантовая двойная пара (sl2, o
n) и
ассоциированная идентичность Капелли, Lett. по математике. Физика 34 (1995), 1–7.
по математике. Физика 34 (1995), 1–7.
[543] Масатоши Нуми, Тору Омеда и Масато Вакаяма, Двойные пары, сферические гармоники
и тождество Капелли в квантовой теории групп, Compositio mathematicae 104 (1996),
227–277.
[544] Абдукадир Обул, Минимальная порождающая система алгебр Рингеля-Холла аффиннозначных квив-
ers, J.Алгебры 297 (2006), 311–332.
[545] Абдукадир Обул и Гуанлиан Чжан, PBW-основы скрученной родовой композиции al-
gebras однозначных колчанов, J.ofAlgebra 297 (2006), 333–360.
[546] Абдукадир Обул, Обобщенные наклоняющие функторы и алгебры Рингеля-Холла, Журнал чистых и прикладных наук.
Алгебра 208 (2007), 445–488.
[547] Адриан Окнеану, Квантованные группы, струнные алгебры и теория Галуа для алгебр, в: D.
Э. Эванс и М. Такесаки, ред., Операторные алгебры и приложения, Том 2, Кембридж
Univ. Press, 1988, 119–172.
[548] Адриан Окнеану, Пути на диаграммах Кокстера: от Платоновых тел и сингулярностей к
минимальным моделям и субфакторам, в: R. Bhata a.o., ред., Лекции по теории операторов, Amer.
Bhata a.o., ред., Лекции по теории операторов, Amer.
математ. Soc., 2000.
[549] О. Огиевецкий, Б. Зумино, Реальность в дифференциальном исчислении на q-евклидовых пространствах,
Lett. по математике. Физика 25 (1992), 121–130.
[550] О.Огиевецкий, А. Валас, Связь между двумя типами характеристических уравнений
для квантовых матриц, Lett. по математике. Физика 65 (2003), 49–57.
[551] Андрей Окуньков, Базис Юнга, формула Вика и высшие тождества Капелли, 1996;
arXiv: q-alg / 9602027v2.
[552] Андрей Окуньков, Квантовые имманенты и высшие тождества Капелли, Преобразование
Группы 1 (1996), 99–126.
[553] Г. И. Ольшанский, Янгианы и универсальные обертывающие алгебры, Зап.Научн. Сем. ЛОМИ
164 (1987), 142–150.
[554] Г. И. Ольшанский, Скрученные янгианы и бесконечные классические размерные алгебры Ли, в: П. П.
Кулиш, ред. Квантовые группы, Springer, 1992, 104–119.
[555] Арупкумар Пал, Индуцированные представления и взаимность Фробениуса для компактных квантовых групп
, Proc. Индийский акад. Sci. (математические науки) 102 (1995), 157–167.
Индийский акад. Sci. (математические науки) 102 (1995), 157–167.
[556] Флорин Панайте, Связь алгебр Конна-Креймера и Гроссмана-Ларсона-Хопфа, построенных на
корневых деревьях, Lett.по математике. Физика 51 (2000), 211–219.
[557] Т. С. Папатеодору, М. Дж. Абловиц, Ю. Г. Саридакис, Правило для быстрых вычислений и
анализа в клеточных автоматах, Stud. в Прил. Математика. 79 (1988), 173–184.
[558] Бодо Парейгис, Некоммутативная некокоммутативная алгебра Хопфа в «природе», J.ofAl-
gebra 70 (1981), 356–374.
[559] Бодо Парейгис, Формы алгебр Хопфа и теория Галуа, Вопросы алгебры, часть 1: кольца
и представления, PWN, 1990, 75–93.
[560] Бодо Парейгис, Vorlesungen ¨uber Quantengruppen und nichtkommutative Geometrie, Uni-
versity of Müunchen, 1993.
[561] Бодо Парейгис, Реконструкция скрытых симметрий, 183 (1996) J.ofAl. –154.
[562] Брайан Паршалл и Цзян-Пан Ван, Квантовые линейные группы, Американская математика. Soc., 1991.
Soc., 1991.
[563] Марио Пашке и Анджей Ситарц, Дискретные спектральные тройки и их симметрии, J.of
math. Phys. 39 (1998), 6191–6205.
Лицензия предоставлена AMS.
К распространению могут применяться лицензии или ограничения авторских прав; см. http://www.ams.org/publications/ebooks/terms
% PDF-1.6
%
1668 0 объект
>
endobj
xref
1668 332
0000000016 00000 н.
0000010262 00000 п.
0000010571 00000 п.
0000010617 00000 п.
0000010750 00000 п.
0000010785 00000 п.
0000010876 00000 п.
0000012007 00000 п.
0000012046 00000 п.
0000012222 00000 п.
0000012393 00000 п.
0000012508 00000 п.
0000013277 00000 п.
0000014061 00000 п.
0000014839 00000 п.
0000015563 00000 п.
0000016272 00000 п.
0000017010 00000 п.
0000017374 00000 п.
0000017743 00000 п.
0000017975 00000 п.
0000018201 00000 п.
0000018915 00000 п.
0000019675 00000 п.
0000022326 00000 п.
0000022387 00000 п.
0000022464 00000 п.
0000022558 00000 п.
0000022604 00000 п. 0000022703 00000 п.
0000022749 00000 п.
0000022898 00000 п.
0000023035 00000 п.
0000023081 00000 п.
0000023250 00000 п.
0000023425 00000 п.
0000023471 00000 п.
0000023606 00000 п.
0000023746 00000 п.
0000023894 00000 п.
0000023939 00000 п.
0000024091 00000 п.
0000024242 00000 п.
0000024397 00000 п.
0000024442 00000 п.
0000024614 00000 п.
0000024759 00000 п.
0000024896 00000 п.
0000024941 00000 п.
0000025074 00000 п.
0000025212 00000 п.
0000025377 00000 п.
0000025422 00000 п.
0000025557 00000 п.
0000025658 00000 п.
0000025702 00000 п.
0000025813 00000 п.
0000025857 00000 п.
0000025970 00000 п.
0000026014 00000 п.
0000026117 00000 п.
0000026160 00000 п.
0000026306 00000 п.
0000026351 00000 п.
0000026439 00000 п.
0000026469 00000 п.
0000026514 00000 п.
0000026610 00000 п.
0000026655 00000 п.
0000026810 00000 п.
0000026855 00000 п.
0000026900 00000 п.
0000027009 00000 н.
0000027054 00000 п.
0000027143 00000 п.
0000027173 00000 п.
0000027218 00000 п.
0000022703 00000 п.
0000022749 00000 п.
0000022898 00000 п.
0000023035 00000 п.
0000023081 00000 п.
0000023250 00000 п.
0000023425 00000 п.
0000023471 00000 п.
0000023606 00000 п.
0000023746 00000 п.
0000023894 00000 п.
0000023939 00000 п.
0000024091 00000 п.
0000024242 00000 п.
0000024397 00000 п.
0000024442 00000 п.
0000024614 00000 п.
0000024759 00000 п.
0000024896 00000 п.
0000024941 00000 п.
0000025074 00000 п.
0000025212 00000 п.
0000025377 00000 п.
0000025422 00000 п.
0000025557 00000 п.
0000025658 00000 п.
0000025702 00000 п.
0000025813 00000 п.
0000025857 00000 п.
0000025970 00000 п.
0000026014 00000 п.
0000026117 00000 п.
0000026160 00000 п.
0000026306 00000 п.
0000026351 00000 п.
0000026439 00000 п.
0000026469 00000 п.
0000026514 00000 п.
0000026610 00000 п.
0000026655 00000 п.
0000026810 00000 п.
0000026855 00000 п.
0000026900 00000 п.
0000027009 00000 н.
0000027054 00000 п.
0000027143 00000 п.
0000027173 00000 п.
0000027218 00000 п. 0000027314 00000 п.
0000027359 00000 п.
0000027455 00000 п.
0000027500 00000 п.
0000027606 00000 п.
0000027651 00000 п.
0000027787 00000 п.
0000027832 00000 н.
0000028014 00000 п.
0000028059 00000 п.
0000028198 00000 п.
0000028243 00000 п.
0000028362 00000 п.
0000028407 00000 п.
0000028527 00000 п.
0000028572 00000 п.
0000028694 00000 п.
0000028739 00000 п.
0000028914 00000 п.
0000028959 00000 п.
0000029113 00000 п.
0000029158 00000 п.
0000029299 00000 н.
0000029344 00000 п.
0000029389 00000 п.
0000029498 00000 п.
0000029543 00000 п.
0000029631 00000 п.
0000029782 00000 п.
0000029812 00000 п.
0000029945 00000 н.
0000029990 00000 н.
0000030078 00000 п.
0000030108 00000 п.
0000030153 00000 п.
0000030249 00000 п.
0000030294 00000 п.
0000030390 00000 п.
0000030435 00000 п.
0000030599 00000 п.
0000030644 00000 п.
0000030807 00000 п.
0000030852 00000 п.
0000031019 00000 п.
0000031064 00000 п.
0000031230 00000 п.
0000031275 00000 п.
0000031320 00000 н.
0000027314 00000 п.
0000027359 00000 п.
0000027455 00000 п.
0000027500 00000 п.
0000027606 00000 п.
0000027651 00000 п.
0000027787 00000 п.
0000027832 00000 н.
0000028014 00000 п.
0000028059 00000 п.
0000028198 00000 п.
0000028243 00000 п.
0000028362 00000 п.
0000028407 00000 п.
0000028527 00000 п.
0000028572 00000 п.
0000028694 00000 п.
0000028739 00000 п.
0000028914 00000 п.
0000028959 00000 п.
0000029113 00000 п.
0000029158 00000 п.
0000029299 00000 н.
0000029344 00000 п.
0000029389 00000 п.
0000029498 00000 п.
0000029543 00000 п.
0000029631 00000 п.
0000029782 00000 п.
0000029812 00000 п.
0000029945 00000 н.
0000029990 00000 н.
0000030078 00000 п.
0000030108 00000 п.
0000030153 00000 п.
0000030249 00000 п.
0000030294 00000 п.
0000030390 00000 п.
0000030435 00000 п.
0000030599 00000 п.
0000030644 00000 п.
0000030807 00000 п.
0000030852 00000 п.
0000031019 00000 п.
0000031064 00000 п.
0000031230 00000 п.
0000031275 00000 п.
0000031320 00000 н. 0000031365 00000 п.
0000031476 00000 п.
0000031521 00000 п.
0000031653 00000 п.
0000031698 00000 п.
0000031814 00000 п.
0000031859 00000 п.
0000032027 00000 н.
0000032072 00000 п.
0000032336 00000 п.
0000032381 00000 п.
0000032537 00000 п.
0000032582 00000 п.
0000032627 00000 н.
0000032736 00000 п.
0000032781 00000 п.
0000032869 00000 п.
0000032899 00000 п.
0000032944 00000 п.
0000033040 00000 п.
0000033085 00000 п.
0000033181 00000 п.
0000033226 00000 н.
0000033345 00000 п.
0000033390 00000 п.
0000033539 00000 п.
0000033584 00000 п.
0000033730 00000 п.
0000033775 00000 п.
0000033901 00000 п.
0000033946 00000 п.
0000033991 00000 п.
0000034100 00000 п.
0000034145 00000 п.
0000034234 00000 п.
0000034352 00000 п.
0000034382 00000 п.
0000034427 00000 п.
0000034457 00000 п.
0000034502 00000 п.
0000034596 00000 п.
0000034641 00000 п.
0000034737 00000 п.
0000034782 00000 п.
0000034898 00000 п.
0000034943 00000 п.
0000035039 00000 п.
0000035084 00000 п.
0000031365 00000 п.
0000031476 00000 п.
0000031521 00000 п.
0000031653 00000 п.
0000031698 00000 п.
0000031814 00000 п.
0000031859 00000 п.
0000032027 00000 н.
0000032072 00000 п.
0000032336 00000 п.
0000032381 00000 п.
0000032537 00000 п.
0000032582 00000 п.
0000032627 00000 н.
0000032736 00000 п.
0000032781 00000 п.
0000032869 00000 п.
0000032899 00000 п.
0000032944 00000 п.
0000033040 00000 п.
0000033085 00000 п.
0000033181 00000 п.
0000033226 00000 н.
0000033345 00000 п.
0000033390 00000 п.
0000033539 00000 п.
0000033584 00000 п.
0000033730 00000 п.
0000033775 00000 п.
0000033901 00000 п.
0000033946 00000 п.
0000033991 00000 п.
0000034100 00000 п.
0000034145 00000 п.
0000034234 00000 п.
0000034352 00000 п.
0000034382 00000 п.
0000034427 00000 п.
0000034457 00000 п.
0000034502 00000 п.
0000034596 00000 п.
0000034641 00000 п.
0000034737 00000 п.
0000034782 00000 п.
0000034898 00000 п.
0000034943 00000 п.
0000035039 00000 п.
0000035084 00000 п. 0000035243 00000 п.
0000035288 00000 п.
0000035409 00000 п.
0000035454 00000 п.
0000035546 00000 п.
0000035591 00000 п.
0000035636 00000 п.
0000035745 00000 п.
0000035790 00000 н.
0000035879 00000 п.
0000035909 00000 п.
0000035954 00000 п.
0000036050 00000 п.
0000036095 00000 п.
0000036140 00000 п.
0000036234 00000 п.
0000036280 00000 п.
0000036369 00000 п.
0000036517 00000 п.
0000036547 00000 п.
0000036644 00000 п.
0000036690 00000 н.
0000036778 00000 п.
0000036989 00000 п.
0000037019 00000 п.
0000037128 00000 п.
0000037173 00000 п.
0000037262 00000 п.
0000037438 00000 п.
0000037468 00000 п.
0000037610 00000 п.
0000037655 00000 п.
0000037744 00000 п.
0000037774 00000 п.
0000037819 00000 п.
0000037930 00000 п.
0000037975 00000 п.
0000038111 00000 п.
0000038156 00000 п.
0000038269 00000 п.
0000038314 00000 п.
0000038449 00000 п.
0000038494 00000 п.
0000038658 00000 п.
0000038703 00000 п.
0000038748 00000 п.
0000038794 00000 п.
0000038890 00000 н.
0000035243 00000 п.
0000035288 00000 п.
0000035409 00000 п.
0000035454 00000 п.
0000035546 00000 п.
0000035591 00000 п.
0000035636 00000 п.
0000035745 00000 п.
0000035790 00000 н.
0000035879 00000 п.
0000035909 00000 п.
0000035954 00000 п.
0000036050 00000 п.
0000036095 00000 п.
0000036140 00000 п.
0000036234 00000 п.
0000036280 00000 п.
0000036369 00000 п.
0000036517 00000 п.
0000036547 00000 п.
0000036644 00000 п.
0000036690 00000 н.
0000036778 00000 п.
0000036989 00000 п.
0000037019 00000 п.
0000037128 00000 п.
0000037173 00000 п.
0000037262 00000 п.
0000037438 00000 п.
0000037468 00000 п.
0000037610 00000 п.
0000037655 00000 п.
0000037744 00000 п.
0000037774 00000 п.
0000037819 00000 п.
0000037930 00000 п.
0000037975 00000 п.
0000038111 00000 п.
0000038156 00000 п.
0000038269 00000 п.
0000038314 00000 п.
0000038449 00000 п.
0000038494 00000 п.
0000038658 00000 п.
0000038703 00000 п.
0000038748 00000 п.
0000038794 00000 п.
0000038890 00000 н. 0000038935 00000 п.
0000039050 00000 п.
0000039095 00000 н.
0000039211 00000 п.
0000039256 00000 п.
0000039378 00000 п.
0000039423 00000 п.
0000039532 00000 п.
0000039577 00000 п.
0000039688 00000 п.
0000039733 00000 п.
0000039850 00000 п.
0000039895 00000 п.
0000039940 00000 н.
0000039986 00000 п.
0000040082 00000 п.
0000040128 00000 п.
0000040174 00000 п.
0000040220 00000 п.
0000040331 00000 п.
0000040377 00000 п.
0000040478 00000 п.
0000040524 00000 п.
0000040642 00000 п.
0000040688 00000 п.
0000040793 00000 п.
0000040839 00000 п.
0000040952 00000 п.
0000040998 00000 н.
0000041044 00000 п.
0000041153 00000 п.
0000041198 00000 п.
0000041287 00000 п.
0000041317 00000 п.
0000041362 00000 п.
0000041491 00000 п.
0000041536 00000 п.
0000041651 00000 п.
0000041696 00000 п.
0000041846 00000 п.
0000041891 00000 п.
0000041990 00000 п.
0000042035 00000 п.
0000042147 00000 п.
0000042192 00000 п.
0000042237 00000 п.
0000042346 00000 п.
0000042392 00000 п.
0000038935 00000 п.
0000039050 00000 п.
0000039095 00000 н.
0000039211 00000 п.
0000039256 00000 п.
0000039378 00000 п.
0000039423 00000 п.
0000039532 00000 п.
0000039577 00000 п.
0000039688 00000 п.
0000039733 00000 п.
0000039850 00000 п.
0000039895 00000 п.
0000039940 00000 н.
0000039986 00000 п.
0000040082 00000 п.
0000040128 00000 п.
0000040174 00000 п.
0000040220 00000 п.
0000040331 00000 п.
0000040377 00000 п.
0000040478 00000 п.
0000040524 00000 п.
0000040642 00000 п.
0000040688 00000 п.
0000040793 00000 п.
0000040839 00000 п.
0000040952 00000 п.
0000040998 00000 н.
0000041044 00000 п.
0000041153 00000 п.
0000041198 00000 п.
0000041287 00000 п.
0000041317 00000 п.
0000041362 00000 п.
0000041491 00000 п.
0000041536 00000 п.
0000041651 00000 п.
0000041696 00000 п.
0000041846 00000 п.
0000041891 00000 п.
0000041990 00000 п.
0000042035 00000 п.
0000042147 00000 п.
0000042192 00000 п.
0000042237 00000 п.
0000042346 00000 п.
0000042392 00000 п. 0000042480 00000 п.
0000042510 00000 п.
0000042556 00000 п.
0000042648 00000 п.
0000042694 00000 п.
0000042825 00000 п.
0000042871 00000 п.
0000042998 00000 н.
0000043044 00000 п.
0000043140 00000 п.
0000043186 00000 п.
0000043366 00000 п.
0000043412 00000 п.
0000043541 00000 п.
0000043587 00000 п.
0000043679 00000 п.
0000043725 00000 п.
0000043836 00000 п.
0000043882 00000 п.
0000043928 00000 п.
0000044037 00000 п.
0000044083 00000 п.
0000044163 00000 п.
0000044193 00000 п.
0000044242 00000 п.
0000044345 00000 п.
0000044391 00000 п.
0000044487 00000 п.
0000044533 00000 п.
0000044634 00000 п.
0000044680 00000 п.
0000044777 00000 п.
0000044823 00000 п.
0000044944 00000 п.
0000044990 00000 н.
0000045096 00000 п.
0000045142 00000 п.
0000045274 00000 п.
0000045320 00000 п.
0000045440 00000 п.
0000045486 00000 п.
0000045621 00000 п.
0000045667 00000 п.
0000045803 00000 п.
0000045849 00000 п.
0000045952 00000 п.
0000045998 00000 п.
0000046044 00000 п.
0000042480 00000 п.
0000042510 00000 п.
0000042556 00000 п.
0000042648 00000 п.
0000042694 00000 п.
0000042825 00000 п.
0000042871 00000 п.
0000042998 00000 н.
0000043044 00000 п.
0000043140 00000 п.
0000043186 00000 п.
0000043366 00000 п.
0000043412 00000 п.
0000043541 00000 п.
0000043587 00000 п.
0000043679 00000 п.
0000043725 00000 п.
0000043836 00000 п.
0000043882 00000 п.
0000043928 00000 п.
0000044037 00000 п.
0000044083 00000 п.
0000044163 00000 п.
0000044193 00000 п.
0000044242 00000 п.
0000044345 00000 п.
0000044391 00000 п.
0000044487 00000 п.
0000044533 00000 п.
0000044634 00000 п.
0000044680 00000 п.
0000044777 00000 п.
0000044823 00000 п.
0000044944 00000 п.
0000044990 00000 н.
0000045096 00000 п.
0000045142 00000 п.
0000045274 00000 п.
0000045320 00000 п.
0000045440 00000 п.
0000045486 00000 п.
0000045621 00000 п.
0000045667 00000 п.
0000045803 00000 п.
0000045849 00000 п.
0000045952 00000 п.
0000045998 00000 п.
0000046044 00000 п. 0000046153 00000 п.
0000046199 00000 п.
0000046288 00000 п.
0000046318 00000 п.
0000046364 00000 н.
0000046460 00000 п.
0000046506 00000 п.
0000046633 00000 п.
0000046679 00000 п.
0000046776 00000 п.
0000046822 00000 п.
0000046939 00000 п.
0000046985 00000 п.
0000047031 00000 п.
0000006936 00000 н.
трейлер
] >>
startxref
0
%% EOF
1999 0 объект
> поток
xYse s & $ Н4t @ «0I @ B» D
0000046153 00000 п.
0000046199 00000 п.
0000046288 00000 п.
0000046318 00000 п.
0000046364 00000 н.
0000046460 00000 п.
0000046506 00000 п.
0000046633 00000 п.
0000046679 00000 п.
0000046776 00000 п.
0000046822 00000 п.
0000046939 00000 п.
0000046985 00000 п.
0000047031 00000 п.
0000006936 00000 н.
трейлер
] >>
startxref
0
%% EOF
1999 0 объект
> поток
xYse s & $ Н4t @ «0I @ B» D
PDF 2017 — Springer — ISBN: 3319570382 — Космология для любопытных Делия Перлов, Алексей Виленкин # 6739
PDF 2017 — Springer — ISBN: 3319570382 — Космология для любопытных Делия Перлова, Алексей Виленкин # 6739
Английский | PDF | 2017 | 365 страниц | | 14.3 МБ
Эта книга представляет собой вводный текст для всех, кто желает узнать о современных взглядах на космос. Наша Вселенная возникла в результате большого взрыва — большого взрыва. На протяжении почти столетия космологи изучали последствия этого взрыва: как Вселенная расширялась и охлаждалась, и как галактики постепенно собирались под действием силы тяжести.
Природа самой челки стала предметом внимания только относительно недавно. Это предмет теории космической инфляции, которая была разработана в последние несколько десятилетий и привела к радикально новому глобальному взгляду на Вселенную.
Студенты и другие заинтересованные читатели найдут здесь нетехнический, но концептуально строгий отчет о современных космологических идеях, описывающий то, что мы знаем, и то, как мы это знаем. Одна из центральных тем книги — это научный поиск ответов на главные космические вопросы: конечна ли вселенная или бесконечна? Он существовал вечно? Если нет, то когда и как он появился? Это когда-нибудь закончится?
Книга основана на курсе бакалавриата, который преподавал Алекс Виленкин в Университете Тафтса.Он не предполагает никаких предварительных знаний по физике или математике, кроме математики в начальной школе. Необходимый физический фон вводится по мере необходимости. Каждая глава включает в себя список вопросов и упражнений разной степени сложности.
Часть I Большой взрыв и наблюдаемая Вселенная
1 Исторический обзор 3
1.1 Большие космические вопросы 3
1.2 Истоки научной космологии 4
1.3 Космология сегодня 7
2 Вселенная Ньютона 13
2.1 Законы движения Ньютона 13
2,2 Ньютоновская гравитация 16
2.3 Ускорение свободного падения 19
2.4 Круговое движение и планетные орбиты 20
2.5 Сохранение энергии и убегающая скорость 22
2,6 Ньютоновская космология 26
2.7 Парадокс Ольберса 27
3 Специальная теория относительности 31
3.1 Принцип относительности 31
3.2 Скорость света и электромагнетизм 35
3. 3 Постулаты Эйнштейна 39
3 Постулаты Эйнштейна 39
3,4 Одновременность 41
3.5 Замедление времени 42
3,6 Уменьшение длины 44
3.6.1 Ускоряющие мюоны 45
3,7 E = mc2 46
3,8 От пространства и времени к пространству-времени 47
3.9 Причинность в пространстве-времени 51
4 Ткань пространства и времени 59
4.1 Поразительная гипотеза 60
4.2 Геометрия пространства 63
4.2.1 Евклидова геометрия 63
4.2.2 Неевклидова геометрия 66
4.3 Изогнутое пространство 67
4.3.1 Кривизна поверхностей 67
4.3.2 Кривизна трехмерного объекта
Космос 70
4.4 Общая теория относительности 72
4.5 Предсказания и проверки общей теории относительности 75
4.5.1 Отклонение света и гравитация
Лицензирование 75
4.5.2 Гравитационное замедление времени 77
4.5.3 Черные дыры 77
4. 5.4 Гравитационные волны 78
5.4 Гравитационные волны 78
5 Расширяющаяся Вселенная 83
5.1 Статическая Вселенная Эйнштейна 83
5.2 Проблемы со статической Вселенной 86
5.3 Расширяющаяся Вселенная Фридмана 89
6 Наблюдательная космология 97
6.1 Отпечатки стихий 98
6.2 Измерение скорости 99
6.3 Измерение расстояний 101
6.4 Рождение внегалактической астрономии 105
7 Закон Хаббла и расширяющаяся Вселенная 109
7.1 Расширяющаяся Вселенная 110
7.2 Начало Вселенной? 113
7.3 Теория устойчивого состояния 114
7,4 Масштабный коэффициент 115
7,5 Космологическое красное смещение 116
7,6 Возраст Вселенной 117
7,7 Расстояние Хаббла и космический горизонт 118
7,8 Не все расширяется 120
8 Судьба Вселенной 125
8.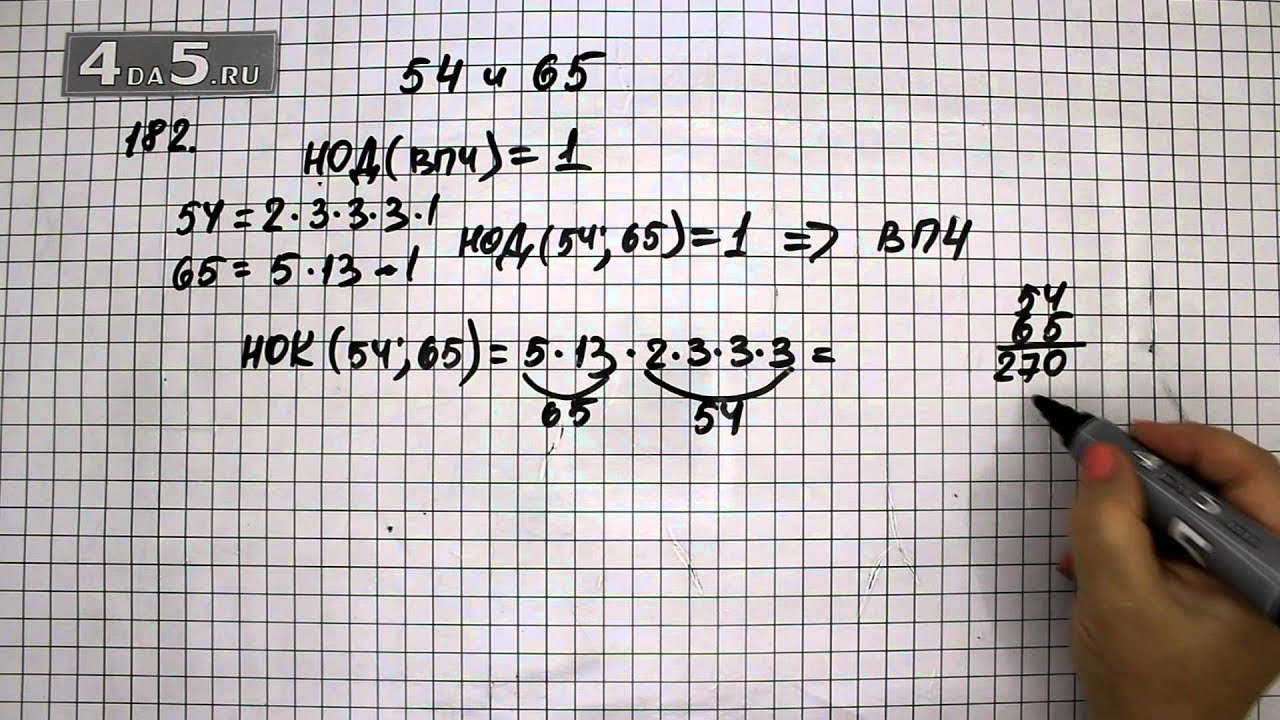 1 Критическая плотность 125
1 Критическая плотность 125
8.2 Параметр плотности 128
9 Темная материя и темная энергия 131
9.1 Средняя массовая плотность Вселенной
и Темная материя 131
9.2 Темная энергия 136
9.3 Судьба Вселенной — снова 140
10 Квантовый мир 143
10.1 Квантовая дискретность 143
10.2 Квантовый индетерминизм 145
10.3 Волновая функция 148
10.4 Интерпретация множества миров 151
11 Большой взрыв 155
11.1 Следуя расширению назад во времени 155
11.2 Тепловое излучение 158
11.3 Модель горячего большого взрыва 161
11.4 Обнаружение первобытного огненного шара 162
11,5 Образы детской вселенной 165
11.6 CMB сегодня и в более ранние эпохи 168
11. 7 Три космических эры 170
7 Три космических эры 170
12 Формирование структуры 175
12,1 Космическая структура 175
12.2 Сборка конструкции 179
12.3 Наблюдение за эволюцией космических структур 180
12.4 Колебания изначальной плотности 182
12,5 Сверхмассивные черные дыры и активные галактики 183
13 Обилие элементов 187
13.1 Почему алхимики не добились успеха 187
13.2 Нуклеосинтез Большого взрыва 189
13,3 Звездный нуклеосинтез 193
13.4 Формирование планетарной системы 194
13,5 Жизнь во Вселенной 196
14 Очень ранняя Вселенная 201
14.1 Физика элементарных частиц и Большой взрыв 201
14.2 Стандартная модель физики элементарных частиц 205
14. 2.1 Частицы 206
2.1 Частицы 206
14.2.2 Силы 206
14.3 Нарушение симметрии 208
14.4 Хронология ранней Вселенной 211
14,5 Физика за пределами стандартной модели 213
14.5.1 Объединение основных сил 213
14,6 Вакуумные дефекты 215
14.6.1 Доменные стены 216
14.6.2 Космические струны 217
14.6.3 Магнитные монополи 220
14,7 Бариогенез 220
Часть II После Большого Взрыва
15 проблем с Большим взрывом 227
15.1 Проблема плоскостности: почему геометрия
Плоской Вселенной? 227
15.2 Проблема горизонта: почему Вселенная
так однороден? 229
15.3 Проблема структуры: каково происхождение
малых колебаний плотности? 232
15.4 Проблема монополей: где они? 232
16 Теория космической инфляции 235
16. 1 Решение проблем плоскостности и горизонта 235
1 Решение проблем плоскостности и горизонта 235
16.2 Космическая инфляция 236
16.2.1 Ложный вакуум 236
16.2.2 Экспоненциальное расширение 238
16.3 Решение проблем Большого взрыва 240
16.3.1 Проблема плоскостности 240
16.3.2 Проблема горизонта 241
16.3.3 Проблема формирования структуры 242
16.3.4 Проблема монополя 242
16.3.5 Расширение и высокая температура
Вселенной 242
16,4 Распад вакуума 243
16.4.1 Кипячение вакуума 243
16.4.2 Задача постепенного выхода 244
16.4.3 Медленная инфляция 245
16.5 Происхождение колебаний малой плотности 247
16,6 Подробнее об инфляции 249
16.6.1 Связь при накачивании
Вселенная 249
16.6.2 Энергосбережение 250
17 Тестирование инфляции: прогнозы и наблюдения 255
17.1 Плоскостность 255
17. 2 Колебания плотности 256
2 Колебания плотности 256
17,3 Гравитационные волны 260
17,4 Открытые вопросы 264
18 Вечная инфляция 269
18.1 Увеличение и уменьшение объема 269
18.2 Случайное блуждание по инфлатонному полю 271
18.3 Вечная инфляция через зарождение пузырьков 274
18,4 Время пространства пузыря 275
18.5 космических клонов 279
18.6 Мультивселенная 281
18.7 Тестирование мультивселенной 284
18.7.1 Столкновения пузырей 284
18.7.2 Черные дыры из Мультивселенной 285
19 Теория струн и мультивселенная 291
19.1 Что такое теория струн? 292
19,2 Дополнительные размеры 294
19,3 Энергетический ландшафт 295
Мультивселенная 19.4 Теория струн 296
19.5 Возвращение к судьбе нашей Вселенной 297
20 Антропный отбор 301
20. 1 Точная настройка природных констант 302
1 Точная настройка природных констант 302
20.1.1 Масса нейтрона 302
20.1.2 Сила слабого взаимодействия 303
20.1.3 Сила тяжести 303
20.1.4 Величина возмущений плотности 303
20.2 Проблема космологической постоянной 304
20.2.1 Динамический квантовый вакуум 304
20.2.2 Настроен на жизнь? 305
20.3 Антропный принцип 307
20.4 Плюсы и минусы антропных объяснений 309
21 Принцип посредственности 313
21,1 Колоколообразная кривая 313
21.2 Принцип посредственности 314
21.3 Получение распределения путем счета
Наблюдатели 315
21.4 Предсказание космологической постоянной 316
21.4.1 Приблизительная оценка 317
21.4.2 Распределение 317
21,5 Задача измерения 319
21.6 Аргумент Судного дня и будущее
нашей цивилизации 321
21.6.1 Большие и малые цивилизации 322
21. 6.2 Лучшее из лучших 323
6.2 Лучшее из лучших 323
22 Было ли у Вселенной начало? 327
22.1 Вселенная, которая существовала всегда? 327
22.2 Теорема BGV 329
22.2.1 Где это нас оставит? 330
22.2.2 Доказательство Бога? 331
23 Создание вселенных из ничего 333
23.1 Вселенная как квантовая флуктуация 333
23.2 Квантовое туннелирование из «ничего» 336
23.2.1 Евклидово время 337
23.3 Мультивселенная квантовой космологии 338
23.4 Значение «ничего» 339
24 Общая картина 343
24.1 Наблюдаемая Вселенная 343
24.1.1 Что мы знаем? 343
24.1.2 Космическая инфляция 344
24.2 Мультивселенная 345
24.2.1 Пузырьковые вселенные 345
24.

 1
1 3
3 2
2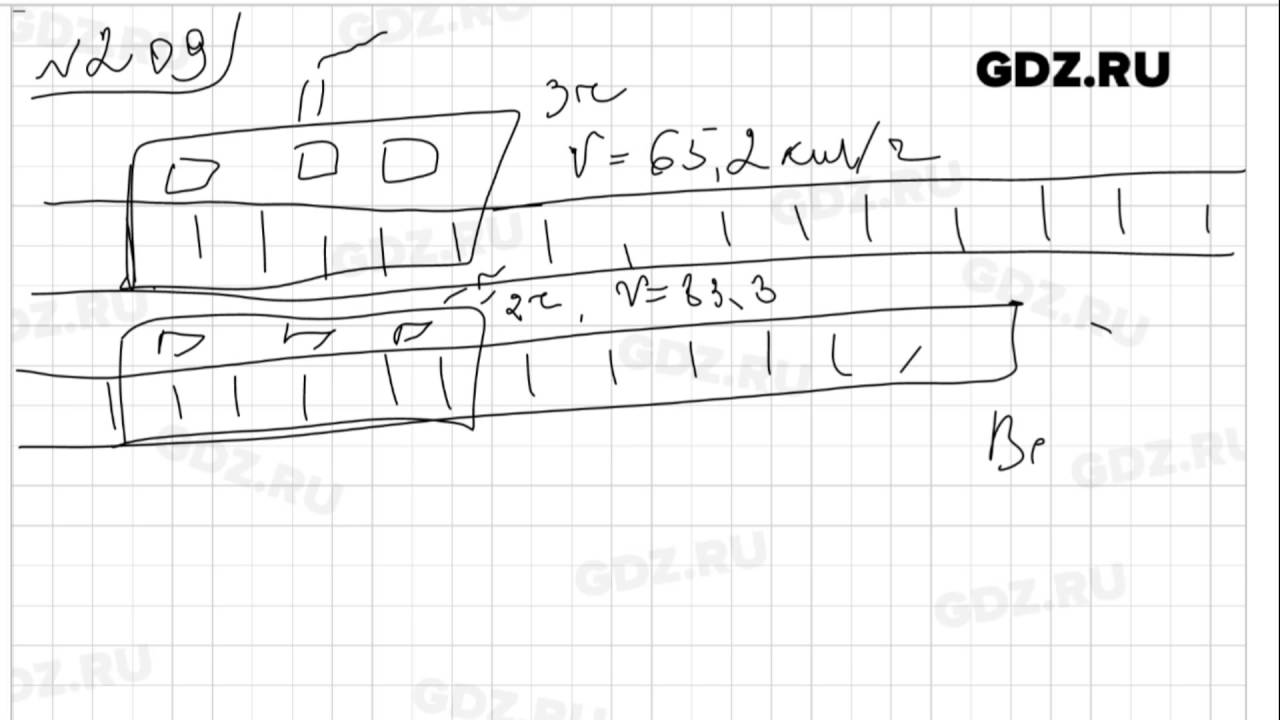 1, 4.7)
1, 4.7) 2
2 Санкт-Петербург)
Санкт-Петербург)