Номер 200 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник)
Номер 200 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
Старая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
ГДЗ Математика 6 класс.
 Виленкин, Жохов. Учебник с подробными ответами
Виленкин, Жохов. Учебник с подробными ответами- Главная
- ГДЗ
- 6 класс
- Математика
- Виленкин, Жохов. Учебник
Старая и новая редакции
Быстрый поиск
Учебник 2018-2022 г.
Новая редакция
Часть 1. Задания
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 385 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897
Задания для самопроверки
Задания для самопроверки § 1 (страницы 39-40)
1 2 3 4 5 6 7 8 9 10
Задания для самопроверки § 2 (страница 77)
1 2 3 4 5 6 7 8 9 10
Задания для самопроверки § 3 (страницы 128-129)
1 2 3 4 5 6 7 8 9 10
Задания для самопроверки § 4 (страница 161)
1 2 3 4 5 6 7 8 9 10
Часть 2. Задания
Задания
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701
Задания для самопроверки
Задания для самопроверки § 5 (страницы 33-34)
1 2 3 4 5 6 7 8 9 10
Задания для самопроверки § 6 (страница 54)
1 2 3 4 5 6 7 8 9 10
Задания для самопроверки § 7 (страница 80)
1 2 3 4 5 6 7 8 9 10
Задания для самопроверки § 8 (страницы 105-106)
1 2 3 4 5 6 7 8 9 10
Задания для самопроверки § 9 (страницы 135-138)
1 2 3 4 5 6 7 8 9 10
Задания для самопроверки § 10 (страница 156)
1 2 3 4 5 6 7 8 9 10
Учебник 2011-2017 г.
Старая редакция
Список заданий
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1052 1053 1054 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074 1075 1076 1077 1078 1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110 1111 1112 1113 1114 1115 1116 1117 1118 1119 1120 1121 1122 1123 1124 1125 1126 1127 1128 1129 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140 1141 1142 1143 1144 1145 1146 1147 1148 1149 1150 1151 1152 1153 1154 1155 1156 1157 1158 1159 1160 1161 1162 1163 1164 1165 1166 1167 1168 1169 1170 1171 1172 1173 1174 1175 1176 1177 1178 1179 1180 1181 1182 1183 1184 1185 1186 1187 1188 1189 1190 1191 1192 1193 1194 1195 1196 1197 1198 1199 1200 1201 1202 1203 1204 1205 1206 1207 1208 1209 1210 1211 1212 1213 1214 1215 1216 1217 1218 1219 1220 1221 1222 1223 1224 1225 1226 1227 1228 1229 1230 1231 1232 1233 1234 1235 1236 1237 1238 1239 1240 1241 1242 1243 1244 1245 1246 1247 1248 1249 1250 1251 1252 1253 1254 1255 1256 1257 1258 1259 1260 1261 1262 1263 1264 1265 1266 1267 1268 1269 1270 1271 1272 1273 1274 1275 1276 1277 1278 1279 1280 1281 1282 1283 1284 1285 1286 1287 1288 1289 1290 1291 1292 1293 1294 1295 1296 1297 1298 1299 1300 1301 1302 1303 1304 1305 1306 1307 1308 1309 1310 1311 1312 1313 1314 1315 1316 1317 1318 1319 1320 1321 1322 1323 1324 1325 1326 1327 1328 1329 1330 1331 1332 1333 1334 1335 1336 1337 1338 1339 1340 1341 1342 1343 1344 1345 1346 1347 1348 1349 1350 1351 1352 1353 1354 1355 1356 1357 1358 1359 1360 1361 1362 1363 1364 1365 1366 1367 1368 1369 1370 1371 1372 1373 1374 1375 1376 1377 1378 1379 1380 1381 1382 1383 1384 1385 1386 1387 1388 1389 1390 1391 1392 1393 1394 1395 1396 1397 1398 1399 1400 1401 1402 1403 1404 1405 1406 1407 1408 1409 1410 1411 1412 1413 1414 1415 1416 1417 1418 1419 1420 1421 1422 1423 1424 1425 1426 1427 1428 1429 1430 1431 1432 1433 1434 1435 1436 1437 1438 1439 1440 1441 1442 1443 1444 1445 1446 1447 1448 1449 1450 1451 1452 1453 1454 1455 1456 1457 1458 1459 1460 1461 1462 1463 1464 1465 1466 1467 1468 1469 1470 1471 1472 1473 1474 1475 1476 1477 1478 1479 1480 1481 1482 1483 1484 1485 1486 1487 1488 1489 1490 1491 1492 1493 1494 1495 1496 1497 1498 1499 1500 1501 1502 1503 1504 1505 1506 1507 1508 1509 1510 1511 1512 1513 1514 1515 1516 1517 1518 1519 1520 1521 1522 1523 1524 1525 1526 1527 1528 1529 1530 1531 1532 1533 1534 1535 1536 1537 1538 1539 1540 1541 1542 1543 1544 1545 1546 1547 1548 1549 1550 1551 1552 1553 1554 1555 1556 1557 1558 1559 1560 1561 1562 1563 1564 1565 1566 1567 1568 1569 1570 1571 1572 1573 1574 1575 1576 1577 1578 1579 1580 1581 1582 1583 1584 1585 1586 1587 1588 1589 1590 1591 1592 1593 1594 1595
Поделись с друзьями в социальных сетях:
Описание ГДЗ
Смотреть ответы
Математика 6 класс
Учебник
Авторы: Виленкин Н.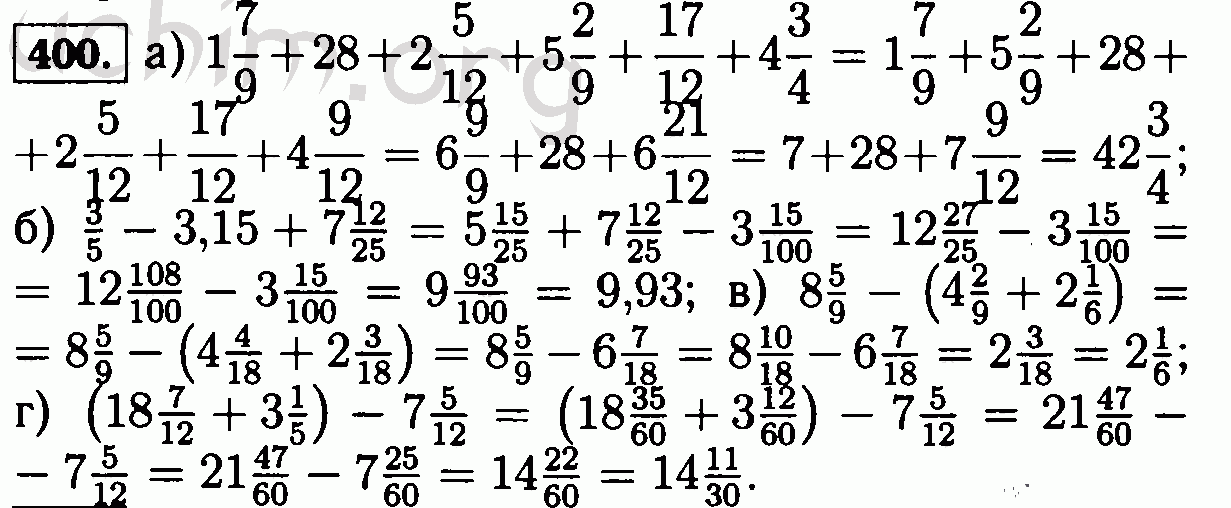 Я., Жохов В.И., Чесноков А.С., Шварцбург С.И.
Я., Жохов В.И., Чесноков А.С., Шварцбург С.И.
2015-2021 год
К списку ответов
ГДЗ по математике для 6 класса Виленкин, Жохов, Чесноков
ГДЗ по математике для 6 класса Виленкин, Жохов, ЧесноковПерейти к содержимому
Вид УМК: Учебник 6 класс
Авторы: Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд
Издательство: Мнемозина 2019
Серия: Математика
На странице решебника представлены ГДЗ с правильными ответами к вопросам и заданиям из учебника по математике для 6 класса авторов Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.
Часть 1 — номера
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897Часть 1 — тесты для самопроверки — страницы
3977128161
Часть 2 — номера
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706
Часть 2- тесты для самопроверки -страницы
2022 gdz-polinkin. ru Все права защищены. Информация взята из открытых источников. По вопросам нарушения авторского права пишите на: gdz-polinkin.ru@yandex.ru
ru Все права защищены. Информация взята из открытых источников. По вопросам нарушения авторского права пишите на: gdz-polinkin.ru@yandex.ru
AMS :: Дополнительные книжные материалы
9*$-Алгебры и конечномерные приближения| Шай Симонсон | В поисках математики не там, где нужно: математика в реальной жизни | 2022 | Спектр, Том. 104 | ||||
| Шай Симонсон | Новое открытие математики | 2011 | Ресурсные материалы для занятий в классе, Vol. 61 | ||||
| Колин Адамс | Книга мозаики: введение в математическую теорию мозаики | 2022 | |||||
| Дэвид Даманик и Джейк Филлман | Одномерные эргодические операторы Шредингера: I. Общая теория | 2022 | Аспирантура по математике, Vol. 221 | ||||
| Дэвид Э. Зитарелли с Деллой Дамбо и Стивеном Ф. Кеннеди | История математики в США и Канаде: Том 2: 1900–1941 | 2022 | Спектр, Том. 103 103 | ||||
| Колин Адамс | Затерянные в математическом музее: история выживания | 2022 | Новая математическая библиотека Аннели Лакс, Vol. 55 | ||||
Лесли Хогбен, Джефиан К.-Х. Лин и Брайан Л. Шейдер | Обратные задачи и форсирование нуля для графиков | 2022 | Математические обзоры и монографии, Vol. 270 | ||||
| Ребекка Рапопорт и Дин Чанг | Математика 2023: ваш ежедневный эпсилон математики: 12-месячный календарь — с января 2023 года по декабрь 2023 года | 2022 | |||||
Катя Ющенко | Аменабельность дискретных групп примерами | 2022 | Математические обзоры и монографии, Vol. 266 | ||||
| Рёта Мацуура | Дружеское введение в абстрактную алгебру | 2022 | Учебники AMS/MAA, Vol. 72 72 | ||||
| Энтони Бонато | Приглашение к играм преследования-уклонения и теории графов | 2022 | Студенческая математическая библиотека, Том. 97 | ||||
| Исаак Голдбринг | Ультрафильтры по всей математике | 2022 | Аспирантура по математике, Vol. 220 | ||||
| Драгана С. Цветкович Илич | Задачи завершения на операторных матрицах | 2022 | Математические обзоры и монографии, Vol. 267 | ||||
| Джон К. Осойнач-младший | Открытие абстрактной алгебры | 2021 | Учебники AMS/MAA, том. 67 | ||||
| Дана С. Эрнст | Введение в доказательство с помощью обучения на основе запросов | 2022 | Учебники AMS/MAA, том. 73 | ||||
| Иларио Аленкар, Уолси Сантос и Грегорио Силва Нето | Дифференциальная геометрия плоских кривых | 2022 | Студенческая математическая библиотека, вып. 96 96 | ||||
| Элис Питерс и Марк Сол | Фестиваль математики: справочник | 2022 | Библиотека математических кружков ИИГС, том. 28 | ||||
| Рустум Чокси | Уравнения с частными производными: первый курс | 2022 | Чистые и прикладные тексты для студентов, том. 54 | ||||
| Делла Дамбо и Дина Хаунспергер | Посчитай меня: сообщество и принадлежность к математике | 2022 | Ресурсные материалы для занятий в классе, том. 68 | ||||
| Джозеф Х. Сильверман | Абстрактная алгебра: комплексный подход | 2022 | Чистые и прикладные тексты для студентов, Vol. 55 | ||||
| Бенджамин Б. Кеннеди | Добро пожаловать в Real Analysis: Непрерывность и исчисление, расстояние и динамика | 2022 | Учебники AMS/MAA, Vol. 70 | ||||
| Уильям Джонстон | Исчисление сложных функций | 2022 | Учебники AMS/MAA, Vol. 71 71 | ||||
| Райан Хейворд | Hex: игривое введение | 2022 | Новая математическая библиотека Аннели Лакс, Vol. 54 | ||||
| Юкио Мацумото | Введение в теорию Морса | 2001 | Переводы математических монографий, Vol. 208 | ||||
| Набиль Х. Мустафа | Отбор проб в комбинаторных и геометрических системах множеств | 2022 | Математические обзоры и монографии, Vol. 265 | ||||
| Рагнар-Олаф Бухвейц. Под редакцией Лучезара Л. Аврамова, Бенджамина Бриггса, Шриканта Б. Айенгара и Янины С. Летц | Максимальные модули Коэна-Маколея и когомологии Тейта | 2021 | Математические обзоры и монографии, Vol. 262 | ||||
| Шири Артштейн-Авидан, Апостолос Яннопулос и Виталий Д. Мильман | Асимптотический геометрический анализ, часть II | 2021 | Математические обзоры и монографии, Vol. 261 261 | ||||
| Гарриет Полласек | Группы Ли: проблемно-ориентированное введение с помощью матричных групп | 2009 | Учебники AMS/MAA, Vol. 13 | ||||
| Дэвид М. Кларк и Сяо Сяо | Числовая линия посредством управляемого запроса | 2021 | Учебники AMS/MAA, Vol. 69 | ||||
| Б. Сетеруман | Доказательства и идея: прелюдия к высшей математике | 2021 | Учебники AMS/MAA, Vol. 68 | ||||
| Исмаилов Вугар Э. | Ридж-функции и приложения в нейронных сетях | 2021 | Математические обзоры и монографии, Vol. 263 | ||||
| Дж. Скотт Картер и Сейити Камада | Диаграмматическая алгебра | 2021 | Математические обзоры и монографии, Vol. 264 | ||||
| Буркард Польстер и Марти Росс | Соединяем два и два: отрывки из файлов Mathologer | 2021 | |||||
| Майкл Йосвиг | Основы тропической комбинаторики | 2021 | Аспирантура по математике, Vol. 219 219 | ||||
| Марсело Виана и Хосе Эспинар | Дифференциальные уравнения: подход динамических систем к теории и практике | 2021 | Аспирантура по математике, Vol. 212 | ||||
| Линдси Н. Чайлдс, Корнелиус Грейтер, Кевин П. Китинг, Алан Кох, Тимоти Коль, Пол Дж. Трумэн и Роберт Г. Андервуд | Алгебры Хопфа и теория модулей Галуа | 2021 | Математические обзоры и монографии, Vol. 260 | ||||
| Брайан Оссерман | Краткое введение в алгебраические многообразия | 2021 | Аспирантура по математике, Vol. 216 | ||||
| Луи-Пьер Арген | Первый курс стохастического исчисления | 2021 | Чистые и прикладные тексты для студентов, Vol. 53 | ||||
| Гизем Караали и Лили С. Хаджави | Математика для социальной справедливости: упор на количественные рассуждения и статистику | 2021 | Ресурсные материалы для занятий в классе, Vol.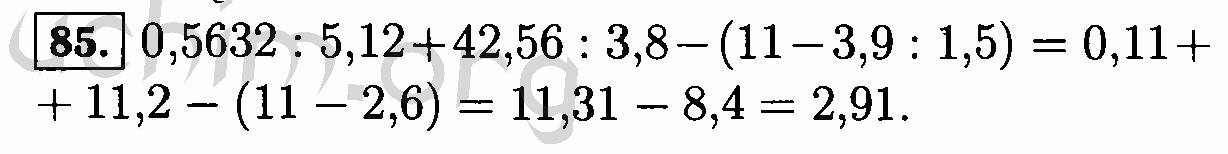 66 66 | ||||
| Имре Барань | Комбинаторная выпуклость | 2021 | Серия университетских лекций, том. 77 | ||||
| Риккардо Бенедетти | Лекции по дифференциальной топологии | 2021 | Аспирантура по математике, том. 218 | ||||
| Уильям Хайнцер, Кристель Роттхаус и Сильвия Виганд | Интегральные домены внутри нётеровских колец степенных рядов: конструкции и примеры | 2021 | Математические обзоры и монографии, вып. 259 | ||||
| Тадао Китадзава, Энди Лю и Джордж Сичерман | Арифметические, геометрические и комбинаторные головоломки из Японии | 2021 | Спектр, том. 102 | ||||
| Майкл Э. Тейлор | Введение в дифференциальные уравнения: второе издание | 2022 | Чистые и прикладные тексты для студентов, том. 52 | ||||
Матильда Гербелли-Готье, Памела Э. Харрис, Майкл А. Хилл, Даган Карп и Эмили Риль, редакторы Харрис, Майкл А. Хилл, Даган Карп и Эмили Риль, редакторы | Беседа о профессиональных нормах в математике | 2021 | |||||
| Стивен Клее, Коля Малкин и Юлия Певцова | Математика вслух: Справочник устной олимпиады | 2021 | Библиотека математических кружков ИИГС, том. 27 | ||||
| Прамод Н. Ачар | Извращенные пучки и приложения к теории представлений | 2021 | Математические обзоры и монографии, вып. 258 | ||||
| Мариус Крайник, Руи Лоха Фернандес и Иоан Маркут | Лекции по пуассоновской геометрии | 2021 | Аспирантура по математике, том. 217 | ||||
| Тай-Пин Лю | Ударные волны | 2021 | Аспирантура по математике, том. 215 | ||||
| Алексей А. Заславский и Михаил Б. Скопенков | Математика через задачи: Часть 2: Геометрия | 2021 | Библиотека математических кружков ИИГС, том. 26 26 | ||||
| Памела Э. Харрис, Алисия Прието-Лангарика, Ванесса Ривера Кионес, Луис Сордо Виейра, Росаура Усканга и Андрес Р. Виндас Мелендес, редакторы | Testimonios: истории латиноамериканских и латиноамериканских математиков | 2021 | Ресурсные материалы для занятий в классе, том. 67 | ||||
| Иоаннис Карацас и Константинос Кардарас | Портфельная теория и арбитраж: курс математических финансов | 2021 | Аспирантура по математике, том 214 | ||||
| Юха Киннунен, Юха Лербек и Антти Вяхакангас | Методы максимальных функций для пространств Соболева | 2021 | Математические обзоры и монографии, вып. 257 | ||||
| Хунг Винь Тран | Уравнения Гамильтона—Якоби: теория и приложения | 2021 | Аспирантура по математике, том. 213 | ||||
| Йорг Беверсдорф | Теория Галуа для начинающих: историческая перспектива, второе издание | 2021 | Студенческая математическая библиотека, вып. 95 95 | ||||
| Мичио Джимбо, Тецудзи Мива и Федор Смирнов | Локальные операторы в интегрируемых моделях I | 2021 | Математические обзоры и монографии, вып. 256 | ||||
| Роберт Мессер | Линейная алгебра: ворота в математику, второе издание | 2021 | Учебники AMS/MAA, том. 66 | ||||
| Александр Боричев и Сергей Куксин | Одномерная турбулентность и стохастическое уравнение Бюргерса | 2021 | Математические обзоры и монографии, вып. 255 | ||||
| Карим Белабас и Анри Коэн | Численные алгоритмы для теории чисел: использование Pari/GP | 2021 | Математические обзоры и монографии, вып. 254 | ||||
| Роберт Р. Брунер и Джон Рогнес | Спектральная последовательность Адамса для топологических модульных форм | 2021 | Математические обзоры и монографии, вып. 253 253 | ||||
| Дэвид Дж. Коверт | Проблема расстояния конечного поля | 2021 | Математические монографии Каруса, том. 37 | ||||
| Томас К. Сибли | Алгебраическое мышление: введение в абстрактную алгебру | 2021 | Учебники AMS/MAA, том. 65 | ||||
Жан-Мари Де Конинк и Николя Дойон | Жизнь простых чисел в 37 сериях | 2021 | |||||
Крейг А. Стефенсон | Периодические орбиты: поиски Ф. Р. Моултоном новой лунной теории | 2021 | История математики, том. 45 | ||||
| Минди Капальди, редактор | Обучение математике с помощью игр | 2021 | Ресурсные материалы для занятий в классе, том. 65 | ||||
| Фрэнк Свец | Влияние и наследие Женского дневника (1704–1840): женская декларация | 2021 | Спектр, том. 101 101 | ||||
| Венди Смит, Мэтью Фойгт, Эйприл Стрём, Дэвид С. Уэбб и У. Гэри Мартин | Усилия по трансформационным изменениям: вовлечение учащихся в математику через институциональную сеть для активного обучения | 2021 | |||||
| Филипп Зауати | Отказ Перельмана: Роман | 2021 | |||||
| Кит Кендиг | Путь к теории чисел: применение силы алгебраических кривых | 2021 | Математические изложения Дольчиани, том. 57 | ||||
| Виктор Прасолов и Юрий Соловьев | Эллиптические функции и эллиптические интегралы | 1997 | Переводы математических монографий, том. 170 | ||||
| Джеймс Р. Кинг | Преобразование геометрии: евклидова плоская геометрия на основе жестких движений | 2021 | Чистые и прикладные тексты для студентов, том. 51 | ||||
| Джули Дезерти | Группа Cremona и ее подгруппы | 2021 | Математические обзоры и монографии, вып. 252 252 | ||||
| Улицы Марио Гарсия-Фернандес и Джеффри | Обобщенный поток Риччи | 2021 | Серия университетских лекций, том. 76 | ||||
| Джеймс Бисгард | Анализ и линейная алгебра: разложение по сингулярным числам и приложения | 2021 | Студенческая математическая библиотека, вып. 94 | ||||
| Аркадий Скопенков | Математика через задачи: Часть 1: Алгебра | 2021 | Библиотека математических кружков ИИГС, том. 25 | ||||
| Итан Д. Болкер и Мора Б. Маст | Математика здравого смысла, второе издание | 2021 | Учебники AMS/MAA, том. 63 | ||||
| Дэвид Хофф | Линейные и квазилинейные параболические системы: теория пространства Соболева | 2020 | Математические обзоры и монографии, вып. 251 | ||||
| Башир Бекка и Пьер де ла Арп | Унитарные представления групп, двойников и символов | 2020 | Математические обзоры и монографии, вып. 250 250 | ||||
| Ива Ставров | Кривизна пространства и времени, с введением в геометрический анализ | 2020 | Студенческая математическая библиотека. об. 93 | ||||
| Дэн Слоутер | Исчисление от приближения к теории | 2020 | Учебники AMS/MAA, №. 64 | ||||
| Киран С. Кедлая, Дэниел М. Кейн, Джонатан М. Кейн, Эван М. О’Дорни | Фитинг Математического конкурса Уильяма Лоуэлла Патнэма 2001–2016: задачи, решения и комментарии | 2020 | Сборники задач, вып. 37 | ||||
| Эли Альджадефф, Антонио Джамбруно, Клаудио Прочези, Амитай Регев | Кольца с полиномиальными тождествами и конечномерными представлениями алгебр | 2020 | Публикации коллоквиума, вып. 66 | ||||
| Чарльз Фефферман и Арье Исраэль | Подгонка сглаженных функций к данным | 2020 | Серия региональных конференций CBMS по математике, нет.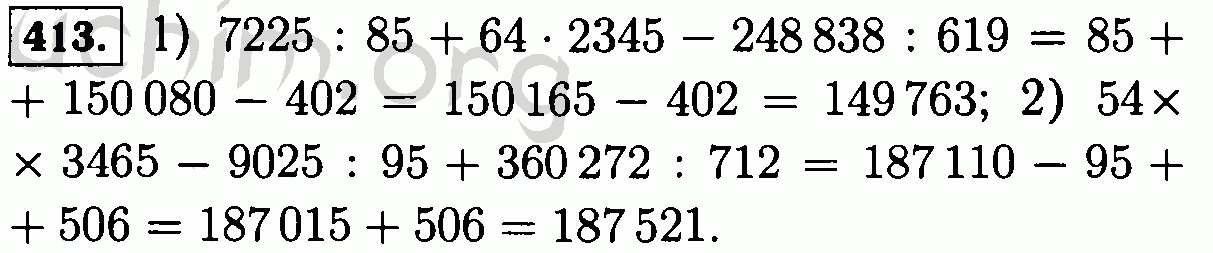 135 135 | ||||
| Карл Г. Вагнер | Первый курс перечислительной комбинаторики | 2020 | Чистые и прикладные тексты для студентов, том. 49 | ||||
| Висенте Муньос, Анхель Гонсалес-Прието и Хуан Анхель Рохо | Геометрия и топология многообразий: поверхности и не только | 2020 | Аспирантура по математике, том. 208 | ||||
| Джун Бэрроу-Грин, Джереми Грей, Робин Уилсон | История математики: подход, основанный на источниках, том 2 | 2021 | Учебники AMS/MAA, том. 61 | ||||
| Диана Дэвис | Иллюстрация математики | 2020 | |||||
| Брюс Э. Саган | Комбинаторика: искусство счета | 2020 | Аспирантура по математике, том. 210 | ||||
| Уоррен П. Джонсон | Введение в $q$-анализ | 2020 | |||||
| Роберт Фрейд и Эдит Дьярмати | Теория чисел | 2020 | Чистые и прикладные тексты для студентов, том. 48 48 | ||||
| Джессика С. Перселл | Теория гиперболических чисел | 2020 | Аспирантура по математике, том. 209 | ||||
Хунг-Хси Ву | Преобразование рациональных чисел в линейные уравнения | 2020 | |||||
| Хунг-Хси Ву | Алгебра и геометрия | 2020 | |||||
| Хунг-Хси Ву | Предварительное исчисление, исчисление и не только | 2020 | |||||
| Роджер Плаймен | Великая гонка простых чисел | 2020 | Студенческая математическая библиотека, вып. 92 | ||||
| Стивен Х. Саперстоун и Макс А. Саперстоун | Взаимодействие с обыкновенными дифференциальными уравнениями | 2020 | Учебники AMS/MAA, том. 62 | ||||
| Дэниел Дж. Веллеман и Стэн Вагон | Велосипед или моноцикл? Коллекция интригующих математических головоломок | 2020 | Сборники задач, том. 36 36 | ||||
| Майкл Э. Тейлор | Введение в анализ с одной переменной | 2020 | Чистые и прикладные тексты для студентов, том. 47 | ||||
| Алисия Дикенштейн и Хуан Сабиа | Matemax: издание на английском и испанском языках | 2020 | |||||
| Майкл Э. Тейлор | Введение в анализ с несколькими переменными: расширенное исчисление | 2020 | Чистые и прикладные тексты для студентов, том. 46 | ||||
| Ральф Абрахам и Джеррольд Э. Марсден | Основы механики | 2008 | AMS Chelsea Publishing, vol. 364.Х | ||||
| Колин С. Адамс | Бунт на экзамене по математике и другие истории с уклоном в математику | 2009 | |||||
| Колин С. Адамс | Книга узлов: элементарное введение в математическую теорию узлов | 2004 | |||||
| Николай Михайлович Адрианов, Федор Пакович и Александр Константинович Звонкин | Полиномы Давенпорта—Занье и детские рисунки | 2020 | Математические обзоры и монографии, том. 249 249 | ||||
| Марсело Агиар и Свапнил Махаджан | Группы Кокстера и алгебры Хопфа | 2006 | Монографии Института Филдса, том. 23 | ||||
| Марсело Агиар и Свапнил Махаджан | Моноидальные функторы, виды и алгебры Хопфа | 2010 | Серия монографий CRM, том. 29 | ||||
| Марсело Агиар и Свапнил Махаджан | Темы в аранжировках гиперплоскости | 2017 | Математические обзоры и монография, вып. 226 | ||||
| Илька Агрикола и Томас Фридрих | Глобальный анализ: дифференциальные формы в анализе, геометрии и физике | 2002 | Аспирантура по математике, том. 52 | ||||
| Илька Агрикола и Томас Фридрих | Элементарная геометрия | 2008 | Студенческая математическая библиотека, вып. 43 | ||||
| Ларс В. Альфорс | Конформные инварианты | 2010 | AMS Chelsea Publishing, vol.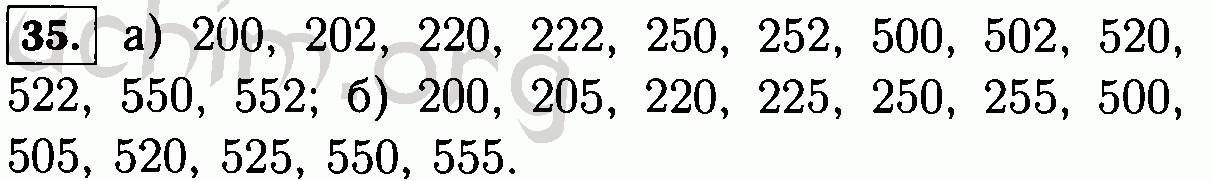 371.Ч 371.Ч | ||||
| Ларс Альфорс, с дополнительными главами: CJ Earle и I. Kra, M. Shishikura и J.H. Хаббард | Лекции по квазиконформным отображениям | 2006 | Серия университетских лекций, том. 38 | ||||
| Мартин Айгнер | Дискретная математика | 2007 | |||||
| Мартин Айгнер и Эрхард Берендс | Математика повсюду | 2010 | |||||
| Майкл Айзенман и Симона Варзель | Случайные операторы: влияние беспорядка на квантовые спектры и динамику | 2015 | Аспирантура по математике, том. 168 | ||||
| С. Альбеверио, Ф. Гестеши, Р. Хёг-Крон и Х. Холден (с приложением Павла Экснера) | Решаемые модели в квантовой механике: второе издание | 2005 | AMS Chelsea Publishing, vol. 350.Х | ||||
| Семен Алескер | Введение в теорию оценок | 2018 | Серия региональных конференций CBMS по математике, № 126 | ||||
Даниэль С. Александр, Феличе Иавернаро и Алессандро Роза Александр, Феличе Иавернаро и Алессандро Роза | Первые дни сложной динамики: история сложной динамики одной переменной в 1906-1942 гг. | 2011 | История математики, том. 38 | ||||
| Серж Алинхак и Патрик Жерар | Псевдодифференциальные операторы и теорема Нэша-Мозера | 2007 | Аспирантура по математике, том. 82 | ||||
| Хараламбос Д. Алипрантис и Раби Турки | Конусы и двойственность | 2007 | Аспирантура по математике, том. 84 | ||||
| Джон М. Алонги и Гейл С. Нельсон | Повторение и топология | 2007 | Аспирантура по математике, том. 85 | ||||
| Клауди Альсина и Роджерт Б. Нельсен | Рог изобилия четырехугольников | 2020 | Математические изложения Дольчиани, том. 55 | ||||
| Клаудия Альсина и Роджер Б. Нельсон | Очаровательные доказательства: путешествие в элегантную математику | 2010 | Математические изложения Дольчиани, том. 42 42 | ||||
| Монтсеррат Альсина и Пилар Байер | Кватернионные порядки, квадратичные формы и кривые Шимуры | 2004 | Серия монографий CRM, том. 22 | ||||
| Туна Алтинель, Александр В. Боровик и Григорий Черлин | Простые группы конечного ранга Морли | 2008 | Математические обзоры и монографии, вып. 145 | ||||
| Саймон Альтманн и Эдуардо Л. Ортис | Математика и социальные утопии во Франции: Олинде Родригес и его время | 2005 | История математики, том. 28 | ||||
| Паоло Алуффи | Алгебра: Глава 0 | 2009 | Аспирантура по математике, том. 104 | ||||
| Алекс Амента и Паскаль Аушер | Эллиптические краевые задачи с данными дробной регулярности: подход первого порядка | 2018 | Серия монографий CRM, том. 37 | ||||
| Хабиб Аммари, Хёнбэ Кан и Хёндэ Ли | Методы определения потенциала слоев в спектральном анализе | 2009 | Математические обзоры и монографии, вып. 153 153 | ||||
| Хабиб Аммари, Брайан Фитцпатрик, Хёнбэ Кан, Матиас Руис, Санхьюон Ю и Хай Чжан | Математические и вычислительные методы фотоники и фононики | 2018 | Математические обзоры и монографии, вып. 235 | ||||
| Кирсти Андерсен | Оптические иллюзии в Риме: математический путеводитель | 2019 | Спектр, том. 99 | ||||
| Титу Андрееску и Марк Сол | Алгебраические неравенства: новые перспективы | 2016 | Библиотека математических кружков ИИГС, том. 19 | ||||
| Фуэнсанта Андреу-Вайо, Хосе М. Масон, Хулио Д. Росси и Х. Хулиан Толедо-Мелеро | Нелокальные задачи диффузии | 2010 | Математические обзоры и монографии, вып. 165 | ||||
| Бен Эндрюс, Беннет Чоу, Кристин Гюнтер и Мэт Лэнгфорд | Внешние геометрические потоки | 2020 | Аспирантура по математике, том. 206 206 | ||||
| В. И. Арнольд | Экспериментальная математика | 2015 | Библиотека математических кружков ИИГС, том. 16 | ||||
| В. И. Арнольд | Математическое понимание природы: очерки удивительных физических явлений и их понимания математиками | 2014 | |||||
| Джеймс Артур | Эндоскопическая классификация представлений | 2013 | Публикации коллоквиума, том. 61 | ||||
| Эмиль Артин и Джон Тейт | Теория поля класса | 2009 | AMS Chelsea Publishing, vol. 366.Ч | ||||
| Шири Артштейн-Авидан, Апостолос А. Яннопулос и В. Д. Мильман | Асимптотический геометрический анализ, часть I | 2015 | Математические обзоры и монографии, вып. 202 | ||||
| Андреас Арванитоёргос | Введение в группы Ли и геометрию однородных пространств | 2003 | Студенческая математическая библиотека, вып.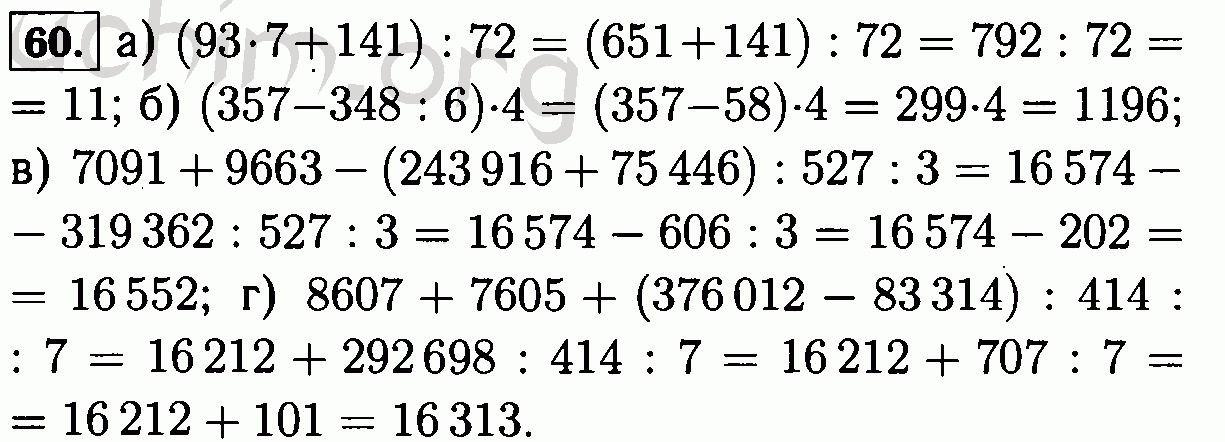 22 22 | ||||
| Майкл Ашбахер и Стивен Д. Смит | Классификация квазитиновых групп: I. Структура сильно квазитиновых $mathcal{K}$-групп | 2004 | Математические обзоры и монографии, вып. 111 | ||||
| Майкл Ашбахер, Ричард Лайонс, Стивен С. Смит и Рональд Соломон | Классификация конечных простых групп: группы характеристики 2 типа | 2011 | Математические обзоры и монографии, вып. 172 | ||||
| Майкл Ашбахер и Стивен С. Смит | Классификация квазитиновых групп: II. Основные теоремы: классификация простых QTKE-групп | 2004 | Математические обзоры и монографии, вып. 112 | ||||
| Гийом Обрун и Станислав Шарек | Алиса и Боб знакомятся с Банахом: интерфейс асимптотического геометрического анализа и квантовой теории информации | 2017 | Математические обзоры и монографии, вып. 223 223 | ||||
| Дэйв Окли, Боб Кляйн, Аманда Сереневи и Татьяна Шубин | Вдохновляющая математика: уроки математических кружков навахо | 2019 | Библиотека математических кружков ИИГС, том. 24 | ||||
| Мишель Оден | Гамильтоновы системы и их интегрируемость | 2008 | Тексты и монографии SMF/AMS, том. 15 | ||||
| Антонио Ауффингер, Майкл Дамрон и Джек Хэнсон | 50 лет перколяции первого прохода | 2017 | Серия университетских лекций, том. 68 | ||||
| Джинхо Байк, Перси Дейфт, Туфик Суидан | Комбинаторная теория и теория случайных матриц | 2016 | Аспирантура по математике, том. 172 | ||||
| Мэтью Бейкер и Роберт Румели | Теория потенциала и динамика на проективной прямой Берковича | 2010 | Математические обзоры и монографии, вып. 159 159 | ||||
| Джон Т. Болдуин | Категория | 2009 | Серия университетских лекций, том. 50 | ||||
| Григорий В. Бард | Мудрец для студентов | 2015 | |||||
| Уильям Баркер и Роджер Хоу | Непрерывная симметрия: от Евклида до Клейна | 2007 | |||||
| Элизабетта Барлетта, Сорин Драгомир и Дришан Л. Дуггал | Слоения в геометрии Коши-Римана | 2007 | Математические обзоры и монографии, вып. 140 | ||||
| Джули Барнс и Джессика М. Либертини | Тактильные обучающие занятия по математике: книга рецептов для бакалавриата | 2018 | Ресурсные материалы для занятий в классе, том. 54 | ||||
| Луис Баррейра и Яков Песин | Введение в теорию гладкой эрготики | 2013 | Аспирантура по математике, том. 148 148 | ||||
| Луис Баррейра и Клаудия Вальс | Обыкновенные дифференциальные уравнения: Качественная теория | 2012 | Аспирантура по математике, том. 137 | ||||
| Джун Бэрроу-Грин, Джереми Грей и Робин Уилсон | История математики: подход, основанный на источниках. Том 1 | 2019 | Учебники AMS/MAA, том. 45 | ||||
| Роберт Г. Бартл | Современная теория интеграции | 2001 | Аспирантура по математике, том 32 | ||||
| Стив Баттерсон | Стивен Смейл: математик, преодолевший пространственный барьер | 2000 | |||||
| Майкл Бин | Вероятность: наука о неопределенности с приложениями к инвестициям, страхованию и инженерии | 2009 | Чистые и прикладные тексты для студентов, том. 6 | ||||
| Йожеф Бек | Неизбежная случайность в дискретной математике | 2009 | Серия университетских лекций, том. 49 49 | ||||
| Матиас Бек и Раман Саньял | Комбинаторные теоремы взаимности: приглашение к перечислительной геометрической комбинаторике | 2018 | Аспирантура по математике, том. 195 | ||||
| Эрхард Берендс | Математика за пять минут | 2008 | |||||
| Эрхард Берендс | Математика за магией | 2019 | |||||
| Александр Бейлинсон и Владимир Дринфельд | Киральные алгебры | 2004 | Публикации коллоквиума, том. 51 | ||||
| Джейсон П. Белл, Драгос Гиока и Томас Дж. Такер | Динамическая гипотеза Морделла-Ланга | 2016 | Математические обзоры и монографии, вып. 210 | ||||
| Александра Беллоу, Карлос Э. Кениг и Пол Маллиавин | Избранные статьи Альберто П. Кальдерона с комментариями | 2008 | Собрание сочинений, том. 21 21 | ||||
| Роберт Л. Бенедетто | Динамика одной неархимедовой переменной | 2019 | Аспирантура по математике, том. 198 | ||||
| Дэвид Дж. Бенсон и Стивен Д. Смит | Классификация пространств спорадических групп | 2008 | Математические обзоры и монографии, вып. 147 | ||||
| А. Бенсуссан, Ж.-Л. Лайонс и Г. Папаниколау | Асимптотический анализ периодических структур | 2011 | AMS Chelsea Publishing, vol. 374.Х | ||||
| Стерлинг К. Берберян | Измерение и интеграция | 2011 | Издательство AMS Chelsea Publishing, том. 241.Х | ||||
| Дж. Л. Берггрен и Р. С. Д. Томас | Феномены Евклида: перевод и изучение эллинистического трактата по сферической астрономии | 2006 | История математики, том. 29 | ||||
Уильям П. Берлингхофф и Фернандо К. Гувеа Берлингхофф и Фернандо К. Гувеа | Математика сквозь века: нежная история для учителей и не только, расширенное второе издание | 2015 | Учебники AMS/MAA, том. 32 | ||||
| Грегори Беруи и Фредерик Огье | Введение в основные простые алгебры и их приложения к беспроводной связи | 2013 | Математические обзоры и монографии, вып. 191 | ||||
| Григорий Берколайко и Петр Кучмент | Введение в квантовые графики | 2012 | Математические обзоры и монографии, вып. 186 | ||||
| Брюс С. Берндт | Теория чисел в духе Рамануджана | 2006 | Студенческая математическая библиотека, вып. 34 | ||||
| Жан Берстель, Аарон Лаув, Кристоф Рейтенауэр и Франко В. Салиола | Комбинторика слов | 2008 | Серия монографий CRM, том. 27 | ||||
| Йорг Беверсдорф | Теория Галуа для начинающих: историческая перспектива | 2006 | Студенческая математическая библиотека, вып. 35 35 | ||||
| Аллан Бикл | Основы теории графов | 2020 | Чистые и прикладные тексты для студентов, том. 43 | ||||
| Лидия Биери и Нина Зипсер | Расширения теоремы об устойчивости пространства Минковского в общей теории относительности | 2009 | AMS/IP Studies in Advanced Mathematics, vol. 45 | ||||
| Роберт Биери и Ральф Стребель | О группах PL-гомеоморфизмов вещественной прямой | 2016 | Математические обзоры и монографии, вып. 215 | ||||
| Эрнст Бинц и Соня Под | Геометрия групп Гейзенберга: с приложениями в теории сигналов, оптике, квантовании и квантовании поля | 2008 | Математические обзоры и монографии, вып. 151 | ||||
| Оливье Бикар | Асимптотически симметричная метрика Эйнштейна | 2006 | Тексты и монографии SMF/AMS, том. 13 13 | ||||
| Павел Блехер и Карл Лихти | Случайные матрицы и шестивершинная модель | 2014 | Серия монографий CRM, том. 32 | ||||
| Бобенко Александр Иванович и Сурис Юрий Борисович | Дискретная дифференциальная геометрия: интегрируемая структура | 2009 | Аспирантура по математике, том. 98 | ||||
| Богачев Владимир Иванович | Слабая сходимость мер | 2018 | Математические обзоры и монографии, вып. 234 | ||||
| Владимир И. Богачев, Николай В. Крылов, Михаэль Рёкнер и С. В. Шапошников | Уравнения Фоккера—Планка—Колмогорова | 2015 | Математические обзоры и монографии, вып. 207 | ||||
| Богачев Владимир Иванович | Дифференцируемые меры и исчисление Маллявена | 2010 | Математические обзоры и монографии, вып. 164 164 | ||||
| Пшемыслав Богацкий | Линейная алгебра: концепции и приложения | 2019 | Учебники AMS/MAA, том. 47 | ||||
| Итан Д. Болкер и Мора Б. Маст | Математика здравого смысла | 2016 | Учебники AMS/MAA, том. 33 | ||||
| Фрэнсис Бонахон | Низкомерная геометрия: от евклидовых поверхностей к гиперболическим узлам | 2009 | Студенческая математическая библиотека, вып. 49 | ||||
| Энтони Бонато | Курс по веб-графике | 2008 | Аспирантура по математике, том. 89 | ||||
| Энтони Бонато и Ричард Дж. Новаковски | Игра в полицейских и грабителей на графиках | 2011 | Студенческая математическая библиотека, вып. 61 | ||||
| Энтони Бонато | Безграничные умы | 2018 | |||||
| Марио Бонк и Даниэль Мейер | Расширение карт Терстона | 2017 | Математические обзоры и монографии, вып. 225 225 | ||||
| Арман Борель | Введение в арифметические группы | 2019 | Серия университетских лекций, том. 73 | ||||
| Матеус К. Бортолан, Александр Н. Карвалью и Хосе А. Ланга | Аттракторы при автономных и неавтономных возмущениях | 2020 | Математические обзоры и монографии, вып. 246 | ||||
| Набиль Бусаид и Эндрю Комеч | Нелинейное уравнение Дирака: спектральная устойчивость уединенных волн | 2019 | Математические обзоры и монографии, вып. 244 | ||||
| Хельмут Брасс и Кнут Петрас | Теория квадратур | 2011 | Математические обзоры и монографии, вып. 178 | ||||
| Силуанос Бразитикос, Апостолос Яннопулос, Петрос Валеттас и Беатрис-Хелен Врициу | Геометрия изотропных выпуклых тел | 2014 | Математические обзоры и монографии, вып. 196 196 | ||||
| Саймон Брендл | Поток Риччи и теорема о сфере | 2010 | Аспирантура по математике, том. 111 | ||||
| Хольгер Бреннер, Юрген Херцог и Орландо Вильямайор | Три лекции по коммутативной алгебре | 2008 | Серия университетских лекций, том. 42 | ||||
| Альберто Брессан | Конспект лекций по функциональному анализу | 2012 | Аспирантура по математике, том. 143 | ||||
| Марк Бриджер | Реальный анализ: конструктивный подход через интервальную арифметику | 2019 | Чистые и прикладные тексты для студентов, том. 38 | ||||
| Кэтрин Брингманн, Аманда Фолсом, Кен Оно и Ларри Ролен | Гармонические формы Маасса и фиктивные модульные формы: теория и приложения | 2017 | Публикации коллоквиума, том. 64 | ||||
Эзра Браун и Ричард К. Гай Гай | Единство комбинаторики | 2020 | Математические монографии Каруса, том. 36 | ||||
| Натаниал П. Браун и Нарутака Одзава | 2008 | Аспирантура по математике, том. 88 | |||||
| Роберт Р. Брунер и Дж. П. К. Гринлис | Связная вещественная K-теория конечных групп | 2010 | Математические обзоры и монографии, вып. 169 | ||||
| Виктор М. Бухштабер и Тарас Э. Панов | Торическая топология | 2015 | Математические обзоры и монографии, вып. 204 | ||||
| Ксавье Бафф, Жером Ференбах, Пьер Лошак, Лейла Шнепс и Пьер Фогель | Пространства модулей кривых, группы классов отображения и теория поля | 2003 | Тексты и монографии SMF/AMS, том. 9 | ||||
| Оливер Бюлер | Краткое введение в классическую, статистическую и квантовую механику | 2006 | Конспект лекций Куранта, том. 13 13 | ||||
| Тео Бюлер и Дитмар А. Саламон | Функциональный анализ | 2018 | Аспирантура по математике, том. 191 | ||||
| Александр Буюм | Основы арифметической дифференциальной геометрии | 2017 | Математические обзоры и монографии, вып. 222 | ||||
| Александр Буюм | Арифметические дифференциальные уравнения | 2005 | Математические обзоры и монографии, вып. 118 | ||||
| Анна Бураго | Дневники математических кружков, 1 класс: полный кружок для 5–7 классов | 2012 | Библиотека математических кружков, том. 11 | ||||
| Анна Бураго | Дневники математических кружков, 2 класс: полный кружок для 5-8 классов | 2018 | Библиотека математических кружков, том. 20 | ||||
| Оуэн Байер, Дейдра Смельцер и Кеннет Ванц | Путешествие в дискретную математику | 2018 | Учебники AMS/MAA, том. 41 41 | ||||
| Луис Каффарелли и Сандро Сальса | Геометрический подход к задачам со свободными границами | 2005 | Аспирантура по математике, том 68 Брайден Кейс | ||||
| Бхаргав Бхатт, Ана Караиани, Киран С. Кедлая, Питер Шольце и Джаред Вайнштейн | Perfectoid Spaces: Лекции Зимней школы в Аризоне 2017 | 2019 | Математические обзоры и монографии, том 242 | ||||
| Овидиу Калин, Дер-Чен Чанг и Питер Грейнер | Геометрический анализ группы Гейзенберга и его обобщения | 2007 | AMS/IP Исследования по высшей математике, том 40 | ||||
| Дафф Кэмпбелл | Открытая дверь в теорию чисел | 2018 | Учебники AMS/MAA, том. 39 | ||||
| Альберто Кандель и Лоуренс Конлон | Расслоения II | 2003 | Аспирантура по математике, том 60 | ||||
Джеймс В. Кэннон Кэннон | Неевклидова геометрия и кривизна: двумерные пространства, том 3 | 2017 | |||||
| Джеймс В. Кэннон | Геометрия длин, площадей и объемов: двумерные пространства, том 1 | 2017 | |||||
| Андреас Чап и Ян Словак | Параболические геометрии I: История вопроса и общая теория | 2009 | Математические обзоры и монографии, том 154 | ||||
| Лука Капонья, Карлос Э. Кениг и Лоредана Ланцани | Гармоническая мера: геометрическая и аналитическая точки зрения | 2005 | Серия университетских лекций, том. 35 | ||||
| Джеймс Карлсон, Артур Джаффе и Эндрю Уайлс | Проблемы премии тысячелетия | 2006 | |||||
| Морин Т. Кэрролл и Элин Риккен | Геометрия: линия и окружность | 2018 | Учебники AMS/MAA, том.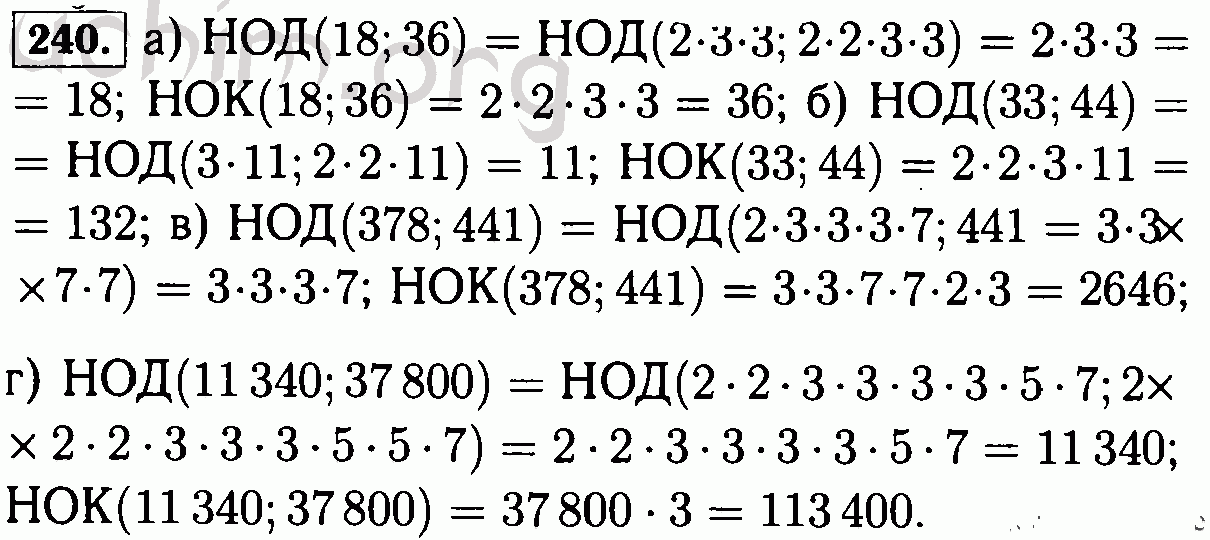 44 44 | ||||
| Тьерри Казенав | Полулинейные уравнения Шрёдингера | 2003 | Конспект лекций Куранта, том. 10 | ||||
| Жоан Серда | Линейный функциональный анализ | 2010 | Аспирантура по математике, том. 116 | ||||
| Чинг-Ли Чай, Брайан Конрад и Франс Оорт | Комплексные задачи на умножение и подъем | 2013 | Математические обзоры и монографии, том. 195 | ||||
| Эрик Шарпантье, Этьен Гис и Анник Лесн | Научное наследие Пуанкаре | 2010 | История математики, том. 36 | ||||
| Г.А. Чечкин, А.Л. Пятницкий, А.С. Шамаев | Гомогенизация: методы и применение | 2007 | Переводы математических монографий, том. 234 | ||||
| Джефф Чигер и Дэвид Г. Эбин | Теоремы сравнения в римановой геометрии | 2008 | AMS Chelsea Publishing, vol. 365.Х 365.Х | ||||
| Эван Чен | Евклидова геометрия в математических олимпиадах | 2016 | Сборники задач, том. 27 | ||||
| Ся Чен | Пересечения со случайным блужданием | 2010 | Математические обзоры и монографии, вып. 157 | ||||
| Уорд Чейни и Уилл Лайт | Курс теории приближений | 2009 | Аспирантура по математике, том. 101 | ||||
| Уорд Чейни и Дэвид Кинкейд | Численный анализ: математика научных вычислений | 2009 | 9p$ Пробелы | 2020 | Серия университетских лекций, том. 75 | ||
| Николай Чернов и Роберто Маркарян | Хаотический бильярд | 2006 | Математические обзоры и монографии, том 127 | ||||
| Паскаль Шерье и Альберт Милани | Линейные и квазилинейные эволюционные уравнения в гильбертовых пространствах | 2012 | Аспирантура по математике, том 135 | ||||
| Стивен Чайлдресс | Введение в теоретическую гидромеханику | 2006 | Конспект лекций Куранта, том.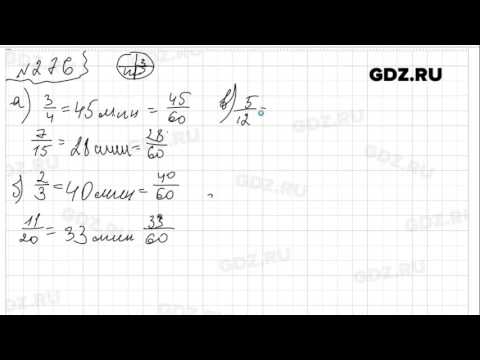 13 13 | ||||
| Беннетт Чоу, Пэн Лу и Лэй Ни | Гамильтон Риччи Флоу | 2006 | Аспирантура по математике, том 77 | ||||
| Беннетт Чоу, Сан-Чин Чу, Дэвид Гликенштейн, Кристин Гюнтер, Джеймс Изенберг, Том Айви, Дэн Кнопф, Пэн Лу, Фэн Луо и Лей Ни | Поток Риччи: методы и приложения: часть I: геометрические аспекты | 2007 | Математические обзоры и монографии, том 135 | ||||
| Беннетт Чоу, Сан-Чин Чу, Дэвид Гликенштейн, Кристин Гюнтер, Джеймс Изенберг, Том Айви, Дэн Кнопф, Пэн Лу, Фэн Луо и Лэй Ни | Поток Риччи: методы и приложения: часть II: аналитические аспекты | 2008 | Математические обзоры и монографии, том 144 | ||||
| Беннетт Чоу, Сан-Чин Чу, Дэвид Гликенштейн, Кристин Гюнтер, Джеймс Изенберг, Том Айви, Дэн Кнопф, Пэн Лу, Фэн Луо и Лей Ни | Поток Риччи: методы и приложения: часть III: геометрически-аналитические аспекты | 2010 | Математические обзоры и монографии, том 163 | ||||
| Беннетт Чоу, Сан-Чин Чу, Дэвид Гликенштейн, Кристин Гюнтер, Джеймс Изенберг, Том Айви, Дэн Кнопф, Пэн Лу, Фэн Луо и Лей Ни | Поток Риччи: методы и приложения: часть IV: долгосрочные решения и связанные темы | 2015 | Математические обзоры и монографии, том 206 | ||||
| Фан Чунг и Линьюань Лу | Сложные графы и сети | 2006 | Серия региональных конференций CBMS по математике, № 107 | ||||
| Беннет Чоу и Дэн Кнопф | Поток Риччи: Введение | 2004 | Математические обзоры и монографии, том 110 | ||||
| Кай Челебак и Яков Элиашберг | От Штейна к Вайнштейну и обратно: симплектическая геометрия и аффинные комплексные многообразия | 2012 | Публикации коллоквиума, том 59 | ||||
Джозеф А. Чима. Алекс Мэтисон и Уильям Т. Росс Чима. Алекс Мэтисон и Уильям Т. Росс | Преобразование Коши | 2006 | Математические обзоры и монографии, том 125 | ||||
| Джозеф А. Чима и Уильям Т. Росс | Обратный сдвиг на космическом корабле Харди | 2000 | Математические обзоры и монографии, том 79 | ||||
| Дэвид Кларк | Евклидова геометрия: метод управляемого исследования | 2012 | Библиотека математических кружков ИИГС, том. 9 | ||||
| Адам Клэй и Дейл Рольфсен | Упорядоченные группы и топология | 2016 | Аспирантура по математике, том 176 | ||||
| Джин Клелланд | От Френе до Картана: метод смешивания кадров | 2017 | Аспирантура по математике, том 178 | ||||
| К. Герберт Клеменс | Двумерные геометрии: подход к решению проблем | 2019 | Чистые и прикладные тексты для студентов, том 34 | ||||
| Вон Клименхага и Анатоль Каток | От групп к геометрии и обратно | 2017 | Студенческая математическая библиотека, том 81 | ||||
Джеймс В. Когделл, Генри Х. Ким и М. Рэм Мурти Когделл, Генри Х. Ким и М. Рэм Мурти | Лекции по автоморфным $L$-функциям | 2004 | Монографии Полевого института, том. 20 | ||||
| Анри Коэн и Фредрик Стромберг | Модульные формы | 2017 | Аспирантура по математике, том. 179 | ||||
| Тобиас Хольк Колдинг и Уильям П. Миникоцци II | Курс минимальных поверхностей | 2011 | Аспирантура по математике, том 121 | ||||
| Фриц Колониус и Вольфганг Климанн | Динамические системы и линейная алгебра | 2014 | Аспирантура по математике, том 158 | ||||
| Группа моделирования сложных систем | Моделирование в здравоохранении | 2010 | |||||
| Ален Конн и Матильда Марколли | Некоммутативная геометрия, квантовые поля и мотивы | 2007 | Публикации коллоквиума, том 55 | ||||
Джон Б.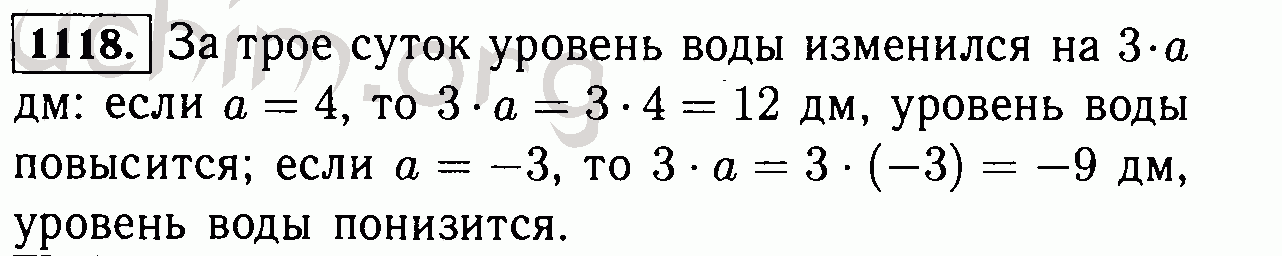 Конвей Конвей | Курс абстрактного анализа | 2013 | Аспирантура по математике, том. 141 | ||||
| Джон Б. Конвей | Математические связи: основной курс | 2010 | |||||
| Мариана Кук | Математики: внешний взгляд на внутренний мир | 2018 | |||||
| Роджер Кук | Самое время: элементарные математические аспекты теории относительности | 2017 | |||||
| Октав Корнеа, Грегори Луптон, Джон Оприа и Даниэль Танре | Люстерник-Шнирельманн Категория | 2003 | Математические обзоры и монографии, том 103 | ||||
| Джеймс Л. Корнетт и Ральф А. Акерман | Расчет для наук о жизни; Подход к моделированию | 2015 | Учебники AMS/MAA | ||||
| Скотт Корри и Дэвид Перкинсон | Делители и песочные кучи | 2018 | |||||
| Кевин Костелло | Перенормировка и эффективная теория поля | 2011 | Математические обзоры и монографии, том 170 | ||||
| Аль Куоко, Кевин Уотерман, Боуэн Каринс, Елена Качоровски и Мишель Мэйнс | Линейная алгебра и геометрия | 2019 | Учебники AMS/MAA, том.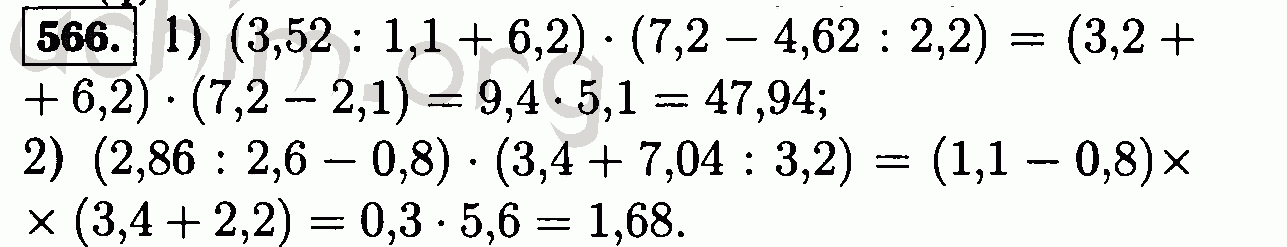 46 46 | ||||
| Дэвид А. Кокс | Применение полиномиальных систем | 2020 | Серия региональных конференций CBMS по математике, нет. 134 | ||||
| Дэвид А. Кокс, Джон Б. Литтл и Генри К. Шенк | Торические разновидности | 2011 | Аспирантура по математике, том 124 | ||||
| Дэвид А. Кокс и Шелдон Кац | Зеркальная симметрия и алгебраическая геометрия | 1999 | Математические обзоры и монографии, том 68 | ||||
| Маргарет Коззенс и Стивен Дж. Миллер | Математика шифрования | 2013 | Математический мир, том. 29 | ||||
| Тереза Креспо и Збигнев Хайто | Алгебраические группы и дифференциальная теория Галуа | 2011 | Аспирантура по математике, том 122 | ||||
| Клифтон Каннингем и Моника Невинс | Оттавские лекции о допустимых представлениях редуктивных $p$-адических групп | 2009 | Монографии Института Филдса, том 26 | ||||
Чарльз У. Кертис Кертис | Пионеры теории репрезентации: Фробениус, Бернсайд, Шур и Брауэр | 1999 | История математики, том. 15 | ||||
| Мел Карри | Математика: рифма и разум | 2018 | Библиотека математических кружков ИИГС, том. 22 | ||||
| Стивен Дейл Катскоки | Введение в алгебраическую геометрию | 2018 | Аспирантура по математике, том 188 | ||||
| Стивен Дейл Катскоки | Разрешение сингулярностей | 2004 | Аспирантура по математике, том 63 | ||||
| Ульрих Депп, Памела Горкин, Эндрю Шаффер и Карл Восс | Нахождение эллипсов: что произведения Бляшке, теорема Понселе и числовой диапазон знают друг о друге | 2018 | Математические монографии Каруса, том 34 | ||||
| Джон П. Д’Анджело | Введение в комплексный анализ и геометрию | 2010 | Чистые и прикладные тексты для студентов, том 12 | ||||
| Анри Дармон | Рациональные точки на модульных эллиптических кривых | 2003 | Серия региональных конференций CBMS по математике, нет.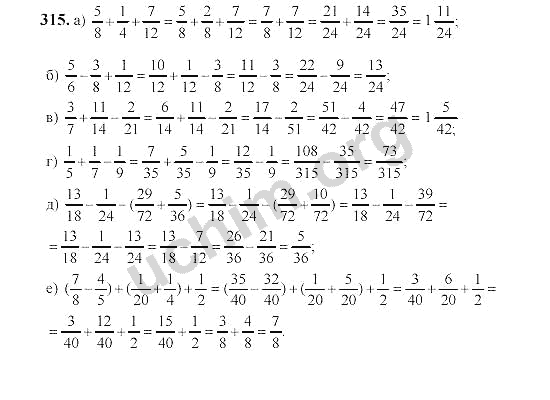 101 101 | ||||
| Роберт Дж. Даверман | Разложения многообразий | 2007 | AMS Chelsea Publishing, vol. 362.Ч | ||||
| Тушар Дас, Дэвид Симмонс и Мариуш Урбански | Геометрия и динамика в гиперболических метрических пространствах Громова | 2017 | Математические обзоры и монографии, вып. 218 | ||||
| Роберт Дж. Даверман и Джерард А. Венема | Вложения в коллекторы | 2009 | Аспирантура по математике, том. 106 | ||||
| Филип Дж. Дэвис | Единство и разобщенность и другие математические очерки | 2015 | |||||
| Оливье Дебарр | Комплексные торы и абелевы многообразия | 2005 | Тексты и монографии SMF/AMS, том. 11 | ||||
| Коррадо де Кончини и Клаудио Прочези | Инвариантная теория матриц | 2017 | Серия университетских лекций, том. 99 99 | ||||
| Ричард Дедекинд и Генрих Вебер | Теория алгебраических функций одной переменной | 2012 | История математики, том. 39 | ||||
| Патрик Дехорной, Иван Дынников, Дейл Рольфсен и Берт Уист | Заказ оплетки | 2008 | Математические обзоры и монографии, вып. 148 | ||||
| Перси Дейфт и Дмитрий Гиоев | Теория случайных матриц: инвариантные ансамбли и универсальность | 2009 | Конспект лекций Куранта, том. 18 | ||||
| Жан-Мари Де Конинк | 1001 Задачи по классической теории чисел | 2007 | |||||
| Жан-Мари Де Конинк | Эти очаровательные числа | 2009 | |||||
| Жан-Мари Де Конинк и Флориан Лука | Аналитическая теория чисел | 2012 | Аспирантура по математике, том. 134 134 | ||||
| Уорвик де Лони и Дейн Фланнери | Теория алгебраического дизайна | 2011 | Математические обзоры и монографии, вып. 175 | ||||
| Б. Н. Делоне | Санкт-Петербургская школа теории чисел | 2005 | История математики, том. 26 | ||||
| Демидов С.С. и Левшин Б.В. | Дело академика Николая Николаевича Лузина | 2016 | История математики, том. 43 | ||||
| Бангминг Дэн, Цзе Ду, Брайан Паршалл и Цзяньпан Ван | Конечномерные алгебры и квантовые группы | 2008 | Математические обзоры и монографии, вып. 150 | ||||
| Франк ден Холландер | Большие отклонения | 2000 | Монографии Института Филдса, том. 14.С | ||||
| Харм Дерксен и Ежи Вейман | Введение в представления Quiver | 2017 | Аспирантура по математике, том. 184 184 | ||||
| Мэтт ДеВос и Дебора А. Кент | Теория игр: игровое введение | 2017 | Студенческая математическая библиотека, вып. 80 | ||||
| Гарольд Г. Даймонд и Вен-Бин Чжан (Чунг Ман Пинг) | Обобщенные числа Берлинга | 2012 | Математические обзоры и монографии, вып. 213 | ||||
| Джо Дистель, Ян Х. Фури и Йохан Сварт | Метрическая теория тензорных произведений: новый взгляд на резюме Гротендика | 2008 | |||||
| Джо Дистель и Анджела Спэлсбери | Радости меры Хаара | 2014 | Аспирантура по математике, том. 150 | ||||
| Шон Динин | Теория вероятностей в финансах: математическое руководство по формуле Блэка-Шоулза, второе издание | 2013 | Аспирантура по математике, том. 70.Р | ||||
| Панделис Додос и Василис Канеллопулос | Теория Рамсея для пространств продуктов | 2016 | Математические обзоры и монографии, вып. 212 212 | ||||
| Сергей Дориченко | Московский математический кружок: наборы задач по неделям | 2012 | Библиотека математических кружков ИИГС, том. 8 | ||||
| Майкл Дорфф, Эллисон Хенрич и Лара Падуэлл | Практическое руководство для математиков по наставничеству студентов | 2019 | Ресурсные материалы для занятий в классе, том. 63 | ||||
| Кристофер Л. Дуглас, Джон Фрэнсис, Андре Г. Энрикес и Майкл А. Хилл | Топологические модульные формы | 2014 | Математические обзоры и монографии, вып. 201 | ||||
| Корнелия Друтю и Михаил Капович | Геометрическая теория групп | 2018 | Публикации коллоквиума, том. 63 | ||||
| Стивен Данбар | Математическое моделирование в экономике и финансах: вероятности, случайные процессы и дифференциальные уравнения | 2019 | Учебники AMS/MAA, том. 49 49 | ||||
| Хавьер Дуоандикоэчеа | Анализ Фурье | 2001 | Аспирантура по математике, том. 29 | ||||
| Питер Дюрен | Приглашение к классическому анализу | 2012 | Чистые и прикладные тексты для студентов, том. 17 | ||||
| Питер Дюрен и Александр Шустер | Пространства Бергмана | 2004 | Математические обзоры и монографии, вып. 100 | ||||
| С.В. Дужин и Б.Д. Чеботаревский | Группы трансформации для начинающих | 2004 | Студенческая математическая библиотека, вып. 25 | ||||
| Уильям Г. Дуайер, Филип С. Хиршхорн, Дэниел М. Кан и Джеффри Х. Смит | Функторы гомотопического предела на модельных категориях и гомотопических категориях | 2004 | Математические обзоры и монографии, вып. 113 | ||||
| Семен Дятлов и Мацей Зворский | Математическая теория резонансов рассеяния | 2019 | Аспирантура по математике, том. 200 200 | ||||
| Гарри Дим | Линейная алгебра в действии, второе издание | 2013 | Аспирантура по математике, том. 78 | ||||
| Дынкин Е.Б. | Супердиффузии и положительные решения нелинейных дифференциальных уравнений в частных производных | 2004 | Серия университетских лекций, том. 34 | ||||
| Вейнан Э., Теджун Ли, Эрик Ванден-Эйнден | Прикладной стохастический анализ | 2010 | Аспирантура по математике, том 199 | ||||
| Вольфганг Эбелинг | Функции нескольких комплексных переменных и их особенности | 2007 | Аспирантура по математике, том 83 | ||||
| Гарольд М. Эдвардс | Высшая арифметика | 2008 | Студенческая математическая библиотека, том 45 | ||||
| Мессуд Эфендиев | Аттракторы для вырожденных уравнений параболического типа | 2013 | Математические обзоры и монографии, том 192 | ||||
| Идо Эфрат | Оценки, заказы и Милнор $K$-теория | 2006 | Математические обзоры и монографии, том 124 | ||||
| Костас Эфтимиу | Введение в функциональные уравнения: теория и стратегии решения задач для математических соревнований и не только | 2011 | Библиотека математических кружков ИИГС, том 6 | ||||
| Юлий Эйдельман, Виталий Мильман и Антонис Цоломитис | Функциональный анализ: введение | 2004 | Аспирантура по математике, том.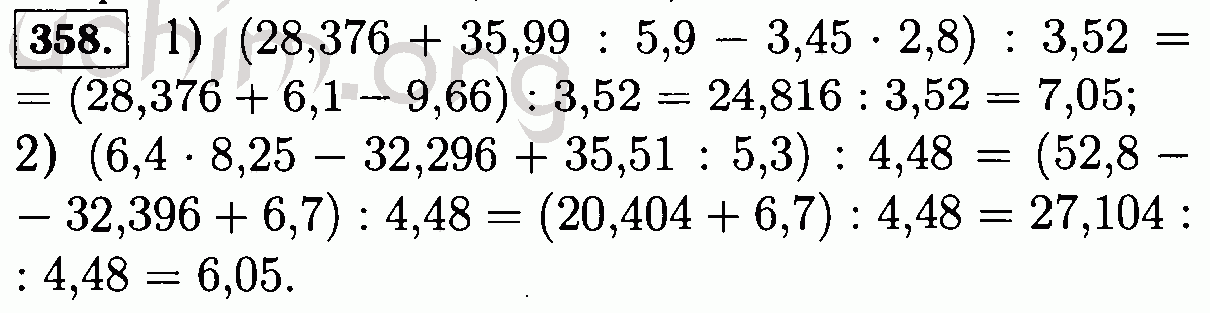 66 66 | ||||
| Альберто Эльдуке и Михаил Кочетов | Оценки простых алгебр Ли | 2013 | Математические обзоры и монографии, вып. 189 | ||||
| Мохамед Эльхамдади и Сэм Нельсон | Quandles: Введение в алгебру узлов | 2015 | Студенческая математическая библиотека, вып. 74 | ||||
| Ричард Эльман, Никита Карпенко и Александр Меркурьев | Алгебраическая и геометрическая теория квадратичных форм | 2008 | Публикации коллоквиума, том. 56 | ||||
| Вивиана Эне и Юрген Херцог | Базы Грёбнера в коммутативной алгебре | 2011 | Аспирантура по математике, том 130 | ||||
| Ласло Эрдёш и Хорнг-Цер Яу | Динамический подход к теории случайных матриц | 2017 | Конспект лекций Куранта, том 28 | ||||
| Грегори Эскин | Лекции по линейным уравнениям с частными производными | 2011 | Аспирантура по математике, том 123 | ||||
| Пьерпаоло Эспозито, Нассиф Гусуб и Юджин Гуо | Математический анализ дифференциальных уравнений в частных производных Моделирование электростатических МЭМС | 2010 | Конспект лекций Куранта, том 20 | ||||
| Павел Иванович Этингоф, Шломо Гелаки, Дмитрий Александрович Никшич, Виктор Острик | Категории тензоров | 2015 | Математические обзоры и монографии, вып. 205 205 | ||||
| Павел Этингоф, Олег Гольберг, Себастьян Хензель, Тянькай Лю, Алекс Швенднер, Дмитрий Вайнтроб и Елена Юдовина | Введение в теорию представлений | 2011 | Студенческая математическая библиотека, том. 59 | ||||
| Лоуренс С. Эванс | Введение в стохастические дифференциальные уравнения | 2013 | |||||
| Лоуренс С. Эванс | Уравнения в частных производных: второе издание | 2010 | Аспирантура по математике, том 19.R | ||||
| Грэм Эверест, Альф ван дер Поортен, Игорь Шпарлински и Томас Уорд | Последовательности повторения | 2003 | Математические обзоры и монографии, том 104 | ||||
| Руй Эксель | Частичные динамические системы, пакеты Fell и приложения | 2017 | Математические обзоры и монографии, том 224 | ||||
| Пьер Эймар и Жан-Пьер Лафон | Число $pi$ | 2004 | |||||
Л. Д. Фаддеев и О.А. Якубовский Д. Фаддеев и О.А. Якубовский | Лекции по квантовой механике для студентов-математиков | 2009 | Студенческая математическая библиотека, том 47 | ||||
| Карл Фейт | Кольца и вещи и прекрасный набор ассоциативной алгебры двадцатого века: второе издание | 2004 | Математические обзоры и монографии, вып. 65.Р | ||||
| Барбара Фантечи, Лотар Готтше, Люк Иллюзи, Стивен Л. Клейман, Нитин Нитсуре, Анджело Вистоли | Фундаментальная алгебраическая геометрия: объяснение FGA Гротендика | 2005 | Математические обзоры и монографии, том 123 | ||||
| Майкл Фарбер | Топология замкнутых форм | 2004 | Математические обзоры и монографии, вып. 108 | ||||
| Джон Фолкнер | Роль неассоциативной алгебры в проективной геометрии | 2014 | Аспирантура по математике, том.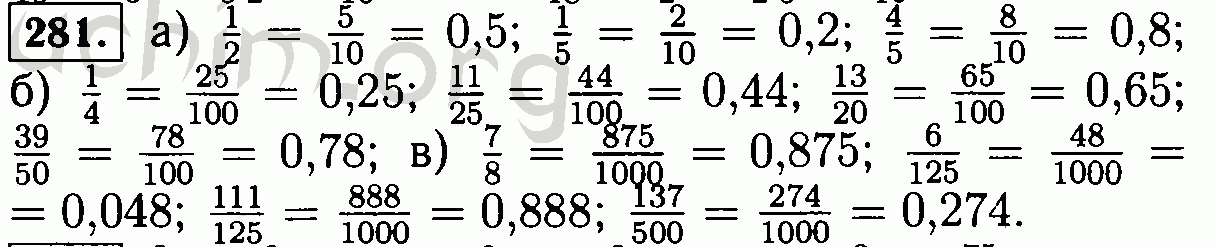 159 159 | ||||
| Роман Федоров, Алексей Белов, Александр Ковальджи и Иван Ященко | Московские математические олимпиады 2000-2005 гг. | 2011 | Библиотека математических кружков ИИГС, том. 7 | ||||
| Роман Федоров, Алексей Белов, Александр Ковальджи и Иван Ященко | Московские математические олимпиады 1993-1999 гг. | 2011 | Библиотека математических кружков ИИГС, том. 4 | ||||
| Джин Фэн и Томас Г. Курц | Большие отклонения для случайных процессов | 2006 | Математические обзоры и монографии, вып. 131 | ||||
| Антонио Фернандес Лопес | Жордановы структуры в алгебрах Ли | 2019 | Математические обзоры и монографии, вып. 240 | ||||
| Феликс Финстер | Принцип фермионного проектора | 2006 | AMS/IP Studies in Advanced Mathematics, vol. 35 35 | ||||
| Патрик Фицпатрик | Расширенное исчисление | 2009 | Чистые и прикладные тексты для студентов, том. 5 | ||||
| Эрика Флапан | Узлы, молекулы и Вселенная: введение в топологию | 2015 | |||||
| Даниэль Флат | Введение в теорию чисел | 2018 | AMS Chelsea Publishing, vol. 384.Х | ||||
| Леопольд Флатто | Теорема Понселе | 2009 | |||||
| Афанассиос С. Фокас, Александр Р. Итс, Андрей А. Капаев и Виктор Ю. Новокшенов | Трансценденты Пенлеве: подход Реймана-Гильберта | 2006 | Математические обзоры и монографии, вып. 128 | ||||
| Джеральд Б. Фолланд | Анализ Фурье и его приложения | 2009 | Чистые и прикладные тексты для студентов, том. 4 | ||||
Джеральд Б. Фолланд Фолланд | Квантовая теория поля: Путеводитель для математиков | 2008 | Математические обзоры и монографии, вып. 149 | ||||
| Фоменко А.Т. и Тужилин Августин | Элементы геометрии и топологии минимальных поверхностей в трехмерном пространстве | 1991 г., переиздано в 2005 г. | Переводы математических монографий, том. 93.С | ||||
| Тимоти Дж. Форд | Сепарабельные алгебры | 2017 | Аспирантура по математике, том. 183 | ||||
| Питер Франкл и Норихидэ Токусигэ | Экстремальные задачи для конечных множеств | 2018 | Студенческая математическая библиотека, вып. 86 | ||||
| Джон Фрэнкс | A (Краткий) Введение в интеграцию Лебега | 2009 | Студенческая математическая библиотека, вып. 48 | ||||
| Эдвард Френкель и Давид Бен-Цви | Алгебры вершин и алгебраические кривые | 2004 | Математические обзоры и монографии, вып. 88.Р 88.Р | ||||
| Бенуа Фресс | Гомотопия операд и групп Гротендика-Тейхмюллера | 2017 | Математические обзоры и монографии, вып. 217 | ||||
| Джон Фридлендер и Хенрик Иванец | Опера де Крибро | 2010 | Публикации коллоквиума, том. 57 | ||||
| Авнер Фридман | Математическая биология | 2018 | Серия региональных конференций CBMS по математике, нет. 127 | ||||
| Курт О. Фридрихс | Математические методы электромагнитной теории | 2014 | Конспект лекций Куранта, том. 25 | ||||
| Роберто Фрихерио | Ограниченные когомологии дискретных групп | 2017 | Математические обзоры и монографии, том. 25 | ||||
| Б. Фристедт, Н. Джейн и Н. Крылов | Фильтрация и прогнозирование: учебник для начинающих | 2007 | Студенческая математическая библиотека, том 38 | ||||
| Дмитрий Фукс и Сергей Табачников | Математический омнибус: тридцать лекций по классической математике | 2007 | |||||
| Кенджи Фукая, Йонг-Гын О, Хироши Охта и Каору Оно | Теория Лагранжевого пересечения Флоера: аномалия и препятствие | 2009 | AMS/IP Studies in Advanced Mathematics, vol.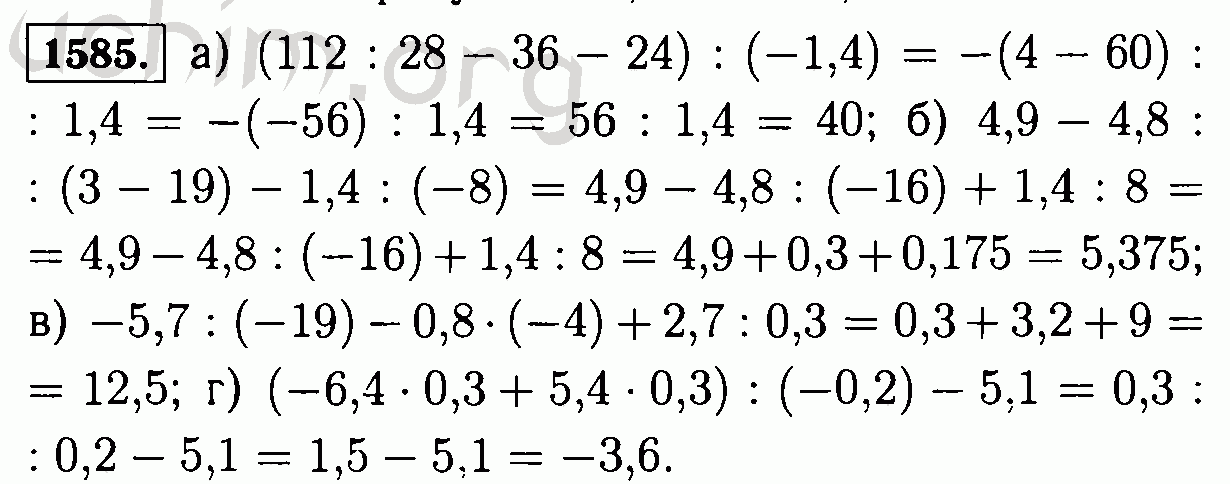 46 46 | ||||
| Гилель Фюрстенберг | Эргодическая теория и фрактальная геометрия | 2014 | Серия региональных конференций CBMS по математике, нет. 120 | ||||
| Микио Фурута | Индекс Теорема. 1 | 2007 | Переводы математических монографий, том 235 | ||||
| Лизл Гал | Математическая галерея | 2017 | |||||
| Деннис Гейтсгори и Никита Розенблюм | Исследование производной алгебраической геометрии, тома I и II | 2017 | Математические обзоры и монографии, вып. 221 | ||||
| Стефан Рамон Гарсия и Стивен Дж. Миллер | 100 лет математических вех: коллекция к столетию Пи Му Эпсилон | 2019 | |||||
| Джулия Гарибальди, Алекс Иосевич и Стивен Сенгер | Проблема расстояния ErdH os | 2011 | Студенческая математическая библиотека, том 56 | ||||
| Томас Гэррити, Ричард Белшофф, Линетт Боос, Райан Браун, Карл Линерт, Дэвид Мерфи, Джуналин Наварра-Мэдсен, Педро Пуатевен, Шон Робинсон, Брайан Снайдер, Кэрин Вернер | Алгебраическая геометрия | 2012 | Студенческая математическая библиотека, том 66 | ||||
| Эдвард Гоган | Введение в анализ | 2009 | Чистые и прикладные тексты для студентов, том.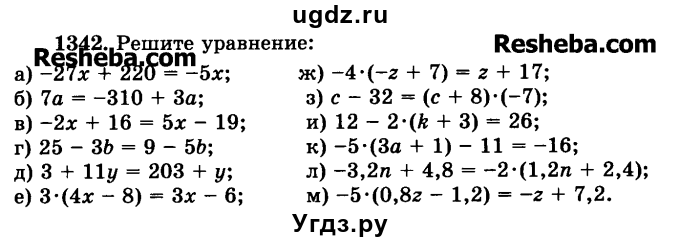 1 1 | ||||
| Фредерик В. Геринг и Кари Хэг | Вездесущий квазидиск | 2012 | Математические обзоры и монографии, вып. 184 | ||||
| Фредерик В. Геринг, Гэвен Дж. Мартин и Брюс П. Палка | Введение в теорию многомерных квазиконформных отображений | 2017 | Математические обзоры и монографии, вып. 216 | ||||
| Михаил Гехтман, Михаил Шапиро и Алек Вайнштейн | Кластерная алгебра и геометрия Пуассона | 2010 | Математические обзоры и монографии, вып. 167 | ||||
| Гельфанд И.М., Шилов Г.Е. | Обобщенные функции, том 1 | 1964 | AMS Chelsea Publishing, vol. 377.Х | ||||
| Гельфанд И.М., Шилов Г.Е. | Обобщенные функции, том 2 | 1968 | AMS Chelsea Publishing, vol. 378.Х | ||||
| Гельфанд И.М., Шилов Г.Е. | Обобщенные функции, том 3 | 1967 | AMS Chelsea Publishing, vol. 379.Х 379.Х | ||||
| Гельфанд И.М., Шилов Г.Е. | Обобщенные функции, том 4 | 1964 | AMS Chelsea Publishing, vol. 380.Х | ||||
| И.М. Гельфанд, М.И. Граев, Н.Я. Виленкин | Обобщенные функции, том 5 | 1966 | AMS Chelsea Publishing, vol. 381.Ч | ||||
| Гельфанд И.М., Граев М.И., Пятецкий-Шапиро И.И. | Обобщенные функции, том 6 | 1969 | AMS Chelsea Publishing, vol. 382.Н | ||||
| Барбара Геллай | Внутренняя природа вещей: жизнь и наука Корнелиуса Ланцоша | 2010 | |||||
| Ларри Дж. Герштейн | Основные квадратичные формы | 2008 | Аспирантура по математике, том. 90 | ||||
| Саугата Гош | Косоортогональные многочлены и теория случайных матриц | 2009 | Серия монографий CRM, том. 28 28 | ||||
| Нассиф Гусуб и Амир Морадифам | Функциональные неравенства: новые перспективы и новые приложения | 2013 | Математические обзоры и монографии, вып. 187 | ||||
| Антонио Джамбруно и Михаил Зайцев | Полиномиальные тождества и асимптотические методы | 2005 | Математические обзоры и монографии, вып. 122 | ||||
| Рик Гиллман и Дэвид Хаусман | Модели конфликта и сотрудничества | 2009 | |||||
| Лаура Гивенталь, Мария Немировская и Илья Захаревич | Математический кружок у залива: темы для 1-5 классов | 2018 | Библиотека математических кружков ИИГС, том. 21 | ||||
| Эли Гласнер | Эргодическая теория через соединение | 2003 | Математические обзоры и монографии, вып. 101 | ||||
| Жиль Годфруа | Приключение чисел | 2004 | Математический мир, том 21 | ||||
Анатолий А. , Гольдберг и Иосиф В. Островский , Гольдберг и Иосиф В. Островский | Распределение значений мероморфных функций | 2008 | Переводы математических монографий, том. 236 | ||||
| Одед Гольдрайх | Учебник по генераторам псевдослучайных чисел | 2010 | Серия университетских лекций, том. 55 | ||||
| Хулио Гонсалес-Диас, Игнасио Гарсия-Хурадо и М. Глория Фиестрас-Жанейро | Вводный курс по математической теории игр | 2010 | Аспирантура по математике, том. 115 | ||||
| Сью Гудман | Начальная топология | 2009 | Чистые и прикладные тексты для студентов, том. 10 | ||||
| Виктор Гудман и Джозеф Стэмпфли | Математика финансов: моделирование и хеджирование | 2009 | Чистые и прикладные тексты для студентов, том. 7 | ||||
| Джудит Р. Гудштейн | Хроники Вольтерры: жизнь и времена выдающегося математика 1860-1819 гг. 40 40 | 2007 | История математики, том. 31 | ||||
| Джудит Р. Гудштейн | Итальянские математики Эйнштейна: Риччи, Леви-Чивита и рождение общей теории относительности | 2018 | |||||
| Сергей Горчинский и Константин Шрамов | Неразветвленная группа Брауэра и ее приложения | 2018 | Переводы математических монографий, том. 246 | ||||
| Дэниел Горенштейн, Ричард Лайонс и Рональд Соломон | Классификация конечных простых групп, номер 6: Часть IV: Особый странный случай | 2004 | Математические обзоры и монографии, вып. 40 | ||||
| Дэниел Горенштейн, Ричард Лайонс и Рональд Соломон | Классификация конечных простых групп, номер 5 | 2002 | Математические обзоры и монографии, вып. 40 | ||||
| Дэниел Горенштейн, Ричард Лайонс и Рональд Соломон | Классификация конечных простых групп, номер 4: часть II, главы 1–4: теоремы единственности | 1999 | Математические обзоры и монографии, вып.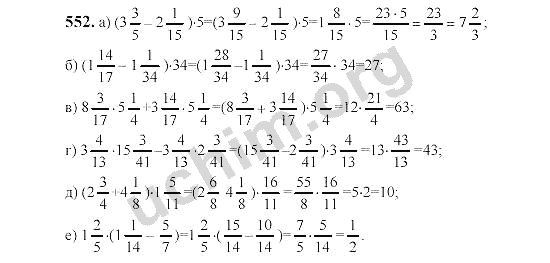 40 40 | ||||
| Дэниел Горенштейн, Ричард Лайонс и Рональд Соломон | Классификация конечных простых групп, номер 3 | 1998 | Математические обзоры и монографии, вып. 40 | ||||
| Дэниел Горенштейн, Ричард Лайонс и Рональд Соломон | Классификация конечных простых групп, номер 2 | 1996 | Математические обзоры и монографии, вып. 40 | ||||
| Дэниел Горенштейн, Ричард Лайонс и Рональд Соломон | Классификация конечных простых групп, номер 1 | 1994 | Математические обзоры и монографии, вып. 40 | ||||
| Эндрю Грэнвилл | Теория чисел раскрыта: мастер-класс | 2019 | |||||
| Эндрю Грэнвилл | Открытие теории чисел: введение | 2019 | |||||
| Джереми Дж. Грей и Карен Хангер Паршалл | Эпизоды истории современной алгебры (1800-1950) | 2007 | История математики, том.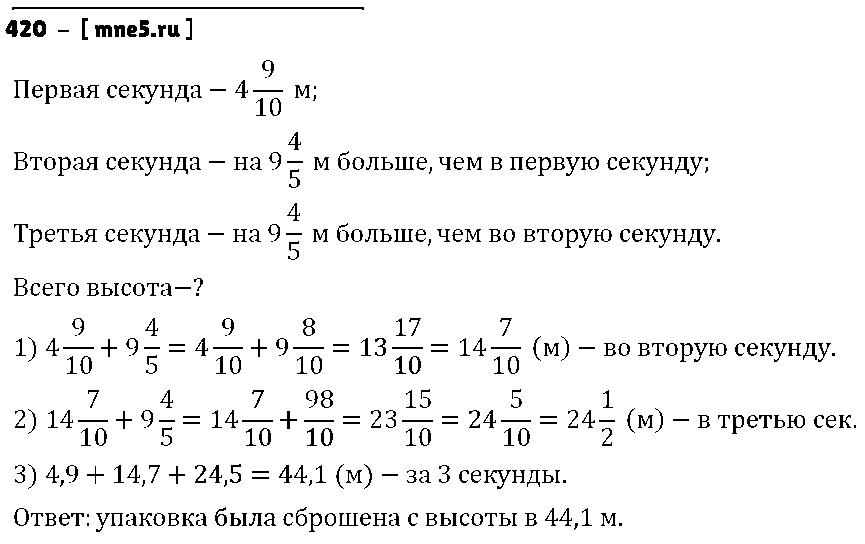 32 32 | ||||
| Джуди Грин и Жанна ЛаДюк | Женщины-первопроходцы в американской математике: кандидаты наук до 1940 года | 2008 | История математики, том. 34 | ||||
| Марк Грин, Филлип Гриффитс, Матта Керр | Теория Ходжа, комплексная теория и теория представлений | 2013 | Серия региональных конференций CBMS по математике, нет. 118 | ||||
| Фредерик П. Гринлиф и Софи Маркес | Линейная алгебра I | 2019 | Конспект лекций Куранта, том. 29 | ||||
| Фредерик П. Гринлиф и Софи Маркес | Линейная алгебра II | 2020 | Конспект лекций Куранта, том. 30 | ||||
| Александр Григорьян | Введение в анализ на графиках | 2018 | Серия университетских лекций, том. 71 | ||||
Чарльз М. Гринстед, Уильям П. Петерсон и Дж. Лори Снелл Лори Снелл | Вероятностные сказки | 2011 | Студенческая математическая библиотека, вып. 57 | ||||
| Марк Гросс | Тропическая геометрия и зеркальная симметрия | 2011 | Серия региональных конференций CBMS по математике, нет. 114 | ||||
| Бранко Грюнбаум | Конфигурации точек и линий | 2009 | Аспирантура по математике, том. 103 | ||||
| Пьер Колмез, Жан-Пьер Серр: | Переписка Гротендика-Серра: двуязычное издание | 2003 | |||||
| Виктор Гийемен и Алан Поллак | Дифференциальная топология | 2010 | AMS Chelsea Publishing, vol. 370.Х | ||||
| Виктор Гиймен и Рейер Сьямар | Свойства выпуклости гамильтоновых групповых действий | 2004 | Серия монографий CRM, том. 26 | ||||
| Элис Гионне | Асимптотика случайных матриц и родственных моделей: использование уравнений Дайсона-Швингера | 2019 | Серия региональных конференций CBMS по математике, нет.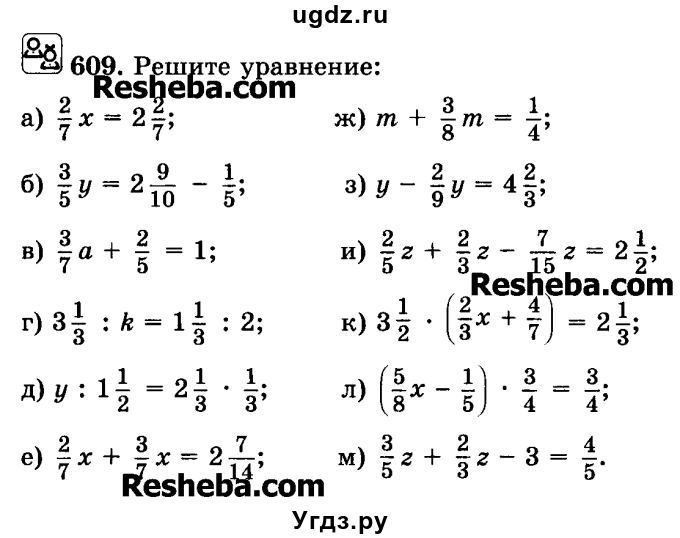 130 130 | ||||
| Роберт С. Ганнинг и Хьюго Росси | Аналитические функции нескольких комплексных переменных | 2009 | AMS Chelsea Publishing, vol. 368.Ч | ||||
| Ларри Гут | Полиномиальные методы в комбинаторике | 2016 | Серия университетских лекций, том. 64 | ||||
| Маркус Хаазе | Функциональный анализ: элементарное введение | 2014 | Аспирантура по математике, том. 156 | ||||
| Жак Адамар | Уроки геометрии. I. Плоская геометрия | 2009 | |||||
| Джеймс Хаглунд | $q,t$-каталонские числа и пространство диагональных гармоник: с приложением по комбинаторике полиномов Макдональда | 2008 | Серия университетских лекций, том. 41 | ||||
| Дегуан Хань, Кери Корнельсон, Дэвид Ларсон и Эрик Вебер | Рамки для бакалавров | 2007 | Студенческая математическая библиотека, том 40 | ||||
| Цин Хань | Нелинейные эллиптические уравнения второго порядка | 2016 | Аспирантура по математике, том 171 | ||||
| Цин Хань | Базовый курс уравнений в частных производных | 2011 | Аспирантура по математике, том 120 | ||||
| Цин Хань и Фанхуа Линь | Эллиптические дифференциальные уравнения с частными производными: второе издание | 2011 | Конспект лекций Куранта, том.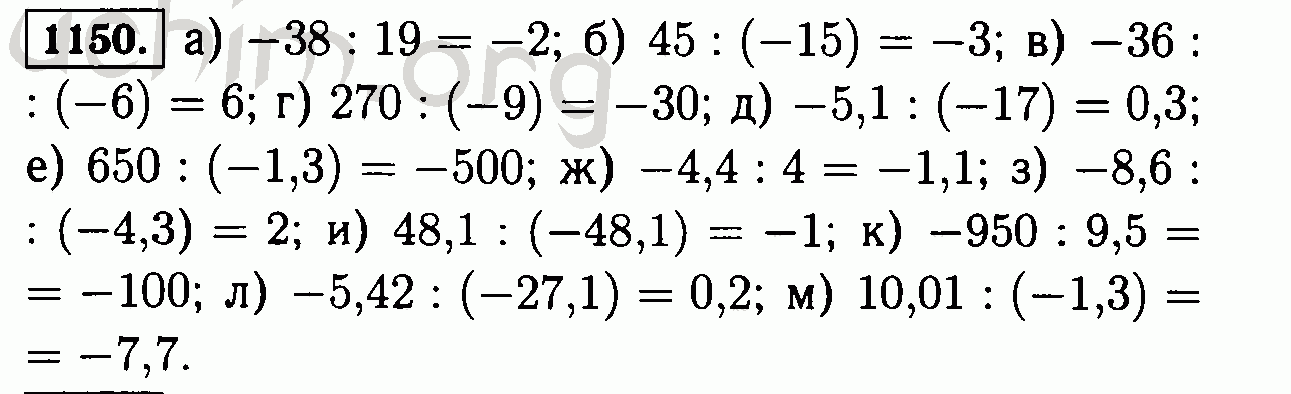 1.Р 1.Р | ||||
| Цин Хань и Цзя-Син Хун | Изометрическое вложение римановых многообразий в евклидово пространство | 2006 | Математические обзоры и монографии, вып. 130 | ||||
| Сариэль Хар-Пелед | Алгоритмы геометрического приближения | 2011 | Математические обзоры и монографии, вып. 173 | ||||
| Шарлотта Ардуэн, Жак Солой и Майкл Сингер | Теории Галуа линейных разностных уравнений: введение | 2016 | Математические обзоры и монографии, вып. 211 | ||||
| Роберт Хардт | Шесть тем на вариацию | 2004 | Студенческая математическая библиотека, том 26 | ||||
| Стюарт П. Гастингс и Дж. Брайс Маклеод | Классические методы в обыкновенных дифференциальных уравнениях: с приложениями к краевым задачам | 2011 | Аспирантура по математике, том 129 | ||||
| Дина Хаунспергер и Роберт Томпсон | 101 Карьера в области математики, четвертое издание | 2019 | Ресурсные материалы для занятий в классе, том. 64 64 | ||||
| Михиль Хазевинкель | Формальные группы и приложения | 2012 | Публикации AMS Chelsea, vol. 375.Х | ||||
| Михиль Хазевинкель, Надежда Губарень и В.В. Кириченко | Алгебры, кольца и модули: алгебры Ли и алгебры Хопфа | 2010 | Математические обзоры и монографии, вып. 168 | ||||
| Иштван Хекенбергер и Ханс-Юрген Шнайдер | Алгебры Хопфа и системы корней | 2020 | Математические обзоры и монографии, вып. 247 | ||||
| А.Я. Хелемский | Квантовый функциональный анализ: некоординатный подход | 2010 | Серия университетских лекций, том 56 | ||||
| А.Я. Хелемский | Лекции и упражнения по функциональному анализу | 2006 | Переводы математических монографий, том 233 | ||||
| Сигурдур Хельгасон | Дифференциальная геометрия, группы Ли и симметричные пространства | 1984 | Аспирантура по математике, том 34 | ||||
| Сигурдур Хельгасон | Геометрический анализ симметричных пространств: второе издание | 2008 | Математические обзоры и монографии, том 39 | ||||
| Сигурдур Хельгасон | Группы и геометрический анализ | 2001 [издание AMS] | Математические обзоры и монографии, вып. 83 83 | ||||
| Джон Хемпель | 3-коллекторный | 2004 | AMS Chelsea Publishing, vol. 349.Х | ||||
| Сэмюэл Херрманн, Петер Имкеллер, Илья Павлюкевич и Дирк Пейтманн | Стохастический резонанс | 2013 | Математические обзоры и монографии, вып. 194 | ||||
| Патрисия Херш, Томас Лам, Павел Пилявский и Виктор Райнер | Математическое наследие Ричарда П. Стэнли | 2016 | |||||
| Рубен Херш | Знакомство с математикой: что мы делаем, когда занимаемся математикой? | 2014 | |||||
| Рубен Херш | Питер Лакс, математик | 2014 | |||||
| Тед Хилл | Раздвигая границы: от Вест-Пойнта до Беркли и дальше | 2017 | |||||
| Мартин Хилс и Франсуа Лозер | Первое путешествие по логике | 2019 | Студенческая математическая библиотека, вып.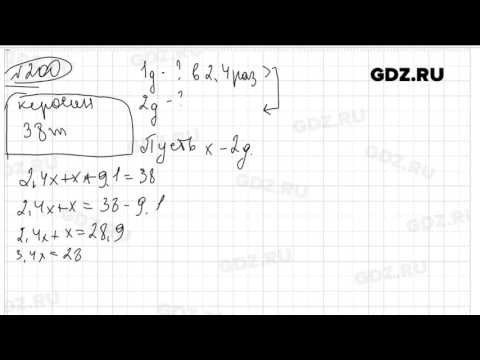 89 89 | ||||
| Джонатан К. Ходж и Ричард Э. Клима | Математика голосования и выборов: практический подход, второе издание | 2018 | Математический мир, том. 30 | ||||
| Джонатан К. Ходж и Ричард Э. Клима | Математика голосования и выборов: практический подход | 2005 | Математический мир, том. 22 | ||||
| Кристофер Холлингс | Математика за железным занавесом: история алгебраической теории полугрупп | 2014 | История математики, том. 41 | ||||
| Кристофер Холлингс и Райнхард Зигмунд-Шультце | Встреча под знаком интеграла?: Конгресс математиков в Осло накануне Второй мировой войны | 2020 | История математики, том. 44 | ||||
| Фрэнк С. Хоппенстедт | Анализ квазистатического состояния дифференциальных, разностных, интегральных и градиентных систем | 2010 | Конспект лекций Куранта, том.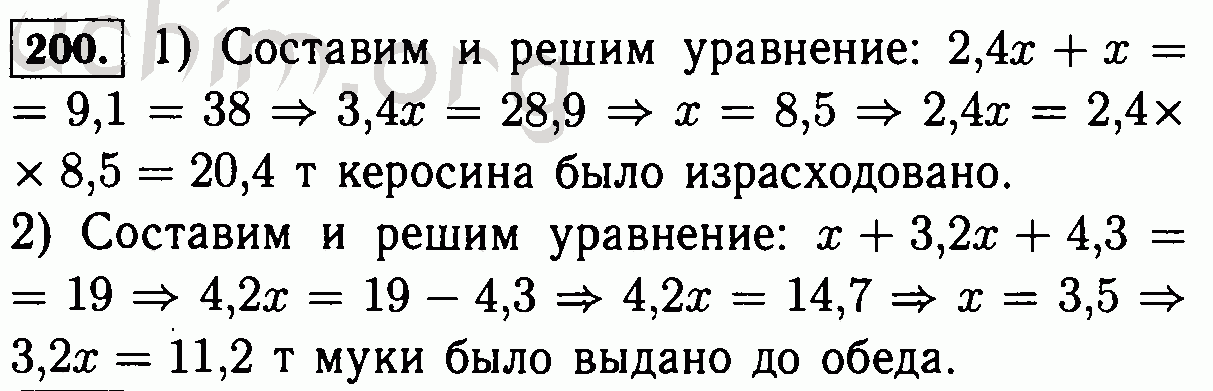 21 21 | ||||
| Фрэнк С. Хоппенстедт | Математические методы анализа сложных заболеваний | 2011 | Конспект лекций Куранта, том. 22 | ||||
| Кентаро Хори, Шелдон Кац, Альбрехт Клемм, Рахул Пандхарипанде, Ричард Томас, Камрун Вафа, Рави Вакил и Эрик Заслоу | Зеркальная симметрия | 2003 | Монография Клэя по математике, том. 1 | ||||
| Фриц Хёрманн | Геометрический и арифметический объем многообразий Симура ортогонального типа | 2014 | Серия монографий CRM, том. 35 | ||||
| Хоссейн Хоссейни Гив | Математический анализ и его сущность | 2016 | Чистые и прикладные тексты для студентов, том. 25 | ||||
| Бернард Хост и Брина Кра | Нильпотентные структуры в эргодической теории | 2018 | Математические обзоры и монографии, вып. 236 236 | ||||
| Сян-дун Хоу | Лекции о конечных полях | 2018 | Аспирантура по математике, том. 190 | ||||
| Дж. Бен Хаф, Манджунат Кришнапур, Юваль Перес и Балинт Вираг | Нули гауссовых аналитических функций и детерминантные точечные процессы | 2009 | Серия университетских лекций, том. 51 | ||||
| Пол Ховард и Джин Э. Рубин | Последствия аксиомы выбора | 1998 | Математические обзоры и монографии, вып. 59 | ||||
| Тим Хсу | Ряды Фурье, преобразования Фурье и функциональные пространства: второй курс анализа | 2020 | Учебники AMS/MAA, том. 59 | ||||
| Клаус Хулек | Элементарная алгебраическая геометрия | 2003 | Студенческая математическая библиотека, вып. 20 | ||||
| Джеймс Э. Хамфрис | Представления полупростых алгебр Ли в категории БГГ $mathscr {O}$ | 2008 | Аспирантура по математике, том. 94 94 | ||||
| Джеймс Э. Хамфрис | Классы сопряженности в полупростых алгебраических группах | 1995 | Математические обзоры и монографии, вып. 43 | ||||
| Бенджамин Хатц | Экспериментальное введение в теорию чисел | 2018 | Чистые и прикладные тексты для студентов, том 31 | ||||
| Патрик Иглесиас-Земмур | Диффеология | 2013 | Математические обзоры и монографии, вып. 195 | ||||
| Рейнхард Иллнер, К. Шон Богун, Саманта МакКоллум и Тея ван Руд | Математическое моделирование: подход к изучению конкретных случаев | 2005 | Студенческая математическая библиотека, том 27 | ||||
| Юлий Ильяшенко и Сергей Яковенко | Лекции по аналитическим дифференциальным уравнениям | 2007 | Аспирантура по математике, том 86 | ||||
| Алексей Иосевич | Вид сверху | 2007 | Студенческая математическая библиотека, том 39 | ||||
И. Мартин Айзекс Мартин Айзекс | Символы разрешимых групп | 2018 | Аспирантура по математике, том. 189 | ||||
| И. Мартин Айзекс | Алгебра: курс для выпускников | 2009 | Аспирантура по математике, том. 100 | ||||
| И. Мартин Айзекс | Теория характеров конечных групп | 2006 | Издательство AMS Chelsea Publishing, том 359.H | ||||
| И. Мартин Айзекс | Теория конечных групп | 2008 | Аспирантура по математике, том 92 | ||||
| И. Мартин Айзекс | Геометрия для студентов | 2009 | Чистые и прикладные тексты для студентов, том. 8 | ||||
| Хосе М. Исидро | Тройные системы Джордана в комплексном и функциональном анализе | 2019 | Математические обзоры и монографии, вып. 243 | ||||
Томас А. Айви и Дж. М. Ландсберг Айви и Дж. М. Ландсберг | Картан для начинающих: дифференциальная геометрия с помощью движущихся рам и внешних дифференциальных систем, второе издание | 2016 | Аспирантура по математике, том 175 | ||||
| Томас А. Айви и Дж. М. Ландсберг | Cartan для начинающих: дифференциальная геометрия с помощью движущихся рам и внешних дифференциальных систем | 2003 | Аспирантура по математике, том 61 | ||||
| Срикант Айенгар, Грэм Дж. Леушке, Антон Лейкин, Клаудия Миллер, Эзра Миллер, Анураг К. Сингх и Ули Вальтер | Двадцать четыре часа локальных когомологий | 2007 | Аспирантура по математике, том 87 | ||||
| Хенрик Иванец и Эммануэль Ковальски | Аналитическая теория чисел | 2004 | Публикации коллоквиума, том. 53 | ||||
| Хенрик Иванец | Лекции о дзета-функции Римана | 2014 | Серия университетских лекций, том. 62 62 | ||||
| Йорг Янель | Группы Брауэра, меры Тамагавы и рациональные точки на алгебраических многообразиях | 2014 | Математические обзоры и монографии, вып. 198 | ||||
| Ханс Нильс Янке | История анализа | 2003 | История математики, том 24 | ||||
| Гэри Р. Дженсен | Арифметика для учителей | 2003 | |||||
| Личжэнь Цзи | Арифметические группы и их обобщения: что, почему и как | 2008 | AMS/IP Исследования по высшей математике, том 43 | ||||
| Шелли М. Джонс | Women Who Count: чествование афроамериканских женщин-математиков | 2019 | |||||
| Палле Э.Т. Йоргенсен | Гармонический анализ | 2018 | Серия региональных конференций CBMS по математике, № 128 | ||||
| Ларс Кэдисон | Новые примеры расширений Фробениуса | 1999 | |||||
| Калюжный-Вербовецкий Дмитрий Сергеевич и Винников Виктор | Основы теории свободных некоммутативных функций | 2014 | Математические обзоры и монографии, вып.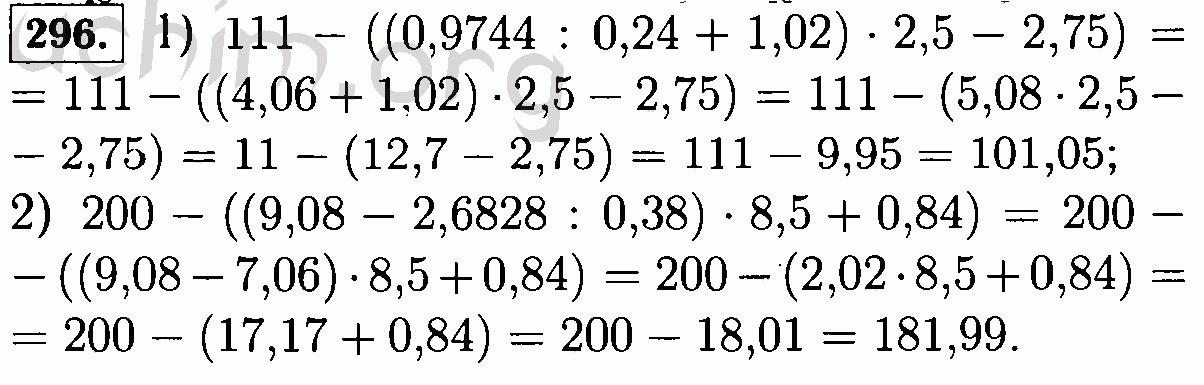 199 199 | ||||
| Дэн Калман, Саша Форгостон и Альберт Гетц | Элементарные математические модели: доступная разработка без исчисления, второе издание | 2019 | Учебники AMS/MAA, том. 50 | ||||
| Эберхард Каниут и Энтони То-Минг Лау | Алгебры Фурье и Фурье-Стилтьеса на локально компактных группах | 2018 | Математические обзоры и монографии, вып. 231 | ||||
| Владимир Кановей | Борелевские отношения эквивалентности | 2008 | Серия университетских лекций, том. 44 | ||||
| Ида Кантор, Иржи Матоусек и Роберт Самал | Математика++ | 2015 | Студенческая математическая библиотека, вып. 75 | ||||
| Гизем Караали и Лили С. Хаджави | Математика для социальной справедливости: ресурсы для занятий в колледже | 2019 | Ресурсные материалы для занятий в классе, Vol.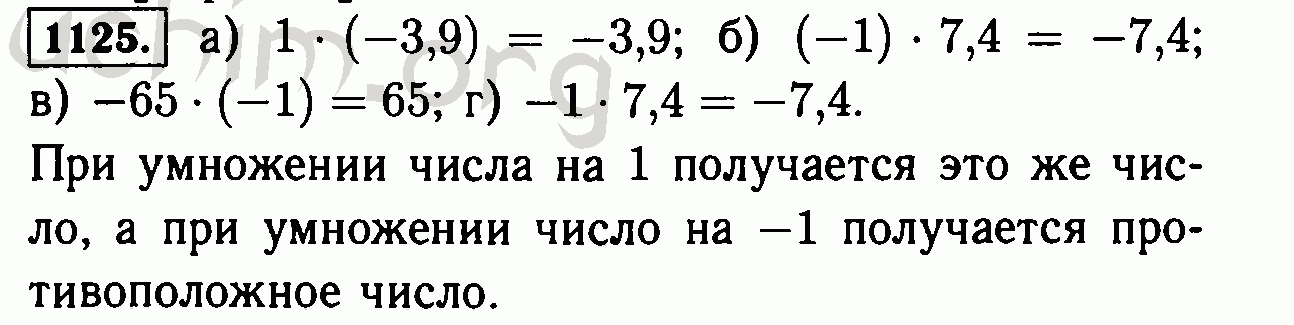 60 60 | ||||
| Анна Карлин и Юваль Перес | Теория игр, живой | 2017 | |||||
| Иоаннис Карацас | Лекции по математике финансов | 1997 | Серия монографий CRM, том. 8 | ||||
| Алекс Касман | Взгляд на теорию солитонов: алгебра и геометрия нелинейных УЧП | 2010 | Студенческая математическая библиотека, вып. 54 | ||||
| Ицхак Кацнельсон и Йонатан Р. Кацнельсон | A (Краткий) Введение в линейную алгебру | 2007 | Студенческая математическая библиотека, вып. 44 | ||||
| Казуя Като, Нобусигэ Курокава и Такеши Сайто | Теория чисел 2: Введение в теорию полей классов | 2011 | Переводы математических монографий, том. 240 | ||||
| Светлана Каток, Алексей Сосинский и Сергей Табачников | МАСС Селекта. Преподавание и изучение высшей математики бакалавриата, Преподавание и изучение высшей математики бакалавриата, | 2003 | |||||
| Каток Светлана | $p$-адический анализ по сравнению с реальным | 2007 | Студенческая математическая библиотека, вып. 37 | ||||
| Анатоль Каток и Вон Клименхага | лекции о поверхностях: (почти) все, что вы хотели о них знать | 2008 | Студенческая математическая библиотека, вып. 46 | ||||
| Михаил Григорьевич Кац | Систолическая геометрия и топология | 2007 | Математические обзоры и монографии, том. 137 | ||||
| Шелдон Кац | Перечислительная геометрия и теория струн | 2006 | Студенческая математическая библиотека, вып. 32 | ||||
| Мэтью Кац и Ян Райманн | Введение в теорию Рамсея: быстрые функции, бесконечность и метаматематика | 2018 | Студенческая математическая библиотека, вып.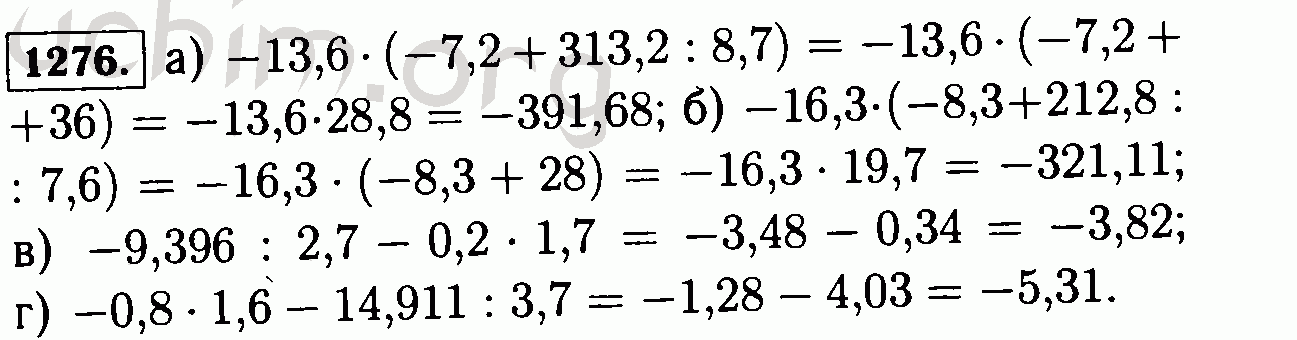 87 87 | ||||
| Такахиро Каваи и Ёсицугу Такей | Алгебраический анализ сингулярного возмущения | 2005 | Переводы математических монографий, том 227 | ||||
| Александр С. Кечрис | Глобальные аспекты эргодических групповых действий | 2010 | Математические обзоры и монографии, том 160 | ||||
| Линда Кин, Ирвин Кра и Руби Э. Родригес | Липман Берс, жизнь в математике | 2015 | |||||
| Кит Кендиг | Никогда не бывает скучно: Хасслер Уитни, пионер математики | 2018 | Спектр, том. 93 | ||||
| Карлос Кениг | Лекции по энергокритическому нелинейному волновому уравнению | 2015 | Серия региональных конференций CBMS по математике, нет. 122 | ||||
| Кацуэй Кенмоцу | Поверхности средней кривизны | 2003 | Переводы математических монографий, том 221 | ||||
| Патрисия Кеншафт | Изменения возможны: истории женщин и меньшинств в математике | 2005 | |||||
Керов С. В. В. | Асимптотическая теория представлений симметричной группы и ее приложения в анализе | 2003 | Переводы математических монографий, том 219 | ||||
| Дмитрий Хавинсон и Эрик Лундберг | Линейные голоморфные уравнения в частных производных и классическая теория потенциала | 2018 | Математические обзоры и монографии, вып. 232 | ||||
| Борис А. Хесин и Сергей Л. Табачников | Арнольд: плыть против течения | 2014 | |||||
| Давар Хошневисан | Вероятность | 2007 | Аспирантура по математике, том. 80 | ||||
| Давар Хошневисан | Анализ стохастических уравнений в частных производных | 2014 | Серия региональных конференций CBMS по математике, нет. 119 | ||||
| Томас Килкелли | Соревнование по силе ARML | 2014 | Библиотека математических кружков ИИГС, №.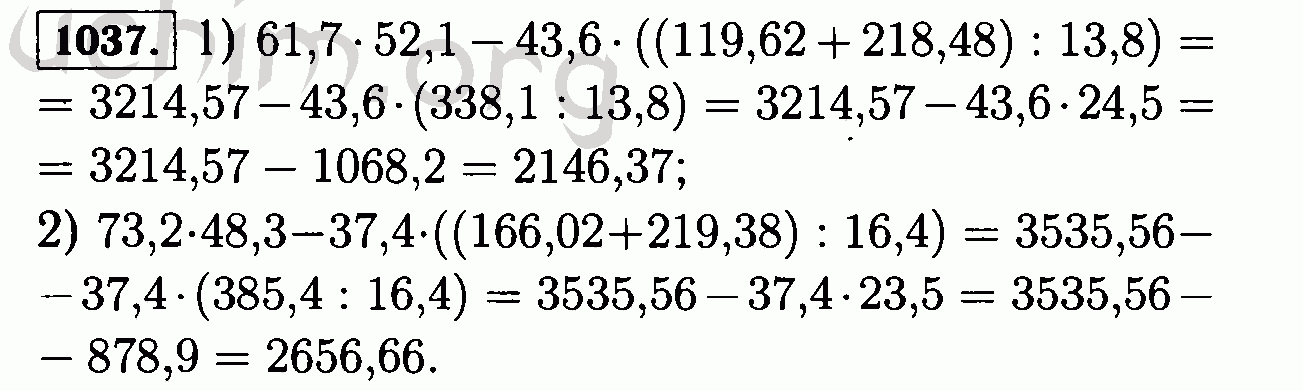 15 15 | ||||
| Кириллов Александр младший | Представления колчанов и разновидности колчанов | 2016 | Аспирантура по математике, том. 174 | ||||
| А.А. Кириллов | Лекции по орбитальному методу | 2004 | Аспирантура по математике, том. 64 | ||||
| Питер Э. Клоден и Мартин Расмуссен | Неавтономные динамические системы | 2011 | Математические обзоры и монографии, вып. 176 | ||||
| Эндрю Найтли и Чарльз Ли | Следы операторов Hecke | 2006 | Математические обзоры и монографии, вып. 133 | ||||
| Роджер Нобель | Введение в математическую теорию волн | 2000 | Студенческая математическая библиотека, вып. 3 | ||||
| Марвин И. Кнопп | Модульные функции в аналитической теории чисел | 1993 | AMS Chelsea Publishing, vol.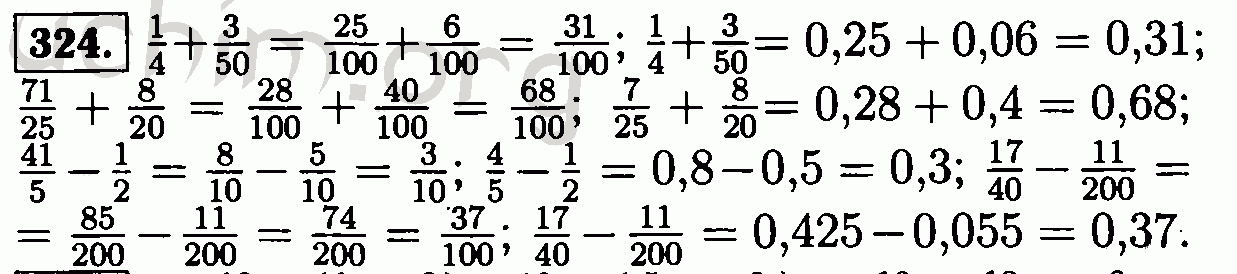 377.Х 377.Х | ||||
| Дональд Э. Кнут | Стабильный брак и его связь с другими комбинаторными задачами | 1997 | CRM Proceedings & Lecture Notes, vol. 10 | ||||
| Александр Колдобский | Анализ Фурье в выпуклой геометрии | 2005 | Математические обзоры и монографии, вып. 116 | ||||
| Александр Колдобский и Владислав Яскин | Интерфейс между выпуклой геометрией и гармоническим анализом | 2008 | Серия региональных конференций CBMS по математике, нет. 108 | ||||
| Акира Коно и Дай Тамаки | Обобщенные когомологии | 2006 | Переводы математических монографий, том 230 | ||||
| Филип Корман | Лекции по дифференциальным уравнениям | 2019 | Учебники AMS/MAA, том. 54 | ||||
| Т. В. Кёрнер | Спутник анализа: второй первый и первый второй курс анализа | 2003 | Аспирантура по математике, том. 62 62 | ||||
| Марк Кот | Первый курс вариационного исчисления | 2014 | Студенческая математическая библиотека, вып. 72 | ||||
| Александр Коростелев и Ольга Коростелева | Математическая статистика: асимптотическая минимаксная теория | 2011 | Аспирантура по математике, том. 119 | ||||
| Димитрис Кукулопулос | Распределение простых чисел | 2019 | Аспирантура по математике, том. 203 | ||||
| Козлов Дмитрий Николаевич | Организованный коллапс: введение в дискретную теорию Морса | 2020 | Аспирантура по математике, том. 207 | ||||
| Стивен Г. Кранц | Учебник по математическому письму: исследование того, как ваши идеи должны быть записаны, набраны, опубликованы, прочитаны и оценены | 2017 | |||||
Стивен Г. Кранц Кранц | Руководство по выживанию математика: аспирантура и раннее развитие карьеры | 2003 | |||||
| Стивен Г. Кранц | Математическое издание: Путеводитель | 2005 | |||||
| Стивен Г. Кранц | Выживание математика: от стажировки до почетного звания | 2009 | |||||
| Стивен Г. Кранц и Роберт Грин | Теория функций одной комплексной переменной, третье издание | 2006 | Аспирантура по математике, том. 40.Р | ||||
| Матиас Крек | Дифференциальная алгебраическая топология | 2010 | Аспирантура по математике, том. 110 | ||||
| Гершон Кресин и Владимир Мазья | Принципы максимума и точные константы для решений эллиптических и параболических систем | 2012 | Математические обзоры и монографии, вып. 183 183 | ||||
| Крылов Н.В. | Лекции по эллиптическим и параболическим уравнениям в пространствах Соболева | 2008 | Аспирантура по математике, том. 96 | ||||
| Крылов Н.В. | Соболев и решения по вязкости для полностью нелинейных эллиптических и параболических уравнений | 2008 | Математические обзоры и монографии, вып. 233 | ||||
| Вольфганг Кюнель | Дифференциальная геометрия: кривые — поверхности — коллекторы, второе издание | 2006 | |||||
| Эрнст Кунц, Дэвид А. Кокс и Алисия Дикенштейн | Вычеты и двойственность для проективных алгебраических многообразий | 2008 | Серия университетских лекций, том. 47 | ||||
| Жан-Пьер Лабес и Жан-Лу Вальдспургер | La Formula des Traces Tordue d’Après le Пятничный утренний семинар | 2013 | Серия монографий CRM, том. 31 31 | ||||
| Л. Лафорг | Хирургия травы | 2003 | Серия монографий CRM, том 19 | ||||
| Дуглас Дж. Лафонтен и Уильям В. Менаско | Слоения кос в топологии малой размерности | 2017 | Аспирантура по математике, том. 185 | ||||
| Джеффри С. Лагариас | Окончательное испытание: задача $3x+1$ | 2010 | |||||
| Тамара Лакинс | Инструменты математического мышления | 2016 | Чистые и прикладные тексты для студентов, том. 26 | ||||
| Т. Ю. Лам | Введение в квадратичные формы над полями | 2005 | Аспирантура по математике, том. 67 | ||||
| Эвелин Лэмб | Страница календаря AMS в день | 2019 | |||||
| Брюс М. Лэндман и Аарон Робертсон | Теория Рамсея о целых числах, второе издание | 2014 | Студенческая математическая библиотека, вып. 73 73 | ||||
| Брюс М. Лэндман и Аарон Робертсон | Теория Рамсея о целых числах | 2003 | Студенческая математическая библиотека, вып. 24 | ||||
| Дж. М. Ландсберг | Тензоры: геометрия и приложения | 2011 | Аспирантура по математике, том. 128 | ||||
| Дж. М. Ландсберг | Тензоры Асимптотическая геометрия и разработки 2016—2018 | 2019 | Серия региональных конференций CBMS по математике, нет. 132 | ||||
| Дэвид Лэнн | Проблема волн на воде | 2013 | Математические обзоры и монографии, вып. 188 | ||||
| Чарльз Лански | Понятия абстрактной алгебры | 2005 | Брукс/Коул: Cengage Learning, vol. 14 | ||||
| Мишель Л. Лапидус | В поисках нулей Римана: струны, фрактальные мембраны и некоммутативное пространство-время | 2008 | |||||
Пол Б. Ларсон и Джиндрих Заплетал Ларсон и Джиндрих Заплетал | Геометрическая теория множеств | 2020 | Математические обзоры и монографии, том. 248 | ||||
| Пол Б. Ларсон | Стационарная башня: заметки о курсе У. Хью Вудина | 2004 | Серия университетских лекций, том. 32 | ||||
| Грегори Ф. Лоулер | Конформно-инвариантные процессы на плоскости | 2005 | Математические обзоры и монографии, вып. 114 | ||||
| Грегори Ф. Лоулер | Случайное блуждание и уравнение теплопроводности | 2010 | Студенческая математическая библиотека, вып. 55 | ||||
| Питер Д. Лакс и Лоуренс Зальцман | Комплексные доказательства реальных теорем | 2011 | Серия университетских лекций, том. 58 | ||||
| Арне Леде | Проблемы со встраиванием типа Brauer | 2005 | Монографии Института Филдса, том. 21 21 | ||||
| Дэн А. Ли | Геометрическая теория относительности | 2009 | Аспирантура по математике, том. 201 | ||||
| Джеффри М. Ли | Многообразия и дифференциальная геометрия | 2009 | Аспирантура по математике, том. 107 | ||||
| Джон М. Ли | Аксиоматическая геометрия | 2013 | Чистые и прикладные тексты для студентов, том. 21 | ||||
| Кьюнг Бай Ли и Фрэнк Рэймонд | Волокна Зайферта | 2010 | Математические обзоры и монографии, вып. 166 | ||||
| Дж. Л. Леман | Теория квадратичных чисел: приглашение к алгебраическим методам в высшей арифметике | 2019 | Математические изложения Дольчиани, том. 52 | ||||
| Олли Лехто | Ларс Альфорс — На вершине математики | 2015 | |||||
| Джованни Леони | Первый курс в пространствах Соболева | 2009 | Аспирантура по математике, том. 105 105 | ||||
| Джованни Леони | Первый курс по пространствам Соболева, второе издание | 2017 | Аспирантура по математике, том. 181 | ||||
| Эммануэль Лезинь | Орел или решка: введение в предельные теоремы теории вероятностей | 2005 | Студенческая математическая библиотека, вып. 28 | ||||
| Дэвид А. Левин и Юваль Перес, при участии Элизабет Л. Уилмер | Цепи Маркова и времена смешивания, второе издание | 2017 | |||||
| Дэвид А. Левин, Юваль Перес и Элизабет Л. Уилмер | Цепи Маркова и время перемешивания | 2009 | |||||
| Марк Леви | Классическая механика с вариационным исчислением и оптимальным управлением: интуитивно понятное введение | 2014 | Студенческая математическая библиотека, вып. 69 | ||||
Грэм Дж. Леушке и Роджер А.. Виганд Леушке и Роджер А.. Виганд | Представления Коэна-Маколея | 2012 | Математические обзоры и монографии, вып. 181 | ||||
| Лоуренс С. Леви и Дж. Крис Робсон | Наследственные неотерианские первичные кольца и идеализаторы | 2011 | Математические обзоры и монографии, вып. 174 | ||||
| Вен-Цзин Винни Ли | Дзета- и $L$-функции в теории чисел и комбинаторике | 2019 | Серия региональных конференций CBMS по математике, № 129 | ||||
| Эллиот Х. Либ и Майкл Лосс | Анализ: второе издание | 2001 | Аспирантура по математике, том 14 | ||||
| Мартин В. Либек и Гэри М. Зейтц | Унипотентные и нильпотентные классы в простых алгебраических группах и алгебрах Ли | 2012 | Математические обзоры и монографии, вып. 180 9*$ Алгебры | 2017 | Чистые и прикладные тексты для студентов, том 29 | ||
Томас Л. Линдстром Линдстром | Пространства: Введение в реальный анализ | 2017 | Чистые и прикладные тексты для студентов, вып. 124 | ||||
| Ю. Н. Линьков | Лекции по математической статистике: части 1 и 2 | 2005 | Переводы математических монографий, том 229 | ||||
| Мартин Лоренц | Экскурсия по теории репрезентации | 2018 | Аспирантура по математике, том 193 | ||||
| Ласло Ловаш | Большие сети и ограничения графа | 2012 | Публикации коллоквиума, том. 60 | ||||
| Ласло Ловаш | Комбинаторные задачи и упражнения: второе издание | 2007 | AMS Chelsea Publishing, vol. 361.Н | ||||
| Ласло Ловаш | Теория соответствия | 2009 | AMS Chelsea Publishing, vol. 367.Х | ||||
| Альваро Лосано-Робледо | Эллиптические кривые, модульные формы и их L-функции | 2011 | Студенческая математическая библиотека, вып. 58 58 | ||||
| Альваро Лосано-Робледо | Теория чисел и геометрия: введение в арифметическую геометрию | 2019 | Чистые и прикладные тексты для студентов, том. 35 | ||||
| Тянь Ма и Шоухинг Ван | Геометрическая теория течений несжимаемой жидкости с приложениями к гидродинамике | 2005 | Математические обзоры и монографии, вып. 119 | ||||
| Барбара Д. МакКлуер, Пол С. Бурдон и Томас Л. Крит | Дифференциальные уравнения: методы, теория и приложения | 2019 | |||||
| Джон М. Маккей и Джереми Т. Тайсон | Конформное измерение: теория и применение | 2010 | Серия университетских лекций, том. 54 | ||||
| Дана Маккензи | Что происходит в математических науках, том 9 | 2013 | Что происходит в математических науках, том. 9 9 | ||||
| Дана Маккензи | Что происходит в математических науках, том 8 | 2011 | Что происходит в математических науках, том. 8 | ||||
| Дана Маккензи | Что происходит в математических науках, том 7 | 2009 | Что происходит в математических науках, том. 7 | ||||
| Дана Маккензи и Барри Сипра | Что происходит в математических науках, том 6 | 2007 | Что происходит в математических науках, том. 6 | ||||
| Диана Маклаган и Бернд Штурмфельс | Введение в тропическую геометрию | 2015 | Аспирантура по математике, том 161 | ||||
| Магарил-Ильяев Г.Г., Тихомиров В.М. | Выпуклый анализ: теория и приложения | 2003 | Переводы математических монографий, том. 222 | ||||
| Казем Махдави и Дебора Кословер | Достижения в области квантовых вычислений | 2009 | Современная математика, том. 482 482 | ||||
| Эндрю Дж. Майда, Рафаил В. Абрамов и Маркус Дж. Гроте | Теория информации и стохастика для многомасштабных нелинейных систем 9*$-Модули | 2005 | Переводы математических монографий, том. 226 | ||||
| Марченко Владимир Александрович | Sturm Liouville Operators and Applications: Revised Edition | 2011 | AMS Chelsea Publishing, vol. 373.Х | ||||
| Владимир Марченко и Виктор Славин | Обратные задачи теории малых колебаний | 2018 | Переводы математических монографий, том. 247 | ||||
| Матильда Марколли | Арифметическая некоммутативная геометрия | 2005 | Серия университетских лекций, том. 33 | ||||
| Мартин Маркл | Теория деформации алгебр и их диаграммы | 2012 | Серия региональных конференций CBMS по математике, нет. 116 > 116 > | ||||
| Мюррей Маршалл | Положительные многочлены и суммы квадратов | 2008 | Математические обзоры и монографии, вып. 146 | ||||
| Иржи Матоусек | Тридцать три миниатюры | 2010 | Студенческая математическая библиотека, вып. 53 | ||||
| Дж. П. Мэй и Дж. Сигурдссон | Параметризованная теория гомотопий | 2006 | Математические обзоры и монографии, вып. 132 | ||||
| Владимир Мазья и Юрген Россманн | Эллиптические уравнения в многогранных областях | 2010 | Математические обзоры и монографии, вып. 162 | ||||
| Владимир Мазья и Гюнтер Шмидт | Приблизительное приближение | 2007 | Математические обзоры и монографии, вып. 141 | ||||
| Карло Мацца, Владимир Воеводский и Чарльз Вайбель | Конспект лекций по мотивным когомологиям | 2006 | Монографии Клэя по математике, том. 2> 2> | ||||
| Дуса Макдафф и Дитмар Саламон | $J$-голоморфные кривые и симплектическая топология, второе издание | 2012 | Публикации коллоквиума, том. 52.Р | ||||
| Генри П. Маккин | Стохастические интегралы | 2005 | AMS Chelsea Publishing, vol. 353.Х | ||||
| Ральф Н. Маккензи, Джордж Ф. Макналти и Уолтер Ф. Тейлор | Алгебры, Решетки, Многообразия | 1987 | AMS Chelsea Publishing, vol. 383.Х | ||||
| Уильям Х. Микс и Хоакин Перес | Обзор классической теории минимальных поверхностей | 2012 | Серия университетских лекций, том. 60 | ||||
| Эккарт Менцлер-Тротт | Потерянный гений логики: жизнь Герхарда Генцена | 2007 | История математики, том. 33 | ||||
| Майк Местертон-Гиббонс | Введение в теоретико-игровое моделирование: второе издание | 2001 | Студенческая математическая библиотека, вып. 11 11 | ||||
| Майк Местертон-Гиббонс | Учебник по вариационному исчислению и теории оптимального управления | 2009 | Студенческая математическая библиотека, вып. 50 | ||||
| Майк Местертон-Гиббонс | Введение в теоретико-игровое моделирование: третье издание | 2019 | Чистые и прикладные тексты для студентов, том. 37 | ||||
| Кристиан Мейер | Модульные тройники Калаби-Яу | 2005 | Монографии Института Филдса, том. 22 | ||||
| Питер В. Мичор | Разделы дифференциальной геометрии | 2008 | Аспирантура по математике, том. 93 | ||||
| Питер Д. Миллер | Прикладной асимптотический анализ | 2006 | Аспирантура по математике, том. 75 96$ | 2015 | |||
| Павел Мнев | Квантовая теория поля: формализм Баталина-Вилковиского и его приложения | 2019 | Серия университетских лекций, том. 72 72 | ||||
| Александр Молев | Янгианы и классические алгебры Ли | 2007 | Математические обзоры и монографии, вып. 143 | ||||
| Александр Молев | Операторы Сугавары для классической алгебры Ли | 2018 | Математические обзоры и монографии, вып. 229 | ||||
| Виктор Х. Молл | Числа и функции | 2012 | Студенческая математическая библиотека, вып. 65 | ||||
| Хью Л. Монтгомери | Ранний анализ Фурье | 2014 | Чистые и прикладные тексты для студентов, том. 22 | ||||
| Себастьян Монтьель и Антонио Рос | Кривые и поверхности: второе издание | 2009 | Аспирантура по математике, том. 69.Р | ||||
| Эмили Х. Мур и Харриет С. Полласек | Наборы разностей: соединение алгебры, комбинаторики и геометрии | 2013 | Студенческая математическая библиотека, вып. 67 67 | ||||
| Джон Дуглас Мур | Введение в глобальный анализ | 2017 | Аспирантура по математике, том. 187 | ||||
| Фабьен Морель | Гомотопическая теория схем | 2006 | Тексты и монографии SMF/AMS, том. 12 | ||||
| Джон В. Морган и Ган Тиан | Гипотеза геометризации | 2014 | Монографии Клэя по математике, том. 5 Джон В. Морган | ||||
| Кенджи Фукая, Доминик Джойс, Дуса Макдафф и Мохаммад Фараджзаде Техрани | Виртуальные фундаментальные циклы в симплектической топологии | 2019 | Математические обзоры и монографии, вып. 237 | ||||
| Карлос Хулио Морено | Расширенная аналитическая теория чисел: L-функции | 2005 | Математические обзоры и монографии, вып. 115 | ||||
Дэвид С. Морган, Дениз М. Халверсон, Спенсер П. Мэглби, Терри С. Бейтман, Ларри Л. Хауэлл Мэглби, Терри С. Бейтман, Ларри Л. Хауэлл | Y Оригами?: Исследования в складывании | 2017 | |||||
| Хитоши Мориёси и Тошикадзе Нацумэ | Алгебра операторов и геометрия | 2008 | Переводы математических монографий, том. 237 | ||||
| Карлос Хулио Морено | Расширенная аналитическая теория чисел: L-функции | 2005 | Математические обзоры и монографии, вып. 115 | ||||
| Фрэнк Морган | Реальный анализ | 2005 | |||||
| Фрэнк Морган | Реальный анализ и приложения: включая ряды Фурье и вариационное исчисление | 2005 | |||||
| Джон В. Морган и Фредерик Цз-Хо Фонг | Течение Риччи и геометризация трехмерных многообразий | 2010 | Серия университетских лекций, том. 53 | ||||
| Джон Морган и Ган Тиан | Поток Риччи и гипотеза Пуанкаре | 2007 | Монография Клэя по математике, том. 3 3 | ||||
| Ацуши Мориваки | Аракелов Геометрия | 2014 | Переводы математических монографий, том. 244 | ||||
| Джеймс Морроу и Кунихико Кодаира | Комплексные коллекторы | 2006 | |||||
| Яннис Н. Мошовакис | Описательная теория множеств: второе издание | 2009 | Математические обзоры и монографии, вып. 155 | ||||
| Гэри Л. Маллен и Карл Маммерт | Конечные поля и приложения | 2007 | Студенческая математическая библиотека, том 41 | ||||
| Джейкоб П. Мурре, Ян Нагель и Крис А. М. Питерс | Лекции по теории чистых мотивов | 2013 | Серия университетских лекций, том. 61 | ||||
| М. Рэм Мерти и Брэндон Фодден | Десятая проблема Гильберта: введение в логику, теорию чисел и вычислимость | 2019 | Студенческая математическая библиотека, вып. 88 88 | ||||
| Ян М. Муссон | Супералгебры Ли и обертывающие алгебры | 2012 | Аспирантура по математике, том. 131 | ||||
| Мясников Алексей Григорьевич, Шпильрайн Владимир и Ушаков Александр Владимирович | Некоммутативная криптография и сложность теоретико-групповых задач | 2011 | Математические обзоры и монографии, вып. 177 | ||||
| Дэвид Начин | Судоку с элементами математики: варианты головоломок всех уровней сложности | 2019 | |||||
| Николай Надирашвили, Владимир Ткачев и Сергей Владуц | Нелинейные эллиптические уравнения и неассоциативные алгебры | 2014 | Математические обзоры и монографии, вып. 200 | ||||
| С.Р. Нагпаул и С.К. Джейн | Темы прикладной абстрактной алгебры | 2005 | Брукс/Коул: Cengage Learning, vol. 15 15 | ||||
| Владимир Некрашевич | Самоподобные группы | 2005 | Математические обзоры и монографии, вып. 117 | ||||
| Роджер Нельсен | Самородки теории чисел: визуальный подход | 2018 | Ресурсные материалы для занятий в классе, том. 55 | ||||
| Гейл С. Нельсон | Удобное введение в меру Лебега и интегрирование | 2015 | Студенческая математическая библиотека, вып. 78 | ||||
| Джон Ной | Сингулярное возмущение в физических науках | 2015 | Аспирантура по математике, том. 167 | ||||
| Мара Д. Нойзель | Теория инвариантов | 2007 | Студенческая математическая библиотека, вып. 36 | ||||
| Мара Д. Нойзел и Ларри Смит | Инвариантная теория конечных групп | 2002 | Математические обзоры и монографии, вып. 94 94 | ||||
| Збигнев Нитецкий | Исчисление в 3D: геометрия, векторы и многомерное исчисление | 2018 | Учебники AMS/MAA, том. 40 | ||||
| Дмитрий Ногин, Михаил А. Цфасман и Серж Владуц | Коды алгебраической геометрии: расширенные главы | 2019 | Математические обзоры и монографии, вып. 238 | ||||
| Дзюндзиро Ногучи | Введение в комплексный анализ | 1998 | Переводы математических монографий, том 168 | ||||
| Вирджиния В. Нунбург | Дифференциальные уравнения: от исчисления к динамическим системам, второе издание | 2019 | Учебники AMS/MAA, том. 43 | ||||
| Масатоши Ноуми | Уравнения Пенлеве через симметрию | 2004 | Переводы математических монографий, том 223 | ||||
И.Я. Новиков, В.Ю. Протасов, М. А. Скопина А. Скопина | Теория вейвлетов | 2011 | Переводы математических монографий, том. 239 | ||||
| С.П. Новиков и И.А. Тайманов | Современные геометрические структуры и поля | 2006 | Аспирантура по математике, том. 71 | ||||
| Дэвид Нуаларт | Исчисление Маллявена и его приложения | 2009 | Серия региональных конференций CBMS по математике, нет. 110 | ||||
| Александр Олевский и Александр Улановский | Функции с отключенным спектром: выборка, интерполяция, преобразование | 2016 | Серия университетских лекций, том. 65 | ||||
| Мартин Олссон | Алгебраические пространства и стеки | 2016 | Публикации коллоквиума, том. 62 | ||||
| Кен Оно | Сеть модульности: арифметика коэффициентов модульных форм и рядов $q$ | 2003 | Серия региональных конференций CBMS по математике, нет. 102 102 | ||||
| Стив Удо | Теория постоянства: от колчанных представлений к анализу данных | 2015 | Математические обзоры и монографии, вып. 209 | ||||
| Сергей Овчинников | Системы счисления: введение в алгебру и анализ | 2015 | Чистые и прикладные тексты для студентов, том. 23 | ||||
| Мариус Оверхолд | Курс аналитической теории чисел | 2014 | Аспирантура по математике, том. 160 | ||||
| Петер С. Озват, Андраш И. Стипшиц и Золтан Сабот | Гомология сетки для узлов и связей | 2015 | Математические обзоры и монографии, вып. 208 | ||||
| Авторы Янош Пах и Миха Шарир | Комбинаторная геометрия и ее приложения к алгоритмам: лекции Alcala | 2009 | Математические обзоры и монографии, вып. 152 | ||||
Виктор М. Бухштабер и Тарас Э. Панов Бухштабер и Тарас Э. Панов | Торическая топология | 2015 | Математические обзоры и монографии, вып. 204 | ||||
| К. Р. Партасарати | Вероятностные меры в метрических пространствах | 2005 | AMS Chelsea Publishing, vol. 352.Х | ||||
| Дональд С. Пассман | Курс теории колец | 2004 | AMS Chelsea Publishing, vol. 348.Х | ||||
| Леонид Пастур и Мария Щербина | Распределение собственных значений больших случайных матриц | 2011 | Математические обзоры и монографии, вып. 171 | ||||
| Сильви Пайча | Регуляризованные интегралы, суммы и следы: аналитическая точка зрения | 2012 | Серия университетских лекций, том. 59 | ||||
| Джером К. Перкус | Математические модели в биологии развития | 2012 | Конспект лекций Куранта, том. 23 23 | ||||
| Джером К. Перкус и Стивен Чайлдресс | Математические методы в иммунологии | 2015 | Конспект лекций Куранта, том. 26 | ||||
| Канишка Перера, Рави П. Агарвал и Донал О’Реган | Теоретико-Морсовские аспекты операторов типа $p$-лапласиана | 2010 | Математические обзоры и монографии, вып. 161 | ||||
| Мария Кристина Перейра и Лесли А. Уорд | Гармонический анализ: от Фурье к вейвлетам | 2012 | Студенческая математическая библиотека, вып. 63 | ||||
| Пестов Владимир | Динамика бесконечномерных групп: феномен Рэмси-Дворецкого-Мильмана | 2006 | Серия университетских лекций, том. 40 | ||||
| Аршак Петросян, Генрик Шахголян и Нина Николаевна Уральцева | Регулярность свободных границ в задачах типа препятствия | 2012 | Аспирантура по математике, том. 136 136 | ||||
| Миодраг С. Петкович | Знаменитые загадки великих математиков | 2009 | |||||
| Марк Пинский | Уравнения с частными производными и краевые задачи с приложениями: третье издание | 2011 | Чистые и прикладные тексты для студентов, том. 15 | ||||
| Марк Пинский | Введение в анализ Фурье и вейвлеты | 2009 | Аспирантура по математике, том. 102 | ||||
| Роберт Платон | Краткая числовая математика | 2003 | Аспирантура по математике, том. 57 | ||||
| Тейн Пламбек и Томас Рокицки | Баррикады и септоку: документы в честь Мартина Гарднера и Тома Роджерса | 2020 | Спектр, том. 100 | ||||
| Дж. М. Плоткин | Hausdorff на заказанных наборах | 2005 | История математики, том. 25 25 | ||||
| Анри Пуанкаре | Статьи по топологии | 2010 | История математики, том. 37 | ||||
| А. Полищук и Л. Посицельский | Квадратичные алгебры | 2005 | Серия университетских лекций, том. 37 | ||||
| Пол Поллак | Разговорное введение в алгебраическую теорию чисел | 2017 | Студенческая математическая библиотека, вып. 84 | ||||
| Пол Поллак | Не всегда глубоко погребенный: второй курс элементарной теории чисел | 2009 | |||||
| Буркхард Польстер | Книга шнурков | 2006 | Математический мир, том. 24 | ||||
| Буркхард Польстер и Марти Росс | Динго съел мой учебник по математике | 2017 | |||||
| Леонид Полтерович и Дэниел Розен | Теория функций на симплектических многообразиях | 2014 | Серия монографий CRM, том. 34 34 | ||||
| Леонид Полтерович, Даниил Розен, Карина Самвелян и Джун Чжан | Топологическое постоянство в геометрии и анализе | 2020 | Серия университетских лекций, том. 74 | ||||
| Алексей Полторацкий | Подход Теплица к проблемам принципа неопределенности | 2015 | Серия региональных конференций CBMS по математике, нет. 121 | ||||
| Бьорн Пунен | Рациональные точки на многообразиях | 2017 | Аспирантура по математике, том. 186 | ||||
| Филипп Пулен | Leçons d’analyse classique: Exposition d’un cours fait by Paul Koosis à l’Universitê McGill, Montreal | 2015 | Серия монографий CRM, том. 36 | ||||
| Прасолов В.В. | Элементы теории гомологии | 2007 | Аспирантура по математике, том. 81 | ||||
| Рэндалл Пруим | Основы и приложения статистики: введение с использованием R | 2011 | Чистые и прикладные тексты для студентов, том. 13 13 | ||||
| Рэндалл Пруим | Основы и приложения статистики: введение в использование R, второе издание | 2018 | Чистые и прикладные тексты для студентов, том. 28 | ||||
| Александр Пухликов | Бирационально жесткие разновидности | 2013 | Математические обзоры и монографии, вып. 190 | ||||
| Женбо Цинь | Схемы Гильберта точек и бесконечномерные алгебры Ли | 2018 | Математические обзоры и монографии, вып. 228 | ||||
| Иэн Реберн | Алгебры графов | 2005 | Серия региональных конференций CBMS по математике, нет. 103 | ||||
| Фирас Расул-Ага и Тимо Сеппалаинен | Курс по большим уклонениям с введением в меры Гиббса | 2015 | Аспирантура по математике, том. 162 | ||||
| Джеффри Раух | Гиперболические дифференциальные уравнения в частных производных и геометрическая оптика | 2012 | Аспирантура по математике, том. 133 133 | ||||
| Миклош Рэдей | Джон фон Нейман: Избранные письма | 2005 | История математики, том. 27 | ||||
| Лассе Гиллен-Ремпе и Ребекка Вальдекер | Тестирование Primality для начинающих | 2014 | Студенческая математическая библиотека, том 70 | ||||
| Беттина Ричмонд и Том Ричмонд | Дискретный переход к высшей математике | 2009 | Чистые и прикладные тексты для студентов, том. 3 | ||||
| Карл Р. Рим | Введение в ортогональные, симплектические и унитарные представления конечных групп | 2011 | Монографии Института Филдса, том. 28 | ||||
| Элейн Маккиннон Рим и Фрэнсис Хоффман | Бурные времена в математике: жизнь Дж. К. Филдса и история медали Филдса | 2011 | |||||
| Р. Кларк Робинсон | Введение в динамические системы: непрерывные и дискретные, второе издание | 2012 | Чистые и прикладные тексты для студентов, том. 19 19 | ||||
| Джон Роу | Обмотка вокруг: число обмоток в топологии, геометрии и анализе | 2015 | Студенческая математическая библиотека, вып. 76 | ||||
| Дейл Рольфсен | Узлы и звенья | 2003 | AMS Chelsea Publishing, vol. 346.Х | ||||
| Майкл Розен | Экспозиция Эмиля Артина: подборка | 2006 | История математики, том 30 | ||||
| Уильям Т. Росс и Гарольд С. Шапиро | Обобщенное аналитическое продолжение | 2002 | Серия университетских лекций, том. 25 | ||||
| Джозеф Дж. Ротман | Продвинутая современная алгебра: второе издание | 2010 | Аспирантура по математике, том. 114 | ||||
| Джозеф Дж. Ротман | Продвинутая современная алгебра: третье издание, часть 1 | 2015 | Аспирантура по математике, том. 165 165 | ||||
| Джозеф Дж. Ротман | Продвинутая современная алгебра: третье издание, часть 2 | 2017 | Аспирантура по математике, том. 180 | ||||
| Луи Галле Роуэн | Высшее образование по алгебре: коммутативный взгляд | 2006 | Аспирантура по математике, том. 73 | ||||
| Луи Галле Роуэн | Высшая алгебра: некоммутативный взгляд | 2008 | Аспирантура по математике, том. 91 | ||||
| Жиль Руайе | Начало логарифмических неравенств Соболева | 2007 | Тексты и монографии SMF/AMS, том. 14 | ||||
| Наташа Рожковская | Математические кружки для учащихся начальной школы | 2014 | ИИГС Mathematical Circles Libra, vol. 13 | ||||
| Сильви Рютт | Хаос в промежутке | 2017 | Серия университетских лекций, том. 67 67 | ||||
| Роберт Румели | Теория емкости с локальной рациональностью | 2013 | Математические обзоры и монографии, вып. 193 | ||||
| Дж. М. М. Руттен, Марта Квятковска, Гетин Норман и Дэвид Паркер | Математические методы анализа параллельных и вероятностных систем | 2004 | Серия монографий CRM, том. 23 | ||||
| Дональд Г. Саари | Столкновения, кольца и другие ньютоновские задачи с $N$-телами | 2005 | |||||
| Лоренцо Садун | Прикладная линейная алгебра: принцип разделения, второе издание | 2008 | |||||
| Лоренцо Садун | Топология мозаичных пространств | 2008 | Серия университетских лекций, том. 46 | ||||
| Такеши Сайто | Великая теорема Ферма: доказательство | 2014 | Переводы математических монографий, том. 245 245 | ||||
| Такеши Сайто | Великая теорема Ферма: основные инструменты | 2013 | Переводы математических монографий, том. 243 | ||||
| Джудит Д. Салли и Пол Дж. Салли-младший | Целые числа, дроби и арифметика: руководство для учителей | 2012 | Библиотека математических кружков, том. 10 | ||||
| Джудит Д. Салли и Пол Дж. Салли-младший | Геометрия: руководство для учителей | 2011 | Библиотека математических кружков, том. 3 | ||||
| Джудит Д. Салли и Пол Дж. Салли-младший | Истоки исследований: вертикальное развитие математических задач | 2007 | |||||
| Пол Дж. Салли мл. | Инструменты торговли: введение в продвинутую математику | 2008 | |||||
| Дональд Сарасон | Теория сложных функций: второе издание | 2007 | |||||
| Марк Сол | Плоская геометрия Адамара | 2010 | |||||
| Жак Солой | Дифференциальная теория Галуа через соответствие Римана-Гильберта: элементарное введение | 2016 | Аспирантура по математике, том. 177 177 | ||||
| Эрик Т. Сойер | Теория функций: интерполяция и проблемы короны | 2009 | Монографии Института Филдса, том. 25 | ||||
| Вильгельм Шлаг | Курс комплексного анализа и римановых поверхностей | 2014 | Аспирантура по математике, том. 154 | ||||
| Дана Шломюк, Андрей Александрович Болибрух, Сергей Яковенко, Вадим Калошин и Александр Буюм | О конечности в дифференциальных уравнениях и диофантовой геометрии | 2005 | Серия монографий CRM, том. 24 | ||||
| Гвидо Шнайдер и Ханнес Юкер | Нелинейные УЧП: подход динамических систем | 2017 | Аспирантура по математике, том. 182 | ||||
| Дженнифер Шультенс | Введение в 3-манифольды | 2014 | Аспирантура по математике, том. 151 | ||||
| Ахилл Шюрманн | Вычислительная геометрия положительно определенных квадратичных форм | 2008 | Серия университетских лекций, том. 48 48 | ||||
| Кристоф Шютте и Марко Сарих | Метастабильность и модели марковского состояния в молекулярной динамике | 2013 | Конспект лекций Куранта, том. 24 | ||||
| Ричард Эван Шварц | Жизнь на бесконечной ферме | 2018 | |||||
| Ричард Эван Шварц | Проективная тепловая карта | 2017 | Математические обзоры и монографии, вып. 219 | ||||
| Ричард Эван Шварц | Галерея Бесконечности | 2016 | |||||
| Ричард Эван Шварц | Действительно большие числа | 2014 | |||||
| Ричард Эван Шварц | Восьмиугольные ПЭТ | 2014 | Математические обзоры и монографии, вып. 197 | ||||
| Ричард Эван Шварц | В основном поверхности | 2011 | Студенческая математическая библиотека, вып. 60 60 | ||||
| Александру Скорпан | Дикий мир 4-многообразия | 2005 | |||||
| Николас А. Сковилл | Дискретная теория Морса | 2019 | Серия студенческих математических библиотек, том. 90 | ||||
| Кристиан Сейп | Интерполяция и дискретизация в пространствах аналитических функций | 2004 | Серия университетских лекций, том. 33 | ||||
| Марк Р. Сепански | Алгебра | 2010 | Чистые и прикладные тексты для студентов, том. 11 | ||||
| Жак Сезиано | Введение в историю алгебры: решение уравнений от месопотамских времен до эпохи Возрождения | 2009 | Математический мир, том. 27 | ||||
| Фрейдун Шахиди | Ряды Эйзенштейна и автоморфные $L$-функции | 2010 | Публикации коллоквиума, том. 58 58 | ||||
| Шахриар Шахриари | Приблизительное исчисление | 2006 | |||||
| Шахриар Шахриари | Алгебра в действии | 2017 | Чистые и прикладные тексты для студентов, том. 27 | ||||
| Элен Шапиро | Линейная алгебра и матрицы: темы для второго курса: | 2015 | Чистые и прикладные тексты для студентов, том. 24 | ||||
| Джоэл Х. Шапиро | Приключения Вольтерры | 2018 | Студенческая математическая библиотека, вып. 85 | ||||
| Томас Р. Шеманске | Современная криптография и эллиптические кривые: руководство для начинающих | 2017 | Студенческая математическая библиотека, том 83 | ||||
| Шень А., Успенский В.А., Верещагин Н. | Колмогоровская сложность и алгоритмическая случайность | 2017 | Математические обзоры и монографии, вып. 220 220 | ||||
| Кодзи Шига и Тошикадзу Сунада | Математический дар, III: взаимодействие между топологией, функциями, геометрией и алгеброй | 2005 | Математический мир, том. 23 | ||||
| Горо Шимура | Арифметические и аналитические теории квадратичных форм и групп Клиффорда | 2004 | Математические обзоры и монографии, том 109 | ||||
| Михаил Шубин | Приглашение к уравнениям в частных производных | 2020 | Аспирантура по математике, том 205 | ||||
| Аарон Н. Сигел | Комбинаторная теория игр | 2013 | Аспирантура по математике, том 146 | ||||
| СЕ Сильва | Приглашение к эргодической теории | 2007 | Студенческая математическая библиотека, том 42 | ||||
| Сезар Э. Сильва | Приглашение к реальному анализу | 2019 | Чистые и прикладные тексты для студентов, том 36 | ||||
Джозеф Х. Сильверман Сильверман | Пространства модулей и арифметическая динамика | 2012 | Серия монографий CRM, том 30 | ||||
| Барри Саймон | Комплексный курс анализа | 2015 | |||||
| Барри Саймон | Функциональная интеграция и квантовая физика: второе издание | 2005 | AMS Chelsea Publishing, vol. 351.Х | ||||
| Барри Саймон | Ортогональные полиномы на единичной окружности: Часть 1: Классическая теория; Часть 2: Спектральная теория | 2004 | Публикации коллоквиума, том. 54 | ||||
| Барри Саймон | Идеалы трассировки и их применение | 2005 | Математические обзоры и монографии, том 120 | ||||
| Эндрю Симосон | Изучение непрерывных дробей: от целых чисел до солнечных затмений | 2019 | Математические выражения Дольчиани, том 53 | ||||
Уильям М. Сингер Сингер | Квадраты Стинрода в спектральных последовательностях | 2006 | Математические обзоры и монографии, том 129 | ||||
| Хэл Л. Смит и Хорст Р. Тиме | Динамические системы и постоянство населения | 2010 | Аспирантура по математике, том. 118 | ||||
| Стивен Д. Смит | Комплексы подгрупп | 2011 | Математические обзоры и монографии, вып. 179 | ||||
| Стивен Д. Смит | Применение классификации конечных простых групп | 2018 | Математические обзоры и монографии, вып. 230 | ||||
| Рональд Соломон | Абстрактная алгебра | 2009 | Чистые и прикладные тексты для студентов, том. 9 | ||||
| Сосинский А.С. | Геометрии | 2012 | Студенческая математическая библиотека, том. 64 | ||||
| Фрэнк Соттайл | Реальные решения уравнений из геометрии | 2011 | Серия университетских лекций, том. 57 57 | ||||
| Джаред Спек | Формирование ударной волны в решениях трехмерных квазилинейных волновых уравнений с малыми данными | 2016 | Математические обзоры и монографии, вып. 214 | ||||
| Джоэл Спенсер | Асимптопия | 2014 | Студенческая математическая библиотека, вып. 71 | ||||
| Джереми П. Спинрад | Эффективные графические представления | 2003 | Монографии Полевого института, том. 19 | ||||
| Звезделина Станкова и Том Рике | Десятилетие математического кружка Беркли: американский опыт, том II | 2015 | Библиотека математических кружков ИИГС, том. 14 | ||||
| Звезделина Станкова и Том Райке | Десятилетие математического кружка Беркли: американский опыт, том I | 2008 | Библиотека математических кружков ИИГС, том. 1 1 | ||||
| Ричард П. Стэнли | Разговорное решение проблем | 2020 | |||||
| Майкл Старберд и Фрэнсис Су | Топология через запрос | 2019 | Учебники AMS/MAA, том. 58 | ||||
| Уильям Штейн | Модульные формы, вычислительный подход | 2007 | Аспирантура по математике, том. 79 | ||||
| Роберт Стейнберг | Лекции по группам Шевалле | 2016 | Серия университетских лекций, том. 66 | ||||
| Джеффри Стром | Современная классическая гомотопическая теория | 2011 | Аспирантура по математике, том. 127> | ||||
| Карл Р. Стромберг | Введение в классический реальный анализ | 2015 | AMS Chelsea Publishing, vol. 376,Ч | ||||
| Дэниел Струк | Математика вероятностей | 2013 | Аспирантура по математике, том. 149> 149> | ||||
| Мартин Стайнс и Дэвид Стайнс | Задачи конвекции-диффузии: введение в их анализ и численное решение | 2018 | Аспирантура по математике, том. 196 | ||||
| Сет Салливант | Алгебраическая статистика | 2018 | Аспирантура по математике, том. 194 | ||||
| Габор Секелихиди | Введение в экстремальные метрики Кэлера | 2014 | Аспирантура по математике, том. 152 | ||||
| Анна Кепеш Семереди | Искусство в жизни математиков | 2015 | |||||
| Джордж Г. Спиро | Математическое попурри: Пятьдесят простых пьес по математике | 2010 | |||||
| Сергей Табачников | Геометрия и бильярд | 2005 | Студенческая математическая библиотека, вып. 30 | ||||
| Гонсало Табуада | Некоммутативные мотивы | 2015 | Серия университетских лекций, том. 63 63 | ||||
| Леон А. Тахтаджан | Квантовая механика для математиков | 2008 | Аспирантура по математике, том. 95 | ||||
| Джеймс Тантон | Насколько круглый куб?: и другие любопытные математические размышления | 2019 | Библиотека математических кружков ИИГС, том. 23 | ||||
| Теренс Тао | Нелинейные дисперсионные уравнения: локальный и глобальный анализ | 2006 | Серия региональных конференций CBMS по математике, нет. 106 | ||||
| Теренс Тао | Структура и случайность: страницы первого года математического блога | 2008 | |||||
| Теренс Тао | Наследие Пуанкаре, часть I: страницы второго года математического блога | 2009 г. | |||||
| Теренс Тао | Наследие Пуанкаре, часть II: страницы второго года математического блога | 2009 | |||||
| Теренс Тао | Эпсилон комнаты, I: реальный анализ: страницы третьего года математического блога | 2010 | Аспирантура по математике, том. 117 117 | ||||
| Теренс Тао | Эпсилон комнаты, II: страницы третьего года математического блога | 2011 | |||||
| Теренс Тао | Введение в теорию меры | 2011 | Аспирантура по математике, том. 126 | ||||
| Теренс Тао | темы в теории случайных матриц | 2012 | Аспирантура по математике, том. 132 | ||||
| Теренс Тао | Анализ Фурье высшего порядка | 2012 | Аспирантура по математике, том. 142 | ||||
| Теренс Тао | Компактность и противоречие | 2013 | |||||
| Теренс Тао | Пятая проблема Гильберта и смежные темы | 2014 | Аспирантура по математике, том. 153 | ||||
| Теренс Тао | Разложение в конечных простых группах лиева типа | 2015 | Аспирантура по математике, том. 164 164 | ||||
| Кристофер Тэпп | Матричные группы для бакалавров, второе издание | 2016 | Студенческая математическая библиотека, вып. 79 | ||||
| Кристофер Тэпп | Матричные группы для бакалавров | 2005 | Студенческая математическая библиотека, вып. 29 | ||||
| Джозеф Л. Тейлор | Комплексные переменные | 2011 | Чистые и прикладные тексты для студентов, том. 16 | ||||
| Джозеф Л. Тейлор | Основы анализа | 2012 | Чистые и прикладные тексты для студентов, том. 18 | ||||
| Майкл Э. Тейлор | Линейная алгебра | 2020 | Чистые и прикладные тексты для студентов, том. 45 | ||||
| Майкл Э. Тейлор | Введение в комплексный анализ | 2019 | Аспирантура по математике, том. 202 202 | ||||
| Майкл Э. Тейлор | Введение в дифференциальные уравнения | 2011 | Чистые и прикладные тексты для студентов, том. 14 | ||||
| Майкл Э. Тейлор | Теория измерений и интеграция | 2006 | Аспирантура по математике, том. 76 | ||||
| Джеральд Тененбаум | Введение в аналитическую и вероятностную теорию чисел, третье издание | 2015 | Аспирантура по математике, том. 163 | ||||
| Уильям Дж. Террелл | Переход к современному анализу | 2019 | AMS Чистые и прикладные тексты для студентов, том. 41 | ||||
| Джеральд Тешл | Математические методы квантовой механики: приложения к операторам Шредингера | 2009 | Аспирантура по математике, том. 99 | ||||
| Джеральд Тешл | Обыкновенные дифференциальные уравнения и динамические системы | 2012 | Аспирантура по математике, том. 140 140 | ||||
| Джеральд Тешл | Математические методы в квантовой механике: с приложениями к операторам Шредингера: второе издание | 2014 | Аспирантура по математике, том. 157 | ||||
| Кристоф Тиле | Анализ волновых пакетов | 2006 | Серия региональных конференций CBMS по математике, нет. 105 | ||||
| Альберто Торчински | Задачи реального и функционального анализа | 2015 | Аспирантура по математике, том. 166 | ||||
| Фреди Трельцш | Оптимальное управление уравнениями в частных производных: теория, методы и приложения | 2010 | Аспирантура по математике, том. 112 | ||||
| Тай-Пэн Цай | Лекции по уравнениям Навье-Стокса | 2018 | Аспирантура по математике, том. 192 | ||||
| Михаил Цфасман, Сергей Владуть и Дмитрий Ногин | Алгебраико-геометрические коды: основные понятия | 2007 | Математические обзоры и монографии, том 139 | ||||
| Левент Тунчел | Полиэдральные и полуопределенные методы программирования в комбинаторной оптимизации | 2010 | Монографии Института Филдса, том. 27 27 | ||||
| Андрей Тюрин | Квантование, классическая и квантовая теория поля и тета-функции | 2003 | Серия монографий CRM, том. 21 | ||||
| Кенджи Уэно | Алгебраическая геометрия 3. Дальнейшее изучение схем | 2003 | Переводы математических монографий, том 218 | ||||
| Кенджи Уэно | Алгебраическая геометрия 1: от алгебраических многообразий к схемам | 1999 | Переводы математических монографий, том 185 | ||||
| Кенджи Уэно | Конформная теория поля с калибровочной симметрией | 2008 | Монографии Института Филдса, том 24 | ||||
| Кенджи Уэно | Введение в алгебраическую геометрию | 1997 | Переводы математических монографий, том 166 | ||||
| Дэвид С. Ульрих | Сложное стало простым | 2008 | Аспирантура по математике, том 97 | ||||
Авторы: Алехандро Урибе А. и Даниэль А. Висшер и Даниэль А. Висшер | Исследования в области анализа, топологии и динамики: введение в абстрактную математику | 2020 | Чистые и прикладные тексты для студентов, том 44 | ||||
| Лесли Джейн Федерер Ваалер, Шинко Кодзима Харпер и Джеймс В. Дэниел | Математическая теория процентов, третье издание | 2019 | Учебники AMS/MAA, том. 57 | ||||
| Ваксман Леонид Львович | квантово-ограниченные симметричные области | 2010 | Переводы математических монографий, том. 238 | ||||
| Сэм Вандервельде | Круг в коробке | 2009 | Библиотека математических кружков ИИГС, том. 2 | ||||
| В.С. Варадараджан | Суперсимметрия для математиков: введение | 2004 | Конспект лекций Куранта, том. 11 | ||||
| В.С. Варадараджан | Эйлер во времени: новый взгляд на старые темы | 2006 | |||||
В. С. Варадараджан С. Варадараджан | Алгебра в древности и современности | 1998 | Математический мир, том. 12 | ||||
| С. Р. С. Варадхан | Теория вероятностей | 2001 | Конспект лекций Куранта, том. 7 | ||||
| С. Р. С. Варадхан | Случайные процессы | 2007 | Конспект лекций Куранта, том. 16 | ||||
| С. Р. С. Варадхан | Большие отклонения | 2007 | Конспект лекций Куранта, том. 27 | ||||
| Александр Варченко | Специальные функции, уравнения типа KZ и теория представлений | 2003 | Серия региональных конференций CBMS по математике, нет. 98 | ||||
| Дрор Варолин | Римановы поверхности посредством комплексной аналитической геометрии | 2011 | Аспирантура по математике, том. 125 | ||||
О. Н. Василенко Н. Василенко | Теоретико-числовые алгоритмы в криптографии | 2007 | Переводы математических монографий, том. 232 | ||||
| В.А. Васильев | Дополнения дискриминантов гладких карт: топология и приложения: исправленное издание | 2002 | Переводы математических монографий, том. 98 | ||||
| Андраш Васи | Уравнения с частными производными: доступный путь через теорию и приложения | 2015 | Аспирантура по математике, том. 169 | ||||
| Сантош С. Вемпала | Метод случайной проекции | 2004 | Серия DIMACS по дискретной математике и теоретической информатике, том. 65 | ||||
| Э. Б. Винберг | Курс алгебры | 2003 | Аспирантура по математике, том. 56 | ||||
| О.Я. Виро, О.А. Иванов, Н.Ю. Нецветаев, В.М. Харламов | Элементарная топология: Сборник задач | 2008 | |||||
| Александр Вольберг | Емкости Кальдерона-Зигмунда и операторы на неоднородных пространствах | 2003 | Серия региональных конференций CBMS по математике, нет. 100 100 | ||||
| А. Р. Уодсворт | Задачи по абстрактной алгебре | 2017 | Студенческая математическая библиотека, вып. 82 | ||||
| Сэмюэл С. Вагстафф-младший | Радость факторинга | 2012 | Студенческая математическая библиотека, вып. 6 | ||||
| Джон Б. Уолш | Зная шансы | 2012 | Аспирантура по математике, том. 139 | ||||
| Нил А. Уотсон | Введение в теорию теплового потенциала | 2012 | Математические обзоры и монографии, вып. 182 | ||||
| Айпин Ван и Антон Зеттл | Обыкновенные дифференциальные операторы | 2019 | Математические обзоры и монографии, вып. 245 | ||||
| Чжэнхан Ван | Топологические квантовые вычисления | 2010 | Серия региональных конференций CBMS по математике, нет. 112 112 | ||||
| Ребекка Вебер | Теория вычислимости | 2012 | Студенческая математическая библиотека, вып. 62 | ||||
| Чарльз А. Вейбель | Книга $K$: Введение в алгебраическую $K$-теорию | 2013 | Аспирантура по математике, том. 145 | ||||
| Стивен Х. Вайнтрауб | Теория представлений конечных групп: алгебра и арифметика | 2003 | Аспирантура по математике, том. 59 | ||||
| Стивен Х. Вайнтрауб | Линейная алгебра для юных математиков | 2019 | AMS Чистые и прикладные тексты для студентов, том. 42 | ||||
| Мартин Х. Вайсман | Иллюстрированная теория чисел | 2017 | |||||
| Лан Вен | Дифференцируемые динамические системы: введение в структурную устойчивость и гиперболичность 9*$-Алгебры | 2019 | Математические обзоры и монографии, вып. 241 241 | ||||
| Финансы | 2006 | Аспирантура по математике, том. 72 | |||||
| Дэниел Т. Уайз | От богатства к Раагу: 3-многообразия, прямоугольные группы Артина и кубическая геометрия | 2012 | Серия региональных конференций CBMS по математике, № 117 | ||||
| Сара Дж. Уизерспун | Когомологии Хохшильда для алгебр | 2019 | Аспирантура по математике, том. 204 | ||||
| Джозеф А. Вольф | Пространства постоянной кривизны: Шестое издание | 2011 | Издательство AMS Chelsea Publishing, том. 372.Н> | ||||
| Джозеф А. Вольф | Гармонический анализ коммутативных пространств | 2007 | Математические обзоры и монографии, вып. 142 | ||||
| Томас Х. Вольф (под редакцией Изабеллы Лаба и Кэрол Шубин) | Лекции по гармоническому анализу | 2003 | Серия университетских лекций, том. 29 29 | ||||
| Скотт А. Вулперт | Семейства римановых поверхностей и геометрия Вейля-Петерссона | 2010 | Серия региональных конференций CBMS по математике, нет. 113 | ||||
| Дэвид Райт | Математика и музыка | 2009 | |||||
| Хунг-Хси Ву | Школа математики: Алгебра | 2016 | |||||
| Хунг-Хси Ву | Преподавание математики в школе: предварительная алгебра | 2016 | |||||
| Хунг-Хси Ву | Понимание чисел в математике начальной школы | 2011 | |||||
| Кэролайн Якель и Сара-Мари Белкастро | Фигурные волокна | 2018 | |||||
| Яфаев Д.Р. | Математическая теория рассеяния: аналитическая теория | 2010 | Математические обзоры и монографии, том 158 | ||||
| Иван Ященко | Приглашение на математический фестиваль | 2013 | Библиотека математических кружков, том 12 | ||||
| Дональд Яу | Цветные оперы | 2016 | Аспирантура по математике, том. 170 170 | ||||
| Дональд Яу и Марк В., Джонсон | Основа для PROPs, алгебр и модулей | 2015 | Математические обзоры и монографии, вып. 203 | ||||
| Энн Л. Янг | Математические шифры: от Цезаря до RSA | 2006 | Математический мир, том. 25 | ||||
| Джузеппе Зампиери | Комплексный анализ и CR-геометрия | 2008 | Серия университетских лекций, том. 43 | ||||
| Оскар Зариски, с приложением Бернара Тейссье | Проблема модулей для плоских ветвей | 2006 | Серия университетских лекций, том. 39 | ||||
| Эдуард Цендер | Примечания по динамическим системам | 2005 | Конспект лекций Куранта, том. 12 | ||||
| Стив Зельдич | Собственные функции лапласиана на римановом многообразии | 2017 | Серия региональных конференций CBMS по математике, нет. 125 125 | ||||
| Антон Зеттл | Теория Штурма-Лиувилля | 2005 | Математические обзоры и монографии, вып. 121 | ||||
| Синчжи Чжань | Матричная теория | 2013 | Аспирантура по математике, том. 147 | ||||
| Пин Чжан | Мера Вигнера и квазиклассические пределы нелинейных уравнений Шрёдингера | 2008 | Конспект лекций Куранта, том. 17 | ||||
| Желобенко Д. | Основные структуры и методы теории представления | 2005 | Переводы математических монографий, том. 228 | ||||
| Роберт Дж. Циммер и Дэйв Витте Моррис | Эргодическая теория, группы и геометрия | 2008 | Серия региональных конференций CBMS по математике, нет. 109 | ||||
| Дэвид Э. Зитарелли | История математики в США и Канаде, Том 1: 1492-1900 | 2019 | Спектр, №. 94 94 | ||||
| Александр Звонкин | Математика от трех до семи: история математического кружка для дошкольников | 2011 | Библиотека математических кружков ИИГС, том. 5 | ||||
| Мачей Зворски | Квазиклассический анализ | 2012 | Аспирантура по математике, том. 138 |
100 лет математической космологии: модели, теории и проблемы, часть B
1. Старобинский А.А. 1980. Новый тип изотропных космологических моделей без сингулярности. физ. лат. Б 91 , 99-102. ( 10.1016/0370-2693(80)-X) [CrossRef] [Google Scholar]
2. Казанас Д. 1980. Динамика Вселенной и спонтанное нарушение симметрии. Ап. Дж. Летт. 241 , Л59. ( 10.1086/183361) [CrossRef] [Google Scholar]
3. Guth AH. 1981.
Инфляционная вселенная: возможное решение проблем горизонта и плоскостности. физ. Преподобный Д 23 , 347-356. ( 10.1103/PhysRevD.23.347) [CrossRef] [Google Scholar]
( 10.1103/PhysRevD.23.347) [CrossRef] [Google Scholar]
4. Стейнхардт П.Дж. 1982. Естественная инфляция. В The Very Early Universe (под редакцией GW Gibbons, SW Hawking, STC Siklos), Proc. Семинар Наффилда, 21 июня – 9 июля 1010 068 г., стр. 251–266. Кембридж, Великобритания: Издательство Кембриджского университета.
5. Вайнберг С.В. 1972. Гравитация и космология. Нью-Йорк, штат Нью-Йорк: Аддисон-Уэсли. [Google Scholar]
6. Brandenberger RH. 1985. Методы квантовой теории поля и инфляционные модели Вселенной. Преподобный Мод. физ. 57 , 1-60. ( 10.1103/RevModPhys.57.1) [CrossRef] [Google Scholar]
7. Колб Э.В., Тернер М.С. 1990. Ранняя Вселенная. Нью-Йорк, штат Нью-Йорк: Аддисон-Уэсли. [Google Scholar]
8. Вайнберг С.В. 2007. Космология. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar]
9. Аде ПАР и др. Сотрудничество BICEP/Keck, 2021 г.
Улучшены ограничения на первичные гравитационные волны с использованием наблюдений Planck , WMAP и BICEP/ Keck в течение сезона наблюдений 2018 года. физ. Преподобный Летт. 127 , 151301. ( 10.1103/PhysRevLett.127.151301) [PubMed] [CrossRef] [Google Scholar]
физ. Преподобный Летт. 127 , 151301. ( 10.1103/PhysRevLett.127.151301) [PubMed] [CrossRef] [Google Scholar]
10. Виленкин А. 1983. Рождение инфляционных вселенных. физ. Преподобный Д 27 , 2848-2855. ( 10.1103/PhysRevD.27.2848) [CrossRef] [Google Scholar]
11. Linde AD. 1986 год. Вечно существующая самовоспроизводящаяся хаотическая инфляционная вселенная. физ. лат. Б 175 , 395-400. ( 10.1016/0370-2693(86)-8) [CrossRef] [Google Scholar]
12. Линде А.Д. 1995. Квантовая космология и структура инфляционной Вселенной. В ПАСКОС / ХОПКИНС 1995 (Совместное собрание Международного симпозиума по частицам, струнам и космологии и 19-го семинара Джона Хопкинса по текущим проблемам теории частиц ), стр. 349–394.
13. Виленкин А. 2004. Вечная инфляция и хаотичная терминология. (http://arxiv.org/abs/gr-qc/0409055 [gr-qc])
14. Кофман Л., Линде А.Д., Муханов В.Ф. 2002.
Инфляционная теория и альтернативная космология. J. Физика высоких энергий. 2002 , 057. ( 10.1088/1126-6708/2002/10/057) [CrossRef] [Google Scholar]
J. Физика высоких энергий. 2002 , 057. ( 10.1088/1126-6708/2002/10/057) [CrossRef] [Google Scholar]
15. Холландс С., Уолд Р.М. 2002. Эссе: альтернатива инфляции. Генерал Отн. Грав. 34 , 2043-2055. ( 10.1023/A:5216055) [CrossRef] [Google Scholar]
16. Linde AD. 1990. Физика элементарных частиц и инфляционная космология. Швейцария: Harwood Academic Publishers. [Google Scholar]
17. Борде А., Гут А.Х., Виленкин А. 2003. Инфляционное пространство-время неполно в прошлых направлениях. физ. Преподобный Летт. 90 , 151301. ( 10.1103/PhysRevLett.90.151301) [PubMed] [CrossRef] [Google Scholar]
18. Aguirre A, Gratton S. 2003. Инфляция без начала: предложение нулевой границы. физ. Преподобный Д 67 , 083515. (10.1103/PhysRevD.67.083515) [CrossRef] [Google Scholar]
19. DeWitt BS. 1967.
Квантовая теория гравитации. I. Каноническая теория. физ. преп. 160 , 1113-1148. ( 10.1103/PhysRev.160.1113) [CrossRef] [Google Scholar]
( 10.1103/PhysRev.160.1113) [CrossRef] [Google Scholar]
20. Wheeler JA. 1968 год. Суперпространство и природа квантовой геометродинамики. В Battelle Rencontres (редакторы CM DeWitt, JA Wheeler), Лекции по математике и физике. Нью-Йорк, штат Нью-Йорк: В. А. Бенджамин.
21. Хартл Дж.Б., Хокинг С.В. 1983. Волновая функция Вселенной. физ. Преподобный Д 28 , 2960-2975. ( 10.1103/PhysRevD.28.2960) [CrossRef] [Google Scholar]
22. Виленкин А. 1985. Граничные условия в квантовой космологии. физ. Преподобный Д 33 , 3560-3569. ( 10.1103/PhysRevD.33.3560) [PubMed] [CrossRef] [Google Scholar]
23. Виленкин А. 1987. Квантовая космология и начальное состояние Вселенной. физ. Преподобный Д 37 , 888-897. ( 10.1103/PhysRevD.37.888) [PubMed] [CrossRef] [Google Scholar]
24. Гиббонс Г.В., Грищук Л.П. 1989.
Какова типичная волновая функция Вселенной?
Нукл. физ. Б 313 , 736-748. ( 10.1016/0550-3213(89)-7) [CrossRef] [Google Scholar]
( 10.1016/0550-3213(89)-7) [CrossRef] [Google Scholar]
25. Halliwell JJ. 1991 Вводные лекции по квантовой космологии. В Квантовая космология и детские вселенные (ред. С. Коулман, Дж. Б. Хартл, Т. Пиран, С. Вайнберг). Сингапур: Мировой научный.
26. Аштекар А. 2021. Краткий обзор петлевой квантовой гравитации. Представитель прог. физ. 84 , 042001. ( 10.1088/1361-6633/абед91) [PubMed] [CrossRef] [Google Scholar]
27. Bojowald M. 2008. Петлевая квантовая космология. Живой преподобный отн. 11 , 044025. ( 10.12942/lrr-2008-4) [PMC free article] [PubMed] [CrossRef] [Google Scholar]
28. Белинский В.А., Грищук Л.П., Зельдович Ю.Б., Халатников И.М. 1985. Инфляционные стадии в космологических моделях со скалярным полем. сов. физ. Дж. Эксп. Теор. физ. 62 , 195. [Google Scholar]
29. Halliwell JJ. 1987.
Скалярные поля в космологии с экспоненциальным потенциалом. физ. лат. Б 185 , 341-344. ( 10.1016/0370-2693(87)-2) [CrossRef] [Google Scholar]
( 10.1016/0370-2693(87)-2) [CrossRef] [Google Scholar]
30. Henneaux M. 1983. Производство энтропии Гиббса в общей теории относительности. Нуово Сим. лат. 38 , 609-614. ( 10.1007/BF02782751) [CrossRef] [Google Scholar]
31. Гиббонс Г.В., Хокинг С.В., Стюарт Дж.М. 1987. Естественная мера на множестве всех вселенных. Нукл. физ. Б 281 , 736-751. ( 10.1016/0550-3213(87)-1) [CrossRef] [Google Scholar]
32. Hawking SW, Page DN. 1988 год. Насколько вероятна инфляция? Нукл. физ. Б 298 , 789-809. ( 10.1016/0550-3213(88)-9) [CrossRef] [Google Scholar]
33. Страница DN. 1987. Вероятность инфляции R2. физ. Преподобный Д 36 , 1607-1624. ( 10.1103/PhysRevD.36.1607) [PubMed] [CrossRef] [Google Scholar]
34. Chmielowski P, Page DN. 1988 год. Вероятность инфляции типа Бьянки I. физ. Преподобный Д 38 , 2392. (10.1103/PhysRevD.38.2392) [PubMed] [CrossRef] [Google Scholar]
35. Gibbons GW, Turok N. 2008.
Проблема меры в космологии. физ. Преподобный Д 77 , 063516. ( 10.1103/PhysRevD.77.063516) [CrossRef] [Google Scholar]
Gibbons GW, Turok N. 2008.
Проблема меры в космологии. физ. Преподобный Д 77 , 063516. ( 10.1103/PhysRevD.77.063516) [CrossRef] [Google Scholar]
36. Стр. DN. 2011. Конечная каноническая мера для неособых космологий. Дж. Космол. Астропарт. физ. 1106 , 038. (10.1088/1475-7516/2011/06/038) [CrossRef] [Google Scholar]
37. Schiffrin JS, Wald RM. 2012. Мера и вероятность в космологии. физ. Преподобный Д 86 , 023521. (10.1103/PhysRevD.86.023521) [CrossRef] [Google Scholar]
38. Linde A, Noorbala M. 2010. Проблема меры для вечной и невечной инфляции. Дж. Космол. Астропарт. физ. 056 , 008. (10.1088/1475-7516/2010/09/008) [CrossRef] [Google Scholar]
39. Ellis GFR, Maartens R, MacCallum MAH. 2012. Релятивистская космология. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]
40. Хокинг С.В. 1988 год.
Червоточины в пространстве-времени. физ. Преподобный Д 37 , 904-910. ( 10.1103/PhysRevD.37.904) [PubMed] [CrossRef] [Google Scholar]
( 10.1103/PhysRevD.37.904) [PubMed] [CrossRef] [Google Scholar]
41. Coleman S. 1988. Почему нет ничего, а не что-то: теория космологической постоянной. Нукл. физ. Б 310 , 643-668. ( 10.1016/0550-3213(88)-1) [CrossRef] [Google Scholar]
42. Fischler W, Susskind L. 1989. Катастрофа червоточины. физ. лат. Б 217 , 48-54. ( 10.1016/0370-2693(89)-1) [CrossRef] [Google Scholar]
43. Коулман С., Хартл Дж. Б., Пиран Т., Вайнберг С. (ред.). 1991. Квантовая космология и детские вселенные. Сингапур: Мировой научный. [Google Scholar]
44. Моррис М.С., Торн К.С. 1988 год. Червоточины в пространстве-времени и их использование для межзвездных путешествий: инструмент для обучения общей теории относительности. Являюсь. Дж. Физ. 56 , 395-412. ( 10.1119/1.15620) [CrossRef] [Google Scholar]
45. Моррис М.С., Торн К.С., Юрцевер Ю. 1988.
Червоточины, машины времени и слабое энергетическое состояние. физ. Преподобный Летт. 61 , 1446-1449. ( 10.1103/PhysRevLett.61.1446) [PubMed] [CrossRef] [Google Scholar]
Преподобный Летт. 61 , 1446-1449. ( 10.1103/PhysRevLett.61.1446) [PubMed] [CrossRef] [Google Scholar]
46. Бронников К.А., Мельников В.Н., Денен Х. 2003. Общий класс черных дыр мира браны. физ. Преподобный Д 68 , 024025. ( 10.1103/PhysRevD.68.024025) [CrossRef] [Google Scholar]
47. Бронников К.А., Скворцова М.В., Старобинский А.А. 2010. Заметки о существовании червоточин в скалярно-тензорной и F(R) гравитации. Грав. Космол. 16 , 216-222. ( 10.1134/S02022830047) [CrossRef] [Google Scholar]
48. Бронников К.А., Lemos JPS. 2009. Цилиндрические червоточины. физ. Преподобный Д 79 , 104019. (10.1103/PhysRevD.79.104019) [CrossRef] [Google Scholar]
49. Visser M. 1995. Лоренцевы червоточины — от Эйнштейна до Хокинга. Нью-Йорк, штат Нью-Йорк: AIP Press. [Google Scholar]
50. Molina-Paris C, Visser M. 1999.
Минимальные условия для создания вселенной Фридмана-Робертсона-Уокера из «отскока». физ. лат. Б 455 , 90-95. ( 10.1016/S0370-2693(99)00469-4) [CrossRef] [Google Scholar]
физ. лат. Б 455 , 90-95. ( 10.1016/S0370-2693(99)00469-4) [CrossRef] [Google Scholar]
51. Freund PGO. 1982. Космологии Калуцы-Клейна. Нукл. физ. Б 209 , 146-156. ( 10.1016/0550-3213(82)-7) [CrossRef] [Google Scholar]
52. Abbott RB, Barr SM, Ellis SD. 1984. Космологии Калуцы-Клейна и инфляция. физ. Преподобный Д 30 , 720-727. ( 10.1103/PhysRevD.30.720) [PubMed] [CrossRef] [Google Scholar]
53. Okada Y. 1982. Эволюция вселенной Калуцы-Клейна. Нукл. физ. Б 264 , 197-220. ( 10.1016/0550-3213(86)-7) [CrossRef] [Google Scholar]
54. Overduin JM, Wesson PS. 1997. Калуца-Кляйн Гравитация. физ. Представитель 283 , 303-378. ( 10.1016/S0370-1573(96)00046-4) [CrossRef] [Google Scholar]
55. Furusawa T, Hosoya A. 1985. Хаотична ли анизотропная модель Калуцы-Клейна Вселенной? прог. Теор. физ. 73 , 467-475. ( 10.1143/PTP.73.467) [CrossRef] [Google Scholar]
56. Барроу Дж.Д., Стейн Шабес Дж.А. 1985.
Миксмастерские вселенные Калуцы-Кляйна. физ. Преподобный Д 32 , 1595-1596. ( 10.1103/PhysRevD.32.1595) [PubMed] [CrossRef] [Google Scholar]
Барроу Дж.Д., Стейн Шабес Дж.А. 1985.
Миксмастерские вселенные Калуцы-Кляйна. физ. Преподобный Д 32 , 1595-1596. ( 10.1103/PhysRevD.32.1595) [PubMed] [CrossRef] [Google Scholar]
57. Demaret J, Henneaux M, Spindel P. 1985. Неколебательное поведение в космологии Калуцы-Клейна в вакууме. физ. лат. Б 164 , 27-30. ( 10.1016/0370-2693(85)-3) [CrossRef] [Google Scholar]
58. Demaret J, Hanquin JL, Henneaux M, Spindel P, Taormina A. 1986. Судьба миксмастерского поведения в неоднородных космологических моделях Калуцы-Клейна в вакууме. физ. лат. Б 175 , 129-132. ( 10.1016/0370-2693(86)-X) [CrossRef] [Google Scholar]
59. Demaret J, de Rop Y, Henneaux M. 1988. Хаос в недиагональных пространственно-однородных космологических моделях в пространственно-временных размерностях ≤10. физ. лат. Б 211 , 37-41. ( 10.1016/0370-2693(88)-9) [CrossRef] [Google Scholar]
60. Хосоя А., Дженсен Л. Г., Стейн Шабес Дж.А. 1987.
Критическое измерение для хаотической космологии. Нукл. физ. Б 283 , 657-668. ( 10.1016/0550-3213(87)-4) [CrossRef] [Google Scholar]
Г., Стейн Шабес Дж.А. 1987.
Критическое измерение для хаотической космологии. Нукл. физ. Б 283 , 657-668. ( 10.1016/0550-3213(87)-4) [CrossRef] [Google Scholar]
61. Гасперини М. 2007. Элементы струнной космологии. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. [Google Scholar]
62. Питер П., Узан Дж. П. 2009. Первичная космология. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar]
63. Гасперини М., Венециано Г. 1993. До большого взрыва в струнной космологии. Астропарт. физ. 1 , 317-339. ( 10.1016/0927-6505(93)-8) [CrossRef] [Google Scholar]
64. Billyard AP, Coley AA, Lidsey JE. 2000. Циклическое поведение в космологиях ранней Вселенной. Дж. Матем. физ. 41 , 6277-6283. ( 10.1063/1.1286878) [CrossRef] [Google Scholar]
65. Барроу Д.Д., Кунце К.Е. 1997.
Пространственно однородные струнные космологии. физ. Преподобный Д 55 , 623-629. ( 10.1103/PhysRevD.55.623) [CrossRef] [Google Scholar]
( 10.1103/PhysRevD.55.623) [CrossRef] [Google Scholar]
66. Барроу Д.Д., Кунце К.Е. 1997. Неоднородные струнные космологии. физ. Преподобный Д 56 , 741-752. ( 10.1103/PhysRevD.56.741) [CrossRef] [Google Scholar]
67. Lidsey JE, Wands D, Copeland EJ. 2000. Суперструнная космология. физ. Представитель 337 , 343-492. ( 10.1016/S0370-1573(00)00064-8) [CrossRef] [Google Scholar]
68. Ланцош К. 1957. Электричество и общая теория относительности. Преподобный Мод. физ. 19 , 337-350. (10.1103/RevModPhys.29.337) [CrossRef] [Google Scholar]
69. Lanczos C. 1957. Расщепление тензора Римана. Преподобный Мод. физ. 34 , 379-389. ( 10.1103/RevModPhys.34.379) [CrossRef] [Google Scholar]
70. Buchdahl HA. 1970. Нелинейные лагранжианы и космологическая теория. Пн. Нет. Р. Астрон. соц. 150 , 1-8. ( 10.1093/mnras/150.1.1) [CrossRef] [Google Scholar]
71. Гурович В. Т. 1971.
Нелинейная поправка к лагранжевой плотности гравитационного поля и космологические решения без сингулярности. сов. физ. Доклады 15 , 1105. [Google Scholar]
Т. 1971.
Нелинейная поправка к лагранжевой плотности гравитационного поля и космологические решения без сингулярности. сов. физ. Доклады 15 , 1105. [Google Scholar]
72. Нариай Х. 1973. Гравитационная неустойчивость регулярных моделей вселенных в модифицированной общей теории относительности. прог. Теор. физ. 49 , 165-180. ( 10.1143/PTP.49.165) [CrossRef] [Google Scholar]
73. Кернер Р. 1982. Космология без сингулярности и нелинейные гравитационные лагранжианы. Генерал Отн. Грав. 14 , 453-469. ( 10.1007/BF00756329) [CrossRef] [Google Scholar]
74. Барроу Д.Д., Оттевилл А.С. 1983. Устойчивость общей релятивистской космологической теории. Дж. Физ. А 16 , 2757-2776. ( 10.1088/0305-4470/16/12/022) [CrossRef] [Google Scholar]
75. Барроу Дж. Д., Коцакис С. 1988. Инфляция и конформная структура теорий гравитации высшего порядка. физ. лат. Б 214 , 515-518. ( 10.1016/0370-2693(88)-4) [CrossRef] [Google Scholar]
76. Mannheim PD, Казанас Д. 1989.
Точное вакуумное решение конформной гравитации Вейля и кривых вращения галактики. Астрофиз. Дж. 342 , 635-638. ( 10.1086/167623) [CrossRef] [Google Scholar]
Mannheim PD, Казанас Д. 1989.
Точное вакуумное решение конформной гравитации Вейля и кривых вращения галактики. Астрофиз. Дж. 342 , 635-638. ( 10.1086/167623) [CrossRef] [Google Scholar]
77. Cotsakis S, Miritzis J, Querella L. 1999. Вариационная и конформная структура нелинейных метрически-связных гравитационных лагранжианов. Дж. Матем. физ. 40 , 3063-3071. ( 10.1063/1.532744) [CrossRef] [Google Scholar]
78. Барроу Дж. Д., Коцакис С. 2020. Инфляция без следа лямбды. Евро. физ. Дж. С. 80 , 839. ( 10.1140/epjc/s10052-020-8428-2) [CrossRef] [Google Scholar]
79. Harrison ER. 1967. Нормальные моды колебаний Вселенной. Преподобный Мод. физ. 39 , 862-882. ( 10.1103/RevModPhys.39.862) [CrossRef] [Google Scholar]
80. Гиббонс Г.В. 1988 год. Энтропия и стабильность Вселенной. Нукл. физ. Б 292 , 784-792. ( 10.1016/0550-3213(87)-5) [CrossRef] [Google Scholar]
81. Гиббонс Г.В. 1988 год.
Неравенство Соболева, теорема Йенсена и масса и энтропия Вселенной. Нукл. физ. Б 310 , 636-642. ( 10.1016/0550-3213(88)-X) [CrossRef] [Google Scholar]
Гиббонс Г.В. 1988 год.
Неравенство Соболева, теорема Йенсена и масса и энтропия Вселенной. Нукл. физ. Б 310 , 636-642. ( 10.1016/0550-3213(88)-X) [CrossRef] [Google Scholar]
82. Ellis GFR, Maartens R. 2004. Эмерджентная Вселенная: инфляционная космология без сингулярности. Учебный класс. Квант. Грав. 21 , 223-232. ( 10.1088/0264-9381/21/1/015) [CrossRef] [Google Scholar]
83. Барроу Д.Д., Эллис Г.Ф.Р., Мартенс Р., Цагас К.Г. 2003. Об устойчивости статической Вселенной Эйнштейна. Учебный класс. Квант. Грав. 20 , L155-L164. ( 10.1088/0264-9381/20/11/102) [CrossRef] [Google Scholar]
84. Барроу Дж. Д., Ямамото К. 2012. Неустойчивости статических вселенных Эйнштейна типа IX Бьянки. физ. Преподобный Д 85 , 083505. ( 10.1103/PhysRevD.85.083505) [CrossRef] [Google Scholar]
85. Барроу Д.Д. 2020.
Пересмотрен принцип конечного действия. физ. Преподобный Д 101 , 023527. (10.1103/PhysRevD.101.023527) [CrossRef] [Google Scholar]
(10.1103/PhysRevD.101.023527) [CrossRef] [Google Scholar]
86. Wainwright J, Ellis GFR. 1993. Динамические системы в космологии. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. [Google Scholar]
87. Барроу Д.Д., Сонода Д.Х. 1985. Асимптотическая устойчивость вселенных типа Бьянки. физ. Респ. 139 , 1-49. ( 10.1016/0370-1573(86)-6) [CrossRef] [Google Scholar]
88. Вальд Р.М. 1983. Асимптотика однородных космологических моделей при наличии положительной космологической постоянной. физ. Преподобный Д 28 , 2118-2120. ( 10.1103/PhysRevD.28.2118) [CrossRef] [Google Scholar]
89. Cotsakis S, Flessas G. 1993. Обобщенные космические теоремы об отсутствии волос. физ. лат. Б 319 , 69-73. ( 10.1016/0370-2693(93)-E) [CrossRef] [Google Scholar]
90. Cotsakis S, Miritzis J. 1998.
Доказательство космической гипотезы об отсутствии волос для некоторых квадратичных однородных космологий. Учебный класс. Квант. Грав. 15 , 2795-2801. ( 10.1088/0264-9381/15/9/024) [CrossRef] [Google Scholar]
Учебный класс. Квант. Грав. 15 , 2795-2801. ( 10.1088/0264-9381/15/9/024) [CrossRef] [Google Scholar]
91. Yokoyama J, Maeda K. 1990. Квантовый космологический подход к космической гипотезе об отсутствии волос в пространстве-времени Бьянки типа IX. физ. Преподобный Д 41 , 1047-1053. ( 10.1103/PhysRevD.41.1047) [PubMed] [CrossRef] [Google Scholar]
92. Wainwright J, Ellis GFR. 1989. Динамический системный подход к космологии Бьянки: ортогональные модели класса А. Класс. Квант. Грав. 6 , 1409-1431. ( 10.1088/0264-9381/6/10/011) [CrossRef] [Google Scholar]
93. Богоявленский О.И. 1985. Методы качественной теории динамических систем в астрофизике и газовой динамике. Нью-Йорк, штат Нью-Йорк: Спрингер. [Google Scholar]
94. Александр С., Бранденбергер Р.Х., Иссон Д.А. 2000. Бранные газы в ранней Вселенной. физ. Преподобный Д 62 , 103509. (10.1103/PhysRevD.62.103509) [CrossRef] [Google Scholar]
95. Barrow JD, Dabrowski MP. 1998.
Струнная космология и хаос. физ. Преподобный Д 57 , 7204. [Google Scholar]
Barrow JD, Dabrowski MP. 1998.
Струнная космология и хаос. физ. Преподобный Д 57 , 7204. [Google Scholar]
96. Дамур Т., Хенно М. 2000. Хаос в суперструнной космологии. физ. Преподобный Летт. 85 , 920-923. ( 10.1103/PhysRevLett.85.920) [PubMed] [CrossRef] [Google Scholar]
97. Damour T, de Buyl S. 2008. Описание общих космологических особенностей переменных Ивасавы. физ. Преподобный Д 77 , 043520. (10.1103/PhysRevD.77.043520) [CrossRef] [Google Scholar]
98. Damour T, Николай. 2008. Симметрии, сингулярности и исчезновение пространства. Междунар. Дж. Мод. физ. Д 17 , 525-531. ( 10.1142/S0218271808012206) [CrossRef] [Google Scholar]
99. Лукас А., Оврут Б.А., Уолдрам Д. 1997. Струнная и М-теория космологических решений с формами Рамона. Нукл. физ. Б 495 , 365-399. ( 10.1016/S0550-3213(97)00194-6) [CrossRef] [Google Scholar]
100. Лукас А., Оврут Б.А., Уолдрам Д. 1998 Космология и М-теория суперструн типа II. (http://arxiv.org/abs/hep-th/41)
1998 Космология и М-теория суперструн типа II. (http://arxiv.org/abs/hep-th/41)
101. Billyard AP, Coley AA, Lidsey JE, Nilsson US. 2000. Динамика космологии М-теории. физ. Преподобный Д 61 , 043504. ( 10.1103/PhysRevD.61.043504) [CrossRef] [Google Scholar]
102. Таунсенд П. 2003 Космическое ускорение и М-теория. (http://arxiv.org/abs/hep-th/0308149 [hep-th])
103. Андерссон Л., Марк Хайнцле Дж. 2007. Вечное ускорение из М-теории. Доп. Теор. Мат. физ. 11 , 371-398. ( 10.4310/ATMP.2007.v11.n3.a2) [CrossRef] [Google Scholar]
104. Townsend P, Wohlfarth MNR. 2004. Космология как геодезическое движение. Учебный класс. Квант. Грав. 21 , 5375-5396. (10.1088/0264-9381/21/23/006) [CrossRef] [Google Scholar]
105. Марольф Д. 1999 Струны/М-браны для релятивистов. (http://arxiv.org/abs/gr-qc/95)
106. Антониадис И. 1990.
Возможное новое измерение в несколько ТэВ. физ. лат. Б 246 , 377-384. ( 10.1016/0370-2693(90)-F) [CrossRef] [Google Scholar]
( 10.1016/0370-2693(90)-F) [CrossRef] [Google Scholar]
107. Антониадис И. 2006. Физика дополнительных измерений. Дж. Физ. конф. сер. 33 , 170-181. ( 10.1088/1742-6596/33/1/015) [CrossRef] [Google Scholar]
108. Randall L, Sundrum R. 1999. Альтернатива компактификации. физ. Преподобный Летт. 83 , 4690-4693. ( 10.1103/PhysRevLett.83.4690) [CrossRef] [Google Scholar]
109. Maartens R. 2004. Космологическая динамика на бране. Живой преподобный отн. 7 , 7. ( 10.12942/lrr-2004-7) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
110. Langlois D. 2003. Космология браны: введение. прог. Теор. физ. Доп. 148 , 181-212. ( 10.1143/PTPS.148.181) [CrossRef] [Google Scholar]
111. Хури Дж., Оврут Б.А., Стейнхардт П.Дж., Турок Н. 2001.
Экпиротическая Вселенная: сталкивающиеся браны и происхождение горячего Большого взрыва. физ. Преподобный Д 64 , 123522. (10.1103/PhysRevD.64.123522) [CrossRef] [Google Scholar]
(10.1103/PhysRevD.64.123522) [CrossRef] [Google Scholar]
112. Lehners JL. 2008. Экпиротическая и циклическая космология. физ. Представитель 465 , 223-263. ( 10.1016/j.physrep.2008.06.001) [CrossRef] [Google Scholar]
113. Brandenberger RH, Patrick P. 2017. Отскакивающие космологии: прогресс и проблемы. Найденный. физ. 47 , 797-850. ( 10.1007/s10701-016-0057-0) [CrossRef] [Google Scholar]
114. Антониадис И., Коцакис С., Клаудату И. 2021. Регулярные бранные миры с нелинейными объемными жидкостями. Евро. физ. Дж. С. 81 , 771. ( 10.1140/epjc/s10052-021-09558-y) [CrossRef] [Google Scholar]
115. Witten E. 1998. Антиде Ситтеровское пространство и голография. Доп. Теор. Мат. физ. 2 , 253-291. ( 10.4310/ATMP.1998.v2.n2.a2) [CrossRef] [Google Scholar]
116. Антониадис I, Коцакис С. 2015.
Образование Σ(1385)± и Ξ(1530)0 в протонно-протонных столкновениях при s=7 ТэВ. Евро. физ. Дж. С. 75 , 1-12. ( 10.1140/epjc/s10052-014-3191-x) [CrossRef] [Google Scholar]
Дж. С. 75 , 1-12. ( 10.1140/epjc/s10052-014-3191-x) [CrossRef] [Google Scholar]
117. Susskind L. 2003 Антропный ландшафт теории струн. (http://arxiv.org/abs/hep-th/0302219 [hep-th])
118. Guth AH. 2007. Вечная инфляция и ее последствия. Дж. Физ. А 40 , 6811-6826. ( 10.1088/1751-8113/40/25/S25) [CrossRef] [Google Scholar]
119. Hawking SW, Hertog T. 2006. Население ландшафта: нисходящий подход. физ. Преподобный Д 73 , 123527. ( 10.1103/PhysRevD.73.123527) [CrossRef] [Google Scholar]
120. Хартл Дж. Б., Хокинг С. В., Хертог Т. 2008. Безграничная мера Вселенной. физ. Преподобный Летт. 100 , 201301. см. также, ( 10.1103/PhysRevLett.100.201301) [PubMed] [CrossRef] [Google Scholar]
121. Тегмарк М. Параллельные вселенные. (http://arxiv.org/abs/astro-ph/0302131 [astro-ph])
122. Трион Э. 1973.
Является ли Вселенная вакуумной флуктуацией?
Природа 246 , 396-397. ( 10.1038/246396a0) [CrossRef] [Google Scholar]
( 10.1038/246396a0) [CrossRef] [Google Scholar]
123. Соколов ДД, Шварцман ВФ. 1974. Оценка размера Вселенной с топологической точки зрения. сов. физ. ЖЭТФ 39 , 196-200. [Google Scholar]
124. Gott JR. 1980. Хаотические космологии и топология Вселенной. Пн. Нет. Р. Астрон. соц. 193 , 153-169. ( 10.1093/mnras/193.1.153) [CrossRef] [Google Scholar]
125. Зельдович Ю.Б., Старобинский А.А. 1984. Квантовое создание Вселенной с нетривиальной топологией. Сов Астрон. лат. 10 , 135-137. [Академия Google]
126. Люминет Ж-П. 2008. Круглая вселенная. Уэлсли, Массачусетс: А.К. Питерс. [Google Scholar]
127. Бэрроу Д.Д. 2014. Космология: поиск двадцати четырех (или более) функций. физ. Преподобный Д 89 , 064022. (10.1103/PhysRevD.89.064022) [CrossRef] [Google Scholar]
128. Fagundes HV. 1985.
Релятивистские космологии с замкнутыми, локально однородными пространственными сечениями. физ. Преподобный Летт. 54 , 1200-1202. ( 10.1103/PhysRevLett.54.1200) [PubMed] [CrossRef] [Google Scholar]
физ. Преподобный Летт. 54 , 1200-1202. ( 10.1103/PhysRevLett.54.1200) [PubMed] [CrossRef] [Google Scholar]
129. Аштекар А., Сэмюэл Дж. 1991. Космологии Бьянки: роль пространственной топологии. Учебный класс. Квантовая Грав. 8 , 2191-2215. ( 10.1088/0264-9381/8/12/005) [CrossRef] [Google Scholar]
130. Koike T, Tanimoto M, Hosoya A. 1993. Компактные однородные вселенные. Дж. Матем. физ. 35 , 4855-4888. ( 10.1063/1.530819) [CrossRef] [Google Scholar]
131. Танимото М., Койке Т., Хосоя А. 1997. Динамика компактных однородных вселенных. Дж. Матем. физ. 38 , 350-368. ( 10.1063/1.531853) [CrossRef] [Google Scholar]
132. Кодама Х. 1998. Каноническое строение локально однородных систем на компактных замкнутых трехмерных многообразиях типов E3, Nil и Sol. прог. Теор. физ. 99 , 173-236. ( 10.1143/PTP.99.173) [CrossRef] [Google Scholar]
133. Барроу Дж. Д., Кодама Х. 2001.
Изотропия компактных вселенных. Учебный класс. Квант. Грав. 18 , 1753-1766 гг. ( 10.1088/0264-9381/18/9/310) [CrossRef] [Google Scholar]
2001.
Изотропия компактных вселенных. Учебный класс. Квант. Грав. 18 , 1753-1766 гг. ( 10.1088/0264-9381/18/9/310) [CrossRef] [Google Scholar]
134. Барроу Дж. Д., Кодама Х. 2001. Все вселенные большие и малые. Междунар. Дж. Мод. физ. Д 10 , 785-790. ( 10.1142/S0218271804) [CrossRef] [Google Scholar]
135. Фишер А.Е., Монкриф В. 1996. Структура квантового конформного суперпространства. В Глобальная структура и эволюция в общей теории относительности (ред. С. Коцакис, Г. В. Гиббонс), том. 460, стр. 111–173. Конспекты лекций по физике. Берлин, Германия: Springer.
136. Фишер А.Е., Монкриф В. 2000.
Приведенный гамильтониан общей теории относительности и сигма-константа конформной геометрии. В (ред. С. Коцакис, Г. Гиббонс), Proc. 2-я Самосская встреча. Космология, геометрия и теория относительности, математические и квантовые аспекты теории относительности и космологии . Конспект лекций по физике, том. 537, стр. 70–101. Берлин, Германия: Springer.
537, стр. 70–101. Берлин, Германия: Springer.
137. Фишер А.Е., Монкриф В. 2006. Гамильтонова редукция уравнений Эйнштейна. Энциклопедия математической физики, стр. 607-623. Нью-Йорк, штат Нью-Йорк: Academic Press. [Google Scholar]
138. Moncrief V, Mondal P. 2019. Может ли Вселенная иметь экзотическую топологию? Чистое приложение Мат. кв. 15 , 921-966. ( 10.4310/PAMQ.2019.v15.n3.a7) [CrossRef] [Google Scholar]
139. Collins CB, Ellis GFR. 1979. Сингулярности в космологиях Бьянки. физ. Представитель 56 , 65-105. ( 10.1016/0370-1573(79)-6) [CrossRef] [Google Scholar]
140. Wald RM. 1990. Доказательство гипотезы повторного коллапса замкнутой вселенной для общих космологий Бьянки типа IX. физ. Преподобный Д 41 , 2444-2448. ( 10.1103/PhysRevD.41.2444) [PubMed] [CrossRef] [Google Scholar]
141. Choquet-Bruhat Y, Cotsakis S. 2002.
Глобальная гиперболичность и полнота. Дж. Геом. физ. 43 , 345-350. ( 10.1016/S0393-0440(02)00028-1) [CrossRef] [Google Scholar]
( 10.1016/S0393-0440(02)00028-1) [CrossRef] [Google Scholar]
142. Choquet-Bruhat Y. 2009. Общая теория относительности и уравнения Эйнштейна. Нью-Йорк, штат Нью-Йорк: Издательство Оксфордского университета. [Google Scholar]
143. Коцакис С., Клаудату И. 2005. Будущие особенности изотропных космологий. Дж. Геом. физ. 55 , 306-315. ( 10.1016/j.geomphys.2004.12.012) [CrossRef] [Google Scholar]
144. Cotsakis S, Klaoudatou I. 2007. Космологические сингулярности и энергия Бела–Робинсона. Дж. Геом. физ. 57 , 1303-1312. ( 10.1016/j.geomphys.2006.10.007) [CrossRef] [Google Scholar]
145. Нодзири С., Одинцов С.Д., Цудзикава С. 2005. Свойства сингулярностей в (фантомной) вселенной темной энергии. физ. Преподобный Д 71 , 063004. (10.1103/PhysRevD.71.063004) [CrossRef] [Google Scholar]
146. Cotsakis S. 2013.
Структура бесконечности в космологии. Междунар. Дж. Мод. физ. Д 23 , 1330003. (10.1142/S0218271813300036) [CrossRef] [Google Scholar]
(10.1142/S0218271813300036) [CrossRef] [Google Scholar]
147. Fernandez-Jambrina L, Lazkoz R. 2006. Классификация космологических вех. физ. Преподобный Д 74 , 064030. ( 10.1103/PhysRevD.74.064030) [CrossRef] [Google Scholar]
148. Каттоен С., Виссер М. 2005. Необходимые и достаточные условия для больших взрывов, отскоков, схлопываний, разрывов, внезапных сингулярностей и экстремальных событий. Учебный класс. Квант. Грав. 22 , 4913-4930. ( 10.1088/0264-9381/22/23/001) [CrossRef] [Google Scholar]
149. Cotsakis S, Barrow JD. 2007. Доминирующий баланс в космологических сингулярностях. Дж. Физ. конф. сер. 68 , 012004. ( 10.1088/1742-6596/68/1/012004) [CrossRef] [Google Scholar]
150. Белинский В.А., Халатников И.М., Лифшиц Е.М. 1963. Исследования по релятивистской космологии. Доп. физ. 12 , 185-249. ( 10.1080/00018736300) [CrossRef][Google Scholar]
151. Старобинский А. А. 1983.
Изотропизация произвольного космологического расширения при заданной эффективной космологической постоянной. сов. физ. ЖЭТФ лат. 37 , 66-69. [Google Scholar]
А. 1983.
Изотропизация произвольного космологического расширения при заданной эффективной космологической постоянной. сов. физ. ЖЭТФ лат. 37 , 66-69. [Google Scholar]
152. Барроу Дж. Д., Коцакис С., Цокарос А. 2010. Общая внезапная космологическая сингулярность. Учебный класс. Квант. Грав. 27 , 165017. ( 10.1088/0264-9381/27/16/165017) [CrossRef] [Google Scholar]
153. Барроу Дж. Д., Коцакис С., Трачилис Д. 2020. Общая внезапная особенность в теории Бранса – Дикке. Евро. физ. Дж. С. 80 , 11-97. ( 10.1140/epjc/s10052-020-08771-5) [CrossRef] [Google Scholar]
154. Марк Хайнцле Дж., Сандин П. 2012. Исходная сингулярность ультражестких идеально-жидких пространств-времен без симметрий. Комм. Мат. физ. 313 , 385-403. ( 10.1007/s00220-012-1496-x) [CrossRef] [Google Scholar]
155. Ландау Л., Лифшиц Э.М. 1975 год.
Классическая теория поля, 4-е исправленное изд. Нью-Йорк, штат Нью-Йорк: Пергамон. [Google Scholar]
[Google Scholar]
156. Халатников И.М., Лифшиц Е.М. 1961. Об особенностях космологических решений уравнений гравитации. И. Сов. физ. ЖЭТФ 12 , 108. [Google Scholar]
157. Халатников И.М., Лифшиц Е.М. 1964. Проблемы релятивистской космологии. сов. физ. Усп. 6 , 495-522. ( 10.1070/PU1964v006n04ABEH003585) [CrossRef] [Google Scholar]
158. Халатников И.М., Каменщик А.Ю., Мартеллини М., Старобинский А.А. 2003. Квазиизотропное решение уравнений Эйнштейна вблизи космологической сингулярности для двухжидкостной космологической модели. Дж. Космол. Астропарт. физ. 03 , 001. ( 10.1088/1475-7516/2003/03/001) [CrossRef] [Google Scholar]
159. Халатников И.М., Каменщик А.Ю., Старобинский А.А. 2002. Комментарий о квазиизотропном решении уравнений Эйнштейна вблизи космологической сингулярности. Учебный класс. Квантовая Грав. 156, 3845-3849. ( 10.1088/0264-9381/19/14/322) [CrossRef] [Google Scholar]
160. Derouelle N, langlois D. 1995.
Длинноволновая итерация уравнений Эйнштейна вблизи пространственно-временной сингулярности. физ. Преподобный Д 52 , 2007-2019 гг. (10.1103/PhysRevD.52.2007) [PubMed] [CrossRef] [Google Scholar]
Derouelle N, langlois D. 1995.
Длинноволновая итерация уравнений Эйнштейна вблизи пространственно-временной сингулярности. физ. Преподобный Д 52 , 2007-2019 гг. (10.1103/PhysRevD.52.2007) [PubMed] [CrossRef] [Google Scholar]
161. Томита К. 1993. Усреднение неоднородных космологических моделей. физ. Преподобный Д 48 , 5634-5641. ( 10.1103/PhysRevD.48.5634) [PubMed] [CrossRef] [Google Scholar]
162. Riess A, et al. 1998. Свидетельства наблюдений сверхновых для ускоряющейся Вселенной и космологической постоянной. Астрон. Дж. 116 , 1009-1038. (10.1086/300499) [CrossRef] [Google Scholar]
163. Perlmutter S, et al. 1999. Измерения Ω и Λ 42 сверхновых с большим красным смещением. Астрофиз. Дж. 517 , 565-586. ( 10.1086/307221) [CrossRef] [Google Scholar]
164. Peebles PJE. 2020. Век космологии. Принстон, Нью-Джерси: Издательство Принстонского университета. [Академия Google]
165. Коупленд Э.Дж., Сами М., Цудзикава С. 2006.
Динамика темной энергии. Междунар. Дж. Мод. физ. Д 15 , 1753-1935. ( 10.1142/S021827180600942X) [CrossRef] [Google Scholar]
Коупленд Э.Дж., Сами М., Цудзикава С. 2006.
Динамика темной энергии. Междунар. Дж. Мод. физ. Д 15 , 1753-1935. ( 10.1142/S021827180600942X) [CrossRef] [Google Scholar]
166. Clifton T, Ferreira PG, Padilla A, Skordis C. 2012. Модифицированная гравитация и космология. физ. Представитель 513 , 1-189. ( 10.1016/j.physrep.2012.01.001) [CrossRef] [Google Scholar]
167. Capozziello S, De Laurentis M. 2011. Расширенные теории гравитации. физ. Представитель 5056, 167-321. ( 10.1016/j.physrep.2011.09.003) [CrossRef] [Google Scholar]
168. Джойс А., Джейн Б., Хури Дж. 2015. За пределами космологической стандартной модели. Представитель физ. 568 , 1-98. ( 10.1016/j.physrep.2014.12.002) [CrossRef] [Google Scholar]
169. Jiménez JB, Heisenberg L, Olmo GJ, Rubiera-Garcia D. 2018.
Борн-Инфельд вдохновил модификации гравитации. Физический отчет 727 , 1-129. ( 10.1016/j.physrep.2017. 11.001) [CrossRef] [Google Scholar]
11.001) [CrossRef] [Google Scholar]
170. Кобаяши Т. 2019. Теория Хорндески и не только: обзор. Представитель прог. физ. 82 , 086901. ( 10.1088/1361-6633/ab2429) [PubMed] [CrossRef] [Google Scholar]
171. Фрушанте Н. 2020. Теория эффективного поля темной энергии: обзор. физ. Представитель 857 , 1-63. ( 10.1016/j.physrep.2020.02.004) [CrossRef] [Google Scholar]
172. Ван С., Ван И, Ли М. 2017. Голографическая темная энергия. физ. Представитель 696 , 1-57. ( 10.1016/j.physrep.2017.06.003) [CrossRef] [Google Scholar]
173. Бранденбергер Р. 2022. Ограничения эффективной теории поля для космологии ранней Вселенной. Фил. Транс. Р. Соц. А 380 , 20210178. ( 10.1098/rsta.2021.0178) [CrossRef] [Google Scholar]
174. Гасперини М. 2022.
От до и после большого взрыва: (почти) самодвойственная космологическая история. Фил. Транс. Р. Соц. А 380 , 20210179. ( 10.1098/rsta. 2021.0179) [CrossRef] [Google Scholar]
2021.0179) [CrossRef] [Google Scholar]
175. Антониадис И., Коцакис С., Клаудату И. 2022. Особенности бранного мира и асимптотика объемных пятимерных жидкостей. Фил. Транс. Р. Соц. А 380 , 20210180. ( 10.1098/rsta.2021.0180) [CrossRef] [Google Scholar]
176. Vanhove P. 2022. S -матричный подход к физике гравитационных волн. Фил. Транс. Р. Соц. А 380 , 20210181. ( 10.1098/rsta.2021.0181) [CrossRef] [Google Scholar]
177. Solà Peracaula J. 2022. Проблема космологической постоянной и бегущий вакуум в расширяющейся Вселенной. Фил. Транс. Р. Соц. А 380 , 20210182. (10.1098/rsta.2021.0182) [CrossRef] [Google Scholar]
178. Erickson CW, Leung R, Stelle KS. 2022. Эффект Хиггса без обеда. Фил. Транс. Р. Соц. А 380 , 20210184. ( 10.1098/rsta.2021.0184) [CrossRef] [Google Scholar]
179. Townsend PK. 2022.
Эфир, темная энергия и струнные компактификации. Фил. Транс. Р. Соц. А 380 , 20210185. (10.1098/rsta.2021.0185) [PubMed] [CrossRef] [Google Scholar]
А 380 , 20210185. (10.1098/rsta.2021.0185) [PubMed] [CrossRef] [Google Scholar]
180. Tan L, Tsamis NC, Woodard RP. 2022. Как инфляционные гравитоны влияют на гравитационное излучение. Фил. Транс. Р. Соц. А 380 , 20210187. ( 10.1098/rsta.2021.0187) [CrossRef] [Google Scholar]
181. Казанас Д., Пападопулос Д., Христодулу Д. 2022. Гравитация выше Эйнштейна? Да, но в каком направлении? Фил. Транс. Р. Соц. А 380 , 20210367. ( 10.1098/rsta.2021.0367) [CrossRef][Google Scholar]
182. Дадхич Н. 2022. О пространственно-временной структуре и Вселенной: некоторые вопросы концепции и принципа. Фил. Транс. Р. Соц. А 380 , 20210405. ( 10.1098/rsta.2021.0405) [CrossRef][Google Scholar]
Существуют ли параллельные вселенные? Мы могли бы жить в мультивселенной
Существуют ли параллельные вселенные? Мы живем только в одной из множества пузырьковых вселенных? (Изображение предоставлено: MARK GARLICK / SCIENCE PHOTO LIBRARY через Getty Images) Параллельные вселенные больше не являются частью хорошей научной фантастики. В настоящее время существует несколько научных теорий, поддерживающих идею существования параллельных вселенных помимо нашей. Однако теория мультивселенной остается одной из самых противоречивых теорий в науке.
В настоящее время существует несколько научных теорий, поддерживающих идею существования параллельных вселенных помимо нашей. Однако теория мультивселенной остается одной из самых противоречивых теорий в науке.
Наша Вселенная невообразимо велика. Сотни миллиардов, если не триллионов, галактик (открывается в новой вкладке) вращаются в пространстве, каждая из которых содержит миллиарды или триллионы звезд (открывается в новой вкладке). Некоторые исследователи, изучающие модели Вселенной, предполагают, что диаметр Вселенной может составлять 7 миллиардов световых лет в поперечнике. Другие думают, что это может быть бесконечно.
Но это все, что там? Научная фантастика любит идею параллельной вселенной и мысль о том, что мы можем жить лишь одной из бесконечного числа возможных жизней. Однако мультивселенная не предназначена для «Звездного пути», «Человека-паука» и «Доктора Кто». Настоящая научная теория исследует и в некоторых случаях поддерживает доводы в пользу существования вселенных вне нашей, параллельных или удаленных от нее, но отражающих нашу. 26 раз в процессе, называемом космической инфляцией (откроется в новой вкладке). И это все до фактического расширения материи, о котором мы обычно думаем как о самом Большом взрыве, которое было следствием всей этой инфляции: по мере замедления инфляции появился поток материи и излучения, создавший классический огненный шар Большого взрыва, и начали формироваться атомы, молекулы, звезды и галактики, населяющие окружающие нас просторы космоса.
26 раз в процессе, называемом космической инфляцией (откроется в новой вкладке). И это все до фактического расширения материи, о котором мы обычно думаем как о самом Большом взрыве, которое было следствием всей этой инфляции: по мере замедления инфляции появился поток материи и излучения, создавший классический огненный шар Большого взрыва, и начали формироваться атомы, молекулы, звезды и галактики, населяющие окружающие нас просторы космоса.
Связанный: Как раздувающаяся вселенная могла создать мультивселенную
Этот загадочный процесс инфляции и Большого взрыва убедил некоторых исследователей в том, что множественные вселенные возможны или даже очень вероятны. По словам физика-теоретика Александра Виленкина из Университета Тафтса в Массачусетсе, инфляция не закончилась везде одновременно. Хотя она закончилась для всего, что мы можем обнаружить на Земле 13,8 миллиарда лет назад, космическая инфляция фактически продолжается в других местах. Это называется теорией вечной инфляции. И поскольку инфляция заканчивается в определенном месте, формируется новый пузырь Вселенной, писал Виленкин для журнала Scientific American в 2011 году.
И поскольку инфляция заканчивается в определенном месте, формируется новый пузырь Вселенной, писал Виленкин для журнала Scientific American в 2011 году.
Эти пузырьковые вселенные не могут контактировать друг с другом, потому что они продолжают бесконечно расширяться. Если бы мы направились к краю нашего пузыря, где он мог бы упереться в следующий пузырь вселенной, мы бы никогда не достигли его, потому что край уносится от нас быстрее, чем скорость света, и быстрее, чем мы сами. мог когда-либо путешествовать.
Родственный: Сколько звезд во Вселенной?
Но даже если бы мы смогли добраться до следующего пузыря, согласно вечной инфляции (в сочетании с теорией струн), наша знакомая вселенная с ее физическими константами и обитаемыми условиями могла бы полностью отличаться от гипотетической вселенной-пузыря рядом с нашей.
«Эта картина Вселенной, или, как ее называют, мультивселенной, объясняет давнюю загадку того, почему константы природы кажутся точно настроенными для возникновения жизни», — писал Виленкин. «Причина в том, что разумные наблюдатели существуют только в тех редких пузырях, в которых по чистой случайности константы оказываются как раз подходящими для развития жизни. Остальная часть мультивселенной остается бесплодной, но никто не может пожаловаться на это. »
«Причина в том, что разумные наблюдатели существуют только в тех редких пузырях, в которых по чистой случайности константы оказываются как раз подходящими для развития жизни. Остальная часть мультивселенной остается бесплодной, но никто не может пожаловаться на это. »
Объяснение Виленкина подразумевает, что в некоторых бесконечных пузырьковых вселенных за пределами нашей могут быть другие разумные наблюдатели. Но с каждым прошедшим мгновением мы удаляемся от них все дальше и никогда не пересечемся.
Квантовая механика и параллельные вселенные
Некоторые исследователи основывают свои представления о параллельных вселенных на квантовой механике, математическом описании субатомных частиц. В квантовой механике множественные состояния существования крошечных частиц возможны одновременно — «волновая функция» заключает в себе все эти возможности. Однако, когда мы на самом деле смотрим, мы наблюдаем только одну из возможностей. Согласно копенгагенской интерпретации квантовой механики, описанной в Стэнфордской энциклопедии философии , мы наблюдаем результат, когда волновая функция «коллапсирует» в единую реальность.
Но вместо этого теория многих миров предполагает, что каждый раз, когда наблюдается одно состояние или результат, существует другой «мир», в котором другой квантовый результат становится реальностью. Это ветвящееся устройство, в котором наша воспринимаемая вселенная разветвляется на почти бесконечные альтернативы. Эти альтернативные вселенные полностью разделены и не могут пересекаться, поэтому, хотя может существовать бесчисленное множество версий вашей жизни, которая немного — или сильно — отличается от вашей жизни в этом мире, вы никогда об этом не узнаете.
Связанный: Черные дыры, инопланетяне, мультивселенная и Марс: Космос Выступления TED, которые вам нужно посмотреть (откроется в новой вкладке)
Теория многих миров — самый «смелый» подход к затруднительному положению квантовой механики, физик Шон Кэрролл написал в своей книге «Что-то глубоко скрытое: квантовые миры и возникновение пространства-времени (открывается в новой вкладке)» (Dutton, 2019). Он также утверждал, что это самая простая теория, хотя и не лишенная недостатков.
Он также утверждал, что это самая простая теория, хотя и не лишенная недостатков.
Одна из этих проблем заключается в том, что идея многих миров на самом деле не поддается фальсификации. Это важный компонент научной мысли, с помощью которого научное сообщество развивает идеи, которые можно исследовать с помощью наблюдений и экспериментов. Если нет возможности найти доказательства против теории, это плохо для науки в целом, утверждает научный журналист Джон Хорган в своем блоге для Scientific American .
Бесконечное пространство, бесконечные вселенные?
Млечный Путь, показанный здесь с Земли, — всего лишь одна из сотен миллиардов, а может быть, и триллионов галактик во Вселенной. Каждая галактика состоит из миллиардов или триллионов звезд, у каждой из которых могут быть планеты. Может ли кто-нибудь из них быть таким же, как наш? (Изображение предоставлено Weerakarn Satitniramai через Getty Images)(открывается в новой вкладке)
Некоторые физики верят в более плоскую версию множественных вселенных. То есть, если вселенная, в которой мы живем, существует вечно, существует не так уж много способов, которыми строительные блоки материи могут упорядочиваться по мере их сборки в бесконечном пространстве. В конце концов, любое конечное число типов частиц должно повторять определенное расположение. Гипотетически в достаточно большом пространстве эти частицы должны повторять расположение целых солнечных систем и галактик.
То есть, если вселенная, в которой мы живем, существует вечно, существует не так уж много способов, которыми строительные блоки материи могут упорядочиваться по мере их сборки в бесконечном пространстве. В конце концов, любое конечное число типов частиц должно повторять определенное расположение. Гипотетически в достаточно большом пространстве эти частицы должны повторять расположение целых солнечных систем и галактик.
Итак, вся ваша жизнь может повториться где-то в другом месте во Вселенной, вплоть до того, что вы съели вчера на завтрак. По крайней мере, это теория.
Но если Вселенная началась в конечной точке, как соглашается почти каждый физик, альтернативной версии вас, скорее всего, не существует, согласно статье астрофизика Итана Сигела 2015 года на Medium .
По словам Зигеля, «количество возможных исходов от частиц в любой Вселенной, взаимодействующих друг с другом, стремится к бесконечности быстрее, чем количество возможных Вселенных увеличивается из-за инфляции».
«Так что это значит для вас?» — написал Сигель. «Это означает, что вы должны сделать эту Вселенную значимой».
Вселенная в зеркальном отражении
Некоторые исследователи предполагают, что на противоположной стороне временной шкалы Большого взрыва, уходящей назад во времени, когда-то существовала вселенная, которая была точным зеркальным отражением нашей собственной. Вот художественная иллюстрация истории Вселенной, представленная WMAP (микроволновым зондом анизотропии Уилкинсона), который потратил девять лет на создание карт всего неба космического микроволнового фона. WMAP изучил свет, выпущенный примерно через 375 000 лет после Большого взрыва, до того, как сформировались звезды и галактики. (Изображение предоставлено NASA / WMAP Science Team)(открывается в новой вкладке)
В относительно недавнем дополнении к пантеону теорий мультивселенной исследователи из Института теоретической физики Периметра в Ватерлоо, Онтарио, предположили, что вселенная началась в момент Большого взрыва — и на противоположной стороне временной шкалы Большого взрыва, растягиваясь назад во времени, когда-то существовала вселенная, которая была точным зеркальным отражением нашей собственной.
«Вместо того, чтобы говорить, что до взрыва существовала другая Вселенная, мы говорим, что вселенная до взрыва на самом деле в некотором смысле является изображением вселенной после взрыва», — Нил Турок, исследователь Института периметра, сообщил дочерний сайт Space.com Live Science (открывается в новой вкладке).
Это означает, что все — протоны, электроны, даже такие действия, как разбивание яйца — будут изменены на противоположные. Антипротоны и положительно заряженные электроны будут составлять атомы, а яйца будут раскалываться и возвращаться внутрь цыплят. В конце концов, эта вселенная сожмется, предположительно, до сингулярности, прежде чем расширится до нашей собственной вселенной.
С другой стороны, обе вселенные были созданы в результате Большого взрыва и одновременно взорвались назад и вперед во времени.
Мультивселенная: аргументы за и против
Аргументы в пользу теории мультивселенной
Космическая инфляция
Наша Вселенная росла экспоненциально в первые моменты своего существования, но было ли это расширение однородным? Если нет, то это предполагает, что разные регионы космоса росли с разной скоростью и могут быть изолированы друг от друга.
Математические константы
Почему законы Вселенной так точны? Некоторые предполагают, что это произошло случайно — мы — единственная вселенная из многих, которая случайно получила правильные числа.
Наблюдаемая Вселенная
Что находится за краем наблюдаемого пространства вокруг нас? Никто не знает наверняка, и до тех пор, пока мы этого не узнаем (а это может быть никогда), мысль о том, что наша Вселенная простирается на неопределенный срок, интересна.
Аргументы против теории мультивселенной
Опровержимость
У нас нет возможности проверить теории мультивселенной. Мы никогда не заглянем за пределы наблюдаемой Вселенной, поэтому, если нет способа опровергнуть теории, стоит ли им вообще верить?
Бритва Оккама
Иногда самые простые идеи оказываются самыми лучшими. Некоторые физики утверждают, что нам вообще не нужна теория мультивселенной. Никаких парадоксов это не решает, а только усложняет.
Нет доказательств
Мы не можем не только не опровергнуть никакую теорию мультивселенной, но и не можем ее доказать. В настоящее время у нас нет доказательств существования мультивселенных, и все, что мы можем видеть, предполагает, что существует только одна вселенная — наша собственная.
Параллельные вселенные в художественной литературе
Главный герой фильма Marvel «Доктор Стрэндж» (2016) может прыгать в разные измерения. (Изображение предоставлено Marvel.com)(открывается в новой вкладке)
Бесчисленные произведения мифов и художественной литературы основаны на идеях параллельных вселенных и мультивселенной. Перекрывающиеся миры появляются в скандинавской мифологии, а также в буддийской и индуистской космологии. Идея соприкосновения нескольких вселенных появилась в печати еще в новелле Эдвина А. Эбботта «Флатландия: многомерный роман» (Seeley & Co., 1884), и ее до сих пор можно увидеть в недавних фильмах, таких как фильм 2016 года. Фильм Марвел «Доктор Стрэндж». Целый жанр японских графических романов, называемый исекай, имеет дело с персонажами, переносимыми в параллельные миры, как описано в Нью-Йоркской публичной библиотеке .
Фильм Марвел «Доктор Стрэндж». Целый жанр японских графических романов, называемый исекай, имеет дело с персонажами, переносимыми в параллельные миры, как описано в Нью-Йоркской публичной библиотеке .
Почти каждый сериал «Звездный путь» включает в себя ту или иную форму зеркальной вселенной, а фильм-перезагрузка 2009 года с Крисом Пайном и Закари Куинто в главных ролях перенес последующие фильмы «Звездного пути» в совершенно новую временную шкалу, явно ответвляющуюся от оригинальной серии.
И комиксы, и соответствующие им фильмы глубоко погружаются в идею параллельных миров. Сюжетные линии недавних комиксов Marvel (как в фильмах, так и в печати), арка DC Flashpoint и «Into the Spider-Verse» 2018 года — все они исследуют несколько вселенных и пересечения между ними.
Это неполный список некоторых проявлений мультивселенных, вселенных с разделенной временной шкалой и параллельных вселенных в художественной литературе: Фильм: Через второе измерение (2011)
Телевидение
- Star Trek: Discovery, множественные эпизоды
- Star Trek: Enterprise, Maily Episodes 10180 10180 10180 10180 10180 10180 10180 10180 10180 10180 10189.
- Звездный путь: Следующее поколение, «Параллели» (Эпизод 11, Сезон 7) (1993)
- Звездный путь: Оригинальный сериал, «Зеркало, Зеркало» (Эпизод 4, Сезон 2) (1967) )
- Доктор Кто, несколько серий
- Слайдеры, вся серия
- Сообщество, «Remedial Chaos Theory» (эпизод 4, сезон 3) (2011)
- Рик и Морти, несколько серий
- Агенты Щ.95-2000) Филипа Пуллмана
- Серия «Плоский мир» (HarperCollins, 1983-2015) Терри Пратчетта
- «Люди как боги» (Макмиллан, 1923) Герберта Уэллса
- Серия «Темная башня» (Дональд М. . Grant, 1982-2012) by Stephen King
 Девять, несколько эпизодов
Девять, несколько эпизодов9 Eka0,0189 Футурама, несколько серий несколько серий
Video games
- BioShock Infinite, 2013
- Kingdom Hearts, 2002-2020
- Chrono Cross, 1999
- Half-Life, 1998-2020
- Metroid Prime 2 : Эхо, 2004
- Zero Escape, 2009-2016
Эта статья частично адаптирована из предыдущей работы автора Space. com Элизабет Хауэлл.
com Элизабет Хауэлл.
Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: community@space.com.
Дейзи Добриевич присоединилась к Space.com в феврале 2022 года в качестве справочного автора, ранее работавшего штатным автором в нашем сестринском журнале All About Space. Прежде чем присоединиться к нам, Дейзи прошла редакционную стажировку в журнале BBC Sky at Night Magazine и работала в Национальном космическом центре в Лестере, Великобритания, где ей нравилось знакомить общественность с космической наукой. В 2021 году Дейзи защитила докторскую диссертацию по физиологии растений, а также имеет степень магистра наук об окружающей среде. В настоящее время она живет в Ноттингеме, Великобритания.0078
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.

- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
1020010- Подача статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подписаться на SCIRP
Связаться с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Наведение мостов в высшем образовании: мультимодальные программы наставничества для поддержки удержания и подготовки к карьере ()
Джеймс Хатсон, Роджер Насер, Майкл Марцано, Райан Кертис, Элизабет Макдональд, Сью Эделе, Барбара Хосто-Марти
Творческое образование Том 13 № 9, 16 сентября 2022 г.

DOI: 10.4236/ce.2022.139178 10 загрузок 51 просмотр
Морфологический признак и физико-химическая характеристика почв под Festuca spp. Доминирующая степь у Высокой горы и горы Хувсгул, Монголия ()
Саруул Нарангерел, Ундармаа Джамсран, Маки Асано, Кенджи Тамура
Открытый журнал почвоведения Том 12 № 9, 16 сентября 2022 г.
DOI: 10.4236/ojss.2022.129018 14 загрузок 82 просмотров
Исследование рассеяния энергии волн в зоне прибоя Гвинейского залива: пример автономного порта Котону в прибрежной зоне Бенина()
Освальд Г.
 Акклассато, Ноукпо Бернар Токпохозин, Кристиан Д. Аковану, Аджимон Матиас Хуекпоэха, Ги Эрве Унге, Бруно Базиль Кунохева
Акклассато, Ноукпо Бернар Токпохозин, Кристиан Д. Аковану, Аджимон Матиас Хуекпоэха, Ги Эрве Унге, Бруно Базиль КунохеваJournal of Modern Physics Vol.13 No.9, 16 сентября 2022 г.
DOI: 10.4236/jmp.2022.139076 8 загрузок 54 просмотров
Модель скалярного поля обеспечивает возможный мост между общей теорией относительности и квантовой механикой()
Рики В. Остин
Международный журнал астрономии и астрофизики Том 12 №3, 16 сентября 2022 г.
DOI: 10.4236/ijaa.2022.123014 8 загрузок 54 просмотров
Характеристики состава тела и взаимосвязь между мышечной массой и мышечной силой у пожилых женщин в разных возрастных группах()
Нао Нишиока Ниши, Норико Танака, Наоми Хирано
Успехи в исследованиях старения Том 11 № 5, 16 сентября 2022 г.

DOI: 10.4236/aar.2022.115010 5 загрузок 37 просмотров
Профиль черепно-мозговой травмы в отделениях неотложной помощи больниц — ретроспективное исследование в Республике Молдова ()
Светлана Кочу, Анжела Казаку-Страту, Лилия Киосеа, Георгий Ройновяну, Сергей Чебану, Коринн Пик-Аса
Открытый журнал профилактической медицины Том 12 № 9, 16 сентября 2022 г.
DOI: 10.4236/ojpm.2022.129013 11 загрузок 74 просмотров
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2022 Scientific Research Publishing Inc. Все права защищены.
верхнийStudia Scientiarum Mathematicarum Hungarica Том 56 Выпуск 1 (2019)
Проблема ЖурналПогасить жетон
Ежемесячное использование контента
| абстрактных просмотров | полнотекстовых просмотров | Загрузка PDF | |
|---|---|---|---|
| Апрель 2022 | 3 | 1 | 0 |
| Май 2022 | 4 | 0 | 0 |
июнь 2022 г. | 2 | 0 | 0 |
| июль 2022 | 9 | 0 | 0 |
| авг. 2022 г. | 1 | 0 | 0 |
| Сентябрь 2022 | 4 | 0 | 0 |
| Октябрь 2022 | 0 | 0 | 0 |
Автор:
Данг Динь Хань
Автор:
Тарек Сайед Ахмед
Автор:
Сун Гуен Ким
Автор:
Александр Лемменс
Авторы:
Ли-Хун Се
и
Шоу Линь
Авторы:
Зеад Мустафа
,
Мона Хандаджи
и
Васфи Шатанави
Авторы:
Абраан, округ Колумбия, Насименту
,
Кассио Ф. Силва
Силва
,
Гаусс М. Кордейро
,
Морад Ализаде
,
Хайтам М. Юсоф
и
Г. Г. Хамедани
Авторы:
Артион Кашури
и
Розана Лико
Авторы:
Мишель Бронятовский
и
Амор Кезиу
Автор:
Т. Мори
Мори
Соло: Философия мультивселенной — Шон Кэрролл
Нажмите выше, чтобы закрыть.
0:00:00.1 Шон Кэрролл: Всем привет и добро пожаловать на подкаст Mindscape. Я ваш ведущий, Шон Кэрролл, и это, хотите верьте, хотите нет, 200-й очередной эпизод Mindscape. Но я говорю регулярно, потому что было намного больше эпизодов, если считать различные бонусы, эпизоды «Спроси меня о чем угодно», праздничные сообщения и тому подобное, но 200 — это неплохо, примерно 50 в год, это четыре года. Это четвертая годовщина Mindscape, так долго по сравнению со многими проектами, которые люди запускают на разных этапах своей карьеры, и я был очень, очень доволен всеми ответами от людей, которые слушают и надеются, что это принесет пользу. Итак, я хочу сделать что-то, чтобы отпраздновать.
0:00:22. 3 СК: Итак, я подумал, что сделаю сольный эпизод, что я часто и делаю в таких ситуациях, а тем временем я переезжаю из Лос-Анджелеса и Калифорнийского технологического института в Балтимор и Джонс Хопкинс, где Я буду профессором натурфилософии, название, которое я придумал, чтобы показать, что я буду заниматься и философией, и физикой, на самом деле тайно это физика, но такая физика очень хорошо вписывается в философский факультет. нет границы между этими двумя областями, в обоих случаях вы напряженно думаете, пытаясь понять фундаментальные принципы работы реальности, это то, что мне интересно делать, поэтому я не вижу барьера, но из-за различных способов, которые научное сообщество развивалось с годами, существует довольно существенный барьер, который воспринимают другие люди.
3 СК: Итак, я подумал, что сделаю сольный эпизод, что я часто и делаю в таких ситуациях, а тем временем я переезжаю из Лос-Анджелеса и Калифорнийского технологического института в Балтимор и Джонс Хопкинс, где Я буду профессором натурфилософии, название, которое я придумал, чтобы показать, что я буду заниматься и философией, и физикой, на самом деле тайно это физика, но такая физика очень хорошо вписывается в философский факультет. нет границы между этими двумя областями, в обоих случаях вы напряженно думаете, пытаясь понять фундаментальные принципы работы реальности, это то, что мне интересно делать, поэтому я не вижу барьера, но из-за различных способов, которые научное сообщество развивалось с годами, существует довольно существенный барьер, который воспринимают другие люди.
0:01:27.9 СК: Итак, я подумал, что, поскольку это происходит, и поскольку это 200-й эпизод моего сольного эпизода, я хотел бы поговорить о конкретном наборе вопросов, которые считаются естественной философией в этом смысле, о пересечении физики и философии. Более того, некоторые способы пересечения физики и философии довольно хорошо известны. Вы слышали о них раньше. Мы много говорили о квантовой механике и коллапсе волновой функции. Основы квантовой механики. Мы также много говорили о времени, стреле времени, энтропии и эмерджентности, связях между фундаментальной физикой и более высоким уровнем, так что все эти вещи являются узнаваемыми, очевидными местами, где и физике, и философии есть что сказать, есть что сказать. еще одна область, на которую иногда обращают внимание, но не так часто, — это космология, а космология — это то, чем я вырос как ученый-исследователь.
Более того, некоторые способы пересечения физики и философии довольно хорошо известны. Вы слышали о них раньше. Мы много говорили о квантовой механике и коллапсе волновой функции. Основы квантовой механики. Мы также много говорили о времени, стреле времени, энтропии и эмерджентности, связях между фундаментальной физикой и более высоким уровнем, так что все эти вещи являются узнаваемыми, очевидными местами, где и физике, и философии есть что сказать, есть что сказать. еще одна область, на которую иногда обращают внимание, но не так часто, — это космология, а космология — это то, чем я вырос как ученый-исследователь.
0:02:04.2 СК: Итак, меня особенно интересуют философские вопросы космологии, и хотя ей уделяется меньше внимания, это действительно совершенно естественное место для философского осмысления вопросов физики, потому что… что еще хуже, тот факт, что проблемы космологии, которые задают большие вопросы, такие как то, что произошло в начале Вселенной? Почему есть что-то, а не ничего? В таких случаях у нас нет данных по этим вопросам, или, по крайней мере, я должен сказать, чтобы быть немного более осторожным, что нет прямого пути решения этих вопросов, просто проведя соответствующий эксперимент.
0:03:00.1 СК: Тем не менее, это важные вопросы, и мы должны думать о них, и поэтому мы должны думать о них тщательно, в физике есть тенденция небрежно думать о вещах. Физики часто полагаются на тот факт, что в конце концов мы будем проводить эксперименты и, следовательно, получим правильный ответ, так что они могут думать довольно небрежно по ходу дела, зная, что они в основном руководствуются данными в вопросах, подобных этому, сделать это труднее, но это не так. Мы снимаем с себя ответственность делать это хорошо, думая о природе пространства и времени во Вселенной. Таким образом, обучение философов тому, как раскапывать наши скрытые предположения, убеждаясь, что мы поступаем логично по ходу дела, подобные вещи имеют безупречный смысл, но на самом деле философия космологии сама по себе довольно широкая область, так что я хотите сосредоточиться на чем-то очень конкретном, что является философией мультивселенной? Теперь, когда я говорю это, на ум приходят две разные вещи, и я хочу поговорить о каждой из них. Во-первых, является ли мультивселенная вообще физикой? Это вообще наука, да? Это своего рода мета-, методологический или эпистемологический вопрос о том, как делается наука, считается ли этот конкретный набор вопросов наукой. Это обсуждалось до смерти, я дам вам свою небольшую точку зрения на это, но я не хочу слишком долго на этом останавливаться.
Во-первых, является ли мультивселенная вообще физикой? Это вообще наука, да? Это своего рода мета-, методологический или эпистемологический вопрос о том, как делается наука, считается ли этот конкретный набор вопросов наукой. Это обсуждалось до смерти, я дам вам свою небольшую точку зрения на это, но я не хочу слишком долго на этом останавливаться.
0:04:12.9 СК: Что я действительно хочу подчеркнуть, так это то, что, помимо этих методологических вопросов, существует реальный онтологический вопрос или набор вопросов о том, как на самом деле устроен мир, которые находятся на стыке физики, космологии и философии. В частности, в случае мультивселенной, как мы рассуждаем, если мы живем в мультивселенной? Как мы говорим о вероятностях, где мы находимся и каковы должны быть наши ожидания, это одна из тех вещей в физике, которая имеет решающее значение, чего мы ожидаем, когда проводим эксперимент? Что мы ожидаем от теории, но обычно нам везет, потому что есть довольно прямой ответ. А в космологии мультивселенной, в частности, не все так однозначно, как мы мыслим антропно? Есть ли вообще смысл думать над всеми этими вопросами антропологически, об этом я хочу поговорить в сегодняшнем подкасте, вот что я имею в виду в данном конкретном случае под философией мультивселенной, и для меня это прекрасный пример такого рода пересечения, которые мы будем исследовать в Университете Джона Хопкинса, не только я, но и другие люди, которые интересуются такого рода междисциплинарными вопросами.
0:05:20.4 СК: Еще одно замечание, которое я хотел сделать, это то, что некоторые люди вполне разумно спросили, будет ли подкаст продолжаться в том же темпе, учитывая, что у меня есть эти новые обязанности, и ответ в том, что я определенно хотел продолжать двигаться в довольно сильном темпе. Но я также должен был быть реалистом, я буду преподавать, и у меня будут другие обязанности, которых у меня не было раньше, поэтому я придумал следующую временную стратегию. Посмотрим, как это сработает, то есть в какой-то момент, я не уверен, сразу или через пару месяцев, мы переключимся на режим, при котором вместо того, чтобы подкаст выходил каждый понедельник плюс и спрашивайте Эпизод Me Anything в середине месяца, в качестве бонуса, я просто начну считать эпизоды Ask Me Anything как обычные эпизоды понедельника, так что у меня все еще будет пронумерованное интервью плюс сольные эпизоды, которые будут появляться по понедельникам, но в один из таких понедельников в течение месяца мы получим эпизод «Спроси меня о чем угодно», тот же эпизод «Спроси меня о чем угодно», который я делал, но это будет тот слот понедельника, так что в целом вместо примерно пяти эпизодов подкастов в месяц будет получение четырех.
0:06:26.1 СК: И я думаю, что это небольшое изменение, но оно сэкономит мне время, и это изменение в экономии времени может иметь решающее значение для моего здравомыслия и моей способности качественно выполнять свою работу. мудрый со всеми вещами, которые я буду делать. Так что посмотрим, как пойдет, кто знает? Может быть, я обнаружу, что у меня есть лишнее время, и вернусь к прежнему графику, я не уверен, что это эксперимент, это то, что мы делаем в этой области.
0:06:47.4 СК: Наконец, для тех из вас, кто не слушает долго, что я имею в виду, когда говорю о чем-то, эпизод, когда люди присылают вопросы, и я отвечаю на них, но люди в в этом случае являются сторонниками Patreon. Так что, если вы хотите стать сторонником Mindscape на Patreon, просто зайдите на Patreon.com/Sean M. Carroll и подпишитесь на доллар в неделю или доллар за эпизод, что угодно… Кстати, эпизоды AMA не взимается с Patreon, поэтому Patreons сэкономят немного денег из-за этого нового соглашения, потому что для Patreons будет на один платный эпизод в месяц меньше, но Patreons смогут задавать вопросы, и они также получат доступ к эпизодам без рекламы. подкаста, а также ощущение того, что они делают что-то правильно и являются частью сообщества, в котором весело, есть отдельный разговор в комментариях на сайте Patreon и тому подобное. Так что, если вы хотите сделать это, пожалуйста.
подкаста, а также ощущение того, что они делают что-то правильно и являются частью сообщества, в котором весело, есть отдельный разговор в комментариях на сайте Patreon и тому подобное. Так что, если вы хотите сделать это, пожалуйста.
0:07:43.1 СК: Я очень ценю поддержку Патреонов. Это помогает мне финансировать различные вещи для подкаста, и это также просто приятно, но, конечно, как я всегда говорю, совершенно нормально не делать этого, особенно для некоторых людей, даже четыре или пять баксов в месяц — это лишнее. расходы, которые они действительно не хотят делать… Это совершенно нормально. В любом случае, я очень ценю поддержку, 200 эпизодов. От всех, кто слушает Mindscape, помогите распространить информацию. Помогите отправить его другим людям. Оставляйте отзывы в iTunes или везде, где вы слушаете свои подкасты. И, надеюсь, в будущем мы добавим еще пару сотен.
[музыка]
0:08:39.7 СК: Моя главная цель здесь действительно состоит в том, чтобы выявить тот факт, что это область, философия мультивселенной, где и физика, и философия имеют реальный интерес и реальные вещи для изучения. скажем, реальные вещи, которые можно предложить в этой дискуссии, и они не так много разговаривают друг с другом, если честно. Иногда философы говорят о мультивселенной, физике или чем-то еще, но они не говорят с физиками столько, сколько должны, а физики никогда не говорят с философами об этих вещах, потому что у физиков такое отношение, что если они сели на 15 минут и думал об этом трудно, они могли понять это.
скажем, реальные вещи, которые можно предложить в этой дискуссии, и они не так много разговаривают друг с другом, если честно. Иногда философы говорят о мультивселенной, физике или чем-то еще, но они не говорят с физиками столько, сколько должны, а физики никогда не говорят с философами об этих вещах, потому что у физиков такое отношение, что если они сели на 15 минут и думал об этом трудно, они могли понять это.
0:09:14.7 СК: И я думаю, что такое отношение часто бывает неправильным, но дело в том, что сегодня я не обязательно сосредотачиваюсь на решении этих проблем, а просто указываю, что проблемы есть, что это область, где должны вестись дискуссии, что мы должны быть непредубежденными, не только иметь отдельных людей, которые заинтересованы в обеих сторонах дискуссии по философии и физике, но и иметь фактическое взаимодействие между людьми с обеих сторон. У меня есть некоторые мнения по некоторым из этих вопросов, поэтому я попытаюсь их изложить, но я очень быстро признаю, что моя позиция здесь еще не полностью определена, поэтому вопросы действительно открыты для меня. Давайте начнем с размышлений о том, что мы имеем в виду, когда говорим слово «мультивселенная». Как вы все знаете, как искушенные слушатели, что существует более одной идеи, которая выражается словом мультивселенная. Мы не говорим о мультивселенной фильмов, таких как «Доктор Стрэндж», или о том, что везде и сразу. Мы говорим о научной мультивселенной, но даже там мы имеем в виду разные идеи, очень, очень разные идеи, но некоторые из одних и тех же философских вопросов являются общими для этих сценариев. Итак, давайте сосредоточимся на трех видах, я думаю, что, возможно, их больше, но в любом случае есть три способа, которыми эти мультивселенные возникают в моей работе.
Давайте начнем с размышлений о том, что мы имеем в виду, когда говорим слово «мультивселенная». Как вы все знаете, как искушенные слушатели, что существует более одной идеи, которая выражается словом мультивселенная. Мы не говорим о мультивселенной фильмов, таких как «Доктор Стрэндж», или о том, что везде и сразу. Мы говорим о научной мультивселенной, но даже там мы имеем в виду разные идеи, очень, очень разные идеи, но некоторые из одних и тех же философских вопросов являются общими для этих сценариев. Итак, давайте сосредоточимся на трех видах, я думаю, что, возможно, их больше, но в любом случае есть три способа, которыми эти мультивселенные возникают в моей работе.
0:10:25.7 СК: Одно из них, и, вероятно, то, что большинство работающих физиков имеют в виду, когда говорят слово мультивселенная, то, что мы могли бы назвать космологической мультивселенной. И это уже немного неправильное название, потому что другие так называемые вселенные и в космологической мультивселенной — это всего лишь области нашей вселенной, которые очень далеки. Космологическая мультивселенная — это идея о том, что мы видим наблюдаемую Вселенную размером примерно в десятки миллиардов световых лет. И причина, по которой мы не можем видеть дальше этого, заключается в том, что есть горизонт, где вы оглядываетесь назад во времени и попадаете в Большой взрыв, так что вы не можете видеть дальше, просто потому, что скорость света конечна. число, один световой год в год.
Космологическая мультивселенная — это идея о том, что мы видим наблюдаемую Вселенную размером примерно в десятки миллиардов световых лет. И причина, по которой мы не можем видеть дальше этого, заключается в том, что есть горизонт, где вы оглядываетесь назад во времени и попадаете в Большой взрыв, так что вы не можете видеть дальше, просто потому, что скорость света конечна. число, один световой год в год.
0:11:12.2 СК: В этой наблюдаемой вселенной, в той части вселенной, которую мы можем видеть, все выглядит довольно гладко, все выглядит довольно однородно в больших масштабах, в малых масштабах есть галактики, звезды и все такое, но если вы усредните миллионы световых лет, вы получите более или менее схожую ситуацию в разных частях наблюдаемой вселенной, то же количество галактик, одинаковую плотность материи и все такое прочее. За пределами Вселенной мы можем наблюдать… Давайте будем честными, мы не знаем, что произойдет, поэтому мы можем догадываться, и это то, что мы традиционно делали в космологии, традиционная вещь в космологии заключалась в том, чтобы сказать: «Ну, давайте просто предположим». что то, что происходит снаружи, является более или менее продолжением того, что происходит внутри». И вы можете сделать это, и тогда у вас появится идея, что Вселенная либо плоская, либо положительно изогнута, либо отрицательно искривлена, на самом деле есть только три варианта, может быть, есть какое-то топологическое препятствие или что-то в этом роде, или осложнения, кто знает. Но идея о том, что Вселенная просто существует бесконечно или, может быть, какое-то конечное время, если это закрытая вселенная, выглядящая точно так же, как в нашей наблюдаемой Вселенной, всегда была просто газом.
что то, что происходит снаружи, является более или менее продолжением того, что происходит внутри». И вы можете сделать это, и тогда у вас появится идея, что Вселенная либо плоская, либо положительно изогнута, либо отрицательно искривлена, на самом деле есть только три варианта, может быть, есть какое-то топологическое препятствие или что-то в этом роде, или осложнения, кто знает. Но идея о том, что Вселенная просто существует бесконечно или, может быть, какое-то конечное время, если это закрытая вселенная, выглядящая точно так же, как в нашей наблюдаемой Вселенной, всегда была просто газом.
0:12:27.9 СК: Принципиальной причины, по которой это должно быть так, нет, и если вы беспокоитесь о мультивселенной или о различных копиях себя, как указывали многие люди, является ли Вселенная пространственно плоской или отрицательно изогнутой, а не топологически искривленный, он будет бесконечным по размеру в этой простодушной идее, согласно которой Вселенная всегда однородна в больших масштабах. И в нашей Вселенной, если мы просто возьмем наблюдаемые нами условия и расширим их до бесконечности, средняя плотность будет числом, тогда вокруг этой плотности будут флуктуации, и существует лишь конечное число способов, которыми количество частиц мы видим в нашей наблюдаемой вселенной, возможно, могли устроиться сами по себе. Правильно, это большое число.
И в нашей Вселенной, если мы просто возьмем наблюдаемые нами условия и расширим их до бесконечности, средняя плотность будет числом, тогда вокруг этой плотности будут флуктуации, и существует лишь конечное число способов, которыми количество частиц мы видим в нашей наблюдаемой вселенной, возможно, могли устроиться сами по себе. Правильно, это большое число.
0:13:16.9 СК: Много возможных способов, потому что у нас есть что-то вроде 10 атомов или массивных частиц в 80-й степени в нашей Вселенной, еще 10 фотонов и нейтрино в 88-й степени и тому подобное, так что частиц очень много. , что они могут расположиться множеством способов, но помните, что бесконечность намного больше любого конечного числа. Итак, если вы действительно думаете, что Вселенная везде одинакова в очень большом масштабе, то есть каждый участок Вселенной, размер нашей наблюдаемой Вселенной, содержит примерно от 10 до 80 атомов, и эти атомы располагаются по-разному от места к месту. , но пространство простирается бесконечно далеко, то все, что только может произойти, произойдет внутри этих вселенных, внутри тех частей вселенной, которые являются сторонами для нашей наблюдаемой вселенной, а их будет бесконечное множество.
0:14:08.9 СК: Значит, где-то еще очень, очень, очень далеко в этой бесконечно большой вселенной будет бесконечное количество людей, точно таких же, как вы и я. Это тут же поднимает эти философские проблемы о том, как иметь дело с мультивселенной, потому что философские проблемы, которые меня будут интересовать, связаны с тем, кто вы в мультивселенной? Какая вы копия этого человека? Как мы можем рассуждать об этом, если существует несколько моих копий, с которыми все происходит в каком-то смысле? Как мы делаем прогнозы для чего-либо. И ни один из этих вопросов не основан на сумасшедших идеях об инфляции, теории струн или квантовой механике. Это просто позволяет нашей Вселенной быть бесконечно большой.
0:14:50.9 СК: Я думаю, это одна из причин, по которой такие люди, как Эйнштейн, поддерживали идею о том, что Вселенная будет пространственно замкнутой, положительно искривленной и конечной по размеру, насколько нам известно, с точки зрения наблюдений, она очень близка до плоского, что соответствовало бы тому, что происходит для Бесконечности, но не… Оно этого не требует. У вас может быть плоская вселенная, которая все еще замкнута на себя, как, например, Телец. Но в любом случае, как я пытался сказать в начале, нет принципиальной причины думать, что Вселенная везде одинакова, это всего лишь предположение. Может быть, это правда, может быть, это не так. Идея космологической мультивселенной состоит в том, что это не так. Что разные области космоса, очень далеко друг от друга, действительно очень разные, даже, может быть, не только разные плотности материи или разные наборы галактик и звезд.
У вас может быть плоская вселенная, которая все еще замкнута на себя, как, например, Телец. Но в любом случае, как я пытался сказать в начале, нет принципиальной причины думать, что Вселенная везде одинакова, это всего лишь предположение. Может быть, это правда, может быть, это не так. Идея космологической мультивселенной состоит в том, что это не так. Что разные области космоса, очень далеко друг от друга, действительно очень разные, даже, может быть, не только разные плотности материи или разные наборы галактик и звезд.
0:15:11.3 СК: Но, может быть, даже разные локальные законы физики, разные вещи, которые мы бы использовали и признали эквивалентными стандартной модели физики элементарных частиц, но с другими частицами, другими силами, разной силой этих сил, может быть. даже разное количество измерений пространства-времени. Однажды я написал статью с Мэттом Джонсоном [0:15:58.0] ____ о том, как вы можете динамически совершать переход от определенного количества измерений пространства в некоторой области к другому количеству измерений пространства, так что это может быть частью космологической мультивселенной. И самое главное, что нужно понять об этой идее космологической мультивселенной, так же, как будет важно помнить и о других версиях мультивселенной, это то, что она не была изобретена, потому что звучит круто, она была изобретена не потому, что физики думали, что вы знаете, было бы забавно подумать об этом.
И самое главное, что нужно понять об этой идее космологической мультивселенной, так же, как будет важно помнить и о других версиях мультивселенной, это то, что она не была изобретена, потому что звучит круто, она была изобретена не потому, что физики думали, что вы знаете, было бы забавно подумать об этом.
0:16:31.1 ШК: Нас с криками и ногами втянули в размышления о космологической мультивселенной против нашей воли, и причина этого в том, что космологическая мультивселенная не является теорией. Это предсказание различных теорий, и оно является следствием этих теорий, но вы должны судить теории, что это следствие не предсказания само по себе, вы не можете отделить предсказание от теории, которая делает это предсказание. . В этом случае, космологическом случае мультивселенной, теории возникли, исходя из инфляционной теории, которую Алан Гут и другие изобрели около 19 г.80, и это было вызвано попыткой понять данные, в частности данные о том, что наша Вселенная гладкая, однородная и изотропная, а также почти пространственно плоская. Кроме того, на самом деле во Вселенной нет наблюдаемых магнитных монополей, что было предсказанием различных теорий великого объединения в то время.
Кроме того, на самом деле во Вселенной нет наблюдаемых магнитных монополей, что было предсказанием различных теорий великого объединения в то время.
0:17:26.2 СК: Итак, Гут использовал эту идею инфляции, которая говорит, что если вселенная начинается или в любом случае в какое-то раннее время, в ее плотности энергии преобладает то, что мы называем энергией ложного вакуума, очень похожее на сегодня мы думаем с 19Когда мы обнаружили, что Вселенная ускоряется, мы подумали, что в пустом пространстве есть энергия, космологическая постоянная, энергия вакуума. Но вы также можете получить временную форму энергии вакуума или энергию ложного вакуума, которая может быть действительно большой энергией в пустом пространстве, и это заставит Вселенную расширяться с огромным ускорением, очень быстрой скоростью. И это вроде как дергать за края мятой простыни или что-то в этом роде, оно стремится все разгладить, сверхускоренное расширение. Итак, Гут занимался физикой и показал, что можно начать с этого ложного вакуума, а затем превратить всю эту вакуумную энергию в обычную материю и излучение. Итак, сначала вы раздуваетесь, над вами доминирует энергия ложного вакуума, вы сглаживаете вселенную и делаете ее плоской, а затем преобразуете всю эту энергию ложного вакуума в обычную материю и излучение. Так вот, он немного ошибся, но он знал, что ошибся, он указал, что в его собственной оригинальной модели вы никогда не покидали инфляцию, вы не получали этого красивого выхода, изящного выхода, как его называли, в ситуация, когда вы превратили эту энергию в обычную материю и излучение.
Итак, сначала вы раздуваетесь, над вами доминирует энергия ложного вакуума, вы сглаживаете вселенную и делаете ее плоской, а затем преобразуете всю эту энергию ложного вакуума в обычную материю и излучение. Так вот, он немного ошибся, но он знал, что ошибся, он указал, что в его собственной оригинальной модели вы никогда не покидали инфляцию, вы не получали этого красивого выхода, изящного выхода, как его называли, в ситуация, когда вы превратили эту энергию в обычную материю и излучение.
0:18:49.4 СК: Итак, вскоре после того, как Андрей Линде, Энди Альбрехт и Пол Стейнхардт предложили модели, в которых можно плавно скатывать скалярное поле от высокой потенциальной энергии к низкой потенциальной энергии, и вы можете преобразовать всю эту энергию в обычное вещество и излучение. Без проблем. Итак, это назвали Новой инфляцией, и это решило проблему изящного выхода. Но вот проблема то ли в старой инфляции, то ли в новой инфляции, это скалярное поле, которое мы постулировали, мы его изобретаем, доказательств этому пока нет, но оно было поставлено и вполне может быть связано с другими идеями в физике.
0:19:24.3 СК: Это не классическое скалярное поле, в мире есть такая вещь, как квантовая механика, и так как скалярное поле скатывает свой потенциал и превращается в материю и энергию, возникают квантовые флуктуации, это не абсолютно одно и то же значение в разных точках пространства. И это принципиально важно. Это объяснение, как мы думаем в теории инфляционной Вселенной, возмущений плотности, которые сегодня приводят к возникновению звезд и галактик. Мы видим отпечаток этих квантовых флуктуаций в космическом микроволновом фоне и в структуре крупномасштабной структуры Вселенной.
0:20:00.9 СК: Если инфляция верна, мы определенно видим колебания плотности и температуры во Вселенной. Инфляция приписывает эти флуктуации квантовым флуктуациям во время инфляционного периода, и вскоре после этого люди заметили, что Пол Стейнхардт, Андрей Линде, Алекс Фланкан и другие, если принять во внимание эти квантовые флуктуации, могут иногда иметь квантовые флуктуации, когда вместо скатывания вниз по склону . Если вы визуализируете потенциальную энергию скалярного поля в виде холма, поле стремится скатиться вниз, как мячик скатывается с холма, но квантовая флуктуация, скажем, вы могли бы время от времени подпрыгивать на холме, это квантовая флуктуация, это редкость, но это может случиться. И эти потенциалы очень плоские, поэтому подпрыгнуть в гору не так уж сложно, а когда вы подпрыгиваете в гору, у вас теперь больше плотность энергии, инфляция происходит быстрее, и вы создаете больший объем пространства. Итак, вы делаете расчет и показываете, что при очень разумных значениях параметров инфляция никогда не заканчивается, она закончится в какой-то области пространства, но где-то еще, поле инфлатона, как мы его называем, это новое скалярное поле, которое мы изобрели, он квантово колебался в гору, и хотя это происходит относительно редко, когда это случается, он генерирует огромное количество пространства, потому что раздувается очень, очень быстро.
Если вы визуализируете потенциальную энергию скалярного поля в виде холма, поле стремится скатиться вниз, как мячик скатывается с холма, но квантовая флуктуация, скажем, вы могли бы время от времени подпрыгивать на холме, это квантовая флуктуация, это редкость, но это может случиться. И эти потенциалы очень плоские, поэтому подпрыгнуть в гору не так уж сложно, а когда вы подпрыгиваете в гору, у вас теперь больше плотность энергии, инфляция происходит быстрее, и вы создаете больший объем пространства. Итак, вы делаете расчет и показываете, что при очень разумных значениях параметров инфляция никогда не заканчивается, она закончится в какой-то области пространства, но где-то еще, поле инфлатона, как мы его называем, это новое скалярное поле, которое мы изобрели, он квантово колебался в гору, и хотя это происходит относительно редко, когда это случается, он генерирует огромное количество пространства, потому что раздувается очень, очень быстро.
0:21:24.2 СК: И затем процесс повторяется, где в той новой области, которую вы создали, в некоторых местах инфляция заканчивается, в других местах она продолжается, но в целом она будет продолжаться где-то во вселенной, так что это это идея, называемая вечной инфляцией.
0:21:38.5 СК: И это не обязательно часть инфляционной теории, но это очень естественная часть инфляционной теории. Это происходит очень легко, не нужно очень много работать, чтобы инфляция была вечной. Так что это уже дает вам своего рода мультистих, потому что он говорит, что инфляция закончится там, где поле инфлатона превратится в обычную материю и излучение, и закончится она по-разному в разных точках пространства в разное время истории Вселенной. , но это стало очень захватывающим только тогда, когда мы поняли, что когда инфляция закончится, локальные законы физики могут быть разными в разных областях пространства. И это было то, о чем люди тоже думали, еще раз, но это стало очень важным для людей, когда мы наткнулись на то, что называется ландшафтом теории струн, и ландшафт теории струн также был в некотором смысле вдохновлен данными еще раз. Когда мы обнаружили в 1998, что Вселенная ускоряется, мы приписываем это космологической постоянной, и это была революция, это единственная революция, которую лично я пережил в фундаментальной физике в свое время, когда мы поняли, что космологическая постоянная, вероятно, не равна нулю, потому что мы все знали, что здесь есть проблема, связанная с космологической постоянной.
0:22:51.0 СК: Энергия пустого пространства может быть в принципе какой угодно, но вы можете оценить, какой она должна быть, вы можете оценить на основе эффективной квантовой теории поля, каким было бы естественное значение космологической постоянной. , и ответ намного, намного, намного больше, чем то, что вы на самом деле наблюдаете. Итак, большинство людей… Когда я учился в аспирантуре, большинство людей твердо верили, что, поскольку энергия вакуума по какой-то неизвестной причине была намного, намного, намного меньше, чем можно было бы предсказать на основе естественности, возможно, даже несмотря на то, что мы не знаю что, был какой-то механизм, который устанавливал его ровно на ноль, потому что просто трудно придумать какую-то причину, по которой ты должен говорить, что он так близок к нулю, а не идти до конца прямо в пространстве всех возможные теоретические идеи, было бы легче придумать гипотетические идеи или вообразить, что они существуют, если бы они просто установили космологическую постоянную точно в ноль.
0:23:44.3 СК: Но потом мы обнаружили, что это не ноль, или, по крайней мере, не похоже на ноль, возможно также, что то, что заставляет вселенную ускоряться, является чем-то вроде динамического скалярного поля, очень похоже на инфляцию, но с гораздо меньшей плотностью энергии, это рассматривается как возможность, но заставить это работать сложнее. Так что мы еще не знаем, мы еще раз проверяем это экспериментально, но самая простая идея заключается в том, что это энергия вакуума.
0:24:11.7 СК: Итак, вернемся к чертежной доске. Мы не можем сказать, что есть какой-то неизвестный механизм, который устанавливает космологическую постоянную в ноль, потому что она не равна нулю. И в теории струн, которая была главным кандидатом на роль квантовой гравитации, определенно было бы легче заставить теорию струн работать, если бы космологическая постоянная не была положительной. На самом деле было гораздо проще заставить его работать, если космологическая постоянная отрицательна, и это хороший способ понять теорию струн. Но если бы он был нулевым, ладно, мы могли бы с этим поладить. Это было очень сложно, очень трудно понять, почему в теории струн нулевая космологическая постоянная, даже если у вас нет явной суперсимметрии при низких энергиях. Суперсимметрия является частью набора инструментов теории струн. Это достаточно легко скрыть, мы не видим экспериментальных доказательств теории струн, но скрыть это достаточно просто, как мы скрываем другие симметрии в физике. Но в целом, когда вы нарушаете суперсимметрию, чтобы скрыть ее, вы не остаетесь с нулевой космологической постоянной, ей легко быть отрицательной, трудно быть ровно равной нулю, предполагается, что легко быть положительной, но слово легко проблематично там мы не знаем.
Но если бы он был нулевым, ладно, мы могли бы с этим поладить. Это было очень сложно, очень трудно понять, почему в теории струн нулевая космологическая постоянная, даже если у вас нет явной суперсимметрии при низких энергиях. Суперсимметрия является частью набора инструментов теории струн. Это достаточно легко скрыть, мы не видим экспериментальных доказательств теории струн, но скрыть это достаточно просто, как мы скрываем другие симметрии в физике. Но в целом, когда вы нарушаете суперсимметрию, чтобы скрыть ее, вы не остаетесь с нулевой космологической постоянной, ей легко быть отрицательной, трудно быть ровно равной нулю, предполагается, что легко быть положительной, но слово легко проблематично там мы не знаем.
0:25:19.6 СК: До сих пор ведутся споры о том, может ли космологическая постоянная быть положительной в теории струн. Но опять же, наивно, кажется, что вы можете получить положительную космологическую постоянную в Теории струн, а затем, как только эта возможность будет выдвинута вперед и в центр, нам нужно понять, как космологическая постоянная может быть положительным числом, люди сели и поняли , Ну да, мы могли бы это сделать, у нас есть все эти дополнительные измерения пространства в теории струн. Теория струн работает наиболее естественно, если пространство-время десятимерно.
Теория струн работает наиболее естественно, если пространство-время десятимерно.
0:25:49.3 ШК: Некоторые версии 11-мерные. Но больше, чем четырехмерное, ладно. Итак, мы должны скрыть эти дополнительные измерения пространства, как нам это сделать? Мы выползаем из них в какую-то геометрически интересную форму, и разные геометрически интересные формы порождают разные низкоэнергетические законы физики, включая разные значения космологической постоянной, и это кажется, по крайней мере многим людям, естественным результатом теории струн. . Что-то, что вам не нужно было вводить, это просто то, что мы не замечали и не уделяли этому слишком много внимания до того, как данные навязали нам это, как это часто бывает в физике. Хорошо, теперь то, что у вас есть, если вы объедините вечную инфляцию с ландшафтом теории струн, вы не только получите инфляцию, порождающую множество различных регионов Вселенной, но и теория струн говорит, что локальные законы физики в этих регионах могут быть нарушены. основанных на различных способах компактификации дополнительных измерений пространства, что может привести к возникновению различных локальных законов физики, включая энергию вакуума.
основанных на различных способах компактификации дополнительных измерений пространства, что может привести к возникновению различных локальных законов физики, включая энергию вакуума.
0:26:47.9 СК: То, что вы вдруг получили, это разные значения энергии вакуума в разных областях пространства, и затем вы применяете старый аргумент, Стивен Вайнберг прославил его, но другие люди указали на него задолго до этого. Его, а именно, что если бы космологическая постоянная была очень, очень большой, либо большой и положительной, либо большой и отрицательной, то очень трудно представить, как могли бы существовать люди или как могла бы существовать жизнь, потому что большая энергия вакуума имеет тенденцию либо взрывать вещи, либо отдельно, если оно положительное, или сломать вселенную за очень короткий период времени, если оно отрицательное. Итак, есть то, что мы называем антропным отбором, если… И это очень, очень большое если. Если есть много разных областей пространства, где энергия вакуума различна, это совершенно естественно, поэтому история идет о том, что живые существа возникают только в том подмножестве всех этих частей вселенной, где энергия вакуума не так велика. И это могло бы объяснить, почему мы наблюдаем небольшую, но не нулевую энергию вакуума.
И это могло бы объяснить, почему мы наблюдаем небольшую, но не нулевую энергию вакуума.
0:27:46.9 СК: И чтобы быть полностью исторически точным, Стивен Вайнберг указал на это за 10 лет до того, как мы открыли космологическую постоянную. Он особо указал, что если объяснение энергии вакуума заключается не в каком-то динамическом механизме, устанавливающем ее равной нулю, а скорее в каком-то антропном отборе, который говорит, что «есть много разных значений энергии вакуума, но мы наблюдаем только те, которые совместимы с нашим существованием, то вы должны предсказать, что космологическая постоянная должна быть наблюдаемой. Он должен быть маленьким, но не настолько маленьким, чтобы мы не могли его наблюдать».
0:28:27.4 СК: Так проще. Наблюдаемых значений космологической постоянной больше, чем ненаблюдаемых, даже совместимых с нашим существованием. И это предсказание, которое он сделал за 10 лет до того, как мы его увидели. Так что это плюс в бухгалтерской книге… Положительная сторона бухгалтерской книги для такого рода рассуждений. В любом случае, это космологическая мультивселенная. Это один из способов получить мультивселенную. Таким образом, в космологической мультивселенной, насколько нам известно, при тех вычислительных методах, которые у нас есть, существует бесконечное число вселенных, по крайней мере, если вы включаете будущее и прошлое, а также настоящий момент.
В любом случае, это космологическая мультивселенная. Это один из способов получить мультивселенную. Таким образом, в космологической мультивселенной, насколько нам известно, при тех вычислительных методах, которые у нас есть, существует бесконечное число вселенных, по крайней мере, если вы включаете будущее и прошлое, а также настоящий момент.
0:29:05.3 СК: И у нас не только разные законы физики во многих из них, но мы также можем иметь в некоторых из них точно такие же законы физики. Это совсем другая идея, чем второй сценарий, о котором мы хотим поговорить, который представляет собой многомировую интерпретацию квантовой механики. Давние слушатели будут знакомы с этим, поэтому мне не нужно вдаваться в подробности. Но многие миры возникают из-за того, что мы, опять же, пытаемся объяснить данные, но данные — это очень разные данные.
0:29:29.8 СК: Здесь мы пытаемся объяснить данные квантовой физики. Тот факт, что когда вы наблюдаете положение электрона, даже если вы описываете положение электрона в терминах волновой функции, разбросанной по всему пространству, когда вы его не наблюдаете, когда вы его наблюдаете, вы всегда увидеть его в положении. Вы никогда не увидите полную волновую функцию. Что с этим делать? Есть много разных вариантов, что с этим делать. Возможности многих миров говорят, что когда вы думаете об этом измерении положения электрона, вам действительно нужно думать о себе как о квантово-механической системе, имеющей волновую функцию.
Вы никогда не увидите полную волновую функцию. Что с этим делать? Есть много разных вариантов, что с этим делать. Возможности многих миров говорят, что когда вы думаете об этом измерении положения электрона, вам действительно нужно думать о себе как о квантово-механической системе, имеющей волновую функцию.
0:30:06.5 ШК: И когда вы моделируете взаимодействие между вами и электроном, которое квалифицируется как измерение, на самом деле происходит то, что вы запутываетесь с электроном. Так что реальность не в том, что электрон коллапсирует в какое-то положение согласно многим мировым представлениям, а в том, что часть волновой функции говорит, что электрон был здесь, и вы его здесь наблюдали. Другая часть, в которой говорится, что электрон был там, и вы наблюдаете его там. И так далее для каждого возможного результата измерения.
0:30:33.4 СК: Что бы там ни предлагалось, так это то, что мы берем эти разные части волновой функции и рассматриваем их как отдельные независимые миры. У него были причины для этого, но я думаю, что лучшие причины, которые существуют после того, как когда-либо… Лучшие причины говорить об этих разных частях волновой функции как о совершенно независимых мирах сводятся к тому, что мы называем декогеренцией. И декогеренция началась в 70-х. Люди предчувствовали это и раньше, но на самом деле теория была разработана в 70-х и 80-х годах, и она объясняет, почему эти разные миры становятся независимыми друг от друга. Чтобы то, что происходит в одном мире, не влияло на то, что происходит в другом мире. Так что они не могут влиять друг на друга в типичных обстоятельствах, и поэтому мы называем их иными мирами.
У него были причины для этого, но я думаю, что лучшие причины, которые существуют после того, как когда-либо… Лучшие причины говорить об этих разных частях волновой функции как о совершенно независимых мирах сводятся к тому, что мы называем декогеренцией. И декогеренция началась в 70-х. Люди предчувствовали это и раньше, но на самом деле теория была разработана в 70-х и 80-х годах, и она объясняет, почему эти разные миры становятся независимыми друг от друга. Чтобы то, что происходит в одном мире, не влияло на то, что происходит в другом мире. Так что они не могут влиять друг на друга в типичных обстоятельствах, и поэтому мы называем их иными мирами.
0:31:19.0 ШК: Совершенно другая идея, чем космологическая мультивселенная. В космологической мультивселенной буквально есть регионы, находящиеся далеко друг от друга в пространстве. Многие миры квантовой механики буквально возникают в моей комнате, когда я измеряю квантовую систему. Я не создаю другую область космоса далеко, я создаю совершенно другую параллельную вселенную. И он нигде не находится, они просто существуют одновременно. Все миры существуют с разными амплитудами, и амплитуды имеют значение, если мы говорим о множестве миров, но сегодня мы говорим не об этом. Мы не говорим о деталях многих миров. Дело в том, что существует множество копий моего будущего «я». Итак, прямо сейчас есть одна моя копия, есть другие копии, которые произошли от меня в прошлом, но я здесь прямо сейчас. Я делаю некоторые измерения, во всех этих разных мирах будет много потомков моего нынешнего «я». Так что это другой вид мультивселенной, который появляется в физике.
И он нигде не находится, они просто существуют одновременно. Все миры существуют с разными амплитудами, и амплитуды имеют значение, если мы говорим о множестве миров, но сегодня мы говорим не об этом. Мы не говорим о деталях многих миров. Дело в том, что существует множество копий моего будущего «я». Итак, прямо сейчас есть одна моя копия, есть другие копии, которые произошли от меня в прошлом, но я здесь прямо сейчас. Я делаю некоторые измерения, во всех этих разных мирах будет много потомков моего нынешнего «я». Так что это другой вид мультивселенной, который появляется в физике.
0:32:14.2 СК: И, наконец, есть идея вечно меняющихся космологий, у которых нет громкого имени. Вот что я буду называть вечно колеблющимися космологиями. Идея такова: Итак, вспомните еще раз ускоряющуюся Вселенную. Итак, в 1998 году мы обнаружили, что Вселенная ускоряется. Самое простое объяснение этому — космологическая постоянная, и есть теорема, доказанная еще в 1980-х Бобом Уолдом из Чикагского университета, которая гласит, что при довольно общих обстоятельствах, если у вас есть Вселенная с положительной космологической постоянной и не слишком другие вещи, тогда эта вселенная всегда будет пустовать.
0:32:57.1 СК: Итак, если у вас есть другие вещи… Если у вас есть положительная космологическая постоянная, но много материи, столько материи, что она скручивает пространство в себя, и вы получаете положительно искривленную вселенную, тогда это в конечном итоге повторный коллапс. Но если материи не слишком много… Итак, если Вселенная близка к плоской, например, тогда Вселенная будет расширяться вечно. А происходит то, что галактики и другие объекты просто отрываются друг от друга. Все возмущения плотности, которые были у нас в ранней Вселенной, выровняются под влиянием этой космологической постоянной ускоренного расширения.
0:33:27.7 СК: Это называется космической теоремой об отсутствии волос. Можно добавить больше деталей, потому что галактики имеют динамику, в них есть звезды, звезды сгорят, попадут в черные дыры. Черные дыры испарятся. Испаряющееся излучение черных дыр будет смещено в красную сторону, по существу, в небытие, и тогда вы действительно останетесь ни с чем, кроме пустого пространства. И название этого пустого пространства, в котором нет ничего, кроме энергии вакуума, называется пространством де Ситтера в честь Виллема де Ситтера, астронома, который первым решил уравнения Эйнштейна и нашел это космологическое решение.
И название этого пустого пространства, в котором нет ничего, кроме энергии вакуума, называется пространством де Ситтера в честь Виллема де Ситтера, астронома, который первым решил уравнения Эйнштейна и нашел это космологическое решение.
0:34:02.2 СК: Одна из вещей, которые мне нравятся в этой космической теореме об отсутствии волос, заключается в том, что все вселенные с положительной космологической постоянной эволюционировали в направлении пространства де Ситтера, точно так же, как все черные дыры эволюционируют в сторону простого массового заряда и черного вращения. Дыры похожи на случай с черной дырой, здесь есть энтропийная интерпретация… Всякий раз, когда у вас есть система, которая неизбежно эволюционирует к какому-то микроскопическому состоянию, а затем просто остается там навсегда, это звучит как приближение системы к равновесию путем термолиза с возрастающей энтропией.
0:34:36.1 СК: Итак, я давно предполагал, что эта космическая теорема об отсутствии волос, вероятно, эквивалентна уравновешиванию. К увеличению энтропии… Ко второму закону термодинамики. И, наконец, с аспирантом Эйданом Чатвином-Дэвисом я смог это доказать. Эйдан сделал большую часть доказательств, которые я должен признать. Но мы в основном нашли определение энтропии, применимое к этим случаям, и мы показали, что даже без уравнения общей теории относительности Эйнштейна, если бы у вас была только расширяющаяся Вселенная с определенным определением энтропии, и вы предположили, что энтропия в области приближается к тогда максимальное значение останется там навсегда, что будет эквивалентно пространству де Ситтера. В эту экспоненциально расширяющуюся, ускоряющуюся вселенную.
К увеличению энтропии… Ко второму закону термодинамики. И, наконец, с аспирантом Эйданом Чатвином-Дэвисом я смог это доказать. Эйдан сделал большую часть доказательств, которые я должен признать. Но мы в основном нашли определение энтропии, применимое к этим случаям, и мы показали, что даже без уравнения общей теории относительности Эйнштейна, если бы у вас была только расширяющаяся Вселенная с определенным определением энтропии, и вы предположили, что энтропия в области приближается к тогда максимальное значение останется там навсегда, что будет эквивалентно пространству де Ситтера. В эту экспоненциально расширяющуюся, ускоряющуюся вселенную.
0:35:21.8 СК: Такова стандартная модель нашей вселенной. Так что, ребята, я ничего не выдумываю про инфляцию, теорию струн или что-то в этом роде, я дразню насчёт выдумок. Я не спекулирую. Это самый распространенный… общепринятый взгляд на то, что делает наша настоящая Вселенная. Он ускоряется, потому что существует космологическая постоянная. Возможно, что космологическая постоянная когда-нибудь в будущем исчезнет, но мы этого не знаем. И можно предположить, что не будет.
Возможно, что космологическая постоянная когда-нибудь в будущем исчезнет, но мы этого не знаем. И можно предположить, что не будет.
0:35:51.7 СК: Итак, проще всего то, что Вселенная просто вечно расширяется под влиянием этой космологической постоянной. В этом случае мы подойдем к пространству де Ситтера. И снова, как и у черных дыр, у пространства де Ситтера есть горизонт, температура и энтропия. И все это придумали Стивен Хокинг и Гэри Гиббонс еще в 19 веке.70-е годы.
0:36:14.4 СК: Точно так же, как черная дыра испускает небольшое количество излучения, в некотором смысле пространство де Ситтера является тепловым состоянием. Состояние черного тела. Состояние с физическими характеристиками тела при фиксированной температуре. И температура будет очень низкой. Мы думаем о космическом микроволновом фоне сегодня с температурой около 2,7 Кельвина. Это будет… О, к сожалению, я забыл цифры. Я думаю, что это что-то вроде 10 до минус 35 кельвинов, когда мы в конечном итоге достигнем равновесия де Ситтера в нашем будущем. Я забыл точное число. Это правильный номер? Я действительно не знаю. Может быть, от 10 до минус 30. Но намного, намного ниже, чем текущая температура космического микроволнового фона.
Я забыл точное число. Это правильный номер? Я действительно не знаю. Может быть, от 10 до минус 30. Но намного, намного ниже, чем текущая температура космического микроволнового фона.
0:37:00.2 СК: Но так же, как и классическая вселенная, которая просто бесконечно велика, вселенная де Ситтера бесконечно стара. Это длится вечно при таком простом способе мышления об этом… Итак, если у вас есть вселенная де Ситтера, которая длится вечно, в этом есть смысл… И это аргумент… Это менее ясно, чем другие вещи, которые я сказал. Итак, позвольте мне просто изложить аргумент, а затем я как бы дам вам предостережения к нему. Это немного похоже на коробку с газом при фиксированной температуре, которая длится вечно. Хорошо.
0:37:29.8 СК: Итак, если у вас есть ящик с газом при фиксированной температуре, которая сохраняется вечно, у вас внутри будет куча частиц, которые бегают внутри и натыкаются друг на друга. И большую часть времени они будут находиться там в состоянии наивысшей энтропии, но только из-за случайных случайных флуктуаций тепловые флуктуации внутри ящика с газом приведут к уменьшению энтропии. Произойдет флуктуация энтропии вниз до более упорядоченной конфигурации, а затем она расслабится обратно.
Произойдет флуктуация энтропии вниз до более упорядоченной конфигурации, а затем она расслабится обратно.
0:38:00.1 СК: И иногда вы действительно можете рассчитать ожидаемую флуктуацию энтропии. И ответ таков: вы получите всевозможные колебания, если будете ждать достаточно долго. Таким образом, очень стандартная вещь для пыток студентов — это подсчитать, как долго вам придется ждать, пока весь воздух в комнате, в классе, который у нас есть прямо сейчас, переместится в одну сторону класса и оставит студентов в одиночестве. другая сторона задыхается. Это во много-много раз превышает нынешний возраст Вселенной, и вам не о чем беспокоиться, но это произойдет, если вы думаете, что ваш класс будет существовать вечно. И вероятность такого колебания больше для малых колебаний, меньше для больших… В этом должен быть смысл. Крошечное отклонение от равновесия будет гораздо более вероятным, чем огромное безумное отклонение от равновесия.
0:38:50.9 СК: Значит, гораздо более вероятно, что газ в комнате попадает в одну половину комнаты, чем то, что весь газ в комнате сжимается до одного маленького кубического сантиметра в углу комнаты. номер. Произойдет и то, и другое, но среднее колебание случается гораздо чаще, чем огромное колебание. И это, конечно, такой способ мышления… Если пространство де Ситтера такое, если будущее нашей Вселенной — это термически флуктуирующий газовый ящик, то в конце концов вы будете колебаться вниз по энтропии. И вы будете колебаться так сильно, что вы знаете, что иногда у вас будет пара частиц, появляющихся из вакуума.
номер. Произойдет и то, и другое, но среднее колебание случается гораздо чаще, чем огромное колебание. И это, конечно, такой способ мышления… Если пространство де Ситтера такое, если будущее нашей Вселенной — это термически флуктуирующий газовый ящик, то в конце концов вы будете колебаться вниз по энтропии. И вы будете колебаться так сильно, что вы знаете, что иногда у вас будет пара частиц, появляющихся из вакуума.
0:39:29.2 СК: Пару раз, реже несколько частиц с высокими энергиями появляются и сталкиваются друг с другом, образуя атомы. Если вы подождете достаточно долго, у вас будет достаточно флуктуирующих веществ, из которых будут создаваться молекулы или микроскопические количества веществ. Если вы будете ждать достаточно долго, вы будете колебаться между звездами, планетами, галактиками или даже всей вселенной. Я написал об этом целую статью с Мэттом Джонсоном и Энтони Агирре. Энтони, разумеется, был предыдущим гостем Mindscape.
0:39:57.8 СК: И… Значит, это произойдет, если вы подождете достаточно долго. А де Ситтеровское будущее нашей вселенной должно длиться бесконечно долго. Таким образом, вы получите все виды этих колебаний. И это приводит к проблеме мозга Больцмана. Идея в том, что если бы у вас были какие-то основания полагать, что вы являетесь типичным наблюдателем во вселенной… Ну, как выглядит типичный наблюдатель в этой вселенной? Это похоже на случайное колебание, верно.
А де Ситтеровское будущее нашей вселенной должно длиться бесконечно долго. Таким образом, вы получите все виды этих колебаний. И это приводит к проблеме мозга Больцмана. Идея в том, что если бы у вас были какие-то основания полагать, что вы являетесь типичным наблюдателем во вселенной… Ну, как выглядит типичный наблюдатель в этой вселенной? Это похоже на случайное колебание, верно.
0:40:25.2 СК: Большинство наблюдателей… Вы получаете кто знает, сколько миллиардов или триллионов таких же наблюдателей, как вы и я, после Большого Взрыва, но тогда вы получаете бесконечное число наблюдателей, которые представляют собой случайные флуктуации в будущем. Так кого волнует, что мы живем сразу после Большого Взрыва. Большинство наблюдателей в этой ситуации будут случайными колебаниями. Это вызывает философскую проблему, к которой мы и подойдем через секунду.
0:40:48.8 СК: Прежде чем я перейду к этому, позвольте мне упомянуть, что мы никоим образом не уверены, что даже если наша Вселенная действительно установится в пустую де Ситтеровскую фазу, будут эти случайные колебания. Потому что здесь происходит сложное взаимодействие между квантовой механикой и гравитацией. Я написал статью с Ким Бодди и Джейсоном Полаком, где мы объяснили, что в очень естественном наборе предположений, где гильбертово пространство квантовой гравитации бесконечномерно… Если вы не знаете, что означает какое-либо из этих слов, не волнуйтесь. об этом. Некоторые из вас, кто следил за ними долгое время, поймут, что они имеют в виду. Но в основном это причудливый способ сказать, что если во Вселенной может произойти сколь угодно большое количество вещей, то это фактически позволяет Вселенной перейти в статическое квантовое состояние.
Потому что здесь происходит сложное взаимодействие между квантовой механикой и гравитацией. Я написал статью с Ким Бодди и Джейсоном Полаком, где мы объяснили, что в очень естественном наборе предположений, где гильбертово пространство квантовой гравитации бесконечномерно… Если вы не знаете, что означает какое-либо из этих слов, не волнуйтесь. об этом. Некоторые из вас, кто следил за ними долгое время, поймут, что они имеют в виду. Но в основном это причудливый способ сказать, что если во Вселенной может произойти сколь угодно большое количество вещей, то это фактически позволяет Вселенной перейти в статическое квантовое состояние.
0:41:38.9 СК: Итак, в этом случае вы интерпретируете утверждение, что де Ситтер — это тепловое состояние, как утверждение, что если бы вы произвели его измерение, то вы бы измерили… Если бы у вас был термометр там буквально… Чего ты не можешь, потому что ты не пустое пространство де Ситтера, потому что ты вещь. Ты не пустота. Но в любом случае, если бы у вас был термометр, вы бы измерили тепловой спектр фотонов.
0:42:02.5 СК: Но в многомировой интерпретации есть разница между тем, что происходит, когда вы не измеряете вещь, где это просто волновая функция, и тем, что вы наблюдаете, когда физически взаимодействуете с ней, чтобы измерить это. И дело в том, что когда ты его не измеряешь… Когда ничего не возмущает состояние, тоже ничего не происходит. Динамических колебаний нет. Термальность этого квантового состояния — это утверждение о том, что вы будете наблюдать, но не утверждение о динамических вещах, возникающих и уходящих, таких как появление мозга или что-то в этом роде.
0:42:36.6 СК: Кстати, я забыл закончить рассказ о мозге Больцмана. Причина, по которой их называют мозгом Больцмана, заключается в том, что типичный наблюдатель будет не просто случайной флуктуацией, а типичной случайной флуктуацией, как мы ожидаем, будет минимальная флуктуация, необходимая для того, чтобы считаться наблюдателем в этой вселенной. Это потому, что легче… Легче получить небольшие колебания энтропии, чем большие. Итак, идея в том, что минимальный наблюдатель — это просто мозг. Вы случайным образом колеблетесь в существовании, мозг, который оглядывается и говорит: «Хм, тепловое равновесие», а затем умирает. Затем он возвращается в… Он снова растворяется в окружающем тепловом равновесии.
Итак, идея в том, что минимальный наблюдатель — это просто мозг. Вы случайным образом колеблетесь в существовании, мозг, который оглядывается и говорит: «Хм, тепловое равновесие», а затем умирает. Затем он возвращается в… Он снова растворяется в окружающем тепловом равновесии.
0:43:14.7 СК: Некоторые люди утверждают, что мы не мозг Больцмана, поэтому мир не может быть таким. И проблема здесь в том, что это не какой-то спекулятивный сценарий о ранней Вселенной. Это самый популярный взгляд на нашу настоящую Вселенную. А так это реальная проблема. Итак, в статье, которую Ким, Джейсон и я написали, мы попытались сказать, что этой проблемы легко избежать, если вы сделаете определенные предположения о квантовой гравитации. Но, конечно, мы не знаем, верны ли эти предположения. Так что над этими идеями все еще очень и очень стоит подумать.
0:43:46.1 СК: Итак, это три разные версии мультивселенной, ориентированной на физику. Космологическая мультивселенная, множество миров квантовой механики и вечная флуктуирующая космология. Вечная флуктуирующая космология – это своего рода мультивселенная во времени. Это не разные регионы пространства или разные вселенные, но если вы подождете достаточно долго, вселенная, о которой вы хотите думать, будет колебаться в существовании. Таким образом, это фактически мультивселенная.
Вечная флуктуирующая космология – это своего рода мультивселенная во времени. Это не разные регионы пространства или разные вселенные, но если вы подождете достаточно долго, вселенная, о которой вы хотите думать, будет колебаться в существовании. Таким образом, это фактически мультивселенная.
0:44:11.6 СК: Следует подчеркнуть одну вещь, о которой я всегда говорил, это то, что каждый из этих трех вариантов является следствием других идей. Он выдвигается не ради самого себя. И это следствие других идей, которые были предложены для учета данных. Для того, чтобы объяснить Вселенную, которую мы видим… Так что здесь происходит 100% стандартный научный процесс. Нет никакого смысла, какого-то отвлечения или отвлечения от занятий настоящей наукой, размышлений об этих разных мультистихах.
0:44:47.7 СК: Тем не менее, не все согласны. Люди возражают. Есть люди, которым не нравятся эти обсуждения мультистиха. И, честно говоря, это вызывает странные эмоции. Люди очень злятся, говоря о мультистихе с обеих сторон. Со всех сторон, надо сказать. Они говорят друг с другом о том, что это ненаучно, и у них появляется что-то наподобие личного и обзывающего. И это действительно утомительно. И это то, о чем я не хочу говорить здесь сегодня.
Со всех сторон, надо сказать. Они говорят друг с другом о том, что это ненаучно, и у них появляется что-то наподобие личного и обзывающего. И это действительно утомительно. И это то, о чем я не хочу говорить здесь сегодня.
0:45:16.7 СК: Я не хочу останавливаться на вопросе, считается ли обсуждение этих сценариев наукой. Я чувствую… Что я хочу сделать, так это разобраться, как говорить об этих сценариях, если вы считаете, что это нормально. Но мне нужно очень быстро прокомментировать вопрос о том, является ли вообще наукой говорить о мультивселенной.
0:45:39.4 СК: Слишком простое возражение против мультивселенной состоит в том, что ее невозможно опровергнуть. Известный сэр Карл Поппер, философ науки, предложил критерий фальсифицируемости для разграничения научных теорий от ненаучных теорий. Так вот, почти никто из физиков, поднимающих вопрос о фальсифицируемости, на самом деле не читал, когда Карл Поппер писал, но они носят на плече соломенного Поппера, которого они упростили до такого девиза, который гласит: «Если вы не можете фальсифицировать теорию с помощью эксперимент, то это не наука». Это не то, что сказал Поппер. Это определенно не то, во что верят философы науки. Они даже не верят, что фальсифицируемость вообще работает… Большинство из них… Как разграничение между наукой и ненаукой.
Это не то, что сказал Поппер. Это определенно не то, во что верят философы науки. Они даже не верят, что фальсифицируемость вообще работает… Большинство из них… Как разграничение между наукой и ненаукой.
0:46:22.6 СК: Но Поппер что-то напутал. У настоящего Поппера были веские причины предложить этот критерий. Даже если я не думаю, что это на самом деле дает вам окончательный ответ. Он заботился о том, чтобы у него были определенные теории, которые что-то говорили. Хорошо… Значит, его беспокоили теории, которые он считал похожими на марксистский анализ истории или фрейдистский психоанализ. По мнению Поппера… И я не собираюсь делать никаких заявлений о том, согласен я с этим или нет. Я действительно не думал об этом.
0:46:53.2 СК: Но в его сознании могло случиться буквально все, что угодно, и сторонники марксистской истории или фрейдистского психоанализа могли постфактум рассказать историю, якобы объясняющую ее. Поэтому он действительно беспокоился о том, что эти теории не имели никакого содержания. И именно поэтому он предложил фальсифицируемость, потому что он сказал: «Послушайте, если вы можете сказать: «Если что-то, происходящее в мире, объяснимо с точки зрения вашей теории… Все, что может произойти, объяснимо, тогда ваша теория не имеет объяснительной ценности».
И именно поэтому он предложил фальсифицируемость, потому что он сказал: «Послушайте, если вы можете сказать: «Если что-то, происходящее в мире, объяснимо с точки зрения вашей теории… Все, что может произойти, объяснимо, тогда ваша теория не имеет объяснительной ценности».
0:47:29.3 СК: В случае мультивселенной это не проблема. Хотя все эти разные сценарии мультивселенной абсолютно бесспорно что-то говорят, а не что-то другое. Проблема в том, что то, что, по их словам, происходит во Вселенной, — это вещи, которые мы не можем видеть. Вещи, которые мы в принципе никогда не сможем увидеть. Мы никогда не сможем коснуться других миров теории многих миров. Мы никогда не сможем увидеть космологическую мультивселенную. Мы никогда не заметим появление мозга Больцмана. Десятки, десятки, десятки… 10, 10, 10 миллиардов лет в будущем или сколько угодно.
0:48:05.2 СК: Значит, он говорит что-то определенное, но ты не знаешь. Вы не сможете проверить это простым способом. Так должны ли мы считать это наукой? Ну, конечно, мы должны. И Поппер, я думаю, согласился бы со мной по этому поводу, потому что ему нужно было жарить другую рыбу. Основная проблема заключается в том, что эти сценарии могут быть правдой, и природа действительно может работать именно так. И это отличается от того, о чем беспокоился Поппер. Там действительно могут быть другие вселенные где-то в другом месте волновой функции, в пространстве или во времени.
И Поппер, я думаю, согласился бы со мной по этому поводу, потому что ему нужно было жарить другую рыбу. Основная проблема заключается в том, что эти сценарии могут быть правдой, и природа действительно может работать именно так. И это отличается от того, о чем беспокоился Поппер. Там действительно могут быть другие вселенные где-то в другом месте волновой функции, в пространстве или во времени.
0:48:36.5 СК: И причина, по которой это имеет значение, заключается в том, что наличие или отсутствие этих других вселенных влияет на то, как мы занимаемся наукой здесь, в этой вселенной, пытаясь объяснить данные, которые у нас есть в наблюдаемой части вселенной. Когда вы занимаетесь космологией или когда вы делаете эти крупномасштабные сценарии для объяснения Вселенной, вещи связаны друг с другом. Они взаимосвязаны. Мы говорим о мультивселенной и вещах, которые мы не можем наблюдать. Но причина, по которой мы говорим о них, заключается в том, что они играют объяснительную роль в том, что мы наблюдаем. И это всего лишь наука. Это не что-то новое.
И это всего лишь наука. Это не что-то новое.
0:49:14.0 СК: Я не сторонник того, что нам нужно подумать о новой парадигме ведения науки из-за мультивселенной. Это точно такая же парадигма, которая была у нас всегда. Мы придумываем теорию, используем ее для учета данных. Так, например, в космологической мультивселенной мы используем космологическую мультивселенную как объяснение наблюдаемого значения энергии вакуума и, возможно, наблюдаемых значений других констант природы, таких как масса бозона Хиггса и так далее. Чтобы объяснить кажущиеся загадочными числа, которые мы наблюдаем в физике. Тонкая настройка некоторых параметров. Именно это пытался сделать Стивен Вайнберг еще до того, как мы узнали, что космологическая постоянная не равна нулю. Итак, дело в том, что если вы работаете физиком и говорите, я хотел бы понять, почему энергия вакуума имеет такую ценность. Считаете ли вы космологическую мультивселенную многообещающей теорией или нет… Абсолютно, бесспорно влияет на то, какие теоретические идеи вы будете рассматривать и выдвигать.
0:50:20.7 СК: Если вы не думаете, что Мультивселенная имеет смысл или существует, тогда вам необходимо придумать какой-нибудь динамический механизм, объясняющий, почему космологическая постоянная имеет то значение, которое мы наблюдаем. Если вы действительно думаете, что мультивселенная существует, то, возможно, вам не нужно этого делать, это просто эффект отбора окружающей среды. Хотя у вас не может быть динамической теории, которая с вероятностью предсказывает, во-первых, что космологическая постоянная имеет определенное значение, и думать, что это хорошая теория, если она имеет другие значения где-то еще.
0:50:51.8 СК: То, как вы занимаетесь наукой, зависит от того, относитесь ли вы к этой теории серьезно. Точно так же во многих мирах квантовой механики вы снова пытаетесь заниматься наукой. Наука не сделана. В физике еще нет теории всего. Вы пытаетесь опираться на то, что мы уже знаем. И на то, как вы это сделаете, сильно повлияет ваше отношение к основам квантовой механики. Если вы не верите, что многие миры… Многие миры просто возникают из-за того, что вы думаете, что существует волновая функция или квантовое состояние, которое подчиняется уравнению Шредингера.
Если вы не верите, что многие миры… Многие миры просто возникают из-за того, что вы думаете, что существует волновая функция или квантовое состояние, которое подчиняется уравнению Шредингера.
0:51:26.0 СК: Если вы в это не верите, то вы должны сказать мне либо что есть помимо волновой функции, либо почему и как волновая функция не подчиняется уравнению Шредингера. Это дополнительная работа, которую вам придется проделать, если вы не верите во многие миры квантовой механики. Скажи мне, что такое скрытые переменные. Скажите мне, что такое явное правило объективного коллапса, если вы верите в подобные вещи.
0:51:49.3 СК: Опять же, на вашу научную практику влияет разумность этого мультивселенного сценария. И, наконец, опять же, аналогично для флуктуирующей космологии, сценариев вечной флуктуирующей космологии, потому что как объяснить Большой взрыв и его состояние с низкой энтропией. Что будет иметь значение, что будет затронуто, если вы думаете, что наша вселенная вечна и изменчива. То, что, по вашему мнению, произойдет в будущем, на нашу вселенную тоже влияет… Влияет то, как вы думаете об этих сценариях.
То, что, по вашему мнению, произойдет в будущем, на нашу вселенную тоже влияет… Влияет то, как вы думаете об этих сценариях.
0:52:19.1 СК: В моем понимании, конечно, это наука. Это не близкий звонок. Это не похоже на квази-науку. Это сложно. Это правда. Это нормально. Я не говорю, что могу предложить вам какой-нибудь простой, простой эксперимент, который я могу себе представить, который раз и навсегда покажет, существует ли одна из этих мультивселенных или нет. Но никто никогда не обещал тебе розарий. То, что я не могу придумать эксперимент, который поможет нам изменить наши убеждения либо к нулю, либо к единице, не означает, что это не наука. Иногда наука просто будет сложной. Иногда нас оставят в неведении относительно того, какой сценарий является правильным.
0:53:00.5 СК: Но есть кое-что верное в отношении того, как выглядит Вселенная за пределами нашего горизонта, как выглядит волновая функция Вселенной в целом и так далее. Поэтому, на мой взгляд, это полностью наука. Сказав все это, я думаю, что… И это всегда опасный подход, когда вы начинаете исследовать психологию людей, с которыми вы не согласны. Но я хочу немного отдать должное людям. Я думаю, что тревога, связанная со сценариями мультивселенной, возникает из совершенно законного беспокойства. И беспокоит то, как вы в таких случаях думаете о нашем месте во вселенной.
Сказав все это, я думаю, что… И это всегда опасный подход, когда вы начинаете исследовать психологию людей, с которыми вы не согласны. Но я хочу немного отдать должное людям. Я думаю, что тревога, связанная со сценариями мультивселенной, возникает из совершенно законного беспокойства. И беспокоит то, как вы в таких случаях думаете о нашем месте во вселенной.
0:53:43.2 СК: Итак, это в основном философская проблема. Просто нет вопросов. Это то, чему учили философов, и часто есть философские статьи, написанные о проблемах, которые обычно не формулируются в приземленных космологических терминах, но, тем не менее, имеют прямое отношение к ним, и затрагивают вопрос о том, какое доверие мы должны иметь к этим проблемам. разные вопросы. Доверие как степень веры. Насколько мы уверены, что все это правда. И, в частности, нам нужно подумать о двух разных наборах доверенностей.
0:54:16.8 СК: Первый — это стандартный научный вопрос о том, какая теория верна. Какая теория существует мультивселенная. .. Космологическая мультивселенная или нет? Верно ли много миров? Или правильная механика Бома или что-то в этом роде. Является ли гильбертово пространство квантовой гравитации конечномерным или бесконечномерным? Приземленные вопросы о том, какая физика лежит в основе того, что происходит.
.. Космологическая мультивселенная или нет? Верно ли много миров? Или правильная механика Бома или что-то в этом роде. Является ли гильбертово пространство квантовой гравитации конечномерным или бесконечномерным? Приземленные вопросы о том, какая физика лежит в основе того, что происходит.
0:54:39.6 СК: Итак, все мы, работающие ученые, доверяем этим различным моделям, и мы хотели бы скорректировать их в соответствии с теоремой Байеса. В правильном пути. Но есть и другое доверие. И вот почему, несмотря на то, что в науке всегда есть какая-то философия науки, философия науки в некотором роде более интересна и забавна. Потому что другое доверие — кто мы во вселенной. Другими словами, это сценарии мультивселенной, в которых участвует много людей. Если это космологическая мультивселенная, то у нас есть разные области пространства, возможно, бесконечное их количество с разными законами физики. Но некоторые из них будут иметь одни и те же законы физики, и мы можем представить, что в них есть множество разных типов разумных наблюдателей.
0:55:28.0 СК: Как мы поместим себя в этот огромный набор разного количества наблюдателей? В случае со многими мирами это очень приземленная и прямолинейная версия этого вопроса. Когда волновая функция разветвляется и теперь есть две разные версии наблюдателя, производившего измерение? Какую вероятность они приписывают нахождению на ветвях со спином вверх или вниз Волновой функции Вселенной, что они измерили спин какого-то электрона, это проблема вывода правила рождения в многомировой интерпретации и квантовой теории? Механика, какая у тебя версия? Чарльз Себенс, мой коллега из Калифорнийского технологического института, и я написали об этом статью, в которой мы назвали это самоопределяющейся неопределенностью, иногда люди также называют ее индексальной неопределенностью. Дело не только в том, что во Вселенной много наблюдателей, существует множество копий одного и того же наблюдателя, они разные, потому что один находится на одной ветви волновой функции, а другой — на другой, но они идентичны, за исключением того, где они расположены во вселенной. Это самостоятельная неуверенность, кто вы? И, наконец, для сценария больцмановский мозг/вечно флуктуирующая вселенная, верно? Вы мозг Больцмана? Ты уверен? Вы больцман, что-то еще, или вы действительно, действительно уверены, что вы обычный наблюдатель, и если да, то заставляет ли это вас отвергать гипотезу о том, что больцмановские мозги вообще существуют?
Это самостоятельная неуверенность, кто вы? И, наконец, для сценария больцмановский мозг/вечно флуктуирующая вселенная, верно? Вы мозг Больцмана? Ты уверен? Вы больцман, что-то еще, или вы действительно, действительно уверены, что вы обычный наблюдатель, и если да, то заставляет ли это вас отвергать гипотезу о том, что больцмановские мозги вообще существуют?
0:56:52.7 СК: Хорошо. Все очень хорошие вопросы. Все вопросы, которые требуют тщательного философского анализа, и опять же, просто чтобы немного отредактировать здесь, одна из причин, почему это весело, интересно, а также продуктивно, чтобы заставить физиков и философов разговаривать друг с другом, заключается в том, что у них есть разные виды слепых зон. , Я бы сказал. Я люблю их обоих, некоторые из моих лучших друзей — физики и/или философы, но у них есть разные вещи, в которых они действительно хороши, и разные вещи, в которых они не так хороши. Философы действительно хороши в том, чтобы объяснить вам, почему ваша теория неверна, говоря более точно, философы хороши в анализе логической цепочки рассуждений, которые приводят вас к какому-то заключению, и говорят вам, где вы ошиблись, вы сделали прыжок здесь это не совсем нормально, физики просто хотят получить правильный ответ, и снова и снова в истории физики они получают правильный ответ по неправильным причинам. Правильно, данные всегда спасают вас в физике, вы в конечном итоге получите правильный ответ, независимо от того, насколько плохи ваши рассуждения, потому что данные просто не позволят вам продолжать ошибаться снова, и снова, и снова. Это как раз тот случай, когда вы попадете в мультивселенную, у вас будут проблемы.
Правильно, данные всегда спасают вас в физике, вы в конечном итоге получите правильный ответ, независимо от того, насколько плохи ваши рассуждения, потому что данные просто не позволят вам продолжать ошибаться снова, и снова, и снова. Это как раз тот случай, когда вы попадете в мультивселенную, у вас будут проблемы.
0:58:06.4 СК: Потому что с чем-то вроде квантовой теории поля вы пишете, что квантовая теория поля существует в 1930-х или 40-х годах, и вы получаете бесконечный ответ. А если бы у вас не было никаких данных, вы могли бы просто сказать: ну, это плохо, теория неверна, ответ бесконечен. Что касается данных, от этого никуда не деться, с этим нужно что-то делать. Итак, вы проделали большую работу, чтобы понять перенормировку, избавление от бесконечности и так далее. Даже изобретение квантовой механики является примером, когда было так много данных, заставляющих вас делать эти сумасшедшие выводы. Но о мультивселенной можно очень небрежно рассуждать и думать, что вы на правильном пути, потому что нет непосредственного эксперимента, который привел бы вас к правильному ответу… Верно, именно здесь философы очень полезны. Это их сильная сторона.
Это их сильная сторона.
0:58:51.0 СК: На мой взгляд, их слабое место в том, что они меньше заботятся о правильном ответе, чем о правильных рассуждениях, которые приведут вас к тому ответу, который вы получаете, это слишком грубый способ говоря это, но то, как это проявляется на практике, заключается в том, что много философских усилий затрачено на выработку следствий теоретических построений, которые, на мой взгляд, я бы сказал, мы знаем, что они неверны.
0:59:14.6 СК: Квантовая теория поля — очень хорошая теория, но она, вероятно, не является правильным ответом на то, что делает природа, потому что она не очень хорошо работает с гравитацией. Общая теория относительности — это очень хорошая теория гравитации с классической точки зрения, но это не окончательный ответ на вопрос о гравитации, потому что она плохо сочетается с квантовой механикой. И есть много моих друзей-философов, которые просто приложили много усилий, чтобы понять последствия на очень, очень детальном уровне этих теорий, потому что это забавная маленькая логическая головоломка и так далее. Но для меня это на самом деле не помогает нам так хорошо понять природу. Поэтому я полагаюсь на философов, которые подскажут мне, в чем моя цепочка рассуждений неверна, но они не так хороши в выборе лучшей теории, а в этом очень хороши физики. Вот почему нам нужно и то, и другое в случае мультивселенной. Ладно, редактура окончена.
Но для меня это на самом деле не помогает нам так хорошо понять природу. Поэтому я полагаюсь на философов, которые подскажут мне, в чем моя цепочка рассуждений неверна, но они не так хороши в выборе лучшей теории, а в этом очень хороши физики. Вот почему нам нужно и то, и другое в случае мультивселенной. Ладно, редактура окончена.
1:00:00.6 СК: К проблеме, с которой мы столкнулись… Вы можете думать об этом с точки зрения байесовского вывода, байесовского рассуждения. У нас есть правило Байеса. Для тех из вас, кто этого не знает, правило Байеса — это способ сказать: «У меня есть некоторые предположения, некоторые из них верны, некоторые — ложны». Давайте выберем набор утверждений, которые являются взаимоисключающими, поэтому они не могут быть истинными одновременно, например, есть космологическая мультивселенная или нет, хорошо, или я есть эта ветвь Волновой Функции, или я какая-то другая ветвь. волновой функции. Ну, Байес дает вам способ обновить эту вероятность, на самом деле доверие, которое вы придаете этим различным утверждениям, когда поступает новая информация, когда приходят новые данные, как мы обычно говорим.
1:00:44.0 СК: И правило Байеса говорит, что вероятность любой данной теории с учетом новых данных пропорциональна вероятности того, что… Вероятность, вы должны были бы получить эти данные, если бы теория была истинной раз исходная априорная вероятность теории. Итак, у вас есть некоторая априорная вероятность для всех различных суждений, таких как эта мультивселенная или та мультивселенная, вы говорите: «Если бы эти различные суждения были истинными, какова вероятность, вероятность, как мы это называем, того, что я получу какие-то данные, вы перемножаете их вместе, и это говорит вам о вероятности вашей теории теперь, когда у вас есть эти данные». И проблема, с которой мы здесь сталкиваемся, заключается в том, что именно вы подразумеваете под функцией правдоподобия байесовского анализа? Вероятность состоит в том, какова вероятность того, что вы увидели бы эти данные, если бы эта теория была верна. И, к сожалению или к счастью, данные, о которых мы говорим, существуют.
1:01:40. 9 СК: Это данные. Хорошо, какова вероятность того, что я существовал бы или вы существовали бы, если бы вы могли пойти дальше и сделать это сами, что мы существовали бы в этом космологическом сценарии.
9 СК: Это данные. Хорошо, какова вероятность того, что я существовал бы или вы существовали бы, если бы вы могли пойти дальше и сделать это сами, что мы существовали бы в этом космологическом сценарии.
1:01:52.1 СК: Что именно это означает? Я имею в виду, является ли это вероятностью существования разумных наблюдателей или того, что существует в этом сценарии, или это вероятность того, что такие наблюдатели, как я или точно такие же, как я, действительно существуют? И должен ли я существовать с какими-то другими свойствами или где-то во вселенной и так далее. На самом деле, это хорошо известная проблема байесовских рассуждений, называемая проблемой старых свидетельств. Помогает ли нам что-то, о чем мы знали все это время, какие-то доказательства, которые у нас были с самого начала, действительно обновить наши априорные данные? Предоставляет ли это дополнительные доказательства, так что тот факт, что мы с вами здесь думаем об этом, считается доказательством чего-либо? Очевидно, что если у вас есть космологический сценарий, в котором я не мог бы существовать, то я должен дать этому нулевое доверие. Мое существование — общеизвестный факт, но могу ли я притвориться, что не знаю этого, записать все космологические сценарии, а затем обновить свое доверие к ним, используя правило Байеса. А с теми данными, которые у меня есть, я не знаю, смогу ли я это сделать? Все хорошо? Или тот факт, что я существую, уже заложил меня в эти доверительные отношения с самого начала, так что я не должен считать это дважды, вот в чем проблема. И затем, более того, на несколько более детальном уровне, если я скажу: «Хорошо, я существую», это должно благоприятствовать сценарию, в котором я существовал бы с вероятностью 0,9?над сценарием, в котором я бы существовал с вероятностью, может быть, 0,1, вероятно… Это кажется разумным, но ладно. А как насчет этого?
Мое существование — общеизвестный факт, но могу ли я притвориться, что не знаю этого, записать все космологические сценарии, а затем обновить свое доверие к ним, используя правило Байеса. А с теми данными, которые у меня есть, я не знаю, смогу ли я это сделать? Все хорошо? Или тот факт, что я существую, уже заложил меня в эти доверительные отношения с самого начала, так что я не должен считать это дважды, вот в чем проблема. И затем, более того, на несколько более детальном уровне, если я скажу: «Хорошо, я существую», это должно благоприятствовать сценарию, в котором я существовал бы с вероятностью 0,9?над сценарием, в котором я бы существовал с вероятностью, может быть, 0,1, вероятно… Это кажется разумным, но ладно. А как насчет этого?
1:03:28.7 СК: Как насчет сравнения вселенной, где есть ровно один такой же человек, как я, с другой вселенной, где есть огромное количество миллиардов квинтиллионов таких же людей, как я? В обеих вселенных вероятность того, что кто-то вроде меня существует, равна единице, но таких людей, как я, больше в другой вселенной, так что я должен считать это, Должен дать этому бонус, Должен ли я считать это дополнительным доказательством в пользу этого космологического сценария. ? Я не уверен, что это вопрос, это то, что мы пытаемся решить прямо здесь, прямо сейчас.
? Я не уверен, что это вопрос, это то, что мы пытаемся решить прямо здесь, прямо сейчас.
1:04:01.9 SC: Итак, позвольте мне, наконец, всякий раз, когда я получаю сольный подкаст, я просто не могу не говорить и продолжаю говорить в течение длительного времени, так что теперь я, наконец, готов поговорить о том, что мы На самом деле мы здесь, чтобы поговорить о том, как мы думаем о вероятностях и достоверности этих теорий мультивселенной, и это вопрос философии космологии. И это… Послушайте, я не первопроходец в этом вопросе, люди, безусловно, немного обеспокоены этим, и есть стандартная стратегия для решения этой проблемы, которая заключается в следующем: мы должны рассуждать так, как если бы мы типично для некоторого эталонного класса наблюдателей. Итак, идея в том, что это называется принципом типичности, или принципом посредственности, или принципом Коперника. Идея в том, что мы не особенные во Вселенной, а мотивация исходит из антропного принципа.
1:04:58.2 СК: Размышляя над этим вопросом, а-ля Вайнберг, если бы у вас было много-много разных частей вселенной, скажем, с разными значениями космологической постоянной, как бы вы использовали это, чтобы сделать предсказание для что вы должны соблюдать? И идея в том, что вы говорите: ну, в этом собрании, в этом ансамбле много наблюдателей, некоторые из них могут жить в высоких значениях космодиальных постоянных частей вселенной, другие могут жить в низких значениях, что угодно, есть какое-то распределение, есть некоторое число, которое вы могли бы вычислить, и я не должен, согласно этому рассуждению, считать себя особенным, я типичный наблюдатель в этом, и поэтому я предсказываю, что я должен наблюдать то, что должен видеть типичный наблюдатель в этом ансамбле .
1:05:43.8 СК: Хорошо, это идея типичности, посредственности, принципа Коперника, называйте это как хотите. И я думаю, что какая-то версия… Две вещи. Во-первых, какая-то версия этой идеи более или менее общепринята среди современных космологов, так думают современные космологи, если они вообще об этом думают. Я откладываю в сторону людей, которые просто не считают наукой говорить о мультивселенной, среди теоретиков мультивселенной эта идея о том, что вы должны предполагать, что мы типичны, является более или менее консенсусной. И, во-вторых, я не думаю, что это очень четко определенная или очень хорошая идея, я думаю, что нам нужно работать лучше, поэтому мы здесь и ведем этот разговор. Так почему я беспокоюсь об этом? Ну, во-первых, почему мы типичны? Почему мы должны думать, что мы типичные наблюдатели? Для меня совершенно очевидно, что я не типичный наблюдатель, даже среди людей здесь, на Земле.
1:06:38.1 СК: У большинства людей на земле нет подкастов, вот так вот, это один из очень многих способов, в которых я не типичный наблюдатель, так что это не доказательство против этого, так что -называется принцип рассуждения, который вы выдвигаете? И что еще более важно, на более техническом уровне я типичен для того, какой именно класс наблюдателей, таких как все живые существа, считает бактерии? Или они должны быть действительно сознательными? Какой уровень сознания мне нужен, чтобы считаться типичным наблюдателем в этом сценарии, Что, если есть коллективный разум, Что, если есть доска, они считаются как один наблюдатель или они считаются как… Считаю ли я их отдельно для всех разных биологических сущностей, которые вошли в их создание, считаю ли я искусственных наблюдателей, считаю ли я искусственный интеллект в кремнии при моделировании в матрице, все это важные вопросы, которые не решаются сразу, поэтому это называется проблемой эталонного класса в этом своего рода принцип типичности образа мышления.
1:07:42.8 SC: Давайте отложим все в сторону, я буду очень, очень великодушен на данный момент, я скажу, хорошо, забудьте о проблеме эталонного класса. Это то, что нужно иметь в виду. Это должно беспокоить нас. Кажется, вы предлагаете фундаментальный принцип рассуждений, который чрезвычайно плохо определен, и это должно вас беспокоить, но давайте предположим, что вы можете его понять, давайте предположим, что это чисто формальность. И тем не менее я бы сказал, что это не… Мы еще не закончили, просто сказать, что мы типичны в каком-то эталонном классе наблюдателей, недостаточно, чтобы позволить нам сделать следующий шаг и превратить это в… Учитывая космологический сценарий, какие вероятности я предсказываю? Итак, чтобы сделать это приземленным, я собираюсь… Я не умею рисовать. Это аудиоподкаст, но я хочу, чтобы вы представили две разные вселенные. Хорошо. Вселенная A и вселенная B. Вселенная a — это маленькая вселенная, в которой, я имею в виду, относительно мало наблюдателей, может быть, этого и не должно быть, когда я говорю относительно мало. Может быть, это как вселенная, которую мы видим, с миллиардами галактик внутри и так далее, но ничего снаружи, не бесконечное количество дополнительных вещей. Это вселенная A, маленькая вселенная, а затем есть большая вселенная, вселенная B большая, и физически она во многом похожа на маленькую вселенную A, но она просто больше, поэтому во вселенной B намного, намного, намного больше наблюдателей, чем в вселенная А.
Может быть, это как вселенная, которую мы видим, с миллиардами галактик внутри и так далее, но ничего снаружи, не бесконечное количество дополнительных вещей. Это вселенная A, маленькая вселенная, а затем есть большая вселенная, вселенная B большая, и физически она во многом похожа на маленькую вселенную A, но она просто больше, поэтому во вселенной B намного, намного, намного больше наблюдателей, чем в вселенная А.
1:09:04.2 СК: Хорошо. Итак, у нас есть два числа для каждого сценария, и когда я говорю об этих вселенных, я должен изо всех сил стараться правильно подобрать словарь, это две разные теории, на самом деле не две разные вселенные, это две разные теории космологической целостной путаницы. , весь ансамбль. Таким образом, теория А имеет относительно мало наблюдателей повсюду в мультивселенной, а теория Б имеет много, много, много наблюдателей в мультивселенной, и поэтому они связаны как с количеством наблюдателей в них, NA и NB, так и с нашими априорными вероятностями. Мы постараемся быть хорошими байесовцами. Мы попытаемся сказать, например, что наблюдения говорят нам об этих двух космологических сценариях, если мы придаем больше правдоподобия теории А или теории Б. Существует априорная вероятность, просто основанная на вопросах простоты и плодотворности и того, насколько хорошо она соответствует в дополнение к другим вещам, которые мы знаем о физике, вероятности, априорной вероятности сценария A и сценария B. Тогда как вы рассуждаете в этом наборе вопросов? Как мы должны обновлять наши априорные данные, когда поступают новые данные, а они действительно есть. Так что, хотя я и сказал, что почти все мультивселенные космологи верят в ту или иную версию принципа типичности, они применяют его совершенно по-разному. И на самом деле есть два разных способа, грубо говоря, два больших популярных лагеря для решения этой проблемы, один популярнее другого.
Мы постараемся быть хорошими байесовцами. Мы попытаемся сказать, например, что наблюдения говорят нам об этих двух космологических сценариях, если мы придаем больше правдоподобия теории А или теории Б. Существует априорная вероятность, просто основанная на вопросах простоты и плодотворности и того, насколько хорошо она соответствует в дополнение к другим вещам, которые мы знаем о физике, вероятности, априорной вероятности сценария A и сценария B. Тогда как вы рассуждаете в этом наборе вопросов? Как мы должны обновлять наши априорные данные, когда поступают новые данные, а они действительно есть. Так что, хотя я и сказал, что почти все мультивселенные космологи верят в ту или иную версию принципа типичности, они применяют его совершенно по-разному. И на самом деле есть два разных способа, грубо говоря, два больших популярных лагеря для решения этой проблемы, один популярнее другого.
1:10:35.1 СК: И у них ужасные имена. Одно из них называется предположением о самовыборке или SSA, а другое называется предположением о самоиндикации или SIA. Мы немного говорили об этом в подкасте с Ником Бостромом некоторое время назад, он частично отвечает за эту номенклатуру. Так что я честно борюсь, потому что, когда вы говорите о допущении самоотбора SSA и допущении о самоиндикации SIA, эти слова ничего не означают в моем мозгу. Я понятия не имею, что должно быть чем, поэтому я переименовал их. Думайте о них как о подходах «сначала мир» и «сначала наблюдатель». Итак, подход «сначала мир» говорит, что вы присваиваете свою априорную вероятность каждому миру, каждому сценарию, сценарию А или сценарию Б, а затем внутри каждого сценария вы предполагаете, что мы являемся типичным наблюдателем, так что это очень разумный поступок. У вас есть первое… Ваше априорное, что теория верна, тогда в теории вы предполагаете, что вы типичны. Но обратите внимание, что это делает. Если бы у вас была в теории A и теории B одна и та же априорная вероятность, они были бы равновероятны априори, но в вашем референтном классе в теории A был только один такой же наблюдатель, как вы, и кто знает 10 из 100 таких же наблюдателей, как вы в теории B.
Мы немного говорили об этом в подкасте с Ником Бостромом некоторое время назад, он частично отвечает за эту номенклатуру. Так что я честно борюсь, потому что, когда вы говорите о допущении самоотбора SSA и допущении о самоиндикации SIA, эти слова ничего не означают в моем мозгу. Я понятия не имею, что должно быть чем, поэтому я переименовал их. Думайте о них как о подходах «сначала мир» и «сначала наблюдатель». Итак, подход «сначала мир» говорит, что вы присваиваете свою априорную вероятность каждому миру, каждому сценарию, сценарию А или сценарию Б, а затем внутри каждого сценария вы предполагаете, что мы являемся типичным наблюдателем, так что это очень разумный поступок. У вас есть первое… Ваше априорное, что теория верна, тогда в теории вы предполагаете, что вы типичны. Но обратите внимание, что это делает. Если бы у вас была в теории A и теории B одна и та же априорная вероятность, они были бы равновероятны априори, но в вашем референтном классе в теории A был только один такой же наблюдатель, как вы, и кто знает 10 из 100 таких же наблюдателей, как вы в теории B. , то вероятность того, что вы являетесь этим наблюдателем в теории А, равна 50 %, а вероятность того, что вы являетесь любым из наблюдателей в теории В, составляет 50 %, умноженное на 10 до минус 100.
, то вероятность того, что вы являетесь этим наблюдателем в теории А, равна 50 %, а вероятность того, что вы являетесь любым из наблюдателей в теории В, составляет 50 %, умноженное на 10 до минус 100.
1:12:12.0 СК: Итак, вы видите, что происходит, это похоже на нетривиальный ход, вы, скорее всего, будете тем конкретным единственным наблюдателем в сценарии с маленькой вселенной, учитывая эти предположения, первый в мире подход , чем вы являетесь любым из наблюдателей в большой вселенной, но предполагается, что общая вероятность того, что вы находитесь в большой вселенной, равна этому набору предположений. Это предположение о самовыборке, SSA, когда другие люди там говорят о предположении о самовыборке, они имеют в виду первый в мире подход к назначению вероятностей, присваивая предшествующий этому сценарию миру, а затем предполагают ваш типичный в нем. Другой подход, предположение о самоиндикации, — это то, что я называю первым подходом наблюдателя, и здесь это своего рода ход, вы можете спорить об этом, но люди так и делают. То есть предположим, что вы типичны среди всех наблюдателей, и это означает, что вы эффективны, поэтому все наблюдатели во всех различных сценариях предполагают, что вы типичны и эффективны, и вам нужно проделать дополнительную работу, чтобы это сработало. на количественном уровне, потому что, если у вас были разные априорные предположения для разных космологических сценариев, то как вы собираетесь приписывать себе типичность в этом ансамбле всех из них?
То есть предположим, что вы типичны среди всех наблюдателей, и это означает, что вы эффективны, поэтому все наблюдатели во всех различных сценариях предполагают, что вы типичны и эффективны, и вам нужно проделать дополнительную работу, чтобы это сработало. на количественном уровне, потому что, если у вас были разные априорные предположения для разных космологических сценариев, то как вы собираетесь приписывать себе типичность в этом ансамбле всех из них?
1:13:28.8 СК: Но ты можешь это сделать, ты можешь посчитать. Вы можете запустить цифры. Смысл этого шага, хотя он и кажется немного нелогичным, заключается в том, что если у вас есть космологический сценарий с большим количеством наблюдателей, то вы должны думать, что этот сценарий с большей вероятностью приведет к появлению такого наблюдателя, как вы, потому что есть просто больше способов. Так что если вы не говорите, что эти наблюдатели рассматривали в нашем эталонном классе точно такие же, как вы. Скажем так, у нас есть эталонный класс всех разумных наблюдателей, верно. А во вселенной А есть буквально один разумный наблюдатель, и мы не знаем, он вроде человекоподобного наблюдателя, может быть, это осьминог или газовый мешок в облаках Юпитера или что-то в этом роде. Верно. А в сценарии B есть от 10 до 100 разумных наблюдателей. Аргументом может быть то, что даже если с точки зрения физики у вас была бы одинаковая априорная вероятность для сценария А и сценария Б, учитывая, что вы человек с определенными характеристиками и т. д., проще представить, что кто-то такой же, как вы, появляется в реальности. сценарий вселенной с большим количеством наблюдателей, поэтому мы должны учитывать это больше. И то, как мы делаем это в этом подходе с первым наблюдателем, предположение о самоиндикации эффективно повышает априорную вероятность на количество наблюдателей в вашем эталонном классе.
А во вселенной А есть буквально один разумный наблюдатель, и мы не знаем, он вроде человекоподобного наблюдателя, может быть, это осьминог или газовый мешок в облаках Юпитера или что-то в этом роде. Верно. А в сценарии B есть от 10 до 100 разумных наблюдателей. Аргументом может быть то, что даже если с точки зрения физики у вас была бы одинаковая априорная вероятность для сценария А и сценария Б, учитывая, что вы человек с определенными характеристиками и т. д., проще представить, что кто-то такой же, как вы, появляется в реальности. сценарий вселенной с большим количеством наблюдателей, поэтому мы должны учитывать это больше. И то, как мы делаем это в этом подходе с первым наблюдателем, предположение о самоиндикации эффективно повышает априорную вероятность на количество наблюдателей в вашем эталонном классе.
1:14:53.3 SC: Грубо говоря, World first говорит: «Укажите ваши априорные вероятности для всех различных сценариев, а затем предположите, что вы типичны для них». Сначала наблюдатель говорит: «Предположим, что вы каким-то образом типичны в пространстве всех наблюдателей во всех возможных мирах, и поэтому отдавайте предпочтение сценариям с большим количеством наблюдателей». Хорошо. И сам Бостром, а также такие люди, как Брэндон Картер и Элис Линкольн, выступали за подход «сначала мир», Кен Олм, другие выступали за подход «сначала наблюдатель», так что они оба отстаивают эти подходы. А вот философы могут нам что-нибудь сказать по этому поводу… Ну да, философы действительно хороши в том, чтобы логично и ясно ставить проблему, а потом расходиться во мнениях о том, как ее решить. Так что есть проблема, что если вы философ или философ, рядом с этими словами я говорил вам о маленькой вселенной А, большой Вселенной Б, присвоение им априорных значений очень сильно напомнит вам очень известную проблему в философии называется проблемой Спящей Красавицы, которая, как я полагаю, была впервые сформулирована в этих словах Адамом Элгой, философом из Принстона. Итак, Проблема Спящей Красавицы следующая, и она не имеет ничего общего с космологией, но вы сразу увидите, какая связь.
Хорошо. И сам Бостром, а также такие люди, как Брэндон Картер и Элис Линкольн, выступали за подход «сначала мир», Кен Олм, другие выступали за подход «сначала наблюдатель», так что они оба отстаивают эти подходы. А вот философы могут нам что-нибудь сказать по этому поводу… Ну да, философы действительно хороши в том, чтобы логично и ясно ставить проблему, а потом расходиться во мнениях о том, как ее решить. Так что есть проблема, что если вы философ или философ, рядом с этими словами я говорил вам о маленькой вселенной А, большой Вселенной Б, присвоение им априорных значений очень сильно напомнит вам очень известную проблему в философии называется проблемой Спящей Красавицы, которая, как я полагаю, была впервые сформулирована в этих словах Адамом Элгой, философом из Принстона. Итак, Проблема Спящей Красавицы следующая, и она не имеет ничего общего с космологией, но вы сразу увидите, какая связь.
1:16:11.6 СК: Итак, это мысленный эксперимент. На самом деле вы этого не сделаете, вы никогда не получите одобрение от Институционального исследовательского совета на проведение этого эксперимента, но идея в том, что у вас есть подопытная Спящая красавица, которую вы собираетесь усыпить, а затем разбудить и попросить вопрос. Хорошо, а происходит то, что вы усыпляете спящую красавицу, а затем подбрасываете монетку, и Спящая красавица точно знает, каким будет экспериментальный протокол, а экспериментальный протокол следующий: вы подбрасываете монету после того, как она уснет, и она будет Орел или решка, и это честная монета. Так что это то, что вы обычно присваиваете 50/50 достоверности 50/50 для орла или решки. Если монета выпадет орлом, то вы усыпите ее в понедельник… В воскресенье, извините. В понедельник вы будите ее, если она выпала орлом, и говорите: «Насколько вы уверены, что монета выпала орлом». Но если выпадет решка, то вы разбудите ее в понедельник, зададите ей этот вопрос, а потом снова усыпите и сотрете ей память, вот почему вы никогда не получите одобрения на это в реальном мире, и ты снова будишь ее во вторник, и снова задаешь ей вопрос.
Хорошо, а происходит то, что вы усыпляете спящую красавицу, а затем подбрасываете монетку, и Спящая красавица точно знает, каким будет экспериментальный протокол, а экспериментальный протокол следующий: вы подбрасываете монету после того, как она уснет, и она будет Орел или решка, и это честная монета. Так что это то, что вы обычно присваиваете 50/50 достоверности 50/50 для орла или решки. Если монета выпадет орлом, то вы усыпите ее в понедельник… В воскресенье, извините. В понедельник вы будите ее, если она выпала орлом, и говорите: «Насколько вы уверены, что монета выпала орлом». Но если выпадет решка, то вы разбудите ее в понедельник, зададите ей этот вопрос, а потом снова усыпите и сотрете ей память, вот почему вы никогда не получите одобрения на это в реальном мире, и ты снова будишь ее во вторник, и снова задаешь ей вопрос.
1:17:24.0 СК: Значит, разница в том, что если монета выпала орлом, ты разбудишь ее только один раз, ты в любом случае помилуешь ее в среду и позволь ей жить своей жизнью, а ты эксперимент, в котором вы будите ее и спрашиваете о достоверности того, что выпадет орел только один раз в понедельник, если выпадет орел. Если выпадет решка, вы разбудите ее и зададите этот вопрос дважды, один раз в понедельник и один раз во вторник. Хорошо, и вопрос в том, когда она проснется и задаст этот вопрос: Как вы верите, что монета… Выпала решка, что она должна сказать? Что рационального сказать? И я считаю, что… Ну, есть два возможных… Есть два способа думать об этом. Существует идея, которую Эльга первоначально отстаивал в своей статье, в которой говорится, что даже несмотря на то, что это монета 50/50, когда Спящая Красавица просыпается, она не знает, понедельник сегодня или вторник, она не знает, выпал орел или решка, и она должна с вероятностью в одну треть поверить в вопрос, выпала ли монета орлом. Почему?
Если выпадет решка, вы разбудите ее и зададите этот вопрос дважды, один раз в понедельник и один раз во вторник. Хорошо, и вопрос в том, когда она проснется и задаст этот вопрос: Как вы верите, что монета… Выпала решка, что она должна сказать? Что рационального сказать? И я считаю, что… Ну, есть два возможных… Есть два способа думать об этом. Существует идея, которую Эльга первоначально отстаивал в своей статье, в которой говорится, что даже несмотря на то, что это монета 50/50, когда Спящая Красавица просыпается, она не знает, понедельник сегодня или вторник, она не знает, выпал орел или решка, и она должна с вероятностью в одну треть поверить в вопрос, выпала ли монета орлом. Почему?
1:18:26.3 СК: Ну, представьте, что вы немного изменили эксперимент и сказали ей, если сегодня понедельник, ладно, так что теперь вы говорите Если вы разбудите ее, если выпадет решка и понедельник, вы сказать Сегодня понедельник, какова вероятность того, что выпал орел, если выпала решка. И в понедельник вы говорите, что это решка, и понедельник, извините, да, это понедельник. Какова вероятность, что выпала решка или решка. И если это вторник, вы говорите, неважно, что это вторник. Ладно, это не считается. Что ж, в таком случае она знает, что сегодня понедельник и вероятность выпадения орла или решки 50/50, и в любом случае это одно и то же, если сегодня понедельник, ничего лишнего не происходит, поэтому 50/50 или… Извините, я не должен сказать, что пропустил вперед. Она должна в равной степени доверять тому, что выпадет орел или решка, если она знает, что сегодня понедельник, потому что, зная, что сегодня понедельник, существует одинаковая вероятность того, что монета выпадет орлом или решкой.
Какова вероятность, что выпала решка или решка. И если это вторник, вы говорите, неважно, что это вторник. Ладно, это не считается. Что ж, в таком случае она знает, что сегодня понедельник и вероятность выпадения орла или решки 50/50, и в любом случае это одно и то же, если сегодня понедельник, ничего лишнего не происходит, поэтому 50/50 или… Извините, я не должен сказать, что пропустил вперед. Она должна в равной степени доверять тому, что выпадет орел или решка, если она знает, что сегодня понедельник, потому что, зная, что сегодня понедельник, существует одинаковая вероятность того, что монета выпадет орлом или решкой.
1:19:24.6 СК: Но вы также можете использовать ту же логику, говорит Эльга, если вы скажете Спящей Красавице, что монета выпала решкой, и спросите ее, понедельник или вторник? Если монета выпала решкой, она будет разбужена дважды, это абсолютно идентичная ситуация, у нее должны быть одинаковые доверительные отношения к понедельнику или вторнику, и, следовательно, у вас равные доверительные отношения к решке и понедельнику.
1:19:49.7 SC: Решка и вторник, орёл и понедельник. Есть только один способ сделать три числа равными, а именно сделать их по одной трети каждое, я не знаю, было ли это очень ясным объяснением того, что вы можете найти в Википедии, это там или вы можете прочитать оригинальную статью Эльги . Я думаю, что это очень разумно… Это совершенно разумно, потому что подумайте о том, чтобы просто проводить эксперимент снова и снова, и подумайте о том, чтобы делать ставки со Спящей Красавицей, вы собираетесь держать пари, что это был орел или решка, вы Буду делать ставки в два раза чаще на версии Спящей Красавицы, где дело выпало решкой, потому что там ее разбудят и в понедельник, и во вторник. И поэтому способ безубыточности для спящей красавицы состоит в том, чтобы присвоить равные вероятности каждой из трех возможностей, орел, решка, понедельник, решка, вторник. Это третья возможность. Но затем появляется Дэвид Льюис, известный философ, который недавно ушел из жизни, и Льюис сказал: «Нет, нет, нет».
1:20:52.7 СК: Перед сном в воскресенье Спящая Красавица присваивала вероятность 50/50 монете, выпавшей орлом или решкой, и когда вы ее будите, она не получает никакой новой информации в В оригинальной версии эксперимента ей не сказали, понедельник сегодня или вторник, поэтому она только что проснулась, и ей следует держаться своего оружия и по-прежнему говорить, что вероятность выпадения монеты, орла или решки, составляет 50/50. Вы не узнаете ничего нового.
1:21:19.0 СК: Хорошо. Так что большинство из нас сказали бы, что третья позиция, вероятно, немного более разумна, во всяком случае, немного более интуитивна, правильная она или нет. И снова люди спорят туда-сюда, Дэвид Льюис, Адам Элга, оба очень умные люди, но подумайте о том, что происходит.
1:21:38.2 СК: Третья позиция в основном говорит: я даю, хотя моя априорная вероятность выпадения орла… Решки… Для выпадения монеты орел или решка была 50/50. Если я знаю, что во вселенной решек будет две мои копии, одна, которая проснулась в понедельник, другая, которая проснулась во вторник, и во вселенной решек, будет только одна моя копия, если я даю равную вероятность все три идеи. Это первый подход наблюдателя. Первый подход наблюдателя в космологии, самоуказывающее предположение заключалось в том, что мы типичны в наборе всех наблюдателей во всех различных вселенных. Аналогия состоит в том, что разные вселенные — это вселенная, где монета выпадает решкой, и вселенная, где монета выпадает решкой. Сценарий, сценарий с орлом, сценарий с решкой, верно. Если вы просто придерживаетесь подхода «сначала мир», вы назначаете а до того, чтобы оказаться в мире решки, 50% до того, чтобы быть решкой, слово 50%, тот факт, что вас больше в мире решки, не имеет значения.
Это первый подход наблюдателя. Первый подход наблюдателя в космологии, самоуказывающее предположение заключалось в том, что мы типичны в наборе всех наблюдателей во всех различных вселенных. Аналогия состоит в том, что разные вселенные — это вселенная, где монета выпадает решкой, и вселенная, где монета выпадает решкой. Сценарий, сценарий с орлом, сценарий с решкой, верно. Если вы просто придерживаетесь подхода «сначала мир», вы назначаете а до того, чтобы оказаться в мире решки, 50% до того, чтобы быть решкой, слово 50%, тот факт, что вас больше в мире решки, не имеет значения.
1:22:45.0 СК: Итак, надеюсь, напряжение здесь немного прояснилось. Когда я описывал, что происходит в контексте космологии, я думаю, что более очевидным и интуитивно привлекательным является первый в мире подход. Вы приписываете вероятность… Априорную вероятность космологическому сценарию, и только после этого вы предполагаете свою типичную внутри нее. Принимая во внимание, что в подходе «Спящей красавицы» наиболее интуитивным кажется подход, ориентированный на наблюдателя, когда мы в равной степени доверяем тому, чтобы быть всеми наблюдателями во всех различных сценариях. Итак, это должно научить нас тому, что нам нужно подумать об этом, [смеется], и это вовсе не очевидный набор вещей, которые нужно делать.
Итак, это должно научить нас тому, что нам нужно подумать об этом, [смеется], и это вовсе не очевидный набор вещей, которые нужно делать.
1:23:29.0 СК: Ладно, теперь будет хуже. Я просто буду копать для нас ямы, потому что, помните, моя цель здесь не в том, чтобы дать вам раз и навсегда окончательный ответ, хотя у меня есть некоторые идеи, а в том, чтобы объяснить, почему это так интересно. философская проблема. И проблема в том, что в любой идее, либо с подходом «сначала мир», назначаются априорные, разные космологические сценарии, а затем предполагаются, что вы типичны в них, либо с подходом «сначала наблюдатель», когда вы предполагаете, что вы типичны в наборе всех возможные наблюдатели, оба они приводят вас к выводам, которые в ретроспективе кажутся необоснованными. Хорошо? Так что есть название, есть то, что называется проблемой самонадеянного философа [смеется], которая возникает при первом подходе наблюдателя. Но я думаю, что при любом подходе возникают одинаково странные проблемы.
1:24:22.8 СК: Итак, позвольте мне рассказать вам, в чем заключаются проблемы, потому что я думаю, что в конечном счете они возникают из-за одной и той же ошибки. В первом в мире подходе, так что помните, я буду повторять это, потому что знаю, что трудно соблюдать жаргон прямо. Подход World First заключается в том, что я сначала присваиваю достоверность различным сценариям, а затем предполагаю, что я типичен для сценария. Итак, проблема здесь в том, что вы, кажется, даете себе рычаги влияния на будущее. Это приводит к тому, что называется аргументом конца света, который вы предсказываете неминуемую гибель человечества. И позвольте мне объяснить, что я имею в виду. Итак, пусть эталонный класс… Сначала запомните мир, итак, у вас есть эталонный класс, мы увидим в нем более типичное, но что мы делаем, так это сначала присваиваем априорную вероятность, а затем предполагаем, что мы типичны внутри него. все наблюдатели в этом сценарии. Итак, пусть теория А, теория маленькой вселенной, будет теорией, согласно которой 200 миллиардов людей будут когда-либо жить, хорошо?
1:25:21. 5 СК: Итак, мы можем идти… Вы можете пойти еще раз, зайти в Википедию и спросить, сколько людей когда-либо жило в истории до сегодняшнего дня? Ответ около 100 миллиардов. Итак, то, что мы предполагаем здесь, в теории А, является космологическим сценарием, при котором в будущем родится примерно такое же количество людей, это не займет много времени, у нас уже есть семь или восемь миллиардов уже живущих, так что, поскольку население рост не займет много лет, прежде чем мы достигнем в общей сложности 200 миллиардов, а затем мы представим, что произойдет какая-то ужасная катастрофа, хорошо? Это теория А, это космологический сценарий в очень широком понимании того, что можно назвать космологией. Теория Б — человечество гораздо успешнее. Итак, теория А такова, что человечество довольно скоро, через 100 или 200 лет, человечество исчезнет.
5 СК: Итак, мы можем идти… Вы можете пойти еще раз, зайти в Википедию и спросить, сколько людей когда-либо жило в истории до сегодняшнего дня? Ответ около 100 миллиардов. Итак, то, что мы предполагаем здесь, в теории А, является космологическим сценарием, при котором в будущем родится примерно такое же количество людей, это не займет много времени, у нас уже есть семь или восемь миллиардов уже живущих, так что, поскольку население рост не займет много лет, прежде чем мы достигнем в общей сложности 200 миллиардов, а затем мы представим, что произойдет какая-то ужасная катастрофа, хорошо? Это теория А, это космологический сценарий в очень широком понимании того, что можно назвать космологией. Теория Б — человечество гораздо успешнее. Итак, теория А такова, что человечество довольно скоро, через 100 или 200 лет, человечество исчезнет.
1:26:10.5 СК: Теория Б говорит, нет, человечество будет процветать долгое время и, может быть, оно исчезнет, но оно не обязательно исчезнет, умирая, может быть, мы превратимся во что-то другое, но кого это волнует? Дело в том, что в теории Б, теории большой вселенной, мы представляем, что когда-либо будет существовать 200 триллионов человеческих существ. Таким образом, в теории А насчитывается всего 200 миллиардов человек, всего в два раза больше, чем существовало на самом деле. Теория Б насчитывает 200 триллионов, то есть более чем в тысячу раз больше, чем уже существовало. Итак, это два наших сценария. У нас есть некоторые предварительные сведения о том, что они вероятны или маловероятны. Что такое априор? Ну, грубо говоря, не знаю, но предположим, что они не слишком отличаются. Это всегда проблема с байесовскими рассуждениями, заключающаяся в том, чтобы определить, какими должны быть априорные доверительные отношения.
Таким образом, в теории А насчитывается всего 200 миллиардов человек, всего в два раза больше, чем существовало на самом деле. Теория Б насчитывает 200 триллионов, то есть более чем в тысячу раз больше, чем уже существовало. Итак, это два наших сценария. У нас есть некоторые предварительные сведения о том, что они вероятны или маловероятны. Что такое априор? Ну, грубо говоря, не знаю, но предположим, что они не слишком отличаются. Это всегда проблема с байесовскими рассуждениями, заключающаяся в том, чтобы определить, какими должны быть априорные доверительные отношения.
1:26:57.8 СК: Но давайте предположим, что они не слишком отличаются, давайте будем достаточно пессимистичны, чтобы сказать: смотрите, вполне вероятно, что человечество уничтожит себя в течение нескольких столетий, верно? Я думаю, что это правдоподобно. Итак, давайте зададим этому какой-нибудь априор, а более успешной теории B дадим какой-нибудь другой априор. Кого волнуют точные цифры, они не будут актуальны. Дело в том, что у нас есть данные в этом сценарии, таким образом думая о вещах с первым в мире сценарием, мы присвоили наш априор и теперь обновляем на основе данных. Что такое данные? Данные таковы, что мы находимся среди первых 100 миллиардов людей, которые когда-либо существовали, хорошо? И рассуждения не вдаваясь в цифры, рассуждения в теории А, что данные действительно вероятны. Вы знаете, если когда-либо будет существовать только 200 миллиардов людей, вероятность того, что случайный человек, типичный человек, окажется в пределах первых 100 миллиардов, составляет 50%. Это чертовски вероятно.
Что такое данные? Данные таковы, что мы находимся среди первых 100 миллиардов людей, которые когда-либо существовали, хорошо? И рассуждения не вдаваясь в цифры, рассуждения в теории А, что данные действительно вероятны. Вы знаете, если когда-либо будет существовать только 200 миллиардов людей, вероятность того, что случайный человек, типичный человек, окажется в пределах первых 100 миллиардов, составляет 50%. Это чертовски вероятно.
1:27:55.1 СК: Но в теории Б, если людей 200 триллионов, то вероятность того, что вы окажетесь среди первых 100 миллиардов, очень мала, меньше 10 с точностью до минус трех, верно? Таким образом, согласно логике, теперь я могу заключить, используя рассуждения, что теория А в 10–3 раза более вероятна, чем я предполагал, исходя из моих априорных вероятностей. Другими словами, я предсказываю только на основании того, что я типичный человек, что человечество долго не протянет. Вот почему это называется аргументом судного дня. И Брэндон Картер, Джон, Лесли, Ричард Готт и другие люди рассуждали именно в этом направлении. Это предсказание первого сценария наблюдателя: поскольку мы с большей вероятностью обладаем определенными качествами, если эти качества типичны, мы можем рассуждать так, чтобы поверить, что если мы типичны, жизнь для людей не будет продолжаться долго. дольше.
Это предсказание первого сценария наблюдателя: поскольку мы с большей вероятностью обладаем определенными качествами, если эти качества типичны, мы можем рассуждать так, чтобы поверить, что если мы типичны, жизнь для людей не будет продолжаться долго. дольше.
1:29:00.2 СК: Это может быть не сценарий Судного дня, например, может быть, мы все поднимемся или сублимируемся в матрицу или что-то в этом роде. Это тоже считается, но люди, какими мы их знаем, не продержатся долго, согласно этим рассуждениям о Судном дне. И Ричард Готт, в частности, получил широкую огласку за то, что продвигал этот способ рассуждения. Есть очень похожий аргумент, выдвинутый Джеймсом Хартлом и Марком Средницки, где они рассматривают два разных сценария, один из которых — это люди, которых сегодня, грубо говоря, 10 миллиардов. Это немного больше, но ладно, это круглое число. Люди — единственные формы жизни, единственные разумные формы жизни в Солнечной системе, верно? Это теория. Предположение. Теория Б состоит в том, что здесь, на Земле, есть люди, но также атмосфера Юпитера кишит формами жизни, разумными существами, там 10 триллионов юпитериан, ясно? Значит, юпитерианцев в тысячу раз больше, чем людей на земле. Это теория Б.
Это теория Б.
1:30:06.3 СК: Итак, два космологических сценария, оба из которых идеально соответствуют нашим данным, полученным с помощью телескопа и так далее. Мы на самом деле не исследовали атмосферу Юпитера, поэтому мы можем присвоить им некоторые априорные значения. Но затем мы делаем рассуждения, мы делаем логику с этой точки зрения в первую очередь, и идея была бы в теории А, если бы мы были типичными наблюдателями, ну, типичными наблюдателями были бы люди, потому что теория А говорит, что единственные наблюдатели в Солнечная система — это люди. Согласно теории Б, типичным наблюдателем в Солнечной системе был бы юпитерианец, верно? Это был бы газовый мешок, плавающий в атмосфере Юпитера. Мы не газовый мешок, плавающий в атмосфере Юпитера, поэтому у нас есть веские доказательства против теории Б. Потому что при таком способе мышления… [хихикает] И, кстати, я имею в виду, что Хартл и Средненицкий приводят этот аргумент, чтобы пошутить. этого, они не верят этому аргументу, они говорят, конечно, вы не верите этому.
1:31:04.4 СК: Они говорят о том, что мы можем заключить, что в атмосфере Юпитера, вероятно, существуют намеренно разумные газовые мешки, даже не глядя на них, просто сидя в креслах и рассуждая подобным образом. , Правильно? И происходит то, что, предполагая, что мы типичные наблюдатели, мы предоставляем себе огромное количество рычагов влияния на то, кем является типичный наблюдатель. Итак, другими словами, как я люблю выражаться, когда вы говорите: «Ну, я типичный наблюдатель, принцип посредственности, это звучит очень скромно». [смех] Похоже, вы на самом деле не говорите ничего грандиозного, но если подумать, то предположение, что вы являетесь типичным наблюдателем во Вселенной, на самом деле предполагает, что типичные наблюдатели во Вселенной такие же, как вы. Типичные наблюдатели примерно в нашу эпоху человеческой истории, типичные наблюдатели здесь, на Земле, а не на Юпитере, верно?
1:31:58.8 СК: Таким образом, вы даете себе огромные рычаги влияния на остальную вселенную, предполагая, что существует не так уж много наблюдателей, не похожих на вас. Потому что если бы был типичный наблюдатель, то не был бы таким, как ты. Итак, это беспокойство вызывает то, что этот первый в мире подход, который казался логичным, когда мы впервые произнесли его вслух, тайно предоставляет вам огромное количество рычагов влияния на вселенную, даже не вставая из своего кресла и не глядя на нее. Итак, вы можете сказать: «Хорошо, я хочу решить эту проблему». Я не верю этим аргументам Судного дня или аргументам инопланетян, давайте перейдем к первому подходу наблюдателя. Помните, что подход, основанный на первом наблюдателе, дает толчок сценариям, в которых больше наблюдателей, потому что вы говорите, что вы типичны в наборе всех наблюдателей по всем различным возможным сценариям.
Потому что если бы был типичный наблюдатель, то не был бы таким, как ты. Итак, это беспокойство вызывает то, что этот первый в мире подход, который казался логичным, когда мы впервые произнесли его вслух, тайно предоставляет вам огромное количество рычагов влияния на вселенную, даже не вставая из своего кресла и не глядя на нее. Итак, вы можете сказать: «Хорошо, я хочу решить эту проблему». Я не верю этим аргументам Судного дня или аргументам инопланетян, давайте перейдем к первому подходу наблюдателя. Помните, что подход, основанный на первом наблюдателе, дает толчок сценариям, в которых больше наблюдателей, потому что вы говорите, что вы типичны в наборе всех наблюдателей по всем различным возможным сценариям.
1:32:48.9 СК: Итак, если бы вы были… Если бы вы усилили, скажем, теорию, согласно которой люди живут дольше, или повысили априорную вероятность, априорное доверие к теории, в которой существует множество инопланетян на Юпитере, так что в обоих сценариях большой вселенной вы получите больше импульса, а затем вы обусловите, наблюдая, что вы находитесь в этом крошечном маленьком кусочке вселенной. Это компенсируется, хорошо? Таким образом, вы не помогаете себе в дополнительных рассуждениях или дополнительных выводах о большой вселенной, но… [смеется] Другими словами, подход, ориентированный на наблюдателя, избавляет от аргумента Судного дня или аргумента Юпитера. У него другая проблема, и технически это то, что Бостром назвал проблемой самонадеянного философа.
Это компенсируется, хорошо? Таким образом, вы не помогаете себе в дополнительных рассуждениях или дополнительных выводах о большой вселенной, но… [смеется] Другими словами, подход, ориентированный на наблюдателя, избавляет от аргумента Судного дня или аргумента Юпитера. У него другая проблема, и технически это то, что Бостром назвал проблемой самонадеянного философа.
1:33:38.4 СК: Итак, еще раз… И я выберу еще один набор цифр, чтобы прояснить ситуацию. Давайте представим, что сценарий А — это некий космологический сценарий с, я не знаю, триллионом наблюдателей, от 10 до 12 наблюдателей в нем. А сценарий Б — это большая вселенная, примерно 10 на 21 наблюдателя в ней. И что касается физики, они одинаково просты, эти два сценария, и нет никаких оснований думать, что большая Вселенная или маленькая вселенная предпочтительнее. Точно так же, как мы бы сказали, простирается ли вселенная за нашим горизонтом в бесконечность или она скручивается в сферу, тор или что-то еще? Между этими двумя сценариями нет большой разницы. Мы живем в бесконечной вселенной или в конечной? Я мог бы придумать хорошие аргументы в пользу любого из них, я бы дал им примерно одинаковое доверие, если бы у меня не было никакой другой информации.
Мы живем в бесконечной вселенной или в конечной? Я мог бы придумать хорошие аргументы в пользу любого из них, я бы дал им примерно одинаковое доверие, если бы у меня не было никакой другой информации.
1:34:33.9 СК: И на что указывает Бостром, так это то, что если вы используете первый подход наблюдателя, то вы даете равные или примерно сопоставимые априорные значения для маленькой вселенной и большой вселенной, но теперь вы говорите, что вы типичный наблюдатель во всем ансамбле, тогда с подавляющей вероятностью, с вероятностью 10 к 9 или около того, плюс один минус 10 к 9, я полагаю, вы окажетесь в большой вселенной, потому что в большой вселенной больше наблюдателей. И поэтому вы заключаете, что теория Б верна, вы заключаете, что наша Вселенная на самом деле простирается бесконечно далеко, она не скручивается в сферу или тор только потому, что в этом сценарии гораздо больше наблюдателей. Итак, Бострому, хотя он и является поклонником аргумента Судного дня, он говорит, что это самонадеянно [смеется] Я не думаю, что я должен быть в состоянии сделать вывод, что вселенная велика, только из того факта, что я существую. Опять же, не вставая с кресла, ничего не делая.
Опять же, не вставая с кресла, ничего не делая.
1:35:31.1 СК: Так вот в чем проблема, как я ее вижу. В обоих случаях вы начинали с подхода «сначала мир» или «сначала наблюдатель», вы начинали с того, что вели себя скромно, говоря: да, я просто типичный наблюдатель, во мне нет ничего особенного. Но в любом случае, просто предположение, что вы типичный наблюдатель, дало вам огромное влияние на то, на что похожа остальная вселенная, без необходимости выходить и смотреть на нее. Итак, дело в том, что типичность на самом деле самонадеянна. Это совсем не скромно. Утверждение, что я типичен, есть утверждение, типичные наблюдатели такие же, как и я, какое право вы имеете так говорить? Это говорит что-то очень, очень сильное о природе вселенной, на что вы не смотрели.
1:36:14.7 СК: Итак, это проблема. Это проблема для антропного мышления. Это проблема для попытки перейти от сценария космологической мультивселенной к предсказанию космологической постоянной, энергии вакуума, верно? Нам нужен какой-то механизм. Нам нужны какие-то формулы, какой-то формализм, который позволит нам подставлять числа, и преимущество принципа типичности в том, что он позволяет нам это делать. Это позволяет нам сказать, что если бы существовали разные конкурирующие теории Вселенной с разным числом наблюдателей и так далее, и у нас были бы распределения по тому, что видели эти наблюдатели, можно было бы предсказать, что эти… Что мы должны увидеть в этот сценарий. И если мы не можем предположить, что мы типичны, то как мы можем делать прогнозы? Как мы вообще используем антропные рассуждения? Можем ли мы его вообще использовать? Итак, есть несколько разных решений, и я хочу рассказать об одном решении, которое мне не нравится, потому что оно немного… Я знаю, почему людям это нравится, это заманчиво, но я действительно… я хочу не согласиться с этим. Это. Итак, [посмеивается] в этом суть статьи Хартла и Средницкого.
Нам нужны какие-то формулы, какой-то формализм, который позволит нам подставлять числа, и преимущество принципа типичности в том, что он позволяет нам это делать. Это позволяет нам сказать, что если бы существовали разные конкурирующие теории Вселенной с разным числом наблюдателей и так далее, и у нас были бы распределения по тому, что видели эти наблюдатели, можно было бы предсказать, что эти… Что мы должны увидеть в этот сценарий. И если мы не можем предположить, что мы типичны, то как мы можем делать прогнозы? Как мы вообще используем антропные рассуждения? Можем ли мы его вообще использовать? Итак, есть несколько разных решений, и я хочу рассказать об одном решении, которое мне не нравится, потому что оно немного… Я знаю, почему людям это нравится, это заманчиво, но я действительно… я хочу не согласиться с этим. Это. Итак, [посмеивается] в этом суть статьи Хартла и Средницкого.
1:37:19.8 СК: Я постараюсь не забыть поставить ссылки на некоторые из этих документов в примечаниях к шоу. Статья Хартла и Средненицкого, которая привела нас к проблеме с инопланетянами, юпитерианцем и прочим, почему она это сделала? Их целью было возразить вообще против типичности. Они думали… И я с ними здесь согласен, но не с их решением, они думали, что считать нас типичными наблюдателями и необоснованно, и вести к неверным выводам, слишком самонадеянно. Так каково их решение? Их решение — то, что они называют нулевым графическим распределением. Итак, они говорят, что когда у вас есть теория, космологическая теория со многими наблюдателями, вместо того, чтобы просто сказать, что мы типичный наблюдатель, другими словами, у нас есть равная вероятность быть любым наблюдателем в этой вселенной в пределах некоторого определенного эталонного класса. , теория приходит не только со списком наблюдателей, но и с распределением по этим наблюдателям. И распределение по этим наблюдателям говорит вам, какова вероятность того, что вы один из этих наблюдателей, хорошо?
Статья Хартла и Средненицкого, которая привела нас к проблеме с инопланетянами, юпитерианцем и прочим, почему она это сделала? Их целью было возразить вообще против типичности. Они думали… И я с ними здесь согласен, но не с их решением, они думали, что считать нас типичными наблюдателями и необоснованно, и вести к неверным выводам, слишком самонадеянно. Так каково их решение? Их решение — то, что они называют нулевым графическим распределением. Итак, они говорят, что когда у вас есть теория, космологическая теория со многими наблюдателями, вместо того, чтобы просто сказать, что мы типичный наблюдатель, другими словами, у нас есть равная вероятность быть любым наблюдателем в этой вселенной в пределах некоторого определенного эталонного класса. , теория приходит не только со списком наблюдателей, но и с распределением по этим наблюдателям. И распределение по этим наблюдателям говорит вам, какова вероятность того, что вы один из этих наблюдателей, хорошо?
1:38:26.9 СК: Другими словами, они рассматривают две разные теории. Итак, вот космологический сценарий, в котором нет мозгов Больцмана. Итак, теория А, теория маленькой вселенной, включает в себя обычных наблюдателей, таких как вы и я, которые появились после Большого Взрыва в результате эволюции, управляемой стрелой времени, и так далее, и так далее, и тому подобное. Обычные термодинамические наблюдатели. Представим, что есть какое-то большое количество этих 10 до 40-го… Не знаю, я придумал цифру и ноль больцмановских мозгов. Итак, давайте представим, что Вселенная просто успокаивается, в ней нет ни флуктуаций, ни больцмановских мозгов, это теория А. Хорошо? Но есть и теория Б. Теория Б имеет такое же количество обычных наблюдателей, но в ней также огромное количество больцмановских мозгов, 10 к 10 к 100 или сколько угодно, 10 к, 10 к, 10 до, от 10 до 100, если хотите. Большое количество больцмановских мозгов.
Итак, вот космологический сценарий, в котором нет мозгов Больцмана. Итак, теория А, теория маленькой вселенной, включает в себя обычных наблюдателей, таких как вы и я, которые появились после Большого Взрыва в результате эволюции, управляемой стрелой времени, и так далее, и так далее, и тому подобное. Обычные термодинамические наблюдатели. Представим, что есть какое-то большое количество этих 10 до 40-го… Не знаю, я придумал цифру и ноль больцмановских мозгов. Итак, давайте представим, что Вселенная просто успокаивается, в ней нет ни флуктуаций, ни больцмановских мозгов, это теория А. Хорошо? Но есть и теория Б. Теория Б имеет такое же количество обычных наблюдателей, но в ней также огромное количество больцмановских мозгов, 10 к 10 к 100 или сколько угодно, 10 к, 10 к, 10 до, от 10 до 100, если хотите. Большое количество больцмановских мозгов.
1:39:19.1 ШК: И мы немного перейдем к тому, что я имею в виду именно под больцмановским мозгом, потому что это важный вопрос. Но наблюдатель, который возник случайным образом, — вот что я имею в виду на данный момент. Итак, типичные космологи на улице, столкнувшись с этими двумя сценариями, сказали бы: хорошо, есть сценарий А, только обычные наблюдатели, без больцмановских мозгов. Сценарий Б, в котором есть и то, и другое. А больцмановских мозгов много. И большинство космологов на улице рассуждают следующим образом: «Ну, я обычный наблюдатель, и вероятность того, что я был бы обычным наблюдателем в теории А, равна единице». Все наблюдатели в теории А — обычные. Таким образом, функция правдоподобия для того, чтобы быть обычным наблюдателем, обусловленным правильностью теории А, равна единице. Это… Данные у меня обычные. Теория в том, что в теории А нет больцмановских мозгов.
Итак, типичные космологи на улице, столкнувшись с этими двумя сценариями, сказали бы: хорошо, есть сценарий А, только обычные наблюдатели, без больцмановских мозгов. Сценарий Б, в котором есть и то, и другое. А больцмановских мозгов много. И большинство космологов на улице рассуждают следующим образом: «Ну, я обычный наблюдатель, и вероятность того, что я был бы обычным наблюдателем в теории А, равна единице». Все наблюдатели в теории А — обычные. Таким образом, функция правдоподобия для того, чтобы быть обычным наблюдателем, обусловленным правильностью теории А, равна единице. Это… Данные у меня обычные. Теория в том, что в теории А нет больцмановских мозгов.
1:40:14.5 СК: Принимая во внимание, что в теории Б вероятность того, что я буду обычным наблюдателем, при предположении типичности исчезающе мала, 10 с минусом, 10 с минусом, 10 с сотней. Хорошо? Если бы теория Б была верна, я был бы больцмановским мозгом, потому что большинство наблюдателей — больцмановы мозги, поэтому, говорит обычный космолог на улице, теория Б исключена. Мне не нужно покидать свое кресло, я знаю, что это неправильно, потому что, если бы это было правильно, я был бы больцмановским мозгом. То, что говорят Хартл и Средненицкий, а это совсем другие ходы, чем делает большинство космологов, они хотят сказать: я не знаю, верна ли теория А или теория Б. Я не покидал своего кресла, и я не должен позволять себе делать выводы, которые касаются только вещей, которые находятся далеко от моего кресла или каких-либо других моих наблюдений. И… Но они… Ничего страшного. [смеется] Но потом они говорят: «Ну, я знаю, что я не больцмановский мозг, и все же я хочу, чтобы он был в некотором смысле типичным, но не совсем».
Мне не нужно покидать свое кресло, я знаю, что это неправильно, потому что, если бы это было правильно, я был бы больцмановским мозгом. То, что говорят Хартл и Средненицкий, а это совсем другие ходы, чем делает большинство космологов, они хотят сказать: я не знаю, верна ли теория А или теория Б. Я не покидал своего кресла, и я не должен позволять себе делать выводы, которые касаются только вещей, которые находятся далеко от моего кресла или каких-либо других моих наблюдений. И… Но они… Ничего страшного. [смеется] Но потом они говорят: «Ну, я знаю, что я не больцмановский мозг, и все же я хочу, чтобы он был в некотором смысле типичным, но не совсем».
1:41:17.1 СК: Вот что они решают с помощью идеи нулевого графического распределения. И поэтому они говорят, что помимо теории А говорят, что это просто обычные наблюдатели. Больцмановских мозгов нет. Теория Б говорит, что есть обычные наблюдатели и мозги Больцмана, теория Б должна прийти вместе с распределением по этим наблюдателям. И они говорят: «Ну, рассмотрим следующее распределение в рамках теории Б. Итак, в теории Б есть и обычные наблюдатели, и больцмановские мозги. Они говорят: что, если моя вероятность быть наблюдателем определенного типа равна нулю для всех больцмановских мозгов и единице по сравнению с числом обычных наблюдателей для всех обычных наблюдателей? Так что я типичен, но только в подмножестве обычных наблюдателей. Итак, они признают, что существуют все эти больцмановские мозги, но они добавляют это дополнительное распределение вероятностей, которое просто говорит Фиату, что я не один из них. Как они могут оправдать это? Ну, они оглядываются и понимают, что они не одни из них.
И они говорят: «Ну, рассмотрим следующее распределение в рамках теории Б. Итак, в теории Б есть и обычные наблюдатели, и больцмановские мозги. Они говорят: что, если моя вероятность быть наблюдателем определенного типа равна нулю для всех больцмановских мозгов и единице по сравнению с числом обычных наблюдателей для всех обычных наблюдателей? Так что я типичен, но только в подмножестве обычных наблюдателей. Итак, они признают, что существуют все эти больцмановские мозги, но они добавляют это дополнительное распределение вероятностей, которое просто говорит Фиату, что я не один из них. Как они могут оправдать это? Ну, они оглядываются и понимают, что они не одни из них.
1:42:12.3 СК: Это можно считать жульничеством, да? Потому что вы используете свои данные, чтобы определить свою теорию заранее. Может быть, это немного обман, но мы доберемся до конкретного способа, которым я думаю, что это терпит неудачу. Но утверждается, что это решает проблему мозга Больцмана без какой-либо работы. Итак, большинство космологов хотят сказать: если ваш космологический сценарий предсказывает, что большинство наблюдателей являются больцмановскими мозгами, тогда ваш космологический сценарий неверен. Что Хартл и Средненицкий хотят сказать, так это то, что все это показывает, что вы не мозг Больцмана. Я совершенно счастлив рассматривать вселенные, в которых есть много мозгов Больцмана, потому что я могу просто сказать, что я не один из них. Это их ход с нулевой графической раздачей. Хорошо? Вот почему я не думаю, что это работает. Я действительно думаю, что это обман. И причина, по которой это мошенничество, несколько более тонкая… Происходит из более тонкого понимания того, что вы подразумеваете под больцмановским мозгом.
Итак, большинство космологов хотят сказать: если ваш космологический сценарий предсказывает, что большинство наблюдателей являются больцмановскими мозгами, тогда ваш космологический сценарий неверен. Что Хартл и Средненицкий хотят сказать, так это то, что все это показывает, что вы не мозг Больцмана. Я совершенно счастлив рассматривать вселенные, в которых есть много мозгов Больцмана, потому что я могу просто сказать, что я не один из них. Это их ход с нулевой графической раздачей. Хорошо? Вот почему я не думаю, что это работает. Я действительно думаю, что это обман. И причина, по которой это мошенничество, несколько более тонкая… Происходит из более тонкого понимания того, что вы подразумеваете под больцмановским мозгом.
1:43:08.8 СК: Типа, люди… Типа, буквально сегодня в твиттере ни с того ни с сего кто-то спрашивал про мозги Больцмана, а что считать мозгом Больцмана? Сколько кислорода вам нужно, сколько тела вам нужно, как долго вам нужно, чтобы выжить, чтобы быть больцмановским мозгом? Итак, я хочу сказать, что ни один из этих вопросов не имеет значения ни в какой реальной точке, потому что вы можете произвести вычисления наоборот. Скажи мне, что ты хочешь считать наблюдателем, хорошо? Вам нужен только мозг? Нужен ли мозг в теле? Нужен ли мозг в теле на планете с атмосферой? Вам нужна семья? [хихикает] Вам нужны другие люди, чтобы быть счастливыми, возможно, вам нужно все, что вы видите? Итак, являетесь ли вы наблюдателем, который буквально находится в точно таком же макроскопическом состоянии, в котором вы лично находитесь прямо сейчас, так что то, что находится в вашем мозгу, все, что вы видите своими глазными яблоками, действительно там.
Скажи мне, что ты хочешь считать наблюдателем, хорошо? Вам нужен только мозг? Нужен ли мозг в теле? Нужен ли мозг в теле на планете с атмосферой? Вам нужна семья? [хихикает] Вам нужны другие люди, чтобы быть счастливыми, возможно, вам нужно все, что вы видите? Итак, являетесь ли вы наблюдателем, который буквально находится в точно таком же макроскопическом состоянии, в котором вы лично находитесь прямо сейчас, так что то, что находится в вашем мозгу, все, что вы видите своими глазными яблоками, действительно там.
1:44:03.2 СК: Ну, типа, давайте все это. Но дело в том, что я определяю все эти вещи с точки зрения вещей, которые существуют прямо сейчас. Хорошо? Нет… Мне не разрешено включать историю того, что привело вас туда. Я говорю, вот разные виды наблюдателей, которые могут существовать в один момент времени. И мы можем в основном классифицировать их на два типа. Существуют термодинамически разумные наблюдатели, верно? Это то, что мы называем обычными наблюдателями, такими как вы и я, людьми, которые появились в результате обычной эволюции, физических процессов, биологии, естественного отбора и так далее, в некотором смысле из прошлого с низкой энтропией. Гипотеза прошлого, о которой вы слышали, как я говорил ранее, идея о том, что около 14 миллиардов лет назад была низкая энтропия, — вот что сразу после этого, спустя несколько десятков миллиардов лет, дает термодинамически чувствительным наблюдателям .
Гипотеза прошлого, о которой вы слышали, как я говорил ранее, идея о том, что около 14 миллиардов лет назад была низкая энтропия, — вот что сразу после этого, спустя несколько десятков миллиардов лет, дает термодинамически чувствительным наблюдателям .
1:44:54.6 СК: Дело в том, что эти наблюдатели, например, смотрят на космический микроволновый фон и говорят: «Ага, это свидетельствует о низкой энтропии в прошлом». Это буквально говорит мне о том, что Вселенная была довольно гладкой в очень, очень ранние времена и, следовательно, имела низкую энтропию. Что ж, в этом есть секрет, [смеется] в этом заключении есть секретный шаг, откуда вы знаете, когда смотрите на Вселенную, что у Вселенной была низкая энтропия? Ответ заключается в том, что она постоянна, но не подразумевается никакими наблюдениями, которые мы делаем. Если вы просто скажете: «Давайте подумаем обо всех возможных способах, которыми фотоны могли попасть в мой телескоп, и дать мне карту космического микроволнового фона, похожую на ту, которую мы видим, большинство из них не соответствуют вселенным, где ранние времена действительно существовали». были гладкими.
были гладкими.
1:45:45.8 СК: Это правда, что если бы ранняя Вселенная была гладкой, мы бы видели то, что видим в наши телескопы. Но неправда, что если мы видим то, что видим в наши телескопы, то ранняя Вселенная должна была быть гладкой. Просто обусловливаем то, что мы видим в наши телескопы, а не какое-то дополнительное предположение об энтропии. Крайне вероятно, что ранняя Вселенная была очень, очень комковатой, дико неоднородной в разных местах, но есть ряд различных эффектов, которые определяют конечную длину волны света, когда мы ее наблюдаем, есть плотность и температура, есть также Эффект Доплера. Есть также гравитационное красное смещение, синее смещение и так далее. Там целая куча эффектов. И хотя это кажется маловероятным, гораздо более вероятно, что происходят дикие флуктуации вещей, которые почти полностью компенсируются к тому времени, когда фотоны достигают точки.
1:46:40.8 СК: И это всего лишь причудливый окольный способ сказать, что при любом состоянии средней энтропии, как мы здесь, в телескоп, смотрим в прошлое, при любом состоянии средней энтропии существует гораздо больше энтропийное прошлое, из которого оно могло развиться посредством случайной флуктуации, Чем есть низкоэнтропийное прошлое, которое естественным образом привело бы к этому. Так что я знаю, что повторяюсь, но это критический и довольно сложный момент, поэтому я повторю его снова. Если вы начнете с вопроса, какие ранние условия естественным образом привели бы к нам? Ответ таков: они должны были иметь низкую энтропию. Я говорил об этом с Дэвидом Уоллесом в подкасте не так давно. Но если вместо этого вы спросите, какие условия, естественно, были бы в прошлом, учитывая, что мы здесь? Вы видите разницу? Вы задаете несколько иной вопрос, не о том, что такое виды вселенных, какие виды начальных условий обычно приводят к нам, а вместо того, какие виды… Каков полный набор вселенных, которые могут привести к нас, хорошо?
Так что я знаю, что повторяюсь, но это критический и довольно сложный момент, поэтому я повторю его снова. Если вы начнете с вопроса, какие ранние условия естественным образом привели бы к нам? Ответ таков: они должны были иметь низкую энтропию. Я говорил об этом с Дэвидом Уоллесом в подкасте не так давно. Но если вместо этого вы спросите, какие условия, естественно, были бы в прошлом, учитывая, что мы здесь? Вы видите разницу? Вы задаете несколько иной вопрос, не о том, что такое виды вселенных, какие виды начальных условий обычно приводят к нам, а вместо того, какие виды… Каков полный набор вселенных, которые могут привести к нас, хорошо?
1:47:45.5 СК: Итак, виды вселенных, которые могут привести к нам, виды начальных условий, сценарии ранних вселенных имеют чрезвычайно высокую энтропию, а мы являемся результатом случайных колебаний. Хорошо, так что все это было отчасти, чтобы сказать, что идея термодинамически разумного наблюдателя — это тот, для кого это не так. Мы не возникли случайно. Гипотеза прошлого, говорящая о низкой энтропии, верна, и поэтому наши выводы из данных о том, что происходило в прошлом нашей Вселенной, надежны и термодинамически разумны. И еще есть наблюдатель другого типа, обобщение идеи больцмановского мозга, которого мы можем назвать наблюдателем со случайными колебаниями, хорошо? Итак, если у вас нет прошлой гипотезы, если вы не настаиваете на предположении, что ранняя Вселенная имела низкую энтропию, все, что вы знаете, — это некоторые особенности вашего текущего состояния.
Гипотеза прошлого, говорящая о низкой энтропии, верна, и поэтому наши выводы из данных о том, что происходило в прошлом нашей Вселенной, надежны и термодинамически разумны. И еще есть наблюдатель другого типа, обобщение идеи больцмановского мозга, которого мы можем назвать наблюдателем со случайными колебаниями, хорошо? Итак, если у вас нет прошлой гипотезы, если вы не настаиваете на предположении, что ранняя Вселенная имела низкую энтропию, все, что вы знаете, — это некоторые особенности вашего текущего состояния.
1:48:37.9 СК: Тогда, если вы живете в тепловой вселенной, которая существует вечно, если вы живете в этой вечной, термально флуктуирующей вселенной, весьма вероятно, что и ваше прошлое, и ваше будущее имели более высокую энтропию, и что вы представляют собой случайное колебание. И это не имеет ничего общего с мозгами или минимальными наблюдателями или чем-то подобным. Утверждение состоит в том, что при любых условиях вашего текущего макроскопического «я», если это все, что вы знаете, вы также не знаете прошлую гипотезу. Если вы просто думаете, что являетесь элементом какого-то случайно колеблющегося ансамбля, то вы появились в результате набора диких совпадений, которые в прошлом сошлись, чтобы перейти от высокой энтропии к созданию вас, хорошо? И если вы живете в этой вселенной со случайными флуктуациями вечно, то количество случайно колеблющихся наблюдателей любого вида. Другими словами, любые макроскопические объекты, живущие на Земле, имеющие солнце, имеющие воспоминания в голове, что бы вы ни говорили, условия, которые вы ставите перед собой в настоящем, число таких случайно флуктуирующих наблюдателей неизмеримо больше, чем число термодинамически такие разумные наблюдатели, если вы живете в этой случайно колеблющейся вселенной.
Если вы просто думаете, что являетесь элементом какого-то случайно колеблющегося ансамбля, то вы появились в результате набора диких совпадений, которые в прошлом сошлись, чтобы перейти от высокой энтропии к созданию вас, хорошо? И если вы живете в этой вселенной со случайными флуктуациями вечно, то количество случайно колеблющихся наблюдателей любого вида. Другими словами, любые макроскопические объекты, живущие на Земле, имеющие солнце, имеющие воспоминания в голове, что бы вы ни говорили, условия, которые вы ставите перед собой в настоящем, число таких случайно флуктуирующих наблюдателей неизмеримо больше, чем число термодинамически такие разумные наблюдатели, если вы живете в этой случайно колеблющейся вселенной.
1:49:44.0 СК: Так вот в чем проблема, если серьезно подумать, способ Хартла и Средненицкого вывернуться из мозговой проблемы Больцмана, потому что они говорят: «Ну, я просто предполагаю, что Fiat что я не мозг Больцмана». Хорошо, давай представим, что я позволил тебе это сделать. Есть еще… Если вы живете в этой вечно изменчивой космологии, все еще есть наблюдатели, которые выглядят точно так же, как вы, но являются случайными флуктуациями. Под точь-в-точь как ты я подразумеваю, где бы ты ни сидел, в комнате вокруг тебя, я подарю тебе всю Землю, если хочешь, хорошо? И весь свет, который приходит на Землю от солнца, звезд, планет и чего-то еще, все такое, я признаю все это, все еще верно, что вы, скорее всего, случайно возникнете в своем существовании. .
Есть еще… Если вы живете в этой вечно изменчивой космологии, все еще есть наблюдатели, которые выглядят точно так же, как вы, но являются случайными флуктуациями. Под точь-в-точь как ты я подразумеваю, где бы ты ни сидел, в комнате вокруг тебя, я подарю тебе всю Землю, если хочешь, хорошо? И весь свет, который приходит на Землю от солнца, звезд, планет и чего-то еще, все такое, я признаю все это, все еще верно, что вы, скорее всего, случайно возникнете в своем существовании. .
1:50:42.1 СК: На самом деле, я мог бы продолжить, я могу сказать, например, давайте возьмем наш световой конус из прошлого, давайте возьмем вас и все ваши наблюдения, расширим их в прошлое и предположим, что все, что вы думаете, правда о вашем прошлом правда. Я собираюсь предоставить вам все это. Но я также говорю, что прошлое, которое, по вашему мнению, вы наблюдаете, на самом деле не является результатом однородной вселенной, это выборка из ансамбля в беспорядочно флуктуирующей вечной вселенной, ясно? Мол, Хартл и Средненицкий хотят допустить, хотят сказать, что все в порядке. Так что, если я расскажу вам все ваше прошлое и скажу, что ставлю условия на подобных наблюдателей, они все еще, вероятно, будут частью более крупного ансамбля теплового равновесия, а это означает, что завтра, когда вы пойдете к телескопу и посмотрите на микроволновый фон, он больше не будет. Это просто… Ваш предыдущий опыт [смеется] был просто случайным колебанием. Нет причин… Потому что…
Так что, если я расскажу вам все ваше прошлое и скажу, что ставлю условия на подобных наблюдателей, они все еще, вероятно, будут частью более крупного ансамбля теплового равновесия, а это означает, что завтра, когда вы пойдете к телескопу и посмотрите на микроволновый фон, он больше не будет. Это просто… Ваш предыдущий опыт [смеется] был просто случайным колебанием. Нет причин… Потому что…
1:51:44.5 ШК: Подумайте об этом… Извините, мне нужно сделать резервную копию, потому что это очевидно для меня, но если вы действительно не задумывались о космологии и общей теории относительности, это не всегда очевидно. Когда мы смотрим на космический микроволновый фон, мы смотрим в прошлое, верно? Мы используем свет, чтобы наблюдать за условиями на расстоянии. Чтобы добраться до нас, требуется световое время, и поэтому прошли миллиарды лет с того момента, как этот фотон, который мы наблюдаем сегодня, в последний раз взаимодействовал с микроволновым фоном. И с течением времени это означает, что между формированием космического микроволнового фона и нами проходит все больше и больше времени. Таким образом, мы все больше и больше оглядываемся назад на области космического микроволнового фона, которые были созданы немного дальше. Горизонт, который мы получаем, растягивая световой конус прошлого до микроволнового фона, постепенно увеличивается с течением времени по мере того, как мы становимся старше.
Таким образом, мы все больше и больше оглядываемся назад на области космического микроволнового фона, которые были созданы немного дальше. Горизонт, который мы получаем, растягивая световой конус прошлого до микроволнового фона, постепенно увеличивается с течением времени по мере того, как мы становимся старше.
1:52:36.1 СК: Итак, мы смотрим на немного разные части космического микроволнового фона. И дело в том, что если все, что мы знаем, является просто случайной флуктуацией, то нет никаких причин для сохранения этого паттерна. Завтра мы должны выглянуть наружу и не увидеть вообще никакого микроволнового фона, это было бы наиболее вероятным, наиболее вероятным способом для Вселенной обусловить наши текущие наблюдения и дать вам все о фактическом прошлом нашего светового конуса. И я бы сказал, я думаю, что Хартл и Средненицкий не согласятся со мной, но я бы сказал, что нет никакой принципиальной причины исключать таких наблюдателей из вашего ксерографического распределения. Если ваша мотивация для исключения наблюдателей заключалась в том, что я хочу рассматривать только тех наблюдателей, у которых были законные справедливые выводы из данных, надежные выводы из прошлого, основанные на их наблюдениях, то наблюдатели, как я только что описал, в полном порядке. И их намного, намного больше, чем те, которые произошли из повсеместно низкой энтропии в очень ранние времена. Те наблюдатели, которые завтра еще увидят там микроволновый фон.
И их намного, намного больше, чем те, которые произошли из повсеместно низкой энтропии в очень ранние времена. Те наблюдатели, которые завтра еще увидят там микроволновый фон.
1:53:51.9 СК: Итак, я бы сказал, что их теория делает предсказания. И их предсказание… Я имею в виду, они сделали его много лет назад, так что оно было сфальсифицировано много-много раз. [хихикает] Другими словами, проблема не в больцмановских мозгах, проблема в больцмановских вас. Проблема в том, что кем бы вы ни были, что бы вы ни думали о своем нынешнем макроскопическом состоянии, вы могли возникнуть случайным образом. И если вы верите, что в космологическом сценарии преобладают случайные флуктуации, то вы, вероятно, действительно флуктуировали. И вы пытаетесь, если вы Хартл и Средненицкий, провести различие между обоими больцмановскими мозгами, но в этом космологическом сценарии нет никаких оснований различать ваш больцмановский мозг, кроме как потому, что он вам просто не нравится. Вы не хотите быть случайной флуктуацией и поэтому говорите: «Я отрицаю, что это то, чем я являюсь».
1:54:44.5 СК: Я думаю, что для этого нет принципиальной причины. Это другая версия самонадеянности. Вы просто приписываете вероятность того, что вы являетесь определенным наблюдателем, не на основе каких бы то ни было данных или даже какого-либо разумно выбранного распределения вероятностей, а просто потому, что вы хотите, чтобы определенный вывод был верным. И я не думаю, что… Наука, космология или философия, если уж на то пошло, обычно работают не так. Но [смеется] я действительно думаю, что есть немного лучший способ делать вещи. И я не думаю, что это раз и навсегда ответ, но он как бы подсказан рассуждениями, которые мы только что прошли, верно? Потому что, в конце концов, я утверждал, что есть своего рода типичность, от которой мы действительно не можем избавиться. В случае с этими вечно колеблющимися вселенными есть больцмановские вы, верно? Это значит, что это ты, Y-O-U, [смеется] на случай, если ты не слышишь мои буквы, когда я говорю.
1:55:44.1 СК: Существуют случайные колебания всех характеристик вашего нынешнего макроскопического «я». И хотя ранее я возражал против мысли, что мы типичны в наборе всех возможных наблюдателей, если вы ограничитесь набором всех наблюдателей, в точности идентичных вам макроскопически, то я действительно думаю, что вы должны быть типичны в этом смысле. , потому что у вас нет критерия, чтобы различать их. Таким образом, в наборе всех людей по имени Шон Кэрролл, у которых есть подкасты под названием Mindscape, и так далее, и так далее, и так далее, людей из мультивселенной, со всеми макроскопическими характеристиками, которые есть у меня, если это все, что я знаю, я должен присвоить равную вероятность будучи ими.
И хотя ранее я возражал против мысли, что мы типичны в наборе всех возможных наблюдателей, если вы ограничитесь набором всех наблюдателей, в точности идентичных вам макроскопически, то я действительно думаю, что вы должны быть типичны в этом смысле. , потому что у вас нет критерия, чтобы различать их. Таким образом, в наборе всех людей по имени Шон Кэрролл, у которых есть подкасты под названием Mindscape, и так далее, и так далее, и так далее, людей из мультивселенной, со всеми макроскопическими характеристиками, которые есть у меня, если это все, что я знаю, я должен присвоить равную вероятность будучи ими.
1:56:25.1 СК: Там есть тонкости с квантовой механикой в разных ветвях волновой функции, но в классическом ансамбле у меня нет причин присваивать себе доверие в этой ситуации самоопределяющейся неопределенности, я у меня нет причин предпочитать одни версии меня другим. Я должен быть типичным в наборе меня во вселенной. И эту идею на самом деле выдвинул Рэдфорд Нил, статистик из Университета Торонто, и он называет эту идею полностью неиндексной обусловленностью. Так что это значит? Итак, это означает, что вы обуславливаете все, что знаете о себе, верно? Итак, вы говорите, я уже знаю, что я землянин, [смеется] все, что вы знаете о себе, о своем возрасте, своем поле и так далее. Все, что вы знаете о себе, ваши воспоминания о прошлом, ваши наблюдения за вселенной, все, что имеет значение, вы можете обусловить этим.
Так что это значит? Итак, это означает, что вы обуславливаете все, что знаете о себе, верно? Итак, вы говорите, я уже знаю, что я землянин, [смеется] все, что вы знаете о себе, о своем возрасте, своем поле и так далее. Все, что вы знаете о себе, ваши воспоминания о прошлом, ваши наблюдения за вселенной, все, что имеет значение, вы можете обусловить этим.
1:57:18.4 СК: За исключением того, где вы находитесь во вселенной, это неиндексальная часть. Это то, что вы не можете обусловить, потому что вы этого не знаете. Итак, вы говорите, что это совсем другой подход, чем обычный космолог, верно? Типичный космолог говорит: «Ну, есть такие… Есть какое-то понятие о наблюдателях. И я не знаю точно, что это значит, но есть умные люди, люди, которые могут заниматься наукой, чего бы это ни стоило. И я типичен в этом наборе, и это позволяет мне делать предсказания, потому что если у меня есть вселенная или мультивселенная с разными значениями космологической постоянной, я могу задать вопросы, например, что видят большинство этих наблюдателей? Проблема с… Очевидная проблема с полностью неиндексной обусловленностью заключалась в том, что я типичен только среди людей… Набор людей, у которых есть точно мои макроскопические данные, как я рассуждаю антропно, верно?
1:58:12. 7 СК: Предлагается, что когда вы делаете байесовские вычисления и говорите о вероятности данных с учетом теории, вы интерпретируете это как вероятность того, что наблюдатель существует точно в вашем макроскопическом пространстве. конфигурация, которая, похоже, исключает возможность предсказания вещей, как космологическая постоянная, потому что мы ее уже наблюдали. Такие люди, как я, знают, что такое космологическая постоянная, поэтому никаких дополнительных предсказаний делать не приходится. Так что это проблема с ним. Итак, я заранее говорю о проблемах. Но я думаю, что проблемы намного перевешивают преимущества, а преимущества не на 100%, поэтому я не думаю, что это окончательный ответ. Но это вместо того, чтобы сказать, что вы типичный наблюдатель, просто сказать, что вы — это вы, и принять это, так что, принимая во внимание все старые свидетельства, к какому выводу это приводит вас?
7 СК: Предлагается, что когда вы делаете байесовские вычисления и говорите о вероятности данных с учетом теории, вы интерпретируете это как вероятность того, что наблюдатель существует точно в вашем макроскопическом пространстве. конфигурация, которая, похоже, исключает возможность предсказания вещей, как космологическая постоянная, потому что мы ее уже наблюдали. Такие люди, как я, знают, что такое космологическая постоянная, поэтому никаких дополнительных предсказаний делать не приходится. Так что это проблема с ним. Итак, я заранее говорю о проблемах. Но я думаю, что проблемы намного перевешивают преимущества, а преимущества не на 100%, поэтому я не думаю, что это окончательный ответ. Но это вместо того, чтобы сказать, что вы типичный наблюдатель, просто сказать, что вы — это вы, и принять это, так что, принимая во внимание все старые свидетельства, к какому выводу это приводит вас?
1:59:05.1 ШЧ: Ну, вернемся к нашим проблемам самонадеянности, да? В первом в мире подходе, когда вы присваивали априорные вероятности различным сценариям, а затем говорили, что вы типичны для них, у нас был аргумент Судного дня. Мы сказали: «Хорошо, если мы типичные люди, то в будущем типичные люди будут в паре поколений от нас, и поэтому человечество умрет». Хорошо? Что ж, полностью неиндексный подход говорит: я — это я, поэтому я знаю, сколько других людей существует, я знаю, сколько лет назад было изобретено сельское хозяйство, была промышленная революция и т. д., и это единственная группа, в которой я Я типичный. Так что я ничего не могу заключить о существовании ни будущих людей, ни инопланетных газовых мешков на Юпитере. Я не претендую на то, чтобы быть типичным в рамках этих наборов, поэтому я не могу привести никаких рассуждений, которые дали бы мне какое-то кабинетное представление о том, законны ли эти сценарии.
Мы сказали: «Хорошо, если мы типичные люди, то в будущем типичные люди будут в паре поколений от нас, и поэтому человечество умрет». Хорошо? Что ж, полностью неиндексный подход говорит: я — это я, поэтому я знаю, сколько других людей существует, я знаю, сколько лет назад было изобретено сельское хозяйство, была промышленная революция и т. д., и это единственная группа, в которой я Я типичный. Так что я ничего не могу заключить о существовании ни будущих людей, ни инопланетных газовых мешков на Юпитере. Я не претендую на то, чтобы быть типичным в рамках этих наборов, поэтому я не могу привести никаких рассуждений, которые дали бы мне какое-то кабинетное представление о том, законны ли эти сценарии.
2:00:05.2 ШК: Так что, с этой точки зрения, нет никакой дополнительной пользы в… Извините, я не могу сказать, что человечество скоро кончится или что на Юпитере нет инопланетян. Как насчет проблемы мозга Больцмана? Если вы типичный наблюдатель, верно? Типичный наблюдатель внутри именно тех наблюдателей, у которых есть ваши данные, ваша макроскопическая информация. Здесь мне приходится немного лукавить, и я пытаюсь быть слишком честным. Я думаю, что это совершенно законная выдумка, но я должен добавить дополнительный принцип размышления об этих вещах. Потому что по этой логике, если вы живете во вселенной, которая вечно колеблется, то действительно большинство… Как я только что сказал, как я только что пытался объяснить, большинство наблюдателей с именно моими макроскопическими данными будут случайными флуктуациями, а не людьми, которые термодинамически термодинамически разумный. И более того, вы можете сказать, что вероятность существования такого же, как я, вообще будет выше, чем вероятность…
Здесь мне приходится немного лукавить, и я пытаюсь быть слишком честным. Я думаю, что это совершенно законная выдумка, но я должен добавить дополнительный принцип размышления об этих вещах. Потому что по этой логике, если вы живете во вселенной, которая вечно колеблется, то действительно большинство… Как я только что сказал, как я только что пытался объяснить, большинство наблюдателей с именно моими макроскопическими данными будут случайными флуктуациями, а не людьми, которые термодинамически термодинамически разумный. И более того, вы можете сказать, что вероятность существования такого же, как я, вообще будет выше, чем вероятность…
2:01:11.0 ШК: Извините, вероятность того, что у кого-то вроде меня в беспорядочно колеблющейся вечной вселенной существует в основном единица, верно? И, учитывая местные законы физики, которые мы собираемся сохранить для этого мысленного эксперимента, в конце концов, кто-то вроде меня появится случайным образом. Принимая во внимание, что вероятность того, что я существую в маленькой вселенной, если я просто верю в обычный Большой взрыв с горячим большим взрывом, который составляет сотни миллиардов галактик, но не бесконечное число, то есть некоторая вероятность получить человека как я, но это небольшая вероятность, верно? Даже если вы думаете, что вероятность получить жизнь где-то во Вселенной довольно велика, вероятность получить именно меня довольно мала. Так что, как и в подходе «сначала наблюдатель», этот подход дает небольшой толчок к более крупным вселенным, потому что я говорю о том, какова вероятность того, что кто-то вроде меня появится на свет?
Так что, как и в подходе «сначала наблюдатель», этот подход дает небольшой толчок к более крупным вселенным, потому что я говорю о том, какова вероятность того, что кто-то вроде меня появится на свет?
2:02:11.0 СК: Значит, важно не общее количество наблюдателей само по себе, а вероятность моего существования. И большая вселенная имеет большую вероятность моего существования, поэтому, для проблемы мозга Больцмана, мне нужно беспокоиться, почему я не мозг Больцмана? А фигня в следующем. Я верю, что не могу поверить, что я больцмановский мозг. Это проблема. Проблема заключается в том, о чем я говорил в своей статье «Почему больцмановские мозги плохи: когнитивная нестабильность сценария больцмановского мозга». Итак, как я уже сказал, если вы верите в сценарий со случайными флуктуациями, вызывающими появление наблюдателей, все виды наблюдателей будут случайным образом флуктуировать. И в том числе, по сути, преобладают наблюдатели, которые совершенно во всем ошибаются. [хихикает] Итак, наблюдатели, у которых есть мысли и убеждения как об эмпирической ситуации во вселенной, так и о законах физики и законах логики, рассуждений и науки, но все эти мысли обо всех этих принципах и части данных случайным образом колебались в их мозгу.
2:03:21.5 СК: Так вот проблема, если вы используете логику и разум, чтобы заключить, что вы, вероятно, флуктуация Больцмана, то вы должны также думать, что вы не имеете права верить ни одному из шагов, которые вы использовали на протяжении способ сделать это рассуждение, потому что все эти шаги были основаны на принципах логики и рассуждений, которые просто случайным образом колебались в вашем мозгу. Итак, это разные вещи. Поэтому я хотел бы сказать, что для того, чтобы быть последовательным в своих размышлениях об этом, я должен модифицировать априорную вероятность, которую я вложил в эти сценарии, с помощью какого-то когнитивного фактора, фактора, который говорит: я не собираюсь давать никакой априорной вероятности. вероятность или нет, может быть, какое-то невероятно маленькое число для сценариев, в которых такие люди, как я, все сделают неправильно, [смеется], потому что я хочу попытаться сделать все правильно. Так что я не могу аргументированно сказать, что я не больцмановский мозг, но я могу рассуждать сам… Мой способ сказать, что я не должен верить, что я больцмановский мозг. А это значит, что я не должен рассматривать космологические сценарии, в которых я должен быть больцмановским мозгом. Это имело смысл?
А это значит, что я не должен рассматривать космологические сценарии, в которых я должен быть больцмановским мозгом. Это имело смысл?
2:04:40.3 СК: В любом случае, дело в том, что причина, по которой я утверждаю, что мы не должны доверять космологии, основанной на больцмановском мозге, не в том, что мы смотрим вокруг и видим, что мы не мозг Больцмана. Это как раз то, что сказал бы мозг Больцмана. [посмеивается] Говорить такое внутренне непоследовательно. Скорее, мы должны исключить их априори, исходя из справедливых принципов рассуждения. И если вы думаете, что это самонадеянно, то это самонадеянно, только если вы думаете, что вы на самом деле можете быть больцмановским мозгом, а я не думаю, что кто-то действительно так думает. Конечно, я не ратую за то, чтобы вы так думали, я просто ратую за то, чтобы мы, работающие космологи, сосредоточились на разработке космологических сценариев, в которых большинство наблюдателей вроде меня не являются больцмановскими мозгами и в то же время такими же, как вы.
2:05:30.0 СК: Следовательно, мне просто нужно принять в качестве принципа рассуждения, что мои рассуждения относительно надежны, другими словами. Хорошо, тогда последний вопрос, который мы должны решить здесь, если это принципы, которые мы принимаем, такого рода полностью неиндексное обусловливание, рассуждение, что мы типичны только в группе людей, точно таких же, как мы сами, тогда как мы реализуем антропный принцип? Как мы делаем предсказания о таких вещах, как космологическая постоянная и так далее? Итак, я утверждаю, что на самом деле, если вы хорошенько об этом подумаете, обычные антропные рассуждения будут действовать до тех пор, пока вы не сделаете ошибку, которую я считаю просто логической ошибкой использования того факта, что вы уже знаете космологическую постоянную. .
2:06:17.8 СК: Итак, если вы думаете, что мы уже знаем значение космологической постоянной, вы на самом деле не предсказываете ее значение, вы должны как бы временно притвориться, что мы не знаем, а затем вы воображаете, что задаете себе вопрос: «Что бы я предсказал в различных космологических сценариях?» Хорошо? И дело в том, что, к лучшему или к худшему, эта идея о том, что у вас есть вероятность вашего существования, зависит от того, как вы интерпретируете вероятность данных с учетом теории, грубо говоря, вероятность вашего существования будет пропорциональна числу наблюдателей, да? Потому что, если мы исключим эти вечные, бесконечно изменчивые вселенные, то чем больше наблюдателей у нас будет во вселенной, которая делает всевозможные вещи, тем больше вероятность того, что мы наткнемся именно на такого наблюдателя, как вы.
2:07:10.6 СК: Грубо говоря, это как бы насыщает, да? Если вы получите достаточное количество наблюдателей, так что, вероятно, таких наблюдателей, как вы, будет больше одного, вы перестанете давать дополнительный бонус большим вселенным. Но если вы сравниваете вселенную, в которой вероятность вас равна 10 минус 10, с вселенной, где вероятность вас равна 10 минус единица, вы бы добавили бонус к вероятности 10 минус единица такой наблюдатель, как вы, и я думаю, что на самом деле это нормально, верно? Я не думаю, что было бы ошибкой отдавать предпочтение вселенным, которые предсказывают, как наблюдатели… Вероятно, такие наблюдатели, как я, будут существовать. И если вы займёте такую позицию, то если вы затем вообразите, что применяете эту проблему к набору различных подвселенных внутри космологической мультивселенной, и эти подвселенные имеют разные значения космологической постоянной, то вы в основном поступаете именно так. что сделал Стивен Вайнберг в 1988.
2:08:02.5 СК: На самом деле, он буквально использовал количество наблюдателей, которые будут измерять космологическую постоянную, как показатель априорной вероятности существования измерения этого значения. А затем он использовал количество галактик в качестве показателя количества наблюдателей. Таким образом, я думаю, другими словами, что использование этой стратегии утверждения, что единственное, что мы типичны внутри, единственный набор наблюдателей, среди которых мы типичны, — это набор наблюдателей, таких же, как я, по-прежнему дает те же антропные предсказания, что и типичный уличный космолог получил бы. Помните, я начал всю дискуссию с того, что физики были очень рады получить правильный ответ, используя неверные рассуждения, и я думаю, что во многих случаях в антропном сценарии антропный принцип, применяемый к космологии, именно это и происходит. Я думаю, что они получают правильный ответ, но по неправильным причинам.
А затем он использовал количество галактик в качестве показателя количества наблюдателей. Таким образом, я думаю, другими словами, что использование этой стратегии утверждения, что единственное, что мы типичны внутри, единственный набор наблюдателей, среди которых мы типичны, — это набор наблюдателей, таких же, как я, по-прежнему дает те же антропные предсказания, что и типичный уличный космолог получил бы. Помните, я начал всю дискуссию с того, что физики были очень рады получить правильный ответ, используя неверные рассуждения, и я думаю, что во многих случаях в антропном сценарии антропный принцип, применяемый к космологии, именно это и происходит. Я думаю, что они получают правильный ответ, но по неправильным причинам.
2:08:58.2 СК: Ладно, последнее, последний вопрос — это другой вид самонадеянности. Итак, я упомянул самонадеянность аргумента Судного дня и так далее, и сказал, что предположение, что я типичен только для таких людей, как я, устраняет эту самонадеянность и избавляет нас от этой проблемы. Помните, что другие виды самонадеянности каким-то образом давали слишком много бонусов большим вселенным, на что Бостром жаловался в подходе, основанном на наблюдателе. И я думаю, что этот подход на самом деле ближе к подходу, ориентированному на наблюдателя, потому что… Он дает дополнительный небольшой толчок вселенным с большим количеством людей в них, потому что вероятность заполучить меня выше, а не потому, что я вроде как априори предпочитаю вселенные с большим количеством людей, но я предпочитаю вселенные, которые предсказывают меня, и я думаю, что это нормально. Я вообще не думаю, что это предвзято. Это хорошо сочетается с третьей позицией в задаче о Спящей красавице, верно?
Помните, что другие виды самонадеянности каким-то образом давали слишком много бонусов большим вселенным, на что Бостром жаловался в подходе, основанном на наблюдателе. И я думаю, что этот подход на самом деле ближе к подходу, ориентированному на наблюдателя, потому что… Он дает дополнительный небольшой толчок вселенным с большим количеством людей в них, потому что вероятность заполучить меня выше, а не потому, что я вроде как априори предпочитаю вселенные с большим количеством людей, но я предпочитаю вселенные, которые предсказывают меня, и я думаю, что это нормально. Я вообще не думаю, что это предвзято. Это хорошо сочетается с третьей позицией в задаче о Спящей красавице, верно?
2:09:56.3 СК: Так что, может быть, в конце концов, все согласовано. Так что наивно, вероятность того, что вы находитесь в большой вселенной, намного, намного больше, чем вероятность того, что вы находитесь в маленькой вселенной, поэтому вы должны позволить себе заключить, что если у вас есть конкурирующие космологические сценарии, которые похожи, физически похожи, то они имеют схожие априорные данные, которые вы хотите им дать, но различаются по количеству наблюдателей, вам следует отдавать предпочтение сценарию с большим количеством наблюдателей. И я думаю, что в статье Рэдфорда Нила он немного лукавит по этому поводу, он не совсем цепляется за пулю и не говорит, что это правда. Я думаю, может быть, это мое предварительное место, на которое я приземляюсь, что нормально отдавать предпочтение вселенным с большим количеством наблюдателей и, следовательно, иметь большую вероятность предсказать меня.
И я думаю, что в статье Рэдфорда Нила он немного лукавит по этому поводу, он не совсем цепляется за пулю и не говорит, что это правда. Я думаю, может быть, это мое предварительное место, на которое я приземляюсь, что нормально отдавать предпочтение вселенным с большим количеством наблюдателей и, следовательно, иметь большую вероятность предсказать меня.
2:10:45.7 СК: Если вы рассматриваете группу вселенных с фактически бесконечным числом наблюдателей, это не имеет значения. Вот в чем для меня заключается разница между полностью неиндексным обусловливанием и более традиционным предположением о самоуказании, также известным как подход, ориентированный на наблюдателя. Потому что при таком подходе вы действительно дали бы импульс в зависимости от того, сколько наблюдателей было на точке. Здесь, в этом подходе, вы просто даете толчок в зависимости от вероятности вашего появления на свет, верно? Так что дело в том, что если вероятность того, что это произойдет, мала, то она будет примерно пропорциональна количеству наблюдателей. По сути, у вас есть шанс, что каждый наблюдатель будет таким же, как вы, поэтому чем больше у вас наблюдателей, тем больше вероятность того, что вы получите именно вас.
По сути, у вас есть шанс, что каждый наблюдатель будет таким же, как вы, поэтому чем больше у вас наблюдателей, тем больше вероятность того, что вы получите именно вас.
2:11:33.4 СК: Но как только число наблюдателей станет настолько большим, что такие люди, как вы, почти неизбежны, я не буду придавать дополнительного значения созданию миллиарда ваших версий вместо создания одной вашей версии. В любом случае, вероятность теории, предсказывающей ваше существование, порядка один, хорошо? Таким образом, ускорение через большие вселенные насыщает при таком способе ведения дел. Это правильный способ делать вещи? Я не знаю. Мне нужно подумать об этом, я думал об этом. Это мой предварительный вывод, мой предварительный способ мышления, я им вполне доволен. Но послушайте, это сложно, вот почему я начал говорить, что не могу провести эксперимент, который легко ответит на эти вопросы. Нам нужно думать как можно тщательнее и быть как можно более честными и строгими в своих рассуждениях, которые приводят нас к этому.
2:12:27.4 СК: И вы знаете, я начал с того, что сказал о разных сильных и слабых сторонах философов и физиков, другой способ охарактеризовать разницу — это просто терпение. [посмеивается] Физики гораздо менее терпеливы, чем философы. Физики хотят получить ответ, они хотят получить его быстро, а философы гораздо более терпеливы, когда думают: «Что означает каждый термин в этом предложении и так далее?» И посмотрите, это не беспримесная хорошая вещь, верно? Вы можете увязнуть и спорить о деталях терминологии и тому подобном, и поэтому не добраться до ответа. Итак, я еще раз повторяю, что подход, которому отдают предпочтение физики, и подход, которому отдают предпочтение философы, имеют свои места. Это место, где вопросы, которые мы задаем, явно являются вопросами физики, но методологии выиграют от тщательного философского анализа.
2:13:19.4 СК: Мне нравится это делать, это весело. Теперь у меня есть работа, которая позволяет мне это делать. Когда я записываю это, я еще не там, но я упаковываю вещи в коробки, [смеется], так что скоро все будет очень официально.
