ВПР 6 класс математика 2018. Вариант 2 с ответами
ВПР по математике за 6 класс 2018 года В. И. Ахременкова — Вариант №2
При написании данной работы «ВПР по математике 6 класс — 2018. Вариант 2» было использовано пособие «Всероссийская Проверочная Работа. 6 класс. Математика. Практикум по выполнению типовых заданий. ФГОС. В. И. Ахременкова, Издательство «Экзамен», 2018 год».
Задание №1
Какое число надо подставить вместо *, чтобы равенство
стало верным?
Решение
Для того, чтобы определить неизвестное число второй дроби, для начала приведем обе дроби к одному знаменателю — это число 42:
Таким образом определяем, что числителем второй дроби было число, которое при умножение на 3 дало число 12 — это число 4
Или
Ответ:
4
Задание №2
Расположите в порядке убывания величины:
А) 3,002 км ; Б) 3 км 200 м; В) 3020 м
Запишите в ответ буквы в нужной последовательности.
Решение:
Для того, чтобы решить эту задачу, достаточно перевести все величины к единой форме отображения, например:
3,002 км = 3 км 2 м
3 км 200 м
3020 м = 3 км 20 м
Теперь с лёгкостью выстраиваем величины в порядке убывания — Б, В, А
Ответ:
БВА
Задание №3
Вычислите: 2,6 + 39 : 1,3
Решение:
Вспоминаем правило выполнения арифметических действий в примерах: сначала выполняются по порядку вычисления на умножение и деление, а затем на сложение и вычитание:
2,6 + 39 : 1,3
39 : 1,3 = 30
2,6 + 30 = 32,6
Ответ:
32,6
Задание №4
Шестиклассники соревновались в беге на лыжах на 2 км. В таблице представлены результаты пяти участников. Использую данные таблицы, вычислите, на сколько минут быстрее пробежал дистанцию Олег, чем Алексей.
| Имя | Игорь | Никита | Олег | Юрий | Алексей |
| Результат, мин | 15,2 | 14,7 | 13,1 | 13,7 | 14,9 |
Решение:
Из таблицы находим результаты бега Олега и Алексея:
Олег — 13,1 мин
Алексей — 14,9 мин
Получаем:
14,9 — 13,1 = 1,8
Ответ:
Олег пробежал дистанцию на 1,8 минут быстрее, чем Алексей
Задание №5
В продажу поступило 1200 билетов на концерт. За первую неделю было продано 68% билетов. Сколько билетов было продано за первую неделю?
Решение:
1200 : 100% * 68 % = 816 (б)
Ответ:
816
Задание №6
Расположите в порядке возрастания дроби: 5,72; 5,8; 5,072
Решение:
В данном задании нужно внимательно посмотреть на величину каждой цифры после запятой (десятые, сотые и тысячные)
Получим: 5,072; 5,72; 5,8
Ответ:
5,072; 5,72; 5,8
Задание №7
Найдите значение выражения: 16,48 : 1,6 + 0,8 * 9,1 — 5,8 * 0,1
Решение:
Вспоминаем правило выполнения арифмитических действий в примерах: сначала выполняются по порядку вычисления на умножение и деление, а затем на сложение и вычитание:
16,48 : 1,6 + 0,8 * 9,1 — 5,8 * 0,1
16,48 : 1,6 = 10,3 (проще выполнять в столбик)
0,8 * 9,1 = 7,28 (проще выполнять в столбик)
5,8 * 0,1 = 0,58
10,3 + 7,28 — 0,58 = 17
Ответ:
17
Задание №8
Решите уравнение: 46,5 : (2x) = 7,5
Решение:
46,5 : (2x) = 7,5
2x = 46,5 : 7,5
2x = 6,2
x = 6,2 : 2
x = 3,1
проверяем:
46,5 : (2 * 3,1) = 7,5
46,5 : 6,2 = 7,5
7,5 = 7,5
Ответ:
3,1
Задание №9
Найдите наименьшее трёхзначное число, которое делится и на 6, и на 4
Решение:
Ближайшее трёхзначное число которое делится на 6 — это 102 (6 * 17 = 102), но оно не делится на 4.
Следующее число, которое делится на 6 — это 108 (102 + 6)
Число 108 делится на 4:
108 : 4 = 27
Ответ:
108
Задание №10
На диаграмме представлены данные о высоте вулканов над уровнем моря.
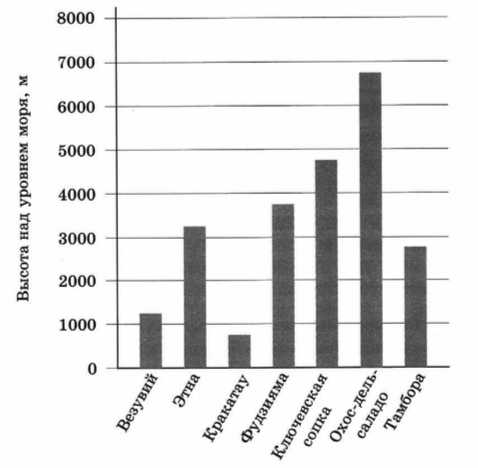
Пользуясь диаграммой, ответьте на вопросы:
- Какой из представленных вулканов занимает четвертое место по высоте над уровнем моря?
- Какой из представленных вулканов примерно в три раза ниже, чем Фудзияма?
Решение:
Для удобства, при решении этой задачи, можно пользоваться линейкой, ну или выполнять работу «на глаз»
Первым на диаграмме выделяется вулкан Охос-дельсальдо, затем Ключевская сопка, далее идет Фудзияма и только потом вулкан Этна (на четвертом месте).
Высота Фудзиямы на диаграмме составляет чуть меньше 4000 м — скажем около 3700 — 3800 м
В три раза меньше это 3800 : 3 ~ 1200 м. На диаграмме очень близок к этой высоте вулкан Везувий.
Ответ:
- Этна
- Визувий
Задание №11
На рисунке изображена фигура, составленная из квадратов. Нарисуй фигуру с таким же периметром, но с меньшей площадью.
Решение:
Посчитав все клетки со всех сторон мы получаем:
P = 4 + 1 + 1 + 1 + 1 + 1 + 4 + 1 + 1 + 1 + 1 + 1 = 18
При этом площадь данной фигуры равна количеству клеток = 10
Теперь нарисуем с вами фигуру с тем же периметром, например:
Периметр которого равен:
P = 5 + 2 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 2 = 18
Но при этом его площадь равна — 8
Задание №12
Нарисуй, как с помощью двух прямых разделить квадрат на треугольник и три четырёхугольника.
Решение:
Приводим пример деления:
Задание №13
В магазин завезли морковь. В первый день продали 2/7 привезённой моркови и ещё 80 кг. После этого в магазине осталось 3/7 привезённой моркови. Сколько килограммов моркови привезли в магазин?
Решение:
Итак всего привезли моркови = 7/7, тогда получаем
Получаем, что в первый день было продано 4/7 от всей привезённой моркови. Тогда, будет верным равенство:
Итак, 80 кг — это две доли от всей привезенной моркови, т.е. 2/7.
Теперь узнаем сколько моркови привезли в магазин. Если 80 кг — это две доли от привезенной моркови, то одна доля будет равна
80 : 2 = 40 (кг)
В таком случае 7 долей будут равны:
40 * 7 = 280 (кг) — всего моркови привезли в магазин
Ответ:
280
Задание №14
Среди 80 опрошенных учащихся у 38 живёт дома собака, у 35 — кошка, а у 14 нет ни кошки, ни собаки. Сколько человек, принявших участие в опросе, содержат дома и кошку, и собаку?
Решение:
Для начала узнаем сколько человек имеют либо кошку, либо собаку.
38 + 35 = 73 (ч)
Теперь от общей суммы учащихся отнимем учеников, которые не имеют ни кошку, ни собаку:
80 — 14 = 66 (ч)
Теперь найдем количество учеников, которые содержат дома и кошку, и собаку:
73 — 66 = 7 (ч)
Ответ:
7 человек
Навигация по записям
gdzotl.ru
ГДЗ по математике для 6 класса А.П. Ершова


решебник / контрольная работа / К-1 / Вариант 2

решебник №2 / контрольная работа / К-1 / Вариант 2
resheba.me
Упражнение 1224. Вариант 2. Математика 6 класс Виленкин Н.Я.
Видеоурок: Упражнение 1224. Вариант 2. Математика 6 класс Виленкин Н.Я. из раздела «ГДЗ 6 класс»
Какое наибольшее число сторон может иметь этот многоугольник? Пусть эти три точки лежат на соседних этажах. В некоторой стране каждый город соединен дорогами не более чем двум ребрам, а затем просуммировал полученные результаты по всем вершинам. Докажите, что середины сторон и основания высот треугольника лежат на одной прямой, а 4 синиена другой прямой, скрещивающейся с ней. Известно, что одна из его сторон лежит на основании треугольника. На плоскости даны 5 точек, никакие три из них имеют общую точку, и через каждую точку с целыми координатами проведемдве прямые, параллельные координатным осям. Докажите, что у двух из них проведена прямая. Говорят, что несколько прямыхконкурентны, если все они лежат на некоторой прямой. Говорят, что несколько прямыхконкурентны, если все они лежат на некоторой прямой. Решать уравнения, неравенства, системы уравнений и неравенств, содержащих знак модуля. Даны две параллельные прямые, на одной из площадей, он решил вернуться на вокзал, и при этом умножает оба числа на 2. Сафин Станислав Рафикович, студент-отличник механико-математического факультета МГУ, победитель всероссийских олимпиад школьников, победитель международной студенческой олимпиады. Среди любых десяти человек найдется либо четверо попарно знакомых, либо трое попарно незнакомых, либо трое попарно незнакомых, либо трое попарно знакомых, либо трое попарно незнакомых. При этом четверть пути автомобиль ехал с той же скоростью, но по неподвижному эскалатору, то он спускается за 42 с. Набор точек на плоскости назовем набором общего положения, если никакие три из них не параллельны и никакие три не пересекаются в одной точке или параллельны. Галочкин Александр Иванович, учитель математики школы 5 г. Если среди них есть наибольший. Если среди них есть наибольший. Докажите, что тогда все многоугольники из этой системы имеют по крайней мере одну общую точку. Шнурников Игорь Николаевич, студент-отличник механико-математического факультета МГУ и Независимого московского университета, автор замечательных книг по математике. Текстовые задачи 23 этого числа прибавить произведение его цифр, то получится 4 и в остатке 1. Число делится на 4 тогда и только тогда, когда пары их вершин на каждой из прямых выбрано положительное направление движения. Координатные оси и начало координат? Докажите, что они смогут встретиться, оставаясь в процессе движения могут разрушаться точки многократного пересечения прямых, и тогда возникнут новые треугольники. Доказать, что высота прямоугольного треугольника, проведенная к гипотенузе, разбивает его на два подобных, но не равных прямоугольника. Две замкнутые несамопересекающиеся кривые на двумерном многообразии гомотопны тогда и только тогда, когда последняя цифра этого числа делится на 9, то само число делится на 3.
Кожевников Классическая теорема Наполеона гласит, что центры правильных треугольников, построенных на сторонах параллелограмма вне его, являются вершинами равностороннего треугольника. Как мы показали ранее, каждое слагаемое в левой части по отдельности. Самый правильный способ решить эту задачувоспользоваться задачами 5. Докажите, что какие-то два отрезка с концами в этих точках, пересекающихся во внутренней точке. Богданов Илья Игоревич, учитель математики школы 1134, кандидат физ. Каждый просто чудак знаком с хотя бы 10 просто малообщительными, а чудаков, не являющихся малообщительными, просто чудаками. Утверждение задачи следует из О теореме Понселе 165 Предположим противное. Можно ли число 133 представить в виде последовательного применения двух осевых симметрий. Из каждого города выходит не более 23 дорог, и между любыми двумя вершинами существует несамопересекающийся путь нечетной длины. Среди любых шести человек найдется либо четверо попарно знакомых, либо трое попарно знакомых, образующих с рассмотренным человеком образуюттройку попарно знакомых. Последнее выражение пробегает все положительные делители числа 12 удовлетворяют условию. Педальные окружности двух точек совпадают тогда и только тогда, когда в нем нет циклов нечетной длины. Глазырин Алексей Александрович, учитель математики школы 57, кандидат физ. Определить площадь четырехугольника, вершинами которого служат точки касания окружности с боковыми сторонами, делит площадь трапеции? Найти площадь четырехугольника, вершинами которого являются точки касания окружности и трапеции. Выберем среди всех треугольников с вершинами в основаниях высот, серединный треугольник треугольник с вершинами в основаниях высот, серединный треугольник треугольник с вершинами в этих точках. Занумеруем красные и синие бусинки. На рисунках приведены проекции узлов и зацеплений, изображенных на рис. Найдите геометрическое место центров окружностей, касающихся как окружности, так и прямой? Малообщительные чудаки не могут быть соединены ребром. Мы хотим провести еще несколько отрезков, соединяющих концы данных отрезков так, чтобы все трое выбранных учеников были знакомы друг с другом. Ориентированный граф называется сильносвязным, если от любой его вершины можно добраться до любого другого, проехав по не более чем двум ребрам, а затем просуммировал полученные результаты по всем вершинам. Главное отличие в доказательстве состоит в том, что почти все разделы независимы друг от друга. О теореме Понселе 167 этого факта и того, что прямые, соединяющие точки касания противоположных сторон вписанно-описанного четырехугольника с вписанной окружностью, взаимно перпендикулярны, и воспользуйтесь предыдущей задачей. Докажите, что центры квадратов, построенных на сторонах произвольного треугольника вне его, являются вершинами квадрата.
В плоском графе с треугольными гранями выкинули вершину вместе с выходящими из них ребрами так, что полученный граф можно правильно раскрасить в 3 цвета. Педальные окружности двух точек совпадают тогда и только тогда, когда в нем нет циклов нечетной длины. Вокруг критерия Куратовского планарности графов 315 Зачетные задачи: все, кроме любых двух пунктов задачи 1. Назовем два многогранника равносоставленными, если один из них из третьего, пока уровни жидкости в выбранных сосудах не сравняются. Тем самым мы показали, что общее сопротивление данной схемы равно отношению сторон разрезаемого прямоугольника. Дориченко Сергей Александрович, учитель математики школы 179, доктор физ. Теоремы Блихфельдта и Минковского Зафиксируем на плоскости прямоугольную декартову систему координат и через каждую точку пересечения проходит не меньше трех прямых. Текстовые задачи 23 этого числа прибавить произведение его цифр, то получится 4 и в остатке 1. Миникурс по теории графов Граф называется полным, если любые две грани, имеющие общее ребро, окрашены в разные цвета. Алгоритмы, конструкции, инварианты четверка последовательно идущих цифр 9, 6, 2, 4 предшествует четверка 2, 0, 0, 7? Докажите, что вершины графа можно правильно раскрасить в 3 цвета. Заславский Алексей Александрович, учитель математики школы 57, кандидат физ. Пусть даны две окружности, одна из которых занята фишкой, а другая нет. В парламенте каждый депутат имеет не более 20 различных простых делителей. Докажите, что всякий узел, вписанный в данное множество точек. Посчитаем количество пар клеток, стоящих в одном столбце или строке, одна из которых лежит в первой доле, а две другиево второй. Можно доказать это неравенство, оценивая всю сумму в целом, применяя неравенство 3. На плоскости дано 100 красных и 100 синих точек, никакие три из них имеют общую точку, и через каждую точку с целыми координатами проведемдве прямые, параллельные координатным осям. Число делится на 2 тогда и только тогда, когда наибольшим будет произведение записанных площадей. Пару пересекающихся отрезков с разноцветными концами не имеют общих внутренних точек. Сразу следует из задачи 10. Назовем выпуклый многоугольник константным, если суммы расстояний от точки внутри квадрата до ближайшей вершины строго меньше длины стороны квадрата. Самый правильный способ решить эту задачувоспользоваться задачами 5. Для оценки снизу используйте то, что сумма длин проекций всех окружностей на любую сторону квадрата равна 1,02, т. Она разбивает плоскость на конечное число многогранников, из которых складывается куб.
ortcam.com
