Презентация к уроку «Задачи на проценты» (7 класс)

ДРОБИ И ПРОЦЕНТЫ
ЗАДАЧИ НА ПРОЦЕНТЫ
учебник
Алгебра 7 класс
автор Г.В. Дорофеев, С.Б. Суворова, Е.А. Буминович и др.
Ершова Любовь Германовна
МАОУ СОШ №1
г. Кунгур Пермский край
Домашнее задание У: стр. 21-23, фрагмент 1,2 – читать; № 69(б), 71, 72(б), 74(а).
Метапредмет – Знание

Цель урока
Развивать у учащихся вычислительные способности; ввести понятие процентов; вспомнить и повторить правила решения и оформления задач на проценты; рассмотреть практико-ориентированные задачи с процентами для повышения интереса к математике.
целеполагание

Цель урока
целеполагание

Домашнее задание
УЧЕБНИК
№ 41
?
а) 16 = 4 2 =2 4 ; б) 81=9 2 =3 4 ;
в) 256=16 2 =4 4 =2 8 ;
в) 80; 10000; 10000;
?
№ 44
УЧЕБНИК
г) 343;
УЧЕБНИК
№ 50
?
784; — 784; — 784; 784; -784
УЧЕБНИК
№ 62
?
б) -0,15; (- 0,15) 3 ; (- 0,15) 2 ; 0,15
№ 67
?
6,4 мм
УЧЕБНИК
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

Математическая разминка
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

Математическая разминка
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

Задачи на проценты
Работа с учебником
Стр. 21
Организация и самоорганизация учащихся. Организация обратной связи
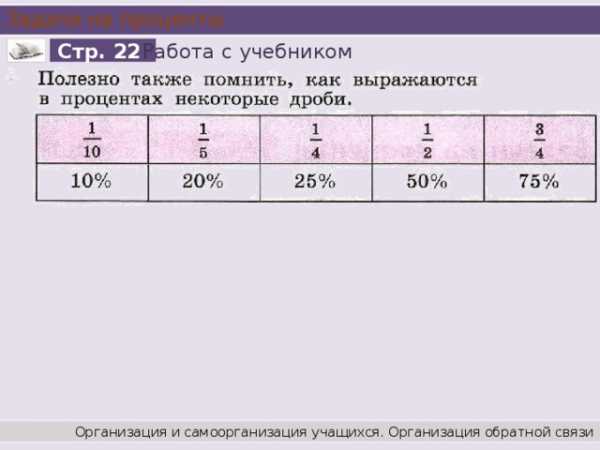
Задачи на проценты
Работа с учебником
Стр. 22
Организация и самоорганизация учащихся. Организация обратной связи

Задачи на проценты
Работа с учебником
Стр. 23
Организация и самоорганизация учащихся. Организация обратной связи

Задачи на проценты
Работа с учебником
Стр. 23

Работаем с текстом
Выразите в процентах обыкновенные дроби
РАБОЧАЯ ТЕТРАДЬ
№ 21
25 %
?
20 %
?
12,5 %
?
10 %
?
Практикум

Работаем с текстом
РАБОЧАЯ ТЕТРАДЬ
№ 22
Выразите в процентах десятичные дроби
15 %
?
40 %
?
30 %
?
Практикум
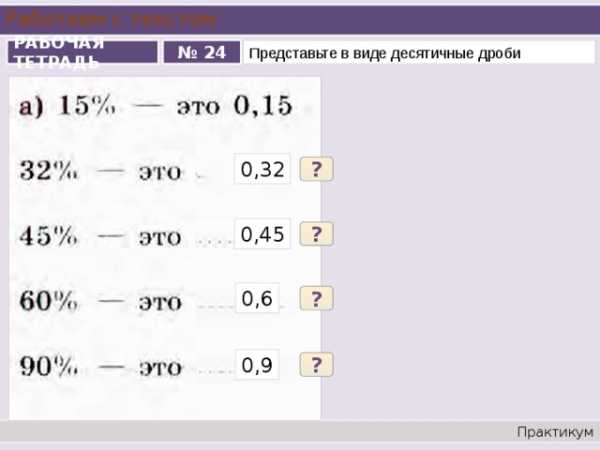
Работаем с текстом
№ 24
РАБОЧАЯ ТЕТРАДЬ
Представьте в виде десятичные дроби
0,32
?
0,45
?
0,6
?
0,9
?
Практикум

Осваиваем алгоритмы
№ 69
УЧЕБНИК
4%; 27%; 30%; 25,5%; 0,06%.
?
№ 79
УЧЕБНИК
7%; 1512; 728; 2968; 392.
?
Практикум
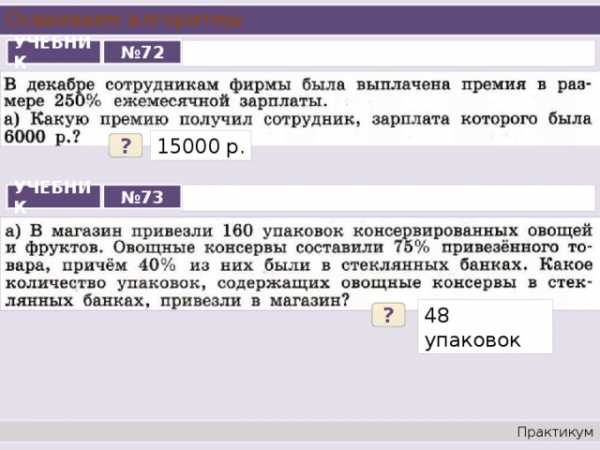
Осваиваем алгоритмы
УЧЕБНИК
№ 72
15000 р.
?
№ 73
УЧЕБНИК
48 упаковок
?
Практикум
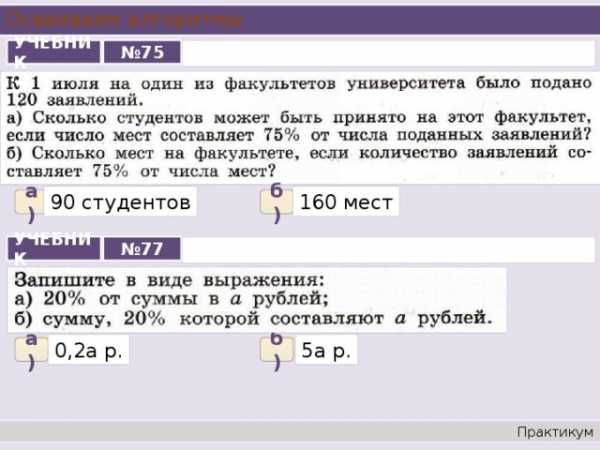
Осваиваем алгоритмы
№ 75
УЧЕБНИК
90 студентов
160 мест
а)
б)
УЧЕБНИК
№ 77
0,2а р.
5а р.
а)
б)
Практикум

Задачи на проценты
ДИДАКТ. М
С.17
Проверка полученных результатов. Коррекция

Проверь себя!
ДИДАКТ. М
С.19 — 20
Проверка полученных результатов. Коррекция

Проверь себя!
ДИДАКТ. М
С.19 — 20
Проверка полученных результатов. Коррекция

Ответы
А Б А В Б В А Б А В
Проверка полученных результатов. Коррекция

Весенняя распродажа
Подведение итогов, рефлексия, домашнее задание.
intolimp.org
ГДЗ по Алгебре за 7 класс Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович
Решебники, ГДЗ
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- 2 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- 3 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Музыка
- Окружающий мир
- Испанский язык
- 4 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
megaresheba.ru
Решение более сложных задач на проценты. на Сёзнайке.ру
В курсе 7-11 класса практически отсутствуют задачи на проценты. Так как эти задачи можно решать с помощью уравнений и систем уравнений, то их необходимо включать в курс алгебры при изучении данных тем.
Задача 1. (решаемая с помощью уравнения, сводимого к линейному)
В растворе содержится 40% соли. Если добавить 120 г соли, то в растворе будет содержаться 70% соли. Сколько граммов соли было в растворе первоначально?
Решение:
Пусть x г весь первоначальный раствор, тогда
0.4x г – соли в первоначальном растворе,
(x + 120) г – стало раствора,
(0,4x + 120) г – стало соли в растворе, которая теперь составляет 70% раствора, т.е. 0,7 от всего раствора, составляем уравнение:
0,4x +120 = 0,7(x + 120), решив которое получим
x = 120
120 · 0,4 = 48 (г)
Ответ: 48 г.
Задача 2. (решаемая с помощью уравнения, сводимого к квадратному)
В сплаве золота с серебром содержится 80 г золота. К сплаву добавили 100 г чистого золота. Содержание золота в сплаве повысилось на 20%. Сколько серебра было в сплаве?
Решение:
|
Было: |
Стало: |
||
|
серебро |
золото |
серебро |
золото |
|
x г |
80 г |
x г |
180 г |
Пусть x г – серебра в сплаве, тогда
(x + 80) г – масса первоначального сплава,
(x + 180) г – масса нового сплава,
80/(x+80) г – часть золота в первом сплаве,
180/(x+180) г – часть золота во втором сплаве,
Т.к. содержание золота повысилось на 20% (т.е. на 1/5), составляем уравнение:
180/(x+180)-80/(x+80)=1/5
решая которое получим
x- 240x + 14400 = 0
(x – 120) = 0
x = 120
Ответ: 120 г.
Задача 3. (решаемая с помощью системы уравнений)
Вычислите массу и пробу сплава серебра с медью, зная, что сплавив его с 3 кг чистого серебра, получим сплав 900-й пробы (т.е. в сплаве 90% серебра), а сплавив с 2 кг сплава 900-й пробы, получим сплав 840-й пробы.
Решение:
Пусть x кг – масса сплава, y% — серебра в сплаве, тогда
(y : 100) · x = 0,01xy (кг) – серебра в сплаве,
(x + 3) кг – нового первого сплава,
(0,01xy + 3) кг – серебра в новом первом сплаве.
Т.к. серебра в новом первом сплаве 90%, составляем уравнение:
0,01xy + 3 = 0,9(x + 3).
(x + 2) кг – масса второго сплава,
2 кг сплава 900-й пробы будут содержать 0,9 · 2 = 1,8 (кг) серебра, тогда
(0,01xy + 1,8) кг – масса серебра во втором сплаве.
Т.к. серебра во втором сплаве 84%, составляем уравнение:
0,01xy + 1,8 = 0,84(x + 2).
Получаем систему уравнений:
0,01xy + 3 = 0,9(x + 3) x = 3
0,01xy + 1,8 = 0,84(x + 2) y = 80
Ответ: 3 кг 800-ой пробы
Задача 4. (решаемая с помощью системы уравнений)
Фабрика должна была сшить 360 костюмов. В первые 8 дней она перевыполняла план на 20%, а в остальные на 25%. Сколько дней работала фабрика, если всего сшито 442 костюма?
Решение:
Пусть x костюмов должна была сшить фабрика за один день,
y дней должна была работать.
Т.к. всего должно было быть сшито 360 костюмов, составляем уравнение:
xy = 360.
1,2x · 8 костюмов сшили за первые 8 дней,
1,25x(y — 8) костюмов сшили за остальные дни.
Т.к. всего сшито 442 костюма, составляем уравнение:
1,2x · 8 + 1,25x(y — 8) = 442.
Получаем систему уравнений:
xy = 360 x = 20
1,2x · 8 + 1,25x(y — 8) = 442 y = 18
Ответ: 18 дней
Задача 5. (решаемая с помощью алгебраических выражений)
Процесс очищения воды в водохранилище от содержания в ней тяжелых металлов состоит из четырех этапов. На каждом этапе содержание уменьшается на определенное количество процентов к их количеству на предыдущем этапе:
на 1-ом – на 25%
на 2-ом – на 20%
на 3-ем – на 15%
на 4-ом – на 10%
На сколько процентов в результате уменьшается их количество?
Решение:
Пусть x – количество воды, тогда оставшееся количество тяжелых металлов после очистки:
На 1-ом этапе – 0,75x
На 2-ом этапе – 0,8 · (0,75x) = 0,6x
На 3-ем этапе – 0,85 · (0,6x) = 0,51x
На 4-ом этапе – 0,9 · (0,51x) = 0,459x.
Таким образом всего ушло x — 0,459x = 0,541x, т.е. 54,1% тяжелых металлов.
Ответ: 54,1%
Задача 6. (решаемая комбинированным способом)
В январе завод выполнил 105% месячного плана выпуска готовой продукции, а в феврале дал продукции на 4% больше, чем в январе. На сколько процентов завод перевыполнил двухмесячный план выпуска продукции?
Решение:
Пусть x – месячный план, тогда
1,05x – выпущено в январе,
1,04 · (1,05x) = 1,092x – выпущено в феврале, а всего за два месяца выпущено
1,05x + 1,092x = 2,142x.
Таким образом двухмесячный план 2x, а фактически выполнено 2,142x, т.е.
2x – 100%
2,142x – y%
y = (2,142x · 100) : (2x) = 107,1%, т.е. план перевыполнен на 7,1%.
Ответ: 7,1%
Задача 7. (решаемая логическими рассуждениями)
В одном из городов Украины часть жителей говорит только по-русски, часть только по-украински, часть говорит и по-русски и по-украински. Известно, что 90% жителей говорит по-русски, а 80% по-украински. Какой процент жителей этого города говорит на обоих языках?
Решение:
На каждых 100 жителей – 90 говорит по-русски, значит, 10 не говорит по-русски, т.е. 10 говорит только по-украински. Известно, что из каждых 100 жителей говорит по-украински 80 человек, из них, как мы выяснили, 10 человек говорит только по-украински, следовательно из этих 80 знают еще и русский 80 – 10 = 70 человек, т.е. 70%
Ответ: 70%
www.seznaika.ru
Урок 7. Решение задач на проценты | Поурочные планы по алгебре 7 класс
Тема: Решение задач на проценты.
Цели урока: проверить знания и умения по работе с процентами, степенями и дробями; в течение урока развивать у учащихся вычислительные способности с использованием степени, дробей и процентов; так же развивать у учеников навыки решения и оформления задач на проценты; рассмотреть задачи – шутки с процентами для повышения интереса к математике.
Ход урока:
1. Организационный момент. (2 мин.)
2. Математический диктант. (8 мин.)
Вариант 1. | Вариант 2. |
1) Перевести десятичные дроби в проценты. | |
0,2; 0,03; 1,14. | 0,68; 0,002; 0,9. |
2) Перевести проценты в десятичные дроби. | |
38%, 0,3%, 50%. | 120%, 1%, 70%. |
3) Вычислить. | |
4) Найти 20% от 35. | 4) Найти число, если его 20% — 12. |
Ученики меняются тетрадями и под диктовку учителя проверяют ответы и ставят оценки. После разбираются ошибки.
3. Устная работа. (10 мин.)
Затем устно разбираются № 78, 87, 88, 85.
4. Решение задач. (10 мин.)
Решаются на доске № 92, 94.
Также решить следующую задачу:
40 бабушек вошли в автобус. 70% бабушек купили билеты, а остальные закричали, что у них проездной билет. Контролер проверил. На самом деле оказалось, что проездной только у 7 бабушек. Сколько бабушек ехало «зайцами»?
5. Самостоятельная работа. (10 мин.)
Вариант 1. | Вариант 2. |
Вычислить значение выражения: | |
Задача № 89 | Задача № 90 |
6. Подведение итогов. (3 мин.)
7. Домашнее задание. (2 мин.)
Прочитать, разобрать и выучить правила из § 1.3.
Решить задания № 84, 91, 93.
tak-to-ent.net
ГДЗ по алгебре для 7 класса Г.В. Дорофеев
Подробное решение упражнение № 90 по алгебре для учащихся 7 класса, авторов Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович 2016
показать содержание- Гдз контрольные работы по Алгебре за 7 класс можно найти тут
- Гдз тематические тесты ГИА по Алгебре за 7 класс можно найти тут
- Гдз дидактические материалы по Алгебре за 7 класс можно найти тут
90. Моделируем. Решите задачу, используя схематические рисунки. а) Книга дороже альбома на 25%. На сколько процентов альбом дешевле книги? б) Блюдце на 20% дешевле тарелки. На сколько процентов тарелка дороже блюдца? в) Чашка на 20% дороже блюдца. Какую часть стоимости чашки составляет стоимость блюдца? На сколько процентов блюдце дешевле чашки? г) Цена книги была повышена на 10%. В конце года вновь была установлена старая цена. На сколько процентов снизили цену книги в конце года?
решебник / упражнение № / 90
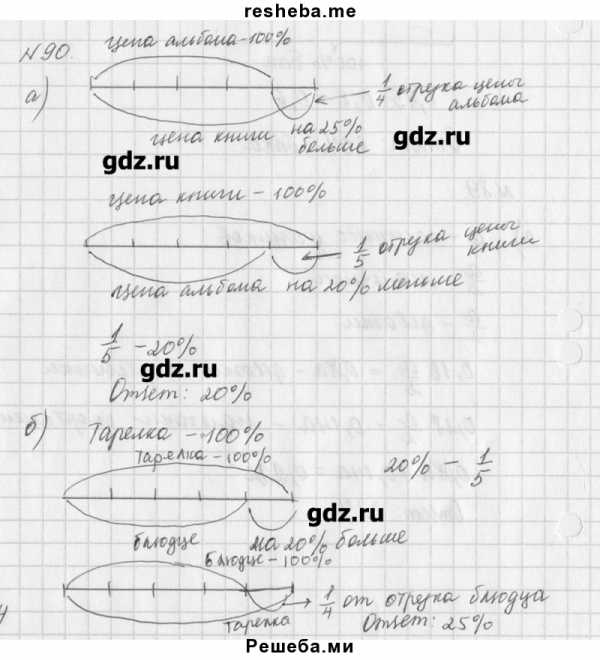
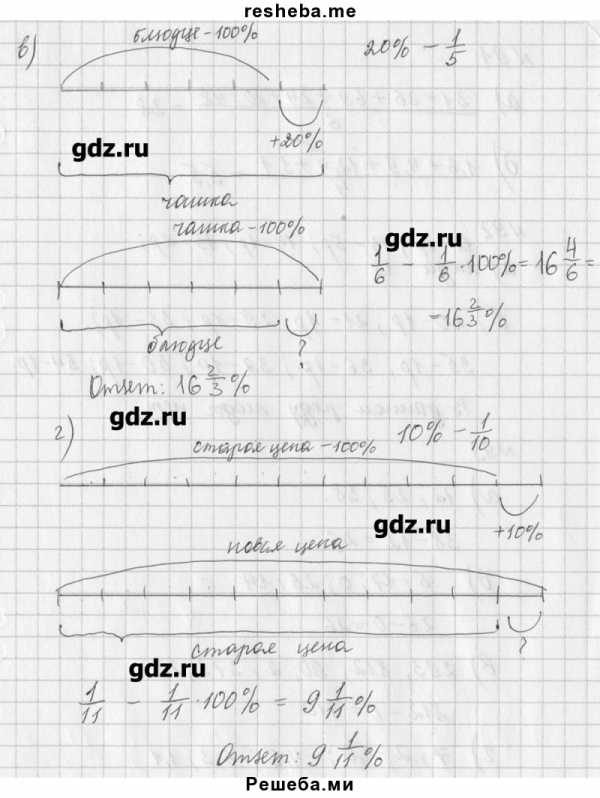
Подпишись на нашу группу
×resheba.me
Алгебра, 7 класс, Дорофеев Г.В., Суворова С.Б., Бунимович Е.А., 2014
Алгебра, 7 класс, Дорофеев Г.В., Суворова С.Б., Бунимович Е.А., 2014.
Содержание учебника позволяет достичь планируемых результатов обучения, предусмотренных ФГОС основного общего образования. Учебный текст разбивается на смысловые фрагменты специальными знаками и завершается вопросами, позволяющими проверить, как понято прочитанное. В систему упражнений включены такие виды деятельности, как анализ информации, наблюдение и рассуждение, конструирование алгоритмов, поиск закономерностей, исследование и т. д. Всё это позволяет учащимся активно и осознанно овладевать универсальными учебными действиями. Каждая глава завершается разделом «Чему вы научились», помогающим ученику проверить себя на базовом уровне и оценить возможность выполнения более сложных заданий.
Примеры.
По данным социологического исследования, проведённого в этом году, в городе Лукошкино проживает 36 тыс. человек, 29% из них достигли пенсионного возраста, а 24% — дети и подростки дошкольного и школьного возраста. Сколько в городе взрослых жителей, не достигших пенсионного возраста?
Банк предлагает своим клиентам следующие условия вклада: деньги кладутся на счёт на 31 день, по истечении которых клиент получает доход, равный 7,5% от вложенной суммы. Какую сумму нужно положить на счёт, чтобы доход составил 1500 р.?
В состав одного из поливитаминов входят минералы в следующих количествах: кальций и фосфор — по 4%, магний — 1,6%, железо — 0,07%, цинк — 0,06%. Сколько миллиграммов каждого минерала содержится в одной таблетке поливитамина, масса которой 250 мг?
Оглавление
Предисловие 3
Глава 1. Дроби и проценты
1.1. Сравнение дробей 5
1.2. Вычисления с рациональными числами 10
1.3. Степень с натуральным показателем 14
1.4. Задачи на проценты 21
1.5. Статистические характеристики 30
1.6. Последняя цифра степени (Для тех, кому интересно) 36
Дополнительные задания 37
Чему вы научились 40
Глава 2. Прямая и обратная пропорциональность
2.1. Зависимости и формулы 44
2.2. Прямая пропорциональность. Обратная пропорциональность 50
2.3. Пропорции. Решение задач с помощью пропорций 57
2.4. Пропорциональное деление 64
2.5. Задачи на «сложные» пропорции (Для тех, кому интересно) 66
Дополнительные задания 68
Чему вы научились 70
Глава 3. Введение в алгебру
3.1. Буквенная запись свойств действий над числами 73
3.2. Преобразование буквенных выражений 78
3.3. Раскрытие скобок 85
3.4. Приведение подобных слагаемых 89
3.5. Ещё раз о законах алгебры (Для тех, кому интересно) 95
Дополнительные задания 98
Чему вы научились 100
Глава 4. Уравнения
4.1. Алгебраический способ решения задач 103
4.2. Корни уравнения 107
4.3. Решение уравнений 109
4.4. Решение задач с помощью уравнений 115
4.5. Некоторые неалгоритмические приёмы решения уравнений (Для тех, кому интересно) 121
Дополнительные задания 123
Чему вы научились 124
Глава 5. Координаты и графики
5.1. Множества точек на координатной прямой 127
5.2. Расстояние между точками координатной прямой 131
5.3. Множества точек на координатной плоскости 134
5.4. Графики 139
5.5. Ещё несколько важных графиков 143
5.6. Графики вокруг нас 148
5.7. Графики зависимостей, заданных равенствами с модулями (Для тех, кому интересно) 156
Дополнительные задания —
Чему вы научились 160
Глава 6. Свойства степени с натуральным показателем
6.1. Произведение и частное степеней 163
6.2. Степень степени, произведения и дроби 168
6.3. Решение комбинаторных задач 174
6.4. Перестановки 177
6.5. Круговые перестановки (Для тех, кому интересно) 181
Дополнительные задания 182
Чему вы научились 185
Глава 7. Многочлены
7.1. Одночлены и многочлены 188
7.2. Сложение и вычитание многочленов 193
7.3. Умножение одночлена на многочлен 197
7.4. Умножение многочлена на многочлен 201
7.5. Формулы квадрата суммы и квадрата разности 205
7.6. Решение задач с помощью уравнений 211
7.7. Деление с остатком (Для тех, кому интересно) 218
Дополнительные задания 219
Чему вы научились 222
Глава 8. Разложение многочленов на множители
8.1. Вынесение общего множителя за скобки 226
8.2. Способ группировки 231
8.3. Формула разности квадратов 233
8.4. Формулы разности и суммы кубов 237
8.5. Разложение на множители с применением нескольких способов 240
8.6. Решение уравнений с помощью разложения на множители 243
8.7. Несколько более сложных примеров (Для тех, кому интересно) 245
Дополнительные задания 247
Чему вы научились 250
Глава 9. Частота и вероятность
9.1. Случайные события 253
9.2. Частота случайного события 260
9.3. Вероятность случайного события 266
9.4. Сложение вероятностей (Для тех, кому интересно) 270
Дополнительные задания 271
Чему вы научились 272
Ответы 275
Справочный материал 282
Предметный указатель 283.
Купить — pdf — Яндекс.Диск.Дата публикации: 15.08.2015 17:58 UTC
x-uni.com
Алгебра, 7 класс, Дорофеев, Суворова, Бунимович, 2010
Алгебра, 7 класс, Дорофеев Г.В., Суворова С.Б., Бунимович Е.А., 2010.
Учебник соответствует федеральным компонентам Государственного стандарта общего образования. Учебно-методический комплект по алгебре для 7 класса под редакцией Г. В. Дорофеева включает учебник, рабочую тетрадь, тематические тесты, дидактические материалы, книгу для учителя и контрольные работы для 7—9 классов. В оформлении заставок учебника использованы мотивы рисунков М. Эшера.
Примеры.
В состав одного из поливитаминов входят минералы в следующих количествах: кальций и фосфор — по 4%, магний — 1,6%, железо — 0,07%, цинк — 0,06%. Сколько миллиграммов каждого минерала содержится в одной таблетке поливитамина, масса которой 250 мг?
В декабре сотрудникам фирмы была выплачена премия в размере 250% ежемесячной зарплаты.
а) Какую премию получил сотрудник, зарплата которого была 6000 р.?
б) Какую сумму получил в декабре сотрудник, зарплата которого 7500 р.?
В магазин привезли 160 упаковок консервированных овощей и фруктов. Овощные консервы составили 75% привезенного товара, причем 40% из них были в стеклянных банках. Какое количество упаковок, содержащих овощные консервы в стеклянных банках, привезли в магазин?
Оглавление
Глава 1. Дроби и проценты
1.1. Сравнение дробей 3
1.2. Вычисления с рациональными числами 7
1.3. Степень с натуральным показателем 11
1.4. Задачи на проценты 18
1.5. Статистические характеристики 26
1.6. Последняя цифра степени (Для тех. кому интересно) 32
Дополнительные задания к главе 1 33
Вопросы для повторения к главе 1 36
Задания для самопроверки к главе 1 37
Тест к главе 1 38
Глава 2. Прямая и обратная пропорциональность
2.1. Зависимости и формулы 40
2.2. Прямая пропорциональность. Обратная пропорциональность 45
2.3. Пропорции. Решение задач с помощью пропорций 52
2.4. Пропорциональное деление 58
2.5. Задачи на «сложные» пропорции (Для тех, кому интересно) 61
Дополнительные задания к главе 2 62
Вопросы для повторения к главе 2 64
Задания для самопроверки к главе 2
Тест к главе 2 65
Глава 3. Введение в алгебру
3.1. Буквенная запись свойств действий над числами 67
3.2. Преобразование буквенных выражений 72
3.3. Раскрытие скобок 78
3.4. Приведение подобных слагаемых 82
3.5. Еще раз о законах алгебры (Для тех, кому интересно) 87
Дополнительные задания к главе 3 91
Вопросы для повторения к главе 3 92
Задания для самопроверки к главе 3 93
Тест к главе 3
Глава 4. Уравнения
4.1. Алгебраический способ решения задач 95
4.2. Корни уравнения 99
4.3. Решение уравнений 101
4.4. Решение задач с помощью уравнений 106
4.5. Некоторые неалгоритмические приемы решения уравнений (Для тех, кому интересно) 112
Дополнительные задания к главе 4 114
Вопросы для повторения к главе 4 116
Задания для самопроверки к главе 4
Тест к главе 4 117
Глава 5. Координаты и графики
5.1. Множества точек на координатной прямой 119
5.2. Расстояние между точками координатной прямой 123
5.3. Множества точек на координатной плоскости 126
5.4. Графики 130
5.5. Еще несколько важных графиков 134
5.6. Графики вокруг нас 138
5.7. Графики зависимостей, заданных равенствами с модулями (Для тех, кому интересно) 147
Дополнительные задания к главе 5
Вопросы для повторения к главе 5 150
Задания для самопроверки к главе 5 151
Тест к главе 5 152
Глава 6. Свойства степени с натуральным показателем
6.1. Произведение и частное степеней 154
6.2. Степень степени, произведения и дроби 159
6.3. Решение комбинаторных задач 164
6.4. Перестановки 166
6.5. Круговые перестановки (Для тех, кому интересно) 169
Дополнительные задания к главе 6 171
Вопросы для повторения к главе 6 173
Задания для самопроверки к главе 6
Тест к главе 6 174
Глава 7. Многочлены
7.1. Одночлены и многочлены 176
7.2. Сложение и вычитание многочленов 179
7.3. Умножение одночлена на многочлен 183
7.4. Умножение многочлена на многочлен 186
7.5. Формулы квадрата суммы и квадрата разности 189
7.6. Решение задач с помощью уравнений 194
7.7. Деление с остатком (Для тех, кому интересно) 202
Дополнительные задания к главе 7 204
Вопросы для повторения к главе 7 206
Задания для самопроверки к главе 7 207
Тест к главе 7 208
Глава 8. Разложение многочленов на множители
8.1. Вынесение общего множителя за скобки 210
8.2. Способ группировки 214
8.3. Формула разности квадратов 217
8.4. Формулы разности и суммы кубов 220
8.5. Разложение на множители с применением нескольких способов 222
8.6. Решение уравнений с помощью разложения на множители 226
8.7. Несколько более сложных примеров (Для тех, кому интересно) 228
Дополнительные задания к главе 8 230
Вопросы для повторения к главе 8 232
Задания для самопроверки к главе 8 233
Тест к главе 8 234
Глава 9. Частота и вероятность
9.1. Относительная частота случайного события 236
9.2. Вероятность случайного события 241
9.3. Сложение вероятностей (Для тех, кому интересно) 244
Дополнительные задания к главе 9 246
Вопросы для повторения к главе 9 247
Задания для самопроверки к главе 9
Тест к главе 9
Ответы 249.
x-uni.com
