Презентация к уроку по алгебре (7 класс) на тему: Числовые выражения
Слайд 1
И снова в позолоте тополя, А школа — как корабль у причала, Где ждут учеников учителя, Чтоб новой жизни положить начало. Пусть счастье в дверь твою стучит, Открой ее скорей пошире. Путь жизни тайною покрыт, Но так прекрасно в этом мире! И пусть всегда – в окошке свет, Улыбка мамина – с порога. Пусть будет много добрых лет И в жизни легкая дорога!Слайд 2
Есть о математике молва, Что она в порядок ум приводит. Поэтому хорошие слова Часто говорят о ней в народе.
Слайд 4
S = v· t a · b = b · a
Слайд 5
Вавилон Египет
Слайд 6
Около 4000 лет назад в Вавилоне и в Египте ученые уже умели составлять линейные уравнения, с помощью которых они решали самые разнообразные задачи землемерия, строительного искусства и военного дела. В Британском музее хранится задача из папируса Ринда (его называли также папирусом Ахмеса)
Слайд 7
В Британском музее хранится задача из папируса Ринда (его называли также папирусом Ахмеса) Найти число, если известно, что от прибавления к нему 2/3 его и вычитая от полученной суммы ее трети получается число 10.
Слайд 8
« Хисаб Ал-джебр Вал-мукабала » («Метод восстановления и противопоставления») – это была первая книга по алгебре. Ал-джебр При решении уравненья, Если в части одной, Безразлично какой, Встретится член отрицательный, Мы к обеим частям, С этим членом сличив. Равный член придадим, Только с знаком другим,— И найдем результат, нам желательный! Вал-мукабала Дальше смотрим в уравненье, Можно ль сделать приведенье, Если члены есть подобны, Сопоставить их удобно. Вычитая равный член из них, К одному приводим их.
Слайд 10
Алгебра уравнение число тождество функция Алгебра, к изучению которой мы приступаем, дает человеку возможность не только выполнять различные вычисления, но и учит его делать это как можно быстрее, рациональнее.
Слайд 11
Тема урока: «Числовые выражения» Повторить и углубить умение учащихся находить значения числовых выражений; Запомнить, что выражение, содержащее действие деление на нуль, не имеет смысла; Развить познавательный интерес учащихся к изучению нового предмета. Цели урока:
Слайд 12
устно Вычислите: 6 7 10 80 289 72 8 5 8100 170
Слайд 13
Запись, составленная из чисел с помощью арифметических действий (сложение, вычитание, умножение, деление, возведение в степень) называет числовым (арифметическим) выражением . 2 2 0 Значением числового выражения называется число, полученное в результате выполнения указанных в числовом выражении действий. Изучение темы
Слайд 14
Два числовых выражения, соединенные знаком «=», образуют числовое равенство . Если значения левой и правой частей числового равенства совпадают, то равенство называют верным , в противном случае – неверным . верное неверное Изучение темы
Слайд 15
Если в данном выражении на некотором этапе вычислений требуется делить на нуль, то это выражение не имеет смысла . Изучение темы
Слайд 16
Киоск задач №1 Установите, какие из следующих выражений имеют смысл и какие не имеют. Для имеющих смысл найдите числа, которым они равны. а) б) в) не имеет смысла -3/7 54/95
Слайд 17
Киоск задач №1 (первая, вторая строчки), №3, №4 (д – з), №5, №6 (первая, третья строчки), №7 (а, б), №13
Слайд 18
Домашнее задание П.1 (изучить, определения выучить), №2, №4 (а – г), №6 (б, д, з)
Слайд 19
Итоги урока О каких выражения мы сегодня говорили? Какое выражение называется числовым? Что называют значением числового выражения? Что такое числовое равенство? Какие виды равенств вы знаете? Когда числовое выражение не имеет смысла?
Слайд 20
Спасибо за урок, Дети Творческих успехов Вам В новом учебном году!
nsportal.ru
Презентация «Повторение. Числовые выражения». Алгебра. 7 класс
Просмотр содержимого документа
«Презентация «Повторение. Числовые выражения». Алгебра. 7 класс»

Первый урок алгебры
в 7 классе
«Повторение. Числовые выражения»
Аверина Анна Игоревна
учитель математики
МБОУ «Тёшинская средняя школа»

6,8
2,3+4,5 =
12,7+ 3,8=
3,12+0,8=
5,7-2,4=
9,1-4,5=
16,5
3,92
3,3
3,6
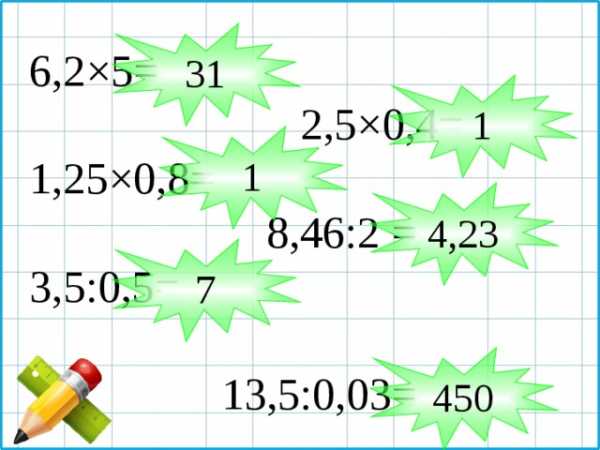
31
6,2×5=
2,5×0,4= 1,25×0,8=
8,46:2 =
3,5:0,5=
13,5:0,03=
1
1
4,23
7
450


-11
-3,3
2,3-5,6= -8,1-2,9=
-6,3+ 2,8=
-3,5
2,7
-8,4
-2,8×3= -5,4×(- )=
0,21×(-0,4)=
-43
12,9: (-0,3)=
-0,084
=-1,5
=5

Ответы:

Самостоятельная работа
№ 5 (2), 6(2,4)
Ответы: № 5 – 10,7
№ 6 – 9/56
4 6/7

«Мне приходится делить время между политикой и уравнениями.
Однако уравнения, по-моему, гораздо важнее.
Политика существует только для данного момента, а уравнения будут существовать вечно»
Альберт Эйнштейн

Самые древние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте умели решать линейные уравнения .

В Индии математики умели решать квадратные уравнения уже в 499 году, но европейцы узнали об этом только из трактата аль-Хорезми

Математик и астроном из г.Хивы
Мухаммед бен Муса аль-Хорезми (787-ок.850г.) написал трактат «Аль-китаб аль мухтасар фи хисаб аль-джебр ва аль-мукабала»
Термин « аль-джебр » постепенно стал употребляться как « алгебра »

ψ
До XVI века изложение алгебры велось словесно,
вот так выглядела запись квадратного уравнения

Знаки «+» и «-» впервые встречаются у немецких математиков XVI века, чуть позже появился знак «×», а знак деления был введён лишь в XVII веке .

Большой вклад в развитие алгебры как науки внесли выдающиеся математики своего времени: Франсуа Виет, Леонардо Фибоначчи, Карл Гаусс, Рене Декарт, Исаак Ньютон, Леонард Лейбниц, Иоганн Бернулли и другие.
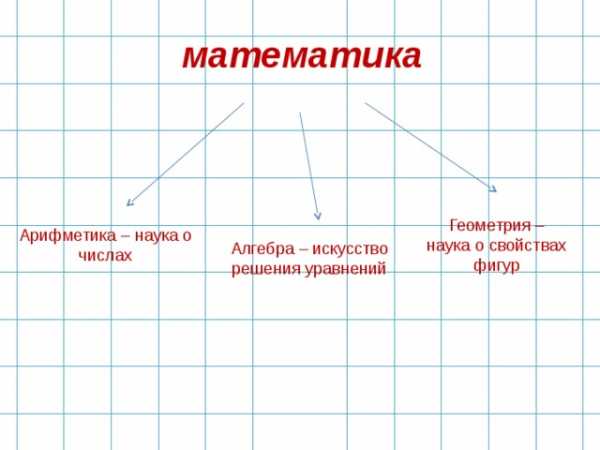
математика
Геометрия – наука о свойствах фигур
Арифметика – наука о числах
Алгебра – искусство решения уравнений

На дом: прочитать пункт 1, выполнить письменно №3 (1,3), №4, №8 (1,3)
Для желающих: прочитать текст на стр.11-13
Алгебра!

Алгебра
новая и незнакомая
удивляет, поражает, восхищает
алгебра – искусство решения уравнений
УСПЕХ!
multiurok.ru
Презентация к уроку по алгебре (7 класс) на тему: Урок математики в 7 классе по теме «Алгебраические выражения».
Слайд 1
Алгебраические выражения.Слайд 2
Проверка домашнего задания. Какие сведения из математики вам пришлось вспомнить в процессе выполнения домашнего задания ?
Слайд 3
Порядок арифметических действий. Переместительный закон сложения: a + b = b + a Переместительный закон умножения: a * b = b * a Сочетательный закон сложения: a + b + c = (a + b) + c = a + (b + c) Сочетательный закон умножения: abc = (ab)c = a(bc) Понятие обыкновенной дроби, десятичной дроби, отрицательного числа. Арифметические операции с десятичными дробями. Арифметические операции с обыкновенными дробями. Основное свойство обыкновенной дроби: Правила действий с десятичными дробями.
Слайд 4
Пример 1 Один холодильник стоит 350 $ . Тогда два холодильника стоят в два раза больше, т.е. 350·2=700 $ ; пять холодильников стоят в пять раз дороже, т.е. 350·5=1750 $ . Легко сообразить, что а холодильников стоят в а раз больше, т.е. 350· а $ С помощью выражения 350· а можно находить стоимость различного числа а холодильников, подставляя различные значения а и выполняя умножение. Так как буква а может принимать различные натуральные значения, то а – переменная 350· а – алгебраическое выражение (или выражение с переменной)
Слайд 5
Пример 2. Пусть длина одной стороны прямоугольника а см, другой – b см. Найдем периметр прямоугольника. b a P = 2 a + 2 b a , b – переменные 2 a + 2 b – алгебраическое выражение
Слайд 6
Пример 3. Запись 2a – 3b + 5 – алгебраическое выражение с переменными a и b . — алгебраическое выражение с переменными x и y .
Слайд 7
Пример 4. Найдем значение выражения при a = 3 , b = 4 и с =2 В данное алгебраическое выражение подставим значения переменных a = 3 , b = 4 , c = 2 . Получаем числовое выражение. Выполнив действия, найдем его значение: = = = 9 Число 9 является значением алгебраического выражения для данных значений переменных. Значение числового выражения , которое получается при подстановке выбранных значений переменных в алгебраическое выражение, называют значением алгебраического выражения.
Слайд 8
Задания. 1.18(а, в) 1.20(а) 1.22(а, г) 1.24(б) 1.29 (а) 1.39(а, б) 1.42(а, в)
Слайд 9
Контрольные вопросы. Чем отличаются числовые и алгебраические выражения? Что называется алгебраическим выражением и переменной? Как вычислить значение алгебраического выражения для данных значений переменных? Всегда ли это можно сделать?
Слайд 10
Задание на дом. 1.18(б, г) 1.20(в) 1.22(б, в) 1.24(г) 1.30(в) 1.40(б, г) 1.42(б, г)
Слайд 11
Спасибо з а урок
nsportal.ru
Презентация — Числовые выражения 7 кл.
Текст этой презентации
Слайд 1
Числовые выражения.7 класс
Слайд 2
Слайд 3
50
Слайд 4
15 + 36 = 51
7² — 3•10 = 9
13•15 + 121:11 = 195 +11= 206
Слайд 5
Слайд 6
0,0081
-100
-1,5
-6,3
— 11,2
Слайд 7
ПРИМЕР: 4 + 8,5 = 8,5 + 4 10•0,5=0,5•10
ПРИМЕР: ( 11 + 3,7)+ 0,3 = 11+(3,7 + 3) ( 258•25)•4= 258•(25•4)
Слайд 8
Слайд 9
(50•0,2) •1,34 = 10 •1,34 =
-75,7•(0,5 •20) = -75,7 •10 =
-15,8 •(4•25) = -15,8 •100 =
0,47 •(0,4•25) = 0,47 •10 =
Слайд 10
(8,91+1,09) +25,7 =
6,64+(7,12 + 2,88) =
18,9-(6,8+5,2+4,1) =
(7,15+12,85) –(9,42+0,58) =
Слайд 11
Сравнение числовых выражений
Для любых двух числовых выражений можно установить,
равны их значения или нет,
и если они равны,
то какое из них больше и какое меньше.
Результат сравнения значений выражений можно записать в виде равенства или неравенства,
c помощью знаков = равно, ≠ не равно, > больше,
Слайд 12
Слайд 13
Если выражения содержат переменные, то для разных значений переменных результат сравнения значений выражений может оказаться различным
Слайд 14
Определение
Неравенства, составленные с помощью знаков > больше или Неравенства, составленные с помощью знаков ≥ больше или равно или ≤ меньше или равно,
называются нестрогими
Слайд 15
СТРОГИЕ НЕРАВЕНСТВА
НЕСТРОГИЕ НЕРАВЕНСТВА
15 > 12
0 ≤ 6+х
х-7 > -9
у ≥ -67+6
-56 ≤ х
а > 497
0,15 ПРОЧИТАЙТЕ НЕРАВЕНСТВА
Слайд 16
ДВОЙНОЕ НЕРАВЕНСТВО
0
-3
4
Х
-3 0 -3 -5 ≤ х 0 > -3
4 > 0
Слайд 17
Слайд 18
11110 ≤ 28 х
Слайд 19
0,50,50,50,5
topslide.ru
Презентация на тему Числовые выражения 7 класс
Презентацию на тему Числовые выражения 7 класс можно скачать абсолютно бесплатно на нашем сайте. Предмет презентации : Математика. Красочные слайды и илюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого презентации воспользуйтесь плеером, или если вы хотите скачать презентацию — нажмите на соответствующий текст под плеером. Презентация содержит 8 слайдов.
Слайд 1Числовые выражения 6-7класс
Умножение и деление десятичных дробей
Задание «Хочу все знать»
На земном шаре обитают птицы- безошибочные составители прогноза погоды на лето. Название этих птиц зашифровано примерами.
Слайд 3Выполните действия №1(2,3 столбики)
д) 6,5*1,22 и) 53,4:15 е) 0,48*2,5 к) 16,94:2,8 ж) 3,725*3,2 л) 75:1,25 з) 0,016*0,25 м) 123,12:30,4
Слайд 4Замените значения выражений буквами и прочтите название этих птиц – метеорологов.
Слайд 5Проверь себя
д) 6,5 е) 0,48 ж) 3,725 з) 0,016 1,22 2,5 3,2 0,25 130 240 7450 80 + 130 96 11175 32 65 1,200 11,9200 0,00400 7,930 Ф Л А М
Слайд 6и) _53,4 /15_ к) _16,94 /28 __ 45 3,56 168 6,05 _84 _140 75 140 _ 90 0 90 0 И Н
Слайд 7л) 756:1,25=7500:125=60 Г м) 123,12:30,4=4,05 О _1231,2 /304 1216 4,05 _1520 1520 0
Это интересно
Фламинго из песка строят гнезда в форме усеченного конуса, в верхнем основании делают углубления, в которые откладывают яйца. Высота гнезда зависит от того каким будет лето : дождливым или сухим. Если лето ожидается дождливым, то гнезда строятся высокими, чтобы их не могла затопить вода, если засушливым – то более низкими.
prezentacii.org
Презентация «Повторение. Числовые выражения». Алгебра. 7 класс
Просмотр содержимого документа
«Презентация «Повторение. Числовые выражения». Алгебра. 7 класс»

Первый урок алгебры
в 7 классе
«Повторение. Числовые выражения»
Аверина Анна Игоревна
учитель математики
МБОУ «Тёшинская средняя школа»

6,8
2,3+4,5 =
12,7+ 3,8=
3,12+0,8=
5,7-2,4=
9,1-4,5=
16,5
3,92
3,3
3,6

31
6,2×5=
2,5×0,4= 1,25×0,8=
8,46:2 =
3,5:0,5=
13,5:0,03=
1
1
4,23
7
450


-11
-3,3
2,3-5,6= -8,1-2,9=
-6,3+ 2,8=
-3,5
2,7
-8,4
-2,8×3= -5,4×(- )=
0,21×(-0,4)=
-43
12,9: (-0,3)=
-0,084
=-1,5
=5

Ответы:

Самостоятельная работа
№ 5 (2), 6(2,4)
Ответы: № 5 – 10,7
№ 6 – 9/56
4 6/7

«Мне приходится делить время между политикой и уравнениями.
Однако уравнения, по-моему, гораздо важнее.
Политика существует только для данного момента, а уравнения будут существовать вечно»
Альберт Эйнштейн

Самые древние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте умели решать линейные уравнения .

В Индии математики умели решать квадратные уравнения уже в 499 году, но европейцы узнали об этом только из трактата аль-Хорезми

Математик и астроном из г.Хивы
Мухаммед бен Муса аль-Хорезми (787-ок.850г.) написал трактат «Аль-китаб аль мухтасар фи хисаб аль-джебр ва аль-мукабала»
Термин « аль-джебр » постепенно стал употребляться как « алгебра »

ψ
До XVI века изложение алгебры велось словесно,
вот так выглядела запись квадратного уравнения

Знаки «+» и «-» впервые встречаются у немецких математиков XVI века, чуть позже появился знак «×», а знак деления был введён лишь в XVII веке .

Большой вклад в развитие алгебры как науки внесли выдающиеся математики своего времени: Франсуа Виет, Леонардо Фибоначчи, Карл Гаусс, Рене Декарт, Исаак Ньютон, Леонард Лейбниц, Иоганн Бернулли и другие.

математика
Геометрия – наука о свойствах фигур
Арифметика – наука о числах
Алгебра – искусство решения уравнений

На дом: прочитать пункт 1, выполнить письменно №3 (1,3), №4, №8 (1,3)
Для желающих: прочитать текст на стр.11-13
Алгебра!

Алгебра
новая и незнакомая
удивляет, поражает, восхищает
алгебра – искусство решения уравнений
УСПЕХ!
multiurok.ru
План-конспект урока по алгебре (7 класс) по теме: Вводный урок в 7 классе, числовые выражения
Алгебра – 7 кл
С.Г. Скороходова учитель математики МБОУ СОШ № 6 ст. Полтавская, Красноармейский район, Краснодарский край.
Урок 1 «Вводный урок в 7 классе, числовые выражения».
Учебник «Алгебра – 7 класс».
Авторы: Ю.Н. Макарычев, Н.Г. Миндюк и др.
Цели урока:
- Привитие интереса к предмету
- Расширение кругозора учащихся
- Систематизировать и обобщить сведения о числовых выражениях, полученных учащимися в 5-6-х классах.
Ход урока
Перед вами учебник «Алгебра – 7 кл.», и конечно сразу возникает вопрос: «Чем мы будем заниматься на уроках алгебры? А поможет нам в этом разобраться легенда:
Однажды некий шах объявил, что щедро вознаградит того, кто лучше всех решит такую задачу:
«В трех чашах хранил я жемчуг. Подарил я старшему сыну половину жемчужин из первой чаши, среднему 1/3 из второй, а младшему — только четверть жемчужин из последней. Затем я подарил старшей дочери четыре лучшие жемчужины из первой чаши, средней – шесть из второй, а младшей только две жемчужины из третьей чаши. И осталось у меня в первой чаше 38, во второй – 12, а в третьей – 19 жемчужин. Сколько жемчужин хранил я в каждой чаше?»
И вот во дворец пришли из разных стран три мудреца. Первый мудрец поклонился и сказал:
-Если в первой чаше, о великий шах, осталось 38 жемчужин, а подарил ты старшей дочери 4 жемчужины, то эти 42 жемчужины и составляют половину того, что было в чаше. Ведь вторую половину ты подарил старшему сын. Значит, в первой чаше хранилось 84 жемчужины. Во второй чаше осталось 12 жемчужин, да 6 ты подарил другой дочери. Эти 18 жемчужин составляют 2/3 того, что хранилось во второй чаше. Ведь 1/3 ты подарил сыну? Значит, во второй чаше было 27 жемчужин. Ну, а в третьей чаше оставалось 19 жемчужин, да 2 ты подарил младшей дочери. Выходит, что 21 жемчужина – это 3/4 содержимого третьей чаши. Ведь 1/3 ты отдал младшему сыну? Значит, в этой чаше 28 жемчужин.
Решить такую задачу помогла мне арифметика – наука о свойствах чисел и правилах вычисления. Это очень древняя наука: люди считают уже много тысяч лет. Название этой науки произошло от греческого слова «арифмос», что означает «число». Ученые Древней Греции больше всех помогли нам разобраться в арифметических правилах.
-Твое решение мне нравится,- одобрил шах, — Рассказывай ты, — обратился он к другому мудрецу.
-О, великий шах! Я не знаю сколько жемчужин было в первой чаше, поэтому я обозначил их число буквой «икс» — х. Выходит, что старшему сыну ты подарил половину – х:2. Если я из х вычту его половину, да еще 4 жемчужины, что ты подарил дочери, то остаток нужно приравнять к 38. Вот какое уравнение я для этого составил: х-(х:2)-4=38
(х:2)=42
Х=84
А для второй чаши надо х-(х:3)-6=12
Х=27
Рассуждая так же, составляю уравнение для третьей чаши: х-(х:4)-2=19
Х=28
-Твое решение мне нравится, — сказал шах.
-А что скажешь ты? – обратился он к третьему мудрецу.
Тот поклонился и молча протянул клочок бумаги, на котором было написано:
х-ах-в=с, а рядом ответ х=(в+с):(1-а)
-Я здесь ничего не понимаю!- рассердился шах.- И почему, у тебя только один ответ? Ведь у меня 3 чаши!
-Все три ответа уместились в одном. Ведь задачи совершенно одинаковые, лишь числа разные. А я не только упростил, но и объединил три решения в одно. Я тоже обозначил через «х» неизвестное число жемчужин в интересующей тебя чаше. Через «а» я обозначил ту часть жемчужин, которую из этой чаши ты подарил сыну, а через «в» — число жемчужин, отданных потом из этой чаши дочери. Наконец, через «с» я обозначил число жемчужин, оставшихся в этой чаши. Подставь вместо этих букв те числа, которые ты задал в своей задаче, и получишь правильные ответы. Будь у тебя 100 чаш, 100 сыновей и 100 дочерей, одного моего уравнения хватит чтобы получить все 100 ответов.
Помогла решить эту задачу алгебра. Она появилась более 1000 лет назад в Хорезме, и создал ее великий узбекский ученый Мухаммед аль-Хорезми. Алгебра почти та же арифметика. Только использует она наравне с числами и буквы. Использовать вместо чисел буквы предложили в 15-16 вв французские ученые Рене Декарт и Франсуа Виет. Под буквой можно разуметь любое число. Алгебра дает самое короткое, самое общее решение для многих похожих друг на друга задач. А когда вы станете старше, вы узнаете и о других, еще более сложных задачах, которые решает алгебра.
Таким образом, на уроках алгебры мы обобщим и систематизируем знания полученные ранее, а так же будем учиться рассуждать, видеть закономерности, объединять их в формулы.
Давайте вспомним:
1)С какими числами мы познакомились, изучая математику.
2)Какие арифметические действия мы умеем выполнять с этими числами?
3)Объясните порядок действий 1,1 + 7 : (3,7 – 1,2)
4)Найдите значение выражений:
-7 * 12 30 * (-5) 15 + (-11) 8 – (-5)
-6 * (-1,5) -180 : 6 -13 – 4 0 : (-56,47)
(-105) : (-15) -4 + 3 (-12) + (-9) 0 — 12
5)Представить десятичные дроби в виде обыкновенных
0,2 0,36 -0,425 0,5 0,75
6)Вычислить:
1,37 : 0,1 + (0,75 + 0,033) * 100
Давайте проанализируем из чего составлены выражения последнего задания (из чисел, знаков, действий, скобок). Таким образом, мы подошли к определению числового выражения.
Числовые выражения составляются из чисел с помощью знаков действий и скобок.
Выполняя действие, мы всегда получаем число.
Число, которое получается в результате выполнения действий в числовом выражении, называют значением выражения.
Например, 315 * 206 + 208 = 65098 -56 – 5*6 = -86
Всегда ли можно найти значение числового выражения? Если в выражении встречается деление на нуль, то значение числового выражения не может быть найдено, так как на нуль делить нельзя. О таких выражениях говорят, что они не имеют смысла.
35 : (4*2-8) или (56 – 52*54) : (24 – 72:3)
Приведите примеры выражений, не имеющих смысла.
Работа по учебнику:
№ 1 (а,б,г,ж,з)
№ 2 (самостоятельно)
№ 4 (б,г,е,з)
№ 5
Д/з: п.1 (правила), № 18, № 1 (в,д,е,и), № 3, № 6.
nsportal.ru
