пособие для учителей общеобразовательных организаций. Сост. Т. А. Бурмистрова
%PDF-1.6 % 378 0 obj > endobj 380 0 obj > endobj 377 0 obj >stream application/pdf

Билеты + ответы по геометрии 7 класс Атанасян
Билет №1
1. Виды треугольников по длине сторон. Периметр треугольника.
Треугольники бывают:
Равнобедренный (равны две стороны), разносторонний (все стороны по величине разные), равносторонний -все стороны равны
2. Смежные углы (определение). Теорема о сумме смежных углов.
Смежными называются два угла, у которых одна сторона общая, а две другие являются дополнительными лучами (т.е. имеют общее начало и дополняют друг друга до прямой).
Сумма смежных углов равна 180°.
Дано: ∠АОВ и ∠ВОС смежные.
Доказать: ∠АОВ + ∠ВОС = 180°
Доказательство:
∠АОС = ∠АОВ + ∠ВОС по свойству измерения углов,
∠АОС = 180°, так как является развернутым, ⇒ ∠АОВ + ∠ВОС = 180°
3.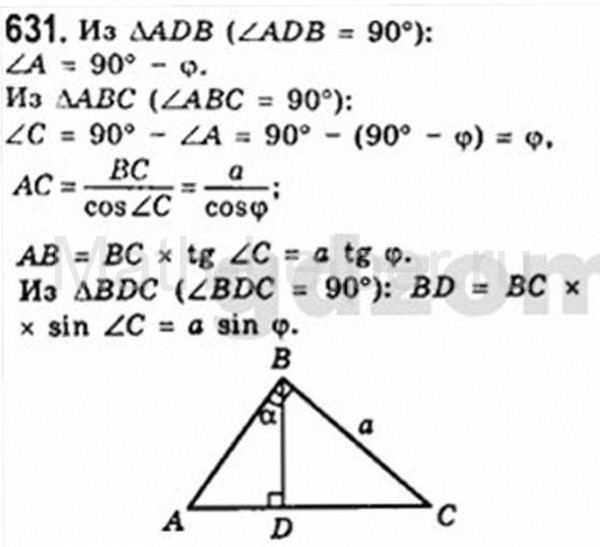
Отрезки AC и BD пересекаются в точке О. AO=OC, BO=OD. При проведении отрезков AB и CD образуются треугольники BAO и OCD. Докажите, что ∆ BAO=∆ OCD.
Билет №2
1. Отрезок (определение). Середина отрезка. Основное свойство расположение точек на прямой.
Отрезок — это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и конец, а значит можно измерить её длину.
Середина отрезка — это точка на заданном отрезке, находящаяся на равном расстоянии от обоих его концов отрезка.
из трёх точек на прямой одна и только одна лежит между двумя другими.
2. Свойства равнобедренного треугольника (доказательство одного из них).
Свойства равнобедренного треугольника:
1. В равнобедренном треугольнике углы при основании равны.
Доказательство:
пусть АВС — равнобедренный треуг с основанием АВ. Докажем, что у него А= В.
Тр САВ равен тр СВА по первому признаку равенства треугДействительно, СА=СВ, СВ=СА, угол С= углу С.Из равенства треугольников следует, что угол А= углу В. Теорема доказана.
2 В равнобедренном треуг биссектриса , проведённая к основанию , является медианной и высотой .
Доказательство:
Рассмотрим треугольники ACF и BCF (важно правильно их назвать!)
1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))
2) ∠ACF=∠BCF (так как CF — биссектриса по условию).
3) сторона CF — общая.
Значит, ∆ ACF=∆ BCF (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон и углов.
Таким образом, AF=BF, следовательно, CF — медиана.
∠AFC=∠BFC. А так как эти углы — смежные, значит, они прямые: ∠AFC=∠BFC=90º.
Значит, CF — высота.
Что и требовалось доказать.
3. Задача по теме «Окружность и ее элементы».
Найдите длину радиуса окружности, если длина диаметра равна 14,5 см.
Билет № 3
1. Основные геометрические фигуры на плоскости. Основное свойство принадлежности точек и прямых.
Основными геометрическими фигурами на плоскости являются точка и прямая. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
2. Построение треугольника по трём сторонам.
Даны три отрезка: a,b иc, равные сторонам искомого треугольника..
В этом случае перед началом построения необходимо убедиться, исполняется ли неравенство треугольника (длина каждого отрезка меньше суммы длин двух остальных отрезков), и эти отрезки могут быть сторонами треугольника.
Если да, то:,
1. Провести прямую.
2. На прямой от выбранной точки A отложить отрезок, равный данному отрезку a, и отметить другой конец отрезка B.
3. Провести окружность с центром A и радиусом, равным отрезку b.
4. Провести окружность с центром B и радиусом, равным отрезку c.
5. Точка пересечения окружностей является третьей вершиной искомого треугольника.
3. Задача по теме «Вертикальные углы».
Один из вертикальных углов равен 45º. Найдите остальные углы.
Билет № 4
Высота, биссектриса, медиана треугольника (определения).
Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса — это отрезок, делящий угол треугольника на две равные части.
Высота треугольника — это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение.
Теорема о свойстве катета, лежащего против угла в 30º.
Так как сумма острых углов прямоугольного треугольника равна 90º, то∠B=90º-∠A=90º-30º=60º.Построим треугольник ADC, равный треугольнику ABC.В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).
Задача по теме » Признаки параллельности прямых».
Один из внутренних накрест лежащих углов, образованных при пересечении двух параллельных прямых третьей прямой, равен 50º. Найдите градусные меры остальных углов.
Билет № 5
Взаимное расположение двух прямых. Основное свойство параллельных прямых.
1)прямые пересекаются (т. е. имеют одну общую точку), 2) прямые параллельны и не совпадают, 3) прямые совпадают( множ-во общих точек)
Через точку не лежащую на прямой, можно провести прямую параллельную данной, причем только одну.
Вертикальные углы (определение). Свойства вертикальных углов.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.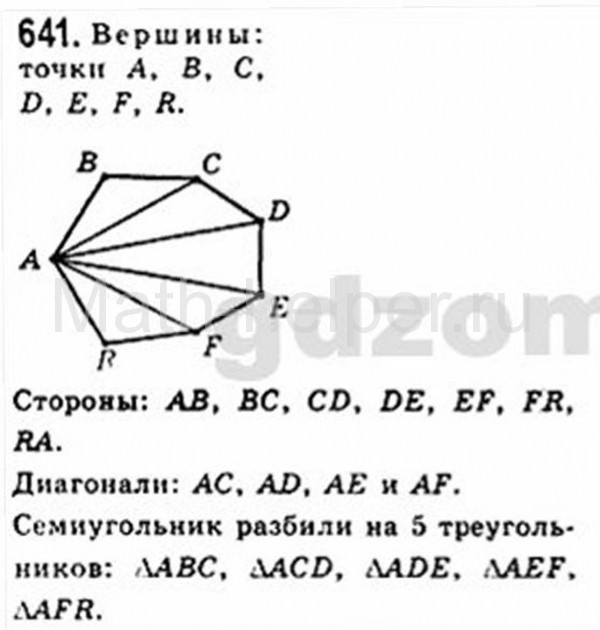
Вертикальные углы равны
Дано: – 1 и – 2 – вертикальные углы.
Доказать: – 1 = – 2.
Доказательство. – 3 является смежным и с – 1, и с – 2. Сумма смежных углов равна 180°, поэтому – 1 + – 3 = 180о , – 2 + – 3 = 180о . Отсюда получаем, что – 1 = 180о –– 3, – 2 = 180о – – 3. Пра- вые части равенств равны, значит, равны и левые. Следовательно, – 1 = – 2. Итак, вертикальные углы равны
3. Задача по теме » Соотношения между сторонами и углами
треугольника».
В треугольнике ABC AB=4 см, AC=6 см,BC=5 см. Какой угол треугольника наименьший, а какой наибольший?
Билет №6
Полуплоскость. Луч (определение). Основное свойство расположения точек относительно прямой на плоскости.
Любая прямая на плоскости разделяет её на две части, которые называются полуплоскостями. Полуплоскость – это часть плоскости, лежащая по одну сторону от любой прямой на этой плоскости. Луч — это часть прямой, состоящая из всех точек этой прямой, лежащих по одну сторону от одной её точки. Эта точка называется началом луча.
Эта точка называется началом луча.
Первый признак равенства треугольников.
Доказать, что треугольник ABC равен треугольнику DEF.
Доказательство:
Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
При этом отрезки СА и СВ наложатся на отрезки FE и FD.
А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
Это в свою очередь даст совмещение вершин А и D, В и Е.
Следовательно, треугольники полностью совместятся, а значит, они равны.
Теорема доказана.
3. Задача по теме » Сумма углов треугольника».
В треугольнике ABC даны два угла: =32º, =57º. Найдите третий угол.
Билет № 7
Угол (определение).
 Измерение углов. Основные свойства измерения углов.
Измерение углов. Основные свойства измерения углов.
У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла).
За единицу измерения углов обычно принимается угол, составляющий одну сто восьмидесятую часть развернутого угла. Считают, что величина этого угла равна одному градусу, обозначают 1о.
Градусная величина угла показывает, сколько раз угол в один градус и его части укладываются в этом угле. Прибор для измерения транспортир.
1)Каждый угол имеет определенную градусную меру большую нуля.
2)Развернутый угол равен 180 градусам.
3) Градусная мера угла равна сумме градусных мер углов,на которые он разбивается любым лучом,проходящим между его сторонами.
Второй признак равенства треугольника.
(Второй признак равенства треугольников — по стороне и двум прилежащим к ней углам)
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.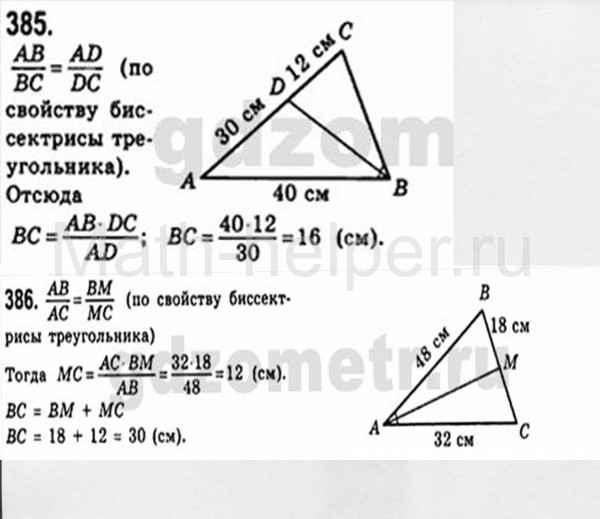
Дано:ΔABC, ΔA1B1C1, AB=A1B1, ∠A=∠A1, ∠B=∠B1.
Доказать: ΔABC= ΔA1B1C1
Доказательство:
Так как AB=A1B1, то треугольник A1B1C1 можно наложить на треугольник ABC так, чтобы
сторона A1B1 совместилась со стороной AB,
точки C1 и С лежали по одну сторону от прямой AB.
Поскольку ∠A=∠A1, сторона A1С1 при этом наложится на луч AC.
Так как ∠B=∠B1, сторона B1C1 наложится на сторону BC.
Точка С1 принадлежит как стороне A1С1, так и стороне B1C1, поэтому С1лежит и на луче AC, и на луче CB.
Лучи AC и CB пересекаются в точке C. Следовательно, точка С1 совместится с точкой C.
Значит, сторона A1С1 совместится со стороной AC, а сторона B1C1 — со стороной BC.
Таким образом, при наложении треугольники ABC и A1B1C1 полностью совместятся.
А это означает, что ΔABC= ΔA1B1C1 (по определению).
Что и требовалось доказать.
Задача по теме » Высота, медиана и биссектриса треугольника».
Отрезок СЕ является медианой ACD. Известно, что AE=2,5 см, AC=3 см, CD=4 см. Найдите периметр треугольника ACD.
Билет № 8
Треугольник (определение). Равные треугольники. Существование треугольника, равному данному.
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника. Соединяющие вершины отрезки называются сторонами треугольника.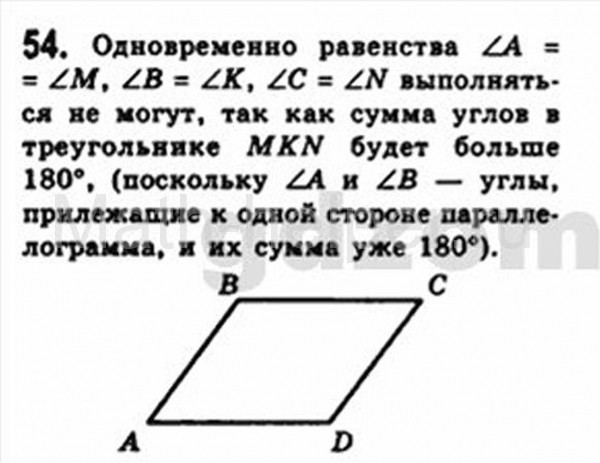 Треугольник обозначается указанием его вершин.
Треугольник обозначается указанием его вершин.
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны.
Каков бы ни был треугольник, существует треугольник, равный данному, отложенный в треугольника, равного данному. заданном направлении, относительно заданной полупрямой.
Третий признак равенства треугольника.
(Третий признак равенства треугольников — по трём сторонам)
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Дано:
ΔABC,
ΔA1B1C1,
AB=A1B1, AC=A1C1, BC=B1C1.
Доказать:
ΔABC= ΔA1B1C1
Доказательство:
Приложим треугольник A1B1C1 к треугольнику ABC так, чтобы
вершина A1 совместилась с вершиной A,
вершина B1 совместилась с вершиной B,
точки C1 и C лежали по разные стороны от прямой AB.

При этом возможны три случая взаимного расположения луча CC1 и угла ACB.
I. Луч CC1 проходит внутри угла ACB.
Проведём отрезок CC1.
По условию AC=A1C1 и BC=B1C1, поэтомутреугольники ACC1 и BCC1 — равнобедренные с основанием CC1.
По свойству равнобедренного треугольника, ∠ACC1=∠AC1C и ∠BCC1=∠BC1C.
Если к равным углам прибывать равные углы, то получим равные углы:
Таким образом, ∠ACB=∠AC1B.
Точки A1 и A, B1 и B совмещены, то есть ∠AC1B и ∠A1C1B1 — один и тот же угол.
Для треугольников ABC и A1B1C1 имеем:
AC=A1C1, BC=B1C1 (по условию), ∠ACB=∠A1C1B1 (по доказанному).
Следовательно, ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
II. Луч CC1 проходит внутри угла ACB.
Так как AC=A1C1 и BC=B1C1, треугольники ACC1и BCC1 — равнобедренные с основанием CC1 и ∠ACC1=∠AC1C и ∠BCC1=∠BC1C (как углы при основании).
Если из равных углов вычесть равные углы, то получим равные углы:
Таким образом, ∠ACB=∠AC1B и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
III. Луч CC1 совпадает со стороной угла ACB.
По условию BC=B1C1, поэтому треугольник BCC1 — равнобедренный с основанием CC1.
Отсюда ∠C1=∠C (как углы при основании) и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
Что и требовалось доказать.
Задача по теме «Неравенства треугольника».
Существует ли треугольник со сторонами 7 см, 2 см и 10 см? Ответ обоснуйте.
Билет № 9
Углы, образованные при пересечении двух прямых секущей. Аксиома параллельности прямых (без доказательства)
При пересечении прямых секущей образуются такие пары углов:
Углы, лежащие между прямыми и по одну сторону секущей, называются внутренними односторонними углами.
Углы, лежащие между прямыми и по разные стороны от секущей, называются внутренними разносторонними углами.
Углы, лежащие по одну сторону секущей, но один из них лежит между заданными прямыми, а другой не лежит между ними, называются соответствующими.
Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной
Внешний угол треугольника (определение).
 Теорема о внешнем угле треугольника.
Теорема о внешнем угле треугольника.
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
Доказательство.
Пусть ABC – данный треугольник. По теореме о сумме углов в треугольнике
- ABС + ∠ BCA + ∠ CAB = 180 º.
Отсюда следует
∠ ABС + ∠ CAB = 180 º — ∠ BCA = ∠ BCD
Теорема доказана.
3. Задача по теме «Признаки равенства прямоугольных треугольников».
У треугольников ABC и DEK: , AC=DK, AB=DE. Докажите, что .
Билет № 10
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников (без доказательства).
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)
Признак равенства прямоугольных треугольников по двум катетам
Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
Признак равенства прямоугольных треугольников по катету и гипотенузе
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Признак равенства по гипотенузе и острому углу
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Признак равенства прямоугольных треугольников по катету и острому углу
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Параллельные прямые (определение). Признаки параллельности двух прямых (доказательство одного из них).
Две прямые a и b на плоскости, которые не пересекаются, называются параллельными и обозначаются a∥b.
Признак 1: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Доказательство:
Через точку К — середину отрезка секущей — проведем перпендикуляр к прямой b — КН, продлим его до пересечения с прямой а.
АК = КВ, так как К середина АВ,
углы при вершине К равны как вертикальные,
∠КВН = ∠КАН’ по условию, ⇒
ΔВКН = ΔАКН’ по стороне и двум прилежащим к ней углам.
Значит ∠АН’К = ∠ВНК = 90°.
Обе прямые а и b перпендикулярны третьей прямой НН’, значит они параллельны.
Признак 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Доказательство:
∠1 = ∠2 по условию (соответственные углы)
∠3 = ∠1 как вертикальные, ⇒
∠2 = ∠3, а это накрест лежащие углы, значит прямые параллельны по первому признаку.
Признак 3: Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Доказательство:
∠1 + ∠2 = 180° по условию (односторонние углы),
∠2 + ∠3 = 180° так как эти углы смежные,
значит ∠1 = ∠3, а это накрест лежащие углы, значит прямые параллельны по первому признаку.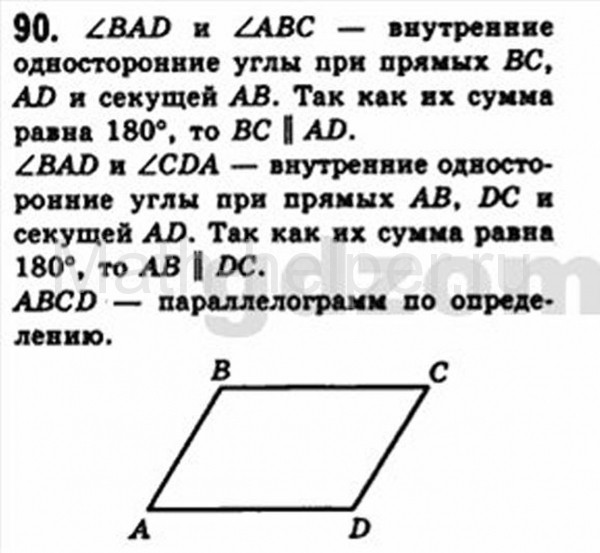
3. Задача по теме » Угол. Измерение углов».
Известно, что =90º. Луч OD делит угол AOB на два угла: и . Найдите , если угол AOD в два раза меньше угла DOB.
Билет № 11
1.Окружность (определение). Радиус, хорда, диаметр окружности.
Окружность-это геометрическая фигура, состоящая из множества точек, находящихся на одинаковом расстоянии от точки, называемой центром окружности.
Радиус- это отрезок, соединяющий центр окружности и любую точку окружности.
Диаметр-это отрезок, соединяющий две точки окружности и проходящий через центр.
Хорда- это отрезок, соединяющий две любые точки окружности.
Треугольник (определение). Теорема о сумме углов треугольника.
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Сумма углов треугольника равна 180 градусам
- Дано: ABC
Доказать: 1+2+3=180o
Доказательство:
1) Проведём а BC, А а
2) 5=1 – накрест лежащие углы при параллельных прямых а и ВС и секущей АВ.
3) 3=4 – накрест лежащие углы при параллельных прямых а и ВС и секущей АС.
4) 5+2+4=180o (развёрнутый угол)
5) 1+ 2+ 3=180oТеорема доказана
Задача по теме «Свойство катета, лежащего против угла в 30º».
В треугольнике ABC =90º, =60º, AB=3,7 см. Найдите длину отрезка BC.
Билет № 12
Высота, биссектриса, медиана треугольника (определения).
Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса — это отрезок, делящий угол треугольника на две равные части.
Высота треугольника — это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение.
Построение треугольника по трём сторонам.
Даны три отрезка, требуется построить из них треугольник.
Данная задача является задачей на построение, для решения которой требуется циркуль и линейка.
При этом следует помнить, что не из каждых трех отрезков можно построить треугольник. Как известно, любая сторона треугольника должна быть меньше суммы двух остальных. Поэтому если один из данных отрезков длиннее, чем два других вместе взятые, то при построении они просто уложатся на первом отрезке, и треугольника не получится.
Алгоритм построения треугольника по трем сторонам сводится к следующему:
Рисуется прямая.
На ней откладывается отрезок, равный одной из данных сторон. Это можно сделать как циркулем, так и линейкой.
Строится окружность (или ее часть) радиусом, равным второму отрезку, и с центром в одной из точек, отложенной на прямой.
Строится окружность (или ее часть) радиусом, равным третьему отрезку, и с центром во второй из точек, отложенных на прямой.
К точке пересечения окружностей проводятся отрезки из точек на прямой. Если были построены не маленькие части окружностей, то таких точек может оказаться две.
 Отрезки надо проводить лишь к одной любой из них.
Отрезки надо проводить лишь к одной любой из них.
В результате получается треугольник, стороны которого равны данным отрезкам. Действительно, ведь одна из его сторон была отмерена на прямой по одному из данных отрезков, а две другие — радиусы, которые равны второму и третьему заданным отрезкам.
Задача по теме «Внешний угол треугольника».
В треугольнике ABC =40º, внешний угол при вершине B равен 70º. Найдите остальные внутренние углы треугольника.
Билет № 13
Перпендикулярные прямые (определение). Перпендикуляр к прямой.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Построение биссектрисы угла.
Построить биссектрису данного угла.
Из точек В и С проведем окружности тем же радиусом r. Пусть точка D – точка их пересечения отличная от A.
Проведем луч AD.
Проведем отрезки BD и CD. Δ ABD = Δ ACD, по третьему признаку равенства треугольников. Отсюда ∠ BAD = ∠ CAD и следовательно AD – биссектриса угла BAC.
3. Задача по теме «Свойства равнобедренного треугольника».
В равнобедренном треугольнике ABC AE – высота, BC- основание. Известно, что BC=12,8 см. Найдите длину отрезка CE.
Билет № 14
Виды треугольников по величине углов.
Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).
Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).
Деление отрезка пополам.
Точки С1 и С2 лежат в разных полуплоскостях от прямой AB. Проведем через точки С1 и С2 прямую. Пусть она пересекает прямую AB в некоторой точке О. Точка О – средина отрезка AB.
Док-во. Δ C1AC2 = Δ C1BC2 по третьему признаку равенства треугольников (AC1 = BC1, AC2 = BC2, по построению и С1С2 — общая). Поэтому ∠ AC1C2 = ∠ BC1C2. Отсюда следует Δ AC1O = Δ BC1O по второму признаку равенства треугольников (∠ AC1C2 = ∠ BC1C2, AC1 = BC1 по построению, OC1 – общая). Следовательно AO = OB и O – середина отрезка AB.
Задача по теме » Смежные углы».
Найдите смежные углы, если один из них в два раза больше другого.
Билет № 15
Расстояние от точки до прямой. Расстояние между параллельными прямыми.
Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на данную прямую.
Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.
Поэтому, чтобы найти расстояние между параллельными прямыми, надо:
1) выбрать на одной из параллельных прямых точку;
2) опустить из выбранной точки к другой прямой перпендикуляр;
3) найти длину этого перпендикуляра.
Неравенство треугольника.
Теорема.
Каждая сторона треугольника меньше суммы двух других сторон.
Доказательство.
Рассмотрим произвольный треугольник ABC и докажем, что AB
В равнобедренном треугольнике BCD 1 = 2, а в треугольнике ABD угол ABD > 1 и, значит, угол ABD > 2. Так как в треугольнике против большего угла лежит большая сторона, то AB < AD. Но AD = AC + CD = AC + CB, поэтому AB < AC + CB. Теорема доказана.
Следствие.
Для любых трех точек A, B и С, не лежащих на одной прямой, справедливы неравенства: AB < AC + CB, AC < AB + BC, BC < BA + AC.
Задача по теме » Взаимное расположение окружностей».
Две окружности диаметром 4 и 8 см касаются внешним образом. Найдите расстояние между центрами этих окружностей.
Билет № 16
Равносторонний треугольник. Свойства равностороннего треугольника
Треугольник называется равносторонним, если все его стороны равны.
Свойства
В равностороннем треугольнике все углы равны между собой и равны 600:
В равностороннем треугольнике высоты, биссектрисы, медианы и пересекаются в одной точке, которая называется центром равностороннего треугольника.
Теорема о соотношении между сторонами и углами треугольника.
Теорема
В треугольнике:
1) против большей стороны лежит больший угол;
1) против большего угла лежит большая сторона.
1) Дано: ∆ ABC, AC>AB.
Доказать: ∠B>∠C.
Доказательство:
Отложим на стороне AC отрезок AK: AK=AB.
Так как AC>AB, то точка K лежит между точками A и C. Следовательно, ∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.
Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.
Значит, у него углы при основании равны: ∠ABK=∠AKB.
Для треугольника BCK ∠AKB — внешний.
Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.
Имеем:
2) Дано: ∆ ABC,
∠B>∠C.
Доказать: AC>AB.
Доказательство:
(методом от противного).Предположим, что неравенство AC>AB — неверное. Тогда либо AC=AB, либо AC∠B=∠C, что противоречит условию.По доказанному в пункте 1), против большей стороны лежит больший угол. Поэтому, если AC∠B<∠C. Снова пришли к противоречию.Значит, выдвинутое нами предположение неверно. Следовательно, AC>AB.
Что и требовалось доказать.
Задача по теме «Смежные и вертикальные углы «.
Сумма данного угла и вертикального ему угла равна 60º. Найдите величину вертикального и смежных с ним углов.
Билет № 17
Равносторонний треугольник. Свойства равностороннего треугольника.
Треугольник называется равносторонним, если все его стороны равны.
Свойства
В равностороннем треугольнике все углы равны между собой и равны 600:
В равностороннем треугольнике высоты, биссектрисы, медианы и пересекаются в одной точке, которая называется центром равностороннего треугольника.
Вертикальные углы (определение). Свойства вертикальных углов
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого
3. Задача по теме «Отрезок. Измерение отрезков «.
На отрезке OD, длина которого 24 см, отмечена точка A. Найдите длину отрезка AD, если отрезок OA на 8 см длиннее отрезка AD.
Билет № 18
Прямоугольный треугольник (определение). Катет. Гипотенуза. Свойства прямоугольного треугольника (без доказательства)
Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами прямоугольного треугольника, а сторона, противолежащая прямому углу – гипотенузой прямоугольного треугольника.
1. Сумма острых углов равна 90
2. Катет лежащий против угла 30 равен половине гипотенузы
3. Обратная теорема: Если катет равен половине гипотенузы, то угол, лежащий против него равен 30
2. Построение угла, равному данному.
Отложить от данного луча угол, равный данному.
Решение. Данный угол с вершиной А и луч ОМ
Проведем произвольную окружность с центром в вершине О данного угла. Пусть В и С — точки пересечения окружности со сторонами угла (рис а). Радиусом ОВ проведем окружность с центром в точке О — начальной точке данного луча (рис. б). Точку пересечения этой окружности с данным лучом обозначим С1. Опишем окружность с центром С1 и радиусом ВС. Точка В1 пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ОBC = Δ ОВ1С1(третий признак равенства треугольников).
Задача по теме «Внутренние и внешние углы треугольника «.
Один из внешних углов прямоугольного треугольника равен 130º. Найдите острые углы треугольника
Билет № 19
Отрезок (определение). Длина отрезка. Основное свойство измерения отрезков.
Отрезок — это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и конец, а значит можно измерить её длину
Расстоянием между двумя точками называется длина отрезка .
1.Каждый отрезок имеет определенную длину, большую нуля.
2.Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой.
3.При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.
4.Два отрезка называются равными, если равны их длины.
Теорема о соотношении между сторонами и углами треугольника.
Теорема
В треугольнике:
1) против большей стороны лежит больший угол;
1) против большего угла лежит большая сторона.
1) Дано: ∆ ABC, AC>AB.
Доказать: ∠B>∠C.
Доказательство:
Отложим на стороне AC отрезок AK: AK=AB.
Так как AC>AB, то точка K лежит между точками A и C. Следовательно, ∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.
Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.
Значит, у него углы при основании равны: ∠ABK=∠AKB.
Для треугольника BCK ∠AKB — внешний.
Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.
Имеем:
2) Дано: ∆ ABC,
∠B>∠C.
Доказать: AC>AB.
Доказательство:
(методом от противного).Предположим, что неравенство AC>AB — неверное. Тогда либо AC=AB, либо AC∠B=∠C, что противоречит условию.По доказанному в пункте 1), против большей стороны лежит больший угол. Поэтому, если AC∠B<∠C. Снова пришли к противоречию.Значит, выдвинутое нами предположение неверно. Следовательно, AC>AB.
Что и требовалось доказать.
Задача по теме «Виды треугольников «.
Периметр равностороннего треугольника DEK равен 18 см. Найдите стороны треугольника DEK .
Билет № 20
1. Угол (определение). Развернутый угол. Внутренняя и внешняя область угла.
Основное свойство откладывания углов.
Угол — это геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.
Лучи называются сторонами угла, а их общее начало — вершиной угла.
Развернутый угол — это угол, стороны которого лежат на одной прямой.Градусная мера развёрнутого угла равна 180º.Каждая сторона развернутого угла дополняет другую сторону до прямой, то есть стороны развёрнутого угла являются дополнительными лучами. Угол разделяет плоскость на две части, каждая из которых также называется углом, то может возникнуть неоднозначность в том, какой именно из углов рассматривается. Чтобы наглядно показать, о каком именно угле идёт речь, на чертеже обычно делается какое-нибудь специальное обозначение.
Тот из углов, который рассматривается, на чертеже обычно отмечают дугой, проведённой от одной стороны угла до другой:
Часть плоскости, расположенная между сторонами рассматриваемого угла называется внутренней областью угла. Часть плоскости не принадлежащая рассматриваемому углу называется внешней областью угла:
От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°,и только один.
3.Теорема о существовании и единственности перпендикуляра к прямой.
Теорема.
Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
Доказательство
Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a.
Значит отрезок AB ⊥ a.
Теперь докажем единственность перпендикуляра AB.
Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.
3. Задача по теме «Сумма углов треугольника «.
Углы треугольника DKC относятся как 2:4:3. Найдите углы треугольника DKC.
Деома — Продукты — Алгебра
Программный продукт «Интерактивная математика», 7 класс, позволяет эффективно вести углублённое изучение математики с использованием возможностей компьютера на уроках алгебры и геометрии в 7 классе. Продукт не привязан к какому-то одному учебнику. Его удобно использовать при работе с учебниками по алгебре таких авторов, как А. Г. Мордкович и Ю. Н. Макарычев; по геометрии — И. Ф. Шарыгин и Л. С. Атанасян.
Последняя версия продукта от 12 августа 2015:
Скачать «Интерактивная математика», Алгебра и геометрия, 7 класс v1.4.3.19 для Windows
Чтобы получить демо-версию, установите программу. При первом запуске выберите демо (из двух вариантов: демо или полный).
В Демо вы можете открыть каждый файл и исследовать интерактивные рисунки. Ограничения демо-версии: недоступны шаги решения и ответы в большинстве файлов.
Возможные варианты покупки и цены вы можете узнать на странице Как купить
Ниже представлены снимки экрана при работе с программой.
Рисунки можно увеличить ↓
Версия 1.4.3.19 от 12 августа 2015 (последняя)
Показать прежние версииВерсия 1.4.3.18 от 9 февраля 2015
Версия 1.4.3.17 от 11 ноября 2012
Версия 1.4.3.16 от 9 октября 2011
Версия 1.4.3.15 от 28 июня 2011
Версия 1.4.3.14 от 6 мая 2011
Версия 1.4.3.13 от 18 апреля 2011
Версия 1.4.3.11 от 23 января 2011
Версия 1.4.3.10 от 4 января 2011
Версия 1.4.3.9 от 4 ноября 2010
Версия 1.4.3.8 от 5 сентября 2010
Версия 1.4.3.7 от 24 августа 2010
Версия 1.4.3.6 от 23 августа 2010
Версия 1.4.3.5 от 16 августа 2010
Версия 1.4.3.3 от 10 мая 2010
Версия 1.4.3.2 от 10 мая 2010
Версия 1.4.3.0 от 23 марта 2010
Версия 1.4.2.0 от 17 марта 2010
Версия 1.4.1.0 от 1 марта 2010
Версия 1.4.0.0 от 20 февраля 2010
Версия 1.3.8.0 от 10 февраля 2010
Версия 1.3.7 от 4 февраля 2010
Версия 1.3.6 от 15 января 2010
Версия 1.3.5 от 18 ноября 2009
Версия 1.3.4 от 13 ноября 2009
Версия 1.3.3 от 1 ноября 2009: изменения в файлах многочлена и степени.
Версия 1.3.2 от 14 октября 2009
Версия 1.3.1 от 13 сентября 2009
Версия 1.3.0 от 25 августа 2009: полная переработка по рекомендациям учителей, работающих с программой.
Версия 1.0.2 от 12 апреля 2009
Версия 1.0.1 от 16 марта 2009
Скрыть прежние версииКак выбрать металлочерепицу — Реальное время
6 критериев выбора кровельного материала
В прошлой статье мы поговорили о достоинствах и недостатках металлочерепицы в качестве кровельного материала. Сегодня разберем, на какие критерии обращать внимание, выбирая ее, ведь строительный рынок предлагает большое разнообразие форм и типоразмеров.
Критерий №1: толщина металлического листа
Лист стали, из которого сделана металлочерепица, может быть разной толщины. Промышленность выпускает этот материал толщиной от 0,4 до 0,7 мм. Чем толще лист, тем дороже стоит металлочерепица. Специалисты рынка рекомендуют присматриваться к толщине не менее 0,5 мм (об этой толщине стального проката говорит и ГОСТ на металлическую черепицу). Варианты с самым тонким листом непрочные: в таком металле остаются вмятины, металл тонкий и легко прогибается, поднимать его на крышу надо аккуратно, потому что он легко гнется.Многие гаражные производства используют самый тонкий металл, до которого могут дотянуться, да еще и покрывают некачественным полимерным покрытием. Поэтому, выбирая толщину листа металлочерепицы, лучше заплатить за материал, который прослужит не 10, а 20 лет, и даже больше.
Критерий №2: качество стали
Есть три генеральных различия между стальным сырьем. Обычно крупные заводы работают с тремя регионами происхождения: с российской сталью, европейской и азиатской. Как водится, самая дорогая — европейская, российская — это среднеценовой сегмент, а самая дешевая (и как говорят многие эксперты рынка, самая сомнительная по качеству) — азиатская. Бывает так, что на гаражных производствах, не мудрствуя лукаво, наносят декоративное покрытие прямо на голую сталь, даже без защитного слоя. Прослужит такая металлочерепица, понятное дело, недолго.Поэтому обязательно при покупке надо требовать маркировку, сопроводительные документы, и не доверять сомнительным продавцам. Особенно сегодня, когда металл подорожал, не нужно вестись на самые дешевые предложения: вполне возможно, что с этой сталью что-то не так.
Критерий №3: слой оцинковки
Оцинковка — это самый популярный, самый традиционный способ защитить сталь от коррозии. Лист стали погружается в расплав цинка, в результате происходит реакция, прочно сплавляющая два металла. Цинк, таким образом, становится со сталью единым целым, а не наносится на нее подобно краске. Цинковое покрытие может быть двух классов — первого (275 г/квадратный метр и больше) и второго (140—275 г/квадратный метр). Соответственно, первый класс — это более долговечная металлочерепица, потому что чем толще слой цинка, тем лучше сталь защищена от коррозии и других популярных проблем.Оцинковка стали контролируется ГОСТом №14918-80. В нем говорится, что в оцинкованных металлических листах цинка должно быть не меньше 142,5 грамма на квадратный метр (получается слой толщиной от 10 мкм). Если меньше — металлочерепицу из такой стали покупать не надо.
Критерий №4: форма волны и цвет
Геометрия поверхности и разнообразие цветов металлочерепицы сегодня очень велики. При этом надо понимать: геометрия волны и ее высота определяют еще и жесткость листа. Поэтому чем выше рельеф поверхности, тем менее гибкая металлочерепица. Изгиб получают путем холодного формования на прокатных станах. Чем выше волна, тем уже будет готовое полотно, потому что листовая заготовка, как правило, имеет одинаковую ширину (1250 мм). И это тоже надо учитывать при выборе: если вам нужно меньше стыков, то лучше выбирать невысокую волну.Если высота волны до 50 мм, то это считается малой волной, если больше — высокой. Металлочерепица с малой высотой волны выпускается практически на всех заводах стальной кровли, и на складах она есть всегда. Металлочерепица с большой высотой волны дороже, потому что выглядит более рельефно и эффектно. Бывает и асимметричная, и асимметрично скошенная волна.
Что выбрать — смотрите сами, в зависимости от вашего кошелька и эстетических предпочтений.
Критерий №5: тип защитного покрытия
От защитного полимерного покрытия металлочерепицы зависит долговечность материала, а значит, и его цена. Самое дорогое покрытие — пластизол. Он сделан на основе ПВХ, у него слегка шероховатая поверхность. Толщина этого покрытия самая серьезная — 200 микрон, оно очень стойкое и к атмосферным воздействиям, и к случайным механическим повреждениям. А вот на цветостойкость пластизола влияет ультрафиолетовое излучение. Поэтому лучше выбирать светлые цвета, если вы остановились на этом покрытии. Палящие солнечные лучи пластизолу на пользу тоже не идут — он может под ними лопнуть.Следом в ценовой линейке идет полимерное покрытие на основе полиуретана с добавлением полиамида. Толщина такого покрытия 50 микрон, у него тоже высокая стойкость к воздействиям окружающей среды. Он устойчив к температурным перепадам, свойственным для нашей климатической полосы, не выгорает под солнцем.
Следом в ценовой линейке — полиэстер (чуть дороже матовый, модифицированный тефлоном, а самый бюджетный — глянцевый). В основе глянцевого покрытия — полиэфирная краска толщиной до 25 микрон. Выцветает она почти всегда, ее легко поцарапать, зато при изгибах металлического листа такое покрытие не нарушается. Все срезы на листах с полиэстеровым покрытием рекомендуют сразу же обрабатывать краской по металлу.
Бывает еще покрытия с каменным гранулятом: он делает поверхность шероховатой. Гранулы придают цвет и защищают металл от механических повреждений.
Словом, покрытий множество, каждый год на рынок выходят новые комбинации полимерных материалов. В каждом случае нужно изучать техническую документацию. Совет: обязательно посмотрите на «живой образец» черепицы, а не выбирайте ее по каталогу: цвет покрытия и его фактуру надо увидеть вживую.
Критерий №6: производство
Выбирая металлочерепицу, нужно отталкиваться от производителя. Желательно, чтобы это не было гаражное производство: завод должен быть крупным и уважаемым.На нем должен использоваться качественный материал: толщина стали — не менее 0,5 мм, содержание цинка — не ниже 225 г/квадратный метр. На производстве должно быть современное оборудование. Важно, чтобы на заводе была собственная лаборатория контроля качества. А еще продукция должна соответствовать ГОСТам и иметь об этом соответствующие документальные подтверждения.
Центр педагогических измерений
Работа по организации и подготовке внедрения системы критериального оценивания в общеобразовательные школы РК
Назарбаев Интеллектуальные школы – прорывной проект в области образования Республики Казахстан, это «точка роста», способствующая модернизации системы среднего образования в Республике Казахстан.
Стратегией развития Автономной организации образования «Назарбаев Интеллектуальные школы» до 2020 года определена миссияИнтеллектуальных школ: «Способствовать повышению интеллектуального потенциала Казахстана через разработку и внедрение модели инновационной, поли язычной системы школьного образования естественно-математического направления, сочетающей в себе лучшие казахстанские традиции, международный опыт и практику».
Одна из стратегических задач АОО – трансляция опыта Интеллектуальных школ в систему среднего образования Казахстана.
Организационной основой реализации этой задачи является Дорожная карта трансляции опыта Назарбаев Интеллектуальных школ в систему образования страны на 2013-2017 годы (скачать), которая будет способствовать дальнейшему реформированию отечественной системы среднего образования.
С целью обеспечения внедрения в процесс обучения на всех уровнях образования современных методик и технологий с учетом опыта автономной организации образования «Назарбаев Интеллектуальные школы» в 2012 году Министерством образования и науки Республики Казахстан определены 30 базовых школ, которые работают в тесном сотрудничестве с АОО.
Система критериального оценивания в рамках внедрения обновленного содержания образования
В соответствии с графиком перехода на обновленное содержание среднего образования, система критериального оценивания учебных достижений обучающихся прошла апробацию в 1 классах 30-ти пилотных школ в 2015-2016 учебном году и с 2016-2017 учебного года внедрена в 1 классы общеобразовательных школ страны. В 2017-2018 учебном году внедряется во 2, 5, 7 классах общеобразовательных школ.
Одним из условий успешной реализации системы критериального оценивания является методическая обеспеченность учителя рекомендациями по оцениванию, качественными инструментами оценки, системой электронного документооборота и отчетности.
Для эффективной и стандартизированной оценки результатов обучения обучающихся разработаны критерии и задания оценивания в соответствии с целями и ожидаемыми результатами обучения. Критерии и задания позволяют определять не только уровень знаний, но и способность обучающимися применять знания и навыки мышления более высокого уровня: анализ, синтез, оценку. Разработанные задания содержат описание уровней их выполнения, шаблоны информирования обучающихся и родителей, что помогает учителю понимать, на каком этапе обучения у обучающегося возникают трудности, какая педагогическая поддержка ему нужна.
В разработке заданий участвуют специалисты и учителя, прошедшие обучение у международных экспертов высокого уровня.
В 2016-2017 гг. для обеспечения процесса оценивания подготовлены:
1. Руководство по критериальному оцениванию для учителей начальной школы на казахском и русском языках
2. Руководство по критериальному оцениванию для учителей основной и общей средней школ на казахском и русском языках
3. Руководство по критериальному оцениванию для региональных и школьных координаторов на казахском и русском языках
4. Сборники заданий для формативного оценивания по предметам 1, 2, 5 и 7 классов на казахском и русском языках
5. Методические рекомендации по суммативному оцениванию по предметам 1, 2, 5 и 7 классов на казахском и русском языках
6. Спецификации суммативного оценивания по предметам для 5, 7 классов на казахском и русском языках
7. Информационные буклеты о критериальном оценивании учебных достижений обучающихся для родителей и учащихся на казахском и русском языках
8. Серия видеофильмов по критериальному оцениванию
Для обеспечения равного и своевременного доступа учителей общеобразовательных школ к инструктивно-методическим материалам создан модуль «Система критериального оценивания» на электронном портале «Системно-методический комплекс» (smk.edu.kz). На данном модуле размещены более 300 инструктивно-методических материалов по критериальному оцениванию, в том числе видео и презентационные ресурсы, формы электронного журнала и инструкции по их заполнению.
Ведется методическая и консультационная поддержка учителей в разделе «Система критериального оценивания» и на дискуссионной площадке Системно-методического комплекса, а также создан форум для региональных и школьных координаторов по критериальному оцениванию в целях эффективного взаимодействия и своевременного информирования.
Диагностическое тестирование
Обновленное содержание образования проходит апробацию в пилотных школах страны, среди которых сельские и городские школы, гимназии, лицеи, средние и малокомплектные школы. Для оценки эффективности учебных программ, системы критериального оценивания и методики преподавания проводится диагностическое тестирование учащихся 30 пилотных и 16 контрольных школ.
Диагностическое тестирование учащихся проводилось трижды: в 1 классе «на входе» – в начале 2015-2016 учебного года и «на выходе» – к концу 2015-2016 учебного года, во 2 классе «на выходе» — к концу 2016-2017 учебного года. В 2017-2018 гг. диагностическое тестирование продолжится в 3 и 4 классах.
Результаты 2015-2017 гг. показали, что обновленное содержание образования и методика преподавания обеспечили серьезное преимущество учащихся пилотных школ. Так, «на выходе» во 2 классе они показали более значимый прогресс среднего балла (+30,2 баллов), чем обучающиеся контрольных школ (+14,7 баллов). Данное преобладание отмечено в разрезе всех трех диагностических тестирований и по всем предметам.
Более подробная информация и результаты диагностического тестирования представлены в отчетах (скачать).
Геометрия 7 Атанасян (Мельникова) | КОНТРОЛЬНЫЕ РАБОТЫ
Геометрия 7 Атанасян (Мельникова) — цитаты контрольных работ в 2-х вариантах с ответами из пособия «Геометрия 7 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных работ по геометрии в 7 классе рекомендуем купить книгу: Наталия Мельникова: Геометрия. 7 класс. Контрольные работы к учебнику Л.С. Атанасяна и др. ФГОС, в которой контрольные работы представлены в 4-х вариантах.
Геометрия 7 класс (Атанасян)
Контрольные работы:
Контрольная работа № 1. Начальные геометрические сведения: измерение отрезков и углов; перпендикулярные прямые; биссектриса угла; смежные и вертикальные углы.
К-1. Вариант 0 К-1. Вариант 1 К-1. Вариант 2 К-1. Вариант 3 К-1. Вариант 4
Контрольная работа № 2. Треугольники: признаки равенства треугольников; медиана, биссектриса, высота треугольника; свойства равнобедренного треугольника; окружность.
К-2. Вариант 0 К-2. Вариант 1 К-2. Вариант 2 К-2. Вариант 3 К-2. Вариант 4
Контрольная работа № 3. Параллельные прямые: свойства углов при параллельных прямых и секущей; признаки параллельности прямых; свойства равнобедренного треугольника; окружность.
К-3. Вариант 0 К-3. Вариант 1 К-3. Вариант 2 К-3. Вариант 3 К-3. Вариант 4
Контрольная работа № 4. Соотношения между сторонами и углами треугольника: сумма углов треугольника; внешний угол треугольника; свойства прямоугольных треугольников; признаки равенства прямоугольных треугольников.
К-4. Вариант 0 К-4. Вариант 1 К-4. Вариант 2 К-4. Вариант 3 К-4. Вариант 4
Контрольная работа № 5 Итоговая за курс 7 класса: медиана, биссектриса, высота треугольника; свойства и признак равнобедренного треугольника; свойства углов при параллельных прямых и секущей; признаки параллельности прямых; окружность; сумма углов треугольника.
К-5. Вариант 0 К-5. Вариант 1 К-5. Вариант 2 К-5. Вариант 3 К-5. Вариант 4
Каждая контрольная работа направлена на проверку усвоения материала главы учебника. Указанные ниже проверяемые элементы знаний отражают только тот материал, который изучался в данной теме. При этом, естественно, задачи тематической контрольной работы могут проверять также и усвоение сведений, изучавшихся в предыдущих темах. Так, например, в контрольной работе № 3 для решения задач нужно применять сведения о вертикальных и смежных углах, о равенстве треугольников, о свойствах равнобедренного треугольника.
Геометрия 7 Атанасян (Мельникова) — цитаты контрольных работ в 2-х вариантах с ответами из пособия «Геометрия 7 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях.
Измерение углов
Измерение угловПонятие угла
Понятие угла — одно из важнейших понятий в геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.Есть две обычно используемые единицы измерения углов.Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минут. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунды, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. |
Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут 7.5 & град.
Когда один угол рисуется на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы. Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла.Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равно π /180 радиани 1 радиан равен 180/ π градусовБольшинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор. |
Краткая справка по истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге Elements of Algebra явно сказал, что углы следует измерять по длине дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e iθ = cos θ + i sin θгде θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, тогда мера в радианах равна 1.5.Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r, в умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, если он измеряется в радианах.Так как площадь всего круга равна πr 2 , а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтомуОбщие углы
Ниже приведена таблица общих углов как при измерении в градусах, так и при измерении радиан. Обратите внимание, что измерение в радианах дано в единицах π . Его, конечно, можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом π . .| Уголок | градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С.Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичные дроби градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, , чтобы найти длину продолжающейся дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, , чтобы найти угол в центре.
(а). л = 0,16296, л = 12,587.
(б). л = 1,3672, л = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286, умноженное на 60, равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но необходимо сначала преобразовать из градусного измерения в радиан .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас есть круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.
14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.
23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.
Насчет цифр точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно теперь, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.Другой пример см. В задаче 3 (а). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, так как ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.
МАТЕМАТИКА — TACOMA
TMATH 109 Финансовые и математические основы (5) QSR
Интерпретирует повседневные финансовые события, используя количественные и алгебраические рассуждения и модели. Студенты изучают графики и уравнения линейных, экспоненциальных и логарифмических функций с упором на личные финансы, практикуя принятие решений и решение проблем. Темы могут включать бюджетирование, ссуды, кредитные карты, налоги, покупку в рассрочку, ипотеку, амортизацию и инвестирование.Предварительное условие: минимум 250 баллов по модифицированному тесту UWT на основе ACC-QAS или минимум 100 баллов по математическому тесту Tacoma Directed Self Placement.
Подробная информация о курсе в MyPlan: TMATH 109
TMATH 110 Вводная статистика с приложениями (5) NW, QSR
Обращается к вводным статистическим концепциям и анализу в современном обществе. Включает описательную статистику, графическое отображение данных, нормальное распределение, сбор данных, вероятность, элементы статистического вывода, проверку гипотез, а также линейную регрессию и корреляцию.Практические примеры, используемые для демонстрации статистических концепций. Предварительные условия: минимальная оценка 2.0 по TMATH 098, MATH 098, TMATH 109, TMATH 124 или MATH 124, минимальный балл 237 на экзамене UWT с измененным размещением на основе экзамена ACC-AAF или минимальный балл 200 по математическому тесту Tacoma Directed Self Placement.
Просмотр сведений о курсе в MyPlan: TMATH 110
TMATH 115 Предварительное исчисление I: функции (5) QSR
Знакомит с концепцией функции, ее обозначениями и готовит студентов к работе с кусочками, экспоненциальными, логарифмическими полиномиальные и рациональные функции.Подчеркивает вычислительные навыки, чтение графиков и решение проблем. Одна из двух частей. Можно подсчитать максимум 10 кредитов из TMATH 115, TMATH 116 и TMATH 120. Предварительные условия: минимальная оценка 2.0 по TMATH 098, MATH 098 или TMATH 109, минимальная оценка 237 по модифицированному тесту UWT на основе ACC-AAF или минимум 300 баллов по математическому тесту Tacoma Directed Self Placement Math. .
Подробная информация о курсе в MyPlan: TMATH 115
TMATH 116 Предварительное исчисление II: тригонометрия (5) NW, QSR
Продолжает изучение концепции функции, ее обозначений, а также тригонометрических и обратных тригонометрических функций.Представляет параметризованные кривые, полярные координаты и комплексные числа. Делает упор на вычислительные навыки, чтение графиков и методы решения проблем. Вторая из двух частей. Можно подсчитать максимум 10 кредитов из TMATH 115, TMATH 116 и TMATH 120. Предварительные условия: минимальная оценка 2,0 по TMATH 115, минимальная оценка 263 по тесту ACC-AAF или минимум 400 баллов по тесту Tacoma Directed Self Placement Math Test.
Просмотрите подробности курса в MyPlan: TMATH 116
TMATH 120 Precalculus (5) NW, QSR
Курс ускоренного обзора, охватывающий содержание TMATH 115 и TMATH 116 за один семестр.Изучает функции и обозначения функций, включая полиномиальные, рациональные, экспоненциальные, логарифмические, тригонометрические и обратные тригонометрические функции. Рекомендуемый сопреквизит: TMATH 158. Необходимое условие: минимальный балл 2,0 в TMATH 098, балл 42-120 на тестовом экзамене ACC-CL, минимальный балл 263 на тестовом экзамене ACC-AAF или минимальный балл. 400 экзаменов по самооценке по математике в Такоме.
Просмотрите подробности курса в MyPlan: TMATH 120
TMATH 124 Исчисление с аналитической геометрией I (5) NW, QSR
Первая четверть в исчислении функций одной переменной.Подчеркивает дифференциальное исчисление. Акцентирует внимание на приложениях и решении проблем с использованием инструментов исчисления. Невозможно получить зачет, если кредит заработан в TMATH 122. Необходимое условие: минимальный балл 2,0 в TMATH 116 или TMATH 120, минимальный балл 68 на MPT-A, минимальный балл 75 на тесте MATHEC, минимальный балл 2 по тесту AP MATH (AB или BC), минимум 276 баллов по тесту ACC-AAF или минимум 500 баллов по тесту Tacoma Directed Self Placement Math Test; рекомендуется: Рекомендуемый совместный реквизит: TMATH 159.
Просмотрите подробности курса в MyPlan: TMATH 124
TMATH 210 Промежуточная статистика с приложениями (5) NW, QSR
Исследует промежуточные концепции статистического вывода и тестирования с использованием статистического программного обеспечения для анализа. Включает выборку и экспериментальный план, t-тесты, дискретные распределения, пропорции, ANOVA, регрессию, преобразования и тесты хи-квадрат. Анализирует наборы данных из различных дисциплин, таких как экологические и социальные науки. Включает критический обзор современных исследований.Предпосылка: минимальная оценка 2.0 по TMATH 110 или STAT 220. Предлагается: WSp.
Подробная информация о курсе в MyPlan: TMATH 210
TMATH 316 Финансовая математика (5) QSR
Знакомит студентов с фундаментальными понятиями финансовой математики: сложный и простой процент, номинальные и эффективные ставки, настоящая и будущая стоимость, ставки дисконтирования, сила представляет интерес. Покрывает аннуитеты как постоянные, так и переменные денежные потоки, ссуды, амортизацию, рефинансирование ссуд и облигации. Исследования могут также включать временную структуру процентных ставок, спотовых ставок, арбитража, продолжительности, выпуклости и иммунизации.Предварительное условие: минимальная оценка 2,0 в TMATH 126 Предлагается: W.
Подробная информация о курсе в MyPlan: TMATH 316
TMATH 390 Probability and Statistics in Engineering and Science (5) NW, QSR
Исследует вероятность и статистику с использованием исследовательского анализа данных и интерактивные вычисления. Темы исследования, включая условную вероятность, независимость, случайные величины, функции распределения, описательную статистику, преобразования, ошибки выборки, доверительные интервалы, наименьшие квадраты и максимальное правдоподобие.Предварительное условие: минимальная оценка 2.0 в TMATH 126 или MATH 126.
Подробная информация о курсе в MyPlan: TMATH 390
TMATH 410 Регрессионное моделирование с приложениями (5) QSR
Исследует регрессионные модели с приложениями; включая множественную линейную регрессию, выбор модели, остаточный анализ, преобразования переменных и категориальные данные. Исследования могут также включать обобщенные линейные модели, нелинейную регрессию, матричную формулировку и смешанные модели. Условие: либо минимум 2 балла.0 в TMATH 210 и TMATH 124 или минимальная оценка 2,0 в TMATH 390.
Подробная информация о курсе в MyPlan: TMATH 410
TMATH 412 Криптография: теория и практика (5) QSR
Охватывает «классические» криптосистемы и их криптоанализ, подход Шеннона к криптографии, включая энтропию и совершенную секретность, блочные шифры и AES. Содержит криптосистему RSA, криптографию с открытым ключом на основе дискретных логарифмов и схемы подписи. Взламывает простые шифры с помощью компьютера.Предварительное условие: минимальная оценка 2.0 по TCSS 321, TMATH 300 или TMATH 308.
Подробная информация о курсе в MyPlan: TMATH 412
Математика 7 класса — Кембриджские государственные школы
В 7 классе учебное время должно быть сосредоточено на четырех важнейших областях:
- развитие понимания и применение пропорциональных отношений;
- развитие понимания операций с рациональными числами и работа с выражениями и линейными уравнениями;
- решение задач, связанных с масштабными чертежами и неформальными геометрическими конструкциями, и работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и
- делает выводы о популяциях на основе выборок.
Поддержка вашего ребенка в 7-м классе по математике
Совет школ большого города создал «дорожные карты» для родителей, чтобы дать родителям рекомендации относительно того, что их ребенок будет изучать по математике и как они могут поддержать это обучение. Эти родительские дорожные карты также предоставляют трехлетние снимки, показывающие, как отобранные стандарты прогрессируют из года в год:
Родительская дорожная карта: поддержка вашего ребенка в математике
Стандарты математической практики
Структура 2011 года вводит Стандарты математической практики.Эти стандарты дополняют стандарты содержания, так что учащиеся все больше вовлекаются в предмет по мере того, как они растут в математической зрелости и опыте в течение начальной, средней и старшей школы. Эти стандарты одинаковы для всех классов от дошкольного до 12 класса.
Здесь можно найти объяснение того, как стандарты могут быть выделены в 7-м классе.
Эти восемь практик можно сгруппировать в следующие категории, как показано в таблице ниже:
Умственные способности продуктивного математического мыслителя: | Рассуждение и объяснение |
Моделирование и использование инструментов | |
Видеть структуру и обобщать |
Стандарты содержания, которые должны быть охвачены в Уровне 7
Направленность обучения в 7-м классе определяется рамками учебной программы по математике штата Массачусетс на 2011 год, которые можно найти на веб-сайте Департамента начального и среднего образования.
Чтобы узнать об основных стандартах Common Core по математике, щелкните здесь.
Средняя учебная программа / Планы и ресурсы по математике для 7-го класса
В 7-м классе учебное время должно быть сосредоточено на четырех критических областях: (1) развитие понимания и применение пропорциональных отношений; (2) развитие понимания операций с рациональными числами и работа с выражениями и линейными уравнениями; (3) решение задач, связанных с масштабными чертежами и неформальными геометрическими конструкциями
, а также работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
(1) Учащиеся расширяют свое понимание соотношений и развивают понимание пропорциональности для решения одно- и многоэтапных задач. Учащиеся используют свое понимание соотношений и пропорциональности для решения широкого круга задач, связанных с процентами, включая те, которые связаны со скидками, процентами, налогами, чаевыми и увеличением или уменьшением процентов
. Учащиеся решают задачи о масштабных чертежах, соотнося соответствующие длины между объектами или используя тот факт, что отношения длин внутри объекта сохраняются в подобных объектах.Учащиеся составляют график пропорциональных соотношений и неформально понимают единицу скорости как меру
крутизны соответствующей линии, называемой наклоном. Они отличают пропорциональные отношения от других отношений.
(2) Учащиеся развивают единое понимание чисел, распознавая дроби, десятичные дроби (которые имеют конечное или повторяющееся десятичное представление) и проценты как различные представления рациональных чисел. Учащиеся распространяют сложение, вычитание, умножение и деление на все рациональные числа, сохраняя свойства операций и отношения между сложением и вычитанием, а также умножением и делением.Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневного контекста (например, суммы задолженности или температуры ниже нуля), учащиеся объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами. Они используют арифметику рациональных чисел, когда формулируют выражения и уравнения с одной переменной и используют эти уравнения для решения задач.
(3) Учащиеся продолжают свою работу с площадью с 6 класса, решая задачи, связанные с площадью и окружностью круга и площадью поверхности трехмерных объектов.При подготовке к работе над соответствием и сходством в 8 классе они рассуждают об отношениях между двумерными фигурами, используя масштабные чертежи и неформальные геометрические конструкции, и они знакомятся с отношениями
между углами, образованными пересекающимися линиями. Учащиеся работают с трехмерными фигурами, связывая их с двухмерными фигурами, исследуя поперечные сечения. Они решают реальные и математические задачи, касающиеся площади, площади поверхности и объема двух- и трехмерных объектов
, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
(4) Учащиеся опираются на свою предыдущую работу с отдельными распределениями данных, чтобы сравнить два распределения данных и ответить на вопросы о различиях между популяциями. Они начинают неформальную работу со случайной выборки для создания наборов данных и узнают о важности репрезентативных выборок для составления выводов.
7 класс | Математика | Iowa Core
В 7 классе учебное время должно быть сосредоточено на четырех критических областях: (1) развитие понимания и применение пропорциональных отношений; (2) развитие понимания операций с рациональными числами и работа с выражениями и линейными уравнениями; (3) решение задач, связанных с масштабными чертежами и неформальными геометрическими конструкциями, и работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
- Учащиеся расширяют свое понимание соотношений и развивают понимание пропорциональности для решения одно- и многоэтапных задач. Учащиеся используют свое понимание соотношений и пропорциональности для решения широкого круга задач, связанных с процентами, включая те, которые касаются скидок, процентов, налогов, чаевых и увеличения или уменьшения процента. Учащиеся решают задачи о масштабных чертежах, соотнося соответствующие длины между объектами или используя тот факт, что отношения длин внутри объекта сохраняются в подобных объектах.Учащиеся составляют график пропорциональных соотношений и неформально понимают единичную ставку как меру крутизны соответствующей линии, называемой наклоном. Они отличают пропорциональные отношения от других отношений.
- Учащиеся развивают единое понимание чисел, распознавая дроби, десятичные дроби (которые имеют конечное или повторяющееся десятичное представление) и проценты как различные представления рациональных чисел. Студенты расширяют сложение, вычитание, умножение и деление на все рациональные числа, сохраняя свойства операций и отношения между сложением и вычитанием, а также умножением и делением.Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневного контекста (например, суммы задолженности или температуры ниже нуля), учащиеся объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами. Они используют арифметику рациональных чисел, когда формулируют выражения и уравнения с одной переменной и используют эти уравнения для решения задач.
- Ученики продолжают свою работу с площадью с 6 класса, решая задачи, связанные с площадью и окружностью круга и площадью поверхности трехмерных объектов.При подготовке к работе над соответствием и сходством в 8 классе они рассуждают о взаимосвязях между двумерными фигурами, используя масштабные чертежи и неформальные геометрические конструкции, и они знакомятся с отношениями между углами, образованными пересекающимися линиями. Учащиеся работают с трехмерными фигурами, связывая их с двухмерными фигурами, исследуя поперечные сечения. Они решают реальные и математические задачи, касающиеся площади, площади поверхности и объема двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
- Учащиеся опираются на свою предыдущую работу с единичными распределениями данных, чтобы сравнить два распределения данных и ответить на вопросы о различиях между популяциями. Они начинают неформальную работу со случайной выборки для создания наборов данных и узнают о важности репрезентативных выборок для составления выводов.
BCISD
Отчет об оценке по геометрии для первокурсников BCISD
Первые 9 недель, интегрированная геометрия
Класс 2011 г. (первокурсники '07 -'08)
Центр математики и науки округа Берриен
G7.1 ТЕСТ NtBk G6.R G7.2 G7.3 G7.4 G7.5 G7.6 Penta G7.7 G7.8 G7.9 MML # 5 CCC-1
28 1/28 Quiz Quiz Quiz Cons Quiz 2/8 proof
Номер ящика P = 23 P = 100 P = 40 P = 175 P = 26 P = 21 P = 10 P = 10 P = 10 P = 50 P = 26 P = 21 P = 10 P = 10 P = 25 процентов Ltr
---------- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ----- ------- ---
620 20 95 40 183 26 21 9 8 10 50 26 19 9 15 --- 98.98% А
657 --- 89 40165 --- --- --- --- --- 0 24 20 6 20 0 96,98% А
451 23 90 40197 25 21 8 9 9 50 25 19 9 15 --- 96,79% А
852 22 95 34 164 24 21 7 7 9 50 25 21 8 15 0 95,45% А
567 21 96 40 189 18 19 7 10 7 50 24 20 8 10 --- 95.43% А
292 23 93 30 163 25 21 10 10 9 50 24 20 8 15 --- 94,34% А
455 21 91 36136 22 16 5 8 8 0 24 20 5 20 0 90,06% А
593 21 86 34 156 25 19 7 7 9 50 24 20 9 10 --- 89,05% А
347 17 87 34 147 22 18 8 8 8 50 21 20 7 15 --- 87.64% А-
453 21 93 30 164 26 17 5 8 10 50 23 19 7 10 0 87,40% A-
563 23 78 39 160 25 21 10 10 10 50 0 20 10 15 --- 87,38% A-
636 22 71 30 163 23 19 5 10 9 50 24 17 9 25 0 87,29% A-
324 23 84 34 192 26 21 7 9 8 50 24 20 9 10 0 86.99% А-
796 21 81 40 167 24 17 7 8 9 50 24 18 9 5 --- 83,78% B +
629 21 76 38 141 24 18 3 7 7 0 8 17 7 15 0 82,97% B +
562 22 80 32 163 25 20 7 5 7 50 26 21 7 5 0 82,54% B +
495 21 68 30 151 24 18 7 7 10 50 24 19 6 15 0 80.23% В +
569 21 72 40 154 24 19 7 10 9 50 23 19 8 10 0 79,90% B +
974 19 73 37180 24 21 9 10 10 50 23 20 9 5 --- 77,86% B
521 19 63 39 192 25 20 5 8 9 50 24 21 8 5 0 77,09% B
457 21 65 39 145 24 21 5 6 10 50 26 21 7 10 0 76.88% В
358 22 58 35 156 25 20 9 9 10 50 24 19 9 5 --- 72,61% B-
751 20 53 38 149 24 19 6 5 9 0 24 19 8 10 0 70,65% B-
498 16 60 32 141 24 17 6 9 6 50 17 18 7 10 --- 69,73% С +
895 22 56 36 160 22 17 6 9 8 50 21 19 5 5 0 69.01% С +
753 0 61 34 127 23 18 8 8 9 0 23 21 8 0 0 63,15% С
346 22 36 0 0 24 11 5 6 10 0 24 20 8 10 0 48,05% D
Среднее значение по классу: 82,53 СО от наивысшего балла до среднего: 1,81
Стандартное отклонение: 9,08 СО от нижнего балла до среднего: -3,80
Асимметрия - среднее значение: -1.26 год
Распределение оценок по буквам: A B C D F
13 10 3 1 0
Доказательства MML и CCC - 1 = ноль, если черновик не сдан (проверка)
8,1 и 8,2 класс, вторник в СУПЕР викторине; alg quiz отложено;
Сумма внутренних углов многоугольника
Возможно, вы уже знаете, что треугольники имеют 180 °, а четырехугольники — 360 °. Однако знаете ли вы, сколько градусов в пятиугольнике или двенадцатиугольнике? Давайте посмотрим на некоторые многоугольники, чтобы найти узор.Обратите внимание, что количество треугольников на 2 меньше, чем количество сторон в каждом примере. Число градусов внутри многоугольника можно определить, умножив количество треугольников в форме на 180 градусов. А количество треугольников на 2 меньше, чем количество сторон.
Давайте воспользуемся формулой на нескольких примерах.
Пример 1 : Сколько градусов в девятиугольнике?
Шаг 1 : Определите количество сторон в шестиугольнике.У нонагонов 9 сторон.
Шаг 2 : Вычислите формулу для n = 9.
(n — 2) 180 °
(9 — 2) 180 °
7 x 180 °
1260 °
Нонагон имеет 1260 ° .
Пример 2 : Сколько градусов в двенадцатиугольнике?
Шаг 1 : Определите количество сторон в двенадцатиугольнике. У додекагонов 12 сторон.
Шаг 2 : Вычислите формулу для n = 12.
(n — 2) 180 °
(12 — 2) 180 °
10 x 180 °
1800 °
Двенадцатигранник имеет 1800 ° .

 Измерение углов. Основные свойства измерения углов.
Измерение углов. Основные свойства измерения углов.
 Теорема о внешнем угле треугольника.
Теорема о внешнем угле треугольника.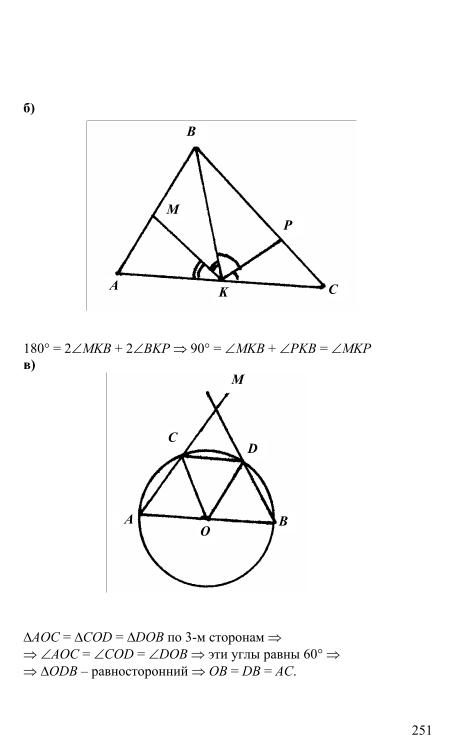
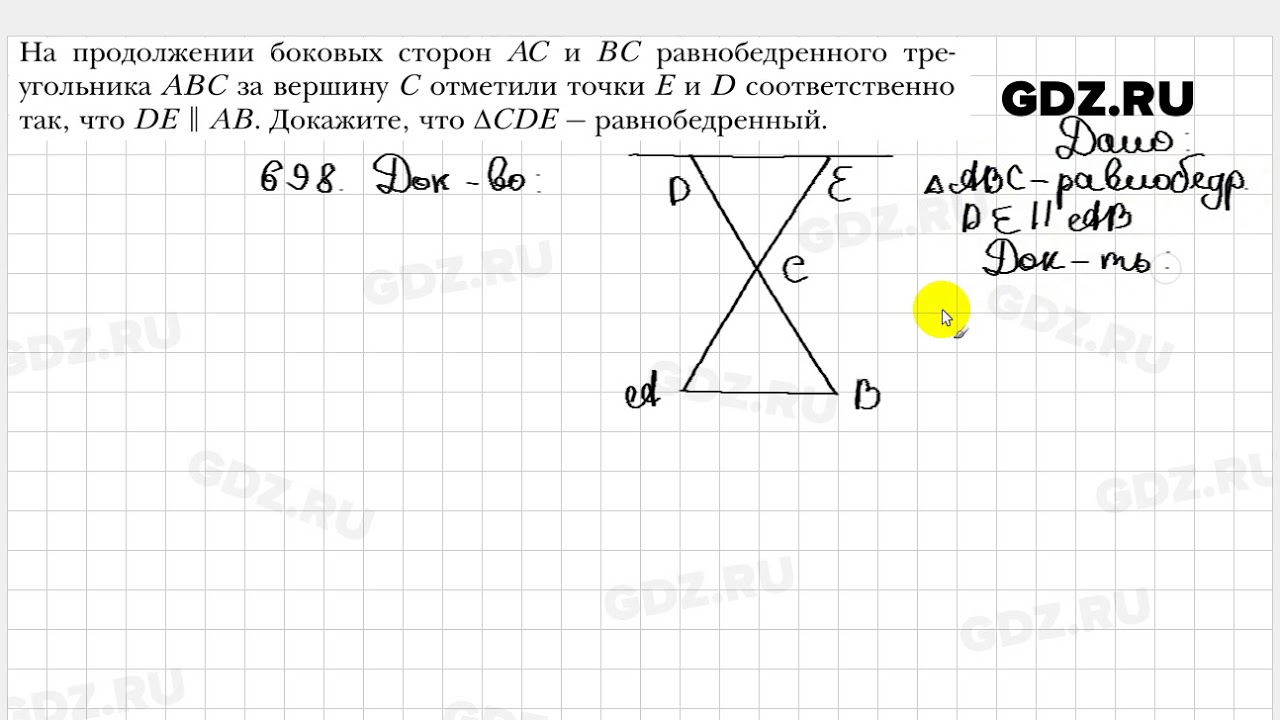 Отрезки надо проводить лишь к одной любой из них.
Отрезки надо проводить лишь к одной любой из них.