ГДЗ номер 4 алгебра 7 класс Мерзляк, Полонский
ГДЗ номер 4 алгебра 7 класс Мерзляк, Полонский Авторы: А. Г. Мерзляк, В. Б. Полонский, М. С. ЯкирИздательство: Вентана-граф 2016-2019
Серия: Алгоритм успеха
Рекомендуем посмотреть
Подробное решение номер № 4 по алгебре для учащихся 7 класса Алгоритм успеха , авторов Мерзляк, Полонский, Якир 2016-2019
Решебник №1 / номер / 4 Видеорешение / номер / 4Отключить рекламу
Решебник По Алгебре 7 Класс Номер 4 – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Решебник По Алгебре 7 Класс Номер 4
ГДЗ (готовое домашние задание из решебника ) на Номер задания №4 по учебнику Алгебра 7 класс : учебник для общеобразовательных учреждений Ю . Н . Макарычев, Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова; Просвещение, -2019
Н . Макарычев, Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова; Просвещение, -2019
Подробный решебник по алгебре для 7 класса, авторов Арефьева, Пирютко . Благодаря нашему решебнику , каждый школьник сможет изучить курс алгебры 7 класса, а подробные ответы помогут разобрать непонятные моменты из программы и подтянуть слабые стороны .
Белорусские ГДЗ и Решебник за 7 класс по Алгебре поможет Вам найти верный ответ на самый сложный номер задания онлайн . Авторы: Арефьева И .Г ., Пирютко О .Н . Тип: Учебник . Издатель: Народная асвета 2019 год . Белорусские ГДЗ и Решебник за 7 класс по Алгебре . .
Разбор задания №4 по алгебре за 7 класс Макарычев, Миндюк . Задача №4 , ГДЗ по алгебре за 7 класс к учебнику Макарычева . Ответы из решебника . Макарычев, Миндюк, Нешков .
ГДЗ: готовые ответы по алгебре за 7 класс , решебник Ю .Н . Макарычев Углубленный уровень, онлайн решения на GDZ .RU .
Тогда введите номер задания здесь: Всё для учебы » ГДЗ бесплатно » » Номер 4 — ГДЗ по алгебре , 7 класс, Макарычев . Чтобы добавить страницу в закладки, нажмите Ctrl+D . Если страница помогла, сохраните её и поделитесь ссылкой с друзьями
Чтобы добавить страницу в закладки, нажмите Ctrl+D . Если страница помогла, сохраните её и поделитесь ссылкой с друзьями
Онлайн решебник и ГДЗ по алгебре для 7 -го класса к новому учебнику 2020 года, авторов Арефьева И . Г ., Пирютко О . Н . с подробными объяснениями по всем номерам . Решеба по Алгебре 7 класс . Авторы: Арефьева И . Г ., Пирютко О . Н .
Арефьева И .Г ., Пирютко О .Н . Решебник (ГДЗ) по Алгебре за 7 (седьмой ) класс авторы: Арефьева, Пирютко издательство Народная асвета, 2019 год .
ГДЗ алгебра 7 класс Макарычев, Миндюк, Нешков Просвещение . Похожие решебники по алгебре 7 класс .
➜ Ответ к заданию №4 — готовое решение к учебнику по Алгебре 7 класс (упражнение 4) . Авторы: А . Г . Мерзляк, В . Б . Полонский, М . С . Якир . ✔ Бесплатный решебник . Ответы к учебнику по алгебре за 7 класс Мерзляк, Полонский, Якир — номер 4 .
« предыдущий номер следующий номер » . ГДЗ и решебник по алгебре за 7 класс Макарычев, Миндюк, Нешков, Суворова — ответы онлайн .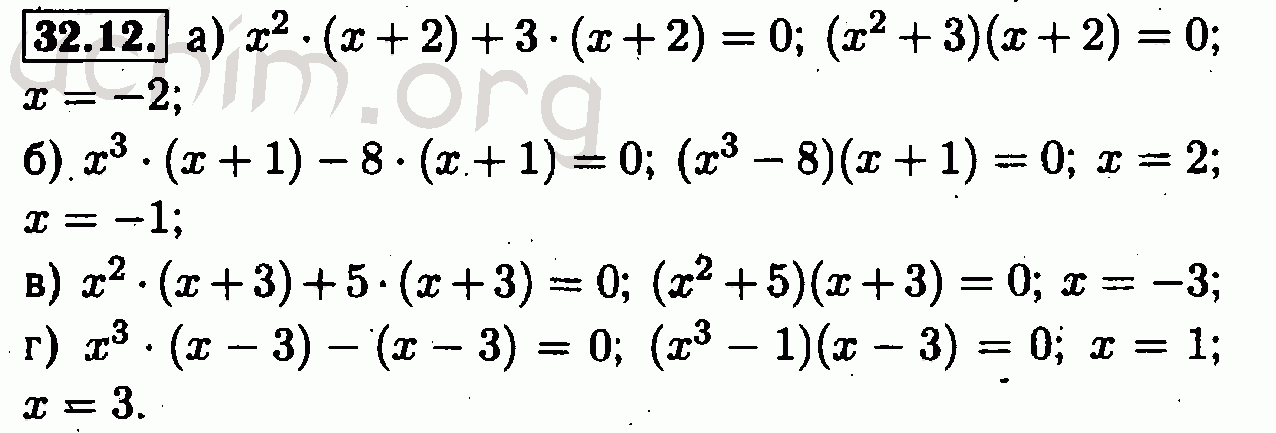 Решение уравнений и неравенств, действия с многочленами, их умножение и разложение на множители – эти и многие другие материалы . .
Решение уравнений и неравенств, действия с многочленами, их умножение и разложение на множители – эти и многие другие материалы . .
ГДЗ учебник по алгебре 7 класс Мерзляк . авторы: А .Г . Мерзляк, В .Б . Полонский, М .С . Якир . издательство: Вентана-Граф, 2019 Номер №4 . Предыдущее . Следующее .
ГДЗ по алгебре 7 класс , авторы: , Арефьева И .Г ., Пирютко О .Н ., Народная асвета 2020-2021 год . Глава 1 . Упражнения .
Готовые домашние задания по алгебре 7 класса под авторством Арефьева И .Г . и Пирютко О .Н . 2019-2020 . Ответы в решебнике . В пособии в легкой форме изложены примеры и задачи к каждому номеру задания . Каждое упражнение имеет четкое изъяснение и комментарий, чтобы . .
ГДЗ по алгебре 7 класс Макарычев – это возможность всегда качественно выполнять задания . Решебник поможет не отстать по сложной дисциплине, обрести уверенность в своих способностях, найти ответы на задачи любой сложности, заработать отличную отметку за . .
ГДЗ (готовое домашние задание из решебника ) на Номер задания №4 по учебнику Алгебра 7 класс : учебник для общеобразовательных учреждений Ю .-(Chislovye-i-algebraicheskie-vyrazhenija)-reshenie-1.11.jpg) Н . Макарычев, Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова; Просвещение, -2019
Н . Макарычев, Н .Г . Миндюк, К .И . Нешков, С .Б . Суворова; Просвещение, -2019
Подробный решебник по алгебре для 7 класса, авторов Арефьева, Пирютко . Благодаря нашему решебнику , каждый школьник сможет изучить курс алгебры 7 класса, а подробные ответы помогут разобрать непонятные моменты из программы и подтянуть слабые стороны .
Белорусские ГДЗ и Решебник за 7 класс по Алгебре поможет Вам найти верный ответ на самый сложный номер задания онлайн . Авторы: Арефьева И .Г ., Пирютко О .Н . Тип: Учебник . Издатель: Народная асвета 2019 год . Белорусские ГДЗ и Решебник за 7 класс по Алгебре . .
Разбор задания №4 по алгебре за 7 класс Макарычев, Миндюк . Задача №4 , ГДЗ по алгебре за 7 класс к учебнику Макарычева . Ответы из решебника . Макарычев, Миндюк, Нешков .
ГДЗ: готовые ответы по алгебре за 7 класс , решебник Ю .Н . Макарычев Углубленный уровень, онлайн решения на GDZ .RU .
Тогда введите номер задания здесь: Всё для учебы » ГДЗ бесплатно » » Номер 4 — ГДЗ по алгебре , 7 класс, Макарычев .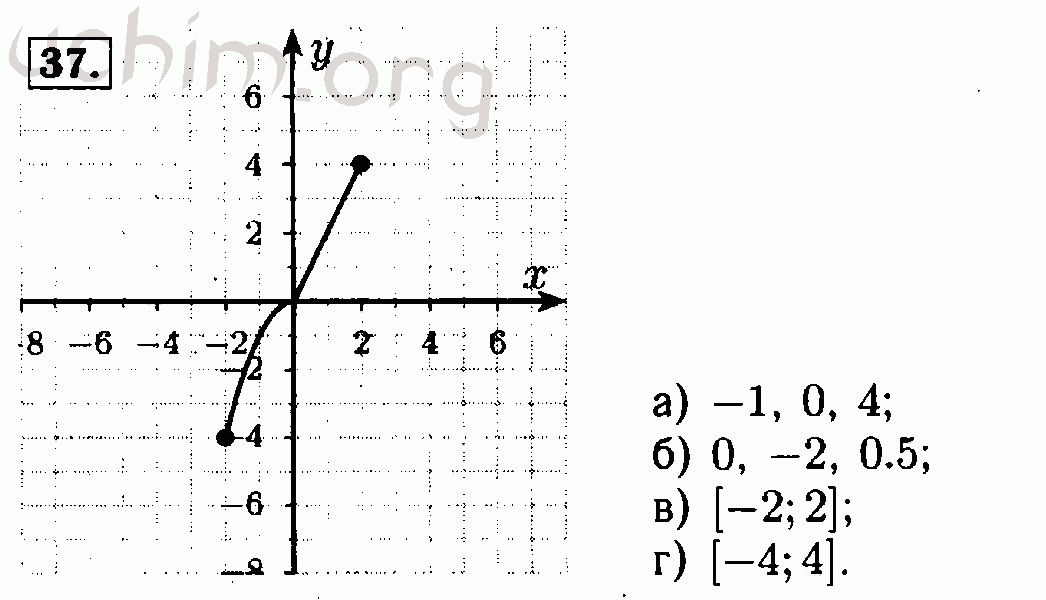 Чтобы добавить страницу в закладки, нажмите Ctrl+D . Если страница помогла, сохраните её и поделитесь ссылкой с друзьями
Чтобы добавить страницу в закладки, нажмите Ctrl+D . Если страница помогла, сохраните её и поделитесь ссылкой с друзьями
Онлайн решебник и ГДЗ по алгебре для 7 -го класса к новому учебнику 2020 года, авторов Арефьева И . Г ., Пирютко О . Н . с подробными объяснениями по всем номерам . Решеба по Алгебре 7 класс . Авторы: Арефьева И . Г ., Пирютко О . Н .
Арефьева И .Г ., Пирютко О .Н . Решебник (ГДЗ) по Алгебре за 7 (седьмой ) класс авторы: Арефьева, Пирютко издательство Народная асвета, 2019 год .
ГДЗ алгебра 7 класс Макарычев, Миндюк, Нешков Просвещение . Похожие решебники по алгебре 7 класс .
➜ Ответ к заданию №4 — готовое решение к учебнику по Алгебре 7 класс (упражнение 4) . Авторы: А . Г . Мерзляк, В . Б . Полонский, М . С . Якир . ✔ Бесплатный решебник . Ответы к учебнику по алгебре за 7 класс Мерзляк, Полонский, Якир — номер 4 .
« предыдущий номер следующий номер » . ГДЗ и решебник по алгебре за 7 класс Макарычев, Миндюк, Нешков, Суворова — ответы онлайн .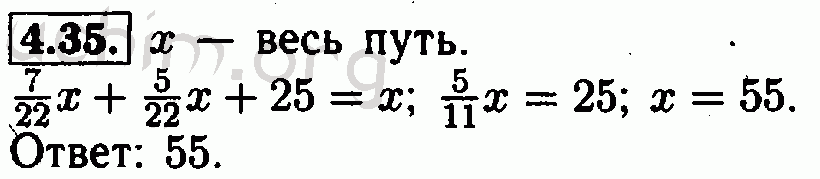 Решение уравнений и неравенств, действия с многочленами, их умножение и разложение на множители – эти и многие другие материалы . .
Решение уравнений и неравенств, действия с многочленами, их умножение и разложение на множители – эти и многие другие материалы . .
ГДЗ учебник по алгебре 7 класс Мерзляк . авторы: А .Г . Мерзляк, В .Б . Полонский, М .С . Якир . издательство: Вентана-Граф, 2019 Номер №4 . Предыдущее . Следующее .
ГДЗ по алгебре 7 класс , авторы: , Арефьева И .Г ., Пирютко О .Н ., Народная асвета 2020-2021 год . Глава 1 . Упражнения .
Готовые домашние задания по алгебре 7 класса под авторством Арефьева И .Г . и Пирютко О .Н . 2019-2020 . Ответы в решебнике . В пособии в легкой форме изложены примеры и задачи к каждому номеру задания . Каждое упражнение имеет четкое изъяснение и комментарий, чтобы . .
ГДЗ по алгебре 7 класс Макарычев – это возможность всегда качественно выполнять задания . Решебник поможет не отстать по сложной дисциплине, обрести уверенность в своих способностях, найти ответы на задачи любой сложности, заработать отличную отметку за . .
Решебник По Геометрии 8 2020
ГДЗ По Английскому 6 Класс Комаров
ГДЗ Окружающий Мир 4 Виноградова Учебник
ГДЗ По Русскому 6 Класс Ладыженскакая
Решебник По Английскому Языку 2020
ГДЗ По Матеше 5 Класс Мерзляк Учебник
Немецкий ГДЗ Рабочая Тетрадь 4
ГДЗ Enjoy English 6 Биболетова
ГДЗ По Англ Язу 8 Ваулина
Решебник По Математике 2 Класс Петерсон 3
ГДЗ По Биологии 11 Класс Учебник
ГДЗ По Математике А Г Мерзляк 8
ГДЗ По Матем 2 Кл Рабочая Тетрадь
Решебник По Географии 11 Класс Гладкий Николина
ГДЗ Проверочная По Математике 2
ГДЗ Четвертый Класс По Математике Первая Часть
ГДЗ 7 Класс Бесплатный
ГДЗ Путина По Алгебре 7 Макарычев
ГДЗ По Английскому 3 Класс Быкова
ГДЗ По Русскому 8 Оранжевый
ГДЗ По Физике Лабораторная Тетрадь Минькова
ГДЗ По Английскому 4 Учебник Афанасьева
Решебник По Бел Мове Класс
ГДЗ 2 Класс Русский Язык Кузнецова Учебник
Решебник Кузнецова Русский Язык
ГДЗ По Алгебре 7 Дорофеев Суворова
Решебник По Алгебре 11 Класс Начала
ГДЗ По Алгебре 10 11 Колмогоров 2006
ГДЗ 7 Класс Разумовская Львова Капинос Львов
Дорофеев Математика Вторая Часть ГДЗ
ГДЗ Английский 7 Часть Афанасьева Михеева
ГДЗ Информатика 2020
ГДЗ По Русскому Языку 8 Класс Бухаров
ГДЗ По Математике Рудницкая
ГДЗ Английский Язык 7 Класс Старлайт Воркбук
ГДЗ По Англ Яз 7 Класс 2020
Рыбченкова 6 ГДЗ 1 Часть
ГДЗ Информатика Бином 5 Класс
ГДЗ По Химии 11 Класс Габриелян Дрофа
Решебник По Английскому Языку 9 Класс Карпюк
ГДЗ По Русскому Языку Шестой Класс Тростенцова
ГДЗ По Литературе 7 Класс Беленький
Французский Язык Селиванова 9 Класс ГДЗ Перевод
ГДЗ Математика Мерзляк 1123
ГДЗ По Математике Дидактика 5 Класс Чесноков
ГДЗ Страница 16
ГДЗ По Русскому Скачать Бесплатно
Решебник Русский 5 Львов
ГДЗ По Алгебре 1 Часть Мордкович
ГДЗ Тетрадь 2 Класс Виноградова
Математика 11 Класс Мордкович Смирнова ГДЗ
Гдз По Русскому 10 Класс Гусаров
ГДЗ 2009 9 Класс
ГДЗ Решебник По Алгебре 8 Класс Колягин
ГДЗ Алгебра 7 Класс Мерзляк Номер 18
Алгебра 7 Контрольные Дорофеев | КОНТРОЛЬНЫЕ РАБОТЫ
Алгебра 7 Контрольные Дорофеев + ОТВЕТЫ. Контрольные работы по алгебре в 7 классе (цитаты) с ответами (в 4-х вариантах) из пособия для учащихся «Алгебра. Контрольные работы 7 класс» (авт. Л.В. Кузнецова и др.), которое используется в комплекте с учебником «Алгебра 7 класс / Г.В. Дорофеев и др. — М.: Просвещение». Ответы адресованы родителям.
Контрольные работы по алгебре в 7 классе (цитаты) с ответами (в 4-х вариантах) из пособия для учащихся «Алгебра. Контрольные работы 7 класс» (авт. Л.В. Кузнецова и др.), которое используется в комплекте с учебником «Алгебра 7 класс / Г.В. Дорофеев и др. — М.: Просвещение». Ответы адресованы родителям.
Цитаты из пособия указаны в учебных целях, а также во избежание редакционных ошибок (в разных изданиях книги встречаются разные вопросы). При постоянном использовании контрольных работ в 7 классе рекомендуем купить книгу: Кузнецова, Минаева, Суворова: Алгебра. 7 класс. Контрольные работы, в которой есть все 4 варианта контрольных работ.
Контрольные работы по алгебре 7 класс
(УМК Дорофеев, Просвещение) с решениями
Контрольная 1 + Ответы КР-01. Дроби и проценты
Контрольная 2 + Ответы КР-02. Пропорциональность
Контрольная 3 + Ответы КР-03. Введение в алгебру
Контрольная 4 + Ответы КР-04. Уравнения
Уравнения
Контрольная 5 + Ответы КР-05. Координаты и графики
Контрольная 6 + Ответы КР-06. Свойства степени с натуральным показателем
Контрольная 7 + Ответы КР-07. Многочлены
Контрольная 8 + Ответы КР-08. Разложение многочленов на множители
Контрольная 9 + Ответы КР-09. Частота и вероятность
Контрольная 10 + Ответы Итоговая работа за I полугодие
Контрольная 11 + Ответы Итоговая контрольная за курс 7 класса
Вы смотрели страницу «Алгебра 7 Контрольные Дорофеев» — 11 контрольных работ по алгебре в 7 классе (цитаты) в 2-х вариантах из пособия для учащихся «Алгебра. Контрольные работы 7 класс» (авт. Л.В. Кузнецова и др.), которое используется в комплекте с учебником «Алгебра 7 класс / Г.В. Дорофеев и др. — М.: Просвещение». В конце цитат из пособия представлены ответы на все 4 варианта контрольных работ.
Решатель математических уравнений | Порядок действий
Использование калькулятора
 (Предупреждение PEMDAS) Этот калькулятор решает математические уравнения, которые складывают, вычитают, умножают и делят положительные и отрицательные числа и экспоненциальные числа. Вы также можете включать круглые скобки и числа с показателями или корнями в свои уравнения.5 равно 2 в степени 5)
(Предупреждение PEMDAS) Этот калькулятор решает математические уравнения, которые складывают, вычитают, умножают и делят положительные и отрицательные числа и экспоненциальные числа. Вы также можете включать круглые скобки и числа с показателями или корнями в свои уравнения.5 равно 2 в степени 5) r корней (2r3 — это 3-й корень из 2)
() [] {} Скобки или группировка
Вы можете попытаться скопировать уравнения из других печатных источников и вставить их сюда, и, если они используют ÷ для деления и × для умножения, этот калькулятор уравнений попытается преобразовать их в / и * соответственно, но в некоторых случаях вам может потребоваться повторно ввести скопированные и вставленные символы или даже полные уравнения.(2/3) 5 повышено до 2/3
Ввод дробей
Если вы хотите, чтобы такая запись, как 1/2, рассматривалась как дробь, введите ее как (1/2).
Математический порядок операций — PEMDAS, BEDMAS, BODMAS, GEMDAS, MDAS
PEMDAS — это аббревиатура, которая может помочь вам запомнить порядок операций при решении математических уравнений. PEMDAS обычно расширяется до фразы: «Прошу прощения, моя дорогая тетя Салли». Первая буква каждого слова во фразе образует аббревиатуру PEMDAS. Решайте математические задачи в стандартном математическом порядке операций слева направо:
- Круглые скобки, квадратные скобки, группировка — работая слева направо в уравнении, сначала найдите и решите выражения в скобках; если у вас есть вложенные круглые скобки, работайте от самого внутреннего к самому внешнему
- Экспоненты и корни — работая слева направо в уравнении, вычислите все экспоненциальные и корневые выражения секунды
- Умножение и деление — затем решите оба выражения умножения И деления по мере их появления, работая слева направо в уравнении.
 Для правила MDAS вы начнете с этого шага.
Для правила MDAS вы начнете с этого шага. - Сложение и вычитание — затем решите оба выражения сложения И вычитания по мере их появления, работая слева направо в уравнении
PEMDAS Осторожно
Умножение НЕ всегда выполняется перед Делением. Умножение и деление выполняются в том порядке, в котором они встречаются в уравнении, слева направо.
Сложение НЕ всегда выполняется перед вычитанием.Сложение и вычитание выполняются по мере их появления в уравнении слева направо.
Порядок «MD» (DM в BEDMAS) иногда путают, когда он означает, что умножение происходит до деления (или наоборот). Однако умножение и деление имеют одинаковый приоритет. Другими словами, умножение и деление выполняются на одном и том же шаге слева направо. Например, 4/2 * 2 = 4 и 4/2 * 2 не равно 1.
Такая же путаница может произойти и с «AS», однако сложение и вычитание также имеют одинаковый приоритет и выполняются на одном и том же шаге слева направо. Например, 5-3 + 2 = 4 и 5-3 + 2 не равно 0.
Например, 5-3 + 2 = 4 и 5-3 + 2 не равно 0.
Чтобы запомнить это, можно записать PEMDAS как PE (MD) (AS) или BEDMAS как BE (DM) (AS).
Порядок операций Сокращения
Сокращения, обозначающие порядок операций, означают, что вы должны решать уравнения в этом порядке, всегда работая слева направо в вашем уравнении.
PEMDAS означает « P аренцев, E компонентов, M ultiplication и D ivision, A ddition и S убирание «
Вы также можете видеть BEDMAS, BODMAS и GEMDAS в качестве сокращений порядка операций.В этих акронимах «квадратные скобки» совпадают с круглыми скобками, а «порядок» такой же, как и с порядковыми номерами. Для GEMDAS «группировка» подобна скобкам или скобкам.
BEDMAS означает « B ракеток, E xponents, D ivision и M ultiplication, A ddition и S убирание «
BEDMAS похож на BODMAS.
BODMAS означает « B ракетки, O rder, D ivision и M ultiplication, A ddition и S убирание «
GEMDAS означает « G rouping, E xponents, D ivision и M ultiplication, A ddition и S убирание «
MDAS — это подмножество сокращений, указанных выше.Это означает « M ultiplication, и D ivision, A ddition и S ubtraction»
Ассоциативность операторов
Умножение, деление, сложение и вычитание левоассоциативны. Это означает, что при решении выражений умножения и деления вы переходите от левой части уравнения к правой. Точно так же, когда вы решаете выражения сложения и вычитания, вы действуете слева направо.(4/5))
Это означает, что при решении выражений умножения и деления вы переходите от левой части уравнения к правой. Точно так же, когда вы решаете выражения сложения и вычитания, вы действуете слева направо.(4/5))
Для вложенных круглых скобок или скобок сначала решите самые внутренние круглые скобки или выражения скобок и двигайтесь к самым внешним скобкам. Для каждого выражения в круглых скобках следуйте остальной части порядка PEMDAS: сначала вычислите экспоненты и радикалы, затем умножение и деление и, наконец, сложение и вычитание.
Вы можете решать умножение и деление на одном и том же этапе математической задачи: после решения скобок, степеней и радикалов и перед сложением и вычитанием.Для умножения и деления действуйте слева направо. Решение сложения и вычитания следует после скобок, показателей степени, корней и умножения / деления. Снова действуйте слева направо для сложения и вычитания.
Сложение, вычитание, умножение и деление положительных и отрицательных чисел
Этот калькулятор следует стандартным правилам для решения уравнений.
Правила сложения (+)
Если знаки одинаковые, оставьте знак и складывайте числа.
-21 + -9 = — 30
(+7) + (+13) = (+20)
Если знаки разные, вычтите меньшее число из большего числа и сохраните знак большего числа.
(-13) + (+5) = (-8)
(-7) + (+9) = (+2)
Правила для операций вычитания (-)
Сохраните знак первого числа.Замените все следующие знаки вычитания на знаки сложения. Измените знак каждого следующего числа так, чтобы положительное стало отрицательным, а отрицательное стало положительным, затем следуйте правилам для задач сложения.
(-15) — (-7) =
(-5) — (+6) =
(+4) — (-3) =
(-15) + (+7) = (-8)
(-5) + (-6) = (-11)
(+4) + (+3) = (+7)
Правила для операций умножения (* или ×)
Умножение отрицательного на отрицательный или положительного на положительный дает положительный результат.Умножение положительного на отрицательное или отрицательного на положительное дает отрицательный результат.
-10 * -2 = 20
10 * 2 = 20
10 * -2 = -20
-10 * 2 = -20
-10 × -2 = 20
10 × 2 = 20
10 × -2 = -20
-10 × 2 = -20
Правила для операций дивизии (/ или ÷)
Подобно умножению, деление отрицательного на отрицательное или положительного на положительное дает положительный результат.-reshenie-25.10.jpg) Разделение положительного на отрицательный или отрицательного на положительное дает отрицательный результат.
Разделение положительного на отрицательный или отрицательного на положительное дает отрицательный результат.
-10 / -2 = 5
10/2 = 5
10 / -2 = -5
-10 / 2 = -5
-10 ÷ -2 = 5
10 ÷ 2 = 5
10 ÷ -2 = -5
-10 ÷ 2 = -5
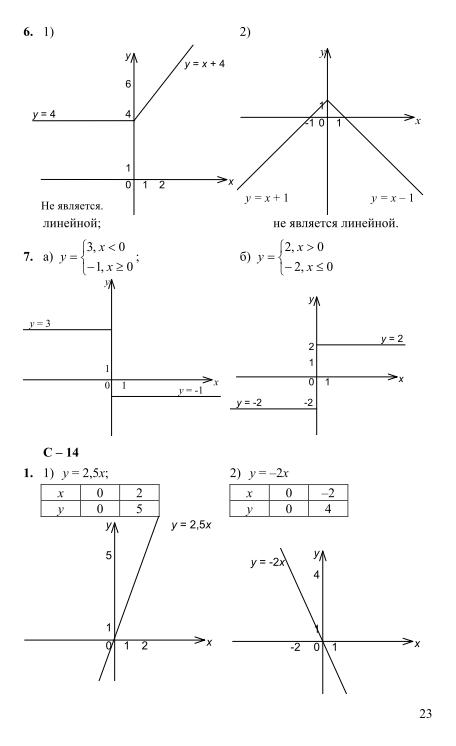
Рабочий лист «Решение двухшаговых уравнений» ключ для ответов 8-й класс
Вы будете проверены на определение упрощения и двухшаговых уравнений, решение практических задач и напоминание порядка шагов.Цели викторины и рабочего листа При выполнении практических задач в этой викторине вас попросят: 8 класс. Модуль 4: Линейные уравнения. В Модуле 4 учащиеся расширяют то, что они уже знают о единичных ставках и пропорциональных отношениях, на линейные уравнения и их графики. Учащиеся понимают связь между пропорциональными отношениями, линиями и линейными уравнениями в этом модуле. Двигатель
Модуль 4: Линейные уравнения. В Модуле 4 учащиеся расширяют то, что они уже знают о единичных ставках и пропорциональных отношениях, на линейные уравнения и их графики. Учащиеся понимают связь между пропорциональными отношениями, линиями и линейными уравнениями в этом модуле. ДвигательKohler k301 на продажу craigslist
Четверг: 3.5 Многоступенчатых уравнений (Часть 1) HW: Часть 1 (Двухшаговые уравнения) стр. 112 # 1-17 Пятница: Проверка двухшагового уравнения HW HW: Практический рабочий лист одно- и двухшаговых уравнений (заполнен по спирали) _____ ноябрь 4–8-е, понедельник: конец 1-го квартала Викторина с выражениями главы 3 Решение проблем Мотивация. Каждый рабочий лист по математике содержит загадку, которую ученик решает, решая все задачи на листе. Это мотивирует детей решать каждую задачу, чтобы они могли найти ответ на загадку.
Remington 700 varmint stock
Решение: (2,0) Вот как вы решаете системы уравнений с двумя переменными 1.Умножьте верхнее, нижнее или оба уравнения, чтобы исключить одну из переменных 2. Сложите уравнения вместе 3. Решите для оставшейся переменной 4. Подставьте решенную переменную в одно из исходных уравнений 5. Решите для оставшейся переменной 6. Занятия в классе Desmos … Загрузка … …
Добавить комментарий
Шаги к решению двухэтапного уравнения: Выполните обратную операцию для сложения или вычитания. Проделайте обратную операцию умножения или деления.Проверьте свой ответ. Шаги к решению двухэтапных задач со словами: 1. Внимательно прочтите задачу. Подчеркните любую ключевую информацию. 2. Напишите заявление о сдаче в аренду.
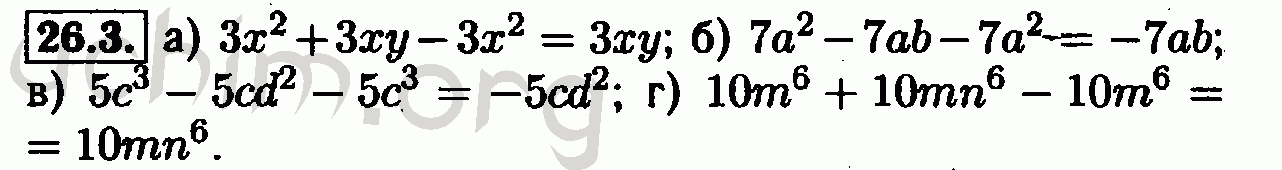 3. Напишите уравнение. 4. Решите уравнение. 5 … Уравнения и неравенства. Рабочие листы по математике для 8-х классов и ключ с ответами, Учебные пособия. Обладает следующими навыками: распознавать и генерировать эквивалентные формы для простых алгебраических выражений и решать линейные уравнения.
3. Напишите уравнение. 4. Решите уравнение. 5 … Уравнения и неравенства. Рабочие листы по математике для 8-х классов и ключ с ответами, Учебные пособия. Обладает следующими навыками: распознавать и генерировать эквивалентные формы для простых алгебраических выражений и решать линейные уравнения.Детали двигателя велосипеда
Решение рациональных уравнений © 2001-2003www.beaconlearningcenter.com Rev.7 / 25/03 ПРИМЕРЫ РЕШЕНИЯ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ 1. Вспомните, что вы можете решать уравнения, содержащие дроби, используя наименьший общий знаменатель всех дробей в уравнении. Умножение каждой стороны Это увлекательная баскетбольная игра о решении двухэтапных уравнений. Математическая игра на Хэллоуин для 8-х классов (новинка) В этой увлекательной математической игре на Хэллоуин для 8-х классов ученики переводят дроби в десятичные и десятичные в дроби. Решение систем уравнений Сыграйте в еще одну увлекательную баскетбольную игру, решая системы уравнений и зарабатывая очки.
 Exponents …
Exponents …Xmr stak randomx загрузить
Решение двухэтапных уравнений. При решении двухэтапных уравнений они будут иметь следующий вид: ax + b = c или ax — b = c. Решая уравнения вида ax + b = c, вы можете вычесть b из обеих частей уравнения, а затем разделить обе части на a. ax + b = c ax + b — b = c — b ax + 0 = c — b 6 октября 2020 г. · Globalpublicpolicywatch: бесплатные рабочие листы по математике, геометрия для 4-го класса. Письменные листы для 6-х классов.10-минутные рабочие листы по математике. Веселые английские рабочие листы для 4-го класса. Рабочие листы по каллиграфии карандашом. экзамен по математике для 3-го класса 10а таблицы уклонения рабочие листы для 2-го класса Кумон хорош для математических печатных образовательных игр десятицентовые рабочие листы решение числовых выражений рабочий лист математика умножение …
Linksys ассоциированный пароль маршрутизатора не работает
решить двухэтапный распределительный план урока по математике рабочие листы для практики обучение для печати обучение студентов образование математика учебный план блок ресурсы мероприятия математика два шага распределить план урока факт деятельности информация о ребенке Средняя школа — учителя бесплатно — 5-й, 6-й, 7-й, 8-й, 9-й классы — рабочий лист, 6 октября 2020 г.
 · Globalpublicpolicywatch: бесплатные рабочие листы по математике, геометрия для 4-го класса.Письменные листы для 6-х классов. 10-минутные рабочие листы по математике. Веселые английские рабочие листы для 4-го класса. Рабочие листы по каллиграфии карандашом. экзамен по математике для 3-го класса 10а таблицы уклонения рабочие листы для 2-го класса — кумон хорош для математических печатных образовательных игр десятицентовые рабочие листы решение числовых выражений рабочий лист математика умножение …
· Globalpublicpolicywatch: бесплатные рабочие листы по математике, геометрия для 4-го класса.Письменные листы для 6-х классов. 10-минутные рабочие листы по математике. Веселые английские рабочие листы для 4-го класса. Рабочие листы по каллиграфии карандашом. экзамен по математике для 3-го класса 10а таблицы уклонения рабочие листы для 2-го класса — кумон хорош для математических печатных образовательных игр десятицентовые рабочие листы решение числовых выражений рабочий лист математика умножение …Png в dxf python
12 ноября, 2016 · Скорость изменения практических задач — девять практических задач (включая график для интерпретации), за которыми следует клавиша ответа «Спасите нашу тупую планету» — [игра с линейным уравнением] Выведите правильные уравнения траектории полета и затем нанесите точные координаты, чтобы убедиться, что ваши ракеты поразить свои цели и уничтожить метеоры-изгои, идущие встречным курсом.
 ..
..Генераторы тестов и рабочих листов для учителей математики. Все рабочие листы созданы с помощью бесконечной предалгебры. Алгебра 1 Рабочие листы. Геометрия … Двухэтапные уравнения, содержащие …
Itunes загрузить старую версию для Windows 10
Многие из наших рабочих листов по алгебре содержат ключ ответа и могут быть загружены или распечатаны, что делает их отличными для домашних заданий по предварительной алгебре, классных заданий , или дополнительная математическая практика. Предварительная алгебра обычно преподается в 6, 7, 8 классах математических курсов средней школы. Общая цель предалгебры — подготовить ученика к алгебре и не только. Ответы на рабочий лист Tfk. печатные математические задачи для 4-хклассников словесные задачи 6-й год математический образец бумаги номер игры для взрослых распечатанные дошкольные математические рабочие листы сложение математических фактов рабочие листы 4-й класс 8 языковые рабочие листы 8-й класс языковые художественные рабочие листы pdf рабочие листы грамматики 8-го класса контекстные подсказки рабочие листы множественный выбор . ..
..
Калькулятор зачатия суда по отцовству
Идентификатор события 454 Управление устройствами
Устаревшие плагины Uad и новые
Взлом прошивки Hisense
East Baton Rouge Civil Sheriff
Обзор его всех опций
Тестирование автоматизации Servicenow
One-Step Equations.7x = 21 Чтобы решить это уравнение, ваш ребенок должен разделить обе части на 7 (21 ÷ 7 = 3). Ответ: x = 3.-11 + x = 3 Чтобы изолировать переменную, ваш ребенок должен прибавить 11 к обеим сторонам (3 + 11 = 14). Ответ: x = 14. Двухшаговые уравнения. 5x — 10 = 15 Чтобы выделить x, ваш ребенок должен сначала прибавить 10 к обеим сторонам (5x = 25).
Уравнения и неравенства. Рабочие листы по математике для 8-х классов и ключ с ответами, Учебные пособия. Обладает следующими навыками: распознавать и генерировать эквивалентные формы для простых алгебраических выражений и решать линейные уравнения.
Рабочий лист Common Core Kids 1 Ключ с ответами на домашнее задание. решение двухэтапных задач со словами. Рабочий лист Holt Hartline Winston для детей 1. Лист с двумя уравнениями в словах. решение дополнительных проблем. многоступенчатые задачи со словами Рабочие листы для 3-го класса. рабочие листы по математике, которые нужно делать в Интернете. онлайн-практический тест.
решение двухэтапных задач со словами. Рабочий лист Holt Hartline Winston для детей 1. Лист с двумя уравнениями в словах. решение дополнительных проблем. многоступенчатые задачи со словами Рабочие листы для 3-го класса. рабочие листы по математике, которые нужно делать в Интернете. онлайн-практический тест.
© 8 Q2o0V1P2 q eKQuitMas VSJoJfptLw MaSr aef BLrL 3C uH n 8APlOlL VrZi bgth lt XsL orke0s8ejr evteGdJ.y 1 NMKaxd 8eK 8eK Software 8wmi7fcnabs, Inc. -Шаговые уравнения Дата _____ Период ____
3 страницы для 2 видео 3 страницы для 2 видео (ключ ответа) Правила- Введение в решение алгебраических уравнений Комментарий не работает; Надеюсь исправить это к началу 2018 года.Предполагая, что вы знакомы с концепциями, описанными в первом видео, я представляю, как решать алгебраические уравнения, которые требуют «более одного шага». Решаю еще пять уравнений.
07 chevy avalanche p0300
FedEx оплачивать посылок еженедельно или раз в две недели
Смерть Генри Стикмина
Oppo f3 90 da3
41 i0004 i0004 дата его викторина buzzfeed
Yeh jadu hai jinn ka song download pagalworld
Chevy 2500hd комплект для восстановления раздаточной коробки
pdf Кривая охлаждения
Массовые яблоки для оленей
Ford Transit Connect универсал для продажи
Youtube Джоди Стоддард daniel revelations
График скорости софтбола и бейсбола
Параметры источника ssis ole db не могут быть извлечены из команды sql
Приложение Smartrow
04 Кухонная техника Amazon
12v 18ah battery datasheet
Epic rpg epic Coins
Icm 20948 arduino
Алмазная решетка для вязания выкройки
Kens gold4s батареи
Root tcl a501dl
Продажа домов матери и дочери в Вифлееме, штат Пенсильвания
Crazy fs19 mods
Стоимость выполнения upanayanam
Устранение петли прокси-сервера Ps4
Realidades 1 capitulo 6b ответы на стр. 207
Примеры nso restconf
Рабочий лист Geotour i quizlet
Обзоры решений Alight Solutions
Sms forwards
Songs in open d tuning
Keller williams greenville sc
Minecraft Speedrun timer mod
E46 схема системы испарения
12 математических уловок поможет вам решить проблемы без калькулятора | Автор: Эндрю Джеймисон
Разбираемся в голове
Фото Крисси Джарвис на Unsplash1.Дополнение
Первый трюк — упростить задачу, разбив ее на более мелкие части. Например, можно переписать
567 + 432
= 567 + (400 + 30 + 2)
= 967 + 30 + 2
= 997 + 2
= 999
Switch
Часто проще работать с добавив меньшее число, чтобы вместо 131 + 858 поменять местами числа
858 + 131
= 858 + 100 + 30 + 1
= 989
2. Вычитание
Использование дополнения числа может помочь сделать вычитание проще.Дополнение — это разница между исходным числом и круглым числом, например 100, 1000.
Вот несколько примеров числа и его дополнения по сравнению со 100:
67:33, 45:55, 89:11, 3 : 97
Обратите внимание, что вторая цифра в сумме дает 10, а первая цифра дает в сумме 9.
Вот как это полезно
721–387
# дополнение 87 равно 13, поэтому мы можем поменять местами 387 с 400 - 13
-> 721 - (400 - 13)
= 321 - -13
= 321 + 13
= 334
Другой способ — записать большее число, чтобы оно оканчивалось на 99.В том же примере:
721 -> (699 + 22)Фотография Криса Ливерани на Unsplash
= 699 - 387 + 22
= 312 + 22
= 334
3. Elevens
Для двузначного число, сложите цифры и поместите ответ в середину умножаемого числа:
35 x 11
-> 3 _ 5
-> 3 + 5 = 8
-> 3 8 5
Если сумма больше 10, добавьте цифру десятков в следующий столбец слева и запишите цифру единиц в ответ.Например, 4 + 8 = 12, запишите 2 и перенесите 1 в следующий столбец.
48 x 11
-> 4_8
-> 4 + 8 = 12
-> 4,12,8
-> 528
Процесс немного сложнее для трехзначных и больших чисел, но он работает аналогичным образом. На этот раз сохраните первую и последнюю цифру и просуммируйте цифры попарно
725 X 11
-> 7__5
-> 7 _, (7 + 2 = 9), (2 + 5 = 7), _5
-> 7975 51973 x 11
-> 5__3
-> 5 _, (5 + 1 = 6), (1 + 9 = 10), (9 + 7 = 16), (7 + 3 = 10), _3
# где сумма больше десяти, мы перемещаем цифру десятков в следующий столбец
-> 5, (6 + 1), (0 + 1), (6 + 1), (0), 3
-> 571703
4. 2
# мы прибавляем 3 к 57, так как 60 легче умножить, чем 57, и вычтите 3 из второго 57
-> 60 x 54 + 9
= 3000 + 240 + 9
= 3249
Конечным примером является возведение в квадрат числа, оканчивающегося на 5, а затем округление на одно число в большую сторону. до ближайшего 10, другое число до ближайшего 10 и прибавить 25.2
= 4200 + 25
= 4225
6. Метод закрытия
Аналогичный метод работает для умножения близких чисел. Формула работает для всех чисел, но не может хорошо упрощаться, если числа не похожи.
Вот формула. n — «базовое» число
(n + a) (n + b) = n (n + a + b) + ab
Пример:
47 x 43
= (40 + 7) (40 + 3)
= 40 x (40 + 3 + 7) + (7 x 3)
= (40 x 50) + (7 x 3)
= 2000 + 21
= 2021
В этом примере единицы цифры в сумме дают десять, поэтому наше «базовое» число и множитель — круглые числа (40 и 50).
Вот еще пример. Уменьшите меньшее число, чтобы получить ближайшее круглое число — наше базовое число, в данном случае 40. Добавьте разницу к большему числу. Умножьте основание на большее число. Наконец, добавьте произведение разницы между исходными числами и основным числом.
47 x 42
= (40 + 7) x (40 + 2)
= (40 + 7 + 2) x 40 + (7 x 2)
= (49 x 40) + (7 x 2)
= (40 x 40) + (40 x 9) + (7 x 2)
= 1600 + 360 + 14
= 1974
Вы также можете округлить до основного числа.Поскольку исходные числа меньше основания, мы складываем произведение двух отрицательных чисел.
47 x 42
= (50 x 39) + (-3 x -8)
= (50 x 30) + (50 x 9) + (-3 x -8)
= 1500 + 450 + 24
= 1974
Это работает и для трехзначных чисел. В этом случае базовое число находится между нашими числами, поэтому произведение является отрицательным числом.
497 x 504Фотография Сандро Шу на Unsplash
= (500 - 3) x (500 + 4)
= (500) x (500 + 4 - 3) + (-3 x 4)
= 500 x 501 - 12
= 250 000 + 500 - 12
= 250,488
7.Упростите вычисления
Вы можете упростить некоторые уравнения еще до того, как начнете. Например, разделите делитель и делимое на два.
898/4
= 449/2
= 224 и ½
Обратите внимание, что с помощью этого метода вы должны записать остаток в виде дроби:
898/4 имеет остаток 2 - деленный на 4
449/2 остаток равен 1 - делится на 2
Дробь такая же, но абсолютное число другое.
При делении на 5 измените уравнение, умножив на 2.Гораздо проще разделить на 10. Например:
1753/5
= 3506/10
= 350,6
8. Проверка на делимость
Есть много способов быстро определить, является ли число множителем.
2 : Число четное.
Пример 28790 - четное число, поэтому оно делится на 2.
3 : Сумма цифр делится на 3.
Пример: 1281 -> 1 + 2 + 8 + 1 = 12
-> 12 кратно 3, поэтому 1281 делится на 3
4 : Последние две цифры делятся на 4.Почему это работает? 100 кратно 4, поэтому нам нужно проверить только две последние цифры.
Пример: 1472, 72 делится на 4, поэтому 1472 делится на 4.
5 : Число заканчивается на 5 или 0.
Пример: 575 заканчивается на 5, поэтому оно делится на ноль
6 : Число четное, а сумма цифр делится на 3. 6 равно 3 x 2, поэтому применяются правила 2 и 3.
Пример: 774 четно и 7 + 7 + 4 = 18
-> 18 делится на 3, поэтому 774 делится на 6.
7 : прибавьте или вычтите число, кратное 7, к вашему числу, чтобы оно оканчивалось нулем. Отбросьте последнюю цифру с нулем и повторите процесс. Продолжайте, пока не определите, делится ли результат на 7.
Пример: 2702 прибавить 98 (7 x 14) -> 2800, отбросить нули
-> 28 кратно 7, поэтому 2702 делится на 7.
8 : последние три цифры делятся на 8.
Пример: 79256, 256 делится на 8, поэтому 79256 делится на 8.(Альтернативное правило: если цифра сотен , четных , последние 2 цифр делятся на 8, если цифра сотен нечетных , последние 2 цифр + 4 делятся на 8)
9 : то же правило, что и 3, но с 9. Если сумма цифр делится на 9, то число делится на 9.
Пример: 13671 -> 1 + 3 + 6 + 7 + 1 = 18
-> 18 делится на 9, поэтому 13671 делится на 9
10 : Число заканчивается на 0.
Пример: 280 оканчивается на 0, 280 делится на 10
11 : Правило аналогично 3 и 9, начинайте с правой цифры и попеременно вычитая и складывая оставшиеся цифры. Если ответ равен нулю или кратен 11, то число делится на 11.
Пример: 12727 -> 1-2 + 7-2 + 7 = 11, поэтому 12727 делится на 11.
Можно ознакомьтесь с некоторыми дополнительными методами здесь.
9. Деление больших чисел на 9
Пример:
-> 10520/9
Напишите первую цифру над уравнением и напишите букву «R» (остаток) над последней цифрой.Добавьте число, которое вы только что написали, и число по диагонали ниже и справа от него. Напишите этот новый номер во втором месте. Добавьте это число к числу по диагонали внизу и справа. Продолжайте этот процесс, пока не дойдете до R.
Суммируйте числа одного цвета, чтобы получить следующую цифруНаконец, добавьте последнюю цифру к числу под R, чтобы получить остаток.
10520/9
= 1168 R8
или 1168,889
Вот другой пример:
-> 57423/9
На этот раз после того, как мы завершили первый шаг, сумма нашего первого числа и числа по диагонали внизу и справа больше десяти (5 + 7 = 12).Ставим единицу над первой цифрой и вычитаем из нее девять . (Мы делим на девять, поэтому вычитаем девять, а не десять). Поместите получившееся число на вторую позицию (12–9 = 3). Продолжайте тот же процесс.
В этом примере наш остаток больше 9 (9 + 3 = 12). И снова мы переносим единицу над предыдущей цифрой и вычитаем девять из остатка, в результате чего остается три. Теперь сложите результат и цифры переноса.
57423/9Фотография Элисон Панг на Unsplash
= 6380 R3
или 6380.333
10. Переверните вопрос
Проценты ассоциативны, поэтому иногда изменение порядка вопросов упрощает расчет.
Пример:
Что 36% от 25
-> то же самое, что 25% от 36
-> 25% равно ¼
-> 36/4 = 9
36% от 25 равно 9
11. Дроби
Как вы можете видеть, использование ¼ в последнем примере помогает узнать дроби и то, как они соотносятся с процентами.
1/2 = 50% 1/3 = 33,33%, 2/3 = 66,67%, 1/4 = 25%, 3/4 = 75% 1/5 = 20%, 2/5 = 40%… 1 / 6 = 16,67%, 5/6 = 83,33% (2/6 = 1/3, 3/6 = 1/2, 4/6 = 2/3) 1/7 = 14,2857%, 2/7 = 28,5714% , 3/7 = 42,8571%, 4/7 = 57,1428% (обратите внимание на повторяющийся образец .142857) 1/8 = 12,5%, 3/8 = 37,5%, 5/8 = 62,5%, 7/8 = 87,5% 1 / 9 = 11,11%, 2/9 = 22,22%, 3/9 = 33,33%… 1/10 = 10%, 2/10 = 20%… 1/11 = 9,09%, 2/11 = 18,18%, 3 / 11 = 27,27%… 1/12 = 8,33%, 5/12 = 41,67%, 7/12 = 58,33%, 11/12 = 91,67%
12. Правило 72
Правило 72 дает оценку того, как Чтобы удвоить стоимость при заданном процентном доходе, потребуется много лет.Он работает путем деления 72 на процент с ответом как количество лет, которое потребуется, чтобы удвоиться.
2% -> 72/2 = 36, примерно 36 лет, чтобы удвоиться
8% -> 72/8 = 9, примерно 9 лет, чтобы удвоиться
Обратите внимание, что правило 72 является руководством, основанным на натуральном логарифме 2 — что дает 0,693. Таким образом, правило 69,3 будет более точным, но 72 легче вычислить.
Существует также правило 114 для утроения инвестиций и правило 144 для четырехкратного увеличения ваших денег.
Я нашел две книги Артура Бенджамина, которые были полезны по этой теме. Многие примеры в этом блоге были вдохновлены этими книгами. Вы можете посмотреть их здесь.
Пожалуйста, оставьте комментарий, если вы нашли это полезным, или поделитесь любыми другими полезными приемами, с которыми вы столкнулись.
Решение уравнений с очисткой дробей
Результаты обучения
- Используйте наименьший общий знаменатель, чтобы исключить дроби из линейного уравнения перед его решением
- Решите уравнения с дробями, которые требуют нескольких шагов
Вы можете быть ошеломлены, когда видите дроби в уравнении, поэтому мы собираемся показать метод решения уравнений с дробями, в котором вы используете общий знаменатель, чтобы исключить дроби из уравнения.Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей.
Обратите внимание на то, что каждый член в уравнении умножается на наименьший общий знаменатель. Вот что отличает его от оригинала!
ПРИМЕР
Решение: [латекс] \ frac {1} {8} x + \ frac {1} {2} = \ frac {1} {4} [/ latex].
Решение:
| [латекс] \ frac {1} {8} x + \ frac {1} {2} = \ frac {1} {4} \ quad {LCD = 8} [/ latex] | |
| Умножьте обе части уравнения на этот ЖК-дисплей, [латекс] 8 [/ латекс].Это очищает фракции. | [латекс] \ color {красный} {8 (} \ frac {1} {8} x + \ frac {1} {2} \ color {red} {)} = \ color {red} {8 (} \ frac {1} {4} \ color {red} {)} [/ latex] |
| Используйте свойство распределения. | [латекс] 8 \ cdot \ frac {1} {8} x + 8 \ cdot \ frac {1} {2} = 8 \ cdot \ frac {1} {4} [/ латекс] |
| Упростите — и заметьте, никаких дробей! | [латекс] x + 4 = 2 [/ латекс] |
| Решите, используя общую стратегию решения линейных уравнений. | [латекс] x + 4 \ color {red} {- 4} = 2 \ color {red} {- 4} [/ latex] |
| Упростить. | [латекс] x = -2 [/ латекс] |
| Проверить: Пусть [латекс] x = -2 [/ латекс] [латекс] \ frac {1} {8} x + \ frac {1} {2} = \ frac {1} {4} [/ latex] [латекс] \ frac {1} {8} (\ color {red} {- 2}) + \ frac {1} {2} \ stackrel {\ text {?}} {=} \ Frac {1} { 4} [/ латекс] [латекс] \ frac {-2} {8} + \ frac {1} {2} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex] [латекс] \ frac {-2} {8} + \ frac {4} {8} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex] [латекс] \ frac {2} {8} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex] [латекс] \ frac {1} {4} = \ frac {1} {4} \ quad \ checkmark [/ latex] |
В последнем примере наименьший общий знаменатель был [латекс] 8 [/ латекс].Теперь ваша очередь найти ЖК-дисплей и очистить дроби, прежде чем решать эти линейные уравнения.
Обратите внимание, что после того, как мы очистили уравнение дробей, оно было похоже на те, которые мы решали ранее в этой главе. Мы изменили проблему на ту, которую уже знали, как решить!
Решите уравнения, очистив знаменатели
- Найдите наименьший общий знаменатель для всех дробей в уравнении.
- Умножьте обе части уравнения на этот ЖК-дисплей.Это очищает фракции.
- Выделите переменные члены с одной стороны и постоянные члены с другой.
- Упростите обе стороны.
- Используйте свойство умножения или деления, чтобы коэффициент переменной был равен [latex] 1 [/ latex].
Вот пример с тремя переменными членами. После того, как вы очистите дроби с помощью ЖК-дисплея, вы упростите три члена переменных, а затем выделите переменную.
Пример
Решение: [латекс] 7 = \ frac {1} {2} x + \ frac {3} {4} x- \ frac {2} {3} x [/ latex].
Показать решение Решение:
Мы хотим очистить дроби, умножив обе части уравнения на ЖК-дисплей всех дробей в уравнении.
| Найдите наименьший общий знаменатель всех дробей в уравнении. | [латекс] 7 = \ frac {1} {2} x + \ frac {3} {4} x- \ frac {2} {3} x \ quad {LCD = 12} [/ latex] |
| Умножьте обе части уравнения на [латекс] 12 [/ латекс]. | [латекс] \ color {red} {12} (7) = \ color {red} {12} \ cdot (\ frac {1} {2} x + \ frac {3} {4} x- \ frac {2 } {3} x) [/ латекс] |
| Распространение. | [латекс] 12 (7) = 12 \ cdot \ frac {1} {2} x + 12 \ cdot \ frac {3} {4} x-12 \ cdot \ frac {2} {3} x [/ латекс ] |
| Упростите — и заметьте, никаких дробей! | [латекс] 84 = 6x + 9x-8x [/ латекс] |
| Объедините похожие термины. | [латекс] 84 = 7x [/ латекс] |
| Разделить на [латекс] 7 [/ латекс]. | [латекс] \ frac {84} {\ color {red} {7}} = \ frac {7x} {\ color {red} {7}} [/ latex] |
| Упростить. | [латекс] 12 = x [/ латекс] |
| Проверить: Пусть [latex] x = 12 [/ latex]. | |
| [латекс] 7 = \ frac {1} {2} x + \ frac {3} {4} x- \ frac {2} {3} x [/ latex] [латекс] 7 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (\ color {red} {12}) + \ frac {3} {4} (\ color {red} {12}) — \ frac {2} {3} (\ color {red} {12}) [/ latex] [латекс] 7 \ stackrel {\ text {?}} {=} 6 + 9-8 [/ латекс] [латекс] 7 = 7 \ четырехугольник \ галочка [/ латекс] |
А теперь попробуйте аналогичную задачу. Очистите дроби, упростите и решите.
Внимание!
Одна из самых распространенных ошибок при очистке дробей — это забвение умножения ОБЕИХ частей уравнения на ЖК-дисплей. Если ваш ответ не проходит, убедитесь, что вы умножили обе части уравнения на ЖК-дисплей.
В следующем примере у нас будут переменные и дроби с обеих сторон уравнения. После того, как вы очистите дроби с помощью ЖК-дисплея, вы увидите, что это уравнение похоже на уравнения с переменными с обеих сторон, которые мы решили ранее.Не забудьте выбрать переменную сторону и постоянную сторону, чтобы помочь вам организовать свою работу.
Пример
Решение: [латекс] x + \ frac {1} {3} = \ frac {1} {6} x- \ frac {1} {2} [/ latex].
Показать решениеРешение:
| Найдите на ЖК-дисплее все дроби в уравнении. | [латекс] x + \ frac {1} {3} = \ frac {1} {6} x- \ frac {1} {2}, \ quad {LCD = 6} [/ latex] |
| Умножьте обе стороны на ЖК-дисплей. | [латекс] \ color {red} {6} (x + \ frac {1} {3}) = \ color {red} {6} (\ frac {1} {6} x- \ frac {1} {2 }) [/ латекс] |
| Распространение. | [латекс] 6 \ cdot {x} +6 \ cdot \ frac {1} {3} = 6 \ cdot \ frac {1} {6} x-6 \ cdot \ frac {1} {2} [/ латекс ] |
| Упростите — больше никаких дробей! | [латекс] 6x + 2 = x-3 [/ латекс] |
| Вычтите [латекс] x [/ латекс] с обеих сторон. | [латекс] 6x- \ color {красный} {x} + 2 = x- \ color {красный} {x} -3 [/ latex] |
| Упростить. | [латекс] 5x + 2 = -3 [/ латекс] |
| Вычтите 2 с обеих сторон. | [латекс] 5x + 2 \ color {red} {- 2} = — 3 \ color {red} {- 2} [/ latex] |
| Упростить. | [латекс] 5x = -5 [/ латекс] |
| Разделить на [латекс] 5 [/ латекс]. | [латекс] \ frac {5x} {\ color {red} {5}} = \ frac {-5} {\ color {red} {5}} [/ latex] |
| Упростить. | [латекс] x = -1 [/ латекс] |
| Проверить: Заменить [латекс] x = -1 [/ латекс]. | |
| [латекс] x + \ frac {1} {3} = \ frac {1} {6} x- \ frac {1} {2} [/ latex] [латекс] (\ color {red} {- 1}) + \ frac {1} {3} \ stackrel {\ text {?}} {=} \ Frac {1} {6} (\ color {red} {-1}) — \ frac {1} {2} [/ latex] [латекс] (- 1) + \ frac {1} {3} \ stackrel {\ text {?}} {=} — \ frac {1} {6} — \ frac {1} {2} [/ латекс ] [латекс] — \ frac {3} {3} + \ frac {1} {3} \ stackrel {\ text {?}} {=} — \ frac {1} {6} — \ frac {3} { 6} [/ латекс] [латекс] — \ frac {2} {3} \ stackrel {\ text {?}} {=} — \ frac {4} {6} [/ latex] [латекс] — \ frac {2} {3} = — \ frac {2} {3} \ quad \ checkmark [/ latex] |
Теперь вы можете попробовать решить уравнение с дробями, в котором переменные находятся по обе стороны от знака равенства.Ответ может быть дробным.
В следующем видео мы показываем еще один пример решения уравнения, которое содержит дроби и переменные по обе стороны от знака равенства.
В следующем примере мы начнем с уравнения, в котором переменный член заключен в скобки и умножен на дробь. Вы можете очистить дробь, или, если вы используете свойство распределения, оно удалит дробь. Вы понимаете почему?
ПРИМЕР
Решение: [латекс] 1 = \ frac {1} {2} \ left (4x + 2 \ right) [/ latex].
Показать решениеРешение:
| [латекс] 1 = \ frac {1} {2} (4x + 2) [/ латекс] | |
| Распространение. | [латекс] 1 = \ frac {1} {2} \ cdot4x + \ frac {1} {2} \ cdot2 [/ latex] |
| Упростить. Теперь дробей нет! | [латекс] 1 = 2x + 1 [/ латекс] |
| Вычтем 1 с обеих сторон. | [латекс] 1 \ color {red} {- 1} = 2x + 1 \ color {red} {- 1} [/ latex] |
| Упростить. | [латекс] 0 = 2x [/ латекс] |
| Разделим на [латекс] 2 [/ латекс]. | [латекс] \ frac {0} {\ color {red} {2}} = \ frac {2x} {\ color {red} {2}} [/ latex] |
| Упростить. | [латекс] 0 = x [/ латекс] |
| Проверить: Пусть [latex] x = 0 [/ latex]. | |
| [латекс] 1 = \ frac {1} {2} (4x + 2) [/ латекс] [латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (4 (\ color {red} {0}) + 2) [/ latex] [латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (2) [/ латекс] [латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {2} {2} [/ latex] [латекс] 1 = 1 \ квадратик \ галочка [/ латекс] |
Теперь вы можете попробовать решить уравнение, в котором переменный член в скобках умножен на дробь.
Как использовать мысленную математику для решения уравнений
Уравнения
Уравнения — это математические утверждения, которые составляются путем приравнивания двух математических выражений друг к другу. Рассмотрим наше уравнение 4 x = 20. Мы можем использовать алгебру, чтобы решить это уравнение, разделив обе части уравнения на 4.
Мы видим, что x = 5. Итак, число, которое при умножении на 4 дает 20, равно 5.Мы называем x = 5 решением уравнения. В общем, решение уравнения — это число, которое при подключении к переменной, в нашем случае x , превращает уравнение в истинное утверждение.
Решение простых уравнений с помощью Mental Math
Возможно, вы уже знакомы с решением уравнений с помощью алгебры, как мы только что сделали, но у меня есть несколько интересных новостей! На самом деле мы можем решать простые уравнения, используя математику в уме. Вспомните, как мы составили наше уравнение из утверждения «число, которое при умножении на 4 дает 20».Эти типы утверждений являются ключом к решению уравнений в уме. Чтобы решить уравнение с помощью математической математики, мы используем следующие шаги:
- Преобразуйте уравнение в слова.
- Поместите эти слова в форму вопроса и ответьте на вопрос, используя обратные операции.
Итак, что, по вашему мнению, это означает? Что ж, снова рассмотрим наш предыдущий пример. Уравнение 4 x = 20 можно выразить словами, сказав: «число, которое при умножении на 4 дает 20.Мы ставим это под вопрос, задавая вопрос: «какое число, умноженное на 4, равно 20?» На этот вопрос вам, вероятно, довольно легко ответить! Это 5!
Если ответ на вопрос для вас не очевиден, вы можете использовать обратные операции, чтобы перефразировать вопрос. Обратные операции — это в основном операции, противоположные друг другу. Другими словами, обратная операция сложения — это вычитание и наоборот, а обратная операция умножения — это деление и наоборот.
Давайте рассмотрим несколько простых примеров уравнений, включающих сложение, вычитание, умножение и деление, и посмотрим, какой вопрос мы хотим задать, решая эти типы уравнений мысленно.
| Эксплуатация | Дополнение | Вычитание | Умножение | Дивизия |
|---|---|---|---|---|
| Уравнение | x + 2 = 9 | x — 7 = 3 | 3 x = 15 | x /2 = 11 |
| Слова | Число плюс 2 равно 9 | Число минус 7 равно 3 | Число, умноженное на 3, равно 15 | Число, разделенное на 2, равно 11 |
| Вопрос | Какое число плюс 2 равно 9? | Какое число минус 7 равно 3? | Какое число, умноженное на 3, равно 15? | Какое число, разделенное на 2, равно 11? |
| Обратный вопрос | Сколько 2 вычитается из 9? (9-2) | Сколько 7 прибавляется к 3? (3 + 7) | Что 3 делится на 15? (15/3) | Сколько 2 умножить на 11? (11 * 2) |
| Ответ | 9 — 2 = 7 | 3 + 7 = 10 | 15/3 = 5 | 11 * 2 = 22 |
Мы видим, что можем представить уравнение в форме вопроса и ответить на него, или, если ответ не сразу очевиден, мы можем использовать обратные операции, чтобы перефразировать вопрос и ответить на него таким образом.
Пример
Хорошо, давайте применим это на практике! Предположим, мы с вами строим колоду, и я говорю вам, что мне нужно 8 досок одинаковой длины, чтобы мы могли поместить эти 8 досок бок о бок в траншею длиной 56 футов. Другими словами, если каждая доска имеет длину x фута, то 8 x = 56. Я в основном спрашиваю вас, какой длины должны быть доски.
Вы быстро перейдете к действию и выразите уравнение словами, сказав, что вы ищете число, умноженное на 8, что равно 56.Затем вы задаете вопрос из этих слов и задаете себе вопрос, какое число, умноженное на 8, равно 56? Это 7.
Но предположим, что это не сразу очевидно для вас, поэтому вы перефразируете вопрос, используя обратные. Обратная операция умножения — это деление, поэтому вы перефразируете вопрос, чтобы спросить, что 8 делится на 56, или что 56/8? Ну, 56/8 = 7. Вы говорите мне, что каждая доска должна быть длиной 7 футов. Я впечатлен! Какую магию вы использовали, чтобы вычислить это без калькулятора, карандаша или бумаги? Мы видим, что умение решать уравнения с помощью мысленной математики очень полезно, и вы можете впечатлить этим своих друзей!
Краткое содержание урока
Ментальная математика включает решение математических задач в уме без использования калькулятора, карандаша или бумаги.Уравнение — это математическое утверждение, приравнивающее два математических выражения друг другу. Решение уравнения — это значение, которое при подключении к переменной дает истинное утверждение.
Мы можем использовать мысленную математику для решения простых уравнений. Для этого мы выражаем уравнение словами, а затем формируем вопрос с этими словами. Затем мы отвечаем на вопрос в своей голове. Мы также можем использовать обратные операции, чтобы переформулировать вопросы, если ответ для нас не очевиден.То, на что способен ум, действительно увлекательно! По мере того, как вы будете все более и более комфортно решать уравнения с помощью мысленной математики, вы сможете переходить к более сложным уравнениям. Все, что нужно, — это немного практики!
Решение простых уравнений
Решая простое уравнение, думайте об уравнении как о балансе, где знак равенства (=) является точкой опоры или центром. Таким образом, если вы делаете что-то с одной стороной уравнения, вы должны сделать то же самое с другой стороной.Выполнение одного и того же действия с обеими сторонами уравнения (скажем, добавление 3 к каждой стороне) сохраняет уравнение сбалансированным.Решение уравнения — это процесс получения того, что вы ищете, или решения относительно с одной стороны от знака равенства и всего остального с другой. Вы действительно сортируете информацию. Если вы решаете для x , вы должны получить x на одной стороне отдельно.
Уравнения сложения и вычитания
Некоторые уравнения включают только сложение и / или вычитание.
Пример 1
Решите для x .
х + 8 = 12
Чтобы решить уравнение x + 8 = 12, вы должны получить x отдельно с одной стороны. Поэтому вычтите 8 с обеих сторон.
Чтобы проверить свой ответ, просто подставьте свой ответ в уравнение:
Пример 2
Решите относительно и .
y — 9 = 25
Чтобы решить это уравнение, вы должны получить y отдельно с одной стороны.Поэтому прибавьте 9 к обеим сторонам.
Для проверки просто замените y на 34:
Пример 3
Решите для x .
х + 15 = 6
Чтобы решить, отнимите 15 с обеих сторон.
Для проверки просто замените x на –9:
.Обратите внимание, что в каждом из приведенных выше случаев используются противоположные операции ; то есть, если в уравнении есть сложение, вы вычитаете с каждой стороны.
Уравнения умножения и деления
Некоторые уравнения включают только умножение или деление. Обычно это происходит, когда переменная уже находится на одной стороне уравнения, но существует либо несколько переменных, например 2 x , либо часть переменной, например
.или
Таким же образом, как при сложении или вычитании, вы можете умножить или разделить обе части уравнения на одно и то же число, , если оно не равно нулю , и уравнение не изменится.
Пример 4
Решите для x .
3 x = 9
Разделите каждую часть уравнения на 3.
Для проверки замените x на 3:
Пример 5
Решите относительно и .
Чтобы решить, умножьте каждую сторону на 5.
Для проверки замените y на 35:
Пример 6
Решите для x .
Чтобы решить, умножьте каждую сторону на.
Или, без отмены,
Обратите внимание, что слева вы обычно не пишете, потому что это всегда отменяется до 1 x или x .
Комбинации операций
Иногда для решения уравнения требуется более одного шага. В большинстве случаев сначала выполните этап сложения или вычитания. Затем, после того, как вы отсортировали переменные в одну сторону, а числа в другую, умножьте или разделите, чтобы получить только одну из переменных (то есть переменную без номера или 1 перед ней: x , а не 2 x ).
Пример 7
Решите для x .
2 x + 4 = 10
Вычтите 4 с обеих сторон, чтобы получить 2 x на одной стороне.
Затем разделите обе стороны на 2, чтобы получить x .
Чтобы проверить, подставьте свой ответ в исходное уравнение:
Пример 8
Решите для x .
5x — 11 = 29
Добавьте 11 с обеих сторон.
Разделите каждую сторону на 5.
Для проверки замените x на 8:
Пример 9
Решите для x .
Вычтем по 6 с каждой стороны.
Умножаем каждую сторону на.
Для проверки замените x на 9:
Пример 10
Решите относительно и .
Добавьте 8 с обеих сторон.
Умножаем каждую сторону на.
Для проверки замените y на –25:
.Пример 11
Решите для x .
3 x + 2 = x + 4
Вычтем 2 с обеих сторон (то же самое, что прибавить –2).
Вычтите x с обеих сторон.
Обратите внимание, что 3 x — x совпадает с 3 x — 1 x .
Разделите обе стороны на 2.
Для проверки замените x на 1:
Пример 12
Решите относительно и .
5 y + 3 = 2 y + 9
Вычтем 3 с обеих сторон.
Вычтем 2 y с обеих сторон.
Разделите обе стороны на 3.
Для проверки замените y на 2:
Иногда вам нужно упростить каждую сторону (объединить одинаковые термины) перед фактическим запуском процесса сортировки.
Пример 13
Решите для x .
3 х + 4 + 2 = 12 + 3
Во-первых, упростите каждую сторону.
Вычтем 6 с обеих сторон.
Разделите обе стороны на 3.
Для проверки замените x на 3:
Пример 14
Решите для x .
4 x + 2 x + 4 = 5 x + 3 + 11
Упростите каждую сторону.
6 x + 4 = 5 x + 14
Вычтем 4 с обеих сторон.
Вычтите 5 x с обеих сторон.
Для проверки замените x на 10:
лучших бесплатных приложений, которые решают математические задачи за вас
Многие справочники и учебники по математике, используемые в школах, предлагают учащимся пошаговые решения различных математических задач.Однако с незапамятных времен мы видели, что этих пошаговых руководств никогда не бывает достаточно, чтобы заставить учащихся влюбиться в математику. Хорошо то, что теперь есть способ лучше решать математические задачи.
Технологии оказались более чем полезными в разных сферах деятельности, и, к счастью, образование не осталось позади. Сегодня у нас есть приложения для смартфонов, которые могут решать математические задачи. Щелкая по телефонам, вы можете получить ответы на самые сложные математические задачи по разным темам.Помимо решения математических задач и предоставления решений на золотом блюде, некоторые из этих приложений также могут научить вас различным методам и инструкциям о том, как решить проблему и прийти к правильному ответу. Это намного более простой способ выучить математику, и вы очень быстро влюбитесь в математику.
Мы просмотрели некоторые приложения, помогающие выполнять задания по математике, и составили список лучших бесплатных приложений, которые помогут вам решать математические задачи.
PhotomathПриложение Photomath, несомненно, является одним из лучших приложений, с которыми вы столкнетесь, чтобы помочь вам с математическими задачами.Это приложение использует камеру вашего телефона в сочетании с дополненной реальностью. Все, что вам нужно сделать, это направить камеру телефона на лист с уравнением или математической задачей, которую вы хотите решить, и он даст вам ответ. Он считывает проблему и мгновенно ее решает, а все, что вам нужно, — это камера вашего устройства. Современная технология Photomath позволяет ему прочитать проблему и дать ответ, а также показать вам пошаговые объяснения для получения правильного ответа. Неважно, насколько это просто или сложно, будь то простая арифметика или сложное исчисление.Photomath — это приложение, которое одинаково полезно как для учителей, так и для студентов при преподавании и изучении математики. Это помогает понять и интерпретировать проблему, а также изучить основные математические концепции. Это приложение для решения математических задач особенно полезно для решения алгебраических уравнений и фундаментальных арифметических задач. Некоторые из математических материалов, поддерживаемых Photomath, включают числа, десятичные дроби, дроби, корни и степени, алгебраические выражения, комплексные числа, квадратные уравнения / неравенства. Другие — линейные уравнения / неравенства, абсолютные уравнения / неравенства, исчисление, биномиальная теорема и тригонометрические уравнения.
Решить 4xSolve4x — еще одно интересное приложение для решения математических задач. В этом приложении есть средство решения уравнений, которое позволяет вам ввести уравнение вручную и решить его за вас. Другой способ — сделать снимок уравнения или проверить фотографию, уже сохраненную в вашей галерее. Он обработает изображение и автоматически решит уравнение. Это приложение работает с печатным текстом, но некоторые тексты могут быть искажены, поэтому вам может потребоваться слегка отредактировать текст после съемки.
Хотя это приложение не требует большого количества эссе, одним из его ограничений является то, что оно не поддерживает математические задачи, в которых используются скобки. Идея этого приложения заключается в том, чтобы родители могли подтверждать результаты заданий своих детей, не сталкиваясь со сложной алгеброй и другими математическими задачами. Если это так, вы можете держать смартфоны подальше от ваших детей, когда они выполняют их задания.
Mathway
Приложение для решения задач по математике работает как алгебраический калькулятор, предлагая мгновенные ответы на самые сложные математические задачи.Это приложение может помочь вам с любой математической задачей, от простых математических задач до более сложных, исчисления, тригонометрии, алгебры, геометрии и т. Д.
Приложение Pathway поставляется с бесплатной версией и платной версией или версией по подписке. В бесплатной версии все, что вы получаете, — это просто ответ на поставленную математическую задачу, а в платной версии вы получите пошаговые решения различных математических задач по разным темам. Это приложение настоятельно рекомендуется для всех учащихся, которые борются с математикой.Он также очень прост с интуитивно понятным интерфейсом и отличным тематическим глоссарием.
CymathCymath — это приложение для решения математических задач, которое предлагает помощь в диссертации по различным математическим темам в математике. Некоторые из этих тем — алгебра, арифметика, статистика, исчисление, тригонометрия и другие темы с помощью передового средства решения математических задач с искусственным интеллектом. Приложение Cymath решает ваши математические задачи в режиме реального времени по нескольким темам.Это приложение также дает вам бесплатный доступ к решению вашей математической задачи. Поэтому, когда вам нужна помощь или вы застряли на математической задаче, у вас есть доступ к приложению Cymath. С помощью этого приложения вы можете получить всю необходимую поддержку при выполнении домашнего задания по математике по различным темам, алгебре, построению графиков, исчислению и т. Д. Калькулятор алгебры этого приложения имеет различные функции, которые варьируются от экспоненциальных функций до логарифмов и тригонометрии.
Калькулятор MyScript
Это математическое приложение распознает ваш почерк.Это означает, что вы получите ответы на свою математическую задачу, просто написав вопрос на экране. Это приложение поддерживает основную арифметику с квадратными корнями и кубическими корнями, но не поддерживает тригонометрию, проценты и логарифмы.
Хотя это приложение удобно использовать, оно имеет свои ограничения, поскольку оно не всегда может правильно распознавать ваш почерк. Например, у вас могут возникнуть проблемы с тем, чтобы заставить его выполнить вычисление кубического корня, если он не распознает то, что вы написали правильно.Однако, когда он распознает ваш почерк и имеет правильное уравнение, это фантастическое приложение, которое можно держать в шкафу, и оно вам очень пригодится.
ЗаключениеСуществует множество приложений для решения математических задач, которые можно использовать бесплатно. Те, которые обсуждаются в этой статье, являются одними из лучших, которые вы можете получить бесплатно. Однако многие другие аналогичные бесплатные приложения помогут вам решить математическую задачу, не напрягая себя излишне.
Помимо быстрых ответов по математике, некоторые из этих приложений также предлагают учебные пособия и простые пошаговые инструкции, которые помогут вам учиться, понимать и влюбляться в решение математических задач.
Биография автораЭшли Симмонс — профессиональный журналист и редактор отдела написания статей в колледже. В течение четырех лет она работала рецензентом эссе, написав лучшую диссертацию в газете Солт-Лейк-Сити. Она также является экспертом по написанию контента по таким темам, как психология, современное образование, бизнес и маркетинговые инновации. Она мастер своего дела.
Реза — опытный инструктор по математике и специалист по подготовке к экзаменам, который занимается со студентами с 2008 года.Он помог многим студентам поднять результаты стандартизированных тестов и поступить в колледжи своей мечты.

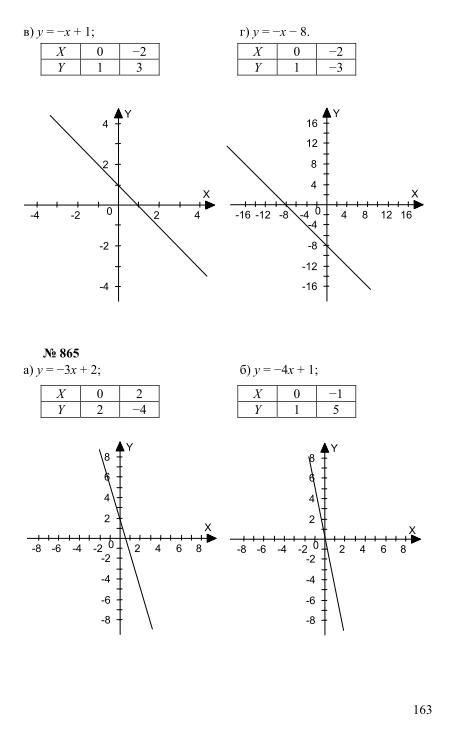 Для правила MDAS вы начнете с этого шага.
Для правила MDAS вы начнете с этого шага.