Примеры по геометрии 7 класс. | Геометрия
Примеры по геометрии 7 класс. | Геометрия — просто!Добрый день!
Сегодня мы с вами разберём несколько примеров по геометрии 7 класса, которые даются в ОГЭ-2015.
Ведь действительно, Основной Государственный Экзамен — ОГЭ, рассчитан не только на знания 9 класса, но и на те знания, которые ученики получают в 7 и 8 классах по геометрии, и, начиная с 5 класса, по математике и алгебре.
Поэтому, в модуле «Геометрия» есть задачи из курса 7 класса.
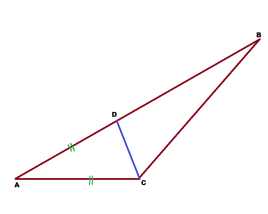
 Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Решение: Из треугольника ADC видно, что он равнобедренный, поскольку 2 боковые стороны его равны.
А в равнобедренном треугольнике углы при основании равны.
Значит, угол ADC равен углу АСВ.
Но сумма внутренних углов треугольника равна 180°.
Отсюда, сумма двух углов при основании равна 180-16=164°.
Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°.
Угол АСВ по условию равен 134°.
А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла.
Т.е. Угол АСВ равен сумме углов АCD и DCB.
Отсюда, угол DCB равен 134 — 82 = 52°.
Ответ: угол DCB равен 52°.
 Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Доказательство: В искомых треугольниках есть по одной равной стороне и одному равному углу. Значит, согласно признакам равенства треугольников, нам необходимо ещё либо по одной равной стороне, либо по одному равному углу.
Стороны как-то не проглядываются, а вот по равному углу можно ещё найти.
Углы АОВ и DOC — вертикальные.
А вертикальные углы, как мы знаем, равны.
В каждом из треугольников мы имеем по равной стороне и двум равным углам, прилежащим к ней.
Треугольники равны по 2 признаку.
 Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Решение: Угол АКС является внешним для треугольника АВК и равным сумме двух внутренних углов, не смежных с ним, т.е. сумме углов В и ВАК.
Отсюда мы можем найти угол ВАК.
Он равен 94 — 62 = 32°.
Поскольку АК — биссектриса угла А, то угол КАС тоже равен 32°.
А теперь, рассматривая треугольник АКС и зная в нём 2 угла, можно найти третий.
∠С = 180 — 32 — 94 = 54°.
Ответ: угол С равен 54°.
 Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Решение: Внешний угол В равен 110°, значит, смежный с ним внутренний угол в треугольнике равен
180-10 = 70°.
Но внутренний угол В равен углу А, как углы при основании равнобедренного треугольника. Значит, угол А равен 70°.
А сумма внутренних углов треугольника равна 180°.
И если 2 из них равны по 70, то на долю третьего угла С приходится 180 — 70 — 70 = 40°.
Ответ: угол с равен 40°.
 Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Решение: Угол ВОМ смежный углу СОМ и равен 180-119 = 61°.
Угол СМА внешний в треугольнике СМВ и равен сумме двух внутренних, не смежных с ним.
Отсюда, угол ОВМ равен 90-61 = 29°.
А из прямоугольного треугольника ВКА можно найти угол А, т.к. сумма острых углов в прямоугольном треугольнике равна 90°.
Значит, угол А равен 90 — 29 = 61°.
Ответ: угол А равен 61°.
На сегодня всё. В следующий раз мы продолжим решение геометрических задач для подготовки к ОГЭ.
Вам так же будет интересно:
Оставить комментарий
geometriyaprosto.ru
Задачи по геометрии на повторение курса 7 класса
Задачи на повторение курса геометрии в 7 классе
1) Найдите величины смежных углов, если один из них в 5 раз больше другого. ( 30 и 50)
2) Отрезки MN и DK пересекаются в их общей середине B. Докажите равенство треугольников MDB и NKB. (по 1 признаку)
3) Найдите периметр равнобедренного треугольника
4) Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126°(63 и 117)
5) Точки М, N и R лежат на одной прямой, MN = 11 см, RN = 20 см. Найдите расстояние MR.(21 или 9)
6) Угол, противолежащий основанию равнобедренного треугольника, равен 50° . Найдите величину внешнего угла при основании.(115)
7) Найдите углы треугольника, на которые высота разбивает равносторонний треугольник.(30, 60 и 90)
8) Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42° .(42 и 138)
9) Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них 126° .(126 и 54)
10) Найдите смежные углы, если один из них на 55° больше другого.(62,5 и 117,5)
11) Луч SR является биссектрисой угла S, а отрезки SM и SN равны. Докажите равенство треугольников SMO и SNO.(1 признак)
12) Найдите длину отрезка AM и градусную меру угла ABK, если BM – медиана, а BK – биссектриса треугольника ABC и известно, что
13) Отрезки AB и CM пересекаются в точке O. Луч OK является биссектрисой угла MOB. Найдите угол MOK, если угол AOM равен 86° .(47)
14) В треугольнике MOK O = 76°, а угол M в 3 раза меньше внешнего угла при вершине K. Найдите неизвестные углы треугольника.(38 и 114)
15) Найдите углы при основании MР равнобедренного треугольника МОР, если MK– его биссектриса и OKM = 96°.(64)
16) Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42°.(42 и 138)
17) Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.(29 и 29)
18) В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см.(8)
19) Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210. Найти эти углы.(110)
20) Найти смежные углы, если один из них на 45 больше другого.(67,5 и 112,5)
21) Один из углов прямоугольного треугольника равен 60, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника.(8,8 и 17,6)
22) Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50 градусам. Найти эти углы.(115 и 65)
23) Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126°.(63 и 117)
24) Основание равнобедренного треугольника равно 8см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2см больше периметра другого. Найти боковую сторону данного треугольника.(6 или 10)
25) В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120, АС+АВ=18см. Найти AC и AB.(6 и 12)
26) Найдите все углы, образованные при пересечении двух параллельных прямых а и в секущей с , если один из углов на 700 больше другого.(105 и 65)
infourok.ru
Решение задач. Видеоурок. Геометрия 7 Класс
На этом уроке мы будем решать задачи по пройденной теме. Вначале повторим изученный материал. Вспомним аксиому о параллельных прямых и следствие из нее. Повторим определение луча и угла и единицы измерения отрезков и углов. Вспомним определение равных геометрических фигур и то, как сравнивают и измеряют отрезки и углы. Вспомним, что такое середина отрезка и биссектриса угла, какие углы называются острыми, прямыми и тупыми. Повторим теоремы о сумме смежных углов и о равенстве вертикальных углов. Вспомним, что такое перпендикулярные прямые и теорему о том, что две перпендикулярные к третьей прямые не пересекаются. И будем решать типовые задачи на повторенный материал.
Вспомним сведения, изученные в текущей теме:
— Аксиома. Через две точки можно провести прямую, и только одну.
— Прямые на плоскости могут пересекаться, могут не иметь общих точек.
— Угол измеряется в градусах. 1 градус – это сто восьмидесятая часть от развернутого угла.
— Сумма смежных углов равна 180о.
— Вертикальные углы равны между собой.
— Прямые, пересекающиеся под углом 90о, называются перпендикулярными.
— Прямые, перпендикулярные одной прямой, не пересекаются.
Пример 1: Найти угол между биссектрисами смежных углов.
Решение:
Рис. 1. Чертеж к примеру 1
Биссектриса BL1 угла ∠DBC = β делит его на два угла, градусная мера которых равна . Биссектриса BL
Ответ: 90о.
Отметим, что в данной задаче нам не было известно, какие градусные меры углов ∠DBC и ∠АBC, однако мы знаем, что их сумма равна 180о.
Пример 2: Отрезок длиной 36 см поделили на 4 неравных части. Расстояние между серединами крайних частей равно 30 см. Найдите расстояние между серединами средних частей отрезка.
Рис. 2. Чертеж к примеру 2
Решение:
Найдем величину суммы отрезков Соответственно,
Вычислим сумму длин оставшихся отрезков:
Найдем расстояние между серединами средних частей отрезка.
Ответ: 12 см.
Пример 3: Отрезок длиной m разделен на три части. Найти расстояние между серединами крайних частей.
Решение:
Выполним рисунок.
Рис. 3. Чертеж к примеру 3
Поскольку длина трети отрезка равна , то длина половины этой части равна . Тогда чтобы найти расстояние между серединами крайних частей, необходимо выполнить действие: .
Ответ: .
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
- Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
Рекомендованные ссылки на интернет-ресурсы
- Геометрические задачи (Источник).
- Обобщающий урок по геометрии в 7-м классе (Источник).
- Прямая линия, отрезок (Источник).
Рекомендованное домашнее задание
- № 14, 16. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
- Определите длину отрезка АВ, если АС : ВС = 3 : 2, а ВС = 3 см.
- При пересечении прямых образовалось 4 неразвернутых угла. Определите градусные меры этих углов, если сумма трех углов 320о.
- Может ли быть такое, что один из смежных углов больше другого в 100 раз?
interneturok.ru
Задачи по геометрии для 7 класса. Равные треугольники, равнобедренный треугольник, свойство биссектрис, высот и серединных перпендикуляров. Уровень С
На этой странице публикуются наиболее интересные задачи по геометрии для 7 класса уровня С, которые или составлены мной лично или проходили через меня в тот или иной период репетиторской работы. Преподавание геометрии способному ребенку — истинное удовольствие для любого репетитора по математике, особенно если под рукой хороший комплект уникальных и содержательных задач. Для маленьких учеников репетитору всегда не хватает хороших задач, их мало, так как дети еще многого не знают. Возможности составителей придумать что-то новое и интересное в рамках программы, сильно ограничены. Одно из направлений работы сайта «профессиональный репетитор по математике» — поиск, сортировка и составление таких задач. Именно тех, над которыми можно и нужно размышлять, задачи, которые не решаются одним взглядом по образцу и подобию, которые можно показать не только одаренным детям. Не путайте их с олимпиадными и конкурсными.
Уважаемые репетиторы по математике: присылайте ссылки и тексты таких задач. Я с удовольствием размещу их на сайте.
1) В четырехугольнике точки и — соответственно середины равных сторон и . Серединные перпендикуляр к стороне пересекает серединный перпендикуляр к стороне в точке . Докажите, что серединный перпендикуляр, проведенный к отрезку проходит через точку .
2) В четырехугольнике серединные перпендикуляры к сторонам и пересекаются на стороне . Известно, что . Докажите, что в четырехугольнике диагонали равны.
3) В квадрате даны точки и соответственно на сторонах и ,причем . Докажите равенство
Комментарий репетитора по математике: для решения этой задачи достаточно элементарных представлений о квадрате. Обычно они у 7 классника есть. И тем более они есть у того, кто пробует решать такие задачи.
4) В треугольнике проведены биссектрисы и , пересекающиеся в точке M, а в треугольнике проведены биссектрисы и , пересекающиеся в точке . Докажите, что и лежат на одной прямой.
5) В равнобедренном треугольнике c основанием на боковых сторонах отложены равные отрезки и . Отрезки и пересекаются в точке. Докажите, что — биссектриса угла .
6) В равнобедренном треугольнике на боковых сторонах и даны точки и так, что . На основании отмечены еще две точки и такие, что . Известно, что и . Докажите, что .
7) В треугольнике проведены две биссектрисы и , пересекающиеся в точке . Известно, что , . Доказать, что — равнобедренный.
8) Дан треугольник ABC, у которого . Докажите, что треугольник, с вершинами в основаниях его биссектрис — прямоугольный.
P.S. Конечно, для решения первых задач семиклассник должен иметь элементарные представления о четырехугольниках. Однако, учитывая низкую смысловую нагрузку на новые понятия и уровень проявляющего интерес к математике школьника, репетитору не придется тратить время на разжевывание и закрепление элементарного. Хватит и пяти минут. При использовании понятия «диагональ» репетитор по математике примитивнейшим образом показывает ее на рисунке. В других ситуациях (когда ученик слабый) придется готовить специальные задания на отработку нового термина.
Обычно дети, проявляющие способности и интерес к математике, легко обучаемы ее основам, поэтому репетитор вполне может немного «забежать вперед» по программе. Если он не собирается опережать школу — следует изменить условия первых задач. Вместо четырехугольника репетитору по математике следует указать самые обычные 4 точки с равными отрезками.
Удачного изучения и использования материалов на индивидуальных занятиях.
Колпаков А.Н. Репетитор по математике Москва, Строгино.
Метки: Геометрия, Задачник по геометрии, Ученикам, Элементарная математика
ankolpakov.ru
Задачи по геометрии за курс 7 класса (для итогового повторения).
Documents войти Загрузить ×- Математика
- Геометрия
Related documents

9 кл входной контроль ГЕОМЕТРИЯ

Специализированное структурное образовательное подразделение Посольства России в Египте средняя

Геометрия для 7 класса

Задания для подготовки

Document 114283

В – 5 ПЛАНИМЕТРИЯ ABC , AC

Тип урока Тема Планируемые результаты :

— pedportal.net
Вариант № 2014

Вспомним о геометрии. представленные задачи.

оригинальный файл 55.5 Кб

В равнобедренном треугольнике ABC с основанием AC боковая
Скачать advertisementstudydoc.ru
Задачи на построение. Геометрия, 7 класс: уроки, тесты, задания.
| 1. |
Отрезки и окружность
Сложность: лёгкое |
4 |
| 2. |
Радиус, диаметр и хорда окружности
Сложность: лёгкое |
1 |
| 3. |
Хорда, радиус и диаметр окружности
Сложность: лёгкое |
1 |
| 4. |
Диаметр окружности
Сложность: лёгкое |
1 |
| 5. |
Радиус окружности
Сложность: лёгкое |
1 |
| 6. |
Окружность или круг
Сложность: лёгкое |
1 |
| 7. |
Расположение окружностей
Сложность: среднее |
1 |
| 8. |
Общая часть окружностей или кругов
Сложность: среднее |
1 |
| 9. |
Радиусы и точки пересечения окружностей
Сложность: среднее |
2 |
| 10. |
Построение по основным конструкциям
Сложность: среднее |
1 |
| 11. |
Равные треугольники в окружности
Сложность: среднее |
3 |
| 12. |
Построение треугольника равного данному
Сложность: среднее |
2 |
| 13. |
Общие точки окружностей
Сложность: среднее |
2 |
| 14. |
Диаметры окружности или круга
Сложность: среднее |
2 |
| 15. |
Построение треугольника по данным сторонам и медиане
Сложность: сложное |
8 |
www.yaklass.ru
Готовые решения задач — Геометрия 7 класс Атанасян Л.С.
Геометрия. Решение задач. 7 класс. К учебнику Атанасяна «Геометрия 7-9» Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Юдина И.И.М.: Физматлит, 2005. — 120с.
Настоящее издание является первой частью учебно-методического пособия, содержащего решения задач из учебника «Геометрия 7-9» Л.С.Атанасяна, В.Ф.Бутузова, С.Б.Кадомцева, Э.Г.Позняка, И.И.Юдиной (М.: Просвещение, 1990 и последующие издания). Данный выпуск содержит решения задач, относящихся к 7 классу.
ОГЛАВЛЕНИЕ
Предисловие
Глава 1. Начальные геометрические сведения
§ 1. Прямая и отрезок
§ 2. Луч и угол
§3. Сравнение отрезков и углов
§4. Измерение отрезков
§5. Измерение углов
§6. Перпендикулярные прямые
Дополнительные задачи
Задачи повышенной трудности к главе 1
Глава 2. Треугольники
§ 1. Первый признак равенства треугольников
§2. Медианы, биссектрисы и высоты треугольника
§3. Второй и третий признаки равенства треугольников
§4. Задачи на построение
Дополнительные задачи
Задачи повышенной трудности к главе 2
Глава 3. Параллельные прямые
§ 1. Признаки параллельности двух прямых
§2. Аксиома параллельных прямых
Дополнительные задачи
Глава 4. Соотношения между сторонами и углами треугольника
§ 1. Сумма углов треугольника
§2. Соотношения между сторонами и углами треугольника
§3. Прямоугольные треугольники
§4. Построение треугольника по трем элементам
Задачи на построение
Дополнительные задачи
Задачи повышенной трудности к главам 3 и 4
proresheno.ru

 Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.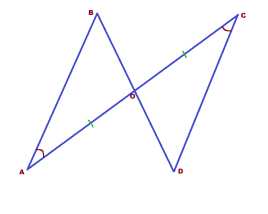 Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.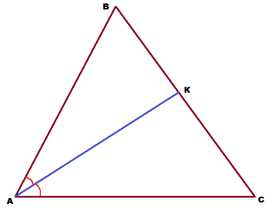 Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.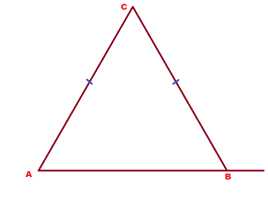 Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.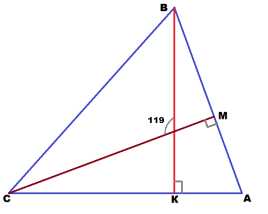 Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.