Занятия онлайн по алгебре 7 класс – Алгебра, 7 класс: уроки, тесты, задания

Алгебра, 7 класс: уроки, тесты, задания

Информация о разделе

Математический язык. Математическая модель

1. Числовые и алгебраические выражения

2. Что такое математический язык

3. Что такое математическая модель

4. Линейное уравнение с одной переменной

5. Координатная прямая

Линейная функция

1. Координатная плоскость

2. Линейное уравнение с двумя переменными и его график

3. Линейная функция y = kx + m и её график

4. Линейная функция y = kx

5. Взаимное расположение графиков линейных функций

Системы двух линейных уравнений с двумя переменными

1. Основные понятия

2. Метод подстановки

3. Метод алгебраического сложения

4. Системы двух линейных уравнений с двумя неизвестными как математические модели реальных ситуаций

Степень с натуральным показателем и её свойства

1. Что такое степень с натуральным показателем

2. Таблица основных степеней

3. Свойства степени с натуральным показателем

4. Умножение и деление степеней с одинаковым показателем

5. Степень с нулевым показателем

Одночлены. Арифметические операции над одночленами

1. Понятие одночлена. Стандартный вид одночлена

2. Сложение и вычитание одночленов

3. Умножение одночленов. Возведение одночлена в натуральную степень

4. Деление одночлена на одночлен

Многочлены. Арифметические операции над многочленами

1. Основные понятия

2. Сложение и вычитание многочленов

3. Умножение многочлена на одночлен

4. Умножение многочлена на многочлен

5. Формулы сокращённого умножения

6. Деление многочлена на одночлен

Разложение многочлена на множители

1. Что такое разложение на множители

2. Вынесение общего множителя за скобки

3. Способ группировки

4. Разложение многочлена на множители с помощью формул сокращённого умножения

5. Разложение многочлена на множители с помощью комбинации различных приёмов

6. Сокращение алгебраических дробей

7. Тождества

Квадратичная функция y = x²

1. Квадратичная функция и её график

2. Графическое решение уравнений

3. Что означает в математике запись у = f(x)

www.yaklass.ru

Конспект «Алгебра 7 класс. Все формулы и определения»

Алгебра 7 класс. Все формулы и определения.
Краткий курс алгебры за 7 класс.

«Алгебра 7 класс. Все формулы и определения» — это краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2013.

---

Выражения и их преобразования

☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а:
Степенью числа а с показателем 1 называют само число а:  а¹ = а.
Степень числа а ≠ 0 с показателем 0 равна 1:  а⁰ = 1.

☑ 2. Свойства степеней с натуральными показателями:

 а^m • аⁿ = а^{m+ n}

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

а^m : аⁿ = а^{m — n}, где а ≠ 0, m ≥ n

(а^m)ⁿ = а^mn

При возведении степени в степень основание оставляют прежним, а показатели перемножают.

(ab)ⁿ = аⁿbⁿ

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

☑ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а²х, –3а²b³, 4, х, у⁵ — одночлены.

 Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а²b⁴ равна 6.

☑ 4. Многочленом называют сумму одночленов. Например, 3х⁵ – 4х² + 1, 7a³b – ab² + ab + 6—многочлены. Одночлены считают многочленами, состоящими из одного члена.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х³у + 3х²у⁵ + ху равна степени одночлена 3х²у⁵, т. е. равна 7.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

☑ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,

(3аb + 5с²) + (ab – с²) = 3ab + 5с² + ab – с² = 4аb + 4с²

При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,

(6x² – у) – (2x² – 8у) = 6х² – у – 2х² + 8у = 4х² + 7у

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,

а² (3аb – b³ + 1) = 3а³b – а²b³ + а²

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,

(5х – 1)(3х + 2) = 15x² – Зx + 10x – 2 = 15x² + 7x – 2

☑ 6. Формулы сокращённого умножения:

(а + b)² = а² + 2аb + b²

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а – b)² = а² – 2аb + b²

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а + b)³ = а³ + 3а²b + 3ab² + b³

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(а – b)³ = а³ – 3а²b + Заb² – b³

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(а – b)(а + b) = а² – b²

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

а³ + b³ = (а + b)(a² – аb + b²)

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

а³ – b³ = (а – b)(a² + ab + b²)

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.

Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х³ – х²у можно разложить на множители, вынеся за скобки х² : 5х³ – х²у = х² (5х – у). Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:

3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).

Многочлен а⁴ – 25x² можно разложить на множители, используя формулу разности квадратов двух выражений:

а⁴ – 25x² = (а²)² – (5x)² = (а² – 5x)(а² + 5x).

Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.

Уравнения

☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x +1 = 5х – 15, так как верно равенство 3•8 + 1= 5•8 – 15.

Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.

☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x² = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.

При решении уравнений с одной переменной используются следующие свойства:

• если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
• если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b, где х — переменная, а и b — числа.

Если а ≠ 0, то уравнение ах = b имеет единственный корень b/a.

Например, уравнение 7х = 2 имеет корень 2/7.

Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.

Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.

☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = —1, у = 4 — решение уравнения 5х + 3у = 7.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.

☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.

☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы
так как является верным каждое из равенств   7 + (–1) = 6   и   2 • 7 – (–1) = 15.

Решить систему уравнений — значит найти все её решения или доказать, что решений нет.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.

☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.

При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:

• если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
• если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.

При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:

• выражают из какого–либо уравнения системы одну переменную через другую;
• подставляют в другое уравнение системы вместо этой переменной полученное выражение;
• решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.

При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:

• умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
• складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.

Функции

☑ 16. Функциональная зависимость, или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа.

Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.

Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b, параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.

Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.

Линейную функцию, задаваемую формулой у – kx при k ≠ 0, называют прямой пропорциональностью.

 График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой координатных четвертях.

☑ 18. График функции у = х² — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.

График функции у = х³ проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.

Статистические характеристики

 ☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.

 Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.

 Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.

Например, медиана ряда чисел  17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел  28, 43, 54, 56, 58, 62 равна 55.

 Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.

Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.

 

---

Вы смотрели Конспект «Алгебра 7 класс. Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:

Алгебра 7 класс. Все формулы и определения

4.6 (91.43%) 7 vote[s]

uchitel.pro

материалы и советы, репетиторы для ребенка 13 лет — Колпаков Александр Николаевич

Предлагаю Вам новый раздел со справочной, учебно-методической и разъяснительно-рекомендательной информацией, связанной с запросом репетитор по математике 7 класс. Также здесь будут публиковаться мои заметки об особенностях работы с маленькими учениками (пока отдельные части этой страницы находятся в стадии доработки).

Меня всегда интересовало, зачем в поисковых строчках яндекса или гугла к главной фразе репетитор по математике приписывают еще и 7 класс? Можно подумать, что есть такие репетиторы, которые работают только семиклассниками и больше ни с какими другими возрастами. Да, математика 7 класса – это особый этап освоения предмета, с весьма своеобразными подходами к обучению, отличие которых от работы со старшеклассниками видят все, в том числе и преподаватели, которые в силу своего образования таковыми не являются. Но одно дело — чувствовать эту разницу, а другое дело – уметь следовать заложенным в программе 7 класса морально-методическим принципам. Видимо те немногие родители, кого интересует выбор репетитора по математике в 7 классе, осознают всю сложность работы с возрастом 12-13 лет и пытаются получить ответы на какие-то поисковые вопросы. Эта страница как раз для таких мам и пап.

Оценивая потребность в информационной поддержке сочетания «репетитор по математике» в паре с «7 классом», я решил изменить традициям и создать практическую страничку, на которой можно было бы соединить дидактический и методический раздел с заданиями и инструкциями по работе преподавателя в 7 классе. Это тесты, перечень тем, изучаемых семиклассниками по разным программам, советы репетитору по работе с математикой 7 класса, родителям по «уходу» за школьниками в младшем и среднем возрасте и др. Читайте, решайте, оценивайте себя или своего ребенка, его репетитора / школьного преподавателя и обращайтесь за помощью в случае необходимости.

Полезные материалы по математике для 7 класса от репетитора

Мой тест по алгебре за 7 класс (повышенной сложности):

Пройдите аналогичный тест за 7 класс. Алгебра, уровень «А», учебник Макарычева.

Доступны дополнительные материалы:
Репетитору по математкие для работы в 7 классе. Тест на формулы сокращенного умножения.

Если Вы занимались какое-то время с учеником 7 класса самостоятельно или нанимали ему преподавателя, то наверняка знаете, как тяжело запрягать новую телегу под названием «геометрия». Далеко не всем профессиональным репетиторам по математике удается в 7 классе растолковать маленькому ученику азы этого весьма специфического предмета. Чрезвычайно трудно понять логику доказательства простых и очевидных фактов, тех, которые видны невооруженным глазом и понятны без лишних слов. Тем не менее, репетитор по математике должен довести технику до полного ее осознания и принятия. Пожалуй, это главная проблема, с которой приходится сталкиваться репетитору. Я решаю ее через сочетание целого ряда методов и упражнений, направленных не только на разъяснение новых принципов, но и на запоминание типичных для ранней геометрии логических переходов.

Как мне кажется, правильная работа репетитора по математике с 7 классом по геометрии в самом начале ее изучения должна быть направлена запоминание наиболее часто используемых образцов записей, стандартных схем и даже результатов некоторых обосновании. Она позволяет сформировать у ученика ощущение близости новых для него форм и методов. Дело в том, что ребенок понимает и принимает в свой мир только то, что хорошо помнит и с чем регулярно приходится сталкиваться в жизни. А запоминает то, что его окружает с утра до вечера, в чем он живет.

Конечно, наивно предполагать, что репетитору по математике в 7 классе удастся погрузить подопечного в планиметрию «на полную катушку», но максимально заполнить мир новыми понятиями и заданиями необходимо. Именно с таким расчетом подбираются упражнения, способные притянуть школьника, а не отбросить его от предмета. При наделении меня достаточным количеством временем на начальном этапе изучения геометрии я предлагаю своему подопечному множество заданий развивающего вводного плана (переходного типа), для выполнения которых нужно просто что-то нарисовать, перечислить изображенные объекты, обозначить их, сравнить их размеры, сопоставить рисунки с их символикой. Идет отработка таких понятий, как пересечение, принадлежность, уяснение обозначений и относительного расположения нескольких объектов по отношению друг другу. Надо сказать, что чем проще задание, тем сложнее его разрабатывать, подбирать и оформлять. Важно провести работу над запоминанием терминов, ибо математическая речь, которой владеет Ваш репетитор математике 7 класс, для ученика может оказаться не соответствующей его словарному запасу и смысловой привязке к определенным картинкам.

Терминологическая работа чрезвычайно важна, ибо аккуратные с точки зрения точной математики разъяснения репетитора в 7 классе кажутся детям чем-то космически далеким и непонятным. Однако не стоит увлекаться терминами и не стоит превращать занятия в уроки рисования, ибо суть геометрии в ином.

Проблем с математикой 7 класса хватит на целый сайт, и нет смысла перечислять их все на этой странице.

Отличия между программами по математике 5 — 6 класса и 7 класса?

Преподавание математики в 7 классе принципиально отличается от аналогичной работы в 5 классе и даже в недавно оконченном 6 классе. Главным образом это связано с разделением предмета на геометрию (планиметрию) и алгебру, а также необходимостью заниматься формированием некоего универсального инструмента для решения практических, текстовых или геометрических задач в будущем. Речь идут об умении решать уравнения, а позже и неравенства. Поэтому все усилия репетитора по математике в работе с курсом алгебры 7 класса направляются на изучение буквенных выражений. Некоторых детей это сильно ломает, так как за годы учебы в 5 — 6 классах они привыкают к определенным схемам и правилам изучения математики: а именно к работе с отдельными числами и отдельными арифметическими действиями. В 7 классе репетитор пытается заставить ребенка по-иному взглянуть на буквенные записи и научить оценивать результаты вычислений без их непосредственного выполнения. Например, нужно догадаться, что ни одно число не является корнем уравнения . Заметим, что 6 классе репетитору не приходится разбирать все варианты ответов линейный уравнений.

Есть несколько качеств и профессиональных навыков, которыми должен обладать преподаватель, работающий с семиклассниками.
Репетитор по математике 7 класс – это:

1) Преподаватель, способный грамотно спланировать разделение уроков на алгебру геометрию

2) Репетитор — методист, ориентирующийся сразу в нескольких программах за 7 класс
Учебников для семиклассников больше чем для шестиклассников. Чего стоит перечисление одних только популярных базовых программ: Мордкович ,Алимов, Макарычев. А еще экспериментальные и профильные курсы. Недавно вышел учебник Петерсона для 7 класса. Репетитор по математике обязан знать и уметь работать с их темами именно в том порядке, в котором они расположены, ибо ученик может придти какой угодно.

3) Репетитор – психолог.
В 7 классе дети вплотную подходят к тяжелому переходному возрасту 14-15 лет. Не исключены ранние конфликты на почве учебы с родителями и учителями. Репетитор, обладающий определенными психологическими знаниями и способностью убедить ребенка в том, что нужно учиться, как правило, добивается хороших результатов даже в работе с трудными подростками.

Существует целый рад принципиальных изменений при переходе от программ 5 — 6 класса к 7 классу. Вот они:

1) Изменение подходов к решению текстовых задач. Если шестиклассники сочетают арифметические действия с уравнениями (в примерном соотношении 1:1), то в 7 классе для решения текстовых задач используются только одни уравнения. В 8 — 9 классе они будут только усложняться, в связи с чем на репетитора по математике сваливается работа по изучению одночленов и многочленов во всех мыслимых и немыслимых сочетаниях степеней, слагаемых, скобок и алгебраических действий.

2) Резкое снижение доли практических задач в 7 классе. Это является следствием заполнения программы заданиями, направленными на формирования алгебраической базы школьника.

3) Полное обоснование используемых теорем, тождеств, выводов и алгоритмов. Никогда ранее ученик не сталкивался с таой математикой. Для того, чтобы репетитор в 7 классе не испытывал с учеников проблем с доказательствами (выводами), необходима подготовка их восприятию на материале олимпиадных задач для 5 — 6 класса определенного вида. Они имеются копилке материалов любого хорошего репетитора.

4) Ведение целого ряда новых фундаментальных понятий, таких как функция, тождество, система уравнений и др. В геометрии их еще больше.

5) Увеличение объема записей в тетрадях (по геометрии) и количества типовых заданий (по алгебре). Следствием этого является увеличение физической нагрузки ученика. Она может привести к первым протестам и конфликтам с репетитором по математике и родителями.

Колпаков А.Н. Репетитор по математике для 7 класса.

ankolpakov.ru

Интернет школа Interneturok — бесплатные школьные уроки по алгебре в 7 классе онлайн, видео уроки по алгебре

Вторым разделом математики, который в 7 классе преподается в качестве отдельной образовательной дисциплины, является алгебра. Если вы видите необходимость в том, чтобы ваш ребенок ознакомился с этим предметом предварительно, видеоматериалы из раздела алгебра 7 класс онлайн к вашим услугам. С их помощью вы можете помочь своему ребенку-школьнику подготовиться к изучению этой дисциплины, а также сделать ее максимально понятной для него.

Анонс курса алгебры 7 класса

 

Знакомство с этим новым разделом математической науки начнется с освоения ее особого языка. Первое, что предстоит узнать учащимся в этом курсе: что такое математическая модель, числовые и алгебраические выражения, какие действия можно выполнять с натуральными и дробными числами. Это очень важные аспекты, без понимания которых невозможно будет продвинуться в дальнейшем усвоении этой сложной дисциплины.

Несколько уроков будут посвящены тому, как связана математическая модель с решением текстовых задач и как в ней использовать числовые и алгебраические выражения. Изучая многочлены и одночлены, каждый пользователь сможет научиться выполнять различные арифметические операции над ними. Знакомясь с тем, что такое линейная функция, учащиеся не только усвоят терминологию, но и научатся решать линейные уравнения с двумя переменными.

 

Школьные уроки алгебры в 7 классе подразумевают под собой обучение составлению буквенных выражений и формул по условиям задач, а также осуществление в формулах и выражениях числовых подстановок и выполнение соответствующих вычислений. Помимо этого, учебник алгебры за 7 класс содержит образовательные материалы по осуществлению подстановки одного выражения в другое, выражению из формул одной переменной через остальные, выполнение действий со степенями с целыми показателями, многочленами , алгебраическими дробями и многое другое. Раздел нашего сайта алгебра 7 класс – бесплатен и содержит множество информации, поясняющей трудные темы в формате видео.

 

Последовательность видеоуроков полностью повторяет учебник алгебры за 7 класс, поэтому вы всегда можете легко контролировать процесс усвоения материала, заранее готовясь к сложным темам и стремясь углубить их понимание. Огромным подспорьем в этом станет сервис онлайн-репетитора, которым снабжен каждый урок этого курса.

Видеоуроки по алгебре 7 класса

Если у вашего ребенка-семиклассника появляются проблемы, связанные с усвоением школьного курса математики, посетите наш сайт вместе с ним. Если темы алгебраических выражений, уравнений с одним неизвестным, алгебраических дробей, уравнений с двумя неизвестными, одночленов и многочленов, разложения на множители, линейных функций и их графиков сложны и он не успевает вовремя усвоить школьный материал,  наш портал поможет ему, поскольку в видеоуроках, снятых с участием опытных педагогов, даже самые сложные темы раскрываются максимально просто и понятно. За довольно небольшое время можно не только сократить отставание по школьной программе, но даже опередить ее, изучая темы, которые только предстоит пройти одноклассникам. В качестве дополнительного самостоятельного образования видеоуроки нашего образовательного портала – это то, что нужно!

interneturok.ru

ГДЗ по алгебре 7 класс

Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст. 1274 п. 1 части четвертой Гражданского кодекса Российской Федерации)

• Алгебра 7 класс. ФГОС Мерзляк, Полонский, Якир Вентана-Граф
• Алгебра 7 класс. Углубленный уровень Макарычев, Миндюк Мнемозина
• Алгебра 7 класс. ФГОС Мордкович, Александрова, Мишустина Мнемозина
• Алгебра 7 класс Алимов Просвещение
• Алгебра 7 класс. ФГОС Дорофеев, Суворова Просвещение
• Алгебра 7 класс. ФГОС Колягин, Ткачева, Фёдорова Просвещение
• Алгебра 7 класс. ФГОС Никольский, Потапов, Решетников Просвещение
• Алгебра 7 класс. ФГОС Макарычев, Миндюк, Нешков Просвещение
• Дидактические материалы по алгебре 7 класс Мерзляк, Полонский, Рабинович Вентана-Граф
• Дидактические материалы по алгебре 7 класс Феоктистов Мнемозина
• Дидактические материалы по алгебре 7 класс Зив, Гольдич Петроглиф
• Дидактические материалы по алгебре 7 класс Евстафьева, Карп Просвещение
• Дидактические материалы по алгебре 7 класс Потапов, Шевкин Просвещение
• Дидактические материалы по алгебре 7 класс Ткачева, Федорова Просвещение
• Дидактические материалы по алгебре 7 класс. ФГОС Звавич, Кузнецова Просвещение
• Дидактические материалы по алгебре 7 класс Попов. К учебнику Мордковича Экзамен
• Дидактические материалы по алгебре 7 класс Звавич, Дьяконова Экзамен
• Контрольные работы по алгебре 7 класс Мордкович Мнемозина
• Контрольные работы по алгебре 7 класс. ФГОС Александрова Мнемозина
• Контрольные работы по алгебра 7 класс. ФГОС Кузнецова Просвещение
• Контрольные и самостоятельные работы по алгебре 7 класс. ФГОС Попов, Мордкович Экзамен
• Самостоятельные и контрольные работы по алгебре 7 класс. ФГОС Глазков, Гаиашвили Экзамен
• Проверочные работы по алгебре 7 класс. ФГОС Александрова Мнемозина
• Самостоятельные работы по алгебре 7 класс. ФГОС Александрова Мнемозина
• Контрольно-измерительные материалы (КИМ) по алгебре 7 класс. ФГОС Мартышова Вако
• Контрольно-измерительные материалы (КИМ) по алгебре 7 класс. ФГОС Глазков, Гаиашвили Экзамен

---

Рабочие тетради

• Рабочая тетрадь по алгебре 7 класс. Часть 1, 2 Мерзляк, Полонский, Якир Вентана-Граф
• Рабочая тетрадь по алгебре 7 класс. Часть 1, 2. ФГОС Муравин Дрофа
• Рабочая тетрадь по алгебре 7 класс. Часть 1, 2. ФГОС Зубарева, Мильштейн Мнемозина
• Рабочая тетрадь по алгебре 7 класс. ФГОС Минаева, Рослова Просвещение
• Рабочая тетрадь по алгебре 7 класс. Часть 1, 2 Потапов, Шевкин Просвещение
• Рабочая тетрадь по алгебре 7 класс. Часть 1, 2. ФГОС Миндюк, Шлыкова Просвещение
• Рабочая тетрадь по алгебре 7 класс. Часть 1, 2. ФГОС Колягин, Ткачева Просвещение
• Рабочая тетрадь по алгебре 7 класс. ФГОС Журавлев, Перепелкина. К учебнику Никольского Экзамен
• Рабочая тетрадь по алгебре 7 класс. ФГОС Ключникова, Комиссарова. К учебнику Мордкович Экзамен
• Рабочая тетрадь по алгебре 7 класс. Часть 1, 2. ФГОС Ерина. К учебнику Макарычева Экзамен

---

Тесты

ГДЗ по алгебре 7 класс. ФГОС

• Как быстро и правильно сделать домашнее задание по алгебре ученику 7 класса без помощи родителей и репетитора? Как сделать так, чтобы и уроки были поучены, и время на отдых на свежем воздухе осталось? А если очень хочется поиграть на компьютере, а в алгебре разбираться до ночи придется? Просто все эти вопросы решить поможет методическое пособие ГДЗ по алгебре 7 за класс. Заботливые авторы математики уже решили все домашние задания по алгебре за весь год! Противные неравенства и уравнения, сложные задачи и примеры. Теперь не нужно ломать голову над тем, правильно ли удалось решить задачу, можно просто сверить с решебником!

Лучше списать вдумчиво из решебника с формулами, чем второпях из тетрадки с ошибками

• Всем известно, что даже отличники иногда не хотят долго сидеть над «домашкой». Первая любовь, интересные премьеры в кинотеатрах или новые игры на приставках, которые так и ждут, когда за них примутся – все это зовет и отвлекает от уроков семиклассников. Правильно, ведь за учебой то и жизни настоящей не увидишь!
• Что делает среднестатистический школьник в таком случае? Ничего. Гуляет. А перед уроками второпях списывает «домашку» у одноклассников из тетрадки с ошибками и без понимания. Достаточно родителям купить и вручить своему ГДЗ по алгебре 7 класс, все проблемы с решением домашнего задания самоустранятся. Время, отведенное на уроки, сократится в 3 раза, а в тетради за домашнюю работу будет гарантированно высокая оценка. Кроме того, в решебнике дается подробное объяснение решения задач и уравнений, нужные формулы и правила. Таким образом, даже при механическом списывании работы, ученик волей-неволей запоминает правила выполнения заданий и систематизирует у себя в голове эти знания.

Родителям с решебниками по алгебре легко проверять уроки семиклассника

• Особенно строгие родители могут купить решебник не ребенку, а себе. Прошло много времени с тех пор, как вы окончили школу, некоторые знания могут исчезнуть или забыться. Неловко попадать впросак перед ребенком, показывая свою неосведомленность в определенном математическом вопросе. А решебник по математике всегда поможет быстро и четко проверить задание, помочь школьнику с пониманием и решением особо трудных упражнений и освежить свои знания.
• В 7-м классе традиционная математика в рамках школьного курса делится на два предмета — геометрию и алгебру. Последнюю семиклассники считают более понятной для изучения. Тем не менее, обилие новой терминологии, законов, практики требует внимательного, скрупулезного и вдумчивого отношения к дисциплине. Зачастую одних школьных уроков для полноценного усвоения материала бывает недостаточно. В этом случае пригодятся специальные учебные материалы и решебники к ним. Но важно помнить, что работа с ГДЗ тогда приносит значимые результаты, когда выполняется:
  — регулярно;
  — на основании специально разработанной схемы, плана изучения;
  — с запоминанием и проработкой рассмотренного материала, возвратом к тем тематикам, заданиям, которые вызвали наибольшие трудности.
• Такая работа полезна еще и тем, что позволяет изучить и запомнить порядок правильной, грамотной записи полученных результатов. Это важно для школьников, поскольку в диагностических работах, ВПР умение излагать и записывать ответы так, как это требуется стандартом, дает дополнительные баллы ученикам. Плюс — все семиклассники — будущие выпускники, а грамотная запись — основа высокого балла на ОГЭ/ЕГЭ. Алгебраических заданий немало в итоговых испытаниях и у девятиклассников, и у одиннадцатиклассников, сдающих математику в обязательном порядке.
• Перед тем, как выбрать оптимальный учебник по алгебре для 7 класс, следует оценить:
  — первоначальный уровень собственных знаний;
  — УМК, программу, по которой дисциплина изучается в школе. Если школьные знания преподаются качественно, имеет смысл выбрать дополнительный учебник по программе, отличной от школьной. Если нет — остановить свой выбор на той книге, которая изучается в классе;
  — понятность изложения материала, задания, ответы на них.
• Проанализировать все вышеперечисленные пункты семиклассники могут в школе, с педагогом-предметником, с репетитором либо самостоятельно. Самоподготовку эксперты называют одной из наиболее эффективных форм работы учащихся средней и старшей школы. Но чтобы она принесла желаемый результат, нужна усидчивость, регулярность и самоконтроль, объективная оценка собственных достигнутых успехов. Можно сочетать самоподготовку с посещением специальных курсов.

© Copyright. Все права защищены. Правообладатель SIA Ksenokss.
Адрес: 1073, Курземес проспект 106/45, Рига, Латвия.
Тел.: +371 29-851-888 E-mail: ekaterina[at]euroki.org

www.euroki.org

7 класс. Алгебра

Рубрика «7 класс. Алгебра»

I. Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.

Пример 1.  Умножить одночлен на многочлен: 2a·(4a²-0,5ab+5a³).

Решение. Одночлен 2а будем умножать на каждый одночлен многочлена:

2a·(4a²-0,5ab+5a³)=2a∙4a²+2a∙(-0,5ab)+2a∙5a³=8a³-a²b+10a⁴. Запишем полученный многочлен в стандартном виде:

10a⁴+8a³-a²b.

Пример 2. Умножить многочлен на одночлен: (3xyz⁵-4,5x²y+6xy³+2,5y²z)∙(-0,4x³).

Решение. Каждое слагаемое, стоящее в скобках, умножаем на одночлен (-0,4x³).

(3xyz⁵-4,5x²y+6xy³+2,5y²z)∙(-0,4x³)=

=3xyz⁵∙(-0,4x³) -4,5x²y∙(-0,4x³)+6xy³∙(-0,4x³)+2,5y²z∙(-0,4x³)=

=-1,2x⁴yz⁵+1,8x⁵y-2,4x⁴y³-x³y²z.

II. Представление многочлена в виде произведения двух или нескольких многочленов называется разложением многочлена на множители.

 III. Вынесение общего множителя за скобки – простейший способ разложения многочлена на множители.

Пример 3. Разложить на множители многочлен:  5a³+25ab-30a².

Решение. Вынесем общий множитель всех членов многочлена за скобки. Это одночлен 5а, потому что на 5а делится каждый из членов данного многочлена. Итак, 5а мы запишем перед скобками, а в скобках запишем частные от деления каждого одночлена на 5а.

5a³+25ab-30a²=5a·(a²+5b-6a). Проверяем себя: если мы умножим 5а на многочлен в скобках a²+5b-6a, то получим данный многочлен 5a³+25ab-30a².

Пример 4.Вынесите общий множитель за скобки: (x+2y)²-4·(x+2y).

Решение. (x+2y)²-4·(x+2y)=(x+2y)(x+2y-4).

Общим множителем здесь являлся двучлен (х+2у). Мы вынесли его за скобки, а в скобках записали частные от деления данных членов (x+2y)² и -4·(x+2y) на их общий делитель

(х+2у). В результате мы представили данный многочлен в виде произведения двух многочленов (x+2y) и (x+2y-4), другими словами, мы разложили многочлен (x+2y)²-4·(x+2y) на множители. Ответ:  (x+2y)(x+2y-4).

IV. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и записать полученные произведения в виде суммы одночленов. При необходимости привести подобные слагаемые.

Пример 5. Выполнить умножение многочленов: (4x²-6xy+9y²)(2x+3y).

Решение. По правилу мы должны каждый член первого многочлена (4x²-6xy+9y²) умножить на каждый член второго многочлена (2x+3y). Чтобы не запутаться, делайте всегда так: сначала умножьте каждый член первого многочлена на 2х, потом опять каждый член первого многочлена умножайте на 3у.

(4x²-6xy+9y²)(2x+3y)=4x²∙2x-6xy∙2x+9y²∙2x+4x²∙3y-6xy∙3y+9y²∙3y=

=8x³-12x²y+18xy²+12x²y-18xy²+27y³=8x³+27y³.

Подобные слагаемые -12x²y и 12x²y, а также 18xy² и -18xy² оказались противоположными, их суммы равны нулю.

Ответ: 8x³+27y³.

 

I.  Сумма одночленов называется многочленом. Одночлены, из которых составлен многочлен, называются членами многочлена.

Например, многочлен 2a+3a²b-6b⁴+3,5a³b состоит из суммы четырех одночленов.

II.  Двучлен – это многочлен, состоящий из двух членов (одночленов).

Примеры двучленов: 2a-3b; 6x²+5; 2x-1.

III. Трехчлен – это многочлен, состоящий из трех членов (одночленов).

Например,  2а+3с-х или x²+4x-5 — трехчлены, так как состоят из трех одночленов.

IV. Степенью многочлена называют наибольшую из степеней входящих в него одночленов.

Например, многочлен 2a²-3b+abc-d² имеет третью степень, так как наибольшей степенью входящих в него одночленов является третья степень одночлена abc (складываем показатели: 1+1+1=3).

Многочлен 4x⁴yz+2x²y³-xz⁴+3x²y² имеет шестую степень, так как наибольшей (шестой) степенью является степень его члена 4x⁴yz (складываем показатели: 4+1+1=6).

V. Многочлен стандартного вида не содержит подобных членов и записан в порядке убывания степеней его членов.

Например, приведенный выше многочлен 4x⁴yz+2x²y³-xz⁴+3x²y² является многочленом стандартного вида, так как записан в порядке убывания степеней его членов.

Пример 1. Упростить многочлен, записав каждый его член в стандартном виде: 4aabb∙(-0,5c²)+5a²bb³-6abcab²c.

Решение.

4aabb∙(-0,5c²)+5a²bb³-6abcab²c=-2a²b²c²+5a²b⁴-6a²b³c², а теперь запишем этот многочлен в стандартном виде (в порядке убывания степеней его членов):

-6a²b³c²-2a²b²c²+5a²b⁴.

Пример 2. Вычислить значение многочлена 5y²-3xy+x²при x=-1, y=2.

Решение.

5y²-3xy+x²=5∙2²-3∙(-1)∙2+(-1)²=5∙4+6+1=27.

Пример 3. Упростить многочлен 2aba-a³bb+7bbbb и найти его числовое значение при a=3, b=2.

Решение.

Упрощаем многочлен: 2aba-a³bb+7bbbb=2a²b-a³b²+7b⁴.

Подставляем значения a и b.

2a²b-a³b²+7b⁴=2∙3²∙2-3³∙2²+7∙2⁴=2∙9∙2-27∙4+7∙16=36-108+112=40.

Пример 4. Привести подобные члены многочлена:

Пример 5. Привести к стандартному виду многочлен:

Напоминание: подобными считают одночлены, имеющие одинаковую буквенную часть.

 I. Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются одночленами.

Примеры одночленов: 

а) a; б) ab; в) 12; г) -3c; д) 2a²∙(-3,5b)³; е) -123,45xy⁵z; ж) 8ac∙2,5a²∙(-3c³).

II. Такой вид одночлена, когда на первом месте стоит числовой множитель (коэффициент), а за ним переменные с их степенями, называют стандартным видом одночлена.

Так, одночлены, приведенные выше, под буквами а), б), в), г)  и е) записаны в стандартном виде, а одночлены под буквами д) и ж) требуется привести к стандартному виду, т. е. к такому виду, когда на первом месте стоит числовой множитель, а за ним записывают буквенные множители с их показателями, причем, буквенные множители стоят в алфавитном порядке. Приведем одночлены д) и ж) к стандартному виду.

д) 2a²∙(-3,5b)³=2a²∙(-3,5)³∙b³=-2a²∙3,5∙3,5∙3,5∙b³=-85,75a²b³;

ж) 8ac∙2,5a²∙(-3c³)=-8∙2,5∙3a³c³=-60a³c³.

III. Сумму показателей степеней всех переменных, входящих в состав одночлена, называют степенью одночлена.

Примеры. Какую степень имеют одночлены а) — ж)?

а) a.  Первую;

б) ab. Вторую: а в первой степени и b в первой степени-сумма показателей 1+1=2;

в) 12. Нулевую, так как буквенных множителей нет;

г) -3c. Первую;

д) -85,75a²b³. Пятую. Мы привели этот одночлен к стандартному виду, имеем а во второй степени и b в третьей. Складываем показатели: 2+3=5;

е)  -123,45xy⁵z. Седьмую. Сложили показатели степеней буквенных множителей: 1+5+1=7;

ж) -60a³c³. Шестую, так как сумма показателей буквенных множителей 3+3=6.

IV.  Одночлены, имеющие одинаковую буквенную часть, называются подобными одночленами.

Пример. Указать подобные одночлены среди данных одночленов 1) -7).

1) 3aabbc; 2) -4,1a³bc; 3) 56a²b²c; 4) 98,7a²bac; 5) 10aaa²x; 6) -2,3a⁴x; 7) 34x²y.

Приведем одночлены 1), 4) и 5) к стандартному виду. Тогда строчка данных одночленов будет выглядеть так:

1) 3a²b²c; 2) -4,1a³bc; 3) 56a²b²c; 4) 98,7a³bc; 5) 10a⁴x;  6) -2,3a⁴x; 7) 34x²y.

Подобными будут те, которые имеют одинаковую буквенную часть, т.е. 1) и 3); 2) и 4); 5) и 6).

1) 3a²b²c и 3) 56a²b²c;

2) -4,1a³bc и 4) 98,7a³bc;

5) 10a⁴x и  6) -2,3a⁴x.

 

Очень большие и очень малые числа принято записывать в стандартном виде: a∙10ⁿ, где 1≤а<10 и n  (натуральное или целое) – есть порядок числа, записанного в стандартном виде.

Например, 345,7=3,457∙10²; 123456=1,23456∙10⁵; 0,000345=3,45∙10^-4.

Примеры. 

Записать в стандартном виде число: 1) 40503; 2) 0,0023; 3) 876,1; 4) 0,0000067.

Решение.

1) 40503=4,0503·10⁴;

2) 0,0023=2,3∙10^-3;

3) 876,1=8,761∙10²;

4) 0,0000067=6,7∙10^-6.

Еще примеры на стандартный вид числа.

5) Число молекул газа в 1 см³ при 0°С и давлении 760 мм.рс.ст равно

27 000 000 000 000 000 000. Записать это число в стандартном виде.

Решение.

27 000 000 000 000 000 000=2,7∙10¹⁹.

6) 1 парсек (единица длины в астрономии) равен 30 800 000 000 000 км. Записать это число в стандартном виде.

Решение.

1 парсек=30 800 000 000 000=3,08∙10¹³ км.

В тему:

Киловатт-час — это внесистемная единица энергии или работы, применяется в электротехнике, обозначается кВт·ч.

1 кВт·ч=3,6∙10⁶ Дж (Джоулей).

 

 I. Определение.  (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:

Примеры. Вычислить:

Решение.

II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:

Примеры. Вычислить:

Решение.

 Свойства степени с натуральным показателем справедливы и для  степеней с любым показателем.

Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.

Примеры на все свойства степени.

Упростить:

Решение.

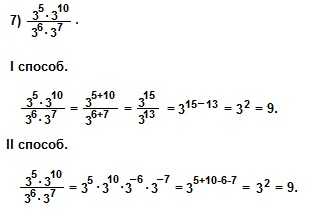       При решении 7) примера  I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями:  a^m∙aⁿ=a^m+n  и a^m:aⁿ=a^m-n. При решении II способом мы использовали понятие степени с отрицательным показателем:  и свойство произведения степеней с одинаковыми основаниями:  a^m∙aⁿ=a^m+n .

 

Пример 8 ) решаем так же, как решали пример 7) вторым способом.

 

 

 

В примере 9) представим 7³как 7²∙7, а степень 4⁵как 4³∙4², а затем сократим дробь на (7²∙4³).

 

В 10) примере применим формулу степени произведения: (ab)ⁿ=aⁿ∙bⁿ, а затем сократим дробь на (2⁶∙3⁵).

                 

I. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аⁿ.

Примеры. Записать произведение в виде степени.

1) mmmm;          2) aaabb;         3) 5·5·5·5·ccc;        4) ppkk+pppk-ppkkk.

Решение.

1) mmmm=m⁴, так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m, будет четвертой степенью числа m.

  2) aaabb=a³b²;    3) 5·5·5·5·ccc=5⁴c³;     4) ppkk+pppk-ppkkk=p²k²+p³k-p²k³.

II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аⁿ – степень, а – основание степени, n – показатель степени. Например:

 2³ — это степень. Число 2 — основание степени, показатель степени равен 3. Значение степени 2³равно 8, так как 2³=2·2·2=8.

Примеры. Написать следующие выражения без показателя степени.

5) 4³;       6) a³b²c³;       7) a³-b³;       8 ) 2a⁴+3b².

Решение.

5) 4³=4·4·4;       6) a³b²c³=aaabbccc;       7) a³-b³=aaa-bbb;       8) 2a⁴+3b²=2aaaa+3bb.

 III. а⁰=1  Любое число (кроме нуля) в нулевой степени равно единице. Например, 25⁰=1. 
 IV. а¹=а  Любое число в первой степени равно самому себе. 

 V. a^m∙aⁿ=a^m+n   При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

Примеры. Упростить:

9) a·a³·a⁷;             10) b⁰+b²·b³;             11) c²·c⁰·c·c⁴.

Решение.

9) a·a³·a⁷=a¹⁺³⁺⁷=a¹¹;           10) b⁰+b²·b³=1+b²⁺³=1+b⁵;             

11) c²·c⁰·c·c⁴=1·c²·c·c⁴=c²⁺¹⁺⁴=c⁷.

VI.  a^m:aⁿ=a^m— n  При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Примеры. Упростить:

12) a⁸:a³;       13) m¹¹:m⁴;         14) 5⁶:5⁴.

12) a⁸:a³=a^8-3=a⁵;       13) m¹¹:m⁴=m^11-4=m⁷;         14) 5⁶:5⁴=5²=5·5=25.

VII. (a^m)ⁿ=a^mn   При возведении степени в степень основание оставляют прежним, а показатели перемножают.

Примеры. Упростить:

15) (a³)⁴;         16) (c⁵)².

15) (a³)⁴=a^3·4=a¹²;         16) (c⁵)²=c^5·2=c¹⁰.

Обратите внимание, что, так как от перестановки множителей произведение не меняется, то:

15) (a³)⁴=(a⁴)³;         16) (c⁵)²=(c²)⁵.

 VIII. (a∙b)ⁿ=aⁿ∙bⁿ   При возведении произведения в степень возводят в эту степень каждый из множителей.

Примеры. Упростить:

17) (2a²)⁵;      18) 0,2⁶·5⁶;        19) 0,25²·40².

Решение.

17) (2a²)⁵=2⁵·a^2·5=32a¹⁰;      18) 0,2⁶·5⁶=(0,2·5)⁶=1⁶=1;

19) 0,25²·40²=(0,25·40)²=10²=100.

       IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.

Примеры. Упростить:

Решение.

 

Функцию вида y=x³ называют кубической функцией. Графиком кубической функции является кубическая парабола, проходящая через начало координат. Ветви кубической параболы y=x³ находятся в I и III четвертях.

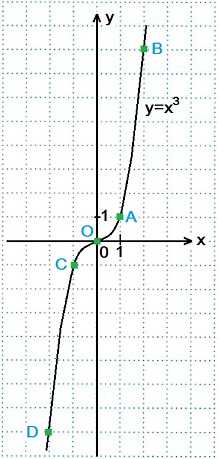Построение графика кубической функции y=x³

Составим таблицу значений функции y=x³ для х=0, х=±1, х=±2.

   x     |    y=x³

   0    |    0³=0            Точка О(0; 0)

   1    |    1³=1            Точка А(1; 1)

  -1    | (-1)³=-1          Точка С(-1; -1)

    2   |   2³=8             Точка В(2; 8 )

  -2   | (-2)³=-8           Точка D(-2; -8)

Функцию вида y=x² называют квадратной функцией. Графиком квадратной функции является парабола с вершиной в начале координат. Ветви параболы y=x² направлены вверх.

Построение графика функции y=x². Составим таблицу значений функции для х=0, х=±1, х=±2, х=±3.

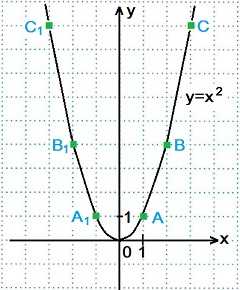х    |   y=x² 

0    |  0²=0  

1    |  1²=1              Точка А(1; 1)

-1   | (-1)²=1           Точка А₁(-1; 1)

2    |   2²=4             Точка В(2; 4)

-2   | (-2)²=4           Точка В₁(-2; 4)

3    |  3²=9              Точка С(3; 9)

-3   | (-3)²=9           Точка С₁(-3; 9)

data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»2890988705″>

1)    Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

       (a+b)² = a²+2ab+b² 

  a) (x + 2y)² = x² + 2 ·x·2y + (2y)² = x² + 4xy + 4y²

б) (2k + 3n)² = (2k)² + 2·2k·3n + (3n)² = 4k² + 12kn + 9n²

2)    Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

        (a-b)² = a²-2ab+b²

 а)   (2a – c)² = (2a)²-2·2a·c + c² = 4a² – 4ac + c²

б)   (3a – 5b)² = (3a)²-2·3a·5b + (5b)² = 9a² – 30ab + 25b²

3)    Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.

         a²–b² = (a–b)(a+b)

a)      9x² – 16y² = (3x)² – (4y)² = (3x – 4y)(3x + 4y)

б)  (6k – 5n)( 6k + 5n) = (6k)² – (5n)² = 36k² – 25n²

4)  Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

        (a+b)³ = a³+3a²b+3ab²+b³

a)  (m + 2n)³ = m³ + 3·m²·2n + 3·m·(2n)² + (2n)³ = m³ + 6m²n + 12mn² + 8n³

б)  (3x + 2y)³ = (3x)³ + 3·(3x)²·2y + 3·3x·(2y)² + (2y)³ = 27x³ + 54x²y + 36xy² + 8y³

5)  Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a-b)³ = a³-3a²b+3ab²-b³

а)  (2x – y)³ = (2x)³-3·(2x)²·y + 3·2x·y² – y³ = 8x³ – 12x²y + 6xy² – y³

б)  (x – 3n)³ = x³-3·x²·3n + 3·x·(3n)² – (3n)³ = x³ – 9x²n + 27xn² – 27n³

6)  Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.

a³+b³ = (a+b)(a²–ab+b²)

a)      125 + 8x³ = 5³ + (2x)³ = (5 + 2x)(5² — 5·2x + (2x)²) = (5 + 2x)(25 – 10x + 4x²)

б)  (1 + 3m)(1 – 3m + 9m²) = 1³ + (3m)³ = 1 + 27m³

7)  Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.

 a³-b³ = (a-b)(a²+ab+b²)

а) 64с³ – 8 = (4с)³ – 2³ = (4с – 2)((4с)² + 4с·2 + 2²) = (4с – 2)(16с² + 8с + 4)

б) (3a – 5b)(9a² + 15ab + 25b²) = (3a)³ – (5b)³ = 27a³ – 125b³

Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.

Страница 1 из 11

www.mathematics-repetition.com