ГДЗ по Алгебре для 8 класса Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов ФГОС
Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов.
Издательства: Просвещение, Мнемозина 2014, 2018
«ГДЗ по алгебре 8 класс углубленный уровень Макарычев, Миндюк, Нешков, Феоктистов (Просвещение, Мнемозина)» эффективно поможет восьмиклассникам на хорошем уровне овладеть материалом в рамках данного технического предмета. Решебник включает в себя не только верные ответы, но и полезные комментарии автора к решению всех номеров из учебного пособия. Благодаря этому, юный пользователь вспомогательного ресурса сможет научиться самостоятельно выполнять сложные задания и разобраться в трудном параграфе из учебника.
Мы выделили и другие полезные свойства учебно-методического пособия ГДЗ:
- – размещено онлайн в глобальной сети «интернет»;
- – наличие мобильной версии сайта для доступа со смартфона;
- – сможет расставить по полочкам в голове у подростка все полученные на уроке знания.
Важным преимуществом является и то, что правильное использование решебника в подготовке к уроку поможет школьникам значительно сэкономить своё личное время при работе с домашним заданием и обеспечит правильность его выполнения.
Кому будет полезно использовать решебник по алгебре для 8 класса углубленного уровня от Макарычева
Данное пособие c ГДЗ абсолютно универсально и может здорово помочь любому типу учеников. Отличникам, преуспевающим в изучении данной технической дисциплины, решебник позволит как следует потренироваться в решении трудных упражнений с возможностью самопроверки по верным ответам. Троечники, использующие вспомогательный ресурс, смогут своевременно справиться с имеющимися в учебе трудностями и оперативно подтянуть свои оценки.
Особенности изучения алгебры в средней школе
На уроках по данной дисциплине ученики восьмого класса познакомятся с множеством популярных математических формул, необходимых для решения различных неравенств и уравнений.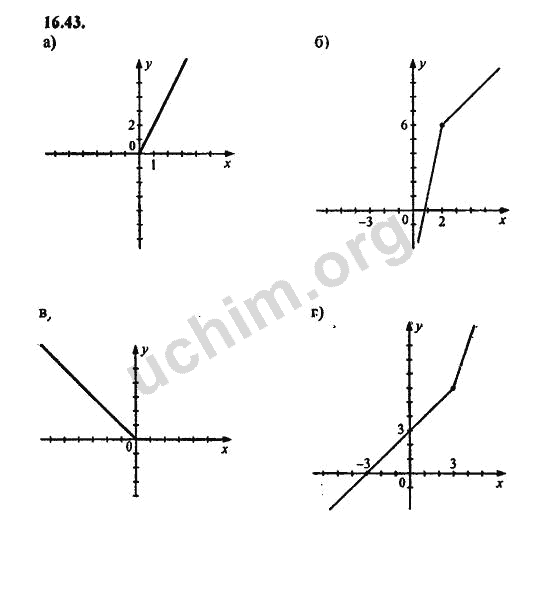
Преподаватель поведает своим воспитанникам о том, какие существуют приемы и хитрости для оперативного и качественного выполнения сложных заданий. Помимо этого, данный курс включает в себя большое количество теоретического материала по следующим важным темам:
- – основное свойство алгебраической дроби;
- – преобразование сложных рациональных уравнений;
- – арифметический квадратный корень.
Грамотно составленное учебно-методическое пособие «ГДЗ по алгебре за 8 класс углубленный уровень Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Феоктистов И. Е. (Просвещение, Мнемозина)» поможет школьникам качественно освоить перечисленные выше параграфы и стать лучшим знатоком точных наук в своём классе.
Привет всем посетителям сайта 
В данный момент здесь Вы можете уже сейчас воспользоваться списком упражнений к учебнику по алгебре Макарычев для седьмого и восьмого классов. С этой страницы Вы можете перейти на соответствующие разделы, например, алгебра 7 класс, где Вашему вниманию представлены список номеров и упражнений к учебнику за 7 класс. Перейдя по выбранному номеру перед Вами откроется страница, на которой Вы можете увидеть условие задачи и ее решение, кроме этого там будет видео-ролик с Youtube, в котором я старался максимально подробно с объяснениями решить данный пример. Кроме этого, еще есть страница — 
| Сезон | Турнир | М | И | В | Н | П | ЗАБ | ПРОП | РАЗН | О | Лучший бомбардир | |
| 2021/2022 | Испания. Ла Лига |
3 | 2 | 1 | 1 | 0 | 7 | 4 | 3 | 4 | Карим Бензема | 2 |
| 2020/2021 | Испания. Ла Лига | 2 | 38 | 25 | 9 | 4 | 67 | 28 | 39 | 84 | Карим Бензема | 23 |
| 2019/2020 | Испания. Ла Лига | 38 | 26 | 9 | 3 | 70 | 25 | 45 | 87 | Карим Бензема | 21 | |
| 2018/2019 | Испания. Ла Лига | 3 | 38 | 21 | 5 | 12 | 63 | 46 | 17 | 68 | Карим Бензема | 21 |
| 2017/2018 | Испания. Ла Лига |
3 | 22 | 10 | 6 | 94 | 44 | 50 | 76 | Криштиану Роналду | 26 | |
| 2016/2017 | Испания. Ла Лига | 1 | 38 | 29 | 6 | 3 | 106 | 41 | 65 | 93 | Криштиану Роналду | 25 |
| 2015/2016 | Испания. Ла Лига | 2 | 38 | 28 | 6 | 4 | 110 | 34 | 76 | 90 | Криштиану Роналду | 35 |
| 2014/2015 | Испания. Ла Лига | 2 | 38 | 30 | 2 | 6 | 118 | 38 | 80 | 92 | Криштиану Роналду | 48 |
| 2013/2014 | Испания. Ла Лига |
3 | 38 | 27 | 6 | 5 | 104 | 38 | 66 | 87 |
|
31 |
| 2012/2013 | Испания. Ла Лига | 2 | 38 | 26 | 7 | 5 | 103 | 42 | 61 | 85 | Криштиану Роналду | 34 |
| 2011/2012 | Испания. Ла Лига | 1 | 38 | 32 | 4 | 2 | 121 | 32 | 89 | 100 | Криштиану Роналду | 46 |
| 2010/2011 | 2 | 38 | 29 | 5 | 4 | 102 | 33 | 69 | 92 | Криштиану Роналду | 40 | |
| 2009/2010 | Испания. Ла Лига |
2 | 38 | 31 | 3 | 4 | 102 | 35 | 67 | 96 | Гонсало Игуаин | 27 |
| 2008/2009 | Испания. Ла Лига | 2 | 38 | 25 | 3 | 10 | 83 | 52 | 31 | 78 | Гонсало Игуаин | 22 |
| 2007/2008 | Испания. Ла Лига | 1 | 38 | 27 | 4 | 7 | 84 | 36 | 48 | 85 | Рауль | 18 |
| 2006/2007 | Испания. Ла Лига | 1 | 38 | 23 | 7 | 8 | 66 | 40 | 26 | 76 | Руд ван Нистелрой | 25 |
| 2005/2006 | Испания. Ла Лига |
2 | 38 | 20 | 10 | 8 | 70 | 40 | 30 | 70 | Роналдо | 14 |
| 2004/2005 | Испания. Ла Лига | 2 | 38 | 25 | 5 | 8 | 71 | 32 | 39 | 80 | Роналдо | 21 |
| 2003/2004 | Испания. Ла Лига | 4 | 38 | 21 | 7 | 10 | 72 | 54 | 18 | 70 | Роналдо | 23 |
| 2002/2003 | Испания. Ла Лига | 1 | 38 | 22 | 12 | 4 | 86 | 42 | 44 | 78 | ||
| 2001/2002 | Испания. Ла Лига |
3 | 38 | 19 | 9 | 10 | 69 | 44 | 25 | 66 | ||
| 2000/2001 | Испания. Ла Лига | 1 | 38 | 24 | 8 | 6 | 81 | 40 | 41 | 80 | ||
| 1999/2000 | Испания. Ла Лига | 5 | 38 | 16 | 14 | 8 | 58 | 48 | 10 | 62 | ||
| 1998/1999 | Испания. Ла Лига | 2 | 38 | 21 | 5 | 12 | 77 | 62 | 15 | 68 | ||
| 1997/1998 | Испания. Ла Лига | 4 | 38 | 17 | 12 | 9 | 63 | 45 | 18 | 63 | ||
| 1996/1997 | Испания. Ла Лига | 1 | 42 | 27 | 11 | 4 | 85 | 36 | 49 | 92 | ||
| 1995/1996 | Испания. Ла Лига | 6 | 42 | 20 | 10 | 12 | 75 | 51 | 24 | 70 |
Квадратное число — элементарная математика
Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или ноль) на само себя, полученное произведение называется квадратным числом, или точным квадратом, или просто «квадратом». ” Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — это квадратные числа.
Более формально: квадратное число — это число в форме n × n или n 2 , где n — любое целое число.
Математический фон
Объекты, расположенные в квадратном массиве
Название «квадратное число» происходит от того факта, что это конкретное количество объектов может быть расположено так, чтобы заполнить идеальный квадрат.
Дети могут поэкспериментировать с монетами (или квадратными плитками), чтобы увидеть, какие из них можно расположить в виде идеально квадратного массива.
Банка по четыре пенни:
Банка девяти пенсов:
И шестнадцать пенсов тоже можно:
Но семь пенсов или двенадцать пенсов не могут быть устроены таким образом. Числа (объектов), которые могут быть организованы в квадратный массив, называются «квадратными числами».
Квадратные массивы должны быть заполнены, если мы хотим считать число квадратным.Здесь 12 пенни расположены в квадрате, но не в полном квадратном массиве, поэтому 12 не является квадратным числом.
Число 12 не квадратное.
Детям может понравиться изучать, какое количество монеток можно расположить на таком открытом квадрате. Их не называют «квадратными числами», но они построены по интересной схеме.
Квадраты из квадратных плиток тоже интересно делать. Число , число квадратных плиток, которые помещаются в квадратный массив, является «квадратным числом».
Вот две платы, 3 × 3 и 5 × 5 .Сколько красных плиток в каждой? Чернить? Желтый?
Есть какие-нибудь из этих квадратных чисел?
Что делать, если таким же образом выложить доску 4 × 4 или 6 × 6 ?
Можете ли вы предсказать количество плиток на доске 7 × 7 или 10 × 10 ?
Квадратные числа в таблице умножения
Квадратные числа появляются по диагонали стандартной таблицы умножения.
Соединения с треугольными числами
Если вы посчитаете зеленые треугольники в каждом из этих рисунков, вы увидите последовательность чисел: 1, 3, 6, 10, 15, 21,…, последовательность, называемую (подходящим образом) треугольными числами.
Если вы посчитаете белые треугольники, которые находятся в «пробелах» между зелеными, последовательность чисел начинается с 0 (потому что у первого рисунка нет пробелов), а затем продолжается: 1, 3, 6, 10, 15,… , снова треугольные числа!
Замечательно, что если вы посчитаете все крошечные треугольники в каждом рисунке — и зеленые, и белые, — цифры будут квадратными числами!
Связь между квадратными и треугольными числами с другой стороны
Постройте ступенчатую систему из стержней Кюизенера, скажем, W, R, G.Затем постройте следующую ступеньку: W, R, G, P.
.Каждая из них «треугольная» (если не учитывать ступенчатую грань). Соедините два последовательных треугольника вместе, и получится квадрат:. Этот квадрат такого же размера, как 16 белых стержней, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).
Вот еще один пример:. Когда они сложены вместе, они образуют квадрат, площадь которого равна 64, опять же, квадрат длины (в белых стержнях) самого длинного стержня.(Коричневый стержень имеет длину 8 белых стержней, а 64 равно 8 умноженным на 8, или «8 в квадрате».)
Ступени из квадратов с номерами
Ступеньки, которые поднимаются, а затем снова опускаются, как эта, также содержат квадратное количество плиток. Когда плитки отмечены шахматной доской, как здесь, дополнительное предложение, описывающее количество красных плиток (10), количество черных плиток (6) и общее количество плиток (16), снова показывает связь между треугольные числа и квадратные числа: 10 + 6 = 16.
Приглашение учеников 2-го (или даже 1-го) класса построить модели ступенек и написать числовые предложения, описывающие эти модели, — хороший способ дать им возможность попрактиковаться в описательных числовых предложениях, а также подружиться с квадратными числами.
Вот два примера. Цвет используется здесь, чтобы помочь вам увидеть, что описывается. Детям нравится цвет, но он им не нужен, и они часто могут увидеть творческие способы описания рисунков ступенек, которые они построили с помощью одноцветных плиток.Или они могут раскрасить миллиметровку на миллиметровой бумаге, чтобы записать свой образец ступенек и показать, как они преобразовали его в числовое предложение.
Ромбовидную форму, сделанную из пенсов, также можно описать числовым предложением 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25.
От одного квадратного числа к другому: два изображения со стержнями Cuisenaire
(1) Начните с W. Добавьте две последовательные штанги, W + R; затем еще два, R + G; тогда G + P; тогда….
| 1; | добавить 1 + 2; | прибавить 2 + 3; | прибавить 3 + 4; | прибавить 4 + 5; | добавить 5 + 6; | добавить 6 + 7 |
(2) Начните с W.Для каждого нового квадрата добавьте два стержня, которые соответствуют сторонам предыдущего квадрата, и новую букву W, чтобы заполнить угол.
Математика — SUNY Canton
Домашняя страница> Описание курсов> Математика
ENGM 101 ВВОДНАЯ МАТЕМАТИКА ДЛЯ ТЕХНИЧЕСКИХ ПРИЛОЖЕНИЙ
Осень / Весна, 3 кредита
Этот курс представляет собой обзор основных математических тем, наиболее активно используемых в основном курсе инженерии и инженерных технологий для второкурсников.К ним относятся алгебраические манипуляции с инженерными уравнениями, тригонометрия, векторы и комплексные числа, а также системы уравнений. Все темы представлены в контексте инженерного приложения и подкреплены обширными примерами их использования в основных инженерных или технологических курсах.
Предварительные требования: Intermediate Algebra (MATH 106) или разрешение преподавателя
МАТЕМАТИКА 099 ОСНОВЫ ПРИКЛАДНОЙ МАТЕМАТИКИ
Осень, 3 условно начисленных кредита
Курс связывает математические концепции и процедуры с реальными приложениями, относящимися к множеству технических областей торговли.Темы включают: обзор фундаментальных арифметических концепций, порядка операций, измерения и преобразования, отношения и пропорции, чисел со знаком, показателей и радикалов, оценки и введения в алгебру. Для студентов без образования алгебры или для тех, кто получил менее 75 баллов на экзамене штата Нью-Йорк по математике A или Integrated Algebra Regents или эквивалентном экзамене, или с разрешения преподавателя. Три часа лекций в неделю.
MATH 100 НАЧАЛО АЛГЕБРЫ
Осень / Весна, 3 кредита
Этот курс предназначен для подготовки студентов к изучению промежуточной алгебры (MATh206).Это предполагает ограниченное образование по алгебре на среднем уровне. Темы включают: обзор арифметических операций, чисел со знаком, показателей степени, основных геометрических понятий (таких как мера угла, формулы площади и объема), операции с многочленами, решение линейных уравнений, введение в построение графиков и элементарные задачи со словами. Для студентов с ограниченным образованием в области алгебры или для тех, кто набирает менее 75 баллов на экзамене штата Нью-Йорк по математике A или Integrated Algebra Regents или эквивалентном экзамене, или с разрешения преподавателя.Три часа лекций в неделю.
MATH 101 ПРИКЛАДНАЯ МАТЕМАТИКА КОЛЛЕДЖА
Осень, 4 кредита
Этот курс разработан, чтобы подготовить студентов к успеху в технических программах и программах подготовки инженеров. Он предполагает наличие алгебраических знаний на начальном уровне. Курс связывает математические концепции и процедуры с реальными приложениями, имеющими отношение к различным областям технической торговли. В этом курсе делается упор на приложения, использующие понятия алгебры.
MATH 106 ПРОМЕЖУТОЧНАЯ АЛГЕБРА
Осень / Весна, 3 кредитных часа GER 1
Этот развивающий курс рассматривает и основывается на основных фундаментальных концепциях алгебры, которые требуются во многих других курсах и областях обучения. Темы включают: обзор фундаментальных понятий, уравнений и неравенств первой степени, построения графиков и систем уравнений, произведений и факторинга, рациональных выражений, показателей степени и радикалов, квадратных уравнений.
Пререквизиты: Начальный курс алгебры (MATH 100) с оценкой C или выше, или экзамен штата Нью-Йорк по математике A или Integrated Math Regents, или эквивалентный экзамен с оценкой 70 или выше, или разрешение преподавателя.
МАТЕМАТИКА 111 ОБЗОР МАТЕМАТИКИ
Осень / Весна, 3 кредитных часа GER 1
Изучение различных математических тем, включая введение в навыки количественного мышления, логику таблицы истинности, множества, вероятность и геометрию.Этот курс предназначен для студентов, не имеющих технической подготовки. Подходит для студентов, изучающих гуманитарные науки. Трехчасовая лекция в неделю.
Пререквизиты: Intermediate Algebra (MATH 106) с оценкой C или выше, или 2 курса математики для старших классов средней школы штата Нью-Йорк с оценкой 75 или выше на втором экзамене по математике штата Нью-Йорк, или разрешение преподавателя.
МАТЕМАТИКА 115 МАТЕМАТИКА ДЛЯ УЧИТЕЛЕЙ НАЧАЛЬНИКОВ I
Осень / Весна, 3 кредитных часа GER 1
Изучение развития, значения и представлений систем счисления, операций с целыми числами, теории чисел и действительной системы счисления.Основное внимание в курсе будет уделяться математическому представлению тем K-8 посредством решения задач. Этот курс открыт только для студентов, участвующих в программе перехода к начальному образованию. Большая часть курса будет основываться на деятельности (изучение тем посредством действий по решению проблем). Три часа лекций в неделю.
Предварительные требования: Intermediate Algebra (MATH 106) с оценкой C или выше, или два (2) курса математики для старших классов средней школы с оценкой 75 или выше на втором экзамене Regents по математике штата Нью-Йорк, или разрешение преподавателя .
МАТЕМАТИКА 116 МАТЕМАТИКА ДЛЯ УЧИТЕЛЕЙ НАЧАЛЬНИКОВ II
Осень / Весна, 3 кредитных часа
Изучение развития, значения и представления статистики, закономерностей и функций, концепций геометрии и измерения двух- и трехмерных фигур. Основное внимание в курсе будет уделяться построению математических представлений для тем K-8 посредством решения задач. Этот курс открыт только для студентов, участвующих в программе перехода к начальному образованию.Большая часть курса будет основываться на деятельности (изучение тем посредством упражнений по решению проблем). Три часа в неделю.
Пререквизиты: Математика для учителей начальных классов I (математика 115) с оценкой C или выше или разрешение преподавателя.
MATH 121 АЛГЕБРА КОЛЛЕДЖА
Осень / Весна, 4 кредитных часа GER 1
Этот курс предоставляет основные алгебраические концепции и введение в тригонометрические и логарифмические функции.Особое внимание уделяется уравнениям и неравенствам; полиномы, рациональные, экспоненциальные и логарифмические функции; а также построение графиков и анализ данных, включая моделирование и линейную регрессию. Дополнительные темы включают комплексные числа; радикальные функции; тригонометрия прямоугольного треугольника; системы уравнений; и элементарные трансцендентные функции. Лекция четыре часа в неделю.
Предварительные требования: Intermediate Algebra (MATH 106) с оценкой C или выше, или два (2) курса математики для старших классов средней школы с оценкой 75 или выше на втором экзамене Regents по математике штата Нью-Йорк, или разрешение преподавателя .Не могут быть приняты на зачет учащимися, имеющими зачет по предисчислительной алгебре (МАТЕМАТИКА 123).
MATH 123 ПРЕДВАРИТЕЛЬНЫЙ РАСЧЕТ
Осень / Весна, 4 кредитных часа GER 1
Этот курс предусматривает интенсивное изучение тем, которые имеют фундаментальное значение для изучения математического анализа. Особое внимание уделяется функциям и их графикам, особое внимание уделяется полиномиальным, рациональным, экспоненциальным, логарифмическим и тригонометрическим функциям, а также аналитической тригонометрии. Дополнительные темы включают комплексные числа; системы уравнений и неравенств; тригонометрические тождества; и тригонометрические приложения.Лекция четыре часа в неделю.
Пререквизиты: Intermediate Algebra (MATH 106) с оценкой C или выше, или 3 курса математики для старших классов средней школы штата Нью-Йорк с оценкой 75 или выше на третьем экзамене по математике штата Нью-Йорк, или разрешение преподавателя. Студенты с кредитами по алгебре колледжа (MATH 121)
не могут принять зачет.MATH 131 ТРИГОНОМЕТРИЯ КОЛЛЕДЖА
Весна, 3 кредитных часа GER 1
Этот курс предназначен для тех студентов, которым не хватает навыков тригонометрии, необходимых для успешной работы по исчислению I.Темы включают: измерение угла; тригонометрия прямоугольного треугольника; тригонометрические тождества; тригонометрические уравнения; графики тригонометрических функций; обратные тригонометрические функции; косые треугольники; и экспоненциальные и логарифмические функции. Три часа лекций в неделю.
Пререквизиты: Алгебра колледжа (MATh221) с оценкой C или выше, или 3 года обучения математике в средней школе с оценкой 75 или выше на третьем экзамене по математике штата Нью-Йорк, или разрешение преподавателя.
MATH 141 СТАТИСТИКА
Осень / Весна, 3 кредитных часа GER 1
Этот курс представляет собой введение в стандартные методы описательной статистики, вероятностной и логической статистики. Темы включают: организацию и представление данных, описательные меры данных, линейный корреляционный и регрессионный анализ, вероятность, распределения вероятностей, включая биномиальные распределения, нормальные распределения, t-распределения Стьюдента и распределения хи-квадрат, оценку параметров и проверку гипотез.Три часа лекций в неделю.
Пререквизиты: Алгебра колледжа (MATH 121), алгебра предварительного исчисления (MATH 123), обзор математики (MATH 111) или математика для учителей начальной школы II (MATH 116) с оценкой C или выше, или 3 года по математике в средней школе с оценкой 75 или выше на третьем экзамене по математике штата Нью-Йорк, или с разрешения преподавателя.
MATH 150 РАСЧЕТ БИЗНЕСА
Осень / Весна, 4 кредитных часа GER 1
Этот курс представляет собой интуитивное введение в математический анализ.Темы включают: обзор функций; аналитическая геометрия линии, свойства пределов; производная с приложениями; трансцендентные функции; и интегралы с приложениями. Выбранные дополнительные темы будут предложены, если позволит время, на усмотрение инструктора. Лекция четыре часа в неделю.
Предварительные требования: Алгебра колледжа (МАТЕМАТИКА 121) или предварительная математическая алгебра (МАТЕМАТИКА 123) с оценкой C или выше, или для учащихся, которые прошли 3 курса математики для старших классов средней школы штата Нью-Йорк с оценкой 75 или выше на третий экзамен Regents по математике штата Нью-Йорк или разрешение преподавателя.
MATH 161 РАСЧЕТ I
Осень, 4 кредитных часа GER 1
Этот курс является первым из трех семестровых курсов по исчислению, разработанных для студентов технических наук, которые планируют перейти в четырехлетний инженерный колледж по завершении программы. Другие квалифицированные студенты также могут пройти эту последовательность. Темы включают: быстрый обзор функций и графиков, ограничения и непрерывность; производная и ее свойства, дифференцирование алгебраических и трансцендентных функций, построение кривых; связанные ставки, прикладные экстремальные задачи; другие приложения дифференцирования, численных методов и антидифференцирования.Лекция четыре часа в неделю.
Предварительные требования: Алгебра колледжа (МАТЕМАТИКА 121), алгебра предварительного исчисления (МАТЕМАТИКА 123) или Тригонометрия колледжа (МАТЕМАТИКА 131) с оценкой C или выше, или для учащихся, которые прошли 3 курса по математике для старших классов средней школы штата Нью-Йорк с оценкой оценка 75 или выше на третьем экзамене по математике штата Нью-Йорк, или разрешение преподавателя.
MATH 162 РАСЧЕТ II
Весна, 4 кредитных часа
Этот курс является вторым из трех семестров курса «Исчисление», который был разработан для студентов, изучающих инженерные науки.Другие квалифицированные студенты также могут пройти этот курс. Темы включают: дифференциалы; определенные интегралы и их приложения; интегрирование экспоненциальных, логарифмических, тригонометрических и обратных тригонометрических функций; методы интеграции; серии; параметрические уравнения и полярные координаты. Лекция четыре часа в неделю.
Пререквизиты: Calculus I (MATH 161) рекомендуется с оценкой C или выше или с разрешения преподавателя.
MATH 263 РАСЧЕТ III
Осенний, 4 кредита
Этот курс является третьим из трех семестровых курсов по исчислению, разработанных для студентов технических наук, которые планируют перейти на инженерную программу в четырехлетнем учебном заведении по окончании учебы.Другие квалифицированные студенты также могут пройти этот курс. Включены темы из аналитической геометрии, плоских кривых и полярных координат, векторов, векторных функций и темы из дифференциальной геометрии, частичного дифференцирования, множественных интегралов, а также избранные темы из векторного исчисления. Лекция четыре часа в неделю.
Пререквизиты: Calculus II (MATH 162) с оценкой C или выше или с разрешения преподавателя.
MATH 341 СТАТИСТИКА II
TBD, 3 кредитных часа
Включает доверительные интервалы и проверку гипотез для пропорций населения, дисперсии и стандартного отклонения; проверка гипотезы на двух выборках на предмет различий между средними значениями; корреляция и регрессия, включая множественную регрессию; поиск интервалов прогноза и проверки гипотез для коэффициента линейной корреляции; Критерии хи-квадрат и F-распределение; непараметрические испытания.Три часа лекций в неделю.
Предварительные требования: Статистика (MATH 141) с оценкой C или выше или разрешение преподавателя
MATH 351 ДИСКРЕТНАЯ МАТЕМАТИКА
Осень / Весна, 3 кредитных часа
Этот курс изучает основные инструменты и методы дискретной математики и их приложения. Темы включают множества, логику, доказательства, функции и отношения, алгоритмы, элементарную теорию чисел, методы подсчета, дискретную вероятность, принцип ящика, рекуррентные отношения, введение в теорию графов и булевы алгебры.Три часа лекции в неделю.
Пререквизиты: Алгебра колледжа (MATH 121) или Предварительная математическая алгебра (MATH 123) с оценкой C или выше или разрешение преподавателя.
MATH 361 ЛИНЕЙНАЯ АЛГЕБРА
Весна / Осень, 3 кредитных часа
Этот курс представляет собой введение в теорию конечномерных абстрактных векторных пространств и линейных преобразований. Темы включают: системы линейных уравнений, матрицы, матричную алгебру, определители и обратные, линейные комбинации и линейную независимость, абстрактные векторные пространства, изменение базиса и координат, внутренние пространства продукта, ортонормированные базисы.Мы также рассматриваем линейные преобразования, изоморфизмы, матричное представление линейных отображений, собственные значения и собственные векторы, диагонализацию и подобие. Приложения включают компьютерную графику, цепи Маркова, химию, линейную регрессию, сетевой поток, электрические схемы и дифференциальные уравнения. Три часа лекции в неделю.
Пререквизиты: Calculus II (MATH 162) с оценкой C или выше или с разрешения преподавателя.
MATH 364 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Весна, 4 кредитных часа
Этот курс представляет собой введение в обыкновенные дифференциальные уравнения.Темы включают: дифференциальные уравнения первого, второго и высшего порядка с постоянными и переменными коэффициентами, преобразования Лапласа, системы линейных дифференциальных уравнений и численные методы, собственные значения и приложения линейных уравнений первого и второго порядка, предназначенные для инженерии. Студенты, изучающие математику и физику, нуждающиеся в практических знаниях дифференциальных уравнений.
Пререквизиты: Calculus II (MATH 162) с оценкой C или выше или с разрешения преподавателя.
MATH 371 ТЕОРИЯ ГРАФА
Весна / Осень, 3 кредитных часа
Этот курс является введением в основные понятия теории графов. Анализируются общие классы графов, такие как пути, деревья и циклы. Мы рассмотрим изоморфизм, связность и проходимость. Если позволяет время, можно рассмотреть планарность и раскраску графиков. Заявки подаются в химии, инженерии и информатике.
Предварительные требования: Calculus II (MATH 162) или разрешение преподавателя.
MATH 461 РАСШИРЕННЫЙ РАСЧЕТ
Весна / Осень, 3 кредитных часа
Этот курс является продолжением Calculus III и служит введением в темы Advanced Calculus. Темы включают линейные, поверхностные и объемные интегралы в двух- и трехмерном пространстве; исследования градиента скалярного поля, обсуждение консервативных полей и потенциальных функций; расходимость и ротор векторных полей; обобщения основной теоремы исчисления для вычисления интегралов; криволинейные координаты, кратные интегралы и преобразование кратных интегралов; неявные функции; Якобианцы; частные производные; частные производные высшего порядка; теоремы о среднем значении; бесконечные ряды; ряды Тейлора и введение в ряды Фурье.Предметные приложения представлены в области механики жидкости и твердого тела, электростатики и электромагнетизма.
Предварительные требования: Исчисление III (MATH 263) и линейная алгебра (MATH 361) с оценкой C или выше или с разрешения преподавателя.
МАТЕМАТИКА 291-295, 391-395 ИЛИ 491-495 СПЕЦИАЛЬНЫЕ ТЕМЫ ПО МАТЕМАТИКЕ
Осень / Весна, 1-4 кредитных часа
Индивидуальные курсы обучения с переменным зачетом (1-4 кредита) могут предлагаться каждый семестр.Эти курсы предназначены для расширения тем в конкретных областях математики.
Верх
Тест ALEKS для MTH 121, 131, 141 — Математический факультет
Кто должен сдавать тест ALEKS PPL?
Все студенты, желающие пройти MTH 121, 131 или 141, за исключением тех, кто имеет оценку C или выше в ULC 148, оценку 4 или 5 по AP Calculus (A / B или B / C), или оценка C или выше в MTH 121, 131 или 141.
Почему я должен сдавать экзамен ALEKS PPL?
Тест используется для оценки вашей готовности к расчету на уровне колледжа.
Взимается ли плата за использование ALEKS PPL?
Плата за размещение по математике оплачивается для одного аккаунта в ALEKS. Эта учетная запись предоставляет вам 5 попыток оценки и шесть месяцев использования учебного модуля. Также есть две дополнительные оценки, которые можно разблокировать, связавшись с координатором ALEKS. Студенты, которые исчерпали бесплатные варианты, должны будут оплачивать любые будущие тесты ALEKS из своего кармана.
Нужно ли мне устанавливать какое-либо программное обеспечение или плагины перед сдачей экзамена ALEKS Placement Assessment?
№При использовании ALEKS PPL не требуются плагины или апплеты. Пока у вас есть доступ к Интернету и вы используете последнюю версию браузера, вы не должны испытывать никаких трудностей при сдаче теста Placement Assessment. Список предпочтительных браузеров можно найти в системных требованиях ALEKS на их сайте поддержки.
Какие темы рассматриваются во время оценки ALEKS PPL?
- Действительные числа (включая дроби, целые числа и проценты).
- Уравнения и неравенства (включая линейные уравнения, линейные неравенства, системы линейных уравнений и квадратные уравнения).
- Линейные и квадратичные функции (включая графики и функции, линейные функции и параболы), показатели и полиномы (включая целые показатели, полиномиальную арифметику, факторизацию и полиномиальные уравнения), рациональные выражения (включая рациональные уравнения и рациональные функции.
- Радикальные выражения (включая высшие корни и рациональные показатели).
- Показатели и логарифмы (включая композиции функций и обратные функции, свойства логарифмов и логарифмические уравнения).
- Геометрия и тригонометрия (включая периметр, площадь и объем, координатную геометрию, тригонометрические функции, тождества и уравнения).
Могу ли я попрактиковаться в использовании инструментов ввода ALEKS, прежде чем приступить к оценке места размещения?
ALEKS начнет с краткого руководства, чтобы убедиться, что вы хорошо знакомы с инструментами математической палитры, прежде чем начнется оценка размещения.В руководстве показано, как вводить разные типы ответов, как использовать калькулятор ALEKS и как строить графики.
Если вы не знаете, как вводить ответ, или вам нужна помощь во время прохождения экзамена ALEKS Placement Assessment, нажмите кнопку Help под инструментами панели ответов. Переход к руководству во время оценки места размещения НЕ повлияет на ваши результаты.
Каков формат вопросов на ALEKS?
ALEKS не является экзаменом с несколькими вариантами ответов.Это открытый ответ и требует, чтобы вы разработали решения с помощью бумаги и карандаша, а затем вводили их в ALEKS. Обязательно возьмите с собой бумагу для заметок.
Могу ли я использовать калькулятор при использовании ALEKS?
ALEKS предоставит экранный калькулятор, если он вам понадобится для решения конкретной задачи. В противном случае вы не сможете пользоваться калькулятором.
Могу ли я использовать какие-либо другие ресурсы во время оценки места размещения?
Вы можете использовать только ручку или карандаш, бумагу и ресурсы, предоставленные в ALEKS.Вы не должны получать помощь от друзей, семьи, других веб-сайтов, учебников или любых других ресурсов, не предоставленных ALEKS. Использование внешних ресурсов приведет к неправильному размещению и, возможно, провалу курса. Это нарушение политики академической честности UB.
Могу ли я просмотреть вопрос после того, как отвечу на него?
Поскольку ALEKS является адаптивным (т.е. каждый последующий вопрос выбирается на основе того, как вы ответили на предыдущие), после отправки ответа вы не можете его изменить.Обязательно внимательно проверьте свой ответ перед тем, как отправлять свой ответ.
Что делать, если я увижу вопросы, которых не знаю?
Вероятно, вам будут заданы вопросы по материалу, который вы еще не изучили. На такие вопросы уместно ответить «Не знаю ».
Однако в любом вопросе, с которым вы знакомы, важно сделать все возможное. « Я не знаю» интерпретируется ALEKS как означающее, что вы не знаете, как решить эту тему, и это будет отражено в результатах оценки места размещения.
Нет штрафных санкций за неправильный ответ на вопрос в Оценке места размещения, это только помогает ALEKS понять, что вы знаете и чего не знаете.
Установлены ли временные аттестации?
Да, у вас есть до 2,5 часов на выполнение экзамена.
Внимание: если вы не ответите на все вопросы в отведенное время, баллы не будут записаны, и вам придется начинать оценку заново.
Что произойдет, если я не пройду оценку места размещения в отведенное время?
Вам придется перезапустить оценку размещения.
Каков мой результат размещения?
Результат вашего размещения (общий балл) — это число от 0 до 100. Оно представляет процент тем, которые, по определению ALEKS, вы освоили. Требуемый балл для прохождения 121 или 131 MTH — 61. Требуемый балл для сдачи 141 MTH — 76.
Где я могу увидеть свой счет?
- Вы получите свой балл сразу после завершения экзамена по зачислению.
- Ваш балл ALEKS можно просмотреть, повторно введя ALEKS, используя ту же ссылку доступа, для которой вы проходили оценку места размещения.
- С апреля 2018 года оценки ALEKS автоматически загружаются в HUB каждую ночь.
- Минимальный требуемый балл для прохождения 121 или 131 MTH — 61. Для MTH 141 это 76.
Как долго действителен результат моего зачисления?
Ваш результат размещения действителен в течение 1 года.
Я не набрал 76/100 или выше.Могу ли я взять 141 MTH?
Нет, вы должны достичь минимального результата зачисления в MTH 141.
Что, если бы я попал в желаемый класс?
Поздравляем! Продолжайте использовать модуль подготовки и обучения, чтобы повысить свои шансы на успех. Требуемый результат размещения — это минимальная подготовка к вашему курсу. Воспользуйтесь преимуществами индивидуального обзора и обучения в ALEKS, чтобы получить лучшую оценку в своем классе.
Могу ли я повторно сдать экзамен ALEKS PPL?
Да, вы можете сдать до пяти экзаменов.Доступ к четвертой и пятой оценке может быть предоставлен после разговора с консультантом. Однако, чтобы сделать каждую попытку стоящей, необходимо, чтобы вы тратили время на работу в модуле подготовки и обучения ALEKS между экзаменами по месту жительства, чтобы вы могли улучшить свои навыки.
Могу ли я сразу же пересдать аттестацию ALEKS?
Как правило, повторная сдача аттестата успеваемости сразу после завершения предыдущей попытки не дает никаких преимуществ.Вы не сможете улучшить свои результаты, просто повторно пройдя оценку размещения, не потратив время на модуль подготовки и обучения, чтобы обновить материал, который вы, возможно, забыли.
Как долго у меня будет доступ к моему модулю подготовки и обучения?
У вас будет шесть месяцев доступа к модулю подготовки и обучения.
Взимается ли дополнительная плата за мой модуль подготовки и обучения?
Доступ к модулю подготовки и обучения включен вместе с дополнительными экзаменами по месту работы.
Должен ли я работать в моем модуле подготовки и обучения ALEKS между экзаменами на место?
Чтобы улучшить свой результат, вы можете пересдать до пяти повторных экзаменов. Вам рекомендуется поработать в учебном модуле не менее 3 часов между попытками, чтобы повысить свои шансы на успех.
Что такое проверки знаний ALEKS?
Работая в модуле подготовки и обучения, вы будете периодически выполнять проверку знаний, чтобы убедиться, что вы освоили темы, полученные в режиме обучения.Если вы не проявите мастерство во время проверки знаний, темы будут добавлены обратно в ваш учебный пирог, чтобы вы могли еще раз просмотреть их.
Учитывается ли прогресс в модуле подготовки и обучения ALEKS при размещении?
Нет. Вы должны пройти новую оценку места размещения, чтобы изменить результат размещения. Выберите вкладку размещения в правом верхнем углу страницы ALEKS, чтобы начать новую оценку размещения.
| Exercise | Проблема | Раствор |
| 1 | Двенадцати студентам был предложен тест по математике, время (в минутах) для его выполнения указано ниже.Найдите диапазон этих времен. 10, 9, 12, 11, 8, 15, 9, 7, 8, 6, 12, 10 | 6, 7, 8, 8, 9, 9, 10, 10, 11, 12, 12, 15 15-6 = 9 Диапазон = 9 |
| 2 | Эстафету завершили 7 участников, время их гонки указано ниже (в секундах). Каков диапазон времени гонок? 13,2, 14,5, 12,9, 13,9, 15,6, 14,1, 12,3 | 12,3, 12,9, 13,2, 13,9, 14,1, 14,5, 15,6 15,6 — 12.3 = 3,3 Диапазон = 3,3 |
| 3 | Каков средний балл по 6 приведенным ниже баллам? 89, 93, 87, 86, 85, 94 | 89 + 93 + 87 + 86 + 85 + 94 = 534 534 ÷ 6 = 89 Среднее значение = 89 |
| 4 | Ниже приведена средняя годовая скорость ветра для 5 самых ветреных городов США в милях в час. Каково среднее значение этих годовых скоростей ветра? 15,4, 14,0, 13,5, 13,1, 12,9 | 15,4 + 14.0 + 13,5 + 13,1 + 12,9 = 68,9 68,9 ÷ 5 = 13,78 Среднее значение = 13,78 миль / ч |
| 5 | Каков средний возраст семи детей, возраст которых указан ниже? 11, 10, 13, 11, 12, 16, 14 | 10, 11, 11, 12, 13, 14, 16 Медиана = 12 |
| 6 | Число торнадо, произошедших в США за последние 8 лет, указано ниже. Найдите медиану. 684, 764, 1133, 656, 702, 1303, 856, 1132 | 656, 684, 702, 764, 856, 1133, 1132, 1303 (764 + 856) ÷ 2 = 810 Медиана = 810 |
| 7 | Ниже приведены суточные высокие температуры в течение одной зимней недели в Олбани, штат Нью-Йорк.Какой режим этих температур? 39, 42, 34, 37, 39, 44, 41 | 34, 37, 39, 39, 41, 42, 44 Режим = 39 |
| 8 | Найдите режим следующих целых чисел. — 18, — 13, 0, + 16, + 3, — 15, 0, + 11, — 14, 0, + 12 | — 18, — 15, — 14, — 13, 0, 0, 0, + 3, + 11, + 12, + 16 Режим 0 |
| 9 | Результаты тестов Хизер: 81, 93, 74 и 95.Какой балл она должна получить на пятом тесте, чтобы получить среднее значение 85 по всем пяти тестам? | (81 + 93 + 74 + 95 + x) ÷ 5 = 85 343 + x = (5) (85) 343 + x = 425 x = 82 Хизер нужно получить 82 на пятом тесте |
| 10 | Среднее значение набора чисел — 108. 2 + 12z} \\
& = \ frac {(z + 6) (z + 11)} {3 (z-11) (z + 11)} \ раз
\ frac {24z (z-11)} {2z (z + 6)} \\
& = \ frac {1} {3} \ times \ frac {24} {2} \\
& = 4
\ end {align *} \ (\ dfrac {3a + 9} {14} \ div \ dfrac {7a + 21} {a + 3} \) \ begin {align *} \ frac {3a + 9} {14} \ div \ frac {7a + 21} {a + 3} & = \ frac {3 (a + 3)} {14} \ div \ frac {7 (a + 3)} {а + 3} \\ & = \ frac {3 (a + 3)} {14} \ div 7 \\ & = \ frac {3 (a + 3)} {14} \ times \ frac {1} {7} \\ & = \ frac {3 (a + 3)} {98} \ end {выровнять *} \ (\ dfrac {a ^ {2} — 5a} {2a + 10} \ times \ dfrac {4a} {3a + 15} \) \ begin {align *} \ frac {{a} ^ {2} — 5a} {2a + 10} \ times \ frac {4a} {3a + 15} & = \ frac {a (a — 5)} {2 (a + 5)} \ times \ frac {4a} {3 (a + 5)} \\ & = \ frac {[a (a — 5)] [4a]} {[2 (a + 5)] [3 (a + 5)]} \\ & = \ frac {4a ^ 2 (a — 5)} {6 (a + 5) ^ 2} \ end {выровнять *}Обратите внимание на ограничение: \ (a \ ne -5 \).2} \ end {выровнять *} Обратите внимание на ограничение: \ (p \ ne 0 \). \ (\ dfrac {24a — 8} {12} \ div \ dfrac {9a — 3} {6} \) \ begin {align *} \ frac {24a — 8} {12} \ div \ frac {9a — 3} {6} & = \ frac {8 (3a — 1)} {12} \ div \ frac {3 (a — 1)} {6} \\ & = \ frac {2 (3a — 1)} {3} \ times \ frac {2} {a — 1} \\ & = \ frac {[2 (3x — 1)] [2]} {[3] [a — 1]} \\ & = \ frac {4 (3a — 1)} {3 (a — 1)} \ end {выровнять *}Обратите внимание на ограничение: \ (a \ ne 1 \).{2} + 2a} {5} \ div \ frac {2a + 4} {20} & = \ frac {a (a + 2)} {5} \ div \ frac {2 (a + 2)} {20} \\ & = \ frac {a (a + 2)} {5} \ times \ frac {10} {a + 2} \\ & = \ frac {[a (a + 2)] [10]} {[5] [a + 2]} \\ & = \ frac {10a} {5} \\ & = 2a \ end {выровнять *} \ (\ dfrac {p ^ {2} + pq} {7p} \ times \ dfrac {21q} {8p + 8q} \) \ begin {align *} \ frac {p ^ {2} + pq} {7p} \ times \ frac {21q} {8p + 8q} & = \ frac {p (p + q)} {7p} \ times \ frac {21q} {8 (p + q)} \\ & = \ frac {[p (p + q)] [21q]} {[7p] [8 (p + q)]} \\ & = \ frac {21pq} {56p} \\ & = \ frac {3q} {8} \ end {выровнять *} \ (\ dfrac {5ab — 15b} {4a — 12} \ div \ dfrac {6b ^ {2}} {a + b} \) \ begin {align *} \ frac {5ab — 15b} {4a — 12} \ div \ frac {6b ^ {2}} {a + b} & = \ frac {5b (a — 3)} {4 (a — 3)} \ div \ frac {6b ^ {2}} {a + b} \\ & = \ frac {5b} {4} \ times \ frac {a + b} {6b ^ {2}} \\ & = \ frac {[5b] [a + b]} {[4] [6b ^ {2}]} \\ & = \ frac {30b ^ {3}} {4 (a + b)} \ end {выровнять *}Обратите внимание на ограничение: \ (a \ ne -b \). 2} \ end {выровнять *} Обратите внимание на ограничение: \ (p \ ne 0 \). математических задач и решений для целых чиселзадач с решениямиЗадача 1: Найдите два последовательных целых числа, сумма которых равна 129. Решение проблемы 1: Задача 2: Найдите три последовательных целых числа, сумма которых равна 366. Решение проблемы 2: Задача 3: Сумма трех последовательных четных целых чисел равна 84.Найдите числа. Решение проблемы 3: Задача 4: Сумма нечетного целого и дважды его последовательного равна 3757.Найдите номер. Решение проблемы 4: Задача 5: Сумма первого и третьего из трех последовательных нечетных целых чисел на 131 меньше второго целого числа в три раза.Найдите три целых числа. Решение проблемы 5: В качестве упражнения проверьте, что сумма первого и третьего на 131 меньше трех раз. Задача 6: Произведение двух последовательных нечетных целых чисел равно 675.Найдите два целых числа. Пусть x, x + 2 — два целых числа. Их произведение равно 144 x (x + 2) = 675. Разверните, чтобы получить квадратное уравнение. х 2 + 2 х — 675 = 0 Решите относительно x, чтобы получить два решения x = 25 или x = -27 если x = 25, то x + 2 = 27 , если x = -27, то x + 2 = -25 У нас есть два решения. Два числа: 25 и 27. или -27 и -25 Убедитесь, что в обоих случаях произведение равно 675. Задача 7: Найдите четыре последовательных четных целых числа так, чтобы сумма первых двух, добавленная к удвоенной сумме последних двух, была равна 742. Решение проблемы 7: Задача 8: Когда наименьшее из трех последовательных нечетных целых чисел складывается с четырехкратным наибольшим, получается результат 729, превышающий среднее целое число более чем в четыре раза.Найдите числа и проверьте свой ответ. Решение проблемы 8: Ответ на проблему правильный. ➤ |