Алгебраические дроби. Видеоурок. Алгебра 8 Класс
Этот урок является одним из итоговых по знаниям алгебры 8-ого класса. Мы с вами вспомним основные определения и примеры решения задач на тему «Алгебраические дроби».
Тема: Повторение курса алгебры 8-ого класса
Урок: Алгебраические дроби
Для начала давайте вспомним, что же такое алгебраические дроби. Алгебраической дробью называют выражение вида , где – многочлены, – числитель, – знаменатель.
Поскольку – многочлены, то необходимо иметь в виду стандартные действия, возможные с многочленами, а именно: приведение к стандартному виду, разложение на множители, а также сокращение числителя и знаменателя.
Пример №1
Сократите дробь
– воспользуемся формулами сокращённого умножения для квадрата суммы и разности квадратов.
Комментарии: вначале мы разложили дробь на множители с помощью формул сокращённого умножения, а дальше воспользовались одним из основных свойств дроби:
Пример №2
Из условия нам пока не ясно, какая связь между этими двумя функциями. Для этого нам необходимо упростить первую из них методом разложения на множители.
однако необходимо не забыть про условие сокращения дроби, т. е. про то, что
лишь с тем отличием, что .
Построим график двух функций.
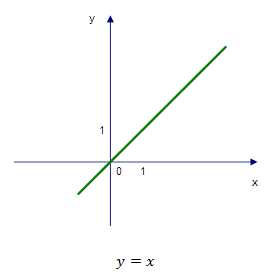
Мы видим яркое различие этих двух графиков: по сути они одинаковы, но на первом графике нам необходимо выколоть точку с координатой (1;0), поскольку эта точна не входит в ОДЗ первой функции.
Итого, мы с вами рассмотрели, что такое дробь, решили пару примеров о том, как важно следить за областью определения (областью допустимых значений), т. е. за теми значениями, которые может принимать .
Дорофеев Г. В. Алгебра. 8 класс
Алгебраические дроби
Алгебра, 8
Никитина Ольга Владимировна,
МОУ СОШ № 81
г. Волгограда
Цели урока:
— сформировать умение применять основное свойство дроби, правила действий с алгебраическими дробями при выполнении действий с алгебраическими дробями;
— продолжить воспитание ответственности перед другими;
— способствовать дальнейшему развитию коммуникативных способностей
Место в учебном плане: перед темой «Примеры на все действия с алгебраическими дробями».
Учебник: Дорофеев Г.В. Алгебра. 8 класс. — М.: Просвещение, 2008.
Ход урока
Работа в группах
Проверка умений:
— демонстрировать теоретические знания по теме «Алгебраические дроби»;
— пользоваться алгоритмами сложения и вычитания дробей с разными знаменателями, умножения и деления дробей;
— находить допустимые значения переменной;
— находить общий знаменатель нескольких дробей;
— работать в группе, прислушиваться к другому мнению.
Целевые установки, составление плана урока (в ходе фронтальной работы).
На доске записан пример (рис. 1). Используется шторка.
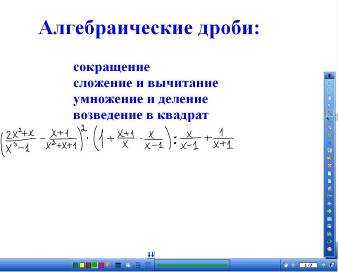
Рис. 1
— Посмотрите на пример (обычно бурная реакция учащихся) (открывается шторка). Красивый?
— Со следующего урока вам предстоит работать с такими примерами. Но как говорят: «Чтобы построить крепкое здание, нужен надежный фундамент». Что для нас на уроках является таким фундаментом? (
— Какие именно знания? (по мере того как называются — открываем на интерактивной доске, дублируются на магнитной доске, где остаются до конца урока). (Определение алгебраической дроби. Основное свойство дроби. Область допустимых значений переменных. Правила действия с алгебраическими дробями. Формулы сокращённого умножения).
— Итак, целью нашего урока мы можем назвать: (Проверка теоретических знаний по теме «Алгебраические дроби», их применение при решении алгебраических задач).
Демонстрация теоретических знаний по теме:
Вы работаете сегодня группами-командами, поэтому результат зависит от каждого. В конце урока я возьму одну тетрадь от группы на проверку.
1. Экспресс-опрос (группам по очереди задаются вопросы, за верный ответ один балл; неверный-переход хода к другой команде).
Дать определение:
а) Какая дробь называется алгебраической?
б) Какие значения переменной называются допустимыми?
в) Что такое общий знаменатель дробей?
г) Что значит найти значение дроби при заданном значении переменной?
2. Составь формулу. Необходимо составить формулу и сформулировать правило. Верный ответ – 1 балл. Если только формула, то – 0,5 балла (рис. 2-3).
Задания по одному открываются стиранием белого цвета ластиком, далее пером записываются результаты справа от знака «равно».
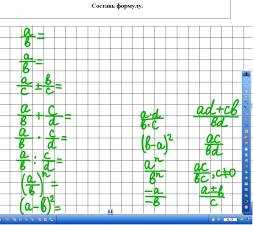
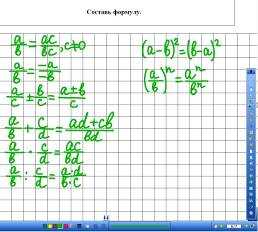
Рис. 2 Рис. 3
Демонстрация умений применять теоретические знания при решении примеров
1) «Найди ошибку» (записаны примеры на интерактивной доске).
— Определите, в каких примерах допущены ошибки? (рис. 4). Решите примеры в тетрадях и исправьте на доске ответы (задание анализируются всем классом) (рис. 5).


Рис. 4 Рис. 5
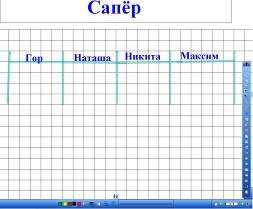
2) «Сапёр» (рис. 7-9)
— Известно, что сапёры – это люди, которым нельзя ошибиться. Напоминаю, что ответ предыдущего примера является элементом следующего. Конечный ответ соответствует определённой букве, её и надо записать на доске.
Контрольные точки — на обороте вашего листочка (приложение 1) (рис. 6).
. 

Рис. 6 Рис. 10
 .
. 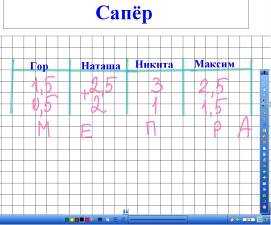
Рис. 7 Рис. 8
Рис. 9
Из этих букв можно сложить фамилию учёного, которого принято считать великим физиком, однако он является и выдающимся математиком. (Ампер).
Историческая пауза
Следует сообщение на французском языке с переводом на русский язык о рассеянности Ампера.
Тест
— Я очень хочу, чтобы вы сейчас не были рассеянными. Ведь предстоит решить тест, выбрать правильный ответ (приложение 2) (рис. 10). Используется шторка.
Собирается по одной тетради от группы.
— А теперь проверьте свои ответы и оцените работу с тестом: «5» — нет ошибок, «4» — одна ошибка, «3» — две ошибки.
Нестандартные задачи
Надо подумать! Задание представлено на доске (рис. 11).
3 минуты подумать, желающий решает на интерактивной доске.
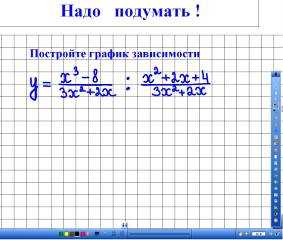
Рис. 11
По гиперссылке осуществляется переход к видеоролику, на котором записан процесс выполнения задания. Ученики выделяют этапы выполнения задания, сравнивая с работой ученика на доске.
Итоги урока (фронтальная беседа)
Обращаемся к записям на доске, сделанным в начале урока! Гиперссылка на первую страницу.
— Какие цели на урок ставили?
— Выполнили?
— Вы готовы к решению примера, с которого начинали урок?
— Какое правило необходимо повторить дома?
gigabaza.ru
Основные понятия связанные с алгебраической дробью (алгебра 8 класс)
Дополнительные сочиненияНа данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется почасти торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Основные понятия
1. Определение и примеры алгебраических дробей
Рациональные выражения делятся на целые и дробные выражения.
Определение. Рациональная дробь – дробное выражение вида , где – многочлены. – числитель, – знаменатель.
Примеры рациональных выражений: – дробные выражения; – целые выражения. В первом выражении, к примеру, в роли числителя выступает , а знаменателя – .
Значение алгебраической дроби, как и любого алгебраического выражения, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной .
2. Вычисление значения алгебраической дроби и две основные задачи на дроби
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.
Пример 1. Вычислить значение дроби при а) , б) , в)
Решение. Подставим значения переменных в указанную дробь: а) , б) , в) – не существует (т. к. на ноль делить нельзя).
Ответ: 3; 1; не существует.
Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных – значения переменных, при которых выражение имеет смысл. Множество всех допустимых значений переменных называется ОДЗ или область определения.
3. Допустимые (ОДЗ) и недопустимые значения переменных в дробях с одной переменной
Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.
Пример 2. Установить, при каких значениях переменной не имеет смысла дробь .
Решение. Чтобы данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не равнялся нулю. Таким образом, недопустимыми будут только те значения переменной, при которых знаменатель будет равняться нулю. Знаменатель дроби , поэтому решим линейное уравнение:
.
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Из решения примера вытекает правило нахождения недопустимых значений переменных – знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.
Рассмотрим несколько аналогичных примеров.
Пример 3. Установить, при каких значениях переменной не имеет смысла дробь.
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменной не имеет смысла дробь .
Решение..
Встречаются и другие формулировки данной задачи – найти область определения или область допустимых значений выражения (ОДЗ). Это означает – найти все допустимые значения переменных. В нашем примере – это все значения, кроме . Область определения удобно изображать на числовой оси.
Для этого на ней выколем точку , как это указано на рисунке:
Рис. 1.
Таким образом, областью определения дроби будут все числа, кроме 3.
Ответ..
Пример 5. Установить, при каких значениях переменной не имеет смысла дробь .
Решение..
Изобразим полученное решение на числовой оси:
Рис. 2.
Ответ..
4. Графическое представление области допустимых (ОДЗ) и недопустимых значений переменных в дробях
Пример 6. Установить, при каких значениях переменных не имеет смысла дробь .
Решение.. Мы получили равенство двух переменных, приведем числовые примеры: или и т. д.
Изобразим это решение на графике в декартовой системе координат:
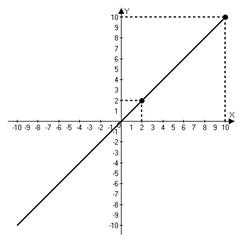
Рис. 3. График функции .
Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.
Ответ. .
5. Случай типа «деление на ноль»
В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа .
Пример 7. Установить, при каких значениях переменных не имеет смысла дробь .
Решение..
Получается, что дробь не имеет смысла при . Но можно возразить, что это не так, потому что: .
Может показаться, что если конечное выражение равно 8 при , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при . Однако, если подставить в исходное выражение, то получим – не имеет смысла.
Ответ..
Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях указанная дробь равна нулю?
(дробь равна нулю, когда ее числитель равен нулю) . Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при , т. к. при этом значении переменной знаменатель равен нулю. Значит, данное уравнение имеет только один корень .
6. Правило нахождения ОДЗ
Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби: для нахождения ОДЗ дроби необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения.
Мы рассмотрели две основные задачи: вычисление значения дроби при указанных значениях переменных и нахождение области допустимых значений дроби.
Рассмотрим теперь еще несколько задач, которые могут возникнуть при работе с дробями.
7. Разные задачи и выводы
Пример 8. Докажите, что при любых значениях переменной дробь .
Доказательство. Числитель – число положительное. . В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.
Доказано.
Пример 9. Известно, что , найти .
Решение. Поделим дробь почленно . Сокращать на мы имеем право, с учетом того, что является недопустимым значением переменной для данной дроби.
Ответ..
На данном уроке мы рассмотрели основные понятия, связанные с дробями. На следующем уроке мы рассмотрим основное свойство дроби.
Список литературы
1. Башмаков М. И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С. М., Потапов М. А., Решетников Н. Н., Шевкин А. В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Фестиваль педагогических идей .
2. Старая школа .
3. Интернет-портал lib2.podelise. ru .
Домашнее задание
1. №4, 7, 9, 12, 13, 14. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Запишите рациональную дробь, областью определения которой является: а) множество , б) множество , в) вся числовая ось.
3. Докажите, что при всех допустимых значениях переменной значение дроби неотрицательно.
4. Найдите область определения выражения . Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.
dp-adilet.kz
Алгебра 8 класс Дорофеев, Суворова, Бунимович
Твитнуть
Поделиться
Плюсануть
Поделиться
Отправить
Класснуть
Запинить
Аннотация
Учебник поможет вам открывать всё новые и новые страницы этой живой, увлекательной, но, как вы уже знаете, совсем не простой науки – алгебры. Устроен он так же, как уже знакомый вам учебник алгебры для 7 класса. Напомним основные принципы построения учебника и условные обозначения.
Пример из учебника
Заглянув в оглавление, вы увидите, что курс разбит на 6 глав -6 важных этапов, которые вам предстоит пройти. Главы делятся на пункты. Если вы откроете учебник наугад, то сориентироваться, где вы находитесь, поможет специальная строка вверху этой страницы (вы уже знаете, что такая строка имеет своё название – колонтитул).
Каждый пункт содержит объяснительный текст и упражнения. Объяснительный текст разбит на несколько фрагментов, поэтому читать его можно в несколько приёмов. Ответив на вопросы и выполнив задания, размещённые в конце текста, вы сможете осмыслить прочитанное, проверить, хорошо ли его поняли.
Содержание
Предисловие 3
Глава 1. Алгебраические дроби
1.1. Что такое алгебраическая дробь 5
1.2. Основное свойство дроби 11
1.3. Сложение и вычитание алгебраических дробей 17
1.4. Умножение и деление алгебраических дробей 26
1.5. Преобразование выражений, содержащих алгебраические дроби 30
1.6. Степень с целым показателем 35
1.7. Свойства степени с целым показателем 43
1.8. Решение уравнений и задач 48
1.9. Сокращение дробей (Для тех, кому интересно) 53
Дополнительные задания 57
Чему вы научились 62
Глава 2. Квадратные корни
2.1. Задача о нахождении стороны квадрата 66
2.2. Иррациональные числа 70
2.3. Теорема Пифагора 78
2.4. Квадратный корень (алгебраический подход) 84
2.5. График зависимости у = 4х 89
2.6. Свойства квадратных корней 93
2.7. Преобразование выражений, содержащих квадратные корни 100
2.8. Кубический корень 106
2.9. Двойные радикалы (Для тех, кому интересно) 111
Дополнительные задания 114
Чему вы научились 117
Глава 3. Квадратные уравнения
3.1. Какие уравнения называют квадратными 122
3.2. Формула корней квадратного уравнения 127
3.3. Вторая формула корней квадратного уравнения 132
3.4. Решение задач 136
3.5. Неполные квадратные уравнения 143
3.6 Теорема Виета 148
3.7. Разложение квадратного трёхчлена на множители 154
3.8. Целые корни уравнения с целыми коэффициентами (Для тех, кому интересно) 159
Дополнительные задания 162
Чему вы научились 166
Глава 4. Системы уравнений
4.1. Линейное уравнение с двумя переменными 170
4.2. График линейного уравнения с двумя переменными 175
4.3. Уравнение прямой вида y = kx + l 182
4.4. Системы уравнений. Решение систем способом сложения 191
4.5. Решение систем уравнений способом подстановки 200
4.6. Решение задач с помощью систем уравнений 205
4.7. Задачи на координатной плоскости 212
4.8. Геометрическая интерпретация неравенств с двумя переменными (Для тех, кому интересно) 216
Дополнительные задания 219
Чему вы научились 223
Глава 5. Функции
5.1. Чтение графиков 227
5.2. Что такое функция 236
5.3. График функции 244
5.4. Свойства функций 252
5.5. Линейная функция 256
5.6. Функция у = k/x и её график 266
5.7. Целая и дробная части числа (Для тех, кому интересно) 272
Дополнительные задания 274
Чему вы научились 279
Глава 6. Вероятность и статистика
6.1. Статистические характеристики 284
6.2. Вероятность равновозможных событий 292
6.3. Сложные эксперименты 298
6.4. Геометрические вероятности (Для тех, кому интересно) 301
Дополнительные задания 303
Чему вы научились 306
Ответы 308
Предметный указатель 318
Учебник можно просто читать в онлайн режиме, переходя сразу на тот параграф или раздел, который Вам сейчас нужен.
znayka.pro
Алгебраические дроби. Методическая разработка
Дополнительные сочиненияЭтот урок является одним из итоговых по знаниям алгебры 8-ого класса. Мы с вами вспомним основные определения и примеры решения задач на тему «Алгебраические дроби».
Тема: Повторение курса алгебры 8-ого класса
Урок: Алгебраические дроби
1. Определение алгебраической дроби
Для начала давайте вспомним, что же такое алгебраические дроби. Алгебраической дробью называют выражение вида , где – многочлены, – числитель, – знаменатель.
Поскольку – многочлены, то необходимо иметь в виду стандартные действия, возможные с многочленами, а именно: приведение к стандартному виду, разложение на множители, а также сокращение числителя и знаменателя.
2. Решение примеров
Пример №1
Сократите дробь
– воспользуемся формулами сокращённого умножения для квадрата суммы и разности квадратов.
Комментарии: вначале мы разложили дробь на множители с помощью формул сокращённого умножения, а дальше воспользовались одним из основных свойств дроби: и числитель, и знаменатель алгебраической дроби можно умножить или разделить на один и тот же многочлен, в том числе число, который не равен 0. Таким образом получается, что мы и числитель, и знаменатель разделили на многочлен , поэтому обязательно необходимо учесть, что этот многочлен не равен 0, т. е. .
Пример №2
Из условия нам пока не ясно, какая связь между этими двумя функциями. Для этого нам необходимо упростить первую из них методом разложения на множители.
однако необходимо не забыть про условие сокращения дроби, т. е. про то, что
После всех сокращений мы получаем, что
лишь с тем отличием, что .
Построим график двух функций.
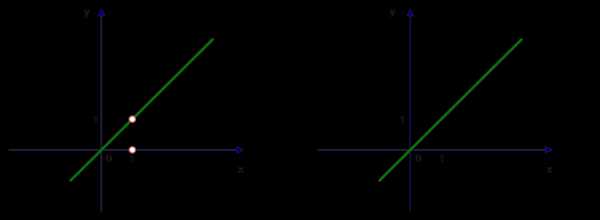
Мы видим яркое различие этих двух графиков: по сути они одинаковы, но на первом графике нам необходимо выколоть точку с координатой (1;0), поскольку эта точна не входит в ОДЗ первой функции.
Итого, мы с вами рассмотрели, что такое дробь, решили пару примеров о том, как важно следить за областью определения (областью допустимых значений), т. е. за теми значениями, которые может принимать .
3. Действия, которые можно производить с алгебраическими дробями
Теперь перейдём к вопросу, какие действия можно производить с алгебраическими дроями, помимо тех, которые уже были упомянуты выше.
Естественно, алгебраические дроби, как и арифметические дроби, можно складывать, вычитать, умножать, делить, возводить в степень, получая при этом рациональные алгебраические выражения (такие выражения, которые составлены из чисел, переменных с помощью арифметических операций и возведения в натуральную степень). После определённых упрощений подобные выражения сводятся к дробям, для которых исходными выражениями также являются алгебраические дроби.
Список действий / условий, с которыми можно столкнуться, решая задачи на алгебраические дроби:
— Упростить рациональные выражения
— Доказать тождества
— Решать рациональное уравнение
— Упростить/вычислить дробь
4. Решение задач
Пример №3
Решить простейшее рациональное уравнение
Дробь равна 0 тогда и только тогда, когда числитель равен 0, а знаменатель не равен 0. В нашем случае знаменатель равен . Значит, решение дроби сводится к линейному уравнению
Ответ:
Пример №4
Решить уравнение
В первую очередь попытаемся сократить дробь
, при условии, что .
Поскольку мы уже упростили дробь в левой части исходного уравнения, то можем подставить новое значение и решить уравнение.
Теперь давайте попробуем выделить полный квадрат из полученного квадратного уравнения
Воспользуемся формулой сокращённого умножения для разности квадратов
Произведение равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. К тому же не забываем, что в начале у нас появилось условие существования нашего выражения в виде . Запишем же систему уравнений.
=> => Мы видим, что противоречит нашему условию, что , поэтому у нас остаётся только один ответ .
Ответ: .
Итак, посмотрим на особенности, которые имеет решённый нами выше пример:
1. Числитель с разностью кубов и знаменатель желательно сократить сразу, поскольку это возможно в данном случае и сильно упростит дальнейшее решение уравнения, однако обязательно нужно помнить о том, что знаменатель дроби не может равняться, 0 и записать это условие.
2. Приведя дробь к квадратному уравнению, мы вспомнили один из методов решения квадратных уравнений – метод выделения полного квадрата.
5. Вывод
Мы с вами на данном уроке вспомнили, что такое алгебраическая дробь, какие действия необходимо производить с числителем и знаменателем при решении таких дробей, какие действия в общем можно производить с дробями такого вида и решили несколько простых задач.
Список литературы
Башмаков М. И. Алгебра 8 класс. – М.: Просвещение, 2004. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010. Никольский С. М., Потапов М. А., Решетников Н. Н., Шевкин А. В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Вся элементарная математика . Школьный помощник . Интернет-портал Testmath. com.
dp-adilet.kz
| 1. |
Перемена знаков числителя и знаменателя дроби
Сложность: лёгкое |
1 |
| 2. |
Сокращение алгебраической дроби, вынесение общего множителя за скобки
Сложность: лёгкое |
2 |
| 3. |
Расширение алгебраической дроби (неизвестный числитель)
Сложность: лёгкое |
1,5 |
| 4. |
Расширение дроби
Сложность: среднее |
2 |
| 5. |
Общий знаменатель (противоположные знаменатели)
Сложность: среднее |
4 |
| 6. |
Дроби с одинаковыми знаменателями
Сложность: среднее |
3 |
| 7. |
Дроби с общим знаменателем (две дроби)
Сложность: среднее |
4 |
| 8. |
Дроби с общим знаменателем (разность квадратов)
Сложность: среднее |
6 |
| 9. |
Дроби с общим знаменателем (три дроби, разность квадратов)
Сложность: среднее |
4 |
| 10. |
Сокращение алгебраической дроби, разложение на множители способом группировки
Сложность: среднее |
3 |
| 11. |
Дроби с одинаковыми знаменателями (общий множитель, способ группировки)
Сложность: сложное |
7 |
www.yaklass.ru
В помощь учителю. Урок 1. Что такое алгебраическая дробь (рациональные выражения) 8 класс
Конспект урока. Что такое алгебраическая дробь (рациональные выражения)
8 класс
Определение 1. Алгебраическая дробь — это выражение вида P/Q, где
Р и Q — многочлены; Р — числитель, а Q — знаменательалгебраической дроби. Алгебраическую дробь также называют рациональной.
Например:
а – b_ , где P = a − b , а Q = b 2−1 ;
b2 — 1
х2 + 3_, где P = x 2+3 , а Q = y 3+x ;
у3 + х
у2 — 1 , где P = y 2−1 , а Q = y −1 .
у — 1
Многочлен — это частный случай алгебраической дроби.
Например, многочлен y 3+2y+7 равен дроби
, а дробь можно записать в виде многочлена 3х2/5 + 5х/5 – 1/5 = 3х2/5 + х — 1/5.Определение 2.
Целые выражения – это выражения,
Определение 3.
Определение 4. Допустимыми значениями переменных, входящих в алгебраическую дробь (рациональное выражение), называют все значения переменных, при которых это выражение имеет смысл.
Закрепляем полученные знания:
Решаем вместе:

Домашнее задание:
infourok.ru
