Как сделать математику 8 класс: Алгебра (математика) 8 класс

Олимпиадные задания (математика) – Олимпиада школьников «Высшая проба» – Национальный исследовательский университет «Высшая школа экономики»

В старых версиях браузеров сайт может отображаться некорректно. Для оптимальной работы с сайтом рекомендуем воспользоваться современным браузером.

Мы используем файлы cookies для улучшения работы сайта НИУ ВШЭ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь, наши правила обработки персональных данных – здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом НИУ ВШЭ и согласны с нашими правилами обработки персональных данных. Вы можете отключить файлы cookies в настройках Вашего браузера.

✖

Обычная версия сайта

2020/2021 учебный год

Для младших классов: максимальная оценка за всю работу — 100 баллов.

Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100. 

Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.

2019/2020 учебный год

Для младших классов: максимальная оценка за всю работу — 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100. 

Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.

2018/2019 учебный год

Задания	Решения и критерии

2017/2018 учебный год

2016/2017 учебный год

2015/2016 учебный год

2014/2015 учебный год

2013/2014 учебный год

2012/2013 учебный год

 Задания 8 класс (задачи 1 и 2 имеют вес 16 баллов, остальные — 17 баллов)

 Задания 9 класс (все задачи имеют равный вес (кроме 4): 17 баллов, задача 4 — 15 баллов)

 Задания 10 класс (все задачи имеют равный вес (кроме 2): 17 баллов, задача 2 — 15 баллов)

 Задания 11 класс (все задачи имеют равный вес (кроме 3): 17 баллов, задача 3 — 15 баллов)

2011/2012 учебный год

Слабый ученик, что делать? Советы репетитору по математике

Каков он — слабый ученик и что творится в его голове? Можно ли его хоть чему-нибудь научить? Эти вопросы мучают многих. Ох, сколько хлопот доставляет преподавателю ленивый и немотивированный двоечник. И не только по математике. Достаточно поработать репетитором хотя бы пару лет и вам обязательно попадется какой-нибудь неподъемный школьник, от которого хочется сразу же убежать. Однако репетитор по математике по долгу службы обязан уметь работать с такими трудными случаями. Но как? Насколько безнадежным может быть типичный двоечник? Можно ли изменить стиль его мышления и дать хоть какие-то знания?

Недавно одному знакомому репетитору по математике потребовался совет в выборе стратегии действий в работе с очень сложным учеником 8 класса. Картина типичная. Ничего не понимает, ничего не знает и ничего не может. Что делать? Привожу детальное описание проблемы и свои соображения относительно данного случая и подобных ему.

Репетитор по математике Ермакова Диана: Помогите советом. Мальчик 8 класс. Обычный, не профильный. Занимается у меня с сентября. Случай очень тяжелый. Во-первых, плохая память и повышенная утомляемость (через 15 минут уже зевает). Проблемы с позвоночником, возможно, причины оттуда. Усиленно лечатся, даже месяц лежал в санатории (оставляла за ним место). Перешли с 1,5 часов занятия на час, поскольку 1,5 он не высиживает. Сказать, что математика дается ему сложно-ничего не сказать. Это для него некий набор магических символов и правил, не подчиняющийся логике. При этом со счетом проблем особых нет, уровень 6 класса он вполне тянет. Но далее, когда начинаются алгебраические выражения, уравнения и т.д. — это кошмар. Мы топчемся практически на одном и том же месте уже полгода. Ленив. ДЗ выполняет из-под родительской палки. При этом каждый мой звонок им — это катастрофа. Его наказывают, всего лишают, и он приходит в слезах. Но изменить сам эту ситуацию и просто работать, чтобы я не звонила родителям — не хочет.

Вот перечень систематических ошибок, которые он делает: или . При переносе слагаемых из одной части уравнения в другую меняет знаки у всех слагаемых уравнения, 2х=5, значит, х=5-2 или х=2:5. Молчу уже про знаки вообще — путает нещадно. Шаг вправо-влево — уже не знает, что надо делать. Не могу сказать, что логика полностью отсутствует, но он предпочитает ею не пользоваться. Я старательный репетитор по математике, и пытаюсь донести до ученика причину, по которой выполняется то или иное действие и то, как как можно его проверить. Никогда не объясняю решение готовых задач: чтобы понять решение, его надо провести полностью самостоятельно, «прочувствовать». Но слушать объяснения репетитора он просто не хочет -«выключается». Говорит, вы мне говорите, что надо делать, и я буду делать. Очень хочет улучшить знания по предмету, но чисто теоретически. Практически это сделать не получается. Говорила: давай подберу тебе другого репетитора по математике. Нет, хочу заниматься с Вами, вдруг другой репетитор окажется злым. Да, еще он очень медлителен. По алгебре на контрольных успевает решить из 5 задач решить 3, а это только на тройку, если решено правильно. По алгебре стабильно три-два. По геометрии стоят даже колы. С геометрией история отдельная: вроде, она ему нравиться, чертежи выполнять любит.

Но практически-теоремы и доказательства зрительно вызубриваются наизусть. Забываются на следующий день. Естественно, применить их к конкретной задаче он просто не может. Кстати, можете взять его «перл» в Вашу коллекцию. Развернутый угол равен 180 градусам, а свернутый угол-не более 10 градусов:))

Под моим присмотром может довести решение до конца без ошибок. Самостоятельно-никак. Нет у меня опыта работы с такими детьми. К тому же жесткие родительские рамки-улучшайте наши оценки в школе и побыстрее. Чего я уже только не придумывала, только что с бубном не танцевала. В какой-то момент стало казаться, что начал понимать, быстрее решать. А на следующее занятие приходит-опять с начала надо начинать. Сил уже нет. Планируем заниматься все лето. Будет высыпаться, будет свободен от других уроков-возможно, станет получше. Подскажите, пожалуйста, из Вашего опыта работы с такими детьми-что делать. Заранее спасибо.

Репетитор по математике Колпаков А.Н.
Ох….как много всего. А частота занятий какая Вас? Сколько раз в неделю? Я в таком случае прошу увеличить ее хотя бы до 3 раз в неделю (если родители конечно серьезно настроены переломить ситуацию).

1) У каждого ученика – свой уровень мышления и свои показатели работы памяти, свой потолок, выше которого поднять ребенка не сможет ни один репетитор по математике. У вас по всей видимости планка очень низкая.

2) Проблема с алгебраическими выражениями чаще всего случается из-за того, что ребенок или не усвоил банального – порядка, в котором выполняются алгебраические действия, или не может его быстро определить, запомнить и связать с правилами. Репетитору по математике здесь нужно провести соответствующую вычислительную работу. До изучения темы «преобразование буквенных выражений» надо поработать над пониманием формы записи числа. Когда в правиле (в формуле) вместо множителя стоит буква, а в примере она заменена числом, дети еще как то соотносят их друг с другом, но как только происходит отождествление буквы и целого выражения – начинаются проблемы.

Я рекомендуб репетиторам по математике чаще использовать прием подстановки: когда ученик понял, что некоторое равенство верно, репетитор переписывает его с заменой числа на сумму или разность других чисел (или на любое другое его представление0.  Например, можно перезаписать так .  Это упростит понимание метода группировки при разложении на множители.  Только применять прием нужно не тогда, когда изучается новая тема, а в процессе работы с другими свойствами и правилами. И делать это надо систематически, чтобы сформировать навык использования и распознания известных законов, формул и схем.

Важно вовремя и точно комментировать каждый переход. При преобразовании выражений я повторяю слабому ученику одно и то же, пока это прочно не застрянет в голове: «В чем смысл знака равно? Он означает, что если мы заменим буквы любыми числами, то результат, который получится в одном выражении окажется точно таким же, как и в другом. Сохранение гарантируют законы и формулы. Поэтому любые преобразования возможны только через них». 2+3x-4)= … три поля и т.д. Чтобы ученик видел конечный формат записи.

4) В возрасте до 7-8 класса у детей почти поголовно отсутствует потребность в чем-либо глубоко разбираться, то есть обосновывать методы. Поэтому он Вам и говорит: «Скажите, что делать и я буду делать». У него просто не хватает объема памяти, чтобы целостно посмотреть на всю пройденную математику и отследить влияние тех или иных условий /фактов. Поэтому не воспринимает логику. И, естественно, не понимает, что в геометрии все нужно доказывать. Я не могу в двух словах описать, что именно должен делать в таком случае репетитор по математике, ибо нужен целый комплекс мер. Могу советовать методику «геометрия в движении», когда репетитор, двигая некоторые части рисунка, показывает несостоятельность неверных суждений. Например, при ошибке формулирования признака параллелограмма (через равенство противоположных сторон) можно показать, что равенство только внутри одной пары не приводит к появлению параллелограмма. Репетитор берет в руки два равных по длине карандаша и попорачивает один из них по отношению к другому.

Ошибка сразу становится очевидной. Параллелограмма нет.

Изменить у умственно слабого ученика его мировосприятие, в частности научить понимать логику линий и растояний, репетитору по математике редко когда удается в сжатые сроки. Это очень долгий процесс. Репетитор создает условия для «погружения» ребенка в предмет, обучая его обращать внимание на мельчайшие детали окружающей действительности (чертежа). Без практической геометрии, в которой размеренно и неспеша, начиная с 4 — 5 класса и заканчивая 6 — 7 классом, школьник учится просто рисовать линии и отклдывать углы, находить пересечения, обозначать, сравнивать, определять «на глазок» параллельность или равенство, — каши не сваришь. При погружении в геометрию в 8 классе репетитору по математике приходится использовать исключительно задачи на вычисление, не требующие никакого обоснования. Иначе не создать фундамента. Стиль работы «от теории к практике» в случае с очень слабым школьником не сработает точно. Репетитор по математике просто запутает подростка строгими рассуждениями.

5) Нельзя наказывать восьмиклассника. Это надо сказать родителям. С ребенком, тем более с подростком, нужно говорить, разъяснять ему многие вещи. Показывайте учебники старших классов. Я заметил, как только репетитор по математике начинает знакомить с содержанием программы в будущем, ребенок заостряет на этой информации свое внимание. Почему? Каждому интересно знать то, что его ожидает. Проблема мотивации изучения математики заключается в том, что дети не могут понять, как эта ненавистная математика поможет в жизни. Открывайте ему глаза какие-то вещи. Например, опишите ему реальную ситуацию: в интернете заказали шкаф, размер коробки которого по длине оказывается больше длины кабины лифта. Поэтому если ее и можно внести в кабину, то только по диагонали. Поэтому нам надо рассчитать удастся ли ее затащить в лифт? Скажите, что это можно выяснить средствами математики 10 классе, для понимания которых сейчас нужно учиться правильно выполнять преобразования. Рисуйте перспективу будущего: говорите о умственном развитии, которое дает изучение математики и которое очень ценится работодателями. Люди, связавшие свою жизнь с математикой, как правило, добиваются много в жизни. Каждый третий обитатель рублевки – выпускник МФТИ, МГТУ или МГУ. Если ребенок хочет зарабатывать, то может быть что то внутри и проснется. При комплексном подходе дети обычно перестраиваются и начинают хотя бы немного работать.

6) Летняя практика с репетитором по математике – самая лучшая стратегия на перспективу. Школа очень сильно мешает дополнительным занятиям. Задавать много не получается, текущая программа, которую ученик не понимает только съедает время впустую. Однако толку от раза в неделю будет мало (именно такой график чаще всего выбирают родители). Нужно не менее 2-3 раз.

7) Не допускайте пропусков занятий. Безусловно, 1.5 месяца санатория добавили «масла в огонь». Зависимость между уровнем развития ученика и необходимой частотой занятий — обратная. Чем ученик слабее, тем чаще и регулярнее он должен заниматься.

Колпаков А.Н. Репетитор по математике, Москва, Строгино.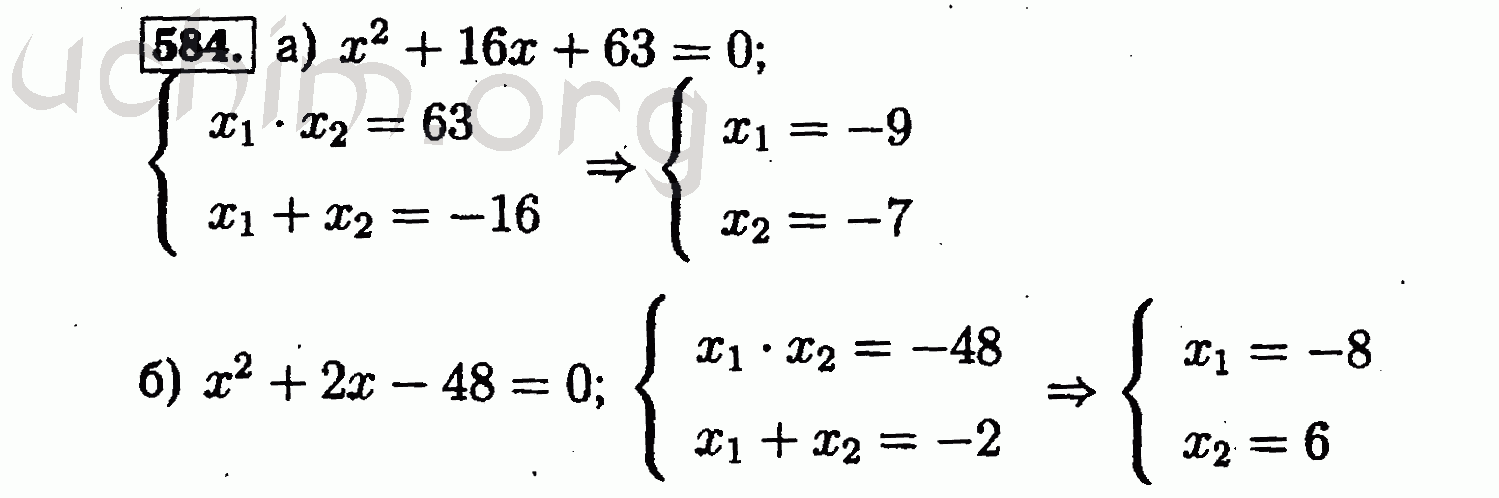

Как самому выучить математику? — Хабр Q&A

Изучать школьную математику, значит уметь решать задачи. Берешь любой задачник и решаешь. Сначала будет тяжко, но потом мозг включится. Начинай с самого начала. С первых классов. В математике знания накладываются одни на другие и буз базы ничего не получится. Хороший сайт: interneturok.ru, и подобные. Отличные сайты на английском. Здесь учебники www.alleng.ru/.
Школьная математика, всего лишь запоминание правил и определений и потом их быстрое применение при решении задач. Ничего сложного. Но она основа, для всего остального. Вот здесь хорошо расписано: viripit.ru/index.htm . Купи старую книгу типа «Энциклопедия юного математика». Читай для удовольствия. Вообще процесс должен занять несколько месяцев, чтобы осилить школьную программу.

Натыкайся на те задачи которые не можешь решить и уделяй им время. Потом пойдет все быстрее и быстрее. Не слушай никого, кто говорит, что учить поздно. У каждого своя судьба, и свои стартовые условия. Но каждый в итоге получает то, что он действительно хочет. Осилить школьную математику, нармально любому человеку. Это общий культурный багаж, без понимания которого, человек будет ограничен. На самом деле все школьные предметы, развивают разные способности мышления. Потом неплохо повторить и физику — чтобы понимать, почему вокруг все так происходит.

Математика программисту в большинстве случаев не нужна. Но нужно знание основ, чтобы быстро разобраться в новом. Обязательно знание некоторых важных разделов:, типа логики и др. Без математики ты не сможешь зазкончить нормальное обучение по ComputerScience.
И самое главное, мозг должен уметь думать и решать задачи. Именно это и развивает в чистом виде — математика.

Но в реальности программисту, кроме умения думать, нужно и воображение, и абстрактное мышление, отличная память, знание английского, и умение общаться; еще умение постоянно учиться, хорошая общая эрудированность и вкус и тд. А так же крепкое здоровье. Так- что не циклись на математике, это всего лишь часть большого целого.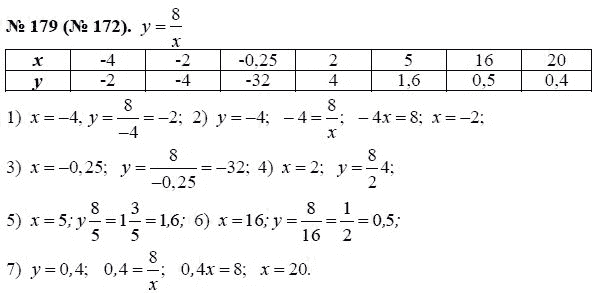

PS: Забудь про криптографию. Ты это не осилишь. Разберись, сейчас — как делить столбиком 🙂

Обзор 8-го класса по математике

    Совсем недавно на нашей платформе стартовал 8 класс по математике. Сегодня мы хотим познакомить вас поближе с нашим новым курсом и рассказать о его главных особенностях. Поэтому скорее к делу!

    Главное:

    Новый курс предназначен для учащихся в возрасте от 13 до 14 лет. Он поможет школьникам седьмых, восьмых и девятых классов улучшить и углубить свои знания по геометрии и алгебре.

    Этот курс содержит 335 задач. Они группируются на две большие категории: упражнения по алгебре и геометрии. В составе каждого такого подкурсах задачи дифференцируются по темам для лучшего восприятия. В уровне всего 30 тем.

    Все задачи определены стандартами МОН Украины для восьмого класса. Также есть упражнения, соответствующие еще и международному стандарту Common Core. С их помощью ученикам удастся еще больше углубить понимание по соответствующей теме.

    Задания только по международным стандартам отмеченные зелеными флажками, а те, которые посвящены более глубокому изучению, — оранжевыми.

    Традиционно:

    Каждая успешно пройденная тема означает новую награду. Это может быть логическая игра, раскраска, лабиринт, пазл, судоку и, конечно, наклейки. Кстати, в личном кабинете у каждого ученика есть своя статистика. Там можно увидеть, сколько задач уже выполнено, сколько из них — правильно, какие баллы были получены и какого рейтинга достигнуто.

    Такая система позволяет родителям и детям контролировать собственные успехи и достигать еще больших результатов.

    Итак, предлагаем перейти к основным темам более детально.

    Алгебра:

    В.13 Решаем степенные уравнения

 

    Решение уравнений — одно из главных упражнений в алгебре, ведь задействует все возможные знания ученика. Именно эта тема рассматривает нахождения неизвестного при действиях со степенями.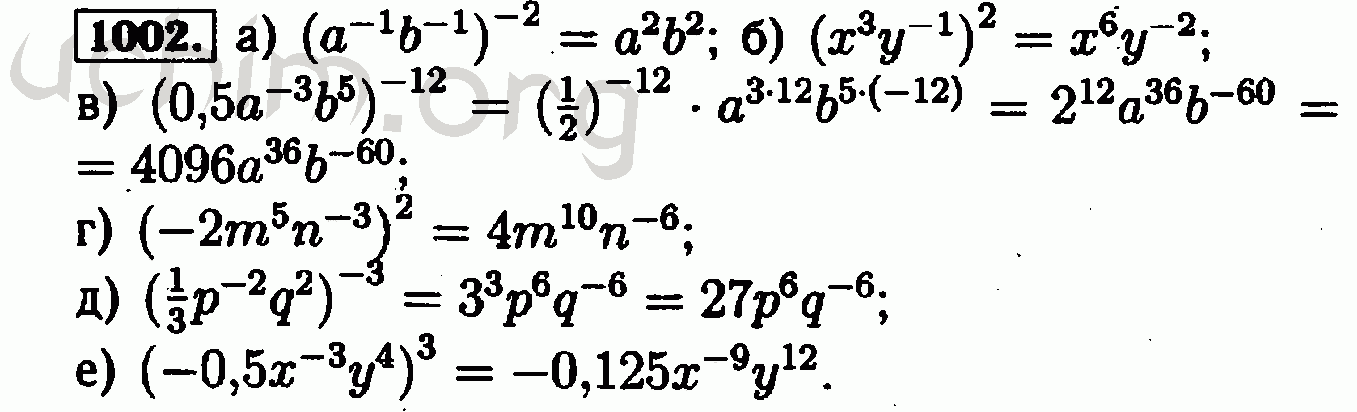 Ученик должен уметь работать с показателями, превращать их, выполнять различные арифметические действия.

    Для решения подобного уравнения необходимо сначала максимально упростить выражение, а потом найти все неизвестные. После того, как решение найдено, нужно просто нажать на правильный вариант и перейти к следующему заданию.

    Ґ.5 Сокращаем рациональные дроби

    Во время прохождения этой задачи ученик потренирует навык работы с дробями. Для того, чтобы в дальнейшем легко и быстро работать с обычными примерами, восьмиклассник должен научиться упрощать числитель и знаменатель дроби до максимально возможных величин. Ведь, если после этого нужно будет подставить любое число вместо буквенного выражения, вычисление будет происходить гораздо быстрее.

    Кроме того, такое упражнение научит школьника быстро ориентироваться между начальной формой выражения и конечной, упрощенной.

    Чтобы выполнить задание, необходимо восстановить равенства правой и левой части, перетащив их мышкой.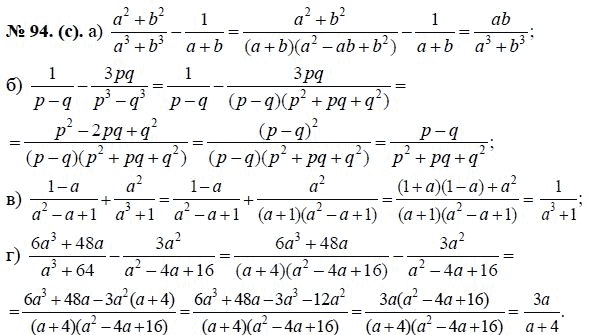

    Ж.4 Графический способ решения системы уравнений

    Кроме того, что восьмиклассник должен уметь удачно решать обычные уравнения, а также системы уравнений, он должен знать, как находить решения с помощью графика функций.

    Это упражнение постепенно вводит ребенка в это умение. Ведь ученику придется просто сравнить записанную систему уравнений и предложенные на экране развязки. Для этого, вместо х и у нужно просто подставить соответствующие значения точки.

    В дальнейшем школьник должен научиться самостоятельно определять, что за функция представлена ​​перед ним и как она будет отображаться на координатной плоскости. А вот точки пересечения этих двух функций — это и есть решения системы уравнения.

    К.6 Считаем сумму платежа

    Основная задача нашей платформы — продемонстрировать ученикам, где в жизни можно применить приобретенные знания. Это упражнение нацелено именно на это.

    Перед учеником — сообщение из банка, а именно — обычная задача на проценты. Однако, такая ситуация может быть реальностью, поэтому ребенку важно научиться решать такие задачи хотя бы в теории.

    С этой задачи восьмиклассник узнает, что такое пеня, откуда она появляется и как рассчитывается. Чтобы решить задачу, нужно вычислить, каким числом является этот процент от первой суммы. Затем результат следует умножить на количество дней, которое начислялась пеня, а потом добавить ответ к исходной сумме.

    Н.1 Свойства делимости чисел

    Знание основных теорий делимости позволит ученикам проще и быстрее ориентироваться в решении и исчислении выражений. Так, благодаря этим теориям, восьмиклассники смогут быстро проанализировать пример и его будущий результат.

    В этом задании перед школьником будут появляться как правильные, так и неправильные утверждения относительно основных признаков делимости. Задача ученика — проанализировать утверждения и дать ответ по их правильности.

    П. 6 Игра «Предприниматель»

    Подобное упражнение является отличной возможностью для того, чтобы развить предпринимательские навыки у ребенка.

    Прежде всего, ученик должен уметь читать статистические данные и диаграммы. Благодаря этому, он легко поймет задачу и решит её.

    Это упражнение также тренирует логику ребенка, расскажет об интересных фактах о разных странах мира. Например, после этой задачи ученик узнает, что наибольший процент на промышленность (по сравнению с другими 3-мя странами) накладывается в Эстонии. Поэтому, если вдруг придется выбирать, чем заниматься и в какой стране, восьмиклассник сможет легко проанализировать представленную информацию и сделать соответствующие решения.

    О.5 Задачи на движение

    Задачи являются неотъемлемой частью любой учебной программы по математике. Они развивают логическое мышление и позволяют на практике применить полученные знания и навыки.

    Тема «Задачи на движение» тренирует умение школьника определять скорость транспорта, расстояние, которое он прошел, а также время, за которое пройдено заданное расстояние.

    Кроме того, для такого транспорта, как яхта, важно учитывать еще и силу ветра, которая будет влиять и на скорость яхты, и на время прохождения расстояния. Именно в этом упражнении, после анализа заданных показателей восьмиклассник должен вычислить скорость яхты и выбрать один из трех возможных вариантов.

    П.9 Строим столбчатые диаграммы

    Статистика помогает систематизировать и упорядочить данные. Однако, для того, чтобы сделать их наглядными, необходимо научиться строить диаграммы. Восьмиклассник уже хорошо знаком с этим понятием. Однако, в восьмом классе диаграммы усложняются.

    В частности, это упражнение требует от ученика построить двойную столбчатую диаграмму. В левой части есть таблица с заданными параметрами, справа — график, на котором нужно нарисовать диаграмму. Школьник анализирует информацию, а затем логично отражает ее благодаря столбчатый двойной диаграмме.

    Геометрия

    Т.13 Изучаем математиков

    Первая тема, которая открывает раздел по геометрии в восьмом классе касается изучения координатной плоскости. Ученик вспомнит главные особенности работы, научится отображать точки на координатной плоскости и строить простые геометрические фигуры.

    Чтобы изучения этого раздела было не просто теоретическим и систематическим, но и познавательным и веселым, мы создали задачу «Изучаем математиков».

    Восьмиклассник увидит перед собой координаты нескольких точек (каждая точка — это часть фамилии математика). После этого он должен найти на координатной плоскости эти точки и выяснить, какие буквы спрятались под ними. Когда все буквы будут найдены, школьник получит имя настоящего математика!

    Х.1 Игра «Какая фигура образовалась?»

    Кроме знакомства с двумерными фигурами, восьмиклассник узнает о возможности их трансформации. В частности, одна фигура может превращаться в другую путем ее вращения или иного изменения относительно своего первоначального положения.

    Школьникам придется хорошо поработать со своим воображением и фантазией, чтобы дать точные ответы на вопросы. А вот в самом задании формулируется ситуация, и необходимо представить себе первоначальную фигуру и правильно определить то, в отношении чего происходит вращение, чтобы понять, какая фигура образовалась.

    Чтобы справиться было проще, под вопросом является маленькая подсказка к заданию.

    Ч.6 Тригонометрические соотношения

    Восьмиклассник должен прекрасно ориентироваться в таких понятиях, как синус, косинус, тангенс и котангенс углов прямоугольного треугольника. Благодаря этим тригонометрическим понятием можно с легкостью узнать неизвестные стороны или углы треугольника.

    Находить неизвестные элементы можно с помощью преобразования формулы, где эти элементы, правильные выражения с дробями, что означают соотношение длин нужных сторон.

    В частности, в этом задании ученик имеет только один известный угол и длину катета, лежащего против него. Выбрав одну из тригонометрических теорем, ученик быстро выяснит, которой все-таки будет длина неизвестной гипотенузы.

    Щ.6 Ищем фигуру по ее описанию

    В процессе изучения геометрии восьмого класса ученик встретится не только с двумерными фигурами. Перед ним предстанут и трехмерные. Один из разделов, который нацелен на то, чтобы объяснить ребенку основные аспекты трехмерных фигур и предоставить теоретическую базу — это раздел «Ищем фигуру по ее описанию».

    Важно, чтобы школьник понимал, что трехмерные фигуры находятся в пространстве, а не на плоскости. Поэтому они имеют более сложнее параметры.

    В этом упражнении ученик должен прочитать определение фигуры и выбрать ту, о которой это определение написано. Такая задача позволит восьмикласснику легко ориентироваться в фигурах и знать их основные особенности. В дальнейшем это умение пригодится для решения более сложных задач и задач с трехмерными фигурами.

    Ш.5 Нахождение неизвестного угла треугольника

   

    Найти неизвестный угол треугольника можно не только при помощи использования известных его углов, но и с помощью прямой, проходящей через точку, принадлежащую его углу, за пределами фигуры. Для этого необходимо знать все свойства углов и прямых, проходящих через них. Это могут быть смежные или соответствующие углы, которые помогут определить градусную меру неизвестных.

    Именно в этом упражнении ученик должен выяснить один из неизвестных углов треугольника, при том, что через одну из его вершин проходит прямая, параллельная одной из сторон данного треугольника. Известен также один угол. Применив свойства прямых, восьмиклассник с легкостью придет к правильному ответу.

    Щ.11 Задачи на объем

    Благодаря тому, что ученик знает формулы для вычисления площадей, периметров и объемов, ему с легкостью будут даваться обычные жизненные ситуации.

    В частности, эта задача. В ней ребенку придется применить свои знания по объемам трехмерных фигур, а именно — параллелепипеда. В задаче предоставлено длины сторон прямоугольного параллелепипеда, что натолкнет восьмиклассника на решение задачи по правильной формуле.

    Упражнение еще раз продемонстрирует школьнику, насколько важно уметь применять свои знания на практике.

    У.11 Площадь ромба

    Изучение двумерных фигур означает, что ученик узнает все об их основных свойствах, а также поймет, как применять их для решения реальных задач.

    Тема «изучение ромба» включает в себя такое понятие, как его площадь. Находить площадь ромба можно несколькими вариантами. Однако, задача восьмиклассника заключается в том, чтобы взглянуть на изображения и проанализировать, какие исходные данные он имеет и какую формулу все-таки следует применять в данном конкретном случае.

    Это упражнение для вычисления площади ромба использует информацию о длине его диагоналей. Зная соотношение длин этих отрезков и площадь фигуры, можно вычислить и сами эти стороны, используя формулу как каркас уравнения. Очень просто, если знать, с какой формулой работать!

    На этом мы предлагаем завершить наш обзор. На самом деле, на этом уровне еще столько всего интересного, яркого и познавательного! Но, если говорить о каждом упражнении отдельно, наш обзор затянется в настоящее небольшое издание 🙂

    Надеемся, теперь у вас есть некоторое представление о новом курсе. А чтобы лучше с ним познакомиться — заходите на уровень и проходите задания!

    Удачи!

«Как построить график функции F(x)+m»

Дата публикации: 09 апреля 2017.

Презентация и урок на тему: «Как построить график функции f(x)+m»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

---

Скачать: Как построить график функции f(x)+m (PPTX)

---

Ребята, сегодня мы научимся еще одному методу построения графиков функций!
Поступим как на прошлом уроке, построим в одной системе координат три параболы: $y=x^2$, $y=x^2+3$, $y=x^2-3$. 2-4, -1<x≤2. \end {cases}$

Представляем MATH! 8 класс от ArgoPrep: более 600 практических вопросов + подробный обзор каждой темы + подробные видео-объяснения включены

Знакомство с математикой! от ArgoPrep — это отмеченная наградами серия, созданная сертифицированными учителями , чтобы предоставить студентам качественные практические задачи. Эта рабочая тетрадь предназначена для предоставления вам исчерпывающего обзора по математике для 8-го класса. Наши рабочие тетради включают обзоры тем с инструкциями, практические вопросы, ответы на объяснения, а также бесплатный цифровой доступ к видеообъяснениям .Практикуйтесь уверенно — с ArgoPrep!

8 класс Математика:

Глава 1 — Система счисления

1.1.A Иррациональные числа

1.1.B Аппроксимация иррациональных чисел

1. 2. Глава Тест

Глава 2 — Выражения и уравнения

2.1.A Свойства экспонент

2.1.B Квадратные корни

2.1.C Полномочия десяти

2.1.D Выполнение операций с научной нотацией

2.2.A График пропорциональных соотношений

2.2.B Определение Y-пересечения и объяснение наклона

2.3.A Решение Линейные уравнения

2.3.B Решение пар линейных уравнений

2.4. Глава Test

Глава 3 — Функции

3.1.A Введение в функции

3.1.B Сравнение функций

3.1.C Нелинейные функции

3.2.A Создание функций

3.2.B Анализ функциональных взаимосвязей

3.3. Глава Тест

Глава 4 — Геометрия

4.1.A Эксперименты с вращениями, отражениями и переводами

4. 1.B Конгруэнтные фигуры

4.1.C Преобразования на координатной плоскости

4 .1.D Подобные рисунки

4.2.A Введение в теорему Пифагора

4.2.B Применение теоремы Пифагора — Часть I

4.2.C Применение теоремы Пифагора — Часть II

4.3 Том конусов, цилиндров и сфер

4.4. Глава Тест

Глава 5 — Статистика

5.1.A Точечные диаграммы

5.1.B Линейные ассоциации

5.1.C Уравнение линейной модели

5.1.D Двусторонние модели

5.1. Глава Тест

Глава 6 — Смешанное оценивание

Независимо от того, следует ли ваша школа по общей основной учебной программе или по программе штата, наш Знакомство с математикой! Рабочие тетради предназначены для предоставления студентам всестороннего обзора.

Мы стремимся предоставить вам потрясающий опыт обучения. Если у вас есть предложения или вам нужна дополнительная помощь, напишите нам по адресу info @ argoprep.com или поговорите с нами в прямом эфире на нашем веб-сайте www.argoprep.com

Подготовка к 8-му классу | Государственные школы Андовера

Добро пожаловать в 8 класс!
Ваши новые учителя математики очень рады встрече с вами в сентябре!

Чтобы помочь вам развить математические навыки в 7-м классе, мы составили список дополнительных летних практических заданий. Все, что от 5 минут в день до 30 минут в неделю, поможет вам быть в курсе математики, которую вы изучали в школе в этом году.

Эта практика представляет собой набор рабочих листов, которые вы можете распечатать дома или в Интернете, используя IXL. Вам следует продолжать использовать Classlink для доступа к своей учетной записи IXL, как и в этом году в школе. Если у вас возникли проблемы с входом в систему, свяжитесь с г-жой Ричард, отправив электронное письмо в конце этого письма. Работа, выполненная с использованием IXL, будет видна вашему учителю осенью.

Прежде чем вы начнете, вот несколько полезных советов, которые помогут вам организовать дополнительную летнюю работу:

1. Всегда полезно хранить работу в одном месте.Так что возьмите скоросшиватель или записную книжку в спиральном переплете, где вы можете записывать. Возможно, вам будет полезно оглянуться на решение вашей проблемы позже. Даже если вы используете IXL, иногда вам нужно что-то записать, чтобы решить проблемы. Если у вас много проблем в какой-либо конкретной области, ваш учитель может позже просмотреть вашу работу, чтобы увидеть, где вы могли допустить ошибки.
2. Выполняйте свою работу карандашом, чтобы при необходимости можно было стереть.
3. Попробуйте выполнить работу без калькулятора, если можете.Практика ваших математических фактов во время решения задач поможет вам развить свои вычислительные навыки.
4. Не расстраивайтесь. Если вы застряли, просто переходите к следующей проблеме. Может, если вы сделаете перерыв, у вас будет мозговой штурм 🙂 А если нет, ничего страшного. Ваш учитель будет рад помочь вам осенью. Запишите свои вопросы, чтобы не забыть задать их позже! Поместите стикер на страницу, чтобы напомнить вам.
5. Удачи! Эта работа не должна вызывать у вас стресс.Это просто летнее упражнение для вашего математического мозга.

Вот ссылки на ваши плейлисты, содержащие инструкции и практические занятия:

• Список для воспроизведения # 1: Выражения: оценка, объединение одинаковых терминов
• Плейлист № 2: Расширяющиеся и разлагаемые на множители выражения: свойство распределения, наибольший общий множитель
• Плейлист № 3 : Решение уравнений и задач с уравнениями
• Плейлист № 4 : Практика построения графиков

Вы можете получить доступ к материалам практики, щелкнув ссылки (или скопировав их в свой браузер). Вам НЕ нужно будет отправлять работу своему учителю, но вы обязательно должны положить ее в свой скоросшиватель (или сделать это в записной книжке со спиральным переплетом). Каждый плейлист посвящен разному набору практических навыков. Вы можете пропускать, смешивать и сочетать, комбинировать печатные работы с навыками IXL или Khan Academy. Получайте удовольствие от работы! Если у вас есть какие-либо вопросы, свяжитесь с г-жой Ричард по адресу [email protected].

Математика для 8 классов — Обучение моего ребенка: ресурсы для родителей

Что изучает ваш подросток

Ученики 8 класса

• вычисление квадратных корней из чисел
• решает проблемы с процентами, превышающими или равными 0%
• выражают проценты в виде дробей и десятичных знаков
• решает линейные уравнения линейное уравнение: уравнение, которое приводит к прямой линии на графике
• используйте таблицы, графики, уравнения и слова для описания числовых шаблонов
• представляют трехмерные объекты в виде сетей и в разных ракурсах
• определяет площадь поверхности прямоугольных призм, треугольных призм и цилиндров
• разработать и применить формулы объема прямоугольных призм, треугольных призм и цилиндров
• понять соответствие полигонов
• критически интерпретировать графики

Подробнее о 8 классе Математика, обратитесь к программе исследований.

Знания и возможности трудоустройства по математике

Знания и возможности трудоустройства учащихся 8-х классов

• Свяжите числовые концепции и операции с ситуациями карьеры и работы
• описывает количества и представляет числа разными способами
• представляет, сравнивает и описывает правильные дроби, смешанные числа и эквивалентные дроби
• выполняет операции с целыми, десятичными и дробными числами с одинаковыми знаменателями
• понимает взаимосвязь между процентами и десятичными знаками
• решать уравнения с одним неизвестным и целыми числами
• делать прогнозы, используя шаблонные правила
• оценить и рассчитать периметр
• выполняет измерения и переводит из метрических (СИ) в британские единицы измерения
• понимает отношения между единицами времени
• : обозначение и рисование линий симметрии на четырехугольниках и треугольниках
• описывает движение фигур в терминах скольжения, поворотов или переворотов
• нанесите на сетку целые числа точек, используя упорядоченные пары
• создание, изучение и управление трехмерными объектами и двухмерными фигурами
• собирать, интерпретировать и отображать данные

Подробнее о знаниях 8-го класса и математику трудоустройства см. в программе исследований.

Как оценивают вашего подростка

Учеба вашего подростка оценивается с помощью разнообразные инструменты и стратегии в классная комната. Спросите учителя вашего подростка какие методы они используют.Разные методы оценки говорят вам и вашему подростку учителя о сильных сторонах вашего подростка, области, в которых они могут расти и как хорошо, что у вашего подростка все в порядке курс. Затем учитель может изменить или доработать свои учебные планы, чтобы учебные мероприятия лучше соответствуют потребностям вашего подростка. В конце курса ваш подросток оценивается и его достижения сообщается, чтобы вы знали, есть ли у них достигли ожидаемых результатов обучения для своего сорта.

Ресурсы в помощь подростку

Для помощи учащимся в обучении доступны разнообразные цифровые и печатные ресурсы, разработанные издателями, преподавателями Альберты или Альберты.Учителя могут выбирать и использовать в классе многочисленные инновационные и творческие ресурсы, чтобы создать богатый опыт обучения для вашего подростка. Посетите LearnAlberta.ca, чтобы узнать больше о ресурсах, с которыми может столкнуться ваш подросток.

Соответствующие ресурсы:

Ваш 8-й класс и математика в соответствии со стандартами Common Core

Математика для восьмого класса может показаться отдельным языком или, по крайней мере, параллельным универсумом определений. Когда ваш ребенок говорит о вещах радикальных, иррациональных и изменчивых, скорее всего, он имеет в виду урок математики, а не размышляет о жизни.

К концу восьмого класса ваш ребенок будет близок к овладению этими навыками:

• Понимание иррациональных чисел и сравнение их с рациональными числами.
• Использование линейных уравнений, линейных функций и систем линейных уравнений для объяснения отношений между двумя переменными или значениями.
• Создание графиков и других диаграмм для иллюстрации этих отношений.
• Понимание концепции функции как одного количества или значения, изменяющего другое количество или значение.
• Вычисление квадратных корней и их противоположностей, степеней.
• Определение идентичности форм путем их поворота, отражения и перемещения на графике.
• Применение теоремы Пифагора для нахождения неизвестных длин в прямоугольных треугольниках и объяснение, почему это работает.
• Найдите объем трехмерных фигур, включая конусы, сферы и цилиндры.
  Иллюстрация взаимосвязей между двумя наборами данных на диаграммах и объяснение закономерностей.

Это так иррационально

Рациональные числа включают положительные или отрицательные целые числа, простые дроби и десятичные дроби (включая те, которые имеют повторяющиеся шаблоны, такие как .2323…). Иррациональные числа — это десятичные дроби, которые продолжаются бесконечно, не повторяя последовательность чисел. Пи — π — самое известное иррациональное число. Он был рассчитан с точностью до квадриллиона десятичных знаков, а закономерности все еще нет! Неудивительно, что у него есть собственный день.

Выражения и уравнения

Большая часть математики для восьмых классов сосредоточена на линейных уравнениях, линейных функциях и системах линейных уравнений, которые используются для демонстрации взаимосвязи между двумя переменными. Идея о них может показаться устрашающей, но вы используете их все время, даже не задумываясь об этом. Посмотрите это видео о GreatSchools, чтобы увидеть реальный пример.

«Это самая важная и сложная концепция для изучения в восьмом классе», — сказал Райан Редд, учитель математики в средней школе Roland-Grise в Уилмингтоне, Северная Каролина.«Это важнейший базовый навык для математики в старших классах».

Восьмиклассники научатся изображать эти отношения на графиках; создание уклонов, которые упрощают сравнение пропорциональных соотношений и которые выглядят следующим образом.

Входы и выходы

Как бы это ни звучало, функция описывает отношения, в которых одно влияет на другое. Например, результат теста вашего ребенка зависит от того, сколько он учился.

Математически функция — это когда одно число, называемое вводом, изменяет следующее число, известное как вывод.Для каждого входа есть только один выход.

Пример. Какая связь между быстрой ездой и пробегом? Вычислите, насколько уменьшается расход топлива на каждую милю сверх установленной вами скорости.

Функции бывают линейными (то есть они создают прямую линию при нанесении на график) или нелинейными (то есть они не образуют линию).

Радикальные корни

Ваш восьмиклассник также узнает около корней , известных как радикальных чисел , и экспонент.Квадратные корни — самые распространенные радикалы. Символ выглядит как галочка √. Когда после знака квадратного корня стоит число, например √49, студентам предлагается найти число, которое при умножении само на себя равно 49. Квадратный корень из 49 равен 7.

Обратной стороной корней является показателей степени. . Они указывают, сколько раз умножить число само на себя. Экспоненты записываются так: 67. Здесь 7, которая, кажется, сидит на плече 6, является показателем. Его также можно было записать так: 6 x 6 x 6 x 6 x 6 x 6 x 6.Ваш ребенок также будет работать с отрицательными показателями в восьмом классе.

Форма вселенной

Ваш восьмиклассник годами играет с формами в классе и за его пределами. Если она занимается полевым спортом, она уже свободно думает треугольниками (три игрока держат точку), меняет их ориентацию, вращает их и перемещает по плоскости (например, к цели) — три ключевых навыка, которые ей предстоит освоить. нужно делать в классе математики в этом году.

Ваш ребенок также познакомится с магией теоремы Пифагора.Забыли этот древний алгоритм? В прямоугольном треугольнике, если a — длина одного из катетов, а b — длина другого катета, то длину третьей стороны, противоположной прямому углу (гипотенуза), можно найти по следующей формуле: a2 + b2 = c2 и c — длина гипотенузы. Ожидается, что ваш ребенок не только будет использовать удобную формулу Пифгаора, но и объяснит, почему она работает.

Наконец, ожидается, что ваш ребенок расширит свое владение объемом: найдет во внутреннем пространстве более сложные трехмерные формы, такие как конусы, сферы и цилиндры.Вот краткое описание этих формул.

С точки зрения статистики

Если ваш восьмиклассник жалуется, что сложная математика, которую она начинает изучать, не имеет отношения к ее повседневной жизни, вы можете поспорить с этим одним простым словом: статистикой.

Понимание статистики поможет вашему ребенку сделать важный жизненный выбор, например, какую машину покупать, какие продукты есть, на какую команду фэнтези-футбола делать большие ставки. В восьмом классе ученики только начинают сравнивать разные наборы данных и узнают, какие выводы они могут из них сделать.

В частности, восьмиклассники должны уметь анализировать данные с помощью диаграмм и графиков и уметь объяснять закономерности в данных. Например, детей могут попросить собрать данные о том, с кем ученикам разрешено встречаться, а какие от них ждут, а затем составить график этих результатов, чтобы увидеть, есть ли корреляция. Дети, которые ходят на свидания, более или менее склонны выполнять работу по дому?

Математика для восьмого класса очень важна для математики большого кахуна в старшей школе. Если вашему ребенку нужна помощь, лучше всего сосредоточиться на самом сложном.Даже несмотря на то, что вам предстоит многое покрыть, если вы сможете помочь своему ребенку справиться с самой большой трудностью, вы пройдете долгий путь, чтобы помочь ему быть готовым к обучению, когда он вернется в класс. И если у вас возникли проблемы с этим, помните, что лучший способ выучить что-то — часто учить этому, поэтому попросите своего ребенка дать вам урок математики в восьмом классе.

Поделиться в Pinterest

Обновлено: 2 декабря 2019 г.

8 класс | Математика | Iowa Core

В 8 классе учебное время должно быть сосредоточено на трех критических областях: (1) формулировка и рассуждение относительно выражений и уравнений, включая моделирование связи двумерных данных с линейным уравнением и решение линейных уравнений и систем линейных уравнений; (2) понимание концепции функции и использование функций для описания количественных отношений; (3) анализ двух- и трехмерного пространства и фигур с использованием расстояния, угла, сходства и конгруэнтности, а также понимание и применение теоремы Пифагора.

1. Студенты используют линейные уравнения и системы линейных уравнений для представления, анализа и решения различных задач. Учащиеся распознают уравнения пропорций ( y / x = m или y = m x ) как специальные линейные уравнения ( y = mx + b ), понимая, что константа пропорциональности ( м ) — это наклон, а графики — это линии, проходящие через начало координат. Они понимают, что наклон ( м, ) линии представляет собой постоянную скорость изменения, так что, если входная или x-координата изменяется на величину A, , выходная или y-координата изменяется на величину m · А .Студенты также используют линейное уравнение для описания связи между двумя величинами в двумерных данных (например, размах рук и росте для студентов в классе). На этом уровне подгонка модели и оценка ее соответствия данным выполняются неформально. Интерпретация модели в контексте данных требует, чтобы учащиеся выразили взаимосвязь между двумя рассматриваемыми величинами и интерпретировали компоненты взаимосвязи (такие как наклон и интервал y ) с точки зрения ситуации.

   Студенты стратегически выбирают и эффективно реализуют процедуры для решения линейных уравнений с одной переменной, понимая, что, когда они используют свойства равенства и концепцию логической эквивалентности, они сохраняют решения исходного уравнения. Студенты решают системы двух линейных уравнений с двумя переменными и связывают системы с парами линий на плоскости; они пересекаются, параллельны или составляют одну и ту же линию. Учащиеся используют линейные уравнения, системы линейных уравнений, линейные функции и свое понимание наклона линии для анализа ситуаций и решения проблем.
   

2. Студенты понимают понятие функции как правило, которое назначает каждому входу ровно один выход. Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводить между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях.
   
3. Учащиеся используют идеи о расстоянии и углах, о том, как они себя ведут при перемещениях, поворотах, отражениях и растяжениях, а также идеи о конгруэнтности и подобии, чтобы описывать и анализировать двумерные фигуры и решать задачи.Учащиеся показывают, что сумма углов в треугольнике — это угол, образованный прямой линией, и что различные конфигурации линий приводят к образованию похожих треугольников из-за углов, возникающих, когда поперечная линия разрезает параллельные линии. Студенты понимают формулировку теоремы Пифагора и ее обратное и могут объяснить, почему теорема Пифагора верна, например, разложив квадрат двумя разными способами. Они применяют теорему Пифагора, чтобы находить расстояния между точками на координатной плоскости, определять длины и анализировать многоугольники.Студенты завершают свою работу над объемом, решая задачи, связанные с конусами, цилиндрами и сферами.

Wolfram | Alpha Примеры: Common Core Math: Grade 8: Expressions & Equations

---

Выражения

Работа с эквивалентными выражениями.

Используйте законы экспоненты для упрощения выражений (CCSS.Math.Content.8.EE.A.1):

Другие примеры

---

Уравнения

Представляйте и решайте задачи с помощью уравнений.

Решите уравнение (CCSS.Content.Math.8.EE.C.7):

Решите уравнение с показателями степени (CCSS.Content.Math.8.EE.A.2):

Найдите уравнение прямой между двумя точками (CCSS.Content.Math.8.EE.B.6):

Решите систему уравнений (CCSS.Content.Math.8.EE.C.8):

Другие примеры

---

Научная нотация

Используйте экспоненциальное представление для представления больших и малых чисел.

Преобразование между стандартной и научной нотацией (CCSS.Content.Math.8.EE.A.3):

Сравните числа, выраженные в экспоненциальном представлении (CCSS.Content.Math.8.EE.A.3):

Выполняйте вычисления в экспоненциальной нотации (CCSS.Content.Math.8.EE.A.4):

Другие примеры

Курс математики для 8-х классов | Центр преподавания и обучения Нью-Джерси

Этот курс находится в процессе обновления и почти завершен.

Все блоки были обновлены, как и годовой план. Полугодовые и полугодовые оценки — это оставшиеся файлы, которые обновляются.

Числа и операции 8 класс

Натуральные числа и целые числа
Сложение, вычитание и целые числа
Умножение и деление целых чисел
Операции с рациональными числами
Преобразование повторяющихся десятичных знаков в дроби

Научная запись

Введение в экспоненты
Свойства экспонентов
Назначение экспоненциальной записи
Запись цифр в экспоненциальной записи
Преобразование: Sci.Обозначение и стандартная форма
Величина
Сравнение номеров в научной записи
Операции с номерами в научной записи

Решение уравнений

Rev: Двухшаговые уравнения
Многоступенчатые уравнения
Решение уравнения, содержащего дроби
Eq с одинаковой переменной на обеих сторонах
Compare Expr.с той же переменной
Написание и решение алгебраического уравнения
Перевод и решение Consec. Int. Проблемы
Решение буквального уравнения.

Вещественные числа

Преобразование повторяющихся десятичных дробей в дроби
Квадратные корни
Кубические корни
Квадратные и кубические корни
Рациональные, иррациональные и действительные #s
Аппроксимация иррациональных квадратных корней

Теорема Пифагора, расстояние и середина

Доказательства
Теорема Пифагора
Формула расстояния
Средние точки

Построение графиков линейных уравнений

Линейные уравнения
Построение графика линейного уравнения с использованием точек пересечения
Горизонтальные и вертикальные линии
Наклон прямой
Наклон и аналогичные треугольники
Форма точечного уклона
Форма наклона-пересечения
Пропорциональные отношения
Решение линейных уравнений

Системы линейных уравнений-8 класс

Решение систем путем построения графиков
Решение систем путем подстановки
Решение систем путем исключения
Выбор стратегии
Написание систем для моделирования ситуаций

2D геометрия

Преобразования
Переводы
Вращения
Отражения
Расширения
Симметрия
Конгруэнтность и сходство
Специальные пары углов
Удаленные внешние углы

Функции

Взаимосвязи и функции
Область и диапазон
Тест вертикальной линии
Линейная зависимость отНелинейный

Моделирование отношений

Интерпретация с помощью функций
Анализ графика
Сравнение различных представлений функций

Данные

Данные с двумя переменными
Линия наилучшего соответствия
Определение уравнения прогнозирования
Двусторонняя таблица

3D геометрия

Трехмерные твердые тела
Объем: призмы и цилиндры
Объем: пирамиды, конусы и сферы

.