Вариант 1 1.Дайте определение параллелограмма. 2.Какая трапеция называется прямоугольной? Равнобедренной? 3.Найдите периметр ромба АВСD, если 0, ВD=8 см. | Вариант 2 1.Какой четырехугольник называется трапецией? 2.Сформулируйте свойства параллелограмма. 3.Докажите, что диагонали прямоугольника равны. |
Вариант 3 1.Дайте определение ромба. 2. Сформулируйте свойства квадрата. 3.Периметр параллелограмма равен 88 см. Найдите стороны параллелограмма, если известно, что одна из них в три раза больше другой. | Вариант 4 1.Какой четырехугольник называется прямоугольником? 2. Сформулируйте свойства ромба. 3.Какая из следующих букв имеет центр симметрии: А, О, М, Х, К? |
Вариант 5 1.Какой многоугольник называется выпуклым? 2. 3.Меньшая сторона параллелограмма равна 4 см. Биссектрисы углов, прилежащих к большей стороне пересекаются в точке, лежащей на противоположной стороне. Найдите периметр параллелограмма. | Вариант 6 1.Дайте определение квадрата. 2. Сформулируйте свойства параллелограмма. 3. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона – 10 см, а один из углов равен 600. |
Вариант 7 1. Дайте определение ромба. 2.Чему равна сумма углов выпуклого четырехугольника? 3.Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 1200. | Вариант 8 1.Приведите примеры фигур, обладающих осевой, центральной симметрией. 2. Является ли параллелограмм выпуклым четыреугольником? 3.Найдите сумму углов выпуклого двенадцатиугольника. |
Вариант 9 1.Начертите четыреугольник и покажите его диагонали, противоположные стороны и противоположные вершины. 2.Докажите, что диагонали ромба взаимноперпендикулярны и делят его углы пополам. 3. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, F? | Вариант 10 1. Какой четырехугольник называется прямоугольником? 2.Какая фигура называется симметричной относительно прямой? 3.Каждый угол выпуклого многоугольника равен 1500. Найдите сумму углов выпуклого многоугольника, число сторон которого в два раза меньше, чем число сторон данного многоугольника. |
Вариант 11 1.Дайте определение ромба. 2.Какая фигура называется симметричной относительно прямой? 3.Периметр параллелограмма АВСD равен 46 см, АВ=14 см. Какую сторону параллелограмма пересекает биссектриса угла? Найдите отрезки, которые образуются при этом пересечении. | Вариант 12 1. 2. Сформулируйте свойства параллелограмма. 3.Найдите сумму углов выпуклого тринадцатиугольника. |
Карточки-задания по геометрии на тему «Параллелограмм и трапеция», 8 класс
Решение задач по теме «Параллелограмм и трапеция»
1. Высота параллелограмма составляет со стороной угол 32°. Найдите углы параллелограмма.
2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из
углов равен 120°.
3. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3,
считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр
равен 88 см.
4. Стороны параллелограмма равны 10см и 3 см. Биссектрисы двух углов, прилегающих к большей стороне,
делят противоположную сторону на три отрезка. Найдите эти отрезки.
5. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая
сторона – 10 см, а один из углов равен 60°. 6. Диагональ АС равнобедренной трапеции АВСD делит пополам угол ВАD. Найти периметр трапеции, если
основание АD равно 12 см, а угол АDС равен 60°.
7. Один угол параллелограмма больше другого на 70°. Найдите больший угол.
8. Периметр параллелограмма равен 46 см. Одна сторона параллелограмма на 3см больше другой.
Найдите меньшую сторону параллелограмм
Решение задач по теме «Параллелограмм и трапеция»
1. Высота параллелограмма составляет со стороной угол 32°. Найдите углы параллелограмма.
2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов
равен 120°.
3. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3,
считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен
88 см.
4. Стороны параллелограмма равны 10см и 3 см. Биссектрисы двух углов, прилегающих к большей стороне,
делят противоположную сторону на три отрезка. Найдите эти отрезки.
5. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая
сторона – 10 см, а один из углов равен 60°.
6. Диагональ АС равнобедренной трапеции АВСD делит пополам угол ВАD. Найти периметр трапеции, если
основание АD равно 12 см, а угол АDС равен 60°.
7. Один угол параллелограмма больше другого на 70°. Найдите больший угол.
8. Периметр параллелограмма равен 46 см. Одна сторона параллелограмма на 3см больше другой.
Найдите меньшую сторону параллелограмм
Решение задач по теме «Параллелограмм и трапеция»
1. Высота параллелограмма составляет со стороной угол 32°. Найдите углы параллелограмма.
2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов
равен 120°.
3. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3,
считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен
88 см.
4. Стороны параллелограмма равны 10см и 3 см. Биссектрисы двух углов, прилегающих к большей стороне,
делят противоположную сторону на три отрезка. Найдите эти отрезки.
5. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая
сторона – 10 см, а один из углов равен 60°.

Карточки-задания для самостоятельной работы геометрии на тему «Параллелограмм», 8 класс
Самостоятельная работа по теме «Параллелограмм» Г 8
1 вариант 2 вариант
42° 54°
1. Найти все углы параллелограмма, если один из них больше другого на
2. Найти периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на
4 см и 9 см 5 см и 11 см
отрезки
Самостоятельная работа по теме «Параллелограмм» Г 8
1 вариант 2 вариант
42° 54°
1.
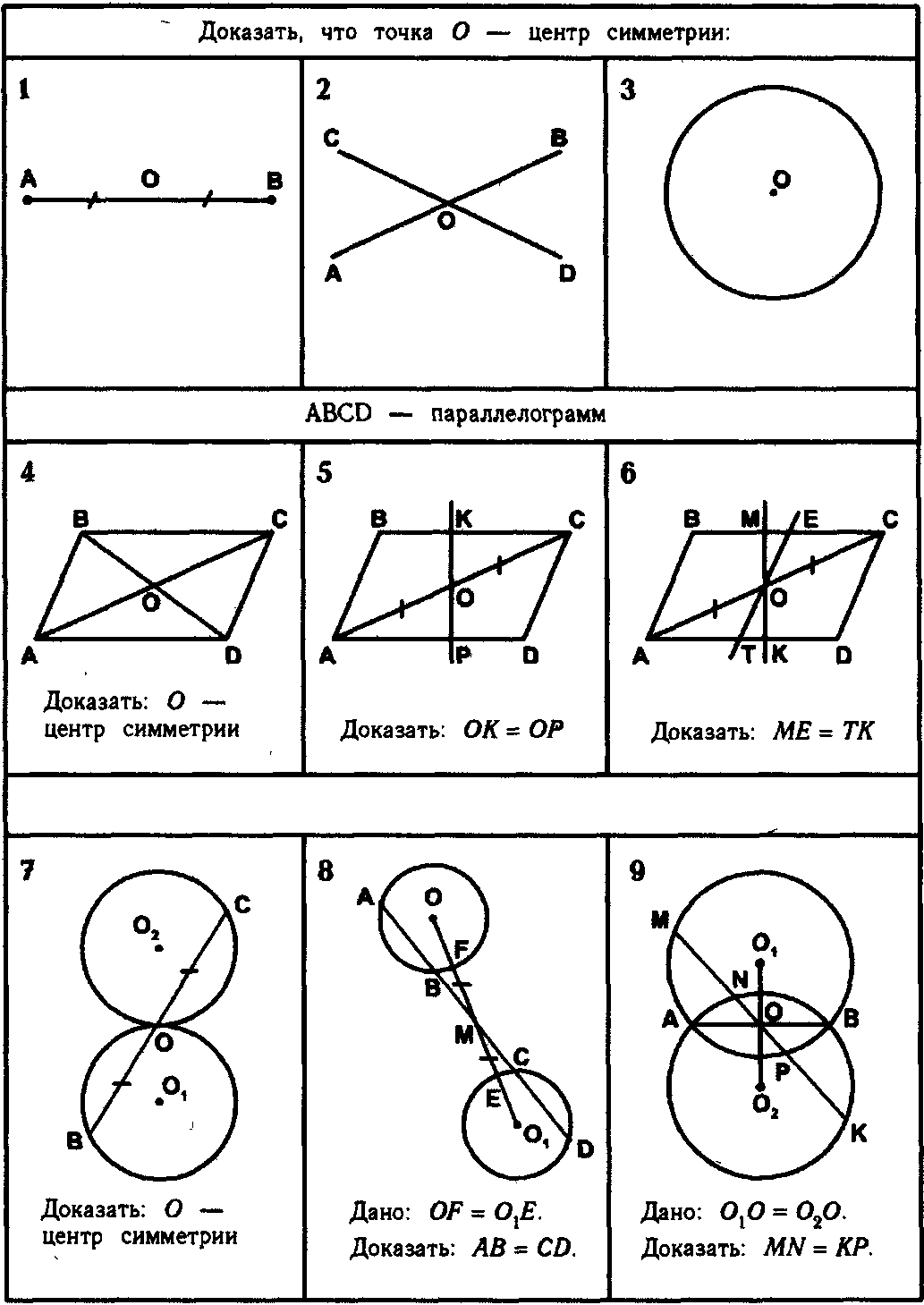
Окружность.
 Геометрия, 8 класс: уроки, тесты, задания.
Вход
Вход
Регистрация
Начало
Новости
ТОПы
Учебные заведения
Предметы
Проверочные работы
Обновления
Переменка
Поиск по сайту
Отправить отзыв
Геометрия, 8 класс: уроки, тесты, задания.
Вход
Вход
Регистрация
Начало
Новости
ТОПы
Учебные заведения
Предметы
Проверочные работы
Обновления
Переменка
Поиск по сайту
Отправить отзыв
-
Касательная и окружность
-
Центральные и вписанные углы.
 Свойство пересекающихся хорд окружности
Свойство пересекающихся хорд окружности
-
Замечательные точки треугольника
-
Вписанная и описанная окружности
|
Этапы урока
|
Деятельность учителя |
Деятельность учащихся
|
Универсальные действия |
|
1 |
2 |
3 |
4 |
|
Самоопределение к деятельности |
— Здравствуйте, ребята! Аристотель говорил: «Ум заключается не только в знании, но и в умении приложить знание на деле».
Тему сегодняшнего урока вы сформулируете сами. Для этого устно выполните следующие задания (раздаются карточки). Назовите букву, стоящую в скобках, соответствующую истинному высказыванию (буквы записать на доске).
Из записанных слов составьте слово.
Что вы понимаете под словом «площадь»?
|
Подготовка класса к работе
Высказывают свои мнения
Площадь Учащиеся приводят различные примеры
|
Личностные: самоопределение; Регулятивные: целеполагание; Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
|
|
Актуализация знаний и фиксация затруднений в деятельности |
В своей практической деятельности человек часто имеет дело с площадями: чтобы найти урожайность, надо знать площадь поля; о площади, занимаемой каким-либо государством, вы узнаёте из курса географии; площадь опоры и площадь поперечного сечения проводника вы должны уметь находить, решая задачи по физике.
Как одним словом назвать фигуры изображённые на экране?
Площади каких фигур вы умеете вычислять?
Чему равна площадь прямоугольника, квадрата?
Умеем ли мы вычислять площадь параллелограмма, ромба, трапеции?
Сформулируйте тему нашего сегодняшнего урока.
Запишите в тетради тему нашего урока.
Сформулируйте цели урока.
Нам предстоит решить несколько проблем по ходу урока. Прежде, чем к этому приступить, давайте определимся с понятием «проблема»? Обратите внимание на слайд и выберите тот вариант трактовки понятия, который вам ближе или составьте своё определение. |
Высказывают свои мнения Многоугольники Прямоугольника, квадрата S = аb, S = а2 Нет Площадь многоугольника Формулируют цели урока. Проблема – сложный вопрос, требующий изучения, разрешения. |
Аргументированный выбор понятия. Личностные: Самоопределение ; поиск и выделение необходимой информации; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. |
|
Создание проблемной ситуации |
Как найти площадь данной фигуры, изображающей силуэт птицы?
|
Разрезать данную фигуру на известные геометрические фигуры, найти сумму их площадей |
Подбор способа решения проблемы.
|
|
Построение проекта выхода из затруднений |
Вы правы, эта фигура является «хитроумным узором из семи частей». С какой трудностью можно столкнуться при выполнении задания? Какую задачу поставим для преодоления этого препятствия? Наша первоначальная проблема пока не решена, наоборот, возникает следующая проблема: как вычислить площадь каждой части, если нам известна только формула площади квадрата и прямоугольника? Перед нами две фигуры, составленные из одних и тех же геометрических фигур. Части, на которые разрезана одна фигура, позволили получить другую фигуру. Какую?
Как называются такие фигуры? Что вам известно о площадях равносоставленных фигур? Как называются фигуры, имеющие равные площади? |
По формулам можно вычислить площади прямоугольника, квадрата. Необходимо попытаться собрать эти семь частей в многоугольник. Работа в парах с геометрической головоломкой «Танграм».
Равносоставленные. Площади равны. Равновеликие. |
Регулятивные: Целеполагание ; выделение и формулирование познавательной цели , анализ ; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. Правильность получения запрограммированного результата. |
|
Открытие новых знаний. |
Вспомните, в чём измеряется площадь? Что означает 1 см2? При выбранной единице измерение площадей площадь каждого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и её части укладываются в данном многоугольнике. Найдите площадь многоугольника АВСD, взяв за единицу измерения закрашенный квадрат. Вычислять площадь многоугольника таким способом не всегда удобно, поэтому и нужны формулы для вычисления площадей. Какие фигуры называются равными? (Фигуры называются равными, если при наложении они совмещаются) Если многоугольники F1 иF2 равны, то, что можно сказать об их площадях? (Площади равны) Ответ объясните. (Площади равны, т.к. в равных фигурах единица измерения укладывается одинаковое число раз) Сформулируйте первое свойство площадей. (Равные многоугольники имеют равные площади) Если многоугольник разбит на несколько частей, как можно найти его площадь? (Площадь равна сумме площадей его частей) Сформулируйте второе свойство площадей. (Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников) Чему равна площадь квадрата со стороной а? (Sкв = а2) Сформулируйте третье свойство. (Площадь квадрата равна квадрату его стороны) Итак, повторим ещё раз свойства площадей. |
мм2, см2, м2, га, а Площадь квадрата со стороной 1 см
20 кв. ед.
Фигуры называются равными, если при наложении они совмещаются
Равные многоугольники имеют равные площади
Площади равны, т.к. в равных фигурах единица измерения укладывается одинаковое число раз
Площадь равна сумме площадей его частей Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников Sкв = а2 Площадь квадрата равна квадрату его стороны |
Регулятивные: Планирование, контроль, коррекция, оценка, саморегуляция ; моделирование, самостоятельное создание алгоритмов деятельности, анализ, синтез, построение логической цепи рассуждения, доказательство; Коммуникативные: управление поведением партнёра.
|
|
Практическая значимость изученного материала |
1. Демонстрируется палетка. Что это? Прибор для вычисления площади фигур – палетка, прозрачная пластинка с нанесенной на неё сеткой линий, предназначенная для вычисления площадей на планах и картах. Где используется: для решения многих инженерных задач при строительстве новых домов, фабрик, водохранилищ и т.п. требуется знать площади отводимых под строительство земельных угодий. Эти площади могут быть рассчитаны по результатам измерений на местности или определены по карте. Для этого применяют способ разбивки участка на простые геометрические фигуры или используют прозрачную плёнку с нанесёнными квадратами – палетку.
С помощью палетки вам предстоит выполнить задание: найти площадь геометрических фигур.
2. |
Мозговой штурм. Учащиеся выдвигают гипотезы по предложенному объекту,
|
Регулятивные: Выбор способа решения задач. Познавательные: Прогнозирование, коррекция; анализ, аналогия, сравнение, выдвижение гипотез и их обоснование, самостоятельное создание способов решения проблем творческого и поискового характера.
|
|
Практическая значимость изученного материала |
3. На ваш взгляд, что общего у данных картинок? Почему они появились на одном слайде перед вами? Это картинки с практической направленностью изучаемого вопроса. Для чего надо знать площадь поверхности дороги? Площадь зеркала водохранилища нужно знать проектировщикам для того, чтобы определить, как станет испаряться из заполненного водохранилища вода. Для чего надо знать площадь поверхности стен в помещении? |
Нахождение площади дороги, стены, водохранилища. При расчете необходимого для её покрытия количества асфальта Чтобы рассчитать необходимое для покрытия количества краски, обоев или кафеля и т.д. |
Коммуникативные: Сотрудничество с учителем и сверстниками, постановка вопросов, умение с достаточной полнотой выражать свои мысли, владение монологической и диалогической формами речи. |
|
Практическая значимость изученного материала |
4. Перед вами на слайде расположена схема оригами – древнего японского искусства складывания из бумаги. Первая схема уже выполнена. Вам предлагается сделать остальные пять. Что в результате получилось? Оцените его площадь, сравните её с площадью первоначального квадрата? Площадь сделанного вашими руками квадрата в 3 раза меньше площади исходного. Это вы и докажите дома. А теперь положите ваше произведение искусства на ладонь квадратом вниз и попробуйте ответить на простой вопрос: что это? Это классический вариант ТАТО. Тато – традиционные японские бумажные плоские коробочки для хранения разных мелочей – булавок, пуговиц, ниток, а в последнее время и марок. Вот таким образом в Японии решили проблему хранения мелочей. Традиционные тато были шестиугольными или восьмиугольными. |
Практическая работа с цветной бумагой. |
Коммуникативные: Сотрудничество с учителем и сверстниками, постановка вопросов, умение с достаточной полнотой выражать свои мысли, владение монологической и диалогической формами речи. Правильность получения запрограммированного результата |
|
Самостоятельная работа с самопроверкой по эталону. |
1.Определи, сколько процентов каждой фигуры закрашено 2. Найдите площадь прямоугольника, если его периметр равен 144 см, а стороны относятся как 5:7. 3. Продолжите фразу так, чтобы утверждение стало неверным. «Площадь прямоугольника равна…» 4. а) если одну пару противоположных сторон прямоугольника увеличить в 2 раза, то площадь …; б) если каждую сторону прямоугольника увеличить в 2 раза, то площадь … 5. АВСD — прямоугольник. Площадь его равна S. Найти площадь треугольника АВМ. |
Выполняют самостоятельную работу с самопроверкой по эталону.
|
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что подлежит усвоению, осознание качества и уровня усвоения; Познавательные: Активная познавательная мыслительная деятельность. Выбор наиболее эффективных способов решения задач, самостоятельное создание алгоритмов деятельности, установление причинно – следственных связей; Коммуникативные: владение монологической и диалогической формами речи.
|
|
Рефлексия |
Итак, на сегодняшнем уроке мы рассмотрели понятие площади.
Прошу подумать и ответить на вопросы: — какое задание для вас оказалось самым лёгким…, трудным…, интересным? — напишите, где в жизни вы сможете применить полученные знания? |
Заполнение листа самооценки
Индивидуальная работа по заполнению листа рефлексии |
Фиксирование своих затруднений и достижений. Оценка; рефлексия, контроль и оценка деятельности . |
Урок по геометрии в 8 классе на тему: «Подготовка к контрольной работе по теме «Четырехугольники»»
Урок по геометрии в 8 классе на тему:
«Подготовка к контрольной работе по теме «Четырехугольники»»
Разработка учителя математики и информатики Егоровой Ольги Владимировны ФГБОУ СОШ №1699 УД Президента РФ
Учебник: «Геометрия 7-9 кл» Л.С. Атанасян, 2008 г
Класс: 8 Б
Предмет: геометрия
Тип урока: урок закрепления знаний
Оборудование: интерактивная доска, компьютер, проектор, программа для компьютера elite Panaboard book, карточки с заданиями, учебник по геометрии, красная и синяя ручка, карандаш, ластик.
Содержание и ход урока
Приветствие.
 Здравствуйте, садитесь.
Здравствуйте, садитесь.
Проверка домашнего задания. (решение на доске, учащиеся сверяются с решением в тетради, учитель проходит и проверяет наличие домашней работы)
Объявление темы урока, целей.
Взаимопроверка геометрических определений (10 мин)
(учащие пишут в тетради геометрические определения по вариантам)
Учащиеся обменяются выполненными заданиями, проверяют, глядя на доску, и ставят оценку соседу по парте:
3 правильно написанных определения – оценка «3»
4 правильно написанных определения – оценка «4»
5 правильно написанных определения – оценка «5»
Подготовка к контрольной работе
Учитель делит учащихся на 4 группы в зависимости от индивидуальных способностей по геометрии, выдает 4 карточки с одной задачей, за 10 минут учащиеся в группе должны решить задачу, решение должен понять каждый учащийся в группе. Затем начиная с 1 задачи, вызывается к интерактивной доске любой из учащихся той группы, в которой решалась эта задача, все остальные учащиеся записывают в тетради решение и т.д.
Учитель ставит оценку отвечающему ученику.
Домашнее задание
Учитель раздает карточки с домашним заданием
Домашняя работа. 8 класс
Подготовка к контрольной работе
Четырехугольники
1. В параллелограмме АВСD через точку О пересечения диагоналей проведена прямая, пересекающая стороны ВС и АD в точках К и Е соответственно, ВО=ОЕ. Найдите КВЕ.
2. В прямоугольной трапеции острый угол равен 60°. Большая боковая сторона и большее основание равны по 20 см. Найдите меньшее основание.
3. В ромбе МРКН с тупым углом К диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен 16°30′. Найдите остальные углы этого треугольника и угол РМН.
4. На катетах АС и ВС прямоугольного треугольника АВС построены квадраты АКМС и СРЕВ. Прямые КМ и РЕ пересекаются в точке Т. Докажите, что ТС АВ.
Подведение итогов урока
Самоанализ урока
Поставленные цели урока были успешно выполнены. Данный урок — традиционный урок с использованием интерактивной доски. На уроке были Использованы приемы индивидуализации обучения: разделение по группам в зависимости от индивидуальных способностей учащихся по геометрии, при решении задач в группах более сильные учащиеся помогали и объясняли слабым. Многократная рефлексия: проверочная работа по определениям, работа в группах, самопроверка и взаимопроверка. В результате урока из 12 учащихся были поставлены следующие оценки: 1) Проверочная работа: «5» — 5, «4» — 5, «3» — 2, 2) У доски: «5» — 1, «4» — 2, «3» — 1. Урок способствовал воспитанию самостоятельности, ответственности, внимания, сообразительности, рациональному использованию времени.
Список использованной литературы
1. «Геометрия 7-9 кл» Л.С. Атанасян, 2008 г
Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии 8 класс»
Картинки оформления к интерактивной доске взяты из электронных учебных пособий по информатики А.А.Дуванова «Азы информатики» и Л.Л. Босовой «УМК по информатике для 5-7 классов»
6
геометрия карточки огэ с ответами
Карточка 1
16095050801) Найти АВ
14986085090
2) Найти угол АСВ, если
угол АОВ = 84°
13906551435
3)
4) Найдите площадь равностороннего треугольника, отсекаемого
от данного треугольника его средней линией,
1998345-350520если площадь данного треугольника равна 48см2.
5) Периметр равностороннего треугольника АВС равен 24см. Найдите длину средней линии этого треугольника.
2086610-916305 Карточка 2
151130-31751) Найти угол АСВ, если угол
АОВ равен 160°
-796083495
2)
3) Найдите площадь данного равностороннего треугольника, если
площадь треугольника, отсекаемого от него
2082165-361315средней линией, равна 6 см2.
2082165109855
4) Средняя линия равностороннего треугольника АВС равна 8см. Найдите периметр этого треугольника
2086610236220
5) Из квадрата со стороной 10см вырезан прямоугольник со сторонами 3см и 4см. Найдите площадь оставшейся части. Карточка 3
152106-27471) Найти угол ВАС, если
угол ВОС = 160°
2) Найдите площадь прямоугольного
треугольника, если его гипотенуза равна 16см,
а один из углов треугольника равен 45°.
15113085725
3) Найти угол ВАС
152105109693
4) Найти длину меньшей средней
линии треугольника
5) В прямоугольнике одна сторона равна 28см, а диагональ равна 35см. Найдите площадь прямоугольника.
1270147955Карточка 4
1) Найти угол ВАС
20348177647
2) Найти угол АОВ, если
угол АСВ = 25°
14986069215
3) Найти площадь
четырёхугольника
20256596520
4) Найти длину большей
высоты
параллелограмма
12827053340
5) Найти косинус угла
2275205295910Карточка 5
1) В треугольнике АВС угол В равен 46°, угол С равен 71°, ВD – биссектриса. Найдите угол АDВ.
161925127635
2) Найти радиус
окружности, если
АВ = 12см, ОА = 13см.
172085145415
3) Найти длину отрезка НМ,
Если АМ=3см, АН=НС=2
2181225200025
4) Найти угол ВОС, если
угол ВАС = 70°
17989551003305) Найти площадь треугольника АВС, если высота, проведённая к одной из его сторон равна 11, а средняя линия, параллельная этой стороне, равна 10. Карточка 6
162560-6351) Найти угол АОВ, если
точки А и В делят
окружность на две дуги в отношении 9 : 11.
2) 162560-4445Найти площадь
параллелограмма
1427480102235
3) КВСD —
параллелограмм.
Найдите длину
отрезка АВ.
1703705622304) Найдите косинус
угла
2096770628655) Найдите площадь
четырёхугольника
Карточка 7
1319530131445
1) Найти угол 3,
если угол 1
равен 40°, а
угол 2 равен
55°.
2) Основания трапеции равны 48 и 24, высота 4. Найдите площадь трапеции.
1372870165103) На рисунке
изображён параллелограмм.
Найти: х.
4) Из квадрата со стороной 8см вырезан прямоугольник со сторонами 3см и 2см. Найдите площадь оставшейся части.
1978660-960755
5) Стороны прямоугольника равны 10 и 24. Найдите радиус окружности, описанной около этого прямоугольника.
Карточка 8
1) Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
18529302529205
1916430132715
2) Найдите угол α
2011680-361953) Прямоугольный треугольник вписан в окружность. Найдите радиус этой окружности.
4) Найдите тангенс угла А.
1720850173990
5) Из прямоугольника со сторонами 8см и 10см вырезан квадрат со стороной 5см. Найдите площадь оставшейся части.
Карточка 9
2139950132080
1) Найдите тангенс угла А.
2154555-317502) Найти длину медианы проведённой из вершины прямого угла.
3) Стороны параллелограмма равны 10 и 35. Высота, опущенная на первую сторону, равна 21. Найдите высоту, опущенную на вторую сторону.
183134026035
4) Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
219329012065
5) Найти площадь трапеции.
Карточка 10
160655-6351) Найти больший угол
параллелограмма АВСD107315-15373
2)
16065538735
3) Найти угол ОСD160655-12704)
ВС = 8, соsВ = 0,8
Найти АВ
5) АВСD — равнобедренная трапеция
Найти угол АВC160655-5715
Карточка 11
161925-6351) Найти меньший угол
параллелограмма АВСD151130122555
2) Найти угол ОСD127001905
3)
182880156845
4)
5) 1619250 Найти тангенс угла СКарточка 12
162737-591) АВСD —
равнобедренная трапеция
Найти угол АDC
28956012065
Найти угол ОDС
2)
28956065405
3) АС = 6, соsA = 0,6
Найти АВ
4) 162560-1270
5) 1625600 Найти площадь параллелограмма
Карточка 13
2063750121285
1) В трапеции АВСD АВ=СD ∟ВDА=18° и ∟ВDС=97°. Найдите угол АВD.
16095075078
2) Найдите тангенс угла АОВ
3) Найдите расстояние от точки А до середины отрезка СВ
4) Найдите угол АВС
1709420-1403985
1949450-28657555) Колесо имеет 8 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
Карточка 14
2086610120650
1) В трапеции АВСD АВ=СD ∟ВDА=40° и ∟ВDС=24°. Найдите угол АВD.
162162650
2) Найдите
расстояние от
точки А до
середины отрезка
СВ165100131445
Найдите котангенс угла АОВ
3)
4) Найдите угол АВС
2044065190500
1586230-1691005
5) Угол АОВ = 63°. Найдите угол АСВ.
Карточка 15
2214245203201) В трапеции АВСD АВ=СD ∟ВDА=24° и ∟ВDС=70°. Найдите угол АВD.
19380201770380
1769745170180
2) Найдите расстояние от точки А до середины отрезка СВ
3) Найдите котангенс угла
АОВ
4) Из квадрата
Вырезали прямоугольник.
Найдите площадь получившейся фигуры.
1765300-9855205) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,6 м и 3,6 м?
Карточка 16
1) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,6 м?
2) Сколько спиц в колесе, если угол между соседними спицами равен 40°?
3) Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
4) Найдите
тангенс угла АОВ
15106651917701510665-1053465
5) Найдите площадь фигуры
Карточка 17
1) Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
2) Сколько спиц в колесе, если угол между соседними спицами равен 9°?
3) Колесо имеет 40 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
1458595111760
4) Найдите
тангенс угла АОВ
5) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 3,1 м, высота большей опоры 3,3 м. Найдите высоту малой опоры.
Карточка 18
1) Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
2) Сколько спиц в колесе, если угол между соседними спицами равен 15°?
3) Колесо имеет 6 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
1433195298454) Найдите котангенс угла АОВ
5) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,5 м, высота средней опоры 2,65 м. Найдите высоту большей опоры.
Карточка 19
1) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,95 м, высота большей опоры 3,65 м. Найдите высоту средней опоры.
2) Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,7 м и 3 м?
3) Человек ростом 1,8 м стоит на расстоянии 10 м от столба, на котором висит фонарь на высоте 7,8 м. Найдите длину тени человека в метрах.
4) Найдите площадь трапеции
1734185135255
5) Прямые m и n параллельны. Найдите ∟3, если
∟1 = 117°, ∟2 = 24°.
Карточка 20
1) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,25 м, высота большей опоры 2,85 м. Найдите высоту средней опоры.
2) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,2 м?
3) Человек ростом 1,6 м стоит на расстоянии 15 м от столба, на котором висит фонарь на высоте 9,6 м. Найдите длину тени человека в метрах.
4) Найдите площадь трапеции
5) Прямые m и n параллельны. Найдите ∟3,
1801495-323850если ∟1 = 74°, ∟2 = 39°.
Карточка 21
1) Лестница соединяет точки А и В. Высота каждой ступени равна 18 см, а длина –
80 см. Расстояние между точками А и В
составляет 41 м. Найдите высоту, на которую поднимается лестница (в метрах).
2) Человек ростом 1,5 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 10,5 м. Найдите длину тени человека в метрах.
3) Найдите площадь трапеции
162737-3602
4)
2129155213995
5) Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27.
Найдите диаметр окружности.
Карточка 22
1992630-44451) Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит
-52070264160сторону на два отрезка. Каковы длины этих отрезков?
2)
3) Найдите тангенс угла АВС
-68580532130
4)
5) На отрезке
AB выбрана точка C так, что AC=6 и
2025650527051542415-2588895BC=4. Построена окружность с центром A , проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.Карточка 23
12700266701)
1809750410210
2) MN и АВ – диаметры окружности. ∟NВА=73°.
Найти угол NMB
127003644903) ∟DMC=24°. Найдите угол СМА.
4)Найти площадь трапеции.
-5143531750
5) Найти площадь параллелограмма
1628775-349250 Карточка 24
1) Прямая касается окружности в точке K . Точка O – центр окружности. Хорда КМ
образует с касательной угол, равный 7°.
Найдите величину угла ОМК
19272254267202076450-880745
2) Найти площадь трапеции
162560108585
3)
224028095250
4) Найти радиус окружности
1958975590555) В треугольнике ABC угол C прямой,
BC=4, sinA=0,8. Найдите AB.
Ответы:
Номер варианта
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
8 80 80 24 94 162 85 17 3 125 65 70 47 76 62 391 3150 1680 3,3 2,55 9 15 11 83
42 17 64 50 5 28 144 40 2,5 2,4 25 55 2 1,5 3,5 9 40 24 360 357 1 3,5 17 6
1,6 24 29 45 3 4,5 5,4 6,5 6 70 9 10 4,5 0,5 0,4 1500 9 60 3 3 22,12 3,5 132 3
12 48 1,5 5 140 -0,8 58 1 1 10 9 15 45 112,5 52 1,5 2 0,5 936 936 13 5 9 4
4 88 588 -0,6 110 40 13 55 324 120 0,75 96 45 31,5 234 30,5 2,9 2,8 39 67 90 6 20 5
Используемая литература:
1) Геометрия. Учебник для 7 класса общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев. Научный редактор – академик А.Н. Тихонова. — 22-е изд. – М.: Просвещение, 2013.
2). Сборник для подготовки ОГЭ. И.В. Ященко, С.А.Шестаков, А.В. Семенов.
3) Сайт: http://www fipi..ru4) Сайт:http://alexlarin.net/ для подготовки ОГЭ
5) Сайт: открытый банк заданий для подготовки ОГЭ по математике.
6–8 классы: Игры по геометрии | Scholastic
Банка Пи
Стандартное соответствие: CCSS.Math.Content.7.G.B.4
Что вам понадобится: Крышки для банок, кнопки, шнурок, сантиметровые линейки, карандаши, калькуляторы (необязательно)
Что делать: Пи — это отношение длины окружности к ее диаметру. Вы можете рассказать об этом студентам или помочь им узнать об этом.
Чтобы начать свое открытие, за неделю до Дня Пи (14 марта) попросите учащихся собрать чистые крышки из банок и бутылок.Работая попарно, они выбирают три крышки из коллекции и обводят их на листе бумаги, чтобы создать круги разного размера. Затем дайте каждой паре веревку длиной не менее 12 дюймов. Попросите одного из партнеров использовать линейку, чтобы найти центр первого круга, удерживайте веревку в центре с помощью кнопки, а затем измерьте диаметр и запишите эту длину. Второй партнер оборачивает веревку по окружности соответствующей крышки и записывает эту длину. Попросите учащихся записать эти два числа для каждого из трех век.
Наконец, спросите учащихся, могут ли они найти связь или определить соотношение между числами. При наличии достаточного количества общих данных и обсуждений дети откроют для себя Пи!
Кто я?
Стандартное соответствие: CCSS.Math.Content.7.G.A.1
Что вам понадобится: Бумага, карандаши
Что делать: Гольф — не единственная игра, в которой побеждает низкий результат. Эта простая игра с геометрией основана на старом режиме «20 вопросов» и является отличным способом попрактиковаться в словарном запасе геометрии.Сначала разбейте учащихся по парам и присвойте каждой паре фигуру (например, острый треугольник) или термин (например, параллельные линии). Партнеры проводят мозговой штурм и записывают список подсказок, описывающих цифру или термин. Чем больше улик, тем лучше. Затем по очереди пригласите группы к классу и попросите их раскрыть одну подсказку. Например, если фигура группы представляет собой прямоугольник, первым может быть «Я четырехугольник» или «У меня есть два набора параллельных линий». Класс делает предположение и продолжает гадать, пока не придет к правильному ответу или не будут использованы все подсказки.За каждую предоставленную подсказку и соответствующее предположение класс получает одно очко. Цель игры — правильно угадать, используя наименьшее количество подсказок и набрав наименьшее количество очков.
Спина к спине
Стандартное соответствие: CCSS.Math.Content.7.G.A.2
Что вам понадобится: Миллиметровка, карандаши
Что делать: Пусть партнеры сядут спиной к спине на стульях с партами перед ними. Шепчите имя фигуры или другой геометрический термин одному партнеру, который будет лидером в этом раунде.Дайте другому партнеру лист миллиметровой бумаги и карандаш. Ведущий партнер описывает фигуру или термин, пока их партнер пытается их нарисовать.
Лидер может использовать столько геометрических терминов, атрибутов и слов направления, сколько необходимо, но никогда не может произносить имя или какую-либо часть имени фигуры или термина. Когда их партнер считает, что они завершили рисунок точно в соответствии со словесными указаниями, лидер проверяет. Если рисунок точный, они меняются ролями. Если это не так, пусть они попробуют еще раз.Рисунки должны быть похожими, но не обязательно совпадать (еще одна возможность поговорить об этих геометрических терминах!).
Концентрация на площади
Стандартное соответствие: CCSS.Math.Content.6.G.A.1
Что вам понадобится: миллиметровая бумага сантиметров, учетные карточки, сантиметровая линейка, карандаши
Что делать: Используя линейку, партнеры рисуют выбранный ими многоугольник на миллиметровой бумаге, вычисляют его площадь, а затем вырезают форму и наклеивают ее на учетную карточку.Фигура не обязательно должна быть правильным многоугольником: она может иметь любой дизайн, если партнеры могут точно рассчитать ее площадь. Попросите учащихся написать на соответствующей учётной карточке площадь нарисованной ими фигуры. Попросите их заполнить не менее восьми таких карт (соответствующих четырем фигурам), чтобы составить набор. Когда все карты готовы, партнерские дуэты объединяются, чтобы сначала перемешать карты, а затем разложить все 16 своих карт на столе или столе лицом вниз.
Партнеры по очереди переворачивают две карты и пытаются найти совпадение по фигуре и площади.Они могут не торопиться, чтобы вычислить площадь получаемых полигонов, при необходимости используя линейку. Если это совпадение, игроки оставляют карты и продолжают переворачивать пары. В противном случае они возвращают карты на их исходные места, и два других игрока делают ход. Побеждает дуэт, набравший наибольшее количество матчей. В качестве дополнительной задачи назначьте определенные области (например, 20 квадратных сантиметров), которые студенты будут использовать при создании своих многоугольников.
Полигональный линкор
Что делать: CCSS.Math.Content.6.G.A.3
Что вам понадобится: Миллиметровка, линейки, карандаши
Что делать: Неизменный фаворит настольных игр — Морской бой. Почему бы не создать свой собственный? Для начала попросите каждого ученика нарисовать координатную плоскость на миллиметровой бумаге и пронумеровать оси от 1 до 12. Попросите учеников нарисовать многоугольник в плоскостях, поставить точку в каждой вершине, а затем записать координаты каждой из вершин. вершины.
Станьте партнером учащихся, и пусть они смотрят друг на друга через стол или стол с разделителем (например, скоросшивателем) между ними.Дайте им новый лист миллиметровой бумаги. Выберите одного из партнеров в качестве лидера и попросите ее начать с того, чтобы сообщить партнеру координаты первой вершины на ее рисунке. Партнер должен отметить эту точку на миллиметровой бумаге. Студенты будут меняться ролями, пока не будут переданы все координаты. Затем, используя линейку, они соединяют вершины на своих листах и завершают многоугольник. Сравните рисунки с оригиналами на точность. Наконец, посмотрите, могут ли учащиеся назвать созданные ими многоугольники в соответствии с количеством сторон.(Застряли? Посетите математический форум Университета Дрекселя, чтобы найти имя для вашего многоугольника — независимо от того, сколько у него сторон. Например, студенты узнают, что нарисованный ими 13-сторонний многоугольник — это трехугольник!)
Нажмите здесь, чтобы подписаться на журнал Scholastic Teacher Magazine
Фото: Philippe Lissac / Godong / Corbis
Критерии зачисления по математике 8-9 классы
Цель этой страницы — познакомить вас с инструментами, используемыми при распределении по математике с восьмого по девятый класс, и предоставить вам диапазоны, которые мы используем в качестве руководства.Распределение по математике — это не то, что происходит в конце года. Скорее, это непрерывный процесс с определенными этапами в течение года. Математический факультет также считает важным включить общее описание каждого курса CCHS.
ОПИСАНИЕ УРОВНЯ CCHS
В CCHS есть четыре уровня математики, разработанные для соответствия различным стилям обучения учащихся. В значительной степени учебная программа и порядок преподавания тем согласованы на каждом из четырех уровней конкретной предметной области.Основные различия между уровнями заключаются в способе представления нового контента, темпах прохождения курса и количестве повторений ранее изученных тем. Ниже приведены более подробные описания каждого уровня.
Honors Geometry: Этот уровень разработан для учащихся, продемонстрировавших высочайший уровень владения нестандартными, абстрактными и сложными математическими понятиями. У студентов есть хорошо развитые, независимые и продуктивные навыки работы. Студенты последовательно демонстрируют владение ранее изученными темами и сохраняют знания без повторного обучения.Студенты изучают новые темы в ускоренном темпе с минимальным повторением и могут легко применять и синтезировать концепции для решения новых задач (в том числе в ситуациях тестирования).
Enriched Geometry: Это расширенный уровень, разработанный для учащихся, продемонстрировавших высокий уровень владения абстрактными и сложными математическими концепциями. Учащиеся выработали привычки продуктивной работы, могут продемонстрировать владение ранее изученными темами и продолжить обучение с ограниченным повторным обучением и повторением.Студенты изучают новые темы в быстром темпе с некоторым повторением. На практике студенты могут применять и синтезировать концепции для решения некоторых новых задач (в том числе в тестовых ситуациях).
Интегрированная математика A: Этот уровень включает в себя последовательность из трех курсов, каждый из которых включает стандарты алгебры, геометрии, статистики и тригонометрии. Теория, лежащая в основе этого подхода, заключается в том, что в реальном мире проблемы не требуют особого подхода. Используя «интегрированный» подход, студенты могут решить, какие навыки использовать для решения конкретной проблемы, независимо от области содержания.Студенты овладевают некоторыми ранее изученными темами и продолжают обучение с повторным обучением и повторением. Студенты узнают, как использовать комбинацию навыков из алгебры, геометрии, статистики и тригонометрии в зависимости от их анализа и подхода к решению проблем. Этот уровень преподается в умеренном темпе с достаточным количеством повторений.
Integrated Math B: Этот уровень включает в себя последовательность из трех курсов, каждый из которых включает стандарты алгебры, геометрии, статистики и тригонометрии.Интегрированный подход, используемый на этом уровне, позволит учащимся решать проблемы, используя различные стратегии. Студенты будут использовать ранее изученный материал и развивать новые навыки в темпе, который дает значительное время для концептуального понимания. Студенты узнают, как использовать комбинацию навыков из алгебры, геометрии, статистики и тригонометрии в зависимости от их анализа и подхода к решению проблем.
Примечание: стрелки указывают типичный путь в математической последовательности, а не препятствует другому перемещению между уровнями.
Процесс зачисления в высшую школу по математике
Для студентов, изучающих независимую и управляемую алгебру 8-го класса, следующие критерии будут использоваться для зачисления в классы математики CCHS.
Отличие геометрии 95 +
Расширенная геометрия 80-94
Интегрированная математика A 60 — 79
Интегрированная математика B — 59
Для тех студентов, изучающих алгебру, которые в настоящее время изучают направленную математику в 8 классе, следующие критерии будут использоваться для зачисления в классы математики CCHS
Интегрированная математика A 80 +
Интегрированная математика B 0 — 79
Перечисленные оценки включают средние оценки за единицу (не средние значения по домашнему заданию / успеваемости).В июне CMS предоставит CCHS текущие оценки учащихся, которые CCHS сверит с диапазонами оценок за февраль на предмет возможных изменений уровня учащихся.
Платоновых тел как пример Вальдорфского образования для всего человека — Вальдорфская школа Орчард-Вэлли
От классного руководителя Линдси Бентон, отрывок из записки для родителей класса:
В дополнение к изучению того, как найти площадь поверхности и объем разнообразных трехмерных форм, 8 класс изучал особую категорию трехмерных форм, называемую Платоновыми телами.У этих фигур есть грани, состоящие из одного и того же правильного многоугольника. Например, если вы возьмете восемь равносторонних треугольников (треугольников со сторонами одинаковой длины) и расположите их рядом друг с другом так, чтобы их края соприкасались, вы можете создать замкнутую форму, называемую октаэдром.
Платоновых тел всего пять. Три из них состоят из равносторонних треугольников, один — из квадратов, а последний — полностью из пятиугольников.
Итак, задача заключалась в создании точных трехмерных моделей Платоновых Тел.Студентам приходилось полагаться на свои навыки транспортира в предыдущие годы, чтобы рисовать точные углы. Им также приходилось набрасывать идеи на макулатуре, и, несмотря на множество попыток и неудач, им приходилось заставлять себя продолжать работу, пока они не обнаружили паттерны, которые действительно можно было сложить в полностью замкнутые трехмерные формы.
Было много тревог и разочарований. Было много скатывающейся макулатуры и желания сдаться. Было много просьб показать, как делать выкройки, чтобы они могли их копировать.
Но, в конце концов, успех был вызван глубоким волнением и удовлетворением! Почти все студенты позвали меня, когда наткнулись на схему, которая работала. В их лицах было такое торжество! Они сделали чистые, окончательные версии форм с золотыми карточками.
Это был опыт, который требовал множества головоломок, принятия ошибок и использования того, что было извлечено из ошибок, для улучшения.
Здесь, в учебной программе, содержится вдохновляющий пример того, что значит обучать человека в целом.Конечно, в нашем блоке геометрии мы вычисляем числа и изучаем формулы. Академическая часть есть и очень живая. Тем не менее, это намного больше! Навыки алгебры, которые они изучали на уроках математики, используются для создания эффективных и действительно работающих формул. Это воодушевляет! Кроме того, учащиеся получают реальный тактильный опыт создания чего-либо своими руками и собственным трудом, делая эти геометрические темы чем-то большим, чем просто понятия, которые живут в голове, но опыт, к которому можно прикоснуться руками.При этом они чувствуют себя воодушевленными и вдохновленными.
Common Core: карточки по математике для 8-х классов
Хотите просмотреть Common Core: 8-й класс по математике, но в данный момент не хотите сесть за весь тест? Varsity Tutors предлагает вам тысячи разные Common Core: карточки по математике для 8-х классов! Наше общее ядро: карточки по математике для 8-х классов позволяют вам практиковаться, задавая как можно меньше, так и как можно больше вопросов. как ты любишь. Начните учиться прямо сейчас с нашими многочисленными дидактическими карточками Common Core: 8th Grade Math.
Образовательные стандартыCommon Core требуют, чтобы к концу восьмого класса ребенок обладал знаниями о рациональных и иррациональных числах, целочисленных показателях, геометрической конгруэнтности, использовании функций при моделировании отношений и закономерностях ассоциации в статистике и вероятности. Некоторым родителям этих тем достаточно, чтобы отправить одного бегом. Впрочем, бояться нечего. Существует множество учебных пособий, которые помогут их сыну или дочери понять домашнее задание по математике.
Varsity Tutors ’Learning Tools предлагают разнообразную помощь в учебе, в том числе полный набор бесплатных онлайн-карточек, в которых особое внимание уделяется математическим понятиям, которые требуются в соответствии со стандартами Common Core. Существуют сотни индивидуальных дидактических карточек, которые вы и ваш ребенок можете использовать для повторения понятий, которые ваш ребенок изучает на уроках математики.
Учебные карточки Common Core по математике для 8-х классов предлагают несколько способов изучить доступный контент. Вы можете попросить вашего сына или дочь начать с конкретных тем, таких как функции, задачи со словами или статистика и вероятность; вы также можете попросить вашего сына или дочь начать с выбора, в котором представлены различные темы в случайном порядке.Независимо от того, как вы подойдете к этому обзору, ваш ребенок увидит один математический вопрос или задачу, которую нужно решить на одной карточке, и будет иметь до пяти ответов на выбор.
Обратная связь с этим инструментом обучения мгновенная. Ваш ребенок увидит правильный ответ и сравнение выбранного им ответа с правильным. Более того, ваш ребенок с самого начала увидит объяснение того, как перейти от математического вопроса к точному ответу в виде пошагового объяснения.
Учебные пособия Карточки уникальны, потому что у вашего ребенка есть доступ к карточкам в любое время, когда у него или нее есть подключение к Интернету, и, по крайней мере, несколько минут для ознакомления с некоторыми концепциями, содержащимися в наборах задач Common Core по математике для 8-х классов. Если вы или ваш ребенок заинтересованы в получении общего обзора каких-либо концепций, которые они могут изучить на уроке математики в восьмом классе, или если есть необходимость сосредоточить внимание на конкретных концепциях для дополнительного обзора, эти онлайн-карточки позволяют пользователям выбирать и выберите вопросы, на которые они хотят ответить.Если ваш ребенок отвечает на вопрос, а затем решает вернуться к той же карточке, система позволяет ему сделать именно это; Кроме того, если ваш ребенок пропускает вопрос, который ему не нравится или который он уже усвоил, штраф не применяется.
Регистрация учетной записи с помощью инструментов обучения Varsity Tutors ‘Learning Tools предоставляет в ваше распоряжение еще более персонализированные инструменты. Вы можете отслеживать конкретные концепции, которые ваш ребенок хорошо знает, или те, которые ему необходимо изучить в дальнейшем, потому что учетная запись отслеживает эту информацию для участников.Если есть концепции, которые вы хотите просмотреть, но не видите карточек, вы можете использовать конструктор карточек, чтобы создать свой собственный инструмент для изучения. Вы также можете создать свои собственные практические тесты или получить доступ к другим инструментам обучения, таким как полные практические тесты, имитирующие то, как может выглядеть фактический экзамен, обучение по концепции (интерактивная программа), короткие практические тесты, охватывающие определенные темы, или даже Серия вопросов дня, в которой каждый день задается один вопрос в задаче.
Настольные игры с 6 геометрическими фигурами для детей младшего и среднего школьного возраста
Как здорово было бы упростить геометрию с помощью некоторых настольных игр с геометрией? Геометрия, как правило, является проблемой для многих учеников начальной и средней школы.Я проверил это для вас.
Сколько доступно настольных игр с геометрией? Сравниваются шесть полезных настольных игр с геометрией для детей от 6 до 14 лет. Их лучше всего использовать в небольших группах или дома. Я очень рекомендую Kitki Three Sticks и Swish, а также, конечно же, Geoboard.
Таблица сравнения настольных игр Geometry
Эти игры помогают изучать концепции геометрии и развивать навыки пространственного мышления, делая обучение увлекательным! Приведенная ниже таблица поможет вам выбрать игру, которая лучше всего подходит для ваших учеников или детей.
| Игра | Возраст | Игроков | Цена | Для | Тема * | Рейтинг |
|---|---|---|---|---|---|---|
| Geoboard | $ 258 9022 9022 9022 9022★★★★ ☆ | |||||
| Ice Cool | 6+ | 2-4 | $ 18 | Home | Уголки | ★★★ ☆☆ |
| Swish | +$ 13 | Home | Spatialization | ★★★★★ | ||
| Kitki Three Stick | 8+ | 2‑4 | $ 35★ | Home, School | Составные формы ★★★★★ ★★ | |
| Shepherd | 13+ | 2‑6 | $ 41 | Школа | Функции | ★★★ ☆ |
| Координаты перекрестного смещения | 10‑22 4 | $ 38 | Школа | Точки построения | ★★★ ☆☆ |
* Более подробное описание тем:
2D Фигуры : Распознавание 2D форм
Углы : определение типов углов
Распространение : Навыки пространственной визуализации
Составные формы : Определение сложных форм, вычисление их площадей
Функции : Построение функций на графике, Определение общих функций, таких как y = x
Точки построения : Нанесение точек на график
Геометрия Настольные игры для детского сада
Географическая доска с карточками геометрической формы (любопытные умы)
★★★★ ☆
Игроков: 2+ | Возраст: 3-8 | Класс CCSS: K1 — класс 2
Geoboards помогает обучать основам геометрических форм так, что это оценят тактильные и визуальные ученики.Эти забавные геодоски позволяют детям детского сада знакомиться с узорами и формами, которые им следует усвоить. Объедините учеников в пары и попросите их соревноваться, чтобы определить, кто сможет воссоздать двумерные фигуры, изображенные на карточках, за наименьшее количество времени.
Одно из основных преимуществ этой игры с геометрическими фигурами — это то, что детских садов позволяет как визуализировать, так и воспроизводить двухмерные формы , такие как круги, квадраты и прямоугольники. Воспитатели могут использовать игру с детскими садами, которые разучивают основные формы.Однако игру также можно использовать с учениками начальной школы, которые изучают такие формы, как восьмиугольник или десятиугольник.
Однако на этом приложение не заканчивается. Учителя могут использовать географические доски и карточки с геометрическими фигурами, чтобы познакомить учеников седьмого класса с концепцией сложных форм. Эта стратегия вдохновляет на творческое мышление, поскольку ученикам предлагается придумать лучшие сложные формы, которые они могут придумать для выбранных пар карточек с образцами.
Представленная здесь геодоска — одна из многих доступных.Вы также можете легко найти учебники для гео-карт, которые предложат несколько рисунков с использованием цветных резинок. Дополнительным преимуществом геобордов является их мелкая моторика, особенно когда вы пытаетесь быстро создавать формы.
Настольные игры с геометрией для начальной / начальной школы
Ice Cool (Brain Games)
★★★ ☆☆
Игроки: 2-4 | Возраст: 6+ | Класс CCSS: от 4 до 6
Настольная игра Ice Cool — это не только то, что кажется на первый взгляд.На первый взгляд, это похоже на настольную игру, в первую очередь направленную на развитие у детей навыков ловкости. Однако родители могут посчитать полезным научить детей практическому использованию углов.
Цель игры состоит в том, чтобы каждый игрок стратегически щелкнул фишкой таким образом, чтобы оппоненты были опрокинуты. Каждый щелчок представляет собой угол. Родители могут посоветовать детям оценить размер угла, под которым можно щелкнуть предметом. Они также могут посоветовать своим детям назвать тип угла.Кроме того, родители могут показать детям старшего школьного возраста связь между углами и движением снаряда по физике.
Однако дети младшего возраста в возрасте от 6 до 10 лет с большей вероятностью сочтут эту игру более привлекательной. Дети старшего возраста старше 10 лет быстрее заскучают. Более того, самая близкая связь с математикой — это определение типов углов; в игре нет настоящего умственного вызова, который помогает развить навыки критического мышления.
Swish (ThinkFun)
★★★★★
Игроков: 2+ | Возраст: 8+ | Класс CCSS: от 6 до 8
Я настоятельно рекомендую Swish , который представляет собой игру с пространственным мышлением и по распознаванию образов с несколькими вариациями, которые могут бросить вызов детям с разным интеллектуальным уровнем.Шестнадцать карточек Swish расположены в сетке 4 x 4. Затем игроки должны сложить ряд карт так, чтобы все сплошные цвета на одной карте совпадали с отверстиями того же цвета на другой карте. Побеждает игрок с наибольшим количеством стеков в конце игры.
В эту игру могут играть дети младшего и старшего школьного возраста. Однако более старшие дети могут быть более заинтригованы задействованными навыками пространственной визуализации. Пространственная визуализация возникает, когда дети должны перевернуть и переставить карты в уме, чтобы создать трехмерную стопку символов.Способность игры развить этот важнейший навык пространственного мышления важна, поскольку детям эти навыки понадобятся для сложных тем, таких как теорема круга.
Китки Три Палки (Kitki)
★★★★★
Игроки: 2-4 | Возраст: 8+ | Класс CCSS: от 7 до 8
Kitki Three Sticks — это более продвинутая версия игры Geoboard with Geometric Pattern Cards с правилами, которые помогают детям создавать и реализовывать свои собственные выигрышные стратегии. Он отлично подходит для демонстрации того, как базовые формы объединяются, чтобы создавать составные формы из-за размера платы и легкости, с которой части могут быть соединены вместе.Например, на протяжении всей игры учащиеся могут понять, что треугольник и прямоугольник можно объединить в трапецию.
Эта игра хорошо подходит для обучения учащихся седьмого и восьмого классов концепции составных фигур. Учителя могут даже добавить более высокий уровень сложности, попросив учащихся вычислить площадь каждой формы, которую они создают. Таким образом, игра может удовлетворить потребности в обучении широкого круга учащихся.
Дополнительно учащиеся развивают навыки критического мышления.Те, кто может создать самые большие составные формы (и определить все формы, которые объединяются, чтобы образовать эти составные фигуры), набирают наибольшее количество очков. Поэтому они должны спросить себя:
- Как я могу соединить эти палочки, чтобы создать осмысленную форму?
- Сколько фигур меньшего размера заключено в созданной мною большей форме?
Эти навыки критического мышления становятся очень полезными по мере того, как учащиеся продвигаются к высшему образованию по геометрии в средней школе и за ее пределами.
Небольшая проблема заключается в том, что кусочки палки начинают падать с доски после использования игры в течение некоторого времени, потому что они свободно входят в отверстия на доске.
Координаты Кросстауна (учебные ресурсы)
★★★ ☆☆
Игроки: 2-4 | Возраст: 10-11 | Класс CCSS: 8
Учебные ресурсыCrosstown Coordinates — это двусторонняя настольная игра , которая учит студентов, как находить координаты на декартовой плоскости. Одна сторона платы имеет только положительную часть осей x и y. Переверните доску, и вы получите полную декартову плоскость.
Студенты часто путают координату x с координатой y.Поэтому они неправильно рисуют точки. Эта игра помогает им четко визуализировать, где должна быть размещена каждая точка , и снижает вероятность того, что они нанесут точки неправильно.
Самая лучшая особенность этой игры — то, что учащиеся могут проверять свои собственные ответы. Если положение их пешек не совпадает с изображением на обратной стороне карты, они неверны. Это увеличивает гибкость учителя в том, что он может ходить по классу, чтобы проверить прогресс каждой группы, вместо того, чтобы его звать со всех сторон для проверки ответов.
Однако игра наскучит примерно через десять минут из-за своей простоты. Поэтому лучше всего использовать его в течение первых десяти или последних десяти минут урока о нанесении точек на график. Учителя не должны планировать, чтобы игра занимала весь класс.
Настольные игры с геометрией для средней школы и старше
Пастух (Coool Toool)
★★★ ☆☆
Игроков: 2-6 | Возраст: 13+ | Класс CCSS: 10
Shepherd помогает учащимся научиться строить линейную функцию s.Чтобы понять, как играть в игру, нужно время, чтобы она больше подходила для более продвинутых учеников. В этой игре студенты будут практиковать:
- Выявление графиков некоторых наиболее общих линейных функций с
- Построение точек на декартовой плоскости
Shepherd имеет два недостатка. Это дорого для учителей, которые хотели бы купить несколько наборов, а правила сложны. поэтому я рекомендую использовать его в математическом клубе, а не в классе со студентами со смешанными способностями.
Другие игры
Существует несколько печатных настольных игр с геометрией, но много настольных игр с печатным рисунком, которые добавляют веселья к более высоким концепциям геометрии. Я планирую сделать для вас сообщение в блоге об этих печатных изданиях. Скажите в комментариях, если вам интересно получить этот новый пост.
Одна из них — настольная игра «Теорема Пифагора», предложенная блогом High School Math Adventures. Теорема Пифагора — это простая для понимания концепция геометрии. Однако некоторые студенты путают стороны прямоугольного треугольника и, следовательно, путают формулу.Это помогает решить эту проблему. Учителя могут использовать эту замечательную игру для повторения после того, как концепция будет изучена.
Франсуа Гели
Я создаю обучающие игры с 2001 года и превратил это увлечение в свою профессиональную деятельность, когда создал ARITMA в 2006 году. Aritma — издатель образовательных карточных игр, который в настоящее время предлагает 18 различных игр и ежегодно увеличивает свою коллекцию. Мне всегда интересно узнать о новых обучающих играх, где бы они ни были и в какой форме.
Недавние сообщения
ссылка на 6 стран мира карточных игр — полное сравнение ссылка на Как игры на память помогают детям?Как игры на запоминание помогают детям?
Моя дочь постоянно обыгрывала меня в играх на запоминание, и ей это очень нравилось, когда она была моложе, но каковы были преимущества этих игр для нее, помимо азарта от победы…
занятий по геометрии, которые нравятся студентам! | Снимки высшего образования
tw Когда дело доходит до математики, кажется, что геометрия находится в совершенно другой лиге. Некоторые дети влюбляются в это мгновенно, в то время как другим детям это кажется сложным. Одна из замечательных особенностей геометрии заключается в том, что мы можем предложить своим ученикам множество практических занятий, что делает их очень увлекательными!Вот некоторые из моих любимых занятий по геометрии:
1.Начните с фигур
Мне нравится, когда ученики начинают с фигур, которые они знают с тех пор, как они были крошечными, например, треугольников, квадратов и кругов. Мы рисуем их на классных досках целым классом. Затем мы рисуем более сложные формы, такие как пятиугольники, шестиугольники, восьмиугольники, трапеции и даже ромб! Это подводит нас к обсуждению многоугольников, и таким образом мы можем классифицировать формы.
Помимо белых досок, есть много способов для детей работать с формами, например, палочки для мороженого (которые также отлично подходят для иллюстрации параллельных, пересекающихся и перпендикулярных линий), LEGOS, геодоски и даже прищепки, которые можно скрепить вместе.
2. Геометрия зефира
Мне нравится это занятие, потому что каждый раз, когда вы добавляете еду, дети уже готовы! Используя зефир и зубочистки, дети могут создавать простые двухмерные фигуры, а также трехмерные фигуры. Кроме того, это упражнение — идеальное место для выделения вершин, поскольку каждый раз, когда вы добавляете зефир, вы кладете его в угол. Если у вас пищевая аллергия или школьные правила запрещают еду, вы можете заменить зефир пластилином.
3.Используйте анкерную диаграмму
После того, как учащиеся провели много времени на изучение форм, пришло время обсудить их атрибуты. Мне нравится делать эту диаграмму привязки с помощью детей. Объясняю, как это будет организовано, от наименьшего количества сторон до наибольшего. Мы также замечаем паттерны сторон и вершин по мере их создания. Я прошу детей привести примеры форм, и иногда они проявляют в этом настоящий творческий подход!
4. Отправляйтесь на поиски мусора формы
Это занятие, которое отлично подойдет для некоторых помощников родителей, если они у вас есть.Я люблю присылать камеры iPad с каждой группой, планшеты, карандаши и протокол. Дети записывают форму, которая была найдена, тип объекта и место его обнаружения. Действительно весело наблюдать, какие формы они могут найти, прогуливаясь по школьному кампусу!
5. Добавьте немного искусства
Я большой сторонник искусства, поэтому добавляю искусство везде, где оно подходит. Геометрия — прекрасное время для создания геометрических животных, роботов или людей. Я обычно выбираю одну из этих категорий, но на самом деле вы тоже можете сделать это широко открытым проектом!
Я поделился другим забавным занятием с геометрическим искусством в своем блоге под названием «Включение искусства в класс».Это от компании «Любит грамотность». В продолжение уроков по геометрии линий и углов я вырезал многоугольники из белого картона для каждого ребенка. У меня есть дети, которые используют линейки и фломастеры и следуют моим пошаговым указаниям, рисую линии, а затем находят тупые углы, прямые углы, перпендикулярные линии и так далее. По окончании урока дети добавляют к ним цвет, превращая его в действительно забавное произведение искусства.
6. Добавьте немного кинестетического обучения
Детям нужно движение, и с помощью этого модуля легко добавить немного движения.В этом упражнении учащиеся будут на полу, работая с партнером, чтобы строить различные виды линий (параллельные, пересекающиеся и перпендикулярные), формы и углы (прямые, острые и тупые), используя свое тело. В качестве альтернативы можно попросить детей встать и использовать руки, чтобы проиллюстрировать эти геометрические концепции.
Еще одно кинестетическое занятие — это сбор китайских скакалок или пакетов с резинками. Если вы используете резинку, одной упаковки хватит на небольшую группу из 5-6 детей. Идея состоит в том, чтобы учащиеся использовали резинку как группу для создания фигур, которые вы называете (особенно хороши типы треугольников) или типов углов.Если две группы работают вместе, можно создать разные виды линий.
7. Добавьте несколько карточек задач и игр
Карточки задач — один из моих любимых инструментов! Детям нравится игровой формат, и я знаю, что они действительно сосредоточены на изучении любой математической концепции, над которой мы работаем. Я использовал их в качестве центров / станций, на протяжении всего урока по математике, для индивидуальных занятий и в качестве выходных листов.
Если вам нужны готовые карточки с математическими задачами специально для геометрии, щелкните здесь;
Набор для геометрии 3-го класса
Набор для геометрии 4-го класса
Набор для геометрии 5-го класса
8.Прочтите текст наставника
Мне нравится, когда я могу связать чтение с математикой! Приведенные выше книги — одни из моих любимых текстов для наставников по геометрии. Мне нравятся все включенные наглядные примеры.
9. Используйте музыку
Я только что нашел эти песни от Numberock на YouTube, и они идеально подходят для этого устройства! Действительно отличные картинки и запоминающиеся мелодии:
параллельных, перпендикулярных и пересекающихся линий
углов
типов треугольников
10. Практика углов
Серьезно, после деления в столбик, измерение углов, вероятно, является самым сложным математическим навыком, с которым студенты столкнутся в начальной школе. годы! Не помогает и то, что он вводится в четвертом классе в общем ядре, а затем даже не упоминается в стандартах пятого класса.Ну что ж!
Одно из полезных занятий — попросить детей использовать миллиметровую бумагу и написать свое имя заглавными печатными буквами. Учащиеся могут измерить любые углы, образованные пересечением линий буквы.
Еще одно любимое занятие для отработки углов — это взять ленту и провести различные линии, которые создают углы на столе, столе или даже на листах мясной бумаги. Дети используют транспортиры для измерения углов, а затем пишут экспозицией (или маркерами на мясной бумаге) прямо на партах / столах! Отличный способ добавить немного веселья к этой сложной концепции!
Надеюсь, вы нашли хотя бы несколько идей, которые можно использовать для своего геометрического блока! Я хотел сообщить вам, что у меня есть комплекты карточек с заданиями по математике для каждого класса с 3-го по 5-й.В каждом наборе 30 наборов из 32 карточек задач, охватывающих ВСЕ СТАНДАРТЫ (CCSS) для этих классов. Я люблю готовить их в начале года, а затем беру любую концепцию, над которой мы работаем, для дополнительной практики.
Если вы хотите взглянуть на:
Комплект карточек заданий по математике для 3-го класса
Комплект карточек заданий по математике для 4-го класса
Комплект карточек заданий по математике для 5-го класса
Спасибо, что заглянули! Если вам понравился этот пост, я был бы рад, если бы вы прикрепили его или поделились с другом-учителем!
Чтобы узнать больше об идеях и стратегиях, касающихся старших классов начальной школы, не забудьте подписаться на бесплатную рассылку новостей The Teacher Next Door по электронной почте прямо ЗДЕСЬ.
Я хотел бы с вами связаться!
Math
Исследования показывают, что качество преподавания и руководство школой являются двумя наиболее важными факторами в повышении успеваемости учащихся. Чтобы учителя и руководители школьных округов были максимально эффективными, непрерывное профессиональное обучение, направленное на углубление и расширение знаний по содержанию и совершенствование учебных навыков, является обязательным условием внедрения передовых образовательных практик.Приверженность педагогов непрерывному профессиональному обучению огромна, когда речь идет об успеваемости учащихся. Суперинтенданты, школьные администраторы, директора, руководители учителей и учителя разделяют ответственность за стратегии профессионального развития и достижения, которые, как доказано, повышают уровень успеваемости педагогов. LearningForward.org — это международная ассоциация лидеров образования, приверженных школьному образованию.
стандарты профессионального обучения для педагогов и автора
Почему важно профессиональное развитие.
Возможности профессионального обучения переходной математике
Чтобы помочь во внедрении переходной математики, Совет по образованию штата Иллинойс (ISBE) создает следующие возможности для профессионального обучения.
Обновленная библиотека информационных вебинаров будет доступна в январе 2020 года. Вебинары будут длиться примерно 10–20 минут и будут посвящены конкретным темам переходной математики, таким как обзор, пути, советы, ресурсы и переносимость.Вебинары будут доступны на веб-сайте штата по переходной математике, расположенном по адресу http://www.iltransitionalmath.org/.В дополнение к серии вебинаров, ISBE предложит серию переходных модулей профессионального обучения математике в режиме онлайн для инструкторов, администраторов и консультантов. Часы профессионального развития доступны по запросу после завершения.
ISBE также доступен для личного профессионального обучения по запросу с округами, учителями и руководителями учебных программ, партнерами по общественным колледжам, региональными управлениями образования и другими группами, такими как системы образования для трудоустройства (EFE), заинтересованных в изучении переходного обучения математике. и реализация.

 Сформулируйте свойства прямоугольника.
Сформулируйте свойства прямоугольника.
 Какой четырехугольник называется прямоугольником?
Какой четырехугольник называется прямоугольником?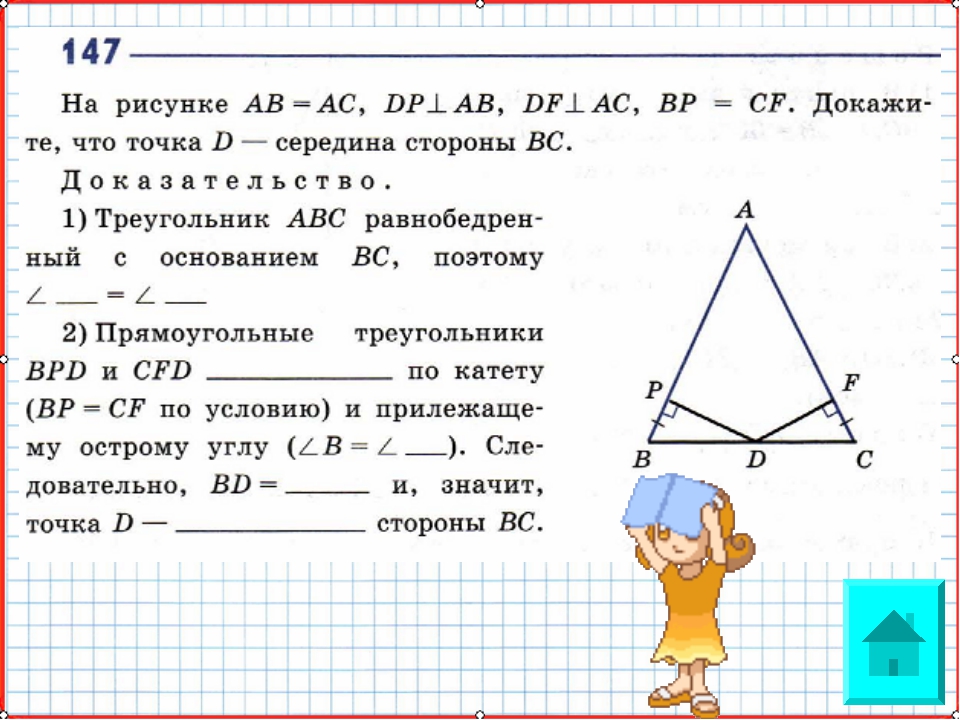 Свойство пересекающихся хорд окружности
Свойство пересекающихся хорд окружности
 Прокомментируйте – как вы понимаете это высказывание.
Прокомментируйте – как вы понимаете это высказывание.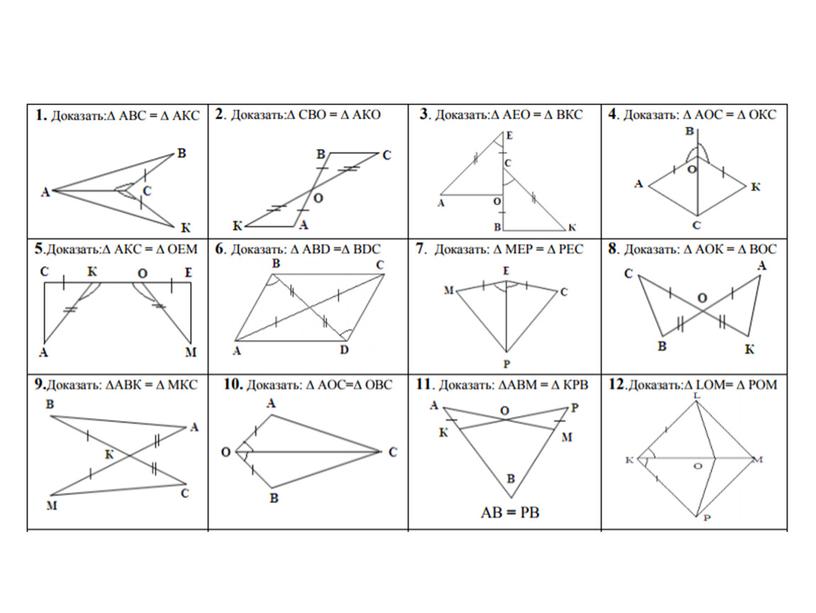
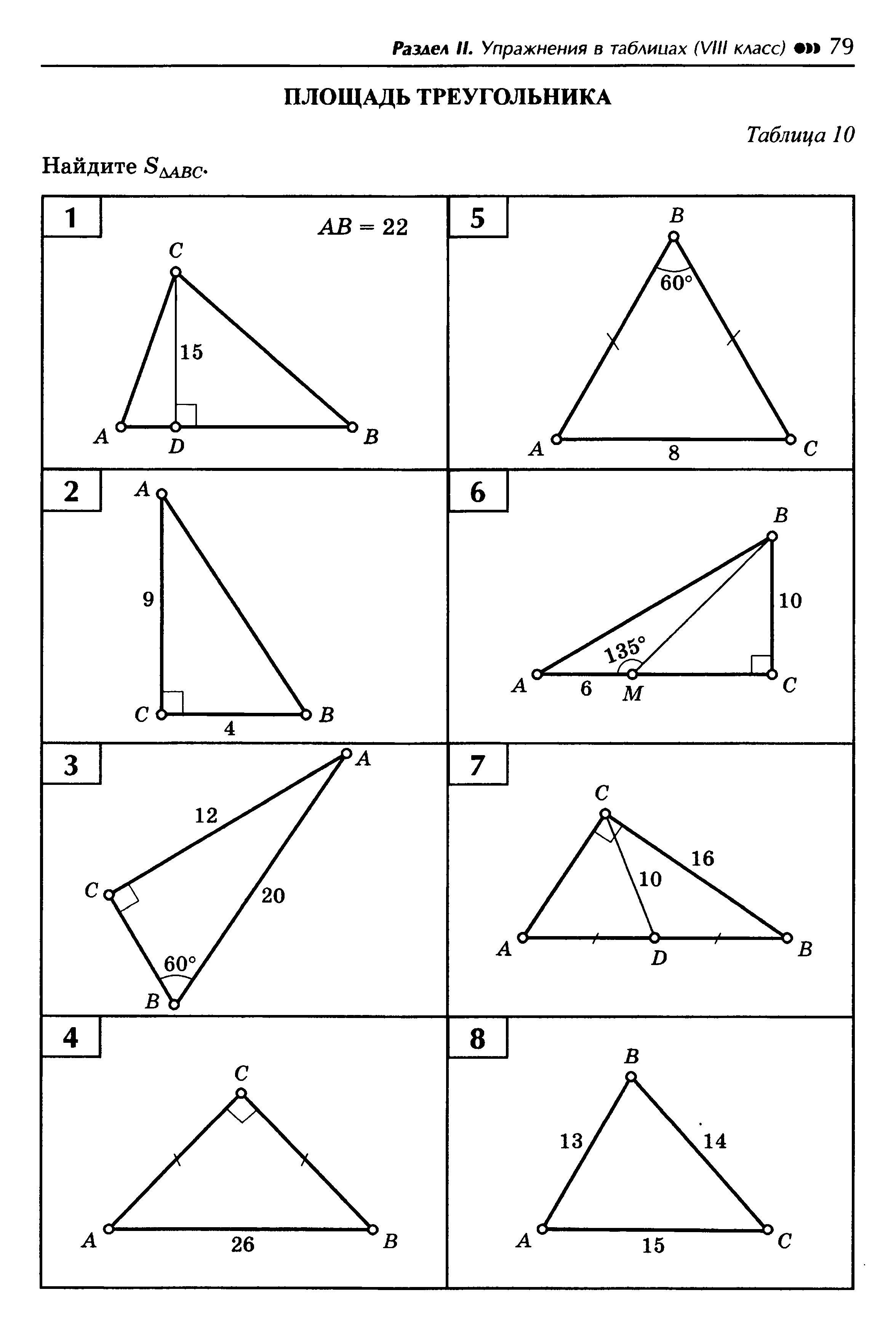
 Площади, каких частей вы можете найти?
Площади, каких частей вы можете найти?
 Вывод этих формул основан на свойствах площадей. Итак, рассмотрим свойства площадей.
Вывод этих формул основан на свойствах площадей. Итак, рассмотрим свойства площадей.

 Сто лет назад немецкий математик Георг Пик обнаружил замечательную формулу для вычисления площади многоугольника с вершинами в узлах клетчатой бумаги. Что же это за формула и как она помогает решить проблему вычисления площади, вы узнаете, изучив информацию на стенде или обратившись к одной из поисковых систем сети Интернет, после чего на следующих уроках мы рассмотрим её применение к определенному виду задач
Сто лет назад немецкий математик Георг Пик обнаружил замечательную формулу для вычисления площади многоугольника с вершинами в узлах клетчатой бумаги. Что же это за формула и как она помогает решить проблему вычисления площади, вы узнаете, изучив информацию на стенде или обратившись к одной из поисковых систем сети Интернет, после чего на следующих уроках мы рассмотрим её применение к определенному виду задач

 Современные мастера часто делают их в форме квадрата, иногда называют конвертами. А как они собираются, открываются, вы узнаете, посетив сайт Страна Мастеров. http://stranamasterov.ru/node/
Современные мастера часто делают их в форме квадрата, иногда называют конвертами. А как они собираются, открываются, вы узнаете, посетив сайт Страна Мастеров. http://stranamasterov.ru/node/ Как продолжить утверждение, чтобы оно стало верным:
Как продолжить утверждение, чтобы оно стало верным: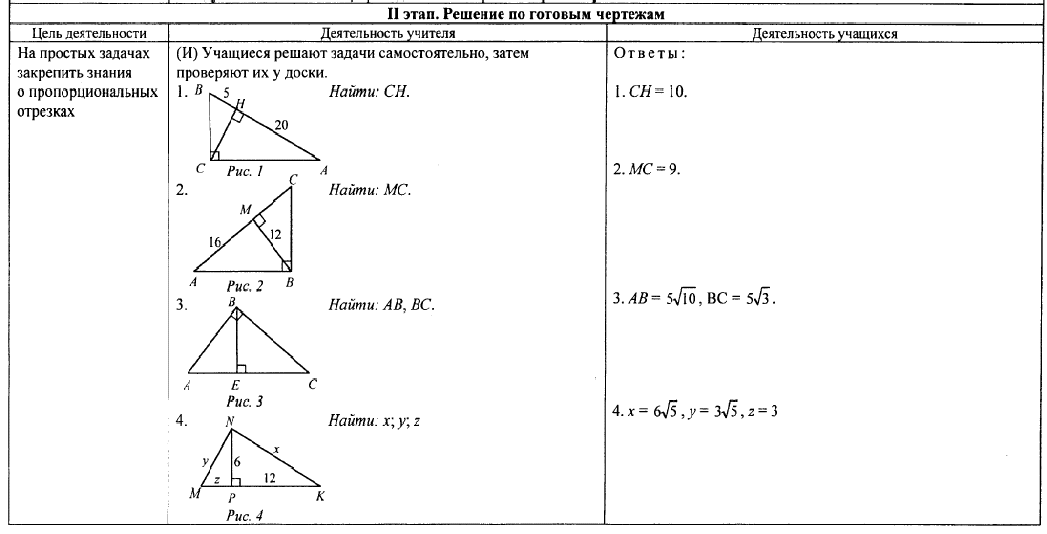

 Здравствуйте, садитесь.
Здравствуйте, садитесь.