Контрольные работы по геометрии 8 класс анастасян: ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян

Содержание

ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян

Геометрия – это один из главных элементов общеобразовательного обучения. Появившись в седьмом классе, эта дисциплина предполагает к повторению все то, что было изучено на уроках математики ранее, но одновременно знакомит школьников с новыми понятиями: многоугольники и их свойства, окружности и векторы, параллелограммы и трапеции. Также ребята учатся находить площади и высоты многих геометрических фигур, узнают о признаках подобия треугольников и правилах работы с теоремами и аксиомами. Чтобы хорошо подготовиться к срезам знаний по итогу каждой темы, можно воспользоваться гдз по геометрии самостоятельные и контрольные работы за 8 класс Иченская, в которых школьники найдут полностью готовые задания. На страницах пособия уже разобраны сложные геометрические задачи, сопровождающиеся не только точными рисунками с соблюдением всех правил, но и пояснения, полноценные алгоритмы решения и т.

д.

Основные группы пользователей сборника готовых ответов

Восьмой класс – это сложный период в жизни любого ученика, потому что помимо огромного количества правил, теорем, аксиом и формул, дети должны регулярно закреплять свои знания и подтверждать их уровень. Для самопроверки хорошо подойдет справочник с онлайн ответами к самостоятельным и контрольным работам по геометрии для 8 класса авторов Иченской, Атанасян, который будет незаменим:

восьмиклассникам, когда нужно дополнительно позаниматься, решая сложные геометрические задачи на поиск площадей, построение высот и углов, с целью обнаружить пробелы в своих знаниях;
при подготовке к предстоящим олимпиадам и конкурсам, где ребята должны знать все, начиная от формул периметра и площади фигур и заканчивая умножением и делением вектора на число и действий между векторами;

если время на проверку работ у учителя ограничено, а нужно полноценно и адекватно оценить каждого ученика, чтобы поставить соответствующие оценки и приступить к изучению нового материала;
для родителей, которые хотят организовать для своего ребенка домашнюю проверку знаний и не знают, какие задания подобрать для этого. Готовые ответы к ним помогут также легко разобраться и с уровнем знаний по данному предмету;
выпускникам 9 и 11 классов в качестве дополнительной литературы, которая поможет не только восполнить знания, изучая готовые алгоритмы решения заданий, но и стать более уверенным в себе на экзаменах.

Неоспоримые плюсы обращения к онлайн справочникам

Благодаря современным технологиям и возможности пользоваться портативными гаджетами, получить доступ к решебнику по геометрии для самостоятельных и контрольных работ по геометрии за 8 класс (авторы Иченская, Атанасян) сегодня может любой школьник. Это является одним из главных преимуществ готовых ответов. Более того, онлайн справочник это:

содержание точных, максимально развернутых и изложенных доступным языком решений, которые помогают в учебе;
удобная навигация, требующая только выбрать вид работы и подходящий вариант, чтобы получить готовые ответы;

адаптивная версия мобильной версии, а значит, доступность в любом месте;
возможность получения оперативного ответа с пояснением, раскрывающим суть задания и служащим примером для дальнейшего самостоятельного решения аналогичных задач.

Подготовка к проверочным работам и выполнение домашних заданий с еуроки ГДЗ будет проходить намного легче и быстрее, как для школьников, так и для их родителей.

Геометрия 8 Контрольные Атанасян (Зив)

Контрольные работы + Ответы

Геометрия 8 Контрольные Атанасян (Зив) — это цитаты контрольных работ из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной, а также ответы на контрольные работы.

Цитаты из пособия указаны в учебных и информационных целях. При постоянном использовании контрольных работ по геометрии в 8 классе рекомендуем купить книгу: Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение, в которой кроме контрольных работ есть еще 39 самостоятельных работ, математические диктанты и задачи повышенной трудности.

Для увеличения изображения — нажмите на картинку !
Чтобы скачать работу — нажмите на правую кнопку мыши и выберите «Сохранить изображение как …»

Контрольная работа № 1.

Четырехугольники

ОТВЕТЫ на Контрольную работу № 1

Контрольная работа № 2.

Площадь

ОТВЕТЫ на Контрольную работу № 2

Контрольная работа № 3.

Подобные треугольники

ОТВЕТЫ на Контрольную работу № 3

Контрольная работа № 4.

Применение подобия, решение прямоугольных треугольников

ОТВЕТЫ на Контрольную работу № 4

Контрольная работа № 5.

Окружность

ОТВЕТЫ на Контрольную работу № 5

Контрольная работа № 6.

Векторы

ОТВЕТЫ на Контрольную работу № 6

Контрольная работа № 7.

Итоговая работа за 8 класс

ОТВЕТЫ на Контрольную работу № 7

Вы смотрели страницу «Геометрия 8 Контрольные Атанасян (Зив)» — Контрольные работы из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной, а также ответы на контрольные работы.

Страница не найдена

Новости

17 авг

Девочка из Москвы Алиса Теплякова, успешно сдавшая ЕГЭ в восемь лет, не поступила на психологический факультет МГУ на бюджет, пишет ТАСС со ссылкой на данные вуза.

17 авг

В Кировской области выбрали педагога, который представит регион в конкурсе «Учитель года России» в 2021 году.

17 авг

Учебный год в Тюменской области планируется начать в очном формате. Власти будут следить за обстановкой по коронавирусу и ОРВИ.

17 авг

Рособрнадзор утвердил расписание проведения всероссийских проверочных работ (ВПР) в 2022 году для обучающихся в общеобразовательных организациях.

17 авг

Пресс-служба Министерства жилищно-коммунального хозяйства Московской области сообщила, что в 50 школах региона установят «ЭКОпункты» в рамках программы экологического воспитания подрастающего поколения.

17 авг

В пресс-службе Роспотребнадзора по Ханты-Мансийскому автономному округу (ХМАО) рассказали, что образовательные учреждения региона в новом учебном году должны будут придерживаться специального графика уроков, перемен и приёма пищи в столовой.

17 авг

В среду, 18 августа, в Тюмени начнёт работать горячая линия по вопросам подготовки детей к учебному году.

▶▷▶ контрольная работа по геометрии 8 класс номер 4 вариант 1

Интерфейс	Русский/Английский
Тип лицензия	Free
Кол-во просмотров	257
Кол-во загрузок	132 раз
Обновление:	11-11-2018

контрольная работа по геометрии 8 класс номер 4 вариант 1 — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольные по геометрии 8 класс, Атанасян, скачать бесплатно mathematics-testscom/algebra- 8 -klass/kontrolnye Cached Контрольная работа № 1 Вариант i Часть А Запишите номера верных ответов к заданию 1 Геометрия в 7 классе, контрольные работы по Атанасяну за 1, 2 mathematics-testscom/algebra-7-klass-novoe/ Cached В 4 -й задаче третьей контрольной ( 1 вариант на параллельные прямые) сказано, что дан равнобедренный треугольник, но не указано какие именно стороны у него равны Контрольная Работа По Геометрии 8 Класс Номер 4 Вариант 1 — Image Results More Контрольная Работа По Геометрии 8 Класс Номер 4 Вариант 1 images контрольная работа по геометрии номер 1 вариант 1 9 класс wwwecaqisaxpgcombr/kontrolnaya-rabota-po-geometrii Cached Контрольная работа 1 ( вариант 1 — 4 ) Контрольная Ответы к учебнику ГДЗ по геометрии 7 класс Зив БГ 10 июн 2012 Методическая разработка (геометрия, 9 класс ) по теме: Контрольные по геометрии 9 класс Контрольные работы по геометрии 8 класс к учебнику Атанасяна ЛС wwwmetod-kopilkaru/kontrolnie-raboti-po Cached Контрольная работа № 1 Г- 8 Вариант — 1 № 1 Диагонали прямоугольника abcd пересекаются в точке О, ∟АВО=36 0 Контрольные работы по геометрии 8 класс infourokru/kontrolnye_raboty_po_geometrii_ 8 Cached КОНТРОЛЬНЫЕ РАБОТЫ Геометрия 8 класс КОНТРОЛЬНАЯ РАБОТА № 1 Вариант 1 1 abcd – ромб Вычислите градусные меры углов ромба Итоговая работа по геометрии 7 класс infourokru/itogovaya_rabota_po_geometrii_7 Cached Скачать: итоговая работа по геометрии 7 класс Вариант 2 1 ) Сумма двух углов треугольника и внешнего угла к третьему равна Контрольные работы по геометрии (8 класс, УМК Атанасяна, 5 шт wwwslavkrugorg/kontrolnye-raboty-po-geometrii- 8 -klass Cached Контрольная работа № 4 1 вариант 1 ) Средние линии треугольника относятся как 2 : 2 : 4 , а периметр треугольника равен 45 см ГДЗ: Самостоятельные и контрольные работы по геометрии 7,8,9 yougdzcom/exesizephp?id=480 Cached ОПИСАНИЕ Готовые самостоятельные и контрольные работы по Геометрии для седьмого, восьмого и девятого классов от автора МА Иченская составлены в соответствии с учебником ЛС Атанасяна Контрольная работа по геометрии, 8 класс Тема: «ОКРУЖНОСТЬ» multiurokru/files/kontrol-naia-rabota-po Cached Разработка — содержание контрольной работы по геометрии для 8 класса по теме : «Окружность», 3 уровня, каждый уровень в двух вариантах Контрольная работа для 8 класса по теме: «Четырехугольники» globuss24ru/doc/kontrolynaya-rabota-dlya- 8 -k Cached Контрольная работа № 1 Четырехугольники 8 класс Вариант 1 1 На сторонах РК и МН Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 29,800 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™

$AD≠AO$ а) ABOD Читать ещё Контрольные работы по геометрии 8 класса (1
( 8 класс ) урокрф › library…po_geometrii_8_klass_181759html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник Контрольных рабор по геометрии 8 класс Пояснительная записка II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов параллелограмма равен 48 Читать ещё Сборник Контрольных рабор по геометрии 8 класс Пояснительная записка Контрольные работы содержат задания на воспроизведение (40%)
$AD≠AO$ а) ABOD – параллелограмм б) ABOD – ромб в) AOCD – ромб г) ∠COD=∠AOD д) ∠AOD=∠BOA Часть В Запишите ответы к заданиям 2 и 3 2 Диагонали прямоугольника ABCD пересекаются в точке O Найдите периметр треугольника AOB

которые имеют 4 равнозначных по сложности варианта Во втором разделе школьники могут ознакомиться из 5-ью математическими диктантами Книга завершается 39 самостоятельными работами

применение (40%) и интеграцию (20%) предметных знаний II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов параллелограмма равен 48 Найти все углы параллелограмма 3Биссектриса угла прямоугольника делит его большую сторону пополам

9 yougdzcom/exesizephp?id=480 Cached ОПИСАНИЕ Готовые самостоятельные и контрольные работы по Геометрии для седьмого
каждый уровень в двух вариантах Контрольная работа для 8 класса по теме: «Четырехугольники» globuss24ru/doc/kontrolynaya-rabota-dlya- 8 -k Cached Контрольная работа № 1 Четырехугольники 8 класс Вариант 1 1 На сторонах РК и МН Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster
скачать бесплатно mathematics-testscom/algebra- 8 -klass/kontrolnye Cached Контрольная работа № 1 Вариант i Часть А Запишите номера верных ответов к заданию 1 Геометрия в 7 классе

контрольная работа по геометрии 8 класс номер 4 вариант 1 — Все результаты Найдите Контрольная работа 4 Вариант 1 № 3 Геометрия 8 Ответы на вопрос – Найдите Контрольная работа 4 Вариант 1 № 3 Геометрия 8 класс Зив БГ – читайте на Рамблер/класс Найдите Контрольная работа 1 Вариант 4 № 4 Геометрия 8 Ответы на вопрос – Найдите Контрольная работа 1 Вариант 4 № 4 Геометрия 8 класс Зив БГ – читайте на Рамблер/класс Найдите углы Контрольная работа 1 Вариант 1 № 1 Геометрия 8 Ответы на вопрос – Найдите углы Контрольная работа 1 Вариант 1 № 1 Геометрия 8 класс Зив БГ – читайте на Рамблер/класс ГДЗ по геометрии 8 класс самостоятельные и контрольные › Геометрия › 8 класс Решебник по геометрии за 8 класс авторы Иченская, Атанасян издательство Картинки по запросу контрольная работа по геометрии 8 класс номер 4 вариант 1 «cb»:9,»cl»:6,»ct»:9,»id»:»GvjJft67ZgNqPM:»,»ml»:»600″:»bh»:90,»bw»:130,»oh»:721,»ou»:» «,»ow»:1503,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_m3″,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcTPdnXrkjNQ5X5zji_1KH_V4L5jt3RyraBCRNFK8q_HD8p9VQSjKQ_ESm48″,»tw»:188 «cl»:6,»cr»:3,»ct»:3,»id»:»fPD9UBWZ-mxvVM:»,»ml»:»600″:»bh»:90,»bw»:88,»oh»:1585,»ou»:» «,»ow»:1510,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_m1″,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:92,»tu»:» \u003dtbn:ANd9GcQ0bX1_Y2Rsw2NzRgifoExSo7O8Rj2PXFosMUq-I0QCfDBKtUidOrjSlw»,»tw»:88 «cl»:3,»cr»:3,»ct»:6,»id»:»lzIMbF4MkUxVHM:»,»ml»:»600″:»bh»:90,»bw»:123,»oh»:1059,»ou»:» «,»ow»:1450,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_86″,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcSgDGmLNRVCLflA0aJnQx9VOEHjVIF5OmlVk25hS_AijlKd9V7s8nsvjQ»,»tw»:123 «cb»:6,»cl»:3,»cr»:3,»id»:»HuwThnqdanccgM:»,»ml»:»600″:»bh»:90,»bw»:123,»oh»:841,»ou»:» «,»ow»:1458,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_1b»,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcQcMYyFD6r3xqsFJmlT7w8UBQTUTmPnWUs-FMdIS6FGCdl3rObBnO7H94Ut»,»tw»:156 «id»:»w-pKLjomk-khCM:»,»ml»:»600″:»bh»:90,»bw»:120,»oh»:435,»ou»:» «,»ow»:1495,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_7c»,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcRmB0Ph_ra2WGpVPik4E4RgiR8dRzcwZblicr67C469b1HeTzzmt5olQDmJ»,»tw»:309 Другие картинки по запросу «контрольная работа по геометрии 8 класс номер 4 вариант 1» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Контрольные работы по геометрии 8 класс (Атанасян) — Инфоурок › Математика Похожие 21 нояб 2014 г — Скачать: контрольные работы по геометрии 8 класс (атанасян) Рейтинг материала: 4 , 1 (голосов: 88) В каждом варианте задания разделены на основной и повышенный уровень Номер материала: 142207 в решении любых вопросов связанных с работой и содержанием сайта Контрольные работы по геометрии 8 класс к учебнику Атанасяна › Математика Похожие 31 окт 2015 г — Контрольная работа № 1 Г – 8 Вариант – 4 1 Периметр параллелограмма 60 см Одна из его сторон на 6 см меньше другой Найдите Контрольные работы по геометрии 8 класс (по Атанасяну) obrazbaseru//888-kontrolnye-raboty-po-geometrii-8-klass-po-atanasyanu-2015021 Похожие Рейтинг: 4 — ‎10 голосов 13 февр 2015 г — Контрольная работа № 1 Четырехугольники; Контрольная работа №2 Площадь; Контрольная работа №3 Подобные треугольники ГДЗ, Ответы по Геометрии 8 класс Дидактические материалы Зив 23 дек 2014 г — Готовые Домашние Задания, Решебник по Геометрии 8 класс В 8-х классах, выполнение домашних работ по геометрии становится Контрольные работы К- 1 Вариант 1 Вариант 2 Вариант 3 Вариант 4 К-2 Видео 17:38 К-4 Соотношения между сторонами и углами треугольника Решайся! YouTube — 17 апр 2017 г 4:40 Контрольная работа 1 Вариант А1 Задание №3 algebra channel YouTube — 9 дек 2015 г 7:58 Контрольная работа по геометрии 8 класс Задание 1 Разбор задачи Галина Сосновская YouTube — 30 сент 2015 г Все результаты Контрольные по геометрии 8 класс, Атанасян, скачать бесплатно Рейтинг: 4 — ‎11 голосов 4 апр 2017 г — Контрольные работы по геометрии 8 класса ( 1 , 2, 3, 4 четверти) к учебнику Часть А Запишите номера верных ответов к заданию 1 1 Ответы на контрольную работу №2 для 8 класса Вариант I 1 а 2 25 3 «Итоговая контрольная работа по геометрии 8 класс» › Контрольная работа 24 мая 2017 г — Cкачать: «Итоговая контрольная работа по геометрии 8 класс » Итоговая контрольная работа по геометрии 8 класс к учебнику ЛС Атанасян по материалам ОГЭ 1 вариант 1 Найдите 4 Какое из следующих утверждений верно? 1 Все углы ромба равны 2 Номер материала, 4154 Диагностическая контрольная работа по геометрии, (8 класс) 21 нояб 2017 г — Учебно-дидактические материалы по Геометрии для 8 класса по УМК любой Вариант 1 1 Один из смежных углов на 450 больше другого 4 Периметр равнобедренного треугольника АВС с основанием ВС ГДЗ к дидактическим материаам по геометрии 8 класс Зив, Мейлер › ГДЗ › 8 класс › Геометрия › БГ Зив Похожие Решебник к дидактическим материалам по геометрии 8 класс Зив Теперь, чтоб выполнить даже простые из 8 вариантов 39 самостоятельных, не говоря уже о 4 разновидностях семи контрольных работ, нужно обращаться к ГДЗ к С- 1 1 2 3 4 5 6 7 8 С-2 1 2 3 4 5 6 7 8 С-3 1 2 3 4 5 6 7 8 С- 4 1 2 3 4 5 6 Геометрия 8 класс Контрольные работы Мельникова НБ allengorg/d/math/math2203htm Предисловие 4 Тематика контрольных работ 6 Задачи для подготовки к контрольной работе 7 Контрольная работа № 1 Четырехугольники 9 Вариант Годовая контрольная работа по геометрии для 8 класса по 1 февр 2017 г — Годовая контрольная работа по геометрии для 8 класса по учебнику ЛС Атанасян и др на 4 варианта Г – 8 Годовая контрольная работа 3 вариант 4 вариант № 1 Укажите номера неверных утверждений «Геометрия 8 класс Контрольные работы к учебнику Л С Интересные рецензии пользователей на книгу Геометрия 8 класс Рейтинг: + 1 Всего представлено 5 контрольных работ по 4 варианта в каждой Перед Сама контрольная работа содержит 6 заданий и состоит из 3 частей (1ч — задания с выбором ответа; 2ч — задачи, которые нужно / город номер Контрольные работы по геометрии 8 класс — Социальная сеть 20 мар 2012 г — Контрольная работа № 1 Четырехугольники Вариант 2 А1 Диагональ квадрата равна 4 см Сторона его равна диагонали другого [PDF] Итоговая контрольная работа по ГЕОМЕТРИИ 8 класс — Основная polaria-1ru/data/documents/Geometriya-8-kl-2018gpdf Структура варианта контрольной работы отвечает цели построения системы 4 Связь экзаменационной модели ОГЭ с моделью промежуточной аттестации Контрольная работа по геометрии содержит 8 заданий: в части 1 – 7 В ответ запишите номера выбранных утверждений без пробелов, Готовые Контрольные Работы По Геометрии 8 Класс Атанасян topikprocessweeblycom//gotovie-kontroljnie-raboti-po-geometrii-8-klass-atanasya Домашняя работа по геометрии за 8 класс к учебникам « Геометрия 7-9 по геометрии Атанасяна с ответами Варианты контрольных за 1 , 2, 3, 4 Входная контрольная работа по геометрии 8 класс — Видеоуроки 18 дек 2017 г — Контрольная работа представлена в виде теста, 2 варианта Ответы@MailRu: Пожайлуста, напишите ссылку на контрольные работы › Образование › Школы Похожие 4 ответа 3 нояб 2016 г — Тематические тесты по геометрии : 8 класс : к учебнику Л С Атанасяна и др 1 / 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK сторона МК = 8 см, RuО компанииРеклама Вакансии геометрия gkryukova40411s002edusiteru/vis_p12aa1html 1 комплект Контрольные работы по геометрии 8 класс 2 комплект ( 4 варианта ) Итоговый тест Самостоятельная работа «Пропорциональные отрезки Книга «Контрольные работы по геометрии 8 класс», Мельникова wwwbgshopru/Catalog/GetFullDescription?id=10404048&type=1 Контрольные работы по геометрии 8 класс в наличии Цена со скидкой 10% в интернет-магазине: 62 1 — 4 классы · Зачетные работы по математике Итоговая контрольная работа по геометрии в 4-х вариантах, 8 класс Похожие Итоговая контрольная работа по геометрии в 4 -х вариантах, 8 класс Скачать материал 1 вариант 8 класс 1 Площадь прямоугольника АВСD равна 15 Укажите в ответе номера верных утверждений в порядке возрастания : 1 ) 8 класса — контрольные работы по геометрии Атанасяна с ответами 8 класса — контрольные работы по геометрии Атанасяна с ответами Варианты контрольных за 1 , 2, 3, 4 четверти контрольная работа по геометрии 8 класс атанасян — SEAE Embu seaembuorg//kontrolnaia-rabota-po-geometrii-8-klass-atanasian-otvety-resheniexm контрольная работа по геометрии 8 класс атанасян ответы решение to Mail» data-nosubject=»[ No Subject]» data-timestamp=’short’ Help Account Info Yahoo Найдите Контрольная работа 4 Вариант 2 № 1 Геометрия 8 Ответы на Контрольные работы по геометрии (8 класс, УМК Атанасяна, 5 шт) uchkopilkaru//3613-kontrolnye-raboty-po-geometrii-8-klass-umk-atanasyana-5-sht Похожие 13 мар 2014 г — Катеты прямоугольного треугольника равны 6и 8 см Контрольная работа № 3 1 вариант 1 ) По рисA = B, СО = 4 , DO= 6, АО = 5 Геометрия 8 класс Контрольные работы по геоиетрии К учебнику Похожие В книжном интернет-магазине OZON можно купить учебник Геометрия 8 класс Контрольные работы по геоиетрии К учебнику Л С Атанасяна и др Итоговая аттестационная работа по геометрии 8 класс — PDF docplayerru/34103917-Itogovaya-attestacionnaya-rabota-po-geometrii-8-klasshtml Итоговая аттестационная работа по геометрии 8 класс 1 ) половине этой стороны 2) этой стороне 3) удвоенной этой стороне 4 ) сумме двух сторон треугольника 3 4 А9 Если Вы обвели не тот номер , то зачеркните обведённый номер крестиком и Контрольная работа 1 Четырехугольники Вариант 1 Контрольная работа 8 класс применение подобияdocx — Знанио Файл Контрольная работа 8 класс применение подобияdocx для Контрольная работа по геометрии «Применение подобия к решению задач» ( 8 класс ) Вариант 1 1 Значение выражения 2sin 30°- 1 равно: а) — 1 /2 ; б) – 1 4 Диагонали прямоугольника АВСD пересекаются в точке О Отрезок ОF – высота КОНТРОЛЬНАЯ РАБОТА № 1 — УРОКИ-КОНСПЕКТЫ ПО КОНТРОЛЬНАЯ РАБОТА № 1 — УРОКИ-КОНСПЕКТЫ ПО ГЕОМЕТРИИ 8 КЛАСС — подробных поурочных разработках по геометрии для 8 класса содержит варианты уроков, справочные и б) Найдите периметр параллелограмма, если СD = 8 см, СМ = 4 см 17 selfies that prove the stupidity knows no limit Контрольная работа по геометрии 8 класс Четырехугольники 1 Контрольная работа по геометрии 8 класса Подобие 1 вариант 1 Контрольная работа № 4 8 класс 1 вариант 1 На рисунке Найдите сторону АВ Ершова Голобородько 8 класс самостоятельные и контрольные › 8 класс › Геометрия игры · Правообладателям · ГДЗ / 8 класс / Геометрия / самостоятельные и контрольные работы ГДЗ К-10 Годовая контрольная работа 1 2 3 4 5 Контрольные работы по геометрии 8-го класса открытыйурокрф/статьи/641227/ Тематические контрольные работы по геометрии для 8-го класса составлены В части А необходимо выбрать правильный ответ из предложенных вариантов , задания Систематическое изложение курса позволяет начать работу по контрольных работ по геометрии 8 класса ( Приложения 1 , 2, 3, 4 , 5) ГДЗ по геометрии 8 класс Гусев Медяник дидактические — GDZme › 8 класс › Геометрия ГДЗ по геометрии 8 класс к дидактическим материалам Гусев Медяник, онлайн ответы из Представленные виды работ разделены на 4 варианта Рабочая программа по геометрии по учебнику ЛСАтанасян (8 7 янв 2015 г — На изучение математики в 8 классе согласно Федеральному базисному учебному плану отводится 5 часов в неделю (всего 170 часов) из них на Контрольная работа № 4 Вариант 1 Номер материала, 42336 Контрольные работы по геометрии 8 класс К учебнику Л С Похожие Контрольные работы по геометрии 8 класс К учебнику Л С Атанасяна и др Кроме того, по каждой теме дается набор заданий для подготовки к контрольной работе Каждый вариант включает задания трех видов: с выбором ответа, Часть 1 Федосова Н 275 ₽ В корзину География 9 класс Атлас Контрольные и самостоятельные работы по алгебре и геометрии 83,00 ₽ — ‎В наличии 8 класс Ко всем действующим учебникам ФГОС» (Журавлев СГ) в Издание ориентировано на работу с любыми учебниками по алгебре и геометрии из Федерального 3-й и 4 -й варианты рассчитаны на учащихся, проявляющих повышенный ISBN, 5-377-11023- 1 , 5-377-08225-5, 978-5-377 -08225-5 Геометрия 8 класс контрольная Контрольные работы по Контрольные работы по геометрии 8 класс к учебнику Атанасяна ЛС Геометрия 8 класс контрольная Контрольная работа № 1 8 класс II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов Запишите номера верных ответов к заданиям 1 и 21 ГДЗ к контрольным и самостоятельным по геометрии 8 класс Зив › ГДЗ › 8 класс › Геометрия › дидактические материалы Зив Похожие Геометрия 8 класс Дидактические материалы Зив В части 1 размещены 7 разных контрольных работ, которые имеют 4 равнозначных по сложности ГДЗ по алгебре 8 класс Мордкович — онлайн решебник — uchimorg ГДЗ по алгебре 8 класс Мордкович — онлайн решебник § 1 Основные понятия § 4 Сложение и вычитание алгебраических дробей с разными знаменателями Домашняя контрольная работа № 1 Вариант 1 Вариант 2 Жохов, Чесноков, Шварцбурд — онлайн решебник · ГДЗ по геометрии 10- 11 класс Контрольная работа по геометрии 8 класс по теме — Продлёнка 22 июл 2016 г — Контрольная работа по геометрии 8 класс по теме: «Окружность» Наименование Вариант 1 Вариант 2 А1 Радиус 1 )8 2)16 3)2 4 )другой ответ А2 Найдите Укажите номера верных утверждений 1 )Длина Геометрия 9 класс: поурочные планы по учебнику А В Погорелова Киселёва Ю А — 2014 — ‎Education Ключ к тесту Задание Вариант 1 2 3 4 5 6 7 8 9 10 Вариант I 78 в 17 8 б 1 Итоговый тест по всему курсу геометрии 2 Итоговая контрольная работа 2 «РЕШУ ВПР»: математика–4 ВПР — 2019: задания, ответы Специально для наших читателей мы ежемесячно составляем варианты для самопроверки Если ваш школьный учитель составил работу и сообщил вам номер , введите его сюда 1 , 2, 3, 4 , 51, 52, 61, 62, 7, 8 , 91, 92, 10, 11 ГДЗ по алгебре для 9 класса Задачник АГ Мордкович Похожие ГДЗ к контрольным работам по алгебре за 9 класс Александрова ЛА 1 ; 2; 3; 4 ; 5; 6; 7; 8 ; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26 математика — Решим всё разворот боковой поверхности конуса сектор, с дугой 1 ,8π дм, а угловой размер дуги 120 градусов просмотры: 8 | математика класс не задан прямоугольник с периметром 4 дм, вращается вокруг прямой, на которой геометрия 7 класс Определите номер подъезда, в котором живет Слава ( L1) Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (50) Показать скрытые результаты В ответ на жалобу, поданную в соответствии с Законом США «Об авторском праве в цифровую эпоху», мы удалили некоторые результаты (1) с этой страницы Вы можете ознакомиться с жалобой на сайте LumenDatabaseorg Вместе с контрольная работа по геометрии 8 класс номер 4 вариант 1 часто ищут контрольная работа по геометрии 8 класс 4 четверть готовые контрольные работы по геометрии 8 класс атанасян готовые контрольные работы по геометрии 8 класс атанасян ответы контрольная работа по геометрии 8 класс четырехугольники контрольная работа номер 1 по геометрии 8 класс атанасян ответы контрольная работа по геометрии 8 класс номер 5 контрольная работа по геометрии 8 класс подобные треугольники годовая контрольная работа по геометрии 8 класс атанасян Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google

Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Музыка Переводчик Диск Почта Коллекции Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 ГДЗ по геометрии 8 класс самостоятельные eurokiorg › gdz…geometriya/8_klass…ichenskaya-274 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян В восьмом классе школьники продолжают изучать геометрию , углубляя и расширяя свои знания по предмету Если в седьмом классе элементарные понятия и аксиомы не вызывали трудностей, то 8 класс часто преподносит Читать ещё ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян В восьмом классе школьники продолжают изучать геометрию , углубляя и расширяя свои знания по предмету Если в седьмом классе элементарные понятия и аксиомы не вызывали трудностей, то 8 класс часто преподносит неприятные сюрпризы Они заключаются в неумении интегрировать формулы и доказательства в единое решение задания Как помочь восьмикласснику понять геометрию ? Отличный способ – ГДЗ по предмету Полностью решенное задание из хорошего учебного пособия поможет наработать базу, понять основные алгоритмы и принципы Скрыть 2 Контрольные работы по геометрии 8 класс к учебнику infourokru › …raboti-po-geometrii-klass…537738html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Инфоурок › Математика › Другие методич материалы › Контрольные работы по геометрии 8 класс к учебнику Контрольная работа № 1 Г- 8 Вариант — 1 № 1 Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360 Читать ещё Инфоурок › Математика › Другие методич материалы › Контрольные работы по геометрии 8 класс к учебнику Атанасяна ЛС Контрольные работы по геометрии 8 класс к учебнику Атанасяна ЛС скачать материал библиотека материалов Контрольная работа № 1 Г- 8 Вариант — 1 № 1 Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360 Найдите угол AOD Скрыть 3 ГДЗ 1 контрольная работа / К-2 геометрия 8 класс GDZru › class-8/geometria/ziv-meiler/e:1-t:1-a:0/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ по геометрии 8 класс БГ Зив дидактические материалы контрольная работа / К-2 — 1 Авторы : БГ Зив, ВМ Мейлер Читать ещё ГДЗ по геометрии 8 класс БГ Зив дидактические материалы контрольная работа / К-2 — 1 Авторы : БГ Зив, ВМ Мейлер Издательство: Просвещение ← предыдущий следующий → Решебник / контрольная работа / К-2 / 1 ← предыдущий следующий → © GDZru 2018 Copyright Подписка About [email protected] google play app store Скрыть 4 Контрольная работа по геометрии 8 класс номер 4 вариант 1 — смотрите картинки ЯндексКартинки › контрольная работа по геометрии 8 класс номер 4 Пожаловаться Информация о сайте Ещё картинки 5 Контрольные работы по геометрии 8 класс infourokru › …po_geometrii_8_klass-342142htm Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте КОНТРОЛЬНЫЕ РАБОТЫ Геометрия 8 класс КОНТРОЛЬНАЯ РАБОТА № 1 Вариант 1 ▲1 ABCD – ромб Вычислите градусные меры углов ромба 2 Периметр параллелограмма равен 30см Одна из его сторон больше другой на 3см 6 Геометрия 8 класс — контрольная работа 1 , вариант gdz-fiveru › Решебники › 8 класс › Геометрия › Зив › k14 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решение варианта 4 контрольной работы 1 к учебнику за 8 класс по геометрии дидактические материалы авторов Зив, Мейлер ГДЗ по геометрии 8 класс Зив, Мейлер дидактические материалы, контрольная работа 1 , вариант 4 7 ГДЗ по геометрии для 8 класса Казаков В В — Тема reshebacom › gdz/geometrija/8-klass/kazakov/e:0-t…3 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробное решение Тема 1 Четырёхугольники / Контрольная работа 1 Вариант 1 4 по геометрии опорные конспекты для учащихся 8 класса , авторов Казаков В В 2016 Читать ещё Подробное решение Тема 1 Четырёхугольники / Контрольная работа 1 Вариант 1 4 по геометрии опорные конспекты для учащихся 8 класса , авторов Казаков В В 2016 показать содержание ← предыдущее Следующее → решебник / Тема 1 Четырёхугольники / Контрольная работа 1 Вариант 1 / 4 ← предыдущее Следующее → Подпишись на нашу группу Скрыть 8 Контрольные работы по геометрии 8 класса mathematics-testscom › algebra-8-klass…geometriya… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольные работы по геометрии 8 класса (1, 2, 3, 4 четверти) к учебнику Атанасяна ЛС с ответами Контрольная работа № 1 Вариант I Часть А Запишите номера верных ответов к заданию 1 1 На рисунке ABCD – трапеция, $AB||OD$, $AO||CD$, $AD=OD$, $AD≠AO$ а) ABOD Читать ещё Контрольные работы по геометрии 8 класса (1, 2, 3, 4 четверти) к учебнику Атанасяна ЛС с ответами Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания Все материалы проверены антивирусной программой Контрольная работа № 1 Вариант I Часть А Запишите номера верных ответов к заданию 1 1 На рисунке ABCD – трапеция, $AB||OD$, $AO||CD$, $AD=OD$, $AD≠AO$ а) ABOD – параллелограмм б) ABOD – ромб в) AOCD – ромб г) ∠COD=∠AOD д) ∠AOD=∠BOA Часть В Запишите ответы к заданиям 2 и 3 2 Диагонали прямоугольника ABCD пересекаются в точке O Найдите периметр треугольника AOB, если AB= 4 , AD=3, BD=5 Скрыть 9 ГДЗ к контрольным и самостоятельным по геометрии reshebacom › gdz/geometrija/8-klass/ziv Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробные решения и ответы к учебнику геометрии по контрольным и самостоятельным работам для 8 класс , авторов В части 1 размещены 7 разных контрольных работ , которые имеют 4 равнозначных по сложности варианта Во втором разделе школьники могут ознакомиться из 5-ью Читать ещё Подробные решения и ответы к учебнику геометрии по контрольным и самостоятельным работам для 8 класс , авторов БГ Зив, ВМ Мейлер, Просвещение 2014 год В части 1 размещены 7 разных контрольных работ , которые имеют 4 равнозначных по сложности варианта Во втором разделе школьники могут ознакомиться из 5-ью математическими диктантами Книга завершается 39 самостоятельными работами , которые предполагают 8 вариантов Самостоятельные работы Скрыть 10 Сборник контрольных работ по геометрии , ( 8 класс ) урокрф › library…po_geometrii_8_klass_181759html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник Контрольных рабор по геометрии 8 класс Пояснительная записка II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов параллелограмма равен 48 Читать ещё Сборник Контрольных рабор по геометрии 8 класс Пояснительная записка Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов параллелограмма равен 48 Найти все углы параллелограмма 3Биссектриса угла прямоугольника делит его большую сторону пополам, меньшая сторона равна 7 см Найдите периметр прямоугольника 4 Один из углов ромба равен 120 , а диагональ, исходящая из вершины этого угла равна 12см Найдите периметр ромба 5Докажите, что если диагонали прямоугольника перпендикулярны, то он является квадратом Скрыть Гдз по Геометрии дидактические материалы за 8 класс GdzPutinacom › Гдз за 8 класс › Геометрия › Зив Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Геометрия 8 класс БГ Зив Дидактические материалы Подробные гдз и решебник по Геометрии для 8 класса дидактические материалы, авторы учебника: БГ Зив, ВМ Мейлер на 2017-2018 год Самостоятельные работы Вместе с « контрольная работа по геометрии 8 класс номер 4 вариант 1 » ищут: итоговая контрольная работа по геометрии 8 класс контрольная работа по алгебре 8 класс контрольные работы по геометрии 8 класс атанасян с ответами и решением контрольная работа по геометрии 7 класс контрольная работа по геометрии 9 класс входная контрольная работа по геометрии 8 класс атанасян диагонали прямоугольника abcd пересекаются в точке o годовая контрольная работа по геометрии 8 класс контрольная работа 1 по геометрии 8 класс гдз по геометрии 7-9 класс атанасян 1 2 3 4 5 дальше Bing Google Mailru Нашлось 373 млн результатов Дать объявление Регистрация Войти 0+ ЯндексБраузер с Алисой, которая готова поболтать Установить Закрыть Попробовать еще раз Включить Москва Настройки Клавиатура Помощь Обратная связь Для бизнеса Директ Метрика Касса Телефония Для души Музыка Погода ТВ онлайн Коллекции Яндекс О компании Вакансии Блог Контакты Мобильный поиск © 1997–2018 ООО «Яндекс» Лицензия на поиск Статистика Поиск защищён технологией Protect Вы всегда успеете к началу На Яндексе можно смотреть любимые телепередачи после эфира Перейти

Геометрия, 8 класс.

Контрольные работы | Методическая разработка по геометрии (8 класс):

Контрольная работа №4

Вариант 2.

Контрольная работа №4

Вариант 1.

№1. А В

8cм

D 15см C

Найти:

А) Площадь прямоугольника АВСD

б) диагональ АС.

№1. В С

5см

А 12см D

Найти:

а) Площадь прямоугольника АВСD

б) диагональ АС.

№2. E

D F

2см Н 4см

Найти площадь треугольника DEF.

(ЕН — высота)

A 5cм Н 3см С

Найти площадь треугольника ABC.

(ВН — высота)

№3.

K N

Найти MN — сторону ромба KMNP, если MP = 16см, KN=12см.

№3.

M P

Найти сторону МР равнобедренного треугольника МNP, если MN=NP=15см и NK=9cм.

(NK — высота )

№4. A 7см B

13cм

D C

Найти площадь равнобедренной трапеции ABCD (AD=BC).

(ВЕ — высота)

№4. F 5см К

10см

Е D

17см

Найти площадь равнобедренной трапеции EFKD (EF=DK)

№5.

O P

5cм

S 7cм Т 3см R

Найти площадь параллелограмма OPRS.

(РТ — высота)

№5.

B C

11515

А 2см Е 12см D

Найти площадь параллелограмма АВСD.

(ВЕ — высота)

Геометрия 8 Контрольные Мерзляк | Контроль знаний

Геометрия 8 Контрольные Мерзляк — это цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Геометрия: дидактические материалы 8 класс: пособие для учащихся общеобразовательных организаций / А. Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович и др. / М.: Вентана-Граф». Представленные ниже контрольные работы в 2-х вариантах ориентированы на учебник «Геометрия 8 класс» авторов

А.Г. Мерзляк, В.Б. Полонский, М.С.Якир системы УМК «Алгоритм успеха». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Нажмите на необходимую вам тему контрольной работы. В начале указана цитата (материал контрольной работы) из вышеуказанного учебного пособия. Каждая цитата представлена в форме удобной для проверки знаний (на одной странице). Затем представлены ответы на оба варианта контрольной. При постоянном использовании данных контрольных работ (в 4-х вариантах) рекомендуем КУПИТЬ книгу: Мерзляк, Рабинович, Полонский: Геометрия. 8 класс. Дидактические материалы. ФГОС

(переход по ссылке в интернет-магазин «Лабиринт.Ру»). Вопросы и ответы представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.

Геометрия 8 класс

Контрольные работы (УМК Мерзляк и др.)

Контрольная работа № 1 КР-1 + ответы

Контрольная работа № 2 КР-2 + ответы

Контрольная работа № 3 КР-3 + ответы

Контрольная работа № 4 КР-4 + ответы

Контрольная работа № 5 КР-5 + ответы

Контрольная работа № 6 КР-6 + ответы

Контрольная работа № 7 Итоговая с ответами

Вы смотрели страницу Геометрия 8 Контрольные Мерзляк. Цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия:

Геометрия: дидактические материалы 8 класс: пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович и др. / М.: Вентана-Граф. Вернуться на страницу «Геометрия 8 класс».

Если Вы считаете, что какой-то пример решен неправильно обязательно напишите нам в поле для Комментариев (ниже) с указанием № контрольной работы, № варианта и № задачи.

Другие контрольные работы по математике в 8 классе:

Контрольные работы по Алгебре в 8 классе (по учебнику Мерзляка А.

Г.)

Контрольные работы по Алгебре в 8 классе (по учебнику Алимова Ш.А.)

Контрольные работы по Алгебре в 8 классе (по учебнику Макарычева Ю.Н.)

Геометрия 8 класс . Тесты и Тренажеры

ГЕОМЕТРИЯ 8 класс. ТЕСТЫ И ТРЕНАЖЕРЫ

Геометрия 8. Свойства параллелограмма (на чертежах) — 8 заданий …

Геометрия 8. ПАРАЛЛЕЛОГРАММ (на чертежах) — 8 заданий …

Геометрия 8. Многоугольники (теория) — 15 вопросов …

Геометрия 8. Свойства и признаки параллелограмма — 15 вопросов …

Геометрия 8. Виды параллелограммов. Трапеция — 15 вопросов …

Геометрия 8. Средние линии треугольника и трапеции — 15 вопросов …

Геометрия 8. Площади многоугольников — 15 вопросов …

Геометрия 8. ТРАПЕЦИЯ (на чертежах) — 7 заданий …

Геометрия 8. Площадь прямоугольника (на чертежах) — 7 заданий …

Геометрия 8 класс.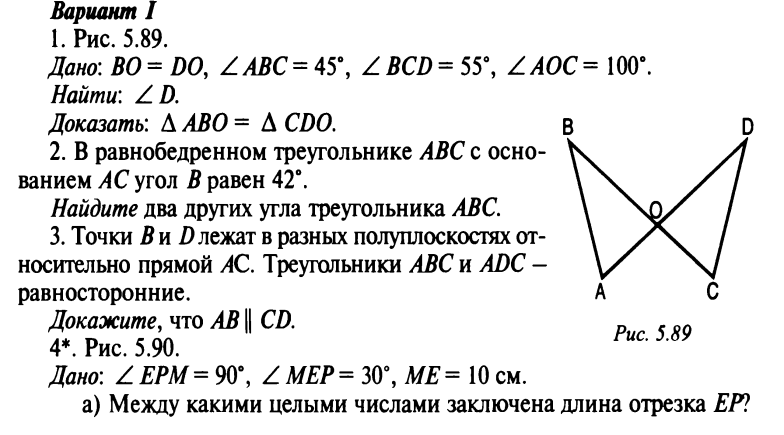 Площадь трапеции — 10 вопросов …

Геометрия 8 класс. Теорема Пифагора — 10 вопросов …

Геометрия 8 класс. Площади (теория) — 10 вопросов …

Геометрия 8. Площадь параллелограмма (на чертежах) — 7 заданий …

Геометрия 8. Площадь треугольника (на чертежах) — 7 заданий …

Геометрия 8. Площадь трапеции (на чертежах) — 7 заданий …

Геометрия 8. Теорема Пифагора (на чертежах) — 7 заданий …

Геометрия 8. Подобные треугольники (на чертежах) — 7 заданий …

Геометрия 8. Определение подобных треугольников — 10 вопросов …

Геометрия 8. Признаки подобия треугольников — 10 вопросов …

Геометрия 8. Применение признаков подобия — 10 вопросов …

Геометрия 8. Соотношения между сторонами и углами — 10 вопросов …

Геометрия 8. Подобные треугольники (теория) — 10 вопросов …

Геометрия 8. Касательная к окружности — 10 вопросов …

Геометрия 8. Центральные и вписанные углы — 10 вопросов …

Геометрия 8. Четыре замечательные точки окружности — 10 вопросов …

Геометрия 8. Вписанные и описанные окружности — 10 вопросов …

Геометрия 8. Окружность (теория) — 10 вопросов …

Геометрия 8. ИТОГОВЫЙ ТЕСТ за год — 16 вопросов …

ГЕОМЕТРИЯ 8 класс. КОНТРОЛЬНЫЕ РАБОТЫ

теорем Чевы и изменение экзамена. Теоремы Чевы и Чевы Пространственные аналоги теорем Чевы и Менелайи

А.В. Шевкин

ФМС № 2007

Теоремы Чевы и Менелая на экзамене

Подробная статья «Вокруг теорем Шевы и Менелая» опубликована на нашем сайте в разделе СТАТЬИ.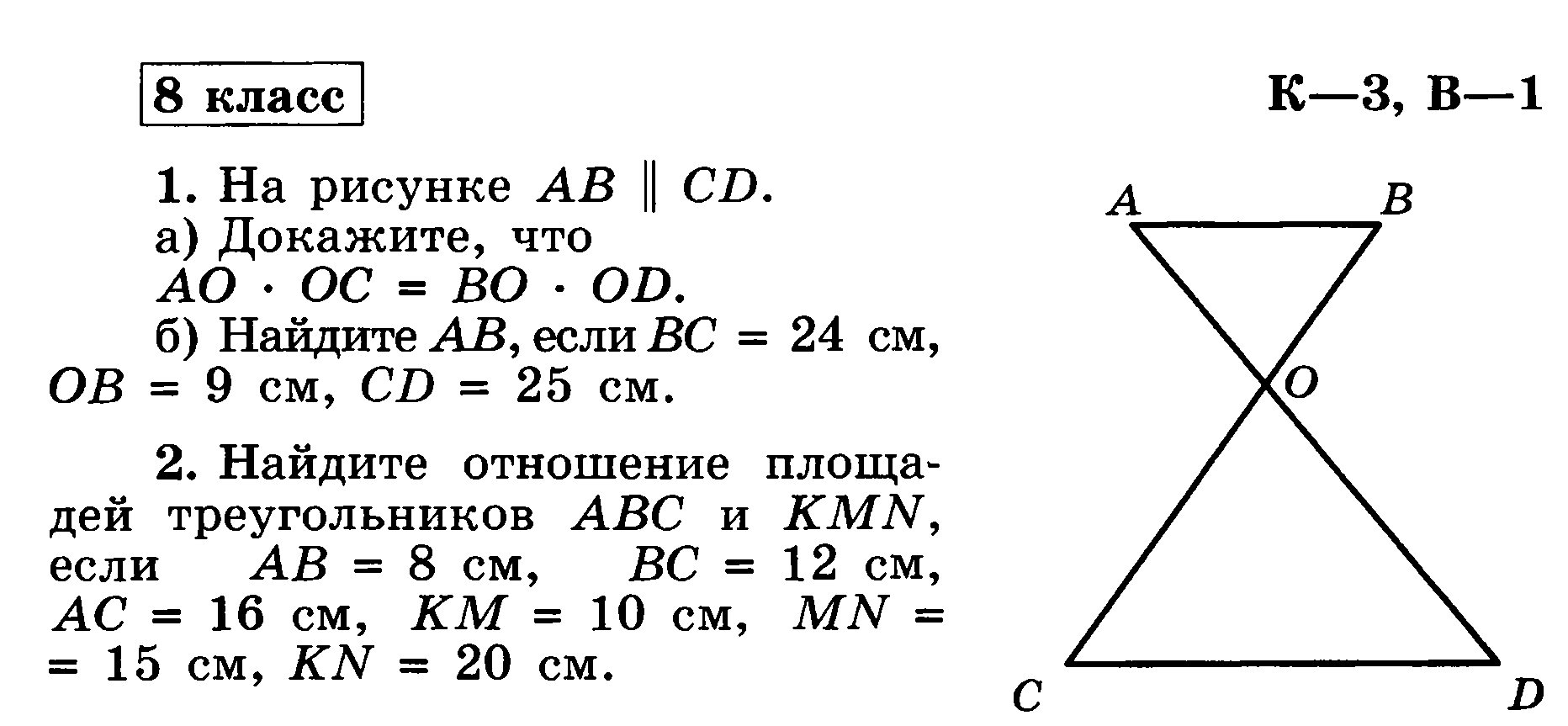 Он адресован учителям математики и старшеклассникам, которые хотят хорошо знать математику.К нему можно вернуться, если есть желание разобраться в вопросе более подробно. В этой заметке мы предоставим краткую информацию из указанной статьи и проанализируем решения задач из сборника для подготовки к ЕГЭ-2016.

Теорема Чевы

Дан треугольник ABC и на его сторонах AB , BC и AC отмечены точки C 1, A 1 и B 1 соответственно (рис.1).

a) Если сегменты AA 1, BB 1 и CC 1 пересекаются в одной точке, то

б) Если равенство (1) верно, то отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке.

На рисунке 1 показан случай, когда сегменты AA 1, BB 1 и CC 1 пересекаются в одной точке внутри треугольника. Это так называемый случай внутренней точки. Теорема Чевы также верна в случае внешней точки, когда одна из точек A 1, B 1 или FROM 1 принадлежит стороне треугольника, а две другие принадлежат продолжениям треугольника. стороны треугольника.В этом случае точка пересечения отрезков AA 1, BB 1 и CC 1 лежит вне треугольника (фиг. 2).

Как вспомнить равноправие Чевы?

Обратим внимание на технику запоминания равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении пересечения вершин треугольника ABC , начиная с точки A … Из точки A идем в точку B , встречаем точку ОТ 1, записываем дробь
… Далее из точки В идем в точку ОТ , встречаем точку A 1, записываем дробь
… Наконец, из точки ИЗ переходим в точку A , встречаем точку IN 1, записываем дробь
… В случае внешней точка, порядок записи дробей сохраняется, хотя две «точки деления» сегмента находятся за пределами своих сегментов. В таких случаях говорят, что точка разделяет сегмент внешне.

Обратите внимание, что любой отрезок, соединяющий вершину треугольника с любой точкой прямой, содержащей противоположную сторону треугольника, называется cheviana .

Рассмотрим несколько способов доказательства части а) теоремы Чевы для случая внутренней точки. Для доказательства теоремы Чевы необходимо доказать утверждение а) любым из предложенных ниже методов, а также доказать утверждение б). Доказательство части b) дается после первого способа доказательства части a).Доказательства теоремы Чевы для случая внешней точки аналогичны.

Доказательство утверждения а) теоремы Чевы с использованием теоремы о пропорциональном отрезке

Пусть три чевиана A A 1, B B 1 и C C 1 пересекаются в точке Z внутри треугольника ABC .

Идея доказательства состоит в том, чтобы заменить отношения отрезков из равенства (1) на отношения отрезков, лежащих на одной прямой.

Через точку IN проведите прямую, параллельную шевиане SS . Прямой AA 1 пересекает построенную линию в точке M , и прямая, проходящая через точку C и параллель AA 1, — в точке T … Через точки A, и FROM проведите прямые, параллельные шевианам BB . Они пересекут линию VM в точках N и R соответственно (рис.3).

P по теореме о пропорциональных отрезках, имеем:

, г.
и
.

Тогда равенства

В параллелограммах ZСTM и ZCRB сегменты TM , CZ и ВR равны как противоположные стороны параллелограмма. Следовательно,
и верно равенство

При доказательстве утверждения б) мы используем следующее утверждение. Рисунок 3

Лемма 1. Если точки ОТ 1 и ОТ 2 делят отрезок AB внутренним (или внешним) способом в одном и том же отношении, считая от одной и той же точки, то эти точки совпадают.

Докажем лемму для случая, когда точки ИЗ 1 и ИЗ 2 делят отрезок AB внутренне одинаково:
.

Доказательства. Из равенства
следуют равенства
и
… Последнее из них выполняется только при условии равенства ОТ 1 B и ОТ 2 B , то есть при условии, что точки ОТ 1 и ИЗ 2 одинаковы.

Доказательство леммы для случая, когда точки ОТ 1 и ОТ 2 делят отрезок AB внешне, проводится аналогично.

Доказательство части б) теоремы Чевы

Пусть теперь выполняется равенство (1). Докажем, что отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке.

Пусть чевианы AA 1 и BB 1 пересекаются в точке Z , проведем через эту точку отрезок CC 2 ( ИЗ 2 лежит на отрезке AB ).Тогда на основании утверждения а) получаем правильное равенство

. (2)

И сравнивая равенства (1) и (2), мы заключаем, что
, то есть точки ОТ 1 и ОТ 2 делят сегмент AB в том же отношении, считая от одной и той же точки. Из леммы 1 следует, что точки ИЗ 1 и ИЗ 2 совпадают. Это означает, что сегменты AA 1, BB 1 и CC 1 пересекаются в одной точке, как требуется.

Можно доказать, что процедура записи равенства (1) не зависит от того, в какой точке и в каком направлении пересекаются вершины треугольника.

Упражнение 1. Найдите длину сегмента A N на рисунке 4, где показаны длины других сегментов.

Ответ. 8.

Задача 2. Chevians AM , BN , CK пересекаются в одной точке внутри треугольника ABC … Найдите отношение
, если
,
… Рисунок: 4

Ответ.
.

P Приведем доказательство теоремы Чевы из статьи. Идея доказательства состоит в том, чтобы заменить отношения отрезков из равенства (1) на отношения отрезков, лежащих на параллельных прямых.

Пусть прямые А А 1, B B 1, C C 1 пересекаются в точке O внутри треугольника ABC (рис.5). Поперек вершины ОТ треугольника ABC проведите прямую, параллельную AB , и ее точки пересечения с прямыми линиями A A 1, B B 1 обозначают соответственно A 2, В 2.

Из подобия двух пар треугольников CB 2 B 1 и ABB 1, BAA 1 и CA 2 A 1, рис.5

имеем равенства

, г.
. (3)

Из подобия треугольников BC 1 O и B 2 CO , A ОТ 1 O и A 2 CO имеем равенства
, из которых следует, что

. (4)

P Умножая равенства (3) и (4), получаем равенство (1).

Утверждение а) теоремы Чевы доказано.

Рассмотрим доказательства утверждения а) теоремы Чевы с использованием площадей для внутренней точки. Это изложено в книге А.Г. Мякишева и опирается на утверждения, которые мы сформулируем в виде задач 3 и 4 .

Задача 3. Отношение площадей двух треугольников с общей вершиной и оснований, лежащих на одной прямой, равно отношению длин этих оснований. Докажите это утверждение.

Задача 4. Докажите, что если
, то
и
… Рисунок: 6

Пусть отрезки AA 1, BB 1 и CC 1 пересекаются в точке Z (рис.6), затем

, г.
. (5)

И из равенств (5) и второго оператора присваивания 4 следует, что
или
… Аналогично находим, что
и
… Умножая последние три равенства, получаем:

, то есть равенство (1) выполняется, как и требуется.

Утверждение а) теоремы Чевы доказано.

Задача 15. Пусть Чевианы пересекаются в одной точке внутри треугольника и разделят его на 6 треугольников, площади которых равны S 1, S 2, S 3, S 4, S 5, S 6 (рис. 7). Докажи это. Рисунок 7

Задача 6. Найдите площадь S треугольника CNZ (площади остальных треугольников показаны на рисунке 8).

Ответ. 15.

Задача 7. Найти площадь S треугольника CNO , если площадь треугольника A NO равна 10 и
,
(рис.9).

Ответ. 30.

Задача 8. Найти площадь S треугольника CNO , если площадь треугольника A BC равна 88 и,
(рис.9).

Раствор R. Так как, то обозначим
,
… как , то обозначим
,
… Из теоремы Чевы следует, что
, а затем
… Если
, то
(рис.10). У нас есть три неизвестных величины ( x , y и S ), поэтому, чтобы найти S , составим три уравнения.

Как
, затем
= 88. Начиная с
, затем
, откуда
… Как
, затем
.

Итак,
откуда
… Цифра: десятка

Назначение 9 . В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и B C .
,
. P AL и CK … Площадь треугольника PBC равна 1. Найдите площадь треугольника ABC .

Ответ. 1,75.

Теорема Т Менелая

Дан треугольник ABC и на его сторонах AC и CB отмечены точки B 1 и A 1 соответственно, а на продолжении стороны AB точка обозначена C 1 (рис.11).

а) Если точки A 1, B 1 и ИЗ 1 лежат на одной прямой, то

. (6)

б) Если выполняется равенство (7), то точки A 1, B 1 и ИЗ 1 коллинеарны. Рисунок: одиннадцать

Как помнить о равенстве Менелая?

Способ запоминания равенства (6) такой же, как и для равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC — сверху вниз, проходя через точки разделения (внутренние или внешние).

Задача 10. Докажите, что запись равенства (6) из любой вершины треугольника в любом направлении дает тот же результат.

Для доказательства теоремы Менелая необходимо доказать утверждение а) любым из предложенных ниже методов, а также доказать утверждение б). Доказательство части b) дается после первого способа доказательства части a).

Доказательство утверждения а) с использованием теоремы о пропорциональном отрезке

I путь. а) Идея доказательства состоит в замене соотношений длин отрезков в равенстве (6) на отношения длин отрезков, лежащих на одной прямой.

Пусть точки A 1, B 1 и ИЗ 1 лежат на одной прямой. Через точку C проведем прямую l , параллельную прямой A 1 B 1, она пересекает линию AB в точке M (рис.12).

R
есть. 12

По теореме о пропорциональных отрезках имеем:
и
.

Тогда верны равенства
.

Доказательство утверждения б) теоремы Менелая

Пусть теперь равенство (6) выполнено, докажем, что точки A 1, B 1 и ИЗ 1 лежат на одной прямой. Пусть прямые AB и A 1 B 1 пересекаются в точке ОТ 2 (рис.13).

Поскольку точки A 1 B 1 и ИЗ 2 лежат на одной прямой, то по утверждению а) теоремы Менелая

. (7)

Сравнивая равенства (6) и (7), получаем
, откуда следует, что равенства

, г.
, г.
.

Последнее равенство верно только при условии
, т.е. если точки ИЗ 1 и ИЗ 2 совпадают.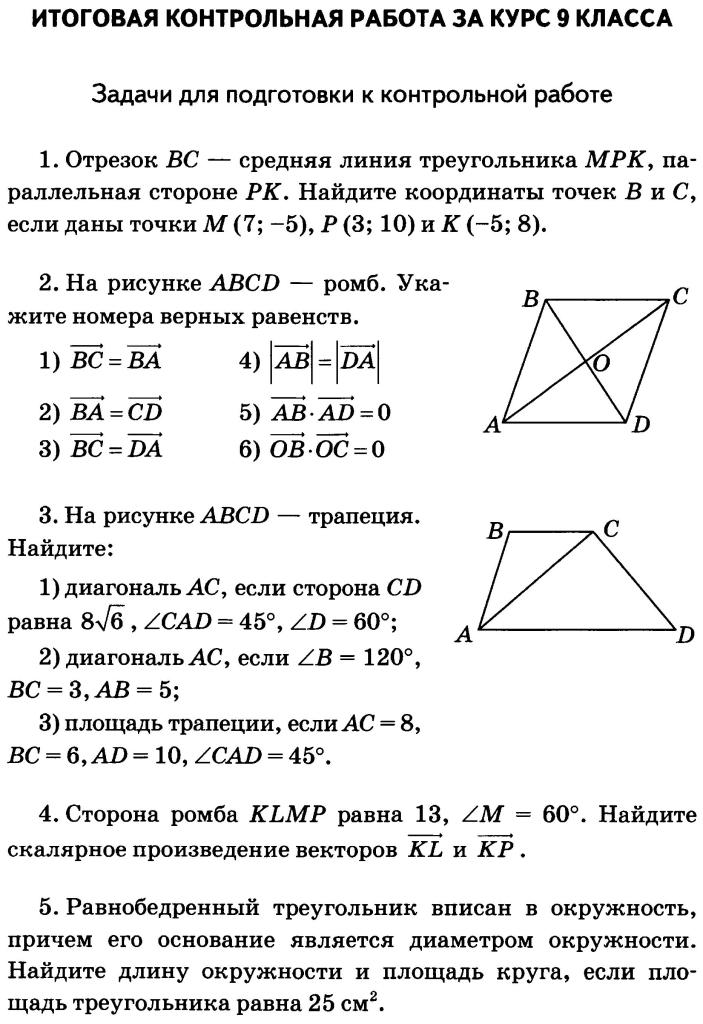

Утверждение б) теоремы Менелая доказано.Рисунок 13

Доказательство утверждения а) с использованием подобия треугольников

Идея доказательства состоит в замене соотношений длин отрезков из равенства (6) на отношения длин отрезков, лежащих на параллельных прямых.

Пусть точки A 1, B 1 и ИЗ 1 лежат на одной прямой. Из точек A , B и C проведите перпендикуляры AA 0, B B 0 и SS 0 к этой прямой (рис.14).

R
есть. 14

Из подобия трех пар треугольников AA 0 B 1 и CC 0 B 1, CC 0 A 1 и BB 0 A 1, C 1 B 0 B и C 1 A 0 A (под двумя углами) имеем правильные равенства

, г.
, г.
,

умножая их, получаем:

Утверждение а) теоремы Менелая доказано.

Доказательство утверждения а) с использованием областей

Идея доказательства состоит в замене отношения длин отрезков из равенства (7) на отношение площадей треугольников.

Пусть точки A 1, B 1 и ИЗ 1 лежат на одной прямой. Соедините точки C и C одну. Обозначим площади треугольников S 1, S 2, S 3, S 4, S 5 (рис.15).

Тогда равенства

, г.
, г.
. (8)

Умножая равенства (8), получаем:

Утверждение а) теоремы Менелая доказано.

R
есть. 15

Точно так же, как теорема Чевы остается верной, если точка пересечения хевианов находится вне треугольника, теорема Менелая остается верной, если секущая пересекает только продолжения сторон треугольника. В этом случае можно говорить о пересечении сторон треугольника во внешних точках.

Доказательство утверждения а) для внешних точек

P секущая устье пересекает стороны треугольника ABC во внешних точках, т.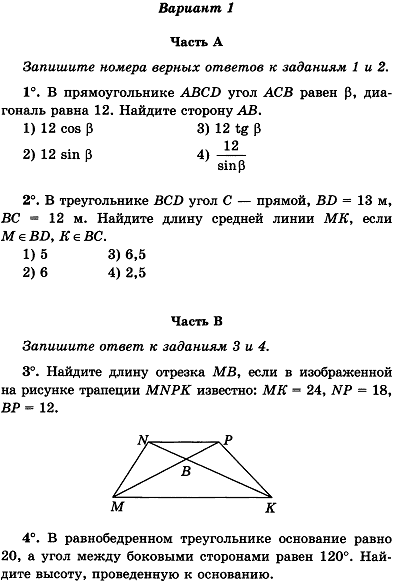 Е. Пересекает продолжения сторон AB , BC и AC в точках C 1, A 1 и B 1 соответственно, и эти точки лежат на одной прямой (рис. 16).

По теореме о пропорциональных отрезках имеем:

и.

Тогда справедливы равенства

Утверждение а) теоремы Менелая доказано. Рисунок 16

Отметим, что приведенное выше доказательство совпадает с доказательством теоремы Менелая для случая, когда секущая пересекает две стороны треугольника во внутренних точках и одну — во внешней.

Доказательство утверждения б) теоремы Менелая для случая внешних точек аналогично приведенному выше доказательству.

Задания 11. В треугольнике ABC точки A 1, IN 1 лежат соответственно на сторонах Sun и A ОТ . P — точка пересечения отрезков AA 1 и BB 1 .
, г.
… Найдите отношение
.

Решение. Обозначим
,
, г.
, г.
(рис.17). По теореме Менелая для треугольника BC IN 1 и секанса PA 1 запишем правильное равенство:

, откуда следует, что

… Рисунок 17

Ответ. .

Задания 12 (МГУ, заочная подготовка). В треугольнике ABC , площадь 6, сбоку AB точка взята TO , разделяет эту сторону относительно
и на стороне AS — точка L , деление AS во взаимосвязи
… точка P пересечения прямых SC и IN L удален от прямой AB на расстоянии 1.5. Найдите длину стороны AB.

Решение. От точек R и ОТ опускаем перпендикуляры PR и CM на прямой AB … Обозначим
,
, г.
, г.
(рис.18). По теореме Менелая для треугольника AKC и секущей PL мы записываем правильное равенство:
, откуда получаем, что
,
. .. Фигурка: восемнадцать

Из подобия треугольников TO MC и TO RP (в двух углах) получаем, что
, откуда следует, что
.

Теперь, зная длину высоты удерживаемой стороны AB треугольника ABC , и площадь этого треугольника, вычисляем длину стороны:
.

Ответ. 4.

Z adania 13. Три окружности с центрами A , IN , ИЗ , , радиусы которых связаны как
, касаются друг друга снаружи в точках X , Y , Z , как показано на рисунке 19.Отрезки AX и BY пересекаются в точке O . В каком отношении, отсчитывая от точки B , отрезок CZ делит отрезок BY ?

Решение. Обозначим
,
, г.
(рис. 19). Как и
, то по утверждению б) теоремы Чевы отрезки A, , X , BY и FROM Z пересекаются в одной точке — точке O . .. Затем сегмент CZ делит сегмент BY в соотношении
… Давайте найдем это отношение. Рисунок 19

По теореме Менелая для треугольника BCY и секущей OX имеем:
, откуда следует, что
.

Ответ. .

Задание 14 (ЕГЭ-2016).

Точки IN 1 и ИЗ AS и AB треугольник ABC и AB 1: B 1 ИЗ =
= КАК 1: ИЗ 1 B … Прямой BB 1 и SS 1 пересекаются в точке ПРО.

а) Докажите, что линия АО пополам сбоку вс.

AB 1 OC 1 на площадь треугольника ABC , если известно, что AB 1: B 1 ОТ = 1: 4.

Решение. а) Пусть прямая АО пересекает сторону BC в точке A 1 (рис.20). По теореме Шевы имеем:

. (9)

Как AB 1: B 1 ИЗ = AS 1: ИЗ 1 B , то равенство (9) означает, что
, то есть CA 1 = A 1 B , как требуется для доказательства. Рисунок двадцать

б) Пусть площадь треугольника AB 1 O равно S . Как AB 1: B 1 ИЗ CB 1 O равняется 4 S , а площадь треугольника AOC равно 5 S … Тогда площадь треугольника AOB — это также 5 S , поскольку треугольники AOB и AOC имеют общее основание AO , а их вершины B и C равноудалены от прямой AO … Причем площадь треугольника AOC 1 равна S , как AS 1: ИЗ 1 B = 1: 4. Тогда площадь треугольника ABB 1 равна 6 S … Так как AB 1: B 1 ОТ = 1: 4, то площадь треугольника CB 1 O равна 24 S , а площадь треугольника ABC равно 30 S … Теперь находим отношение площадей четырехугольника AB 1 OC 1 (2 S ) на площадь треугольника ABC (30 S ), он равен 1:15.

Ответ. 1:15.

Задание 15 (ЕГЭ-2016).

Точки IN 1 и ОТ 1 лежат по сторонам соответственно AS и AB треугольник ABC и AB 1: B 1 ОТ =
= AS 1: ИЗ 1 B … Прямой BB 1 и SS 1 пересекаются в точке ПРО.

а) Докажите, что линия АО пополам сбоку вс.

б) Найдите отношение площади четырехугольника AB 1 OC 1 к площади треугольника ABC , если известно, что AB 1: B 1 ИЗ = 1: 3.

Ответ. 1:10.

Z adania 1 6 (ЕГЭ-2016). На отрезке BD взято точка ОТ … Биссектриса BL ABC с фундаментом Sun BLD с фундаментом BD .

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что cos
ABC DL, т. е. треугольник BD точка взята ИЗ … Биссектриса BL равнобедренный треугольник ABC с основанием Солнце является боковой стороной равнобедренного треугольника. BLD с фундаментом BD .

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что cos ABC =.В каком отношении прямая DL разделяет сторону AB ?

Ответ. 4:21.

Литература

1. Смирнова И.М., Смирнов В.А. Замечательные точки и линии треугольника. М .: Математика, 2006, № 17.

2. Мякишев А.Г. Элементы геометрии треугольника. (Серия «Библиотека« Математическое образование »). М .: МЦНМО, 2002. — 32 с.

3. Геометрия. Дополнительные главы к учебнику для 8-х классов: Учебник для учащихся школ и классов с углубленным изучением / Л.С. Атанасян, В.Ф. Бутузов, С. Кадомцев и др. — М .: Вита-Пресс, 2005. — 208 с.

4. Эрдниев П., Манцаев Н. Теоремы Чевы и Менелая. М .: Квант, 1990, № 3. С. 56–59.

5. Шарыгин И.Ф. Теоремы Чевы и Менелая. М .: Квант, 1976, № 11. С. 22–30.

6. Вавилов В.В. Медианы и средние линии треугольника. М .: Математика, 2006, № 1.

7. Ефремов Дм. Новая геометрия треугольника. Одесса, 1902. — 334 с.

8. Математика.50 вариантов типовых тестовых заданий / И.В. Ященко, М.А.Волькевич, И. Высоцкий и другие; изд. И.В. Ященко. — М .: Издательство «Экзамен», 2016. — 247 с.

Теорема Менелая или теорема о полном четырехугольнике известна со времен Древней Греции. Свое название он получил в честь своего автора — древнегреческого математика и астронома Менелай Александрийский (ок. 100 г. н.э.). Эта теорема очень красивая и простая, но, к сожалению, в современном школьном курсе ей не уделяется должного внимания.А между тем во многих случаях он помогает очень легко и изящно решать довольно сложные геометрические задачи.

Теорема 1 (теорема Менелая) .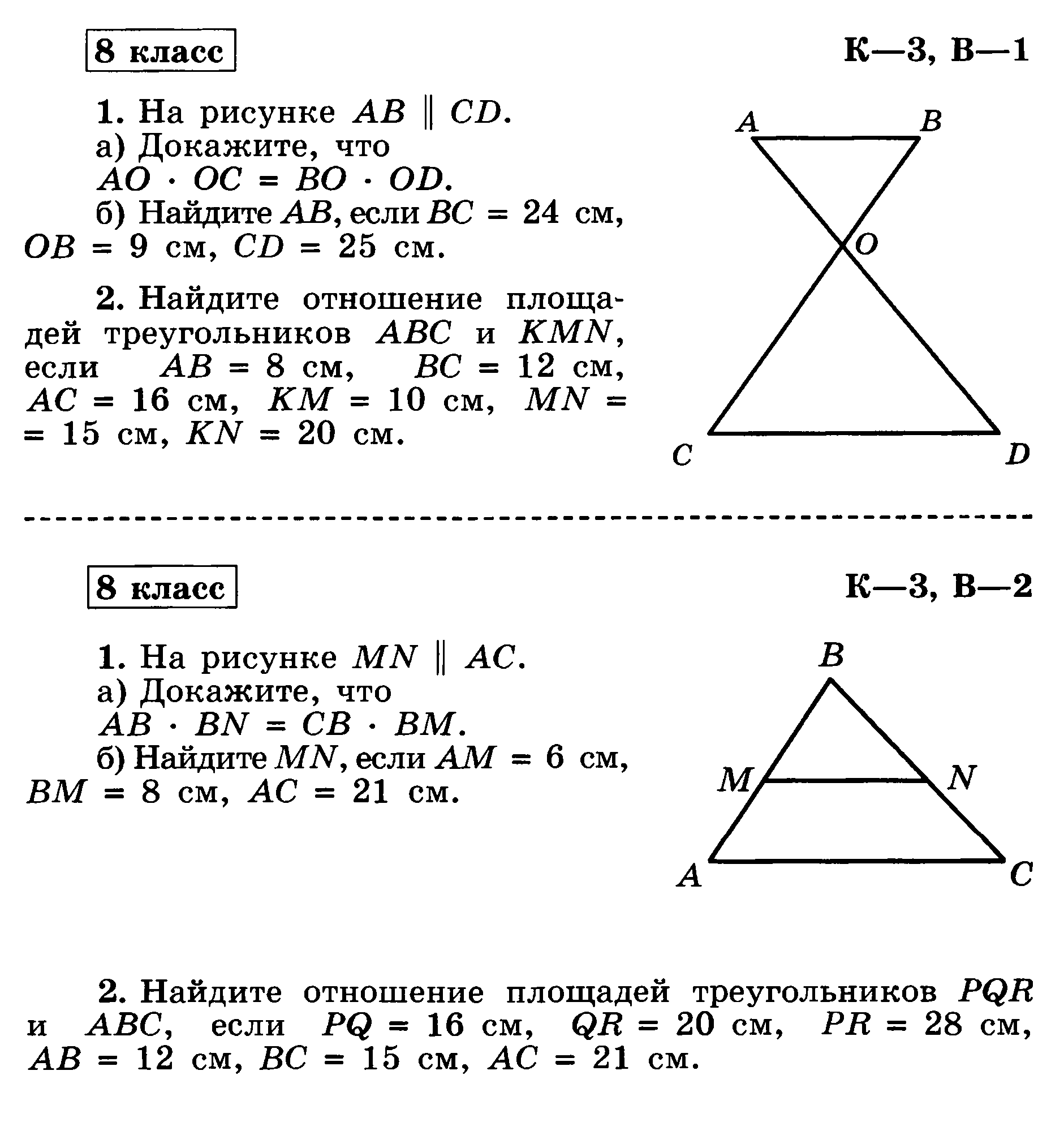 .. Пусть ∆ABC пересекает прямая, которая не параллельна стороне AB и пересекает две ее стороны AC и BC соответственно в точках F и E, а прямая AB в точках F и E точка D (рис.1) ,

, затем A F FC * CE EB * BD DA = 1

Примечание. Чтобы легко запомнить эту формулу, вы можете использовать следующее правило: двигайтесь по контуру треугольника от вершины к точке пересечения с прямой и от точки пересечения к следующей вершине.

Доказательства. Из вершин A, B, C треугольника проведите соответственно три параллельные прямые до пересечения с секущей линией. Получаем три пары одинаковых треугольников (знак сходства в двух углах). Подобие треугольников влечет следующие равенства

А теперь умножаем полученные данные на равенства:

Теорема доказана.

Чтобы ощутить всю красоту этой теоремы, попробуем решить предложенную ниже геометрическую задачу двумя разными способами: с помощью вспомогательной конструкции и с помощью теорем менелая .

Цель 1.

В ∆ABC биссектриса AD делит сторону BC в соотношении 2: 1. В каком соотношении медиана CE делит эту биссектрису?

Решение.

Использование вспомогательной конструкции:

Пусть S — точка пересечения биссектрисы AD и медианы CE. Дополним ∆ASB до параллелограмма ASBK. (рис. 2)

Очевидно SE = EK, так как пересечение параллелограмма делит диагонали пополам.Рассмотрим теперь треугольники ∆CBK и ∆CDS. Нетрудно заметить, что они похожи (признак сходства в двух углах: и как внутренние односторонние углы с параллельными линиями AD и KB и секущей CB). Подобие треугольника подразумевает следующее:

Используя условие, получаем:

CB CD = CD + DB CD = CD + 2CD CB = 3CD CD = 3

Теперь обратите внимание, что KB = AS как противоположные стороны параллелограмма. Тогда

AS SD = KB SD = CB CD = 3

Использование теоремы Менелая.

Рассмотрим ∆ABD и применим к нему теорему Менелая (прямая, проходящая через точки C, S, E, является секущей):

BE EA * AS SD * DC CB = 1

По условию теоремы у нас BE / EA = 1, так как CE — медиана, а DC / CB = 1/3, как мы рассчитали ранее.

1 * КАК СД * 1 3 = 1

Отсюда получаем AS / SD = 3 На первый взгляд оба решения достаточно компактны и примерно равны. Однако идея дополнительной конструкции для школьников часто оказывается очень сложной и совсем не очевидной, тогда как, зная теорему Менелая, ему нужно только правильно ее применить.

Рассмотрим другую задачу, в которой теорема Менелая работает очень элегантно.

Цель 2.

На сторонах AB и BC ∆ABC даны точки M и N соответственно такие, что выполняются следующие равенства

AM MB = CN NA = 1 2

В каком соотношении точка пересечения S отрезков BN и CM делит каждый из этих отрезков (рис. 3)?

Решение.

Рассмотрим ∆ABN.Применим теорему Менелая для этого треугольника (прямая, проходящая через точки M, S, C, является секущей)

AM MB * BC SN * CN CA = 1

Из условия задачи имеем: AM MB = 1 2

NC CA = NC CN + NA = NC CN + 2NC = NC 3 NC = 1 3

Подставляем эти результаты и получаем:

1 2 * БС СН * 1 3 = 1

Отсюда BS / SN = 6. А, значит, точка пересечения S отрезков BN и CM делит отрезок BN в соотношении 6: 1.

Рассмотрим ∆ACM. Применим теорему Менелая для этого треугольника (прямая, проходящая через точки N, S, B, является секущей):

AN NC * CS SM * MB BA = 1

Из постановки задачи имеем: AN NC = 2

МБ BA = MB BM + MA = 2MA 2MA + MA = 2MB 3MA = 2 3

Подставляем эти результаты и получаем:

2 * КС СМ * 2 3 = 1

Отсюда CS / SM = 3/4

Это означает, что точка S пересечения отрезков BN и CM делит отрезок CM в соотношении 3: 4.

Верна и обратная теорема Менелая. Часто это бывает даже полезнее. Это особенно хорошо работает в задачах доказательства. Часто с его помощью даже олимпиадные задачи решаются красиво, легко и быстро.

Теорема 2 (обратная теорема Менелая). Пусть дан треугольник ABC и точки D, E, F принадлежат прямым BC, AC, AB соответственно (обратите внимание, что они могут лежать как на сторонах треугольника ABC, так и на их продолжениях) (рис. 4) .

Тогда если AF FC * CE EB * BD DA = 1

то точки D, E, F лежат на одной прямой.

Доказательства. Докажем теорему от противного. Предположим, что соотношение из условий теоремы выполнено, но точка F не лежит на прямой DE (рис. 5).

Обозначим точку пересечения прямых DE и AB буквой O. Теперь применим теорему Менелая и получим: AE EC * CD DB * BO OA = 1

Но, с другой стороны, равенство BF FA = BO OA

не может быть выполнен.

Следовательно, соотношение из условий теоремы не может быть выполнено. Получили противоречие.

Теорема доказана.

Сайт

, при полном или частичном копировании материала ссылка на источник обязательна.

Класс: 9

Задачи урока:

обобщить, расширить и систематизировать знания и умения студентов; научить использовать знания при решении сложных задач;
способствовать развитию навыков самостоятельного применения знаний при решении задач;
для развития логического мышления и математической речи учащихся, умения анализировать, сравнивать и обобщать;
воспитывать у студентов уверенность в себе, трудолюбие; умение работать в команде.

Задачи урока:

Воспитательная: повторить теоремы Менелая и Чевы; применяйте их при решении проблем.
Развивающие: учат выдвигать гипотезы и умело отстаивать свое мнение доказательствами; проверьте умение обобщать и систематизировать свои знания.
Образовательные: повысить интерес к предмету и подготовить к более сложным задачам.

Тип урока: урок по обобщению и систематизации знаний.

Оборудование: карточки для коллективной работы на уроке по данной теме, индивидуальные карточки для самостоятельной работы, компьютер, мультимедийный проектор, экран.

В классах

I этап. Организационный момент (1 мин.)

Учитель разъясняет тему и цель урока.

II этап. Обновление базовых знаний и навыков (10 мин.)

Учитель: На уроке мы вспоминаем теоремы Менелая и Чевы, чтобы успешно перейти к решению задач.Давайте вместе с вами посмотрим на экран. Для какой теоремы дана эта цифра? (Теорема Менелая). Постарайтесь четко сформулировать теорему.

Рисунок 1

Пусть точка A 1 лежит на стороне BC треугольника ABC, точка C 1 — на стороне AB, точка B 1 — на продолжении стороны AC за точку C. Точки A 1, B 1 и C 1 лежат на одной прямой, если и только если равенство

Учитель: Давайте вместе посмотрим на следующий рисунок. Сформулируйте теорему для этого рисунка.

Изображение 2

Линия AD пересекает две стороны и является продолжением третьей стороны треугольника BMC.

По теореме Менелая

Линия MB пересекает две стороны и является продолжением третьей стороны треугольника ADC.

По теореме Менелая

Учитель: Какой теореме соответствует цифра? (Теорема Чевы). Сформулируйте теорему.

Рисунок 3

Пусть в треугольнике ABC точка A 1 лежит на стороне BC, точка B 1 — на стороне AC, точка C 1 — на стороне AB.Отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство

III этап. Решаю задачи. (22 мин.)

Класс делится на 3 команды, каждая из которых получает карточку с двумя разными задачами. Дается время на решение, затем на экране отображается … По готовым чертежам задач представители команд поочередно объясняют свое решение. Каждое объяснение сопровождается обсуждением, ответами на вопросы и проверкой правильности решения на экране.В обсуждении принимают участие все члены команды. Чем активнее команда, тем выше ее оценивают при подведении итогов.

Карточка 1.

1. В треугольнике ABC на стороне BC берется точка N так, чтобы NC = 3BN; на продолжении стороны АС за точку А берется точка М так, чтобы МА = АС. Прямая MN пересекает сторону AB в точке F. Найдите отношение

2. Докажите, что медианы треугольника пересекаются в одной точке.

Решение 1

Рисунок 4

По условию задачи MA = AC, NC = 3BN.Пусть MA = AC = b, BN = k, NC = 3k. Прямая MN пересекает две стороны треугольника ABC и продолжение третьей.

По теореме Менелая

Ответ:

Проба 2

Рисунок 5

Пусть AM 1, BM 2, CM 3 — медианы треугольника ABC. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что

Тогда по (обратной) теореме Чева отрезки AM 1, BM 2 и CM 3 пересекаются в одной точке.

У нас:

Итак, доказано, что медианы треугольника пересекаются в одной точке.

Карточка 2.

1. На стороне PQ треугольника PQR берется точка N, а на стороне PR — точка L, а NQ = LR. Пересечение QL и NR делит QL относительно m: n, считая от точки Q. Найдите

2. Докажите, что биссектрисы треугольника пересекаются в одной точке.

Решение 1

Рисунок 6

По условию NQ = LR, Пусть NA = LR = a, QF = км, LF = kn.Линия NR пересекает две стороны треугольника PQL и продолжение третьей.

По теореме Менелая

Ответ:

Проба 2

Рисунок 7

Покажем, что

Тогда по (обратной) теореме Шевы AL 1, BL 2, CL 3 пересекаются в одной точке. По свойству биссектрис треугольника

Почленно умножая полученные равенства, получаем

Для биссектрис треугольника выполняется равенство Чевы, следовательно, они пересекаются в одной точке.

Карточка 3.

1. В треугольнике ABC AD — медиана, точка O — середина медианы. Прямой BO пересекает сторону AC в точке K. В каком соотношении точка K делит AC, считая от точки A?

2. Докажите, что если окружность вписана в треугольник, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке.

Решение 1

Рисунок 8

Пусть BD = DC = a, AO = OD = m.Линия BK пересекает две стороны и продолжение третьей стороны треугольника АЦП.

По теореме Менелая

Ответ:

Проба 2

Рисунок 9

Пусть A 1, B 1 и C 1 — точки касания вписанной окружности треугольника ABC. Чтобы доказать, что отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:

Используя свойство касательных, проведенных к окружности из одной точки, введем обозначения: C 1 B = BA 1 = x, AC 1 = CB 1 = y, BA 1 = AC 1 = z.

Равенство Чевы выполняется, что означает, что биссектрисы треугольника пересекаются в одной точке.

IV этап. Решение задач (самостоятельная работа) (8 мин.)

Учитель: Работа команд окончена и теперь мы приступим к самостоятельной работе над индивидуальными карточками по 2 вариантам.

Материалы к уроку для самостоятельной работы студентов

Вариант 1. В треугольнике ABC, площадь которого равна 6, на стороне AB берется точка K, разделив эту сторону в соотношении AK: BK = 2: 3, а на стороне AB. сторона AC — точка L, делящая AC в соотношении AL: LC = 5: 3.Точка Q пересечения прямых SK и BL удалена от линии AB на некоторое расстояние. Найдите длину стороны AB. (Ответ: 4.)

Вариант 2. Точка K берется на стороне переменного тока в треугольнике ABC. Найти длину высоты треугольника ABC, выпавшего из вершины B. (ответ: 1.5.)

Работы переданы учителю для проверки.

Этап V. Подведение итогов (2 мин.)

Ошибки проанализированы, оригинальные ответы и комментарии отмечены.Подведены итоги работы каждой команды и выставлены оценки.

VI этап. Домашнее задание (1 мин.)

Домашнее задание состоит из задач № 11, 12 с. 289-290, № 10, с. 301.

Заключительное слово преподавателя (1 мин).

Сегодня вы услышали математические речи друг друга и оценили свои способности. В будущем мы будем применять такие обсуждения, чтобы лучше понять предмет. Аргументы на уроке дружили с фактами, а теория — с практикой.Спасибо вам всем.

Литература:

В.В. Ткачук Математика для соискателя. — М .: МЦНМО, 2005.

ТЕОРЕМА ЧЕВЫ И МЕНЕЛЫ

Теорема Чевы

Большинство замечательных точек треугольника можно получить, используя следующую процедуру. Пусть существует какое-то правило, по которому мы можем выбрать некоторую точку A 1 , на стороне BC (или ее продолжении) треугольника ABC (например, выберите середину этой стороны).Затем строим аналогичные точки B 1, C 1 на двух других сторонах треугольника (в нашем примере еще две середины сторон). Если правило выбора выполнено успешно, то прямые AA 1, BB 1, CC 1 пересекаются в некоторой точке Z (выбор середин сторон в этом смысле, конечно, удачный, так как медианы треугольника пересекаются в точках один пункт).

Я хотел бы иметь какой-нибудь общий метод, который позволяет по положению точек на сторонах треугольника определять, пересекаются ли соответствующие тройки прямых в одной точке или нет.

Универсальное условие, которое «закрыло» эту проблему, было найдено в 1678 году итальянским инженером. Джованни Чева .

Определение. Отрезки, соединяющие вершины треугольника с точками на противоположных сторонах (или их продолжениях), называются шевианами, если они пересекаются в одной точке.

Есть два варианта расположения чевианов. В одном варианте точки

,
,

пересечение является внутренним, а концы шевианов лежат на сторонах треугольника.Во втором варианте точка пересечения внешняя, конец одного шевиана лежит сбоку, а два других имеют концы на продолжениях сторон (см. Рисунки).

Теорема 3. ( Прямая теорема Чевы) В произвольном треугольнике ABC на сторонах BC, CA, AB или их продолжениях взяты точки A соответственно 1 , IN 1 , ИЗ 1 такие, что прямые AA 1 , BB 1 , SS 1 пересекаются в некоторой общей точке, затем

Обоснование: есть несколько оригинальных доказательств теоремы Чевы; мы рассмотрим доказательство, основанное на двукратном применении теоремы Менелая. Впервые выпишем соотношение теоремы Менелая для треугольника ABB 1 и секущей CC 1 (точка пересечения шевиана будет Z):

, г.

и второй раз для треугольника B 1 BC и секанс AA 1 :

Умножая эти два отношения и делая необходимые сокращения, мы получаем соотношение, содержащееся в формулировке теоремы.

Теорема 4. (обратная теорема Чевы) . Если для выбранных по сторонам треугольника ABC или их продолжение точек А 1 , IN 1 и С 1 Состояние чевы выполнено:

, г.

затем прямо AA 1 , г. BB 1 и CC 1 пересекаются в одной точке .

Доказательство этой теоремы проводится от противного, как и доказательство теоремы Менелая.

Рассмотрим примеры применения прямой и обратной теорем Чевы.

Пример 3. Докажите, что медианы треугольника пересекаются в одной точке.

Решение. Рассмотрим отношение

для вершин треугольника и середин его сторон. Очевидно, что в каждой дроби в числителе и знаменателе есть равные отрезки, поэтому все эти дроби равны единице.Следовательно, соотношение Чевы выполняется, следовательно, по обратной теореме медианы пересекаются в одной точке.

Теорема (теорема Шевы) … Пусть точки лежат на сторонах и треугольнике соответственно. Пусть отрезки и пересекаются в одной точке. Затем

(обойти треугольник по часовой стрелке).

Доказательства. Обозначим через точку пересечения отрезков прямой и … Опустим от точек и перпендикуляров к прямой, прежде чем пересекать ее в точках и соответственно (см. Рисунок).

Поскольку треугольники и имеют общую сторону, то их площади называются высотами, проведенными с этой стороны, то есть:

Последнее равенство верно, поскольку прямоугольные треугольники и имеют одинаковый острый угол.

Аналогично получаем

Умножим эти три равенства:

q.E.D.

О медианах:

1. Поместите единичные массы в вершины треугольника ABC.
2.Центр масс точек A и B находится в середине AB. Центр масс всей системы должен находиться посередине к стороне AB, так как центр масс треугольника ABC является центром масс центра масс точек A и B, и точки C.
(как оказалось сбивает с толку)
3. Точно так же CM должна лежать на медиане сторон AC и BC
4. Поскольку CM является единственной точкой, все эти три медианы должны пересекаться в ней.

Кстати, сразу следует, что они делятся перекрестком в соотношении 2: 1.Поскольку масса центра масс точек A и B равна 2, а масса точки C равна 1, следовательно, общий центр масс, согласно теореме о пропорции, будет делить медианное значение на соотношение 2/1.

Большое спасибо, четко сказано, думаю, будет не лишним представить документ методами массовой геометрии, например:
Линии AA1 и CC1 пересекаются в точке O; AC1: C1B = p и BA1: A1C = q. Нам нужно доказать, что прямая BB1 проходит через точку O тогда и только тогда, когда CB1: B1A = 1: pq.
Поместите гири 1, p и pq в точки A, B и C соответственно. Тогда точка C1 — это центр масс точек A и B, а точка A1 — центр масс точек B и C. Следовательно, центр масс точек A, B и C с этими массами является точкой O пересечения. прямых CC1 и AA1. С другой стороны, точка O лежит на отрезке, соединяющем точку B с центром масс точек A и C. Если B1 является центром масс точек A и C с массами 1 и pq, то AB1: B1C = pq: 1.Остается заметить, что на отрезке AC есть одна точка, разделяющая его в этом отношении AB1: B1C.

2. Теорема Чевы

Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется cheviana … Таким образом, если в треугольнике ABC х , Y и Z — точки лежащие по бокам до н.э. , CA , AB соответственно сегменты AX , BY , CZ являются чевианцами.Этот термин происходит от имени итальянского математика Джованни Чева, который опубликовал следующую очень полезную теорему в 1678 году:

Теорема 1,21. Если три шевиана AX, BY, CZ (по одной из каждой вершины) треугольника ABC конкурируют, то

| BX || XC | · | CY || YA | · | AZ || ZB | = 1 .

Когда мы говорим, что три линии (или сегмента) конкурентоспособны , то имеем в виду, что все они проходят через одну точку, которую обозначим P … Чтобы доказать теорему Чевы, напомним, что площади треугольников одинаковой высоты пропорциональны основаниям треугольников. Ссылаясь на рисунок 3, мы имеем:

| BX || XC | = SABXSAXC = SPBXSPXC = SABX − SPBXSAXC − SPXC = SABPSCAP.

Аналогично

| CY || YA | = SBCPSABP, | AZ || ZB | = SCAPSBCP.

Теперь, если мы их умножим, мы получим

| BX || XC | · | CY || YA | · | AZ || ZB | = SABPSCAP · SBCPSABP · SCAPSBCP = 1 .

Верна и обратная теорема к этой теореме:

Теорема 1.22. Если три чевиана AX, BY, CZ удовлетворяют соотношению

| BX || XC | · | CY || YA | · | AZ || ZB | = 1 ,

то они конкурентоспособны .

Чтобы показать это, предположим, что первые два Чевиана пересекаются в точке P , как и прежде, и третья шевиана, проходящая через точку P , составит CZ ′ … Тогда по теореме 1.21

| BX || XC | · | CY || YA | · | AZ ′ || Z′B | = 1 .

Но по предположению

| BX || XC | · | CY || YA | · | AZ || ZB | = 1 .

Следовательно,

| AZ || ZB | = | AZ ′ || Z′B | ,

точка Z ′ совпадает с точкой Z , и мы доказали, что сегменты AX , BY и CZ соревновательные (стр. 54 и, стр. 48, 317).

В курсе геометрии есть теоремы, которые в школе недостаточно подробно изучаются, но которые могут быть полезны при решении самых сложных задач ОГЭ и ЕГЭ. К ним относится, например, теорема Менелая.Традиционно ее изучают в классах с углубленным изучением математики в 8-м классе, а в обычную учебную программу (по учебнику Атанасяна) теорема Менелая входит в учебники 10-11 классов.
Между тем, результат изучения интернет-ресурсов, где упоминается теорема Менелая, показывает, что обычно она формулируется не полностью, а потому неточно, и не приводятся все случаи ее использования, а также доказательство обратной теоремы. Цель этой статьи — понять, что такое теорема Менелая, как и почему она используется, а также поделиться с учениками методикой преподавания этой теоремы на индивидуальных уроках с репетитором.
Рассмотрим типичную проблему (Задача № 26, ОГЭ), встречающуюся на экзаменах в различных вариантах, которые различаются только числами в условии.

Само решение проблемы несложное — вы можете ознакомиться с ним ниже. В этой статье нас в основном интересует немного другой момент, который часто опускается, понимается как самоочевидный, как очевидный. Но очевидное — это то, что можно доказать. И это можно доказать по-разному — обычно это доказывают исключительно с помощью подобия, — но это можно сделать и с помощью теоремы Менелая.
Из условия следует, что, поскольку углы у нижнего основания трапеции в сумме составляют 90 °, то, если удлинить стороны, получится прямоугольный треугольник. Далее из полученной точки пересечения продолжений боковых сторон проводится отрезок, проходящий через средние точки оснований. Почему этот отрезок проходит через все эти три точки? Обычно об этом не говорится ни слова в решениях проблем, найденных в Интернете. Нет даже ссылки на теорему о четырех точках трапеции, не говоря уже о доказательстве этого утверждения.Между тем, это можно доказать с помощью теоремы Менелая, которая является условием того, что три точки принадлежат одной прямой.

Формулировки теоремы Менелая
Пришло время сформулировать теорему. Следует отметить, что в разных учебниках и учебных пособиях встречаются довольно разные его формулировки, хотя суть остается неизменной. В учебнике Атанасяна и соавт. Для 10-11 классов дана следующая формулировка теоремы Менелая, назовем ее «вектор»:

В учебнике «Геометрия 10-11 классы» Александрова и др., Так же, как и в учебнике тех же авторов «Геометрия. 8 класс», дана несколько иная формулировка теоремы Менелая, и она одинакова для 10-11 и 8 классов:
Здесь нужно отметить три момента. .
Примечание 1. На экзаменах нет задач, которые нужно решать только с помощью векторов, для которых используется ровно «минус один». Поэтому для практического использования наиболее удобная формулировка является, по сути, следствием теоремы для отрезков (это вторая формулировка, выделенная жирным шрифтом).Мы ограничимся им для дальнейшего изучения теоремы Менелая, поскольку наша цель — научиться применять ее для решения задач.
Примечание 2. Несмотря на то, что во всех учебниках также четко прописан случай, когда все три точки A 1, B 1 и C 1 могут лежать на продолжениях сторон треугольника (или на прямых, содержащих стороны треугольника ), на нескольких обучающих сайтах в Интернете сформулирован только случай, когда две точки лежат на двух сторонах, а третья лежит на продолжении третьей стороны.Вряд ли это может быть оправдано тем фактом, что на экзаменах встречаются только проблемы первого типа, а проблемы не могут встречаться, когда все эти точки лежат на продолжении трех сторон.
Примечание 3. Обратная теорема, т.е. условие, что три точки лежат на одной прямой, обычно вообще не рассматривается, и некоторые преподаватели даже советуют (???) иметь дело только с прямой теоремой, а не рассматривать обратную. теорема. Между тем доказательство обратного утверждения достаточно поучительно и позволяет доказать утверждения, аналогичные приведенным в решении задачи 1.Опыт доказательства обратной теоремы, несомненно, принесет студенту заметную пользу при решении задач.

Рисунки и шаблоны

Чтобы научить студента видеть теорему Менелая в задачах и использовать ее в решениях, важно обращать внимание на изображения и шаблоны в записи теоремы для конкретного случая. А поскольку сама теорема находится в «чистом» виде, т.е. не окружена другими отрезками, стороны разных фигур в задачах обычно не встречаются, то целесообразнее показывать теорему на конкретных задачах.А если в качестве объяснения показывать картинки, то сделайте их многомерными. При этом выделите одним цветом (например, красным) прямую, образованную тремя точками, а синим — отрезки треугольника, участвующие в записи теоремы Менелая. При этом те элементы, которые не участвуют, остаются черными:

На первый взгляд может показаться, что формулировка теоремы довольно сложна и не всегда ясна; потому что в нем задействованы три фракции.Ведь если у ученика недостаточно опыта, то он легко может ошибиться в письменной форме и, как следствие, неправильно решить задачу. И здесь иногда начинаются проблемы. Дело в том, что учебники обычно не акцентируют внимание на том, как «сделать обходной путь» при написании теоремы. О законах написания самой теоремы ничего не сказано. Поэтому некоторые репетиторы даже рисуют разные стрелки, в каком порядке записывать формулу. И они предлагают студентам строго следовать этим рекомендациям. Отчасти это правильно, но гораздо важнее понять суть теоремы, чем записывать ее чисто механически, используя «правило обхода» и стрелки.
На самом деле важно только понимать логику «обхода», но она настолько точна, что невозможно ошибиться при написании формулы. В обоих случаях а) и б) запишем формулу треугольника AMC.
Для начала определим для себя три точки — вершины треугольника. У нас есть эти точки A, M, C. Затем мы определяем точки, лежащие на пересекающейся прямой (красная линия), это B, P, K. Начинаем «движение» с вершины треугольника, например, с точка C.От этой точки «идем» до точки, которая образована пересечением, например, стороны AC и пересекающейся прямой — у нас есть эта точка K. Пишем в числителе первой дроби — SK. Далее от точки K «идем» до оставшейся точки на прямой AC — в точку A. В знаменателе первой дроби пишем — KA. Поскольку точка A также принадлежит прямой AM, то же самое проделываем с отрезками на прямой AM. И здесь мы снова начинаем сверху, затем «идем» до точки на пересекающейся прямой, а затем переходим к вершине M.«Оказавшись» на прямой BC, мы делаем то же самое с отрезками на этой прямой. Из M мы, естественно, «идем» в B, после чего возвращаемся в C. Этот «объезд» можно делать как по часовой стрелке, так и против часовой стрелки. Важно только понять правило обхода — от вершины к точке на прямой и от точки на прямой к другой вершине. Так обычно объясняют правило написания произведения дробей. Результат:
Обратите внимание на то, что весь «обход» отражен в записи и для удобства показан стрелками.
Однако итоговая запись может быть получена без выполнения какого-либо «обхода». После того, как точки — вершины треугольника (A, M, C) и точки — лежащие на пересекающейся прямой (B, P, K) выписаны, они также записывают тройки букв, обозначающих точки, лежащие на каждой из три строки. В наших случаях это I) B, M, C; II) A, P, M и III) A, C, K. После этого правильную левую часть формулы можно записать, даже не глядя на рисунок, и в любом порядке. Нам достаточно из каждой тройки букв написать правильные дроби, подчиняющиеся правилу — условно «средние» буквы — это точки пересекающейся прямой (красная).Условно «крайними» буквами являются точки вершин треугольника (синие). При написании формулы таким образом вам нужно только убедиться, что любая «синяя» буква (вершина треугольника) попадет и в числитель, и в знаменатель один раз. Например.
Этот метод особенно полезен для случаев типа b), а также для самопроверки.

Теорема Менелая. Доказательство
Есть несколько разных способов доказать теорему Менелая. Иногда доказывают, используя подобие треугольников, для которых из точки M проводится отрезок, параллельный AC (как на этом чертеже).Другие проводят дополнительную прямую линию, не параллельную пересекающейся линии, а затем прямыми линиями, параллельными пересекающейся линии, они, кажется, «проецируют» все необходимые отрезки на эту линию и, используя обобщение теоремы Фалеса (т. Е. теорема о пропорциональных отрезках), выведите формулу. Однако, возможно, самый простой способ доказательства получается, если провести из точки M прямую линию, параллельную пересечению. Докажем таким образом теорему Менелая.
Дано: Треугольник ABC.Линия PK пересекает стороны треугольника и продолжение стороны MC в точке B.
Докажите, что выполняется равенство:
Доказательство. Нарисуйте луч MM 1 параллельно BK. Запишем соотношения между отрезками, которые входят в обозначения формулы теоремы Менелая. В одном случае рассмотрим прямые, пересекающиеся в точке A, а в другом случае — в точке C. Умножим левую и правую части этих уравнений:

Теорема доказана.
Теорема доказывается аналогично для случая б).

Из точки C проведите отрезок CC 1, параллельный линии BK. Запишем отношения между отрезками, которые входят в обозначения формулы теоремы Менелая. В одном случае рассмотрим прямые, пересекающиеся в точке A, а в другом — в точке M. Поскольку в теореме Фалеса не сказано Что-нибудь о расположении отрезков на двух пересекающихся прямых, отрезки могут располагаться по разные стороны от точки M. Следовательно,

Теорема доказана.

Теперь докажем обратную теорему.
Дано:
Докажите, что точки B, P, K лежат на одной прямой.
Доказательства. Пусть прямая BP пересекает AC в некоторой точке K 2, которая не совпадает с точкой K. Поскольку BP — прямая, содержащая точку K 2, для нее верна только что доказанная теорема Менелая. Итак, для нее мы пишем
. Однако мы только что доказали, что
. Отсюда следует, что точки K и K 2 совпадают, поскольку они разделяют сторону AC в одинаковом соотношении.
Для случая б) теорема доказывается аналогично.

Решение проблем с использованием теоремы Менелая

Во-первых, давайте вернемся к проблеме 1 и решим ее. Прочитаем еще раз. Сделаем рисунок:

Дана трапеция ABCD. ST — средняя линия трапеции, то есть одно из заданных расстояний. Углы A и D в сумме составляют 90 °. Продлим стороны AB и CD и получим точку K на их пересечении. Соедините точку K с точкой N — серединой BC. Теперь докажем, что точка P, являющаяся серединой основания AD, также принадлежит прямой KN.Рассмотрим последовательно треугольники ABD и ACD. Две стороны каждого треугольника пересекает линия KP. Предположим, что прямая KN пересекает базу AD в некоторой точке X. По теореме Менелая:
Поскольку треугольник AKD прямоугольный, точка P, которая является серединой гипотенузы AD, равноудалена от A, D и K. Аналогично , точка N равноудалена от точек B, C и K. Отсюда одна база равна 36, а другая — 2.
Решение. Рассмотрим треугольник BCD. Его пересекает луч AX, где X — точка пересечения этого луча с продолжением стороны BC.По теореме Менелая:
Подставляя (1) в (2), получаем:

Решение. Обозначим буквами S 1, S 2, S 3 и S 4 площади треугольников AOB, AOM, BOK и четырехугольника MOKC соответственно.

Поскольку BM — медиана, то S ABM = S BMC.
Следовательно, S 1 + S 2 = S 3 + S 4.
Так как нам нужно найти соотношение площадей S 1 и S 4, разделим обе части уравнения на S 4:
Подставим эти значения. К формуле (1): Из треугольника BMC с секущей AK по теореме Менелая имеем: Из треугольника AKC с секущей BM по теореме Менелая имеем: Все необходимые отношения выражаются через k и теперь вы можно подставить их в выражение (2):
Решение этой проблемы с помощью теоремы Менелая обсуждается на странице.

Примечание репетитора по математике. Применение теоремы Менелая в этой задаче — тот самый случай, когда этот метод позволяет существенно сэкономить время на экзамене. Эта задача предложена в демо-версии вступительного экзамена в 9-й лицей НИУ ВШЭ (2019).

Решайте сами

1) Задача попроще. Точка M отмечается на медиане BD треугольника ABC так, чтобы BM: MD = m: n.Линия AM пересекает сторону BC в точке K.
Найдите соотношение BK: KC.
2) Задача посложнее. Биссектриса угла A параллелограмма ABCD пересекает сторону ВС в точке P, а диагональ BD — в точке T. Известно, что AB: AD = k (0 3) Задача № 26 ОГЭ. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 36. Найдите стороны треугольника ABC.
Совет репетитора по математике. В Интернете есть решение такой задачи с помощью дополнительного построения и затем либо подобия, либо нахождения площадей, и только после этого сторон треугольника.Те. оба эти метода требуют дополнительной конструкции. Однако решение такой задачи с использованием свойства биссектрисы и теоремы Менелая не требует дополнительных построений. Это намного проще и рациональнее.

Круглые тела Солнечной системы. Презентация на тему «Круглые геометрические тела» Круглые тела в повседневной жизни

Слайд 2

Цилиндр Конус Сфера Исторические факты Интересные Авторы

Slide 3

Цилиндр Цилиндр — это тело, ограниченное цилиндрической поверхностью и двумя окружностями с границами.Боковая поверхность — цилиндрическая поверхность Основание — окружности Генераторы — образующие цилиндрической поверхности Ось — прямая OO1 Радиус — радиус основания Высота — длина образующей

Slide 4

Типы секций:

Осевой Если плоскость резания проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого являются образующими, а две другие — диаметрами оснований цилиндра. Круговой Если плоскость сечения перпендикулярна оси цилиндра, то сечение представляет собой круг.Цилиндр можно получить, повернув прямоугольник вокруг одной из его сторон

Слайд 5

Площадь цилиндра

Общая площадь поверхности цилиндра складывается из площадей боковой поверхности и двух оснований. S = 2πr (r + h) Площадь боковой поверхности цилиндра равна произведению окружности основания и высоты цилиндра. Площадь его стреловидности принимается за площадь боковой поверхности цилиндра.S = 2πrh

Slide 6

Историческая справка о цилиндре

ЦИЛИНДР .. Слово «цилиндр» происходит от греческого kylindros, что означает «ролик», «ролик».

Slide 7

Cone Cone — тело, ограниченное конической поверхностью и окружностью с границей. Коническая поверхность — боковая поверхность конуса Основание-окружность Образующие конусов — образующие конической поверхности Ось-прямая линия, проходящая через центр основания и вершину конуса

Slide 8

Типы секций:

Осевой — Если плоскость сечения проходит через ось конуса, то сечение представляет собой равнобедренный треугольник.Основание которого составляет диаметр основания конуса, а боковые стороны образуют конус. Круговой — если секущая плоскость перпендикулярна оси конуса, то сечение представляет собой круг. Конус можно получить, вращая прямоугольный треугольник вокруг одной из ножек.

Слайд 9

Площадь конуса

Площадь общей поверхности конуса называется суммой площадей боковой поверхности и основания S = πr (l + r) Площадь боковой поверхности конуса равна на произведение половины окружности основания генератором.S = πrl Площадь его развертки принимается за площадь боковой поверхности конуса.

Слайд 10

Основные формулы

Slide 11

Историческая справка о конусе

ЦИЛИНДР .. Слово «цилиндр» происходит от греческого kylindros, что означает «ролик», «ролик». КОНУС. Латинское слово conus заимствовано из греческого языка (konos — пробка, пробка, сосновая шишка). В XI книге «Начала» дается следующее определение: если прямоугольный треугольник, вращающийся вокруг одной из ног, возвращается в то же положение, из которого он начал движение, то описанная фигура будет конусом.Евклид считает только

Slide 12

Сфера Сфера — поверхность, состоящая из всех точек в пространстве, расположенных на заданном расстоянии от заданной точки. Сегмент радиуса, соединяющий центр с любой точкой на сфере Сегмент диаметра, соединяющий две точки сферы и проходящий через ее центр. Хорда — это отрезок прямой, соединяющий любые две точки сферы.

Слайд 13

Область сферы

За площадь сферы мы берем предел последовательности площадей описываемых поверхностей вокруг сферы многогранников, так как наибольший размер каждой грани стремится к нулю.2

Сдвиг 14

Касательная плоскость к сфере

Касательная плоскость к сфере — это плоскость, которая имеет только одну общую точку со сферой. Точка касания — это их общая точка. Теорема: радиус сферы, проведенный к точке касания сферы и плоскости, перпендикулярен касательной плоскости. Теорема: Если радиус сферы перпендикулярен плоскости, проходящей через ее конец, лежащий на сфере, то эта плоскость касается сферы

Slide 15

Историческая справка о сфере

Однако оба слова «шар» и «сфера» происходят от одного и того же греческого слова «сфира» — шар.В данном случае слово «шар» образовалось от перехода согласных звуков sf на w. В древности сфера была в почете. Астрономические наблюдения над небосводом неизменно вызывали образ шара. Пифагорейцы учили о существовании десяти сфер Вселенной, по которым якобы движутся небесные тела. Они утверждали, что расстояния этих тел друг от друга пропорциональны интервалам музыкальной гаммы. В этом просматривались элементы мировой гармонии.В таких полумистических рассуждениях была пифагорейская «музыка сфер». Аристотель считал, что сферическая форма, как наиболее совершенная, характерна для Луны, Солнца, Земли и всех тел мира. Развивая взгляды Евдокса, он считал, что Земля окружена рядом концентрических сфер. Сфера всегда широко использовалась в различных областях науки и техники. В XI Книге начал Евклид определяет шар как фигуру, описываемую полукругом, вращающимся вокруг фиксированного диаметра.

Slide 16

Водовзводная башня Водовзводная башня построена в 1488 году. Прежнее название башни — Свиблова — связано с находившимся поблизости двором боярина Свиблова. В 1633 году в башне установили водяной насос для перекачки воды в резервуар, расположенный наверху башни. По трубам вода разливалась по Кремлю. В 1805-1806 годах башню разобрали и перестроили по проекту архитектора И.В. Еготов. В 1812 году башня была взорвана французами, а в 1819 году восстановлена под руководством О.И. Бове. Высота башни до звезды составляет 57,7 метра, со звездой — 61,25 метра. Башня представляет собой цилиндр. В сечении башня круглая.

Слайд 17

Описание слайда:

Кривоарбатский переулок, дом 10. Два огромных белых цилиндра, прислоненных друг к другу. По периметру шестьдесят небольших ромбовидных окошек, создающих образ улья.На фасаде — гигантское окно длиной в несколько метров. Над окном надпись: «Константин Мельников. Архитектор». Самое известное (даже знаковое) здание 1920-х годов в Москве. Константин Степанович Мельников родился в Москве в семье строителя, выходца из крестьян, в 1890 году. После окончания церковно-приходской школы работал «мальчиком» в фирме «Торговый дом Залесский и Чаплин». Чаплин помог ему поступить в 1905 г. в Московское училище живописи, ваяния и зодчества, а затем после окончания Мельникова в 1913 г.Кафедра живописи посоветовала продолжить обучение на архитектурном факультете, который Константин Степанович окончил в 1917 году. В старших классах училища и в первые годы после его окончания Мельников работает в духе неоклассицизма. Однако уже в начале 20-х годов Константин Степанович резко порывает с разного рода традиционалистскими стилизациями. Сам факт широкой реализации его произведений заставляет по-другому относиться к тем его произведениям, которые остались в проектах и которые в 1920-е годы в острой полемике того периода часто объявлялись «фантастическими».В проектах Мельникова поражает степень раскованности творческой фантазии мастера в вопросах формообразования. Можно с полной уверенностью сказать, что в ХХ в. не было другого архитектора, который создал бы столько принципиально новых проектов и такой уровень новизны, что их оригинальность не только сильно отделяла их от работ других мастеров, но и столь же отличалась от работ самого их автора. Кривоарбатский переулок, дом 10. Два огромных белых цилиндра, прислоненных друг к другу.По периметру шестьдесят небольших ромбовидных окошек, создающих образ улья. На фасаде — гигантское окно длиной в несколько метров. Над окном надпись: «Константин Мельников. Архитектор». Самое известное (даже знаковое) здание 1920-х годов в Москве. Константин Степанович Мельников родился в Москве в семье строителя, выходца из крестьян, в 1890 году. После окончания церковно-приходской школы работал «мальчиком» в фирме «Торговый дом Залесский и Чаплин».Чаплин помог ему поступить в 1905 году. Б Московское училище живописи, ваяния и зодчества, а затем после окончания Мельникова в 1913 году. Отделение живописи посоветовало продолжить учебу на архитектурном факультете, который Константин Степанович окончил в 1917 году. На старших курсах училища и в первые годы после окончания школы Мельников работает в духе неоклассицизма. Однако уже в начале 20-х годов Константин Степанович резко порывает с разного рода традиционалистскими стилизациями.Сам факт широкой реализации его произведений заставляет по-другому относиться к тем его произведениям, которые остались в проектах и которые в 1920-е годы в острой полемике того периода часто объявлялись «фантастическими». В проектах Мельникова поражает степень раскованности творческой фантазии мастера в вопросах формообразования. Можно с полной уверенностью сказать, что в ХХ в. не было другого архитектора, который создал бы столько принципиально новых проектов и такой уровень новизны, что их оригинальность не только сильно отделяла их от работ других мастеров, но и столь же отличалась от работ самого их автора.

Согласно определению, принятому в 2006 году Международным астрономическим союзом, планета называется телом, вращающимся вокруг Солнца, достаточно массивным, чтобы иметь сферическую форму под действием собственной гравитации, кроме того, у нее должно быть пространство вблизи своей орбиты. , бесплатно от других. Если обратить внимание на первую часть этой формулировки, то можно задать вопрос — каков общий минимальный размер тела, чтобы оно имело форму шара?

Считается, что эта цифра составляет примерно 400 километров.По крайней мере, в нашей Солнечной системе Мимас длиной 397 километров имеет сферическую форму и, следовательно, является самым маленьким из известных круглых тел.

Mimas

При этом этот показатель зависит от того, из чего состоит корпус — поэтому для ледяных спутников он меньше, для каменных предметов больше. Например, астероид Гигея длиной 530 километров определенно не является круглым. Протей (спутник Нептуна) протяженностью 420 километров тоже совсем не похож на Мимас.

Proteus

Информация ниже показывает все круглые тела Солнечные системы диаметром менее 10 тысяч километров.Сюда входят как сферические объекты, так и тела, такие как Хаумеа и Варуна, которые имеют эллиптическую форму. Также почему-то здесь были записаны уже упомянутые Гигея и Протей — но даже с ними, думаю, картина достаточно наглядная.

Еще одна версия инфографики, включающая только те тела, которые побывали на космическом корабле. Обе картинки хороши для визуального сравнения, чтобы понять, какую часть Солнечной системы мы еще не исследовали.

Включить эффекты

1 из 9

Отключить эффекты

Посмотреть похожие

Код для вставки

Связаться с

Одноклассники

Телеграмма

Обзоры

Добавьте свой отзыв

Зарегистрируйтесь, чтобы добавить отзыв.

Слайд 1

КРУГЛЫЕ ТЕЛА / пресс-конференция / ЦИЛИНДР КОНУСНЫЙ ШАР Презентация к уроку геометрии в 11 классе.

Slide 2

Обобщение и углубление знаний о круглых телах; их применение (круглые тела) на практике в быту; Развитие логического мышления, творческой активности, речи; Воспитание самостоятельности, активности, культуры общения. ЦЕЛИ УРОКА

Slide 4

ШАР, СФЕРА Я глобус, апельсин и шар.Я круглый шар, я даже чайник.

Slide 5

КОНУС Вы легко найдете меня в воронке, На дереве, в шляпке гриба. Да, конус не в стороне, Морковь тоже я.

Slide 6

УРЕЗАННЫЙ КОНУС Заводской дымоход и маяк с подсветкой — Этот конус совсем не простой — усеченный!

Slide 7

Задача не для робких: упаковать мяч в коробку. Он должен плотно прилегать, чтобы в пути не трясло.

Slide 8

И что в итоге? Смотрите: куб — это коробочка, шарик внутри.

Slide 9

Геометрия: Учебное пособие. для 10-11 классов / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. -М .: Просвещение. 2007 Microsoft Office Power Point / сборник картинок / http://iskystvo.ru/2008/10/ Использованная литература и Интернет-ресурсы:

Посмотреть все слайды

Аннотация

2. Учебное заведение.

3. Геометрия, 11 класс

5. Тема урока. « Цилиндр, конус, шар » / ПРЕСС-КОНФЕРЕНЦИЯ /

Список использованной литературы.

http://www.salda.ru/dishes/profi/

http://www.cook.freecopy.su/cookbook/?l\u003d23&w\u003d4306

http://www.srbp.ru/offers/20/805/2456.html

http://fotki.yandex.ru/users/mamuka532/view/60544/

http://arsel.flamber.ru/photos/1200076904/

http: // www.vikar-plastic.com.ua/index.php?categoryID=301

http://yogaclassic.ru/post/2343

http://fantasyflash.ru/anime/index.php?kont=sea&n=

http://fantasyflash.ru/anime/index.php?kont\u003ddisney&n\u003d1

http://www.liveinternet.ru/photo/ha8xa7/post15454746/

http://s99-omsk.narod.ru/projects/v/mozaika.htm

http://iskystvo.ru/metka/forma/

http://www.russika.ru/ef.php?s=3346

http: // akinfeev.livejournal.com/17482.html?page=26

http://mega.km.ru/bes_2004/encyclop.asp?TopicNumber=34130&rubr=156

http://www.board74.ru/articles/geometry/tcone.html

http://iskystvo.ru/2008/10/

http://flamber.ru/photos/tags/%E4%EE%F0%EE%E3%E0/1181070512/

http://slavyane.cddk.ru/publ/20-1-0-272

http://media.meta.ua/files/pic/0/26/108/mIR6YnZXGo.jpg

противень

оранжевый

анимашки (маяк)

анимашки (микки и принцесса)

усеченная вершина

заводская труба

2. Учебное заведение. Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 15, село Березайка» Бологовский район, Тверская область

3. Предмет, класс, в котором используется товар. Геометрия, 11 класс

5. Тема урока. « Цилиндр, конус, шар » / ПРЕСС-КОНФЕРЕНЦИЯ /

6. Необходимое оборудование и материалы для занятия. Модели круглых тел, «черный ящик» для вопросов-головоломок, интерактивная доска для просмотра презентации или мультимедийной инсталляции.

7. Описание мультимедийного продукта. Презентация создана с помощью офисного приложения Power Point. Смена слайдов осуществляется щелчком мыши. Содержание презентации: тема урока, цели, затем слайды, представляющие цилиндр, шар, конус, усеченный конус, которые были созданы студентами, ответившими на вопросы во время пресс-конференции. Затем слайд, на котором написан вопрос практического содержания, затем ответ на него, результаты урока и список интернет-ресурсов.Слайды содержат рисунки и фотографии, заимствованные из Интернета. Формулы, стихи составлены автором работы

8. Цель создания и использования медиа-продукта в классе. Для большей ясности. Урок должен быть неограниченным.

9. Как это реализовано на уроке (время и место). Используется в начале урока при постановке целей и знакомстве детей — представителей научных обществ: «Цилиндр», «конус», «шар», «усеченный конус».Затем он используется после подведения итогов первой части урока, когда ученики приступают к практическому заданию (вписать сферу в куб). В конце урока при подведении итогов.

Список использованной литературы.

1.Алтыпов П.И. Геометрия. Тесты. 10-11 классы: учебно-методическая. Учебное пособие.-М .: Дрофа, 2001

2. Зив Б.Г. Задания для уроков геометрии 7-11 класс. — Санкт-Петербург, 2000, изд. «Акация»

3. Геометрия: Учебное пособие. для 10-11 классов / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. -М .: Просвещение. 2007

4. Энциклопедический словарь молодого математика / Составитель А.П. Савин.- М.6 Педагогика, 1989

5. ИНТЕРНЕТ-ресурсы (список картинок по порядку)

http://www.salda.ru/dishes/profi/

http://www.cook.freecopy.su/cookbook/?l\u003d23&w\u003d4306

http://www.srbp.ru/offers/20/805/2456.html

http://fotki.yandex.ru/users/mamuka532/view/60544/

http: // arsel.flamber.ru/photos/1200076904/

http://www.vikar-plastic.com.ua/index.php?categoryID=301

http://yogaclassic.ru/post/2343

http://fantasyflash.ru/anime/index.php?kont=sea&n=

http://fantasyflash.ru/anime/index.php?kont\u003ddisney&n\u003d1

http://www.liveinternet.ru/photo/ha8xa7/post15454746/

http://s99-omsk.narod.ru/projects/v/mozaika.htm

http://iskystvo.ru/metka/forma/

http: // www.russika.ru/ef.php?s=3346

http://akinfeev.livejournal.com/17482.html?page=26

http://mega.km.ru/bes_2004/encyclop.asp?TopicNumber=34130&rubr=156

http://www.board74.ru/articles/geometry/tcone.html

http://iskystvo.ru/2008/10/

http://flamber.ru/photos/tags/%E4%EE%F0%EE%E3%E0/1181070512/

http://slavyane.cddk.ru/publ/20-1-0-272

http://media.meta.ua/files/pic/0/26/108/mIR6YnZXGo.jpg

противень

оранжевый

анимашки (маяк)

анимашки (микки и принцесса)

усеченная вершина

Готовые школьные домашние задания: фото ответы на задания APK

Готовые школьные домашние задания по фотографиям — мечта каждого, кто учится в средней или старшей школе! Это приложение поможет вам найти готовые домашние задания по всем школьным предметам с 1 по 11 класс.Достаточно сфотографировать на смартфон страницу с домашним заданием из учебника или рабочей тетради, и приложение найдет ответ. Также вы можете получить решения задач, уравнения и примеры по фото.

Преимущество нашего образовательного приложения — это широкая база авторов учебников, рабочих тетрадей, тестов и викторин по основным школьным предметам.

Вы найдете готовые домашние задания по самым популярным школьным предметам:
— Математика
— Русский
— Алгебра
— Английский
— Геометрия
— Физика
— Биология
— История
— География
— Литература
— Химия
— Немецкий
— Компьютерные науки
— Социальные науки

В приложении вы найдете готовые домашние задания к учебникам, рабочие тетради, контрольные материалы, дидактические материалы, тесты, викторины, тренажеры и сборники заданий от следующих авторов: Александрова, Алимов, Атанасян , Афанасьева, Баранов, Баранова, Бархударов, Башмаков, Боголюбова, Босова, Бунеев, Бунимович, Бутузов, Быстрова, Ваулина, Виленкин, Волкова, Габриелян, Гаврилова, Гамбарин, Глазков, Гольцова, Дорогорцова, Дорогорцова, Евроцкий , Ерина, Ефремова, Желтовская, Жохов, Звавич, Зив, Зубарева, Иванов, Истомина, Иченская, Канакина, Кауфман, Кибирева, Климанова, Ключникова, Козлов, Колягин, Комарова, Коровин а, Кузнецова, Кузовлева, Купалова, Ладыженская, Ларионова, Литвинова, Львова, Макарычева, Мартышова, Мерзляк, Меркин, Минаева, Миндюк, Миракова, Мищенко, Мордкович, Моро, Муравин, Мякишев, Никитерсышва, Никитины, Никитина, Никольский Пичугов, Погорелов, Полонский, Попов, Попова, Потапов, Разумова, Разумовская, Рамзаева, Рубин, Рудницкая, Рыбченкова, Смирнова, Соловейчик, Ткачева, Тростенцова, Чекин, Чесноков, Чулков, Шарыгин, Шмелев и другие.

Скачать презентационные полигоны. Многоугольник и его элементы. Сообщение Темы урока

Для просмотра презентаций создайте себе аккаунт (аккаунт) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Учитель математики МБОУ ООШ №14 Томререйюк Краснодарского края Боярко Ирина Геннадьевна УРОК

ACFGB ABCDEFG- многоугольник. Соседние отрезки AB, BC, CD, DE, EF, FG, GA не лежат на одной прямой.Неумение резать не имеет общих точек. Назовите несколько пар несгибаемых сегментов. D E.

A C F G B A, B, C, D, E, F, G — многоугольник. D e vertices

CFGB AB, BC, CD, DE, EF, FG, GA — Образцы многоугольника DEA

CFGB Сумма длин сторон AB, BC, CD, DE, EF, FG, GA — называется DE и периметр многоугольника P = AB + BC + CD + DE + EF + FG + GA Образовательный портал «Мой университет» — www. Мои — Университет. RU Факультет «Реформа образования» — www.EDU — РЕФОРМА. Ru

Многоугольник, имеющий n углов, называется N-яйцом. Сколько сторон у N-картриджа? Образовательный портал «Мой университет» — www. Мои — Университет. RU Факультет «Реформа образования» — www. EDU — РЕФОРМА. Ru

A C F G B Соседние вершины D E -Две вершины, принадлежащие одной стороне Образовательный портал «Мой университет» — www. Мои — Университет. RU Факультет «Реформа образования» — www. EDU — РЕФОРМА. Ru

C F G B D E A AC, AD, AE, AF-диагональ многоугольника, проведенная из вершины A.Определение: отрезок, соединяющий две неосновные вершины, называется диагональю. Образовательный портал «Мой университет» — www. Мои — Университет. RU Факультет «Реформа образования» — www. EDU — РЕФОРМА. Ru

Определение: Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой части, содержащей его сторону. Образовательный портал «Мой университет» — www. Мои — Университет. RU Факультет «Реформа образования» — www. EDU — РЕФОРМА. Ru

Внешний регион Внутренний район

Задача 2.Сколько диагоналей у пятиугольника? Образовательный портал «Мой университет» — www. Мои — Университет. RU Факультет «Реформа образования» — www. EDU — РЕФОРМА. Ru

Задание. Сколько диагоналей у шестиугольника? Образовательный портал «Мой университет» — www. Мои — Университет. RU Факультет «Реформа образования» — www. EDU — РЕФОРМА. Ru

А этот многоугольник делим на несколько треугольников, проводим сверху и все по диагонали. Сколько работали треугольники? Найдите сумму углов многоугольника

Какова сумма углов треугольника? Найдите сумму всех углов этого пятиугольника.A S = 180 ° ∙ 3 = 540 °

Зависит ли сумма углов пятиугольника от: размера? Формы? Цвета? От чего зависит эта сумма?

Сумма углов n-яиц равна S = 180 ° ∙ (N -2)

Вариант 1 Вариант 2 1. Найдите количество диагоналей прямоугольника 1. Найдите количество диагоналей квадрата 2. Вычислите количество всех углов прямоугольника 2. Вычислите сумму всех углов квадрата 3. Найдите сумму углов выпуклого 12-квадрата 3.Найдите сумму углов выпуклого 8-квадрата 4. Количество точек неразрывных многоугольников 1 2 3 4 4. Количество точек выпуклых многоугольников 1 2 3 4 5. Найдите периметр прямоугольника со сторонами 4 см и 7 см 5. Найдите периметр квадрата со стороной 12 см. Образовательный портал «Мой университет» — www. Мои — Университет. RU Факультет «Реформа образования» — www. EDU — РЕФОРМА. Ru

Вариант 1 Вариант 2 1. Найти количество диагоналей прямоугольника 2 1. Найти количество диагоналей квадрата 2 2.Вычислите сумму всех углов прямоугольника 360 ° 2. Вычислите сумму всех квадратов квадрата 360 ° 3. Найдите сумму углов выпуклого 12-квадрата 1800 ° 3. Найти сумму углов выпуклого 8-квадрата 1080 ° 4. Номера точек неразрывных многоугольников 1 2 3 4 4. Номера точек выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 22 см 5. Найдите периметр квадрата со стороной 12 см 48 см

Использованная литература: L.С. Атанасян, геометрия 7-9 (учебник для общеобразовательных учреждений). — М .: Просвещение, 2005 г. Фотографии: http://www.gifzona.ru/pozd_1s.htm http://images-photo.ru/photo/7-2-0-0-2 http://www.webman .ru / Animation / Main.htm

1. Многоугольник 2. Выпуклый многоугольник 3. Решение задач 4. Лабораторная работа 5. Самостоятельная работа

Презентация на тему «Многоугольники» (геометрия, 8 класс) состоит из 9 слайдов. Материал может быть использован при изучении новой темы: вводится понятие многоугольника, его элементов, понятие выпуклых и неразрывных многоугольников, отображается формула для расчета количества углов.выпуклый многоугольник. Рассматривается частный тип многоугольника — четырехугольник.

Загрузить:

Предпросмотр:

Для предварительного просмотра презентаций создайте себе аккаунт (аккаунт) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Полигоны 8 класс Учитель Володина О.Н.

Многоугольник AC с DFGE Многоугольник — фигура, составленная из сегментов таким образом, что: соседние сегменты не лежат на одной прямой 2. Несгибаемые сегменты не имеют общих точек

Многоугольник AC с D Многоугольник — фигура состоит из сегментов таким образом, что: Связанные сегменты не лежат на одной прямой 2.Несгибаемые сегменты не имеют общих точек AVS D — не многоугольник около

Многоугольник AB с DFGE Точки A, B, C, D, E, F, G — вершины сегментов многоугольника AB, Sun, CD, DE, EF , FG, GA — Пираты Многоугольник P = AB + Солнце + CD + DE + EF + FG + GA — Периметр AU, AD — Диагональ

Многоугольник ACCD Внутренняя область Внешняя область

Выпуклый многоугольник AB с DE

Не отсоединяется многоугольник AV с DEF

Сумма углов выпуклого N-холодного числа сторон треугольников 4 2 5 3 6 4 N n-2 Сумма углов выпуклого N-угла: (N-2 ) 180 o

Четырехугольники 4 стороны AB с D 4 Стихи 2 диагонали P = AB + Солнце + CD + Da Сумма углов выпуклого четырехугольника равна

По теме: Методические разработки, презентации и тезисы

Тест по геометрии составлен по учебнику Л.С. Атанасян «Геометрия 7-9», но также может быть использован при работе над учебником А. В. Погорелова. Освещен весь материал по теме «Квадрат Петуго …

Круг описан возле правого многоугольника и вписан в правильный многоугольник

абстрактный урок« Круг описан возле правого многоугольника и вписан в правильный многоугольник »Атанасян ..

Конспект занятия «Правые многоугольники. Петриттер «График» 5 класс

Цель урока: формирование концепции полигонзадачи урока — познакомиться с понятием многоугольника, диагональю многоугольника, периметром многоугольника; — развивать измерительные, математические навыки…

«Урок прямоугольного квадрата» — 5 см. Оформите квадрат со стороной 5 см. 3 см. А = 5 см. Определение цели урока. 2 Метод: 3 + 3 + 3 + 3 + 3 = 3 * 5 = 15 (см2). Нарисуйте прямоугольник со сторонами 5 см и 3 см. 5 + 5 + 5 + 5 + 5 = 5 * 5 = 25 (см 2). 1 Метод: 5 + 5 + 5 = 5 * 3 = 15 (см2). Как найти квадратный квадрат? В = 3 см. Гребенникова Елена Викторовна, учитель начальных классов МОУ СОШ №5 ДЕСТРЕВЫЙ.

«Romble Roma Rectangle» — ромб.D. Площадь. Решение задач по готовым чертежам. Ответы на проверку test. Решение задач по теме «Прямоугольник. Контрольный тест. К.А. Дано: АВД — ромб. Теоретическая самостоятельная работа. Заполните таблицу, отметив знаками + (да), — (нет). Цель занятия: закрепить теоретический материал по теме «Прямоугольник.

«Многоугольник в квадрате» — 1. 7. V. S. Workout Z A D A N E 1. 2. Запишите правильную последовательность чисел. Цвет (один или несколько)? Перед тем как приступить к задаче, раскрасьте дом! 3.? 5. 4.

«Квадрат геометрических фигур» — S = AD * BH.б. А. Педагог: Ивняминова Л.А. Фигуры одинаковой площади имеют ареометрическую форму. S = (a? B): 2. С. а. Материал к уроку геометрии в 8 классе. Х. Д. Квадрат фигур. Равные формы имеют равные площади. S = а? Б.

«Математика Прямоугольник 2 класс» — 39. 6. Какие цифры под №4 и №5, чем отличаются? 1. Создайте «цепочку» 90 — 45 -9 + 14 -12 +6 — 8 + 3 =. 60. 42. 45. 2. Введите каждое число от 3 до 60. Я не хочу сегодня играть в прятки. Периметр прямоугольника.Геометрический материал. 57. Устный отчет. Прочтите стихотворение.

«Урок 2 класс Квадрат прямоугольник» — Формулы. Мы отлично учимся! Б Л. Ключ. Мы старательны! D. Математика. Второй урок. Открытие урока. Прямоугольник. Квадрат. Вырезать треугольник Многоугольник Прямоугольник Quadrilateer Square. А. С нами все будет! Р — ? Площадь — ? Выражения с переменной. 8: A p = (a + b) · 2 4 — x C: 3 p = a + b + a + b p = a · 2 + b · 2 14 + y.

Устный счет Сравните тексты заданий. Как они выглядят
Разные?
Из автобуса вышло 10 человек, из автобуса
С другой — 20.На сколько пассажиров меньше
Это было в автобусе?
На одной остановке из автобуса
вышло 10 человек, на другой — 20,
Сколько человек вышло из автобуса
?
Можно ли утверждать, что решения
задач одинаковы?

Сообщение Темы урока

Рассмотрим чертежи.
Какой узор вы нашли?
Какие цифры вы знаете?
Какие у вас трудности?
Как можно назвать все цифры одной
Короче?
Поговорим об этом.Читать.

Определение целей урока

Многоугольник и его элементы
Определим цели урока, используя вспомогательные слова:
Познакомимся с …
Узнаем …
Мы запомним …
Мы сможем to …
Сможем отразить …
Познакомимся с концептом
«Многоугольник», научимся находить и обозначать
его вершины.

Вы уже умеете различать и изображать на бумаге
такие формы, как треугольник, квадриль
, пятиугольник.Такие фигуры
обычно называют
полигонами.
Посмотрите на рисунок на стр. 42
учебник.

Этюд по новому материалу Стр. 42, № 1 (у.)

На кондитерской фабрике Печенье
выполнено в виде многоугольника,
изображено в учебнике. Как можно позвонить по
каждому из них?
треугольник
Quirhugon
пятиугольник
Сколько углов у каждой фигуры?

Изучение нового материала

Рассмотрим желтый многоугольник.
Вывод: в желтом многоугольнике
5 углов, 5 сторон, 5 вершин.
Сколько в нем углов?
Какая фигура у каждой партии?
Сколько у него сторон?
Какая фигура верхняя?
Сколько у него вершин?

Изучение нового материала

Что вы можете сказать о количестве углов,
сторон и вершин в каждом
многоугольнике?
Вывод: в любых углах многоугольника
,
сторон и вершин одинаково.

Изучение нового материала

Сколько углов в семифлене?
Сколько вершин в десятиугольнике?
Сколько сторон у Б.
Пятнадцать тритонов?

Изучение нового материала

Как определить имя этого многоугольника?
Что считать легче всего?
Рассмотрим вершины многоугольника.
Как это называется?

Изучение нового материала

Есть ли ученые степени?
А Другольники?
У какого многоугольника
наименьшее количество углов?
Как называется многоугольник с
100 вершинами?

Изучение нового материала

Давайте научимся отображать элементы
полигоном.
Стихи — баллы.
Стороны сегменты.
Углы покажут
Повернуть заостренно.

Изучение нового материала

Вершины треугольника обозначены
буквами.
Считать обозначение
можно разными способами, начиная с
С любой вершины
ABC, вы, Sav, BCA,
QA, SPE.
ВХОД
НО
ОТ

Выход

Чтение.

Работа по учебнику Стр. 43, № 2

Что изображено на картинке?
Какие данные называются
полигонами?

Работа по учебнику П.43, номер 3

Работа над учебником стр. 43, № 4

Работа в тетради стр. 16, № 1

Работа в тетради стр. 16, № 2

стр. 44, № 7 ( учебник)

Найдите сумму I.
Разница между числами: 9 и 7.
9 + 7 = 16 90 10 5 9–7 = 2

С.44, № 7 (учебник)

Найдите сумму I.
Разница между числами: 8 и 5.
8 + 5 = 13 90 10 5 8–5 = 3

С.44, № 7 (учебник)

Найдите сумму I.
Разница между числами: 10 и 3.
10 + 3 = 13 90 10 5 10 — 3 = 7

С.44, № 7 (учебник)

Найдите сумму I.
Разница между числами: 7 и 7.
7 + 7 = 14 90 10 5 7–7 = 0

Презентация урока. Определение подобных треугольников. Презентация по геометрии «Определение подобия треугольников». Практическое применение подобия треугольников

Презентация «Определение таких треугольников» охватывает этап внедрения нового понятия на уроке геометрии в 8 классе — подобия треугольников.Уточнив понятие пропорциональности отрезков, на основе которого строится понятие подобия, студенты переходят к рассмотрению достаточно сложного для них материала — подобия. С помощью презентации учитель во время объяснения формирует четкое представление учащихся об изучаемом предмете — аналогично треугольникам, продолжает развивать навыки использования математической речи, формирует навыки применения выученного концепция для решения практических задач.

слайды 1-2 (Тема презентации «Определение похожих треугольников», примеры)

Следующие инструменты используются для объяснения свойства подобия треугольников в презентации:

выделение красным цветом основных понятий;
анимированная конструкция графической части для уточнения определения, ясности при объяснении материала;
рамки основных алгебраических выражений по теме;
использование рисунков для понимания практического смысла изучаемого понятия.

Такая демонстрация позволяет углубить понимание материала, облегчить его запоминание.

Презентация начинается с демонстрации предметов, на контурах которых построены похожие геометрические фигуры. Например, футбол и гандбол, узорчатые тарелки разных размеров. Справа от предметов — очертания похожих друг на друга фигур — большого и малого квадрата, большого и малого круга.

слайды 3-4 (определение одинаковых треугольников)

Такая демонстрация, знакомящая ученика с изучением данного понятия через практическое применение, очень эффективна и помогает решить одну из важных задач урока — закрепить представление ученика об изучаемом предмете.

На следующем слайде концепция подобия разложена на компоненты с помощью двух построенных треугольников ABC и A1B1C1. Используя анимацию, постепенно соответствующие углы помечаются как равные. Соответствующие углы обозначены одинаково — A и A1 в одном полукруге, B и B1 в двух, C и C1 в трех. Несмотря на то, что эти треугольники имеют равные углы, соответствующие их стороны называются одинаковыми. Это выражение в дальнейшем необходимо использовать при решении геометрических задач, поэтому выражение выделено зеленым цветом, что означает необходимость запомнить его и использовать в будущем.

слайд 5 (сайт)

Теперь мы можем сформулировать определение подобия треугольников с соответствующим равенством углов и пропорциональностью одинаковых сторон. Далее демонстрируются алгебраические обозначения условий подобия треугольников — равенства углов и пропорциональности всех трех сторон. Условие соразмерности сторон заключено в рамку для запоминания. Результатом взаимоотношений каждой пары является одно и то же число.Он обозначается k и определяется как коэффициент подобия треугольников.

Исходя из изучаемой концепции, следует изучить следующие темы курса геометрии — соотношение площадей одинаковых треугольников, признаки подобия треугольников.

Данную презентацию «Определение таких треугольников» можно рекомендовать не только как демонстрационный материал на уроке геометрии, сопровождающем объяснения учителя. Это может помочь студенту самостоятельно изучить материал, а также помочь объяснить концепцию сходства на уроке с дистанционным обучением.

1.1. Пропорциональные отрезки Определение подобных треугольников 1.2. Определение подобных треугольников 1.3. Соотношение площадей подобных треугольников Соотношение площадей похожих треугольников Свойства сходства.

1.1 Пропорциональные сегменты. Отношение отрезков AB и CD — это отношение их длин, то есть говорят, что отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1, если ПРИМЕР 1. Отрезки AB и CD , длина которых составляет 2 см и 1 см, пропорциональны сегментам A 1 B 1 и C 1 D 1, длина которых составляет 3 см и 1.5 см. Верно,

1.2. Определение подобных треугольников. В повседневной жизни встречаются предметы одинаковой формы, но разного размера, например, футбольные и теннисные мячи, круглая тарелка и большое круглое блюдо. В геометрии фигуры одинаковой формы принято называть похожими. Итак, любые два квадрата, любые два круга подобны. Введем понятие таких треугольников.

1.2. Определение подобных треугольников. ПОДОБИЕ, геометрическое понятие, характеризующее наличие одной и той же формы в геометрических фигурах, независимо от их размера.Две фигуры F1 и F2 называются подобными, если между их точками можно установить взаимно однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек фигур F1 и F2 равно одинаковому константа k, называемая коэффициентом подобия. Углы между соответствующими линиями таких фигур равны. Аналогичные цифры у F1 и F2.

Определение Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны аналогичным сторонам другого треугольника.Другими словами, два треугольника подобны, если их можно обозначить буквами ABC и A 1 B 1 C 1 так, чтобы A = A 1, B = B 1, C = C 1, число k равно Соотношение одинаковых сторон треугольников называется коэффициентом подобия.

1.3. Соотношение площадей одинаковых треугольников. Теорема. Отношение площадей двух одинаковых треугольников равно квадрату коэффициента подобия. Доказательство. Пусть треугольники ABC и A1B1C1 подобны, а коэффициент подобия равен k.Пусть S и S1 обозначают площадь этих треугольников. Поскольку A = A1, то

Свойства подобия. Задача 2. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные смежным сторонам треугольника. Решение. Пусть AD — биссектриса треугольника ABC. Докажем, что треугольники ABD и ACD имеют общую высоту AH, поэтому 12 A H B D C

Доказательство: По теореме о сумме углов: C = A — B, а C 1 = A 1 — B 1, значит C = C 1.Поскольку A = A 1 и C = C 1, то и из этого следует: Получается, что одинаковые стороны пропорциональны. Дано: ABC и A 1 B 1 C 1 A = A 1 B = B 1 Докажите: ABC A 1 B 1 C 1 A C B A1A1 B1B1 S1C1

ABC 2 A 1 B 1 C 1 (по первому знаку), что означает, с другой стороны, из этих равенств получаем AC = = AC 2. ABC = ABC 2 — с двух сторон и угол между их (AB — общая сторона, AC = AC 2 и, потому что и).Итак, а затем ABC A1B1C1 Дано: ABC и A 1 B 1 C 1 D: Доказательство: Рассмотрим ABC 2, для которого и

Доказательство: A 1 B 1 — средняя линия, а A 1 B 1 // AB, следовательно, и, следовательно, AOW A 1 OB 1 (два угла), то AB = A 1 B 1, поэтому AO = 2A 1 O и BO = 2B 1 O. Итак, точка O является пересечением медиан AA 1 и BB 1 делит каждую из них в соотношении 2: 1, считая сверху.Аналогично доказывается, что точка O — пересечение медиан BB 1 и CC 1 делит каждую из них в соотношении 2: 1, считая сверху. Итак, точка O — пересечение медиан AA 1, BB 1 и CC 1 делит их в соотношении 2: 1, считая сверху.

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

МБОУ Гимназия №14

Учитель математики: Э.Д. Лазарев

Пропорциональные сегменты

Отношение сегментов AB и CD называется отношением их длин, т.е.е.

Сегменты AB и CD пропорциональные сегменты A 1 B 1 и C 1 D 1, если

Определение похожих треугольников

Два треугольника называются , как , если их углы соответственно равны и стороны одного треугольника пропорциональны аналогичным сторонам другого.

Число k, равное отношению одинаковых сторон треугольников, называется коэффициентом подобия

B 1

А 1

К 1

Отношение площадей одинаковых треугольников

Отношение площадей двух одинаковых треугольников составляет квадрат коэффициента подобия

Биссектриса треугольника делит противоположную сторону на сегменты, пропорциональные соседним сторонам треугольника.

Б 1

А 1

К 1

Если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны

 ABC,  A 1 B 1 C 1,

 A =  A 1,  B \ u003d  B 1

Доказательство:

 ABC  A 1 B 1 C 1

B 1

А 1

К 1

Признаки подобия треугольников
II признак подобия треугольникам
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
 ABC,  A 1 B 1 C 1,
Доказательство:
 ABC  A 1 B 1 C 1
B 1
А 1
К 1

Признаки подобия треугольников
III признак подобия треугольникам
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
 ABC,  A 1 B 1 C 1,
Доказательство:
 ABC  A 1 B 1 К 1
Б 1
А 1
К 1

Средняя линия треугольника
Средняя линия треугольника — это линия, соединяющая середины двух сторон
Средняя линия треугольника
, параллельная одной из его сторон
и равная половине этой стороны
 ABC, MN — средняя линия
Prove:
MN  AC, MN = AC

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в соотношении 2: 1, считая от вершины
A 1
К 1
Б 1

Применение подобия для решения проблем
Высота прямоугольного треугольника, начерченного из вершины прямого угла, делит треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
 ABC  ACD,

Применение подобия к доказательству теорем
1. Высота прямоугольного треугольника, начерченного из вершины прямого угла, является средней величиной, пропорциональной отрезкам, на которые делится гипотенуза, на эту высоту

Применение подобия к доказательству теорем
2. Сторона прямоугольного треугольника — это среднее значение, пропорциональное гипотенузе и отрезку гипотенузы, заключенному между стороной и высотой, проведенной из вершины прямого угла.
Данную презентацию можно использовать на любом этапе урока. Содержит элементы повторения пройденного материала, нового теоретического материала, решения задач.
Просмотр содержания документа

«Презентация по геометрии« Определение подобия треугольников »»
Геометрия, класс 8
Определение подобных треугольников

Задачи урока:
Повторить понятие «отношение двух чисел»,
«Пропорция»; помню основное свойство
пропорций.
2. Представьте понятие пропорциональных сегментов и
подобных треугольников.
3. Закрепить полученные знания через решение задач
.

А теперь вспомните:
Что называется отношением двух чисел?
Что показывает отношение?
2. Отношение AM к AC 2: 3. О чем это говорит?
Найдите соотношение 3: 2.
3. В треугольнике ABC AB: BC: AC = 1: 3: 2 его периметр равен 42 см.Найдите стороны треугольника ABC.
4. Что называется пропорцией? Верны ли пропорции?
1,2: 3,6 = 6: 18; 15: 3 = 4: 20?

Продолжение:
5. В пропорции a: b = c: d указать крайний и средний
стержня. Сформулируйте основное свойство пропорции.
6. Переставив средний и крайний элементы пропорции,
Сделайте правильные пропорции:
и). 14: 0,2 = 35: 0,5; б) АБ: МН = С Д: КР.
7. Найдите неизвестный член пропорции:
и). 2х: 3 = 16: 9; б) х: АВ = МН: КР.

Что называется соотношением сегментов?
Соотношение сегментов AB и CD называется отношением их длин, т.е. AB: C D.
AB: C D = 4 : 6 или AB : C D = 2: 3

Какие сегменты называются пропорциональными?
AB = 2 см, A 1 B 1 = 5 см
C 1 D 1 = 6 см
Отрезки AB и CD пропорциональны отрезкам A 1 B 1 и
C 1 D 1 если
A 1 B 1 C 1 D 1.

Два треугольника называются как , если их углы равны соответственно и стороны один треугольник пропорционально аналогичным сторонам другой треугольник.
AB и A 1 In 1
связанные стороны
BC и B 1 C 1
CA и C 1 A 1

Итак, Δ ABC и Δ И 1 AT 1 С 1 аналогично, если выполнено условий :
k, где k — коэффициент
A 1 B 1 B 1 C 1 A 1 C 1

Даны отрезки: AB = 12 см, CD = 8 см, EF = 15 см, KL = 30 см, MN = 16 см, PQ = 20 см.Найдите среди них пары пропорциональных отрезков.
EF 15 5 получил, что
MN 16 4 AB MN, затем сегменты AB и MN
PQ 20 5 EF PQ пропорционально
сегментов EF и PQ.
(Самостоятельно найти еще две пары пропорциональных отрезков)

В таких треугольниках ABC и EDF стороны AB и AC, BC и DF подобны
жил. Найдите стороны AB и AC треугольника ABC, если ED = 3 см, EF = 7 см,
1.Зная значения одинаковых сторон BC и DF треугольников ABC и EDF, определить коэффициент подобия k.
2. Определим AB = k · ED и AC = k · EF.

Подержанные книги:
1.Гаврилова Н.Ф. Разрабатывающие работы по геометрии: 8 класс.: ВАКО, 2008.
2. Геометрия. Рабочая тетрадь 8 класса. Учебное пособие для учащихся общеобразовательных школ. Авторы: Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, И. Юдина. М .: Просвещение, 2011
3.Геометрия, 7-9: учебник для общеобразовательных. учреждений / (Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.). М .: Просвещение, 2012.
изложение других презентаций
«Геометрия« Подобные треугольники »» — основная тригонометрическая идентичность. Второй признак подобия треугольников. Синус, косинус и тангенс. Значения синуса, косинуса и тангенса для углов 30 °, 45 °, 60 °. Подобные треугольники. Подобие прямоугольных треугольников. Продолжение сторон. Пропорциональные сегменты. Теорема о соотношении площадей таких треугольников.Значения синуса, косинуса и тангенса. Две стороны треугольника соединены отрезком, не параллельным третьему.
«Нахождение площади трапеции» — Результаты. Свойства прямоугольного треугольника. Найдите площадь трапеции. Сравните площадь. Обозначьте площадки. Задачи на самоконтроль. Площадь трапеции. Повторение пройденного материала. Ловушка. Запишите формулы. Сформируйте умение применять формулу. Найдите область.Площадь ячейки. Решение проблемы. Подвести итоги. Площадь.
«Четырехугольники, их признаки и свойства» — Ромб. Четырехугольники, их признаки и свойства. Представьте типы четырехугольников. Прямоугольник. Свойства параллелограмма. Прямоугольник, у которого все стороны равны. Четырехугольник, вершины которого находятся посередине сторон. Диагонали. Виды четырехугольников. Тесты. Из каких двух равных треугольников можно сделать квадрат. Виды трапеции. Углы ромба. Квадрат. Знаки параллелограмма.Четырехугольники.
«Теорема о вписанном угле» — Радиус окружности 4 см. Отвечать. Острый угол. Обеспечение изученного материала. Обновление знаний студентов. Актуализация знаний. Изучение нового материала. Радиус круга. Как называется угол с вершиной в центре окружности. Найдите угол между хордами. Понятие вписанного угла. Треугольник. Найдите угол между ними. Решение. Попробуй себя. Правильный ответ. Круги пересекаются. Теорема о вписанном угле.
«Теорема Пифагора для прямоугольного треугольника» — прямоугольный треугольник. Имя Пифагора. Сочетание двух противоречащих друг другу принципов. Геродот. Утверждение теоремы. Античные авторы. Пифагор Самосский. Монета с изображением Пифагора. Теорема Пифагора. Учение Пифагора.
«Понятие площади многоугольника» — Смежные стороны параллелограмма. Площадь треугольника. Математический диктант. Параллелограмм. Площадь ромба.Понятие о многоугольной области. Площадь прямоугольника. Площадь трапеции. Высоты. Площадь полигонов. Площадь прямоугольного треугольника. Теорема. Острый угол. Площадь параллелограмма. Вычислите площадь ромба. Найдите площадь прямоугольного треугольника. Треугольники. Единицы площади.
теорем Чевы и Менделая. Теорема Чевы и измененная теорема для треугольника
Класс: 9
Задачи урока:
обобщить, расширить и систематизировать знания и умения студентов; научить использовать знания при решении сложных задач;
способствовать развитию навыков самостоятельного применения знаний при решении задач;
для развития логического мышления и математической речи учащихся, умения анализировать, сравнивать и обобщать;
воспитывать у студентов уверенность в себе, трудолюбие; умение работать в команде.
Задачи урока:
Воспитательная: повторить теоремы Менелая и Чевы; применяйте их при решении проблем.
Развивающие: учат выдвигать гипотезы и умело отстаивать свое мнение доказательствами; проверьте умение обобщать и систематизировать свои знания.
Образовательные: повысить интерес к предмету и подготовить к более сложным задачам.
Тип урока: урок по обобщению и систематизации знаний.
Оборудование: карточки для коллективной работы на уроке по данной теме, индивидуальные карточки для самостоятельной работы, компьютер, мультимедийный проектор, экран.
В классах
I этап. Организационный момент (1 мин.)
Учитель разъясняет тему и цель урока.
II этап. Обновление базовых знаний и навыков (10 мин.)
Учитель: На уроке мы вспоминаем теоремы Менелая и Чевы, чтобы успешно перейти к решению задач.Давайте вместе с вами посмотрим на экран. Для какой теоремы дана эта цифра? (Теорема Менелая). Постарайтесь четко сформулировать теорему.
Рисунок 1
Пусть точка A 1 лежит на стороне BC треугольника ABC, точка C 1 — на стороне AB, точка B 1 — на продолжении стороны AC за точку C. Точки A 1, B 1 и C 1 лежат на одной прямой, если и только если равенство
Учитель: Давайте вместе посмотрим на следующий рисунок. Сформулируйте теорему для этого рисунка.

Рисунок 2
Линия AD пересекает две стороны и является продолжением третьей стороны треугольника BMC.
По теореме Менелая
Линия MB пересекает две стороны и является продолжением третьей стороны треугольника ADC.
По теореме Менелая
Учитель: Какой теореме соответствует цифра? (Теорема Чевы). Сформулируйте теорему.

Рисунок 3
Пусть в треугольнике ABC точка A 1 лежит на стороне BC, точка B 1 — на стороне AC, точка C 1 — на стороне AB.Отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство
III этап. Решаю задачи. (22 мин.)
Класс делится на 3 команды, каждая из которых получает карточку с двумя разными задачами. Дается время на решение, затем на экране отображается … Используя готовые чертежи задач, представители команд поочередно объясняют свое решение. Каждое объяснение сопровождается обсуждением, ответами на вопросы и проверкой правильности решения на экране.В обсуждении принимают участие все члены команды. Чем активнее команда, тем выше ее оценивают при подведении итогов.
Карточка 1.
1. В треугольнике ABC на стороне BC берется точка N так, чтобы NC = 3BN; на продолжении стороны AC за точку A берется точка M так, чтобы MA = AC. Прямая MN пересекает сторону AB в точке F. Найдите отношение
.
2. Докажите, что медианы треугольника пересекаются в одной точке.
Решение 1

Рисунок 4
По условию задачи MA = AC, NC = 3BN.Пусть MA = AC = b, BN = k, NC = 3k. Прямая MN пересекает две стороны треугольника ABC и продолжение третьей.
По теореме Менелая
Ответ:
Проба 2

Рисунок 5
Пусть AM 1, BM 2, CM 3 — медианы треугольника ABC. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что
Тогда по (обратной) теореме Чева отрезки AM 1, BM 2 и CM 3 пересекаются в одной точке.
У нас:
Итак, доказано, что медианы треугольника пересекаются в одной точке.
Карточка 2.
1. На стороне PQ треугольника PQR берется точка N, а на стороне PR — точка L, а NQ = LR. Пересечение отрезков QL и NR делит QL в соотношении m: n, считая от точки Q. Найдите
2. Докажите, что биссектрисы треугольника пересекаются в одной точке.
Решение 1

Рисунок 6
По условию NQ = LR, Пусть NA = LR = a, QF = км, LF = kn.Линия NR пересекает две стороны треугольника PQL и продолжение третьей.
По теореме Менелая
Ответ:
Проба 2

Рисунок 7
Покажем, что
Тогда по (обратной) теореме Шевы AL 1, BL 2, CL 3 пересекаются в одной точке. По свойству биссектрис треугольника
Почленно умножая полученные равенства, получаем
Для биссектрис треугольника выполняется равенство Чевы, следовательно, они пересекаются в одной точке.
Карточка 3.
1. В треугольнике ABC AD — это медиана, точка O — это середина медианы. Прямая BO пересекает сторону AC в точке K. В каком отношении точка K делит AC, считая от точки A?
2. Докажите, что если окружность вписана в треугольник, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке.
Решение 1

Рисунок 8
Пусть BD = DC = a, AO = OD = m.Линия BK пересекает две стороны и продолжение третьей стороны треугольника АЦП.
По теореме Менелая
Ответ:
Проба 2

Рисунок 9
Пусть A 1, B 1 и C 1 — точки касания вписанной окружности треугольника ABC. Чтобы доказать, что отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:
Используя свойство касательных, проведенных к окружности из одной точки, введем обозначения: C 1 B = BA 1 = x, AC 1 = CB 1 = y, BA 1 = AC 1 = z.
Равенство Чевы выполняется, что означает, что биссектрисы треугольника пересекаются в одной точке.
IV этап. Решение задач (самостоятельная работа) (8 мин.)
Учитель: Работа команд окончена и теперь мы приступим к самостоятельной работе над индивидуальными карточками по 2 вариантам.
Материалы к уроку для самостоятельной работы студентов
Вариант 1. В треугольнике ABC, площадь которого равна 6, на стороне AB берется точка K, разделив эту сторону в соотношении AK: BK = 2: 3, а на стороне AB сторона AC — точка L, делящая AC в соотношении AL: LC = 5: 3.Точка Q пересечения прямых SK и BL удалена от линии AB на некоторое расстояние. Найдите длину стороны AB. (Ответ: 4.)
Вариант 2. Точка K берется на стороне переменного тока в треугольнике ABC. Найти длину высоты треугольника ABC, выпавшего из вершины B. (ответ: 1.5.)
Работы переданы учителю для проверки.
Этап V. Подведение итогов (2 мин.)
Ошибки проанализированы, оригинальные ответы и комментарии отмечены.Подведены итоги работы каждой команды и выставлены оценки.
VI этап. Домашнее задание (1 мин.)
Домашнее задание состоит из задач № 11, 12 с. 289-290, № 10, с. 301.
Заключительное слово преподавателя (1 мин).
Сегодня вы услышали математические речи друг друга и оценили свои способности. В будущем мы будем применять такие обсуждения, чтобы лучше понять предмет. Аргументы на уроке дружили с фактами, а теория — с практикой.Спасибо вам всем.
Литература:
В.В. Ткачук Математика для соискателя. — М .: МЦНМО, 2005.
.
А.В. Шевкин
ФМС № 2007
Теоремы Чевы и Менелая на экзамене
Подробная статья «Вокруг теорем Шевы и Менелая» опубликована на нашем сайте в разделе СТАТЬИ. Он адресован учителям математики и старшеклассникам, которые заинтересованы в хороших знаниях математики.Вы можете вернуться к нему, если хотите разобраться в проблеме более подробно. В этой заметке мы предоставим краткую информацию из указанной статьи и проанализируем решения задач из сборника для подготовки к ЕГЭ-2016.
Теорема Чевы
Дан треугольник ABC и на его сторонах AB , BC и AC отмечены точки C 1, A 1 и B 1 соответственно (рис.1).
a) Если сегменты AA 1, BB 1 и CC 1 пересекаются в одной точке, то
б) Если равенство (1) верно, то отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке.
На рисунке 1 показан случай, когда сегменты AA 1, BB 1 и CC 1 пересекаются в одной точке внутри треугольника. Это так называемый случай внутренней точки. Теорема Чевы также верна в случае внешней точки, когда одна из точек И 1, B 1 или ОТ 1 принадлежит стороне треугольника, а две другие принадлежат продолжениям треугольника. стороны треугольника.В этом случае точка пересечения отрезков AA 1, BB 1 и CC 1 лежит вне треугольника (фиг. 2).
Как вспомнить равноправие Чевы?
Обратим внимание на технику запоминания равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении пересечения вершин треугольника ABC , начиная с точки A … Из точки A идем в точку B , встречаем точку ОТ 1, записываем дробь
… Далее из точки IN идем в точку ОТ , встречаем точку И 1, записываем дробь
… Наконец, из точки ИЗ переходим в точку И , встречаем точку В 1, записываем дробь
… В случае внешней точка, порядок записи дробей сохраняется, хотя две «точки деления» сегмента находятся за пределами своих сегментов.В таких случаях говорят, что точка разделяет сегмент внешне.
Обратите внимание, что любой отрезок, соединяющий вершину треугольника с любой точкой прямой, содержащей противоположную сторону треугольника, называется cheviana .
Рассмотрим несколько способов доказательства утверждения а) теоремы Чевы для случая внутренней точки. Для доказательства теоремы Чевы необходимо доказать утверждение а) любым из предложенных ниже методов, а также доказать утверждение б).Доказательство утверждения б) проводится после первого способа доказательства утверждения а). Доказательства теоремы Чевы для случая внешней точки аналогичны.
Доказательство утверждения а) теоремы Чевы с использованием теоремы о пропорциональном отрезке
Пусть три чевиана A A 1, B B 1 и C C 1 пересекаются в точке Z внутри треугольника ABC .
Идея доказательства состоит в том, чтобы заменить отношения отрезков из равенства (1) на отношения отрезков, лежащих на одной прямой.
Через точку IN проведите прямую, параллельную шевиане SS 1. Прямой AA 1 пересекает построенную линию в точке M , и прямая, проходящая через точку C и параллель AA 1, — в точке T … Через точки И и ОТ проведем прямые параллельные шевианы BB 1. Они пересекут линию VM в точках N и R соответственно (рис.3).
P по теореме о пропорциональных отрезках, имеем:
, г.
и
.
Тогда равенства
.
В параллелограммах ZСTM и ZCRB отрезки TM , СZ и ВR равны противоположным сторонам параллелограмма. Следовательно,
и верно равенство
.
При доказательстве утверждения б) мы используем следующее утверждение. Рисунок 3
Лемма 1. Если точки ОТ 1 и ОТ 2 делят отрезок AB внутренним (или внешним) способом в одном и том же отношении, считая от одной и той же точки, то эти точки совпадают.
Докажем лемму для случая, когда точки ИЗ 1 и ИЗ 2 делят отрезок AB внутренне одинаково:
.
Доказательства. Из равенства
следуют равенства
и
… Последнее из них выполняется только при условии равенства ОТ 1 B и ОТ 2 B , то есть при условии, что точки ОТ 1 и ИЗ 2 одинаковы.
Доказательство леммы для случая, когда точки ОТ 1 и ОТ 2 делят отрезок AB внешне, проводится аналогично.
Доказательство части б) теоремы Чевы
Пусть теперь выполняется равенство (1). Докажем, что отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке.
Пусть чевианы AA 1 и BB 1 пересекаются в точке Z , проведем через эту точку отрезок CC 2 ( ИЗ 2 лежит на отрезке AB ).Тогда на основании утверждения а) получаем правильное равенство
. (2)
И сравнивая равенства (1) и (2), мы заключаем, что
, то есть точки ОТ 1 и ОТ 2 делят сегмент AB в том же отношении, считая от одной и той же точки. Из леммы 1 следует, что точки ИЗ 1 и ИЗ 2 совпадают. Это означает, что сегменты AA 1, BB 1 и CC 1 пересекаются в одной точке, как требуется.
Можно доказать, что процедура записи равенства (1) не зависит от того, в какой точке и в каком направлении пересекаются вершины треугольника.
Упражнение 1. Найдите длину сегмента И N на рисунке 4, где показаны длины других сегментов.
Ответ. 8.
Задача 2. Chevians AM , BN , CK пересекаются в одной точке внутри треугольника ABC … Найдите отношение
, если
,
… Рисунок: 4
Ответ.
.
P Приведем доказательство теоремы Чевы из статьи. Идея доказательства состоит в том, чтобы заменить отношения отрезков из равенства (1) на отношения отрезков, лежащих на параллельных прямых.
Пусть прямые А А 1, B B 1, C C 1 пересекаются в точке O внутри треугольника ABC (рис.5). Поперек вершины ОТ треугольника ABC проведите прямую, параллельную AB , и ее точки пересечения с прямыми линиями A A 1, B B 1 обозначают соответственно A 2, В 2.
Из подобия двух пар треугольников CB 2 B 1 и ABB 1, BAA 1 и CA 2 A 1, рис.пять
имеем равенства
, г.
. (3)
Из подобия треугольников BC 1 O и B 2 CO , A ОТ 1 O и A 2 CO имеем равенства
, из которых следует, что
. (4)
P Умножая равенства (3) и (4), получаем равенство (1).
Утверждение а) теоремы Чевы доказано.
Рассмотрим доказательства утверждения а) теоремы Чевы с использованием площадей для внутренней точки.Это изложено в книге А.Г. Мякишева и опирается на утверждения, которые мы сформулируем в виде задач 3 и 4 .
Задача 3. Отношение площадей двух треугольников с общей вершиной и оснований, лежащих на одной прямой, равно отношению длин этих оснований. Докажите это утверждение.
Задача 4. Докажите, что если
, то
и
… Рисунок: 6
Пусть отрезки AA 1, BB 1 и CC 1 пересекаются в точке Z (рис.6), затем
, г.
. (5)
И из равенств (5) и второй постановки задачи 4 следует, что
или
… Аналогично находим, что
и
… Умножая последние три равенства, получаем:
,
, то есть равенство (1) выполняется, как и требуется.
Утверждение а) теоремы Чевы доказано.
Задача 15. Пусть Чевианы пересекаются в одной точке внутри треугольника и разделят его на 6 треугольников, площади которых равны S 1, S 2, S 3, S 4, S 5, S 6 (рис.7). Докажи это. Рисунок 7
Задача 6. Найдите площадь S треугольника CNZ (площади остальных треугольников показаны на рисунке 8).
Ответ. 15.
Задача 7. Найдите площадь S треугольника CNO , если площадь треугольника AND NO равна 10 и
,
(рис.9).
Ответ. 30.
Задача 8. Найти площадь S треугольника CNO , если площадь треугольника И BC равна 88 и,
(рис.9).
Раствор R. Так как, то обозначим
,
… как , то обозначим
,
… Теорема Чевы означает, что
, а затем
… Если
, то
(рис.10). У нас есть три неизвестных величины ( x , y и S ), поэтому, чтобы найти S , составим три уравнения.
Как
, затем
= 88. Начиная с
, затем
, откуда
… Как
, затем
.
Итак,
откуда
… Цифра: десятка
Назначение 9 . В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и B C .
,
. P AL и CK … Площадь треугольника PBC равна 1. Найдите площадь треугольника ABC .
Ответ. 1,75.
Теорема Т Менелая
Дан треугольник ABC и на его сторонах AC и CB отмечены точки B 1 и A 1 соответственно, а на продолжении стороны AB точка обозначена C 1 (рис.11).
а) Если точки И 1, B 1 и ИЗ 1 лежат на одной прямой, то
. (6)
б) Если равенство (7) верно, то точки И 1, B 1 и ИЗ 1 коллинеарны. Рисунок: одиннадцать
Как помнить о равенстве Менелая?
Техника запоминания равенства (6) такая же, как и для равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC — сверху вниз, проходя через точки разделения (внутренние или внешние).
Задача 10. Докажите, что запись равенства (6) из любой вершины треугольника в любом направлении дает тот же результат.
Для доказательства теоремы Менелая необходимо доказать утверждение а) любым из предложенных ниже методов, а также доказать утверждение б). Доказательство утверждения б) проводится после первого способа доказательства утверждения а).
Доказательство утверждения а) с использованием теоремы о пропорциональном отрезке
I путь. а) Идея доказательства состоит в замене соотношений длин отрезков в равенстве (6) на отношения длин отрезков, лежащих на одной прямой.
Пусть точки И 1, B 1 и ИЗ 1 лежат на одной прямой. Через точку C проведем прямую l , параллельную прямой AND 1 B 1, она пересекает линию AB в точке M (рис.12).
R
есть. 12
По теореме о пропорциональных отрезках имеем:
и
.
Тогда верны равенства
.
Доказательство утверждения б) теоремы Менелая
Пусть теперь равенство (6) верно, докажем, что точки И 1, B 1 и ИЗ 1 лежат на одной прямой. Пусть прямые AB, и И 1 B 1 пересекаются в точке ОТ 2 (рис.13).
Поскольку точки И 1 B 1 и ИЗ 2 лежат на одной прямой, то по утверждению а) теоремы Менелая

. (7)
Сравнивая равенства (6) и (7), получаем
, откуда следует, что равенства
, г.
, г.
.
Последнее равенство верно только при условии
, т.е. если точки ИЗ 1 и ИЗ 2 совпадают.
Утверждение б) теоремы Менелая доказано.Рисунок 13
Доказательство утверждения а) с использованием подобия треугольников
Идея доказательства состоит в замене соотношений длин отрезков из равенства (6) на отношения длин отрезков, лежащих на параллельных прямых.
Пусть точки И 1, B 1 и ИЗ 1 лежат на одной прямой. Из точек A , B и C проведите перпендикуляры AA 0, B B 0 и SS 0 к этой прямой (рис.14).
R
есть. четырнадцать
Из подобия трех пар треугольников AA 0 B 1 и CC 0 B 1, CC 0 A 1 и BB 0 A 1, C 1 B 0 B и C 1 A 0 A (под двумя углами) имеем правильные равенства
, г.
, г.
,
умножая их, получаем:
.
Утверждение а) теоремы Менелая доказано.
Доказательство утверждения а) с использованием областей
Идея доказательства состоит в замене отношения длин отрезков из равенства (7) на отношение площадей треугольников.
Пусть точки И 1, B 1 и ИЗ 1 лежат на одной прямой. Соедините точки C и C 1. Обозначим площади треугольников S 1, S 2, S 3, S 4, S 5 (рис.15).
Тогда равенства
, г.
, г.
. (8)
Умножая равенства (8), получаем:
Утверждение а) теоремы Менелая доказано.
R
есть. 15
Точно так же, как теорема Чевы остается в силе, если точка пересечения хевианов находится вне треугольника, теорема Менелая остается верной также, если секущая пересекает только продолжения сторон треугольника. В этом случае можно говорить о пересечении сторон треугольника во внешних точках.
Доказательство утверждения а) для внешних точек
P секущая устье пересекает стороны треугольника ABC во внешних точках, т. Е. Пересекает продолжения сторон AB , BC и AC в точках C 1, A 1 и B 1 соответственно, и эти точки лежат на одной прямой (рис. 16).
По теореме о пропорциональных отрезках имеем:
и.
Тогда справедливы равенства
Утверждение а) теоремы Менелая доказано. Рисунок: sixteen
Отметим, что приведенное выше доказательство совпадает с доказательством теоремы Менелая для случая, когда секущая пересекает две стороны треугольника во внутренних точках и одну — во внешней.
Доказательство утверждения б) теоремы Менелая для случая внешних точек аналогично приведенному выше доказательству.
Задания 11. В треугольнике ABC точки И 1, IN 1 лежат соответственно на сторонах Солнца и A ОТ . P — точка пересечения отрезков AA 1 и BB 1 .
, г.
… Найдите отношение
.
Решение. Обозначим
,
, г.
, г.
(рис.17). По теореме Менелая для треугольника BC IN 1 и секанса PA 1 запишем правильное равенство:
,
, откуда следует, что
… Рисунок 17
Ответ. .
Задания 12 (МГУ, заочная подготовка). В треугольнике ABC , площадь 6, сбоку AB точка взята TO , разделяет эту сторону относительно
и на стороне AS — точка L , деление AS во взаимосвязи
… Точка P пересечения прямых SC и IN L удален от прямой AB на расстоянии 1.5. Найдите длину стороны AB.
Решение. От точек R и ОТ опускаем перпендикуляры PR и CM на прямой AB … Обозначим
,
, г.
, г.
(рис.18). По теореме Менелая для треугольника AKC и секущей PL мы записываем правильное равенство:
, откуда получаем, что
,
… Рисунок 18
Из подобия треугольников TO MC и TO RP (под двумя углами) получаем, что
, откуда следует, что
.
Теперь, зная длину высоты удерживаемой стороны AB треугольника ABC , и площадь этого треугольника, вычисляем длину стороны:
.
Ответ. 4.
Z adania 13. Три окружности с центрами И , IN , ИЗ , , радиусы которых связаны как
, касаются друг друга снаружи в точках X , Y , Z , как показано на рисунке 19.Отрезки AX и BY пересекаются в точке O . В каком отношении, считая от точки B , раздел CZ делит отрезок BY ?
Решение. Обозначим
,
, г.
(рис. 19). Как и
, то по утверждению б) теоремы Шевы отрезки И X , BY и ОТ Z пересекаются в одной точке — точке O … Затем сегмент CZ делит сегмент BY в соотношении
… Давайте найдем это отношение. Рисунок: девятнадцать
По теореме Менелая для треугольника BCY и секущей OX имеем:
, откуда следует, что
.
Ответ. .
Задание 14 (ЕГЭ-2016).
Точки IN 1 и ИЗ AS и AB треугольник ABC и AB 1: B 1 ИЗ =
= КАК 1: ИЗ 1 B … Прямой BB 1 и SS 1 пересекаются в точке ПРО.
, а) Докажите, что линия АО половинки сбоку вс.
AB 1 OC 1 на площадь треугольника ABC , если известно, что AB 1: B 1 ОТ = 1: 4.
Решение. а) Пусть прямая АО пересекает сторону BC в точке A 1 (рис.20). По теореме Шевы имеем:
. (9)
Как AB 1: B 1 ИЗ = AS 1: ИЗ 1 B , тогда равенство (9) означает, что
, то есть CA 1 = AND 1 B , как требуется для доказательства. Рисунок 20
б) Пусть площадь треугольника AB 1 O равно S . Как AB 1: B 1 ИЗ CB 1 O равняется 4 S , а площадь треугольника AOC равно 5 S … Тогда площадь треугольника AOB — это также 5 S , поскольку треугольники AOB и AOC имеют общее основание AO , а их вершины B и C равноудалены от прямой AO … Причем площадь треугольника AOC 1 равна S , как AS 1: ИЗ 1 B = 1: 4. Тогда площадь треугольника ABB 1 равна 6 S … Так как AB 1: B 1 ОТ = 1: 4, то площадь треугольника CB 1 O равна 24 S , а площадь треугольника ABC равно 30 S … Теперь находим отношение площадей четырехугольника AB 1 OC 1 (2 S ) на площадь треугольника ABC (30 S ), он равен 1:15.
Ответ. 1:15.
Задание 15 (ЕГЭ-2016).
Точки IN 1 и ОТ 1 лежат по сторонам соответственно AS и AB треугольник ABC и AB 1: B 1 ОТ =
= AS 1: ИЗ 1 B … Прямой BB 1 и SS 1 пересекаются в точке ПРО.
а) Докажите, что линия АО пополам сбоку вс.
б) Найдите отношение площади четырехугольника AB 1 OC 1 к площади треугольника ABC , если известно, что AB 1: B 1 ИЗ = 1: 3.
Ответ. 1:10.
Z adania 1 6 (ЕГЭ-2016). На отрезке BD взято точка ОТ … Биссектриса BL ABC с фундаментом Sun BLD с фундаментом BD .
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что cos
ABC DL, т.е. треугольник BD точка взята ИЗ … Биссектриса BL равнобедренный треугольник ABC с основанием Солнце является боковой стороной равнобедренного треугольника. BLD с фундаментом BD .
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что cos ABC =.В каком отношении прямая DL разделяет сторону AB ?
Ответ. 4:21.
Литература
1. Смирнова И.М., Смирнов В.А. Замечательные точки и линии треугольника. М .: Математика, 2006, № 17.
.
2. Мякишев А.Г. Элементы геометрии треугольника. (Серия «Библиотека« Математическое образование »»). М .: МЦНМО, 2002. — 32 с.
3. Геометрия. Дополнительные главы к учебнику для 8-х классов: Учебник для учащихся школ и классов с углубленным изучением / Л.С. Атанасян, В.Ф. Бутузов, С. Кадомцев и др. — М .: Вита-Пресс, 2005. — 208 с.
4. Эрдниев П., Манцаев Н. Теоремы Чевы и Менелая. М .: Квант, 1990, № 3. С. 56–59.
5. Шарыгин И.Ф. Теоремы Чевы и Менелая. М .: Квант, 1976, № 11. С. 22–30.
6. Вавилов В.В. Медианы и средние линии треугольника. М .: Математика, 2006, № 1.
.
7. Ефремов Дм. Новая геометрия треугольника. Одесса, 1902. — 334 с.
8. Математика.50 вариантов типовых тестовых заданий / И.В. Ященко, М.А.Волькевич, И. Высоцкий и другие; изд. И.В. Ященко. — М .: Издательство «Экзамен», 2016. — 247 с.

В курсе геометрии есть теоремы, которые в школе недостаточно подробно изучаются, но которые могут быть полезны при решении самых сложных задач ОГЭ и ЕГЭ. К ним относится, например, теорема Менелая. Традиционно ее изучают в классах с углубленным изучением математики в 8-м классе, а в обычную учебную программу (по учебнику Атанасяна) теорема Менелая входит в учебники 10-11 классов.
Между тем, результат изучения интернет-ресурсов, где упоминается теорема Менелая, показывает, что обычно она формулируется не полностью, а потому неточно, и не приводятся все случаи ее использования, а также доказательство обратной теоремы. Цель этой статьи — понять, что такое теорема Менелая, как и почему она используется, а также поделиться с учениками методикой преподавания этой теоремы на индивидуальных уроках с репетитором.
Рассмотрим типичную проблему (Задача № 26, ОГЭ), встречающуюся на экзаменах в различных вариантах, которые различаются только числами в условии.

Само решение проблемы несложное — вы можете ознакомиться с ним ниже. В этой статье нас в основном интересует немного другой момент, который часто опускается, понимается как самоочевидный, как очевидный. Но очевидное — это то, что можно доказать. И это можно доказать по-разному — обычно это доказывают исключительно с помощью подобия, — но это можно сделать и с помощью теоремы Менелая.
Из условия следует, что, поскольку углы у нижнего основания трапеции в сумме составляют 90 °, то, если удлинить стороны, получится прямоугольный треугольник.Далее из полученной точки пересечения продолжений боковых сторон проводится отрезок, проходящий через средние точки оснований. Почему этот отрезок проходит через все эти три точки? Обычно об этом не говорится ни слова в решениях проблем, найденных в Интернете. Нет даже ссылки на теорему о четырех точках трапеции, не говоря уже о доказательстве этого утверждения. Между тем, это можно доказать с помощью теоремы Менелая, которая является условием того, что три точки принадлежат одной прямой.
Формулировки теоремы Менелая
Пришло время сформулировать теорему. Следует отметить, что в разных учебниках и учебных пособиях встречаются довольно разные его формулировки, хотя суть остается неизменной. В учебнике Атанасяна и соавт. Для 10-11 классов дана следующая формулировка теоремы Менелая, назовем ее «векторной»:
В учебнике «Геометрия 10-11 классы» Александрова и др., А также в учебнике тех же авторов. «Геометрия.8-й класс «, дается немного другая формулировка теоремы Менелая, и она одинакова для 10-11 и 8-го классов:
Здесь нужно отметить три момента.
Примечание 1. На экзаменах нет задач, которые необходимо сдать. решаться только с помощью векторов, для которых используется ровно «минус один». Поэтому для практического использования наиболее удобная формулировка является, по сути, следствием теоремы для отрезков (это вторая формулировка, выделенная жирным шрифтом Мы ограничимся им для дальнейшего изучения теоремы Менелая, поскольку наша цель — научиться применять ее для решения задач.
Примечание 2. Несмотря на то, что во всех учебниках также четко прописан случай, когда все три точки A 1, B 1 и C 1 могут лежать на продолжениях сторон треугольника (или на прямых, содержащих стороны треугольника ), на нескольких обучающих сайтах в Интернете сформулирован только случай, когда две точки лежат на двух сторонах, а третья лежит на продолжении третьей стороны. Вряд ли это может быть оправдано тем фактом, что на экзаменах встречаются только проблемы первого типа, а проблемы не могут встречаться, когда все эти точки лежат на продолжении трех сторон.
Примечание 3. Обратная теорема, т.е. условие, что три точки лежат на одной прямой, обычно вообще не рассматривается, и некоторые преподаватели даже советуют (???) иметь дело только с прямой теоремой, а не рассматривать обратную. теорема. Между тем доказательство обратного утверждения достаточно поучительно и позволяет доказать утверждения, аналогичные приведенным в решении задачи 1. Опыт доказательства обратной теоремы, несомненно, принесет студенту ощутимую пользу при решении задач.
Рисунки и шаблоны
Чтобы научить студента видеть теорему Менелая в задачах и использовать ее в решениях, важно обращать внимание на изображения и шаблоны в записи теоремы для конкретного случая. А поскольку сама теорема находится в «чистом» виде, т.е. не окружена другими отрезками, стороны разных фигур в задачах обычно не встречаются, то целесообразнее показывать теорему на конкретных задачах. А если в качестве объяснения показывать картинки, то сделайте их многомерными.При этом выделите одним цветом (например, красным) прямую, образованную тремя точками, а синим — отрезки треугольника, участвующие в записи теоремы Менелая. При этом те элементы, которые не участвуют, остаются черными:
На первый взгляд может показаться, что формулировка теоремы довольно сложна и не всегда ясна; потому что в нем задействованы три фракции. Ведь если у ученика недостаточно опыта, то он легко может ошибиться в письменной форме и, как следствие, неправильно решить задачу.И здесь иногда начинаются проблемы. Дело в том, что учебники обычно не акцентируют внимание на том, как «сделать обходной путь» при написании теоремы. О законах написания самой теоремы ничего не сказано. Поэтому некоторые репетиторы даже рисуют разные стрелки, в каком порядке записывать формулу. И они предлагают студентам строго следовать этим рекомендациям. Отчасти это правильно, но гораздо важнее понять суть теоремы, чем записывать ее чисто механически, используя «правило обхода» и стрелки.
На самом деле важно только понимать логику «обхода», и она настолько точна, что невозможно ошибиться при написании формулы. В обоих случаях а) и б) запишем формулу треугольника AMC.
Для начала определим для себя три точки — вершины треугольника. У нас есть эти точки A, M, C. Затем мы определяем точки, лежащие на пересекающейся прямой (красная линия), это B, P, K. Начинаем «движение» с вершины треугольника, например, с точка C.От этой точки «идем» до точки, которая образована пересечением, например, стороны AC и пересекающейся прямой — у нас есть эта точка K. Пишем в числителе первой дроби — SK. Далее от точки K «идем» до оставшейся точки на прямой AC — в точку A. В знаменателе первой дроби пишем — KA. Поскольку точка A также принадлежит прямой AM, то же самое проделываем с отрезками на прямой AM. И здесь мы снова начинаем сверху, затем «идем» до точки на пересекающейся прямой, после чего переходим к вершине M.«Оказавшись» на прямой BC, мы делаем то же самое с отрезками на этой прямой. Из M мы, естественно, «идем» в B, после чего возвращаемся в C. Этот «объезд» можно делать как по часовой стрелке, так и против часовой стрелки. Важно только понять правило обхода — от вершины к точке на прямой и от точки на прямой к другой вершине. Так обычно объясняют правило написания произведения дробей. Результат:
Обратите внимание на то, что весь «обход» отражен в записи и для удобства показан стрелками.
Однако итоговая запись может быть получена без выполнения какого-либо «обхода». После того, как точки — вершины треугольника (A, M, C) и точки — лежащие на пересекающейся прямой (B, P, K) выписаны, они также записывают тройки букв, обозначающих точки, лежащие на каждой из три строки. В наших случаях это I) B, M, C; II) A, P, M и III) A, C, K. После этого правильную левую часть формулы можно записать, даже не глядя на рисунок, и в любом порядке. Нам достаточно из каждой тройки букв написать правильные дроби, подчиняющиеся правилу — условно «средние» буквы — это точки пересекающейся прямой (красная).Условно «крайними» буквами являются точки вершин треугольника (синие). При написании формулы таким образом вам нужно только убедиться, что любая «синяя» буква (вершина треугольника) попадет и в числитель, и в знаменатель один раз. Например.
Этот метод особенно полезен для случаев типа b), а также для самопроверки.
Теорема Менелая. Доказательство
Есть несколько разных способов доказать теорему Менелая. Иногда это доказывается с помощью подобия треугольников, для которых из точки M (как на этом чертеже) проводится отрезок, параллельный AC.Другие проводят дополнительную прямую линию, не параллельную пересекающейся линии, а затем прямые линии, параллельные пересекающейся линии, как будто они «проецируют» все необходимые отрезки на эту линию и, используя обобщение теоремы Фалеса (т. Е. теорема о пропорциональных отрезках), выведите формулу. Однако, возможно, самый простой способ доказательства получается, если провести из точки M прямую линию, параллельную пересечению. Докажем таким образом теорему Менелая.
Дано: Треугольник ABC.Линия PK пересекает стороны треугольника и продолжение стороны MC в точке B.
Докажите, что выполняется равенство:
Доказательство. Нарисуйте луч MM 1 параллельно BK. Запишем соотношения между отрезками, которые входят в обозначения формулы теоремы Менелая. В одном случае рассмотрим прямые, пересекающиеся в точке A, а в другом случае — в точке C. Умножим левую и правую части этих уравнений:

Теорема доказана.
Теорема доказывается аналогично для случая б).

Из точки C проведите отрезок CC 1, параллельный линии BK. Запишем соотношения между отрезками, которые входят в обозначения формулы теоремы Менелая. В одном случае рассмотрим прямые, пересекающиеся в точке A, а в другом случае — в точке M. Поскольку теорема Фалеса ничего не говорит о расположении отрезков на двух пересекающихся прямых, отрезки могут быть расположены на противоположных сторонах линии. точка M. Следовательно,

Теорема доказана.
Теперь докажем обратную теорему.
Дано:
Докажите, что точки B, P, K лежат на одной прямой.
Доказательства. Пусть прямая BP пересекает AC в некоторой точке K 2, которая не совпадает с точкой K. Поскольку BP — прямая, содержащая точку K 2, для нее верна только что доказанная теорема Менелая. Итак, для нее мы пишем
. Однако мы только что доказали, что
. Отсюда следует, что точки K и K 2 совпадают, поскольку они разделяют сторону AC в одинаковом соотношении.
Для случая б) теорема доказывается аналогично.
Решение проблем с использованием теоремы Менелая
Во-первых, давайте вернемся к проблеме 1 и решим ее. Прочитаем еще раз. Сделаем рисунок:

Дана трапеция ABCD. ST — средняя линия трапеции, то есть одно из заданных расстояний. Углы A и D в сумме составляют 90 °. Продлим стороны AB и CD и получим точку K на их пересечении. Соедините точку K с точкой N — серединой BC. Теперь докажем, что точка P, являющаяся серединой основания AD, также принадлежит прямой KN.Рассмотрим последовательно треугольники ABD и ACD. Две стороны каждого треугольника пересекает линия KP. Предположим, что прямая KN пересекает базу AD в некоторой точке X. По теореме Менелая:
Поскольку треугольник AKD прямоугольный, точка P, которая является серединой гипотенузы AD, равноудалена от A, D и K. Аналогично , точка N равноудалена от точек B, C и K. Отсюда одна база равна 36, а другая — 2.
Решение. Рассмотрим треугольник BCD. Его пересекает луч AX, где X — точка пересечения этого луча с продолжением стороны BC.По теореме Менелая:
Подставляя (1) в (2), получаем:
Решение. Обозначим буквами S 1, S 2, S 3 и S 4 площади треугольников AOB, AOM, BOK и четырехугольника MOKC соответственно.

Поскольку BM — медиана, то S ABM = S BMC.
Отсюда S 1 + S 2 = S 3 + S 4.
Так как нам нужно найти соотношение площадей S 1 и S 4, разделим обе части уравнения на S 4:
Подставим эти значения К формуле (1): Из треугольника BMC с секущей AK по теореме Менелая имеем: Из треугольника AKC с секущей BM по теореме Менелая имеем: Все необходимые отношения выражаются через k, и теперь мы можно подставить их в выражение (2):
Решение этой проблемы с помощью теоремы Менелая обсуждается на странице.
Примечание репетитора по математике. Применение теоремы Менелая в этой задаче — тот самый случай, когда этот метод позволяет существенно сэкономить время на экзамене. Эта задача предложена в демо-версии вступительного экзамена в 9-й лицей НИУ ВШЭ (2019).
© Репетитор по математике в Москве, Александр Анатольевич, 8-968-423-9589.
Решайте сами
1) Задача попроще. Точка M отмечается на медиане BD треугольника ABC так, чтобы BM: MD = m: n.Линия AM пересекает сторону BC в точке K.
Найдите соотношение BK: KC.
2) Задача посложнее. Биссектриса угла A параллелограмма ABCD пересекает сторону ВС в точке P, а диагональ BD — в точке T. Известно, что AB: AD = k (0 3) Задача № 26 ОГЭ. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 36. Найдите стороны треугольника ABC.
Совет репетитора по математике. В Интернете есть решение такой проблемы с помощью дополнительного построения и затем либо подобия, либо нахождения площадей, и только после этого сторон треугольника.Те. оба эти метода требуют дополнительной конструкции. Однако решение такой задачи с использованием свойства биссектрисы и теоремы Менелая не требует дополнительных построений. Это намного проще и рациональнее.
Математика — 10 класс Мендель Виктор Васильевич, декан факультета естественных наук, математики и информационных технологий Дальневосточного государственного экономического университета ТЕОРЕМЫ ЧЕВЫ И МЕНЕЛАЯ Особое место в планиметрии занимают две замечательные теоремы: теорема Чевы и теорема Менелая.Эти теоремы не включены в базовую программу курса геометрии в средней школе, но их изучение (и применение) рекомендуется всем, кто немного больше интересуется математикой, чем это возможно в школьной программе. Чем интересны эти теоремы? Прежде всего отметим, что при решении геометрических задач продуктивно сочетаются два подхода: — один основан на определении базовой конструкции (например: треугольник — круг; треугольник — секущая; треугольник — три прямые. проходящий через его вершины и пересекающийся в одной точке; четырехугольник с двумя параллельными сторонами и т. д.), а второй — метод опорных задач (простых геометрических задач, к которым сводится процесс решения сложной задачи). Итак, теоремы Менелая и Шевы относятся к числу наиболее распространенных построений: первая рассматривает треугольник, стороны или продолжения сторон которого пересекаются некоторой прямой (секущей), вторая имеет дело с треугольником и тремя прямыми линиями. проходящие через его вершины, пересекающиеся в одной точке. Теорема Менелая Эта теорема, соблюдая (вместе с обратными) соотношениями, показывает отрезки, образец, соединяющий вершины треугольника и точки пересечения секущей со сторонами (продолжениями сторон) треугольника.На рисунках показаны два возможных случая расположения треугольника и секущей. В первом случае секущая пересекает две стороны треугольника и продолжение третьей, во втором — продолжение всех трех сторон треугольника. Теорема 1. (Менелай). Пусть ABC пересекает прямая, которая не параллельна стороне AB и пересекает две ее стороны AC и BC соответственно в точках B1 и A1, а прямая AB в точке C1, тогда AB1 CA1 BC1    1. B1C A1B C1 A Теорема 2.(обратная теореме Менелая). Пусть в треугольнике ABC точки A1, B1, C1 принадлежат прямым BC, AC, AB соответственно, тогда если AB1 CA1 BC1   1 B1C A1B C1 A, то точки A1, B1, C1 лежать на одной прямой. Доказательство первой теоремы можно провести следующим образом: перпендикуляры из всех вершин треугольника опускаются на секущую. В результате получились три пары одинаковых прямоугольных треугольников. Соотношения отрезков, фигурирующие в формулировке теоремы, заменяются соотношениями перпендикуляров, соответствующих им по подобию.Получается, что каждый отрезок — перпендикуляр в дробях будет присутствовать дважды: один раз в одной дроби в числителе, второй раз в другой дроби, в знаменателе. Таким образом, произведение всех этих соотношений будет равно единице. Обратная теорема доказывается от противного. Предполагается, что в условиях теоремы 2 точки A1, B1, C1 не лежат на одной прямой. Тогда прямая A1B1 пересечет сторону AB в точке C2, отличной от точки C1. В этом случае в силу теоремы 1 для точек A1, B1, C2 будет выполнено то же соотношение, что и для точек A1, B1, C1.Отсюда следует, что точки C1 и C2 будут делить отрезок AB в одинаковом соотношении. Тогда эти точки совпадают — мы получили противоречие. Рассмотрим примеры приложений теоремы Менелая. Пример 1. Докажите, что медианы треугольника в точке пересечения делятся в соотношении 2: 1, считая от вершины. Решение. Запишем соотношение, полученное в теореме Менелая для треугольника ABMb и прямой McM (C): AM c BM M bC    1. M c B MM b CA Первая дробь в этом произведении, очевидно, равна 1 , а третье второе отношение равно 1.Следовательно, 2 2: 1, как и требуется. Пример 2. Секущая пересекает продолжение стороны AC треугольника ABC в точке B1, так что точка C является серединой отрезка AB1. Этот секанс делит сторону AB пополам. Найдите, в каком отношении он разделяет сторону BC? Решение. Запишем для треугольника и секанса произведение трех соотношений из теоремы Менелая: AB1 CA1 BC1    1. B1C A1B C1 A Из условий задачи следует, что первое отношение равно единице, а третье — 1, 2, поэтому второе отношение равно 2, т.е.е. То есть секущая делит сторону BC в соотношении 2: 1. Мы встретимся со следующим примером применения теоремы Менелая, когда рассмотрим доказательство теоремы Шевы. Теорема Чевы Большинство замечательных точек треугольника можно получить с помощью следующей процедуры. Пусть существует какое-то правило, по которому мы можем выбрать некоторую точку A1 на стороне BC (или ее продолжении) треугольника ABC (например, выбрать середину этой стороны). Затем построим аналогичные точки B1, C1 на двух других сторонах треугольника (в нашем примере еще две середины сторон).Если правило выбора выполнено успешно, то прямые AA1, BB1, CC1 пересекаются в некоторой точке Z (выбор середин сторон в этом смысле, конечно, удачный, так как медианы треугольника пересекаются в одной точке) . Я хотел бы иметь какой-то общий метод, который позволяет по положению точек на сторонах треугольника определять, пересекаются ли соответствующие тройки прямых в одной точке или нет. Универсальное условие, которое «закрыло» эту проблему, было найдено в 1678 году итальянским инженером Джованни Чева.Определение. Отрезки, соединяющие вершины треугольника с точками на противоположных сторонах (или их продолжения), называются шевианами, если они пересекаются в одной точке. Есть два варианта расположения чевианов. В одном варианте осуществления точка пересечения является внутренней, а концы шевианов лежат на сторонах треугольника. Во втором варианте точка пересечения внешняя, конец одного шевиана лежит сбоку, а два других имеют концы на продолжениях сторон (см. Рисунки).Теорема 3. (Прямая теорема Шевы) В произвольном треугольнике ABC на сторонах BC, CA, AB или их продолжениях выбираются точки A1, B1, C1 соответственно так, что прямые AA1, BB1, CC1 пересекаются в некоторой общей точке. точка, то BA1 CB1 AC1   1 CA1 AB1 BC1. Доказательство: существует несколько оригинальных доказательств теоремы Шевы, мы рассмотрим доказательство, основанное на двукратном применении теоремы Менелая. Впервые запишем связь теоремы Менелая для треугольника ABB1 и секущей CC1 (обозначим точку пересечения хевианов через Z): AC1 BZ B1C    1, C1B ZB1 CA и второй раз для треугольника B1BC и секущая AA1: B1Z BA1 CA    1.ZB A1C AB1 Умножая эти два соотношения и делая необходимые сокращения, получаем соотношение, содержащееся в формулировке теоремы. Теорема 4. (обратная теорема Чевы). Если для точек A1, B1 и C1, выбранных на сторонах треугольника ABC или их продолжений, выполняется условие Cheva: BA1 CB1 AC1   1 CA1 AB1 BC1, то прямые AA1, BB1 и CC1 пересекаются в одной точке. Доказательство этой теоремы проводится от противного, как и доказательство теоремы Менелая. Рассмотрим примеры применения прямой и обратной теорем Чевы.Пример 3. Докажите, что медианы треугольника пересекаются в одной точке. Решение. Рассмотрим отношение AC1 BA1 CB1   C1B A1C B1 A для вершин треугольника и середин его сторон. Очевидно, что в каждой дроби в числителе и знаменателе есть равные отрезки, поэтому все эти дроби равны единице. Следовательно, соотношение Чевы выполняется, следовательно, по обратной теореме медианы пересекаются в одной точке. Задания для самостоятельного решения Предлагаемые здесь задания — это тест №1 для учащихся 9 класса.Решите эти задачи, запишите решения в отдельную (помимо физики и информатики) тетрадь. Укажите на обложке следующую информацию о себе: 1. Фамилия, имя, класс, профиль класса (например: Пупкин Василий, 9 класс, математический) 2. Почтовый индекс, адрес проживания, e-mail (если есть), телефон ( дом или мобильный) 3. Данные о школе (например: МБОУ №1, Бикин) 4. Фамилия, имя учителя математики (например: учитель математики Петрова М.И.) Рекомендуется решить не менее четырех задач.М 9.1.1. Может ли секущая из теоремы Менелая разрезать стороны треугольника (или их продолжения) на отрезки длины: а) 3, 3, 5, 7,10, 14; в) 3, 5, 6, 7, 7, 10, Если такие варианты возможны, приведите примеры. Сегменты могут быть в разном порядке. M 9.1.2. Могут ли внутренние шевианы треугольника делить его стороны на отрезки: а) 3, 3, 5, 7,10, 14; в) 3, 5, 6, 7, 7, 10, Если такие варианты возможны, приведите примеры. Сегменты могут быть в разном порядке. Подсказка: придумывая примеры, не забывайте проверять неравенство треугольника.M 9.1.3. Используя обратную теорему Чевы, докажите, что: а) биссектрисы треугольника пересекаются в одной точке; б) отрезки, соединяющие вершины треугольника с точками на противоположных сторонах, в которых эти стороны касаются вписанной окружности, пересекаются в одной точке. Направления: а) запомните, в каком отношении биссектриса делит противоположную сторону; б) использовать то свойство, что отрезки двух касательных, проведенных из одной точки в определенную окружность, равны. М 9.1.4. Завершите доказательство теоремы Менелая, начатое в первой части статьи.M 9.1.5. Докажите, что высоты треугольника пересекаются в одной точке, используя обратную теорему Чевы. М 9.1.6. Докажите теорему Симпсона: из произвольной точки M, взятой на окружности, описанной вокруг треугольника ABC, опускаются перпендикуляры к сторонам или продолжениям сторон треугольника, докажите, что основания этих перпендикуляров лежат на одной прямой. Подсказка: используйте обратную теорему Менелая. Попробуйте выразить длину отрезков линии, используемых во взаимосвязях, через длины перпендикуляров, проведенных к их точке M.Также полезно запомнить свойства углов вписанного четырехугольника.
Теорема Менелая или теорема о полном четырехугольнике известна со времен Древней Греции. Свое название он получил в честь своего автора — древнегреческого математика и астронома Менелай Александрийский (ок. 100 г. н.э.). Эта теорема очень красивая и простая, но, к сожалению, в современном школьном курсе ей не уделяется должного внимания. А между тем во многих случаях он помогает очень легко и изящно решать довольно сложные геометрические задачи.
Теорема 1 (теорема Менелая) … Пусть ∆ABC пересекает прямая, которая не параллельна стороне AB и пересекает две ее стороны AC и BC в точках F и E соответственно, а прямая AB в точках точка D (рис.1) ,
, затем A F FC * CE EB * BD DA = 1
Примечание. Чтобы легко запомнить эту формулу, вы можете использовать следующее правило: двигайтесь по контуру треугольника от вершины к точке пересечения с линией и от точки пересечения к следующей вершине.
Доказательства. Из вершин A, B, C треугольника проведите соответственно три параллельные линии, пока они не пересекутся с секущей линией. Получаем три пары одинаковых треугольников (знак сходства в двух углах). Подобие треугольников влечет следующие равенства
А теперь умножаем полученные данные на равенства:
Теорема доказана.
Чтобы ощутить всю красоту этой теоремы, попробуем решить предложенную ниже геометрическую задачу двумя разными способами: с помощью вспомогательной конструкции и с помощью теорем менелая .
Цель 1.
В ∆ABC биссектриса AD делит сторону BC в соотношении 2: 1. В каком соотношении медиана CE делит эту биссектрису?
Решение.
Использование вспомогательной конструкции:
Пусть S — точка пересечения биссектрисы AD и медианы CE. Построим ∆ASB до параллелограмма ASBK. (рис. 2)
Очевидно SE = EK, так как пересечение параллелограмма делит диагонали пополам.Рассмотрим теперь треугольники ∆CBK и ∆CDS. Нетрудно заметить, что они похожи (признак сходства в двух углах: и как внутренние односторонние углы с параллельными линиями AD и KB и секущей CB). Подобие треугольника подразумевает следующее:
Используя условие, получаем:
CB CD = CD + DB CD = CD + 2CD CB = 3CD CD = 3
Теперь обратите внимание, что KB = AS, как противоположные стороны параллелограмма. Тогда
AS SD = KB SD = CB CD = 3
Использование теоремы Менелая.
Рассмотрим ∆ABD и применим к нему теорему Менелая (прямая, проходящая через точки C, S, E, является секущей):
BE EA * AS SD * DC CB = 1
По условию теоремы у нас BE / EA = 1, так как CE — медиана, а DC / CB = 1/3, как мы рассчитали ранее.
1 * КАК СД * 1 3 = 1
Отсюда получаем AS / SD = 3 На первый взгляд оба решения достаточно компактны и примерно равны. Однако идея дополнительной конструкции для школьников часто оказывается очень сложной и совсем не очевидной, тогда как, зная теорему Менелая, ему нужно только правильно ее применить.
Рассмотрим другую задачу, в которой теорема Менелая работает очень элегантно.
Цель 2.
На сторонах AB и BC ∆ABC даны точки M и N соответственно такие, что выполняются следующие равенства
AM MB = CN NA = 1 2
В каком соотношении точка пересечения S отрезков BN и CM делит каждый из этих отрезков (рис. 3)?
Решение.
Рассмотрим ∆ABN.Применим теорему Менелая для этого треугольника (прямая, проходящая через точки M, S, C, является секущей)
AM MB * BC SN * CN CA = 1
Из условия задачи имеем: AM MB = 1 2
NC CA = NC CN + NA = NC CN + 2NC = NC 3 NC = 1 3
Подставляем эти результаты и получаем:
1 2 * БС СН * 1 3 = 1
Отсюда BS / SN = 6. А, значит, точка S пересечения отрезков BN и CM делит отрезок BN в соотношении 6: 1.
Рассмотрим ∆ACM. Применим теорему Менелая для этого треугольника (прямая, проходящая через точки N, S, B, является секущей):
AN NC * CS SM * MB BA = 1
Из условия задачи имеем: AN NC = 2
МБ BA = MB BM + MA = 2MA 2MA + MA = 2MB 3MA = 2 3
Подставляем эти результаты и получаем:
2 * КС СМ * 2 3 = 1
Отсюда CS / SM = 3/4
Это означает, что точка S пересечения отрезков BN и CM делит отрезок CM в соотношении 3: 4.
Верна и обратная теорема Менелая. Часто это бывает даже полезнее. Это особенно хорошо работает в задачах доказательства. Часто с его помощью красиво, легко и быстро решаются даже олимпиадные задачи.
Теорема 2 (обратная теорема Менелая). Пусть дан треугольник ABC и точки D, E, F принадлежат прямым BC, AC, AB соответственно (обратите внимание, что они могут лежать как на сторонах треугольника ABC, так и на их продолжениях) (рис. 4) .
Тогда если AF FC * CE EB * BD DA = 1
то точки D, E, F лежат на одной прямой.
Доказательства. Докажем теорему от противного. Предположим, что соотношение из условий теоремы выполнено, но точка F не лежит на прямой DE (рис. 5).
Обозначим точку пересечения прямых DE и AB буквой O. Теперь применим теорему Менелая и получим: AE EC * CD DB * BO OA = 1
Но, с другой стороны, равенство BF FA = BO OA
не может быть выполнен.
Следовательно, соотношение из условий теоремы не может быть выполнено.

Контрольные работы по геометрии 8 класс анастасян: ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян

ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян

Основные группы пользователей сборника готовых ответов

Неоспоримые плюсы обращения к онлайн справочникам

Геометрия 8 Контрольные Атанасян (Зив)

Геометрия 8 Контрольные Атанасян (Зив)

Контрольная работа № 1.

Контрольная работа № 2.

Контрольная работа № 3.

Контрольная работа № 4.

Контрольная работа № 5.

Контрольная работа № 6.

Контрольная работа № 7.

Страница не найдена

Новости

▶▷▶ контрольная работа по геометрии 8 класс номер 4 вариант 1

Геометрия, 8 класс.

Геометрия 8 Контрольные Мерзляк | Контроль знаний

Геометрия 8 класс

Другие контрольные работы по математике в 8 классе:

Контрольные работы по Алгебре в 8 классе (по учебнику Мерзляка А.

Контрольные работы по Алгебре в 8 классе (по учебнику Алимова Ш.А.)

Контрольные работы по Алгебре в 8 классе (по учебнику Макарычева Ю.Н.)

Геометрия 8 класс . Тесты и Тренажеры

ГЕОМЕТРИЯ 8 класс. ТЕСТЫ И ТРЕНАЖЕРЫ

ГЕОМЕТРИЯ 8 класс. КОНТРОЛЬНЫЕ РАБОТЫ

Рекомендуемые материалы для очного контроля знаний

Программа обучения по геометрии в 8 классе (основные темы)

теорем Чевы и изменение экзамена. Теоремы Чевы и Чевы Пространственные аналоги теорем Чевы и Менелайи

В классах

I этап. Организационный момент (1 мин.)

II этап. Обновление базовых знаний и навыков (10 мин.)

III этап. Решаю задачи. (22 мин.)

IV этап. Решение задач (самостоятельная работа) (8 мин.)

Этап V. Подведение итогов (2 мин.)

VI этап. Домашнее задание (1 мин.)

Заключительное слово преподавателя (1 мин).

2. Теорема Чевы

Круглые тела Солнечной системы. Презентация на тему «Круглые геометрические тела» Круглые тела в повседневной жизни

Типы секций:

Площадь цилиндра

Историческая справка о цилиндре

Типы секций:

Площадь конуса

Основные формулы

Историческая справка о конусе

Область сферы

Касательная плоскость к сфере

Историческая справка о сфере

Обзоры

И что в итоге? Смотрите: куб — это коробочка, шарик внутри.

Аннотация

Готовые школьные домашние задания: фото ответы на задания APK

Скачать презентационные полигоны. Многоугольник и его элементы. Сообщение Темы урока

Подписи к слайдам:

Загрузить:

Предпросмотр:

Подписи к слайдам:

По теме: Методические разработки, презентации и тезисы

Сообщение Темы урока

Определение целей урока

Этюд по новому материалу Стр. 42, № 1 (у.)

Изучение нового материала

Изучение нового материала

Изучение нового материала

Изучение нового материала

Изучение нового материала

Изучение нового материала

Изучение нового материала

Выход

Работа по учебнику Стр. 43, № 2

Работа по учебнику П.43, номер 3

Работа над учебником стр. 43, № 4

Работа в тетради стр. 16, № 1

Работа в тетради стр. 16, № 2

стр. 44, № 7 ( учебник)

С.44, № 7 (учебник)

С.44, № 7 (учебник)

С.44, № 7 (учебник)

Просмотр содержания документа