Краткий курс алгебры 8 класс.
8 класс алгебра Рациональные дроби и их свойства.
Целые и дробные выражения называют рациональными выражениями.
Значения переменных при которых выражение имеет смысл , называют допустимыми значениями переменных.
Дробь , числитель и знаменатель которой многочлены , называют рациональной дробью.
Основное свойство рациональной дроби: если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен , то получится равная ей дробь.
Тождеством называется равенство , верное при всех допустимых значениях входящих в него переменных.
Если изменить знак числителя ( или знак знаменателя ) дроби и знак перед дробью , то получим выражение , тождественно равное данному.
Сумма и разность дробей.
Чтобы сложить рациональные дроби с одинаковыми знаменателями , надо сложить их числители , а знаменатель оставить тем же.
Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями , надо из числителя первой дроби вычесть числитель второй дроби , а знаменатель оставить тем же.
Сложение и вычитание рациональных дробей с разными знаменателями сводится к сложению и вычитанию рациональных дробей с одинаковыми знаменателями .Для этого дроби приводят к общему знаменателю.
Произведение и частное дробей.
Чтобы умножить дробь на дробь , нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем , а второе – знаменателем дроби.
Чтобы возвести дробь в степень , надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе , а второй – в знаменателе дроби.
Чтобы разделить одну дробь на другую , нужно первую дробь умножить на дробь , обратную второй.
Функция у= и её график.
Обратной пропорциональностью называется функция , которую можно задавать формулой у= , где х – незави симая переменная и k – не равное нулю число.
Областью определения функции у= является множество всех чисел , отличных от нуля.
Кривую , являющуюся графиком обратной пропорциональности , называют гиперболой. Гипербола состоит из двух ветвей.
Действительные числа.
Всякое рациональное число , как целое , так и дробное , можно представить в виде дроби , где m- целое число , а n – натуральное. Одно и то же рациональное число
можно представить в таком виде разными способами.Среди дробей , с помощью которых записывается данное рациональное число , всегда можно указать дробь с наименьшим знаменателем. Эта дробь несократима. Для целых чисел такая дробь имеет знаменатель , равный 1.
Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби.
Каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число.
Среди рациональных чисел нет такого числа , квадрат которого равен 2.
Если к положительным бесконечным десятичным дробям присоединить противоположные им им числа и число нуль , то получим множество чисел , которые называют действительными числами.
Множество действительных чисел состоит из рациональных и иррациональных чисел.
Арифметический квадратный корень.
Квадратным корнем из числа а называют число , квадрат которого равен а.
Арифметическим квадратным корнем из числа а называется неотрицательное число , квадрат которого равен
= b , если выполняются два условия : 1) b ≥ 0 ; 2) = а.
При а ‹ 0 выражение не имеет смысла.
При любом а , при котором выражение имеет смысл , верно равенство ( = а.
Выражение имеет смысл при любом а ≥ 0
Если а ≥ 0 и b 0 , то Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Если а ≥ 0 и b 0 , то = . Корень из дроби , числитель которой неотрицателен , а знаменатель положителен , равен корню из числителя , делённому на корень из знаменателя.
При любом значении х верно равенство = |
Функция у = и её график.
Если х = 0 , то у = 0 , поэтому начало координат принадлежит графику функции. 0
Если х › 0 , у › 0 : график расположен в первой координатной четверти.
Большему значению аргумента соответствует дольше значение функции ; график функции идёт вверх.
Квадратное уравнение и его корни.
Квадратным уравнением называется уравнение вида a+bx +c = 0 , где а,b и с – некоторые числа , причём а ≠ 0.
Квадратное уравнение в котором а = 1, называют приведённым квадратным уравнением.
Если в квадратном уравнении a+bx +c = 0 хотя бы один из коэффициентов b или с равен нулю , то такое уравнение называют неполным квадратным уравнением
При решении квадратного уравнения a+bx +c = 0 целесообразно поступать следующим образом: 1. Вычислить дискриминант и сравнить его с нулём ; 2. Если дискриминант положителен , то воспользоваться формулой корней , если дискриминант отрицателен , то записать , что корней нет.
Сумма корней приведённого квадратного уравнения равна второму коэффициенту , взятому с противоположным знаком, а произведение корней равно свободному члену.(Теорема Виета).
Если числа m и n таковы , что их сумма равна — p , а произведение равно g , то эти числа являются корнями уравнения +px +g = 0 ( Обратная теореме Виета )
Дробные рациональные уравнения.
При решении дробных рациональных уравнений поступают следующим образом:
1 Найти общий знаменатель дробей , входящих в уравнение;
2 Умножить обе части уравнения на их общий знаменатель;
3Решить получившееся целое уравнение;
4 Исключить из его корней те , которые обращают в нуль общий знаменатель.
Числовые неравенства и их свойства.
Число а больше числа b , если разность а – b – положительное число ; число а меньше числа b , если разность а – b – отрицательное число.
Если а › b ,то b ‹ а; если а ‹ b ,то b › а.
Если а ‹ b и b ‹ с , то а ‹ с .
Если а ‹ b и с— любое число ,то а + с ‹ b + с. Если к обеим частям верного неравенства прибавить одно и то же число , то получится верное неравенство.
Если а ‹ b и с— положительное число ,то ас ‹ bс. Если а ‹ b и с— отрицательное число ,то ас › bс.
Если обе части верного неравенства умножить или разделить на одно и то же положительное число , то получится верное равенство.
Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный , то получится верное равенство.
Если а и b – положительные числа и а ‹ b ,то ‹
Если а ‹ b и с ‹ d ,то а + с ‹ b + d. Если почленно сложить верные неравенства одного знака , то получится верное неравенство.
Если а ‹ b и с ‹ d , где а, b, с , d – положительные числа ,то ас ‹ bd.
Если почленно перемножить верные неравенства одного знака , левые и правые части которых – положительные числа , то получится верное неравенство.
Если а и b – положительные числа и а ‹ b ,то ‹ , где n – натуральное число.
Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения.
Неравенства с одной переменной и их системы.
Пересечением двух множеств называют множество , состоящее из всех общих элементов этих множеств.
Объединением двух множеств называют множество , состоящее из всех элементов , принадлежащих хотя бы одному из этих множеств.
Решением неравенства с одной переменной называется значение переменной , которое обращает его в верное числовое неравенство.
Решением системы неравенств с одной переменной называется значение переменной , при котором верно каждое из неравенств системы.
Степень с целым показателем и её свойства.
Если а ≠ 0 и n – целое отрицательное число , то = .
Выражению при целом отрицательном n ( так же как и при n = 0 ) не приписывают никакого значения ; это выражение не имеет смысла.
Для каждого а ≠ 0 и любых целых m и n
= ; = ; = ;
Для каждых а ≠ 0 и b ≠ 0 и любого n
= ; ( = ;
Стандартным видом числа а называют его запись в виде а* , где 1≤ а ≤ 10 и
n – число. Число n называется порядком числа а.
Геометрия 8 класс
Многоугольники
Если несмежные звенья замкнутой ломаной не имеют общих точек , то эта ломаная называется многоугольником, её звенья называют сторонами многоугольника , а длина ломаной называется периметром многоугольника.
Отрезок соединяющий любые две несоседние вершины , называеся диагональю многоугольника.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой , проходящей через две его соседние вершины.
Сумма углов выпуклого n- угольника равна ( n – 2 )*
Внешним углом выпуклого многоугольника называется угол , смежный с углом многоугольника.
Сумма внешних углов выпуклого многоугольника равна
Две несмежные стороны четырехугольника называются противоположными.
Сумма углов выпуклого четырехугольника равна
Параллелограммом называется четырехугольник , у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
В параллелограмме противоположные стороны равны и противоположные углы равны.
Диагонали параллелограмма точкой пересечения делятся пополам.
Признаки параллелограмма:
Если в четырёхугольнике две стороны равны и параллельны , то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике две стороны попарно равны , то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам , то этот четырёхугольник – параллелограмм.
Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые , пересекающие вторую прямую , то они отсекут на второй прямой равные между собой отрезки.
Трапецией называется четырёхугольник у которого две стороны параллельны , а две другие стороны не параллельны.
Трапеция называется равнобедренной , если её боковые стороны равны.
Трапеция называется прямоугольной , если один из её углов прямой.
Прямоугольником называется параллелограмм , у которого все углы прямые.
Свойства прямоугольника:
В прямоугольнике противоположные стороны равны и все углы равны.
Диагонали прямоугольника точкой пересечения делятся пополам.
Диагонали прямоугольника равны.
Признаки прямоугольника:
Если в параллелограмме диагонали равны , то этот параллелограмм – прямоугольник.
Ромбом называется параллелограмм , у которого все стороны равны.
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадратом называется прямоугольник у которого все стороны равны.
Свойства квадрата:
Все углы квадрата прямые.
Диагонали квадрата равны , взаимно перпендикулярны , точкой пересечения делятся пополам и делят углы квадрата пополам.
Осевая и центральная симметрии.
Две точки А и В называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АВ и перпендикулярна к нему.
Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется ось симметрии фигуры.
Две точки А и В называются симметричными относительно точки О , если О – середина отрезка АВ.
Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Тока О называется центром симметрии фигуры.
Площадь многоугольника.
Равные многоугольники имеют равные площади.
Если многоугольник составлен из нескольких многоугольников , то его площадь равна сумме площадей этих многоугольников.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если высоты двух треугольников равны , то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника , то площади этих треугольников относятся как произведения сторон , заключающих равные углы.
Площадь трапеции равна произведению полу суммы её оснований на высоту.
Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетеов.
Обратная теорема: если квадрат одной стороны треугольника равен сумме квадратов двух других сторон , то треугольник прямоугольный.
Формула Герона : площадь S треугольника со сторонами a,b,c выражается формулой S = , где p = (a + b + c) — полупериметр треугольника.
Определение подобных фигур.
Отношение отрезков АВ и СD называется отношение их длин , т.е. АВ/CD.
Говорят ,что отрезки АВ и СD пропорциональны отрезкам А₁В₁ и С₁D₁ , если
АВ/ А₁В₁ = СD/ С₁D₁ .
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Число k равное отношению сходственных сторон подобных треугольников , называется коэффициентом подобия.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников.
1 признак: если два угла одного треугольника соответственно равны двум углам другого , то такие треугольники подобны.
2 признак: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы , заключённые между этими сторонами , равны , то такие треугольники подобны.
3 признак: если три стороны одного треугольника пропорциональны трём сторонам другого треугольника , то такие треугольники подобны.
Средней линией треугольника называется отрезок , соединяющий середины двух его сторон.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Отрезок ХУ называется средним пропорциональным ( или средним геометрическим) для отрезков АВ и СD , если ХУ =
Высота прямоугольного треугольника , проведённая из вершины прямого угла , есть среднее пропорциональное для отрезков , на которые делится гипотенуза этой высотой.
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы , заключенного между катетом и высотой , проведённой из вершины прямого угла.
Соотношения между сторонами и углами прямоугольного треугольника.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Тангенс угла равен отношению синуса к косинусу этого угла.
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника , то синусы этих углов равны , косинусы этих углов равны и тангенсы этих углов равны.
Основное тригонометрическое тождество: = 1
Касательная к окружности.
Если расстояние от центра окружности до прямой меньше радиуса окружности (d ‹ r ) , то прямая и окружность имеют две общие точки.
Если расстояние от центра окружности до прямой равно радиусу окружности (d = r ) , то прямая и окружность имеют одну общую точку.
Если расстояние от центра окружности до прямой больше радиуса окружности (d › r ) , то прямая и окружность не имеют общих точек.
Прямая , имеющая с окружностью одну общую точку , называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности.
Касательная к окружности перпендикулярна к радиусу , проведенному к точке касания.
Отрезки касательных к окружности , проведённые из одной точки , равны и составляют равные углы с прямой , проходящей через эту точку и центр окружности.
Если прямая проходит через конец радиуса , лежащий на окружности , и перпендикулярна к этому радиусу , то она является касательной.
Центральные и вписанные углы.
Дуга называется полуокружностью , если отрезок , соединяющий её концы , является диаметром окружности.
Если дуга АВ окружности с центром О меньше полуокружности или является полуокружностью , то её градусная мера считается равной градусной мере центрального угла АОВ. Если же дуга АВ больше полуокружности , то уё градусная мера считается равной – уг.АОВ –
Сумма градусных мер двух дуг окружности с общими концами равна
infourok.ru
Интернет школа Interneturok — бесплатные школьные уроки по алгебре в 8 классе онлайн, видео уроки по алгебре
Современный учебник по алгебре 8 класса содержит в себе материалы, ориентированные на повторение пройденного за предыдущий год, а также дальнейшее изучение квадратичных функций, их свойств, графиков, сравнение значений, произведение и частное дробей т.д. Школьные уроки алгебры в 8 классе – это изучение параболы, действительных чисел, иррациональных выражений, нулей, квадратных уравнений (полных и неполных), теоремы Виета, алгебраических дробей и многое другое.
Видеоуроки по алгебре
Во избежание проблем с усвоением этих и других тем воспользуйтесь разделом алгебра 8 класс онлайн, входящим в структуру нашего сайта, и вы увидите, как эффектно работают обучающие материалы в формате видео. Учитывая то, что уроки алгебры за 8 класс бесплатны и круглосуточно доступны всем пользователям, их использование становится действительно стоящим делом. Необходимость в посещении дополнительных занятий в школе или в вызове платного домашнего репетитора теперь может отпасть!
Программа по алгебре 8 класса
Числовые неравенства, неравенства с одной переменной, их системы и решение уравнений, понятие и свойства степеней с целым показателем, запись и действия с приближенными значениями – вот что предстоит узнать школьникам в рамках изучения алгебры в 8 классе.
Продолжая в этом курсе знакомство с одной из наиболее сложных математических дисциплин, пользователи смогут уделить особое внимание тому, как осуществляется решение задач по алгебре, и попрактиковаться в этом вместе с преподавателем, а потом и самостоятельно, используя тесты и тренажеры. Задачи на сложение и вычитание дробей, решения рациональных уравнений и многое другое представлено на страницах нашего портала. И для того, чтобы все это уметь успешно решать необходимо знать формулы по алгебре, изучение которых началось еще в предыдущем курсе алгебры 7 класса.
Серьезные темы, которым будет уделено внимание в 8 классе, связаны с изучением различных алгебраических функций, среди которых квадратичная функция. В течение нескольких уроков преподаватель будет знакомить учащихся с ее свойствами и построением графика, поскольку любая алгебраическая функция имеет графическое отражение. В этом классе они также продолжат изучать действительные числа, узнав, что такое его модуль и какие бывают основные числовые множества, а также другие аспекты этой важной темы.
В конце курса будет уделено внимание закреплению изученных формул по алгебре и новым математическим понятиям. Это очень важный материал, поскольку для тех, кто хорошо понимает его суть в дальнейшем, решение задач по алгебре не составит особого труда.
На страницах нашего портала имеется множество видеоуроков, которые позволят ученикам средних общеобразовательных школ лучше ориентироваться в этой довольно сложной науке. Здесь размещены видеоуроки, которые были сняты с участием опытных преподавателей школьных дисциплин. С их помощью сложные темы в алгебре будут раскрыты максимально быстро, и восьмиклассникам будет намного легче продолжать освоение этой науки. Дробные рациональные уравнения и их решение графическим способом, формулы коней квадратного уравнения, свойства арифметического квадратного корня и материалы на многие другие темы в формате видео находятся на нашем портале в соответствующих разделах.
interneturok.ru
Школьная программа по алгебре для 8 класса
Математика известна как царица наук и гимнастика для ума. По сути, наша жизнь наполнена числами, причем речь не идет о простой арифметике для подсчета чего-либо — фактически каждое явление, закон, процесс могут быть выражены в определенной математической модели. Программа по алгебре для учащихся 8-х классов общеобразовательных школ ставит своей целью повысить теоретический уровень обучения, постепенно усиливая роль теории обобщений, анализа и дедуктивных заключений. И все это поможет в дальнейшем понять более сложные темы, разобраться в том, что преподается старшеклассникам.
Задачи по алгебре: цели и значение курса
Даже по сравнению с курсом математики 7-го класса, задачи по алгебре в 8-ом классе становятся заметно более сложными, да и изучаемые темы более специфичны. Программа по алгебре сегодня является не просто одним из методов интеллектуального развития учащегося и мотивации его мыслительной деятельности. Курс направлен на формирование у школьников представлений об идеях и используемых методах математики, о ней как об одной из форм познания действительности и способе описания (мат.моделирование явлений и процессов). Что в свою очередь неразрывно связано с общечеловеческой культурой, общественным и техническим прогрессом.
Задачи по алгебре ставят целью овладение учащимися конкретными математическими знаниями, которые необходимы для применения в практической деятельности, включая логическую. Кроме того, освоение программы по алгебре за 8-ой класс, включающей такие специфические темы как рациональные дроби, рациональные и иррациональные числа и их свойства, просто необходимо для изучения смежных дисциплин и дальнейшего образования. Также в список тем в этот период входят квадратные корни, квадратные уравнения, неравенства и системы неравенств, понятие степеней и элементы статистики. Все это крайне важно для школьника, понадобится ему и позже для изучения других вопросов.
Возможные трудности
Еще не так давно алгебра за 8 класс бесплатно была доступна для освоения только на школьных занятиях или самостоятельно, дома по учебникам. Школьный курс рассчитан на то чтобы дать учащемуся все необходимые знания. Тем не менее, программа по алгебре просто не в состоянии учесть индивидуальные особенности каждого школьника и применять индивидуальный подход. Это представляет основную сложность при изучении предмета, в котором важную роль играет именно самообразовательная часть.
Альтернативные методы обучения
Учебный портал InternetUrok.ru предлагает в качестве достойной альтернативы репетиторам, или учащимся, испытывающим определенные сложности, заниматься по курсу алгебра 8 класс бесплатно в удобное время и не выходя из дома. Система обучения основана на использовании эффективной дидактики с мотивационным и психологическим компонентом. Кроме того, теоретический материал и разбор задачи по алгебре по той или иной теме подробно представлен в видеоуроках, есть возможность выбрать и пройти задания для самоконтроля, закрепив материал, а также задать интересующие вопросы опытным педагогам.
Таким образом, изучая алгебру 8 класс бесплатно в качестве дополнительного способа обучения с применением интернета, вы получаете широкие возможности для познавательной деятельности, а также фактически индивидуальный подход, что особенно важно при подготовке к контрольным, экзаменам, аттестациям. Полезен портал будет также и родителям, желающим держать руку на пульсе образовательного процесса своего чада.
interneturok.ru
8 класс Алгебра — Математика онлайн
Меню- Обучение
- Закрыть
- Вебинары
- Закрыть
- Все вебинары
- Вебинар#1.ЕГЭ №9,13,18
- Вебинар#2. ЕГЭ №14
- Вебинар#3. ЕГЭ №16
- Вебинар#4.ЕГЭ №17
- Вебинар#5.ЕГЭ №13,18
- Вебинар#6.ЕГЭ №13,18
- Вебинар#7. ЕГЭ №15,18
- Вебинар#8. ЕГЭ. № 13,15
- Вебинар#9. ЕГЭ. №15
- Вебинар#10. ЕГЭ. №14
- Вебинар #11. ЕГЭ №14
- Вебинар#12 .ЕГЭ №16
- Вебинар#13. ЕГЭ №16
- Вебинар#14. ЕГЭ №18
- Вебинар#15. ЕГЭ №18
- Вебинар#16. ЕГЭ №18
- Вебинар#17. ЕГЭ №13
- Вебинар#18. ЕГЭ №15
- Вебинар#19. ЕГЭ №14
- Закрыть
- Пути обучения и темы
- Закрыть
- Пути обучения
- Что такое пути обучения
- Ваш первый учебный путь
- Все пути обучения
- Доступные темы
- Список бесплатных тем
- Полный список доступных тем
- Закрыть
- Подготовка к ЕГЭ
- Закрыть
- ЕГЭ Профиль
- Задание №4
- Задание №5
- Задание №6
- Задание №8
- Задание №9
- Задание №11
- Задание №13
- Задание №14
- Задание №17
- Задание №18
- ЕГЭ База
- Задание №7
- Задание №10
- Пути обучения
- Не помню как работают формулы приведения
- Хочу вспомнить как решать тригонометрические ур.
- Как отбирать корни тригонометрических ур.
- Учимся решать комбинированные ур.
- Учимся решать тригонометрические ур. с параметром
- Объем пирамиды. От простого к сложному.
- Вебинары
- Вебинар#1.ЕГЭ №9,13,18
- Вебинар #2.ЕГЭ №14
- Вебинар#3. ЕГЭ №16
- Вебинар#4.ЕГЭ №17
- Вебинар#5.ЕГЭ №13,18
- Вебинар#6.ЕГЭ №13,18
- Вебинар#7. ЕГЭ №15,18
- Вебинар#8.ЕГЭ № 13,15
- Вебинар#9.ЕГЭ. №15
- Вебинар#10. ЕГЭ. №14
- Вебинар #11. ЕГЭ №14
- Вебинар#12. ЕГЭ №16
- Вебинар#13. ЕГЭ №16
- Вебинар#14. ЕГЭ №18
- Вебинар#15. ЕГЭ №18
- Вебинар#16. ЕГЭ №18
- Вебинар#17. ЕГЭ №13
- Вебинар#18. ЕГЭ №15
- Вебинар#19. ЕГЭ №14
- Закрыть
- 11 класс
- Закрыть
- Алгебра
- Уравнения
- Показательные уравнения
- Комбинированные уравнения
- Уравнения
- Геометрия
- Многогранники
- Пути обучения
- Закрыть
- 10 Класс
- Закрыть
- Алгебра
- Повторение 7-9
- Числовые функции
- Тригонометрические уравнения
- Преобразование тригонометрических выражений
- Геометрия
- Введение
- Параллельность прямых и плоскостей
- Перпендикулярность прямых и плоскостей
- Подготовка к ЕГЭ
- Задание №13
- Задание №18
- Пути обучения
- Закрыть
- ОГЭ
- Закрыть
- ОГЭ
- Задание №4
- Задание №9
- Задание №17
- Задание №21
- Задание №22
- Пути обучения
- Закрыть
- 9 Класс
- Закрыть
- Алгебра
- Текстовые задачи
- Геометрия
- Факультатив
- Уравнения
- Уравнения повышенной сложности
- Уравнения
- Пути обучения
- Закрыть
- 8 Класс
- Закрыть
- Алгебра
- Уравнения
- Квадратные уравнения
- Рациональные уравнения
- Текстовые задачи
- Уравнения
- Геометрия
- Окружности
- Факультатив
- Уравнения
- Рациональные уравнения с параметром
- Уравнения
- Пути обучения
- Закрыть
- 7 Класс
- Закрыть
- Алгебра
- Текстовые задачи
- Уравнения
- Линейные уравнения
- Геометрия
- Факультатив
- Уравнения
- Линейные уравнения с параметром
- Уравнения
- Пути обучения
- Закрыть
- Для учителя
- Закрыть
- Алгебра
- Вероятность и статистика
- Повторение 7-9
- Числовые функции
- Текстовые задачи
- Алгебраические уравнения
- Тригонометрические уравнения
- Показательные уравнения
- Иррациональные уравнения
- Комбинированные уравнения
- Преобразование тригонометрических выражений
- Геометрия
- 10 класс Стереометрия
- Многогранники
- Планиметрия
- Закрыть
- Вебинары
- Закрыть
- Информация
- Закрыть
- Учителям и школам
- Для учителей и школ
- Учителям и школам
- Ученикам и родителям
- Для родителей
- Родительский доступ
- Руководство учащегося
- Ученикам и родителям
- Общая информация
- Новости
- Как это работает
- Отзывы
- Акции
- Список слушателей
- Общая информация
- Закрыть
- Вебинары
- Закрыть
- Закрыть
- Вход
- Регистрация
- Как это работает
- Новости
- Поддержка
ВХОД НА САЙТ
Забыл парольЗапомнить
- Регистрация
- Обучение
- Закрыть
- Вебинары
- Закрыть
- Все вебинары
- Вебинар#1.ЕГЭ №9,13,18
- Вебинар#2. ЕГЭ №14
- Вебинар#3. ЕГЭ №16
- Вебинар#4.ЕГЭ №17
- Вебинар#5.ЕГЭ №13,18
- Вебинар#6.ЕГЭ №13,18
- Вебинар#7. ЕГЭ №15,18
- Вебинар#8. ЕГЭ. № 13,15
- Вебинар#9. ЕГЭ. №15
- Вебинар#10. ЕГЭ. №14
- Вебинар #11. ЕГЭ №14
- Вебинар#12 .ЕГЭ №16
- Вебинар#13. ЕГЭ №16
- Вебинар#14. ЕГЭ №18
- Вебинар#15. ЕГЭ №18
- Вебинар#16. ЕГЭ №18
- Вебинар#17. ЕГЭ №13
- Вебинар#18. ЕГЭ №15
- Вебинар#19. ЕГЭ №14
- Закрыть
- Пути обучения и темы
- Закрыть
- Пути обучения
- Что такое пути обучения
- Ваш первый учебный путь
- Все пути обучения
- Доступные темы
- Список бесплатных тем
- Полный список доступных тем
- Закрыть
- Подготовка к ЕГЭ
- Закрыть
- ЕГЭ Профиль
- Задание №4
- Задание №5
- Задание №6
- Задание №8
- Задание №9
- Задание №11
- Задание №13
- Задание №14
- Задание №17
- Задание №18
- ЕГЭ База
- Задание №7
- Задание №10
- Пути обучения
- Не помню как работают формулы приведения
- Хочу вспомнить как решать тригонометрические ур.
- Как отбирать корни тригонометрических ур.
- Учимся решать комбинированные ур.
- Учимся решать тригонометрические ур. с параметром
- Объем пирамиды. От простого к сложному.
- Вебинары
- Вебинар#1.ЕГЭ №9,13,18
- Вебинар #2.ЕГЭ №14
- Вебинар#3. ЕГЭ №16
- Вебинар#4.ЕГЭ №17
- Вебинар#5.ЕГЭ №13,18
- Вебинар#6.ЕГЭ №13,18
- Вебинар#7. ЕГЭ №15,18
- Вебинар#8.ЕГЭ № 13,15
- Вебинар#9.ЕГЭ. №15
- Вебинар#10. ЕГЭ. №14
- Вебинар #11. ЕГЭ №14
- Вебинар#12. ЕГЭ №16
- Вебинар#13. ЕГЭ №16
- Вебинар#14. ЕГЭ №18
- Вебинар#15. ЕГЭ №18
- Вебинар#16. ЕГЭ №18
- Вебинар#17. ЕГЭ №13
- Вебинар#18. ЕГЭ №15
- Вебинар#19. ЕГЭ №14
- Закрыть
- 11 класс
- Закрыть
- Алгебра
- Уравнения
- Показательные уравнения
- Комбинированные уравнения
- Уравнения
- Геометрия
- Многогранники
- Пути обучения
- Закрыть
- 10 Класс
- Закрыть
- Алгебра
- Повторение 7-9
- Числовые функции
- Тригонометрические уравнения
- Преобразование тригонометрических выражений
- Геометрия
- Введение
- Параллельность прямых и плоскостей
- Перпендикулярность прямых и плоскостей
- Подготовка к ЕГЭ
- Задание №13
- Задание №18
- Пути обучения
- Закрыть
- ОГЭ
- Закрыть
- ОГЭ
- Задание №4
- Задание №9
- Задание №17
- Задание №21
- Задание №22
- Пути обучения
- Закрыть
- 9 Класс
- Закрыть
- Алгебра
- Текстовые задачи
- Геометрия
- Факультатив
- Уравнения
- Уравнения повышенной сложности
- Уравнения
- Пути обучения
- Закрыть
- 8 Класс
- Вебинары
mathcourse.ru
Учебный курс по математике «Мир алгебры» для 8 класса
«Рассмотрено» Руководитель МО _____ /Бутко Е.Ю./ ФИО Протокол №_1__ от «__» августа 2014 г. | «Согласовано» Заместитель руководителя по УВР МБОУ «СОШ № 14» _____ /__Рубанова Е.А./ ФИО «__» августа 2016 г. | «Утверждено» Руководитель МБОУ «СОШ № 14» ___________ /_Полякова_В.А.__ / ФИО Приказ № от «___» _августа_2014г. |
РАБОЧАЯ ПРОГРАММА ПЕДАГОГА
Зыковой Ларисы Николаевны,
Учебный курс «Мир алгебры»
8 класс
Утверждено на заседании педагогического совета
протокол № _1___
от «_ » августа 2016 г.
2014 – 2015 учебный год
город Нижневартовск
Пояснительная записка
Данный курс «Мир алгебры» направлен на коррекцию знаний учащихся за курс 7 — 8 классов по алгебре, повышение уровня математической подготовки через решение большого класса задач, на формирование у школьников навыков решения линейных и квадратных уравнений, неравенств. Материал, предусмотренный данным курсом, примыкает к курсу алгебры для 7-8 классов. Изучение курса «Мир алгебры» поможет учащимся приобрести умения решать задачи, точно и грамотно формулировать изученные теоретические положения, правильно пользоваться алгебраической терминологией и символикой, применять рациональные способы решения, строить графики линейных и квадратичных функций. В ходе изучения материала данного курса целесообразно сочетать такие формы организации учебной работы, как практикумы по решению задач и тестирование, Изучение материала данного курса обеспечивает успешность обучения учащихся 8 классов для качественной подготовки к ГИА.
Программа курса «Мир алгебры» рассчитана на 19 часов.
Цель курса – обеспечение прочного и сознательного овладения учащимися системой математических знаний и умений в начале курса изучения алгебры 7-9.
Образовательные задачи курса.
Научить школьников выполнять тождественные преобразования выражений;
Научить учащихся решать линейные уравнения и неравенства;
Научить учащихся решать квадратные уравнения и неравенства;
Научить строить графики линейных и квадратичных функций;
Помочь овладеть умениями на уровне свободного их использования.
Содержание курса
1. Алгебраические дроби. Что такое алгебраическая дробь. Основное свойство дроби. Сложение и вычитание алгебраических дробей. Умножение и деление алгебраических дробей. Степень с целым показателем. Свойства степени с целым показателем. Решение уравнений и задач.
2. Квадратные корни. Задача о нахождении стороны квадрата. Иррациональные числа. Теорема Пифагора. Квадратный корень (алгебраический подход). Свойства квадратных корней. Преобразование выражений, содержащих квадратные корни. Кубический корень.
3. Квадратные уравнения. Какие уравнения называют квадратными. Формула корней квадратного уравнения. Вторая формула корней квадратного уравнения. Решение задач. Неполные квадратные уравнения. Теорема Виета. Разложение квадратного трехчлена на множители.
4. Системы уравнений. Линейное уравнение с двумя переменными и его график. Уравнение прямой вида y=kx+l. Системы уравнений. Решение систем способом сложения. Решение систем уравнений способом подстановки. Решение задач с помощью систем уравнений. Задачи на координатной плоскости.
5. Функции. Чтение графиков. Что такое функция. График функции. Свойства функций. Линейная функция. Функция и её график.
Учебно-тематический план
3
2
Квадратные корни
4
3
Квадратные уравнения
4
4
Системы уравнений
5
5
Функции
3
Всего
19
Тест
5
Календарно-тематический план
п/п
Наименование разделов
Всего часов
Дата проведения
Форма контроля
1. Алгебраические дроби (3 часа)
1
Способы решения уравнений
1
Практикум
Тестирование
https://oge.sdamgia.ru/
2
Решение задач с помощью уравнений
2
2. Квадратные корни (4 часа)
1
Иррациональные числа
1
Практикум
Тестирование
https://oge.sdamgia.ru/
2
Квадратный корень (алгебраический подход). Свойства квадратных корней
1
3
Преобразование выражений, содержащих квадратные корни
1
4
Кубический корень
1
3. Квадратные уравнения (4 часа)
1
Формулы корней квадратного уравнения
1
Практикум
Тестирование
https://oge.sdamgia.ru/
2
Неполные квадратные уравнения
1
3
Теорема Виета
1
4
Разложение квадратного трехчлена на множители
1
4. Системы уравнений (5часов)
1
Системы уравнений. Решение систем способом сложения
1
Практикум
Тестирование
https://oge.sdamgia.ru/
2
Системы уравнений. Решение систем способом подстановки
1
3
Решение задач с помощью систем уравнений
2
4
Задачи на координатной плоскости
1
5. Функции (3 часа)
1
Графики функций.
1
Практикум
Тестирование
https://oge.sdamgia.ru/
2
Свойства функций
2
ВСЕГО
19ч
Требования к уровню подготовки учащихся
В результате изучения курса ученик должен
знать/понимать
• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
уметь
• выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
• решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
• решать линейные и квадратные неравенства с одной переменной и их системы;
• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи;
• изображать числа точками на координатной прямой;
• определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
• описывать свойства изученных функций, строить их графики;
Учебно-методическое и информационное обеспечение курса:
Алгебра: учебник для 7, 8 класса общеобразовательных учреждений. Под ред. А. Г. Мордковича . М.: Просвещение, 2010;
https://oge.sdamgia.ru/-
Образовательный портал для подготовки к экзаменам;
Математика: алгебра. Функции, анализ данных: учебник для 8 класса общеобразовательных учреждений. Под ред. Г.В.Дорофеева. М.: Просвещение, 2007.
Алгебра 8. Тематические тесты. ГИА. Л.В. Кузнецова;
5. www. school.edu -Российский общеобразовательный портал.
6. www.school-collection.edu.ru
Единая коллекция цифровых образовательных ресурсов.
7. www.it-n.ru — Сеть творческих учителей.
8. www . festival.1september.ru -Фестиваль педагогических идей «Открытый урок».
Техническое обеспечение:
1. Мультимедийный проектор.
2. Доска Mimio.
3. Система голосования Mimio Vote.
4. Документ-камера.
infourok.ru
Курс по алгебре для 8 классов «Подготовка к поступлению в лицей»
Занятие №1 «Числовые выражения»
Задание №1 Вычислите:
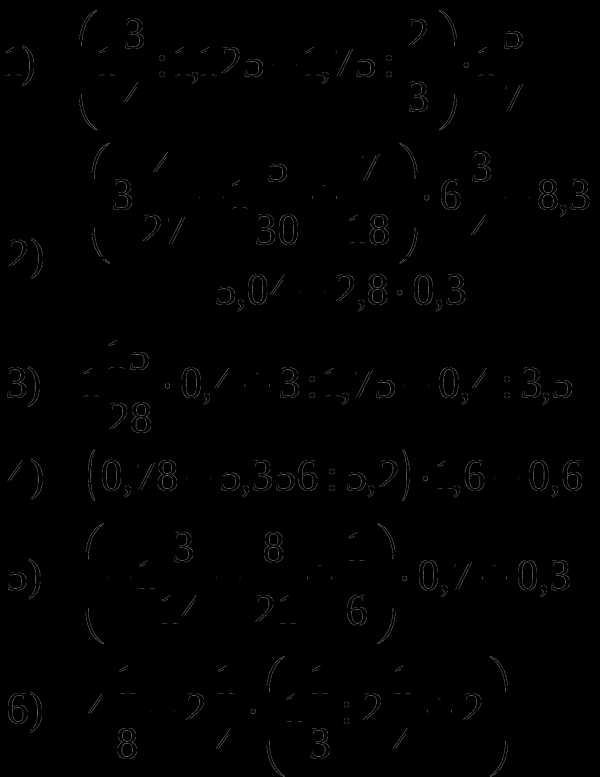
Задание №2 Вычислите:
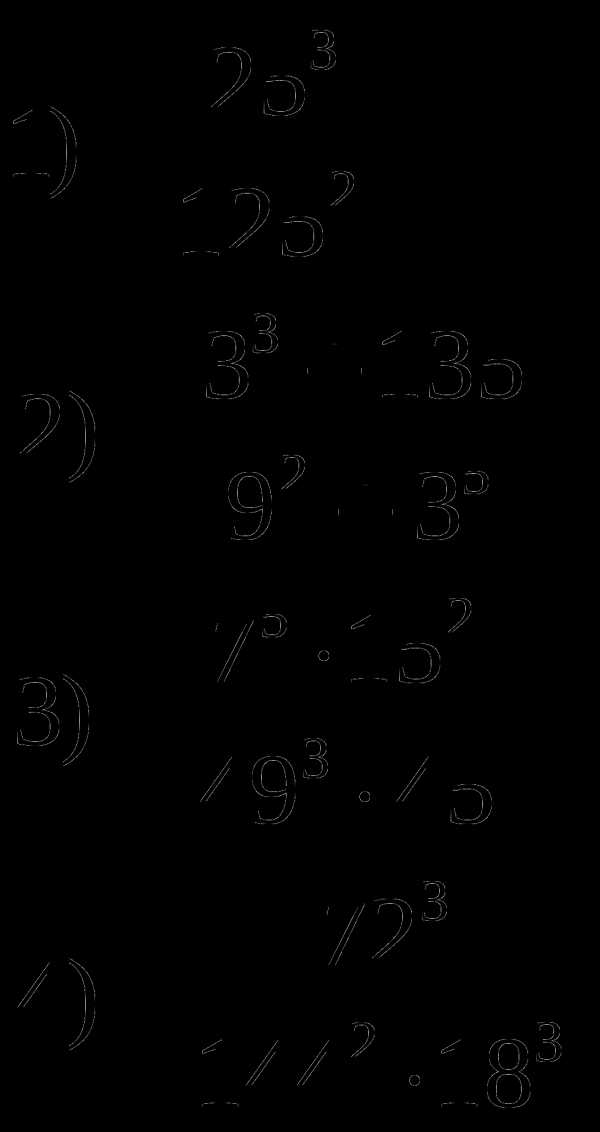
Задание №3 Решите задачи:
Если каждому из своих друзей Сергей даст 4 персика, то у него останется 2 персика; если он станет давать по 5 персиков, то не хватит одного персика. Сколько друзей у Сергея и сколько персиков у него было?
На соревнованиях по настольному теннису участвовали равные по составу команды, всего 123 мальчика и 82 девочки. Во всех командах было одинаковое количество мальчиков и девочек. Сколько команд участвовало в соревнованиях? Сколько мальчиков и девочек было в каждой команде?
Какое наименьшее число метров материала должно быть в рулоне, чтобы его можно было продать без остатка по 2м, по 6м, по 10м?
Домашнее задание №1
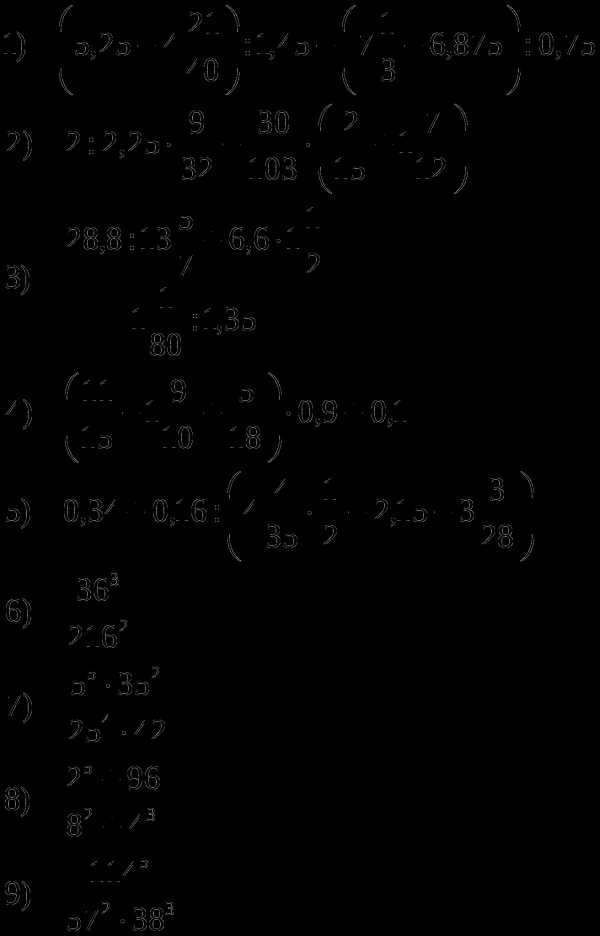
10) Используя только арифметические действия и скобки, представьте первые десять чисел натурального ряда, обходясь только одной цифрой 3, применяя ее в точности четыре раза.
Занятие №2 «Многочлены и одночлены»
Задание №1 Упростите
Задание №2 Разложите на множители
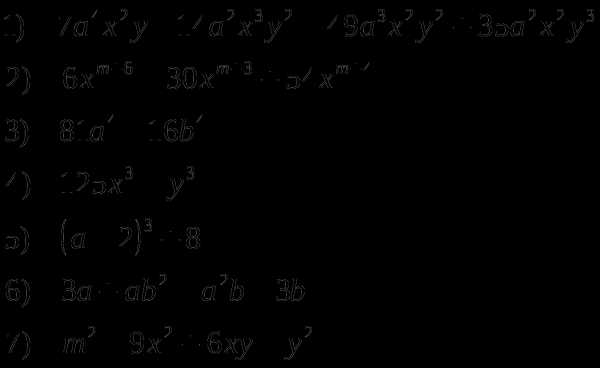
Задание №2 Сократите дробь
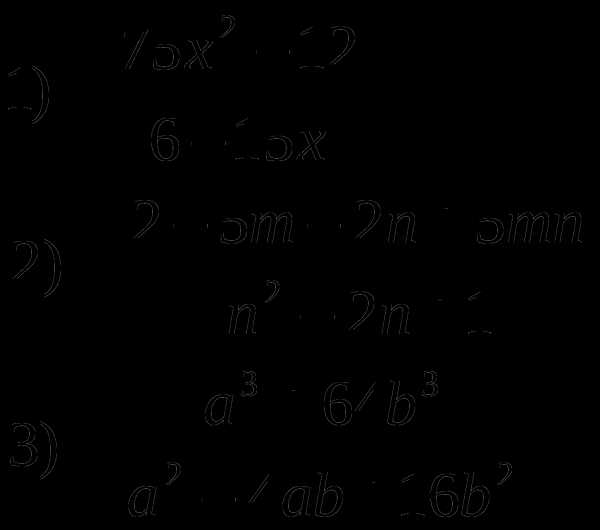
Задание №3 Упростите выражение
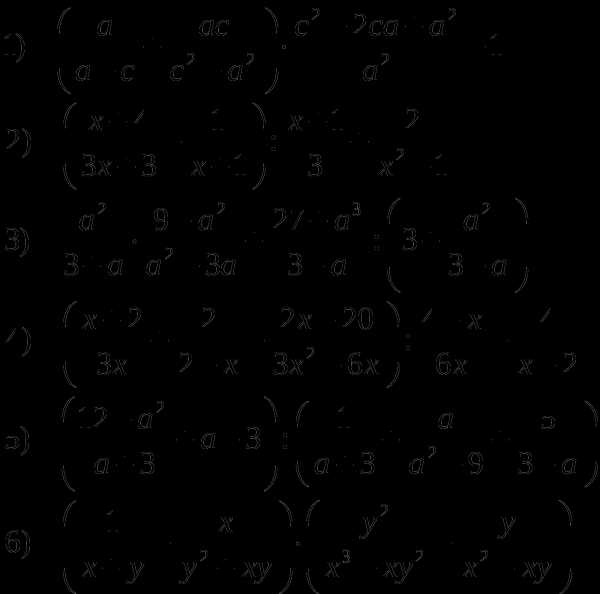
Задание №4
Пусть 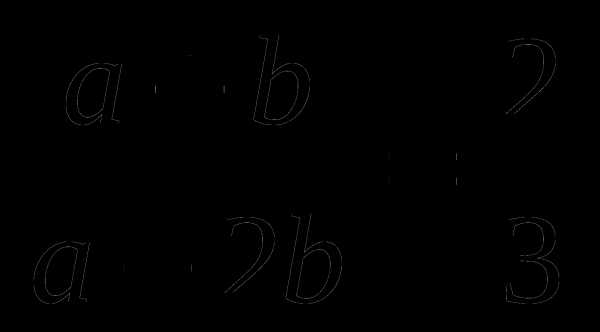 . Вычислите
. Вычислите 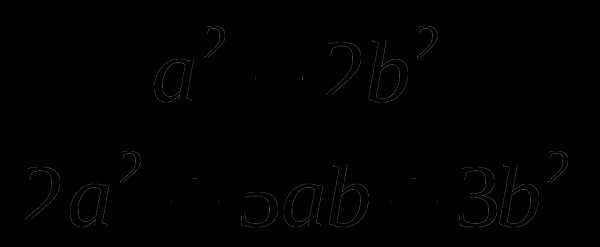 .
.
Задание №5
Известно, что  . Не вычисляя
. Не вычисляя  , найдите
, найдите 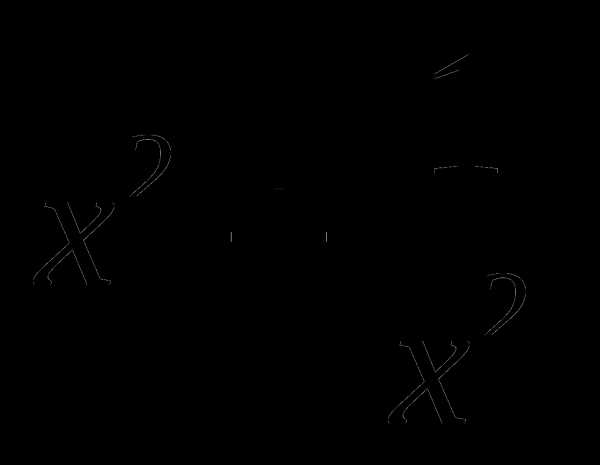 .
.
Задание №6. Вычислите
.
Домашнее задание №2
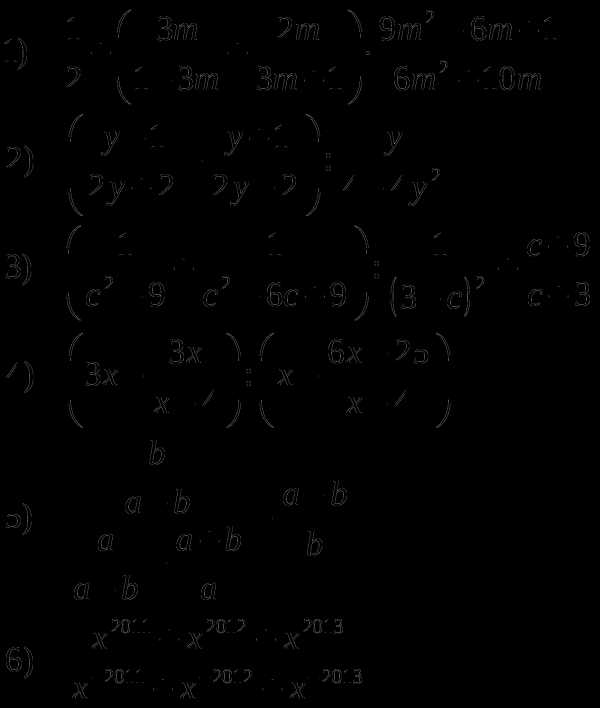
Занятие №3 «Функции и их графики»
Задание №1
Найдите угловой коэффициент прямой и постройте ее график.
Задание №2
При каком значении  прямая проходит через точку
прямая проходит через точку 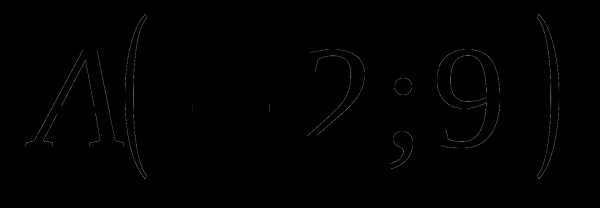 .
.
Задание №3
Найдите координаты точки пересечения графиков функций и .
Задание №4
Составьте уравнение прямой, проходящей через точки 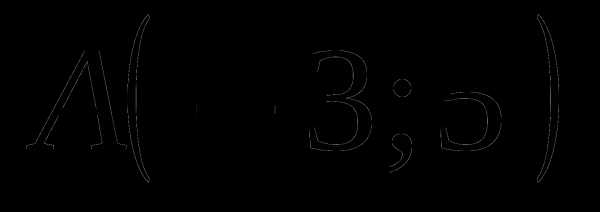 и
и  .
.
Задание №5
Решите графически уравнение  .
.
Задание №6
Решите графически систему уравнений 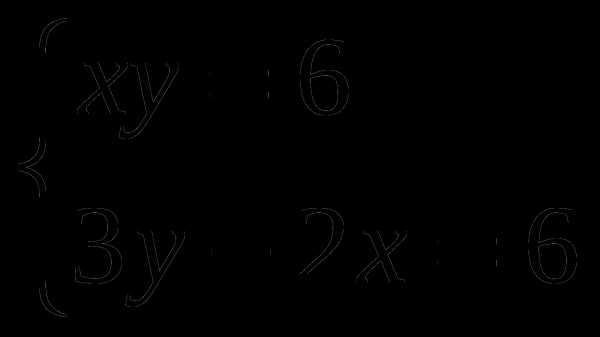
Задание №7
Определите, какие из указанных точек принадлежат графику данной функции 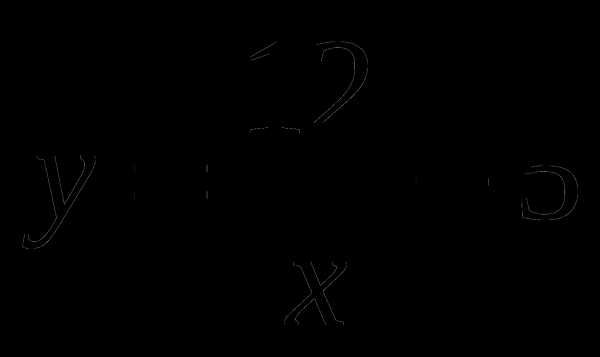 .
.
.
Задание №8
Найдите координаты точек пересечения графика функции 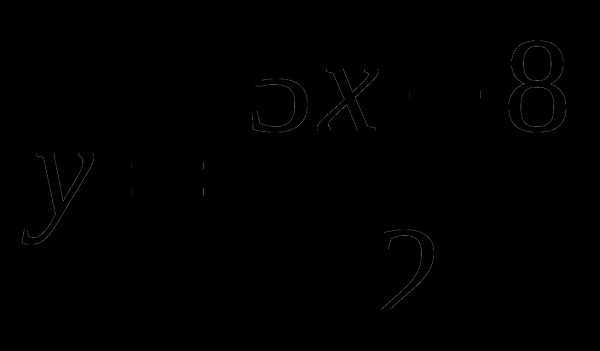 с осями координат.
с осями координат.
Домашнее задание №3
1) Решите графически уравнения:
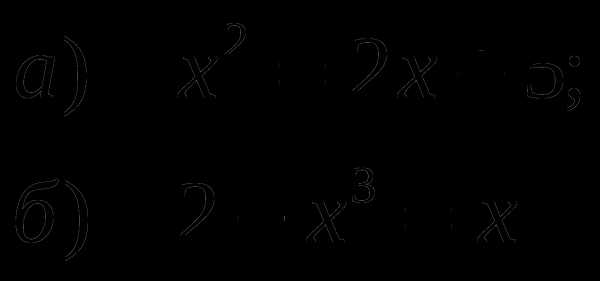
2) Решите графически системы
уравнений:
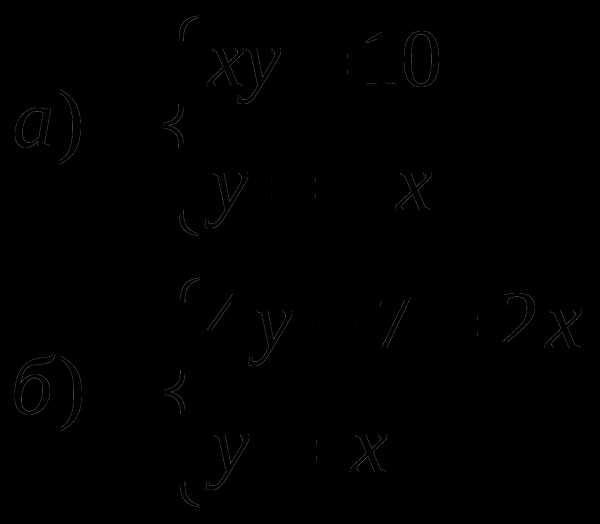
3) Прямые , 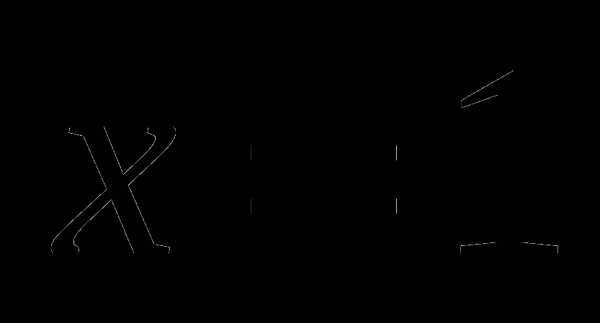 ,
,
 попарно пересекаясь,
попарно пересекаясь,
образуют треугольник. Вычислите
координаты его вершин, длины
сторон и постройте этот
треугольник.
Составьте уравнение прямой, проходящей через точку пересечения графиков функций , , угловой коэффициент которой равен
 .
.
Занятие №4 «Модуль числа. Арифметический квадратный корень. Линейные уравнения»
Задание №1
Вычислите:
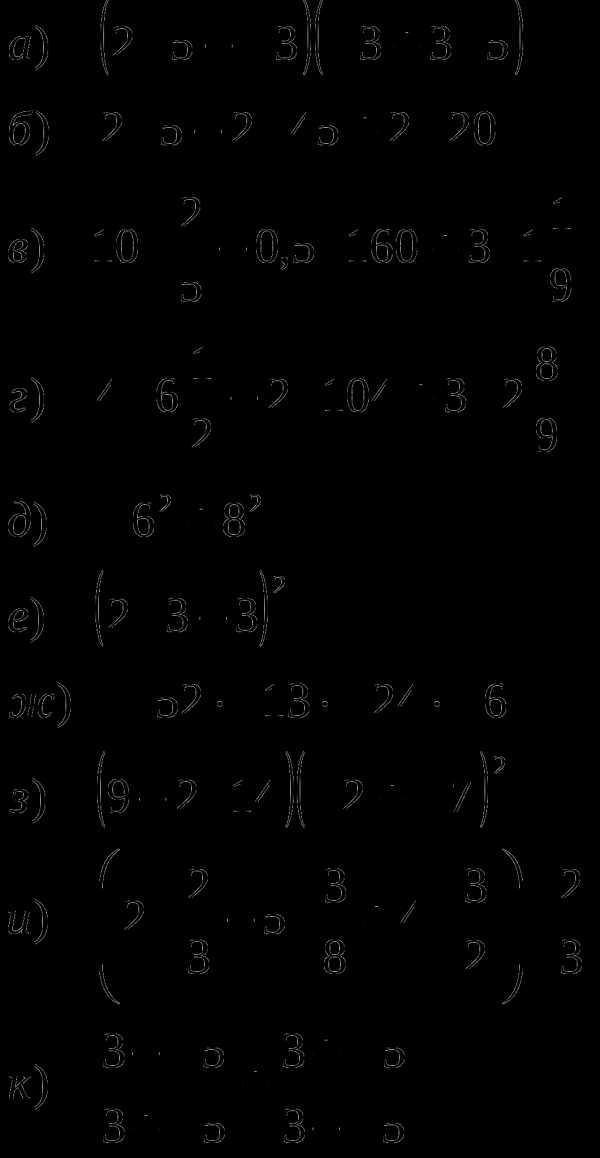
Задание №2
Сократите дробь:
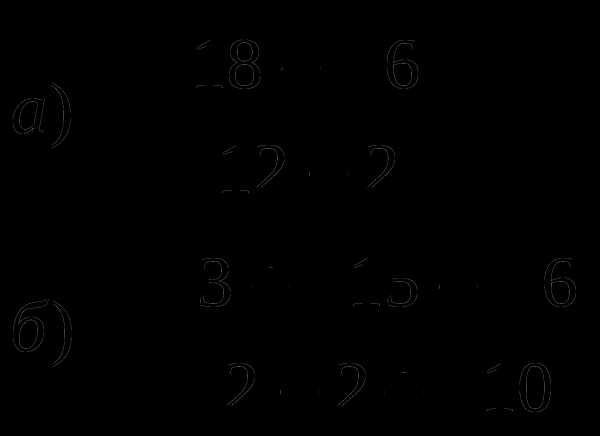
Задание №3
Решите уравнения:
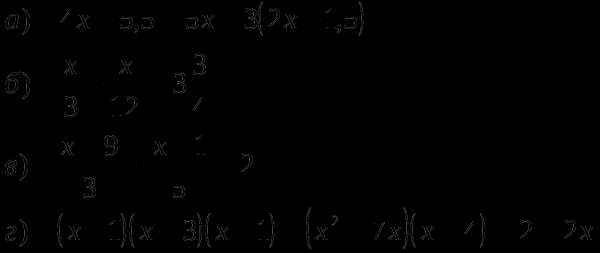
Домашнее задание №4
Вычислите:
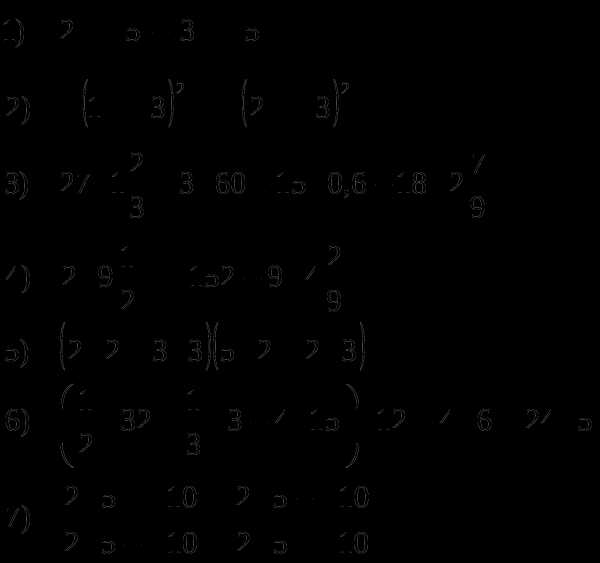 Решите уравнение:
Решите уравнение:
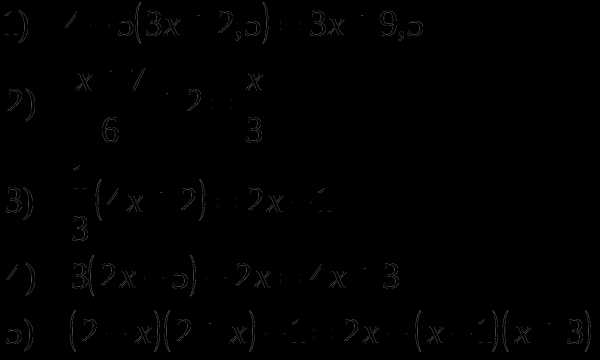
Упростите:

Постройте график функции:
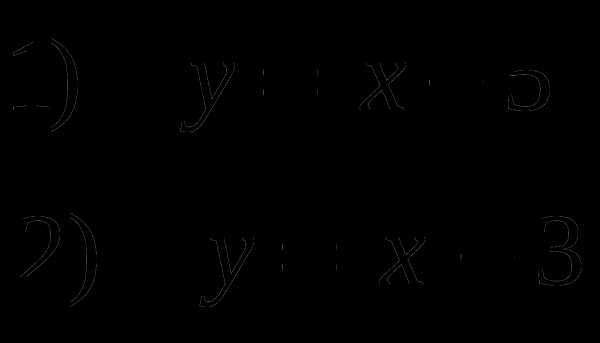
Решите задачу:
Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.
Занятие №5 «Квадратные уравнения. Теорема Виета»
Задание №1
Решите уравнения:
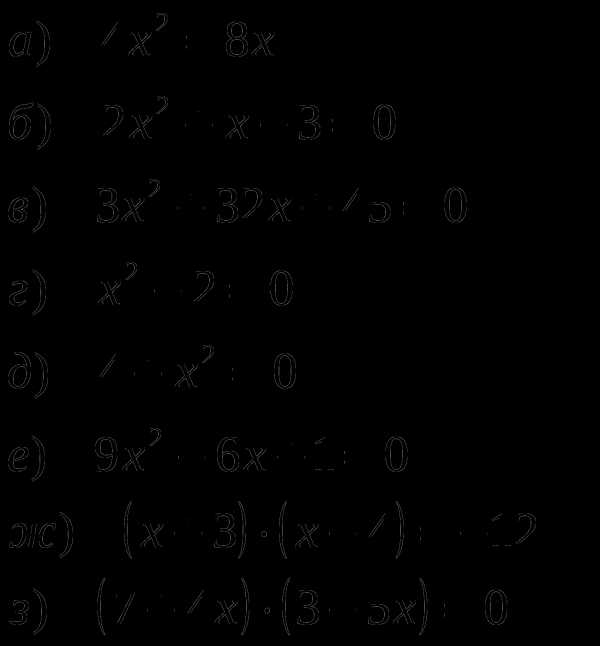
Задание №2
При каких значениях  уравнение имеет одно решение?
уравнение имеет одно решение?
Задание №3
Составьте квадратное уравнение, корни которого равны .
Задание №4
Вычислите  , где
, где 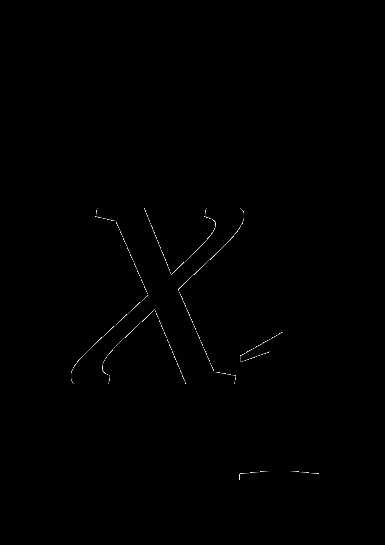 и
и  — корни уравнения .
— корни уравнения .
Задание №5
Вычислите  , где
, где  и
и  — корни уравнения .
— корни уравнения .
Задание №6
Один из корней уравнения в 3 раза больше другого. Найдите 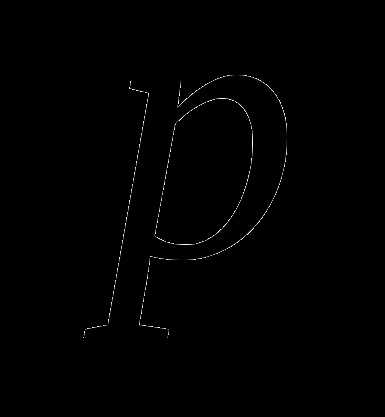 .
.
Задание №7
При каких значениях  значения многочленов и равны.
значения многочленов и равны.
Домашнее задание №5
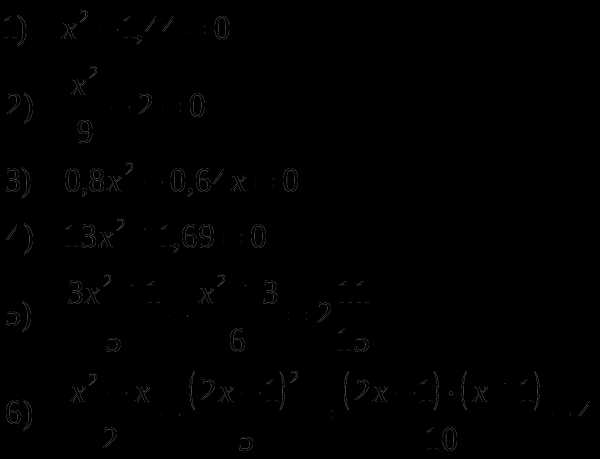
 и
и  — корни уравнения . Разность корней равна
— корни уравнения . Разность корней равна 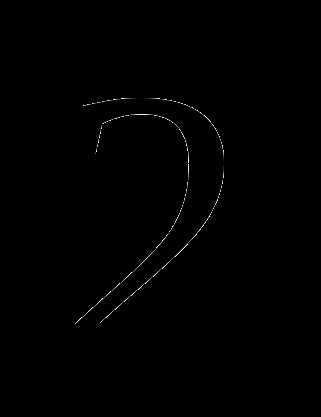 . Найдите
. Найдите 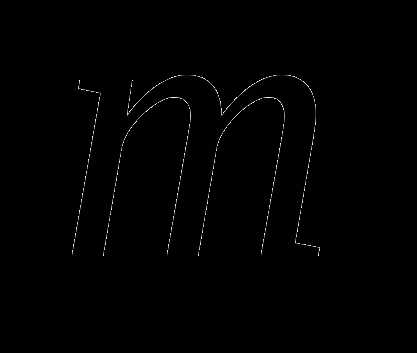 .
.
 При каких
При каких  значение выражения равно
значение выражения равно 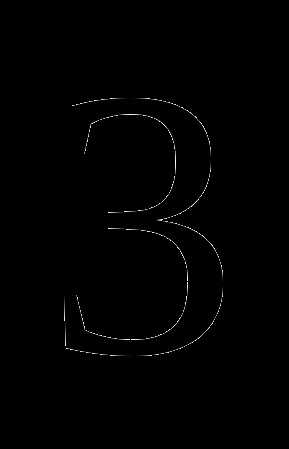 ?
?
 Найдите
Найдите  , если один из корней уравнения равен
, если один из корней уравнения равен 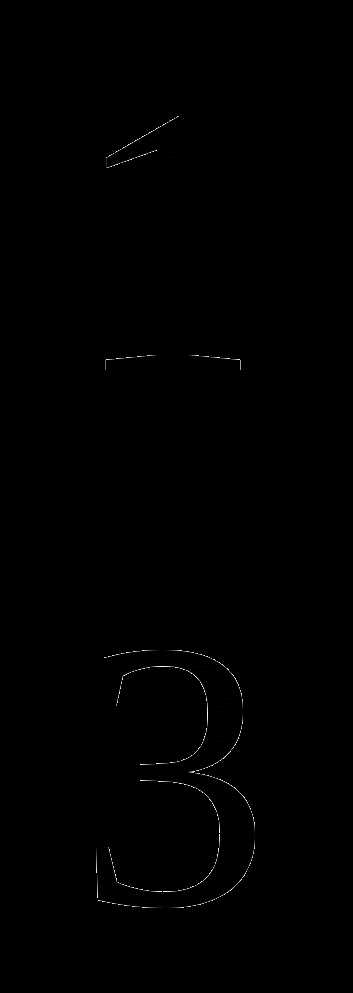 .
.
 Из пунктов А и В, расстояние между которыми равно 270 км, одновременно навстречу друг другу выехали два автомобиля. Скорость одного автомобиля на 10 км/ч меньше скорости другого. Через 2 ч расстояние между автомобилями составило 50 км. Найдите скорость каждого автомобиля.
Из пунктов А и В, расстояние между которыми равно 270 км, одновременно навстречу друг другу выехали два автомобиля. Скорость одного автомобиля на 10 км/ч меньше скорости другого. Через 2 ч расстояние между автомобилями составило 50 км. Найдите скорость каждого автомобиля.
Занятие №6 «Системы линейных уравнений»
Задание №1
Решите системы линейных уравнений:
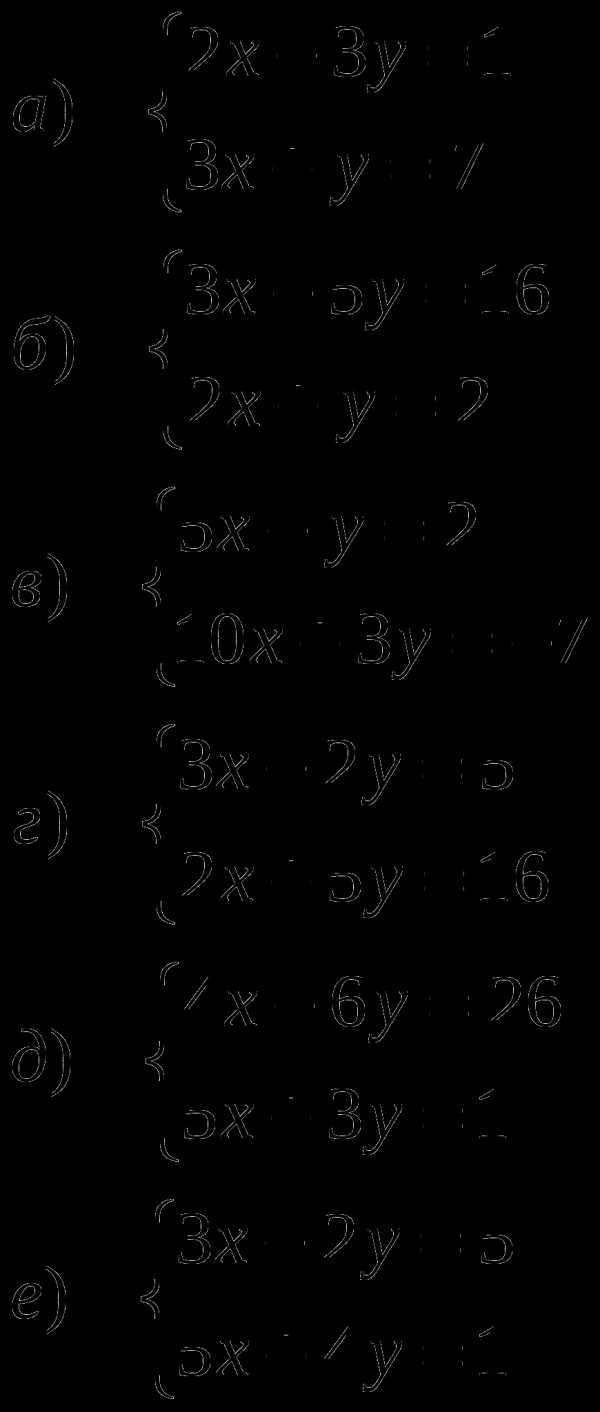
Задание №2
Найдите координаты точки пересечения прямых и .
Задание №3
Составьте уравнение прямой, проходящей через точки 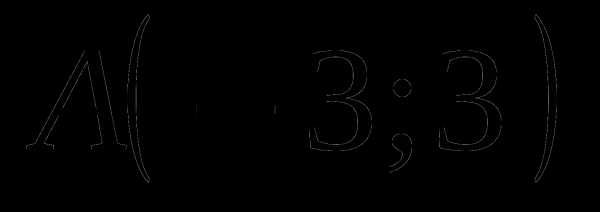 и
и 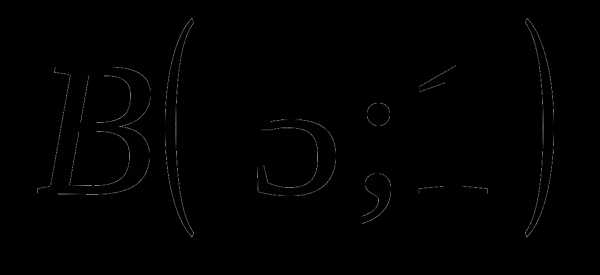 .
.
Задание №4
Решите задачи, составив системы линейных уравнений:
а) На турбазе имеются палатки и домики; всего их 25. В каждом домике живут 4 человека, а в каждой палатке 2 человека. Сколько на турбазе палаток и сколько домиков, если на турбазе отдыхают 70 человек?
б) В саду посадили одинаковыми рядами 60 кустов смородины. Рядов оказалось на 7 меньше, чем кустов в каждом ряду. Сколько кустов в каждом ряду?
в) Сумма двух чисел равна 137, а их разность 19. Найдите эти числа.
г) В волейбольной и баскетбольной секциях занимается 132 школьника. Число волейболистов относится к числу баскетболистов, как 5 к 6. Сколько школьников занимается в каждой секции?
Домашнее задание №6
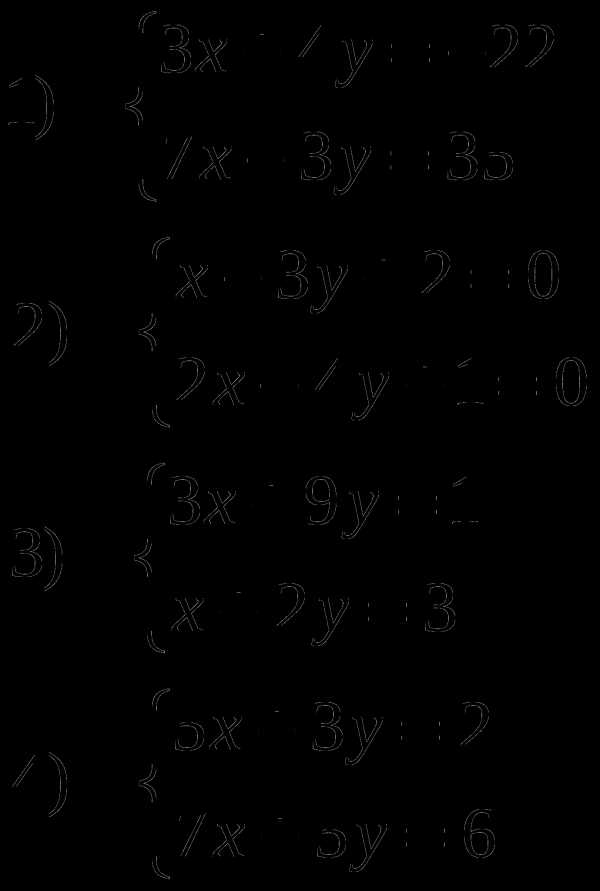
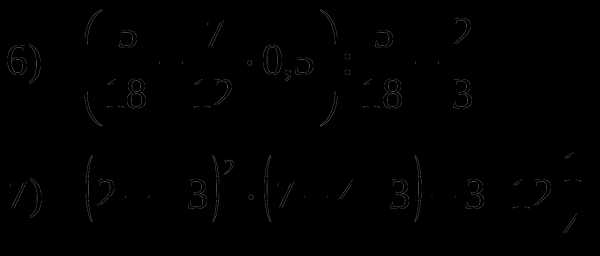
 Найдите с помощью графиков
Найдите с помощью графиков
число корней уравнения
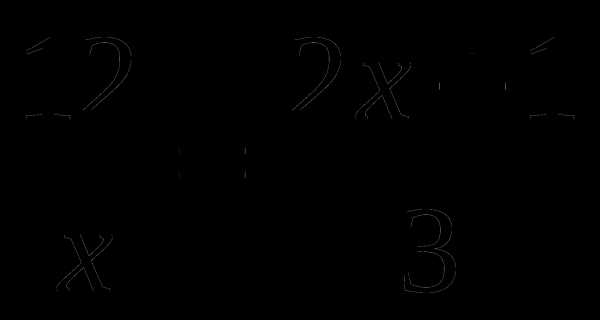
Занятие №7 «Дробно-рациональные уравнения»
Задание №1
Решите уравнения:
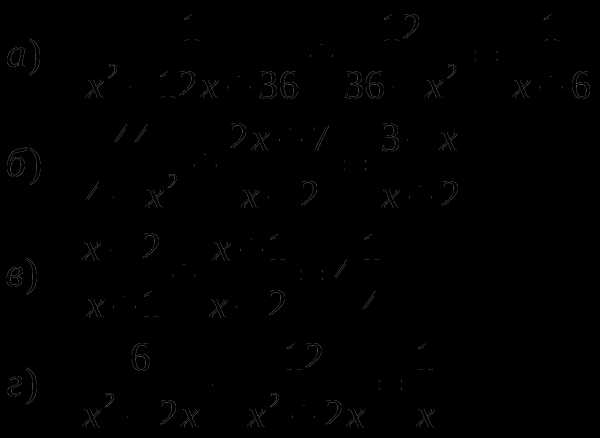
Задание №2
Решите задачи:
а) Из города А в город В выехали велосипедист и мотоциклист. Скорость велосипедиста на 10 км/ч меньше скорости мотоциклиста, поэтому он затратил на весь путь на 6 ч больше. С какой скоростью ехал мотоциклист, если расстояние между городами 120 км?
б) Теплоход прошел 4 км против течения реки и затем прошел еще 33 км по течению, затратив на весь путь 1 ч. Найдите скорость теплохода в стоячей воде, если скорость течения реки равна 6,5 км/ч.
в) Товарный поезд был задержан в пути на 12 мин., а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/ч. Найдите первоначальную скорость поезда.
г) Автомобиль едет из города А в город В со скоростью 48 км/ч и возвращается обратно со скоростью 50 км/ч по другой дороге, которая длиннее первой на 5 км. На обратный путь автомобиль затрачивает времени на 2 мин. больше, чем на путь от А к В. Определить длину каждой дороги от А до В.
д) Велосипедист проехал расстояние 67 км за 4ч, причем на последних 27 км пути его скорость была на 2 км/ч больше, чем на предыдущем участке пути. Сколько времени затратил велосипедист на последние 27 км пути?
Домашнее задание №7
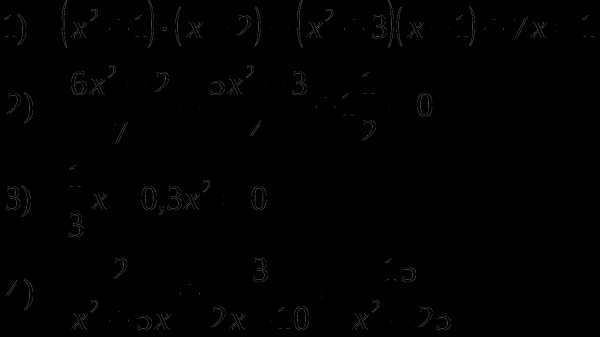
 Скорый поезд был задержан у семафора на 16 мин и ликвидировал опоздание на перегоне в 80 км, идя со скоростью на 10 км/ч больше, чем по расписанию. Определите скорость поезда по расписанию.
Скорый поезд был задержан у семафора на 16 мин и ликвидировал опоздание на перегоне в 80 км, идя со скоростью на 10 км/ч больше, чем по расписанию. Определите скорость поезда по расписанию.
 Моторная лодка прошла по течению реки 10 км, а против течения 15 км, затратив на весь путь 1ч 10 мин. Найдите скорость лодки по течению, если скорость течения реки равна 2 км/ч.
Моторная лодка прошла по течению реки 10 км, а против течения 15 км, затратив на весь путь 1ч 10 мин. Найдите скорость лодки по течению, если скорость течения реки равна 2 км/ч.
Занятие №8 «Решение текстовых задач»
Задание №1
Решите задачи:
Две бригады рабочих должны к некоторому сроку изготовить по 300 деталей. Первая бригада, изготовляя в день на 10 деталей больше второй, затратила на выполнение задания на 1 день меньше. Сколько деталей в день изготовляла каждая бригада?
Две бригады, работая совместно, закончили посадку деревьев за 4 дня. Сколько дней потребовалось бы на эту работу каждой бригаде в отдельности, если одна из них может выполнить работу на 15 дней быстрее другой?
Бригада рабочих обязалась изготовить 432 шины для колес. Однако 4 рабочих заболели и не вышли на работу. Каждому из оставшихся пришлось изготовлять на 9 шин в день больше, чтобы выполнить обязательство. Сколько рабочих числилось в бригаде?
На строительстве железной дороги работали две путевые бригады. Первая бригада ежедневно прокладывала на 40 м путей больше второй и проложила 270 м путей. Вторая бригада работала на 2 дня больше первой и проложила 250 м. Сколько дней работала каждая бригада?
Для перевозки 60 т груза затребовали некоторое количество машин. В связи с тем, что на каждую машину погрузили на 0,5 т меньше, дополнительно было затребовано еще 4 машины. Сколько машин было запланировано первоначально?
Один рабочий затрачивает на изготовление болта на 6 мин меньше, чем второй. Сколько болтов может изготовить каждый из них за 7ч, если первый обрабатывает за это время на 8 болтов больше?
Две машинистки получили рукопись для перепечатки. Известно, что второй машинистке потребовалось бы на перепечатку всей рукописи на 3 дня больше, чем первой. За какое время смогла бы перепечатать всю рукопись каждая машинистка, если вторая работала 6 дней, а первая – на 4 дня больше, чем вторая?
Площадь прямоугольника 60, а его периметр равен 32. Найдите стороны прямоугольника и длину его диагонали.
Задания экзаменационных работ прошлых лет
Вычислите:
Упростите:
Решите уравнения:
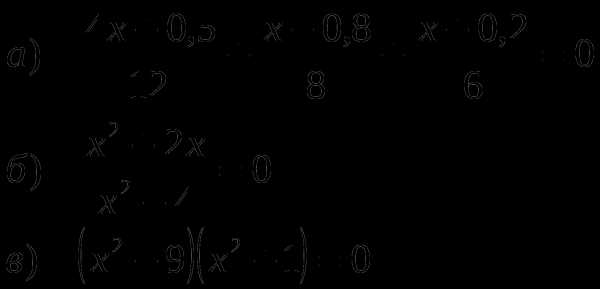
Решите систему уравнений
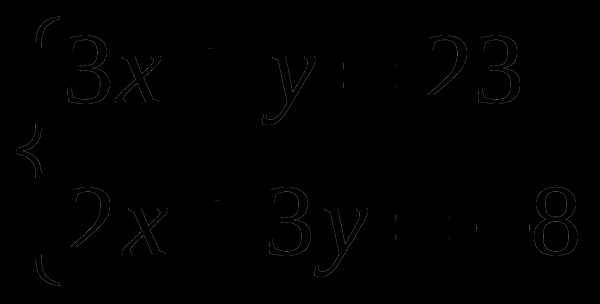
Решите задачу: сумма катетов прямоугольного треугольника равна 40 м, а гипотенуза имеет длину 32 м. Найдите площадь треугольника.
Постройте график функции
 . Принадлежит ли точка
. Принадлежит ли точка  графику?
графику?Упростите
Выполните действия
Упростите выражение
Упростите выражение
Найдите число, которое на 60% меньше корня уравнения
 .
.Решите уравнения:
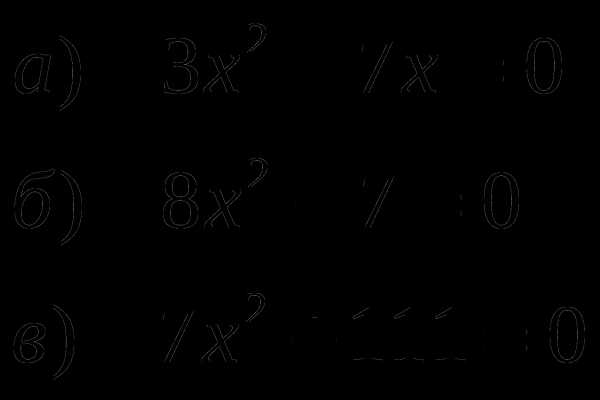
Решите графически уравнение:

Найдите корни квадратного уравнения , если его дискриминант .
Контрольная работа
Вычислите:
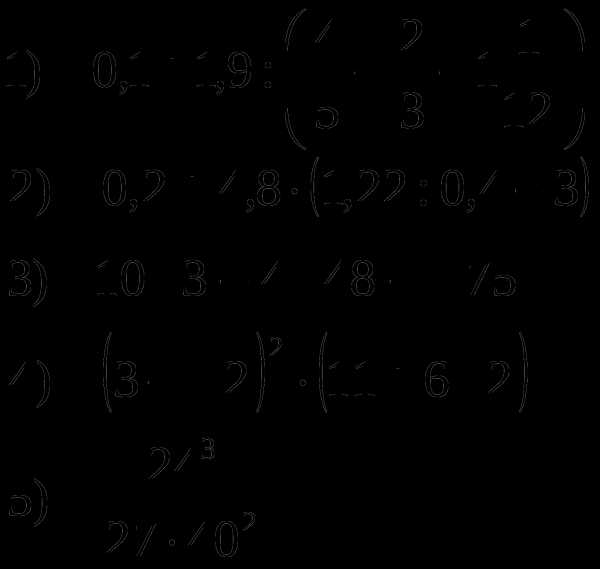
Решите уравнения:
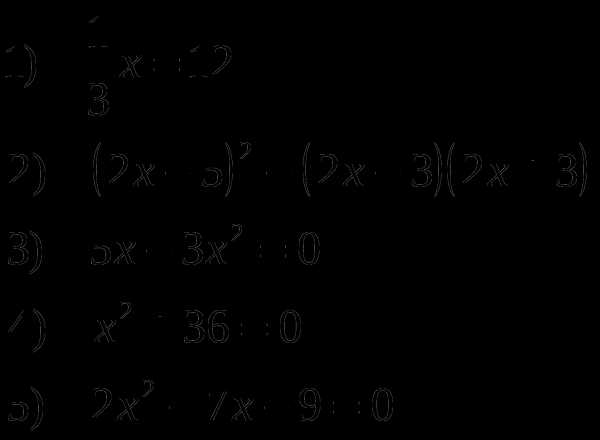
Решите графически систему уравнений:
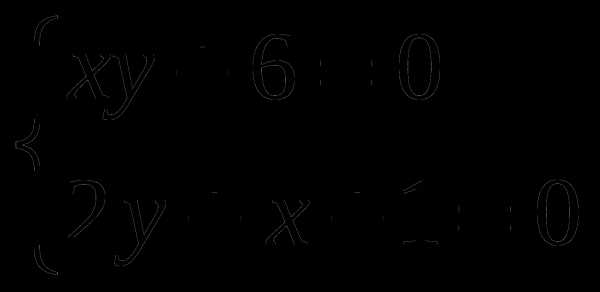
Упростите выражение:
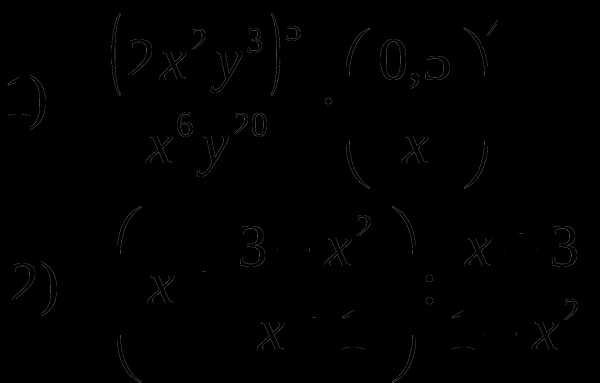
Решите задачу: на одно платье и три сарафана пошло
 ткани, а на три таких же платья и пять таких же сарафанов —
ткани, а на три таких же платья и пять таких же сарафанов —  ткани. Сколько ткани потребуется на одно платье и сколько на один сарафан?
ткани. Сколько ткани потребуется на одно платье и сколько на один сарафан?
Контрольная работа
Вычислите:
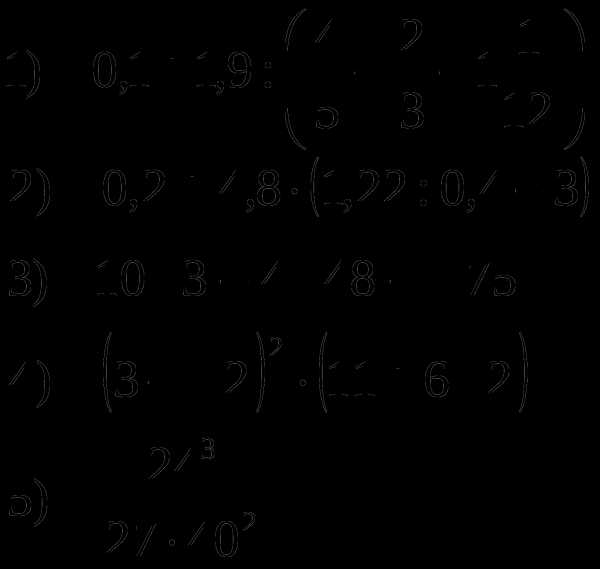
Решите уравнения:
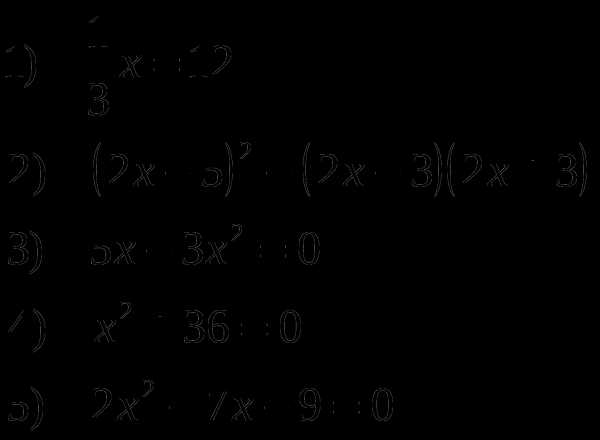
Решите графически систему уравнений:
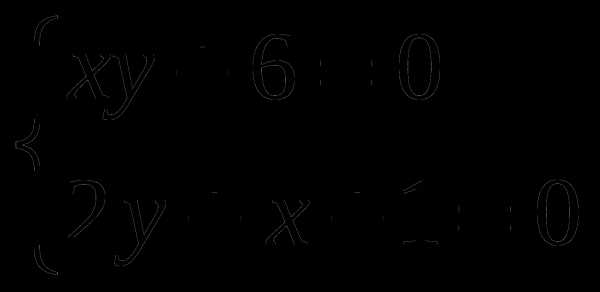
Упростите выражение:
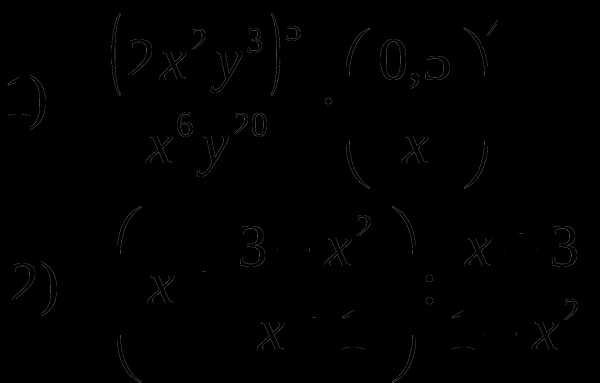
Решите задачу: на одно платье и три сарафана пошло
 ткани, а на три таких же платья и пять таких же сарафанов —
ткани, а на три таких же платья и пять таких же сарафанов —  ткани. Сколько ткани потребуется на одно платье и сколько на один сарафан?
ткани. Сколько ткани потребуется на одно платье и сколько на один сарафан?
Занятие №5 «Арифметический квадратный корень»
Задание №1
Решите графически уравнение:
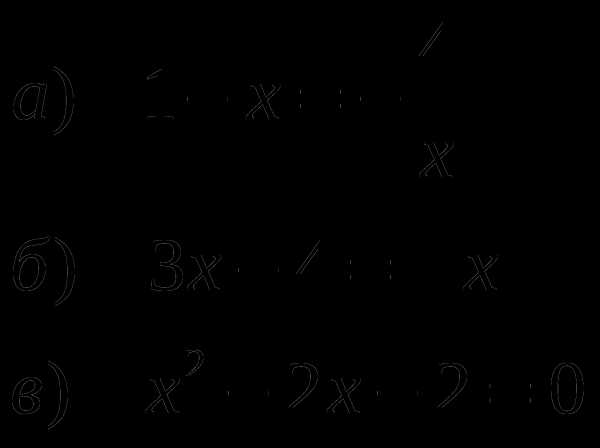
Задание №2
Решите графически систему уравнений:
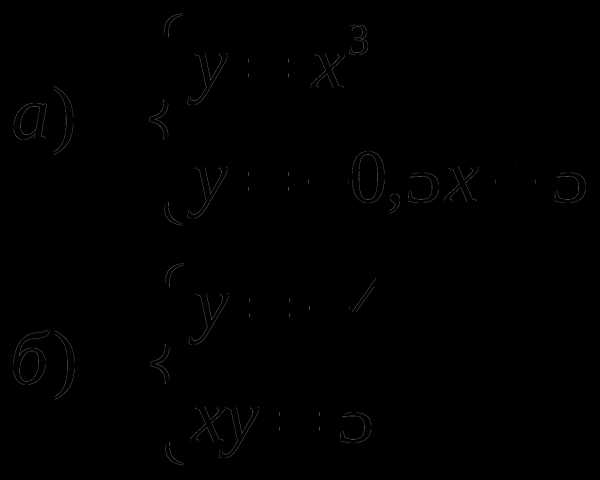
Задание №3
Вычислите:
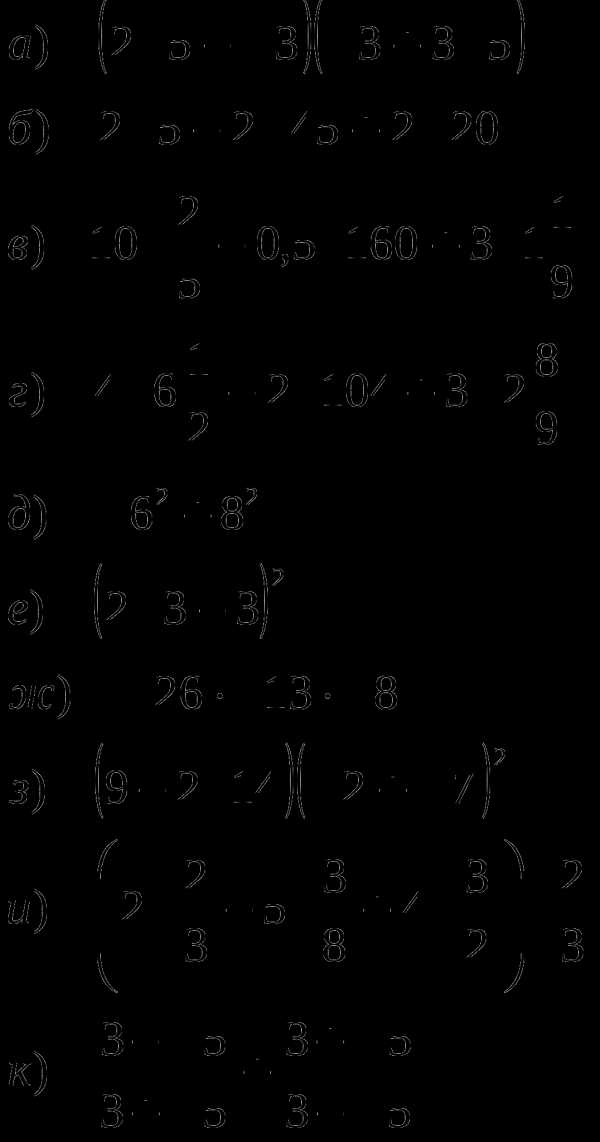
Задание №4
Сократите дробь:
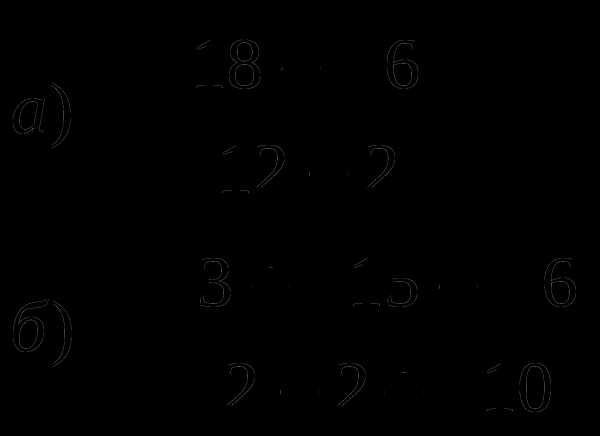
Домашнее задание №4
Вычислите:
 Решите графическим способом:
Решите графическим способом:
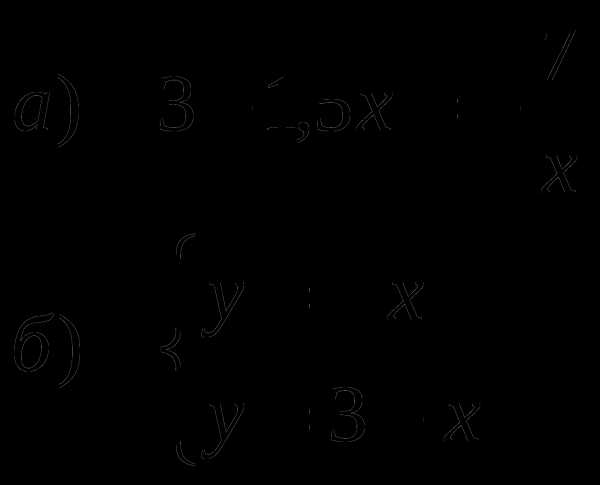
Задания экзаменационных работ прошлых лет
Вычислите:
Упростите:
Решите уравнения:
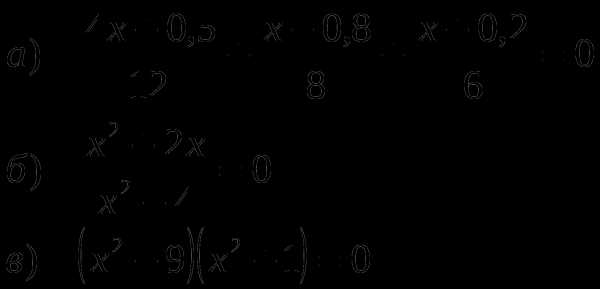
Решите систему уравнений
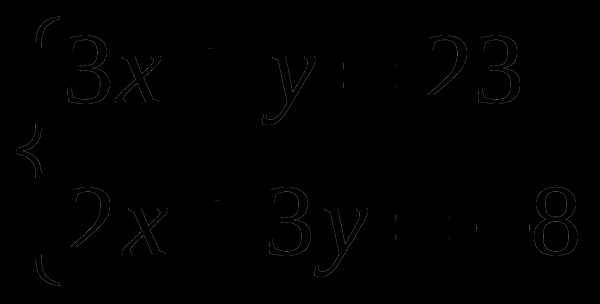
Решите задачу: сумма катетов прямоугольного треугольника равна 40 м, а гипотенуза имеет длину 32 м. Найдите площадь треугольника.
Постройте график функции
 . Принадлежит ли точка
. Принадлежит ли точка  графику?
графику?Упростите
Выполните действия
Упростите выражение
Упростите выражение
Найдите число, которое на 60% меньше корня уравнения
 .
.Решите уравнения:
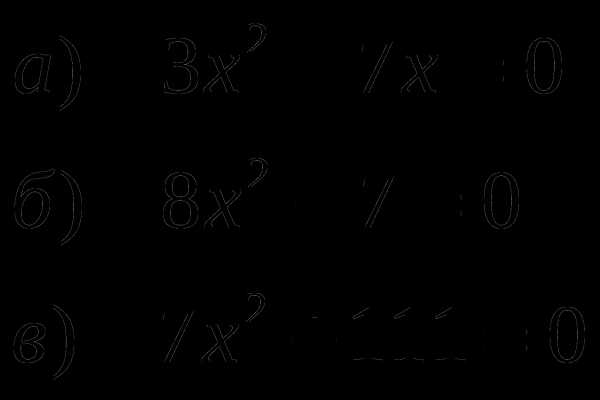
Решите графически уравнение:

Найдите корни квадратного уравнения , если его дискриминант .
infourok.ru
Рабочая программа по алгебре (8 класс) на тему: Спец курс по математике
Спецкурс «За пределами школьного курса математики»
8 класс
Пояснительная записка.
Данная программа спецкурса может привлечь внимание учащихся 8 класса, которым интересна и нужна математика. Программа направлена на расширение знаний учащихся, повышение уровня математической подготовки обучающихся через решение большого класса задач. Занятия этого курса являются развитием системы ранее приобретенных знаний. Его цель создать целостное о теме и значительно расширить спектр задач посильных для учащихся.
Успешное усвоение учениками данного спецкурса должно помочь им сдать и поступить на избранный ими профиль. Школьники смогут приобрести умения, которые позволят им быть успешными на следующей ступени образовательной вертикали. Стоить отметить, что навыки в решении уравнений, неравенств, исследовании и построении графиков элементарных функций совершенно необходимы любому ученику, желающему не только успешно выступать на математических конкурсах и олимпиадах, но и хорошо подготовиться к поступлению в дальнейшем в высшие учебные заведения.
Наряду с основной задачей обучения математики – обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений программа данного спецкурса предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.
Данная программа спецкурса предназначена для платных образовательных услуг.
Цель:
Создание условий, способствующих интеллектуальному развитию обучающихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
Задачи:
- расширить рамки школьной программы;
- раскрыть прикладную направленность школьного курса математики как инструмента деятельности;
- повысить уровень математической культуры учащихся;
- формировать умения выбирать задания, соответствующие направленности познавательного интереса;
- способствовать развитию логического мышления, памяти, внимания;
- формирование положительной мотивации к изучению математики;
- сформировать высокий уровень активности, раскованности мышления, проявляющейся в продуцировании большого количества разных идей, возникновении нескольких вариантов решения задач.
Требования к математической подготовке учащихся 8 класса.
В результате изучения курса учащиеся должны уметь:
- Решать задачи на проценты, производить процентные вычисления в жизненных ситуациях
- Решать задачи на смеси, растворы, сплавы
- Преобразовывать выражения, содержащие модуль
- Решать уравнения, неравенства, содержащие модуль
- Строить графики элементарных функций, содержащие модуль
- Уметь решать квадратные уравнения всеми способами , рассмотренными в рамках курса
- Овладеть понятием трехчлен и его приложением
Содержание обучения.
2 часа в неделю, всего 50 часов.
- Процентные расчеты на каждый день. (8 часов)
- Модуль (8 часов)
- Графики «улыбаются» (10 часов)
- Способы решения квадратного уравнения (10 часов)
- Квадратный трехчлен и его приложения (10 часов)
- Тестовые проверочные работы ( 4 часа)
В каждой теме курса предусмотрены лекции, практические занятия, самостоятельные и проверочные работы.
Номер Занятия. | Кол-во Часов. | Тема. | Лекция. | Практика. | Самост. работа. | Тест. |
1-8 | 8 ч | Процентные расчеты на каждый день. | ||||
1-2 | 2 ч | Проценты. Основные задачи на проценты. | 0,5 | 1 | 0,5 | |
3-4 | 2 ч | Процентные вычисления в жизненных ситуациях. | 0,5 | 1 | 0,5 | |
5-6 | 2 ч | Банковские операции. | 0,5 | 1 | 0,5 | |
7-8 | 2 ч | Задачи на смеси, растворы, сплавы. | 0,5 | 1 | 0,5 | |
9 | 1 ч | Тест №1. | ||||
10-17 | 8 ч | Модуль. | ||||
10-11 | 2 ч | Модуль: общие сведения, геометрический смысл. | 0,5 | 1,5 | ||
12-13 | 2 ч | Преобразование выражений, содержащих модуль. | 0,5 | 1 | 0,5 | |
14-15 | 2 ч | Графики функций, содержащих модуль. | 0,5 | 1 | 0,5 | |
16-17 | 2 ч | Модуль в задачах ГИА и ЕГЭ. | 0,5 | 1 | 0,5 | |
18 | 1 ч | Тест №2. | ||||
19-28 | 10 ч | Графики «улыбаются». | ||||
19-20 | 2 ч | Графики вокруг нас. | 1 | 1 | ||
21-22 | 2 ч | Геометрические преобразования графиков функций. | 0,5 | 1 | 0,5 | |
23-24 | 2 ч | Построение графиков функций, содержащих модуль, на основе геометрических представлений. | 0,5 | 1 | 0,5 | |
25-26 | 2 ч | Графики кусочно-заданных функций. | 0,5 | 1 | 0,5 | |
27-28 | 2 ч | Презентация проектов «Графики улыбаются» | ||||
29-40 | 10 ч. | Способы решения квадратного уравнения. | 1 | |||
29 | 1 ч | Разложение левой части уравнения на множители. | 0,5 | 0,5 | ||
30 | 1 ч | Метод выделения полного квадрата. | 0,5 | 0,5 | ||
31 | 1 ч | Решение квадратных уравнений по формулам. | 0,5 | 0,5 | ||
32 | 1 ч | Решение уравнений с использованием теоремы Виета (прямой и обратной). | 0,5 | 0,5 | ||
34 | 1 ч | Решение уравнений способом «переброски». | 0,5 | 0,5 | ||
35 | 1 ч | Свойства коэффициентов квадратного уравнения. | 0,5 | 0,5 | ||
36 | 1 ч | Графическое решение квадратного уравнения. | 0,5 | 0,5 | ||
37 | 1 ч | Решение квадратного уравнения с помощью циркуля и линейки. | 0,5 | 0,5 | ||
38 | 1ч | Решение квадратных уравнений с помощью номограммы. | 0,5 | 0,5 | ||
39 | 1 ч | Геометрический способ решения квадратных уравнений. | 1 | 0,5 | ||
40 | 1 ч | Тест №3. | ||||
41-49 | 10 ч | Квадратный трехчлен и его приложения. | ||||
41-42 | 2 ч | Квадратный трехчлен. | 0,5 | 1 | 0,5 | |
43-45 | 3 ч | Исследование корней квадратного трехчлена. Расположение корней квадратного трехчлена. | 0,5 | 2 | 0,5 | |
46-47 | 2 ч | Примеры применения свойств квадратного трехчлена при решении задач. | 0,5 | 1 | 0,5 | |
48-49 | 2 ч | Решение задач, основанных на исследовании корней квадратного трехчлена. | 0,5 | 1 | 0,5 | |
50 | 1 ч | Тест №4. |
Литература:
- Сборник элективных курсов. Математика. Автор – составитель М. Е. Козина. Волгоград, Учитель, 2007.
- И. Н. Вольхина, В. В. Благодарова, О. И. Гареева и др. Предпрофильная подготовка школьников по математике. Учебные программы курсов по выбору. Под ред. И. Н. Вольхиной. – Новосибирск: Изд–во НИПКиПРО, 2004.
- Е. С. Смирнова Интеллект и творчество. Развивающий курс. 5 — 7 класс. — М.: УЦ Перспектива, 2004.
- А. В. Фарков. Математические олимпиады в школе. 5 – 11 классы. – М.: Айрис пресс, 2003.
- Н. П. Кострикина. Задачи повышенной трудности в курсе алгебры 7 – 9 классов. Книга для учителя. – М.: Просвещение, 1991.
- Никольская И.Л. Факультативный курс по математике. – М.: Просвещение, 1991.
- Пичурин Л.Ф. За страницами учебника алгебры. – М.: Просвещение, 1990.
- Н. К. Антонович. Когда кончается урок математики. – Новосибирск, Наука, 1989.
- Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. – М.: Просвещение, 1988.
- Алимов Ш.А., Ильин В.А. и др. Алгебра 6-8 // Пробный учебник для 6-8 классов средней школы – М. Просвещение 1981 г.
- Брадис В.М. Четырехзначные математические таблицы для средней школы. – Изд.57-е М.Просвещение, 1990
- Гусев В.М., Мордкович А.Г. Математика: Справ.материалы // Книга для учащихся. – 2-е издание. М.Просвещение, 1990
- Кужепов А.К., Рубанов А.Т.. Задачник по алгебре и элементарным функциям: учеб.пособ. для сред.спец.завед. –М: Высшая школа, 1969
- Пресман А.Л. Решение квадратного уравнения с помощью циркуля и линейки. -1972. -№4/72. –М.: Квант
- Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. –изд.4-е, дополн. –М.: Высшая школа, 1973
- Худобин А.И. Сборник задач по алгебре и элементарным функциям: Пособ для учителя. Изд.2-е. –М.Просвещение, 1970
Спецкурс «За пределами школьного курса математики»
8 класс
Пояснительная записка.
Данная программа спецкурса может привлечь внимание учащихся 8 класса, которым интересна и нужна математика. Программа направлена на расширение знаний учащихся, повышение уровня математической подготовки обучающихся через решение большого класса задач. Занятия этого курса являются развитием системы ранее приобретенных знаний. Его цель создать целостное о теме и значительно расширить спектр задач посильных для учащихся.
Успешное усвоение учениками данного спецкурса должно помочь им сдать и поступить на избранный ими профиль. Школьники смогут приобрести умения, которые позволят им быть успешными на следующей ступени образовательной вертикали. Стоить отметить, что навыки в решении уравнений, неравенств, исследовании и построении графиков элементарных функций совершенно необходимы любому ученику, желающему не только успешно выступать на математических конкурсах и олимпиадах, но и хорошо подготовиться к поступлению в дальнейшем в высшие учебные заведения.
Наряду с основной задачей обучения математики – обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений программа данного спецкурса предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.
Данная программа спецкурса предназначена для платных образовательных услуг.
Цель:
Создание условий, способствующих интеллектуальному развитию обучающихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
Задачи:
- расширить рамки школьной программы;
- раскрыть прикладную направленность школьного курса математики как инструмента деятельности;
- повысить уровень математической культуры учащихся;
- формировать умения выбирать задания, соответствующие направленности познавательного интереса;
- способствовать развитию логического мышления, памяти, внимания;
- формирование положительной мотивации к изучению математики;
- сформировать высокий уровень активности, раскованности мышления, проявляющейся в продуцировании большого количества разных идей, возникновении нескольких вариантов решения задач.
Требования к математической подготовке учащихся 8 класса.
В результате изучения курса учащиеся должны уметь:
- Решать задачи на проценты, производить процентные вычисления в жизненных ситуациях
- Решать задачи на смеси, растворы, сплавы
- Преобразовывать выражения, содержащие модуль
- Решать уравнения, неравенства, содержащие модуль
- Строить графики элементарных функций, содержащие модуль
- Уметь решать квадратные уравнения всеми способами , рассмотренными в рамках курса
- Овладеть понятием трехчлен и его приложением
Содержание обучения.
2 часа в неделю, всего 50 часов.
- Процентные расчеты на каждый день. (8 часов)
- Модуль (8 часов)
- Графики «улыбаются» (10 часов)
- Способы решения квадратного уравнения (10 часов)
- Квадратный трехчлен и его приложения (10 часов)
- Тестовые проверочные работы ( 4 часа)
В каждой теме курса предусмотрены лекции, практические занятия, самостоятельные и проверочные работы.
Номер Занятия. | Кол-во Часов. | Тема. | Лекция. | Практика. | Самост. работа. | Тест. |
1-8 | 8 ч | Процентные расчеты на каждый день. | ||||
1-2 | 2 ч | Проценты. Основные задачи на проценты. | 0,5 | 1 | 0,5 | |
3-4 | 2 ч | Процентные вычисления в жизненных ситуациях. | 0,5 | 1 | 0,5 | |
5-6 | 2 ч | Банковские операции. | 0,5 | 1 | 0,5 | |
7-8 | 2 ч | Задачи на смеси, растворы, сплавы. | 0,5 | 1 | 0,5 | |
9 | 1 ч | Тест №1. | ||||
10-17 | 8 ч | Модуль. | ||||
10-11 | 2 ч | Модуль: общие сведения, геометрический смысл. | 0,5 | 1,5 | ||
12-13 | 2 ч | Преобразование выражений, содержащих модуль. | 0,5 | 1 | 0,5 | |
14-15 | 2 ч | Графики функций, содержащих модуль. | 0,5 | 1 | 0,5 | |
16-17 | 2 ч | Модуль в задачах ГИА и ЕГЭ. | 0,5 | 1 | 0,5 | |
18 | 1 ч | Тест №2. | ||||
19-28 | 10 ч | Графики «улыбаются». | ||||
19-20 | 2 ч | Графики вокруг нас. | 1 | 1 | ||
21-22 | 2 ч | Геометрические преобразования графиков функций. | 0,5 | 1 | 0,5 | |
23-24 | 2 ч | Построение графиков функций, содержащих модуль, на основе геометрических представлений. | 0,5 | 1 | 0,5 | |
25-26 | 2 ч | Графики кусочно-заданных функций. | 0,5 | 1 | 0,5 | |
27-28 | 2 ч | Презентация проектов «Графики улыбаются» | ||||
29-40 | 10 ч. | Способы решения квадратного уравнения. | 1 | |||
29 | 1 ч | Разложение левой части уравнения на множители. | 0,5 | 0,5 | ||
30 | 1 ч | Метод выделения полного квадрата. | 0,5 | 0,5 | ||
31 | 1 ч | Решение квадратных уравнений по формулам. | 0,5 | 0,5 | ||
32 | 1 ч | Решение уравнений с использованием теоремы Виета (прямой и обратной). | 0,5 | 0,5 | ||
34 | 1 ч | Решение уравнений способом «переброски». | 0,5 | 0,5 | ||
35 | 1 ч | Свойства коэффициентов квадратного уравнения. | 0,5 | 0,5 | ||
36 | 1 ч | Графическое решение квадратного уравнения. | 0,5 | 0,5 | ||
37 | 1 ч | Решение квадратного уравнения с помощью циркуля и линейки. | 0,5 | 0,5 | ||
38 | 1ч | Решение квадратных уравнений с помощью номограммы. | 0,5 | 0,5 | ||
39 | 1 ч | Геометрический способ решения квадратных уравнений. | 1 | 0,5 | ||
40 | 1 ч | Тест №3. | ||||
41-49 | 10 ч | Квадратный трехчлен и его приложения. | ||||
41-42 | 2 ч | Квадратный трехчлен. | 0,5 | 1 | 0,5 | |
43-45 | 3 ч | Исследование корней квадратного трехчлена. Расположение корней квадратного трехчлена. | 0,5 | 2 | 0,5 | |
46-47 | 2 ч | Примеры применения свойств квадратного трехчлена при решении задач. | 0,5 | 1 | 0,5 | |
48-49 | 2 ч | Решение задач, основанных на исследовании корней квадратного трехчлена. | 0,5 | 1 | 0,5 | |
50 | 1 ч | Тест №4. |
Литература:
- Сборник элективных курсов. Математика. Автор – составитель М. Е. Козина. Волгоград, Учитель, 2007.
- И. Н. Вольхина, В. В. Благодарова, О. И. Гареева и др. Предпрофильная подготовка школьников по математике. Учебные программы курсов по выбору. Под ред. И. Н. Вольхиной. – Новосибирск: Изд–во НИПКиПРО, 2004.
- Е. С. Смирнова Интеллект и творчество. Развивающий курс. 5 — 7 класс. — М.: УЦ Перспектива, 2004.
- А. В. Фарков. Математические олимпиады в школе. 5 – 11 классы. – М.: Айрис пресс, 2003.
- Н. П. Кострикина. Задачи повышенной трудности в курсе алгебры 7 – 9 классов. Книга для учителя. – М.: Просвещение, 1991.
- Никольская И.Л. Факультативный курс по математике. – М.: Просвещение, 1991.
- Пичурин Л.Ф. За страницами учебника алгебры. – М.: Просвещение, 1990.
- Н. К. Антонович. Когда кончается урок математики. – Новосибирск, Наука, 1989.
- Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. – М.: Просвещение, 1988.
- Алимов Ш.А., Ильин В.А. и др. Алгебра 6-8 // Пробный учебник для 6-8 классов средней школы – М. Просвещение 1981 г.
- Брадис В.М. Четырехзначные математические таблицы для средней школы. – Изд.57-е М.Просвещение, 1990
- Гусев В.М., Мордкович А.Г. Математика: Справ.материалы // Книга для учащихся. – 2-е издание. М.Просвещение, 1990
- Кужепов А.К., Рубанов А.Т.. Задачник по алгебре и элементарным функциям: учеб.пособ. для сред.спец.завед. –М: Высшая школа, 1969
- Пресман А.Л. Решение квадратного уравнения с помощью циркуля и линейки. -1972. -№4/72. –М.: Квант
- Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. –изд.4-е, дополн. –М.: Высшая школа, 1973
- Худобин А.И. Сборник задач по алгебре и элементарным функциям: Пособ для учителя. Изд.2-е. –М.Просвещение, 1970
nsportal.ru

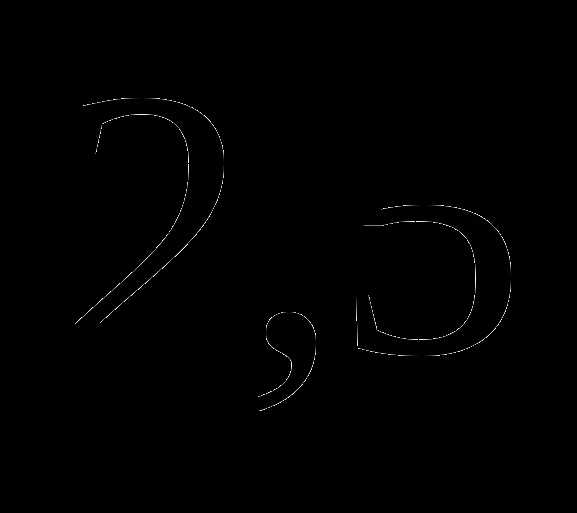 .
. . Принадлежит ли точка
. Принадлежит ли точка  графику?
графику?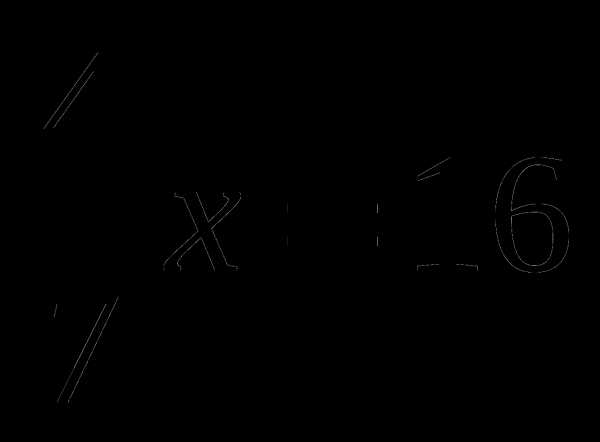 .
.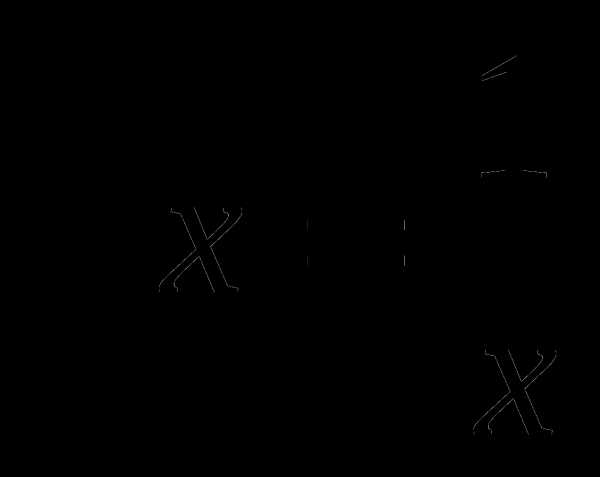
 ткани, а на три таких же платья и пять таких же сарафанов —
ткани, а на три таких же платья и пять таких же сарафанов — 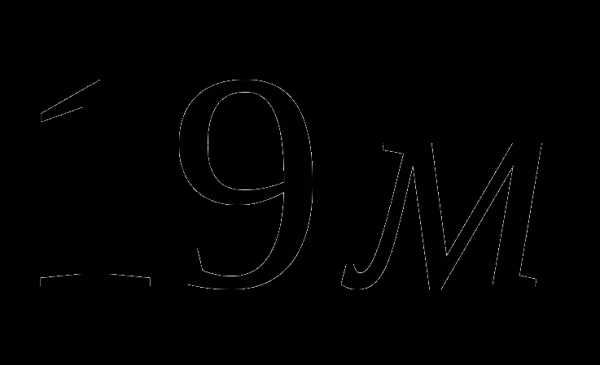 ткани. Сколько ткани потребуется на одно платье и сколько на один сарафан?
ткани. Сколько ткани потребуется на одно платье и сколько на один сарафан?