Гдз по алгебре 8 класс макарычев 184
ГДЗ 184 номер алгебра 8 класс,.Н
С его помощью ученик изучит и проанализировать понятие «рациональные дроби выявить их свойства, научится находить сумму и разность дробей, а также произведение и частное, познакомится с квадратным корнем, усвоит его качество, где они применяются, сумеет справляться с квадратными уравнениями. это решебник, практическое пособие, которое содержит готовые ответы на задачи и примеры второй части одноименного учебника, составленного коллективом российских авторов:.Н. Издательство: Просвещение предыдущий следующий, решебник 2 / номер / 184 предыдущий следующий.
ГДЗ по Алгебре для 8 класса Ю.
 Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова на 5
Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова на 5Издательство: Просвещение 2015
«ГДЗ по алгебре 8 класс Макарычев, Миндюк, Нешков, Суворова (Просвещение)» включает верные ответы на все номера заданий основного издания и является отличным подспорьем восьмиклассникам в изучении математики. Учебник разработан в соответствии с требованиями Федерального государственного образовательного стандарта коллективом признанных специалистов в данной сфере и состоит из более чем 1000 упражнений и контрольных вопросов.
В восьмом классе ребята продолжают постигать точную науку, программа становится все сложнее, учебная нагрузка по другим предметам также возрастает, поэтому хороший помощник в учении школьникам очень пригодится. Такой поддержкой ученикам станет данное методическое пособие, включающее самые подробные ответы на все номера. Решебник как нельзя лучше подойдет ребятам, кому необходимо сэкономить время на приготовлении домашних заданий, и тем, кто желает углубить свои знания по дисциплине и научиться решать самые сложные задачи.
Такой поддержкой ученикам станет данное методическое пособие, включающее самые подробные ответы на все номера. Решебник как нельзя лучше подойдет ребятам, кому необходимо сэкономить время на приготовлении домашних заданий, и тем, кто желает углубить свои знания по дисциплине и научиться решать самые сложные задачи.
Решебник – виртуальный репетитор школьников
- – сложение и вычитание алгебраических дробей с разными знаменателями;
- – понятие квадратного корня из неотрицательного числа;
- – преобразование графиков функций.
Решебник упрощает и систематизирует знания, полученные от преподавателя и из других источников, экономит время школьников. Достаточно зайти в ресурс и найти верное решение.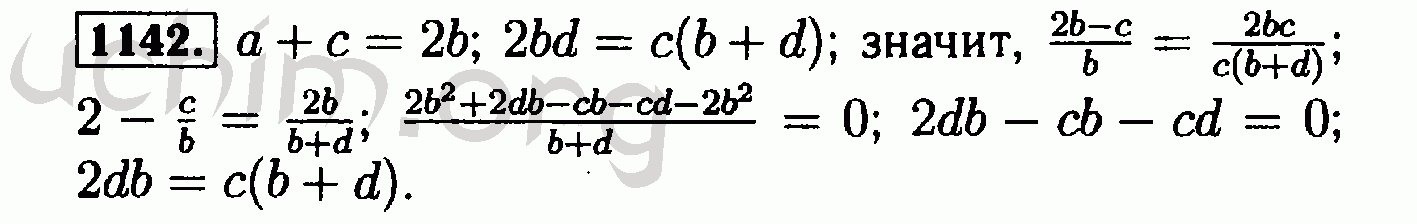 Однако не стоит увлекаться бездумным списыванием готовых ответов. Гораздо полезнее применять онлайн-сборник в качестве виртуального репетитора. Для этого надо выполнить упражнения самостоятельно, затем проверить себя по решебнику, отыскать допущенные ошибки и проанализировать их, выявив тем самым пробелы в знаниях. Возможно плохо усвоенную тему придётся повторить ещё раз по учебнику.
Однако не стоит увлекаться бездумным списыванием готовых ответов. Гораздо полезнее применять онлайн-сборник в качестве виртуального репетитора. Для этого надо выполнить упражнения самостоятельно, затем проверить себя по решебнику, отыскать допущенные ошибки и проанализировать их, выявив тем самым пробелы в знаниях. Возможно плохо усвоенную тему придётся повторить ещё раз по учебнику.
Подробнее о решебнике по алгебре для 8 класса от Макарычева и его преимуществах
Систематические занятия с решебником способствуют:
- – стопроцентной подготовке к каждому уроку и проверочным работам;
- – повышению уровня знаний и успеваемости по предмету;
- – появлению уверенности в своих силах, что отражается в ответах на уроках и письменных работах.
Привет всем посетителям сайта математика дома. Сейчас Вы находитесь на главной странице ресурса, который посвящен алгебре по учебнику автора Макарычев и другие. В данный момент здесь Вы можете уже сейчас воспользоваться списком упражнений к учебнику по алгебре Макарычев для седьмого и восьмого классов. С этой страницы Вы можете перейти на соответствующие разделы, например, алгебра 7 класс, где Вашему вниманию представлены список номеров и упражнений к учебнику за 7 класс. Перейдя по выбранному номеру перед Вами откроется страница, на которой Вы можете увидеть условие задачи и ее решение, кроме этого там будет видео-ролик с Youtube, в котором я старался максимально подробно с объяснениями решить данный пример. Кроме этого, еще есть страница —
Сейчас Вы находитесь на главной странице ресурса, который посвящен алгебре по учебнику автора Макарычев и другие. В данный момент здесь Вы можете уже сейчас воспользоваться списком упражнений к учебнику по алгебре Макарычев для седьмого и восьмого классов. С этой страницы Вы можете перейти на соответствующие разделы, например, алгебра 7 класс, где Вашему вниманию представлены список номеров и упражнений к учебнику за 7 класс. Перейдя по выбранному номеру перед Вами откроется страница, на которой Вы можете увидеть условие задачи и ее решение, кроме этого там будет видео-ролик с Youtube, в котором я старался максимально подробно с объяснениями решить данный пример. Кроме этого, еще есть страница —
 На каждой страничке с решениями внизу имеется возможность оставить комментарии, если есть какой-либо вопрос по данному примеру, возможно не совсем полное объяснение или же, например, Вы нашли ошибку (такое очень мало вероятно, но все же возможно, все могут ошибаться, в том числе и я) укажите в чем, по Вашему мнению, она заключается, я обязательно дам пояснение или исправлю неточность. Также там Вы можете прямо в комментариях писать пожелания и просьбы по решению каких-либо упражнений по алгебре и не только. Учебники под авторством Макарычева и компании переиздавались много раз, поэтому если год издания Вашего учебника не совпадает с тем, по которому работал я, то Вам необходимо самостоятельно найти соответствие, в основном упражнения во всех изданиях одинаковые, но возможны небольшие отклонения, возможно в нумерации. Обращаем Ваше внимание, что я работал по учебникам
На каждой страничке с решениями внизу имеется возможность оставить комментарии, если есть какой-либо вопрос по данному примеру, возможно не совсем полное объяснение или же, например, Вы нашли ошибку (такое очень мало вероятно, но все же возможно, все могут ошибаться, в том числе и я) укажите в чем, по Вашему мнению, она заключается, я обязательно дам пояснение или исправлю неточность. Также там Вы можете прямо в комментариях писать пожелания и просьбы по решению каких-либо упражнений по алгебре и не только. Учебники под авторством Макарычева и компании переиздавались много раз, поэтому если год издания Вашего учебника не совпадает с тем, по которому работал я, то Вам необходимо самостоятельно найти соответствие, в основном упражнения во всех изданиях одинаковые, но возможны небольшие отклонения, возможно в нумерации. Обращаем Ваше внимание, что я работал по учебникам 
Решение номер №184 по Алгебре за 8 класс Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров
184. Пусть а За – 2b; 4) а + b > 4а-5b.
Видеорешение/ номер / 184
youtube.com/embed/_Kh-LBOqMsQ?start=15503″ frameborder=»0″ allowfullscreen=»»/>
Решебник №2/ номер / 184
Множителииз 184 — Найдите простые множители / множители 184
Факторы 184 — это целые числа, которые можно равномерно разделить на 184.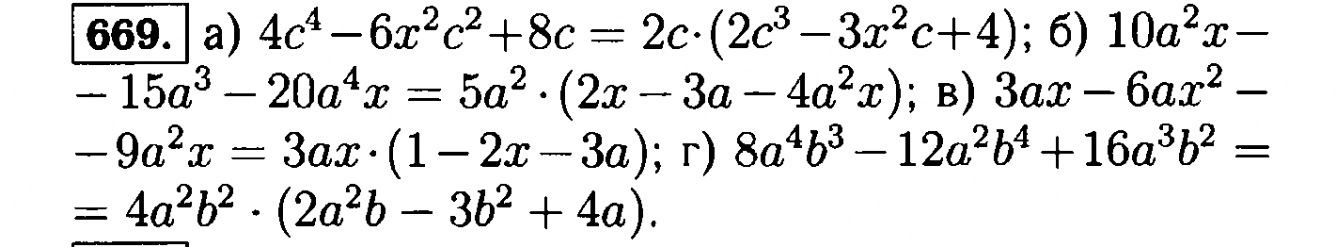 Всего имеется 8 факторов 184, то есть 1, 2, 4, 8, 23, 46, 92, 184, где 184 — самый большой множитель. Парные множители числа 184 равны (1, 184), (2, 92), (4, 46), (8, 23), а его простые множители равны 2 × 23.
Всего имеется 8 факторов 184, то есть 1, 2, 4, 8, 23, 46, 92, 184, где 184 — самый большой множитель. Парные множители числа 184 равны (1, 184), (2, 92), (4, 46), (8, 23), а его простые множители равны 2 × 23.
- Все множители 184: 1, 2, 4, 8, 23, 46, 92 и 184
- Отрицательные множители 184: -1, -2, -4, -8, -23, -46, -92 и -184
- Подводя итоги 184: 2, 23
- Простая факторизация 184: 2 3 × 23 1
- Сумма множителей 184: 360
Какие множители числа 184?
Факторы 184 — это пары тех чисел, произведения которых дают 184.Эти множители могут быть простыми или составными числами.
Как найти множители 184?
Чтобы найти множители 184, нам нужно найти список чисел, которые делили бы 184 без остатка.
- 184/1 = 184; следовательно, 1 — множитель 184.
- 184/4 = 46; следовательно, 4 — это множитель 184.

☛ Также проверьте:
- Факторы 70 — Факторы 70: 1, 2, 5, 7, 10, 14, 35, 70
- Факторы 5 — Факторы 5 равны 1, 5
- Факторы 23 — Факторы 23 равны 1, 23
- Множители 9 — Множители 9 равны 1, 3, 9
- Факторы 52 — Факторы 52: 1, 2, 4, 13, 26, 52
Факторы из 184 по прайм-факторизации
Число 184 составное, поэтому оно состоит из простых делителей.Теперь давайте узнаем, как вычислить простые множители 184. Первый шаг — разделить число 184 на наименьший простой множитель, здесь он равен 2. Мы продолжаем деление, пока оно не даст ненулевой остаток.- 184 ÷ 2 = 92
- 92 ÷ 2 = 46
- 46 ÷ 2 = 23
Дальнейшее деление 23 на 2 дает ненулевой остаток. Итак, мы останавливаем процесс и продолжаем делить число 23 на следующий наименьший простой множитель. В конце концов, мы останавливаемся, если следующего основного фактора не существует или когда мы не можем дальше делиться.
В конце концов, мы останавливаемся, если следующего основного фактора не существует или когда мы не можем дальше делиться.
Итак, разложение числа 184 на простые множители можно записать как 2 3 × 23 1 , где 2, 23 — простые числа.
Фактор 184 в парах
Парные множители 184 — это пары чисел, которые при умножении дают произведение 184. Попарно множители 184 составляют:
- 1 × 184 = (1, 184)
- 2 × 92 = (2, 92)
- 4 × 46 = (4, 46)
- 8 × 23 = (8, 23)
Отрицательные парные множители 184:
- -1 × -184 = (-1, -184)
- -2 × -92 = (-2, -92)
- -4 × -46 = (-4, -46)
- -8 × -23 = (-8, -23)
ПРИМЕЧАНИЕ: Если (a, b) является парным множителем числа, то (b, a) также является парным множителем этого числа.
Факторы 184 решенных примеров
Пример 1.
 Сколько факторов у 184?
Сколько факторов у 184? Решение:
Факторы 184: 1, 2, 4, 8, 23, 46, 92, 184. Следовательно, 184 имеет 8 факторов.
Пример 2: Найдите НОК и наибольший общий коэффициент (GCF) 184 и 20.
Решение:
Факторы 184 — это 1, 2, 4, 8, 23, 46, 92, 184, а множители 20 — 1, 2, 4, 5, 10, 20.
Следовательно, НОК 184 и 20 равно 920, а наибольший общий коэффициент (GCF) 184 и 20 равен 4.
Пример 3. Найдите, если 8, 22, 23, 92 и 184 делятся на 184.
Решение:
Когда мы делим 184 на 22, остается остаток. Следовательно, число 22 не делится на 184. Все числа, кроме 22, делятся на 184.
Пример 4. Найдите произведение всех простых делителей числа 184.
Решение:
Так как простые множители 184 равны 2, 23. Следовательно, произведение простых множителей = 2 × 23 = 46.

перейти к слайду перейти к слайду перейти к слайду
Готовы увидеть мир глазами математиков?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых занятиях и станьте экспертом во всем.
Забронируйте бесплатную пробную версию Класс
Часто задаваемые вопросы по факторам 184
Какие факторы у 184?
Факторы числа 184: 1, 2, 4, 8, 23, 46, 92, 184, а отрицательные факторы — -1, -2, -4, -8, -23, -46, -92, -184.
Какова сумма всех множителей числа 184?
Сумма всех множителей 184 = (2 3 + 1 — 1) / (2 — 1) × (23 1 + 1 — 1) / (23 — 1) = 360
Каковы парные множители числа 184?
Парные множители 184: (1, 184), (2, 92), (4, 46), (8, 23).
Какой наибольший общий множитель чисел 184 и 147?
Множители 184 равны 1, 2, 4, 8, 23, 46, 92, 184, а делители 147 равны 1, 3, 7, 21, 49, 147. 184 и 147 имеют только один общий делитель, равный 1. .Это означает, что 184 и 147 взаимно просты.
184 и 147 имеют только один общий делитель, равный 1. .Это означает, что 184 и 147 взаимно просты.
Следовательно, наибольший общий коэффициент (GCF) 184 и 147 равен 1.
Сколько факторов из 57 являются общими для факторов из 184?
Так как множители 184 равны 1, 2, 4, 8, 23, 46, 92, 184, а множители 57 — 1, 3, 19, 57. Следовательно, 184 и 57 имеют только один общий множитель, равный 1. Следовательно, 184 и 57 взаимно просты.
8 РАЗВИТИЕ МАТЕМАТИЧЕСКИХ ЗНАНИЙ НЕ ЧИСЛА | Сложим: помощь детям в изучении математики
Лерер Р., & Chazan, D. (Редакторы). (1998). Создание учебной среды для развития понимания геометрии и пространства . Махва, Нью-Джерси: Эрлбаум.
Лерер, Р., Якобсон, К., Кемени, В., и Стром, Д. (1999). Использование детской интуиции для развития математического понимания пространства. В E.Fennema & T.R.Romberg (Eds.), Classrooms, которые способствуют пониманию, (стр. 63–87). Махва, Нью-Джерси: Эрлбаум.
Лерер, Р., Якобсон, К., Тойр, Г., Демени, В., Стром, Д., Хорват, Дж., Ганс, С., и Келер, М. (1998). Развитие понимания геометрии и пространства в начальных классах. В R.Lehrer & D.Chazan (Eds.), Разработка обучающей среды для развития понимания геометрии и пространства (стр. 169–200). Махва, Нью-Джерси: Эрлбаум.
Лерер Р., Дженкинс М. и Осана Х. (1998). Продольное исследование детских рассуждений о пространстве и геометрии. В R.Lehrer & D.Chazan (Eds.), , Проектирование обучающей среды для развития понимания геометрии и пространства (стр.137–167). Махва, Нью-Джерси: Эрлбаум.
Лерер Р., Рэндл Л. и Сансилио Л. (1989). Изучение геометрии предварительной проверки с помощью Logo. Познание и обучение , 6 , 159–184.
Лерер Р. и Шаубле Л. (2000a). Изобретая структуры данных для репрезентативных целей: модели классификации учащихся начальных классов. Математическое мышление и обучение , 2 , 49–72.
Лерер Р., & Шаубле, Л. (2000b). Моделирование в математике и естественных науках. В R.Glaser (Ed.), Достижения в педагогической психологии (том 5, стр. 101–159). Махва, Нью-Джерси: Эрлбаум.
Лерер Р. и Шаубле Л. (2000c). Развитие модельных рассуждений. Журнал прикладной психологии развития , 21 (1), 39–48.
Лерер Р., Шаубле Л., Стром Д. и Плайдж М. (2001). Сходство формы и содержания: Вид модельного материала.В S.Carver & D.Klahr (Eds.), Познание и обучение: Двадцать пять лет прогресса (стр. 39–74). Махва, Нью-Джерси: Эрлбаум.
Линчевски, Л., и Виннер, С. (1990). Вложенные фигуры и структуры алгебраических выражений. В G.Booker, P.Cobb, & T.N.de Mendicuti (Eds.), Proceedings of the XIV International Conference for the Psychology of Mathematics Education (vol. 2, pp. 85–92). Оастепек, Мексика: Программный комитет PME. (ERIC Document Reproduction Service No.ЕД 411 138).
Линдквист, М. (1989). Стандарты измерений. Учитель арифметики , 37 , 22–26.
Лоххед Дж. (1980). Факультетские интерпретации простых алгебраических утверждений: профессорская сторона уравнения. Журнал математического поведения , 3 , 29–37.
МакГрегор, М., и Стейси, К. (1993). Когнитивные модели, лежащие в основе формулировок учащимися простых линейных уравнений. Журнал исследований в области математического образования , 24 , 217–232.
Мейсон, Дж. (1996). Выражение общности и корней алгебры. В N.Bednarz, C.Kieran, & L.Lee (Eds.), Подходы к алгебре: Перспективы исследований и преподавания (стр. 65–86). Дордрехт, Нидерланды: Kluwer.
Мейсон, Дж., Грэм, А., Пимм, Д., и Говар, Н. (1985). Пути к / корням алгебры . Милтон Кейнс, Великобритания: Open University Press.
Matos, J.M.L.de. (1999). Когнитивные модели для концепции угла (Неопубликованная докторская диссертация, Университет Джорджии, 1999). Международные тезисы диссертаций , 60 (05), 1491A. Резюме доступно: http://wwwlib.umi.com/dissertations/fullcit/9928965. [10 июля 2001 г.].
Макклейн, К., Кобб, П., Гравемейер, К., и Эстес, Б. (1999). Развитие математических рассуждений в контексте измерения. В Л.В. Стифф и Ф.Р. Курсио (ред.),
Перейти по математике 7 класс. Ключ ответов на вопросы Глава 6 Алгебраические выражения — Перейти по математике. Ключ ответов
Получите подробные решения для учеников 7-х классов в HMH Go Math Answer Key Глава 6 Алгебраические выражения. Мы советуем студентам, которые хотят набрать наивысшие оценки на экзаменах, пройти курс математики по математике для 7-го класса, глава 6, «Алгебраические выражения». Изучите концепции мысленных вычислений из нашей ключевой главы 6 «Математические выражения для 7-го класса» «Алгебраические выражения».
Перейти к математике 7 класс Ответы на ключевые слова Глава 6 Алгебраические выражения
Получите ответы на свои вопросы, загрузив ключ к ответам по математике для 7 класса, глава 6, Алгебраические выражения, pdf. Мы предоставили пошаговое объяснение по теме. Итак, ознакомьтесь с темами, прежде чем начинать подготовку. После подготовки у вас есть возможность проверить свои математические навыки, решив вопросы, приведенные в конце главы.
Глава 6 Алгебраические выражения — Урок: 1
Глава 6 Алгебраические выражения — Урок: 2
Глава 6 Алгебраические выражения — Урок: 3
Глава 6 Алгебраические выражения — Урок: 4
Глава 6 Алгебраические выражения
Практическое руководство — стр.176
Вопрос 1.
У менеджера летнего лагеря 14 бейсбольных и 23 теннисных мяча. Менеджер покупает несколько коробок с бейсбольными мячами по 12 бейсбольных мячей в коробке и такое же количество коробок с теннисными мячами с 16 теннисными мячами в коробке. Напишите выражение, представляющее общее количество шаров.
______ + ______ №
Ответ: 37 + 28n
Пояснение:
При этом,
У менеджера летнего лагеря 14 бейсбольных и 23 теннисных мяча.
Менеджер покупает несколько коробок с бейсбольными мячами по 12 бейсбольных мячей в коробке и такое же количество коробок с теннисными мячами с 16 теннисными мячами в коробке.
Пусть n будет количеством коробок каждого типа.
Бейсбольные мячи: 14 + 12n
Теннисные мячи: 23 + 16n
Теперь добавьте похожие термины
14 + 12n + 23 + 16n
(14 + 23) + (12 + 16) n
37 + 28n
Таким образом, общее количество шаров выражается следующим образом: 37 + 28n
Вопрос 2.
Используйте выражение, которое вы нашли выше, чтобы найти общее количество бейсбольных и теннисных мячей, если менеджер купил 9 коробок каждого типа.
Ответ: 289
Пояснение:
Выражение, которое мы нашли в предыдущем вопросе, это 37 + 28n
n = 9 квадратов
Подставьте значение n в выражение
37 + 28 (9) = 37 + 252 = 289
Таким образом, общее количество шаров = 289
Используйте свойство распределения, чтобы развернуть каждое выражение.
Вопрос 3.
0,5 (12м — 22н)
______ м — ______ номер
Ответ: 6м — 11н
Explanation:
Мы используем свойство распределения, чтобы расширить выражение.
0,5 (12m — 22n) = 0,5 (12m) — 0,5 (22n)
= 16m — 11n
Таким образом, расширение 0,5 (12m — 22n) составляет 16m — 11n
Вопрос 4.
\ (\ frac {2} {3} \) (18x + 6z)
______ x + ______ z
Ответ: 12x + 4z
Explanation:
Мы используем свойство распределения, чтобы расширить выражение.
\ (\ frac {2} {3} \) (18x + 6z) = \ (\ frac {2} {3} \) (18x) + \ (\ frac {2} {3} \) (6z)
= \ (\ frac {36} {3} \) + \ (\ frac {12} {3} \)
= 12x + 4z
Таким образом, расширение \ (\ frac {2} {3} \) ( 18x + 6z) равно 12x + 4z
Разложите каждое выражение на множители.
Вопрос 5.
2x + 12
Введите ниже:
_____________
Ответ: 2 (x + 6)
Пояснение:
Общий множитель равен 2. Фактор выражения:
2x + 12 = 2 (x + 6)
Вопрос 6.
12x + 24
Введите ниже:
_____________
Ответ: 12 (x + 2)
Пояснение:
Общий множитель — 12.Разложим выражение на множители:
12x + 24 = 12 (x + 2)
Вопрос 7.
7x + 35
Введите ниже:
_____________
Ответ: 7 (x + 5)
Пояснение:
Общий множитель равен 7. Фактор выражения:
7x + 35 = 7 (x + 5)
Регистрация основных вопросов
Вопрос 8.
Какая связь между умножением и факторингом?
Ответ:
Разложение числа на множители означает запись его в виде произведения — списка чисел, которые при умножении дают вам исходное число, таким образом, разложение на множители подразумевает умножение.
С другой стороны, мы можем интерпретировать взаимосвязь между факторизацией и умножением как одну противоположность, потому что разложение выражения на множители означает деление каждого члена выражения на одно и то же число / коэффициент.
Независимая практика — стр. № 177
Напишите и упростите выражение для каждой ситуации.
Вопрос 9.
Компания сдает в аренду 15 продовольственных киосков и 20 игровых киосков на ярмарке графства. Плата за продуктовый киоск составляет 100 долларов плюс 5 долларов в день.Плата за игровую будку составляет 50 долларов плюс 7 долларов в день. Ярмарка длится d дней, а все киоски сданы в аренду на все время. Напишите и упростите выражение для суммы в долларах, которую платят компании.
______ + ______ д
Ответ: 2500 + 215d
Пояснение:
Учитывая это,
Компания сдает в аренду 15 продовольственных киосков и 20 игровых киосков на ярмарке графства.
Стоимость киоска с едой составляет 100 долларов плюс 5 долларов в день.
Плата за игровую будку составляет 50 долларов плюс 7 долларов в день.
Позвольте d быть количеством дней, на которые арендуются будки.
Мы должны написать выражение для суммы денег для продуктовых киосков
15 (100 + 5d)
Мы должны написать выражение для суммы денег для игровых будок
20 (50 + 7d)
Мы должны напишите выражение для суммы денег для всех будок
15 (100 + 5d) + 20 (50 + 7d)
1500 + 75d + 1000 + 140d
Объедините одинаковые термины
2500 + 215d
Таким образом, выражение для суммы в долларах, которые платят компании 2500 + 215d
Вопрос 10.
Изготовитель ковров использует узор, который представляет собой прямоугольник длиной 96 дюймов и шириной 60 дюймов. Производитель ковров хочет увеличить каждое измерение на разную величину. Пусть l и w — увеличение длины и ширины в дюймах. Напишите и упростите выражение для периметра нового узора.
______ + ______ l + ______ w
Ответ:
Ковровщик использует узор, который представляет собой прямоугольник длиной 96 дюймов и шириной 60 дюймов. Производитель ковров хочет увеличить каждое измерение на разную величину.
Формула для периметра прямоугольника: 2 Длина + 2 Ширина
2 × (96 + l + 60 + w)
= 2 × (156 + l + w)
= (312 + 2l + 2w) дюймов
В 11–12 определите два множителя, которые были умножены вместе, чтобы сформировать массив плиток. Затем определите произведение двух факторов.
Вопрос 11.
______ x + ______
Ответ: 3x + 6
Пояснение:
Два множителя равны
Ширина = 3
Длина = x + 2
Площадь является произведением двух чисел:
3 (x + 2) = 3 (x) + 3 (2)
3x + 6
Вопрос 12.
______ х — ______
Ответ: 8x — 4
Пояснение:
Два множителя равны
Ширина = 4
Длина = 2x — 1
Площадь является произведением двух чисел:
4 (2x — 1) = 4 (2x) + 4 (-1) = 8x — 4
Вопрос 13.
Объясните, как на рисунке показано, что 6 (9) = 6 (5) + 6 (4).
Тип ниже:
___________
Ответ:
Обратите внимание, что левая часть рисунка имеет 6 единиц сверху вниз и 5 единиц слева направо, что составляет 6 × 5.С другой стороны, правая часть также имеет 6 единиц сверху вниз, но 4 единицы слева направо, что составляет 6 × 4. Сложение двух выражений даст (6 × 5) + (6 × 4).
В 14–15 указан периметр фигуры. Найдите длину указанной стороны.
Вопрос 14.
Введите ниже:
_____________
Ответ: 3x — 7
Пояснение:
Мы знаем, что периметр фигуры — это сумма всех сторон. Следовательно, мы можем определить длину другой стороны, представив ее переменной s
сторона + сторона + сторона = периметр
s + (x + 3) + (2x +4) = 6x
s + 3x + 7 = 6x
s = 6x — 3x — 7
Объедините похожие термины
s = 3x — 7
Вопрос 15.
Тип ниже:
_____________
Ответ: 2x + 6
Пояснение:
Мы знаем, что периметр фигуры — это сумма всех сторон. Следовательно, мы можем определить длину другой стороны, представив ее переменной s
2side + 2side = периметр
2s + 2 (3x — 3) = 10x + 6
2s + 6x — 6 = 10x + 6
2s = 10x + 6 -6x + 6
2s = 4x + 12
2s = 2 (2x + 6)
s = 2x + 6
Стр. № 178
Вопрос 16.
Настойчиво решайте проблемы
На рисунках показаны размеры теннисного корта и баскетбольной площадки, выраженные в ширине x в футах теннисного корта.
а. Напишите выражение для периметра каждого корта.
Тип ниже:
_____________
Ответ:
Поскольку корты прямоугольные, мы можем сложить все стороны корта, используя следующие выражения:
Теннис:
x + x + (2x + 6) + (2x + 6)
= 2x + 4x + 12
= 6x + 12
Баскетбол:
(1/2 x + 32) + (1/2 x + 32) + (3x — 14) + (3x — 14)
x + 64 + 6x — 28
Теперь объедините похожие условия
7х + 36
Вопрос 16.
б. Напишите выражение, описывающее, насколько периметр баскетбольной площадки больше, чем периметр теннисного корта.
Тип ниже:
_____________
Ответ: x + 24
Пояснение:
Поскольку периметр баскетбольной площадки больше, мы вычитаем из него периметр теннисного корта.
Следовательно, выражение (7x + 36) — (6x + 12)
= 7x + 36 — 6x — 12 = x + 24
Вопрос 16.
c. Предположим, теннисный корт имеет ширину 36 футов. Найдите все размеры двух кортов.
Ширина теннисного корта: _________ футов
Длина теннисного корта: _________ футов
Ширина баскетбольной площадки: _________ футов
Длина баскетбольной площадки: _________ футов
Ответ:
Чтобы найти все размеры, подставляем 36 в x теннисного корта и решаем длину.
Для теннисного корта:
Ширина: x = 36 футов
Длина: 2x + 6 = 2 (36) + 6 = 72 + 6 = 78 футов
Для баскетбольной площадки:
Ширина: 1/2 x + 32 = 1 / 21 (36) + 32 = 18 + 32 = 50 футов
Длина: 3x — 14 = 3 (36) — 14 = 108-14 = 94 футов
Вопрос 17.
Выводы нарисуйте
Используйте цифру, чтобы найти произведение (x + 3) (x + 2). (Подсказка: найдите площадь каждого маленького квадрата или прямоугольника, затем сложите.)
Введите ниже:
_____________
Ответ: x² + 5x + 6
Пояснение:
Мы можем сложить площади меньших квадратов, чтобы найти площадь всей фигуры.
Обратите внимание, что есть один xx = x²
Есть 3 (x.1) = 3x
Есть 2 (x.1) = 2x
Есть 6 (1.1) = 6
Сложив их вместе, мы получим x² + 3x + 2x + 6 = x² + 5x + 6
Вопрос 18.
Сообщайте математические идеи
Десмонд утверждает, что продукт, показанный справа, иллюстрирует свойство распределения. Ты согласен? Объясните, почему да или почему нет.
________
Ответ: Да
Пояснение:
Умножение можно записать:
58 × 23 = 58 (20 + 3)
58 (20) + 58 (3)
1160 + 174
Мы замечаем, что произведения 174 и 1160 были получены с использованием свойства распределения. .
Вопрос 19.
Обоснуйте рассуждение
Опишите два разных способа найти произведение 8 × 997, используя математические вычисления. Найдите продукт и объясните, почему ваши методы работают.
Тип ниже:
_____________
Ответ:
Дано произведение
8 × 997
Для мысленных вычислений мы используем тот факт, что 997 близко к 1000
8 × 997 = 8. (1000 — 3)
8 × 1000 — 8 × 3
8000 — 24
7976
Другой метод:
8 × 997 = 8. (900 + 90 + 7)
8 (900) + 8 (90) + 8 (7)
7200 + 720 + 56
7976
Практическое руководство — стр.182
В таблице показана средняя температура в Барроу, Аляска, за три месяца в течение одного года.
Вопрос 1.
На сколько градусов выше средняя температура в ноябре, чем в январе?
________ ° F
ответ: 11,7 ° F
Пояснение:
Пусть x представляет количество градусов, на которое температура в ноябре теплее, чем в январе.
x + (-13,4) = -1,7
x — 13,4 + 13,4 = -1,7 + 3,4
x = 11,7
Таким образом, средняя температура в ноябре составляет 11.На 7 ° F теплее.
Вопрос 2.
Предположим, что в течение одного периода сильного холода средняя дневная температура снижалась на 1 \ (\ frac {1} {2} \) ° F каждый день. Сколько дней понадобилось, чтобы температура снизилась на 9 ° F?
________ дней
Ответ: 6 дней
Пояснение:
Пусть x будет количеством дней, которое потребовалось для понижения температуры на 9 ° F
(-1 1/2) x = -9
-3 / 2x = -9
-3x = -18
x = 6
Понижение температуры на 9 ° F заняло 6 дней.
Используйте обратные операции для решения каждого уравнения.
Вопрос 3.
−2x = 34
________
Ответ: -17
Пояснение:
Дано уравнение:
−2x = 34
x = -17
Вопрос 4.
г — 3,5 = −2,1
________
Ответ: 1.4
Пояснение:
Дано уравнение:
y — 3,5 = −2,1
y = -2,1 + 3,5
y = 1,4
Вопрос 5.
\ (\ frac {2} {3} \) z = −6
________
Ответ: -9
Пояснение:
Дано уравнение:
\ (\ frac {2} {3} \) z = −6
z = -6 × \ (\ frac {3} {2} \)
z = -9
Регистрация основных вопросов
Вопрос 6.
Как написание уравнения помогает решить проблему?
Тип ниже:
_____________
Ответ:
Составление уравнения помогает нам смоделировать проблему. После того, как уравнение написано, мы можем применить математические правила для определения неизвестного в уравнении.
Независимая практика — стр. № 183
В таблице показана высота в футах на пиках нескольких гор. Используйте таблицу для 7–9.
Вопрос 7.
Эверест — 8707.На 37 футов выше, чем гора Мак-Кинли. На какой высоте находится Эверест?
________ футов
Ответ: 29 087,87
Пояснение:
Учитывая, что
гора Эверест на 8 707,37 футов выше, чем гора Мак-Кинли.
Добавьте 8707,37 к высоте горы Мак-Кинли, чтобы найти высоту горы Эверест.
20 321,5 + 8 707,37 = 29 028,87
Таким образом, высота Эвереста составляет 29 087,87 футов
Вопрос 8.
Лиам спустился с вершины К2 на высоту 23 201.06 футов. На сколько футов спустился Лиам? Каково было его изменение высоты?
________ футов
Ответ: 5050,25 футов
Пояснение:
Дано,
Лиам спустился с вершины К2 на высоту 23 201,06 фута.
Вычтите высоту горы K2 и ее высоту после спуска, чтобы найти количество футов, на которые он спустился. Поскольку он спустился с горы, изменение высоты является отрицательной величиной для количества футов, на которые он спустился.
спуск: 28 251.31 — 23 201,06 = 5050,25 футов
изменение высоты: -5050,25 футов
Вопрос 9.
K2 на 11 194,21 футов выше горы Кения. Напишите и решите уравнение, чтобы найти высоту горы Кения.
________ футов
Ответ: 17 057,1
Пояснение:
Пусть h будет высотой горы Кения.
Напишите уравнение, используя данную информацию, что К2 с высотой 28 251,31 фута на 11 194,21 фута выше горы Кения.
ч + 11,194,21 = 28,251,31
ч = 17057.1 фут
Вопрос 10.
Воздушный шар начинает снижаться со скоростью 22 \ (\ frac {1} {2} \) футов в минуту. За какое время высота воздушного шара изменится на -315 футов?
________ минут
Ответ: 14 минут
Пояснение:
Воздушный шар начинает снижаться со скоростью 22 \ (\ frac {1} {2} \) футов в минуту.
315/22 \ (\ frac {1} {2} \) = 315 / \ (\ frac {45} {2} \)
= 315 × \ (\ frac {2} {45} \) = 14 минут
Вопрос 11.
Во время другой части полета аэростат в Упражнении 10 изменил высоту на -901 фут за 34 минуты.Какова была скорость его спуска?
________ \ (\ frac {□} {□} \) футов в минуту
Ответ:
Разделите количество футов на количество минут
\ (\ frac {901} {34} \) = 26,5 футов в минуту
(Или)
\ (\ frac {901} {10} \) = 90,1 футов на минута
В таблице показаны средние температуры в нескольких штатах с января по март. Используйте таблицу для 12–14.
Вопрос 12.
Напишите и решите уравнение, чтобы определить, насколько средняя трехмесячная температура в Монтане выше, чем в Миннесоте.
________ ° С
ответ: 1,8 ° C
Пояснение:
Напишите уравнение, где t — количество градусов выше, чем температура в Монтане по сравнению с температурой Миннесоты
-2,5 + t = -0,7
t = -0,7 + 2,5
t = 1,8 ° C
Вопрос 13.
Насколько теплее средняя трехмесячная температура во Флориде, чем в Монтане?
________ ° С
ответ: 18,8 ° C
Пояснение:
Вычтем температуры Флориды и Монтаны
18,1 — (-0,7) = 18.1 + 0,7 = 18,8 ° С
Вопрос 14.
Как должна измениться средняя температура в Техасе, чтобы соответствовать средней температуре во Флориде?
________ ° С
Ответ: увеличить на 5,6 ° C
Пояснение:
Вычтем температуры Флориды и Техаса
18,1–12,5 = 5,6 ° C
Вопрос 15.
У футбольной команды чистый ярд -26 \ (\ frac {1} {3} \) ярдов за серию розыгрышей. Команде нужно чистое расстояние в 10 ярдов, чтобы получить первый удар. Сколько ярдов им нужно пройти в следующем розыгрыше, чтобы получить первый даун?
________ \ (\ frac {□} {□} \) ярдов
Ответ: 36 \ (\ frac {1} {3} \) ярдов
Пояснение:
Вычтите окончательный чистый метр и текущий чистый метр, чтобы определить, сколько еще ярдов им нужно
10 — (−26 \ (\ frac {1} {3} \)) = 10 + 26 \ (\ frac { 1} {3} \)
= 36 \ (\ frac {1} {3} \)
Им нужно набрать 36 \ (\ frac {1} {3} \) ярдов в следующей игре, чтобы получить первый даун. .
Стр. № 184
Вопрос 16.
Дайвер начинает на уровне моря и спускается вертикально со скоростью 2 \ (\ frac {1} {2} \) футов в секунду. Сколько времени нужно дайверу, чтобы достичь -15,6 футов?
________ секунд
Ответ: 6,24 секунды
Пояснение:
Разделите количество футов, на которое спускается дайвер, на скорость спуска.
время = расстояние / скорость
\ (\ frac {-15.6} {- 2.5} \)
= 6,24 секунды
Вопрос 17.
Анализ взаимосвязей
В упражнении 16, какова взаимосвязь между скоростью, с которой дайвер спускается, высотой, которую он достигает, и временем, необходимым для достижения этой отметки?
Тип ниже:
_____________
Ответ: Высота, которую он достигает (y), прямо пропорциональна времени, необходимому для достижения этой высоты (x), а скорость снижения (k) — константа пропорциональности.
Вопрос 18.
Проверка на разумность
Джейн снимала деньги со своего сберегательного счета каждые 5 месяцев. Средняя сумма, которую она снимала в месяц, составляла 45,50 долларов. Сколько всего она сняла за 5 месяцев? Покажите, что ваш ответ разумный.
$ ________
Ответ: 227,50 $
Пояснение:
Умножьте сумму, которую она снимала в месяц, на количество месяцев.
45,50 × 5 = 227,50
Поскольку 45,50 ≈ 50 и 50 × 5 = 250, что близко к 227.50, ответ разумный.
Вопрос 19.
Обоснование рассуждений
Рассмотрим две проблемы, указанные ниже. Какие значения в задачах представлены отрицательными числами? Объяснить, почему.
(1) Дайвер ниже уровня моря поднимается на 25 футов к рифу на глубине -35,5 футов. Какая высота была у дайвера до того, как она поднялась на риф?
(2) Самолет снижается на 1,5 мили до высоты 3,75 мили. Какой была высота самолета перед спуском?
Тип ниже:
_____________
Ответ:
Высота -35.5 и высота после подъема представлены отрицательными числами. Изменение высоты обозначается отрицательным числом, так как самолет спускается.
Вопрос 20.
Анализировать взаимосвязи
Чем решение -4x = -4,8 отличается от решения — \ (\ frac {1} {4} \) x = -4,8? Как связаны решения?
Тип ниже:
_____________
Ответ:
Когда вы решаете -4x = -4,8, вы делите обе части на -4, чтобы найти x.
Когда вы решаете — \ (\ frac {1} {4} \) x = -4.8, вы умножаете обе части на -4, чтобы найти x.
Тогда ответы на второе уравнение будут в 16 раз больше, чем на первую задачу, поскольку 4 × 4 = 16
Вопрос 21.
Сообщайте математические идеи
Флинн открывает сберегательный счет. За один трехмесячный период он делает депозиты в размере 75,50 и 55,25 долларов. Он снимает 25,15 и 18,65 долларов. Его баланс на конец трехмесячного периода составляет 210,85 доллара. Объясните, как узнать сумму его первоначального депозита.
$ ________
Ответ: 123 $.90
Пояснение:
Пусть x будет его начальным депозитом. Напишите уравнение его баланса после внесения дополнительных депозитов и снятия средств.
x + 75,50 + 55,25 — 25,15 — 18,65 = 210,58
x + 86,95 = 210,85
Упростим левую часть уравнения
x = 123,90
Таким образом, начальная сумма депозита составляет 123,90 доллара США
Практическое руководство — Страница № 188
Нарисуйте плитки алгебры, чтобы смоделировать данное двухэтапное уравнение.
Вопрос 1.
2x + 5 = 7
Введите ниже:
_____________
Ответ: 1
Пояснение:
Сначала нарисуйте два положительных прямоугольника слева, чтобы представить 2x, и пять положительных квадратов, чтобы представить 5.На правой стороне нарисуйте 7 положительных квадратов, чтобы представить 7.
Вопрос 2.
−3 = 5 — 4x
Введите ниже:
_____________
Ответ: 2
Пояснение:
Нарисуйте 3 отрицательных квадрата с левой стороны, чтобы представить -3. С правой стороны нарисуйте 5 положительных квадратов, представляющих 5, и 4 отрицательных прямоугольника, представляющих -4x.
Вопрос 3.
Группа взрослых и один ребенок посещают фильм в Cineplex 15. Билеты стоят 9 долларов для взрослых и 6 долларов для детей.Общая стоимость фильма 78 долларов. Напишите уравнение, чтобы найти количество взрослых в группе.
________ взрослых
Ответ: 8 взрослых
Пояснение:
Дано,
Группа взрослых и один ребенок посещают фильм в Cineplex 15.
Билеты стоят 9 долларов для взрослых и 6 долларов для детей.
Полная стоимость фильма 78 долларов.
Напишите уравнение для общей стоимости, пусть a будет количеством взрослых.
9a + 6 = 78
9a = 72
a = 8
Следовательно, в группе 8 взрослых.
Вопрос 4.
Разбейте уравнение 2x + 10 = 16, чтобы проанализировать каждую часть.
Тип ниже:
_____________
Ответ:
Поскольку x — это значение, которое мы пытаемся найти, x — это решение. Это означает, что 2x — это количество, которое мы ищем, умноженное на 2. 10 прибавляется к 2x = 16, что означает, что результат равен 16.
Вопрос 5.
Напишите соответствующую реальную проблему для представления 2x — 125 = 400.
Введите ниже:
_____________
Ответ:
Реальная проблема может заключаться в следующем: однажды летом вы продаете лимонад.Вы заплатили 125 долларов за все необходимые материалы. Если вы взимаете с клиентов 2 доллара за чашку лимонада, сколько чашек лимонада вам нужно продать, чтобы получить прибыль в 400 долларов?
Регистрация основных вопросов
Вопрос 6.
Опишите шаги, которые вы должны выполнить, чтобы написать двухэтапное уравнение, которое можно использовать для решения реальной проблемы.
Тип ниже:
_____________
Ответ:
Сначала вы должны определить, что вы ищете, с помощью переменной.В реальной задаче я написал задачу 5, где переменная x представляет количество проданных чашек. Затем решите, как остающаяся информация связана с переменной. Поскольку x — это количество проданных чашек, а 2 доллара — цена за чашку, тогда в уравнении должно быть 2x.
Поскольку прибыль = доход — стоимость расходных материалов, стоимость 125 долларов необходимо вычесть из 2x, и уравнение должно равняться прибыли в 400 долларов. Это даст уравнение 2x — 125 = 400.
Независимая практика — стр.189
Вопрос 7.
Опишите, как смоделировать -3x + 7 = 28 с помощью плиток алгебры.
Тип ниже:
_____________
Ответ:
На левой стороне нарисуйте 3 отрицательных прямоугольника, чтобы представить -3x, и 7 положительных квадратов, чтобы представить 7. С правой стороны нарисуйте 28 положительных квадратов, чтобы представить 28.
Вопрос 8.
Вэл взяла напрокат велосипед, пока была в отпуске. Она платила фиксированную арендную плату в размере 55 долларов плюс 8,50 долларов каждый день. Общая стоимость составила 123 доллара. Напишите уравнение, которое вы сможете использовать, чтобы определить количество дней, на которые она арендовала велосипед.
________ дней
Ответ: 8 дней
Пояснение:
Пусть x будет количеством дней, тогда ежедневная комиссия составит 8,50x.
Поскольку существует фиксированная комиссия в размере 55 долларов, общая сумма комиссии составляет 8,50x + 55
8,50x + 55 = 123
8,50x = 123-55
8,50x = 68
x = 68 / 8,50
x = 8
Таким образом, она арендовал велосипед на 8 дней.
Вопрос 9.
Ресторан продает кружку для наполнения кофе за 6,75 доллара. Стоимость каждого пополнения составляет 1,25 доллара США. В прошлом месяце Кейт потратил 31,75 доллара на кружку и заправку.Напишите уравнение, которое вы можете использовать, чтобы найти количество добавок, которые купил Кейт.
________ заправки
Ответ: 20 заправок
Пояснение:
Учитывая это,
Ресторан продает кружку для наполнения кофе за 6,75 доллара.
Стоимость каждого пополнения составляет 1,25 доллара США. В прошлом месяце Кейт потратил 31,75 доллара на кружку и заправку.
Пусть x представляет количество заправок, тогда общее количество заправок будет 1,25x.
Поскольку стоимость кружки составляла 6,75 доллара, общая стоимость составляет 6,75 + 1,25x
6,75 + 1,25x = 31,75
1.25x = 31,75 — 6,75
1,25x = 25
x = 25 / 1,25
x = 20
Таким образом, Кейт купил 20 картриджей.
Вопрос 10.
В тренажерном зале проводится одно 60-минутное занятие по субботам и несколько 45-минутных занятий в течение недели. На прошлой неделе все занятия длились в общей сложности 285 минут. Напишите уравнение, которое вы можете использовать, чтобы найти количество уроков в будние дни.
________ классы
Ответ: 5 классов
Пояснение:
Given,
В тренажерном зале проводится одно 60-минутное занятие по субботам и несколько 45-минутных занятий в течение недели.
На прошлой неделе все занятия длились в общей сложности 285 минут.
Пусть x будет количеством 45-минутных занятий, тогда общее время 45-минутных занятий, если 45x общее время всех классов будет тогда 60 + 45x = 285
45x = 285-60
45x = 225
x = 225/45
x = 5
Таким образом, количество занятий в будний день равно 5.
Вопрос 11.
Множественные представления
В зоопарке Спрингдейла обитают 172 южноамериканских животного. Это на 45 больше, чем половина африканских животных в зоопарке.Напишите уравнение, которое вы могли бы использовать, чтобы найти n — количество африканских животных в зоопарке.
________ животные
Ответ: 254 животных
Пояснение:
В зоопарке Спрингдейла обитают 172 южноамериканских животного. Это на 45 больше, чем половина африканских животных в зоопарке.
n / 2 + 45 = 172
n / 2 = 172 — 45
n / 2 = 127
n = 127 × 2
n = 254 животных
Таким образом, количество африканских животных в зоопарке составляет 254.
Вопрос 12.
Школа купила баскетбольное оборудование и форму на 548 долларов на сумму 29 долларов.50 каждый. Общая стоимость составила 2023 доллара. Напишите уравнение, которое вы сможете использовать, чтобы найти количество школьной формы, купленной в школе.
________ форменная
Ответ: 50 униформ
Пояснение:
Общая стоимость равна стоимости баскетбольного инвентаря плюс стоимость формы.
Пусть x представляет количество униформ. Поскольку каждая форма стоит 29,50 долларов, то стоимость x униформы составляет 29,50 долларов.
Стоимость баскетбольного инвентаря 548 долларов, итого 548 + 29.50x
Предполагается, что общая стоимость составляет 2023 доллара, поэтому, если установить это значение равным выражению, которое мы получили для общей стоимости, мы получим уравнение 548 + 29,50x = 2023
29,50x = 2023 — 548
29,50x = 1475
x = 1475 / 29,50
x = 50
Таким образом, школа купила 50 единиц формы.
Вопрос 13.
Финансовая грамотность
У Хизер 500 долларов на сберегательном счете. Она снимает 20 долларов в неделю за бензин. Напишите уравнение, которое Хизер может использовать, чтобы узнать, сколько недель ей понадобится, чтобы иметь баланс в 220 долларов.
________ недель
Ответ: 14 недель
Пояснение:
Учитывая,
Хизер имеет 500 долларов на ее сберегательном счету. Она снимает 20 долларов в неделю за бензин.
Пусть x будет количеством недель. Так как она снимает 20 долларов каждую неделю, то через x недель ее счет изменится на -20 долларов.
Ее первоначальный баланс составлял 500 долларов, поэтому через x недель ее конечный баланс составляет 500–20 долларов.
Предполагается, что ее конечный баланс составляет 220 долларов, поэтому уравнение:
500 — 20x = 220
-20x = 220-500
-20x = -280
x = 280/20
x = 14
Потребуется 14 недель, чтобы иметь баланс 220 долларов.
Вопрос 14.
Critique Reasoning
Для 9x + 25 = 88 Дина написала ситуацию: «Я купила в магазине несколько рубашек по 9 долларов за штуку и получила скидку в 25 долларов. Мой общий счет составил 88 долларов. Сколько рубашек я купил? »
а. Какую ошибку допустила Дина?
Тип ниже:
_____________
Ответ: Ее ошибка заключалась в том, что скидка уменьшила бы сумму, которую она заплатила, поэтому в ее уравнении нужно было вычесть 25, а не прибавить.
Вопрос 14.
б. Перепишите уравнение, чтобы оно соответствовало ситуации Дины.
Тип ниже:
_____________
Ответ: Замена сложения в 9x + 25 = 88 на вычитание дает 9x — 25 = 88
Вопрос 14.
c. Как бы вы могли переписать ситуацию, чтобы она соответствовала уравнению?
Тип ниже:
_____________
Ответ: Вместо скидки ситуацию можно переписать так, чтобы она покупала другой товар, например брюки или свитер, который стоит 25 долларов.
Стр. № 190
Вопрос 15.
Multistep
Сэнди взимает с каждой семьи, где она нянчится, фиксированную плату в размере 10 долларов за ночь и дополнительно 5 долларов за ребенка.Кимми берет 25 долларов за ночь, независимо от того, сколько детей в семье.
а. Напишите двухэтапное уравнение, в котором сравниваются суммы, взимаемые двумя девушками, и выясняется, когда их гонорары одинаковы.
Тип ниже:
_____________
Ответ: 10 + 5x = 25
Объяснение:
Пусть x будет количеством потомков.
Сэнди взимает с каждой семьи, где она нянчится, фиксированную плату в размере 10 долларов за ночь и дополнительно 5 долларов за ребенка. Кимми берет 25 долларов за ночь, независимо от того, сколько детей в семье.
Это означает, что она взимает в сумме 10 + 5x за ночь.
Kimmi взимает только фиксированную плату в размере 25 долларов за ночь.
Поскольку вам нужно сравнить их расходы, установите эти выражения равными друг другу.
Сэнди: 10 + 5x
Кимми: 25
Уравнение: 10 + 5x = 25
Вопрос 15.
б. Сколько детей должно быть в семье, чтобы Сэнди и Кимми взимали одинаковую сумму?
________ детей
Ответ: 3 ребенка
Пояснение:
Вычтите 10 с обеих сторон, а затем разделите обе стороны на 5, чтобы найти x.
10 + 5x = 25
5x = 25-10
5x = 15
x = 3 ребенка
Вопрос 15.
c. В семье Сандерсонов пятеро детей. Какую няню им выбрать, если они хотят сэкономить на присмотре за детьми и почему?
_____________
Ответ: Кимми экономит им $ 10
Объяснение:
Подставьте x = 5 в приведенное выше уравнение для Сэнди.
10 + 5 (5) = 10 + 25 = 35
Это на 10 долларов больше, чем 25 долларов, которые взимает Кимми, поэтому им следует выбрать Kimmi, потому что это сэкономит им 10 долларов.
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 16.
Анализируйте взаимосвязи
Каждый ученик написал двухэтапное уравнение. Питер написал уравнение 4x — 2 = 10, а Андрес — уравнение 16x — 8 = 40. Учитель посмотрел на их уравнения и попросил их сравнить их. Опишите один способ, в котором уравнения похожи.
Тип ниже:
_____________
Ответ:
Каждый ученик написал двухэтапное уравнение.Питер написал уравнение 4x — 2 = 10, а Андрес написал уравнение 16x — 8 = 40.
4x — 2 = 10
4x = 10 + 2
4x = 12
x = 3
16x — 8 = 40
16x = 40 + 8
16x = 48
x = 48/16
x = 3
Они также похожи, потому что если вы умножите обе части 4x — 2 = 10 на 4, вы получите 16x — 8 = 40
Вопрос 17.
Что за ошибка?
У Дэймона в кармане 5 десятицентовиков и несколько пятак на общую сумму 1,20 доллара. Чтобы найти количество пятаков, которое есть у Деймона, студент написал уравнение 5n + 50 = 1.20. Найдите ошибку в уравнении ученика.
Тип ниже:
_____________
Ответ:
Ошибка в том, что он написал сумму денег в левой части уравнения в центах, а сумму денег в левой части уравнения написал в долларах. Ему нужно записать уравнение как 5n + 50 = 120. или 0,05n + 0,50 = 1,20
Вопрос 18.
Представьте реальные проблемы
Напишите реальную проблему, на которую вы могли бы ответить, решив уравнение -8x + 60 = 28.
Тип ниже:
_____________
Ответ:
Возможная реальная проблема: у вас есть 60 долларов, которые можно потратить на одежду. Вы хотите купить футболки по 8 долларов каждая. После того, как вы пошли за покупками, у вас осталось 28 долларов. Сколько футболок ты купил?
Практическое руководство — Страница № 194
Уравнение 2x + 1 = 9 смоделировано ниже
Вопрос 1.
Чтобы решить уравнение с помощью плиток алгебры, сначала удалите _____
Затем разделите каждую сторону на _____
Введите ниже:
_____________
Ответ:
Первый шаг — удалить по одному положительному квадрату с каждой стороны.Затем разделите каждую сторону на 2 равные группы.
Вопрос 2.
Решение: x = _____
x = ______
Ответ: x = 4
Пояснение:
Решение — x = 4, поскольку удаление одного квадрата с каждой стороны дает 2x = 8, а затем деление каждой стороны на две равные группы дает x = 4.
Решите каждую проблему, написав и решив уравнение.
Вопрос 3.
Прямоугольная рамка для картины имеет периметр 58 дюймов. Высота рамы 18 дюймов.Какая ширина рамки?
______ дюймов
Ответ: 11 дюймов
Пояснение:
Прямоугольная рамка для картины имеет периметр 58 дюймов. Высота рамы 18 дюймов.
Периметр прямоугольника равен P = 2w + 2h.
Принято, что периметр прямоугольной рамки P = 58 дюймов, а высота h = 18 дюймов.
P = 2w + 2h
58 = 2w + 2 (18)
2w = 58 — 36
2w = 22
w = 11 дюймов
Таким образом, ширина рамки составляет 11 дюймов.
Вопрос 4.
Школьный магазин имеет на складе 1200 карандашей и продает в среднем 24 карандаша в день. Менеджер повторно заказывает, когда количество карандашей на складе составляет 500. Через сколько дней менеджеру придется делать повторный заказ?
______ дней
Ответ: 30 дней
Пояснение:
Школьный магазин имеет на складе 1200 карандашей и продает в среднем 24 карандаша в день.
Менеджер меняет заказ, когда количество карандашей на складе составляет 500.
Пусть x будет количеством дней
1200 — 24x = 500
-24x = -700
x ≈ 30
Таким образом, менеджер должен переупорядочить 30 дней.
Регистрация основных вопросов
Вопрос 5.
Как решить, какие операции использовать для решения двухэтапного уравнения?
Тип ниже:
_____________
Ответ:
При решении двухэтапного уравнения необходимо использовать обратные операции. Вы удаляете сложение, вычитая обратную операцию вычитания. Вы избавитесь от умножения, используя обратную операцию деления.
Стр. № 195
Вопрос 6.
9s + 3 = 57
______
Ответ: 6
Пояснение:
Дано уравнение
9s + 3 = 57
9s = 57 — 3
9s = 54
s = 54/9
s = 6
Вопрос 7.
4д + 6 = 42
______
Ответ: 9
Пояснение:
Дано уравнение
4d + 6 = 42
4d = 42-6
4d = 36
d = 36/4
d = 9
Вопрос 8.
−3y + 12 = −48
______
Ответ: 20
Пояснение:
Дано уравнение
−3y + 12 = −48
-3y = -48-12
-3y = -60
3y = 60
y = 20
Вопрос 9.
\ (\ frac {k} {2} \) + 9 = 30
______
Ответ: 42
Пояснение:
Дано уравнение
\ (\ frac {k} {2} \) + 9 = 30
\ (\ frac {k} {2} \) = 30 — 9
k / 2 = 21
к = 42
Вопрос 10.
\ (\ frac {g} {3} \) — 7 = 15
______
Ответ: 66
Пояснение:
Дано уравнение
\ (\ frac {g} {3} \) — 7 = 15
\ (\ frac {g} {3} \) = 15 + 7
г / 3 = 22
г = 22 × 3
г = 66
Вопрос 11.
\ (\ frac {z} {5} \) + 3 = −35
______
Ответ: -190
Пояснение:
Дано уравнение
\ (\ frac {z} {5} \) + 3 = −35
\ (\ frac {z} {5} \) = −35 — 3
z / 5 = -38
z = -38 × 5
z = -190
Вопрос 12.
−9ч — 15 = 93
______
Ответ: -12
Пояснение:
Дано уравнение
−9h — 15 = 93
-9h = 93 + 15
-9h = 108
-h = 108/9
h = -12
Вопрос 13.
−3 (n + 5) = 12
______
Ответ: -9
Пояснение:
Дано уравнение
−3 (n + 5) = 12
-3n — 15 = 12
-3n = 12 + 15
-3n = 27
-n = 27/3
n = -9
Вопрос 14.
−17 + \ (\ frac {b} {8} \) = 13
______
Ответ: 240
Пояснение:
Дано уравнение
−17 + \ (\ frac {b} {8} \) = 13
b / 8 = 13 + 17
b / 8 = 30
b = 30 × 8
b = 240
Вопрос 15.
7 (с — 12) = −21
______
Ответ: 9
Пояснение:
Дано уравнение
7 (c — 12) = −21
7c — 84 = -21
7c = -21 + 84
7c = 63
c = 63/7
c = 9
Вопрос 16.
−3 + \ (\ frac {p} {7} \) = −5
______
Ответ: -14
Пояснение:
Дано уравнение
−3 + \ (\ frac {p} {7} \) = −5
\ (\ frac {p} {7} \) = -5 + 3
\ (\ frac {p} {7} \) = -2
p = -2 × 7
p = -14
Вопрос 17.
46 = −6 т — 8
______
Ответ: -9
Пояснение:
Дано уравнение
46 = −6t — 8
-6t — 8 = 46
-6t = 46 + 8
-6t = 54
-t = 54/6
t = -9
Вопрос 18.
После внесения депозита на сберегательном счете Пуджи было 264 доллара. Она заметила, что если она добавит 26 долларов к сумме, изначально находящейся на счете, и удвоит сумму, она получит новую сумму. Сколько у нее изначально было на счету?
$ ______
Ответ: 106 $
Пояснение:
Пусть x будет исходной суммой.Прибавление 26 долларов к исходной сумме дает сумму x + 26.
Затем удвоение суммы дает 2 (x + 26), так что новая сумма равна 2 (x + 26) долларам.
Предполагается, что новая сумма составляет 264 доллара, поэтому 2 (x + 26) = 264
2 (x + 26) = 264
x + 26 = 264/2
x + 26 = 132
x = 132 — 26
x = 106
Таким образом, у нее изначально на счету 106 долларов.
Вопрос 19.
Текущая температура в Смоллтауне составляет 20 ° F. Это на 6 градусов меньше, чем вдвое выше, чем шесть часов назад.Какой была температура в Смоллтауне шесть часов назад?
______ ° F
ответ: 13 ° F
Пояснение:
Текущая температура в Смоллтауне 20 ° F. Это на 6 градусов меньше, чем вдвое выше, чем шесть часов назад.
Пусть x будет температурой шесть часов назад
2x — 6 = 20
2x = 20 + 6
2x = 26
x = 13
Таким образом, шесть часов назад температура в Смоллтауне была 13 ° F.
Вопрос 20.
Одно измерение на арктической исследовательской станции показало, что температура была -35 ° C.Что это за температура в градусах Фаренгейта?
______ ° F
Ответ: -31 ° F
Пояснение:
Одно измерение на арктической исследовательской станции показало, что температура была -35 ° C.
Замените C = -35 в формулу для преобразования температур Цельсия и Фаренгейта
C = 5/9 (F — 32)
-35 = \ (\ frac {5} {9} \) (F — 32)
-35 × \ (\ frac {9} {5} \) = F — 32
-7 × 9 = F — 32
-63 = F — 32
F = -63 + 32
F = -31 ° F
Таким образом, температура в градусах Фаренгейта составляет -31 ° F
Вопрос 21.
Арто заметил, что если он возьмёт противоположное его возрасту и прибавит 40, он получит число 28. Сколько лет Арто?
______ лет
Ответ: 12 лет
Пояснение:
Арто заметил, что если он возьмет противоположность своего возраста и прибавит 40, он получит число 28.
Пусть x будет его возрастом
-x + 40 = 28
x = 40 — 28
x = 12
Таким образом Арто 12 лет.
Вопрос 22.
У Свена 11 клиентов более чем в два раза больше, чем когда он начал продавать газеты.Сейчас у него 73 клиента. Сколько у него было, когда он начал?
______ клиентов
Ответ: 31 покупатель
Пояснение:
Пусть x будет количеством клиентов, с которыми он начал
11 + 2x = 73
2x = 73-11
2x = 62
x = 62/2
x = 31
Таким образом, у Свена было 31 покупатель, когда он начал.
Вопрос 23.
Паула купила лыжную куртку на распродаже за 6 долларов меньше половины ее первоначальной цены. За пиджак она заплатила 88 долларов. Какая была первоначальная цена?
$ ______
Ответ: 188 $
Пояснение:
Учитывая это,
Паула купила лыжную куртку на распродаже за 6 долларов меньше половины ее первоначальной цены.За пиджак она заплатила 88 долларов.
Пусть x будет исходной ценой
1/2 x — 6 = 88
1/2 x = 88 + 6
1/2 x = 94
x = 94 × 2
x = 188
Таким образом, исходная цена составляет 188 долларов.
Вопрос 24.
Семья Макинтош пошла собирать яблоки. Всего было собрано 115 яблок. Семья съедала в общей сложности 8 яблок каждый день. Через сколько дней у них осталось 19 яблок?
______ дней
Ответ: 12 дней
Пояснение:
Семья МакИнтош пошла собирать яблоки.Всего было собрано 115 яблок. Семья съедала в общей сложности 8 яблок каждый день
Пусть x будет количеством дней.
115 — 8x = 19
115-19 = 8x
8x = 96
x = 96/8
x = 12
Таким образом, ответ на вышеуказанный вопрос составляет 12 дней.
Используйте калькулятор для решения каждого уравнения.
Вопрос 25.
−5,5x + 0,56 = −1,64
______
Ответ: 0,4
Пояснение:
Дано уравнение
−5,5x + 0,56 = −1,64
Вычесть 0.56 с обеих сторон
-5,5x = -2,2
Разделите обе стороны на -5,5
x = 0,4
Вопрос 26.
−4,2x + 31,5 = −65,1
______
Ответ: 23
Пояснение:
Дано уравнение
−4,2x + 31,5 = −65,1
Вычтем 31,5 с обеих сторон
-4,2x = -96,6
4,2x = 96,6
x = 96,6 / 4,2
x = 23
Вопрос 27.
\ (\ frac {k} {5.2} \) + 81,9 = 47,2
______
Ответ: -180,44
Пояснение:
Дано уравнение
\ (\ frac {k} {5.2} \) + 81,9 = 47,2
k / 5,2 = 47,2 — 81,9
k / 5,2 = -34,7
k = -180,44
Стр. № 196
Вопрос 28.
Напишите двухэтапное уравнение, которое включает умножение и вычитание, включает отрицательный коэффициент и имеет решение x = 7.
Введите ниже:
____________
Ответ:
Возможное двухэтапное уравнение, которое включает умножение и вычитание, включает отрицательный коэффициент и имеет решение x = 7: -2x — 7 = -21
-2x = -21 + 7
-2x = -14
2x = 14
x = 14/2
x = 7
Вопрос 29.
Напишите двухэтапное уравнение, включающее деление и сложение, которое имеет решение x = -25
Введите ниже:
____________
Ответ: \ (\ frac {x} {5} \) + 20 = 15
Пояснение:
Возможное двухэтапное уравнение, которое включает деление и сложение и имеет решение x = -25: \ (\ frac {x} {5} \) + 20 = 15
\ (\ frac {x} { 5} \) = 15-20
\ (\ frac {x} {5} \) = -5
x = -25
Вопрос 30.
Объясните ошибку
Показано решение учащегося уравнения 3x + 2 = 15.Опишите и исправьте ошибку, допущенную учащимся.
3x + 2 = 15 Разделим обе стороны на 3.
x + 2 = 5 Вычтем 2 с обеих сторон.
x = 3
\ (\ frac {□} {□} \)
Ответ:
Ее ошибка была в том, что она разделила обе стороны на 3.
Она не разделила 2 на 3. Она должна была получить x + \ (\ frac {2} {3} \) = 5 после разделения обеих сторон. на 3.
Ее первым шагом должно было быть вычитание обеих сторон на 2 вместо деления обеих сторон на 3.
3x + 2 = 15
3x = 15 — 2
3x = 13
x = 13/2
Вопрос 31.
Множественные представления
Объясните, как можно использовать обратную стратегию решения задач для решения уравнения \ (\ frac {x} {4} \) — 6 = 2.
______
Ответ: Работать в обратном направлении означало бы назвать результат 2 и прибавить к нему 6, чтобы получить 8. Затем умножив это на 4, чтобы получить 32.
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 32.
Reason Abstractly
Формула F = 1,8C + 32 позволяет найти температуру по Фаренгейту (F) для данной температуры по Цельсию (C).Решите уравнение для C, чтобы получить формулу для определения температуры по Цельсию для заданной температуры по Фаренгейту.
Тип ниже:
____________
Ответ:
F = 1,8C + 32
F — 32 = 1,8C
1,8C = F — 32
C = (F — 32) / 1,8
Вопрос 33.
Reason Abstractly
Уравнение P = 2 (l + w) можно использовать для определения периметра P прямоугольника длиной l и шириной w. Решите уравнение для w, чтобы получить формулу для определения ширины прямоугольника с учетом его периметра и длины.
Тип ниже:
____________
Ответ:
P = 2 (l + w)
P / 2 = l + w
P / 2 — l = w
w = P / 2 — l
Вопрос 34.
Причина абстрактно
Решите уравнение ax + b = c относительно x.
Тип ниже:
____________
Ответ:
Вычтем обе части на b
ax = c — b
x = (c — b) / a
6.1 Алгебраические выражения — Страница № 197
Вопрос 1.
Научный клуб совершил двухдневную экскурсию. В первый день участники заплатили 60 долларов за проезд плюс 15 долларов за билет в планетарий.На второй день они заплатили 95 долларов за проезд плюс 12 долларов за билет в геологический музей. Напишите выражение, представляющее общую стоимость двух дней для n членов клуба.
Тип ниже:
____________
Ответ: 155 + 27n
Пояснение:
Пусть n будет количеством элементов. Тогда n также представляет количество билетов.
В первый день билеты стоят 15 долларов каждый, поэтому для n участников стоимость билета составляет 15 миллионов долларов. Члены также должны заплатить 60 долларов за транспорт, поэтому общая стоимость первого дня составит 60 + 15 долларов.
На второй день билеты стоят 12 долларов каждый, поэтому для n участников стоимость билета составляет 12n долларов. Члены также должны заплатить 95 долларов за транспорт, поэтому общая стоимость первого дня составит 95 + 12 долларов.
Общая стоимость двух дней составит (60 + 15n) + (95 + 12n).
Объедините похожие термины.
27н + 155
6.2 Одношаговые уравнения с рациональными коэффициентами
Решить.
Вопрос 2.
ч + 9,7 = −9,7
______
Ответ: h = -19.4
Пояснение:
Дано уравнение
h + 9,7 = -9,7
h = -9,7 — 9,7
h = -19,4
Вопрос 3.
\ (- \ frac {3} {4} + p = \ frac {1} {2} \)
\ (\ frac {□} {□} \)
Ответ: p = 1 \ (\ frac {1} {4} \)
Пояснение:
Дано уравнение
\ (- \ frac {3} {4} + p = \ frac {1} {2} \)
-3/4 + p = 1/2
p = 1 / 2 + 3/4
p = 1 \ (\ frac {1} {4} \)
Вопрос 4.
−15 = −0,2k
______
Ответ: k = 75
Пояснение:
Дано уравнение
−15 = −0.2k
0,2k = 15
k = 15 / 0,2
k = 150/2
k = 75
Вопрос 5.
\ (\ frac {y} {- 3} = \ frac {1} {6} \)
\ (\ frac {□} {□} \)
Ответ: y = — \ (\ frac {1} {2} \)
Пояснение:
Дано уравнение
\ (\ frac {y} {- 3} = \ frac {1} {6} \)
y = -3/6
y = -1/2
Вопрос 6.
— \ (\ frac {2} {3} \) m = −12
______
Ответ: m = 18
Пояснение:
Дано уравнение
— \ (\ frac {2} {3} \) m = −12
\ (\ frac {2} {3} \) m = 12
m = 12 × 3 / 2
м = 6 × 3
м = 18
Вопрос 7.
2,4 = — \ (\ frac {t} {4.5} \)
______
Ответ: t = -10,8
Пояснение:
Дано уравнение
2,4 = — \ (\ frac {t} {4.5} \)
-t = 2,4 × 4,5
t = -10,8
6.3 Написание двухшаговых уравнений
Вопрос 8.
Джерри начал делать приседания каждый день. В первый день он сделал 15 приседаний. Каждый день после этого он делал на 2 приседания больше, чем накануне. Сегодня Джерри сделал 33 приседания. Напишите уравнение, которое можно решить, чтобы найти количество дней, в течение которых Джерри приседал, не считая первого дня.
______ дней
Ответ: 2x + 15 = 33
Пояснение:
Пусть x будет количеством дней, тогда количество дополнительных приседаний равно 2x, так как он делает еще 2 приседания за каждый день, не считая первого дня.
Поскольку он начал делать 15 приседаний в первый день, общее количество приседаний после x будет 2x +15
2x + 15 = 33
6.4 Решение двухшаговых уравнений
Решить.
Вопрос 9.
5n + 8 = 43
______
Ответ: n = 7
Пояснение:
Дано уравнение
5n + 8 = 43
5n = 43-8
5n = 35
n = 35/5
n = 7
Вопрос 10.
\ (\ frac {y} {6} \) — 7 = 4
______
Ответ: y = 66
Пояснение:
Дано уравнение
\ (\ frac {y} {6} \) — 7 = 4
\ (\ frac {y} {6} \) = 4 + 7
\ (\ frac {y } {6} \) = 11
y = 11 × 6
y = 66
Вопрос 11.
8w — 15 = 57
______
Ответ: w = 9
Пояснение:
Дано уравнение
8w — 15 = 57
8w = 57 + 15
8w = 72
w = 72/8
w = 9
Вопрос 12.
\ (\ frac {g} {3} \) + 11 = 25
______
Ответ: g = 42
Пояснение:
Дано уравнение
\ (\ frac {g} {3} \) + 11 = 25
\ (\ frac {g} {3} \) = 25 — 11
\ (\ frac {g } {3} \) = 14
г = 14 × 3
г = 42
Вопрос 13.
\ (\ frac {f} {5} \) — 22 = −25
______
Ответ: f = -15
Пояснение:
Дано уравнение
\ (\ frac {f} {5} \) — 22 = −25
\ (\ frac {f} {5} \) = -25 + 22
\ (\ frac {f} {5} \) = -3
f = -3 × 5
f = -15
Вопрос 14.
−4p + 19 = 11
______
Ответ: p = 2
Пояснение:
Дано уравнение
−4p + 19 = 11
-4p = 11-19
-4p = -8
p = 2
Основной вопрос
Вопрос 15.
Как можно использовать двухэтапные уравнения для представления и решения реальных проблем?
Тип ниже:
___________
Ответ:
Для представления и решения реальных проблем можно использовать пошаговые двухэтапные уравнения, переведя слова в алгебраическое уравнение, решив уравнение и затем интерпретировав решение уравнения.
Выбранный ответ — Страница № 198
Вопрос 1.
Такси стоит 1,50 доллара за первую милю и 0,75 доллара за каждую дополнительную милю.Какое уравнение можно решить, чтобы определить, сколько миль вы можете проехать на такси за 10 долларов, учитывая, что x — это количество дополнительных миль?
Опции:
а. 1,5x + 0,75 = 10
б. 0,75x + 1,5 = 10
с. 1,5х — 0,75 = 10
г. 0,75x — 1,5 = 10
Ответ: 0,75x + 1,5 = 10
Пояснение:
Пусть x будет количеством дополнительных миль, тогда плата за дополнительные мили составит 0,75x, тогда общая стоимость будет 1,50 + 0,75x = 10
Таким образом, правильный ответ — вариант B.
Вопрос 2.
Какое решение является \ (\ frac {t} {2.5} \) = −5,2?
Опции:
а. -13
б. -2.08
с. 2.08
г. 13
Ответ: -13
Пояснение:
t / 2,5 = -5,2
t = -5,2 × 2,5
t = -13
Таким образом, правильный ответ — вариант A.
Вопрос 3.
Какое выражение эквивалентно 5x — 30?
Опции:
а. 5 (х — 30)
б. 5 (х — 6)
с. 5х (х — 6)
г. х (5–30)
Ответ: 5 (x — 6)
Пояснение:
Выносим за скобки 5 из каждого члена.
5x — 30 = 5 (x — 6)
Таким образом, правильный ответ — вариант B.
Вопрос 4.
В научном эксперименте температура вещества изменяется с 42 ° F до -54 ° F со средней скоростью -12 градусов в час. Через сколько часов происходит смена?
Опции:
а. -8 часов
б. 18 часов
c. 1 час
д. 8 часов
Ответ: 8 часов
Пояснение:
В научном эксперименте температура вещества изменяется с 42 ° F до -54 ° F со средней скоростью -12 градусов в час.
Пусть x будет количеством часов.
42 — 12x = -54
-12x = -54-42
-12x = -96
12x = 96
x = 96/12
x = 8 часов
Таким образом, правильный ответ — вариант D.
Вопрос 5.
Какое утверждение лучше всего представляет расстояние на числовой прямой между -14 и -5?
Опции:
а. −14 — (−5)
б. −14 + (−5)
с. −5 — (−14)
д. -5 + (-14)
Ответ: −5 — (−14)
Пояснение:
Расстояние — это разница между наибольшим числом и наименьшим числом, поэтому расстояние между -5 и -14 равно -5 — (-14), поскольку -5 больше, чем -14.
Таким образом, правильный ответ — вариант C.
Вопрос 6.
Какая крупа стоит больше всего за унцию?
Опции:
а. 4,92 доллара за 12 унций
b. 4,25 доллара за 10 унций
c. 5,04 доллара за 14 унций
d. 3,92 доллара США за 8 унций
Ответ: 3,92 доллара за 8 унций
Пояснение:
Найдите стоимость единицы для каждого варианта ответа, разделив стоимость на количество унций и округлив до двух десятичных знаков, если необходимо.
а. 4,92 доллара за 12 унций
4,92 / 12 = 0 долларов.41 за унцию
б. 4,25 доллара за 10 унций
4,25 / 10 ≈ 0,43 за унцию
c. 5,04 доллара за 14 унций
5,04 / 14 = 0,36 за унцию
d. 3,92 доллара за 8 унций
3,92 / 8 = 0,49 за унцию
Таким образом, правильный ответ — вариант D.
Мини-задание
Вопрос 7.
Кейси купил 9 билетов на концерт. Общая стоимость составила 104 доллара, включая 5 долларов за обслуживание.
а. Напишите уравнение, которое вы можете решить, чтобы найти c, стоимость одного билета.
Тип ниже:
_____________
Ответ: 9c + 5 = 104
Пояснение:
Пусть c будет стоимость каждого билета, общая стоимость 9 билетов до платы за обслуживание составит 9 центов, добавив плату за обслуживание, получим общую сумму 9 центов + 5
Вопрос 7.
г. Объясните, как вы можете оценить решение своего уравнения.
Тип ниже:
_____________
Ответ:
104 — это примерно 105. вычитание 5 из этого дает 100. 9 — это примерно 10, а 100, деленное на 10, дает 10, поэтому цена билета составляет около 10 долларов.
Вопрос 7.
c. Решите уравнение. Сколько стоил каждый билет?
$ ______
Ответ:
9c = 99
c = 99/9
c = 11
Заключение:
Концепция алгебры помогает студентам в реальной жизни. dL.029 809. 12 7) 78. 25 Пример <3 десятичных разряда <2 десятичных разряда <5 десятичных знаков UUUUU UUU UU Пример делителя> 0. • Умножьте десятичные дроби на целые числа и выполните деление на ненулевые целые числа, когда результат заканчивается десятичные дроби, с цифровыми технологиями и без них (ACMNA129). 78 12. 92 16. Раздайте копии сотых сеток (M12). 853 7. 48 → 0. 02 12. 01 = одна сотая 0. Раздайте лист задания с округлением десятичных до ближайшего целого числа каждому учащемуся и четырем генераторам чисел от 0 до 9 и просмотрите указания со студентами.Округление десятичных знаков Десятичная точка. 768 7 3 Поскольку 7 больше 5, мы увеличиваем до 4. 112 4) 48. 172 11. 73 10) 58. 3 6 11. 0196 до тысячных 4) 5. Головоломки с округлением десятичных дробей. 95 5) 4. 547 3) i) Округлить до ближайшего целого числа. 3 3) 98. Попросите добровольца выполнить Бесконечную предалгебру — округление десятичных дробей. Дата создания: 19.02.2016, 20:05:05. 12. 7. 7 Раздаточный материал / распечатка или файл для использования на проекторе / накладной для обучения / просмотра десятичных операций Простое округление с десятичными знаками — это бесплатные рабочие листы, доступные для вас.02 4 десятое целое число 4. (чаще называется. Эти рабочие листы были загружены администратором 24 октября 2020 г. на Рабочие листы. 065965 5) 8. 8 Шаг 4: a) При округлении до левой части десятичной дроби, все цифры справа от цифры округления станут 0 до десятичной точки. 51 29. 8 31. 001 = одна тысячная ДОБАВЛЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ЗНАЧЕНИЙ При ДОБАВЛЕНИИ И ВЫЧИСЛЕНИИ десятичных знаков используйте свой калькулятор! КРУГЛЫЙ свой ответ. б. Часть точки Часть. Округление десятичных дробей: поля ввода и вывода Здесь представлен интересный способ резюмировать округление десятичных дробей.249 5. »Десятичные дроби являются частью системы счисления Base-10, как и целые числа. Десятичное целое число. NBT. 1 3.. 5 11. Десятичные дроби также основаны на простом шаблоне десятков, где каждое место в десять раз превышает значение места справа от него. 922 4. Изучите подчеркнутую цифру, определите ее разрядное значение и затем округлите десятичные дроби до требуемого разрядного значения. 1) 8. Например: 0. 96 4. 88. Упражнение 1. Округлите следующее число до тысячных разрядов. 05 1. 5) Обведите десятичные дроби, округляющие до 12.Подчеркните число до тысячных разрядов и посмотрите на цифру справа от последней подчеркнутой цифры: 4. 43 2. 9 целое десятое число 2. 317 3. Этот базовый арифметический навык Округление десятичных дробей до указанного места. Просмотр округления целых чисел и десятичных знаков. 28 3. Десятичные знаки) Число, записанное в. 76873 с точностью до тысячных. 67385 3) 243. а. Десятичные числа. Рабочие листы отредактированы @ 2009 MLC Стр. 4 из 21 Упражнение 3 Указания: Округлите следующие десятичные числа до указанного места 1).27 1. 317 5. 4 + 5. 2 3. 85 14. Для округления десятичных дробей можно также использовать разрядные значения. Округлите до ближайшей десятой. 479 → 4) 8. 4 Округление десятичных знаков (A) Округлите каждое десятичное число до ближайшего указанного. 474 0. 8. 613 → 2. Число Ближайшая единица Ближайшая десятая 3. 26. 1325 тысячных 2). 1 4) 6. 14 → • 12 3) 23. 945 0. 21 3. 6 8) 85. 2 6. 63 2. 4278 3-х сотое целое число 5. 16 3. 14415. 1) Обведите десятичные дроби, которые округляют в большую сторону. до 2. 76873 до 4. ID: 1484363 Язык: английский Школьный предмет: математика Оценка / уровень: 10 класс Возраст: 14–16 Основное содержание: десятичные дроби Другое содержание: десятичные дроби Добавить в мои рабочие тетради (27) Загрузить файл pdf Вставить на мой веб-сайт или блог> Поместите десятичную дробь прямо вверх в том месте, где вы пишете свой ответ, перепишите задачу> Разделите как обычно 6005 24020.LDLXCz. 3 13. 6 350. 4. 5. 75 2) 62. If 22 Rounding Decimals Robot. р) и дробная номенклатура. 5 4. Попросите учащихся перевернуть страницу и закрасить 1. 2. состоит из трех частей. • больше или равно пяти прибавить 1 к указанному разряду. 25 2) 2. com Округление чисел с десятичными знаками Имя: _____ 1. com 1 Округление десятичных знаков Округление до ближайшего целого числа. 2182 десятитысячные 3. 5 6 12. 636 Поскольку следующая цифра справа меньше 5, округлите до 5. 95 [1] 3) Округлите числа в таблице. 8446 2.68. 682269; тысячные 4) 5. 2 628. 82 6. 3. 61884 до тысячных Деление десятичных знаков в деление десятичных знаков на десятичные классы 6-й класс Рабочий лист Десятичные дроби Найдите частное и округлите ответы до шести знаков после запятой. http: // math. 636, округленное до ближайшего целого числа, равно 6. 785 до ближайшей сотой Решение: Если цифра справа от данного места: • меньше 5, не меняйте данное место. 201 х. pdf. 124 31. 43 11. 06 343. Десятичные числа Число, содержащее десятичную точку, называется «десятичным числом» или «десятичным числом».3 5. 31. Подчеркните все места, где вы округляете до следующей цифры. 3) Обведите десятичные дроби, округляющие до 5. 22 3. Десятичные дроби до сотых, десятичные до ближайшей десятой, округление десятичных дробей Общие основные стандарты: число 5-го уровня и операции в системе счисления с основанием десяти CCSS. 4 588. Я перебираю первые несколько задач со студентами. pdf из ERT 123 в колледже Аль-Сират. 1 Простое округление с десятичными знаками — это бесплатные рабочие листы, доступные для вас. 77 9. 41 U U 3 14. Округление целых чисел и десятичных дробей Чтобы округлить целое число: 1.12 3. 54 2. 6138 88. 563976; десятитысячные Пример 4: Раунд 4. Число 1 десятичный разряд 2 десятичных знака 0. ДЕСЯТИЧНЫЕ ЧАСТИ Десятичные дроби — это дробные части целого. 800. 90 5. Округляя число, вы получаете другое число, которое можно использовать, чтобы определить, насколько велико исходное число. 415; десятые 3) 4. 96 = 793. 777450 8) 0. 0. 547 30. 1-12 21-21 0 4. 4) Обведите десятичные дроби, которые округляют до 31. Математика. 6. 44 _____ Округление десятичных знаков (B) Ответы Округлите каждое десятичное число до ближайшего указанного.52 = 891. Округлите до ближайшей десятой: 1) 12. 336 9) 92. 284 6) 60. 785 Итак, ответ: 3. название даты округление до 2 знаков после запятой лист 2 ответа 1) 0. 693 2) i) Округлить до ближайшего целого числа. (b) Часть цифры в десятичной дроби определяет значение разряда цифр. 951 → 8. Округление десятичных знаков до подчеркнутого разряда. Просмотрите концепцию округления десятичных знаков в этом наборе рабочих листов в формате pdf для 6-го класса. 1. 1 1 15. 2) Обведите десятичные дроби, которые округляют до 7. 184. оценка и округление для проверки правильности ответов (ACMNA128).453 5) 39. Округлить до имени Дата ОКРУГЛЕНИЕ ДО 2-х ДЕСЯТИЧНЫХ МЕСТ. ЛИСТ 1 ОТВЕТ. Округлить эти числа до ближайшего целого. 1) 3. 7057 [1] Округление, десятичные разряды и значащие числа. 24 3. 3. 01 37. Число ближайших 10 ближайших 100 423 420 482 535 799 [1] 2) Округлите числа в таблице. 60 десятичных знаков. 43 7. 736 → 4. 0 1 целое число целое число 6. 76 7. 731 2) 2. Любые нули в конце десятичной дроби можно опустить — они занимают место. 1) 0. 17126 6) 3. 74 6) 8. 30025 1. b) При округлении до правой части десятичной дроби опустите все цифры справа от цифры округления.Без десятичного числа. Округление до ближайшего целого числа. Округление до ближайшего десятого. Округление до ближайшей сотой. 5. 4 Округлите каждое десятичное число до указанного разряда. 97 1. 63. ii) Округлите до ближайшей десятой. 121 11. 186 Округление десятичных знаков Заполните приведенную ниже таблицу. 6967 целое число тысячный Q. 642 _____ 4) 3. 18 3. Десятичное представление. 007 94.Округление десятичных дробей до ближайшего целого числа. Рабочий лист — Отличные, приятные и бесплатные математические рабочие листы смогут представить математическую задачу по-другому. Округление десятичных чисел (A) Округление каждого десятичного числа до ближайшего указанного места. 83 Итак, ответ — 6. Напишите название каждого десятичного разряда, подчеркнутого. 7 7. Если число справа — 4, 3, 2, 1 или 0, это говорит о той же цифре, которая уже есть. 23 3. 9 2. • Умножьте и разделите десятичные дроби на 10 (ACMNA130). 871 = 53. 94 → 4 2) 12.607 = 349. 54 + 90. iii) Округлить до сотых. 7. 61263; десятитысячные 2) 1. 79 Пример № 2: Раунд 6. 6 4. Округление десятых, сотых и целых. Это похоже на округление целых чисел. 2 23 Добавление / вычитание десятичных знаков (A) Ответы. Подсчитайте каждую сумму или разницу. 651 13. 82 7. 41 3 7. 6. Все цифры после округляемой становятся нулями. 89 4. 941. об. Содержание. 769 и опустите цифры вправо, оставив 4. com Округление десятичных дробей Округлите до ближайшего целого числа. А.84 целое число сотых 3. 769 как наше округленное число. 865 целое число целое число 2. Учащиеся решают две головоломки с округлением десятичных дробей. 61 3) 5. Десятичные дроби — пакет обзора — упражнения Hanlonmath. Напишите число, которое нужно округлить. 11-04-19 Округление десятичных знаков. 636 Так как цифра справа равна 5 или больше, округлите до 6. Теперь учащиеся перенесут свой опыт представления десятичных дробей на числовой строке на округление десятичных дробей до ближайшего целого числа с использованием числовой строки. Загрузка… Округление десятичных знаков: округление десятичных знаков аналогично округлению целых чисел, за исключением того, что цифры справа от заданного значения разряда отбрасываются, а не заменяются нулями.1234 с точностью до тысячных 5) 6. Примечание: (а) Десятичная часть числа представляет собой число меньше единицы. Рабочий лист округления десятичных знаков A Пункт 3078-A www. Если цифра справа от данного разряда меньше 5, опустите цифру и все цифры вправо. 4 2. 0982 Имя: Дата: Округление десятичных знаков Меч 3. 6967 целое число тысячные 1) Округлите числа в таблице. 31. Самостоятельная практика Студенты работают над рабочим листом самостоятельно. 3 1. 07 3. 405 4) i) Округлить до ближайшего целого числа.xlsx Автор: Владелец Дата создания: 27.12.2015 12:09:46. 1 13. 83 с точностью до десятой Решение: 6. tlsbooks. округление десятичных знаков pdf
.

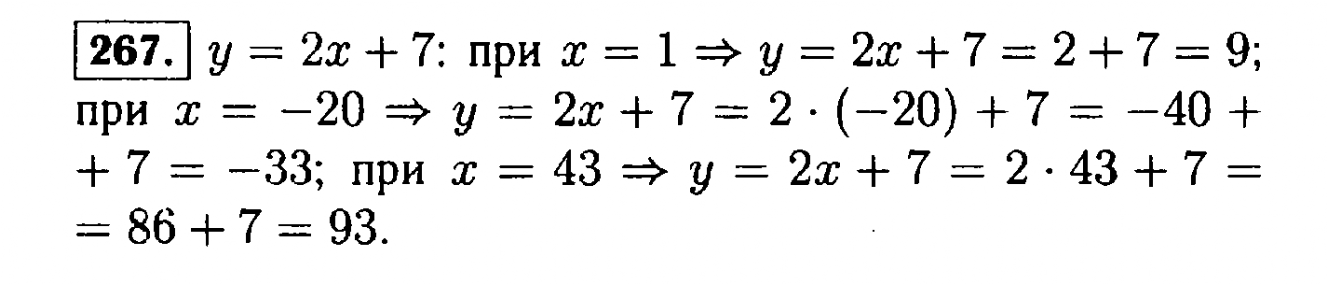 Сколько факторов у 184?
Сколько факторов у 184? 