ГДЗ Алгебра 8 класс А.Г. Мордкович, Л.И. Звавич (2013) . Ответы и решения на VipGDZ.ru
Стоит отметить, что готовые домашние задания появились в учебном процессе не так давно, около десяти лет назад. Достаточно интересным является тот факт, что родиной этих книг-помощниц считается такая строгая страна как Германия. Создал первый образец решебников учитель обычной берлинской школы, который пытался хоть как-то облегчить изучение сложных тем учениками. Его разработка очень быстро завоевала популярность и распространилась по всему миру.
Популярные решебники по алгебре за восьмой класс
В нашей стране одной из самых востребованных книг такого формата является ГДЗ по алгебре 8 класс Мордкович. Почему стоит обратить свое внимание на этот учебник, который находиться на нашем сайте VIPGDZ? Ответ на данный вопрос кроется в положительном влиянии, которое решебники этого автора оказывают на школьников.
В первую очередь, хочется начать с того, что ГДЗ становятся основной причиной развития такой черты как самостоятельность.
Также, с использованием справочников такого формата в течение длительного времени, школьник проявляет уверенность в себе и учится защищать свое мнение. Конечно, нельзя не сказать и о таком плюсе ГДЗ Мордковича А.Г., как рост мотивации к обучению. Давайте вспомним, что всегда становилось главной причиной увеличения желания приобретать новые знания? Безусловно, высокие оценки, которые легко зарабатывать с помощью данного решебника.
Используем только лучшие правильные решения на VIPGDZ.ru
Наш образовательный сайт VIPGDZ не мог обойти стороной такое надежное пособие, как качественные ответы по алгебре Мордковича, поэтому выложил его на своих страницах. Теперь каждый желающий сможет использовать этот решебник в любое время суток, просто заходя на наш портал.-(Itogovoe-povtorenie)-reshenie-66.jpg)
Отметим, что VIPGDZ.ru выгодно отличается от своих коллег. Все дело в том, что все книги, предложенные нашим ресурсом, можно просматривать абсолютно бесплатно. Кроме того, Вам даже не нужно проходить какую-либо регистрацию для этого.
Мы также позаботились о том, чтобы ученикам 8 класса было комфортно пользоваться ГДЗ самостоятельно. Именно поэтому VIPGDZ получил удобный интерфейс, с которым поиск нужных материалов на сайте и работа с ними не принесет никаких хлопот.
Одной из последних инноваций нашего портала является появление его мобильной версии. Теперь сотрудничать со справочниками по алгебре в режиме онлайн станет возможно как дома, так и в любом другом месте. Для этого необходимо просто иметь под рукой смартфон или планшет.
Изучайте алгебру без проблем, используя для этого только качественные решебники на нашем сайте VIPGDZ.ru!
Страница не найдена
Новости
Афганский телеканал TOLOnews проинформировал о гибели 63 человек в результате серии взрывов около женской школы в Кабуле.
Об этом сообщили источники и родственники погибших.
9 май
Число погибших в результате серии взрывов около женской школы в Кабуле превысило 50, пострадавших более 100, сообщает TOLOnews со ссылкой на данные Министерства внутренних дел.
9 май
В колледжах и школах России началась проверка программ обучения истории на предмет полноты сведений о Великой Отечественной войне, заявил РИА Новости министр просвещения Сергей Кравцов.
По меньшей мере 15 человек погибли и 20 получили ранения в результате серии взрывов в Кабуле, в частности, атака произошла около школы, когда ученики покидали здание, пишет TOLOnews со ссылкой на источник в МВД.-(Itogovoe-povtorenie)-reshenie-53.jpg)
8 май
По меньшей мере 15 человек погибли и 20 получили ранения в результате серии взрывов в Кабуле, в частности, атака произошла около школы, когда ученики покидали здание, пишет Tolo News со ссылкой на источник в МВД.
8 май
Мэр Москвы Сергей Собянин рассказал о программе благоустройства школьных дворов в столице, он выразил мнение о перспективах и «подводных камнях» в данном вопросе.
Глава российского правительства Михаил Мишустин утвердил список поручений, подготовленных для реализации тезисов послания президента Федеральному собранию.
В частности, премьер-министр распорядился до 17 августа подготовить доклад о предоставлении единовременных выплат семьям с детьми школьного возраста, а также оказания помощи неполным нуждающимся семьям с детьми и беременным женщинам. В общей сложности в перечень поручений вошли 58 пунктов, касающихся в том числе поддержки семей, российской туристической отрасли и обеспечения финансовой устойчивости региональных бюджетов.
ГДЗ: Алгебра 8 класс Мордкович, Александрова, Мишустина
Алгебра 8 класс
Тип: Сборник задач
Авторы: Мордкович, Александрова, Мишустина
Издательство: Мнемозина
Алгебра для некоторых восьмиклассников становится непреодолимым препятствием.-reshenie-30.21.jpg)
Описываемые темы книги
Авторы Мордкович, Александрова, Мишустина в своём учебнике для 8 класса помимо повторения пройденного материала прошлого года, разобрали множество новых тем, разбитых по главам на параграфы, среди которых можно встретить такие, как:
- Сложение и вычитание алгебраических дробей.
- Понятие квадратного корня из неотрицательного числа.
- Квадратичная функция.
- Квадратные уравнения. Неравенства.
После разобранных тем, авторы предлагают задания на повторение и закрепление изученного материала.
Что вошло в пособие с готовыми задачами
В решебник с «ГДЗ по Алгебре 8 класс Мордкович» вошли все задачи с учебника. Решения заданий подробно расписаны по названиям параграфов и номерам упражнений в точном порядке, установленном книгой. Описаны ответы как новых тем, так и упражнения для повторения. В пособие включены:
- задания различного уровня сложности;
- материал для контроля ранее изученных тем;
- подробные точные ответы, изучив которые, ученик без проблем сможет выполнить аналогичные упражнения на контрольной работе без посторонней помощи.
Основная задача решебника — заменить восьмикласснику профессионального репетитора, который в любую минуту подскажет не просто верный ответ, но и точный алгоритм работы, помогая запомнить не только основной смысл, но и правильное оформление решения.
Польза готовых заданий
Учебник Мордковича издательства книги Мнемозина с её задачами воспринимается некоторыми учениками как серьёзное препятствие.
ГДЗ по алгебре 8 класс Ключникова рабочая тетрадь 1, 2 часть
ГДЗ готовые домашние задания рабочей тетради по алгебре 8 класс Ключникова Комиссарова часть 1, 2 ФГОС от Путина. Решебник (ответы на вопросы и задания) учебников и рабочих тетрадей необходим для проверки правильности домашних заданий без скачивания онлайн
Часть 1
§1. Основные понятия
1 2 3 4 5 6 7 8 9 10
§2. Основное свойство алгебраической дроби
1 2 3 4 5 6 7 8 9 10 11
§3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
1 2 3 4 5 6 7 8 9
§4.
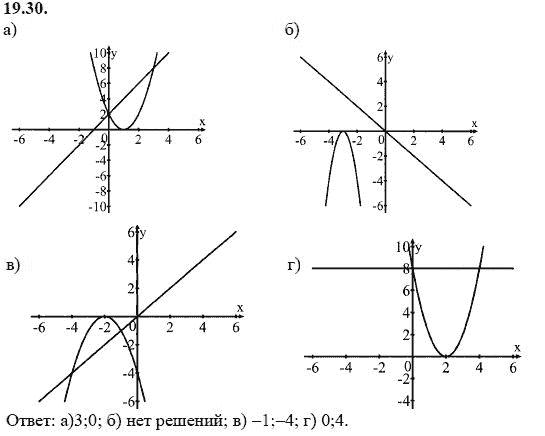Сложение и вычитание алгебраических дробей с разными знаменателями1 2 3 4 5 6 7 8 9 10 11
§5. Сложение и деление алгебраических дробей. Возведение алгебраической дроби в степень
1 2 3 4 5 6 7 8 9 10
§6. Преобразование рациональных выражений
1 2 3 4 5 6 7 8 9 10
§7. Первые представления о решении рациональных уравнений
1 2 3 4 5
§8. Степень с отрицательным целым показателем
1 2 3 4 5 6 7 8 9 10 11
§9. Рациональные числа
1 2 3 4 5 6 7 8 9 10
§10. Понятие квадратного корня из неотрицательного числа
1 2 3 4 5 6 7 8 9 10 11 12
§11. Иррациональные числа
1 2 3 4 5 6
§12. Мнножество действительных чисел
1 2 3 4 5 6 7 8 9 10
§13. Функция игрек равно корень из икс, её свойства и график
1 2 3 4 5 6 7 8 9 10 11 12
§14. Свойства квадратных корней
1 2 3 4 5 6 7 8 9 10 11
§15. Преобразование выражений, содержащих операцию извлечения квадратного корня
1 2 3 4 5 6 7 8 9 10 11 12
§16.
Модуль действительного числа1 2 3 4 5 6 7 8 9 10 11
§17. Функция y = kx в квадрате, её свойства и график
1 2 3 4 5 6 7 8 9 10 11
§18. Функция y = k делить на x, её свойства и график
1 2 3 4 5 6 7 8 9
§19. Как построить график функции y = f(x + l), если известен график функции y = f(x)
1 2 3 4 5 6 7 8 9
Часть 2
§20. Как построить график функции y=f(x)+m, если известен график функции y=f(x)
1 2 3 4 5 6 7 8 9
§21. Как построить график функции y=f(x+l)+m, если известен график функции y=f(x)
1 2 3 4 5 6 7 8
§22. Функция y равно ax в квадрате плюс bx плюс c, её свойства и график
1 2 3 4 5 6 7 8 9 10
§23. Графическое решение квадратных уравнений
1 2 3 4 5 6 7 8 9 10
§24. Основные понятия
1 2 3 4 5 6 7 8 9 10 11
§25. Формулы корней квадратного уравнения
1 2 3 4 5 6 7 8 9 10
§26. Рациональные уравнения
1 2 3 4 5 6 7
§27.
Рациональные уравнения как математические модели реальных ситуаций1 2
§28. Ещё одна формула корней квадратного уравнения
1 2 3 4 5 6 7
§29. Теорема Виета
1 2 3 4 5 6 7 8
§30. Иррациональные уравнения
1 2 3 4 5 6 7
§31. Свойства числовых неравенств
1 2 3 4 5 6 7 8 9 10 11
§32. Исследование функций на монотонность
1 2 3 4 5 6 7 8 9
§33. Решение линейных неравенств
1 2 3 4 5 6 7 8 9 10 11 12
§34. Решение квадратных неравенств
1 2 3 4 5 6 7
§35. Приближённые значения действительных чисел
1 2 3 4 5 6 7 8 9 10
§36. Стандартный вид положительного числа
1 2 3 4 5 6 7 8 9 10 11
Гдз решебник по алгебре 8 класс Мордкович ответы к задачнику
Готовые домашние задания по алгебре для задачника 8 класса автора А.Г. Мордкович — лучшее пособие после учебника и задачника. Оно экономит время и нервы тысячам семей по всей стране.
Не каждый родитель разбирается в алгебре. Даже, если в школьные годы он был круглым отличником, в том возрасте, когда ребенок учится в 8 классе, вряд ли что- то вспомнится из школьной программы. Как проверить домашнюю работу? ГДЗ по алгебре 8 класс Мордкович раскроет все схемы и правильные способы решения номеров. Даже самые трудные задания покажутся пустяком.
Решебник по алгебре с ответами к задачнику Мордковича будут также полезны учителям, которые работают сразу с несколькими классами, но при этом проверяют домашнее задание каждый урок. Ответы сэкономят время, помогут правильно выбрать решение.
1.11.21.31.41.51.61.71.81.91.101.111.121.131.141.151.161.171.181.191.201.211.221.231.241.251.261.271.281.291.301.311.321.331.341.351.361.371.381.391.401.412.12.22.32.42.52.62.72.82.92.102.112.122.132.142.152.162.172.182.192.202.212.222.232.242.252.262.272.282.292.302.312.322.332.342.352.362.372.382.392.402.412.422.432.442.452.463.13.23.33.43.53.63.73.83.93.103.113.123.133.143.
153.163.173.183.193.203.213.223.233.243.253.263.273.283.294.14.24.34.44.54.64.74.84.94.104.114.124.134.144.154.164.174.184.194.204.214.224.234.244.254.264.274.284.294.304.314.324.334.344.354.364.374.384.394.404.414.424.434.444.454.464.474.484.494.504.514.524.534.544.554.565.15.25.35.45.55.65.75.85.95.105.115.125.135.145.155.165.175.185.195.205.215.225.235.245.255.265.275.285.295.305.315.325.335.345.355.365.375.385.395.405.415.425.435.445.455.466.16.26.36.46.56.66.76.86.96.106.116.126.136.146.156.166.176.186.196.206.216.226.236.247,97,107,117,127,137,147,157,167,177,187,197,207,217,227,277,287,297,307,317,327,337,347,357,367.17.27.37.47.57.67.77.87.377.387.397.408.18.28.38.48.58.68.78.88.98.108.118.128.138.148.168.178.188.198.208.218.228.238.248.258.268.278.288.298.308.318.329.19.29.39.49.59.69.79.89.99.109.119.129.139.149.159.169.179.189.199.209.219.229.239.249.259.269.279.289.2910.110.210.310.410.510.610.710.810.910.1010.1110.1210.1310.1410.1510.1610.1710.1810.1910.2010.2110.2210.2310.
2410.2510.2610.2710.2810.2910.3010.3110.3210.3310.3410.3510.3610.3710.3810.3910.4010.4110.4210.4311.111.211.311.411.511.611.711.811.911.1011.1111.1211.1311.1411.1511.1611.1712.112.212.312.412.512.612.712.812.912.1012.1112.1212.1312.1412.1512.1612.1712.1812.1912.2012.2112.2213.113.213.313.413.513.613.713.813.913.1013.1113.1213.1313.1413.1513.1613.1713.1813.1913.2013.2113.2213.2313.2413.2513.2613.2713.2813.2913.3013.3113.3214.114.214.314.414.514.614.714.814.914.1014.1114.1214.1314.1414.1514.1614.1714.1814.1914.2014.2114.2214.2314.2414.2514.2614.2714.2814.2914.3014.3114.3214.3314.3414.3514.3615.115.215.315.415.515.615.715.815.915.1015.1115.1215.1315.1415.1515.1615.1715.1815.1915.2015.2115.2215.2315.2415.2515.2615.2715.2815.2915.3015.3115.3215.3315.3415.3515.3615.3715.3815.3915.4015.4115.4215.4315.4415.4515.4615.4715.4815.4915.5015.5115.5215.5315.5415.5515.5615.5715.5815.5915.6015.6115.6215.6315.6415.6515.6615.6715.6815.6915.7015.7115.7215.7315.7415.7515.7615.7715.7815.7915.8015.8115.8215.8315.
8415.8515.8615.8715.8815.8915.9015.9115.9215.9315.9415.9515.9616.116.216.316.416.516.616.716.816.916.1016.1116.1216.1316.1416.1516.1716.1816.1916.2016.2116.2216.2316.2416.2516.2616.2716.2816.2916.3016.3116.3216.3316.3416.3516.3616.3716.3816.3916.4016.4116.4216.4316.4417.117.217.317.417.517.617.717.817.917.1017.1117.1217.1317.1417.1517.1617.1717.1817.1917.2017.2117.2217.2317.2517.2617.2717.2817.2917.3017.3117.3217.3317.3417.3517.3617.3717.3817.3917.4017.4117.4217.4317.4417.4517.4617.4717.4817.4917.5017.5117.5217.5317.5417.5517.5617.5717.5817.5917.6017.6117.6217.6317.6417.6517.6618.118.218.318.418.518.618.718.818.918.1018.1118.1218.1318.1418.1518.1618.1718.1818.1918.2018.2118.2218.2318.2418.2518.2618.2718.2818.2918.3018.3118.3218.3318.3418.3518.3618.3718.3819.119.219.319.419.519.619.719.819.919.1019.1119.1219.1319.1419.1519.1619.1719.1819.1919.2019.2119.2219.2319.2419.2519.2619.2719.2819.2919.3019.3119.3219.3319.3419.3519.3619.3719.3819.3919.4019.4119.4219.4319.4419.4519.4619.4719.4819.4919.
5019.5119.5219.5319.5419.5519.5619.5719.5820,120,220,320,420,520,620,720,820,920.1020.1120.1220.1320.1420.1520.1620.1720.1820.1920.2020.2120.2220.2320.2420.2520.2620.2720.2820.2920.3020.3120.3220.3320.3420.3520.3620.3720.3820.3920.4020.4120.4221.121.221.321.421.521.621.721.821.921.1021.1121.1221.1321.1421.1521.1621.1721.1821.1921.2021.2121.2221.2321.2421.2521.2621.2721.2821.2922.122.222.322.422.522.622.722.822.922.1022.1122.1222.1322.1422.1522.1622.1722.1822.1922.2022.2122.2222.2322.2422.2522.2622.2722.2822.2922.3022.3122.3222.3322.3422.3522.3622.3722.3822.3922.4022.4122.4222.4322.4422.4522.4622.4722.4822.4922.5022.5122.5222.5322.5422.5523.823.923.1023.1123.1223.1323.1423.1523.1623.1723.1823.1923.2023.2123.2223.2323.2424.124.224.324.424.524.624.724.824.924.1024.1124.1224.1324.1424.1524.1624.1724.1824.1924.2024.2124.2224.2324.2424.2524.2624.2724.2824.2924.3024.3124.3224.3324.3424.3524.3624.3724.3824.3925.125.225.325.425.525.625.725.825.925.1025.1125.1225.1325.1425.1525.1625.1725.1825.1925.
2025.2125.2225.2325.2425.2525.2625.2725.2825.2925.3025.3125.3225.3325.3525.3625.3725.3825.3925.4025.4125.4225.4325.4425.4525.4625.4725.4826.126.226.326.426.526.626.726.826.926.1026.1126.1226.1326.1426.1526.1626.1726.1826.1926.2026.2126.2226.2326.2426.2526.2626.2726.2827.127.227.327.427.527.627.727.827.927.1027.1127.1227.1327.1427.1527.1627.1827.1927.2027.2127.2227.2327.2527.2627.2727.2827.2927.3027.3127.3227.3327.3427.3527.3627.3727.3827.3927.4027.4127.4227.4327.4427.4528.128.228.328.428.528.628.728.828.928.1028.1128.1228.1328.1428.1528.1628.1728.1828.1928.2028.2128.2228.2328.2428.2528.2628.2728.2829.129.229.329.429.529.629.729.829.929.1029.1129.1229.1329.1429.1529.1629.1729.1829.1929.2029.2129.2229.2329.2429.2529.2629.2729.2829.2929.3029.3129.3229.3329.3429.3529.3629.3729.3829.3929.4029.4129.4229.4329.4429.4529.4629.4729.4829.4929.5029.5129.5229.5329.5429.5530.130.230.330.430.530.630.730.830.930.1030.1130.1230.1330.1430.1530.1630.1730.1830.1930.2030.2130.2230.2330.2431.131.231.331.431.531.631.731.831.931.1031.1131.1231.1331.1431.1531.1631.1731.1831.1931.2031.2131.2231.2331.2431.2531.2631.2731.2831.2931.3031.3131.3231.3331.3431.3531.3631.3731.3831.3931.4031.4131.4231.4331.4431.4531.4631.4731.4831.4931.5031.5131.5231.5331.5431.5531.5631.5731.5831.5931.6031.6131.6231.6331.6431.6532.132.232.332.432.532.632.732.832.932.1032.1132.1232.1332.1433.133.233.333.433.533.633.733.833.933.1033.1133.1233.1333.1533.1633.1733.1833.1933.2033.2133.2233.2333.2433.2533.2633.2733.2833.2933.3033.3133.3233.3333.3433.3533.3633.3733.3834.134.234.334.434.534.634.734.834.934.1034.1134.1234.1334.1434.1534.1634.1734.1834.1934.2034.2134.2234.2334.2434.2534.2634.2734.2834.2934.3034.3134.3234.3334.3434.3534.3634.3734.3834.3934.4034.4134.4234.4334.4434.4534.4635.135.235.335.435.535.635.735.835.935.1135.1236.136.236.336.436.536.636.736.836.936.1036.1136.1236.1336.1436.1536.1636.1736.1836.19Похожие решебники
ГДЗ, Ответы по Алгебре 8 класс Мордкович. Все решебники тут GDZ-na5.info
Готовые Домашние Задания, Решебник по Алгебре 8 класс. Мордкович
ГДЗ: 8 класс. Алгебра.Мордкович А.Г. 2014 г. |
Здравствуй, дорогой ученик. Ты изучаешь алгебру уже второй год! В седьмом классе, надеемся, ты справился с этим предметом успешно. В этом году школьная программа будет ещё сложнее, поэтому для успешного освоения алгебры в восьмом классе тебе будет необходим помощник. И таковой у нас имеется!
Мы предлагаем тебе сборник ответов и решений, который носит название «ГДЗ по алгебре для 8 класса». Открыв его, ты найдёшь ответы на все задачи! Он пригодится тебе, если ты, к примеру, не смог справиться с задачей или пропустил что-то на уроке. Навёрстывай упущенное вместо с ГДЗ!
Ответы к домашним заданиям по Алгебре 8 класс. Мордкович
Задачи на повторение.
§-01.
§-02.
§-03.
§-04.
§-05.
§-06.
§-07.
§-08.
§-09.
§-10.
§-11.
§-12.
§-13.
§-14.
§-15.
§-16.
§-17.
§-18.
§-19.
§-20.
§-21.
§-22.
§-23.
§-24.
§-25.
§-26.
§-27.
§-28.
§-29.
§-30.
§-31.
§-32.
§-33.
§-34.
§-35.
§-36.
Страница 106 решения задач и ответы к учебнику Алгебра 8 класс Мордкович А.Г., Алексанрова Л.А., Мишустина Т.Н., Тульчинская Е.Е.
Страницы содержания: 1, 2, 3
страницы ответов:
Задачи на повторение
4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22,
Глава 1. Алгебраические дроби
23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69,
Глава 2. Функция . Свойства квадратного корня
70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113,
Глава 3. Квадратичная функция у = k/x
114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199,
Глава 4. Квадратные уравнения
200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273,
Глава 5. Неравенства
274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311,
Глава 6. Итоговое повторение
312, 313, 314, 315, 316, 317, 318, 319, 320, 321, 322, 323, 324, 325, 326, 327, 328, 329, 330, 331, 332, 333, 334, 335, 336, 337, 338, 339, 340, 341, 342, 343, 344, 345, 346, 347, 348
Как решить алгебраические дроби? Теория и практика. Основные понятия Как понять основные понятия алгебраических дробей
§ 1 Понятие алгебраической дроби
Алгебраическая дробь — это выражение
, где P и Q — многочлены; P — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.
Вот несколько примеров алгебраических дробей:
Любой многочлен — это частный случай алгебраической дроби, потому что любой многочлен можно записать как
Например:
Значение алгебраической дроби зависит от значения переменных.
Например, рассчитаем значение дроби
1)
2)
В первом случае получаем:
Обратите внимание, что эта дробь может быть уменьшена:
Таким образом, вычисление значения алгебраической дроби упрощается. Воспользуемся этим.
Во втором случае получаем:
Как видите, значение алгебраической дроби изменилось с изменением значений переменных.
§ 2 Допустимые значения переменных алгебраической дроби
Рассмотрим алгебраическую дробь
Значение x = -1 недопустимо для этой дроби, потому что знаменатель дроби при этом значении x обращается в нуль. При таком значении переменной алгебраическая дробь не имеет смысла.
Таким образом, допустимые значения переменных алгебраической дроби — это те значения переменных, для которых знаменатель дроби не обращается в нуль.
Давайте решим несколько примеров.
При каких значениях переменной алгебраическая дробь не имеет смысла:
Для поиска недопустимых значений переменных знаменатель дроби приравнивается к нулю, и находятся корни соответствующего уравнения.
При каких значениях переменной алгебраическая дробь равна нулю:
Дробь равна нулю, если числитель равен нулю.Приравняем числитель нашей дроби к нулю и найдем корни получившегося уравнения:
Таким образом, при x = 0 и x = 3 эта алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.
Итак, на этом уроке вы узнали основные понятия алгебраической дроби: числитель и знаменатель дроби, а также допустимые значения переменных алгебраической дроби.
Список использованной литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 14.00 Часть 1 Учебное пособие для общеобразовательных учреждений / А.Г. Мордкович. — 9 изд., Перераб. — М .: Мнемосина, 2007. — 215 с .: ил.
- Мордкович А.Г. «Алгебра» 8 класс. В 14.00 ч. 2 Задача для образовательных учреждений / А.Г. Мордкович, Т. Мишустина, Е.Е.Тульчинская. — 8-е изд., — М .: Мнемосина, 2006 — 239с.
- Алгебра. 8 класс. Контрольные работы для студентов образовательных учреждений Л.Александрова под ред. А.Г. Мордковича 2-е изд., Стерт. — М .: Мнемосина 2009. — 40 с.
- Алгебра. 8 класс. Самостоятельная работа для студентов образовательных учреждений: к учебнику А.Г. Мордковича, под ред. Л.А. Александрова. А.Г. Мордкович. 9-е изд., Стер. — М .: Мнемосина 2013. — 112с.
Когда ученик поступает в среднюю школу, математика делится на 2 предмета: алгебру и геометрию. Понятий становится все больше, задачи усложняются. Некоторым людям трудно понимать дроби.Пропустил первый урок по этой теме, и вуаля. фракции? Вопрос, который будет мучить всю школьную жизнь.
Понятие алгебраической дроби
Начнем с определения. Под алгебраической дробью понимается выражение P / Q, где P — числитель, а Q — знаменатель. Буквенный ввод может скрывать число, числовое выражение, числово-буквенное выражение.
Прежде чем задаться вопросом, как решать алгебраические дроби, сначала вам нужно понять, что такое выражение является частью целого.
Обычно целое равно 1. Число в знаменателе показывает, на сколько частей была разделена единица измерения. Числитель нужен, чтобы знать, сколько элементов берется. Дробная черта соответствует знаку деления. Допускается записывать дробное выражение в виде математической операции «Деление». В этом случае числитель — делимое, знаменатель — делитель.
Основное правило обыкновенных дробей
Когда ученики изучают эту тему в школе, им дают примеры для подкрепления.Чтобы их правильно решать и находить различные пути выхода из сложных ситуаций, нужно применить основное свойство дробей.
Это звучит так: если умножить числитель и знаменатель на одно и то же число или выражение (ненулевое), то значение обыкновенной дроби не изменится. Частным случаем этого правила является деление обеих частей выражения на одно и то же число или многочлен. Такие преобразования называются тождественными равенствами.
Ниже мы рассмотрим, как решать сложение и вычитание алгебраических дробей, умножение, деление и сокращение дробей.
Математические операции с дробями
Рассмотрим, как решить основное свойство алгебраической дроби, как применить его на практике. Если вам нужно умножить две дроби, сложить их, разделить одну на другую или вычесть, вы всегда должны следовать правилам.
Итак, для операций сложения и вычитания необходимо найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби указаны с одинаковыми Q-выражениями, то этот пункт следует опустить.Когда общий знаменатель найден, как вы решаете алгебраические дроби? Сложите или вычтите числители. Но! Следует помнить, что если перед дробью стоит знак «-», все знаки в числителе меняются местами. Иногда не следует делать никаких замен и математических операций. Достаточно поменять знак перед дробью.
Часто используется такое понятие, как уменьшение дробей … Это означает следующее: если числитель и знаменатель делятся выражением, отличным от единицы (одинаковым для обеих частей), то получается новая дробь.Дивиденд и делитель меньше, чем предыдущие, но из-за основного правила дробей они остаются равными исходному примеру.
Цель этой операции — получить новое неприводимое выражение. Эту проблему можно решить, уменьшив числитель и знаменатель на наибольший общий множитель. Алгоритм работы состоит из двух точек:
- Нахождение НОД для обеих частей дроби.
- Деление числителя и знаменателя на найденное выражение и получение неразложимой дроби, равной предыдущей.
Ниже приведена таблица со списком формул. Для удобства его можно распечатать и носить с собой в записной книжке. Однако, чтобы в дальнейшем при решении контрольного или экзамена не возникало затруднений в вопросе, как решать алгебраические дроби, указанные формулы необходимо выучить наизусть.
Несколько примеров с решениями
С теоретической точки зрения рассматривается вопрос о том, как решать алгебраические дроби.Приведенные в статье примеры помогут лучше усвоить материал.
1. Переведите дроби и приведите их к общему знаменателю.
2. Переведите дроби и приведите их к общему знаменателю.
После изучения теоретической части и рассмотрения практических вопросов больше возникнуть не должно.
Но тогда мы сформулировали его в «упрощенном» виде, удобном и достаточном для работы с обыкновенными дробями. В этой статье мы рассмотрим основное свойство дроби применительно к алгебраическим дробям (то есть к дробям, числитель и знаменатель которых являются полиномами, в некоторых учебниках алгебры такие дроби называются не алгебраическими, а рациональными дробями).Сначала сформулируем основное свойство алгебраической дроби , обосновываем его, а после перечислим основные области его применения.
Навигация по страницам.
Формулировка и обоснование
Для начала напомним, как было сформулировано основное свойство дроби для обыкновенной дроби: если числитель и знаменатель обыкновенной дроби одновременно умножить или разделить на какое-то натуральное число, то значение дроби не изменится.На это утверждение отвечают равенства и (которые также верны с переставленными частями в форме и), где a, b и m — некоторые.
На самом деле о делении числителя и знаменателя на число говорить не приходится — этот случай покрывается равенством формы. Например, равенство можно обосновать посредством деления, используя равенство как, но оно также может быть оправдано на основе равенства как … Поэтому в дальнейшем мы будем связывать основное свойство дроби с равенством (и) и будем не зацикливайтесь на равенстве (а).
Теперь мы покажем, что основное свойство дроби применимо и к дробям, числитель и знаменатель которых есть. Для этого докажем, что записанное равенство справедливо не только для натуральных чисел, но и для любых действительных чисел. Другими словами, мы докажем, что равенство верно для любых действительных чисел a, b и m, а b и m ненулевые (иначе мы столкнемся с делением на ноль).
Пусть дробь a / b будет записью числа z, то есть ,. Докажем, что дробь также соответствует числу z, т. Е. Докажем это.Это докажет равенство.
Стоит отметить, что если алгебраическая дробь имеет дробные коэффициенты, то умножение ее числителя и знаменателя не на определенное число позволяет перейти к целым коэффициентам и тем самым упростить ее форму. Например, … А правила изменения знаков членов алгебраической дроби основаны на умножении числителя и знаменателя на минус один.
Вторая по важности область применения основного свойства дроби — это редукция алгебраических дробей.В общем случае сокращение осуществляется в два этапа: сначала числитель и знаменатель факторизуются, что позволяет найти общий множитель m, а затем на основе равенства переход к дроби вида a / b без этого общего множителя выполняется. Например, алгебраическая дробь после факторизации числителя и знаменателя принимает форму www.site, включая внутренние материалы и внешний дизайн, не может быть воспроизведена в любой форме или использована без предварительного письменного разрешения правообладателя.
В § 42 было сказано, что если деление многочленов не может быть выполнено полностью, то частное записывается в форме дробного выражения, в котором делимое является числителем, а делитель — знаменателем.
Примеры дробных выражений:
Числитель и знаменатель дробного выражения могут сами быть дробными выражениями, например:
Из дробных алгебраических выражений нам чаще всего приходится иметь дело с теми, в которых числитель и знаменатель являются многочленами (в частности, одночленами).Каждое такое выражение называется алгебраической дробью.
Определение. Алгебраическое выражение, представляющее собой дробь, числитель и знаменатель которой являются полиномами, называется алгебраической дробью.
Как и в арифметике, числитель и знаменатель алгебраической дроби называются членами дроби.
В будущем, изучив операции с алгебраическими дробями, мы сможем преобразовать любое дробное выражение в алгебраическую дробь, используя идентичные преобразования.
Примеры алгебраических дробей:
Обратите внимание, что целое выражение, то есть многочлен, можно записать в виде дроби, для этого достаточно записать это выражение в числителе, а в знаменателе 1. Например:
2. Допустимые значения букв.
Буквы, входящие только в числитель, могут принимать любые значения (если по условию задачи не вводятся дополнительные ограничения).
Для букв, включенных в знаменатель, допускаются только те значения, которые не обращаются в нуль знаменатель.Поэтому в дальнейшем мы всегда будем предполагать, что знаменатель алгебраической дроби не равен нулю.
На этом уроке обсуждается понятие алгебраической дроби. Человек встречает дроби в простейших жизненных ситуациях: когда необходимо разделить предмет на несколько частей, например, торт разрезать поровну на десять человек. Очевидно, каждому достанется кусок пирога. В данном случае мы сталкиваемся с понятием числовой дроби, но возможна ситуация, когда объект делится на неизвестное количество частей, например, по x.В этом случае возникает понятие дробного выражения. Вы уже встречались с целочисленными выражениями (не содержащими разделения на выражения с переменными) и их свойствами в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Рациональные выражения делятся на целых и дробных выражений.
Определение. Рациональная дробь — дробное выражение вида, где — многочлены.- знаменатель числителя.
Примеры рациональных выражений : — дробные выражения; — целые выражения. Например, в первом выражении он действует как числитель и знаменатель.
Значение алгебраической дроби , как и любое алгебраическое выражение , зависит от числового значения тех переменных, которые в него включены. В частности, в первом примере значение дроби зависит от значений переменных и, а во втором только от значения переменной.
Рассмотрим первую типичную задачу: вычисление значения рациональной дроби для разных значений входящих в нее переменных.
Пример 1. Рассчитайте значение дроби в пунктах а), б), в)
Решение. Подставьте значения переменных в указанную дробь: а), б), в) — не существует (так как на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видите, для любой дроби возникают две типичные задачи: 1) вычисление дроби, 2) поиск действительных и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — значения переменных, для которых выражение имеет смысл. Набор всех допустимых значений переменных называется ODZ или домен .
Значение буквальных переменных может быть недопустимым, если знаменатель дроби для этих значений равен нулю.Во всех остальных случаях значения переменных действительны, так как дробь может быть вычислена.
Пример 2.
Решение. Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю. Таким образом, недействительными будут только те значения переменной, у которых знаменатель равен нулю. Знаменатель дроби, поэтому решим линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Решение примера подразумевает правило поиска недопустимых значений переменных — знаменатель дроби равен нулю и находятся корни соответствующего уравнения.
Давайте рассмотрим несколько похожих примеров.
Пример 3. Узнать, при каких значениях переменной дробь не имеет смысла .
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменной дробь не имеет смысла.
Решение. .
Есть и другие постановки этой задачи — найти домен или диапазон допустимых значений выражения (ODZ) … Это означает — найти все допустимые значения переменных. В нашем примере это все значения кроме. На числовой оси удобно нанести область определения.
Для этого проткнем на нем точку, как показано на рисунке:
Рисунок: один
Таким образом, в домене дроби будут все числа кроме 3.
Ответ. .
Пример 5. Установить, при каких значениях переменной дробь не имеет смысла.
Решение. .
Изобразим получившееся решение на числовой оси:
Рисунок: 2
Ответ..
Пример 6.
Решение. … Мы получили равенство двух переменных, приведем числовые примеры: или и т. Д.
Постройте это решение в декартовой системе координат:
Рисунок: 3. График функций
Координаты любой точки на этом графике не входят в диапазон допустимых значений дроби.
Ответ. .
В рассмотренных примерах мы столкнулись с ситуацией, когда происходило деление на ноль.Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типов.
Пример 7. Установить, при каких значениях переменных дробь не имеет смысла.
Решение. .
Оказывается, дробь не имеет смысла. Но кто-то может возразить, что это не так, потому что: .
Может показаться, что если итоговое выражение равно 8 at, то исходное тоже может быть вычислено, и, следовательно, имеет смысл при.Однако если подставить его в исходное выражение, мы получим — смысла нет.
Ответ. .
Чтобы разобраться в этом примере более подробно, решим следующую задачу: при каких значениях указанная дробь равна нулю?
Было бы полезно прочитать:
Дети и учеба — Информационный портал
В § 42 было сказано, что если деление многочленов не может быть выполнено целенаправленно, частное записывается в форме дробного выражения, в котором делимое является числителем, а делитель — знаменателем.
Примеры дробных выражений:
Числитель и знаменатель дробного выражения и сами могут быть дробными выражениями, например:
Из дробных алгебраических выражений чаще всего приходится иметь дело с теми, в которых числитель и знаменатель являются многочленами (в частности, и одинарными). Каждое такое выражение называется алгебраической дробью.
Определение. Алгебраическое выражение, представляющее собой дробь, числитель и знаменатель которой являются многочленами, называется алгебраической дробью.
Как и в арифметике, числитель и знаменатель алгебраической дроби называются членами дроби.
В будущем, изучив действия над алгебраическими дробями, мы сможем преобразовать любое дробное выражение с помощью идентичных преобразований в алгебраическую дробь.
Примеры алгебраических дробей:
Обратите внимание, что целое выражение, то есть многочлен, можно записать в виде дроби, для этого достаточно записать в числителе это выражение, а в знаменателе — 1.Например:
2. Допустимые значения букв.
Буквы, входящие в числитель, могут принимать любые значения (если не введены дополнительные ограничения).
Для букв, входящих в знаменатель, действительны только те значения, которые не уплачены до нуля. Поэтому в будущем мы всегда будем предполагать, что знаменатель алгебраической дроби не равен нулю.
В этом уроке рассматривается понятие алгебраической дроби.С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить определенный предмет на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, всем достанется лучше торта. В данном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект разбивается на неизвестное количество частей, например, по x. В этом случае возникает понятие дробного выражения. С общими выражениями (не содержащими разделения на выражения с переменными) и их свойствами уже познакомился в 7 классе.Далее рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Рациональные выражения делятся на целых и дробных выражений.
Определение. Рациональная дробь — дробное выражение вида, где — многочлены. — знаменатель числителя.
Примеры рациональных выражений: — дробные выражения; — целые выражения.В первом выражении, например, роль числителя выступает, а знаменатель -.
Значение алгебраического дроби , как и любое алгебраическое выражение , зависит от числового значения переменных, которые в него включены. В частности, в первом примере значение дроби зависит от значений переменных и, а во втором только от значения переменной.
Рассмотрим первую типичную задачу: расчет значения рационального дроби с разными значениями входящих в него переменных.
Пример 1. Рассчитайте значение дроби в пунктах а), б), в)
Решение. Подставляем значения переменных в указанную дробь: а), б), в) — ее нет (так как делить невозможно).
Ответ: а) 3; б) 1; Б) не существует.
Как видите, есть две типовые задачи для любой дроби: 1) Расчет фруктов, 2) допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — Переменные, в которых выражение имеет смысл. Многие из всех допустимых значений переменных называются Нечетным или доменом .
Значение буквенных переменных может быть неприемлемым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значения переменных допустимы, так как дробь может быть вычислена.
Пример 2.
Решение. Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю. Таким образом, недопустимыми будут только те значения переменной, у которых знаменатель будет равен нулю. Знаменатель дроби, так пусть линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Решение примера следует правилу поиска недопустимых значений переменных — обозначение дроби равно нулю и расположены корни соответствующего уравнения.
Рассмотрим несколько похожих примеров.
Пример 3. Установить, при каких значениях переменной не имеет смысла .
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменная нет смысла ломать.
Решение. .
Есть и другие постановки этой задачи — найти домен или область допустимых значений выражения (ОТЗ) .Это значит — найти все допустимые значения переменных. В нашем примере это все значения кроме. Область определения удобно отображать на числовой оси.
Для этого накидываем точку, как указано на картинке:
Рис. Один
Таким образом, объем определения трещины Будут все числа, кроме 3.
Ответ. .
Пример 5. Установить, при каких значениях переменная нет смысла ломать.
Решение. .
Отображение полученного решения на числовой оси:
Рис. 2.
Ответ. .
Пример 6.
Решение. . Получили равенство двух переменных, приводим числовые примеры: или и т. Д.
Показать это решение на расписании в декартовой системе координат:
Рис. 3. Функциональный график
Координаты любой точки, лежащей на этом графике, не входят в область допустимых значений дроби.
Ответ. .
В рассмотренных примерах мы столкнулись с ситуацией, когда деление возникало на ноль. Теперь рассмотрим случай, когда более интересная ситуация возникает с типовым делением.
Пример 7. Установить, при каких значениях переменных нет смысла ломать.
Решение. .
Получается, что дробь не имеет смысла. Но можно утверждать, что это не так, потому что: .
Может показаться, что если конечное выражение равно 8 at, то можно вычислить и начальное, а значит, имеет смысл при. Однако, если подставить в исходное выражение, я понял — это не имеет смысла.
Ответ. .
Чтобы разобраться с этим примером более подробно с этим примером, следующая задача: при каких значениях указанная дробь равна нулю?
§ 1 Понятие алгебраической дроби
Алгебраической дроби называют выражение
, где расположены p и q; P — числитель алгебраической дроби, q — знаменатель алгебраической дроби.
Вот примеры алгебраических дробей:
Любой многочлен — это частный случай алгебраической дроби, потому что любой многочлен можно записать как
Например:
Значение алгебраической дроби зависит от значения переменных.
Например, вычисляем значение дроби
1)
2)
В первом случае получаем:
Обратите внимание, эту дробь можно разрезать:
Таким образом, расчет значения алгебраической дроби упрощается.Мы этим пользуемся.
Во втором случае получаем:
Как видно, значение алгебраической дроби изменилось с изменением переменных.
§ 2 Допустимые значения алгебраических дробей
Рассмотрим алгебраическую дробь
Значение x = -1 недопустимо для этой дроби, т.к. знаменатель дроби с таким значением x обращается к нулю. В этом случае значение переменной алгебраической дроби не имеет смысла.
Таким образом, значения переменных алгебраических дробей являются значениями переменных, в которых знаменатель не применяется к нулю.
Пусть решают некоторые примеры.
При каких значениях переменной не имеет смысла алгебраическая дробь:
Для поиска недопустимых значений переменных знаменатель равен нулю, а корни соответствующего уравнения равны.
При каких значениях переменной стоит нулевая алгебраическая дробь:
Дробь равна нулю, если числитель равен нулю.Приравниваем к нулю числитель нашей дроби и находим корни получившегося уравнения:
Таким образом, при x = 0 и x = 3 эта алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.
Итак, на этом уроке вы изучили основные понятия алгебраических дробей: числитель и знаменатель дроби, а также допустимые значения переменных алгебраических дробей.
Список литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 2 час. 1 учебник для общеобразовательных учреждений / А.Г. Мордкович. — 9-е изд., Перераб. — М .: Мнемозина, 2007. — 215 с .: Ил.
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Л. 2 задания для общеобразовательных учреждений / А.Г. Мордкович, т. Н. Мишустина, Е.Е.Тульчинская. — 8-е изд., — М .: Мнемозина, 2006 — 239с.
- Алгебра. 8 класс. Экзамен для студентов образовательных учреждений Александрова Л.А. Под ред. А.Г. Мордковича 2-е изд., Чед. — М.: Мнемозина 2009. — 40С.
- Алгебра. 8 класс. Самостоятельная работа для студентов образовательных учреждений: к учебнику А.Г. Мордкович, Л.А. Александрова Под ред. А.Г. Мордкович. 9-е изд., Чед. — М .: Мнемозина 2013. — 112с.
Когда ученик идет в старшую школу, математика делится на 2 предмета: алгебру и геометрию. Концепции становятся все более и более задачами. У некоторых возникают трудности с восприятием дробей. Они пропустили первый урок по этой теме, и вуаля.Фрукты? Вопрос, который будет мучить всю школьную жизнь.
Понятие алгебраического дробления
Начнем с определения. Под алгебраической дробью понимается выражение P / Q, где p — числитель, а q — знаменатель. Под буквенной записью может быть скрыто число, числовое выражение, числовое выражение.
Прежде чем задаться вопросом, как решать алгебраические дроби, сначала необходимо понять, что такое выражение является частью целого.
Как правило, целое равно 1. Число в знаменателе показывает, сколько частей было разделено на единицу. Числитель нужен для того, чтобы узнать, сколько элементов взято. Дробный знак соответствует знаку деления. Допускается записывать дробное выражение в виде математической операции «Решение». В этом случае числитель делится, знаменатель — делитель.
Основное правило обыкновенных дробей
Когда ученики изучают эту тему в школе, им дают примеры для закрепления.Чтобы правильно их решать и находить различные пути из сложных ситуаций, необходимо применить основное свойство дробей.
Это звучит так: если умножить числитель и знаменатель на одно и то же число или выражение (отличное от нуля), то значение обыкновенной дроби не изменится. Частным случаем этого правила является разделение обеих частей выражения на одно и то же число или многочлен. Такие преобразования называются тождественными равенствами.
Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.
Математические операции с дробями
Рассмотрим, как решить, главное свойство алгебраической дроби, как применить его на практике. Если вам нужно умножить две дроби, сложить их, разделить одну на другую или вычесть, вы всегда должны придерживаться правил.
Итак, для операции сложения и вычитания необходимо найти дополнительный множитель, чтобы привести выражения к общему знаменателю.Если изначально дроби указаны с одинаковыми q выражениями, то вам нужно понизить этот пункт. Когда находят общий знаменатель, как решать алгебраические дроби? Вам нужно складывать или вычитать цифры. Но! Необходимо помнить, что если перед дробью стоит знак «-», то все знаки в числителе меняются на противоположные. Иногда не следует производить никаких замен и математических операций. Достаточно поменять знак перед дробью.
Часто используется такое понятие, как уменьшающая дробь .Это означает следующее: если числитель и знаменатель разделены на выражение, отличное от единицы (одинаковое для обеих частей), то получается новая дробь. Разделитель и разделитель меньше прежнего, но из-за основных правил дроби остаются равными в исходном примере.
Цель этой операции — получить новое неинтерпретируемое выражение. Вы можете решить эту задачу, если сократите числитель и знаменатель до наибольшего общего делителя. Алгоритм работы состоит из двух точек:
- Нахождение узла для обеих частей дроби.
- Деление числителя и знаменателя для найденного выражения и получение неустойчивой дроби, равной предыдущей.
Ниже представлена таблица, в которой расписаны формулы. Для удобства его можно распечатать и носить с собой в блокноте. Однако для того, чтобы решать контрольный или экзамен в будущем в будущем, не было затруднений решить, как решать алгебраические дроби, эти формулы нужно выучить наизусть.
Некоторые примеры с решениями
С теоретической точки зрения вопрос, как решать алгебраические дроби.Приведенные в статье примеры помогут лучше усвоить материал.
1. Преобразуйте дроби и приведите их к общему знаменателю.
2. Преобразуйте дроби и приведите их к общему знаменателю.
После изучения теоретической части и поиска практических вопросов больше не должно быть.
формулировка, доказательство, примеры применения Значение алгебраической дроби не определяется, если ее
В этом уроке рассматривается понятие алгебраической дроби.С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить определенный предмет на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, всем достанется лучше торта. В данном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В этом случае возникает понятие дробного выражения. С общими выражениями (не содержащими разделения на выражения с переменными) и их свойствами уже познакомился в 7 классе.Далее рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Основные понятия
1. Определение и примеры алгебраических дробейРациональные выражения делятся на целых и дробных выражений.
Определение. Рациональная дробь — дробное выражение вида, где — многочлены. — знаменатель числителя.
Примеры рациональных выражений: — дробные выражения; — целые выражения. В первом выражении, например, роль числителя выступает, а знаменатель -.
Значение алгебраического дроби , как и любое алгебраическое выражение , зависит от числового значения переменных, которые в него включены. В частности, в первом примере значение дроби зависит от значений переменных и, а во втором только от значения переменной.
2. Расчет значения алгебраической дроби и две основные задачи по дробиРассмотрим первую типичную задачу: вычисление значения рационального дроби с разными значениями входящих в него переменных.
Пример 1. Рассчитайте значение дроби как а), б), Б)
Решение. Подставляем значения переменных в указанную дробь: а), б), в) — ее нет (так как делить невозможно).
Ответ: 3; один; не существует.
Как видите, есть две типовые задачи для любой дроби: 1) Расчет фруктов, 2) допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — Переменные, в которых выражение имеет смысл. Многие из всех допустимых значений переменных называются Нечетным или доменом .
3. Допустимые (ОТЗ) и недопустимые значения переменных в долях с одной переменнойЗначение буквенных переменных может быть неприемлемым, если знаменатель дроби при этих значениях равен нулю.Во всех остальных случаях значения переменных допустимы, так как дробь может быть вычислена.
Пример 2. Установить, при каких значениях переменная нет смысла ломать.
Решение. Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю. Таким образом, недопустимыми будут только те значения переменной, у которых знаменатель будет равен нулю. Знаменатель дроби, так пусть линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Решение примера следует правилу поиска недопустимых значений переменных — обозначение дроби равно нулю и расположены корни соответствующего уравнения.
Рассмотрим несколько похожих примеров.
Пример 3. Установить, при каких значениях переменной нет смысла ломать.
Решение. .
Ответ. .
Пример 4. Установить при каких значениях переменной не имеет смысла хилать.
Решение ..
Есть и другие постановки этой задачи — найти домен или область допустимых значений выражения (ОТЗ) . Это значит — найти все допустимые значения переменных. В нашем примере это все значения кроме. Область определения удобно отображать на числовой оси.
Для этого накидываем точку, как указано на картинке:
Таким образом, объем определения трещины Там будут все числа, кроме 3.
Ответ ..
Пример 5. Установить, при каких значениях переменной нет смысла ломать.
Решение ..
Отображение полученного решения на числовой оси:
Ответ ..
4. Графическое изображение области допустимых (ОТЗ) и недопустимых значений переменных в дробяхПример 6. Установить при каких значениях переменных не имеет смысла хилать.
Решение .. Получили равенство двух переменных, приводим числовые примеры: или и т. Д.
Показать это решение на расписании в декартовой системе координат:
Рис. 3. Функциональный график.
Координаты любой точки, лежащей на этом графике, не входят в область допустимых значений дроби.
Ответ. .
5. Шкаф типа «деление на ноль»В рассмотренных примерах мы столкнулись с ситуацией, когда деление возникало на ноль.Теперь рассмотрим случай, когда более интересная ситуация возникает с типовым делением.
Пример 7. Установить, при каких значениях переменных нет смысла ломать.
Решение ..
Получается, что дробь не имеет смысла. Но можно утверждать, что это не так, потому что:.
Может показаться, что если конечное выражение равно 8 at, то можно вычислить и начальное, а значит, имеет смысл при. Однако, если подставить в исходное выражение, я понял — это не имеет смысла.
Ответ ..
Чтобы разобраться с этим примером более подробно с этим примером, следующая задача: при каких значениях указанная дробь равна нулю?
(дробь равна нулю, если ее числитель равен нулю). Но необходимо решить исходное уравнение с дробью, и это не имеет смысла при, потому что значение переменной равно нулю. Итак, это уравнение имеет только один корень.
6. Правило нахождения …Таким образом, можно сформулировать точное правило нахождения площади допустимых значений дроби: найти Нечетное дроби. Необходимо и достаточно приравнять его знаменатель к нулю и найти корни полученного уравнения.
Мы рассмотрели две основные задачи: вычисление дробного значения при заданных значениях переменных и нахождение области допустимых значений троя .
Рассмотрим еще несколько задач, которые могут возникнуть при работе с дробями.
7. Разные задачи и выводыПример 8.Докажите, что в любых значениях переменной дроби.
Доказательства. Числитель — число положительное. . В итоге числитель и знаменатель — числа положительные, значит, и дробь — это положительное число.
Доказано.
Пример 9. Как известно, найти.
Решение. Делим долю замера. Уменьшать мы имеем право с учетом того, что является недопустимым значением переменной для этой дроби.
Ответ..
В этом уроке мы рассмотрели основные понятия, связанные с дробями. В следующем уроке мы рассмотрим — главное свойство трещины .
Библиография
1. Башмаков М. И. Алгебра 8 класс. — М .: Просвещение, 2004.
.2. Дорофеев Г.В., Суворова С.Б., Байнович Е.А. и другие. Алгебра 8. — 5-е изд. — М .: Просвещение, 2010.
.3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс.Учебник для общеобразовательных учреждений. — М .: Просвещение, 2006.
.1. Фестиваль педагогических идей.
2. Старая школа.
3. Интернет-портал LIB2.Podelise. RU.
Домашнее задание
1. №4, 7, 9, 12, 13, 14. Дорофеев Г.В., Суворов С.Б., Байнович Е.А. и другие. Алгебра 8. — 5-е изд. — М .: Просвещение, 2010.
.2. Запишите рациональную дробь, площадь определения которой составляет: а) множество, б) множество, в) всю числовую ось.
3. Докажите, что при всех допустимых значениях переменной дробь неотрицательна.
4. Найдите область выражения. Примечание. Рассмотрим отдельно два случая: когда знаменатель младшей дроби равен нулю, и когда знаменатель исходной дроби равен нулю.
В § 42 было сказано, что если деление многочленов не может быть выполнено целенаправленно, частное записывается в форме дробного выражения, в котором делимое является числителем, а делитель — знаменателем.
Примеры дробных выражений:
Числитель и знаменатель дробного выражения и сами могут быть дробными выражениями, например:
Из дробных алгебраических выражений чаще всего приходится иметь дело с теми, в которых числитель и знаменатель являются многочленами (в частности, и одинарными). Каждое такое выражение называется алгебраической дробью.
Определение. Алгебраическое выражение, представляющее собой дробь, числитель и знаменатель которой являются многочленами, называется алгебраической дробью.
Как и в арифметике, числитель и знаменатель алгебраической дроби называются членами дроби.
В будущем, изучив действия над алгебраическими дробями, мы сможем преобразовать любое дробное выражение с помощью идентичных преобразований в алгебраическую дробь.
Примеры алгебраических дробей:
Обратите внимание, что целое выражение, то есть многочлен, можно записать в виде дроби, для этого достаточно записать в числителе это выражение, а в знаменателе — 1.Например:
2. Допустимые значения букв.
Буквы, входящие в числитель, могут принимать любые значения (если не введены дополнительные ограничения).
Для букв, входящих в знаменатель, действительны только те значения, которые не уплачены до нуля. Поэтому в будущем мы всегда будем предполагать, что знаменатель алгебраической дроби не равен нулю.
Когда ученик идет в старшую школу, математика делится на 2 предмета: алгебру и геометрию.Концепции становятся все более и более задачами. У некоторых возникают трудности с восприятием дробей. Они пропустили первый урок по этой теме, и вуаля. Фрукты? Вопрос, который будет мучить всю школьную жизнь.
Понятие алгебраического дробления
Начнем с определения. Под алгебраической дробью понимается выражение P / Q, где p — числитель, а q — знаменатель. Под буквенной записью может быть скрыто число, числовое выражение, числовое выражение.
Прежде чем задаться вопросом, как решать алгебраические дроби, сначала необходимо понять, что такое выражение является частью целого.
Как правило, целое равно 1. Число в знаменателе показывает, сколько частей было разделено на единицу. Числитель нужен для того, чтобы узнать, сколько элементов взято. Дробный знак соответствует знаку деления. Допускается записывать дробное выражение в виде математической операции «Решение». В этом случае числитель делится, знаменатель — делитель.
Основное правило обыкновенных дробей
Когда ученики изучают эту тему в школе, им дают примеры для закрепления. Чтобы правильно их решать и находить различные пути из сложных ситуаций, необходимо применить основное свойство дробей.
Это звучит так: если умножить числитель и знаменатель на одно и то же число или выражение (отличное от нуля), то значение обыкновенной дроби не изменится. Частным случаем этого правила является разделение обеих частей выражения на одно и то же число или многочлен.Такие преобразования называются тождественными равенствами.
Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.
Математические операции с дробями
Рассмотрим, как решить, главное свойство алгебраической дроби, как применить его на практике. Если вам нужно умножить две дроби, сложить их, разделить одну на другую или вычесть, вы всегда должны придерживаться правил.
Итак, для операции сложения и вычитания необходимо найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби указаны с одинаковыми q выражениями, то вам нужно понизить этот пункт. Когда находят общий знаменатель, как решать алгебраические дроби? Вам нужно складывать или вычитать цифры. Но! Необходимо помнить, что если перед дробью стоит знак «-», то все знаки в числителе меняются на противоположные. Иногда не следует производить никаких замен и математических операций.Достаточно поменять знак перед дробью.
Часто используется такое понятие, как уменьшающая дробь . Это означает следующее: если числитель и знаменатель разделены на выражение, отличное от единицы (одинаковое для обеих частей), то получается новая дробь. Разделитель и разделитель меньше прежнего, но из-за основных правил дроби остаются равными в исходном примере.
Цель этой операции — получить новое неинтерпретируемое выражение.Вы можете решить эту задачу, если сократите числитель и знаменатель до наибольшего общего делителя. Алгоритм работы состоит из двух точек:
- Нахождение узла для обеих частей дроби.
- Деление числителя и знаменателя для найденного выражения и получение неустойчивой дроби, равной предыдущей.
Ниже представлена таблица, в которой расписаны формулы. Для удобства его можно распечатать и носить с собой в блокноте.Однако для того, чтобы решать контрольный или экзамен в будущем в будущем, не было затруднений решить, как решать алгебраические дроби, эти формулы нужно выучить наизусть.
Некоторые примеры с решениями
С теоретической точки зрения вопрос, как решать алгебраические дроби. Приведенные в статье примеры помогут лучше усвоить материал.
1. Преобразуйте дроби и приведите их к общему знаменателю.
2.Преобразуйте дроби и приведите их к общему знаменателю.
После изучения теоретической части и поиска практических вопросов больше не должно быть.
§ 1 Понятие алгебраической дроби
Алгебраической дроби называют выражение
, где расположены p и q; P — числитель алгебраической дроби, q — знаменатель алгебраической дроби.
Вот примеры алгебраических дробей:
Любой многочлен — это частный случай алгебраической дроби, потому что любой многочлен можно записать как
Например:
Значение алгебраической дроби зависит от значения переменных.
Например, вычисляем значение дроби
1)
2)
В первом случае получаем:
Обратите внимание, эту дробь можно разрезать:
Таким образом, расчет значения алгебраической дроби упрощается. Мы этим пользуемся.
Во втором случае получаем:
Как видно, значение алгебраической дроби изменилось с изменением переменных.
§ 2 Допустимые значения алгебраических дробей
Рассмотрим алгебраическую дробь
Значение x = -1 недопустимо для этой дроби, т.к. знаменатель дроби с таким значением x обращается к нулю.В этом случае значение переменной алгебраической дроби не имеет смысла.
Таким образом, значения переменных алгебраических дробей являются значениями переменных, в которых знаменатель не применяется к нулю.
Пусть решают некоторые примеры.
При каких значениях переменной не имеет смысла алгебраическая дробь:
Для поиска недопустимых значений переменных знаменатель равен нулю, а корни соответствующего уравнения равны.
При каких значениях переменной стоит нулевая алгебраическая дробь:
Дробь равна нулю, если числитель равен нулю. Приравниваем к нулю числитель нашей дроби и находим корни получившегося уравнения:
Таким образом, при x = 0 и x = 3 эта алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.
Итак, на этом уроке вы изучили основные понятия алгебраических дробей: числитель и знаменатель дроби, а также допустимые значения переменных алгебраических дробей.
Список литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 2 час. 1 учебник для общеобразовательных учреждений / А.Г. Мордкович. — 9-е изд., Перераб. — М .: Мнемозина, 2007. — 215 с .