Контрольная работа по геометрии 1 9 класс 1 вариант: ГДЗ Контрольные работы / К-1. Варианты 1 геометрия 9 класс дидактические материалы Зив

• 1 класс
  • Математика
  • Английский язык
  • Русский язык
  • Музыка
  • Литература
  • Окружающий мир

• 2 класс
  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Технология

• 3 класс
  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Казахский язык

• 4 класс
  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Казахский язык

• 5 класс
  • Математика
  • Английский язык
  • Русский язык
  • Физика
  • Немецкий язык
  • Украинский язык
  • Биология

Контрольные работы по геометрии 9 класс | Материал по геометрии (9 класс):

Геометрия 9 Атанасян (Мельникова) | КОНТРОЛЬНЫЕ РАБОТЫ

Геометрия 9 Атанасян (Мельникова) — контрольные работы с ответами, цитаты из пособия «Геометрия 9 класс. Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др»  (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных работ по геометрии в 9 классе рекомендуем купить книгу: Наталия Мельникова: Геометрия. 9 класс. Дидактические материалы к учебнику Л.С. Атанасяна и др. ФГОС, в которой контрольные работы представлены в 4-х вариантах, а также есть набор заданий по каждой теме для подготовки к контрольным работам. Структура контрольных работ и форма заданий соответствуют структуре и форме заданий Основного государственного экзамена (ОГЭ).

Контрольные работы по геометрии в 9 классе:

Контрольная работа 1 К-1. Векторы. Метод координат

Контрольная работа 2 К-2. Соотношения в треугольнике

Контрольная работа 3 К-3. Длина окружности и площадь круга

Контрольная работа 4 К-4. Движения

Контрольная работа 5 К-5. Начальные сведения из стереометрии

Контрольная работа 6 К-6. ИТОГОВАЯ за 9 класс

Контрольная работа 7 К-7.  ИТОГОВАЯ за 7-9 классы

Структура контрольной работы

Каждая контрольная работа рассчитана на один урок. Все работы составлены в четырех вариантах одинакового уровня сложности (только в пособии). Каждая работа состоит из трех частей, соответствующих форме предлагаемых заданий.

В часть А включаются задания с выбором ответа. Учащимся нужно выбрать из предложенных вариантов либо верное утверждение, либо нужный рисунок. При этом верных ответов может быть несколько, и учащимся необходимо записать номера ответов, которые, по их мнению, верны. Заметим, что, вообще говоря, в заданиях с выбором ответа применяются два подхода. При первом подходе среди предлагаемых вариантов ответа имеется только один правильный. При втором — верных ответов может быть несколько, и результатом решения задачи является не один номер, а все номера верных ответов. При этом задание считается выполненным верно, если указаны номера всех верных ответов.

В часть В входят вычислительные задачи, которые необходимо решить и записать число, которое получилось в результате вычислений.

При выполнении частей А и В контрольной работы учащиеся не записывают ни обоснования, ни вычисления, нужные для решения задач. Все записи или рисунки учащиеся, в случае необходимости, могут делать в черновике. Черновик не сдается учителю и не влияет на оценку за выполнение работы.

В части С имеются и задачи на доказательство, и задачи на вычисление геометрических величин. Решение этих задач должно быть оформлено письменно, как в традиционной контрольной работе. Следует иметь в виду, что при записи решения вычислительных задач, так же как и при решении задач на доказательство, необходимо приводить обоснования с использованием изученных геометрических фактов.

Последняя задача, в каждом варианте отмеченная звездочкой, предназначена для наиболее подготовленных учащихся, успевающих достаточно быстро выполнить все предыдущие задания. В зависимости от уровня подготовленности класса эту задачу можно считать дополнительной и оценивать ее решение отдельно.
Перед проведением первой контрольной работы необходимо проинструктировать учащихся о том, как они должны оформить решение задач. Полезно привести пример, показывающий, как должны выглядеть ответы на задачи частей А и В.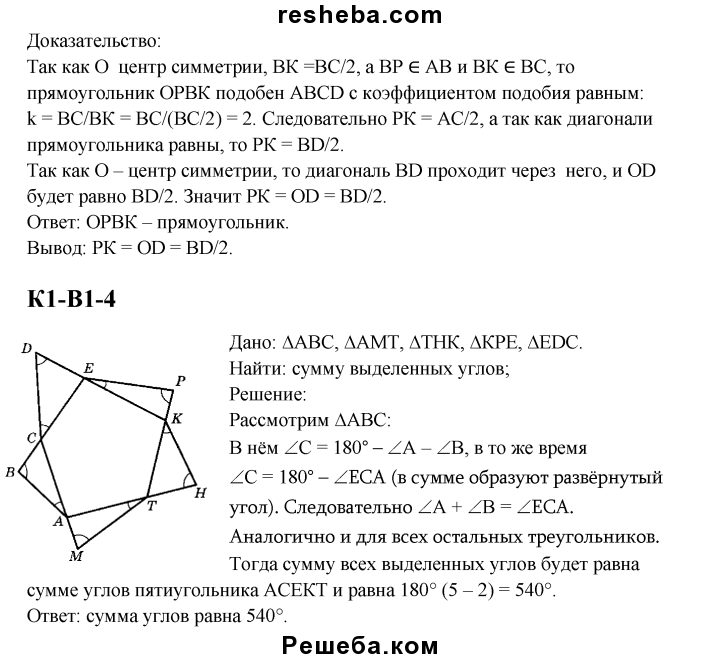

Следует напомнить эти инструкции и при проведении каждой последующей контрольной работы.

Дифференцированный подход к учащимся осуществляется за счет того, что в работах представлены задания разного уровня, которые, как правило, расположены по мере возрастания уровня сложности. Стереометрический материал может изучаться в ознакомительном плане без обязательной проверки его усвоения. Поэтому контрольную № 5 по усмотрению учителя можно не проводить или полученные за нее оценки выставлять в журнал по желанию учащегося.

Номера заданий обязательного уровня, посильных для менее подготовленных учащихся, отмечены кружком. Такие задания представлены во всех трех частях работы.

Следует заметить, что при традиционном письменном оформлении решения задач предлагаемое в контрольных работах количество задач было бы нереально решить за один урок. Однако нужно иметь в виду, что задания с выбором ответа и с кратким ответом не требуют времени на оформление решения и очень часто ответы на них могут быть получены устно. Поэтому основные затраты времени будут связаны с решением задач части С.

Тематика контрольных работ

Каждая тематическая контрольная работа направлена на проверку усвоения материала главы учебника. Одна из итоговых контрольных работ проверяет усвоение материала, изучавшегося в 9 классе, другая составлена по материалу всего курса планиметрии. Указанные ниже проверяемые элементы знаний отражают только тот материал, который изучался в данной теме. При этом, естественно, задачи тематической контрольной работы могут проверять также и усвоение сведений, изучавшихся в предыдущих темах.

Контрольная работа № 1. Векторы. Метод координат
• равенство векторов, координаты и модуль вектора, сложение векторов и умножение вектора на число;
• координаты середины и длина отрезка, заданного координатами концов;
• уравнение окружности;
• средняя линия трапеции.

Контрольная работа № 2. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
• теорема синусов, теорема косинусов;
• формула площади треугольника;
• скалярное произведение векторов.

Контрольная работа № 3. Длина окружности и площадь круга
• правильные многоугольники;
• длина окружности и длина дуги окружности;
• площадь круга и кругового сектора.

Контрольная работа № 4. Движения
• понятие движения;
• симметрия относительно прямой, симметрия относительно точки, параллельный перенос; поворот.

Контрольная работа № 5. Начальные сведения из стереометрии
• геометрические тела: призма, параллелепипед, пирамида, цилиндр, конус;
• свойства правильной призмы и правильной пирамиды;
• объемы тел, боковая поверхность цилиндра и конуса;
• сечение прямоугольного параллелепипеда плоскостью.

Итоговая контрольная работа за курс 9 класса
• координаты середины отрезка, заданного координатами концов;
• равенство векторов, модуль вектора;
• скалярное произведение векторов;
• теорема синусов, теорема косинусов;
• длина окружности и площадь круга;
• площадь правильного многоугольника.

Итоговая контрольная работа за курс 7-9 классов
• свойства параллелограмма, прямоугольника и ромба;
• признаки подобия треугольников;
• средняя линия треугольника;
• формулы площади треугольника;
• теорема Пифагора и определения синуса, косинуса и тангенса острого угла прямоугольного треугольника;
• теорема синусов, теорема косинусов.

Геометрия 9 Атанасян (Мельникова) — контрольные работы с ответами, цитаты из пособия «Геометрия 9 класс. Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др»  (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях.

Контрольная работа вариант №1 — 1 гдз по геометрии 9 класс Мерзляк, Полонский дидактические материалы

Решебники, ГДЗ

• 1 Класс
  • Математика
  • Русский язык
  • Английский язык
  • Информатика
  • Немецкий язык
  • Литература
  • Человек и мир
  • Природоведение
  • Основы здоровья
  • Музыка
  • Окружающий мир
  • Технология
• 2 Класс
  • Математика
  • Русский язык
  • Белорусский язык
  • Английский язык
  • Информатика
  • Украинский язык
  • Французский язык
  • Немецкий язык
  • Литература
  • Человек и мир
  • Природоведение
  • Основы здоровья
  • Музыка
  • Окружающий мир
  • Технология
  • Испанский язык
• 3 Класс
  • Математика
  • Русский язык
  • Белорусский язык
  • Английский язык
  • Информатика
  • Украинский язык
  • Французский язык
  • Немецкий язык
  • Литература

Контрольные и самостоятельные работы по алгебре и геометрии 9 класс

АЛГЕБРА

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

KBАДРАТИЧНАЯ ФУНКЦИЯ

C1. Функции и их свойства

C2. Квадратный трехчлен

C3. График квадратичной функции

C4. Квадратичная функция: задачи с параметрами (домашняя самостоятельная работа)

C5. Решение квадратичных неравенств

C6. Решение неравенств методом интервалов

УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ

C7. Решение целых уравнений

C8. Уравнения высших степеней: методы решения, задачи с параметрами (домашняя самостоятельная работа)

C9. Решение систем уравнений второй степени

C10. Решение задач с помощью систем уравнений. Графическое решение систем

C11. Системы рациональных уравнений, (домашняя самостоятельная работа)

АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ

C12. Арифметическая прогрессия. Формула n-го члена

C13. Формула суммы n первых членов арифметической прогрессии

C14. Геометрическая прогрессия. Формула n-го члена

C15. Формула суммы первых n членов геометрической прогрессии. Бесконечная геометрическая прогрессия

C16. Комбинированные задачи на прогрессии (домашняя самостоятельная работа)

СТЕПЕНЬ ЧИСЛА

C17. Четные и нечетные функции. Функция у = xn

C18. Корень n-й степени и его свойства

C19. Определение и свойства степени с дробным показателем

C20. Преобразование степенных выражений с рациональными показателями

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ

C21. Элементы комбинаторики

C22. Начальные сведения из теории вероятностей

C23. Элементы статистики и теории вероятностей

ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ

C24. Определение тригонометрических функций

C25. Свойства тригонометрических функций. Радианная мера угла

C26. Тригонометрические тождества и их применение

C27. Формулы приведения

C28. Формулы сложения

C29. Формулы двойного угла

C30. Формулы суммы и разности тригонометрических функций

C31. Дополнительные тригонометрические задачи (домашняя самостоятельная работа)

КОНТРОЛЬНЫЕ РАБОТЫ

К1. Квадратичная функция

К2. Решение неравенств

К3. Целые уравнения и системы уравнений

К4. Арифметическая прогрессия

К5. Геометрическая прогрессия

К6. Степень с рациональным показателем

К7. Элементы комбинаторики и теории вероятностей

К8. Свойства тригонометрических функций. Тригонометрические тождества. Формулы приведения

К9. Формулы сложения и их следствия

К10. Итоговая контрольная работа

ГЕОМЕТРИЯ

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику Л.C. Атанасяна и др.)

МЕТОД КООРДИНАТ

C1. Координаты вектора

C2. Простейшие задачи в координатах

C3. Уравнение окружности

C4. Уравнение прямой

C5. Применение векторов и координат к решению задач (домашняя самостоятельная работа)

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

C6. Синус, косинус, тангенс угла

C7. Теорема о площади треугольника. Теорема синусов

C8. Теорема косинусов.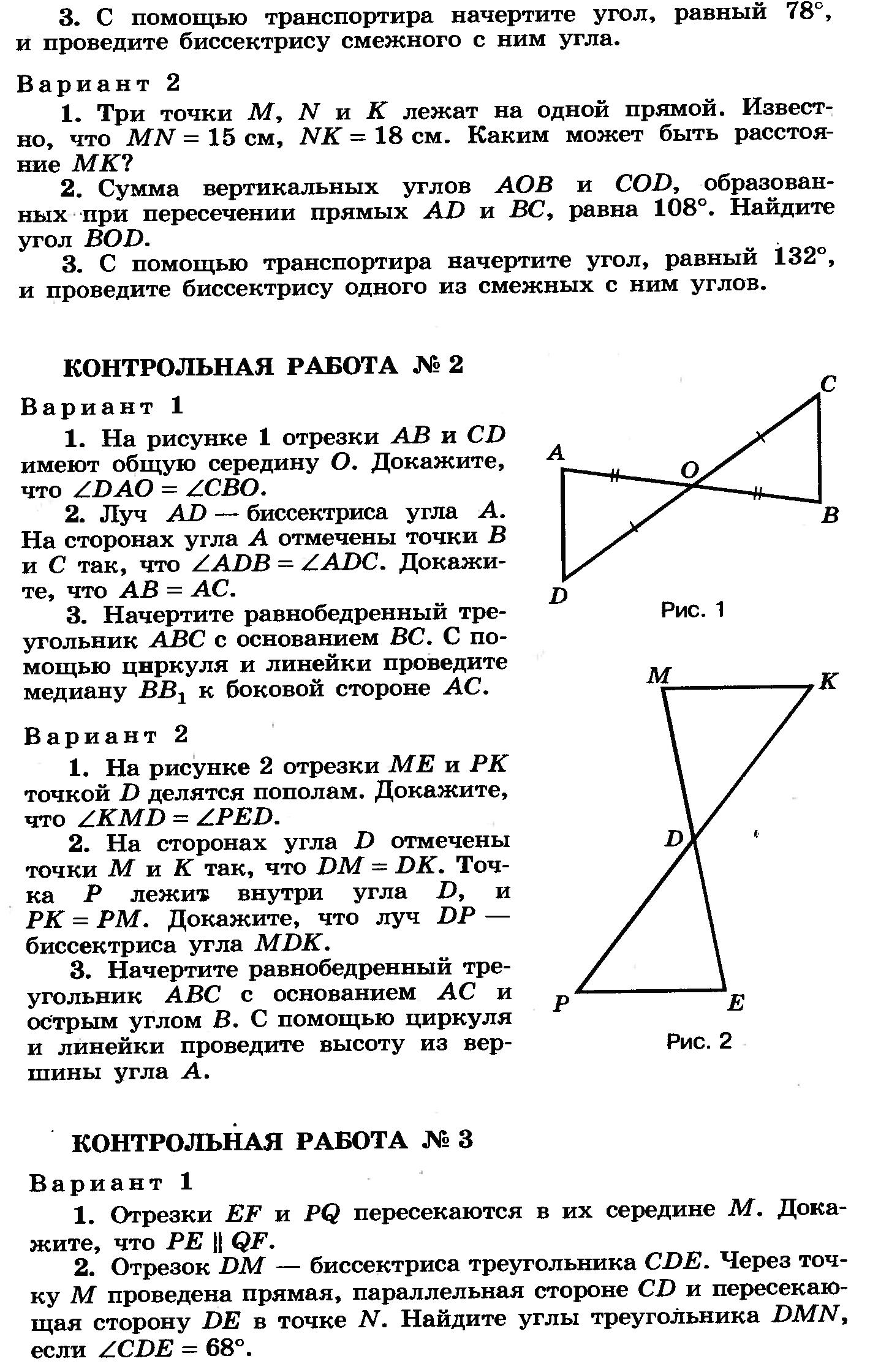 Решение треугольников

C9. Скалярное произведение векторов

C10. Решение треугольников. Скалярное произведение (домашняя самостоятельная работа)

ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА

C11. Правильные многоугольники

C12. Длина окружности, площадь круга, площадь кругового сектора

ДВИЖЕНИЯ

C13. Понятие движения

C14. Параллельный перенос и поворот

КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику Л.С. Атанасяна и др.)

K1. Метод координат

K2. Соотношение между сторонами и углами треугольника

K3. Длина окружности й площадь круга

K4. Движение

K5. Итоговая контрольная работа

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)

ПОДОБИЕ ФИГУР

C1. Преобразование подобия и его свойства

C2. Признаки подобия треугольников

C3. Подобие прямоугольных треугольников. Свойство биссектрисы угла треугольника

C4. Подобие треугольников (домашняя самостоятельная работа)

C5. Теорема о вписанных углах и ее следствия

C6. Применение теоремы о вписанных углах и ее следствий в задачах (домашняя самостоятельная работа)

РЕШЕНИЕ ТРЕУГОЛЬНИКОВ

C7. Теорема косинусов. Соотношение диагоналей и сторон параллелограмма

C8. Теорема синусов и ее следствия

C9. Теоремы косинусов и синусов (домашняя самостоятельная работа)

МНОГОУГОЛЬНИКИ

C10. Выпуклый многоугольник

C11. Правильные многоугольники. Формулы для радиусов вписанных и описанных окружностей правильных многоугольников

C12. Длина окружности. Радианная мера угла

ПЛОЩАДИ ФИГУР

C13. Площадь прямоугольника, квадрата, параллелограмма

C14. Площадь треугольника

C15. Площадь трапеции, площадь четырехугольника

C16. Окружность и многоугольники (домашняя самостоятельная работа)

C17. Площади подобных фигур. Площадь круга и его частей

C18. Площади фигур (домашняя самостоятельная работа)

КОНТРОЛЬНЫЕ РАБОТЫ (по учебни

Формула расстояния, Формула сечения | Примечания, видео, контроль качества и тесты | 9 класс> Математика по выбору> Координатная геометрия

Формула расстояния, формула сечения

Формула расстояния

Можно выполнить расчет расстояния между любыми двумя точками на плоской поверхности. 2} \)

Примечания

1. Формула остается прежней, если точки P (x ₁ , y ₁ ) и Q (x ₂ , y ₂ ) взяты в разных квадрантах.
2. Если точка лежит на оси x, ее ордината равна нулю. Следовательно, любую точку на оси x можно принять как (x, 0).
3. Если точка лежит на оси Y, ее абсцисса равна нулю. поэтому любую точку на оси y можно принять как (0, y).
4. Чтобы доказать, что четырехугольник — это:
   а) ромб, покажите, что все стороны равны.
   б) квадрат, показать, что все равны и диагонали тоже равны.
   c) параллелограмм, показать, что противоположные стороны равны.
   г) прямоугольник, показать, что противоположные стороны равны и диагонали также равны.
5. Чтобы доказать, что треугольник a:
   a) разносторонний, покажите, что все стороны не равны.
   б) равнобедренный, показывает, что две стороны равны.
   c) равносторонний, показать, что все стороны равны.
   d) прямоугольный треугольник, показать, что квадрат на одной стороне равен сумме квадратов двух других сторон.

Формула сечения

Формула внутреннего деления

Формула внутреннего деления ^{_{Источник: www.onlinemath5all.com}}

Найти координаты точки, которая разделяет внутреннюю линию, соединяющую две точки (x ₁ , y ₁ ) и (x ₂ , y ₂ ) в заданном соотношении m ₁ : м ₂ .

Пусть A (x, y) и B (x ₁ , y ₁ ) — две заданные точки. Пусть точка P (x ₂ , y ₂ ) делит линию, соединяющую AB внутри, в соотношении ₁ : m ₂

Тогда AP: PB = m ₁ : m ₂

Нарисуйте перпендикуляры AL, PN и BM от A, P и B соответственно к оси x.Тогда OL = x ₁ , ON = x, OM = x ₂ , AL = y ₁ , PN = y и BM = y ₂ . Снова проведите соответственно AQ и PR от A и P к отрезкам PN и BM соответственно.

AQ = LN = ON -OL = x — x ₁ PR = NM = OM — ON = x ₂ -x
PQ = PN — QN = PN -AL = y — y ₁ BR = BM — RM = BM — PN = y ₂ — y

In Δ ^с PQA и BRA, ∠PQA = ∠ BRP, ∠QAP = ∠RPB и ∠APQ = ∠PBR

Итак, Δ ^s PQA и BRP аналогичны.

Тогда
\ (\ frac {AP} {PB} \)
= \ (\ frac {AQ} {PR} \)
= \ (\ frac {QP} {RB} \)
= \ (\ frac {m_1} {m_2} \)
= \ (\ frac {x-x_1} {x_2-x} \)
= \ (\ frac {y-y_1} {y_2y} \)

Принимая первые два соотношения, получаем,
или, \ (\ frac {m_1} {m_2} \) = \ (\ frac {x-x_1} {x_2-x} \)
или, m ₂ x — m ₂ x ₁ = m ₁ x ₂ -m ₁ x
или, м ₂ x + m ₁ x = m ₁ x ₂ + m ₂ x ₁
или, x (m ₁ + m ₂ ) = m ₁ x ₂ + m ₂ x ₁
или, x = \ (\ frac {m_1x_2 + m_2x_1} {m_1 + m_2} \)

Аналогично из отношений

\ (\ frac {m_1} {m_2} \) = \ (\ frac {y-y_1} {y_2-y} \)
получаем
y = \ (\ frac {m_1y_2 + m_2y_1} {m_1 + m_2} \)
∴ Координаты P: \ (\ frac {m_1x_2 + m_2x_1} {m_1 + m_2} \), \ (\ frac {m_1y_2 + m_2y_1} {m_1 + m_2} \)

Формула для внешнего деления

Формула внешнего деления ^{_{Источник: www.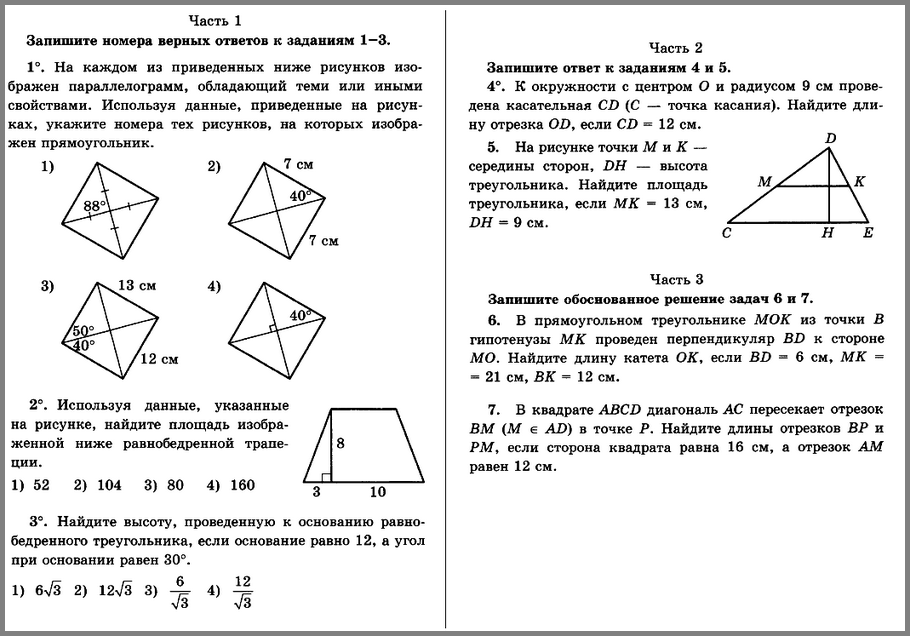 onlinemath5all.com}}

Если точка P (x, y) делит AB снаружи в соотношении m ₁ : m ₂ , то разделенный сегмент BP измеряется в противоположном направлении и, следовательно, m ₂ принимается как отрицательный.
\ (\ следовательно \) Формулы сечения для внешнего деления:
(x, y) = (\ (\ frac {m_1x_2 — m_2x_1} {m_1 — m_2} \)), (\ (\ frac {m_1y_2 — m_2y_1 } {m_1 — m_2} \))

Формула средней точки

Формула средней точки ^{_{Источник: www.studyblue.com}}

В особых случаях также используются формулы средней точки ».
m ₁ : m ₂ = 1: 1, т.е. m ₁ = m ₂
\ (\ следовательно \) x = \ (\ frac {x_1 + x_2} {2} \) и y = \ (\ frac {y_1 + y_2} {2} \)
Таким образом, координаты P (x, y) равны P (\ (\ frac {x_1 + x_2} {2} \), \ (\ frac {y_1 + y_2} {2} \)), которая называется формулой средней точки.

K-формула

Если точка P (x, y) делит соединяющиеся две точки A (x ₁ , y ₁ ) и B (x ₂ , y ₂ ) в соотношении k: 1, то
x = \ (\ гидроразрыва {к. х_2 + 1. x_1} {k + 1} \) = \ (\ frac {kx_2 + x_1} {k + 1} \)
и, y = \ (\ frac {k. y_2 + 1. y_1} {k + 1} \ ) = \ (\ frac {ky_2 + y_1} {k + 1} \)

∴ Координата P равна (\ (\ frac {kx_2 + x_1} {k + 1}, \ frac {ky_2 + y_1} {k + 1} \))
Для задач, в которых требуется найти соотношение когда данная точка делит соединение двух данных точек, удобно взять соотношение k: 1.

Формула центроида

Centroid ^{_{Источник: math.tutorvista.com}}

Пусть P (x ₁ , y ₁ ), Q (x ₂ , y ₂ ) и R (x ₃ , y ₃ ) являются вершинами треугольника PQR.Пусть S, T и U — середины сторон QR, RP и PQ соответственно. Тогда PS, QT и RU называются медианами треугольника PQR. Если эти медианы пересекаются друг с другом в точке N, то N называется центроидом треугольника PQR.
Поскольку S — средняя точка стороны QR, ее координаты равны (\ (\ frac {x_2 + x_3} {2}, \ frac {y_2 + y_3} {2} \))
Из геометрии плоскости мы знаем что центроид треугольника делит медиану в соотношении 2: 1. Теперь, если координаты N равны (x, y), то по формуле сечения.
x = \ (\ frac {2. \ Frac {x_2 + x_3} {2} + 1. X_1} {2 + 1} \) = \ (\ frac {x_1 + x_2 + x_3} {3} \) и y = \ (\ frac {2. \ frac {y_2 + y_3} {2} + 1. y_1} {2 + 1} \) = \ (\ frac {y_1 + y_2 + y_3} {3} \)

Следовательно, координаты N равны (\ (\ frac {x_1 + x_2 + x_3} {3}, \ frac {y_1 + y_2 + y_3} {3} \))

MPM2D Grade 10 Math Analytic Geometry Test — onstudynotes

Средняя точка

• M = ((x1 + x2) / (2)), ((y1 + y2) / (2))

Длина

Должен знать: Поиск формул уклона, середины и длины

Уравнения кругов

Свойства треугольников

• Свойство 1: Каждая медиана делит площадь треугольника
пополам.
• Свойство 2: В любом треугольнике три медианы пересекаются в одной и той же точке, центр тяжести
• Свойство 3: средний сегмент составляет половину площади и половину длины и параллелен противоположным сторонам
• Свойство 4: Центроид разделяет линию в соотношении 2: 1

Свойства параллелограммов

• Свойство 1: Середины смежных сторон любого четырехугольника образуют параллелограмм
• Свойство 2: Противоположные стороны любого параллелограмма имеют одинаковую длину
• Свойство 3 : диагонали параллелограмма делят друг друга пополам

Свойства трапеций

• Свойство 1: Отрезки трапеции параллельны параллельным сторонам
• Свойство 2: Сегменты линии, соединяющие середины непараллельных сторон, равны средней длине параллельных сторон. Верхняя сторона плюс сторона среднего сегмента, деленная на 2, равна длине непараллельной стороны

Свойства ромба

• Свойство 1: Все стороны равны по длине
• Свойство 2: Противоположные стороны параллельны, но не перпендикулярны

Собственность кругов

• Свойство 1: Диаметры окружности пересекаются в центре
• Свойство 2: Правая биссектриса хорды проходит через центр окружности
• Свойство 3: Серединные перпендикулярные линии трех точек пересекаются в центре
• Свойство 4: Центр окружности — точка интереса правой биссектрисы сторон треугольника
.

Найти кратчайшее расстояние от отрезка AB до C

1. найдите наклон, затем точку пересечения оси Y отрезка AB
2. Найдите наклон перпендикуляра линии AB
3. Сопоставьте координаты точки C с уклоном перпендикуляра в формате y = mx + b
4. Найдите точку интереса на линиях C и AB, чтобы увидеть, где ^ линия пересекается с линией AB путем замены исключения
5. Найдите расстояние между POI и точкой C

Найдите центр круга с точками A, B и C, лежащими на окружности

1. Предполагая, что AB и BC — хорды на окружности, мы находим их наклоны
2. Получите перпендикулярный наклон этих хорд и средней точки
3. Используя среднюю точку и перпендикулярные линии этих уклонов, получите уравнение правой биссектрисы этих хорд.
4. Найдите POI этих двух линий, и это ваш центр круга

С Днем Республики 🇮🇳 Скидка до 70% на ежедневные цели CAT 2021.Запишитесь сейчас

• MBA Mocks
  • CAT Mocks
  • Моки IIFT
  • Моки XAT
  • CMAT Mocks
  • Моки SNAP
  • NMAT Mocks
  • MAH MBA CET Mocks
  • Маки TISSNET
• Прошлые статьи
  • CAT Предыдущие статьи
  • IIFT Предыдущие статьи
  • XAT Предыдущие статьи
  • MAT Предыдущие статьи
  • CMAT Предыдущие статьи
  • PGDBA Предыдущие статьи
  • Предыдущие статьи TISS
  • SNAP Предыдущие статьи
  • SRCC GBO Предыдущие статьи
  • TS ICET Предыдущие статьи
  • AP ICET Предыдущие статьи
• Подготовить

  • Бесплатный контент

    • Решенные вопросы о CAT
    • Ежедневные тесты
    • Бесплатные макеты
    • Тесты на бесплатные темы
    • Бесплатные видео CAT
    • Предыдущие статьи
    • GK Тесты
    • Информация об экзамене CAT

    Учись и практикуй

    • CAT Ежедневная цель
    • Моки
    • Моки ОМЕЦ
    • В разрезе
    • Концептуальные видео
    • Классные видео
    • XAT DM Практика
    • CAT Study Material
    • Заметки
    • Примеры наборов
    • Видео с вопросами

    Консультация колледжа

    • Процентильный предсказатель
    • Лучшие колледжи MBA
    • Предсказание вызовов IIM
    • Истории успеха CAT
• Другие экзамены
  • МБА
  • SSC
  • RRB
  • БАНКОВСКИЙ
  • СТРАХОВАНИЕ
  • FCI
  • ИНЖИНИРИНГ
    • RRB JE Mocks
    • RRB JE Предыдущие статьи
    • ISRO Предыдущие статьи
    • SSC JE Предыдущие статьи
    • DMRC Предыдущие статьи
  • ОБОРОНА
    • IB ACIO Mocks
    • IB SA Предыдущие статьи
    • ISRO Предыдущие статьи
  • ПОЛИЦИЯ
    • RPF SI Предыдущие статьи

.