Контрольная работа по геометрии 9 класс 1 четверть – Контрольная работа по геометрии за 1 полугодие в 9 классе по учебнику Атанасяна

Контрольная работа по геометрии за 1 полугодие в 9 классе по учебнику Атанасяна

Контрольная работа по геометрии за I-е полугодие. 9 класс

Вариант 1.

Часть 1

1. В трапеции ABCD, основания которой равны 5 и 8 см, MN – средняя линия.

Отрезок BE параллелен стороне CD. Найдите длину отрезка MK.

Ответ:__________________

2. Какие из равенств являются верными? Укажите в ответе их номера.

1. 2. 3.

Ответ:__________________

3. Начертите два неколлинеарных вектора a и b. Постройте векторы, равные:

а) 2a +3b; б) a – b.

4. Даны векторы: a {6; -4}, b =i-2j, c=a + 2b

   . Найдите координаты вектора с.

5. Даны векторы: a {6; -4}, b =i-2j, c=a + 2b. Найдите длину вектора с.

6. Выберите верные утверждения, запишите их номера без пробелов и запятых:

1) Вектор — это направленный отрезок, для которого указано, какая из его точек является началом, а какая концом.

2) Векторы называются противоположными, если они сонаправлены и длины их равны.

3) Средняя линия трапеции — это отрезок, соединяющий середины её оснований

4) Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов

5) Вычисление длины вектора по его координатам вычисляется по формуле |a|=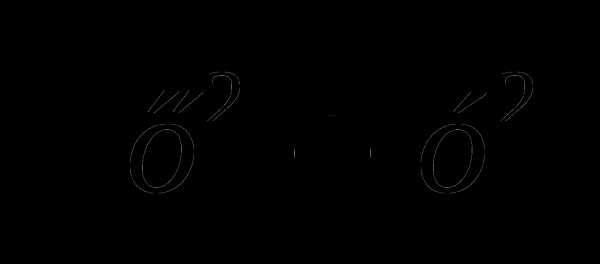

4. Найдите координаты центра окружности (х — 2)² + (у + 1)² = 16

1) (-2; 1) 2) (2; -1) 3) (1; -2) 4) (-1; 2)

Часть 2

(запишите подробное решение задач)

4. Радиус окружности равен 4. Центр окружности принадлежит оси Оу и имеет отрицательную координату. Окружность проходит через точку (0; -2). Напишите уравнение окружности.

5. Высота , проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание на два отрезка, меньший из которых равен 2 см. Найдите большее основание, если её средняя линия равна 8 см.

Контрольная работа по геометрии за I-е полугодие. 9 класс

Вариант 2

Часть 1

1. В трапеции ABCF, основания которой равны 7 и 10 см, MN – средняя линия.

Отрезок BE параллелен стороне CF. Найдите длину отрезка MK.

Ответ:__________________

2. Какие из равенств являются верными? Укажите в ответе их номера.

1. 2. 3.

Ответ:__________________

3. Начертите два неколлинеарных вектора c и d. Постройте векторы, равные:

а) 3c +2d; б) c – 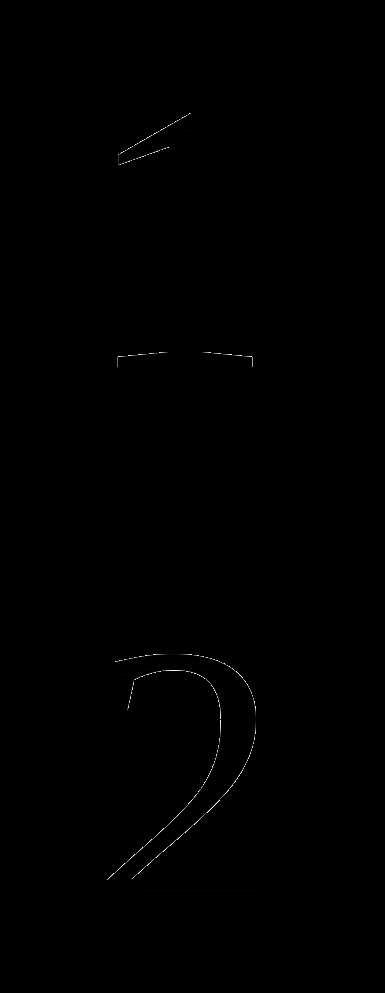d.

4. Даны векторы: b{-12;18}, a=2i+j, c=2a – b.Найдите координаты вектора с.

4. Даны векторы: b

   {-12;18}, a=2i+j, c=2a – b. Найдите длину вектора с.

5. Выберите верные утверждения, запишите их номера без пробелов и запятых:

1) От любой точки можно отложить вектор, равный данному и притом только один.

2) Векторы называются равными, если они сонаправлены

3) Средняя линия трапеции параллельна его основаниям и равна их полусумме

4) каждая координата суммы двух и более векторов равна разности соответствующих координат этих векторов.

5) Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

4. Найдите координаты центра окружности (х + 4)² + (у — 3)² = 9

1) (3; 4) 2) (-3; 4) 3) (-4; 3) 4) (4; -3)

Часть 2

(запишите подробное решение задач)

4. Напишите уравнение прямой, проходящей через две точки А(-3;-3) и В(3;5)

5. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию на два отрезка, равные 2 см и 6 см. Найдите основания трапеции.

infourok.ru

Административная контрольная работа по геометрии 9 класс

Административная контрольная работа по геометрии 9 класс

(октябрь/ноябрь)

1 вариант

Верно ли утверждение (отвечаем «да» или «нет»)?

1. Все углы ромба равны.

2. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

3. Площадь квадрата равна произведению двух его смежных сторон.

4. Если два угла одного треугольника равны 60° и 50°, а два угла другого треугольника равны 50° и 80°, то такие треугольники подобны.

5. Сумма углов равнобедренного треугольника равна 180 градусам.

6. Два треугольника подобны, если их углы соответственно равны и соответственные стороны пропорциональны.

7. Диагонали параллелограмма равны.

8. В треугольнике со сторонами АВ=2см, ВС=3см и АС=4см наибольшим является угол А.

9. В тупоугольном треугольнике все углы тупые.

10. В любом параллелограмме диагонали точкой пересечения делятся пополам.

Записать формулу:

11. Запишите теорему синусов для треугольника MPK. 

12. Запишите теорему косинусов для нахождения МР треугольника МРК.

Решите задачи и запишите только ответы:

13. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

14.Пол комнаты, имеющей форму прямоугольника со сторонами

6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?

15.Один из углов параллелограмма в 3 раза меньше другого. Найдите больший угол этого параллелограмма.

16.Периметр прямоугольника равен 40см, одна из его сторон в 1,5 раза больше другой. Найдите большую сторону.

17.Стороны треугольника 5 см и 4 см, а угол между ними равен 60°. Найти третью сторону треугольника.

18.СТО=ДВА;  С = 114° , ВД=АД. Найдите угол В.

Административная контрольная работа по геометрии 9 класс

(октябрь/ноябрь)

2 вариант

Верно ли утверждение (отвечаем «да» или «нет»)?

1. Основания равнобедренной трапеции равны.

2. Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?

3. Две прямые, параллельные третьей прямой, перпендикулярны друг другу.

4. Вертикальные углы равны.

5. Если один из двух смежных углов острый, то другой тупой.

6. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

7. Диагонали ромба равны.

8. Существует треугольник с углами 47° , 56° и 87°

9. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

10. В треугольнике ABC угол В — наибольший. Сторона ВС треугольника наибольшая?

Записать формулу:

11. Запишите теорему синусов для треугольника BCD. 

12. Запишите теорему косинусов для нахождения ВС треугольника BCD.

Решите задачи и запишите только ответы:

13. На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

14. Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?

15. Периметр квадрата равен 116. Найдите площадь квадрата.

16. Один из углов параллелограмма в 2 раза больше другого. Найдите больший угол этого параллелограмма.

17. Стороны треугольника 5 см и 3 см, а угол между ними 60°. Найдите третью сторону треугольника.

18. Стороны прямоугольного треугольника равны 11см, 60см и 61см. Найдите

его площадь.

Ответы

1 вариант

2 вариант

1. нет

1. нет

2. да

2. нет

3. да

3. нет

4. нет

4. да

5. да

5. да

6. да

6. нет

7. нет

7. нет

8. нет

8. нет

9. нет

9. да

10. да

10. нет

11. МР²=МК² +КР² – 2МK·РК·cosK

12. BC²=BD² +DC²– 2BD·DC·cosD

13. 6

13. 7

14. 1680

14. 3150

15. 135

15. 841

16. 12

16. 120

18. 114

18.  330

Критерии оценивания:

№ 1-12 — «1 балл» за верный ответ.

№ 13-18 — «2 балла» за верный ответ.

Всего 24 баллов

Результат:

0-11 баллов – оценка «2»

12-16 баллов – оценка «3»

17-20 баллов – оценка «4»

21-22 баллов – оценка «5»

infourok.ru

контрольные работы по геометрии 9 класс по учебнику А.В. Погорелова

Контрольные работы Г-9 по Бурмистрову

Контрольная работа №1 «Подобие фигур» вариант-1

№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см

№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см

а) вычислите длину проекции стороны ВС на прямую СD.

в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СД)

Контрольная работа № 1 «Подобие фигур» вариант 2

а) вычислите длины отрезков ВО и ОD.

в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).

Контрольная работа №2 «Углы, вписанные в окружность» вариант-1

№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.

№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:

а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.

в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см

Контрольная работа №2 «Углы, вписанные в окружность» вариант-2

№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.

№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:

а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.

в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.

Контрольная работа №3 «Решение треугольников» 1 вариант.

1. В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.

2. Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5 см и 3 см.

3. Сторона параллелограммам равна 2см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.

4. *Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.

Контрольная работа №3 «Решение треугольников» 2 вариант.

1. В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.

2. Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4 см и 7 см.

3. Найдите углы равнобокой трапеции, в которой боковая сторона равна 2 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.

4. *Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.

Контрольная работа №4 «Многоугольники» вариант-1

№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.

№2. Около правильного треугольника со стороной 5см описана окружность. Найдите

а) радиус описанной окружности;

в) сторону правильного шестиугольника, вписанного в эту окружность.

№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.

Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.

Контрольная работа №4 «Многоугольники» вариант-2

№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.

№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите

а) радиус окружности;

в) сторону правильного треугольника, описанного около данной окружности.

№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.

Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.

Контрольная работа №5 «Площади многоугольников» вариант-1

№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.

№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.

№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.

Контрольная работа №5 «Площади многоугольников» вариант-2

№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм.

№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.

№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45 . Вычислите площадь трапеции, если основания её равны 24см и 60см.

Контрольная работа №6 «Площадь круга и его частей» вариант-1

№1. Найдите площадь круга, диаметр которого 6см.

№2. Площади двух подобных многоугольников пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.

№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.

№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.

Контрольная работа №6 «Площадь круга и его частей» вариант-2

№1. Найдите площадь круга, диаметр которого 8см.

№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников.

№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.

№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.

Контрольная работа № 1

«Подобие фигур»

вариант-1

№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см

№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см

а) вычислите длину проекции стороны ВС на прямую СD.

в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)

Контрольная работа № 1

«Подобие фигур»

вариант -2

а) вычислите длины отрезков ВО и ОD.

в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).

Контрольная работа №1

«Подобие фигур»

вариант-1

№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см

№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см

а) вычислите длину проекции стороны ВС на прямую СD.

в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)

Контрольная работа № 1

«Подобие фигур»

вариант -2

а) вычислите длины отрезков ВО и ОD.

в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).

Контрольная работа № 1

«Подобие фигур»

вариант-1

№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см

№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см

а) вычислите длину проекции стороны ВС на прямую СD.

в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)

Контрольная работа № 1

«Подобие фигур»

вариант -2

а) вычислите длины отрезков ВО и ОD.

в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).

Контрольная работа №2

«Углы, вписанные в окружность»

вариант-1

№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.

№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:

а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.

в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см

Контрольная работа №2 «Углы, вписанные в окружность»

вариант-2

№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.

№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:

а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.

в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.

Контрольная работа №2

«Углы, вписанные в окружность»

вариант-1

№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.

№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:

а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.

в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см

Контрольная работа №2 «Углы, вписанные в окружность»

вариант-2

№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.

№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:

а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.

в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.

Контрольная работа №2

«Углы, вписанные в окружность»

вариант-1

№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.

№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:

а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.

в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см.

Контрольная работа №2 «Углы, вписанные в окружность»

вариант-2

№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.

№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:

а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.

в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.

Контрольная работа №3

«Решение треугольников»

вариант-1

1. В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.

2. Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5 см и 3 см.

3. Сторона параллелограммам равна 2см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.

4. *Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.

Контрольная работа №3

«Решение треугольников»

вариант-2

1. В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.

2. Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4 см и 7 см.

3. Найдите углы равнобокой трапеции, в которой боковая сторона равна 2 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.

4. *Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.

Контрольная работа №3

«Решение треугольников»

вариант-1

1. В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.

2. Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5 см и 3 см.

3. Сторона параллелограммам равна 2см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.

4. *Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.

Контрольная работа №3

«Решение треугольников»

вариант-2

1. В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.

2. Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4 см и 7 см.

3. Найдите углы равнобокой трапеции, в которой боковая сторона равна 2 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.

4* Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.

Контрольная работа №3

«Решение треугольников»

вариант-1

.

1. В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.

2. Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5 см и 3 см.

3. Сторона параллелограммам равна 2см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.

4. *Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.

Контрольная работа №3

«Решение треугольников»

вариант-2

1. . В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.

2. Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4 см и 7 см.

3. Найдите углы равнобокой трапеции, в которой боковая сторона равна 2 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.

4* Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.

Контрольная работа №4

«Многоугольники»

вариант-1

№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.

№2. Около правильного треугольника со стороной 5см описана окружность. Найдите

а) радиус описанной окружности;

в) сторону правильного шестиугольника, вписанного в эту окружность.

№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.

Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.

Контрольная работа №4

«Многоугольники»

вариант-2

№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.

№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите

а) радиус окружности;

в) сторону правильного треугольника, описанного около данной окружности.

№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.

Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.

Контрольная работа №4

«Многоугольники»

вариант-1

№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.

№2. Около правильного треугольника со стороной 5см описана окружность. Найдите

а) радиус описанной окружности;

в) сторону правильного шестиугольника, вписанного в эту окружность.

№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.

Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.

Контрольная работа №4

«Многоугольники»

вариант-2

№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.

№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите

а) радиус окружности;

в) сторону правильного треугольника, описанного около данной окружности.

№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.

Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.

Контрольная работа №4

«Многоугольники»

вариант-1

№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.

№2. Около правильного треугольника со стороной 5см описана окружность. Найдите

а) радиус описанной окружности;

в) сторону правильного шестиугольника, вписанного в эту окружность.

№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.

Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.

Контрольная работа №4

«Многоугольники»

вариант-2

№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.

№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите

а) радиус окружности;

в) сторону правильного треугольника, описанного около данной окружности.

№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.

Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.

Контрольная работа №5

«Площади многоугольников»

вариант-1

№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.

№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.

№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.

Контрольная работа №5

«Площади многоугольников»

вариант-2

№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм

.

№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.

№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.

Контрольная работа №5

«Площади многоугольников»

вариант-1

№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.

№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.

№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.

Контрольная работа №5

«Площади многоугольников»

вариант-2

№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм

.

№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.

№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.

Контрольная работа №5

«Площади многоугольников»

вариант-1

№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.

№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.

№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.

Контрольная работа №5

«Площади многоугольников»

вариант-2

№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм

.

№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.

№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.

Контрольная работа №6

«Площадь круга и его частей»

вариант-1

№1. Найдите площадь круга, диаметр которого 6см.

№2. Площади двух подобных многоугольников

пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.

№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.

№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.

Контрольная работа №6

«Площадь круга и его частей»

вариант-2

№1. Найдите площадь круга, диаметр которого 8см.

№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников

№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.

№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.

Контрольная работа №6

«Площадь круга и его частей»

вариант-1

№1. Найдите площадь круга, диаметр которого 6см.

№2. Площади двух подобных многоугольников

пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.

№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.

№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.

Контрольная работа №6

«Площадь круга и его частей»

вариант-2

№1. Найдите площадь круга, диаметр которого 8см.

№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников

№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.

№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.

Контрольная работа №6

«Площадь круга и его частей»

вариант-1

№1. Найдите площадь круга, диаметр которого 6см.

№2. Площади двух подобных многоугольников

пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.

№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.

№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.

Контрольная работа №6

«Площадь круга и его частей»

вариант-2

№1. Найдите площадь круга, диаметр которого 8см.

№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников

№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.

№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.

infourok.ru

ПОЛУГОДОВАЯ КОНТРОЛЬНАЯ РАБОТА (геометрия — 9 класс)

Просмотр содержимого документа
«ПОЛУГОДОВАЯ КОНТРОЛЬНАЯ РАБОТА (геометрия — 9 класс)»

ПОЛУГОДОВАЯ КОНТРОЛЬНАЯ РАБОТА ДЛЯ УЧАЩИХСЯ 9 класса (геометрия)

Вариант 1

1. Зная координаты М(-3;0) и К(7;4) найдите:

координаты вектора , середины отрезка МК и длину МК

1. Запишите:

а)координаты вектора

б) разложение вектора по координатным векторам и

в) координаты вектора , если

3. Найдите sinα, tgα если cosα=

4. Найдите скалярное произведение и угол между векторами 

5. Решите треугольник АВС, если А=60^о, В=40, с=14.

Найдите площадьАВС

Вариант 2

1. Зная координаты М(-5;3) и N(4;9) найдите:

координаты вектора , середины отрезка МN и длину МN

2. Запишите:

а)координаты вектора

б) разложение вектора по координатным векторам и

в) координаты вектора , если

3. Найдите cosά, tgα, если sinά=

4. Найдите скалярное произведение и угол между векторами  

5. Решите треугольник АВС, если А=120^о, в=32, с=45

Найдите площадьАВС

multiurok.ru

Методическая разработка (геометрия, 9 класс) по теме: Контрольные работы по геометрии 9 класс

         

    Контрольные работы

            по геометрии  

                  9 класс

 

                Контрольная работа №1.

                          Вариант 1.

1. Начертите два неколлинеарных вектора  и . Постройте векторы, равные:

а) +3;               б) 2-.

    2. На стороне ВС ромба ABCD лежит точка К так, что      ВК=КС, О – точка пересечения диагоналей. Выразите векторы , ,  через векторы = и =.

1. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.

4*. В треугольнике АВС О – точка пересечения медиан. Выразите вектор  через векторы = =.

 

Контрольная работа №1.

                    Вариант 2.

1. Начертите два неколлинеарных вектора  и . Постройте векторы, равные:

а) +;               б) 3-.

2. На стороне СD квадрата ABCD лежит точка P так, что CP=PD, О – точка пересечения диагоналей. Выразите векторы , ,  через векторы = и =.

3.В равнобедренной трапеции один из углов равен 60°, боковая сторона равна 8 см, а меньшее основание

7 см.  Найдите среднюю линию трапеции.

4*. В треугольнике MNK О – точка пересечения медиан, = =, =k·(+).

        Контрольная работа №2.

                            Вариант 1.

1. Найдите координаты и длину вектора, если

 = -+, , .

2. Даны координаты вершин треугольника АВС : А(-6;1), В(2;4), С(2;-2). Докажите, что треугольник АВС равнобедренный, и найдите высоту треугольника, проведённую из вершины А.

3. Окружность задана уравнением +=9. Напишите уравнение прямой, проходящей через её центр и параллельной оси ординат.

                Контрольная работа №2.

                            Вариант 2.

1. Найдите координаты и длину вектора, если

 = , , .

2. Даны координаты вершин четырёхугольника АВСD :

А(-6;1), В(0;5), С(6;-4)? D(0;-8). Докажите, что АВСD — прямоугольник, и найдите координаты точки пересечения его диагоналей.

3. Окружность задана уравнением +=16. Напишите уравнение прямой, проходящей через её центр и параллельной оси абсцисс.

                Контрольная работа №3.

              Вариант 1.

1. Найдите угол между лучом ОА и положительной полуосью Ох, если А (-1;3).

2. Решите треугольник АВС, если  см.

3. Найдите косинус угла М треугольника KLM, если

К (1;7), L(-2;4), M (2;0).

         

                Контрольная работа №3.

              Вариант 2.

1. Найдите угол между лучом ОВ и положительной полуосью Ох, если В (3;3).

2. Решите треугольник ВСD, если

             ВС= см.

3. Найдите косинус угла A треугольника ABC, если

A (3;9), B(0;6), C (4;2).

               Контрольная работа №4 .

                            Вариант 1.

1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

2.  Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72.

3.  Найдите длину дуги окружности радиуса 3 см, если её градусная мера равна 150°.

              Контрольная работа №4 .

                             Вариант 2.

1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 см. Найдите сторону квадрата, вписанного в ту же окружность.

2.  Найдите длину окружности, если площадь вписанного в неё правильного шестиугольника равна 72.

3.  Найдите площадь кругового сектора, если  градусная мера его дуги  равна 120°, а радиус круга равен 12 см.

      Контрольная работа №5.

                  Вариант 1.

1. Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую

сторону АВ.

2. Две окружности с центрами  и , радиусы которых равны, пересекаются в точках M и N. Через точку М проведена прямая, параллельная    и пересекающая окружность с центром  в точке D. Используя параллельный перенос, докажите, что четырёхугольник MD является параллелограммом.

      Контрольная работа №5.

                  Вариант 2.

1. Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой

стороны CD.

2. Дан шестиугольник . Его стороны  и ,  и ,  и  попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали , ,  данного шестиугольника пересекаются в одной точке.

Итоговая контрольная работа.

              Вариант 1.

Часть 1.

1.Какое утверждение относительно треугольника со сторонами 5,9,15 верно?

а) треугольник остроугольный;

б) треугольник тупоугольный;

в) треугольник прямоугольный;

г) такого треугольника не существует.

2.Если одна из сторон треугольника на 3 см меньше другой, высота делит третью сторону на отрезки 5 см и 10 см, то периметр треугольника равен:

а) 25 см;     б) 40 см;      в) 32 см;       г) 20 см.

3.Если один из углов ромба равен 60°, а диагональ, проведённая из вершины этого угла, равна4 см, то периметр ромба равен:

а) 16 см;     б) 8 см;     в) 12 см;     г) 24 см.

4.Величина одного из углов треугольника равна 20°. Найдите величину острого угла между биссектрисами двух других углов треугольника.

а) 84°;     б) 92°;     в) 80°;     г) 87°.

5.В треугольнике АВС сторона а=7, сторона b=8, сторона с=5. Вычислите угол А.

а) 120°;     б) 45°;     в) 30°;     г) 60°.

Часть 2.

1.В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.

2.В треугольнике ВСЕ .

3.Найдите площадь треугольника КМР, если сторона КР равна 5, медиана РО равна 3,

4.Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если её средняя линия равна 5.

5.Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС соответственно в точках Е и D. Найдите величину угла АВС (в градусах), если известно, что АЕ=1, ВD=3.

Итоговая контрольная работа.

              Вариант 2.

Часть 1.

1.Какое утверждение относительно треугольника со сторонами 12,9,15 верно?

а) треугольник остроугольный;

б) треугольник тупоугольный;

в) треугольник прямоугольный;

г) такого треугольника не существует.

2.Если сходственные стороны подобных треугольников равны 2 см и 5 см, площадь первого треугольника равна 8  , то площадь второго треугольника равна:

а) 5 ;    б) 40   в) 60 ;       г) 20 .

3.Если в равнобедренном треугольнике длина основания равна 12 см, а его периметр равен 32 см , то радиус окружности, вписанной в треугольник, равен::

а) 4 см;     б) 3 см;     в) 6 см;     г) 5 см.

4.В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите катеты треугольника.

 а)12 см и 16 см;    б)7 см и 11 см;    в) 10 см и 13 см;    г) 8 см и 15 см.

5.Стороны прямоугольника равны a и k. Найдите радиус окружности, описанной около этого прямоугольника.

а) ;        б) ;        в) ;        г) .

 Часть 2.

1.Окружность с центром О, вписанная в равнобедренный треугольник АВС с основанием АС, касается стороны ВС в точке К, причём СК:ВК=5:8. Найдите площадь треугольника, если его периметр равен 72.

2.Около треугольника АВС описана окружность. Медиана треугольника АМ продлена до пересечения с окружностью в точке К. Найдите сторону АС, если АМ=18, МК=8, ВК=10.

3.Найдите основание равнобедренного треугольника , если угол при основании равен 30°, а взятая внутри треугольника точка находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии  2 от основания.

4.Пусть М – точка пересечения диагоналей выпуклого четырёхугольника  ABCD, в котором стороны АВ, АD, и ВС равны между собой. Найдите угол СМD (в градусах), если известно, что DМ=МС, а угол САВ не равен углу DBA.

5.На боковой стороне ВС равнобедренного треугольника АВС как на диаметре построена окружность, пересекающая основание этого треугольника в точке D. Найдите квадрат расстояния от вершины А до центра окружности, если АD=, а угол АВС равен 120°.

nsportal.ru

Контрольная работа по геометрии за 3 четверть, 9 класс

1 вариант 1. Определите стороны параллелограмма, если его периметр равен 38 дм, а одна из сторон на 11 дм больше другой. 2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120°. 3. Периметр ромба равен 12 см. Найдите длины его сторон. 4. Стороны параллелограмма 10 см и 6 см, а угол между этими сторонами 150°. Найдите площадь этого параллелограмма. 5. Найти с, если а = 6 см; b = 8 см. 6. Найти Х 7. В прямоугольном треугольнике АВС А = 90°, АВ = 20 см; высота АD = 12 см. Найдите АС и cos C и тангенс угла С 8. Точки А, В, С лежат на окружности с центром О, АОВ = 80° Найдите ВСА

2 вариант 1. Определите стороны параллелограмма, если его периметр равен 48 дм, а одна из сторон на 6 дм больше другой. 2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 10 см и 6 см, а один из углов равен 60°. 3. Периметр ромба равен 30 см. Найдите его стороны. 4. Стороны параллелограмма 10 см и 6 см, а угол между этими сторонами 30°. Найдите площадь этого параллелограмма. 5. Найти а, если с = 5 см, b = 3 см. 6. Найти Х 7. В прямоугольном треугольнике АВС А = 90°, АВ = 5 см; высота АD = 4 см. Найдите АС, cos C синус угла С 8. Точки А, В, С лежат на окружности с центром О, АСВ = 80° Найдите ВОА

infourok.ru

Входная контрольная работа по геометрии, 9 класс

Пояснительная записка

Тестовая контрольная работа по геометрии составлена в форме ГИА. Контрольная работа состоит из двух частей. 1 часть – 7 заданий, 2 часть – 2 задания.

Задания 1 части оцениваются в 1 балл, задания 2 части – 2 балла.

Задания, оцениваемые одним баллом, считаются выполненными верно, если указан верный ответ.

Задания, оцениваемые двумя баллами, считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.

Контрольная работа рассчитана на 45 минут.

11-13 б – оценка «5»

9-10 б – оценка «4»

7-8 б – оценка «3»

При составлении контрольной работы использовались задания открытого банка заданий по математике. ( http://mathgia.ru/or/gia12/Main.html )

Административная контрольная работа по геометрии

Класс: 9

1 вариант

1. Площадь прямоугольника АВСD равна 15. Найдите сторону ВС прямоугольника, если известно, что АВ = 3.

2. Найдите медиану прямоугольного треугольника, проведенную к гипотенузе, равной 14.

3. Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол треугольника. Ответ дайте в градусах.

4. В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что

ÐАСD = 25^°.

1. В прямоугольном треугольнике АВК гипотенуза АВ равна 13, катет АК равен 12, катет ВК равен 8. Найдите тангенс угла А.

2. На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах

3. Укажите в ответе номера верных утверждений в порядке возрастания:

   1. в прямоугольном треугольнике высота может совпадать с одной из его сторон.

   2. точка пересечения высот произвольного треугольника – центр окружности, описанной около этого треугольника.

   3. высота может лежать и вне треугольника.

   4. треугольник со сторонами 6,8,10 — прямоугольный.

   5. существует треугольник со сторонами 6, 8, 15.

4. Человек ростом 1,7 м стоит на расстоянии 12 шагов от столба, на котором висит фонарь. Тень человека равна двум шагам. На какой высоте (в метрах) расположен фонарь?

5. Пря­мая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окруж­но­сти. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 83°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в гра­ду­сах.

Административная контрольная работа по геометрии

Класс: 9

2 вариант

1. Площадь параллелограмма АВСD равна 35. Найдите сторону ВС параллелограмма, если известно, что высота, проведенная к этой стороне, равна 7 .

2. Найдите гипотенузу прямоугольного треугольника, если медиана, проведенная к этой гипотенузе, равна 4.

3. Один из двух острых угла прямоугольного треугольника на 20⁰ больше другого. Найдите больший острый угол. Ответ дайте в градусах.

4. В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно,

что ÐАСD = 15°.

1. В прямоугольном треугольнике АВК гипотенуза АВ равна 16, катет АК равен 12, катет ВК равен 8. Найдите синус угла А.

2. На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах

3. Укажите в ответе номера верных утверждений в порядке возрастания:

   1. в равностороннем треугольнике все высоты равны.

   2. точка пересечения медиан произвольного треугольника – это центр окружности, описанной около этого треугольника.

   3. медиана, это отрезок соединяющий середины двух сторон треугольника.

   4. треугольник со сторонами 6,8,9 — не существует.

   5. треугольник со сторонами 3, 4, 5 — прямоугольный.

4. Найдите длину солнечной тени от здания высотой 16 м, если солнечная тень от человека ростом 1 м 80 см равна 2 м 70 см.

5. Ка­са­тель­ные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 72°. Най­ди­те угол ABO. Ответ дайте в гра­ду­сах.

Административная контрольная работа по геометрии

Класс: 9

3 вариант

1. Площадь прямоугольника АВСD равна 45. Найдите сторону ВС прямоугольника, если известно, что АВ = 9.

2. Найдите гипотенузу прямоугольного треугольника, если радиус описанной окружности равен 11.

3. Один из острых углов прямоугольного треугольника на 24⁰ больше другого. Найдите больший острый угол. Ответ дайте в градусах.

4. В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что ÐАСD = 10°.

5. В прямоугольном треугольнике АВК гипотенуза АВ равна 13, катет АК равен 12, катет ВК равен 8. Найдите косинус угла А.

6. На клетчатой бумаге с клетками размером 1 см х1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах

7. Укажите в ответе номера верных утверждений в порядке возрастания:

   1. точка пересечения биссектрис является центром вписанной окружности любого треугольника.

   2. отношение периметров подобных многоугольников равно квадрату коэффициента подобия.

   3. в прямоугольнике диагонали перпендикулярны.

   4. в равнобокой трапеции диагонали равны

   5. треугольник со сторонами 5, 12, 13 – прямоугольный.

8. Человек ростом 1,6 м стоит на расстоянии 10 шагов от столба, на котором висит фонарь. Тень человека равна пяти шагам. На какой высоте (в метрах) расположен фонарь?

9. Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

Административная контрольная работа по геометрии

Класс: 9

4 вариант

1. Площадь параллелограмма АВСD равна 45. Найдите сторону ВС параллелограмма, если известно, что высота, проведенная к этой стороне, равна 5.

2. Найдите медиану прямоугольного треугольника, проведенную к гипотенузе, если гипотенуза равна 14.

3. Два острых угла прямоугольного треугольника относятся как 1:9. Найдите больший острый угол. Ответ дайте в градусах.

4. В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что ÐАСD = 20°.

5. В прямоугольном треугольнике АВК гипотенуза АВ равна 17, катет АК равен 15, катет ВК равен 8. Найдите тангенс угла А.

6. На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах

7. Укажите в ответе номера верных утверждений в порядке возрастания:

   1. у прямоугольника диагонали равны.

   2. медиана всегда делит пополам один из углов треугольника.

   3. радиус описанной около прямоугольного треугольника окружности равен одной из его медиан.

   4. отношение площадей подобных треугольников равно квадрату коэффициента подобия.

   5. треугольник со сторонами 3, 4, 6 – не существует.

8. Длина солнечной тени от дерева равна 24 м. Вертикальный шест высотой 1 м 50 см в тот же момент отбрасывает тень длиной 1 м 60 см. Вычислите высоту дерева.

9. На от­рез­ке AB вы­бра­на точка C так, что AC = 75 и BC = 10. По­стро­е­на окруж­ность с цен­тром A, про­хо­дя­щая через C. Най­ди­те длину от­рез­ка ка­са­тель­ной, про­ведённой из точки B к этой окруж­но­сти.

Ключ:

1	2	3	4	5	6	7	8	9
4,5	7	5	130	2/3	28	134	11,9	7

Вариант 1

Задание 8.

Рассм. два подобных треугольника: первый с катетами — 1,7 м и 2 шага, а второй х (высота столба) и 14 шагов (2+12), т.к.  эти треугольники подобны, Составим пропорцию: 1,7 м /2 шага=х/14 шаг, х= 1,7 м * 7 = 11,9 метров высота столба.

Задание 9.

Угол, об­ра­зо­ван­ный хор­дой и ка­са­тель­ной равен по­ло­ви­не дуги, ко­то­рую он за­клю­ча­ет, по­это­му ве­ли­чи­на дуги MK равна 2 · 83° = 166°. Угол MOK — цен­траль­ный, по­это­му он равен ве­ли­чи­не дуги, на ко­то­рую опи­ра­ет­ся. Зна­чит, угол MOK равен 166°. В тре­уголь­ни­ке OMK сто­ро­ны OK и OM равны как ра­ди­у­сы окруж­но­сти, по­это­му тре­уголь­ник OMK — рав­но­бед­рен­ный, сле­до­ва­тель­но, углы при ос­но­ва­нии равны. Сумма углов тре­уголь­ни­ка равна 180°, по­это­му ∠OKM = ∠OMK = (180° − ∠KOM)/2 = (180° − 166°)/2 = 7°.

Вариант 2

1	2	3	4	5	6	7	8	9
5	8	55	150	3	76	48	24	36

Задание 8.

Переведем см в м: 1 м 80 см = 1,8 м; 2 м 70 см =  2,7 м

Составим пропорцию:  

1,8 /16= 2,7/x

х = (16*2,7) / 1,8

х = 24

Задание 9.

Введём обо­зна­че­ние (см. ри­суно­к). Ка­са­тель­ные, про­ведённые к окруж­но­сти из одной точки равны, по­это­му  сле­до­ва­тель­но, тре­уголь­ник  — рав­но­бед­рен­ный. От­ку­да  Угол между ка­са­тель­ной и хор­дой равен по­ло­ви­не дуги, ко­то­рую он за­клю­ча­ет, зна­чит, дуга  равна 108°. Угол AOB — цен­траль­ный, по­это­му он равен дуге, на ко­то­рую опи­ра­ет­ся, сле­до­ва­тель­но, равен 108°. Рас­смот­рим тре­уголь­ник AOB, он рав­но­бед­рен­ный, сле­до­ва­тель­но, 

Вариант 3

1	2	3	4	5	6	7	8	9
5	22	57	160	12/13	10	145	4,8	4

Задание 8.

Пусть х м — высота фонаря, 10+5=15м — расстояние от столба до конца тени.

Составляем пропорцию:

х/1,6 = 15/5;   X=1.6*15/5= 4,8

Задание 9.

Опу­стим ра­ди­у­сы на каж­дую ка­са­тель­ную. Со­еди­ним точки A и O. По­лу­чив­ши­е­ся тре­уголь­ни­ки — пря­мо­уголь­ные, так как ра­ди­ус, про­ве­ден­ный в точку ка­са­ния, пер­пен­ди­ку­ля­рен ка­са­тель­ной. По ги­по­те­ну­зе и ка­те­ту эти тре­уголь­ни­ки равны, таким об­ра­зом, мы по­лу­чи­ли, что угол, ле­жа­щий на­про­тив ка­те­та равен  Катет, ле­жа­щий на­про­тив угла в равен по­ло­ви­не ги­по­те­ну­зы, тогда ра­ди­ус равен 4.

Вариант 4

1	2	3	4	5	6	7	8	9
53	2.5	2	431	4	65	20	22,5	40

Задание 8.

Пусть х м — высота дерева.

Составим пропорцию:

х/1,5 = 24/1,6;   X=1,5*24/1,6= 22,5

Задание 9.

Про­ведём ра­ди­ус  в точку ка­са­ния. Из пря­мо­уголь­но­го тре­уголь­ни­ка  по тео­ре­ме Пи­фа­го­ра найдём 

 

 

12.10.2015 г.

Административная контрольная работа

по геометрии

Ученика (цы) 9__ класса

ФИО (в родительном падеже)

Вариант______

Задания 1-7, считаются выполненными верно, если указан верный ответ. Эти задания оцениваются одним баллом.

Задания 8,9 (задания с развернутым ответом), считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.

Отметка	«2»	«3»	«4»	«5»
Кол-во баллов	0-2	3-5	6-8	9-11

12.10.2015 г.

Административная контрольная работа

по геометрии

Ученика (цы) 9__ класса

ФИО (в родительном падеже)

Вариант______

Задания 1-7, считаются выполненными верно, если указан верный ответ. Эти задания оцениваются одним баллом.

Задания 8,9 (задания с развернутым ответом), считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.

Отметка	«2»	«3»	«4»	«5»
Кол-во баллов	0-2	3-5	6-8	9-11

12.10.2015 г.

Административная контрольная работа

по геометрии

Ученика (цы) 9__ класса

ФИО (в родительном падеже)

Вариант______

Задания 1-7, считаются выполненными верно, если указан верный ответ. Эти задания оцениваются одним баллом.

Задания 8,9 (задания с развернутым ответом), считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.

Отметка	«2»	«3»	«4»	«5»
Кол-во баллов	0-2	3-5	6-8	9-11

kopilkaurokov.ru