Самостоятельные работы по геометрии 9 класс
Понятие вектора
Вариант 1А1. Перечертите рисунок в тетрадь. Постройте векторы , такие, что .
А2. АВСD – параллелограмм. Докажите, что .
А3. Можно ли утверждать, что из равенства следует равенство ?
Вариант 2
А1. Перечертите рисунок в тетрадь. Постройте векторы , такие, что .
А2. Тоски М, К, N и P не лежат на одной прямой и . Докажите, что KMNP – параллелограмм.
А3. Можно ли утверждать, что из равенства следует равенство ?
Сложение и вычитание векторов
Вариант 1А1. Начертите четыре попарно неколлинеарных вектора .
Постройте вектор .
А2. Упростите выражение .
А3. Дан прямоугольный треугольник АВС с гипотенузой ВС. Постройте вектор и найдите , если АВ = 8 см.
Вариант 2
А1. Начертите пять попарно неколлинеарных вектора .
Постройте вектор .
А2. Упростите выражение .
А3. Дан прямоугольный треугольник АВС с гипотенузой АВ. Постройте вектор и найдите , если ВС = 9 см
Простейшие задачи в координатах
Вариант 1А1. Найдите координаты вектора , если А(-2; 5), В(1; 4).
А2. Даны векторы . Найдите координаты векторов и .
А3. Найдите координаты середины отрезка с концами А(1; 3), В(3; 1).
________________
В1. Даны точки М(3; 1), К(0; 0), Р(0; 2). Будет ли треугольник МРК равносторонним?
Вариант 2
А1. Найдите координаты вектора , если А(-2; -4), В(4; 0).
А2. Даны векторы . Найдите координаты векторов и .
А3. Найдите координаты середины отрезка с концами А(2; 2), В(6; 6).
_________________
В1. Даны точки А(4; 2), В(0; -6), С(-4; -2). Будет ли треугольник АВС равносторонним?
Уравнение окружности. Уравнение прямой
Вариант 1 А1. Начертите окружность, заданную уравнением .
Начертите окружность, заданную уравнением .
А2. Запишите уравнение окружности с центром в точке С(3;-5), касающейся оси ординат.
А3. Прямая задана уравнением .
а) Начертите эту прямую.
б) Запишите координаты пересечения прямой с осями координат.
в) Найдите площадь треугольника, образованного осями координат и этой прямой.
________________
В1. Окружность задана уравнением . Напишите уравнения касательных к окружности, которые параллельны оси ординат.
Вариант 2
А1. Начертите окружность, заданную уравнением .
А2. Запишите уравнение окружности с центром в точке С(-2;4), касающейся оси ординат.
А3. Прямая задана уравнением .
а) Начертите эту прямую.
б) Запишите координаты пересечения прямой с осями координат.
в) Найдите площадь треугольника, образованного осями координат и этой прямой.
________________
В1. Окружность задана уравнением .
Синус, косинус, тангенс угла
Вариант 1А1. Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найдите косинус меньшего острого угла этого треугольника.
А2. Найдите .
А3. Найдите .
А4. Постройте угол
Вариант 2
А1. Стороны прямоугольного треугольника равны 5 см, 12 см и 13 см. Найдите тангенс большего острого угла этого треугольника.
А2. Найдите .
А3. Найдите .
А4. Постройте угол
Решение треугольников
Вариант 1А1. Найдите площадь равнобедренного треугольника, если его боковая сторона равна 1 м, а угол при вершине равен 45о.
А2. В треугольнике АВС АС = 0,59 дм, А = 40о, С = 35о. Вычислите ВС.
А3. Две стороны треугольника равны 1,3 и 42,5, угол между ними 100о. Вычислите третью сторону треугольника.
Вариант 2
А1. Найдите площадь равностороннего треугольника со стороной, равной 1 м.
А2. В треугольнике АВС АС = 15,2 см, А = 25о, С = 80о. Вычислите ВС.
А3. Две стороны треугольника равны 27,4 и 16,3, угол между ними 70
Скалярное произведение векторов
Вариант 1А1. Даны точки А(2; 4), В(5; 8), С(-7; -1), D(5; 8). Найдите скалярное произведение векторов .
А2. Даны векторы . Найдите скалярное произведение векторов.
А3. Вычислите скалярное произведение векторов, если , а угол между ними равен 60о.
Вариант 2
А1. Даны точки А(2; 4), В(-1; 6), С(-4; -2), D(3; 2). Найдите скалярное произведение векторов и .
А2. Даны векторы . Найдите скалярное произведение векторов.
А3. Вычислите скалярное произведение векторов, если , а угол между ними равен 30
Геометрия 9 класс Контрольная № 2 с ответами
Контрольная работа № 1 по геометрии в 9 классе «Метод координат» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 7 класса (Н.Ф. Гаврилова, ВАКО). Урок 14. Геометрия 9 класс Контрольная № 2 «Метод координат».
Смотреть Список всех контрольных по геометрии в 9 классе (УМК Атанасян)
Контрольная работа № 2
«Метод координат»
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока
ХОД УРОКА
1. Организационный момент
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
2. Контрольная работа «Метод координат»
I уровень сложности
Вариант 1
- Найдите координаты и длину вектора а, если а = m/3 – n, m{–3; 6}, n{2; – 2}.

- Напишите уравнение окружности с центром в точке А(–3; 2), проходящей через точку В(0; –2).
- Треугольник MNK задан координатами своих вершин: М(–6; 1), N(2; 4), К(2; –2).
а) Докажите, что ΔMNK — равнобедренный. - * Найдите координаты точки N, лежащей на оси абсцисс и равноудаленной от точек Р(–1; 3) и K(0; 2).
Вариант 2
- Найдите координаты и длину вектора b, если b = с/2 – d, с{6; –2}, d{ 1; –2}.
- Напишите уравнение окружности с центром в точке С(2; 1), проходящей через точку D(5; 5).
- Треугольник CDE задан координатами своих вершин: С(2; 2), D(6; 5), Е(5; –2).
а) Докажите, что ΔCDE – равнобедренный.
б) Найдите биссектрису, проведенную из вершины С. - * Найдите координаты точки А, лежащей на оси ординат и равноудаленной от точек В(1; –3) и С(2; 0).
II уровень сложности
III уровень сложности
3. Рефлексия учебной деятельности
Рефлексия учебной деятельности
В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.
Ответы на контрольную I уровня сложности
Ответы на контрольную II уровня сложности
Ответы на контрольную III уровня сложности
Вы смотрели: Геометрия 9 класс Контрольная № 2. Поурочное планирование по геометрии для 9 класса. УМК Атанасян (Просвещение). Урок 24. Контрольная работа по геометрии «Метод координат» + ОТВЕТЫ.
Смотреть Список всех контрольных по геометрии в 9 классе по УМК Атанасян.
Вернуться к Списку уроков Тематического планирования в 9 классе.
Геометрия 9 Атанасян (Мельникова) | КОНТРОЛЬНЫЕ РАБОТЫ
Геометрия 9 Атанасян (Мельникова) — контрольные работы с ответами, цитаты из пособия «Геометрия 9 класс. Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных работ по геометрии в 9 классе рекомендуем купить книгу: Наталия Мельникова: Геометрия. 9 класс. Дидактические материалы к учебнику Л.С. Атанасяна и др. ФГОС, в которой контрольные работы представлены в 4-х вариантах, а также есть набор заданий по каждой теме для подготовки к контрольным работам. Структура контрольных работ и форма заданий соответствуют структуре и форме заданий Основного государственного экзамена (ОГЭ).
Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных работ по геометрии в 9 классе рекомендуем купить книгу: Наталия Мельникова: Геометрия. 9 класс. Дидактические материалы к учебнику Л.С. Атанасяна и др. ФГОС, в которой контрольные работы представлены в 4-х вариантах, а также есть набор заданий по каждой теме для подготовки к контрольным работам. Структура контрольных работ и форма заданий соответствуют структуре и форме заданий Основного государственного экзамена (ОГЭ).
Контрольные работы по геометрии в 9 классе:
Контрольная работа 1 К-1. Векторы. Метод координат
Контрольная работа 2 К-2. Соотношения в треугольнике
Контрольная работа 3 К-3. Длина окружности и площадь круга
Контрольная работа 4 К-4. Движения
Контрольная работа 5 К-5. Начальные сведения из стереометрии
Контрольная работа 6 К-6. ИТОГОВАЯ за 9 класс
ИТОГОВАЯ за 9 класс
Контрольная работа 7 К-7. ИТОГОВАЯ за 7-9 классы
Структура контрольной работы
Каждая контрольная работа рассчитана на один урок. Все работы составлены в четырех вариантах одинакового уровня сложности (только в пособии). Каждая работа состоит из трех частей, соответствующих форме предлагаемых заданий.
В часть А включаются задания с выбором ответа. Учащимся нужно выбрать из предложенных вариантов либо верное утверждение, либо нужный рисунок. При этом верных ответов может быть несколько, и учащимся необходимо записать номера ответов, которые, по их мнению, верны. Заметим, что, вообще говоря, в заданиях с выбором ответа применяются два подхода. При первом подходе среди предлагаемых вариантов ответа имеется только один правильный. При втором — верных ответов может быть несколько, и результатом решения задачи является не один номер, а все номера верных ответов. При этом задание считается выполненным верно, если указаны номера всех верных ответов.
В часть В входят вычислительные задачи, которые необходимо решить и записать число, которое получилось в результате вычислений.
При выполнении частей А и В контрольной работы учащиеся не записывают ни обоснования, ни вычисления, нужные для решения задач. Все записи или рисунки учащиеся, в случае необходимости, могут делать в черновике. Черновик не сдается учителю и не влияет на оценку за выполнение работы.
В части С имеются и задачи на доказательство, и задачи на вычисление геометрических величин. Решение этих задач должно быть оформлено письменно, как в традиционной контрольной работе. Следует иметь в виду, что при записи решения вычислительных задач, так же как и при решении задач на доказательство, необходимо приводить обоснования с использованием изученных геометрических фактов.
Последняя задача, в каждом варианте отмеченная звездочкой, предназначена для наиболее подготовленных учащихся, успевающих достаточно быстро выполнить все предыдущие задания. В зависимости от уровня подготовленности класса эту задачу можно считать дополнительной и оценивать ее решение отдельно.
Перед проведением первой контрольной работы необходимо проинструктировать учащихся о том, как они должны оформить решение задач. Полезно привести пример, показывающий, как должны выглядеть ответы на задачи частей А и В.
Следует напомнить эти инструкции и при проведении каждой последующей контрольной работы.
Дифференцированный подход к учащимся осуществляется за счет того, что в работах представлены задания разного уровня, которые, как правило, расположены по мере возрастания уровня сложности. Стереометрический материал может изучаться в ознакомительном плане без обязательной проверки его усвоения. Поэтому контрольную № 5 по усмотрению учителя можно не проводить или полученные за нее оценки выставлять в журнал по желанию учащегося.
Номера заданий обязательного уровня, посильных для менее подготовленных учащихся, отмечены кружком. Такие задания представлены во всех трех частях работы.
Следует заметить, что при традиционном письменном оформлении решения задач предлагаемое в контрольных работах количество задач было бы нереально решить за один урок. Однако нужно иметь в виду, что задания с выбором ответа и с кратким ответом не требуют времени на оформление решения и очень часто ответы на них могут быть получены устно. Поэтому основные затраты времени будут связаны с решением задач части С.
Однако нужно иметь в виду, что задания с выбором ответа и с кратким ответом не требуют времени на оформление решения и очень часто ответы на них могут быть получены устно. Поэтому основные затраты времени будут связаны с решением задач части С.
Тематика контрольных работ
Каждая тематическая контрольная работа направлена на проверку усвоения материала главы учебника. Одна из итоговых контрольных работ проверяет усвоение материала, изучавшегося в 9 классе, другая составлена по материалу всего курса планиметрии. Указанные ниже проверяемые элементы знаний отражают только тот материал, который изучался в данной теме. При этом, естественно, задачи тематической контрольной работы могут проверять также и усвоение сведений, изучавшихся в предыдущих темах.
Контрольная работа № 1. Векторы. Метод координат
• равенство векторов, координаты и модуль вектора, сложение векторов и умножение вектора на число;
• координаты середины и длина отрезка, заданного координатами концов;
• уравнение окружности;
• средняя линия трапеции.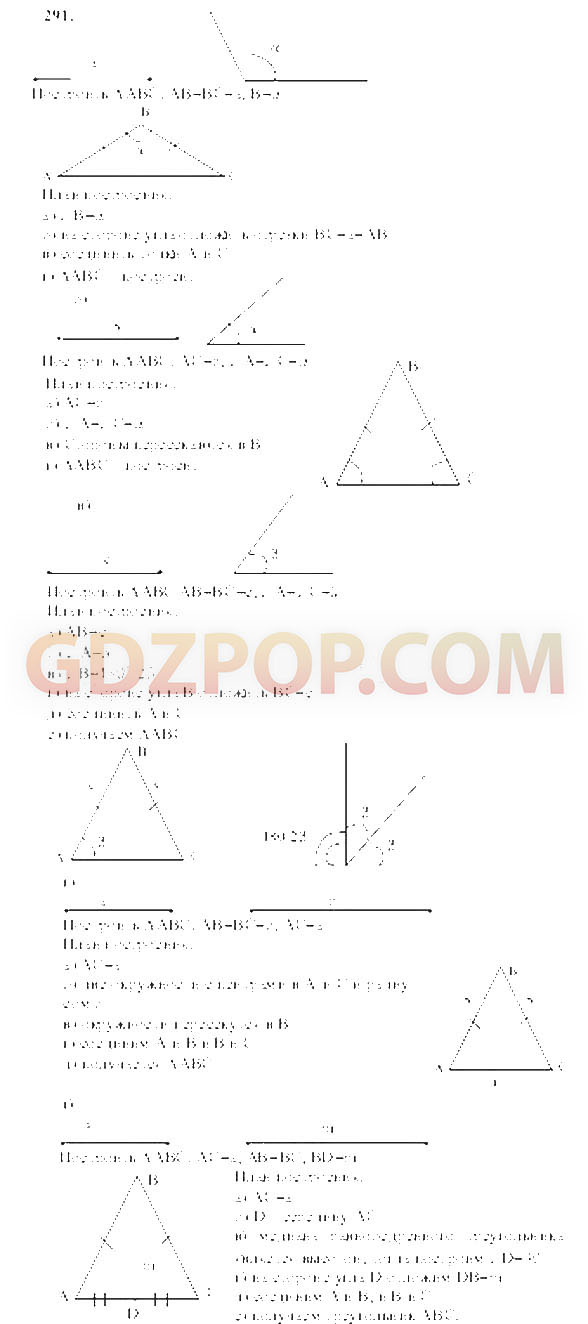
Контрольная работа № 2. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
• теорема синусов, теорема косинусов;
• формула площади треугольника;
• скалярное произведение векторов.
Контрольная работа № 3. Длина окружности и площадь круга
• правильные многоугольники;
• длина окружности и длина дуги окружности;
• площадь круга и кругового сектора.
Контрольная работа № 4. Движения
• понятие движения;
• симметрия относительно прямой, симметрия относительно точки, параллельный перенос; поворот.
Контрольная работа № 5. Начальные сведения из стереометрии
• геометрические тела: призма, параллелепипед, пирамида, цилиндр, конус;
• свойства правильной призмы и правильной пирамиды;
• объемы тел, боковая поверхность цилиндра и конуса;
• сечение прямоугольного параллелепипеда плоскостью.
Итоговая контрольная работа за курс 9 класса
• координаты середины отрезка, заданного координатами концов;
• равенство векторов, модуль вектора;
• скалярное произведение векторов;
• теорема синусов, теорема косинусов;
• длина окружности и площадь круга;
• площадь правильного многоугольника.
Итоговая контрольная работа за курс 7-9 классов
• свойства параллелограмма, прямоугольника и ромба;
• признаки подобия треугольников;
• средняя линия треугольника;
• формулы площади треугольника;
• теорема Пифагора и определения синуса, косинуса и тангенса острого угла прямоугольного треугольника;
• теорема синусов, теорема косинусов.
Геометрия 9 Атанасян (Мельникова) — контрольные работы с ответами, цитаты из пособия «Геометрия 9 класс. Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях.
Геометрия Самостоятельные и контрольные работы 7-9 класс Иченская
Читать онлайн (cкачать в формате PDF) — Щелкни!
<Вернуться> | <Пояснение: Как скачать?> Пояснение: Для скачивания книги (с Гугл Диска), нажми сверху справа — СТРЕЛКА В ПРЯМОУГОЛЬНИКЕ .
 Затем в новом окне сверху справа — СТРЕЛКА ВНИЗ . Для чтения — просто листай колесиком страницы вверх и вниз.
Затем в новом окне сверху справа — СТРЕЛКА ВНИЗ . Для чтения — просто листай колесиком страницы вверх и вниз.Текст из книги:
к М. А. Иченская
М. А. Иченская
ГЕОМЕТРИЯ
САМОСТОЯТЕЛ ЬН Ы Е И КОНТРОЛЬНЫЕ РАБОТЫ
У
м
►
КЛАССЫ
Учебное пособие
для общеобразователь
организаций
5-е издание
Москва
«Просвещение»
2017
УДК 373.167.1:514 ББК 22.151я72 И96
6+
Иченская М. А.
И96 Геометрия. Самостоятельные и контрольные работы. 7—9 классы: учеб, пособие для общеобразоват. организаций / М. А. Иченская. — 5-е изд. — М. : Просвещение, 2017. — 144 с.: ил. — ISBN 978-5-09-045910-5.
Пособие содержит самостоятельные и контрольные работы, а также карточки к итоговым зачётам по курсу геометрии 7—9 классов. Оно ориентировано на учебник «Геометрия. 7—9 классы» авторов Л. С. Атанасяна и др.
Пособие адресовано школьникам, учителям математики и студентам педвузов.
УДК 373.167.1:514 ББК 22.151я72
Учебное издание Иченская Мира Александровна
ГЕОМЕТРИЯ
Самостоятельные и контрольные работы 7—9 классы
Учебное пособие для общеобразовательных организаций
Центр естественно-математического образования Редакция математики и информатики Зав.
 Начертите прямую и обозначьте её буквой Ь. Отметьте точку М, лежащую на прямой Ъ. Отметьте точку N, не лежащую на прямой Ъ. Используя символы е и запишите предложение: «Точка М лежит на прямой Ъ, а точка N не лежит на ней».
2. Начертите прямые а и пересекающиеся в точке М. На прямой а отметьте точку N, отличную от точки М. Являются ли прямые MN и а различными прямыми? Может ли прямая Ъ проходить через точку N1 Ответы обоснуйте.
7 класс
С—1, В—2
1. Начертите прямую и обозначьте её буквой а. Отметьте точку К, лежащую на прямой а. Отметьте точку С, не лежащую на прямой а. Используя символы е и
запишите предложение: «Точка К лежит на прямой а, а точка С не лежит на ней».
2. Начертите прямые тип, пересекающиеся в точке А. На прямой т отметьте точку В, отличную от точки А. Являются ли прямые АВ и т различными прямыми? Может ли прямая п проходить через точку В? Ответы обоснуйте.
7 класс
1. На прямой даны три точки А, В и С. Назовите:
а) пары совпадающих лучей;
б) пары противоположных лучей.
2.
Начертите прямую и обозначьте её буквой Ь. Отметьте точку М, лежащую на прямой Ъ. Отметьте точку N, не лежащую на прямой Ъ. Используя символы е и запишите предложение: «Точка М лежит на прямой Ъ, а точка N не лежит на ней».
2. Начертите прямые а и пересекающиеся в точке М. На прямой а отметьте точку N, отличную от точки М. Являются ли прямые MN и а различными прямыми? Может ли прямая Ъ проходить через точку N1 Ответы обоснуйте.
7 класс
С—1, В—2
1. Начертите прямую и обозначьте её буквой а. Отметьте точку К, лежащую на прямой а. Отметьте точку С, не лежащую на прямой а. Используя символы е и
запишите предложение: «Точка К лежит на прямой а, а точка С не лежит на ней».
2. Начертите прямые тип, пересекающиеся в точке А. На прямой т отметьте точку В, отличную от точки А. Являются ли прямые АВ и т различными прямыми? Может ли прямая п проходить через точку В? Ответы обоснуйте.
7 класс
1. На прямой даны три точки А, В и С. Назовите:
а) пары совпадающих лучей;
б) пары противоположных лучей.
2.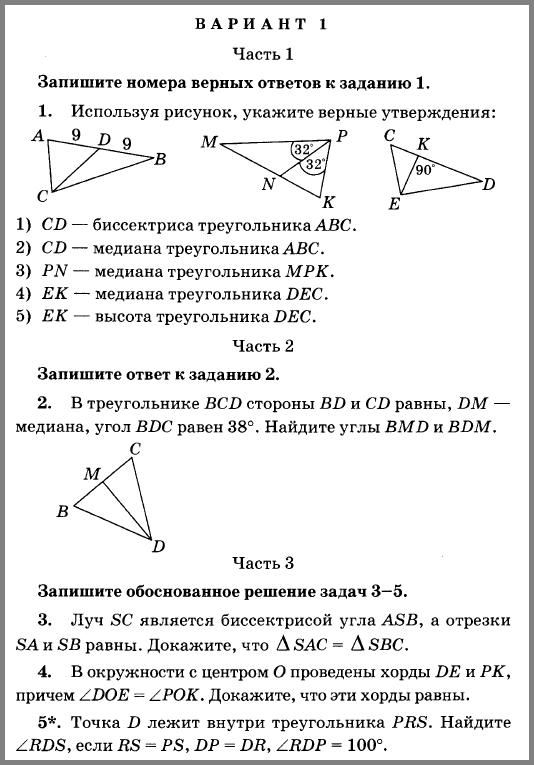 Назовите:
а) луч, который делит угол BOD на два угла;
б) луч, который не делит угол BOD на два угла.
С—2, В—1
С В
7 класс
1. На прямой даны три точки М, N Vi К. Назовите:
а) совпадающие лучи среди лучей MN, NK, МК, КМ;
б) пары противоположных лучей.
2. Назовите:
а) луч, который делит угол РОМ на два угла;
б) луч, который не делит угол РОМ на два угла.
М
С—2, В—2
N К
7 класс
С—3, В—1
1. На луче h с началом в точке О отметьте точки А и В так, чтобы точка А лежала между точками О и Б. Сравните отрезки ОА и ОБ и запишите результат сравнения.
2. Изобразите неразвёрнутый угол АВС и проведите какой-нибудь луч ББ, делящий этот угол на два угла. Сравните:
а) угол АВС и угол ABD;
б) угол АВС и угол ВВС.
Запишите результаты сравнения.
7 класс
С—3, В—2
1. На луче k с началом в точке О отметьте точки М и N так, чтобы точка N лежала между точками О и М. Сравните отрезки ОМ и ON и запишите результат сравнения.
2. Изобразите неразвёрнутый угол DBA и проведите какой-нибудь луч БС, делящий этот угол на два угла.
Назовите:
а) луч, который делит угол BOD на два угла;
б) луч, который не делит угол BOD на два угла.
С—2, В—1
С В
7 класс
1. На прямой даны три точки М, N Vi К. Назовите:
а) совпадающие лучи среди лучей MN, NK, МК, КМ;
б) пары противоположных лучей.
2. Назовите:
а) луч, который делит угол РОМ на два угла;
б) луч, который не делит угол РОМ на два угла.
М
С—2, В—2
N К
7 класс
С—3, В—1
1. На луче h с началом в точке О отметьте точки А и В так, чтобы точка А лежала между точками О и Б. Сравните отрезки ОА и ОБ и запишите результат сравнения.
2. Изобразите неразвёрнутый угол АВС и проведите какой-нибудь луч ББ, делящий этот угол на два угла. Сравните:
а) угол АВС и угол ABD;
б) угол АВС и угол ВВС.
Запишите результаты сравнения.
7 класс
С—3, В—2
1. На луче k с началом в точке О отметьте точки М и N так, чтобы точка N лежала между точками О и М. Сравните отрезки ОМ и ON и запишите результат сравнения.
2. Изобразите неразвёрнутый угол DBA и проведите какой-нибудь луч БС, делящий этот угол на два угла. Сравните:
а) угол DBA и угол ВВС;
б) угол DBA и угол СВ А.
Запишите результаты сравнения.
7 класс
С—4, В—1
1. На прямой Ъ отмечены точки С, D, Е, причём CD = б см, DE = 8 см. Чему может быть равна длина отрезка СЕ7
2. Точка М — середина отрезка АВ, МВ = 4,3 дм. Найдите длину отрезка АВ в миллиметрах.
3. Отрезки PQ и EF пересекаются, точка К лежит на отрезке EF, причём PQ = 21 см, РК = 14 см, QK = 8 см. Является ли точка К точкой пересечения отрезков PQ и EF7 Ответ обоснуйте.
7 класс
С—4, В—2
1. На прямой а отложены точки М, К, N, причём МК = 7 см, KN = 10 см. Чему может быть равна длина отрезка MN1
2. Точка Е — середина отрезка CD, СЕ = 2,8 см. Найдите длину отрезка CD в миллиметрах.
3. Отрезки АВ и CD пересекаются. Точка N лежит на отрезке CD, причём AN = 13 см, NB = 12 см и АВ = 8 см. Является ли точка N точкой пересечения отрезков АВ и СЛ? Ответ обоснуйте.
7 класс
С—5, В—1
1. Начертите луч О А и с помощью транспортира отложите от луча О А углы: Z.AOB = 25®, Z.AOC = 78®. Чему равен угол ВОС1
2.
Сравните:
а) угол DBA и угол ВВС;
б) угол DBA и угол СВ А.
Запишите результаты сравнения.
7 класс
С—4, В—1
1. На прямой Ъ отмечены точки С, D, Е, причём CD = б см, DE = 8 см. Чему может быть равна длина отрезка СЕ7
2. Точка М — середина отрезка АВ, МВ = 4,3 дм. Найдите длину отрезка АВ в миллиметрах.
3. Отрезки PQ и EF пересекаются, точка К лежит на отрезке EF, причём PQ = 21 см, РК = 14 см, QK = 8 см. Является ли точка К точкой пересечения отрезков PQ и EF7 Ответ обоснуйте.
7 класс
С—4, В—2
1. На прямой а отложены точки М, К, N, причём МК = 7 см, KN = 10 см. Чему может быть равна длина отрезка MN1
2. Точка Е — середина отрезка CD, СЕ = 2,8 см. Найдите длину отрезка CD в миллиметрах.
3. Отрезки АВ и CD пересекаются. Точка N лежит на отрезке CD, причём AN = 13 см, NB = 12 см и АВ = 8 см. Является ли точка N точкой пересечения отрезков АВ и СЛ? Ответ обоснуйте.
7 класс
С—5, В—1
1. Начертите луч О А и с помощью транспортира отложите от луча О А углы: Z.AOB = 25®, Z.AOC = 78®. Чему равен угол ВОС1
2. если МК = 10 см, KF = 8 см.
Е
7 класс
С—7, В—2
1. Докажите равенство треуголь
если МК = 10 см, KF = 8 см.
Е
7 класс
С—7, В—2
1. Докажите равенство треугольСборник контрольных работ по геометрии, (9 класс)
СБОРНИК
КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ
9 класс
Пояснительная записка
Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию.
.
Контрольная работа №1 9 класс.
Тема: «Векторы на плоскости».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач скалярное произведение векторов и его свойства, условия перпендикулярности и коллинеарности векторов,
находить координаты вектора и его абсолютную величину, выполнять действия с векторами;
— умение оформлять решение задачи.
I вариант. |
1.Даны точки А(-2;4) и В(5;1).Найдите координаты вектора и его абсолютную величину. 2. Дан параллелограмм АВСD. О- точка пересечения диагоналей. Найдите векторы -, +2, + + 3.Даны векторы (2;0), (1;2), (-3;m). Найдите значение m, при котором векторы А) и -2 перпендикулярны. В) + коллинеарны 4. Даны точки А(-1;4) и В(3;1), С(3;4). Найдите угол между векторами и . 5. Вычислите , если =5, =8, а угол между векторами и равен 600. |
II вариант. |
1. Даны точки А(3;-1) и В(1;4).Найдите координаты вектора АВ и его абсолютную величину. 2. Дан параллелограмм АВСD. О- точка пересечения диагоналей. Найдите векторы — 2 + + + 3. Даны векторы (2;0), (1;2), (-3;m). Найдите значение m, при котором векторы А) и 2 перпендикулярны. В) векторы — коллинеарны. 4. Даны точки А(2;-1) и В(2;3), С(-1;-1). Найдите угол между векторами и 5. Вычислите , если =3, =4, а угол между векторами и равен 600 |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Координаты вектора и его абсолютная величина. | №1, | 20 % | ||
Действия с векторами. Геометрический смысл. | №2 | 20% | ||
Условия перпендикулярности и коллинеарности векторов. | №3 | 20% | ||
Скалярное произведение и его свойства. | №4 | №5 | 40 % | |
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Координаты вектора и его абсолютная величина. | Формула нахождения координат вектора. | 1 балл | 3 балла |
Формула абсолютной величины. | 1 балл | |||
Вычисления. | 1 балл | |||
2 | Действия с векто-рами. Геометричес-кий смысл. | Правило треугольника. | 1 балл | 3 балла |
Правило параллелограмма. | 1 балл | |||
Правило многоугольника. | 1 балл | |||
3 | Условия перпенди-кулярности и кол-линеарности векторов. | Условие коллинеарности векторов и вычисление . | 2 балла | 5 баллов |
Условие перпендикулярности векторов и вычисления. | 2 балла | |||
Оформление решения задачи. | 1 балл | |||
4 | Нахождение косинуса угла между векторами. | Нахождение координат вектора. | 1 балл | 5 баллов |
Знание формулы нахождения косинуса угла между векторами. | 1 балл | |||
Нахождение абсолютной величины. | 1 балл | |||
Вычисление по формуле. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
5 | Скалярное произведение и его свойства. | Скалярный квадрат. | 2 балла | 5 баллов |
ФСУ. | 1 балл | |||
Вычисление. | 1 балл | |||
Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №2 9 класс.
Тема: «Преобразования плоскости».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач свойств симметрии относительно точки и прямой, параллельного переноса;
— знание и умение применять при решении задач свойств подобия;
— умение выполнять чертежи по условию задачи;
— умение оформлять решение задачи.
I вариант. |
1. Найдите координаты точек симметричных данным А(-2;-1), В(1;3) и С(2;0) относительно: А)оси Ох в) оси Оу С) начала координат 2. При параллельном переносе точка А(3;-1) переходит в точку А1(5,-4). В какую точку в результате данного переноса перейдет точка В(-7;0) 3.Стороны треугольника равны 6см, 7см и 8см. Найдите периметр подобного ему треугольника, периметр которого равен 84см. 4. Доказать: МВN АВС. Найти АС. А С 5. Найдите две стороны треугольника, если их сумма равна 91см, а биссектриса угла между ними делит третью сторону в отношении 5:8. |
II вариант. |
1. Найдите координаты точек симметричных данным А(0;-1), В(1;-3) и С(-2;5) относительно: А)оси Ох в) оси Оу С) начала координат 2. При параллельном переносе точка А(-3;-4) переходит в точку А1(7,3). В какую точку в результате данного переноса перейдет точка В(0;5) 3. Стороны треугольника относятся как 2:5:6. Найдите периметр подобного ему треугольника, периметр которого равен 39см. 4. Дано: АО=15см, ВО=8см, АС=27см,DO=10cм , BC=16см. Доказать: AOD COB. Найти АD. 5. Найдите две стороны треугольника, если их разность равна 28см, а биссектриса угла между ними делит третью сторону на отрезки 43см и 29см. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Симметрия относительно точки и прямой. | №1, | 20 % | ||
Параллельный перенос. | №2 | 20% | ||
Подобие треугольников. | №3,№4 | 40% | ||
Подобие треугольников. | №5 | 20 % | ||
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Симметрия относительно точки и прямой. | Симметрия относительно оси Ох. | 1 балл | 3 балла |
Симметрия относительно оси Оу. | 1 балл | |||
Симметрия относительно начала координат. | 1 балл | |||
2 | Параллельный перенос. | Формула, задающая параллельный перенос. | 1 балл | 3 балла |
Вычисление вектора параллельного переноса. | 1 балл | |||
Нахождение точки В 1. | 1 балл | |||
3 | Подобие треугольников. | Запись сторон подобного треугольника. | 1 балл | 5 баллов |
Составление уравнения. | 1 балл | |||
Вычисление коэффициента подобия. | 1 балл | |||
Нахождение сторон подобного треугольника. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
4 | Подобие треугольников. | Применение признака подобия для доказательства. | 2 балла | 5 баллов |
Нахождение стороны. | 2 балла | |||
Оформление решения задачи. | 1 балл | |||
5 | Подобие треугольников. Свойство биссектрисы. | Знание свойства биссектрисы. | 1 балл | 5 баллов |
Выполнение чертежа по условию задачи. | 1 балл | |||
Введение неизвестного и составление уравнения. | 2 балла | |||
Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №6 9 класс.
Тема: «Многоугольники».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач пропорциональность отрезков хорд и секущих, формулы, связывающие стороны, периметр, площадь и радиусы вписанной и описанной окружностей связи величины центрального и вписанного углов
— умение выполнять чертеж по условию задачи;
— умение оформлять решение задачи..
I вариант. |
1. По данным рисунка найдите угол х (О- центр окружности. 2. Дано: AB=0.7 см, ВЕ=0.5 см, СЕ=0.4 см. Найти: DE, DC 3.Внутренний угол правильного многоугольника в 3 раза больше внешнего угла. Найдите сторону многоугольника, если периметр равен 96 см. 4.Сторона правильного треугольника, описанного около окружности, равна 12см. 5.Сторона правильного вписанного многоугольника стягивает в окружности радиуса 6 см дугу длиной 3 см. Найдите периметр многоугольника. |
II вариант. |
1. По данным рисунка найдите угол х (О- центр окружности. 2. Дано: СD=0.8 см, DЕ=0.2 см, AЕ=0.24 см Найти: BE, AB 3.Сторона правильного многоугольника равна 5 см, а его внутренний угол на 108о больше внешнего угла. Найдите периметр многоугольника. 4.Сторона правильного шестиугольника, вписанного в окружность, равна 8см. Найдите сторону квадрата описанного около данной окружность. 5. Точки касания двух соседних сторон описанного многоугольника ограничивают в окружности радиуса 6см дугу длиной 4 см. Найдите периметр многоугольника. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Центральные и вписанные углы. | №1 | 20% | ||
Пропорциональность отрезков хорд и секущих | №2 | 20% | ||
Правильные многоугольники | №3, №4 | №5 | 60% | |
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Центральные и вписанные углы. | Знание связи величины цент-рального и вписанного углов. | 1 балл | 4 балла |
Умение применять. | 1 балл | |||
Нахождение угла. | 1 балл | |||
Сопутствующие пояснения. | 1 балл | |||
2 | Пропорциональность отрезков хорд и секущих. | Знание формулы. | 1 балл | 3 балла |
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
3 | Правильные многоугольники. | Составление уравнения по условию. | 1 балл | 5 баллов |
Знание формулы нахождения уг-ла правильного многоугольника. | 1 балл | |||
Определение числа сторон многоугольника. | 1 балл | |||
Нахождение периметра | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
4 | Формулы, связы-вающие стороны, периметр, площадь и радиусы вписан-ной и описанной окружностей. | Нахождение радиуса окружности. | 2 балла | 5 баллов |
Нахождение стороны многоугольника. | 2 балла | |||
Вычисления и оформление решения задачи. | 1 балл | |||
5 | Правильные многоугольники. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
Определение количества сторон. | 2 балла | |||
Вычисления. | 1 балл | |||
Нахождение периметра. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
Контрольная работа №4 9 класс.
Тема: «Решение треугольников».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач теоремы синусов и косинусов, решать задачи на нахождение неизвестных элементов в треугольнке;
— умение оформлять решение задачи.
I вариант. |
1.В треугольнике АВС =350,=250. Укажите наибольшую сторону треугольника. Ответ объясните. 2. Две стороны треугольника равны 3см и 8см, а угол между ними равен 600. Найдите периметр треугольника. 3. Решите треугольник АВС, если=750,=450, АВ=2см. 4. Диагонали параллелограмма равны 12см и 20см, а угол между ними равен 600. Найдите стороны параллелограмма. 5. В прямоугольном треугольнике один из углов равен α, а катет, прилежащий к данному углу, равен а. Найдите биссектрису прямого угла. |
II вариант. |
1. В треугольнике АВС ⦟В=550, ⦟А=1100. Укажите наименьшую сторону треугольника. Ответ объясните. 2. Две стороны треугольника равны 3см и 5см, а угол между ними равен 1200. Найдите периметр треугольника. 3. Решите треугольник АВС, если ⦟В=300, ⦟С=1050, АС=4см. 4. Стороны параллелограмма равны 10см и 16см, а угол между ними равен 600. Найдите диагонали параллелограмма. 5. В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен β. Найдите биссектрису второго острого угла. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Теорема синусов | №1, | №5 | 40% | |
Теорема косинусов | №2 | №4 | 40% | |
Решение треугольника | №3 | 20% | ||
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Теорема синусов. | Нахождение угла треугольника. | 1 балл | 3 балла |
Знание следствия из теоремы синусов. | 1 балл | |||
Запись ответа. | 1 балл | |||
2 | Теорема косинусов. | Знание теоремы косинусов. | 1 балл | 4 балла |
Умение находить периметр. | 1 балл | |||
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
3 | Решение треугольника. | Нахождение угла треугольника. | 1 балл | 5 баллов |
Применение теоремы синусов. | 2 балла | |||
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
4 | Теорема косинусов. | Определение неизвестных элементов. | 1 балл | 5 баллов |
Нахождение катета. | 1 балл | |||
Нахождение острых углов. | 1 балл | |||
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
5 | Теорема синусов. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
Применение определения биссектрисы. | 1 балл | |||
Нахождение угла. | 1 балл | |||
Нахождение биссектрисы. | 1 балл | |||
Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
Контрольная работа №5 9 класс.
Тема: «Длина окружности и площадь круга».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач формулы площадей круга и его частей, длин окружности и дуги;
— умение оформлять решение задачи.
I вариант. |
1. Длина окружности равна 8π. Вычислить площадь круга, ограниченного данной окружностью.
2. Градусная мера дуги окружности с радиусом 6см равна 300. Вычислите площадь кругового сектора, соответствующего этой дуге. 3.Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 720, а радиус окружности равен 6см. 4. Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 см2. 5.Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4см, а градусная мера дуги равна 600. |
II вариант. |
1. Площадь круга равна 324π. Вычислите длину окружности, ограничивающую данный круг. 2. Градусная мера дуги окружности с радиусом 4см равна 450. Вычислите площадь кругового сектора, соответствующего этой дуге. 3. Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 360, а радиус окружности равен 12см. 4. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 см2. 5. Найдите площ |
Решебник контрольно-измерительные материалы по Геометрии за 9 класс Рурукин А.Н. на Гитем ми
ГДЗ 9 класс Геометрия контрольно-измерительные материалы Рурукинавтор: Рурукин А.Н..
Данное пособие содержит решебник (ГДЗ) контрольно-измерительные материалы по Геометрии за 9 класс . Автора: Рурукин А.Н. Издательство: ВАКО. Полные и подробные ответы к упражнениям на Гитем
ГДЗ к учебнику по геометрии за 7-9 классы Атанасян Л.С. можно скачать здесь.
ГДЗ к учебнику по геометрии за 7-9 классы Погорелов А.В. можно скачать здесь.
ГДЗ к сборнику заданий по геометрии за 9 класс Ершова А.П. можно скачать здесь.
ГДЗ к рабочей тетради по геометрии за 9 класс Глазков Ю.А. можно скачать здесь.
ГДЗ к рабочей тетради по геометрии за 9 класс Мищенко Т.М. можно скачать здесь.
Тесты
Тест 1. Варианты
1 2Тест 2. Варианты
1 2Тест 3. Варианты
1 2Тест 4. Варианты
1 2Тест 5. Варианты
1 2Тест 6. Варианты
1 2Тест 7. Варианты
1 2Тест 8. Варианты
1 2Тест 9. Варианты
1 2Тест 10. Варианты
1 2Тест 11. Варианты
1 2Тест 12. Варианты
1 2Тест 13. Варианты
1 2Тест 14. Варианты
1 2Тест 15. Варианты
1 2Тест 16. Варианты
1 2Девятый класс (9 класс) Вопросы по координатной геометрии для тестов и рабочих листов
Вы можете создавать печатные тесты и рабочие листы из этих Класс 9 Координатная геометрия вопроса! Выберите один или несколько вопросов, установив флажки над каждым вопросом. Затем нажмите кнопку добавить выбранные вопросы к тесту перед переходом на другую страницу.
Предыдущая Страница 1 из 2 Следующие Выбрать все вопросы Найдите точку пересечения [math] x — [/ math] и точку пересечения [math] y — [/ math] графика [math] y = -x + 3 [/ math].- (0,3), (3,0)
- (0,3), (-3,0)
- (0,1), (2,0)
- (0, -1), (-1,0)
Для учащихся 9–10 классов, занимающихся геометрией. Используйте кликер для ответов на вопросы.
Презентация на тему: «Для учащихся 9-10 классов, занимающихся геометрией. Ответьте на вопросы с помощью кликера» — стенограмма презентации:
1 Для учащихся 9-10 классов, занимающихся геометрией. Используйте кликер, чтобы ответить на вопросы.
2 Q1: Что это за теорема? Если три стороны одного треугольника конгруэнтны трем сторонам другого треугольника, то треугольники конгруэнтны A.Конгруэнтность бокового угла-стороны (SAS) B. Конгруэнтность угла-стороны-угла (ASA) C. Сопоставление стороны-стороны-стороны (SSS) D. Конгруэнтность угла-угла-стороны (AAS)
3 Q2: Что это за теорема? Если две стороны и прилегающий угол одного треугольника совпадают с соответствующими частями другого треугольника, треугольники конгруэнтны. A. Конгруэнтность угол-угол-сторона (AAS) B. Сопоставление сторон-угла-стороны (SAS) C. Сопоставление стороны-стороны-стороны (SSS) D.Угол-боковой-угол (ASA) Конгруэнтность
4 Q3: Что это за теорема? Если два угла и включенная сторона одного треугольника совпадают с соответствующими частями другого треугольника, треугольники конгруэнтны. A. Конгруэнтность «угол-сторона-угол» (ASA) B. Сопоставление «сторона-угол-сторона» (SAS) C. Сопоставление «сторона-сторона-сторона» (SSS) D. Конгруэнтность «угол-угол-сторона» (AAS)
5 Q4: Что это за теорема? Если два угла и не включенная сторона одного треугольника конгруэнтны соответствующим частям другого треугольника, треугольники конгруэнтны.A. Сопоставление сторон-сторон-сторон (SSS) B. Сопоставление сторон-угла-сторон (SAS) C. Сопоставление угла-стороны-угла (ASA) D. Сопоставление угла-угла-стороны (AAS)
Пересекающиеся линии. (Координатная геометрия) — Math Open Reference
Пересекающиеся линии. (Координатная геометрия) — Открытый справочник по математике Смысл пересечение из двух непараллельный линии можно найти изуравнения двух линий.
Попробуй это Перетащите любую из 4 точек ниже, чтобы переместить линии.Отметьте, где они пересекаются.
Чтобы найти пересечение двух прямых:
- Для начала нам понадобятся уравнения двух линий. Если у вас нет уравнений, см. Уравнение прямой — форма наклона / пересечения и Уравнение линии — форма точки / уклона (Если одна из линий вертикальная, см. Раздел ниже).
- Тогда, поскольку в точке пересечения два уравнения будут иметь одинаковые значения x и y, мы полагаем два уравнения равными друг другу.Это дает уравнение, которое мы можем решить относительно x
- Мы подставляем это значение x в одно из линейных уравнений (неважно какое) и решаем его относительно y.
Пример
Так, например, если у нас есть две линии, которые имеют следующие уравнения (в форме пересечения наклона):г = 3х-3
y = 2,3x + 4
В точке пересечения они оба будут иметь одинаковое значение координаты y, поэтому мы приравниваем уравнения друг другу:3х-3 = 2.3x + 4
Это дает нам уравнение с одним неизвестным ( x ), которое мы можем решить: Измените порядок, чтобы осталось x терминов3x — 2,3x = 4 + 3
Объединение похожих терминов0,7x = 7
Даватьх = 10
Чтобы найти y, просто установите x равным 10 в уравнении любой строки и решите относительно y: Уравнение для линии (подойдет любая линия)у = 3х — 3
Установите x равным 10г = 30 — 3
Даватьг = 27
Теперь у нас есть как x, так и y, поэтому точка пересечения равна (10, 27)Какую форму уравнения использовать?
Напомним, что линии можно описать форма уклона / пересечения и форма точки / наклона уравнения.Поиск пересечения работает одинаково для обоих. Просто установите уравнения, как указано выше. Например, если у вас есть два уравнения в форме точечного уклона:у = 3 (х-3) + 9
у = 2,1 (х + 2) — 4
просто установите их равными:3 (х-3) + 9 = 2,1 (х + 2) — 4
и действуйте, как указано выше, решая для x, а затем подставляя это значение в любое уравнение, чтобы найти y.Два уравнения не обязательно должны иметь одинаковую форму. Просто приравняйте их друг к другу и действуйте обычным образом.
Когда одна линия вертикальная
Когда одна из линий вертикальна, у нее нет определенного наклона, поэтому ее уравнение будет выглядеть примерно как x = 12. См. Раздел Вертикальные линии (координатная геометрия). Мы находим пересечение несколько иначе. Предположим, у нас есть прямые, уравнения которых| y = 3x-3 | Линия с уклоном вверх и вправо |
| х = 12 | Вертикальная линия |
На вертикальной линии все точки на ней имеют координату x 12 (определение вертикальной линии), поэтому мы просто устанавливаем x равным 12 в первом уравнении и решаем его относительно y.
Уравнение для линии:
у = 3х — 3
Установите x равным 12 Используя уравнение для второй (вертикальной) линииг = 36 — 3
Даватьг = 33
Итак, точка пересечения находится в (12,33).
Если обе линии вертикальные, они параллельны и не пересекаются (см. Ниже).
Когда они параллельны
Когда две прямые параллельны, они нигде не пересекаются. Если вы попытаетесь найти пересечение, уравнения будут абсурдными.Например, строки y = 3x + 4 и y = 3x + 8 параллельны, потому что их наклоны (3) равны. См. Параллельные линии (координатная геометрия). Если вы попробуете описанный выше процесс, вы напишете 3х + 4 = 3х + 8. Очевидная невозможность.Сегменты и лучи могут вообще не пересекаться
Рис 1. Сегменты не пересекаются
В случае двух непараллельных линий пересечение всегда будет где-то на линиях. Но в случае сегменты линии или же лучи которые имеют ограниченную длину, они могут не пересекаться.
На рис.1 мы видим два отрезка, которые не перекрываются и поэтому не имеют точки пересечения. Однако если вы примените к ним описанный выше метод, вы найдете точку, где они пересеклись бы, если бы они были достаточно длинными.
Что попробовать
- На приведенной выше диаграмме нажмите «сброс».
- Перетащите любую из точек A, B, C, D и обратите внимание на место пересечения линий.
- Перетащите точку, чтобы получить две параллельные линии, и обратите внимание, что они не пересекаются.
- Нажмите «скрыть детали» и «показать координаты». Переместите точки в любое новое место, где перекресток все еще виден. Рассчитайте наклоны линий и точки пересечения. Нажмите «Показать подробности», чтобы проверить результат.
Ограничения
Для большей ясности в приведенном выше апплете координаты округлены до целых чисел, а длины округлены до одного десятичного знака. Это может привести к небольшому отклонению расчетов.
Подробнее см.


 Рефлексия учебной деятельности
Рефлексия учебной деятельности




 Дано: АВ=24см, ВС=16см, МВ=15см,NC=6cм , MN=20см.
Дано: АВ=24см, ВС=16см, МВ=15см,NC=6cм , MN=20см.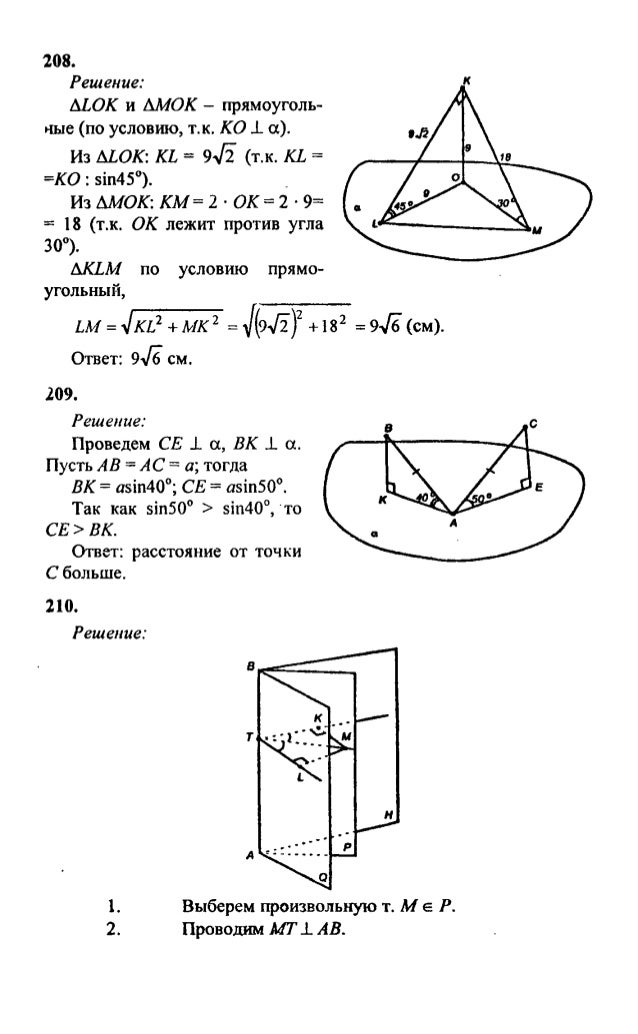
 Свойство биссектрисы.
Свойство биссектрисы.


 Найдите сторону правильного шестиугольника, вписанного в данную окружность.
Найдите сторону правильного шестиугольника, вписанного в данную окружность.