Страница 142 №540-548 ГДЗ к учебнику «Математика» 5 класс Дорофеев, Шарыгин, Суворова
Задание 540. Для каждого утверждения укажите рисунок, который его опровергает (рис. 7.11).
а) Прямоугольник − это четырехугольник, у которого есть две пары равных сторон.
б) Квадрат − это четырехугольник, у которого все стороны равны.
в) Прямоугольник − это четырехугольник, у которого есть прямые углы.
Ответ
а) Рисунок 2
б) Рисунок 3
в) Рисунок 1
Задание 541. Найдите периметр квадрата со стороной, равной:
а) 5 см;
б) 7 см 5 мм;
в) 10 см 3 мм.
Решение
а) P = 5 * 4 = 20 см
б) P = 7 см 5 мм * 4 = 75 мм * 4 = 300 мм = 30 см
в) P = 10 см 3 мм * 4 = 103 мм * 4 = 412 мм = 41 см 2 мм
Задание 542. Найдите периметр прямоугольника со сторонами, равными:
а) 22 м и 14 м;
б) 3 м 45 см и 1 м 70 см.
Решение
а) P = 2 * (22 + 14) = 2 * 36 = 72 м
б) P = 2 * (3 м 45 см + 1 м 70 см) = 2 * 515 см = 1030 см = 10 м 30 см
Задание 543. а) Периметр прямоугольника равен 36 см, длина одной стороны − 10 см. Найдите длину другой стороны прямоугольника.
б) Периметр квадрата равен 36 см. Чему равна его сторона?
Решение
а) 1) 36 : 2 = 18 (см) − полупериметр прямоугольника;
2) 18 − 10 = 8 (см) − длина другой стороны прямоугольника.
Ответ: 8 см.б) 36 : 4 = 9 (см) − периметр квадрата.
Ответ: 9 см.
Задание 544. Разметили два земельных участка прямоугольной формы. Размеры одного − 110 м и 190 м, а другого − 150 м и 140 м. У какого участка длина ограды будет больше?
Решение
1) 2 * (110 + 190) = 2 * 300 = 600 (м) − длина ограды первого участка;
2) 2 * (150 + 140) = 2 * 290 = 580 (м) − длина ограды второго участка.
3) 600 > 580
Ответ: длина ограды первого участка больше.
Задание 545. Скопируйте рисунок 7.12 на лист нелинованной бумаги и раскрасьте его по−своему. Расскажите алгоритм построения.
Решение
Нужно построить квадрат и поделить его на 4 равные части. Затем при помощи циркуля построить дуги с вершинами в серединах сторон квадрата.
Задание 546. Начертите в тетради какой−нибудь прямоугольник с периметром, равным 24 см. Укажите длины его сторон. Начертите еще один прямоугольник с таким же периметром, но с другими сторонами. Может ли среди таких прямоугольников быть квадрат?
Решение
P = 2 * (8 + 4) = 2 * 12 = 24 (см)
P = 2 * (7 + 5) = 2 * 12 = 24 (см)
24 : 4 = 6 (см) − сторона квадрата.
Задание 547. Представьте, что вам надо определить периметр вашей классной комнаты, а у вас нет измерительных инструментов.
Решение
Определите на глаз длину комнаты, а затем ширину. Далее найдите периметр.
Задание 548. Представьте, что вам надо начертить план комнаты, имеющей форму прямоугольника, длина которого равна 4 м, ширина 3 м. Пусть сторона одной клетки тетради изображает 1 м. Начертите такой прямоугольник. Затем начертите прямоугольник с такими же размерами, если 1 м изображается отрезком, равным 1 см.
Решение
МАОУ ЛИЦЕЙ № 142 Г.ЧЕЛЯБИНСК
Уважаемые гости нашего сайта!
В связи с проведением ремонтных работ телефон 7 (351) 232-96-71 не работает!
Для связи с нами вы можете воспользоваться электронной почтой [email protected].
6 сентября начинаются занятия в «Школе будущего первоклассника» (Подробнее)
«Школа будущего первоклассника» лицея объявляет набор дошкольников в группы по подготовке
к школе на 2021/2022 учебный год. (Подробнее)
(Подробнее)
«Технологии будущего» в образовательном комплексе «Смена»
«Образовательный Комплекс «Смена» по адресу Степана Разина 8, приглашает детей с 9 лет для изучения «Технологий будущего». Подробнее
Заявление на возврат и согласие на обработку данных
«Южно-Уральский государственный гуманитарно-педагогический университет» приглашает учащихся 9, 10, 11 классов в группы по подготовке к итоговой аттестации в форме и по материалам (ЕГЭ, ОГЭ, ГВЭ). Подробнее
Подробнее
3 сентября в 10-х классах прошел необычный урок «Физика и музыка». Десятиклассники МАОУ «Лицей № 142 г. Челябинска» получили уникальную возможность увидеть и услышать музыкальные портреты физиков.
Урок подготовили и провели Свирская Людмила Моисеевна музыкант и преподаватель Южно-Уральского государственного гуманитарно-педагогического университета, доцент кафедры физики и методики обучения физики, кандидат физико-математических наук и Шефер Ольга Робертовна, доктор педагогических наук, профессор Южно-Уральского государственного гуманитарно-педагогического университета.
Людмила Моисеевна рассказала учащимся, как можно языком музыки охарактеризовать деятельность выдающихся физиков. Ребята узнали об известных ученых-физиках, которые не только занимались наукой и совершали великие открытия, сидя в своих лабораториях, но и были успешными музыкантами, в их числе: один из основателей современной теоретической физики Альберт Эйнштейн, основоположник квантовой теории Макс Планк, основатель матричной квантовой механики Вернер Гейзенберг, автор фундаментальных работ по термодинамике необратимых процессов Илья Романович Пригожин, глава уральской школы физиков-теоретиков Сергей Васильевич Вонсовский.
Выражаем благодарность Людмиле Моисеевне и Ольге Робертовне за подготовку и проведение познавательного интересного урока.
На торжественной линейке произошло очень памятное и знаковое событие. Почетные гости линейки — первый заместитель председателя Комитета Законодательного Собрания по строительной политике и жилищно-коммунальному хозяйству, депутат Законодательного собрания Челябинской области Александр Александрович Мотовилов и депутат Челябинской городской думы Максим Константинович Калинин вручили плакетку и нагрудный знак учителю физической культуры Вадиму Михайловичу Позднякову. Повод более чем приятный, Вадим Михайлович стал лауреатом Премии Законодательного Собрания Челябинской области в сфере физической культуры и спорта.
Отметим, Премия Законодательного Собрания Челябинской области в сфере физической культуры и спорта является ежегодной и присуждается за добросовестный и безупречный труд, высокое профессиональное мастерство, создание благоприятных условий для всестороннего развития личности.
1 сентября в лицее прошел настоящий праздничный бум!
Целый калейдоскоп мероприятий прошел в этот день у лицеистов. В статье подробно о том, как прошел первый осенний день.
Спешите найти себя в альбоме
19 августа был запущен уникальный проект
1. Онлайн-каникулы в Челябинске — это море конкурсов, жаркие состязания, яркие призы! Возможность продлить летние каникулы аж до 19 сентября, но в онлайне!
2. Отличный шанс прокачать свои соцсети и научиться генерировать контент.
Прояви себя и получи билет на финальное шоу в Челябинске!
Чтобы принять участие, нужно выполнить первое задание:
— быть подписчиком Онлайн-каникулы в Челябинске
— рассказать своим друзьям про онлайн-каникулы в Челябинске в видео-формате (также можно сделать репост анонса или опубликовать пост с афишей проекта) в своём личном аккаунте с отметкой @mol_chelyabinsk и хэштегом: #КаникулыВЧелябинске
Срок проведения: с 19.08.2021 по 19.09.2021. Победителей определит жюри среди тех участников, которые выполнят больше всего заданий. Призы можно получить на финальном шоу или по почте. От тебя всего-то и нужно: выполняй задания и получай призы! iPhone 12, AirPods, электросамокат, гаджеты Xiaomi и многое другое!
Организаторы конкурса: Всероссийская общественная организация «Союз добровольцев России» и сетевое СМИ «МОЛ.РФ (Молодёжь в онлайне)». Подробные правила участия: vk.com/@mol_chelyabinsk-rules
Номер №142 — гдз по математике 4 класс Моро, Бантова, Бельтюкова
Умножение и деление на однозначное число
Задачи-расчеты:
1 2 3Странички для любознательных:
1 2 3 4Умножение на числа, оканчивающиеся нулями
Странички для любознательных:
1 2 3 4 5 6Страница 23, Проверочные работы:
1 2Странички для любознательных:
1 2 3 4 5 6 7 8 9 10 11 12Деление на числа, оканчивающиеся нулям
Страница 37, Проверочные работы:
1 2Математика вокруг нас:
1 2 3 4 5 6Умножение на двузначное и трехзначное число
Странички для любознательных:
1 2 3 4 5Страница 56, Проверочные работы:
1 2Деление на двузначное число
Странички для любознательных:
1 2 3 4 5 6Деление на трехзначное число
Странички для любознательных:
1 2 3 4 5 6 7Страница 86, Нумерация:
Страница 89, Выражения и уравнения:
Страница 90, Сложение и вычитание:
Страница 92, Умножение и деление:
Страница 94, Правила о порядке выполнения действий:
Страница 95, Величины:
Страница 96, Геометрические фигуры:
Страница 97, Задачи:
Страница 6, Странички для любознательных:
1 2 3 4 5 6 7 8 9 10 11 12 13 14Страница 104, Доли:
Страница 105, Единицы площади — ар и гектар:
Страница 108, Диагонали прямоугольника(квадрата), и их свойства:
Страница 110, Куб:
Страница 111, Прямоугольный параллелепипед:
Страница 112, Пирамида:
Страница 113, Цилиндр:
Страница 113, Шар:
Тексты для контрольных работ
Страница 114, Задания базового уровня:
1 2 3 4 5 6 7 8Страница 115, Задания повышенного уровня сложности:
1 2 3 4 5 6 7 8 9Число 142 — Факты о целом числе
Как выглядит число 142?
Эта визуализация показывает соотношение между двумя простыми множителями (большие кружки) и четырьмя делителями.
142 — четное составное число. Он состоит из двух разных простых чисел, перемноженных. Всего у него четыре делителя.
Разложение на простые множители 142:
2
× 71Ниже приведены интересные математические факты о числе 142 из базы данных Numbermatics.
Быстрые ссылки:имен Факторы Делители Базы Корнеплоды Весы Веселье
Имена 142
- Кардинал: 142 можно записать как Сто сорок два.
Научная нотация
- Научная нотация: 1.42 × 10 2
Факторы 142
- Количество различных простых множителей ω ( n ): 2
- Общее количество простых множителей Ω ( n ): 2
- Сумма простых множителей: 73
Делители 142
- Число делителей d (n) : 4
- Полный список делителей:
- Сумма всех делителей σ ( n ): 216
- Сумма собственных делителей (ее аликвотная сумма) s ( n ): 74
- 142 является недостаточным числом, потому что сумма его собственных делителей (74) меньше его самого.
 Его дефицит 68
Его дефицит 68
Базы 142
- Двоичный: 10001110 2
- Шестнадцатеричный: 0x8E
- База-36: 3 года
Квадраты и корни 142
- 142 в квадрате (142 2 ) равно 20164
- 142 куба (142 3 ) это 2863288
- Квадратный корень из 142 равен 11,9163752879 .
- Кубический корень из 142 равен 5,2171034461 .
Весы и сравнения
Насколько велик 142?- 142 секунды равно 2 минутам 22 секундам.
- Чтобы сосчитать от 1 до 142, вам потребуется около одиннадцати секунд.
Это очень приблизительная оценка, основанная на скорости речи в полсекунды на каждый третий порядок величины. Если вы говорите быстро, вы, вероятно, сможете сказать любое случайно выбранное число от единицы до тысячи примерно за полсекунды. Очевидно, что для определения очень больших чисел требуется больше времени, поэтому мы добавляем полсекунды на каждые дополнительные x1000.
 (Мы не учитываем непроизвольные паузы, перерывы в туалет или необходимость спать в наших расчетах!)
(Мы не учитываем непроизвольные паузы, перерывы в туалет или необходимость спать в наших расчетах!) - Куб объемом 142 кубических дюйма будет около 0.4 фута высотой.
Развлекательная математика с 142
- 142 назад — это 241
- Количество десятичных цифр: 3
- Сумма цифр 142 равна 7.
- Скоро будет больше!
Ссылка на эту страницу
HTML: чтобы создать ссылку на эту страницу, просто скопируйте и вставьте ссылку ниже в свой блог, веб-страницу или электронную почту.
Число 142 — Факты о целых числахBBCODE: чтобы разместить ссылку на эту страницу в сообщении или поле для комментариев на форуме, просто скопируйте и вставьте код ссылки ниже:
[url = https: // числовая математика.com / n / 142 /] Number 142 — Факты о целых числах [/ url]Цитируйте эту страницу
MLA style:
«Число 142 — Факты о целых числах». Numbermatics.com. 2021. Интернет. 15 сентября 2021 г.
Numbermatics.com. 2021. Интернет. 15 сентября 2021 г.
APA style:
Numbermatics. (2021 г.). Число 142 — Факты о целом числе . Получено 15 сентября 2021 г. с https://numbermatics.com/n/142/
Чикагский стиль:
Numbermatics. 2021. «Число 142 — Факты о целых числах». https://numbermatics.com/n/142/
Имеющаяся у нас информация для 142 включает математические данные и числовую статистику, рассчитанную с использованием стандартных алгоритмов и методов.Мы все время добавляем больше. Если вы хотели бы увидеть какие-либо функции, свяжитесь с нами. Информация предоставлена для образовательного использования, интеллектуального любопытства и развлечения!
Ключевые слова: делители 142, математика, множители 142, учебная программа, школа, колледж, экзамены, университет, разложение на простые множители 142, STEM, наука, технология, инженерия, физика, экономика, калькулятор, сто сорок два.
Фрэнк Торн
Фрэнк ТорнФрэнк Торн Университет Южной Каролины |
Текущее обучение (осень 2021 г.

Математика 532, Современная геометрия.
Математика 701, Аспирантура по алгебре I.
Предыдущий:
Math 550 (вектор), Math 788 (Эл. Кривые), Математика 142 (Calc II), Математика 782 (Распределение простых чисел), Math 374 (Дискретный для CS), Math 701-2 (Alg I / II), Математика 141 (Расчет I), Математика 735 (Группы Ли), Math 788 (Эл. Кривые), Математика 141 (Расчет I), Математика 544 (Лин Алг), Math 547 / 702I (Alg II), Math 374 (Дискретный для CS), Math 546 (Alg I), Математика 142H, (Calc II), Математика 788G (GON), Математика 580 (Введение в NT), Математика 142 (Calc II), Математика 788P (Alg NT), Математика 531 (Геометрия), Математика 141 (Расчет I), Математика 574 (дискретный), Математика 141 (Расчет I), Math 782 (Anal NT), (ссылки 2020-21 будут добавлены).
Математика игровых шоу (с примечаниями к курсу — не стесняйтесь использовать!)
Я занимаюсь теорией чисел. Некоторые из моих конкретных интересов:
- Классическая аналитическая теория чисел. Моей первой задачей в аспирантуре было прочитать весь Давенпорт. Меня интересуют методы сита, L-функции и связанные темы, а также их классические приложения, а также приложения, выходящие за рамки их традиционных настроек.
- Распределение числовых полей, кручение групп классов и связанные темы.Я особенно интересует это с аналитической точки зрения, включая дзета-функций Синтани , связанных с предоднородными векторными пространствами . Меня также интересуют другие точки зрения на эти вопросы: теория полей классов и теория Куммера; принцип отражения Шольца; алгебро-геометрические перспективы по этим темам; и другие связанные с этим точки зрения.
Резюме.
Семинары в Университете Южной Каролины:
(ссылки устарели)Алгебраическая геометрия, арифметическая геометрия и коммутативная алгебра по пятницам после обеда.
Теория чисел, в четверг утром.
Коллоквиум.
Аспирантам также предлагается посещать выпускной коллоквиум.
См. Здесь список других семинаров, проводимых в USC.
Публикации и препринты:
1. Ограниченные промежутки между произведениями простых чисел с приложениями к эллиптическим кривым и идеальные группы классов.
Уведомления о международных исследованиях в области математики (2008), 41 с.
2.
Неравномерности в распределении простых чисел в функциональных полях.
Журнал теории чисел 128 (2008), 1784-1794.
3. Пузыри конгруэнтных простых чисел.
Математические материалы Кембриджского философского общества 157 (2014), нет. 3, 443–456.
4. Принцип неопределенности для функциональных полей.
Журнал теории чисел 131 (2011), 1363-1389.
5. Матрицы Майера за пределами Z.
Протоколы
Конференция по целым числам 2007.
6.
Аналитические свойства дзета-функций Шинтани.
Труды
симпозиум RIMS по автоморфным формам, автоморфным представлениям и связанным темам (Киото, 2010).
7. Вторичный член в счетной функции для кубических полей, с Такаши Танигучи.
Duke Mathematical Journal 162 (2013), нет.13, 2451-2508.
8.
Дзета-функция Шинтани не является
конечная сумма произведений Эйлера.
Труды Американского математического общества , 142 (2014), нет. 6, 1943-195 гг. 2.
9. Орбитальные L-функции для пространства бинарных кубических форм, с Такаши Танигучи.
Канадский математический журнал 65 (2013), нет. 6,
1320-1383.
10. Четыре точки зрения на вторичные члены в теоремах Давенпорта-Хейльбронна.
Целые числа, том 12B, Труды конференции по целым числам, 2011 г.
11. Оценка ошибок для подсчета полей S_3-секстических чисел с Такаши Танигучи.
Международный журнал теории чисел 10 (2014), вып. 4,
935-948.
12. Книжный обзор Opera de Cribro и Введение в ситовые методы и их применение .
Бюллетень Американского математического общества 50 (2013), нет. 2, 359-366.
13. О существовании представлений Галуа большой степени для полей малого дискриминанта
с Джереми Роузом.
Тихоокеанский математический журнал 271 (2014), нет. 1, 243-256.
14. Ряды Дирихле, связанные с кубическими полями с заданной квадратичной резольвентой, с Анри Коэном.
Мичиганский математический журнал 63 (2014), нет. 2, 253-273.
15. Ряды Дирихле, ассоциированные с полями четвертой степени с заданной резольвентой, с Анри Коэном.
Исследования в области теории чисел 2 (2016), ст. 29, 40 с.
16. Нули L-функций вне критической полосы, Эндрю Букер.
Алгебра и теория чисел 8 (2014), вып. 9, 2027-2042.
17. Тождества для расширений полей, обобщающих отношения Оно-Накагавы, с
Анри Коэн и Симон Рубинштейн-Сальзедо.
Compositio Mathematica 151 (2015), вып. 11, 2059-2075.
18. Количество разветвленных простых чисел в числовых полях малой степени,
с Робертом Лемке Оливером.
Труды Американского математического общества 145 (2017), вып. 8, 3201–3210.
19. Аналитическая теория чисел и методы дзета-функции.
Поданный. Запрошено для включения в Материалы Летней школы 2014 г.
по подсчету арифметических объектов, Монреаль.
20. Орбитальные экспоненциальные суммы для предоднородных векторных пространств,
с Такаши Танигучи.
Американский журнал математики .
Журнал Лондонского математического общества, № , чтобы выйти.
22. Границы на 2-кручение в группах классов числовых полей и целых точек на эллиптических
кривые.
С Манджулом Бхаргавой, Арулом Шанкаром, Такаши Танигучи, Якобом
Цимерман и Юнцян Чжао.
Журнал Американского математического общества, № , чтобы выйти.
23. Уровни распределения решетовых задач в предоднородных векторных пространствах,
с Такаши Танигучи.
Mathematische Annalen, , чтобы появиться.
24. Распределение полей КМ G-Вейля и гипотеза Колмеса,
с Адрианом Баркеро-Санчесом и Риадом Масри.
Поданный.
25. Равномерные оценки для подсчета точек решетки и частичных сумм дзета-функций,
с Дэвидом Лоури-Дуда и Такаши Танигучи.
Поданный.
26. Ранговый рост эллиптических кривых в неабелевых расширениях,
с Робертом Лемке Оливером.
Уведомления о международных математических исследованиях, , чтобы появиться.
27. Верхние оценки многочленов с малой группой Галуа,
с Робертом Лемке Оливером.
Математика, появляться.
28. Улучшены нижние оценки количества полей с альтернированной группой Галуа,
с Аароном Ландесманом и Робертом Лемке Оливером.
Поданный.
29.
Гипотеза Малла для G × A, где G = S_3, S_4, S_5,
с Риадом Масри, Вэй-Лун Цай и Цзюя Ван.
Поданный.
30.
Верхние оценки числовых полей заданной степени и ограниченного дискриминанта,
с Робертом Дж. Лемке Оливером.
Поданный.
31.
Считая квинтичные поля с родом номер один,
с Кевином Дж. Макгауном и Амандой Такер.
Поданный.
32.
Асимптотические тождества для аддитивных сверток сумм делителей,
с Робертом Дж.Лемке Оливер и Санроуз Шреста.
Будет представлено в ближайшее время.
Еще несколько в стадии подготовки.
Предстоящая / недавняя профессиональная деятельность:
Международная конференция по теории чисел и дискретной математике, Кочи, Индия, 11-14 декабря 2020 г.
Failed Login
Failed Login Спасибо, что посетили Encyclopædia Britannica Online .
Сожалеем, но нам не удалось подтвердить ваш доступ.
Если вы знаете свое имя пользователя и пароль, введите их ниже. (Обратите внимание, что пароли чувствительны к регистру).
Если вам нужна помощь, обратитесь в службу поддержки.
Для индивидуальных членовНужна помощь? Посетите нашу страницу часто задаваемых вопросов, чтобы получить ответы на общие вопросы.Или вы можете связаться со службой поддержки клиентов Britannica по электронной почте, используя нашу онлайн-форму справки, или по телефону или факсу. Персонал службы поддержки клиентов доступен с 8:00 утра. до 18:00. Центральное время США, понедельник-пятница.
- Телефон (США и Канада): (800) 323-1229
- Телефон (для всех других стран): (312) 347-7159
- Факс: (312) 294-2104
Школы, библиотеки и учреждения
Если вы являетесь подписчиком и считаете, что получили это сообщение по ошибке, обратитесь к системному администратору. Служба технической поддержки Britannica по адресу 1.800.621.3900 доб. 7160, или отправьте запрос в службу поддержки Britannica.
Если вы не являетесь подписчиком, но хотели бы получить дополнительную информацию о доступе к предварительному просмотру, обратитесь в офис продаж Britannica. В Северной и Южной Америке звоните по телефону 1.800.621.3900, напишите нам, или посетите www.info.eb.com. По всем другим регионам мира обращайтесь в соответствующий местный офис.
Вниманию пользователей «Афин»: если вы являетесь пользователем системы управления доступом «Афины»,
, пожалуйста, щелкните здесь, чтобы войти на сайт Афин.Пользователи Афин должны войти на сайт Афин перед доступом к сайту.
Математический колледж — CLEP | Совет колледжа
Обзор
Экзамен по математике в колледже охватывает материал, который обычно преподается в курсе колледжа для нематематических специальностей и специальностей в областях, не требующих углубленных знаний математики.
Экзамен содержит примерно 60 вопросов, на которые нужно ответить за 90 минут. Некоторые из этих вопросов представляют собой предварительные вопросы, которые не будут оцениваться.
Требуемые знания и навыки
Вопросы на экзамене по математике в колледже требуют, чтобы кандидаты продемонстрировали следующие способности в примерных пропорциях:
- Решение рутинных, простых задач (около 50% экзамена)
- Решение нестандартных задач, требующих понимания концепций и применения навыков и концепций (около 50% экзамена)
Научный калькулятор
Научный калькулятор TI-30XS MultiView ™ интегрирован в программу экзамена и доступен студентам в течение всего периода тестирования.
Чтобы использовать калькулятор во время экзамена, студенты должны выбрать значок Калькулятор . Информация об использовании калькулятора доступна на значке Help на вкладке Calculator . Ожидается, что студенты знают, как и когда правильно пользоваться калькулятором.
Посетите ETS, чтобы узнать больше и попрактиковаться в использовании научного калькулятора. Предмет экзамена по математике в колледже основан на следующих темах.Проценты рядом с основными темами указывают приблизительный процент экзаменационных вопросов по этой теме.
Алгебра и функции (20%)
1- Решение уравнений, линейных неравенств и систем линейных уравнений аналитическими и графическими методами
- Интерпретация, представление и оценка функций: числовые, графические, символьные и описательные методы
- Графики функций: смещения, горизонтальные и вертикальные отражения и симметрия относительно оси x, оси y и начала координат
- Линейный и экспоненциальный рост
- Приложения
Подсчет и вероятность (10%)
- Задачи подсчета: правило умножения, комбинации и перестановки
- Вероятность: объединение, пересечение, независимые события, взаимоисключающие события, дополнительные события, условные вероятности и математическое ожидание
- Приложения
Анализ и статистика данных (15%)
- Интерпретация и представление данных: таблицы, гистограммы, линейные диаграммы, круговые диаграммы, круговые диаграммы, диаграммы рассеяния и гистограммы
- Числовые сводки данных: среднее (среднее), медиана, мода и диапазон
- Стандартное отклонение и нормальное распределение (только концептуальные вопросы)
- Приложения
Финансовая математика (20%)
- Проценты, изменение в процентах, наценки, скидки, налоги, прибыль и убыток
- Проценты: простые, сложные, непрерывные проценты, эффективная процентная ставка, эффективная годовая доходность или годовая процентная ставка (APR)
- Текущая стоимость и будущая стоимость
- Приложения
Геометрия (10%)
- Свойства треугольников и четырехугольников: периметр, площадь, подобие и теорема Пифагора
- Параллельные и перпендикулярные прямые
- Свойства окружностей: окружность, площадь, центральные углы, вписанные углы и секторы
- Приложения
Логика и наборы (15%)
- Логические операции и утверждения: условные утверждения, союзы, дизъюнкции, отрицания, гипотезы, логические выводы, обратные, обратные, контрпримеры, контрапозитивы и логическая эквивалентность
- Связи множеств, подмножества, непересекающиеся множества, равенство множеств и диаграммы Венна
- Операции над множествами: объединение, пересечение и дополнение
- Приложения
Числа (10%)
- Свойства чисел и их операции: целые и рациональные, иррациональные и действительные числа (включая распознавание рациональных и иррациональных чисел)
- Элементарная теория чисел: множители и делимость, простые и составные числа, нечетные и четные целые числа, а также основная теорема арифметики
- Измерение: преобразование единиц измерения, экспоненциальное представление и числовая точность
- Абсолютное значение
- Приложения
1 Рассматриваются следующие типы функций: линейные, полиномиальные, радикальные, экспоненциальные, логарифмические и кусочно определенные.
Обучение математике | Совершенное и простое числа
Идеальное число: Среди различных типов чисел, которые мы изучаем в математике, Идеальное число — одно из самых увлекательных и интересных чисел. Если сумма всех положительных делителей или множителей, исключая само число, равна данному числу, то это число называется Совершенным числом. Иногда его называют идеальным или полным числом. Математически положительное целое число «n» называется Совершенным числом, если o (n) = 2n, где «o» — маленькая сигма.
Пример: Положительные делители 6 (исключая само число) равны 1, 2 и 3, сумма всех положительных делителей (1 + 2 + 3) = 6, что равно самому числу. Следовательно, «6» — это наименьшее совершенное число.
Примерно за 300 лет до нашей эры греческий математик Евклид показал в Книге элементов IV, что если (2m-1) — простое число, то (2m-1) 2m-1 — совершенное число. Первые четыре совершенных числа, то есть 6, 28, 496 и 8128, были единственными, известными ранней греческой математике, а математик Никомах (introductio Arithmeticae) отметил 8128 еще в 100 году нашей эры.Только эти четыре совершенных числа меньше 10 000. Но пятый Perfect No. 33,550,336 = 212 (213-1) был изобретен египетским математиком Исмаилом ибн Фаллусом (1194–1252) почти через 1700 лет после последнего изобретения. Исмаил упомянул следующие два совершенных числа: 8,589,869,056 = [216 (217 — 1)] и 137, 438, 691, 328.
В 1588 году итальянский математик Пьетро Катальди также определил шестое (8, 589, 869, 056) и седьмое (137, 438, 691, 328) совершенные числа, а также доказал, что каждое совершенное число, полученное из правила Евклида, оканчивается на 6 или 8.Возможно, вы заметили, что все идеальные числа — четные.
Первые четыре совершенных числа образуются по формуле 2m- 1 (2m-1), где m является простым числом, как показано ниже:
Если m = 2, то 21 (22-1) = 6
Если m = 3, то 22 (23-1) = 28
Если m = 4, то 24 (25-1) = 496
Если m = 7, то 26 ( 27 — 1) = 8128
Никомах (60–120 гг. Н. Э.) Предположил, что каждое совершенное число имеет вид 2m — 1 (2m — 1), где (2m — 1) простое число.
В XVIII веке Леонард Эйлер доказал, что формула 2m — 1 (2m-1) дает все четные совершенные числа.Таким образом, существует взаимно однозначное соответствие между четным совершенным числом и простыми числами Мерсенна, каждое простое число Мерсенна порождает одно четное совершенное число, и наоборот. Помните, что простые числа вида (2m-1), m — простое число, известны как простые числа Мерсенна, после того, как монах 17-го века Марин Мерсенн ввел эту формулу, он изучал теорию чисел и совершенные числа, а также имел форму 2m1. (2m-1), каждое четное совершенное число является (2m1) -м треугольным числом (и, следовательно, равно сумме целых чисел от 1 до 2m — 1) и 2m-1-м гексагональным числом.
Кроме того, каждое четное совершенное число, за исключением 6, является (2m + 1) / 3-м центрированным неагональным числом и равно сумме первых двух нечетных кубиков.
Остается без ответа вопрос, существует ли какое-нибудь нечетное совершенное число, хотя были получены различные результаты. В 1496 году Жак Лефевр заявил, что правило Евклида дает все совершенные числа, подразумевая, таким образом, отсутствие нечетного совершенного числа. Совсем недавно Карл Померанс представил эвристический аргумент, предполагающий, что на самом деле не должно существовать нечетного совершенного числа.
Пара чисел считается дружной, если каждое из них является суммой собственных делителей других чисел.
Наименьшая пара — 220 и 284. Разложение 220 на простые множители = 22 x 5 x 11
Сумма собственных делителей = 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
И аналогично 284 = 22 × 71 и сумма его собственных делителей = 1 + 2 + 4 + 71 + 142 = 220
Эти числа имеют особое влияние на установление союза и дружбы между людьми. Сабит ибн Курра (ок. 850 г.) в своей книге об определении Дружественных чисел отметил, что если вы выберете так, что каждое из выражений a = 3.2P-1, b = 3.2P-1 — 1 и c = 9.22P-1 — 1 — это простое число, тогда 2Pab и 2PC — дружественные числа. Вторая пара, 17 296 и 18 416, была обнаружена Ибн аль-Банной (1256 — 1321) и повторно описана Пирре де Ферма в 1636 году. Декарт нашел третью пару 9 363 584 и 9 437 056, используя формулы Табита в этом случае P = 7. Теперь другой тип. из дружной пары — paganini Дружная пара, 1184 и 1210, названа в честь Николо Паганини, открывшего их в 1866 году. С помощью компьютеров было найдено более 7500 дружеских пар.
ПРЕМЬЕРНЫЕ НОМЕРАПосле смерти Евклида александрийский математик Эратосфен из Кирены (276 — 194 гг. До н.э.) работал в области теории чисел. Он был известен как 2-й Платон. Он первым дал понятие простых чисел. Слово «Prime» происходит от древнеанглийского «Prim», которое происходит от латинского «Prima hora», что означает первый час. Положительное число, которое делится только на I и само по себе называется простым числом, целые числа 2, 3, 5, 7, 11, 13… 113 и т.д. являются примерами простых чисел.
Число «2» — наименее простое и только четное. Все остальные простые числа нечетные. Математически целое число n> 1 называется простым числом или просто простым числом, если его единственные положительные делители равны 1 и n.
Целое число> 1, которое не является простым, называется составным числом. Проще говоря, мы можем сказать, что положительное число, у которого есть другие делители, кроме 1 и самого числа, называется составным числом. Целые числа 4, 6, 8, 9 …… и т. Д. (В порядке возрастания) являются примерами составных чисел.Любое составное число может быть представлено как произведение простых чисел (так называемая факторизация простых чисел), например, 504 = 23 x 32 x 71
Условно. Единство не является ни простым, ни составным числом.
Таблица простых чисел от 1 до 1000 приведена ниже.
С древних времен многие известные математики работали над простыми числами, Евклид (в книге IX его «Элементов») первым доказал, что в теории чисел существует бесконечно много простых чисел.Раздел математики, обогащенный понятиями простых чисел, известен как теория чисел. Многие великие математики, такие как Эйлер (1707–1783), Ферма (1601–1665), Гаусс (1775–1855), Абель, Харди (1877–1947), Райт и др., Развивали эту ветвь математики. Особенно удивил весь мир вклад индийского математика Шриниваса Рамануджана (1887-1920).
Предложение 14 книги IX «Элементов Евклида» воплощает результат, который позже стал известен как Фундаментальная теорема арифметики, а именно, что каждое составное число может быть представлено как произведение простых чисел одним и только одним способом.Например, 21 = 3 x 7, но ’21’ нельзя выразить как произведение двух других простых чисел 2 и 5.
Процитируем само предложение: «Если число будет наименьшим из тех, что измеряются простыми числами, оно не будет измеряться никакими другими простыми числами, кроме тех, которые первоначально его измеряли»
N.B .: Основная теорема арифметики: каждое натуральное число, n> 1, является либо простым, либо произведением простых чисел. Это представление уникально и является частью порядка, в котором встречаются факторы.
На основе простых чисел есть счетное количество составных чисел.В 1845 году Джозеф Бертран предположил, что простые числа хорошо распределены в том смысле, что между n> 2 и 2n есть по крайней мере одно простое число. Между 1 и 10 есть одно четыре простых числа, а именно 2, 3, 5, 7, между 11 и 20 также четыре простых числа, то есть 11, 13, 17, 19, но между 21 и 30 есть только два простых числа 23 и 29.
Всего простых чисел меньше 100 равно 25, то есть 25% простых чисел меньше 100, 16,8% простых чисел меньше 1000, но общее количество простых чисел меньше 10000 равно 1219.Теперь мы готовим диаграмму, чтобы показать существование простых чисел в разных диапазонах.
Очевидно, что количество простых чисел постепенно уменьшается с увеличением числового ряда. Можете ли вы сказать, исходя из наблюдения, что простые числа заканчиваются, если числовой ряд продолжает расти? Есть ли самое большое простое число? Греческий математик Евклид (300 г. до н.э.) ответил на этот вопрос в своей знаменитой книге «Элементы» части IV. Он доказал простым методом (Reductio ad absurdum), что источник простых чисел неограничен.Это бесконечно; не существует самого большого простого числа. Его способ эксперимента: если возможно, скажем, что простые числа счетны.
Пусть 2, 3, 5 и 7 будут простыми числами в порядке возрастания, и предположим, что есть последнее простое число 7 (а затем все составные числа), тогда 2x3x5x7 + 1 = 220 + 1 = 221, что является простым числом, потому что если число делится на 2, 3, 5 и 7 соответственно, мы всегда получаем 1 в качестве остатка.
Следовательно, наше предположение неверно, т.е. 7 не является самым большим простым числом.Нет уверенности в том, что если последовательное произведение некоторых конкретных простых чисел увеличивается на единицу, то результирующее может быть, а может и не быть простым.
Как 2 x 1 + 1 = 2 + 3 = 3 2 x 3 + 1 = 6 + 1 = 7 2 x 3 x 5 + 1 = 30 + 1 = 31 и 2 x 3 x 5 x 7 x 11 + 1 = 2310 + 1 = 2311 — все простые числа, но 2 x 3 x 5 x 7 x 11 x 13 + 1 = 30031 не является простым числом, потому что 30031 = 59 x 509.
Аналогичным образом мы видим, что 2 x 3 x 5 x 7 x 11 x 13 x 17 + 1 = 510510 + 1 = 510511 = 19 x 97 x 277 и 2 x 3 x 5 x 7 x 11 x 13 x 17 x 19 + 1 = 9699 690 + 1 = 9 699 691 не являются Prime.Но они могут показать, что доказательство Евклида неверно.
Из контекста доказательства Евклида мы можем предположить, что число ’11’ является самым большим числом, очевидно, что 30031 — не простое число, делители которого равны 59 и 509, оба являются простыми числами. Каждый из чем ’11’. Таким образом, мы можем сделать вывод, что наше предположение о том, что «11» — это наибольшее простое число, неверно.
Аналогичным образом, если возможно, мы предполагаем, что 13 или 17 — наибольшее простое число. Затем мы можем выяснить, что 19, 97 или 277 больше простых чисел, чем 11.Таким образом, предположение о существовании наибольшего простого числа неверно.
Расположение — это особенность простых чисел теории чисел. Между двумя последовательными точными квадратными числами есть по крайней мере одно простое число. 2 и 3 — простые числа от 1 до 4 и 5, 7 — простые числа от 4 до 9. Но 17, 19, 23 — простые числа от 16 до 25.
Мы можем подготовить диаграмму, показывающую количество простых чисел между двумя числами совершенного квадрата.
Существует ли какое-либо правило, регулирующее существование простого числа между двумя последовательными числами Совершенного квадрата? Это вопрос без ответа.Есть еще одна особенность простых чисел. Между числом и его двойным числом существует минимум одно простое число. Например, 3 — это простое число от 2 до 4, 5 и 7 также являются простыми числами от 4 до 8. Точно так же 17, 19, 23, 29, 31 — простые числа от 16 до 32. Доказательство этой теории было разработано. русским математиком П.Л. Чебычевым в 1852 году.
Тайна простых чисел настолько привлекательна, что она привлекает каждого математика. Французского юриста и математика Пьера де Ферма (1601–1665) также привлекла настоящая любовь к математике, особенно к теории чисел, которую он спас из царства суеверий и оккультизма, где она долгое время находилась в заточении.Он изобрел формулу для определения простых чисел. Но это не везде так. Число Ферма — это целое число в форме.
Но если n = 6, 7, 8 ……. тогда получим ли мы какое-нибудь простое число? Сколько простых чисел? Бесконечное или конечное количество простых чисел?
Греческие математики поняли, что искать простые числа в теории чисел непросто. Итак, в 300 г. до н.э. математик Эратосфен из Кирены изобрел новый процесс нахождения всех простых чисел из числового ряда.Этот простой процесс называется Решетом Эратосфена. Теперь мы объясним процесс, записав целые числа от 2 до 100 в их естественном порядке, а затем систематически найдем простые числа. Рассмотрим последовательность последовательных целых чисел.
Признание того, что «2» является простым числом, поэтому его большее кратное, то есть 4, 6, 8, 10… 100 и т. Д., Не являются числами. Зачеркните их знаком «X». Первое из оставшихся целых чисел — «3», которое должно быть простым.
Мы оставляем 3, но вычеркиваем все кратные 3, а именно 6, 9, 12, 15… 99 и т. Д.символом «___» (четные числа, кратные «3», были удалены на предыдущем шаге). Таким образом, все числа, кратные 5, 12, 10, 15, 20 …… и т. Д., Являются составными числами, мы вычеркиваем их с помощью «\», сохраняя при этом 5. Первое оставшееся целое число 7 является простым числом, поскольку оно не делится на 2, 3 или 5 — единственные числа, предшествующие ему. После исключения числа, кратного 7, наибольшее простое число меньше? 100 = 10, а числа, кратные 7, зачеркнуты по символу. Оставшиеся положительные целые числа, а именно 2, 3, 5, 7, 11, 13 …….97 — все простые числа меньше 100.
Различные типы простых чисел Почти простые числа: Почти простые числа имеют ограниченное количество простых множителей. Два почти простых числа имеют два основных фактора (включая повторяющиеся факторы) и также называются полупростыми числами. Пары 4, 6; 8, 12; 18, 27 и т. Д. Являются примерами двух — почти простых чисел. У трех почти простых чисел есть три простых множителя и так далее. Последовательность из трех — почти простых чисел начинается с 8, 12, 18, 20, 27, 28, 30, 42, 44, 45, 50 …….. Последовательность n — почти простых чисел начинается с 2n, 3.2n-1, …….
Относительно простое или простое по отношению друг к другу: Если общий делитель двух целых чисел равен единице, то говорят, что эти числа являются простыми по отношению друг к другу или относительно простыми числами, а иногда их также называют параллельными числами. Целые числа p и q называются простыми между собой, если gcd (p, q) = 1. Например, 3, 5 и 4, 9 являются двумя парами простых чисел друг для друга, так как gcd (3, 5) = 1 и gcd ( 4, 9) = 1. Очевидно, что два составных числа могут быть простыми друг другу.
[Примечание: пусть p и q — целые числа, а не оба равны нулю. Тогда p и q взаимно просты или взаимно просты тогда и только тогда, когда существуют такие целые числа u и v, что pu + qv = 1]
Кузен Праймс
Простые числа двоюродных братьев — это пары, различающиеся на 4, поэтому они более далеки, чем простые числа-близнецы, но менее далеки, чем сексуальные простые числа.
Есть 14 пар простых чисел-близнецов меньше 200, а также 14 пар простых чисел-близнецов: 3-7, 7-11, 13-17, 19-23, 37-41, 43-47, 67-71, 79-83. , 97-101, 103-107, 109-113, 127-131, 163-167 и 193-197.Еще двадцать — шесть пар ниже 1000.
Разница между парой простых чисел-близнецов равна 2. Это форма пары следующих друг за другом нечетных целых чисел p и P + 2, чем оба простых числа. Между 0 и 1000 34 пары простых чисел-близнецов. Количество пар простых чисел-близнецов в указанном интервале:
Если первая из гипотез Харди — Литтла Вуда верна, то простые числа-близнецы и двоюродные братья имеют одинаковую плотность, поскольку мы движемся к бесконечности на основе простых чисел Кузена до 242, исключая исключительную начальную пару, 3- 7, поскольку 3 не имеет формы 6n + 1, ряд 1/7 + 1/11 + 1/13 + 1/17 + 1/19 + 1/23 + 1/37 + 1/41 имеет сумму 1 .1970449.
Простые числа Каллена: Числа в форме Cn = n, 2n +1 названы в честь преподобного Дж. Каллена, который в 1905 году заметил, что, за исключением C1 = 3 и еще одного возможного исключения, все они составны для n — 1. до 100. Исключением был C53, который, как обнаружил подполковник Аллан Джозеф Каннингем (1842-1928), делится на 5591. Хотя для низких значений n простые числа Каллена редки, было высказано предположение, что их бесконечное количество.
Известные простые числа Каллена встречаются, когда n = 1, 141, 4713, 6611, 18496, 32292, 32469, 59656,
, 262419, 361275 и 481899.
Числа вида n.bn + 1, называемые обобщенными числами Каллена, также редко бывают простыми, когда b = 3, n. 3n + 1 простое для n = 2, 8, 3, 54, 114, 414, 1400, 2850. , 2848, 4874, 7268, 19290.
Самый большой известный Каллен Прайм — C481899 из 145 072 цифр, обнаруженный Масакату Мори в 1998 году.
ПОСЛЕДУЮЩИЕ ПЕРВИЧНЫЕ И СУММЫ
Последовательная последовательность целых чисел выглядит так: 1, 12, 123, 1234, 12345 ……… ..
Среди первых 13 500 членов простых чисел нет.Какими способами можно записать целое число n как сумму одного или нескольких последовательных простых чисел? Если мы вызываем if f (n), то f (5) = 2, потому что 5 = 5 и 5 = 2 + 3, и f (41) = 3, потому что 41 = 11 + 13 + 17 = 2 + 3 + 5 + 7 + 11 + 13 Лео Мозер доказал, что среднее значение f (n) от n = 1 до N равно log 2, поскольку N стремится к бесконечности.
Удаляемые простые числа: Крис Колдуэлл определяет делатируемое простое число как такое, которое остается простым, поскольку цифры удаляются в определенном выбранном порядке. Это его пример: 410256793, 41256793, 4125673, 415673, 45673, 4567, 467, 67, 7.
Неизвестно, существует ли бесконечность таких простых чисел.
Усекаемые простые числа: Усекаемое справа число является простым и остается простым, поскольку цифры удаляются справа. Следовательно, он не содержит нулевой цифры, а цифры 2 и 5 могут быть только самой левой цифрой. В базе 10 восемьдесят три усекаемых справа простых числа, начиная с 2, 3, 5, 7, 23, 29, 31, 37, 53, 59, 71, 73, 79, 233, 239, 293, 311, 313, 317, 373 …… Имеется бесконечное количество простых чисел, усекаемых слева, если допускаются нули, например.грамм. 1087. Если нули недопустимы, в базе 10 будет 4260 усекаемых слева простых чисел, начиная с 2, 3, 5, 7, 13, 17, 23, 37, 43, 47, 53, 67, 73, 83, 97, 113, 137, 167, 173 …… и т. Д.
ОПИСАТЕЛЬНЫЕ ПРИМЕРЫ
В описательной (или самоописательной) последовательности каждый термин описывает предыдущий термин. Например, 2 2 1112 один 2, 1 один 2 один 2 Три Один Один два. начиная с 1, последовательность продолжается 1, 11, 21, 1211, 111221, 312211, 13112221 …… Первые два простых числа — 11 и 312211.
Простые числа Мерсенна: Французский священник отец Марин Мерсенн (1588–1648) был одним из самых необычных и выдающихся математиков своего времени. Он был автором различных математических наук, включая Synopsis Mathematicae (1626), Traite del Harmonie Universile (1636-1637) и Universal Geomaterie Synopsis (1644). Числа вида Mn = 2n — 1 (n> 1) называются числами Мерсенна в честь Менина Мерсенна.
Примальность Mn требует, чтобы n было простым числом.В предисловии к своей Cogitata Physica — Mathematica (1644) Мерсенн заявил, что Mn Prime для n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257 и составной для всех других простых чисел n < 257. Первые четыре простых числа Мерсенна, а именно 3, 7, 31 и 127 заменяются на n в формуле 2n - 1.
Эйлер и число, обратное простым числам: Леонард Эйлер был одним из ее величайших математиков всех времен, наряду с Архимедом, Ньютоном и Гауссом. Как и они, он преуспел в чистой и прикладной математике и создал концепции и методы непреходящей важности.
В 1737 году он доказал, что сумма обратных простых чисел 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + 1/13 + 1/17 + расходится. Он также утверждал, что в журнале современной записи, что он расходится, как и журналы журнала функций. Это настолько медленно, что требуется более 360 000 членов, чтобы сумма превысила 3. Чередующаяся сумма взаимных простых чисел сходится, поскольку ее значение всегда находится в диапазоне от 1/2 до 0: 1/2 — 1/3 + 1/5 — 1/7 + 1/11 — 1/13 + …… = 0,2696063519
Сумма обратного квадрата простых чисел также сходится к 0.4522474200 т.е. 1/22 + 1/32 + 1/52 + 1/72 + 1/112 + 1/132 + ……… = 0,4522474200
[N.B.:(i) Целое число a называется делимым на целое число b = / 0 в символах b a, если существует такое целое число C, что a = bc. Мы пишем b a, чтобы указать, что a не делится на b.
(ii) Если a и b заданы целые числа, а не оба нуля, наибольший общий делитель a и b, обозначенный gcd (a, b), будет ее положительным целым числом d, удовлетворяющим.
(и) д / а и д / б, и
(ii) если c / a и c / b, то c 3. Наименьшее общее кратное двух ненулевых целых чисел a и b, обозначенных 1 cm (a, b), является положительным целым числом m, удовлетворяющим и) а / м и б / м ii) Если a / c и b / c, при c> 0, то m 4. Наибольшее простое число с цифрами от 1 до 9 — 98765431. Если можно использовать 0, то это 987654103. 5. Число является треугольным тогда и только тогда, когда оно имеет вид (n (n + 1)) / 2 для некоторого n> 1. (Самар Чандра Дей — учитель математики в школе Силигури) Доцент кафедры преподавания На p-типичном комплексе де Рама-Витта над W (k) .3 и соответствующие суммы персонажей , с Томми Окчипинти. J. Теория чисел. 168 (2016), 13-38. Версия от 26.09.2014. Склоны Ньютона для башен Артин-Шрайер-Витт , с Дацин Ван и Лян Сяо. Математика. Анна. 364 (2016), нет. 3-4, 1451-1468. Версия от 20.10.2013. Характеристика строго APF расширений с Брайденом Кайсом и Джонатаном Любином. J. Théor. Nombres Bordeaux. 28 (2016), нет. 2, 417-430. Версия от 20.02.2014. Почти чистые и сверхконвергентные векторы Витта , с Кираном Кедлая.J. Алгебра. 422 (2015), 373-412. Версия от 16.08.2014. Канонические кольца Коэна для полей норм , с Bryden Cais. Int. Математика. Res. Нет. 2015 (2015), 5473-5517. Версия от 30.12.2013. Интегральная структура на когомологиях Монски-Вашницера и сверхконвергентный комплекс де Рама-Витта , с Дэвидом Зурейком-Брауном. Математика. Res. Lett. 21 (2014), нет. 2, 281-288. Версия от 01.05.2013. Какие конечные простые группы являются группами единиц? , с Томми Окчипинти.J. Pure Appl. Алгебра 218 (2014), вып. 4, 743-744. Версия от 06.08.2013. Какие чередующиеся и симметричные группы являются группами единиц? , с Томми Окчипинти. J. Algebra Appl. 13 (2014), 12 с. Версия от 16.07.2013. L-функции p-адических символов , с Дацин Ван. Nagoya Math. J. 213 (2014), 77-104. Версия от 30.03.2013. На векторе Витта Фробениус , с Кираном Кедлая. Proc. Амер. Математика. Soc. 142 (2014), 2211-2226.Версия от 01.10.2012. Сверхконвергентные векторы Витта , с Андреасом Лангером и
Томас Зинк. J. Reine Angew. Математика. 668 (2012), 1-34. Сверхконвергентные когомологии Рама-Витта , с Андреасом
Лангер и Томас Зинк.
Анна. Научный. Éc. Норма. Как дела. (4) 44 (2011), нет. 2, 197-262. Сверхконвергентный комплекс де Рама-Витта , Ph.D. Диссертация, Массачусетский технологический институт. Посоветовал Киран Кедлая. 2009. Вы можете увидеть его здесь, щелкнув ссылку «Предварительный просмотр, не для печати».Однако обратите внимание, что результаты первых четырех разделов улучшены и расширены в моих совместных статьях с Андреасом Лангером и Томасом Цинком, а результаты последних двух разделов улучшены и расширены в моих совместных статьях с Кираном Кедлая. Полностью геодезические поверхности Зейферта в гиперболическом узле и зацеплении
дополняет II (доступ по подписке) с Колином Адамсом, Ханной Беннетт, Майклом
Дженнингс, Дженнифер Новак, Николас Перри и Эрик Шенфельд.
J. Differ. Геом. 79 (2008), нет.1, 1-23. Я изучаю проблемы низкоразмерной топологии, используя такие инварианты, как гомологии Хованова и гомологии Хегора Флоера.
Совсем недавно это включало работу с окаймленными гомологиями Флоера, чтобы понять связь между тугими слоениями, левыми порядками и не-L-пространствами.Мои исследования поддерживаются грантом Совета по естественным наукам и инженерным исследованиям Канады (NSERC),
и мне выпала честь выполнять свою работу на традиционной, исконной и не уступившей территории народа х w mǝθk w y̓ǝm (Musqueam). Я являюсь членом топологической группы UBC. Я участвую в разработке новых методов PIMS CRG в низком измерении. Мой офис находится в области математики 219. Лучший способ связаться со мной — по электронной почте: liam [at] math [dot] ubc [dot] ca Instagram: @mathonmydeskrightnow Мои документы на
arXiv,
MathSciNet и
zbMATH.Они перечислены ниже в (приблизительном) обратном хронологическом порядке. Вычислительное программное обеспечение, связанное с этими инвариантами, благодаря Gurkeerat Chhina и Claudius Zibrowius, доступно на GitHub.
Образцы клубков и связанные с ними вычисления собраны в зарождающемся атласе клубков, составленном Леоном Яо. Это включает в себя некоторые более ранние записи о гомологическом твердотеле Heegaard Floer , которые никогда не появлялись, хотя есть видео разговоров по этому материалу от BIRS.
и из SCGP, а также слайды с совместных заседаний AMS (2013 г.) и зимних заседаний CMS (2013 г.). слайдов с Математического конгресса Америки (2017 г.). Слайды с совместных заседаний EMS / SCM (2015). Некоторые дополнительные комментарии по разделению мутантов, которые упрощают / уточняют / обобщают конструкцию в этой статье, можно найти здесь.
Они будут включены в опубликованную версию статьи; вот последняя версия статьи. Раньше эта статья называлась Таутовскими слоениями на графовых многообразиях . Сопровождающий блокнот Mathematica для некоторых расчетов для этой статьи с использованием KnotTheory`. Слайды из моего выступления на конференции по топологии в Джорджии. Сопровождающий блокнот Mathematica, выполняющий вычисления в этой статье с использованием KnotTheory`. Осень 2018 Зима 2019 Зима 2020 Осень 2020 Зима 2021 Осень 2021 г. Зима 2022 года Дизайн страницы этого веб-сайта был украден у моего друга Патрика Ингрэма;
фото было сделано Риком Деспардом на Венис-Бич. Домашняя страница Кристофера Дэвиса
Департамент математики
Калифорнийский университет, Ирвин Контактная информация:
Электронная почта: [email protected] (всегда лучший способ связаться со мной)
Офис: Rowland Hall, Room 440J
Веб-сайт: http: // www.math.uci.edu/~davis
Рабочий телефон: 949.824.5313 Я перед мостом Золотые Ворота в Сан-Франциско О себе:
Я во второй раз учусь в Калифорнийском университете в Ирвине. С 2010 по 2013 год я здесь был приглашенным доцентом, а сейчас я доцент кафедры математики. Это позиция, ориентированная на преподавание, и я надеюсь, что буду участвовать во многих различных аспектах обучения на математическом факультете.С 2013 по 2015 год я работал постдоком в Копенгагенском университете в рамках профессуры Нильса Бора Ларса Хессельхолта. Я был аспирантом Массачусетского технологического института, где моим руководителем был Киран.
Кедлая. Мои математические интересы лежат в области теории чисел и алгебраической геометрии. Более конкретно, ниже вы увидите, что во многих моих статьях используются векторы Витта. Публикаций:
Ссылка arXiv на многие мои статьи. Препринтов:
векторов Витта с p-адическими коэффициентами и кольца Фонтена ,
с Кираном Кедлая. Версия от 21.02.11. Большая часть этого материала была перенесена в нашу бумагу Frobenius и нашу бумагу почти чистоты . Текущее преподавание:
Прошлое преподавание UCI:
Другое:
Слайды рекомендаций первокурсников и второкурсников, февраль 2017 г.
резюме по состоянию на февраль 2017 г.
Лабораторные инструкции по математике 173, Введение в криптологию.
Код Sage для Math 173, Введение в криптологию.
Криптография и шалфей. Видео из моего выступления на Sage Education Days 5.
Слайды из моего выступления на JMM в 2013 году на тему «Базовые кольца для глобальных (phi, Gamma) -модулей». Лиам Уотсон
Лиам Уотсон Исследования
Публикации
Препринты и работа в подготовке
Отправлено, arXiv.2105.06308.
, arXiv.2005.02792.
Отправлено, arXiv.2004.01619.
Отправлено, arXiv.1910.14584.
Отправлено, arXiv.1810.10355.
Отправлено, arXiv.1604.03466.
Видео выступлений по этому материалу от CMO (2017):
Часть 1
а также
Часть 2.
Другие разговоры по этому материалу были записаны в INI (2017) в рамках программы Гомологические теории в малых размерностях .
Видео переговоров по (более старым версиям) этого материала от BIRS (2016):
Часть 1.
а также
Часть 2 Опубликован, в печати или принят
Появиться в The Open Book Series , arXiv.2104.13592.
Появится в Geometry & Topology , arXiv.1908.04397.
Появиться в Geometry & Topology , arXiv.1508.05445.
Появиться в Geometry & Topology , arXiv.1908.00082.
Compositio Mathematica Volume 156 Number 3 (2020), arXiv.1508.05911.
Selecta Mathematica , Volume 24 Number 2 (2018).
Успехи по математике , том 313 (2017).
Журнал топологии , том 10, номер 1 (2017).
Pacific Journal of Mathematics , Volume 267, Number 2 (2014).
Труды Американского математического общества , том 142, номер 4 (2014).
Алгебраическая и геометрическая топология , том 13, номер 4 (2013).
Mathematische Annalen , том 356, выпуск 4 (2013).
Квантовая топология , Volume 4 Number 4 (2013).
Бюллетень Лондонского математического общества , том 45, номер 5 (2013).
Уведомления о международных исследованиях в области математики , номер 12 (2013).
Selecta Mathematica Volume 18 Number 2 (2012).
Mathematical Research Letters , Volume 18 Number 6 (2011)
Низкоразмерная и симплектическая топология , Том 82 Труды симпозиумов по чистой математике (2011)
Американский журнал математики , том 132, номер 5 (2010).
Pacific Journal of Mathematics , Volume 245 Number 2 (2010).
Алгебраическая и геометрическая топология , том 7 (2007).
Труды 19-й Канадской конференции по вычислительной геометрии , (2007).
Журнал теории узлов и ее разветвлений , том 15 номер 9 (2006). Отредактированные тома
Редакторы: Оливье Коллин,
Кэмерон Гордон,
Стефан Фридл,
Стефан Тилльманн,
и Лиам Уотсон
Современная математика 760. Научно-исследовательский центр математики. Тезисов
UQÀM
Кандидатская диссертация (июнь 2009 г.)
Научный руководитель: Стив Бойер
UBC
Диссертация на степень магистра (октябрь 2004 г.)
Научный руководитель: Дейл Рольфсен Надзор
Докторантура
Докторантура
Мастера
Бакалавриат
Атлас клубков Леона.
Gurkeerat, связанное с инвариантами из погруженных кривых в гомологии Хованова , доступно на GitHub.
Компьютерная реализация Кевина алгоритма скольжения по стрелке из раздела 3 документа Bordered Floer homology для многообразий с торической границей через погруженные кривые доступна здесь.
: Роторы в гомологии Хованова, Canadian Mathematical Bulletin Volume 59 Number 1 (2016)
Примечания: Модульные теории и теории гомологии фильтрованных узлов
: Открытые книги первого рода с неупорядочиваемой слева фундаментальной группой, Труды Американского математического общества , том 142, номер 4 (2014).
: упрощение эквивалентности сетки, Involve Volume 8 Number 5 (2015).
Вот обновленный отчет о проекте Нэнси. Глазго, уровень 4
Сиан Гриффитс (2013)
Нил Хендерсон (2013) Обучение
Об этой странице

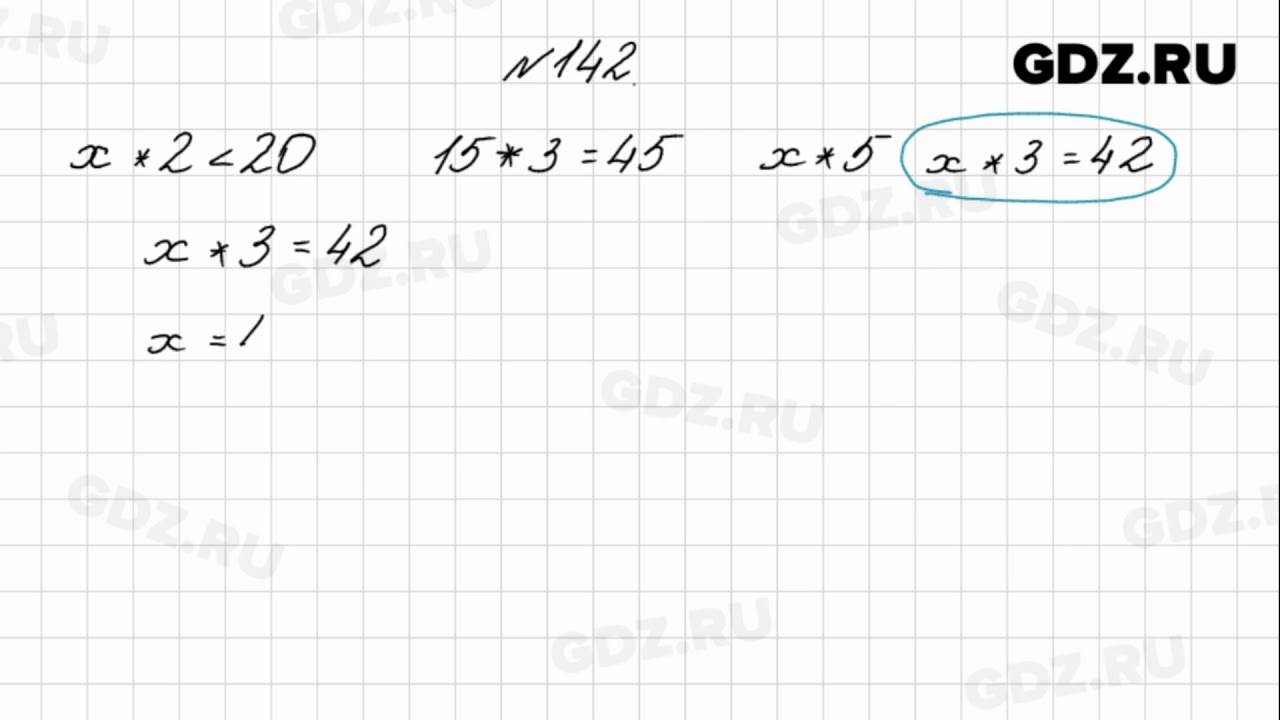
 Его дефицит 68
Его дефицит 68 (Мы не учитываем непроизвольные паузы, перерывы в туалет или необходимость спать в наших расчетах!)
(Мы не учитываем непроизвольные паузы, перерывы в туалет или необходимость спать в наших расчетах!)