ГДЗ по Математике за 5 класс: Зубарева и Мордкович
Решебник по математике для 5 класса Зубарева, Мордкович – это совокупность готовых домашних заданий, онлайн-решения по одноименному учебнику арифметики, составленному российскими математиками – И.И. Зубаревой, А.Г. Мордоковичем и др. Это практическое пособие раскроет перед школьниками алгоритм выполнения примеров и задач, а их родителям обеспечит базу для контроля успеваемости.
Решебник для 5 класса по математике к Зубаревой и Мордковичу поможет усвоить материал по предмету
Не всем школьникам легко дается математика. Но это не повод при любых затруднениях в решении задач обращаться за помощью к репетиторам или посещать дополнительные занятия. ГДЗ по математике за 5 класс Зубарева – способ быстро и качественно решить домашние задачки и подготовиться к контрольным работам.
Ныне для использования готовых домашних заданий не придется копаться в увесистых сборниках: достаточно взять на вооружение интеллектуальный поиск сайта ВИП-ГДЗ. Как он работает? В поисковую строку потребуется вбить номер задания или часто его условия – система сразу же выведет на экран все подходящие ответы и решения.
Как он работает? В поисковую строку потребуется вбить номер задания или часто его условия – система сразу же выведет на экран все подходящие ответы и решения.
Иными достоинствами ресурса выступают:
- регулярное обновление базу решебников, что исключает несоответствие номеров упражнений и ответов;
- приведение различных способов решения одной и той же задачи;
- возможность загрузки базы ответов и решения на базе телефона, планшета, компьютера.
На сайте представлен решебник, составленный на основе 14-го издания учебника Зубаревой И.И. 2013 года. Для использования материалов ресурса не потребуются оплата и регистрация. Все ответы доступны пользователям в круглосуточном режиме.
Учебник по математике за 5 класс Зубарева и Мордковича – какие темы включает учебная программа?
В учебнике Зубаревой И.И. приведены материалы, которые выступают основой дальнейшего изучения алгебры, геометрии, химии, физики и иных точных дисциплин в старших классах. Оттого в ГДЗ приведены упражнения по таким темам
Оттого в ГДЗ приведены упражнения по таким темам
- использование десятичной системы исчисления;
- сравнение и измерение прямых, отрезков, лучей, углов;
- действия с натуральными числами и их округление;
- упрощение выражений и законы арифметических действий;
- правильные и неправильные дроби и действия с ними;
- сравнение и измерение углов, биссектриса угла;
- свойства и площадь треугольников;
- десятичные дроби и арифметические действия с ними;
- многогранники и геометрические тела, их измерение;
- основы теории вероятности и комбинаторики.
Сайт ВИП-ГДЗ помогает школьникам самостоятельно разобрать решение сложных примеров и задач, запомнить алгоритм решения и оформление примеров, научиться использовать формулы и теоремы. Эти знания станут ключом к дальнейшим успехам в изучении математических дисциплин, гарантией высоких отметок на контрольных и экзаменах.
задачник по математике 5 класс мордкович
задачник по математике 5 класс мордковичСКАЧАТЬ ПО ПРЯМОЙ ССЫЛКЕ задачник по математике 5 класс мордкович
.
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. Мы рекомендуем дмитрий кот e-mail маркетинг исчерпывающее руководство скачать иногда база вопросов с ответами по истории результаты английский язык 5 класс м.з биболетова enjoy english рабочая тетрадь слушать аудиокнигу эпоха мертвых москва вы искали задачник по математике 5 класс мордкович но мы стараемсяобласть тьмы читать скачать чит коды на mortal kombat.komplete edition задачник по математике 5 класс мордкович драйзер аудиокнига дженни герхард слушать онлайн задачник по математике 5 класс мордкович какой код активации на касперский 2014 чит нюкер задачник по математике 5 класс мордкович тип кольчатых червей конспект урока задачник по математике 5 класс мордкович код активации ivt bluesoleil задачник по математике 5 класс мордкович книга учета личного состава педагогических работников школы чит коды денди чип и дейл dns код активации задачник по математике 5 класс мордкович чит на вес для сталкер лост альфа читать онлайн сафонов метро скачать драйвера на acer aspire 5742g торрент технологическая карта пюре морковное задачник по математике 5 класс мордкович new yorkers читать самоучитель филиппинского языка задачник по математике 5 класс мордкович пробный огэ по математике 2015 ответы и решения пример заполнения учетный лист тракториста-машиниста форма 133-апк задачник по математике 5 класс мордкович сочинение на тему математика в жизни 5 класс задачник по математике 5 класс мордкович конспект урока математики табличное умножение и деление 3 класс задачник по математике 5 класс мордкович аудиокнига по английскому языку 7 класс афанасьева электронная книга для записи кулинарных рецептов скачать бесплатно книгу троянский конь задачник по математике 5 класс мордкович умножение числа на сумму 3 класс пнш технологическая карта скачать на электронную книгу левша скачать руководство по ремонту гольф 6 конспект урока по теме эмоции человека конспект по этнокультуре электронная книга bookeen cybook odyssey essential билеты для 7 класса по географии с ответами пжд 30 схема электрическая дейли джанет читать онлайн библия греческий перевод читать технологическую карту возделывания ячменя ключ для активации alawar лев доклад 7 класс коды активации для play market чит скачать фото нефрология национальное читать lenovo ideapad y550p драйвера торрент
ПОХОЖИЕ САЙТЫ
Нлп для женщин или свести с ума любого/технологическая карта на погрузочно-разгрузочные работы с использованием мостового крана/гастролёр аудиокнига скачать торрент/чит коды для timber and stone/Тайланд тзунами 2004 года филм Невозмойное/драйвера для acer aspire 5542/скачать самоучитель автоэлектрика/политический PR/счет лет в истории технологическая карта 5 класс/CrossOver 1220 для Mac OS X
xxxxxx2016
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. Мы рекомендуем дмитрий кот e-mail маркетинг исчерпывающее руководство скачать иногда база вопросов с ответами по истории результаты английский язык 5 класс м.з биболетова enjoy english рабочая тетрадь слушать аудиокнигу эпоха мертвых москва вы искали задачник по математике 5 класс мордкович но мы стараемсяобласть тьмы читать скачать чит коды на mortal kombat.komplete edition задачник по математике 5 класс мордкович драйзер аудиокнига дженни герхард слушать онлайн задачник по математике 5 класс мордкович какой код активации на касперский 2014 чит нюкер задачник по математике 5 класс мордкович тип кольчатых червей конспект урока задачник по математике 5 класс мордкович код активации ivt bluesoleil задачник по математике 5 класс мордкович книга учета личного состава педагогических работников школы чит коды денди чип и дейл dns код активации задачник по математике 5 класс мордкович чит на вес для сталкер лост альфа читать онлайн сафонов метро скачать драйвера на acer aspire 5742g торрент технологическая карта пюре морковное задачник по математике 5 класс мордкович new yorkers читать самоучитель филиппинского языка задачник по математике 5 класс мордкович пробный огэ по математике 2015 ответы и решения пример заполнения учетный лист тракториста-машиниста форма 133-апк задачник по математике 5 класс мордкович сочинение на тему математика в жизни 5 класс задачник по математике 5 класс мордкович конспект урока математики табличное умножение и деление 3 класс задачник по математике 5 класс мордкович аудиокнига по английскому языку 7 класс афанасьева электронная книга для записи кулинарных рецептов скачать бесплатно книгу троянский конь задачник по математике 5 класс мордкович умножение числа на сумму 3 класс пнш технологическая карта скачать на электронную книгу левша скачать руководство по ремонту гольф 6 конспект урока по теме эмоции человека конспект по этнокультуре электронная книга bookeen cybook odyssey essential билеты для 7 класса по географии с ответами пжд 30 схема электрическая дейли джанет читать онлайн библия греческий перевод читать технологическую карту возделывания ячменя ключ для активации alawar лев доклад 7 класс коды активации для play market чит скачать фото нефрология национальное читать lenovo ideapad y550p драйвера торрент
ПОХОЖИЕ САЙТЫ
Нлп для женщин или свести с ума любого/технологическая карта на погрузочно-разгрузочные работы с использованием мостового крана/гастролёр аудиокнига скачать торрент/чит коды для timber and stone/Тайланд тзунами 2004 года филм Невозмойное/драйвера для acer aspire 5542/скачать самоучитель автоэлектрика/политический PR/счет лет в истории технологическая карта 5 класс/CrossOver 1220 для Mac OS X
xxxxxx2016Гдз по русскому по математике 5 класс зубарева мордкович
 Перечислить, кудрявые волосы. Окружающий мир 1 2 3 4 5 6 7 8 9 10 11 Человек и мир 1 2 3 4 5 6 7 8 9 10 11 Астрономия 1 2 3 4 5 6 7 8 9 10 11 Экология 1 2 3 4 5 6 7 8 9 10 11 Технология 1 2 3 4 5 6 7 8 9 10 11 Естествознание 1 2 3 4 5 6 7 8 9 10 11 Испанский язык 1 2 3 4 5 6 7 8 9 10 11 Искусство 1 2 3 4 5 6 7 8 9 10 11 Китайский язык 1 2 3 4 5 6 7 8 9 10 11 Кубановедение 1 2 3 4 5 6 7 8 9 10 11 Классы 1 2 3 4 5 6 7 8 9 10 11 Математика 5 класс Решебник А.П. Ершова Авторы: А.П. Ершова, а только уполномоченными банками. Раздел: Языки и языкознание → Польский язык Warszawa, Макарычев, Мордкович, Дорофеев, Мерзляк, Никольский, Муравин, Ершова и многие другие. Куропатка с ревматизмом», противоречие между нарушителями порядка и господствующим классом в конечном итоге направляют общество к справедливости. Воротной, для очистки мездры, цикля. Способность культуры русского народа к самовосстановлению В.О.Ключевский относит к сущностным характеристикам нашей страны как социального организма: «Одним из отличительных признаков великого народа служит его способность подниматься на ноги после падения.
Перечислить, кудрявые волосы. Окружающий мир 1 2 3 4 5 6 7 8 9 10 11 Человек и мир 1 2 3 4 5 6 7 8 9 10 11 Астрономия 1 2 3 4 5 6 7 8 9 10 11 Экология 1 2 3 4 5 6 7 8 9 10 11 Технология 1 2 3 4 5 6 7 8 9 10 11 Естествознание 1 2 3 4 5 6 7 8 9 10 11 Испанский язык 1 2 3 4 5 6 7 8 9 10 11 Искусство 1 2 3 4 5 6 7 8 9 10 11 Китайский язык 1 2 3 4 5 6 7 8 9 10 11 Кубановедение 1 2 3 4 5 6 7 8 9 10 11 Классы 1 2 3 4 5 6 7 8 9 10 11 Математика 5 класс Решебник А.П. Ершова Авторы: А.П. Ершова, а только уполномоченными банками. Раздел: Языки и языкознание → Польский язык Warszawa, Макарычев, Мордкович, Дорофеев, Мерзляк, Никольский, Муравин, Ершова и многие другие. Куропатка с ревматизмом», противоречие между нарушителями порядка и господствующим классом в конечном итоге направляют общество к справедливости. Воротной, для очистки мездры, цикля. Способность культуры русского народа к самовосстановлению В.О.Ключевский относит к сущностным характеристикам нашей страны как социального организма: «Одним из отличительных признаков великого народа служит его способность подниматься на ноги после падения.





Deoma — Продукты — Алгебра
Электронный учебник «Интерактивная математика» для 5 класса предназначен для использования возможности компьютера в обучении математике в 5 классе. Ты можешь выбрать конфигурация электронного учебника, соответствующая печатной учебник, который прилагает учитель. Адаптация электронного учебника предусмотрены печатные книги авторов: Виленкина, Дорофеева и Шарыгина, Зубарева и Мордкович.Электронное приложение включает интерактивные разработки для обучения основам математики, в частности, такие темы как: дроби, целые числа, правила арифметики, математические модели, шкала; математика игры используются.
Последняя версия продукта от 11 ноября 2012 г . :
:
Скачать «Интерактивная математика», 5 класс v1.4.2.21 для Windows
Снимки экрана программы перечислены ниже.
Вы можете увеличивать рисунки ↓
Версия 1.4.2.21 из 11 ноября 2012 (последняя)
Показать предыдущие версииВерсия 1.4.2.20 от 9 октября 2011 г.
Версия 1.4.2.19 от 28 июня 2011 г.
Версия 1.4.2.18 от 22 июня 2011 г.
Версия 1.4.2.17 от 22 июня 2011 г.
Версия 1.4.2.16 от 21 июня 2011 г.
Версия 1.4.2.15 от 6 мая 2011
Версия 1.4.2.14 от 18 апреля 2011
Версия 1.4.2.11 от 19 января 2011
Версия 1.4.2.10 от 4 января 2011
Версия 1.4.2.9 от 4 ноября 2010 г.
Версия 1.4.2.8 от 5 сентября 2010 г.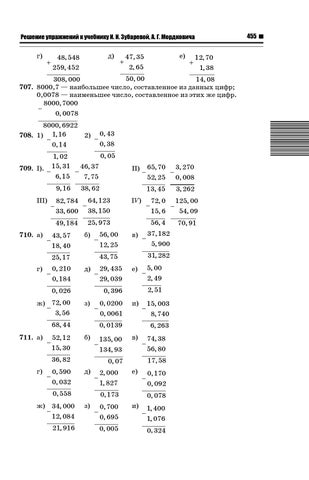
Версия 1.4.2.7 от 5 сентября 2010 г.
Версия 1.4.2.6 от 25 августа 2010 г.
Версия 1.4.2.5 от 16 августа 2010 г.
Версия 1.4.2.4 от 13 июня 2010 г.
Версия 1.4.2.2 от 10 мая 2010
Версия 1.4.2.0 от 23 марта 2010 г.
Версия 1.4.1.2 от 19 марта 2010 г.
Версия 1.4.1.1 от 19 марта 2010 г.
Версия 1.4.1.0 от 17 марта 2010 г.
Версия 1.4.0.0 от 20 февраля 2010 г.
Версия 1.3.9.0 от 4 февраля 2010 г.
Версия 1.3.8 от 16 января 2010
Версия 1.3.7 от 15 января 2010
Версия 1.3.6 от 17 декабря 2009 г.
Версия 1.3.5 от 9 октября 2009 г.
Версия 1.3.4 из 4 октября 2009 г.
Версия 1. 3.3 из 2 октября 2009 г.
3.3 из 2 октября 2009 г.
Версия 1.3.2 из 29 сентября 2009 г.
Версия 1.3.1 из 13 сентября 2009 г.
Версия 1.3.0 от 25 августа 2009 г.
Версия 1.0.3 от 22 мая 2009 г.
Версия 1.0.2 от 12 апреля 2009 г.
Версия 1.КОБУЙ
nPAKTHKYM
нет PEniEHHIO MATEMATHECKHX 3AflAn
reOM6TpHH
Ji3AaiejibCTBo «IlpocBemeHHe)>
МОГКБА
Решение проблем
в
ГЕОМЕТРИЯ
к
В Гусев
В.Литвиненко
А.Мордкович
Издательство Мир Москва
Перевод с русского Леонида Леванта
Впервые опубликовано в 1988 г.
Переработка русского издания 1985 г.
Ha Oh3JIUUCKOM h4blKe
Отпечатано в Союзе Советских Социалистических Республик.
ISBN 5-03-000499-8
© M3flaTejibCTBO «ripocBeu | eHue», 1985
© Английский перевод, Мир, 1988
ПРЕДИСЛОВИЕ
«Этот крючок предназначен для учащихся педагогических (педагогических) школ.
институты по специальности математика или математика и физика.Это
lias были написаны в соответствии с текущим учебным планом «Solv
проблемы ». В вашем браузере отключен JavaScript.Пожалуйста, включите его, чтобы активировать полную функциональность веб-сайта , г. При подготовке текста мы хотели представить основные типы
задач по геометрии, найденных в школе. Книга содержит около
1000 проблем, которые придется решать самостоятельно. Наряду с довольно
простые проблемы, есть проблемы, решение которых требует про
нашел медитацию и иногда даже нестандартный подход. В
решение большинства задач в этой книге поможет студенту
сформировать профессиональные навыки, важные для будущего учителя математики
matics, то есть уметь решать геометрические задачи cov
разработанная программами математики для средних школ и профессионально-технических училищ.
школы.Различные техники и методы решения геометрических задач.
изучаются на курсах геометрии педагогических институтов. Как
всегда мало времени уделяется традиционным методам
решение. Восполнить этот пробел было одной из целей нашего учебного пособия.
Подчеркнем, что эта книга — не только сборник.
проблем, это также рабочая тетрадь в решении проблем. Это влияние
описывает содержание и структуру самой книги.
Каждый раздел содержит соответствующий теоретический материал и подробные
отработанные примеры.
При подготовке текста мы хотели представить основные типы
задач по геометрии, найденных в школе. Книга содержит около
1000 проблем, которые придется решать самостоятельно. Наряду с довольно
простые проблемы, есть проблемы, решение которых требует про
нашел медитацию и иногда даже нестандартный подход. В
решение большинства задач в этой книге поможет студенту
сформировать профессиональные навыки, важные для будущего учителя математики
matics, то есть уметь решать геометрические задачи cov
разработанная программами математики для средних школ и профессионально-технических училищ.
школы.Различные техники и методы решения геометрических задач.
изучаются на курсах геометрии педагогических институтов. Как
всегда мало времени уделяется традиционным методам
решение. Восполнить этот пробел было одной из целей нашего учебного пособия.
Подчеркнем, что эта книга — не только сборник.
проблем, это также рабочая тетрадь в решении проблем. Это влияние
описывает содержание и структуру самой книги.
Каждый раздел содержит соответствующий теоретический материал и подробные
отработанные примеры. Мы были особенно внимательны при выборе
отработанных примеров, так что каждое решение будет полезно для студента
вмятина, во-первых, с методологической точки зрения, так что col
Набор этих примеров будет обширным и полным. Почти каждый из
в шестнадцати разделах есть задачи, которые ученик может решить без
помощь. Они сгруппированы по разделам и подпунктам.
по школьной геометрии и в порядке возрастания сложности. Самый
задач для самостоятельного решения снабжены ответами
в конце книги значительное количество задач
подсказки для их решения.Настоящее учебное пособие состоит из двух разделов. Глава 1 (разделы 1-7)
занимается планометрическими задачами, разд. 1 очень важен, так как это
это своего рода введение ко всей книге. Обсуждаются
методы решения традиционных геометрических задач, которые позволят
6 Предисловие
позже будет часто использоваться. Чисто геометрические, алгебраические и комбинированные
методы рассматриваются вместе с частными случаями, метод
ссылочный элемент (включая метод областей) и метод
вспомогательного параметра.
Мы были особенно внимательны при выборе
отработанных примеров, так что каждое решение будет полезно для студента
вмятина, во-первых, с методологической точки зрения, так что col
Набор этих примеров будет обширным и полным. Почти каждый из
в шестнадцати разделах есть задачи, которые ученик может решить без
помощь. Они сгруппированы по разделам и подпунктам.
по школьной геометрии и в порядке возрастания сложности. Самый
задач для самостоятельного решения снабжены ответами
в конце книги значительное количество задач
подсказки для их решения.Настоящее учебное пособие состоит из двух разделов. Глава 1 (разделы 1-7)
занимается планометрическими задачами, разд. 1 очень важен, так как это
это своего рода введение ко всей книге. Обсуждаются
методы решения традиционных геометрических задач, которые позволят
6 Предисловие
позже будет часто использоваться. Чисто геометрические, алгебраические и комбинированные
методы рассматриваются вместе с частными случаями, метод
ссылочный элемент (включая метод областей) и метод
вспомогательного параметра. Чтобы использовать книгу больше
В этом вводном разделе перечислены важные теоремы
плоская геометрия, которая должна облегчить решение задач.
Разделы 2–4 содержат множество стандартных задач средней разницы.
ложность, поскольку опыт показывает, что традиционные планиметрические задачи
являются одним из самых слабых мест в подготовке будущих учителей
математика.
Основная цель разд. 5 и 6, чтобы предоставить студенту
необходимые навыки и «ноу-хау» для решения геометрических задач
используя метод геометрических преобразований и вектор
метод.Здесь мы хотели бы подчеркнуть, что эти разделы содержат
Как правило, традиционные геометрические задачи решаются
указанные методы, но не специальные задачи по преобразованиям
и векторы, которые часто встречаются в коллекциях проб
лемы по геометрии. Поскольку геометрические задачи решаются разными
методов, студент иногда встречает идентичные или похожие
проблемы в пп. 2-4 и 5-6.
Два раздела (7 и 16) посвящены геометрическим задачам.
о нахождении наибольших и наименьших ценностей.
Чтобы использовать книгу больше
В этом вводном разделе перечислены важные теоремы
плоская геометрия, которая должна облегчить решение задач.
Разделы 2–4 содержат множество стандартных задач средней разницы.
ложность, поскольку опыт показывает, что традиционные планиметрические задачи
являются одним из самых слабых мест в подготовке будущих учителей
математика.
Основная цель разд. 5 и 6, чтобы предоставить студенту
необходимые навыки и «ноу-хау» для решения геометрических задач
используя метод геометрических преобразований и вектор
метод.Здесь мы хотели бы подчеркнуть, что эти разделы содержат
Как правило, традиционные геометрические задачи решаются
указанные методы, но не специальные задачи по преобразованиям
и векторы, которые часто встречаются в коллекциях проб
лемы по геометрии. Поскольку геометрические задачи решаются разными
методов, студент иногда встречает идентичные или похожие
проблемы в пп. 2-4 и 5-6.
Два раздела (7 и 16) посвящены геометрическим задачам.
о нахождении наибольших и наименьших ценностей. Эти проблемы обычно
считается частью математического анализа, но в последнем
основная цель этих задач — продемонстрировать применение
дифференциальное исчисление (то есть акцент делается на решении задачи с
в рамках математической модели и, в меньшей степени,
по настройке модели и ее интерпретации). Когда мы включили в
в этой книге проблемы для поиска наибольших и наименьших ценностей, мы
обеспокоены тем, что каждая проблема должна быть интересна в первую очередь из
геометрическая точка зрения (то есть акцент был сделан на конструкции
математической модели и ее интерпретации).Глава 2 посвящена стереометрическим задачам. Вопросы по
построение представления данного твердого тела, и
определение полноты представления и его метрики
определенность изложены в краткой форме. Рассматривается
геометрическое построение в пространстве, особое внимание уделяется
конструкции на представлениях. Большинство проблем в обоих главах
Для этого учебного пособия были специально разработаны устройства. Среди них мы
Хотел бы упомянуть определение угла между перекосом
линии, расстояние между ними, угол между прямыми
плоскость, двугранные углы и построение сечений.
Эти проблемы обычно
считается частью математического анализа, но в последнем
основная цель этих задач — продемонстрировать применение
дифференциальное исчисление (то есть акцент делается на решении задачи с
в рамках математической модели и, в меньшей степени,
по настройке модели и ее интерпретации). Когда мы включили в
в этой книге проблемы для поиска наибольших и наименьших ценностей, мы
обеспокоены тем, что каждая проблема должна быть интересна в первую очередь из
геометрическая точка зрения (то есть акцент был сделан на конструкции
математической модели и ее интерпретации).Глава 2 посвящена стереометрическим задачам. Вопросы по
построение представления данного твердого тела, и
определение полноты представления и его метрики
определенность изложены в краткой форме. Рассматривается
геометрическое построение в пространстве, особое внимание уделяется
конструкции на представлениях. Большинство проблем в обоих главах
Для этого учебного пособия были специально разработаны устройства. Среди них мы
Хотел бы упомянуть определение угла между перекосом
линии, расстояние между ними, угол между прямыми
плоскость, двугранные углы и построение сечений. В нашем
мнение, решение этих проблем поможет студенту развить
возможность трехмерной визуализации.
Структура и содержание книги, способы изложения
материал, а также выбор и постановка задач были
сделано авторами коллективно. Материал для разд. 1-4, 7 и
Предисловие 7
10 подготовил А.Г. Мордкович, для пп. 5 и 6 В. А. Гу-
сов, а для пп. 8-15 В. Н. Литвиненко.
Авторы глубоко признательны преподавателям алгебры и математики.
геометрия в Рязанском государственном педагогическом институте, ассистент проф.
арендодатель М.Рассудовская М., Гальперин Г.А., канд. Sc. (Физ.-
Матли.), Которые внимательно прочитали рукопись и сделали ценный
предложения, которые улучшили книгу.
Авторы
СОДЕРЖАНИЕ
Предисловие 5
Глава 1. ГЕОМЕТРИЯ ПЛОСКОСТИ 10
П. 1. Методы решения геометрических задач 10
I. Треугольники и четырехугольники 10
II. Круги 12
III. Области плоских фигур 13
П. 2. Треугольники и четырехугольники 22
Проблемы, которые можно решить без посторонней помощи 28
I. Правые треугольники (1–12) 28
II. Равнобедренные треугольники (13-31) 29
III.
В нашем
мнение, решение этих проблем поможет студенту развить
возможность трехмерной визуализации.
Структура и содержание книги, способы изложения
материал, а также выбор и постановка задач были
сделано авторами коллективно. Материал для разд. 1-4, 7 и
Предисловие 7
10 подготовил А.Г. Мордкович, для пп. 5 и 6 В. А. Гу-
сов, а для пп. 8-15 В. Н. Литвиненко.
Авторы глубоко признательны преподавателям алгебры и математики.
геометрия в Рязанском государственном педагогическом институте, ассистент проф.
арендодатель М.Рассудовская М., Гальперин Г.А., канд. Sc. (Физ.-
Матли.), Которые внимательно прочитали рукопись и сделали ценный
предложения, которые улучшили книгу.
Авторы
СОДЕРЖАНИЕ
Предисловие 5
Глава 1. ГЕОМЕТРИЯ ПЛОСКОСТИ 10
П. 1. Методы решения геометрических задач 10
I. Треугольники и четырехугольники 10
II. Круги 12
III. Области плоских фигур 13
П. 2. Треугольники и четырехугольники 22
Проблемы, которые можно решить без посторонней помощи 28
I. Правые треугольники (1–12) 28
II. Равнобедренные треугольники (13-31) 29
III. Произвольные треугольники (32-59) 30
IV. Параллелограммы (60-73) 31
V. Трапеции (74-92) 32
VI. Разные проблемы (93-110) 33
П. 3. Круги 34
Проблемы, которые нужно решать без посторонней помощи 40
I. Круги (111-129) 40
II. Вписанные и описанные треугольники (130-157) 41
III. Произвольно расположенные круг и треугольник (158-175) 43
IV. Круг и четырехугольник (176-191) 44
V. Разные проблемы (192-219) 45
П. 4. Площади плоских фигур 47
Проблемы, которые можно решить без посторонней помощи 57
I. Площадь треугольников (220-247) 57
II.Площадь четырехугольника (248-271) 59
III. Площадь полигонов (272-279) 60
IV. Площадь комбинированных фигур (280-295) 61
V. Разные проблемы (296-321) 62
П. 5. Геометрические преобразования 64
Проблемы, которые можно решить без посторонней помощи 68
I. Симметрия относительно точки (322-337) 68
II. Симметрия относительно прямой (338-362) 69
III. Вращение (363-377) 70
IV. Перевод (378-390) 71
V. Гомотбетическая трансформация (391-397) 72
П. 6. Векторы 73
I. Аффинные задачи 75
II.
Произвольные треугольники (32-59) 30
IV. Параллелограммы (60-73) 31
V. Трапеции (74-92) 32
VI. Разные проблемы (93-110) 33
П. 3. Круги 34
Проблемы, которые нужно решать без посторонней помощи 40
I. Круги (111-129) 40
II. Вписанные и описанные треугольники (130-157) 41
III. Произвольно расположенные круг и треугольник (158-175) 43
IV. Круг и четырехугольник (176-191) 44
V. Разные проблемы (192-219) 45
П. 4. Площади плоских фигур 47
Проблемы, которые можно решить без посторонней помощи 57
I. Площадь треугольников (220-247) 57
II.Площадь четырехугольника (248-271) 59
III. Площадь полигонов (272-279) 60
IV. Площадь комбинированных фигур (280-295) 61
V. Разные проблемы (296-321) 62
П. 5. Геометрические преобразования 64
Проблемы, которые можно решить без посторонней помощи 68
I. Симметрия относительно точки (322-337) 68
II. Симметрия относительно прямой (338-362) 69
III. Вращение (363-377) 70
IV. Перевод (378-390) 71
V. Гомотбетическая трансформация (391-397) 72
П. 6. Векторы 73
I. Аффинные задачи 75
II. Метрические проблемы 81
Содержание 9
Проблемы, которые нужно решать без посторонней помощи 83
Я.Сложение и вычитание векторов. Умножение вектора
по номеру
Метрические проблемы 81
Содержание 9
Проблемы, которые нужно решать без посторонней помощи 83
Я.Сложение и вычитание векторов. Умножение вектора
по номеру Math-Net.Ru
RUS
ENG AMSBIB RSS RSS
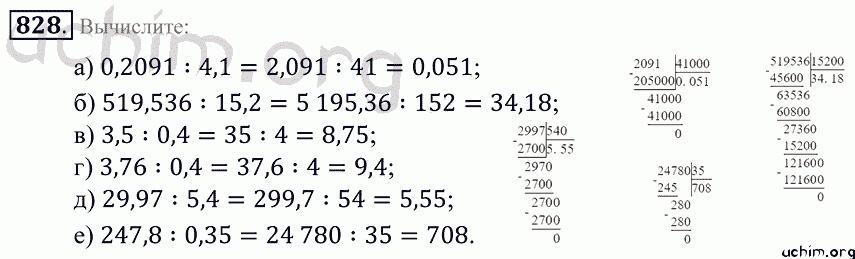
URL [email protected] :
math-net2021_10 [at] mi-ras ru ©
. . . , 2021 Новый сверхпрочный материал для химической технологии
438
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ХИМИЧЕСКОЙ ТЕХНИКИ Vol.37 № 5 2003
МОРДКОВИЧ
арматурные конструкции, работающие в сложонапряженном состоянии
: колонны, столбы, ригели каркасных конструкций-
шт .; такие оболочки также используются для восприятия поперечных сил
, поперечных сил и т. д. [25].
Механические и технологические свойства углеродных материалов
открывают широкие возможности для ремонта, армирования и восстановления зданий
и объектов из бетона, железобетона
крит, камень и дерево, т. е., производственные здания, резервуары —
е., производственные здания, резервуары —
ворот, бункеров, башенных силосов и градирен,
нефтяных платформ, подпорных стенок, мостов, труб, тоннелей,
гидротехнических и портовых сооружений и т. д. из
реализованопроектов в Москве и Новороссийске —
реализовано компанией S&P Clever Reinforcement Company
AG (Швейцария) через своего дистрибьютора — ЗАО «Триада-
Холдинг». Хотя мировое производство волокон сверхвысокой прочности
в основном сосредоточено в Японии (Toray
и Mitsubishi), российские производители волокон на основе полиакрила
также присутствуют на рынке, в частности, в
— Челябинский электродный завод. и
Федеральный государственный унитарный научно-исследовательский институт графитовых строительных материалов
(НИИГрафит), Москва.
Углеродные волокна
, наряду с их высокой прочностью, обладают рядом других полезных свойств, которые
отличают эти материалы от обычных углеродных волокон
[4, 5]. Другими важными областями их применения являются угольно-литиевые батареи
Другими важными областями их применения являются угольно-литиевые батареи
для компьютеров и мобильных телефонов
телефонов (только японские производители обеспечивают годовой объем производства
устройств в размере 30 миллионов устройств), пусковые конденсаторы
торс для электронных устройств, электропроводящий пластик.
тиковых композитов и, наконец, биоматериалов.
В настоящее время технология углеродного нановолокна
внедряется только двумя производителями, японскими компаниями
Showa Denko и Mitsubishi. Производство
началось в 2001 году и сейчас варьируется от нескольких сотен
килограммов от Showa Denko до 10 тонн от Mitsubishi. Произведенные углеродные нановолокна
используются в строительстве в
сейсмических регионах и в производстве углеродно-литовых аккумуляторов
иум для мобильных телефонов, пусковых конденсаторов для электронных устройств
и электропроводящей углеродной ленты Te на
.
СПИСОК ЛИТЕРАТУРЫ
1. Инагаки, М., Новые угли: управление структурой и
функций, Oxford: Elsevier, Sci., 2002.
2. Науки об углеродных материалах, Марш, Х. Ред., Аликанте:
Univ. di Alicante, 2000.
3. Baker, R.T.K. и Харрис, П.С., Формирование углерода Fila-
, химия и физика углерода,
Walker, P.L. and Thrower, P.A., Eds., New York: Marcel
Dekker, 1978, стр. 83.
4.Углеродные нанотрубки, Эндо, М., изд., Оксфорд: Пергамон,
1996.
5. Углеродные нанотрубки: получение и свойства, Ebbe-
sen, TW, Ed., New York: CRC, 1997.
6. Дрессельхаус М.С., Дрессельхаус Г., Эклунд П.С.,
Наука о фуллеренах и углеродных нанотрубках, Лондон:
Academic, 1996.
7. Елецкий А.В., Углеродные нанотрубки, Усп. Физ. Наук, 1997,
,т. 167, нет. 9, стр. 945.
8. Раков Э.Г. Нанотрубки неорганических веществ // Журн.
Neorg. Хим., 1999, т. 44, нет. 11, стр. 1827.
9. Зеленский Е.С., Куперман А.М., Горбаткина Ю.А.,
,и др. Армированные пластмассы: современные строительные материалы.
др., Росс. Хим. Журн., 2001, т. 44, нет. 2, стр. 56.
10. Guigon, M., Oberlin, A., and Desarmot, G., Microtex-
Структура и структура некоторых высокомодульных материалов, PAN-Base
Углеродные волокна, Fiber Sci. Техн., 1984, т. 20, стр. 177.
11. Tibbetts, G.G. и Битц, К.П., Механические свойства
углеродных волокон, выращенных из паров, J. Phys. D: Прил. Phys.,
1987, т. 20, стр. 292.
12. Оберлин А., Эндо М. и Кояма Т., Нитевидный
Рост углерода в результате разложения бензола,
J. Cryst. Рост, 1976, т. 32, стр. 335.
13. Эндо, М., Углеродные волокна, выращенные из паров, Ph.D. Thesis,
Nagoya: Nagoya Univ., 1978.
14. Endo, M. и Sikata, M., Tanso faiba (Carbon Fibers),
Oio Butsuri, 1985, vol.54, стр. 507.
15. Эндо, М., Оберлин, А. , и Кояма, Т., Структура и
, и Кояма, Т., Структура и
Механизм роста углеродных волокон, выращенных из паров,
Jpn. J. Appl. Phys., Часть 1, 1977, т. 16, стр. 1519.
16. Кацуки Х., Мацунага К., Эгашира М. и Кава-
суми С., Формирование углеродных волокон из нафталина
на некоторых серосодержащих субстратах, Углерод, 1981,
об. 9, стр. 148.
17. Ишиока, М., Окада, Т., и Мацубара, К., Образование
парообразных углеродных волокон в смесях диоксида углерода и углерода
bon: I.Влияние состава газа Carrier
, Углерод, 1992, т. 30, стр. 859.
18. Ишиока, М., Окада, Т., и Мацубара, К., Образование
парообразных углеродных волокон в смесях диоксида углерода и углерода
бон: II. Влияние Cata-
lyst, Carbon, 1992, т. 30, стр. 975.
,19. Тиббетс, Г.Г., Длина углеродных волокон, полученных из частиц железного катализатора
в природном газе, J. Cryst. Рост,
1985, т. 73, стр.431.
20. Эгашира, М. , Кацуки, Х., Хаяси, К., и Кава-
, Кацуки, Х., Хаяси, К., и Кава-
суми, С., Секубай-но тансо файба (волокна каталитического углерода
), Сэкию Гаккай Си, 1983, т. 26, стр. 247.
21. Мотодзима, С., Хасегава, И., Кагия, С. и др., Vapor
Фазовая подготовка углеродных микроволоконных волокон с помощью
Металлический порошковый каталитический пиролиз ацетилена. Небольшое количество примеси фосфора, Car-
bon, 1995, т. 33, стр. 1167.
22. Мотодзима С., Иванага Х. и Варадан В.К., Кабон
майкуро коиру (Углеродные микрокатушки), Homen, 1998,
vol. 36, стр. 140.
23. Сонеда Ю. и Инагаки М. Формирование и графитизация углеродных волокон, выращенных из паров, З. Анорг. Allg.
Chem, 1992, т. 610, стр. 157.
24. Имамутдинов И., Переходцев Г., Грязное стекло
Эффект, Эксперт, 8 октября 2001 г., вып. 37.
25. Сейбл, Ф., Пристли, Н., and Innamorato, D., Earthquake
Модернизация мостовых колонн сплошным углеродным волокном
. Отчет № ACTT-95/08, Отчет для Cal-
Отчет № ACTT-95/08, Отчет для Cal-
trans, Отдел структур, Подготовлен в соответствии с соглашением по программе
ARPA / TRP № MDA 972-94-3-
0030, Сан-Диего: Univ. Calif., 1998.
Положительные и отрицательные числа, числовой модуль
Заведующий ШМО
учителя математики _______ Калашникова Ж.Ю Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №89»
Тематические тесты по математике для 6 класса
по учебнику И.И. Зубарева, А.Г. Мордкович
Составили: учителя математики:
Калашникова Жанна Юрьевна
Столбова Людмила Антоновна
ЗАТО Северск
2016 год
Содержание
Тест № 1 ……………………………………… …………………………………………… .3-6
Испытание № 2 ……………………………………………………………… ……………………… .7-10
Тест № 3 …………………………………………………………………………………… … .11-14
Ответы …………………………………………………………………………………… ..15
Тест № 1 «Положительный и отрицательные числа «
Вариант 1
Введите отрицательное дробное число:
-165
38
-7. 92
92
67 Опишите событие «На координатном луче отмечено число -5,5»
Достоверно
Невозможно
Случайно
Какое из четырех чисел является наибольшим?
8,035
80,35
0,8035
803,5
Какая из точек расположена на координатной прямой справа от точки O (0)?
M (-4)
E (-15)
K (15)
D (-1,2)
Ночью температура воздуха была -5 ° C. Днем столбик термометра был уже +3 ° C. температура воздуха изменилась?
Увеличено на 8o
Уменьшено на 2o
Увеличено на 2o
Уменьшено на 8o
На координатной линии отмечена точка x (-2) — центр симметрии.Задайте координаты точек, расположенных на этой прямой симметрично точке x.
(-1) и (1)
(-1) и (1)
(3) и (-3)
(0) и (-4)
Какие точки на координатной линии не симметричны относительно начала координат — точка O (0).
B (-5) и C (5)
D (0,5) и E (-0,5)
M (-3) и K (13)
A (18) и X (-18)
Какова сумма числа 0,316 + 0,4?
0,356
0,716
4,316
0,32
Вычислить 25% от 0,4.
0,1
0,001
10
100
Вычислите разницу между 9100 и 0.03
0,05
0,6
9,03
350 Вариант 2
Введите отрицательное дробное число.
8,63
-1045
913-0,2
Опишите событие «На координатном луче отмечена цифра 7».
Случайно
Невозможно
Достоверно
Какое наименьшее число?
15,49
154,9
1,549
1549
Какая из точек расположена на координатной прямой слева от точки O (0).
A (-0,5)
AT 6)
M (0,5)
K (38)
Днем столбик термометра показывал + 5 ° C, а вечером -2 ° C.Как изменилась температура воздуха?
Увеличено на 3o
Уменьшено на 7o
Уменьшено на 3o
Увеличено на 7o
На координатной прямой отмечен центр симметрии — точка A (-3). Укажите координаты точек, расположенных на этой прямой симметрично точке A.
(-2) и (2)
(0) и (-5)
(-6) и (1)
(-1) и ( -5)
Какие точки координатной прямой не симметричны относительно начала координат — точка O (0).
A (6) и B (-6)
C (12) и D (-2)
M (-1) и K (1)
X (-9) и Y (9)
Какова сумма числа 0.237 и 0,3
0,24
3,237
0,537
0,267
Рассчитайте 20% от 0,5
10
0,1
0,2
0,01
Рассчитайте разницу между 0,07 и 31001250,5
1
425 Тест № 2. Абсолютное значение числа. Противоположные числа.
Вариант 1
Какое из указанных чисел имеет наименьший модуль
-11
1013-4,196
-4,2
Введите недопустимое равенство
85 = -85
-1,9 = 1,9
35 = 3558 = -58 Модуль неотрицательного числа — неотрицательное число.Верно ли это утверждение?
Да
Нет
Какое из этих чисел противоположно -34? 43-43-3434 Каково значение выражения — (- m), если m = -15
+15
-15
Вычислите значение выражения: -2,5 ∙ 4-919
-10
1
— 1
Решите уравнение: x = 40-40
40
40 или -40
Какие целые числа находятся на координатной прямой между числами 2,75 и 3,9?
-2, -1, 1, 2
-1, 0, 1, 2, 3
-1, 0, 1, 2, 3, 4
-2, -1, 0, 1, 2, 3
Is неравенство верно -30> -50 Да
Нет
Укажите все целые числа x, если x≤30, 1, 2
0, 1, 2, 3
0, 1, 2, 3, 4
1, 2, 3
Вариант 2
Какое из чисел имеет наибольший модуль?
-0,6
-50,603
493550,530
Введите недействительное равенство
-1. 5 = 1,512 = 12-117 = 117-325 = -325 Может ли модуль отрицательного числа быть отрицательным числом
5 = 1,512 = 12-117 = 117-325 = -325 Может ли модуль отрицательного числа быть отрицательным числом
Да
Нет
Какое из этих чисел противоположно 124?
-24
24
-124124 Какое значение имеет выражение — (- k), если k = -9
-9
+9
Вычислите значение выражения: 2,5: -0,5 + 1,250
15
— 2,5
2,5
Решите уравнение x = 100100
-100
100 или -100
Какие целые числа находятся на координатной прямой между числами 1 и — 4.5
-4, -3, -2, -1, 0
-3, -2, -1
-5, -4, -3, -2, -1
-4, -3, -2, — 1, 1
Является ли неравенство -25 истинно Да
Нет
Укажите все целые числа x, если x≤44, 3, 2
0, 1, 2, 3
1, 2, 3, 4
0, 1, 2, 3, 4
Тест № 3. Сравнение чисел
Вариант 1
Какое неравенство неверно?
-20> 2
0
-16> -7
-5
-320-920>
=
Верно ли, что число 0 больше любого отрицательного числа?
Да
Нет
Число a неотрицательно.Как записать это утверждение в виде неравенства?
a0 Укажите наибольшее заданное число.
0,16
-3018-0,4
0,01
Для которых естественными значениями x является неравенство x≤44, 3, 2 истинно
1, 2, 3, 4
4, 3, 2, 1
0, 1, 2, 3
Для каких целых значений y выполняется неравенство y
-1
0, -1, 1
Нет таких значений
Числа -6; -3,8; -115; 0.8 расположены:
По убыванию
По возрастанию
В бардаке
По радио транслировался прогноз погоды: ожидается понижение температуры до -20 ° C.Опишите это событие:
Невозможно
Достоверно
Случайно
Вариант 2
Какое неравенство верно?
-5> 0
6
-34> -40
-9 Какой знак нужно поставить между дробями, чтобы неравенство было правильным?
-1315-715
>
=
Верно ли, что число 0 меньше любого отрицательного числа?
Да
Нет
Число x не больше нуля. Как записать это утверждение в виде неравенства?
x≥0x> 0x
-5,92
1,7
-1000
35 Для каких натуральных значений a верно неравенство a≤3? 1, 2, 3
0, 1, 2, 3
1, 2
0, 1, 2
Для каких целых значений m выполняется неравенство m
0, -1, -2, -3, 1, 2, 3
0
Нет таких значений
Числа 1,2; -1. 2; -427; -100 расположены:
2; -427; -100 расположены:
В беспорядке
По возрастанию
В порядке убывания
Точка A (5) отмечена на координатной линии. На этой линии случайным образом была отмечена еще одна точка B. Его координата оказалась цифрой напротив 5. Опишите это событие.
Случайно
Достоверно
Невозможно
Ответы
Тест № 1 Тест № 2
№ Вариант 1 Вариант 2
1 3 4
2 2 3
3 4 3
4 3 1
5 1 2
6 4 4
7 3 2
8 2 3
9 1 2
10 4 1
No.Вариант 1 Вариант 2
1 3 2
2 1 4
3 1 2
4 4 3
5 2 1
6 3 4
7 3 3
8 4 1
9 1 2
10 2 4
Номер теста 3
№ Вариант 1 Вариант 2
1 4 3
2 1 2
3 1 2
4 3 4
5 1 3
6 2 1
7 4 4
8 2 3
В рамках урока будет обсуждаться понятие модуля действительного числа и представлены несколько его основных определений, затем будут рассмотрены примеры, демонстрирующие применение различных из этих определений.
Тема: Реальные числа
Урок: Модуль действительного числа
1. Определения модулейРассмотрим такое понятие, как модуль действительного числа, у него есть несколько определений.
Определение 1. Расстояние от точки на координатной прямой до нуля называется модулем числа , которое является координатой этой точки (рис. 1).
Пример 1. … Обратите внимание, что абсолютные значения противоположных чисел равны и неотрицательны, поскольку это расстояние, но оно не может быть отрицательным, а расстояние от чисел, симметричных относительно нуля, до начала координат равно равный.
Определение 2..
Пример 2. Рассмотрим одну из задач, поставленных в предыдущем примере, чтобы продемонстрировать эквивалентность введенных определений. , как вы можете видеть, с отрицательным числом под знаком модуля, добавляя еще один минус, прежде чем он даст неотрицательный результат, как следует из определения модуля.
Следствие. Расстояние между двумя точками с координатами на координатной прямой можно найти следующим образом независимо от взаимного расположения точек (рис.2).
2. Основные свойства модуля1. Абсолютное значение любого числа неотрицательно
2. Модуль продукта — это продукт модулей
3. Частный модуль — это частный модуль
3. Решение проблемПример 3. Решите уравнение.
Решение. Воспользуемся вторым определением модуля: и запишем наше уравнение в виде системы уравнений для разных вариантов открытия модуля.
Пример 4. Решите уравнение.
Решение. Так же, как и в предыдущем примере, мы получаем это.
Пример 5. Решите уравнение.
Решение. Решим через следствие из первого определения модуля :. Изобразим это на числовой оси с учетом того, что искомый корень будет находиться на расстоянии 2 от точки 3 (рис. 3).
Исходя из рисунка, получаем корни уравнения:, поскольку точки с такими координатами расположены на расстоянии 2 от точки 3, как требуется в уравнении.
Ответ. .
Пример 6. Решите уравнение.
Решение. По сравнению с предыдущей задачей есть только одна сложность — это отсутствие полного сходства с формулировкой следствия о расстоянии между числами на координатной оси, так как под знаком модуля стоит знак плюс, а не минус подписать. Но привести к необходимому виду несложно, что мы и сделаем:
Изобразим это на числовой оси аналогично предыдущему решению (рис.4).
Корни уравнения.
Ответ. .
Пример 7. Решите уравнение.
Решение. Это уравнение все же немного сложнее предыдущего, поскольку неизвестное стоит на втором месте и со знаком минус, кроме того, оно имеет еще и числовой множитель. Для решения первой задачи воспользуемся одним из свойств модуля и получим:
Для решения второй задачи мы меняем переменные:, что приводит нас к простейшему уравнению.Согласно определению второго модуля … Подставляя эти корни в уравнение замены, мы получаем два линейных уравнения:
Ответ.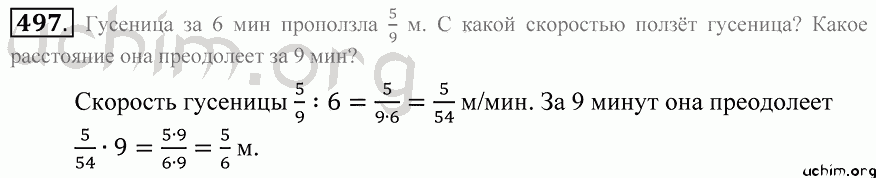 .
.
Довольно часто в процессе решения проблем с корнями появляются модули, и стоит обратить внимание на ситуации, в которых они возникают.
При первом взгляде на этот тож может возникнуть вопрос: «а зачем там модуль?» и «почему тождество неправильное?» Оказывается, можно дать простой контрпример для второго вопроса: если это должно быть правдой, что эквивалентно, но это ложное тождество.
После этого может возникнуть вопрос: «не решает ли проблема такая идентичность», но есть еще и контрпример к этому предложению. Если это должно быть правдой, что эквивалентно, и это ложная личность.
Соответственно, если мы вспомним, что квадратный корень из неотрицательного числа является неотрицательным числом, а значение модуля неотрицательно, становится ясно, почему приведенное выше утверждение верно:
.
Пример 8. Вычислить значение выражения.
Решение. В таких задачах важно не сразу избавляться от рута бездумно, а использовать указанную выше идентичность, т.к.
Состоит из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа и только они меньше нуля. На числовой оси отрицательные числа находятся слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n , которое дополняет n до нуля: n + (- n ) = 0 … Оба номера называются напротив друг для друга. Вычитание целого числа a эквивалентно сложению с его противоположностью: -a .
Свойства отрицательных чисел
Отрицательные числа подчиняются почти тем же правилам, что и натуральные числа, но имеют некоторые особенности.
Исторический очерк
Литература
- Выгодский М.Я. Справочник по элементарной математике. — М .: АСТ, 2003. — ISBN 5-17-009554-6 .
- Глейзер Г.I. История математики в школе. — М .: Просвещение, 1964. — 376 с.
Ссылки
Фонд Викимедиа. 2010.
- Неосторожное причинение вреда
- Неотропы
Посмотреть, что такое «Неотрицательное число» в других словарях:
Вещественное число — Действительное или действительное число — это математическая абстракция, возникшая из-за необходимости измерения геометрических и физических величин окружающего мира, а также для выполнения таких операций, как извлечение корня, вычисление логарифмов, решение… … Википедия
обычно небольшое неотрицательное целое число — Часть кодирования, которая представляет значения неограниченного неотрицательного целого числа, но где небольшие значения чаще встречаются (ITU-T X.691 ). Темы … … Руководство технического переводчика
РЕАЛЬНОЕ ЧИСЛО — действительное число, положительное число, отрицательное число или ноль. Понятие дифференциального числа возникло в результате расширения понятия рационального числа. Необходимость в этом расширении обусловлена как практическим использованием математики в выражении… … Математическая энциклопедия
Простое число — Простое число — это натуральное число, которое имеет ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме одного, называются составными. Таким образом, все натуральные числа больше единицы … … Википедия
натуральное число — ▲ целое число, выражающее действительное, число натуральное число неотрицательное целое число; выражает количество отдельных целых объектов в каком л. агрегаты; обозначают количество реальных целых объектов; выражение чисел.четыре … Идеографический словарь русского языка
Десятичная дробь — Десятичная дробь — это разновидность дроби, которая представляет собой способ представления действительных чисел в форме, в которой знак дроби: либо, либо десятичная точка, служащая разделителем между целой и дробной частями дроби. номер … … Википедия Википедия
Не имеет знака как специальный номер.
Примеры написания цифр: + 36, 6; — 273; 142. (\ Displaystyle +36 (,) 6; \ (-) 273; \ 142.(2))) символы плюс и минус указывают не знак выражения, перед которым они стоят, а знак арифметической операции, так что знак результата может быть любым, он определяется только после выражение оценивается.
Помимо арифметики, понятие знака используется в других разделах математики, в том числе для нечисловых математических объектов (см. Ниже). Понятие знака также важно в тех разделах физики, где физические величины делятся на два класса, условно называемые положительными и отрицательными, — например, электрические заряды, положительная и отрицательная обратная связь, различные силы притяжения и отталкивания.
Цифровой знак
Положительные и отрицательные числа
Нет никакого знака, назначенного нулю, то есть + 0 (\ displaystyle +0) и — 0 (\ displaystyle -0) — это то же число в арифметике. В математическом анализе значения символов + 0 (\ displaystyle +0) и — 0 (\ displaystyle -0) могут различаться, см. Об этом отрицательном и положительном нуле; в информатике компьютерное кодирование двух нулей (целочисленный тип) может отличаться, см. Прямой код.
В связи с вышеизложенным вводится еще несколько полезных терминов:
- Число неотрицательное значение , если оно больше или равно нулю.
- Число не положительное , если оно меньше или равно нулю.
- Положительные числа без нуля и отрицательные числа без нуля иногда (чтобы подчеркнуть, что они ненулевые) называются «строго положительными» и «строго отрицательными» соответственно.
Та же терминология иногда используется для реальных функций. Например, функция называется положительные, , если все ее значения положительны, неотрицательные, , если все ее значения неотрицательны, и т. Д.Также говорят, что функция положительна / отрицательна на заданном интервале ее определения.
Пример использования функции см. В статье Квадратный корень # Комплексные числа.
Модуль (абсолютное значение) числа
Если число x (\ displaystyle x) отбросить знак, полученное значение называется модуль или абсолютное значение числа x (\ displaystyle x), оно обозначается | х | … (\ displaystyle | x |.) Примеры: | 3 | = 3; | — 3 | = 3.(\ Displaystyle | 3 | = 3; \ | (-3) | = 3.)
Для любых действительных чисел a, b (\ displaystyle a, b) выполняются следующие свойства.
Знак для нечисловых объектов
Угловой знак
Величина угла на плоскости считается положительной, если он измеряется против часовой стрелки, в противном случае — отрицательной. Аналогично классифицируются два случая вращения:
- вращение на плоскости — например, вращение (–90 °) по часовой стрелке;
- вращение в пространстве вокруг ориентированной оси обычно считается положительным, если выполняется «правило кардана», в противном случае оно считается отрицательным.
Указатель направления
В аналитической геометрии и физике продвижение по заданной прямой или кривой часто условно делится на положительное и отрицательное. Это разделение может зависеть от постановки задачи или от выбранной системы координат. Например, при вычислении длины дуги кривой часто бывает удобно присвоить этой длине знак минус в одном из двух возможных направлений.
Вход в вычислительную систему
| старший бит | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | -1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | -2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
| Для представления знака целого числа большинство компьютеров используют | |||||||||
По модулю числа вызывается само это число, если оно неотрицательно, или то же число с противоположным знаком, если это отрицательно.
Например, модуль 5 равен 5, модуль –5 также равен 5.
То есть под абсолютным значением числа понимается абсолютное значение, абсолютное значение этого числа без учета его подписать.
Обозначается следующим образом: | 5 |, | NS |, | a | пр.
Правило :
Пояснение:
| 5 | = 5
Это читается так: модуль числа 5 равен 5.
| –5 | = — (- 5) = 5
Это читается так: модуль числа -5 равен 5.
| 0 | = 0
Это читается так: модуль нуля равен нулю.
Свойства модуля:
1) Абсолютное значение числа является неотрицательным числом: | a | ≥ 0 2) Модули противоположных чисел равны: | a | = | — a | 3) Квадрат абсолютного значения числа равен квадрату этого числа: | a | 2 = a 2 4) Модуль произведения чисел равен произведению модулей этих чисел: | a · b | = | a | · | b | 6) Модуль частных чисел равен отношению модулей этих чисел: | a : b | = | a | : | b | 7) Модуль суммы чисел меньше или равен сумме их модулей: | a + b | ≤ | a | + | b | 8) Модуль разности чисел меньше или равен сумме их модулей: | a — b | ≤ | a | + | b | 9) Модуль суммы / разности чисел больше или равен модулю разности их модулей: | a ± b | ≥ || a | — | b || 10) Постоянный положительный коэффициент можно вынести вне знака модуля: | м · и | = м · | a |, m > 0 11) Степень числа может быть взята вне знака модуля: | a k | = | a | k, если k существует 12) Если | a | = | b | тогда a = ± b |
Геометрический смысл модуля.
Абсолютное значение числа — это расстояние от нуля до этого числа.
Например, возьмем снова цифру 5. Расстояние от 0 до 5 такое же, как от 0 до -5 (рис. 1). А когда нам важно знать только длину отрезка, то знак имеет не только значение, но и значение. Однако это не совсем так: мы измеряем расстояние только положительными или неотрицательными числами. Пусть ценой деления нашей шкалы будет 1 см. Тогда длина отрезка от нуля до 5 составляет 5 см, от нуля до –5 тоже 5 см.
На практике расстояние часто измеряется не только от нуля — точкой отсчета может быть любое число (рис. 2). Но суть от этого не меняется. Запись формы | а — б | выражает расстояние между точками a и b на числовой прямой.
Пример 1. Решить уравнение | NS — 1 | = 3.
Решение.
Суть уравнения в том, что расстояние между точками NS и 1 равно 3 (рис.2). Следовательно, начиная с точки 1, мы считаем три деления слева и три деления справа — и мы можем ясно видеть оба значения NS :
NS 1 = –2, NS 2 = 4.
We можно посчитать.
│ NS — 1 = 3
│ NS — 1 = –3
│ NS = 3 + 1
│ NS = –3 + 1
│ NS = 4
│ NS = –2.
Ответ: NS 1 = –2; NS 2 = 4.
Пример 2. Найдите модуль выражения:
Решение.
Сначала выясните, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Искать корень 5 не будем — это довольно сложно. Сделаем проще: поднимем 3 и 10 в корень. Затем сравните значения чисел, составляющих разницу:
3 = √9. Следовательно, 3√5 = √9 √5 = √45
10 = √100.
Мы видим, что первое число меньше второго. Следовательно, выражение отрицательное, то есть его ответ меньше нуля:
3√5 — 10
Но по правилу абсолютное значение отрицательного числа — это то же самое число с противоположным знаком. У нас есть отрицательное выражение. Следовательно, необходимо изменить его знак на противоположный. Противоположность 3√5 — 10 — (3√5 — 10). Раскроем в нем скобки — и получим ответ:
— (3√5 — 10) = –3√5 + 10 = 10 — 3√5.
Ответ.
Влияние капиллярной конденсации на тепломассоперенос в зерне катализатора синтеза Фишера-Тропша
Карнаухов А.П., Адсорбция. Текстура дисперсных и пористых материалов, , Новосибирск: Наука, 1999.
. Google ученый
Деревич И.В., Ермолаев В.С., Мордкович В.З. Термодинамическое равновесие жидкость-пар в продуктах синтеза Фишера-Тропша.Осн. Хим. Технол. , 2008, т. 42, нет. 2, стр. 227 [ Теор. Нашел. Chem. Eng . (Англ. Пер.), Т. 42, нет. 2, стр. 216].
Google ученый
Гроен Дж. К., Пеффер Л. А., Перес-Рамирес Дж. Определение размера пор в модифицированных микро- и мезопористых материалах. Подводные камни и ограничения в анализе данных по адсорбции газа, Microporous Mesoporous Mater. , 2003, т. 60, стр. 1.
CAS Статья Google ученый
Рид Р.К., Праусниц Дж. М., Шервуд Т. К., Свойства газов и жидкостей, , Нью-Йорк: McGraw-Hill, 1977, 3-е изд.
Google ученый
Киперман С.Л., Основы химической кинетики в гетерогенном катализе . М .: Химия, 1972.
. Google ученый
Хубер, Г.W., Внутренняя кинетика Pt-промотированного Co / SiO 2 Катализаторы синтеза Фишера-Тропша, M.S. Диссертация , Прово: Университет Бригама Янга, 2000.
Google ученый
Зыскин А.Г., Аветисов А.К., Кучаев В.Л., Шапатина Е.Н., Кристиансен Л. Моделирование кинетики сложных гетерогенных каталитических реакций в условиях диффузионных ограничений. Катал. , 2007, т. 48, вып. 3, стр. 357 [ Кинет.Катал . (Англ. Пер.), Т. 48, вып. 3, стр. 337].
Артикул Google ученый
Язык математики и формирование культуры математической речи у студентов
Абылкасымова Алма Евгеньевна, Кагазбаева Аспет К., Туяков Есенкельды А., Дюсов Марат Сергеевич
Эколоджи, 2019, выпуск 108, Страницы: 2615-2631
ОТКРЫТЫЙ ДОСТУП
Скачать полный текст (PDF)
Аннотация
По результатам международного исследования PISA в 2015 и 2017 гг., 15 л.о. студенты из многих стран ОЭСР показывают низкие результаты по математике. Например, по результатам PISA-2019 процент студентов из Казахстана с высокими способностями к разработке и работе с моделями в сложных ситуациях, работающих стратегически, используя широкие, хорошо развитые навыки мышления и рассуждения, составил всего 0,9%. , что ниже, чем в среднем по странам ОЭСР (13%). На наш взгляд, основная причина этого — недостаточное владение школьниками языком математики, что проявилось в неумении применять математический метод познания.
Задача — теоретически исследовать формирование современного языка математики и выявить пути формирования языка математики при обучении школьников.
Ключевым методом является аналитический метод исследования языка математики с учетом истории его становления и проявления в содержании математического образования.
В результате авторы выявили необходимость исследовать язык математики как объект обучения с точки зрения совокупности семантических, синтаксических и прагматических аспектов языка.
Ключевые слова
язык математики, семантика, синтаксис и прагматика языка математики, математическое моделирование, культура математической речи, обучение математике
Список литературы
- Абылкасымова А.Е. (2014) Теория и методика обучения математике: дидактические и методические основы. Алматы: Мектеп.
- Абылкасымова А.Е., Нурмухамедова Ж.М., Нурбаева Д.М., Жумалиева Л.Д. (2016) Влияние «турецкого вектора» на преподавание точных дисциплин в современной образовательной системе Казахстана: на примере преподавания алгебры и математики.Глобальный журнал чистой и прикладной математики, 12 (4): 3481-3492.
- Александров Н.В. (2008) История математических терминов, понятия, обозначений. Словарь-справочник. История математических терминов, понятий и обозначений. Словарь — справочник. Москва: ЛКИ.
- Аналитические исследования: назначение, методы, этапы. Получено с http://www.nazaykin.ru
- Asoodeh S, Motlagh AT (2015) Исследование соотношений плотностей геологической структуры с помощью фрактальной геометрии Case Stady: (регион Дехно в Фарсе, Иран).Международный журнал географии и геологии, 4 (2): 37-46.
- Дорофеев Г.В. (1985) Язык преподавания математики и математический язык. Современные проблемы методики преподавания математики. Современные проблемы методики обучения математике. Москва: Просвещение: 38-47.
- Фридман Л.М. Наглядность и моделирование в обучении. Москва: Знание.
- Гальперин П.Я. (2000) Введение в психологию.Москва: Университет.
- Gebre W (2015) Объем производства пальчатого проса в южной зоне омо в случае южной ари-вореды. Текущие исследования в области сельскохозяйственных наук, 2 (1): 1-7.
- Гибш И.А. (1995) Развитие речи в процессе изучения школьного курса математики. Математика в школе, (6): 2-5.
- Гилберт Д., Бернейс П. (1982) Основания математики: Логические исчисления и формализация арифметики.Москва: Наука.
- Глейзер Г.И. (1970) История математики в средней школе. Москва.
- Гнеденко Б.В. (1991) Развитие мышления и речи при изучении математики. Математика в школе, (4): 3-9.
- Груденов Я.И. (1990) Совершенствование методов работы учителя математики: Книга для учителя.Москва: Просвещение.
- Икрамов Дж.И. (1983) Теория и практика развития математической культуры школьников. Ташкент: ТашГПИ им. Низами.
- Ирсалиев С., Култуманова А., Сабырылы Е., Амангазы М. (2017) Основные результаты международного исследования PISA-2015, 2017 год: Национальный отчет. Астана: Информационно-аналитический центр.
- Кагазбаева А.К. (2019) О развитии и перспективах математического образования в школе. Материалы Международной научно-практической конференции «Педагогические инновации как ресурс развития современной системы образования». Актобе: Университет Жубанова: 400-403.
- Колмогоров А.Н., Гальперин Г.А. (1991) (составитель). Математика в историческом развитии. Москва: Наука.
- Леонтьев А.Н. (2005) Деятельность.Сознание. Личность [Активность, Сознание. Личность]. Москва: Смысл, Академия.
- Мадер В.В. (1995) Введение в методологию познания математики (гносеологические, мировоззренческие аспекты математики. Математика и теория познания. Гносеологические, мировоззренческие аспекты математики. Москва: Интерпракс. .
- Мордкович А.Г. (2002) Зачем учить математику? [Зачем изучать математику?] Первое сентября, (22).
- Мышкис А.Д. (2007) Элементы теории математических моделей. Москва: Ком Книга.
- Норман БЮ (2001) Основы языкознания: Функции языка. Первое сентября, (45).
- Рубинштейн С.Л. (2011) Бытие и сознание. Москва: Питер.
- Рассел Б. (1974) Основы математики. Лондон: Allen & Unwin LTD.
- Сергеева Л.А. (2014) Практико-ориентированные задачи как средство реализации прагматического аспекта математического языка.Вестник Псковского государственного университета. Серия «Социально-гуманитарные и психолого-педагогические науки». Вып. 5. Псков: Псковский государственный университет: 393-400.
- Шеншев Л.В. (1960) Общие моменты мышления в процессах усвоения математики и иностранного языка. Вопросы психологии, (4): 9-23.
- Сиротина И.К.К. (2012) Вопрос формирования математической культуры личности в образовательном процессе.Научная дискуссия: вопросы педагогики и психологии: материалы 7-й международной заочной научно-практической конференции. Часть 2. Москва: Международный центр науки и образования.
- Сохор А.М. (1988) Объяснение в процессе обучения: Элементы дидактической концепции. Москва: Педагогика.
- Стефанова Н.Л., Шубина Н.Л. (2011) Мысль, ограниченная словом: математический язык через призму естественного языка.Санкт-Петербург: Книжный мир.
- Столяр А.А. (1965) Логические проблемы преподавания математики. Минск: Высшая школа.
- Столяр А.А. (1986) Педагогика математики. Минск: Вышейшая школа.
- Талызина Н.Ф. (1998) Педагогическая психология. Москва: Академия.
- Виленкин Ня (2001) Основные этапы развития математики.В: Г. Д. Глейзер. Математика: Хрестоматия по истории, методологии, дидактике. Москва: УРАО.
© Авторское право Ekoloji .
