Контрольная работа номер 2 по геометрии 2 вариант: ГДЗ 7 класс / контрольные работы / К-2. вариант 2 геометрия 7‐9 класс самостоятельные и контрольные работы Иченская

ГДЗ 7 класс / контрольные работы / К-2. вариант 2 геометрия 7‐9 класс самостоятельные и контрольные работы Иченская

Решение есть!
  • 1 класс
    • Математика
    • Английский язык
    • Русский язык
    • Музыка
    • Литература
    • Окружающий мир
  • 2 класс
    • Математика
    • Английский язык
    • Русский язык
    • Немецкий язык
    • Информатика
    • Музыка
    • Литература
    • Окружающий мир
    • Технология
  • 3 класс
    • Математика
    • Английский язык
    • Русский язык
    • Немецкий язык
    • Информатика
    • Музыка
    • Литература
    • Окружающий мир
    • Казахский язык
  • 4 класс
    • Математика
    • Английский язык
    • Русский язык
    • Немецкий язык
    • Информатика
    • Музыка
    • Литература
    • Окружающий мир
    • Казахский язык
  • 5 класс
    • Математика
    • Английский язык
    • Русский язык
    • Физика
    • Немецкий язык
    • Украинский язык
    • Биология
    • История
    • Информатика
    • ОБЖ
    • География
    • Музыка

Контрольные работы по геометрии по учебнику Атанасян Л. С. | Учебно-методический материал по геометрии (7 класс) по теме:

  1.                              1 вариант.

1). Диагонали прямоугольника ABCD пересекается в точке О, ABO = 36°. Найдите AOD.

2).  Найдите углы прямоугольной трапеции, если один из ее углов равен 20°.

3).  Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма.

4). В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.

5).* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, АМ = 4 см. Найдите длину диагонали BD ромба, если точка М лежит на стороне AD.

  1.                                 2 вариант.

1).  Диагонали прямоугольника MNKP  пересекаются в точке О,MON= 64°. Найдите  ОМР.       2).  Найдите углы равнобокой трапеции, если один из ее углов на 30° больше второго.

3). Стороны  параллелограмма  относятся  как       3 : 1, а его периметр равен 40 см. Найдите стороны параллелограмма.

4).  В прямоугольной трапеции разность углов при одной из боковых сторон равна 48°. Найдите углы трапеции.

5).* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, длина диагонали  АС  равна 6 см. Найдите AM, если точка М лежит на продолжении стороны AD.

  1.                                1 вариант.

1).  Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.

2).  Катеты  прямоугольного  треугольника  равны    6 и 8 см. Найдите гипотенузу и площадь треугольника.

3).  Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.

4).* В прямоугольной трапеции АВСК большая боковая сторона равна 3см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции.

                                     2 вариант.

1).  Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника.

2).  Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и гипотенузу треугольника.

3).  Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр.

4).* В прямоугольной трапеции ABCD большая боковая сторона равна 8 см, угол А равен 60°, а высота ВН делит основание AD пополам. Найдите площадь трапеции.

                                   1 вариант.

1).  По рис. A = B, СО = 4, DO = 6, АО = 5.

Найти: а).  ОВ;  б).  АС : BD;  в).  .

2).  В треугольнике  ABC  сторона АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK  сторона МК = 8 см, MN =12 см, KN = 14 см. Найдите углы треугольника MNK, если A = 80°, B = 60°.        

3). Прямая пересекает стороны треугольника ABC в точках М и К соответственно так, что МК || АС, ВМ : АМ = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника  ABC  равен  25 см.

4).  В трапеции  ABCD  (AD и ВС основания)  диагонали  пересекаются  в точке О, AD = 12 см,  ВС = 4 см. Найдите площадь треугольника  ВОС, если  площадь треугольника  AOD  равна 45 см2. 

                                   2 вариант.

1).  По рис. РЕ || NK, MP = 8, MN = 12, ME = 6. Найти: а) .  МК;  б).  РЕ : NК;  в). .

                       

2).  В  ∆ АВС  АВ = 12 см, ВС = 18 см, В = 70 0, а  в  ∆ МNК  МN = 6 см, NК = 9 см, N = 70 0. Найдите сторону  АС  и  угол  С  треугольника  АВС, если  МК =  7 см, К = 60 0.

3).  Отрезки АВ и CD пересекаются в точке  О так, что ACO = BDO, АО : ОВ = 2:3. Найдите периметр треугольника  АСО, если  периметр  треугольника  BOD равен 21 см.

4). В трапеции ABCD ( AD и ВС основания) диагонали пересекаются в точке О,  = 32 см2,  = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см.

Контрольная работа вариант 2 — 2 гдз по геометрии 7 класс Мерзляк, Полонский дидактические материалы

Решебники, ГДЗ

  • 1 Класс
    • Математика
    • Русский язык
    • Английский язык
    • Информатика
    • Немецкий язык
    • Литература
    • Человек и мир
    • Природоведение
    • Основы здоровья
    • Музыка
    • Окружающий мир
    • Технология
  • 2 Класс
    • Математика
    • Русский язык
    • Белорусский язык
    • Английский язык
    • Информатика
    • Украинский язык
    • Французский язык
    • Немецкий язык
    • Литература
    • Человек и мир
    • Природоведение
    • Основы здоровья
    • Музыка
    • Окружающий мир
    • Технология
    • Испанский язык
  • 3 Класс
    • Математика
    • Русский язык
    • Белорусский язык
    • Английский язык
    • Информатика
    • Украинский язык
    • Французский язык
    • Немецкий язык
    • Литература
    • Человек и мир
    • Музыка
    • Окружающий мир
    • Технология
    • Испанский язык

Контрольные работы по геометрии 7 класс, учебник А. В.Погорелов


7 класс Контрольная работа № 1

по теме «Основные геометрические свойства простейших фигур»

Вариант 1

1.  MNF = DEF, MN = 13 см,  FE = 75°. Найдите длину стороны DE и градусную меру угла N.

2. Точка О лежит между точками Р и Н, причем ОР = 7 см, ОН = 11,3 см. Найдите расстояние между точками Р и Н.

3. Прямой угол АОВ разделен лучом ОС на два угла. Один из них на 12° больше другого. Найдите градусную меру полученных углов.

Вариант 2

1.  BCD = JST, JS = 18 см,  D = 115°. Найдите градусную меру угла Т и длину стороны ВС.

2. Точка С лежит между точками А и В, причем АВ = 15 см, АС = 6,8 см.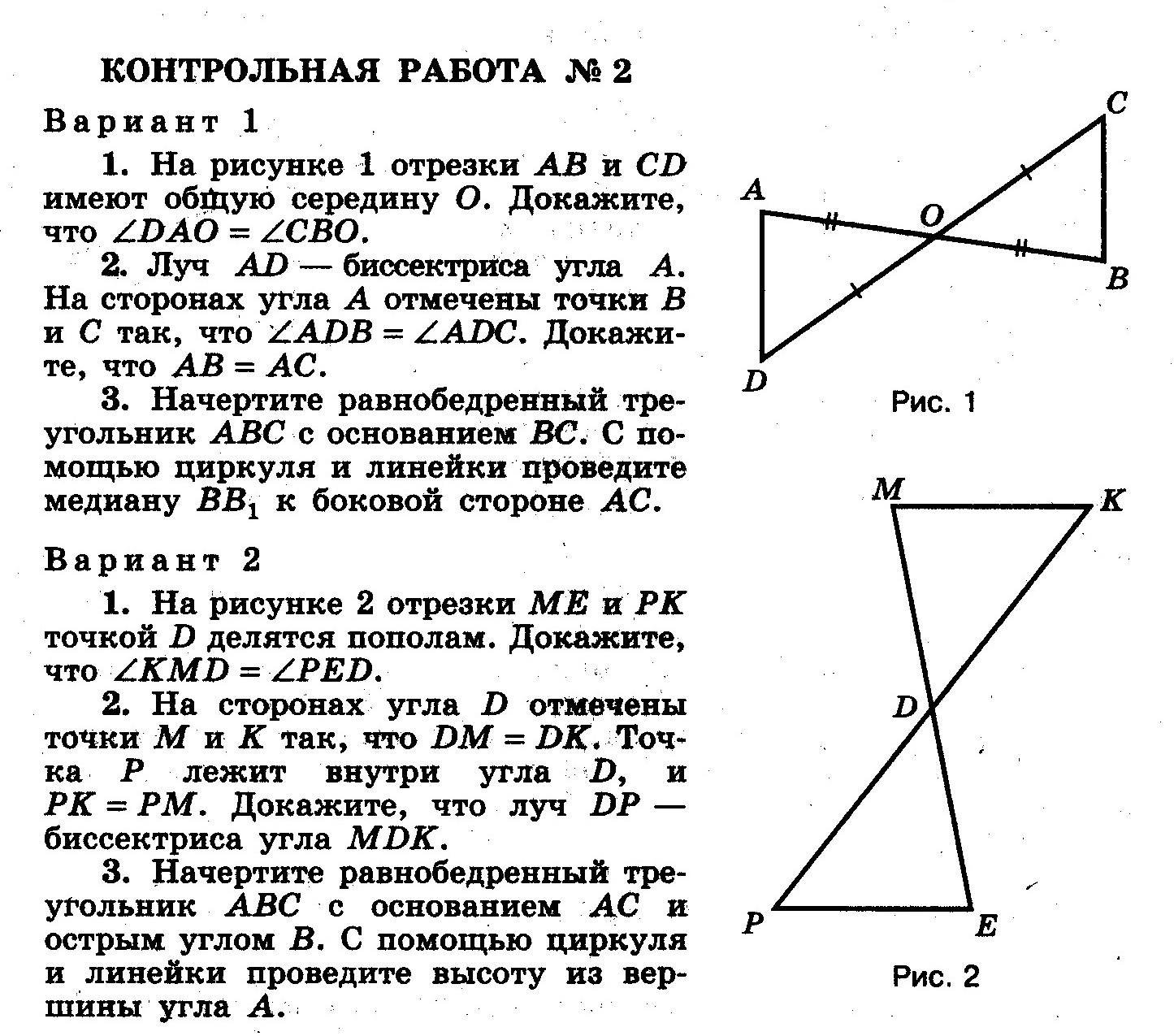 Найдите расстояние между точками В и С .

3. Прямой угол АОВ разделен лучом ОС на два угла. Один из них в 4 раза больше другого. Найдите градусную меру полученных углов.

7 класс Контрольная работа № 1

по теме «Основные геометрические свойства простейших фигур»

Вариант 1

1.  MNF = DEF, MN = 13 см,  FE = 75°. Найдите длину стороны DE и градусную меру угла N.

2. Точка О лежит между точками Р и Н, причем ОР = 7 см, ОН = 11,3 см. Найдите расстояние между точками Р и Н.

3. Прямой угол АОВ разделен лучом ОС на два угла. Один из них на 12° больше другого. Найдите градусную меру полученных углов.

Вариант 2

1.  BCD = JST, JS = 18 см,  D = 115°. Найдите градусную меру угла Т и длину стороны ВС.

2. Точка С лежит между точками А и В, причем АВ = 15 см, АС = 6,8 см. Найдите расстояние между точками В и С .

3. Прямой угол АОВ разделен лучом ОС на два угла. Один из них в 4 раза больше другого. Найдите градусную меру полученных углов.


7 класс Контрольная работа № 2

по теме «Смежные и вертикальные углы»

Вариант 1

1. Прямые АВ и СD пересекаются в точке О.

а) Выпишите две пары смежных углов. Каким свойством они обладают?

б) Какие из углов, образовавшихся при пересечении этих прямых, равны? Как они называются?

2. а) Один из смежных углов в 3 раза меньше другого. Найдите эти углы.

б) Могут ли два смежных угла быть тупыми? Ответ обоснуйте.

Вариант 2

1. Прямые РН и ОМ пересекаются в точке Х.

а) Выпишите две пары смежных углов. Каким свойством они обладают?

б) Какие из углов, образовавшихся при пересечении этих прямых, равны? Как они называются?

2. а) Один из смежных углов на 50° меньше другого. Найдите эти углы.

б) Может ли один из вертикальных углов быть тупым? Ответ обоснуйте.

7 класс Контрольная работа № 2

по теме «Смежные и вертикальные углы»

Вариант 1

1. Прямые АВ и СD пересекаются в точке О.

а) Выпишите две пары смежных углов. Каким свойством они обладают?

б) Какие из углов, образовавшихся при пересечении этих прямых, равны? Как они называются?

2. а) Один из смежных углов в 3 раза меньше другого. Найдите эти углы.

б) Могут ли два смежных угла быть тупыми? Ответ обоснуйте.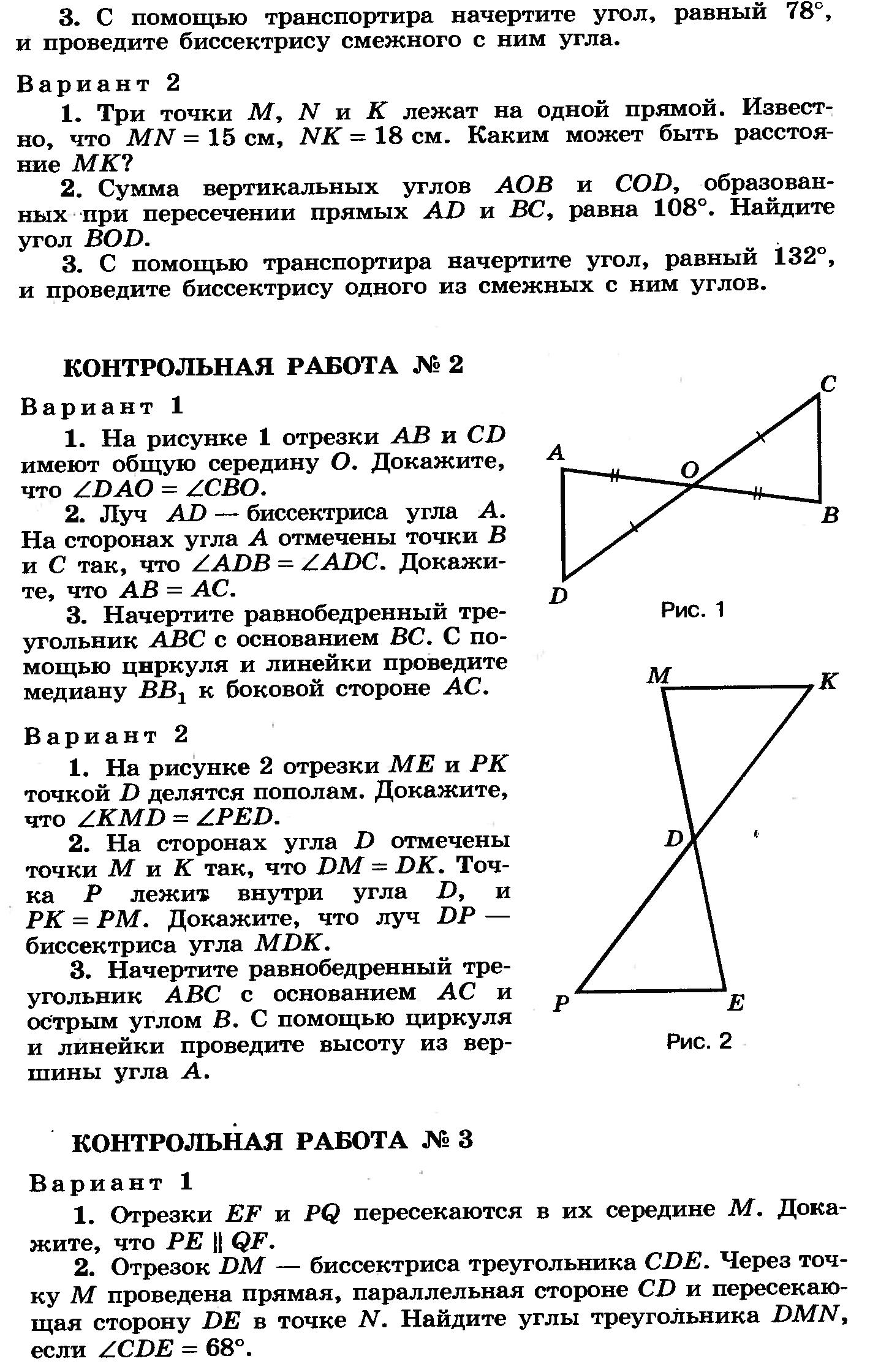

Вариант 2

1. Прямые РН и ОМ пересекаются в точке Х.

а) Выпишите две пары смежных углов. Каким свойством они обладают?

б) Какие из углов, образовавшихся при пересечении этих прямых, равны? Как они называются?

2. а) Один из смежных углов на 50° меньше другого. Найдите эти углы.

б) Может ли один из вертикальных углов быть тупым? Ответ обоснуйте.


7 класс Контрольная работа № 3

по теме «Признаки равенства треугольников»

Вариант 1

1. Отрезки МК и OD пересекаются в точке Е и делятся ею пополам. Докажите, что МО = DK.

2. В АNС AN = CN, NE – медиана, CNE = 35°. Найдите АNС.

3. Периметр равнобедренного треугольника равен 15,6 см. Его основание больше боковой стороны на 3 см.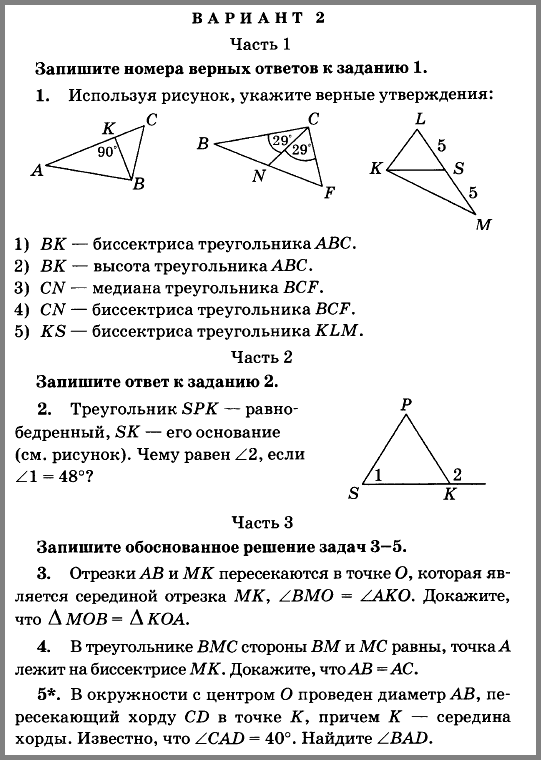 Найдите стороны треугольника.
__________________________________________________________________

Вариант 2

1. МР = NK и MN = PK. Докажите, что МРК = MNK.

2. В DFL DF = FL, FC – медиана, DFL = 130°. Найдите CFL.

3. Периметр равнобедренного треугольника равен 13 см. Сумма основания и боковой стороны 8,3 см. Найдите стороны треугольника.

7 класс Контрольная работа № 3

по теме «Признаки равенства треугольников»

Вариант 1

1. Отрезки МК и OD пересекаются в точке Е и делятся ею пополам. Докажите, что МО = DK.

2. В АNС AN = CN, NE – медиана, CNE = 35°. Найдите АNС.

3. Периметр равнобедренного треугольника равен 15,6 см. Его основание больше боковой стороны на 3 см. Найдите стороны треугольника.
__________________________________________________________________

Вариант 2

1. МР = NK и MN = PK. Докажите, что МРК = MNK.

2. В DFL DF = FL, FC – медиана, DFL = 130°. Найдите CFL.

3. Периметр равнобедренного треугольника равен 13 см. Сумма основания и боковой стороны 8,3 см. Найдите стороны треугольника.


7 класс Контрольная работа № 4

по теме «Сумма углов треугольника»

Вариант 1

1. Параллельные прямые а и b пересекаются прямой с, 1 = 123°. Найдите угол 2 (см. рис.).

2. Прямая m пересекает стороны треугольника АВС, АВ в точке Р, ВС в точке Е. АВС = 35°, АСВ = 84°, АРЕ = 119°.

а) Докажите, что прямые m и АС параллельны.

б) Найдите внешний угол треугольника АВС при вершине А.

Вариант 2

1. Прямая k пересекает параллельные прямые m и n, 1 = 64°. Найдите угол 2 (см. рис.).

2. Прямая а пересекает стороны треугольника MNK KM в точке А, KN в точке В. MNK = 24°, MKN = 138°, MАВ = 162°.

а) Докажите, что прямые l и MN параллельны.

б) Найдите внешний угол треугольника MNK при вершине M.

7 класс Контрольная работа № 4

по теме «Сумма углов треугольника»

Вариант 1

1. Параллельные прямые а и b пересекаются прямой с, 1 = 123°. Найдите угол 2 (см. рис. ).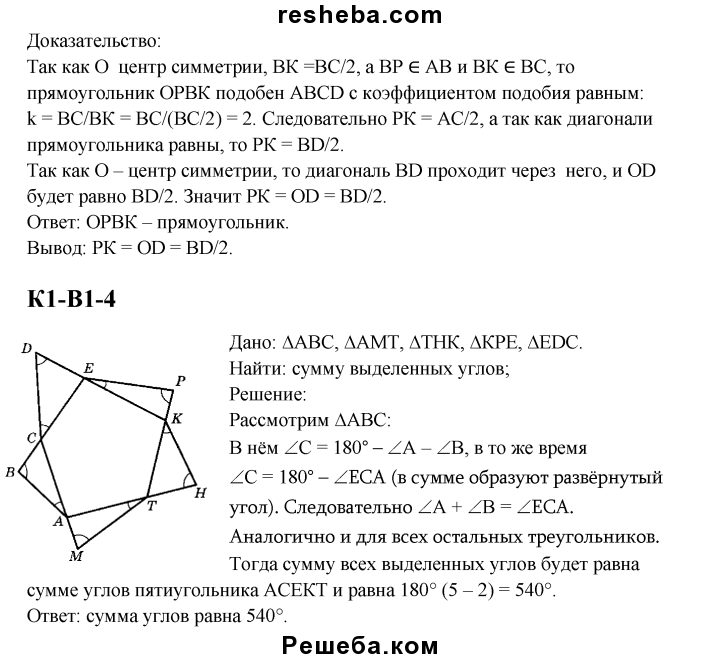

2. Прямая m пересекает стороны треугольника АВС, АВ в точке Р, ВС в точке Е. АВС = 35°, АСВ = 84°, АРЕ = 119°.

а) Докажите, что прямые m и АС параллельны.

б) Найдите внешний угол треугольника АВС при вершине А.

Вариант 2

1. Прямая k пересекает параллельные прямые m и n, 1 = 64°. Найдите угол 2 (см. рис.).

2. Прямая а пересекает стороны треугольника MNK KM в точке А, KN в точке В. MNK = 24°, MKN = 138°, MАВ = 162°.

а) Докажите, что прямые l и MN параллельны.

б) Найдите внешний угол треугольника MNK при вершине M.

7 класс Контрольная работа № 5

по теме «Геометрические построения»

Вариант 1

1. Углы треугольника пропорциональны числам 2, 3, и 4. Найдите все углы треугольника.

2. Постройте равнобедренный треугольник по боковой стороне и углу при вершине.

3. АС – касательная, АВ – хорда окружности с центром в точке О, угол ВАС равен 75°. Чему равен угол АОВ?

4. АD и СЕ – биссектрисы равнобедренного треугольника АВС с основанием АС. Докажите, что треугольник АЕС равен треугольнику СDА.

Вариант 2

1. Угол при вершине равнобедренного треугольника на 30° больше угла при вершине основании. Найдите все углы треугольника.

2. Постройте равнобедренный треугольник по основанию и углу при основании.

3. АС – касательная, АВ – хорда окружности с центром в точке О, угол АОВ равен 70°. Чему равен угол ВАС?

4.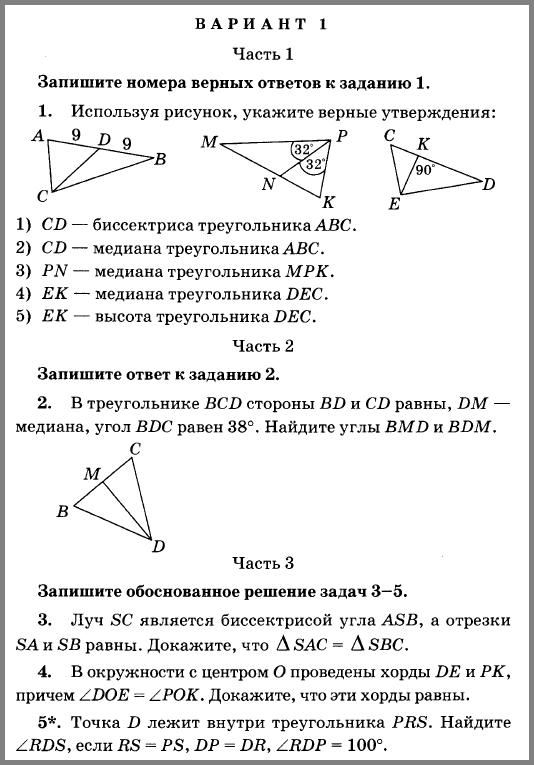 АЕ и КМ – медианы равнобедренного треугольника АРК с основанием АК. Докажите, что треугольник АРЕ равен треугольнику КРМ.

7 класс Контрольная работа № 5

по теме «Геометрические построения»

Вариант 1

1. Углы треугольника пропорциональны числам 2, 3, и 4. Найдите все углы треугольника.

2. Постройте равнобедренный треугольник по боковой стороне и углу при вершине.

3. АС – касательная, АВ – хорда окружности с центром в точке О, угол ВАС равен 75°. Чему равен угол АОВ?

4. АD и СЕ – биссектрисы равнобедренного треугольника АВС с основанием АС. Докажите, что треугольник АЕС равен треугольнику СDА.

Вариант 2

1. Угол при вершине равнобедренного треугольника на 30° больше угла при вершине основании. Найдите все углы треугольника.

2. Постройте равнобедренный треугольник по основанию и углу при основании.

3. АС – касательная, АВ – хорда окружности с центром в точке О, угол АОВ равен 70°. Чему равен угол ВАС?

4. АЕ и КМ – медианы равнобедренного треугольника АРК с основанием АК. Докажите, что треугольник АРЕ равен треугольнику КРМ.


Итоговая контрольная работа

Вариант 1

1. Прямые а и с параллельны, угол 1 равен 140°. Найдите угол 2 (см. рис. 1).

2. Треугольник АВС – равнобедренный с основанием ВС, отрезок ВК – его биссектриса. Найдите АКВ, если С = 70°.

3. Найдите угол В треугольника ВСЕ, если он на 30° меньше угла С, а внешний угол при вершине Е равен 130°.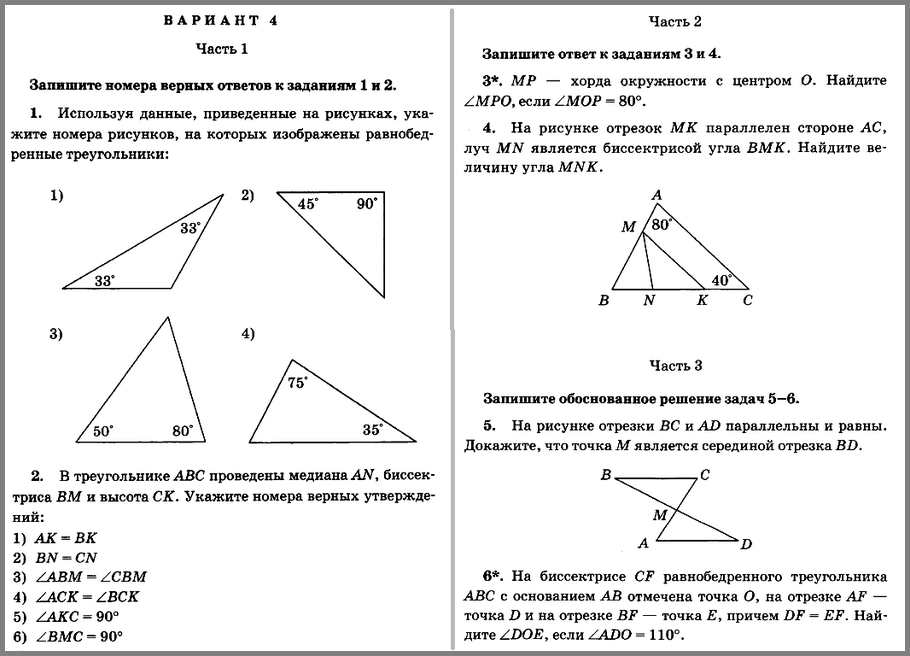

4. Найдите угол Р треугольника РМD, если D = 45°, АКD = 85°, а прямые КА и РМ параллельны.

5. В треугольнике АВС и АЕС известны элементы: САВ = 45°, АВС = 70°, САЕ = 65°, АВ = 6 см. Какое равенство верно?

а) АЕ = 6 см; в) СЕ = 6 см;

б) АС = 6 см; г) ВС = 6 см.

6. Дан треугольник АВС с прямым углом в точке А, С = 30°, АВ = 6 см. Какое равенство верно?

а) АС = 6 см; в) ВС = 12 см;

б) АС = 12 см; г) ВС = 6 см.

Ответы: 1) 40°, 2) 105°, 3) 50°, 4) 50°, 5) в, 6) в.

Вариант 2

  1. Прямые а и с параллельны, угол 1 равен 120°. Найдите угол 2 (см. рис.1).

2. Треугольник АВС – равнобедренный с основанием ВС, отрезок ВК – его высота. Найдите АВК, если С = 70°.

3. Найдите угол В треугольника АВЕ, если он на 30° меньше угла Е, а угол А равен 80°.

4. Найдите угол КСЕ, если в треугольнике ОКМ, О = 50°, М = 60°, а прямые СЕ и КМ параллельны.

5. В треугольниках АВС и ВАЕ известны элементы: АВС = 30°, ВАС = 70°, ВЕА = 80°, ВАЕ = 30°, АС = 4 см. Какое равенство неверно?

а) АЕ = 4 см; в) АВ = 4 см;

б) ВЕ = 4 см; г) ВС = 4 см.

6. Дан треугольник АВС, В = 90°, С = 45°, АВ = 6 см. Какое равенство верно?

а) АС = 6 см; в) АС = 12 см;

б) ВС = 12 см; г) ВС = 6 см.

Контрольная работа по геометрии по теме «Площадь многоугольника. Теорема Пифагора» – УчМет

Контрольная работа по геометрии по теме

«Теорема Пифагора. Площадь многоугольника.»

Вариант 1

№1

Выберите верные утверждения:

  1. Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

  2. Площадь трапеции равна произведению оснований на высоту.

  3. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

  4. Площадь прямоугольного треугольника равна произведению его катетов.

№2

Вычислите площадь фигуры, изображенной на рисунке:

1) 2) 3)

№3

Смежные стороны параллелограмма 32 и 26 см, а один из углов 1500. Найти площадь параллелограмма.

№4

Основания трапеции ВС и АD равны 12 и 24 см, боковая сторона СD = 10 см образует с большим основанием угол 450. Найти площадь трапеции.

№5

В треугольнике АВС АВ = 12 см, ВС = 13 см, АС =5 см. Найти площадь треугольника АВС и высоту АК, проведенную к стороне ВС.

Критерии оценивания

№1 -1 балл, если верно указаны все верные утверждения;

№2- за каждое верное выполненное задание по 1 баллу;

№ 3 -2 балла;

№4,5 – 3 балла. В заданиях 3-5 ставится на 1 балл ниже, если допущена вычислительная ошибка, но ход решения верный.

Оценка «3» — 4-6 баллов

«4» — 7-9 баллов

«5» — 10-12-баллов.

Контрольная работа по геометрии по теме

«Теорема Пифагора. Площадь многоугольника.»

Вариант 1

№1

Выберите верные утверждения:

  1. Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.

  2. Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.

  3. Площадь трапеции равна произведению полусуммы оснований на боковую сторону.

  4. Площадь ромба равна произведению его диагоналей.

№2

Вычислите площадь фигуры, изображенной на рисунке:

  1. 2) 3)

№3

Основания трапеции равны 12 и 17 см, боковая сторона 8 см образует с большим основанием угол 300. Найти площадь трапеции.

№4

В параллелограмме АВСD смежные стороны равны 20 и 28 см, а один из углов 450. Найти площадь параллелограмма.

№5

В треугольнике MNP MN = 10 см, MP = 8 см, NP =6 см. Найти площадь треугольника MNP и высоту PК, проведенную к стороне MN.

Критерии оценивания

№1-1 балл, если верно указаны все верные утверждения;

№2- за каждое верное выполненное задание по 1 баллу.

№ 3 -2 балла;

№4,5 – 3 балла. В заданиях 3-5 ставится на 1 балл ниже, если допущена вычислительная ошибка, но ход решения верный.

Оценка «3» — 4-6 баллов

«4» 7-9 баллов

«5» — 10-12-баллов

Ячейки

S2 | S2Geometry

Библиотека S2 определяет структуру для разложения единичной сферы на иерархия ячеек .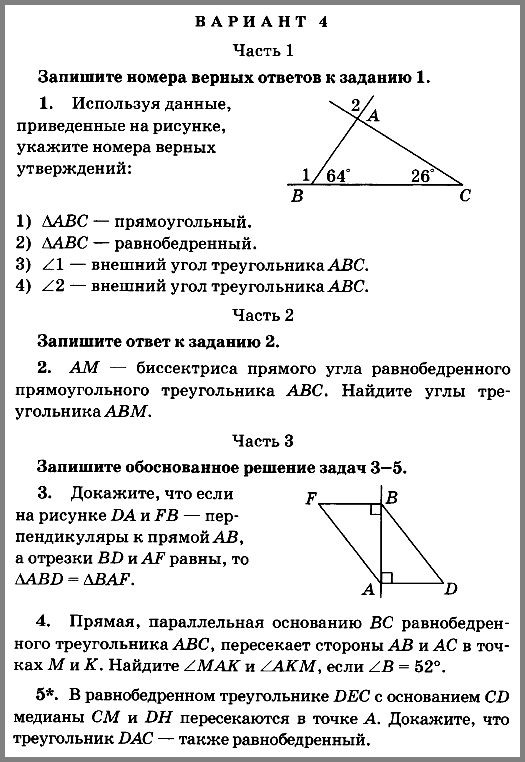 Каждая клетка представляет собой четырехугольник, ограниченный четырьмя геодезическими. Верхний уровень иерархии получается путем проецирования шести граней куб на единичную сферу, а нижние уровни получаются разделением каждого ячейку рекурсивно на четырех дочерних элементов. Например, на следующем изображении показано две из шести лицевых ячеек , одна из которых несколько раз подразделялась:

Обратите внимание, что края ячеек выглядят изогнутыми; это потому что они сферические геодезические , и.е., прямые на сфере (аналогично маршруты, по которым летают самолеты).

Каждая ячейка в иерархии имеет уровень , определяемый как количество раз ячейка разделена (начиная с ячейки лица). Уровни ячеек варьируются от От 0 до 30. Наименьшие ячейки на уровне 30 называются конечными ячейками ; имеются 6 * 4 30 из них всего около 1 см в поперечнике Земли поверхность. (Подробную информацию о размерах ячеек на каждом уровне можно найти на S2 Страница статистики ячейки. )

Иерархия S2 полезна для пространственной индексации и аппроксимации регионов. как набор ячеек. Ячейки могут использоваться для представления как точек, так и регионы: точки обычно представлены как листовые ячейки, а регионы — представлены как совокупности ячеек на любом уровне (ах). Например здесь приближение Гавайев как совокупность 22 ячеек:

S2 Нумерация CellId

Каждая ячейка однозначно идентифицируется 64-битным S2CellId .Ячейки S2 пронумерованы особым образом, чтобы максимально увеличить местонахождение ссылка когда они используются для пространственной индексации (по сравнению с другими методами нумерация ячеек).

В частности, ячейки S2 упорядочены последовательно по кривая заполнения пространства (разновидность фрактала). Конкретная кривая, используемая S2, называется кривой заполнения пространства S2 , и состоит из шести кривых Гильберта, соединенных вместе, чтобы образовать единую непрерывная петля по всей сфере. Вот иллюстрация Кривая S2 после 5 уровней деления:

Желтая кривая — аппроксимация кривой заполнения пространства S2.Это представляет собой одиночный непрерывный цикл с фрактальной структурой, такой что проходит около каждой точки на сфере. (Если бы вы разрезали желтой линией, это разделит сферу на две равные половины.) зеленые линии показывают границы ячеек S2 на уровнях 0, 1, 2, 3, 4 и 5, нарисованные в виде линий разной ширины. (Вы можете нажать на изображение, чтобы увидеть увеличенную версию.)

Ячейки на уровне 5 пронумерованы в порядке возрастания вдоль этой кривой. Это приводит к тому, что , если S2CellIds двух ячеек близко друг к другу, то клетки тоже близко вместе . Это свойство значительно улучшает местность ссылки, когда ячейки используются для индексации.

В оставшейся части этого раздела приведены дополнительные сведения о том, как ячейка S2 иерархия организована. (Вам не нужно понимать этот фон информацию для использования библиотеки — вы можете пропустить вперед, если желательно. )

Кривая Гильберта

Кривая S2 основана на кривой Гильберта. Кривая Гильберта — это функция от единичного интервала [0,1] до единичного квадрата [0,1] × [0,1], то есть заполняет пространство , что означает, что он посещает каждую точку единичного квадрата.В Кривая Гильберта непрерывна, но не дифференцируема, и ее можно рассматривать как иметь бесконечную длину.

Его проще всего определить как предел итеративного процесса, который создает более детальная аппроксимация кривой на каждом шаге. Вот часть первая страница Статья Гильберта 1891 года, определяющая его кривую (ср. Марк МакКлюр ):

Как видите, первая итерация делит единичный квадрат на 4 квадраты поменьше. Кривая посещает эти квадраты в определенном порядке. который выглядит как перевернутая буква «U» (рис. 1).Вторая итерация занимает каждый квадрат из первой итерации и d

тест на способности, вопросы, ярлыки, решенные примеры видео

Числа

Важные формулы:

1) Геометрическая прогрессия: x, xr, xr 3 , xr 4 , — находятся в геометрической прогрессии. Здесь a — первый член, а r — обычное отношение.
a) n th term = xr (n -1)

b) Сумма n членов = x (1 — r n ), здесь r <1
(1 — r)
c) Сумма n членов = x (r n — 1), здесь r> 1
(r — 1)

2) Арифметическая прогрессия: говорят, что x, x + y, x + 2y, x + 3y находятся в A.P. Здесь x — первый член, а общая разница — y.
a) n th член = x + (n — 1) y
b) сумма n членов = n [2x + (n — 1) y]
2

3) 1 + 2 + 3 ± — — — — + n = n (n + 1)
2

4) (1 2 + 2 2 + 3 2 — — — — + n 2 ) = n (n + 1) (2n + 1)
6

5) (1 3 + 2 3 + 3 3 — — — — + n 3 ) = n (n + 1) 2
2

Что следует помнить:

Разница между арифметической прогрессией и геометрической прогрессией:
Arithmetic Pro gression: Это последовательность чисел, в которой каждый член после первого получается добавлением константы к предыдущему члену. Постоянный член называется общей разницей.
Геометрическая прогрессия: Это последовательность ненулевых чисел. Соотношение любого члена и предшествующего ему члена всегда постоянно.

Типы чисел Определение Пример Следует запомнить
Натуральные числа Числа, используемые для подсчета и упорядочения 1, 2, 3, 4, 5, — — натуральные числа
Целые числа Все счетные числа вместе с нулем образуют набор целых чисел 0, 1, 2, 3, 4 —— целые числа Любое натуральное число — это целое число
0 — это целое число.что не является естественным нет.
Целые числа Счетные числа + отрицательные счетные числа + ноль, все являются целыми числами -2, -1, 0, 1, 2, —- целые числа Положительные целые числа: 0 , 1, 2, 3, ——-
Целые отрицательные числа: -1, -2, -3, -4, ———
Четные числа Число , кратное 2 , называется четным числом 0, 2, 4, 6, 8, —— четные числа
Нечетные числа Число не делится на 2 называется четным числом 1, 3, 5, 7, 9, —— нечетные числа
Простые числа Число, имеющее ровно два множителя i. e 1 и само по себе называется простым числом 2, 3, 5, 7, 11, —— простые числа
Составные числа Натуральные числа, не являющиеся простыми числами, называются составными номерами 4, 6, 8, 9, 10, —— составными номерами.
Co Простые числа Любые два натуральных числа x и y являются взаимно простыми, если их HCF 1 (4, 5), (7, 9), — Сопоставимое число числа

Делимость чисел

1) Число, кратное 2
Цифра единиц — 0, 2, 4, 6, 8
Пример: 42, 66, 98, 1124

2 ) Число делится на 3
Сумма цифр делится на 3
Пример: 267 — (2 + 6 + 7) = 15
15 делится на 3

3) Число делится на 4
Число образованный двумя последними цифрами, делится на 4
EX: 832
Последние две цифры делятся на 4, следовательно, 832 делится на 4

4) Число делится на 5
Цифра единиц равна нулю или пяти
Пример: 50, 20, 55, 65 и т. Д.

5) Число, кратное 6
Число делится на 2 и 3
Пример: 168
Последняя цифра = 8 —- (8 делится на 2)
Сумма цифр = (1 + 6 + 8) = 15 —— (делится на 3)
Следовательно, 168 делится на 6

6) Число делится на 11
Если разница между суммами цифр в четных местах и ​​суммой цифр в нечетных местах равна 0 или делится на 11.
Пример: 4527039
Цифры на четных местах: 4 + 2 + 0 + 9 = 15
Цифры на нечетных местах: 5 + 7 + 3 = 15
Разница между нечетными и четными = 0
Следовательно, число делится на 11

7) Число, кратное 12
Число делится как на 4, так и на 3
Пример: 1932
Последние две цифры делятся на 4
Сумма цифр = (1 + 9 + 3 + 2) = 15 — — (Делится на 3)
Следовательно, число 1932 делится на 12

Основные формулы: (Необходимо помнить)
1) (a — b) 2 = (a 2 + b 2 — 2ab)
2) (a + b) 2 = (a 2 + b 2 + 2ab)
3) (a + b) (a — b) = (a 2 — b 2 )
4) (a 3 + b 3 ) = (a + b) (a 2 — ab + b 2 )
5) (a 3 — b 3 ) = (a — b) (a 2 — ab + b 2 )
6) (a + b + c) 2 = a 2 + b 2 + c 2 + 2 (ab + bc + ca)
7) (a 3 + b 3 + c 3 — 3abc) = ( a + b + c) (a 2 + b 2 + c 2 — ab — bc — ac)

Советы и приемы:

1) Если H. C.F двух чисел равен 1, тогда числа называются взаимно простыми.
Чтобы найти число, скажем, b делится на a, найдите два числа m и n, такие что m * n = a, где m и n — взаимно простые числа, а если b делится как на m, так и на n, то оно равно делится на.

2) Сумма первых n нечетных чисел = n 2

3) Сумма первых n четных чисел = n (n + 1)

4) Четные числа, делящиеся на 2, могут быть выражается как 2n, n — целое число, отличное от нуля.

5) Нечетные числа, не делящиеся на 2, можно выразить как 2 (n + 1), n ​​- целое число.

6) Дивиденд = [(Делитель × Частное)] + Остаток

7) Если Дивиденд = a n + b n или a n — b n
a) Если n четно: a n — b n делится на (a + b)
b) Если n нечетное: a n + b n делится на (a + b)
c) a n — b n всегда делится на (a — b)

8) Чтобы найти единичную цифру числа, которая имеет вид a b . (Пример: 7 105 , 9 125 )
1) Если b не делится на 4
Шаг 1: Разделите b на 4, если оно не делится, найдите остаток от b при делении на 4.
Шаг 2: Цифра единиц измерения = r , r — остаток.

2) Если b кратно 4
Цифра единиц равна 6: Когда четные числа 2, 4, 6, 8 увеличиваются до кратного 4.
Цифра единиц измерения равна 1: Когда нечетные числа 3, 7 и 9 увеличиваются до кратного 4.

Разнообразие вопросов

Как правило, в этой главе задаются вопросы о 6 типах чисел. Понимание и изучение концепций поможет в решении численных задач, связанных с этой главой.

Тип 1: Найдите цифру единиц в числе в форме ab


Q 1. Найдите цифру единиц в (4137) 754

a. 9
г. 7
г. 3
г. 1
Посмотреть решение

Правильный вариант: (a)

Подсказка: Разделите b на 4, если оно не делится, найдите остаток от b при делении на 4.
Цифра единиц = a r , r — остаток
Число имеет вид a b , т.е. (4137) 754
4 × 188 = 752, следовательно, мы получаем остаток как 2
Цифра единиц = (4137) 2 = 17114769
9 — это цифра в разложении единиц


Q 2. Найдите цифру единицы в произведении (3 65 × 6 59 × 7 71 )

a. 1
г. 4
г. 5
г. 9
Просмотреть решение

Правильный вариант: (b)

Подсказка:
Если b кратно 4
Цифра единиц равна 6: Когда четные числа 2, 4, 6, 8 увеличиваются до кратного 4.
Цифра единиц равна 1: Когда нечетные числа 3, 7 и 9 увеличиваются до кратного 4.
Используя данную подсказку, мы можем легко решить произведение больших чисел.
[3 (4) 16 × 3] = (1 × 3) = 3
[6 59 ] = 6
[7 71 ] = [7 (4) 17 × 7 3 ] = [1 × 3] = 3
Следовательно, (3 × 6 × 3) = 54
Требуемая цифра единицы — 4.

Тест уровня английского языка (A1-C2) • Онлайн-тест по английскому

Гражданство * AfghanistanÅland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarcticaAntigua И BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBosnia И HerzegovinaBotswanaBouvet IslandBrazilBritish Индийский океан TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCape VerdeCayman IslandsCentral африканских RepublicChadChileChinaChristmas IslandCocos (Кокосовые) IslandsColombiaComorosCongoCongo, Демократическая Республика TheCook IslandsCosta RicaCÔte D’ivoireCroatiaCubaCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland (Мальвинские) острова Фарерские IslandsFijiFinlandFranceFrench GuianaFrench PolynesiaFrench Южный TerritoriesGabonGambiaGeorgiaGermanyGhanaGibraltarGreeceGreenlandGrenadaGuadeloupeGuamGuatemalaGuernseyGuineaGuinea-bissauGuyanaHaitiHeard острова И острова Макдональд, Гондурас, Гонконг, Венгрия, Исландия, Индия. iaIndonesiaIran, Исламская Республика OfIraqIrelandIsle Из ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKorea, Корейская Народно-Демократическая Республика OfKorea, Республика OfKuwaitKyrgyzstanLao Народная Демократическая RepublicLatviaLebanonLesothoLiberiaLibyan Арабская JamahiriyaLiechtensteinLithuaniaLuxembourgMacaoMacedonia, бывшая югославская Республика OfMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesia, Федеративные Штаты OfMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNetherlands AntillesNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorthern Mariana IslandsNorwayOmanPakistanPalauPalestinian край, OccupiedPanamaPapua Новый GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarRÉunionRomaniaRussian FederationRwandaSaint BarthÉlemySaint HelenaSaint Киттс И NevisSaint LuciaSaint МартинСент-Пьер и МикелонСент-Винсент и ГренадиныСамоаСан-МариноСао Фолиант И PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Джорджия и Южные Сандвичевы IslandsSpainSri LankaSudanSurinameSvalbard и Ян MayenSwazilandSwedenSwitzerlandSyrian Arab RepublicTaiwan, провинция ChinaTajikistanTanzania, Объединенная Республика OfThailandTimor-lesteTogoTokelauTongaTrinidad И TobagoTunisiaTurkeyTurkmenistanTurks И Кайкос IslandsTuvaluUgandaUkraineUnited Арабских EmiratesUnited KingdomUnited StatesUnited Внешнего Малый IslandsUruguayUzbekistanVanuatuVatican город StateVenezuelaViet NamVirgin остров, BritishVirgin остров, U.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

➤