ГДЗ Геометрия 7-9 класс Атанасян
- Геометрия 7-9 класс
- Тип пособия: Учебник
- Авторы: Атанасян
- Издательство: «Просвещение»
Задания
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310Похожие ГДЗ Геометрия 7-9 класс
- Геометрия 7 класс
- Рабочая тетрадь
- Атанасян, Бутузов, Глазков
- Просвещение
- Геометрия 7-9 класс
- Самостоятельные и контрольные работы
- Иченская, Атанасян
- Просвещение
- Геометрия 7 класс
- Тесты
- Фарков
- Экзамен
Задания: 1
Условие
Решебник №1
Решебник №2
Седьмой класс — первое знакомство с геометрией
С седьмого класса школьники начинают постигать новый для себя предмет — геометрию. Он позволяет расширить пространственное мышление, а так же весьма пригодится для тех из ребят, которые в дальнейшем захотят связать свою жизнь со строительством и инженерией. По началу данная дисциплина кажется относительно простой. Что же сложного в рисовании геометрических фигур? Однако потом начинают вылезать скрытые нюансы.
Он позволяет расширить пространственное мышление, а так же весьма пригодится для тех из ребят, которые в дальнейшем захотят связать свою жизнь со строительством и инженерией. По началу данная дисциплина кажется относительно простой. Что же сложного в рисовании геометрических фигур? Однако потом начинают вылезать скрытые нюансы.
Программа по геометрии, которая отражена в ГДЗ
Предельного внимания требует запоминание теоретического материала, формул и теорем. Кроме того, необходимо научиться применять новообретенные знания на практике. В этом в ближайшие три года школьникам должен помочь учебник «Геометрия 7-9 класс» Атанасян, Бутузов, Кадомцев, выпущенный издательством «Просвещение» в 2017 г. За это время учащимся предстоит освоить такие темы, как:
- углы, отрезки, прямые;
- треугольники;
- параллельные прямые;
- векторы и окружности;
- площади;
- четырехугольники;
- синусы, косинусы, тангенсы;
- метод координат;
- длины и окружности.

Так же предстоит узнать и много другой информации. Сложность программы идет по нарастающей, поэтому у учеников еще есть возможность вникнуть в материал. Однако если подзапустить учебу или невнимательно относиться к ней, то потом будет трудно наверстать нужные знания.
Содержимое решебника по геометрии
В наше время учителя не могут уделять много времени на разъяснение тематики, поэтому учащимся приходится самостоятельно осваивать некоторые моменты. А если это не получается, то этот процесс облегчит решебник к учебнику «Геометрия 7-9 класс» Атанасян, Бутузов, Кадомцев, в котором прописаны все необходимое для понимания предмета.
Сборник разработан с учетом всех недочетов, которые могут возникнуть у ребят во время учебы. В совокупности в нем даны исчерпывающие ответы по 1310 номерам, которые представлены в учебнике. Кроме того, в ГДЗ по геометрии 7-9 класс Атанасян включены многочисленные графики и чертежи, наглядно демонстрирующие решение некоторых задач.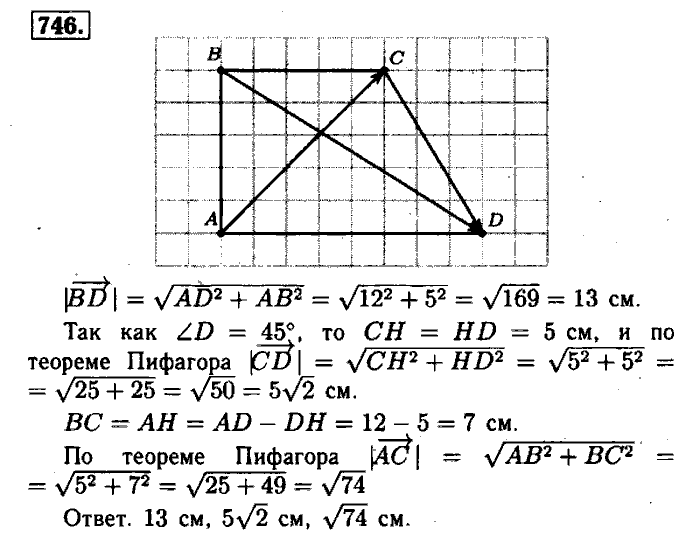
ГДЗ помогут выполнить домашние задания
На нашем сайте собрано несколько вариантов
Некоторым ученикам учеба дается очень сложно, или иногда возникают ситуации, когда задача крайне непонятна. Сложность материала постоянно возрастает, а требования становятся все жестче. Не многие сейчас могут позволить себе нанять репетитора. Поэтому все больше школьников начинают обращаться к ГДЗ, которые помогают сделать учебу проще. Решебник к учебнику
- запомнить теорию;
- понять принцип выполнения задач;
- подтянуть знания и восполнить пробелы;
- улучшить свою успеваемость;
- качественно и быстро проверять д/з.

У решебников много положительных качеств, но чтобы это понять, надо им правильно пользоваться. А для этого всего-то и требуется — не списывать!
Есть ли польза от решебников в 7 классе
По многочисленным отзывам, в том числе учителей и репетиторов, учебник построен не очень профессионально. Некоторые задания расположены не от простого к сложному, а наоборот. А, главное, авторы все время объясняют действия через принцип наложения, Из-за чего у детей вообще может сложиться неверное представление о предмете. Поэтому ГДЗ элементарно поможет понять, что же именно подразумевали авторы, составляя задачи таким образом.
Мы постоянно работаем над обновлением информации и следим за ее качеством. Если вам что-то непонятно, то можете написать об этом в комментариях — мы вам обязательно ответим!
Поиск материала «Готовые домашние задания по геометрии — 9 класс
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.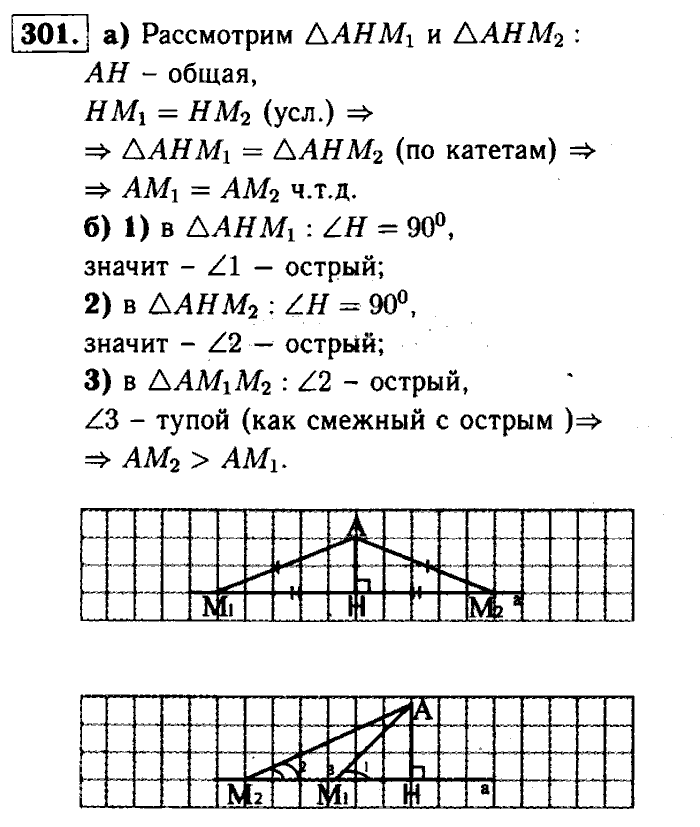
Search results:
- ГДЗ — Геометрия. 9 класс — Атанасян Л.С.
ГДЗ — Геометрия. 9 класс — Атанасян Л.С. Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по геометрии.
Готовые домашние задания.
11klasov.net
- ГДЗ по Геометрии за 7-9 класс: Атанасян. Решебник…
ГДЗ по геометрии 7-9 класс Атанасян, Бутузов, Кадомцев. Геометрия – наука, требующая от школьника умения эффективно визуализировать задание. Стандартным применением типовых формул здесь не обойтись. Оттого не все школьники могут качественно усвоить этот предмет.
Достаточно лишь воспользоваться ГДЗ по геометрии для 7-9 класса Атанасяна. В учебном пособии приведены пошаговые алгоритмы выполнения геометрических задач с комментариями и готовыми ответами.

otvetkin.info
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- ГДЗ
7класс. ГДЗ по геометрии за 7, 8 и 9 класс к учебнику Атанасяна с решением номеров и задач. Атанасян, Бутузов, Кадомцев.
pomogalka.me
- Гдз по геометрии 7-9 класс Атанасян скачать бесплатно | 4ЕГЭ
Готовое домашнее задание (ГДЗ) к учебнику по Геометрии 7-9 кл., Атанасян.
 Решебник к учебнику — Геометрия. 7—9 классы Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Ссылки удалены.
Решебник к учебнику — Геометрия. 7—9 классы Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Ссылки удалены.Задания по теме «Местоимение». Пробные работы ОГЭ по русскому языку | Сегодня, 14:01.
4ege.ru
- ГДЗ по Геометрии 7, 8, 9 класс: Атанасян (Решебник)
Готовые домашние задания по геометрии за 7, 8, 9 класс Атанасян, Бутузов, Кадомцев – онлайн-решебники с ответами и решениями примеров и задач бесплатно и без регистрации, поиск ответов в один клик.
Готовые домашние задания – важное подспорье в изучении сложного предмета, а также основа для поверки успеваемости школьников родителями. Авторы: Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев. Годы актуальности: 2014-2018г. Просвещение, 2 издание.
gdegdz.ru
- Решебник по геометрии Атанасян 7-9 класс
Сборник ГДЗ геометрии Атанасян 7 класс 8 класс 9 класс, доступный прямо онлайн на сайте reshak.
 ru, содержит подробные решения всех задач.
ru, содержит подробные решения всех задач.Сборник задач Атанасян 7 класс 8 класс 9 класс – один из наиболее распространённых учебников по геометрии. Именно этот учебник вызывает наибольшие затруднения у школьников. Поэтому был подготовлен этот сборник ГДЗ Атанасян, который содержит ответы на задачи с разными путями решения, что помогает школьнику решить задачку так, чтобы учитель не догадался, что он списал.
reshak.ru
- Решебник по геоментрии Атанасян Л.С. для 7,8,9 класса 2015 год
Решебники по геометрии 7 класс.
Решебник по геометрии для 11 класса Атанасян Л.С.
resh-ege.ru
- ГДЗ: Геометрия 7-9 класс Атанасян — Учебник
Решения с подробным объяснением и ГДЗ: Геометрия 7-9 класс Атанасян — Учебник.
 В первую очередь, это касается точных наук: именно в этот период относительно простая математика разделяется на сложнейшие предметы – алгебру и геометрию.
В первую очередь, это касается точных наук: именно в этот период относительно простая математика разделяется на сложнейшие предметы – алгебру и геометрию.gdzbezmoroki.com
- ГДЗ Рабочая тетрадь по Геометрии 9 класс Атанасян
ГДЗ решебник Геометрия 9 класс рабочая тетрадь Атанасян Л.С. Просвещение 2014 ФГОС с ответами онлайн бесплатно!
- Домашняя работа по Геометрия. 7 класс — Атанасян Л.С.
Главная » Решебники, ГДЗ » Домашняя работа по Геометрия.
7 класс — Атанасян Л.С. Предлагаемое учебное пособие содержит образцы выполнения всех задач и упражнений из учебника «Геометрия.
Telegram. скачать учебник ГДЗ — Геометрия. 7 класс — Атанасян Л.С.
Готовые домашние задания.
11klasov.
 net
net - Геометрия. 7-9 класс. Учебник — Атанасян
Учебник «Геометрия. 7—9 классы», являющийся завершённой предметной линии учебников по геометрии для учащихся 7—9 классов общеобразовательных организаций. Классический практико-ориентированный курс геометрии, подкорректирован с учетом реализации проверенных временем принципов обучения; Максимальное использование принципа наглядности в подаче материала позволяет обеспечить вариативность, дифференцируемость и другие принципы обучения; Дана широкая система задач
Готовые домашние задания.
11klasov.net
- ГДЗ Геометрия 7-9 класс Атанасян — Учебник
Седьмой класс — первое знакомство с геометрией. С седьмого класса школьники начинают постигать новый для себя предмет — геометрию . Он позволяет расширить пространственное мышление, а так же весьма пригодится для тех из ребят, которые в дальнейшем захотят связать свою
Кроме того, в ГДЗ по геометрии 7-9 класс Атанасян включены многочисленные графики и чертежи, наглядно демонстрирующие решение некоторых задач.
 ГДЗ помогут выполнить домашние задания. На нашем сайте собрано несколько вариантов решебников , в которых вы…
ГДЗ помогут выполнить домашние задания. На нашем сайте собрано несколько вариантов решебников , в которых вы…megashpora.com
- Мегарешеба — ГДЗ и решебники по Геометрии за 9 класс онлайн
Добро пожаловать на мегарешеба — с лучшими ГДЗ по Геометрии за 9 класс. Здесь Вы найдете готовые ответы на домашнюю работу. Смотрите решения и получайте пятерки.
ГДЗ по Геометрии за 9 класс. Геометрия 9 класс контрольно-измерительные материалы.
megaresheba.net
- ГДЗ по геометрии 7-9 класс Атанасян — онлайн
При помощи гдз по геометрии за 7-9 класс, ученики получают навыки вычисления и решения геометрических задач. Решебник по геометрии Атанасян Л.С. 7-9 класс описывает вычисление площади различных фигур, дает знания о синусе, косинусе, тангенсе, котангенсе.
 Готовые домашние задания Атанасян позволят вам понять, как вычисляются тригонометрические функции, значения углов, площади фигур, длины дуг окружности.
Готовые домашние задания Атанасян позволят вам понять, как вычисляются тригонометрические функции, значения углов, площади фигур, длины дуг окружности.uchim.org
- Гдз и решебник Геометрия 7-9 класс Атанасян — Учебник
Достоинства ГДЗ. Освоенный теоретический материал сразу нужно закрепить, выполнив практические задания. И тут тоже пригодится справочник. На его страницах можно найти правильно оформленные чертежи, снабженные развернутыми комментариями
Регулярное использование сборника позволит школьникам получать высокие оценки и за ответы у доски, и за проверочные работы. Польза решебника. Благодаря правильному использованию «ГДЗ по геометрии 7-9 класс Атанасян Л.С. (Просвещение)» у школьников улучшается успеваемость.
spishi.ltd
- ГДЗ решебник по геометрии 7-9 класс Атанасян, Бутузов.
 ..
..С ГДЗ домашнее задание перестанет быть чем-то страшным и невыполнимым, его можно будет легко делать, опираясь на верные ответы. Решебник – не только про ответы. Готовые домашние задания дают возможность понять шаблоны, по которым решаются те или иные сложные
Хорошие оценки, вследствие правильного решения и оформления. Геометрия тесно связана с чертежами. Для задач постоянно требуются приблизительные изображения той или иной фигуры, и « ГДЗ по геометрии 10-11 классов Атанасяна Л.С. Просвещение»…
GDZ.world
- ГДЗ по Геометрии 7‐9 класс Атанасян
ГДЗ РФ — У нас подобраны готовые решения домашних заданий по Геометрии за 7 класс, Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин Просвещение. Вы найдете ответы на вопросы, краткое и полное решение задач.
ГДЗ по геометрии за 7, 8, 9 класс Л.С. Атанасян, В.Ф. Бутузов.
 Тип: Учебник. Авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин. Издательство: Просвещение 2016. Геометрия – это наука о фигурах, занимающаяся взаимным расположением и размерами их частей, выражающихся в…
Тип: Учебник. Авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин. Издательство: Просвещение 2016. Геометрия – это наука о фигурах, занимающаяся взаимным расположением и размерами их частей, выражающихся в…xn--c1acj.xn--p1ai
- ГДЗ по геометрии 9 класс, решебники и ответы
ГДЗ по геометрии 9 класс – это не просто перечень ответов. В пособии собраны упражнения с подробным пояснением, рисунками. Справочник структурирован, поэтому работать с ним легко. Такой помощник можно смотреть круглосуточно с ПК или смартфона.
Даже при простом, но вдумчивом и качественном переписывании готового решения с данного сборника получится подтянуть свои знания. Кому понадобятся готовые домашние задания. Поскольку онлайн-решебник полностью соответствует школьной программе, то он становится незаменим
pomogalka.me
- ГДЗ (решебник) по геометрии 7-9 класс Атанасян, Бутузов.
 ..
..Использовать гдз по геометрии 7-9 класс Атанасян нужно с осторожностью и всей ответственностью, чтобы не нарушить естественный процесс обучения и не подарить ученику губительную возможность постоянно подсматривать ответы из решебника. ГДЗ Атанасяна должно применяться только в присутствии родителей и использоваться только для проверки домашней работы, полученных за все обучение предмета, знаний, проверки усвоения материала. Также ответы по геометрии за 7 класс автора Атанасян помогают в подготовке к…
reshator.me
- ГДЗ решебник по Геометрии 7, 8, 9 класс — Атанасян
Готовые домашние задания по геометрии для 7, 8 и 9 класса – решебник Атанасян Л.С. и др., ответы в один клик, круглосуточно, бесплатно и без регистрации. Самая актуальная база сборников решений.
ГДЗ по геометрии за 7, 8 и 9 класс Атанасян – это онлайн-решебник ответов по учебнику Л.
 С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева и др. Если задачи по геометрии ставят вас в тупик, то подробные решения сборника помогут разобраться с алгоритмом выполнения заданий и их оформлением, развить абстрактное мышление, усвоить…
С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева и др. Если задачи по геометрии ставят вас в тупик, то подробные решения сборника помогут разобраться с алгоритмом выполнения заданий и их оформлением, развить абстрактное мышление, усвоить…spishigdz.ru
- ГДЗ по геометрии 7-9 класс Атанасян, Бутузов, Кадомцев
Особым спросом пользуется ГДЗ по геометрии 7-9 класс Атанасян. Здесь собраны детальные ответы на упражнения из соответствующего учебника. Нужно лишь найти в сборнике требуемые номера и переписать решения. Для улучшения успеваемости этого будет достаточно.
проверить корректность выполнения упражнений. Предлагаемый сборник ГДЗ по геометрии 7, 8 и 9 класс к учебнику Атанасяна, Бутузова представлен на нашем сайте в последней редакции, благодаря чему пользователи ресурса могут быть твердо уверены в правильности…
otvet.
 plus
plus - ГДЗ по геометрии 7-9 класс Атанасян, Бутузов с подробным…
ГДЗ по геометрии за 7-9 класс авторов Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. с пошаговыми решениями задач. Все упражнения даны с подробным описанием всего решения и подробными пояснениями, а не только ответы к заданиям.
Чтобы лучше разобраться с новым материалом по геометрии, целесообразно пользоваться сборниками с уже выполненными задачами, в которых можно найти как численные ответы так и пункты решения. В данном издании решебника подробно рассмотрены методы работы с типовыми упражнениями.
LoveGDZ.com
- ГДЗ по геометрии 7-9 класс Атанасян учебник
ГДЗ по геометрии 7-9 класс к учебнику Атанасян с подробным решением, онлайн ответы с пояснениямииз
Cамые актуальные готовые домашние задания по всем предметам.

Геометрия – наука, требующая внимательности и развитого пространственного мышления.
GDZ.me
- Мегарешеба — ГДЗ по Геометрии за 7‐9 класс Л.С. Атанасян…
Убедись в правильности решения задачи вместе с ГДЗ по Геометрии за 7‐9 класс Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин . Ответы сделаны к книге 2016 года от Просвещение ФГОС.
В любом случае рекомендуем вам рассмотреть возможность использования решебника по алгебре для 7-9 класса под авторством Атанасяня Л.С.В.Ф. Бутузова,С.Б. Кадомцева, который позволит делать следующее: выполнять домашнее задание любой сложности за считанные минуты
megaresheba.net
- Онлайн ГДЗ рабочая тетрадь Атанасян 9 класс
С данным ГДЗ вы забудете, что такое домашняя работа и полностью окунетесь в мир своих интересов, освободившись от бремени нудной учебы.

Рабочая тетрадь Атанасяна 9 класс состоит из глав и разделов, которые разделены на параграфы. Именно с учетой данных навигационных признаков построен наш решебник Атанасяна рабочей тетради. Мы надеемся, что данный решебник не оставит вас равнодушным и вы будете возвращаться сюда снова и снова!
reshak.ru
- ГДЗ для 9 класса — Геометрия
Проверяем задания с помощью ГДЗ по геометрии. Чтобы качественно готовиться к урокам и хорошо отвечать в школе, необходимо точно проанализировать свои знания, выявить в них пробелы. Для этого нужно, чтобы с учеником рядом постоянно был надежный консультант, который поможет работать эффективно, но в то же время очень быстро.
Все разделы данного «ГДЗ по геометрии, 9 класс» послужат отличным справочником и в старших классах, когда на основе изучаемого сейчас материала начнётся проработка более сложных тем.
gdzbezmoroki.
 com
com - Решебники ГДЗ по геометрии 9 класс
ГДЗ по геометрии 9 класс являются наиболее востребовательными среди школьников средней школы. Причем популярность данных решебников только возрастает, так как задания становятся всё более сложными для школьников, особенно для девушек, кто не любит математику.
Кроме того, решебники Атанасяна и Погорелова можно использовать как на компьютере, так и на мобильном телефоне, имеющим выход глобальную сеть интернет. ГДЗ по геометрии смогут помочь Вам обрести бОльшую свободу в плане свободного времени, а также повысят вашу…
reshak.ru
- Геометрия 9 класс Атанасян Учебник
Содержание учебника «Геометрия 9 класс» УМК Атанасян позволяет достичь планируемых результатов обучения, предусмотренных ФГОС основного общего образования. Учебник включает трёхступенчатую систему задач, а также исследовательские задачи, темы рефератов, список рекомендуемой литературы, что позволит учащимся расширить и углубить свои знания по геометрии.
 Специально для родителей и только у нас даны ОТВЕТЫ и РЕШЕНИЯ на задачи из учебника (ГДЗ).
Специально для родителей и только у нас даны ОТВЕТЫ и РЕШЕНИЯ на задачи из учебника (ГДЗ).xn--9-8sb3ae5aa.xn--p1ai
- Геометрия 7 8 9 класс Атанасян
Геометрия 7 8 9 класс Атанасян. Геометрия 7 8 9 класс Атанасян.
vcevce.ru
- Номер №9 — ГДЗ по Геометрии 7-9 класс: Атанасян Л.С.
ГДЗ (готовое домашние задание из решебника) на Номер №9 по учебнику Геометрия 7-9 классы: учебник для общеобразовательных организаций / Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — 2-е издание. Просвещение, 2014-2019г.
Ответ на Номер №9 из ГДЗ по Геометрии 7-9 класс: Атанасян Л.С.
otvetkin.info
- Классы
Видеоуроки, тесты и тренажёры по предмету Геометрия за 9 класс по учебнику Атанасян Л.
 С.
С.interneturok.ru
- Онлайн Учебник Геометрия 7 — 9 класс Атанасян бесплатно читать
Чтобы читать и смотреть Учебник Геометрия 7 — 9 класс Атанасян, нажмите на нужные страницы. Появятся изображения с бесплатными учебными материалами.
В комментариях вы можете сверяться и делиться готовыми ответами на домашнее задание, создавая свой интерактивный решебник к сложным упражнениям.
rabochaya-tetrad-i-uchebnik.com
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Готовые домашние задания по геометрии — 9 класс — Атанасян Л.С.»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 34 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
ГДЗ по геометрии 7-9 класс Атанасян учебник
Авторы: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Позняк Э.Г., Юдина И.И.
Просвещение
Подробное решение задач из учебника по геометрии за 7-9 класс Атанасян Л.С., а также Бутузов В.Ф. и других. Пособие предлагает готовые правильные пошаговые решения с ответами на представленные в учебнике упражнения. Что же касается дополнительных вопросов после глав, они здесь так же включены и расписаны четко и подробно.
В учебнике предусмотрено разделение на разделы, темы и параграфы с отдельным списком подтем. Подобный порядок изложенного материала позволяет школьникам быстро производить решения на определенные темы. Решебник рассчитан для базового и высокого уровня подготовки. Перед выполнением какого-либо упражнения учащиеся знакомятся с вводными вопросами и новыми геометрическими терминами. Весь учебный материал опирается на представленные решения именно с пояснениями, помогающие наладить процесс усвоения и закрепления нового материала.
Весь учебный материал опирается на представленные решения именно с пояснениями, помогающие наладить процесс усвоения и закрепления нового материала.
Геометрия – наука, требующая внимательности и развитого пространственного мышления. Понять суть теорем и формул непросто без подробных объяснений решения тех или иных задач. Чтобы усвоить все темы и разобраться в вариантах решения практических заданий, достаточно ознакомиться с методическим пособием. В ГДЗ приведены сами задачи, ответы к ним и объяснения решений. Такой вариант обучения отлично подходит ученикам средней и старшей школы.
Что содержится в решебнике Атанасяна за 7-9 класс
В учебнике представлены следующие темы:
- Начальные геометрические сведения. В этот раздел входят ответы по темам «Прямая и отрезок», «Луч и угол», «Изменение отрезков», «Градусные меры угла», «Построение прямых на плоскости».
- Треугольники. В данном разделе представлены ответы на такие темы как «Равенство треугольников», «Перпендикуляр к прямой» и др.
 В этом разделе объясняются теоремы и доказательства по равнобедренным треугольникам, а также приводятся задачи на построение разных геометрических окружностей.
В этом разделе объясняются теоремы и доказательства по равнобедренным треугольникам, а также приводятся задачи на построение разных геометрических окружностей. - Параллельные прямые. Здесь представлены теоремы о пересечении прямых и представлены практические способы построения двух параллельных прямых.
- Площадь, окружность, векторы. В этих разделах онлайн-сборника объясняются теоремы и приведены примеры их доказательств. Вычисление площадей и длин сторон разных геометрических фигур выполняется последовательно и с объяснениями.
Сборник с готовыми домашними заданиями позволяет школьникам, родителям и учителям быстро находить решения задач и выполнять практические задания. Простые объяснения решений позволяют повышать успеваемость и облегчают процесс обучения. В пособии представлены решения задач повышенной сложности, расположенные в конце каждой главы. К каждому из них прилагается подробное объяснение, рисунки, графики и чертежи для построений.
Учебник делится на 3 части – 7, 8 и 9 класс, соответственно.
- Задачи для 7 класса. В решебнике тесно переплетается теоретический и практический материал таких тем: «Четырехугольник», «Окружность», «Терема Пифагора», «Подобные треугольники», «Векторы» и др. Структура данного издания достаточно проста, поэтому поиск необходимого задания не займет много времени.
- Решения к заданиям за 8 класс. В этой части учебника рассматриваются практические упражнения, в которых, например, нужно доказать, что если все углы выпуклого четырехугольника равны друг другу, то хотя бы один из них тупой. Также в некоторых требуется доказательство того, что если в четырехугольнике все углы прямые, то четырехугольник – прямоугольник и т.д. Сюда вошли задания на такие темы: «Многоугольники», «Параллелограмм и трапеция», «Площади параллелограмма, треугольника и трапеции», «Применение подобия к доказательству теорем и решению задач», «Центральные и вписанные углы», «Понятие вектора».
- Решение с пояснениями упражнений для 9 класса.
 Здесь вы найдете решение задач, в которых нужно определить, сколько граней и ребер имеет прямоугольный параллелепипед и октаэдр, либо доказать, что площадь боковой поверхности прямой призмы равна произведению периметра основания на боковое ребро. Также здесь даны ответы на задания, требующие построить правильный треугольник по заданным данным, найти объемы частей призмы или длину окружности.
Отдельно в пособии произведены вычисления сечения куба; доказано, что площадь закрашенной фигуры равна площади круга на представленном рисунке; построены трапеция и треугольник по трем медианам. Также школьники найдут здесь построенные отрезки по заданным данным и сечение параллелепипеда, вычисленную площадь круга и призмы, и т.д.
Здесь вы найдете решение задач, в которых нужно определить, сколько граней и ребер имеет прямоугольный параллелепипед и октаэдр, либо доказать, что площадь боковой поверхности прямой призмы равна произведению периметра основания на боковое ребро. Также здесь даны ответы на задания, требующие построить правильный треугольник по заданным данным, найти объемы частей призмы или длину окружности.
Отдельно в пособии произведены вычисления сечения куба; доказано, что площадь закрашенной фигуры равна площади круга на представленном рисунке; построены трапеция и треугольник по трем медианам. Также школьники найдут здесь построенные отрезки по заданным данным и сечение параллелепипеда, вычисленную площадь круга и призмы, и т.д.
Кому пригодится данное пособие
Использовать ГДЗ по геометрии Атанасяна для учащихся средней школы могут:
- Родители, которые часто помогают своим детям в выполнении домашних заданий. Однако бывает сложно сразу понять тему и найти верные ответы.
 Онлайн решебник поможет проконтролировать правильность выполнения работы и объяснить ребёнку решение задачи любой сложности.
Онлайн решебник поможет проконтролировать правильность выполнения работы и объяснить ребёнку решение задачи любой сложности. - Учащиеся. Школьникам решебник помогает повышать уровень знаний при выполнении домашних заданий во время повышенной учебной нагрузки. Пособие помогает в подготовке к олимпиадам.
- Школьники, которые делают упор на другие дисциплины. Когда нужны высокие оценки по геометрии, но времени на глубокое изучение предмета не хватает, поможет выполнение домашних заданий с помощью сборника готовых ответов. Такой подход позволяет снизить риск получения низкой оценки, а также позволяет быстро понять принципы решения практических задач и доказательства теорем.
- Учителя и репетиторы. При проверке большого количества тетрадей приходится автоматизировать работу. Готовые решения помогут справиться с большими объемами проверяемых материалов.
ГДЗ по Геометрии для 7-9 класса Учебник Атанасян, Позняк, Кадомцев, Бутузов
ГДЗ по геометрии для 7-9 класса Атанасяна, Позняка, Кадомцева, Бутузова разработано для школьников, которые только начали изучать данный предмет. Многие считают, что геометрия это один из самых сложных предметов из школьного курса. Поэтому, если у ученика возникли трудности с изучением геометрии в 7-9 классе, то тогда это пособие для них.
Многие считают, что геометрия это один из самых сложных предметов из школьного курса. Поэтому, если у ученика возникли трудности с изучением геометрии в 7-9 классе, то тогда это пособие для них.
Решебник содержит все темы из данного учебника. Материал изложенный в ГДЗ безусловно поможет лучше ориентироваться в данном предмете, даст возможность развить навыки в правильном и последовательном доказательстве утверждений. Ребенок не только сможет улучшить оценку по геометрии, но и также использовать пособие в подготовке к сдаче ОГЭ и ЕГЭ.
Материал изложенный в ГДЗ полный, удобный в использовании, понятен. Сборник заданий могут использовать как школьники, так и студенты. Также он может быть полезен и родителям, которые хотят проверить правильность выполнения заданий по такому сложному предмету ‒ геометрия.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310
Вопросы для повторения
Глава 1
123456789101112131415161718192021
Глава 2
123456789101112131415161718192021
Глава 3
123456789101112131415
Глава 4
1234567891011121314151617181920
Глава 5
1234567891011121314151617181920
Глава 6
12345678910
Глава 7
123456789101112131415161718
Глава 8
1234567891011121314151617181920212223242526
Глава 9
1234567891011121314151617181920
Глава 10
123456789101112131415161718192021
Глава 11
123456789101112131415161718192021
Глава 12
123456789101112
Глава 13
1234567891011121314151617
Глава 14
1234567891011121314151617181920212223242526
ГДЗ к учебнику по геометрии 7-9 класс Атанасян
Авторы: Л. С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина.
С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина.
Год издания: 2018
7 класс
12345678910111213141516171819202122232425262728293031323334353637 (а)37 (б)3839404142434445464748495051525354555657585960616465 (а)65 (б)666768697071727374757677 (а)77 (б)787980818283848586878890919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291 (а-в)291 (г-д)292293294295296297298299300301302303304305306307308309310311312313314 (а-б)314 (в)315316317318319320321322323324325326327328329330331332333334335336337338 (1)338 (2)339340341342343344345346347348349350351352353354355356357358359360361362Учебник за 8 класс
Когда в расписании школьника появляется геометрия, подростки уже имеют некоторое представление об этом предмете. Родители делятся впечатлениями о своих трудностях с особой математической дисциплиной. Поэтому мамы и папы чаще всего не могут помочь с домашней работой, как это делали в младшей школе.
Родители делятся впечатлениями о своих трудностях с особой математической дисциплиной. Поэтому мамы и папы чаще всего не могут помочь с домашней работой, как это делали в младшей школе.
По-разному воспринимая учебный материал, часто даже отличники не успевают на уроке разобраться во всех тонкостях планиметрии и стереометрии, не могут самостоятельно решить задачи и уравнения. Чтобы помочь ребенку, родители ищут репетиторов, вместе с которыми сын или дочь будет размышлять над каждой задачей.
Но занятия с репетитором — это не всегда удобный график и значительные расходы. Сегодня оптимальным способом освоения геометрии становится решебник
363364365366367368370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412ном 413413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511. 513514516517519520521523524525526 (1)526527528529530532533534535536537538539540541542543544545546547548549550551552553554555557558559560561562563564565566567570571572573574575576577579580581582583585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717719720721722723725726727728729730731733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801803804805806807808809810
513514516517519520521523524525526 (1)5265275285295305325335345355365375385395405415425435445455465475485495505515525535545555575585595605615625635645655665675705715725735745755765775795805815825835855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177197207217227237257267277287297307317337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018038048058068078088098109 класс
911912913914 (а)914 (б)914 (в)915916917918919920921922923924925926927928929930931932933934935936937938939940941942943944945946947 (а)947 (б)948 (а)948 (б)949 (а)949 (б)950951 (а)951 (б)954955956957958959 (а-б)959 (в-г)959 (д)960961962963964965966967968969970971972973974975976977978979980981983985986987988989990991992993994995996 (а)996 (б-в)997998999100010011002-(а)1002-(б)1003 (в)1003-(а)1003-(б)1004100510061007100810091010 (а)1010 (б)101110121013101410151016101710181019102010211022102310241025 (а-б)1025-(в-д)1025-(е-;)1025-(з-и)102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310561057105810591060 (а-б)1060 (в-г)1061 (а)1061 (б-в)10621063106410651066106710681069107010711072107810791080108110821083108410851086108710881089109010911092109310941095109610971098109911001101110211031104 (а)1104 (б-г)1104 (д)1105-(а-б)1105-(в-г)110611071108110911101111111211131114111511161117 (а-б)1117 (в-г)11181119112011211122112311241125112611271128112911301131113211331134 (а-б)1134 (в)113511371139114011441147 (а)1147 (б)1148 (а)1148 (б)115011511152115311541156115811591160116111621163116411651166 (а)1166 (б-в)11671168116911701171117211731174 (а)1174 (б)117511761177117811791180 (1)1180 (2)118111821183118411851186118711881189 (а)1189 (б)11901191119211931194119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231224122512261227122812291230Почему решебник лучше репетитора
Сборник ГДЗ к учебнику по геометрии для 7 — 9 классов, написанному Атанасяном, полностью совпадает с учебником. Единственное отличие двух пособий в том, что в решебнике все задания уже выполнены.
Единственное отличие двух пособий в том, что в решебнике все задания уже выполнены.
Решебник составлен опытными педагогами, которые знают самые последние требования ФГОС. Не каждый репетитор в курсе актуальных методических новшеств.
Работа с ГДЗ возможна в любое удобное школьникам время. При этом разбираться в материале, обращаться повторно к одним и тем же задачам каждый ученик может столько, сколько нужно именно ему. Ведь решебник не объявит о том, что занятие закончено, не повысит цену за дополнительное время консультаций.
Чем может помочь решебник
Сборник ГДЗ незаменим при подготовке к урокам геометрии в течение учебного года. С его помощью станут понятными даже задания повышенной трудности. В отличие от учебника, в решебнике даны не просто правильные ответы, а представлен полный вариант оформления задания, в том числе схематический.
Особенно важен ресурс, содержащий готовые домашние задания по геометрии, для учеников, которые пропустили уроки во время лечения.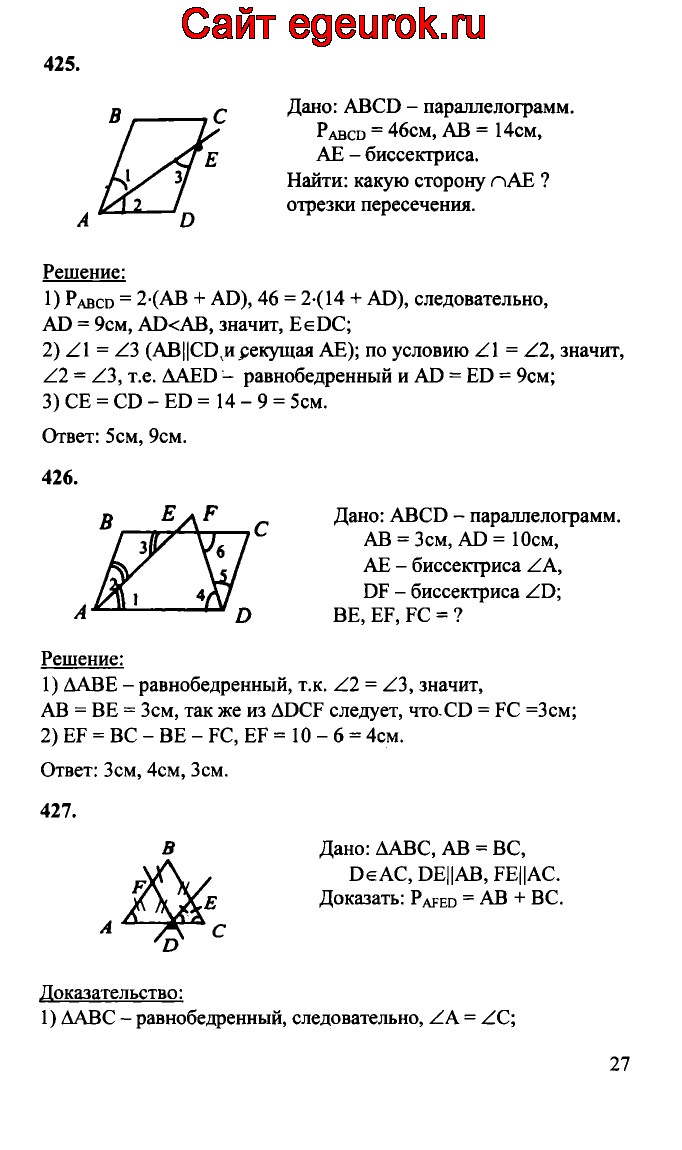 Они смогут увидеть, как одноклассники решали задачи и уравнения, и самостоятельно разберутся в новом материале.
Они смогут увидеть, как одноклассники решали задачи и уравнения, и самостоятельно разберутся в новом материале.
Не обойтись без ГДЗ и при подготовке к проверочным и контрольным работам, к итоговой аттестации. Решая задачи, подростки также получают возможность проверить их, исправить допущенные ошибки, повторить пройденное, устранить пробелы в знаниях.
Решебник — это прямая, открывающая школьникам дверь в мир геометрии.
Почему решебник — это надежно
Сборник готовых домашних заданий составлен профессионалами. Создателями ГДЗ стали квалифицированные педагоги-математики. Они не только предложили пользователям ресурса правильные ответы, но и объяснили ход мыслей с опорой на теоретический материал конкретных тем.
Ценность решебника повышается, благодаря грамотному оформлению заданий, которое соответствует требованиям учебной программы по геометрии.
В каких случаях нужен решебник
Сборник ГДЗ по геометрии будет сопровождать школьника в течение каждого учебного года, с 7 по 9 класс.
Решебник понадобится при выполнении и проверке домашних заданий, будет необходим для самостоятельного изучения материала, а также при подготовке к проверочным работам разного уровня.
Не обойтись без ГДЗ и при подготовке к государственной итоговой аттестации. Сборник поможет вспомнить учебный материал, систематизировать знания, потренироваться в решении задач на разные темы.
Результаты работы с решебником
ГДЗ обеспечит результаты с учетом индивидуальных особенностей школьников.
Гуманитарии, для которых геометрия сложна и непостижима, освоят ее основы, справятся с заданиями и получат хорошие оценки по предмету.
Ребята, увлекающиеся математической наукой, смогут углубить знания и самостоятельно проработать задания повышенной трудности.
Даже педагоги заинтересованы в использовании ГДЗ: результаты качества знаний по предмету повышаются, когда ученики, кроме основных и дополнительных пособий, занимаются с решебником.
ГДЗ Решебник Геометрия 7-9 класс Учебник «Просвещение» Атанасян, Бутузов.
ГДЗ Решебник Геометрия 7-9 класс Учебник «Просвещение» Атанасян, Бутузов.Геометрия 7-9 классУчебникАтанасян, Бутузов«Просвещение»
Зачастую обучение в школе проходит не так гладко, как хотелось бы большинству родителей. Да это и не удивительно, учитывая сложность учебной программы. Поэтому учащимся может весьма пригодится решебник к учебнику «Геометрия 7-9 класс Учебник, авторы: Атанасян, Бутузов» от издательства Просвещение, которое входит в серии УМК «». В сборнике подробно приводятся решения всех заданий, которые так же сопровождаются условиями.
ГДЗ «Геометрия 7-9 класс Учебник, авторы: Атанасян, Бутузов» поможет преодолеть множество трудностей в ходе обучения:
- дополнить и углубить свои познания;
- разобраться в мельчайших аспектах предмета Геометрия;
- исправить допущенные ошибки;
- повысить успеваемость.
Делитесь решением с друзьями, оставляйте комментарии — они помогают нам становится лучше!
Упражнения
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310Вопросы к главе 1
123456789101112131415161718192021Вопросы к главе 2
123456789101112131415161718192021Вопросы к главе 3
1234567891011121314151617Вопросы к главе 4
12345678910111213141516171819202122Вопросы к главе 5
12345678910111213141516171819202122Вопросы к главе 6
123456789101112Вопросы к главе 7
123456789101112131415161718Вопросы к главе 8
1234567891011121314151617181920212223242526Вопросы к главе 9
1234567891011121314151617181920Вопросы к главе 10
123456789101112131415161718192021222324Вопросы к главе 11
12345678910111213141516171819202122Вопросы к главе 12
12345678910111213Вопросы к главе 13
1234567891011121314151617Вопросы к главе 14
1234567891011121314151617181920212223242526Похожие ГДЗ Геометрия 7-9 класс
Геометрия 7 классРабочая тетрадьАтанасян, Бутузов, Глазков«Просвещение»
Упражнения: 1
Предыдущее
Следующее
Условие
Решебник №1
Решебник №2
Решебник №3
Решебник №4
Предыдущее
Следующее
закрытьГДЗ и решебники
Здание с вписанной и описанной окружностью Презентация.
 Окружность, описанная рядом с треугольником. Искомая формула радиуса окружности
Окружность, описанная рядом с треугольником. Искомая формула радиуса окружностиЧтобы насладиться просмотром презентаций, создайте себе учетную запись (аккаунт) Google и войдите в нее: https://accounts.google.com
Подписи к слайдам:
8 класс Л.С. Атанасян Геометрия 7-9 вписанная и описанная окружность
O D C Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник. A E Многоугольник называется описанным около этой окружности.
D каким из двух четырехугольников ABC D или AEK D описывается? И е примерно
D в с прямоугольником нельзя вписать в круг. А О.
D В каких известных свойствах нам пригодятся при изучении вписанной окружности? A E о свойстве касательности касательных отрезков f p
D C в любом описанном четырехугольнике суммы противоположных сторон равны. A E O A A R N F B B C C C D D
D C Сумма двух противоположных сторон описанного четырехугольника равна 15 см. Найдите периметр этого четырехугольника. И про номер 695 в С + AD = 15 AB + DC = 15 P ABCD = 30 см
Найдите периметр этого четырехугольника. И про номер 695 в С + AD = 15 AB + DC = 15 P ABCD = 30 см
D f Найти FD A O N? 4 7 6 5
D в равновесной трапеции описана около окружности. Основания трапеции равны 2 и 8. Найдите радиус вписанной окружности. А в c + ad = 1 0 ab + dc = 1 0 2 8 5 5 2 n f 3 3 4 s l
D B верно и обратное утверждение. o Если суммы противоположных сторон выпуклого четырехугольника равны, то его можно вставить в него. Солнце + А Д = АВ + ДЦ
D в C можно ли вписать окружность в этот четырехугольник? А О 5 + 7 = 4 + 8 5 7 4 8
В С и в любом треугольнике можно вписать окружность. Теорема Докажите, что в треугольнике можно войти в окружность дано: ABC
K в C и L M о 1) DP: биссектриса углов треугольника 2) при OL = CO M, по гипотенузе и восток. Угол L = М проводят из точки перпендикуляра к сторонам треугольника 3) МОА = СоА, по гипотенузе и ОСТ. Угол МО = КО 4) L О = М О = К относительно точки о равноудаленной от стороны треугольника. Итак, окружность с центром в So проходит через точки k, l и m. Стороны треугольника ABC касаются этой окружности. Значит, в окружность вписана буква АВС.
Итак, окружность с центром в So проходит через точки k, l и m. Стороны треугольника ABC касаются этой окружности. Значит, в окружность вписана буква АВС.
К в С и в любой треугольник можно вписать круг. Л М О теореме
Д в с докажите, что площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности. A № 69 7 F R A 1 A 2 A 3 R O R … + K
O D C Если все вершины многоугольника лежат на окружности, то окружность называется описанным многоугольником. A E Многоугольник называется вписанным в эту окружность.
О Д каким из многоугольников, изображенных на рисунке, вписана окружность? А Е Л П Х Е О Г Б В А Е
О и в D какие известные свойства пригодятся нам при изучении описываемой окружности? Теорема о вписанном угле
O и D В любом вписанном четырехугольнике сумма противоположных углов равна 180 0. C + 360 0
59 0? 90 0? 65 0? 100 0 D A B C O 80 0 115 0 D A B C O 121 0 Найдите неизвестные углы четырехугольников.
D — истинное и обратное утверждение. Если сумма противоположных углов четырехугольника равна 180 0 , то возле него можно написать окружность. А Б В О 80 0 100 0 113 0 67 0 О Г А Б В 790 99 0 123 0 77 0
В С и о любом треугольнике можно описать окружность. Теорема Докажите, что окружность может быть описана: АВС
К в С и лм о 1) ДП: середина перпендикулярна сторонам = СО 2) в ОЛ = СО Л, по разрядам 3) сом = и о м, согласно к КАТЕМС СО = АО 4) ат = со = АО, т. е. Точка равна вершинам треугольника. Значит, окружность с центром в Т.ОО и радиусом ОА будет проходить через все три вершины треугольника, т.е. это описываемая окружность.
К в С и про любой треугольник можно описать окружность. Л М Теорема о
Треугольник АВС так, что диаметр окружности вписан в С и С и С С А № 702. Найти углы треугольника, если: а) Солнце = 134 0 134 0 67 0 23 0 б ) ас = 70 0 70 0 55 0 35 0
О в С и № 703 Между прочим вписан равный треугольник АВС с основанием самолета. Найдите углы треугольника, если Солнце = 102 0. 102 0 51 0 (180 0 — 51 0): 2 = 1290:2 = 128 0 60 /: 2 = 64 0 30 /
Найдите углы треугольника, если Солнце = 102 0. 102 0 51 0 (180 0 — 51 0): 2 = 1290:2 = 128 0 60 /: 2 = 64 0 30 /
О в С и № 704 (а) Окруженный с центром О описан возле прямоугольного треугольника. Докажите, что эта точка лежит на середине гипотенузы. 180 0 d и a m e t p
O в C № 704 (b) Циркумстиальная с центром O описана около прямоугольного треугольника. Найдите стороны треугольника, если диаметр окружности равен D и один из острых углов треугольника равен. Д.
О с С № 705 (а) Возле прямоугольного треугольника АВС с прямым углом с описанной окружностью. Найдите радиус этой окружности, если копье = 8 см, Солнце = 6 см. 8 6 10 5 5
О с и в № 705 (б) возле прямоугольного треугольника АВС с прямым углом с описанной окружностью. Найдите радиус этой окружности, если динамик = 18 см, 18 30 0 36 18 18
О в С и боковые стороны треугольника, изображенного на рисунке, равны 3 см. Найдите радиус окружности, описанной рядом с ним. 180 0 3 3
O в C, а радиус окружности, описанной возле треугольника, изображенного на рисунке, равен 2 см. Найдите сторону АВ. 180 0 2 2 45 0?
Найдите сторону АВ. 180 0 2 2 45 0?
На тему: Методическая разработка, презентации и конспекты
Презентация к занятию включает определения основных понятий, создание проблемной ситуации, а также развитие творческих способностей учащихся….
Рабочая программа для элективный курс по геометрии «Решение контурных задач на вписанные и описанные окружности» 9
Статистические данные анализа результатов состояния ЭЭГ говорят о том, что наименьший процент правильных ответов традиционно дают студенты по геометрическим задачам. Задания по планиметрии входят в…
Слайд 1.
Клада 2.
Определение: Окружность называется описанной около треугольника, если все вершины треугольника лежат на этой окружности. Если окружность описана рядом с треугольником, то треугольник вписан в окружность.
Слайд 3.
Теорема. Возле треугольника можно описать круг, и притом только один. Ее центр является точкой пересечения средних перпендикуляров к сторонам треугольника. Доказательство: Проведем срединные перпендикуляры Р, К, N к сторонам АВ, Солнца, АС по свойству серединных перпендикуляров к сторонам треугольника (чудесная точка треугольника): они пересекаются в одной точке — о, для чего ОА = ОС = ОС. То есть все вершины треугольника равноудалены от точки о, значит, они лежат на окружности с центром О. Итак, окружность описана вблизи треугольника АБС.
Ее центр является точкой пересечения средних перпендикуляров к сторонам треугольника. Доказательство: Проведем срединные перпендикуляры Р, К, N к сторонам АВ, Солнца, АС по свойству серединных перпендикуляров к сторонам треугольника (чудесная точка треугольника): они пересекаются в одной точке — о, для чего ОА = ОС = ОС. То есть все вершины треугольника равноудалены от точки о, значит, они лежат на окружности с центром О. Итак, окружность описана вблизи треугольника АБС.
Слайд 4.
Важное свойство: если окружность описана около прямоугольного треугольника, то его центр — середина гипотенузы. R = ½ АВ Задача: найти радиус окружности, описанной возле прямоугольного треугольника, карты которого равны 3 см и 4 см.
Слайд 5.
Формулы радиуса описанной около треугольника окружности Задача: найти радиус описанной окружности около равностороннего треугольника, сторона которого равна 4 см. Решение:
Слайд 6.
Задание: В окружность, радиус которой 10 см, вписан равноправный треугольник. Высота до основания 16 см. Найдите сторону и площадь треугольника. Решение: Т. К. Окружность описана около равноцепного треугольника АВС, тогда центр окружности лежит на высоте ВН. АО = СО = СО = 10 см, ит = вн — ат = 16 — 10 = 6 (см) ас = 2ан = 2 · 8 = 16 (см), САВС = ½ AS · ВН = ½ · 16 · 16 = 128 (см2)
Слайд 7.
Определение: Окружность называется описанной около четырехугольника, если все вершины четырехугольника лежат на окружности. Теорема. Если вокруг окружности описан четырехугольник, то сумма его противоположных углов равна 1800. Доказательство: другая формулировка теоремы: Сумма противоположных углов равна 1800, вписанной в окружность величины.
Слайд 8.
Обратная теорема: Если сумма противолежащих углов четырехугольника равна 1800, то около него можно описать окружность. Доказательство: № 729(учебник) вокруг какого квадролона нельзя описать окружность?
Доказательство: № 729(учебник) вокруг какого квадролона нельзя описать окружность?
«Алгебра и геометрия» — женщина учит детей геометрии. Бале был уже, по словам мамы, последним представителем греческой геометрии. Вне 4-й степени таких формул нет уравнения для общего решения. Интерлоганы и новоевропейская наука были арабами. Был поднят вопрос о геометрии физики.
«Термины геометрии» — биссектриса треугольника. Точка абстракции. Диагональ. Словарь по геометрии. Круг. Радиус. Периметр треугольника. Вертикальные углы. Условия. Угол. Окружность хорды. Вы можете добавить свои условия. Теорема. Выберите первую букву. Геометрия. Электронный словарь. Хлеб. Компас. Родственные углы. Срединный треугольник.
«Геометрия 8 класс» — так выворачивая теоремы, можно добраться до аксиомы. Понятие теоремы. Квадрат гипотенузы равен сумме квадратов катетов. А2+В2=С2. Понятие аксиомы. Каждое математическое утверждение, полученное логическим доказательством, является теоремой. У любого здания есть фундамент. Каждое утверждение опирается на уже доказанное.
Каждое утверждение опирается на уже доказанное.
«Визуальная геометрия» — Квадрат. Конверт номер 3. Помогите, пожалуйста, ребята, а то Матроскин меня жидко разжижит. Все стороны квадрата равны. Площади вокруг нас. Сколько квадратов изображено на картинке? Задания на внимательность. Конверт № 2. Все углы квадрата прямые. Дорогой мяч! Зрительная геометрия, 5 класс. Отличные свойства разной длины сторон разного цвета.
«Исходная геометрическая информация» — Евклид. Чтение. Что говорят о нас цифры. На рисунке выделен участок прямой, ограниченный двумя точками. Через одну точку можно проводить любые разные прямые линии. Математика. В геометрии нет царского пути. Записывать. Дополнительные задания. Планиметрия. Обозначение. Страницы «Начало» Евклида. Платон (477-347 до н.э.) — древнегреческий философ, ученик Сократа.
«Таблицы по геометрии» — таблицы. Умножение вектора на число осевой и центральной симметрии. Касательная к окружности Центральный и вписанный углы вписаны и описывают окружность. Концепция вектора. Сложение и вычитание векторов. Содержание: многоугольники Паралимлограммы и трапеция Прямоугольник, ромб, квадрат Многоугольник Квадрат Квадрат треугольника, параллелограмм и трапеция Теорема Пифагора Подобные треугольники Признаки подобия треугольников между сторонами и углами прямоугольного треугольника, ограничение прямого и круг.
Концепция вектора. Сложение и вычитание векторов. Содержание: многоугольники Паралимлограммы и трапеция Прямоугольник, ромб, квадрат Многоугольник Квадрат Квадрат треугольника, параллелограмм и трапеция Теорема Пифагора Подобные треугольники Признаки подобия треугольников между сторонами и углами прямоугольного треугольника, ограничение прямого и круг.
На каком рисунке изображена окружность, вписанная в треугольник?
Если окружность вписана в треугольник,
, то треугольник описан вблизи окружности.
Теорема. В треугольник можно вписать круг, и притом только один. Его центр является точкой пересечения биссектрисы треугольника.
Dano: ABC
Докажите: Существует OCC. (O; R),
вписанный в треугольник
Доказательство:
Проведем биссектрису треугольника: АА 1, ВВ 1, СС 1.
По свойству (чудесная точка треугольника)
биссектрисы пересекаются в одной точке — о,
и эта точка равноудалена от всех сторон треугольника, т. е.
е.
ОК = ОЕ = ИЛИ, где ОК АВ, ОЕ Солнце, ИЛИ АС, означает
О — центр окружности, а АВ, Солнце, АС — касательные к ней.
Итак, окружность вписана в ABC.
Дано: OCP. (O; R), вписанный в ABC,
р = ½ (АВ+Вс+АС) — половинная версия.
Доказать S. ABC = p · r
Доказательство:
соединить центр окружности с вершинами
треугольника и провести точку радиуса окружности
23 9.
Эти радиусы являются
высотами треугольников AOs, Vos, Soa.
S ABC = S AOB + S Boc + S AOC = ½ AB · R + ½ BC · R + ½ AC · R =
= ½ (AB + BC + AC) · R = ½ P · Р.
Задача: в равносторонний треугольник со стороной 4 см
вписана окружность. Найдите ее радиус.
Вывод формулы радиуса вписанной в треугольник окружности
S = p · r = ½ p · r = ½ (a + b + c) · r
2s = ( A + B + C) · R
Искомая формула радиуса окружности,
вписанной в прямоугольный треугольник
— карт, C — гипотенуза
Определение: Окружность называется вписанной в четырехугольник, если его касаются все стороны квадролона.
В какой фигуре окружность вписана в четырехугольник:
Теорема: если в четырехугольник вписана окружность,
то суммы противоположных сторон
в любом описанном
кадриль сумма противоположностей
стороны равны).
АВ + СК = ВС + АК.
Обратная теорема: если суммы противоположных сторон
выпуклого четверика равны,
то в нем можно войти в окружность.
Задача: В ромб, острый угол которого равен 60 0 , вписана окружность,
радиус которой 2см. Найдите периметр ромба.
Разделение задач
Данар: OCP. (О; Р) вписан в АВСК,
Р Авск = 10
Найти: Вс + АК
Дано: АВСМ описан возле ОКР. (О;R)
ВС = 6, ам = 15,
Оа = ОБ О Б => ОБ = ОС => О к середине перпендикуляра к АС => о тр. ABC Можно описать окружность Ba => OA = OC => «TITLE=» (!Lang: Теорема 1 Доказательство: 1) A — Средняя перпендикулярность к AB 2) B — Средняя перпендикулярность к BC 3) АВ = О 4) О А => ОА = ОВ О Б => ОБ = ОС => О к середине перпендикуляра к АС => о ТР. ABC Можно описать окружность Ba => oa = OC =>»>
8
!} Теорема 1 Доказательство: 1) А — средняя перпендикулярность к АВ 2) В — средняя перпендикулярность к ВС 3) АВ = О 4) О А => ОА = ОВ О В => ОВ = ОС = > o Твердый перпендикуляр к АС => о тр. ABC Можно описать окружность Ba => oa = OC => Oa = OB O B => OB = OC => O к середине перпендикуляра к AC => о тр. ABC Можно описать окружность Ba => oa = OC => «> OA = OB O B => OB = OC => O к середине перпендикуляра к AC => о тр. ABC можно описать окружностью Ba => oa = OC =>»> Oa = OB O B => OB = OC => O к середине перпендикуляра к AC => о тр. ABC Можно описать окружность Ba => OA = OC => «TITLE=» (!Lang: Теорема 1 Доказательство: 1) A — Средняя перпендикулярность к AB 2) B — Средняя перпендикулярность к BC 3) АВ = О 4) О А => ОА = ОВ О Б => ОБ = ОС => О к середине перпендикуляра к АС => о ТР.
ABC Можно описать окружность Ba => OA = OC => «TITLE=» (!Lang: Теорема 1 Доказательство: 1) A — Средняя перпендикулярность к AB 2) B — Средняя перпендикулярность к BC 3) АВ = О 4) О А => ОА = ОВ О Б => ОБ = ОС => О к середине перпендикуляра к АС => о ТР. ABC Можно описать окружность Ba => oa = OC =>»>
8
!} Теорема 1 Доказательство: 1) А — средняя перпендикулярность к АВ 2) В — средняя перпендикулярность к ВС 3) АВ = О 4) О А => ОА = ОВ О В => ОВ = ОС = > o Твердый перпендикуляр к АС => о тр. ABC Можно описать окружность Ba => oa = OC => Oa = OB O B => OB = OC => O к середине перпендикуляра к AC => о тр. ABC Можно описать окружность Ba => oa = OC => «> OA = OB O B => OB = OC => O к середине перпендикуляра к AC => о тр. ABC можно описать окружностью Ba => oa = OC =>»> Oa = OB O B => OB = OC => O к середине перпендикуляра к AC => о тр. ABC Можно описать окружность Ba => OA = OC => «TITLE=» (!Lang: Теорема 1 Доказательство: 1) A — Средняя перпендикулярность к AB 2) B — Средняя перпендикулярность к BC 3) АВ = О 4) О А => ОА = ОВ О Б => ОБ = ОС => О к середине перпендикуляра к АС => о ТР. ABC Можно описать окружность Ba => oa = OC =>»>
title=»Теорема 1 Доказательство: 1) А — средняя перпендикулярность к АВ 2) В — средняя перпендикулярность к ВС 3) АВ = О 4) О А => ОА = ОВ О В => ОВ = ОС \ u003d>o Твердый перпендикуляр к AC => о тр.ABC Можно описать окружность Ba => oa = OC =>»>
!}
ABC Можно описать окружность Ba => oa = OC =>»>
title=»Теорема 1 Доказательство: 1) А — средняя перпендикулярность к АВ 2) В — средняя перпендикулярность к ВС 3) АВ = О 4) О А => ОА = ОВ О В => ОВ = ОС \ u003d>o Твердый перпендикуляр к AC => о тр.ABC Можно описать окружность Ba => oa = OC =>»>
!}
Свойства треугольника и трапеции, входящих в Схему Схема ОКР-ТП, описанная около п/у, лежит посередине гипотенузы ОКР, описанная вблизи острой тр-ки, лежит в ТП -КЭ ОКР-ТП, описываемое про тупую тр-ку, не лежит в тр-ке, если возле трапеции можно описать, это уравновешиваемое
Построение треугольника по двум углам, прилежащим к стороне. Построение треугольника тремя элементами
Представляем вашему вниманию видеоурок на тему «Построение треугольника по трем элементам». Вы сможете решить несколько примеров из класса задач на строительство. Учитель подробно разберет задачу о построении треугольника по трем элементам, а также вспомнит теорему о равенстве треугольников.
Данная тема имеет широкое практическое применение, поэтому рассмотрим некоторые виды решения задач. Напомним, что любые построения выполняются исключительно с помощью циркуля и линейки.
Пример 1:
Постройте треугольник по двум сторонам и углу между ними.
Дано: Предположим, что анализируемый треугольник выглядит так
Рис. 1.1. Анализируемый треугольник на примере 1
Пусть заданы отрезки с и а, а задан угол
Рис. 1.2. Установить Предметы например 1
Здание:
Сначала нужно отложить угол 1
Рис. 1.3. Отложенный угол 1 например 1
Затем на сторонах данного угла откладываем циркулем две заданные стороны: длину стороны измеряем циркулем а и кладем острие циркуля в вершину угла 1, а с другой частью делаем надрез со стороны угла 1. Такую же процедуру проделываем со стороной С
Рис. 1.4. Откладываем стороны на и С например 1
Затем соединяем получившиеся надрезы, и получается искомый треугольник АВС
Рис. 1.5. Построен треугольник ABC например 1
1.5. Построен треугольник ABC например 1
Будет ли заданный треугольник равным ожидаемому? Будет, потому что элементы получившегося треугольника (две стороны и угол между ними) соответственно равны двум сторонам и углу между ними, заданным в условии. Следовательно, по первому свойству равенства треугольников — — искомое.
Строительство завершено.
Примечание:
Вспомним, как отложить угол, равный заданному.
Пример 2
Отложить от данного луча угол, равный данному. Угол A и луч OM заданы. Строить .
Здание:
Рис. 2.1. Условие для примера 2
1. Построить окружность Okr(A, r = AB). Точки В и С — точки пересечения со сторонами угла А
Рис. 2.2. Пример решения 2
1. Построить окружность Okr(D, r = CB). Точки Е и М — точки пересечения со сторонами угла А
Рис. 2.3. Решение для примера 2
1. Угол MOE является искомым, так как .
Строительство завершено.
Пример 3
Построить треугольник ABC по известной стороне и двум смежным углам.
Пусть анализируемый треугольник выглядит так:
Рис. 3.1. Условие например 3
Тогда данные сегменты выглядят так
Рис. 3.2. Состояние например 3
Корпус:
Отложите угол на плоскости
Рис. 3.3. Решение для примера 3
На стороне заданного угла отложим длину стороны a
Рис. 3.4. Решение для примера 3
Затем откладываем угол от вершины С. Необщие стороны углов γ и α пересекаются в точке А
Рис. 3.5. Решение для примера 3
Является ли построенный треугольник искомым? Так и есть, так как сторона и два прилежащих к ней угла построенного треугольника соответственно равны стороне и углу между ними, заданным в условии
Требуется по второму критерию равенства треугольников
Построение выполнено
Пример 4
Построить треугольник на двух катетах
Пусть анализируемый треугольник выглядит так
3
4. 1. Состояние например 4
1. Состояние например 4
Известные элементы — ножки
Рис. 4.2. Условие например 4
Эта задача отличается от предыдущих тем, что по умолчанию можно определить угол между сторонами — 90 0
Здание:
Отложите угол, равный 90 0 . Сделаем это точно так же, как показано в примере 2.
Рис. 4.3. Решение для примера 4
Затем на сторонах этого угла откладываем длины сторон а и b , заданные в условии
Рис. 4.4. Решение например 4
В результате полученный треугольник и есть искомый, так как две его стороны и угол между ними соответственно равны двум сторонам и углу между ними, заданным в условии
Обратите внимание, что угол 90 0 можно отложить, построив две перпендикулярные линии. Как выполнить эту задачу, см. дополнительный пример
Дополнительный пример
Восстановить перпендикуляр к прямой p, проходящей через точку A,
, прямую p и точку A, лежащую на этой прямой
Рис. 5.1. Условие для дополнительного примера
5.1. Условие для дополнительного примера
Здание:
Сначала построим окружность произвольного радиуса с центром в точке А
Рис. 5.2. Решение для дополнительного примера
Эта окружность пересекает прямую R в точках K и E. Затем строим две окружности Okr(K, R = KE), Okr(E, R = KE). Эти окружности пересекаются в точках С и В. Искомым является отрезок SV,
Рис. 5.3. Ответ на дополнительный пример
- Единая коллекция цифровых образовательных ресурсов ().
- Репетитор по математике ().
- № 285, 288. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Е. Г., Юдина И. И. под редакцией Тихонова А. Н. Геометрия 7-9 классы. М.: Просветление. 2010
- Постройте равнобедренный треугольник по стороне и углу, противоположному основанию.
- Построить гипотенузу прямоугольного треугольника и острый угол
- Построить треугольник по углу, высоте и биссектрисе, проведенной из вершины заданного угла.

§ 1 Построение треугольника по двум сторонам и углу между ними
Построение геометрической фигуры — одна из интересных задач геометрии. Только с помощью циркуля и линейки без делений получить необходимую цифру непросто.
Форма треугольника часто используется при решении задач, но как правильно ее построить?
Пусть необходимо построить треугольник по двум сторонам и углу между ними.
Во-первых, что такое две стороны — это два произвольных отрезка, например, P1Q1 и P2Q2, а также произвольный угол альфа. Все эти элементы уже построены, другими словами, этим элементам даны задания.
Во-вторых, нужно определить последовательность построения: сначала нужно построить одну сторону треугольника, затем угол, а затем вторую сторону треугольника.
Итак, перед нами белый лист, проводим прямую а и отмечаем на ней точку А, затем берем циркуль и откладываем отрезок АВ, равный отрезку Р1Q1. Далее выбираем произвольное отверстие компаса и рисуем одну окружность с центром в вершине угла альфа и другую окружность с центром в точке А. Первая окружность будет пересекать лучи угла альфа в точках Р и К, а вторая окружность будет пересекают прямую а в точке М. Проведите отрезок RK. Затем берем отверстие циркуля, равное отрезку RK, и строим окружность с центром в точке М. Окружность с центром в точке М пересекает окружность с центром в точке А, пусть эта точка будет М1. Нарисуем балку AM1. Затем на луче AM1 откладываем отрезок AC, равный отрезку P2Q2. Соедините точки B и C отрезком. Получившийся треугольник ABC и есть искомый.
Первая окружность будет пересекать лучи угла альфа в точках Р и К, а вторая окружность будет пересекают прямую а в точке М. Проведите отрезок RK. Затем берем отверстие циркуля, равное отрезку RK, и строим окружность с центром в точке М. Окружность с центром в точке М пересекает окружность с центром в точке А, пусть эта точка будет М1. Нарисуем балку AM1. Затем на луче AM1 откладываем отрезок AC, равный отрезку P2Q2. Соедините точки B и C отрезком. Получившийся треугольник ABC и есть искомый.
Теперь докажем, что получившийся треугольник ABC является искомым. Фактически отрезок AB равен отрезку P1Q1, а отрезок AC равен отрезку P2Q2 по построению. Угол альфа также по построению равен углу CAB. При заданном ходе построения для любых заданных отрезков P1Q1 и P2Q2 и развернутого угла альфа можно построить искомый треугольник. Поскольку прямую а и точку А на ней можно выбрать произвольно, треугольников, удовлетворяющих условиям задачи, бесконечно много. Все эти треугольники равны между собой по первому критерию равенства треугольников, поэтому принято говорить, что данная задача имеет единственное решение.
§ 2 Построение треугольника по стороне и двум прилежащим углам
Теперь рассмотрим задачу построения треугольника по стороне и двум прилежащим углам.
Итак, нам дан отрезок PQ и два угла альфа и бета. Проведите прямую a и отметьте на ней произвольную точку A. Отложите от точки A отрезок AB, равный отрезку PQ. Затем строим угол М1АВ с вершиной в точке А, равный углу альфа, и угол М2ВА с вершиной в точке В, равный углу бета. Точкой пересечения лучей AM1 и VM2 будет точка C. Треугольник ABC искомый.
Докажем: отрезок AB по построению равен отрезку PQ, также по построению угол CAB равен углу alpha, а угол CBA равен углу beta.
Как известно, сумма углов в треугольнике равна 180 градусам, поэтому при заданном ходе построения искомый треугольник АВС можно построить только в том случае, если сумма углов альфа и бета меньше 180 градусов. Если сумма этих углов больше или равна 180 градусам, треугольник построить нельзя.
В этой задаче, как и в предыдущей, прямую а и точку А на ней можно выбрать произвольно, а значит, существует бесконечно много треугольников, удовлетворяющих условиям задачи. Все эти треугольники равны между собой по второму критерию равенства треугольников, поэтому мы говорим, что эта задача имеет единственное решение.
Все эти треугольники равны между собой по второму критерию равенства треугольников, поэтому мы говорим, что эта задача имеет единственное решение.
§ 3 Построение треугольника по трем сторонам
Построение треугольника по трем сторонам — третья задача построения треугольника.
Пусть даны три сегмента P1Q1, P2Q2 и P3Q3. необходимо построить треугольник ABC, в котором AB равен P1Q1, BC равен P2Q2 и CA равен P3Q3.
Проведите прямую а и на ней с помощью циркуля отложите отрезок АВ, равный отрезку Р1Q1. Затем строим две окружности: одну — с центром в точке A и радиусом P3Q3, а другую — с центром в точке B и радиусом P2Q2. Пусть точка C будет одной из точек пересечения этих окружностей. Проведя отрезки AC и BC, получим искомый треугольник ABC. Действительно, по построению AB равен P1Q1, BC равен P2Q2, а CA равен P3Q3, то есть стороны треугольника равны этим отрезкам.
Рассматриваемая задача не всегда имеет решение из-за неравенства треугольника, то есть в любом треугольнике сумма любых двух сторон больше третьей стороны, поэтому, если какой-либо из этих отрезков больше или равен сумме двух других, то невозможно построить треугольник, стороны которого были бы равны данным отрезкам.
Список использованной литературы:
- Атанасян Л.С. Учебник: Геометрия. 7-9 классы: учеб. для общеобразовательных организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. – 383 с.
- Геометрия. Часть I Планиметрия: учебное пособие/ И.Б. Барский, Г.Н. Тимофеев. — Йошкар-Ола: изд-во Марийского государства. ун-та, 2006 и 2008 гг. — 636с
Тема урока: Построение треугольника по трем элементам
Цель урока: научиться строить треугольники по трем элементам
Цели урока: Построение треугольника с помощью линейки и циркуля
На занятиях:
1 этап : организационный момент, приветствие, проверка домашнего задания
Этап 2: новая тема
Построение треугольника по двум сторонам и углу между ними .
Даны два отрезка a и b, равные сторонам искомого треугольника, а угол ∡
1
равен углу треугольника между сторонами. Необходимо построить треугольник с элементами, равными данным отрезкам и углу.
1. Проведите прямую линию.
Аа.
∡ 1 (угол верх А
4. С другой стороны угла откладываем отрезок равный этому отрезку б.
5. Соедините концы сегментов.
По критерию равенства треугольников по двум сторонам и углу между ними построенный треугольник равен всем треугольникам, имеющим эти элементы.
Построение треугольника по стороне и двум прилежащим углам .
Даны отрезок и два угла∡
1
и∡
2
, равноугольный треугольник, примыкающий к данной стороне. Необходимо построить треугольник с элементами равными данному отрезку и углам.
1. Проведите прямую линию.
2. На прямой из выбранной точки А провести отрезок, равный заданному отрезку аВ.
3. Построить угол, равный заданному∡ 1 (угол А, одна сторона угла лежит на прямой).
4. Построить угол, равный заданному∡ 2 (угол topB, одна сторона угла лежит на прямой).
5. Точка пересечения других сторон углов является третьей вершиной искомого треугольника.
По критерию равенства треугольников по стороне и двум прилежащим к ней углам построенный треугольник равен всем треугольникам, имеющим эти элементы.
Построение треугольника с тремя сторонами .
Даны три сегмента: а,
bandc, равный сторонам искомого треугольника. Необходимо построить треугольник со сторонами, равными данным отрезкам.
В этом случае перед началом построения необходимо убедиться, что выполняется неравенство треугольника (длина каждого отрезка меньше суммы длин двух других отрезков), и эти отрезки могут быть сторонами треугольник.
1. Проведите прямую линию.
2. На прямой из выбранной точки А провести отрезок, равный данному отрезку а, и отметить другой конец отрезка В.
3. Нарисуйте окружность с центром A и радиусом, равным отрезку b.
4. Нарисуйте окружность с центром и радиусом, равным отрезку c.
5. Точка пересечения окружностей – третья вершина искомого треугольника
По критерию равенства треугольников по трем сторонам построенный треугольник равен всем треугольникам, имеющим заданные стороны.
3 этап: решение задач
№ 239 стр. 74
построить прямоугольный треугольник по двум катетам образуется при соединении отрезками трех точек, не принадлежащих одной прямой. Он однозначно определяется совокупностью трех данных: трех сторон, двух сторон и угла между ними или стороны и двух смежных углов.
В качестве примера попробуем построить треугольник по стороне и двум прилежащим углам?
Быстрая навигация по статьям
Построение треугольника
Прежде всего, на прямой откладывается отрезок, равный длине данной стороны. Концы отрезка отмечены точками А и В.
Для построения треугольника нужно отложить заданные углы от точек А и В. Если значения углов заданы, то использовать транспортир построить:
- Нижний брусок транспортира выравниваем по отрезку прямой;
- Устанавливаем точку отсчета в точке А для первого угла и в точке В для второго;
- Затем отложите углы. Ставим точки возле соответствующего деления шкалы и обозначаем их М и Н;
- Точки А и М, В и N соединяем прямыми линиями.
 Пересечение построенных прямых будет третьей и последней вершиной треугольника C.
Пересечение построенных прямых будет третьей и последней вершиной треугольника C.
Итак, по заданной стороне и двум заданным углам построен треугольник.
Графический угол
Часто для построения треугольника по стороне и двум прилежащим углам углы задаются графически. Задача усложняется, так как необходимо построить угол, равный по величине заданному графическому углу.
Можно измерить значение заданного графически угла с помощью транспортира и получить значения прилежащих углов, а затем использовать метод, описанный в предыдущем пункте, и построить треугольник.
Использование циркуля
Для другого способа построения угла, соответствующего по величине заданному, вам потребуется циркуль:
- Циркуль при произвольном решении чертит окружность с центром в начальной точке угла . Пересечения окружности и сторон угла будем обозначать М и N;
- Теперь вернемся к отрезку АВ, равным сторонам искомого треугольника.
 Не меняя решения, проводим из точки А окружность и отмечаем точку пересечения ее с отрезком АВ — получаем точку М1;
Не меняя решения, проводим из точки А окружность и отмечаем точку пересечения ее с отрезком АВ — получаем точку М1; - Возврат к заданному углу. Поместите ножку циркуля в точку М и сделайте раствор равным МN;
- Теперь, не меняя решения компаса, проводим окружность из точки М1 до пересечения с первой окружностью — получаем точку N1;
- Соедините прямые точки A и N1. Угол М1АН1 и будет равен заданному;
- Второй угол также строим в точке B. Пересечение сторон построенных углов будет недостающей вершиной C.
Таким способом строится треугольник с помощью циркуля вдоль стороны и двух заданных вложенных углов с помощью циркуля.
Наконец, рассмотрим задачу, решение которой приводит к построению треугольника по стороне и двум углам:
На другом берегу реки (рис. 72) виден верстовой столб А . Требуется, не переходя реку, узнать расстояние до нее от вехи В на этом берегу.
Давайте сделаем это. Измеряйте от точки В на некотором расстоянии по прямой ВС и на концах В и ОТ отмерим углы 1 и 2 (рис. 73). Если теперь на удобной местности отмерить расстояние д.е. равняется солнцу , и строят на его концах углы а и б (рис. 74), равные углам 1 и 2, тогда в точке пересечения их сторон получаем третью вершину F треугольника ДЕФ. Легко видеть, что треугольник DEF равно треугольнику ABC ; Действительно, если представить, что треугольник DEF наложен на ABC так, что сторона DE совпала с равной ему стороной солнце , то уг. а совпадает с углом 1, угол b- с углом 2, а сторона D.F. пойдет на сторону VA , а сторона EF на сторону SA. Поскольку две прямые могут пересекаться только в одной точке, вершина F должен соответствовать верхнему A . Таким образом, расстояние д.ф. равно желаемому расстоянию ВА.
73). Если теперь на удобной местности отмерить расстояние д.е. равняется солнцу , и строят на его концах углы а и б (рис. 74), равные углам 1 и 2, тогда в точке пересечения их сторон получаем третью вершину F треугольника ДЕФ. Легко видеть, что треугольник DEF равно треугольнику ABC ; Действительно, если представить, что треугольник DEF наложен на ABC так, что сторона DE совпала с равной ему стороной солнце , то уг. а совпадает с углом 1, угол b- с углом 2, а сторона D.F. пойдет на сторону VA , а сторона EF на сторону SA. Поскольку две прямые могут пересекаться только в одной точке, вершина F должен соответствовать верхнему A . Таким образом, расстояние д.ф. равно желаемому расстоянию ВА.
Задача, как видим, имеет только одно решение. В общем случае по стороне и двум углам, примыкающим к этой стороне, можно построить только один треугольник; не может быть других треугольников с той же стороной и теми же двумя углами, примыкающими к ней в тех же местах. Все треугольники, имеющие одну одинаковую сторону и два одинаковых угла, примыкающих к ней в одних и тех же местах, могут быть совмещены до полного совпадения. Итак, это признак, по которому можно установить полное равенство треугольников.
Все треугольники, имеющие одну одинаковую сторону и два одинаковых угла, примыкающих к ней в одних и тех же местах, могут быть совмещены до полного совпадения. Итак, это признак, по которому можно установить полное равенство треугольников.
Вместе с ранее установленными знаками равных треугольников мы теперь знаем следующие три:
Треугольники:
по р е м т о р о н и м;
на два этажа на м и угол между ними;
Пор он и д в у м у г л м .
Для краткости обозначим эти три случая равенства треугольников следующим образом:
по трем сторонам: ССС ;
с двух сторон и угол между ними: SUS ;
боковые и два уголка: УСУ .
Заявки
14. Чтобы узнать расстояние до точки А на другом берегу реки от В на этом берегу (рис. 5), отмерьте по прямой некоторую линию солн., , затем в точке В построить угол, равный АВС , с другой стороны ВС , а в точке ОТ — таким же образом угол, равный ДИА. Расстояние между точками D пересечение сторон обеих сторон углов до точки AT равно искомому расстоянию AB . Почему?
Расстояние между точками D пересечение сторон обеих сторон углов до точки AT равно искомому расстоянию AB . Почему?
Решение: Треугольники ABC и VDC равны по одной стороне солнцу ) и двум углам (угл. DCB = угл. DIA ; угол DBC = 4угл.) 304, 93 ABC 9 = 4 угл. AB = BD, как стороны, лежащие в равных треугольниках против равных углов.
Следствия теоремы изменены. Теорема Чевы и измененная. Зачем все это нужно
Класс: 9
Задачи урока:
- обобщать, расширять и систематизировать знания и умения учащихся; научить использовать знания при решении сложных задач;
- способствовать развитию навыков самостоятельного применения знаний при решении задач;
- развивать логическое мышление и математическую речь учащихся, умение анализировать, сравнивать и обобщать;
- воспитывать у студентов уверенность в себе, трудолюбие; умение работать в команде.

Цели урока:
- Образовательные: повторить теоремы Менелая и Хевы; применять их при решении задач.
- Развивающие: учить выдвигать гипотезу и умело отстаивать свое мнение в доказательствах; проверить умение обобщать и систематизировать свои знания.
- Образовательные: повышают интерес к предмету и готовят к более сложным задачам.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: карточки для коллективной работы на уроке по данной теме, индивидуальные карточки для самостоятельной работы, компьютер, мультимедийный проектор, экран.
I этап. Организационный момент (1 мин.)
Преподаватель сообщает тему и цель урока.
Этап II. Актуализация базовых знаний и навыков (10 мин.)
Учитель: На уроке вспоминаем теоремы Менелая и Хева, чтобы успешно перейти к решению задач. Давайте вместе с вами посмотрим на экран. Для какой теоремы дан этот рисунок? (теорема Менелая). Постарайтесь четко сформулировать теорему.
Для какой теоремы дан этот рисунок? (теорема Менелая). Постарайтесь четко сформулировать теорему.
Рисунок 1
Пусть точка A 1 лежит на стороне BC треугольника ABC, точка C 1 — на стороне AB, точка B 1 — на продолжении стороны AC за точку C. Точки A 1, B 1 и C 1 лежат на одной прямой тогда и только тогда, когда выполняется равенство
Учитель: Давайте вместе посмотрим на следующий рисунок. Сформулируйте теорему для этого рисунка.
Рисунок 2
Линия AD пересекает две стороны и является продолжением третьей стороны треугольника BMC.
По теореме Менелая
Линия MB пересекает две стороны и является продолжением третьей стороны треугольника ADC.
По теореме Менелая
Учитель: Какой теореме соответствует рисунок? (теорема Чевы). Сформулируйте теорему.
Рисунок 3
Пусть в треугольнике ABC точка A 1 лежит на стороне BC, точка B 1 — на стороне AC, точка C 1 — на стороне AB. Отрезки АА 1, ВВ 1 и СС 1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство
Этап III.
 Решения проблем. (22 мин.)
Решения проблем. (22 мин.)Класс делится на 3 команды, каждая получает карточку с двумя разными заданиями. На решение дается время, затем на экран выводится… Используя готовые рисунки к заданиям, представители команд поочередно объясняют свое решение. Каждое объяснение сопровождается обсуждением, ответами на вопросы и проверкой правильности решения на экране. В обсуждении принимают участие все члены команды. Чем активнее команда, тем выше она оценивается при подведении итогов.
Карточка 1.
1. В треугольнике ABC на стороне BC взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А берется точка М так, что МА = АС. Прямая MN пересекает сторону AB в точке F. Найдите отношение
2. Докажите, что медианы треугольника пересекаются в одной точке.
Решение 1
Рисунок 4
По условию задачи MA = AC, NC = 3BN. Пусть MA = AC = b, BN = k, NC = 3k. Прямая MN пересекает две стороны треугольника ABC и продолжение третьей.
По теореме Менелая
Ответ:
Доказательство 2
Рис. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что
Тогда по (обратной) теореме Чевы отрезки AM 1 , BM 2 и CM 3 пересекаются в одной точке.
Имеем:
Итак, доказано, что медианы треугольника пересекаются в одной точке.
Карточка 2.
1. На стороне PQ треугольника PQR берется точка N, а на стороне PR точка L, причем NQ = LR. Пересечение отрезков QL и NR делит QL в отношении m:n, считая от точки Q. Найти
2. Доказать, что биссектрисы треугольника пересекаются в одной точке.
Решение 1
Прямая NR пересекает две стороны треугольника PQL и является продолжением третьей.
от Menelaus ‘Теорема
Ответ:
Доказательство 2
Рисунок 7
Давайте показываем, что
Тогда, по Cheva (обратная), теом в одной точке. По свойству биссектрис треугольника
По свойству биссектрис треугольника
Умножая полученные равенства почленно, получаем
Для биссектрис треугольника выполняется равенство Чевы, следовательно, они пересекаются в одной точке.
Карточка 3.
1. В треугольнике ABC AD – медиана, точка O – середина медианы. Прямая ВО пересекает сторону АС в точке К. В каком отношении точка К делит АС, считая от точки А?
2. Докажите, что если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке.
Решение 1
Рисунок 8
Пусть BD = DC = a, AO = OD = m. Линия BK пересекает две стороны и продолжение третьей стороны треугольника ADC.
По теореме Менелая
Ответ:
Доказательство 2
Рис. Чтобы доказать, что отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:
Пользуясь свойством касательных, проведенных к окружности из одной точки, введем обозначение : С 1 В = ВА 1 = х, АС 1 = СВ 1 = у, БА 1 = АС 1 = z.
Равенство Чевы выполняется, что означает, что биссектрисы треугольника пересекаются в одной точке.
Стадия IV. Решение задач (самостоятельная работа) (8 мин.)
Учитель: Работа команд окончена и теперь приступим к самостоятельной работе по индивидуальным карточкам по 2 вариантам.
Материалы к занятию для самостоятельной работы учащихся
Вариант 1. В треугольнике АВС, площадь которого равна 6, на стороне АВ взята точка К, делящая эту сторону в отношении АК:ВК=2:3, а на стороне АС — точка L, делящая АС в отношении AL:LC=5:3. Точка Q пересечения прямых SK и BL есть удален от линии АВ на расстоянии. Найдите длину стороны АВ. (Ответ: 4.)
Вариант 2. На стороне АС в треугольнике АВС взята точка К. АК = 1, КС = 3. Со стороны АВ берется точка L. AL: LВ = 2:3, Q — точка пересечения прямых BK и CL. Найдите длину высоты треугольника ABC, опущенного из вершины B. (Ответ: 1.5.)
Работы сдаются учителю для проверки.
Этап V. Конспект урока (2 мин.)
Анализируются ошибки, отмечаются оригинальные ответы и комментарии. Подводятся итоги работы каждой команды и выставляются оценки.
Этап VI. Домашнее задание (1 мин.)
Домашнее задание составляется из задач №11, 12 стр. 289-290, №10, с. 301.
Заключительное слово преподавателя (1 мин).
Сегодня вы слушали математическую речь друг друга и оценивали свои возможности. В дальнейшем мы будем применять такие обсуждения для лучшего понимания предмета. Аргументы на уроке дружили с фактами, а теория с практикой. Спасибо вам всем.
Литература:
- Ткачук В.В. Математика для абитуриента. — М.: МЦНМО, 2005.
ТЕОРЕМА ХЕВЫ И МЕНЕЛЫ
Теорема Чевы
Большинство замечательных точек треугольника можно получить с помощью следующей процедуры. Пусть существует некоторое правило, по которому мы можем выбрать некоторую точку A 1
, на стороне BC (или ее продолжении) треугольника ABC (например, выбираем середину этой стороны). Затем строим аналогичные точки B 1 , C 1 на двух других сторонах треугольника (в нашем примере еще две середины сторон). Если правило выбора выполнено успешно, то прямые АА 1, ВВ 1, СС 1 пересекаются в некоторой точке Z (выбор середин сторон в этом смысле, конечно, удачен, так как медианы треугольника пересекаются в точках Z). один пункт).
Затем строим аналогичные точки B 1 , C 1 на двух других сторонах треугольника (в нашем примере еще две середины сторон). Если правило выбора выполнено успешно, то прямые АА 1, ВВ 1, СС 1 пересекаются в некоторой точке Z (выбор середин сторон в этом смысле, конечно, удачен, так как медианы треугольника пересекаются в точках Z). один пункт).
Хотелось бы иметь некий общий метод, позволяющий по положению точек на сторонах треугольника определять, пересекается ли соответствующая тройка прямых в одной точке или нет.
Универсальное условие, «закрывающее» эту проблему, было найдено в 1678 г. итальянским инженером Джованни Чева .
Определение. Отрезки, соединяющие вершины треугольника с точками на противоположных сторонах (или их продолжениями), называются чевианами, если они пересекаются в одной точке.
Есть два варианта расположения чевианцев. В одном варианте точка
пересечения является внутренней, а концы шевианы лежат на сторонах треугольника. Во втором варианте точка пересечения внешняя, конец одного шевиана лежит сбоку, а два других имеют концы на продолжениях сторон (см. чертежи).
Во втором варианте точка пересечения внешняя, конец одного шевиана лежит сбоку, а два других имеют концы на продолжениях сторон (см. чертежи).
Теорема 3. ( прямая теорема Чевы) В произвольном треугольнике АВС на сторонах ВС, СА, АВ или их продолжениях взяты точки А соответственно 1 , В 1 , ОТ 1 такой, что прямые линии AA 1 , ББ 1 , СС 1 пересекаются в какой-то общей точке, тогда
.
Доказательства: имеется несколько оригинальных доказательств теоремы Чевы; мы рассмотрим доказательство, основанное на двойном применении теоремы Менелая. Запишем впервые соотношение теоремы Менелая для треугольника ABB 1 и секущей CC 1 (точка пересечения чевиана обозначена Z):
,
и второй раз для треугольника B 1 BC и секущая AA 1 :
.
Перемножая эти два отношения и делая необходимые сокращения, мы получаем соотношение, содержащееся в формулировке теоремы.
Теорема 4. (обратная теорема Чевы) . Если для выбранных по сторонам треугольника Азбука или их расширения точек А 1 , В 1 и С 1 условие чевы выполнено:
,
затем сразу АА 1 , ББ 1 и СС 1 пересекаются в одной точке .
Доказательство этой теоремы проводится от противного, как и доказательство теоремы Менелая.
Рассмотрим примеры применения прямой и обратной теорем Чевы.
Пример 3. Докажите, что медианы треугольника пересекаются в одной точке.
Решение. Рассмотрим отношение
вершин треугольника к серединам его сторон. Очевидно, что в каждой дроби в числителе и знаменателе равные отрезки, значит, все эти дроби равны единице. Следовательно, выполняется отношение Чевы, поэтому по обратной теореме медианы пересекаются в одной точке.
Теорема (теорема Чевы) … Пусть точки лежат на сторонах треугольника соответственно. Пусть отрезки и пересекаются в одной точке. Затем
(обходим треугольник по часовой стрелке).
Доказательства. Обозначим через точки пересечения отрезков и… Опустим из точек и перпендикуляры к прямой до пересечения ее в точках и соответственно (см. рисунок).
Так как треугольники и имеют общую сторону, то их площади называются высотами, проведенными к этой стороне, т.е. и:
Последнее равенство верно, так как прямоугольные треугольники подобны острому углу.
Аналогично получаем
и
Перемножим эти три равенства:
q.E.D.
О медианах:
1. Разместите единичные массы в вершинах треугольника ABC.
2. Центр масс точек А и В находится в середине АВ. Центр масс всей системы должен находиться посередине стороны АВ, так как центр масс треугольника АВС является центром масс центра масс точек А и В и точки С.
(получилось запутанно)
3. Аналогично ЦМ должна лежать на медиане к сторонам АС и ВС
4. Так как ЦМ единственная точка, значит, все эти три медианы должны в ней пересекаться.
Кстати, сразу следует, что они делятся пересечением в соотношении 2:1. Так как масса центра масс точек А и В равна 2, а масса точки С равна к 1, следовательно, общий центр масс по теореме о пропорции будет делить медиану в отношении 2/1.
Большое спасибо, ясно изложено, думаю не лишним будет представить док методами масс геометрии, например:
Прямые AA1 и CC1 пересекаются в точке O; АС1: С1В = р и ВА1: А1С = q. Нам нужно доказать, что прямая ВВ1 проходит через точку О тогда и только тогда, когда СВ1: В1А = 1: pq.
Поместите грузы 1, p и pq в точки A, B и C соответственно. Тогда точка C1 является центром масс точек A и B, а точка A1 является центром масс точек B и C. Следовательно, центр масс точек A, B и C с этими массами является точкой O пересечения линий CC1 и AA1. С другой стороны, точка О лежит на отрезке, соединяющем точку В с центром масс точек А и С. Если В1 — центр масс точек А и С с массами 1 и pq, то АВ1: В1С = pq: 1. Остается заметить, что на отрезке AC есть единственная точка, делящая его в этом отношении AB1:B1C.
Если В1 — центр масс точек А и С с массами 1 и pq, то АВ1: В1С = pq: 1. Остается заметить, что на отрезке AC есть единственная точка, делящая его в этом отношении AB1:B1C.
2. Теорема Чевы
Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевиана … Таким образом, если в треугольнике ABC х , Д и Z — точки, лежащие по бокам г. до н.э. г. , СА , АБ соответственно сегменты AX , BY , ЧЗ являются чевианцами. Этот термин происходит от имени итальянского математика Джованни Чевы, опубликовавшего в 1678 году следующую очень полезную теорему:
Теорема 1.21. Если три чевиана AX, BY, CZ (по одному из каждой вершины) треугольника ABC состязательны, то
| БХ || ХС |· | КИ || ЮА |· | Аризона || ЗБ |=1 .
Рисунок: 3. |
Когда мы говорим, что три линии (или сегмента) конкурентоспособны , то имеем в виду, что все они проходят через одну точку, которую обозначим через P . .. Чтобы доказать теорему Чевы, вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников. Ссылаясь на рисунок 3, мы имеем:
.. Чтобы доказать теорему Чевы, вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников. Ссылаясь на рисунок 3, мы имеем:
| БХ || ХС |= SABXSAXC= SPBXSPXC= SABX-SPBXSAXC-SPXC= САБПСКАП.
Аналогично
| КИ || Я |= СБКПСАБП, | Аризона || ЗБ |= SCAPSBCP.
Теперь, если их перемножить, получится
| БХ || ХС |· | КИ || ЮА |· | Аризона || ЗБ |= САБПСКАП· СБКПСАБП· SCAPSBCP=1 .
Верна и обратная теорема к этой теореме:
Теорема 1.22. Если три чевиана AX, BY, CZ удовлетворяют соотношению
| БХ || ХС |· | КИ || ЮА |· | Аризона || ЗБ |=1 ,
тогда они конкурентоспособны .
Чтобы показать это, предположим, что первые два чевиана пересекаются в точке P , как и раньше, и третья шевиана, проходящая через точку P , будет CZ ′ … Тогда по теореме 1.21
| БХ || ХС |· | КИ || ЮА |· | АЗ ′ || Z′B |=1 .
Но по предположению
| БХ || ХС |·
| КИ || ЮА |·
| Аризона || ЗБ |=1
.
Следовательно,
| Аризона || ЗБ |= | АЗ ′ || З’Б | ,
точка Z ′ совпадает с точкой Z , и мы доказали, что отрезки AX , BY и ЧЗ соревновательный (с. 54 и, с. 48, 317).
Теорема Менелая или теорема о полном четырехугольнике известна еще со времен Древней Греции. Свое название он получил в честь своего автора — древнегреческого математика и астронома Менелая Александрийского (ок. 100 г. н.э.). Эта теорема очень красивая и простая, но, к сожалению, в современном школьном курсе ей не уделяется должного внимания. А, между тем, во многих случаях помогает очень легко и изящно решать достаточно сложные геометрические задачи.
Теорема 1 (теорема Менелая) … Пусть ∆ABC пересекает прямая, не параллельная стороне AB и пересекающая две ее стороны AC и BC в точках F и E соответственно, а прямая AB в точка D (рис. 1) ,
затем A F FC * CE EB * BD DA = 1
Примечание. Чтобы легко запомнить эту формулу, можно воспользоваться следующим правилом: двигаться по контуру треугольника от вершины до точки пересечения с прямой и от точки пересечения до следующей вершины.
Чтобы легко запомнить эту формулу, можно воспользоваться следующим правилом: двигаться по контуру треугольника от вершины до точки пересечения с прямой и от точки пересечения до следующей вершины.
Доказательства. Из вершин треугольника А, В, С провести соответственно три параллельные прямые до пересечения с секущей. Получаем три пары подобных треугольников (признак подобия в двух углах). Из подобия треугольников следуют следующие равенства
А теперь перемножим полученные данные на равенства:
Теорема доказана.
Чтобы почувствовать всю прелесть этой теоремы, попробуем решить предложенную ниже геометрическую задачу двумя разными способами: с помощью вспомогательной конструкции и с помощью теорем Менелая .
Задача 1.
В ∆ABC биссектриса AD делит сторону BC в отношении 2:1. В каком отношении медиана CE делит эту биссектрису?
Решение.
Используя вспомогательную конструкцию:
Пусть S — точка пересечения биссектрисы AD и медианы CE. Построим ∆ASB к параллелограмму ASBK. (рис. 2)
Построим ∆ASB к параллелограмму ASBK. (рис. 2)
Очевидно SE = EK, так как пересечение параллелограмма делит диагонали пополам. Рассмотрим теперь треугольники ∆CBK и ∆CDS. Легко видеть, что они подобны (признак подобия по двум углам: и как внутренние односторонние углы с параллельными прямыми AD и KB и секущей CB). Из подобия треугольника следует следующее:
Используя условие, получаем:
CB CD = CD + DB CD = CD + 2CD CB = 3CD CD = 3
Теперь обратите внимание, что KB = AS, как противоположные стороны параллелограмма. Тогда
AS SD = KB SD = CB CD = 3
Используя теорему Менелая.
Рассмотрим ∆ABD и применим к нему теорему Менелая (прямая, проходящая через точки C, S, E, является секущей):
BE EA * AS SD * DC CB = 1
По условию теореме, имеем BE/EA=1, так как CE медиана, а DC/CB=1/3, как мы вычислили ранее.
1 * AS SD * 1 3 = 1
Отсюда получаем AS/SD = 3 На первый взгляд оба решения достаточно компактны и примерно эквивалентны. Однако идея дополнительной конструкции для школьников часто оказывается очень сложной и вовсе не очевидной, тогда как, зная теорему Менелая, ему нужно только правильно ее применить.
Однако идея дополнительной конструкции для школьников часто оказывается очень сложной и вовсе не очевидной, тогда как, зная теорему Менелая, ему нужно только правильно ее применить.
Рассмотрим еще одну задачу, в которой теорема Менелая работает очень элегантно.
Цель 2.
На сторонах AB и BC ∆ABC соответственно заданы точки M и N такие, что выполняются равенства
AM MB = CN NA = 1 2
отрезки BN и CM делят каждый из этих отрезков (рис. 3)?
Решение.
Учитывать ∆ABN. Применим к этому треугольнику теорему Менелая (прямая, проходящая через точки M, S, C, является секущей)
AM MB * BC SN * CN CA = 1
Из условия задачи имеем: AM MB = 1 2
NC CA = NC CN + NA = NC CN + 2NC = NC 3 NC = 1 3
Подставляем эти результаты и получаем:
1 2 * BS SN * 1 3 = 1
Отсюда BS / SN = 6. И, следовательно, точка S пересечения отрезков BN и CM делит отрезок BN в отношении 6:1.
Рассмотрим ∆ACM. Применим к этому треугольнику теорему Менелая (прямая, проходящая через точки N, S, B, является секущей):
AN NC * CS SM * MB BA = 1
Из условия задачи имеем: AN NC = 2
MB BA = MB BM + MA = 2MA 2MA + MA = 2MB 3MA = 2 3
Подставляем эти результаты и получаем:
2 * CS SM * 2 3 = 1
Отсюда CS / SM = 3/4
Это означает, что точка S пересечения отрезков BN и CM делит отрезок CM в соотношении 3:4.
Верна и теорема, обратная теореме Менелая. Часто даже полезнее. Это особенно хорошо работает в задачах доказательства. Часто с его помощью даже олимпиадные задачи решаются красиво, легко и быстро.
Теорема 2 (обратная теорема Менелая). Пусть дан треугольник ABC и точки D, E, F принадлежат прямым BC, AC, AB соответственно (заметим, что они могут лежать как на сторонах треугольника ABC, так и на их продолжениях) (рис. 4) .
Тогда если AF FC * CE EB * BD DA = 1
то точки D, E, F лежат на одной прямой.
Доказательства. Докажем теорему от противного. Предположим, что соотношение из условий теоремы выполнено, но точка F не лежит на прямой DE (рис. 5).
Обозначим точку пересечения прямых DE и AB буквой О. Теперь применим теорему Менелая и получим: AE EC * CD DB * BO OA = 1
Но, с другой стороны, равенство БФ ФА = БО ОА
не может быть выполнено.
Следовательно, соотношение из условий теоремы не может быть выполнено. Получили противоречие.
Теорема доказана.
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
А.В. Шевкина
ФМС №2007
Теоремы Чевы и Менелая на ЕГЭ
Подробная статья «Вокруг теорем Чевы и Менелая» опубликована на нашем сайте в разделе СТАТЬИ. Он адресован учителям математики и старшеклассникам, заинтересованным в хорошем знании математики. Вы можете вернуться к нему, если хотите более подробно разобраться в вопросе. В этой заметке мы приведем краткую информацию из упомянутой статьи и разберем решения задач из сборника для подготовки к ЕГЭ-2016.
В этой заметке мы приведем краткую информацию из упомянутой статьи и разберем решения задач из сборника для подготовки к ЕГЭ-2016.
Теорема Чевы
Дан треугольник ABC и на его сторонах AB , BC и AC отмечены точки C 5 4 35 , 90 и В 1 соответственно (рис. 1).
а) Если отрезки АА 1 , ВВ 1 и СС 1 пересекаются в одной точке, то
б) Если верно равенство (1), то отрезки АА 1 ,
5 ВВ0346 1 и CC 1 пересекаются в одной точке. На рис. 1 показан случай, когда отрезки AA 1 , BB 1 и CC 1 пересекаются в одной точке внутри треугольника. Это так называемый внутренний точечный случай. Теорема Чевы справедлива и в случае внешней точки, когда одна из точек И 1 , В 1 или ОТ 1 принадлежит стороне треугольника, а две другие принадлежат продолжениям треугольника. стороны треугольника. В этом случае точка пересечения отрезков AA 1 , BB 1 и CC 1 лежит вне треугольника (рис. 2).
2).
Как запомнить равенство Чевы?
Обратим внимание на технику запоминания равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC начиная с пункта А … Из пункта А идем в пункт Б , встречаем пункт ИЗ 1 , записываем дробь
… Далее из пункта В идем в пункт точка ИЗ , встречаем точку И 1, записываем дробь
… Наконец, из точки ИЗ идем к точке И , встречаем точку В 1, записываем дробь
. .. В случае внешней точки порядок записи дробей сохраняется, хотя две «точки деления» отрезка находятся вне своих отрезков. В таких случаях говорят, что точка делит отрезок снаружи.
Обратите внимание, что любой отрезок, соединяющий вершину треугольника с любой точкой прямой, содержащей противоположную сторону треугольника, называется cheviana .
Рассмотрим несколько способов доказательства утверждения а) теоремы Чевы для случая внутренней точки. Для доказательства теоремы Чевы необходимо доказать утверждение а) любым из предложенных ниже способов, а также доказать утверждение б). Доказательство утверждения б) дается после первого способа доказательства утверждения а). Доказательства теоремы Чевы для случая внешней точки аналогичны.
Доказательство утверждения а) теоремы Чевы с использованием теоремы о пропорциональных отрезках
Пусть три чевиана А А 1 , B B 1 и C C 1 пересекаются в точке Z внутри треугольника ABC .
Идея доказательства состоит в том, чтобы заменить отношения отрезков из равенства (1) отношениями отрезков, лежащих на одной прямой.
Через точку В провести прямую, параллельную чевиану СС 1 . Прямая AA 1 пересекает построенную прямую в точке M , и прямую, проходящую через точку С и параллель АА 1, — в точке Т . .. Через точки И и ОТ проведем прямые, параллельные чевианы ВВ 1 . Они пересекут линию VM в точках N и R соответственно (рис. 3).
.. Через точки И и ОТ проведем прямые, параллельные чевианы ВВ 1 . Они пересекут линию VM в точках N и R соответственно (рис. 3).
P по теореме о пропорциональных отрезках имеем:
,
и
.
Тогда равенства
.
В параллелограммах ЗСТМ и ЗЦРБ отрезки ТМ , СZ и ВR равны как противоположные стороны параллелограмма. Следовательно,
и равенство
верно.
При доказательстве утверждения б) мы используем следующее утверждение. Рис. 3
Лемма 1. Если точки ОТ 1 и ОТ 2 делят отрезок АВ внутренним (или внешним) способом в одном и том же отношении, считая от одной точки, то эти точки совпадают.
Докажем лемму для случая, когда точки ОТ 1 и ОТ 2 делят отрезок АВ внутренне в одинаковом отношении:
.
Доказательства. Из равенства
следуют равенства
и
. . Последнее из них выполняется только при условии, что ИЗ 1 В и ИЗ 2 В равны, то есть при условии равенства точек ИЗ 1 и ИЗ 2 одинаковый.
. Последнее из них выполняется только при условии, что ИЗ 1 В и ИЗ 2 В равны, то есть при условии равенства точек ИЗ 1 и ИЗ 2 одинаковый.
Доказательство леммы для случая, когда точки ОТ 1 и ОТ 2 делят внешне отрезок АВ , проводится аналогично.
Доказательство части b) теоремы Чевы
Пусть теперь верно равенство (1). Докажем, что отрезки AA 1 , BB 1 и CC 1 пересекаются в одной точке.
Пусть чевианы AA 1 и BB 1 пересекаются в точке Z , проведем через эту точку отрезок CC 2 ( ОТ 2 лежит на отрезке АВ ). Тогда на основании утверждения а) получаем правильное равенство
. (2)
И сравнивая равенства (1) и (2), заключаем, что
, т.е. точки ОТ 1 и ОТ 2 делят отрезок АВ в одинаковом отношении, считая от одной и той же точки. Из леммы 1 следует, что точки ИЗ 1 и ИЗ 2 совпадают. Это означает, что отрезки AA 1 , BB 1 и CC 1 пересекаются в одной точке, что и требовалось.
Это означает, что отрезки AA 1 , BB 1 и CC 1 пересекаются в одной точке, что и требовалось.
Можно доказать, что порядок записи равенства (1) не зависит от того, в какой точке и в каком направлении проходятся вершины треугольника.
Упражнение 1. Найдите длину отрезка И N на рисунке 4, на котором показаны длины других отрезков.
Ответ. 8.
Задание 2. Чевианы АМ , BN , CK пересекаются в одной точке внутри треугольника ABC … Найдите отношение
, если
,
… Рисунок: 4
Ответ.
.
P приведем доказательство теоремы Чевы из статьи. Идея доказательства состоит в том, чтобы заменить отношения отрезков из равенства (1) отношениями отрезков, лежащих на параллельных прямых.
Пусть прямые А А 1 , B B 1 , C C 1 пересекаются в точке O внутри треугольника ABC (рис. 5). Через вершину С треугольника АВС провести прямую, параллельную АВ , а ее точки пересечения с прямыми А А 1 , B B 1 обозначают соответственно A 2 , Б 2 .
5). Через вершину С треугольника АВС провести прямую, параллельную АВ , а ее точки пересечения с прямыми А А 1 , B B 1 обозначают соответственно A 2 , Б 2 .
Из подобия двух пар треугольников CB 2 B 1 и АББ 1, БАА 1 и СА 2 А 1, рис. 5
имеем равенства
,
.
(3)
From the similarity of triangles BC 1 O and B 2 CO , A FROM 1 O and A 2 CO we have the equalities
из чего следует, что
. (4)
P Перемножив равенства (3) и (4), получим равенство (1).
Утверждение а) теоремы Чевы доказано.
Рассмотрим доказательства утверждения а) теоремы Чевы с использованием площадей в качестве внутренней точки. Изложено в книге А.Г. Мякишева и опирается на утверждения, которые мы сформулируем в виде задач 3 и 4 .
Задание 3. Отношение площадей двух треугольников с общей вершиной и основаниями, лежащих на одной прямой, равно отношению длин этих оснований. Докажите это утверждение.
Задание 4. Докажите, что если
, то
и
… Рис. 6), затем
,
.
(5)
И из равенств (5) и второй постановки задачи 4
Из следует, что
или
… Аналогично находим, что
и
… Перемножая последние три равенства, получаем:
,
то есть равенство (1) верно, что и требовалось.
Утверждение а) теоремы Чевы доказано.
Задание 15. Пусть шевианы пересекаются в одной точке внутри треугольника и делят его на 6 треугольников, площади которых равны S 1 , с 2 , с 3 , с 4 , с 5 , S 6 (рис. 7). Докажи это. Рис. 7
Задача 6. Найти площадь S треугольник CNZ (площади остальных треугольников показаны на рис. 8).
Ответ. 15.
15.
Задача 7. Найти площадь S треугольника СНО , если площадь треугольника А А НО равна 10 и
,(рис. 9).
Ответ. 30.
Задача 8. Найти площадь S треугольника СНО если площадь треугольника И до н.э. равно 88 и,
(рис. 9).
Р раствор. Так как, то обозначим
,
… Как , то обозначим
,
… Из теоремы Чевы следует, что
, а затем
… Если
, то
(рис. 10). У нас есть три неизвестных величины ( x , y и S ), поэтому для нахождения S составим три уравнения.
Как
то
= 88. Так как
то
откуда
… Как
то
.
Итак,
откуда
… Рис. десятка
Присвоение 9 . В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и В С .
В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и В С .
,
. Р АЛ и СК … Площадь треугольника ПВС равна 1. Найдите площадь треугольника АВС .
Ответ. 1,75.
Теорема Менелая
Дан треугольник ABC и на его сторонах AC и CB отмечены точки B 1 и A
6 1 5 соответственно и на продолжении стороны AB точка с маркировкой C 1 (рис. 11).
а) Если точки И 1 , В 1 и ОТ 1 лежат на одной прямой, то
. (6)
б) Если верно равенство (7), то точки И 1 , Б 1 и ОТ 1 коллинеарны. Рис. одиннадцать
Как запомнить равенство Менелая?
Способ запоминания равенства (6) тот же, что и для равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC — сверху вниз, проходя через точки деления (внутренние или внешние).
Задание 10. Докажите, что запись равенства (6) из любой вершины треугольника в любом направлении дает один и тот же результат.
Для доказательства теоремы Менелая необходимо доказать утверждение а) любым из предложенных ниже способов, а также доказать утверждение б). Доказательство утверждения б) дается после первого способа доказательства утверждения а).
Доказательство утверждения а) с помощью теоремы о пропорциональных интервалах
I путь. а) Идея доказательства состоит в том, чтобы заменить отношения длин отрезков в равенстве (6) отношениями длин отрезков, лежащих на одной прямой.
Пусть точки И 1 , В 1 и ОТ 1 лежат на одной прямой. Через точку С проведем прямую l параллельно прямой И 1 В 1, она пересекает прямую АВ в точке М (рис. 12).
Р
есть. 12
По теореме о пропорциональных отрезках имеем:
и
.
Тогда верны равенства
.
Доказательство утверждения б) теоремы Менелая
Теперь пусть выполняется равенство (6), докажем, что точки И 1 , В 1 и ОТ 1 лежат на одной прямой. Пусть прямые АВ и И 1 Б 1 пересекаются в точке С 2 (рис. 13).
Так как точки И 1 В 1 и ОТ 2 лежат на одной прямой, то по утверждению а) теоремы Менелая
. (7)
Сравнивая равенства (6) и (7), имеем
, откуда следует равенство
,
,
.
Последнее равенство верно только при условии
, т. е. если точки ОТ 1 и ОТ 2 одинаковы.
Утверждение б) теоремы Менелая доказано. Рис. 13
Доказательство утверждения а) с использованием подобия треугольников
Идея доказательства состоит в том, чтобы заменить отношения длин отрезков из равенства (6) на отношения длин отрезков, лежащих на параллельных прямых.
Пусть точки И 1 , В 1 и С 1 коллинеарны. Из точек А , В и С к этой прямой провести перпендикуляры АА 0 , В В 0 и SS 0 (рис. 14).
Р
есть. четырнадцать
Из подобия трех пар треугольников AA 0 B 1 и CC 0 B 1 , СС 0 А 1 и ВВ 0 А 1 , C 1 B 0 B и C 1 A 0 A (под двумя углами) имеем правильные равенства
,
,
,
умножив их, получим:
.
Утверждение а) теоремы Менелая доказано.
Подтверждение утверждения а) с использованием областей
Идея доказательства состоит в том, чтобы заменить отношение длин отрезков из равенства (7) отношением площадей треугольников.
Пусть точки И 1 , В 1 и ОТ 1 лежат на одной прямой. Соедините точки C и C 1 . Обозначим площади треугольников S 1 , S 2 , S 3 , S 4 , S 5 (рис. 15).
Соедините точки C и C 1 . Обозначим площади треугольников S 1 , S 2 , S 3 , S 4 , S 5 (рис. 15).
Тогда равенства
,
,
. (8)
Умножая равенства (8), получаем:
Утверждение а) теоремы Менелая доказано.
Р
есть. 15
Точно так же, как теорема Чевы остается верной, если точка пересечения шевианцев находится вне треугольника, теорема Менелая остается верной, если секущая пересекает только продолжения сторон треугольника. В этом случае можно говорить о пересечении сторон треугольника во внешних точках.
Доказательство утверждения а) для случая внешних точек
P секущая устье пересекает стороны треугольника ABC во внешних точках, т. е. пересекает продолжения сторон AB , BC и AC в точках C 1 , A 1 и B 1 , лежащих соответственно в этих точках на одной прямой (рис. 16).
16).
По теореме о пропорциональных отрезках имеем:
а.
Тогда верны равенства
Утверждение а) теоремы Менелая доказано. Рис. шестнадцать
Заметим, что приведенное выше доказательство совпадает с доказательством теоремы Менелая для случая, когда секущая пересекает две стороны треугольника во внутренних точках и одну во внешних.
Доказательство утверждения б) теоремы Менелая для случая внешних точек аналогично приведенному выше доказательству.
Задание 11. В треугольнике АВС точки И 1 , В 1 лежат соответственно на сторонах ВС и А ОТ . P — точка пересечения сегментов AA 1 и ВВ 1 .
,
… Найти отношение
.
Решение. Обозначим
,
,
,
(рис. 17). По теореме Менелая для треугольника BC IN 1 и секанса PA 1 запишем правильное равенство:
,
откуда следует, что
. .. Рис. 17
.. Рис. 17
2 9. .
Задания 12 (МГУ, заочное подготовительное отделение). В треугольнике ABC , площадь которого равна 6, на стороне АВ точка взята К , разделяет эту сторону по отношению к
и по стороне AS — точка L , деление AS в отношении
… Точка P пересечения прямых SC и IN L удалены от прямой АВ на расстоянии 1,5. Найдите длину стороны АБ.
Решение. Из точек R и ИЗ опускаем перпендикуляры ПР и СМ на прямую АВ … Обозначим
,
,
,
(рис. 18). По теореме Менелая для треугольника AKC и секущей PL запишем правильное равенство:
, откуда получаем, что
,
… Рис. 18
Из подобия треугольников К MC и ТО RP (в двух углах) получаем, что
, откуда следует, что
.
Теперь, зная длину высоты, проведенной к стороне AB треугольника ABC , и площадь этого треугольника, вычисляем длину стороны:
.
Ответ. 4.
Задание 13. Три круга с центрами И , В , С , , радиусы которых связаны как
, касаются друг друга внешне в точках X , Y , Z , как показано на рисунке 19. Отрезки AX и BY пересекаются в точке O . В каком отношении, считая от точки B , участок CZ делит отрезок BY ?
Решение. Обозначим
,
,
(рис. 19). Так как
, то по утверждению б) теоремы Чевы отрезки И X , BY и ОТ Z пересекаются в одной точке — точка O … Тогда отрезок CZ делит отрезок BY 4 …. это отношение. Рис. девятнадцать
По теореме Менелая для треугольника BCY и секанса OX имеем:
, откуда следует, что
.
Ответ. .
Задание 14 (ЕГЭ-2016).
Очки В 1 и ИЗ AS и AB треугольник ABC , и AB 1: 4 6 4 ROM
=
= AS 1: ОТ 1 B … Прямой BB 1 и нержавеющая сталь 1 пересекаются в точке ОБ.
а ) Докажите, что линия АО пополам сторона ВС.
АВ 1 ОС 1 в площадь треугольника АВС если известно, что АВ 1: Б 1 ОТ = 1:4.
Решение. а) Пусть прямая АО пересекает борт до н.э. в точке А 1 (рис. 20). По теореме Чевы имеем:
. (9)
Как AB 1: B 1 ОТ = КАК 1: С 1 B , то из равенства (9) следует, что
, т.е. CA 1 = И 1 B , что и требуется доказать. Рис. 20
б) Пусть площадь треугольника АВ 1 О равно S . Как AB 1: B 1 ОТ CB 1 O равно 4 S , а площадь треугольника AOC равно 5 S … Тогда площадь треугольника АОБ тоже 5 S так как треугольники AOB и АОС имеют общее основание АО , а их вершины В и С равноудалены от прямой АО . При этом площадь треугольника
Как AB 1: B 1 ОТ CB 1 O равно 4 S , а площадь треугольника AOC равно 5 S … Тогда площадь треугольника АОБ тоже 5 S так как треугольники AOB и АОС имеют общее основание АО , а их вершины В и С равноудалены от прямой АО . При этом площадь треугольника
Ответ. 1:15.
Задание 15 (ЕГЭ-2016).
Points IN 1 and FROM 1 lie on the sides respectively AS and AB triangle ABC , and AB 1: B 1 FROM =
= КАК 1: ОТ 1 В … Прямая ВВ 1 и нержавеющая сталь 1 пересекаются в точке ОБ.
а) Докажите, что линия АО пополам стороны ВС.
б) Найдите отношение площади четырехугольника АВ 1 ОС 1 к площади треугольника АВС , если известно, что 6 В 4 АВ 1 : 1 ИЗ = 1:3.
Ответ. 1:10.
Задание 1 6 (ЕГЭ-2016). На отрезке BD точка взята ОТ … Биссектриса BL ABC с основанием ВС BLD с основанием BD .
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что cos
ABC DL, т.е. точка треугольника BD взята ОТ . .. Биссектриса BL равнобедренный треугольник ABC с основанием Солнце является боковой стороной равнобедренного треугольника BLD с основанием BD .
.. Биссектриса BL равнобедренный треугольник ABC с основанием Солнце является боковой стороной равнобедренного треугольника BLD с основанием BD .
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что cos ABC =. В каком отношении прямой DL делит сторону AB ?
Ответ. 4:21.
Литература
1. Смирнова И.М., Смирнов В.А. Чудесные точки и линии треугольника. М.: Математика, 2006, № 17.
2. Мякишев А.Г. Элементы геометрии треугольника. (Серия «Библиотека «Математическое образование»). М.: МЦНМО, 2002. – 32 с.
3. Геометрия. Дополнительные главы к учебнику 8 класса: Учебное пособие для учащихся школ и классов с углубленным изучением / Л.С. Атанасян, Бутузов В. Ф., Кадомцев С. Б. и др. – М.: Вита-Пресс, 2005. – 208 с.
4. Эрдниев П., Манцаев Н. Теоремы Чевы и Менелая.М.: Квант, 1990, №3, С. 56–59
5. Шарыгин И. Ф. Теоремы Чевы и Менелая, М.: Квант, 1976, № 11, стр. 22–30.
Шарыгин И. Ф. Теоремы Чевы и Менелая, М.: Квант, 1976, № 11, стр. 22–30.
6. Вавилов В.В. Медианы и срединные линии треугольника. М.: Математика, 2006, №1.
7. Ефремов Дм. Новая геометрия треугольника. Одесса, 1902. — 334 с.
8. Математика. 50 вариантов типовых тестовых заданий / И.В. Ященко, М.А. Волкевич, И.Р. Высоцкий и др.; изд. И.В. Ященко. — М.: Издательство «Экзамен», 2016. — 247 с.
Математика — 10 класс Мендель Виктор Васильевич, декан факультета естественных наук, математики и информационных технологий ДВГГУ ТЕОРИИ ЧЕВА И МЕНЕЛАЯ Особое место в планиметрии отведено двум замечательным теоремам: теореме Чевы и теореме Менелая. Эти теоремы не входят в базовую программу курса геометрии средней школы, но их изучение (и применение) рекомендуется всем, кто интересуется математикой чуть больше, чем это возможно в рамках школьной программы… К чему эти теоремы интересны? Прежде всего отметим, что при решении геометрических задач продуктивно сочетаются два подхода: — один основан на определении базовой структуры (например: треугольник — это окружность; треугольник — секущая; треугольник — три прямые линии). проходящий через его вершины и пересекающийся в одной точке; четырехугольник с двумя параллельными сторонами и др.), а второй — метод опорных задач (простых геометрических задач, к которым сводится процесс решения сложной задачи). Так, теоремы Менелая и Хевы относятся к числу наиболее распространенных построений: первая рассматривает треугольник, стороны или продолжения сторон которого пересекаются некоторой прямой линией (секущей), вторая имеет дело с треугольником и тремя прямые, проходящие через его вершины и пересекающиеся в одной точке. Теорема Менелая Эта теорема, являющаяся наблюдаемым (вместе с обратными) отношениями, показывает отрезки, закономерность, соединяющую вершины треугольника и точки пересечения секущей со сторонами (продолжениями сторон) треугольника. На рисунках показаны два возможных случая расположения треугольника и секущей. В первом случае секущая пересекает две стороны треугольника и продолжение третьей, во втором — продолжение всех трех сторон треугольника. Теорема 1.
проходящий через его вершины и пересекающийся в одной точке; четырехугольник с двумя параллельными сторонами и др.), а второй — метод опорных задач (простых геометрических задач, к которым сводится процесс решения сложной задачи). Так, теоремы Менелая и Хевы относятся к числу наиболее распространенных построений: первая рассматривает треугольник, стороны или продолжения сторон которого пересекаются некоторой прямой линией (секущей), вторая имеет дело с треугольником и тремя прямые, проходящие через его вершины и пересекающиеся в одной точке. Теорема Менелая Эта теорема, являющаяся наблюдаемым (вместе с обратными) отношениями, показывает отрезки, закономерность, соединяющую вершины треугольника и точки пересечения секущей со сторонами (продолжениями сторон) треугольника. На рисунках показаны два возможных случая расположения треугольника и секущей. В первом случае секущая пересекает две стороны треугольника и продолжение третьей, во втором — продолжение всех трех сторон треугольника. Теорема 1. (Менелай) Пусть ABC пересекает прямая, не параллельная стороне AB и пересекающая две ее стороны AC и BC соответственно в точках B1 и A1, а прямая AB в точке C1, тогда AB1 CA1 BC1 1. B1C A1B C1 A Теорема 2. (обратная теореме Менелая) Пусть точки A1, B1, C1 треугольника ABC принадлежат прямым BC, AC, AB соответственно, тогда если AB1 CA1 BC1 1 B1C A1B C1 A, то точки A1, B1, C1 лежат на одной прямой. Доказательство первой теоремы можно провести следующим образом: на секущую опустить перпендикуляры из всех вершин треугольника. В результате получится три пары подобных прямоугольных треугольников. Отношения отрезков, фигурирующие в формулировке теоремы, заменяются отношениями перпендикуляров, соответствующих им по подобию. Получается, что каждый отрезок — перпендикуляр в дробях будет присутствовать дважды: один раз в одной дроби в числителе, второй раз в другой дроби в знаменателе. Таким образом, произведение всех этих отношений будет равно единице. Обратная теорема доказывается от противного.
(Менелай) Пусть ABC пересекает прямая, не параллельная стороне AB и пересекающая две ее стороны AC и BC соответственно в точках B1 и A1, а прямая AB в точке C1, тогда AB1 CA1 BC1 1. B1C A1B C1 A Теорема 2. (обратная теореме Менелая) Пусть точки A1, B1, C1 треугольника ABC принадлежат прямым BC, AC, AB соответственно, тогда если AB1 CA1 BC1 1 B1C A1B C1 A, то точки A1, B1, C1 лежат на одной прямой. Доказательство первой теоремы можно провести следующим образом: на секущую опустить перпендикуляры из всех вершин треугольника. В результате получится три пары подобных прямоугольных треугольников. Отношения отрезков, фигурирующие в формулировке теоремы, заменяются отношениями перпендикуляров, соответствующих им по подобию. Получается, что каждый отрезок — перпендикуляр в дробях будет присутствовать дважды: один раз в одной дроби в числителе, второй раз в другой дроби в знаменателе. Таким образом, произведение всех этих отношений будет равно единице. Обратная теорема доказывается от противного. Предполагается, что в условиях теоремы 2 точки A1, B1, C1 не лежат на одной прямой. Тогда прямая A1B1 пересекает сторону AB в точке C2, отличной от точки C1. В этом случае в силу теоремы 1 для точек A1, B1, C2 будет выполняться то же соотношение, что и для точек A1, B1, C1. Отсюда следует, что точки С1 и С2 будут делить отрезок АВ в одинаковом отношении. Тогда эти точки совпадают — получили противоречие. Рассмотрим примеры применения теоремы Менелая. Пример 1. Докажите, что медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины. Решение. Запишем полученное в теореме Менелая соотношение для треугольника ABMb и прямой McM (C): AM c BM M bC 1. M c B MM b CA Первая дробь в этом произведении, очевидно, равна 1. , а третье второе соотношение равно 1. Следовательно, 2 2 : 1, что и требовалось. Пример 2. Секанс пересекает продолжение стороны AC треугольника ABC в точке B1 так, что точка C является серединой отрезка AB1. Эта секущая делит сторону АВ пополам. Найдите, в каком отношении она делит сторону ВС? Решение.
Предполагается, что в условиях теоремы 2 точки A1, B1, C1 не лежат на одной прямой. Тогда прямая A1B1 пересекает сторону AB в точке C2, отличной от точки C1. В этом случае в силу теоремы 1 для точек A1, B1, C2 будет выполняться то же соотношение, что и для точек A1, B1, C1. Отсюда следует, что точки С1 и С2 будут делить отрезок АВ в одинаковом отношении. Тогда эти точки совпадают — получили противоречие. Рассмотрим примеры применения теоремы Менелая. Пример 1. Докажите, что медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины. Решение. Запишем полученное в теореме Менелая соотношение для треугольника ABMb и прямой McM (C): AM c BM M bC 1. M c B MM b CA Первая дробь в этом произведении, очевидно, равна 1. , а третье второе соотношение равно 1. Следовательно, 2 2 : 1, что и требовалось. Пример 2. Секанс пересекает продолжение стороны AC треугольника ABC в точке B1 так, что точка C является серединой отрезка AB1. Эта секущая делит сторону АВ пополам. Найдите, в каком отношении она делит сторону ВС? Решение. Запишем для треугольника и секущей произведение трех соотношений из теоремы Менелая: AB1 CA1 BC1 1. B1C A1B C1 A Из условий задачи следует, что первое отношение равно единице, а третья равна 1, 2, значит вторая пропорция равна 2, т.е. то есть секущая делит сторону ВС в соотношении 2:1. Со следующим примером применения теоремы Менелая мы столкнемся, когда будем рассматривать доказательство теоремы Чевы. Теорема Чевы Большинство замечательных точек треугольника можно получить с помощью следующей процедуры. Пусть существует какое-то правило, по которому мы можем выбрать некоторую точку A1 на стороне BC (или ее продолжении) треугольника ABC (например, выбрать середину этой стороны). Затем построим аналогичные точки B1, C1 на двух других сторонах треугольника (в нашем примере еще две середины сторон). Если правило выбора выполнено успешно, то прямые AA1, BB1, CC1 пересекаются в некоторой точке Z (выбор середины сторон в этом смысле, конечно, удачен, так как медианы треугольника пересекаются в одной точке) .
Запишем для треугольника и секущей произведение трех соотношений из теоремы Менелая: AB1 CA1 BC1 1. B1C A1B C1 A Из условий задачи следует, что первое отношение равно единице, а третья равна 1, 2, значит вторая пропорция равна 2, т.е. то есть секущая делит сторону ВС в соотношении 2:1. Со следующим примером применения теоремы Менелая мы столкнемся, когда будем рассматривать доказательство теоремы Чевы. Теорема Чевы Большинство замечательных точек треугольника можно получить с помощью следующей процедуры. Пусть существует какое-то правило, по которому мы можем выбрать некоторую точку A1 на стороне BC (или ее продолжении) треугольника ABC (например, выбрать середину этой стороны). Затем построим аналогичные точки B1, C1 на двух других сторонах треугольника (в нашем примере еще две середины сторон). Если правило выбора выполнено успешно, то прямые AA1, BB1, CC1 пересекаются в некоторой точке Z (выбор середины сторон в этом смысле, конечно, удачен, так как медианы треугольника пересекаются в одной точке) . Хотелось бы иметь некий общий метод, позволяющий по положению точек на сторонах треугольника определять, пересекается ли соответствующая тройка прямых в одной точке или нет. Универсальное условие, «закрывающее» эту проблему, было найдено в 1678 году итальянским инженером Джованни Чева. Определение. Отрезки, соединяющие вершины треугольника с точками на противоположных сторонах (или их продолжениями), называются чевианами, если они пересекаются в одной точке. Возможны два варианта расположения чевианцев. В одном варианте точка пересечения является внутренней, а концы шевианов лежат на сторонах треугольника. Во втором варианте точка пересечения внешняя, конец одного шевиана лежит сбоку, а два других имеют концы на продолжениях сторон (см. чертежи). Теорема 3. (Прямая теорема Чевы) В произвольном треугольнике ABC на сторонах BC, CA, AB или их продолжениях берутся точки A1, B1, C1 соответственно такие, что прямые AA1, BB1, CC1 пересекаются в некоторых общих точку, затем BA1 CB1 AC1 1 CA1 AB1 BC1.
Хотелось бы иметь некий общий метод, позволяющий по положению точек на сторонах треугольника определять, пересекается ли соответствующая тройка прямых в одной точке или нет. Универсальное условие, «закрывающее» эту проблему, было найдено в 1678 году итальянским инженером Джованни Чева. Определение. Отрезки, соединяющие вершины треугольника с точками на противоположных сторонах (или их продолжениями), называются чевианами, если они пересекаются в одной точке. Возможны два варианта расположения чевианцев. В одном варианте точка пересечения является внутренней, а концы шевианов лежат на сторонах треугольника. Во втором варианте точка пересечения внешняя, конец одного шевиана лежит сбоку, а два других имеют концы на продолжениях сторон (см. чертежи). Теорема 3. (Прямая теорема Чевы) В произвольном треугольнике ABC на сторонах BC, CA, AB или их продолжениях берутся точки A1, B1, C1 соответственно такие, что прямые AA1, BB1, CC1 пересекаются в некоторых общих точку, затем BA1 CB1 AC1 1 CA1 AB1 BC1. Доказательство: Существует несколько оригинальных доказательств теоремы Чевы, мы рассмотрим доказательство, основанное на двойном применении теоремы Менелая. Запишем соотношение теоремы Менелая первый раз для треугольника ABB1 и секущей CC1 (точку пересечения шевианов обозначим через Z): AC1 BZ B1C 1, C1B ZB1 CA и второй раз для треугольника B1BC и секанс AA1: B1Z BA1 1. ZB A1C AB1 Перемножив эти два отношения и сделав необходимые сокращения, получим соотношение, содержащееся в формулировке теоремы. Теорема 4. (обратная теорема Чевы). Если для точек A1, B1 и C1, выбранных на сторонах треугольника ABC или их продолжений, выполняется условие Чева: BA1 CB1 AC1 1 CA1 AB1 BC1, то прямые AA1, BB1 и CC1 пересекаются в одной точке. Доказательство этой теоремы проводится от противного, как и доказательство теоремы Менелая. Рассмотрим примеры применения прямой и обратной теорем Чевы. Пример 3. Докажите, что медианы треугольника пересекаются в одной точке. Решение. Рассмотрим отношение AC1 BA1 CB1 C1B A1C B1 A для вершин треугольника и середины его сторон.
Доказательство: Существует несколько оригинальных доказательств теоремы Чевы, мы рассмотрим доказательство, основанное на двойном применении теоремы Менелая. Запишем соотношение теоремы Менелая первый раз для треугольника ABB1 и секущей CC1 (точку пересечения шевианов обозначим через Z): AC1 BZ B1C 1, C1B ZB1 CA и второй раз для треугольника B1BC и секанс AA1: B1Z BA1 1. ZB A1C AB1 Перемножив эти два отношения и сделав необходимые сокращения, получим соотношение, содержащееся в формулировке теоремы. Теорема 4. (обратная теорема Чевы). Если для точек A1, B1 и C1, выбранных на сторонах треугольника ABC или их продолжений, выполняется условие Чева: BA1 CB1 AC1 1 CA1 AB1 BC1, то прямые AA1, BB1 и CC1 пересекаются в одной точке. Доказательство этой теоремы проводится от противного, как и доказательство теоремы Менелая. Рассмотрим примеры применения прямой и обратной теорем Чевы. Пример 3. Докажите, что медианы треугольника пересекаются в одной точке. Решение. Рассмотрим отношение AC1 BA1 CB1 C1B A1C B1 A для вершин треугольника и середины его сторон. Очевидно, что в каждой дроби в числителе и знаменателе равные отрезки, значит, все эти дроби равны единице. Следовательно, соотношение Чевы выполняется, поэтому по обратной теореме медианы пересекаются в одной точке. Задания для самостоятельного решения Предлагаемые здесь задания являются тестом №1 для учащихся 9 класса.. Решите эти задачи, запишите решения в отдельную (от физики и информатики) тетрадь. Укажите на обложке следующую информацию о себе: 1. Фамилию, имя, класс, профиль класса (например: Пупкин Василий, 9 класс, математический) 2. Почтовый индекс, адрес проживания, e-mail (если есть), телефон ( домашний или мобильный ) 3. Информация о школе (например: МБОУ №1, пос. Бикин) 4. Фамилия, имя учителя математики (например: учитель математики Петрова М.И.) Рекомендуется решить не менее четырех задач. М 9.1.1. Может ли секущая из теоремы Менелая разрезать стороны треугольника (или их продолжения) на отрезки длины: а) 3, 3, 5, 7, 10, 14; в) 3, 5, 6, 7, 7, 10, Если возможны такие варианты, приведите примеры.
Очевидно, что в каждой дроби в числителе и знаменателе равные отрезки, значит, все эти дроби равны единице. Следовательно, соотношение Чевы выполняется, поэтому по обратной теореме медианы пересекаются в одной точке. Задания для самостоятельного решения Предлагаемые здесь задания являются тестом №1 для учащихся 9 класса.. Решите эти задачи, запишите решения в отдельную (от физики и информатики) тетрадь. Укажите на обложке следующую информацию о себе: 1. Фамилию, имя, класс, профиль класса (например: Пупкин Василий, 9 класс, математический) 2. Почтовый индекс, адрес проживания, e-mail (если есть), телефон ( домашний или мобильный ) 3. Информация о школе (например: МБОУ №1, пос. Бикин) 4. Фамилия, имя учителя математики (например: учитель математики Петрова М.И.) Рекомендуется решить не менее четырех задач. М 9.1.1. Может ли секущая из теоремы Менелая разрезать стороны треугольника (или их продолжения) на отрезки длины: а) 3, 3, 5, 7, 10, 14; в) 3, 5, 6, 7, 7, 10, Если возможны такие варианты, приведите примеры. Сегменты могут быть в другом порядке. М 9.1.2. Могут ли внутренние шевианы треугольника делить его стороны на отрезки: а) 3, 3, 5, 7, 10, 14; в) 3, 5, 6, 7, 7, 10, Если возможны такие варианты, приведите примеры. Сегменты могут идти в разном порядке. Подсказка: Придумывая примеры, не забывайте проверять неравенство треугольника. М 9.1.3. Используя обратную теорему Чевы, докажите, что: а) биссектрисы треугольника пересекаются в одной точке; б) отрезки, соединяющие вершины треугольника с точками на противоположных сторонах, в которых эти стороны касаются вписанной окружности, пересекаются в одной точке. Указания: а) запомнить, в каком отношении биссектриса делит противоположную сторону; б) воспользоваться тем свойством, что отрезки двух касательных, проведенных из одной точки в некоторую окружность, равны. М 9.1.4. Завершите доказательство теоремы Менелая, начатое в первой части статьи. М 9.1.5. Докажите, что высоты треугольника пересекаются в одной точке, используя обратную теорему Чевы.
Сегменты могут быть в другом порядке. М 9.1.2. Могут ли внутренние шевианы треугольника делить его стороны на отрезки: а) 3, 3, 5, 7, 10, 14; в) 3, 5, 6, 7, 7, 10, Если возможны такие варианты, приведите примеры. Сегменты могут идти в разном порядке. Подсказка: Придумывая примеры, не забывайте проверять неравенство треугольника. М 9.1.3. Используя обратную теорему Чевы, докажите, что: а) биссектрисы треугольника пересекаются в одной точке; б) отрезки, соединяющие вершины треугольника с точками на противоположных сторонах, в которых эти стороны касаются вписанной окружности, пересекаются в одной точке. Указания: а) запомнить, в каком отношении биссектриса делит противоположную сторону; б) воспользоваться тем свойством, что отрезки двух касательных, проведенных из одной точки в некоторую окружность, равны. М 9.1.4. Завершите доказательство теоремы Менелая, начатое в первой части статьи. М 9.1.5. Докажите, что высоты треугольника пересекаются в одной точке, используя обратную теорему Чевы. М 9.1.6. Докажите теорему Симпсона: из произвольной точки М, взятой на окружности, описанной вокруг треугольника АВС, опущены перпендикуляры к сторонам или продолжениям сторон треугольника, докажите, что основания этих перпендикуляров лежат на одной прямой. Подсказка: используйте обратную теорему Менелая. Попробуйте выразить длины отрезков, используемых в отношениях, через длины перпендикуляров, проведенных к их точке М. Также полезно помнить свойства углов вписанного четырехугольника.
М 9.1.6. Докажите теорему Симпсона: из произвольной точки М, взятой на окружности, описанной вокруг треугольника АВС, опущены перпендикуляры к сторонам или продолжениям сторон треугольника, докажите, что основания этих перпендикуляров лежат на одной прямой. Подсказка: используйте обратную теорему Менелая. Попробуйте выразить длины отрезков, используемых в отношениях, через длины перпендикуляров, проведенных к их точке М. Также полезно помнить свойства углов вписанного четырехугольника.
Инструменты | Бесплатный полнотекстовый | Разработка быстрого времяпролетного детектора на основе КФУ для эксперимента AMS-100 в космосе
1. Введение
заменить действующий в настоящее время AMS-02 [2] на борту Международной космической станции. Он служит обсерваторией космических лучей, развернутой возле точки Лагранжа 2 Солнце-Земля в течение следующего десятилетия.
Как показано на рис. 1а, AMS-100 состоит из набора цилиндрических субдетекторов радиусом 2 м и длиной 6 м, окруженных магнитом и компенсационной катушкой, и оснащен внешними солнечными панелями. , радиатор, солнцезащитный козырек и служебный модуль космического корабля.
, радиатор, солнцезащитный козырек и служебный модуль космического корабля.
Вдоль прибора времяпролетные детекторы (TOF) расположены внутри и снаружи соленоидного магнита, как показано на рис. 1b.
TOF покрывает цилиндрическую поверхность длиной 6 м и радиусом 2 м, в результате чего общая площадь составляет 75 м 2 . Он состоит из четырех отдельных слоев. Каждый слой состоит из отдельных сцинтилляционных плиток, соединенных с двумя Si-ФЭУ с временным разрешением σt=20 пс, где σt определяется уравнением (2). Временное разрешение системы TOF составляет σt/2. Это временное разрешение позволяет идентифицировать изотопы космических лучей, такие как 2 H, 3 He, 10Be, с высокой точностью в широком диапазоне импульсов.
Недавно в экспериментах PANDA [3] и MEG II [4] были разработаны временные детекторы на основе считывания сцинтилляционной плитки серией Si-ФЭУ и получено временное разрешение в диапазоне σt = 50∼60 пс [3,4 ,5]. В этой статье мы приняли аналогичные концепции дизайна, нацеленные на лучшее временное разрешение, в основном за счет увеличенной активной области SiPM. Кроме того, мы ожидаем снижения электронных шумов при низкой температуре окружающей среды 200 К, при которой будет работать TOF в AMS-100.
Кроме того, мы ожидаем снижения электронных шумов при низкой температуре окружающей среды 200 К, при которой будет работать TOF в AMS-100.
2. Детектор времени пролета (Tof) на основе SiPM
Как и в экспериментах PANDA и MEG II, для быстрых временных измерений была выбрана пластиковая сцинтилляционная плитка с коротким временем затухания сцинтилляций и высокой статистикой фотонов.
Основной вклад во временное разрешение (σtph) фотонной статистики, обнаруженный SiPM, может быть выражен как [6]
где τr и τd — время нарастания и затухания сцинтиллятора, Ndet — число зарегистрированных фотонов. Ndet можно выразить как произведение количества фотонов (Nph), квантовой эффективности (QE), эффективности сбора (CE) и коэффициента усиления (G) SiPM. Произведение QE·CE широко определяется как эффективность обнаружения фотонов (PDE). Здесь исключаются шумовые помехи от перекрестных помех, послеимпульса, темнового тока и электронного шума. Согласно уравнению (1), временное разрешение улучшается, когда τr и τd становятся короче.
Согласно уравнению (1), временное разрешение улучшается, когда τr и τd становятся короче.
В целях быстрой синхронизации были выбраны пластиковые сцинтилляторы Eljen-228 и Eljen-232 на основе поливинилтолуола из-за их высокого светового выхода 10 200 фотонов/1 МэВ e − , низкой плотности 1,023 г/см 3 и быстродействия. времена нарастания и затухания мерцаний менее 500 пс и 1600 пс соответственно. Приведенный показатель преломления равен 1,58, а светоотдача постоянна в диапазоне температур от −60 °C до +20 °C [7]. Размеры используемой сцинтилляционной плитки составляют 25 мм (ширина) × 6 мм (толщина) × 120 мм (длина). Толщина регулируется в соответствии с высотой одноканального SiPM.
SiPM представляет собой полупроводниковый детектор фотонов, состоящий из прямоугольной матрицы микроячеек. Каждая микроячейка состоит из лавинного фотодиода (ЛФД), работающего в режиме Гейгера, и гасящего резистора. Все ЛФД и гасящие резисторы идентичны, а микроячейки подключены к одному общему выходу параллельно. В настоящее время SiPM является хорошо известным фотодатчиком, поскольку его технология достигла впечатляющей зрелости. Подобно обычному фотоумножителю, SiPM обеспечивает быстрое реагирование. Превосходные свойства, такие как компактность, высокий коэффициент усиления, низкая стоимость и высокая устойчивость к магнитным полям, позволяют использовать гибкую и высокосегментированную конструкцию детектора TOF для крупномасштабных экспериментов [8]. Низкое напряжение смещения и низкое энергопотребление являются дополнительными преимуществами для длительной работы в космосе.
В настоящее время SiPM является хорошо известным фотодатчиком, поскольку его технология достигла впечатляющей зрелости. Подобно обычному фотоумножителю, SiPM обеспечивает быстрое реагирование. Превосходные свойства, такие как компактность, высокий коэффициент усиления, низкая стоимость и высокая устойчивость к магнитным полям, позволяют использовать гибкую и высокосегментированную конструкцию детектора TOF для крупномасштабных экспериментов [8]. Низкое напряжение смещения и низкое энергопотребление являются дополнительными преимуществами для длительной работы в космосе.
Для быстрых SiPM выбрана серия S14161 от Hamamatsu Photonics (HPK). По сравнению с серией S13360, используемой PANDA [3], он обеспечивает более высокий PDE (50% при λpeak = 450 нм, Vbias = VBD + 2,7 В) с низкими перекрестными помехами, более высоким коэффициентом усиления порядка 106 и более низким напряжением пробоя. (VBD=38 В). Послеимпульсные эффекты и темновая скорость счета также значительно снижены на два порядка по сравнению с серией S12571/S12572 [9].
Этот SiPM состоит из N=16(4×4) каналов. Каждый канал имеет эффективную площадь (6 × 6) мм 2 с шагом пикселя 50 мкм, что приводит к большому динамическому диапазону из-за большого количества микроячеек (14 тыс.).
Существует несколько способов объединения N каналов SiPM, таких как последовательное, параллельное и гибридное соединения, как подробно описано в ссылке [3]. Оптимальным сценарием, который используется в данном исследовании, является гибридная схема. Он использует функцию параллельного соединения общего Vbias среди N каналов и функцию последовательного соединения, относящуюся к качеству сигнала, но с использованием развязывающего конденсатора между каналами.
3. Экспериментальная установка
Создан прототип счетчика TOF для количественной оценки временного разрешения. Как показано на рисунке 2а, одна сцинтилляционная плитка считывается двумя массивами SiPM, установленными на двух противоположных краях сцинтиллятора длиной 120 мм. Каждый SiPM состоит из четырех последовательных каналов, как показано на рисунке 2b.
Каждый SiPM состоит из четырех последовательных каналов, как показано на рисунке 2b.
Ожидается, что по сравнению с детектором PANDA TOF увеличенная активная площадь Si-ФЭУ улучшит временное разрешение в ≃ 2 раза, определяемом разным покрытием поверхности [10], что соответственно улучшит количество регистрируемых фотонов (Ndet) ( Уравнение (1)).
В этой статье мы используем как временное разрешение совпадения (σΔt), так и временное разрешение (σt), которые определяются как
где tL,R обозначает отметку времени левого или правого SiPM, а t — среднее время для совпадающего события, как показано на рисунке 2a.
3.1. Конструкция DAQ
Схема экспериментальной тестовой установки изображена на рисунке 3. На ней показан прототип TOF, состоящий из сцинтилляционной плитки, соединенной с Si-ФЭУ, и передних плат внутри климатической камеры. Внутренняя часть климатической камеры светонепроницаема, чтобы избежать попадания фонового света на сцинтиллятор. Сигнальные, силовые, коммуникационные и другие служебные линии соединяются с внешними приборами через специальный ввод.
Сигнальные, силовые, коммуникационные и другие служебные линии соединяются с внешними приборами через специальный ввод.
Сигналы, индуцируемые светодиодом или радиоактивным источником, подаются на интерфейсную плату, а затем считываются с помощью высокоскоростного оцифровщика формы сигнала Domino Ring Sampling (DRS4) [11]. Оценочная плата DRS4 способна одновременно оцифровывать четыре входных канала с частотой дискретизации до 5 гигавыборок в секунду с 1024 точками выборки на канал. Этого достаточно для определения пикосекундной (пс) синхронизации. Усовершенствованные внутренние схемы калибровки времени позволяют получить разрешение по времени меньше пс. Плата питается через USB-порт и содержит встроенный модуль триггерной логики.
Плата предусилителя используется для управления усилением двух фаз операционного усилителя. Встроенный модуль питания (Hamamatsu C11204-01 [12]) обеспечивает напряжение смещения для SiPM. Микроконтроллер USB (FTDI-FT4222H [13]) используется для считывания показаний датчика температуры на SiPM. Модуль источника питания смещения имеет встроенную функцию температурной компенсации, так что SiPM может работать в оптимальных условиях даже в средах с переменными температурами. Он управляется через мост USB FT4222H с протоколом последовательного периферийного интерфейса (SPI).
Модуль источника питания смещения имеет встроенную функцию температурной компенсации, так что SiPM может работать в оптимальных условиях даже в средах с переменными температурами. Он управляется через мост USB FT4222H с протоколом последовательного периферийного интерфейса (SPI).
Все данные мониторинга напряжения, тока внешнего источника питания, температуры и других условий работы климатической камеры записываются цифровым мультиметром (DMM, Keithley 2700E), подключенным к программе LabVIEW. ПК на базе Linux используется для управления и мониторинга всех аппаратных устройств.
3.2. Ультрафиолетовый (УФ) светодиод и радиоактивный источник
90 Sr На рис. 4 показан прототип испытательной установки внутри климатической камеры. Светодиод ультрафиолетового (УФ) света (375 нм, Thorlabs LED375L) расположен в центре сцинтиллятора, как показано на рисунке 4а. Он используется для генерации сверхкоротких световых импульсов малой мощности (<1 мВт) и длительностью 10 нс (FWHM) в пределах узкого угла обзора (±20°). Свет передается путем полного отражения к SiPM. Светодиод крепится на механическом держателе с отверстием диаметром 2 мм, которое служит коллиматором генерируемых световых импульсов. УФ-светодиод использовался для количественной оценки вклада считывающей электроники во временное разрешение. Мы получили вклад около 5 пс, который в настоящее время пренебрежимо мал по сравнению с наблюдаемым полным временным разрешением ≃ 40 пс, описанным в разделе 4.6.
Свет передается путем полного отражения к SiPM. Светодиод крепится на механическом держателе с отверстием диаметром 2 мм, которое служит коллиматором генерируемых световых импульсов. УФ-светодиод использовался для количественной оценки вклада считывающей электроники во временное разрешение. Мы получили вклад около 5 пс, который в настоящее время пренебрежимо мал по сравнению с наблюдаемым полным временным разрешением ≃ 40 пс, описанным в разделе 4.6.
Для оценки характеристик прототипа используется радиоактивный источник стронция ( 90 Sr), как показано на рисунке 4b. Электроны, испускаемые его дочерним элементом, иттрием ( 90 Y), имеют непрерывное распределение энергии с максимальной энергией 2,28 МэВ. Электроны коллимируются с отверстием (диаметром 2 мм) на дне алюминиевого контейнера корпуса. Электроны отдают энергию сцинтиллятору, и возникающий в результате свет регистрируется обоими SiPM. SiPM считываются DRS4. Порог его дискриминатора настроен на низкий уровень σnoise×20≈10 мВ. Записанные данные используются для автономного анализа. В редких случаях электрон может выделять в сцинтилляторе свою максимальную энергию 2,28 МэВ. Вклад оценивается по максимуму спектра сигнального импульса в режиме самовозбуждения и составляет менее 1‰.
Записанные данные используются для автономного анализа. В редких случаях электрон может выделять в сцинтилляторе свою максимальную энергию 2,28 МэВ. Вклад оценивается по максимуму спектра сигнального импульса в режиме самовозбуждения и составляет менее 1‰.
Электроны в диапазоне энергий 1∼3 МэВ осаждают 2 МэВ см 2 /г в пластиковом сцинтилляторе на основе винилтолуола [14], эквивалентном МИП. Поэтому в этом отчете мы предполагаем, что электрон с энергией 1 МэВ выделяет ту же энергию, что и MIP.
3.3. Напряжение пробоя и зависимость от температуры
Напряжение пробоя (VBD) уменьшается при низких температурах из-за большей подвижности носителей. Его можно определить по измерениям высоты импульса как функции напряжения смещения (Vbias). Он получен как точка пересечения на оси Vbias. VBD был определен как 38,1 В для левого Si-ФЭУ и 37,8 В для правого Si-ФЭУ при +23 °C.
В широком диапазоне температур окружающей среды VBD линейно коррелирует с температурой (см. рис. 5):
рис. 5):
где α обозначает температурный коэффициент, а VBD(T0) напряжение пробоя при эталонной температуре T0. Измеренный средний температурный коэффициент α = (34,2 ± 0,1 ± 0,3) мВ/°С. Ошибки представляют собой статистическую и систематическую неопределенность соответственно. Систематическая ошибка в 1% была оценена путем изменения диапазонов подгонки для определения напряжения пробоя при заданной температуре. Это соответствует эталонному значению 34 мВ/°C, предоставленному поставщиком [9].].
Модуль источника питания с контуром обратной связи по температуре и напряжению генерирует напряжение смещения в соответствии со следующей формулой.
Общий заряд сигнала пропорционален усилению. Коэффициент усиления (G) увеличивается линейно с перенапряжением и определяется выражением
где Ccell обозначает емкость микроячейки SiPM. Если предположить, что температурный градиент Ccell пренебрежимо мал, коэффициент усиления уменьшается с повышением температуры при том же напряжении смещения, если только не применяется температурная компенсация.
4. Анализ данных и результаты
4.1. Сигналы с быстрым передним фронтом
Быстрые передние фронты сигналов используются для оценки постоянной времени, времени нарастания, базовой линии и амплитуды импульса после вычитания базовой линии. На рис. 6 показаны необработанные сигналы при ΔV=3 В, индуцированные источником 90 Sr и зарегистрированные обоими Si-ФЭУ. Каждая форма сигнала хорошо описывается ступенчатой функцией вида
где a и b описывают базовую линию импульса и амплитуду сигнала соответственно. t0 относится ко времени полувысоты амплитуды импульса, а tτ к постоянной времени. Время нарастания оценивается временем, необходимым для увеличения амплитуды импульса с 10% до 90% от его максимума.
Точно так же время затухания определяется как время, необходимое для уменьшения амплитуды импульса с 90% до 10% от своего максимума. Общий собранный заряд оценивается по площади между графиком и осью времени.
4.2. Разрешение по времени совпадения (CTR)
Точность измерения времени ограничена дрожанием из-за шума и отклонением во времени из-за колебаний амплитуды. Вклад джиттера во временное разрешение обычно выражается в первом приближении как
где σn обозначает электронный шум, dV/dt — наклон амплитуды сигнала при заданном пороге, который можно аппроксимировать как отношение амплитуды пика (Vpeak) к времени нарастания (tr), а SNR — отношение сигнал/шум. коэффициент шума. Следовательно, временное разрешение улучшается непосредственно с уменьшением времени нарастания сигнала и увеличением пиковой амплитуды сигнала.
Наилучшее временное разрешение достигается при использовании метода постоянной дробной синхронизации, поскольку он устраняет зависящее от амплитуды отклонение сигналов во времени [15,16]. В этой статье этот метод реализуется как процедура запуска с постоянной дробной высотой импульса в автономном анализе формы волны.
На рис. 7 распределения постоянной времени, времени нарастания и меток времени для левого и правого Si-ФЭУ представлены с постоянным дробным порогом 0,2 (20%). Необработанные данные собираются с помощью триггера 70 мВ при максимальной высоте импульса 170 мВ, которая оценивается при максимальной энергии электронов 2,28 МэВ. События отбираются для совпадающих пар сигналов в окне временной разницы, фиксированном на уровне 10 нс, с эффективностью 99,9%. Измеренные временные распределения аппроксимируются с использованием асимметричной функции Гаусса со средним значением μ, амплитудой C и ее стандартным отклонением σ, определяемым как
где σ=σ1, если t<µ, и σ=σ2 в противном случае.
Постоянная времени и время нарастания одинаковы для обоих Si-ФЭУ и имеют значения 0,8 нс и 3,6 нс соответственно.
Разница во времени между совпадающими парами импульсов, то есть между левым и правым Si-ФЭУ (Δt=tleft-tright), показана на рисунке 8 для двух образцов, собранных при низком и высоком уровнях запуска 20 мВ и 70 мВ. С учетом основных гауссовских подгонок измеренный CTR равен σ Δt = (100 ± 0,8) пс и σ Δt = (82 ± 0,2) пс при КПД 70 % и 98 % соответственно. Систематическая погрешность оценивается в 1% при многократном повторении измерения. Он включает влияние колебаний температуры в климатической камере на ±0,1 °С и положения источника на ±2 мм. Вклад этой систематической неопределенности в посадки незначителен.
С учетом основных гауссовских подгонок измеренный CTR равен σ Δt = (100 ± 0,8) пс и σ Δt = (82 ± 0,2) пс при КПД 70 % и 98 % соответственно. Систематическая погрешность оценивается в 1% при многократном повторении измерения. Он включает влияние колебаний температуры в климатической камере на ±0,1 °С и положения источника на ±2 мм. Вклад этой систематической неопределенности в посадки незначителен.
4.3. Сравнительное исследование CTR двух сцинтилляторов
На рисунке 9 мы сравниваем CTR между сцинтилляторами Eljen-228 и Eljen-232 в зависимости от перенапряжения. Это исследование было выполнено путем изменения перенапряжения от 0,5 В до 7 В при фиксированном пороге дискриминатора 10 мВ и постоянной температуре окружающей среды +23 °C. Минимальный CTR оценивается равным σΔt=(96,4±0,8) пс и σΔt=(122,9±1,2) пс для Eljen-228 и Eljen-232 соответственно. Результаты показывают лучшую производительность для Eljen-228, что связано с более высоким световым выходом на 20%, который компенсирует увеличение времени нарастания на 30% по сравнению с Eljen-232.
Количественное понимание этого результата потребует подробного исследования с помощью моделирования методом Монте-Карло для моделирования переноса оптических фотонов в пластиковом сцинтилляторе, соединенном с SiPM, как сообщается в статьях [17,18].
CTR сильно зависит от напряжения смещения, порогового уровня срабатывания, оптических связей и температурных условий.
Для следующих измерений CTR сцинтиллятор (Eljen-228) обернут одним слоем алюминированного майлара для улучшения сбора сцинтилляционного света. Возможное влияние смазки оптической связи между сцинтиллятором и Si-ФЭУ в этом исследовании не изучалось.
4.4. Позиционная зависимость временного разрешения
Позиционная зависимость временного разрешения изучалась с шагом 5 мм в продольном направлении при напряжении смещения 41,0 В (или ΔV=3,0 В) и пороге дискриминатора 40 мВ для регистрации электронов, которые близко к MIP (Ee−≃1 МэВ). Разница во времени Δt двух SiPM может быть выражена как линейная функция положения источника как
где ts представляет время начала, xi — положение источника относительно центра сцинтиллятора, а l — длина сцинтиллятора. ttrig.L(R) обозначает отметку времени каждого SiPM, а veff — эффективная скорость света в сцинитляторе.
ttrig.L(R) обозначает отметку времени каждого SiPM, а veff — эффективная скорость света в сцинитляторе.
Как показано на рисунке 10, мы можем получить эффективную скорость света в сцинтилляторе, vэфф=19,1±0,1(стат)±0,7(сист) см/нс, подгоняя данные линейной функцией по положению источника. Систематическая ошибка оценивается путем изменения постоянного дробного порога на 0,1 (10%). Измеренный veff дает показатель преломления n=c/veff=1,57±0,01(стат)±0,06(сист), что согласуется со значением n=1,58, указанным в паспорте продукта.
Средний CTR равен (86,8±0,3) пс, что эквивалентно σt=(43,4±0,1) пс. Это указывает на хорошую однородность вдоль продольного направления сцинтиллятора. Этот результат также может быть переведен в разрешение по положению (8,29 ± 0,02) мм.
4.5. Временное разрешение в зависимости от напряжения смещения
При низком постоянном пороге дискриминатора 10 мВ мы изменяли напряжение смещения Vbias Si-ФЭУ от 38,5 В до 45,0 В и регистрировали форму импульса при температуре +23 °C. Этот низкий порог собирает события, соответствующие средней энергии электронов 0,5 МэВ. При каждом напряжении смещения дробный пороговый уровень изменяется от 0,1 до 0,9с шагом 0,1. Полученные значения CTR показаны на рисунке 11.
Этот низкий порог собирает события, соответствующие средней энергии электронов 0,5 МэВ. При каждом напряжении смещения дробный пороговый уровень изменяется от 0,1 до 0,9с шагом 0,1. Полученные значения CTR показаны на рисунке 11.
Минимальное временное разрешение получено для постоянного дробного порогового уровня между 0,2 и 0,3, антикоррелированного с напряжением смещения и согласующегося с ожиданием из уравнения (7), что оптимальная разрешение по времени достигается, когда производная амплитуды импульса (dV/dt) максимальна.
Временное разрешение явно улучшается, когда напряжение смещения увеличивается выше VBD=38 В из-за увеличения PDE, коэффициента усиления и отношения сигнал-шум, как показано в уравнениях (1) и (7), но начинает ухудшаться при превышении Vbias>43 В ( или ΔV>5 В) из-за шума темнового тока, перекрестных помех и эффектов послеимпульса, которые, как ожидается, будут увеличиваться с увеличением ΔV [19].].
Наилучшее временное разрешение σt=(48,2±0,2)пс при перенапряжении ΔV=3,25 В.
4.6. Временное разрешение в зависимости от порога дискриминатора
При постоянном перенапряжении ΔV=3,0 В и рабочей температуре +23 °C зависимость временного разрешения от вложенной энергии электронов оценивается путем изменения уровня порога дискриминатора от 10 мВ до 80 мВ с шагом 10 мВ.
На рис. 12 показаны измерения CTR. Оптимальное временное разрешение достигается при постоянном дробном пороге 0,2 (20%), согласующемся с предыдущим результатом сканирования напряжения смещения.
Влияние временного джиттера на CTR наиболее существенно при низких порогах дискриминатора, поскольку при высоких порогах создается больше фотоэлектронов. По мере увеличения порога дискриминатора собираются электроны с более высокой энергией. Вложенную энергию можно оценить, сравнив среднюю высоту импульса с конечной точкой спектра амплитуды импульса. При пороге дискриминатора 45 мВ средняя высота импульса соответствует электронам с энергией около 1 МэВ, близким к MIP. В этот момент временное разрешение составляет σt=(42,8±0,1±0,5) пс. Первая ошибка представляет собой статистическую ошибку аппроксимации, а вторая — систематическую ошибку, оцененную с учетом погрешности температуры 0,1 °C и неопределенности положения источника ±2 мм.
В этот момент временное разрешение составляет σt=(42,8±0,1±0,5) пс. Первая ошибка представляет собой статистическую ошибку аппроксимации, а вторая — систематическую ошибку, оцененную с учетом погрешности температуры 0,1 °C и неопределенности положения источника ±2 мм.
Внешний триггерный счетчик был установлен за 120-мм сцинтиллятором для выбора MIP из 90 Sr для проверки временного разрешения, полученного с помощью внутреннего автоматического триггера. Внешний триггерный счетчик состоит из сцинтиллятора 10 × 10 × 6 мм 3 (EJ-232), считываемого двумя Si-ФЭУ (S14520-6050VS) для запуска по совпадению.
В настройке внешнего триггера события выбираются с использованием того же порога дискриминатора 45 мВ при ΔV=3,0 В. На рис. 13 высота импульса и результаты CTR сравниваются с режимом внутреннего триггера. На рис. 13а показаны амплитудный спектр внешнего и внутреннего триггерных импульсов. По сравнению с режимом внутреннего триггера среднее значение амплитуды импульса на 10% выше, а выбранные события — это в основном электроны между 1 и 2 МэВ, т. е. MIP-подобные частицы [14]. В режиме внутреннего триггера не-MIP-подобные низкоэнергетические электроны вносят вклад в сигналы и ухудшают измеренное временное разрешение, как показано на рисунке 13b. Измеренное временное разрешение с внешним триггером составляет σt=(39.3±0,1±0,7) пс. Систематическая ошибка оценивается путем изменения порога внешнего триггера.
е. MIP-подобные частицы [14]. В режиме внутреннего триггера не-MIP-подобные низкоэнергетические электроны вносят вклад в сигналы и ухудшают измеренное временное разрешение, как показано на рисунке 13b. Измеренное временное разрешение с внешним триггером составляет σt=(39.3±0,1±0,7) пс. Систематическая ошибка оценивается путем изменения порога внешнего триггера.
4.7. Разрешение по времени в зависимости от рабочей температуры
Чувствительность SiPM зависит от произведения эффективности обнаружения фотонов (PDE) и коэффициента усиления (G), как описано в уравнении (1). Оба фактора зависят от перенапряжения (ΔV), которое сильно коррелирует с температурой из-за сильной температурной зависимости напряжения пробоя (VBD(T)), как это выражено в уравнении (3). Это вызванное температурой изменение VBD влияет не только на ΔV, но и на другие характеристики SiPM, такие как PDE, усиление, темновая скорость счета, перекрестные помехи и вероятность послеимпульса [19]. ]. Однако световой поток сцинтиллятора постоянен в диапазоне температур от −60 °C до +20 °C, как обсуждалось ранее.
]. Однако световой поток сцинтиллятора постоянен в диапазоне температур от −60 °C до +20 °C, как обсуждалось ранее.
Температурная зависимость CTR исследуется путем снижения рабочей температуры с +23 °C до −30 °C, при этом напряжение смещения изменяется для сохранения того же перенапряжения (ΔV) в соответствии с уравнением (4), а дискриминатор пороговые значения устанавливаются, как в Разделе 4.5 и Разделе 4.6. Следует отметить, что напряжение смещения применяется с учетом температурной компенсации.
Чтобы сравнить результаты поведения CTR для обеих температур, CTR исследуется как функция перенапряжения и порога дискриминатора, как показано на рисунке 14.
Как уже упоминалось в разделе 3.3, напряжение пробоя (VBD) сместилось от 38 В до 36 В при снижении рабочей температуры с +23 °C до −30 °C. На рис. 14а показан измеренный CTR при низком пороге дискриминатора 10 мВ. Для обеих температур CTR в зависимости от перенапряжения имеет минимум σt=(48,2±0,2) пс при ΔV=3,25±0,01 В.
Это означает, что для изучаемого здесь диапазона температур временное разрешение не зависит от температуры при условии, что перенапряжение остается неизменным. Небольшая разница в CTR выше ΔV>5 В может быть результатом уменьшенного темнового счета и уменьшенной вероятности оптических перекрестных помех при низких температурах [19,20].
На рис. 14б CTR измерен, как описано в разделе 4.6, при том же перенапряжении 3,0±0,1 В при изменении рабочей температуры. При −30 °C временное разрешение достигает σt=(42,4±0,5) пс при пороге 45 мВ, где средняя энергия энерговклада электронов близка к MIP (Ee−≃1 МэВ). Этот факт согласуется с результатом, полученным при +23 °С.
5. Выводы
Был построен прототип TOF для эксперимента AMS-100, и его характеристики были изучены в различных условиях эксплуатации и окружающей среды. Этот прототип состоит из сцинтилляционной плитки длиной 120 мм с площадью поверхности (25 × 6 мм 2 ), соединенной с двумя Si-ФЭУ на противоположных сторонах. Для оптимизации временного разрешения каждый SiPM объединяет четыре канала в один канал считывания с помощью гибридного соединения, а его сигнал подается на высокоскоростной дигитайзер. С помощью радиоактивного 90 Sr, получено временное разрешение σt=[39,3±0,1(стат)±0,7(сист)] пс для MIP-подобных частиц в режиме внешнего триггера.
Для оптимизации временного разрешения каждый SiPM объединяет четыре канала в один канал считывания с помощью гибридного соединения, а его сигнал подается на высокоскоростной дигитайзер. С помощью радиоактивного 90 Sr, получено временное разрешение σt=[39,3±0,1(стат)±0,7(сист)] пс для MIP-подобных частиц в режиме внешнего триггера.
Этот результат значительно улучшает временное разрешение 50-60 пс, о котором ранее сообщали PANDA и MEG II. Это достижение является результатом использования нового типа Si-ФЭУ, который не только покрывает все поперечное сечение сцинтиллятора на обоих концах, но также обеспечивает улучшенное временное разрешение в широком диапазоне перенапряжения по сравнению с предыдущими Si-ФЭУ. Более того, эта работа демонстрирует тот факт, что даже в различных температурных условиях временное разрешение времяпролетного счетчика остается стабильным при сохранении одного и того же перенапряжения.
Не удалось продемонстрировать ожидаемое улучшение временного разрешения в два раза за счет улучшенного покрытия поверхности сцинтиллятора. Для этой цели емкость (C) выбранного Si-ФЭУ (S14161-6050HS, C=2000 пФ, площадь 6 × 6 мм 2 , 16 каналов) слишком велика. SiPM от Hamamatsu (S14161-3050HS, C=500 пФ, площадь 3 × 3 мм 2 , 64 канала) будет использоваться для детального исследования влияния емкости при сохранении покрытия поверхности сцинтиллятора на том же уровне.
Для этой цели емкость (C) выбранного Si-ФЭУ (S14161-6050HS, C=2000 пФ, площадь 6 × 6 мм 2 , 16 каналов) слишком велика. SiPM от Hamamatsu (S14161-3050HS, C=500 пФ, площадь 3 × 3 мм 2 , 64 канала) будет использоваться для детального исследования влияния емкости при сохранении покрытия поверхности сцинтиллятора на том же уровне.
Кроме того, можно ожидать дальнейших улучшений от новых технологий SiPM [21,22].
Вклад авторов
Концептуализация, C.C., T.K. и С.С.; методология, C.C. и Т.К.; программное обеспечение, C.C. и компакт-диск; проверка, Т.К. и В.К.; формальный анализ, CC; расследование, Д.Л., В.К. и М.В.; ресурсы, Т.К., Г.С. и С.С.; курирование данных, C.C., T.B. и компакт-диск; написание — первоначальная черновая подготовка, C.C.; написание — обзор и редактирование, C.C., T.K. и С.С.; визуализация, MW и CC; надзор, С.С.; администрирование проекта, GS и SS; финансирование приобретения, S.S. Все авторы прочитали и согласились с опубликованной версией рукописи.
Финансирование
Это исследование было поддержано RWTH Aachen University, Германия.
Заявление Институционального контрольного совета
Неприменимо.
Заявление об информированном согласии
Неприменимо.
Заявление о доступности данных
Данные, представленные в этом исследовании, доступны по запросу от соответствующего автора.
Благодарности
Мы признательны за постоянную превосходную поддержку цехов механики и электроники 1-го физического института Рейнско-Вестфальского технического университета Ахена. Мы благодарим Софию Чуриду за внутренний обзор этой статьи.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Сокращения
В данной рукописи используются следующие сокращения:
| AMS-02 | Alpha Magnetic Spectrometer |
| AMS-100 | A Magnetic Spectrometer with an acceptance of 100 m 2 · sr |
| TOF | Time-of-Flight |
| SiPM | Кремниевый фотоумножитель |
| DRS | Domino Ring Sampling |
| SPI | Serial Peripheral Interface |
| CTR | Coincidence Time Resolution |
| SNR | Signal-to-Noise Ratio |
| MIP | Минимальная ионизирующая частица |
| PDE | Эффективность обнаружения фотонов |
Ссылки
- «> Schael, S.; Атанасян, А.; Бердуго, Дж.; Брец, Т .; Чупалла, М .; Дахвальд, Б.; фон Дутинхем, П.; Дюранти, М .; Гаст, Х .; Карпински, В .; и другие. AMS-100: космический магнитный спектрометр нового поколения — международная научная платформа для физики и астрофизики в точке Лагранжа 2. Nucl. Инструм. Мет. физ. Рез. А 2019 , 944, 162561. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Агилар, М.; Кавасонца, Лос-Анджелес; Амброси, Г.; Арруда, Л.; Аттиг, Н.; Барао, Ф.; Баррин, Л.; Бартолони, А .; Башегмез-дю Пре, С.; Бейтс, Дж.; и другие. Альфа-магнитный спектрометр (AMS) на международной космической станции: Часть II — Результаты первых семи лет. физ. Респ. 2021 , 894, 1–116. [Google Scholar] [CrossRef]
- Сотрудничество PANDA. Отчет о техническом проектировании ствола PANDA Time-of-Flight. Доступно в Интернете: https://panda.gsi.de/system/files/user_uploads/ken.suzuki/RE-TDR-2016-003_0.pdf (по состоянию на 4 июля 2018 г.
 ).
). - Бальдини, А.М.; Бараккини, Э.; Бемпорад, К.; Берг, Ф .; Биазотти, М .; Бока, Г.; Каттанео, PW; Кавото, Г.; Цей, Ф .; Кьяппини, М .; и другие. Схема эксперимента MEG II. Евро. физ. J. C 2018 , 78, 380. [Google Scholar] [CrossRef]
- Cattaneo, P.W.; Героне, доктор медицины; Гатти, Ф.; Нисимура, М .; Оотани, В. Разработка высокоточного счетчика времени на основе пластикового сцинтиллятора с считыванием SiPM. IEEE транс. Нукл. науч. 2014 , 61, 2657–2666. [Google Scholar] [CrossRef][Зеленая версия]
- Виноградов С.А. Аппроксимации моделей временного разрешения совпадения сцинтилляционных детекторов с дискриминатором переднего фронта. Нукл. Инструм. Мет. физ. Рез. А 2018 , 912, 143–153. [Google Scholar] [CrossRef]
- Eljen Technology. Доступно в Интернете: https://eljentechnology.com/products/plastic-scintillators/ej-228-ej-230 (по состоянию на 28 июня 2019 г.
 ).
). - Ренкер Д.; Лоренц, Э. Достижения в области твердотельных детекторов фотонов. Дж. Инструм. 2009 , 4, P04004. [Академия Google] [CrossRef]
- Ямамото, К.; Нагано, Т .; Ямамда, Р.; Ито, Т .; Охаси, Ю. Недавняя разработка MPPC в Хамамацу для приложений подсчета фотонов. В материалах 5-го Международного семинара по новым детекторам фотонов (PD18), Токио, Япония, 27–29 ноября 2018 г. [Google Scholar]
- Böhm, M.; Леманн, А .; Моц, С .; Улиг, Ф. Быстрое считывание SiPM детектора PANDA TOF. Дж. Инструм. 2016 , 11, C05018. [Google Scholar] [CrossRef]
- Оценочная плата DRS4. Доступно в Интернете: https://www.psi.ch/en/drs/evaluation-board (по состоянию на 3 июня 2020 г.).
- Спецификация Hamamatsu C11204-01. Доступно в Интернете: https://www.hamamatsu.com/resources/pdf/ssd/c11204-01_kacc1203e.pdf (по состоянию на 9 февраля 2021 г.). «> Технический паспорт микросхемы FT4222H. Доступно в Интернете: https://ftdichip.com/products/ft4222h (по состоянию на 28 октября 2020 г.).
- Программа NIST-ESTAR. Доступно в Интернете: https://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html (по состоянию на 2 декабря 2020 г.).
- Гедке, Д.А.; Макдональд, В. Дж. Триггер постоянной доли высоты импульса для оптимального временного разрешения. Нукл. Инструм. Мет. 1967 , 55, 377. [Google Scholar] [CrossRef]
- Гедке Д.А.; Макдональд, В. Дж. Разработка триггера постоянной доли амплитуды импульса для оптимального временного разрешения. Нукл. Инструм. Мет. 1968 , 58, 253. [Google Scholar] [CrossRef]
- Seifert, S.; Ван Дам, HT; Винке, Р .; Дендувен, П.; Лонер, Х .; Бикман, Ф.Дж.; Шаарт, Д.Р. Комплексная модель для прогнозирования временного разрешения сцинтилляционных детекторов на основе SiPM: теория и экспериментальная проверка.
 IEEE транс. Нукл. науч. 2012 , 59, 190. [Google Scholar] [CrossRef]
IEEE транс. Нукл. науч. 2012 , 59, 190. [Google Scholar] [CrossRef] - Acerbi, F.; Гандакер, С. Понимание и моделирование SiPM. Нукл. Инструм. Мет. А 2019 , 626, 16–35. [Google Scholar] [CrossRef]
- Непомук Отте, А.; Гарсия, Д.; Нгуен, Т .; Пурушотэм, Д. Характеристика трех высокоэффективных и чувствительных к синему кремнию фотоумножителей. Нукл. Инструм. Мет. A 2017 , 846, 106. [Google Scholar] [CrossRef][Green Version]
- Collazuol, G.; Бизоньи, М.; Маркатили, С .; Пьемонте, К.; Герра А.Г. Исследования кремниевых фотоумножителей при криогенных температурах. Нукл. Инструм. Мет. А 2011 , 628, 389–392. [Google Scholar] [CrossRef]
- Лекок, П. Раздвигая границы во времяпролетной ПЭТ-визуализации. IEEE транс. Радиат. Плазма Мед. науч. 2019 , 1, 473–485. [Google Scholar] [CrossRef]
- Испытание TOF-PET за 10 пс.
 Доступно в Интернете: https://the10ps-challenge.org (по состоянию на 11 сентября 2021 г.).
Доступно в Интернете: https://the10ps-challenge.org (по состоянию на 11 сентября 2021 г.).
Рисунок 1. ( a ) Изображение AMS-100, развернутого в космосе: прибор AMS-100 имеет цилиндрическую форму с радиусом 2 м и длиной 6 м, окруженную компенсационной катушкой. Перед солнцезащитным козырьком он оснащен солнечными панелями, электрической двигательной установкой и служебным модулем космического корабля. Задний радиатор отводит тепло от инструмента. ( b ) Поперечное сечение детектора AMS-100 с его цилиндрическими субдетекторными слоями.
Рисунок 1. ( a ) Изображение AMS-100, развернутого в космосе: прибор AMS-100 имеет цилиндрическую форму с радиусом 2 м и длиной 6 м, окруженную компенсационной катушкой. Перед солнцезащитным козырьком он оснащен солнечными панелями, электрической двигательной установкой и служебным модулем космического корабля. Задний радиатор отводит тепло от инструмента. ( b ) Поперечное сечение детектора AMS-100 с его цилиндрическими субдетекторными слоями.
Рисунок 2. Тестовый счетчик TOF состоит из сцинтиллятора и двух SiPM, соединенных со сцинтиллятором на противоположных сторонах. ( a ) Вид сверху: радиоактивный источник, 90 Sr, помещен в середину сцинтиллятора. Сцинтилляционный свет собирается на обоих SiPM. ( b ) Вид сбоку: Каждая сторона сцинтиллятора полностью обращена к четырем каналам SiPM.
Рисунок 2. Тестовый счетчик TOF состоит из сцинтиллятора и двух SiPM, соединенных со сцинтиллятором на противоположных сторонах. ( a ) Вид сверху: радиоактивный источник, 90 Sr, помещен в середину сцинтиллятора. Сцинтилляционный свет собирается на обоих SiPM. ( b ) Вид сбоку: Каждая сторона сцинтиллятора полностью обращена к четырем каналам SiPM.
Рисунок 3. Испытательная установка прототипа TOF внутри климатической камеры. В качестве источника света используется светодиод, управляемый генератором импульсов, а для подачи сигналов, эквивалентных MIP, используется радиоактивный источник. Выходные сигналы SiPM усиливаются, а затем подаются на высокоскоростной дигитайзер сигналов (DRS4). Все устройства управляются ПК на базе Linux.
Выходные сигналы SiPM усиливаются, а затем подаются на высокоскоростной дигитайзер сигналов (DRS4). Все устройства управляются ПК на базе Linux.
Рисунок 3. Испытательная установка прототипа TOF внутри климатической камеры. В качестве источника света используется светодиод, управляемый генератором импульсов, а для подачи сигналов, эквивалентных MIP, используется радиоактивный источник. Выходные сигналы SiPM усиливаются, а затем подаются на высокоскоростной дигитайзер сигналов (DRS4). Все устройства управляются ПК на базе Linux.
Рисунок 4. Прототип испытательной установки TOF: ( a ) Светодиод (375 нм) направляет свет в сцинтиллятор для систематического исследования; ( b ) поверх поверхности сцинтиллятора используется радиоактивный источник ( 90 Sr) для исследования характеристик прототипа.
Рисунок 4. Прототип испытательной установки TOF: ( a ) Светодиод (375 нм) направляет свет в сцинтиллятор для систематического исследования; ( b ) поверх поверхности сцинтиллятора используется радиоактивный источник ( 90 Sr) для исследования характеристик прототипа.
Рисунок 5. Зависимость напряжения пробоя (VBD) от температуры для двух Si-ФЭУ. Напряжение пробоя получено путем измерения высоты импульса сигнала с источником 90 Sr. При снижении температуры с +23 °C до −30 °C VBD уменьшается с 38 В до 36 В. Черная и красная полосы ошибок указывают на 95%-й уровень достоверности подгонки.
Рисунок 5. Зависимость напряжения пробоя (VBD) от температуры для двух Si-ФЭУ. Напряжение пробоя получают путем измерения высоты импульса сигнала с помощью 90 Ср источник. При снижении температуры с +23 °C до −30 °C VBD уменьшается с 38 В до 36 В. Черная и красная полосы ошибок указывают на 95%-й уровень достоверности подгонки.
Рисунок 6. Быстрые импульсные сигналы, индуцированные источником 90 Sr и зарегистрированные обоими КФЭУ: ( и ) левый КФЭУ(Л) и ( б ) правый КФЭУ(П). Также показаны результат подгонки (красные линии) на быстром переднем фронте сигналов, время нарастания и время на половине высоты импульса, t0.
Рисунок 6. Быстрые импульсные сигналы, индуцированные источником 90 Sr и зарегистрированные обоими КФЭУ: ( и ) левый КФЭУ(Л) и ( б ) правый КФЭУ(П). Также показаны результат подгонки (красные линии) на быстром переднем фронте сигналов, время нарастания и время на половине высоты импульса, t0.
Рисунок 7. Измеренная временная информация от обоих SiPM для сцинтиллятора Eljen-228. Каждое распределение показывает постоянную времени ( a ), время нарастания ( b ) и отметка времени ( c ), отмеченные с заданным постоянным дробным порогом 0,2 (20%). Данные соответствуют асимметричной функции Гаусса, определенной в уравнении (8).
Рисунок 7. Измеренная временная информация от обоих SiPM для сцинтиллятора Eljen-228. Каждое распределение показывает постоянную времени ( a ), время нарастания ( b ) и отметку времени ( c ), отмеченные при заданном пороге дробной константы 0,2 (20%). Данные соответствуют асимметричной функции Гаусса, определенной в уравнении (8).
Данные соответствуют асимметричной функции Гаусса, определенной в уравнении (8).
Рисунок 8. Распределения разницы во времени между левым и правым Si-ФЭУ (Δt=tleft-tright) для порогов ( a ) 20 мВ с низким и ( b ) 70 мВ с высоким порогом для сцинтиллятора Eljen-228. Каждое распределение аппроксимируется наложением двух гауссиан с одинаковым средним значением. CTR представляет собой основное стандартное отклонение функции Гаусса (σΔt) и показывает (100 ± 0,8) пс и (82 ± 0,2) пс соответственно.
Рисунок 8. Распределения разницы во времени между левым и правым Si-ФЭУ (Δt=tleft−tright) для ( a ) 20 мВ низкий и ( b ) 70 мВ высокий пороги для сцинтиллятора Eljen-228. Каждое распределение аппроксимируется наложением двух гауссиан с одинаковым средним значением. CTR представляет собой основное стандартное отклонение функции Гаусса (σΔt) и показывает (100 ± 0,8) пс и (82 ± 0,2) пс соответственно.
Рисунок 9. Сравнение Eljen-228 и Eljen-232. Перенапряжение варьировалось от 0,5 В до 7 В при фиксированном пороге дискриминатора 10 мВ и температуре окружающей среды +23 °С. Серые и красные полосы ошибок указывают на 95% уровень достоверности подгонки.
Перенапряжение варьировалось от 0,5 В до 7 В при фиксированном пороге дискриминатора 10 мВ и температуре окружающей среды +23 °С. Серые и красные полосы ошибок указывают на 95% уровень достоверности подгонки.
Рисунок 9. Сравнение Eljen-228 и Eljen-232. Перенапряжение варьировалось от 0,5 В до 7 В при фиксированном пороге дискриминатора 10 мВ и температуре окружающей среды +23 °С. Серые и красные полосы ошибок указывают на 95% уровень достоверности подгонки.
Рисунок 10. Разница во времени между левым и правым КФЭУ в зависимости от положения источника на сцинтилляторе. CTR рассчитывается при постоянном дробном пороге 0,2 (20%). Черные и красные полосы ошибок указывают на 95% уровень достоверности подгонки.
Рисунок 10. Разница во времени между левым и правым КФЭУ в зависимости от положения источника на сцинтилляторе. CTR рассчитывается при постоянном дробном пороге 0,2 (20%). Черные и красные полосы ошибок указывают на 95% уровень достоверности подгонки.
Рисунок 11. CTR как функция постоянного дробного порога для различных напряжений смещения. Минимальные значения CTR (пурпурные точки) распределяются вокруг постоянного дробного порога от 0,2 (20%) до 0,3 (30%). Как показано пунктирной линейной линией, она смещается от 0,3 до 0,2 по мере увеличения напряжения смещения. Вкладка указывает минимальный CTR в зависимости от напряжения смещения и перенапряжения (ΔV). Лучший CTR для электронов с энергией 0,5 МэВ показывает (96,4 ± 0,4) пс при ΔV = 3,25 В. Цветная полоса ошибок указывает на 95% уровень достоверности подгонки.
Рисунок 11. CTR как функция постоянного дробного порога для различных напряжений смещения. Минимальные значения CTR (пурпурные точки) распределяются вокруг постоянного дробного порога от 0,2 (20%) до 0,3 (30%). Как показано пунктирной линейной линией, она смещается от 0,3 до 0,2 по мере увеличения напряжения смещения. Вкладка указывает минимальный CTR в зависимости от напряжения смещения и перенапряжения (ΔV). Лучший CTR для электронов с энергией 0,5 МэВ показывает (96,4 ± 0,4) пс при ΔV = 3,25 В. Цветная полоса ошибок указывает на 95% уровень достоверности подгонки.
Лучший CTR для электронов с энергией 0,5 МэВ показывает (96,4 ± 0,4) пс при ΔV = 3,25 В. Цветная полоса ошибок указывает на 95% уровень достоверности подгонки.
Рисунок 12. CTR как функция постоянного дробного порога для различных порогов дискриминатора, пропорциональных энергии электрона. Минимальные значения CTR (пурпурные точки) распределяются вокруг постоянного дробного порога 0,2 (20%). Вкладка показывает минимальный CTR как функцию порога дискриминатора. CTR постепенно улучшается с увеличением энергии электронов от (9от 8 ± 0,4) пс до (78 ± 0,3) пс. Цветные полосы ошибок указывают на 95% уровень достоверности подгонки.
Рисунок 12. CTR как функция постоянного дробного порога для различных порогов дискриминатора, пропорциональных энергии электрона. Минимальные значения CTR (пурпурные точки) распределяются вокруг постоянного дробного порога 0,2 (20%). Вкладка показывает минимальный CTR как функцию порога дискриминатора. CTR постепенно улучшается с увеличением энергии электронов от (9от 8 ± 0,4) пс до (78 ± 0,3) пс. Цветные полосы ошибок указывают на 95% уровень достоверности подгонки.
Цветные полосы ошибок указывают на 95% уровень достоверности подгонки.
Рисунок 13. Сравнение нормализованной высоты импульса сигнала ( a ) и CTR ( b ) между внешним (закрашенный черный кружок) и внутренним (открытый синий квадрат) режимами запуска. Средняя амплитуда высоты импульса составляет (75,2±8,6) мВ и (68,7±12,9) мВ для внешнего и внутреннего триггерных режимов соответственно. CTR представляет собой основное стандартное отклонение функции Гаусса и показывает (78,7 ± 0,3) пс и (83,3 ± 0,3) пс для режимов внешнего и внутреннего запуска соответственно.
Рисунок 13. Сравнение нормализованной высоты импульса сигнала ( a ) и CTR ( b ) между внешним (закрашенный черный кружок) и внутренним (открытый синий квадрат) режимами запуска. Средняя амплитуда высоты импульса составляет (75,2±8,6) мВ и (68,7±12,9) мВ для внешнего и внутреннего триггерных режимов соответственно. CTR представляет собой основное стандартное отклонение функции Гаусса и показывает (78,7 ± 0,3) пс и (83,3 ± 0,3) пс для режимов внешнего и внутреннего запуска соответственно.
Рисунок 14. CTR для двух различных температур в зависимости от перенапряжения ( a ) и в зависимости от порога дискриминатора ( b ). Серые и красные полосы ошибок указывают на 95% уровень достоверности подгонки в обоих случаях.
Рисунок 14. CTR для двух различных температур в зависимости от перенапряжения ( a ) и в зависимости от порога дискриминатора ( b ). Серые и красные полосы ошибок указывают на 95% уровень достоверности подгонки в обоих случаях.
Примечание издателя: MDPI остается нейтральным в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности. |
© 2022 авторами. Лицензиат MDPI, Базель, Швейцария. Эта статья находится в открытом доступе и распространяется на условиях лицензии Creative Commons Attribution (CC BY) (https://creativecommons.org/licenses/by/4.0/).
Средняя линия треугольника, средняя линия трапеции.
 Средняя линия трапеции Средняя линия трапеции atanasyan презентация
Средняя линия трапеции Средняя линия трапеции atanasyan презентация Определение: Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон. АК = КС БЭ = СЕ КЕ — средняя линия АВС Определение: средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. A BC K N E AH = HB KE = CE NOT — средняя линия ABC A B C K E Сколько средних линий в треугольнике? Сколько средних линий в трапеции?
Средняя линия треугольника Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. А С В М К Дано: АВС, МК — средняя линия Доказательство: Так как по условию МК — средняя линия, то АМ = МБ = ½ АВ, СК = КВ = ½ ВС, Значит, ВМ АВ ВК ВС 1 2 В — общее для АВС и МВК, значит, АВС и МВК подобны по второму признаку подобия, следовательно, ВМК = А, значит, МК АС. Докажите: МК AS, MK = ½ AS MK AS 1 2 Из подобия треугольников также следует, что, то есть MK = ½ AS.
Решить проблему F R N? А Б
Доказательство: Проведем А 1 В 1 А В С А1А1 В1В1 О С1С1 По условию АА 1, ВВ 1 — средние средние, БА 1 = СА 1, АВ 1 = СВ 1, т. е. А 1 В 1 — средние линия. Отсюда А 1 В 1 АВ, следовательно, 1 = 2, 3 = 4. Следовательно, треугольники АОВ и А 1 ОВ 1 подобны в двух углах. Это означает, что их стороны пропорциональны: AO VO AB A1OA1O B1OB1O A1B1A1B1 По свойству средней линии треугольника AB = 2 A 1 B 1 , т.е.
е. А 1 В 1 — средние линия. Отсюда А 1 В 1 АВ, следовательно, 1 = 2, 3 = 4. Следовательно, треугольники АОВ и А 1 ОВ 1 подобны в двух углах. Это означает, что их стороны пропорциональны: AO VO AB A1OA1O B1OB1O A1B1A1B1 По свойству средней линии треугольника AB = 2 A 1 B 1 , т.е.
Средняя линия трапеции Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме. А В С К М Р Дано: АВСК — трапеция МР — средняя линия Докажите: МР АК, МР ВС МР = Доказательство: О Проведите прямую МЭ АК через точку М, докажите, что МЭ пройдет через Р.Т.К. АБСК — трапеция, тогда ВС АК, а, следовательно, ВС МЕ АК. Так как МР — средняя линия, то АМ = МВ, КР = СР Е Следовательно, МР лежит на МЕ, а значит, МР АК, МР ВС. Запустим ВК. По теореме Фалеса О — середина ВК, значит, МО — средняя линия АВК, ОП — средняя линия ВСК МР = МО + ОП = ½ АК + ½ ВС = ½ (АК + ВС ) = По теореме Фалеса МЭ пересечет СК в середине СК т.е. в точке Р.
«Площадь занятия трапецией» — В прямоугольной трапеции основания 5см. и 17см., а меньшая сторона 10см. Учитель подводит итоги, задавая вопросы: Кто набрал 5, 4, 3 балла? В каждом случае сформулируйте доказанную теорему. Решение задачи. Как рассчитать площадь трапеции? Какие элементы плоских фигур используются в формулах площади?
и 17см., а меньшая сторона 10см. Учитель подводит итоги, задавая вопросы: Кто набрал 5, 4, 3 балла? В каждом случае сформулируйте доказанную теорему. Решение задачи. Как рассчитать площадь трапеции? Какие элементы плоских фигур используются в формулах площади?
«Задачи на теорему Пифагора» — №21 Находка: Х. №18 Находка: Х. №27 Находка: X. Задачи на готовые рисунки («Теорема Пифагора»). №23 Находка: Х. №25 Находка: Х. №26 Находка: Х. №13 Находка: Х. №20 Находка: Х. №19Находка: Х. №14 Находка: Х. Вы выполнили все предложенные задания. №29 Находка: Х. №28 Находка: Х. №30 Находка: Х. №22 Находка: Х.
Теорема Фалеса — Фалес широко известен как геометр. Астрономия. Милетский материалист. Проведем через точку В2 прямую ЕF, параллельную линии А1А3. Из равенства треугольников следует равенство сторон В1В2 = В2В3. Теорема Фалеса. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Треугольники B2B1F и B2B1E равны по второму знаку равенства треугольников.
«Теорема синусов» — Стороны треугольника пропорциональны синусам противоположных углов. Решение: Устная работа: Ответы на задания по рисункам: Проверка домашнего задания. Тема урока: Теорема синусов. Теорема синусов:
Решение: Устная работа: Ответы на задания по рисункам: Проверка домашнего задания. Тема урока: Теорема синусов. Теорема синусов:
«Урок по теореме Пифагора» — Определить вид треугольника: Знакомство с теоремой. Доказательство теоремы. Разогревать. Теорема Пифагора. И вы найдете лестницу длиной 125 футов. План урока: Историческая справка. Отображение картинок. Решение простейших задач. Вычислите высоту CF трапеции ABCD. Доказательство. Определить тип четырехугольника КМНП.
«Теорема Пифагора 8 класс» — ЦИФРЫ. Деление чисел на четные и нечетные, простые и составные. Дано: прямоугольный треугольник a,b катет c- гипотенуза. Высота. Доказательство Бхаскари. Открытия пифагорейцев в математике. Дано: Треугольник прямоугольный, а, b — катеты, с — гипотенуза Докажите: с2 = а2 + b2. Меньшая сторона прямоугольного треугольника.
резюме других презентаций
«Построение правильных многоугольников» -? = 60?. ? 180. Геометрия. ? =. н. п — 2. Работу выполнила учитель математики МОУ «Гимназия №11» Лисицына Е.Ф.
Работу выполнила учитель математики МОУ «Гимназия №11» Лисицына Е.Ф.
«Теорема Фалеса» — Теорема Фалеса. Геометрическая теорема названа в честь Фалеса. Астрономия. Проведем через точку В2 прямую ЕF, параллельную линии А1А3. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Презентация по геометрии ученицы 9 «А» класса Сорогиной Полины. Милетский материалист. Геометрия. По свойству параллелограмма A1A2 = FB2, A2A3 = B2E. Фалес широко известен как геометр. А так как А1А2=А2А3, то FB2=B2E.
«Разложение вектора на два неколлинеарных» — Пусть p коллинеарно b. Доказательство: Разложение вектора на два неколлинеарных вектора. Доказательство. Пусть a и b — неколлинеарные векторы. Лемма: Если векторы a и b коллинеарны и a? 0, то существует число k такое, что b = ka. Докажем, что любой вектор p можно разложить по векторам a и b. Геометрия 9 класс. Тогда p = yb, где y — некоторое число.
«Правильные многоугольники 9 класс» — Урок геометрии в 9 классе. Луковникова Н. М., учитель математики. Построение правильного пятиугольника 1 способ. МОУ гимназия №56 Томск-2007г. Правильные многоугольники.
М., учитель математики. Построение правильного пятиугольника 1 способ. МОУ гимназия №56 Томск-2007г. Правильные многоугольники.
«Симметрия фигур» — Линия а называется осью симметрии фигуры. D. Одна форма получается из другой путем трансформации. Оглавление. Обратное преобразование движения есть тоже движение. А1. Выполнил: Пантюков Е. А. Существует множество различных типов симметрии. М1. Трансформация фигур.
«Симметрия относительно прямой» — Фигура может иметь одну или несколько осей симметрии. Симметрия в природе. Савченко Миша, 9Б класс. Угол. Кто изображен на оригинальном фото? Л.С. Атанасяна «Геометрия 7-9». Равнобедренная трапеция. Постройте отрезок А1В1, симметричный отрезку АВ относительно прямой. Сколько осей симметрии имеет каждая фигура? Прямоугольник.
Для использования предпросмотра презентаций создайте себе учетную запись Google (аккаунт) и войдите в it: https://accounts.google.com
Подписи к слайдам:
Средняя линия (8 класс)
Средняя линия треугольника
Средняя линия треугольника Определение: Отрезок, соединяющий середины Две стороны треугольника называются СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА. 0003
0003
Теорема Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. то есть: КМ ║ АС КМ = ½ АС А Б В К М
Решить задачу устно: А Б В К М 7 см Дано: М К — среднее. Строковый поиск: AU?
Работая в парах:
Решим задачу: Дано: MN — ср. линия Найти: P ∆ ABC M N A B C 3 4 3, 5
Работая в парах:
Средняя линия трапеции
Напомним: Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны A D B C BC || AD — основания AB łł CD — стороны
Средняя линия трапеции. Определение: средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. A D B C M N MN — средняя линия трапеции ABCD
Теорема о средней линии трапеции Средняя линия трапеции параллельна ее основаниям и равна их полусумме. то есть: M N ║BC║A D M N = ½ (ВС + А D) M N A D B C
Решить устно: M N A D B C 6,3 см 18,7 см?
Решите устно в парах: Дано: АВ = 16 см; CD = 18 см; М Н = 15 см. Найти: Р ABCD = ? М Н А Д Б В
Найти: Р ABCD = ? М Н А Д Б В
Самостоятельная работа Задача: Средняя линия трапеции равна 5см. Найдите основания трапеции, если известно, что нижнее основание в 1,5 раза больше верхнего. Решение: A D B C 5 см Пусть ВС = Х см тогда AD = 1,5Х см ВС + AD = 10 см Х + 1,5Х = 10 Х = 4 Значит: ВС = 4 см AD = 6 см
СПАСИБО ЗА УРОК!!!
Презентация разработана Лугвиной Натальей Анатольевной Лугвиной, учителем математики, СОШ № 467 г. Санкт-Петербурга, Колпинский район
По теме: методические разработки, презентации и конспекты
Урок обобщения и закрепления знаний по теме «Средняя линия треугольника. Средняя линия трапеции» в 8 классе с использованием ИКТ….
Рабочая тетрадь – индивидуальное творческое задание учащегося. который предполагает самостоятельную работу с текстом по теме «Трапеция. Средняя линия трапеции», применение знаний при решении задач. …
Тема «Средняя линия трапеции» является одной из важных тем курса геометрии. Эта фигура довольно часто встречается в различных задачах, как и ее средняя линия. Задания, содержащие данные по этой теме, часто встречаются в выпускных экзаменах и аттестационных работах. Знания по этой теме также могут пригодиться при обучении в средних и высших учебных заведениях.
Эта фигура довольно часто встречается в различных задачах, как и ее средняя линия. Задания, содержащие данные по этой теме, часто встречаются в выпускных экзаменах и аттестационных работах. Знания по этой теме также могут пригодиться при обучении в средних и высших учебных заведениях.
Хоть в теме и заявлена фигура трапеция, но рассмотрение данной темы может проходить в ходе изучения темы «Векторы» и «Использование векторов при решении задач». Понять это можно, взглянув на слайд презентации.
Здесь автор определяет срединную линию как отрезок, соединяющий середины сторон. Причем здесь также отмечено, что средняя линия трапеции параллельна ее основаниям, а также равна их полусумме. Именно в ходе доказательства этого утверждения и пригодятся знания, связанные с векторами. Применяя правила сложения векторов по рисунку, приведенному в качестве иллюстрации условия, получаются равенства. Эти равенства имеют одну и ту же левую часть, и это средняя линия трапеции в виде вектора. Складывая эти равенства, мы получаем большое выражение в правой части равенства.
Складывая эти равенства, мы получаем большое выражение в правой части равенства.
слайды 1-2 (Тема презентации «Средняя линия трапеции», определение средней линии трапеции)
Если внимательно рассмотреть, то в двух случаях получается сложение противоположных векторов, в результате чего получается ноль . Тогда остается, что двойной вектор, содержащий среднюю линию трапеции, равен сумме векторов, содержащих основания. Разделив это равенство на 2, получается, что вектор, содержащий среднюю линию, составляет половину суммы векторов, содержащих основания. Теперь векторы сравниваются. Получается, что все эти векторы имеют одинаковое направление. Это означает, что знаки векторов можно смело опускать. И тогда получается, что самая средняя линия трапеции равна полусумме оснований.
Презентация содержит один слайд, несущий много информации. Здесь дано определение средней линии трапеции и указано ее основное свойство. В курсе геометрии это свойство является теоремой. Вот как доказывается теорема, используя знание понятия векторов и действий над ними.
Вот как доказывается теорема, используя знание понятия векторов и действий над ними.
Преподаватель может дополнить эту презентацию своими примерами и заданиями, но здесь публикуется все, что требуется для среднего уровня знаний по данному предмету. Тем более, что так автор оставил возможность учителю пофантазировать, доработать то, что ему самому хотелось бы, чтобы создать соответствующую атмосферу на уроке. Не забывайте о настрое на само занятие. Тогда с помощью этой презентации вы точно сможете добиться желаемого результата.
Что такое биссектриса? Окружность, описывающая треугольник. Треугольник, вписанный в окружность. Теорема синусов. Отрывок, характеризующий биссектрису
В предыдущем уроке мы рассмотрели свойства биссектрисы угла, как вложенной в треугольник, так и свободной. Треугольник включает в себя три угла, и для каждого из них сохраняются рассматриваемые свойства биссектрисы.
Теорема:
Биссектрисы треугольника AA 1, BB 1, CC 1 пересекаются в одной точке O (рис. 1).
1).
Рис. 1. Иллюстрация к теореме
Доказательство:
Рассмотрим первые две биссектрисы BB 1 и СС 1 . Они пересекаются, точка пересечения O существует. Чтобы доказать это, предположим противное: пусть данные биссектрисы не пересекаются, тогда они параллельны. Тогда прямая ВС есть секущая и сумма углов , это противоречит тому, что во всем треугольнике сумма углов равна .
Итак, точка O пересечения двух биссектрис существует. Рассмотрим его свойства:
Точка O лежит на биссектрисе угла , значит, она равноудалена от его сторон BA и BC. Если ОК перпендикулярен ВС, а ОЛ перпендикулярен ВА, то длины этих перпендикуляров равны -. При этом точка О лежит на биссектрисе угла и равноудалена от его сторон СВ и СА, перпендикуляры ОМ и ОК равны.
Получились следующие равенства:
, то есть все три перпендикуляра, опущенные из точки О на стороны треугольника, равны между собой.
Нас интересует равенство перпендикуляров OL и OM. Это равенство говорит о том, что точка O равноудалена от сторон угла, а значит, лежит на его биссектрисе AA 1.
Это равенство говорит о том, что точка O равноудалена от сторон угла, а значит, лежит на его биссектрисе AA 1.
Таким образом, мы доказали, что все три биссектрисы треугольника пересекаются в одной точке.
Кроме того, треугольник состоит из трех сегментов, а это значит, что мы должны рассматривать свойства одного сегмента.
Сегмент AB дан. Любой отрезок имеет середину, и через нее можно провести перпендикуляр — обозначим его через р. Таким образом, p — серединный перпендикуляр.
Рис. 2. Иллюстрация к теореме
Любая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка.
Докажите, что (рис. 2).
Доказательство:
Рассмотрим треугольники и . Они прямоугольные и равные, так как имеют общий катет ОМ, а катеты АО и ОВ равны по условию, таким образом, имеем два прямоугольных треугольника, равных по двум катетам. Отсюда следует, что гипотенузы треугольников тоже равны, что и требовалось доказать.
Верна обратная теорема.
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Дан отрезок AB, биссектриса к нему равна p, точка M равноудалена от концов отрезка. Докажите, что точка M лежит на серединном перпендикуляре к отрезку (рис. 3).
Рис. 3. Иллюстрация к теореме
Доказательство:
Рассмотрим треугольник. Он равнобедренный, как по условию. Рассмотрим медиану треугольника: точка О — середина основания АВ, ОМ — медиана. Согласно свойству равнобедренного треугольника медиана, проведенная к его основанию, является одновременно и высотой, и биссектрисой. Отсюда следует, что . Но прямая p также перпендикулярна AB. Мы знаем, что единственный перпендикуляр к отрезку AB можно провести в точку O, а это значит, что прямые OM и p совпадают, отсюда следует, что точка M принадлежит прямой p, что и требовалось доказать.
Прямая и обратная теоремы могут быть обобщены.
Точка лежит на серединном перпендикуляре к отрезку тогда и только тогда, когда она равноудалена от концов этого отрезка.
Итак, повторим, что в треугольнике три отрезка и к каждому из них применимо свойство серединного перпендикуляра.
Теорема:
Серединные перпендикуляры треугольника пересекаются в одной точке.
Дан треугольник. Перпендикулярно его сторонам: 1 изн в сторону ВС, 2 изн в сторону АС, 3 изн в сторону АВ.
Докажите, что перпендикуляры Р 1 , Р 2 и Р 3 пересекаются в точке О (рис. 4).
Рис. 4. Иллюстрация к теореме
Доказательство:
Рассмотрим два срединных перпендикуляра P 2 и P 3 , они пересекаются, точка пересечения O существует. Докажем этот факт от противного — пусть перпендикуляры Р 2 и Р 3 параллельны. Тогда угол прямой, что противоречит тому факту, что сумма трех углов треугольника равна . Итак, существует точка O пересечения двух из трех серединных перпендикуляров. Свойства точки О: она лежит на серединном перпендикуляре к стороне АВ, а значит, равноудалена от концов отрезка АВ:. Он также лежит на серединном перпендикуляре к стороне AC, поэтому . Мы получили следующие равенства.
Мы получили следующие равенства.
В предыдущем уроке мы рассмотрели свойства биссектрисы угла, как вложенной в треугольник, так и свободной. Треугольник включает в себя три угла, и для каждого из них сохраняются рассматриваемые свойства биссектрисы.
Теорема:
Биссектрисы треугольника AA 1, BB 1, CC 1 пересекаются в одной точке O (рис. 1).
Рис. 1. Иллюстрация к теореме
Доказательство:
Рассмотрим первые две биссектрисы BB 1 и СС 1 . Они пересекаются, точка пересечения O существует. Чтобы доказать это, предположим противное: пусть данные биссектрисы не пересекаются, тогда они параллельны. Тогда прямая ВС есть секущая и сумма углов , это противоречит тому, что во всем треугольнике сумма углов равна .
Итак, точка O пересечения двух биссектрис существует. Рассмотрим его свойства:
Точка O лежит на биссектрисе угла , а значит, равноудалена от его сторон BA и BC. Если ОК перпендикулярен ВС, а ОЛ перпендикулярен ВА, то длины этих перпендикуляров равны -. При этом точка О лежит на биссектрисе угла и равноудалена от его сторон СВ и СА, перпендикуляры ОМ и ОК равны.
При этом точка О лежит на биссектрисе угла и равноудалена от его сторон СВ и СА, перпендикуляры ОМ и ОК равны.
Получили следующие равенства:
, то есть все три перпендикуляра, опущенные из точки О на стороны треугольника, равны между собой.
Нас интересует равенство перпендикуляров OL и OM. Это равенство говорит о том, что точка O равноудалена от сторон угла, а значит, лежит на его биссектрисе AA 1.
Таким образом, мы доказали, что все три биссектрисы треугольника пересекаются в одной точке.
Кроме того, треугольник состоит из трех сегментов, а это значит, что мы должны рассматривать свойства одного сегмента.
Сегмент AB дан. Любой отрезок имеет середину, и через нее можно провести перпендикуляр — обозначим его через р. Таким образом, p — серединный перпендикуляр.
Рис. 2. Иллюстрация к теореме
Любая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка.
Докажите, что (рис. 2).
Доказательство:
Рассмотрим треугольники и . Они прямоугольные и равные, так как имеют общий катет ОМ, а катеты АО и ОВ равны по условию, таким образом, имеем два прямоугольных треугольника, равных по двум катетам. Отсюда следует, что гипотенузы треугольников тоже равны, что и требовалось доказать.
Верна обратная теорема.
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Дан отрезок AB, биссектриса к нему равна p, точка M равноудалена от концов отрезка. Докажите, что точка M лежит на серединном перпендикуляре к отрезку (рис. 3).
Рис. 3. Иллюстрация к теореме
Доказательство:
Рассмотрим треугольник. Он равнобедренный, как по условию. Рассмотрим медиану треугольника: точка О — середина основания АВ, ОМ — медиана. Согласно свойству равнобедренного треугольника медиана, проведенная к его основанию, является одновременно и высотой, и биссектрисой. Отсюда следует, что . Но прямая p также перпендикулярна AB. Мы знаем, что единственный перпендикуляр к отрезку AB можно провести в точку O, а это значит, что прямые OM и p совпадают, отсюда следует, что точка M принадлежит прямой p, что и требовалось доказать.
Отсюда следует, что . Но прямая p также перпендикулярна AB. Мы знаем, что единственный перпендикуляр к отрезку AB можно провести в точку O, а это значит, что прямые OM и p совпадают, отсюда следует, что точка M принадлежит прямой p, что и требовалось доказать.
Прямая и обратная теоремы могут быть обобщены.
Точка лежит на серединном перпендикуляре к отрезку тогда и только тогда, когда она равноудалена от концов этого отрезка.
Итак, повторим, что в треугольнике три отрезка и к каждому из них применимо свойство серединного перпендикуляра.
Теорема:
Серединные перпендикуляры треугольника пересекаются в одной точке.
Дан треугольник. Перпендикулярно его сторонам: 1 изн в сторону ВС, 2 изн в сторону АС, 3 изн в сторону АВ.
Докажите, что перпендикуляры Р 1 , Р 2 и Р 3 пересекаются в точке О (рис. 4).
Рис. 4. Иллюстрация к теореме
Доказательство:
Рассмотрим два срединных перпендикуляра P 2 и P 3 , они пересекаются, точка пересечения O существует. Докажем этот факт от противного — пусть перпендикуляры Р 2 и Р 3 параллельны. Тогда угол прямой, что противоречит тому факту, что сумма трех углов треугольника равна . Итак, существует точка O пересечения двух из трех серединных перпендикуляров. Свойства точки О: она лежит на серединном перпендикуляре к стороне АВ, а значит, равноудалена от концов отрезка АВ:. Он также лежит на серединном перпендикуляре к стороне AC, поэтому . Мы получили следующие равенства.
Докажем этот факт от противного — пусть перпендикуляры Р 2 и Р 3 параллельны. Тогда угол прямой, что противоречит тому факту, что сумма трех углов треугольника равна . Итак, существует точка O пересечения двух из трех серединных перпендикуляров. Свойства точки О: она лежит на серединном перпендикуляре к стороне АВ, а значит, равноудалена от концов отрезка АВ:. Он также лежит на серединном перпендикуляре к стороне AC, поэтому . Мы получили следующие равенства.
Глоссарий терминов планиметрии — Здесь собраны определения терминов планиметрии. Ссылки на термины в этом словаре (на этой странице) выделены курсивом. # А Б В Г Д Е Ж Ж З И К Л М Н О П Р С … Википедия
коллинеарных точек
Конкурсный прямой — Здесь собраны определения терминов из планиметрии. Ссылки на термины в этом словаре (на этой странице) выделены курсивом. # А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Окружность Аполлония — Здесь собраны определения терминов из планиметрии. Ссылки на термины в этом словаре (на этой странице) выделены курсивом. # А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Ссылки на термины в этом словаре (на этой странице) выделены курсивом. # А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Преобразование плоскости — Здесь собраны определения терминов из планиметрии. Ссылки на термины в этом словаре (на этой странице) выделены курсивом. # А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Чевиана — Здесь собраны определения терминов из планиметрии. Ссылки на термины в этом словаре (на этой странице) выделены курсивом. # А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Глоссарий планиметрии — Эта страница представляет собой глоссарий. См. также основную статью: Планиметрия Здесь собраны определения терминов из планиметрии. Ссылки на термины в этом словаре (на этой странице) выделены курсивом … Википедия
Задача Аполлония — Задача Аполлония состоит в том, чтобы построить окружность, касающуюся трех данных окружностей, используя циркуль и линейку. Согласно легенде, задача была сформулирована Аполлонием Пергским около 220 г. до н.э. е. в книге «Прикосновение», которая была утеряна… Википедия
до н.э. е. в книге «Прикосновение», которая была утеряна… Википедия
Задача Аполлония — Задача Аполлония состоит в том, чтобы построить окружность, касающуюся трех данных окружностей, используя циркуль и линейку. Согласно легенде, задача была сформулирована Аполлонием Пергским около 220 г. до н.э. е. в книге «Прикосновение», которая была утеряна, но была… … Википедия
Диаграмма Вороного — случайное множество точек на плоскости Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, в котором ка … Википедия

Раздаточный материал (Приложение №1)
Задачи на построение с циркулем и линейкой без делений чаще всего решаются по определенной схеме: данные задачи и желаемые элементы.
II. Дом : По плану строят с циркулем и линейкой.
III. Доказательство : Докажите, что построенная фигура удовлетворяет условиям задачи.
IV. Исследование : Проведите исследование по любым данным, есть ли у задачи решение и если да, то сколько решений (не выполнять во всех задачах).
Вот несколько примеров элементарных строительных задач, которые мы рассмотрим:
1. Отложите отрезок, равный этому (изучался ранее).
2. Построение серединного перпендикуляра к отрезку:
- построить середину данного отрезка;
- построить прямую, проходящую через данную точку и перпендикулярную данной прямой (точка может лежать или не лежать на данной прямой).
3. Построение биссектрисы угла.
4. Построение угла, равного заданному.
Построение угла, равного заданному.
Медиана, перпендикулярная сегменту.
Определение: Биссектриса отрезка — это прямая, проходящая через середину отрезка и перпендикулярная ей.
Задание: «Построить серединный перпендикуляр к отрезку». Презентация
О — середина АВ
Описание конструкции ( номер слайда 4 ):
Балка а; А — начало луча
Окружность (А; r =м)
Окружность а = В; AB = m
Круг 1 (A; r 1 > m/2)
Круг 2 (B; r 1)
Круг 1 Круг 2 =
MN ; MN AB =0, (MN = L)
, где MN AB, O — середина AB
III. Доказательство (слайд № 5, 6)
1. Рассмотрим AMN и BNM:
AM = MB=BN=AN=r 2 , поэтому AM = BN , AN = BM MN — общая сторона
(рисунок 3)
Следовательно, AMN = BNM (по 3 сторонам),
Следовательно,
1= 2 (по определению равны)
3= 4 (по определению равны)
и MAN 2. НБМ равнобедренные (по определению) ->
1 = 4 и 3 = 2 (по свойству равнобедренных)
3. Из точек 1 и 2 -> 1 = 3 поэтому МО является биссектрисой равнобедренного АМВ
Из точек 1 и 2 -> 1 = 3 поэтому МО является биссектрисой равнобедренного АМВ
4. Таким образом, мы доказали, что MN является серединным перпендикуляром к отрезку AB
IV. Исследование
Эта задача имеет единственное решение, т.к. любой отрезок имеет только одну середину, и через данную точку можно провести единственную прямую, перпендикулярную данной.
Определение: Геометрический набор точек (GMT) — это набор точек, обладающих некоторым свойством. (Приложение №2)
Известный вам GMT:
- Биссектрисой отрезка называется множество точек, равноудаленных от концов отрезка.
- Биссектриса угла — множество точек, равноудаленных от сторон угла
Итак, докажем теорему:
Теорема: «Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка».
(рисунок 4)
Дано: AB; МО — перпендикулярная биссектриса
Доказать: AM = VM
| Доказательство: 1. 2. Рассмотрим АМО и ВМО — прямоугольные МО — общая ветвь | АО = ВО (О — середина АВ) -> АМО = БМО (на 2-х ножках) -> АМ = ВМ (по определению равных треугольников, как соответствующих сторон) Q.E.D |
Домашнее задание: «Докажите теорему, обратную заданной»
Теорема: «Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку».
(Рисунок 5)
Дано: AB; MA=MV
Докажите : Точка M лежит на серединном перпендикуляре
Доказательство:
То. МО — биссектриса, содержащая все точки, равноудаленные от концов отрезка.
Свойство серединных перпендикуляров к сторонам треугольника
Они пересекаются в одной точке и эта точка является центром описанной вокруг треугольника окружности, которую мы будем изучать в восьмом классе.
Мастерская
Материально-техническое оснащение:
Распространение: 29 574 КБ
ОС: Windows 9x/2000/XP
Сайт: http://www.ascon.ru
Теперь перенесем построение в графическую среду компьютера (слайд №7)
Полученные ранее знания и навыки необходимо применить к конкретной задаче. Вы увидите, что построение займет у вас не больше времени, чем построение в блокноте. Среди прочего интересно посмотреть, как компьютерная среда выполняет человеческие команды для построения плоских фигур. Перед вами приложение №3, в котором подробно описаны ваши этапы построения. Загрузите программу и откройте новый чертеж ( номер слайда 8 , 9).
Нарисуйте геометрические объекты, указанные в условии задачи: луч a с началом в точке А и отрезок равный м – произвольная длина ( номер слайда 10 ).
Ввести обозначение балки, сегмента, начала балки на чертеже с помощью вкладки «Инструменты » текста.
Построить окружность радиусом, равным отрезку м с центром в вершине в заданной точке НО ( номер слайда 11 ).
м с центром в вершине заданной точки А ( слайд №12, 13 ).
Построить окружность с радиусом, равным отрезку больше 1/2 м Для этого выбираем пункт « Между 2 точками» ( слайд №14, 15, 16 ).
Через точки пересечения окружностей М и N провести прямую ( слайд №17,18 ).
Подержанные книги:
- Угринович Н.Д. «Информатика. Базовый курс» 7 класс. — М.: БИНОМ — 2008 — 175 с.
- Угринович Н.Д. «Практикум по информатике и информационным технологиям». Руководство. — М.: БИНОМ, 2004-2006. —
- Угринович Н.Д. «Преподавание курса «Информатика и ИКТ» в 8-11 классах начальной и старшей школы М.: Лаборатория знаний БИНОМ, 2008. — 180 с.
- Угринович Н.Д. Компьютерная мастерская на CD-ROM. — М.: БИНОМ, 2004-2006.
- Богуславский А.
 А., Третьяк Т.М. Фарафонов А.А. «Компас — 3D v 5.11-8.0 Мастерская для начинающих» — М.: СОЛОН — ПРЕСС, 2006 — 272 с.
А., Третьяк Т.М. Фарафонов А.А. «Компас — 3D v 5.11-8.0 Мастерская для начинающих» — М.: СОЛОН — ПРЕСС, 2006 — 272 с. - Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. «Геометрия 7-9. Учебник для общеобразовательных школ» — М: Просвещение 2006 — 384 с.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. «Изучение геометрии 7-9 классы. Методические указания к учебнику» — М: Просвещение 1997 — 255 с.
- Афанасьева Т.Л., Тапилина Л.А. «Планы уроков к учебнику 8 класса Атанасяна Л.С.» — Волгоград «Учитель» 2010, 166 с.
Заявка №1
План решения задач на построение циркуля и линейки.
- Анализ.
- Строительство.
- Доказательство.
- Исследование.
Объяснение
- При выполнении анализа схематически вычерчивается требуемый рисунок и устанавливается связь между данными задания и требуемыми элементами.
- По плану построение ведется с помощью циркуля и линейки.

- Доказывают, что построенная фигура удовлетворяет условиям задачи.
- Провести исследование: для любых данных есть ли у задачи решение, и если да, то сколько решений?
Примеры задач на элементарное построение
- Отложите отрезок, равный заданному.
- Построить серединный перпендикуляр к отрезку.
- Построить середину отрезка.
- Построить прямую, проходящую через заданную точку перпендикулярно заданной прямой (точка может лежать или не лежать на заданной прямой).
- Построить биссектрису угла.
- Постройте угол, равный заданному.
Приложение №2
Геометрическое место точек (GMT) представляет собой набор точек, обладающих некоторым свойством.
Примеры GMT:
- Серединным перпендикуляром к отрезку называется множество точек, равноудаленных от концов отрезка.
- Окружность — это множество точек, равноудаленных от данной точки — центра окружности.
 92), где нижний индекс указывает на сторону, к которой проведен перпендикуляр, S — площадь треугольника, а также предполагается, что стороны связаны неравенствами a\geqslant b\geqslant c. p_a\geq p_b и p_c\geq p_b. Другими словами, для треугольника наименьший биссектриса относится к среднему отрезку.
92), где нижний индекс указывает на сторону, к которой проведен перпендикуляр, S — площадь треугольника, а также предполагается, что стороны связаны неравенствами a\geqslant b\geqslant c. p_a\geq p_b и p_c\geq p_b. Другими словами, для треугольника наименьший биссектриса относится к среднему отрезку.Написать отзыв о статье «Средний перпендикуляр»
Примечания
Отрывок, характеризующий серединный перпендикуляр
Кутузов, перестав жевать, удивленно уставился на Вольцогена, как бы не понимая, что ему говорят. Вольцоген, заметив волнение des alten Herrn, [старый джентльмен (немец)], сказал с улыбкой:
— Я не счел себя вправе скрывать от вашей светлости то, что видел… Войска в полном беспорядке. ..
— Видели? Вы видели? .. — нахмурившись, крикнул Кутузов, быстро вставая и наступая на Вольцогена. «Как ты смеешь… как ты смеешь…!» — закричал он, делая угрожающие жесты, тряся руками и задыхаясь. — Как вы смеете, милостивый государь, говорить мне это. Вы ничего не знаете. Передайте от меня генералу Барклаю, что его сведения неверны и что действительный ход сражения известен мне, главнокомандующему, лучше, чем ему.
Вы ничего не знаете. Передайте от меня генералу Барклаю, что его сведения неверны и что действительный ход сражения известен мне, главнокомандующему, лучше, чем ему.
Вольцоген хотел что-то возразить, но Кутузов перебил его.
— Противник отброшен на левом и разгромлен на правом фланге. Если вы плохо видели, милостивый государь, то не позволяйте себе говорить того, чего вы не знаете. Сходи, пожалуйста, к генералу Барклаю и передай ему мое непременное намерение завтра атаковать неприятеля, — сурово сказал Кутузов. Все молчали, и слышно было одно тяжелое дыхание запыхавшегося старого генерала. — Везде отбиты, за что благодарю Бога и нашу храбрую армию. Враг разбит, и завтра мы его прогоним со святой русской земли, — сказал Кутузов, перекрестившись; и вдруг расплакалась. Вольцоген, пожав плечами и скривив губы, молча отошел в сторону, удивляясь uber diese Eingenommenheit des alten Herrn. [об этой тирании старого джентльмена. (немецкий)]
— Да вот он, мой богатырь, — сказал Кутузов пухлому, красивому черноволосому генералу, входившему в это время в курган.


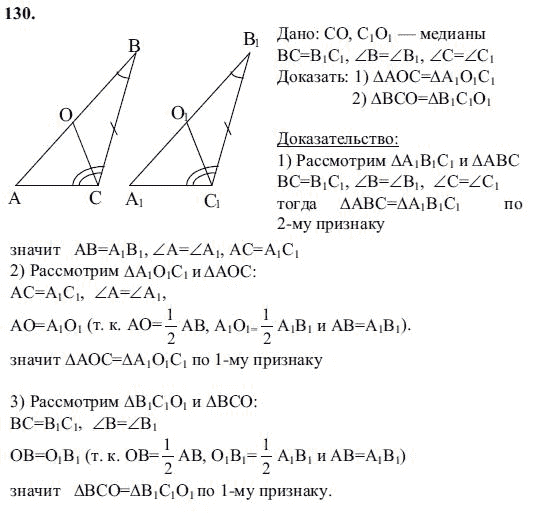

 Решебник к учебнику — Геометрия. 7—9 классы Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Ссылки удалены.
Решебник к учебнику — Геометрия. 7—9 классы Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Ссылки удалены. ru, содержит подробные решения всех задач.
ru, содержит подробные решения всех задач. В первую очередь, это касается точных наук: именно в этот период относительно простая математика разделяется на сложнейшие предметы – алгебру и геометрию.
В первую очередь, это касается точных наук: именно в этот период относительно простая математика разделяется на сложнейшие предметы – алгебру и геометрию. net
net ГДЗ помогут выполнить домашние задания. На нашем сайте собрано несколько вариантов решебников , в которых вы…
ГДЗ помогут выполнить домашние задания. На нашем сайте собрано несколько вариантов решебников , в которых вы… Готовые домашние задания Атанасян позволят вам понять, как вычисляются тригонометрические функции, значения углов, площади фигур, длины дуг окружности.
Готовые домашние задания Атанасян позволят вам понять, как вычисляются тригонометрические функции, значения углов, площади фигур, длины дуг окружности. ..
.. Тип: Учебник. Авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин. Издательство: Просвещение 2016. Геометрия – это наука о фигурах, занимающаяся взаимным расположением и размерами их частей, выражающихся в…
Тип: Учебник. Авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин. Издательство: Просвещение 2016. Геометрия – это наука о фигурах, занимающаяся взаимным расположением и размерами их частей, выражающихся в… ..
.. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева и др. Если задачи по геометрии ставят вас в тупик, то подробные решения сборника помогут разобраться с алгоритмом выполнения заданий и их оформлением, развить абстрактное мышление, усвоить…
С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева и др. Если задачи по геометрии ставят вас в тупик, то подробные решения сборника помогут разобраться с алгоритмом выполнения заданий и их оформлением, развить абстрактное мышление, усвоить…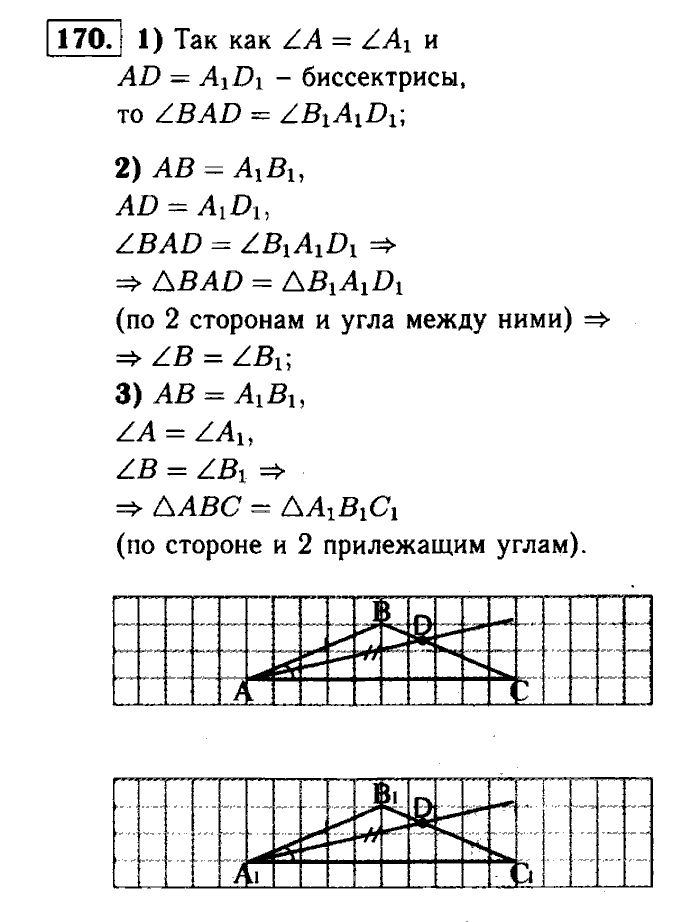 plus
plus
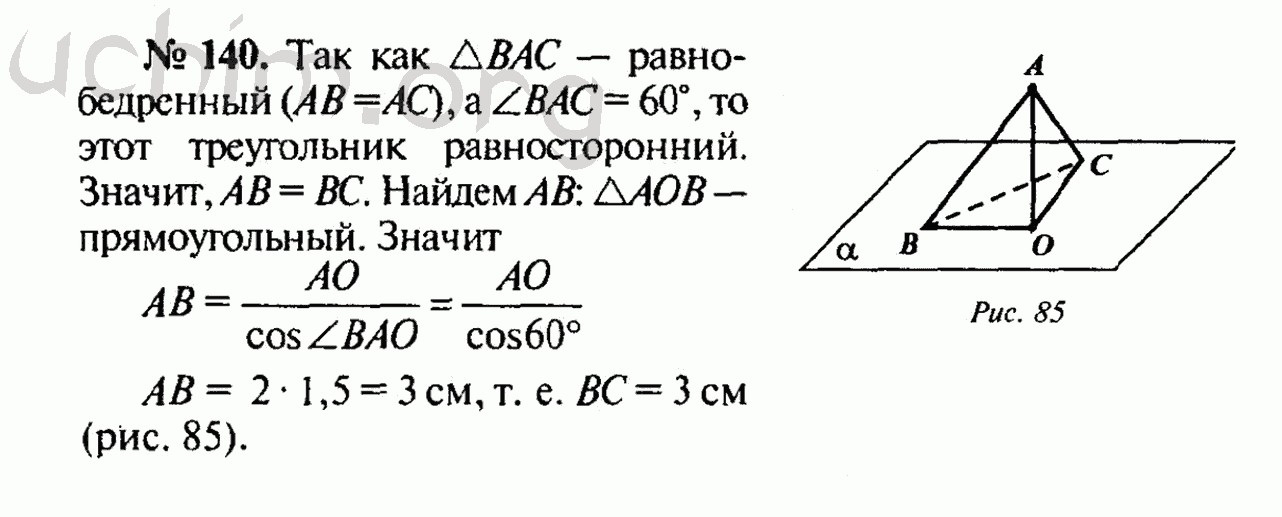
 com
com Специально для родителей и только у нас даны ОТВЕТЫ и РЕШЕНИЯ на задачи из учебника (ГДЗ).
Специально для родителей и только у нас даны ОТВЕТЫ и РЕШЕНИЯ на задачи из учебника (ГДЗ).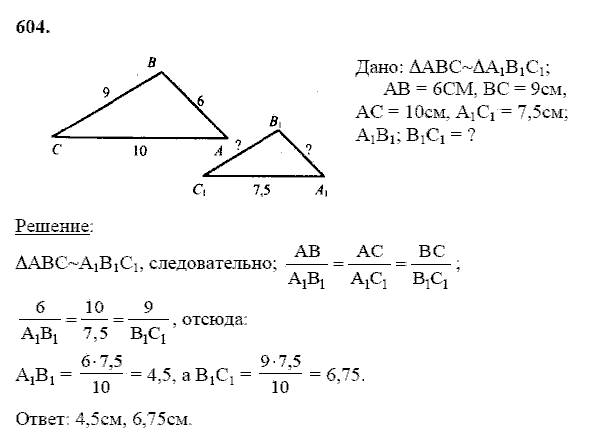 С.
С. В этом разделе объясняются теоремы и доказательства по равнобедренным треугольникам, а также приводятся задачи на построение разных геометрических окружностей.
В этом разделе объясняются теоремы и доказательства по равнобедренным треугольникам, а также приводятся задачи на построение разных геометрических окружностей. Здесь вы найдете решение задач, в которых нужно определить, сколько граней и ребер имеет прямоугольный параллелепипед и октаэдр, либо доказать, что площадь боковой поверхности прямой призмы равна произведению периметра основания на боковое ребро. Также здесь даны ответы на задания, требующие построить правильный треугольник по заданным данным, найти объемы частей призмы или длину окружности.
Отдельно в пособии произведены вычисления сечения куба; доказано, что площадь закрашенной фигуры равна площади круга на представленном рисунке; построены трапеция и треугольник по трем медианам. Также школьники найдут здесь построенные отрезки по заданным данным и сечение параллелепипеда, вычисленную площадь круга и призмы, и т.д.
Здесь вы найдете решение задач, в которых нужно определить, сколько граней и ребер имеет прямоугольный параллелепипед и октаэдр, либо доказать, что площадь боковой поверхности прямой призмы равна произведению периметра основания на боковое ребро. Также здесь даны ответы на задания, требующие построить правильный треугольник по заданным данным, найти объемы частей призмы или длину окружности.
Отдельно в пособии произведены вычисления сечения куба; доказано, что площадь закрашенной фигуры равна площади круга на представленном рисунке; построены трапеция и треугольник по трем медианам. Также школьники найдут здесь построенные отрезки по заданным данным и сечение параллелепипеда, вычисленную площадь круга и призмы, и т.д. Онлайн решебник поможет проконтролировать правильность выполнения работы и объяснить ребёнку решение задачи любой сложности.
Онлайн решебник поможет проконтролировать правильность выполнения работы и объяснить ребёнку решение задачи любой сложности.