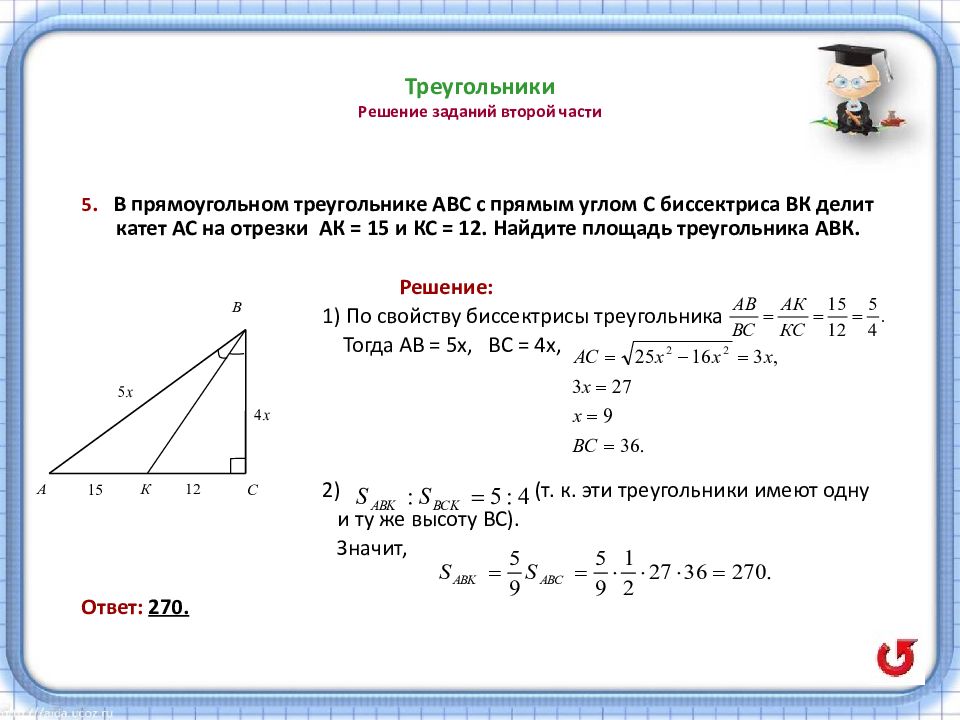
Методы решения геометрических задач — Пособие по геометрии
При решении геометрических задач обычно используются три основных метода: геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем; алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений; комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других — алгебраическим.
Какой бы путь решения ни был выбран, успешность его использования зависит, естественно, от знания теорем и умения их применять.
Метод дополнительного построения
Всякое геометрическое
решение геометрической задачи начинается с работы над чертежом. При этом иногда
на «естественном» чертеже (т.е. на чертеже, на котором изображено только
условие) трудно заметить связи между данными и искомыми величинами, а если
фигуру достроить, эти связи становятся очевидными.
Метод подобия
Подобие треугольников
Две фигуры F и F1 называются подобными, если они переводятся друг в друга преобразованием подобия, т.е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз.
Признаки подобия треугольников:
1) Если два угла одного соответственно равны двум углам другого;
2) Если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами равны;
3) Если три стороны одного треугольника пропорциональны трем сторонам другого.
Метод замены
Метод
замены широко применяется в алгебре, но не менее эффективно «замена» может быть
применена в геометрии. Сущность этого приема решения геометрических задач
состоит в следующем: фигура, о которой идет речь в условии задачи, так
заменяется фигурой с той же искомой величиной, чтобы найти эту величину было
легче.
Сущность этого приема решения геометрических задач
состоит в следующем: фигура, о которой идет речь в условии задачи, так
заменяется фигурой с той же искомой величиной, чтобы найти эту величину было
легче.
Суть метода заключается в том, что исходя из условия задачи составляют уравнение (или систему уравнений). В качестве вспомогательных аргументов удобно выбирать величины, которые вместе с данными из условия задачи дают набор элементов, однозначно задающих некоторую фигуру.
Метод площадей
В
математических задачах часто бывает полезен такой прием: двумя способами найти
одну и ту же величину и приравнять полученные для нее выражения. Пусть мы,
например, двумя способами нашли площадь некоторой фигуры. Если в одном из
выражений для площади входит, скажем синус какого-либо угла α, то при помощи
соотношения
из
полученного равенства можно получить некоторое неравенство, порой интересное.
Метод «вспомогательных объёмов»
Для нахождения расстояния от точки до плоскости или при нахождении углов между прямой и плоскостью метод «вспомогательного объёма» во многих случаях оказывается наиболее эффективным. Суть метода заключается в том, что объём некоторой фигуры выражается двумя способами, а затем из полученных равенств выражается искомая величина. Причём в этом методе нет необходимости строить проекцию прямой на плоскость или проекцию точки, что во многих случаях оказывается очень затруднительным.
Векторный метод
Применение критериев коллинеарности и компланарности векторов в решении задач.
Критерии
коллинеарности и компланарности векторов служат основной для применения
векторной алгебры в решении стереометрических задач. Они позволяют выразить в
виде векторных равенств различные утверждения о расположенных точках, прямых и
плоскостей в пространстве. Переход от векторных равенств к скалярным происходит
на основе единственности разложения вектора по двум неколлинеарным и трём
некомпланарным векторам.
Координатный метод
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. И, решая ту или иную геометрическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще, удобнее. Некоторые виды координатных систем, отличные от прямоугольных.
1.Косоугольные (аффинные) координаты.
2.Полярные координаты.
3.Цилиндрические координаты.
4.Сферические координаты.
5.Прямоугольные координаты.
Рассмотрим самые употребительные и простые координаты в пространстве, называемые прямоугольными. Их называют ещё декартовыми по имени Рене Декарта (1596-1650) – французского учёного и философа, впервые ввёдшего координаты в геометрию (на плоскость).
Как решать задачи по геометрии. Часть 1
Геометрическая логика при решении задач
Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.
Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.
Это про тебя? Тогда ты попал туда, куда нужно!
Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.
Сразу оговорюсь — без знания теории в геометрии никак. В смысле, вообще никак, от слова «совсем». Чтоб тебе было полегче при чтении этой статьи, я буду внутри решений задач в скобках курсивом указывать используемые свойства и теоремы. Но помни: если вдруг в знании теории у тебя пробел – закрытие его за тобой! Бери учебник и читай. Причем главные вещи – заучивай (или понимай). Знать теорию – обязательно!
Ладно, к делу.
Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?
Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.
Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.
А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.
К чему весь этот разговор? Решение задачи по геометрии это точно такой же «квест», только математический . Вдумайся: у нас всегда есть некоторые исходные данные и есть то, что нужно найти (или доказать – разницы на самом деле практически нет). И наша задача – построить логическую цепочку от исходных данных к цели. Строительным материалом при этом у нас будут данные (исходные и полученные при рассуждениях), а также теоремы и свойства.
Ладно, давай уже конкретный пример разберем.
Задача. В треугольнике \(ABC\) из точки \(B\) проведена высота \(BH\). Найти длину отрезка \(AH\), если известно, что сторона \(AC\; =\; 14\) см и угол \(A\) равен углу \(C\).
Так.
В геометрии это означает:
- построить чертежа выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
- выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
Хорошо. Значит, текущая ситуация у нас такова:
Давайте потихоньку развеивать туман. Нам известно, что углы \(А\) и \(С\) равны, а это значит, что треугольник \(АВС\) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.
Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что \(BH\) – высота. А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.
А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.
А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка \(H\) делит сторону \(AC\) пополам. То есть \(AH = HC\).
Стоп. Так у нас же есть длина стороны \(AC\)! И если мы знаем, что точка \(H\) делит сторону \(AC\) пополам, значит, \(AH\) равен половине \(AC\)! Таким образом, получаем, что \(AH = AC/2 = 14/2=7\) см.
Готово. Ответ получен.
Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:
А записывается примерно так:
Решение задач по геометрии по фото
Даже прилежный ученик может столкнуться со сложностями при подготовке уроков. Если вам требуется найти решение трудных задач по геометрии по фотографии, читайте эту статью. Из нее будет ясно, какие ресурсы и программы стоят внимания.
Znanija — приложение, которое поможет решить уравнение по геометрии
На сайте znanija.com пользователи могут выкладывать фотографии с геометрическими задачками. Это русскоязычный сегмент проекта brainly.com. Он позволяет ученикам обращаться за квалифицированной помощью специалистов со всего мира.
Вы можете найти приложение «Знания» по запросу «Brainly» на платформе App Store или Google Play. Скачайте эту программу на свой телефон, чтобы пообщаться с экспертами и отличниками.
Основные достоинства приложения для решения сложных задач по геометрии:
| Преимущества приложения: | Пояснения: |
|---|---|
Здесь разбирающиеся в предмете люди могут оказать посильную помощь тем, кто в этом нуждается. | Набирайте за это баллы и получайте увеличение статуса. Чтобы увидеть размер вознаграждения, посмотрите на иконку в правом верхнем углу от вопроса. Наведите на нее курсор, и вы сможете узнать больше о системе баллов. |
| Если не хотите ожидать ответа, воспользуйтесь поиском по архиву. | В библиотеке «Знания» накопилось уже немало готовых решений задач. Наверняка там найдется и нужная вам информация. |
| В приложении есть встроенные покупки. | Однако цена годовой подписки на App Store сравнительно невелика. |
| Сообщество работает круглосуточно. | Пользователи проживают в разных часовых поясах, поэтому могут отвечать на вопросы в любое время. |
Для записи геометрических функций и математических знаков работает клавиатура LaTeX.
В приложении можно получить помощь по всем базовым предметам, включая геометрию. Доступны такие языки как украинский, казахский, белорусский.
Чтобы вас не ввели в заблуждение, эксперты сообщества просматривают ответы к задачам и оставляют пометку «Проверенный». Если вы ее увидите, то можете полагаться на такой комментарий.
Если вы ее увидите, то можете полагаться на такой комментарий.
Ответы находятся очень быстро. Решение большинства задач по геометрии находится в течение первых 10 минут с момента загрузки фото в приложение. Однако на всякий случай постарайтесь скидывать снимки заранее. Даже если вы получите ответ сразу, у вас останется больше времени на то, чтобы понять объяснение и подготовиться к уроку.
Photomath — быстрое выполнение задач по фотографии
Некоторые задачи из тригонометрии можно решить с помощью приложения Photomath. Однако это касается примеров, записанных с помощью цифр и математических формул. Разобраться с рисунками геометрических фигур Photomath не сможет.
Чтобы скачать приложение для OS Android, переходите на площадку Google Play. Версия для Айфонов лежит на сайте App Store.
Desmos Graphing Calculator — онлайн-калькулятор по геометрии
Продвинутый графический калькулятор Десмос позволяет решать задачки по алгебре и геометрии на компьютере по фотографии. Аддон для Google Chrome можно установить в магазине расширений. Официальный сайт программы находится по адресу https://www.desmos.com/calculator?lang=ru.
Аддон для Google Chrome можно установить в магазине расширений. Официальный сайт программы находится по адресу https://www.desmos.com/calculator?lang=ru.
Своя версия приложения для Android представлена и в магазине Google Play. Владельцы Айфонов и Айпадов могут загрузить программу из App Store. Это абсолютно бесплатный софт, который доступен любому желающему.
«Геометрия» — приложение, которое решает формулы по фото
Большинство выложенных в онлайн-магазинах приложений содержат лишь справочники формул. Хотя они могут быть полезны в процессе самоподготовки или в качестве шпоры, поручить им решение заданий не получится. Однако это не относится к бесплатной программе «Геометрия» от NaNSolvers.
Данный софт выложен в Google Market. Он зарабатывает на показах рекламы, которую пользователю требуется просмотреть для перехода к решению задач. Также есть возможность докупить PRO-версию, чтобы получить доступ к дополнительной информации на более сложные темы.
Как работать с этим софтом для решения сложных задач по предмету геометрия:
- Просто перенесите рисунок из вашего учебника в приложение с помощью встроенных инструментов.
- В результате программа выдаст решение, снабженное подробными пояснениями к каждому шагу.
- Если приложение сразу же не запускается на русском языке, выберите его самостоятельно в «Настройках», или «Settings».
Программа справится с любой задачкой по геометрии. Если вы столкнулись с ошибкой, напишите разработчикам. Они продолжают работать над софтом, чтобы сделать его еще полезнее.
Это может быть полезным: Uchi.ru вход на сайт: Регистрация — Я родитель.
Allcalc Geometry — бесплатная программа для помощи в решении задач
Скачать программу можно с платформы Google Play. Она функционирует по аналогии с приложением «Геометрия». Из недостатков данного ПО стоит отметить невозможность выгрузить результат расчетов на онлайн-ресурс или сохранить его на телефон. Его придется либо запоминать, либо переписывать вручную.
Его придется либо запоминать, либо переписывать вручную.
Приложение вышло уже давно, однако по-прежнему поддерживается разработчиками. С изображениями оно не работает, однако вы можете перенести информацию с фотографии вручную. Это удобный калькулятор, в котором легко делать простые расчеты для строительства, при сборке мебели и в процессе выполнения других повседневных работ.
Видео-инструкция
В данном видео вы узнаете, каким образом делать решение разных задач по геометрии через приложение Brainly по фотографии.
App Store: Пифагория
Изучайте геометрию, играя на клетчатом поле.
> Более 350 уровней: от элементарных до настоящих головоломок
> 28 разделов для исследования
> 70+ геометрических терминов в словаре
> Простое управление
> Легкий и удобный интерфейс
> Развивайте воображение и тренируйте память
***О Пифагории***
Пифагория – это коллекция геометрических задач различной тематики, которые можно решить без сложных построений и вычислений. Все фигуры изображены на клетчатом поле, как в тетрадке. Многие уровни можно пройти просто за счет геометрической интуиции или самостоятельно, без всяких теорем, находя закономерности и симметрию.
Все фигуры изображены на клетчатом поле, как в тетрадке. Многие уровни можно пройти просто за счет геометрической интуиции или самостоятельно, без всяких теорем, находя закономерности и симметрию.
*** Просто играйте ***
Здесь нет сложных и хитрых инструментов. Вы можете только строить отрезки или прямые и ставить точки в пересечениях линий. Но этого оказывается достаточно, чтобы обеспечить бесконечное множество интересных построений и неожиданных задач.
*** Все определения под рукой ***
Если вы забыли какое-нибудь определение, можно посмотреть его в глоссарии. Термины, упоминающиеся в условии задачи, всегда под рукой – просто нажмите на кнопку «Информация».
*** Для кого эта игра ***
Пользователи Euclidea смогут взглянуть на построения по-другому, открыть для себя новые подходы к решению задач и проверить свою геометрическую интуицию.
Пользователи Пифагории с треугольной сеткой тоже не будут скучать – клетчатое поле требует другой подход к решению задач.
Тем, кто только начинает своё знакомство с геометрией, игра поможет понять важные идеи и свойства Евклидовой геометрии.
Тем, кто считает, что изучил геометрию, игра будет очень полезна, потому что задачи охватывают большинство понятий начального курса элементарной геометрии.
Если же у вас не сложились отношения с геометрией, Пифагория поможет вам взглянуть на этот предмет по-новому. Мы получаем множество отзывов, что Пифагория и Euclidea позволили увидеть красоту и естественность геометрических построений и даже втянуться в решение задач. Попробуйте!
Если у вас есть дети, не упустите возможности приобщить их к математике. Пифагория – отличный способ подружиться с геометрией и провести время с пользой.
*** Охваченные темы ***
> Длина, расстояние, площадь
> Параллели и перпендикуляры
> Углы и треугольники
> Биссектрисы, медианы, высоты, серединные перпендикуляры
> Теорема Пифагора
> Окружности и касательные
> Параллелограммы, квадраты, ромбы, прямоугольники и трапеции
> Симметрия, отражение, вращение
*** Почему Пифагория ***
Пифагор Самосский – древнегреческий философ и математик, живший в VI в.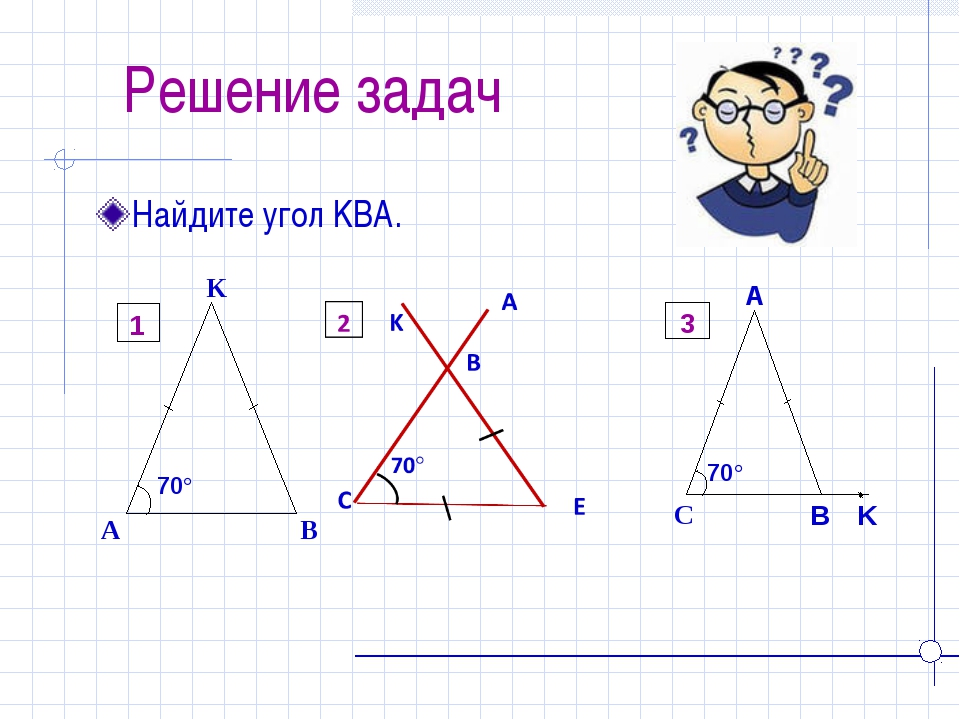 до н.э. Его имя носит один из самых известных геометрических фактов – теорема Пифагора. В ней утверждается, что в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе (стороне, противоположной прямому углу), равна сумме площадей квадратов, построенных на двух других сторонах (катетах). Играя в Пифагорию, вы часто встречаете прямые углы и опираетесь на теорему Пифагора, чтобы сравнивать длины отрезков и расстояния между точками. Вот почему игра названа в честь Пифагора.
до н.э. Его имя носит один из самых известных геометрических фактов – теорема Пифагора. В ней утверждается, что в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе (стороне, противоположной прямому углу), равна сумме площадей квадратов, построенных на двух других сторонах (катетах). Играя в Пифагорию, вы часто встречаете прямые углы и опираетесь на теорему Пифагора, чтобы сравнивать длины отрезков и расстояния между точками. Вот почему игра названа в честь Пифагора.
*** Дерево ***
Дерево Пифагора – это фрактал, состоящий из квадратов и прямоугольных треугольников или, другими словами, из фигур, известных как «Пифагоровы штаны». Ваше дерево подрастает с каждой решённой задачей и получается уникальным, отличаясь от других по форме. А после того, как все уровни решены, вы увидите его цветение. Всё зависит от вас. Удачи!
*** Вопросы? Комментарии? ***
Отправляйте ваши запросы и будьте в курсе последних новостей о Пифагории на https://www.euclidea.xyz/
Задачи с синусом.
 Задачи на синусы и косинусы. Задачи косинусы синусы решение. Многие ученики путаются в решении задач используя синус и косинус угла, мы подробно разберём решение таких задач, ведь если разобраться и верно нарисовать рисунок, то это не так уж и сложно. В этой статье вместе с myalfaschool.ru мы научимся решать такие задачи, также ты можешь записаться на бесплатный пробный урок здесь.
Задачи на синусы и косинусы. Задачи косинусы синусы решение. Многие ученики путаются в решении задач используя синус и косинус угла, мы подробно разберём решение таких задач, ведь если разобраться и верно нарисовать рисунок, то это не так уж и сложно. В этой статье вместе с myalfaschool.ru мы научимся решать такие задачи, также ты можешь записаться на бесплатный пробный урок здесь.Задача 1: \(10\)-метровая лестница опирается на здание таким образом, что угол подъема от земли до здания составляет \(30˚\) градусов. Найдите расстояние от вершины лестницы до земли, кроме того, найдите расстояние от здания до подножья лестницы.
Решение.
\(AB-\)длина лестница, \(BC-\)расстояние от вершины лестницы до земли, \(AC-\)расстояние от здания до подножья лестницы. Угол \(∠BCA\) равен \(90˚\).
- 1. Рассмотрим синус угла \(∠BAC\) и найдем \(BC-\) :
\(sin30=\frac{BC}{AB}\)
\(\frac{1}{2}=\frac{BC}{10}—>1*10/2=5—>BC=5\)
- 2.
 Далее рассмотрим косинус угла \(∠BAC\) и найдем \(AC:\)
Далее рассмотрим косинус угла \(∠BAC\) и найдем \(AC:\)
\(cos30=\frac{AC}{AB}\)
\(\frac{\sqrt{3}}{2}=\frac{AC}{10}—>\sqrt{3}*10/2=5—>AC=5\sqrt{3}\)
Ответ: \(BC=5\) м, \(AC=5\sqrt{3}\) м.
Задача 2. Смотритель маяка видит корабль под углом 60˚ . Найдите расстояние от верха маяка до коробля и от низа маяка до корабля, если высота маяка 50 м.
Решение.
\(AB-\)высота маяка, \(BC-\)расстояние от верха маяка до коробля, \(AC-\) расстояние от низа маяка до корабля. Угол \(∠BCA\) равен \(90˚\).
- 1. Рассморим синус угла \(∠BAC\) и найдем \(AB\):
\(sin60=\frac{BC}{AB}\)
\(\frac{\sqrt{3}}{2}=\frac{50}{AB}—>2*50/\sqrt{3}=10/1,73=57,8—>AB≈57,8\)
- 2. Рассморим косинус угла \(∠BAC\) и найдем \(AC\) :
\(cos60=\frac{AC}{AB}\)
\(\frac{1}{2}=\frac{AC}{57,8}—>1*57,8/2=28,9—>AC≈28,9\)
Ответ: \(AB≈57,8\) м, \(AC≈28,9 \) м.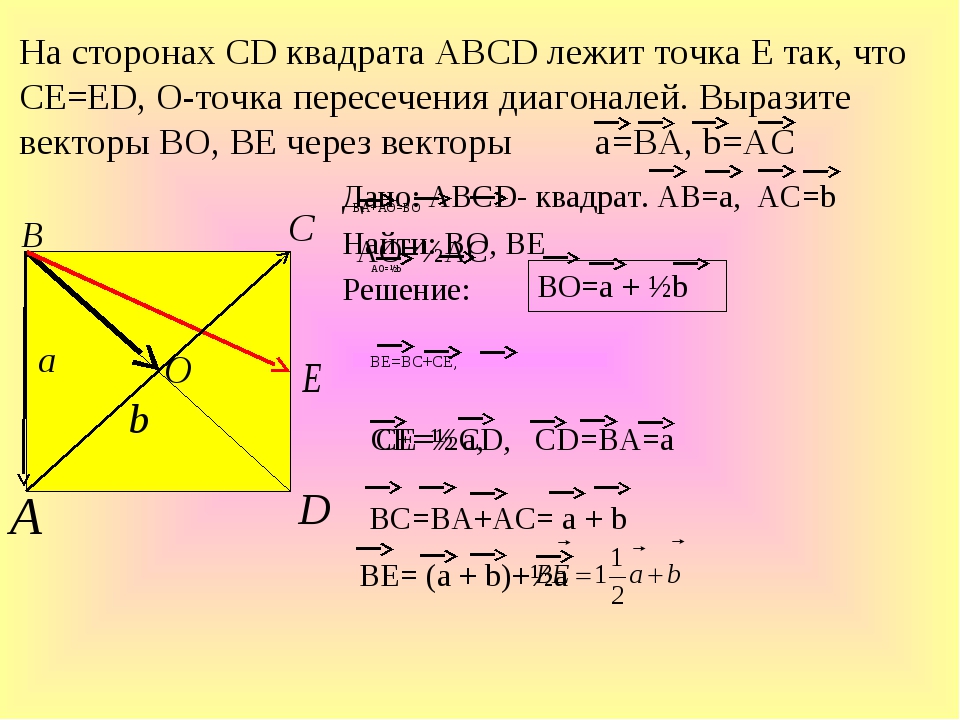
Задача 3. Скалолаз поднимается на 15-градусный уклон у подножья горы. Если он поднимается с постоянной скоростью 3 м в час, то на какой высоте он будет через 5 часов?
Решение.
- 1. Вычислим расстояние \(AB\) через \(5\) часов: \(5*3=15\) м под уклоном \(15˚\).
- 2. \(AB-15\) м , угол \(∠BAC\) = \(15˚\). Рассмотрим синус угла \(∠BAC\):
\(sin(15)=\frac{BC}{AB}\)
\(0,65=\frac{BC}{15}—> BC = 9,75\)
Ответ: \(9,75 \) м.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Пермский государственный гуманитарно-педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике.
Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике.
Репетитор по математике
Донецкий государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 7-11 классов. Математика двигает человечество вперёд. Она помогает учёным познать окружающий мир.
Я люблю математику за то, что она дисциплинирует и воспитывает ум. Это очень важно в современном быстроменяющемся мире. Недаром говорят, что математика – это гимнастика ума.
Приоритетом для меня является всестороннее развитие умственных способностей своих учеников, в особенности логического и творческого мышления на основе глубокого знания и понимания предмета. Мне важно видеть реальную позитивную динамику роста моего ученика от урока к уроку, применять индивидуальный подход для достижения необходимого результата.
Самое главное в работе с детьми — настроиться на их волну. Для меня главное, чтобы обучение проходило в непринужденной и доброжелательной атмосфере, чтобы, получая новые знания, ребенок раскрыл и приумножил свои способности, чтобы полученный результат порадовал его и послужил основой для дальнейшего развития.
Математика двигает человечество вперёд. Она помогает учёным познать окружающий мир.
Я люблю математику за то, что она дисциплинирует и воспитывает ум. Это очень важно в современном быстроменяющемся мире. Недаром говорят, что математика – это гимнастика ума.
Приоритетом для меня является всестороннее развитие умственных способностей своих учеников, в особенности логического и творческого мышления на основе глубокого знания и понимания предмета. Мне важно видеть реальную позитивную динамику роста моего ученика от урока к уроку, применять индивидуальный подход для достижения необходимого результата.
Самое главное в работе с детьми — настроиться на их волну. Для меня главное, чтобы обучение проходило в непринужденной и доброжелательной атмосфере, чтобы, получая новые знания, ребенок раскрыл и приумножил свои способности, чтобы полученный результат порадовал его и послужил основой для дальнейшего развития.
Репетитор по математике
Национальный исследовательский ядерный университет «МИФИ»
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Считаю, что математика доступна для каждого: это увлекательный мир чисел и операций над ними.
Со мной вы поймёте, что математика может быть очень интересной, если найти свой путь к ней!
Считаю, что математика доступна для каждого: это увлекательный мир чисел и операций над ними.
Со мной вы поймёте, что математика может быть очень интересной, если найти свой путь к ней!
Логарифмы (урок)
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Алгоритм решения задач на доказательство равенства треугольников
Проблемы преподавания геометрии в 7 классе общеизвестны. Учителю необходимо добиться, что бы ученики осознали необходимость доказательства различного рода положений; выработать у них навык решения таких задач.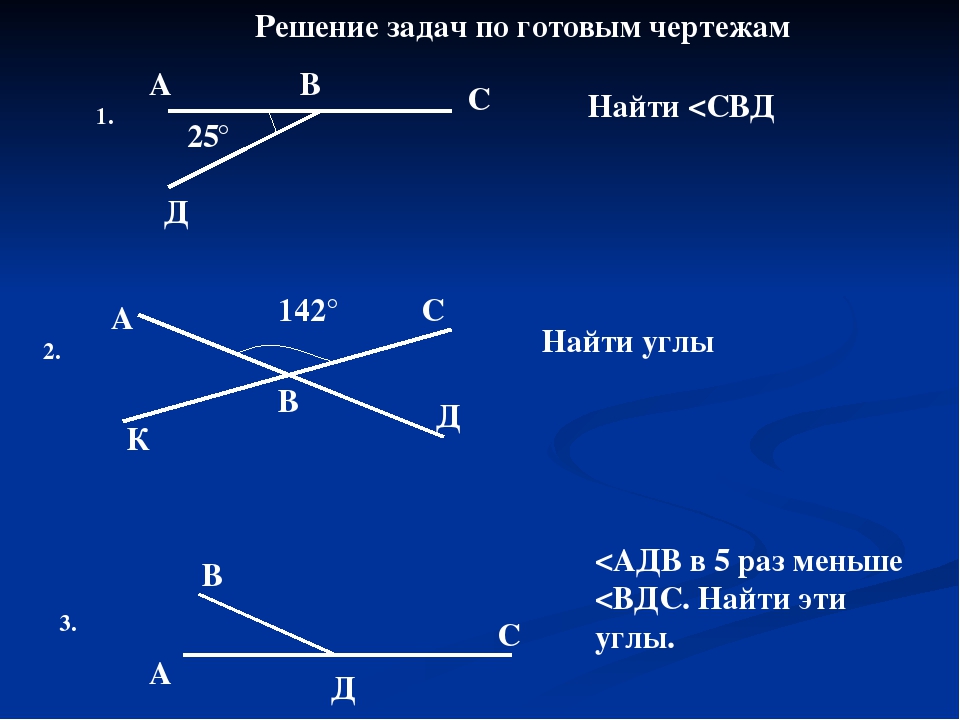
Единство теории и практики — один из основных принципов преподавания геометрии. Решению задач отводится большая роль. Задачи по геометрии следует решать не от случая к случаю, а повседневно, на каждом уроке, в тесной связи с изучаемой теорией. На уроках геометрии надо чаще решать задачи на доказательство и построение. Очень важно научить ученика понимать чертеж, выделять на чертеже необходимые детали. Часто ученик не понимает содержание теоремы или решение задачи из-за того, что не видит отчетливо на чертеже те фигуры, о которых идет речь и рассмотрение которых дает решение вопроса.
Я предлагаю для обучения учащихся решению задач на доказательство равенства треугольников воспользоваться следующим алгоритмом, который содержит некоторые подсказки, помогает отыскать на чертеже необходимые для доказательства фигуры.
Алгоритм решения задач на доказательство равенства треугольников
1. РАССУЖДАЕМ
РАССУЖДАЕМ
Чтобы доказать, что два треугольника равны, необходимо найти три пары соответственно равных элементов:
- две стороны и угол между ними (1 признак)
- сторону и два прилежащих к ней угла (2 признак)
- три стороны (3 признак)
Равные элементы (стороны или углы) могут быть указаны в условии задачи, либо анализируем чертёж (вертикальные углы, общая сторона, биссектриса угла, медиана в треугольнике или середина отрезка). Равные элементы необходимо отметить на чертеже – это облегчит рассуждения.
2. ЗАПИСЫВАЕМ РЕШЕНИЕ
Рассмотрим треугольник… и треугольник….
- … =… (по условию)
- … =… (по условию)
- …=… (почему данные элементы равны?)
Значит треугольник… равен треугольнику… по (указать признак равенства треугольников)
Итак, как выписать равные элементы.
1. Выписываем те элементы, равенство которых дано в условии.
2. Недостающие равные углы можно получить из следующих условий:
|
1 |
|
(по св-ву вертикальных углов) |
|
2 |
|
DC – биссектриса. Это означает равенство углов: (т. к. DC – биссектриса) |
|
3 |
|
RO – высота. (т. к. RO – высота)
|
|
4 |
|
RO QP. Это означает равенство углов: (т. к. RO QP)
|
|
5 |
|
Для треугольников ВСЕ и АСD угол С общий: — общий |
|
6 |
|
Углы, смежные с равными – равны. (как смежные с равными) |
Недостающие равные стороны можно получить из следующих условий:
|
1 |
|
Общая сторона DC (общая) |
|
2 |
|
RO – медиана. Это означает равенство отрезков, сторон: QO=OP (т. к. RO – медиана) |
|
3 |
|
O – середина отрезка QP. QO=OP (т. к. O – середина QP) |
Кроме того, равенство сторон или углов треугольников может следовать из равенства других треугольников.
Пример оформления задачи.
В
Дано: ВО=OD, АО=СО С
Док-ть: О
А D
Доказательство:
АО= СО (по усл. )
)
ВО= DO (по усл.) по 1 признаку
(верт.)
Ч.т.д.
Методы решения геометрических задач.
Методы решения геометрических задач
Сегодня важнейшей задачей школьного математического образования является привлечение внимания школьников и учителей к геометрии, понимание необходимости систематических занятий геометрией, развивающих мышление и пространственные представления. Только такие занятия могут дать необходимое качество математического образования школьников, позволят им не только подготовиться к успешной сдаче экзамена, но и заложат основу для дальнейшей творческой жизни.
Количество геометрических задач, встречающихся в контрольно-измерительных материалах (КИМ) единого экзамена, невелико. Их доля составляет не более 13 % от общего числа задач (3-4 задания). Однако умение решать такие задачи может оказаться решающим аргументом при поступлении в престижные или популярные вузы.
Анализируя результаты решения абитуриентами геометрических задач на вступительных испытаниях по математике, видим печальную статистику: с задачами по геометрии справляются не более 10 % поступающих, решают неправильно – около 30 %, а порядка 60 % абитуриентов полностью игнорируют такие задачи.
Приступая к решению задач по геометрии, учащиеся сталкиваются с целым рядом трудностей, которые одним не дают получить верный ответ, а другим – даже просто начать решение. В чем причины? Они связаны не только с пробелами в знании предмета, но и с отсутствием у учащегося серьезного опыта в решении многослойных геометрических задач. Вполне возможно, что часть учащихся, потенциально обладающих уровнем подготовки, достаточным для решения геометрических задач, помещаемых в варианты ЕГЭ, просто не доверяет своим знаниям и умениям и, полагая заранее, что задачи очень трудные, не берется за их решение.
Если для большинства задач по алгебре и началам анализа существуют шаблонные подходы и алгоритмы решений, то в геометрии такого нет. Решение почти каждой геометрической задачи – это маленькая исследовательская работа. Чтобы с ней справиться, ученик должен иметь солидный опыт такого рода деятельности. И тут мы сталкиваемся с противоречием – опыт должен быть большой, а часов на изучение геометрии в школьном курсе отводится мало. Частичный выход из этого положения видится в использовании времени, отведенного в средней школе на повторение всего курса геометрии, исключительно для решения геометрических задач, взятых из вариантов ЕГЭ и ГИ
.
Трудности решения геометрических задач обусловлены как объективными, так и субъективными факторами, среди которых
Неалгоритмичность задач
Необходимость выбора метода решения задачи и теоремы для решения конкретной задачи (нескольких теорем) из большого набора известных фактов
Нужно решить довольно много задач, чтобы научиться их решать
Причины ошибок в решении геометрических задач
Незнание и/или непонимание аксиом, определений, теорем;
неумение их применять
невнимательное чтение условия и вопроса задания;
вычислительные ошибки;
нарушения логики в рассуждениях; принятие ошибочных гипотез;
недостатки в работе с рисунком
При решении геометрических задач обычно используются три основных метода:
геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем;
алгебраический – когда искомая геометрическая величина
вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений;
комбинированный – когда на одних этапах
решение ведется геометрическим методом, а на других — алгебраическим.
Метод треугольника
Метод подобия
Метод дополнительного построения
Метод замены
Метод площадей
Метод введения вспомогательного неизвестного
Метод «вспомогательных объёмов»
Координатный метод
Какой бы путь решения ни был выбран, успешность его использования зависит,
естественно, от знания теорем и умения их применять.
Метод дополнительного построения
Всякое геометрическое решение геометрической задачи начинается с работы над
чертежом. При этом иногда на «естественном» чертеже (т.е. на чертеже, на
котором изображено только условие) трудно заметить связи между данными и
искомыми величинами, а если фигуру достроить, эти связи становятся очевидными.
Метод подобия
Подобие треугольников
Две фигуры F и F1 называются подобными, если они переводятся друг в друга преобразованием
подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются
е. таким преобразованием, при котором расстояния между точками изменяются
(увеличиваются или уменьшаются) в одно и то же число раз.
Признаки подобия треугольников:
1) Если два угла одного соответственно равны двум углам другого;
2) Если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами равны;
3) Если три стороны одного треугольника пропорциональны трем сторонам другого.
Метод замены Метод
Метод замены широко применяется в алгебре, но не менее эффективно «замена» может быть
применена в геометрии. Сущность этого приема решения геометрических задач состоит в
следующем: фигура, о которой идет речь в условии задачи, так заменяется фигурой с той же
искомой величиной, чтобы найти эту величину было легче.
Метод введения вспомогательного неизвестного
Суть метода заключается в том, что исходя из условия задачи составляют
уравнение (или систему уравнений). В качестве вспомогательных аргументов
удобно выбирать величины, которые вместе с данными из условия задачи дают
набор элементов, однозначно задающих некоторую фигуру.
Метод площадей
В математических задачах часто бывает полезен такой прием: двумя
способами найти одну и ту же величину и приравнять полученные для нее
выражения. Пусть мы, например, двумя способами нашли площадь некоторой
фигуры. Если в одном из выражений для площади входит, скажем синус
какого-либо угла α, то при помощи соотношения из полученного равенства
можно получить некоторое неравенство, порой интересное.
Метод «вспомогательных объёмов»
Для нахождения расстояния от точки до плоскости или при нахождении
углов между прямой и плоскостью метод «вспомогательного объёма» во
многих случаях оказывается наиболее эффективным. Суть метода заключается
Суть метода заключается
в том, что объём некоторой фигуры выражается двумя способами, а затем из
полученных равенств выражается искомая величина. Причём в этом методе
нет необходимости строить проекцию прямой на плоскость или проекцию точки,
что во многих случаях оказывается очень затруднительным.
Векторный метод
Применение критериев коллинеарности и компланарности векторов в решении задач.
Критерии коллинеарности и компланарности векторов служат основной для
применения векторной алгебры в решении стереометрических задач. Они
позволяют выразить в виде векторных равенств различные утверждения о
расположенных точках, прямых и плоскостей в пространстве. Переход от
векторных равенств к скалярным происходит на основе единственности
разложения вектора по двум неколлинеарным и трём некомпланарным векторам.
Координатный метод
Координаты на плоскости и в пространстве можно вводить бесконечным числом
разных способов. И, решая ту или иную геометрическую задачу методом координат,
И, решая ту или иную геометрическую задачу методом координат,
можно использовать различные координатные системы, выбирая ту из них, в
которой задача решается проще, удобнее. Некоторые виды координатных систем,
отличные от прямоугольных.
1.Косоугольные (аффинные) координаты.
2.Полярные координаты.
3.Цилиндрические координаты.
4.Сферические координаты.
5.Прямоугольные координаты.
Рассмотрим самые употребительные и простые координаты в пространстве, называемые прямоугольными. Их называют ещё декартовыми по имени Рене Декарта (1596-1650) – французского учёного и философа, впервые ввёдшего координаты в геометрию (на плоскость).
Задач и вопросов по свободной геометрии с решениями
Бесплатные учебники по геометрии по таким темам, как отражение, серединный перпендикуляр, центральный и вписанный углы, описанные окружности, закон синуса и свойства треугольника для решения задач треугольника. Также включены геометрические задачи с подробными решениями для треугольников, многоугольников, параллелограммов, трапеций, пирамид и конусов. Также включены уравнения полярных координат, преобразование и построение графиков. Также включены более сложные геометрические задачи.
Также включены геометрические задачи с подробными решениями для треугольников, многоугольников, параллелограммов, трапеций, пирамид и конусов. Также включены уравнения полярных координат, преобразование и построение графиков. Также включены более сложные геометрические задачи.
Проблемы геометрии
- Прямоугольник. Прямоугольные задачи по площади, размерам, периметру и диагонали с подробными решениями.
- Задачи геометрии на квадратах. Квадратные задачи по площади, диагонали и периметру, с подробными решениями.

- Проблемы с полигонами. Проблемы, связанные с правильными многоугольниками.
- Задачи о параллельных прямых и углах. Проблемы, связанные с параллельными линиями и чередующимися и соответствующими углами.
- Проблема перекрывающихся кругов.Найдите область перекрытия двух кругов: проблема с подробным решением.
- Проблемы секторов и кругов. Проблемы, с подробными решениями, относящиеся к секторам и кругу.
- Проблемы закона косинуса.
 Закон косинуса используется для решения словесных задач.
Закон косинуса используется для решения словесных задач. - Проблемы закона синуса. Синус-закон используется для решения словесных задач.
- Проблемы треугольника. Проблемы треугольника с подробным решением.
- Задачи о равносторонних треугольниках с решениями.
- Равнобедренные треугольники. Задачи с решениями.
- Проблемы объема 3D-фигур.
 Трехмерные формы, такие как призмы, проблемы объема с подробными решениями.
Трехмерные формы, такие как призмы, проблемы объема с подробными решениями. - Площадь восьмиугольника — проблема с решением. Найдите длину одной стороны, периметр и площадь правильного восьмиугольника, учитывая расстояние между двумя противоположными сторонами (пролет).
- Площадь и периметр прямоугольных треугольников. Задачи с решением.
- Два квадрата и круг — проблема с решением. Представлена задача с подробным решением о круге, вписанном в один квадрат и описанном в другом.
- Два круга и квадрат — проблема с решением.
 Представлена задача с подробным решением на квадрате, вписанном в один круг и описанном в другом.
Представлена задача с подробным решением на квадрате, вписанном в один круг и описанном в другом. - Треугольник, вписанный в круг — проблема с решением. Вписанная задача прямоугольного треугольника с подробным решением.
- Примеры подобных треугольников и проблемы с решениями. Определение и теоремы о подобных треугольниках, включая примеры и задачи с подробными решениями.
- Теорема о перехвате и проблемы с решениями.
- Круг, касающийся прямоугольного треугольника — проблема с решением.
 Решите прямоугольный треугольник, все стороны касаются окружности. Представлены как проблема, так и ее подробное решение.
Решите прямоугольный треугольник, все стороны касаются окружности. Представлены как проблема, так и ее подробное решение. - Примеры конгруэнтных треугольников и задачи с решениями.
- Сравните объемы трехмерных фигур. Задача сравнить объемы конуса, цилиндра и полусферы.
- Как построить усеченную пирамиду ?. Если отрезать верхнюю часть конуса плоскостью, перпендикулярной высоте конуса, получится усеченный конус.Как построить усеченную вершину с учетом радиуса основания, радиуса вершины и высоты?
- Задачи параллелограмма.
 Проблемы со словами, относящиеся к параллелограммам, представлены вместе с подробными решениями.
Проблемы со словами, относящиеся к параллелограммам, представлены вместе с подробными решениями. - Проблемы с конусом. Представлены проблемы, связанные с площадью поверхности и объемом конуса, с подробными решениями.
- Проблемы пирамиды. Проблемы пирамиды, связанные с площадью и объемом поверхности, с подробными решениями.
- Проблемы трапеции. Проблемы трапеции представлены вместе с подробными решениями.
- Решите трапецию с учетом ее оснований и ножек.
- Проблемы ромба.
 Описание и свойства ромба представлены вместе с проблемами с подробными решениями.
Описание и свойства ромба представлены вместе с проблемами с подробными решениями.
Challenge Geometry Problems
Учебники по геометрии
- Простые доказательства теоремы Пифагора и проблемы с решениями.
- Треугольники. Определения и свойства треугольников в геометрии.
- Вписанные и центральные углы в кругах.
 На примерах и задачах обсуждаются определения и теоремы, относящиеся к вписанным и центральным углам в кругах.
На примерах и задачах обсуждаются определения и теоремы, относящиеся к вписанным и центральным углам в кругах. - Вопросы теоремы о пересечении хорд с решениями.
- Области треугольников. Задачи с решениями. Используйте разные формулы площади треугольника, чтобы вычислить площади треугольников и фигур.
- Параллельные линии и углы. Этот урок посвящен соответствующим внутренним и внешним углам, которые образуются при пересечении поперечной линией двух параллельных линий.
- Свойства треугольников.
 Апплет используется для интерактивного исследования свойств треугольников.
Апплет используется для интерактивного исследования свойств треугольников. - Теорема Фалеса. Аплет используется для проверки теоремы Фалеса: угол, вписанный в полукруг, является прямым углом.
- Правильные многоугольники. Учебник по разработке полезных формул для площади правильных многоугольников.
- Симметрия вращения в правильных многоугольниках. Интерактивное руководство для изучения симметрии вращения правильных многоугольников и вывода формулы для угла поворота.
- Симметрия вращения геометрических фигур.
 Интерактивное руководство для изучения симметрии вращения геометрических фигур.
Интерактивное руководство для изучения симметрии вращения геометрических фигур. - Углы в геометрии. Определения и свойства углов в геометрии.
- Закон синуса — неоднозначный случай — апплет. Неоднозначный случай синусоидального закона при решении задач треугольника исследуется в интерактивном режиме с помощью апплета.
- Высота, медиана и биссектриса угла треугольника.
- Центральные и вписанные углы — Интерактивный апплет. Свойства центрального и вписанного углов, пересекающих общую дугу в окружности, исследуются с помощью апплета интерактивной геометрии.

- Перпендикулярные биссектрисы с решениями.
- Треугольники, биссектрисы и окружности — интерактивный апплет. Свойства серединных перпендикуляров в треугольниках и описанных окружностях исследуются в интерактивном режиме с помощью геометрического Java-апплета.
- Таблица формул для геометрии. Представлена таблица формул геометрии, относящаяся к площади и периметру треугольников, прямоугольников, окружностей, секторов и объему сферы, конуса, цилиндра.
Полярные координаты
Геометрические преобразования
Геометрические калькуляторы и рабочие таблицы
Автор — электронная почтаДомашняя страница
1. 1 1 | Точки, линии и плоскости | Упражнения | стр.8 |
| 1,2 | Измерение и построение сегментов | Упражнения | стр.16 |
| 1,3 | Использование формул средней точки и расстояния | Упражнения | с.24 |
| Викторина | стр.28 | ||
| 1,4 | Периметр и площадь в координатной плоскости | Упражнения | стр. 34 34 |
| 1,5 | Измерение и построение углов | Упражнения | с.43 |
| 1,6 | Описание пар углов | Упражнения | с.52 |
| Обзор главы | с.56 | ||
| Глава Test | с.59 | ||
| Оценка стандартов | с. 60 60 |
Графики и геометрия — WebMath
Быстро! Мне нужна помощь с: Выберите элемент справки по математике … Исчисление, Производное вычисление, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех сложных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование площади, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика полиномов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторинг триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Общая математика — WebMath
Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Find allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные числа, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Образцы, Упрощение, Пример Правые треугольники, Ветер, рисунок
K-8 — WebMath
Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Find allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные числа, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Образцы, Упрощение, Пример Правые треугольники, Ветер, рисунок
| Вот Самая сложная простая задача геометрии в мире, как можно найти на веб-странице Кейта Эневольдсена Think Zone: Решения обеих этих проблем можно найти далеко ниже, так что будьте осторожны. как далеко вы прокрутите ниже, если не хотите видеть ответ. Что делает эти геометрические задачи такими интересными (и «трудными»), так это то, что только разрешена элементарная геометрия (без тригонометрии). Типа, основные правила о параллельные и пересекающиеся прямые и углы образуются: а также простой факты о треугольнике:
Решения, приведенные ниже, являются по замыслу не строгими доказательствами , а скорее предоставьте достаточно информации, чтобы решение очень очевидно для большинства читателей. Вы должны щелкнуть, чтобы найти изображения, связанные с этими решениями, чтобы не портить удовольствие тем, кто хочет попробовать найти решение для себя первый. Решение проблемы первое Решение One Image 1. Рассчитайте известные углы:
5. Проведите линию CG, который делит ACB пополам и заключает:
Решение второй проблемы Изображение второго решения 1.Рассчитайте известные углы:
|
Решение | Нет решений или бесконечно много? | Геометрия уравнений
Найдите значение \ (k \), для которого системы уравнений \ [\ begin {align *} 2x — ky & = 1 \\ (k + 3) x — 9y & = k \ конец {выравнивание *} \]имеют
- бесконечное количество решений,
- решений нет.2 + 3k — 18 \ вправо) y + 3 — k = 0.
\] Квадратичный коэффициент для \ (y \) можно разложить на множители, получив уравнение \ [
(К + 6) (К-3) У + 3-К = 0.
\]
Итак, \ ((k + 6) (k-3) y- (k-3) = 0 \), факторизуя, получаем
\ [\ begin {уравнение} \ label {уравнение: линейное уравнение по оси y и k} (к-3) ((к + 6) у-1) = 0. \ конец {уравнение} \]Таким образом, \ (k = 3 \) или \ ((k + 6) y-1 = 0 \).
Необходимо рассмотреть три случая:
Случай 1: \ (k \ ne 3 \) и \ (k \ ne -6 \)
В этом случае мы имеем единственное решение, а именно \ [ y = \ frac {1} {k + 6} \ quad \ text {и} \ quad x = \ frac {(k + 6) + k} {2 (k + 6)} = \ frac {k + 3} {k + 6}.\]
Случай 2: \ (k = 3 \)
Если \ (k = 3 \), уравнение \ (\ eqref {eq: linear-Equation-in-y-and-k} \) верно для при любом выборе \ (y \) и любом выборе \ (y \) дает уникальное значение \ (x \) (а именно значение, полученное из уравнения \ (\ eqref {eq: eq-for-x-in-terms-of-k-and-y} \) ). Таким образом, существует бесконечно много решений \ ((x, y) \).
Случай 3: \ (k = -6 \)
В этом случае уравнение \ (\ eqref {eq: linear-Equation-in-y-and-k} \) никогда не может выполняться, так как оно приводит к противоречивому утверждению, что \ (9 = 0 \).Поэтому решений нет.
Подход 2: Использование координатной геометрии
Каждое из двух уравнений можно рассматривать как уравнение прямой.
Обычно эти две линии пересекаются в одной точке.
Но если их градиенты равны, то они либо не имеют решений (если прямые разные и параллельны), либо бесконечно много (если прямые совпадают).
Какие у них градиенты? Линия \ (2x — ky = 1 \) имеет градиент \ (\ dfrac {2} {k} \) (если \ (k \ neq 0 \), и вертикальный, если \ (k = 0 \)) и \ ((k + 3) x — 9y = k \) имеет градиент \ (\ dfrac {k + 3} {9} \).2 + 3к -18 = 0 \). (Если \ (k = 0 \), вторая линия имеет градиент \ (\ frac13 \), который не является вертикальным, поэтому линии не параллельны.)
Это множится в \ ((k + 6) (k-3) = 0 \), поэтому их градиенты равны, когда \ (k = 3 \) и когда \ (k = -6 \).
Если \ (k = 3, \), то исходными уравнениями являются \ (2x-3y = 1 \) и \ (6x-9y = 3 \), которые совпадают, и поэтому существует бесконечно много решений \ ((x , у) \).
Если \ (k = -6 \), то исходные уравнения становятся \ (2x + 6y = 1 \), или \ (x + 3y = 0,5 \), и \ (- 3x-9y = -6 \), или \ (x + 3y = 2 \).В этом случае линии параллельны и различны, поэтому решений нет.
Этот апплет GeoGebra помогает нам увидеть, что происходит.
.

 Далее рассмотрим косинус угла \(∠BAC\) и найдем \(AC:\)
Далее рассмотрим косинус угла \(∠BAC\) и найдем \(AC:\) Это означает равенство углов:
Это означает равенство углов:

 Это означает равенство отрезков, сторон:
Это означает равенство отрезков, сторон:
 Закон косинуса используется для решения словесных задач.
Закон косинуса используется для решения словесных задач. Трехмерные формы, такие как призмы, проблемы объема с подробными решениями.
Трехмерные формы, такие как призмы, проблемы объема с подробными решениями.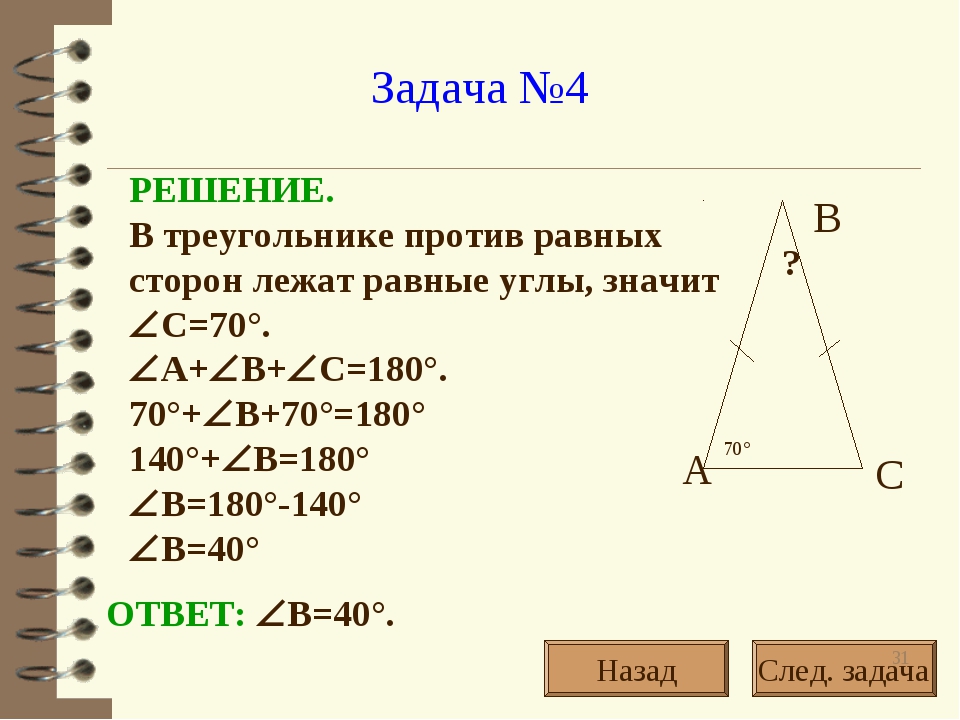 Представлена задача с подробным решением на квадрате, вписанном в один круг и описанном в другом.
Представлена задача с подробным решением на квадрате, вписанном в один круг и описанном в другом.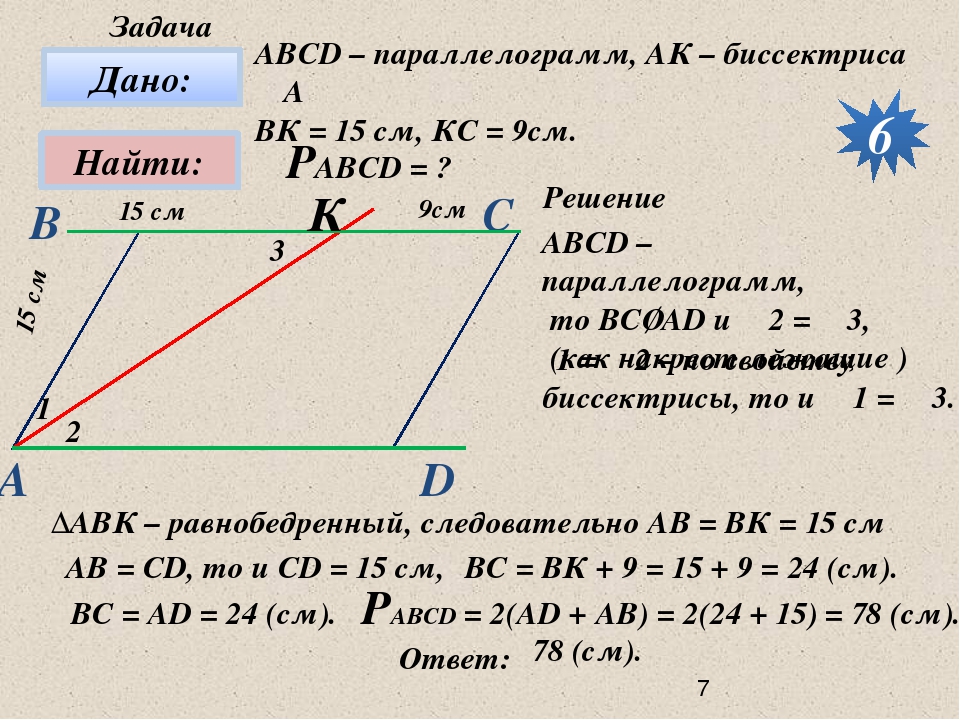 Решите прямоугольный треугольник, все стороны касаются окружности. Представлены как проблема, так и ее подробное решение.
Решите прямоугольный треугольник, все стороны касаются окружности. Представлены как проблема, так и ее подробное решение.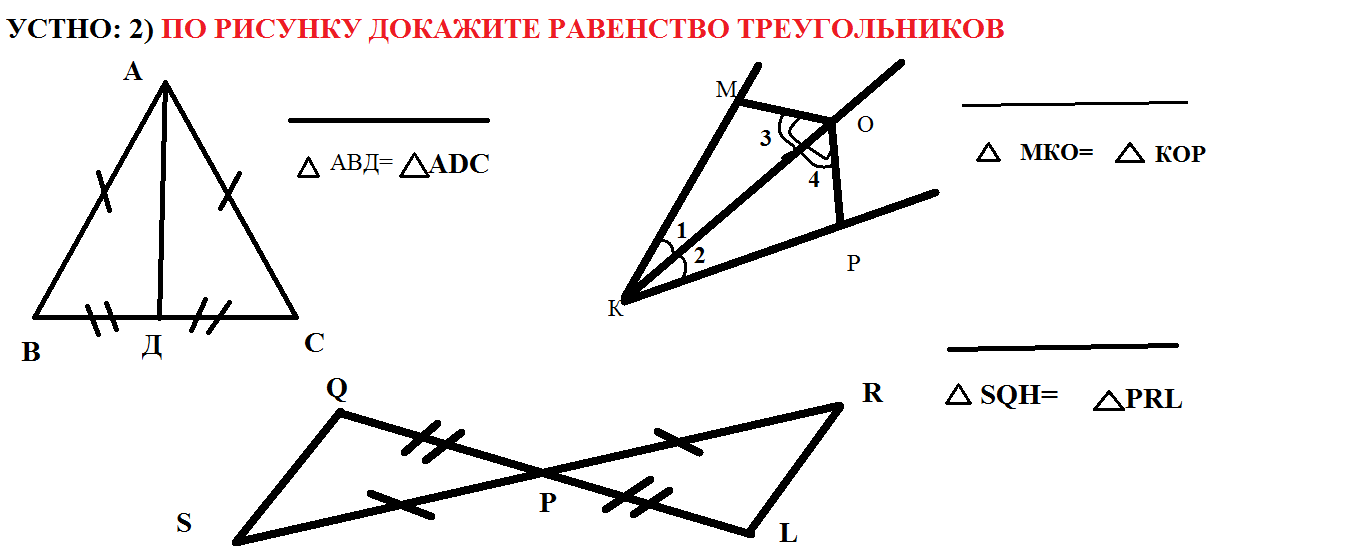 Проблемы со словами, относящиеся к параллелограммам, представлены вместе с подробными решениями.
Проблемы со словами, относящиеся к параллелограммам, представлены вместе с подробными решениями. Описание и свойства ромба представлены вместе с проблемами с подробными решениями.
Описание и свойства ромба представлены вместе с проблемами с подробными решениями. На примерах и задачах обсуждаются определения и теоремы, относящиеся к вписанным и центральным углам в кругах.
На примерах и задачах обсуждаются определения и теоремы, относящиеся к вписанным и центральным углам в кругах. Апплет используется для интерактивного исследования свойств треугольников.
Апплет используется для интерактивного исследования свойств треугольников. Интерактивное руководство для изучения симметрии вращения геометрических фигур.
Интерактивное руководство для изучения симметрии вращения геометрических фигур.