Решение задачи по геометрии 7: Книга: «Геометрия. 7-8 классы. Решение задач на готовых чертежах. ФГОС». Купить книгу, читать рецензии | ISBN 978-5-7057-4904-1

Урок геометрии в 7-м классе по теме «Свойства прямоугольного треугольника. Решение задач»

Цели урока:

• дидактические – совершенствование навыков решения задач на применение свойств прямоугольного треугольника;
• развивающие – развитие специального учебного навыка решения геометрических задач;
• воспитательные – воспитание интереса к математике.

Ход урока

1. Орг. момент.

Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело, чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием.

Сегодня у нас заключительный урок по теме «Свойства прямоугольного треугольника».

Перед вами стоит задача – закрепить умение применять свойства прямоугольного треугольника при решении задач; проверить свои знания в ходе выполнения самостоятельной работы.

2. Актуализация опорных знаний.

Работа с буклетами( напротив каждого пункта «Памятки» записать правильный ответ)

1. Сумма двух острых углов прямоугольного треугольника равна 90°.
2. Катет прямоугольного треугольника, лежащий против угла в 30° равен половине гипотенузы.
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
4. В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
5. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

3. Решение задач.

а) по готовым чертежам ( готовые чертежи в буклетах и на интерактивной доске).

Устно.

1. Найти: N 

2. АВ=12см. Найти: ВС

3. PD = 1,2cм. Найти: PQ

Возле доски с решением.

4. АВ = 4,2см. ВС = 8,4см. Найти: B

5.DCM = 70° Найти: DAM

6. C = 90°, PC = СM; CA = 8 см Найти: MP.

б) Решение текстовых задач.

7. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.

Дано: ΔАВС, С=90°, А=60°, АВ+АС=18см Найти: АВ, АС. Решение: В=90° – 60°=30°, значит, АС – меньший катет, тогда АС=0,5АВ АВ+0,5АВ=18 АВ=12см, АС=6см Ответ: АВ=12см, АС=6см.

8. В прямоугольном треугольнике АВС С=90° и А=30°, проведена медиана СМ и биссектриса MD ΔСМА. Найдите MD, если ВС=23см.

Дано: ΔАВС, С=90°, А=30°, СМ-медиана С, МD – биссектриса ΔСМА, ВС=23см. Найти: MD. Решение: Т.к. СМ – медиана, то СМ-ВМ=МА=0,5АВ Т.к. А=30° и ВС=24см, то АВ=46см и = СМ=ВМ=МА=23см. Т.к. СМ=МА, то ΔСМА равнобедренный, следовательно, МD – высота. Т.к. А=30°, АDM= 90° и МА=23см, то MD=0,5МА= 11,5см. Ответ: MD=11,5см.

Физ.пауза

1. разминка шейного отдела позвоночника;
2. разминка для глаз.

4. Самостоятельная работа.

Прежде чем приступить к этой работе, запишем домашнее задание.

П.34, №259, №260, №265.

Самостоятельная работа
Вариант 1. 1. Найти: 1) острые углы ΔАВС; 2) высоту СК, если ВС=3,8см. 2. В прямоугольном треугольнике СDЕ с прямым углом Е проведена высота ЕF. Найдите СF и FD, если CD=18см, а DCE=30°.	Вариант 2 1. Найти: 1) острые углы ΔАВС; 2) высоту СК, если ВС=5,6см. 2. В прямоугольном треугольнике MNK с гипотенузой MN и углом M равным 60° проведена высота KН. Найдите MH и NН, если MН=6см.

5. Итог урока.

Чем мы сегодня занимались на уроке?

Какие свойства применяли при решении задач?

Приложение.

Как решать задачи по геометрии. Часть 1

Геометрическая логика при решении задач

Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.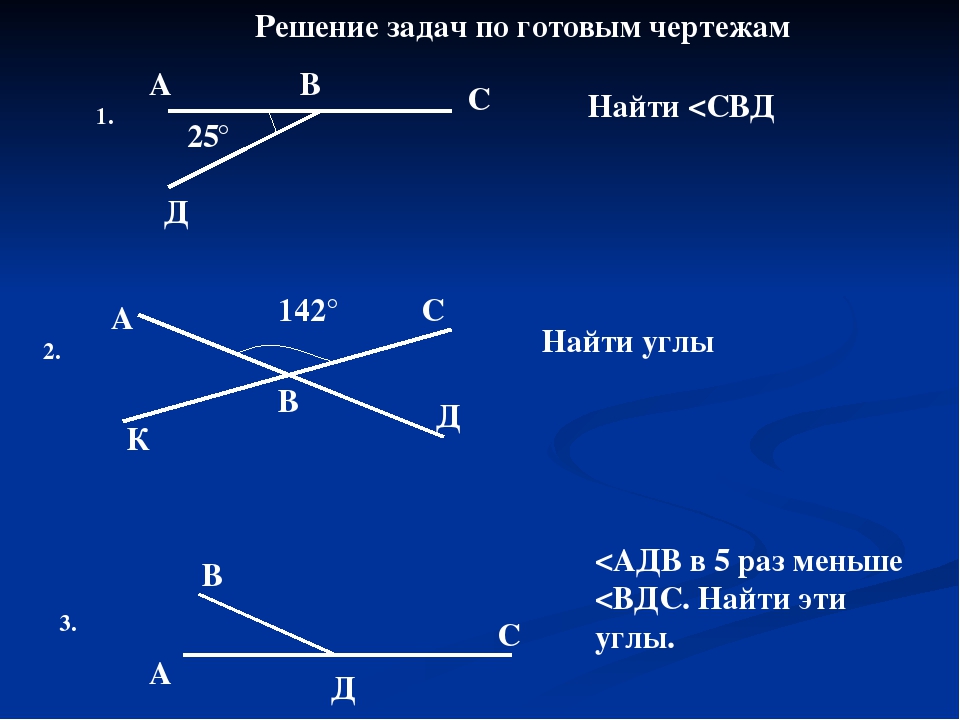

Это про тебя? Тогда ты попал туда, куда нужно!

Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.

Сразу оговорюсь — без знания теории в геометрии никак

. В смысле, вообще никак, от слова «совсем». Чтоб тебе было полегче при чтении этой статьи, я буду внутри решений задач в скобках курсивом указывать используемые свойства и теоремы. Но помни: если вдруг в знании теории у тебя пробел – закрытие его за тобой! Бери учебник и читай. Причем главные вещи – заучивай (или понимай). Знать теорию – обязательно!

Ладно, к делу.

Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.

д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?

Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.

Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.

К чему весь этот разговор? Решение задачи по геометрии это точно такой же «квест», только математический . Вдумайся: у нас всегда есть некоторые исходные данные и есть то, что нужно найти (или доказать – разницы на самом деле практически нет). И наша задача – построить логическую цепочку от исходных данных к цели. Строительным материалом при этом у нас будут данные (исходные и полученные при рассуждениях), а также теоремы и свойства.

Ладно, давай уже конкретный пример разберем.

Задача. В треугольнике \(ABC\) из точки \(B\) проведена высота \(BH\). Найти длину отрезка \(AH\), если известно, что сторона \(AC\; =\; 14\) см и угол \(A\) равен углу \(C\).

Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.

В геометрии это означает:

1. построить чертежа выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
2. выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
   

Хорошо. Значит, текущая ситуация у нас такова:

Давайте потихоньку развеивать туман. Нам известно, что углы \(А\) и \(С\) равны, а это значит, что треугольник \(АВС\) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.

Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что \(BH\) – высота. А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.

А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка \(H\) делит сторону \(AC\) пополам. То есть \(AH = HC\).

Стоп. Так у нас же есть длина стороны \(AC\)! И если мы знаем, что точка \(H\) делит сторону \(AC\) пополам, значит, \(AH\) равен половине \(AC\)! Таким образом, получаем, что \(AH = AC/2 = 14/2=7\) см.

Готово. Ответ получен.

Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:

Зачёт по геометрии за 7 класс

Вопросы по геометрии. 7 класс

1. Сколько прямых можно провести через две точки?

2. Сколько общих точек могут иметь две прямые?

3. Что такое отрезок? Начертить, обозначить и объяснить? Какая точка называется серединой отрезка?

4. Что такое луч? Как обозначаются лучи?

5. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.

6. Какие фигуры называются равными?

7. Как сравнить два угла? Какой луч называется биссектрисой угла?

8. Какой угол называется острым? прямым? тупым?

9. Какие углы называются смежными? Чему равна сумма смежных углов? Уметь их строить.

10. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? Уметь их строить.

11. Какие прямые называются перпендикулярными? Уметь их строить Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются?

12. Объясните, какая фигура называется треугольником. Начертите треугольник и покажите его стороны, вершины и углы. Что такое периметр треугольника?

13. Какие треугольники называются равными?

14. Что такое теорема и доказательство теоремы?

15. Сформулируйте первый признак равенства треугольников.

16. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? Уметь их строить.

17. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Уметь их строить.

18. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Уметь их строить.

19. Какой треугольник называется равнобедренным? Уметь его строить. Как называются его стороны?

20. Какой треугольник называется равносторонним? Уметь его строить. Сформулировать основные свойства равнобедренного треугольника.

21. Сформулируйте второй признак равенства треугольников.

22. Сформулируйте третий признак равенства треугольников.

23. Что такое определение? Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности?

24. Объясните, как отложить от данного луча в данную плоскость угол, равный данному.(с помощью циркуля и линейки)

25. Объясните как построить биссектрису данного угла.( с помощью циркуля и линейки)

26. Объясните, как построить прямую, проходящую через данную точку, лежащую на данной прямой, и перпендикулярную к этой прямой. .(с помощью циркуля и линейки)

27. Объясните, как построить середину данного отрезка. .(с помощью циркуля и линейки)

28. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?

29. Что такое секущая? Назовите пары углов, которые образуются при пересечении двух прямых секущей. Уметь их построить , показать и обозначить.

30. Сформулируйте признаки параллельности прямых ?

31. Что такое аксиома? Приведите примеры. Сформулируйте аксиому параллельных прямых.

32. Какая теорема называется обратная данной теореме? Приведите примеры теорем, обратных данным.

33. Сформулируйте теоремы об углах, образованных двумя параллельными прямыми и секущей.

34. Сформулируйте теорему о сумме углов треугольника.

35. Какой угол называется внешним углом треугольника? Уметь его строить. Сформулируйте, чему равен внешний угол в треугольнике.

36. Какой треугольник называют остроугольным? Какой треугольник называется тупоугольным? Уметь их строить.

37. Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?

38. Сформулируйте соотношения между сторонами и углами. Почему в прямоугольном треугольнике гипотенуза больше катета?

39. Сформулируйте теорему о неравенстве треугольника.

40. Сформулируйте некоторые свойства прямоугольных треугольников.

41. Сформулируйте признаки равенства прямоугольных треугольников.

42. Что называется расстоянием от точки до прямой?

43. Что называется расстоянием между двумя параллельными прямыми?

44. Объясните, как построить треугольник по двум сторонам и углу между ними.

45. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.

46. Объясните, как построить треугольник по трём сторонам. Всегда ли эта задача имеет решение?

Задачи к зачету по геометрии. 7 класс

Задача №1. В равнобедренном треугольнике угол при основании в 2 раза меньше, чем угол при вершине. Найдите все углы треугольника.

Задача №2. Высота АD равностороннего треугольника ВАС с основанием ВС равна 10 см, периметр треугольника АDС равен 70 см. Найдите периметр треугольника АВС.

Задача №3. Первый угол треугольника равен 40градусов, а второй больше третьего на 16 градусов. Найдите эти углы треугольника.

Задача №4. В равнобедренном треугольнике периметр равен 150 см, боковая сторона больше основания на 15 см. Найдите все стороны треугольника.

Задача №5. В равнобедренном прямоугольном треугольнике гипотенуза равна 42 см. Найдите высоту проведённую из вершины прямого угла.

Задача №6. В равнобедренном треугольнике внешний угол при вершине равен 40 градусов. Найдите углы этого треугольника.

Задача №7. В равнобедренном треугольнике СDЕ с основанием СЕ проведена биссектриса СF. Найдите угол ЕСF, если угол D равен 54 градуса.

Задача №8. Один из углов прямоугольного треугольника равен 60 градусов, а сумма гипотенузы и меньшего катета равна 30 см. Найдите гипотенузу треугольника.

Задача №9. Один из внешних углов равнобедренного треугольника равен 110 градусов. Найдите все углы данного треугольника.

Задача №10. Периметр равнобедренного треугольника равен 65 см, его боковая сторона на 5 см меньше основания. Найдите стороны треугольника.

Задача №11. Периметр равнобедренного тупоугольного треугольника равен 77 см, а одна из его сторон больше другой на 17см. Найдите стороны этого треугольника.

Задача №12. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108 градусов. Найдите угол ВОD.

Задача №13. В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NК в точке О. причём ОК равно 9 см.
Найдите расстояние от точки О до прямой МN.

Задача №14. Отрезки АВ и СD- диаметры окружности с центром О. Найдите периметр треугольника АОD, если хорда СВ равна 10 см, диаметр АВ равен 12 см.

Задача №15. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 296 градусов.

Задача №16. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если угол АОВ равен 110 градусов, а угол АОС на 18 градусов меньше угла ВОС.

Задача №17. Углы треугольника относятся как 2: 3: 4. Найдите их градусные меры.

Задача №18. В равнобедренном треугольнике АВС с основанием АС равно 38 см внешний угол при вершине В равен 60 градусов. Найдите расстояние от вершины С до прямой АВ.

Задача №19. Один из углов при пересечении двух параллельных прямых третьей прямой в 2 раза больше другого. Найдите остальные углы.

Задача №20. Один из углов при пересечении двух параллельных прямых третьей прямой на 20 градусов меньше другого. Найдите остальные углы.

Задача №21. В равнобедренном треугольнике АВС с основанием АС равно 42см, внешний угол при вершине С равен 120 градусов. Найдите боковые стороны треугольника АВС.

geo7.docx

ГДЗ Геометрия 7-9 класс Балаян

Геометрия 7-9 класс

Задачи на готовых чертежах

Балаян

Большая перемена

Феникс

Впереди школьников ждут довольно напряженные годы в освоении многих предметов. Особое место среди них занимает геометрия, которая хоть и кажется простой, на деле не так-то легко дается ребятам. Самым основным, чем нужно овладеть подросткам — свободно работать с всевозможными моделями и графиками. Научившись понимать их, они смогут наглядно показывать решения многих задач. Решебник к учебнику «Геометрия. Задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ 7-9 класс» Балаян поможет ученикам получить необходимые навыки, а так же значительно улучшит знание материала, если отнестись в его использованию достаточно внимательно.

Что имеется в издании

Сборник включает в себя сорок девять таблиц с заданиями, которые распределены между классами. Каждая таблица содержит несколько упражнений, которые относятся к какой-либо изучаемой теме. ГДЗ по геометрии 7-9 класс Балаян поможет подготовиться к экзаменационной части, так как авторы дают исчерпывающие решения по всем номерам.

Действенен ли решебник

Учитывая сложность и серьезность современной программы, следует заранее осуществлять подготовку к проверочным работам. Периодическое повторение поможет школьникам лучше усвоить и запомнить материал, так как сделать это во время уроков просто не удается. А поняв принцип решений задач они могут отточить свои навыки до автоматизма, чтобы не испытывать проблем во время тестирований. Однако не стоит рассчитывать на то, что дополнительные пособия можно использовать в качестве шпаргалки, так как информация довольно обширная и проработать ее за пару дне точно не удастся. Так что решебник к учебнику «Геометрия. Задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ 7-9 класс» Балаян требует серьезного подхода и лучше начинать им пользоваться после первой же изученной темы. «Феникс», 2018 г.

Название

Условие

Решение

МАТЕМАТИКА В ШКОЛЕ 448 — Домашние задания — геометрия

Домашнее задание №07 «Смежные и вертикальные углы» — 7в — на 3 октября. 7б, 7а — на 29 сентября. Не забудьте прочитать п. 11 учебника и выучить ответы на вопросы 17 , 18 на стр. 26

Домашнее задание №1 «Прямая и отрезок» — на 8 сентября

Домашнее задание №10 «Треугольник» — н 17 октября.

Домашнее задание №11 «Первый признак равенства треугольников» — на 20 октября

Домашнее задание №12 «Первый признак равенства треугольников» — на 24 октября

Домашнее задание №13 «Медианы, биссектрисы и высоты треугольника» — на 27 октября.

Домашнее задание №14 «Свойства равнобедренного треугольника» — на 10 ноября

Домашнее задание №15 «Свойства равнобедренного треугольника» — на 14 ноября

Домашнее задание №16 «Второй признак равенства треугольников» — на 17 ноября

Домашнее задание №17 «Третий признак равенства треугольников» — на 24 ноября

Домашнее задание №18 «Все признаки равенства треугольников» — на 28 ноября

Домашнее задание №19 «Окружность» — на 1 декабря

Домашнее задание №2 «Луч и угол» — на 12 сентября. Не забудьте выучить ответы на вопросы 4 — 6 на стр. 25!

Домашнее задание №20 «Задачи на построение» — на 5 декабря

Домашнее задание №21 «Задачи на построение» — на 8 декабря.

Домашнее задание №22 «Подготовка к контрольной работе» — на 12 декабря.

Домашнее задание №23 Подготовка к контрольной работе — на 15 декабря. Не забудьте чертежные инструменты принести на урок!

Домашнее задание №24 «Параллельные прямые» — на 12 января

Домашнее задание №25 «Признаки параллельности прямых» — на 16 января.

Домашнее задание №26 Аксиома параллельных прямых — на 19 января

Домашнее задание №27 Свойства параллельных прямых — на 23 января.

Домашнее задание №28 Свойства параллельных прямых — на 26 января

Домашнее задание №29 Свойства и признаки параллельных прямых — на 30 января

Домашнее задание №3 «Сравнение отрезков и углов» — на 15 сентября. Читать пункты 5 и 6 в учебнике. Знать ответы на вопросы 7 — 11 на стр. 25

Домашнее задание №30 Свойства и признаки параллельных прямых — на 2 февраля

Домашнее задание №31 «Подготовка к контрольной работе» — на 6 февраля

Домашнее задание №32 Сумма углов треугольника — на 27 февраля. Не забудьте выучить теорему с доказательством и свойство внешнего угла (п.31 в учебнике). Самостоятельно изучите материал п.32

Домашнее задание №33 «Сумма углов треугольника» — на 2 марта

Домашнее задание №34 «Соотношения между сторонами и углами треугольника» — на 6 марта

Домашнее задание №35 «Неравенство треугольника» — на 13 марта

Домашнее задание №36 «Неравенство треугольника» — на 20 марта

Домашнее задание №37 «Свойства прямоугольного треугольника» — на 3 апреля

Домашнее задание №38 «Признаки равенства прямоугольных треугольников» — на 10 апреля

Домашнее задание №39 «Признаки равенства прямоугольных треугольников» — на 17 апреля

Домашнее задание №4 «Измерение отрезков» — на 19 сентября. Читать пункты 7, 8. Знать ответы на вопросы 12 и 13 на стр. 25.

Домашнее задание №40 «Расстояние от точки до прямой и между параллельными прямыми» — на 24 апреля

Домашнее задание №41 Решение задач — на 4 мая. Не забудьте принести циркуль!

Домашнее задание №42 Задачи на построение — на 8 мая. На уроке снова будет нужен циркуль!

Домашнее задание №43 Подготовка к контрольной работе — на 15 мая. Удачи!

Домашнее задание №5 «Измерение углов» — на 22 сентября. Не забудьте про устную часть задания

Домашнее задание №6 «Измерение углов» — на 26 сентября

Домашнее задание №8 «Смежные и вертикальные углы» — 7а, 7в — на 6 октября, 7б — на 3 октября

Домашнее задание №9 «Подготовка к контрольной работе» — на 10 октября

ГДЗ по Геометрии для 7‐9 класса задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ Балаян Э.Н.

Автор: Балаян Э. Н..

Издательство: Феникс 2018

«ГДЗ по геометрии 7-9 класс задачи на готовых чертежах Балаян (Феникс)» включает верные ответы на все номера заданий основного издания и является надежной поддержкой учеников в подготовке к ОГЭ и ЕГЭ. Учебное пособие разработано в соответствии с требованиями Федерального государственного образовательного стандарта и состоит из практических задач по разделам программы седьмого, восьмого и девятого классов.

Итоговые испытания требуют серьезной подготовки школьников, начиная уже с седьмого класса. В этот период ученики постепенно, шаг за шагом, осваивают все разделы и учатся решать задачи различной тематики и сложности. Данное учебно-методическое пособие содержит самые подробные ответы на все номера и как нельзя лучше подойдет ребятам в учебном процессе по изучению дисциплины.

Правильное использование решебника в учебе

С «ГДЗ к задачам на готовых чертежах по геометрии за 7-9 класс Балаян Э. Н. (Феникс)» ученики смогут выполнить задания по всем темам курса и систематизировать информацию, полученную из различных источников. Самыми трудными для освоения разделами, по мнению методистов, являются:

• – разложение вектора по двум неколлинеарным, скалярное произведение;
• – окружность, описанная около правильного многоугольника;
• – признаки равенства и подобия треугольников, их основные элементы и замечательные точки.

Любое решение можно найти в ресурсе. Однако не стоит им пользоваться как шпаргалкой. Целесообразно применять решебник для проверки самостоятельно выполненных упражнений. Важным условием является внимательный анализ ошибок и недочетов, позволяющий выявить пробелы в знаниях и темы, нуждающиеся в проработке. Вдумчивый подход к ГДЗ обеспечивает не только отличную успеваемость, но и глубокие фундаментальные знания по предмету.

Плюсы решебника задач на готовых чертежах по геометрии для 7-9 классов Балаян и его участия в овладении дисциплиной

Имея под рукой ресурс, ребята получат возможность:

• – потратить на подготовку к урокам и проверочным работам гораздо меньше времени, чем обычно;
• – потренироваться в решении задач на проблемные темы и разобрать сложные номера;
• – увереннее чувствовать себя на уроках и получать отличные оценки;
• – планомерно подготавливаться к итоговой аттестации.

Решебник находится в круглосуточном онлайн-доступе, воспользоваться им можно в любое время со всех гаджетов с выходом в интернет.

Решайте линейные и квадратные уравнения с помощью программы «Пошаговое решение математических задач»

Решение уравнений — центральная тема алгебры. В этой главе мы изучим некоторые методы решения уравнений с одной переменной. Для этого мы будем использовать навыки, полученные при манипулировании числами и символами алгебры, а также операциями с целыми числами, десятичными знаками и дробями, которые вы изучили в арифметике.

УСЛОВНЫЕ И ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Классифицируйте уравнение как условное или тождественное.
2. Решите простые уравнения мысленно.
3. Определите, эквивалентны ли определенные уравнения.

Уравнение — это указание в символах того, что два числовых выражения равны.

Уравнения можно разделить на два основных типа:

1. Идентификатор верен для всех значений буквальных и арифметических чисел в нем.

Пример 1 5 x 4 = 20 — это идентификатор.

Пример 2 2 + 3 = 5 — это идентификатор.

Пример 3 2x + 3x = 5x — это тождество, поскольку любое значение, замененное на x, даст равенство.

2. Условное уравнение верно только для определенных значений буквальных чисел в нем.

Пример 4 x + 3 = 9 верно, только если буквальное число x = 6.

Пример 5 3x — 4 = 11 верно, только если x = 5.

Буквальные числа в уравнении иногда называют переменными .

Поиск значений, которые делают условное уравнение истинным, является одной из основных целей этого текста.

Решение или корень уравнения — это значение переменной или переменных, которые делают уравнение истинным.

Говорят, что решение или корень для удовлетворяет уравнению .

Решение уравнения означает нахождение решения или корня.

Многие уравнения можно решить мысленно.Умение мысленно решить уравнение будет зависеть от умения манипулировать числами в арифметике. Чем лучше вы знаете факты умножения и сложения, тем более искусными вы будете в умении решать уравнения.

Пример 6 Решить относительно x: x + 3 = 7

Решение

Чтобы получить истинное утверждение, нам нужно значение для x, которое при добавлении к 3 даст 7. Наши знания арифметики показывают, что 4 является необходимым значением. Следовательно, решение уравнения — x = 4.

Какое число, добавленное к 3, равно 7?

Пример 7 Решить относительно x: x — 5 = 3

Решение

Из какого числа вычитаем 5, чтобы получить 3? Опять же наш опыт с арифметикой говорит нам, что 8 — 5 = 3. Следовательно, решение — x = 8.

Пример 8 Решить относительно x: 3x = 15

Решение

Какое число нужно умножить на 3, чтобы получить 15? Наш ответ: x = 5.

Решение

На какое число разделим 2, чтобы получить 7? Наш ответ — 14.

Пример 10 Решить относительно x: 2x — 1 = 5

Решение

Мы бы вычли 1 из 6, чтобы получить 5. Таким образом, 2x = 6. Тогда х = 3.

Независимо от того, как решается уравнение, решение всегда следует проверять на правильность.

Пример 11 Студент решил уравнение 5x — 3 = 4x + 2 и нашел ответ x = 6. Правильно это или нет?

Решение

Удовлетворяет ли x = 6 уравнению 5x — 3 = 4x + 2? Чтобы проверить, мы подставляем 6 вместо x в уравнение, чтобы увидеть, получим ли мы истинное утверждение.

Это неверное утверждение, поэтому ответ x = 6 неверен.

Другой студент решил то же уравнение и нашел x = 5.

Это верное утверждение, поэтому x = 5 верно.

Многие студенты думают, что, когда они нашли решение уравнения, проблема решена. Не так! Последним шагом всегда должна быть проверка решения.

Не все уравнения можно решить мысленно.Теперь мы хотим представить идею, которая является шагом к упорядоченному процессу решения уравнений.

Является ли x = 3 решением x — 1 = 2? Является ли x = 3 решением 2x + I = 7? Что можно сказать об уравнениях x — 1 = 2 и 2x + 1 = 7?

Два уравнения эквивалентны , если они имеют одно и то же решение или решения

Пример 12 3x = 6 и 2x + 1 = 5 эквивалентны, потому что в обоих случаях x = 2 является решением.

Методы решения уравнений включают процессы преобразования уравнения в эквивалентное уравнение. Если сложное уравнение, такое как 2x — 4 + 3x = 7x + 2 — 4x, можно заменить на простое уравнение x = 3, а уравнение x = 3 эквивалентно исходному уравнению, то мы решили уравнение.

Два вопроса теперь становятся очень важными.

1. Эквивалентны ли два уравнения?
2. Как мы можем заменить уравнение другим уравнением, которое ему эквивалентно?

Ответ на первый вопрос находится по принципу подстановки.

Пример 13 Являются ли 5x + 2 = 6x — 1 и x = 3 эквивалентными уравнениями?

Решение

Ответ на второй вопрос включает методы решения уравнений, которые будут обсуждаться в следующих нескольких разделах.

Чтобы правильно использовать принцип подстановки, мы должны подставить цифру 3 вместо x везде, где x появляется в уравнении.

ПОДРАЗДЕЛЕНИЕ ПРАВИЛО

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Используйте правило деления для решения уравнений.
2. Решите некоторые основные прикладные задачи, решение которых связано с использованием правила деления.

Как упоминалось ранее, мы хотим представить упорядоченную процедуру решения уравнений. Эта процедура включает четыре основных операции, первая из которых представлена ​​в этом разделе.

Если каждый член уравнения представляет собой деление на одно и то же ненулевое число, полученное уравнение будет равно эквивалентно исходному уравнению.

Чтобы подготовиться к использованию правила деления для решения уравнений, мы должны обратить внимание на следующий процесс:

(Мы обычно пишем 1x как x с пониманием коэффициента 1.)

Пример 1 Решить относительно x: 3x = 10

Решение

Наша цель — получить x = некоторое число. Правило деления позволяет нам разделить каждый член 3x = 10 на одно и то же число, и наша цель найти значение x будет означать, что мы делим на 3. Это дало бы нам коэффициент 1 для x.

Проверить: 3x = 10 и x = эти эквивалентные уравнения?

Подставляем вместо x в первое уравнение, получая

Уравнения эквивалентны, поэтому решение правильное.

Пример 2 Решить относительно x: 5x = 20

Решение

Обратите внимание, что правило деления не позволяет нам делить на ноль. Поскольку деление на ноль недопустимо в математике, такие выражения, как бессмысленны.

Пример 3 Решить относительно x: 8x = 4

Решение

Ошибки иногда допускаются в очень простых ситуациях.Не обращайте внимания на эту проблему и приходите к x = 2! Обратите внимание, что правило деления позволяет нам разделить каждый член уравнения на любое ненулевое число, и полученное уравнение эквивалентно исходному уравнению. Следовательно, мы можем разделить каждую часть уравнения на 5 и получить, что эквивалентно исходному уравнению. Однако деление на 5 не помогает найти решение. На какое число нужно разделить, чтобы найти решение?

Пример 4 Решить относительно x: 0.5x = 6

Решение

Пример 6 Формула для определения длины окружности (C) круга: C = 2πr, где π представляет радиус круга, и он составляет приблизительно 3,14. Найдите радиус круга, если измеренная длина окружности равна 40,72 см. Дайте правильный ответ с точностью до двух знаков после запятой.

Решение

Чтобы решить задачу, связанную с формулой, мы сначала используем принцип подстановки.

Окружность означает «расстояние вокруг».»Это периметр круга. Радиус — это расстояние от центра до круга.

ПРАВИЛО ВЫЧИСЛЕНИЯ

ЗАДАЧИ

По завершении этого раздела вы сможете использовать правило вычитания для решения уравнений.

В этом разделе будет обсуждаться второй шаг к упорядоченной процедуре решения уравнений. Вы будете использовать свои знания одинаковых терминов из главы 1, а также методы из раздела ПРАВИЛО ПОДРАЗДЕЛЕНИЯ .Обратите внимание, как новые идеи в алгебре основываются на предыдущих знаниях.

Если та же величина равна , вычитая из обеих частей уравнения, полученное уравнение будет равно , эквивалентному исходному уравнению.

Пример 1 Решить относительно x, если x + 7 = 12.

Решение

Хотя это уравнение легко решить в уме, мы хотим проиллюстрировать правило вычитания. Мы должны думать так:

«Я хочу решить относительно x, поэтому мне нужно, чтобы x был сам по себе на одной стороне уравнения.Но у меня x + 7. Так что, если я вычту 7 из x + 7, у меня будет только x с левой стороны ». (Помните, что величина, вычтенная из себя, дает ноль.) Но если мы вычтем 7 из одной стороны от числа. уравнение, правило требует, чтобы мы вычли 7 из другой стороны. Итак, мы действуем следующим образом:

Обратите внимание, что x + 0 можно записать просто как x, поскольку ноль, добавленный к любой величине, равен самой величине.

Пример 2 Решить относительно x: 5x = 4x + 3

Решение

Здесь наше мышление должно развиваться таким же образом.«Я хочу получить все неизвестные величины с одной стороны уравнения и все арифметические числа с другой, поэтому у меня есть уравнение в форме x = некоторое число. Таким образом, мне нужно вычесть Ax с обеих сторон».

Наша цель — получить x = некоторое число. Помните, что проверка вашего решения — важный шаг в решении уравнений.

Пример 3 Решить относительно x: 3x + 6 = 2x + 11

Здесь у нас более сложная задача.Сначала вычтите 6 с обеих сторон.

Теперь мы должны исключить 2x с правой стороны, вычтя 2x с обеих сторон.

Теперь мы рассмотрим решение, которое требует использования как правила вычитания, так и правила деления.

Обратите внимание, что вместо первого вычитания 6 мы могли бы сначала вычесть 2x с обеих сторон, получив 3x — 2x + 6 = 2x — 2x + 11 x + 6 = 11. Затем, вычитая 6 из обеих сторон, мы имеем х + 6-6 = 11-6 х = 5. Имейте в виду, что наша цель — x = некоторое число.

Пример 4 Решить относительно x: 3x + 2 = 17

Решение

Сначала мы используем правило вычитания, чтобы вычесть 2 из обеих сторон, получая

Затем мы используем правило деления, чтобы получить

Пример 5 Решить относительно x: 7x + 1 = 5x + 9

Решение

Сначала воспользуемся правилом вычитания.

Тогда правило деления дает нам

Пример 6 Периметр (P) прямоугольника находится по формуле P = 2l + 2w, где l обозначает длину, а w обозначает ширину.Если периметр прямоугольника 54 см, а длина 15 см, какова ширина?

Решение

Периметр — это расстояние вокруг. Вы понимаете, почему формула P = 2l + 2w?

ДОПОЛНИТЕЛЬНОЕ ПРАВИЛО

ЗАДАЧИ

По завершении этого раздела вы сможете использовать правило сложения для решения уравнений.

Теперь мы переходим к следующей операции в нашей цели разработки упорядоченной процедуры решения уравнений.Еще раз, мы будем полагаться на предыдущие знания.

Если одна и та же величина равна и прибавляется к обеим сторонам уравнения, полученное уравнение будет равно , эквивалентному к исходному уравнению.

Пример 1 Решить относительно x, если x — 7 = 2.

Решение

Как всегда, решая уравнение, мы хотим прийти к форме «x = некоторое число». Мы замечаем, что 7 было вычтено из x, поэтому, чтобы получить только x в левой части уравнения, мы прибавляем 7 к обеим частям.

Не забывайте всегда проверять свое решение.

Пример 2 Решить относительно x: 2x — 3 = 6

Решение

Помня о нашей цели получить только x, мы замечаем, что, поскольку 3 было вычтено из 2x, мы добавляем 3 к обеим частям уравнения.

Теперь мы должны использовать правило деления.

Почему мы добавляем 3 к обеим сторонам? Обратите внимание, что в примере простое использование правила сложения не решает проблему.

Пример 3 Решить относительно x: 3x — 4 = 11

Решение

Сначала воспользуемся правилом сложения.

Затем, используя правило деления, получаем

Здесь снова нам нужно было использовать как правило сложения, так и правило деления для решения уравнения.

Пример 4 Решить относительно x: 5x = 14 — 2x

Решение

Здесь наша цель получить только x с одной стороны предполагает, что мы удалим 2x справа, поэтому мы добавляем 2x к обеим сторонам уравнения.

Далее мы применим правило деления.

Здесь снова нам нужно было использовать как правило сложения, так и правило деления для решения уравнения. Обратите внимание, что мы проверяем, всегда подставляя решение в исходное уравнение.

Пример 5 Решить относительно x: 3x — 2 = 8 — 2x

Решение

Здесь наша задача более сложная. Мы должны подумать об удалении числа 2 из левой части уравнения, а также lx из правой части, чтобы получить только x с одной стороны.Сначала мы можем сделать что-то из этого. Если мы выберем сначала прибавить 2x к обеим сторонам, мы получим

Теперь прибавляем 2 к обеим сторонам.

Наконец, правило деления дает

Можем ли мы сначала добавить 2 к обеим сторонам? Попытайся!

ПРАВИЛО УМНОЖЕНИЯ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Используйте правило умножения для решения уравнений.
2. Решите пропорции.
3. Решите основные прикладные задачи, используя правило умножения.

Теперь мы подошли к последней из четырех основных операций при разработке нашей процедуры решения уравнений. Мы также введем соотношение и пропорции и воспользуемся правилом умножения для определения пропорций.

Если каждый член уравнения равен , умноженному на на такое же ненулевое число, полученное уравнение будет эквивалентно исходному уравнению.

В элементарной арифметике одними из самых сложных операций являются операции с дробями. Правило умножения позволяет нам избежать этих операций при решении уравнения, содержащего дроби, путем нахождения эквивалентного уравнения, содержащего только целые числа.

Помните, что когда мы умножаем целое число на дробь, мы используем правило

Теперь мы готовы решить уравнение, содержащее дроби.

Обратите внимание, что в каждом случае только числитель дроби умножается на целое число.

Пример 4

Решение

Имейте в виду, что мы хотим получить только x на одной стороне уравнения. Мы также хотели бы получить уравнение в целых числах, которое эквивалентно данному уравнению. Чтобы исключить дробь в уравнении, нам нужно умножить на число, которое делится на знаменатель 3. Таким образом, мы используем правило умножения и умножаем каждый член уравнения на 3.

Теперь у нас есть эквивалентное уравнение, которое содержит только целые числа.Используя правило деления, получаем

Чтобы исключить дробь, нам нужно умножить ее на число, которое делится на знаменатель. В этом примере нам нужно умножить на число, которое делится на 3. Мы могли бы умножить обе части на 6, 9, 12 и так далее, но уравнение проще и легче работать, если мы используем наименьшее несколько.

Пример 5

Решение

Посмотрите, получите ли вы такое же решение, умножив каждую часть исходного уравнения на 16. Всегда проверяйте исходное уравнение.

Пример 6

Решение

Здесь наша задача такая же, но немного сложнее. Нам нужно исключить две фракции. Мы должны умножить каждый член уравнения на число, которое делится как на 3, так и на 5. Лучше всего использовать наименьшее из таких чисел, которое, как вы помните, — это наименьшее общее кратное . Поэтому мы умножим на 15.

В арифметике вы могли использовать наименьшее общее кратное как «наименьший общий знаменатель».»

Пример 7

Решение

Наименьшее общее кратное для 8 и 2 равно 8, поэтому мы умножаем каждый член уравнения на 8.

Теперь воспользуемся правилом вычитания.

Наконец, правило деления дает нам

Перед умножением замените смешанные числа на неправильные дроби. В этом примере измените. Помните, что каждый член нужно умножить на 8. Обратите внимание, что в этом примере мы использовали три правила для поиска решения.

Решение простых уравнений путем умножения обеих частей на одно и то же число часто встречается при изучении соотношения и пропорции.

Соотношение — это частное двух чисел.

Отношение числа x к числу y можно записать как x: y или. В общем, дробная форма более значима и полезна. Таким образом, мы запишем отношение 3 к 4 как.

Пропорция — это утверждение, что два соотношения равны.

Пример 8

Решение

Нам нужно найти такое значение x, чтобы отношение x к 15 было равно отношению 2 к 5.

Умножая каждую часть уравнения на 15, получаем

Почему мы умножаем обе стороны на 15? Проверьте это решение в исходном уравнении.

Пример 9 Какое число x имеет такое же отношение к 3, как 6 к 9?

Решение

Чтобы найти x, сначала запишем пропорцию:

Затем мы умножаем каждую часть уравнения на 9.

Скажите себе: «2 равно 5, как x равно 10». Проверить!

Пример 11 Отношение количества женщин к количеству мужчин в классе математики составляет 7 к 8. Если в классе 24 мужчины, сколько женщин в классе?

Решение

Пример 12 Два сына должны были разделить наследство в соотношении 3 к 5. Если сын, получивший большую часть, получил 20 000 долларов, какова была общая сумма наследства?

Решение

Теперь мы добавляем 20 000 долларов США + 12 000 долларов США, чтобы получить общую сумму в 32 000 долларов США.

Проверить! Опять же, будьте осторожны при настройке пропорций. В соотношении 3/5 доля 5 является большей. Следовательно, поскольку 20 000 долларов — это большая часть, она также должна быть указана в знаменателе.

Пример 13 Если юридические требования к вместимости комнаты требуют 3 кубических метров воздушного пространства на человека, сколько людей могут законно занимать комнату шириной 6 метров, длиной 8 метров и высотой 3 метра?

Решение

Итак, вместимость юридической комнаты составит 48 человек.

Это означает, что «1 человек составляет 3 кубических метра, а x люди — 144 кубических метра». Проверьте решение.

ОБЪЕДИНЕНИЕ ПРАВИЛ ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Используйте комбинации различных правил для решения более сложных уравнений.
2. Применяйте упорядоченные шаги, описанные в этом разделе, для систематического решения уравнений.

Многие упражнения в предыдущих разделах требовали использования более чем одного правила в процессе решения.Фактически, вполне возможно, что одна задача может включать все правила

.

Не существует обязательного процесса для решения уравнений, включающего более одного правила, но опыт показал, что следующий порядок дает более плавную и безошибочную процедуру.

Первые Исключите дроби, если они есть, умножив каждый член уравнения на наименьшее общее кратное всех знаменателей дробей в уравнении.
Второй Упростите, объединив одинаковые члены с каждой стороны уравнения.
Третий Сложите или вычтите необходимые количества, чтобы получить неизвестное количество с одной стороны и арифметические числа с другой стороны.
Четвертый Разделите на коэффициент неизвестной величины.
Пятый Проверьте свой ответ.

Помните, коэффициент — это число, умноженное на букву. (То есть в выражении 5x коэффициент равен 5.)

Еще раз убедитесь, что каждый термин умножить на 3.

Решение

Умножение каждого члена на 15 дает

Вы можете оставить свой ответ в виде неправильной дроби вместо смешанного числа. Любая форма верна, но неправильная форма дроби будет более полезной при проверке вашего решения.

Обратите внимание, что в этом уравнении есть четыре члена.

Пример 3 Цена продажи (S) определенного товара составляла 30 долларов.00. Если маржа (M) составляла одну пятую стоимости (C), найдите стоимость товара. Используйте формулу C + M = S.

Решение

Поскольку маржа составляла одну пятую от стоимости, мы можем написать

РЕЗЮМЕ

Ключевые слова

• Уравнение — это утверждение в символах, что два числовых выражения равны.
• Идентификатор верен для всех значений буквальных и арифметических чисел в нем.
• Условное уравнение верно только для определенных значений буквальных чисел в нем.
• Решение или корень уравнения — это значение переменной, которая делает уравнение истинным утверждением.
• Два уравнения эквивалентны , если они имеют один и тот же набор решений.
• Соотношение — это частное двух чисел.
• Пропорция — это утверждение, что два соотношения равны.

Процедуры

• Если каждый член уравнения разделить на одно и то же ненулевое число, полученное уравнение эквивалентно исходному уравнению.
• Если из обеих частей уравнения вычесть одну и ту же величину, полученное уравнение эквивалентно исходному уравнению.
• Если одна и та же величина добавляется к обеим сторонам уравнения, полученное уравнение эквивалентно исходному уравнению.
• Если каждая сторона уравнения умножается на одно и то же ненулевое число, полученное уравнение эквивалентно исходному уравнению.
• Чтобы решить уравнение, выполните следующие действия:
  Шаг 1 Исключите дроби, умножив каждый член на наименьшее общее кратное всех знаменателей в уравнении.
  Шаг 2 Объедините одинаковые члены с каждой стороны уравнения.
  Шаг 3 Сложите или вычтите члены, чтобы получить неизвестную величину с одной стороны и числа арифметики с другой.
  Шаг 4 Разделите каждый член на коэффициент неизвестной величины.
  Шаг 5 Проверьте свой ответ.
  

GRE Стратегии решения проблем (для тестируемых)

Вопросов по критерию количественного мышления в Общем тесте GRE® предлагается моделировать и решать проблемы, используя количественные или математические методы.Как правило, решение математической задачи состоит из трех основных шагов:

• Шаг 1. Разберитесь в проблеме
• Шаг 2: Реализуйте стратегию решения проблемы
• Шаг 3. Проверьте свой ответ

Вот описание трех шагов, за которым следует список полезных стратегий для решения математических задач.

Шаг 1. Понять проблему

Первый шаг — внимательно прочитать формулировку проблемы, чтобы убедиться, что вы понимаете предоставленную информацию и проблему, которую вас просят решить.

Некоторая информация может описывать определенные количества. Количественная информация может быть дана словами или математическими выражениями, или их комбинацией. Кроме того, в некоторых задачах вам может потребоваться прочитать и понять количественную информацию в представлениях данных, геометрических фигурах или системах координат. Другая информация может принимать форму формул, определений или условий, которым должны удовлетворять количества. Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые могут быть переведены в уравнения или неравенства.

Помимо понимания информации, которую вам дают, важно понимать, что вам нужно сделать, чтобы решить проблему. Например, какие неизвестные количества необходимо найти? В какой форме они должны быть выражены?

Шаг 2: Реализация стратегии решения проблемы

Решение математической задачи требует большего, чем понимание описания проблемы, то есть больше, чем понимание величин, данных, условий, неизвестных и всех других математических фактов, связанных с проблемой.Это требует определения того, какие математические факты использовать, а также когда и как использовать эти факты для разработки решения проблемы. Это требует стратегии.

Математические задачи решаются с использованием самых разных стратегий. Также могут быть разные способы решения данной проблемы. Поэтому вам следует разработать репертуар стратегий решения проблем, а также представление о том, какие стратегии могут лучше всего работать при решении конкретных проблем. Попытка решить проблему без стратегии может привести к большому объему работы без получения правильного решения.

После того, как вы определились со стратегией, вы должны ее реализовать. Если вы застряли, проверьте свою работу, чтобы увидеть, не допустили ли вы ошибки в своем решении. Важно иметь гибкий и непредвзятый настрой. Если вы проверяете свое решение и не можете найти ошибку, или если ваша стратегия решения просто не работает, поищите другую стратегию.

Шаг 3. Проверьте свой ответ

Когда вы придете к ответу, вы должны проверить его разумность и правильность вычислений.

• Вы ответили на заданный вопрос?
• Разумен ли ваш ответ в контексте вопроса? Проверить разумность ответа можно так же просто, как вспомнить основной математический факт и проверить, соответствует ли ваш ответ этому факту.Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы убедиться, что ваш ответ обоснован. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть между 300 и 600.
• Вы допустили вычислительную ошибку при получении ответа? Ошибка ввода ключа с помощью калькулятора? Вы можете проверять наличие ошибок на каждом этапе своего решения.Или вы можете напрямую проверить правильность вашего решения. Например, если вы решили уравнение для x и получили ответ, вы можете проверить свой ответ, подставив его в уравнение, чтобы увидеть это.

Стратегии

Нет никаких установленных правил — применимых ко всем математическим задачам — для определения наилучшей стратегии. Способность определять стратегию, которая будет работать, растет по мере того, как вы решаете все больше и больше проблем. Далее следует краткое описание полезных стратегий.Вместе с каждой стратегией дается один или два типовых вопроса, на которые вы можете ответить с помощью стратегии. Эти стратегии не составляют полный список, и, за исключением группирования первых четырех стратегий вместе, они не представлены в каком-либо определенном порядке.

Первые четыре стратегии — это стратегии трансляции, когда одно представление математической задачи переводится в другое.

Вирусная математическая задача с двумя ответами разделяет Интернет

• Пользователь Twitter @pjmdoll поделился математической задачей: 8 ÷ 2 (2 + 2) =?
• Некоторые люди получили ответ 16, а некоторые — 1.
• Путаница связана с различием между современными и историческими интерпретациями порядка действий.
• Правильный ответ сегодня — 16. Ответ 1 был бы правильным 100 лет назад.
• Посетите домашнюю страницу INSIDER, чтобы узнать больше.

Идет загрузка.

Известно, что вирусные математические уравнения разделяют людей в Интернете.Некоторые задачи настолько сложны, что кажутся невозможными, даже если они предназначены для учеников начальной школы.

Подробнее : 10 вирусных математических уравнений, которые поставили в тупик Интернет

Эта последняя вирусная проблема, о которой поделился пользователь Twitter @pjmdoll, является одним из таких уравнений.

—em ♥ ︎ (@pjmdolI) 28 июля 2019 г.

Уравнение: 8 ÷ 2 (2 + 2) =?

Каждый получает разные ответы.

—laur♏️ (@lauram_williams) 30 июля 2019 г.

—becca 10✧ * .✰LILY + BARBS DAY (@spaceywhy) 30 июля 2019 г.

—maggie (@BatmanOfficial_) 29 июля 2019 г.

—George В. Куш (@supermaddd) 29 июля 2019 г.

—Light💜 ᴮᵃⁿᵍᵗᵃⁿ ᶠᵒʳᵉᵛᵉʳ 💜 (@SakuraTsukimine) 29 июля 2019 г.

Вот правильный способ решить 8 ÷ 2 (2 + 2) =?

Сначала сложите числа в скобках.

8 ÷ 2 (4) =?

Теперь произведите умножение и деление слева направо.

8 ÷ 2 (4) = 4 (4) = 16.

Путаница вызвана различием между современными и историческими интерпретациями порядка операций, известными как PEMDAS:

1. Круглые скобки
2. Экспоненты
3. Умножение и деление (слева направо)
4. Сложение и вычитание (слева направо)

Похожая математическая задача стала вирусной в 2011 году, когда люди не смогли прийти к единому мнению относительно ответа на 48 ÷ 2 (9 + 3). Преш Талуокер, автор книги «Радость теории игр: введение в стратегическое мышление», объяснил противоречие на своем канале YouTube MindYourDecisions и в сообщении в своем блоге.

Люди, получившие число 1 как ответ на эту проблему, использовали устаревшую версию порядка операций, сначала умножая 2 (4), а затем деля 8 на 8, согласно Талуокеру. Этот ответ был бы правильным 100 лет назад. Но если вставить уравнение в современный калькулятор как есть, ответ будет 16. Вы должны добавить еще один набор круглых скобок, чтобы получить ответ 1.

Люди получают разные ответы в зависимости от того, как они применяют порядок действий.Талия Лакриц / ИНСАЙДЕР

Талуокер объясняет, что часть путаницы также вызвана неоднозначностью символа разделения в задаче.

«В учебниках всегда есть правильные скобки, или они объясняют, что нужно разделять», — пишет он в своем блоге. «Поскольку математический набор текста сегодня намного проще, мы почти никогда не видим ÷ как символ, а вместо этого дроби записываются с числителем вертикально над знаменателем.«

Вы можете посмотреть полное объяснение этого уравнения Талуокером ниже.

Если вы сможете решить одну из этих 6 основных математических задач, вы выиграете приз в 1 миллион долларов | The Independent

В 2000 году Институт математики Клэя объявил задачи Премии тысячелетия. Это был сборник из семи важнейших математических задач, которые остались нерешенными.

Отражая важность проблем, Институт предложил приз в размере 1 миллиона долларов каждому, кто сможет предоставить строгое и рецензируемое решение любой из проблем.

В то время как одна из проблем, гипотеза Пуанкаре, была классно решена в 2006 году (математик, решивший ее, Григорий Перельман, одинаково хорошо отверг и приз в миллион долларов, и желанную медаль Филдса), остальные шесть проблем остаются нерешенными. .

Вот шесть математических задач, настолько важных, что решение любой из них стоит 1 миллион долларов.

P vs NP

(Getty Images / iStockphoto)

Некоторые проблемы простые, а некоторые сложные.

В мире математики и информатики существует множество задач, которые мы знаем, как запрограммировать компьютер для «быстрого» решения — основы арифметики, сортировка списка, поиск по таблице данных. Эти проблемы могут быть решены за «полиномиальное время», сокращенно «P». Это означает, что количество шагов, необходимых для сложения двух чисел или сортировки списка, управляемо растет вместе с размером чисел или длиной списка.

Но есть еще одна группа проблем, для которой легко проверить, является ли возможное решение проблемы правильным, но мы не знаем, как эффективно найти решение.Найти простые множители большого числа — такая проблема — если у меня есть список возможных множителей, я могу перемножить их и посмотреть, верну ли я свое исходное число. Но нет известного способа быстро найти множители произвольно большого числа. Действительно, безопасность Интернета зависит от этого факта.

По историческим и техническим причинам проблемы, для которых мы можем быстро проверить возможное решение, называются разрешимыми за «недетерминированное полиномиальное время» или «NP».

Любая проблема в P автоматически находится в NP — если я могу решить проблему быстро, я могу так же быстро проверить возможное решение, просто решив проблему и посмотрев, соответствует ли ответ моему возможному решению.Суть вопроса P vs NP заключается в том, верно ли обратное: если у меня есть эффективный способ проверить решения проблемы, есть ли эффективный способ на самом деле найти эти решения?

Большинство математиков и компьютерных ученых считают, что ответ отрицательный. Алгоритм, который мог бы решать задачи NP за полиномиальное время, имел бы ошеломляющие последствия для большей части математики, науки и технологий, и эти последствия настолько необычны, что дают основания сомневаться в том, что это возможно.

Конечно, доказать, что такого алгоритма не существует, само по себе является невероятно сложной задачей. Возможность окончательно сделать такое заявление о подобных проблемах, вероятно, потребует гораздо более глубокого понимания природы информации и вычислений, чем мы имеем в настоящее время, и почти наверняка будет иметь глубокие и далеко идущие последствия.

Прочтите официальное описание P vs NP от Института математики Клэя здесь.

Уравнения Навье-Стокса

На удивление сложно объяснить, что происходит, когда вы добавляете сливки в утренний кофе.

Уравнения Навье-Стокса представляют собой гидродинамическую версию трех законов движения Ньютона. Они описывают, как поток жидкости или газа будет развиваться в различных условиях. Подобно тому, как второй закон Ньютона описывает, как скорость объекта будет изменяться под действием внешней силы, уравнения Навье-Стокса описывают, как скорость потока жидкости будет изменяться под действием внутренних сил, таких как давление и вязкость, а также внешних сил. силы, подобные гравитации.

Уравнения Навье-Стокса представляют собой систему дифференциальных уравнений.Дифференциальные уравнения описывают, как конкретная величина изменяется с течением времени при некоторых начальных начальных условиях, и они полезны при описании всех видов физических систем. В случае уравнений Навье-Стокса мы начинаем с некоторого начального потока жидкости, а дифференциальные уравнения описывают, как этот поток развивается.

Решение дифференциального уравнения означает нахождение некоторой математической формулы для определения того, каким будет ваше интересующее количество на самом деле в любой конкретный момент времени, на основе уравнений, описывающих, как это количество изменяется.Многие физические системы, описываемые дифференциальными уравнениями, такие как вибрирующая гитарная струна или поток тепла от горячего объекта к холодному, имеют хорошо известные решения этого типа.

Однако уравнения Навье-Стокса сложнее. С математической точки зрения инструменты, используемые для решения других дифференциальных уравнений, здесь не оказались полезными. Физически жидкости могут демонстрировать хаотическое и турбулентное поведение: дым, исходящий от свечи или сигареты, имеет тенденцию сначала течь плавно и предсказуемо, но быстро превращается в непредсказуемые вихри и завитки.

Возможно, такое турбулентное и хаотическое поведение означает, что уравнения Навье-Стокса не могут быть решены точно во всех случаях. Возможно, удастся построить некую идеализированную математическую жидкость, которая, следуя уравнениям, в конечном итоге станет бесконечно турбулентной.

Любой, кто сможет построить способ решения уравнений Навье-Стокса во всех случаях или показать пример, в котором уравнения не могут быть решены, получит премию тысячелетия за эту задачу.

Прочтите официальное описание уравнений Навье-Стокса Институтом математики Клэя здесь.

Теория Янга-Миллса и квантовый разрыв масс

Математика и физика всегда были взаимовыгодными отношениями. Развитие математики часто открывало новые подходы к физической теории, а новые открытия в физике стимулировали более глубокие исследования лежащих в их основе математических объяснений.

Квантовая механика, пожалуй, самая успешная физическая теория в истории.Материя и энергия ведут себя по-разному в масштабе атомов и субатомных частиц, и одним из величайших достижений 20-го века стало теоретическое и экспериментальное понимание этого поведения.

Одной из основных опор современной квантовой механики является теория Янга-Миллса, которая описывает квантовое поведение электромагнетизма, а также слабых и сильных ядерных взаимодействий в терминах математических структур, возникающих при изучении геометрических симметрий. Предсказания теории Янга-Миллса были подтверждены бесчисленными экспериментами, и эта теория является важной частью нашего понимания того, как атомы устроены вместе.

Несмотря на этот физический успех, теоретические математические основы теории остаются неясными. Одна из проблем, представляющих особый интерес, — это «массовая щель», которая требует, чтобы определенные субатомные частицы, которые в некотором роде аналогичны безмассовым фотонам, вместо этого действительно имели положительную массу. Разрыв в массах — важная часть того, почему ядерные силы чрезвычайно сильны по сравнению с электромагнетизмом и гравитацией, но имеют чрезвычайно малый радиус действия.

Задача Премии тысячелетия, таким образом, состоит в том, чтобы показать общую математическую теорию, лежащую в основе физической теории Янга-Миллса, и получить хорошее математическое объяснение разрыва между массами.

Прочтите официальное описание теории Янга-Миллса и проблемы массового разрыва в Институте математики Клея.

Гипотеза Римана

Возвращаясь к древним временам, простые числа — числа, делящиеся только сами на себя и 1 — были объектом восхищения математиков. На фундаментальном уровне простые числа являются «строительными блоками» целых чисел, поскольку любое целое число может быть однозначно разбито на произведение простых чисел.

Учитывая центральную роль простых чисел в математике, вопросы о том, как простые числа распределяются вдоль числовой прямой, то есть как далеко простые числа находятся друг от друга, представляют собой активные области интереса.

К 19 веку математики открыли различные формулы, которые дают приблизительное представление о среднем расстоянии между простыми числами. Однако остается неизвестным, насколько близко к этому среднему остается истинное распределение простых чисел — то есть, есть ли части числовой прямой, где имеется «слишком много» или «слишком мало» простых чисел в соответствии с этими средними формулами.

Гипотеза Римана ограничивает эту возможность, устанавливая границы того, насколько далеко от среднего может отклоняться распределение простых чисел. Гипотеза эквивалентна и обычно формулируется в терминах того, лежат ли все решения уравнения, основанного на математической конструкции, называемой «дзета-функцией Римана», вдоль определенной линии в плоскости комплексных чисел. Действительно, изучение функций, подобных дзета-функции, стало отдельной областью математических интересов, что сделало гипотезу Римана и связанные с ней проблемы еще более важными.

Как и несколько задач, связанных с Премией тысячелетия, существуют значительные свидетельства того, что гипотеза Римана верна, но строгое доказательство остается неуловимым. На сегодняшний день вычислительные методы показали, что около 10 триллионов решений уравнения дзета-функции попадают в требуемую линию, и никаких контрпримеров не найдено.

Конечно, с математической точки зрения, 10 триллионов примеров истинности гипотез абсолютно не заменяют полного доказательства этой гипотезы, в результате чего гипотеза Римана остается одной из открытых проблем, связанных с присуждением Премии тысячелетия.

Прочтите официальное описание гипотезы Римана Институтом математики Глина здесь.

Гипотеза Берча и Суиннертона-Дайера

Одним из самых старых и обширных объектов математического исследования являются диофантовы уравнения или полиномиальные уравнения, для которых мы хотим найти целочисленные решения. Классическим примером, который многие могут вспомнить из школьной геометрии, являются тройки Пифагора или наборы из трех целых чисел, удовлетворяющие теореме Пифагора x2 + y2 = z2.

В последние годы алгебраисты особенно изучали эллиптические кривые, которые определяются особым типом диофантовых уравнений. Эти кривые имеют важные приложения в теории чисел и криптографии, и поиск целочисленных или рациональных решений для них является важной областью исследования.

Одним из самых ошеломляющих математических достижений последних нескольких десятилетий было доказательство Эндрю Уайлсом классической Великой теоремы Ферма, в котором говорилось, что версий пифагоровых троек более высокой степени не существует.Доказательство этой теоремы Уайлсом явилось следствием более широкого развития теории эллиптических кривых.

Гипотеза Берча и Суиннертона-Дайера предоставляет дополнительный набор аналитических инструментов для понимания решений уравнений, определяемых эллиптическими кривыми.

Прочтите здесь официальное описание гипотезы Берча и Суиннертона-Дайера от Института математики Клэя.

Гипотеза Ходжа

Математическая дисциплина алгебраической геометрии, в широком смысле, представляет собой изучение многомерных форм, которые могут быть определены алгебраически, когда решение задается алгебраическими уравнениями.

В качестве чрезвычайно простого примера вы можете вспомнить из школьной алгебры, что уравнение y = x2 приводит к параболической кривой, когда решения этого уравнения вычерчиваются на миллиметровой бумаге. Алгебраическая геометрия имеет дело с многомерными аналогами этого вида кривой, когда рассматривают системы множественных уравнений, уравнений с большим количеством переменных и уравнения на плоскости комплексных чисел, а не действительные числа.

В 20 веке процветали изощренные методы понимания кривых, поверхностей и гиперповерхностей, являющихся предметами алгебраической геометрии.Сложные для представления формы можно сделать более управляемыми с помощью сложных вычислительных инструментов.

Гипотеза Ходжа предполагает, что определенные типы геометрических структур имеют особенно полезный алгебраический аналог, который можно использовать для лучшего изучения и классификации этих форм.

Прочтите официальное описание гипотезы Ходжа Институтом математики Клэя здесь.

Подробнее:

• Сколько зарабатывают самые высокооплачиваемые работники в 20 профессиях
• Семь устаревших «правил» мужского стиля, которые вы теперь можете игнорировать
• 16 навыков, которым трудно научиться, но которые окупятся навсегда

Прочтите оригинальную статью на Business Insider UK.© 2017. Следите за новостями Business Insider UK в Twitter.

Как решать практические задачи геометрии

Цели

o Определить некоторые важные этапы процесса решения практических задач геометрии

o Применять методы решения геометрических задач в практических ситуациях

Geometry имеет множество реальных приложений в повседневных ситуациях. В этой статье мы научимся применять геометрические принципы и методы для решения задач.Ключом к решению практических задач геометрии является перевод реальной ситуации в цифры, измерения и другую информацию, необходимую для концептуального представления ситуации. Например, вы уже знаете, как рассчитать площадь составной фигуры; Если бы вас попросили определить, сколько места на полу доступно в определенном здании с составной формой, вам просто нужно было бы применить те же принципы, которые вы использовали бы для расчета площади составной фигуры. Конечно, могут потребоваться некоторые измерения здания, но применяются те же методы решения проблем.

Нам следует представить базовый подход к решению практических задач геометрии. Этот подход аналогичен подходу к решению почти задачи со словом, но немного больше ориентирован на характеристики задач геометрии, в частности.

1. Определите, что вам нужно вычислить для решения проблемы. В некоторых случаях может потребоваться длина; в других случаях — измерение площади или угла. Если вы на протяжении всего процесса осознаете, что вам нужно определить, вы можете сэкономить значительное количество времени.

2. Нарисуйте диаграмму. Иногда могут быть полезны линейка, циркуль, транспортир или комбинация этих инструментов. Однако даже если вы используете только грубый набросок, визуальное представление проблемы может помочь вам организовать свои мысли и отслеживать важную информацию, такую ​​как соотношение отрезков линии и углов, а также их размеры.

3. Запишите все соответствующие измерения. Например, если вы рассчитываете площадь, вам может потребоваться измерить определенную длину (в качестве альтернативы, они могут быть предоставлены вам).В любом случае запишите их и отметьте каким-либо образом на диаграмме.

4. Обратите внимание на единицы. Использование единиц измерения длины или угла в квадратных метрах может быть досадной ошибкой! Внимательно следите за приборами, которые вы используете, на протяжении всей задачи. Если единицы не указаны, просто используйте, например, общий термин «единицы» вместо дюймов или метров.

5. При необходимости разделите цифру на небольшие части. Если ваша диаграмма представляет собой составную фигуру, ее можно разделить на небольшие части, с которыми вы сможете справиться.

6. Определите все подходящие геометрические отношения. Этот шаг может значительно упростить проблему. Возможно, вы можете показать два совпадающих или похожих треугольника, или, возможно, вы сможете определить конгруэнтные сегменты или углы. Используйте этот шаг, чтобы заполнить как можно больше недостающей информации на диаграмме.

7. Посчитайте. На этом этапе вам необходимо применить полученные знания для анализа фигуры и других данных для решения проблемы. Например, вам может потребоваться применить теорему Пифагора или вычислить периметр фигуры.Какими бы ни были детали проблемы, вам нужно будет применить свои навыки в геометрии соответствующим образом.

8. Проверьте свои результаты. Взгляните на свой ответ в контексте вашей диаграммы — имеет ли ваш ответ смысл? Результат в миллионы квадратных метров для площади фигуры с размерами в пределах нескольких метров должен говорить вам о том, что вы допустили ошибку в какой-то момент своего анализа.

Не каждый шаг описанного выше подхода потребуется для решения каждой проблемы.Вы должны руководствоваться здравым смыслом при определении того, что необходимо для удовлетворительного и быстрого решения проблемы. Кроме того, вы не всегда можете думать о том, чтобы использовать точную последовательность шагов, описанных выше; План — это просто способ описать систематический подход к решению проблем. Оставшаяся часть этой статьи дает вам возможность проверить свои навыки геометрии с помощью нескольких практических задач. Очевидно, что эти проблемы не требуют, чтобы вы выходили на улицу и измеряли длину или углы, но имейте в виду, что проблемы, с которыми вы сталкиваетесь в повседневной жизни, могут потребовать этого!

Практическая задача : План дома показан ниже.Определите площадь, занимаемую домом.

Решение : Давайте сначала разделим диаграмму дома на два прямоугольника и трапецию, так как мы можем вычислить площадь каждой из этих фигур. Используя свойства каждой фигуры, мы также можем заполнить некоторую неизвестную информацию.

Итак, площадь большего прямоугольника равна произведению 40 футов и 20 футов, или 800 квадратных футов. Площадь меньшего прямоугольника составляет 25 футов на 6 футов, или 150 квадратных футов.Площадь трапеции следующая:

Высота ( h ) составляет 6 футов, а две базы ( b ₁ и b ₂ ) — 8 и 11 футов.

Сложив все три области, мы получим общую площадь дома 1007 квадратных футов.

Практическая задача : Путешественник поднимается по крутому холму. Уклон холма между двумя деревьями постоянный, а основание одного дерева на 100 метров выше другого.Если расстояние между деревьями по горизонтали составляет 400 метров, как далеко турист должен пройти, чтобы добраться от одного дерева к другому?

Решение : Поскольку эту проблему сложно представить, диаграмма чрезвычайно полезна. Обратите внимание, что основания деревьев различаются по высоте на 100 метров — это наша вертикальная дистанция для прогулки. Горизонтальное расстояние 400 метров.

Обратите внимание, что мы показали прямой угол, потому что горизонтальный и вертикальный сегменты перпендикулярны.Теперь мы можем использовать теорему Пифагора, чтобы вычислить расстояние d , которое должен пройти турист.

Таким образом, турист должен пройти около 412 метров. Обратите внимание, что, хотя турист делает значительное (100 метров) изменение высоты во время этой прогулки, разница между фактическим расстоянием, которое он проходит, и горизонтальным расстоянием невелика — всего около 12 метров.

Практическая задача : У домовладельца есть прямоугольный огороженный двор, и он хочет положить мульчу в свои треугольные сады, как показано ниже.Внутренняя граница каждого сада всегда встречается с забором под одним и тем же углом. Если мешок с мульчей покрывает около 50 квадратных футов, сколько мешков с мульчей домовладелец должен купить, чтобы укрыть свой сад?

Решение : В задаче говорится, что внутренняя граница каждого сада встречается с забором под одинаковым углом во всех случаях; таким образом, мы можем сделать вывод (как показано ниже), что все треугольники равнобедренные (и что треугольники с одинаковой длиной сторон совпадают по условию ASA).Таким образом, мы можем пометить каждую сторону неизвестной переменной x или y .

Напомним, что огороженная территория прямоугольная; таким образом, угол в каждом углу составляет 90 °. Затем мы можем найти x и y , используя теорему Пифагора. Однако сначала обратите внимание, что x и y — это высота и оснований соответствующих треугольников.

Поскольку сады состоят из двух треугольников каждой формы, общая площадь сада представляет собой просто сумму x ² и y ² .(Если вы не следуете этому пункту, просто используйте в каждом случае формулу площади треугольника — вы получите тот же результат.)

Таким образом, домовладельцу нужно шесть мешков мульчи (всего 300 квадратных футов), чтобы покрыть свой сад. (Конечно, мы предполагаем, что он должен купить целое число мешков.)

Математика / Решение задач в общем ядре

Обзор

Использование моделей — важный шаг, помогающий студентам перейти от конкретной манипулятивной работы с задачами со словами к абстрактному этапу создания уравнения для решения контекстных задач.Научившись использовать простые модели для представления ключевых математических отношений в словесной задаче, учащиеся могут легче разбираться в словесных задачах, распознавать как числовые отношения в данной задаче, так и связи между типами задач, а также успешно решать задачи с уверенностью в том, что их решения разумны.

Важность

Почему моделирование текстовых задач важно?

У студентов часто возникают проблемы со словами.Многие студенты просто ищут какие-то числа и что-то с ними делают, надеясь, что они решат проблему.

Учащиеся должны выработать привычку сначала разбираться в проблеме. Диаграмма или модель часто фокусируются на понимании проблемы, а не просто на получении ответа. Затем модель можно использовать для создания продуманного уравнения. Модель и уравнение можно использовать в качестве проверки рассуждений после того, как учащийся получит решение.

Решение проблем не заканчивается на ответе.Процесс должен продолжаться после «получения ответа» на рассуждение о том, имеет ли ответ смысл.

Что такое моделирование текстовых задач?

Модели на любом уровне могут варьироваться от простых до сложных, от реалистичных до представительных. Молодые студенты часто решают начальные словесные задачи, разыгрывая их и моделируя их с реальными объектами проблемной ситуации, например плюшевых мишек или игрушечных машинок. Со временем они расширяются до использования репрезентативных рисунков, сначала рисуя рисунки, которые реалистично изображают элементы проблемы, а затем переходят к многоцелевым представлениям, таким как круги или счетные метки.После множества конкретных опытов с реальными задачами со словами, включающими соединение и разделение, или умножение и разделение объектов, учителя могут переводить учащихся на рисунки модели с перевернутой буквой V и гистограммы, которые являются многоцелевыми графическими организаторами, привязанными к определенным типам задач со словами.

Моделирование базовых числовых соотношений

Простые диаграммы, иногда известные как числовые связи, треугольники фактов, ситуационные диаграммы или графические изображения, все чаще появляются в учебных материалах.Но способности учащихся решать проблемы и относительное мышление выиграют, если они будут чаще использовать эти диаграммы и модели.

Маленькие дети могут начать видеть числовые отношения, существующие в семье фактов, благодаря использованию модели, из которой они выводят уравнения. Связь чисел и перевернутая буква V — это одна простая модель, которая помогает учащимся увидеть отношения сложения / вычитания в семействе фактов и может использоваться с задачами со словами, требующими простого соединения и разделения.Связь чисел, а затем модель перевернутой буквы V могут быть адаптированы для семейств фактов умножения и деления. Кроме того, учащиеся могут подумать о соотношениях между числами в перевернутой букве V в формальных терминах, слагаемых и в сумме , или проще говоря, часть и итого , как показано на диаграммах ниже.

Конкретный пример для данной суммы 10 будет следующим, в зависимости от того, какой элемент проблемы неизвестен.

6 + 4 =? 6+? = 10? + 4 = 1

4 + 6 =? 10-6 =? 10 — 4 =?

Несмотря на то, что они часто используются с семействами фактов и изучением основных фактов, диаграммы с числовыми связями и перевернутые буквы V также могут хорошо работать при решении текстовых задач. Студентам необходимо подумать о том, что они знают и чего не знают в словесной задаче — известны ли обе части или только одна из них? Правильно разместив известные величины на перевернутой V-диаграмме, учащиеся с большей вероятностью определят полезное уравнение для решения проблемы и увидят результат как разумный для ситуации.Например, рассмотрим следующую задачу:

У Захария было 10 вагонов. Захари подарил своему брату 3 вагона. Сколько вагонов сейчас у Закари?

Студенты должны определить, со сколькими суммами Захари начал ( всего или целых ), и сколько он отдал ( часть от общего числа ). Итак, им нужно узнать, сколько осталось (остальная часть из ). Следующая перевернутая V-диаграмма представляет отношения между номерами этой проблемы:

3 +? = 10 или 10 — 3 =?, Значит, у Закари осталось 7 вагонов.

По мере того, как учащиеся переходят к умножению и делению, модель перевернутой буквы V все еще может использоваться либо в режиме повторного сложения, либо в режиме умножения. Ситуации разделения не требуют новой модели; деление рассматривается как обратное умножению или ситуация, когда один из факторов неизвестен.

Опять же, перевернутая V-диаграмма может быть полезна при решении задач умножения и деления слов. Например, рассмотрим следующую задачу:

Фонг посадил 18 растений томатов в 3 ряда.Если в каждом ряду было одинаковое количество растений, сколько растений было в каждом ряду?

Студенты могут видеть, что они знают продукт и количество строк. Число В строке неизвестно. Любая из приведенных ниже диаграмм может помочь решить эту проблему, убедив учащихся, что шесть раз подряд — разумный ответ.

Хотя перевернутая V-диаграмма может быть расширена до многозначных чисел, она обычно используется с проблемами, связанными с базовыми семействами фактов. Расширение использования модельной диаграммы перевернутой буквы V должно усилить взаимосвязь между числами в семействе фактов, что сделает его полезным и быстрым визуальным средством для решения простых задач со словами с дополнительным преимуществом использования и увеличения удержания основных фактов.

Модели и типы задач для вычислений

По мере того, как дети переходят к работе с многозначными числами, учителя могут переводить учащихся на чертежи ленточных диаграмм / гистограмм, быстрые наброски, которые помогают учащимся увидеть взаимосвязь между важными числами в словесной задаче и определить, что известно и неизвестно в ситуации.

Знакомя учащихся с грифельными моделями, учитель получает важные наглядные пособия, помогающие учащимся думать о математических отношениях между числами в заданной задаче со словом.

С ленточной диаграммой / гистограммой взаимосвязь между числами во всех этих типах задач становится более прозрачной и помогает студенту переходить от работы с манипуляторами и рисования картинок к символической стадии написания уравнения для ситуации. При рутинном использовании диаграмм и хорошо организованных обсуждениях учителями ученик начнет понимать части словесной задачи и то, как эти части соотносятся друг с другом.

Проблемы частично-частично-целиком. Задачи «частично-частично-целое» полезны с задачами со словами, которые относятся к совокупности вещей, например коллекции. Обычно это более статичные ситуации, включающие два или более подмножества целого набора. Рассмотрим проблему,

У Коула 11 красных блоков и 16 синих блоков. Сколько всего блоков у Коула?

Учащиеся могут построить простой прямоугольник из двух частей, чтобы обозначить два известных набора блоков (части / дополнения). Неважно, чтобы части прямоугольника были точно пропорциональны числам в задаче, но некоторое внимание к их относительному размеру может помочь в решении проблемы.Неизвестным в этой задаче является то, сколько их всего (всего / всего / суммы), что обозначено скобкой (или перевернутой буквой V) над полосой, обозначающей общее количество двух наборов блоков. Первая барная модель ниже отражает информацию в задаче о блоках Коула.

11 + 16 =? Итак, у Коула всего 27 блоков.

Аналогичная модель будет работать для задачи, когда известна вся сумма, но одна из частей (недостающее слагаемое) неизвестна. Например:

У Коула было 238 блоков.100 из них были желтыми. Если все блоки Коула синие или желтые, сколько их было синими?

Следующая модель стержня может быть полезна в решении этой проблемы.

100+? = 238 или 238 — 100 =? Итак, у Коула 138 синих блоков.

Ответ должен быть немного больше 100, потому что 100 + 100 равно 200, но здесь всего 238, поэтому синих блоков должно быть чуть больше 100.

Модель стержня «часть-часть-целая» легко может быть расширяется до больших чисел и других числовых типов, таких как дроби и десятичные дроби.Рассмотрим задачу:

Летисия прочитала 7 ½ книг для читателей. Всего она хочет прочитать 12 книг. Сколько еще книг ей нужно прочитать?

Первая диаграмма ниже отражает эту проблему. Любая проблема со словом, которую можно рассматривать как части и целое, реагирует на диаграммы моделирования стержней. Если у задачи есть несколько слагаемых, учащиеся просто рисуют на полосе достаточно частей, чтобы отразить количество слагаемых или частей, и указывают, является ли одна из частей или целое / сумма неизвестными, как показано на втором рисунке ниже.

12 — 7 ½ =? или 7 ½ +? = 12, поэтому Летиции нужно прочитать еще 4 ½ книги.

Задачи соединения (сложения) и разделения (вычитания).

Студенты, которые не могут решить, нужно ли им прибавлять или вычитать, а затем умножать или делить, находят организационный потенциал гистограммы невероятно полезным.

У Марии было 20 долларов. Она получила еще 11 долларов за присмотр за детьми. Сколько у нее сейчас денег? Рассмотрим эту задачу объединения:

Учащиеся могут определить, что начальная сумма в 20 долларов является одной из частей, 11 долларов — другая часть (дополнительная сумма), а неизвестным является сумма / вся сумма или сколько денег она есть сейчас.Первая диаграмма ниже помогает представить эту проблему.

Рассмотрим соответствующую ситуацию с вычитанием:

У Марии был 31 доллар. Часть денег она потратила на новый компакт-диск. У Марии осталось 16 долларов.

Вторая диаграмма выше представляет эту ситуацию. Студенты могут использовать модель, чтобы помочь им определить, что общая сумма сейчас составляет 31 доллар, одна из частей (вычитающее изменение) неизвестна, поэтому другая часть — это те 16 долларов, которые у нее остались.

Проблемы сравнения. Проблемы со сравнением обычно считались трудными для детей. Частично это может быть связано с акцентом на вычитание, который используется в задачах со словами, которые включают ситуации «убрать», а не нахождение «разницы» между двумя числами. Интересно, что исследования в странах, которые часто используют гистограммы, показали, что учащиеся не находят задачи сравнения намного более сложными, чем задачи «часть-часть-целое» (Yeap, 2010, стр. 88-89).

Модель с двумя стержнями может помочь сделать задачи сравнения менее загадочными.В основном, задачи сравнения включают две величины (либо одна величина больше другой, либо они равны) и разницу между величинами. Можно нарисовать две полосы, по одной представляющей каждое количество, с разницей, представленной пунктирной областью, добавленной к меньшему количеству. Например, учитывая задачу:

Тамека участвовал в 26 окружных ярмарках. Ее друг Джексон проехал 19 поездок. На сколько аттракционов ездил Тамека больше, чем Джексон?

Учащиеся могут создать диаграмму столбцов сравнения, показанную ниже, где большее количество, 26, является более длинным столбцом.Пунктирная секция показывает разницу между количеством поездок Джексона и Тамеки, или насколько больше у Тамека, чем у Джексона, или на сколько дополнительных поездок Джексону пришлось бы проехать, чтобы у него было такое же количество поездок, как у Тамека.

26-19 =? или 19+? = 26; разница в 7, так что Тамека проехал еще 7 аттракционов.

Задачи сравнения выражают несколько различных формулировок отношений. Если Тамека проехал на 7 аттракционов больше, чем Джексон, то Джексон проехал на 7 аттракционов меньше, чем Тамека.Варианты схемы модели с двойной полосой могут сделать для учащихся более наглядными отношения, сформулированные по-разному. Студентам часто бывает полезно осознать, что в какой-то момент обе величины имеют одинаковое количество, как показано на модели ниже пунктирной линией, проведенной от конца прямоугольника, представляющего меньшее количество. Но у одной из величин больше, чем указано в области справа от пунктирной линии на более длинной полоске. Разницу между количествами можно определить путем вычитания 19 из 26 или сложения от 19 до 26 и получения 7, что означает, что 26 на 7 больше, чем 19, или 19 означает, что на 7 меньше 26.

Проблемы со сравнительными словами особенно проблематичны для изучающих английский язык, поскольку вопрос можно задать несколькими способами. Изменение полос сравнения может сделать вопросы более прозрачными. Вот несколько вариантов вопросов о двух количествах поездок, на которых проехали Тамека и Джексон:

• На сколько аттракционов проехал Тамека больше, чем Джексон?
• На сколько поездок Джексон совершил меньше поездок, чем Тамека?
• Сколько еще поездок пришлось бы проехать Джексону, чтобы проехать столько же поездок, что и Тамека?
• На сколько меньше поездок пришлось бы проехать Тамеке, чтобы проехать столько же поездок, что и Джексон?

Сравнения также могут быть мультипликативными.Рассмотрим проблему:

В коллекции Хуана 36 компакт-дисков. Это в 3 раза больше дисков, чем у его брата Маркоса. Сколько компакт-дисков у Маркоса?

В этой ситуации учащиеся должны построить модель стержня, показанную ниже слева, из 3 частей. Студенты могут разделить 36 на 3 равные группы, чтобы показать количество, которое нужно взять 3 раза, чтобы создать в 3 раза больше компакт-дисков для Хуана.

36 ¸ 3 =? или 3 раза? = 36 12 + 12 + 12 =? (или 3 x 12 =?)

, так что у Маркоса 12 компакт-дисков.Итак, у Хуана 36 компакт-дисков.

Аналогичная модель может использоваться, если большее количество неизвестно, но меньшее количество и мультипликативное отношение известны. Если проблема была:

У Хуана есть компакт-диски. У него в 3 раза больше компакт-дисков, чем у Маркоса, у которого 12 компакт-дисков. Сколько компакт-дисков у Хуана?

Как видно на диаграмме вверху справа, студенты могут положить 12 в коробку, чтобы показать количество компакт-дисков, которые есть у Маркоса; затем продублируйте это 3 раза, чтобы увидеть, что у Хуана в 3 раза больше компакт-дисков.Тогда общее количество, которое есть у Хуана, будет суммой этих трех частей.

Задачи умножения и деления. Та же модель, что и для мультипликативных сравнений, также будет работать для основных задач умножения слов, начиная с однозначных множителей. Рассмотрим проблему:

У Аланы было 6 упаковок жевательной резинки. В каждой упаковке 12 штук жевательной резинки. Сколько всего жевательных резинок у Аланы?

В следующей линейчатой ​​модели для визуализации проблемы используется повторное сложение умножения.

12 + 12 + 12 + 12 + 12 + 12 = 72 (или 6 x 12 = 72)

, так что у Аланы 72 кусочка жевательной резинки.

По мере того, как учащиеся переходят к многозначным множителям, они могут использовать модель с многоточием, чтобы упростить гистограмму. Например:

Сэм пробегает 32 км в день в течение апреля, чтобы подготовиться к гонке. Если Сэм бегает каждый день месяца, сколько всего километров он пробежал в апреле?

30 x 32 км = 30 x 30 км + 30 x 2 км = 960 км

Сэм пробежал 960 км за 30 дней апреля.

Поскольку деление — это обратное умножение, в задачах деления слов будет использоваться модель мультипликативного столбца, в которой произведение (делимое) известно, но один из факторов (делитель или частное) неизвестен.

Задачи, связанные со ставками, дробями, процентами и несколькими шагами. По мере того, как учащиеся переходят в старшие классы, они могут применять новые концепции и многоступенчатые задачи со словами к чертежам моделей грифов. Скемп (1993) определил, что реляционное мышление имеет решающее значение для развития математики.Учащийся должен уметь расширять свое мышление на основе моделей, которые они использовали ранее, связывая и адаптируя то, что он знает, к новым ситуациям.

Рассмотрим следующую задачу о скорости и расстоянии:

Фонг проехала 261 милю, чтобы увидеться с бабушкой. В среднем она разгонялась до 58 миль в час. Как долго она добиралась до дома бабушки?

Следующая модель основана на модели «часть-часть-целое» с использованием формата повторяющегося сложения для умножения и деления. Предполагается, что учащиеся имеют опыт использования модели для задач деления, частные которых являются не просто целыми числами.По мере того, как они наращивают (или делят) 261 милю, они вычисляют, что пять 58 будут представлять 5 часов путешествия, а оставшиеся 29 миль будут представлены половинным квадратом, поэтому решение состоит в том, что Фонг займет 5½ часов. времени в пути, чтобы добраться до дома бабушки.

Даже более сложную проблему скорости можно решить с помощью комбинации подобных моделей. Рассмотрим эту задачу:

Сью и ее подруга Энн вместе отправились в путешествие. Сью проехала первые 2/5 поездки, а Энн проехала 210 миль за последние 3/5 поездки.Средняя скорость Сью составляла 60 миль в час, а Энн — 70 миль в час. Сколько времени у них заняла поездка?

Есть несколько способов, которыми учащиеся могут комбинировать или изменять базовую модель столбцов. Одно из решений может заключаться в следующем, где первое неизвестное — сколько миль проехала Сью. Полоса, разделенная на пятые части, показывает, как рассчитать километры, которые проехала Сью. Поскольку мы знаем, что 210 миль, которые проехала Энн, составляют 3/5 всего пути, каждая из ящиков Анны, каждая из которых представляет 1/5 пути, составляет 70 миль. Таким образом, Сью проехала две части по 70 миль, или 140 миль, что составляет 2/5 от общей поездки.

Теперь диаграмму необходимо расширить, чтобы показать, как рассчитать количество часов. Участок 210 миль Анны, разделенный на ее скорость 70 миль в час, займет 3 часа, как указано в следующем расширении диаграммы. Расстояние Сью в 140 миль теперь необходимо разделить на сегменты со скоростью 60 миль в час, чтобы определить время ее вождения, равное 2 1/3 часа. Таким образом, общая поездка в 350 миль займет 5 1/3 часа времени вождения, учитывая две нормы вождения.

Рассмотрим более простую многоступенчатую задачу:

Роберто купил 5 спортивных напитков по 1 доллару.25 каждый. Роберто дал кассиру 20 долларов. Сколько сдачи он получил обратно?

Опять же, у учащихся могут быть вариации, когда они начнут расширять использование диаграмм в многоэтапных или более сложных задачах. Некоторые ученики могут использовать сразу две диаграммы, как показано ниже слева. Другие могут указывать вычисления на одной диаграмме, как показано на диаграмме справа.

Имея рутинный опыт моделирования стержней, студенты могут расширить использование моделей для решения задач, связанных с отношениями, которые могут быть выражены с помощью переменных.Рассмотрим эту простую задачу, которую можно представить алгебраически:

Каллан и Авриель собрали в общей сложности 190 ошибок для научного проекта. Каллан собрал на 10 ошибок больше, чем Авриель. Сколько жуков собрал Каллан?

Пусть n равно количеству ошибок, собранных Авриель, а n + 10 равно количеству ошибок, собранных Калланом. Студенты могут создать следующую модель:

Поскольку n + n = 180 (или 2 n = 180), n = 90.Таким образом, Каллан собрал 90 + 10 или 100 ошибок, а Авриэль собрала 90 ошибок, всего 190 ошибок, собранных вместе.

При использовании модельного метода учащиеся должны переводить информацию и отношения в словах в визуальные представления, которые являются моделями. Они также должны манипулировать и преобразовывать визуальные представления, чтобы генерировать информацию, полезную при решении заданных проблем.

Понимание структуры словесной задачи включает в себя знание того, как связана математическая информация в данной текстовой задаче и как выделить компоненты, необходимые для решения проблемы.Чертежи ленточной диаграммы / гистограммы могут помочь учащимся лучше определять переменные, участвующие в проблеме, а также отношения между ними. Эта способность сосредотачиваться на отношениях между числами в данной задаче и распознавать математическую структуру как особый тип проблемы является частью реляционного мышления — критически важным навыком для успеха в алгебре. Использование перевернутой буквы V и гистограммы в предалгебраическую работу в классах K-7 может сделать учащихся более подготовленными к формальному изучению алгебры.

Это отличный сайт для практики решения проблем — моделирования проблем с помощью ленточной диаграммы / гистограммы

7 лучших приложений и веб-сайтов для решения математических задач

Мы уже говорили о приложениях для изучения математики для Android и iOS. Эти приложения позволяют изучать математические концепции и освежить их в памяти независимо от того, где вы находитесь. Но что делать, если вы застряли на проблеме, и некому помочь? Ответ прост. Существует множество приложений и веб-сайтов, которые можно использовать для решения математических задач в кратчайшие сроки.Итак, если вы не хотите ни от кого зависеть, вот несколько лучших приложений и веб-сайтов для решения математических задач, которые вы можете попробовать. Давай начнем.

Как выполнять домашнее задание с помощью приложений Math Solver

1. Mathway: сканирование фотографий, решение проблем

Mathway — это наиболее рекомендуемое приложение, когда речь идет о приложениях для решения математических задач. Он охватывает большую область математики, такую ​​как базовая математика, алгебра, тригонометрия, исчисление и т. Д. Итак, хотите ли вы решить основные квадратные корни или вычислить сложные пределы и производные, это единственный инструмент, который может вам понадобиться.

Mathway также позволяет вам общаться с экспертами. Вы можете отправить свой вопрос за плату в размере 5 долларов США в месяц (один нерешенный вопрос за раз) или 30 долларов США в месяц (1-й план + 20 сеансов в прямом эфире с экспертами).

Чтобы приступить к решению проблем, все, что вам нужно сделать, это выбрать предметную область и сфотографировать вопрос. Более того, если вы хотите ввести вопрос, вы также можете сделать это с клавиатуры. Цифры на клавиатуре меняются в зависимости от выбранной вами темы.Самое приятное то, что он показывает вам шаги для решения каждой проблемы. Однако он находится за платным доступом и будет стоить вам 9,99 доллара в месяц. Это также удаляет рекламу.

Плюсы

• Охватывает несколько областей (алгебра, тригонометрия, исчисление и т. Д.)
• Поддерживает три типа ввода (клавиатура, камера, голос)
• Пошаговое решение проблем
• Вход в систему не требуется

Минусы

• Спросите эксперта, может быть дорого для многих

Получить Mathway для (iOS | Android | Интернет)

2.Slader Homework Answers

Если у вас много математических вопросов, фотографировать или печатать каждую задачу может стать большой проблемой. Поскольку большинство математических задач извлечено из учебников, почему бы просто не пролистать вопросы / ответы в самой книге? Это приложение делает именно это. Вы можете отсканировать штрих-код книги или выбрать категорию уже решенных книг.

В дополнение к математике средней школы (предварительная алгебра, геометрия, тригонометрия) и математике высшего уровня (дифференциальные уравнения, статистика и т. Д.)), оно также охватывает другие темы, такие как английский язык, менеджмент, бухгалтерский учет и т. д. Хотя приложение имеет большую базу данных книг, есть вероятность, что вы не найдете книгу, которую ищете. Более того, большинство учебных пособий по математике заблокированы. Таким образом, вы можете просматривать их, только перейдя на премиальный план, который стоит 3,99 доллара в месяц.

Плюсы

• Найдите математические решения по книге
• Четко показывает номер главы, страницу и номер упражнения
• Пользователи могут оценивать и комментировать решения

Минусы

• Очень медленно загружается
• Тонны рекламных баннеров
• Ограниченная база данных книг
• Нет возможности сканировать вопросы

Получить ответы на домашнее задание Slader для (iOS | Android)

3.Cymath — решатель математических задач

Cymath похож на Mathway, но мне он нравится больше из-за нескольких дополнительных функций. Но перед этим давайте сначала поговорим об общих чертах. Оба приложения для решения математических задач позволяют решать математические задачи, а также вводить данные с клавиатуры. Однако в Mathway гораздо больше подполей математики по сравнению с Cymath. Я попробовал ответить на несколько вопросов по алгебре, и оба из них показали хорошие результаты. Однако Cymath часто показывал ошибки, когда я задавал вопросы по тригонометрии.

В заключение, если вы хотите охватить большую область объектов и хотите максимальной точности, Mathway все равно лучше.

Cymath выделяется несколькими другими аспектами, например, разделом истории и возможностью добавлять решения в закладки. Это пригодится, когда вы застряли и хотите обратиться к старой проблеме. Кроме того, в нем также есть вкладка обучения, на которой есть общие ссылки, практические вопросы, а также обсуждается одна проблема каждую неделю. Плюс версия стоит 4,99 доллара в месяц. Он удаляет рекламу, показывает пошаговые решения и даже отвечает, почему используется определенный шаг (помимо того, как).

Плюсы

• Охватывает большинство тем (алгебра, исчисление, построение графиков)
• Чистый интерфейс (простой для просмотра в браузере)
• Поддерживает ввод изображений и клавиатуры
• Возможность истории и закладок

Минусы

• Немного спотыкается о точности
• Не так полно, как Mathway

Get Cymath — средство решения математических задач для (iOS | Android)

4.Решатель геометрии ² lite

Большинство приложений для математических вычислений не работают с геометрией, но вот приложение, которое с этим справляется. Так что в следующий раз, когда вам будет сложно найти площадь фигуры или вы не сможете вспомнить конкретную формулу, вы знаете, где искать. Вы можете легко переключаться между 2D и 3D фигурами на боковой панели. Кроме того, все рисунки приведены в виде списка вместе с линейной диаграммой для облегчения понимания.

Расчет также очень прост. Все, что вам нужно сделать, это добавить переменные, и приложение покажет вам все результаты в реальном времени, когда вы измените эти переменные в режиме реального времени.Если вы не хотите полагаться на функцию автоматического расчета, она также отображает все формулы на одной вкладке для быстрого ознакомления. Пока все формулы бесплатны, калькулятор для нескольких цифр заблокирован. С другой стороны, вы можете просто посмотреть 15-секундную видеорекламу, чтобы разблокировать их. Если вы не хотите видеть рекламу, у вас есть возможность удалить рекламу и разблокировать все цифры, заплатив единовременную плату в размере 3,99 доллара США.

Плюсы

• 2D и 3D раздел фигуры
• Автоматический калькулятор с переменными
• Список всех формул (площадь, периметр, центроид и т. Д.))

Минусы

Получить решатель геометрии ² lite для (iOS | Android)

5. Google Lens (домашнее задание)

Знаете ли вы, что приложение Google Search можно использовать для решения математических задач? Очень немногие люди знают об этом, и я уверен, что на самом деле им пользуются еще меньше. Чтобы использовать эту функцию, у вас должно быть установлено приложение Google Search. Просто нажмите на значок камеры и выберите опцию «Домашнее задание» снизу. Теперь все, что вам нужно сделать, это направить камеру на вопрос и соответствующим образом настроить рамку.

Если приложение может успешно просканировать вопрос, вы получите его предварительный просмотр. Если неточность, у вас есть возможность отредактировать вопрос. Вы также можете просмотреть решение поэтапно. У Google также есть еще одно приложение для решения проблем, Socratic (iOS, Android), которое охватывает все темы. Вы также можете попробовать это, но это не позволяет вам загружать вопросы из своей галереи. Следовательно, когда ваши друзья отправляют вам проблему в WhatsApp, использование приложения Google Search — лучшее решение.

Плюсы

• Бесплатное приложение
• Показывает пошаговое решение
• Позволяет редактировать вопрос
• См. Похожие вопросы / концепции с результатами поиска Google

Минусы

• Не специальное приложение для решения математических задач
• Может не работать для углубленного изучения математики

Загрузите приложение Google Search для (iOS | Android)

6.QuickMath

Если вы предпочитаете использовать компьютер по телефону для обучения, вам следует посетить веб-сайт QuickMath. Сайт не изящный, но легко решает базовые математические задачи. Подобно приложениям для решения математических задач, которые мы обсуждали выше, оно автоматически решает математические задачи. Учитесь ли вы в школе или колледже, он охватывает широкий спектр предметов. Вы можете решать простые уравнения, алгебру, исчисление, процентные задачи и т. Д.

Веб-сайт легко просматривать, и все варианты хорошо продуманы.Вы можете нажать на тип вопроса на боковой или верхней панели. Прокрутив страницу вниз, вы также сможете просмотреть пошаговое решение любой проблемы. В дополнение к этому, он также предоставляет краткое объяснение каждого шага.

Плюсы

• Легко переключаться между типами вопросов
• Решает как базовые, так и сложные математические задачи
• Функции справочного и учебного раздела
• Пошаговое объяснение

Минусы

• Нет возможности загружать вопросы
• Экранная клавиатура — ненадежный способ ввода (личный выбор)

Получить QuickMatch для (iOS | Android | Интернет)

7.WolframAlpha

Wolfram часто называют поисковой машиной для решения проблем. В отличие от Google, который в значительной степени полагается на результаты поиска, Wolfram использует глубокие вычислительные мощности (чрезвычайно собранные и тщательно отобранные данные) для решения математических уравнений и имеет широкий спектр областей, с которыми он работает. Вы можете решать задачи, связанные с элементарной математикой, алгеброй, геометрией исчисления и т. Д. Для начала введите вопрос, загрузите изображение или даже просто вставьте ссылку, содержащую вопрос.

Wolfram Alpha наверняка решит все ваши проблемы.Единственная проблема заключается в том, что множество замечательных функций являются эксклюзивными для профессиональной версии, которая стоит 5,59 доллара в месяц. Это не только открывает пошаговые решения, но также добавляет полезные функции, такие как практические задачи, управляемые калькуляторы (финансы, питание и т. Д.), Возможность загрузки результатов и т. Д. Если вы студент, я настоятельно рекомендую вам попробовать это. Это отличный фактический ресурс не только для решения математических задач, но и для решения других предметов, таких как химия, инженерия, экономика, статистика и т. Д.

Плюсы

• Решения, основанные на фактических данных
• Охватывает большинство предметов, помимо математики

Минусы

• Полезные функции за платным доступом (пошаговое решение, результаты загрузки и т.